2013Matlab上机作业2

合集下载

matlab作业-2013

作业注意事项1、作业以matlab的m文件递交，并以附件的方式发到老师的matlab工作邮箱clrongmatlab@，m文件的命名规则为m+课程序号+作业次序（A，B，C，…）+题次，如m89A1代表序号为89，同学的课程序号请看教学平台的文件。

第一次作业（A）的第1道题的函数文件。

如果一道题有多个的程序，可以在后面添加相应的序号，如m89A12。

2、作业最好是调试成功的代码。

如部分同学缺少必要的数学基础，可以做作业的其中一部分，但需要同学自己实践调试完成。

3、m文件建立方法1)在命令窗口输入命令edit，即进入命令窗口2)输入命令3)保存(默认文件夹\matlab\work，最好建立自己专门的文件夹)4)在命令窗口运行第一次作业（数值与符号计算）1、利用至少三种不同的matlab 实现方法求解线性方程组6+2-3=445+5+4=233+4-2=12x y z x y z x y z ⎧⎪⎨⎪⎩2、已知2143D ⎡⎤=⎢⎥⎣⎦，(1,2,3,4,5)m m D D m ==，请生成矩阵（选做） 1111m m m m D D D D H D D D D −⎡⎤⎢⎥−⎢⎥⎢⎥=⎢⎥−⎢⎥⎢⎥−⎣⎦% 3、设有两个多项式5432()352756f x x x x x x =−+−++，2()353g x x x =+−，求()f x +()g x ；()()f x g x ⋅；()f x -()g x ；()f x /()g x 。

4、已知：2222()x y xy z x y e +=+，求222,,z z z x x x y∂∂∂∂∂∂∂。

5、南京中山陵的台阶有392级台阶，分为10个部分。

一个人每一步可以爬1、2、3阶，假如不考虑各部分的间断性，计算他爬完这些台阶可能的步骤种类数目；假如考虑各部分的间断性（假设台阶在各部分均匀分布，其中2部分40阶，其余部分39阶），计算他爬完这些台阶可能的步骤种类数目；要求写出建模方法和编程计算。

MATLAB 上机习题及答案

15、今有多项式P1(x)=x4-2x+1,P2(x)=x2+4x-0.5，要求先求得P(x)=P1(x)+P2(x)，然后计算xi=0.2*i各点上的P(xi)（i=0,1,2,…,5）值。

p1=[1.0 0.0 0.0 -2.0 1.0];>> p2=[0.0 0.0 1.0 4.0 -0.5];>> p1x=poly2sym(p1);p2x=poly2sym(p2);>> p=p1x+p2xp =x^4+2*x+1/2+x^2>> x=0:5;>> x.^4+2*x+1/2+x.^2ans =0.5000 4.5000 24.5000 96.5000 280.5000 660.50001、试个MATLAB的工作空间中建立以下2个矩阵：A＝[1 2]1234B⎡⎤=⎢⎥⎣⎦，求出矩阵A和B的乘积，并将结果赋给变量C。

>> A=[1 2]A =1 2>> B=[1 23 4]B =1 23 4>> C=A*BC =7 102、利用MATLAB提供的帮助信息，了解inv命令的调用格式，并作简要说明。

help invINV Matrix inverse.INV(X) is the inverse of the square matrix X.A warning message is printed if X is badly scaled ornearly singular.See also SLASH, PINV, COND, CONDEST, LSQNONNEG, LSCOV. Overloaded methodshelp gf/inv.mhelp zpk/inv.mhelp tf/inv.mhelp ss/inv.mhelp lti/inv.mhelp frd/inv.mhelp sym/inv.mhelp idmodel/inv.m3、使用help命令查询函数plot的功能以及调用方法，然后利用plot命令绘制函数y=sin(x)的图形，其中0xπ≤≤。

matlab 上机练习1-2 (2)

第一次上机:基础准备及入门2.1 指令窗运行入门2.1.1 最简单的计算器使用法【例2.5.1-1】求23)]47(212[÷-⨯+的算术运算结果。

（1）用键盘在MATLAB 指令窗中输入以下内容 >> (12+2*(7-4))/3^2（2）在上述表达式输入完成后，按【Enter 】键，该就指令被执行。

（3）在指令执行后，MATLAB 指令窗中将显示以下结果。

ans = 2【例2.5.1-2】简单矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321A 的输入步骤。

（1）在键盘上输入下列内容A = [1,2,3; 4,5,6; 7,8,9]（2）按【Enter 】键，指令被执行。

（3）在指令执行后，MATLAB 指令窗中将显示以下结果：A =1 2 3 4 5 6 7 8 9【例2.5.1-3】矩阵的分行输入A=[1,2,3 4,5,6 7,8,9]（以下是显示结果）A =1 2 3 4 5 6 7 8 9【例2.5.1-4】指令的续行输入（以下格式在除Notebook 外的MATLAB 环境中可运行）S = 1 – 1/2 + 1/3 –1/4 + 1/5 – 1/6 ... + 1/7 – 1/8 S =0.63452.1.2数值、变量和表达式2.1.2.1复数和复数矩阵【例2.5.2.5-1】复数ieziziz63212,21,43π=+=+=表达，及计算321zzzz=。

（1）经典教科书的直角坐标表示法z1= 3 + 4iz1 =3.0000 +4.0000i（2）采用运算符构成的直角坐标表示法和极坐标表示法z2 = 1 + 2 * i %运算符构成的直角坐标表示法z3=2*exp(i*pi/6) %运算符构成的极坐标表示法z=z1*z2/z3z2 =1.0000 +2.0000iz3 =1.7321 + 1.0000iz =0.3349 + 5.5801i【例2.5.2.5-2】复数矩阵的生成及运算A=[1,3;2,4]-[5,8;6,9]*iB=[1+5i,2+6i;3+8*i,4+9*i]C=A*BA =1.0000 - 5.0000i 3.0000 - 8.0000i2.0000 - 6.0000i 4.0000 - 9.0000iB =1.0000 + 5.0000i2.0000 + 6.0000i3.0000 + 8.0000i4.0000 + 9.0000iC =1.0e+002 *0.9900 1.1600 - 0.0900i1.1600 + 0.0900i 1.3700【例2.5.2.5-3】求上例复数矩阵C的实部、虚部、模和相角。

matelab作业2参考答案

matelab作业2参考答案Matlab作业2参考答案Matlab作业2是一项综合性的任务，要求学生运用Matlab编程语言解决一系列数学问题。

本文将为大家提供一份参考答案，帮助学生更好地理解和完成这项作业。

首先，我们将讨论作业的第一个问题，即给定一个矩阵A，求解其特征值和特征向量。

在Matlab中，可以使用eig函数来实现这一功能。

例如，假设我们有一个3×3的矩阵A，可以按照以下方式计算其特征值和特征向量：```A = [1 2 3; 4 5 6; 7 8 9];[eigenvectors, eigenvalues] = eig(A);```在上述代码中，变量eigenvectors将存储A的特征向量，而变量eigenvalues 将存储A的特征值。

通过打印这两个变量的值，我们可以得到矩阵A的特征值和特征向量。

接下来，我们将探讨作业的第二个问题，即求解线性方程组。

假设我们有一个3×3的系数矩阵A和一个3×1的常数向量b，我们需要求解方程组Ax=b。

在Matlab中，可以使用backslash运算符来求解线性方程组。

例如，假设我们有以下方程组：```A = [1 2 3; 4 5 6; 7 8 9];b = [10; 20; 30];x = A \ b;```在上述代码中，变量x将存储方程组的解。

通过打印变量x的值，我们可以得到方程组的解。

此外，作业的第三个问题要求学生使用Matlab绘制函数图像。

在Matlab中，可以使用plot函数来实现这一功能。

例如，假设我们要绘制函数y=sin(x)，其中x的取值范围为0到2π，可以按照以下方式绘制函数图像：```x = 0:0.1:2*pi;y = sin(x);plot(x, y);```在上述代码中，变量x将存储x的取值范围，变量y将存储对应的函数值。

通过调用plot函数，我们可以将函数y=sin(x)的图像绘制出来。

MATLAB 上机2 2013-10-21

3
（1） [1 2; 3 4]+10-2i
4
（2） [1 2; 3 4].*[0.1 0.2; 0.3 0.4]
5
（3） [1 2; 3 4].\[20 10; 9 2]
6
（4） [1 2; 3 4].^2
7
（5） exp([1 2; 3 4])
8
（6） log([1 2; 3 4])
9
36
37
实验 2 MATLAB命令操作（二）
l 熟悉矩阵和向量求和sum与求积prod X是一个向量，A是一个矩阵 l 函数的调用格式
（1） sum(X)：返回向量 X 各元素的积（2） prod(X)：返回向量 X 各元素的乘积（3） sum(A)：返回一个行向量，其第 i 个元素是A的第i列的元素乘积（4） prod(A)：返回一个行向量，其第 i 个元素是 A 的第 i 列的元素乘积（5） sum(A，dim)：当dim为1时，该函数等同于prod(A)；当dim为2时，返回一个列向量，其第i个 10 元素是A的第i行的各元素和
17
（6） prod([1 2; 3 4], 2)
当dim=2时，第2个元素是第二行各元素之积
>> prod(A) ans = 3 8 >>
当dim=1，同 prod(A)
18
实验 3 MATLAB命令操作（三）
（1）创建一个矩阵，并保存到D盘的\test目录中
1 2 3 A = 6 5 4 8 7 9
实验 2 MATLAB命令操作（二）
（1） sum([1 2 3 4]) （2） prod([1 2 3 4]) （3） sum([1 2; 3 4]) （4） prod([1 2; 3 4]) （5） sum([1 2;3 4], 2) （6） prod([1 2; 3 4], 2)

MATLAB期末上机试题带答案

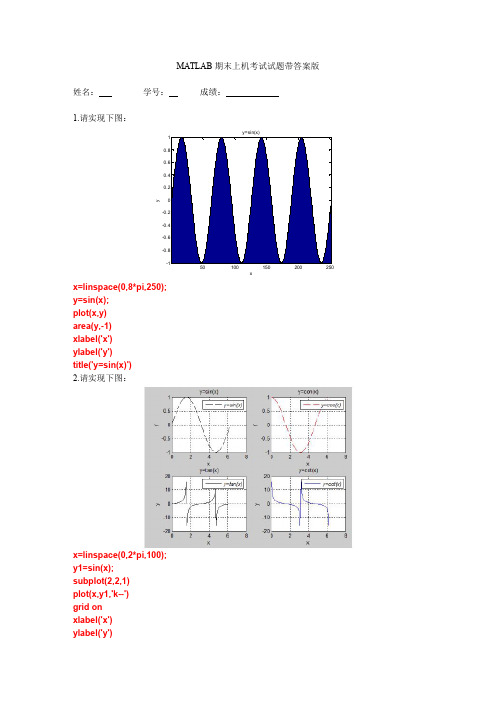
MATLAB 期末上机考试试题带答案版姓名：学号：成绩：1.请实现下图：50100150200250x y x=linspace(0,8*pi,250);y=sin(x);plot(x,y)area(y,-1)xlabel('x')ylabel('y')title('y=sin(x)')2.请实现下图：x=linspace(0,2*pi,100);y1=sin(x);subplot(2,2,1)plot(x,y1,'k--')grid onxlabel('x')ylabel('y')title('sin(x)')legend('y=sin(x)')y2=cos(x);subplot(2,2,2)plot(x,y2,'r--')grid onxlabel('x')ylabel('y')title('cos(x)')legend('y=cos(x)')y3=tan(x);subplot(2,2,3)plot(x,y3,'k-')grid onxlabel('x')ylabel('y')title('tan(x)')legend('y=tan(x)')y4=cot(x);subplot(2,2,4)plot(x,y4)grid onxlabel('x')ylabel('y')title('cot(x)')legend('y=cot(x)')3.解方程组：a=[321;1-13;24-4]；b=[7;6;-2]；x=a\b4.请实现下图：x y x=linspace(0,4*pi,1000);y1=sin(x);y2=sin(2*x);plot(x,y1,'--',x,y2,'b*')grid onxlabel('x');ylabel('y');title('耿蒙蒙')legend('sin(x)','sin(2*x)')5.请在x ，y 在（-2，2）内的z=xexp (-x 2-y 2)绘制网格图[x,y]=meshgrid(-2:0.1:2);z=x.*exp (-x.^2-y.^2);mesh(x,y,z)6.请实现peaks 函数：-33x Peaksy [x,y]=meshgrid(-3:1/8:3);z=peaks(x,y);mesh(x,y,z)surf(x,y,z)shading flataxis([-33-33-88])xlabel('x');ylabel('y');title('Peaks')7.请在x=[0,2],y=[-0.5*pi,7.5*pi],绘制光栅的振幅为0.4的三维正弦光栅。

matlab上机练习题答案(可编辑修改word版)

a ⎣ ⎦ 1. 计算 a = 5⎦ >> a=[6 9 3;2 7 5]; >> b=[2 4 1;4 6 8]; >> a.*b ans =⎣4 8⎦>> d=deconv([3 13 6 8],[1 4]) d =312⎡2 4 7 4⎤⎡8⎤1236 36 求欠定方程组⎢9 3 5 6⎥ x = ⎢5⎥ 的最小范数解84240⎡4 9 2⎤⎡37⎤⎣ >> a=[2 4 7 4;9 3 5 6]; >> b=[8 5]'; ⎦ ⎣ ⎦2. 对于 AX = B ，如果 A = ⎢7 6 4⎥ ， B = ⎢26⎥ ，求解 X 。

>> x=pinv(a)*b⎢ ⎥ ⎢ ⎥x =>> A=[4 9 2;7 6 4;3 5 7]; >> B=[37 26 28]’; >> X=A\B X =⎢⎣3 5 7⎥⎦ ⎢⎣28⎥⎦-0.2151 0.4459 0.7949 0.27077 用符号函数法求解方程 a t 2+b*t +c=0-0.5118 >> r=solve('a*t^2+b*t+c=0','t') 4.0427 r =1.3318[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))] ⎡1 2 5 ⎤ ⎡8 - 7 4⎤ [ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]3. a = ⎢3 6 - 4⎥ ， b = ⎢3 6 2⎥ ，观察 a 与 b 之间的⎣ ⎦ ⎣ ⎦⎡a 11 a 12 ⎤六种关系运算的结果 >> a=[1 2 3;4 5 6];8 求矩阵 A = ⎢ ⎣ 21 ⎥ 的行列式值、逆和特征根a 22 ⎦>> b=[8 –7 4;3 6 2];>> syms a11 a12 a21 a22;>> a>b >> A=[a11,a12;a21,a22] ans =>> AD=det(A) % 行列式 0 1 0 >> AI=inv(A) % 逆 11>> AE=eig(A) % 特征值 >> a>=b ans =0 1 0 1 01>> a<b ans =1 0 1 0 1>> a<=b ans =1 0 1 010 A = [ a11, a12][ a21, a22] AD =a11*a22-a12*a21 AI =[ -a22/(-a11*a22+a12*a21), a12/(-a11*a22+a12*a21)] [ a21/(-a11*a22+a12*a21), -a11/(-a11*a22+a12*a21)] AE = [1/2*a11+1/2*a22+1/2*(a11^2- 2*a11*a22+a22^2+4*a12*a21)^(1/2)] [1/2*a11+1/2*a22-1/2*(a11^2->> a==b2*a11*a22+a22^2+4*a12*a21)^(1/2)] ans =9 因式分解： x 4 - 5x 3 + 5x 2 + 5x - 60 0 0 >> syms x;0 00 >> f=x^4-5*x^3+5*x^2+5*x-6; >> a~=b ans =>> factor(f) ans =(x-1)*(x-2)*(x-3)*(x+1)4 计算多项式乘法(x 2+2x +2)(x 2+5x +4) ⎡10 f = ⎢ x 21 x ⎤⎥ ，用符号微分求 df/dx 。

MATLAB练习2013

1、用GUI建立函数极限可视化显示绘制函数y=(sin(x)/x)在-100≤x≤100,-0.24≤y≤1.1下的曲线，并观察和推断当x→-∞，x→+∞，x→∞，x→0-，x→0+，x→0时，函数的变化趋势。

要求：（1）要有菜单；（2）界面上能改变函数；（3）界面友好，使用方便，设计要人性化；（4）、尽量要动画显示函数的极限趋势。

2、用MATLAB设计一个计算器。

要求：（1）用户能任意输入数据；（2）至少要能进行基本计算；（3）、计算的方式有用户选；（4）、界面友好，使用方便，设计要人性化；（5）、使用效果要能达到一般的电子计算器3、用MATLAB设计一个方程或方程组解答器。

要求：（1）、有用户任意输入方程或方程组；（2）、方程的输入方式一matlab方式，并要求按习惯显示出答案（即字符形式显示）。

（3）、界面友好，使用方便，设计要人性化。

4、用MATLAB设计一个曲线拟合。

要求：（1）、曲线拟合的方法自选（给出选项）；（2）、参数由用户设定（有提示）；（3）、显示输入的数据及拟合后的多项式（3）、界面友好，使用方便，设计要人性化。

（4）、数据可以输入，也可以导入。

5、制作函数t*exp(-t/b)的动画。

要求：（1）、参数t和b由用户设定；（2）、任意带t，b参数的式子均能动画显示（2）、界面友好，使用方便，设计要人性化。

6、制作一个学生综合考评系统要求：（1）界面要能显示全班综合考评的排名。

（2）（行操作）操作人员在界面上能通过姓名，学号，名次调出考评的相关信息。

（3）（列操作）操作人员在界面上能调出被加分和被扣分的同学的姓名及加分情况。

7、成绩处理系统要求：（1）从excel文档里读出相关的信息；（2）把处理后的数据添加在excel文档相应的栏；（3）计算：学习成绩：各科平均成绩×70%德育成绩：班级评20+辅导员/班主任10（4）界面友好，使用方便，设计要人性化8、做一个专业方面的仿真系统要求：（1）要求相关的文档介绍，介绍该仿真系统的意义；（2）文档里要有程序框图，对程序说明；（3）、仿真和后部程序；（4）、对系统的仿真进行校验，并对仿真效果给予评价。

matlab第二章作业 2

2.1创建一个有七个元素的一维数组，并做如下处理（1）直接寻访一维数组的第六个元素（2）寻访一维数组的第一、三、五个元素（3）寻访一维数组中第四个至最后一个元素（4）寻访一维数组中大于70的元素A=linspace(1,200,7)%创建一个有七个元素的一维数组>>A =Columns 1 through 31.0000 34.1667 67.3333Columns 4 through 6100.5000 133.6667 166.8333Column 7200.0000（5）>> A(6)%直接寻访一维数组的第六个元素ans =166.8333（6）>> A([1,3,5])%寻访一维数组的第一、三、五个元素ans =1.0000 67.3333 133.6667（7）>> A(4:end)%寻访一维数组中第四个至最后一个元素ans =100.5000 133.6667 166.8333 200.0000>> b=A>70%判断A中的各元素是否大于70b =0 0 0 1 1 1 1>> A(b)%显示A 中大于70的元素ans =100.5000 133.6667 166.8333 200.00002.3找出数组A=⎥⎦⎤⎢⎣⎡----5311342024中所有绝对值大于3的元素 >> A=[-4,-2,0,2,4;-3,-1,1,3,5]%创建AA =-4 -2 0 2 4-3 -1 1 3 5>> b=abs(A)>3%判断A 中各元素绝对值是否大于3b =1 0 0 0 10 0 0 0 1>> A(b)%显示逻辑值为1的各元素ans =-4452.5求1)1)(4)(232+++++s s s s s （的商及余多项式 >> p1=[1,5,6,10,8];%创建分子多项式>> ps1=poly2str(p1,'s')%以s 作为未知数显示多项式ps1 =s^4 + 5 s^3 + 6 s^2 + 10 s + 8>> p2=[1,1,1];%创建分母多项式>> ps2=poly2str(p2,'s')%以s 作为未知数显示多项式ps2 =s^2 + s + 1>> [q,r]=deconv(p1,p2)%求商及余多项式q =1 4 1r =0 0 0 5 7>> disp(['商：',poly2str(q,'s')])%显示商多项式商： s^2 + 4 s + 1>> disp(['余：',poly2str(r,'s')])%显示余多项式余： 5 s + 72.6求3阶方阵A 的特征多项式构造方阵A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡200030001 A=[1,0,0;0,3,0;0,0,2;];%构造方阵A>> B=poly(A);%B 为A 的特征多项式>> poly2str(B,'s')ans =s^3 - 6 s^2 + 11 s - 6>> p=roots(B)%求B 的根p =3.00002.00001.0000。

Matlab第二、三次上机作业-推荐下载

第二次上机作业一. 任务：用MATLAB 语言编写连续函数最佳平方逼近的算法程序（函数式M 文件）。

并用此程序进行数值试验，写出计算实习报告。

二. 程序功能要求：1.用Lengendre 多项式做基，并适合于构造任意次数的最佳平方逼近多项式。

可利用递推关系0112()1,()()(21)()(1)()/2,3,.....n n n P x P x x P x n xP x n P x nn --===---⎡⎤⎣⎦=2.程序输入：（1）待求的被逼近函数值的数据点(可以是一个数值或向量)0x （2）区间端点：a,b 。

3. 程序输出：（1）拟合系数：012,,,...,nc c c c （2）待求的被逼近函数值00001102200()()()()()n n s x c P x c P x c P x c P x =++++ 三：数值试验要求：1.试验函数：；也可自选其它的试验函数。

()cos ,[0,4]f x x x x =∈+2.用所编程序直接进行计算，检测程序的正确性，并理解算法。

3.分别求二次、三次、。

最佳平方逼近函数。

）x s (4.分别作出逼近函数和被逼近函数的曲线图进行比较。

）x s ()(x f （分别用绘图函数plot(,s())和fplot(‘x cos x ’,[x 1 x 2,y 1,y 2])）0x 0x 解题思路：参照应用数值分析书P259“算法7-1”，利用Legendre 多项式对f(x)∈C(a,b)的最佳平方逼近写出以下算法：M 文件1：%文件名：GLAppro.mfunction[poly,yy,delta]=GLAppro(f,n,a,b,xx)%功能：利用Gauss Legendre 多项式求函数的最佳平方逼近%输入：f ——被逼近函数；a,b ——逼近区间；xx ——欲求的逼近点%n ——逼近的L 多项式的次数（标量时为最高次数，向量时为其所选择的的逼近次数）%输出：poly ——所求的逼近多项式系数（降序）；yy ——逼近店的值；delta ——逼近误差N=numel(n);if N>1id=n+1;elseN=n+1;enddelta=quad(@myfun,-1,1,[],[],f,a,b);c=zeros(1,N);poly=zeros(1,id(N)); for k=1:Nc(k)=(2*id(k)-1)*quad(@fLegPoly,-1,1,[],[],f,id(k)-1,a,b)/2;delta=delta-c(k)^2*2/(2*id(k)-1);endif nargin==5t0=(2*xx-a-b)/(b-a);yy=zeros(size(xx));for k=1:Np=LegPoly(id(k)-1);yy=yy+c(k)*polyval(p,t0);poly(id(N)-id(k)+1:(id(N)))=poly(id(N)-id(k)+1:(id(N)))+c(k)*p;endelsefor k=1:Np=LegPoly(k-1);poly(N-k+1:N)=poly(N-k+1:N)+c(k)*p;endendM文件2：function y=myfun(t,f,a,b)%功能：GLAppro子函数，变换到区间[-1,1]x=(b-a)*t/2+(b+a)/2;y=f(x).*f(x);M文件3：function f=fLegPoly(t,f1,n,a,b)%功能：GLAppro子函数，求变换后的积分函数p=LegPoly(n);x=(b-a)*t/2+(b+a)/2;f=f1(x).*polyval(p,t);M文件4：function p=LegPoly(n)%功能：递归法求n次Gauss Legendre多项式%输入：n——多项式次数%输出：p——降幂排列的多项式系数p0=1;p1=[1,0];if n==0p=p0;elseif n==1p=p1;elsep=((2*n-1)*[LegPoly(n-1),0]-(n-1)*[0,0,LegPoly(n-2)])/n;end%文件名：homework2.mf=@(x)(x.*cos(x));n=cell(3,1);n{1}=2;n{2}=3;n{3}=4;a=0;b=4;x0=linspace(a,b)';color=['k','g','b'];y=f(x0);plot(x0,y,'r-','linewidth',1.5);hold on;syms t x;for i=1:3[poly,py,delta]=GLAppro(f,n{i},a,b,x0);pt=vpa(poly2sym(poly,t),4);poly=simple(subs(pt,t,(2*x-a-b)/(b-a)));poly=vpa(poly,4);disp(['所求的最佳评分那个逼近多项式为（n=' int2str(n{i}) '):']);disp(poly);disp(['误差为:' num2str(delta)]);plot(x0,py,color(i),'linewidth',1.5)end分别求两次、三次和四次最佳平方逼近函数s(x)输入：homework2输出：所求的最佳评分那个逼近多项式为（n=2):- 0.1599*x^2 - 0.572*x + 0.8268误差为:0.45032所求的最佳评分那个逼近多项式为（n=3):0.3818*x^3 - 2.45*x^2 + 3.093*x - 0.3948误差为:0.02393所求的最佳评分那个逼近多项式为（n=4):0.08539*x^4 - 0.3014*x^3 - 0.6939*x^2 + 1.531*x - 0.08255误差为:0.002258调整图象并标注：yx第三次上机作业一. 任务一：用MATLAB 语言编写化工原理流体力学中d-u-Re-λ试差法的算法程序（函数式M 文件）。

实验作业2 MATLAB作图

实验作业2 MATLAB作图1、用plot,fplot 绘制函数y=cos(tan( x))的图形。

解：代码如下:x=linspace(-0.5,0.5,30);y=cos(tan(pi*x));plot(x,y)结果：fplot('[cos(tan(pi*x))]',[-0.5,0.5])结果：注意事项： fplot('[cos(tan(pi*x))]',[-0.5,0.5])不能写成fplot('[cos(tan(pi*x))]',（-0.5,0.5）)否则是错误程序。

2. 用ezplot绘制函数exy-sin(x+y)=0 在[-3, 3]上的图形。

解：代码如下：ezplot('exp(x*y)-sin(x+y)=0',[-3,3])3.用matlab以动画的方式绘制出摆线x=a(t-sint) y=a(1-cost) （a自己赋值）的渐屈线clear;clc;close;a=1;syms tx=a*(t-sin(t));y=a*(1-cos(t));ezplot(x,y,[0,2*pi]),grid on ;hold on;dy=diff(y)/diff(x);dyy=diff(dy)/diff(x);xx=x-(1+dy^2)*dy/dyy;%渐屈线的坐标yy=y+(1+dy^2)/dyy;M=50;t=0;xxx=subs(xx);yyy=subs(yy);H1=plot(xxx,yyy,'r');hold on;grid on ;axis([0,7,-2.5,2.5]);x1=subs(x);y1=subs(y);H2=plot([x1,xxx],[y1,yyy],'k--');H3=plot(x1,y1,'ko');H4=plot(xxx,yyy,'ro');tt=linspace(0,2*pi,M);for i=1:Mpause(0.2);t=tt(1:i);xxx=subs(xx);yyy=subs(yy);x1=subs(x);y1=subs(y);set(H1,'xdata',xxx,'ydata',yyy);set(H2,'xdata',[x1(i),xxx(i)],'ydata',[y1(i),yyy(i)]);set(H3,'xdata',x1(i),'ydata',y1(i));set(H4,'xdata',xxx(i),'ydata',yyy(i));end绘制函数⎩⎨⎧-=-=)cos 1()sin (t a y t t a x 在]2,0[π∈t 上的图形。

MATLAB上机题.doc

西北农林科技大学本科课程试卷2011—2012学年第1学期《MATLAB与科学计算》课程A卷（上机考试）专业班级：09农水班命题教师：王增红审题教师：马孝义学生姓名学号：考试成绩：考试须知：1、所有考生请在规定时间内，完成以下操作内容，并将.m文件和操作结果粘贴到试卷中。

2、考试过程中，请注意保存文件，因个人操作造成的文件丢失，按0分计。

3、编程题请注意编程规范，否则酌情扣分。

4、请将姓名和学号填入试卷中指定位置，word文件名请按“s机号-学号-姓名”规则保存。

5、考试结束后停止操作，学生和教师确认文件拷贝无误后，方可离开考场，否则后果自负。

y2=[2 5 4;9 10 5]plot(x1,y1)%x1的列与y1的行相等，与y1的每列对应一条直线，两条直线plot(x1,x2)%x1的列与x2的列相等，与x2的每行对应一条直线，两条直线plot(x1,y2)%x1的列与y2的列相等，与y2的每行对应一条直线，两条直线plot(y1,x1)%y1的行与x1的列相等，与x1的每行对应一条直线，两条直线plot(x2,x1)%x2的列与x1的列相等，与x1的每行对应一条直线，两条直线plot(y2,x1)%y2的列与x1的列相等，与x1的每行对应一条直线，两条直线plot(x2,y2)%x2与y2的行列相等，与y2的每列对应一条直线，三条直线plot(y2,x2)%y2与x2的行列相等，与x2的每列对应一条直线，三条直线其图形如下所示：二、绘图题（根据题意，对下列各题进行绘图，共20分）得分：分（本大题中的3个小题编辑M文件，运行查看图形，并将M文件粘贴到试卷中）1、画一二维饼形图，至少包含三个元素。

（5分）答：x=[100 200 300 400]explode=[1 1 1 1]pie(x,explode,{'一','二','三','四'})2、在同一窗口绘制6个子图，已知t=::2*pi，每个子图分别绘制（其中y1=sin(t),y2=cos(2t),y3=sin(t)+cos(t),y4=3t,y5=2ln(t),y6=e t）（10分）答：t=::2*pisubplot(2,3,1)y1=sin(t)plot(t,y1)title('y1=sin(t)')subplot(2,3,2)y2=cos(2*t)plot(t,y2)title('y2=cos(2t)')subplot(2,3,3)y3=sin(t)+cos(t)plot(t,y3)title('y3=sin(t)+cos(t)')subplot(2,3,4)y4=3*tplot(t,y4)title('y4=3t') subplot(2,3,5) y5=2*log(t) plot(t,y5)title('y5=2ln(t)') subplot(2,3,6) y6=exp(t) plot(t,y6) title('y6=e^t')3、在matlab 的图形窗口中写出标题为表达式⎰⎰±=m mzdx ydx qt 00，字体大小为14号，如右图所示。

MATLAB_上机试题

一、作业；1.下面是一个线性方程组：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.03216/15/14/15/14/13/14/13/12/1x x x 求方程的解。

2、输入一个电压等级，要求输出为变电站的主接线方式。

输入500时，输出为“一个半断路器接线”输入为220时，输出为“双母线带旁路接线。

输入为110时，输出为“单母分段接线“输入为35时，输出为“单母线接线”输入为其他时，输出为“请输入正确的电压等级”要求：（1）用if 语句实现。

（2）用switch 语句实现。

3、输出九九乘法表4、画图功能(1)单窗口单曲线x=[0, 0.48,0.84,1,0.91,0.6,0.14]只上述X 来画图(2)单窗口多曲线t=0:pi/100:2*pi;y=sin(t);y1=sin(t+0.25);y2=sin(t+0.5);横坐标为t ，纵坐标为y,y1,y2的曲线画在一个图上面。

（3）多窗口曲线图将（2）里面提供的数据分别画在3个窗口里面。

二、仪器设备；计算机、MATLAB软件。

三、实验原理；1、任何算法功能都可以通过程序模块组成的三种基本程序结构的组合来实现: 顺序结构：程序按程序语句或模块在执行流中的顺序逐个执行。

选择结构：程序按设定的条件实现程序执行流的多路分支。

循环结构：程序按给定的条件重复地执行指定的程序段或模块。

if表达式1程序模块1elseif 表达式2程序模块2…elseif 表达式n程序模块nelse程序模块n+1endswitch 表达式case 数值1程序模块1；case 数值2程序模块2；……case 数值n程序模块n；otherwise程序模块n+1endfor 循环变量 = v语句段endwhile 条件表达式语句段endFunction 输出变量＝函数名称（输入变量）语句；end；2、画图的基本形式(1)plot(y)(2)plot(x,y)(3)plot(x1,y1，x2,y2，…)(4)subplot（n,m,l）意思是把一个窗口分成n*m个窗口，现在取其中第l个四、注意事项；1、关键字与end标识语句段的起止。

《MATLAB及其应用》上机作业.doc(修订于2009.11.19)

《MATLAB及其应用》上机作业学院名称：（四号宋体）专业班级：（四号宋体）学生姓名：（四号宋体）学生学号：（四号宋体）年月作业11.用MATLAB 可以识别的格式输入下面两个矩阵12342357135732391894A ⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,144367723355422675342189543i i B i +⎛⎫ ⎪+⎪= ⎪+ ⎪⎪⎝⎭再求出它们的乘积矩阵C ,并将C 矩阵的右下角23⨯子矩阵赋给D 矩阵。

赋值完成后,调用相应的命令查看MATLAB 工作空间的占有情况。

2.设矩阵16231351110897612414152⎛⎫⎪⎪ ⎪ ⎪⎝⎭,求A ,1A -,3A ,12A A -+,1'3A A --,并求矩阵A 的特征值和特征向量。

3.解下列矩阵方程:010100143100001201001010120X -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭4.一球从100米高度自由落下,每次落地后反跳回原高度的一半,再落下。

求它在第10次落地时,共经过多少米?第10次反弹有多高?5.用MATLAB 语言实现下面的分段函数5,1(),25,y f x x ⎧⎪⎪==⎨⎪-⎪⎩101010x x x >≤<-6.分别用for 和while 循环编写程序,求出6323626312122222i i K ===++++++∑并考虑一种避免循环的简洁方法来进行求和,并比较各种算法的运行时间。

7.应用MA TLAB 语言及二分法编写求解一元方程32()1459700f x x x x =-+-=在区间[3，6]的实数解的算法，要求绝对误差不超过0.001。

8.二阶系统的单位阶跃响应为1cos )t y a ζζ-=+，在同一平面绘制ζ分别为0，0.3，0.5，0.707的单位阶跃响应曲线。

要求：(1)四条曲线的颜色分别为蓝、绿、红、黄，线型分别为“——”、“……”、“oooooo”、“++++++”； (2)添加横坐标轴和纵坐标轴名分别为“时间t”和“响应y”，并在平面图上添加标题“二阶系统曲线”和网格；(3)在右上角添加图例（即用对应的字符串区分图形上的线），并分别在对应的响应曲线的第一个峰值处标示“zeta ＝0”、“zeta ＝0.3”、“zeta ＝0.5”、“zeta ＝0.707”。

MATLAB上机内容及作业

MATLAB上机内容及作业无约束优化求解函数fminsearch和fminunc求解无约束非线性优化问题的函数有fminsearch 函数、fminunc 函数。

函数fminsearch和fminunc功能相同，但fminunc函数可以得到目标函数在最优解处的梯度和Hessian矩阵值。

无约束优化数学模型为：min f(X) X∈R n求解无约束非线性优化问题的步骤为：第一步：先编写目标函数的M文件；第二步：再在命令窗口中调用相应的优化函数。

1、fminsearch函数调用格式为[x, fval]=fminsearch(@myfun, x0)输出参数的含义：x：返回最优解的设计变量的值；fval：在最优设计变量值时，目标函数的最小值；exitflag：返回算法终止的标志，有以下几种情况，＞0 表示算法收敛于最优解处；＝0 表示算法已经达到迭代的最大次数；＜0 表示算法不收敛。

output：返回优化算法信息的一个数据结构，有以下信息：output.iteration 表示迭代次数output.algorithm 表示所采用的算法output.funcCount 表示函数评价次数输入参数的含义：@myfun：目标函数的M文件，在其前要加“@”，或表示为'myfun' ，myfun自己可以任意命名；x0：在调用该优化函数时，需要先对设计变量赋一个初始值；2、fminunc函数的调用格式[x, fval]=fminunc (@myfun, x0)grad：返回目标函数在最优解处的梯度信息；hessian：返回目标函数在最优解处的hessian矩阵信息。

其余含义同上。

3、实例已知某一优化问题的数学模型为：min f(X)=3x12+2x1x2+x22X∈R n用MA TLAB程序编写的代码为：第一步：首先编写目标函数的.m文件，并保存为examplefsearch.m文件（先单击file菜单，后点击New 命令中的M—file，即可打开M文件编辑窗口进行代码的编辑，在英文状态下输入程序代码），代码为：function f=examplefsearch（x）f=3*x(1)^ 2+2*x(1)*x(2)+x(2)^2;第二步：在Command窗口中调用fminsearch函数，代码为：x0=[1;1]; %赋初值[x,fval]=fminsearch(@examplefsearch,x0) %回车即可调用fminsearch函数，得到结果输出最优解结果为：x=1.0e-0.08* -0.7914 0.2260 %分别为x1和x2的最优点的值（近似为0）fval=1.5722e-016 %对应最优点的最优目标函数值（近似为0）4、作业已知几个优化问题的数学模型分别为：（1）min f(X)=0.1935x1 x22 x32(4+6x4) X∈R4（2）min f(X)= (x13+cos x2+log x3）/ e x1 X∈R3（3）min f(X)=2x13+4x1x23 -10x1x2+x33X∈R3试用MATLAB编程分别求解上述优化问题的最优解。

Matlab上机练习二答案

1、求⎥⎦⎤⎢⎣⎡+-+-+-+-++=i 44i 93i 49i 67i 23i 57i 41i 72i 53i 84x 的共轭转置。

>> x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i];>> x’ans =4.0000 - 8.0000i 3.0000 - 2.0000i3.0000 - 5.0000i 7.0000 + 6.0000i2.0000 + 7.0000i 9.0000 - 4.0000i1.0000 - 4.0000i 3.0000 + 9.0000i7.0000 + 5.0000i 4.0000 - 4.0000i2、计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。

>> a=[6 9 3;2 7 5];>> b=[2 4 1;4 6 8];>> a.*bans =12 36 38 42 403、对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。

>> A=[4 9 2;7 6 4;3 5 7];>> B=[37 26 28]’;>> X=A\BX =-0.51184.04271.33184、 ⎥⎦⎤⎢⎣⎡-=463521a ，⎥⎦⎤⎢⎣⎡-=263478b ，观察a 与b 之间的六种关系运算的结果。

>> a=[1 2 3;4 5 6];>> b=[8 –7 4;3 6 2];>> a>bans =0 1 01 0 1>> a>=bans =0 1 01 0 1>> a<bans =1 0 10 1 0>> a<=bans =1 0 10 1 0>> a==bans =0 0 00 0 0>> a~=bans =1 1 11 1 15、[]7.0802.05--=a ，在进行逻辑运算时，a 相当于什么样的逻辑量。

2013年matlab应用作业

为滑行距离，计算滑行多长距离后，速度可降至。
程序为：
>> fun=inline('5400*v./(8.276*v.^2+2000)','v');
>> quad(fun,15,30)
ans =
291.8696
结果为：291.8696
五、（15分）在一天24小时内，从零点开始每间隔2小时测得的环境温度数据分别为（℃）
X =
30.0000 30.0000 2.0000
Fmin =
-900.0000
结果为：围墙的长和宽都是30米,高为2米,围城的面积为900平方米.
12，9，9，10，18，24，28，27，25，20，18，15,13，推测中午1点（13时）的温度，绘出温度变化曲线。
程序为：
>> x=0:2:24;
>> y=[12 9 9 10 18 24 28 27 25 20 18 15 13];
>> x1=13;y1=interp1(x,y,x1,'spline')
程序为：
function[C,Ceq]=nonlconstr(x)
C=(x(1)+x(2))*x(3)-120;Ceq=[];
>> objfun='-x(1)*x(2)';
>> LB=[0 0 2];
>> x0=[10 10 2];
>> [X,Fmin]=fmincon(objfun,x0,[],[],[],[],LB,[],'nonlconstr')
2012-2013年度第二学期