黑龙江省大庆铁人中学2013-2014学年度高三下学期4月月考数学(理科)
2014大庆铁人中学三模
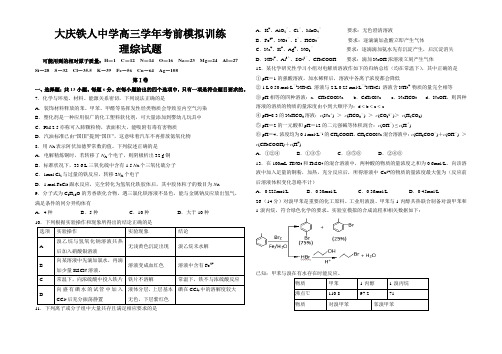
大庆铁人中学高三学年考前模拟训练理综试题可能用到的相对原子质量:H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27Si-28 S-32 Cl-35.5 K-39 Fe-56 Cu-64 Ag-108第Ⅰ卷一、选择题:共13小题。
每题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
7.化学与环境、材料、能源关系密切,下列说法正确的是A.装饰材料释放的苯、甲苯、甲醛等易挥发性烃类物质会导致室内空气污染B.塑化剂是一种应用很广的化工塑料软化剂,可大量添加到婴幼儿玩具中C.PM 2.5亦称可入肺颗粒物,表面积大,能吸附有毒有害物质D.汽油标准已由―国Ⅲ‖提到―国Ⅳ‖,这意味着汽车不再排放氮氧化物8.用N A表示阿伏加德罗常数的值。
下列叙述正确的是A.电解精炼铜时,若转移了N A个电子,则阴极析出32 g铜B.标准状况下,33.6 L三氧化硫中含有1.5 N A个三氧化硫分子C.1mol Cl2与过量的铁反应,转移3N A个电子D.1 mol FeCl3跟水反应,完全转化为氢氧化铁胶体后,其中胶体粒子的数目为N A9.分子式为C8H10O的芳香族化合物,遇三氯化铁溶液不显色,能与金属钠反应放出氢气,满足条件的同分异构体有A.4种B.5种C.10种D.大于10种10.下列根据实验操作和现象所得出的结论正确的是11.下列离子或分子组中大量共存且满足相应要求的是A.K+、AlO2-、Cl-、MnO4-要求:无色澄清溶液B.Fe3+、NO3-、I-、HCO3-要求:逐滴滴加盐酸立即产生气体C.Na+、K+、Ag+,NO3-要求:逐滴滴加氨水先有沉淀产生,后沉淀消失D.NH4+、Al3+、SO42-、CH3COOH 要求:滴加NaOH浓溶液立刻产生气体12.某化学研究性学习小组对电解质溶液作如下的归纳总结(均在常温下),其中正确的是① pH=1的强酸溶液,加水稀释后,溶液中各离子浓度都会降低② 1 L 0.50 mol·L-1NH4Cl 溶液与2 L 0.25 mol·L-1NH4Cl 溶液含NH4+ 物质的量完全相等③ pH相等的四种溶液:a.CH3COONa b.C6H5ONa c.NaHCO3 d.NaOH,则四种溶液的溶质的物质的量浓度由小到大顺序为:d < b < c < a④ pH=8.3的NaHCO3溶液:c(Na+) >c(HCO3-) >c(CO32-)>c(H2CO3)⑤ pH=2的一元酸和pH=12的二元强碱等体积混合:c(OH-) ≤ c(H+)⑥ pH=4、浓度均为0.1mol·L-1的CH3COOH、CH3COONa混合溶液中:c(CH3COO-)+c(OH-) >c(CH3COOH)+c(H+)A.①②④B.①③⑤C.③⑤⑥D.②④⑥13.在100mL HNO3和H2SO4的混合溶液中,两种酸的物质的量浓度之和为0.6mol/L。
黑龙江大庆铁人中学2013-2014学年高二下学期四月月考文科数学试卷(带解析)

黑龙江大庆铁人中学2013-2014学年高二下学期四月月考文科数学试卷(带解析)1()A【答案】C 【解析】C.考点:直角坐标与极坐标的转化2)A【答案】B【解析】试题分析:根据规律发现,后一项与前一项的差为公差为3故选B.考点:不完全归纳3)A【答案】D【解析】故选D.考点:导数的定义4是参数),则曲线是()A、线段B、直线C、圆D、射线【答案】D【解析】试题分析:消去参数t故是一条射线,故选D.考点:参数方程与普通方程的互化5.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )①若K 2的观测值满足K 2≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;②从独立性检验可知有99%的把握认为吸烟与患病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;③从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误 A .① B .①③ C .③ D .② 【答案】C 【解析】个吸烟的人中必有99人患有肺病,不表示某人吸烟,考点:独立性检验 6) A【答案】A 【解析】考点:利用导数求最值7.设△ABC 的三边长分别为a 、b 、c ,△ABC 的面积为S ,内切圆半径为r ,则r 类比这个结论可知:四面体S -ABC 的四个面的面积分别为S 1、S 2、S 3、S 4,内切球的半径为r ,四面体S -ABC 的体积为V ,则r =() A.B.C.D.【答案】C 【解析】故选C.考点:不完全归纳8)A【答案】C【解析】故选C.考点:参数方程9)A.一条射线和一个圆 B.两条直线 C.一条直线和一个圆 D.一个圆【答案】C【解析】试题分析:化简为,得到故选C.考点:极坐标方程与普通方程的互化10为参数),则直线的倾斜角为( )A.40° B.50° C.140° D.130°【答案】C【解析】C.考点:直线的参数方程11.若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( ) A. 2 B. 3 C. 6 D. 9【答案】D【解析】试题分析所以故选D.考点:函数极值的应用12部分对应值如下表,函:( )A.【答案】D【解析】故选D.考点:1.利用导数解不等式;2.线性规划问题.13.与直线2x-6y+1=0垂直,且与曲线f(x)=x3+3x2-1相切的直线方程是________.【解析】代考点:1.导数的几何意义;2.直线的垂直.14.对具有线性相关关系的变量x和y,由测得的一组数据已求得回归直线的斜率为6.5,且恒过(2,3)点,则这条回归直线的方程为________.【解析】所以回归方考点:线性回归方程15________。
黑龙江省大庆市铁人中学2014-2015学年高一4月阶段性检测数学试题

大庆铁人中学2015年第一次月考(数学)一.选择(共12小题,每题5分)1.在△ABC 中,若C cB b A acos cos cos ==,则ABC ∆是( )A .直角三角形B .等边三角形C .钝角三角形D .等腰直角三角形2.在ABC ∆中,角A ,B ,C 的对边分别为a,b,c ,若bc c b a 3222-=--,则A 等于 A .6π B .4π C .3π D .23π3.在ABC ∆中,32=a ,22=b ,︒=45B ,则=AA .︒30B .︒60C .︒30或︒150D .︒60或︒1204.在ABC ∆中,60A ∠=,a =3b =,则ABC ∆解的情况A .有一解B .有两解C .无解D .不能确定5.若,011<<b a 则下列不等式:(1)b a b a ⋅<+;(2)b a >(3) b a <中,正确的不等式有() A. 1个 B.2个 C.3个 D.0个6.在各项均为正数的等比数列{}n a 中,若389a a =,则31310log log a a +=( )A 、1B 、4C 、2D 、3log 57.已知数列{}n a 满足{}12430,,103n n n a a a a ++==-则的前项和等于A .()-10-61-3B .()-1011-39 C .()-1031-3 D .()-1031+38.如果等差数列{}n a 中,34512a a a ++=,那么=7SA 、14B 、21C 、28D 、359.等差数列}{n a 中,20,873==a a ,若数列}1{1+n n a a 的前n 项和为254,则n 的值为( )A 、14B 、15C 、16D 、1810.在数列{}n a 中,12a =, n n a a n n 1ln 1++=+,则n a = ( )A .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++11.已知0,0a b >>,且12=+b a ,则21a b +的最小值为( ) A .7 B .8 C .9 D .1012. 已知不等式()27)1(log 114313212112-+->++⋅⋅⋅+⨯+⨯+⨯a a n n 对一切正整数n 恒成立,则实数a 的范围为A .()3,0B .)3,1(C .)4,2(D .),3(+∞二.填空题(共4小题,每题5分)13.在下列图形中,小黑点的个数构成一个数列{}n a 的前3项.数列n a 的一个通项公式n a = ;14.在△ABC 中三边之比a:b:c=2:3:19,则△ABC 中最大角= ;15.在ABC ∆中,内角,,A B C 所对的边长分别是,,a b c , 已知4A π=,4cos 5B =,若10,BCD =为AB 的中点,则CD = ;16.设S n 是公差不为零的等差数列{}n a 的前n 项和,且a 1 > 0,若S 5 = S 9,则当S n 最大时,n=三.解答题(本题共6小题)17. (本题满分10分)已知等差数列{}n a 为递增数列,其前三项和为-3,前三项的积为8(1)求等差数列{}n a 的通项公式;(2)求数列{}n a 的前n 的和n S 。
黑龙江大庆铁人中学2013-2014学年高二下学期四月月考理科数学试卷(带解析)

黑龙江大庆铁人中学2013-2014学年高二下学期四月月考理科数学试卷(带解析)1)A【答案】D【解析】故选D.考点:利用导数求函数的单调区间2.已知随机变量X服从正态分布N(3.1),.6826,则p(X>4)=()A.0.1588 B.0.1587 C.0.1586 D.0.1585【答案】B【解析】故选B.考点:正态分布3.已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为()AC【答案】C【解析】故选C.考点:求回归直线方程4()A【答案】D【解析】故选D.考点:利用导数求函数的单调区间5)A【答案】D【解析】故选D.考点:恒成立问题6时则()AC【答案】B【解析】知得函数关于对称,根据单调增,可得:故选B.考点:1.导数分析函数的单调性;2.利用函数性质比较大小.7.箱中装有标号为1,2,3,4,5,6且大小相同的6个球.从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖,恰好有3人获奖的概率是()A【答案】B【解析】试题分析:所以4人中恰好有3故选B.考点:1.古典概型;2.二项分布.8()ABC【答案】A【解析】利用导数的几何意义得:解,直线,切,即与抛物线因为相切,故选A.考点:1.导数的几何意义;2.求切线方程.9.把半圆弧分成4等份,以这些分点(包括直径的两端点)为顶点,作出三角形,从这些三角形中任取3个不同的三角形,则这3个不同的三角形中钝角三角形的个数X的期望为()A.2 C.3 D【答案】D【解析】试题分析:共57个,钝角三角形的个数,,,D.考点:1.超几何分布;2.离散型随机变量的分布.10R当x>0()(A)(2,0) ∪(2,+∞) (B)(2,0) ∪(0,2)(C)(∞,2)∪(2,+∞) (D)(∞,2)∪(0,2)【答案】D【解析】试题分析:D.考点:1.函数的性质解不等式;2.利用导数求函数的单调性;3.函数的图像.11.从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数, 则这个数不能被 3整除的概率为()A【答案】C【解析】试题分析:解:从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,这个数不能被3整除.10个数字分成三组,即被3除余1的有{1,4,7}、被3除余2的有{2,5,8},被3整除的有{3,6,9,0},若要求所得的三位数被3整除,则可以分类讨论:②若三个数字均取自第三组,则要考虑取出的数字中有无数字0③若三组各取一个数字,第三组中不取0④若三组各取一个数字,第三组中取03整除的数共有228个,不能被3整除的数有420个,考点:1.排列,组合的应用;2古典概型的应用.12( )ABC D【答案】A【解析】故选A . 考点:1.利用导游求函数的单调性;2.比较大小.13m 的取值范围是 .【解析】函数在R 上单调,考点:利用导数解决恒成立问题14.若随机变量X的概率分布密度函数∈R),则E(2X1)=_________.【答案】5【解析】考点:正态分布的期望15.点P的曲线y=x3P处的切线的倾斜角为α,则α的取值范围是_________.【解析】试题分析:根据导数的几何意义,,所以倾斜角考点:1.导数的几何意义;2.倾斜角与斜率.16.设函数,若是偶函数,则.【解析】考点:三角函数的性质17.已知5个乒乓球,其中3个新的,2个旧的,每次取1个,不放回的取两次,求:(1)第一次取到新球的概率.(2)第二次取到新球的概率.(3)在第一次取到新球的条件下第二次取到新球的概率.【答案】(1(2(3【解析】试题分析:(1)此问为古典概型的概率,总的基本事件的个数为5个,第一次取到新球的基本事件包含3(2)第二次取到新球包含两种情况,第一次取到新球,或是第一次没有取到新球;(3设第i j(i,j=1,2)(1分(2)第二次取到新球为C事件,分(3分考点:1.古典概型的概率问题;2.条件概率.18(1y=x+ln2时,求a的值.(2)1,5)时,求a的取值集合.【答案】【解析】试题分析:(1)(2根据根与系数的关系得到.(1分(2),的解集为即的取分考点:1.导数的几何意义;2.导数求函数的单调区间.19.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为35.(1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由; 临界值表供参考:【答案】详见解析 【解析】试题分析:(1)根据在全部50人中随机抽取1肺疾病的人数,即可得到列联表;(2(2)因为K2所以K2≈8.333,又P(K2≥7.789)=0.005=0.5%.那么,我们有99.5%的把握认为是否患心肺疾病是与性别有关系的.考点:独立性检验20.一种电脑屏幕保护画面,每次p q,若第k次出(1)(2)【答案】(1)详见解析;【解析】试题分析:(1)3,同理其他情况,(2)次,i=1,2,3,4),可分前4次有2,3,或4解:(2)前4次有2前4次有3前4次有4考点:1.相互独立事件的概率;2.分布列和期望21.某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门。
黑龙江省大庆铁人中学2013-2014学年高二下学期四月月考数学理科

黑龙江省大庆铁人中学2013-2014学年高二下学期四月月考数学理科时间:120分钟 满分:150分一、选择题(本大题共12小题,每小题5分,共60分) 1.函数32()31f x x x =-+的单调递减区间是( )A (2,)+∞B (,2)-∞C (,0)-∞D (0,2) 2.已知随机变量X 服从正态分布N(3.1),且(24)P X ≤≤=0.6826,则 p (X>4)=( )A. 0.1588B. 0.1587C. 0.1586D. 0.1585 3.已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回 归直线方程为( )A . 1.234y x =+B . 1.235y x =+C . 1.230.08y x =+D .0.08 1.23y x =+4.函数xe x xf )3()(-=的单调递增区间是 ( ))2,.(-∞A )3,0.(B )4,1.(C ),2.(+∞D5.函数]1,()(3-∞-=在ax x x f 上递增,则a 的范围是( )3.>a A 3.≥a B 3.<a C 3.≤a D 6.已知函数)(x f 满足)()(x f x f -=π且当)2,2(ππ-∈x 时,x x x f sin )(+=, 则( ))3()2()1(.f f f A << .)2()1()3(.f f f B << )1()3()2(.f f f C << )1()2()3(.f f f D <<7.箱中装有标号为1,2,3,4,5,6且大小相同的6个球.从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖,恰好有3人获奖的概率是 ( ) .A 16625 .B 96625 .C 624625 .D 46258.若存在过点(1,0)的直线与曲线3y x =和21594y ax x =+-都相切,则a 等于( ) A .1-或25-64 B .1-或214 C .74-或25-64 .D 74-或79.把半圆弧分成4等份,以这些分点(包括直径的两端点)为顶点,作出三角形, 从这些三角形中任取3个不同的三角形,则这3个不同的三角形中钝角三角形的个数X 的期望为 ( ) A.1019 B. 2 C. 3 D. 1021 10.设)(x f 是定义在R 上的奇函数,且0)2(=f ,当x>0时,有2()()0xf x f x x '-<恒成立,则不等式2()0x f x >的解集是 ( ) (A) (-2,0) ∪(2,+∞) (B) (-2,0) ∪(0,2) (C) (-∞,-2)∪(2,+∞) (D) (-∞,-2)∪(0,2) 11.从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数, 则这个数不能被 3整除的概率为 ( ) A .5419 B . 5438 C . 5435 D .6041 12.已知)(x f 是可导的函数,且)()(x f x f <'对于R x ∈恒成立,则( ) A . )0()2014(),0()1(2014f e f ef f <<B .)0()2014(),0()1(2014f ef ef f >> C .)0()2014(),0()1(2014f e f ef f <> D .)0()2014(),0()1(2014f ef ef f ><二、填空题(本大题共4小题,每小题5分,共20分)13.函数123+++=mx x x y 在实数集上是单调函数,则m 的取值范围是 .14.若随机变量X 的概率分布密度函数是8)2(,2221)(+-=x e x πϕδμ (x ∈R ),则 E (2X -1)=_________. 15.点P 的曲线y=x 3-x+32上移动,在点P 处的切线的倾斜角为α,则α的取 值范围是_________.16.设函数)0)(3cos()(πϕϕ<<+=x x f ,若)()(x f x f '+是偶函数,则 =ϕ__________.三、解答题(18题10分,其余每题12分,共70分.)17. 已知5个乒乓球,其中3个新的,2个旧的,每次取1个,不放回的取两次, 求:(1)第一次取到新球的概率. (2)第二次取到新球的概率.(3)在第一次取到新球的条件下第二次取到新球的概率.18.已知函数1()ln 1af x x ax x-=-+- ()a R ∈. (1)当()y f x =在点(2, (2))f 处的切线方程是y=x+ln2时,求a 的值. (2)当)(x f y =的单调递增区间是(1,5)时,求a 的取值集合.19.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行了问卷调查得到了如下的列联表:已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为35.(1)请将上面的列联表补充完整;(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由; 临界值表供参考:⎝ ⎛⎭⎪⎫参考公式:K 2=(a +b )(c +d )(a +c )(b +d ),其中n =a +b +c +d20..某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门。
黑龙江省大庆铁人中学2013-2014学年高二下学期期末考试数学(理)试题

一选择题1已知集合,,则()A B C D2已知是i虚数单位,若,则()A 1BC D3函数在点处的切线方程是()A B C D4函数的值域为()A B C D5若函数有大于零的极值点,则实数的取值范围是()A B C D6用数学归纳法证明“”时,从到,等式的左边需要增乘的代数式是()A B C D7由算得,参照附表,得到的正确结论是:A有99%以上的把握认为“爱好该项运动与性别有关”B有99%以上的把握认为“爱好该项运动与性别无关”C在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”8一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数是一个随机变量,则的值为()A B C D9设是一个随机变量,其分布列为:则()A 1BC D10从1,2,3,4,5中任取2个不同的数,事件A:取到的2个数之和为偶数;事件B:取到的2个数均为偶数;则()A B C D11国庆节放假,甲去北京旅游的概率为,乙、丙去北京旅游的概率分别为,。
假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为()A B C D12已知定义在上的函数,其导函数为,且恒成立,则()A B C D二填空题13函数的定义域为;14由直线与曲线所围成的封闭图形的面积为;15下列命题:①线性相关系数越大,两个变量的线性相关性越强;反之,线性相关性越弱;②残差平方和越小的模型,拟合效果越好;③用相关指数来刻画回归效果,越小,说明模型拟合效果越好;④随机误差是衡量预报精确度的一个量,它满足。
其中正确的是(填序号)。
16在中,两直角边分别为设为斜边上的高,则;由此类比三棱锥中的三条侧棱两两垂直,且长度分别为,设棱锥底面上的高为,则(填一个)。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
黑龙江省大庆铁人中学2013-2014学年高一下学期期末考试理科综合试题(文科用)

黑龙江省大庆铁人中学2013-2014学年高一下学期期末考试理科综合试题(文科用)一、选择题(生物每小题6分,共60分;化学每题6分,共60分;物理每题6分,共72分。
生物,化学为单选........;.物理,...每小题至少一个正确选项,全对得6分,选对但不全得3分,错选不得分)1.下图能正确表示基因分离定律实质的是()2.下列表示测交的组合是()A.AA×Aa B.aa×aa C.Aa×aa D.Aa×Aa3.基因突变发生在()A.DNA→RNA的过程中B.DNA→DNA的过程中C.RNA→蛋白质的过程中D.mRNA→氨基酸的过程中4.基因型为DdTt和ddTT的亲本杂交,子代中不可能出现的基因型是()A.DDTT B.ddTT C.DdTt D.ddTt5.下列关于现代生物进化理论的叙述,不合理的是()A.生物进化的基本单位是种群B.自然选择决定基因突变的方向C.四倍体西瓜与二倍体西瓜不是同一物种D.生态系统多样性形成的原因可以概括为共同进化6.果蝇的精子内有4条染色体。
它的初级精母细胞内的DNA、染色体、染色单体数目分别是()7.下列四组成分中,属于DNA分子组成成分的是()A.脱氧核糖、核酸、磷酸B.脱氧核糖、碱基、磷酸C.核糖、碱基、磷酸D.核糖、脱氧核酸、磷酸8.有关基因工程的叙述正确的是()A.限制性内切酶只有在获得目的基因时使用B.基因工程的工具是限制酶、DNA连接酶和运载体C.质粒都可以作为运载体D.重组质粒的形成在细胞内完成9.下图为某家族白化病遗传系谱图(正常肤色基因为A,致病基因为a)。
下列相关叙述中判断错误的是()A.2号个体的基因型为aa B.4号个体的基因型为AaC.6号个体的基因型为Aa D.9号个体的基因型为AA10.下列各种遗传病中属于染色体病的是()A.多指B.先天性聋哑C.冠心病D.21三体综合征11.下列气体大量存在不会造成空气污染的是()A.N2B.CO C.SO2D.NO212.盛有浓硫酸的烧杯敞口放置一段时间后,质量增加。
黑龙江省大庆铁人中学2013-2014学年高一下学期4月月考理科数学试题

黑龙江省大庆铁人中学2013-2014学年高一下学期4月月考理科数学试题试卷说明:1、本试卷满分150分,答题时间120分钟。
2、请将答案直接填涂在答题卡上,考试结束只交答题卡。
第Ⅰ卷(选择题 满分60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.在△ABC 中,若A =30°,B =60°,b =3,则a 等于( )A .3B .1C .2D.122.△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,若a cos B =b cos A ,则△ABC 是( ) A .直角三角形 B .等腰三角形 C .等边三角形 D .等腰直角三角形 3.在等差数列{a n }中,若a 3+a 4+a 5+a 6+a 7=450,则a 2+a 8的值等于( )A .45B .75C .180D .3004.已知等比数列{a n }满足a 1+a 2=3,a 2+a 3=6,则a 7等于( )A .64B .81C .128D .2435.已知数列{a n }满足a n +1=⎩⎨⎧2a n ⎝⎛⎭⎫0≤a n <12,2a n-1 ⎝⎛⎭⎫12≤a n<1.若a 1=67,则a 2014的值为( )A .67B .57C .37D .176.设S n 是等差数列{a n }的前n 项和,若 a 5a 3=59,则S 9S 5等于( )A .1B .-1C .2D .127.数列{a n }满足a 1,a 2-a 1,a 3-a 2,…,a n -a n -1是首项为1,公比为2的等比数列,那么a n 等于( )A .2n -1B .2n -1-1 C .2n +1 D .4n -18.在△ABC 中,sin 2A ≤sin 2B +sin 2C -sin B sin C ,则A 的取值范围是 ( )A .⎝⎛⎦⎤0,π6 B .⎝⎛⎦⎤0,π3C .⎣⎡⎭⎫π6,π D .⎣⎡⎭⎫π3,π9.△ABC 中,角A ,B ,C 的对边边长分别为a =3,b =4,c =6,则bc cos A +ca cos B +ab cosC = ( ) A .61B .612C .614D .12210.设S n 是等差数列{a n }的前n 项和,若S 3S 6=13,则S 6S 12等于( )A .18B .13C .310 D .1911.已知a n =n -98n -99,则这个数列的前30项中最大项和最小项分别是( )A .a 1,a 30B .a 1,a 9C .a 10,a 30D .a 10,a 9 12.在△ABC 中,已知a 4+b 4+c 4=2c 2(a 2+b 2),则角C 为 ( )A .30°B .60°C .120°D .45°或135°第Ⅱ卷 (非选择题 满分90分)二、填空题(本大题共4小题,每小题5分,共20分) 13.在△ABC 中,2a sin A -b sin B -c sin C=______。
黑龙江省大庆铁人中学高三化学4月月考试题新人教版

大庆铁人中学2013-2014学年度高三4月月考化学试题可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 K 39 Mn 55 Fe 56 Cu 64 Ba 137第Ⅰ卷一、选择题:本卷共13小题。
每小题6分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
7.已知NA代表阿伏加德罗常数,下列说法正确的是A.1mol重甲基(-CD3)含有电子数为9NAB.标准状况下,22.4 L O2和O3组成的混合物中原子总数为2NAC.在含Al3+总数为NA的AlCl3溶液中,Cl-总数为3NAD.1 mol铁铝混合物与足量稀盐酸反应时,转移电子数是3NA8.下列是三种有机物的结构简式:下列说法正确的是A.三种有机物都能发生水解反应B.三种有机物苯环上的氢原子若被氯原子取代,其一氯代物都只有2种C.三种物质中,其中有两种互为同分异构体D.三种物质在一定条件下,均可以与H2发生加成反应9.常温下,有下列4种溶液:①②③④0.1mol/L NaOH溶液pH =11NaOH溶液0.1mol/LCH3COOH溶液pH =3CH3COOH溶液下列说法正确的是A.由水电离出的C (H+ ): ①>③B.②与④混合,若溶液显酸性,则所得溶液中离子浓度可能为:c(CH3COO-) >c(H+)>c(Na+)>c(OH-)C.③稀释到原来的100倍后,pH与④相同D.①与③混合,若溶液pH = 7 则V(NaOH) > V(CH3COOH)10.下列解释事实或实验现象的化学用语正确的是A.铁溶于稀硝酸,溶液变为浅绿色:Fe + 4H+ + NO3—== Fe3+ + NO ↑ + 2H2OB.澄清石灰水与过量的苏打溶液混合,溶液变混浊:Ca2+ + 2OH- + 2 HCO3- = CaCO3↓+ CO32- + 2H2OC.1mo·L-1 的 NaAlO2 溶液和2.5mol· L-1 的盐酸等体积混合:2AlO2- + 5 H+=Al(OH)3 ↓+ Al3+ + H2 OD.过氧化钠固体与水反应制氧气:2O22—+2H2O=4OH-+O2↑11.某水溶液中只可能含有下列离子中的若干种:K+、Mg2+、Fe3+、Al3+、NH4+、NO3—、Cl—、CO32—和SO42—。
大庆铁人中学2014年高二下数学期末试卷(附答案理科)

大庆铁人中学2014年高二下数学期末试卷(附答案理科)大庆铁人中学2014年高二下数学期末试卷(附答案理科)一选择题1已知集合,,则()ABCD2已知是i虚数单位,若,则()A1BCD3函数在点处的切线方程是()ABCD4函数的值域为()ABCD5若函数有大于零的极值点,则实数的取值范围是()ABCD6用数学归纳法证明“”时,从到,等式的左边需要增乘的代数式是()ABCD7通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女总计爱好402060不爱好203050总计60501103.8416.63510.828由算得,参照附表,得到的正确结论是:A有99%以上的把握认为“爱好该项运动与性别有关”B有99%以上的把握认为“爱好该项运动与性别无关”C在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”8一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数是一个随机变量,则的值为()ABCD-1019设是一个随机变量,其分布列为:则()A1BCD10从1,2,3,4,5中任取2个不同的数,事件A:取到的2个数之和为偶数;事件B:取到的2个数均为偶数;则()ABCD11国庆节放假,甲去北京旅游的概率为,乙、丙去北京旅游的概率分别为,。
假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为()ABCD12已知定义在上的函数,其导函数为,且恒成立,则()ABCD二填空题13函数的定义域为;14由直线与曲线所围成的封闭图形的面积为;15下列命题:①线性相关系数越大,两个变量的线性相关性越强;反之,线性相关性越弱;②残差平方和越小的模型,拟合效果越好;③用相关指数来刻画回归效果,越小,说明模型拟合效果越好;④随机误差是衡量预报精确度的一个量,它满足。
铁中高一2014期末

黑龙江省大庆铁人中学2013-2014学年高一下学期期末考试数学(理)试题满分150分时间120分钟一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求)1、若数列}{n a 的前n 项和12-=n S n ,则=4a ( )A.7B.8C.9D.172、直线l 过点)2,1(-,且与直线0432=+-y x 垂直,则l 的方程是( )A .0123=-+y xB .0723=++y xC .0532=+-y xD .0832=+-y x 3、在ABC ∆中,若B b A a cos cos =,则ABC ∆一定是 ( ) A 等腰三角形 B 直角三角形 C 等腰三角形或直角三角形 D 等腰直角三角形4、在ABC ∆中,c b a ,,分别是角C B A ,,的对边,若,24,34,600===b a A 则=B ( ) A 0013545或 B 0135 C 045 D 以上答案都不对5、若,01,0<<-<b a 则下列不等式成立的是 ( )A 2ab ab a >>B a ab ab >>2C 2ab b ab >>D a ab ab >>2 6、已知m 、n 是两条不同的直线,α、β是两个不同的平面,给出下列命题: ①若,//m αβα⊥,则m β⊥;②若,m n αβ⊥⊥,且,m n ⊥则αβ⊥;③若,m β⊥//m α,则αβ⊥;④若//m α,//n β,且//m n ,则//αβ. 其中正确命题的个数是( ) A 1 B 2 C 3 D 47、已知等差数列}{n a 的前n 项和为n S ,若6,11641-=+-=a a a ,则当n S 取最小值时,n 等于( ) A 6 B 7 C 8 D 98、如图所示,棱长皆相等的四面体ABC S -中,D 为SC 的中点,则BD 与SA 所成角的余弦值是( ) A.33 B. 32 C. 63 D. 629、设n S 是等比数列}{n a 的前n 项和,693,,S S S 成等差数列,且,252m a a a =+则m 等于 ( ) A 6 B 7 C 8 D 1010、已知直线0323=-+y x 和016=++my x 互相平行,则它们之间的距离是 ( ) A. 4 B.13132 C. 26135 D. 26137 11、三棱锥BCD A -的外接球为球O ,球O 的直径是AD ,且BCD ABC ∆∆,都是边长为1的等边三角形,则三棱锥BCD A -的体积是( ) A122 B 81 C 61D 82 12、在ABC ∆中,设AD 为BC 边上的高,且BC AD =,c b ,分别表示角C B ,所对的边长,则bcc b +的取值范围是( )A ]5,2[B ]6,2[C ]5,3[D ]6,3[ 二、填空题(本大题共4小题,每小题5分,共20分)13、若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥≤-+≥-0070x y x x y 则y x +2的最大值为__________14、已知直线01=-+-k y kx 恒过定点A ,若点A 在直线)0,(01>=-+n m ny mx 上,则nm 11+的最小值为15、一个几何体的三视图如图所示,其中正视图是一个正三角形,俯视图是一个等腰直角三角形,则该几何体的外接球的表面积为俯视图侧视图正视图31116、ABC ∆中,060=∠A ,点M 为边AC 的中点,32=BM ,则AC AB +的最大值为________ 三、解答题:本大题共6小题,共70分, 解答时应写出必要的文字说明、证明过程或演算步骤. 17、(本题满分10分) 已知直线l 在两坐标轴上的截距相等,且点)3,1(A 到直线l 的距离为2,求直线l 的方程. 18、(本题满分12分)在ABC ∆中,c b a ,,分别是角C B A ,,的对边,045=B ,10=b ,552cos =C . (1)求a 边长;(2)设AB 中点为D ,求中线CD 长. 19、(本题满分12分)已知ABC ∆中, 角C B A ,,对边分别为c b a ,,,已知3,2π==C c .(1)若ABC ∆的面积等于3,求b a ,(2)若A A B C 2sin 2)sin(sin =-+,求ABC ∆的面积. 20、(本题满分12分)如图,四边形ABCD 是边长为2的正方形,AF DE DE AF ABCD DE 2,//,=⊥平面,BE 与平面ABCD 所成角的正切值为22 (1)求证:EFB AC 平面//(2)求二面角A BE F --的大小FEDCBA21、(本题满分12分)已知数列}{n a 是公差不为0的等差数列,4213,,,6a a a a 且=成等比数列,数列}{n b 满足*1,12N n b b n n ∈+=+,且31=b(1)求数列}{n a 和}{n b 的通项公式 (2)设数列}{n c 的前n 项和为n S ,且)1(log 12+∙=n n n b a c ,证明:21<n S22、(本题满分12分)已知数列{}n a 的前n 项和是n S ,12-=n n a S ()*n N ∈. (1)求数列{}n a 的通项公式;(2)若数列{}n b 满足n n a n b ⋅=2,求数列{}n b 的前n 项和n T ; (3)若数列{}n c 满足()n n nn a c λ1123--+=(λ为非零常数),确定λ的取值范围,使*n N ∈时,都有n n c c >+1.大庆铁人中学高一学年下学期期末考试数学答案(理科) 2014.7二、填空题 13、221 14、 4 15、π316 16、 74 三、解答题18、【解析】(1)()10103sin sin =+=C B A ,23=a ; --------6分 (2)2=c ,13=CD . --------12分 19、【解析】20、【解析】(I )设AC ,BD 交于O ,取EB 中点G ,连结FG ,GO , 在BDE ∆中,11//,//,//22OG DE FA DE OG FA ∴,即四边形FAOG 是平行四边形 //,FG AO ∴又AO ⊄平面EFB ,FG ⊂平面EFB ,所以直线AC//平面EFB.……5分(II )分别以AD ,DC ,DE 为,,x y z 轴,建立空间直角坐标系O xyz -(2,2,0),(0,0,2),(2,0,1),B E F (0,2,1)(2,2,2)BF BE =-=--平面AEB 的法向量(1,0,1)m =……8分设平面FBE 的法向量(,,)n x y z =22220n BFz y x y z n BE⎧⊥=⎧⎪⇒⎨⎨--+=⊥⎩⎪⎩令1y =,则(1,1,2)n =设二面角F-BE-A 的大小为θ,||3|cos |2||||m n m n θ==,所以二面角F-BE-A 的大小为6π……12分21、【解析】(1)12,21-==+n n n b n a ; ------------------------------------6分 (2)21)111(21<+-=n S n -------------------------------------12分(3)∵112)1(23-+-⋅+=n n n n C λn n n2)1(31λ+-+=∴n n C C >+1即 >-+++112)1(3n n n λn n n 2)1(3λ-+即02)1(2)1(33111>---+--++n n n n n n λλ即0)22()1(321>+-+⋅+n n nnλ即023)1(32>⋅-+⋅nnnλ∴>-λn)1(nn 2332⋅⋅- 即>-λn )1(1)23(--n ………………………8分 当n 为偶数时≤--1)23(n 23-∴23->λ…………………………10分当n 为奇数时≤--1)23(n 1- ∴1->-λ 即 1<λ 又∵0λ≠ ∴ 123<<-λ且0λ≠ ………………………………………………12分。
黑龙江省大庆市铁人中学高一数学下学期4月段考试卷(含解析)

2014-2015学年黑龙江省大庆市铁人中学高一(下)4月段考数学试卷一、选择题(共12小题,每小题5分,满分60分)1.在△ABC中,若==,则△ABC是()A.直角三角形B.等边三角形C.钝角三角形D.等腰直角三角形2.在△ABC中,角A,B,C的对边分别为a,b,c,若a2﹣b2﹣c2=﹣bc,则A等于()A.B.C.D.3.在△ABC中,a=,b=,B=45°,则A等于()A.30°B.60°C.30°或150°D.60°或120°4.在△ABC中,∠A=60°,a=,b=3,则△ABC解的情况()A.无解B.有一解C.有两解D.不能确定5.若则下列不等式:(1)a+b<a•b;(2)|a|>|b|(3)a<b中,正确的不等式有()A. 1个B. 2个C. 3个D. 0个6.在各项均为正数的等比数列{a n}中,若a3a8=9,则log3a1+log3a10=()A. 1 B. 2 C. 4 D. log357.已知数列{a n}满足3a n+1+a n=0,a2=﹣,则{a n}的前10项和等于()A.﹣6(1﹣3﹣10) B.C. 3(1﹣3﹣10)D. 3(1+3﹣10)8.如果等差数列{a n}中,a3+a4+a5=12,那么S7=()A. 14 B. 21 C. 28 D. 359.等差数列{a n}中,a3=8,a7=20,若数列{}的前n项和为,则n的值为()A. 14 B. 15 C. 16 D. 1810.在数列{a n}中,a1=2,a n+1=a n+ln(1+),则a n=()A. 2+lnn B. 2+(n﹣1)lnn C. 2+nlnn D. 1+n+lnn11.已知a>0,b>0,且2a+b=1,则+的最小值为()A. 7 B. 8 C. 9 D. 1012.已知不等式对一切正整数n恒成立,则实数a的范围为()A.(0,3)B.(1,3)C.(2,4)D.(3,+∞)二、填空题(共4小题,每小题5分,满分20分)13.在如图图形中,小黑点的个数构成一个数列{a n}的前3项.(1)a5= ;(2)数列{a n}的一个通项公式a n= .14.在△ABC中三边之比a:b:c=2:3:,则△ABC中最大角= .15.在△ABC中,内角A,B,C所对的边长分别是a,b,c,已知A=,cosB=,若BC=10,D为AB的中点,则CD= .16.设S n是公差不为零的等差数列{a n}的前n项和,且a1>0,若S5=S9,则当S n最大时,n= .三、解答题(共6小题,满分70分)17.已知等差数列{a n}为递增数列,其前三项和为﹣3,前三项的积为8(1)求等差数列{a n}的通项公式;(2)求数列{a n}的前n的和S n.18.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,.(1)求A的大小;(2)若,,求a.19.已知△ABC中,角A,B,C的对边分别为a,b,c,且,b=1.(Ⅰ)若,求c;(Ⅱ)若a=2c,求△ABC的面积.20.在数列{a n}中,已知a1=2,a n+1=4a n﹣3n+1,n∈N•.(1)设b n=a n﹣n,求证:数列{b n}是等比数列;(2)求数列{a n}的前n项和S n.21.数列{a n}的前n项和为S n,a1=2,S n=a n﹣1(n∈N*)(1)求数列{a n}的通项公式;(2)设b n=na n,求数列{b n}的前n项和T n.22.若函数为f(x)=x2﹣2mx﹣2m﹣1(1)求f(x)>0的解集;(2)若f(x)>﹣4m﹣2对满足0≤x≤1的所有实数x都成立,求m的取值范围.2014-2015学年黑龙江省大庆市铁人中学高一(下)4月段考数学试卷参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.在△ABC中,若==,则△ABC是()A.直角三角形B.等边三角形C.钝角三角形D.等腰直角三角形考点:正弦定理的应用.专题:计算题.分析:先根据正弦定理将边的关系变为角的关系,进而再由两角和与差的正弦公式确定B=C 得到三角形是等腰三角形.解答:解:由=,得=.又=,∴=.∴=.∴sinAcosB=cosAsinB,sin(A﹣B)=0,A=B.同理B=C.∴△ABC是等边三角形.故选B.点评:本题主要考查正弦定理和两角和与差的正弦公式的应用.三角函数公式比较多,要对公式强化记忆.2.在△ABC中,角A,B,C的对边分别为a,b,c,若a2﹣b2﹣c2=﹣bc,则A等于()A.B.C.D.考点:余弦定理.专题:解三角形.分析:利用余弦定理即可得出.解答:解:∵a2﹣b2﹣c2=﹣bc,∴b2+c2﹣a2=bc.∴cosA==,又A∈(0,π),∴A=.故选:A.点评:本题考查了余弦定理的应用,属于基础题.3.在△ABC中,a=,b=,B=45°,则A等于()A.30°B.60°C.30°或150°D.60°或120°考点:正弦定理.专题:计算题.分析:根据B的度数求出sinB的值,再由a,b的值,利用正弦定理求出sinA的值,然后根据A为三角形的内角,利用特殊角的三角函数值即可求出A的度数.解答:解:由a=,b=,B=45°,根据正弦定理得:,所以,又A∈(0,180°),所以A等于60°或120°.故选D点评:此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.4.在△ABC中,∠A=60°,a=,b=3,则△ABC解的情况()A.无解B.有一解C.有两解D.不能确定考点:正弦定理.专题:计算题;解三角形.分析:由a,b及sinA的值,利用正弦定理即可求出sinB的值,求解即可.解答:解:由正弦定理得:即,解得sinB=,因为,sinB∈[﹣1,1],故角B无解.即此三角形解的情况是无解.故选A.点评:此题考查学生灵活运用正弦定理化简求值,掌握正弦函数的图象与性质,是一道基础题.5.若则下列不等式:(1)a+b<a•b;(2)|a|>|b|(3)a<b中,正确的不等式有()A. 1个B. 2个C. 3个D. 0个考点:不等式的基本性质.专题:不等式的解法及应用.分析:由,可得b<a<0.利用不等式的性质即可得出.解答:解:∵,∴b<a<0.则下列不等式:(1)a+b<0<a•b,正确;(2)|a|>|b|,不正确;(3)a<b不正确.故正确的不等式只有1个.故选:A.点评:本题考查了不等式的基本性质,属于基础题.6.在各项均为正数的等比数列{a n}中,若a3a8=9,则log3a1+log3a10=()A. 1 B. 2 C. 4 D. log35考点:等比数列的性质;对数的运算性质.专题:计算题.分析:根据等比数列的性质可知a1a10=a3a8=9,再利用对数的性质即可得到答案.解答:解:log3a1+log3a10=log3(a1a10)=2故选B.点评:本题主要考查了等比数列的性质.即若 m、n、p、q∈N*,且m+n=p+q,则a m a n=a p a q.7.已知数列{a n}满足3a n+1+a n=0,a2=﹣,则{a n}的前10项和等于()A.﹣6(1﹣3﹣10) B.C. 3(1﹣3﹣10)D. 3(1+3﹣10)考点:等比数列的前n项和.专题:计算题;等差数列与等比数列.分析:由已知可知,数列{a n}是以﹣为公比的等比数列,结合已知可求a1,然后代入等比数列的求和公式可求解答:解:∵3a n+1+a n=0∴∴数列{a n}是以﹣为公比的等比数列∵∴a1=4由等比数列的求和公式可得,S10==3(1﹣3﹣10)故选C点评:本题主要考查了等比数列的通项公式及求和公式的简单应用,属于基础试题8.如果等差数列{a n}中,a3+a4+a5=12,那么S7=()A. 14 B. 21 C. 28 D. 35考点:等差数列的前n项和.专题:等差数列与等比数列.分析:利用等差中项可知a4=4,进而可得结论.解答:解:∵a3+a4+a5=12,∴a4=4,∴S7=(a1+a7)+(a2+a6)+(a3+a5)+a4=7a4=28,故选:C.点评:本题考查等差中项的性质,注意解题方法的积累,属于中档题.9.等差数列{a n}中,a3=8,a7=20,若数列{}的前n项和为,则n的值为()A. 14 B. 15 C. 16 D. 18考点:数列的求和;等差数列的性质.专题:计算题.分析:根据a3=8,a7=20等差数列的通项公式为3n﹣1,然后根据数列的前n项的和S n=+…+,因为=(﹣)可得S n=解出n即可.解答:解:设等差数列的首项为a,公差为d,因为a3=8,a7=20,所以a+2d=8,a+6d=20,解得a=3,a=2.a n=3n﹣1;又因为==(﹣),所以S n=(﹣+﹣+﹣+…+﹣)=(﹣)=25,解得n=16故选C点评:考查学生运用等差数列性质解决问题的能力,灵活运用做差方法求数列的和.10.在数列{a n}中,a1=2,a n+1=a n+ln(1+),则a n=()A. 2+lnn B. 2+(n﹣1)lnn C. 2+nlnn D. 1+n+lnn考点:数列的概念及简单表示法.专题:点列、递归数列与数学归纳法.分析:把递推式整理,先整理对数的真数,通分变成,用迭代法整理出结果,约分后选出正确选项.解答:解:∵,,…∴=故选:A.点评:数列的通项a n或前n项和S n中的n通常是对任意n∈N成立,因此可将其中的n换成n+1或n﹣1等,这种办法通常称迭代或递推.解答本题需了解数列的递推公式,明确递推公式与通项公式的异同;会根据数列的递推公式写出数列的前几项.11.已知a>0,b>0,且2a+b=1,则+的最小值为()A. 7 B. 8 C. 9 D. 10考点:基本不等式.专题:不等式的解法及应用.分析:利用“乘1法”、基本不等式的性质即可得出.解答:解:∵a>0,b>0,2a+b=1,∴+=(2a+b)=5+=9,当且仅当a=b=时取等号.∴+的最小值为9.故选:C.点评:本题考查了“乘1法”、基本不等式的性质,属于基础题.12.已知不等式对一切正整数n恒成立,则实数a的范围为()A.(0,3)B.(1,3)C.(2,4)D.(3,+∞)考点:数列的求和.专题:等差数列与等比数列.分析:由于,于是原不等式化为>,由于不等式对一切正整数n 恒成立,可得log2(a﹣1)+a﹣,化简整理利用对数函数的单调性即可得出.解答:解:∵,∴不等式,化为>,由于不等式对一切正整数n 恒成立,∴log2(a﹣1)+a﹣,化为4﹣a>log2(a﹣1),∴1<a<3.故选:B.点评:本题考查了数列“裂项求和”、恒成立问题的等价转化方法、对数函数的单调性,考查了推理能力与计算能力,属于中档题.二、填空题(共4小题,每小题5分,满分20分)13.在如图图形中,小黑点的个数构成一个数列{a n}的前3项.(1)a5= 13 ;(2)数列{a n}的一个通项公式a n= 3n﹣2 .考点:归纳推理.专题:推理和证明.分析:观察图形特点,从中找出规律,它们的点数分别是;1,4,7,…,总结出其规律,根据规律求解.解答:解:通过观察,得到点的个数分别是:a1=1,a2=4,a3=7,…可归纳推理为:数列{a n}是一个以1为首项,以3为公差的等差数列,故a n=3n﹣2,当n=5时,a5=13,故答案为:13,3n﹣2点评:此题主要考查了学生分析问题、观察总结规律的能力.关键是通过观察分析得出规律,数列{a n}一个首项是1,公差是3的等差数列.14.在△ABC中三边之比a:b:c=2:3:,则△ABC中最大角= .考点:解三角形.专题:计算题.分析:根据三边的比,设出三边的长,利用大边对大角的原则,判断出△ABC中最大角,进而利用余弦定理求得cosC的值,进而求得C.解答:解:依题意可设a=2t,b=3t,c=t,依据大边对大角的原则,判断出C为最大角由余弦定理可知 cosC==﹣∴C=故答案为:.点评:本题主要考查了余弦定理的应用.涉及已知三边求三角形的内角的问题,常用余弦定理来解决.15.在△ABC中,内角A,B,C所对的边长分别是a,b,c,已知A=,cosB=,若BC=10,D为AB的中点,则CD= .考点:余弦定理.专题:解三角形.分析:利用正弦定理可得:b,c,再利用中线长定理即可得出.解答:解:如图所示,∵cosB=,B∈(0,π),∴=.sinC=sin(B+)==.由正弦定理可得:=,∴=6,c==14.由中线长定理可得:a2+b2=2CD2+,∴=2CD2+,解得CD=.故答案为:.点评:本题考查了正弦定理、中线长定理,考查了推理能力与计算能力,属于中档题.16.设S n是公差不为零的等差数列{a n}的前n项和,且a1>0,若S5=S9,则当S n最大时,n= 7 .考点:等差数列的前n项和.专题:等差数列与等比数列.分析:由题意可得a7+a8=0,判断数列的前7项为正数,从第8项开始为负数,可得结论.解答:解:∵a1>0,若S5=S9,∴S9﹣S5=a6+a7+a8+a9=0,∴2(a7+a8)=0,∴a7+a8=0,又a1>0,∴该等差数列的前7项为正数,从第8项开始为负数,即前7项和最大,∴当S n最大时,n=7故答案为:7点评:本题考查等差数列的前n项和的最值,得出数列项的正负变化以及利用等差数列的性质是解决问题的关键.三、解答题(共6小题,满分70分)17.已知等差数列{a n}为递增数列,其前三项和为﹣3,前三项的积为8(1)求等差数列{a n}的通项公式;(2)求数列{a n}的前n的和S n.考点:等差数列的前n项和;等差数列的通项公式.专题:等差数列与等比数列.分析:(1)设等差数列{a n}的公差为d,(d>0),根据条件,建立方程组,解方程组可得a1、d,进而可得通项公式;(2)利用等差数列的求和公式可得结论.解答:解:(1)设等差数列{a n}的公差为d,d>0∵等差数列{a n}前三项的和为﹣3,前三项的积为8,∴,∴或,∵d>0,∴a1=﹣4,d=3,∴a n=3n﹣7;(2)∵a n=3n﹣7,∴a1=3﹣7=﹣4,∴S n==.点评:本题考查等差数列的前n项和公式和通项公式,正确运用公式是关键.考查学生的计算能力.18.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,.(1)求A的大小;(2)若,,求a.考点:余弦定理;正弦定理.专题:三角函数的求值;解三角形.分析:(1)已知等式利用正弦定理化简,根据sinB不为0求出sinA的值,即可确定出A的度数;(2)由b,c,cosA的值,利用余弦定理求出a的值即可.解答:解:(1)由b=asinB,根据正弦定理得:sinB=sinAsinB,∵在△ABC中,sinB≠0,∴si nA=,∵△ABC为锐角三角形,∴A=;(2)∵b=,c=+1,cosA=,∴根据余弦定理得:a2=b2+c2﹣2bccosA=6+4+2﹣2××(+1)×=4,则a=2.点评:此题考查了正弦、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.19.已知△ABC中,角A,B,C的对边分别为a,b,c,且,b=1.(Ⅰ)若,求c;(Ⅱ)若a=2c,求△ABC的面积.考点:解三角形;正弦定理;余弦定理的应用.专题:综合题.分析:(Ⅰ)由,利用辅助角公式化简,结合B的范围,可得B,利用A,求得C,结合正弦定理可求c的值;(Ⅱ)确定△ABC为直角三角形,再求其面积.解答:解:(Ⅰ)由已知,∵,∴sin(B﹣)=.…(2分)∵0<B<π,∴.故B﹣=,解得B=.…(4分)由,且A+B+C=π,得C=.由,即,解得c=.…(7分)(Ⅱ)因为b2=a2+c2﹣2accosB,a=2c,B=,所以b2=4c2+c2﹣4c2×,解得b=c.…(10分)由此得a2=b2+c2,故△ABC为直角三角形,A=,c=.其面积S=bc=.…(13分)点评:本题考查三角函数的化简,考查正弦定理、余弦定理的运用,考查三角形面积的计算,确定三角形的边与角是关键.20.在数列{a n}中,已知a1=2,a n+1=4a n﹣3n+1,n∈N•.(1)设b n=a n﹣n,求证:数列{b n}是等比数列;(2)求数列{a n}的前n项和S n.考点:数列的求和;等比关系的确定.专题:计算题.分析:(1)确定数列{b n}是等比数列,则要证明是个不为0的定值,结合题干条件即可证,(2)首先根据(1)求出数列{b n}的通项公式,然后根据题干条件求得a n=b n+n=4n﹣1+n,结合等差数列和等比数列的求和公式即可解答.解答:解:(1)∵,(5分)且b1=a1﹣1=1∴b n为以1为首项,以4为公比的等比数列,(7分)(2)由(1)得b n=b1q n﹣1=4n﹣1(8分)∵a n=b n+n=4n﹣1+n,(9分)∴=,(12分)点评:本题主要考查数列求和和等比关系的确定的知识点,解答本题的关键是熟练掌握等差和等比数列的性质和求和公式,本题难度一般.21.数列{a n}的前n项和为S n,a1=2,S n=a n﹣1(n∈N*)(1)求数列{a n}的通项公式;(2)设b n=na n,求数列{b n}的前n项和T n.考点:数列的求和;数列递推式.专题:等差数列与等比数列.分析:(1)利用递推式、等比数列的通项公式即可得出;(2)b n=na n=2n•3n﹣1.利用“错位相减法”、等比数列的前n项和公式即可得出.解答:解:(1)∵S n=a n﹣1(n∈N*),∴当n≥2时,,a n=S n﹣S n﹣1=a n﹣1﹣,化为a n=3a n﹣1.当n=1时,,解得a1=2.∴数列{a n}是等比数列,首项为2,公比为3.∴.(2)b n=na n=2n•3n﹣1.∴数列{b n}的前n项和T n=2(1+2×3+3×32+…+n•3n﹣1),3T n=2(3+2×32+3×33+…+n×3n),∴﹣2T n=2(1+3+32+…+3n﹣1﹣n×3n)==(1﹣2n)×3n﹣1.∴T n=.点评:本题考查了递推式的应用、等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.22.若函数为f(x)=x2﹣2mx﹣2m﹣1(1)求f(x)>0的解集;(2)若f(x)>﹣4m﹣2对满足0≤x≤1的所有实数x都成立,求m的取值范围.考点:二次函数的性质;函数恒成立问题.专题:函数的性质及应用;不等式的解法及应用.分析:(1)解x2﹣2mx﹣2m﹣1=0得:x=2m+1或x=﹣1,结合二次函数的图象和性质,讨论2m+1与﹣1的大小,可得不等式f(x)>0的解集.(2)首先对提议进行转换,考虑二次函数的对称轴和已知区间之间的关系进行分类讨论,最后求出参数的取值范围.解答:解:(1)解x2﹣2mx﹣2m﹣1=0得:x=2m+1或x=﹣1,当2m+1<﹣1,即m<﹣1时,不等式f(x)>0的解集是:(﹣∞,2m+1)∪(﹣1,+∞),当2m+1=﹣1,即m=﹣1时,不等式f(x)>0的解集是:(﹣∞,﹣1)∪(﹣1,+∞),当2m+1>﹣1,即m>﹣1时,不等式f(x)>0的解集是:(﹣∞,﹣1)∪(2m+1,+∞),(2)若f(x)>﹣4m﹣2对满足0≤x≤1的所有实数x都成立,即x2﹣2mx+2m+1>0对满足0≤x≤1的所有实数x都成立,设函数g(x)=x2﹣2mx+2m+1所以函数是开口方向向上,对称轴为x=m的抛物线.由于g(x)=x2﹣2mx+2m+1在0≤x≤1的所有实数x对g(x)>0都成立,所以①当m<0时,只需g(0)>0成立即可.即:2m+1>0解得:m>﹣所以:﹣<m<0②当0≤m≤1时,只需满足f(m)>0即可.即:m2﹣2m2+2m+1>0解得:1﹣≤m≤1+所以:0≤m≤1③当m>1时,只需满足f(1)>0即可.即:2>0恒成立所以:m>1综上所述:m的取值范围为:m>﹣点评:本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.。
黑龙江省大庆铁人中学2014届高三数学考前模拟冲刺试题 理(含解析)

某某铁人中学高三学年考前模拟训练数学试题(理科)【试卷综析】这套试题,具体来说比较平稳,基本符合高考复习的特点,稳中有变,变中求新,适当调整了试卷难度,体现了稳中求进的精神。
考查的知识涉及到函数、三角函数、数列、解析几何、立体几何、排列组合 、概率、复数等几章知识,重视学科基础知识和基本技能的考察,同时侧重考察了学生的学习方法和思维能力的考察,有相当一部分的题目灵活新颖,知识点综合与迁移。
试卷的整体水准应该说可以看出编写者花费了一定的心血。
但是综合知识、创新题目的题考的有点少。
这套试题以它的知识性、思辨性、灵活性,基础性充分体现了考素质,考基础,考方法,考潜能的检测功能。
试题中无偏题,怪题,起到了引导高中数学向全面培养学生数学素质的方向发展的作用。
考试时间:120分钟 总分:150分一、选择题(本大题共12小题,每题5分,共计60分,在每题给出的四个选项中,只有一个是正确的) 1.已知集合}|{2x y y M ==,}2|{22=+=y x y N ,则N M =( ).A )}1,1(),1,1{(-.B }1{.C ]1,0[.D ]2,0[【知识点】数集与点集的区别;交集.【答案解析】D 解析:解:由于集合M 、N都是数集,所以{}{}|0,|22M y y N y y =≥=-≤≤,则N M ={}|02y y ≤≤,故选D.【思路点拨】先确定集合M 、N 都是数集,避免出现解方程组的错误,然后再求交集. 2.复数ii321+-在复平面内对应的点位于( ) .A 第一象限 .B 第二象限 .C 第三象限 .D 第四象限【知识点】复数;复数的实部与虚部复平面.【答案解析】C 解析:解:可化为()()()22123151513131323i i i i i ----==---,所以在第三象限. 故选C.【思路点拨】可依据题意先把复数化简为实部加虚部的形式,对应坐标可知结果.3.已知p :a >3,q :∃x ∈R ,使x 2+ax +1<0是真命题,则p 是q 的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【知识点】必要条件、充分条件与充要条件的判断. 【答案解析】A 解析:解:【思路点拨】根据二次函数的图象和性质,可得命题q :∃x ∈R ,使x 2+ax+1<0是真命题,表示对应函数的最小值小于0,即对应方程有两个实根,进而构造不等式求出a 的X 围,再根据充要条件的定义可得答案.【典型总结】本题考查的知识点是充要条件,存在性问题,其中根据存在性问题与极值问题的关系,求出命题q 为真时a 的X 围,是解答的关键. 4.设,,l m n 表示不同的直线,αβγ,,表示不同的平面,给出下列四个命题:①若m ∥l ,且.m α⊥则l α⊥; ②若m ∥l ,且m ∥α.则l ∥α;③若,,l m n αββγγα===,则l ∥m ∥n ; ④若,,,m l n αββγγα===且n ∥β,则l ∥m .其中正确命题的个数是( ) .A 1 .B 2.C 3 .D 4【知识点】线线平行、线面平行、线面垂直等定理.【答案解析】B 解析:解:①平行线中的一条垂直于一个平面则另一条也垂直于这个平面m ⊥α则l ⊥α正确.②l 可能属于α,所以不正确.③l,m,n 可能交于一点,所以不正确. ④n ∥β∴n ∥l ∴l ∥α∴l ∥m ∴正确.【思路点拨】可由直线与平面平行的判定定理和性质定理推出各种说法的正误.5.已知数列}{n a 中,11=a ,n a a n n +=+1,若利用如图所示的程序框图计算该数列的第10项,则判断框内的条件是( ) .A ?8≤n .B ?9≤n.C ?10≤n .D ?11≤n【知识点】当型循环结构,程序框图 【答案解析】B 解析:解:【思路点拨】n=1,满足条件,执行循环体,S=2,依此类推,当n=10,不满足条件,退出循环体,从而得到循环满足的条件.【典型总结】本题主要考查了当型循环结构,算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题. 6.已知向量(1,2),(4,)a x b y =-=,若a b ⊥,则93x y +的最小值为( ).A .B 12 .C 6 .D【知识点】向量的运算;基本不等式. 【答案解析】C 解析:解:()142022a b x y x y ⊥∴-⋅+=⇒+=又293336x x y y +=+≥=,233xy=时等号成立即2x y =时等号成立. 【思路点拨】本题可由向量的基本运算求出x 和y 的关系,利用基本不等式即可. 7.已知函数()()sin 2f x x ϕ=+,其中02ϕπ<<,若()6f x f π⎛⎫≤∈⎪⎝⎭对x R 恒成立,且()2f f ππ⎛⎫> ⎪⎝⎭,则ϕ等于 ( ) .A 6π.B 56π .C 76π.D 116π【知识点】y=Asin (ωx+φ)的部分图象确定其解析式.数的最大值或最小值,由此可以确定满足条件的初相角φ的值,结合f (2π)>f (π),易求出满足条件的具体的φ值.8.已知三棱锥的三视图如图所示,则它的外接球表面积为( ).A 16π.B 4π .C 8π.D 2π 【知识点】三视图 ;球的表面积公式. 【答案解析】B 解析:解:由三棱锥的三视图可知中点位置即为球心,因为斜边长为223+1=2,斜边上的中线等于斜边的一半,三棱锥的高为1,所以三棱锥的外接球的半径为1,所以根据球的表面积公式可得2S=4R =4ππ【思路点拨】由几何体的三视图可求出底面三角形为直角三角形,斜边长为2,高为1,所以可得球的半径为1,代入公式可求. 9.从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,则这个数能被 3整除的概率为 ( ).A 5419.B 5438 .C 5435.D 6041 【知识点】古典概型及其概率计算公式.【答案解析】A 解析:解:0到9这10个数字中,任取3个数字组成一个没有重复数字的三位数,所有的三位数的个数为32109A A -=648个.将10个数字分成三组,即被3除余1的有{1,4,7}、被3除余2的有{2,5,8},被3整除的有{3,6,9,0}.若要求所得的三位数被3整除,则可以分类讨论: ①三个数字均取第一组,或均取第二组,有233A =12个;②若三个数字均取自第三组,则要考虑取出的数字中有无数字0,共有3243A A -=18个;③若三组各取一个数字,第三组中不取0,有11133333•••C C C A =162个, ④若三组各取一个数字,第三组中取0,有112332••2C C A =36个,这样能被3整除的数共有228个.故这个三位数能被3整除的概率是2281964854=,故选A .【思路点拨】由题意可得所有的三位数有32109A A -=648个,然后根据题意将10个数字分成三组:即被3除余1的有1,4,7;被3除余2的有2,5,8;被3整除的有3,6,9,0,若要求所得的三位数被3整除,则可以分类讨论:每组自己全排列,每组各选一个,再利用排列与组合的知识求出个数,进而求出答案. 10.函数)(x f y =为定义在R 上的减函数,函数)1(-=x f y 的图像关于点(1,0)对称, y x ,满足不等式)2(2x x f -0)2(2≤-+y y f ,)2,1(M ,),(y x N , O 为坐标原点,则当41≤≤x 时, ON OM ⋅的取值X 围为( ).A [)+∞,12.B []3,0.C []12,3.D []12,0【知识点】函数的奇偶性;线性规划;向量.【答案解析】D 解析:解:函数y=f (x-1)的图象关于点(1,0)对称,所以f(x )为 奇函数.22220f x x f y y ∴-≤-+≤()(),2222x x y y ∴-≥-+,222214x x y yx ⎧-≥-⎨≤≤⎩即()()2014x y x y x -+-≥⎧⎪⎨≤≤⎪⎩由图可得可行域为2OM ON x y ⋅=+可取的X 围是[]0,12.故选D .【思路点拨】本题是考查函数性质的一综合题,多个知识点交汇的典型题型,利用函数的性质把两个变量的关系转化成可行域,利用用线性规划的方法可解.11.已知双曲线1322=-x y 与抛物线ay x =2有相同的焦点F ,O 为原点,点P 是抛物线准线上一动点,点A 在抛物线上,且4=AF ,则PO PA +的最小值为( ).A 132.B 24.C 133.D 64【知识点】双曲线与抛物线的几何性质;抛物线的几何意义;【思路点拨】利用抛物线的定义由|AF|=4得到A 到准线的距离为4,即可求出点A 的坐标,根据:“|PA|+|PO|”相当于在准线上找一点,使得它到两个定点的距离之和最小,最后利用平面几何的方法即可求出距离之和的最小值.【典型总结】此题考查学生灵活运用抛物线的简单性质解决最小值问题,灵活运用点到点的距离、对称性化简求值.12.已知定义在R 上的可导函数)(x f 满足:0)()('<+x f x f ,则122)(+--m m em m f 与)1(f (e是自然对数的底数)的大小关系是( ).A 122)(+--m m em m f >)1(f .B 122)(+--m m em m f <)1(f.C 122)(+--m m em m f ≥)1(f .D 不确定【知识点】利用导数判断单调性;构造新函数,不等式.2m m --2(m m )g -【思路点拨】设出()(),xg x e f x =是本题的关键,然后利用函数()g x 的单调性即可. 二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)13.在边长为1的等边ABC ∆中,D 为BC 边上一动点,则AB AD ⋅的取值X 围是.【知识点】平面向量数量积的运算.两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,2AB 与BD 的夹角∴AB AD ⋅=AB ⋅(AB BD +)=2AB AB BD +⋅=1+1×||BD cos120°=12||BD .由于BC 边上一动点,故 0≤|BD|≤1,∴12≤1-12•||BD ≤1,即AB AD ⋅的取值X 围是1[2故答案为1[,1]2【思路点拨】由题意可得AB 与BD 的夹角等于120°,利用两个向量的数量积的定义计算AB AD ⋅=1-12||BD ,结合0≤|BD|≤1 求得AB AD ⋅ 的取值14.(x x+2)6)1(x -的展开式中x 的系数是【知识点】二项式定理;二项式展开式的系数. 【答案解析】31解析:解:x 的系数为2x与6)1(x -展开式中2x 项的乘积的系数加上x 与6)1(x -展开式中常数项的乘积的系数,6)1(x -的展开式中常数项为1,2x 的项为4426115C x x ⎛⎫-= ⎪⎝⎭所以221530x x x ⨯=,13031x x x ⨯+=,所以x 的系数为31.【思路点拨】可依据展开式中一次项得到的过程进行分析,是由那些项合并得到,就可以分开求出一次项,最后合并,找出系数即可.15.抛物线342-+-=x x y 及其在点)0,1(A 和点)0,3(B 处的切线所围成图形的面积为【知识点】直线与圆锥曲线的关系. 【答案解析】23解析:解:对y=x 2-4x+3求导可得,y′=2x -4∴抛物线y=x 2-4x+3及其在点A(1,0)和B (3,0)处的两条切线的斜率分别为-2,2从而可得抛物线y=x 2-4x+3及其在点A (1,0)和B (3,0)处的两条切线方程分别为 l 1:2x+y-2=0,l 2:2x-y-6=0(2)由2226y x y x =-+⎧⎨=-⎩可得交点P (2,-2)S=221432[2]x x x dx -+--+⎰()()+23243[26]x x x dx -+--⎰()()=22121[x x dx -+⎰() +23269[x x dx -+⎰()=3213x x x -+()|21+321393x x x -+()|32=23,故选A 【思路点拨】欲求切线的方程,只须求出其斜率的值即可,故先利用导数求出在切点处的导函数值,再结合A (1,0),B (3,0)都在抛物线上,即可求出切线的方程,然后可得直线与抛物线的交点的坐标和两切线与x 轴交点的坐标,最后根据定积分在求面积中的应用公式即可求得所围成的面积S 即可.16.函数)(x f 的定义域为D ,若存在闭区间],[b a D ⊆,使得函数)(x f 满足:(1))(x f 在],[b a 内是单调函数;(2))(x f 在],[b a 上的值域为]2,2[b a ,则称区间],[b a 为函数)(x f y =的“和谐区间”。
黑龙江省大庆铁人中学2014届高三数学4月月考试题 文 新人教A版

黑龙江省大庆铁人中学2013-2014学年度高三下学期4月月考数学试题(文科)考试时间:120分钟 总分:150分一、选择题〔本大题共12小题,每题5分,共计60分,在每题给出的四个选项中,只有一个是正确的〕1.{},01|2>-∈=x R x A {}2)3(log |2≤+∈=x Z x B ,如此()RC A B ⋂=〔 〕(A) ]1,1[- (B) )1,3(--(C){}1,0,1-( D){}0,12.i 是虚数单位,复数i iZ -+=221,如此Z =〔 〕〔A 〕5 〔B 〕 2 〔C 〕 55〔D 〕13.某程序框图如下列图,假设3a =,如此该程序运行后,输出的x 的值为〔 〕(A) 33 ( B) 31 ( C)29 ( D) 27 4.某几何体的三视图如右图,(其中侧视图中的圆弧是半圆),如此该几何体的外表积为(A)π1492+ (B)π1482+ (C)π2492+ (D)π2482+ 5.假设等比数列{}n a 中满足483a a +=-,如此62610(2)a a a a ++=( )(A)3-(B) 3(C) 6 (D)96.y x ,满足约束条件,设),(y x 表示的平面区域为M ,在区域M 内任 取一点 ,如此此点到直线2-=x y 的距离大于2的概率为( )(A) 41 (B)43 (C)21 ( D) 917.设c b a ,,是三条不同直线,α,β,γ是三个不同平面,如此如下命题正确题是〔 〕 ①假设αγ⊥,βγ⊥,如此//αβ;②假设b a ,异面,a α⊂,b β⊂,//a β,//b α,如此//αβ; ③假设a αβ=,b βγ=,c γα=,且//a b ,如此//c β;④假设b a ,为异面直线,//a α,//b α,c a ⊥,c b ⊥,如此c α⊥. (A) ①②④ (B) ②④ (C) ②③④ (D) ③④8.如下关于函数()2sin(2)13f x x π=-+的命题正确的答案是〔 〕(A) 函数()f x 在区间(,)63ππ-上单调递增(B) 函数()f x 的对称轴方程是5212k x ππ=+〔k Z ∈〕(C) 函数()f x 的对称中心是〔,06k ππ+〕〔k Z ∈〕(D) 函数()f x 以由函数()2cos 21g x x =+向右平移6π个单位得到9.函数()sin f x x x =,如此π()11f ,(1)f -,π3f -()的大小关系为第5题图俯视图侧视图54246〔A)ππ()(1)()311f f f ->-> ( B)ππ(1)()()311f f f ->-> (C)ππ()(1)()113f f f >->- ( D)ππ()()(1)311f f f ->>-10.在ABC ∆中,角A ,B ,C 对应边分别是a ,b ,c ,5a =,8b =,60C =︒, 如此||BC CA CA CB ⋅+-等于( )(A)13- (B) 27(C) 5(D)5-11.双曲线22221x y a b -=〔0,0>>b a 〕的两个焦点为12,F F ,假设P 为其上的一点,且12||2||PF PF =,如此双曲线离心率的取值范围为〔 〕(A)(1,3)(B) (1,3](C)(3,)+∞(D)[3,)+∞12. 关于x 的方程1x e --0kx =〔其中e 是自然对数的底数〕的有三个不同实根,如此k 的取值范围是(A) {k |k > e } (B) {k |2k > 2e } (C) {k |1k >} (D) {k |21k >} 二、填空题〔本大题共4小题,每一小题5分,共20分,把答案填在题中横线上〕13. 假设α为锐角,且3cos()65πα+=,如此sin(2)3πα+=. 14.1234212,21334,2135456,213575678,⨯=⨯⨯=⨯⨯⨯⨯=⨯⨯⨯⨯⨯⨯=⨯⨯⨯…依此类推,第n 个等式为 . 15. 如下说法:①“,23x n x R ∃∈>使〞的否认是“,3x x R ∀∈≤使2〞; ②假设正数y x ,满足xy y x 53=+,如此y x 43+的最小值为528;③命题“函数()f x x x =在处有极值,如此0'()0f x =〞的否命题是真命题;④()f x ∞∞是(-,0)(0,+)上的奇函数,0x >时的解析式是()2xf x =,如此0x <时的解析式为()2.xf x -=- 其中正确的说法是 ______________16.球O 的球面上有三点C B A ,,,且︒=∠=30,3BAC BC ,过C B A ,,三点作球O 的截面,球心O 到截面的距离为4,如此该球的体积为________________ 三、解答题〔本大题共6小题,其中17~22每题各12分,22~24三选一10分,共70分〕17.〔本小题总分为12分〕{}n a 是一个公差小于0的等差数列,且满足372827,6a a a a =-+=(I)求数列{}n a 的通项公式;(Ⅱ)设数列{}n a 的前n 项和为n S ,在由所有前n 项和n S 组成的数列{}n S 中,哪一项最大,最大项是多少?18〔本小题总分为12分〕对某校高一年级学生参加社区服务次数进展统计,随机抽取M 名学生作为样本,得到这M下:10 15 20 25 30次数⑴求出表中M 、p 、、n 的值;⑵补全频率分布直方图;假设该校高一学生有360人,试估计他们参加社区服务的次数在区间[)15,20内的人数;⑶在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[)20,25内的概率.19.〔本小题总分为12分〕 如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,AD//BC ,⊥PD 底面ABCD ,∠ADC=90°,BC=12AD=1, PD=CD=2,Q 为AD 的中点. 〔Ⅰ〕假设点M 在棱PC 上,设PM=tMC ,是否存在实数t ,使得PA//平面BMQ ,假设存在,给出证明并求t 的值,假设不存在,请说明理由; 〔Ⅱ〕在〔Ⅰ〕的条件下,求三棱锥BMQ P -的体积.20. 〔本小题总分为12分〕如图,(10)F ,,直线:1l x =-,P 为平面上的动点,过点P 作l 的垂线,垂足为点Q ,且QP QF FP FQ ⋅=⋅.〔Ⅰ〕求动点P 的轨迹C 的方程; 〔Ⅱ〕过点F 的直线交轨迹C 于A B ,两点,交直线l 于点M . 〔1〕1MA AF λ=,2MB BF λ=,求12λλ+的值;〔2〕求MA MB⋅的最小值.21. 〔本小题总分为12分〕 设)1()(+-=x a e x f x〔1〕求函数)(x f 的单调区间;〔2〕设x e ax f x g +=)()(,且))(,(),,(212211x x y x B y x A ≠是曲线)(x g y =上任意两点,假设对任意的1-≤a ,直线AB 的斜率大于常数,求实数的取值范围PABCDQM22,23,24为选修题目,三题选择一个作答,如果三题都答,如此按第一题评分。
黑龙江省大庆铁人中学2013-2014学年高二下学期四月月考数学文科

黑龙江省大庆铁人中学2013-2014学年高二下学期四月月考数学文科2014.4.15时间:120分钟 满分:150分 一、选择题(本大题共12小题,每小题5分,共60分) 1.点()3,1-P ,则它的极坐标是.( ) A .⎪⎭⎫ ⎝⎛3,2π B .⎪⎭⎫ ⎝⎛34,2π C .⎪⎭⎫ ⎝⎛-3,2π D .⎪⎭⎫⎝⎛-34,2π2.数列2,5,11,20,,47,x …中的x 等于( ) A .28 B .32 C .33 D .273. 若'0()3f x =-,则000()(3)limh f x h f x h h→+--=( )A .3-B .6-C .9-D .12-4. 曲线的参数方程为⎩⎨⎧-=+=12322t y t x (t 是参数),则曲线是( ) A 、线段 B 、直线 C 、圆 D 、射线5.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )①若K 2的观测值满足K 2≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;②从独立性检验可知有99%的把握认为吸烟与患病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;③从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误 A .① B .①③ C .③ D .② 6.函数xxy ln =的最大值为( ) A .1-e B .e C .2e D .310 7.设△ABC 的三边长分别为a 、b 、c ,△ABC 的面积为S ,内切圆半径为r ,则r =2Sa +b +c;类比这个结论可知:四面体S -ABC 的四个面的面积分别为S 1、S 2、S 3、S 4,内切球的半径为r ,四面体S -ABC 的体积为V ,则r =( ) A.VS 1+S 2+S 3+S 4B.2V S 1+S 2+S 3+S 4 C.3V S 1+S 2+S 3+S 4 D.4VS 1+S 2+S 3+S 48.直线l 的参数方程为()x a tt y b t=+⎧⎨=+⎩为参数,l 上的点1P 对应的参数是1t ,则点1P 与(,)P a b 之间的距离是( )A .1tB .12tC .12tD .122t 9..极坐标方程cos 2sin 2ρθθ=表示的曲线为( )A .一条射线和一个圆B .两条直线C .一条直线和一个圆D .一个圆 10.直线的参数方程为⎩⎪⎨⎪⎧x =t sin50°-1y =-t cos50°(t 为参数),则直线的倾斜角为( )A .40°B .50°C .140°D .130°11.若a>0, b>0, 且函数f(x)=4x 3-ax 2-2bx+2在x=1处有极值,则ab 的最大值等于( )A . 2B . 3C . 6D . 9 12.已知函数)(x f 的定义域为—2,)∞+,部分对应值如下表,)('x f 为)(x f 的导函数,函数)('x f y =的图象如右图所示:若两正数,a b 满足(2)1f a b +<,则44b a -+的取值范围是( )A . )34,76(B .)37,53(C .)56,32(D .1(1,)2--二、填空题(本大题共4小题,每小题5分,共20分)13.与直线2x -6y +1=0垂直,且与曲线f (x )=x 3+3x 2-1相切的直线方程是________. 14. 对具有线性相关关系的变量x 和y ,由测得的一组数据已求得回归直线的斜率为6.5,且恒过(2,3)点,则这条回归直线的方程为________.15. 函数322(),f x x ax bx a =+++在1=x 时有极值10,那么b a ,的值分别为________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黑龙江省大庆铁人中学2013-2014学年度高三下学期4月月考数学试题(理科)2014.4考试时间:120分钟 总分:150分一、选择题(本大题共12小题,每题5分,共计60分,在每题给出的四个选项中,只有一个是正确的) 1. 已知集合{1,2},{,},a A B a b ==若⎭⎬⎫⎩⎨⎧=⋂21B A ,则A B 为 ( )A . 1{1,,1}2- B .1{1,}2- C .1{1,}2 D . 1{,1,}2b2.设i 是虚数单位,若复数10()3a a R i-∈-是纯虚数,则a 的值为( ) A .3- B . 1- C .1 D .33.已知m ,n 为两条不同的直线,α,β为两个不同的平面,下列命题中正确的是( )A .l m ⊥,l n ⊥,且,m n α⊂,则l α⊥B .若平面α内有不共线的三点到平面β的距离相等,则βα//C .若n m m ⊥⊥,α,则α//nD .若α⊥n n m ,//,则α⊥m 4.给出下列三个结论:(1)若命题p 为假命题,命题q ⌝为假命题,则命题“q p ∨”为假命题;(2)命题“若0xy =,则0x =或0y =”的否命题为“若0xy ≠,则0x ≠或0y ≠”; (3)命题“,20xx ∀∈>R ”的否定是“ ,20xx ∃∈≤R ”.则以上结论正确的个数为( ) A .3 B .2 C .1 D .05.设等比数列{}n a 中,前n 项和为n S ,已知7863==S S ,,则=++987a a a ( )A .81 B .81- C .857 D .855 6. 将4名实习教师分配到高一年级三个班实习,每班至少安排一名教师,则不同的分配方案有 ( )种 A .12B . 36C .72D .1087. 函数()()sin 0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的最小正周期是π,若其图象向右平移6π个单位后得到的函数为奇函数,则函数()f x 的图象( )A .关于点)0,6(π对称B .关于6π=x 对称C .关于点,012π⎛⎫⎪⎝⎭对称 D .关于12x π=对称8. 若1ln ln 1(,1),ln ,(),,2xx x e a x b c e -∈===则,,a b c 的大小关系为 ( ) A .c b a >> B .b c a >> C .a b c >> D .b a c >>9. 程序框图如图所示,该程序运行后输出的S 的值是 ( )A .12- B .13 C .3- D . 210. 已知向量()3,z x +=,()z y -=,2,且⊥,若实数y x ,满足不等式1≤+y x ,则实数z 的取值范围为( )A .[-3,3]B .[]2,2- C .[]1,1- D .[]2,2- 11. 若抛物线24x y =上有一条长为6的动弦AB ,则AB 的中点到x 轴的最短距离为( )A .34B .32C .1D .2 12.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的体积最大时,其高的值为( )A B . C . D .二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)13. 6)1(xx -的展开式的常数项为 14.某几何体的三视图如图,则它的体积是________15.0(21)nna x dx =+⎰,则数列1{}na 的前n 项和n S =____________ 16.过双曲线22221(0,0)x y a b a b-=>>的左焦点(,0)(0)F c c ->,作倾斜角为6π的直线FE 交该双曲线右支于点P ,若1()2OE OF OP =+且0OE EF ⋅=,则双曲线的离心率为________ 三、解答题(本大题共6小题,其中17-21每题各12分,22-24三选一10分,共70分) 17.在ABC ∆中,角A B C 、、对边分别是a b c 、、,满足222()AB AC a b c ⋅=-+. (Ⅰ)求角A 的大小;(Ⅱ)求24sin()23C B π--的最大值,并求取得最大值时角B C 、的大小.18.某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):(1) 指出这组数据的众数和中位数; (2)若幸福度不低于9.5分,则称该人 的幸福度为“极幸福”.求从这16人中随机 选取3人,至多有1人是“极幸福”的概率;(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记ξ表示抽到“极幸福”的人数,求ξ的分布列及数学期望.19. 如图,直三棱柱111C B A ABC -中,4=AC ,3=BC ,41=AA ,BC AC ⊥,点D 在线段AB 上.(Ⅰ)若D 是AB 中点,证明1AC ∥平面CD B 1; (Ⅱ)当13BD AB =时,求二面角1B CD B --的余弦值。
20. 已知椭圆C :)0(12222>>=+b a by a x 经过点)23,1(P ,离心率21=e ,直线l 的方程为 4=x .(1)求椭圆C 的方程;(2)AB 是经过右焦点F 的任一弦(不经过点P ),设直线AB 与l 相交于点M ,记P A ,PB ,PM 的斜率分别为321,,k k k ,问:是否存在常数λ,使得321k k k λ=+?若存在,求出λ的值,若不存在,说明理由。
21. 已知函数32,1()ln ,1x x bx c x f x a x x ⎧-+++<=⎨≥⎩,当23x =时, ()f x 有极大值427。
(1)求实数,b c 的值;(2)若存在0[1,2]x ∈-,使得0()37f x a ≥-成立,求实数a 的取值范围。
三选一:22.(本题满分10分)选修4—1几何证明选讲:如图,AB 是⊙O 的直径,AC 是弦,∠BAC 的平分线AD 交⊙O 于点D ,DE ⊥AC ,交AC的延长AA 1BC DB 1C 1线于点E ,OE 交AD 于点F 。
(I )求证:DE 是⊙O 的切线; (II )若2,5AC AFAB DF=求的值. 23.(本题满分10分)选修4—4:坐标系与参数方程在极坐标系中,已知圆C 的圆心)4C π,半径r = (Ⅰ)求圆C 的极坐标方程; ,直线l 的参数方程为⎩⎨⎧+=+=ααsin 2cos 2t y t x (t 为参数),直线l 交圆C 于A B 、两点,求弦长 24.(本题满分10分)选修4—5:不等式选讲 已知函数||)(a x x f -=。
(1)若m x f ≤)(的解集为}51|{≤≤-x x ,求实数m a ,的值。
(2)当2=a 且20<≤t 时,解关于x 的不等式()(2)f x t f x +≥+。
2014.4 高三考试理科数学试题答案 一、选择题ADDCC BDBAA DB二、填空题15 283π- 1n n + 1三、解答题 17、18. 解:(1)众数:8.6; 中位数:8.75 ;……………………………2分(2)设i A 表示所取3人中有i 个人是“极幸福”,至多有1人是“极幸福”记为事件A ,则140121)()()(3162121431631210=+=+=C C C C C A P A P A P ; …………………6分(3)ξ的可能取值为0,1,2,3.6427)43()0(3===ξP ;6427)43(41)1(213===C P ξ; 64943)41()2(223===C P ξ;641)41()3(3===ξP ……..……………..10分所以ξ的分布列为:ξE 27279101230.7564646464=⨯+⨯+⨯+⨯=. ………..……….…12分 另解:ξ的可能取值为0,1,2,3.则1~(3,)4B ξ,3313()()()44k k kP k C ξ-==.所以ξE =75.0413=⨯. 19.证明:如图,以C 为原点建立空间直角坐标系C-xyz .则B (3, 0, 0),A (0, 4, 0),1A (0, 4, 4),1B (3, 0, 4),1C (0, 4, 4)(1)解法一:)4,4,0(1-=AC设平面B 1 CD 的法向量为),,(z y x m =,由043),,()4,0,3(1=--=⋅--=⋅z x z y x m C B 且0223),,()0,2,23(=+=⋅=⋅y x z y x , 令x = 4得)3,3,4(--=,所以 0)3,3,4()4,4,0(1=--⋅-=⋅AC 又CD B AC 11平面⊄ 所以 AC 1∥平面B 1CD ; 解法二:证明:连结BC 1,交B 1C 于E ,DE . 因为 直三棱柱ABC -A 1B 1C 1,D 是AB 中点, 所以侧面B B 1C 1C 为矩形,DE 为△ABC 1的中位线,所以 DE // AC 1. 因为 DE ⊂平面B 1CD , AC 1⊄平面B 1CD , 所以 AC 1∥平面B 1CD . (2)解:由(Ⅰ)知AC ⊥BC ,设D (a , b , 0)(0a >,0b >),因为 点D 在线段AB 上,且13BD AB =, 即13BD BA =. 所以 2a =,43b =,4(1,,0)3BD =-.所以)4,0,3(1--=C B ,4(2,,0)3CD =.平面BCD 的法向量为1(0,0,1)n =. 设平面B 1 CD 的法向量为2(,,1)n x y =,由 120B C n ⋅=,20CD n ⋅=, 得 3404203x x y +=⎧⎪⎨+=⎪⎩, 所以 43x =-,2y =,24(,2,1)3n =-. 设二面角1B CD B --的大小为θ, 所以 1212cos 61n n n n θ⋅==. 所以 二面角1B CD B --的余弦值为61. 20.解:(1)由点3(1,)2P 在椭圆上得,221914a b += ①11,22c e a ==又所以 ② 由 ①②得2221,4,3c a b ===,故椭圆C 的方程为22143x y +=……………………..4分 (2)假设存在常数λ,使得123k k k λ+=.由题意可设,AB k AB 的斜率为则直线的方程为(1)y k x =- ③代入椭圆方程22143x y +=并整理得2222(43)84(3)0k x k x k +-+-= 设1122(,),(,)A x y B x y ,则有2212122284(3),4343k k x x x x k k -+==++ ④ ……………6分在方程③中,令4x =得,(4,3)M k ,从而2121213322,,11y y k k x x --==-- 33312412k k k -==--.又因为B F A 、、共线,则有BF AF k k k ==, 即有k x yx y =-=-112211 所以=+21k k =--+--1231232211x y x y )1111(2311212211-+---+-x x x y x y=.232-k 1)(2212121++--+x x x x x x ⑤ 将④代入⑤得=+21k k .232-k 12134834)3(42348222222-=++-+--+k k k k k k k ,又213-=k k , 所以=+21k k 32k故存在常数2=λ符合题意……………………………………………………………12分 21.(1)当1x <时,'2()32f x x x b =-++则'2222()3()20333f b =-⨯+⨯+=,所以0b = (2分) 因为322224()()()33327f c =-++=,所以0c = (4分)(2)因为存在0[1,2]x ∈-,使得0()37f x a ≥-所以问题可转化为当[1,2]x ∈-时,max ()37f x a ≥- 由(1)知,32,1()ln ,1x x x f x a x x ⎧-+<=⎨≥⎩○1当11x -≤<时,'22()323()3f x x x x x =-+=-- 令'()0f x =得0x =或23x =当x 变化时,',f(x)变化情况如下表又f(-1)=2,f(3)=27,f(0)=0 所以f(x)在[-1,1)上的最大值为2 (6分) ○2当12x ≤≤时,f(x)=alnx 当0a ≤时,()0f x ≤,所以f(x)的最大值为0当a>0时,f(x)在[1,2]上单调递增,所以f(x)在[1,2]上的最大值为aln2 (8分) 由此可知,当0a ≤时,f(x)在[-1,2]上的最大值为2;由max 0()237a f x a ≤⎧⎨=≥-⎩得0a ≤当a>0时,若ln 22a ≤即2ln 2a ≤时,f(x)在区间[-1,2]上的最大值为2;由max 20ln 2()237a f x a ⎧<≤⎪⎨⎪=≥-⎩得20ln 2a <≤ (10分) 若ln 22a >即2ln 2a >时,f(x)在区间[-1,2]上的最大值为ln 2a由max 2ln 2()ln 237a f x a a ⎧>⎪⎨⎪=≥-⎩得27ln 23ln 2a <≤- 综上可知,a 的取值范围为7(,]3ln 2-∞- (12分)… 22.(I )证明:连结OD ,可得∠ODA=∠OAD=∠DAC …………………2分 ∴OD//AE 又AE ⊥DE …………………………………3分 ∴OE ⊥OD ,又OD 为半径∴DE 是的⊙O 切线 ………………………5分 (II )解:过D 作DH ⊥AB 于H ,则有∠DOH=∠CAB2cos cos 5AC DOH CAB AB ∠=∠== …………6分 设OD=5x ,则AB=10x ,OH=2x , 7AH x ∴=由△AED ≌△AHD 可得AE=AH=7x ……………8分 又由△AEF ∽△DOF 可得7::5AF DF AE OD ==75AF DF ∴= ……………………………………………………10分 23.(1)由)4C π得,C 直角坐标(1,1),所以圆C 的直角坐标方程为22(1)(1)3x y -+-=,由cos sin x y ρθρθ=⎧⎨=⎩得,圆C 的直角坐标方程为 22cos 2sin 10ρρθρθ---=(2)将2cos 2sin x t y t αα=+⎧⎨=+⎩带入C 的直角坐标方程22(1)(1)3x y -+-= 得22(cos sin )10t t αα++-= 则0∆>设A,B对应参数分别为12,t t ,则122(cos sin )t t αα+=-+,121t t =-12||||AB t t =-=因为[0,)4πα∈,所以sin 2[0,1)α∈所以84sin 2[8,12)α+∈所以||AB 的取值范围为分解集为(成立时当成立时当舍去时,当)(分)解:(10..........................................................] (2)2,2,0,2202,20,20,222225.................................................................32,5151,1.24+∞-∴∴-≥+-<+≤≤∴≥+-<≤∴<≤≥+-≥≥+-∴=⎩⎨⎧==∴⎩⎨⎧=+-=-∴≤≤-+≤≤-∴≤-t x t x x t x x t x x t x t x x x t x a m a m a m a x m a x m a m a x。
