Cohomologie des alg`{e}bres de Kr{o}necker g'{e}n'{e}rales
NBR ISO 14001 - 2004 - Sistema de gesto ambiental

Anexo A (informativo) Orientações para uso desta Norma .......................................................................11 Anexo B (informativo) Correspondência entre a ABNT NBR ISO 14001:2004 e a ABNT NBR ISO 9001:2000..............................................................................................................21 Bibliografia..................................................................................................................................................27
Prefácio
A Associação Brasileira de Normas Técnicas (ABNT) é o Fórum Nacional de Normalização. As Normas Brasileiras, cujo conteúdo é de responsabilidade dos Comitês Brasileiros (ABNT/CB), dos Organismos de Normalização Setorial (ABNT/ONS) e das Comissões de Estudo Especiais Temporárias (ABNT/CEET), são elaboradas por Comissões de Estudo (CE), formadas por representantes dos setores envolvidos, delas fazendo parte: produtores, consumidores e neutros (universidades, laboratórios e outros). A ABNT NBR ISO 14001 foi elaborada no Comitê Brasileiro de Gestão Ambiental (ABNT/CB-38), pela Comissão de Estudo de Gestão Ambiental (CE-38:001.01). O Projeto circulou em Consulta Nacional conforme Edital nº 08, de 31.08.2004, com o número Projeto NBR ISO 14001. Esta Norma é equivalente à ISO 14001:2004. Esta Norma contém os anexos A e B, de caráter informativo. Esta segunda edição cancela e substitui a edição anterior (ABNT NBR ISO 14001:1996), a qual foi tecnicamente revisada.
西班牙语前缀详表

Dos o doble
Bifurcación: dividir en dos
Circun
Alrededor
Circunvalar: rodear
Co, col, con, com
Unión o colaboración
Colegir: juntar.
Cuadri, cuatri, cuatro
psicosocial
quiro-
mano
quirúrgico
rino-
nariz
rinorrea
sacar(o)-
azúcar
sacarosa
sarco-
carne
sarcoma
seudo-
falso
seudónimo
sider(o)
hierro
siderurgia
taqui-
rápido
taquicardia
di(a)-
a través de,
Diagonal: línea recta que va de un vértice a otro.
dis-
con dificultad
Disconforme: no conforme
ecto-
fuera de
Ectoplasma: exteriordelcitoplasma
pato-
enfermedad
patológico
ped-
niño
pediatría
pir(o)
fuego
pirómano
plast-
formar
plástica
pod(o)-
pie
podología
苹果手机和平板电脑设置指南说明书

Manual para configurar la cuenta enun Iphone o Ipad de apple con iOS 5.x Aviso. Este manual está pensado para una determinada versión de un programaespecífico, con la configuración por defecto de cada fabricante. Si Ud. tiene una configuracióndistinta o no comprende alguno de los pasos especificados en este manual, puede consultartelefónicamente con el Consejo General de COP, teléfono 91 444 90 20, horario de lunes ajueves: 10h a 18h y viernes: 9h a 16h.En este manual se configurará el correo para acceder a él de forma segura a través de un certificado SSL. Los certificados SSL permiten que la información que se envíe o reciba desde internet al acceder a su cuenta de correo este siempre cifrada, protegida y con emisores verificados. La tecnología SSL (Secure Sockets Layer)es una herramienta de encriptación que protege todas las transacciones que puedan realizarse a través de él. Los certificados están emitidos por una autoridad de certificación que verifica la identidad del propietario del certificado. Puede encontrar más información en http://www.cop.es/sslSi lo desea o tiene problemas puede configurar el correo de forma segura puede hacerlo con los parámetros de configuración estándar que aparecen en http://www.cop.es/manuales.Paso 1.- Busque el icono Ajustes e inícielo."Añadir cuenta".Paso 3.- Seleccione "Otras" en tipo de cuenta.especificados en la carta de alta y pulse "Siguiente".Paso 5.-Selecione "IMAP"como tipo de cuenta. Especifique mail.cop.es como nombre de host en el servidor de correo entrante y saliente. Escriba el nombre de usuario y la contraseña que se le ha asignado en la carta de alta, normalmente su número de colegiado_cop, tanto en "Servidor de correo entrante"como en "Servidor de correosaliente", tal como se muestra en la figura.Paso 6.- Tras introducir los datos se mostrará el mensaje "Verificando" durante un período de tiempo que puede llegar a varios minutos. En este instante el dispositivo comprueba los servicios disponibles y configurará la cuenta. Los parámetros que introdujimos en el paso anterior son para configurar el correo eletrónico de forma segura tal como se indica en http://www.cop.es/ssl. Se podría configurar igualmente de forma estándar tal como se indicaen http://www.cop.es/manuales.Paso 7.- Tras la verificación el dispositivo detectará que existen dos servicios, el correo electrónico y el de notas. Debemos de marcar el de correo electrónico y si lo deseamos el de notas. Las notas podrán consultarse desde el dispositivo y desde el correo web https://mail.cop.es. En nuestro ejemplo sólo marcamos el correo electrónico. Pulsaremosguardar y ya tendremos la cuenta creada.Pasos opcionalesPor defecto los mail que enviemos a través del ipad/iphone, los borradores y elementos eliminados se guardarán sólo en el dispositivo. Si queremos que estos correos se guarden en las carpetas del servidor y que puedan ser accesibles también desde el correo web https://mail.cop.es. o, cualquier otro dispositivo configurado como IMAP deberemos configuralo. A continuación exponemos los pasos para configurar esta caraterística si así se desea.Paso 1.- En ajustes, seleccionaremos"Correo, contactos y calendario", selecccionaremos la cuenta del COP y damos al enlace con el nombre de la cuenta.Paso 2.- Seleccionamos "Avanzado".Paso3.- En Buzones seleccionamos por ejemplo "Buzón Enviado".pasos los repetiríamos para la "Papelera" y "Borradores".。
Esquisse d'un Programme(grothendieck的纲领)

ESQUISSE D’UN PROGRAMMEpar Alexandre GrothendieckSommaire:1.Envoi.2.Un jeu de“Lego-Teichm¨u ller”et le groupe de Galois de Q sur Q.3.Corps de nombres associ´e s`a un dessin d’enfant.4.Poly`e dres r´e guliers sur les corpsfinis.5.Haro sur la topologie dite“g´e n´e rale”,et r´eflexions heuristiques vers unetopologie dite“mod´e r´e e”.6.“Th´e ories diff´e rentiables”(`a la Nash)et“th´e ories mod´e r´e es”.7.A la Poursuite des Champs.8.Digressions de g´e om´e trie bidimensionnelle.9.Bilan d’une activit´e enseignante.10.Epilogue.NotesN.B.Les ast´e risques(*)renvoient aux notesfigurant au bas de la mˆe me page,les renvois num´e rot´e s de(1)`a(7)aux notes(rajout´e es ult´e rieurement) r´e unies`a lafin du rapport.ESQUISSE D’UN PROGRAMMEpar Alexandre Grothendieckme la conjoncture actuelle rend de plus en plus illusoire pour moi lesperspectives d’un enseignement de recherche`a l’Universit´e,je me suis r´e solu `a demander mon admission au CNRS,pour pouvoir consacrer mon´e nergie`a d´e velopper des travaux et perspectives dont il devient clair qu’il ne se trou-vera aucun´e l`e ve(ni mˆe me,semble-t-il,aucun cong´e n`e re math´e maticien) pour les d´e velopper`a ma place.En guise de document“Titres et Travaux”,on trouvera`a la suite de ce texte la reproduction int´e grale d’une esquisse,par th`e mes,de ce que je con-sid´e rais comme mes principales contributions math´e matiques au moment d’´e crire ce rapport,en1972.Il contient´e galement une liste d’articles pu-bli´e s`a cette date.J’ai cess´e toute publication d’articles scientifiques depuis 1970.Dans les lignes qui suivent,je me propose de donner un aper¸c u au moins sur quelques th`e mes principaux de mes r´eflexions math´e matiques depuis lors.Ces r´eflexions se sont mat´e rialis´e es au cours des ann´e es en deux volumineux cartons de notes manuscrites,difficilement d´e chiffrables sans doute`a tout autre qu’`a moi-mˆe me,et qui,apr`e s des stades de d´e cantations successives,attendent leur heure peut-ˆe tre pour une r´e daction d’ensemble tout au moins provisoire,`a l’intention de la communaut´e math´e matique.Le terme“r´e daction”ici est quelque peu impropre,alors qu’il s’agit bien plus de d´e velopper des id´e es et visions multiples amorc´e es au cours de ces douze derni`e res ann´e es,en les pr´e cisant et les approfondissant,avec tous les rebondissements impr´e vus qui constamment accompagnent ce genre de travail–un travail de d´e couverte donc,et non de compilation de notes pieusement accumul´e es.Et je compte bien,dans l’´e criture des“R´eflexions Math´e matiques”commenc´e e depuis f´e vrier1983,laisser apparaˆıtre claire-ment aufil des pages la d´e marche de la pens´e e qui sonde et qui d´e couvre, en tˆa tonnant dans la p´e nombre bien souvent,avec des trou´e es de lumi`e re 12subites quand quelque tenace image fausse,ou simplement inad´e quate,se trouve enfin d´e busqu´e e et mise`a jour,et que les choses qui semblaient de guingois se mettent en place,dans l’harmonie mutuelle qui leur est propre.Quoi qu’il en soit,l’esquisse qui suit de quelques th`e mes de r´eflexions des derni`e res dix ou douze ann´e es,tiendra lieu en mˆe me temps d’esquisse de pro-gramme de travail pour les ann´e es qui viennent,que je compte consacrer au d´e veloppement de ces th`e mes,ou au moins de certains d’entre eux.Elle est destin´e e,d’une part aux coll`e gues du Comit´e National appel´e s`a statuer sur ma demande,d’autre part`a quelques autres coll`e gues,anciens´e l`e ves,amis,8Alexandre Grothendieckdans l’´e ventualit´e o`u certaines des id´e es esquiss´e es ici pourraient int´e resser l’un d’entre eux.2.Les exigences d’un enseignement universitaire,s’adressant donc`a des´e tudiants(y compris les´e tudiants dits“avanc´e s”)au bagage math´e matique modeste(et souvent moins que modeste),m’ont amen´e`a renouveler de fa¸c on draconienne les th`e mes de r´eflexion`a proposer`a mes´e l`e ves,et defil en aiguille et de plus en plus,`a moi-mˆe me´e galement.Il m’avait sembl´e important de partir d’un bagage intuitif commun,ind´e pendant de tout lan-gage technique cens´e l’exprimer,bien ant´e rieur`a tout tel langage–il s’est av´e r´e que l’intuition g´e om´e trique et topologique des formes,et plus parti-culi`e rement des formes bidimensionnelles,´e tait un tel terrain commun.Il s’agit donc de th`e mes qu’on peut grouper sous l’appellation de“topologie des surfaces”ou“g´e om´e trie des surfaces”,´e tant entendu dans cette derni`e re appellation que l’accent principal se trouve sur les propri´e t´e s topologiques des surfaces,ou sur les aspects combinatoires qui en constituent l’expression technique la plus terre-`a-terre,et non sur les aspects diff´e rentiels,voire con-formes,riemaniens,holomorphes et(de l`a)l’aspect“courbes alg´e briques complexes”.Une fois ce dernier pas franchi cependant,voici soudain la g´e om´e trie alg´e brique(mes anciennes amours!)qui fait irruption`a nou-veau,et ce par les objets qu’on peut consid´e rer comme les pierres de con-struction ultimes de toutes les autres vari´e t´e s alg´e briques.Alors que 23dans mes recherches d’avant1970,mon attention syst´e matiquement´e tait dirig´e e vers les objets de g´e n´e ralit´e maximale,afin de d´e gager un langage d’ensemble ad´e quat pour le monde de la g´e om´e trie alg´e brique,et que je ne m’attardais sur les courbes alg´e briques que dans la stricte mesure o`u cela s’av´e rait indispensable(notamment en cohomologie´e tale)pour d´e velopper des techniques et´e nonc´e s“passe-partout”valables en toute dimension et en tous lieux(j’entends,sur tous sch´e mas de base,voire tous topos annel´e s de base...),me voici donc ramen´e,par le truchement d’objets si simples qu’un enfant peut les connaˆıtre en jouant,aux d´e buts et origines de la g´e om´e trie alg´e brique,familiers`a Riemann et`a ses´e mules!Depuis environ1975,c’est donc la g´e om´e trie des surfaces(r´e elles),et `a partir de1977les liens entre les questions de g´e om´e trie des surfaces et la g´e om´e trie alg´e brique des courbes alg´e briques d´efinies sur des corps tels que C,R ou des extensions de typefini de Q,qui ont´e t´e ma principale source d’inspiration,ainsi que monfil conducteur constant.C’est avec surprise et avec´e merveillement qu’aufil des ans je d´e couvrais(ou plutˆo t, sans doute,red´e couvrais)la richesse prodigieuse,r´e ellement in´e puisable,la profondeur insoup¸c onn´e e de ce th`e me,d’apparence si anodine.Je crois y sentir un point n´e vralgique entre tous,un point de convergence privil´e gi´eEsquisse d’un Programme9 des principaux courants d’id´e es math´e matiques,comme aussi des princi-pales structures et des visions des choses qu’elles expriment,depuis lesplus sp´e cifiques,(tels les anneaux Z,Q,Q,R,C ou le groupe Sl(2)sur l’unde ces anneaux,ou les groupes alg´e briques r´e ductifs g´e n´e raux)aux plus“abstraits”,telles les“multiplicit´e s”alg´e briques,analytiques complexes ouanalytiques r´e elles.(Celles-ci s’introduisent naturellement quand il s’agitd’´e tudier syst´e matiquement des“vari´e t´e s de modules”pour les objets g´e om´e triques envisag´e s,si on veut d´e passer le point de vue notoirement insuffisant des“modules grossiers”,qui revient`a“tuer”bien malencontreusement les groupesd’automorphismes de ces objets.)Parmi ces multiplicit´e s modulaires,cesont celles de Mumford-Deligne pour les courbes alg´e briques“stables”degenre g,`aνpoints marqu´e s,que je note M g,ν(compactification de la34multiplicit´e“ouverte”M g,νcorrespondant aux courbes lisses),qui depuisquelques deux ou trois ann´e es ont exerc´e sur moi une fascination parti-culi`e re,plus forte peut-ˆe tre qu’aucun autre objet math´e matique`a ce jour.A vrai dire,il s’agit plutˆo t du syst`e me de toutes les multiplicit´e s M g,νpour g,νvariables,li´e es entre elles par un certain nombre d’op´e rationsfondamentales(telles les op´e rations de“bouchage de trous”i.e.de“gom-mage”de points marqu´e s,celle de“recollement”,et les op´e rations inverses),qui sont le reflet en g´e om´e trie alg´e brique absolue de caract´e ristique z´e ro(pour le moment)d’op´e rations g´e om´e triques famili`e res du point de vue de la“chirurgie”topologique ou conforme des principale raison sansdoute de cette fascination,c’est que cette structure g´e om´e trique tr`e s richesur le syst`e me des multiplicit´e s modulaires“ouvertes”M g,νse r´efl`e te parune structure analogue sur les groupo¨ıdes fondamentaux correspondants,les“groupo¨ıdes de Teichm¨u ller” T g,ν,et que ces op´e rations au niveau des T g,νont un caract`e re suffisamment intrins`e que pour que le groupe de Galois IΓdeQ/Q op`e re sur toute cette“tour”de groupo¨ıdes de Teichm¨u ller,en respec-tant toutes ces structures.Chose plus extraordinaire encore,cette op´e rationestfid`e le–`a vrai dire,elle estfid`e le d´e j`a sur le premier“´e tage”non triv-ial de cette tour,`a savoir T0,4–ce qui signifie aussi,essentiellement,quel’action ext´e rieure de IΓsur le groupe fondamental π0,3de la droite projec-tive standard P1sur Q,priv´e e des trois points0,1,∞,est d´e j`afid`e le.Ainsile groupe de Galois IΓconcrets,respectant d’ailleurs certaines structures essentielles de ce groupe.Il s’ensuit qu’un´e l´e ment de IΓpeutˆe tre“param´e tr´e”(de diverses fa¸c ons´e quivalentes d’ailleurs)par un´e l´e ment convenable de ce groupe profiniπ0,3(un groupe profini libre`a deux g´e n´e rateurs),ou par un syst`e me detels´e l´e ments,ce ou ces´e l´e ments´e tant d’ailleurs soumis`a certaines con-ditions simples,n´e cessaires(et sans doute non suffisantes)pour que ce ouces´e l´e ments corresponde(nt)bien`a un´e l´e ment de IΓ.Une des tˆa ches les10Alexandre Grothendieckplus fascinantes ici,est justement d’appr´e hender des conditions n´e cessaires et suffisantes sur un automorphisme ext´e rieur de π0,3i.e.sur le ou les 45param`e tres correspondants,pour qu’il provienne d’un´e l´e ment de IΓ–ce qui fournirait une description“purement alg´e brique”,en termes de groupes profinis et sans r´e f´e rence`a la th´e orie de Galois des corps de nombres,du groupe de Galois IΓ=Gal(Q/Q)!Peut-ˆe tre une caract´e risation mˆe me conjecturale de IΓcomme sous-groupe de Autext( π0,3)est-elle pour le moment hors de port´e e(1);je n’ai pas de conjecture`a proposer encore.Une autre tˆa che par contre est abordable imm´e diatement,c’est celle de d´e crire l’action de IΓsur toute la tour de Teichm¨u ller,en termes de son action sur le“premier´e tage” π0,3,i.e.ex-primer un automorphisme de cette tour,en termes du“param`e tre”dans π0,3,qui rep`e re l’´e l´e ment courantγde IΓ.Ceci est li´e`a une repr´e sentation de la tour de Teichm¨u ller(en tant que groupo¨ıde muni d’une op´e ration de “recollement”)par g´e n´e rateurs et relations,qui donnera en particulier une pr´e sentation par g´e n´e rateurs et relations,au sens ordinaire,de chacun des T g,ν(en tant que groupo¨ıde profini).Ici,mˆe me pour g=0(donc quand les groupes de Teichm¨u ller correspondants sont des groupes de tresses“bien connus”),les g´e n´e rateurs et relations connus`a ce jour dont j’ai eu con-naissance,me semblent inutilisables tels quels,car ils ne pr´e sentent pas les caract`e res d’invariance et de sym´e trie indispensables pour que l’action de IΓsoit directement lisible sur cette pr´e sentation.Ceci est li´e notamment au fait que les gens s’obstinent encore,en calculant avec des groupes fondamen-taux,`afixer un seul point base,plutˆo t que d’en choisir astucieusement tout un paquet qui soit invariant par les sym´e tries de la situation,lesquelles sont donc perdues en route.Dans certaines situations(comme des th´e or`e mes de descente`a la Van Kampen pour groupes fondamentaux)il est bien plus ´e l´e gant,voire indispensable pour y comprendre quelque chose,de travailler avec des groupo¨ıdes fondamentaux par rapport`a un paquet de points base convenable,et il en est certainement ainsi pour la tour de Teichm¨u ller.Il semblerait(incroyable,mais vrai!)que la g´e om´e trie mˆe me du premier´e tage de la tour de Teichm¨u ller(correspondant donc aux“modules”soit pour des droites projectives avec quatre points marqu´e s,soit pour des courbes el-56liptiques(!))n’ait jamais´e t´e bien explicit´e e,par exemple la relation entre le cas de genre0avec la g´e om´e trie de l’octa`e dre,et celle du t´e tra`e dre.A fortiori les multiplicit´e s modulaires M0,5(pour les droites projectives avec cinq points marqu´e s)et M1,2(pour les courbes de genre1avec deux points marqu´e s),d’ailleurs quasiment isomorphes entre elles,semblent-elles terre vierge–les groupes de tresses ne vont pas nous´e clairer`a leur sujet!J’ai commenc´e`a regarder M0,5`a des moments perdus,c’est un v´e ritable joyau, d’une g´e om´e trie tr`e s riche´e troitement li´e e`a celle de l’icosa`e dre.Esquisse d’un Programme11 L’int´e rˆe t a priori d’une connaissance compl`e te des deux premiers´e tages de la tour(savoir,les cas o`u la dimension modulaire N=3g−3+νest≤2) r´e side dans ce principe,que la tour enti`e re se reconstitue`a partir des deux premiers´e tages,en ce sens que via l’op´e ration fondamentale de“recolle-ment”,l’´e tage1fournit un syst`e me complet de g´e n´e rateurs,et l’´e tage2un syst`e me complet de relations.Il y a une analogie frappante,et j’en suis persuad´e,pas seulement formelle,entre ce principe,et le principe analogue de Demazure pour la structure des groupes alg´e briques r´e ductifs,si on rem-place le terme“´e tage”ou“dimension modulaire”par“rang semi-simple du groupe r´e ductif”.Le lien devient plus frappant encore,si on se rappelle que le groupe de Teichm¨u ller T1,1(dans le contexte discret transcendant maintenant,et non dans le contexte alg´e brique profini,o`u on trouve les compl´e tions profinies des premiers)n’est autre que Sl(2,Z),i.e.le groupe des points entiers du sch´e ma en groupes simple de rang1“absolu”Sl(2).Ainsi,sentiellement la mˆe me que celle pour“la tour”des groupes r´e ductifs detous rangs–un groupe d’ailleurs dont on peut dire sans doute qu’il est pr´e sent dans toutes les disciplines essentielles des math´e matiques.Ce principe de construction de la tour de Teichm¨u ller n’est pas d´e montr´e`a l’heure actuelle–mais je n’ai aucun doute qu’il ne soit valable.Il r´e sulterait (via une th´e orie de d´e vissage des structures stratifi´e es–en l’occurrence les M g,ν–qui resterait`a´e crire,cf.par.5)d’une propri´e t´e extrˆe mementplausible des multiplicit´e s modulaires ouvertes M g,νdans le contexte ana-67lytique complexe,`a savoir que pour une dimension modulaire N≥3,le groupe fondamental de M g,ν(i.e.le groupe de Teichm¨u ller habituel T g,ν) est isomorphe au“groupe fondamental`a l’infini”i.e.celui d’un“voisinage tubulaire de l’infini”.C’est l`a une chose bien famili`e re(due`a Lefschetz essentiellement)pour une vari´e t´e lisse affine de dimension N≥3.Il est vrai que les multiplicit´e s modulaires ne sont pas affines(sauf pour des petites valeurs de g),mais il suffirait qu’une telle M g,νde dimension N(ou plutˆo t, un revˆe tementfini convenable)soit r´e union de N−2ouverts affines,donc que M g,νne soit pas“trop proche d’une vari´e t´e compacte”.N’ayant aucun doute sur ce principe de construction de la tour de Teich-m¨u ller,je pr´e f`e re laisser aux experts de la th´e orie transcendante,mieux outill´e s que moi,le soin de prouver le n´e cessaire(s’il s’en trouve qui soit int´e ress´e),pour expliciter plutˆo t,avec tout le soin qu’elle m´e rite,la struc-ture qui en d´e coule pour la tour de Teichm¨u ller par g´e n´e rateurs et relations, dans le cadre discret cette fois et non profini–ce qui revient,essentielle-ment,`a une compr´e hension compl`e te des quatre multiplicit´e s modulaires M0,4,M1,1,M0,5,M1,2,et de leurs groupo¨ıdes fondamentaux par rap-port`a des“points base”convenablement choisis.Ceux-ci s’offrent tout12Alexandre Grothendiecknaturellement,comme les courbes alg´e briques complexes du type(g,ν) envisag´e,qui ont un groupe d’automorphismes(n´e cessairementfini)plus grand que dans le cas g´e n´e rique(*).En y incluant la sph`e re holomorphe `a trois points marqu´e s(provenant de M0,3i.e.de l’´e tage0),on trouve 78douze“pi`e ces de construction”fondamentales(6de genre0,6de genre1) dans un“jeu de L´e go-Teichm¨u ller”(grande boˆıte),o`u les points marqu´e s sur les surfaces envisag´e es sont remplac´e s par des“trous”`a bord,de fa¸c on `a avoir des surfaces`a bord,donc des pi`e ces de construction qui peuvent s’assembler par frottement doux comme dans le jeu de L´e go ordinaire cher `a nos enfants(ou petits-enfants...).Par assemblage on trouve un moyen tout ce qu’il y a de visuel pour construire tout type de surface(ce sont ces assemblages essentiellement qui seront les“points base”pour notre fameuse tour),et aussi de visualiser les“chemins”´e l´e mentaires par des op´e rations tout aussi concr`e tes telles des“twists”,ou des automorphismes des pi`e ces du jeu,et d’´e crire les relations fondamentales entre chemins compos´e s.Suiv-ant la taille(et le prix!)de la boˆıte de construction utilis´e e,on trouve d’ailleurs de nombreuses descriptions diff´e rentes de la tour de Teichm¨u ller par g´e n´e rateurs et boˆıte la plus petite est r´e duite`a des pi`e ces toutes identiques,de type(0,3)–ce sont les“pantalons”de Thurston,et le jeu de L´e go-Teichm¨u ller que j’essaie de d´e crire,issu de motivations et de r´eflexions de g´e om´e trie alg´e brique absolue sur le corps Q,est tr`e s proche du jeu de“chirurgie g´e od´e sique hyperbolique”de Thurston,dont j’ai ap-pris l’existence l’an dernier par Yves Ladegaillerie.Dans un micros´e minaire avec Carlos Contou-Carr`e re et Yves Ladegaillerie,nous avons amorc´e une r´eflexion dont un des objets est de confronter les deux points de vue,qui se compl`e tent mutuellement.J’ajoute que chacune des douze pi`e ces de construction de la“grande boˆıte”se trouve munie d’une d´e composition cellulaire canonique,stable par toutes les sym´e tries,ayant comme seuls sommets les“points marqu´e s”(ou centres des trous),et comme arˆe tes certains chemins g´e od´e siques(pour la structure riemanienne canonique sur la sph`e re ou le tore envisag´e)en-tre certaines paires de sommets(savoir ceux qui se trouvent sur un mˆe me “lieu r´e el”,pour une structure r´e elle convenable de la courbe alg´e brique (*)Il faut y ajouter de plus les“points-base”provenant par op´e rations de recollement de“pi`e ces”du mˆe me type en dimension modulaire inf´e rieure.D’autre part,en dimension modulaire2(cas de M0,5et M1,2),il convient d’exclure les points de certaines familles`a un param`e tre de courbes admet-tant un automorphisme exceptionnel d’ordre2.Ces familles constituent d’ailleurs sur les multiplicit´e s envisag´e es des courbes rationnelles remar-quables,qui me paraissent un ingr´e dient important de la structure de ces multiplicit´e s.Esquisse d’un Programme13 complexe envisag´e e).Par suite,toutes les surfaces obtenues dans ce jeu par assemblage sont munies de structures cellulaires canoniques,qui`a leur tour(cf.§3plus bas)permettent de consid´e rer ces surfaces comme as-89soci´e e`a des courbes alg´e briques complexes(et mˆe me sur Q)canoniquement d´e termin´e es.Il y a l`a un jeu de chass´e-crois´e typique entre le combinatoire, et l’alg´e brique complexe(ou mieux,l’alg´e brique sur Q).La“petite boˆıte”aux pi`e ces toutes identiques,qui a le charme de l’´e cono-mie,donnera sans doute une description relativement compliqu´e e pour les relations(compliqu´e e,mais nullement inextricable!).La grande boˆıte don-nera lieu`a des relations plus nombreuses(du fait qu’il y a beaucoup plus de points-bases et de chemins remarquables entre eux),mais`a structure plus transparente.Je pr´e vois qu’en dimension modulaire2,tout comme dans le cas plus ou moins familier de la dimension modulaire1(avec notamment la description de Sl(2,Z)par(ρ,σ|ρ3=σ2,ρ4=σ6=1)),on trouvera un engendrement par les groupes d’automorphismes des trois types de pi`e ces pertinentes,avec des relations simples que je n’ai pas d´e gag´e es`a l’heure d’´e crire ces lignes.Peut-ˆe tre mˆe me trouvera-t-on un principe de ce genre pour tous les T g,ν,ainsi qu’une d´e composition cellulaire de M g,νg´e n´e ralisant celles qui se pr´e sentent spontan´e ment pour M0,4et M1,1,et que j’entrevois d`e s`a pr´e sent pour la dimension modulaire2,en utilisant les hypersurfaces correspondant aux diverses structures r´e elles sur les structures complexes envisag´e es,pour effectuer le d´e coupage cellulaire voulu.3.Plutˆo t que de suivre(comme pr´e vu)un ordre th´e matique rigoureux,jeme suis laiss´e emporter par ma pr´e dilection pour un th`e me particuli`e rement riche et brˆu lant,auquel je compte me consacrer d’ailleurs prioritairement pendant quelques temps,`a partir de la rentr´e e84/85.Je reprends donc l’expos´e th´e matique l`a o`u je l’ai laiss´e,tout au d´e but du paragraphe pr´e c´e dent.Mon int´e rˆe t pour les surfaces topologiques commence`a poindre en1974, o`u je propose`a Yves Ladegaillerie le th`e me de l’´e tude isotopique des plonge-ments d’un1-complexe topologique dans une surface compacte.Dans les deux ann´e es qui suivent,cette´e tude le conduit`a un remarquable th´e or`e me d’isotopie,donnant une description alg´e brique compl`e te des classes d’isoto-910pie de plongements de tels1-complexes,ou de surfaces compactes`a bord, dans une surface compacte orient´e e,en termes de certains invariants com-binatoires tr`e s simples,et des groupes fondamentaux des protagonistes.Ce th´e or`e me,qui doit pouvoir s’´e tendre sans mal aux plongements d’un es-pace compact quelconque(triangulable pour simplifier)dans une surface compacte orient´e e,redonne comme corollaires faciles plusieurs r´e sultats classiques profonds de la th´e orie des surfaces,et notamment le th´e or`e me d’isotopie de Baer.Il vafinalementˆe tre publi´e,s´e par´e ment du reste(et14Alexandre Grothendieckdix ans apr`e s,vu la duret´e des temps...),dans Topology.Dans le travail de Ladegaillerie figure ´e galement une description purement alg´e brique,en ter-mes de groupo¨ıdes fondamentaux,de la cat´e gorie “isotopique”des surfaces compactes X ,munies d’un 1-complexe topologique K plong´e dans X .Cette description,qui a eu le malheur d’aller `a l’encontre du “goˆu t du jour”et de ce fait semble impubliable,a n´e anmoins servi (et sert encore)comme un guide pr´e cieux dans mes r´e flexions ult´e rieures,notamment dans le contexte de la g´e om´e trie alg´e brique absolue de caract´e ristique nulle.Le cas o`u (X,K )est une “carte”2-dimensionnelle,i.e.o`u les composantes connexes de X \K sont des 2-cellules ouvertes (et o`u de plus K est muni d’un ensemble fini S de “sommets”,tel que les composantes connexes de K \S soient des 1-cellules ouvertes)attire progressivement mon attention dans les ann´e es cat´e gorie isotopique de ces cartes admet une description alg´e brique particuli`e rement simple,via l’ensemble des “rep`e res”(ou “drapeaux”ou “biarcs”)associ´e s `a la carte,qui se trouve naturellement muni d’une structure d’ensemble `a groupe d’op´e rateurs,sous le groupe C 2= σ0,σ1,σ2|σ20=σ21=σ22=(σ0σ2)2=1 ,que j’appelle le groupe cartographique (non orient´e )de dimension 2.Il admet comme sous-groupe d’indice 2le groupe cartographique orient´e en-gendr´e par les produits en nombre pair des g´e n´e rateurs,qui peut aussi se d´e crire comme 1011C +2= ρs ,ρf ,σ|ρs ρf =σ,σ2=1 ,(avecρs =σ2σ1,ρf =σ1σ0,σ=σ0σ2=σ2σ0,op´e rations de rotation ´e l´e mentaire d’un rep`e re autour d’un sommet,d’une face et d’une arˆe te respectivement).Il y a un dictionnaire parfait entre la situation topologique des cartes compactes,resp.cartes compactes ori-ent´e es,d’une part,et les ensembles finis `a groupe d’op´e rateurs C 2resp.C +2de l’autre,dictionnaire dont l’existence ´e tait d’ailleurs plus ou moins connue,mais jamais ´e nonc´e e avec la pr´e cision n´e cessaire,ni d´e velopp´e e tant soit peu.Ce travail de fondements est fait avec le soin qu’il m´e rite dans un excellent travail de DEA,fait en commun par Jean Malgoire et Christine Voisin en 1976.Cette r´e flexion prend soudain une dimension nouvelle,avec cette remar-que simple que le groupe C +2peut s’interpr´e ter comme un quotient du groupe fondamental d’une sph`e re orient´e e priv´e e de trois points,num´e rot´e s 0,1,2,les op´e rations ρs ,σ,ρf s’interpr´e tant comme les lacets autour de ces points,satisfaisant la relation famili`e rel 0l 1l 2=1,alors que la relation suppl´e mentaireσ2=1i.e.l21=1signifie qu’ons’int´e resse au quotient du groupe fondamental correspondant`a un indicede ramification impos´e2au point1,qui classifie donc les revˆe tements de lasph`e re,ramifi´e s au plus en les points0,1,2,avec une ramification´e gale`a1ou2en les points au dessus de1.Ainsi,les cartes orient´e es compactesforment une cat´e gorie isotopique´e quivalente`a celle de ces revˆe tements,soumis de plus`a la condition suppl´e mentaire d’ˆe tre des revˆe tementsfi-nis.Prenant maintenant comme sph`e re de r´e f´e rence la sph`e re de Riemann,ou droite projective complexe,rigidifi´e e par les trois points0,1et∞(cedernier rempla¸c ant donc2),et se rappelant que tout revˆe tement ramifi´efinid’une courbe alg´e brique complexe h´e rite lui-mˆe me d’une structure de courbealg´e brique complexe,on aboutit`a cette constatation,qui huit ans apr`e sme paraˆıt encore toujours aussi extraordinaire:toute carte orient´e e“finie”se r´e alise canoniquement sur une courbe alg´e brique complexe!Mieux en-1112core,comme la droite projective complexe est d´efinie sur le corps de baseabsolue Q,ainsi que les points de ramification admis,les courbes alg´e briquesobtenues sont d´efinies non seulement sur C,mais sur la clˆo ture alg´e briqueQ de Q dans C.Quant`a la carte de d´e part,elle se retrouve sur la courbealg´e brique,comme image inverse du segment r´e el[0,1](o`u0est consid´e r´ecomme un sommet,et1comme milieu d’une“arˆe te pli´e e”ayant1commecentre),lequel constitue dans la sph`e re de Riemann la“2-carte orient´e euniverselle”(*).Les points de la courbe alg´e brique X au dessus de0,de1et de∞ne sont autres que les sommets,et les“centres”des arˆe tes et desfaces respectivement de la carte(X,K),et les ordres des sommets et desfaces ne sont autres que les multiplicit´e s des z´e ros et des pˆo les de la fonctionrationnelle(d´efinie sur Q)sur X,exprimant sa projection structurale versP1C.Cette d´e couverte,qui techniquement se r´e duit`a si peu de choses,a fait surmoi une impression tr`e s forte,et elle repr´e sente un tournant d´e cisif dans lecours de mes r´eflexions,un d´e placement notamment de mon centre d’int´e rˆe ten math´e matique,qui soudain s’est trouv´e fortement localis´e.Je ne croispas qu’un fait math´e matique m’ait jamais autant frapp´e que celui-l`a,et aiteu un impact psychologique comparable(2).Cela tient sˆu rement`a la naturetellement famili`e re,non technique,des objets consid´e r´e s,dont tout dessin (*)Il y a une description analogue des cartesfinies non orient´e es,´e ventuellement avec bord,en termes de courbes alg´e briques r´e elles,plus pr´e cis´e ment derevˆe tement de P1R ramifi´e seulement en0,1,∞,la surface`a bord associ´e e`a un tel revˆe tement´e tant X(C)/τ,o`uτest la conjugaison carte non orient´e e“universelle”est ici le disque,ou h´e misph`e re sup´e rieur de la sph`e re de Riemann,muni comme pr´e c´e demment du1-complexe plong´e K=[0,1].。
西班牙语经典语法
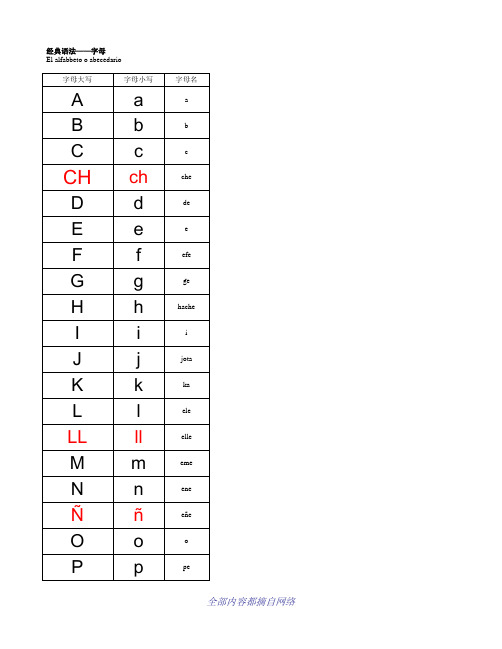
经典语法——字母El alfabbeto o abecedario2. 2.其中CH语LL已经在1994年被西班牙皇家语言学院取消。
注:经典语法系列基本覆盖了主要的西班牙语语法现象,编写过程中参考了.tw/firework/educacion/educacion.htm 的相关资料经典语法——重音规则Reglas de acentuación单词包含一个以上的音节是,有一个音节应该重读(acento tónico):1. 1.在没有重音符号的情况下,如果单词是除了n,s以外的辅音结尾的,重读位置为最后一个音节,其他情况重读音节为单词的倒数第2个音节,如:camisa 重读mi 这个音节,因为ca-mi-sa mi是倒数第二,lucas重读lu这个音节,因为虽然是辅音结尾,但这个辅音是s,所以也重读倒数第二个音节,profesor 为一般辅音结尾,所以重读最后一个音节sor2. 2.有重音符号的情况下,重读重音符号所在音节,如:médico重读me 这个音节相关的名词解释:元音:分3类1. 1.单元音A ,E,I,O,U,其中A,E,O为强元音,I,U为弱元音2. 2.双元音分3种情况一强一弱:ai re, p ei ne, au la;一弱一强:hac ie ndo, nov io;两弱:c iu dad, c ui dado;共有如下14重组合两个强元音会形成2个音节,如aéreo可分为a-é-re-o3. 3.三元音(Triptongo)为弱元音+强元音+弱元音组成,如b uey Parag uay辅音:除元音以外的音节:有元音和辅音或者单独的元音组成的发音片段,如estudiante 就可以分为es-du-dian-de几个音节重音符号(tilde):á,É,Él es chino字母上面的符号注:经典语法系列基本覆盖了主要的西班牙语语法现象,编写过程中参考了.tw/firework/educacion/educacion.htm 的相关资料经典语法——前置词(介词)Las Preposiciones/gram34.htm注:经典语法系列基本覆盖了主要的西班牙语语法现象,编写过程中参考了.tw/firework/educacion/educacion.htm 的相关资料经典语法——指小词Los diminutivos指小词也有叫做缩小词的,是一种词缀,作用类似于汉语的“小”和“点”,缩小或者减轻词根所表达的意义,常常起到缓和语气,表达亲切感和好感的作用,在口语中使用很多,比如:Tu camisa es fea.你的夹克是难看的。
华为逆变器WIFI模块快速指南说明书

Guía rápidaMódulo WIFIAviso:Lea este manual detenidamente antes de usar el producto y guárdelo en unlugar donde pueda encontrarlo fácilmente.Debido a la actualización del producto y otros factores,el contenido de estemanual puede cambiar de vez en cuando.Tome el producto real como estándary obtenga el manual más reciente en www.grupotemper.es.A menos que seacuerde lo contrario, este manual solo se utilizarácomo guía.Cualquierdeclaración,información o sugerencia en este manual no tomaráningún tipo deresponsabilidad. Sin permiso por escrito,queda prohibido que cualquierempresa o individuo pueda extraer,copiar o transmitir de ninguna forma elcontenido de este documento(en parte o ensu totalidad).Advertencia:Retire el módulo WIFI después de apagarlo.Nota:Este módulo WIFI viene como accesorio con nuestra gama de inversores monofásicos y trifásicos con tecnología ONGRID.SOLARMAN inteligentepara usuario finalNegocios SOLARMANpara negocios4.Métodos de uso y avisos para el botón de reinicio4.1Métodos de uso y descripciones de pulsaciones de teclas para el botón de reinicioiPhone:busque"SOLARMAN Smart"en Apple Store.Android:busque"SOLARMAN Smart"en Google Play.1.Instalación del registrador revestidoTipo1Conecte el inversor como semuestra en elTipo2Conecte el registrador en la interfaz de comunicación del inversor comose muestra en el diagramaMANUAL DE USUARIO para SOLARMAN Smart APP1.RegistroAccede a SOLARMAN Smart y regístrate.Haga clic en"Registrarse"y cree su cuenta aquí.2.Estado del registrador2.Crear una plantaHaga clic en"Agregar ahora"para crear su planta.Complete la información básica de la planta y otra información aquí.El estado de funcionamiento normal del registrador,cuando el enrutador está conectado ala rednormalmente:1.Estado de conexión correcta y con servicio:la luz NET se mantiene encendida después deencender el registrador.2.El registrador funciona normalmente:la luz READY parpadea.3.Estado de conexión exisotda con el inversor:la luz COM sigue encendida.3.Procesamiento de estado anormalSi los datos en la plataforma son anormales cuando el registrador está funcionando, consulte la tablaque se muestra a continuación de acuerdo con el estado de las luces indicadoras para comprobar losproblemas.Si aún no se pueden resolver o el estado de las luces indicadoras no se muestra en la tabla ,comuníquesecon nuestro Servicio al Cliente.(Nota:utilice la siguiente consulta de tabla después del encendido durante al menos2 minutos).3. Agregar un registradorMétodo 1:Ingrese el SN del registrador manualmente.Método 2:Haga clic en el icono a la derecha y escanee para ingresar el SN del registrador.Puede encontrar el SN del registrador en la caja o en el propio aparato.Paso 3:Configuración automáticaEspere un momento para completar la configuración.Entonces el sistema cambiaráa la página siguiente.Haga clic en "Listo"para verificar los datos de la planta.(Por lo general,los datos se actualizaránen 10minutos)4.Configuración de redDespués de agregar el registrador,configure la red para garantizar un funcionamiento normal.Vaya a "Detalles de la planta"Lista de dispositivos", busque el SN de destino y haga clic en "Redes".Si se produce un error de configuración,compruebe los siguientes puntos e inténtelo de nuevo.(1)Asegúrese de que WLAN estéENCENDIDO.(2)Asegúrese de que WiFi sea normal.(3)Asegúrese de que el router inalámbrico no implemente la lista blanca-negra.(4)Elimine los caracteres especiales en la red Wi-Fi.(5)Acorte la distancia entre el teléfono y el dispositivo.(6) Intente conectarse a otro Wi-Fi.Advertencia:Asegúrese de que el registrador estéfuncionando correctamente antes de abandonar lainstalación. Si hay algo anormal,no abandone el lugar y comuníquese con el servicio al cliente.Paso 1:Confirmar información Wi-FiAsegúrese de que su teléfono se haya conectado a la red WiFi correcta. Haga clic en "Inicio".Aviso:No se admite Wi-Fi 5G.Si tiene alguna consulta técnica sobre nuestros productos,contáctenos y proporcione la siguiente información:1.Modelo del producto y número de serie del registrador.2.Modelo del producto y número de serie del inversor conectado.¡Gracias por su apoyo y cooperación!Queridos clientes,Muchas gracias por usar nuestros productos.Para brindarle un mejor servicio,complete la tarjeta de garantía y guárdela cuidadosamente.Paso 2:Conéctese a la red APHaga clic en "Ir a conectar"y busque la red "AP_XXXXX"correcta (XXXXXse refiere al SN del registrador).Si se requiere la contraseña,puede encontrar la contraseña en el cuerpo del registrador. Vuelva a SOLARMAN Smart APP,después de conectarse ala red AP.。
现代西班牙语第一册课后习题答案.

课后习题答案第一课:II. 1.Paco es cubano.2.Ana y Pepe son amigos.3.Ella es Ana.4.¿Quien es él?5.Son Ana y Ema amigas?Sí,ellas son amigas.第二课:VII. 1.¿Son ellos amigos de Ana?No,ellos no son anigos de Ana .Son amigos de Ema.2.¿Qué es Lucía? Es enfermera.3.¿Es usted hermana de Paco ?Sí,yo soy hermana de Paco.4.¿Quién es cantante? Lucía es cantante.5.¿Eres cocinero? No,no soy cocinero.Soy médico.6.¿Lucía y Ema son hermanas.VIII.1.Ema es enfermera.Es esposa de manolo.2.¿Qué son ellos? Ellos son cocineros.3.¿Sois médicos? No,no somos médicos.Somos enfermeros.这里也可以全用阴性的词.4.Hola,¿usted es ....? (¿quién es usted?5. Me llamo Zhang bin .Soy padre de zhang weinan.¡Hola!5.Estos dos son Paco y Li xin. Paco es chileno. Li xin es china.Ellos son amigos de Lucía.自我测试题(1--2课VIII. 1.¿Quiénes sois? (¿Quiénes son ustedes?2.¿Qué es Paco? ¿Es médico?3.¿Quién es ella?¿Es hermana de Ema?4.Este es Manolo. Es cubano.Es cantante.5.Estos dos son Lucía y Pepe.Lucía es enfermera.Pepe es cocinero.somos amigos.6.¡Hola!Me llamo Li Xin.¡Hola!Me llamo Manolo.Este es Pepe.7.¿Es usted esposa de Paco?No,no soy esposa de Paco.(no soy su esposa soy su hermana.第三课:V. la el,la lael el lasel la loslas los lasVI. mi casa nuestra casanuestras casas el amigo tuyovuestra amiga vuestros hijosnuestros esposos sus esposassus hermanos(los hermanos de élsus hermanos (los hermanos de ellossu habitación su oficina(la oficina de ustedes vuestros dormitorios nuestros camas el cuarto de Ana(la habi tación de Ana la mesa de Pacola casa de Lucía el tormitorio de de Lin xinel cuarto de nuestro padre la mesa de su hijala fábrica de nuestro amigo la oficina de nuestro padrelas camas de vuestros hermanos la oficina de su madre这道题的答案都不是唯一的.VIII. 1.En 2. El el de Su en el4.sus(tus5.En de del de mi(suX. Esta es mi casa. En ella hay una sala,una cocinay dos dormitorios.En la sala hay tres sofás y una mesa. Este es el dormitorio de mi hijo.En él hay dos camas. Yo soy funcionario.Mi oficina está en el centro de la ciudad.第四课:VIII. 1. la de Es En hay2. es maestro amable La de3. señora la de amable somos4. En un En el5. el es en de本题中第一个el似乎可以不用填单词的。
法语常见前缀后缀

a- quatre 四
thalasso- mer 海
théo- dieu 神
therm(o)- chaleur 热
top(o)- lieu 地方
typo- caractère 型,版
syn-/sym- avec, ensemble 共,同,合
tachy- rapide 快,迅速
tauto- le même 同样
taxi- arrangement 安排,整理
techn(o)- art, science 技术,工艺
télé- de loin à distance 远,远距离
cycl(o)- cercle 圈,环;循环
cyto- cellule 细胞
dactyl(o)- doigt 指,趾
démo- peuple 人民;人口
derm(o)-/dermato- peau 皮,皮肤
di- deux 二,双;二重
di(a)- séparé de, à travers 分离;通过,横过
hypn(o)- sommeil 睡眠;催眠
hypo- sous; insuffisance 下,在…下;少,不足
hystér(o)- utérus 子宫
icon(o)- image 像,肖像;图像
idé(o)- idée 思想,观念
idi(o)- particulier 特有的,个人的
hépat(o)- foie 肝
hept(a)- sept 七
hét
éro- autre 异
hex(a)- six 六
hiér(o)- sacré 圣,神圣
hipp(o)- cheval 马
Bosch Serie 4 积分式洗衣机说明书

Serie 4, Lavastoviglie integrabile, 60 cm, acciaio inox, XXLSBI4HCS48EAccessori specialiSGZ0BI11 Kit di adattamento e fissaggio NiroSGZ0IC00 :SGZ1010 Prolunga acqua-stop sgs/gi/gv/guSMZ1051EU :SMZ2014 Cestello per bicchieri a stelo lungoSMZ5000 Set completo spazio 51SMZ5003 Cerniera ribaltabile per dimensioni alte SMZ5045 :SMZ5100 Cestello porta posateSMZ5300 Accessorio lavastoviglie da incasso Caricare facilmente le stoviglie e gestirela lavastoviglie tramite l'app Home Connect.• ExtraDry: opzione selezionabile per un'ulteriore asciugatura.• CestelloVario - Flessibilità nel terzo livello di carico• Home Connect: elettrodomestici interconnessi di Bosch per unapiù facile gestione della quotidianità• AquaStop: protezione antiallagamento, con una garanzia a vita al 100%.Dati tecniciClasse di efficienza energetica: ........................................................D Consumo energetico del programma Eco per 100 cicli : .........85 kWh Numero massimo di coperti: .. (14)Consumo di acqua del programma eco in litri per ciclo: ..............9.5 l Durata del programma: .............................................................4:55 h Emissioni di rumore aereo: ......................................44 dB(A) re 1 pW Classe di emissioni di rumore aereo: ................................................B Da incasso / a libera installazione: .....................................Da incasso Altezza senza piano di lavoro: ....................................................0 mm Dimensioni (lxp): ................................................865 x 598 x 573 mm Dimensioni del vano per l'installazione: .......865-925 x 600 x 550 mm Profondità con porta aperta a 90 gradi: ...............................1200 mm piedini regolabili: ...................................................Yes - all from front Regolazione massima dei piedini: ............................................60 mm Zoccolo regolabile: ..........................................verticale ed orizontale Peso netto: ..............................................................................37.6 kg Peso lordo: ..............................................................................39.5 kg Potenza: ..................................................................................2400 W Corrente: .....................................................................................10 A Tensione: .............................................................................220-240 V Frequenza: ...........................................................................50; 60 Hz Lunghezza del cavo di alimentazione elettrica: .....................175.0 cm Tipo di spina: ..........................................................................Schuko Lunghezza tubo entrata: ..........................................................165 cm Lunghezza tubo uscita: ............................................................190 cm Codice EAN: (4242005184019)Installazione: ......................................................................IntegrabileSerie 4, Lavastoviglie integrabile, 60cm, acciaio inox, XXLSBI4HCS48ECaricare facilmente le stoviglie e gestire la lavastoviglie tramite l'app Home Connect.Prestazioni e consumo- Classe di efficienza energetica¹: D- Energia² / Acqua³: 85 kWh / 9.5 litri- Capacità: 14 coperti- Durata del programma⁴: 4:55 (h:min)- Livello sonoro: 44 dB(A) re 1 pW- Livello di rumore programma Silence: 41(A) re 1 pW- Classe di efficienza di rumore: BProgrammi e opzioni- 6 Programmi: Eco 50 °C, Auto 45-65°, Intensive 70 °C, Express 65°, Silence- Prelavaggio- 4 Programmi supplementari: Home Connect, Asciugatura extra, Mezzo carico, SpeedPerfect+- Home Connect-capibile via WLAN- Programma manutenzione- Silence on demand (tramite App)Tecnologia lavaggio- Scambiatore di calore.- DosageAssist- EcoSilence Drive- Automatismo di pulizia- Sistema di filtri autopulenti con ondulazione a 3 livelli- Contenitore interno: Materiale della vasca interna in acciaio inox Sistema Cestelli- Cestelli Flex- VarioCestello- Ruote con scorrimento facile nel cestello inferiore e nel terzo cestello- Cestello inferiore con blocco (rackStopper) per evitare che fuoriesca dalle guide.- Cestello superiore regolabile in altezza con Rackmatic (3 livelli)- Griglie abbattibili nel cestello superiore (2x)- Griglie abbattibili nel cestello inferiore (2x)- Ripiani per tazze nel cestello superiore (2x)- Carrello inferiore con ripiani per tazze (2x)Indicazione e funzionamento- Iscrizioni di testo in chiaro (inglese)- Indicazione tempo residuo (min.)- Programmatore inizio lavaggio (1-24 h)Sicurezza- AquaStop: una garanzia Bosch per danni causati dall'acqua - durata del dispositivo*- Sicurezza bambini (Tasti)- Tecnologia di protezione del vetro - Aiuto per il riempimento del sale (Imbuto)- Protezione contro il vaporeDimensioni- Dimensioni del prodotto (HxLxP): 86.5 x 59.8 x 57.3 cm¹ In una scala di classi di efficienza energetica da A a G² Consumo di energia in kWh per 100 cicli (nel programma Eco 50°C)³ Consumo di acqua in litiri per ciclo (nel programma Eco 50 °C)⁴ Durata del programma Eco 50 °C* Verificare i termini di garanzia al link/ch/it/condizioni-generali-di-garanziaSerie 4, Lavastoviglie integrabile, 60 cm, acciaio inox, XXLSBI4HCS48E。
UGREEN磁吸无线充电器15W使用说明书

尸裁切线辅助线压痕线牙刀V 槽线画线半穿刀·外表面视图门内表面视图4EID -ICIBIA版本I变更描述I变更日期设计者A01 I 初始发行2021/05/14 李雪嫂A02 I增加F CCID/ICID 警语2021/07/9 李雪嫂A03 I变更FCCID \ ICID警语2021/12/01李雪嫂忙UGREENHow It WorksDE,Wlees fcn如omert I F Nonctionnement I ES, Como Fcnclona IT; Come Fcn,lona IJP; 使用方法I CN; 使用卫叫屯§1ARMagnetic Wireless Charger 15WModel: CD245 I P/N: 302333FCC 1Dc2AQl5-30233 IC,26850-30233Lisee Maocal I Becct,echaodbcch IMao e el de l'ctmsatec「Maocal de cscado I Maocale Uteate I取扳说明各用户手Ill It''比.,,凶,。
勹EN: Coccectthe pcoduct to powec outle DE: S chlle�e, Sle das Pcodukt ac eloe Steckdose a, FR: Coccecte, le p尺dult au chacgeucES: Cocecte el pcoducto a la fuecte de ahmeclaci6, I T: Collegan, ii pcodotto a uoa pcesa d, cocceote JP: 当裂品在家庭用O习y七y卜忆接統匕去丸CN: 将无线充连接电淙通电。
生,凶丿4严泸凶护士�:AReEN: A ttach y ou, pho,e o, the pcoduct , the, start cha「gt,gDE:Schlie胫,Ste the Haody a , das Prod"kt a, ood starte, Siede, Ladevocga,gFR: Mette,vot「e telepho门e sue le pcoduit, p uts ii commeocera a s e cha「ge「ES: Coloque su m6vil e, el pcoducto,luego come, 芘治a cacga函I T: Collegace ii telefono al prodotto, q uindi awl a ce la ncacica JP: 又,-卜7才y宅当掣品1二取D付lt-r分5、充霆抒鹃始含杠李才。
Uma forma bidimensional que maximiza a resist^encia aerodin^amica newtoniana

Abstract. In a previous work [18, 19] it is investigated, by means of computational simulations, shapes of nonconvex bodies that maximize resistance to its motion on a rarefied medium, considering that bodies are moving forward and at the same time slowly rotating. Here the previous results are improved: we obtain a two-dimensional geometric shape that confers to the body a resistance very close to the supremum value (R = 1.4965 < 1.5). Resumo Um corpo bidimensional, apresentando um ligeiro movimento rotacional, deslocase num meio rarefeito de part´ ıculas que colidem com ele de uma forma perfeitamente el´ astica. Em investiga¸ c˜ oes que os dois primeiros autores realizaram anteriormente [18, 19], procuraram-se formas de corpos que maximizassem a for¸ ca de travagem do meio ao seu movimento. Dando continuidade a esse estudo, encetam-se agora novas investiga¸ c˜ oes que culminam num resultado que representa um grande avan¸ co qualitativo relativamente aos ent˜ ao alcan¸ cados. Esse resultado, que agora se apresenta, consiste numa forma bidimensional que confere ao corpo uma resistˆ encia muito pr´ oxima do seu limite te´ orico. Mas o seu interesse n˜ ao se fica pela maximiza¸ c˜ ao da resistˆ encia newtoniana; atendendo ` as suas caracter´ ısticas, apontam-se ainda outros dom´ ınios de aplica¸ c˜ ao onde se pensa poder vir a revelar-se de grande utilidade. Tendo a forma ´ optima encontrada resultado de estudos num´ ericos, ´ e objecto de um estudo adicional de natureza anal´ ıtica, onde se demonstram algumas propriedades importantes que explicam em grande parte o seu virtuosismo.
仓颉造字西语版 -回复

仓颉造字西语版-回复仓颉造字西语版: El Método de Creación de Caracteres de CangjieIntroducción:La escritura ha sido una herramienta esencial para la comunicación humana durante miles de años. En diferentes partes del mundo, se han desarrollado diversos sistemas de escritura para representar los sonidos y las palabras de los lenguajes hablados. Uno de los sistemas de escritura más antiguos y sofisticados es el chino, que cuenta con miles de caracteres.En la antigua civilización china, se desarrollaron varios métodos para crear nuevos caracteres, y uno de los más famosos es el método de "Cangjie", una leyenda literaria en la historia china. Según la leyenda, Cangjie fue un funcionario del legendario emperador amarillo, Huangdi, durante la antigua era Xia. Cangjie es conocido como el invento de los caracteres chinos y el creador del método de Cangjie para la creación de caracteres chinos.Paso 1: La idea del carácterEl primer paso en el método de Cangjie es tener una idea de cómo se ve el carácter. Esto puede ser inspirado por la forma de un objeto, una imagen o la combinación de otros caracteres existentes. Por ejemplo, si queremos crear un carácter para representar la palabra "sol", podríamos imaginar un círculo con rayos saliendo de él.Paso 2: División de los elementosUna vez que tenemos la idea básica del carácter, el siguiente paso es dividirlo en elementos más pequeños llamados "trazos". Los trazos son los componentes fundamentales de los caracteres chinos y se pueden combinar de varias maneras para formar diferentes caracteres. Por lo general, los caracteres chinos se componen de cuatro a cinco trazos.Paso 3: Clasificación de los trazosDespués de dividir el carácter en trazos, el siguiente paso es clasificar los trazos en diferentes categorías según su posición y forma. En el método de Cangjie, hay ocho categorías principales de trazos: punto, línea horizontal, línea vertical, línea diagonal, gancho izquierdo, gancho derecho, gancho arriba y gancho abajo.Paso 4: Selección de trazosUna vez que se han clasificado los trazos, puede seleccionar trazos de diferentes categorías para formar el carácter deseado. Por ejemplo, utilizando el ejemplo anterior del carácter para "sol", podemos seleccionar un trazo circular para representar el círculo del sol y agregar trazos diagonales para representar los rayos.Paso 5: Orden de los trazosDespués de seleccionar los trazos, es importante determinar el orden en el que se deben escribir. El orden de los trazos puede afectar la legibilidad del carácter y el flujo de la escritura. En el método de Cangjie, generalmente se sigue un orden de escritura de arriba a abajo o de izquierda a derecha.Paso 6: Práctica y perfeccionamientoLa creación de caracteres chinos no es un proceso instantáneo, requiere práctica y perfeccionamiento. A medida que practicas más, puedes experimentar con diferentes combinaciones de trazos ymejorar tu habilidad para crear caracteres únicos y originales. Conclusión:El método de Cangjie ha sido utilizado durante miles de años para crear nuevos caracteres chinos. A través de la división de caracteres en trazos, la clasificación de trazos en diferentes categorías y la selección y orden de trazos, es posible crear caracteres chinos únicos y comprensibles. Aunque el método de Cangjie se basa en principios antiguos, sigue siendo relevante hoy en día y continúa siendo utilizado para crear nuevos caracteres chinos en la era digital.。
葡萄牙语安徒生童话:AS_ROUPAS_NOVAS_DO_IMPERADOR【皇帝的新装】

Há muito, muito tempo, vivia em um reino distante um imperador vaidosíssimo. Seuúnico interesse eram as roupas. Pensava apenas em trocar de roupas, várias vezes ao dia; desfilava vestes belíssimas, luxuosas e muito caras para a corte. Um belo dia, chegaram à capital do reino dois pilantras, muito habilidosos em viver às custas do próximo. Assim que os dois souberam da fraqueza do imperador por belas roupas, espalharam a notícia de que eles eram especialistas em tecer um pano único no mundo, de cores e padr?es deslumbrantes. E — o mais impressionante, segundo eles: as roupas confeccionadas com aquele tecido tinham o poder de serem invisíveis para as pessoas tolas, ou que ocupassem um cargo sem merecê-lo. O imperador logo se entusiasmou com a idéia de ter roupas n?o só bonitas, mas também úteis para desmascarar os bobos e os que n?o mereciam cargos na corte. E tratou de mandar chamar t?o habilidosos tecel?es.— Ponham-se logo a meu servi?o. Quero uma roupa sob medida, a mais linda que játenham feito.— Majestade, necessitamos de uma sala, de um tear, de fios de seda e de ouro e, principalmente, de que ninguém nos incomode. Foram logo atendidos. Uma hora depois estavam diante do tear, fingindo tecer sem parar. E assim continuaram por muitos dias, pedin do cada vez mais seda, mais ouro… e mais dinheiro, é claro! O imperador estava curioso e um dia resolveu enviar seu velho primeiro-ministro para inspecionar a obra dos tecel?es. “é ele um ministro sábio e fiel”, pensou o rei. “Com certeza, conseguirá ver e sse tecido t?o extraordinário e nada me esconderá.” Mas, quando o velho ministro chegou em frente ao tear, nada viu. Preocupou-se. Ficou em dúvida.— Mas isso n?o significa que eu n?o seja digno do cargo que ocupo — disse a si mesmo, aflito. Aos tecel?es, porém, que lhe perguntavam com insistência se o padr?odo tecido era de seu agrado, se as cores se harmonizavam, ele respondeu entusiasmado: — Mas claro! é magnífico. Nunca vi coisa igual. O ministro levou ao conhecimento do imperador os progressos da confec??o e, por precau??o elogiou o extraordinário bom gosto dos dois profissionais. Por nada neste mundo admitiria ter olhado para um tear vazio. Na cidade já n?o se falava em outra coisa, sen?o da nova roupa do imperador e de seus poderes mágicos. Diziase que custaria uma fortuna, mas que bem valia o pre?o: poderia desmascarar ministros e secretários! Na corte, em compensa??o, muitos impostores e aproveitadores do cofre do reino n?o dormiam tranqüilos e aguardavam com temor o momento em que o imperador iria, enfim, vestir a t?o famosa e denunciadora roupa. Transcorreram mais cinco ou seis dias, e o imperador, que n?oagüentava mais esperar, resolveu ir em pessoa visitar os tecel?es. Com uma comitiva de guardas e escudeiros,e acompanhado por seu fiel primeiro-ministro, que tremia de medo, foi ver o trabalho dos dois impostores, sendo recebido com enorme solenidade e muitas explica??es.— Nunca teríamos ousado esperar tanto, Majestade. Sua visita e sua satisfa??o s?o o maior reconhecimento ao nosso trabalho… Aprovando Vossa Majestade nosso humilde trabalho, ficaremos extremamente lisonjeados. Será muita honra. Após tanta bajula??o, o imperador e sua comitiva foram conduzidos à sala do tear.— Majestade, observe a extraordinária beleza e perfei??o do desenho — disse o velho ministro com voz trêmula. O imperador permanecia calado: estava assombrado! Ele n?ovia nada, apenas o tear vazio, totalmente vazio! Isto queria dizer que era um bobo, ou n?o era digno de ser imperador. “Coitado de mim!”, pensou. “Nada poder ia ser pior, tenho que dar um jeito para n?o descobrirem a verdade.” Resolveu reagir e afastar o perigo de um possível desmascaramento. Aproximou-se do tear, segurando seumonóculo, fingindo admirar o tecido invisível.—Hein?… Sim, é claro… é realmente u ma beleza. Um trabalho e tanto. E a comitiva toda fez um coro de elogios e mais elogios. Nenhum membro do séquito iria confessar n?o estar vendo nada de nada, pois ninguém queria passar por tonto, ou ser considerado indigno do cargo que ocupava. Os espertos tecel?es sorriam, satisfeitos. O temor dos poderosos representava mais seda, mais ouro e mais dinheiro.— Vossa Majestade, ent?o, aprova o nosso trabalho?— perguntaram— perguntaram eles, com malícia e ironia. O imperador disse que estava satisfeito e, para demonstrar seu reconhecimento, presenteou os dois pilantras com um saco cheio de ouro. Mas continuava preocupado e perplexo. Seria indigna sua realeza? Seria ele um incompetente?— Majestade — falou o primeiro-ministro. — Por que com esse tecido n?o manda confeccionar uma roupa especial para o torneio do próximo domingo?— Sim, sim, claro — resmungou o imperador.— Estou mesmo querendo uma roupa nova para o torneio. Foi dada nova incumbência aos tecel?es, que pegaram a fita métrica e tiraram as medidas do rei, fingindo entender do ofício.— A cauda, Majestade, deverá ser muito longa?— Claro que sim, muito comprida. Arrastando-se por metros atrás de mim.— E o la?o? Prefere de veludo ou de cetim?— Podem sugerir, confio no gosto de vocês. O imperador voltou ao palácio transformado, e os dois impostores continuaram a trabalhar na frente do tear vazio. Nem sequer pararam durante a noite. Empenhados na farsa, trabalhavam à luz de vela.Alguém que, por curiosidade, foi espiar por uma fresta da porta, viu-os atarefados, cortando o ar com uma grande tesoura e costurando com uma agulha sem linha. Dois dias depois, na manh? do domingo, os tecel?es se apresentaram na corte, levando a roupa para o torneio. Mantinham os bra?os levantados, como se estivessem segurando algo muito delicado e volumoso. Ninguém via nada— pois nada havia para ser visto —, mas ninguém, também, ousou confessar. Quem assumiria ser tolo ou incompetente? Os dois charlat?es correram ao encontro do imperador, assim que este apareceu na porta do sal?o.— Vossa Majestade gostaria de vestir suas roupas novas agora? — perguntou, ir?nico, o primeiro. O imperador disse que queria vesti-las logo. Foi para a frente de um grande espelho e tirou as roupas que vestia. Os tecel?es fingiram entregar ao imperadorprimeiro a túnica, depois a cal?a e, enfim a capa com sua longa cauda. O imperador, meio despido, sentia muito frio. Até espirrou, mas n?o podia nem pensar em perguntar se continuava em trajes íntimos.— N?o é um pouco leve demais este tecido? — arriscou.— Majestade, a leveza é uma de suas qualidades mais apreciadas. Nem uma aranha poderia tecer uma tela t?o impalpável, apesar de termos empregado muitos fios de ouro.E o imperador se convenceu de que estava vestindo uma roupa fabulosa, embora o espelho refletisse apenas a imagem de um homem de cueca e camiseta. Em volta dele, os cortes?os se desmanchavam em elogios à nova roupa. Finalmente, a toalete terminou: tomara banho, perfumara-se, penteara-se e vestira a t?o falada roupa. No pátio dopalácio já estavam a postos quatro soldados em trajes de gala, segurando um dossel sob o qual o imperador se protegeria até a pra?a dos torneios.— Vossa Majestade está pronta? A roupa é do seu agrado? — Perguntou um dos charlat?es.— N?o deseja mais nenhuma mudan?a? — Perguntou o outro trapaceiro. O imperador deu mais uma olhada no espelho, perplexo e desconfiado, e respondeu:— Claro. Podemos ir. Os criados de quarto ficaram fingindo recolher do ch?o a cauda do manto real, os soldados seguraram bem alto o dossel, e o cortejo come?ou a caminhar. Ao longo das ruas uma multid?o estava à espera do cortejo, a fim de admirar as fabulosas roupas do imperador. Nas janelas e nas sacadas os curiosos se espremiam, e os comentários eram intermináveis.— é a roupa mais linda de todo o guarda-roupa imperial.— Que luxo, que elegancia! Naturalmente, ninguém via a roupa t?o comentada, mas n?o iria confessar isso, pois correria o risco de passar por bobo ou incompetente. O cortejo já tinha atravessado meia cidade, chegando próximo à pra?a dos torneios. De repente, um menininho que conseguira um lugar bem na frente, gritou, desapontado: — O imperador n?o está vestido. Como é ridículo, assim quase pelado! Cadê as roupas novas? Muitos o escutaram, alguém repetiu o comentário.—Um garotinho está gritando que o imperador está sem roupas…— Oh! é a voz da inocência! Crian?a diz tudo que vê. As palavras, primeiro murmuradas, aumentaram de volume e agora eram ditas aos brados pela gente do povo, que ria até n?o poder mais. O imperador escutou e ficou corado como um tomate, pois a cada passo que dava, se convencia de que aquela gente tinha raz?o e que ele tinha sido redondamente enganado e que, na verdade a t?o elogiada roupa n?o existia. Mas, e agora? Faria o quê? Continuou a caminhar, todo orgulhoso, como se nada de estranho ocorresse, acompanhado pelas gargalhadas cada vez mais intensas de seus súditos. Os dois charlat?es nunca mais foram vistos. Fugiram com todo o ouro, e o imperador aprendeu que a vaidade é a pior inimiga do reino.皇帝的新装许多年以前有一位皇帝,他非常喜欢穿好看的新衣服。
Th'eorie de jauge et groupoi des (Gauge theory and groupoids)

4. w(c, z · g) = w(c, z ) · g. Par exemple, si X = ∗, alors C est un groupe topologique et w correspond ` a une repr´ esentation (= homomorphisme continu) de C dans G. Plus g´ en´ eralement, si w est une repr´ esentation de C sur ξ , l’´ equation w(c, ˜ ∗) = w ˜ ∗ · h(c) d´ efinit un homomorphisme continu h : ΩC → G appel´ e l’holonomie de w. Les r´ esultats de cet article concernent l’existence et la classification de repr´ esentations d’un X -groupo¨ ıde C sur un G-fibr´ e principal ξ donn´ es. Nos hypoth` eses principales seront que C est un X -groupo¨ ıde localement trivial et G un groupe SIN (d´ efinitions ci-dessous). Soit C un X -groupo¨ ıde. Une C -contraction est une application continue ∗ ρ : Uρ → C , o` u Uρ est un ouvert de X , telle que α(ρ(x)) = x. Soit Cont C (X ) l’ensemble des C -contractions. Le X -groupo¨ ıde C est dit localement trivial si {Uρ | ρ ∈ Cont C (X )} est un recouvrement ouvert de X ([Ma, p. 32]; cette d´ efinition co¨ ıncide avec la terminologie de [Eh] si C est transitif). Si le recouvrement {Uρ } est de plus num´ erisable1 , c’est-` a-dire s’il existe une partition de l’unit´ e {µρ : X → [0, 1]} qui lui est subordonn´ ee, on dira que C est un X -groupo¨ ıde localement trivial num´ erisable. Plusieurs exemples naturels de tels groupo¨ ıdes sont pr´ esent´ es au paragraphe 6. Reprenant les id´ ees de Ch. Ehresmann [Eh], nous d´ emontrerons au § 2 l’existence d’une repr´ esentation universelle de C et d’un principe de reconstruction : Th´ eor` eme 1.1 (Th´ eor` eme A) Soit C un X -groupo¨ ıde localement trivial num´ erisable. Alors : a) l’application β : C∗ → X est un ΩC -fibr´ e principal num´ erisable (que nous appellerons ξC ). La formule w ˜ (c, u) := c u d´ efinit une repr´ esentation de C sur ξC . p b) soit ξ := (E −→ X ) un G-espace principal muni d’une repr´ esentation w de C . Alors ξ est le fibr´ e associ´ ea ` ξC E = C∗ ×ΩC G = C∗ ×hw G , o` u ΩC agit a ` gauche sur G via l’holonomie hw de w. En particulier, ξ est un G-fibr´ e principal num´ erisable. De plus, la repr´ esentation w est obtenue de w ˜ par la formule w(c, [u, g]) = [w ˜(c, u), g] = [cu, g].
《godisagirl》歌词

groove cove rage- god is a girlreme mberi ng me,dis cover andsee all o ver t he wo rld,she's know n asa gir lto thos e who a fr ee,t he mi nd sh all b e keyfor gotte n asthe p ast 'caus e his torywilllastgodis agirl,wher everyou a re,d o you beli eve i t, ca n you reci eve i t? go d isa gir l,wh ateve r you say,do y ou be lieve it,can y ou re cieve it?god i s a g irl,howev er yo u liv e,do youbelie ve it, can yourecie ve it? god is a girl,she's on ly agirl,do y ou be lieve it,can y ou re cieve it?she w antsto sh ine,forev er in time,she is s o dri ven,she's alwa ys mi ne c leanl y and free,she want s you to b eapartof th e fut ure,a gir l lik e mether e isa sky,ill umina tingus, s omeon e isout t herethat we t rulytrustthe re is a ra inbow foryou a nd mea b eauti ful s unris e ete rnall ygo d isa gir lwh ereve r you are,do y ou be lieve it,can y ou re cieve it?god i s a g irl whate ver y ou sa y,do youbelie ve it, can yourecie ve it? god is a girlhow everyou l ive,do yo u bel ieveit, c an yo u rec ieveit? g od is a gi rls he'sonlya gir l,do youbelie ve it, can yourecie ve it? end。
关于法语专业毕业论文选题参考题目[精选范文]
![关于法语专业毕业论文选题参考题目[精选范文]](https://img.taocdn.com/s3/m/25ff50c748649b6648d7c1c708a1284ac85005c3.png)
关于法语专业毕业论文选题参考题目(1)victorhugoetlhommedanssesromans(2)psychanalysedespersonnagesdemadamebovary(3)latragdiemodernedelhommedanslesoeuvresdecam us(4)lalinationdespersonnagesderougeetnoir(5)linfluenceprofondedesciv i lisationsg r ecqueethbr a a?q uesurlac u u lturefran?a a ise(6)die u u ouhomme?la r eligionetl a a littrature f ran?aise(77)montaigne:dequoidout e e-t-il?(8)l edrameclas s s iquelatrag d d ieduhros(99)lacompara i sonentreal e e xandreduma s s etdejingyo n n g:l abiogra p p hiedeschev a a lierserran t(10)lepet i tprince:le c c onteduving t imesicle(111)lacompar a a isonentrer o o usseauetvo l taire(12)l epregoriot e e tlasocitbo u u rgeoisedu199sicle(13)l aculturedu m m oyenageche z z fran?oisvi l lon(14)em i lezolaetle r omanralist e e p;(15)les f ablesdelaf o o ntaine(16)lacorrespo n n dancedansl a a littrature f ran?aise(117)lesperso n n nagesdestr o o ismousquet a a ires(18)l e e sdiffrente s s colesdelit t raturefran??aise(19)l a a chinevuepa r lesphiloso p p hesdeslumi r esenfrance(20)lefoot-b b allfran?ai s s2.指导教师:李培西西(1)lacult u u refran?ais e e(2)lesann e e scroises(33)refletsre f ltelacivil i sationfran??aise(4)la f rancophoni e e(5)lacult u u refran?ais e e traverslab a a ndedessine(6)levigno b b lefran?ais(7)lacompar a a isondelaco n n ceptionest h h tiqueentre l achin eetla f rance(8)l a a comparaiso n n desculture s s entrelevin f ran?aisetl a a lco olchino i s(9)compa r aisondespo l itessesfra n n?aisesetch i noises(10)lartdelang o o ciationave c c lesfran?ai s s(11)ladif f usiondelal l iancefran?a a isechengdu(12)lapress e e(lesmdias)e e nfranceete n n chine:deux s s ystm ediffr e e nts(13)la n n alysedesgr v v esenfrance(14)lefroma g g e:ungo?ttr s s fran?ais(115)comparai s s ondelaprot e e ctiondesmo n n umentshist o o riquesenfr a a nceetench i ne(16)les m m diasfran?a i s(17)pens e e delasignif i ancedelins t allationdu c c onsulatfra n n aischengd u u(18)lacom m m unautfran?a a iseenchine(19)lescoop r ationsuniv e e rsitairess i no-fran?ai s s es(20)les c c hangescomm e e rciauxentr e e lafranceet l achine3.指导导教师:邹燕舞(1)l acuisinefr a a n?aisep;(22)lecinmafr a a n?ais(3)l e e sparfumsen f rance(4)l a a haute-cout u u reenfrance(5)linflue n n cedesgrand e e smarquesfr a a n?aisesenc h h ine(6)lam o o defran?ais e e(7)laffin i tetladiffr e e nceentrele s s proverbesf r an?aisetch i n ois(8)le m m ploidupron o o mindfinion(9)lannedef r anceenchin e e chengdu(100)lesmotsde f ran?aisfam i lier(11)l e e scaractris t iquesdelal a a nguefran?a i sedanslapr e e sse(12)la b b rviationde l alanguefra n n?aise(13)l esentrepri s s esfran?ais e e senchine(114)lesentre p p risesfran?a a isesimplan t esausichua n n(15)lhist o o ireduconsu l atdefrance c c hengdunbsp;(16)lesco m m paraisonse n n trelenseig n n ementsupri e e urenfr ance e e tenchine(117)fran?ais l anguetrang r eenchine(118)lesystme d d ucatifenfr a a nce(19)le n n seignement d d ufran?aise n n chine(20)l efran?aise n n chine4.指导教教师:陶涛(1)le c c anadafranc o o phone(2)l a a franceauqu o o tidien(3)l esrelation s s entrelachi n n eetlafranc e e depuislafi n n dela2e guer r emondi关于法语语专业毕业论文选题参考题题目相关内容:优秀毕业论论文选题原则选题题是毕业论文写作的开始,,也是论文整个写作过程的的第一步。
西班牙语虚拟式过去完成时和复合条件式的语法讲义

西班⽛语虚拟式过去完成时和复合条件式的语法讲义语法⼀、虚拟式过去完成时和复合条件句 pretérito pluscuamperfecto de subjuntivo y condicional compuesto⾸先我们先要了解各⾃的变位⽅式,并熟练掌握,在此前提下,我们才能明⽩他们在条件句中的应⽤。
1、虚拟式过去完成时变位。
我们之前已经学习了完成时haber +变位动词的过去分词,如haber estado 的形式,这⾥只需要把助动词haber 根据主语进⾏变位,变为虚拟式过去时即可。
2、复合条件句的变位。
也是由助动词haber的简单条件式变位加上动词过去分词构成的。
⽐如⼆、虚拟式过去完成时和复合条件式在条件句中的应⽤。
◆在此之前先让我们来回顾⼀下我们已经学过的三种条件句。
1、从句:陈述式现在时表⽰:现在或将来可能实现和达到的条件和结果。
例句:Si me llaman buscándote, les digo que estás ocupado.Si sabes la verdad, dímela no más.2、从句:陈述式过去未完成时主句:可以是陈述式过去未完成时,简单条件式。
表⽰:过去或过去将来可能实现和达到的条件和结果。
例句:En aquellos días, si hacía buen tiempo, siempre salíamos de excursión.La madre pensó que si el ni?o seguía con la fiebre, lo llevaría para que lo viera el médico.3、从句:虚拟式过去未完成时表⽰:现在不现实的或极少可能实现和达到的条件和结果。
例句:Si estuviéramos en semejante situación, nos quejaríamos.◆本节课我们学习的主句:复合条件式表⽰:对已经发⽣的事情做不符合事实的设想例句: Si te hubieras puesto el abrigo, no habrías estado frío.Si me hubieras avisado la hora del tren, no lo habría perdido.(事实上结果已经发⽣,你没穿所以着凉了,你没通知我所以我错过了,这只是做出了完全不可能实现的⼀种设想,)是⼀种假设性的条件句我们以⼀句话为例,来分析⼀下以上各种情况下,所表现出的不同意思:Si andamos en moto, le alcanzaremos en media hora. 我们要是骑摩托的话,半⼩时就能赶上他们。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
arXiv:math/0509551v1 [math.KT] 23 Sep 2005
B. Bendiffalah (ben@math.univ-montp2.fr)
Institut de Math´ ematiques et de Mod´ elisation de Montpellier (UMR CNRS 5149) D´ epartement de Math´ ematiques, Case 051 Universit´ e de Montpellier II, Place Eug` ene Bataillon MONTPELLIER 34095 Cedex 5, FRANCE
la g´ en´ eralisation de [Ci] et [MP] de la suite exacte longue de D. Happel [Hap] (cf. aussi [GMS],[GS],[GG],[K]) :
Abstract for “Cohomology of General Kr¨ onecker Algebras”. The computation of the Hochschild cohomology HH ∗ T = H ∗ (T, T ) of a triangular M algebra T = A 0 B was performed in [BG2], by the means of a certain triangular complex. We use this result here to show how HH ∗ T splits in little pieces whenever the bimodule M is ∞ decomposable. As an example, we express the Hilbert-Poincar´ e serie i=0 dimK (HH i Tm )ti m M as a function of m ≥ 1 and those of T of the “general” Kr¨ onecker algebra Tm = A 0 B (here the ground ring K is a field and dimK T < +∞). The Lie algebra structure of HH 1 T is also considered. Sommaire. 1. Introduction Cohomologie des alg` ebres triangulaires. R´ eductions. Alg` ebres de Krœnecker d’un bimodule. 2. Premier Th´ eor` eme de R´ eduction Cohomologie triangulaire. Preuve du Lemme 1. Preuve du Th´ eor` eme 1 (cf. 1.2.3). 3. Second Th´ eor` eme de R´ eduction Cohomologie modifi´ ee. Suite exacte de Mayer-Vietoris. 4. L’Alg` ebre de Lie HH 1 T Preuve du Th´ eor` eme 3. 1 Scindage de HH T . 5. R´ ef´ erences Bibliographiques
D. Guin (dguin@math.univ-montp2.fr)
Institut de Math´ ematiques et de Mod´ elisation de Montpellier (UMR CNRS 5149) D´ epartement de Math´ ematiques, Case 051 Universit´ e de Montpellier II, Place Eug` ene Bataillon MONTPELLIER 34095 Cedex 5, FRANCE
` ´ ERALES ´ COHOMOLOGIE DES ALGEBRES DE KRŒNECKER GEN B. Bendiffalah (Montpellier II) et D. Guin (Montpellier II)
1. Introduction De nombreux travaux ont montr´ e l’importance du calcul de la cohomologie de Hochschild des alg` ebres associatives. Il existe cependant peu de r´ esultats g´ en´ eraux concernant les alg` ebres triangulaires (cf. §1.1). Pourtant, la connaissance de leur cohomologie est suffisante (par des proc´ ed´ es de r´ ecurrence) pour obtenir le calcul de la cohomologie d’alg` ebres tr` es g´ en´ erales, comme les alg` ebres de poset (e.g. [M]) ou les alg` ebres h´ er´ editaires artiniennes (e.g. [Har]). L’objectif de ce travail est d’´ etudier l’incidence de la d´ ecomposabilit´ e du bimodule M sur la cohomologie de Hochschild de l’alg` ebre triangulaire. En particulier, nous ´ etudierons la s´ erie de Hilbert-Poincar´ e des alg` ebres de Krœnecker “g´ en´ erales” (cf. §1.3). Un anneau commutatif K est fix´ e et ⊗ = ⊗K ; nous dirons “module” pour tout ` l’exception notable de la section §4, o` module sur K . A u il est question d’alg` ebres de Lie, toutes nos alg` ebres sont des K -alg` ebres associatives unitaires. Pour toute alg` ebre T , les “T modules” sont des modules (unitaires) ` a gauche sur T . Pour les T -modules-` a-droite, nous o utiliserons plutˆ ot l’alg` ebre oppos´ ee T . §1.1 Cohomologie des alg` ebres triangulaires. Nous renvoyons ` a [CE] pour toutes les questions basiques sur la cohomologie de Hochschild. Fixant deux alg` ebres A et B et un A ⊗ B o -module M (un “bimodule”), on s’int´ eresse ` a l’alg` ebre “triangulaire” (e.g. [ARS,III.§2]) : (1.1.1)
M T = [A 0B ] , aa m a m [a 0 b ][ 0 b′ ] = [ 0
′ ′ ′
am′ +mb′ ] bb′
.
Sa cohomologie, HH ∗ T := H ∗ (T, T ), n’est pas connue dans le cas g´ en´ eral alors que son homologie (de Hochschild) est “triviale” : H∗ (T, T ) = H∗ (A, A) ⊕ H∗ (B, B ) ([Lo]). Hormis la section §4, nous supposerons syst´ ematiquement que le K -module T est n mi projectif (donc aussi A, B et M ) et nous nous int´ eressons au cas o` u M = i=1 Mi (mi ≥ 1), sans aucune hypoth` ese sur la famille de A ⊗ B o -modules E = {M1 , ...,Mn} (autre que les Mi soient e calcul de la cohomologie de Mi M l’alg` ebre [A eduit de ceux des alg` ebres [A a l’aide de deux sortes de r´ eductions 0 B ] se d´ 0 B ], ` ∗ AM M′ (cf. §1.2). La premi` ere (Th´ eor` eme 1) ram` ene le calcul de HH [ 0 B ] ` a celui de HH ∗ [A 0 B ], o` u M ′ = i Mi : nous en d´ eduisons la cohomologie des alg` ebres de Krœnecker g´ en´ erales (cf. §1.3). La seconde r´ eduction (Th´ eor` eme 2) est une famille de suites exactes longues de Mi M′ type Mayer-Vietoris ramenant le calcul de HH ∗ [A a ceux des HH ∗ [A 0B ] ` 0 B ], 1 ≤ i ≤ n. Ce travail fait suite ` a [BG2], o` u la cohomologie de T est exprim´ ee ` a l’aide d’un certain complexe “triangulaire” (M est suppos´ e K -projectif). Ce r´ esultat, que nous rappelons dans §2.1 pour le confort du lecteur, avait permis entre autres choses de retrouver ——
