Maple内核
MAPLE软件简介及其应用

1.2 Maple 命令的输入与显示 1. > 命令提示符;大小写敏感。
2. Maple命令以;或:结尾,以;结尾 显示结果,而以:结尾则不显示结果。 3. Maple的赋值号为:=。
4. 光标放在命令行的任意位置,然后 回车即可运行此命令;在书写命令时如需 换行,须按Shift+回车。
1.3 Maple 的数值与解析计算
if 条件 then 语句组 elif 条件 then 语句 组 else 语句组 fi 3. 循环语句
for 循环变量名 from 初值 by 步长 to 终 值 do 语句组 od
考察下列程序中的循环和条件语句。
restart: n:=10000: count:=0: for i from 1 to n do r1:=rand(0..1): r2:=rand(0..1): if r1()=1 or r2()=1 then count:=count+1: fi: od: prizeA:=1000*evalf(count/n);
Maple可进行无误差的符号计算和高精 度的数值计算。例如, 100!, Pi, sqrt(2), sin(3)。
1.4 Maple 的图形显示
1. 一般函数做图
plot(f(x),x=a..b,option); plot3d(f(x,y),x=a..b,y=c..d,option);
2. 极坐标做图
od;
3. 布尔表达式和逻辑运算
Maple中的关系运算符为<,<=,>,>=,=, <>;逻辑运算符为and, or, not。 “表达式 关系运算符 表达式”称为关 系式,其值为true或false。
由关系式、逻辑运算符和括号组成的 表达式称为布尔表达式。例如,
maple数学软件的应用原理

Maple数学软件的应用原理1. Maple数学软件概述Maple是一款强大的数学软件,被广泛应用于科学、工程和数学领域。
它提供了丰富的功能和工具,支持数值计算、符号计算、图形绘制和数据分析等。
Maple在解决数学问题、模拟和建模方面有着广泛的应用,其核心原理在于运用数学算法、符号计算技术和计算引擎。
2. Maple数学软件的优势2.1 强大的符号计算能力Maple的核心优势在于其强大的符号计算能力。
它能够精确计算各种数学表达式,包括重积分、微分方程和级数等。
通过符号计算,Maple可以进行精确的数学推导和变换,从而解决复杂的数学问题。
2.2 丰富的数值计算功能除了符号计算外,Maple还具有丰富的数值计算功能。
它支持高精度数值计算和数值优化算法,可以用于求解数值解、数值逼近和数值积分等问题。
Maple还提供了众多的数值绘图函数,可以直观地展示数学模型的图像。
2.3 可视化建模和数据分析Maple不仅可以进行数学计算,还能进行可视化建模和数据分析。
它提供了丰富的图形绘制功能,可以绘制二维和三维图形,并进行交互式操控。
同时,Maple还支持数据分析、统计建模和机器学习等领域的应用,使得用户能够更好地理解和分析数据。
2.4 高度可定制和扩展Maple具有高度可定制和扩展性,用户可以根据自己的需要编写自定义的函数和算法。
它提供了友好的编程环境,支持多种编程语言,如Maple语言、C语言和Java等。
用户可以利用这些编程语言和Maple的函数库,开发自己的数学算法和应用。
3. Maple数学软件的应用场景3.1 科学研究Maple在科学研究中有着广泛的应用。
它能够处理各种复杂的数学问题,提供准确的数学推导和分析工具,为科学研究提供了强大的支持。
科学家可以使用Maple进行模拟、建模和数据分析,从而深入研究物理现象、化学反应和生物过程等。
3.2 工程设计与优化在工程设计和优化中,Maple也发挥着重要作用。
Maple软件的介绍 使用方法

一、基本概念和操作
• 目前在科技、工程、教育界比较流行和著名的 数 学 软 件 主 要 有 五 个 : Maple、MATLAB、 MathCAD、Mathematica和SAS。它们功能全面, 各有特色。 • Maple 的功能主要包括符号计算、数值计算、 图形处理、程序设计等 (MATLAB、MathCAD 的符号计算功能来源于Maple) 。 • Maple 包括处理用户命令输入、管理内部数据 的“内核”;外挂函数库(工具包,在需要时可 以由用户自行加载) ;交互式图形用户界面(通 过这个接口,用户才能够向 Maple 发出指令并 得到执行)。
一、基本概念和操作(6)
• 清除变量 :一旦定义了变量,Maple将在整个 工作过程中记得变量的值。再次赋值可以覆盖 前一次赋值。 • 有时我们需要从内存中清除变量的值。 • 使用 x:=‘x’;格式可清除变量x的值。注意这里 使用单引号。 • 立即清除内存中所有变量的值使用 restart 命令。 在开始新问题时可以使用 restart 命令确保无赋 过值的变量。
一、基本概念和操作(8)
命令: evalf:用来把非浮点数的计算结果或者表达式转 化为浮点数形式的近似结果。其基本的命令格 式为evalf(expr,n) expr:任意的算术表达式 n:计算结果的精度,当n缺省时采用环境变量 Digits的值
一、基本概念和操作(9)
simplify(expr):对计算的结果进行化简 combine(f):对数的乘积的合并 coeff(p,x,n)或coeff(p,x^n)以x为变量的 多项式p中x^n项的系数 degree(p,x):计算多项式p中变量x的最高次 数 sort(p,[x,y]):对多项式p按字典序排列 subs(x=a,expr):用表达式a替换表达式expr 中出现的所有子表达式x。 eval(expr,x=a) eval(name)完全求值命令
计算机数学软件Maple概述

控制系统分析与设计
系统建模
Maple可用于建立控制系统的数学模型,包括传递函数、状态 空间表示和频率响应等。它支持控制系统的时域和频域分析。
稳定性分析
Maple提供了多种稳定性分析方法,如劳斯判据、奈奎斯特图和根轨 迹等。它可用于评估控制系统的稳定性,并指导控制器的设计。
控制器设计
Maple支持多种控制器设计方法,如PID控制、最优控制和鲁棒控制等。 它可以帮助工程师设计高效且稳定的控制系统,以满足不同的工程需求。
控制结构
Maple提供条件语句(如if-else)、 循环语句(如for、while)等控制结 构,用于实现复杂的逻辑功能。
函数定义与调用
用户可以自定义函数,并在程序中调 用这些函数。函数可以接受参数,并 返回计算结果。
03
Maple在数学计算中的应用
符号计算
代数运算
Maple可以进行各种代数运算,如多项式运算、因式分解、求根 等。
方面更具优势。此外,Maple的编程语言相对更简单易用。
03
与Python的比较
Python是一种通用编程语言,通过安装额外的库(如NumPy、SciPy
等)可以实现数学计算功能。然而,与Maple相比,Python在符号计
算和图形可视化方面功能相对较弱。
02
Maple基础知识
Maple的界面Maple与MATLAB之间的数据交换和算 法调用。
与其他科学计算软件的接口
如与Mathematica、SageMath等软件的互 操作性。
Maple在科研与教学中的应用案例
数学研究
用于解决复杂数学问题,如微分方程求解、符号积分等。
物理工程
在物理模拟、工程设计等领域进行数学建模和仿真。
数学软件Maple使用教程

数学软件Maple使⽤教程数学实验数学软件Maple使⽤教程序⾔⼀.什么是数学实验?我们都熟悉物理实验和化学实验,就是利⽤仪器设备,通过实验来了解物理现象、化学物质等的特性。
同样,数学实验也是要通过实验来了解数学问题的特性并解决对应的数学问题。
过去,因为实验设备和实验⼿段的问题,⽆法解决数学上的实验问题,所以,⼀直没有听说过数学实验这个词。
随着计算机的飞速发展,计算速度越来越快,软件功能也越来越强,许多数学问题都可以由计算机代替完成,也为我们⽤实验解决数学问题提供了可能。
数学实验就是以计算机为仪器,以软件为载体,通过实验解决实际中的数学问题。
⼆.常⽤的数学软件⽬前较流⾏的数学软件主要有四种:1.MathACD其优点是许多数学符号键盘化,通过键盘可以直接输⼊数学符号,在教学⽅⾯使⽤起来⾮常⽅便。
缺点是⽬前仅能作数值运算,符号运算功能较弱,输出界⾯不好。
2.Matlab优点是⼤型矩阵运算功能⾮常强,构造个⼈适⽤函数⽅便很⽅便,因此,⾮常适合⼤型⼯程技术中使⽤。
缺点是输出界⾯稍差,符号运算功能也显得弱⼀些。
不过,在这个公司购买了Maple公司的内核以后,符号运算功能已经得到了⼤⼤的加强。
再⼀个缺点就是这个软件太⼤,按现在流⾏的版本5.2,⾃⾝有400多兆,占硬盘空间近1个G,⼀般稍早些的计算机都安装部下。
我们这次没⽤它主要就是这个原因。
3.Mathematica其优点是结构严谨,输出界⾯好,计算功能强,是专业科学技术⼈员所喜爱的数学软件。
缺点是软件本⾝较⼤,⽬前流⾏的3.0版本有200兆;另⼀个缺点就是命令太长,每⼀个命令都要输⼊英⽂全名,因此,需要英语⽔平较⾼。
4.Maple优点是输出界⾯很好,与我们平常书写⼏乎⼀致;还有⼀个最⼤的优点就是它的符号运算功能特别强,这对于既要作数值运算,⼜要作符号运算时就显得⾮常⽅便了。
除此之外,其软件只有30兆,安装也很⽅便(直接拷贝就可以⽤)。
所以,我们把它放到学校⽹上直接调⽤。
maple 编程语言类型 -回复

maple 编程语言类型-回复Maple 编程语言类型Maple 是一种高级的编程语言,用于科学计算和数学建模。
它提供了丰富的数学函数库,可以进行符号计算、数值计算和数据可视化。
Maple 具有类似于MATLAB 的矩阵操作能力,以及类似于Python 的面向对象编程特性。
本文将深入讨论Maple 的编程语言类型。
1. 命令式编程:Maple 是一种命令式编程语言,其中的指令按照特定的顺序执行。
命令式编程强调计算机中指令的顺序和执行方式,开发人员需要详细描述每个操作步骤。
在Maple 中,开发者可以使用内置函数和运算符来实现这些操作。
例如,使用`solve` 函数来求解方程,使用`int` 函数来进行积分计算。
2. 符号计算:Maple 的一个重要特点是其强大的符号计算能力。
符号计算是一种处理数学表达式的方法,它可以保留变量和未知数的符号形式,而不是仅仅进行数值计算。
这使得开发者能够进行精确的数学推导和计算。
在Maple 中,通过定义变量和使用内置函数,开发者可以进行代数运算、微积分、线性代数等数学操作。
3. 数值计算:Maple 还支持数值计算,它可以在处理数学表达式时对变量进行数值替代,以获得近似的数值结果。
这对于处理复杂的数学公式和方程组非常有用。
Maple 提供了大量的数值计算函数和算法,例如求解方程组的数值解、数值积分和数值微分等。
4. 函数式编程:Maple 具有函数式编程的特性,它支持函数作为一等对象。
这意味着函数可以像其他数据类型一样进行传递和操作。
开发者可以定义自己的函数,并将其用作参数传递给其他函数或赋值给变量。
这种函数式编程的特性使得Maple 具有优雅而强大的抽象能力,可以更方便地进行代码复用和模块化。
5. 面向对象编程:与函数式编程相反,Maple 还支持面向对象编程。
开发者可以定义类和对象,通过封装属性和方法来创建复杂的数据结构和行为。
这种面向对象的编程方式使得代码更加易于理解和维护,并提供了更高级的抽象和封装能力。
数学软件四大家Maple

数学软件四大家Maple、MATLAB、MathCAD和Mathematica目前在科技和工程界上比较流行和著名的数学软件主要有四个,分别是MATLAB、Maple、MathCAD和Mathematica。
它们在各自针对的目标都有不同的特色。
下面就让我为你一一道来。
一、Maple 系统Maple 是由Waterloo大学开发的数学系统软件,它不但具有精确的数值处理功能,而且具有无以伦比的符号计算功能。
Maple 的符号计算能力还是MathCAD和MATLAB等软件的符号处理的核心。
Maple提供了2000余种数学函数,涉及范围包括:普通数学、高等数学、线性代数、数论、离散数学、图形学。
它还提供了一套内置的编程语言,用户可以开发自己的应用程序,而且Maple自身的2000多种函数,基本上是用此语言开发的。
Maple采用字符行输入方式,输入时需要按照规定的格式输入,虽然与一般常见的数学格式不同,但灵活方便,也很容易理解。
输出则可以选择字符方式和图形方式,产生的图形结果可以很方便地剪贴到Windows应用程序内。
二、MATLAB 系统MATLAB原是矩阵实验室(Matrix Laboratory)在70年代用来提供Linpack和Eispack软件包的接口程序,采用C语言编写。
从80年代出现3.0的DOS版本,逐渐成为科技计算、视图交互系统和程序语言。
MATLAB可以运行在十几个操作平台上,比较常见的有基于Windows 9X/NT、OS/2、Macintosh、Sun、Unix、Linux等平台的系统。
MATLAB程序主要由主程序和各种工具包组成,其中主程序包含数百个内部核心函数,工具包则包括复杂系统仿真、信号处理工具包、系统识别工具包、优化工具包、神经网络工具包、控制系统工具包、μ分析和综合工具包、样条工具包、符号数学工具包、图像处理工具包、统计工具包等。
而且5.x版本还包含一套几十个的PDF文件,从MATLAB的使用入门到其他专题应用均有详细的介绍。
01-Maple基础和实践教程

Maple基础和实践教程Maple基础和实践教程Maple是应用最为广泛的科学计算软件之一,具有非常强大的符号计算和数值计算功能。
Maple 提供智能界面求解复杂数学问题和创建技术文件,用户可在易于使用的智能文件环境中完成科学计算、建模仿真、可视化、程序设计、技术文件生成、报告演示等,从简单的数字计算到高度复杂的系统,满足各个层次用户的需要。
与传统工程软件不同,甚至有别于旧版本的Maple,新版本Maple 为工程师提供了大量的专业计算功能,庞大的数学求解器可用于各种工程领域,如微分方程、矩阵、各种变换包括FFT、统计、小波、等等,超过5,000个计算命令让用户通常只需要一个函数就可以完成复杂的分析任务。
本章主要介绍Maple的基本功能,包括:数值和符号计算计算、求解方程、微积分计算、向量及矩阵计算、微分方程求解等。
Maple是一个全面的系统,提供多种方式完成同一个任务。
在本章中,我们将通过简单、易于重复的方式求解常见的问题,但它不是唯一的操作方式。
当用户熟悉本章中的各种操作方式后,用户可以通过帮助系统了解如何使用相似的技术完成各种任务。
Maple环境Maple的用户界面是一个典型的Windows或Mac风格的操作环境。
工作环境界面如图2-1所示。
图2-1:Maple工作界面在图2-1的工作界面中,窗体的主要部分包括:●主文档,即主工作区。
事实上,用户大可以把它想象成包含有各种数学和绘图工具的Microsoft Word。
●面板区。
汇集了数学工具和特殊的数学符号,用户可以将它们直接拖拽到工作区中使用。
面板区中最重要的面板当属Expressions,Matrix,Common Symbols和Greek。
Maple提供了总共约30个面板,用户可以在面板区空白处单击鼠标右键,并单击Arrange Palettes 来进行选择。
●工具条。
Maple提供了两个主要的工具条。
默认状态下,标准工具条含有保存、缩放等通用按钮和一些Maple特定用途的按钮。
MAPLE软件简介及其应用

Maple有非常强大、完善的在线帮助功 能。Maple可通过Introduction, Topic Search 和键盘命令等方式寻求帮助。
例如,?interp; ?dsolve;
1.8 Maple 的函数库 Maple有数以千计的函数,这些函数被 分成四大类: 标准库、混合库、专用软件包 和共享软件包。
Maple 有几十个专用软件包,分别处 理不同数学分支问题。
专用软件包在使用时要用命令with(软 件包名)调入。
4. 共享库
共享库是由 Maple 爱好者开发的软件 包。这些程序用户可上网搜寻。
第二章 Maple语言基础
Maple 是一个可编程的数学环境。本 章介绍 Maple 的符号集、语句、表达式、 基本数据类型以及基本的程序语言。 2.1 标识符与变量名
Maple可进行无误差的符号计算和高精 度的数值计算。例如, 100!, Pi, sqrt(2), sin(3)。
1.4 Maple 的图形显示
1. 一般函数做图
plot(f(x),x=a..b,option); plot3d(f(x,y),x=a..b,y=c..d,option);
2. 极坐标做图
所有分支。 Maple支持函数、序列、集合、列表、 数组、表等多种数据结构。 用户可以查看 Maple的非内部函数的源程序,也可以将自 己编和函数、过程添加到Maple的函数库中 或建立自己的函数库。 Maple 的一个突出 特点是它的界面非常友好。它有一个非常 好的帮助系统,可以很方便地查找函数和 命令的用法。
od;
3. 布尔表达式和逻辑运算
Maple中的关系运算符为<,<=,>,>=,=, <>;逻辑运算符为and, or, not。 “表达式 关系运算符 表达式”称为关 系式,其值为true或false。
Maple的内部常数
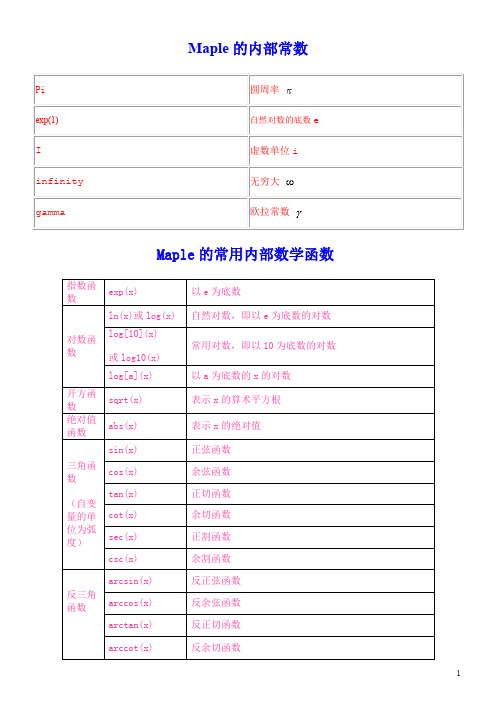
Maple的内部常数Maple的常用内部数学函数)Maple中的数学运算符Maple的关系运算符函数的连续性四大数学软件(mathcad,mathematica,maple,matlab)中,只有Maple才有判断函数连续性的命令,其命令如下:如何用Maple求极限(1)极限:(2)单侧极限:左极限:右极限:如何用Maple求导数如何用Maple求高阶导数如何在Maple中求隐函数的导数在Maple中,没有直接求参数方程确定的函数的导数的命令,只能根据参数方程确定的函数的求导公式一步一步地进行推导;或者,干脆自己编一个小程序,应用起来会更加方便。
如何用Maple求不定积分求定积分、广义积分如何用Maple先加载student函数库,加载方法为:with(student);如何用Maple进行分部积分的计算先加载student函数库,加载方法为:with(student);在Maple中,如何用矩形法、梯形法和辛普森法求近似积分在计算之前,首先要加载student函数库,加载方法为:with(student);矩形法梯形法辛普森法如何用Maple对数列和级数进行求和如何用Maple进行连乘如何用Maple展开级数如何在Maple中进行积分变换在进行拉普拉斯变换及其逆变换、傅立叶变换及其逆变换、傅立叶正弦变换和傅立叶余弦变换时,必须要先加载积分变换函数库,加载方法为:with(inttrans),但在进行Z变换及其逆变换时,不用加载任何函数库。
如何用Maple解微分方程如何用Maple解微分方程组如何用maple求多变量函数的极限以两个变量为例说明,多于两个变量的函数极限可以依次类推。
计算极限如何用maple 求多元函数的偏导数求偏导数如何用maple 求多变量函数的泰勒展开式首先要加载mtaylor 链接库,加载方法为:readlib (mtaylor )(在maple7、maple8、maple9中不用加载)如何用maple 求重积分可以利用数个int ()指令的组合来完成。
mapleforMATLAB安装说明

第五步:在MATLAB命令提示行里面输入pathtool,这是会弹出一个对话框,下拉到最后,选中最后两个,然后点击左边的”Move to Top“(移动到顶端)按钮,然后选择保存。exit退出matlab,现在设置好了。重新启动matlab,现在可以用maple内核了�
第一步:下载并安装Maple;
第二步:安装Maple Toobox for Matlab 13,安装到你的maple安装目录下;
第三步:拷贝MapleToolboxForMatlab.dat 到 ~\Maple 13\toolbox\MapleToolboxForMatlab\license ("~"指maple安装根目录)。
第四步:运行matlab2010a,cmd窗口执行`toolbox_version`。会返回结ple工具箱安装成功,但是不经设置的话matlab仍然使用内置的MuPAD, 即便是toolbox_version=maple,并不是说你现在的符号运算都是使用maple内核,其实现在的使用还是matlab默认的MuPad。现在我们开始设置最关键的一个东西,也是让maple内核工作的关键!
MATLAB 常用函数检索表

909附录 MATLAB 常用函数检索表Aabs 函数——数值的绝对值与复数的幅值。
acos 、acosh 函数——反余弦函数与反双曲余弦函数。
acot 、acoth 函数——反余切函数与反双曲余切函数。
acsc 、acsch 函数——反余割函数与反双曲余割函数。
angle 函数——计算复数的相角。
asec 、asech 函数——反正割函数与反双曲正割函数。
asin 、asinh 函数——反正弦函数与反双曲正弦函数。
atan 、atanh 函数——反正切函数与反双曲正切函数。
Bbar 函数——二维垂直条形图。
barh 函数——二维水平条形图。
bdclose 函数——关闭正在打开的仿真系统窗口。
besselap 函数——设计Bessel 低通滤波器。
Bessel 函数——设计Bessel 滤波器。
betafit 函数——计算β分布的参数估计。
Betalike 函数——负分布的对数似然函数。
bicgstab 函数——稳定双共轭梯度方法解方程组。
bicg 函数——双共轭梯度法解方程组。
bilinear 函数——用双线性变换法将模拟滤波器转化为数字滤波器。
binocdf 函数——二项分布的累积概率值。
binofit 函数——二项分布的参数估计。
binopdf 函数——二项分布的密度函数。
binornd 函数——二项分布的随机数据的产生。
binostat 函数——二项分布的均值和方差。
blkdiag 函数——产生以输入元素为对角线元素的矩阵。
boxplot 函数——样本数据的盒图。
break 函数——结束循环。
brighten 函数——色图控制函数。
buttap 函数——设计巴特沃思模拟滤波器。
butter 函数——设计巴特沃思数字滤波器。
Ccapaplot 函数——样本的概率图形。
cat 函数——创建多维数组。
ccode 函数——符号表达式的C 语言代码。
cdf2rdf 函数——复对角矩阵转化为实对角矩阵。
maple

Maple系统内置高级技术解决建模和仿真中的数学问题,包括世界上最强大的符号计算、无限精度数值计算、创新的互联网连接、强大的4GL语言等,内置超过5000个计算命令,数学和分析功能覆盖几乎所有的数学分支,如微积分、微分方程、特殊函数、线性代数、图像声音处理、统计、动力系统、等。
Maple不仅仅提供编程工具,更重要的是提供数学知识。
Maple是教授、研究员、科学家、工程师、学生们必备的科学计算工具,从简单的数字计算到高度复杂的非线性问题,Maple都可以帮助您快速、高效地解决问题。
用户通过Maple产品可以在单一的环境中完成多领域物理系统建模和仿真、符号计算、数值计算、程序设计、技术文件、报告演示、算法开发、外部程序连接等功能,满足各个层次用户的需要,从高中学生到高级研究人员。
主要技术特征强大的求解器:数学和分析软件的领导者★ 内置超过5000个符号和数值计算命令,覆盖几乎所有的数学领域,如微积分,线性代数,方程求解,积分和离散变换,概率论和数理统计,物理,图论,张量分析,微分和解析几何,金融数学,矩阵计算,线性规划,组合数学,矢量分析,抽象代数,泛函分析,数论,复分析和实分析,抽象代数,级数和积分变换,特殊函数,编码和密码理论,优化等。
★ 各种工程计算:优化,统计过程控制,灵敏度分析,动力系统设计,小波分析,信号处理,控制器设计,集总参数分析和建模,各种工程图形等。
★ 提供世界上最强大的符号计算和高性能数值计算引擎,包括世界上最强大的微分方程求解器(ODEs,PDEs,高指数DAEs)。
★ 智能自动算法选择。
★ 强大、灵活、容易使用的编程语言,让您能够开发更复杂的模型或算法。
★ 与多学科复杂系统建模和仿真平台MapleSim紧密集成。
技术文件环境:重新定义数学的使用性★ 大量易学易用的工具和特征,提供“数学版office”工作环境,用户即使没有任何语法知识也可以完成大量数学问题的计算,戏剧性缩短学习曲线。
Maple的常用内部数学函数要点
5、3D图象
Maple可以生成由显函数、参数型、微分 方程的解给出的3D曲线和曲面。图像的外观如:字体、光照、着色等也可随便更改。
下例将生成二元函数: 的图 象。
>plot3d(x*exp(-x^2-y^2),x=-2..2,y=-2..2,axes=BOXED,
title=`ASurfacePlot`);
六、maple在微积分方面的运用
Maple提 供多种强力工具用以解决一元或多元微积分问题。Maple可被用于求解微分、积分、极 限、级数展开、级数求和、求、积分变换(如拉普拉斯变换、Z变换、梅林变换、傅利 叶变换等)、以及分段函数等诸多领域的问题。Maple不仅能够给出以上问题的数值解 ,他强大的引擎同样提供解析解(符号解)。
>solve({eqn1,eqn2,eqn3,eqn4},{a,b,c,d});
使用所得解验证:eqn1,eqn2
>eval({eqn1,eqn2},%);
5、解不等式
下例演示在Maple中解不等式如何方 便。
解不等式组: .
>solve({x^2<1,y^2<=1,x+y<1/2},{x,y});
>200!;
Maple使用百分号%代表对前面输出 的引用。(详情请参考在线帮助)下面的ifactor命令对前面的结果进行因数分解。
>ifactor(%);
下面的命令又将上式乘开,重新得到200!
>expand(%);
2、浮点运算
Maple的威力首先表现在它的精确运算能 力。无论是分数还是无理数,都不会在运预算过程中自动取近似的十进制小数。这样 避免了误差的叠加。当然如果需要,Maple将给出任意精度的近似小数。
Maple内核

如何在Matlab2010a中使用Maple内核的符号工具箱/viewthread.php?tid=6061MathWorks自从2008年10开始,在Matlab的新版本(Matlab2008a,即7.6之后)中使用MuPAD内核替换原来的Maple符号计算内核!至于为什么?我们很容易想到MathWorks和MapleSoft两大公司的利益冲突。
开始的时候虽然Matlab的符号工具箱不再提供Maple内核(默认为MuPAD),但是还是支持Maple内核滴,只要你安装的对应版本的Maple或者Maple Toolbox for Matlab,就可以使用1.>>symengine命令切换你习惯的符号计算引擎!比如我就比较喜欢Maple内核,至于切换符号计算引擎的具体步骤,建议您参考下面的帖子:如何设置选择Matlab的符号计算引擎,Maple或MuPAD可是,令人沮丧的是,MATLAB2010a爆出冷门——Matlab2010a不再支持maple 引擎。
以我个人的使用经历和体会来说,MuPAD和Maple内核压根不是一个级别的,很多东西在Maple上可以轻松的得到结果,可是在MuPAD内核却很让人失望!并且Maple计算速度明显优于MuPAD,下面举一个例子说明在基于MuPAD内核的Matlab2010上运行1.>> evalin(symengine,'diff(sin(x),x$n)')2.3.ans =4.5.diff(sin(x), x $ n)在基于Maple内核的Matlab2008a上(最后一个使用Maple内核的Matlab)1.>> maple('diff(sin(x),x$n)')2.3.ans =4.5.sin(x+1/2*n*pi)是不是感慨万分呀,很为MathWorks感到惋惜!还好天无绝人之路,其实对于热衷于Maple内核的MATLABer来说,我们还是再次重新看到了希望!这就是安装Maple Toolbox for Matlab 13,不过由于Matlab没法直接支持Maple 引擎,因此我们还需要做其他相关配置工作,具体参见下面的教程!============================================以下内容由论坛会员zwither原创,再次表示感谢。
电磁场理论实验指导(Maple简明版)

为避免前面Maple结果的影响,可使用restart指令。
4.1 启动矢量运算包、设置坐标系、定义矢量
1. 启动函数包: with(VectorCalculus): 2.设置坐标系 SetCoordinates( ' cartesian'[x,y,z] ); SetCoordinates( ' cylindrical '[rho,theta,z] ); SetCoordinates( 'spherical'[r,phi,theta] ); 矢量的坐标系转换: SetCoordinates(spherical[r,phi,theta]); VF:= VectorField(<r,0,0>); VF:=MapToBasis(VF, cartesian[x,y,z]);
(cartesian、cylindrical、spherical名称要小写)
查看坐标系GetCoordinates( );
maple定义的柱坐标、球坐标系可help: cylindrical coordinates spherical coordinates 特别说明: 1.VectorCalculus定义的球坐标与柱坐标如图.跟教材不相同.
第3章 Maple解方程
3.1 代数方程形式: express1=express2 1.解代数方程: solve(方程,var) 例:a:=solve(x^2-x-6=0,x); 如果精确解过于复杂,可求近似解: 将方程中任意元素的整数系数改为小数,再求. 例:solve(x^3-12*x^2+3=0,x); solve(x^3-12*x^2+3.0=0,x); 验证解的正确性: eval(expr,x=解); subs(x=解,expr); 2. 解代数方程组 solve({x+y+z=1,4*x+2*y+z=4,3*x+y=3});线性方程组 solve({x^2+y=5,x+y=3});非线性方程组
MAXIMA,Mathematica和Maple的区别

MAXIMA,Mathematica和Maple的区别1)MAXIMA。
这个程序基于世界上最老的计算机代数系统之一: MACSYMA 系统。
它是用 Common Lisp 实现的。
很多现在的符号计算程序比如 Maple 都从 MAXIMA 身上学到很多东西。
我为MAXIMA 写了一个简单的介绍,通过这个介绍你会发现MAXIMA 的光辉历史,体会到自由软件的重要优势。
MAXIMA现在以GPL发行,永远是一个自由软件。
2)Maple是在1980年9月,由加拿大滑铁卢大学(Waterloo University)的符号计算研究小组研制的一种计算机代数系统。
经过近20年的不断发展,数学软件Maple已成为当今世界上最优秀的几个数学软件之一,它具有良好的使用环境、强有力的符号计算能力、高精度的数字计算、灵活的图形显示和高效的可编程功能。
Maple的大部分数学函数和过程是用Maple自身的语言写成的,存于外部函数库中。
当一个函数调用时,在多数情况下,Maple会自动将该函数的过程调入内存,一些不常用的函数才需要用户自己将它们调入。
另外有一些特别的函数包也需要用户自己调入,如线性代数包、统计包,这使得Maple在资源的利用上具有很大的优势,只有最有用的东西才留住内存,这是Maple可以在较小内存的计算机上正常运行的原因。
Maple目前已有大量的专用软件包。
很适合进行符号运算,最近这些年的关于计算规范形系数的电算程序大多数是利用Maple软件编写而成的。
由于该软件有较强的符号运算能力及内存消耗小等优点,很适合用于规范形理论的研究,尤其在求解高维非线性系统的高阶规范形方面有较明显的优势。
3)Mathematica系统是美国Wolfram研究公司开发的一个功能强大的计算机数学系统。
它提供了范围广泛的数学计算功能,支持在各个领域工作的人们做科学研究和过程中的各种计算。
这个系统可以帮助人们解决各种领域里的涉及比较复杂的符号计算和数值计算的理论和实际问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何在Matlab2010a中使用Maple内核的符号工具箱
/viewthread.php?tid=6061
MathWorks自从2008年10开始,在Matlab的新版本(Matlab2008a,即7.6之后)中使用MuPAD内核替换原来的Maple符号计算内核!
至于为什么?我们很容易想到MathWorks和MapleSoft两大公司的利益冲突。
开始的时候虽然Matlab的符号工具箱不再提供Maple内核(默认为MuPAD),但是还是支持Maple内核滴,只要你安装的对应版本的Maple或者Maple Toolbox for Matlab,就可以使用
1.>>symengine
命令切换你习惯的符号计算引擎!比如我就比较喜欢Maple内核,至于切换符号计算引擎的具体步骤,建议您参考下面的帖子:
如何设置选择Matlab的符号计算引擎,Maple或MuPAD
可是,令人沮丧的是,MATLAB2010a爆出冷门——Matlab2010a不再支持maple 引擎。
以我个人的使用经历和体会来说,MuPAD和Maple内核压根不是一个级别的,很多东西在Maple上可以轻松的得到结果,可是在MuPAD内核却很让人失望!并且Maple计算速度明显优于MuPAD,下面举一个例子说明
在基于MuPAD内核的Matlab2010上运行
1.>> evalin(symengine,'diff(sin(x),x$n)')
2.
3.ans =
4.
5.diff(sin(x), x $ n)
在基于Maple内核的Matlab2008a上(最后一个使用Maple内核的Matlab)
1.>> maple('diff(sin(x),x$n)')
2.
3.ans =
4.
5.sin(x+1/2*n*pi)
是不是感慨万分呀,很为MathWorks感到惋惜!
还好天无绝人之路,其实对于热衷于Maple内核的MATLABer来说,我们还是再次重新看到了希望!
这就是安装Maple Toolbox for Matlab 13,不过由于Matlab没法直接支持Maple 引擎,因此我们还需要做其他相关配置工作,具体参见下面的教程!
============================================
以下内容由论坛会员zwither原创,再次表示感谢。
本人仅仅重新整理方便大家了解和学习,原帖参见/redirec ...
84528&fromuid=1
第一步:下载Maple Toolbox for Matlab 13,(12好像不行,我没有尝试过)在verycd 上面有,有32位,64位的,windows linux SunOS的,各取所需,是带有license 文件的。
放心使用。
第二步:安装Maple Toobox for Matlab 13,安装到你的 ~\MATLAB\2010a 下("~"指Matlab程序安装根目录,比如 "C:\Program Files")。
第三步:拷贝crack/MapleToolboxForMatlab.dat 到~\Maple
13\toolbox\MapleToolboxForMatlab\license ("~"指程序安装根目录,比如"C:\Program Files")。
第四部:运行matlab2010a,cmd窗口执行`toolbox_version`。
1.>> toolbox_version
2.
3.toolbox_version =
4.
5.maple
上面说明maple工具箱安装成功,但是不经设置的话matlab仍然使用内置的MuPAD!
注意:即便是toolbox_version=maple,并不是说你现在的符号运算都是使用maple内核,其实现在的使用还是matlab默认的MuPad。
不信的话可以试试执行:
1.>> maple('sin(x)')
2.
3.??? Error using ==> maple at 54
4.
5.The MAPLE command is not available.
6.
7.>> syms x
8.
9.>> int('atan(x)/x^(3/2)',0,1)
10.
11.ans =
12.
13.- pi/2 + 2^(1/2)*atan(2^(1/2)*(1/2 - i/2))*(i + 1) +
2^(1/2)*atan(2^(1/2)*(i/2 + 1/2))*(1 - i)
注意这个结果是和maple内核得到的是不一样的,一会我们设置好了大家可以看到!
现在我们开始设置最关键的一个东西,也是让maple内核工作的关键!
在命令提示行里面输入(当然也可以从File菜单的set Path...选项直接操作)
1.>>pathtool
这是会弹出一个对话框,下拉到最后,选中最后两个(他们是和maple相关的)。
然后点击左边的”Move to Top“(移动到顶端)按钮,然后选择保存。
exit退出matlab,现在设置好了。
重新启动matlab,现在可以用maple内核了,试试:
1.>> maple('sin(x)')
2.
3.ans =
4.
5. sin(x)
6.
7.>> syms x;
8.
9.>> int('atan(x)/x^(3/2)',0,1)
10.
11.ans =
12.
13. 1/2 1/2 1/2 1/2
14.
15. - 1/2 pi + 2 log(2 + 2 ) - 1/2 2 log(2) + 1/2 2 pi
注意:如果你安装有Maple 13,可以在Maple计算那个积分试试,保证和上面使用Maple Toolbox for Matlab 13计算具有相同的结果,而不是MuPAD上面得到的那个结果。
大家可以用这个式子来试验是否安装好了。
Maple内核得到的结果明显精简许多,虽然两个的数值解是一样的。
如果你有matlab2008b,也就是matlab第一次引入mupad(5.1版)作为其符号引擎的那个版本,你会发现下面的结果:
1.>> int('arctan(x)/x^(3/2)',0,1)
2.
3.Warning: Explicit integral could not be found.
找不到解。
可见MuPad能力是没有Maple强的,虽然2010a的MuPad升级到了5.4能够求解这个问题了,但是结果还是不够精简。
而在matlab2010a中通过键入symengine来设置引擎已经被mathwork和谐掉了,想必是想抛开maple自己单做(mathwork收购了mupad,所以mupad现在是mathwork自家人了),最后还是想垄断符号和数值计算两个领域。
但显然远没有那么容易。
呵呵,做大了就想垄断了。
