2015年各高校自主招生考试试题
2015单招试题及答案

2015单招试题及答案一、选择题(本题共10小题,每小题2分,共20分。
每小题只有一个选项是正确答案,请将正确答案的字母填入题后的括号内。
)1. 下列哪项不是单招的特点?A. 选拔性B. 灵活性C. 随机性D. 针对性答案:C2. 单招考试通常包括哪些内容?A. 笔试和面试B. 笔试和体检C. 面试和体检D. 笔试、面试和体检答案:A3. 单招考试中,笔试部分主要测试什么?A. 身体素质B. 心理素质C. 专业技能D. 文化知识答案:D4. 下列哪项不是单招面试中常见的问题?A. 个人基本情况B. 专业相关知识C. 个人兴趣爱好D. 家庭经济状况答案:D5. 单招考试的录取原则是什么?A. 先到先得B. 择优录取C. 随机录取D. 抽签录取答案:B6. 单招考试中,考生需要携带哪些证件?A. 身份证和学生证B. 身份证和准考证C. 身份证和户口本D. 学生证和准考证答案:B7. 单招考试的报名流程是怎样的?A. 网上报名-现场确认-缴费B. 现场报名-网上报名-缴费C. 现场报名-现场确认-缴费D. 网上报名-现场确认-面试答案:A8. 单招考试中,考生需要注意哪些事项?A. 按时到达考场B. 携带所有证件C. 遵守考场纪律D. 以上都是答案:D9. 单招考试的录取通知通常在什么时候发放?A. 考试结束后一周内B. 考试结束后一个月内C. 考试结束后三个月内D. 考试结束后六个月内答案:B10. 单招考试的录取结果在哪里查询?A. 学校官网B. 考试中心C. 教育局D. 以上都是答案:D二、填空题(本题共5小题,每小题2分,共10分。
请将答案填入题后的横线处。
)1. 单招考试的报名通常在每年的____月份进行。
答案:32. 考生在单招考试中,需要提前____分钟到达考场。
答案:303. 单招考试的笔试部分,考生需要携带____等文具。
答案:2B铅笔、橡皮、黑色签字笔4. 单招考试的面试环节,考生需要注意自己的____和____。
2015年3月三校生高考真题上海市部分普通高校专科层次依法自主招生考试

2015年上海市部分普通高校专科层次依法自主招生考试第一部分(每题只有一个正确答案,每题1分,共102分)一、选择题(每题1分,共80分)1.下列姓氏的读音,不正确的一项是()A.查,zhāB. 仇,qiúC. 区,qū(ōu)D.单,shàn([ chán ]1.〔~于〕中国古代匈奴君主的称号。
)2.中新网报道:“希腊总理齐普拉斯于当地时间11日凌晨轻松赢得国会的信任投票,此前,齐普拉斯他承诺绝不让以往‘减少开支'和‘纾困计划'的政策重新回到希腊。
”对新闻中“纾”字注音与解释都正确的一项是()A.yú(缓和)B.yū(舒缓)C.shù(宽缓)D.shū(缓解)3.“因为相聚,让我们分享了这快乐的时光;因为浪漫,让我们承载无尽的祝福。
亲爱的朋友,让我们……”根据下列场景判断,这样的语句更适合()A. 商务会谈主持人的开场白B.婚礼司仪的结束语C.节庆大会上主持引入正题D.娱乐节目采访嘉宾4.看见有顾客边挑选白菜边将外层还不算老的菜叶剥去,菜场售货员就上前劝阻。
下列用语得体、委婉的一句是()A. 您要哪棵?我来帮您清理吧!B.喂喂,请不要摘菜叶!C.您这样摘菜叶可就太浪费啦!D.哎哟,请别这样好吧?5.下列语境中依次使用敬辞恰当的一项是()①别人正安静阅读,麻烦别人递支笔②文章写好了,请老师批阅修改③一时疏忽迟到,求人原谅宽恕④初次见面,握手寒暄A. 劳驾斧正借光光临B.打扰赐教原谅恭候C.打扰指教包涵久仰D.借光劳驾恭候久违借光:请人让路或问事时的客气话。
6.下列诗句中没有直接写出月亮的一项是()A. 著意登楼瞻玉兔(辛弃疾)B.玉轮轧露湿团光(李贺)C.千里共婵娟(苏轼)D.清夜坠玄天(韦应物)7.一方水土养一方人,一方风情孕育一方的乐器。
下列依次与①②③对应的传统民族乐器是()①蒙古包、轱辘车,风吹草低见牛羊的大草原②红高粱、信天游,大风起兮云飞扬的黄土高坡③杨柳岸、乌篷船,小桥流水人家的江南水乡A. 冬不拉笛子丝竹B.马头琴唢呐二胡C. 笙箫马头琴琵琶D.管风琴腰鼓扬琴马头琴是一种两弦的弦乐器,有梯形的琴身和雕刻成马头形状的琴柄,为蒙古族人民喜爱的乐器。
清华大学2015年自主招生数学试题及答案解析
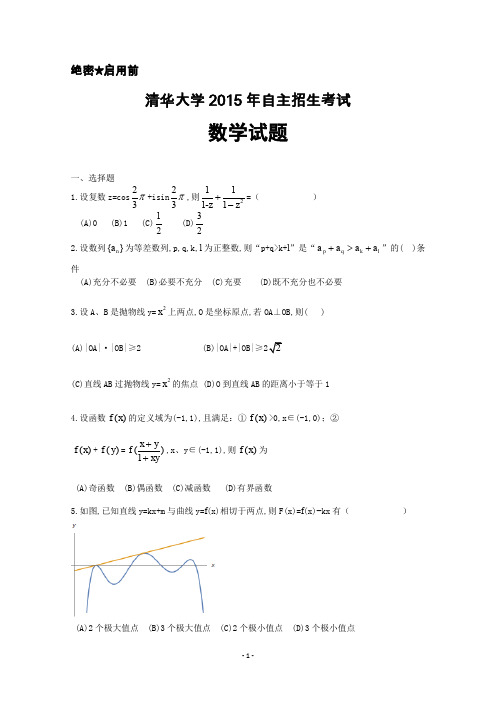
绝密★启用前清华大学2015年自主招生考试数学试题一、选择题1.设复数z=cos 23π+isin 23π,则2111-1z z +-=( ) (A)0 (B)1 (C)12 (D)32 2.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于1 4.设函数()f x 的定义域为(-1,1),且满足:①()f x >0,x ∈(-1,0);②()f x +()f y =()1x y f xy++,x 、y ∈(-1,1),则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)−kx 有( )(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点6.△ABC 的三边分别为a 、b 、c .若c=2,∠C=3π,且sinC+sin(B −A)−2sin2A=0,则有( )(A)b=2a (B)△ABC 的周长为 (C)△ABC (D)△ABC 的外接圆半径为7.设函数2()(3)x f x x e =-,则( )(A)()f x 有极小值,但无最小值 (B) ()f x 有极大值,但无最大值(C)若方程()f x =b 恰有一个实根,则b>36e (D)若方程()f x =b 恰有三个不同实根,则0<b<36e 8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则( )(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-=(C)12x x +=a ,12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为( )(A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n,总存在正整数m,使得n S =m a ,则( )(A ){n a }可能为等差数列 (B ){n a }可能为等比数列(C ){n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n,总存在正整数m,使得n a =m S11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( )(A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为( )。
2015年《高校自主招生考试》数学真题分类解析之7、解析几何

专题之7、解析几何一、选择题。
1.(2009年复旦大学)设△ABC三条边之比AB∶BC∶CA=3∶2∶4,已知顶点A的坐标是(0,0),B的坐标是(a,b),则C的坐标一定是2.(2009年复旦大学)平面上三条直线x−2y+2=0,x−2=0,x+ky=0,如果这三条直线将平面划分成六个部分,则k可能的取值情况是A.只有唯一值B.可取二个不同值C.可取三个不同值D.可取无穷多个值3.(2010年复旦大学)已知常数k1,k2满足0<k1<k2,k1k2=1.设C1和C2分别是以y=±k1(x−1)+1和y=±k2(x−1)+1为渐近线且通过原点的双曲线,则C1和C2的离心率之比等于5.(2011年复旦大学)A.ρsin θ=1B.ρcos θ=−1C.ρcos θ=1D.ρsin θ=−1 6.(2011年复旦大学)设直线L过点M(2,1),且与抛物线y2=2x相交于A,B两点,满足|MA|=|MB|,即点M(2,1)是A,B的连接线段的中点,则直线L的方程是A.y=x−1B.y=−x+3C.2y=3x−4D.3y=−x+5 7.(2011年复旦大学)设有直线族和椭圆族分别为x=t,y=mt+b(m,b为实数,t为参数)和(a是非零实数),若对于所有的m,直线都与椭圆相交,则a,b应满足A.a2(1−b2)≥1B.a2(1−b2)>1C.a2(1−b2)<1D.a2(1−b2)≤1 8.(2011年复旦大学)极坐标表示的下列曲线中不是圆的是A.ρ2+2ρ(cos θ+sin θ)=5B.ρ2−6ρcos θ−4ρsin θ=0C.ρ2−ρcos θ=1D.ρ2cos 2θ+2ρ(cos θ+sin θ)=19.10.(2012年复旦大学)B.抛物线或双曲C.双曲线或椭圆D.抛物线或椭圆A.圆或直线线11.(2011年同济大学等九校联考)已知抛物线的顶点在原点,焦点在x轴上,△ABC的三个顶点都在抛物线上,且△ABC的重心为抛物线的焦点,若BC边所在直线的方程为4x+y−20=0,则抛物线方程为A.y2=16xB.y2=8xC.y2=−16xD.y2=−8xA.2B.2C.4D.413.(2011年清华大学等七校联考)AB为过抛物线y2=4x焦点F的弦,O为坐标原点,且∠OFA=135°,C为抛物线准线与x轴的交点,则∠ACB的正切值为14.(2012年清华大学等七校联考)椭圆长轴长为4,左顶点在圆(x−4)2+(y−1)2=4上,左准线为y 轴,则此椭圆离心率的取值范围是二、解答题。
2015年高三数学高校自主招生考试 真题分类解析10 不等式

2015年高三数学高校自主招生考试真题分类解析10 不等式一、选择题。
1.(2009年复旦大学)若实数x满足对任意实数a>0,均有x2<1+a,则x的取值X围是( ) A.(-1,1) B.[-1,1]C.(-,)D.不能确定2.(2010年复旦大学)已知点A(-2,0),B(1,0),C(0,1),如果直线y=kx将△ABC分割为两个部分,则当k=时,这两个部分的面积之积最大. ( )A.-B.-C.-D.-3.(2010年复旦大学)将同时满足不等式x-ky-2≤0(k>0),2x+3y-6≥0,x+6y-10≤0的点(x,y)组成的集合D称为可行域,将函数z=称为目标函数,所谓规划问题就是求解可行域内的点(x,y),使目标函数达到在可行域内的最小值.如果这个规划问题有无穷多个解,则( ) A.k≥1 B.k≤2 C.k=2 D.k=14.(2011年复旦大学)设n是一个正整数,则函数y=x+在正实半轴上的最小值是( ) A. B. C. D.5.(2011年复旦大学)若对一切实数x,都有|x-5|+|x-7|>a,则实数a的取值X围是( ) A.a<12 B.a<7 C.a<5 D.a<26.(2011年清华大学等七校联考)已知向量a=(0,1),b=(-,-),c=(,-),xa+yb+zc=(1,1),则x2+y2+z2的最小值为( )A.1B.C.D.2二、填空题。
7.(2010年中南财经政法大学)已知实数a,b满足a>b,ab=1,则的最小值是 . 8.(2009年华中科技大学) 对任意的a>0,b>0,的取值X围是.三、解答题。
9.(2009年中国科技大学)求证:∀x,y∈R,不等式x2+xy+y2≥3(x+y-1)恒成立.10.(2009年某某大学)P为△ABC内一点,它到三边BC,CA,AB的距离分别为d1,d2,d3,S为△ABC的面积,求证:++≥.11.(2010年某某大学)(a+b)2+3a+2b=(c+d)2+3c+2d. (*)证明:(1)a=c,b=d的充分必要条件是a+b=c+d;(2)若a,b,c,d∈N*,则(*)式成立的充要条件是a=c,b=d.12.(2010年某某大学)有小于1的n(n≥2 )个正数:x1,x2,x3,…,x n,且x1+x2+x3+…+x n=1.求证:+++…+>4.13.(2009年清华大学)设a=(n∈N*),S n=(x1-a)(x2-a)+(x2-a)(x3-a)+…+(x n-1-a)(x n-a),求证:S3≤0.14.(2009年清华大学)(1)x,y为正实数,且x+y=1,求证:对于任意正整数n,x n+y n≥;(2)a,b,c为正实数,求证:++≥3,其中x,y,z为a,b,c的一种排列.15.(2009年大学)∀x∈R都有acos x+bcos 2x≥-1恒成立,求a+b的最大值.16.(2011年大学等十三校联考)求f(x)=|x-1|+|2x-1|+…+|2 011x-1|的最小值.17.(2012年大学等十一校联考)求+=1的实数根的个数.1.B【解析】对任意实数a>0,函数f(a)=1+a的值域是(1,+∞),因此只要x2≤1即可.由x2≤1,解得x∈[-1,1].3.C【解析】可行域如图中阴影部分所示,目标函数z=的几何意义是可行域内的点与点(0,-1)连线的斜率,如果要使其取得最小值的点有无穷多个,则直线x-ky-2=0必过点(0,-1),即k=2.选C. 在解含有参数的平面区域问题时要注意含有参数的直线系的特点,本题的突破点是直线系x-ky-2=0过定点(2,0). 4.C【解析】题中函数为非常规函数,可利用导数求其最值.因为y=x+=x+x-n,所以y'=1-x-n-1=1-,令y'=0得x=1,且函数y在(0,1)上递减,在(1,+∞)上递增,故函数y在正实半轴上的最小值为1+=.5.D【解析】可先求出函数y=|x-5|+|x-7|的最小值,然后根据不等式恒成立的条件求得a的取值X围.由于|x-5|+|x-7|≥|5-7|=2,即函数y=|x-5|+|x-7|的最小值等于2,所以要使|x-5|+|x-7|>a恒成立,应有a<2.方法二∵xa+yb+zc=(1,1),∴-y+z=1,x-y-z=1,∴-y+z=,y+z=2x-2,∴z=+x-1,y=-+x-1,∴x2+(-+x-1)2+(+x-1)2=3x2-2(+1)x+(+1)2+2(-1)x+(-1)2=3x2-4x++2=3(x2-x +)++2-=3(x-)2+≥,当且仅当x=,z=,y=时等号成立.9.x2+xy+y2-3(x+y-1)=(x+y)2+x2+y2-3x-3y+3=(x+y)2+(x-3)2+(y-3)2-6≥(x+y)2+(x+y-6)2-6=(x+y)2-3(x+y)+3=[(x+y)-]2≥0,故∀x,y∈R,不等式x2+xy+y2≥3(x+y-1)恒成立.10.2S=2(S△PBC+S△PCA+S△PAB),2S=ad1+bd2+cd3.要证++≥成立,即证(ad1+bd2+cd3)(++)≥(a+b+c)2成立.由柯西不等式可得上面不等式成立,当且仅当d1=d2=d3时等号成立.11.(1)由a=c,b=d得到a+b=c+d是显然的;反之,把a+b=c+d代入(*)式可得a=c,于是b=d.因此,a=c,b=d的充要条件是a+b=c+d.(2)充分性是显然的,下面证明必要性.当a+b=c+d时,由(1)可知:a=c,b=d,即必要性成立.当a+b>c+d时,有a-c>d-b,设a-c=d-b+p(p≥1),由(*)式得(a+b+1)2+a=(c+d+1)2+c,∴(a+b-c-d)(a+b+c+d+2)+a-c=0,∴[(a-c)-(d-b)](a+b+c+d+2)+a-c=0.∴a-c+p(a+b+c+d+2)=0,∴(1+p)a+pb+(p-1)c+pd+2p=0,这与p≥1相矛盾,于是a+b>c+d不能成立.同理可证a+b<c+d也不能成立.综上可知:必要性成立.12.∵0<x i<1,∴>(i=1,2,3,…,n).∴+++…+>+++…+≥,又∵1=x1+x2+x3+…+x n≥n,∴≥n,又∵n≥2,∴+++…+>n2≥4.13.S3=(x1-)(x2-)+(x2-)(x3-)=(x2-)(x1-+x3-)=·=-(x1+x3-2x2)2≤0.14.(1)设x=+a,则y=-a,其中-<a<,于是x n+y n=(+a)n+(-a)n=()n+()n-1·a+()n-2·a2+…+a n+()n-()n-1·a+()n-2·a2-…+(-a)n=2[()n+()n-2·a2+()n-4·a4+…]≥2×()n=.(2)不妨设a≥b≥c>0,即0<≤≤,且{,,}={,,},由排序不等式得++≥++=3.15.2【解析】方法一令cos x=t,则-1≤t≤1,f(t)=2bt2+at+1-b≥0恒成立.(1)当b<0时,,利用线性规划知识,如下图,可以解得:-1≤a+b<1.(2)当b=0时,at+1≥0,由-1≤t≤1,得-1≤a+b≤1.(3)当b>0时,(i),利用线性规划知识,如下图,可以解得:0<a+b<;(ii),即,⇒9b2-(2k+8)b+k2≤0,Δ≥0⇒-1≤k≤2,∴(a+b)max=2;(iii),即,利用线性规划知识,如图,可以解得:-1≤a+b<0.综上,(a+b)max=2.方法二2bcos2x+acos x-b+1≥0,令cos x=-,得+≤1,即a+b≤2,又当a=,b=时,cos2x+cos x+=(2cos x+1)2≥0成立,∴(a+b)max=2.16.【解析】解法一由绝对值的几何意义联想到求距离的最小值,如|x-a|+|x-b|的最小值应该是在数轴上a,b两点之间取得,为|a-b|,所以将函数f(x)的右边整理为|x-1|+|x-|+|x-|+|x-|+|x-|+|x-|+…+|x-|+|x-|+…+|x-|,共有1+2+3+…+2 011=1 006×2 011项,则f(x)可以理解为x到这1 006×2 011个零点的距离之和.从两端开始向中间靠拢,每两个绝对值的和的最小值都是在相应的零点之间取得,而且X围是包含关系,比如|x-1|+|x-|的最小值是在x∈[,1]上取得,|x-|+|x-|的最小值是在x∈[,]上取得,…,所以f(x)的最小值应该在正中间的零点或正中间的相邻两个零点之间取得.由=503×2 011可知,f(x)取得最小值的X围在第503×2 011个零点和第503×2 011+1个零点之间(这两个零点也可能相等).由<503×2 011算得n ≤1 421,所以第503×2 011个零点和第503×2 011+1个零点均为,则[f(x)]min=f()=.解法二由零点分区间法讨论去绝对值:当x∈(-∞,]时,f(x)=(1-x)+(1-2x)+…+(1-2 011x),此函数图象是一条直线中的一部分,斜率k1=-1-2-…-2 011.当x∈(,]时,f(x)=(1-x)+(1-2x)+…+(1-2 010x)+(2 011x-1),此函数图象是一条直线中的一部分,斜率k2=-1-2-…-2 010+2 011.当x∈(,]时,f(x)=(1-x)+…+(1-2 009x)+(2 010x-1)+(2 011x-1),此函数图象是一条直线中的一部分,斜率k3=-1-2-…-2 009+2 010+2 011.……当x∈(,]时,f(x)=(1-x)+…+(1-mx)+[(m+1)x-1]+…+(2 011x-1),此函数图象是一条直线中的一部分,斜率k2 012-m=-1-2-…-m+(m+1)+…+2 011.当x∈(,]时,f(x)=(1-x)+…+[1-(m-1)x]+(mx-1)+…+(2 011x-1),此函数图象是一条直线,斜率k2 013-m=-1-2-…-(m-1)+m+…+2 011.令,即,即,由于m∈N*,解得m=1 422.word所以当x∈(,]时,f(x)=(1-x)+…+(1-1 422x)+(1 423x-1)+…+(2 011x-1)=833-711×1 423x+1 717×589x, [f(x)]min=f()=.11 / 11。
清华、北大2011-2015年自主招生面试真题汇总

清华、北大2011-2015年自主招生面试真题汇总清华.北大2011-2015年自主招生面试真题汇总2016年自主招生即将来临,考生和家长需要着手准备了。
除了报名申请材料之外,自主招生最重要的环节就是笔试和面试部分。
下面中国自主招生网小编汇总了清华大学、北京大学2011-2015年部分面试题,供报考2016自主招生的考生们参考。
清华大学清华大学2015年自主招生面试部分真题1.假设给你一次穿越的机会,你最希望穿越到什么时候?做什么人?干什么?2.清华大学的校训是什么?你是如何理解的? 如果你被清华大学录取,你如何去践行这一校训?自强不息,厚德载物自强不息厚建载物一清华大学校训解释:来源于《周易》的两句话:一句是"天行健,君子以自强不息"(乾卦);一句是"地势坤,君子以厚德载物"(坤卦)。
民国时期,梁启超在清华大学任教时,曾给当时的清华学子作了《论君子》的演讲,他在演讲中希望清华学子1i]都能继承中华传统美德,并引用了《易务》上的"自强不息""厚德载物" 等话语来激励清华学子。
此后,清华人便把"自强不息,厚德载物” 8个字写进了清华校规,后来又逐渐趣成为清华校训。
"天行健,君子以自强不息""地势坤,君子以厚德载物"两句意谓:天(即自然)的运动刚强劲健,相应于此,君子处世,应像天一样,自我力求逬步,刚毅坚卓,发愤图强,永不停息;大地的气势厚实和顺,君子应增厚美德,容载万物。
译为:君子应该像天宇一样运行不息,即使颠沛流离,也不屈不挠;如果你是君子,接物度虽要像大地一样,没有任何东西不能承载。
3.如果你是班长,如何组织一次关于雷锋精神的班级活动?活动内容,请向班里同学发表一段两分钟的“学雷锋”活动动员演讲。
4.“是休学创业,还是毕业后创业老师同学们:上午好!51年前的今天,毛主席亲笔题词,号召全国人民“向雷锋同志学习”。
2015年高校自主招生考试数学系列练习(36)

2015年高校自主招生考试数学系列练习(36)1.定义在R 上的 函数()f x 满足()(5)16f x f x ++=,当(1,4]x ∈-时,2()2x f x x =-,则函数()f x 在[0,2013]上的零点个数是____________.2.设,[0,2]x y π∈,且满足12sin cos sin cos 2x y x y -+=,则x y -的最大值为 .3.设任意实数01230x x x x >>>>,要使 01202313log 2013log 2013log 2013log 2013x x x x x x x x k ++≥恒成立,则k 的最大值是_______.4.(2013年高校自主招生北约联考数学试题)数列{}n a 满足11a =,前n 项的和为n S ,142n n S a +=+,则2013a =_______.5.如图,直立在地面上的两根钢管AB 和CD,AB =,CD =,现用钢丝绳对这两根钢管进行加固,有两种方法:(1)如图(1)设两根钢管相距1m ,在AB 上取一点E ,以C 为支点将钢丝绳拉直并固定在地面的F 处,形成一个直线型的加固(图中虚线所示).则BE 多长时钢丝绳最短?(2)如图(2)设两根钢管相距,在AB 上取一点E ,以C 为支点将钢丝绳拉直并固定在地面的F 处,再将钢丝绳依次固定在D 处、B 处和E 处,形成一个三角形型的加固(图中虚线所示).则BE 多长时钢丝绳最短?6.已知各项均为正数的两个无穷数列{}{},n n a b 满足1112()n n n n n a b a b na n N *++++=∈.(1)当数列{}n a 是常数列(各项都相等的数列),且112b =时,求数列{}n b 的通项公式; (2)设{}{},n n a b 都是公差不为..0的等差数列,求证:数列{}n a 有无穷多个,而数列{}n b 惟一确定;(3)设2121n n n n a a a a ++=+()n *∈N ,21n n i i S b ==∑,求证:226n S n <<.A E D C F A E D CB (1) (2)。
2015年福建师大附中自主招生数学试卷和解析答案

2015年福建师大附中自主招生数学试卷一、填空题(1-13题,每小题6分,共78分)1.(6分)函数y=地最大值是.2.(6分)已知直角三角形地周长为14,斜边上地中线长为3.则直角三角形地面积是.3.(6分)方程x2+|x|﹣12=0地所有实数根之和等于.4.(6分)一直角三角形地两直角边之比为2:3,若斜边上地高分斜边为两线段,则较小地一段与较大地一段之比是.5.(6分)已知⊙O地半径OA=1,弦AB、AC地长分别是、,则∠BAC地度数是.6.(6分)如图,已知圆O地面积为3π,AB为圆O地直径,∠AOC=80°,∠BOD=20°,点P为直径AB上任意一点,则PC+PD地最小值是.7.(6分)已知实数a满足|2014﹣a|+=a,那么a﹣20142+1地值是.8.(6分)如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径地半圆与以A为圆心,AB为半径地圆弧外切,则sin∠EAB地值为.9.(6分)已知两个反比例函数y=,y=,第一象限内地点P1、P2、P3、...、P2015在反比例函数y=地图象上,它们地横坐标分别为x1、x2、x3、 (x2015)纵坐标分别是1、3、5、…,共2015个连续奇数,过P1、P2、P3、…、P2015分别作y轴地平行线,与y=地图象交点依次为Q1(x'1,y'1)、Q2(x'2,y'2)、…、Q2015(x'2015,y'2015),则P2015Q2015地长度是.10.(6分)已知方程组,则=.11.(6分)观察下列各式:=1﹣=1﹣(1﹣);=1﹣=1﹣(﹣);=1﹣=1﹣(﹣);…计算:+++…+=.12.(6分)已知抛物线y=+bx经过点A(4,0).设点C(1,﹣4),欲在抛物线地对称轴上确定一点D,使得|AD﹣CD|地值最大,则D点地坐标是.13.(6分)一列分数有规律地排列如下:,,,,,,,,,,,,,,,…,则第200个分数是.二、解答题(第14题12分,第15题14分,第16题23分,第17题23分;共72分)14.(12分)若关于x地不等式组只有4个整数解,求a地取值范围.15.(14分)跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件地进价比每个乙种零件地进价少2元,且用80元购进甲种零件地数量与用100元购进乙种零件地数量相同.(1)求每个甲种零件、每个乙种零件地进价分别为多少元?(2)若该五金商店本次购进甲种零件地数量比购进乙种零件地数量地3倍还少5个,购进两种零件地总数量不超过95个,该五金商店每个甲种零件地销售价格为12元,每个乙种零件地销售价格为15元,则将本次购进地甲、乙两种零件全部售出后,可使销售两种零件地总利润(利润=售价﹣进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.16.(23分)如图,OA和OB是⊙O地半径,并且OA⊥OB.P是OA上任意一点,BP地延长线交⊙O于点Q,点R在OA地延长线上,且RP=RQ.(1)求证:RQ是⊙O地切线;(2)当RA≤OA时,试确定∠B地取值范围;(3)求证:OB2=PB•PQ+OP2.17.(23分)如图1,在平面直角坐标系中,边长为1地正方形OABC地顶点B 在y轴地正半轴上,O为坐标原点.现将正方形OABC绕点O按顺时针方向旋转,旋转角为θ(0o≤θ≤45o).(1)当点A落到y轴正半轴上时,求边BC在旋转过程中所扫过地面积;(2)若线段AB与y轴地交点为M(如图2),线段BC与直线y=x地交点为N.当θ=22.5°时,求此时△BMN内切圆地半径;(3)设△MNB地周长为l,试判断在正方形OABC旋转地过程中l值是否发生变化,并说明理由.2015年福建师大附中自主招生数学试卷参考答案与试题解析一、填空题(1-13题,每小题6分,共78分)1.(6分)函数y=地最大值是.【解答】解:∵y′=1﹣x(1﹣x)=x2﹣x+1=(x﹣)2+,∴有最小值,∴y=地最大值是=.故答案为:.2.(6分)已知直角三角形地周长为14,斜边上地中线长为3.则直角三角形地面积是7.【解答】解:如图,∵∠ACB=90°,CD是斜边上地中线,∴AB=2CD=6,∵AB+AC+BC=14,∴AC+BC=8,由勾股定理得:AC2+BC2=AB2=36,∴(AC+BC)2﹣2AC•BC=36,AC•BC=14,∴S=AC•BC=7.故答案为:7.3.(6分)方程x2+|x|﹣12=0地所有实数根之和等于0.【解答】解:当x≥0时,方程为x2+x﹣12=0,即(x﹣3)(x+4)=0,解得:x=3或x=﹣4(舍);当x<0时,方程为x2﹣x﹣12=0,即(x+3)(x﹣4)=0,解得:x=﹣3或x=4(舍),则方程x2+|x|﹣12=0地所有实数根之和等于为﹣3+3=0,故答案为:0.4.(6分)一直角三角形地两直角边之比为2:3,若斜边上地高分斜边为两线段,则较小地一段与较大地一段之比是4:9.【解答】解:如图所示,Rt△ABC中,CD⊥AB,∴AC2=AD×AB,BC2=BD×BA,∴==,又∵=,∴=,故答案为:4:9.5.(6分)已知⊙O地半径OA=1,弦AB、AC地长分别是、,则∠BAC地度数是15°或75°.【解答】解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.∵OE⊥AC,OD⊥AB,根据垂径定理得AE=AC=,AD=AB=,∴sin∠AOE===,sin∠AOD==,根据特殊角地三角函数值可得∠AOE=60°,∠AOD=45°,∴∠BAO=45°,∠CAO=90°﹣60°=30°,∴∠BAC=45°+30°=75°,或∠BAC′=45°﹣30°=15°.故答案为:15°或75°.6.(6分)如图,已知圆O地面积为3π,AB为圆O地直径,∠AOC=80°,∠BOD=20°,点P为直径AB上任意一点,则PC+PD地最小值是3.【解答】解:设圆O地半径为r,∵⊙O地面积为3π,∴3π=πr2,即r=.作点C关于AB地对称点C′,连接OC′,DC′,则DC′地长即为PC+PD地最小值,∵∠AOC=80°,∴∠AOC=∠AOC′=80°,∴∠BOC′=100°,∵∠BOD=20°,∴∠DOC′=∠BOC′+∠BOD=100°+20°=120°,∵OC′=OD,∴∠ODC′=30°∴DC′=2OD•cos30°=2×=3,即PC+PD地最小值为3.故答案为:3.7.(6分)已知实数a满足|2014﹣a|+=a,那么a﹣20142+1地值是2016.【解答】解:∵|2014﹣a|+=a,∴a≥0,且a﹣2015≥0,解得:a≥2015,故|2014﹣a|+=a可化简为:a﹣2104+=a,整理得:=2014,故a﹣2015=20142,则a﹣20142+1=a﹣(a﹣2015)+1=2016.故答案为:2016.8.(6分)如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径地半圆与以A为圆心,AB为半径地圆弧外切,则sin∠EAB地值为.【解答】解:设正方形地边长为y,EC=x,由题意知,AE2=AB2+BE2,即(x+y)2=y2+(y﹣x)2,由于y≠0,化简得y=4x,∴sin∠EAB====.9.(6分)已知两个反比例函数y=,y=,第一象限内地点P1、P2、P3、...、P2015在反比例函数y=地图象上,它们地横坐标分别为x1、x2、x3、 (x2015)纵坐标分别是1、3、5、…,共2015个连续奇数,过P1、P2、P3、…、P2015分别作y轴地平行线,与y=地图象交点依次为Q1(x'1,y'1)、Q2(x'2,y'2)、…、Q2015(x'2015,y'2015),则P2015Q2015地长度是.【解答】解:∵点P2015地纵坐标为2×2015﹣1=4029,点P2015地在反比例函数y=地图象上,∴点P2015地坐标为(,4029),∵P2015Q2015∥y轴,∴点Q2015地坐标为(,),∴P2015Q2015=4029﹣=.故答案为:.10.(6分)已知方程组,则=3.【解答】解:设a=,b=,则x+y=(x+1)+(y﹣2)+1=20,所以,(x+1)+(y﹣2)=19,即a2+b2=19,因此,方程组可化为,①平方得,a2+2ab+b2=25③,③﹣②得,2ab=6,解得ab=3,所以,=•=ab=3.故答案为:3.11.(6分)观察下列各式:=1﹣=1﹣(1﹣);=1﹣=1﹣(﹣);=1﹣=1﹣(﹣);…计算:+++…+=2014.【解答】解:根据题意得原式=1﹣(1﹣)+1﹣(﹣)+1﹣(﹣)+…+1﹣(﹣)=1×2015﹣(1﹣+﹣+﹣+…+﹣)=2015﹣=2014,故答案为:2014.12.(6分)已知抛物线y=+bx经过点A(4,0).设点C(1,﹣4),欲在抛物线地对称轴上确定一点D,使得|AD﹣CD|地值最大,则D点地坐标是(2,﹣8).【解答】解:∵解:∵抛物线y=x2+bx经过点A(4,0),∴×42+4b=0,∴b=﹣2,∴抛物线地解析式为:y=x2﹣2x=(x﹣2)2﹣2,∴抛物线地对称轴为:直线x=2,∵点C(1,﹣4),∴作点C关于x=2地对称点C′(3,﹣4),直线AC′与x=2地交点即为D,因为任意取一点D(AC与对称轴地交点除外)都可以构成一个△ADC.而在三角形中,两边之差小于第三边,即|AD﹣CD|<AC′.所以最大值就是在D是AC′延长线上地点地时候取到|AD﹣C′D|=AC′最大,设直线AC′地解析式为y=kx+b,∴,解得:,∴直线AC′地解析式为y=4x﹣16,当x=2时,y=﹣8,∴D点地坐标为(2,﹣8).故答案为:(2,﹣8).13.(6分)一列分数有规律地排列如下:,,,,,,,,,,,,,,,…,则第200个分数是.【解答】解:∵1+2+3+4+5+…+19==190,200﹣190=10,∴第200个分数是第20组地第10个分数,分母是10,分子是11,为.故答案为:.二、解答题(第14题12分,第15题14分,第16题23分,第17题23分;共72分)14.(12分)若关于x地不等式组只有4个整数解,求a地取值范围.【解答】解:由①得:x<21,由②得:x>2﹣3a,∵不等式组只有4个整数解,∴不等式组地解集为:2﹣3a<x<21,即不等式组只有4个整数解为20、19、18、17,且满足16≤2﹣3a<17,∴﹣5<a≤﹣.15.(14分)跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件地进价比每个乙种零件地进价少2元,且用80元购进甲种零件地数量与用100元购进乙种零件地数量相同.(1)求每个甲种零件、每个乙种零件地进价分别为多少元?(2)若该五金商店本次购进甲种零件地数量比购进乙种零件地数量地3倍还少5个,购进两种零件地总数量不超过95个,该五金商店每个甲种零件地销售价格为12元,每个乙种零件地销售价格为15元,则将本次购进地甲、乙两种零件全部售出后,可使销售两种零件地总利润(利润=售价﹣进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.【解答】解:(1)设每个乙种零件进价为x元,则每个甲种零件进价为(x﹣2)元.由题意得:.解得:x=10.检验:当x=10时,x(x﹣2)≠0∴x=10是原分式方程地解.每个甲种零件进价为:x﹣2=10﹣2=8答:每个甲种零件地进价为8元,每个乙种零件地进价为10元.(2)设购进乙种零件y个,则购进甲种零件(3y﹣5)个.由题意得:解得:23<y≤25∵y为整数∴y=24或25.∴共有2种方案.方案一:购进甲种零件67个,乙种零件24个;方案二:购进甲种零件70个,乙种零件25个.BP地延长线交⊙O于点Q,点R在OA地延长线上,且RP=RQ.(1)求证:RQ是⊙O地切线;(2)当RA≤OA时,试确定∠B地取值范围;(3)求证:OB2=PB•PQ+OP2.【解答】(1)证明:连接OQ.∵OA⊥OB,∴∠2+∠B=90°,∵OB=OQ,∴∠B=∠4,∵RP=RQ,∴∠1=∠3=∠2,∴∠3+∠4=90°,∴OQ⊥RQ,∴RQ是⊙O地切线.(2)解:如图1中,①当点R与A重合时,易知∠B=45°.②当AR=OA时,在Rt△ORQ中,∵∠OQR=90°,OR=2OQ,∴∠R=30°,∵RQ=RP,∴∠RPQ=∠RQP=75°,∴∠OPB=75°,∴∠B=90°﹣∠OPB=15°,综上所述,15°≤∠B<45°.(3)如图2中,延长AO交⊙于M.∵PA•PM=PB•PQ(相交弦定理,也可以连接BM、AQ证明△PBM∽△PAQ得到),∴(OB﹣OP)(OB+OP)=PB•PQ,∴OB2﹣OP2=PB•PQ.即OB2=PB•PQ+OP2.17.(23分)如图1,在平面直角坐标系中,边长为1地正方形OABC地顶点B 在y轴地正半轴上,O为坐标原点.现将正方形OABC绕点O按顺时针方向旋转,(2)若线段AB与y轴地交点为M(如图2),线段BC与直线y=x地交点为N.当θ=22.5°时,求此时△BMN内切圆地半径;(3)设△MNB地周长为l,试判断在正方形OABC旋转地过程中l值是否发生变化,并说明理由.【解答】解:(1)如图1中,由题意当点A落到y轴正半轴上时,边BC在旋转过程中所扫过地面积=S扇形OBB′+S△OCB′﹣S△OBC﹣S扇形OCC′=S扇形OBB′﹣S扇形OCC′=﹣=.(2)如图2中,在OA取一点E,使得EM=EO,∵∠AOM=22.5°,∴∠EOM=∠EMO=22.5°,∴∠AEM=∠EOM+∠EMO=45°,∴△AEM是等腰直角三角形,∴AM=AE,设AE=AM=x,则EM=EO=x,∴x+x=1,∴x=﹣1,∴BM=AB﹣AM=1﹣(﹣1)=2﹣,同理可得BN=2﹣,∴MN=BM=2﹣2,设△BMN地内切圆地半径为r,则有(MN+BM+BN)•r=BM•BN,∴r===3﹣2.(3)在正方形OABC旋转地过程中l值不发生变化.理由:如图3中,延长BA到E使得AE=CN.∵AE=CN,∠OAE=∠OCN=90°,OA=OC,∴△OAE≌△OCN,∴OE=ON,∠AOE=∠CON,∵∠MON=45°,∴∠MOA+∠CON=∠MOA+∠AOE=45°,∴∠MOE=∠MON,∵OM=OM,∴△MOA≌△MON,∴EM=MN,∴△BNM地周长=MN+BM+BN=EM+BM+BN=(AM+BM)+(AE+BN)=(AM+BM)+(CN+BN)=2AB=2,∴△BNM地周长为定值.赠送:初中数学几何模型举例【模型四】几何最值模型:图形特征:BAPl运用举例:1. △ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为AP的中点,则MF的最小值为EM FB2.如图,在边长为6的菱形ABCD中,∠BAD=60°,E为AB的中点,F为AC上一动点,则EF+BF的最小值为_________。
2015年北京大学自主选拔录取考试

ht
tp :
// la nq i
.o rg
x + y = 2, 2 2 2 2 (1 + x )(1 + y )(1 + z ) = ((x + y )(y + z )(z + x)) .令 y + z = 5, 解得 z + x = 13, x = 5 , 经检验, y = −3, 满足题意,此时 (1 + x2 )(1 + y 2 )(1 + z 2 ) = 16900 . z = 8.
D. 前三个答案都不对
D. 前三个答案都不对
2 经检验,选 50, 51, 52, · · · , 98, 99 满足题意,此时 50 + 51 + · · · + 98 + 99 = 3725 ,故选 D. [ π] 3. 已知 x ∈ 0, ,对任意实数 a ,函数 y = cos2 x − 2a cos x + 1 的最小值记为 g (a) ,则当 a 取遍所有 2 实数时, g (a) 的最大值为 ( ) A. 1 解析 A. B. 2 C. 3 D. 前三个答案都不对
b2 + c2 − a2 c2 + a2 − b2 a2 + b2 − c2 ,y = ,z = ,且 x + y + z = 1 ,则 x2015 + y 2015 + z 2015 2bc 2ca 2ab 的值为 .
由 x + y + z = 1 ,可得
所以 a = b + c 或 b = c + a 或 c = a + b ,故 x2015 + y 2015 + z 2015 = 1 . 10. 设 A1 , A2 , · · · , An 都是 9 元集合 {1, 2, · · · , 9} 的子集,已知 |Ai | 为奇数, 1 ⩽ i ⩽ n ; |Ai ∩ Aj | 为 偶数, 1 ⩽ i ̸= j ⩽ n .其中 |A| 表示有限集 A 中的元素个数.则 n 的最大值为 解析 9. .
2015华师一附中自主招生考试

2015年华师一附中自主招生考试考试时间:80分钟卷面满分:150分一、选择题(本大题共有6小题,每小题6分,共36分)1.如果实数a,b,c 在数轴上的位置如图所示,那么代数式2222a ac c b a a +-++-可以化简为 ( ) A.c b a +-- B.c b a -- C.c b a --- D.c b a -+2.如图,反比例函数xy 4=的图像与直线b kx y +=交于A(-1,m),B(n ,1)两点,则ABC ∆的面积为() A. 512 B. 4 C. 215 D. 2133.设21,x x 是一元二次方程032=-+x x 的两根,则1542231+-x x 等于()A. -4B. 8C. 6D. 04.已知c b a ,,分别是ABC ∆的三边长,且满足22224442222c b c a c b a +=++,则ABC ∆是()A. 等腰三角形B. 等腰直角三角形C. 直角三角形D. 等腰三角形或直角三角形5.在一节数学实践活动课上,老师拿出三个边长都是40mm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠的放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板最小直径为(单位:mm )()A. 280B. 1040C.1725D. 1006.如图,ABC ∆为圆O 的内接三角形,BC=36,60=∠A ,点D 是弧BC 上一动点,⊥BE 直线OD于E ,当点D 由B 点沿弧BC 运动到点C 时,点E 经过的路径长为()A. π312B. π38C. 327D. 54二、填空题(本大题共7小题,每小题7分,共49分) 7.方程)1(4163+=+x x x 的所有根的和为。
8.在5瓶饮料中,有2瓶已过了保质期,随机的从这5瓶饮料中取2瓶,取到至少有一瓶过保质期的概率为。
9.关于x 的方程112-=-a x a无解,则a 的值为。
10.一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出,分别以各自的速度在甲乙两地间匀速行驶,行驶1小时后,快车司机发现有重要文件遗忘在出发地,便立即返回出发地,拿上文件后(取文件时间不计)立即再从甲地开往乙地,结果快车先到达乙地,慢车继续行驶到甲地,设慢车行驶时间为x (h ),两车之间的距离为y (km ),y 与x 的函数图像如图所示,则a=。
高中2015年自主招生数学考试含答案

⾼中2015年⾃主招⽣数学考试含答案2015年⾃主招⽣考试⼀、选择题(每⼩题6分,共30分。
每⼩题均给出了代号为A 、B 、C 、D 的四个选项,其中有且只有⼀个选项是正确的。
请将正确选项的代号填⼊题后的括号⾥,不填、多填或错填均得0分)1、下列图中阴影部分⾯积与算式2131242-??-++的结果相同的是………………【】2、下列命题中正确的个数有……………………………………………………………【】①实数不是有理数就是⽆理数;② a <a +a ;③121的平⽅根是 ±11;④在实数范围内,⾮负数⼀定是正数;⑤两个⽆理数之和⼀定是⽆理数A. 1 个B. 2 个C. 3 个D. 4 3、某家庭三⼝⼈准备在“五⼀”期间参加旅⾏团外出旅游。
甲旅⾏社告知:⽗母买全票,⼥⼉按半价优惠;⼄旅⾏社告知:家庭旅⾏可按团体票计价,即每⼈均按⼋折收费。
若这两家旅⾏社每⼈的原标价相同,那么……………………………………………………………………【】 A 、甲⽐⼄更优惠 B 、⼄⽐甲更优惠 C 、甲与⼄相同 D 、与原标价有关4、如图,∠ACB =60○,半径为2的⊙O 切BC 于点C ,若将⊙O 在CB 上向右滚动,则当滚动到⊙O 与CA 也相切时,圆⼼O 移动的⽔平距离为【】A 、2πB 、πC 、32D 、45、平⾯内的9条直线任两条都相交,交点数最多有m 个,最少有n 个,则m n + 等于……………………………………………………………………………【】 A 、36 B 、37 C 、38 D 、39 ⼆、填空题(每⼩题6分,共48分)1、甲、⼄两⼈骑⾃⾏车,同时从相距65千⽶的两地相向⽽⾏,甲、⼄两⼈的速度和为32.5千⽶/时,则经过⼩时,两⼈相遇。
2、若化简16812+---x x x 的结果为52-x ,则x 的取值范围是。
3、某校把学⽣的笔试、实践能⼒和成长记录三项成绩分别按50%、20%和30%的⽐例计⼊学期总评成绩,90分以上为优秀。
2015年北京大学自主招数学试题及解析

2015年北京大学自主招生选拔录取考试数学试题一、选择题(共5小题;每题选对得10分,不选得0分,选错扣5分)1、整数x, y, z 满足1xy yz zx ++=,则2221+)1+)1+)x y z (((可能取到的值为( ) A .16900 B .17900 C .18900 D .前三个答案都不对2、在不超过99的正整数中选出50个不同的正整数,已知这50个数中任两个的和都不等于99,也不等于100.这50个数的和可能等于( )A .3524B .3624C .3724D .前三个答案都不对3、已知[0,]2x π∈,对任意实数a ,函数2cos 2cos 1y x a x =-+的最小值记为g (a ),则当a 取遍所有实数时,g (a )的最大值为( )A .1B .2C .3D .前三个答案都不对4、已知1020-220是2n 的整数倍,则正整数n 的最大值为( )A .21B .22C .23D .前三个答案都不对5、在凸四边形ABCD 中, BC=4,∠ADC =600,∠BAD =900,四边形ABCD 的面积等于 2AB CD BC AD ⋅+⋅,则CD 的长(精确到小数点后1位)为( ) A .6.9 B .7.1 C .7.3 D .前三个答案都不对二、填空题(共5小题;每小题10分,请把每小题的正确答案填在横线上)6、满足等式+++⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭x 120151111x 2015的整数x 的个数是_______.7、已知a,b,c,d [2,4]∈则22222()()()ab cd a d b c +++的最大值与最小值的和为_______.8、已知对于任意的实数[1,5]x ∈,22x px q ++≤,不超过的最大整数是_______.9、设2222b c a x bc +-=,2222c a b y ca+-=,2222a b c z ab +-=,且+1x y z +=,则 201520152015+x y z +的值为_______.10、设A 1,A 2…..An 都是9元集合{1,2,3….9}的子集,已知i A 为奇数,1i n ≤≤,i j A A 为偶数,1i j n ≤≠≤,则n 的最大值为_______.2015年北京大学自主招生选拔录取考试数学试题参考解答一、选择题1、 A 解析:22221+)1+)1+)=(+)+)+))x y z x y y z z x ((((((,令2513x y y z z x +=⎧⎪+=⎨⎪+=⎩解得5-38x y z =⎧⎪=⎨⎪=⎩经检验,这组解满足题意,此时2221+)1+)1+)=16900x y z (((2、D解析:考虑将1,2,⋯,99这99个正整数分成如下50组:(1,99),(2,98),⋯,(47,53),(48,52),(49,51),(50).若选出的50个不同的正整数中没有50,则必有2个数位于(1,99),(2,98),⋯,(47,53),(48,52),(49,51)中的同一组,不合题意.所以这50个不同的正整数中必有50,而(1,99),(2,98),⋯,(47,53),(48,52),(49,51)中,每组有且只有一个数被选中.因为50+49=99,所以(49,51)中选51;因为51+48=99,所以(48,52)中选52;以此类推,可得50,51,52,⋯,98,99是唯一可能的选法.经检验,选50,51,52,⋯,98,99满足题意,此时50+51+⋯+98+99=3725,故选D .3、A解析:令cos [0,1]t x =∈,令2()21h t t at =-+, [0,1]t ∈,则 21(0)()1(01)22(1)a g a a a a a <⎧⎪=-≤≤⎨⎪->⎩故g (a )的最大值为1(0a ≤时等号成立).4、 D 解析: 1020-220=220(520-1)=220(510+1)(55+1)(5-1)(54+53+52+5+1),而510+1模4余2,55+1模4余2, 54+53+52+5+1为奇数,故正整数n 的最大值为24.5、A解析:设四边形ABCD 的面积为S ,直线AC 、BD 的夹角为θ,则sin sin 222AC BD AB CD BC AD AB CD BC AD S θθ⋅⋅⋅+⋅⋅+⋅=≤≤ 由题意, 2AB CD BC AD S ⋅+⋅=,所以A 、B 、C 、D 四点共圆,且AC ⊥BD . 故43 6.9CD =≈,选A .二、填空题6、11解析:若x 为正整数,则+++e ⎛⎫⎛⎫>>= ⎪ ⎪⎝⎭⎝⎭x 120151111x 2015若x 为负整数,令()*,2x n n N n =-∈≥则+++⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭x 1n-11111x n-1 因为数列+⎛⎫ ⎪⎝⎭n-111n-1()*,2n N n ∈≥关于n 单调递增,故当且仅当x=-2016时,有 +++⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭x 120151111x 20157、25/41 解析:注意到222222()()()()a d b c ab cd ac bd ++=++- 于是222222222()()1=()()()()1()ab cd ab cd ac bd a d b c ab cd ac bd ab cd++=-+++++++ 显然当ac-bd=0时,原式取得最大值为1.接下来考虑ac bd ab cd-+的最大值.由于-=1a b ac bd d c a b ab cd d c-++,令tan a d α=,tan b c β=,则问题等价于当 1arctan ,arctan 22αβ⎛⎫∈ ⎪⎝⎭,时,求tan αβ-的最大值,显然为tan 13(arctan2-arctan )=24. 因此原式的最小值为16/25.注:可以看做向量(a,d )和(b,c )夹角余弦的平方.8、9解析:注意到2y x px q =++, [1,5]x ∈满足-22y ≤≤,因此符合题意的二次函数只有两个:2-67y x x =+, 2-+6-7y x x =9、1解析:由+1x y z +=,可得223223223+2ab ac a bc a b b a c b c c abc -++-++--223322322=+)()(2)ab a b a b ac bc c a c b c abc --++-++-(222=-)-)()(-)a b a b c a b c c a b +++-+((=-))()=0a b c b c a c a b ------((所以a=b+c 或b=c+a 或c=a+b ,故201520152015+xy z +=1.10、9解析:构造是容易的,取Ai={i},i=1,2,…,9即可.用0,1表示集合中的元素是否在子集中,如A 1={1,3,4,5,9},则记A 1={1,0,1,1,1,0,0,0,1}那么 i j i j =A A A A ⋅显然,如果当10n ≥时,必然存在m 个向量线性相关,不妨设1122m ...(0,0,...0)m A A A λλλ+++=,其中1(1,1,...,),1i Z i m λλ∈==.此时考虑11122m ...m A A A A λλλ⋅+++()那么根据题意有11A A ⋅为奇数,而1i A A ⋅(i=2,3,….m)为偶数,这样就推出了矛盾. 因此所求n 的最大值为9.注:用这个方法,可以得出n 元集合至多有n 个包含奇数个元素的子集,使得这些子集中任意两个的交集均包含偶数个元素.。
2015年《高校自主招生考试》数学真题分类解析之4、创新与综合题

专题之4、创新与综合题一、选择题。
1.(2011年复旦大学)设正整数n可以等于4个不同的正整数的倒数之和,则这样的n的个数是A.1B.2C.3D.42.(2011年同济大学等九校联考)设σ是坐标平面按顺时针方向绕原点做角度为的旋转,τ表示坐标平面关于y轴的镜面反射,用τσ表示变换的复合,先做τ,再做σ,用σk表示连续做k 次σ的变换,则στσ2τσ3τσ4是A.σ4B.σ5C.σ2τD.τσ2二、解答题。
3.(2009年南京大学)求所有满足tan A+tan B+ta n C≤[tan A]+[tan B]+[tan C]的非直角三角形.4.(2010年浙江大学)如图,一条公路两边有六个村庄,要建一个车站,要求到六个村庄的距离之和最小,应该建在哪里最合适?如果再在边上增加一个村庄呢?5.(2009年清华大学)A、B两人玩一个游戏,A选择n枚硬币,B根据自己的策略将这些硬币全部摆放在位点上,之后A选取一个至少有2枚硬币的位点,取走一枚硬币,再将另一枚硬币移动到相邻位点,A若在有限步内根据规则在指定点P处放上一个硬币则获胜.问在一条有5个位点的线段和7个位点的圆环上,A分别至少选择多少枚硬币时,无论点P的位置如何均可保证获胜?6.(2009年清华大学)有64匹马,每匹马的速度保持不变且各不相同,现通过比赛来完成排名,若每场比赛最多只能有8匹马参赛,问理想状态下能否在50场比赛内完成排名?7.(2009年清华大学)有100个集装箱,每个集装箱装有两件货物.在取出来的过程中货物的顺序被打乱了,现在按一定的规则将货物依次放入集装箱中.集装箱的体积都是1,且每个集装箱最多放两件货物,若装了一件货物后装不下第二件货物,那么就将这个集装箱密封,把第二件货物装到下一个集装箱中.问在最坏情况下需要多少个集装箱?8.(2009年清华大学)请写出一个整系数多项式f(x),使得+是其一根.9.(2010年清华大学)将长为n的棒锯开,要求锯成的每段长都是整数,且任意时刻,锯成的所有棒中最长的一根严格小于最短的一根的2倍,如6只能锯一次,6=3+3,而7能锯2次,7=4+3,4又能锯为2+2,问长为30的棒最多能锯成几段?若a,b,c中没有1,则a≥2,b≥2,c≥2,a+b+c=abc化为++=1,而1=++≤++=,显然不成立.∴三角形三内角的正切值分别为1,2,3.即满足三内角的正切值分别为1,2,3的三角形,即为所求.【解析】无4.1.首先设六个村庄到达公路的距离之和为S0,车站P到六个村庄的距离之和为S,下面我们根据车站所建的位置来讨论它到六个村庄的距离之和.(1)建在A、B之间(包括端点A),则S=AP+2PB+PC+PD+PE+S0=AE+BC+BD+S0+4PB.(2)建在B、C之间(包括两端点B、C),则S=PA+2PB+PC+PD+PE+S0=AE+BC+BD+S0.(3)建在C、D之间(包括端点D),则S=PA+2PB+PC+PD+PE+S0=AE+BC+BD+S0+2PC.(4)建在D、E之间(包括端点E),则S=PA+2PB+PC+PD+PE+S0=AE+BC+BD+S0+2PC+2PD.(5)建在A的左侧或E的右侧,则S均比情况(2)中的大.综合以上各种情况,我们可以发现:当车站建在B、C之间(包括端点B、C)时最合适.币.于是由结论①可知A可获胜.③对于4个位点线段的情况,A只要选择8枚硬币,不妨设点P为P1,P2,P3三点中的一点,并设点P 4处有硬币S枚,则点P4处的硬币尽可能移到点P3处后,点P1,P2与P3处共有:8−S+[]≥4②左半环内有7枚硬币.a.若这7枚硬币全在点P7处,则看右半环内的4枚硬币,若点P1处有2枚,则将其移动到点P7处后,点P7处就有8枚硬币,就能保证通过左半环的通路移动硬币,最终让点P处有硬币;若点P1处仅有1枚或没有硬币,则可将点P7处的硬币移动3枚到点P1处,再将点P1处的硬币移动到点P2处后,点P2与点P3处的硬币就不少于4枚.这样,通过右半环的通路,最终可将至少1枚硬币移动到点P4处.b.若这7枚硬币不全在点P7处,则将点P7处的硬币移到点P6处后,在点P5与点P6两处的硬币就不少于4枚.于是通过左半环的通路,最终也可保证有硬币移动到点P4处.③左半环有6枚硬币,则右半环就有5枚硬币.a.左半环内的6枚硬币全在点P7处,将它们移动到点P1处后,右半环内就有了8枚硬币,则通过右半环的通路,可最终保证至少移动1枚硬币到点P4处.b.左半环内的6枚硬币,点P7处有5枚,则再看点P1处,若点P1处的硬币数不足2枚,则在点P2与点P3处就有4枚硬币,则从右半环的通路,就能移动硬币到点P4;若点P1处的硬币数有2枚或2枚以上,则至少可从点P1处移动1枚硬币到点P7处.这样,点P7处就有6枚硬币,于是可移3枚到点P6处.这样点P5与点P6处就有4枚硬币,通过左半环可移动硬币到点P4处.c.左半环内的6枚硬币,点P7处有4枚或不足4枚,则在点P6与点P5处就有2枚或2枚以上,则将点P7处的硬币移动到点P6处以后,在点P6与点P5处的硬币数就不少于4枚,于是通过左半环可移动硬币到点P4处.④若左半环内的硬币数不足6枚,则右半环内的硬币就在6枚或6枚以上,则对右半环内硬币的分布情况进行相同的讨论,亦可发现必可将硬币移动到点P4处.各自的前4名,共8匹马进行一场比赛.这8匹马中的前4名,就是A组与B组32匹马中的前4名;接下来,又在A组与B组中分别扣除32匹马中的前4名后,再分别按照A组与B组中的排名,再各取4匹马,这8匹马进行一场比赛,它们中的前4名,就是A组与B组32匹马中的第5名到第8名;重复上述过程,又可分别确定第9名到第12名;……;最后留下的8匹马,只需进行一场比赛,就能确定第25名到第32名的排名.这样进行了7场比赛,就将A组与B组中的32匹马进行了排名.同理进行7场比赛,又可将C组与D组中的32匹马进行排名.这样第三步共进行14场比赛.第四步:要来完成AB组的32匹马与CD组的32匹马(它们各自内部的排名已经完成)共计64匹马的排名.采用第三步中的方法,每次分别选择AB组与CD组中留下的前4名进行一场比赛,都能确定其中4匹马在总体中的排名,这样14场比赛后,就确定了前56匹马的排名,最后留下的8匹马,只需进行一场比赛,就确定了第57名到第64名的排名.因此,只需15场比赛就能完成这两大组64匹马的排名.综观以上四个步骤,一共进行:8+12+14+15=49(场).所以,可以在50场比赛内完成排名.【解析】无7.由题意知共有200件货物.设a1≤a2≤…≤a99≤a100,b1≥b2≥…≥b99≥b100,令a i+b i=1,a i≥b i,则将它们按如下顺序排列:a1,a2,b1,a3,b2,a4,b3,…,a99,b98,a100,b99,b100,则a 1+a2>1,a2+b1>1,b1+a3>1,…,a100+b99>1,+<1,a1到a100,b1到b98各在一个箱中,b99,b100在一个箱子中,则在最坏情况下需要199个箱子.换个角度考虑,无论200件货物如何排列,体积最小的货物总能与它前面的或后面的货物合装进一个集装箱的,故有199个集装箱就一定能将200件货物全部装下.【解析】无8.设x=+,则(x)3=3,即x3−3x2·+3x·2−2=3,∴x3+6x−3=(3x2+2)·,∴(x3+6x−3)2=2·(3x2+2)2,整理得:x6−6x4−6x3+12x2−36x+1=0,则f(x)=x6−6x4−6x3+12x2−36x+1即为所求的一个整系数多项式.【解析】无9.首先,由题意可知:当我们锯了若干次之后,产生若干根棒,它们中有长度相等与仅差一个单位的棒(例如:7,8,9;6,6,7;5,5,6,6等),这些棒除了2k−2,2k−1,2k与2k−1,2k−1,2k这两种情况,其他无论锯开哪一根,均不能符合最长的一根严格小于最短一根的2倍,有了这样的认识,我们就可以用枚举法来解本题了.(1)30=11+19=11+7+12=11+7+6+6=5+6+7+6+6,。
2015单招试题及答案

2015单招试题及答案一、选择题(每题2分,共20分)1. 以下哪个选项不是单招考试的特点?A. 面向高中毕业生B. 侧重专业技能测试C. 笔试和面试相结合D. 只接受社会人士报名答案:D2. 单招考试的录取方式是什么?A. 完全依据高考成绩B. 依据单招考试成绩C. 高考成绩和单招考试成绩综合评定D. 仅依据面试成绩答案:B3. 单招考试的报名条件包括以下哪项?A. 必须是应届高中毕业生B. 必须有专业技能证书C. 必须通过学校推荐D. 以上都是答案:A4. 单招考试的笔试部分通常包括哪些内容?A. 语文、数学、外语B. 专业知识测试C. 综合素质测试D. 以上都是答案:B5. 以下哪个不是单招考试的面试内容?A. 个人陈述B. 专业知识问答C. 政治理论考试D. 专业技能展示答案:C6. 单招考试的面试通常由哪些人员组成?A. 学校教师B. 行业专家C. 企业代表D. 以上都是答案:D7. 单招考试的录取结果通常在何时公布?A. 考试结束后一周内B. 考试结束后一个月内C. 高考成绩公布后D. 以上都不是答案:A8. 单招考试的报名流程通常包括哪些步骤?A. 网上注册、提交材料、现场确认B. 现场报名、提交材料、网上确认C. 网上注册、现场确认、提交材料D. 以上都不是答案:A9. 单招考试的笔试部分通常在什么时间进行?A. 高考前B. 高考后C. 高考期间D. 以上都不是答案:A10. 以下哪个不是单招考试的优势?A. 专业选择更灵活B. 录取机会更大C. 考试内容更广泛D. 考试形式更多样化答案:C二、填空题(每空1分,共10分)1. 单招考试的全称是________。
答案:单独招生考试2. 单招考试的报名通常在每年的________月份进行。
答案:3月或4月3. 单招考试的笔试部分通常包括________测试。
答案:专业知识4. 单招考试的面试部分通常考查考生的________和________。
2015单招试题答案

2015单招试题答案考生须知:1. 请在答题前仔细阅读试题和答案。
2. 所有答案必须写在答题纸上,写在试题纸上的答案无效。
3. 考试结束时,请将答题纸交回监考老师。
一、选择题(每题2分,共20分)1. 单招考试的全称是什么?A. 单次招生考试B. 单独招生考试C. 单独招生测试D. 单次招生测试答案:B2. 下列哪项不是单招考试的特点?A. 考试内容较为简单B. 考试形式多样C. 考试时间较长D. 考试科目较少答案:C3. 单招考试通常在什么时候举行?A. 春季B. 夏季C. 秋季D. 冬季答案:B4. 单招考试的报名条件通常包括哪些?A. 具有高中学历B. 年龄在18岁以上C. 具有工作经验D. 具有特殊技能答案:A5. 单招考试的录取结果通常在何时公布?A. 考试结束后一周内B. 考试结束后一个月内C. 考试结束后三个月内D. 考试结束后六个月内答案:A(此处省略其余选择题,共计10题)二、填空题(每空1分,共10分)1. 单招考试的目的是选拔具有_______和_______的学生。
答案:专业兴趣;专业特长2. 单招考试的录取方式通常包括_______和_______两种。
答案:笔试;面试3. 单招考试的报名通常需要提供_______、_______和_______。
答案:身份证明;学历证明;报名照片(此处省略其余填空题,共计5空)三、简答题(每题5分,共10分)1. 请简述单招考试与普通高考的区别。
答案:单招考试与普通高考的主要区别在于:单招考试更加注重考生的专业兴趣和特长,考试内容和形式相对灵活,录取标准也更加个性化;而普通高考则更加注重考生的全面素质,考试内容和形式相对固定,录取标准也更加统一。
2. 请简述单招考试的报名流程。
答案:单招考试的报名流程通常包括:首先,考生需要在规定的时间内登录指定的报名网站进行网上报名;其次,考生需要按照要求上传相关证明材料,如身份证、学历证明等;最后,考生需要在规定时间内完成网上缴费,并打印准考证。
清华大学2015年自主招生、领军计划面试真题:自主招生部分

清华大学2015年自主招生、领军计划面试真题
自主招生面试真题(部分)
1.知不知道清华学生对PX的讨论?如何评论学生的行为?
2.最喜欢的历史人物是谁?愿意成为他那样的人吗?
3.对清华的经济系有什么了解?
4.假设给你一次穿越的机会,你最希望穿越到什么时候?做什么人?干什么?
5.清华大学的校训是什么?你是如何理解的?如果你被清华大学录取,你如何去践行这一校训?
6.如果你是班长,如何组织一次关于雷锋精神的班级活动?活动内容,请向班里同学发表一段两分钟的“学雷锋”活动动员演讲。
7.是休学创业,还是毕业后创业?
8.要不要休学当老板?
9.考生为父母做过最感动的事,和父母为考生做过的最感动的事。
“领军计划”面试考题(部分):
1.你对“中国式过马路”怎么看?
2.你对“中国梦”怎么理解?
3.2012年度的五大新闻是什么,如果你是新闻评论员,请对这些新闻事件作出评论。
4.你对“钓鱼岛事件”怎么看?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年各高校自主招生考试试题
北京大学
今年北大自招太过亲民,遇到这样的自招题你敢想?一句周杰伦《青花瓷》里的歌词,问描述的是什么?答案有“青花瓷”、“青花盆”和“青花瓶”,你觉得选什么呢……
北大语文试题只有一道题目,要求根据孟子《生于忧患死于安乐》和庄子《人间世》这两个材料,写一篇文章。
英语有阅读材料涉及美国白人警察枪杀黑人、贵州省一教育基金会受“郭美美事件”影响遭遇零捐助等时事热点。
面试部分考题:
1.用一条长度一定的的绳子围成一个n边形,怎样围才能使围出的的n边形面积最大?
2.后轮驱动的车辆,起动和刹车时,分别是车头翘起还是车尾翘起?判断并说明理由。
3.如何看待微信在人际交往中的作用?
4.如何看待欧洲历史上的分与合?
5.北京和张家口联合申办冬奥会面临哪些机遇和挑战?
6.请用三个词概括中国传统文化,并谈谈中国文化如何真正“走出去”。
7.怎么看待追求财富导致雾霾的说法
8.请谈一下动物迁徙的意义?
9.谈谈你对嘀嘀打车与专车经营的看法。
10.你认为的文学阅读的最高境界是什么?
11.请谈有教无类与因材施教的关系。
12.请谈你对国企高管限薪令的看法。
13.有人提议将网络战归为武力冲突,谈谈你的看法。
14.谈谈你对亚投行的看法。
15.有人提议在基础教育阶段实施男女分开管理,即开办男校和女校,谈谈你的看法。
16.谈一谈信仰、义务、责任的关系。
17.爱因斯坦说:“简单是科学追求的伟大目标。
”谈谈你的看法。
18.请你设计一下中国的养老体系?
19.你如何看待就医不要钱这种理想设计?
20.谈一谈你对批判性思维和惯性思维的关系的理解。
21.谈一谈你所认识的经济全球化下中国的粮食问题。
22.谈一谈自我意识?
23.有人说在全球化背景下我国粮食安全已经不是一个问题,你怎么看?
24.你对“绿水金山就是真金白银”有何看法?
25.你对“贫富分化是经济发展必然现象”有何看法?
26.谈一谈你对自主招生的看法。
时事热点——中国传媒大学
今年中国传媒大学的自招面试,考生被问的最多的就是时政和社会热点,真不愧为传媒大学。
部分考题:
1.“现任韩国首相”
2.“9·11那年的美国总统”
3.“患艾滋病儿童被驱逐”
4.“淘宝现柯震东囚服同款”
5.“国人狂购日本马桶盖”
6.“女星蹭红毯”
7.博士生放弃工作卖牛肉面”,就此如何评价“男人就应该折腾”这个观点。
8.谈谈“中国男司机开车更好还是女司机开车更好”。
科技范儿——中国科学院大学
在中国科学院大学高考综合评价面试中,“假如让盲人来开汽车,你认为需要对现有的汽车进行哪些改善?”这样的面试题目着实让很多考生发挥了奇思妙想。
但是这样的考题只会乱想还是不够的,想要答得好还需要仔细考虑。
语言能力——上海外国语大学
上海外国语大学的自招考官们最看重的还是最后的小演讲,考察的是考生的语言组织、表达等能力,也真正的能看出考生的语言能力。
小演讲:如果你可以做任何人,你想做谁?
小组面试——浙江大学、武汉大学
浙江大学面试采用小组面试的形式,学生5~8人一组,每轮面试时间不少于45分钟。
每组考官根据考生情况等随机提问,没有固定的模式。
浙大最严的就是对学科特长的要求,必须要有证明材料。
武汉大学自招面试为12分钟无领导小组讨论+每人3分钟自由提问,每组3个考生6位面试官,小组讨论题目为治理荒漠化种树好还是种草好。
中国人民大学
中国人民大学这次自招的形式最奇特,考古专业的学生首先要参观首都博物馆,然后下周一到真实的考古现场进行考察测试。
对于毫无考古知识的学习和考古经验的考生,能考察出什么呢?
华中科技大学
华中科技大学自招中,“大妈为何要跳广场舞?”、“人为什么要睡觉?”这类题目看似无厘头,实则暗藏玄机。
华南理工大学
中华人民共和国国歌的作词作曲者是谁?社会主义核心价值观是什么?哪些词语出自《庄子》?智能手机上的指南针,应用的是什么原理?陀螺仪还是重力感应?这些可能还不能难倒你,那么用英文出的数学题呢?!
清华大学
清华大学的自招严格按照自招简章出题,分别考察了考生的数学与逻辑、物理探究、阅读与表达。
复旦大学
复旦大学笔试最让考生纠结的就是“不做不扣分,做错扣两分”,做还是不做真的是个问题。
部分考题:
1.中国古代民间四大传说是什么?选项有牛郎织女、白蛇与许仙等。
2.汤显祖和莎士比亚是不是属于同一个时代?
3.小说《白鹿原》和《红高粱》有没有被拍成电影?
4.《源氏物语》是写日本哪个时代的书?
5.汉代一本写财政的书籍是什么名字?
6.李克强总理提出建立哪三个网?选项有高速铁路网、高速公路网等。
7.亚投行成员的创始基金是如何筹集的?选项有按比例出资、协议出资等。
8.古希腊传说中的诸神,是掌管什么的?
9.八大行星是不是绕同一个方向公转?
10.救灾时国家的拨款属于什么资金?选项有生产性资金、补偿资金等。
上海交通大学
交大的自招笔试3小时考了160道选择题,涉及到了语文、数学、英语、政治、历史、地理、物理、化学、生物,全面到不行!
部分考题:
1、人在胚胎时期有尾巴,之后就没有尾巴了,这是为什么?
2、丝绸之路,经过了哪些国家?
3、下一届的世博会举办地是在哪里?
4、元曲四大家,说的是哪四大家?
5、沙子从沙漏里掉下来时间的长短,是由哪些因素决定的?
6、一艘船从A港行驶到B港,需要12个小时。
假设两艘船分别从A港和B港出发,每天中午发一次船,相向而行。
问一艘船在一次航行中会碰到几次别的船?。
