山西省阳泉市2016年中考数学一轮复习专题1实数的有关概念

合集下载

山西省阳泉市中考数学一轮复习专题1实数的有关概念含答案

实数的有关概念题组练习一（问题习题化） 1. 下列各数中，最小的数是( )A ．3-B ．2-C ．2)3(-D ．3102⨯2. 在实数，，0，，，﹣1.414，有理数有（）个.A.1B.2C.3D.4 3.下列运算正确的是（） A.-87×(-83)=7221 B.-2.68-7.42=-10 C.3.77-7.11=-4.66 D.101102102103-<- 4.下列说法正确的是（） A.一个数的绝对值一定比0大B.一个数的相反数一定比它本身小C.绝对值等于它本身的数一定是正数D.最小的正整数是1 5.设n 为正整数，且n ＜＜n +1，则n 的值为_____.6.实数a ，b 在数轴上对应的点的位置如图所示，计算||a b -的结果为（）7. 某市在一次扶贫助残活动中，共捐款5280000元，将5280000用科学记数法表示为 _______________. ◆ 知识梳理题组练习二（知识网络化）8. 在实数0 、π 、722、2 、9 - 中，无理数的个数有 .9.设a n 为正整数n 4的末位数，如a 1＝1，a 2＝6，a 3＝1,a 4＝6. 则a 1＋a 2＋a 3＋…＋a 2013＋a 2014＋a 2015＝ .10.数轴上实数b 的对应点的位置如图所示．比较大小：21b ＋1________0＞ (用“＜”或“＞”填空）．11.估计12介于 ( ) A ．0.4与0.5之间 B ．0.5与0.6之间 C ．0.6与0.7之间 D ．0.7与0.8之间12石墨烯是现在世界上最薄的纳米材料，其理论厚度仅是0.00000000034m ,这个数用科学记数法表示正确的是（） A. 3.4×109- B. 0.34×109-实数的概念；实数与数轴上的C. 3.4×1010- D. 3.4×1011-`13如图，四个有理数在数轴上的对应点M ，P ，N ，Q ，若点M ，N 表示的有理数互为相反数，则图中表示绝对值最小的数的点是（） A. 点M B. 点N C. 点P D. 点Q14. 如图，M ，N 两点在数轴上表示的数分别是m ，n ，则下列式子中成立的是（）A ．m+n ＜0B ． ﹣m ＜﹣nC ．|m|﹣|n|＞0D ． 2+m ＜2+n 15.将6.18×10﹣3化为小数的是（）16.如图，正方形ODBC 中，OC=1，OA=OB ，则数轴上点A 表示的数是．第16题图17.如图3，已知数轴上的点A 、B 、C 、D 分别表示数-2、1、2、3，则表示3P 应落在线段（）18.在数轴上表示数－1和2014的两点分别为A 和B ，则A 、B 两点间的距离为( )A ．2013B ．2014C ．2015D ．201619.已知2-x +（y-4）2=0，求以x ，y 为两边长的等腰三角形的周长？20. 一组数1,1,2,x,5,y ，…,满足“从第三个数起，每个数都等于它前面的两个数之和”，那么这组数中y 表示的数为AA.8B.9C.13D.15题组练习三（中考考点链接） 21.若（±3）2=a 2则a 的值是_______ .22. 我市2015年参加中考的考生人数约为43400人，将43400用科学记数法表为． 23.32)1(-的立方根是( )A ．－1B ．OC ．1D ． ±124.设边长为3的正方形的对角线长为a ．下列关于a 的四种说法：①a 是无理数；②a 可以用数轴上的一个点来表示；③3＜a ＜4；④a 是18的算术平方根．其中，所有正确说法的序号是（） A ．①④ B ．②③ C ．①②④ D. ①③④25. 若﹣2x m ﹣n y 2与3x 4y 2m+n 是同类项，则m ﹣3n 的立方根是______．26.2210b b -+=，则221||a b a+-＝ _____________。

实数的有关概念(1)

中考大一轮复习讲义◆ 数学
中考大一轮复习讲义◆ 数学 2
中考大一轮复习讲义◆ 数学
夯实基本知已知彼
知识结构梳理
整数正零整数
有理数
实数
负整数
分数正负分分数数
有限小数或无限循环小数
无理数正负无无理理数数无限不循环小数
1
2
3
3
中考大一轮复习讲义◆ 数学
夯实基本知已知彼
基础知识回顾
B 2. (2014·广东珠海)－的相反数是( )
A. 2 B. C. －2 D. －
B 3. (2014·河北)－2是2的( )
A. 倒数 B. 相反数 C. 绝对值 D. 平方根
A 1 4. (2014·重庆B卷)某地连续四天每天的平均气温分别是：1℃，－1℃，
0℃，2℃，则平均气温中最低的是( ) A. －1℃ B. 0℃ C. 1℃ D. 2℃
B 2 5. (2014·湖南怀化)我国南海海域面积约为3500000 km2，用科学记数法
表示正确的是( ) A. 3.5×105 km2 B. 3.5×106 km2 C. 3.5×107 km2 D. 3.5×108 km2
3
6
中考大一轮复习讲义◆ 数学
热点看台快速提升
热点一绝对值热点搜索理解绝对值的意义及性质是难点，由于|a|的含义是：表示数 a的点到原点的距离，因此|a|≥0. 可运用|a|的非负性进行求解或判断某些字母的取值．
数意义化简绝对值．
∵－2013 是负数，－2013的相反数是2013，∴|－2013|＝2013，故选C.23
7
中考大一轮复习讲义◆ 数学
c 点对点训练
1. (2012·湖南衡阳)－3的绝对值是( ) A. B. －3

(完整word版)数学人教版九年级下册中考第一轮复习第1讲(实数有关的概念)

m0 1n2016中考数学第一轮复习第1讲-------实数的有关概念知识点1：实数平行练习1： 1. 四个数-5，-0.1，21，3中为无理数的是（） A. -5 B. -0.1 C. 21D.32. 在实数：3.14159，364，1.010010001…，4.21&&，π，227中，无理数的个数有（） A ． 1个 B ．2个 C ．3个 D ．4个3. 如图，在数轴上表示15的点可能是（）A. P 点B. Q 点C. M 点D. N 点4. 如图,已知在数轴上有点A 和点B 两个点，估计点A 和点B 之间表示整数的点有个，它们分别是 .第3题图第4题图知识点2：数轴（三要素：1、原点；2、正方向；3、单位长度.）平行练习2：1. 如图为四位同学所画的数轴，其中正确的是（） A. B. C. D.2. 如图，在数轴上点A 表示的数可能是（） A. 1.5 B.－1.5 C.－2.6 D. 2.63. 已知实数m 、n 在数轴上的对应点的位置如图所示，1.整数(包括：正整数、0、负整数)和分数（可以表示为有限小数和无限循环小数）都是有理数．如：－3，，0.231，0.737373…，，.2.无限不环循小数叫做无理数．◆常见的几种无理数： ①根号型：如35,2等开方开不尽的数；②圆周率π型:如π，π-1等； ③构造型：如1.121121112…等无限不循环小数.112AB则下列判断正确的是( )A.0m >B.0n <C.0mn <D.0m n ->知识点3：相反数、倒数平行练习3：1. 如果向东走80m 记为80m ，那么向西走60m 记为（） A. -60m B. 60-m C. -(-60)m D. 601m 2. 下列各组数中，互为相反数的是（） A ．2和－2B ．－2和12C ．－2和－12D ．12和23. a （0a ≠）的相反数是（）A. a -B. aC. aD. 1a4．实数3的倒数是（） A. 31-B.31C. 3-D. 35. 如图，数轴上表示数﹣2的相反数的点是（） A ．点P B ．点Q C ．点M D ．点N6.12-的相反数是 .7. 若实数a 、b 互为相反数，则a+b= ；若实数m 、n 互为倒数，，则 .知识点4：绝对值⎩⎨⎧-≥=.,,00＜；a a a a a 平行练习4：1. 6-的值是（）A ．6-B ．16-C ．16D ．62. 计算： 12-=_____； 3-π=_____；32=__________.（结果保留根号）3. 绝对值等于3的数是__ ___.4. 对任意的实数a ，总有 0.知识点5：科学计数法平行练习5：1. 世界文化遗产长城的总长约为6700000m ，这个数字用科学计数法表示为；把一个数写成a ×10n 的形式(其中1≤a ＜10，n 是整数)，这种记数法叫做科学记数法．如： 40700＝4.07×105，0.000043＝4.3×10-5．已知一粒米的质量为0.000021千克，这个数字用科学计数法表示为 . 2. 根据2011年第六次全国人中普查主要数据公报，江西省常住人口约为4456万人；这个数据可以用科学计数法表示为人.知识点6：实数的运算p p aa 1=-， ()010≠=a a平行练习6：1. 昆明今年1月份某天的最高气温为5℃，最低气温为-1℃，则昆明这天的温差为（） A ．4℃ Ｂ．6℃ C ．-4℃ Ｄ．-6℃2. 25-+的相反数是( )A. 3B. -3C. -7D. 7 3. 计算：（1）()()0332011422---+÷- （2）011130321)(tan ---︒+-π）（4. 定义一种新运算：⊗，a ⊗b=41a-b变式探究：1. 320x y -++=，则x y +的值为 .2. 设实数a b 、在数轴上对应的位置如图所示，化简式子b a a ++.3. 已知2x =9，1+y =2，且xy ＜0，求x+y 的值.b0a课后作业1.如果零上5 ℃记做+5 ℃，那么零下7 ℃可记作（） A ．－7 ℃ B ．+7 ℃ C ．+12 ℃ D ．－12 ℃2.下列各数：3π，sin30°，3-，4，其中无理数的个数是（） A. 1个 B. 2个 C. 3个 D. 4个 3.下列各数中，最小的数是（） A ．－l B ．O C ．1D ．3 4.下列四个数中，负数是（） A. -2B. ()2-2 C. -2D.()2-25. 7-的相反数是（）A. 7-B. 7C.71-D. 71 6. 12-的绝对值是（）A ．2B ．2-C ．12D ．12-7. 实数a 在数轴上的位置如图所示，则|a －2.5|=（） A. a －2.5 B. 2.5－ a C. a +2.5 D. －a －2.58. 地球半径约为6400000米，用科学记数法表示为（） A ． 0.64×107 B ．6.4×106 C.64×105D ．640×1049. PM 2.5是指大气中直径小于或等于0.0000025 m 的颗粒物，将0.0000025用科学记数法表示为（）A. -50.2510⨯B. -60.2510⨯C. -52.510⨯D. -62.510⨯10. 实数3的倒数是（）A ．﹣B ．C ．﹣3D ．3 11. 下列运算正确的是（）A 4=2B ．（﹣3）2=﹣9C ．2﹣3=8 D ．20=0 12. 已知a 1+7+b =0-，则a+b=（）A ．﹣8B ．﹣6C ．6D ．8 13. 若（a －1）2+|b －2|=0，则（a －b ）2012的值是（）A. －1B. 1C. 0D. 2012 14. 如图，在数轴上的点M 表示的数可能是（） A ．1.5 B ．－1.5 C ．－2.4 D ．2.415. 实数a 、b 在数轴上的位置如图所示，下列式子错误．．的是（）A. a ＜bB.a b >C. －a ＜－bD.b －a ＞016. 点A 、B 、C 在同一条数轴上，其中点A 、B 表示的数分别为-3、1，若线段BC=2，则AC 等于（）A. 3B. 2C.3 或5D. 2或6 17. 下列计算正确的是（）A. 2221243x x x =⋅B. 1553x x x =⋅C. 34x x x =÷ D. 725x x =)(18. 实数m 、n 在数轴上的位置如图所示，则|n ﹣m|= .19. 一个数的绝对值等于3，则这个数是 . 20. 计算：（1）11312+2sin 60+3-⎛⎫-- ⎪⎝⎭（2）()()12121+20122π-⎛⎫----- ⎪⎝⎭21. 先化简，再求值：()()()2212-+-+x x x ，其中23=x .22. 观察下面的变形规律：211211-=⨯；3121321-=⨯；4131431-=⨯；…… （1）若n 为正整数,请你猜想=+⨯)(11n n ；（2）证明（1）题中你猜想的结论；（3）求和：+⨯+⨯+⨯431321211 (2012)20111⨯+.23. 2013年3月，某煤矿发生瓦斯爆炸，该地救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A 、B 两个探测点探测到C 处有生命迹象．已知A 、B 两点相距4米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C 的深度.。

中考数学第一轮复习资料第1_2课时实数的有关概念

第1——2课时实数的有关概念【知识梳理】1.实数的分类：整数(包括:正整数、0、负整数)和分数(包括:有限小数和无限环循小数)都是有理数. 有理数和无理数统称为实数.2.数轴：规定了原点、正方向和单位长度的直线叫数轴．实数和数轴上的点一一对应.3.绝对值：在数轴上表示数a的点到原点的距离叫数a的绝对值，记作∣a∣，正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值是0.4.相反数：符号不同、绝对值相等的两个数，叫做互为相反数．a的相反数是-a，0的相反数是0.5.有效数字：一个近似数,从左边笫一个不是0的数字起,到最末一个数字止,所有的数字,都叫做这个近似数的有效数字.6.科学记数法：把一个数写成a×10n的形式(其中1≤a<10,n是整数),这种记数法叫做科学记数法.如:407000=4.07×105,0.000043=4.3×10－5.7.大小比较：正数大于0，负数小于0，两个负数，绝对值大的反而小.8.数的乘方：求相同因数的积的运算叫乘方，乘方运算的结果叫幂.9.平方根：一般地，如果一个数x的平方等于a,即x2=a那么这个数x就叫做a的平方根（也叫做二次方根）．一个正数有两个平方根，它们互为相反数；0只有一个平方根，它是0本身；负数没有平方根．10.开平方：求一个数a的平方根的运算，叫做开平方．11.算术平方根：一般地，如果一个正数x的平方等于a,即x2=a，那么这个正数x就叫做a的算术平方根，0的算术平方根是0．12.立方根：一般地，如果一个数x的立方等于a,即x3=a，那么这个数x就叫做a的立方根（也叫做三次方根）,正数的立方根是正数;负数的立方根是负数；0的立方根是0．13.开立方：求一个数a的立方根的运算叫做开立方．【思想方法】数形结合，分类讨论【例题精讲】例1.下列运算正确的是（）A． B．C．D．例2.的相反数是（）A． B． C． D．例3.2的平方根是（）A．4 B． C． D．例4.《广东省重点建设项目计划（草案）》显示，港珠澳大桥工程估算总投资726亿元，用科学记数法表示正确的是（）A．元B．元C．元D．元例5.实数在数轴上对应点的位置如图所示，则必有（）a0 例5图A ．B ．C ．D ．例6.（改编题）有一个运算程序，可以使：⊕= (为常数)时，得（+1）⊕= +2，⊕（+1）= -3现在已知1⊕1= 4，那么2009⊕2009=．【当堂检测】1.计算的结果是（）A ．B ．C ．D ．2.的倒数是（）A ．B ．C ．D ．3.下列各式中，正确的是（）A ．B ．C ．D ．4.已知实数在数轴上的位置如图所示，则化简的结果为（） A．1 B ．C ．D ．5.的相反数是（）A ．B ．C ．D ．6.-5的相反数是____,-的绝对值是____,=_____.7.写出一个有理数和一个无理数，使它们都是小于－1的数.8.如果，则“”内应填的实数是（）A．B．C ．D ．第4题图。

中考数学复习之实数,与实数有关的概念与练习题

一．实数知识过关1.实数有关的概念1. 有理数:__________________2. 无理数:无限不循环小数叫做无理数.3. 实数：有理数和_______统称为实数.4. 实数的分类：(1) 按定义分： (2)按性质分：5. 数轴：(1)规定了______、_______、_______的直线叫做数轴；(2)______和实数是一一对应的关系.6. 相反数、绝对值、倒数考点分类考点1 相反数、倒数和绝对值例1：2023-的相反数是( )A.1B.-1C.2023D.20231已知点M 、N 、P 、Q 在数轴上的位置如图所示，则其中对应的绝对值最大的点是( )A. NB.MC.PD.Q考点2 无理数的识别例2 在实数389722，，，π-中，是无理数的是( ) A. 722- B.9 C.π D.38考点3 科学记数法例3 (1) 一天时间为86400秒，用科学记数法表示这一数字是( )A. 210864⨯B. 3104.86⨯C. 41064.8⨯D.510864.0⨯(2) 目前世界上能制造出的最小晶体管的长度只有0.00000004m ，将0.00000004用科学记数法表示为( )A. 8104⨯B. 8104-⨯C.8104.0⨯D.8104⨯-考点4 非负数的性质例4 已知x,y 为实数，且0|2|31=-+-y x 则x -y 的值为( ) A.3 B.-3 C.1 D.-1考点5 绝对值的化简例5 已知有理数a,b 在数轴上如图所示，且||||b a =，则可化简为( )A.a -bB.a+bC.2aD.2b真题演练1．两千多年前，中国人就开始使用负数，如果收入100元记作+100元，那么支出60元应记作（） A ．﹣60元B ．﹣40元C ．+40元D ．+60元2．下列各数不是有理数的是（） A ．1.21B ．﹣2C ．2πD ．123．下列各数：−74，1.010010001，833，0，﹣π，﹣2.626626662…，0.1⋅2⋅，其中有理数的个数是（） A ．2B ．3C ．4D ．54．在−13，227，0，﹣1，0.12，14，﹣2，﹣1.5这些数中，正有理数有m 个，非负整数有n 个，分数有k 个，则m ﹣n +k 的值为（） A ．3B ．4C ．6D ．55．有理数a ，b 在数轴上的对应点的位置如图所示，下列结论中正确的是（）A ．a ＞﹣2B ．|a |＞bC ．a ＞﹣bD ．|b |＞|a |6．已知数a ，b ，c 在数轴上的位置如图所示，化简|a +b |﹣|a ﹣b |+|a ﹣c |的结果为（）A ．﹣a ﹣2b ﹣cB ．﹣a ﹣b ﹣cC ．﹣a ﹣cD ．﹣a ﹣2b +c7．﹣2022的相反数是（） A ．﹣2022B ．2022C ．﹣2021D ．20218．−43的相反数是（） A ．34B ．43C ．−34D ．−439．新的一年到来了，中考也临近了，你是否准备好了？请选出2023的相反数是（） A ．12023 B ．−12023C ．2023D ．﹣202310．下列各数中，属于分数的是（）A．﹣0.2B．π2C．234D．|a|a11．已知：（a﹣2）2+|b+3|+|c+4|＝0，请求出：5a﹣b+3c的值是（）A．0B．﹣1C．1D．无法确定12．数据2060000000用科学记数法表示为（）A．206×107B．2.06×10C．2.06×109D．20.6×108 13．2022年11月27日，宁波舟山港累计完成集装箱吞吐量超过3108万标准箱，提前34天达到去年全年总水平．将3108万用科学记数法表示应为（）A．3.108×106B．3.108×107C．31.08×106D．0.3108×108 14．新型冠状病毒是承载在飞沬上传播的，而飞沬的直径是5um（提示：1m＝1000000um），只要能够过滤小于5um的颗粒的空气净化器都有用，我们常用的医用口罩等都是有用的，飞沬直径用科学记数法可表示为（）A．5×106m B．5×10﹣6m C．50×10﹣6m D．0.5×10﹣5m 15．华为麒麟990芯片采用了最新的0.000000007米的工艺制程，数0.000000007用科学记数法表示为（）A．7×10﹣9B．7×10﹣4C．0.7×10﹣9D．0.7×10﹣8课后练习1．中国是最早采用正负数表示相反意义的量，并进行负数运算的国家．在一部中国古代数学著作中，涉及用不同颜色的算筹（小棍形状的记数工具）分别表示正数和负数，这部著作是（）A．《几何原本》B．《九章算术》C．《孙子算经》D．《四元玉鉴》2．有理数a、b、c、d在数轴上的对应点如图所示，这四个数中绝对值最小的是（）A．a B．b C．c D．d3．下列各数中最小的负整数是（）A．﹣2021B．﹣2022C．﹣2023D．﹣14．2022年11月13日，第十四届中国国际航空航天博览会在珠海圆满落幕，本届航展参展规模远超预期、参展展品全领域覆盖、商贸交流活动成效显著．航展6天，共签订总值超过398亿美元的合作协议书，39800000000用科学记数法表示为（）A．3.98×1011B．0.398×1010C．3.98×1010D．0.398×1011 5．已知|3a+1|+（b﹣3）2＝0，则（ab）2022的值是（）A．1B．﹣1C．0D．36．若（a+1）2+|b﹣2|＝0，则（b+a）2021的值是（）A．1B．﹣2021C．﹣1D．2021填空题（共21小题）7．2022年全国粮食达到13731亿斤，数据13731用四舍五入法精确到1000，并用科学记数法表示是．8．某头非洲大象的体重大约3880千克，则将3880千克精确到100千克用科学记数法表示记为千克．9．观察下面式子：21＝2，22＝4，23＝8，24＝16，25＝32，26＝64…，那么22023的结果的个位上的数字是．10．如图，周长为6个单位长度的圆上的六等分点分别为A，B，C，D，E，F，点A落在2的位置，将圆在数轴上沿负方向滚动，那么落在数轴上﹣2023的点是．11．数轴上，点B在点A的右边，已知点A表示的数是﹣1，且AB＝2023，那么点B表示的数是．12．若a的相反数等于它本身，b是最小的正整数，c是最大的负整数，则代数式a﹣b+c ＝．13．若a．b互为相反数，c的倒数是−35，则a+b﹣6c的值是．冲击A+如图1所示，△ABC是以AB为底的等腰三角形，AC=BC=6，延长CB至P，使得BP=BC，连接AP，AP=4.(1)求证：直线AP为圆O的切线；(2)如图2所示，将△ABC沿着AC翻折至△ACQ处，QC边与圆交于点D，连接AD，求△ACD的面积.。

中考数学一轮复习专题实数知识点、对应习题及答案

实数考点1 实数的大小比较两实数的大小关系如下：正实数都大于0，负实数都小于0，正数大于一切负数；两个正实数，绝对值大的实数较大；两个负实数，绝对值大的实数反而小．实数和数轴上的点一一对应，在数轴上表示的两个实数，右边的数总大于左边的数．例1 比较3－2与2－1的大小．分析：比较3－2与2－1的大小，可先将各数的近似值求出来，即3－2≈1.732－1.414=0.318，2－1≈1.414－1=0.414，再比较大小例2 在-6,0,3,8这四个数中，最小的数是（）A.-6B.0C.3D.8 答：2－1，A 利用数轴考点2 无理数常见的无理数类型(1) 一般的无限不循环小数，如：1.41421356¨··· (2) 看似循环而实际不循环的小数，如0.1010010001···(相邻两个1之间0的个数逐次加1)。

(3) 有特定意义的数，如：π=3.14159265···(4).开方开不尽的数。

如：35,3注意：（1）无理数应满足：①是小数；②是无限小数；③不循环；（2）无理数不是都带根号的数（例如π就是无理数），反之，带根号的数也不一定都是无理数（例如4，327就是有理数）．例3 下列是无理数的是（）A.-5/2B.πC. 0D.7.131412例4在实数中－23 ，0 3.14 ）A ．1个B ．2个C ．3个D ．4个答：B ，A考点3 实数有关的概念实数的分类（1）按实数的定义分类：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎩⎪⎨⎧无限不循环小数负无理数正无理数无理数数有限小数或无限循环小负分数正分数分数负整数零正整数整数有理数实数（2）按实数的正负分类：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧负无理数负分数负整数负有理数负实数负数）零（既不是正数也不是正无理数正分数正整数正有理数正实数实数例5若a 为实数,下列代数式中,一定是负数的是( ) A. －a 2 B. －( a +1)2 C.－2a D.－(a -+1)分析：本题主要考查负数和非负数的概念,同时涉及考查字母表示数这个知识点.由于a 为实数, a 2、( a +1)2、2a 均为非负数，∴－a 2≤0，－( a +1)2≤0，－2a ≤0．而0既不是正数也不是负数，是介于正数与负数之间的中性数．因此，A 、B 、C 不一定是负数．又依据绝对值的概念及性质知－(a -+1)﹤0．故选D例6实数a 在数轴上的位置如图所示, 化简:2)2(1-+-a a =分析：这里考查了数形结合的数学思想,要去掉绝对值符号,必须清楚绝对值符号内的数是正还是负.由数轴可知:1﹤a ﹤2,于是,22)2(,112a a a a a -=-=--=-所以, 2)2(1-+-a a =a －1+2－a =1.例7 如图所示,数轴上A 、B 两点分别表示实数1，5，点B 关于点A 的对称点为C ，则点C 所表示的实数为（）A. 5－2B. 2－5C.5－3 D.3－5分析：这道题也考查了数形结合的数学思想,同时又考查了对称的性质．B 、C 两点关于点A 对称，因而B 、C 两点到点A 的距离是相同的，点B 到点A 的距离是5－1，所以点C 到点A 的距离也是5－1，设点C 到点O 的距离为a ，所以a +1=5－1，即a =5－2．又因为点C 所表示的实数为负数，所以点C 所表示的实数为2－5．例8已知a 、b 是有理数，且满足（a －2）2+3-b =0，则a b的值为分析：因为（a －2）2+3-b =0，所以a －2=0，b －3=0。

2016年中考数学总复习第1讲_实数的有关概念与运算

2016年中考数学总复习第1讲：实数的有关概念与运算【基础知识回顾】一、实数的分类：1、按实数的定义分类：实数有限小数或无限循环数注：1、正确理解实数的分类．如：2π是数，不是数，722是数，不是数．二、实数的基本概念和性质1、数轴：规定了、、的直线叫做数轴，和数轴上的点是一一对应的．2、相反数：只有不同的两个数叫做互为相反数，a 的相反数是，0的相反数是， a 、b 互为相反数⇔ ；a+b 的相反数为；a-b 的相反数为；-a+b 的相反数为．3、倒数：实数a 的倒数是，没有倒数，a 、b 互为倒数⇔ ．4、绝对值：在数轴上表示一个数的点到的距离叫做这个数的绝对值．⎪⎩⎪⎨⎧<=>=)0()0(0)0(a a a a ； ⎪⎩⎪⎨⎧<=>=-)()(0)(b a b a b a b a ．因为绝对值表示的是距离，所以一个数的绝对值是数，我们学过的非负数有三个：、、．注：0是唯一一个没有倒数的数，相反数等于本身的数是，倒数等于本身的数是，绝对值等于本身的数是．三、科学记数法、近似数和有效数字1、科学记数法：把一个较大或较小的数写成的形式叫做科学记数法．其中a 的取值范围是．如:407000=4.07×105,0.000043=4.3×10－5. 2、近似数和有效数字：一般的，将一个数四舍五入后得到的数称为这个数的近似数，这时，从数字起到近似数的最后一位止，中间所有的数字都叫这个数的有效数字．注：1、科学记数法不仅可以表示较大的数，也可以表示较小的数，其中a 的取值范围一样，n 的取值不同，当表示较大数时，n 的值是原整数数位减一，表示较小的数时，n 是负整数，它的绝对值等于原数中左起第一个非零数字前零的个数（含整数数位上的零）．四、数的乘方与开方1、数的乘方：求相同因数的积的运算叫乘方，乘方运算的结果叫幂.2、平方根：一般地，如果一个数x 的平方等于a,即x 2=a 那么这个数x 就叫做a 的平方根（也叫做二次方根）．一个正数有平方根，它们互为；0只有平方根，它是0本身；没有平方根．3、开平方：求一个数a 的平方根的运算，叫做开平方．4、算术平方根：一般地，如果一个正数x 的平方等于a ，即x 2=a ，那么这个正数x 就叫做a 的算术平方根， 0的算术平方根是0．5、立方根：一般地，如果一个数x 的立方等于a ，即x 3=a ，那么这个数x 就叫做a 的立方根（也叫做三次方根）,正数的立方根是正数;负数的立方根是负数；0的立方根是0．6、开立方：求一个数a 的立方根的运算叫做开立方．特别注意的两个运算公式：a 0=1（a ≠0），ppa a1=-五、实数的运算1、加法法则：同号两数相加，取相同的符号，并把绝对值相加；异号两数相加，绝对值相等时和为0；绝对值不等时，取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值；一个数同0相加，仍得这个数． 2、减法法则：减去一个数，等于加上这个数的相反数．3、乘法法则：两个有理数相乘，同号得正，异号得负，再把绝对值相乘；任何数与0相乘，积仍为0．4、除法法则：两个有理数相除，同号得正，异号得负，并把绝对值相除；0除以任何非0的数都得0；除以一个数等于乘以这个数的倒数．5、混合运算法则：先算乘方，再算乘除，最后算加减；如果有括号，先算括号里面的．⎪ ⎪ ⎪⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数无理数负分数＿零正整数整数有理数无限不循环小数6、运算律：加法交换律：a +b =b +a (a 、为任意有理数)；加法结合律：(a+b)+c=a+(b+c)(a, b,c 为任意有理数)7、实数运算公式：【重点考点例析】考点一、无理数的识别例1 ．（2012•盐城）下面四个实数中，是无理数的为（）A ．0 BC ．﹣2D ．0.5 考点二、实数的有关概念例2 ．（2012•乐山）如果规定收入为正，支出为负．收入500 元记作500元，那么支出237元应记作（） A ．﹣500元 B ． ﹣237元 C ． 237元 D ． 500元例3 ．（2012•怀化）64的立方根是（） A ．4 B ． ±4 C ． 8 D ． ±8 例4 ．（2012•|3|x y --互为相反数，则x+y 的值为（）A ．3B ． 9C ． 12D ． 27 考点三、实数与数轴例5．（2012•乐山）如图，A 、B 两点在数轴上表示的数分别为a 、b ，下列式子成立的是（） A ．ab ＞0 B ．a+b ＜0 C ．（b-1）（a+1）＞0 D ．（b-1）（a-1）＞0 例6．（2012•常德）实数a ，b 在数轴上的位置如图所示，下列各式正确的是（） A ．a+b ＞0 B ．ab ＞0 C ．|a|+b ＜0 D ．a-b ＞0例7．下列各式中，正确的是（） A ．3152<<B ．4153<<C ．5154<<D ．161514<<例8．已知实数a在数轴上的位置如图所示，则化简|1|a - ）A ．1B ．1-C ．12a -D ．21a -例9．如果2()13⨯-=，则“”内应填的实数是（）A ． 32B ． 23C ．23-D ．32-考点四、实数的计算（必考：5分）例10．（2015•昆明）计算：202015)21()6()1(9----+-+π．例11．（2015•曲靖）计算：2)22()31()1(022015---+---．例12．（2015•衢州）计算：(0214sin 60-+-︒ .例13．（2015•庆阳）计算：27330cos 4)31()23(1--++--o ．例14．（2015•天水）计算：10)81(45sin 218)3(---+-oπ．例15．（2015•宿迁）计算：021)3()2(260cos ---+--πo ．第11题图。

中考数学复习《实数的有关概念》

（C）
类型4
规律探究题
例6 （2018•益阳）小李用围棋排成下列一组有规律
的图案，其中第1个图案有1枚棋子，第2个图案有3 枚棋子，第3个图案有4枚棋子，第4个图案有6枚棋子……那么第9个图案的棋子数是 13 枚.
…
（ 1）（ 2）（ 3）（ 4）（ 5）
…
（ 1）（ 2）
（ 3）（ 4）（ 5）
且到原点的距离相等 .
3.乘积为 1 的两个数互为倒数. 倒数是它本身， 0 没有倒数.
1和-1 的
4.在数轴上，表示数a的点与原点的距离，
称为数a的绝对值，记作 |a| ， |a| ≥ 0.
当a≥0时，|a|= a ；当a≤0时，|a|= -a 5. 有理数和无理数统称为实数. 其中，整数和分数是有理数，无限不循环小数是无理数. .
解设第n个图形有an个棋子，观察得出：
a1=1，a2=3×1，a3=4=3×1+1，a4=6=3×2，
a5=7=3×2+1，… 发现当n为奇数时，an=3k+1(其中n=2k+1)
当n为偶数时，an=3(k+1)(其中n=2k+2) ∴当n=9时，9=2k+1，解得k=4，
∴a9=3×4+1=13.
考点2
近似数与科学记数法
1.科学记数法：
把一个绝对值大于1的数写成 a×10n ，n比原来的
数的整数部分少 1 ；把一个绝对值小于1的数写 -n a × 10 成，n等于原来的数从左边数起第一个非
零数字前面的零的个数.其中，1≤|a|＜10.
2.近似数：
一个数四舍五入到哪一位，就称这个数精确

中考数学专题01 实数的有关概念及运算(原卷版)

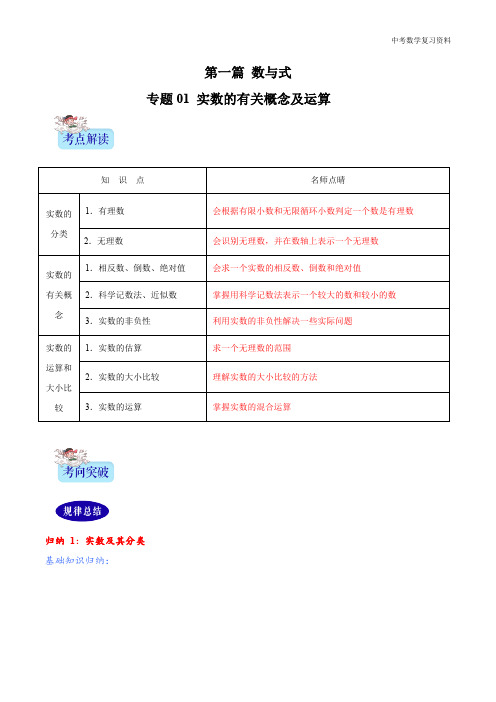
归纳 4：科学记数法与近似数基础知识归纳：根据科学记数法的定义，科学记数法的表示形式为 a×10n，其中 1≤|a|＜10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值．基本方法归纳：利用科学记数法表示一个数，在确定 n 的值时，看该数是大于或等于 1 还是小于 1．当该数大于或等于 1 时，n 为它的整数位数减 1；当该数小于 1 时，－n 为它第一个有效数字前 0 的个数（含小
中考数学复习资料
的克数记为负数，下面检测过的四个排球，在其上方标注了检测结果，其中质量最接近标准的一个是（）A．B．Fra bibliotek C．D．
3．（2019 内蒙古通辽市，第 1 题，3 分） 1 的相反数是（） 2019
A．2019 B． 1 C．﹣2019 D． 1
（）
A．5×106 B．107 C．5×107 D．108 14．（2019 重庆 A，第 8 题，4 分）按如图所示的运算程序，能使输出 y 值为 1 的是（）
A．m=1，n=1 B．m=1，n=0 C．m=1，n=2 D．m=2，n=1
归纳 5：实数的混合运算基础知识归纳：实数混合运算时，将运算分为三级，加减为一级运算，乘除为二级运算，乘方为三级运算．同级运算时，从左到右依次进行；不是同级的混合运算，先算乘方，再算乘除，而后才算加减；运算中如有括号时，先做括号内的运算，按小括号、中括号、大括号的顺序进行基本方法归纳：实数的混合运算经常涉及到零指数幂、负整数指数幂、特殊角的三角函数值、绝对值的化简、二次根式等内容，要熟练掌握这些知识．注意问题归纳：实数的混合运算经常以选择、填空和解答的形式出现，是中考是热点，也是比较容易出错的地方，在解答此类问题时要注意基本性质和运算的顺序．

太原市数学中考《第二章实数》知识点聚焦

知能图谱平方根⎩⎪⎨⎪⎧算术平方根的定义及性质平方根的定义及性质开平方运算立方根⎩⎨⎧立方根的定义及性质开立方运算实数与数轴的关系→实数与数轴上的点一一对应正有理数⎩⎨⎧正整数正分数负有理数⎩⎨⎧负整数负分数无理数⎩⎨⎧⎭⎬⎫正无理数负无理数无限不循环小数实数的运算及运算律⎩⎪⎨⎪⎧实数的加、减法实数的乘、除法实数的乘方、开方交换律结合律分配律实数的大小比较⎩⎨⎧直接法间接法第3讲平方根与立方根知识能力解读知能解读(一)算术平方根、平方根的定义及性质1．算术平方根的定义、表示及性质(1)定义：一般地，如果一个正数x的平方等于a，即2x a=，那么这个正数x叫作a的算术平方根．规定：0的算术平方根是0．(2)表示方法：()0a a≥a”，a叫作被开方数．(3)性质：一个非负数的算术平方根的平方等于它本身，即()2a a=≥．注意：2(1)区别：①2两者运算顺序不同．②2中a的取值范围是0a≥a取正数、零、负数都可以．(2)联系：当0a≥时，2=．2．平方根的定义及性质(1)定义：一般地，如果一个数的平方等于a，那么这个数叫作a的平方根或二次方根．这就是说，如果2x a=，那么x叫作a的平方根．平方根与立方根有理数实数的分类实数(2)表示方法：正数a 的平方根表示为a ”．(3)性质：正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根． 3．开平方运算求一个数a 的平方根的运算，叫作开平方．平方与开平方互为逆运算．根据这种互逆关系，可以求一个数的平方根．如4±的平方为()2416±=，所以，16的平方根为4±，即4=±．4．平方根与算术平方根的区别及联系 (1)区别： ①定义不同：“一个正数”与“一个数”含义不同．②个数不同：一个正数有两个平方根，而一个正数的算术平方根只有一个．③表示方法不同：正数a 的平方根表示为a (2)联系：①具有包含关系：平方根包含算术平方根，算术平方根是平方根中的一种． ②存在条件相同：平方根和算术平方根都只有非负数才有． ③0的平方根、算术平方根均为0．④可以利用平方和开平方的互逆关系求一个非负数的算术平方根和平方根． 5．平方根(或算术平方根)的几个结论(1)式子0a ≥；)0a ≥表示a 0≥．(二)立方根的定义及性质(1)定义：一般地，如果一个数的立方等于a ，那么这个数叫作a 的立方根或三次方根．这就是说，如果3x a =，那么x 叫作a 的立方根．(2)表示方法：a 的立方根(或三次方根)a 为被开方数，3为根指数(根指数3不能省略)a ”或“a 的立方根”． (3)性质：正数的立方根是正数，负数的立方根是负数，0的立方根是0． (4)有关立方根的补充说明和公式：被开方数a 可为正数、零、负数，a 一致；=③3a ==．(5)开立方：求一个数的立方根的运算，叫作开立方．开立方与立方是互为逆运算的关系，负数(在实数范围内)不能开平方，但可以进行开立方运算．如12-的立方为18-，即31128⎛⎫-=- ⎪⎝⎭，反过来，18-的立方根为12-，12=-；3的立方为27，即3327=，反过来，27的立方根为33=．(三)(1)利用计算器求一个非负数的算术平方根时，只需要直接按书写顺序按键即可；求一个非负数的平方根时，则先求出它的算术平方根，再在前面添加符号．(不同计算器有不同的按键顺序)注意：(1)用计算器求一个非负数的负的平方根时，一般先求出算术平方根，然后再求其相反数，即负的平方根．(2)被开方数是分数时应化为小数；被开方数后面的0或小数点后的0比较多时，可先10n =将被开方数化简．(2)利用计算器求一个数的立方根时，只需要直接按书写顷序按键即可，若遇到被开方数是负数时，“－”的输入可按()-，也可以按-．方法技巧归纳方法技巧 (一)平方根与立方根的求法我们知道，平方与开平方、立方与开立方都互为逆运算，根据这种互逆关系，可以求一个数的平方根和立方根．(二)平方根与立方根性质的应用平方根的性质：一个正数有两个平方根，0的平方根是0，负数没有平方根，即只有非负数才有平方根．立方根的性质：一个正数有一个正的立方根，一个负数有一个负的立方根，0的立方根是0．(三)算术平方根与立方根的综合应用 (四)用计算器求算术平方根、立方根 (五)根据一个数的平方根求这个数易混易错辨析易混易错知识12．2a 的算术平方根，a 可以取任意实数；2表示a 的算术平方根的平方，a 只能取非负数．23．误认为负数没有立方根．任何数都有立方根，正数的立方根是正数，负数的立方根是负数，0的立方根是0．易混易错 (一)审题不认真，忽视语言叙述中含有的运算 (二)混淆平方根与算术平方根(三)在求形如“()20x a a =≥”的等式中的x 值时易漏掉x 为负值的情况中考试题研究中考命题规律本讲是中考的热点内容，注重考查对概念、性质和意义的理解，如平方根、算术平方根的概念以及它们的性质和意义，另外对算术平方根非负性的考查也是重中之重，题型以填空题、选择题为主，有时也与其他知识点综合以解答题的形式出现．中考试题 (一)平方根、立方根、算术平方根的概念、性质 (二)算术平方根的非负性第4讲实数知识能力解读知能解读 (一)无理数、实数的定义及分类1．无理数的定义无限不循环小数叫作无理数．点拨：判断一个数是不是无理数，应看这个数是否满足“小数”“无限”和“不循环”这三个条件．2．实数的定义及分类有理数和无理数统称实数，实数分类如下： (1)按定义分类实数⎩⎪⎨⎪⎧有理数⎩⎨⎧⎭⎬⎫整数分数有限小数和无限循环无理数：无限不循环小数(2)按性质分类正有理数⎩⎨⎧正整数正分数正无理数零负有理数⎩⎨⎧负整数负分数负无理数(二)实数的有关性质数的范围从有理数扩充到实数以后，实数范围内的相反数、绝对值的意义和有理数范围内的相反数、绝对值的意义完全一样．(1)实数a 的相反数为a -；0的相反数是其本身；若a 与b 互为相反数，则0a b +=，反之亦然．(2)实数a 的绝对值表示为a ；一个正实数的绝对值是它本身，一个负实数的绝对值是它的相反数，0的绝对值是0，即()()()0000a a a a a a >⎧⎪==⎨⎪-<⎩．(3)实数与数轴上的点是一一对应的，每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都表示一个实数．点拨：已知实数a ，b 在数轴上对应的点分别为A ，B ，则用a ，b 分别表示点A 、点B 到原点的距离；a b -表示点A 到点B 的距离．这是绝对值的几何意义．与规定有理数的大小一样，对于数轴上的两个点，右边的点表示的实数总比左边的点表示的实数大． (三)实数的运算实数和有理数一样，可进行加、减、乘、除、乘方、开方运算；有理数范围内的运算律、运算法则在实数范围内仍适用．交换律：a b b a +=+，ab ba =；结合律：()()a b c a b c ++=++，()()ab c a bc =；分配律：()a b c ab ac +=+． (四)实数的大小比较(1)数轴比较法： (2)代数比较法； (3)差值比较法；(4)商值比较法；(5)倒数比较法：若11a b>，0a >，0b >，则a b <；实数正实数负实数(6)平方比较法：若0a >，0b >，22a b >，则a b >；(7)开方比较法：若0a >，0b >>a b >；(8)估算法：在实数的大小比较中，当遇到无理数时，可以按照所要求的精确度用相应的近似有限小数去代替，再进行比较．方法技巧归纳方法技巧 (一)无理数的识别识别无理数，常常与有理数综合在一起进行辨析，主要把握“无限”和“不循环”两个特点．初中所学的无理数归纳起来有三类：(1)(2)化简后含有π的数，如π5-；(3)特殊结构的无限不循环小数(构造型的无理数)，如0.020020002⋅⋅⋅(相邻两个2之间依次多一个0)． (二)实数大小比较的方法实数的大小比较包括有理数的大小比较和无理数的大小比较，另外还包括有理数与无理数的大小比较．有时综合多个知识点进行考查．常用的方法有特殊值法、平方法等． (三)实数与数轴的关系所有的有理数都可以用数轴上的点来表示，但数轴上的点不全表示有理数，因此有理数与数轴上的点之间不是一一对应关系；所有的无理数都能用数轴上的点来表示，但数轴上的点并不都表示无理数，所以无理数与数轴上的点也不是一一对应关系；数轴上的每一个点都表示实数，且所有的实数都能用数轴上的点来表示，所以实数与数轴上的点是一一对应关系．拓展：有序实数对与坐标平面上的点之间也是一一对应关系． (四)实数的运算当数的范围从有理数扩充到实数以后，实数之间不仅可以进行加、减、乘、除(除数不为0)、乘方运算，而且正数及0可以进行开平方运算，任意一个实效可以进行开立方运算．在进行实数运算时，有理数的运算法则及运算律等同样适用． (五)实数性质的应用 (六)借助数轴化简易混易错辨析易混易错知识1．对无理数的概念理解不透彻，只看表面形式．(1)是有理数； (2)不带根号的不一定不是无理数，如是无理数． 2．误认为有分数线的数就是分数，导致判断失误，如π2不是分数，它是无理数． 3．混淆有理数与数轴和实数与数轴的关系，误认为有理数和数轴上的点也是一一对应的．易混易错混淆无理数与有理数中考试题研究中考命题规律本讲主要考查实数的概念、性质及计算，尤其是实数的大小比较、实数与数轴的关系、实数中的新定义运算及规律探究等，是中考热点，无理数的估算是近几年中考的热点题目．题型以填空题、选择题为主．中考试题(一)实数的大小比较 (二)无理数的估算 (三)无理数的识别 (四)实数的运算(五)实数中的新定义题(六)实数运算中的规律探究问题(探究性考点)。

中考数学一轮复习考点专练实数的相关概念课件

C．带根号的数都是无理数
D．实数包括正实数、负实数
2．(202X·乐山)如果规定收入为正，那么支出为负，收入2元
记作＋2元，支出5元记作(
)
A．5元 B．－5元
C．－3元 D．7元
3．(202X·潜江)下列实数中是无理数的是(
)
A．3.14
B. 9 C. 3
D. 1
7
4．向指定方向变化用正数表示，向指定方向的相反方向变化用负数表示，“体重减少1.5kg”换一种说法可以叙述为“体重增加 _－__1_._5_kg”．
为( )
A．0.10909×105
B．1.0909×104
C．10.909×103
D．109.0报网，中国科学技术大学的潘建伟、陆
朝阳等人构建了一台76个光子100个模式的量子计算机“九章”．它
处理“高斯玻色取样”的速度比目前最快的超级计算机“富岳”快一
百万亿倍．也就是说，超级计算机需要一亿年完成的任务，“九
18．算筹是在珠算发明以前我国独创并且有效的计算工具，为我国古代数学的发展做出了很大的贡献．在算筹计数法中，以“纵式”和“横式”两种方式来表示数字如图：
表示多位数时，个位用纵式，十位用横式，百位用纵式，千位用
横式，以此类推，遇零则置空．示例如图：
6728,6708)，
则
表示的数是 _9_1_6_7_．
1.对于含有计数单位或计量单位并需转换单位的科学记数法，可以利用1亿＝108，1万＝104，1mm＝10－3m，1μm＝10－6m，1nm＝ 10－9m等来表示，能提高解题的效率． 2．用科学记数法表示数时，要注意已知数据是否与表达数据单位一致．
8.(202X·兴安盟)用四舍五入法把某数取近似值为5.2×10－2，

山西中考数学一轮复习考点突破训练第1讲实数课件

解：原式＝8－4＋13 ×6＋1＝8－4＋2＋1＝7.
13.(2019·山西16(1)题5分)计算： 27 ＋(－12 )－2－3tan 60°＋(π－ 2 )0. 解：原式＝3 3 ＋4－3 3 ＋1＝5.
14．(2017·山西16(1)题5分)计算：(－2)3＋(13 )－2 － 8 ·sin 45°.
2．(2020·太原一模)若a＝－20120 ，则|a|的结果为( B ) A.－20120 B．20120 C．－2020 D．2020
3．(2020·郴州)如图，表示互为相反数的两个点是( B )
A．点A与点B B．点A与点D C．点C与点B D．点C与点D
重难点2 科学记数法
【例2】 (2020·河北)已知光速为300000千米/秒，光经过t秒(1≤t≤10)传播的
A．2.2×108 B．2.2×10－8 C．0.22×10－7 D．22×10－9
6．(2020·宜昌)我国渤海、黄海、东海、南海海水含有不少化学元素，其
中铝、锰元素总量均约为8×106 吨．用科学记数法表示铝、锰元素总量的和，
接近值是(
)C
A．8×106 B．16×106
C．1.6×107 D．16×1012
A．2.5×10－5 m B．0.25×10－7 m C．2.5×10－6 m D．25×10－5 m
考点3 实数的大小比较(仅2018年考查，3分)
8．(2018·山西1题3分)下面有理数比较大小，正确的是( B ) A．0＜－2 B．－5＜3 C．－2＜－3 D．1＜－4
考点4 实数的运算(必考)
重难点3 实数的大小比较
【例3】 (2020·温州)数1，0，－23 ，－2中最大的是( A ) A．1 B．0 C．－23 D．－2

中考数学一轮复习：实数

中考数学一轮复习
实数
知识点一数的有关概念
1．数轴规定了原点、正方向、单位长度的直线，叫做数轴．实数和数轴上的点是一一对应的．数轴是数形结合的基础，也是平面直角坐标系的基础． 2．相反数 (1)实数 a 的相反数为－a； (2)a 与 b 互为相反数⇔a＋b＝0； (3)相反数的几何意义：在数轴上，表示相反数的两个点位于原点的两侧，且到原点的距离相等．这两个点关于原点对称； (4)相反数是它本身的数是 0.
【思路点拨】分母相同 → 比较 5－1与1的大小 →
5－1>1 → 结论
【解析】 > ∵ 5>2，∴ 5－1>2－1，∴ 5－1>1， 5－1 1 ∴ > . 2 2
如图，数轴上的两点A、B分别表示实数a、b，则下列四个数中，最大的是( ) 1 C. a 1 D. b
Aቤተ መጻሕፍቲ ባይዱa
B．b
答案：D
类型四实数的运算
3．倒数 1 ，其中 a≠0； a (2)a 和 b 互为倒数⇔ab＝1 ； (3)倒数是它本身的数有 1、－1. 4．绝对值一个正数的绝对值等于它本身；0 的绝对值是 0；负数的绝对值是它的相反数． (1)实数 a 的倒数是 a a＞0 即|a|＝0 a＝0 －a a＜0
【解析】D ∵该小数左起第一个非0数前有6个0，∴n＝－6，－ ∴0.000 002 5＝2.5×10 6.
据某域名统计机构公布的数据显示，截至 2012 年 5 月 21 日，我国“.NET” 域名注册量约为 560 000 个，居全球第三位．将 560 000 用科学记数法表示应为( ) 3 4 A．560×10 B．56×10 5 C．5.6×10 D．0.56×106

2016中考数学实数复习

把握命题趋势，提高复习效率，提升解题能力，打造中考高分！2016年中考数学专题复习第一讲实数【基础知识回顾】一、实数的分类：1．按实数的定义分类：2．按实数的正负分类：【名师提醒】：1．正确理解实数的分类。

如：2π是数，不是数； 722是数，不是数。

2．0既不是数，也不是数，但它是自然数。

二、实数的基本概念和性质1．数轴：规定了、、的直线叫做数轴，和数轴上的点是一一对应的，数轴的作用有、、等。

实数 ⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩正实数零负实数 ⎧⎪⎨⎪⎩正无理数 ⎧⎪⎨⎪⎩负有理数实数 ⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩有理数无理数 ⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩整数 ⎧⎪⎨⎪⎩正整数零 ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭有限小数或无限循环小数负分数 ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭正无理数无限不循环小数2．相反数：只有不同的两个数叫做互为相反数，a 的相反数是，0的相反数是，a 、b 互为相反数⇔3．倒数：实数a 的倒数是，没有倒数，a 、b 互为倒数⇔4．绝对值：在数轴上表示一个数的点离开的距离叫做这个数的绝对值。

因为绝对值表示的是距离，所以一个数的绝对值是数，我们学过的非负数有三个：、、。

【名师提醒】：a+b 的相反数是，a-b 的相反数是,0是唯一一个没有倒数的数，相反数等于本身的数是，倒数等于本身的数是，绝对值等于本身的数是。

三、科学记数法、近似数和有效数字。

1．科学记数法：把一个较大或较小的数写成的形式叫做科学记数法。

其中a 的取值范围是。

2．近似数和有效数字：一般的，将一个数四舍五入后的到的数称为这个数的近似数，这时，从数字起到近似数的最后一位止，中间所有的数字都叫这个数的有效数字。

【名师提醒】：1．科学记数法不仅可以表示较大的数，也可以表示较小的数，其中a 的取值范围一样，n 的取值不同，当表示较大数时，n 的值是原整数数位减一，表示较小的数时，n 是负整数，它的绝对值等于原数中左起第一个非零数字前零的个数（含整数数位上的零）。

中考一轮：实数

`力行教育学科教师辅导讲义学员编号：LXWH01XS 年级：九年级课时数： 3学员姓名：肖胜辅导科目：数学学科教师：朱老师授课类型1v3 授课日期及时段 2015年3月29日13:00-15:00教学内容实数的概念与运算1.实数的有关概念（1）相反数：只有不同的两个数互为相反数。

若a 、b 互为相反数，则。

（2）数轴：规定了、和的直线叫做数轴。

（3）倒数：乘积的两个数互为倒数。

若a （a≠0）的倒数为1a.则。

（4）绝对值：（5）实数和的点一一对应。

2.科学记数法、近似数和有效数字（1）科学记数法：把一个数记成±a×10n 的形式（其中1≤a<10，n 是整数）（2）近似数是指根据精确度取其接近准确数的值。

取近似数的原则是“四舍五入”。

有效数字：从左边第一个不是0的数字起，到精确到的数位止，所有的数字，都叫做这个数字的有效数字。

3.实数的运算顺序：在同一个算式里，先、，然后，最后．有括号时，先算里面，再算括号外。

同级运算从左到右，按顺序进行。

4.实数的大小比较（1）差值比较法：a b -＞0a ⇔＞b ，a b -=0a b ⇔=，a b -＜0a ⇔＜ b（2）商值比较法：若a b 、为两正数，则a b ＞1a ⇔＞b ；1;a a b b=⇔=a b ＜1a ⇔＜b （3）绝对值比较法：若a b 、为两负数，则a ＞b a ⇔＜b a b a b a =⇔=；；＜b a ⇔＞b5．二次根式的性质①20,a ≥=若则(a) ；③ab = (0,0)a b ≥≥ ②2()()a a a a ⎧==⎨-⎩；④(0,0)a a a b b b =≥二:例题讲解1．下列各数中：-1，0，169，2π，1.1010016.0, ,12-, 45cos ,- 60cos , 722,2,π-722.有理数集合{ …}；正数集合{ …}；整数集合{ …}；自然数集合{ …}；分数集合{ …}；无理数集合{ …}；2. 已知(x-2)2+|y-4|+6z -=0，求xyz 的值．．3．已知a 与 b 互为相反数，c 、d 互为倒数，m 的绝对值是2求32122()2()m m a b cd m -+-÷的值4. a 、b 在数轴上的位置如图所示，且a ＞b ，化简a a b b a -+--5.比较大小:(1)35211,(2)155137,(3)103++-与与与3-226.探索规律:31=3，个位数字是3；32=9，个位数字是9；33=27，个位数字是7；34=81，个位数字是1；35=243，个位数字是3；36=729，个位数字是9；…那么37的个位数字是；320的个位数字是；7.计算：（1）1002211()(2001tan30)(2)31621--++-⋅+-（2）20080＋|-1|-3cos30°＋ (21)3；（3）232(2)2sin 60---+.0b a8. 已知△ABC 的三边长分别为a 、b 、c, 且a 、b 、c 满足a 2－6a+9+4|5|0b c -+-=，试判断△ABC 的形状三：【中考演练】1.（08常州）-3的相反数是______,-12的绝对值是_____,2-1=______,2008(1)-= ． 2. 某种零件，标明要求是φ20±0.02 mm （φ表示直径，单位：毫米），经检查，一个零件的直径是19.9 mm ，该零件 .（填“合格” 或“不合格”）3. 下列各数中：－3，14，0，32，364，0.31，227，2π，2.161 161 161…，（－2 005）0是无理数的是___________________________．4．(08湘潭)全世界人民踊跃为四川汶川灾区人民捐款，到6月3日止各地共捐款约423.64亿元，用科学记数法表示捐款数约为__________元．（保留两个有效数字）5．（06北京）若0)1(32=++-n m ，则m n +的值为．6. 2.40万精确到__________位，有效数字有__________个.7．（06荆门）点A 在数轴上表示+2，从A 点沿数轴向左平移3个单位到点B ，则点B 所表示的实数是（）A ．3B ．-1C ．5D ．-1或38．(08扬州)如果□＋2＝0，那么“□”内应填的实数是（）A ．21B ．21-C ．21± D ．2 9．（08梅州）下列各组数中，互为相反数的是（） A ．2和21 B ．-2和－21 C ．-2和|-2| D ．2和21 10．（08无锡）16的算术平方根是（）A.4B.－4C.±4D.1611．若x 的相反数是3，│y│＝5，则x ＋y 的值为（）A ．－8B ．2C ．8或－2D ．－8或212．(08湘潭) 如图，数轴上A 、B 两点所表示的两数的（）A. 和为正数B. 和为负数C. 积为正数D. 积为负数AB O -3字母表示数与整式一：知识点梳理1. 代数式的分类:2. 代数式的有关概念(1)代数式: 用 (加、减、乘、除、乘方、开方)把数或表示数的字母连结而成的式子叫代数式。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实数的有关概念
题组练习一（问题习题化） 1. 下列各数中，最小的数是( )
A ．3-
B ．2-
C ．2)3(-
D ．3102⨯
2. 在实数
，，0，，，﹣1.414，有理数有（）个.
A.1
B.2
C.3
D.4 3.下列运算正确的是（） A.-87×(-83)=7221 B.-2.68-7.42=-10 C.3.77-7.11=-4.66 D.101102
102103
-
<- 4.下列说法正确的是（） A.一个数的绝对值一定比0大
B.一个数的相反数一定比它本身小
C.绝对值等于它本身的数一定是正数
D.最小的正整数是1 5.设n 为正整数，且n ＜
＜n +1，则n 的值为_____.
6.实数a ，b 在数轴上对应的点的位置如图所示，计算||a b -的结果为（）
7. 某市在一次扶贫助残活动中，共捐款5280000元，将5280000用科学记数法表示为 _______________. ◆ 知识梳理
题组练习二（知识网络化）
8. 在实数0 、π 、7
22
、2 、9 - 中，无理数的个数有 .
9.设a n 为正整数n 4的末位数，如a 1＝1，a 2＝6，a 3＝1,a 4＝6. 则a 1＋a 2＋a 3＋…＋a 2013＋a 2014＋a 2015＝ .
10.数轴上实数b 的对应点的位置如图所示．比较大小：2
1
b ＋1________0＞ (用“＜”或“＞”填空）．
11.
估计
1
2
介于 ( ) A ．0.4与0.5之间 B ．0.5与0.6之间 C ．0.6与0.7之间 D ．0.7与0.8之间
12石墨烯是现在世界上最薄的纳米材料，其理论厚度仅是0.00000000034m ,这个数用科学记数法表示正确的是（） A. 3.4×10
9
- B. 0.34×10
9
-
实数的概念；实数与数轴上的
C. 3.4×10
10
- D. 3.4×10
11
-
`13如图，四个有理数在数轴上的对应点M ，P ，N ，Q ，若点M ，N 表示的有理数互为相反数，则图中表示绝对值最小的数的点是（） A. 点M B. 点N C. 点P D. 点Q
14. 如图，M ，N 两点在数轴上表示的数分别是m ，n ，则下列式子中成立的是（）
A ．m+n ＜0
B ． ﹣m ＜﹣n
C ．|m|﹣|n|＞0
D ． 2+m ＜2+n 15.将6.18×10
﹣3
化为小数的是（）
16.如图，正方形ODBC 中，OC=1，OA=OB ，则数轴上点A 表示的数是．
第16题图
17.如图3，已知数轴上的点A 、B 、C 、D 分别表示数-2、1、2、3，则表示3P 应落在线段（）
18.在数轴上表示数－1和2014的两点分别为A 和B ，则A 、B 两点间的距离为( )
A ．2013
B ．2014
C ．2015
D ．2016
19.已知2-x +（y-4）2
=0，求以x ，y 为两边长的等腰三角形的周长？
20. 一组数1,1,2,x,5,y ，…,满足“从第三个数起，每个数都等于它前面的两个数之和”，那么这组
数中y 表示的数为A
A.8
B.9
C.13
D.15
题组练习三（中考考点链接） 21.若（±3）2
=a 2
则a 的值是_______ .
22. 我市2015年参加中考的考生人数约为43400人，将43400用科学记数法表为． 23.
3
2)1(-的立方根是( )
A ．－1
B ．O
C ．1
D ． ±1
24.设边长为3的正方形的对角线长为a ．下列关于a 的四种说法：①a 是无理数；②a 可以用数轴上的一个点来表示；③3＜a ＜4；④a 是18的算术平方根．其中，所有正确说法的序号是（） A ．①④ B ．②③ C ．①②④ D. ①③④
25. 若﹣2x m ﹣
n y 2与3x 4y 2m+n 是同类项，则m ﹣3n 的立方根是______．
26.2210b b -+=，则2
21
||a b a
+-＝ _____________。

答案：
1.A ；
2.D ；
3.A ；
4.A ；
5.8；
6. b a -；
7. 5.28×106；
8. 2个； 9.6652； 10. ＞； 11.； C 12.C ； 13.C ； 14.D ； 15. 0.00618； 16.﹣；
17. ．OB 上； 18.C ； 19.10； 20. A
21. 4.34×104 22. 2.5×103
；23.C ；24.C ；25.2；
26.2(1)0b -=
∴23101
a a
b ⎧-+=⎨=⎩，由2
310a a -+=，得1a a +＝3，两边平方，得2
21a a
+＝7，∴原式＝7－1＝6。