高中奥林匹克物理竞赛专题讲座第5部分 振动和波
物理竞赛讲义十四振动、波

当振源按简谐振动的规律振动时,在媒质中所形成的波称为简谐波。
任何复杂形式的机械波,都是由各种不同频率的简谐波叠加而成的。
简谐波的波动方程和它的解——波函数 在播的传播方向上,平衡位置为x 的质点在t 时刻偏离平衡位置的位移的函数形式——波函数y (x 、t )。
对于平面简谐波的波函数,可以表述为下面三种形式:])(2c o s [])(2c o s [])(c o s [000),(φλνπφλπφϖ+±=+±=+±=xt A x Tt A v x t A y t x 机械波是机械振动在媒质中的传播,而媒质中的每一个质点都在做受迫振动,因而对这些物理量应当分别从波动和振动两个方面去理解。
在坐标系建立后,波函数y (x 、t )描述的是:在播的传播方向上,平衡位置距离坐标原点为x 处的媒质质点,在t 时刻偏离平衡位置的位移。
波(振)幅A ,从波动角度讲,描述机械波的强度,对于横波,是波峰的高度或是波谷的深度;对于纵波,是从平衡位置到疏部(或密部)中心的距离。
从振动角度讲,是媒质质点做受迫振动的振幅。
在不考虑能量损失的情况下,平面简谐波的波幅由振源决定。
波长λ,从波动角度讲,在同一传播方向上,两个相邻的具有相同振动状态(位相相差2π)的媒质质点的平衡位置之间的距离,从振动角度讲,媒质中的某一质点在完成一次全振动时,这个质点的振动状态在波传播方向上传播的距离。
当波源相对媒质静止不动时,波长由媒质和振源的频率决定。
周期T ,从波动角度讲,媒质中的某一质点的振动状态在波传播方向上传播一个波长的距离所用的时间,从振动角度讲,媒质中的某一质点完成一次全振动所用的时间。
频率ν,从波动角度讲,单位时间通过媒质中的某一质点的完整波的个数,从振动角度讲,媒质中的某一质点在单位时间内完成的全振动的个数。
圆频率ω,从波动角度讲,2π秒内通过媒质中的某一质点的完整波的个数,从振动角度讲,媒质中的某一质点在2π秒内完成的全振动的个数。
高中物理奥林匹克竞赛专题振动和波(共113张PPT)

——简谐振动的 运动学方程
也可用复数表示:x(t)Aeit Aeit
计算结果一般取实部
x,q
x,q
t
t
6
9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/62021/9/6Monday, September 06, 2021 10、阅读一切好书如同和过去最杰出的人谈话。2021/9/62021/9/62021/9/69/6/2021 6:53:21 AM 11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/62021/9/62021/9/6Sep-216-Sep-21 12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/62021/9/62021/9/6Monday, September 06, 2021
You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
8
2. 简谐振动的速度、加速度
由xA cots(), 得
x d d x t A s itn ) ( A c( o t s 2 ) a x d d tx 2 A c o t s) ( 2 A c o t s ()
(B)1:2 ;
(C) 3:1 ; 正确答案:(C)
(D) 2:1。
简谐振动的总能量为:E
Ek
Ep
1k 2
A2
当物体的位移为振幅的一半时
其势能为:
Ep
1kx2 1kA2
2
2 2
高中物理竞赛 振动和波共55页

•
46、寓形宇内复几时,曷不委心任去 留。•ຫໍສະໝຸດ 47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
高二物理竞赛振动和波动课件

可以求得波在两介质分界面处折射波的方向问题, 即得到折射定律。
波的叠加原理
☆
几列波可以保持各自的特点通过同一媒质, 好像没有其他波一样;
在它们相重叠的区域内, 每一点的振动都是各个波单独 在该点产生的振动的矢量和。
波的干涉
☆
波的干涉现象
由频率相同、振动方向相同、相位相同 或相位差恒定的两个波源所发出的波,
在空间相遇,出现某些点振动始终加强, 某些点振动始终减弱或完全抵消
的现象称为波的干涉现象。
能产生干涉现象的波叫做相干波, 相应的波源叫做相干波源。
波的相干条件
频率相同、 振动方向相同、 相位相同或相位差恒定
反映了能量的传播过程
能量密度 单位体积媒质的波动能量
☆
w E 2 A2 sin 2 t x
V
u
在一个周期内的平均值 w 1 T wdt 1 2 A2
叫做平均能量密度
T0
2
平均能流密度
单位时间通过垂直于传播方向的单位面积的平均能流
I u 2 A2 / 2 A2
能流密度是矢量,方向与波速方向相同, 它的大小表示波的强度。
y Acost x / u Acos2 t / T x / Acos t 2 x /
“-”表示波沿x 轴正方向传播;“十”表示波x沿 轴负方向传播
波函数的物理意义
☆
它描述了波线上所有质点 离开自己平衡位置的位移随时间的变化规律。
y(t t, x ut) y(t, x) 表示了波的传播。
波长 同一波线上相位差为 2 的两相邻质点之间的距离,
即一个完整波形的长度。它反映波在空间上的周期性。
高二物理竞赛振动和波动课件

了解波的衍射。
比位移的相位超前 。
加速度的相位比速度的相位超前
,
3.掌握简谐振动的基本特征,
单位时间内振动的次数称为频率。
自由运动的物体所组成的振动系统,
这样的振动称为简谐振动。
绳的上端固定,这样的系统叫做单摆。
10.理解机械波产生的条件。
了解波的能量传播特征及能流、能流密度的概念。
,
并理解其物理意义。
M mgLsin 7.了解不同频、相互垂直的两个简谐振动的合成结果。
能够作简谐振动的物体,称为谐振子。 绳的上端固定,这样的系统叫做单摆。
ft
另一端连结一个可以视为质点的
m
理解惠更斯原理和波的叠加原理。
(1)同方向、同频率的两简谐振动的合成,仍为简谐振动。
加速度的相位比速度的相位超前
圆频率 k / m 周期 T 2 / 2 m / k
单摆
一个可以看做质点的小球系于不可伸长、 质量可以忽略不计的细绳的下端,
绳的上端固定,这样的系统叫做单摆。
如果物体振动的位移随时间按正(余)弦函数规律变化 了解波的衍射。 单位时间内振动的次数称为频率。
L T
加速度的相位比速度的相位超前
☆
能够作简谐振动的物体,称为谐振子。
这个物体连同对它施加回复力的物体组成振动系统。
弹簧振子
k
f
一个质量可忽略不计的弹簧一端固定,
m
另一端连结一个可以视为质点的 自由运动的物体所组成的振动系统, 便是一个弹簧振子。
x
O
x
f
d2x kx ma m
m 2 x
dt2
d2 dt
x
2
高中物理竞赛 振动和波55页PPT

56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。 60、迢迢新秋夕,亭亭月将圆。
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
高中物理竞赛讲座:第五章波动1

二. 机械波的形成
0 t=0 4 8 16 12 20 · · · · · · · · · ·· · · · ·· · · ·· · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·t = T/4 · 24
· · · t = T/2 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · t = 3T/4 · · · · · · t=T · · · · · · · · · · · · · · · · · · · · · ·
3. 波长 :
u
波线上相邻的振动状态相同的两质元间的距离。 x
uT
由波源和媒质共同决定。 波长反映波的“空间周期”。
四、波动的传播特征:
· · · · · · · · · · ·· · · · · ·· · · · · · · t = T/4 · · · · · · · · · · · · · · · · · · · · · · · · · · · · t = T/2 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · t = 3T/4 · · · · · t=T · · · · · · · · · · · · · · · · · · · · · · ·
0 4 8
12
16
24
20
t=0
§5-2
一、波的几何描述
波的基本概念
(1)波面:由振动相位相同的点所组成的面
高中物理竞赛机械振动和机械波知识点讲解

高中物理竞赛机械振动和机械波知识点讲解知识点击1.简谐运动的描述和基本模型⑴简谐振动的描述:当一质点,或一物体的质心偏离其平衡位置x ,且其所受合力F 满足(0)F kx k =->,故得2ka x x m ω=-=-,k mω= 则该物体将在其平衡位置附近作简谐振动。
⑵简谐运动的能量:一个弹簧振子的能量由振子的动能和弹簧的弹性势能构成,即222111222E m kx kA υ=+=∑⑶简谐运动的周期:如果能证明一个物体受的合外力F k x =-∑,那么这个物体一定做简谐运动,而且振动的周期22mT kππω==,式中m 是振动物体的质量。
⑷弹簧振子:恒力对弹簧振子的作用:只要m 和k 都相同,则弹簧振子的振动周期T 就是相同的,这就是说,一个振动方向上的恒力一般不会改变振动的周期。
多振子系统:如果在一个振动系统中有不止一个振子,那么我们一般要找振动系统的等效质量。
悬点不固定的弹簧振子:如果弹簧振子是有加速度的,那么在研究振子的运动时应加上惯性力.⑸单摆及等效摆:单摆的运动在摆角小于50时可近似地看做是一个简谐运动,振动的周期为2lT gπ=,在一些“异型单摆”中,l g 和的含义及值会发生变化。
(6)同方向、同频率简谐振动的合成:若有两个同方向的简谐振动,它们的圆频率都是ω,振幅分别为A 1和A 2,初相分别为1ϕ和2ϕ,则它们的运动学方程分别为111cos()x A t ωϕ=+ 222cos()x A t ωϕ=+因振动是同方向的,所以这两个简谐振动在任一时刻的合位移x 仍应在同一直线上,而且等于这两个分振动位移的代数和,即12x x x =+由旋转矢量法,可求得合振动的运动学方程为cos()x A t ωϕ=+这表明,合振动仍是简谐振动,它的圆频率与分振动的圆频率相同,而其合振幅为221212212cos()A A A A A ϕϕ=++-合振动的初相满足11221122sin sin tan cos cos A A A A ϕϕϕϕϕ+=+2.机械波:(1)机械波的描述:如果有一列波沿x 方向传播,振源的振动方程为y=Acos ωt ,波的传播速度为υ,那么在离振源x 远处一个质点的振动方程便是cos ()x y A t ωυ⎡⎤=-⎢⎥⎣⎦,在此方程中有两个自变量:t 和x ,当t 不变时,这个方程描写某一时刻波上各点相对平衡位置的位移;当x 不变时,这个方程就是波中某一点的振动方程.(2)简谐波的波动方程:简谐振动在均匀、无吸收的弹性介质中传播所形成的波叫做平面简谐波。
物理竞赛--振动和波复习
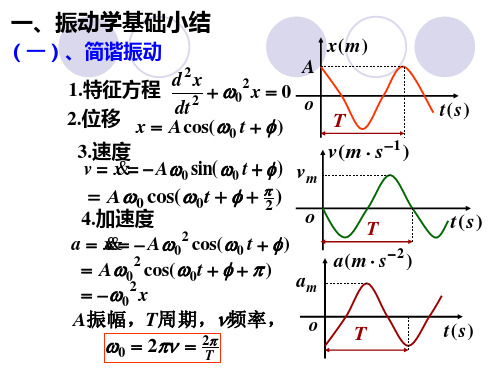
1 cos 0
3
cos
2
1(m)
tan 0
Asin 0 A cos0
3
0 3或4 3 据题意 0 3
27
[解法二] 因为x x1 x2 cos t 3 cos( t 2)
x
12
3
2
1 cos t
12 32123来自32sint
2 1 cos t 3 sin t
0
作t=0时刻矢量图
AArr22
ArAr
20
x2
100
rr AA11
x
x1
x
A A12 A22 2 A1 A2 cos( 20 10 )
tan 0
A s in 0 Acos 0
A1 sin10 A1 cos 10
A2 sin20 A2 cos 20
注意:
Asin0 0
Acos0
0 (0,
xB 5
5cm
2;
5 4
5
Acos(
2
)
Asin
振动方程为: x 5
2
cos(
4
t
5 4
)cm
v x
t 6s
t 4s
5
2
4
sin(4
t
5 4
)
vA v0 5
2
4
sin
5 4
A
B
o
x
5 cm s1
4
t0
t 2s
习题集p50题2. 如图为用余弦函数表示的一质
点作谐振动曲线, 振动圆频率为
E1212kkAx22mEp1022ckoA12s2k2cA(o2s02t(120mt)02 A) 2
高中物理竞赛讲座:第五章波动3

S
u vB u v B u s
频率升高 若观察者以速度 v B离开波源运动 频率降低。
vB
u
3)观察者不动,波源以速度
vs 向着观察者运动
s
s'
vsT
'
A
S
vs
' vsT (u vs )T
波源趋近观察者
vsT
u u ' ( u v s )T
§ 5-7
一、驻波
驻波
1。概念 :一对振幅相同、在同一条直线上沿反向传播的 相干波叠加而形成的波。 2。驻波方程 两波的波动方程分别为:
波腹
波节
3。驻波特征分析
(1).各点振幅
波腹(A 2 A)位置:
随x作周期性变化
波节(A 0)位置:
相邻波节(或波腹)的距离:
波腹
波节
(2).相邻两波节之间的质点振动相位相同,波节两侧质点 的振动相位相反。 (3).能量只在两波节间的波腹与波节转移,而无能量的 定向传播。 (4).形式象波,本质却是介质的一种特殊振动状态。
多普勒效应 (Doppler effect)
人耳相对于媒质的运动速度。
vs ——波源相对于媒质的运动速度。
波源的频率 s 波速 u
观察者接收到的频率
波长
1) 波源和观察者都不动的情况 频率不变
2)波源不动,观察者以速度
vB向着波源运动
波源远离观察者
(4) 相对于媒质波源和观察者同时运动
当波源和观察者彼此趋近时
当波源和观察者彼此离开时
u VB u VB s u Vs u VB s u Vs
高中物理竞赛讲座:第五章波动2

通过垂直于波的传播方向的单位面积的平均能流。
P 1 I u 2 2u s 2
—单位:焦耳/秒米2
波动在无吸收的、均匀无限大介质中传播,
1、平面波:A保持不变。
2、球面波:A与r成反比。 证明:1、
无吸收, P 1 P 2
1 2 2 A1 us 2 1 2 2 P2 us A2 us 2 P 1 us
波动(体元)
(非孤立系统) 体元在不断接受或放出 能量
x) u
振动(系统) (孤立系统)
(5)能量密度:单位体积内的能量
W / V A22 sin2 (t x / u)
(6)平均能量密度:能量密度在一个周期内的平均值
T 1 T 0
2 2 1 A dt A {[ 0 sin (t x / u)dt] / T } 2
[例] 已知:T 4S
Y(cm) 0.2
u
t2
p
x(cm)
求:P点的振动方程 解:yP A cos (t p) o
2 方法一: T 2
t0
t p
ห้องสมุดไป่ตู้
2
2
p
2
方法二:由 t 0波形图可知: p
[例] 已知:波动T 2 S, t 0时刻波形如图示 求:( 1 )波动方程, (2) OB长度。
二、应用
1、用惠更斯原理确定下一时刻波的波前 (1)平面波
t + Δt 时刻的波面
. . . . . . .
.
.
子波波源
t 时刻的波面
(2)球面波
t + Δt 时刻
第五讲 振动与波
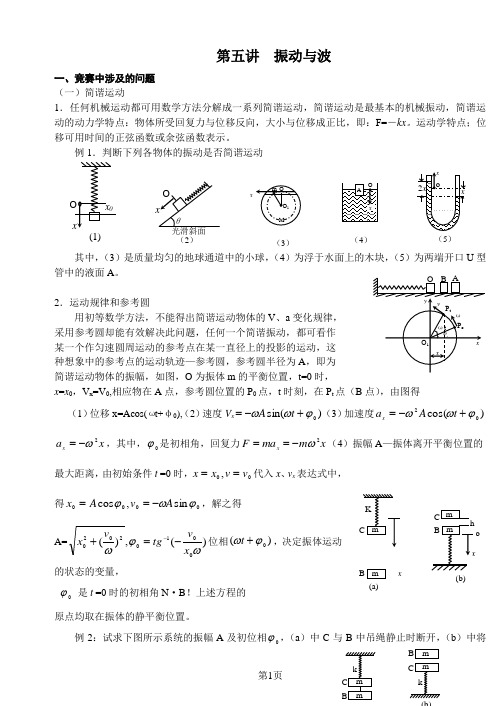
第五讲 振动与波一、竞赛中涉及的问题 (一)简谐运动1.任何机械运动都可用数学方法分解成一系列简谐运动,简谐运动是最基本的机械振动,简谐运动的动力学特点:物体所受回复力与位移反向,大小与位移成正比,即:F=-kx 。
运动学特点;位移可用时间的正弦函数或余弦函数表示。
例1.判断下列各物体的振动是否简谐运动其中,(3)是质量均匀的地球通道中的小球,(4)为浮于水面上的木块,(5)为两端开口U 型管中的液面A 。
2.运动规律和参考圆用初等数学方法,不能得出简谐运动物体的V 、a 变化规律,采用参考圆却能有效解决此问题,任何一个简谐振动,都可看作 某一个作匀速圆周运动的参考点在某一直径上的投影的运动,这 种想象中的参考点的运动轨迹—参考圆,参考圆半径为A ,即为 简谐运动物体的振幅,如图,O 为振体m 的平衡位置,t=0时,x =x 0,V x =V 0,相应物在A 点,参考圆位置的P 0点,t 时刻,在P t 点(B 点),由图得(1)位移x=Acos(ωt +φ0),(2)速度V x )sin(0ϕωω+-=t A (3)加速度)cos(02ϕωω+-=t A a x x a x 2ω-=,其中,0ϕ是初相角,回复力x m ma F x 2ω-==(4)振幅A —振体离开平衡位置的最大距离,由初始条件t =0时,00,v v x x ==代入x 、v x 表达式中,得0000sin ,cos ϕωϕA v A x -==,解之得A=)(,)(00102020ωϕωx v tg v x -=+-位相)(0ϕω+t ,决定振体运动的状态的变量,0ϕ 是t =0时的初相角N ·B !上述方程的 原点均取在振体的静平衡位置。
例2:试求下图所示系统的振幅A 及初位相0ϕ,(a )中C 与B 中吊绳静止时断开,(b )中将(1)(2)(4)(a)xo (b)(3)(5)物B 无初速地放在物C 上。
3.简谐运动的圆频率,频率与周期(1)圆频率 即x 、v x 、a x 表达式中的ω ,由F=-kx =m k x m =∴-ωω,2(2)周期T ,T=k m πωπ2/2=。
高中物理竞赛讲座讲稿子:第五部分《振动和波》

第五部分 振动和波第一讲 基本知识介绍《振动和波》的竞赛考纲和高考要求有很大的不同,必须做一些相对详细的补充。
一、简谐运动1、简谐运动定义:∑F = -k x①凡是所受合力和位移满足①式的质点,均可称之为谐振子,如弹簧振子、小角度单摆等。
谐振子的加速度:a= -mk x2、简谐运动的方程回避高等数学工具,我们可以将简谐运动看成匀速圆周运动在某一条直线上的投影运动(以下均看在x 方向的投影),圆周运动的半径即为简谐运动的振幅A 。
依据:∑F x = -m ω2Acos θ= -m ω2x对于一个给定的匀速圆周运动,m 、ω是恒定不变的,可以令:m ω2= k这样,以上两式就符合了简谐运动的定义式①。
所以,x方向的位移、速度、加速度就是简谐运动的相关规律。
从图1不难得出——位移方程:x= Acos(ωt + φ) ②速度方程:v= -ωAsin(ωt +φ) ③加速度方程:a = -ω2A cos(ωt +φ) ④ 相关名词:(ωt +φ)称相位,φ称初相。
运动学参量的相互关系:a = -ω2xA = 202)v (x ω+ tg φ= -x v ω 3、简谐运动的合成a 、同方向、同频率振动合成。
两个振动x 1 = A 1cos(ωt +φ1)和x 2 = A 2cos(ωt +φ2) 合成,可令合振动x = Acos(ωt +φ) ,由于x = x 1 + x 2 ,解得A = )cos(A A 2A A 12212221φ-φ++ ,φ= arctg 22112211cos A cos A sin A sin A φ+φφ+φ显然,当φ2-φ1 = 2k π时(k = 0,±1,±2,…),合振幅A 最大,当φ2-φ1 = (2k + 1)π时(k = 0,±1,±2,…),合振幅最小。
b 、方向垂直、同频率振动合成。
当质点同时参与两个垂直的振动x = A 1cos(ωt + φ1)和y = A 2cos(ωt + φ2)时,这两个振动方程事实上已经构成了质点在二维空间运动的轨迹参数方程,消去参数t 后,得一般形式的轨迹方程为212A x +222A y -221A A xy cos(φ2-φ1) = sin 2(φ2-φ1) 显然,当φ2-φ1 = 2k π时(k = 0,±1,±2,…),有y = 12A A x ,轨迹为直线,合运动仍为简谐运动;当φ2-φ1 = (2k + 1)π时(k = 0,±1,±2,…),有212A x +222A y = 1 ,轨迹为椭圆,合运动不再是简谐运动;当φ2-φ1取其它值,轨迹将更为复杂,称“李萨如图形”,不是简谐运动。
高中物理竞赛普通物理学专题第5章机械波第三节波的能量和声强

单位为分贝(dB) 人耳对响度的主观感觉由声强级和频率共同决定
12
设 x=0 时, A=A0
c ln A0
A A0e x
I I0e 2x
10
*四、声压、声强和声强级
声压:介质中有声波传播时的压力与无声波时的 静压力之间的压差.
平面简谐波,声压振幅为
声强:声波的能流密度。
频率越高越容易获得较大的声压和声强 引起人听觉的声波有频率范围和声强范围
11
通常把最低声强作为测定声强的标准,用I0表示. 声强级
势能亦为零;此时动能等于零。
2.能量密度 单位体积介质中所具有的波的能量。
5
平均能量密度: 一个周期内能量密度的平均值。
w 1 A2 2
2
6
二、波的能流和能流密度
1.能流:单位时间内通过介质中某一 截面的能量。
u
S
u
平均能流:在一个周期内能流的平均值。
2. 能流密度(波的强度): 通过垂直于波动传播方向的单位面积的平均能量
单位:瓦·米-2
7
3.平面波和球面波的振幅 在均匀不吸收能量的媒质中传播的平面波在行进
方向上振幅不变,球面波的振幅与离波源的距离成 反比。
对平面波:
在一个周期T内通过S1和S2面的能量应该相等
u
S
S
所以,平面波振幅相等。
8
对球面波:
r2
r1
所以振幅与离波源的距离成反比。如果距波源单位 距离的振幅为A则距波源r 处的振幅为A/r
由于振动的相位随距离的增加而落后的关系, 与平面波类似,球面简谐波的波函数:
9
三、波的吸收
波在实际介质中,由于波动能量总有一部分会被 介质吸收,波的机械能不断减少,波强亦逐渐减弱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五部分 振动和波第一讲 基本知识介绍一、简谐运动1、简谐运动定义:∑F= -k x①凡是所受合力和位移满足①式的质点,均可称之为谐振子,如弹簧振子、小角度单摆等。
谐振子的加速度:a= -mk x2、简谐运动的方程回避高等数学工具,我们可以将简谐运动看成匀速圆周运动在某一条直线上的投影运动(以下均看在x 方向的投影),圆周运动的半径即为简谐运动的振幅A 。
依据:∑Fx = -m ω2Acos θ= -m ω2x对于一个给定的匀速圆周运动,m 、ω是恒定不变的,可以令:m ω2 = k这样,以上两式就符合了简谐运动的定义式①。
所以,x 方向的位移、速度、加速度就是简谐运动的相关规律。
从图1不难得出——位移方程:x= Acos(ωt + φ) ②速度方程:v= -ωAsin(ωt +φ) ③加速度方程:a= -ω2A cos(ωt +φ) ④ 相关名词:(ωt +φ)称相位,φ称初相。
运动学参量的相互关系:a= -ω2x A =2020)v (x ω+ , tg φ= -00x vω 3、简谐运动的合成a 、同方向、同频率振动合成。
两个振动x 1 = A 1cos(ωt +φ1)和x 2 = A 2cos(ωt +φ2) 合成,可令合振动x = Acos(ωt +φ) ,由于x = x 1 + x 2 ,解得A = )cos(A A 2A A 12212221φ-φ++ ,φ= arctg22112211cos A cos A sin A sin A φ+φφ+φ 显然,当φ2-φ1 = 2k π时(k = 0,±1,±2,…),合振幅A 最大,当φ2-φ1 = (2k + 1)π时(k = 0,±1,±2,…),合振幅最小。
b 、方向垂直、同频率振动合成。
当质点同时参与两个垂直的振动x = A 1cos(ωt + φ1)和y = A 2cos(ωt + φ2)时,这两个振动方程事实上已经构成了质点在二维空间运动的轨迹参数方程,消去参数t 后,得一般形式的轨迹方程为212A x +222A y -221A A xy cos(φ2-φ1) = sin 2(φ2-φ1)当φ2-φ1 = 2k π时(k = 0,±1,±2,…),有y =12A A x ,轨迹为直线,合运动仍为简谐运动; 当φ2-φ1 = (2k + 1)π时(k = 0,±1,±2,…),有212A x +222A y = 1 ,轨迹为椭圆,合运动不再是简谐运动;当φ2-φ1取其它值,轨迹将更为复杂,称“李萨如图形”,不是简谐运动。
c 、同方向、同振幅、频率相近的振动合成。
令x 1 = Acos(ω1t + φ)和x 2 = Acos(ω2t + φ) ,由于合运动x = x 1 + x 2 ,得:x =(2Acos 212ω-ωt )cos (212ω+ωt +φ)。
合运动是振动,但不是简谐运动,称为角频率为212ω+ω的“拍”现象。
4、简谐运动的周期 由②式得:ω=mk,而圆周运动的角速度和简谐运动的角频率是一致的,所以T = 2πkm⑤ 5、简谐运动的能量一个做简谐运动的振子的能量由动能和势能构成,即∑E =21mv 2 + 21kx 2 = 21kA 2 注意:振子的势能是由(回复力系数)k 和(相对平衡位置位移)x 决定的一个抽象的概念,而不是具体地指重力势能或弹性势能。
当我们计量了振子的抽象势能后,其它的具体势能不能再做重复计量。
6、阻尼振动、受迫振动和共振二、机械波1、波的产生和传播 产生的过程和条件;传播的性质,相关参量(决定参量的物理因素)2、机械波的描述a 、波动图象。
和振动图象的联系b 、波动方程如果一列简谐波沿x 方向传播,振源的振动方程为y = Acos (ωt + φ),波的传播速度为v ,那么在离振源x 处一个振动质点的振动方程便是y = Acos 〔ωt + φ -λx·2π〕= Acos 〔ω(t - vx )+ φ〕 这个方程展示的是一个复变函数。
对任意一个时刻t ,都有一个y (x )的正弦函数,在x-y 坐标下可以描绘出一个瞬时波形。
所以,称y = Acos 〔ω(t -vx)+ φ〕为波动方程。
3、波的干涉a 、波的叠加。
几列波在同一介质种传播时,能独立的维持它们的各自形态传播,在相遇的区域则遵从矢量叠加(包括位移、速度和加速度的叠加)。
b 、波的干涉。
两列波频率相同、相位差恒定时,在同一介质中的叠加将形成一种特殊形态:振动加强的区域和振动削弱的区域稳定分布且彼此隔开。
我们可以用波程差的方法来讨论干涉的定量规律。
如图2所示,我们用S 1和S 2表示两个波源,P 表示空间任意一点。
当振源的振动方向相同时,令振源S 1的振动方程为y 1 = A 1cos ωt ,振源S 1的振动方程为y 2 = A 2cos ωt ,则在空间P 点(距S 1为r 1 ,距S 2为r 2),两振源引起的分振动分别是y 1′= A 1cos 〔ω(t − vr1)〕y 2′= A 2cos 〔ω(t − vr 2)〕 P 点便出现两个频率相同、初相不同的振动叠加问题(φ1 = v r 1ω ,φ2 =v r 2ω),且初相差Δφ= vω(r 2 – r 1)。
根据前面已经做过的讨论,有 r 2 − r 1 = k λ时(k = 0,±1,±2,…),P 点振动加强,振幅为A 1 + A 2 ;r 2 − r 1 =(2k − 1)2λ时(k = 0,±1,±2,…),P 点振动削弱,振幅为│A 1-A 2│。
4、波的反射、折射和衍射 5、多普勒效应当波源或者接受者相对与波的传播介质运动时,接收者会发现波的频率发生变化。
多普勒效应的定量讨论可以分为以下三种情况(在讨论中注意:波源的发波频率f 和波相对介质的传播速度v 是恒定不变的)——a 、只有接收者相对介质运动(如图3所示) 设接收者以速度v 1正对静止的波源运动。
如果接收者静止在A 点,他单位时间接收的波的个数为f ,当他迎着波源运动时,设其在单位时间到达B 点,则AB = v 1 ,、 在从A 运动到B 的过程中,接收者事实上“提前”多接收到了n 个波 n =λAB= f /v v 1= vf v 1 显然,在单位时间内,接收者接收到的总的波的数目为:f + n =v v v 1+ f ,这就是接收者发现的频率f 1 。
即f 1 = v v v 1+ f 显然,如果v 1背离波源运动,只要将上式中的v 1代入负值即可。
如果v 1的方向不是正对S ,只要将v 1出正对的分量即可。
b 、只有波源相对介质运动(如图4所示) 设波源以速度v 2正对静止的接收者运动。
如果波源S 不动,在单位时间内,接收者在A 点应接收f 个波,故S 到A 的距离:S A = f λ在单位时间内,S 运动至S ′,即S S '= v 2 。
由于波源的运动,事实造成了S 到A 的f 个波被压缩在了S ′到A 的空间里,波长将变短,新的波长λ′=fAS '= f S S S A '-= f v f 2-λ= f v v 2-而每个波在介质中的传播速度仍为v ,故“被压缩”的波(A 接收到的波)的频率变为f 2 =λ'v = 2v v v - f 当v 2背离接收者,或有一定夹角的讨论,类似a 情形。
c 、当接收者和波源均相对传播介质运动当接收者正对波源以速度v 1(相对介质速度)运动,波源也正对接收者以速度v 2(相对介质速度)运动,我们的讨论可以在b 情形的过程上延续…f 3 = v v v 1+ f 2 = 21v v v v -+ f 关于速度方向改变的问题,讨论类似a 情形。
6、声波a 、乐音和噪音b 、声音的三要素:音调、响度和音品c 、声音的共鸣第二讲 重要模型与专题一、简谐运动的证明与周期计算物理情形:如图5所示,将一粗细均匀、两边开口的U 型管固定,其中装有一定量的水银,汞柱总长为L 。
当水银受到一个初始的扰动后,开始在管中振动。
忽略管壁对汞的阻力,试证明汞柱做简谐运动,并求其周期。
模型分析:对简谐运动的证明,只要以汞柱为对象,看它的回复力与位移关系是否满足定义式①,值得注意的是,回复力∑F系指振动方向上的合力(而非整体合力)。
当简谐运动被证明后,回复力系数k 就有了,求周期就是顺理成章的事。
本题中,可设汞柱两端偏离平衡位置的瞬时位移为x 、水银密度为ρ、U 型管横截面积为S ,则次瞬时的回复力ΣF = ρg2xS =L mg 2x 。
由于L 、m 为固定值,可令:Lmg2 = k ,而且ΣF 与x 的方向相反,故汞柱做简谐运动。
周期T = 2πk m= 2πg 2L。
答:汞柱的周期为2πg2L。
学生活动:如图6所示,两个相同的柱形滚轮平行、登高、水平放置,绕各自的轴线等角速、反方向地转动,在滚轮上覆盖一块均质的木板。
已知两滚轮轴线的距离为L 、滚轮与木板之间的动摩擦因素为μ、木板的质量为m ,且木板放置时,重心不在两滚轮的正中央。
试证明木板做简谐运动,并求木板运动的周期。
思路提示:找平衡位置(木板重心在两滚轮中央处)→力矩平衡和ΣF 6= 0结合求两处弹力→求摩擦力合力… 答案:木板运动周期为2πg2Lμ 。
巩固应用:如图7所示,三根长度均为L = 2.00m 地质量均匀直杆,构成一正三角形框架ABC ,C 点悬挂在一光滑水平轴上,整个框架可绕转轴转动。
杆AB 是一导轨,一电动松鼠可在导轨上运动。
现观察到松鼠正在导轨上运动,而框架却静止不动,试讨论松鼠的运动是一种什么样的运动。
解说:由于框架静止不动,松鼠在竖直方向必平衡,即:松鼠所受框架支持力等于松鼠重力。
设松鼠的质量为m 即:N = mg ①再回到框架,其静止平衡必满足框架所受合力矩为零。
以C 点为转轴,形成力矩的只有松鼠的压力N 、和松鼠可能加速的静摩擦力f ,它们合力矩为零,即:M N = M f现考查松鼠在框架上的某个一般位置(如图7,设它在导轨方向上距C 点为x ),上式即成:N ·x = f ·Lsin60° ②解①②两式可得:f = L3mg2x ,且f 的方向水平向左。
根据牛顿第三定律,这个力就是松鼠在导轨方向上的合力。
如果我们以C 在导轨上的投影点为参考点,x 就是松鼠的瞬时位移。
再考虑到合力与位移的方向因素,松鼠的合力与位移满足关系——∑F= -k x其中k =L3mg 2 ,对于这个系统而言,k 是固定不变的。
显然这就是简谐运动的定义式。
答案:松鼠做简谐运动。
