第十四章复习题
第十四章 整式的乘法与因式分解复习题--解答题(含解析)

人教版八年级上14章整式的乘除与分解因式复习题(解答题)一.解答题1.(2018秋•雨花区校级月考)规定两数a,b之间的一种运算,记作(a,b),如果a c=b,则(a,b)=c.我们叫(a,b)为“雅对”.例如:因为23=8,所以(2,8)=3.我们还可以利用“雅对”定义说明等式(3,3)+(3,5)=(3,15)成立.证明如下:设(3,3)=m,(3,5)=n,则3m=3,3n=5,故3m⋅3n=3m+n=3×5=15,则(3,15)=m+n,即(3,3)+(3,5)=(3,15).(1)根据上述规定,填空:(2,4)=;(5,1)=;(3,27)=.(2)计算(5,2)+(5,7)=,并说明理由.(3)利用“雅对”定义证明:(2n,3n)=(2,3),对于任意自然数n都成立.2.(2018春•苏州期中)规定a*b=2a×2b,求:(1)求2*3;(2)若2*(x+1)=16,求x的值.3.(2018春•开福区校级期中)阅读材料:n个相同的因数a相乘,可记为a n,如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若a n=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为log a b(即log a b=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).根据以上材料,解决下列问题:(1)计算以下各对数的值:log24=,log216=,log264=;(2)根据(1)中的计算结果,写出log24,log216,log264满足的关系式;(3)根据(2)中的关系式及4,16,64满足的关系式猜想一般性结论:log a M+log a N=(a>0且a≠1,M>0,N>0);(4)根据幂的运算法则说明(3)中一般性结论的正确性.4.(2018春•苏州期中)若33×9m+4÷272m﹣1的值为729,求m的值.5.(2018春•利津县期末)若x m=16,x n=128,求x2m﹣n的值.6.(2018秋•安溪县期中)规定两数a,b之间的一种运算,记作(a,b):如果a c=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.(1)根据上述规定,填空:(5,125)=,(﹣2,4)=,(﹣2,﹣8)=;(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4),他给出了如下的证明:设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n∴3x=4,即(3,4)=x,∴(3n,4n)=(3,4).请你尝试运用上述这种方法说明下面这个等式成立的理由.(4,5)+(4,6)=(4,30)7.(2018秋•松北区校级期中)(1)计算:﹣82018×(﹣0.125)2018(2)已知a m=6,a n=2,求a2m+3n的值.8.(2018•安庆一模)特殊两位数乘法的速算﹣﹣如果两个两位数的十位数字相同,个位数字相加为10,那么能立即说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.如:47×43=2021,61×69=4209.(1)请你直接写出83×87的值;(2)设这两个两位数的十位数字为x(x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz.(3)99991×99999=.9.(2017秋•武昌区期末)如图,某小区有一块长为4a米(a>1),宽为(4a﹣2)米的长方形地块.该长方形地块正中间是一个长为(2a+1)米的长方形,四个角是大小相同的正方形,该小区计划将阴影部分进行绿化,对四个角的正方形用A型绿化方案,对正中间的长方形采用B型绿化方案.(1)用含a的代数式表示采用A型绿化方案的四个正方形边长是米,B型绿化方案的长方形的另一边长是米.(2)请你判断使用A型,B型绿化方案的面积哪个少?并说明理由.(3)若使用A型,B型绿化方案的总造价相同,均为1350元,每平方米造价高的比低的多元,求a的值.10.(2018春•三原县期末)如图所示,长方形ABCD是“阳光小区”内一块空地,已知AB=(2a+6b)米,BC=(8a+4b)米.(1)该长方形ABCD的面积是多少平方米?(2)若E为AB边的中点,DF=BC,现打算在阴影部分种植一片草坪,这片草坪的面积是多少平方米?11.(2018秋•开福区校级月考)如图1,长方形的两边长分别为m+3,m+13;如图2的长方形的两边长分别为m+5,m+7.(其中m为正整数)(1)写出两个长方形的面积S1,S2,并比较S1,S2的大小;(2)现有一个正方形的周长与图1中的长方形的周长相等.试探究该正方形的面积与长方形的面积的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由.(3)在(1)的条件下,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有19个,求m的值.12.(2018秋•海安县期中)若(x2+px﹣)(x2﹣3x+q)的积中不含x项与x3项,求p、q的值;13.(2018秋•宜宾县期中)小明在计算一个多项式乘﹣2x2+x﹣1时,因看错运算符号,变成了加上﹣2x2+x﹣1,得到的结果为4x2﹣2x﹣1,那么正确的计算结果为多少?14.(2018秋•德惠市校级月考)已知(x+a)(x2﹣x+c)的乘积中不含x2和x项,求a,c的值.15.(2018秋•临清市校级月考)计算:(1)(3a+b2)(b2﹣3a)(2)(m﹣2n)216.(2018秋•龙凤区校级月考)利用乘法公式计算:(1)5002﹣499×501.(2)50×4917.(2018秋•武邑县校级月考)化简:(2x+3y)2﹣2(2x+3y)(2x﹣3y)+(2x﹣3y)218.(2018秋•襄汾县期中)已知(x+y)2=9,(x﹣y)2=25,分别求x2+y2和xy的值.19.(2018秋•德惠市校级月考)已知a+b=2,a2+b2=10,求:(1)ab的值.(2)a﹣b的值.20.(2018春•福田区校级期末)乘法公式的探究及应用:(1)如图,可以求出阴影部分的面积是(写成两数平方差的形式);(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是,长是,面积是(写成多项式乘法的形式);(3)比较左、右两图的阴影部分面积,可以得到乘法公式:(用式子表达);(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)21.(2018春•常熟市期末)(1)如图1,阴影部分的面积是.(写成平方差的形式)(2)若将图1中的阴影部分剪下来,拼成如图2的长方形,面积是.(写成多项式相乘的积形式)(3)比较两图的阴影部分的面积,可以得到公式:.(4)应用公式计算:(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).22.(2018秋•思明区校级期中)如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b)连结AF、CF、AC,若a+b=10,ab=20,求阴影部分的面积.23.(2018秋•路南区期中)已知图甲是一个长为2a,宽为2b的长方形,沿图甲中虚线用剪刀均匀分成四个小长方形,然后按图乙的形状拼成一个正方形.(1)请将图乙中阴影部分正方形的边长用含a、b的代数式表示;(2)请用两种不同的方法求图乙中阴影部分的面积S;(3)观察图乙,并结合(2)中的结论,写出下列三个整式:(a+b)2,(a﹣b)2,ab 之间的等式;(4)根据(3)中的等量关系,解决如下问题:当a+b=8,ab=12时,求(a﹣b)2的值.24.(2018春•大田县期中)乘法公式的探究及应用.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B 种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.(1)请用两种不同的方法求图2大正方形的面积.方法1:;方法2:(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.(3)类似的,请你用图1中的三种纸片拼一个图形验证:(a+b)(a+2b)=a2+3ab+2b2(4)根据(2)题中的等量关系,解决如下问题:①已知:a+b=5,a2+b2=11,求ab的值;②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.25.(2018春•杏花岭区校级期中)已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均剪成四个小长方形,然后拼成如图乙所示的一个大正方形.(1)你认为图乙中的阴影部分的正方形的边长=;(2)请用两种不同的方法求图乙中阴影部分的面积:方法一:方法二:(3)观察图乙,请你写出下列代数式之间的等量关系:(m+n)2、(m﹣n)2、mn.(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=7,求a﹣b的值.26.(2018春•埇桥区期末)(1)因式分解:9(m+n)2﹣(m﹣n)2(2)已知:x+y=1,求x2+xy+y2的值.27.(2018春•沧县期末)请给4x2+1添上一个单项式,使新得到的多项式能运用完全平方公式分解因式.请写出两种情况,并对其分别进行因式分解.28.(2018春•宿豫区期中)把下列各式因式分解:(1)a4﹣1(2)(x+2)(x+4)+x2﹣429.(2017秋•前郭县期末)下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程解:设x2﹣4x=y,原式=(y+2)(y+6)+4(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)(1)该同学第二步到第三步运用了因式分解的(填序号).A.提取公因式B.平方差公式C.两数和的完全平方公式D.两数差的完全平方公式(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后?.(填“是”或“否”)如果否,直接写出最后的结果.(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.30.(2018春•郓城县期末)下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.解:设x2﹣4x=y,原式=(y+2)(y+6)+4 (第一步)=y2+8y+16 (第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)(1)该同学第二步到第三步运用了因式分解的.A.提取公因式B.平方差公式C.两数和的完全平方公式D.两数差的完全平方公式(2)该同学因式分解的结果是否彻底?.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果.(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.31.(2018春•诸城市期末)因式分解:(1)x2y﹣2xy2+y3(2)4ax2﹣48ax+128a;(3)(x2+16y2)2﹣64x2y232.(2018春•雨城区校级期中)分解因式:(1)a2(a﹣b)+b2(b﹣a)(2)a2﹣4ab+4b2﹣2a+4b33.(2018春•市中区期末)先阅读下面的村料,再分解因式.要把多项式am+an+bm+bn分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得am+an+bm+bn=a(m+n)+b(m+n).这时,由于a(m+n)+b(m+n)中又有公困式(m+n),于是可提公因式(m+n),从而得到(m+n)(a+b),因此有am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b).这种因式分解的方法叫做分组分解法,如果把一个多项式各个项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以利用分组分解法来因式分解.请用上面材料中提供的方法因式分解:(1)ab﹣ac+bc﹣b2=a(b﹣c)﹣b(b﹣c)(请你完成分解因式下面的过程)=(2)m2﹣mn+mx﹣nx;(3)x2y2﹣2x2y﹣4y+8,34.(2018春•揭阳期末)甲、乙两个同学分解因式x2﹣4x+m+ax+b时,甲看错了b,分解结果为(x+2)(x+4);乙看错了a,分解结果为(x+1)(x+9),求a+b的值.35.(2018春•迁安市期末)常用的分解因式的方法有提取公因式法、公式法及十字相乘法,但有更多的多项式只用上述方法就无法分解,如x2﹣4y2﹣2x+4y,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了.过程为:x2﹣4y2﹣2x+4y=(x+2y)(x﹣2y)﹣2(x﹣2y)=(x﹣2y)(x+2y﹣2).这种分解因式的方法叫分组分解法.利用这种方法解决下列问题:(1)分解因式x2﹣2xy+y2﹣16;(2)△ABC三边a,b,c满足a2﹣ab﹣ac+bc=0,判断△ABC的形状.36.(2018春•滦县期末)下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.解:设x2﹣4x=y原式=(y+2)(y+6)+4(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)我们把这种因式分解的方法称为“换元法”,请据此回答下列问题;(1)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”),若不彻底,请直接写出因式分解的最后结果:.(2)请模仿上面的方法尝试对多项式(m2﹣2m)(m2﹣2m+2)+1进行因式分解.37.(2018春•山亭区期末)解下列各题:(1)分解因式:9a2(x﹣y)+4b2(y﹣x);(2)甲,乙两同学分解因式x2+mx+n,甲看错了n,分解结果为(x+2)(x+4);乙看错了m,分解结果为(x+1)(x+9),请分析一下m,n的值及正确的分解过程.38.(2018春•常熟市期末)将下列各式分解因式(1)3x(a﹣b)﹣9y(b﹣a);(2)a2﹣4a﹣12;(3)81x4﹣72x2y2+16y4人教版八年级上14章整式的乘除与分解因式复习题(解答题)参考答案与试题解析一.解答题1.(2018秋•雨花区校级月考)规定两数a,b之间的一种运算,记作(a,b),如果a c=b,则(a,b)=c.我们叫(a,b)为“雅对”.例如:因为23=8,所以(2,8)=3.我们还可以利用“雅对”定义说明等式(3,3)+(3,5)=(3,15)成立.证明如下:设(3,3)=m,(3,5)=n,则3m=3,3n=5,故3m⋅3n=3m+n=3×5=15,则(3,15)=m+n,即(3,3)+(3,5)=(3,15).(1)根据上述规定,填空:(2,4)=2;(5,1)=0;(3,27)=3.(2)计算(5,2)+(5,7)=(5,14),并说明理由.(3)利用“雅对”定义证明:(2n,3n)=(2,3),对于任意自然数n都成立.【分析】(1)根据上述规定即可得到结论;(2)设(5,2)=x,(5,7)=y,根据同底数幂的乘法法则即可求解;(3)设(2n,3n)=x,于是得到(2n)x=3n,即(2x)n=3n根据“雅对”定义即可得到结论.【解答】解:(1)∵22=4,∴(2,4)=2;∵50=1,∴(5,1)=0;∵33=27,∴(3,27)=3;故答案为:2,0,3;(2)设(5,2)=x,(5,7)=y,则5x=2,5y=7,∴5x+y=5x•5y=14,∴(5,14)=x+y,∴(5,2)+(5,7)=(5,14),故答案为:(5,14);(3)设(2n,3n)=x,则(2n)x=3n,即(2x)n=3n所以2x=3,即(2,3)=x,所以(2n,3n)=(2,3).2.(2018春•苏州期中)规定a*b=2a×2b,求:(1)求2*3;(2)若2*(x+1)=16,求x的值.【分析】(1)直接利用已知a*b=2a×2b,将原式变形得出答案;(2)直接利用已知得出等式求出答案.【解答】解:(1)∵a*b=2a×2b,∴2*3=22×23=4×8=32;(2)∵2*(x+1)=16,∴22×2x+1=24,则2+x+1=4,解得:x=1.3.(2018春•开福区校级期中)阅读材料:n个相同的因数a相乘,可记为a n,如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若a n=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为log a b(即log a b=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).根据以上材料,解决下列问题:(1)计算以下各对数的值:log24=2,log216=4,log264=6;(2)根据(1)中的计算结果,写出log24,log216,log264满足的关系式;(3)根据(2)中的关系式及4,16,64满足的关系式猜想一般性结论:log a M+log a N=log a MN(a>0且a≠1,M>0,N>0);(4)根据幂的运算法则说明(3)中一般性结论的正确性.【分析】(1)根据a n=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为log a b (即log a b=n),进而得出答案;(2)利用(1)中所求进而得出答案;(3)利用(2)中所求规律进而得出答案;(4)利用发现的规律进而分析得出答案.【解答】解:(1)log24=2,log216=4,log264=6;故答案为:2,4,6;(2)由(1)得:log2 4+log2 16=log2 64;(3)由(2)得:log a M+log a N=log a MN;故答案为:log a MN;(4)记log a M=m,log a N=n,则M=a m,N=a n,所以MN=a m•a n=a m+n,所以log a MN=log a a m+n=m+n,所以log a M+log a N=log a MN.4.(2018春•苏州期中)若33×9m+4÷272m﹣1的值为729,求m的值.【分析】直接利用幂的乘方运算法则、同底数幂的乘除运算法则将原式变形进而得出答案.【解答】解:∵33×9m+4÷272m﹣1的值为729,∴33×32m+8÷36m﹣3=36,∴3+2m+8﹣(6m﹣3)=6,解得:m=2.5.(2018春•利津县期末)若x m=16,x n=128,求x2m﹣n的值.【分析】直接利用幂的乘方运算法则以及同底数幂的乘除运算法则将原式变形得出答案.【解答】解:∵x m=16,x n=128,∴x2m﹣n=(x m)2÷x n=162÷128=2.6.(2018秋•安溪县期中)规定两数a,b之间的一种运算,记作(a,b):如果a c=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.(1)根据上述规定,填空:(5,125)=3,(﹣2,4)=2,(﹣2,﹣8)=3;(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4),他给出了如下的证明:设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n∴3x=4,即(3,4)=x,∴(3n,4n)=(3,4).请你尝试运用上述这种方法说明下面这个等式成立的理由.(4,5)+(4,6)=(4,30)【分析】(1)根据规定的两数之间的运算法则解答;(2)根据积的乘方法则,结合定义计算.【解答】解:(1)53=125,(5,125)=3,(﹣2)2=4,(﹣2,4)=2,(﹣2)3=﹣8,(﹣2,﹣8)=3,故答案为:3;2;3;(2)设(4,5)=x,(4,6)=y,(4,30)=z,则4x=5,4y=6,4z=30,4x×4y=4x+y=30,∴x+y=z,即(4,5)+(4,6)=(4,30).7.(2018秋•松北区校级期中)(1)计算:﹣82018×(﹣0.125)2018(2)已知a m=6,a n=2,求a2m+3n的值.【分析】(1)直接利用积的乘方运算法则计算得出答案;(2)直接利用同底数幂的乘法运算法则将原式变形得出答案.【解答】解:(1)﹣82018×(﹣0.125)2018=﹣(8×0.125)2018=﹣1;(2)∵a m=6,a n=2,∴a2m+3n=(a m)2×(a n)3=36×8=288.8.(2018•安庆一模)特殊两位数乘法的速算﹣﹣如果两个两位数的十位数字相同,个位数字相加为10,那么能立即说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.如:47×43=2021,61×69=4209.(1)请你直接写出83×87的值;(2)设这两个两位数的十位数字为x(x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz.(3)99991×99999=9999000009.【分析】(1)根据“前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积”进行计算;(2)这两个两位数的十位数字为x(x>3),个位数字分别为y和z,则由题知y+z=10,利用多项式乘多项式的计算法则解答;(3)利用1×9=9,91×99=909,991×999=99009…找出规律解答.【解答】解:(1)83和87满足题中的条件,即十位数都是8,8>3,且个位数字分别是3和7,之和为10,那么它们的乘积是一个4位数,前两位数字是8和9的乘积,后两位数字就是3和7的乘积,因而,答案为:7221;(2)这两个两位数的十位数字为x(x>3),个位数字分别为y和z,则由题知y+z=10,因而有:(10x+y)(10x+z)=100x2+10xz+10xy+yz=100x2+10x(y+z)+yz=100x2+100x+yz=100x(x+1)+yz得证;(3)1×9=991×99=909991×999=99009…99991×99999=9999000009.故答案是:9999000009.9.(2017秋•武昌区期末)如图,某小区有一块长为4a米(a>1),宽为(4a﹣2)米的长方形地块.该长方形地块正中间是一个长为(2a+1)米的长方形,四个角是大小相同的正方形,该小区计划将阴影部分进行绿化,对四个角的正方形用A型绿化方案,对正中间的长方形采用B型绿化方案.(1)用含a的代数式表示采用A型绿化方案的四个正方形边长是(a﹣)米,B 型绿化方案的长方形的另一边长是(2a﹣1)米.(2)请你判断使用A型,B型绿化方案的面积哪个少?并说明理由.(3)若使用A型,B型绿化方案的总造价相同,均为1350元,每平方米造价高的比低的多元,求a的值.【分析】(1)根据题意表示出A、B型绿化方案的边长或另一边长即可;(2)分别表示出A、B型的面积,利用作差法判断大小即可;(3)根据题意列出分式方程,求出方程的解即可得到结果.【解答】解:(1)A型绿化方案的四个正方形边长是(a﹣)米,B型绿化方案的长方形的另一边长是(2a﹣1)米;故答案为:(a﹣);(2a﹣1);(2)记A型面积为S A,B型面积为S B,根据题意得:S A=4(a﹣)2=4a2﹣4a+1,S B=(2a+1)(2a﹣1)=4a2﹣1,∴S A﹣S B=﹣4a+2,∵4a﹣2>0,∴﹣4a+2<0,即S A﹣S B<0,则S A<S B;(3)由(2)得S A<S B,∴﹣=,即﹣=,解得:a=2,经检验a=2是分式方程的解.10.(2018春•三原县期末)如图所示,长方形ABCD是“阳光小区”内一块空地,已知AB=(2a+6b)米,BC=(8a+4b)米.(1)该长方形ABCD的面积是多少平方米?(2)若E为AB边的中点,DF=BC,现打算在阴影部分种植一片草坪,这片草坪的面积是多少平方米?【分析】(1)根据长方形的面积公式,多项式与多项式相乘的法则计算;(2)根据题意分别求出AE,AF,根据多项式与多项式相乘的法则计算.【解答】解:(1)长方形ABCD的面积=AB×BC=(2a+6b)(8a+4b)=16a2+56ab+24b2;(2)由题意得,AF=AD﹣DF=BC﹣BC=(8a+4b)﹣(8a+4b)=(6a+3b),AE=(2a+6b)=a+3b,则草坪的面积=×AE×AF=×(a+3b)(6a+3b)=3a2+ab+b2.11.(2018秋•开福区校级月考)如图1,长方形的两边长分别为m+3,m+13;如图2的长方形的两边长分别为m+5,m+7.(其中m为正整数)(1)写出两个长方形的面积S1,S2,并比较S1,S2的大小;(2)现有一个正方形的周长与图1中的长方形的周长相等.试探究该正方形的面积与长方形的面积的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由.(3)在(1)的条件下,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有19个,求m的值.【分析】(1)利用矩形的面积公式计算即可;(2)求出正方形的面积即可解决问题;(3)构建不等式即可解决问题;【解答】解:(1)∵S1=(m+13)(m+3)=m2+16m+39,S2=(m+7)(m+5)=m2+12m+35,∴S1﹣S2=4m+4>0,∴S1>S2.(2)∵一个正方形的周长与图1中的长方形的周长相等,∴正方形的边长为m+8,∴正方形的面积=m2+16m+64,∴m2+16m+64﹣(m2+16m+39)=25,∴该正方形的面积与长方形的面积的差是一个常数;(3)由(1)得,S1﹣S2=4m+4,∴当19<4m+4≤20时,∴<m≤4,∵m为正整数,m=4.12.(2018秋•海安县期中)若(x2+px﹣)(x2﹣3x+q)的积中不含x项与x3项,求p、q的值;【分析】利用多项式乘多项式法则及合并同类项法则化简式子,找出x项与x3令其系数等于0求解.【解答】解:(x2+px﹣)(x2﹣3x+q)=x4+(p﹣3)x3+(q﹣3p﹣)x2+(qp+1)x+q,∵积中不含x项与x3项,∴p﹣3=0,qp+1=0,∴p=3,q=﹣.13.(2018秋•宜宾县期中)小明在计算一个多项式乘﹣2x2+x﹣1时,因看错运算符号,变成了加上﹣2x2+x﹣1,得到的结果为4x2﹣2x﹣1,那么正确的计算结果为多少?【分析】根据整式的加减混合运算求出原多项式,根据多项式乘多项式法则求出正确的结果.【解答】解:原多项式为:(4x2﹣2x﹣1)﹣(﹣2x2+x﹣1)=4x2﹣2x﹣1+2x2﹣x+1=6x2﹣3x(6x2﹣3x)(﹣2x2+x﹣1)=﹣12x4+6x3﹣6x2+6x3﹣3x2+3x=﹣12x4+12x3﹣9x2+3x.14.(2018秋•德惠市校级月考)已知(x+a)(x2﹣x+c)的乘积中不含x2和x项,求a,c的值.【分析】根据多项式乘多项式的法则计算,让x2项和x项的系数为0,即可求得a,c的值.【解答】解:(x+a)(x2﹣x+c)=x3﹣x2+cx+ax2﹣ax+ac=x3+(a﹣1)x2+(c﹣a)x+ac,∵(x+a)(x2﹣x+c)的乘积中不含x2和x项,∴a﹣1=0且c﹣a=0,则a=c=1.15.(2018秋•临清市校级月考)计算:(1)(3a+b2)(b2﹣3a)(2)(m﹣2n)2【分析】(1)根据平方差公式求出即可;(2)根据完全平方公式求出即可.【解答】解:(1)(3a+b2)(b2﹣3a)=(b2)2﹣(3a)2=b4﹣9a2;(2)(m﹣2n)2=m2﹣4mn+4n2.16.(2018秋•龙凤区校级月考)利用乘法公式计算:(1)5002﹣499×501.(2)50×49【分析】(1)原式变形后,利用平方差公式计算即可求出值;(2)原式变形后,利用平方差公式计算即可求出值.【解答】解:(1)原式=5002﹣(500﹣1)×(500+1)=5002﹣(5002﹣1)=5002﹣5002+1=1;(2)原式=(50+)×(50﹣)=2500﹣=2499.17.(2018秋•武邑县校级月考)化简:(2x+3y)2﹣2(2x+3y)(2x﹣3y)+(2x﹣3y)2【分析】先根据完全平方公式和平方差公式展开,再去括号、合并同类项即可得.【解答】解:原式=4x2+12xy+9y2﹣2(4x2﹣9y2)+4x2﹣12xy+9y2=4x2+12xy+9y2﹣8x2+18y2+4x2﹣12xy+9y2=36y2.18.(2018秋•襄汾县期中)已知(x+y)2=9,(x﹣y)2=25,分别求x2+y2和xy的值.【分析】直接利用完全平方公式将原式变形,进而得出答案.【解答】解:∵(x+y)2=9,(x﹣y)2=25,∴两式相加,得(x+y)2+(x﹣y)2=2x2+2y2=34,则x2+y2=17;两式相减,得(x+y)2﹣(x﹣y)2=4xy=﹣16,则xy=﹣4.19.(2018秋•德惠市校级月考)已知a+b=2,a2+b2=10,求:(1)ab的值.(2)a﹣b的值.【分析】(1)根据(a+b)2=a2+b2+2ab求出即可;(2)先求出(a﹣b)2的值,再开方即可.【解答】解:(1)∵a+b=2,a2+b2=10,∴(a+b)2=4,∴a2+b2+2ab=4,∴10+2ab=4,∴ab=﹣3;(2)∵ab=﹣3,a2+b2=10,∴(a﹣b)2=a2+b2﹣2ab=10﹣2×(﹣3)=16,∴a﹣b==±4.20.(2018春•福田区校级期末)乘法公式的探究及应用:(1)如图,可以求出阴影部分的面积是a2﹣b2(写成两数平方差的形式);(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是a﹣b,长是a+b,面积是(a+b)(a﹣b)(写成多项式乘法的形式);(3)比较左、右两图的阴影部分面积,可以得到乘法公式:(a+b)(a﹣b)=a2﹣b2(用式子表达);(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)【分析】(1)由图形的面积关系即可得出结论;(2)由图形即可得到长方形的长,宽以及面积;(3)依据两图的阴影部分面积相等,可以得到乘法公式;(4)依据平方差公式以及完全平方公式,即可得到计算结果.【解答】解:(1)由图可得,阴影部分的面积=a2﹣b2;故答案为:a2﹣b2;(2)由图可得,矩形的宽是a﹣b,长是a+b,面积是(a+b)(a﹣b);故答案为:a﹣b,a+b,(a+b)(a﹣b);(3)依据两图的阴影部分面积相等,可以得到乘法公式(a+b)(a﹣b)=a2﹣b2;故答案为:(a+b)(a﹣b)=a2﹣b2;(4)(2m+n﹣p)(2m﹣n+p)=(2m)2﹣(n﹣p)2=4m2﹣(n2﹣2np+p2)=4m2﹣n2+2np﹣p2.21.(2018春•常熟市期末)(1)如图1,阴影部分的面积是a2﹣b2.(写成平方差的形式)(2)若将图1中的阴影部分剪下来,拼成如图2的长方形,面积是(a﹣b)(a+b).(写成多项式相乘的积形式)(3)比较两图的阴影部分的面积,可以得到公式:a2﹣b2=(a﹣b)(a+b).(4)应用公式计算:(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).【分析】(1)根据面积的和差,可得答案;(2)根据矩形的面积公式,可得答案;(3)根据图形割补法,面积不变,可得答案;(4)根据平方差公式计算即可.【解答】解:(1)如图(1)所示,阴影部分的面积是a2﹣b2,故答案为:a2﹣b2;(2)根据题意知该长方形的长为a+b、宽为a﹣b,则其面积为(a+b)(a﹣b),故答案为:(a+b)(a﹣b);(3)由阴影部分面积相等知a2﹣b2=(a﹣b)(a+b),故答案为:a2﹣b2=(a﹣b)(a+b);(4)(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣)=(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)=××××…××=×=.22.(2018秋•思明区校级期中)如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b)连结AF、CF、AC,若a+b=10,ab=20,求阴影部分的面积.【分析】根据完全平方公式即可求出答案.【解答】解:∵a2+b2=(a+b)2﹣2ab=100﹣40=60,∴阴影部分的面积=a2+b2﹣(a+b)•b﹣a2=60﹣×ab﹣b2﹣a2=60﹣×20﹣×60=60﹣10﹣30=20.23.(2018秋•路南区期中)已知图甲是一个长为2a,宽为2b的长方形,沿图甲中虚线用剪刀均匀分成四个小长方形,然后按图乙的形状拼成一个正方形.(1)请将图乙中阴影部分正方形的边长用含a、b的代数式表示;(2)请用两种不同的方法求图乙中阴影部分的面积S;(3)观察图乙,并结合(2)中的结论,写出下列三个整式:(a+b)2,(a﹣b)2,ab 之间的等式;(4)根据(3)中的等量关系,解决如下问题:当a+b=8,ab=12时,求(a﹣b)2的值.【分析】(1)根据图形即可得出图乙中阴影部分小正方形的边长为a﹣b;(2)直接利用正方形的面积公式得到图中阴影部分的面积为(a﹣b)2;也可以用大正方形的面积减去4个长方形的面积得到图中阴影部分的面积为(a+b)2﹣4ab;(3)根据图中阴影部分的面积是定值得到(a+b)2,(a﹣b)2,ab之间的等量关系式;(4)利用(3)中的公式得到(a﹣b)2=(a+b)2﹣4ab,进而得出(a﹣b)2的值.【解答】解:(1)图乙中小正方形的边长为a﹣b.(2)方法①:S=(a﹣b)2;方法②:S=(a+b)2﹣4ab;(3)因为图中阴影部分的面积不变,所以(a﹣b)2=(a+b)2﹣4ab;(4)由(3)得:(a﹣b)2=(a+b)2﹣4ab,∵a+b=8,ab=12,∴(a﹣b)2=82﹣4×12=64﹣48=16.24.(2018春•大田县期中)乘法公式的探究及应用.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B 种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.(1)请用两种不同的方法求图2大正方形的面积.方法1:(a+b)2;方法2:a2+b2+2ab(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.(a+b)2=a2+2ab+b2(3)类似的,请你用图1中的三种纸片拼一个图形验证:(a+b)(a+2b)=a2+3ab+2b2(4)根据(2)题中的等量关系,解决如下问题:①已知:a+b=5,a2+b2=11,求ab的值;②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.【分析】(1)依据正方形的面积计算公式即可得到结论;(2)依据(1)中的代数式,即可得出(a+b)2,a2+b2,ab之间的等量关系;(3)画出长为a+2b,宽为a+b的长方形,即可验证:(a+b)(a+2b)=a2+3ab+2b2;(4)①依据a+b=5,可得(a+b)2=25,进而得出a2+b2+2ab=25,再根据a2+b2=11,即可得到ab=7;②设2018﹣a=x,a﹣2017=y,即可得到x+y=1,x2+y2=5,依据(x+y)2=x2+2xy+y2,即可得出xy==﹣2,进而得到(2018﹣a)(a﹣2017)=﹣2.【解答】解:(1)图2大正方形的面积=(a+b)2图2大正方形的面积=a2+b2+2ab故答案为:(a+b)2,a2+b2+2ab;(2)由题可得(a+b)2,a2+b2,ab之间的等量关系为:(a+b)2=a2+2ab+b2故答案为:(a+b)2=a2+2ab+b2;(3)如图所示,(4)①∵a+b=5,∴(a+b)2=25,∴a2+b2+2ab=25,又∵a2+b2=11,∴ab=7;②设2018﹣a=x,a﹣2017=y,则x+y=1,∵(2018﹣a)2+(a﹣2017)2=5,∴x2+y2=5,∵(x+y)2=x2+2xy+y2,∴xy==﹣2,即(2018﹣a)(a﹣2017)=﹣2.25.(2018春•杏花岭区校级期中)已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均剪成四个小长方形,然后拼成如图乙所示的一个大正方形.(1)你认为图乙中的阴影部分的正方形的边长=m﹣n;(2)请用两种不同的方法求图乙中阴影部分的面积:方法一:(m﹣n)2方法二:(m+n)2﹣4mn(3)观察图乙,请你写出下列代数式之间的等量关系:(m+n)2、(m﹣n)2、mn(m﹣n)2=(m+n)2﹣4mn.(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=7,求a﹣b的值.【分析】(1)根据图乙中的阴影部分的正方形的边长等于小长方形的长减去宽进行判断;(2)图乙中阴影部分的面积既可以用边长的平方进行计算,也可以用大正方形的面积减去四个小长方形的面积进行计算;(3)根据(m﹣n)2和(m+n)2﹣4mn表示同一个图形的面积进行判断;(4)根据(a﹣b)2=(a+b)2﹣4ab,进行计算即可得到a﹣b的值.【解答】解:(1)由题可得,图乙中的阴影部分的正方形的边长等于m﹣n;故答案为:m﹣n;(2)方法一:图乙中阴影部分的面积=(m﹣n)2方法二:图乙中阴影部分的面积=(m+n)2﹣4mn;故答案为:(m﹣n)2,(m+n)2﹣4mn;(3)∵(m﹣n)2和(m+n)2﹣4mn表示同一个图形的面积;∴(m﹣n)2=(m+n)2﹣4mn;故答案为:(m﹣n)2=(m+n)2﹣4mn;(4)∵(a﹣b)2=(a+b)2﹣4ab,而a+b=8,ab=7,∴(a﹣b)2=82﹣4×7=64﹣28=36,∴a﹣b=±6.26.(2018春•埇桥区期末)(1)因式分解:9(m+n)2﹣(m﹣n)2(2)已知:x+y=1,求x2+xy+y2的值.【分析】(1)直接利用平方差公式分解因式得出答案;(2)直接提取公因式,再利用完全平方公式分解因式,进而把已知代入求出答案.【解答】解:(1)9(m+n)2﹣(m﹣n)2=[3(m+n)+(m﹣n)][3(m+n)﹣(m﹣n)]=(4m+2n)(2m+4n)=4(2m+n)(m+2n);(2)x2+xy+y2=(x2+2xy+y2)=(x+y)2,当x+y=1时,原式=×12=.27.(2018春•沧县期末)请给4x2+1添上一个单项式,使新得到的多项式能运用完全平方公式分解因式.请写出两种情况,并对其分别进行因式分解.【分析】添加4x或﹣4x,利用完全平方公式分解即可.【解答】解:添加4x,得4x2+4x+1=(2x+1)2,添加﹣4x,得4x2﹣4x+1=(2x﹣1)2.28.(2018春•宿豫区期中)把下列各式因式分解:(1)a4﹣1(2)(x+2)(x+4)+x2﹣4【分析】(1)直接利用平方差公式计算得出答案;(2)直接将原式分解因式进而提取公因式得出答案.【解答】解:(1)a4﹣1=(a2+1)(a2﹣1)=(a2+1)(a+1)(a﹣1);(2)(x+2)(x+4)+x2﹣4=(x+2)(x+4)+(x+2)(x﹣2)=(x+2)(2x+2)=2(x+2)(x+1).29.(2017秋•前郭县期末)下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程解:设x2﹣4x=y,原式=(y+2)(y+6)+4(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)(1)该同学第二步到第三步运用了因式分解的C(填序号).A.提取公因式B.平方差公式C.两数和的完全平方公式D.两数差的完全平方公式(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后?否.(填“是”或“否”)如果否,直接写出最后的结果(x ﹣2)4.(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.【分析】(1)根据分解因式的过程直接得出答案;(2)该同学因式分解的结果不彻底,进而再次分解因式得出即可;(3)将(x2﹣2x)看作整体进而分解因式即可.【解答】解:(1)该同学第二步到第三步运用了因式分解的两数和的完全平方公式;故选:C;(2)这个结果没有分解到最后,原式=(x2﹣4x+4)2=(x﹣2)4;故答案为:否,(x﹣2)4;(3)(x2﹣2x)(x2﹣2x+2)+1=(x2﹣2x)2+2(x2﹣2x)+1=(x2﹣2x+1)2=(x﹣1)4.30.(2018春•郓城县期末)下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.解:设x2﹣4x=y,原式=(y+2)(y+6)+4 (第一步)。
期末专题复习第十四章欧姆定律+动态电路分析 苏科版九年级物理上册【有答案】

期末专题复习第十四章欧姆定律动态电路分析一、单选题1.从2020年5月1日起,驾驶员酒醉后驾车要负刑事责任。
酒精测试仪可检测驾驶员是否酒后驾车,如图所示是它的原理图。
图中R1为定值电阻,酒精气体传感器R2的电阻值倒数与酒精气体浓度成正比,如果测得酒精气体浓度变大,那么测试仪的()A.电压表示数不变B.电压表示数越大C.通过传感器的电流越小D.传感器两端的电压越大2.如图所示的电路中,电源电压不变。
当闭合开关S,滑动变阻器的滑片P向右移动时,下列判断正确的是()A.电流表示数变大,电压表示数变小B.电流表示数变小,电压表示数不变C.电流表示数变小,电压表示数变大D.电流表示数变大,电压表示数不变3.如图所示,电源电压不变,R为滑动变阻器,R0为定值电阻;忽略温度对灯丝电阻的影响。
闭合开关S,将滑动变阻器的滑片P向左滑动时,下列说法正确的是()A.电流表A示数减小B.电压表V2示数和电压表V1示数之差变大C.灯两端电压变化量小于滑动变阻器两端电压变化量D.电压表V2和电流表A示数之比增大4.如图所示,电源电压保持不变,闭合开关,滑动变阻器的滑片向左移动的过程中,下列说法正确的是()A.电压表V1示数变大,电路表示数变小B.电压表V2示数不变,电流表示数变大C.电压表V1示数和电流表示数的乘积变大D.电压表V2示数和电流表的比值不变5.货车超限超载运输对公路交通安全危害极大,严查货车超限超载是治理公路交通运输乱象的重点之一。
现在,高速公路入口一般均设有公路超限超载检测站。
如图所示R1是定值电阻,起保护作用;R2是压敏电阻(阻值随压力增加而减小)。
将S闭合后,以下说法正确的是()A.压力表实际是一个电流表B.当升降机静止不动时,检测物越重压力表示数越大C.压力表示数不变时升降机一定在做匀速直线运动D.检测物被取走时电路电流最大6.如图是小海设计的温度测量仪的电路,R1是定值电阻,R2是阻值随温度升高而减小的热敏电阻,当R2的温度随环境温度降低时()A.R2的阻值变小B.电流表的示数增大C.电压表V1的示数增大D.电压表V2的示数变化量与电流表示数变化量的比值不变7.如图所示,电源电压保持不变。
八年级生物上册 第十四章 生物的生殖与发育试题 苏教版

第十四章 生物的生殖与发育(复习)第一课 生物的生殖与发育1、无性生殖是指一类不经过的结合,由母体直接产生的生殖方式。
2、常见的无性生殖方式有植物组织培养:在无菌,含有多种营养物质和植物激素的培养基上3、嫁接就是把一株植物体的芽或带芽的枝接到另一株植物体上。
接上去的芽或枝叫做接穗,别接的植物体叫做砧木。
无论是芽接还是枝接都要使接穗和砧木的形成层紧密地结合在一起,这样才能提高成活率。
4、植物园引进了一种稀有花卉,技术人员想在短时间内将其大量繁殖,最理想的方法是( ) A 、种子繁殖B 、植物组织培养C 、扦插 D 、压条5、X 明同学想在一株菊花开出几种不同颜色的花朵,他可以采用的方法是( ) A 、扦插 B 、压条C 、嫁接 D 、植物组织培养6、下列那种繁殖方式不是营养生殖( )A 、把蒜瓣种下,使之长成新个体B 、把马铃薯的块茎种下,使之长成新个体C 、把核桃种下,使之长成新个体D 、把大丽花的块茎种下,使之长成新个体 7、下列哪一项不是营养生殖的优点()A 、操作简便B 、能保持品种的优良特性C 、能加快繁殖速度D 、能改良后代的品质第二课 植物的有性生殖1、有性生殖是指通过两性生殖细胞的结合,成为受精卵,进而发育成新个体的生殖方式。
2、雄蕊花药中的花粉通过不同的途径传送到雌蕊柱头上的过程,叫做传粉。
3、传粉有自花传粉和异花传粉两种方式。
4、花的基本结构见书本P 、85、子房的基本结构构见书本P 、96、子房与果实之间的关系: 子房发育成 子房壁发育成 胚珠发育成 珠被发育成 受精卵发育成7、 8、一朵花的主要部分是( ) A 、 花托 B 、花冠 B 、 花萼 D 、雄蕊、雌蕊9、我们平常吃下的桃肉是由桃花的那一部分发育而来的( ) A 、 子房壁 B 、珠被 C 、胚乳 D 、果皮10、一个南瓜内有多粒种子,对此现象的下列解释中,正确的是( ) A 、 一朵花内有多个雌蕊 B 、一朵花内有多个子房C 、一个子房内有多个胚珠D 、一个胚珠内有多个卵细胞同时受精11、下列各特征属于风煤花的是()①芬芳的气味②花粉多而轻③柱头有分叉或黏液④甘甜的花蜜⑤花大而鲜艳A、①④⑤B、②③C、②⑤D、③④12、“麻屋子、红帐子、白胖子”,关于花生的描述中,“麻屋子”,“红帐子”,“白胖子”,分别由什么结构发育而来的()A、子房壁、珠被、子房B、子房壁、珠被、受精卵C、柱头、珠被、子房D、花柱、珠被、受精卵第三课昆虫的生殖与发育1、家蚕的发育过程要经过受精卵、幼虫、蛹、成虫四个时期。
物理化学——第14章-胶体与大分子溶液复习题

本章练习题
4、制备BaSO4溶胶,反应物Ba(SCN)2过量,请写出胶团 的结构并判断胶粒带电情况。
答:胶核是(BaSO4)m,优先吸附相同离子Ba2+,吸附层 中还有负离子SCN-离子。 所以胶粒为[(BaSO4)m· n Ba2+· (2n-x) SCN-]x+。 中性胶团为[(BaSO4)m· n Ba2+· (2n-x) SCN-]x+· xSCN-。
判断题
1、能产生丁铎尔现象的分散系统就是溶胶。(
X )
2、通过超显微镜可以直接看到胶体粒子的形状和大小。 ( X ) 3、加入电解质有时可以使胶体稳定,有时也可以使胶体 聚沉。( √ ) 4、大分子溶液与溶胶一样是多相不稳定体系。( X )
选择题
1.将高分子溶液作为胶体体系来研究,因为它:(D) (A) 是多相体系 ; (B)热力学不稳定体系 ; (C) 对电解质很敏感 ;(D) 粒子大小在胶体范围内 。 (D) 2.溶胶与大分子溶液的区别主要在于: (A)粒子大小不同 ; (B) 渗透压不同 ; (C) 丁铎尔效应的强弱不同 ; (D)相状态和热力学稳定性不同
第十四章 胶体分散系统 和大分子溶液
本章练习题
1、为什么燃烧不完全时烟囱冒黑烟,而燃烧较完全时烟 囱冒青烟? 答:燃烧不完全时,烟灰颗粒较大,属于粗分散系统,对入 射光主要是反射,看到的是黑色。燃烧较完全时,烟灰颗粒 小,属于胶体系统,看到的是散射光。由于蓝光、紫光的散 射强,所以看到的是青烟。
本章练习题
选择题
3. 下列电解质对某溶胶的聚沉值分别为c(NaNO3) = 300, c(Na2SO4) = 295,c(MgCl2) = 25,c(AlCl3) = 0.5(mol· dm-3), 可确定该溶液中粒子带电情况为: (C) (A)不带电 ;(B)带正电 ;(C) 带负电 ;(D)不能确定 。 4. 在AgNO3溶液中加入稍过量 KI溶液,得到溶胶的胶团 结构可表示为: (A) (A)[(AgI)m•nI-•(n-x) •K+]x-•xK+ ; (B)[(AgI)m•nNO3-•(n-x)K+]x-•xK+ ; (C)[(AgI)m•nAg+•(n-x)I-]x-•xK+ ; (D)[(AgI)m•nAg+•(n-x)NO3-]x+•xNO3- 。
病理生理学复习题14

第十四章呼吸功能不全一、选择题A型题⒈海平面条件下,诊断呼吸衰竭的根据之一是PaO2A <40mmHg (5.3kPa)B <50mmHg (6.7kPa)C <60mmHg (8.0kPa)D <70mmHg (9.3kPa)E <80mmHg (10.6kPa)[答案]C⒉呼吸衰竭是指A肺泡通气量严重不足B外呼吸功能严重障碍C内呼吸功能严重障碍D CO2排出障碍E O2吸入及CO2排出障碍[答案]B⒊限制性通气不足的原因是A呼吸中枢抑制B肺泡壁厚度增加C气道阻力增高D肺泡膜面积减少E肺内通气血流比失调[答案]A⒋造成阻塞性通气不足的原因是A呼吸肌活动障碍B 气道阻力增加C 胸廓顺应性降低D 肺顺应性降低E 弥散障碍[答案]B⒌影响气道阻力的主要因素是A 气道内径B 气道长度C 气道形态D气流形式E 气流速度[答案]A⒍反应肺泡通气量的最佳指标是A 肺活量B 潮气量C PaCO2D P A CO2E PaO2[答案]D⒎呼吸衰竭引起肺动脉高压的主要机制是A 血液粘滞性增高B 缺氧所致血量增多C 肺泡气氧分压减低引起肺血管收缩D 外周血管扩张血液回流增加E 肺小动脉壁增厚[答案]E⒏肺气肿患者易产生呼气性呼吸困难,其机制为A 小气道阻塞B 小气道管壁增厚C 小气道管壁顺应性减低D 小气道痉挛E 气道等压点移至膜性气道[答案]E⒐ARDS患者发生呼吸衰竭的主要机制是A 阻塞性通气功能障碍B 限制性通气功能障碍C 通气血流比失调D 肺泡膜面积↓E 肺泡膜厚度↑[答案]C⒑功能性分流是指A 部分肺泡通气不足B 部分肺泡血流不足C 肺泡通气不足而血流正常或增加D 肺泡血流不足而通气正常E A-V吻合支开放[答案]C⒒呼吸衰竭时最常发生的酸碱平衡紊乱是()A 呼吸性酸中毒B 呼吸性碱中毒C 代谢性酸中毒D 代谢性碱中毒E 混合性酸碱平衡紊乱[答案]E⒓正常人P A O2略高于PaO2的主要原因是A 生理性通气/血流比例不协调B 功能性死腔增多C 功能性分流增多D 解剖分流增多E 正常静息时仅部分肺泡参与气体交换[答案]A⒔能够引起ARDS的原因是A 吸入毒气B 休克C 肺挫伤D败血症E 以上都是[答案]E⒕急性呼吸性酸中毒的主要代偿机制是A 肺代偿B 细胞内缓冲和细胞内外离子交换C肾脏泌H+ 增多D 肾脏产NH3增多E 肾脏重吸收NaHCO3增多[答案]B⒖下列哪种情况可引起吸气性呼吸困难?A 声带麻痹B 肿瘤压迫气管胸内部分C COPD患者D 张力性气胸压迫肺E 细支气管慢性炎症[答案]A⒗呼吸衰竭引起的缺氧类型是A 循环性缺氧B 低张性缺氧C 组织性缺氧D 血液性缺氧E 组织性缺氧+血液性缺氧[答案]B⒘关于死腔样通气的叙述下列哪项是错误的?A 由部分肺泡血流不足而通气仍正常引起B 可见于肺内微血栓形成时C 肺部疾病时功能死腔可占潮气量的30%左右D 其通气血流比常大于0.8E 引起的血气特点主要是PaO2减低[答案]C⒙真性分流是指A 部分肺泡血流不足B 部分肺泡通气不足C 肺泡完全不通气但仍有血流D 肺泡完全无血流但仍有通气E 部分肺泡通气与血流的不足[答案]C⒚不能引起呼吸衰竭而致机体缺氧的是A 气道阻塞B 支气管哮喘C贫血D胸膜纤维化E 严重胸廓畸形[答案]C⒛呼吸衰竭患者吸纯氧15分钟变化不大是属何种异常?A通气血流比小于0.8B通气血流比大于0.8C功能分流增加D解剖分流增加E 弥散障碍[答案]D21.呼吸衰竭患者血气分析:pH 7.02,PaCO2 8.0kPa( 60mmHg) , PaO2 5.0kPa( 37.5mmHg ) HCO3- 15mmol/L,患者可能为哪种类型的酸碱平衡紊乱A急性呼吸性酸中毒B慢性呼吸性酸中毒C急性呼吸性酸中毒合并代谢性酸中毒D代谢性酸中毒E慢性呼吸性酸中毒合并代谢性酸中毒[答案]C22.肺性脑病的主要发病机制是A脑血流量增加和脑细胞酸中毒B缺氧使脑血管扩张C脑细胞内ATP生成减少D缺氧使脑血管壁通透性增加E缺氧使脑细胞内酸中毒[答案]A23.完整的呼吸过程是指A肺通气功能B肺换气功能C细胞呼吸功能D内、外呼吸功能E内、外呼吸功能及气体在血液中的运输[答案]E24.胸膜广泛增厚的病人可发生A限制性通气不足B阻塞性通气不足C气体弥散障碍D功能分流增加E真性分流增加[答案]A25.下列哪项不会引起限制性通气不足A低钾血症B呼吸中枢抑制C气道痉挛D气胸E肺组织广泛纤维化[答案]C26.以下可引起限制性通气不足的原因是A喉头水肿B气管异物C支气管哮喘D多发性肋骨骨折E肺水肿[答案]D27.胸内中央型气道阻塞可发生A呼气性呼吸困难B吸气性呼吸困难C呼气吸气同等困难D呼气吸气均无困难E阵发性呼吸困难[答案]A28.阻塞性通气不足可见于以下哪种情况?A低钾血症B多发性肋骨骨折C 大量胸腔积液D化脓性胸膜炎E慢性支气管炎[答案]E29.阻塞性通气不足是由于A弹性阻力增加B肺泡通气/血流比例失调C非弹性阻力增加D肺泡扩张受限制E 肺A-V交通支大量开放[答案]C30.因部分肺泡通气/血流比例大于0.8而发生呼吸衰竭可见于A肺不张B肺水肿C肺动脉栓塞D慢性阻塞性肺病患者E支气管肺炎[答案]C31.氧疗对于下列哪种情况引起的病变基本无效A通气障碍B气体弥散障碍C功能性分流D死腔样通气E肺内动静脉交通支大量开放[答案]E32.II型呼吸衰竭的氧疗原则是A间歇低浓度给氧B慢速高浓度给氧C正压低浓度给氧D持续低流量低浓度给氧E持续高流量高浓度给氧[答案]D33.判断呼吸衰竭的一个重要标准是A呼吸节律异常B发绀的程度C血气分析参数D呼吸困难程度E组织细胞受损程度[答案]C34.支气管肺炎引起I型呼吸衰竭的主要发病环节是A肺内动静脉短路开放B肺泡通气/血流比例失调C阻塞性通气障碍D限制性通气障碍E弥散障碍[答案]B35.有关通气/血流比例失调下列哪项不正确?A可以是部分肺泡通气不足B可以是部分肺泡血流不足C是引起呼吸衰竭的最重要机制D PaO2↓,而PaCO2可以正常E可见于气管阻塞,总肺泡通气量下降而肺血流未相应减少[答案]EB型题A PaCO2↑B PaO2↓C PaO2正常, PaCO2↑D PaO2↓, PaCO2↓E PaO2↓, PaCO2↑1.通气障碍时2.换气障碍时[答案]1E2BA 过量麻醉药使用B COPD患者C肺血管病变D ARDSE 肺实变1.可引起呼气性呼吸困难2.因急性肺泡毛细血管膜受损而致呼吸衰竭[答案]1B 2DA 生理性通气/血流比例不协调B 功能性分流增加C 死腔样通气增加D 解剖分流增加E 弥散功能障碍1.阻塞性肺气肿时2.常人P A O2略高于PaO2的主要原因[答案] 1B 2AA限制性通气不足B阻塞性通气不足C功能性分流增加D解剖分流增加E弥散障碍1.支气管异物可引起2.静麻醉药过量可引起3.大叶性肺炎(早期)4.大量胸腔积液5.一侧肺叶切除可引起6.肺内动静脉短路大量开放[答案]1B 2A 3C 4A 5E 6D C型题A 呼气性呼吸困难B吸气性呼吸困难C两者均有D两者均无1.中央性气道胸内部分阻塞时2.中央性气道胸外部分阻塞时3.外周性气道阻塞[答案]1A 2B 3AA PaO2<60mmHg (8.0kPa)B PaCO2>50mmHg (6.7kPa)C 两者均可D 两者均否1.贫血时2.一侧肺叶切除患者活动时3.II型呼吸衰竭患者用纯氧治疗可出现4.ARDS(早期)5.严重支气管哮喘6.异物阻塞主支气管[答案]1D 2A 3B 4A 5C 6CX型题⒈肺换气功能障碍包括A 弥散障碍B 通气/血流比例失调C 解剖分流增加D 功能性分流增加E 限制性通气不足[答案]ABCD⒉呼吸衰竭造成机体损害的主要原因是A 低氧血症B 酸碱平衡紊乱C 电解质紊乱D 内分泌功能障碍E 高碳酸血症[答案]AE⒊ARDS时通气/血流比例失调的原因是A 肺不张,肺水肿引起的部分气道阻塞B 炎性介质引起的支气管痉挛而致肺内分流C 肺内DIC及炎性介质引起肺血管收缩D 肺泡总通气量不足而血流未减少E 肺部病变的分布不均匀[答案]ABCDE⒋某青年突发高热.咳嗽.胸痛.呼吸急促,查WBC15×109/L,次日出现烦躁,四肢厥冷,出汗,静脉塌陷,口唇紫绀,脉搏111次/分,BP 9.7KPa/7.3Kpa,PaO2 6.7Kpa。
(必考题)人教版初中物理九年级第十四章综合经典复习题(答案解析)(1)

一、选择题1.小明做热学实验时将一瓶煤油用去一半,则剩下的一半()A.比热容不变,热值变为原来的一半B.比热容和热值都没有发生变化C.热值不变,比热容变为原来的一半D.比热容和热值都变为原来的一半B解析:B比热容是物质本身的一种性质和物质种类,物态有关,热值是燃料本身的一种性质,和燃料种类有关,一瓶煤油用去一半,物质的种类不变,物态不变,所以比热容和热值都不变。
故选B。
2.下列关于能量的转化正确的是()A.钻木取火﹣﹣﹣内能转化为机械能B.光合作用﹣﹣﹣光能转化为内能C.日光灯﹣﹣﹣光能转化为电能D.电饭锅﹣﹣﹣电能转化为内能D解析:DA.钻木取火是把机械能转化为内能,故A不符合题意;B.光合作用是把光能转化为化学能,故B不符合题意;C.日光灯是把电能转化为光能,故C不符合题意;D.电饭锅是应用电流热效应工作的,把电能转化为内能,故D符合题意。
故选D。
3.如图所示,甲、乙两图中的装置是研究不同物质的热值实验、下列说法正确的是()A.甲、乙两装置实验时,需要保持加热时间相同B.甲、乙两装置中液体升高的温度越高,燃料的热值越大C.甲、乙两装置实验时,不需要保持液体质量相同D.甲、乙两装置实验时,不需要保持燃料质量相同B解析:B研究不同物质的热值实验中,采用了控制变量法,需要控制燃料的质量相同;为了比较不同燃料的热值,要用不同的燃料,应加热同一种液体,让液体的质量相同,通过温度计的示数高低得出吸热多少,进而判断热值大小,液体升高的温度越高,燃料的热值越大。
实验中不需要控制燃料的加热时间相同,一定要让两种液体完全燃烧,故B正确,ACD错误。
故选B。
4.柴油机与汽油机相比,下列说法错误的是()A.柴油机有喷油嘴没有火花塞B.柴油机吸气冲程进入汽缸的只有空气C.柴油机效率更低一些D.压缩冲程中,柴油机缸内气体被压缩程度更大C解析:CA.柴油机有喷油嘴,而汽油机的顶部有火花塞,故A正确,不符合题意;B.柴油机吸气冲程进入汽缸的只有空气,汽油机在吸气冲程中吸入的是空气和汽油的混合物,故B正确,不符合题意;CD.由于柴油机和汽油机的结构和点燃方式不同,使得柴油机的效率比汽油机的效率高,且在压缩冲程中,柴油机缸内气体被压缩程度更大,故C错误,符合题意,D正确,不符合题意。
《常考题》人教版初中物理九年级第十四章综合经典复习题(含答案解析)

一、选择题1.下列关于内能、热量、温度和做功的说法中正确的是( )A .在汽油机的压缩冲程中,内能转化为机械能B .物体的比热容跟物体的质量、吸收或放出的热量、温度有关C .物体从外界吸收了热量,温度一定升高D .一个物体温度升高,内能一定增加D解析:DA .汽油机在压缩冲程中,将机械能转化为内能,故A 错误;B .物质的比热容与物质的种类和状态有关,与物体的质量大小、吸收或放出的热量多少、温度高低是无关的,故B 错误;C .晶体熔化时,吸收热量,内能增加,但温度不变,故C 错误;D .一个物体的温度升高,物体内能增加,故D 正确。
故选D 。
2.甲、乙两种燃料,甲的质量是乙质量的2倍,甲、乙完全燃烧后放出热量之比3:2,则甲乙两种燃料热值之比为( )A .3:4B .4:3C .2:3D .3:2A解析:A由题意可知,m 甲=2m 乙,Q 甲=1.5Q 乙,根据Q 放=mq 可知 1.5324q Q m Q m q m Q Q m =⨯=⨯=甲甲乙乙乙乙甲乙乙乙 故选A 。
3.2020年11月24日04时30分,中国首个月球采样返回任务“嫦娥五号”发射升空,火箭飞行约2200秒后,顺利将探测器送入预定轨道,开启我国首次地外天体采样返回之旅,下列说法正确的是( )A .火箭发射时,尾部产生大量白气,这是水汽化产生的水蒸气B .火箭加速升空时,将燃料的化学能转化为重力势能C .火箭使用液氢做燃料,是因为液氢热值大D .火箭升空过程中,与空气摩擦,通过热传递使内能增加C解析:CA .火箭发射时,尾部产生大量白气,这些白气人眼可以看到,不是水蒸气,是小水滴,这是水蒸气遇冷液化成的,A 错误;B .火箭加速升空时,速度不断变大,动能在变大,高度也在变大,那么重力势能也在变大,那么燃料的化学能转化为动能和重力势能,B 错误;C .火箭使用液氢做燃料,是因为液氢比其他燃料的热值大,根据Q qm =可知,在燃料的质量相同时,液氢完全燃烧放出的热量较多,C 正确;D .火箭升空过程中,与空气摩擦,这是在做功,不是热传递,是通过做功使内能增加,D 错误。
沪科版九年级物理 第十四章 了解电路 复习题(包含答案)
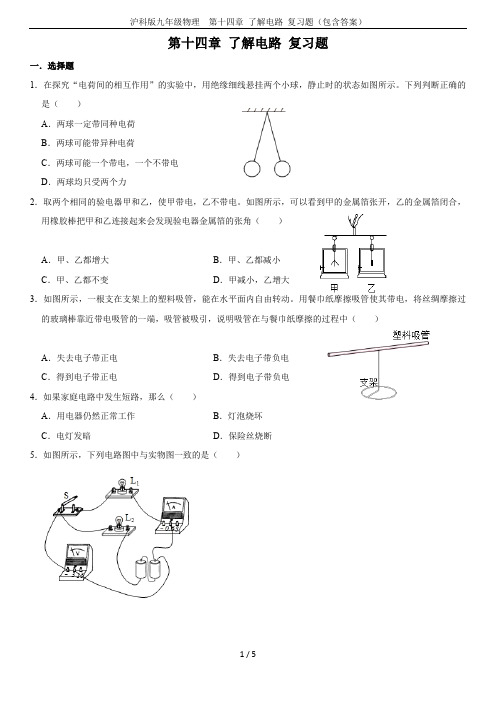
第十四章了解电路复习题一.选择题1.在探究“电荷间的相互作用”的实验中,用绝缘细线悬挂两个小球,静止时的状态如图所示。
下列判断正确的是()A.两球一定带同种电荷B.两球可能带异种电荷C.两球可能一个带电,一个不带电D.两球均只受两个力2.取两个相同的验电器甲和乙,使甲带电,乙不带电。
如图所示,可以看到甲的金属箔张开,乙的金属箔闭合,用橡胶棒把甲和乙连接起来会发现验电器金属箔的张角()A.甲、乙都增大B.甲、乙都减小C.甲、乙都不变D.甲减小,乙增大3.如图所示,一根支在支架上的塑料吸管,能在水平面内自由转动。
用餐巾纸摩擦吸管使其带电,将丝绸摩擦过的玻璃棒靠近带电吸管的一端,吸管被吸引,说明吸管在与餐巾纸摩擦的过程中()A.失去电子带正电B.失去电子带负电C.得到电子带正电D.得到电子带负电4.如果家庭电路中发生短路,那么()A.用电器仍然正常工作B.灯泡烧坏C.电灯发暗D.保险丝烧断5.如图所示,下列电路图中与实物图一致的是()A.B.C.D.6.如图所示的电路中,小灯泡L1、L2规格相同,闭合开关S后,发现L1不亮,L2发光。
此电路的故障可能是()A.灯L1短路B.灯L2短路C.灯L1断路D.开关S 接触不良7.如图所示,某一型号的锁设置了三种打开方式:密码(S1),特定指纹(S2)或应急钥匙(S3),三者都可以单独使电动机M工作而打开门锁,下列电路设计符合要求的是()A.B.C.D.8.下列操作能使图中的小灯泡L1和L2组成串联电路的是()A.闭合开关S1、S2和S3B.只闭合开关S1和S2C.只闭合开关S2和S3D.只闭合开关S39.如图所示,开关S闭合时,灯泡L1、L2组成并联电路的是()A.B.C.D.10.如图中两灯规格不同,能测出通过灯L1电流的电路是()A.B.C.D.11.将两只不同规格的灯泡L1、L2接在如图所示的电路中,闭合开关S1、S2后下列说法中正确的是()A.电流表测量干路电流B.L1与L2的亮度一定相同C.通过L1和L2的电流一定相等D.只断开S2,L1发光且亮度不变12.如图所示的电路图中,电流表能够测出总电流的是()A.B.C.D.13.在如图中,要使L1与L2串联,在“〇”处接入电流表或电压表,测量电路中的电流、L1两端的电压。
高考物理一轮复习 习题:第十四章 碰撞与动量守恒定律 第3课时 原子结构 氢原子光谱【含解析】

一、原子的核式结构1.α粒子散射实验的结果.绝大多数α粒子穿过金箔后,基本上仍沿原来的方向前进,但少数α粒子发生了大角度偏转,极少数α粒子的偏转超过了90°,有的甚至被撞了回来,如图所示.2.卢瑟福的原子核式结构模型.在原子的中心有一个很小的核,叫原子核,原子的所有正电荷和几乎所有质量都集中在原子核里,带负电的电子在核外绕核旋转.3.原子核的尺度:原子核直径的数量级为10-15 m,原子直径的数量级约为10-10m.二、玻尔理论1.定态:原子只能处于一系列不连续的能量状态中,在这些能量状态中原子是稳定的,电子虽然绕核运动,但并不向外辐射能量.2.跃迁:原子从一种定态跃迁到另一种定态时,它辐射或吸收一定频率的光子,光子的能量由这两个定态的能量差决定,即hν=E m-E n(h是普朗克常量,h=6.63×10-34 J·s).3.轨道:原子的不同能量状态跟电子在不同的圆周轨道绕核运动相对应.原子的定态是不连续的,因此电子的可能轨道也是不连续的.4.氢原子的能级、能级公式.(1)氢原子的能级图(如图所示).(2)氢原子的能级和轨道半径.①氢原子的能级公式:E n=1n2E1(n=1,2,3,…),其中E1为基态能量,其数值为E1=-13.6_e V.②氢原子的半径公式:r n=n2r1(n=1,2,3,…),其中r1为基态半径,又称玻尔半径,其数值为r1=0.53×10-10_m.1.α粒子散射实验说明了原子的正电荷和绝大部分质量集中在一个很小的核上.(√) 2.阴极射线来源于原子核.(×)3.原子的核式结构模型是由英国物理学家卢瑟福提出的.(√)4.原子光谱是不连续的,是由若干频率的光组成的.(√)5.氢原子由能量为E n的定态向低能级跃迁时,氢原子辐射的光子能量为hν=E n. (×) 6.电子跃迁时辐射的光子的频率等于电子绕核做圆周运动的频率.(×)7.氢原子吸收光子后,将从高能级向低能级跃迁.(×)8.原子的能量量子化现象是指原子的能量状态是不连续的.(√)1.(2015·开封模拟)在卢瑟福α粒子散射实验中,金箔中的原子核可以看作静止不动,下列各图画出的是其中两个α粒子经历金箔散射过程的径迹,其中正确的是()解析:金箔中的原子核与α粒子都带正电,α粒子接近原子核过程中受到斥力而不是引力作用,选项A、D错误;由原子核对α粒子的斥力作用及物体做曲线运动的条件,知曲线轨迹的凹侧应指向受力一方,选项B错误,C正确.答案:C2.(多选)(2016·芜湖模拟)按照玻尔原子理论,下列表述正确的是()A.核外电子运行轨道半径可取任意值B.氢原子中的电子离原子核越远,氢原子的能量越大C.原子跃迁时,辐射或吸收光子的能量由能级的能量差决定,即hν=|E m-E n|D.氢原子从激发态向基态跃迁的过程,可能辐射能量,也可能吸收能量解析:由玻尔理论知核外电子轨道是不连续的,不可以取任意值,故选项A错误;电子离原子核越远,能级越高,故原子的能量越大,选项B正确;原子发生跃迁时,若从低能级向高能级跃迁,吸收能量,从高能级向低能级跃迁,释放能量,且吸收和放出的光子的能量,由能级的能量差决定,故选项C 正确,D 错误.答案:BC3.(2015·西安模拟)用频率为ν0的光照射大量处于基态的氢原子,在所发射的光谱中仅能观测到频率分别为ν1、ν2、ν3的3条谱线,且ν3>ν2>ν1,则( )A .ν0<ν1B .ν3=ν2+ν1C .ν0=ν1+ν2+ν3D.1ν1=1ν2+1ν3解析:大量氢原子跃迁时,只有3个频率的光谱,这说明是从n =3能级向低能级跃迁,根据能量守恒有h ν3=h ν2+h ν1,解得ν3=ν2+ν1,B 正确.答案:B4.(2016·株洲模拟)根据玻尔原子结构理论,氦离子(He +)的能级图如图所示.电子处在n =3轨道上比处在n =5轨道上离氦核的距离________(填“近”或“远”).当大量He +处在n =4的激发态时,由于跃迁所发射的谱线有______条.解析:根据玻尔原子理论,量子数n 越小,轨道越靠近原子核,所以n =3比n =5的轨道离原子核近,大量处于n =4 激发态的原子跃迁一共有6种情形,即产生6条谱线.答案:近 6一、单项选择题1.(2014·上海卷)不能用卢瑟福原子核式结构模型得出的结论是()A.原子中心有一个很小的原子核B.原子核是由质子和中子组成的C.原子质量几乎全部集中在原子核内D.原子的正电荷全部集中在原子核内解析:为了解释α粒子散射实验,卢瑟福提出了原子核式结构模型:在原子的中心有一个很小的核,叫原子核,原子的全部正电荷和几乎全部质量都集中在原子核里,但不能得到原子核内的组成,故选项B不能用卢瑟福原子核式结构模型得出,A、C、D可以.答案:B2.(2015·安阳模拟)已知处于某一能级n上的一群氢原子向低能级跃迁时,能够发出10种不同频率的光,下列能表示辐射光波长最长的那种跃迁的示意图是()解析:由图示可知,在A 所示能级间跃迁中释放光子的能量最小,辐射光波的波长最长.选项A 正确.答案:A3.(2016·大同模拟)氢原子的核外电子从距核较近的轨道跃迁到距核较远的轨道过程中( )A .原子要吸收光子,电子的动能增大,原子的电势能增大,原子的能量增大B .原子要放出光子,电子的动能减小,原子的电势能减小,原子的能量也减小C .原子要吸收光子,电子的动能增大,原子的电势能减小,原子的能量增大D .原子要吸收光子,电子的动能减小,原子的电势能增大,原子的能量增大解析:根据玻尔理论,氢原子核外电子在离核越远的轨道上运动时,其能量越大,由能量公式E n =E 1n 2(E 1=-13.6 eV),可知电子从低轨道(量子数n 小)向高轨道(n 值较大)跃迁时,要吸收一定能量的光子,选项B 可排除;氢原子核外电子绕核做圆周运动,其向心力由原子核对电子的库仑引力提供,即ke 2r 2=mv 2r ,电子运动的动能E k =12mv 2=ke 22r,由此可知电子离核越远,r 越大时,则电子的动能就越小,选项A 、C 均可排除;由于原子核带正电荷,电子带负电荷,事实上异种电荷远离过程中需克服库仑引力做功,即库仑力对电子做负功,则原子系统的电势能将增大,系统的总能量增大,选项D 正确.答案:D4.(2016·宝鸡模拟)氢原子的部分能级如图所示,氢原子吸收以下能量时,可以从基态跃迁到n =2能级的是( )A .10.2 eVB .3.4 eVC.1.89 eV D.1.51 eV解析:氢原子基态能量为-13.6 eV,n=2能级的能量为-3.4 eV,两者的差值为10.2 eV,即所需要吸收的能量,故选项A正确.答案:A5.(2015·东营模拟)仔细观察氢原子的光谱,发现它只有几条分立的不连续的亮线,其原因是()A.氢原子只有几个能级B.氢原子只能发出平行光C.氢原子有时发光,有时不发光D.氢原子辐射的光子的能量是不连续的,所以对应的光的频率也是不连续的解析:光谱中的亮线对应不同频率的光,“分立的不连续的亮线”对应着不同频率的光,选项B、C错误;氢原子在不同的能级之间跃迁时,辐射不同能量的光子,并且满足E=h ν,能量不同,相应光子频率不同,体现在光谱上是一些不连续的亮线,选项A错误,D 正确.答案:D6.(2015·秦皇岛模拟)如图所示为氢原子能级示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出若干种不同频率的光,下列说法正确的是()A.这些氢原子总共可辐射出3种不同频率的光B.由n=2能级跃迁到n=1能级产生的光频率最小C.由n=4能级跃迁到n=1能级产生的光最容易发生衍射现象D.用n=2能级跃迁到n=1能级辐射出的光照射逸出功为6.34 eV的金属铂能发生光电效应解析:由原子跃迁、光电效应的规律分析.这些氢原子向低能级跃迁时可辐射出6种光子,选项A错误;由n=4能级跃迁到n=3能级产生的光子能量最小,光频率最小,选项B错误;由n=4能级跃迁到n=1能级产生的光子能量最大,光频率最大,光波长最小,最不容易发生衍射现象,选项C错误;由n=2能级跃迁到n=1能级辐射出的光子能量为10.20 eV>6.34 eV,所以能使金属铂发生光电效应,选项D正确.答案:D二、多项选择题7.如图所示为卢瑟福和他的同事们做α粒子散射实验装置的示意图.荧光屏和显微镜一起分别放在图中的A、B、C、D四个位置时,观察到以下现象,其中正确的是()A.放在A位置时,相同时间内观察到屏上的闪光次数最少B.放在B位置时,相同时间内观察到屏上的闪光次数只比A位置时稍少些C.放在C、D位置时,屏上观察不到闪光D.放在D位置时,屏上仍能观察到一些闪光,但次数极少解析:根据α粒子散射现象,绝大多数α粒子沿原方向前进,少数α粒子发生较大偏转,放在A位置时,相同时间内观察到屏上的闪光次数最多.答案:BD8.(2016·大连模拟)如图所示为氢原子的能级示意图,锌的逸出功是3.34 eV,那么对氢原子在能级跃迁过程中发射或吸收光子的特征认识正确的是()A.用氢原子从高能级向基态跃迁时发射的光照射锌板一定不能产生光电效应现象B.一群处于n=3能级的氢原子向基态跃迁时,能放出3种不同频率的光C.一群处于n=3能级的氢原子向基态跃迁时,发出的光照射锌板,锌板表面所发出的光电子的最大初动能为8.75 eVD.用能量为10.3 eV的光子照射,可使处于基态的氢原子跃迁到激发态E.用能量为14.0 eV的光子照射,可使处于基态的氢原子电离解析:当氢原子从高能级向低能级跃迁时,辐射出光子的能量有可能大于3.34 eV,锌板有可能产生光电效应,选项A错误;由跃迁关系可知,选项B正确;从n=3能级向基态跃迁时发出的光子最大能量为12.09 eV,由光电效应方程可知,发出光电子的最大初动能为8.75 eV,选项C正确;氢原子在吸收光子能量时需满足两能级间的能量差,因此选项D 错误;14.0 eV>13.6 eV,因此可以使处于基态的氢原子电离,选项E正确.答案:BCE9.(2016·烟台模拟)已知氢原子的能级如图所示,现用光子能量在10~12.9 eV范围内的光去照射一群处于基态的氢原子,则下列说法中正确的是()A.在照射光中可能被吸收的光子能量有无数种B.在照射光中可能被吸收的光子能量只有3种C.照射后可能观测到氢原子发射不同波长的光有6种D.照射后可能观测到氢原子发射不同波长的光有3种解析:n=1→n=5,hν=E5-E1=13.06 eV,故能量在10~12.9 eV范围内的光子,仅吸收符合n=1→n=2,n=1→n=3,n=1→n=4的能级差的三种光子,选项A错误,B 正确;照射后处于最高能级的原子的量子数n=4,故向低能级跃迁能辐射的光谱条数N=n(n-1)-12=6,选项C正确,D错误.答案:BC三、非选择题10.玻尔氢原子模型成功解释了氢原子光谱的实验规律,氢原子能级图如图所示.当氢原子从n=4的能级跃迁到n=2的能级时,辐射出频率为____Hz的光子,用该频率的光照射逸出功为 2.25 eV的钾表面,产生的光电子的最大初动能为____eV(电子电荷量e=1.60×10-19C,普朗克常量h=6.63×10-34J·s).解析:氢原子从n=4的能级跃迁到n=2的能级时,释放出光子的能量为E=-0.85 eV -(-3.40eV)=2.55 eV,由hν=E解得光子的频率ν=6.2×1014Hz.用此光照射逸出功为2.25 eV的钾时,由光电效应方程知,产生光电子的最大初动能为E k=hν-W=(2.55-2.25) eV=0.30 eV.答案:6.2×10140.3011.氢原子基态能量E1=-13.6 eV,电子绕核做圆周运动的半径r1=0.53×10-10m.求氢原子处于n=4激发态时:(1)原子系统具有的能量;(2)电子在n=4轨道上运动的动能(已知能量关系E n=1n2E1,半径关系r n=n2r1,k=9.0×109N ·m 2/C 2,e =1.6×10-19C);(3)若要使处于n =2轨道上的氢原子电离,至少要用频率为多大的电磁波照射氢原子 (普朗克常量h =6.63×10-34 J ·s)?解析:(1)由E n =1n 2E 1得 E 4=E 142=-0.85 eV . (2)因为r n =n 2r 1,所以r 4=42r 1,由圆周运动知识得k e 2r 24=m v 2r 4, 所以E k4=12mv 2=ke 232r 1=9.0×109×(1.6×10-19)232×0.53×10-10J ≈0.85eV(3)要使处于n =2的氢原子电离,照射光的光子能量应能使电子从第2能级跃迁到无限远处,最小频率的电磁波的光子能量应为h ν=0-E 14, 得ν≈8.21×1014Hz.答案:(1)-0.85 eV (2)0.85 eV (3)8.21×1014 Hz。
人教版九年级 第14章 内能的利用 期中复习练习题(有答案)

第14章内能的利用期中复习练习题2022—2023学年人教版九年级上册一、选择题。
1、如图所示的四个情景,下列说法中正确的是()A.甲图中蓝墨水在热水中扩散得快,说明温度越高分子无规则运动越剧烈B.乙图中两个铅块紧压在一起后能吊住重物。
说明分子间存在斥力C.丙图中厚玻璃筒内的空气被压缩时,空气的内能减小D.丁图中进气门和排气门均关闭且活塞向下运动,这是内燃机的做功压缩冲程2、(多选)关于四冲程内燃机,下面说法正确的是()A.内燃机是利用内能来做功的机器B.在压缩冲程,内能转化为机械能C.在做功冲程,内能转化为机械能D.四个冲程依次为吸气、压缩、做功、排气冲程3、下列关于“热机”的说法中,正确的是()A.热机使用的燃料热值越大,热机效率越高B.做功冲程将机械能转化为内能C.热机常用水做冷却剂,是因为水的沸点高D.火箭发动机属于热机4、在学习了内能及能量的转化和守恒后,同学们在一起梳理知识时交流了以下想法。
你认为其中正确的是()A.只有做功可以改变物体的内能B.热传递过程中,温度从高温物体传给低温物体C.在一定条件下各种形式的能量都可以相互转化D.能量守恒定律证明了能量既不会产生,也不会消失5、在四冲程汽油机的工作过程中,内能转化为机械能的冲程是()A. 吸气冲程B. 压缩冲程C. 做功冲程D. 排气冲程6、下列关于汽油机和柴油机的说法,正确的是()A.柴油机的工作过程分为吸气、压缩、排气三个冲程B.汽油机和柴油机都属于内燃机C.在吸气冲程中,汽油机吸入的是汽油和空气的混合物,而柴油机吸入的是柴油和空气的混合物D. 汽油机顶部有喷油嘴,而柴油机顶部有火花塞7、有关四冲程汽油机,下列说法正确的是()A.吸气冲程吸入的是空气B.压缩冲程内能转化为机械能C.做功冲程把机械能转化为内能D.做功冲程把内能转化为机械能8、目前长沙城区的老居民小区正在进行水路改造,改造中用到了一种打孔工具——冲击钻,冲击钻工作时,钻头在电动机的带动下不断地冲击墙壁,打出圆孔。
第十四章《内能的利用》复习训练题

第十四章《内能的利用》复习训练题1.(2020巴中)下列四幅图是汽油机一个工作循环的四个冲程,其中不是靠飞轮惯性完成的是()2.(2020南京)如图是内燃机某冲程的工作示意图,下面四个事例中能量转化与之相同的是()3.(2020东营)如图是四冲程汽油机工作循环中的一个冲程,下列关于冲程及其能量转化判断正确的是()A.做功冲程,将机械能转化为内能B.做功冲程,将内自能转化为机械能C.压缩冲程,将机械能转化为内能D.压缩冲程,将内能转化为机械能4.(2020衡阳)如图所示为内燃机四冲程工作示意图,下列说法正确的是()A.一个工作循环的正确顺序是:甲乙丙丁B.乙图冲程能获得动力C.丁图冲程有明显机械能转化为内能的过程D.丙图冲程存在化学能转化为内能的过程5.(2020甘孜)下列关于热值和热机效率的说法,正确的是()A.使燃料燃烧更充分,可以增大热值B.使燃料燃烧更充分,可以提高热机效率C.柴油机的热机效率通常为100%D.燃料燃烧释放的热量越大,热值越大6.(2020枣庄)关于热机的效率,下列说法正确的是()A.在做功同样多的情况下,热机的效率越高消耗的燃料越多B.一般情况下柴油机的效率比汽油机的高C.热机的效率越高说明做功越快D.热机损失的能量中,废气带走的能量较少,主要是由于机械摩擦损失的7.(2020安徽)物理学习过程中,对物理知识的正确认识是非常重要的。
以下说法正确的是()A.物体的运动速度越大,惯性越大B.磁场和磁感线都是真实存在的C.电动机工作时消耗的电能主要转化成机械能D.热机工作的实质是把机械能转化为内能8.(2020湘西州)关于能量守恒定律的下列说法中。
正确的是()A.能量既可以凭空消失B.能量也可以凭空产生C.热机的工作过程不遵循能量守恒定律D.能量转化和转移过程中,能量的总量保持不变9.(2020·黑龙江)目前长沙城区的老居民小区正在进行水路改造,改造中用到了一种打孔工具-一冲击钻,冲击钻工作时,钻头在电动机的带动下不断地冲击墙壁,打出圆孔,如图所示,冲击钻在工作过程中,其能量转化关系是()A.内能转化为机械能B.内能转化为电能C.只有机械能和内能的转化D.有电能、机械能和内能的转化10.(2020通辽)下列说法正确的是()A.热量总是从内能大的物体向内能小的物体传递B.雪花纷飞,说明分子不停地做无规则运动C.同一物体,温度降低得越多,放出的热量越多D.汽油机的压缩冲程,汽缸内的混合物内能增加,温度升高11.(2020鄂州)夜幕下的广场,孩子们都喜欢骑上能发光的滑板车遛弯,这种滑板车在人的助力下可以滑行起来,同时轮子会发光,停下来时就不发光。
病理学试题

第十四章心功能不全【学习要求】♦掌握心功能不全、心力衰竭的概念。
♦掌握心力衰竭的发病机制。
♦熟悉心功能不全的原因和诱因。
♦熟悉心功能不全的代偿方式及其意义。
♦熟悉心功能不全时的代谢与功能的变化。
♦了解心功能不全的分类和防治的病理生理基础。
【复习题】一、选择题A型题1.心力衰竭最具特征性的血流动力学变化是A.肺动脉循环充血B.动脉血压下降C.心输出降低D.毛细血管前阻力增大E.体循环静脉淤血2.下列哪种疾病可引起低输出量性心力衰竭A.甲状腺功能亢进B.严重贫血C.心肌梗死D.脚气病(VitB1缺乏)E.动-静脉瘘3.下列哪项是心肌向心性肥大的特征A.肌纤维长度增加B.心肌纤维呈并联性增生C.心腔扩大D.室壁增厚不明显E.室腔直径与室壁厚度比值大于正常4.下列哪个肌节长度收缩力最大A.1.8μm B.2.0μmC.2.2μm D.2.4μmE.2.6μm5.心力衰竭时心肌收缩性减弱与下列哪项因素无关A.ATP供给不足B.心肌细胞坏死C.肌浆网Ca2+摄取能力下降D.肌浆网Ca2+释放能力下降E.肌钙蛋白活性下降6.下列哪项因素与心室舒张功能障碍无关A.甲状腺功能亢进B.心室舒张势能减弱C.心肌顺应性降低D.心室僵硬度加大E.肌浆网Ca2+释放能力下降7.下列哪种疾病可引起左心室后负荷增大A.甲状腺功能亢进B.严重贫血C.心肌炎D.心肌梗死E.高血压病8.下列哪种情况可引起右心室前负荷增大A.肺动脉高压B.肺动脉栓塞C.室间隔缺损D.心肌炎E.肺动脉瓣狭窄9.下列哪项变化在急性心力衰竭不会发生A.心率加快B.肺水肿C.心肌肥大D.血压下降E.皮肤苍白10.下列哪种情况可引起心肌向心性肥大A.心肌梗死B.主动脉瓣闭锁不全C.脚气病D.高血压病E.严重贫血11.心功能不全时,通过增加血容量起代偿作用的主要器官是A.心B.肝C.脾D.肺E.肾12.下列哪项因素与心肌兴奋-收缩耦联障碍无关A.肌钙蛋白活性下降B.肌球蛋白A TP酶活性下降C.肌浆网Ca2+释放能力下降D.肌浆网Ca2+储存量下降E.Ca2+内流障碍13.心肌缺血引起的心肌收缩性减弱与下列哪个因素无关A.ATP生成减少B.心肌细胞死亡C.酸中毒D.肌浆网Ca2+摄取能力降低E.肌钙蛋白与Ca2+结合障碍14.下列哪项不是心脏向心性肥大的特点A.肌纤维变粗B.室壁增厚C.心腔无明显扩大D.心肌纤维呈串联性增大E.室腔直径与室壁厚度比值小于正常15.下列哪种疾病引起的心力衰竭不属于低输出量性心力衰竭A.冠心病B.心肌炎C.二尖瓣狭窄D.甲状腺功能亢进E.主动脉瓣狭窄16.下列哪项属于心力衰竭时肺循环淤血的表现A.肝颈静脉返流征阳性B.夜间阵发性呼吸困难C.下肢水肿D.肝肿大压痛E.颈静脉怒张17.心功能不全时,下列哪项反应已失去代偿意义A.心率加快B.心肌肥大C.肌源性扩张D.红细胞增多E.血流重分布18.下列哪项不是心力衰竭时心输出量减少的表现A.皮肤苍白B.脉压变小C.端坐呼吸D.尿少E.嗜睡19.心力衰竭病人使用静脉扩张剂可以A.增强心肌收缩功能B.改善心肌舒张功能C.降低心脏后负荷D.降低心脏前负荷E.控制水肿20.心力衰竭时,下列哪项代偿反应主要由肾脏引起A.红细胞增多B.血流重分布C.紧张源性扩张D.肌红蛋白增加E.细胞线粒体数量增多B型题A.左室前负荷增大B.右室前负荷增大C.左室后负荷增大D.右室后负荷增大E.左、右室后负荷均增大1.高血压病时2.肺动脉瓣狭窄时3.慢性支气管炎及肺气肿时4.主动脉瓣关闭不全时5.肺动脉栓塞时6.甲状腺功能亢进时7.主动脉瓣狭窄时X型题1.酸中毒引起心肌收缩性减弱的机制是A.使Ca2+与肌浆网钙储存蛋白结合紧密B.降低β-受体对去甲肾上腺素的敏感性C.H+与肌钙蛋白结合增加D.H+进入心肌细胞,与K+进入交换,形成高钾血症2.心力衰竭时血容量增多的负面影响是A.增加心室充盈B.维持动脉压C.水钠潴留D.心脏容量负荷增大3.心力衰竭引起血容量增多主要是通过下列哪些环节实现的A.降低肾小球滤过率B.增加淋巴回流C.扩张血管D.增加肾小管对水钠的重吸收4.心肌肥大的不平衡生长引起心肌收缩性减弱的主要机制是A.心肌交感神经分布密度下降B.心肌线粒体数量增加不足C.肥大心肌毛细血管数量不足D.肌球蛋白ATP酶活性下降5.心肌缺血引起心力衰竭的发病机制是A.ATP生成不足B.酸中毒C.心肌细胞死亡D.肌浆网钙处理功能障碍6.心肌离心性肥大的特点是A.心肌并联性增生B.心脏明显扩大C.心肌纤维长度增大D.室腔直径与室壁厚度比值大于正常7.下列哪些情况可阻止Ca2+内流A.酸中毒B.高钾血症C.高钠血症D.高钙血症8.下列哪些情况可引起低输出量性心力衰竭A.主动脉瓣狭窄B.妊娠C.严重贫血D.冠心病9.下列哪些因素可引起心肌细胞凋亡A.TNFB.氧自由基C.线粒体功能异常D.细胞钙稳态失衡10.下列哪些因素可造成心肌能量生成及利用障碍而引发心力衰竭A.严重贫血B.心肌肥大C.VitB1缺乏D.冠心病二、名词解释1.heart failure2.congestive heart failure3.low output heart failure4.paroxysmal nocturnal dyspnea5.concentric hypertrophy三、填空题1.心力衰竭时心脏的代偿反应有,和。
《医学微生物学》第十四章分枝杆菌属和第第十七章其他细菌复习题及答案

《医学微生物学》第十四章分枝杆菌属和第第十七章其他细菌复习题及答案第十四章分枝杆菌属一、单项选择题1.关于结核分枝杆菌生物学特性的叙述,错误的是:A.抗酸染色,呈红色B.专性需氧,生长缓慢C.菌落表面粗糙呈菜花状D.耐酸碱,在6%H2SO4或4%NaOH中可存活30minE.耐煮沸,100℃15min才死亡2.下列细菌中,繁殖速度最慢的是:A.大肠埃希菌B.丙型链球菌C.脑膜炎奈瑟菌D.结核分支杆菌E.肺炎链球菌3.在液体培养基中形成菌膜生长的细菌是:A.变形杆菌B.布氏杆菌C.肉毒梭菌D.结核分枝杆菌E.产气荚膜梭菌4.结核分枝杆菌常用的培养基是:A.沙保培养基B.罗氏培养基C.疱肉培养基D.巧克力色培养基E.亚碲酸钾培养基5.细胞壁中含脂类最多的细菌是:A.结核分枝杆菌B.白喉棒状杆菌C.衣氏放线菌D.霍乱弧菌E.幽门螺杆菌6.与结核分枝杆菌抗酸性有关的成分是:A.索状因子B.磷脂C.分枝菌酸D.蜡脂DE.硫酸脑苷脂7.结核分枝杆菌侵入机体的途径,不可能的是:A.呼吸道B.消化道C.破损的皮肤D.泌尿道E.节肢动物叮咬8.不以内毒素或外毒素为致病物质的细菌是:A.白喉棒状杆菌B.炭疽杆菌C.结核分枝杆菌D.绿脓假单胞杆菌E.布氏杆菌9.人体对结核分枝杆菌的免疫特点是:A.以体液和细胞免疫并重B.以体液免疫为主C.为有菌免疫D.不能通过人工主动免疫获得E.可引起I型超敏反应10.卡介苗是:A.经甲醛处理后的人型结核分枝杆菌B.加热处理后的人型结构分枝杆菌C.发生了抗原变异的牛型结核分枝杆菌D.保持免疫原性,减毒的牛型结核分枝杆菌E.保持免疫原性,减毒的活的人型结核分枝杆菌11.卡介苗的接种对象主要是:A.结核性脑膜炎患者B.结核菌素试验阳性者C.严重结核病人,结核菌素试验阴性患者D.新生儿和结核菌素试验阴性的儿童E.C + D12.有关结核菌素试验,下述错误的是:A.属于皮肤迟发型超敏反应B.可检测机体对结核分枝杆菌的免疫状况C.皮肤反应程度以局部红肿,硬结的直径为标准.D.可检测机体细胞免疫功能状况E.12-18小时观察结果13.结核菌素试验为阳性反应,下述可能情况错误的是:A.表明机体已感染过结核分枝杆菌B.表明机体接种卡介苗成功C.表明机体对结核分枝杆菌有一定的特异性免疫力D.表明机体对结核分枝杆菌有迟发型超敏反应E.表明机体对结核分枝杆菌无免疫力14.从痰中检出具有临床诊断意义的细菌是:A.表皮葡萄球菌B.金黄色葡萄球菌C.甲型溶血性链球菌D.脑膜炎奈瑟菌E. 结核分枝杆菌二、多项选择题1.结核杆菌对下列化学因素具有抵抗力:A.70—75%酒精B.4%NaOHC.3%HCID.6%H2SO4E.5%石炭酸2.结核杆菌培养特性表现为:A.严格厌氧B.专性需氧C.营养要求高D.生长缓慢E.液体培养基中呈均匀混浊生长3.结核菌素试验主要用途是:A.用于选择卡介苗接种对象及免疫效果测定B.结核菌素试验阴性反应,不宜接种卡介苗C.结核菌素试验强阳性者,婴幼儿可作结核病诊断D.作为机体细胞免疫力功能状态的检测E.在未接种卡介苗人群中,作结核杆菌感染的流行病学调查4.麻风杆菌所致的瘤型麻风,其特点:A.潜伏期长,病变严重B.主要侵犯皮肤粘膜.神经等C.病灶组织不易找到麻风杆菌D.麻风菌素试验呈阳性E.血清中查到大量抗体5.麻风杆菌所致的结核样型麻风,其特点:A.病程缓慢.稳定B.病变主要发生在皮肤.神经C.病灶组织查到大量麻风杆菌D.麻风菌素试验呈阴性E.该型麻风传染性小三、名词解释1.BCG2. acid-fast bacilli3.结核菌素试验4.感染性免疫5.麻风细胞四、问答题1.简述抗酸染色方法。
苏州景城学校八年级数学上册第十四章《整式的乘法与因式分解》复习题(答案解析)

一、选择题1.下列计算正确的是( )A .248a a a •=B .352()a a =C .236()ab ab =D .624a a a ÷= D 解析:D【分析】分别根据同底数幂的乘法,幂的乘方,积的乘方法则以及同底数幂的除法法则逐一计算判断即可.【详解】解:A 、a 2∙a 4=a 6,故选项A 不合题意;B 、(a 2)3=a 6,故选项不B 符合题意;C 、(ab 2)3=a 3b 6,故选项C 不符合题意;D 、a 6÷a 2=a 4,故选项D 符合题意.故选:D .【点睛】本题主要考查了幂的运算,熟练掌握幂的运算法则是解答本题的关键.2.已知: 13m m +=, 则: 331m m +的值为( ) A .15B .18C .21D .9B 解析:B【分析】 把13m m +=两边平方得出221m m +的值,再把331m m+变形代入即可得出答案 【详解】 解:∵13m m+=, ∴219⎛⎫+= ⎪⎝⎭m m , ∴221=7+m m ∴()3232111=m+m 1+=371=18m m ⎛⎫⎛⎫+-⨯- ⎪⎪⎝⎭⎝⎭m m 故选:B【点睛】本题考查了完全平方公式的应用,熟练掌握公式是解题的关键3.计算()201920180.52-⨯的值( ) A .2 B .2- C .12 D .12- D解析:D【分析】 将原式变形为201920181-22⎛⎫⨯ ⎪⎝⎭,再利用同底数幂的乘法逆运算变为2018201811--222⎛⎫⎛⎫⨯⨯ ⎪ ⎪⎝⎭⎝⎭,然后运用乘法交换律及积的乘方的逆运算计算即可. 【详解】 解:原式=201920181-22⎛⎫⨯ ⎪⎝⎭=2018201811--222⎛⎫⎛⎫⨯⨯ ⎪ ⎪⎝⎭⎝⎭ =2018201811-2-22⎛⎫⎛⎫⨯⨯ ⎪ ⎪⎝⎭⎝⎭=201811-2-22⎛⎫⎛⎫⨯⨯ ⎪ ⎪⎝⎭⎝⎭ =()20181-1-2⎛⎫⨯ ⎪⎝⎭=1×1-2⎛⎫ ⎪⎝⎭=12- 故选:D .【点睛】本题主要考查了整式的乘法,熟练掌握同底数幂的乘法、积的乘方的逆运算是解题的关键.4.下列计算中能用平方差公式的是( ).A .()()a b a b -+-B .1133x y y x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭C .22x x D .()()21x x -+ B解析:B【分析】根据平方差公式()()22a b a b a b -+=-一项一项代入判断即可. 【详解】A 选项:两项都是互为相反数,故不能用平方差公式;B 选项:两项有一项完全相同,另一项为相反数,故可用平方差公式;C 选项:两项完全相同,故不能用平方差公式;D 选项:有一项2-与1不同,故不能用平方差公式.故选:B .【点睛】此题考查平方差的基本特征:()()22a b a b a b -+=-中a 与b 两项符号不同,难度一般.5.下列运算正确..的是( ) A .246x x x ⋅=B .246()x x =C .3362x x x +=D .33(2)6x x -=- A 解析:A【分析】根据同底数幂的乘法、幂的乘方、积的乘方以及合并同类项进行判断即可.【详解】A 选项246x x x ⋅=,选项正确,故符合题意;B 选项248()x x =,选项错误,故不符合题意;C 选项3332x x x +=,选项错误,故不符合题意;D 选项33(2)8x x -=-,选项错误,故不符合题意.故选:A .【点睛】本题考查同底数幂的乘法、幂的乘方、积的乘方以及合并同类项,属于基础题,熟练掌握这些计算公式和方法是解决本题的关键.6.如图是一所楼房的平面图,下列式子中不能表示它的面积的是( )A .x 2+3x +6B .(x +3)(x +2)﹣2xC .x (x +3)+6D .x (x +2)+x 2D解析:D【分析】 根据S 楼房的面积=S 矩形ABCD +S 矩形DEFC +S 矩形CFHG 代入数值求出图形面积,再根据计算各整式判断即可.【详解】S 楼房的面积=S 矩形ABCD +S 矩形DEFC +S 矩形CFHG=AD •AB +DC •DE +CF •FH .∵AB =DC =AD =x ,DE =CF =3,FH =2,∴S 楼房的面积=x 2+3x +6.∵(x+3)(x+2)﹣2x= x 2+3x +6,x (x +3)+6= x 2+3x +6,x (x +2)+x 2=2 x 2+2x ,故选:D ..【点睛】此题考查列整式求图形面积,整式的混合运算,掌握整式的运算法则是解题的关键. 7.已知5a b +=,2ab =-,则a 2+b 2的值为( )A .21B .23C .25D .29D 解析:D【分析】根据完全平方公式得()2222a b a b ab +=+-,再整体代入即可求值.【详解】解:∵()2222a b a b ab +=++,∴()2222a b a b ab +=+-, ∵5a b +=,2ab =-,∴原式()252225429=-⨯-=+=. 故选:D .【点睛】本题考查完全平方公式,解题的关键是熟练运用完全平方公式进行计算.8.下列运算正确的是( )A .3515x x x ⋅=B .()3412x x -=C .()32628y y = D .623x x x ÷= C解析:C【分析】根据整式的同底数幂相乘法则、幂的乘方法则、积的乘方法则、同底数幂相除法则进行计算并判断.【详解】A 、358⋅=x x x ,故该项错误;B 、()3412x x -=-,故该项错误; C 、()32628y y =,故该项正确;D 、624x x x ÷=,故该项错误;故选:C .【点睛】本题考查了整式的计算,熟记整式的同底数幂相乘法则、幂的乘方法则、积的乘方法则、同底数幂相除法则是解题的关键.9.计算()()202020213232 -⨯的结果是( ) A .32- B .23- C .23 D .32D 解析:D【分析】利用积的乘方的逆运算解答.【详解】()()202020213232 -⨯ =20202020233322⎛⎫⎛⎫-⨯⨯ ⎪ ⎪⎝⎭⎝⎭=2020233322⎛⎫-⨯⨯ ⎪⎝⎭=32. 故选:D .【点睛】此题考查积的乘方的逆运算,掌握积的乘方的计算公式是解题的关键.10.若|a |=13,b|=7,且a +b>0,则a -b 的值是( ).A .6或20B .20 或-20C .6或-6D .-6或20A解析:A【分析】先求出a b ,的值,根据条件+a b >0,确定=13a ,b=7±,分类代入-a b 求值即可.【详解】|a |=13,=13a ±,|b|=7,b=7±,∵+a b >0,∴=13a ,b=7±,当=13a ,b=7时,=1376a b --=,当=13a ,7b =-时,=13+720a b -=,则6a b -=或20.故选择:A .【点睛】本题考查条件限定求值问题,会根据限定条件求出字母的值,掌握分类思想求代数式的值是解题关键.二、填空题11.如果210x x m -+是一个完全平方式,那么m 的值是__________.25【分析】利用完全平方公式的结构特征即可求出m 的值【详解】解:∵x2-10x+m 是一个完全平方式∴m==25故答案为:25【点睛】此题考查了完全平方式熟练掌握完全平方公式是解本题的关键解析:25【分析】利用完全平方公式的结构特征,即可求出m 的值.【详解】解:∵x 2-10x +m 是一个完全平方式,∴m=210()2-=25. 故答案为:25.【点睛】 此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.12.已知18m x =,16n x =,则2m n x +的值为________.【分析】根据同底数幂的乘法可得再根据幂的乘方可得然后再代入求值即可【详解】解:故答案为【点睛】此题主要考查了同底数幂的乘法和幂的乘方关键是掌握同底数幂的乘法法则:同底数幂相乘底数不变指数相加;幂的乘 解析:14【分析】根据同底数幂的乘法可得22m n m n x x x +=⋅,再根据幂的乘方可得()22m m x x =,然后再代入18mx =,16n x =求值即可. 【详解】 解:()2222111684m n m n m n x x x x x +⎛⎫=⋅=⋅=⨯= ⎪⎝⎭ , 故答案为14. 【点睛】 此题主要考查了同底数幂的乘法和幂的乘方,关键是掌握同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加;幂的乘方法则:底数不变,指数相乘.13.计算:248(21)(21)(21)(21)1+++++=___________.216【分析】在原来的算式前面乘上(2-1)根据平方差公式进行计算即可求解【详解】原式======216故答案是:216【点睛】本题主要考查有理数的运算掌握平方差公式是解题的关键 解析:216【分析】在原来的算式前面乘上(2-1),根据平方差公式,进行计算,即可求解.【详解】原式=248(21)(21)(21)(21)(21)1-+++++=2248(21)(21)(21)(21)1-++++=448(21)(21)(21)1-+++=88(21)(21)1-++=16(21)1-+=216.故答案是:216.【点睛】本题主要考查有理数的运算,掌握平方差公式,是解题的关键.14.已知x 2-3x -1=0,则2x 3-3x 2-11x +1=________.4【分析】根据x2-3x -1=0可得x2-3x =1再将所求代数式适当变形后分两次整体代入即可求得值【详解】解:∵x2-3x -1=0∴x2-3x =1∴==将x2-3x =1代入原式==将x2-3x =1代解析:4【分析】根据x 2-3x -1=0可得x 2-3x =1,再将所求代数式适当变形后分两次整体代入即可求得值.【详解】解:∵x 2-3x -1=0,∴x 2-3x =1,∴3223111x x x --+=223132611x x x x -+-+=()22233111x x x x x -+-+将x 2-3x =1代入原式=221113x x x +-+=23)13(x x -+将x 2-3x =1代入原式=314+=,故答案为:4.【点睛】本题考查代数式求值,因式分解法的应用.解决此题的关键是掌握“降次”思想和整体思想.15.已知102m =,103n =,则32210m n ++=_______.7200【分析】根据幂的乘方法则分别求出和的值然后根据同底数幂的乘法运算法则计算即可【详解】解:∵∴∴故答案为:7200【点睛】本题考查同底数幂的乘法和幂的乘方解题的关键是掌握运算法则解析:7200【分析】根据幂的乘方法则分别求出3m 10和210n 的值,然后根据同底数幂的乘法运算法则计算即可.【详解】解:∵102m =,103n =,∴()33m 10108m ==,()22n 10109n ==, ∴3m+2n+232210101010891007200m n =⋅⋅=⨯⨯=,故答案为:7200.【点睛】本题考查同底数幂的乘法和幂的乘方,解题的关键是掌握运算法则.16.一个三角形的面积为3xy -4y ,一边长是2y ,则这条边上的高为_____.3x -4【分析】利用面积公式计算即可得到答案【详解】设这条边上的高为a 由题意得:∴ay=3xy-4y ∴a=3x-4故答案为:3x-4【点睛】此题考查多项式除以单项式法则:用多项式中的每一项分别除以单解析:3x -4【分析】利用面积公式计算即可得到答案.【详解】设这条边上的高为a , 由题意得:12342y a xy y ⋅⋅=-, ∴ay=3xy-4y ,∴a=3x-4,故答案为:3x-4.【点睛】 此题考查多项式除以单项式法则:用多项式中的每一项分别除以单项式,再把结果相加. 17.对于2(34)x y --的计算,追风学习小组进行了激烈的讨论,①小杰说只能用公式()2222a b a ab b -=-+;②小聪说可以看成普通的多项式乘以多项式即(34)(34)x y x y ----;③小懿说可以用公式222()2a b a ab b +=++但要看准谁是a 谁是b ;④小王说口算就是22916x y +;⑤小亮说可以转化计算2(34)x y +,你认为谁的说法正确请写出序号____.①②③⑤【分析】根据多项式乘以多项式和完全平方公式计算即可【详解】①正确;②正确;③正确;④错误;⑤正确;故答案为:①②③⑤【点睛】此题考查了多项式乘以多项式和完全平方公式计算熟练掌握运算法则是解答解析:①②③⑤【分析】根据多项式乘以多项式和完全平方公式计算即可.【详解】①22222(34)(3)2(3)4(4)92416x y x x y y x xy y --=--⋅-⋅+=++,正确;②22222(34)(34)(34)(3)3443(4)92416x y x y x y x x y y x y x xy y --=----=-+⋅+⋅+=++,正确;③22222(34)(3)2(3)(4)(4)92416x y x x y y x xy y --=-+⋅-⋅-+-=++,正确; ④错误;⑤222222(34)(34)(3)234(4)92416x y x y x x y y x xy y --=+=+⋅⋅+=++,正确; 故答案为:①②③⑤【点睛】此题考查了多项式乘以多项式和完全平方公式计算,熟练掌握运算法则是解答此题的关键. 18.已知有理数a ,b 满足0ab <,a b a b +=+,521a b b a ++=--,则()31222a b a b ⎛⎫++⋅- ⎪⎝⎭的值为______.0【分析】分情况讨论或根据绝对值的性质化简得到即可求出结果【详解】解:①时(矛盾)舍去;②时原式故答案是:0【点睛】本题考查代数式的求值解题的关键是掌握绝对值的化简利用整体代入的思想求值解析:0【分析】分情况讨论,0a >,0b <或0a <,0b >,根据绝对值的性质化简,得到312022a b ++=,即可求出结果. 【详解】解:①0a >,0b <时,()521a b b a b a b a ++=--=---=-⎡⎤⎣⎦,610a b ∴++=,0a b a b +=+≥,()61510a b a a b ∴++=+++>(矛盾),∴舍去;②0a <,0b >时,()521a b b a b a a b ++=--=--=-,4310a b ∴++=,312022a b ∴++=, ∴原式()00a b =-=.故答案是:0.【点睛】本题考查代数式的求值,解题的关键是掌握绝对值的化简,利用整体代入的思想求值. 19.若6x y +=,3xy =-,则2222x y xy +=_____.【分析】先将原式因式分解得再整体代入即可求出结果【详解】解:∵∴原式故答案是:【点睛】本题考查因式分解解题的关键是熟练运用因式分解和整体代入的思想求值解析:36-【分析】先将原式因式分解得()2xy x y +,再整体代入即可求出结果.【详解】解:()22222x y xy xy x y +=+, ∵6x y +=,3xy =-,∴原式()23636=⨯-⨯=-.故答案是:36-.【点睛】本题考查因式分解,解题的关键是熟练运用因式分解和整体代入的思想求值. 20.若方程22(1)8m x mx x --+=是关于x 的一元一次方程,则代数式2008|1|m m --的值为________.1【分析】根据一元一次方程的定义可求出m 的值在将m 代入代数式计算即可【详解】原方程可整理为根据题意可知且所以所以故答案为:1【点睛】本题考查一元一次方程的定义以及代数式求值利用一元一次方程的定义求出解析:1【分析】根据一元一次方程的定义,可求出m 的值.在将m 代入代数式计算即可.【详解】原方程可整理为22(1)(1)80m x m x --++=.根据题意可知210m -=且10m +≠,所以1m =. 所以2008200811111m m --=--=.故答案为:1.【点睛】本题考查一元一次方程的定义以及代数式求值.利用一元一次方程的定义求出m 的值是解答本题的关键.三、解答题21.计算(1)(65x 2y -4xy 2)•13xy (2)[(x +3y )•(x -3y )-(x -y )2]÷(-2y ) 解析:(1)25x 3y 2-43x 2y 3;(2)5y -x 【分析】(1)按照多项式乘单项式的计算法则进行计算求解;(2)整式的混合运算,先算乘方,然后算乘除,最后算加减,有小括号先算小括号里面的.【详解】解:(1)(65x 2y -4xy 2)•13xy =25x 3y 2-43x 2y 3 (2)[(x +3y )•(x -3y )-(x -y )2]÷(-2y )=[x 2-9y 2-(x 2-2xy +y 2)]÷(-2y )=(x 2-9y 2-x 2+2xy-y 2)÷(-2y )=(-10y 2+2xy )÷(-2y )=5y -x【点睛】本题考查整式的混合运算,掌握运算顺序和计算法则正确计算是解题关键.22.阅读下面材料,完成任务.多项式除以多项式可以类比于多位数的除法进行计算,先把多项式按照某个字母的降幂进行排列,缺少的项可以看做系数为零,然后类比多位数的除法利用竖式进行计算.∴26445123215÷= ∴()()32223133x x x x x +-÷-=++ 请用以上方法解决下列问题:(计算过程要有竖式)(1)计算:()()3223102x x x x +--÷- (2)若关于x 的多项式43225x x ax b +++能被二项式2x +整除,且a ,b 均为自然数,求满足以上条件的a ,b 的值.解析:(1)()()3222310245x x x x x x +--÷-=++;(2)0a =,8b =;1a =,4b =;2a =,0b =【分析】(1)直接利用竖式计算即可;(2)竖式计算,根据整除的意义,利用对应项的系数对应倍数求得答案即可.【详解】解:(1)列竖式如下:()()3222310245x x x x x x +--÷-=++ (2)列竖式如下:∵多项式43225x x ax b +++能被二项式2x +整除∴余式()420b a +-=∵a ,b 均为自然数∴0a =,8b =;1a =,4b =;2a =,0b =【点睛】此题考查利用竖式计算整式的除法,解题时要注意同类项的对应.23.分解因式:(1)25105x x ++(2)()()2249a x y b y x -+-解析:(1)()251x +;(2)()()()2323x y a b a b -+-【分析】(1)先提取公因式5,再利用完全平方公式分解因式;(2)先提公因式(x-y ),再利用平方差公式分解因式.【详解】(1)解:原式()2521x x =++ ()251x =+;(2)解:原式()()2249x y a b =--()()()2323x y a b a b =-+-.【点睛】此题考查因式分解:将多项式写成整式的积的形式,叫做将多项式因式分解,因式分解的方法:提公因式法和公式法,掌握因式分解的方法并熟练应用是解题的关键.24.如果2()()41x m x n x x ++=+-.①填空:m n +=______,mn =______.②根据①的结果,求下列代数式的值:(1)225m mn n ++;(2)2()m n -.解析:①4,−1;②(1)13;(2)20【分析】①据多项式乘多项式的运算法则求解即可;②根据完全平方公式计算即可.【详解】①∵(x +m )(x +n )=x 2+(m +n )x +mn =x 2+4x−1,∴m +n =4,mn =−1.故答案为:4,−1;②(1)m 2+5mn +n 2=(m +n )2+3mn =42+3×(−1)=16−3=13;(2)(m−n )2=(m +n )2−4mn =42−4×(−1)=16+4=20.【点睛】本题主要考查了完全平方公式以及多项式乘多项式,熟记相关公式与运算法则是解答本题的关键.25.利用乘法公式计算:(1)198×202(2)(2y +1)(﹣2y -1)解析:(1)39996;(2)2441y y ---.【分析】(1)将两个数化为200与2的和与差,用平方差公式计算即可;(2)第二个括号内提取一个负号可与第一个括号合成两数和的平方,利用完全平方公式展开即可.【详解】解:(1)原式=(2002)(2002)-+=222002-=400004-=39996;(2)原式=(21)(21)y y -++=2(21)y -+=2441y y ---.【点睛】本题考查利用完全平方公式和平方差公式计算.熟记公式是解题关键.26.好学的晓璐同学,在学习多项式乘以多项式时发现:(12x +4)(2x +5)(3x ﹣6)的结果是一个多项式,并且最高次项为:12x •2x •3x =3x 3,常数项为:4×5×(﹣6)=﹣120,那么一次项是多少呢? 根据尝试和总结她发现:一次项就是:12x ×5×(﹣6)+2x ×4×(﹣6)+3x ×4×5=﹣3x . 请你认真领会晓璐同学解决问题的思路、方法,仔细分析上面等式的结构特征,结合自己对多项式乘法法则的理解,解决以下问题:(1)计算(x +2)(3x +1)(5x ﹣3)所得多项式的最高次项为 ,一次项为 ; (2)若计算(x +1)(﹣3x +m )(2x ﹣1)(m 为常数)所得的多项式不含一次项,求m 的值;(3)若(x +1)2021=a 0x 2021+a 1x 2020+a 2x 2019+…+a 2020x +a 2021,则a 2020= .解析:(1)15x 3,﹣11x ;(2)m =-3;(3)2021【分析】(1)求多项式的最高次项,把每个因式的多项式最高次项相乘即可;求一次项,含有一次项的有x ,3x ,5x ,这三个中依次选出其中一个再与另外两项中的常数相乘最终积相加,或者展开所有的式子得出一次项即可.(2)先根据(1)所求方法求出一次项系数,最后用m 表示,列出等式,求出m ; (3)根据前两问的规律可以计算出第(3)问的值.【详解】(1)由题意得:(x +2)(3x +1)(5x ﹣3)所得多项式的最高次项为x ×3x ×5x =15x 3,一次项为:1×1×(﹣3)x +2×3×(﹣3)x +2×1×5x =﹣11x ,故答案为:15x 3,﹣11x ;(2)依题意有:1×m ×(﹣1)+1×(﹣3)×(﹣1)+1×m ×2=0,解得m =﹣3;(3)根据题意可知2020a 即为2021(1)x +所得多项式的一次项系数,∵2021(1)x +展开之后x 的一次项共有2021个,且每一项的系数都为2021(111)1⨯⨯⨯=, ∴20202021202120212021(111)+(111)(111)2021a =⨯⨯⨯⨯⨯⨯++⨯⨯⨯=故答案为:2021.【点睛】本题考查多项式乘多项式以及对多项式中一次项系数的理解,根据题意找出多项式乘多项式所得结果的一次项系数与多项式乘多项式中每个多项式的一次项系数和常数项关系规律是解题关键.27.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式. 例如由图①可以得到两数和的平方公式:(a +b )2=a 2+2ab +b 2.请解答下列问题:(1)写出由图②可以得到的数学等式 ;(2)利用(1)中得到的结论,解决下面问题:若a +b +c =6,a 2+b 2+c 2=14,求ab +bc +ac 的值;(3)可爱同学用图③中x 个边长为a 的正方形,y 个宽为a ,长为b 的长方形,z 个边长为b 的正方形,拼出一个面积为(2a +b )(a +4b )的长方形,则x +y +z = . 解析:(1)(a +b +c )2=a 2+b 2+c 2+2ab +2ac +2bc ;(2)11;(3)15【分析】(1)观察图形可得:大正方形的边长为:a+b+c ,该正方形的面积等于3个小正方形的面积加上6个长方形的面积,由此可得出等式;(2)将a+b+c =6,a 2+b 2+c 2=14代入(1)中所得的等式,计算即可;(3)由题意得:(2a+b )(a+4b )=xa 2+yab+zb 2,将等式左边展开,再比较系数即可得出x ,y ,z 的值,然后求和即可.【详解】解:(1)观察图形可得:大正方形的边长为:a +b +c ,该正方形的面积等于3个小正方形的面积加上6个长方形的面积,∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,a+b+c=6,a2+b2+c2=14,∴62=14+2(ab+ac+bc),∴ab+ac+bc=(36﹣14)÷2=11.(3)由题意得:(2a+b)(a+4b)=xa2+yab+zb2,∴2a2+8ab+ab+4b2=xa2+yab+zb2,∴2a2+9ab+4b2=xa2+yab+zb2,∴x=2,y=9,z=4,∴x+y+z=2+9+4=15.故答案为:15.【点睛】本题考查了因式分解的应用、完全平方公式的几何背景及多项式乘法等知识点,数形结合并熟练掌握相关运算法则是解题的关键.28.把下列多项式因式分解(要写出必要的过程):(1)﹣x2y+6xy﹣9y;(2)9(x+2y)2﹣4(x﹣y)2;(3)1﹣x2﹣y2+2xy.解析:(1)﹣y(x﹣3)2;(2)(5x+4y)(x+8y);(3)(1+x﹣y)(1﹣x+y)【分析】(1)先提取公因式,再按照完全平方公式分解;(2)分别把前后两项看成某项的平方并根据平方差分解因式,然后对每个因式去括号及合并同类项进行化简;(3)首先把后面三项看成一组并化成完全平方式,然后与第一项组合并利用平方差公式分解后对每个因式去括号化简即可.【详解】解:(1)﹣x2y+6xy﹣9y=﹣y(x2﹣6x+9)=﹣y(x﹣3)2;(2)9(x+2y)2﹣4(x﹣y)2;=[3(x+2y)+2(x﹣y)][3(x+2y)﹣2(x﹣y)]=(5x+4y)(x+8y);(3)1﹣x2﹣y2+2xy=1﹣(x2+y2﹣2xy)=1﹣(x﹣y)2=[1+(x﹣y)][1﹣(x﹣y)]=(1+x﹣y)(1﹣x+y).【点睛】本题考查了因式分解,熟练掌握因式分解的各种方法并灵活运用是解题关键.。
外科学复习题

外科学复习题外科学复习题第十四章急诊一.名词解释.1.休克2.有效循环血量3.心肺脑复苏二.填空题1.休克类型有_____________、_____________、____________和____________。
2.休克的一般监测包括______________、_____________、______________、___________和____________。
3.人工呼吸与心外按压的比例单人为______:_______,双人为________:___________。
4.初期复苏步骤是___________、____________和_____________。
三.单项选择题1.防治休克的措施中错误的是A.汽车运送时,病人头部置于车头方向B保暖、止痛C.输液、输血 D.控制原发疾病 E.预防过敏反应2.下列哪项是休克早期的表现A.血压下降B脉压变小C皮肤瘀斑D体温不升E无尿3.抗休克的最基本措施是A.应用血管活性药B扩充血容量C纠正酸中毒D应用抗生素E增强心功能4.各种类型休克的共同特点是A心排血量减少B有效循环血量减少C外周血管阻力升高D血压下降 E. CVP 降低5.初期复苏应在心跳呼吸骤停后( )开始A尽早 B 6min C 4min D 4—6min E 8min6.发现某病人心跳呼吸骤停,应立即A 吸氧B测量血压C做心电图检查D事实初期复苏E应用复苏药物7.胸外心脏按压与人工呼吸次数比双人是A 1:1B 2:1C 3:1D 4:1E 5:18.判断口对口人工呼吸是否有效的主要依据A 吹入时阻力的大小B 胸廓明显起伏C瞳孔是否缩小D口唇紫绀是否有改善E 心跳是否改善四.问答题1.休克早期有哪些临床表现?2.休克的治疗原则是什么?3.休克的病因有哪些?4.如果进行初期复苏?第十五章体液平衡失调一.名词解释1.渗透压2.低钾血症3.代谢性酸中毒二.填空题1.静脉补钾应注意______________ ____________ ____________和____________。
(必考题)人教版初中物理九年级第十四章综合经典复习题(提高培优)(1)

一、选择题1.提高汽油机效率最有效的做法是()A.减小机械间的摩擦B.把火花塞改为喷油嘴C.加大进入汽缸的油量D.改烧热值更高的氢气A解析:A热机的效率是指用来做有用功的能量与燃料完全燃烧放出的能量之比,要提高热机的效率,要尽量使燃料充分燃烧放热,并尽量减少能量的各种损失。
把火花塞改为喷油嘴、加大进入汽缸的油量、改烧热值更高的氢气不能显著提高汽油机的效率;减小机械间的摩擦可以减少能量损失,是最有效的做法。
故选A。
2.如图所示,试管内的高温高压水蒸气从玻璃管中喷出,使小叶轮转动,与这一实验过程中能量的转化相同的是汽油机的()A.吸气冲程B.压缩冲程C.做功冲程D.排气冲程C解析:C试管内的高温高压水蒸气从玻璃管中喷出,水蒸气具有内能,水蒸气使小叶轮转动,小叶轮的机械能变大,这是水蒸气的内能转化为小叶轮的机械能;而汽油机的四冲程中,吸气冲程和排气冲程没有能量的转化,压缩冲程是机械能转化为内能,做功冲程是内能转化为机械能,那么与这一实验过程中能量的转化相同的是汽油机的做功冲程。
故选C。
3.2020年11月24日,搭载着“嫦娥五号”探测器的长征五号火箭发射成功,标志着中国“探月工程”第三步拉开序幕,长征五号运载火箭采用无毒,无污染的液氢液氧燃料作推进剂,属于绿色环保大型液体运载火箭,下列说法正确的是()A.液氢燃烧得越充分,其热值就越大B.燃料燃烧产生高温高压的燃气对火箭做功,燃气的内能会增加C.高温高压的燃气推动火箭升空把内能转化成机械能D.通常情况下气态的氢氧是采用高温高压方式进行加注的C解析:CA.热值是燃料的一种特性,它只与燃料的种类有关,与有无充分燃烧无关,故A错误;B.燃气对火箭做功,内能转化为机械能,燃气的内能会减小,故B错误;C.燃气对火箭做功,内能转化为机械能,故C正确;D.令气体液化的方法有两种,一是降低温度,二是压缩体积。
通常情况下气态的氢氧是采用低温、高压进行加注的。
故选C。
4.一桶水用去一半,剩下的半桶水不变的物理量是()A.热值,内能B.比热容,密度C.质量,体积D.热量,温度B解析:BA.热值是反应燃料燃烧时放热能力的物理量,与水无关;水的内能与质量有关,用去一半的水内能会改变,故A不符合题意;B.比热容和密度均是物质的一种特性,与质量和体积无关,故B符合题意;C.水用去一半后,其质量和体积均变为原来的一半,故C不符合题意;D.热量不是状态量,不能用具有来描述热量;水的温度受环境的影响,故有可能改变,故D不符合题意。
人教版八年级上第十四章整理与复习练习题

人教版八年级上第十四章整理与复习练习题一、选择题(共4小题;共20分)1. 下列各式从左到右的变形是因式分解的是A. B.C. D.2. 分解因式,结果正确的是A. B.C. D.3. 多项式分解因式的正确结果是A. B.C. D.4. 已知,则的值为B. C. D.二、填空题(共3小题;共15分)5. 根据,,,的规律,则可以得出的结果可以表示为.6. 当时,代数式,则当时,代数式的值为.7. 如图是我国数学家发明的“杨辉三角”,此图揭示了(为非负整数)的展开式的项数及其系数的有关规律.请你观察,并根据此规律写出的展开式共有项,第二项的系数是,的展开式共有项,各项的系数和是.三、解答题(共3小题;共39分)8. 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:,善于思考的小明进行了以下探索:设(其中,,,均为整数),则有,,,这样小明就找到了一种把部分的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:(1)当,,,均为正整数时,若,用含,的式子分别表示,,得,.(2)若,且,,均为正整数,求的值.9. 因式分解:.10. 分解因式:答案第一部分1. D2. D 【解析】3. D4. C 【解析】,,,.第二部分5.【解析】6.7. ,,,【解析】的展开式有项;的展开式有项;的展开式有项;故的展开式共有项.由题中规律得的展开式中第二项的系数为,的展开式中第二项的系数为,故的展开式中第二项的系数为.的展开式中各项的系数和为;的展开式中各项的系数和为;的展开式中各项的系数和为;故的展开式中各项的系数和为.第三部分8. (1);(2)由题意,得,且,为正整数,或或.或.9. .10. 设,则原式.。
第14章--勾股定理复习练习题

★第14章 勾股定理★★1.已知直角三角形的斜边长为20cm,一直角边长为12cm,则另一直角边长为【 】(A )15cm (B )16cm (C )8cm (D )14cm★2.一直角三角形的两边长分别为3和4,则第三边的长为【 】(A )5 (B )7 (C )5 (D )5或7★3.若正方形的边长为1,则它的对角线长为【 】(A )1 (B )2 (C )3 (D )2★4.等腰三角形的底边长为10cm,面积为60cm 2,则该等腰三角形的周长是【 】(A )33cm (B )34cm (C )35cm (D )36cm ★5.在△ABC 中,∠A=90°,BC=a ,AC=b ,AB=c ,则下列各式不成立的是【 】(A )222c b a += (B )222b a c +=(C )222b a c -= (D )222c a b -=★6.已知一个正三角形的边长为2,则它的面积是【 】(A )2 (B )3 (C )2 (D )4★7.在△ABC 中,AB=15,AC=13,高AD=12,则△ABC 的面积是【 】(A )42 (B )37 (C )42或37 (D )42或32★8.若把一个直角三角形的两条直角边同时扩大为原来的2倍,则其斜边扩大为原来的【 】(A )2倍 (B )4倍 (C )2倍 (D )3倍★9.如图(1)所示,在△ABC 中,AD ⊥BC 于点D,AB=3,BD=2,CD=1,则2AC 的值是【 】(A )14 (B )6 (C )4 (D )8★10.如图(2)所示,点E 在正方形ABCD 内,满足∠AEB=90°,AE=6,BE =8,则阴影部分的面积是【 】(A )48 (B )60 (C )76 (D )80★11.如图(3)所示,正方形网格中,每个小正方形的边长为1,在网格上的△ABC 中,边长为无理数的边数是【 】(A )0 (B )1 (C )2 (D )3★12.如图(4)所示,三个正方形中的两个面积为144,16921==S S ,则另一个正方形的面积3S 为【 】(A )50 (B )25 (C )100 (D )30★13.如图(5)所示,以直角三角形三边为直径,向三角形外部作半圆,图(1)图(2)图(3)图(4)图(5)图(6)BC A它们的面积分别为,,,321S S S 若321,16,12S S S 则ππ==等于【 】(A )π28 (B )π25 (C )π20 (D )π18★14.如图(6)所示,△ABC 为等腰三角形,底边BC 长为6,底边上的中线AD=4,它的腰长为【 】(A )7 (B )6 (C )5 (D )4★15.若一个直角三角形的三边长分别为4, 3 , x ,则以x 为边长的正方形的面积是【 】(A )25 (B )7 (C )25或7 (D )以上都不对★16.如图(7)所示,一棵大树在离地面9米高的B 处折断,树顶A 落在离树底C 处12米的A 点,则大树折断之前的高度为【 】(A )9米 (B )15米 (C )21米 (D )24米★17.如图(8)所示,在Rt △ABC 中,∠C=90°,AC=6cm,BC=8cm,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,则CD 的长度为【 】(A )2cm (B )3cm (C )4cm (D )5cm★18.如图(9)所示,分别以直角三角形的三边为一边作三个等边三角形,其面积分别为n m p ,,,则这些面积之间的关系是【 】图(7)图(8)图(9)(A )2224343p n m =+ (B )p n m =+ (C )222p n m =+ (D )p n m =+4343 ★19.在△ABC 中,已知3:2:1::=∠∠∠C B A ,则该三角形是【 】(A )锐角三角形 (B )直角三角形(C )钝角三角形 (D )等腰直角三角形★20.由下列条件不能判定△ABC 是直角三角形的是【 】(A )5:4:3::=∠∠∠C B A(B )B C A ∠=∠-∠(C )5:3:2::=∠∠∠C B A(D )18=∠-∠C B °,且B C ∠=∠32 ★21.下列长度的四组线段中,不能组成直角三角形的是【 】(A )3 , 3 , 23 (B )8 , 15 , 17 (C )1 , 2 , 3 (D )6 , 8 , 10 ★22.三角形的三边c b a 、、满足()ab c b a 222=-+,则这个三角形的形状是【 】(A )等边三角形 (B )钝角三角形(C )直角三角形 (D )锐角三角形★23.△ABC 的三边长c b a 、、满足()022233=+-+++b a c ab b a b a ,则△ABC 的形状是【 】(A )直角三角形 (B )等边三角形(C )等腰三角形 (D )等腰直角三角形★24.下列各项中,能组成勾股数的是【 】第29题(A )514131、、 (B )222543、、 (C )5、11、12 (D )5、12、13 ★25.如果△ABC 的三边长分别为c b a 、、,且,2,22mn b n m a =-= 22n m c +=都是正整数)且n m n m ,,(>,则此三角形是【 】(A )锐角三角形 (B )直角三角形(C )钝角三角形 (D )等腰直角三角形★26.如果一个三角形满足下列条件:①三边长分别为1 , 1 , 2;②三边长分别为4 , 3 , 4;③三边长分别为7 , 24 , 25;④三边长之比为5 : 12 : 13.其中能判定该三角形是直角三角形的有【 】(A )1个 (B )2个 (C )3个 (D )4个★27.若一个三角形的两边长分别为6cm 、8cm,要使这个三角形成为直角三角形,则第三边的长应该是【 】(A )10cm (B )8cm (C )28cm (D )28cm 或10cm ★28.在△ABC 中,AB=17,BC=30,BC 边上的中线AD=8,则△ABC 的形状是【 】(A )直角三角形 (B )等腰三角形(C )等边三角形 (D )等腰直角三角形★29.如图所示,在单位正方形的网格中有AB 、CD 、EF 、GH 四条线段,其中能构 成一个直角三角形三边的线段是【 】 (A )CD,EF,GH (B )AB,CD,GH(C )AB,EF,GH (D )AB,CD,EF ★30.已知等腰三角形的腰长为10,一腰上的高为6,则以底边为边长的第36题正方形的面积是【 】(A )40 (B )80 (C )40或360 (D )80或360 ★31.如果一个直角三角形的两条直角边长分别为)1(2,12>-n n n ,那么斜边长应为【 】(A )n 2 (B )1+n (C )12-n (D )12+n★32.如果线段c b a 、、能组成直角三角形,则它们的比可以是【 】(A )1 : 2 : 4 (B )1 : 3 : 5 (C )3 : 4 : 7 (D )5 : 12 : 13 ★33.△ABC 的三边之长分别是c b a 、、,且48,14==+ab b a ,10=c ,则△ABC 是【 】(A )等边三角形 (B )直角三角形(C )等腰直角三角形 (D )直角三角形或钝角三角形 ★34.一架25 dm 长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7 dm,如果梯子的顶端沿墙下滑4 dm,那么梯足将滑出【 】(A )9 dm (B )15 dm (C )5 dm (D )8 dm★35.如果梯子的底端离建筑物9 m,那么15 m 长的梯子可以到达建筑物的高度是【 】(A )10 m (B )11 m (C )12 m (D )13 m★36.如图所示,已知蚂蚁从长、宽都是3,高是8的长方体纸箱的A 点沿纸箱表面爬到B点,那么它爬行的最短路线的长是【 】(A )10 (B )14(C )130 (D )73第37题第40题★37.如图所示,有一长、宽、高分别是5 cm 、4 cm 、3 cm 的长方体木块,一只蚂蚁要从长方体的一个顶点A 处沿长方体的表面爬到长方体上和A 相对的顶点B 处,则需要爬行的最短路径长为【 】(A )50 cm (B )74 cm(C )80 cm (D )90 cm★38.以下列各组数据为三角形三边的长,其中能构成直角三角形的是【 】(A )2 , 3 , 4 (B )4 , 5 , 6 (C )1 , 2 , 3 (D )3 , 2 , 5 ★39.直角三角形的直角边为,,b a 斜边为c ,斜边上的高为h ,则以h c +、b a +、h 为边的三角形是【 】(A )直角三角形 (B )锐角三角形(C )钝角三角形 (D )不能确定★40.如图所示,点A 和点B 分别是棱长为20 cm 的正方体盒子上两个相邻面的中心,一只蚂蚁在盒子的表面由A 处向B 处爬行,所走的最短距离是【 】(A )40 cm (B )220 cm(C )20 cm (D )210 cm★41.如图所示,一艘轮船以16海里/时的速度从港口A 出发向东北方向航行,另一艘轮船以12海里/时的速度从港口A 出发向东南方向航行,离开港口2小时后,两船相距【 】(A )25海里 (B )30海里 (C )35海里 (D )40海里★42.如图所示,是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形.已知大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边是a ,较长直角边是b ,则()2b a +的值为【 】 (A )13 (B )19 (C )25 (D )169★43.在Rt △ABC 中,∠B=90°,BC=15,AC=17,以AB 的长为直径作半圆,则此半圆的面积为【 】(A )π4 (B )π8 (C )π16 (D )以上都不对 ★44.已知在Rt △ABC 中,∠C=90°,10,14==+c b a ,则Rt △ABC 的面积为【 】(A )24 (B )36 (C )48 (D )60★45.在Rt △ABC 中,∠C=90°,若AB=10,AC=8,则BCAC 等于【 】 (A )53 (B )45 (C )34 (D )43 ★46.在Rt △ABC 中,∠A=90°,AB=AC=2,则高AD 的长是【 】(A )1 (B )2 (C )3 (D )以上都不对★47.已知Rt △ABC 的三边长分别为2,15,8,,,c b a c b a 那么若==的值第41题c b a第42题D C AB为【 】(A )161 (B )289 (C )225 (D )161或289★48.已知在Rt △ABC 中,∠C=90°,AC=9,BC=12,则点C 到AB 的距离是【 】(A )536 (B )1512 (C )49 (D )433 ★49.在Rt △ABC 中, 为三边长,则下列关系中正确的是【 】(A )222c b a =+ (B )222b c a =+(C )222a b c =+ (D )以上都有可能★50.已知y x ,为正数,且()034222=-+-y x ,以y x ,为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为【 】(A )5 (B )25 (C )7 (D )15★51.在△ABC 中,∠C=90°,若===c b a 则,5,12________.★52.在Rt △ABC 中,其中两条边长为3和4,则其第三边长为_______. ★53.在△ABC 中,∠C=90°,若===b c a 则,10,6________. ★54.在△ABC 中,∠C=90°,若===a c b a 则,20,4:3:________,=b __ _______.★55.等腰直角三角形的面积为2,则其周长为__________.★56.一根旗杆从离地面4.5米处被折断,旗杆顶端落在地面离旗杆底部6米处,则旗杆折断前的高为________.★57.若直角三角形的两直角边长为b a ,,且04962=-++-b a a ,则该直角三角形的斜边长为________.题★58.如图所示,一根筷子长度为20 cm,斜放在半径为3 cm 的圆柱形水杯内,露在水杯外面的部分AD 的长为10 cm,则水杯高AC=_____cm.★59.如图所示是用1 m 的正方形地砖铺设的地面示意图,小明沿图中所示的折线A→B→C 所走的路程为________m.(保留根号)★60.如图所示,已知圆柱体底面圆的半径为π2,高为2,CD,AB 分别是上、下底面的直径,AD 、BC 是母线,若一只小虫从A 点出发,从侧面爬行到C 点,则小虫爬行的最短路线的长度是________.(保留根号) ★61.已知△ABC 的三边长为c b a ,,,且()05432=-+-+-c b a ,那么该三角形是________三角形.★62.如图所示,图中所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A 、B 、C 、D 的面积之和为________cm 2.★63.如果一个长方形的长为24 cm,宽为7 cm,在里面放一根铁条,那么铁条最长可以是________.★64.若直角三角形的三边长分别为2 , 4 , x ,则x 的值为__________.第59题第60题第62题★65.有一长为12 cm 、宽为4 cm 、高为3 cm 的长方形铁盒,在其内部要放一根笔直的铁丝,则铁丝最长是________.★66.如图所示,一长方体底面长12 cm,宽3 cm,高4 cm,则该长方体中相对的两个顶点M 、N 之间的距离是________.★67.如图,四边形ABCD 中,AC ⊥BD,O 为垂足,设22CD AB m +=,22BC AD n +=,则n m 、的大小关系是________.★68.如图所示,一牧童在A 处放羊,牧童家在B 处,A 、B 两处距河岸的距离AC 、BD 的长分别是500 m 、700 m,且C 、D 两地相距500 m,天黑前牧童将羊赶往河边喝水再回家,那么牧童至少应走________. ★69.在等腰△ABC 中,AB=AC=10 cm,BC=12 cm,则BC 边上的高AD 的长是________.★70.若三角形的三边长分别为,32,1+++m m m 和则当=m ______时,此三角形是直角三角形.★71.若一个三角形的三边之比为5 : 12 : 13,且周长为60 cm,则它的面积为________cm 2.★72.若△ABC 的三边c b a 、、满足()()0222=-+-c b a b a ,且b a ≠,则该三角形的形状是____________.★73.如图所示,我国古代数学家赵爽的“勾股方图”是由四个全等的直第66题第67题第68题DCB A角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为b a ,,那么()=+2b a ________.★74.如图所示,AD ⊥CD,AB=13,BC=12,CD=3,AD=4,则△ABC 的面积为________.★75.如图所示,在等边△ABC 中,AB=6,点D 是BC 的中点,将△ABD 绕点A 旋转得到△ACE,那么线段DE 的长度为________.★76.如图所示,在操场上竖立着一根长为2米的测影竿CD,早晨测得它的影长BD 为4米,中午测得它的影长AD 为1米,则A 、B 、C 三点_______构成直角三角形(填“能”或“不能”).★77.如图所示,正方体的棱长为2cm,用经过A 、B 、C 三点的平面截这个正方体,所得截面的周长是________cm.第73题第74题第75题EAC第76题DCBA第77题CAB第78题★78.如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走捷径,在花圃内走出了一条路,他们仅仅少走了________m 的路,却踩伤了花草.★79.在△ABC 中,,5,7,252222==-=+c b a b a 则该三角形最大边上的高是________.★80.若直角三角形的两边的长为3和4,则此三角形的周长为______. ★81.一个直角三角形的三边为三个连续偶数,则该直角三角形的斜边长为________.★82.直角三角形中,以直角边为边长的两个正方形的面积分别为7 cm 2、8 cm 2,则以斜边为边长的正方形的面积为________ cm 2. ★83.已知c b a ,,是△ABC 的三边长,且满足0222=-+--b a b a c ,则△ABC 的形状为____________.★84.若直角三角形两直角边之比为 3 : 4 , 斜边长为 20 ,则它的面积为________.★85.在△ABC 中,∠C=90°,若AB=5,则AB 2+AC 2+BC 2=________. ★86.在△ABC 中,点D 为BC 的中点,BD=3,AD=4,AB=5,则AC 的长度为________.★87.在△ABC 中,AB=AC,BD ⊥AC 于点D,若BD=3,DC=1,则AD 的长度是________.★88.如图所示,某市在“旧城改造”中计划在市内一块三角形空地上种植某种草皮以美化环境,已知这种草皮每平方米售价a 元,则购买这种草皮至少需要________元.★89.如图所示为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要________米.★90.如图所示,地面上有一块砖,宽AB=5 cm,长BC=10 cm,CD 上的点G 距地面的高CG=8 cm,地面上一只蚂蚁从A 处爬到G 处,要爬行的最短路程是________.★91.如图,在△ABC 中,∠ACB=90°,以△ABC 的各边为边在△ABC 外作三个正方形,321,,S S S 分别表示这三个正方形的面积,若811=S ,==32,225S S 则________.★92.如图所示,求图中直角三角形中未知边的长度:=b ________,=c ________.★93.如图所示,在△ABC 中,∠ACB=90°,点O 为在△ABC 的三条角平分线的交点,OD ⊥BC,OE ⊥AC,OF ⊥AB,点D 、E 、F 分别是垂足,且17m15m8m 第88题C AB5米3米第89题第90题G第91题第92题BC=8 cm,CA=6 cm,则点O 到三边AB,AC 和BC 的距离均等于______ _____cm.★94.如图所示,在△ABC 中,CE 平分∠ACB,CF 平分∠ACD,连结EF,则=+22CF CE ________.★95.如图所示,一棵大树在一次强台风中于离地面3 m 处折断倒下,树干顶部落在距根部4 m 处,这棵大树在折断前的高度为_______.★96.如图所示,请你根据这个图形写出一个代数恒等式为__________ ________________,它可以用来验证____________.★97.如图所示,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是________米.★98.如果一个三角形两边的平方分别为16,25,那么第三条边的平方是________时,这个三角形是直角三角形.★99.如果一个直角三角形的两条直角边之比为5 : 12,则斜边上的高第93题第94题EACFD4m3m第95题第96题第97题与斜边之比为________.★100.将一根长24 cm的筷子,置于底面直径为15 cm、高8 cm的圆柱形水杯中,设筷子露在杯子外面的长度为h cm,则h的取值范围是__ _____________.★101.如图所示,在△ABC中,AB=10,BC=21,AC=17,求BC边上的高AD的长度.第101题★102.如图所示,在△ABC中,∠C=90°,BD平分∠ABC,把△ABC沿BD折叠,点C落在点E处.若AC=6,BC=8,求AD的长.第102题★103.如图所示,在△ABC中,AB=AC=20,BC=32,D是BC边上一点,且AD⊥AC,求BD的长.AB C第103题★104.在△ABC中,AB=15,AC=13,BC边上的高AD=12,求△ABC 的面积.(提示:分为两种情况)★105.如图所示,在△ABC中,AB=5cm,BC=6cm,BC边上的中线AD=4cm,求△ABC的面积.第107题DFB CA★106.如图所示,在等腰△ABC 中,AB=AC,AD 是∠BAC 的平分线,BC=24,△ABC 的面积是60. (1)求∠ADB 的度数; (2)求AB 的长度.★107.如图所示,在△ABC 中,∠ABC=90°,AB=16,正方形BCEF 的面积为144,BD ⊥AC 于D,求BD 的长.第105题DB CA第106题DB CA★108.如图所示,是一块地的平面图,其中AD=4 m,CD=3 m,AB=13 m, BC=12 m,∠ADC=90°,求这块地的面积.★109.△ABC 的三边c b a ,,满足c b a c b a 201612200222++=+++,试判断△ABC 的形状.★110.如图所示,四边形ABCD 中,∠B=90°,AB=3,BC=4,CD=12,AD= 13,求四边形ABCD 的面积.第108题★111.如图所示,在正方形ABCD 中,点E 为AD 的中点,点F 在DC 上,且DF : FC=1 : 3,试判断△BEF 的形状,并说明理由.★112.如图所示,在△ABC 中,AC=8,BC=6.在△ABE 中,DE 为AB 边上的高,DE=12,S △ABE =60,求∠C 的度数.第110题BCAD第111题FED ABC第112题CBAD E★113.如图所示,点D为BC边上一点,已知AB=13,AD=12,AC=15,BD =5,试求BC的长.AC第113题★114.如图所示,在△ABC中,∠C=90°,点D为AC边上一点,且AD=BD=5,又△ABD的面积为10,求CD的长.第114题★115.如图所示,矩形ABCD中,AD=4 cm,AB=10 cm,按图的方式折叠,使点B与点D重合,折痕为EF,求DE的长.第115题★116.如图所示,折叠长方形的一边AD,使点D 落在边BC 上的F 点,已知AB=8 cm,BC=10 cm,求EC 的长.★117.如图所示,在△ABC 中,∠C=90°,AC=6,BC=8,现将直角边AC 沿∠CAB 的角平分线AD 折叠,使它落在斜边AB 上,且与AE 重合,求CD 的长.第116题第117题★118.如图所示,折叠Rt△ABC,使两个锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,求线段BD的长.第118题★119.如图所示,有两棵树,一棵树高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了_______米.第6题图★120.如图所示,在△ABC中,AB=20,AC=12,BC=16,把△ABC折叠,使AB落在直线AC上,求重叠部分(阴影部分)的面积.第120题★121.如图所示,将矩形ABCD 沿直线BD 折叠,使点C 落在点C′处,已知AD=8,AB=4,求△BED 的面积.★122.如图所示,将矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上的点F 处,已知CE=3 cm,AB=8 cm,求图中阴影部分的面积.★123.如图所示,在△ABC 中,点D 在BC 边上,若AB=10,BD=6,AD=8, AC=17.(1)判断△ABD 的形状;第121题第122题EABCD F(2)求△ABC 的面积.★124.如图所示,在铁路CD 的同侧有两个煤矿A 、B,它们到铁路的距离分别为AC 、BD,并且AC=6 km,BD=8 km,CD=14 km,为了方便煤炭外运,铁路部门和两个煤矿决定在铁路旁修建一个货运中转站,请你帮助他们解决下面两种方案中的问题:方案一:货运中转站M 到煤矿A 、B 的距离相等,即BM AM =,求AM 的长;方案二:货运中转站M 到A 、B 两个煤矿的距离之和最短,即BM AM +最小,求BM AM +的值.第123题DAB C第124题★125.如图所示,铁路上有两点A 、B 相距40千米,铁路两侧有C 、D 两村庄(看作两个点),DA ⊥AB,CB ⊥AB,垂足分别为A 、B,DA=24千米,CB=16千米,现在要在铁路旁修建一个煤栈,使得C 、D 两村庄到煤栈的距离相等,问:煤栈应建在距A 点多少千米处?★126.如图所示,是用硬纸板做成的四个全等的直角三角形和一个边长为c 的正方形,请你将它们拼成一个能验证勾股定理的图形. (1)画出拼成的这个图形; (2)根据你画的图,验证勾股定理.第125题a cb acbbc ab ca cc第126题★127.如图所示,有两个完全相同的如图甲所示用硬纸板做成的直角三角形,两直角边长分别为,,b a 斜边长为c .图乙是以c 为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个能证明勾股定理的图形.(1)画出拼成的这个图形的示意图,写出它是什么图形; (2)用这个图形证明勾股定理;(3)假设图甲的直角三角形有若干个,你能运用图甲所给的直角三角形拼出另一种能证明勾股定理的图形码?请画出图形.★128.如图,甲、乙两船从港口A 同时出发,甲船以16海里/时的速度向北偏东40°方向航行,乙船向南偏东50°方向航行,3小时后,甲船到达C 岛,乙船到达B 岛.若C 、B 两岛相距60海里,问乙船的速度是多少?第127题★129.如图,D 、E 分别是△ABC 的边BC 和AB 上的点,△ABD 与△ACD 的周长相等,△CAE 与△CBE 的周长相等.设BC=,a AC=,b AB=c .(1)求AE 和BD 的长;(2)若∠BAC=90°,△ABC 的面积为S,求证:S=AE·BD.50°40°东北A CBACE★130.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画三角形:①使三角形的三边长分别为3、8、5(在图甲中画一个即可); ②使三角形为钝角三角形且面积为4(在图乙中画一个即可).★131.如图所示,在梯形ABCD 中,AB ∥CD,∠A=90°,AB=2,BC=3,CD =1,点E 是AD 的中点,试判断EC 与EB 的位置关系,并写出推理过程. (提示:作辅助线构造全等三角形并利用等腰三角形的性质)甲乙第131题★132.如图所示,AD 是△ABC 的边BC 上的高,且CD BD AD ⋅=2,试证明△ABC 是直角三角形.附加题★133.已知c b a 、、分别为△ABC 的三边长. (1)当ac c ab b 2222+=+时,请判断△ABC 的形状; (2)试说明02222<-+-ac c b a .第132题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四章 线性动态电路的复频域分析
一、是非题
1. 若已知F(s)=(3s+3)/[(s+1)(s+2)],•则可知其原函数中必含有t
e -项。
2. 某电路有两个3V电压源,其中一个在t=0时接入电路,而另一个在(-∞,∞)区间一直接在电路中,则这两个电源在t≥0时的象函数均为 3/s.
3. 用拉普拉斯变换分析电路时,电路的初始值无论取0-或0+时的值,所求得的响应总是相同的.
4.系统的网络函数与其阶跃响应是一对拉氏变换对。
5.若系统的网络函数有一个位于右半s 平面的极点,则该系统必不稳定。
6.稳定系统的自然响应全部是零输入响应。
7.网络函数的定义为()()()
R s H s E s =
,其中R(S)为全响应的象函数。
8.在采用运算法分析电路的响应时,对于含有初值电流非零的电感元件,其运算模型用运算阻抗sL 和附加电压源Li (0-)的串联形式表示时,附加电压源Li (0-)的方向与初始电流参考方向无关。
二、选择题
1. 已知£[δ(t)]=1,则£[0()t t δ-]=______。
(A) 1; (B) 0
st e - (C) 0
st e
(D) 0
0()st e
t t ε--
2. 已知£[2()t
e
t ε-]=1/(s+2), 则£[2(1)t e t ε--]=_____。
(A) 2S e S -+ (B) 22S e S -+ (C) (2)2S e S -+ (D) (2)
2
S e S -++
3. 已知()(21)
S
e F S S S -=+, 则f(t)=_____。
(A) (1)/2
[1]()t e
t ε--- (B) (1)/2[1](1)t e t ε---- (C) (1)/2
[12]()t e
t ε--- (D) (1)/2[12](1)t e t ε----
4. f(t)的波形如图所示, 则F(s)=_____。
(A) 2
2211[]2
2S S S e Se ---- (B) 2221
[1]S S e Se S ---- ( C) 2221[1]2S S
e Se S ---- (D) 222111[]22
S S e Se S ----
5. R、L、C串联电路的复频域阻抗为_______。
(A)R+S L+S C (B)R+jS L+1/jS C (C)R+S L-1/S C (D)R+S L+1/S C
6. 已知双口网络N在零状态时的阶跃响应为 23/(9)S +, 若激励改为E(s)=
23/(9)S +, 则网络N的响应象函数U(s)=_____。
(A)
229(9)S + (B) 22
9(9)
S
S + (C)
223(9)S S + (D) 22
9
(9)S S +
7. 图示电路中,L=1H,C=1F,其中输入阻抗Z(s)=_____。
(A)
2
2(1)
S S + (B) 22(1)S
S + (C)
2(1)S S + (D) 2(1)S
S -+
8.()245
56
s F s s s +=
++的原函数为:
A .()3237t
t f t e e --=-+; B . ()2373t t f t e e --=-+ ;
C .()2337t
t f t e
e --=-+; D .()3723t t
f t e e --=-+。
9.已知某网络函数的极点为1224,p j =-±,则对应的时域冲激响应波形为: A .等幅振荡型; B .衰减振荡型; C .指数衰减型; D .发散振荡型。
10.已知函数()f t 的象函数为()F s ,则由微分性质可知,
()
df t dt
的象函数为: A .()()0sF s f -- B .()()0F s sf -- C .()()0sf F s -- D .()()0f sF s --
11.已知某电路中电感电流的初始值(0)5A L i -=,电容电压的初始值(0)8V C u -=。
则在该其运算模型中,由这两个初值所引起的附加电压源的大小分别为 A .5L 、
8C B . 5L 、8
s
C . 5L 、8C
D . 5s 、8s
三、填空题
1. 如图所示电路,已知(0)c u -=4V, (0)L i -=2A(与i 方向相同), 2()S u t e =), 则
电流i 的零状态响应的象函数为__________, 电流i 的 零输入响应的象函数为__________。
u C -
2.某系统的网络函数()23
12
H s s s =+++,则相应单位冲激响应()h t =( )。
3.网络函数()()
1
3s H s s s -=
+的两个极点分别为1p =0,2p =( )。
4.已知某线性电路的单位冲激响应()35t h t e -=,则对应此电路的网络函数
()H s =( )。
5.某系统是稳定的,系统网络函数的极点应全部位于s 平面的( )
6.网络函数极点在复平面上的位置,决定了网络动态响应的性质。
当极点位于复平面的左半平面时,极点离虚轴越远,动态响应衰减得越慢。
7.如果时间函数()f t 的拉氏变换为()F s ,则
()f t dt ⎰的拉氏变换为
四、计算题
1. 如图所示电路在S断开前处于稳态试画出S断开后的运算电路图。
2. 如图所示动态电路的激励12u u 、如图B所示,求C u =?
Ω
u
(s)
3. 如图所示电路, 开关动作前电路已稳定.t=0时,断开开关S,当t≥0时,试求:
(1)画出运算电路. (2)求出电流i(t)的象函数I(s); (3)求电流i(t).
4. 求图示电路的入端复频域阻抗Z(s)。
5. 电路如图所示,求1()L u t (t >0).
Ωi 2
6.如图所示电路,开关S 断开已久,t=0时S 闭合, (1)画出运算电路; (2) 求t ≥0时的1()i t 。
7.图示电路,开关S 闭合已久。
0=t 时,开关S 断开。
(1)画出运算电路;(2)应用运算法求电流()t i L 。
i 1
3H 2V Ω
8.图示电路原处于稳定状态。
0=t 时开关S 闭合,试用运算法求电流()t i L 。
本章作业:计算题的第6、7、8小题
10V Ω。
