DSP讲义15-4
dsp学习资料

一DSP定点算数运算1 数的定标在定点DSP芯片中,采用定点数进行数值运算,其操作数一般采用整型数来表示。
一个整型数的最大表示范围取决于DSP芯片所给定的字长,一般为16位或24位.显然,字长越长,所能表示的数的范围越大,精度也越高。
如无特别说明,本书均以16位字长为例。
DSP芯片的数以2的补码形式表示。
每个16位数用一个符号位来表示数的正负,0表示数值为正,l则表示数值为负。
其余15位表示数值的大小.因此,二进制数0010000000000011b=8195 二进制数1111111111111100b= -4 对DSP芯片而言,参与数值运算的数就是16位的整型数。
但在许多情况下,数学运算过程中的数不一定都是整数。
那么,DSP芯片是如何处理小数的呢?应该说,DSP芯片本身无能为力。
那么是不是说DSP 芯片就不能处理各种小数呢?当然不是。
这其中的关键就是由程序员来确定一个数的小数点处于16位中的哪一位。
这就是数的定标。
通过设定小数点在16位数中的不同位置,就可以表示不同大小和不同精度的小数了。
数的定标有Q表示法和S表示法两种。
表1.1列出了一个16位数的16种Q表示、S表示及它们所能表示的十进制数值范围。
从表1.1可以看出,同样一个16位数,若小数点设定的位置不同,它所表示的数也就不同。
例如,16进制数2000H=8192,用Q0表示16进制数2000H=0。
25,用Q15表示但对于DSP芯片来说,处理方法是完全相同的。
从表1。
1还可以看出,不同的Q所表示的数不仅范围不同,而且精度也不相同。
Q越大,数值范围越小,但精度越高;相反,Q越小,数值范围越大,但精度就越低。
例如,Q0 的数值范围是一32768到+32767,其精度为1,而Q15的数值范围为—1到0.9999695,精度为1/32768=0.00003051.因此,对定点数而言,数值范围与精度是一对矛盾,一个变量要想能够表示比较大的数值范围,必须以牺牲精度为代价;而想精度提高,则数的表示范围就相应地减小。
DSP讲义

DSP芯片的主要应用领域
3. DSP系统的基本构成 系统的基本构成
3.1 信号处理系统的不同实现方式 在通用计算机上软件实现; 在通用计算机中加入专用的加速处理机; 利用通用单片机; 通用可编程DSP芯片; 专用DSP芯片; 基于通用DSP芯片内核的ASIC. 3.2. 系统的一般框图: 系统的一般框图:
3. 寻址方式
TMS320C240指令集提供三种基本的存储器寻址方式:直接寻址,间 接寻址和立即寻址. 在直接寻址中,指令字包含数据存储器地址的最低7位.这7位数 据与数据存储器页指针的9位相连,形成16位的数据存储器地址., 数据存储器共被分为512页,每页128个字.直接寻址包括两个步 骤:1,设置数据页 2,指定偏移量 间接寻址通过辅助寄存器来访问数据存储器.在这种寻址方式中, 指令操作数的地址被包含在当时被选中的辅助寄存器中.八个辅 助寄存器(AR0~AR7).共有四种间接寻址方式: .无增/减 .增/减1(后增/减) .增/减一个指针值(指针值存于AR0) .增/减逆序寻址(仅用于FFT,进位取反) 在立即寻址中,实际的操作数是是作为指令字的一部分来提供的. 该寻址方式对于数据无需存储或在程序执行中被多次使用,如初 始值或常数,非常有用.
芯片价格(包括配件),硬件资源,开发工具,功耗,封装形式 等因素.
4.4 DSP发展历史和主要的供应商 发展历史和主要的供应商
第一片DSP是1978年由AMI公司发布的S2811; 第一片具有乘法器的DSP是NEC公司的PD7720; 最成功的DSP为TI公司的五代产品和三大系列,市场分额达到50 %; AD公司的ADSP2101,ADSP2111, ADSP2171, ADSP21000等系列; Motolora公司的MC56001,MC96002等.
dsp课件Chapter15

Bilinear Transform Method
a b b00 b01 b02 a01 a02
bb aa
Matlab code for calculating coefficients:
tan(pi*2/8) % cut-off 2kHz, fsample 8 kHz, input < 580 mVpp (1 + 2^0.5 + (a*a)) (a*a)/b 2*b00 b00 2*(a^2 -1)/b (1 + a^2 - (2^0.5)*a)/b
Chapter 15 Infinite Impulse Response (IIR) Filters
Learning Objectives
Introduction to the theory behind IIR filters:
Properties. Coefficient calculation. Structure selection.
z z1 z z 2 z z N Y z z p1 z p2 z p N X z
For the implementation of the above equation we need the difference equation:
1
p
p
0 -3 pass-band ripple
1
1
p
s
stop-band ripple
s
fsb : stop-band frequency fc : cut-off frequency fpb : pass-band frequency (b)
DSP讲义15-4(精)

第四讲DSP 最小硬件系统的设计4.1引言一个DSP 硬件系统可以分为最小硬件系统设计和外围接口设计两个部分。
本讲主要介绍DSP 最小硬件系统的设计,包括复位、时钟、电源及存储器接口等.5402系统原理图继续最小系统电源图5402最小返回第四讲DSP 最小硬件系统的设计第四讲DSP 最小硬件系统的设计第四讲DSP 最小硬件系统的设计第四讲DSP最小硬件系统的设计第四讲DSP最小硬件系统的设计第四讲DSP最小硬件系统的设计第四讲DSP 最小硬件系统的设计返回4.2DSP系统的基本硬件设计4.2.1 复位电路电压公式:提问:输入方式比较,阻容颠倒可以不?电源刚加上电时,TMS320 DSP 芯片处于复位状态,/RS低使芯片复位为使芯片初始化正确,一般应保证/RS为低至少持续3 个CLKOUT 周期但是,在上电后,系统的晶体振荡器一般需要儿百毫秒的稳定期,一般为100~200ms。
选择R = 100K , C = 47μ,可得t1= 167ms 。
●此种复位特点:简单存在不足:有时不能可靠复位4.2DSP系统的基本硬件设计4.2DSP系统的基本硬件设计4.2.2 时钟电路4.2DSP系统的基本硬件设计4.2.2 时钟电路TMS320VC5402内部具有一个可编程锁相环(PLL),它可以配置为两种模式:( 1 ) PLL 模式。
输入时钟乘以一个1~31之间的常数;( 2 ) DIV 模式。
输入时钟除以2 或4 。
软件可编程PLL 受一个存储器映射(地址为58h )的时钟模式寄存器CLKMD 控制,CLKMD 用于定义PLL 时钟模块的配置。
复位后CLKMD的值根据DSP 芯片三根输入引脚CLKMD1~CLKMD3 确定,从而确定DSP 的工作时钟。
4.2DSP系统的基本硬件设计4.2.2 时钟电路由于DSP 的程序需要从外部低速EPROM 、EEPROM中调入,可以采用较低工作频率的DSP 复位时钟模式,待RAM CLKMD 的值,使芯片工作在较高的频率上。
DSP基础知识专业复习资料(ppt 150页)_252

程序总线PB 传送取自程序存储器的指令代码 和立即操作数。
数据总线CB、DB和EB这3条数据总线将内部 各单元(如CPU、数据地址生成电路、程
序地址产生逻辑、在片外围电路以及数据 存储器)连接在一起,其中CB和DB传送读 自数据存储器的操作数,EB传送写到存储 器的数据。 *为什么要用2条数据线(CB、DB)读数?
3
二、选择芯片考虑的因素
1.DSP芯片的运算速度
MAC 时 间 : 一 次 乘 法 和 一 次 加 法 的 时 间 。 大 部 分 DSP芯片可在一个指令周期内完成一次乘法和一次加 法操作。
FFT执行时间:运行一个N点FFT程序所需时间。由
于FFT运算在数字信号处理中很有代表性,因此FFT运 算时间常作为衡量DSP芯片运算能力的一个指标。
MIPS:每秒执行百万条指令。 MOPS:每秒执行百万次操作。 MFLOPS:每秒执行百万次浮点操作。 BOPS:每秒执行十亿次操作。
4
三、系统调试和评价工具 : TMS320有一系 列系统调试工具用于代替或协助目标系统进行 软件评价和开发。
现有的产品有: DSK初学者开发套件(DSP Starter Kit) EVM软件评估模块(Evaluation Module) XDS510硬件仿真器(Extend Development Support Emulators)。 TI公司还提供集成开发工具CCS(Code Composer Studio),CCS可从网上下载,可进 行软、硬件仿真和系统分析,受到广泛应用。
14
2乘法器/加法器
17X17乘法 40位加法
检零 饱和 取整
15
为了使修正系数的量化误差最小,要 进行舍入处理。 C54X的CPU中是一个17×17位的硬件乘 法器,它与一个40位的专用加法器相连。 因此,乘法器可以在一个时钟周期内完成 一次乘法累加(MAC)运算。
DSP(数字信号处理)课件

第1章 绪论 章
DSP定义:利用数字计算机或专用数字硬件,对数字信号进行 DSP定义:利用数字计算机或专用数字硬件, 定义 的一切处理运算称为数字信号处理。 的一切处理运算称为数字信号处理。 DSP芯片:解决实时处理要求,适合DSP运算需求的单片可编程 DSP芯片:解决实时处理要求,适合DSP运算需求的单片可编程 芯片 DSP 微处理器芯片。 微处理器芯片。
用于初始化
LD LD LD LD LD
# 80h, A ;80h A # 32767,B ;32767 B # 23,DP ;23 DP # 15,ASM ;15 ASM # 3,ARP ;3 ARP
OVLY=0, 则片内RAM只映象到数据存储空间 若OVLY=0, 则片内RAM只映象到数据存储空间 若OVLY=1, 则片内 , 则片内RAM映象到程序和数据空间 映象到程序和数据空间
DROM位 位
当DROM=1,则部分片内 ,则部分片内ROM映象到数据空间 映象到数据空间 映象与MP/MC的有关 当DROM=0,则片内 ,则片内ROM映象与 映象与 的有关
返回首页
2.5 TMS320C54x片内外设简介 片内外设简介
1.通用 引脚 .通用I/O引脚 2.定时器 . 3.时钟发生器 . 4.主机接口(HPI) 4.主机接口(HPI) 5.串行口 . 6.软件可编程等待状态发生器 . 7.可编程分区转换逻辑 .
返回首页
第3章 TMS320C54x的数据寻址方式 章 的数据寻址方式
除程序存储器空间和数据存储器空间外, 除程序存储器空间和数据存储器空间外,C54x系 系 列器件还提供了I/O存储器空间 利用I/O空间可 存储器空间, 列器件还提供了 存储器空间,利用 空间可 以扩展外部存储器。 以扩展外部存储器。 I/O存储器空间为 存储器空间为64K字(0000h~FFFFh),有 ),有 存储器空间为 字 ~ ), 两条指令PORTR和PORTW可以对 存储器空 可以对I/O存储器空 两条指令 和 可以对 间操作, 间操作,读写时序与程序存储器空间和数据存储 器空间有很大不同。 器空间有很大不同。 使用片内存储器没有等待状态,速度快; 使用片内存储器没有等待状态,速度快; 使用片外存储器可以对更大的存储空间寻址, 使用片外存储器可以对更大的存储空间寻址,但 是速度较慢。 是速度较慢。
DSP培训讲义[1]
![DSP培训讲义[1]](https://img.taocdn.com/s3/m/01cec8955901020207409cc0.png)
PPT文档演模板
2020/10/30
DSP培训讲义[1]
CCS IDE
TI公司的DSP集成开发环境CCS(Code Composer Studio),集成除了最基本的 C编译器、汇编优化器、汇编器、连接 器,还有文档管理器、运行支持库、交 叉列表工具、建库工具、十六进制转化 工具等;为用户提供了环境配置、源文 件编辑、程序调试、跟踪和分析等功能
PPT文档演模板
——DSP培训DS之P培C训C讲S义I[1D] E
CCS IDE——数据可视化(Data Visualization)
Amplitude vs Time Diagram
PPT文档演模板
——DSP培训DS之P培C训C讲S义I[1D] E
CCS IDE——数据可视化(Data Visualization)
CCS IDE——项目管理(Project Manager)
项目级/文件级编译链接选项
项目配置:项目编译链接选项的集合
PPT文档演模板
——DSP培训DS之P培C训C讲S义I[1D] E
CCS IDE——项目管理(Project Manager)
多项目管理
当前激活 项目黑体 显示
PPT文档演模板
——DSP培训DS之P培C训C讲S义I[1D] E
PPT文档演模板
——DSP培训DS之P培C训C讲S义I[1D] E
CCS IDE
PPT文档演模板
设备驱动 工程项目创建 项目管理
编辑技巧 调试工具
数据可视化
Profile功能S义I[1D] E
CCS IDE——设备驱动(Setup Studio)
根据用户目标为CCS开发环境选择合适 的驱动并进行配置,可以是软件仿真 ( Simulation ) 也 可 是 硬 件 仿 真 (Emulation)。
DSP2812寄存器汇总
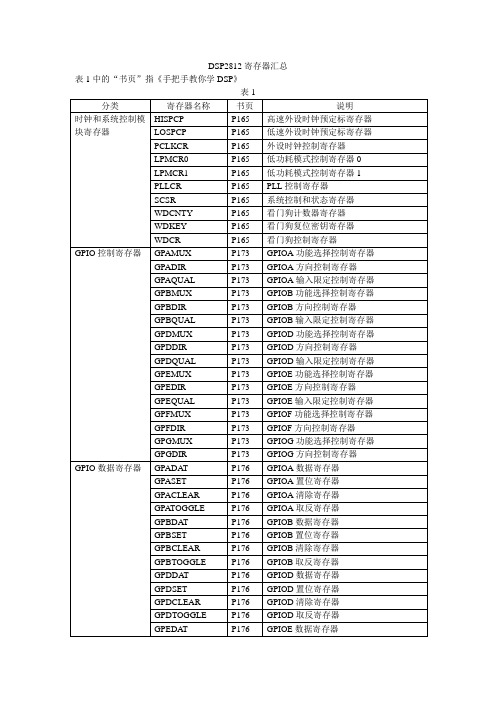
PIE, INT9组使能寄存器
PIEIFR9
P201
PIE, INT9组标志寄存器
PIEIER10
P201
PIE, INT10组使能寄存器
PIEIFR10
P201
PIE, INT10组标志寄存器
PIEIER11
P201
PIE, INT11组使能寄存器
PIEIFR11
P201
PIE, INT11组标志寄存器
P187
CPU定时器2控制寄存器
TIMER2TPR
P187
CPU定时器2预定标寄存器低位
TIMER2TPRH
P187
CPU定时器2预定标寄存器高位
CPU中断寄存器
IER
P196
CPU中断使能寄存器
IFR
P196
CPU中断标志寄存器
INTM
P196
CPU全局中断标志位
PIE(外设中断控制器)中断寄存器
EVAIFRA
P257
EVA中断标志寄存器A
EVAIMRA
P257
EVA中断屏蔽寄存器A
EVAIFRB
P257
EVA中断标志寄存器B
EVAIMRB
P257
EVA中断屏蔽寄存器B
EVAIFRC
P257
EVA中断标志寄存器C
EVAIMRC
P257
EVA中断屏蔽寄存器C
EVBIFRA
P257
EVB中断标志寄存器A
P293
ADC自动序列状态寄存器
ADCRESULT0
P293
ADC转换结果缓冲寄存器0
ADCRESULT1
P293
ADC转换结果缓冲寄存器1
dsp原理及应用课件ppt演示文稿

条件存储指令。 从中断快速返回指令。
第五页,共52页。
在片外围电路(如图2-1所示) 软件可编程等待状态发生器。 可编程分区转换逻辑电路。 带有内部振荡器。 外部总线关断控制,以断开外部的数据总线、地
址总线和控制信号。 数据总线具有总线保持器特性。 可编程定时器。并行主机接口(HPl)。
第六页,共52页。
电源 可用IDLEl、IDLE2和IDLE3指令控制功耗,以工
作在省电方式。 可以控制关断CLKOUT输出信号。
第七页,共52页。
在片仿真接口 具 有 符 合 IEEEll49.1 标 准 的 在 片 仿 真 接 口
(JTAG)。 速度 单周期定点指令的执行时间为25/20/15/12.5/10-
第三十三页,共52页。
15~13
12 11 10 9
ARP
TC C OV OV
AB
8~0 DP
图2-9 状态寄存器ST0位结构
第三十四页,共52页。
表2-2 状态寄存器ST0
第三十五页,共52页。
15 14 13 12 11 10 9
8
7
6
5 4~
0
BR CP XF HM INT 0 OV SX C16 FR CM AS
1 3FFFH 1 4000H
Page1: 低16K
外部
Page1: 高48K
外部
2 0000H
2 3FFFH 2 4000H
Page2: 低16K
外部
Page2: 高48K
外部
... F 0000H
... F 3FFFH
... F 4000H
Page15: 低16K 外部
DSP完整课件第1315章,dsp课件,

01100000(60h) 反向进位 00001000 加+ = 01101000(68h) 反向进位 00001000 加+ = 01100100(64h) 反向进位 00001000 加+ = 01101100(6ch) 01100111(67h) 反向进位 00001000 加+ = 01101111(6fh)
【例5】 采用直接寻址的ADD指令。 LDP ADD #4 9h,5 ;设臵数据页为4(地址0200h-027Fh) ;将数据地址0209h单元的内容左移5位后加至ACC
指令寄存器(IR) 0 0 1 0 ADD操作码 高9位来自DP 0000 0010 0 000 0 0 1 0 移5位 低7位来自IR 1001 0 000 1001 9h
.sect
·未初始化的块 符号 .bss
2010
‚块名‛,地址
.usect
自定义块
‚块名‛,字数
符号,字数(在RAM中保留空间) 退出
TMS320LF240x的寻址方式
当硬件执行指令时,寻找指令操作码及所指定的参与运 算的操作数的方法——寻址方式。
根据程序的要求采用不同的寻址方式,可以有效地缩短 程序的运行时间和提高代码执行效率。
2010
退出
• 位码倒序(位反转)寻址功能
存储单元地址 变换结果 位码倒序 位码倒序寻址结果 0000(60h) X(0) 0000 X(0) 0001 (61h) X(8) 1000 X(1) 0010 (62h) X(4) 0100 X(2) 0011 (63h) X(12) 1100 X(3) 0100 (64h) X(2) 0010 X(4) 0101 (65h) X(10) 1010 X(5) 0110 (66h) X(6) 0110 X(6) 0111 (67h) X(14) 1110 X(7) 1000 (68h) X(1) 0001 X(8) 1001 (69h) X(9) 1001 X(9) 1010 (6ah) X(5) 010l X(10) 1011 (6bh) X(13) 110l X(11) 1100 (6ch) X(3) 0011 X(12) 1101 (6dh) X(11) 1011 X(13) 1110 (6eh) X(7) 011l X(14)
数字信号处理经典 (15)Moving Average Filters

CHAPTER15EQUATION 15-1Equation of the moving average filter. Inthis equation, is the input signal, isx[]y[] the output signal, and M is the number of points used in the moving average. This equation only uses points on one side of the output sample being calculated.y[i]'1Mj M&1j'0x[i%j]y[80]'x[80]%x[81]%x[82]%x[83]%x[84]5Moving Average FiltersThe moving average is the most common filter in DSP, mainly because it is the easiest digital filter to understand and use. In spite of its simplicity, the moving average filter is optimal for a common task: reducing random noise while retaining a sharp step response. This makes it the premier filter for time domain encoded signals. However, the moving average is the worst filter for frequency domain encoded signals, with little ability to separate one band of frequencies from another. Relatives of the moving average filter include the Gaussian, Blackman, and multiple-pass moving average. These have slightly better performance in the frequency domain, at the expense of increased computation time.Implementation by ConvolutionAs the name implies, the moving average filter operates by averaging a numberof points from the input signal to produce each point in the output signal. Inequation form, this is written:Where is the input signal, is the output signal, and M is the numberx[]y[]of points in the average. For example, in a 5 point moving average filter, point80 in the output signal is given by:277The Scientist and Engineer's Guide to Digital Signal Processing278y [80]'x [78]%x [79]%x [80]%x [81]%x [82]5100 'MOVING AVERAGE FILTER 110 'This program filters 5000 samples with a 101 point moving 120 'average filter, resulting in 4900 samples of filtered data.130 '140 DIM X[4999] 'X[ ] holds the input signal 150 DIM Y[4999] 'Y[ ] holds the output signal 160 '170 GOSUB XXXX 'Mythical subroutine to load X[ ]180 '190 FOR I% = 50 TO 4949'Loop for each point in the output signal 200 Y[I%] = 0'Zero, so it can be used as an accumulator 210 FOR J% = -50 TO 50'Calculate the summation220 Y[I%] = Y[I%] + X(I%+J%]230 NEXT J%240 Y[I%] = Y[I%]/101'Complete the average by dividing 250 NEXT I%260 '270 ENDTABLE 15-1As an alternative, the group of points from the input signal can be chosen symmetrically around the output point:This corresponds to changing the summation in Eq. 15-1 from: ,j '0to M &1to: . For instance, in a 10 point moving average j '&(M &1)/2to (M &1)/2filter, the index, j , can run from 0 to 11 (one side averaging) or -5 to 5(symmetrical averaging). Symmetrical averaging requires that M be an odd number. Programming is slightly easier with the points on only one side;however, this produces a relative shift between the input and output signals.You should recognize that the moving average filter is a convolution using a very simple filter kernel. For example, a 5 point filter has the filter kernel: . That is, the moving average filter is a þ0,0,1/5,1/5,1/5,1/5,1/5,0,0þconvolution of the input signal with a rectangular pulse having an area of one .Table 15-1 shows a program to implement the moving average filter.Noise Reduction vs. Step ResponseMany scientists and engineers feel guilty about using the moving average filter.Because it is so very simple, the moving average filter is often the first thing tried when faced with a problem. Even if the problem is completely solved,there is still the feeling that something more should be done. This situation is truly ironic. Not only is the moving average filter very good for many applications, it is optimal for a common problem, reducing random white noise while keeping the sharpest step response.Chapter 15- Moving Average Filters279Sample number 0100200300400500-12FIGURE 15-1Example of a moving average filter. In (a), arectangular pulse is buried in random noise. In (b) and (c), this signal is filtered with 11 and 51point moving average filters, respectively. As the number of points in the filter increases, thenoise becomes lower; however, the edges becoming less sharp. The moving average filteris the optimal solution for this problem,providing the lowest noise possible for a given edge sharpness. Sample numberA p l i t u d A m p i t u d A m p l i t u d e Figure 15-1 shows an example of how this works. The signal in (a) is a pulse buried in random noise. In (b) and (c), the smoothing action of the moving average filter decreases the amplitude of the random noise (good), but also reduces the sharpness of the edges (bad). Of all the possible linear filters that could be used, the moving average produces the lowest noise for a given edge sharpness. The amount of noise reduction is equal to the square-root of the number of points in the average. For example, a 100 point moving average filter reduces the noise by a factor of 10.To understand why the moving average if the best solution, imagine we want to design a filter with a fixed edge sharpness. For example, let's assume we fix the edge sharpness by specifying that there are eleven points in the rise of the step response. This requires that the filter kernel have eleven points. The optimization question is: how do we choose the eleven values in the filter kernel to minimize the noise on the output signal? Since the noise we are trying to reduce is random, none of the input points is special; each is just as noisy as its neighbor. Therefore, it is useless to give preferential treatment to any one of the input points by assigning it a larger coefficient in the filter kernel. The lowest noise is obtained when all the input samples are treated equally, i.e., the moving average filter. (Later in this chapter we show that other filters are essentially as good. The point is, no filter is better than the simple moving average).The Scientist and Engineer's Guide to Digital Signal Processing 280EQUATION 15-2Frequency response of an M point moving average filter. The frequency, f, runs between 0 and 0.5. For , use:f'0H[f]'1H[f]'sin(B f M)M sin(B f)FrequencyChapter 15- Moving Average Filters281Sample number 0618240.00.21.01.2FrequencyFFT20 Log( )Aplit u deA mp itudFrequencyThe Scientist and Engineer's Guide to Digital Signal Processing282Figure 15-4 shows the frequency response of two other relatives of the movingaverage filter. When a pure Gaussian is used as a filter kernel, the frequencyresponse is also a Gaussian, as discussed in Chapter 11. The Gaussian isimportant because it is the impulse response of many natural and manmadesystems. For example, a brief pulse of light entering a long fiber optictransmission line will exit as a Gaussian pulse, due to the different paths takenby the photons within the fiber. The Gaussian filter kernel is also usedextensively in image processing because it has unique properties that allowfast two-dimensional convolutions (see Chapter 24). The second frequencyresponse in Fig. 15-4 corresponds to using a Blackman window as a filterkernel. (The term window has no meaning here; it is simply part of theaccepted name of this curve). The exact shape of the Blackman window isgiven in Chapter 16 (Eq. 16-2, Fig. 16-2); however, it looks much like aGaussian.How are these relatives of the moving average filter better than the movingaverage filter itself? Three ways: First, and most important, these filters havebetter stopband attenuation than the moving average filter. Second, the filterkernels taper to a smaller amplitude near the ends. Recall that each point inthe output signal is a weighted sum of a group of samples from the input. If thefilter kernel tapers, samples in the input signal that are farther away are givenless weight than those close by. Third, the step responses are smooth curves,rather than the abrupt straight line of the moving average. These last two areusually of limited benefit, although you might find applications where they aregenuine advantages.The moving average filter and its relatives are all about the same at reducingrandom noise while maintaining a sharp step response. The ambiguity lies inhow the risetime of the step response is measured. If the risetime is measuredfrom 0% to 100% of the step, the moving average filter is the best you can do,as previously shown. In comparison, measuring the risetime from 10% to 90%makes the Blackman window better than the moving average filter. The pointis, this is just theoretical squabbling; consider these filters equal in thisparameter.The biggest difference in these filters is execution speed. Using a recursivealgorithm (described next), the moving average filter will run like lightning inyour computer. In fact, it is the fastest digital filter available. Multiple passesof the moving average will be correspondingly slower, but still very quick. Incomparison, the Gaussian and Blackman filters are excruciatingly slow,because they must use convolution. Think a factor of ten times the number ofpoints in the filter kernel (based on multiplication being about 10 times slowerthan addition). For example, expect a 100 point Gaussian to be 1000 timesslower than a moving average using recursion.Recursive ImplementationA tremendous advantage of the moving average filter is that it can beimplemented with an algorithm that is very fast. To understand thisChapter 15- Moving Average Filters283FIGURE 15-4Frequency response of the Blackman windowand Gaussian filter kernels. Both these filtersprovide better stopband attenuation than themoving average filter. This has no advantage inremoving random noise from time domainencoded signals, but it can be useful in mixeddomain problems. The disadvantage of thesefilters is that they must use convolution, aterribly slow algorithm.FrequencyThe Scientist and Engineer's Guide to Digital Signal Processing284100 'MOVING AVERAGE FILTER IMPLEMENTED BY RECURSION 110 'This program filters 5000 samples with a 101 point moving 120 'average filter, resulting in 4900 samples of filtered data.130 'A double precision accumulator is used to prevent round-off drift.140 '150 DIM X[4999] 'X[ ] holds the input signal 160 DIM Y[4999] 'Y[ ] holds the output signal 170 DEFDBL ACC 'Define the variable ACC to be double precision 180 '190 GOSUB XXXX 'Mythical subroutine to load X[ ]200 '210 ACC = 0 'Find Y[50] by averaging points X[0] to X[100]220 FOR I% = 0 TO 100 230 ACC = ACC + X[I%]240 NEXT I%250 Y[50] = ACC/101260 ' 'Recursive moving average filter (Eq. 15-3)270 FOR I% = 51 TO 4949280 ACC = ACC + X[I%+50] - X[I%-51]290 Y[I%] = ACC/101300 NEXT I% 310 '320 END TABLE 15-2is used in future calculations. (The term "recursive" also has other meanings,especially in computer science). Chapter 19 discusses a variety of recursive filters in more detail. Be aware that the moving average recursive filter is very different from typical recursive filters. In particular, most recursive filters have an infinitely long impulse response (IIR), composed of sinusoids and exponentials. The impulse response of the moving average is a rectangular pulse (finite impulse response, or FIR).This algorithm is faster than other digital filters for several reasons. First,there are only two computations per point, regardless of the length of the filter kernel. Second, addition and subtraction are the only math operations needed,while most digital filters require time-consuming multiplication. Third, the indexing scheme is very simple. Each index in Eq. 15-3 is found by adding or subtracting integer constants that can be calculated before the filtering starts (i.e., p and q). Fourth, the entire algorithm can be carried out with integer representation. Depending on the hardware used, integers can be more than an order of magnitude faster than floating point.Surprisingly, integer representation works better than floating point with this algorithm, in addition to being faster . The round-off error from floating point arithmetic can produce unexpected results if you are not careful. For example,imagine a 10,000 sample signal being filtered with this method. The last sample in the filtered signal contains the accumulated error of 10,000 additions and 10,000 subtractions. This appears in the output signal as a drifting offset.Integers don't have this problem because there is no round-off error in the arithmetic. If you must use floating point with this algorithm, the program in Table 15-2 shows how to use a double precision accumulator to eliminate this drift.。
《DSP实训讲义》word版

DSP 实训讲义目录:第一章电子系统设计总论第一节电子系统设计方法第二节电子系统的调试、组装与总结第三节电子系统的电磁兼容第二章DTMF信号发生和接受器系统设计第一节什么是DTMF信号第二节DTMF信号发生器的要求第三节DTMF信号检测方法第三章DTMF信号发生/检测器的设计第一节基于DSP的DTMF信号发生器硬件设计第二节基于DSP的DTMF 信号检测器硬件设计第三节DTMF信号发生器软件设计第四节DTMF 信号检测器软件设计附录一 protel 简介附录二 CCS2.0简介第一章电子系统设计总论从一般系统到电子系统以系统的观点分析电子系统,那么一个电子系统应该有输入,输出,以及输入输出之间的映射关系,如果,输入和输出之间的映射关系,那么输入输出之间有:对于一个物理可实现的系统来说首先确定的是系统输入输出之间的映射关系对于一个系统来说往往工作在某种环境或者是某些环境下因此往往要求系统能在这种环境下可靠工作也就是环境在一定范围变化的情况下系统输入输出之间的关系还要能保持。
因此在设计一个系统的时候应该考虑两个至少是两个特性:一系统输入和输出之间的关系这个关系可以说就是系统要完成的功能或者说是任务二当系统的工作环境在一定范围变化的时候,系统仍然能够完成设计时的输入和输出之间关系的能力这种能力就叫做可靠性电子系统的设计时应考虑的基本问题在电子系统设计阶段应考虑以下两个问题:一、功能设计二、可靠性设计电子系统的功能是一个电子系统的主要特性,在设计的时候是设计人员主要考虑问题。
设计一个电子系统是为了能在一定的环境和一定的时间段内完成一定的任务,因此设计者在设计电子系统的时候不但要考虑电子系统功能,还要考虑设计的电子系统能不能在规定的环境和时间段上完成设计的功能,也就是要考虑设计的电子系统在一定的环境变化范围内和期望的时间长度上能不能可靠的完成设计时的功能因此电子系统的可靠性是电子系统在规定的时间和环境条件下完成设计的功能的能力,度量可靠性能力的指标就是可靠性度量电子系统功能设计方法电子系统设计方法一般有:A 自下向上设计方法,B 自顶向下设计方法电子系统传统的设计方法是自下向上设计方法这种方法是采用中小规模集成电路和分立元件对电路板设计,采用这种方法对一个复杂电子系统进行设计的时候往往是先设计好底层的电路然后搭积木一般用设计好的底层电路搭建复杂的电子系统。
dsp培训讲义

DSP培训讲义DSP培训讲义 (1)第1节功能概述 (3)1.1概念 (3)1.2如何认识DSP (3)1.3特性概述 (3)1.4 器件概述 (5)1.5 功能框图 (7)1.6 封装 (7)第2节存储器 (27)2.1存储器映像 (27)2.1.1片内的程序/数据 (27)2.1.2 保留区 (27)2.1.3 CPU中断向量 (27)2.2存储器接口 (28)2.2.1地址和数据总线 (28)2.2.2特殊总线操作 (29)2.2.3对偶地址进行32位存取的排列 (29)XMAC (30)第3节C28X的寻址方式 (31)第4节CCS使用 (65)第1节功能概述1.1概念●数字信号处理(Digital Signal Processing)是指利用计算机或专用设备,以数值计算的方式对实时信号进行采集、变换、综合、估计与识别等加工处理,从而达到提取信息和便于应用的目的。
●而DSP芯片(数字信号处理器(Digital Signal Processors)就是这样的一种微处理器。
其中TI公司推出的TMS320F28X处理器具有较高的信号处理和控制功能,在数字控制领域拥有广阔的应用前景。
●TMS320F2810及TMS320F2812是工业界首批32位的控制专用、内含闪存以及高达150MIPS的数字信号处理器,专门为工业自动化、光学网络及自动化控制等应用而设计。
1.2如何认识DSP1.DSP就是一种处理器,它无非是一种数据处理能力极其强大、片内资源十分丰富的处理器;它的使用与单片机有许多类似之处,比如片内外设的使用亦是通过读写相应的控制寄存器来实现的,它的学习与使用并不难。
微处理器2.相对于单片机,DSP为我们开发高品质的产品搭建了一个更为广阔的平台,但学通DSP并不是开发优秀产品的充分条件。
在具体的DSP应用领域,相应的专业知识和对该行业的深刻理解仍然是最重要的。
比如我们做仪器,扎实的测量和计量知识基础,对测量测试行业的国内国际标准以及对用户需求的深刻理解是第一位的,我们只是用DSP来实现我们的设计思路和理念。
阿尔派dsp15调音教程

阿尔派dsp15调音教程
01、确认系统左右声道及喇叭相位是否正确,相位仪。
对主机以及功放电平进行匹配,最大不失真,示波器。
除前声场之外,关闭后声场及超低音,对前声场进行高通HPF切频,频点根据每套喇叭频响范围确认,市面上大部分喇叭都可以切在80Hz以上高通,喇叭素质高的可以切到60Hz。
02、这时,我们要听到饱满有力度的中低音。
歌曲(MACE第9首,Bass清晰饱满有量感,脚鼓清晰结实,鼓槌敲击鼓皮声,电吉他纤细明亮,音量适中,跟其他乐器明显不同,军鼓的音量在听感上比其他器件音量要大一些。
03、有腔体共鸣声,要有力度,明亮度适中,通通鼓的音色音高与军鼓不同,嚓片有金属感,但不能听上去表现太大,比军鼓音量小,过大容易出现高音失真)。
这里被动分频下,高音的量感可以通过分频器来调整,分频器调整不了的要从主机着手啦。
主动分频中,可以单独调整高、中、中低的量感来保证前声场各喇叭之间的平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四讲DSP 最小硬件系统的设计4.1引言一个DSP 硬件系统可以分为最小硬件系统设计和外围接口设计两个部分。
本讲主要介绍DSP 最小硬件系统的设计,包括复位、时钟、电源及存储器接口等.5402最小系统原理图5402最小系统5402最小系统电源图继续返回返回返回4.2DSP系统的基本硬件设计4.2.1 复位电路电压公式:电源刚加上电时,TMS320 DSP 芯片处于复位状态,/RS低使芯片复位为使芯片初始化正确,一般应保证/RS为低至少持续3 个CLKOUT 周期但是,在上电后,系统的晶体振荡器一般需要儿百毫秒的稳定期,一般为100~200ms。
选择R = 100K , C = 47μ,可得t1= 167ms 。
●此种复位特点:提问:输入方式比较,阻容颠倒可以不?存在不足:有时不能可靠复位简单如何设计复位电路4.2.1 复位电路上电触发掉电保护触发4.2.2 时钟电路4.2.2 时钟电路TMS320VC5402内部具有一个可编程锁相环(PLL),它可以配置为两种模式:( 1 ) PLL 模式。
输入时钟乘以一个1~31之间的常数;( 2 ) DIV 模式。
输入时钟除以2 或4 。
软件可编程PLL 受一个存储器映射(地址为58h )的时钟模式寄存器CLKMD 控制,CLKMD 用于定义PLL 时钟模块的配置。
复位后CLKMD的值根据DSP芯片三根输入引脚CLKMD1~CLKMD3 确定,从而确定DSP 的工作时钟。
4.2.2 时钟电路由于DSP 的程序需要从外部低速EPROM 、EEPROM 中调入,可以采用较低工作频率的DSP 复位时钟模式,待程序全部调入到内部快速RAM 后,再用软件重新配置CLKMD 的值,使芯片工作在较高的频率上。
例如: 设外部晶体频率是10MHz ,设置CLKMD1~CLKMD3 = 111,则复位后DSP的工作频率是10MH/2 = 5MHz。
用软件重新设置CLKMD =9007H , 就可以使DSP 工作在10x10MHz = 100 MHz 的频率。
4.2.3 电源设计为了降低芯片功耗,近来推出的DSP 芯片大部分采用低电压供电方式,并月采用内核电压和I/O 电压分开的方式。
电源分两种,即内核电源(Cvdd )和I/O 电源(Dvdd ) ,其中I/O电源一般采用3.3V 电压,而内核电源电压分为3.3V 或2.5V 甚至更低,降低内核电压的主要目的还是降低功耗。
以TMS320VC5402为例子:CV DD=1.8V DV DD=3.3V4.2.3 电源设计4.2.3 电源设计4.2.3 电源设计1.电源电压结构及要求4.2.3 电源设计2.电流要求电流消耗主要取决于器件的激活度,CVdd 消耗的电流主要取决于CPU 的激活度,外设消耗的电流取决于正在工作的外设及其速度。
与CPU 相比,外设消耗的电流是比较小的。
时钟电路也需要消耗一小部分电流,而且这部分电流是恒定的,与CPU和外设的激活程度无关。
4.2.3 电源设计2.电流要求CVdd(int) 为器件的所有内部逻辑提供电流,包括CPU、时钟电路和所有外设。
DVdd(IO) 只为外部接口引脚提供电压,消耗的电流取决于外部输出的速度和数量,以及在这些输出上的负载电容。
例如:TMS320VC549的每MHz(CLKOUT)消耗的平均电流是0.45mA,峰值电流为每MHz(CLKOUT ) 1.1mA 。
按1.5mA来计算,TMS320VC549工作在100MHz的最大估计电流为:( 1.5mA/MHz) X (100MHz) = 150mA4.2.3 电源设计3.加电次序由于有两个电源,需要考虑的问题是加电次序。
理想情况下,DSP 芯片上的两个电源同时加电,但是在一些场合很难做到。
如果不能做到同时加电,应先对DVdd 加电,然后对CVdd 加电。
DVdd应不超过CVdd 电压2V 。
CVdd不能超过DVdd 的电压为1个二极管压降(约0.5V),否则有可能损坏器件。
FPGA的顺序4.2.3 电源设计4. 电压的产生4.2.3 电源设计5. 电源解决方案(1)单3.3V电压输出。
TI 公司的TPS7133、TPS7233、TPS7333,或其他公司的芯片,如Maxim 的Max604Linear公司的LT1117、LT1764等。
(2)单电源可调电压输出。
TI公司的TPS7101、TPS7201 等芯片能够提供可调节的输出电压(1.2~9.75v )。
电压调节是通过改变外接的两个电阻的阻值实现的。
可调的应用:不是主流电压4.2.3 电源设计5. 电源解决方案(3)双电源输出。
TI公司的TPS73HD301、TPS73HD325和TPS73HD318。
TPS73 HD301的输出电压为一路3.3V、一路可调输出(1.2~9.75v ) ;TPS73HD325的输出电压为一路3.3V、一路2.5V;TPS73HD318 的输出电压为一路3.3V、一路1.8V 。
每路电源的最大输出电流为750mA 。
4.2.3 电源设计5. 电源解决方案4.2.3 电源设计5. 电源解决方案1.8V 4.2.3 电源设计5. 电源解决方案4.2.3 电源设计5. 电源解决方案4.2.3 电源设计5. 电源解决方案4.2.3 电源设计5. 电源解决方案输出提高4.2.3 电源设计5. 电源解决方案DC-DC模块4.2.4 等待状态发生器DSP 芯片中有了锁相环(PLL),输入时钟频率与CPU 工作频率之间的关系不再是2:1了。
TMS320C54x-40 的DSP 芯片,其尾数40 表示CPU 运行的最高频率(单位为MHz),由于大多数指令都是单周期指令,所以这种DSP 的运行速率也就是40MIPs (每秒执行4000万条指令)。
一个40MIPs 的DSP芯片,其机器周期为25ns 。
如果不插等待状态,就要求外部器件的存取时间ta < 15ns。
如果C54x 与慢速器件相接口,这就需要通过软件或硬件的方法插入等待状态。
4.2.4 等待状态发生器4.2.4 等待状态发生器(1) 采用硬件等待C54x 有一个输入引脚READY,CPU利用这个引脚检测外部器件是否已经做好传送数据的准备。
若READY=1 ,表示外部器件已准备好;若READY=0,表示没有准备好,处理器就自动插入一个等待状态(所有外部地址线、数据线以及控制信号均延长一个机器周期),之后再次检测READY 信号。
4.2.4 等待状态发生器(1) 采用硬件等待如果软件等待0和1个状态,CPU是不检测READY 信号的。
当软件等待2~7 个状态,且执行到最后一个软件等待状态结束时,/MSC引脚(为状态完成信号,输出信号)变成低电平,表示n 个软件等待状态已经过去。
如果需要,可以在此软件等待状态的基础上,再加外部硬件等待也就是说,只有/MSC信号变成低电平后,CPU才采样READY 信号,如果在这种情况(插入2~7 个软件等待状态)下,不需要再增加硬件等待,只要将/MSC脚与READY引脚相连。
4.2.4 等待状态发生器(1) 采用硬件等待4.2.4 等待状态发生器(2) 采用软件等待C54x 片内有一个软件等待状态寄存器(SWWSR ) ,可以用来设置等待状态。
SWWSR 映像到数据存储器。
28h 单元,它由6 个部分组成,最高位为保留位,或外部扩展程序存储器地址控制位:4.2.4 等待状态发生器(2) 采用软件等待●可以通过软件为以上5 个存储空间分别插入0~7 个软件等待状态。
(2) 采用软件等待例:试为TMS320C54x-40配置:程序存储器(EPROM)8K×16 位,ta=70 ns数据存储器(SRAM)8K×16 位,ta=12nsA/D和D/A转换器16 位,转换时间= 120ns 画出系统的接口连线图.(2) 采用软件等待程序存储器(EPROM)8K×16 位,ta=70 ns数据存储器(SRAM)8K×16 位,ta=12nsA/D和D/A转换器16 位,转换时间= 120ns●数据存储器可以不插入等待状态,●程序存储器插入3个等待●A/D、D/A外部设备插入5个等待●状态软件等待状态寄存器(SWWSR)应配置为:(2) 采用软件等待●数据存储器可以不插入等待状态,●程序存储器插入3个等待●A/D、D/A外部设备插入5个等待●状态软件等待状态寄存器(SWWSR)应配置为:(3) 采用软硬件混合等待(3) 采用软硬件混合等待如图:当CPU 寻址外部程序存储器时,将SWWSR 中相应的字段值加载到计数器。
如果这个字段值不为000 ,就会向CPU 发出一个“没有准备好”信号,等待状态计数器启动工作。
没有准备好的情况一直保持到计数器减到0和外部READY 线置高电平为止。
外部READY 信号和内部等待状态的READY 信号经过一个与门产生CPU等待信号,加到CPU的/WAIT 端。
当计数器减到0 (内部等待状态的READY 信号变为高电平),且外部READY 也为高电平时,CPU的/WAIT端由低变高,结束等待状态。
(3) 采用软硬件混合等待等待一个周期TMS320C54x 等新一代DSP 芯片的I/O工作电压是3.3V,因此,其I/O电平也是3.3V逻辑电平。
在设计DSP 系统时,如果外围芯片的工作电压也是3.3V ,那么就可以直接连接。
但是,由于现有很多外围芯片的工作电压都是5V ,如EPROM 、EEPROM、SRAM 、模数转换芯片等,因此,就存在一个如何将3.3V DSP 芯片与这些5V供电芯片的可靠接口的问题。
DSP、FPGA、MCU1. 各种电平的转换标准COMS的特点?VOLmax<VILmaxV OHmin>VH Lmin Vo、Vi:很高2. 3.3V与5V电平转换的4种情形2. 3.3V与5V电平转换的4种情形( 1 ) 5V TTL器件驱动3.3V TTL器件。
由于5V TTL和3.3V TTL的电平转换标准是一样的,因此,如果3.3V 的器件能够承受5V 电压,直接相接从电平上来说是完全可以的。
2. 3.3V与5V电平转换的4种情形( 2 ) 3.3V TTL器件(LVC)驱动5V TTL器件。
由于两者的的电平转换标准是一样的,因此不需要额外的器件就可以将两者直接相接。
只要3.3V 器件的V OH和V OL电平分别是2.4V 和0.4V, 5V器件就可以将输入读为有效电平,因为它的V IH和V IL 电平分别是2V和0.8V。
2. 3.3V与5V电平转换的4种情形(3) 5V CMOS 驱动3.3V TTL 器件(LVC)。
显然,两者的转换电平是不一样的。
