基础小练习:动态平衡问题分析
高三物理练习题(28)

2019届高三二轮复习专题—基础综合—力与平衡核心知识考点一受力分析、物体的平衡明确六种常见力规律方法1.受力分析的顺序一般按照“一重、二弹、三摩擦、四其他”的程序,结合整体法与隔离法分析物体的受力情况.2.处理平衡问题的基本思路典例分析1 . 如图所示,一根弹性杆的一端固定在倾角为30°的斜面上,杆的另一端固定一个质量为1kg的小球,小球处于静止状态。
取g=10m/s2。
则弹性杆对小球的作用力A.大小为10N,方向竖直向上B.大小为10N,方向垂直于斜面向上C.大小为5N,方向垂直于斜面向上D.大小为5N,方向垂直于斜面向上【答案】A【解析】【详解】小球受到竖直向下的重力G=10N,杆对小球的作用力F,小球静止,处于平衡状态,由平衡条件得:F与重力G是一对平衡力,则F=G=10N,方向竖直向上;故A正确,BCD错误。
故选:A.考点二整体与隔离在静态平衡中的应用核心知识1.整体法在研究物理问题时,把所研究的对象作为一个整体来处理的方法称为整体法.采用整体法可以避免对系统内部进行繁琐的分析,常常使问题解答更简便明了.2.隔离法把所研究对象从整体中隔离出来进行研究,最终得出结论的方法称为隔离法.采用隔离物体法能排除与研究对象无关的因素,使事物的特征明显地显示出来,从而进行有效的处理.3.隔离法与整体法的关系隔离法与整体法,在一般问题的求解中,随着研究对象的转化,往往两种方法交叉运用,研究系统外力时往往用整体法而研究单个物体受力,则用隔离法.规律方法整体法、隔离法处理静态平衡问题的思路典例分析2 . 如图,一质量为M="10" kg的正方形小物块置于固定在水平地面上的斜面体上,物块M与斜面间动摩擦因数μ="0.5" ,一平行于斜面的轻质细绳一端系于物块M上,另一端绕过定滑轮与人相连(不计定滑轮处的一切摩擦),定滑轮质量m0="2" kg.当人以T="100" N的力斜向下拉绳子时(人不移动位置,只是手中收绳子),为保证物块M 沿斜面向上做匀速直线运动,需同时施加一垂直物块M上表面向下作用力F. 人的质=" 50" kg,斜面倾角和绳子与水平面的夹角都是量m人θ=30∘,sin30∘=1/2,cos30∘=/2,重力加速度取g="10" m/s2求:(1)人对地面的压力N多大;(2)人与地面的摩擦力f的大小和方向;地大小;(3)定滑轮上方竖直悬杆OA对定滑轮的拉力F杆(4)作用力F的大小。
对蹦床运动员平衡能力和训练方法的分析

221对蹦床运动员平衡能力和训练方法的分析赵微娜 南通市儿童业余体育学校摘要:本文以我国蹦床运动员为研究对象,采用文献资料法、专家访谈法、逻辑分析法等研究方法,着重分析视觉、本体感觉对蹦床运动员平衡能力的影响,探究蹦床运动员在平衡训练中所遵循的全面发展原则、培养良好的身体形态以及科学针对性原则,并通过瑞士球、平行垫、核心板、拉力器等道具如何进行平衡能力训练,从中总结出适合我国蹦床运动员具体实际的训练方法,从而为提高我国的蹦床运动水平提供理论依据。
关键词:蹦床运动员;平衡能力;训练方法蹦床运动引进我国的时间虽然不长,却获得了蓬勃发展,获得了大力推广,加上蹦床技术的不断革新,我国的蹦床运动水平提升很快,并在多届奥运会的舞台上取得了良好的成绩。
如今,世界蹦床运动在传统竞技的基础上提出了“高、难、准、美”的新要求,标志着蹦床运动跨入了更高难度的新时代,这也对蹦床运动员的身体和心理素质提出了更高的要求。
而影响蹦床运动员在比赛中稳定发挥的主要因素将是身体素质的强弱,这其中平衡能力更是成为了蹦床运动员能否高质量地完成技术动作获得高分的关键。
一、对蹦床运动员平衡能力影响因素的分析(一)视觉的影响视觉系统主要提供给运动员周围环境以及自身身体运动和方向的信息。
根据运动员日常训练的观察和查阅资料显示,运动员在闭上眼睛睁开眼睛分别做动作时各项指标都会出现显著的差异,以单足站立为例,运动员在闭眼时,动作的精确度和规范程度明显低于睁眼的状态,平衡能力也会下降,当运动员睁眼时各项指标明显提高,这就从侧面反映了视觉对平衡能力的重要性。
而相关资料显示,在蹦床训练中,运动员长期采用睁眼和闭眼交叉的方法进行平衡训练,运动员的平衡能力都会得到有效的提高。
因此建议蹦床运动员在训练平衡能力时可以采用此方法。
(二)本体感觉的影响蹦床运动在运动过程中需要通过高速跳跃和变换动作,完成一系列的动作需要运动员迅速调整自己的身体姿态改变运动轨迹以保持身体的支撑平衡。
化学平衡与浓度变化的计算练习题

化学平衡与浓度变化的计算练习题一. 前置知识概述在进行化学反应中,平衡态是指反应物和生成物在一定条件下浓度保持稳定的状态。
化学平衡的理论基础是利用平衡常数来描述反应进程。
当平衡态建立时,正反应速率相等,化学反应呈现动态平衡的特征。
在化学平衡反应中,浓度变化是非常重要的,通过浓度的变化可以了解反应的进行情况。
浓度变化可以通过平衡反应方程式和平衡常数来计算和推导。
二. 练习题1. 对于反应:A(g) + B(g) ⇌ 2C(g),平衡常数Kc为0.4。
当初始时,A、B、C的浓度分别为0.2mol/L、0.5mol/L和0.1mol/L。
求在平衡时,A、B和C的浓度是多少?解析:假设A(g)和B(g)的浓度变化为x,C(g)的浓度变化为2x,则在平衡时,A的浓度为0.2-x,B的浓度为0.5-x,C的浓度为0.1+2x。
根据平衡常数的定义,有Kc = [C]^2 / ([A] * [B]),代入平衡时的浓度得到0.4 = (0.1+2x)^2 / ((0.2-x) * (0.5-x)),解方程得到x = 0.02。
因此,在平衡时,A的浓度为0.2-0.02=0.18mol/L,B的浓度为0.5-0.02=0.48mol/L,C的浓度为0.1+2*0.02=0.14mol/L。
2. 对于反应方程式:2A(aq) + B(aq) ⇌ 3C(aq),平衡常数Kc为2.0×10^4。
在初始时,A的浓度为0.1mol/L,B的浓度为0.2mol/L,C的浓度为0.3mol/L。
求在平衡时,A、B和C的浓度分别是多少?解析:假设A(aq)和B(aq)的浓度变化为x,C(aq)的浓度变化为3x,则在平衡时,A的浓度为0.1-2x,B的浓度为0.2-x,C的浓度为0.3+3x。
根据平衡常数的定义,有Kc = [C]^3 / ([A]^2 * [B]),代入平衡时的浓度得到2.0×10^4 = (0.3+3x)^3 / ((0.1-2x)^2 * (0.2-x)),解方程得到x =0.015。
高一力学动态平衡—相似三角形、动态三角形

高一力学动态平衡—相似三角形、动态三角形在高一力学的学习中,动态平衡问题是一个重要且具有一定难度的知识点。
其中,相似三角形和动态三角形的方法在解决这类问题时常常能发挥关键作用。
我们先来理解一下什么是动态平衡。
简单来说,动态平衡就是指物体在运动过程中,其合力始终为零,保持平衡状态,但某些力的大小、方向在不断变化。
想象一个用绳子悬挂的物体,绳子的长度不变,但悬挂点在移动,这就是一种动态平衡的情况。
相似三角形法在处理动态平衡问题时,基于的原理是在力的矢量三角形与几何三角形相似的情况下,对应边成比例。
这意味着我们可以通过几何关系来确定力的变化情况。
比如说,有一个物体放在斜面上,用一个力 F 沿着斜面向上推,同时受到斜面的支持力 N 和重力 G 的作用。
我们可以分别画出力的矢量三角形和由物体、斜面构成的几何三角形。
如果这两个三角形相似,那么力之间的比例关系就与三角形边的比例关系相同。
举个具体的例子吧。
一个光滑的圆球放在一个斜面上,被一根细绳斜拉着处于静止状态。
我们画出圆球受到的重力 G、绳子的拉力 T 和斜面的支持力 N 所构成的矢量三角形。
同时,观察圆球、绳子与斜面接触点以及斜面顶点构成的几何三角形。
如果这两个三角形相似,那么我们就可以根据边的比例关系来判断力的大小变化。
再来看动态三角形法。
这种方法主要用于一个力的大小和方向不变,另一个力的方向不变,第三个力大小和方向都在变化的情况。
比如,还是一个物体放在斜面上,重力大小和方向不变,斜面的支持力方向不变,而施加在物体上的一个外力的大小和方向都在改变。
我们可以通过平移力的矢量,构建一个动态的三角形来分析力的变化。
具体来讲,我们先画出重力,然后根据支持力的方向画出支持力,再把外力的起始点与重力的末端连接起来,这样就构成了一个三角形。
随着外力的变化,这个三角形的形状也在改变,但我们可以通过其中一些不变的条件来分析力的变化规律。
比如说,当外力与支持力垂直时,外力取得最小值。
高三受力分析动态平衡模型总结(解析版)

动态平衡受力分析在有关物体平衡的问题中,有一类涉及动态平衡。
这类问题中的一部分力是变力,是动态力,力的大小和方向均要发生变化,故这是力平衡问题中的一类难题。
解决这类问题的一般思路是:把“动”化为“静”,“静”中求“动”。
物体受到往往是三个共点力问题,利用三力平衡特点讨论动态平衡问题是力学中一个重点和难点。
基础知识必备方法一:三角形图解法特点:三角形图象法则适用于物体所受的三个力中,有一力的大小、方向均不变(通常为重力,也可能是其它力),另一个力的方向不变,大小变化,第三个力则大小、方向均发生变化的问题。
方法:先正确分析物体所受的三个力,将三个力的矢量首尾相连构成闭合三角形。
然后将方向不变的力的矢量延长,根据物体所受三个力中二个力变化而又维持平衡关系时,这个闭合三角形总是存在,只不过形状发生改变而已,比较这些不同形状的矢量三角形,各力的大小及变化就一目了然了。
【例1】如图所示,一个重力为G的匀质球放在光滑斜面上,斜面倾角为,在斜面上有一光滑的不计厚度的木板挡住球,使之处于静止状态.今使板与斜面的夹角β缓慢增大,问:在此过程中,挡板对球的压力F N1和斜面对球的支持力F N2变化情况为()A.F N1、F N2都是先减小后增加B.F N2一直减小,F N1先增加后减小C.F N1先减小后增加,F N2一直减小D.F N1一直减小,F N2先减小后增加答案C【练习1】如图所示,小球被轻质细绳系着,斜吊着放在光滑劈面上,小球质量为m,斜面倾角为θ,向右缓慢推动劈一小段距离,在整个过程中()A.绳上张力先增大后减小B.绳上张力先减小后增大C.劈对小球支持力减小D.劈对小球支持力增大答案D方法二:相似三角形法。
特点:相似三角形法适用于物体所受的三个力中,一个力大小、方向不变,其它二个力的方向均发生变化,且三个力中没有二力保持垂直关系,但可以找到力构成的矢量三角形相似的几何三角形的问题原理:先正确分析物体的受力,画出受力分析图,将三个力的矢量首尾相连构成闭合三角形,再寻找与力的三角形相似的几何三角形,利用相似三角形的性质,建立比例关系,把力的大小变化问题转化为几何三角形边长的大小变化问题进行讨论。
高考化学化学平衡知识点总结与题型练习 2024

高考化学化学平衡知识点总结与题型练习2024一、化学平衡概述化学平衡是指在封闭系统中,各物质的摩尔数处于动态平衡的状态。
在这种状态下,正向反应和逆向反应的速率相等,且各物质的浓度保持不变。
二、化学平衡的条件1. 封闭系统:化学反应发生在封闭的反应容器中,不受外界影响。
2. 反应物浓度:反应物的浓度要足够高,以保证反应能够进行。
当反应物浓度过低时,反应会偏向生成物的一侧。
3. 反应温度:温度的变化会影响反应的平衡位置。
根据Le Chatelier 原理,提高反应温度会使平衡位置偏向反应物的一侧,降低反应温度则使平衡位置偏向生成物的一侧。
4. 压力:对于气相反应而言,压力变化也可以影响平衡位置。
增加压力会偏向摩尔数较少的一侧,减小压力则会偏向摩尔数较多的一侧。
三、化学平衡的表达式化学反应达到平衡时,可以根据反应物与生成物的摩尔比例,得到化学平衡的表达式。
一般形式为:aA + bB ↔ cC + dD,其中a、b、c、d分别表示反应物与生成物的摩尔系数。
四、平衡常数1. 平衡常数的定义:对于化学平衡表达式aA + bB ↔ c C + dD,定义平衡常数Kc为平衡时各物质摩尔浓度的乘积商的比值,即Kc =[C]^c[D]^d / [A]^a[B]^b,方括号表示浓度。
2. 平衡常数的大小:平衡常数表示正向反应与逆向反应在平衡状态下的相对强度。
当Kc > 1时,平衡偏向生成物的一侧;当Kc < 1时,平衡偏向反应物的一侧;当Kc = 1时,反应物和生成物的浓度相等。
3. 改变平衡常数:平衡常数受温度的影响,温度升高或降低都会改变平衡常数的值。
五、平衡常数与反应系数的关系平衡常数与反应系数之间存在着一定的关系。
对于化学平衡表达式aA + bB ↔ cC + dD,平衡常数Kc = ([C]^c[D]^d) / ([A]^a[B]^b)。
当反应方程式中的系数发生改变时,平衡常数也会相应发生变化。
力的合成与分解知识点与例题讲解

力的合成与分解知识点与例题讲解Prepared on 22 November 2020力的合成(基础篇)命题人:rain1.合力:一个物体受到几个力共同作用产生的效果与一个力对物体作用产生的效果相同时,这个力就叫做那几个力的合力2.合成:求几个力的合力叫做力的合成.三、合力的求法1.力的平行四边形定则:如果用表示两个共点力F1和F2的线段为邻边作平行四边形,那么,合力F的大小和方向就可以用这两个邻边之间的对角线表示出来。
2.共点力:几个力如果都作用在物体的同一点,或者它们的作用线相交于同一点,这几个力叫做共点力。
3.平行四边形定则的两种应用方法(1)图解法a.两个共点力的合成:从力的作用点作两个共点力的图示,然后以F1、F2为边作平行四边形,对角线的长度即为合力的大小,对角线的方向即为合力的方向。
b.两个以上共点力的合成:先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到所有的力都合成进去,最后得到的结果就是这些力的合力。
(2)计算法先依据平行四边形定则画出力的平行四边形,然后依据数学公式(如余弦定理)算出对角线所表示的合力的大小和方向。
当两个力互相垂直时,有:F=√F12+F22、tanθ=F2/F1四、合力大小的范围(1)合力F随θ的增大而减小(2)当θ=0°时,F有最大值Fmax=F1+F2,当θ=180°时,F有最小值Fmin=F1-F2(3)合力F既可以大于,也可以等于或小于原来的任意一个分力一般地 | F1-F2≤ F ≤ F1+F2五、矢量与标量矢量:即有大小,又有方向,并遵循平行四边形定则的物理量叫做矢量。
标量:只有大小而没有方向,遵循代数求和法则的物理量叫做标量。
矢量和标量的根本区别就在于它们分别遵循两种不同的求和运算法则.力的分解(基础篇)命题人:尚瑞阳一、分力及力的分解概念1.力的分力:几个力共同产生的效果跟原来一个力产生的效果相同,这几个力就叫做原来那个力的分力。
高一物理:共点力平衡与动态分析练习及答案

高一物理:共点力平衡与动态分析练习及
答案
引言
本文档提供了高一物理共点力平衡与动态分析的练题及答案,旨在帮助学生巩固和加深对该知识点的理解。
练题
1. 一个物体在水平地面上受到两个力的作用,一个力的大小为10N,方向为向右,另一个力的大小为6N,方向为向左。
求物体的净力大小和方向。
2. 一个物体质量为2kg,受到一个大小为12N的向右的力和一个大小为8N的向左的力的作用。
求物体的加速度。
3. 一个质量为5kg的物体静止在水平地面上,受到一个大小为25N的向右的力和一个大小为20N的向左的力的作用。
求静摩擦力的大小和方向。
4. 一个物体质量为3kg,受到一个大小为15N的向右的力和一个大小为12N的向左的力的作用。
已知物体的加速度为2m/s^2,求物体受到的摩擦力的大小和方向。
答案
1. 物体的净力大小为4N,方向为向右。
2. 物体的加速度为2m/s^2。
3. 静摩擦力的大小为5N,方向为向左。
4. 物体受到的摩擦力的大小为6N,方向为向左。
以上是共点力平衡与动态分析的练题及答案,希望对学生们的研究有所帮助。
人教版(2019)高中物理必修一第三章3.5 共点力的平衡学案

第5节 共点力的平衡学习目标核心素养形成脉络1.理解平衡状态的运动特点,并熟练掌握运动状态与受力之间的关系.2.理解共点力平衡的条件,应用条件解决实际问题.3.掌握动态平衡的特征,熟练解决其问题.4.掌握整体法与隔离法的应用.1.对平衡状态的理解 (1)两种平衡状态:共点力作用下的平衡状态包括静止状态和匀速直线运动状态.(2)“静止”和“v =0”的区别与联系v =0⎩⎪⎨⎪⎧a =0时,是静止,是平衡状态a ≠0时,不是平衡状态 总之,平衡状态是指a =0的状态.2.共点力平衡的条件表达式:F 合=0.基础理解(1)图示是幽默大师卓别林一个常用的艺术造型,他身子侧倾,依靠手杖的支持使身躯平衡.下列说法正确的是( )A .水平地面对手杖没有摩擦力的作用B .水平地面对卓别林没有摩擦力的作用C .水平地面对手杖的弹力方向沿杆向上D .水平地面对卓别林的作用力方向一定不是竖直向上的提示:选D.手杖有向右滑动的趋势,卓别林有向左滑动的趋势,水平地面对手杖和卓别林均有摩擦力的作用,选项A 、B 错误;水平地面对手杖的弹力方向垂直于地面向上,选项C 错误;地面对卓别林的摩擦力方向向右,所以水平地面对卓别林的作用力方向斜向右上方,一定不是竖直向上的,选项D 正确.(2)如图,一小球放置在木板与竖直墙面之间.设墙面对球的弹力大小为F N1,木板对球的弹力大小为F N2.以木板与墙连接点所形成的水平直线为轴,将木板从图示位置开始缓慢地转到水平位置.不计摩擦,在此过程中( )A.F N1始终减小,F N2始终增大B.F N1始终减小,F N2始终减小C.F N1先增大后减小,F N2始终减小D.F N1先增大后减小,F N2先减小后增大提示:选B.法一:解析法如图所示,由平衡条件得F N1=mgtan θF N2=mgsinθ,θ逐渐增大到90°,tan θ、sin θ都增大,F N1、F N2都逐渐减小,所以选项B正确.法二:图解法对球受力分析,球受3个力,分别为重力G、墙对球的弹力F N1和板对球的弹力F N2.当板逐渐放至水平的过程中,球始终处于平衡状态,即F N1与F N2的合力F始终竖直向上,大小等于球的重力G,如图所示,由图可知F N1的方向不变,大小逐渐减小,F N2的方向发生变化,大小也逐渐减小,故选项B正确.对共点力平衡条件的理解问题导引我们处在一个异彩纷呈的世界里,世界上的物体可谓千姿百态.远古的巨石千百年来一直神奇地矗立着(如图).都市里的人,却自有动中取静的办法,到了大商场里,你只要站着不动,自动扶梯就会安稳匀速地送你上楼下楼(如图).从物理学角度来看,如果一个物体保持静止或做匀速直线运动,我们就说这个物体是处于平衡状态.因此,巨石、匀速电梯上站立的人都是处于平衡状态.那么,保持物体平衡需要什么条件呢?要点提示如果物体受两个力作用而平衡,这两个力一定等大反向且作用在一条直线上,即合力为零.如果物体受多个力而平衡,根据力的合成定则,我们可以把任意两个共点力用一个合力来等效代替,据此,三个以上的共点力最终都可以等效简化为两个共点力.可见,三个以上共点力的平衡,最终也都可以简化为二力平衡.根据二力平衡条件,我们就可以得出在共点力作用下物体的平衡条件是合力为零,即F合=0.【核心深化】物体受共点力作用,下列说法正确的是()A.物体的速度等于零,物体就一定处于平衡状态B.物体相对另一物体保持静止时,物体一定处于平衡状态C.物体所受合力为零时,就一定处于平衡状态D.物体做匀加速运动时,物体处于平衡状态[解析]处于平衡状态的物体,从运动形式上看是处于静止或匀速直线运动状态,从受力上来看,物体所受合外力为零.速度为零的物体,受力不一定为零,故不一定处于平衡状态,选项A错;物体相对于另一物体静止时,该物体相对地面不一定静止,如当另一物体做变速运动时,该物体也做变速运动,此物体处于非平衡状态,故选项B错;选项C符合平衡条件,为正确选项;物体做匀加速运动,所受合力不为零,故不是平衡状态,选项D 错.[答案] C(多选)关于共点力,下列说法中正确的有()A.作用在一个物体上的两个力,如果大小相等,方向相反,那么这两个力是共点力B.作用在一个物体上的两个力,如果是一对平衡力,那么这两个力是共点力C.作用在一个物体上的几个力,如果它们的作用点不在同一点上,那么这几个力也可能是共点力D.作用在一个物体上的几个力,如果它们的作用线可以汇交于一点,那么这几个力是共点力解析:选BCD.作用在一个物体上的几个力,如果作用在物体的同一点或者虽不作用在物体的同一点,但力的作用线交汇于一点,那么这几个力是共点力,所以选项C、D正确;大小相等、方向相反的力不一定作用在同一点,但一对平衡力必作用于同一物体的同一直线上,是共点力,所以选项A错误,选项B正确.解决平衡问题常用方法问题导引如图所示,重物的重力为G,轻绳AO与BO的A、B端是固定的,平衡时AO是水平的,BO与竖直方向的夹角为θ,能否用分解法和合成法两种方法求出AO的拉力F T1和BO的拉力F T2的大小?要点提示选取O点为研究对象,其受力如图甲所示,O点受到三个力的作用:重物对O的拉力大小为G,AO绳的拉力F T1,BO绳的拉力F T2.如图乙所示,作出F T1和F T2的合力等于重力大小,在三角形中解出两绳拉力大小.如图丙所示,将重力沿两绳的方向分解,在三角形中解出两绳拉力大小.【核心深化】1.处理静态平衡问题的常用方法方法内容合成法物体受三个共点力的作用而平衡,则任意两个力的合力一定与第三个力大小相等,方向相反分解法物体受三个共点力的作用而平衡,将某一个力按力的效果分解,则其分力和其他两个力满足平衡条件正交分解法物体受到三个或三个以上力的作用而平衡,将物体所受的力分解为相互垂直的两组,每组力都满足平衡条件力的三角形法对受三个力作用而平衡的物体,将力的矢量图平移使三个力组成一个首尾依次相接的矢量三角形,根据正弦定理、余弦定理或相似三角形等数学知识求解未知力在科学研究中,可以用风力仪直接测量风力的大小,其原理如图所示.仪器中一根轻质金属丝悬挂着一个金属球.无风时,金属丝竖直下垂;当受到沿水平方向吹来的风时,金属丝偏离竖直方向一个角度.风力越大,偏角越大.通过传感器,就可以根据偏角的大小指示出风力.那么风力大小F跟金属球的质量m、偏角θ之间有什么样的关系呢?[解析]选取金属球为研究对象,它受到三个力的作用,如图甲所示.金属球处于平衡状态,这三个力的合力为零.可用以下四种方法求解.法一:力的合成法如图乙所示,风力F和拉力F T的合力与重力等大反向,由平行四边形定则可得F=mg tan θ.法二:效果分解法重力有两个作用效果:使金属球抵抗风的吹力和使金属丝拉紧,所以可以将重力沿水平方向和金属丝的方向进行分解,如图丙所示,由几何关系可得F=F′=mg tan θ.法三:正交分解法以金属球为坐标原点,取水平方向为x轴,竖直方向为y轴,建立坐标系,如图丁所示.由水平方向的合力F x合和竖直方向的合力F y合分别等于零,即F x合=F T sin θ-F=0F y合=F T cosθ-mg=0解得F=mg tan θ.法四:三角形法三个力的示意图首尾相连构成一个直角三角形,如图戊所示,由三角函数可求得F=mg tan θ.由所得结果可见,当金属球的质量m一定时,风力F只跟偏角θ有关.因此,偏角θ的大小就可以指示出风力的大小.[答案] F =mg tan θ如图所示,光滑半球形容器固定在水平面上,O 为球心.一质量为m 的小滑块,在水平力F 的作用下静止于P 点,设滑块所受支持力为F N ,OP 与水平方向的夹角为θ.下列关系正确的是( )A .F =mg tan θB .F =mg tan θC .F N =mg tan θD .F N =mg tan θ解析:选A .法一:合成法滑块受力如图甲,由平衡条件知:mg F =tan θ,mg F N =sin θ⇒F =mg tan θ,F N =mg sin θ.法二:效果分解法将重力按产生的效果分解,如图乙所示,F =G 2=mg tan θ,F N =G 1=mg sin θ. 法三:正交分解法将滑块受的力水平、竖直分解,如图丙所示,mg =F N sin θ,F =F N cos θ,联立解得:F =mg tan θ,F N =mg sin θ. 法四:封闭三角形法如图丁所示,滑块受的三个力组成封闭三角形,解直角三角形得:F =mg tan θ,F N =mg sin θ. 动态平衡问题问题导引如图所示,人通过跨过定滑轮的轻绳牵引一物体,人向右缓慢移动时,地面对人的支持力和摩擦力如何变化?要点提示人受重力、绳子的拉力及地面对人的支持力和摩擦力,当人缓慢向右移动时,绳子拉力的大小不变,但在水平方向的分力增大,竖直方向的分力减小,故地面对人的支持力和摩擦力都变大.【核心深化】1.动态平衡:“动态平衡”是指物体所受的力一部分是变力,是动态力,力的大小和方向均要发生变化,但变化过程中的每一个状态均可视为平衡状态,所以叫动态平衡.2.分析动态平衡问题的方法方法步骤解析法(1)列平衡方程求出未知量与已知量的关系表达式(2)根据已知量的变化情况来确定未知量的变化情况图解法(1)根据已知量的变化情况,画出平行四边形边、角的变化(2)确定未知量大小、方向的变化相似三角形法(1)根据已知条件画出两个不同情况对应的力的三角形和空间几何三角形,确定对应边,利用三角形相似知识列出比例式(2)确定未知量大小的变化情况(多选)(2019·湖南衡阳高一月考)如图所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a 、b两点,悬挂衣服的衣架挂钩是光滑的,挂于绳上处于静止状态.如果只人为改变一个条件,当衣架静止时,下列说法正确的是()A.绳的右端上移到b′,绳子拉力不变B.将杆N向右移一些,绳子拉力变大C.绳的两端高度差越小,绳子拉力越小D.若换挂质量更大的衣服,则衣架悬挂点右移[解析]如图所示,两个绳子是对称的,与竖直方向夹角是相等的.假设绳子的长度为x,两竖直杆间的距离为L,则x cos θ=L,绳子一端在上下移动的时候,绳子的长度不变,两杆之间的距离不变,则θ角度不变;两个绳子的合力向上,大小等于衣服的重力,由于夹角不变,所以绳子的拉力不变,A正确,C错误;当杆向右移动后,根据x cos θ=L,即L变大,绳长不变,所以θ角度减小,绳子与竖直方向的夹角变大,绳子的拉力变大,B正确;绳长和两杆距离不变的情况下,θ不变,所以挂的衣服质量变化,不会影响悬挂点的移动,D错误.[答案]AB关键能力2图解法如图所示,小球用细绳系住,绳的另一端固定于O点.现用水平力F缓慢推动斜面体,小球在斜面上无摩擦地滑动,细绳始终处于直线状态,当小球升到接近斜面顶端时细绳接近水平,此过程中斜面对小球的支持力F N以及绳对小球的拉力F T的变化情况是()A.F N保持不变,F T不断增大B.F N不断增大,F T不断减小C.F N保持不变,F T先增大后减小D.F N不断增大,F T先减小后增大[思路点拨] 要注意采用动态分析法.在小球所受的重力、斜面的支持力、细绳的拉力三个力中,重力大小方向都不变,斜面的支持力方向不变,而绳的拉力大小方向都变化.[解析]如图所示,先对小球进行受力分析,重力mg、支持力F N、拉力F T组成一个闭合的矢量三角形,由于重力不变、支持力F N方向不变,斜面向左移动的过程中,拉力F T 与水平方向的夹角β减小,当F T⊥F N时,细绳的拉力F T最小,由图可知,随β的减小,斜面的支持力F N不断增大,F T先减小后增大,故选项D正确,A、B、C错误.[答案] D关键能力3相似三角形法光滑半球面上的小球被一通过定滑轮的力F由底端缓慢拉到顶端的过程中,试分析绳的拉力F及半球面对小球的支持力F N的变化情况(如图所示).[解析]如图所示,作出小球的受力示意图,注意弹力F N总与球面垂直,从图中可得到相似三角形.设球体半径为R,定滑轮到球面最高点的距离为h,定滑轮与小球间绳长为L,根据三角形相似得F L=mgh+R,F N R=mg h+R由以上两式得绳中的张力F=mg Lh+R球面的弹力F N=mg Rh+R由于在拉动过程中h、R不变,L变小,故F减小,F N不变.[答案]F减小F N不变动态平衡问题的常见解题思路:适用于三力平衡问题(1)若已知一个力不变,另一个力F1方向不变大小变,则用三角形法(或图解法)处理问题,另一个力F2有最小值的条件为F1⊥F2.(2)若已知一个力不变,另一个力大小不变方向变,则用画图法处理问题.(3)若已知一个力不变,另一个力大小、方向都变,则采用相似三角形法处理问题.解决问题时,要寻找一个力的三角形和一个边的三角形,根据对应边比例相等求解.【达标练习】1.如图所示,两根等长的绳子AB和BC在结点B吊一重物静止,两根绳子与水平方向夹角均为60°.现保持绳子AB与水平方向的夹角不变,将绳子BC逐渐缓慢地变化到沿水平方向,在这一过程中,绳子BC拉力的变化情况是()A.增大B.先减小后增大C.减小D.先增大后减小解析:选B.以结点B为研究对象,分析受力情况,根据三力平衡条件知,绳AB的拉力T AB与绳子BC的拉力T BC的合力与重力大小相等、方向相反.作出绳子BC逐渐缓慢地变化到沿水平方向过程中多个位置力的合成图,由几何知识得,绳子BC拉力先减小后增大.2.如图所示是一个简易起吊设施的示意图,AC是质量不计的撑杆,A端与竖直墙用铰链连接,一滑轮固定在A点正上方,C端吊一重物.现施加一拉力F缓慢将重物P向上拉,在AC杆达到竖直前()A .BC 绳中的拉力F T 越来越大B .BC 绳中的拉力F T 越来越小C .AC 杆中的支撑力F N 越来越大D .AC 杆中的支撑力F N 越来越小解析:选B.作出C 点的受力示意图,如图所示,由图可知力的矢量三角形与几何三角形ABC 相似.根据相似三角形的性质得F T BC =F N AC=G AB ,解得BC 绳中的拉力为F T =G BC AB ,AC 杆中的支撑力为F N =G AC AB.由于重物P 向上运动时,AB 、AC 不变,BC 变小,故F T 减小,F N 不变.选项B 正确.1.(2019·集宁校级月考)如图所示,人站在自动扶梯的水平踏板上,随扶梯斜向上匀速运动,不计空气阻力,以下说法正确的是( )A .人受到重力和支持力的作用B .人受到重力、支持力和摩擦力的作用C .人的重力和人对踏板的压力是一对平衡力D .人对踏板的压力就是人的重力解析:选A.人站在自动扶梯上,人受到竖直向下的重力作用和竖直向上的支持力作用,人相对于扶梯是静止的,没有运动也没有运动趋势,人不受摩擦力作用,故A 正确,B 错误;重力和支持力是一对平衡力,人的重力和人对踏板的压力不是平衡力,C 错误;人对踏板的压力属于弹力,人的重力是万有引力,二者是不同性质的力,故D 错误.2.(多选)(2019·湖北八校联考)如图所示,A 、B 两球质量均为m ,固定在轻弹簧的两端,分别用细绳悬于O 点,其中球A 处在光滑竖直墙面和光滑水平墙面的交界处,已知两球均处于平衡状态,OAB 恰好构成一个正三角形,则下列说法正确的是(重力加速度为g )( )A .球A 可能受到四个力的作用B .弹簧对球A 的弹力大于对球B 的弹力C .绳OB 对球B 的拉力大小一定等于mgD .绳OA 对球A 的拉力大小等于或小于1.5mg解析:选ACD.对球B 受力分析,据共点力平衡可知弹簧和绳对球B 的作用力大小均为mg ,选项C 正确;对同一弹簧而言,产生的弹力处处相等,故弹簧对球A 的弹力等于对球B 的弹力,选项B 错误;对球A 分析可知,一定受重力、弹簧的弹力、墙面的支持力作用,可能受地面的支持力和绳的拉力,地面的支持力和绳的拉力也可能有一个为0,当地面对球A 的支持力为0时,绳上的拉力最大,等于重力和弹簧竖直方向的分力之和,即1.5mg ,故选项A 、D 正确.3.如图所示,一条不可伸长的轻质细绳一端跨过光滑钉子b 悬挂一质量为m 1的重物,悬挂点为d ,另一端与另一轻质细绳相连于c 点,ac =l 2,c 点悬挂质量为m 2的重物,平衡时ac 正好水平,此时d 点正好与ac 在同一水平线上,且到b 点的距离为l ,到a 点的距离为54l ,则两重物的质量的比值m 1m 2为( ) A.52B .2 C.54D.35 解析:选C.法一:合成法因c 点处于平衡状态,所以任意两个力的合力均与第三个力大小相等,方向相反,如图甲所示,根据平行四边形定则将力F 与m 1g 合成,则sin θ=m 2g m 1g,而sin θ=l l 2+⎝⎛⎭⎫3l 42=45,所以m 1m 2=54,选项C 正确.法二:分解法因c 点处于平衡状态,所以可在F 、m 1g 方向上分解m 2g ,如图乙所示,则同样有sin θ=m 2g m 1g ,所以m 1m 2=54,选项C 正确. 法三:正交分解法将倾斜绳拉力m 1g 沿竖直方向和水平方向分解,如图丙所示,则m 1g ·sin θ=m 2g ,同样可得m 1m 2=54,选项C 正确. 4.如图所示,质量为m 的球放在倾角为α的光滑斜面上,在斜面上有一光滑且不计厚度的木板挡住球,使之处于静止状态.今使挡板与斜面的夹角β缓慢增大,在此过程中,斜面对球的支持力N 1和挡板对球的压力N 2的变化情况为( )A .N 1、N 2都是先减小后增大B .N 1一直减小,N 2先增大后减小C .N 1先减小后增大,N 2一直减小D .N 1一直减小,N 2先减小后增大解析:选D.法一 图解法:对球受力分析,如图甲所示.球始终处于平衡状态,故三个力的合力始终为零,三力构成矢量三角形.挡板逆时针转动时,N 2方向也逆时针转动,作出图甲所示的动态矢量三角形.由图甲可见,N 1随β的增大一直减小,N 2先减小后增大.法二 正弦定理法:对球受力分析,如图乙所示.球受重力mg 、斜面支持力N 1、挡板压力N 2.由正弦定理得mg sin β=N 1sin (180°-α-β)=N 2sin α解得N 1=sin (α+β)sin βmg =sin αtan β+cos α,N 2=sin αsin βmg 故随着β的增大,N 1一直减小,N 2先减小后增大,β=90°时,N 2达到最小值,为mg sin α.一、单项选择题1.(2019·绥化联考)L 形木板P (上表面光滑)放在固定斜面上,轻质弹簧一端固定在木板上,另一端与置于木板上表面的滑块Q 相连,如图所示.若P 、Q 一起沿斜面匀速下滑,不计空气阻力.则木板P的受力个数为( )A .3B .4C .5D .6解析:选C.P 、Q 一起沿斜面匀速下滑时,木板P 的上表面光滑,整体分析,受力平衡,受重力、斜面支持力、斜面的摩擦力;隔离滑块Q 分析受力,受到三个力:重力、P 对Q 的支持力、弹簧对Q 沿斜面向上的弹力;再隔离木板P 分析受力:P 的重力、Q 对P 的压力、弹簧对P 沿斜面向下的弹力、斜面对P 的支持力、斜面对P 的摩擦力,故选项C 正确.2.(2019·四川彭州中学月考)如图所示,a 、b 两个质量相同的球用线连接,a 球用线挂在天花板上,b 球放在光滑斜面上,系统保持静止,以下图示哪个是正确的( )解析:选B.对b球受力分析,受重力、垂直斜面向上的支持力和细线的拉力,由于三力平衡时三个力中任意两个力的合力与第三个力等值、反向、共线,故细线拉力向右上方,故A图错误;再对a、b两个球整体受力分析,受总重力、垂直斜面向上的支持力和上面细线的拉力,再次根据共点力平衡条件判断,上面的细线的拉力方向斜向右上方,故C、D图均错误.3.倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上.下列结论正确的是()A.木块受到的摩擦力大小是mg cos αB.木块对斜面体的压力大小是mg sin αC.桌面对斜面体的摩擦力大小是mg sin αcos αD.桌面对斜面体的支持力大小是(M+m)g解析:选D.以木块为研究对象,如图甲所示,有F f=mg sin α,F N=mg cos α,故选项A、B均错误;以木块与斜面体所组成的整体为研究对象,如图乙所示,有F f桌=0,F N桌=(M+m)g,故选项C错误,D正确.4.(2019·哈三中期中)如图所示,两段等长细线分别连接着两个质量相等的小球a、b,悬挂于O点.现在两个小球上分别加上水平方向的外力,其中作用在b球上的力大小为F、作用在a球上的力大小为2F,则此装置平衡时的位置可能是下列哪幅图()解析:选B.设每个球的质量为m,Oa与ab和竖直方向的夹角分别为α、β.以两个小球组成的整体为研究对象,分析受力情况,如图1,根据平衡条件可知,Oa 绳的方向不可能沿竖直方向,否则整体的合力不为零,不能保持平衡.由平衡条件得:tan α=F2mg,以b球为研究对象,分析受力情况,如图2,由平衡条件得:tan β=Fmg,则α<β,故B正确.5.如图所示,用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂,小球处于静止状态,弹簧A与竖直方向的夹角为30°,弹簧C水平,则弹簧A、C的伸长量之比为()A.3∶4B.4∶ 3C.1∶2 D.2∶1解析:选D.将两小球及弹簧B视为整体进行受力分析有F C=F A sin 30°F C=kx CF A=kx AF A F C=1sin 30°=2∶1x Ax C=2∶1故D正确,A、B、C错误.6.如图所示,内壁及碗口光滑的半球形碗固定在水平面上,碗口保持水平.A 球、C 球与B 球分别用两根轻质细线连接,当系统保持静止时,B 球对碗壁刚好无压力,图中θ=30°,则A 球、C 球的质量之比为( )A .1∶2B .2∶1C .1∶ 3 D.3∶1 解析:选C.设A 球、C 球的质量分别m A 、m C .由几何知识可知,两细线相互垂直.由A 、C 两球平衡得T 1=m A g ,T 2=m C g .以B 球为研究对象,分析受力情况:受重力G 、两细线的拉力T 1、T 2.由平衡条件得T 1=T 2tan θ 得T 1T 2=tan θ=13,则得m A m C =T 1T 2=13 . 7.(2019·长沙模拟)如图所示,质量不等的盒子A 和物体B 用细绳相连,跨过光滑的定滑轮,A 置于倾角为θ的斜面上,与斜面间的动摩擦因数μ=tan θ,B 悬于斜面之外而处于静止状态.现向A 中缓慢加入砂子,下列说法正确的是( )A .绳子拉力逐渐减小B .A 对斜面的压力逐渐增大C .A 所受的摩擦力一定逐渐增大D .A 可能沿斜面下滑解析:选B .当m A g sin θ>m B g 时,对A 受力分析,由平衡条件有:m A g sin θ=F f +m B g ,随m A 的增大,摩擦力不断增大;当m A g sin θ<m B g 时,由平衡条件有:m A g sin θ+F f =m B g ,随m A 的增大,摩擦力不断减小,C 项错;在垂直斜面方向上,始终有:F N =m A g cos θ,因此随着不断加入砂子,A 对斜面的压力不断增大,B 项对;由μ=tan θ,可知最大静摩擦力F fmax =μm A g cos θ=m A g sin θ,故增加的重力的分力与增加的摩擦力大小相等,方向相反,故A 不会滑动,保持静止,D 项错;绳子所受拉力等于B 的重力,故拉力保持不变,A 项错.8.(2019·河北高三模拟)如图,一不可伸长的光滑轻绳,其左端固定于O 点,右端跨过位于O ′点的固定光滑轴悬挂一质量为M 的物体;OO ′段水平,长度为L ;绳子上套一可沿绳滑动的轻环.现在轻环上悬挂一钩码,平衡后,物体上升L ,则钩码的质量为( )A.22MB.32M C.2M D.3M解析:选D.重新平衡后,绳子形状如图,由几何关系知:绳子与竖直方向夹角为30°,则环两边绳子的夹角为60°,根据平行四边形定则,环两边绳子拉力的合力为 3 Mg,根据平衡条件,则钩码的质量为3M,故选项D正确.二、多项选择题9.如图所示,一木板B放在水平面上,木块A放在木板B的上面,A的右端通过一不可伸长的轻绳固定在直立墙壁上.用力F向左拉动木板B,使它以速度v做匀速直线运动,这时轻绳的张力为F T.下列说法中正确的是() A.木板B受到的滑动摩擦力大小等于FB.水平面受到的滑动摩擦力大小等于F TC.木块A受到的滑动摩擦力大小等于F TD.若木板B以2v的速度匀速运动,则拉力等于2F解析:选AC.由于木板B匀速向左运动,所以木板B受到木块A及地面的滑动摩擦力的合力大小等于F;水平面受到的滑动摩擦力大小等于F-F T,对木块A受力分析知,木块A受到的滑动摩擦力大小等于F T;若木板B以2v的速度匀速运动,则拉力仍等于F,故选项A、C正确.10.有一堆砂子在水平面上堆成圆锥形,稳定时底角为α,如图所示.如果视每粒砂子完全相同,砂子与砂子之间,砂子与地面之间的动摩擦因数均为μ,砂子之间的最大静摩擦力可近似认为与滑动摩擦力相等,以下说法正确的是()A.砂子稳定时,砂堆底面受到地面的摩擦力一定为零B.砂子稳定时,只有形成严格规则的圆锥底面受到地面的摩擦力才为零C.砂子稳定形成的圆锥底角最大时,tan α=μD.砂子稳定形成的圆锥底角最大时,sin α=μ解析:选AC.把所有砂子看成一个整体,对整体受力分析,由水平方向合力为零可得,砂子稳定时,砂堆底面受到地面的摩擦力一定为零,与形状无关,故A正确,B错误;取斜面上的一粒质量为m的砂子为研究对象,若砂子恰好平衡,则倾角α最大,砂子受力平衡,根据平衡条件得:mg sin α=μmg cos α,得tan α=μ,故C正确,D错误.11.一根长为L的易断的均匀细绳,两端固定在天花板上的A、B两点.若在细绳的C处悬一重物,已知AC>CB,如图所示,则下列说法中正确的是()A.增加重物的重力,BC段先断B.增加重物的重力,AC段先断C.将A端往左移时绳子容易断D.将A端往右移时绳子容易断。
生物一轮复习第一编考点通关考点26人体的内环境与稳态练习含解析

考点26 人体的内环境与稳态一、基础小题1.如图表示淋巴和另外三种液体之间相互关系的示意图,下列相关判断错误的是()A.丙与乙之间的关系不存在B.如果甲与乙之间的水分交换失去平衡,可能会引起组织水肿C.淋巴不仅可以调节甲与乙之间的水分平衡,而且能将甲中少量的蛋白质运回乙D.四种液体之间不断发生物质交换,为细胞提供了必需的物质并排出了代谢废物答案A解析观察题图,根据所学知识:淋巴中的物质只能来自组织液,而淋巴通过淋巴循环汇入到血液循环中,故可以确定甲、乙和丙分别表示组织液、血浆和细胞内液。
甲与乙之间的水分交换是维持细胞生活环境保持正常渗透压的重要条件,如果这个平衡被破坏,则会引起组织水肿等病变,B正确;淋巴循环有三个作用:免疫、调节血浆和组织液之间水分交换、将组织液中的少量蛋白质运回血浆,C正确;细胞所必需的物质及代谢废物只有通过体液各个成分之间的相互交换才能正常地获得和排出,D正确;血浆中也存在多种细胞,细胞内液与血浆之间可以进行双向物质交换,A错误。
2.关于内环境稳态,以下说法正确的是()A.下丘脑渗透压感受器能感受细胞外液渗透压下降、产生渴觉B.血液中CO2增多引起呼吸频率加快,是由体液和神经共同调节的C.正常情况下生成与回流的组织液中氧气含量相等D.毛细血管处血浆和组织液之间相互转化的量总是平衡的答案B解析下丘脑不能产生渴觉,各种感觉都是在大脑皮层产生的,A错误;血液中CO2增多刺激呼吸中枢兴奋,属于体液调节,而呼吸中枢兴奋引起呼吸肌收缩加快,则呼吸频率加快,是神经调节的结果,B正确;一般情况下,富含氧气的血浆从毛细血管动脉端渗出生成组织液,生活在组织液中的组织细胞通过有氧呼吸消耗部分氧气,导致毛细血管静脉端回流的组织液氧气含量相对较低,C错误;血浆和组织液能够直接相互转化,同时组织液通过转化为淋巴,间接转化为血浆,从而维持血浆的量相对稳定,所以血浆和组织液之间相互转化的量并不总是平衡的,D 错误。
共点力平衡之动态平衡问题

共点力平衡之动态平衡问题公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]共点力平衡之动态平衡问题(一)共点力的平衡1.平衡状态:在共点力的作用下,物体处于静止或匀速直线运动的状态.2.共点力作用下物体的平衡条件:合力为零,即=F0.合(二)物体的动态平衡问题物体在几个力的共同作用下处于平衡状态,如果其中的某个力(或某几个力)的大小或方向,发生变化时,物体受到的其它力也会随之发生变化,如果在变化的过程中物体仍能保持平衡状态,我们称之为动态平衡。
解决这类问题的一般思路是:把“动”化为“静”,“静”中求“动”。
分析方法:(1)三角形图解法如果物体在三个力作用下处于平衡状态,其中只有一个力的大小和方向发生变化,而另外两个力中,一个大小、方向均不变化;一个只有大小变化,方向不发生变化的情况。
例1.半圆形支架BAD上悬着两细绳OA和OB,结于圆心O,下悬重为G的物体,使OA绳固定不动,将OB绳的B端沿半圆支架从水平位置缓慢移到竖直位置C的过程中(如图),分析OA绳和OB绳所受力的大小如何变化。
练习1.如图所示,质量为m 的小球被轻绳系着,光滑斜面倾角为θ,向左缓慢推动劈,在这个过程中( ) A .绳上张力先增大后减小 B .斜劈对小球支持力减小C .绳上张力先减小后增大D .斜劈对小球支持力增大 (2)相似三角形法例2.一轻杆BO ,其O 端用光滑铰链固定在竖直轻杆AO 上,B 端挂一重物,且系一细绳,细绳跨过杆顶A 处的光滑小滑轮,用力F 拉住,如图2-1所示。
现将细绳缓慢往左拉,使杆BO 与杆AO 间的夹角θ逐渐减少,则在此过程中,拉力F 及杆BO 所受压力FN 的大小变化情况是( )A .FN 先减小,后增大 始终不变 C .F 先减小,后增大 始终不变练习2.光滑的半球形物体固定在水平地面上,球心正上方有一光滑的小滑轮,轻绳的一端系一小球,靠放在半球上的A 点,另一端绕过定滑轮后用力拉住,使小球静止,如图所示。
动态平衡问题的几种解法

动态平衡问题的几种解法在有关物体平衡的问题中,有一类涉及动态平衡。
这类问题中的一部分力是变力,是动态力,力的大小和方向均要发生变化,故这是力平衡问题中的一类难题。
解决这类问题的一般思路是:把“动”化为“静”,“静”中求“动”。
下面就介绍几种动态平衡问题的解题方法。
方法一:图解法(三角形法则)原理:当物体受三力作用而处于平衡状态时,其合力为零,三个力的矢量依次恰好首尾相连,构成闭合三角形,当物体所受三个力中二个发生变化而又维持平衡关系时,这个闭合三角形总是存在,只不过形状发生改变而已,比较这些不同形状的矢量三角形,各力的大小及变化就一目了然了。
例题1:如图1所示,一个重力G的匀质球放在光滑斜面上,斜面倾角为,在斜面上有一光滑的不计厚度的木板挡住球,使之处于静止状态。
今使板与斜面的夹角缓慢增大,问:在此过程中,挡板和斜面对球的压力大小如何变化?解析:取球为研究对象,球受重力G、斜面支持力F1、挡板支持力F2。
因为球始终处于平衡状态,故三个力的合力始终为零,三个力构成封闭的三角形。
挡板逆时针转动时,F2的方向也逆时针转动,F1的方向不变,作出如图2所示的动态矢量三角形。
由图可知,F2先减小后增大,F1随增大而始终减小。
点评:三角形法则适用于物体所受的三个力中,有一力的大小、方向均不变(通常为重力,也可以是其它力),另一个力的大小变化,第三个力则大小、方向均发生变化的问题,对变化过程进行定性的分析。
方法二:解析法原理:物体处于动态平衡状态时,对研究对象的任一状态进行受力分析,根据具体情况引入参量,建立平衡方程,求出应变参量与自变参量的一般函数关系,然后根据自变量的变化确定应变量的变化。
例题2:如图3所示,小船用绳索拉向岸边,设船在水中运动时所受水的阻力不变,那么小船在匀速靠岸过程中,下面说法哪些是正确的()A. 绳子的拉力F不断增大B. 绳子的拉力F不变C. 船所受的浮力不断减小D. 船所受的浮力不断增大解析:小船共受四个力作用:重力G、浮力F浮、水的阻力f、绳子拉力F。
幼儿园小班动态平衡教育教案

幼儿园小班动态平衡教育教案课题名称:小班动态平衡教育教学目标:1. 技能目标:掌握动态平衡动作,并能够在不稳定基础上保持平衡;2. 知识目标:了解动态平衡的概念,认识到动态平衡在日常生活中的重要性;3. 情感目标:培养幼儿勇于尝试、勇于挑战、勇于进取、勇于探索的精神。
教学内容:小班动态平衡教学。
教学方法:情境教学、游戏教学、实践操作。
教学用具:椅子、球、平衡板、其他小工具等。
教学过程:Step1. 热身教师引入“平衡”概念,让幼儿谈一谈平衡是什么,有哪些场合需要平衡。
为了提高幼儿兴趣,可以展示一些常见的平衡场合的图片或视频。
Step2. 谈论平衡幼儿围坐在一起,教师以问题的方式引导幼儿讨论日常生活中的平衡场合,如:踩高跷、骑自行车、跳绳等。
然后引入动态平衡的概念,引导幼儿讨论动态平衡场合,如:平衡车、滑板车、滑雪等。
Step3. 模仿动态平衡动作教师在场地中准备好各种材料,让幼儿模仿一些动态平衡动作,如:骑平衡车、跳跃着踩过去平衡球、在平衡板上保持平衡等。
教师要在一旁帮助幼儿练习,让他们掌握动态平衡技巧,并获得成功体验。
Step4. 小游戏教师带领幼儿进行小游戏,让他们在玩中感受到动态平衡的重要性。
例如,让幼儿手拿篮球,用脚尖踩在平衡板上,尽可能长时间保持平衡;或者让幼儿围绕一圈做小动作,最后在狭小的空间上跳掉落推球等。
这些游戏不仅提高了幼儿动态平衡技巧,还锻炼了幼儿的身体协调性、反应力和手脚配合能力。
Step5. 小结教师在课程结束前,与幼儿一起回顾学习内容,让幼儿把动态平衡的知识重新整合,深化印象。
同时也可以让他们自由发挥,讲述自己的学习收获和对动态平衡的认识。
Step6. 家庭作业教师可以让家长和孩子一起在家做一些有关平衡的活动,例如:走沙发、踩空中地板、踩步阶梯等。
通过家庭作业,巩固幼儿在课堂上所学的动态平衡技巧,让他们认识到动态平衡在生活中的重要性。
教学评价:1. 教学效果评价:通过小组活动、个人展示等方式评估幼儿动态平衡能力的提高情况;2. 教学过程评价:对教学过程中教师的表现、幼儿的主动性、活跃性、参与度等情况进行评价;3. 教学材料评价:评估所选教具是否合适,并通过幼儿意见等方式进行收集。
常考的“动态平衡”模型之晾衣杆模型

常考的“动态平衡”模型之晾衣杆模型典例(2020·河南省实验中学高一期中)如图所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b 两点,悬挂衣服的衣架钩是光滑的,挂于绳上处于静止状态.如果只人为改变一个条件,当衣架静止时,下列说法正确的是()A.绳的右端上移到b ,绳子拉力不变B.绳的两端高度差越小,绳子拉力越小C.将杆N向左移一些,绳子拉力变小D.若换挂质量更大的衣服,则衣服架悬挂点右移【答案】AC【详解】1、目前,我市每个社区均已配备了公共体育健身器材。
图5所示器材为一秋千,用两根等长轻绳将一座椅悬挂在竖直支架上等高的两点。
由于长期使用,导致两根支架向内发生了稍小倾斜。
如图中虚线所示,但两悬挂点仍等高,座椅静止时用F表示所受合力的大小,F1表示单根轻绳对座椅拉力的大小,与倾斜前相比()A.F不变,F1变小B.F不变,F1变大C.F变小,F1变小D.F变大,F1变大解析:选A木板静止时,受重力和两个拉力而平衡,故三个力的合力为零,即:F=0;根据共点力平衡条件,有:2F 1cos θ=mg解得:F 1=mg2cos θ由于长期使用,导致两根支架向内发生了稍小倾斜,故图中的θ角减小了,故F 不变,F 1减小;故选A 。
结论:相当于杆宽d 减小,sin θ=L d θ减小 ,T=θcos 2mg所以细线拉力减小2、(2021·全国高三专题练习)如图所示,水平直杆AB 的中点O 为转轴,一轻绳跨过轻质滑轮,两端分别固定在A 、B 两点,滑轮通过另一根轻绳连接一重物,不计滑轮与轻绳之间的摩擦。
现让直杆AB 绕O 逆时针缓慢转过角度θ(θ<90°),轻绳的张力( )A .逐渐减小B .逐渐增大C .先增大后减小D .先减小后增大【答案】A 【详解】由题意可知,让直杆AB 绕O 逆时针缓慢转过角θ(θ<90°)的过程中可认为重物处于平衡状态,滑轮左、右两侧轻绳绳长记为l 1、l 2,与竖直方向的夹角记为α1、α2,轻绳张力大小记为F T ,受力分析如图所示:水平方向上有 F T sin α1=F T sin α2 竖直方向上有F T cos α1+F T cos α2=mg 由几何关系知l 1sin α1+l 2sin α2=AB cos θ解得 α1=α2 F T =12cos mg α sin α1=12cos AB l l θ+ 由该过程中角度θ逐渐增大可知,α1逐渐减小,故轻绳的张力逐渐减小,选项A 正确,BCD 错误。
动平衡实训总结

动平衡实训总结动平衡实训总结一、实训背景二、实训目的三、实训内容1.理论学习2.设备操作3.实际练习四、实训收获1.技能提升2.团队合作能力增强3.解决问题的能力提高五、不足之处及改进方案一、实训背景动平衡是机械制造和维修中非常重要的一个环节,涉及到机械的运转平稳性和寿命。
为了提高学生的动平衡技能,加强理论和实践的结合,学校安排了动平衡实训课程。
二、实训目的本次动平衡实训旨在通过理论学习、设备操作和实际练习等环节,加深学生对动平衡原理和方法的理解,提高其在机械制造和维修中的应用水平。
三、实训内容1. 理论学习在开始设备操作前,老师先为我们介绍了动平衡相关知识,包括静态平衡和动态平衡的区别、不同类型转子的不同要求等等。
这些知识为后续的设备操作和实际练习打下了坚实的理论基础。
2. 设备操作在理论学习后,我们开始进行设备操作。
老师为我们介绍了动平衡仪的结构和使用方法,并演示了如何进行动平衡测试。
接着,我们分组进行了设备操作,每个小组都有机会亲自操作动平衡仪,对转子进行测试和调整。
3. 实际练习最后,我们进行了实际的练习。
老师提供了一些不同类型的转子,让我们根据之前学到的知识进行动平衡测试和调整。
通过实际练习,我们更加深入地理解了动平衡原理和方法,并掌握了相关技能。
四、实训收获1. 技能提升通过本次实训,我们掌握了动平衡相关知识和技能,在机械制造和维修中具备更强的应用能力。
2. 团队合作能力增强在设备操作和实际练习中,每个小组都需要充分合作才能完成任务。
这锻炼了我们的团队合作意识和能力。
3. 解决问题的能力提高在实践过程中,我们遇到了一些问题,如转子测试不准确、调整不到位等。
通过分析问题原因和采取相应措施,我们成功解决了这些问题,提高了自己的解决问题能力。
五、不足之处及改进方案本次实训虽然收获颇丰,但也存在一些不足之处。
比如,在设备操作和实际练习中,时间安排有些紧张,导致一些同学没有充分掌握相关技能。
为了改进这一情况,可以考虑增加实训时间或者减少理论学习时间。
3-6岁幼儿平衡能力影响因素分析

3-6岁幼儿平衡能力影响因素分析摘要:平衡能力对于一个人来说有着重要的作用,在幼儿时期身体快速发育的阶段中,同时这也是平衡能力发展的最为关键的阶段,如今我国在全面倡导提升幼儿的身体素质,且在“3-6岁幼儿发展指南”中,也将平衡能力作为幼儿重点提升的身体素质之一。
从意识上,幼儿家长需要开始全面重视对幼儿平衡能力的发展,从行动上,家长乃至幼儿园更需要重视对幼儿的平衡训练,以此才能为幼儿平衡能力的发展奠定良好的基础。
本文从幼儿的外在环境以及内在因素等各个方面进行了分析,探讨会影响3-6岁幼儿平衡能力发展的因素,然后进一步阐述了3-6岁幼儿平衡能力发展的必要性,最后就影响因素进行了进一步的研究探讨。
关键词:3-6岁幼儿;平衡能力;影响因素平衡能力是表现身体素质的一种,是在不同范围的支撑面上可以进行有效控制身体重心的一项能力,在临床当中,具有强大平衡能力的人,无论是处在哪种状态下,或是运动过程中或是外力作用下,都能够自然而然的维持并调整好自身的姿势[1]。
人体平衡能力主要分为以下两点,其一是当人体身体位置在改变的过程中具备的控制和调整姿势和重心的动态平衡能力,其二是当人体姿势和重心在相对静止的状态下保持的静态平衡能力,而对于幼儿来说,在幼儿的生长发育正常规律下,平衡能力也是相对重要的,有研究表明,在幼儿的3-4岁时期,是幼儿平衡能力发展的敏感阶段,无论是男孩还是女孩,在这个时期的平衡能力都处于快速增长的阶段,对幼儿平衡能力发展进行细致的划分,可以得出在3-4岁幼儿平衡能力发展的增幅最快,4-5岁是其次,5-6岁是最末,所以说在幼儿阶段,幼儿的各项身体素质都在快速的发展,因此更需要重点关注其平衡能力的发展,要知道平衡能力的发展并不是一蹴而就的,而是一个系统性、长期性的过程[2]。
1 3-6岁幼儿平衡能力影响因素分析本文以我市3-6岁幼儿为研究对象,旨在分析影响3-6岁幼儿平衡能力发展的相关因素,并为提高3-6岁幼儿平衡能力提供有效的参考。
基础体能的训练方法有哪些

基础体能的训练方法有哪些体能训练在人体成长的过程中扮演着很重要的一个角色,不但是在军队训练中,即便是在普通的工作生活中也需要有一个健康的体魄才可以更好的生活工作,练就健康的体魄需要掌握相应的方式方法,那么基础体能训练的方法有哪些,接下来小编为大家介绍主要训练基础体能的方法,一起来看看吧!基础体能训练主要表现在下面的几点上:一、耐力训练1、长跑:要求为400米跑道,女子每次15圈,男子每次20圈,平均速度为每圈不得低于2分20秒。
2、负重越野:自己背负不低于30公斤的背囊(女子为20公斤),在不低于海拔2000米的小路、山脊行走,时间为一整天或两天,每周或两周一次。
3、如果时间和其他条件不允许,也可用游泳、自行车等代替长跑,运动量相当。
二、力量训练1、大腿力量训练:大腿与地面平行,做“鸭步”状行走,30米一组,5组一次,中间不休息。
2、小腿力量训练:踮脚跳,大腿不用力,30米一组,5组一次,中间不休息。
3、上肢力量训练:俯卧撑8个一组,做5组;引体向上6个一组,做5组。
4、腰腹力量训练:仰卧起坐带转体,15或20次一组,做3组。
三、平衡训练1、单脚平衡:单脚站立完成前仰后俯动作多次。
2、动态平衡:选择一离地窄坎,像走平衡木样行走;或单脚跳格子。
四、柔韧训练1、单杠悬垂,拉伸肢体。
2、压腿,下腰。
3、拉伸身体两侧肌肉。
力量、平衡和柔韧训练每周不少于3次,并接在长跑之后完成。
在俱乐部组织的每次行动之前,长跑每周不得少于4次。
在行动前10天减少运动量,以免行动中肌肉疲劳。
膀胱功能的训练方法是什么身体健康是至关重要的,膀胱问题在现在不少见,因为各种各样原因,不少朋友的身体健康亮出红灯,要怎样才可以让膀胱恢复健康,要怎样才可以更好的生活,接下来小编为大家介绍膀胱功能的训练方法,一起来看看吧!膀胱是一个储尿器官。
在哺乳类,它是由平滑肌组成的一个囊形结构,位于骨盆内,其后端开口与尿道相通。
膀胱与尿道的交界处有括约肌,可以控制尿液的排出。
高中化学第二册化学平衡 例题解析

煌敦市安放阳光实验学校化学平衡例题解析(一)典型例题【例1】在密闭容器中进行如下反:X2(g)+Y2(g) 2Z(g),已知X2、Y2、Z 的起始浓度分别为0.1mol/L、0.3mol/L、0.2mol/L,在一条件下当反达到平衡时,各物质的浓度有可能是A.Z为0.3mol/LB.Y2为0.35mol/LC.X2为0.2mol/LD.Z为0.4mol/L【分析】理解“可逆反”的义:在同一条件下,反既能向生成物方向移动,又能向反物方向移动。
任何可逆反,反物都不可能百分之百地转化为生成物。
若反向右进行,则X2、Y2、Z三种物质的浓度范围依次是:0~0.1mol/L、0.2mol/L~0.3mol/L、0.2mol/L~0.4mol/L;若反向左进行,则X2、Y2、Z三种物质的浓度范围依次是:0.1~0.2mol/L、0.3mol/L~0.4mol/L、0mol/L~0.2mol/L。
【答案】A、B。
【例2】在一温度下,反A2(g)+B2(g) 2AB(g)达到平衡的标志是A.单位时间内生成n mol A2,同时生成n mol ABB.容器内总压强不随时间改变C.单位时间内生成2n mol AB同时生成n mol B2D.任何时间内A2、B2的物质的量之比为值【知识】一条件下可逆反中正反与逆反的速率相,反混和物中各组分的浓度保持不变的状态叫化学平衡状态。
化学反达到平衡后,反混和物的百分组成一可引伸为物质的物质的量浓度、质量分数、体积(物质的量)分数一、反物的转化率(利用率)一。
化学平衡的特征:⑴化学平衡是一种动态平衡,即v正=v逆≠0。
(动)⑵外界条件(如浓度、温度和压强)不改变时,化学平衡状态不变。
()说明:化学平衡状态与反从正反开始还是从逆反无关。
⑶当外界条件发生改变时,化学平衡发生移动,直至达到的化学平衡。
(变)【分析】因为左边化学计量数之和为2,右边也为2,所以无论从左边反开始,还是从右边加入生成物开始,总过程,气体压强始终不变,所以B是错误的。
九年级杠杆课课解析与练习
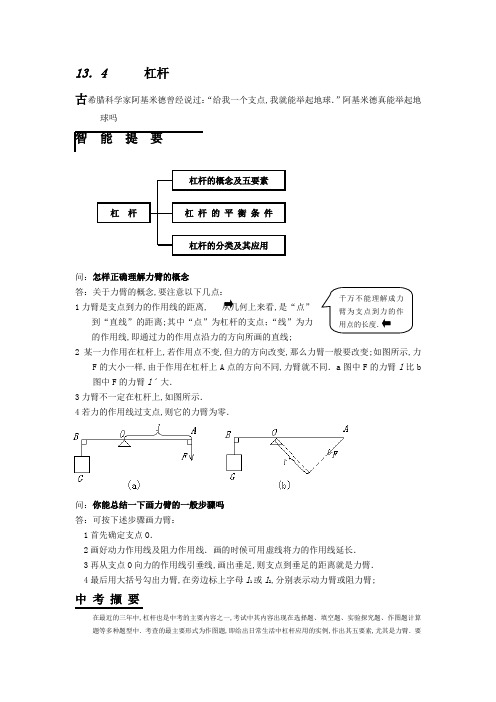
13.4 杠杆古希腊科学家阿基米德曾经说过:“给我一个支点,我就能举起地球.”阿基米德真能举起地球吗智 能 提 要问:怎样正确理解力臂的概念答:关于力臂的概念,要注意以下几点:1力臂是支点到力的作用线的距离, 从几何上来看,是“点”到“直线”的距离;其中“点”为杠杆的支点;“线”为力的作用线,即通过力的作用点沿力的方向所画的直线;2某一力作用在杠杆上,若作用点不变,但力的方向改变,那么力臂一般要改变;如图所示,力F 的大小一样,由于作用在杠杆上A 点的方向不同,力臂就不同.a 图中F 的力臂l 比b 图中F 的力臂l ˊ大. 3力臂不一定在杠杆上,如图所示. 4若力的作用线过支点,则它的力臂为零.问:你能总结一下画力臂的一般步骤吗 答:可按下述步骤画力臂: 1首先确定支点O .2画好动力作用线及阻力作用线.画的时候可用虚线将力的作用线延长. 3再从支点O 向力的作用线引垂线,画出垂足,则支点到垂足的距离就是力臂. 4最后用大括号勾出力臂,在旁边标上字母l 1或l 2,分别表示动力臂或阻力臂;中 考 撷 要在最近的三年中,杠杆也是中考的主要内容之一,考试中其内容出现在选择题、填空题、实验探究题、作图题计算题等多种题型中.考查的最主要形式为作图题,即给出日常生活中杠杆应用的实例,作出其五要素,尤其是力臂.要杠 杆 杠杆的概念及五要素杠 杆 的 平 衡 条 件杠杆的分类及其应用千万不能理解成力臂为支点到力的作用点的长度.善于把日常生活中涉及到杠杆知识又不容易联想到杠杆的应用实例与杠杆联系起来,分析其中的五要素.智 能 拓 展用不准确的天平进行准确的测量我们实验室力测量物体质量的天平是等臂杠杆,它是根据杠杆的平衡条件制作的测量仪器. 因为动力臂等于阻力臂,所以左盘中的物重等于右盘中的砝码重,左盘中的物体质量等于右盘中的砝码质量.由于使用不当和部分被损,一些天平实际上的不等臂杠杆,用这样的天平直接测量,不管你是怎样认真地进行正确操作,称量结果与物体的真实值之间总有偏差.在粗略测量和练习使用天平时,都可以忽略由于仪器本身造成的误差.但是在精确测量中,这是不允许的,如何用不准确的天平进行准确的测量呢第一种方法“是恒载法”.先将另外一个物体放到天平的一只托盘上,然后把砝码放在另外一只托盘上,直至天平平衡.接着,把待测物体放到放砝码的托盘上,并将其中的一部分砝码逐渐取出,使天平恢复平衡. 此时,被测物体的质量就等于被取出的砝码的质量.由于砝码是准确的,所称出的值就是它的真实值.第二种方法是“替代法”.把待测物体放到天平的一只盘上,另外拿些沙粒加到另外一只盘上,一直加到使天平平衡.然后,把待测物体拿下沙粒别动,逐渐把砝码加到这只盘上,直到天平重新恢复平衡为止.这样,被测物体的质量就等于盘上砝码的质量.第三种方法是“复称法”.首先把待测物体设质量为m 放在左盘,然后往右盘加砝码质量为m 1使之平衡. 此时,便有mgl 1=m 1gl 2l 1、l 2分别为左、右盘到天平中央刀口的距离.接着,又将待测物体放到右盘,然后往左盘加砝码质量为m 2至天平平衡.此时,也有m 2gl 1=mgl 2.将两式相比可得21m m m ,只要将m 1、m 2的值代入上式,便可以得出待测物体的质量了.智 能 归 例题型一 会确认并画出杠杆的动力臂和阻力臂例 如图甲所示,杠杆OA 处于平衡状态,在图中分别画出力F 1和F 2对支点0的力臂L 1和L 2;知识点 力臂的概念,会画力臂 闯关点拨 再次提醒:画力臂时必须注意力臂是“支点到力的作用线的距离”,而不是“支点到力的作用点的距离”; 答 如图乙所示变形题1 如下图甲所示,杠杆OA 在力F 1、F 2的作用下处于静止状态,L 2是力F 2的力臂.在图中画出力F 1的力臂L 1和力F 2.甲乙甲乙闯关点拨 根据已知的力臂画力时,力的作用线应与力臂垂直,且要注意力的作用点应画在杠杆上. 答 如上图乙所示变形题2 如下图甲所示的钢丝钳,其中A 为剪钢丝处,B 为手的用力点,O 为转动轴,图乙为单侧钳柄及相连部分示意图,请在图乙中画出剪钢丝时的动力F 1、阻力F 2、动力l 1、阻力臂l 2 ;闯关点拨 动力作用在B 点,方向竖直向下,阻力作用在A 点,方向竖直向下;表示F 1的线段应比表示F 2的线段短一些,因为钢丝钳是省力杠杆.答 如图丙所示题型二 有关探究杠杆平衡条件的实验题例 1 某同学用如右图所示装置验证杠杆的平衡条件,所用的4只钩码每只质量都是50g,在图示情况时,杠杆AB 处于水平平衡状态,这时弹簧秤的读数为.设F 1的力臂为l 1,F 2的力臂l 2,则=21l l .若在杠杆左端钩码下方增加一个相同的钩码,重新调节弹簧秤对杠杆右端拉力的方向后,使杠杆AB 再次恢复水平平衡,则这时弹簧秤的拉力与对应力臂的乘积应是未增加钩码前弹簧秤的拉力与对应力臂乘积的____倍.知识点 探究杠杆的平衡条件闯关点拨 图中的杠杆平衡时,应满足F 1l 1=F 2l 2, 则10780.296.11221===F F l l . 增加钩码后,再次平衡时,由杠杆的平衡条件得F 1ˊl 1ˊ=F 2ˊl 2ˊ,那么还要注意力的方向不要画反了.丙注意:F 1的力臂并非杠杆的OA 段,不能直接比较OA 与OB .452'222'2'211'1'1===F F l F l F l F l F . 答 7/10 5/4例2 在右图所示的实验装置中:①实验前没有挂钩码时,发现杠杆左端下倾,应将杠杆右端螺母向_______左或右边旋一些,使杠杆在水平位置平衡;②实验时只有8个相同的钩码,杠杆上每格等距,当在A 点挂4个钩码时,则怎样挂钩码可以使杠杆在水平位置平衡请设计两种方案答:①_______________________________ ②__________________________ __; 知识点 杠杆平衡条件的应用闯关点拨 解题的关键是依据杠杆的平衡条件,看左、右两边的力和力臂的乘积是否相等.解 1右 2①2个钩码挂在“6”处;②3个钩码挂在“4” 处.题型三 有关杠杆的动态平衡问题例1 如图12-16所示,用始终与杠杆垂直的力F ,将杠杆缓慢地由位置A 拉至位置B ,阻力G 的力臂 ,动力F ;填“变大”或“变小”“不变”知识点 杠杆的平衡条件及其应用闯关点拨 关键是要先弄清哪些是不变量,哪些是改变量,再根据杠杆的平衡条件作出判断分析和解 分别画出杠杆在A 、B 两位置的阻力G 的力臂可看出,阻力臂l G 将变大,由于F 的方向始终与杠杆垂直,所以F 的力臂始终等于杠杆长,故F 的力臂l F 不变;根据公式变大。
健身练习题

一、填空题1、经过长期而有规律的___________训练,肌肉力量会增加,这是由于肌纤维的围度增加,募集更多的运动神经元和骨骼强壮引起的。
2、发展力量耐力,可采用________ 、________ 和________ 的练习方法。
3、血管是指血液流过的一系列管道。
人体除角膜、毛发、指(趾)甲、牙质及上皮等处外,血管遍布全身。
按血管的构造功能不同,分为_________、_________、和_________三种。
4、肌肉酸痛分成两种,在训练中或训练后立即感觉到的酸痛是________ ,剧烈运动后1-2天产生的肌肉酸痛称为________ 。
5、在有氧锻炼中,运动中_________是生理出力程度表现最简单最可靠的指标。
6、有氧锻炼方法主要可以分为________ 和________ 。
7、构成关节的两个关节面弧度差即关节头与关节窝的弧度越大, ________就越好,反之就越差。
8、位觉是由颞骨中一个膜性的复杂管道结构-膜通路实现的。
膜通路由_________、_________、和_________、三部分组成,其中充满淋巴,称为内淋巴。
9、健身锻炼计划的制定中锻炼者的_________、_________、和_________、的起始状态是制定健身锻炼目标的基础10、运动强度即每次运动的_________和难度,主要指_________的运动量11、血管是指血液流过的一系列管道。
人体除角膜、毛发、指(趾)甲、牙质及上皮等处外,血管遍布全身。
按血管的构造功能不同,分为_________、_________和_________三种。
12、个体的健身综合需求包括三个方面,即__ ______ 、__ ______ 和________ 。
13、身体质量指数的正常范围是__ ______ ,超过或低于该范围的危险性都增高。
14、体育锻炼对人的情绪状态具有__ ______ 和__ ______ ,其中________ 产生于活动过程中和活动结束时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础小练习:动态平衡问题分析
(时间:20分钟)
选择题
图2-5-1
1.[2016·全国卷Ⅱ] 质量为m的物体用轻绳AB悬挂于天花板上.用水平向左的力F 缓慢拉动绳的中点O,如图2-5-1所示.用T表示绳OA段拉力的大小,在O点向左移动的过程中()
A.F逐渐变大,T逐渐变大
B.F逐渐变大,T逐渐变小
C.F逐渐变小,T逐渐变大
D.F逐渐变小,T逐渐变小
图2-5-2
2.如图2-5-2所示,与水平方向成θ角的推力F作用在物块上,随着θ逐渐减小直到为零的过程中,物块始终沿水平面做匀速直线运动.关于物块受到的外力,下列判断正确的是()
A.推力F先增大后减小
B.推力F一直减小
C.物块受到的摩擦力先减小后增大
D.物块受到的摩擦力一直不变
图2-5-3
3.如图2-5-3所示,在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A 与竖直墙面间放一光滑圆球B,整个装置处于静止状态.现对B施加一竖直向下的力F,F 的作用线通过球心,设墙对B的作用力为F1,A对B的作用力为F2,地面对A的摩擦力为F3.若F缓慢增大而整个装置仍保持静止,在此过程中()
A.F1保持不变,F3缓慢增大
B.F1缓慢增大,F3保持不变
C.F2缓慢增大,F3缓慢增大
D.F2缓慢增大,F3保持不变
4.如图2-5-4所示,用OA、OB两根轻绳将物体悬于两竖直墙之间,开始时OB绳水
平.现保持O 点位置不变,改变OB 绳长使绳末端由B 点缓慢上移至B ′点,此时OB ′与OA 的夹角θ<90°.设此过程中OA 、OB 的拉力分别为F OA 、F OB ,下列说法正确的是( )
图2-5-4
A .F OA 逐渐增大
B .F OA 逐渐减小
C .F OB 逐渐增大
D .F OB 逐渐减小 5.如图2-5-5所示,轻绳与轻杆承受弹力的最大值一定,杆的O 端用铰链固定,光滑
轻小滑轮在O 的正上方,B 端吊一重物,现将绳的一端拴在杆的B 端,用拉力F 将B 端缓慢上拉,在OB 杆达到竖直前(均未断),关于绳子的拉力F 和杆受的弹力F N 的变化,下列判断正确的是( )
图2-5-5
A .F 变大
B .F 变小
C .F N 变大
D .F N 变小 6.如图2-5-6所示,三根长度均为L 的轻绳分别连接于C 、D 两点,A 、B 两端被悬挂
在水平天花板上,相距2L ,现在C 点上悬挂一个质量为m 的重物,为使CD 绳保持水平,在D 点上可施加力的最小值为( )
图2-5-6
A .mg B.
33
mg C.12mg D.14
mg
图2-5-7
7.在固定于地面的斜面上垂直安放着一个挡板,截面为1
4圆的柱状物体甲放在斜面上,
半径与甲相等的光滑圆球乙被夹在甲与挡板之间,没有与斜面接触而处于静止状态,如图2-5-7所示.现在从圆心O 1处对甲施加一平行于斜面向下的力F ,使甲沿斜面方向极其缓慢地移动,直至甲与挡板接触为止.设乙对挡板的压力为F 1,甲对斜面的压力为F 2,在此过程中( )
A .F 1缓慢增大,F 2缓慢增大
B .F 1缓慢增大,F 2缓慢减小
C .F 1缓慢减小,F 2缓慢增大
D .F 1缓慢减小,F 2不变
基础小练习:动态平衡问题分析——参考答案
选择题
1.A 2.B 3.C 4.B
5.B [解析] 设重物的重力为G .以B 端为研究对象,分析受力情况,作出受力分析图,如图所示:作出力F N 与F 的合力F 2,根据平衡条件得知,F 2=F 1=G .由△CDB ∽△ABO 得F N F 2=BO AO ,解得F N =BO AO G ,式中,BO 、AO 、G 不变,则F N 大小不变,C 、D 错误;由△CDB ∽△ABO 得
F N OB =F
AB
,AB 减小,则F 一直减小,A 错误,B 正确.
6.C [解析] 由题图可知,要想CD 水平,各绳均应绷紧,则AC 与水平方向的夹角为60°;结点C 受力平衡,受力分析图如图所示,则CD 绳的拉力F T =mg tan 30°=
3
3
mg ;D 点受CD 绳拉力大小等于F T ,方向向左;要使CD 水平,D 点所受两绳的拉力与外界的力的合力应为零,CD 绳对D 点的拉力可分解为沿BD 绳的F 1及另一分力F 2,由几何知识可知,当力F 2与BD 垂直时,F 2最小,而F 2的大小为拉力的大小,故最小力F =F T sin 60°=1
2
mg ,故C 正确. 7.D [解析] 先对球乙进行受力分析,其受重力、挡板的支持力和物体甲的支持力,如图a 所示.根据平衡条件,结合几何知识可以看出挡板的支持力不断减小,根据牛顿第三定律,球乙对挡板的压力不断减小,故A 、B 错误;再对甲与乙整体进行受力分析,其受重
力、斜面的支持力、挡板的支持力和已知力F,如图b所示.
根据平衡条件得,x方向:F+(M+m)g sin θ-F′1=0,y方向:F2-(M+m)g cos θ=0,解得F2=(M+m)g cos θ,由牛顿第三定律可知,物体甲对斜面的压力不变,C错误,D正确.。
