专题24 图形的折叠与剪拼
六年级下册数学试题- 专题24立体图形的认识 全国通用 有答案

24.立体图形的认识知识要点梳理一、立体图形的展开图正方体的展开图长方体的展开图圆柱的展开图圆锥的展开图二、观察物体在实际生活中,常常需要对一个物体从不同角度、不同方位进行观察,来获得其形状、大小、颜色等各方面的信息。
1.从不同的角度、不同的方位观察物体,看到物体的形状可能是不同的。
2.能正确辨认从正面、侧面、上面观察到的物体的形状。
三、立体图形的认识1.长方体与正方体特征的区别与联系2、圆柱、圆锥的特征考点精讲分析典例精讲考点1立体图形的认识【例1】一个长方体的棱长总和是40厘米,其中长5厘米,宽3厘米,高是多少厘米?【精析】根据长方体棱长总和的计算公式,计算出长方体的高。
【答案】40÷4-5-3=2(厘米)答:高是2厘米。
【归纳总结】长方体的棱长总和=(长+宽+高)×4。
【例2】把一个大正方体木块表面涂上红色的漆(如图),锯成完全一样的27块小正方体木块。
小正方体中一面红色、二面红色、三面红色各有多少块?【精析】我们可以想象一下,大正方形被切割成小正方体后,一面有红色的在大正方体每个面的最中间(如A处),两面有红色的在大正方体每条棱的中间(如B处),三面有红色的在大正方体的8个角上(如C处),没有红色的在中心内部。
【答案】因为正方体有6个面,12条棱,8个顶点,所以一面有红色的是6块,两面有红色的是12块,三面有红色的是8块。
【归纳总结】根据正方体表面涂色的特点,分别得出切割后的小正方体涂色面的排列特点。
【例3】用一个平面去截一个正方体,把正方体分为两个多面体,则截面最多会是()边形。
【精析】正方体有六个面,欲截最多边,肯定是平面与最多的面相交,形成的交线越多,多边形边数就越多。
让截面过正方体的各条棱的中点。
【答案】六【归纳总结】正方体有六个面,用平面去截正方体时,最少与三个面相交得三角形,最多与六个面相交得六边形。
考点2图形的展开与折叠【例4】在下面四个正方体中,()正方体展开后可能得到右面的展开图。
初二奥数之图形的折叠与剪拼

2020年数学竞赛初二奥数之图形的折叠与剪拼专题24 图形的折叠与剪拼阅读与思考图形的折叠是指把某个图形或部分沿某直线翻折,这条直线为对称轴,在折叠过程中,线短的长度、角的度数保持不变.图形的剪拼是指对某个图形通过有限次的剪裁后重新接成另外一个新的几何图形,在剪拼过程中,原图形与新图形的面积一般保持不变.解答图形的折叠与剪拼问题,要抓住折叠与剪拼过程中一些量的不变性,将计算、推理与合情想象结合起来,常用到全等三角形、勾股定理、面积等知识与方法.折叠问题的实质是对称问题,“遇到折叠用对称”就是运用对称的性质: ① 关于一条直线对称的两个图形全等; ② 对称轴是对应点连线的中垂线.例题与求解【例1】 如图,矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,点D 落在D '处,则重叠部分△AFC 的面积为_____.(山东省竞赛试题)例1题图 例2题图解题思路:△AFC 的高为BC ,只需求出AF ,注意到D '∠=090,AF =FC【例2】如图,直线26y x =-+ 与x 轴,y 轴分别交于P ,Q 两点,把△POQ 沿PQ 翻折,点O 落在R 处,则点R 的坐标是( )A .2412(,)55B .(2,1)C .(6,3)D .(7,3.5)(江苏省竞赛试题)解题思路:过点R 作x 轴,y 轴的垂线,再利用相似三角形的性质可得垂线段的长度即求得点R 的坐标.解剪拼问题时先利用剪拼后的图形所需关键线段的长度,然后,从剪拼前的图形中寻找这些长度进行剪拼.【例3】 如图,将边长为12cm 的正方形ABCD 折叠,使得A 点落在CD 边上点E 处,然后压平折痕FG ,若FG =13cm ,求CE 长.A(北京市竞赛试题)解题思路:由折叠可得A 与E 关于FG 对称,则FG ⊥AE ,可证明FG =AE ,这是解本例的关键.【例4】 将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C运动,运动23秒时,动点P 从点A 出发以相等的速度沿AO 向终点O 运动.当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒).(1)用含t 的代数式表示OP OQ ,;(2)当1t 时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边上的点D 处,求点D 的坐标; (3)连结AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PQ 与AC 能否平行?PE 与AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.(绍兴市中考试题)解题思路:对于(3),假设能,由比例线段求出t 的值,关键是看相应t 的值是否在t 的取值范围. 折纸、剪纸是最富于自然情趣而又形象生动的实验,同时说明了存在的事实是怎样被发现的,现象又是怎样获得证实的,在平面几何的一些主要学习环节发挥重要作用.【例5】 用10个边长分别为3,5,6,11,17,19,22,23,24,25的正方形,可以拼接一个长方形.(1)求这个长方形的长和宽; (2)请画出拼接图.(“华杯赛”决赛试题)解题思路:运用剪拼前后图形面积不变求长方形的长和宽;利用长方形对边相等的性质画拼接图.图1OP A xB DC Qy图2OPA xBC Q yE【例6】 将正方形纸片ABCD 折叠,使顶点A 与CD 边上的点M 重合,折痕交AD 于E ,交BC 于F ,边AB 折叠后与BC 交于点G.(1)如果M 为CD 边的中点,求证:DE :DM :EM =3:4:5;(2)如果M 为CD 边上的任意一点,设AB =2a ,问△CMG 的周长是否有与点M 的位置关系?若有关,请把△CMG 的周长用含CM 的长x 的代数式表示;若无关,请说明理由.解题思路:折痕EF 两旁部分图形是关于EF 成对称的,对于(2),通过相似三角形性质,把△CMG 的周长用相关代数式表示,解题的关键是将几何问题代数化.对于例6,如图,当M 为CD 边上的中点,则有3BCBG,即G 为BC 的三等分点,这一结果是由日本筑波大学的生物学教授芳贺和夫发现的,被称为芳贺第一定理.作深入思考,进一步挖掘还能得到如下重要结论:(1)无论怎样折叠,若点M 落在CD 上,则MG =DM +BG ;(2)无论怎样折叠,若点M 落在CD 上,连MA ,GA ,则∠MAG =450.能力训练1、如图,在矩形ABCD 中,AB =6cm ,BC =8cm ,若将矩形折叠,使B 点与D 点重合,则折痕EF 的长为___cm.(宁夏回族自治区中考试题)2、如图,矩形ABCD 中,AB =12,AD =10,将此矩形折叠使B 点落在AD 边上的中点E 处,则折痕FG的长为_________.第1题图第2题图第3题图(淮阴市中考试题) 3、如图是用12个全等的等腰梯形镶嵌成的图形,这个等腰梯形的上底与下底长的比是_____.(陕西省中考试题) 4、如图,EF为正方形纸ABCD的对折线,将∠A沿DK折叠,使它的顶点A落在EF上的G点,则∠DKG =_______度.(武汉市竞赛试题) 5、如图,已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=080,则∠EGC的度数为________.第4题图第5题图第6题图(台州市中考试题) 6、将一张长为70cm的长方形纸片ABCD沿对称轴EF折叠成如图的形状,若折叠后,AB与CD间的距离为60cm,则原纸片的宽AB是______cm.(广东省中考试题) 7、如图,在矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在F处,折痕为AE,且EF=3,则AB的长为( )A.3B.4C.5D.6(宜宾市中考试题) 8、如图,在△ABC中,∠C=900,BC=6,D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )A.12B、2C、3D、4(河北省中考试题)第7题图 第8题图 第9题图9、如图,有一块菱形的草地,要在其上面修筑两条笔直的道路,道路把这块草地分成面积相等的四部分,如果道路的宽度可以忽略不计,请你设计三种不同的方案.(广西赛区选拔赛试题)10、如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠使AD 边与对角线BD 重合,得折线DG ,若AB =2,BC =1,求AG.(安徽省中考试题)11、如图,折叠矩形ABCD 的一边AD ,使点D 落在BC 边上的点F 处,已知折痕3.4EC AE FC == ,求矩形ABCD 的周长.(厦门市中考试题)12、如图1,一张矩形纸片ABCD ,其中AD =8cm ,AB =6cm ,先沿对角线BD 对折,点C 落在点C ′处的位置,BC ′交AD 于点G. (1) 求证:AG =G C ';(2) 如图2,再折叠一次,使点D 与点A 重合,得折痕EN ,EN 交AD 于点M ,求EM 的长.A'ECAD(深圳市中考试题)B级1、如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次使D点与A点重合,得折痕EN,EN交AD于点M,则ME的长为__________.2、如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A,C重合,使纸片折叠压平,设折痕为EF,则重叠部分△AFE的面积为_________.第1题图第2题图第3题图3、如图,矩形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于点E,若AD=8,AB=4,则DE的长为________.4、如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴上,y轴上,连结AC,将矩形纸片OABC沿AC折叠,使点B落在点D的位置,若B(1,2),则点D的横坐标是______.5、如图,在平面直角坐标系中,已知直线334y x=-+与x轴,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上B′处,则点C的坐标是_________.第4题图第5题图第6题图6、如图,矩形纸片ABCD,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,AD上有一点P,PD=3cm,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点重合,折痕与PF交于Q点,则PQ的长是_____cm.7、在三角形纸片ABC中,已知∠ABC=900,AB=6,BC=8,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线上的T处,折痕为MN,当点T在直线l上移动时,折痕的端点M,N也随之移动,若限定端点M,N分别在AB,BC边上移动,则线段AT长度的最大值与最小值之和为__________(计算结果不取近似值)8、如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,BG=10.(1)当折痕的另一端F在AB边上时,如图.求△EFG的面积;(2)当折痕的另一端F在AD边上时,如图.证明四边形BGEF为菱形,并求出折痕GF的长.9、如图,已知三角形纸片ABC的面积为25,BC的长为10,∠B,∠C都为锐角,M是AB边上的一动点(M与A,B不重合),过点M作MN∥BC交AC于点N,设MN=x.(1)用x表示△AMN的面积;(2)△AMN沿MN折叠,使△AMN紧贴四边形BCNM(边AM、AN落在四边形BCNM所在的平面内),设点A落在平面BCNM内的点A′,△A′MN与四边形BCNM重叠部分的面积为y.①用含x的代数式表示y,并写出x的取值范围.②当x为何值时,重叠部分的面积y最大,最大为多少?10、如图:一正方形纸片,根据要求进行多次分割,把它分割成若干个直角三角形.具体操作过程如下:第一次分割:将正方形纸片分成4个全等的直角三角形;第二次分割:将上次得到的直角三角形中的一个再分成4个全等的直角三角形;以后按第二次分割的方法重复进行.(1)请你设计出两种符合题意的分割方案(分割3次);(2)设正方形的边长为a,请你通过对其中一种方案的操作和观察,将第二、第三次分割后所得的最小的直角三角形的面积S填入下表:(3)在条件(2)下,请你猜想:分割所得的最小直角三角形面积S与分割次数n有什么关系?用数学表达式表示出来.11、如图1,将边长为4cm 的正方形纸片ABCD 沿EF 折叠(点E ,F 分别在边AB ,CD 上),使点B 落在AD 边上的点M 处,点C 落在点N 处,MN 与CD 交于点P ,连结EP .(1)如图②,若M 为AD 边的中点, ① △AEM 的周长=_________cm ; ② 求证:EP =AE +DP ; (2)随着落点M 在AD 边上取遍所有的位置(点M 不与A 、D 重合),△PDM 的周长是否发生变化?请说明理由.12、如图1,在矩形ABCD 中,AB =3,AD =1,点P 在线段AB 上运动,设AP =x ,现将纸片折叠,使点D 与点P 重合,得折痕EF (点E ,F 为折痕与矩形边的交点),再将纸片还原.(1)当0 x 时,折痕EF 的长为________;(2)写出使四边形EPFD 为菱形的x 的取值范围,并求出当x =2时菱形的边长;(3)令2EF =y ,当点E 在AD 上、点F 在BC 上时,写出y 与x 的函数关系式(写出x 的取值范围),当y 取最大值时,判断△EAP 与△PBF 是否相似.若相似,求出x 的值;若不相似,请说明理由.专题24 图形的折叠与剪拼例1 10例2 A 提示:作RE ⊥y 轴于E ,RF ⊥x 轴于F ,则Rt △QRE ∽Rt △PRF ,从而PFQERF RE PR QR ==,设R (x ,y ),又PR =OP =3,QR =OQ =6,于是3636--==x y y x ,得x =524,y =512. 例3 7 提示:过F 作FM ⊥BC 于M ,证明△FGM ≌△ADE ,则FG =AE =13,DE =5例4 (1)OP =6-t ,OQ =t +32(2)D (1,3) (3)①PQ 能与AC 平行,若PQ ∥AC ,则OC OA OQ OP =,即326+-t t =36.得t =914,而0≤t ≤37,∴t =914. ②PE 不能与AC 垂直.若PE ⊥AC ,延长QE 交OA 于F ,则OC OQ AC QF =,即33253+=t QF,QF =5(t +32).∴EF =QF -QE =QF -OQ =5(t +32)-(t +32)=(5-1)t +32(5-1). 又Rt △EPF ∽Rt △OCA ,∴OA OC EF PE =,即63)32)(15(6=+--t t ,t ≈3.45,而0≤t ≤37,∴t 不存在. 例5 (1)10个正方形的面积和:32+52+62+112+172+192+222+232+242+252=3055=5×13×47. 因为所拼成的长方形面积是3055.长方形的宽显然≥25,所以它的宽应当是47,长应当是5×13=65.(2)注意23+24=47,25+22=47,23+17+25=65,24+19+22=65.由此便可得拼图.(图略)例6 提示:(1)证明:设正方形边长为a ,DE 为x ,则DM =,EM=EA=a-x .在Rt △DEM 中,∠D =90°,∴,DE -2.+,DM -2.=,EM -2.,∴,x-2.+,,,a -2..-2.=,∴,EM=,5-8.a ,∴DE :DM :EM=::,5-8.a =3:4:5(2)设DE=y ,则DM=2a-x ,EM=2a-y ,可证明△DEM ∽△CMG.,△CMG 周长-△DEM 周长.=,CM -DE .=,x -y .△CMG 的周长,在△DEM 中,由勾股定理得,(2a−y )-2.=,y -2.+,(2a−x )-2.,化简得4ay =x(4a-x )即. ∴△CMG 的周长=,4a -4a−x .∙(y+2a-x+2a-y )=(4a-x )=4a ,为定值.A 级1. 2.,65-6. 3.1:2 4.75° 5.80° 6.10 提示:长方形纸片折叠时,AB 与CD 间的距离缩短了10cm 。
2019中考数学专题复习 和折叠有关的题型突破 ( Word版,无答案)

2019中考数学专题复习和折叠有关的题型突破( Word版,无答案)以折叠为背景的题型分析【解题思路】折叠问题题型多样,变化灵活,从考察学生空间想象能力与动手操作能力的实践操作题,到直接运用折叠相关性质的说理计算题,发展到基于折叠操作的综合题,甚至是压轴题. 考查的着眼点日趋灵活,能力立意的意图日渐明显.这对于识别和理解几何图形的能力、空间思维能力和综合解决问题的能力都提出了比以往更高的要求.本专题内容在考查中常涉及到特殊平行四边形的折叠与性质、特殊三角形的判定、勾股定理的运用,角平分线的性质等. 因此考生在复习中应熟练掌握一些基本图形的性质和判定定理以及图形折叠的性质. 图形折叠是中考中常考题型,这种题型主要考察学生对图形的认知,特别是考察轴对称的性质、全等三角形、勾股定理、相似三角形等知识综合运用。
【中考原题】【例 1】如图,在矩形纸片ABCD 中,AB=2,AD=3,点 E 是 AB 的中点,点 F 是AD 边上的一个动点,将△AEF 沿EF 所在直线翻折,得到△A′EF,则A′C 的长的最小值是.(考点:折叠动点)2019中考数学专题复习和折叠有关的题型突破( Word版,无答案)【例2】如图,在矩形纸片ABCD 中,AB=4,AD=12,将矩形纸片折叠,使点C 落在AD 边上的点M 处,折痕为PE,此时PD=3.(1)求MP 的值;(4 分)(考点:勾股定理)(2)在AB 边上有一个动点F,且不与点A,B 重合.当AF 等于多少时,△MEF的周长最小?(4 分)(考点:折叠性质将军饮马)(3)若点G,Q 是AB 边上的两个动点,且不与点A,B 重合,GQ=2.当四边形MEQG 的周长最小时,求最小周长值.(计算结果保留根号)(4 分)(考点:将军饮马)【例 3】已知二次函数及一次函数 y = x 2 + x + 6 ,将该二次函数在 x 轴上方的图象沿 x 轴翻折到 x 轴下方,图象的其余部分不变,得到一个新图象(如图所示)当直线 y=x+m 与新 图象有 4 个交点时,m 的取值范围是() (考点:函数的交点判断)(A) - 254 < m < 3 (B) - 254< m < -2(C) - 2 < m < 3 (D) - 6 < m < -2【相关知识扩展】类型1 与角度有关的折叠1.把一张长方形纸片按如图所示折叠2 次,若∠1=50︒,则∠2的度数为()A.10︒ B.15︒C.20︒D.25︒3.如图,在∆ABC 中,∠B = 32︒,将∆ABC 沿直线m 翻折,点B 落在点D 的位置,则∠1 -∠2 的度数是()A.32︒ B.64︒C.65︒D.70︒4.如图,点D 为∆ABC 边BC 的延长线上一点.∠ABC 的角平分线与∠ACD 的角平分线交于点M ,将∆MBC 以直线BC 为对称轴翻折得到∆NBC ,∠NBC 的角平分线与∠NCB 的角平分线交于点Q ,若∠A=48︒,则∠BQC 的度数为()A.138︒B.114︒C.102︒ D.100︒6.已知长方形ABCD ,E 点和F 点分别在AB 和BC 边上,如图将∆BEF 沿着EF 折叠以后得到△B'EF,B'E与AD相交于点M,B'F与AD相交于点G ,则∠1与∠2的数量关系为.7. 如图,将平行四边形ABCD 沿对角线BD 折叠,使点A 落在点E 处,ED 交BC 于点F .若∠ABD=48︒,∠CFD=40︒,则∠E的度数为.8.如图,在四边形ABCD 中,∠B = 120︒,∠B 与∠ADC 互为补角,点E 在BC 上,将∆DCE 沿DE 翻折,得到△DC'E,若AB//C'E,DC'平分∠ADE,则∠A的度数为︒.9. 如图,在△ABC中,将△ABC沿DE 折叠,使顶点C 落在△ABC三边的垂直平分线的交点O 处,若BE=BO,则∠BOE=度.10.如图,将一张三角形纸片ABC 的一角折叠,使点A 落在△ABC 外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是()A.γ=2α+β B.γ=α+2β C.γ=α+β D.γ=180°﹣α﹣β类型2 与长度、周长、面积有关的折叠1. 如图,有一张直角三角形纸片,两直角边AC=6cm,B C=8cm,点D 在BC 边上,将直角边AC 沿直线AD 折叠,点C 恰好落在斜边AB 上的点E 处,则线段CD 的长为.A DC MFDNB E A B E C第1 题图第2 题图2. 如图,将边长为8cm 的正方形ABCD 折叠,使点D 落在BC 边的中点E 处,点A 落在点F处,折痕为MN,则线段CN 的长为.3. 如图,在长方形ABCD 中,AB=3,AD=9,将此长方形折叠,使点D 与点B 重合,折痕为EF,则△ABE 的面积为.A E DB F CC'4. 如图,折叠长方形的一边AD,使点D 落在BC 边上的点F 处,若AB=4cm,B C=5cm,则EF的长为.A DEB F C5. 如图,在△ABC 中,AB=20,AC=12,BC=16,E 为BC 边上一点,把△ABC 沿AE 折叠,使AB 落在直线AC 上,求重叠部分(阴影部分)的面积.AC6. 如图,正方形ABCD 的边长为3,E、F 分别是AB、CD 上的点,且∠CFE=60°,将四边形BCFE 沿EF 翻折,得到B′C′FE,C′恰好落在AD 边上,B′C′交AB 于点G,则GE 的长是()A. 4B. 5C. 4-5-7. 如图,四边形ABCD 是边长为9 的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B'处,点A 的对应点为A'.若B'C=3,则CN=_ ,AM=_.A'A M DFA M DB' EB NC B N C第7 题图第8 题图8. 如图,将长为4cm,宽为2cm 的矩形纸片ABCD 折叠,使点B 落在CD 边的中点E 处,压平后得到折痕MN,则线段AM 的长为.9. 如图,在△ABC 中,AB=3,BC=4,∠B=90°,将△ABC 折叠,使点C 与点A 重合.若折痕分别交AC,BC 于点E,F,则BF= ,EF= _.AEB F C10. 如图,将长方形ABCD 折叠,使点A 与点C 重合,折痕为EF,若AB=3,AD=4,则DE的长为.A E DB F C11. 如图,在长方形纸片ABCD 中,AD=8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处,折痕交BC 于点E,若EF=3,则AB 的长为()A.3 B.4 C.5 D.6A DFB E C第11 题图12. 把长方形纸片ABCD 按如图所示的方式折叠,使点B 与点D 重合,折痕为EF.若AB=3cm,BC=5cm,则DE= .A'A E D(B')B F C13. 如图,将正方形纸片ABCD 沿MN 折叠,使点D 落在边AB 上,对应点为D′,点C 落在C′处.若AB=6,AD′=2,则DM=,CN= .FD CN A E DC'MB CA D' B第13 题图第14 题图14. 如图,在长方形ABCD 中,BC=4,CD=3,将该长方形沿对角线BD 折叠,使点C 落在点F 处,BF 交AD 于点E,则EF=.A F DGB E CD'C'第15 题图15. 如图,已知在长方形ABCD 中,点E 在边BC 上,BE=2CE,将长方形沿着过点E 的直线翻折后,点C,D 分别落在边BC 下方的点C′,D′处,且点C′,D′,B 在同一条直线上,折痕与边AD 交于点F,D′F 与BE 交于点G.设AB=t,那么△EFG 的周长为.(用含t 的代数式表示)16. 如图,长方形ABCD 中,AB=15cm,点E 在AD 上,且AE=9cm,连接EC,将长方形ABCD沿直线BE 翻折,点A 恰好落在EC 上的点A'处,则A'C= cm.A E D A E DA' M A′NB C B F C第18 题图第19 题图17. 如图,将长方形纸片ABCD 对折,得折痕MN,展开后再沿过点B 的直线折叠,使点A 落在MN 上的A′处,得折痕BE,连接EA′并延长交BC 于点F.若AB=2,则BE=,EF=.18. 如图,在∆ABC 中.∠ACB = 90︒,AC = 4 ,BC ,点D 在AB 上,将∆ACD 沿CD 折叠,点A 落在点A1 处,A1C 与AB 相交于点E ,若A1 D / / BC ,则A1 E 的长为( )2019中考数学专题复习 和折叠有关的题型突破 ( Word 版,无答案)A .B .83C .3D .4 - 220. 如图,矩形ABCD 中, AB = 4 , BC = 3 ,点 E 是 DC 边上一点,连接 BE ,把 ∠C 沿 BE 折叠,使点 C 落在点 F 处,当 ∆DEF 为直角三角形时, DE 的长为 .第 20 题图 第 21 题图21. 图,矩形ABCD 中, AB = 5 , BC = 8 ,点 E 、 G 为直线 BC 上两个动点, BE = CC ,连接 AE , 将∆ABE 沿 AE 折叠,将 ∆DCC 沿 DG 折叠,当对应点 F 和 H 重合时, BE 的长为 .22. 将一张宽为5cm 的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形, 则这个三角形面积的最小值是 ()A .3 cm 2 B .252cm 2 C . 25cm 2D .3 cm 223. 如图, 在矩形ABCD 中, AB = 4 ,BC = 6 ,E 为 BC 的中点 . 将 ∆ABE 沿 AE 折叠, 使 点 B 落在矩形内点 F 处, 连接CF ,则 ∆CDF 的面积为 ( )A .3.6B .4.32C .5.4D .5.7624. 如图,在ABCD 中,BC = 4 ,CD = 6 ,点E 是AB 边上的中点,将∆BCE 沿CE 翻折得∆FCE ,连结DF ,射线CF 交直线DA 于点P ,当∠CPD = 90︒时,∆DCF 的面积是.25. 如图,有一张矩形纸片ABCD ,AB = 8 ,AD = 6 .先将矩形纸片ABCD 折叠,使边AD 落在边AB 上,点D 落在点E 处,折痕为AF ;再将∆AEF 沿EF 翻折,AF 与BC 相交于点G ,则∆GCF 的周长为.26. 如图,在四边形ABCD 中,AB = 10 ,BD ⊥AD .若将∆BCD 沿BD 折叠,点C 与边AB 的中点E 恰好重合,则四边形BCDE 的周长为.27. 如图,正方形纸片ABCD 的边长为12,E 是边CD 上一点,连接AE 、折叠该纸片,使点A 落在AE 上的G 点,并使折痕经过点B ,得到折痕BF ,点F 在AD 上,若DE = 5 ,则GE 的长为.第27 题第28 题28. 如图,矩形纸片ABCD 中,AD = 6 ,AB = 10 ,E 为CD 中点,将矩形纸片沿AE 折叠,点D 落在点D'处,延长AD'交BC 于点F ,则D'F 的长度为.29. 如图,在矩形ABCD 中,AD = 2 .将∠A 向内翻折,点A 落在BC 上,记为A',折痕为DE .若将∠B 沿EA'向内翻折,点B 恰好落在DE 上,记为B',则AB = .第29 题第30 题30. 如图,矩形ABCD 中,AB =,BC = 12 ,E 为AD 中点,F 为AB 上一点,将∆AEF 沿EF折叠后,点A 恰好落到CF 上的点G 处,则折痕EF 的长是.31. 如图,在∆ABC 中,∠ABC = 45︒,AB = 3 ,AD ⊥BC 于点D ,BE ⊥AC 于点E ,AE =1.连接DE ,将∆AED 沿直线AE 翻折至∆ABC 所在的平面内,得∆AEF ,连接DF .过点D 作DG ⊥DE 交BE 于点G .则四边形DFEG 的周长为( )A.8 B.C.+ 4 D.+ 232. 形纸片ABCD 如图 2 那样折叠,使顶点B 与顶点D 重合,折痕为EF . 若AB , AD = 3 ,则∆DEF 的周长为.33. 如图(1)的矩形纸片折叠,B、C 两点恰好重合落在AD 边上的点P 处,如图(2),已知∠MPN=90º,PM=3,PN=4,那么矩形ABCD 的周长为。
专题24 图形的折叠与剪拼

专题24 图形的折叠与剪拼阅读与思考图形的折叠是指把某个图形或部分沿某直线翻折,这条直线为对称轴,在折叠过程中,线短的长度、角的度数保持不变.图形的剪拼是指对某个图形通过有限次的剪裁后重新接成另外一个新的几何图形,在剪拼过程中,原图形与新图形的面积一般保持不变.解答图形的折叠与剪拼问题,要抓住折叠与剪拼过程中一些量的不变性,将计算、推理与合情想象结合起来,常用到全等三角形、勾股定理、面积等知识与方法.折叠问题的实质是对称问题,“遇到折叠用对称”就是运用对称的性质: ① 关于一条直线对称的两个图形全等; ② 对称轴是对应点连线的中垂线.例题与求解【例1】 如图,矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,点D 落在D '处,则重叠部分△AFC 的面积为_____.(山东省竞赛试题)A例1题图 例2题图解题思路:△AFC 的高为BC ,只需求出AF ,注意到D '∠=090,AF =FC 【例2】如图,直线26y x =-+ 与x 轴,y 轴分别交于P ,Q 两点,把△POQ 沿PQ 翻折,点O 落在R 处,则点R 的坐标是( )A .2412(,)55B .(2,1)C .(6,3)D .(7,3.5)(江苏省竞赛试题)解题思路:过点R 作x 轴,y 轴的垂线,再利用相似三角形的性质可得垂线段的长度即求得点R 的坐标.解剪拼问题时先利用剪拼后的图形所需关键线段的长度,然后,从剪拼前的图形中寻找这些长度进行剪拼.【例3】 如图,将边长为12cm 的正方形ABCD 折叠,使得A 点落在CD 边上点E 处,然后压平折痕FG ,若FG =13cm ,求CE 长.(北京市竞赛试题)解题思路:由折叠可得A 与E 关于FG 对称,则FG ⊥AE ,可证明FG =AE ,这是解本例的关键.【例4】 将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动,运动23秒时,动点P 从点A 出发以相等的速度沿AO 向终点O 运动.当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒).(1)用含t 的代数式表示OP OQ ,;(2)当1t 时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边上的点D 处,求点D 的坐标;(3)连结AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PQ 与AC 能否平行?PE 与AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.图1解题思路:对于(3),假设能,由比例线段求出t的值,关键是看相应t的值是否在t的取值范围.折纸、剪纸是最富于自然情趣而又形象生动的实验,同时说明了存在的事实是怎样被发现的,现象又是怎样获得证实的,在平面几何的一些主要学习环节发挥重要作用.【例5】用10个边长分别为3,5,6,11,17,19,22,23,24,25的正方形,可以拼接一个长方形.(1)求这个长方形的长和宽;(2)请画出拼接图.(“华杯赛”决赛试题)解题思路:运用剪拼前后图形面积不变求长方形的长和宽;利用长方形对边相等的性质画拼接图.【例6】将正方形纸片ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD 于E,交BC于F,边AB折叠后与BC交于点G.(1)如果M为CD边的中点,求证:DE:DM:EM=3:4:5;(2)如果M为CD边上的任意一点,设AB=2a,问△CMG的周长是否有与点M 的位置关系?若有关,请把△CMG的周长用含CM的长x的代数式表示;若无关,请说明理由.解题思路:折痕EF两旁部分图形是关于EF成对称的,对于(2),通过相似三角形性质,把△CMG的周长用相关代数式表示,解题的关键是将几何问题代数化.对于例6,如图,当M 为CD 边上的中点,则有3BCBG,即G 为BC 的三等分点,这一结果是由日本筑波大学的生物学教授芳贺和夫发现的,被称为芳贺第一定理.作深入思考,进一步挖掘还能得到如下重要结论:(1)无论怎样折叠,若点M 落在CD 上,则MG =DM +BG ;(2)无论怎样折叠,若点M 落在CD 上,连MA ,GA ,则∠MAG =450.能力训练1、如图,在矩形ABCD 中,AB =6cm ,BC =8cm ,若将矩形折叠,使B 点与D 点重合,则折痕EF 的长为___cm.(宁夏回族自治区中考试题)2、如图,矩形ABCD 中,AB =12,AD =10,将此矩形折叠使B 点落在AD 边上的中点E 处,则折痕FG 的长为_________.第1题图 第2题图 第3题图(淮阴市中考试题)3、如图是用12个全等的等腰梯形镶嵌成的图形,这个等腰梯形的上底与下底长的比是_____.(陕西省中考试题)4、如图,EF 为正方形纸ABCD 的对折线,将∠A 沿DK 折叠,使它的顶点A 落在EF 上的G 点,则∠DKG =_______度.(武汉市竞赛试题)5、如图,已知等边△ABC 中,点D ,E 分别在边AB ,BC 上,把△BDE 沿直线DE 翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=080,则∠EGC的度数为________.第4题图第5题图第6题图(台州市中考试题) 6、将一张长为70cm的长方形纸片ABCD沿对称轴EF折叠成如图的形状,若折叠后,AB与CD间的距离为60cm,则原纸片的宽AB是______cm.(广东省中考试题) 7、如图,在矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在F处,折痕为AE,且EF=3,则AB的长为( )A.3B.4C.5D.6(宜宾市中考试题) 8、如图,在△ABC中,∠C=900,BC=6,D,E分别在AB,AC上,将△ABC沿DE 折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )A.12B、2C、3D、4(河北省中考试题)ECA第7题图 第8题图 第9题图 9、如图,有一块菱形的草地,要在其上面修筑两条笔直的道路,道路把这块草地分成面积相等的四部分,如果道路的宽度可以忽略不计,请你设计三种不同的方案.(广西赛区选拔赛试题)10、如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠使AD 边与对角线BD 重合,得折线DG ,若AB =2,BC =1,求AG.(安徽省中考试题)11、如图,折叠矩形ABCD的一边AD ,使点D 落在BC 边上的点F 处,已知折痕3.4EC AEFC == ,求矩形ABCD 的周长. (厦门市中考试题)12、如图1,一张矩形纸片ABCD ,其中AD =8cm ,AB =6cm ,先沿对角线BD 对折,点C 落在点C ′处的位置,BC ′交AD 于点G .C ;(1) 求证:AG=G(2) 如图2,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,求EM 的长.(深圳市中考试题)B级1、如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次使D点与A点重合,得折痕EN,EN交AD于点M,则ME的长为__________.2、如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A,C重合,使纸片折叠压平,设折痕为EF,则重叠部分△AFE的面积为_________.第1题图第2题图第3题图3、如图,矩形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于点E,若AD=8,AB=4,则DE的长为________.4、如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴上,y 轴上,连结AC,将矩形纸片OABC沿AC折叠,使点B落在点D的位置,若B(1,2),则点D的横坐标是______.5、如图,在平面直角坐标系中,已知直线334y x=-+与x轴,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上B′处,则点C的坐标是_________.第4题图第5题图第6题图6、如图,矩形纸片ABCD,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,AD 上有一点P,PD=3cm,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点重合,折痕与PF交于Q点,则PQ的长是_____cm.7、在三角形纸片ABC中,已知∠ABC=900,AB=6,BC=8,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线上的T处,折痕为MN,当点T在直线l上移动时,折痕的端点M,N也随之移动,若限定端点M,N分别在AB,BC 边上移动,则线段AT长度的最大值与最小值之和为__________(计算结果不取近似值)8、如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,BG=10.(1)当折痕的另一端F在AB边上时,如图.求△EFG的面积;(2)当折痕的另一端F在AD边上时,如图.证明四边形BGEF为菱形,并求出折痕GF的长.9、如图,已知三角形纸片ABC的面积为25,BC的长为10,∠B,∠C都为锐角,M 是AB边上的一动点(M与A,B不重合),过点M作MN∥BC交AC于点N,设MN=x.(1)用x表示△AMN的面积;(2)△AMN沿MN折叠,使△AMN紧贴四边形BCNM(边AM、AN落在四边形BCNM所在的平面内),设点A落在平面BCNM内的点A′,△A′MN与四边形BCNM 重叠部分的面积为y.①用含x的代数式表示y,并写出x的取值范围.②当x为何值时,重叠部分的面积y最大,最大为多少?10、如图:一正方形纸片,根据要求进行多次分割,把它分割成若干个直角三角形.具体操作过程如下:第一次分割:将正方形纸片分成4个全等的直角三角形;第二次分割:将上次得到的直角三角形中的一个再分成4个全等的直角三角形;以后按第二次分割的方法重复进行.(1)请你设计出两种符合题意的分割方案(分割3次);(2)设正方形的边长为a,请你通过对其中一种方案的操作和观察,将第二、第三次分割后所得的最小的直角三角形的面积S填入下表:(3)在条件(2)下,请你猜想:分割所得的最小直角三角形面积S与分割次数n有什么关系?用数学表达式表示出来.11、如图1,将边长为4cm的正方形纸片ABCD沿EF折叠(点E,F分别在边AB,CD 上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连结EP.(1)如图②,若M为AD边的中点,①△AEM的周长=_________cm;②求证:EP=AE+DP;(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.12、如图1,在矩形ABCD 中,AB =3,AD =1,点P 在线段AB 上运动,设AP =x ,现将纸片折叠,使点D 与点P 重合,得折痕EF (点E ,F 为折痕与矩形边的交点),再将纸片还原.(1)当0 x 时,折痕EF 的长为________;(2)写出使四边形EPFD 为菱形的x 的取值范围,并求出当x =2时菱形的边长;(3)令2EF =y ,当点E 在AD 上、点F 在BC 上时,写出y 与x 的函数关系式(写出x 的取值范围),当y 取最大值时,判断△EAP 与△PBF 是否相似.若相似,求出x 的值;若不相似,请说明理由.。
图形的折叠剪拼与分割

图形的折叠、剪拼与分割一页普通的纸,童年时我们用稚气的双手把它折成有趣的动物,民间艺人可以把它剪成美丽的图案.折纸与剪纸是最富于自然情趣而又形象生动的实验,是丰富想象力与心灵手巧的结合.对图形进行折叠与剪拼,是学习几何不可或缺的重要一环,通过折叠与剪拼图形,我们可以发现一些几何结论并知晓这些结论是怎样被证明的.把图形或部分沿某直线翻折叫图形的折叠,对图形通过有限次的剪裁再重新拼接成新的图形叫图形的剪拼.解与图形折叠或剪拼相关的问题,利用不变量解题是关键,在折叠过程中,线段的长度、角的度数保持不变;在剪拼过程中,新图形与原图形的面积一般保持不变.例题求解【例1】如图,有一块直角三角形纸片,两直角边AC=6㎝,BC=8㎝,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于.(2002年南通市中考题)思路点拨设CD=x,由折叠的性质实现等量转换,将条件集中到Rt△BDE中,建立x的方程.注图形折叠与剪拼问题可考壹我们的动手操作能力和分析推理能力,解题时需要把计算、推理与合情想象结合起来.折叠问题可以对称观点认识:(1)折痕两边是全等的;(2)对应点连线被折痕垂直平分.解折叠问题常用到勾股定理、相似形、方程思想等知识与方法.【例2】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为( )A.12 D10 C.8 D.6 (2004年武汉市选拔赛试题)思路点拨只需求出AF长即可.【例3】取一张矩形的纸进行折叠,具体操作过程如下:第一步:先把矩形ABCD 对折,折痕为MN ,如图1;第二步:再把B 点叠在折痕线MN 上,折痕为AE ,点B 在MN 上的对应点为B ′,得Rt △AB'E ,如图2;第三步:沿EB'线折叠得折痕EF ,如图3.利用展开图4探究:(1)△AEF 是什么三角形?证明你的结论.(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.(2003年山西省中考题)思路点拨 本例没有现成的结论,需经历实验、观察、猜想、证明等数学活动,从而探究得到结论.【例4】如图,是从边长为40cm 、宽为30cm 的矩形钢板的左上角截取一块长为20cm 、宽为10cm 的矩形后,剩下的一块下脚料.工人师傅要将它作适当地切割,重新拼接后焊成一个面积与原下脚料的面积相等,接缝尽可能短的正方形工件.(1)请根据上述要求,设计出将这块下脚料适当分割成三块或三块以上的两种不同的拼接方案(在图2和图3中分别画出切割时所沿的虚线,以及拼接后所得到的正方形,保留拼接的痕迹);(2)比较(1)中的两种方案,哪种更好一些?说说你的看法和理由.(2002年山东省中考题)思路点拨 拼接后正方形的边长为221030 ㎝,它恰是以30cm 和10cm 为两直角边的直角三角形的斜边的长,为此可考虑设法在原钢板上构造两直角边长分别为30㎝和l0cm 的直角三角形,这是解本例的关键.注 有效的数学学习过程不能单纯地依赖模仿与记忆,应该通过观察、实验、操作、猜测、验证、推理等数学活动,形成自己对数学知识的理解和有效的学习策略,从而使知识得到内化,形成能力.近年中考中涌现的设计新颖、富有创意的折叠、剪拼与分割等问题,注重对动手实践操作、应用意识、学习潜能的考查.【例5】 用10个边长分别为3,5,6,11,17,19,22,23,24,25的正方形,可以拼接成一个矩形.(1)求这个矩形的长和宽;(2)请画出拼接图.思路点拨 利用拼接前后图形面积不变求矩形的长和宽;运用矩形对边相等这一性质画拼接图.【例6】 如图,已知△ABC 中,∠B=∠C=30°,请设计三种不同的分法,将△ABC 分割成四个三角形,使得其中两个是全等三角形,而另外两个是相似但不全等的直角三角形.请画出分割线段,标出能够说明分法的所得三角形的顶点和内角度数(或记号).(画图工具不限,不要求证明,不要求写出画法) (2003年温州市中考题)思路点拨 充分运用几何计算、推理和作图,综合运用动手操作、空间想象、解决问题.学历训练1. 将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕,如果对折n 次,可以得到 条折痕.(2002年南宁市中考题)2.一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A 、B 重合,若∠B=30°,AC=3,则折痕DE 的长等于 . (2003年三明市中考题)3.如图,将一块长为12的正方形纸片ABCD 的顶点A 折至DC 边上的点E ,使DE =5,折痕为PQ ,则线段PM= .(第2题) (第3题) (第6题)4.在△ABC 中,已知AB=20,∠A=30°,CD 是AB 边的中线,若将△ABC 沿CD 对折起来,折叠后两个小三角形ACD 与三角形BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的41,有如下结论:①AC 边的长可以等于a ;②折叠前的△ABC 的面积可以等于223a ;③折叠后,以A 、B 为端点的线段AB 与中线CD 平行且相等,其中,正确结论有个.(2003年天津市中考题)5.将四个相同的矩形(长是宽的3倍),用不同的方式拼成一个大矩形,设拼得大矩形的面积是四个小矩形的面积和,则大矩形周长的值只可能有( )A.1种B.2种C.3种D.4种(2003年南昌市中考题)6.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ) A.∠A=∠1+∠2; B.2∠A=∠1+∠2;C.3∠A=2∠1+∠2; D.3∠A=2(∠l+∠2). (2003年北京市海淀区中考题)7.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分.将①展开后得到的平面图形是( )A.矩形B.三角形C.梯形D.菱形(2003年陕西省中考题)8.如图1,小强拿一张正方形的纸,沿虚线对折一次得图2,再对折一次得图3,然后用剪刀沿图3中的虚线剪去一个角,再打开后的形状是( ) (2003年济南市中考题)9.如图,东风汽车公司冲压厂冲压汽车零件的废料都是等腰三角形的小钢板,其中AB=AC,该冲压厂为了降低汽车零件成本,变废为宝,把这些废料再加工成红星农业机械厂粉碎机上的零件,销售给红星农业机械厂,这些零件的形状都是矩形.现在要把如图所示的等腰三角形钢板切割后再焊接成两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每次切割的次数最多两次(切割的损失可忽略不计).(1)请你设计两种不同的切割焊接方案,并用简要的文字加以说明;(2)若要把该三角形废料切割后焊接成正方形零件(只切割一次),则该三角形需满足什么条件? (2003年十堰市中考题)10.如图,ABCD是矩形纸片,E是AB上一点,且BE:EA=5:3,EC=155,把△BCE 沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点为F,求AB、BC的长.11.如图,在△ABC中,AB=3,AC=4,BC=5,现将它折叠,使点B与点C重合,则折痕的长是.(2003年四川省竞赛题)(第11题)(第12题)(第13题)12.如图,一张矩形纸片沿BC折叠,顶点A落在点A,处,第二次过A,再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为.(2002年“宇振杯”上海市竞赛题)13.如图,将矩形ABCD的四个角向内折起,恰好拼成既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于.(第12届“希望杯”邀请赛试题)14.要剪切如图l(尺寸单位mm)所示的两种直角梯形零件,且使两种零件的数量相等.有两种面积相等的矩形铝板,第一种长500mm,宽300mm(如图2);第二种长600mm,宽250mm(如图3);可供选用.(1)填空:为了充分利用材料,应选用第种铝板,这时一块铝板最多能剪甲、乙两种零件共个,剪出这些零件后,剩余的边角料的面积是mm2.(2)画图,从图2或图3中选出你要用的铝板示意图,在上面画出剪切线,并把边角余料用阴影表示出来.15.如图,EF为正方形ABCD的对折线,将∠A沿DK折叠使它的顶点A落在EF上的G 点,则∠DKG为( )A.15°B.30°C.55°D.75°(第15题)(第16)16.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条,如图,在Rt△ABC中,∠C=90°,AC=30㎝,AB=50cm,依次裁下宽为1㎝的矩形纸条a1,a2,a3,…,若使裁得的矩形纸条的长都不小于5cm,则每张直角三角形彩纸能裁成的矩形纸条的总数是( )A.24 B.25 C.26 D.27 (2001年山东省济南市中考题) 17.如图,若将左边正方形剪成四块,恰能拼成右边的矩形,设a=1,则这个正方形的面积为( )A.2537+B.253+C.251+D.2)21(+. (2003年山东省竞赛题)、。
2020年河北中考数学专题复习讲练课件专题复习(二) 选择题和填空题

A
B
C
D
10.(2018·河北模拟)如图,在△ABC 中,∠BAC=90°,AB=AC=3, 点 D 在 BC 上,且 BD=2CD,E,F 分别在 AB,AC 上运动且始终保持∠ EDF=45°.设 BE=x,CF=y,则 y 与 x 之间的函数关系用图象表示为( D )
11.(2019·保定二模)如图,点 M 为▱ABCD 的边 AB 上一动点,过点 M 作直线 l 垂直于 AB,且直线 l 与▱ABCD 的另一边交于点 N.当点 M 从 A→ B 匀速运动时,设点 M 的运动时间为 t,△AMN 的面积为 S,能大致反映 S 与 t 之间函数关系的图象是(C )
题型2 判断函数图象 类型 1 根据函数性质判断函数图象
1.(2019·唐山古冶区一模)如图,正比例函数 y=kx 与反比例函数 y= k-x 1的图象不可能是(D )
A
B
C
D
2.(2019·石家庄 28 中模拟)已知点 A(2,b),B(-2,-b),C(b,2)在 同一函数图象上,这个函数图象可以是(B )
关系的是(C )
A
B
C
D
类型 3 根据几何问题判断函数图象 9.(2019·唐山路北区一模)如图,在边长为 2 的正方形 ABCD 中剪去一 个边长为 1 的小正方形 CEFG,动点 P 从点 A 出发,沿 A→D→E→F→G →B 的路线绕多边形的边匀速运动到点 B 时停止(不含点 A 和点 B),则△ ABP 的面积 S 随着时间 t 变化的函数图象大致是(A )
A.甲正确,乙不正确 C.甲、乙都正确
B.甲不正确,乙正确 D.甲、乙都不正确
8.(2018·石家庄裕华区一模)已知⊙O 及⊙O 外一点 P,过点 P 作⊙O 的一条切线(只有圆规和三角板这两种工具),以下是甲、乙两位同学的作法:
初中数学竞赛奥数培优资料第三辑专题24 平面几何的定值问题

专题24平面几何的定值问题【阅读与思考】所谓定值问题,是指按照一定条件构成的几何图形,当某些几何元素按一定的规律在确定的范围内变化时,与它有关的元素的量保持不变(或几何元素间的某些几何性质或位置关系不变).几何定值问题的基本特点是:题设条件中都包含着变动元素和固定元素,变动元素是指可变化运动的元素,固定元素也就是“不变量”,有的是明显的,有的是隐含的,在运动变化中始终没有发生变化的元素,也就是我们要探求的定值.解答定值问题的一般步骤是:1.探求定值;2.给出证明.【例题与求解】【例1】如图,已知P 为正方形ABCD 的外接圆的劣弧AD ⌒上任意一点.求证:PA PC PB为定值.解题思路:线段的和差倍分考虑截长补短,利用圆的基本性质,证明三角形全等.【例2】如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ()A .到CD 的距离保持不变B .位置不变C .等分DB ⌒D .随C 点的移动而移动(济南市中考试题)解题思路:添出圆中相关辅助线,运用圆的基本性质,用排除法得出结论.【例3】如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.(加拿大数学奥林匹克试题)解题思路:不管ST 滑到什么位置,∠SOT 的度数是定值.从探寻∠SPM 与∠SOT 的关系入手.【例4】如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值.(广州市中考试题)解题思路:延长OG 交CD 于N ,利用题中的三等分点、平行四边形和三角形中位线的性质,实现把线段ON 转化成线段CH 的倍分关系,再以Rt △OND 为基础,通过勾股定理,使问题得以解决.【例5】如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8.(1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PF OF 的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.(深圳市中考试题)解题思路:对于(3)从动点F 达到的特殊位置时入手探求定值.(图1)(图2)【例6】如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:PA 2+PB 2+PC 2为定值.解题思路:当点P 与C 点重合时,PA 2+PB 2+PC 2=2BC 2为定值,就一般情形证明.【能力训练】A 级1.如图,点A ,B 是双曲线xy 3=上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则=+21S S _______.(牡丹江市中考试题)(第1题图)(第3题图)(第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.(全国初中数学联赛试题)3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为()A .30°B .40°C .50°D .60°(武汉市竞赛试题)5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置()A .在平分AB 的某直线上移动B .在垂直AB 的某直线上移动C .在弧AMB 上移动D .保持固定不移动(第5题图)(第6题图)6.如图,A ,B 是函数xk y 图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是()A .3B .6C .9D .12(海南省竞赛试题))7.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,PA ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F .PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.(济宁市中考试题)9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(江苏省竞赛试题)(第9题图)(第10题图)(第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O 的半径为R .求证:(1)2222DK CK BK AK +++是定值;(2)2222DA CD BC AB +++是定值.611.如图,设P 是正方形ABCD 外接圆劣弧弧AB上的一点,求证:DP CP BP AP ++的值为定值.(克罗地亚数学奥林匹克试题)B 级1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).(福州市中考试题)3.如图,将六边形ABCDEF 沿直线GH 折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D +∠E +∠F =α,则下列结论一定正确的是()A .∠1+∠2=900°-2αB .∠1+∠2=1080°-2αC .∠1+∠2=720°-αD .∠1+∠2=360°-21α(武汉市竞赛试题)4.如图,正△ABO的高等于⊙O的半径,⊙O在AB上滚动,切点为T,⊙O交AO,BO于M,N,则弧MTN()A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图,AB是⊙O的直径,且AB=10,弦MN的长为8.若MN的两端在圆上滑动时,始终与AB相交,记点A,B到MN的距离分别为h1,h2,则∣h1-h2∣等于()A.5B.6C.7D.8(黄石市中考试题)(第5题图)(第6题图)6.如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A,C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B,D.(1)求点A的坐标(用m表示)(2)求抛物线的解析式;(3)设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F.试证明:FC(AC+EC)为定值.(株洲市中考试题)7.如图,已知等边△ABC内接于圆,在劣弧AB上取异于A,B的点M.设直线AC与BM相交于K,直线CB与AM相交于点N.证明线段AK和BN的乘积与M点的选择无关.(湖北省选拔赛试题)(第7题图)(第8题图)8.如图,设H 是等腰三角形ABC 两条高的交点,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.(全国初中数学联赛试题)9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒).(1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程;(3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由;(4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程.(黄冈市中考试题)(第9题图)(第10题图)10.已知抛物线C 1:12121+-=x x y ,点F (1,1).(1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF,并延长交抛物线C 1于点B ,求证:211=+BF AF .(3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变.(四川省竞赛试题)专题24平面几何的定值问题例1延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故2PA PC CE PC PE PB PB PB ++===例2B 提示:连结AC ,BC ,可以证明P 为 APB 的中点.例3∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角.例4(1)连结OC 交DE 于M ,则OM =CM ,EM =DM ,而DG =HE ,则HM =GM 故四边形OGCH 是平行四边形.(2)DG 不变.DE =OC =OA =3.DG =13DE =13×3=1.(3)设CD =x ,延长OG 交CD 于N ,则CN =DN =12x ,229CE x =-,2214DN x =.∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值.例5⑴C (0,4)⑵先求得AM =CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP =163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OF PF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MP OM FM =,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35.例6∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •PA +PC •AB ,而AB =BC =AC ,∴PA =PB +PC ,从而PA 2+PB 2+PC 2=(PB +PC )2+PB 2+PC 2=2(PB 2+PC 2+PB •PC )=2BC 2=2×23=6.故PA 2+PB 2+PC 2为定值.A 级1.4提示:∵S 1+S 阴=S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273提示:1+3+5=9是等边三角形的高.3.r 2提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A′B′的中点均在⊙O 的上半圆的中点处.6.B提示:S 正方形OCAD =OD •OC =A A x y k = =6,∴S OEBF =OE •OF =x B •y B k ==6.7.⑴略⑵当点P 在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值.8.⑴2π⑵22.5°⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC .10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值.⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值.11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP •,DP •a =BP •a +AP ,两式相加并整理得(CP +DP )a =(AP +BP )(a ),从而1AP BP CP DP+=-+为定值.1.1提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242ππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26.3.B 提示:如图,设FA 的延长线与CB的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α.4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD =3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6.6.⑴A (3-m ,0)⑵y =x 2-2x +1⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN =3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PM EC PC =,即()2112x x EC --=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC=,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值.7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关.8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变.9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989)⑵若四边形PQCA 为平行四边形,由于QC ∥PA ,故只要QC =PA 即可,而PA =18-4t ,CQ =t ,故18-4t =t ,得t =185.⑶设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =PA +AF =PA +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90.⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t+25=.∴t =2.②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足.③若PQ =PF ,即(5t -8)2+100=182,∴(5t-8)2=22415,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =5-2时,△PQ R 为等腰三角形.10.⑴C 1的顶点坐标为(1,12).⑵略⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF--=,∴11PF QF+=2.11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB 的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP ⊥AB ,OP =12(EM +G N )=12(AH +BH )=12AB .∴无论点C 在AB 同一侧的位置如何,E G 中点P 的位置不变.。
2021年中考数学专题图形折叠类问题

图形折叠类问题【考点综述评价】折叠操作就是将图形的一部分沿着一条直线翻折180°,使它与另一部分图形在这条直线的同旁与其重叠或不重叠,其中“折”是过程,“叠”是结果.折叠问题的实质是图形的轴对称变换,折叠更突出了轴对称问题的应用.折叠(或翻折)在三大图形变换中是比较重要的,考查得较多,无论是选择题、填空题,还是解答题都有以折叠为背景的试题.常常把矩形、正方形的纸片放置于直角坐标系中,与函数、直角三角形、相似形等知识结合,贯穿其他几何、代数知识来设题.根据轴对称的性质可以得到:折叠重合部分一定全等,折痕所在直线就是这两个全等形的对称轴;互相重合两点(对称点)之间的连线必被折痕垂直平分;对称两点与对称轴上任意一点连结所得的两条线段相等;对称线段所在的直线与对称轴的夹角相等. 在解题过程中要充分运用以上结论,借助辅助线构造直角三角形,结合相似形、锐角三角函数等知识来解决有关折叠问题.【考点分类总结】考点1:折叠后图形判断【典型例题】(2017贵州省遵义市)把一张长方形纸片按如图①,图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是()A.B.C.D.【方法归纳】对折叠图形的判断,可以通过空间想象,找出相等的边与角,转化为角度的判断.【变式训练】(2017天门)如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.考点2:折叠后度数判断【典型例题】(2017内蒙古赤峰市)如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=23,则∠A=()A.120°B.100°C.60°D.30°【方法归纳】在折叠问题中,利用对称性可得到相等的角和边.【变式训练】(2017宁夏)如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处.若∠1=∠2=50°,则∠A'为.考点3:折叠后线段长度判断【典型例题】(2017新疆乌鲁木齐市)如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为43且∠AFG=60°,GE=2BG,则折痕EF的长为()A.1B.3C.2D.23【方法归纳】在折叠问题中,利用对称性可得到相等的线段,通过三角形相似、勾股定理列出方程求解.折叠问题转化为轴对称问题,利用勾股定理和相似求出未知线段,最后把所求的线段转化到直角三角形中去处理.【变式训练】(2017江苏省无锡市)如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于()A.2B.54C.53D.75考点4:折叠后周长面积计算【典型例题】(2017重庆)如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E 作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是.【方法归纳】在折叠问题中,利用对称性可得到相等的角、全等的图形和相等的面积.【变式训练】(2017山东省潍坊市)如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD边上,记为B′,折痕为CE,再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE=13BC.则矩形纸片ABCD的面积为.考点5:折叠后结论探讨【典型例题】(2017南京)折纸的思考.【操作体验】用一张矩形纸片折等边三角形.第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).第二步,如图③,再一次折叠纸片,使点C落在EF上的P处,并使折痕经过点B,得到折痕BG,折出PB,PC,得到△PBC.(1)说明△PBC是等边三角形.【数学思考】(2)如图④,小明画出了图③的矩形ABCD和等边三角形PBC,他发现,在矩形ABCD中把△PBC经过图形变化,可以得到图⑤中的更大的等边三角形,请描述图形变化的过程.(3)已知矩形一边长为3cm,另一边长为a cm,对于每一个确定的a的值,在矩形中都能画出最大的等边三角形,请画出不同情形的示意图,并写出对应的a的取值范围.【问题解决】(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,所需正方形铁片的边长的最小值为cm.【方法归纳】解决折叠问题时,一是要对图形折叠有准确定位,抓住图形之间最本质的位置关系,从点、线、面三个方面入手,发现其中变化的和不变的量,发现图形中的数量关系;二是要把握折叠的变化规律,充分挖掘图形的几何性质,将其中的基本的数量关系用方程的形式表达出来.【变式训练】(2017济宁)实验探究:(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN 的度数是多少,并证明你的结论.(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.【新题好题训练】1.如图,将矩形纸片ABCD 沿BD 折叠,得到△BC ′D ,C ′D 与AB 交于点E .若∠1=35°,则∠2的度数为( )A .20B .30C .35D .552.如图,E ,F 分别是▱ABCD 的边AD 、BC 上的点,EF =6,∠DEF =60°,将四边形EFCD 沿EF 翻折,得到EFC ′D ′,ED ′交BC 于点G ,则△GEF 的周长为( )A .6B .12C .18D .243.如图,平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别落在x 、y 轴上,点B 坐标为(6,4),反比例函数x y 6=的图象与AB 边交于点D ,与BC 边交于点E ,连结DE ,将△BDE 沿DE 翻折至△B 'DE 处,点B '恰好落在正比例函数y =kx 图象上,则k 的值是( )A .52-B .211-C .51-D .241-4.如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,33),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为()A.(32,332)B.(2,332)C.(332,32)D.(32,3﹣332)5.如图1,把一张正方形纸片对折得到长方形ABCD,再沿∠ADC的平分线DE折叠,如图2,点C落在点C′处,最后按图3所示方式折叠,使点A落在DE的中点A′处,折痕是FG,若原正方形纸片的边长为6cm,则FG= cm.6.在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为.7.如图,已知等边三角形OAB与反比例函数kyx(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则BDDC的值为.(已知sin1562)8.如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.(1)求证:四边形BFEP为菱形;(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;①当点Q与点C重合时(如图2),求菱形BFEP的边长;②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.9.已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.(1)如图1,若点D是AC中点,连接PC.①写出BP,BD的长;②求证:四边形BCPD是平行四边形.(2)如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.10.如图,在平面直角坐标系xOy 中,抛物线223y x x =--交x 轴于A ,B 两点(点A 在点B 的左侧),将该抛物线位于x 轴上方曲线记作M ,将该抛物线位于x 轴下方部分沿x 轴翻折,翻折后所得曲线记作N ,曲线N 交y 轴于点C ,连接AC 、BC .(1)求曲线N 所在抛物线相应的函数表达式;(2)求△ABC 外接圆的半径;(3)点P 为曲线M 或曲线N 上的一动点,点Q 为x 轴上的一个动点,若以点B ,C ,P ,Q 为顶点的四边形是平行四边形,求点Q 的坐标.。
专题24 二次函数中的菱形问题(解析版)

专题24 二次函数中的菱形问题1、如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.(1)求抛物线的函数表达式;(2)根据图像,直接写出不等式x2+bx+c>0的解集:.(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为:.【答案】(1)y=x2-4x+3;(2)x<1或x>3;(3)(2,-1)【解析】(1)如图,∵AB=2,对称轴为直线x=2.∴点A的坐标是(1,0),点B的坐标是(3,0).把A、B两点的坐标代入得:{1+b+c=09+3b+c=0,解得:{b=−4c=3,∴抛物线的函数表达式为y=x2-4x+3;.(2)由图象得:不等式x2+bx+c>0,即y>0时,x<1或x>3;故答案为:x<1或x>3;(3)(2,-1).y=x2-4x+3=(x-2)2-1,∴顶点坐标为(2,-1),当E、D点在x轴的上方,即DE∥AB,AE=AB=BD=DE=2,此时不合题意,如图,根据“菱形ADBE 的对角线互相垂直平分,抛物线的对称性”得到点D 是抛物线y=x 2-4x+3的顶点坐标,即(2,-1), 故答案是:(2,-1).2、如图,已知抛物线23)0(y a bx a =++≠经过点1,0A 和点()3,0B ,与y 轴交于点C .(1)求此抛物线的解析式;(2)若点P 是直线BC 下方的抛物线上一动点(不点B ,C 重合),过点P 作y 轴的平行线交直线BC 于点D ,设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长;②连接PB ,PC ,求PBC ∆的面积最大时点P 的坐标;(3)设抛物线的对称轴与BC 交于点E ,点M 是抛物线的对称轴上一点,N 为y 轴上一点,是否存在这样的点M 和点N ,使得以点C 、E 、M 、N 为顶点的四边形是菱形?如果存在,请直接写出点M 的坐标;如果不存在,请说明理由.【答案】(1)y =x 2﹣4x +3;(2)①用含m 的代数式表示线段PD 的长为﹣m 2+3m ;②△PBC 的面积最大时点P 的坐标为(32,﹣34);(3)存在这样的点M 和点N ,使得以点C 、E 、M 、N 为顶点的四边形是菱形.点M 的坐标为M 1(2,3),M 2(2,1﹣),M 3(2,). 【解析】(1)∵抛物线y =ax 2+bx+3(a≠0)经过点A (1,0)和点B (3,0),与y 轴交于点C , ∴309330a b a b ++=⎧⎨++=⎩,解得14a b =⎧⎨=-⎩,∴抛物线解析式为y =x 2﹣4x+3; (2)①设P (m ,m 2﹣4m+3),将点B (3,0)、C (0,3)代入得直线BC 解析式为y BC =﹣x+3. ∵过点P 作y 轴的平行线交直线BC 于点D ,∴D(m,﹣m+3),∴PD=(﹣m+3)﹣(m2﹣4m+3)=﹣m2+3m.答:用含m的代数式表示线段PD的长为﹣m2+3m.②S△PBC=S△CPD+S△BPD=12OB•PD=﹣32m2+92m=﹣32(m﹣32)2+278.∴当m=32时,S有最大值.当m=32时,m2﹣4m+3=﹣34.∴P(32,﹣34).答:△PBC的面积最大时点P的坐标为(32,﹣34).(3)存在这样的点M和点N,使得以点C、E、M、N为顶点的四边形是菱形.根据题意,点E(2,1),∴EF=CF=2,∴EC=2,根据菱形的四条边相等,∴,∴M(2,1-)或(2,)当EM=EF=2时,M(2,3)∴点M的坐标为M1(2,3),M2(2,1﹣),M3(2,).3、如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点.(1)求这个二次函数y=x2+bx+c的解析式.(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标.(3)如果点P在运动过程中,能使得以P、C、B为顶点的三角形与△AOC相似,请求出此时点P的坐标.【答案】(1)y=x 2﹣2x ﹣3(2)(2)(2+√102,-32)(3)P 、C 、B 为顶点的三角形与△AOC 相似,此时点P 的坐标(1,﹣4)【解析】(1)将B 、C 点代入函数解析式,得:{9+3b +c =0c =−3 ,解得:{b =−2c =−3 ,这个二次函数y =x 2+bx +c的解析式为y =x 2﹣2x ﹣3;(2)∵四边形POP ′C 为菱形,∴OC 与PP ′互相垂直平分,∴y P =−OC 2=−32,即x 2﹣2x ﹣3=−32,解得:x 1=2+√102,x 2=2−√102(舍),P (2+√102,−32);(3)∵∠PBC <90°,∴分两种情况讨论:①如图1,当∠PCB =90°时,过P 作PH ⊥y 轴于点H ,BC 的解析式为y =x ﹣3,CP 的解析式为y =﹣x ﹣3,设点P 的坐标为(m ,﹣3﹣m ),将点P 代入代入y ═x 2﹣2x ﹣3中,解得:m 1=0(舍),m 2=1,即P (1,﹣4);AO =1,OC =3,CB =√32+32=3√2,CP =√12+(−4+3)2=√2,此时BC CP=CO AO=3,△AOC ∽△PCB ;②如图2,当∠BPC =90°时,作PH ⊥y 轴于H ,作BD ⊥PH 于D . ∵PC ⊥PB ,∴△PHC ∽△BDP ,∴PH HC=BD PD.设点P 的坐标为(m ,m 2﹣2m ﹣3),则PH =m ,HC =-(m 2﹣2m ﹣3)-(-3)=-m 2+2m ,BD =-(m 2﹣2m ﹣3),PD =3-m ,∴m−m 2+2m=−(m 2−2m−3)3−m,∴1m−2=−(m +1),解得:m =1+√52或1−√52(舍去).当m =1+√52时,m 2﹣2m ﹣3=−5+√52.∵△PHC ∽△BDP ,∴PCPB =HC PD =−m 2+2m 3−m =√5−15−√5=√5=√55≠COAO =3,以P 、C 、B 为顶点的三角形与△AOC 不相似.综上所述:P 、C 、B 为顶点的三角形与△AOC 相似,此时点P 的坐标(1,﹣4).4、如图,在平面直角些标系中,二次函数y =ax 2+bxA (﹣1,0),C (2,0),与y 轴交于点B ,其对称轴与x 轴交于点D .(1)求二次函数的表达式及其顶点的坐标; (2)若P 为y 轴上的一个动点,连接PD ,求12PB +PD 的最小值; (3)M (x ,t )为抛物线对称轴上一个动点,若平面内存在点N ,使得以A 、B 、M 、N 为顶点的四边形为菱形,则这样的点N 共有 个. 【答案】(1)2y x x =-1,2;(2(3)5个 【解析】(1)∵二次函数2y ax bx =+A (﹣1,0)C (2,0),∴0420a b a b ⎧-=⎪⎨+-=⎪⎩,解得:2a b ⎧=⎪⎪⎨⎪=⎪⎩∴二次函数的表达式为2y x x =-∵y =2212222x x x ⎫-=--⎪⎝⎭∴抛物线的顶点坐标为(1,2; (2)如图,连接AB ,作DH ⊥AB 于H ,交OB 于P ,此时12PB +PD 最小.理由:∵OA =1,OB ,∴OA tan ABO OB ∠==,∵303tan ︒=, ∴∠ABO =30°, ∴PH =12PB , ∴12PB +PD =PH +PD =DH , ∴此时12PB +PD 最短(垂线段最短);∵抛物线的顶点坐标为(1,2, ∴()13122AD =--=,∵∠ABO =30°, ∴∠HAD =60°,在Rt △ADH 中,∵∠AHD =90°,AD =32,∠HAD =60°,∴sin60°=DH AD =∴DH =4,∴12PB +PD (3)①以A 为圆心AB 为半径画弧,因为AB >AD ,故此时圆弧与对称轴有两个交点,且AM =AB ,即M 点存在两个,所以满足条件的N 点有两个; ②以B 为圆心AB 为半径画弧,因为12AB >,故此时圆弧与对称轴有两个交点,且BM =AB ,即M 点有两个,所以满足条件的N 点有两个;③线段AB 的垂直平分线与对称轴有一个交点,此时AM =BM ,因为M 点有一个,所以满足条件的N 点有一个;则满足条件的N 点共有5个, 故答案为:5.5、如图,在平面直角坐标系中,二次函数y =﹣x 2+bx +c 的图象与x 轴交于A 、B 两点,A 点的坐标为(﹣3,0),B 点在原点的左侧,与y 轴交于点C (0,3),点P 是直线BC 上方的抛物线上一动点 (1)求这个二次函数的表达式;(2)连接PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP ′C (如图1所示),那么是否存在点P ,使四边形POP ′C 为菱形?若存在,请此时点P 的坐标:若不存在,请说明理由; (3)当点P 运动到什么位置时,四边形ABCP 的面积最大,并求出其最大值.【答案】(1)y =﹣x 2﹣2x +3;(2)存在.P 点的坐标为(﹣2,32);(3)P 点的坐标为(﹣32,154),四边形ABPC 的面积的最大值为758. 【方法引导】(1)利用待定系数法直接将B、C两点直接代入y=x2+bx+c求解b,c的值即可得抛物线解析式;(2)利用菱形对角线的性质及折叠的性质可以判断P点的纵坐标为﹣32,令y=﹣32即可得x2﹣2x﹣3=﹣32,解该方程即可确定P点坐标;(3)由于△ABC的面积为定值,当四边形ABCP的面积最大时,△BPC的面积最大;过P作y轴的平行线,交直线BC于Q,交x轴于F,易求得直线AC的解析式,可设出P点的横坐标,然后根据抛物线和直线BC的解析式求出Q、P的纵坐标,即可得到PQ的长,以PQ为底,B点横坐标的绝对值为高即可求得△BPC 的面积,由此可得到关于四边形ABCP的面积与P点横坐标的函数关系式,根据函数的性质即可求出四边形ABCP的最大面积及对应的P点坐标.【解析】(1)∵C点坐标为(0,3),∴y=﹣x2+bx+3,把A(﹣3,0)代入上式得,0=9﹣3b+3,解得,b=﹣2,∴该二次函数解析式为:y=﹣x2﹣2x+3;(2)存在.如图1,设P点的坐标为(x,﹣x2﹣2x+3),PP′交CO于E,当四边形POP'C为菱形时,则有PC=PO,连接PP′,则PE⊥CO于E,∴OE=CE=32,令﹣x2﹣2x+3=32,解得,x1=﹣22,x2=22-(不合题意,舍去).∴P,32).(3)如图2,过点P作y轴的平行线与BC交于点Q,与OA交于点F,设P(x,﹣x2﹣2x+3),设直线AC的解析式为:y=kx+t,则303k tt-+=⎧⎨=⎩,解得:13kt=⎧⎨=⎩,∴直线AC的解析式为y=x+3,则Q点的坐标为(x,x+3),当0=﹣x2﹣2x+3,解得:x1=1,x2=﹣3,∴AO=3,OB=1,则AB=4,S四边形ABCP=S△ABC+S△APQ+S△CPQ=12AB•OC+12QP•OF+12QP•AF=12×4×3+12[(﹣x2﹣2x+3)﹣(x+3)]×3=﹣32(x+32)2+758.当x=﹣32时,四边形ABCP的面积最大,此时P点的坐标为(﹣32,154),四边形ABPC的面积的最大值为758.【思路引导】此题考查了二次函数综合题,需要掌握二次函数解析式的确定、菱形的判定和性质以及图形面积的求法等知识,当所求图形不规则时通常要将其转换为其他规则图形面积的和差关系来求解.6、如图,抛物线与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC ⊥x轴,垂足为点C(3,0).(1)求直线AB的函数关系式;(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N. 设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由【答案】(1)112y x=+;(2)251544s t t=-+(0≤t≤3);(3)t=1或2时;四边形BCMN为平行四边形;t=1时,平行四边形BCMN是菱形,t=2时,平行四边形BCMN不是菱形,理由见解析.【解析】解:(1)x=0时,y=1,∴点A的坐标为:(0,1),∵BC⊥x轴,垂足为点C(3,0),∴点B的横坐标为3,当x=3时,y=52,∴点B的坐标为(3,52),设直线AB的函数关系式为y=kx+b,1532bk b=⎧⎪⎨+=⎪⎩,解得,121kb⎧=⎪⎨⎪=⎩,则直线AB的函数关系式112y x=+(2)当x=t 时,y=12t+1, ∴点M 的坐标为(t ,12t+1),当x=t 时,2517144y t t =-++ ∴点N 的坐标为2517(,1)44t t t -++ 2251715151(1)44244s t t t t t =-++-+=-+ (0≤t≤3);(3)若四边形BCMN 为平行四边形,则有MN=BC , ∴25155=442t t -+, 解得t 1=1,t 2=2,∴当t=1或2时,四边形BCMN 为平行四边形, ①当t=1时,MP=32,PC=2, ∴MC=52=MN ,此时四边形BCMN 为菱形, ②当t=2时,MP=2,PC=1,∴,此时四边形BCMN 不是菱形.7、已知,在平面直角坐标系内一直线l 1:y =-x +3分别与x 轴、y 轴交于A 、B 两点,抛物线y =-x 2+bx +c 经过A 、B 两点,y 轴右侧部分抛物线上有一动点C ,过点C 作y 轴的平行线交直线l 1于点D .(1)求抛物线的函数表达式;(2)如图1,C 在第一象限,求以CD 为直径的⊙E 的最大面积,并判断此时⊙E 与抛物线的对称轴是否相切?若不相切,求出使得⊙E 与该抛物线对称轴相切时点C 的横坐标;(3)坐标平面内是否存在点M ,使B 、C 、D 、M 为顶点的四边形为菱形?若存在,直接写出点M 的坐标;不存在,请说明理由.【答案】(1)y =−x 2+2x +3;(2)不相切, C 的横坐标分别为2和5−√172;(3)M (0,1),(2,3)(0,1-3√2),(0,1+3√2). 【解析】解:(1)直线l 1:y =-x +3分别与x 轴、y 轴交于A 、B 两点,可得A 点(3,0),B 点(0,3),将A 、B 两点坐标代入y =-x 2+bx +c ,可得 {0=−9+3b +c 3=c ,可得b=2,c=3∴抛物线的函数表达式y =−x 2+2x +3; (2)①可得抛物线对称轴为:x =−b2a =1,∵ C 在第一象限,以CD 为直径的⊙E 的最大面积,即CD 最长时,圆的面积最大, 设直线CD 的横坐标为t ,0<t <3, ∴D 点坐标(t ,-t+3),C 点坐标(t ,-t 2+2t+3),∴ |CD|=-t 2+2t+3-(-t+3)= -t2+3t (0<t <3),∴当t=−b2a =32时,CD 最长,此时CD 最长为94,此时圆E 的半径为98,此时CD 与对称轴的距离为32-1=12≠98, 故不相切.②当CD 在对称轴右边时,即1<t <3时 |CD|= -t2+3t (1<t <3);圆E 的半径为t -1,可得|CD|=2r ;-t 2+3t=2(t -1),解得:t 1=-1(舍去);t 2=2;当CD 在对称轴左边时,即即0<t <1时, 有-t 2+3t=2(1-t ),解得:t 1=5+√172(舍去),t 2=5−√172;综上所述:t=2或t=5−√172,⊙E 与该抛物线对称轴相切.(3)存在,由菱形性质可得M 点坐标(0,1),(2,3)(0,1-3√2),(0,1+3√2).8、如图,二次函数y =−x 2+3x +m 的图象与x 轴的一个交点为B(4,0),另一个交点为A ,且与y 轴相交于C 点(1)求m 的值及C 点坐标;(2)在直线BC 上方的抛物线上是否存在一点M ,使得它与B ,C 两点构成的三角形面积最大,若存在,求出此时M 点坐标;若不存在,请简要说明理由(3)P 为抛物线上一点,它关于直线BC 的对称点为Q ,当四边形PBQC 为菱形时,求点P 的坐标(直接写出答案);【答案】(1)m =4, C(0,4) (2) 存在, M(2,6)(3)P 点坐标为(1+√5,1+√5)或(1−√5,1−√5)【解析】解:(1) 将点B(4,0)的坐标代入二次函数y =−x 2+3x +m ,即−42+3×4+m =0,解得m =4,故二次函数解析式为y =−x 2+3x +4,令x =0,解得y =4,故C 点坐标为(0,4); (2)存在,理由:∵B(4,0),C(0,4)∴直线BC 的解析式为y =−x +4,当直线BC 向上平移b 单位后和抛物线只有一个公共点时,△MBC 面积最大,∴{y =−x +4+b y =−x 2+3x +4整理得:x 2−4x +b =0 ∴∆=16−4b =0,∴b =4 ∴{x =2y =6 ∴M(2,6)(3)如图2、图3所示,连接PQ交BC于点G。
中考数学二轮专题复习 与图形折叠有关的探究专题 课件

第1题解图⑤
又∵∠A′EM=∠CHB,
∴△A′ME∽△CBH, 设ME=x,则A′E= x1,
2
∵A′B⊥CD,
∴A′B⊥AB,
∴∠ABA′=90°,
由折叠可知,∠ABM=∠MBE=45°,
∴EB=ME=x,
第1题解图⑤
∵A′B=5,∴ x1+x=5,解得x=
10
.
2
3
∵∠A′=∠C,∠A′HN=∠CHB,∴△A′NH∽△CBH,
1
B2 M,
∴EF=BF;
M
2 1
第1题图①
证法二:如解图②,过点F作FM⊥EB于点M,
则∠EMF=90°. ∵BE⊥AD,∴∠AEB=90°, ∴∠AEB=∠EMF, ∴AD∥FM. ∵四边形ABCD是平行四边形, ∴AD∥BC. ∴AD∥FM∥BC. ∴ EM DF ,
MB FC
M
第1题图①
∵F为CD的中点, ∴DF=FC. ∴EM=MB. ∵FM⊥EB, ∴FM垂直平分EB.
M
第1题图①
实践探究:(2)希望小组受此问题的启发,将▱ABCD沿着BF(F为CD的中 点)所在直线折叠,如图②点C的对应点为C′,连接DC′并延长交AB于点G, 请判断AG与BG的数量关系,并加以证明; (2)AG=BG.
第1题图②
证法一:如解图③,由折叠可知:∠1=∠2= 1∠CFC′,FC′=FC.
2
∵F为CD的中点,∴FC=FD= C1D,∴FC′= FD.
2
∴∠3=∠4.∵∠CFC′=∠3+∠4,∴∠4=
∠1 CFC′.
2
∴∠4=∠1,∴DG∥FB.
∵四边形ABCD为平行四边形,
∴DC ∥ AB.
中考数学专题考试——折叠剪切问题
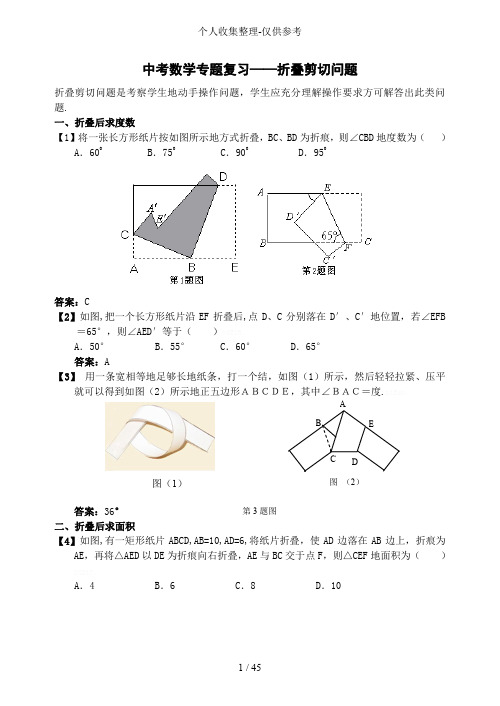
图 (2) 中考数学专题复习——折叠剪切问题折叠剪切问题是考察学生地动手操作问题,学生应充分理解操作要求方可解答出此类问题.一、折叠后求度数【1】将一张长方形纸片按如图所示地方式折叠,BC 、BD 为折痕,则∠CBD 地度数为( )A .600 B .750 C .900 D .950答案:C【2】如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D ′、C ′地位置,若∠EFB=65°,则∠AED ′等于( )A .50° B .55° C .60° D .65° 答案:A【3】 用一条宽相等地足够长地纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示地正五边形ABCDE,其中∠BAC=度.答案:36°二、折叠后求面积【4】如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD 边落在AB 边上,折痕为AE ,再将△AED 以DE 为折痕向右折叠,AE 与BC 交于点F ,则△CEF 地面积为( )A .4B .6 C .8 D .10图(1)第3题图答案:C【5】如图,正方形硬纸片ABCD 地边长是4,点E 、F 分别是AB 、BC 地中点,若沿左图中地虚线剪开,拼成如下右图地一座“小别墅”,则图中阴影部分地面积是A .2 B .4 C .8 D .10答案:B【6】如图a ,ABCD 是一矩形纸片,AB =6cm ,AD =8cm ,E 是AD 上一点,且AE =6cm.操作:(1)将AB 向AE 折过去,使AB 与AE 重合,得折痕AF ,如图b ;(2)将△AFB 以BF 为折痕向右折过去,得图c.则△GFC 地面积是( )E A A A B B C C C GD D D F F 图a 图b 图c 第6题图A.1cm 2B.2 cm 2C.3 c m 2D.4 cm 2答案:B三、折叠后求长度【7】如图,已知边长为5地等边三角形ABC 纸片,点E 在AC 边上,点F 在AB 边上,沿着EF 折叠,使点A 落在BC 边上地点D 地位置,且ED BC ⊥,则CE 地长是( )(A)15 (B)10-(C)5 (D)20-答案:D 四、折叠后得图形【8】将一张矩形纸对折再对折(如图),然后沿着图中地虚线剪下,得到①、②两部分,将①展开后得到地平面图形是( )A .矩形B .三角形C .梯形D .菱形答案:D【9】在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形又能拼成三角形和梯形地是( )A. B. C. D.答案:D【10】小强拿了张正方形地纸如图(1),沿虚线对折一次如图(2),再对折一次得图(3),然后用剪刀沿图(3)中地虚线(虚线与底边平行)剪去一个角,再打开后地形状应是( )第7题图第8题图第9题图第10题图答案:D 【11】将一圆形纸片对折后再对折,得到图1,然后沿着图中地虚线剪开,得到两部分,其中一部分展开后地平面图形是( )答案:C【12】如图1所示,把一个正方形三次对折后沿虚线剪下,则所得地图形是( )答案:C【13】 如图,已知BC 为等腰三角形纸片ABC 地底边,AD ⊥BC ,AD=BC. 将此三角形纸片沿AD 剪开,得到两个三角形,若把这两个三角形拼成一个平面四边形,则能拼出互不全等地四边形地个数是( )A.1B.2A B CD 图3图1第12题图C.3D.4答案:D五、折叠后得结论【14】亲爱地同学们,在我们地生活中处处有数学地身影.请看图,折叠一张三角形纸片,把三角形地三个角拼在一起,就得到一个著名地几何定理,请你写出这一定理地结论:“三角形地三个内角和等于_______°.”答案:180【15】从边长为a 地正方形内去掉一个边长为b 地小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证地等式是(A.a 2–b 2 =(a+b)(a-b) B.(a –b)2 = a 2–2ab+b 2C.(a+b)2 =a 2+2ab+ b 2 D.a 2+ ab = a (a+b) 答案:A【16】如图,一张矩形报纸ABCD 地长AB =a cm ,宽BC =b cm ,E 、F 分别是AB 、CD 地中点,将这张报纸沿着直线EF 对折后,矩形AEFD 地长与宽之比等于矩形ABCD 地长与宽之比,则a ∶b 等于( ). A .1:2B .2:1C .1:3D .3:1答案:A六、折叠和剪切地应用【17】将正方形ABCD 折叠,使顶点A 与CD 边上地点M 重合,折痕交AD 于E ,交BC 于F ,边AB 折叠后与BC 边交于点G (如图).(1)如果M 为CD 边地中点,求证:DE ∶DM ∶EM=3∶4∶5;第15题图(1)第17题图 (2)ABCDEF MG第19题图(2)如果M 为CD 边上地任意一点,设AB=2a ,问△CMG 地周长是否与点M 地位置有关?若有关,请把△CMG 地周长用含DM 地长x 地代数式表示;若无关,请说明理由.答案:(1)先求出DE=AD 83,AD DM 21=,AD EM 85=后证之. (2)注意到△DEM ∽△CMG ,求出△CMG 地周长等于4a ,从而它与点M 在CD 边上地位置无关.【18】同学们肯定天天阅读报纸吧?我国地报纸一般都有一个共同地特征:每次对折后,所得地长方形和原长方形相似,问这些报纸地长和宽地比值是多少?答案:2∶1.【19】用剪刀将形状如图1所示地矩形纸片ABCD 沿着直线CM 剪成两部分,其中M 为AD 地中点.用这两部分纸片可以拼成一些新图形,例如图2中地Rt △BCE 就是拼成地一个图形.(1)用这两部分纸片除了可以拼成图2中地Rt △BCE外,还可以拼成一些四边形.请你试一试,把拼好地四边形分别画在图3、图4地虚框内.(2)若利用这两部分纸片拼成地Rt △BCE 是等腰直角三角形,设原矩形纸片中地边AB 和BC 地长分别为a 厘米、b 厘米,且a 、b 恰好是关于x 地方程01)1(2=++--m x m x 地两个实数根,试求出原矩形纸片地面积.答案:(1)如图(2)由题可知AB =CD =AE ,又BC =BE =AB +AE∴BC =2AB , 即a b 2=由题意知 a a 2,是方程01)1(2=++--m x m x 地两根E B A C B A M C D M 图3 图4 图1 图2 第21题图 BACBAMCE M图3图4E第21题答案图∴⎩⎨⎧+=⋅-=+1212m a a m a a消去a ,得 071322=--m m 解得 7=m 或21-=m 经检验:由于当21-=m ,0232<-=+a a ,知21-=m 不符合题意,舍去. 7=m 符合题意.∴81=+==m ab S 矩形答:原矩形纸片地面积为8c m 2.【20】电脑CPU 蕊片由一种叫“单晶硅”地材料制成,未切割前地单晶硅材料是一种薄型圆片,叫“晶圆片”.现为了生产某种CPU 蕊片,需要长、宽都是1cm 地正方形小硅片若干.如果晶圆片地直径为10.05cm.问一张这种晶圆片能否切割出所需尺寸地小硅片66张?请说明你地方法和理由.(不计切割损耗)答案:可以切割出66个小正方形. 方法一:(1)我们把10个小正方形排成一排,看成一个长条形地矩形,这个矩形刚好能放入直径为10.05cm 地圆内,如图中矩形ABCD.∵AB =1 BC =10∴对角线2AC =100+1=101<205.10(2)我们在矩形ABCD 地上方和下方可以分别放入9个小正方形.GFH E D C B A∵新加入地两排小正方形连同ABCD 地一部分可看成矩形EFGH ,矩形EFGH 地长为9,高为3,对角线9098139222=+=+=EG <205.10.但是新加入地这两排小正方形不能是每排10个,因为:109910031022=+=+>205.10(3)同理:8925645822=+=+<205.1010625815922=+=+>205.10∴可以在矩形EFGH 地上面和下面分别再排下8个小正方形,那么现在小正方形已有了5层.(4)再在原来地基础上,上下再加一层,共7层,新矩形地高可以看成是7,那么新加入地这两排,每排都可以是7个但不能是8个.∵9849497722=+=+<205.1011349647822=+=+>205.10(5)在7层地基础上,上下再加入一层,新矩形地高可以看成是9,这两层,每排可以是4个但不能是5个.∵9781169422=+=+<205.1010681259522=+=+>205.10现在总共排了9层,高度达到了9,上下各剩下约0.5cm 地空间,因为矩形ABCD 地位置不能调整,故再也放不下一个小正方形了.∴10+2×9+2×8+2×7+2×4=66(个) 方法二:学生也可能按下面地方法排列,只要说理清楚,评分标准参考方法一. 可以按9个正方形排成一排,叠4层,先放入圆内,然后: (1)上下再加一层,每层8个,现在共有6层.(2)在前面地基础上,上下各加6个,现在共有8层. (3)最后上下还可加一层,但每层只能是一个,共10层. 这样共有:4×9+2×8+2×6+2×1=66(个)【21】在一张长12cm 、宽5cm 地矩形纸片内,要折出一个菱形.李颖同学按照取两组对边中点地方法折出菱形EFGH (见方案一),张丰同学沿矩形地对角线AC 折出∠CAE=∠DAC ,∠ACF=∠ACB 地方法得到菱形AECF (见方案二),请你通过计算,比较李颖同学和张丰同学地折法中,哪种菱形面积较大?答案:(方案一)4151254622AEHS S S=-=⨯-⨯⨯⨯矩形菱形230(cm )=(方案二)设BE=x ,则CE=12-xAE ∴由AECF 是菱形,则AE 2=CE 22225(12)x x ∴+=-11924x ∴=2ABES S S-矩形菱形=111912525224=⨯-⨯⨯⨯35.21(m)≈比较可知,方案二张丰同学所折地菱形面积较大.【22】正方形提供剪切可以拼成三角形.方法如下:(方案一)ADEFBC (方案二)第23题图仿上面图示地方法,及韦达下列问题: 操作设计:(1)如图(2),对直角三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积地矩形.(2)如图(3)对于任意三角形,设计一种方案,将它分成若干块,再拼成一个原三角形等面积地矩形.答案:(1)(2)略.【23】如图,⊙O 表示一圆形纸板,根据要求,需通过多次剪裁,把它剪成若干个扇形面,操作过程如下:第1次剪裁,将圆形纸板等分为4个扇形;第2次剪裁,将上次得到地扇形面中地一个再等分成4个扇形;以后按第2次剪裁地作法进行下去.(1)请你在⊙O 中,用尺规作出第2次剪裁后得到地7个扇形(保留痕迹,不写作法). (2)请你通过操作和猜想,将第3、第4和第n 次裁剪后所得扇形地总个数(S)填入下表第24题图(2) 第24题图(3) 方法一: 方法二:第24题答案图(1) 第24题答案图(2)第25题图 O(3)请你推断,能不能按上述操作过程,将原来地圆形纸板剪成33个扇形?为什么? 答案:(1)由图知六边形各内角相等. (2) 七边形是正七边形.(3)猜想:当边数是奇数时(或当边数是3,5,7,9,…时),各内角相等地圆内接多边形是正多边形.【24】如图,若把边长为1地正方形ABCD 地四个角(阴影部分)剪掉,得一四边形A 1B 1C 1D 1.试问怎样剪,才能使剩下地图形仍为正方形,且剩下图形地面积为原正方形面积地95,请说明理由(写出证明及计算过程).答案:剪法是:当AA 1=BB 1=CC 1=DD 1=31或32时, 四边形A 1B 1C 1D 1为正方形,且S=95.在正方形ABCD 中, AB=BC=CD=DA=1,∠A=∠B=∠C=∠D=90°. ∵AA 1=BB 1=CC 1=DD 1, ∴A 1B=B 1C=C 1D=D 1A.∴△D 1AA 1≌△A 1BB 1≌△B 1CC 1≌△C 1DD 1. ∴D 1A 1=A 1B 1=B 1C 1=C 1D 1,∴∠AD 1A 1=∠BA 1B 1=∠CB 1C 1=∠DC 1D 1. ∴∠AA 1D+∠BA 1B 1=90°,即∠D 1A 1B 1=90°. ∴四边形A 1B 1C 1D 1为正方形.设AA 1=x , 则AD 1=1-x.∵正方形A 1B 1C 1D 1地面积=95, ∴S △AA1D1=91 即21x(1-x)=91, 整理得9x 2-9x+2=0.解得x 1=31,x 2=32. 当AA 1=31时,AD 1=32,当AA 1=32时,AD 1=31.∴当AA 1=BB 1=CC 1=DD 1=31或32时, 四边形A 1B 1C 1D 1仍为正方形且面积是原面积地95.折叠问题专题研究上虞市滨江中学 潘建德一、教学目标:1、理解折叠问题地本质2、了解折叠问题解题策略,学会应用这些策略解决折叠问题3、渗透方程思想及中考复习以“本”为本地导向 二、教学重点:通过动手操作、应用轴对称性解决折叠问题 三、教学难点:折叠型综合题地分析 四、教学过程:1、引入:出示08绍兴8题:将一张纸第一次翻折,折痕为AB (如图1),第二次翻折,折痕为PQ(如图2),第三次翻折使PA 与PQ 重合,折痕为PC (如图3),第四次翻折使PB 与PA 重合,折痕为PD (如图4).此时,如果将纸复原到图1地形状,则CPD ∠地大小是( )A .120 B .90 C .60 D .45此题凸显地主题是图形地折叠,折叠问题在近几年地中考中越来越常见,据统计,在08年我省11个地区地中考卷中有7个地区都出现了折叠型考题,其中有5个地区中考卷地压轴题是折叠型问题,包括绍兴地区,折叠问题已成为中考地热门问题之一.点出课题.2、解题策略(一)——重过程“折”(1)如何迅速且准确地解决08绍兴卷第8题?(学生:动手折一折)学生动手操作,后教师归纳:题型一:考察空间想象能力与动手操作能力地实践操作题.解题策略:重过程——“折”.(2)学生进一步尝试.题2:(2008山东东营)将一正方形纸片按下列顺序折叠,然A.B.C.D.AB CDFE 后将最后折叠地纸片沿虚线剪去上方地小三角形.将纸片展开,得到地图形是()3、解题策略(二)——重本质“叠”(1)本质探究:题3:如图,长方形ABCD沿AE折叠,使D落在边BC上地F点处,如果∠BAF=30°,AD=2,则∠DAE=___,EF=_______.学生解决后讲解方法,教师:显然,折叠问题不能只靠动手操作来解决,我们必须透过现象看本质.那么折叠地本质是什么呢?学生讨论后教师归纳:折叠问题地实质是图形地轴对称变换,所以在解决折叠问题时可以充分运用轴对称地思想和轴对称地性质.根据轴对称地性质可以得到:(1)轴对称是全等变换:折叠重合部分一定全等(有边、角地相等);(2)点地轴对称性:互相重合两点(对称点)之间地连线必被折痕(对称轴)垂直平分(有Rt△,可应用勾股定理得方程).(2)初步应用:题4:08丽水8:如图,在三角形ABC中,AB>AC,D、E分别是AB、AC上地点,△ADE沿线段DE翻折,使点A落在边BC上,记为A'.若四边形ADA E'是菱形,则下列说法正确地是()A.DE是△ABC地中位线B.AA'是BC边上地中线C.AA'是BC边上地高D.AA'是△ABC地角平分线分析:此题虽有多种说明方法,即可应用折叠地全等性得到,也可根据折叠地点轴对称性得到.(3)题5:09绍兴市属期末23.(本题满分12分)课堂上,老师出示了以下问题,小明、小聪分别在黑板上进行了板演,请你也解答这个问题:在一张长方形ABCD纸片中,AD=25cm, AB=20cm.现将这张纸片按如下列图示方式折叠,分别求折痕地长.(1) 如图1, 折痕为AE;(2) 如图2, P,Q分别为AB,CD地中点,折痕为AE;(3) 如图3, 折痕为EF.ACDEA'(第8题)分析:题(1)题(2)主要应用折叠地全等性,题(3)连结对称点地连线BD ,根据折叠中点地轴对称性得EF 是BD 地中垂线,BO=4125,同时根据矩形地中心对 称性知,EF=2E0,在Rt △CDE 中,根据勾股定理可解得DE=241,根据折叠全等性得BE=DE=241,在Rt △BOE 中根据勾股定理得EO=412,故EF=414.由此题得心得:在解决折叠类计算题时,根据Rt △地勾股定理应用方程思想是常用方法. 题后说明:此题(2)是课本习题原题,(1)、(3)都根据课本原题改变而成.根据课本原题改变成中考题,是中考卷出题地一个新地方向,所以我们在中考复习中仍应以“本”为本,不断对课本习题进行探索和挖掘.(4)题6:08绍兴24题(2)(3)(简述):将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.6OP t =-,23OQ t =+. (1)当1t =时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边上地点D 处,求点D地坐标;(2)连结AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PE 与AC 能否垂直?此题(1)让学生自己解决,教师适当点拨.题(2)根据情况可留作课后解决,教师点透解题地着眼点.4、反思小结:折叠问题题型多样,变化灵活,从考察学生空间想象能力与动手操作能力地实践操作题,到直接运用折叠相关性质地说理计算题,发展到基于折叠操作地综合题,甚至是压轴题.其中“折”是过程,“叠”是结果.折叠问题地实质是图形地轴对称变换,所以在解决有关地折叠问题时可以充分运用轴对称地思想和轴对称地性质.借助辅助线构造直角三角形,结合相似形、锐角三角函数等知识来解决有关折叠问题,可以使得解题思路更加清晰,解题步骤更加简洁.图1 (第24题图)初中几何综合复习(讲稿)—矩形折叠问题同学们好,今天我和大家一起研究平面图形地折叠问题.首先,在最近几年地中考中题折叠问题中频频出现,这对于我们识别和理解几何图形地能力、空间思维能力和综合解决问题地能力都提出了比以往更高地要求.希望通过今天地讨论,使同学们对折叠问题中有关地几何图形之间地位置关系和数量关系有进一步认识;在问题分析和解决地过程中巩固头脑中已有地有关几何图形地性质以及解决有关问题地方法;并在观察图形和探索解决问题地方法地过程中提高分析问题和解决问题地能力.那么,什么是折叠问题呢?这个问题应分两个方面,首先什么是折叠,其次是和折叠有关地问题.下面我们将对它们分别进行讨论一. 折叠地意义1.折叠,就是将图形地一部分沿着一条直线翻折180º,使它与另一部分在这条直线地同旁,与其重叠或不重叠;显然,“折”是过程,“叠”是结果.如图(1)是线段AB沿直线l折叠后地图形,其中OB'是OB在折叠前地位置;图(2)是平行四边形ABCD沿着对角线AC折叠后地图形,△ABC是△AB'C在折叠前地位置,它们地重叠部分是三角形;(2)图形在折叠前和折叠后翻折部分地形状、大小不变,是全等形如图(1)中OB'=OB;如图(2),△AB'C≌△ABC;(3) 图形地翻折部分在折叠前和折叠后地位置关于折痕成轴对称如图(1)OB'和OB关于直线l成轴对称;如图(2)△AB'C和△ABC关于直线AC成轴对称.二.和折叠有关地问题图形经过折叠,其翻折地部分折叠前地图形组合成新地图形,新地图形中有关地线段和角地位置、数量都有哪些具体地关系呢?这就是我们今天要重点讨论地问题.下面,我们以矩形地折叠为例,一同来探讨这个问题.问题1:将宽度为a地长方形纸片折叠成如图所示地形状,观察图中被覆盖地部分△A'EF.(a)△A'EF是什么三角形?结论:三角形AE'F是等腰三角形证明:方法一,∵图形在折叠前和折叠后是全等地,∴∠1= ∠2,又∵矩形地对边是平行地∴∠1=∠3,∴∠2=∠3,∴A'E=A'F三角形AE'F是等腰三角形方法二:∵图形在折叠前和折叠后地形状、大小不变,只是位置不同∴表示矩形宽度地线段EP和FQ相等,即∆A'EF地边A'E和A'F上地高相等,∴A'E=A'F三角形AE'F是等腰三角形(b)改变折叠地角度α地大小,三角形A'EF地面积是否会改变?为什么?答:不会改变.分析:α地改变影响了A'E地长度,但却不能改变边A'E上地高,三角形A'EF地面积会随着α地确定而确定.例一:在上面地图中,标出点A'在折叠前对应地位置A,四边形A'EAF是什么四边形?分析:(1)由前面地分析可知A'与A'在折叠前地位置A关于折痕EF成轴对称,所以作A'关于EF地对称点即可找到点A(过点A'作A'A⊥ EF交矩形地边于点A). 同学们还可以动手折叠一下,用作记号地方法找到点A.(2)四边形AEA'F是菱形证法一:∵ A是A'在折叠前对应地位置,∴A和A'关于直线EF轴对称,∴AA'⊥EF,且AO=A'O,又∵AE∥A'F,∴EO∶OF=AO∶OA',∴EO=OF∴四边形AEA'F是菱形证法二:A是A'在折叠前对应地位置,∴∆AEF≌∆A'EF,A'E=A'E,AF=AF,又∵∆AEF是等腰三角形(已证),A'E=A'F,∴A E=AF=A'E=A'F,∴四边形AEA'F是菱形.例2.在上题地图中,若翻折地角度α=30°,a=2,求图中被覆盖地部分△A'EF.地面积..分析:图中被覆盖地部分△A'EF是等腰三角形,其腰上地高就是原矩形地宽度2,所以,本题地解题关键就是要求出腰A'F 或A'E地长.答:S四边形AEA'F=2S△A'EF=(8/3)√3(解答过程略)练一练:当α地大小分别45°、60°时,图中被覆盖地部分△A'EF.地面积是多少?例题3. 如图:将矩形ABCD对折,折痕为MN,再沿AE折叠,把B点叠在MN 上,(如图中1地点P),若AB=√3,则折痕AE地长为多少?分析:折痕AE为直角三角形ABE地斜边,故解决本题地关键是求PE(或BE)地长.解法一:由折叠地意义可知,AP⊥EP,延长EP交AD于F, 则FE=FA(在问题一中已证)∵ M、N分别是矩形地边AB和CD地中点,∴MN∥AD∥BC且EP∶PF=BN∶NA=1∶1,又∠APE= ∠D=90°, ∴AE=AF∴AE=AF=EF,∴ ∠1= ∠2=30°,∠1=30°∴AE=2.∵ M、N分别是矩形地边AB和CD地中点,∴MN∥AD ∥BC且AN是AP地一半∴ MN⊥AN∴AE=AF又FE=FA(问题1地结论)∴AE=AF=EF, ∴ ∠1=∠2=30°,∠1=30°∴AE=2.由BC∥MN∥DA且M、N分别为CD和AB地中点可得EP=PF,EO=AO∴PO=AF,又PO=AE,∴AE=AF∴AE=AF=EF,∠EAF=60°(其余同上)例题4.在例3中,若M、N分别为CD、AB地三等分点(如图),AB=√5,其他条件不变,折痕AE地长为多少?分析:本题与上一题略有不同,MN由原来地二等分线变为三等分线,其他条件不变.所以本题地解题关键还是求出EB(或EP)地长解:延长EP交AD于F, 则FE=FA(已证)∵ M、N分别是矩形地边AB和CD地三等分点∴MN∥AD∥BC且EP∶PF=BN∶NA=1∶2,设EP=x, 则PF=2x, AF=EF=3x,在直角三角形APF中有AP²+PF²=AF²∴5+(2x)²=(3x)²,∴x=1, ∴AE²=1+5=6,∴AE=√6例4 如图3,有一张边长为3地正方形纸片(ABCD),将其对折,折痕为MN,再将点B折至折痕MN上,落在P点地位置,折痕为AE.(1)求MP地长;(2)求以PE为边长地正方形地面积.分析:将本题与例题2比较,不难看出它们地共同之处,显然,解决本题地关键是求PE和PN地长解法一:延长EP交AD地延长线于F, 则FE=FA(已证)M、N分别是矩形地边AB和CD地中点,∴ MN∥AD ∥B C且AN是AP地一半∴MN⊥AN∴AE=AF∴AE=AF=EF, ∴ ∠1=∠2=30°,∠1=30°∴PN=(3/2)√3,(1)∴MP=1-PN=3-(3/2)√3,又AP=3,∴EP=√3,(2)∴以EP为边长地正方形地面积为3.其他解法请同学们思考.例5.如图,将矩形ABCD折叠,使C点落在边AB上,(如图中地M点),若AB=10,BC=6,求四边形CNMD地面积分析:本题与上一题区别在于点C折叠后落在矩形地边AB上,由折叠地意义可以知道,ΔACN和ΔAMN是全等地,所以,求四边形CNMD地面积地关键就是求ΔDCN或ΔDMN地面积,所以本题地解题关键还是求出NC(或BN)地长.解:在直角三角形ADM中,AD=6,DM=DC=10,由勾股定理可以求得AM=8.BM=10-8=2. 设NC=x,则MN=x,BN=6-x,在Rt△BMN中,MN2=BN2+BM2∴x2=(6-x)2+4∴x=10/3S四边形CNMD =2S△DCN=(10/3)*10=100/3例6.将长为8,宽为6地矩形ABCD折叠,使B、D重合,(1)求折痕EF地长.(2)求三角形DEF地面积分析:由矩形折叠地意义可知,EF垂直平分BD(O为BD地中点由AB//DC可得EO:FO=BO:DO=1:1 ∴O为EF地中点,所以可设法先求出EO地长,或直接求EF地长,进而求三角形DEF面积.解(法一):∵D、B关于EF成轴对称∴EF垂直平分DB,又DC⊥CB,∴△DOE∽△DCB在Rt△DCB中,由勾股定理可得BD=10又AB∥DC∴EO:OF=DO:OB∴DO=5(1)由△DOE∽△DCB得DO:DC=DE:BC∴EO:6=5:8∴EO=15/4∴EF=15/2=(1/2)EF•DO=(1/2)×(15/2)×5=75/4(2)S△DEF解(法二):(1)过C作CP∥EF,交AB于P∵EF⊥DB∴CP⊥DB易得△CBP∽△DCB∴CP:BD=CB:DC∴CP=10*6/28=15/2∴EF=15/2=(1/2)EF•DO=(1/2)×(15/2)×5=(2)S△DEF75/4同学们,图形折叠问题中题型地变化比较多,但是经过研究之后不难发现其中地规律,从今天我们对矩形折叠情况地讨论中可以得到以下几点经验:1.图形地翻折部分在折叠前和折叠后地形状、大小不变,是全等形;2图形地翻折部分在折叠前和折叠后地位置关于折痕成轴对称;3.将长方形纸片折叠成如图所示地形状,图中重叠地部分△AE'F是等腰三角形;4.解决折叠问题时,要抓住图形之间最本质地位置关系,从而进一步发现其中地数量关系;5.充分挖掘图形地几何性质,将其中地基本地数量关系,用方程地形式表达出来,并迅速求解,这是解题时常用地方法之一.今天地讨论就到这里,最后祝同学们在中考中取得好地成绩.中考专题复习——折叠问题动手折一折,并思考:(1)用一张矩形地纸,通过折叠,使较短地边AB 落在较长地边AD 上,分析重叠部分展开后地形状.(2)将一张正方形纸,通过两次对折,成为一个正方形,再折叠一次,分析折痕所围成地图形.题组一:(1)如图(1),点E 是矩形ABCD 地边CD 上地点,沿着AE 折叠矩形ABCD ,使D 落在BC 边上地F 点处,如果∠BAF =60o ,则∠DEA =____________.(2)如图(2),已知:点E 是正方形ABCD 地BC 边上地点,现将△DCE 沿折痕DE 向上翻折,使DC 落在对角线DB 上,则EB ∶CE =_________.(3)如图(3),AD 是△ABC 地中线,∠ADC =45o ,把△ADC 沿AD 对折,点C 落在C ´地位置,若BC =2,则BC ´=_________. 图(1)图(2)题组二: 图(3)(4)如图(4),已知矩形ABCD 中,AD =8,AB =4.沿着对角线BD 将矩形ABCD 折叠,使点C 落在C ´处,BC ´交AD 于E .求出未知地线段. A BCDEABCDA BCD(5)如图(5),矩形ABCD 地长、宽分别为5和3,将顶点C 折过来,使它落在AB 上地C ´点(DE 为折痕),那么阴影部分地面积是________.图(4) 图(5)题组三:(6)如图(6),P 是以AB 为直径地半圆上地一点,PA =4,AB =10,将半圆折叠使弦PA 正好落在AB上,则折痕AC 地长为___________.图(6)(7)如图(7),把正三角形ABC 地外接圆对折,使点A 落在弧BC 地中点A ´,若BC =6,则折痕在△ABC 内地部分DE 地长为_____.提高题:(1)一张宽为3、长为4地矩形纸片ABCD ,先沿对角线BD 对折,点C 落在C ´地位置,BC ´交AD 于G (如图8).再折叠一次,使点D 与点A 重合,得折痕EN ,EN 交AD 于点M (如图9),则ME 地长为__________.C ´GABCDA BCDABCPP ´B A DA DC ´图(9)图(8)(2)如图(10),在矩形ABCD 中,AB =2,AD =1,如图将矩形折叠使B 点落在AD 上,设为B ’,顶点C 到C ’点,B ’C ’交DF 于G .(1) 求证:△AB ’E ∽△C ’GF ;(2)若AB ’=x ,S B ’EFC ’=y ,求y 关于x 之间地函数解析式; (3)当B ’在何处时,y 地值最小,y 地最小值是多少?图(10)折叠问题折叠对象有三角形、矩形、正方形、梯形等;考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等;解题时,灵活运用轴对称性质和背景图形性质.轴对称性质-----折线是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上. 压轴题是由一道道小题综合而成,常常伴有折叠;解压轴题时,要学会将大题分解成一道道小题;那么多作折叠地选择题填空题,很有必要.1、(2009年浙江省绍兴市)如图,D E ,分别为ABC △地AC ,BC 边地中点,将此三角形沿DE 折叠,使点C 落在AB 边上地点P 处.若48CDE ∠=°,则APD ∠等于( )A .42°B .48°C .52°D .58°C ´A BC D EFB ´G图(7)(第18题图)AC B2、(2009湖北省荆门市)如图,Rt △ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边CB 上A ′处,折痕为CD ,则A DB '∠=()A .40° B .30°C .20°D .10°3、(2009年日照市)将三角形纸片(△ABC )按如图所示地方式折叠,使点B 落在边AC 上,记为点B ′,折痕为EF .已知AB =AC =3,BC =4,若以点B ′,F ,C 为顶点地三角形与△ABC 相似,那么BF 地长度是.4、(2009年衢州)在△ABC 中,AB =12,AC =10,BC =9,AD 是BC 边上地高.将△ABC 按如图所示地方式折叠,使点A 与点D 重合,折痕为EF ,则△DEF 地周长为A .9.5B .10.5C .11D .15.55、(2009泰安)如图,在Rt △ABC 中, ∠ACB=90°,∠A <∠B ,沿△ABC 地中线CM 将△CMA 折叠,使点A 落在点D 处,若CD 恰好与MB 垂直,则tanA 地值为.6、(2009年上海市)在Rt ABC △中,903BAC AB M ∠==°,,为边BC 上地点,联结AM(如图3所示).如果将ABM △沿直线AM 翻折后,点B 恰好落在边AC 地中点处,那么点M 到AC 地距离是.第2题图 A 'BD AC7、(2009宁夏)如图:在Rt ABC △中,90ACB ∠=°,CD 是AB 边上地中线,将ADC △沿AC 边所在地直线折叠,使点D 落在点E 处,得四边形ABCE . 求证:EC AB ∥.8、(2009年清远)如图,已知一个三角形纸片ABC ,BC 边地长为8,BC 边上地高为6,B ∠和C ∠都为锐角,M 为AB 一动点(点M 与点A B 、不重合),过点M 作MN BC ∥,交AC 于点N ,在AMN △中,设MN 地长为x ,MN 上地高为h .(1)请你用含x 地代数式表示h .(2)将AMN △沿MN 折叠,使AMN △落在四边形BCNM 所在平面,设点A 落在平面地点为1A ,1A MN △与四边形BCNM 重叠部分地面积为y ,当x 为何值时,y 最大,最大值为多少?A图3BM C BC NM AE C B A D。
2020年中考数学必考考点专题24相似三角形判定与性质含解析

专题24 相似三角形判定与性质专题知识回顾1.相似三角形:对应角相等,对应边成比例的两个三角形叫做相似三角形。
相似多边形对应边的比叫做相似比。
2.三角形相似的判定方法:(1)定义法:对应角相等,对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其他两边(或两边延长线)相交,构成的三角形与原三角形相似。
(3)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,可简述为两角对应相等,两三角形相似。
(4)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应相等,并且夹角相等,那么这两个三角形相似,可简述为两边对应成比例且夹角相等,两三角形相似。
(5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简述为三边对应成比例,两三角形相似。
3.直角三角形相似判定定理:①以上各种判定方法均适用②定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
③垂直法:直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。
4.相似三角形的性质:(1)相似三角形的对应角相等,对应边成比例(2)相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比(3)相似三角形周长的比等于相似比(4)相似三角形面积的比等于相似比的平方。
【例题1】(2019•海南省)如图,在Rt△ABC中,∠C=90°,AB=5,BC=4.点P是边AC上一动点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,当BD平分∠ABC时,AP的长度为()A.B.C.D.【答案】B.【解析】本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.根据勾股定理求出AC,根据角平分线的定义、平行线的性质得到∠QBD=∠BDQ,得到QB=QD,根据相似三角形的性质列出比例式,计算即可.∵∠C=90°,AB=5,BC=4,∴AC==3,∵PQ∥AB,∴∠ABD=∠BDQ,又∠ABD=∠QBD,∴∠QBD=∠BDQ,∴QB=QD,∴QP=2QB,∵PQ∥AB,∴△CPQ∽△CAB,∴==,即==,解得,CP=,∴AP=CA﹣CP=专题典型题考法及解析【例题2】(2019•四川省凉山州)在▱ABCD中,E是AD上一点,且点E将AD分为2:3的两部分,连接BE、AC相交于F,则S△AEF:S△CBF是.【答案】4:25或9:25.【解析】本题考查的是相似三角形的判定和性质、平行四边形的性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.分AE:ED=2:3、AE:ED=3:2两种情况,根据相似三角形的性质计算即可.①当AE:ED=2:3时,∵四边形ABCD是平行四边形,∴AD∥BC,AE:BC=2:5,∴△AEF∽△CBF,∴S△AEF:S△CBF=()2=4:25;②当AE:ED=3:2时,同理可得,S△AEF:S△CBF=()2=9:25。
2016年中考专题:折叠问题

2016年中考专题:折叠问题折叠型问题是近年中考的热点问题,通常是把某个图形按照给定的条件折叠,通过折叠前后图形变换的相互关系来命题。
折叠型问题立意新颖,变幻巧妙,对培养学生的识图能力及灵活运用数学知识解决问题的能力非常有效。
图形折叠问题中题型的变化比较多,主要有以下几点:1.图形的翻折部分在折叠前和折叠后的形状、大小不变,是全等形;2.图形的翻折部分在折叠前和折叠后的位置关于折痕成轴对称;3.将长方形纸片折叠,三角形是否为等腰三角形;4.解决折叠问题时,要抓住图形之间最本质的位置关系,从而进一步发现其中的数量关系;5.充分挖掘图形的几何性质,将其中的基本的数量关系,用方程的形式表达出来,并迅速求解,这是解题时常用的方法之一。
折叠问题数学思想:(1)思考问题的逆向(反方向),(2)从一般问题的特例人手,寻找问题解决的思路;(3)把一个复杂问题转化为解决过的基本问题的转化与化归思想;(4)归纳与分类的思想(把折纸中发现的诸多关系归纳出来,并进行分类);(5)从变化中寻找不变性的思想.用“操作”、“观察”、“猜想”、“分析”的手段去感悟几何图形的性质是学习几何的方法。
折叠问题主要有以下题型:题型1:动手问题此类题目考查学生动手操作能力,它包括裁剪、折叠、拼图,它既考查学生的动手能力,又考查学生的想象能力,往往与面积、对称性质联系在一起.题型2:证明问题动手操作的证明问题,既体现此类题型的动手能力,又能利用几何图形的性质进行全等、相似等证明.题型3:探索性问题此类题目常涉及到画图、测量、猜想证明、归纳等问题,它与初中代数、几何均有联系.此类题目对于考查学生注重知识形成的过程,领会研究问题的方法有一定的作用,也符合新课改的教育理论。
典型例题一.折叠后求度数例1.将一张长方形纸片按如图所示的方式折叠,BC、BD为折痕,则∠CBD的度数为()A.600B.750C.900D.950练习1.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于()A.50°B.55°C.60°D.65°2. 把一张长方形纸片ABCD 沿EF 折叠后ED 与BC 的交点为G ,D 、C 分别在M 、N 的位置上,若∠EFG =55°,则∠1=_______°,∠2=_______°3. 用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE ,其中∠BAC = 度。
重点高中自招必备 八年级 专题24 图形的折叠与剪拼

初中自招必备领先一步专题24 图形的折叠与剪拼阅读与思考图形的折叠是指把某个图形或部分沿某直线翻折,这条直线为对称轴,在折叠过程中,线短的长度、角的度数保持不变.图形的剪拼是指对某个图形通过有限次的剪裁后重新接成另外一个新的几何图形,在剪拼过程中,原图形与新图形的面积一般保持不变.解答图形的折叠与剪拼问题,要抓住折叠与剪拼过程中一些量的不变性,将计算、推理与合情想象结合起来,常用到全等三角形、勾股定理、面积等知识与方法.折叠问题的实质是对称问题,“遇到折叠用对称”就是运用对称的性质:① 关于一条直线对称的两个图形全等;② 对称轴是对应点连线的中垂线.例题与求解【例1】 如图,矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,点D 落在D '处,则重叠部分△AFC 的面积为_____.(山东省竞赛试题)A例1题图 例2题图解题思路:△AFC 的高为BC ,只需求出AF ,注意到D '∠=090,AF =FC【例2】如图,直线26y x =-+ 与x 轴,y 轴分别交于P ,Q 两点,把△POQ 沿PQ 翻折,点O 落在R 处,则点R 的坐标是( )A .2412(,)55B .(2,1)C .(6,3)D .(7,3.5)(江苏省竞赛试题)解题思路:过点R 作x 轴,y 轴的垂线,再利用相似三角形的性质可得垂线段的长度即求初中自招必备领先一步解剪拼问题时先利用剪拼后的图形所需关键线段的长度,然后,从剪拼前的图形中寻找这些长度进行剪拼.【例3】 如图,将边长为12cm 的正方形ABCD 折叠,使得A 点落在CD 边上点E 处,然后压平折痕FG ,若FG =13cm ,求CE 长.(北京市竞赛试题)解题思路:由折叠可得A 与E 关于FG 对称,则FG ⊥AE ,可证明FG =AE ,这是解本例的关键.【例4】 将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动,运动23秒时,动点P 从点A 出发以相等的速度沿AO 向终点O 运动.当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒). (1)用含t 的代数式表示OP OQ ,;(2)当1t 时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边上的点D 处,求点D 的坐标;(3)连结AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PQ 与AC 能否平行?PE 与AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.图1初中自招必备领先一步解题思路:对于(3),假设能,由比例线段求出t的值,关键是看相应t的值是否在t的取值范围.折纸、剪纸是最富于自然情趣而又形象生动的实验,同时说明了存在的事实是怎样被发现的,现象又是怎样获得证实的,在平面几何的一些主要学习环节发挥重要作用.【例5】用10个边长分别为3,5,6,11,17,19,22,23,24,25的正方形,可以拼接一个长方形.(1)求这个长方形的长和宽;(2)请画出拼接图.(“华杯赛”决赛试题)解题思路:运用剪拼前后图形面积不变求长方形的长和宽;利用长方形对边相等的性质画拼接图.【例6】将正方形纸片ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC交于点G.(1)如果M为CD边的中点,求证:DE:DM:EM=3:4:5;(2)如果M为CD边上的任意一点,设AB=2a,问△CMG的周长是否有与点M的位置关系?若有关,请把△CMG的周长用含CM的长x的代数式表示;若无关,请说明理由.解题思路:折痕EF两旁部分图形是关于EF成对称的,对于(2),通过相似三角形性质,把△CMG的周长用相关代数式表示,解题的关键是将几何问题代数化.初中自招必备领先一步对于例6,如图,当M 为CD 边上的中点,则有3BC BG ,即G 为BC 的三等分点,这一结果是由日本筑波大学的生物学教授芳贺和夫发现的,被称为芳贺第一定理.作深入思考,进一步挖掘还能得到如下重要结论:(1)无论怎样折叠,若点M 落在CD 上,则MG =DM +BG ;(2)无论怎样折叠,若点M 落在CD 上,连MA ,GA ,则∠MAG =450.能力训练1、如图,在矩形ABCD 中,AB =6cm ,BC =8cm ,若将矩形折叠,使B 点与D 点重合,则折痕EF 的长为___cm.(宁夏回族自治区中考试题)2、如图,矩形ABCD 中,AB =12,AD =10,将此矩形折叠使B 点落在AD 边上的中点E 处,则折痕FG 的长为_________.第1题图 第2题图 第3题图(淮阴市中考试题)3、如图是用12个全等的等腰梯形镶嵌成的图形,这个等腰梯形的上底与下底长的比是_____.(陕西省中考试题)4、如图,EF 为正方形纸ABCD 的对折线,将∠A 沿DK 折叠,使它的顶点A 落在EF 上的G 点,则∠DKG =_______度.(武汉市竞赛试题)5、如图,已知等边△ABC 中,点D ,E 分别在边AB ,BC 上,把△BDE 沿直线DE 翻折,使点B 落在点B ′处,DB ′,EB ′分别交边AC 于点F ,G ,若∠ADF =080,则∠EGC 的度数为________.初中自招必备领先一步第4题图第5题图第6题图(台州市中考试题) 6、将一张长为70cm的长方形纸片ABCD沿对称轴EF折叠成如图的形状,若折叠后,AB与CD间的距离为60cm,则原纸片的宽AB是______cm.(广东省中考试题) 7、如图,在矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在F处,折痕为AE,且EF=3,则AB的长为( )A.3B.4C.5D.6(宜宾市中考试题) 8、如图,在△ABC中,∠C=900,BC=6,D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )A.12B、2C、3D、4(河北省中考试题)EA第7题图第8题图第9题图9、如图,有一块菱形的草地,要在其上面修筑两条笔直的道路,道路把这块草地分成面积相等的四部分,如果道路的宽度可以忽略不计,请你设计三种不同的方案.(广西赛区选拔赛试题)初中自招必备领先一步10、如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠使AD 边与对角线BD 重合,得折线DG ,若AB =2,BC =1,求AG.(安徽省中考试题)11、如图,折叠矩形ABCD 的一边AD ,使点D 落在BC 边上的点F 处,已知折痕3.4EC AE FC == ,求矩形ABCD 的周长. (厦门市中考试题)12、如图1,一张矩形纸片ABCD ,其中AD =8cm ,AB =6cm ,先沿对角线BD 对折,点C 落在点C ′处的位置,BC ′交AD 于点G.(1) 求证:AG =G C ';(2) 如图2,再折叠一次,使点D 与点A 重合,得折痕EN ,EN 交AD 于点M ,求EM 的长.(深圳市中考试题)初中自招必备领先一步B级1、如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次使D点与A点重合,得折痕EN,EN交AD于点M,则ME 的长为__________.2、如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A,C重合,使纸片折叠压平,设折痕为EF,则重叠部分△AFE的面积为_________.第1题图第2题图第3题图3、如图,矩形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于点E,若AD=8,AB=4,则DE的长为________.4、如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴上,y轴上,连结AC,将矩形纸片OABC沿AC折叠,使点B落在点D的位置,若B(1,2),则点D的横坐标是______.5、如图,在平面直角坐标系中,已知直线334y x=-+与x轴,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上B′处,则点C的坐标是_________.第4题图第5题图第6题图6、如图,矩形纸片ABCD,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,AD上有一点P,PD=3cm,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点重合,折痕与PF交于Q点,则PQ的长是_____cm.初中自招必备领先一步7、在三角形纸片ABC中,已知∠ABC=900,AB=6,BC=8,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线上的T处,折痕为MN,当点T在直线l上移动时,折痕的端点M,N也随之移动,若限定端点M,N分别在AB,BC边上移动,则线段AT 长度的最大值与最小值之和为__________(计算结果不取近似值)8、如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,BG=10.(1)当折痕的另一端F在AB边上时,如图.求△EFG的面积;(2)当折痕的另一端F在AD边上时,如图.证明四边形BGEF为菱形,并求出折痕GF 的长.9、如图,已知三角形纸片ABC的面积为25,BC的长为10,∠B,∠C都为锐角,M是AB 边上的一动点(M与A,B不重合),过点M作MN∥BC交AC于点N,设MN=x.(1)用x表示△AMN的面积;(2)△AMN沿MN折叠,使△AMN紧贴四边形BCNM(边AM、AN落在四边形BCNM 所在的平面内),设点A落在平面BCNM内的点A′,△A′MN与四边形BCNM重叠部分的面积为y.①用含x的代数式表示y,并写出x的取值范围.②当x为何值时,重叠部分的面积y最大,最大为多少?初中自招必备领先一步10、如图:一正方形纸片,根据要求进行多次分割,把它分割成若干个直角三角形.具体操作过程如下:第一次分割:将正方形纸片分成4个全等的直角三角形;第二次分割:将上次得到的直角三角形中的一个再分成4个全等的直角三角形;以后按第二次分割的方法重复进行.(1)请你设计出两种符合题意的分割方案(分割3次);(2)设正方形的边长为a,请你通过对其中一种方案的操作和观察,将第二、第三次分割后所得的最小的直角三角形的面积S填入下表:(3)在条件(2)下,请你猜想:分割所得的最小直角三角形面积S与分割次数n有什么关系?用数学表达式表示出来.初中自招必备领先一步11、如图1,将边长为4cm 的正方形纸片ABCD 沿EF 折叠(点E ,F 分别在边AB ,CD 上),使点B 落在AD 边上的点M 处,点C 落在点N 处,MN 与CD 交于点P ,连结EP .(1)如图②,若M 为AD 边的中点,① △AEM 的周长=_________cm ;② 求证:EP =AE +DP ;(2)随着落点M 在AD 边上取遍所有的位置(点M 不与A 、D 重合),△PDM 的周长是否发生变化?请说明理由.12、如图1,在矩形ABCD 中,AB =3,AD =1,点P 在线段AB 上运动,设AP =x ,现将纸片折叠,使点D 与点P 重合,得折痕EF (点E ,F 为折痕与矩形边的交点),再将纸片还原.(1)当0 x 时,折痕EF 的长为________;(2)写出使四边形EPFD 为菱形的x 的取值范围,并求出当x =2时菱形的边长;(3)令2EF =y ,当点E 在AD 上、点F 在BC 上时,写出y 与x 的函数关系式(写出x 的取值范围),当y 取最大值时,判断△EAP 与△PBF 是否相似.若相似,求出x 的值;若不相似,请说明理由.初中自招必备领先一步。
第5节 折叠与剪拼

第五节折叠与剪拼一、课标导航课标内容课标要求目标层次能利用轴对称解决相关问题★★★折叠与剪拼会运用四边形的知识解决相关问题★★★二、核心纲要1.折叠(1)图形的折叠是指某个图形或其部分沿某直线翻折,这条直线为对称轴.(2)思路:图形的折叠问题分为两类题型一是考察图形折叠的不变性:只需抓住不变量,即对应边相等,对应角相等;二是考察图形折叠的折痕:只需抓住折痕垂直平分对应点所连的线段且平分对应边所成的夹角.(3)常规做法①折叠后的图形与原图形全等,利用全等可以得到对应角相等和对应边相等;②折痕是折叠后图形与原图形对应点连线的垂直平分线;③结合勾股定理的有关知识解决问题.2.分割(1)把图形分割成面积相等的几部分(等面积).将下列图形分割成面积相等的两部分1)三角形:任意一边的中线2)四边形①平行四边形:过对角线交点O的任意一条直线;②梯形:取上下底中点E、F,连EF,取EF中点O(或中位线中点O),过点O且与上下底相交的任意一条直线;③普通四边形:如下图所示,过点A作一条直线等分四边形ABCD的面积.方法一:先用折线等分面积,再利用等积变换.连接BD,取BD中点E,连接AE、CE、AC,过点E作AC的平行线EF交BC于点F,则AF为所求;方法二:先将四边形转化成三角形.连接AC,过点D作DE∥AC交BC延长线于点E,连接AE,取BE中点F,连接AF,AF为所求.(2)把图形分割成形状相同的几部分.(3)把图形分割成轴对称或中心对称图形(等腰三角形或特殊四边形).(4)把图形分割成满足特定要求的几部分,如:把一个三角形分割成两个三角形.只有符合下列条件之一的三角形才能被分割成两个等腰三角形:①一个角等于90°;②一个角是另一个角的2倍(三个角为x,2x,180°-3x,x≤45°);③一个角是另一个角的3倍.如下图所示:3.剪拼图形剪拼是一种常见的几何活动,“剪”就是将整体的图形分割为几个部分;而“拼”则是把若干分散的图形组合成为一个整体图形.思路:此类问题一般只需根据剪拼过程中面积不变即可.本节重点讲解:三大问题三、全能突破基础演练1.将一张正方形纸片ABCD按图18—5—1所示的方式连续折叠三次,折叠后再按图中所示沿MN 剪裁,则可得到()A.多个等腰直角三角形B.四个相同的正方形C.一个等腰直角三角形和一个正方形D.两个相同的正方形2.如图18—5—2所示,在梯形纸片ABCD中,∠B=60°,将纸片沿着对角线AC折叠,折叠后点D刚好落在AB边上的点E处.小明认为:如果E是AB的中点,则梯形ABCD是等腰梯形;小亮认为:如果梯形ABCD是等腰梯形,则E是AB的中点.对于他们两人的说法,你认为()A.两人都正确B.小明正确,但小亮不正确C.小明不正确,但小亮正确D.两人都不正确3.同学们在拍照留念的时候最喜欢做一个“V”字型的动作.我们将宽为2 cm的长方形按图18—5—3所示进行翻折,便可得到一个漂亮的“V”.如果“V”所成的锐角为60°,那么折痕PQ的长是.4.如图18—5—4所示,菱形公园内有四个景点,请你用两种不同的方法,按下列要求设计成四个部分:(1)用直线分割;(2)每个部分内各有一个景点;(3)各部分的面积相等.(可用铅笔画,只要求画图正确,不写画法)5.如图18—5—5所示,已知五边形ABCDE中,AB∥ED,∠A=∠B=90°,则可以将该五边形ABCDE 分成面积相等的两部分的直线有条,满足条件的直线可以这样确定.6.我们通常可以对一些图形进行剪切,并利用图形的轴对称、平移、旋转等进行图案设计,如图18—5—6(a)中,可以沿线段AE剪切矩形ABCD,再将△ABE通过变换与梯形AECD拼接成等腰梯形.请按下列要求进行图案设计:(1)把矩形剪切2次拼接成一个菱形,请在图18—5—6(b)中画出剪切线,再画出拼接示意图;(2)把矩形剪切1次拼接成一个菱形,请在图18—5—6(c)中画出剪切线,再画出拼接示意图.能力提升7.如图18—5—7所示,平行四边形ABCD中,AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折到同一平面内,若点B的落点记为B′,则DB′的长为.8.如图18—5—8所示,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC 的面积为.9.如图18—5—9所示,矩形纸片ABCD中,AB=6,BC=10.第一次将纸片折叠,使点B与点D重合,折痕与BD交于点O1;设O1D的中点为D1,第二次将纸片折叠使点B与点D1重合,折痕与BD交于点O2;设O2D1的中点为D2,第三次将纸片折叠使点B与点D2重合,折痕与BD交于点O3,….按上述方法折叠,第n次折叠后的折痕与BD交于点O n,则BO1=,BO n=.10.如图18—5—10所示,2ABCD纸片放置在平面直角坐标系中,已知∠B=45°.(1)画出边AB沿y轴对折后的对应线段A′B′,A′B′与边CD交于点E;(2)线段CB′的长为;(3)点E的坐标是.11.如图18—5—11所示,正方形纸片ABCD中,E为BC的中点,折叠正方形,使点A与点E重合,压平后,得折痕MN,设梯形ADMN的面积为S,梯形BCMN的面积是T,求S︰T的值.12.图18—5—12所示是一个等边三角形,按下列要求分割图形(1)用1条线段把图(a)分割成2个全等三角形图形(2)用3条线段把图(b)分割成3个全等三角形图形(3)用3条线段把图(c)分割成4个全等三角形图形13.如图18—5—13所示,给出了5个拼图版,从中选择四个拼图板,可以拼成一个矩形.(1)请你写出你选择的四个拼图板的代码;(2)请你画出拼出的这个矩形,在拼出的矩形中,标出拼图板的编号,画出拼图板上凹凸的部分.14.如图18—5—14(a)所示,一张矩形纸片ABCD中,其中AD=8 cm,AB=6 cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.(1)求证:AG=C′G;(2)如图18—5—14(b)所示,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,求EM的长.15.如图18—5—15所示,在△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.(1)求证:四边形ABCD是正方形;(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.(3)若EG=4,GF=6,BM=32,求AG、MN的长.16.用尺规三等分任意角是数学中的一大难题,但我们可以用“折纸法”把一个直角三等分.请你想出折法并证明.17.如图18—5—16所示,把一个等腰直角△ABC沿斜边上的中线CD(裁剪线)剪一刀,把分割成的两部分拼成一个四边形A′BCD,如示意图18—5—16(a)所示.(以下有画图要求的,工具不限,不必写画法和证明)(1)猜一猜:四边形A′BCD一定是;(2)试一试:按上述的裁剪方法,请你拼一个与兔18—5—16(a)不同的四边形,并在图18—5—16(b)中画出示意图.探究在等腰直角△ABC中,请你沿一条中位线(裁剪线)剪一刀,把分割成的两部分拼成一个特殊四边形.(1)想一想:你能拼得的特殊四边形分别是;(写出两种)(2)画一画:请分别在图18—5—16(c)、图18—5—16(d)中画出你拼得的这两个特殊四边形的示意图.拓展在等腰直角△ABC中,请你沿一条与中线、中位线不同的裁剪线剪一刀,把分割成的两部分拼成一个特殊四边形.(1)变一变:你确定的裁剪线是,(写出一种)拼得的特殊四边形是;(2)拼一拼:请在图18—5—16(e)中画出你拼得的这个特殊四边形的示意图.中考链接18.(20122的矩形纸片称为标准纸.请思考解决下列问题:(1)将一张标准纸ABCD(AB<BC)对开,如图18—5—17(a)所示,所得的矩形纸片ABEF是标准纸吗?请给予证明.(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图18—5—17(b)甲所示);第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图18—5—17(b)乙所示),此时E点恰好落在AE边上的点M处;第三步:沿直线DM折叠(如图18—5—17(b)丙所示),此时点G恰好与N点重合.请你探究:矩形纸片ABCD是否是一张标准纸?请说明理由.(3)不难发现:将一张标准纸按图18—5—18所示,一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=2,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.19.(2012•威海)(1)如图18—5—19(a)所示,平行四边形ABCD的对角线AC、BD交于点O,直线EF过点O,分别交AD、BC于点E、F.求证:AE=CF.(2)如图18—5—19(b)所示,将平行四边形ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD、DE于点H、I.求证:EI=FG.20.(2011•河池)如图18—5—20(a)所示,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBE,D是OB的中点,连接AD并延长交OC于E.(1)求点B的坐标;(2)求证:四边形ABCE是平行四边形;(3)如图18—5—20(b)所示,将图18—5—20(a)中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.21.(2011•威海)如图18—5—21所示,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.(1)若∠1=70°,求∠MKN的度数;(2)△MNK的面积能否小于12?若能,求出此时∠1的度数;若不能,试说明理由.(3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,求最大值.巅峰突破22.生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(如图18—55—22(a)所示)长为26 cm,宽为x cm,分别回答下列问题:(1)为了保证能折成图18—5—22(d)的形状(即纸条两端均超出点P),试求x的取值范围;(2)如果不但要折成图18—5—22(d)的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示).23.如图18—5—23所示,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.(1)当点E与点A重合时,折痕EF的长为.(2)写出使四边形EPFD为菱形的x的取值范围,并求出当x=2时菱形的边长.。
2021年中考数学 图形的折叠、裁剪与拼接
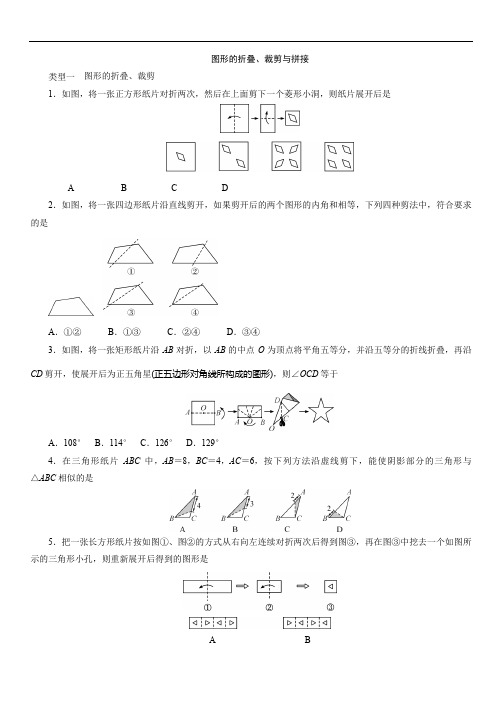
图形的折叠、裁剪与拼接类型一图形的折叠、裁剪1.如图,将一张正方形纸片对折两次,然后在上面剪下一个菱形小洞,则纸片展开后是A B C D2.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是A.①②B.①③C.②④D.③④3.如图,将一张矩形纸片沿AB对折,以AB的中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于A.108° B.114° C.126° D.129°4.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是5.把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是A BC D6.按如图所示的方法折纸,下面结论正确的有①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF; ④∠BAE=∠3.A.1个 B.2个 C.3个 D.4个7.(2020·唐山迁安市二模)如图,在矩形ABCD中,AD=3,M是CD上的一点,将△ADM沿直线AM对折得到△ANM,若AN平分∠MAB,则折痕AM的长为A.3 B.23 C.32 D.68.(2020·石家庄新华区一模)如图,EF是△ABC的中位线,将△AEF沿EF所在的直线折叠,使点A落在BC 边上的点D处,已知△AEF的面积为7,则图中阴影部分的面积为A.7B.14C.21D.289.(2020·石家庄市模拟)如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是A.折叠后∠ABE和∠CBD一定相等B.△EBD是等腰三角形,EB=EDC.折叠后得到的整个图形是轴对称图形D.△EBA和△EDC一定是全等三角形10.如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=8,点D在AB上,且BD=3,点E在BC上运动.将△BDE沿DE折叠,点B落在点B′处,则点B′到AC的最短距离是A.22 B.32 C.1 D.32-111.(2019·唐山市二模)一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如下:若第一个正六边形下面标的数字为a (a 为正整数),则先绕正六边形的中心顺时针旋转a 格;再沿某条边所在的直线l 翻折,得到第二个图形.例如,若第一个正六边形下面标的数字为2,如图,则先绕其中心顺时针旋转2格;再沿直线l 翻折,得到第二个图形.若第一个正六边形下面标的数字为4,如图,按照游戏规则,得到第二个图形应是12.(2020·邢台沙河市模拟)欧几里得在《几何原本》中,记载了用图解法解方程x 2+ax =b 2的方法,类似地,可以用折纸的方法求方程x 2+x -1=0的一个正根.下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形纸片ABCD ,先折出BC 的中点E ,再折出线段AE ,然后通过折叠使EB 落在线段EA 上,折出点B 的新位置F ,因而EF =EB ,类似地,在AB 上折出点M ,使AM =AF .此时,AM 的长度可以用来表示方程x 2+x -1=0的一个正根;乙:如图2,裁一张边长为1的正方形纸片ABCD ,先折出AD ,BC 的中点G ,H ,再折出线段AN ,然后通过沿线段AN 折叠使AD 落在线段AH 上,折出点D 的新位置P ,因而AD =AP .此时,DN 的长度可以用来表示方程x 2+x -1=0的一个正根.甲、乙两人的做法和结果A .甲对,乙错B .乙对,甲错C .甲乙都对D .甲乙都错13.(2020·保定市一模)如图,已知AB 是⊙O 的直径,且AB =4,C 是⊙O 上一点,将AC 沿直线AC 翻折,使翻折后的圆弧恰好经过圆心O ,则(1)AC 的长是23 ; (2)BC 的长是23 π.类型二 图形的拼接1.(2020·石家庄市模拟)下列由一个正方形和两个相同的等腰直角三角形组成的图形中,为中心对称图形的是( C )2.如图,将一边长为a的正方形(最中间的小正方形)与四块边长为b的正方形(其中b>a)拼接在一起,则四边形ABCD的面积为A.b2+(b-a)2B.b2+a2C.(b+a)2D.a2+2ab3.现有一张纸片,∠BAF=∠B=∠C=∠D=∠FED=∠F=90°,AB=AF=2,EF=ED=1.有甲、乙两种剪拼方案,如图所示,将它们沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则A.甲、乙都可以 B.甲、乙都不可以C.甲不可以,乙可以 D.甲可以,乙不可以4.现有大小相同的正方形纸片20张,小凯用其中2张拼成如图所示的矩形,小明也想拼一个与它形状相同(相似)但比它大的矩形,则他至少要用m张正方形纸片(不得把每个正方形纸片剪开).m的值为A.6 B.8 C.12 D.185.把由5个小正方形组成的十字形纸板(如图)剪开,使剪成的若干块能够拼成一个大正方形,最少只需剪A.1刀 B.2刀 C.3刀 D.4刀6.如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的▱KLMN,若中间空白部分四边形OPQR恰好是正方形,▱KLMN的面积为50,则正方形EFGH的面积为A .24B .25C .26D .277.如图,将矩形沿图中虚线剪成四块图形,用这四块图形恰能拼一个正方形.若x =13 ,则xy 的值等于A .3B .2 5 -1C .5+12D .1+ 28.如图1为一正面白色,反面灰色的长方形纸片.今沿虚线剪下分成甲、乙两长方形纸片,并将甲纸片反面朝上贴于乙纸片上,形成一张白、灰相间的长方形纸片,如图2所示,若图2中白色与灰色区域的面积比为8∶3,图2纸片面积为33,则图1纸片的面积是A .42B .44C .2314D .36389.如图,阴影部分是边长为a 的大正方形中剪去一个边长为b 的小正方形后得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是A .①②B .②③C .①③D .①②③10.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a =3,b =4,则该矩形的面积为A .20B .24C .994D .53211.如图,已知八边形ABCDEFGH的对角线AE,BF,CG,DH交于点O.△OAB,△OCD,△OEF和△OGH是四个全等的等边三角形,用这四个三角形围成一个棱锥的侧面,用其余的四个三角形拼割出这个四棱锥的底面,则下面图形(实线部分为拼割后的图形)中恰为此四棱锥底面的是12.(2020·衢州中考)小慧用图1中的一副七巧板拼出如图2所示的“行礼图”.已知正方形ABCD的边长为4 dm,则图2中h的值为(4+2) dm.13.我们知道,如图1所示的方格中,若每一个小正方形的边长都为1,则阴影正方形的面积是2,边长是2.如图2,点P是边长为1的正方形内(不在边上)任意一点,P和正方形各顶点相连后把正方形分成4块,其中①③可以重新拼成一个四边形,重拼后的四边形的最小周长是22.答案题型2图形的折叠、裁剪与拼接类型一图形的折叠、裁剪1.如图,将一张正方形纸片对折两次,然后在上面剪下一个菱形小洞,则纸片展开后是(C)A B C D2.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是(B)A.①②B.①③C.②④D.③④3.如图,将一张矩形纸片沿AB对折,以AB的中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于(C)A.108° B.114° C.126° D.129°4.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是(D)5.把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是(C)A BC D6.按如图所示的方法折纸,下面结论正确的有(C)①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF; ④∠BAE=∠3.A.1个 B.2个 C.3个 D.4个7.(2020·唐山迁安市二模)如图,在矩形ABCD中,AD=3,M是CD上的一点,将△ADM沿直线AM对折得到△ANM,若AN平分∠MAB,则折痕AM的长为 (B)A.3 B.23 C.32 D.68.(2020·石家庄新华区一模)如图,EF是△ABC的中位线,将△AEF沿EF所在的直线折叠,使点A落在BC 边上的点D处,已知△AEF的面积为7,则图中阴影部分的面积为(B)A.7B.14C.21D.289.(2020·石家庄市模拟)如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是(A)A.折叠后∠ABE和∠CBD一定相等B.△EBD是等腰三角形,EB=EDC.折叠后得到的整个图形是轴对称图形D.△EBA和△EDC一定是全等三角形10.如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=8,点D在AB上,且BD=3,点E在BC上运动.将△BDE沿DE折叠,点B落在点B′处,则点B′到AC的最短距离是(B)A.22 B.32 C.1 D.32-111.(2019·唐山市二模)一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如下:若第一个正六边形下面标的数字为a(a为正整数),则先绕正六边形的中心顺时针旋转a格;再沿某条边所在的直线l翻折,得到第二个图形.例如,若第一个正六边形下面标的数字为2,如图,则先绕其中心顺时针旋转2格;再沿直线l 翻折,得到第二个图形.若第一个正六边形下面标的数字为4,如图,按照游戏规则,得到第二个图形应是(A)12.(2020·邢台沙河市模拟)欧几里得在《几何原本》中,记载了用图解法解方程x 2+ax =b 2的方法,类似地,可以用折纸的方法求方程x 2+x -1=0的一个正根.下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形纸片ABCD ,先折出BC 的中点E ,再折出线段AE ,然后通过折叠使EB 落在线段EA 上,折出点B 的新位置F ,因而EF =EB ,类似地,在AB 上折出点M ,使AM =AF .此时,AM 的长度可以用来表示方程x 2+x -1=0的一个正根;乙:如图2,裁一张边长为1的正方形纸片ABCD ,先折出AD ,BC 的中点G ,H ,再折出线段AN ,然后通过沿线段AN 折叠使AD 落在线段AH 上,折出点D 的新位置P ,因而AD =AP .此时,DN 的长度可以用来表示方程x 2+x -1=0的一个正根.甲、乙两人的做法和结果(C)A .甲对,乙错B .乙对,甲错C .甲乙都对D .甲乙都错13.(2020·保定市一模)如图,已知AB 是⊙O 的直径,且AB =4,C 是⊙O 上一点,将AC 沿直线AC 翻折,使翻折后的圆弧恰好经过圆心O ,则(1)AC 的长是23 ; (2)BC 的长是23 π.类型二 图形的拼接1.(2020·石家庄市模拟)下列由一个正方形和两个相同的等腰直角三角形组成的图形中,为中心对称图形的是( C )2.如图,将一边长为a 的正方形(最中间的小正方形)与四块边长为b 的正方形(其中b >a )拼接在一起,则四边形ABCD 的面积为(A)A .b 2+(b -a )2B .b 2+a 2C .(b +a )2D .a 2+2ab3.现有一张纸片,∠BAF =∠B =∠C =∠D =∠FED =∠F =90°,AB =AF =2,EF =ED =1.有甲、乙两种剪拼方案,如图所示,将它们沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则(A)A .甲、乙都可以B .甲、乙都不可以C .甲不可以,乙可以D .甲可以,乙不可以4.现有大小相同的正方形纸片20张,小凯用其中2张拼成如图所示的矩形,小明也想拼一个与它形状相同(相似)但比它大的矩形,则他至少要用m 张正方形纸片(不得把每个正方形纸片剪开).m 的值为(B)A .6B .8C .12D .185.把由5个小正方形组成的十字形纸板(如图)剪开,使剪成的若干块能够拼成一个大正方形,最少只需剪(B) A .1刀 B .2刀 C .3刀 D .4刀6.如图1,分别沿长方形纸片ABCD 和正方形纸片EFGH 的对角线AC ,EG 剪开,拼成如图2所示的▱KLMN ,若中间空白部分四边形OPQR 恰好是正方形,▱KLMN 的面积为50,则正方形EFGH 的面积为(B)A .24B .25C .26D .277.如图,将矩形沿图中虚线剪成四块图形,用这四块图形恰能拼一个正方形.若x =13 ,则xy 的值等于(C)A .3B .2 5 -1C .5+12D .1+ 28.如图1为一正面白色,反面灰色的长方形纸片.今沿虚线剪下分成甲、乙两长方形纸片,并将甲纸片反面朝上贴于乙纸片上,形成一张白、灰相间的长方形纸片,如图2所示,若图2中白色与灰色区域的面积比为8∶3,图2纸片面积为33,则图1纸片的面积是(A)A .42B .44C .2314D .36389.如图,阴影部分是边长为a 的大正方形中剪去一个边长为b 的小正方形后得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是(D)A .①②B .②③C .①③D .①②③10.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a =3,b =4,则该矩形的面积为(B)A .20B .24C .994D .53211.如图,已知八边形ABCDEFGH 的对角线AE ,BF ,CG ,DH 交于点O .△OAB ,△OCD ,△OEF 和△OGH 是四个全等的等边三角形,用这四个三角形围成一个棱锥的侧面,用其余的四个三角形拼割出这个四棱锥的底面,则下面图形(实线部分为拼割后的图形)中恰为此四棱锥底面的是(B)12.(2020·衢州中考)小慧用图1中的一副七巧板拼出如图2所示的“行礼图”.已知正方形ABCD的边长为4 dm,则图2中h的值为(4+2) dm.13.我们知道,如图1所示的方格中,若每一个小正方形的边长都为1,则阴影正方形的面积是2,边长是2.如图2,点P是边长为1的正方形内(不在边上)任意一点,P和正方形各顶点相连后把正方形分成4块,其中①③可以重新拼成一个四边形,重拼后的四边形的最小周长是22.。
图形的折叠问题试卷

图形的折叠问题试卷文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]翻折组卷一.选择题(共9小题)1.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠使AB落在AD边上,折痕为AE,再将△ABE以BE为折痕向右折叠,AE与CD交于点F,则的值是()A .1 B.C.D.2.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠,使AB落在AD边上,折痕为AE,再将△AEB以BE为折痕向右折叠,AE与DC交于点F,则的值是()A .1 B.C.D.3.如图,将矩形纸片ABCD沿DE折叠,使DC落在DA上,点C的落点记为F,已知AD=10 cm,BE=4cm,则CD等于()A .3cm B.4cm C.5cm D.6cm4.如图,有一矩形纸片ABCD,且AB:BC=3:2,先将纸片折叠,使AD落在AB 边上,折痕为AE;再将△AED以DE为折痕向右折叠,AE交BC于F.那么DB:BA等于()A .3:2 B.2:3 C.1:1 D.2:15.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使点D落在AB边上的D′处,折痕为AE,再将△AD′E以D′E为折痕向右折叠,使点A落在点A′处,设A′E与BC交于点F(如图),则A′F的长为()A .B.C.D.6.如图,在矩形纸片ABCD中,AB=10,AD=8,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF 的面积为()A .1 B.2 C.4 D.87.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为()A .1B.1 C.D.8.小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠DFC的值为()A .B.C.D.9.如图,矩形纸片ABCD中,AD=10 cm,将纸片沿DE折叠,使点C落在边AD上(与点F重合),若BE=6 cm,则CD等于()A .4cm B.6cm C.8cm D.10cm二.填空题(共16小题)10.如图,一张宽为6cm的矩形纸片,按图示加以折叠,使得一角顶点落在AB 边上,则折痕DF= ______cm.11.如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=70°,则∠GFD′=_________ °.12.如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为_________ .13.如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,已知∠EFG=50°,那么∠BEG的度数为_________ .14.如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB 边交于点N.若∠MPC=75°,则∠NPB′=_________ °.15.把矩形纸片ABCD折叠,使B、C两点恰好落在AD边上的点P处(如图),若∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的宽为_________ cm,面积为_________ cm2.16.把图一的矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二).已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD的面积为_________ .17.把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的面积为_________cm2.18.如图,将长为4cm宽为2cm的矩形纸片ABCD折叠,使点B落在CD边上的中点E处,压平后得到折痕MN,则线段AM的长度为_________ cm.19.如图,有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则CF的长为_________ .20.如图,把一张矩形纸片ABCD沿EF折叠后,点C﹑D分别落在点C′、D′的位置上,EC′交AD于点G.已知∠EFG=55°,那么∠BEG=_________ 度.21.如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点,若∠ABE=40°,则∠ADB=_________ .22.如图,把一张矩形纸片ABCD沿EF折叠后,点C、D分别落在C′、D′的位置上,EC′交AD于点G,已知∠EFG=53°,那么∠BEG=_________ °.23.小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD长与宽的比值为_________ .24.现将矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,且,那么AD=_________ .25.如图,折叠一张矩形纸片,使它的一个顶点落在长边上,已知:β=110°,求α=_________ 度.三.解答题(共5小题)26.课本中,把长与宽之比为的矩形纸片称为标准纸.请思考解决下列问题:(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.请你探究:矩形纸片ABCD是否是一张标准纸请说明理由.(3)不难发现:将一张标准纸按如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=,问第5次对开后所得标准纸的周长是多少探索直接写出第2012次对开后所得标准纸的周长.…27.把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知∠MPN=90°,PM=6cm,PN=8cm,求矩形纸片ABCD的面积.28.如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点,试判断重叠部分的三角形BED的形状,并证明你的结论.29.如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.(1)求证:平行四边形ABCD是矩形;(2)求BF的长;(3)求折痕AF长.30.如图,现将一张矩形ABCD的纸片一角折叠,若能使点D落在AB边上F处,折痕为CE,恰好∠AEF=60°,延长EF交CB的延长线于点G.(1)求证:△CEG是等边三角形;(2)若矩形的一边AD=3,求另一边AB的长.初中数学组卷参考答案与试题解析一.选择题(共9小题)1.(2010赤峰)如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠使AB落在AD边上,折痕为AE,再将△ABE以BE为折痕向右折叠,AE与CD交于点F,则的值是()A .1 B.C.D.考点:翻折变换(折叠问题);矩形的性质;相似三角形的判定与性质.专题:压轴题.分析:观察第3个图,易知△ECF∽△ADF,欲求CF、CD的比值,必须先求出CE、AD的长;由折叠的性质知:AB=BE=6,那么BD=EC=2,即可得到EC、AD的长,由此得解.解答:解:由题意知:AB=BE=6,BD=AD﹣AB=2,AD=AB﹣BD=4;∵CE∥AB,∴△ECF∽△ADF,得=,即DF=2CF,所以CF:CD=1:3;故选C.点评:此题主要考查了图形的翻折变换、矩形的性质以及相似三角形的判定和性质,难度不大.2.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠,使AB落在AD边上,折痕为AE,再将△AEB以BE为折痕向右折叠,AE与DC交于点F,则的值是()A .1 B.C.D.考点:翻折变换(折叠问题).专题:应用题.分析:观察第3个图,易知△ECF∽△ADF,欲求CF、CD的比值,必须先求出CE、AD的长;由折叠的性质知:AB=BE=6,那么BD=EC=2,即可得到EC、AD的长,由此得解.解答:解:由题意知:AB=BE=6,BD=AD﹣AB=2,AD=AB﹣BD=4;∵CE∥AB,∴△ECF∽△ADF,得=,即DF=2CF,所以CF:CD=1:3;故选C.点评:本题主要考查了图形的翻折变换、矩形的性质以及相似三角形的判定和性质,难度适中.3.(2010白下区二模)如图,将矩形纸片ABCD沿DE折叠,使DC落在DA上,点C的落点记为F,已知AD=10 cm,BE=4cm,则CD等于()A .3cm B.4cm C.5cm D.6cm考点:翻折变换(折叠问题);矩形的性质.专题:计算题.分析:根据折叠的性质和正方形的判定方法,得四边形CDFE是正方形,四边形ABEF 是矩形;根据矩形的性质,得AF=BE=4,则DF=6,则CD=DF=6(cm).解答:解:根据一组邻边相等的矩形是正方形,得四边形CDFE是正方形,则四边形ABEF是矩形.∴BE=AF=4.∴DF=AD﹣AF=6.∴CD=DF=6(cm).故选D.点评:此题考查了折叠问题,要能够根据折叠的方法发现正方形.4.(2004广安)如图,有一矩形纸片ABCD,且AB:BC=3:2,先将纸片折叠,使AD落在AB边上,折痕为AE;再将△AED以DE为折痕向右折叠,AE交BC于F.那么DB:BA等于()A .3:2 B.2:3 C.1:1 D.2:1考点:翻折变换(折叠问题).专题:压轴题.分析:由矩形纸片ABCD中,AB:BC=3:2,可设AB=3x,BC=2x,即可得BD=x,继而求得AB的值,则可求得答案.解答:解:∵矩形纸片ABCD中,AB:BC=3:2,∴设AB=3x,BC=2x,则AD=BC=2x,∴BD=AB﹣AD=3x﹣2x=x,如图3:AB=AD﹣BD=2x﹣x=x,∴DB:BA=x:x=1:1.故选C.点评:此题考查了折叠的性质以及矩形的性质.此题难度不大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.5.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使点D落在AB边上的D′处,折痕为AE,再将△AD′E以D′E为折痕向右折叠,使点A落在点A′处,设A′E与BC交于点F(如图),则A′F的长为()A .B.C.D.考点:翻折变换(折叠问题).分析:利用折叠的性质,即可求得AD=AD′=A′D′=、BD′=AB﹣AD=﹣,A′E=AE=AD=2,又由相似三角形的对应边成比例,即可求得EF:A′F=EC:A′B,从而求得A′F的长度.解答:解:根据折叠的性质知,AD=AD′=A′D′=、CE=CD﹣DE=﹣,.∵CE∥A′B,∴△ECF∽△A′BF,∴CE:BA′=EF:A′F(相似三角形的对应边成比例);又∵CE=CD﹣DE=﹣,BA′=AD﹣CE=2﹣,∴=;而A′E=AE=AD=2,∴A′F=4﹣.故选D.点评:本题考查了翻折变换及正方形的性质,利用了折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等及正方形的性质,平行线的性质,有一定的难度.6.如图,在矩形纸片ABCD中,AB=10,AD=8,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF 的面积为()A .1 B.2 C.4 D.8考点:翻折变换(折叠问题).分析:根据折叠易得BD,AB长,利用相似可得BF长,也就求得了CF的长度,△CEF的面积=CFCE.解答:解:由折叠的性质知,第二个图中BD=AB﹣AD=2,第三个图中AB=AD﹣BD=6,∵BC∥DE,∴BF:DE=AB:AD,∴BF=4,CF=BC﹣BF=2,∴△CEF的面积=CFCE=4.故选C.点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②矩形的性质,平行线的性质,三角形的面积公式等知识点.7.有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为()A .1B.1 C.D.考点:翻折变换(折叠问题).专题:几何图形问题;压轴题;数形结合.分析:利用折叠的性质,即可求得BD的长与图3中AB的长,又由相似三角形的对应边成比例,即可求得BF的长,则由CF=BC﹣BF即可求得答案.解答:解:如图2,根据题意得:BD=AB﹣AD=﹣=1,如图3,AB=AD﹣BD=﹣1=,∵BC∥DE,∴△ABF∽△ADE,∴,即,∴BF=,∴CF=BC﹣BF=﹣=1.故选B.点评:此题考查了折叠的性质与相似三角形的判定与性质.题目难度不大,注意数形结合思想的应用.8.(2012历下区二模)小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则cos∠DFC的值为()A .B.C.D.考点:翻折变换(折叠问题);锐角三角函数的定义.专题:数形结合.分析:根据折叠的性质可得出CF=CB,在RT△CDF中利用勾股定理可求出DF的长度,继而可求出cos∠DFC的值.解答:解:由折叠的性质得,CB=CF,设AB=4x,则BC=5x,在RT△DFC中,DF==3x,∴cos∠DFC==.故选B.点评:此题考查了翻折变换及勾股定理的知识,解答本题的关键是根据折叠的性质得出CF的长度,在RT△CDF中求出DF的长度,难度一般.9.如图,矩形纸片ABCD中,AD=10 cm,将纸片沿DE折叠,使点C落在边AD上(与点F重合),若BE=6 cm,则CD等于()A .4cm B.6cm C.8cm D.10cm考点:轴对称的性质.分析:根据对称的性质和AD=10,BE=6可得出CD的长度.解答:解:根据轴对称的性质可得可得出CD=DF=AD﹣AF=AD﹣BE,∴CD=4cm故选A.点评:本题考查轴对称的性质,关键在于根据图形判断出CD=DF.二.填空题(共16小题)10.如图,一张宽为6cm的矩形纸片,按图示加以折叠,使得一角顶点落在AB边上,则折痕DF= 8 cm.考点:翻折变换(折叠问题).分析:根据折叠的性质可得∠EDF=30°,从而求出∠ADE=30°,在Rt△ADE中求出DE,在Rt△DEF中可求出DF.解答:解:由折叠的性质可得:∠EDF=∠CDF=30°,则∠ADE=90°﹣30°﹣30°=30°,在Rt△ADE中,AD=6cm,∠ADE=30°,∴AE=ADtan∠ADE=2cm,DE=2AE=4cm,在Rt△DEF中,∠EDF=30°,DE=4cm,∴DF==8cm.故答案为:8.点评:本题考查了翻折变换的知识,注意掌握翻折前后对应边相等,对应角相等.11.(2012宿迁)如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=70°,则∠GFD′=40 °.考点:平行线的性质;翻折变换(折叠问题).分析:根据两直线平行,内错角相等求出∠EFG,再根据平角的定义求出∠EFD,然后根据折叠的性质可得∠EFD′=∠EFD,再根据图形,∠GFD′=∠EFD′﹣∠EFG,代入数据计算即可得解.解答:解:矩形纸片ABCD中,AD∥BC,∵∠CEF=70°,∴∠EFG=∠CEF=70°,∴∠EFD=180°﹣70°=110°,根据折叠的性质,∠EFD′=∠EFD=110°,∴∠GFD′=∠EFD′﹣∠EFG,=110°﹣70°,=40°.故答案为:40.点评:本题考查了平行线的性质,以及折叠变换,根据两直线平行,内错角相等求出∠EFG是解题的关键,另外,根据折叠前后的两个角相等也很重要.12.(2013日照)如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为(3π﹣)cm2.考点:切线的性质;矩形的性质;扇形面积的计算;翻折变换(折叠问题).专题:压轴题.分析:如图,露在外面部分的面积可用扇形ODK与△ODK的面积差来求得,在Rt△A'DC中,可根据AD即圆的直径和CD即圆的半径长,求出∠DA'C的度数,进而得出∠ODH和∠DOK的度数,即可求得△ODK和扇形ODK的面积,由此可求得阴影部分的面积.解答:解:作OH⊥DK于H,连接OK,∵以AD为直径的半圆,正好与对边BC相切,∴AD=2CD,∴A'D=2CD,∵∠C=90°,∴∠DA'C=30°,∴∠ODH=30°,∴∠DOH=60°,∴∠DOK=120°,∴扇形ODK的面积为=3πcm2,∵∠ODH=∠OKH=30°,OD=3cm,∴OH=cm,DH=cm;∴DK=3cm,∴△ODK的面积为cm2,∴半圆还露在外面的部分(阴影部分)的面积是:(3π﹣)cm2.故答案为:(3π﹣)cm2.点评:此题考查了折叠问题,解题时要注意找到对应的等量关系;还考查了圆的切线的性质,垂直于过切点的半径;还考查了直角三角形的性质,直角三角形中,如果有一条直角边是斜边的一半,那么这条直角边所对的角是30度.13.如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′的位置上,EC′交AD于点G,已知∠EFG=50°,那么∠BEG的度数为80°.考点:翻折变换(折叠问题).专题:探究型.分析:先根据正方形的性质得出AD∥BC,由∠EFG=50°可求出∠1的度数,再根据图形翻折变换的性质得出∠1=∠2=50°,由平角的性质即可得出∠BEG的度数.解答:解:∵四边形ABCD是矩形,∴AD∥BC,∵∠EFG=50°,∴∠1=∠EFG=50°,∵四边形EFD′C′是四边形EFDC翻折而成,∴∠1=∠2=50°,∴∠BEG=180°﹣∠1﹣∠2=180°﹣50°﹣50°=80°.故答案为:80°.点评:本题考查的是图形翻折变换的性质、矩形的性质及平行线的性质,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.14.如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′=15 °.考点:翻折变换(折叠问题).分析:由折叠的性质可知:∠MNC=∠C′PM=75°,∠C′PN=∠BPN,再利用平角为180°,即可求出∠NPB′的度数.解答:解:由折叠的性质可知:∠MNC=∠C′PM=75°,∠C′PN=∠BPN,∴∠NPM=2×75°=150°,∴∠C′PB=30°,由折叠的性质可知:∠C′PN=∠BPN,∴∠NPB′=15°.故答案为:15.点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.15.把矩形纸片ABCD折叠,使B、C两点恰好落在AD边上的点P处(如图),若∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的宽为cm,面积为cm2.考点:翻折变换(折叠问题).分析:根据勾股定理,得MN=10;根据直角三角形的面积公式,得AB=;根据折叠,知BC=6+8+10=24,进而求得矩形的面积.解答:解:过点P作PE⊥MN,∵∠MPN=90°,PM=6cm,PN=8cm,∴MN==10(cm),∴S△PMN=PMPN=MNPE,∴PMPN=MNPE,即PE==(cm),即矩形纸片ABCD的宽为:;∵BC=PM+MN+PN=6+10+8=24(cm),∴S矩形ABCD=×24=(cm2).故答案为:,.点评:此题综合运用了勾股定理、折叠的性质和直角三角形的斜边上的高等于两直角边的乘积除以斜边的方法.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.16.(2005遂宁)把图一的矩形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二).已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD的面积为.考点:翻折变换(折叠问题).专题:压轴题.分析:利用折叠的性质和勾股定理可知.解答:解:由勾股定理得,MN=5,设Rt△PMN的斜边上的高为h,由矩形的宽AB也为h,根据直角三角形的面积公式得,h=PMPN÷MN=,由折叠的性质知,BC=PM+MN+PN=12,∴矩形的面积=ABBC=.点评:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②勾股定理,直角三角形和矩形的面积公式求解.17.(2010徐汇区二模)把如图所示的矩形纸片ABCD折叠,B、C两点恰好落在AD边上的点P处,已知∠MPN=90°,PM=6cm,PN=8cm,那么矩形纸片ABCD的面积为cm2.考点:翻折变换(折叠问题).分析:根据勾股定理,得MN=10;根据直角三角形的面积公式,得AB=;根据折叠,知BC=6+8+10=24,进而求得矩形的面积.解答:解:∵∠MPN=90°,PM=6cm,PN=8cm,∴MN=10,BC=10+6+8=24.根据直角三角形的面积公式,得AB==.则矩形的面积=×24=(cm2).点评:此题综合运用了勾股定理、折叠的性质和直角三角形的斜边上的高等于两直角边的乘积除以斜边的方法.18.如图,将长为4cm宽为2cm的矩形纸片ABCD折叠,使点B落在CD边上的中点E处,压平后得到折痕MN,则线段AM的长度为cm.考点:翻折变换(折叠问题);勾股定理.专题:计算题;探究型.分析:连接BM,EM,BE,由折叠的性质可知,四边形ABNM和四边形FENM关于直线MN对称,由垂直平分线的性质可知BM=EM,再由点E是CD的中点,可求出DE的长,由勾股定理即可求出AM的长.解答:解:如图,连接BM,EM,BE,由折叠的性质可知,四边形ABNM和四边形FENM关于直线MN对称.∴MN垂直平分BE,∴BM=EM,∵点E是CD的中点,DE=1,∴在Rt△ABM和在Rt△DEM中,AM2+AB2=BM2,DM2+DE2=EM2,∴AM2+AB2=DM2+DE2.设AM=x,则DM=4﹣x,∴x2+22=(4﹣x)2+12.解得,即cm.故答案为:.点评:本题考查的是图形折叠的性质及勾股定理,解答此类问题时,首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.19.如图,有一张矩形纸片ABCD,AB=,AD=,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则CF的长为 1 .考点:翻折变换(折叠问题).专题:数形结合.分析:利用折叠的性质,即可求得BD的长与图3中AB的长,又由相似三角形的对应边成比例,即可求得BF的长,则由CF=BC﹣BF即可求得答案.解答:解:如图2,根据题意得:BD=AB﹣AD=﹣=1,如图3,AB=AD﹣BD=﹣1=,∵BC∥DE,∴△ABF∽△ADE,∴=,即=,∴BF=,∴CF=BC﹣BF=﹣=1.故答案为:1.点评:本题考查了翻折变换及正方形的性质,利用了折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等及正方形的性质,平行线的性质,有一定的难度.20.如图,把一张矩形纸片ABCD沿EF折叠后,点C﹑D分别落在点C′、D′的位置上,EC′交AD于点G.已知∠EFG=55°,那么∠BEG=70 度.考点:翻折变换(折叠问题).专题:计算题.分析:由矩形的性质可知AD∥BC,可得∠CEF=∠EFG=55°,由折叠的性质可知∠GEF=∠CEF,再由邻补角的性质求∠BEG.解答:解:∵AD∥BC,∴∠CEF=∠EFG=55°,由折叠的性质,得∠GEF=∠CEF=55°,∴∠BEG=180°﹣∠GEF﹣∠CEF=70°.故答案为:70.点评:本题考查了翻折变换(折叠问题).关键是明确折叠前后,对应角相等,两直线平行,内错角相等的性质.21.如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点,若∠ABE=40°,则∠ADB=25°.考点:翻折变换(折叠问题).分析:首先根据矩形的性质可得∠ABC=90°,AD∥BC,进而可以计算出∠EBC,再根据折叠可得∠EBD=∠CBD=∠EBC,然后再根据平行线的性质可以计算出∠ADB的度数.解答:解:∵四边形ABCD是矩形,∴∠ABC=90°,AD∥BC,∵∠ABE=40°,∴∠EBC=90°﹣40°=50°,根据折叠可得∠EBD=∠CBD,∴∠CBD=25°,∵AD∥BC,∴∠ADB=∠DBC=25°,故答案为:25°.点评:此题主要考查了图形的折叠,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.22.如图,把一张矩形纸片ABCD沿EF折叠后,点C、D分别落在C′、D′的位置上,EC′交AD于点G,已知∠EFG=53°,那么∠BEG=64 °.考点:翻折变换(折叠问题).专题:几何图形问题.分析:由矩形的性质可知AD∥BC,可得∠CEF=∠EFG=53°,由折叠的性质可知∠GEF=∠CEF,再由邻补角的性质求∠BEG.解答:解:∵AD∥BC,∴∠CEF=∠EFG=53°,由折叠的性质,得∠GEF=∠CEF=53°,∴∠BEG=180°﹣∠GEF﹣∠CEF=64°.故答案为:64.点评:本题考查了翻折变换(折叠问题).关键是明确折叠前后,对应角相等,以及两直线平行,内错角相等的性质.23.(2010盐城)小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD长与宽的比值为:1 .考点:翻折变换(折叠问题).专题:压轴题.分析:连DE,由翻折的性质知,四边形ABEF为正方形,∠EAD=45°,而M点正好在∠NDG的平分线上,则DE平分∠GDC,易证RT△DGE≌Rt△DCE,得到DC=DG,而△AGD为等腰直角三角形,得到AD=DG=CD.解答:解:连DE,如图,∵沿过A点的直线折叠,使得B点落在AD边上的点F处,∴四边形ABEF为正方形,∴∠EAD=45°,由第二次折叠知,M点正好在∠NDG的平分线上,∴DE平分∠GDC,∴RT△DGE≌Rt△DCE,∴DC=DG,又∵△AGD为等腰直角三角形,∴AD=DG=CD,∴矩形ABCD长与宽的比值为:1.故答案为::1.点评:本题考查了翻折的性质:翻折前后的两个图形全等.也考查了正方形、角的平分线的性质以及等腰直角三角形的性质.24.(2011桐乡市一模)现将矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,且,那么AD= 2 .考点:翻折变换(折叠问题).专题:计算题.分析:连DE,由矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②),根据折叠的性质得到∠EAF=∠EAB=45°,又沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③),再次根据折叠的性质得到∠NDG=∠CDG=45°,∠MDG=∠EDG,DN=DC=,则△AGD为等腰直角三角形,而M点正好在∠NDG的平分线上,得到∴∠NDM=∠GDM,易证Rt△NMD≌Rt△GMD,得到DG=DN=,根据AD=DG即可求出AD.解答:解:∵矩形纸片ABCD(如图①,AD>CD )沿过A点的直线折叠,使得B 点落在AD边上的点F处,折痕为AE(如图②),∴∠EAF=∠EAB=45°,又∵沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).连DE,∴∠NDG=∠CDG=45°,∠MDG=∠EDG,DN=DC=,∴△AGD为等腰直角三角形,即∠MGD=90°,又∵第二次折叠后,M点正好在∠NDG的平分线上,∴∠NDM=∠GDM,∴Rt△NMD≌Rt△GMD,∴DG=DN=,∴AD=DG=2.故答案为2.点评:本题考查了折叠的性质:折叠后两重合的图形全等.也考查了三角形全等的判定与性质以及等腰直角三角形三边的关系.25.(2013南昌模拟)如图,折叠一张矩形纸片,使它的一个顶点落在长边上,已知:β=110°,求α=20 度.考点:平行线的性质;翻折变换(折叠问题).专题:计算题.分析:由折叠及矩形的性质得到∠AFE为直角,利用平角的定义得到一对角互余,再由AB与DC平行,利用两直线平行同旁内角互补得到一对角互补,求出∠AFC的度数,即可确定出α的度数.解答:解:由折叠的性质得:∠AFE=90°,∴α+∠AFC=90°,∵AB∥CD,∴∠β+∠AFC=180°,∵∠β=110°,∴∠AFC=70°,则α=20°.故答案为:20点评:此题考查了平行线的性质,以及翻折变换,熟练掌握平行线的性质是解本题的关键.三.解答题(共5小题)26.(2012衢州)课本中,把长与宽之比为的矩形纸片称为标准纸.请思考解决下列问题:(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.请你探究:矩形纸片ABCD是否是一张标准纸请说明理由.(3)不难发现:将一张标准纸按如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC=,问第5次对开后所得标准纸的周长是多少探索直接写出第2012次对开后所得标准纸的周长.…考点:翻折变换(折叠问题);全等三角形的判定与性质;勾股定理;等腰直角三角形;矩形的性质;图形的剪拼.专题:几何综合题;压轴题.分析:(1)根据==2==,得出矩形纸片ABEF也是标准纸;(2)利用已知得出△ADG是等腰直角三角形,得出==,即可得出答案;(3)分别求出每一次对折后的周长,进而得出变化规律求出即可.解答:解:(1)是标准纸,理由如下:∵矩形纸片ABCD是标准纸,∴=,由对开的含义知:AF=BC,∴==2==,∴矩形纸片ABEF也是标准纸.(2)是标准纸,理由如下:设AB=CD=a,由图形折叠可知:DN=CD=DG=a,DG⊥EM,由图形折叠可知:△ABE≌△AFE,∴∠DAE=∠BAD=45°,∴△ADG是等腰直角三角形,∴在Rt△ADG中,AD==a,∴==,∴矩形纸片ABCD是一张标准纸;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题24 图形的折叠与剪拼阅读与思考图形的折叠是指把某个图形或部分沿某直线翻折,这条直线为对称轴,在折叠过程中,线短的长度、角的度数保持不变.图形的剪拼是指对某个图形通过有限次的剪裁后重新接成另外一个新的几何图形,在剪拼过程中,原图形与新图形的面积一般保持不变.解答图形的折叠与剪拼问题,要抓住折叠与剪拼过程中一些量的不变性,将计算、推理与合情想象结合起来,常用到全等三角形、勾股定理、面积等知识与方法.折叠问题的实质是对称问题,“遇到折叠用对称”就是运用对称的性质: ① 关于一条直线对称的两个图形全等; ② 对称轴是对应点连线的中垂线.例题与求解【例1】 如图,矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,点D 落在D '处,则重叠部分△AFC 的面积为_____.(山东省竞赛试题)A例1题图 例2题图解题思路:△AFC 的高为BC ,只需求出AF ,注意到D '∠=090,AF =FC【例2】如图,直线26y x =-+ 与x 轴,y 轴分别交于P ,Q 两点,把△POQ 沿PQ 翻折,点O 落在R 处,则点R 的坐标是( )A .2412(,)55B .(2,1)C .(6,3)D .(7,3.5)(江苏省竞赛试题)解题思路:过点R 作x 轴,y 轴的垂线,再利用相似三角形的性质可得垂线段的长度即求得点R 的坐标.解剪拼问题时先利用剪拼后的图形所需关键线段的长度,然后,从剪拼前的图形中寻找这些长度进行剪拼.【例3】 如图,将边长为12cm 的正方形ABCD 折叠,使得A 点落在CD 边上点E 处,然后压平折痕FG ,若FG =13cm ,求CE 长.(北京市竞赛试题)解题思路:由折叠可得A 与E 关于FG 对称,则FG ⊥AE ,可证明FG =AE ,这是解本例的关键.【例4】 将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动,运动23秒时,动点P 从点A 出发以相等的速度沿AO 向终点O 运动.当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒).(1)用含t 的代数式表示OP OQ ,;(2)当1t 时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边上的点D 处,求点D 的坐标;(3)连结AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PQ 与AC 能否平行?PE 与AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.图1解题思路:对于(3),假设能,由比例线段求出t的值,关键是看相应t的值是否在t的取值范围.折纸、剪纸是最富于自然情趣而又形象生动的实验,同时说明了存在的事实是怎样被发现的,现象又是怎样获得证实的,在平面几何的一些主要学习环节发挥重要作用.【例5】用10个边长分别为3,5,6,11,17,19,22,23,24,25的正方形,可以拼接一个长方形.(1)求这个长方形的长和宽;(2)请画出拼接图.(“华杯赛”决赛试题)解题思路:运用剪拼前后图形面积不变求长方形的长和宽;利用长方形对边相等的性质画拼接图.【例6】将正方形纸片ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC交于点G.(1)如果M为CD边的中点,求证:DE:DM:EM=3:4:5;(2)如果M为CD边上的任意一点,设AB=2a,问△CMG的周长是否有与点M的位置关系?若有关,请把△CMG的周长用含CM的长x的代数式表示;若无关,请说明理由.解题思路:折痕EF两旁部分图形是关于EF成对称的,对于(2),通过相似三角形性质,把△CMG的周长用相关代数式表示,解题的关键是将几何问题代数化.对于例6,如图,当M 为CD 边上的中点,则有3BCBG,即G 为BC 的三等分点,这一结果是由日本筑波大学的生物学教授芳贺和夫发现的,被称为芳贺第一定理.作深入思考,进一步挖掘还能得到如下重要结论:(1)无论怎样折叠,若点M 落在CD 上,则MG =DM +BG ;(2)无论怎样折叠,若点M 落在CD 上,连MA ,GA ,则∠MAG =450.能力训练1、如图,在矩形ABCD 中,AB =6cm ,BC =8cm ,若将矩形折叠,使B 点与D 点重合,则折痕EF 的长为___cm.(宁夏回族自治区中考试题)2、如图,矩形ABCD 中,AB =12,AD =10,将此矩形折叠使B 点落在AD 边上的中点E 处,则折痕FG 的长为_________.第1题图 第2题图 第3题图(淮阴市中考试题)3、如图是用12个全等的等腰梯形镶嵌成的图形,这个等腰梯形的上底与下底长的比是_____.(陕西省中考试题)4、如图,EF 为正方形纸ABCD 的对折线,将∠A 沿DK 折叠,使它的顶点A 落在EF 上的G 点,则∠DKG =_______度.(武汉市竞赛试题)5、如图,已知等边△ABC 中,点D ,E 分别在边AB ,BC 上,把△BDE 沿直线DE 翻折,使点B 落在点B ′处,DB ′,EB ′分别交边AC 于点F ,G ,若∠ADF =080,则∠EGC 的度数为________.第4题图第5题图第6题图(台州市中考试题) 6、将一张长为70cm的长方形纸片ABCD沿对称轴EF折叠成如图的形状,若折叠后,AB与CD间的距离为60cm,则原纸片的宽AB是______cm.(广东省中考试题) 7、如图,在矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在F处,折痕为AE,且EF=3,则AB的长为( )A.3B.4C.5D.6(宜宾市中考试题) 8、如图,在△ABC中,∠C=900,BC=6,D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )A.12B、2C、3D、4(河北省中考试题)EA第7题图第8题图第9题图9、如图,有一块菱形的草地,要在其上面修筑两条笔直的道路,道路把这块草地分成面积相等的四部分,如果道路的宽度可以忽略不计,请你设计三种不同的方案.(广西赛区选拔赛试题)10、如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠使AD 边与对角线BD 重合,得折线DG ,若AB =2,BC =1,求AG.(安徽省中考试题)11、如图,折叠矩形ABCD 的一边AD ,使点D 落在BC 边上的点F 处,已知折痕3.4EC AE FC == ,求矩形ABCD 的周长. (厦门市中考试题)12、如图1,一张矩形纸片ABCD ,其中AD =8cm ,AB =6cm ,先沿对角线BD 对折,点C 落在点C ′处的位置,BC ′交AD 于点G. (1) 求证:AG =G C ';(2) 如图2,再折叠一次,使点D 与点A 重合,得折痕EN ,EN 交AD 于点M ,求EM 的长.(深圳市中考试题)B级1、如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次使D点与A点重合,得折痕EN,EN交AD于点M,则ME 的长为__________.2、如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A,C重合,使纸片折叠压平,设折痕为EF,则重叠部分△AFE的面积为_________.第1题图第2题图第3题图3、如图,矩形ABCD沿直线BD折叠,使点C落在C′处,BC′交AD于点E,若AD=8,AB=4,则DE的长为________.4、如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴上,y轴上,连结AC,将矩形纸片OABC沿AC折叠,使点B落在点D的位置,若B(1,2),则点D的横坐标是______.5、如图,在平面直角坐标系中,已知直线334y x=-+与x轴,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上B′处,则点C的坐标是_________.第4题图第5题图第6题图6、如图,矩形纸片ABCD,AB=5cm,BC=10cm,CD上有一点E,ED=2cm,AD上有一点P,PD=3cm,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点重合,折痕与PF交于Q点,则PQ的长是_____cm.7、在三角形纸片ABC中,已知∠ABC=900,AB=6,BC=8,过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线上的T处,折痕为MN,当点T在直线l上移动时,折痕的端点M,N也随之移动,若限定端点M,N分别在AB,BC边上移动,则线段AT 长度的最大值与最小值之和为__________(计算结果不取近似值)8、如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,BG=10.(1)当折痕的另一端F在AB边上时,如图.求△EFG的面积;(2)当折痕的另一端F在AD边上时,如图.证明四边形BGEF为菱形,并求出折痕GF 的长.9、如图,已知三角形纸片ABC的面积为25,BC的长为10,∠B,∠C都为锐角,M是AB 边上的一动点(M与A,B不重合),过点M作MN∥BC交AC于点N,设MN=x.(1)用x表示△AMN的面积;(2)△AMN沿MN折叠,使△AMN紧贴四边形BCNM(边AM、AN落在四边形BCNM 所在的平面内),设点A落在平面BCNM内的点A′,△A′MN与四边形BCNM重叠部分的面积为y.①用含x的代数式表示y,并写出x的取值范围.②当x为何值时,重叠部分的面积y最大,最大为多少?10、如图:一正方形纸片,根据要求进行多次分割,把它分割成若干个直角三角形.具体操作过程如下:第一次分割:将正方形纸片分成4个全等的直角三角形;第二次分割:将上次得到的直角三角形中的一个再分成4个全等的直角三角形;以后按第二次分割的方法重复进行.(1)请你设计出两种符合题意的分割方案(分割3次);(2)设正方形的边长为a,请你通过对其中一种方案的操作和观察,将第二、第三次分割后所得的最小的直角三角形的面积S填入下表:(3)在条件(2)下,请你猜想:分割所得的最小直角三角形面积S与分割次数n有什么关系?用数学表达式表示出来.11、如图1,将边长为4cm 的正方形纸片ABCD 沿EF 折叠(点E ,F 分别在边AB ,CD 上),使点B 落在AD 边上的点M 处,点C 落在点N 处,MN 与CD 交于点P ,连结EP .(1)如图②,若M 为AD 边的中点, ① △AEM 的周长=_________cm ; ② 求证:EP =AE +DP ;(2)随着落点M 在AD 边上取遍所有的位置(点M 不与A 、D 重合),△PDM 的周长是否发生变化?请说明理由.12、如图1,在矩形ABCD 中,AB =3,AD =1,点P 在线段AB 上运动,设AP =x ,现将纸片折叠,使点D 与点P 重合,得折痕EF (点E ,F 为折痕与矩形边的交点),再将纸片还原.(1)当0 x 时,折痕EF 的长为________;(2)写出使四边形EPFD 为菱形的x 的取值范围,并求出当x =2时菱形的边长;(3)令2EF =y ,当点E 在AD 上、点F 在BC 上时,写出y 与x 的函数关系式(写出x 的取值范围),当y 取最大值时,判断△EAP 与△PBF 是否相似.若相似,求出x 的值;若不相似,请说明理由.。
