《图形的位似》PPT课件2 (共6张PPT)
合集下载
图形的位似 PPT课件 人教版

老师寄语:
心有多宽,天地就有多广.良 好的心态是成功的内在因 素.把我们的主要精力,投放 在学习上,未来一定是美好 的.
皮影是我国传统的民 间艺术,艺人是如何 把这种“无声电影” 展示给观众的呢?
图形的位似在的幻过灯程机中放 ,映 这图 些片 图
片有什么关系呢?
幻灯机在哪儿
制作:呢张? 伟亮
我的实验室: 墙上的影子
•
76、好习惯成就一生,坏习惯毁人前程。
•
77、年轻就是这样,有错过有遗憾,最后才会学着珍惜。
•பைடு நூலகம்
78、时间不会停下来等你,我们现在过的每一天,都是余生中最年轻的一天。
•
79、在极度失望时,上天总会给你一点希望;在你感到痛苦时,又会让你偶遇一些温暖。在这忽冷忽热中,我们学会了看护自己,学会了坚强。
•
80、乐观者在灾祸中看到机会;悲观者在机会中看到灾祸。
13、人生最大的错误是不断担心会犯错。
•
14、忍别人所不能忍的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获。
•
15、不管怎样,仍要坚持,没有梦想,永远到不了远方。
•
16、心态决定命运,自信走向成功。
•
17、第一个青春是上帝给的;第二个的青春是靠自己努力的。
•
18、励志照亮人生,创业改变命运。
•
利用位似形可以将一个图形放大或缩小。
位似图形的任意一对对应点到位似中心的距离之 比等于位似比。
1.按如下方法将△ABC的三边缩小来原来的 1 : 如图所示,任取一点O,•连AO,•BO,CO,并2取它们
的中点D,E,F,得△DEF,则下列说法中正确的个数
是( )
①△ABC与△DEF是位似图形;
48图形的位似二精品PPT课件

第四章 图形的相似
第8节 图形的位似(二)
复习提问:
什么是位似图形?
如何判断两个图形是否位似?
怎样求两个位似图形的相似比?
如何将画在纸上的一个图片放大, 使放大前后对应线段的比为1:2? 你有哪些方法?
探究1
在直角坐标系中,△OAB三个顶点的坐标 分别为O(0,0),A(3,0),B(2,3).
原坐标
y O(0,0) 8 A(6,0)
B(3,6)
C(-3,3)
横纵坐标×-23
O′(0,0) A′(-9,0)
6
B
B′(-4.5,-9)
C′(4.5,-4.5)
4
C
以原点O为位 似中心,与
2
四边形OABC
A
相似比为3:
-8 -6 -4 -2 OO 2 4 6 8 x 2的位似图形
-2
有两个,它
-4
们关于原点
成中心对称。
-6
原坐标 O(0,0) A(6,0) B(3,6)
C(-3,3)
横纵坐标×23 O′(0-8,0) A′(9,0) B′(4.5,9) C′(-4.5,4.5)
练习
• 如图,在直角坐标系中,四边形 OABC的顶点坐标分别是O(0,0),A (3,0),B(4,4),C(-2,3).画 出四边形OABC以O为位似中心的位似 图形,使它与四边形OABC的相似比是 2:1.
6
5
4
验
3 2
证
1
O 1234567
结论
在直角坐标系中,将一个多边形每 个顶点的横、纵坐标都乘以同一个数k (k≠0),所对应的图形与原图形位似, 位似中心是坐标原点,他们的相似比为 ∣k∣.
第8节 图形的位似(二)
复习提问:
什么是位似图形?
如何判断两个图形是否位似?
怎样求两个位似图形的相似比?
如何将画在纸上的一个图片放大, 使放大前后对应线段的比为1:2? 你有哪些方法?
探究1
在直角坐标系中,△OAB三个顶点的坐标 分别为O(0,0),A(3,0),B(2,3).
原坐标
y O(0,0) 8 A(6,0)
B(3,6)
C(-3,3)
横纵坐标×-23
O′(0,0) A′(-9,0)
6
B
B′(-4.5,-9)
C′(4.5,-4.5)
4
C
以原点O为位 似中心,与
2
四边形OABC
A
相似比为3:
-8 -6 -4 -2 OO 2 4 6 8 x 2的位似图形
-2
有两个,它
-4
们关于原点
成中心对称。
-6
原坐标 O(0,0) A(6,0) B(3,6)
C(-3,3)
横纵坐标×23 O′(0-8,0) A′(9,0) B′(4.5,9) C′(-4.5,4.5)
练习
• 如图,在直角坐标系中,四边形 OABC的顶点坐标分别是O(0,0),A (3,0),B(4,4),C(-2,3).画 出四边形OABC以O为位似中心的位似 图形,使它与四边形OABC的相似比是 2:1.
6
5
4
验
3 2
证
1
O 1234567
结论
在直角坐标系中,将一个多边形每 个顶点的横、纵坐标都乘以同一个数k (k≠0),所对应的图形与原图形位似, 位似中心是坐标原点,他们的相似比为 ∣k∣.
图形的位似ppt课件

点O就是它们的位似中心,位似比为 .
由作图还可以看到,
C
D
位似多边形必定是
C′
D′
相似多边形,位似比
A
也就是相似比.
B
A′
B′
O
11
11
探究新知
例1
判断下列各图形哪些是位似图形:
若是,请指出位似中心
(1)正五边形ABCDE与正五边形A'B'C'D'E';
(1‘)五边形ABCDE与五边形A'B'C'D'E';
E
x
-6
OA,OB,OC,OD,
-8
-10
F′
-12
G′
-14
就得到四边形G′C′E′F′,也是所求作的四
边形.
23
23
探究新知
如图,例题中平行四边形ABCD的顶点坐标分别为 A(0,4),
B(2,0),C(6,0),D(4,4).
(1)写出平行四边形GCEF的各个顶点坐标.
y
14
G
F
12
10
8
G(0,12),C(6,0),
2.确定关键点(一般是多边形的顶点);
3.找出新图形的关键点;
4.顺次连接各点,得到所求作的图形.
18
18
探究新知
放缩尺是将图形进行放大或缩小的工具.
如图,点O位置固定不变,在A,A'处装
有画笔.当画笔A沿图形F运动时,画笔A'
画出图形F',图形F'将图形F放大了.反之,
图形F是图形F'的缩小图形.
△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是
图形的位似(公开课)PPT课件

课堂作业
全品P28 11 13
完整版ppt课件
16
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
完整版ppt课件 17
27.3.1 图形的位似
完整版ppt课件
1
学习目标
1.掌握位似图形的概念和性质; 2.会利用“位似图形的性质”将一个图 形放大和缩小,画出一个图形的位似图 形。
完整版ppt课件
2
自学指导:
(认真看课本P47-P48练习前:)
1.结合课本P47页思考归纳“位似图 形”的概念; 2.结合P47思考及P48页探究归纳 “位似图形”的性质; 3.利用“位似图形”的性质画一个图形 的位似图形。
5分钟后比谁能正确做对检测题!
完整版ppt课件
3
自学检测
课本P48页练习 1 2
完整版ppt课件
4
在日常生活中,我们经常见到这样一类相似的图形,
例如,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕 上(如图显示了它工作的原理).在照相馆中,摄影师通过照 相机,把人物的形象缩小在底片上.
这样的放大缩小,没有改变图形形状,经过放大或缩小的图
完整版ppt课件
11
3.位似图形的画法
以0为中心把△ABC 缩小为原来的一半。
A B
C
O C’
B’ A’
如何作位似图形? 1.定位(位似中心);2.定量(位似比)
完整版ppt课件
12
4.已知四边形ABCD,如图所示,画一个四边形 A‘B’C‘D’,使四边形A‘B’C‘D’与原图
形相似比为2.5.
完整版ppt课件
14
小结 本节课你有哪些收获?
图形的位似ppt课件

各角分别相等,各边成比例的两个多边形叫做相似多边形.
相似三角形对应边的比叫做相似比.
探索与思考
如图是一幅宣传海报,它由一组形状相同的图片组成.在图片①和图片②上任取一组对应点A,A’,可以发现:直线AA’都经过镜头中心点O,且 都等于一个固定值.请你实际试一试.
下图是两个相似五边形,设直线AA’与BB’相交于点O,那么直线CC’,DD’,EE’是否也都经过点O? , , , , 有什么关系?
D
EFΒιβλιοθήκη AOBC
D
E
F
A
O
B
C
结果会得到一个放大了的△DEF,且△DEF的三边是△ABC三边的2倍.即它们的位似比是2∶1.
做一做:
利用橡皮筋将一个图形放大
交流小结,收获感悟
1. 对自己说,你有什么收获? 2. 对同学说,你有什么温馨提示? 3. 对老师说,你还有什么困惑?
布置作业,强化目标 作业:习题4.13
教学目标
1.了解位似图形及其有关概念,能够利用作位似图形等方法将一个图形放大或缩小. 2.学生经历将一个图形放大或缩小的方法,并且在学习和运用过程中发展数学应用意识. 3.培养学生动手操作的良好习惯,以积极进取的思想探究数学学科知识,体会本节知识的实际应用价值和文化价值.
问题:什么叫相似多边形?什么叫相似多边形的相似比?
F
E
D
做一做:
例题讲解
(1)如果在射线OA,OB,OC上分别取D,E,F,使OD=2OA, OE=2OB, OF=2OC,那么,结果又会怎样?
(2)如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样呢? 结果会得到一个与△ABC全等的△DEF,.即它们的位似比是1∶1.
相似三角形对应边的比叫做相似比.
探索与思考
如图是一幅宣传海报,它由一组形状相同的图片组成.在图片①和图片②上任取一组对应点A,A’,可以发现:直线AA’都经过镜头中心点O,且 都等于一个固定值.请你实际试一试.
下图是两个相似五边形,设直线AA’与BB’相交于点O,那么直线CC’,DD’,EE’是否也都经过点O? , , , , 有什么关系?
D
EFΒιβλιοθήκη AOBC
D
E
F
A
O
B
C
结果会得到一个放大了的△DEF,且△DEF的三边是△ABC三边的2倍.即它们的位似比是2∶1.
做一做:
利用橡皮筋将一个图形放大
交流小结,收获感悟
1. 对自己说,你有什么收获? 2. 对同学说,你有什么温馨提示? 3. 对老师说,你还有什么困惑?
布置作业,强化目标 作业:习题4.13
教学目标
1.了解位似图形及其有关概念,能够利用作位似图形等方法将一个图形放大或缩小. 2.学生经历将一个图形放大或缩小的方法,并且在学习和运用过程中发展数学应用意识. 3.培养学生动手操作的良好习惯,以积极进取的思想探究数学学科知识,体会本节知识的实际应用价值和文化价值.
问题:什么叫相似多边形?什么叫相似多边形的相似比?
F
E
D
做一做:
例题讲解
(1)如果在射线OA,OB,OC上分别取D,E,F,使OD=2OA, OE=2OB, OF=2OC,那么,结果又会怎样?
(2)如果在射线AO,BO,CO上分别取点D,E,F使DO=OA,EO=OB,FO=OC,那么,结果又会怎样呢? 结果会得到一个与△ABC全等的△DEF,.即它们的位似比是1∶1.
位似精品PPT课件 (2)

少? x
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
17
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
讲师:XXXXXX XX年XX月XX日
掌握图形位似的性质。 4.掌握直角坐标系中图形的位似变化与对应 点坐标变化的规律。
动手操作
1.已知点O和△ABC,连接OA、OB、OC,在线段OA、 OB、OC上分别取点A′、B′、C′,使
OA OB OC 1 OA OB OC 2
画△A′B′C′
2.已知点O和△ABC,连接OA、OB、OC,在 线段OA、OB、OC的反向延长线上分别取点 A"、B"、C",使 OA'' OB'' OC'' 1
3 位似与平移、旋转等图形变换等有何不同点? 位似不仅改变了图形的位置,而且还可以改变图
形的大小.
当堂检测
1.下列语句正确的是( ) A.相似图形一定是位似图形,位似图形一定是相似图形 B.位似图形一定是相似图形,而且位似比等于相似比 C.利用位似变换只能放大图形,不能缩小图形 D.利用位似变换只能缩小图形,不能放大图形
在平面直角坐标系中, △ABC三个顶点的坐标分别为
A(4,2)、B(8,2)、C(4,6),以原点O为位似中心,按
相似比1:2把它缩小.
1.缩小后对应点的坐标分别是多少?
2.将位似中心点O沿y轴向上或向下移动a个
单位,对应点的坐标分别是多少?
3.将位似中心点O沿x轴向
y
左或向右移动b个单位,
图形的位似变换PPT课件
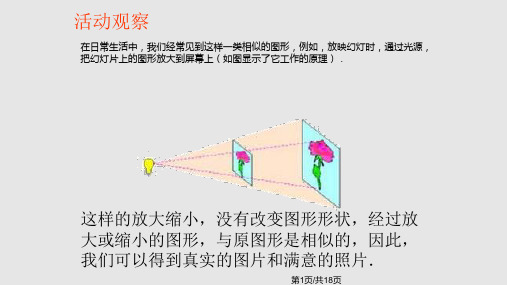
C' D ' ,使 OA' OB ' OC ' OD' 2;
OA OB OC OD
(4)连接A ' B ',B ' C ',C ' D ',D ' A '.
所得四边形A ' B ' C ' D'即为所求.
第5页/共18页
观察下述图形有什么共同特点?
C
C'
B' A'
O C'
A'
B'
B'
A
BA
第9页/共18页
探索:
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心, 相似比为3:1,把线段AB缩小.
y
A′(2,1),B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现? 第10页/共18页
在平面直角坐标系中,有两点A(6,3),B(6,0),
以原点O为位似中心,相似比为1:3,把线段AB缩小.
y
A C
B
o
x
第14页/共18页
小结:
如果两个图形不仅形状相同,而且每组对应点所在的 直线都经过同一点,那么这样的两个图形叫做位似图 形, 这个点叫做位似中心. 在平面直角坐标系中,如果位似变换是以原点为位 似中心,相似比为k,那么位似图形对应点的坐标的 比等于k或-k.
第15页/共18页
布置作业
课堂作业:P97练习; 家庭作业 : (1)P99习题第2、3题; (2)预习下一节内容.
第16页/共18页
教学反思
第17页/共18页
感谢您的欣赏
第18页/共18页
y
A′(2,1),B′(2,0)
A〞(-2,-1), B〞 (-2,0)
OA OB OC OD
(4)连接A ' B ',B ' C ',C ' D ',D ' A '.
所得四边形A ' B ' C ' D'即为所求.
第5页/共18页
观察下述图形有什么共同特点?
C
C'
B' A'
O C'
A'
B'
B'
A
BA
第9页/共18页
探索:
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心, 相似比为3:1,把线段AB缩小.
y
A′(2,1),B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现? 第10页/共18页
在平面直角坐标系中,有两点A(6,3),B(6,0),
以原点O为位似中心,相似比为1:3,把线段AB缩小.
y
A C
B
o
x
第14页/共18页
小结:
如果两个图形不仅形状相同,而且每组对应点所在的 直线都经过同一点,那么这样的两个图形叫做位似图 形, 这个点叫做位似中心. 在平面直角坐标系中,如果位似变换是以原点为位 似中心,相似比为k,那么位似图形对应点的坐标的 比等于k或-k.
第15页/共18页
布置作业
课堂作业:P97练习; 家庭作业 : (1)P99习题第2、3题; (2)预习下一节内容.
第16页/共18页
教学反思
第17页/共18页
感谢您的欣赏
第18页/共18页
y
A′(2,1),B′(2,0)
A〞(-2,-1), B〞 (-2,0)
图形的位似ppt课件

一般地,位似图形有以下性质:
位似图形上任意一对对应点到位似中心的距离之比等于位似
比.
完整版课件
12
作位似图形
例: 如图,请以坐标原点O为位似中心,作位似图形, 并把对应的边长放大3倍.
完整版点坐标变化的规律
想一想:
1.所画的两个四边形具有怎样的对称性? 2.怎样运用原图形与位似图形对应点的坐标关系,画出以 原点为位似中心的位似图形?
完整版课件
4
如图,D,E分别AB,AC上的点.
A
(1)如果DE∥BC,那么∆ADE和 D E
∆ABC是位似图形吗?为什么? B
C
解:(1) ∆ADE和 ∆ABC是位似图形.理由是:
因为DE∥BC,所以∆ADE∽ ∆ABC.
又因为 点A是∆ADE和 ∆ABC的公共点,点D和
点B是对应点,点E和点C是对应点,直线BD
与CE交于点A,所以∆ADE和 ∆ABC是位似图
形.
完整版课件
5
如图,D,E分别AB,AC上的点. (1)如果DE∥BC,那么∆ADE和 ∆ABC是位似图形吗?为什么? B
A DE
C
(2)如果∆ADE和 ∆ABC是位似图形,那么 DE∥BC吗?为什么?
解:(2) DE∥BC.理由是:
∆ADE和 ∆ABC是位似图形
(7)△ABC与△ADE(①DE∥BC; ②∠AED=∠B)
完整版课件
10
2.如图P,E,F分别是AC,AB,AD的中点,四边 形AEPF与四边形ABCD是位似图形吗?如果是位似图 形,说出位似中心和位似比.
完整版课件
11
位似图形的性质
(1)从上面练习第 1(1)(4)题图中,我们可以看到,△OAB∽△O A′B′, 则OOAA′ =OBO′B =A′ABB′ .从第 2 题的图中同样可以看到AAFD =AACP =AAEB =EBPC =DFCP
初中数学《图形的位似(第2课时)》教学课件

y A′(2,1),B′(2,0)
A〞(-2,-1),B〞(-2,0)
A
A'
B〞
x
o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比 为k,那么位似图形对应点的坐标的比等于k或-k.
反过来有以下性质:
如果多边形有一个顶点在坐标原点,有一条边在X轴上, 那么将这个多边形的顶点坐标分别扩大(或缩小)相同的倍 数,所得到的图形与原图形是位似图形,坐标原点是它们的 位似中心.
图形的位似
第2课时
1.会用图形的坐标的变化来表示图形的位似变换,掌握 把一个图形按一定大小比例放大或缩小后,点的坐标变 化的规律. 2.了解四种变换(平移、轴对称、旋转和位似)的异同, 并能在复杂图形中找出这些变换.
1.什么叫位似图形? 对应边互相平行(或共线)且每对对应点所在的直线都经过 同一点的两个相似多边形叫做位似图形,这个交点叫做位似 中心. 2.位似图形的性质.
④位似图形上任意两点与位似中心的距离之比等于位似
比. 【答案】②③
3.两个位似图形中的对应角__相__等__,对应线段的_比__相__等__, 对应顶点的连线必经过_位__似__中__心___.
4.位似图形上某一对对应点到位似中心的距离分别为5和 10,则它们的位似比为_1__:2___.
5.四边形ABCD和四边形A′B′C′D′位似,O为位似中 心,若OA:OA′=1:4,那么S四边形ABCD :S四边形A′B′C′D′ =_1_:_1_6_.
在平面直角坐标系中, △ABC三个顶点的坐标分别为
A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,
北师版九年级数学上册《图形的位似》PPT课件

感悟新知
知3-导
第二步;画出图形各顶点与位似中心O的连线; 第三步:按相似比取点; 第四步:顺次连接各点,所得的图形就是所求的图形.
感悟新知
知3-导
2.要点精析: (1)位似中心的选取要使画图方便且符合要求,一般以多边形
的一个顶点为位似中心画图最简便. (2)画位似图形时,要弄清相似比,即分清是已知图形与新图
课堂小结
图形的位似
知识总结
知识方法要点
关键总结
注意事项
每组对应点所在直线交于一 画位似图形时要找准对应点,
位
点的相似多边形是位似多边 理解相似比.注意位似中心的位
似 多
形; 位似多边形的对应边平 置:①位似中心在多边形的一
边
行或在一条直线上,多边形 侧;②两个多边形分居在位似
形
上任意一组对应点到位似中 中心的两侧;③位似中心在两
感悟新知
知识点 3 位似图形的画法
知3-导
1.画位似图形的步骤:
第一步:确定位似中心O(位似中心可以在图形外部,也可以在
图形内部,还可以在图形的边上,还可以在某一个顶点上);
特别提醒: ◆位似中心的选取一般考虑使画图方便且符合要求. ◆以一点为位似中心画位似图形时,符合要求的图形往往
不唯一,一般情况下,同一个位似中心的两侧各有一 个符合要求的图形.
求出AD的长,然后根据△OAD∽△OBG,求出
OB的长,即可确定C点的坐标.
∵正方形BEFG的边长是6,∴BE=EF=6,
∵两正方形的相似比为1∶3. ∴ CB CB 1 .
EF 6 3
∴AB=BC=CD=AD=2.
根据位似图形的性质可知,OA=1,即 OB 2 1 .
OB 3
公开课图形的位似PPT
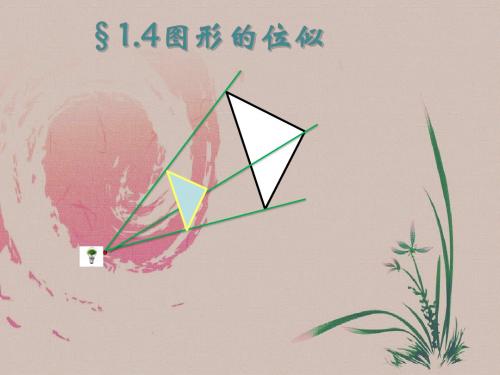
操作:已知ABC与点O,以点O为位似中心, 画出ABC,使它与ABC是位似图形,且相似比 为3:2;
交流:1.总结画法; 2.有什么注意事项? 3.你能画出几个已知图形的位似图形;
问君何所疑议——垂画线法的总画结法
B′
. ①选点:确定位似中心(可以在图 形外部、内部或边上) .
B
②作射线:以位似中心为端点向 O
对应点连线过
一点;
C
问君何所疑——位似中心位置
释疑:两图形外部; 两图形之间; 两图形的性质
同桌合作1:证明位似图形上任意一对 对应点到位似中心的距离之比等于相似比 (任选一图证明)
问君何所疑议——垂位线似的图画形法的画法
• 小组合作2:已知位似中心,如何作一 个图形的位似图形?有几种画法?
A
各关键点作射线.
C
A′ C′
③定对应点:根据已知的相似比分别在射线上取各
关键点的对应点,满足放缩比例.
④连线:顺次连接各关键点的对应点,即可得到要求
的新图形.
问君何所移——迁移应用
• 个性超市练习第4题
问君何所易——牛刀小试
• 1. OAB与 OAB是以点O为位似中心的位似 图形,OA=2cm,AA 5cm,则它们的位似 比为______.
问君何所已——颗粒归仓
位似
位似的定义 位似的性质 位似图形的画法
注意事项
勤思善问,一日千里!
O
问君何所疑——理解位似图形的概念
问题一:所有相似图形都是位似图 形吗;满足什么条件的两个相似图 形才是位似图形;
释疑:对应边互相平行(或共线); 对应点连线过同一点;
问君何所移——迁移应用
如图,在△ABC中,AB∥DE,△ABC与 △ADE位似吗?
交流:1.总结画法; 2.有什么注意事项? 3.你能画出几个已知图形的位似图形;
问君何所疑议——垂画线法的总画结法
B′
. ①选点:确定位似中心(可以在图 形外部、内部或边上) .
B
②作射线:以位似中心为端点向 O
对应点连线过
一点;
C
问君何所疑——位似中心位置
释疑:两图形外部; 两图形之间; 两图形的性质
同桌合作1:证明位似图形上任意一对 对应点到位似中心的距离之比等于相似比 (任选一图证明)
问君何所疑议——垂位线似的图画形法的画法
• 小组合作2:已知位似中心,如何作一 个图形的位似图形?有几种画法?
A
各关键点作射线.
C
A′ C′
③定对应点:根据已知的相似比分别在射线上取各
关键点的对应点,满足放缩比例.
④连线:顺次连接各关键点的对应点,即可得到要求
的新图形.
问君何所移——迁移应用
• 个性超市练习第4题
问君何所易——牛刀小试
• 1. OAB与 OAB是以点O为位似中心的位似 图形,OA=2cm,AA 5cm,则它们的位似 比为______.
问君何所已——颗粒归仓
位似
位似的定义 位似的性质 位似图形的画法
注意事项
勤思善问,一日千里!
O
问君何所疑——理解位似图形的概念
问题一:所有相似图形都是位似图 形吗;满足什么条件的两个相似图 形才是位似图形;
释疑:对应边互相平行(或共线); 对应点连线过同一点;
问君何所移——迁移应用
如图,在△ABC中,AB∥DE,△ABC与 △ADE位似吗?
浙教版数学九年级上册4.7《图形的位似》ppt课件2

C
F
P
A
E
B
四、探索新知
(2)从上面练习 1 的位似图形中,我们可以 看到,△OAB∽△O A′B′,则
OA OB
AB
OA′ =OB′ =A′B′ .
从第 2 题的图中同样可以看到
AF AD
=AAPC
=AAEB
=BECP
=DFCP
位似图形上任意一对对应点到位似 中心的距离之比等于位似比.
四、动手做一做
1.两图形相似. 2.每组对应点所在直线都经过同一点.
显然,位似图形是相似图形的特殊情形
,其相似比又叫做它们的位似比.
二、知识应用
判断下列各图形哪些是位似图形:
(1)五边形ABCDE与五边形A′B′C′D′E′;
(1)-1
(1)-2
(2)正方形ABCD∽正方形A′B′C′D′.
(3)等边三角形ABC与等边三角形A′B′C′
浙教版初中数学九年级(上)
4.7 图形的位似
请同学们仔细观察下列两幅图有什 么共同特点?
1)两个图形形状相同 2)每组对应点所在的直线都经过同一点
如果两个图形不仅形状相同,而且每组对应 点所在的直线都经过同一点,那么这样的两个图
形叫做位似图形, 这个点叫做位似中心.
一、知识总结
同时满足下面两个条件的两个图形才 叫做位似图形.两条件缺一不可.
B′C′,CD与C′D′,AD与A′D′是否平
行?为什么?
不经过位似中
心的对应线段
平行.
1、课本P123例题 8
6
A
D
4
2
-10-5ຫໍສະໝຸດ OB5C10
-2
-4
2、以坐标原点为位似中心的位似变换有 一下性质:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总结
如果多边形有一个顶点在坐标原点,有一 条边在X轴上,那么将这个多边形的顶点坐 标分别扩大(或缩小)相同的倍数,所得 到的图形与原图形是位似图形,坐标原点 是它们的位似中心。
1.天行健,君子以自强不息。 ——《周易》 译:作为君子,应该有坚强的意志,永不止息的奋斗精神,努力加强自我修养,完成并发展自己的学业或事业,能这样做才体现了天的意志,不辜负宇宙给予君子的职 责和才能。 2.勿以恶小而为之,勿以善小而不为。 ——《三国志》刘备语 译:对任何一件事,不要因为它是很小的、不显眼的坏事就去做;相反,对于一些微小的。却有益于别人的好事,不要因为它意义不大就不去做它。 3.见善如不及,见不善如探汤。 ——《论语》 译:见到好的人,生怕来不及向他学习,见到好的事,生怕迟了就做不了。看到了恶人、坏事,就像是接触到热得发烫的水一样,要立刻离开,避得远远的。 4.躬自厚而薄责于人,则远怨矣。 ——《论语》 译:干活抢重的,有过失主动承担主要责任是“躬自厚”,对别人多谅解多宽容,是“薄责于人”,这样的话,就不会互相怨恨。 5.君子成人之美,不成人之恶。小人反是。 ——《论语》 译:君子总是从善良的或有利于他人的愿望出发,全心全意促使别人实现良好的意愿和正当的要求,不会用冷酷的眼光看世界。或是唯恐天下不乱,不会在别人有失败、 错误或痛苦时推波助澜。小人却相反,总是“成人之恶,不成人之美”。 6.见贤思齐焉,见不贤而内自省也。 ——《论语》 译:见到有人在某一方面有超过自己的长处和优点,就虚心请教,认真学习,想办法赶上他,和他达到同一水平;见有人存在某种缺点或不足,就要冷静反省,看自己 是不是也有他那样的缺点或不足。 7.己所不欲,勿施于人。 ——《论语》 译:自己不想要的(痛苦、灾难、祸事……),就不要把它强加到别人身上去。 8.当仁,不让于师。 ——《论语》 译:遇到应该做的好事,不能犹豫不决,即使老师在一旁,也应该抢着去做。后发展为成语“当仁不让”。 9.君子欲讷于言而敏于行。 ——《论语》 译:君子不会夸夸其谈,做起事来却敏捷灵巧。 10.二人同心,其利断金;同心之言,其臭如兰。 ——《周易》 译:同心协力的人,他们的力量足以把坚硬的金属弄断;同心同德的人发表一致的意见,说服力强,人们就像嗅到芬芳的兰花香味,容易接受。 11.君子藏器于身,待时而动。 ——《周易》 译:君子就算有卓越的才能超群的技艺,也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。 12.满招损,谦受益。 ——《尚书》 译:自满于已获得的成绩,将会招来损失和灾害;谦逊并时时感到了自己的不足,就能因此而得益。 13.人不知而不愠,不亦君子乎? ——《论语》 译:如果我有了某些成就,别人并不理解,可我决不会感到气愤、委屈。这不也是一种君子风度的表现吗?知缘斋主人 14.言必信 ,行必果。 ——《论语》 译:说了的话,一定要守信用;确定了要干的事,就一定要坚决果敢地干下去。 15.毋意,毋必,毋固,毋我。 ——《论语》 译:讲事实,不凭空猜测;遇事不专断,不任性,可行则行;行事要灵活,不死板;凡事不以“我”为中心,不自以为是,与周围的人群策群力,共同完成任务。 16.三人行,必有我师焉,择其善者而从之,其不善者而改之。——《论语》 译:三个人在一起,其中必有某人在某方面是值得我学习的,那他就可当我的老师。我选取他的优点来学习,对他的缺点和不足,我会引以为戒,有则改之。 17.君子求诸己,小人求诸人。 ——《论语》 译:君子总是责备自己,从自身找缺点,找问题。小人常常把目光射向别人,找别人的缺点和不足。 18.君子坦荡荡,小人长戚戚。 ——《论语》 译:君子心胸开朗,思想上坦率洁净,外貌动作也显得十分舒畅安定。小人心里欲念太多,心理负担很重,就常忧虑、担心,外貌、动作也显得忐忑不安,常是坐不定, 站不稳的样子。
2.已知△OAB的顶点O是坐标原点,A(-1, 2),B(-3, 0),△OAB 各个顶点的横、纵坐标都扩大为原来的3倍,得到点O′,A,′B′.连接
OA′,OB′,OC′, △OA′B′与△OAB是位似图形吗?如果是,位似中心是哪个点?
y
A(-1, 2),
B(-3, 0)
o
x
想一想:一个图形的各顶点的坐标扩大或缩小相同 的倍数,所得的图形和原图形是什么关系?坐标原 点又是什么?
(3,0)
(3,2)
(0,2)
4 5 x
(0,0)
-3
-4
顺次Байду номын сангаас接下列各点,你得到什么图形? (0,0) (6,0)
y 8
(6,4)
(0,4)
(0,0)
(2)你能发现这两个图形有什么关系吗?
7
6 5 4 3 2 1 0 -1 -2 1 2 3 6 7 8 9 10
两个图 形位似
4 5 x
-3
-4
练一练:
课前回顾: 什么是位似图形?即它的特征是:
相似,对应点的连线相交于一点;对应 线段平行(或共线)
顺次连接下列各点,你得到什么图形? (0,0) (6,4) (0,4) (0,0)
(6,0)
(1)把上面各点坐标的横坐标、纵坐标都除2,画出这 个新图形。 y 8 (0,0)
7
5 4 3 2 1 0 -1 -2 1 2 3 6 7 8 9 10 6
