二次函数中考2014
2014年全国各地中考数学真题分类解析汇编(13)二次函数
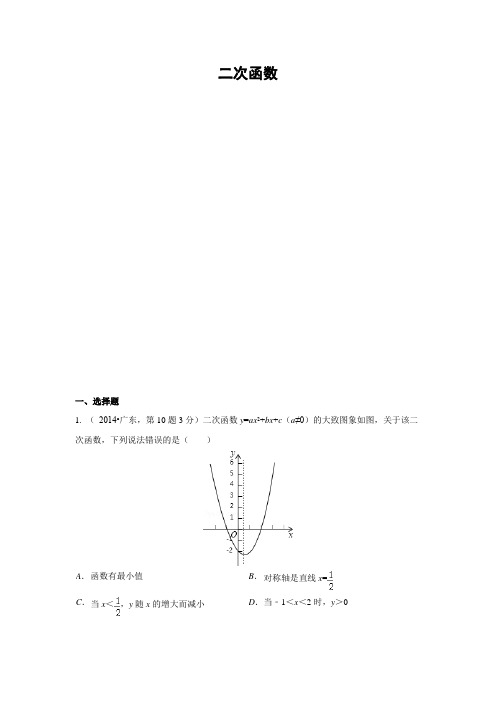
二次函数一、选择题1. (2014•广东,第10题3分)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是()A.函数有最小值B.对称轴是直线x=C.当x<,y随x的增大而减小D.当﹣1<x<2时,y>0考点:二次函数的性质.分析:根据抛物线的开口方向,利用二次函数的性质判断A;根据图形直接判断B;根据对称轴结合开口方向得出函数的增减性,进而判断C;根据图象,当﹣1<x<2时,抛物线落在x轴的下方,则y<0,从而判断D.解答:解:A、由抛物线的开口向下,可知a<0,函数有最小值,正确,故本选项不符合题意;B、由图象可知,对称轴为x =,正确,故本选项不符合题意;C、因为a>0,所以,当x <时,y随x的增大而减小,正确,故本选项不符合题意;D、由图象可知,当﹣1<x<2时,y<0,错误,故本选项符合题意.故选D.点评:本题考查了二次函数的图象和性质,解题的关键是利用数形结合思想解题.2. (2014•广西贺州,第10题3分)已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx +与反比例函数y =在同一坐标系内的大致图象是()A.B.C.D.考点:二次函数的图象;一次函数的图象;反比例函数的图象.分析:先根据二次函数的图象得到a>0,b<0,c<0,再根据一次函数图象与系数的关系和反比例函数图象与系数的关系判断它们的位置.解答:解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x=﹣>0,∴b<0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴一次函数y=cx+的图象过第二、三、四象限,反比例函数y=分布在第二、四象限.故选B.点评:本题考查了二次函数的图象:二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象为抛物线,当a>0,抛物线开口向上;当a<0,抛物线开口向下.对称轴为直线x=﹣;与y轴的交点坐标为(0,c).也考查了一次函数图象和反比例函数的图象.3.(2014年四川资阳,第10题3分)二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是()A.4个B.3个C.2个D.1个考点:二次函数图象与系数的关系.分析:利用二次函数图象的相关知识与函数系数的联系,需要根据图形,逐一判断.解答:解:∵抛物线和x轴有两个交点,∴b2﹣4ac>0,∴4ac﹣b2<0,∴①正确;∵对称轴是直线x﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,∴4a+c>2b,∴②错误;∵把(1,0)代入抛物线得:y=a+b+c<0,∴2a+2b+2c<0,∵b=2a,∴3b,2c<0,∴③正确;∵抛物线的对称轴是直线x=﹣1,∴y=a﹣b+c的值最大,即把(m,0)(m≠0)代入得:y=am2+bm+c<a﹣b+c,∴am2+bm+b<a,即m(am+b)+b<a,∴④正确;即正确的有3个,故选B.点评:此题主要考查了二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特殊点的关系,也要掌握在图象上表示一元二次方程ax2+bx+c=0的解的方法.同时注意特殊点的运用.4.(2014年天津市,第12 题3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x 的一元二次方程ax2+bx+c﹣m=0没有实数根,有下列结论:①b2﹣4ac>0;②abc<0;③m>2.其中,正确结论的个数是()A.0 B.1C.2D.3考点:二次函数图象与系数的关系.分析:由图象可知二次函数y=ax2+bx+c与x轴有两个交点,进而判断①;先根据抛物线的开口向下可知a<0,由抛物线与y轴的交点判断c与0的关系,根据对称轴在y轴右侧得出b与0的关系,然后根据有理数乘法法则判断②;一元二次方程ax2+bx+c﹣m=0没有实数根,则可转化为ax2+bx+c=m,即可以理解为y=ax2+bx+c和y=m没有交点,即可求出m的取值范围,判断③即可.解答:解:①∵二次函数y=ax2+bx+c与x轴有两个交点,∴b2﹣4ac>0,故①正确;②∵抛物线的开口向下,∴a<0,∵抛物线与y轴交于正半轴,∴c>0,∵对称轴x=﹣>0,∴ab<0,∵a<0,∴b>0,∴abc<0,故②正确;③∵一元二次方程ax2+bx+c﹣m=0没有实数根,∴y=ax2+bx+c和y=m没有交点,由图可得,m>2,故③正确.故选D.点评:本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.5.(2014•新疆,第6题5分)对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是()﹣,的顶点坐标是(﹣,6.(2014•舟山,第10题3分)当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为()或C或或﹣或,.y=2x2,y=﹣2x2,共有的性质是()=<﹣>﹣﹣<﹣>﹣﹣8.(2014•孝感,第12题3分)抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为()=1=1﹣9.(2014·台湾,第26题3分)已知a、h、k为三数,且二次函数y=a(x﹣h)2+k在坐标平面上的图形通过(0,5)、(10,8)两点.若a<0,0<h<10,则h之值可能为下列何者?() A.1 B.3 C.5 D.7分析:先画出抛物线的大致图象,根据顶点式得到抛物线的对称轴为直线x=h,由于抛物线过(0,5)、(10,8)两点.若a<0,0<h<10,则点(0,5)到对称轴的距离大于点(10,8)到对称轴的距离,所以h﹣0>10﹣h,然后解不等式后进行判断.解:∵抛物线的对称轴为直线x=h,而(0,5)、(10,8)两点在抛物线上,∴h﹣0>10﹣h,解得h>5.故选D.点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点.抛物线与y 轴交于(0,c );抛物线与x 轴交点个数由△决定,△=b 2﹣4ac >0时,抛物线与x 轴有2个交点;△=b 2﹣4ac =0时,抛物线与x 轴有1个交点;△=b 2﹣4ac <0时,抛物线与x 轴没有交点.10.(2014·浙江金华,第9题4分)如图是二次函数2y x 2x 4=-++的图象,使y 1≤成立的x 的取值范围是【 】A .1x 3-≤≤B .x 1≤-C .x 1≥D .x 1≤-或x 3≥【答案】D . 【解析】试题分析:由图象可知,当y 1≤时,x 1≤-或x 3≥. 故选D . 考点:1.曲线上点的坐标与方程的关系;2.数形结合思想的应用11.(2014•浙江宁波,第12题4分)已知点A (a ﹣2b ,2﹣4ab )在抛物线y =x 2+4x +10上,则点A 关于抛物线对称轴的对称点坐标为( )﹣=12.(2014•菏泽第8题3分)如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是()....,13.(2014•济宁,第8题3分)“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是()14.(2014年山东泰安,第17题3分)已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是()A.B C D.分析:根据二次函数图象判断出m<﹣1,n=1,然后求出m+n<0,再根据一次函数与反比例函数图象的性质判断即可.解:由图可知,m<﹣1,n=1,所以,m+n<0,所以,一次函数y=mx+n经过第二四象限,且与y轴相交于点(0,1),反比例函数y=的图象位于第二四象限,纵观各选项,只有C选项图形符合.故选C.点评:本题考查了二次函数图象,一次函数图象,反比例函数图象,观察二次函数图象判断出m、n的取值是解题的关键.15.(2014年山东泰安,第20题3分)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为()A.4个B.3个C.2个D.1个分析:根据表格数据求出二次函数的对称轴为直线x=1.5,然后根据二次函数的性质对各小题分析判断即可得解.解:由图表中数据可得出:x=1时,y=5值最大,所以二次函数y=ax2+bx+c开口向下,a <0;又x=0时,y=3,所以c=3>0,所以ac<0,故(1)正确;∵二次函数y=ax2+bx+c开口向下,且对称轴为x==1.5,∴当x>1.5时,y的值随x 值的增大而减小,故(2)错误;∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程ax2+(b ﹣1)x+c=0的一个根,故(3)正确;∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+(b﹣1)x+c=0,∵x=3时,ax2+(b﹣1)x+c=0,且函数有最大值,∴当﹣1<x<3时,ax2=(b﹣1)x+c>0,故(4)正确.故选B.点评:本题考查了二次函数的性质,二次函数图象与系数的关系,抛物线与x轴的交点,二次函数与不等式,有一定难度.熟练掌握二次函数图象的性质是解题的关键.16.(2014•滨州,第9题3分)下列函数中,图象经过原点的是()==二.填空题1. (2014•安徽省,第12题5分)某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y=a(1+x)2.考点:根据实际问题列二次函数关系式.分析:由一月份新产品的研发资金为a元,根据题意可以得到2月份研发资金为a×(1+x),而三月份在2月份的基础上又增长了x,那么三月份的研发资金也可以用x表示出来,由此即可确定函数关系式.解答:解:∵一月份新产品的研发资金为a元,2月份起,每月新产品的研发资金与上月相比增长率都是x,∴2月份研发资金为a×(1+x),∴三月份的研发资金为y=a×(1+x)×(1+x)=a(1+x)2.故填空答案:a(1+x)2.点评:此题主要考查了根据实际问题二次函数列解析式,此题是平均增长率的问题,可以用公式a(1±x)2=b来解题.2.(2014年云南,第16题3分)抛物线y=x2﹣2x+3的顶点坐标是.考点:二次函数的性质.专题:计算题.分析:已知抛物线的解析式是一般式,用配方法转化为顶点式,根据顶点式的坐标特点,直接写出顶点坐标.解答:解:∵y=x2﹣2x+3=x2﹣2x+1﹣1+3=(x﹣1)2+2,∴抛物线y=x2﹣2x+3的顶点坐标是(1,2).点评:此题考查了二次函数的性质,二次函数y=a(x﹣h)2+k的顶点坐标为(h,k),对称轴为x=h,此题还考查了配方法求顶点式.3.(2014•浙江湖州,第16题4分)已知当x1=a,x2=b,x3=c时,二次函数y=x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c 时,都有y1<y2<y3,则实数m的取值范围是.分析:根据三角形的任意两边之和大于第三边判断出a最小为2,再根据二次函数的增减性和对称性判断出对称轴在2、3之间偏向2,即不大于2.5,然后列出不等式求解即可.解:∵正整数a,b,c恰好是一个三角形的三边长,且a<b<c,∴a最小是2,∵y1<y2<y3,∴﹣<2.5,解得m>﹣.故答案为:m>﹣.点评:本题考查了二次函数图象上点的坐标特征,三角形的三边关系,判断出a最小可以取2以及对称轴的位置是解题的关键.4. (2014•株洲,第16题,3分)如果函数y=(a﹣1)x2+3x+的图象经过平面直角坐标系的四个象限,那么a的取值范围是a<﹣5.=<﹣轴的正半轴相交.因此5. (2014年江苏南京,第16题,2分)已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:则当y<5时,x的取值范围是.考点:二次函数与不等式分析:根据表格数据,利用二次函数的对称性判断出x=4时,y=5,然后写出y<5时,x的取值范围即可.解答:由表可知,二次函数的对称轴为直线x=2,所以,x=4时,y=5,所以,y<5时,x的取值范围为0<x<4.故答案为:0<x<4.点评:本题考查了二次函数与不等式,观察图表得到y=5的另一个x的值是解题的关键.6. (2014•扬州,第16题,3分)如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a﹣2b+c的值为0.(第3题图)7.(2014•菏泽,第12题3分)如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则= _______.,,的横坐标相同,为2=3,,﹣=﹣.8. (2014•珠海,第9题4分)如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,則它的对称轴为直线x=2.=三.解答题1. (2014•安徽省,第22题12分)若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.(1)请写出两个为“同簇二次函数”的函数;(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A (1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.考点:二次函数的性质;二次函数的最值.专题:新定义.分析:(1)只需任选一个点作为顶点,同号两数作为二次项的系数,用顶点式表示两个为“同簇二次函数”的函数表达式即可.(2)由y1的图象经过点A(1,1)可以求出m的值,然后根据y1+y2与y1为“同簇二次函数”就可以求出函数y2的表达式,然后将函数y2的表达式转化为顶点式,在利用二次函数的性质就可以解决问题.解答:解:(1)设顶点为(h,k)的二次函数的关系式为y=a(x﹣h)2+k,当a=2,h=3,k=4时,二次函数的关系式为y=2(x﹣3)2+4.∵2>0,∴该二次函数图象的开口向上.当a=3,h=3,k=4时,二次函数的关系式为y=3(x﹣3)2+4.∵3>0,∴该二次函数图象的开口向上.∵两个函数y=2(x﹣3)2+4与y=3(x﹣3)2+4顶点相同,开口都向上,∴两个函数y=2(x﹣3)2+4与y=3(x﹣3)2+4是“同簇二次函数”.∴符合要求的两个“同簇二次函数”可以为:y=2(x﹣3)2+4与y=3(x﹣3)2+4.(2)∵y1的图象经过点A(1,1),∴2×12﹣4×m×1+2m2+1=1.整理得:m2﹣2m+1=0.解得:m1=m2=1.∴y1=2x2﹣4x+3=2(x﹣1)2+1.∴y1+y2=2x2﹣4x+3+ax2+bx+5=(a+2)x2+(b﹣4)x+8∵y1+y2与y1为“同簇二次函数”,∴y1+y2=(a+2)(x﹣1)2+1=(a+2)x2﹣2(a+2)x+(a+2)+1.其中a+2>0,即a>﹣2.∴.解得:.∴函数y2的表达式为:y2=5x2﹣10x+5.∴y2=5x2﹣10x+5=5(x﹣1)2.∴函数y2的图象的对称轴为x=1.∵5>0,∴函数y2的图象开口向上.①当0≤x≤1时,∵函数y2的图象开口向上,∴y2随x的增大而减小.∴当x=0时,y2取最大值,最大值为5(0﹣1)2=5.②当1<x≤3时,∵函数y2的图象开口向上,∴y2随x的增大而增大.∴当x=3时,y2取最大值,最大值为5(3﹣1)2=20.综上所述:当0≤x≤3时,y2的最大值为20.点评:本题考查了求二次函数表达式以及二次函数一般式与顶点式之间相互转化,考查了二次函数的性质(开口方向、增减性),考查了分类讨论的思想,考查了阅读理解能力.而对新定义的正确理解和分类讨论是解决第二小题的关键.2. (2014•福建泉州,第22题9分)如图,已知二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).(1)写出该函数图象的对称轴;(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?OA OB(+的图象经过原点OA=,﹣的顶点.)的顶点坐标为(﹣),对称轴直线x=﹣,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:<﹣时,﹣取得最小值,即顶<﹣时,时,3. (2014•福建泉州,第25题12分)如图,在锐角三角形纸片ABC中,AC>BC,点D,E,F分别在边AB,BC,CA上.(1)已知:DE∥AC,DF∥BC.①判断四边形DECF一定是什么形状?②裁剪当AC=24cm,BC=20cm,∠ACB=45°时,请你探索:如何剪四边形DECF,能使它的面积最大,并证明你的结论;(2)折叠请你只用两次折叠,确定四边形的顶点D,E,C,F,使它恰好为菱形,并说明你的折法和理由.=12=12====6 =124. (2014•广东,第25题9分)如图,在△ABC中,AB=AC,AD⊥AB于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t 秒(t>0).(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.考点:相似形综合题.分析:(1)如答图1所示,利用菱形的定义证明;(2)如答图2所示,首先求出△PEF的面积的表达式,然后利用二次函数的性质求解;(3)如答图3所示,分三种情形,需要分类讨论,分别求解.解答:(1)证明:当t=2时,DH=AH=2,则H为AD的中点,如答图1所示.又∵EF⊥AD,∴EF为AD的垂直平分线,∴AE=DE,AF=DF.∵AB=AC,AD⊥AB于点D,∴AD⊥BC,∠B=∠C.∴EF∥BC,∴∠AEF=∠B,∠AFE=∠C,∴∠AEF=∠AFE,∴AE=AF,∴AE=AF=DE=DF,即四边形AEDF为菱形.(2)解:如答图2所示,由(1)知EF∥BC,∴△AEF∽△ABC,∴,即,解得:EF=10﹣t.S△PEF=EF•DH=(10﹣t)•2t=﹣t2+10t=﹣(t﹣2)2+10∴当t=2秒时,S△PEF存在最大值,最大值为10,此时BP=3t=6.(3)解:存在.理由如下:①若点E为直角顶点,如答图3①所示,此时PE∥AD,PE=DH=2t,BP=3t.∵PE∥AD,∴,即,此比例式不成立,故此种情形不存在;②若点F为直角顶点,如答图3②所示,此时PE∥AD,PF=DH=2t,BP=3t,CP=10﹣3t.∵PF∥AD,∴,即,解得t=;③若点P为直角顶点,如答图3③所示.过点E作EM⊥BC于点M,过点F作FN⊥BC于点N,则EM=FN=DH=2t,EM∥FN∥AD.∵EM∥AD,∴,即,解得BM=t,∴PM=BP﹣BM=3t﹣t=t.在Rt△EMP中,由勾股定理得:PE2=EM2+PM2=(2t)2+(t)2=t2.∵FN∥AD,∴,即,解得CN=t,∴PN=BC﹣BP﹣CN=10﹣3t﹣t=10﹣t.在Rt△FNP中,由勾股定理得:PF2=FN2+PN2=(2t)2+(10﹣t)2=t2﹣85t+100.在Rt△PEF中,由勾股定理得:EF2=PE2+PF2,即:(10﹣t)2=(t2)+(t2﹣85t+100)化简得:t2﹣35t=0,解得:t=或t=0(舍去)∴t=.综上所述,当t=秒或t=秒时,△PEF为直角三角形.点评:本题是运动型综合题,涉及动点与动线两种运动类型.第(1)问考查了菱形的定义;第(2)问考查了相似三角形、图形面积及二次函数的极值;第(3)问考查了相似三角形、勾股定理、解方程等知识点,重点考查了分类讨论的数学思想.5. (2014•珠海,第22题9分)如图,矩形OABC的顶点A(2,0)、C(0,2).将矩形OABC绕点O逆时针旋转30°.得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段GF、GH、GO和x轴于点M、P、N、D,连结MH.(1)若抛物线l:y=ax2+bx+c经过G、O、E三点,则它的解析式为:y=x2﹣x;(2)如果四边形OHMN为平行四边形,求点D的坐标;(3)在(1)(2)的条件下,直线MN与抛物线l交于点R,动点Q在抛物线l上且在R、E两点之间(不含点R、E)运动,设△PQH的面积为s,当时,确定点Q的横坐标的取值范围.OF点右边时,所求三角形为两三角形的差.得关系式再代入,=2,=3=,,,x=﹣,,,,﹣x﹣,x<.①当﹣,﹣••••••[x(x(﹣+时,,﹣•)﹣•..,<﹣x+,解得﹣<<,<.6. 2014•广西贺州,第26题12分)二次函数图象的顶点在原点O,经过点A(1,14);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.(1)求二次函数的解析式;(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM 平分∠OFP;(3)当△FPM是等边三角形时,求P点的坐标.考点:二次函数综合题.专题:综合题.分析:(1)根据题意可设函数的解析式为y=ax2,将点A代入函数解析式,求出a的值,继而可求得二次函数的解析式;(2)过点P作PB⊥y轴于点B,利用勾股定理求出PF,表示出PM,可得PF=PM,∠PFM=∠PMF,结合平行线的性质,可得出结论;(3)首先可得∠FMH=30°,设点P的坐标为(x,14x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.解答:(1)解:∵二次函数图象的顶点在原点O,∴设二次函数的解析式为y=ax2,将点A(1,14)代入y=ax2得:a=14,∴二次函数的解析式为y=14x2;(2)证明:∵点P在抛物线y=14x2上,∴可设点P的坐标为(x,14x2),过点P作PB⊥y轴于点B,则BF=14x2﹣1,PB=x,∴Rt△BPF中,PF==14x2+1,∵PM⊥直线y=﹣1,∴PM=14x2+1,∴PF=PM,∴∠PFM=∠PMF,又∵PM∥x轴,∴∠MFH=∠PMF,∴∠PFM=∠MFH,∴FM平分∠OFP;(3)解:当△FPM是等边三角形时,∠PMF=60°,∴∠FMH=30°,在Rt△MFH中,MF=2FH=2×2=4,∵PF=PM=FM,∴14x2+1=4,解得:x=±2,∴14x2=14×12=3,∴满足条件的点P的坐标为(2,3)或(﹣2,3).点评:本题考查了二次函数的综合,涉及了待定系数法求函数解析式、角平分线的性质及直角三角形的性质,解答本题的关键是熟练基本知识,数形结合,将所学知识融会贯通.7. (2014•广西玉林市、防城港市,第26题12分)给定直线l:y=kx,抛物线C:y=ax2+bx+1.(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a 的值;(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点.①求此抛物线的解析式;②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ.=0中,若不能使其结果为﹣x),∴顶点(﹣,﹣=1﹣.==,==0=xx xx==﹣(﹣x8.(2014年四川资阳,第22题9分)某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的,且空调采购单价不低于1200元,问该商家共有几种进货方案?(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润.考点:二次函数的应用;一元一次不等式组的应用.分析:(1)设空调的采购数量为x台,则冰箱的采购数量为(20﹣x)台,然后根据数量和单价列出不等式组,求解得到x的取值范围,再根据空调台数是正整数确定进货方案;(2)设总利润为W元,根据总利润等于空调和冰箱的利润之和整理得到W与x的函数关系式并整理成顶点式形式,然后根据二次函数的增减性求出最大值即可.解答:解:(1)设空调的采购数量为x台,则冰箱的采购数量为(20﹣x)台,由题意得,,解不等式①得,x≥11,解不等式②得,x≤15,所以,不等式组的解集是11≤x≤15,∵x为正整数,∴x可取的值为11、12、13、14、15,所以,该商家共有5种进货方案;(2)设总利润为W元,y2=﹣10x2+1300=﹣10(20﹣x)+1300=10x+1100,则W=(1760﹣y1)x1+(1700﹣y2)x2,=1760x﹣(﹣20x+1500)x+(1700﹣10x﹣1100)(20﹣x),=1760x+20x2﹣1500x+10x2﹣800x+12000,=30x2﹣540x+12000,=30(x﹣9)2+9570,当x>9时,W随x的增大而增大,∵11≤x≤15,∴当x=15时,W最大值=30(15﹣9)2+9570=10650(元),答:采购空调15台时,获得总利润最大,最大利润值为10650元.点评:本题考查了二次函数的应用,一元一次不等式组的应用,(1)关键在于确定出两个不等关系,(2)难点在于用空调的台数表示出冰箱的台数并列出利润的表达式.9.(2014年四川资阳,第24题12分)如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A (3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.(1)求抛物线的解析式;(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.考点:二次函数综合题.分析:(1)根据对称轴可知,抛物线y=ax2+bx+c与x轴的另一个交点为(﹣1,0),根据待定系数法可得抛物线的解析式为y=﹣x2+2x+3.(2)分三种情况:①当MA=MB时;②当AB=AM时;③当AB=BM时;三种情况讨论可得点M的坐标.(3)平移后的三角形记为△PEF.根据待定系数法可得直线AB的解析式为y=﹣x+3.易得直线EF的解析式为y=﹣x+3+m.根据待定系数法可得直线AC的解析式.连结BE,直线BE交AC于G,则G(,3).在△AOB沿x轴向右平移的过程中.分二种情况:①当0<m≤时;②当<m<3时;讨论可得用m的代数式表示S.解答:解:(1)由题意可知,抛物线y=ax2+bx+c与x轴的另一个交点为(﹣1,0),则,解得.故抛物线的解析式为y=﹣x2+2x+3.(2)①当MA=MB时,M(0,0);②当AB=AM时,M(0,﹣3);③当AB=BM时,M(0,3+3)或M(0,3﹣3).所以点M的坐标为:(0,0)、(0,﹣3)、(0,3+3)、(0,3﹣3).(3)平移后的三角形记为△PEF.设直线AB的解析式为y=kx+b,则,解得.则直线AB的解析式为y=﹣x+3.△AOB沿x轴向右平移m个单位长度(0<m<3)得到△PEF,易得直线EF的解析式为y=﹣x+3+m.设直线AC的解析式为y=k′x+b′,则,解得.则直线AC的解析式为y=﹣2x+6.连结BE,直线BE交AC于G,则G(,3).在△AOB沿x轴向右平移的过程中.①当0<m≤时,如图1所示.设PE交AB于K,EF交AC于M.则BE=EK=m,PK=P A=3﹣m,联立,解得,即点M(3﹣m,2m).故S=S△PEF﹣S△P AK﹣S△AFM=PE2﹣PK2﹣AF•h=﹣(3﹣m)2﹣m•2m=﹣m2+3m.②当<m<3时,如图2所示.设PE交AB于K,交AC于H.因为BE=m,所以PK=P A=3﹣m,又因为直线AC的解析式为y=﹣2x+6,所以当x=m时,得y=6﹣2m,所以点H(m,6﹣2m).故S=S△P AH﹣S△P AK=P A•PH﹣P A2=﹣(3﹣m)•(6﹣2m)﹣(3﹣m)2=m2﹣3m+.综上所述,当0<m≤时,S=﹣m2+3m;当<m<3时,S=m2﹣3m+.点评:考查了二次函数综合题,涉及的知识点有:抛物线的对称轴,待定系数法求抛物线的解析式,待定系数法求直线的解析式,分类思想的应用,方程思想的应用,综合性较强,有一定的难度.10.(2014•温州,第21题10分)如图,抛物线y=﹣x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(﹣1,0).(1)求该抛物线的解析式及顶点M的坐标.(2)求△EMF与△BNE的面积之比.=))11.(2014•舟山,第22题10分)实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x 刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=(k>0)刻画(如图所示).(1)根据上述数学模型计算:①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?②当x=5时,y=45,求k的值.(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.,则=12.(2014•舟山,第24题12分)如图,在平面直角坐标系中,A是抛物线y=x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED 的面积为S.(1)当m=时,求S的值.(2)求S关于m(m≠2)的函数解析式.(3)①若S=时,求的值;②当m>2时,设=k,猜想k与m的数量关系并证明.=====k,代入即可得出k的值;②可得====22;=,即的面积为,,===========13.(2014年广东汕尾,第25题10分)如图,已知抛物线y=x2﹣x﹣3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.(1)直接写出A、D、C三点的坐标;(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.分析:(1)令y=0,解方程x2﹣x﹣3=0可得到A点和D点坐标;令x=0,求出y=﹣3,可确定C点坐标;(2)根据抛物线的对称性,可知在在x轴下方对称轴右侧也存在这样的一个点;再根据三角形的等面积法,在x轴上方,存在两个点,这两个点分别到x轴的距离等于点C到x轴的距离;(3)根据梯形定义确定点P,如图所示:①若BC∥AP1,确定梯形ABCP1.此时P1与D点重合,即可求得点P1的坐标;②若AB∥CP2,确定梯形ABCP2.先求出直线CP2的解析式,再联立抛物线与直线解析式求出点P2的坐标.解:(1)∵y=x2﹣x﹣3,∴当y=0时,x2﹣x﹣3=0,解得x1=﹣2,x2=4.当x=0,y=﹣3.∴A点坐标为(4,0),D点坐标为(﹣2,0),C点坐标为(0,﹣3);(2)∵y=x2﹣x﹣3,∴对称轴为直线x==1.∵AD在x轴上,点M在抛物线上,∴当△MAD的面积与△CAD的面积相等时,分两种情况:①点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,∵C点坐标为(0,﹣3),∴M点坐标为(2,﹣3);。
2014中考含答案 二次函数的综合问题

二次函数的综合问题【教学目标】(一)培养学生灵活掌握和运用二次函数知识的能力;(二)提高分析问题和解决问题的能力.【重点、难点】重点:使学生初步会把二次函数概念和性质综合在一起灵活运用;熟悉数与形的相互联系,相辅相成.难点:善于选择恰当的解法;善于把问题与函数的有关性质联系起来.【知识要点】1.二次函数y=ax2+bx+c图象的顶点坐标是____.2.y=ax2+bx+c图象的顶点坐标公式.3.y=ax2+bx+c图象的画法.4.用待定系数法求二次函数的解析式.5.图象法解ax2+bx+c>0的几何意义.6.有关二次函数的最大值、最小值问题【经典例题】例1.已知y=x2-4x-9(1)把它配方成y=a(x+h)2+k形式;(2)写出它的开口方向、顶点M的坐标、对称轴方程和最值;(3)求出图象与y轴、x轴的交点坐标;(4)作出函数图象;(5)x取什么值时y>0,y<0;(6)设图象交x轴于A,B两点,求△AMB面积.例2.已知图22是二次函数y=ax2+bx+c的图象,判断以下各式的值是正值还是负值.(1)a;(2)b;(3)c;(4)b2-4ac;(5)2a+b;(6)a+b+c;(7)a-b+c.例3 .k取什么值时,对于任意实数x,二次不等式(4-k)x2-3x+k+4>0都成立.例4 .k取什么值时,对于任意实数x,二次不等式(4-k)x2-3x+k+4>0都成立.例5.如图32有一个半径为R的圆的内接等腰梯形,其下底是圆的直径.(1)写出周长y与腰长x的函数关系及自变量x的范围;(2)腰长为何值时周长最大,最大值是多少?例6.抛物线c+=2与x轴交于A、B两点,抛物线的顶点为P.axbxy+(1)若ABP∆为等边三角形,则∆= .(2)若ABP∆为等腰直角三角形,则∆= .例7.如图所示,ABC ∆为直角三角形,D AC BC C ,4,3,90==︒=∠为AC 上任意一点,E 在BC 上,G 、F 在AB 上,四边形DEFG 为矩形,设x CD =,四边形DEFG 的面积为y ,则y 与x 的函数关系式为 .例8.如图,抛物线2812y mx mx n =++与x 轴交于A 、B 两点(点A 在点B 的左边),在第二象限内抛物线上的一点C ,使△OCA ∽△OBC ,且:AC B C =,若直线AC 交y 轴于P 。
2014中考含答案 二次函数y=ax2的图象

二次函2ax y =的图象【教学目标】1.会用描点法画出二次函数()02≠=a ax y 的图象,知道抛物线的有关概念; 2.了解抛物线()02≠=a ax y 的顶点、对称轴的概念; 3.理解二次函数()02≠=a ax y 的最值;4.了解二次函数()02≠=a ax y ,函数值y 随自变量x 变化的变化规律.【重点、难点】重点:会用描点法画出二次函数()02≠=a ax y 的图象.难点:由抛物线的图象直观得到二次函数()02≠=a ax y 的有关性质.【知识要点】1.二次函数2x y =的图象.用描点法画出二次函数2x y =的图象,如图, 它是一条关于y 轴对称的曲线,这样的曲线叫做抛物线.2.二次函数2x y =的有关性质.因为抛物线2x y =关于y 轴对称,所以y 轴是这条抛物线的对称轴,对称轴与抛物线的交点是抛物线的顶点,从图上看,抛物线2x y =的顶点是图象的最低点,因为抛物线2x y =有最低点,所以函数2x y =有最小值,它的最小值就是最低点的纵坐标. 3.二次函数2ax y =的图象画法.用描点画二次函数2ax y =的图象时,应在顶点的左、右两侧对称地选取自变量x 的值,然后计算出对应的y 值,这样的对应值选取越密集,描出的图象越准确。
4.二次函数2ax y =的性质.2(2).抛物线2ax y =的对称轴是y 轴,顶点是原点,当0>a 时,抛物线开口向上,在对称轴左侧部分,y 随x 的增大而减小;在对称轴右侧部分,y 随x 的增大而增大.当0<a 时,抛物线开口向下,在对称轴左侧部分,y 随x 的增大而增大;在对称轴右侧部分,y 随x 的增大而减小;a 的大小决定抛物线2ax y =的开口大小,a 越大,抛物线开口越小;a 越小,抛物线开口越大.【典型例题】例1 画图.在同一坐标系内,画出下列函数的图象(1)y=2x 2 (2)y=-2x 2例2 填空1.函数y=31x 2的图象开口 ,顶点坐标为 ,对称轴为 ,当x=时,y 有最 值。
2014中考含答案 二次函数:由图象判断 的符号

二次函数:由图象判断∆,,,c b a 的符号教学目的: 掌握抛物线的()02≠++=a c bx ax y 图像与系数∆,,,c b a 的关系 教学重点:通过抛物线的位置判断∆,,,c b a 的符号. 教学难点:通过∆,,,c b a 的符号判断抛物线的位置 教学过程:前面,我们已经学过二次函数c bx ax y ++=2的一些基本性质,现在我们简单地回顾一下这些性质:二次函数c bx ax y ++=2的图象是 ,应用配方法可将其化为=y .其中=h ,=k .其图象与函数2ax y =的图象的 相同,开口方向相同, 那么,我们今天一起来学习抛物线的位置与∆,,,c b a 之间的关系.上面讲过,对于抛物线来说:(1)a 决定抛物线的开口方向:⇔>0a ;⇔<0a .(2)C 决定抛物线与y 轴交点的位置, 0>c ⇔抛物线交y 轴于 ;0<c ⇔抛物线交y 轴于 ; 0=c ⇔ .(3)直线abx 2-=是抛物线的对称轴,当b a ,同号时⇔对称轴在y 轴 ;0=b ⇔对称轴为 ;b a ,异号⇔对称轴在y 轴 ,简称为 .(4)当042>-ac b 时,抛物线与x 轴 交点;当042=-ac b 时,抛物线与x 轴 交点; 当042<-ac b 时,抛物线与x 轴 交点.[典型例题]一.通过抛物线的位置判断∆,,,c b a 的符号.例1 二次函数c bx ax y ++=2的图象,如图所示,则a 0,b 0,c 0.(填“>”或“<”)例2. 已知二次函数)0(2≠++=a c bx ax y 的图象是(1)a 0,b 0,c 0(填“>”或“(2)点(bc ac ,)在直角坐标系中的第 象限.(3)二次函数,满足ac b 42- 0.(4)一次函数c ax y +=的图象不经过第 象限.例3. 二次函数c bx ax y ++=2的图象如上图所示,则点⎪⎭⎫⎝⎛c b c a ,在直角坐标系中的( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限例4.二次函数c bx ax y ++=2的图象如图所示,则ac 0. A 、> B 、< C 、= D 、无法确定例5. 二次函数c bx ax y ++=2的图象,如图(1)所示,则系数b ax y +=的图象只可能是图( )Cx[课堂练习:]1.二次函数c bx ax y ++=2的图象如图所示,则下列条件不正确的是( )A 、0,0,0<><c b aB 、042<-ac bC 、0<++c b aD 、0>+-c b a2.如图,为二次函数c bx ax y ++=2的图象,则 一次函数bc ax y +=的图象不经过( ) A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限3.二次函数c bx ax y ++=2的图象如图,则点⎪⎭⎫⎝⎛-+b ac ac b b a ,42在.( ) A 、第一象限 B 、第二象限C 、第三象限D 、第四象限4. 下列图象中,当0>ab 时,函数2ax y =与b ax y +=的图象是( )5.二次函数c bx ax y ++=2与一次函数c ax y +=在同一坐标系中的图象大致是( )xx二.通过∆,,,c b a 的符号判断抛物线的位置:例,<cax =例2.若0,0,0,0>∆>>>c b a ,那么抛物线c bx ax y ++=2经过象限.例3.已知二次函数c bx ax y ++=2且0,0>+-<c b a a ;则一定有ac b 42- 0(填“>”“<”“=”“≥”或“≤”)例4.如图,为二次函数c bx ax y ++=2则一次函数bc ax y +=的图象不经过( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限例5.已知抛物线c bx ax y ++=2的系数有0=+-c b a ,则这条抛物线经过点 .例6.如果函数b kx y +=的图象在第一、二、三象限内,那么函数12-+=bx kx y 的大致图象是( )xxxx[课堂练习]1.若直线c bx ax y ++=2开口向上,则直线3+=ax y 经过 象限. 2.函数c bx ax y ++=2和b ax y +=在同一从标系中,如图所示,正确的3.二次函数c bx ax y ++=2()0≠a 的图象,如图,下列结论①0<c ②0>b ③024>++c b a ④()22b c a <+其中正确的有()A 、1个B 、2个C 、3个D 、4个4.已知函数c bx ax y ++=2的图象如图所示,关于系数c b a ,,有下列不等式( ) ①0<a ②0<b ③0>c ④02<+b a ⑤0>++c b a 其中正确个数为.5.若一抛物线2ax y =与四条直线,1,2,1===y x x 2=y 围成的正方形有公共点,则a 的取值范围是 .6.已知二次函数bx ax y +=2(0≠a ),当x 取()2121,x x x x ≠时,函数值相等那么当x 取21x x +时,函数值为 .7.已知抛物线52-+=mx x y 经过点(2,-3),则=m ;当x 时,y 随x 增大而增大yx8.已知二次函数()m mx x m y 34222+--=图像开口向下,对称轴是2=x . (1)求m 值;(2)若函数图像顶点为A ,与x 轴两交点为B 、C ,求经过A 、B 、C 三点的圆的半径.9.已知抛物线122-++=m x x y .(1)若抛物线与x 轴只有一个交点,求m 值;(2)若抛物线与直线m x y 2+=只有一个交点,求m 值.10.已知抛物线q px x y ++-=2与x 轴的正半轴交于点A ,与x 轴负半轴交于点B ,与y 轴正半轴交于点C .(1)若︒=∠︒=∠60,45CAB CBA ,求q p ,的值;(2)3tan tan ,90=∠-∠︒=∠CBA CAB ACB ,求q p ,的值.11.已知二次函数c bx ax y ++=2的图象经过点(c,2),且0=+b b a a ,不等式022>-++c bx ax 无解,试求出二次函数c bx ax y ++=2的解析式。
2014中考27题二次函数专项:直角、相似、等腰问题及答案

直角三角形问题1.已知:如图一次函数112y x =+的图象与x 轴交于点A ,与y 轴交于点B ;二次函数212y x bx c =++的图象与一次函数112y x =+的图象交于B C ,两点,与x 轴交于D E ,两点且D 点坐标为(1,0) (1)求二次函数的解析式;(2)求四边形BDEC 的面积S ;(3)在x 轴上是否存在点P ,使得PBC △是以P 为直角顶点的直角三角形?若存在,求出所有的点P ,若不存在,请说明理由.(4)在抛物线上是否存在点P ,使得PBC △是以∠B 或∠C 为直角顶点的直角三角形?若存在,求出所有的点P ,若不存在,请说明理由.2. 在平面直角坐标系中,现将一块等腰直角三角板ABC 放在第一象限,斜靠在两坐标轴上,且点()02A ,,点()10C ,,如图所示;抛物线22y ax ax =--经过点B . (1)求点B 的坐标; (2)求抛物线的解析式;(3)在抛物线上是否还存在点P (点B 除外),使ACP △仍然是以AC 为直角边的等腰直角三角形?若存在,求所有点P 的坐标;若不存在,请说明理由.3.如图,在平面直角坐标系中,将一块等腰直角三角板ABC 斜靠在两坐标轴上放在第二象限,点C 的坐标为()10-,.B 点在抛物线211222y x x =+-的图象上,过点B 作BD x ⊥轴,垂足为D ,且B 点横坐标为3-.(1)求证:BDC COA △≌△; (2)求BC 所在直线的函数关系式;(3)抛物线的对称轴上是否存在点P ,使ACP △是以AC 为直角边的直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.4. 如图,在平面直角坐标系中,△ABC 是直角三角形,∠ACB=900,AC=BC ,OA=1,OC=4,抛物线2y x bx c =++经过A ,B 两点,抛物线的顶点为D . (1)求b ,c 的值;(2)点E 是直角三角形ABC 斜边AB 上一动点(点A 、B 除外),过点E 作x 轴的垂线交抛物线于点F ,当线段EF 的长度最大时,求点E 的坐标;(3)在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上是否存在一点P ,使△EFP 是以EF 为直角边的直角三角形? 若存在,求出所有点P 的坐标;若不存在,说明理由.备用图5. 如图,已知抛物线y =x 2+bx +c 与x 轴交于A 、B 两点(A 点在B 点左侧),与y 轴交于点(03)C ,,对称轴是直线x =1,直线BC 与抛物线的对称轴交于点D . (1)求抛物线的函数表达式; (2)求直线BC 的函数表达式;(3)点E 为y 轴上一动点,CE 的垂直平分线交CE 于点F ,交抛物线于P 、Q 两点,且点P 在第三象限. ①当线段PQ =34AB 时,求tan ∠CED 的值; ②当以点C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标. 温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.角与相似6.如图,四边形ABCO 是平行四边形,42AB OB ==,,抛物线过A B C 、、三点,与x 轴交于另一点D .一动点P 以每秒1个单位长度的速度从B 点出发沿BA 向点A 运动,运动到点A 停止,同时一动点Q 从点D 出发,以每秒3个单位长度的速度沿DC 向点C 运动,与点P 同时停止. (1)求抛物线的解析式;(2)若抛物线的对称轴与AB 交于点E ,与x 轴交于点F ,当点P 运动时间t 为何值时,四边形POQE 是等腰梯形?(3)当t 为何值时,以P B O 、、为顶点的三角形与以点Q B O 、、为顶点的三角形相似?7. 如图①,已知抛物线2(0)y ax bx a =+≠经过(30)A ,、(44)B ,两点. (1)求抛物线的解析式;(2)将直线OB 向下平移m 个单位长度后,得到的直线与抛物线只有一个公共点D ,求m 的值及点D 的坐标; (3)如图②,若点N 在抛物线上,且 NBO ABO ∠=∠,则在(2)的条件下,求出所有满足POD NOB △∽△的点P 的坐标(点P 、O 、D 分别与点N 、O 、B 对应).8.如图,已知抛物线的方程C :()()()120y x x m m =-+->与x 轴相交于点B 、C ,与y 轴相交于点E ,且点B 在点C 的左侧.(1)若抛物线1C 过点M (2,2),求实数m 的值. (2)在(1)的条件下,求BCE △的面积.(3)在(1)的条件下,在抛物线的对称轴上找一点H ,使BH EH +最小,并求出点H 的坐标. (4)在第四象限内,抛物线1C 上是否存在点F ,使得以点B 、C 、F 为顶点的三角形与BCE △相似?若存在,求m 的值;若不存在,请说明理由.9.在平面直角坐标系中,抛物线32++=bx ax y 与x 轴的两个交点分别为A (-3,0)、B (1,0),过顶点C 作CH ⊥x 轴于点H .(1)直接填写:a = ,b = ,顶点C 的坐标为 ;(2)在y 轴上是否存在点D ,使得△ACD 是以AC 为斜边的直角三角形?若存在,求出点D 的坐标;若不存在,说明理由;(3)若点P 为x 轴上方的抛物线上一动点(点P 与顶点C 不重合),PQ ⊥AC 于点Q ,当△PCQ 与△ACH 相似时,求点P 的坐标.等腰三角形10.已知抛物线2y ax bx c =++经过()10A -,、()30B ,、()03C ,三点,直线l 是抛物线的对称轴. (1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当PAC △的周长最小时,求点P 的坐标;(3)在直线l 上是否存在点M ,使MAC △为等腰三角形,若存在,直接写出....所有符合条件的点M 的坐标;若不存在,请说明理由.11. 已知直线24y x =+与x 轴、y 轴分别交于A D 、两点,抛物线212y x bx c =-++经过点A D 、,点B是抛物线与x 轴的另一个交点.(1)求这条抛物线的解析式及点B 的坐标;(2)设点M 是直线AD 上一点,且13AOM OMD S S =△△::,求点M 的坐标; (3)如果点(2)C y ,在这条抛物线上,在y 轴的正半轴上是否存在点P ,使BCP △为等腰三角形,若存在,请求出点P 的坐标;若不存在,请说明理由.12.如图,在平面直角坐标系中,直线22+=x y 交x 轴于点A ,交y 轴于点B ,将△AOB 绕原点O 顺时针旋转90º后得到△COD ,抛物线l 经过点A 、C 、D . (1)求点A 、B 的坐标; (2)求抛物线l 的解析式;(3)已知在抛物线l 与线段AD 所围成的封闭图形(不含边界....)中,存在点),(b a P ,使得△PCD 是等腰三角形,求a 的取值范围.答案1. 解:(1)()()0110B D ,,,的坐标代入212y x bx c =++ 1102c b c =⎧⎪⎨++=⎪⎩得解析式213122y x x =-+ 3分(2)设()00C x y ,,则有00200011213122y x y x x ⎧=+⎪⎪⎨⎪=-+⎪⎩解得0043x y =⎧⎨=⎩,()43C ∴,. 6分由图可知:ACB ABD S S S =-△△又由对称轴为32x =可知()20E ,011119433122222S AE y AD OB ∴=-⨯=⨯⨯-⨯⨯=·8分(3)设符合条件的点P 存在,令()0P a ,.当P 为直角顶点时,如图,过C 作CF x ⊥轴于F . Rt Rt BO OP BOP PFC PF CF∴= △∽△,,即143aa =-.整理得2430a a -+=,解得1a =或3a = ∴所求的点P 的坐标为()10,或()30,综上所述:满足条件的点P 共有二个. 12分2. 解:(1)过点B 作BD x ⊥轴,垂足为D ,9090BCD ACO ACO OAC ∠+∠=︒∠+∠=︒ ,,BCD CAO ∴∠=∠. 又90BDC COA ∠=∠=︒ ,CB AC =,∴12BDC CAO BD OC CD OA ∴====△≌△,,.∴点B 的坐标为()31,. (2)抛物线22y ax ax =--经过点()31B ,,则得到1932a a =--,解得12a=,所以抛物线的解析式为211222y x x =--; (3)假设存在点P ,使得ACP △是直角三角形;①若以AC 为直角边,点C 为直角顶点;则延长BC 至点1P 使得1PC BC =,得到等腰直角三角形1ACP ,过点1P ,作1PMx ⊥轴,如图. 11CP BC MCP BCD =∠=∠ ,,190PMC BDC ∠=∠=︒, 1MPC DBC ∴△≌△2CM CD ∴==,11PM BD ∴==, 可求得点()111P --,;经检验点()111P --,在抛物线211222y x x =--上; ②若以AC 为直角边,点A 为直角顶点;则过点A 作2AP CA ⊥,且使得2AP AC =,得到等腰直角三角形2ACP ,过点2P 作2P N y ⊥轴, 如图同理可证2AP N CAO △≌△;221NP OA AN OC ∴====,,可求得点()221P -,;经检验点()221P -,也在抛物线211222y x x =--上; ③若以AC 为直角边,点A 为直角顶点; 则过点A 作3AP CA ⊥,且使得3APAC =, 得到等腰直角三角形3ACP ,过点3P 作3P H y ⊥轴,如图. 同理可证3AP H CAO △≌△;321HP OA AH OC ∴====,,可求得点()323P ,;经检验点()323P ,不在抛物211222y x x =--上. 故符合条件的点有()()121121P P ---,,,两点. 3. 解:(1)∵ 90BCD ACO ∠+∠=︒,90ACO OAC ∠+∠=︒,∴BCD OAC ∠=∠. ∵ABC △为等腰直角三角形,∴BC AC =.在BDC △和COA △中,90BDC COA BCD OAC BC AC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴BDC COA △≌△(AAS ).(2)∵C 点坐标为()10-,,∴BD =CO =1.∵B 点的横坐标为3-,∴B 点坐标为()31-,.设BC 所在直线的函数关系式为y kx b =+,则有0,31,k b k b -+=⎧⎨-+=⎩解之,得 1,21.2k b ⎧=-⎪⎪⎨⎪=-⎪⎩∴BC 所在直线的函数关系式为1122y x =--. (3)存在.二次函数解析式为211222y x x =+-=21117228x ⎛⎫+- ⎪⎝⎭,∴对称轴为直线12x =-.若以AC 为直角边,点C 为直角顶点,对称轴上有一点1P ,使1CPAC ⊥.∵BCAC ⊥, ∴点1P 为直线BC 与对称轴直线12x =-的交点. 由题意,得 112212y x x ⎧=--⎪⎪⎨⎪=-⎪⎩解之,得111214x y ⎧=-⎪⎪⎨⎪=-⎪⎩∴11124P ⎛⎫-- ⎪⎝⎭,. 若以AC 为直角边,点A 为直角顶点,对称轴上有一点2P ,使2AP AC ⊥,过点A 作2AP BC ∥,交对称轴直线12x =-于点2P . ∵CD =OA , ∴A (0,2).易求得直线2AP 的解析式为122y x =-+,由12212y x x ⎧=-+⎪⎪⎨⎪=-⎪⎩ 得221294x y ⎧=-⎪⎪⎨⎪=⎪⎩ ∴21924P ⎛⎫- ⎪⎝⎭,.∴满足条件的点有两个,坐标分别为1211192424P P ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭-,-、-,. 4. 解:(1)由已知得:A (-1,0) B (4,5)∵二次函数2y x bx c =++的图像经过点A (-1,0)B (4,5) ∴101645b c b c -+=⎧⎨++=⎩解得:b=-2 c=-3(2)∵直线AB 经过点A (-1,0) B (4,5)∴直线AB 的解析式为:y=x +1 ∵二次函数223y x x =--∴设点E (t , t +1),则F (t ,223t t --)∴EF= 2(1)(23)t t t +--- =2325()24t --+ ∴当32t =时,EF 的最大值=254∴点E 的坐标为(32,52)(3)①如图:顺次连接点E 、B 、F 、D可求出点F 的坐标(32,154-),点D 的坐标为(1,-4) S EBFD 四边行=S BEF +S DEF=12531253(4)(1)242242⨯-+⨯-=758② ⅰ)过点E 作a ⊥EF 交抛物线于点P ,设点P (m ,223m m --)则有:25232mm --=解得:122m =,222m -=∴15)2p, 25)2p ⅱ)过点F 作b ⊥EF 交抛物线于3P ,设3P (n ,223n n --) 则有:215423n n --=- 解得:112n =,232n =(与点F 重合,舍去)∴3P 115-24(,) 综上所述:所有点P的坐标为125()22p +,225()22p 3P (115-24(,). 5. (1)∵抛物线的对称轴为直线x =1,∴1221b ba -=-=⨯,∴2b =-. ∵抛物线与y 轴交于点C (0,-3), ∴c =-3,∴抛物线的函数表达式为y =x 2-2x -3.(2)∵抛物线与x 轴交于A 、B 两点,当y =0时,x 2-2x -3=0. ∴x 1=1-,x 2=3. ∵A 点在B 点左侧, ∴A (1-,0),B (3,0).设过点B (3,0)、C (0,-3)的直线的函数表达式为y =kx +m ,则033k m m =+⎧⎨-=⎩,∴13k m =⎧⎨=-⎩∴直线BC 的函数表达式为y =x -3. (3)①∵AB =4,PO =34AB ,∴PO =3. ∵PO ⊥y 轴,∴PO ∥x 轴,则由抛物线的对称性可得点P 的横坐标为12-,∴P 1724⎛⎫-- ⎪⎝⎭,. ∴F 704⎛⎫- ⎪⎝⎭,,∴FC =3-OF =3-74=54.∵PO 垂直平分CE 于点F ,∴CE =2FC =52. ∵点D 在直线BC 上,∴当x =1时,y =2-,则D (1,-2).过点D 作DG ⊥CE 于点G ,∴DG =1,CG =1,∴GE =CE -CG =52-1=32.在Rt △EGD 中,tan ∠CED =23GD EG =.②P 1(1,2-),P 2512⎛⎫- ⎪ ⎪⎝⎭,. 6. 解:(1) 四边形ABCO 是平行四边形,4.OC AB ∴==(42)(02)(40)A B C ∴-,,,,,. 1分 抛物线2y ax bx c =++过点B , 2.c ∴= 2分由题意,有1642016422a b a b -+=⎧⎨++=⎩,.解得1161.4a b ⎧=-⎪⎪⎨⎪=⎪⎩,3分∴所求抛物线的解析式为211 2.164y x x =-++4分(2)将抛物线的解析式配方,得211(2)2.164y x =--+∴抛物线的对称轴为 2.x = 5分(80)(22)(2).D E F ∴,,,,,0欲使四边形POQE 为等腰梯形,则有..OP QE BP FQ ==即363.2t t t ∴=-=,即7分(3)欲使以点P B O 、、为顶点的三角形与以点Q B O 、、为顶点的三角形相似, 90PBO BOQ ∠=∠=∴ °,有BP OQOB BO=或BP BOOB OQ=,即PB OQ =或2OB PB QO =·.①若P Q 、在y 轴的同侧.当BP OQ =时,t =83t -,2t ∴=.8分当2OB PB QO =·时,(83)4t t -=,即23840.t t -+=解得1222.3t t ==, 9分 ②若P Q 、在y 轴的异侧.当PB OQ =时,38t t -=,4t ∴=.10分当2OB PBQO =·时,(38)4t t -=,即23840t t --=.解得43t ±=403t -=< .故舍去. 43t +∴=11分∴当2t =或23t =或4t =或43t +=秒时,以P B O 、、为顶点的三角形与以点Q B O 、、为顶点的三角形相似.7. 解:(1) ∵ 抛物线2(0)y ax bx a =+≠经过点(30)A ,、(44)B ,.∴9301644a b a b +=⎧⎨+=⎩,.解得:13a b =⎧⎨=-⎩,.∴ 抛物线的解析式是23y x x =-.(2) 设直线OB 的解析式为1y k x =,由点(44)B ,,得:144k =,解得11k =. ∴ 直线OB 的解析式为y x =.∴ 直线OB 向下平移m 个单位长度后的解析式为:y x m =-.∵ 点D 在抛物线23y x x =-上.∴ 可设2(3)D x x x -,.又点D 在直线y x m =-上,∴ 23x x x m -=-,即240x x m -+=.∵ 抛物线与直线只有一个公共点, ∴∆=16-4m =0,解得:m =4.此时1x =2x =2,y =2x -3x =-2,∴ D 点坐标为(2,-2).(3) ∵ 直线OB 的解析式为y x =,且(30)A ,,∴ 点A 关于直线OB 的对称点A '的坐标是(0,3). 设直线A B '的解析式为23y k x =+,过点(44)B ,,∴ 2434k +=,解得:214k =. ∴ 直线A B '的解析式是134y x =+.∵ NBO ABO ∠=∠, ∴ 点N 在直线A B '上, ∴ 设点134N n n ⎛⎫+ ⎪⎝⎭,,又点N 在抛物线23y x x =-上,∴21334n n n +=-, 解得:134n =-,24n = (不合题意,会去),∴ 点N 的坐标为345416⎛⎫- ⎪⎝⎭,.方法一:如图,将NOB △沿x 轴翻折,得到11N OB △,则1345416N ⎛⎫-- ⎪⎝⎭,,1(44)B -,, ∴ O 、D 、1B 都在直线y x =-上.∵ 1POD NOB △∽△,∴ 111POD N OB △∽△, ∴11OP ON =1OD OB =12,∴ 点P 1的坐标为345832⎛⎫-- ⎪⎝⎭,.将1OPD △沿直线y x =-翻折,可得另一个满足条件的点2453328P ⎛⎫⎪⎝⎭,.综上所述,点P 的坐标是345832⎛⎫-- ⎪⎝⎭,或453328⎛⎫⎪⎝⎭,.方法二:如图,将△NOB 绕原点顺时针旋转90°,得到22N OB △, 则2453164N ⎛⎫⎪⎝⎭,,2(44)B -,.∴O 、D 、2B 都在直线y x =-上.∵ 1POD NOB △∽△,∴ 122POD N OB △∽△,∴ 12OP ON =2OD OB =12,∴ 点1P 的坐标为453328⎛⎫ ⎪⎝⎭,. 将1OPD △沿直线y x =-翻折,可得另一个满足条件的点2345832P ⎛⎫-- ⎪⎝⎭,.综上所述,点P 的坐标是345832⎛⎫-- ⎪⎝⎭,或453328⎛⎫⎪⎝⎭,. 8. 解:(1)依题意将()22M ,代入得2=()()1222m m-+-,解得4m =. (2)令()()12404x x -+-=,得1224x x =-=,.∴()20B -,,()40C ,.在1C 中,令0x =得2y =. ∴()02E ,.∴162BCE S BC OE ==△·. (3)当4m =时,易得对称轴1x =,又B 、C 关于1x =对称.连EC 交1x =于H ,则H 使BH EH +最小. 设直线EC :y kx b =+,将()02E ,,()40C ,代入得122y x =-+,将1x =代入得312H ⎛⎫ ⎪⎝⎭,. (4)分两种情况讨论(每写出一种相似情形给1分)右图当BEC BCF △∽△时,45EBC CBF∠=∠=°,2BE BCBC BE BF BC BF=∴=,·,作FT x ⊥轴,垂足为T ,则BT TF =.∴可令()2F x x --,()0x >,又点F 在抛物线上,∴()()122x x x m m--=-+-.∵2x +>0(∵x >0),∴2x m =,()222F m m --,, 此时)1BFm ==+,2BE BC m ==+.又∵2BCBE =·()22BF m∴+=,·)1m +,∴2m =±0m >,∴2m =. 如图(同上图略)当BEC FCB △∽△,则BC ECBF BC=,同①∵EBC CFB BTF COE ∠=∠,△∽△,2TF OE BT OC m ==,∴可令()22F x x m ⎛⎫-+ ⎪⎝⎭,()0x >,又F 在抛物线上,∴()()()2122x x x m m m-+=-+-.∵()200x x +>> ,2x m =+,∴()2422m F m EC BC m m +⎛⎫+-==+ ⎪⎝⎭,,.又2BC ECBF=·,∴()22m +=整理得:0=16,显然不成立. 综合①②得,在第四象限内,抛物线上存在点F ,使以点B 、C 、F 为顶点的三角形与BCE △相似,2m =.9. 解:(1)12a b =-=-,,顶点C 的坐标为(-1,4)(2)假设在y 轴上存在满足条件的点D , 过点C 作CE ⊥y 轴于点E .由∠CDA =90°得,∠1+∠2=90°. 又∠2+∠3=90°,∴∠3=∠1. 又∵∠CED =∠DOA =90°,∴△CED ∽△DOA ,∴AODO ED CE =.设D (0,c ),则341cc =-.变形得0342=+-c c ,解之得1231c ,c ==. 综合上述:在y 轴上存在点D (0,3)或(0,1),使△ACD 是以AC 为斜边的直角三角形. (3)①若点P 在对称轴右侧(如图①),只能是△PCQ ∽△CAH ,得∠QCP =∠CAH .延长CP 交x 轴于M ,∴AM =CM , ∴AM 2=CM 2.设M (m ,0),则( m +3)2=42+(m +1)2,∴m =2,即M (2,0).设直线CM 的解析式为y=k 1x+b 1,则⎩⎨⎧=+=+-0241111b k b k , 解之得341-=k ,381=b .∴直线CM 的解析式3834+-=x y . 联立⎪⎩⎪⎨⎧+--=+-=3238342x x y x y ,解之得13209x y ⎧=⎪⎪⎨⎪=⎪⎩或14x y =-⎧⎨=⎩(舍去).∴)92031(,P . ②若点P 在对称轴左侧(如图②),只能是△PCQ ∽△ACH ,得∠PCQ =∠ACH .过A 作CA 的垂线交PC 于点F ,作FN ⊥x 轴于点N .由△CFA ∽△CAH 得2==AHCHAF CA , 由△FNA ∽△AHC 得21===CA AF HC NA AH FN .∴12==FN AN ,, 点F 坐标为(-5,1). 设直线CF 的解析式为y=k 2x+b 2,则⎩⎨⎧=+-=+-1542222b k b k ,解之得419,4322==b k .∴直线CF 的解析式41943+=x y . 联立⎪⎩⎪⎨⎧+--=+=32419432x x y x y ,解之得⎪⎪⎩⎪⎪⎨⎧=-=165547y x 或 14x y =-⎧⎨=⎩(舍去). ∴)165547(,-P . ∴满足条件的点P 坐标为)92031(,或)165547(,- 10. 解:(1)由题意得09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩,,. 解得123a b c =-⎧⎪=⎨⎪=⎩,,. ∴抛物线的函数关系式为:223y x x =-++.(2)∵()2121x =-=⨯-,∴抛物线的对称轴l 为:直线1x =. 连接BC 交对称轴l 于点P ,因为点A 与点B 关于对称轴l 成轴对称,所以点P 为所求的点.6分解法一:设直线l 交x 轴于点N ,则1ON =.∵()30B ,,∴3OB =,∴2BN =.∵l y ∥轴, ∴BPN BCO △∽△,∴PN BN CO BO =,∴233PN =,∴2PN =. ∵点P 在l 上,∴点P 的坐标是()12,. (图①)(图②)解法二:设直线BC 的函数关系式为y kx m =+,将()30B ,、()03C ,代入,得303k m m +=⎧⎨=⎩,.解得:13k m =-⎧⎨=⎩,.∴3y x =-+. ∵点P 在对称轴l 上,∴点P 的横坐标为1.当1x =时,132y =-+=,∴点P 的坐标是(1,2).(3)符合条件的点M 共有4个:(1,0),(1),(1-,(1,1).11题11. 解:(1)当0x =时,4y =,(04)D ∴,.当0y =时,2x =-,(20)A ∴-,. 抛物线212y x bx c=-++经过点A D 、,4220c b c =⎧∴⎨--+=⎩,.解得1b =,4c =.∴这条抛物线的解析式为2142y x x =-++.当0y =时,整理得2280x x --=,解得12x =-,24x =,∴点(40)B ,. (2)①当点M 在线段AD 上时,过点M 作MEx ⊥轴于E ,13AOM OMD S S = △△::,13AM MD ∴=::,又ME y ∥轴,Rt Rt AME ADO ∴△∽△,14ME AM DO AD ∴==,又(04)41D OD ME ∴=∴= ,,,,133241(1)22x x M ∴+=∴=-∴-,,,. ②当点M 在DA 的延长线上时,过点M 作MF x ⊥轴于F ,13AOM OMD S S = △△::,13AM MD ∴=::,12AM AD ∴=::,又M F y ∥轴,R t R tA M F A D O ∴△∽△,12MF AM DO AD ∴==. 2422423(32)OD MF x x M =∴=∴+=-∴=-∴-- ,,,,,.(3)在y 轴的正半轴上存在符合条件的点P . 点(2)C y ,在这条抛物线上,4y ∴=,∴点()24C ,, 连接CD ,(04)D ,,90CDO ∴∠=°,①设11(0)P y ,,满足11PB PC =,其中10y >.在1Rt BOP △中,22211PB OB OP =+;在1Rt CDP △中,22211PC DC DP =+.222211OB DP DC DP ∴+=+,即2221142(4)y y +=+-.解得112y =,即11(0)2P ,,符合题意.②设22(0)P y ,,满足2P B BC =,其中20y >. 点(24)C ,,点(40)B ,,2224220BC ∴=+=,在2Rt BOP △中,22222P B OB OP =+,22220OB OP ∴+=,即222420y +=,解得22y =-(舍去)或22y =,即2(02)P ,,符合题意.③设33(0)P y ,,满足3PC BC =,其中30y >.在3Rt CDP △中,22233PC DP CD =+,22320DP CD ∴+=,即223(4)220y -+=,解得30y =(舍去)或38y =,即3(08)P ,. 直线3P B 的解析式为28y x =-+,而(24)C ,在直线3P B 上,∴3P 不符合题意,舍去. ∴在y 轴的正半轴上存在符合条件的点P ,点1(0)2P ,或(02)P ,. 12. 解:(1)当x =0时,y =2当y =0时,由2x+2=0得x =-1∴ A (-1,0) B (0,2) (答对一个坐标得2分)(2)由旋转可知:OC =OA =1,OD =OB =2∴ C (0,1), D (2,0) 设抛物线l 的解析式是c bx ax y ++=2)0(≠a依题意得⎪⎩⎪⎨⎧=++==+-02410c b a c c b a 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=12121c b a ∴ 抛物线l 的解析式是121212++-=x x y(3)在COD Rt ∆中,由C (0,1), D (2,0)可得512C 22=+=D 若△PCD 是等腰三角形,则有以下三种情况:①当C P =CD 时,此时点P 在抛物线l 与线段AD 所围成的封闭图形外,不合题意;(学生未答不扣分),②当DP =DC 时,以点D 为圆心,DC 长为半径画弧交x 轴于点H ,此时点P 在\s\up4 (⌒(⌒)CH ⌒上(不含点C 、H ),此时a 的取值范围是025<<+-a ; ③当P C=PD 时,作线段CD 的垂直平分线FG ,交CD 于点E ,交x 轴于点F ,交抛物线于点G .此时点P 在线段FG 上(不含点F 、G 、E ),求得 E (1,21),DE =25.在DOC Rt DEF Rt ∆∆,中,DC DO DF DE CDO ==∠cos ,∴5225=DF ,解得45=DF ,∴43452=-=OF ,即F(43,0).易得过E 、F 的直线解析式是232-=x y ,联立方程组得⎪⎪⎩⎪⎪⎨⎧++-=-=121212322x x y x y 解得2293,229321--=+-=x x (舍去)∴点G 的横坐标是2293+-, 此时a 的取值范围是229343+-<<a ,且1≠a . 综合①②③,当△PCD 是等腰三角形时,a 的取值范围是025<<+-a 或229343+-<<a ,且1≠a .。
2014年中考二次函数压轴题

2014年中考数学总复习《二次函数》一.解答题(共30小题)1.(2013•自贡)如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD 交抛物线于点D,并且D(2,3),tan∠DBA=.(1)求抛物线的解析式;(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q 点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.2.(2013•株洲)已知抛物线C1的顶点为P(1,0),且过点(0,).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).(1)求抛物线C1的解析式的一般形式;(2)当m=2时,求h的值;(3)若抛物线C1的对称轴与直线AB交于点E,与抛物线C2交于点F.求证:tan∠EDF﹣tan∠ECP=.3.(2013•舟山)如图,在平面直角坐标系xOy中,抛物线y=(x﹣m)2﹣m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.(1)当m=2时,求点B的坐标;(2)求DE的长?(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以,A,B,D,P为顶点的四边形是平行四边形?4.(2013•重庆)如图,对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A 的坐标为(﹣3,0).(1)求点B的坐标;(2)已知a=1,C为抛物线与y轴的交点.①若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.5.(2013•张家界)如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.(1)求直线CD的解析式;(2)求抛物线的解析式;(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.6.(2013•湛江)如图,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,﹣5).(1)求此抛物线的解析式;(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.7.(2013•枣庄)如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.8.(2013•岳阳)如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C 点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F.(1)求A,B,C三点的坐标;(2)求抛物线的解析式及顶点F的坐标;(3)已知M为抛物线上一动点(不与C点重合),试探究:①使得以A,B,M为顶点的三角形面积与△ABC的面积相等,求所有符合条件的点M的坐标;②若探究①中的M点位于第四象限,连接M点与抛物线顶点F,试判断直线MF与⊙E的位置关系,并说明理由.9.(2013•玉林)如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).(1)求点B,C的坐标;(2)判断△CDB的形状并说明理由;(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.10.(2013•营口)如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.(1)求该抛物线的解析式与顶点D的坐标.(2)试判断△BCD的形状,并说明理由.(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.11.(2013•益阳)阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1,y1),B(x2,y2),AB中点P的坐标为(x p,y p).由x p﹣x1=x2﹣x p,得x p=,同理,所以AB的中点坐标为.由勾股定理得AB2=,所以A、B两点间的距离公式为.注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.(1)求A、B两点的坐标及C点的坐标;(2)连结AB、AC,求证△ABC为直角三角形;(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.12.(2013•烟台)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=ax2+bx+c的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(﹣,0),以0C为直径作半圆,圆心为D.(1)求二次函数的解析式;(2)求证:直线BE是⊙D的切线;(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.13.(2013•孝感)如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);(2)如图2,若点E在线段BC上滑动(不与点B,C重合).①AE=EF是否总成立?请给出证明;②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=﹣x2+x+1上,求此时点F的坐标.14.(2013•湘西州)如图,已知抛物线y=﹣x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).(1)求抛物线的解析式及它的对称轴方程;(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;(3)试判断△AOC与△COB是否相似?并说明理由;(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.15.(2013•湘潭)如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx﹣2的图象过C点.(1)求抛物线的解析式;(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为相等的两部分?(3)点P是抛物线上一动点,是否存在点P,使四边形PACB为平行四边形?若存在,求出P点坐标;若不存在,说明理由.16.(2013•咸宁)为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?17.(2013•梧州)如图,抛物线y=a(x﹣h)2+k经过点A(0,1),且顶点坐标为B(1,2),它的对称轴与x 轴交于点C.(1)求此抛物线的解析式.(2)在第一象限内的抛物线上求点P,使得△ACP是以AC为底的等腰三角形,请求出此时点P的坐标.(3)上述点是否是第一象限内此抛物线上与AC距离最远的点?若是,请说明理由;若不是,请求出第一象限内此抛物线上与AC距离最远的点的坐标.18.(2013•无锡)如图,直线x=﹣4与x轴交于点E,一开口向上的抛物线过原点交线段OE于点A,交直线x=﹣4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.(1)求点A的坐标;(2)若△OBC是等腰三角形,求此抛物线的函数关系式.19.(2013•乌鲁木齐)如图.在平面直角坐标系中,边长为的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.(1)求证:△OAD≌△EAB;(2)求过点O、E、B的抛物线所表示的二次函数解析式;(3)在(2)中的抛物线上是否存在点P,其关于直线BF的对称点在x轴上?若有,求出点P的坐标;(4)连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,求点M的坐标.20.(2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,)在抛物线上,直线l是一次函数y=kx﹣2(k≠0)的图象,点O是坐标原点.(1)求抛物线的解析式;(2)若直线l平分四边形OBDC的面积,求k的值;(3)把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线l交于M,N两点,问在y轴正半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴对称?若存在,求出P点坐标;若不存在,请说明理由.21.(2013•铜仁地区)如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).(1)求抛物线的解析式;(2)求△ABC的面积;(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.22.(2013•铁岭)某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y(1的函数关系式:_________(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?23.(2013•天津)已知抛物线y1=ax2+bx+c(a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:(Ⅰ)求y1与x之间的函数关系式;(Ⅱ)若经过点T(0,t)作垂直于y轴的直线l′,A为直线l′上的动点,线段AM的垂直平分线交直线l于点B,点B关于直线AM的对称点为P,记P(x,y2).(1)求y2与x之间的函数关系式;(2)当x24.(2013•泰安)如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.25.(2013•太原)综合与探究:如图,抛物线y=x2﹣x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.(1)求点A,B,C的坐标.(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.26.(2013•台州)如图1,已知直线l:y=﹣x+2与y轴交于点A,抛物线y=(x﹣1)2+k经过点A,其顶点为B,另一抛物线y=(x﹣h)2+2﹣h(h>1)的顶点为D,两抛物线相交于点C.(1)求点B的坐标,并说明点D在直线l上的理由;(2)设交点C的横坐标为m.①交点C的纵坐标可以表示为:_________或_________,由此进一步探究m关于h的函数关系式;②如图2,若∠ACD=90°,求m的值.27.(2013•遂宁)如图,抛物线y=x2+bx+c与x轴交于点A(2,0),交y轴于点B(0,).直线y=kx过点A与y轴交于点C,与抛物线的另一个交点是D.(1)求抛物线y=x2+bx+c与直线y=kx的解析式;(2)设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为l,点P的横坐标为x,求l与x的函数关系式,并求出l的最大值.28.(2013•绥化)如图,已知抛物线y=(x﹣2)(x+a)(a>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.(1)若抛物线过点M(﹣2,﹣2),求实数a的值;(2)在(1)的条件下,解答下列问题;①求出△BCE的面积;②在抛物线的对称轴上找一点H,使CH+EH的值最小,直接写出点H的坐标.29.(2013•宿迁)如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣3(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.(1)求a和b的值;(2)求t的取值范围;(3)若∠PCQ=90°,求t的值.30.(2013•深圳)如图1,过点A(0,4)的圆的圆心坐标为C(2,0),B是第一象限圆弧上的一点,且BC⊥AC,抛物线y=x2+bx+c经过C、B两点,与x轴的另一交点为D.(1)点B的坐标为(_________,_________),抛物线的表达式为_________;(2)如图2,求证:BD∥AC;(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长.。
2014年中考二次函数综合

二次函数综合板块一:旋转、翻折、平移1、点P为抛物线y=x2-2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A 在点B的上方),点Q为点P旋转后的对应点.(1)当m=2,点P横坐标为4时,求Q点的坐标;(2)设点Q(a,b),用含m、b的代数式表示a;(3)如图,点Q在第一象限内,点D在x轴的正半轴上,点C为OD的中点,QO平分∠AQC,AQ=2QC,当QD=m时,求m的值.2、已知抛物线L1:23212-+=x x y 的顶点为C ,与x 轴交于A 、B ,将抛物线L1沿x 轴翻折得到抛物线L2(1)求抛物线L2的解析式及顶点M 的坐标. (2)点P 为y 轴右侧的抛物线L2上一点点Q 为抛物线L1上一点若以M 、C 、P 、Q 为顶点的四边形为矩形求点P 、Q 的坐标.(3)N 点在抛物线L2上以MN 为斜边作等腰直角三角形其直角顶点E 正好在x 轴上求N 点坐标.3、如图,直线33y x b =+经过点B(3-,2),且与x 轴交于点A .将抛物线213y x=沿x 轴作左右平移,记平移后的抛物线为C ,其顶点为P .(1)求∠BAO 的度数;(2)抛物线C 与y 轴交于点E ,与直线AB 交于两点,其中一个交点为F .当线段EF ∥x 轴时,求平移后的抛物线C 对应的函数关系式; (3)在抛物线213y x=平移过程中,将△PAB 沿直线AB 翻折得到△DAB ,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.OABxyOABxy213y x =4、已知抛物线C1:y=-x2-2x+3与x轴的正半轴交于B,交y轴于C,将C1绕平面内的一点旋转180得到抛物线C2,且所得抛物线经过B,C两点.(1)求C2的解析式(2)将C2沿x轴平移得到抛物线C3,设C2的顶点为D,C3的顶点为E,抛物线 C3与C2交于M,若△MDE为等腰直角三角形。
2014中考数学压轴题精选(二次函数)(16题)-附详细解答和评分标准

1、(08广东茂名25题)(本题满分10分)如图,在平面直角坐标系中,抛物线y =-32x 2+b x +c 经过A (0,-4)、B (x 1,0)、 C (x 2,0)三点,且x 2-x 1=5.(1)求b 、c 的值;(4分)(2)在抛物线上求一点D ,使得四边形BDCE 是以BC 为对角线的菱形;(3分)(3)在抛物线上是否存在一点P ,使得四边形B P O H 是以OB 为对角线的菱形?若存在,求出点P 的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.(3分)解:(08广东茂名25题解析)解:(1)解法一: ∵抛物线y =-32x 2+b x +c 经过点A (0,-4), ∴c =-4 ……1分又由题意可知,x 1、x 2是方程-32x 2+b x +c =0的两个根, ∴x 1+x 2=23b , x 1x 2=-23c =6 ·························································· 2分 由已知得(x 2-x 1)2=25 又(x 2-x 1)2=(x 2+x 1)2-4x1x 2=49b 2-24 ∴49b 2-24=25 解得b =±314···························································································· 3分当b =314时,抛物线与x 轴的交点在x 轴的正半轴上,不合题意,舍去.∴b =-314. ··························································································· 4分 解法二:∵x 1、x 2是方程-32x 2+b x +c=0的两个根, 即方程2x 2-3b x +12=0的两个根.∴x =4969b 32-±b , ································································· 2分(第25题图)x∴x 2-x 1=2969b 2-=5,解得 b =±314 ·················································································· 3分 (以下与解法一相同.)(2)∵四边形BDCE 是以BC 为对角线的菱形,根据菱形的性质,点D 必在抛物线的对称轴上, ···················································································· 5分又∵y =-32x 2-314x -4=-32(x +27)2+625····························· 6分 ∴抛物线的顶点(-27,625)即为所求的点D . ································· 7分(3)∵四边形BPOH 是以OB 为对角线的菱形,点B 的坐标为(-6,0),根据菱形的性质,点P 必是直线x =-3与抛物线y =-32x 2-314x -4的交点, ···················································· 8分∴当x =-3时,y =-32×(-3)2-314×(-3)-4=4,∴在抛物线上存在一点P (-3,4),使得四边形BPOH 为菱形. ··············· 9分 四边形BPOH 不能成为正方形,因为如果四边形BPOH 为正方形,点P 的坐标只能是(-3,3),但这一点不在抛物线上. ············································· 10分 2、(08广东肇庆25题)(本小题满分10分)已知点A (a ,1y )、B (2a ,y 2)、C (3a ,y 3)都在抛物线x x y 1252+=上. (1)求抛物线与x 轴的交点坐标; (2)当a =1时,求△ABC 的面积;(3)是否存在含有1y 、y 2、y 3,且与a 无关的等式?如果存在,试给出一个,并加以证明;如果不存在,说明理由.(08广东肇庆25题解析)(本小题满分10分)解:(1)由5x x 122+=0, ··································································· (1分)得01=x ,5122-=x . ······································································· (2分) ∴抛物线与x 轴的交点坐标为(0,0)、(512-,0). ································· (3分)(2)当a =1时,得A (1,17)、B (2,44)、C (3,81), ·························· (4分) 分别过点A 、B 、C 作x 轴的垂线,垂足分别为D 、E 、F ,则有ABC S ∆=S ADFC 梯形 -ADEB S 梯形 -BEFC S 梯形 ············································· (5分)=22)8117(⨯+-21)4417(⨯+-21)8144(⨯+ ······························· (6分)=5(个单位面积) ······························································ (7分)(3)如:)(3123y y y -=. ······························································· (8分)事实上,)3(12)3(523a a y ⨯+⨯= =45a 2+36a .3(12y y -)=3[5×(2a )2+12×2a -(5a 2+12a )] =45a 2+36a . ··········· (9分) ∴)(3123y y y -=. ········································································ (10分) 3、(08辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =,矩形ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD .点A 的对应点为点E ,点B的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,.(1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.(08辽宁沈阳26题解析)解:(1)点E 在y 轴上 ············································ 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =,BO =,2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上. ······························································· 3分 (2)过点D 作DM x ⊥轴于点M1OD =,30DOM ∠=x第26题图∴在Rt DOM △中,12DM =,OM =点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎝⎭, ············································································· 5分 由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A的坐标为( ··············································································· 6分抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(A,122D ⎛⎫ ⎪ ⎪⎝⎭,代入22y ax bx =++中得321312422a a ⎧-+=⎪⎨++=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为:28299y x x =--+ ················································ 9分(3)存在符合条件的点P ,点Q . ······························································ 10分 理由如下:矩形ABOC 的面积3AB BO ==∴以O B P Q ,,,为顶点的平行四边形面积为由题意可知OB 为此平行四边形一边, 又3OB =OB ∴边上的高为2 ···················································································· 11分 依题意设点P 的坐标为(2)m ,点P在抛物线28299y x x =--+上28229m ∴--+=解得,10m =,2m =1(02)P ∴,,228P ⎛⎫- ⎪ ⎪⎝⎭以O B P Q ,,,为顶点的四边形是平行四边形,PQ OB ∴∥,PQ OB == ∴当点1P 的坐标为(02),时,点Q的坐标分别为1(2)Q,2Q ; 当点2P的坐标为2⎛⎫⎪ ⎪⎝⎭时,点Q的坐标分别为32Q ⎛⎫ ⎪ ⎪⎝⎭,42Q ⎫⎪⎪⎝⎭. ········································ 14分4、(08辽宁12市26题)(本题14分)26.如图16,在平面直角坐标系中,直线y =与x 轴交于点A ,与y 轴交于点C ,抛物线2(0)3y ax x c a =-+≠经过A B C ,,三点. (1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标;(2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由; (3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.(08辽宁12市26题解析)解:(1)直线y =-x 轴交于点A ,与y 轴交于点C .(10)A ∴-,,(0C , ············································································· 1分点A C ,都在抛物线上,03a c c⎧=++⎪∴⎨⎪=⎩3a c ⎧=⎪∴⎨⎪=⎩ ∴抛物线的解析式为2y x x =-················································· 3分x∴顶点1F ⎛ ⎝⎭ ·················································································· 4分 (2)存在 ································································································ 5分1(0P ······························································································ 7分2(2P ····························································································· 9分 (3)存在 ······························································································ 10分 理由: 解法一:延长BC 到点B ',使BC B C '=,连接B F '交直线AC 于点M ,则点M 就是所求的点. ········································································· 11分 过点B '作B H AB '⊥于点H .B点在抛物线233y x x =-(30)B ∴, 在Rt BOC △中,tan OBC ∠=,30OBC ∴∠=,BC =在Rt BB H '△中,12B H BB ''==6BH H '==,3OH ∴=,(3B '∴--, ········································ 12分设直线B F '的解析式为y kx b =+3k b k b ⎧-=-+⎪∴⎨=+⎪⎩解得6k b ⎧=⎪⎪⎨⎪=⎪⎩y x ∴=················································································· 13分62y y x ⎧=⎪∴⎨=-⎪⎩解得377x y ⎧=⎪⎪⎨⎪=-⎪⎩37M ⎛∴ ⎝⎭ ∴在直线AC 上存在点M ,使得MBF △的周长最小,此时377M ⎛⎫- ⎪ ⎪⎝⎭,. ·· 14分x5、(08青海西宁28题)如图14,已知半径为1的1O 与x 轴交于A B ,两点,OM 为1O 的切线,切点为M ,圆心1O 的坐标为(20),,二次函数2y x bx c =-++的图象经过A B ,两点.(1)求二次函数的解析式;(2)求切线OM 的函数解析式;(3)线段OM 上是否存在一点P ,使得以P O A ,,为顶点的三角形与1OO M △相似.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.(08青海西宁28题解析)解:(1)圆心1O 的坐标为(20),,1O 半径为1,(10)A ∴,,(30)B ,……1分二次函数2y x bx c =-++的图象经过点A B ,,∴可得方程组10930b c b c -++=⎧⎨-++=⎩····································································· 2分解得:43b c =⎧⎨=-⎩∴二次函数解析式为243y x x =-+- ······································· 3分(2)过点M 作MF x ⊥轴,垂足为F . ······················································ 4分OM 是1O 的切线,M 为切点,1O M OM ∴⊥(圆的切线垂直于经过切点的半径). 在1Rt OO M △中,1111sin 2O M O OM OO ∠== 1O OM ∠为锐角,130O OM ∴∠= ························ 5分1cos3022OM OO ∴==⨯=, 在Rt MOF △中,3cos30322OF OM ===.1sin 3032MF OM ===.∴点M 坐标为32⎛ ⎝⎭············································································· 6分图14设切线OM 的函数解析式为(0)y kx k =≠32k =,k ∴= ····· 7分∴切线OM 的函数解析式为y =··························································· 8分 (3)存在. ····························································································· 9分 ①过点A 作1AP x ⊥轴,与OM 交于点1P .可得11Rt Rt APO MO O △∽△(两角对应相等两三角形相似)113tan tan 30P A OA AOP =∠==113P ⎛⎫∴ ⎪ ⎪⎝⎭, ····································· 10分 ②过点A 作2AP OM ⊥,垂足为2P ,过2P 点作2P H OA ⊥,垂足为H . 可得21Rt Rt AP O O MO △∽△(两角对应相等两三角开相似) 在2Rt OP A △中,1OA =,23cos30OP OA ∴==在2Rt OP H △中,223cos 4OH OP AOP =∠==,2221sin 2P H OP AOP =∠==2344P ⎛⎫∴ ⎪ ⎪⎝⎭, ································· 11分∴符合条件的P 点坐标有13⎛ ⎝⎭,,344⎛⎫⎪ ⎪⎝⎭, ·············································· 12分6、(08山东济宁26题)(12分)ABC △中,90C ∠=,60A ∠=,2AC =cm .长为1cm 的线段MN 在ABC △的边AB 上沿AB 方向以1cm/s 的速度向点B 运动(运动前点M 与点A 重合).过M N ,分别作AB 的垂线交直角边于P Q ,两点,线段MN 运动的时间为t s .(1)若A M P △的面积为y ,写出y 与t 的函数关系式(写出自变量t 的取值范围);(2)线段MN 运动过程中,四边形MNQP 有可能成为矩形吗?若有可能,求出此时t 的值;若不可能,说明理由;(3)t 为何值时,以C P Q ,,为顶点的三角形与ABC △相似?(08山东济宁26题解析)解:(1)当点P 在AC 上时,A M t =,tg 603PM AM t ∴==.2133(01)2y tt t t ∴==≤≤. ······························································ 2分 当点P 在BC 上时,3tan 30(4)3PM BM t ==-.213(4)(13)2363y t t t t t =-=-+≤≤. ··········································· 4分(2)2AC =,4AB ∴=.413BN AB AM MN t t ∴=--=--=-.3tan 30)QN BN t ∴==-. ······························································ 6分 由条件知,若四边形MNQP 为矩形,需PM QN =)3t =-, 34t ∴=. ∴当34t =s 时,四边形MNQP 为矩形.························································ 8分(3)由(2)知,当34t =s 时,四边形MNQP 为矩形,此时PQ AB ∥,PQC ABC ∴△∽△. ··············································································· 9分除此之外,当30CPQ B ∠=∠=时,QPC ABC △∽△,此时3tan 30CQ CP ==. 1cos602AM AP ==,22AP AM t ∴==.22CP t ∴=-. ························ 10分3cos302BN BQ ==,)3BQ t ∴==-.又2BC =)33CQ t ∴=-=. ·································· 11分 322t ∴=-,12t =.∴当12t =s 或34s 时,以C P Q ,,为顶点的三角形与ABC △相似. ··············· 12分7、(08四川巴中30题)(12分)30.已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E .(1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?(08四川巴中30题解析)解:(1)在2334y x =-+中,令0y =23304x ∴-+=12x ∴=,22x =-(20)A ∴-,,(20)B , ········································· 1分又点B 在34y x b =-+上 302b ∴=-+32b =BC ∴的解析式为3342y x =-+ ··································································· 2分 (2)由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩,得11194x y =-⎧⎪⎨=⎪⎩2220x y =⎧⎨=⎩ ············································· 4分 914C ⎛⎫∴- ⎪⎝⎭,,(20)B ,。
二次函数中考历年真题

1:(2014北京)在平面直角坐标系中,抛物线y=2x²+mx+n经过点A(0,—2),B(3,4)(1)求抛物线的表达式及对称轴(2)设点B关于原点的对称点C,点D是抛物线对称轴上一动点,记抛物线在A,B,之间的部分为图像G(包含A,B两点)若直线CD与图像G有公共点,结合函数图像,求点D纵坐标t的取值范围。
2(2013北京)在平面直角坐标系中抛物线y=mx²-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B(1)求A,B的坐标(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;(3)若该抛物线在—2<x<—1这一段位于l的上方并且在2<x<3这一段位于直线AB的下方,求该抛物线的解析式考1:已知二次函数y=ax²+bx+c的图像与x轴交于点A(—1,0),B(3,0)与y轴交于C(0,—3)。
求该二次函数的解析式考点一:抛物线沿x轴翻折与平移直线的交点问题:将二次函数的图像在x轴下方的部分沿x轴翻折,其余部分保持不变,另得到一个新的图像,请你结合新图像回答,直线y=x+n与新图像的交点情况。
考点二:抛物线沿x轴翻折与旋转直线交点的问题:将二次函数的图像在x轴下方的部分沿x轴翻折,其余部分不变得到一个新图像,请你结合图像回答,直线y=kx-3(k≠0)于新图像的交点情况。
考点三:抛物线沿平行于x轴的动直线翻折与平移的交点问题将二次函数的图像在y=-b下方的部分沿y=-b翻折,其余部分保持不变,得到一个新的图象,请你新图象回答直线y=x+b与新图象交点的情况。
考点四:抛物线沿x轴翻转后再平移与定直线的交点情况将二次函数图象在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象G,再将G向上平移n个单位,若图像G与过(0,5)且与x轴平行的直线4的交点,直接写出n的取值范围;考点五:抛物线部分沿y轴翻折与平移直线的交点问题将二次函数y轴左侧的部分沿y轴翻折,其余部分保持不变,得到一个新的图象,庆你结合新图象回答,直线y=x+n与新图像有两个交点时,n的取值范围考点六:抛物线部分沿y轴翻折与旋转直线的交点问题保留二次函数的图象y轴右侧的部分,同时将其关于y轴作轴对称,得到新图象为G,若一次函数y=—kx-3与图像G有三个公共点,求m的取值范围考点七:抛物线部分沿平行于y轴的直线翻折与平移直线的交点问题过C点作y轴的垂线l,将抛物线在y轴左侧的部分翻折到直线l下方,构成鑫的图象G,若一次函数y=x+m与图像G有两个公共点,求m的值考点八:过定点的动直线和部分抛物线的交点问题若D(—2,d)在二次函数图象上,过点E(2,—7)的一次函数为y=kx+m,记抛物线在C,D两点的部分为G,若一次函数与图像G有公共点,求m的取值范围。
2014年中考全国考题二次函数的图象和性质汇编

2014年中考全国数学试题二次函数的图象和性质专题一、选择题1. (2012重庆市4分)已知二次函数)0(2≠++=a c bx ax y 的图象如图所示对称轴为21-=x 。
下列结论中,正确的是【 】 A .0abc > B .0a b += C .20b c >+ D .42a c b +<2. (2012浙江衢州3分)已知二次函数y=﹣x 2﹣7x+,若自变量x 分别取x 1,x 2,x 3,且0<x 1<x 2<x 3,则对应的函数值y 1,y 2,y 3的大小关系正确的是【 】A .y 1>y 2>y 3B .y 1<y 2<y 3C .y 2>y 3>y 1D .y 2<y 3<y 13. (2012浙江义乌3分)如图,已知抛物线y 1=﹣2x 2+2,直线y 2=2x+2,当x 任取一值时,x 对应的函数值分别为y 1、y 2.若y 1≠y 2,取y 1、y 2中的较小值记为M ;若y 1=y 2,记M=y 1=y 2.例如:当x=1时,y 1=0,y 2=4,y 1<y 2,此时M=0.下列判断:①当x >0时,y 1>y 2; ②当x <0时,x 值越大,M 值越小;③使得M 大于2的x 值不存在; ④使得M=1的x 值是或.其中正确的是【 】A .①②B .①④C .②③D .③④4. (2012江苏常州2分)已知二次函数()()2y=a x 2+c a 0>-,当自变量x 分别取2,3,0时,对应的值分别为123y y y ,,,则123y y y ,,的大小关系正确的是【 】A. 321y y y <<B. 123y y y <<C. 213y y y <<D. 312y y y <<5. (2012江苏镇江3分)关于x 的二次函数()()y=x+1x m -,其图象的对称轴在y 轴的右侧,则实数m 的取值范围是【 】A. m<1-B. 1<m<0-C. 0<m<1D. m>15. (2012湖北天门、仙桃、潜江、江汉油田3分)已知二次函数y=ax 2+bx+c 的图象如图所示,它与x 轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b ﹣2a=0;②abc <0;③a ﹣2b+4c <0;④8a+c >0.其中正确的有【 】A .3个B .2个C .1个D .0个6. (2012湖北宜昌3分)已知抛物线y=ax 2﹣2x+1与x 轴没有交点,那么该抛物线的顶点所在的象限是【 】A .第四象限B .第三象限C .第二象限D .第一象限7. (2012湖南郴州3分)抛物线2y x 12=-+()的顶点坐标是【 】 A .(-1,2) B .(-1,-2) C .(1,-2) D .(1,2)8. (2012湖南衡阳3分)如图为二次函数y=ax 2+bx+c (a≠0)的图象,则下列说法:①a >0 ②2a+b=0 ③a+b+c >0 ④当﹣1<x <3时,y >0其中正确的个数为【 】A .1B .2C .3D .49. (2012湖南株洲3分)如图,已知抛物线与x 轴的一个交点A (1,0),对称轴是x=﹣1,则该抛物线与x 轴的另一交点坐标是【 】A .(﹣3,0)B .(﹣2,0)C .x=﹣3D .x=﹣210. (2012四川乐山3分)二次函数y=ax 2+bx+1(a≠0)的图象的顶点在第一象限,且过点(﹣1,0).设t=a+b+1,则t 值的变化范围是【 】A .0<t <1B .0<t <2C .1<t <2D .﹣1<t <111. (2012四川广元3分) 若二次函数22y ax bx a 2=++-(a ,b 为常数)的图象如图,则a 的值为【 】A. 1B. 2C. 2-D. -212. (2012四川德阳3分)设二次函数2y x bx c =++,当x 1≤时,总有y 0≥,当1x 3≤≤时,总有y 0≤,那么c 的取值范围是【 】A.c 3=B.c 3≥C.1c 3≤≤D.c 3≤13. (2012四川巴中3分) 对于二次函数y 2(x 1)(x 3)=+-,下列说法正确的是【 】A. 图象的开口向下B. 当x>1时,y 随x 的增大而减小C. 当x<1时,y 随x 的增大而减小D. 图象的对称轴是直线x=-114. (2012辽宁鞍山3分)如图,二次函数y=ax 2+bx+c (a≠0)的图象与x 轴交于A 、B 两点,与y 轴交于点C ,点B 坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c <0;③ac >0;④b 2﹣4ac >0.其中正确的结论是【 】A .①④B .①③C .②④D .①②15. (2012山东滨州3分)抛物线234y x x =--+ 与坐标轴的交点个数是【 】 A .3 B .2 C .1 D .016. (2012山东济南3分)如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是【 】A .y 的最大值小于0B .当x=0时,y 的值大于1C .当x=-1时,y 的值大于1D .当x=-3时,y 的值小于017. (2012山东日照4分)二次函数y=ax 2+bx +c(a≠0)的图象如图所示,给出下列结论:① b 2-4ac>0;② 2a +b<0;③ 4a -2b +c=0;④ a ︰b ︰c= -1︰2︰3.其中正确的是【 】(A) ①② (B) ②③ (C) ③④ (D)①④18. (2012山东泰安3分)二次函数2y ax bx =+的图象如图,若一元二次方程20ax bx m ++=有实数根,则m 的最大值为【 】 A .3- B .3 C .6- D .919. (2012山东泰安3分)设A 1(2)y -,,B 2(1)y ,,C 3(2)y ,是抛物线2(1)y x a =-++上的三点,则1y ,2y ,3y 的大小关系为【 】A .213y y y >>B .312y y y >>C .321y y y >>D .312y y y >>20. (2012山东威海3分)已知二次函数()2y=ax +bx+c a 0≠的图象如图所示,下列结论错误的是【 】A.abc >0B.3a >2bC.m (am +b )≤a -bD.4a -2b +c <021. (2012山东烟台3分)已知二次函数y=2(x ﹣3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=﹣3;③其图象顶点坐标为(3,﹣1);④当x <3时,y 随x 的增大而减小.则其中说法正确的有【 】A .1个B .2个C .3个D .4个22. (2012山东枣庄3分)抛物线2y ax bx 3=+-经过点(2,4),则代数式8a 4b 1++的值为【 】A .3B .9C .15D .15-23. (2012河北省3分)如图,抛物线y 1=a (x +2)2-3与y 2=12(x -3)2+1交于点A (1,3),过点A 作x 轴的平行线,分别交两条抛物线于点B ,C .则以下结论:①无论x 取何值,y 2的值总是正数;②a=1;③当x=0时,y 2-y 1=4;④2AB=3AC ;其中正确结论是【 】A .①②B .②③C .③④D .①④24. (2012甘肃白银3分)二次函数2y ax bx c =++的图象如图所示,则函数值y 0<时x 的取值范围是【 】A .x 1<-B .x >3C .-1<x <3D .x 1<-或x >325. (2012甘肃兰州4分)抛物线y =-2x 2+1的对称轴是【 】A .直线1x=2 B .直线1x=2- C .y 轴 D .直线x =2 26. (2012甘肃兰州4分)已知二次函数y =a(x +1)2-b(a≠0)有最小值,则a ,b 的大小关系为【 】A .a >bB .a <bC .a =bD .不能确定27. (2012青海西宁3分)如图,二次函数y =ax 2+bx +c 的图象过点(-1,1)、(2,-1).下列关于这个二次函数的叙述正确的是【 】A .当x =0时,y 的值大于1B .当x =3时,y 的值小于0C .当x =1时,y 的值大于1D .y 的最大值小于028. (2012黑龙江黑河、齐齐哈尔、大兴安岭、鸡西3分)已知二次函数y=ax 2+bx+c(a≠O)的图象如图所示,现有下列结论:①abc>0 ②b 2-4ac<0 ⑤c<4b ④a +b>0,则其中正确结论的个数是【 】 A .1个 B .2个 C .3个 D .4个29. (2012黑龙江牡丹江3分)抛物线2y ax bx c =++与x 轴的交点坐标是(-l ,0)和(3,0),则这条抛物线的对称轴是【 】.A .直线x=-1 8.直线x=0 C .直线x=1 D .直线x= 3二、填空题1. (2012广东深圳3分)二次函数622+-=x x y 的最小值是 .2. (2012江苏苏州3分)已知点A (x 1,y 1)、B (x 2,y 2)在二次函数y=(x -1)2+1的图象上,若x 1>x 2>1,则y 1 y 2.3. (2012江苏无锡2分)若抛物线y=ax 2+bx+c 的顶点是A (2,1),且经过点B (1,0),则抛物线的函数关系式为 .4. (2012湖北咸宁3分)对于二次函数2y x 2mx 3=--,有下列说法:①它的图象与x 轴有两个公共点;②如果当x ≤1时y 随x 的增大而减小,则m 1=;③如果将它的图象向左平移3个单位后过原点,则m 1=-;④如果当x 4=时的函数值与x 2008=时的函数值相等,则当x 2012=时的函数值为3-.其中正确的说法是 .(把你认为正确说法的序号都填上)5. (2012湖北孝感3分)二次函数y =ax 2+bx +c(a≠0)的图象的对称轴是直线x =1,其图象的一部分如图所示.下列说法正确的是 (填正确结论的序号).①abc <0;②a -b +c <0;③3a +c <0;④当-1<x <3时,y >0.6. (2012辽宁营口3分)二次函数n x x y +-=62的部分图像如图所示,若关于x 的一元二次方程062=+-n x x 的一个解为11=x ,则另一个解2x = .7. (2012山东枣庄4分)二次函数2y x 2x 3=--的图象如图所示.当y <0时,自变量x 的取值范围是 .8. (2012新疆区5分)当x= 时,二次函数y=x 2+2x ﹣2有最小值.9. (2012吉林长春3分)如图,在平面直角坐标系中,点A 是抛物线()2y=a x 3+k -与y 轴的交点,点B 是这条抛物线上的另一点,且AB ∥x 轴,则以AB 为边的等边三角形ABC 的周长为 .10. (2012黑龙江牡丹江3分)若抛物线2y ax bx c =++经过点(-1,10),则a b c -+= .11. (2012黑龙江大庆3分)已知二次函数y=-x 2-2x +3的图象上有两点A(-7,1y ),B(-8,2y ),则1y 2y .(用>、<、=填空).三、解答题1. (2012北京市7分)已知二次函数23y (t 1)x 2(t 2)x 2=++++在x 0=和x 2=时的函数值相等。
2014年中考数学二次函数综合试题

2014中考数学二次函数综合训练1、如图1,已知二次函数图象的顶点坐标为C(1,0),直线mxy+=与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.(1)求m的值及这个二次函数的关系式;(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;AB上是否存在一点P,使得四边形DCEP是平行四边P点的坐标;若不存在,请说明理由.2、如图2,已知二次函数24y ax x c=-+的图像经过点A和点B.(1)求该二次函数的表达式;(2)写出该抛物线的对称轴及顶点坐标;m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的图13、如图3,已知抛物线c x b x a y ++=2经过O(0,0),A(4,0),B(3,3)三点,连结AB ,过点B 作BC ∥x 轴交该抛物线于点C.(1) 求这条抛物线的函数关系式.(2) 两个动点P 、Q 分别从O 、A 两点同时出发,以每秒1个单位长度的速度运动. 其中,点P 沿着线段0A 向A 点运动,点Q 沿着折线A →B →C 的路线向C 点运动. 设这两个动点运动的时间为t (秒) (0<t <4),△PQA 的面积记为S.① 求S 与t 的函数关系式; ② 当t 为何值时,S 有最大值,最大值是多少?并指出此时△PQA 的形状;③ 是否存在这样的t 值,使得△PQA 是直角三角形?若存在,请直接写出此时P 、Q 两点的坐标;若不存在,请说明理由.4、某公司推出了一种高效环保型除草剂,年初上市后,公司经历了从亏损到盈利的过程. 图4的二次函数图象(部分)刻车了该公司年初以来累积利润S (万元)与时间t (月)之间的关系(即前t 个月的利润总和S 与t 之间的关系). 根据图象提供信息,解答下列问题:(1)公司从第几个月末开始扭亏为盈;(2)累积利润S 与时间t 之间的函数关系式;(3)求截止到几月末公司累积利润可达30万元;(4)求第8个月公司所获利是多少元?5、如图5,已知抛物线cxbxay++=2的顶点坐标为E(1,0),与y轴的交点坐标为(0,1).(1)求该抛物线的函数关系式.(2)A、B是x轴上两个动点,且A、B间的距离为AB=4,A在B的左边,过A作AD⊥x轴交抛物线于D,过B作BC⊥x 轴交抛物线于C. 设A点的坐标为(t,0),四边形ABCD的面积为S.P,使得△PAE的周长最小,若存在,请求出点.图5 备用图6)如图6,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2。
二次函数图像与性质中考真题(含详细答案和分析)

二次函数图像与性质中考真题一.填空题(共26小题)1.(2014•天津)抛物线y=x2﹣2x+3的顶点坐标是_________.2.(2014•长沙)抛物线y=3(x﹣2)2+5的顶点坐标是_________.3.(2014•大连)函数y=(x﹣1)2+3的最小值为_________.4.已知抛物线y=ax2+bx+c与x轴的公共点是(﹣4,0),(2,0),则这条抛物线的对称轴是直线_________5.(2014•温州一模)二次函数y=(x+3)2﹣5的对称轴是直线_________.6.(2014•奉贤区二模)二次函数y=x2+3图象的顶点坐标是_________.7.(2014•青浦区一模)函数y=(x+5)(2﹣x)图象的开口方向是_________.8.(2014•金山区一模)抛物线y=x2+2x的对称轴是_________.9.(2014•杨浦区二模)抛物线y=2x2+4x﹣2的顶点坐标是_________.10.如果二次函数y=(2k﹣1)x2﹣3x+1的图象开口向上,那么常数k的取值范围是_________.11.(2014•天河区二模)二次函数y=x2﹣4x的顶点坐标是_________.12.(2014•泰兴市二模)二次函数y=2(x+1)(x﹣3)图象的顶点坐标为_________.13.(2014•崇明县一模)抛物线y=x2﹣4x+5的对称轴是直线_________.14.(2014•成都高新区一模)抛物线y=x2﹣12x+9的顶点坐标是_________.15.(2014•和平区一模)求抛物线y=﹣2x2+8x﹣8的开口方向、对称轴及顶点坐标.16.(2014•鄂托克旗模拟)抛物线y=﹣x2+4x﹣5的顶点坐标是_________.17.(2014•奉贤区一模)二次函数y=﹣2(x﹣2)2的图象在对称轴左侧部分是_________.“上升或下降”18.(2014•历城区一模)抛物线y=2(x﹣3)2+1的顶点坐标是_________.19.(2014•青浦区一模)如果二次函数y=x2+2kx+k﹣4图象的对称轴为x=3,那么k=_________.20.(2014•奉贤区一模)抛物线y=3x2﹣1的顶点坐标为_________.21.抛物线y=﹣(x﹣1)2+1在对称轴的右侧的部分是_________的.(从“上升”或“下降”中选择)22.(2014•黄浦区一模)若抛物线y=(x+m)2+m﹣1的对称轴是直线x=1,则它的顶点坐标是_________.23.(2014•安徽模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0.其中所有正确结论的序号是_________.24.(2014•靖江市模拟)已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,b2﹣4ac,a+b+c,a﹣b+c,2a+b中,其值为正的式子的个数为_________个.25.二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过_________象限.26.(2014•长宁区一模)已知抛物线y=mx2+4x+m(m﹣2)经过坐标原点,则实数m的值是二.解答题(共4小题)27.(2012•宿迁模拟)已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.28.(2009•衡阳)已知二次函数的图象过坐标原点,它的顶点坐标是(1,﹣2),求这个二次函数的关系式.29.(2009•临沂)如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.求出抛物线的解析式;30.(2008•镇江)推理运算:二次函数的图象经过点A(0,﹣3),B(2,﹣3),C(﹣1,0).(1)求此二次函数的关系式;(2)求此二次函数图象的顶点坐标;(3)填空:把二次函数的图象沿坐标轴方向最少平移_________个单位,使得该图象的顶点在原点.参考答案与试题解析一.填空题(共26小题)1.(2014•天津)抛物线y=x2﹣2x+3的顶点坐标是(1,2).考点:二次函数的性质.专题:计算题.分析:已知抛物线的解析式是一般式,用配方法转化为顶点式,根据顶点式的坐标特点,直接写出顶点坐标.解答:解:∵y=x2﹣2x+3=x2﹣2x+1﹣1+3=(x﹣1)2+2,∴抛物线y=x2﹣2x+3的顶点坐标是(1,2).点评:此题考查了二次函数的性质,二次函数y=a(x﹣h)2+k的顶点坐标为(h,k),对称轴为x=h,此题还考查了配方法求顶点式.2.(2014•长沙)抛物线y=3(x﹣2)2+5的顶点坐标是(2,5).考点:二次函数的性质.分析:由于抛物线y=a(x﹣h)2+k的顶点坐标为(h,k),由此即可求解.解答:解:∵抛物线y=3(x﹣2)2+5,∴顶点坐标为:(2,5).故答案为:(2,5).点评:此题主要考查了二次函数的性质,解题的关键是熟练掌握抛物线y=a(x﹣h)2+k的顶点坐标为(h,k).3.(2014•大连)函数y=(x﹣1)2+3的最小值为3.专题:常规题型.分析:根据顶点式得到它的顶点坐标是(1,3),再根据其a>0,即抛物线的开口向上,则它的最小值是3.解答:解:根据非负数的性质,(x﹣1)2≥0,于是当x=1时,函数y=(x﹣1)2+3的最小值y等于3.故答案为:3.点评:本题考查了二次函数的最值的求法.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.4.(2014•南通)已知抛物线y=ax2+bx+c与x轴的公共点是(﹣4,0),(2,0),则这条抛物线的对称轴是直线x=﹣1.考点:抛物线与x轴的交点.专题:待定系数法.分析:因为点(﹣4,0)和(2,0)的纵坐标都为0,所以可判定是一对对称点,把两点的横坐标代入公式x=求解即可.解答:解:∵抛物线与x轴的交点为(﹣4,0),(2,0),∴两交点关于抛物线的对称轴对称,则此抛物线的对称轴是直线x==﹣1,即x=﹣1.故答案是:x=﹣1.点评:本题考查了抛物线与x轴的交点,以及如何求二次函数的对称轴,对于此类题目可以用公式法也可以将函数化为顶点式来求解,也可以用公式x=求解,即抛物线y=ax2+bx+c与x轴的交点是(x1,0),(x2,0),则抛物线的对称轴为直线x=.5.(2014•温州一模)二次函数y=(x+3)2﹣5的对称轴是直线x=﹣3.考点:二次函数的性质.分析:对照顶点式y=a(x﹣h)2+k的对称轴是x=h,求本题中二次函数的对称轴.解答:解:因为二次函数y=(x+3)2﹣5的顶点坐标是(﹣3,﹣5),故对称轴是直线x=﹣3.点评:顶点式y=a(x﹣h)2+k,顶点坐标是(h,k),对称轴是x=h,此题考查了学生的应用能力.6.(2014•奉贤区二模)二次函数y=x2+3图象的顶点坐标是(0,3).考点:二次函数的性质.分析:根据二次函数的性质,利用顶点式直接得出顶点坐标即可.解答:解:∵二次函数y=x2+3,∴二次函数y=x2+3图象的顶点坐标是:(0,3).点评:此题主要考查了利用二次函数顶点式求顶点坐标,此题型是中考中考查重点,同学们应熟练掌握.7.(2014•青浦区一模)函数y=(x+5)(2﹣x)图象的开口方向是向下.考点:二次函数的性质.分析:首先将二次函数化为一般形式,然后根据二次项系数的符号确定开口方向.解答:解:y=(x+5)(2﹣x)=﹣x2+3x+10,∵a=﹣1<0,∴开口向下,故答案为:向下.点评:本题考查了二次函数的性质,解题的关键是正确的化为一般形式.8.(2014•金山区一模)抛物线y=x2+2x的对称轴是直线x=﹣1.考点:二次函数的性质.专题:计算题.分析:先把一般式配成顶点式,根据二次函数的性质即可得到抛物线的对称轴.解答:解:y=x2+2x=(x2+2x+1)﹣1=(x+1)2﹣1,抛物线的对称轴为直线x=﹣1.故答案为直线x=﹣1.点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=﹣;抛物线与y轴的交点坐标为(0,c);当b2﹣4ac>0,抛物线与x轴有两个交点;当b2﹣4ac=0,抛物线与x轴有一个交点;当b2﹣4ac<0,抛物线与x轴没有交点.9.(2014•杨浦区二模)抛物线y=2x2+4x﹣2的顶点坐标是(﹣1,﹣4).考点:二次函数的性质.分析:利用顶点的公式首先求得横坐标,然后把横坐标的值代入解析式即可求得纵坐标.解答:解:x=﹣=﹣1,把x=﹣1代入得:y=2﹣4﹣2=﹣4.则顶点的坐标是(﹣1,﹣4).故答案是:(﹣1,﹣4).点评:本题考查了二次函数的顶点坐标的求解方法,可以利用配方法求解,也可以利用公式法求解.10.(2014•嘉定区一模)如果二次函数y=(2k﹣1)x2﹣3x+1的图象开口向上,那么常数k的取值范围是k>.考点:二次函数的性质.分析:根据二次函数的开口向上列出关于k的不等式,求出k的取值范围即可.2∴2k﹣1>0,解得k>.故答案为:k>.点评:本题考查的是二次函数的性质,熟知二次函数y=ax2+bx+c(a≠0),当a>0时,抛物线的开口向上是解答此题的关键.11.(2014•天河区二模)二次函数y=x2﹣4x的顶点坐标是(2,﹣4).考点:二次函数的性质.分析:用配方法将抛物线的一般式转化为顶点式,确定顶点坐标即可.解答:解:∵y=x2﹣4x=(x﹣2)2﹣4,∴抛物线顶点坐标为(2,﹣4).故本题答案为:(2,﹣4).点评:本题考查了抛物线解析式与顶点坐标的关系,求顶点坐标可用配方法,也可以用顶点坐标公式.12.(2014•泰兴市二模)二次函数y=2(x+1)(x﹣3)图象的顶点坐标为(1,﹣8).考点:二次函数的性质.分析:根据函数解析式的相互转化,可得顶点式解析式,根据顶点式解析式,可得答案.解答:解:y=2(x+1)(x﹣3)转化成y=2(x﹣1)2﹣8,故答案为:(1,﹣8).点评:本题考查了二次函数的性质,转化成顶点式解析式是解题关键.13.(2014•崇明县一模)抛物线y=x2﹣4x+5的对称轴是直线x=2.考点:二次函数的性质.专题:数形结合.分析:首先把y=x2﹣4x+5进行配方,然后就可以确定抛物线的对称轴,也可以利用公式x=﹣确定.解答:解:y=x2﹣4x+5,=x2﹣4x+4+1,=(x﹣2)2+1,∴对称轴是直线x=2.故答案为:x=2.点评:此题主要考查了二次函数的性质,解题的关键是会配方法或对称轴的公式x=﹣.14.(2014•成都高新区一模)抛物线y=x2﹣12x+9的顶点坐标是(6,﹣27).考点:二次函数的性质.分析:把抛物线解析式整理成顶点式形式,然后写出顶点坐标即可.解答:解:y=x2﹣12x+9=(x﹣6)2﹣27,故答案为:(6,﹣27).点评:本题考查了二次函数的性质,把抛物线解析式整理成顶点式形式求解更简便.15.(2014•和平区一模)求抛物线y=﹣2x2+8x﹣8的开口方向、对称轴及顶点坐标.考点:二次函数的性质.分析:根据二次项系数得出抛物线的开口方向,将一般式转化为顶点式即可得出对称轴和顶点坐标.解答:解:y=2x2+8x﹣8,∵a=﹣2<0,∴抛物线开口向下.∵y=﹣2x2+8x﹣8=﹣2(x2﹣4x+4)=﹣2(x﹣2)2,∴对称轴为直线x=﹣2,顶点坐标为(2,0).点评:本题考查了二次函数的性质及配方法的应用,用到的知识点:二次函数y=a(x﹣h)2+k,当a >0时,抛物线开口向上;对称轴是直线x=h,顶点坐标是(h,k).利用配方法将一般式转化为顶点式是解题的关键.16.(2014•鄂托克旗模拟)抛物线y=﹣x2+4x﹣5的顶点坐标是(2,﹣1).考点:二次函数的性质.分析:根据所给的二次函数,把a=﹣1、b=4、c=﹣5代入顶点公式即可求.解答:解:∵y=﹣x2+4x﹣5∴,.故答案为:(2,﹣1).点评:本题考查了二次函数的性质,解题的关键是熟练掌握二次函数顶点公式.17.(2014•奉贤区一模)二次函数y=﹣2(x﹣2)2的图象在对称轴左侧部分是上升.“上升或下降”考点:二次函数的性质.分析:直接根据二次函数的性质进行解答即可.解答:解:∵二次函数y=﹣2(x﹣2)2中,a=﹣2<0,∴抛物线开口向下,∴函数图象在对称轴左侧部分是上升.故答案为:上升.点评:本题考查的是二次函数的性质,熟知当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<﹣时,y随x的增大而增大是解答此题的关键.18.(2014•历城区一模)抛物线y=2(x﹣3)2+1的顶点坐标是(3,1).考点:二次函数的性质.分析:已知抛物线解析式为顶点式,可直接求出顶点坐标.解答:解:由抛物线解析式可知,抛物线顶点坐标为(3,1),点评:本题考查了二次函数的性质,将解析式化为顶点式y=a(x﹣h)2+k,顶点坐标是(h,k),对称轴是x=h.19.(2014•青浦区一模)如果二次函数y=x2+2kx+k﹣4图象的对称轴为x=3,那么k=﹣3.考点:二次函数的性质.分析:直接利用对称轴公式求解即可.解答:解:∵二次函数y=x2+2kx+k﹣4图象的对称轴为x=3,∴对称轴为:x=﹣=3,解得:k=﹣3,故答案为:﹣3点评:本题主要考查二次函数的性质,解此题的关键是对二次函数的性质的理解和掌握,知对称轴.20.(2014•奉贤区一模)抛物线y=3x2﹣1的顶点坐标为(0,﹣1).考点:二次函数的性质.分析:根据形如y=ax2+k的顶点坐标为(0,k),据此可以直接求顶点坐标.解答:解:∵抛物线的解析式为y=3x2﹣1,∴其顶点坐标为(0,﹣1).故答案为:(0,﹣1).点评:本题考查了二次函数的性质.二次函数的顶点式方程y=a(x﹣k)2+h的顶点坐标是(k,h),对称轴方程是x=k.21.(2014•嘉定区一模)抛物线y=﹣(x﹣1)2+1在对称轴的右侧的部分是下降的.(从“上升”或“下降”中选择)考点:二次函数的性质.分析:根据a<0,知抛物线开口向下,则在对称轴右侧的部分呈下降趋势.解答:解:∵a<0,∴抛物线开口向下,∴对称轴右侧的部分呈下降趋势.故答案为:下降.点评:考查了二次函数的性质,能够根据抛物线的开口方向分析对称轴左右两侧的变化规律.22.(2014•黄浦区一模)若抛物线y=(x+m)2+m﹣1的对称轴是直线x=1,则它的顶点坐标是(1,﹣2).考点:二次函数的性质.分析:首先根据对称轴是直线x=1,从而求得m的值,然后根据顶点坐标公式直接写出顶点坐标;解答:解:∵抛物线y=(x+m)2+m﹣1的对称轴是直线x=1,∴m=﹣1,∴解析式y=(x﹣1)2﹣2,∴顶点坐标为:(1,﹣2),点评:本题主要考查了二次函数的性质,熟练掌握顶点式是解题的关键,难度适中.23.(2014•安徽模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0.其中所有正确结论的序号是②③.考点:二次函数图象与系数的关系.专题:压轴题.分析:由x=1时,y=a+b+C>0,即可判定①错误;由x=﹣1时,y=a﹣b+c<0,即可判定②正确;由抛物线的开口向下知a<0,与y轴的交点为在y轴的正半轴上得到c>0,又对称轴为x=<1,得到2a+b<0,由此可以判定③正确;由对称轴为x=>0即可判定④错误.解答:解:①当x=1时,y=a+b+C>0,∴①错误;②当x=﹣1时,y=a﹣b+c<0,∴②正确;③由抛物线的开口向下知a<0,与y轴的交点为在y轴的正半轴上,∴c>0,∵对称轴为x=<1,∴﹣b>2a,∴2a+b<0,∴③正确;④对称轴为x=>0,∴a、b异号,即b>0,∴abc<0,∴④错误.∴正确结论的序号为②③.故填空答案:②③.点评:二次函数y=ax2+bx+c系数符号的确定:(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0;(2)b由对称轴和a的符号确定:由对称轴公式x=判断符号;(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0;(4)当x=1时,可以确定y=a+b+C的值;当x=﹣1时,可以确定y=a﹣b+c的值.24.(2014•靖江市模拟)已知二次函数y=ax2+bx+c的图象如图所示,则下列7个代数式ab,ac,bc,2考点:二次函数图象与系数的关系.分析:由抛物线开口向上,得到a>0,再由对称轴在y轴右侧,得到a与b异号,可得出b<0,又抛物线与y轴交于正半轴,得到c大于0,可得出ab<0,ac>0,由抛物线与x轴有2个交点,得到根的判别式b2﹣4ac>0,当x=1时,y=a+b+c<0,x=﹣1时,y=a﹣b+c>0,由﹣=1得b+2a=0.解答:解:∵抛物线的开口向上,∴a>0,∵﹣>0,∴b<0,∵抛物线与y轴交于正半轴,∴c>0,∴ab<0,ac>0,bc<0∵抛物线与x轴有2个交点,∴b2﹣4ac>0∵x=1时的函数值小于0,∴y=a+b+c<0又∵x=﹣1时的函数值大于0∴y=a﹣b+c>0∵对称轴为直线x=1,∴﹣=1,即2a+b=0,所以一共有3个式子的值为正.故答案为:3.点评:此题考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c(a≠0),a的符号由抛物线开口方向决定;b的符号由对称轴的位置及a的符号决定;c的符号由抛物线与y轴交点的位置决定;抛物线与x轴的交点个数,决定了b2﹣4ac的符号,此外还要注意x=1,﹣1对应函数值的正负来判断其式子的正确与否.25.(2014•平原县二模)二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过二、三、四象限.分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.解答:解:∵抛物线的顶点(﹣m,n)在第四象限,∴﹣m>0,n<0,∴m<0,∴一次函数y=mx+n的图象经过二、三、四象限,故答案是:二、三、四.点评:此题考查了二次函数的图象,用到的知识点是二次函数的图象与性质、一次函数的图象与性质,关键是根据抛物线的顶点在第四象限,得出n、m的符号.26.(2014•长宁区一模)已知抛物线y=mx2+4x+m(m﹣2)经过坐标原点,则实数m的值是2.考点:二次函数图象上点的坐标特征.分析:把原点坐标代入函数解析式进行计算即可得解.解答:解:∵抛物线y=mx2+4x+m(m﹣2)经过坐标原点,∴m(m﹣2)=0,解得m1=0,m2=2,当m=0时,函数为一次函数,不是抛物线,所以,m≠0,因此,实数m的值是2.故答案为:2.点评:本题考查了二次函数图象上点的坐标特征,要注意二次项系数不等于0.二.解答题(共4小题)27.(2012•宿迁模拟)已知抛物线的顶点坐标为M(1,﹣2),且经过点N(2,3),求此二次函数的解析式.考点:待定系数法求二次函数解析式.分析:因为抛物线的顶点坐标为M(1,﹣2),所以设此二次函数的解析式为y=a(x﹣1)2﹣2,把点(2,3)代入解析式即可解答.解答:解:已知抛物线的顶点坐标为M(1,﹣2),设此二次函数的解析式为y=a(x﹣1)2﹣2,把点(2,3)代入解析式,得:a﹣2=3,即a=5,∴此函数的解析式为y=5(x﹣1)2﹣2.点评:本题考查了用待定系数法求函数解析式的方法.若题目给出了二次函数的顶点坐标,则采用顶点式求解简单.28.(2009•衡阳)已知二次函数的图象过坐标原点,它的顶点坐标是(1,﹣2),求这个二次函数的关系式.考点:待定系数法求二次函数解析式.分析:此题告诉了二次函数的顶点坐标,采用顶点式比较简单.解答:解:设这个二次函数的关系式为y=a(x﹣1)2﹣2,∵二次函数的图象过坐标原点,∴0=a(0﹣1)2﹣2解得:a=2故这个二次函数的关系式是y=2(x﹣1)2﹣2,即y=2x2﹣4x.点评:本题考查了用待定系数法求函数解析式的方法,设解析式时要根据具体情况选择适当形式.29.(2009•临沂)如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.(1)求出抛物线的解析式;(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.考点:二次函数综合题.专题:压轴题.分析:(1)已知抛物线经过A(4,0),B(1,0),可设抛物线解析式的交点式,再把C(0,﹣2)代入即可;(2)∵△OAC是直角三角形,以A,P,M为顶点的三角形与其相似,由于点P可能在x轴的上方,或者下方,分三种情况,分别用相似比解答;(3)过D作y轴的平行线交AC于E,将△DCA分割成两个三角形△CDE,△ADE,它们的底相同,为DE,高的和为4,就可以表示它们的面积和,即△DCA的面积,运用代数式的变形求最大值.解答:解:(1)∵该抛物线过点C(0,﹣2),设该抛物线的解析式为y=ax2+bx﹣2.将A(4,0),B(1,0)代入,得,解得,∴此抛物线的解析式为y=﹣x2+x﹣2.(2)存在.如图,设P点的横坐标为m,则点P的纵坐标为,当1<m<4时,AM=4﹣m,PM=,又∵∠COA=∠PMA=90°,∴①当==2时,△APM∽△ACO,∴=2,即|4﹣m|=2(),∴4﹣m=m2+5m﹣4,∴m2﹣6m+8=0,∴(m﹣2)(m﹣4)=0,解得:m1=2,m2=4(舍去)∴P(2,1)②当,△APM∽△CAO,那么有:2|4﹣m|=,∴2(4﹣m)=﹣m2+m﹣2,∴m2﹣9m+20=0,∴(m﹣4)(m﹣5)=0,解得:m1=4(舍去),m2=5(舍去),∴当1<m<4时,P(2,1),类似地可求出当m>4时,P(5,﹣2),当m<1时,P(﹣3,﹣14),当P,C重合时,△APM≌△ACO,P(0,﹣2).综上所述,符合条件的点P为(2,1)或(5,﹣2)或(﹣3,﹣14)或(0,﹣2);(3)如图,设D点的横坐标为t(0<t<4),则D点的纵坐标为﹣t2+t﹣2.过D作y轴的平行线交AC于E.由题意可求得直线AC的解析式为y=x﹣2.∴E点的坐标为(t,t﹣2).∴DE=﹣t2+t﹣2﹣(t﹣2)=﹣t2+2t.∴S△DAC=×(﹣t2+2t)×4=﹣t2+4t=﹣(t﹣2)2+4.∴当t=2时,△DAC面积最大.∴D(2,1).点评:本题综合考查了抛物线解析式的求法,抛物线与相似三角形的问题,坐标系里表示三角形的面积及其最大值问题,要求会用字母代替长度,坐标,会对代数式进行合理变形.30.(2008•镇江)推理运算:二次函数的图象经过点A(0,﹣3),B(2,﹣3),C(﹣1,0).(1)求此二次函数的关系式;(2)求此二次函数图象的顶点坐标;(3)填空:把二次函数的图象沿坐标轴方向最少平移5个单位,使得该图象的顶点在原点.考点:待定系数法求二次函数解析式;二次函数的性质;二次函数图象与几何变换.分析:(1)可用一般式来求二次函数的关系式;(2)把二次函数的关系式整理为顶点式即可求得顶点;(3)应看顶点坐标是如何经过最短距离之和到达原点.解答:解:(1)设y=ax2+bx﹣3,(1分)把点(2,﹣3),(﹣1,0)代入得,(2分)解方程组得∴y=x2﹣2x﹣3;(3分)(也可设y=a(x﹣1)2+k)(2)y=x2﹣2x﹣3=(x﹣1)2﹣4,(4分)∴函数的顶点坐标为(1,﹣4);(5分)(3)|1﹣0|+|﹣4﹣0|=5.(6分)点评:一般用待定系数法来求函数解析式;抛物线y=ax2+bx+c(a≠0)通过配方,将一般式化为y=a(x ﹣h)2+k的形式,可确定其顶点坐标为(h,k).进一步考查了平移的知识.。
2014年新观察中考数学二次函数

例、如图,已知直线y=kx与抛物线交于点A(3,6).若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点0、A不重合),且满足∠BAO=∠AOD.(1)求B点的坐标;(2)若D(n,0),∠DEB=∠AOD,且符合条件的E点只有一个,求n.1、如图,已知抛物线y=+2x+8与x轴交于点A、B两点,与y轴交于点C,D为抛物线的顶点,直线CD交x轴于E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点,试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?2、已知抛物线y=a—6ax+5a与x轴交于A、B两点(A左、B右)。
(1)若抛物线与直线y=2x的最近点之间的距离为,求a的值;(2)若抛物线不通过直线y=2x上方的点,求抛物线顶点纵坐标的取值范围。
(2)若抛物线不通过直线y=2x上方的点,求抛物线顶点纵坐标的取值范围。
例、如图,点P是直线l:y=—2x—2上的点,过点P的另一条直线优交抛物线y=于A、B两点.试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得P A=AB成立。
1、已知二次函数y=a(x2—6x+8)(a>0)的图象与x轴分别交于点A、B,与y轴交于点C,点D是抛物线的顶点,对称轴交x轴于M点,如图,当点P在抛物线对称轴上时,设点P的纵坐标t是大于3的常数,试问:是否存在一个正数a,使得四条线段P A、PB、PC、PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)?请说明理由。
2、如图,抛物线y=a(x—1)2+4 与x轴交于A、B两点,与y轴交于C点,D是抛物线的顶点,已知CD=.在抛物线上共有三个点到直线BC的距离为m,求m的值。
例、已知关于x的二次函数y=x2—2mx+m2+m的图象与关于x的函数y=kx+1的图象交于两点A(x1,y1)、B(x2,y2);(x1<x2)。
(1)当k=1,m为任何值时,猜想AB的长是否不变?并证明你的猜想.(2)当m=0,无论k为何值时,猜想△AOB的形状.证明你的猜想.(2)当m=0,无论k为何值时,猜想△AOB的形状.证明你的猜想.1、如图,抛物线y=—2x—3与坐标轴交于A、B、C三点,直线y=kx—1与抛物线交于P、Q两点,且y轴平分△CPQ的面积,求k的值。
辽宁中考--二次函数-2014

1.函数y=(x-1)2+3的最小值为2.将抛物线y=(x-3)2+1先向上平移2个单位,再向左平移1个单位后,得到的抛物线解析式为3.如图,平面直角坐标系中,点M 是直线y=2与x 轴之间的一个动点,且点M 是抛物线y=21x 2+bx+c 的顶点,则方程21x 2+bx+c=1的解的个数是( ) A .0或2B .0或1C .1或2D .0,1或24.二次函数y=ax 2+bx+c (a≠0,a ,b ,c 为常数)的图象如图,ax 2+bx+c=m 有实数根的条件是( )A .m≥-2B .m≥5C .m≥0D .m >45.如图,二次函数y=ax 2+bx+3的图象经过点A (-1,0),B (3,0),那么一元二次方程ax 2+bx=0的根是6.如图1,抛物线y=ax 2+bx-1经过A (-1,0)、B (2,0)两点,交y 轴于点C .点P 为抛物线上的一个动点,过点P 作x 轴的垂线交直线BC 于点D ,交x 轴于点E .(1)请直接写出抛物线表达式和直线BC 的表达式.(2)如图1,当点P 的横坐标为32时,求证:△OBD ∽△ABC . (3)如图2,若点P 在第四象限内,当OE=2PE 时,求△POD 的面积.(4)当以点O、C、D为顶点的三角形是等腰三角形时,请直接写出动点P的坐标.7.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(6,0),C(-4,0)两点,与y轴交于点B(0,3).(1)求抛物线的解析式;(2)点D、点E同时从点O出发以每秒1个单位长度的速度分别沿x轴正半轴,y轴正半轴向点A、点B方向移动,当点D运动到点A时,点D、E同时停止移动.过点D作x轴的垂线交抛物线于点F,交AB于点G,作点E关于直线DF的对称点E′,连接FE′,射线DE′交AB于点H.设运动时间为t秒.①t为何值时点E′恰好在抛物线上,并求此时△DE′F与△ADG重叠部分的面积;②点P是平面内任意一点,若点D在运动过程中的某一时刻,形成以点A、E′、D、P为顶点的四边形是菱形,那么请直接写出点P的坐标.8.如图,抛物线y=a(x-m)2+2m-2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m-1).连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.(1)该抛物线的解析式为(用含m的式子表示);(2)求证:BC∥y轴;(3)若点B′恰好落在线段BC′上,求此时m的值.9.如图1,在平面直角坐标系中,二次函数122742+-=x y 的图象与y 轴交于点A ,与x 轴交于B ,C 两点(点B 在点C 的左侧),连接AB ,AC .(1)点B 的坐标为 ,点C 的坐标为 ;(2)过点C 作射线CD ∥AB ,点M 是线段AB 上的动点,点P 是线段AC 上的动点,且始终满足BM=AP (点M 不与点A ,点B 重合),过点M 作MN ∥BC 分别交AC 于点Q ,交射线CD 于点N (点 Q 不与点P 重合),连接PM ,PN ,设线段AP 的长为n . ①如图2,当n <21AC 时,求证:△PAM ≌△NCP ; ②直接用含n 的代数式表示线段PQ 的长;③若PM 的长为97,当二次函数122742+-=x y 的图象经过平移同时过点P 和点N 时,请直接写出此时的二次函数表达式.10.如图,直线y=x-4与x 轴、y 轴分别交于A 、B 两点,抛物线y=31x 2+bx+c 经过A 、B 两点,与x 轴的另一个交点为C ,连接BC .(1)求抛物线的解析式及点C 的坐标;(2)点M 在抛物线上,连接MB ,当∠MBA+∠CBO=45°时,求点M 的坐标;(3)点P 从点C 出发,沿线段CA 由C 向A 运动,同时点Q 从点B 出发,沿线段BC 由B 向C 运动,P 、Q 的运动速度都是每秒1个单位长度,当Q 点到达C 点时,P 、Q 同时停止运动,试问在坐标平面内是否存在点D ,使P 、Q 运动过程中的某一时刻,以C 、D 、P、Q为顶点的四边形为菱形?若存在,直接写出点D的坐标;若不存在,说明理由.11.如图,抛物线y=-x2+bx+c交x轴于点A,交y轴于点B,已知经过点A,B的直线的表达式为y=x+3.(1)求抛物线的函数表达式及其顶点C的坐标;(2)如图①,点P(m,0)是线段AO上的一个动点,其中-3<m<0,作直线DP⊥x轴,交直线AB于D,交抛物线于E,作EF∥x轴,交直线AB于点F,四边形DEFG为矩形.设矩形DEFG的周长为L,写出L与m的函数关系式,并求m为何值时周长L最大;(3)如图②,在抛物线的对称轴上是否存在点Q,使点A,B,Q构成的三角形是以AB为腰的等腰三角形?若存在,直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.12.在机器调试过程中,生产甲、乙两种产品的效率分别为y1、y2(单位:件/时),y1、y2与工作时间x(小时)之间大致满足如图所示的函数关系,y1的图象为折线OABC,y2的图象是过O、B、C三点的抛物线一部分.(1)根据图象回答:•调试过程中,生产乙的效率高于甲的效率的时间x(小时)的取值范围是; 说明线段AB的实际意义是.(2)求出调试过程中,当6≤x≤8(3)时,生产甲种产品的效率y1(件/时)与工作时间x (小时)之间的函数关系式.(3)调试结束后,一台机器先以图中甲的最大效率生产甲产品m 小时,再以图中乙的最大效率生产乙产品,两种产品共生产6小时,求甲、乙两种产品的生产总量Z (件)与生产甲所用时间m (小时)之间的函数关系式.13.如图,平行四边形ABCO 在平面直角坐标系中,点A 的坐标为(-2,0),点B 的坐标为(0,4),抛物线y=-x 2+mx+n 经过点A 和C .(1)求抛物线的解析式.(2)该抛物线的对称轴将平行四边形ABCO 分成两部分,对称轴左侧部分的图形面积记为S 1,右侧部分图形的面积记为S 2,求S 1与S 2的比.(3)在y 轴上取一点D ,坐标是(0,27),将直线OC 沿x 轴平移到O′C′,点D 关于直线O′C′的对称点记为D′,当点D′正好在抛物线上时,求出此时点D′坐标并直接写出直线O′C′的函数解析式.13.如图,抛物线y=ax 2+23x+c 与x 轴交于点A (4,0)、B (-1,0),与y 轴交于点C ,连接AC ,点M 是线段OA 上的一个动点(不与点O 、A 重合),过点M 作MN ∥AC ,交OC 于点N ,将△OMN 沿直线MN 折叠,点O 的对应点O′落在第一象限内,设OM=t ,△O′MN 与梯形AMNC 重合部分面积为S .(1)求抛物线的解析式;(2)①当点O′落在AC 上时,请直接写出此时t 的值;②求S 与t 的函数关系式;(3)在点M 运动的过程中,请直接写出以O 、B 、C 、O′为顶点的四边形分别是等腰梯形和平行四边形时所对应的t 值.14.已知:抛物线y=ax 2+bx+c (a≠0)经过点A (1,0),B (3,0),C (0,-3).(1)求抛物线的表达式及顶点D 的坐标;(2)如图①,点P 是直线BC 上方抛物线上一动点,过点P 作y 轴的平行线,交直线BC 于点E .是否存在一点P ,使线段PE 的长最大?若存在,求出PE 长的最大值;若不存在,请说明理由;(3)如图②,过点A 作y 轴的平行线,交直线BC 于点F ,连接DA 、DB .四边形OAFC 沿射线CB 方向运动,速度为每秒1个单位长度,运动时间为t 秒,当点C 与点B 重合时立即停止运动.设运动过程中四边形OAFC 与四边形ADBF 重叠部分面积为S ,请求出S 与t 的函数关系式.15.如图,在Rt △ABC 中,∠C=90°,顶点A 、C 的坐标分别为(-1,2),(3,2),点B 在x 轴上,点B 的坐标为(3,0),抛物线y=-x 2+bx+c 经过A 、C 两点.(1)求该抛物线所对应的函数关系式;(2)点P 是抛物线上的一点,当S △PAB =45S △ABC 时,求点P 的坐标; (3)若点N 由点B 出发,以每秒56个单位的速度沿边BC 、CA 向点A 移动,31秒后,点M 也由点B 出发,以每秒1个单位的速度沿线段BO 向点O 移动,当其中一个点到达终点时另一个点也停止移动,点N 的移动时间为t 秒,当MN ⊥AB 时,请直接写出t 的值,不必写出解答过程.16.如图,在平面直角坐标系中,将抛物线y=33x 2先向右平移1个单位,再向下平移334个单位,得到新的抛物线y=ax 2+bx+c ,该抛物线与y 轴交于点B ,与x 轴正半轴交于点C .(1)求点B 和点C 的坐标;(2)如图1,有一条与y 轴重合的直线l 向右匀速平移,移动的速度为每秒1个单位,移动的时间为t 秒,直线l 与抛物线y=ax 2+bx+c 交于点P ,当点P 在x 轴上方时,求出使△PBC 的面积为23的t 值;(3)如图2,将直线BC 绕点B 逆时针旋转,与x 轴交于点M (1,0),与抛物线y=ax 2+bx+c 交于点A ,在y 轴上有一点D (0,332),在x 轴上另取两点E ,F (点E 在点F 的左侧),EF=2,线段EF 在x 轴上平移,当四边形ADEF 的周长最小时,先简单描述如何确定此时点E 的位置?再直接写出点E 的坐标.17.如图,平面直角坐标系中,抛物线y=ax 2+bx+4经过点D (2,4),且与x 轴交于A (3,0),B (-1,0)两点,与y 轴交于点C ,连接AC ,CD ,BC(1)直接写出该抛物线的解析式(2)点P 是所求抛物线上的一个动点,过点P 作x 轴的垂线l ,l 分别交x 轴于点E ,交直线AC 于点M .设点P 的横坐标为m .①当0≤m≤2时,过点M 作MG ∥BC ,MG 交x 轴于点G ,连接GC ,则m 为何值时,△GMC 的面积取得最大值,并求出这个最大值②当-1≤m≤2时,试探求:是否存在实数m,使得以P,C,M为顶点的三角形和△AEM相似?若存在,求出相应的m值;若不存在,请说明理由.。
2014中考二次函数性质拔高真题

二次函数一、基本知识点:<1>、二次函数的概念:形如)0(2≠++=a c bx ax y 的函数.<2>、抛物线)0(2≠++=a c bx ax y 的顶点坐标是 (a b ac a b 44,22--);对称轴是直线ab x 2-=. <3>、当a >0时抛物线的开口向上;当a <0时抛物线的开口向下.a 越大,抛物线的开口越小;a 越小,抛物线的开口越大.a 相同的抛物线,通过平移(或旋转、轴对称)一定能够重合. <4>、抛物线y=ax*2+bx+c 的a ,b ,c 符号的确定a 的符号:由抛物线的开口方向确定。
开口向上a>0;开口向下a<0。
b 的符号:a 、b 同号时抛物线的对称轴在y 轴的左侧;a 、b 异号时抛物线的对称轴在y 轴的 右侧。
(简称:左同右异)b=0时抛物线的对称轴是y 轴。
C 的符号:由抛物线与y 轴的交点位置确定。
交点在x 轴上方时c>0;交点在x 轴下方时c<0;经过坐标原点时c=0。
<5>、二次函数解析式的三种形式:(1)已知抛物线上的三点,设一般式:)0(2≠++=a c bx ax y (2)已知抛物线顶点坐标(h, k ),设顶点式:k h x a y +-=2)((3)已知抛物线与x 轴的两个交点(X1,0)、 (X2,0)交点式:))((21x x x x a y --=,抛物线与x轴的交点坐标是(0,1x )和(0,2x ).<6>、抛物线的平移规律:从2ax y =到k h x a y +-=2)(,抓住顶点从(0,0)到(h ,k ). <7>、(1)当ac b 42->0时,一元二次方程)0(02≠=++a c bx ax 有两个实数根21,x x ,抛物线)0(2≠++=a c bx ax y 与x 轴的交点坐标是A (0,1x )和B (0,2x )。
二次函数、中考题集

2
15
解:(1)当 x=0 时,y=-2, ∴A(0,-2), 抛物线的对称轴为直线 x=-−2m /2m =1, ∴B(1,0); (2)易得 A 点关于对称轴直线 x=1 的对称点 A′(2,-2), 则直线 l 经过 A′、B, 设直线 l 的解析式为 y=kx+b(k≠0), 则 2k+b=−2 ,k+b=0 , 解得 k=−2 , b=2 , 所以,直线 l 的解析式为 y=-2x+2; (3)∵抛物线的对称轴为直线 x=1, ∴抛物线在 2<x<3 这一段与在-1<x<0 这一段关于对称轴对称, 结合图象可以观察到抛物线在-2<x<-1 这一段位于直线 l 的上方, 在-1<x<0 这一段位于 直线 l 的下方, ∴抛物线与直线 l 的交点的横坐标为-1, 当 x=-1 时,y=-2×(-1)+2=4, 所以,抛物线过点(-1,4), 当 x=-1 时,m+2m-2=4, 解得 m=2, 2 ∴抛物线的解析式为 y=2x -4x-2.
2.(2014•潍坊)如图,已知矩形 ABCD 的长 AB 为 5,宽 BC 为 4,E 是 BC 边上的一个动点, AE⊥EF,EF 交 CD 于点 F.设 BE=x,FC=y,则点 E 从点 B 运动到点 C 时,能表示 y 关于 x 的 函数关系的大致图象是( )
A.
B.
C.
D.
1
3.(2014•牡丹江)如图,点 P 是菱形 ABCD 边上一动点,若∠A=60°,AB=4,点 P 从点 A 出 发,以每秒 1 个单位长的速度沿 A→B→C→D 的路线运动,当点 P 运动到点 D 时停止运动, 那么△APD 的面积 S 与点 P 运动的时间 t 之间的函数关系的图象是( )
二次函数15年14年中考真题
2015年08月06日XX的初中数学组卷一.选择题(共30小题)1.(2015•兰州)下列函数解析式中,一定为二次函数的是()A.y=3x﹣1 B.y=ax2+bx+c C.s=2t2﹣2t+1 D.y=x2+ 2.(2015•宁夏)函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A.B.C.D.3.(2015•湖北)二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的图象可能是()A.B.C.D.4.(2015•泰安)某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:x …﹣2 ﹣1 0 1 2 …y …﹣11 ﹣2 1 ﹣2 ﹣5 …由于粗心,他算错了其中一个y值,则这个错误的数值是()A.﹣11 B.﹣2 C.1D.﹣55.(2015•沈阳)在平面直角坐标系中,二次函数y=a(x﹣h)2(a≠0)的图象可能是()A.B.C.D.6.(2015•黔东南州)如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有()A.1个B.2个C.3个D.4个7.(2015•包头)如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣;④4ac﹣b2>8a;其中正确的结论是()A.①③④B.①②③C.①②④D.①②③④8.(2014•泰安)已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是()A.B.C.D.9.(2014•泰安)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:X ﹣1 0 1 3y ﹣1 3 5 3下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为()A.4个B.3个C.2个D.1个10.(2014•汕头)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是()A.函数有最小值B.对称轴是直线x=C.D.当﹣1<x<2时,y>0当x<,y随x的增大而减小11.(2014•淄博)已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是()A.6B.5C.4D.312.(2014•三明)已知二次函数y=﹣x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是()A.b≥﹣1 B.b≤﹣1 C.b≥1 D.b≤113.(2014•宿迁)若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为()A.y=(x+2)2+3 B.y=(x﹣2)2+3 C.y=(x+2)2﹣3 D.y=(x﹣2)2﹣314.(2014•海南)将抛物线y=x2平移得到抛物线y=(x+2)2,则这个平移过程正确的是()A.向左平移2个单位B.向右平移2个单位C.向上平移2个单位D.向下平移2个单位15.(2014•衢州)在同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是()A.(﹣3,﹣6)B.(1,﹣4)C.(1,﹣6)D.(﹣3,﹣4)16.(2014•淄博)如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣的图象交于点A(m,4),则这个二次函数的解析式为()A.y=x2﹣x﹣2 B.y=x2﹣x+2 C.y=x2+x﹣2 D.y=x2+x+217.(2014•东营)若函数y=mx2+(m+2)x+m+1的图象与x轴只有一个交点,那么m的值为()A.0B.0或2 C.2或﹣2 D.0,2或﹣218.(2014•义乌市)如图是二次函数y=﹣x2+2x+4的图象,使y≤1成立的x的取值范围是()A.﹣1≤x≤3 B.x≤﹣1 C.x≥1 D.x≤﹣1或x≥319.(2013•宿迁)下列三个函数:①y=x+1;②;③y=x2﹣x+1.其图象既是轴对称图形,又是中心对称图形的个数有()A.0B.1C.2D.320.(2013•聊城)如图,在平面直角坐标系中,抛物线y=经过平移得到抛物线y=,其对称轴与两段抛物线所围成的阴影部分的面积为()A.2B.4C.8D.16 21.(2013•株洲)二次函数y=2x2+mx+8的图象如图所示,则m的值是()A.﹣8 B.8C.±8 D.6 22.(2012•衢州)已知二次函数y=﹣x2﹣7x+,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是()A.y1>y2>y3B.y1<y2<y3C.y2>y3>y1D.y2<y3<y123.(2015•崇左)如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是()A.sinA=B.cosA=C.tanA=D.tanB=24.(2015•乐山)如图,已知△ABC的三个顶点均在格点上,则cosA的值为()A.B.C.D.25.(2015•温州)如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是()A.B.C.D.26.(2015•厦门)已知sin6°=a,sin36°=b,则sin26°=()A.a2B.2a C.b2D.b27.(2015•山西)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2B.C.D.28.(2015•丽水)如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是()A.B.C.D.29.(2015•包头)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是()A.B.3C.D.230.(2015•庆阳)在△ABC中,若角A,B满足|cosA﹣|+(1﹣tanB)2=0,则∠C的大小是()A.45°B.60°C.75°D.105°2015年08月06日XX的初中数学组卷参考答案与试题解析一.选择题(共30小题)1.(2015•兰州)下列函数解析式中,一定为二次函数的是()A.y=3x﹣1 B.y=ax2+bx+c C.s=2t2﹣2t+1 D.y=x2+考点:二次函数的定义.分析:根据二次函数的定义,可得答案.解答:解:A、y=3x﹣1是一次函数,故A错误;B、y=ax2+bx+c (a≠0)是二次函数,故B错误;C、s=2t2﹣2t+1是二次函数,故C正确;D、y=x2+不是二次函数,故D错误;故选:C.点评:本题考查了二次函数的定义,y=ax2+bx+c (a≠0)是二次函数,注意二次函数都是整式.2.(2015•宁夏)函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A.B.C.D.考点:二次函数的图象;反比例函数的图象.专题:压轴题;数形结合.分析:本题可先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.解答:解:由解析式y=﹣kx2+k可得:抛物线对称轴x=0;A、由双曲线的两支分别位于二、四象限,可得k<0,则﹣k>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上;本图象与k的取值相矛盾,故A错误;B、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象符合题意,故B正确;C、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故C错误;D、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故D错误.故选:B.点评:本题主要考查了二次函数及反比例函数和图象,解决此类问题步骤一般为:(1)先根据图象的特点判断k取值是否矛盾;(2)根据二次函数图象判断抛物线与y轴的交点是否符合要求.3.(2015•湖北)二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的图象可能是()A.B.C.D.考点:二次函数的图象;一次函数的图象;反比例函数的图象.分析:根据二次函数图象开口向下得到a<0,再根据对称轴确定出b,根据与y轴的交点确定出c>0,然后确定出一次函数图象与反比例函数图象的情况,即可得解.解答:解:∵二次函数图象开口方向向下,∴a<0,∵对称轴为直线x=﹣>0,∴b>0,∵与y轴的正半轴相交,∴c>0,∴y=ax+b的图象经过第一、二、四象限,反比例函数y=图象在第一三象限,只有C选项图象符合.故选C.点评:本题考查了二次函数的图形,一次函数的图象,反比例函数的图象,熟练掌握二次函数的有关性质:开口方向、对称轴、与y轴的交点坐标等确定出a、b、c的情况是解题的关键.4.(2015•泰安)某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:x …﹣2 ﹣1 0 1 2 …y …﹣11 ﹣2 1 ﹣2 ﹣5 …由于粗心,他算错了其中一个y值,则这个错误的数值是()A.﹣11 B.﹣2 C.1D.﹣5考点:二次函数的图象.分析:根据关于对称轴对称的自变量对应的函数值相等,可得答案.解答:解:由函数图象关于对称轴对称,得(﹣1,﹣2),(0,1),(1,2)在函数图象上,把(﹣1,﹣2),(0,1),(1,﹣2)代入函数解析式,得,解得,函数解析式为y=﹣3x2+1x=2时y=﹣11,故选:D.点评:本题考查了二次函数图象,利用函数图象关于对称轴对称是解题关键.5.(2015•沈阳)在平面直角坐标系中,二次函数y=a(x﹣h)2(a≠0)的图象可能是()A.B.C.D.考点:二次函数的图象.分析:根据二次函数y=a(x﹣h)2(a≠0)的顶点坐标为(h,0),它的顶点坐标在x轴上,即可解答.解答:解:二次函数y=a(x﹣h)2(a≠0)的顶点坐标为(h,0),它的顶点坐标在x轴上,故选:D.点评:本题考查了二次函数的图象,解决本题的关键是明二次函数的顶点坐标.6.(2015•黔东南州)如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有()A.1个B.2个C.3个D.4个考点:二次函数图象与系数的关系.分析:首先根据二次函数y=ax2+bx+c的图象经过原点,可得c=0,所以abc=0;然后根据x=1时,y<0,可得a+b+c<0;再根据图象开口向下,可得a<0,图象的对称轴为x=﹣,可得﹣,b<0,所以b=3a,a>b;最后根据二次函数y=ax2+bx+c图象与x轴有两个交点,可得△>0,所以b2﹣4ac>0,4ac﹣b2<0,据此解答即可.解答:解:∵二次函数y=ax2+bx+c图象经过原点,∴c=0,∴abc=0∴①正确;∵x=1时,y<0,∴a+b+c<0,∴②不正确;∵抛物线开口向下,∴a<0,∵抛物线的对称轴是x=﹣,∴﹣,b<0,∴b=3a,又∵a<0,b<0,∴a>b,∴③正确;∵二次函数y=ax2+bx+c图象与x轴有两个交点,∴△>0,∴b2﹣4ac>0,4ac﹣b2<0,∴④正确;综上,可得正确结论有3个:①③④.故选:C.点评:此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c).7.(2015•包头)如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣;④4ac﹣b2>8a;其中正确的结论是()A.①③④B.①②③C.①②④D.①②③④考点:二次函数图象与系数的关系.分析:①先由抛物线的对称性求得抛物线与x轴令一个交点的坐标为(3,0),从而可知当x>3时,y<0;②由抛物线开口向下可知a<0,然后根据x=﹣=1,可知:2a+b=0,从而可知3a+b=0+a=a<0;③设抛物线的解析式为y=a(x+1)(x﹣3),则y=ax2﹣2ax﹣3a,令x=0得:y=﹣3a.由抛物线与y轴的交点B在(0,2)和(0,3)之间,可知2≤﹣3a≤3.④由4ac﹣b2>8a得c﹣2<0与题意不符.解答:解:①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为(3,0),当x>3时,y<0,故①正确;②抛物线开口向下,故a<0,∵x=﹣=1,∴2a+b=0.∴3a+b=0+a=a<0,故②正确;③设抛物线的解析式为y=a(x+1)(x﹣3),则y=ax2﹣2ax﹣3a,令x=0得:y=﹣3a.∵抛物线与y轴的交点B在(0,2)和(0,3)之间,∴2≤﹣3a≤3.解得:﹣1≤a≤﹣,故③正确;④.∵抛物线y轴的交点B在(0,2)和(0,3)之间,∴2≤c≤3,由4ac﹣b2>8a得:4ac﹣8a>b2,∵a<0,∴c﹣2<∴c﹣2<0∴c<2,与2≤c≤3矛盾,故④错误.故选:B.点评:本题主要考查的是二次函数的图象和性质,掌握抛物线的对称轴、开口方向与系数a、b、c之间的关系是解题的关键.8.(2014•泰安)已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是()A.B.C.D.考点:二次函数的图象;一次函数的图象;反比例函数的图象.专题:数形结合.分析:根据二次函数图象判断出m<﹣1,n=1,然后求出m+n<0,再根据一次函数与反比例函数图象的性质判断即可.解答:解:由图可知,m<﹣1,n=1,∴m+n<0,∴一次函数y=mx+n经过第一、二、四象限,且与y轴相交于点(0,1),反比例函数y=的图象位于第二、四象限;故选:C.点评:本题考查了二次函数图象,一次函数图象,反比例函数图象,观察二次函数图象判断出m、n的取值是解题的关键.9.(2014•泰安)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:X ﹣1 0 1 3y ﹣1 3 5 3下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为()A.4个B.3个C.2个D.1个考点:二次函数的性质;二次函数图象与系数的关系;抛物线与x轴的交点;二次函数与不等式(组).专题:压轴题;图表型.分析:根据表格数据求出二次函数的对称轴为直线x=1.5,然后根据二次函数的性质对各小题分析判断即可得解.解答:解:(1)由图表中数据可得出:x=1时,y=5,所以二次函数y=ax2+bx+c开口向下,a<0;又x=0时,y=3,所以c=3>0,所以ac<0,故(1)正确;(2)∵二次函数y=ax2+bx+c开口向下,且对称轴为x==1.5,∴当x≥1.5时,y的值随x值的增大而减小,故(2)错误;(3)∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程ax2+(b﹣1)x+c=0的一个根,故(3)正确;(4)∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+(b﹣1)x+c=0,∵x=3时,ax2+(b﹣1)x+c=0,且函数有最大值,∴当﹣1<x<3时,ax2+(b﹣1)x+c>0,故(4)正确.故选:B.点评:本题考查了二次函数的性质,二次函数图象与系数的关系,抛物线与x轴的交点,二次函数与不等式,有一定难度.熟练掌握二次函数图象的性质是解题的关键.10.(2014•汕头)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是()A.函数有最小值B.对称轴是直线x=C.D.当﹣1<x<2时,y>0当x<,y随x的增大而减小考点:二次函数的性质.专题:压轴题;数形结合.分析:根据抛物线的开口方向,利用二次函数的性质判断A;根据图形直接判断B;根据对称轴结合开口方向得出函数的增减性,进而判断C;根据图象,当﹣1<x<2时,抛物线落在x轴的下方,则y<0,从而判断D.解答:解:A、由抛物线的开口向上,可知a>0,函数有最小值,正确,故A选项不符合题意;B、由图象可知,对称轴为x=,正确,故B选项不符合题意;C、因为a>0,所以,当x<时,y随x的增大而减小,正确,故C选项不符合题意;D、由图象可知,当﹣1<x<2时,y<0,错误,故D选项符合题意.故选:D.点评:本题考查了二次函数的图象和性质,解题的关键是利用数形结合思想解题.11.(2014•淄博)已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是()A.6B.5C.4D.3考点:二次函数的性质.专题:计算题.分析:根据抛物线的顶点式得到抛物线的对称轴为直线x=h,由于所给数据都是正数,所以当对称轴在y轴的右侧时,比较点A和点B到对称轴的距离可得到h<4.解答:解:∵抛物线的对称轴为直线x=h,∴当对称轴在y轴的右侧时,A(0,2)到对称轴的距离比B(8,3)到对称轴的距离小,∴x=h<4.故选:D.点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣,),对称轴直线x=﹣,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<﹣时,y随x的增大而减小;x>﹣时,y随x的增大而增大;x=﹣时,y取得最小值,即顶点是抛物线的最低点.②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<﹣时,y随x的增大而增大;x>﹣时,y随x的增大而减小;x=﹣时,y取得最大值,即顶点是抛物线的最高点.12.(2014•三明)已知二次函数y=﹣x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是()A.b≥﹣1 B.b≤﹣1 C.b≥1 D.b≤1考点:二次函数的性质.专题:数形结合.分析:先根据抛物线的性质得到其对称轴为直线x=b,且当x>b时,y随x的增大而减小,由于已知当x>1时,y的值随x值的增大而减小,则可得判断b≤1.解答:解:∵抛物线y=﹣x2+2bx+c的对称轴为直线x=﹣=b,而a<0,∴当x>b时,y随x的增大而减小,∵当x>1时,y的值随x值的增大而减小,∴b≤1.故选:D.点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点式为y=a(x+)2+,的顶点坐标是(﹣,),对称轴直线x=﹣b/2a,当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<﹣时,y随x的增大而减小;x>﹣时,y随x的增大而增大;②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x <﹣时,y随x的增大而增大;x>﹣时,y随x的增大而减小,13.(2014•宿迁)若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为()A.y=(x+2)2+3 B.y=(x﹣2)2+3 C.y=(x+2)2﹣3 D.y=(x﹣2)2﹣3考点:二次函数图象与几何变换.分析:根据二次函数图象的平移规律解答即可.解答:解:将抛物线y=x2向右平移2个单位可得y=(x﹣2)2,再向上平移3个单位可得y=(x﹣2)2+3,故选:B.点评:本题考查了二次函数的几何变换,熟悉二次函数的平移规律是解题的关键.14.(2014•海南)将抛物线y=x2平移得到抛物线y=(x+2)2,则这个平移过程正确的是()A.向左平移2个单位B.向右平移2个单位C.向上平移2个单位D.向下平移2个单位考点:二次函数图象与几何变换.分析:根据图象左移加,可得答案.解答:解:将抛物线y=x2平移得到抛物线y=(x+2)2,则这个平移过程正确的是向左平移了2个单位,故选:A.点评:本题考查了二次函数图象与几何变换,函数图象平移规律是:左加右减,上加下减.15.(2014•衢州)在同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是()A.(﹣3,﹣6)B.(1,﹣4)C.(1,﹣6)D.(﹣3,﹣4)考点:二次函数图象与几何变换.专题:动点型.分析:根据函数图象向右平移减,向下平移减,可得目标函数图象,再根据顶点坐标公式,可得答案.解答:解:函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象y=2(x﹣2)2+4(x﹣2)﹣3﹣1,即y=2(x﹣1)2﹣6,顶点坐标是(1,﹣6),故选:C.点评:本题考查了二次函数图象与几何变换,利用了图象的平移规律:上加下减,左加右减.16.(2014•淄博)如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣的图象交于点A(m,4),则这个二次函数的解析式为()A.y=x2﹣x﹣2 B.y=x2﹣x+2 C.y=x2+x﹣2 D.y=x2+x+2考点:待定系数法求二次函数解析式;反比例函数图象上点的坐标特征.专题:计算题.分析:将A坐标代入反比例解析式求出m的值,确定出A的坐标,将A与B坐标代入二次函数解析式求出b与c的值,即可确定出二次函数解析式.解答:解:将A(m,4)代入反比例解析式得:4=﹣,即m=﹣2,∴A(﹣2,4),将A(﹣2,4),B(0,﹣2)代入二次函数解析式得:,解得:b=﹣1,c=﹣2,则二次函数解析式为y=x2﹣x﹣2.故选:A.点评:此题考查了待定系数法求二次函数解析式,以及反比例函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.17.(2014•东营)若函数y=mx2+(m+2)x+m+1的图象与x轴只有一个交点,那么m的值为()A.0B.0或2 C.2或﹣2 D.0,2或﹣2考点:抛物线与x轴的交点.专题:分类讨论.分析:分为两种情况:函数是二次函数,函数是一次函数,求出即可.解答:解:分为两种情况:①当函数是二次函数时,∵函数y=mx2+(m+2)x+m+1的图象与x轴只有一个交点,∴△=(m+2)2﹣4m(m+1)=0且m≠0,解得:m=±2,②当函数是一次函数时,m=0,此时函数解析式是y=2x+1,和x轴只有一个交点,故选:D.点评:本题考查了抛物线与x轴的交点,根的判别式的应用,用了分类讨论思想,题目比较好,但是也比较容易出错.18.(2014•义乌市)如图是二次函数y=﹣x2+2x+4的图象,使y≤1成立的x的取值范围是()A.﹣1≤x≤3 B.x≤﹣1 C.x≥1 D.x≤﹣1或x≥3考点:二次函数与不等式(组).专题:几何图形问题.分析:根据函数图象写出直线y=1以及下方部分的x的取值范围即可.解答:解:由图可知,x≤﹣1或x≥3时,y≤1.故选:D.点评:本题考查了二次函数与不等式,此类题目,利用数形结合的思想求解是解题的关键.19.(2013•宿迁)下列三个函数:①y=x+1;②;③y=x2﹣x+1.其图象既是轴对称图形,又是中心对称图形的个数有()A.0B.1C.2D.3考点:二次函数的图象;一次函数的图象;反比例函数的图象;轴对称图形;中心对称图形.专题:压轴题.分析:根据一次函数图象,反比例函数图象,二次函数图象的对称性分析判断即可得解.解答:解:①y=x+1的函数图象,既是轴对称图形,又是中心对称图形;②y=的函数图象,既是轴对称图形,又是中心对称图形;③y=x2﹣x+1的函数图象是轴对称图形,不是中心对称图形;所以,函数图象,既是轴对称图形,又是中心对称图形的是①②共2个.故选C.点评:本题考查了二次函数图象,一次函数图象,正比例函数图象,熟记各图形以及其对称性是解题的关键.20.(2013•聊城)如图,在平面直角坐标系中,抛物线y=经过平移得到抛物线y=,其对称轴与两段抛物线所围成的阴影部分的面积为()A.2B.4C.8D.16考点:二次函数图象与几何变换.专题:压轴题.分析:根据抛物线解析式计算出y=的顶点坐标,过点C作CA⊥y轴于点A,根据抛物线的对称性可知阴影部分的面积等于矩形ACBO的面积,然后求解即可.解答:解:过点C作CA⊥y,∵抛物线y==(x2﹣4x)=(x2﹣4x+4)﹣2=(x﹣2)2﹣2,∴顶点坐标为C(2,﹣2),对称轴与两段抛物线所围成的阴影部分的面积为:2×2=4,故选:B.点评:本题考查了二次函数的问题,根据二次函数的性质求出平移后的抛物线的对称轴的解析式,并对阴影部分的面积进行转换是解题的关键.21.(2013•株洲)二次函数y=2x2+mx+8的图象如图所示,则m的值是()A.﹣8 B.8C.±8 D.6考点:抛物线与x轴的交点.专题:压轴题.分析:根据抛物线与x轴只有一个交点,△=0,列式求出m的值,再根据对称轴在y轴的左边求出m的取值范围,从而得解.解答:解:由图可知,抛物线与x轴只有一个交点,所以,△=m2﹣4×2×8=0,解得m=±8,∵对称轴为直线x=﹣<0,∴m>0,∴m的值为8.故选B.点评:本题考查了二次函数图象与x轴的交点问题,本题易错点在于要根据对称轴确定出m 是正数.22.(2012•衢州)已知二次函数y=﹣x2﹣7x+,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是()A.y1>y2>y3B.y1<y2<y3C.y2>y3>y1D.y2<y3<y1考点:二次函数图象上点的坐标特征.专题:压轴题.分析:根据x1、x2、x3与对称轴的大小关系,判断y1、y2、y3的大小关系.解答:解:∵二次函数y=﹣x2﹣7x+,∴此函数的对称轴为:x=﹣=﹣=﹣7,∵0<x1<x2<x3,三点都在对称轴右侧,a<0,∴对称轴右侧y随x的增大而减小,∴y1>y2>y3.故选:A.点评:此题主要考查了函数的对称轴求法和函数的单调性,利用二次函数的增减性解题时,利用对称轴得出是解题关键.23.(2015•崇左)如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是()A.sinA=B.cosA=C.tanA=D.tanB=考点:锐角三角函数的定义.分析:先利用勾股定理求出AC的长,然后根据锐角三角函数的定义对各选项分别进行计算,再利用排除法求解即可.解答:解:∵∠ACB=90°,AB=13,BC=12,∴AC===5,A、sinA==,故本选项正确;B、cosA==,故本选项错误.C、tanA==,故本选项错误;D、tanB==,故本选项错误;故选A.点评:本题考查了锐角三角函数的定义,勾股定理的应用,熟记在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边是解题的关键.24.(2015•乐山)如图,已知△ABC的三个顶点均在格点上,则cosA的值为()A.B.C.D.考点:锐角三角函数的定义;勾股定理;勾股定理的逆定理.专题:网格型.分析:过B点作BD⊥AC,得AB的长,AD的长,利用锐角三角函数得结果.解答:解:过B点作BD⊥AC,如图,由勾股定理得,AB==,AD==2cosA===,故选:D.点评:本题主要考查了锐角三角函数和勾股定理,作出适当的辅助线构建全等三角形是解答此题的关键.25.(2015•温州)如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是()A.B.C.D.考点:锐角三角函数的定义.分析:根据锐角的余弦等于邻边比斜边求解即可.解答:解:∵AB=5,BC=3,∴AC=4,∴cosA==.故选D.点评:本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边26.(2015•厦门)已知sin6°=a,sin36°=b,则sin26°=()A.a2B.2a C.b2D.b考点:锐角三角函数的定义.分析:根据一个数的平方的含义和求法,由sin6°=a,可得sin26°=a2,据此解答即可.解答:解:∵sin6°=a,∴sin26°=a2.故选:A.点评:(1)此题主要考查了锐角三角函数的定义,要熟练掌握,解答此题的关键是要明确:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.(2)此题还考查了一个数的平方的含义和求法,要熟练掌握.27.(2015•山西)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2B.C.D.考点:锐角三角函数的定义;勾股定理;勾股定理的逆定理.专题:网格型.分析:根据勾股定理,可得AC、AB的长,根据正切函数的定义,可得答案.解答:解:如图:,由勾股定理,得AC=,AB=2,BC=,∴△ABC为直角三角形,∴tan∠B==,故选:D.点评:本题考查了锐角三角函数的定义,先求出AC、AB的长,再求正切函数.28.(2015•丽水)如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是()A.B.C.D.考点:锐角三角函数的定义.分析:利用垂直的定义以及互余的定义得出∠α=∠ACD,进而利用锐角三角函数关系得出答案.解答:解:∵AC⊥BC,CD⊥AB,∴∠α+∠BCD=∠ACD+∠BCD,∴∠α=∠ACD,∴cosα=cos∠ACD===,只有选项C错误,符合题意.故选:C.点评:此题主要考查了锐角三角函数的定义,得出∠α=∠ACD是解题关键.29.(2015•包头)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是()A.B.3C.D.2考点:锐角三角函数的定义;勾股定理.分析:设BC=x,则AB=3x,由勾股定理求出AC,根据三角函数的概念求出tanB.解答:解:设BC=x,则AB=3x,由勾股定理得,AC=2x,tanB===2,故选:D.点评:本题考查的是锐角三角函数的概念和勾股定理的应用,应用勾股定理求出直角三角形的边长、正确理解锐角三角函数的概念是解题的关键.30.(2015•庆阳)在△ABC中,若角A,B满足|cosA﹣|+(1﹣tanB)2=0,则∠C的大小是()A.45°B.60°C.75°D.105°考点:特殊角的三角函数值;非负数的性质:绝对值;非负数的性质:偶次方.分析:根据非负数的性质得出cosA=,tanB=1,求出∠A和∠B的度数,继而可求得∠C 的度数.解答:解:由题意得,cosA=,tanB=1,则∠A=30°,∠B=45°,则∠C=180°﹣30°﹣45°=105°.故选D.点评:本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数中考一、选择题 1. (2014•海南)将抛物线y=x 2平移得到抛物线y=(x+2)2,则这个平移过程正确的是( )A . 向左平移2个单位B .向右平移2个单位 C . 向上平移2个单位 D . 向下平移2个单位 2. (2014•黑龙江绥化,第17题3分)如图是二次函数y=ax 2+bx+c 图象的一部分,且过点A (3,0),二次函数图象的对称轴是x=1,下列结论正确的是( )第2题图 第4题图 第7题图 第9题图A . b 2>4acB . a c >0C . a ﹣b+c >0D . 4a+2b+c <0 3.(2014•宁夏)已知a ≠0,在同一直角坐标系中,函数y=ax 与y=ax 2的图象有可能是( )A .B .C .D .4.(2014•陕西)二次函数y=ax 2+bx+c (a ≠0)的图象如图,则下列结论中正确的是( )A . c >﹣1B . b >0C . 2a+b ≠0D . 9a+c >3b5.(2014•四川成都)将二次函数y=x 2﹣2x+3化为y=(x ﹣h )2+k 的形式,结果为( )A . y =(x+1)2+4B . y =(x+1)2+2C . y =(x ﹣1)2+4D . y =(x ﹣1)2+26.(2014•哈尔滨)将抛物线y=﹣2x 2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为( )A . y =﹣2(x+1)2﹣1B . y ﹣2(x+1)2+3C . y =﹣2(x ﹣1)2+1D . y =﹣2(x ﹣1)2+37. (2014年湖北黄石) 二次函数y=ax 2+bx+c (a ≠0)的图象如图,则函数值y >0时,x 的取值范围是( )A . x <﹣1B . x >3C .﹣1<x <3D . x <﹣1或x >38. (2014•湖北荆门)将抛物线y=x 2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )A .y=(x ﹣4)2﹣6B .y=(x ﹣4)2﹣2C .y=(x ﹣2)2﹣2D . y =(x ﹣1)2﹣39.(2014•莱芜)已知二次函数y=ax 2+bx+c 的图象如图所示.下列结论:①abc >0;②2a ﹣b <0;③4a ﹣2b+c <0;④(a+c )2<b 2其中正确的个数有( )A . 1B . 2C . 3D .410. (2014•丽水)在同一平面直角坐标系内,将函数y=2x 2+4x ﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是()A . (﹣3,﹣6) B . (1,﹣4) C . (1,﹣6) D . (﹣3,﹣4)11.(2014年广西南宁)如图,已知二次函数y=﹣x 2+2x ,当﹣1<x <a 时,y 随x 的增大而增大,则实数a 的取值范围是( )第11题图 第12题图 填空第1题图A . a >1B . ﹣1<a ≤1C . a >0D . ﹣1<a <212.(2014年贵州安顺)如图,二次函数y=ax 2+bx+c (a >0)图象的顶点为D ,其图象与x 轴的交点A 、B 的横坐标分别为﹣1,3.与y 轴负半轴交于点C ,在下面五个结论中:①2a ﹣b=0;②a+b+c >0;③c=﹣3a ;④只有当a=时,△ABD 是等腰直角三角形;⑤使△ACB 为等腰三角形的a 值可以有四个.其中正确的结论是 .(只填序号)二、填空题1. (2014•浙江绍兴)如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是.2.(2014•黑龙江牡丹江)已知二次函数y=kx2+(2k﹣1)x﹣1与x轴交点的横坐标为x1,x2(x1<x2),则对于下列结论:①当x=﹣2时,y=1;②方程kx2+(2k﹣1)x﹣1=0有两个不相等的实数根x1,x2;③x2﹣x1=.其中正确的结论有(只需填写序号即可).三、解答题1.(2014•海南)如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.2.(2014•黑龙江龙东)如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)请直接写出D点的坐标.(2)求二次函数的解析式.(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.3.(2014•绥化)如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.(1)求tan∠DBC的值;(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.4.(2014•湖南永州)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.(1)求抛物线的解析式,并写出其顶点坐标;(2)当S△MFQ:S△MEB=1:3时,求点M的坐标.5.(2014•四川成都)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m 长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.(1)若花园的面积为192m2,求x的值;(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.6.(2014•四川绵阳)如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2,),顶点坐标为N(﹣1,),且与x轴交于A、B两点,与y轴交于C点.(1)求抛物线的解析式;(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.7.(2014•浙江绍兴)如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.(2)探究下列问题:①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?8. (2014•黑龙江牡丹江)某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.(1)试确定y与x之间的函数关系式;(2)若该体育用品商店试销的这款排球所获得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.9. (2014•湖北荆门)我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;(2)求售价x的范围;(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?10.(2014•莱芜,第24题12分)如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4﹣x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.(1)求抛物线的表达式;(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.11. (2014•青岛)某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)12. (2014•乐山)如图,抛物线y=x2﹣2mx(m>0)与x轴的另一个交点为A,过P(1,﹣m)作PM⊥x轴与点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.(1)若m=2,求点A和点C的坐标;(2)令m>1,连接CA,若△ACP为直角三角形,求m的值;(3)在坐标轴上是否存在点E,使得△PEC是以P为直角顶点的等腰直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.。
