山东省平邑县曾子学校高中数学必修四导学案(无答案)1.2.1任意角的三角函数 (第一课时)
高中数学第一章三角函数1.2任意角的三角函数导学案(无答案)新人教A版必修4(最新整理)

高中数学第一章三角函数1.2 任意角的三角函数导学案(无答案)新人教A版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第一章三角函数1.2 任意角的三角函数导学案(无答案)新人教A版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第一章三角函数1.2 任意角的三角函数导学案(无答案)新人教A版必修4的全部内容。
1oyx1P(a,b)任意角的三角函数一、学习目标:1.借助单位圆理解任意角三角函数(正、余、正切)的定义;2。
从任意角三角函数的定义认识其定义域,函数值的符号;3.根据定义理解公式一;4。
能初步应用定义分析和解决与三角函数值有关的一些简单问题。
二、学习重点、难点:重点:任意角的三角函数的定义;难点:用单位圆上点的坐标刻画三角函数。
三、学习任务:阅读教材P11——15(到例5前止)完成下列问题:问题(一):Ⅰ. 观察三角函数定义的“进化”过程,完成填空.sinα=_____ sinα=______sinα=______ sinα=______三角函数定义需要经历一个逐步化归的过程,即由直角三角形中____________到直角坐标系中_____________再到用单位圆上点的________定义三角函数.Ⅱ. 完成下列问题:1。
任意角的三角函数设α是一个任意角,它的始边与x轴的非负半轴重合,顶点在原点,终边与单位圆的交点为P(x,y).3yox(-)(-)(+)(+)yox(-)(-)(+)(+)(1) y 叫做α的正弦,记作____________,即_____________;(2) x 叫做α的余弦,记作____________,即_____________;(3) xy叫做α的正切,记作____________,即_____________.2. 三角函数的定义域如表所示:3。
山东省高一数学人教A必修四1.2.11任意角的三角函数导学案

§1.2.1 任意角三角函数(1)1.掌握任意角的正弦,余弦,正切的定义.2.掌握正弦,余弦,正切函数的定义域和这三种函数的值在各象限的符号.一、课前准备(预习教材P11~ P15,找出疑惑之处)在初中,我们利用直角三角形来定义锐角三角函数,你能说出锐角三角函数的定义吗?二、新课导学※探索新知问题1:你能用直角坐标系中角的终边上的点的坐标来表示锐角三角函数吗?问题2:改变终边上的点的位置这三个比值会改变吗?为什么?问题3:怎样将锐角三角函数推广到任意角?问题4:锐角三角函数的大小仅与角A的大小有关,与直角三角形的大小无关,任意角的三角函数大小有无类似性质?问题5:随着角 的确定,三个比值是否唯一确定?依据函数定义,可以构成一个函数吗?问题6:对于任意角的三角函数思考下列问题:①定义域;②函数值的符号规律③三个函数在坐标轴上的取值情况怎样?④终边相同的角相差π2的整数倍,那么这些角的同一三角函数值有何关系?※ 典型例题例1:已知角α的终边经过点P (2,-3),求αααtan cos sin 2++变式训练⑴:已知角α的终边经过点P (2a ,-3a ) (a ≠0),求αααtan cos sin 2++的值.变式训练⑵:角α的终边经过点P (-x ,-6)且135cos -=α,求x 的值.例2:确定下列三角函数值的符号(1)cos127π (2)sin(-465º) (3)tan 311π变式训练⑴:若cos α>0且tan α<0,试问角α为第几象限角变式训练⑵:使sin αcos α<0成立的角α的集合为( ) A. ⎭⎬⎫⎩⎨⎧∈+<<+Z k k k ,2ππαππα B. ⎭⎬⎫⎩⎨⎧∈+<<+Z k k k ,222ππαππα C. ⎭⎬⎫⎩⎨⎧∈+<<+Z k k k ,22232ππαππαD. ⎭⎬⎫⎩⎨⎧∈+<<+Z k k k ,23222ππαππα※ 动手试试1、函数x x y cos sin -+=的定义域是( )A .))12(,2(ππ+k k ,Z k ∈B .])12(,22[πππ++k k ,Z k ∈ C .])1(,2[πππ++k k , Z k ∈D .[2,(21)]k k ππ+ ,Z k ∈2、若θ是第三象限角,且02cos<θ,则2θ是( ) A .第一象限角B .第二象限角C .第三象限角D .第四象限角3、已知点P (ααcos ,tan )在第三象限,则角α在 ( )A .第一象限B .第二象限C .第三象限D .第四象限4、已知sin αtan α≥0,则α的取值集合为 .三、小结反思三角函数的定义及性质,特殊角的三角函数值,三角函数的符号问题. 各象限的三角函数的符号规律可概括为:“一正二正弦,三切四余弦”.※ 当堂检测(时量:5分钟 满分:10分)计分:1、若角α终边上有一点)0|)(|,(≠∈a R a a a P 且,则αsin 的值为 ( )A 、22B 、-22C 、±22 D 、以上都不对 2、下列各式中不成立的一个是 ( )A 、0260cos <B 、0)1032tan(>-C 、056sin >⎪⎭⎫ ⎝⎛-π D 、0317tan >π3、已知α终边经过)12,5(-P ,则=αsin .4、若α是第二象限角,则点)cos ,(sin ααA 是第 几 象限的点.5、已知角θ的终边在直线y =33 x 上,则sin θ= ;θtan = .6、设角x 的终边不在坐标轴上,求函数|tan |tan |cos |cos |sin |sin x x x x x x y ++=的值域.7、(1) 已知角α的终边经过点P(4,-3),求2sin α+cos α的值;(2)已知角α的终边经过点P(4a,-3a)(a ≠0),求2sin α+cos α的值;(3)已知角α终边上一点P与x轴的距离和与y轴的距离之比为3∶4(且均不为零),求2sinα+cosα的值.。
1.2.1任意角的三角函数(一)导学案-2021-2022学年高一数学人教A版必修4

1.2任意角的三角函数
1.2.1 任意角的三角函数(一)
一、学习目标、细解考纲
1.借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义.(重点、难点)
2.掌握任意角三角函数(正弦、余弦、正切)在各象限的符号.(易错点)
3掌握公式——并会应用.
4.借助单位圆给出任意角三角函数的定义,培养了学生数学抽象和数学建模的核心素养.
5.通过利用三角函数定义及符号特点求值,提升了学生直观想象和数学运算的核心素养.
二、自主学习—————(素养催化剂)
(阅读教材第11—14页内容,完成以下问题:)
1.任意角的正弦,余弦,正切是怎样定义的?明确函数定义域
2.各函数在每个象限的符号怎么判断?
3.理解公式一,明确公式一的作用
三、探究应用,“三会培养”-------(素养生长剂)
四、拓展延伸、智慧发展--------(素养强壮剂)
五、备选例题
六、本课总结、感悟思考--------(素养升华剂)。
山东省平邑县曾子学校高中数学必修四导学案:1.2.1任

1.2.1任意角的三角函数(第一课时)【学习目标】1.理解任意角的正弦、余弦、正切的定义,会用定义求任意角的三角函数值;2. 会用三角函数值的符号解决问题;3. 掌握并能初步运用定义分析和解决与三角函数值有关的一些问题.【新知自学】知识回顾:1. 弧度制的定义长度等于__________的圆弧所对的圆心角叫做1弧度角,记作1rad,或1弧度,2.弧度数的求法一个半径为r的圆的圆心角α所对的弧长是l,那么角α的弧度数的绝对值是:α________.α的正负由 __决定.=正角的弧度数是一个,负角的弧度数是一个,零角的弧度数是 .3.角度与弧度的换算(1)3600=________rad;(2)________=πrad;新知梳理:1. 三角函数定义在直角坐标系中,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:(1)______叫做α的正弦,记作_______,即________;(2)_______叫做α的余弦,记作_______,即_________;(3)_______叫做α的正切,记作_______,即_________.推广:α终边上任意一点P错误!未找到引用源。
(除了原点)的坐标为(x,y)错误!未找到引用源。
,它与原点的距离为r,那么sinα=____ ;cosα=___ ____,tan α=____ _ __.(三角函数值的大小与P 点的位置有关吗?)2.三角函数的符号(1)正弦值错误!未找到引用源。
对于第一、二象限为____(y>0,r>0)错误!未找到引用源。
,对于第三、四象限为____(y<0,r>0) (2)余弦值错误!未找到引用源。
对于第一、四象限为_____(x>0,r>0),对于第二、三象限为___ (x<0,r>0)(3)正切值x y 错误!未找到引用源。
对于第一、三象限为____(x,y 错误!未找到引用源。
山东省平邑县高中数学 第一章 三角函数 1.2.1 任意角的三角函数(第2课时)导学案(无答案)新人教A版必修4

1.2.1任意角的三角函数(第二课时)【学习目标】1.进一步理解任意角的正弦、余弦、正切的定义;2. 了解角α的正弦线、余弦线、正切线,认识三角函数的定义域;3. 掌握并能初步运用定义、公式一分析和解决与三角函数值有关的一些问题.【新知自学】知识回顾:1. 三角函数定义在直角坐标系中,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:(1)____叫做α的正弦,记作____,即____;(2)___叫做α的余弦,记作____,即____;(3)___叫做α的正切,记作___,即_____.2.三角函数的符号对于第一、二象限为____(y>0,r>0),对于第三、四象限为____(y<0,r>0) 正弦值yr余弦值x对于第一、四象限为_____(x>0,r>0),对于第二、三象限为___ (x<0,r>0)ry对于第一、三象限为____(x,y同号),对于第二、四象限为____(x,y异号).正切值x新知梳理:1. 诱导公式终边相同的角的_________________相等.公式一: ____ ___=sinα,__________ __=cosα,_____ ____=tanα.∈)(其中,k Z2.正弦线、余弦线、正切线:如上图,分别称有向线段,,MP OM AT 为正弦线、余弦线、正切线.对点练习:1sin(-1654°)的大小.2.用三角函数线比较sin1和cos1的大小,结果是_______________.3.利用三角函数线比较下列各组数的大小(用“>”或“<”连接):(1)sin 23π________sin 34π;(2)cos 23π________cos 34π;(3)tan 23π________tan 34π.【合作探究】 典例精析:题型一:诱导公式的应用例1. 求下列三角函数值:(1)325cos π; (2))45sin(π-; (3)π3tan变式练习(1)sin(-13950)cos11100+cos(-10200)sin7500;变式练习(2)sin(πππ4tan 511cos 611-⋅+).题型二:三角函数线的应用例2.在单位圆中,画出满足21cos =α的角α的终边.变式练习(3)已知40πθ<<,确定θθcos ,sin 的大小关系.变式练习(4):如果4<α<2,那么下列不等式成立的是( )A .cos α<sin α<tan αB .tan α<sin α<cos αC .sin α<cos α<tan αD .cos α<tan α<sin α【课堂小结】【当堂达标】1.)34sin(π-=( ) A.21 B.21- C.23 D.23- 2.若53πα=,则αααtan ,cos ,sin 的大小关系是3.求值:︒+︒-︒750cos 450sin 405tan .4、利用三角函数线比较下列各组数的大小:(1)sin 2π3与sin 4π5; (2)tan 2π3与tan 4π5; (3)cos 2π3与cos 4π5.【课时作业】1. 若1sin sin -=x x,则角x 一定是( )A. 第三象限角B. 第四象限角C. 第三象限角或第四象限角D. 不确定 2. x xx x cos cos sin sin +的值为( )A. 2B. 2或0C. 2或0或2-D.不确定3. 求下列各式的值:(1));415tan(325cos ππ-+(2)︒-︒+︒360cos 765tan 810sin .*4. 用三角函数线,比较sin1与cos1的大小.**5.在单位圆中,用阴影部分表示出满足21sin ≥α的角的集合,并写出该集合.6.用三角函数线证明:|sin α|+|cos α|≥1【延伸探究】利用单位圆中的三角函数线,分别确定角θ的取值范围.(1)sin θ≥32; (2)-12≤cos θ<32.规律提示:用单位圆中的三角函数线求解简单的三角不等式,应注意以下两点:(1)先找到“正值”区间,即0~2π间满足条件的角θ的范围,然后再加上周期;(2)注意区间是开区间还是闭区间.。
山东省平邑县曾子学校高中数学必修四导学案全集43份人教课标版34实用教案

两角和与差的正弦、余弦、正切公式()编审:周彦魏国庆【学习目标】.理解以两角差的余弦公式为基础,推导两角和、差正弦和正切公式的方法;.掌握两角和与差的余弦、正弦和正切公式的应用.【新知自学】知识回顾.两角差的余弦公式是(公式).化简cos cos sin sin2 2 2 2sin( );2cos( );2sin( );2cos().2新知梳理两角和的余弦公式中的角,可以是随意角,那么,作以下的代换,你会有什么发现?、把()式中的角“”换成“”,可得(公式)、把()式中的角“”换成“”,可得(公式)2、把()式中的角“”换成“”,可得(公式)2、把()式除以()式,可得(公式)、把()式除以()式,可得(公式)思虑感悟、上述个公式之间还有哪些联系,你能发现吗?、在正切公式中,应满足什么条件?、如何娴熟记忆公式?对点练习、sin72cos42 c os72sin42;cos105;cos20cos70 sin20sin70;tan15tan15、3cos sin的值为()12..2.2【合作研究】典例精析:例、求以下各式的值.()sin165;7()tan. 12变式练习:、求值:cos75cos15变式练习:、已知sin5)10,均为锐角,求的值。
,sin(,5103,是第四象限角,求sin,cos,tan的值.例、已知sin5444变式练习:、已知sin1,则cos.43 4【课堂小结】【当堂达标】.25π11π-11π5π的值是()12 612 6.- 2 . 22 2.π.π1212.若(αβ)β-(αβ)β,则(αβ)(α-β)等于()..-..±.求值:()°;()°°°°.【课时作业】. oooo的值是().3.12.3.12.sin20cos40 cos20sin40;sin15 sin75..tan75tan15;1tan75tan153 tan15.13tan15.已知sin4,2,,cos5,若是第三象限角,求cos.513.已知tan2,求tan的值. 4*.已知tan 1,tan2,(0,),求tan()与的值. 322山东省平邑县曾子学校高中数学必修四导学案全集43份人教课标版34实用教案*.在35ABC中,sinA,cosB,求cosC的值.513山东省平邑县曾子学校高中数学必修四导学案全集43份人教课标版34实用教案、已知sin(3)5,cos( )3,且03,求cos( ) 的值。
山东省平邑县曾子学校高中数学四导学案:1.1.1任意角缺答案

1.1 任意角和三角函数1。
1。
1 任意角编审:周彦魏国庆【学习目标】1、解任意角的概念.2、边相同的角的含义及表示.【新知自学】知识回顾:回忆初中角的概念:从一个点引出的两条_________构成的几何图形.新知梳理:1.角的定义高中:一条射线OA由原来的位置,绕着它的________按一定方向旋转到另一位置OB,就形成了角α。
其中射线OA叫角α的_______,射线OB叫角α的_______,O叫角α的_______.2.正角、负角、零角概念把按__________方向旋转所形成的角叫正角;按_______方向旋转所形成的角叫负角;如果一条射线_______________,我们称它形成了一个零角.在不引起混淆的前提下,“角α”或“∠α”可简记为α。
感悟:角的概念推广到任意角,其中包括_________、________、_______,正角可以到正无穷大,负角可以到负无穷大.对点练习:1、如果你的手表慢了25分钟,有比较简单的两种校正方式,请问校正时分针分别转过的角度是多少?3.象限角角的顶点与原点重合,角的始边与x轴的________________重合,那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角。
思考:任意角都可以归结为象限角吗?锐角都是第一象限角吗?第一象限角都是锐角吗?4.终边相同的角所有与角α终边相同的角,连同角α在内,可构成一个集合________________________,即任一与角α终边相同的角,都可以表示成角α与________________的和。
对点练习:2、在与角10030°终边相同的角中,求满足下列条件的角.(1)最大的负角;(2)最小的正角;(3)360°~720°的角.3.若角α满足180°〈α<360°,角5α与α有相同的始边,且又有相同的终边,那么角α=________。
【合作探究】 典例精析:一、角的基本概念例1。
山东省平邑县曾子学校高中数学必修四导学案:1.2.2同角三角函数的基本关系 Word版缺答案

1.2.2同角三角函数的基本关系【学习目标】1.掌握同角三角函数的基本关系式;2.灵活运用公式解决变形、求值、证明等问题.【新知自学】预习课本P30---33页的内容, 知识回顾:1、知识回顾:(1)任意角的三角函数是如何定义的?(2)在单位圆中,任意角的正弦、余弦、正切函数线分别是什么?对于一个任意角ααααtan ,cos ,sin ,是三个不同的三角函数,从联系的观点来看,三者之间应存在一定的内在联系,你能找出这种同角三角函数之间的基本关系吗?新知梳理:1、(1)同角三角函数的基本关系①平方关系:αα22cos sin +=_______;(运用三角函数线,体现数形结合) ②商的关系:=ααcos sin ___________ (Z k k ∈+≠,2ππα).(运用定义)(2)文字叙述:同一个角错误!未找到引用源。
的正弦、余弦的_________等于1,商等于角错误!未找到引用源。
的_______. 感悟:在同角的三个三角函数中,可“知一求二”. 对点练习:1.化简7sin -12π的结果是( ) A.sin7π B.-sin 7π C.cos 7π D.-cos 7π 2.已知α是第二象限角,且sin α=53,则cos α=_________,tan α=_________. 3.已知sin α=31,则 sin 4α-cos 4α=_______________.4.化简:(1)θθtan cos ∙=;(2)αα22sin 211cos 2--=;(3)02100sin 1- =;(4)0010cos 10sin 21- =;【合作探究】 典例精析:题型一:利用同角三角函数关系求值例1. 若sin θ=-45,tan θ>0,求cos θ.变式1.(1)已知α是第二象限角且tan α=-512,求sin α、cos α的值. (2)已知tan α=3,求sin 2α+2sin α·cos α的值.题型二:利用同角三角函数关系化简、证明例2.求证cos1sin 1sin cosx xx x+=-变式2. 化简(,)2πθπ∈题型三:正余弦的和、差、积之间的转化例3、已知sin θ+cos θ=15,θ∈(0,π),试分别求①sin θcos θ;②sin θ-cos θ;③ta n θ+θtan 1.的值。
山东省平邑县曾子学校高中数学必修四导学案:第三章 三角恒等变换 章末小结 Word版缺答案

第三章 三角恒等变换 章末小结编审:周彦 魏国庆【复习目标】进一步掌握三角恒等变换的方法,如何利用正、余弦、正切的和差公式与二倍角公式,对三角函数式进行化简、求值和证明:【知识与方法】1、熟练记忆三角恒等变换公式:2、三角恒等变换过程与方法,实际上是对三角函数式中的角、名、形的变换,即:(1)找差异:角、名、形的差别;(2)建立联系:角的和差关系、倍半关系等,名、形之间可以用哪个公式联系起来;(3)变公式:在实际变换过程中,往往需要将公式加以变形后运用或逆用公式。
如:升降幂公式22cos 1cos 2αα+=; 22cos 1sin 2αα-=; ααα2cos 12cos 1tan 2-+=; tan α±tan β=tan(α±β)(1 tan αtan β);1= sin 2α+cos 2α(1的代换);拆角cos α= cos βcos(α-β)- sin βsin(α-β);切化弦等。
3.asin α+bcos α=22b a +sin(α+φ),其中cos φ=___,sin φ=___,即tan φ=b a.【题型总结】题型1、化简求值:综合使用三角函数的定义、性质、公式,求出三角函数式的值。
化简要求:________、________、__________、__________、__________、__________;1、化简(1)0070sin 120sin 3-;1(2)sin2αsin2β+cos2αcos2β-cos2αcos2β。
22、求值:)5tan 5tan 1(10sin 20sin 220cos 100000--+题型2、条件求值:综合考虑要求值的式子和条件式的关联,对于已知条件式的应用及其变形是解决此类问题的关键。
3、已知)sin(βα+=32,)sin(βα-=51,求βαtan tan 的值。
4. 已知,135)4sin(,40=-<<x x ππ 求)4cos(2cos x x+π的值。
山东省平邑县高中数学第一章三角函数1.4三角函数的图象和性质小结导学案(无答案)新人教A版必修4

【学习目标】1.4三角函数的图象和性质1 .能画出y = sin x, y= cos x, y= tan x的图象,了解三角函数的周期性.2 .理解正弦函数、余弦函数在区间[0,2 n ]上的性质(如单调性、最大值和最小值以及与X轴的交点等),理解正切函数在区间内的单调性.【新知自学】知识梳理:1.周期函数及最小正周期对于函「数f(X),如果存在一个非零常数T,使得当X取定义域内的每一个值时,都有________________ ,则称f(x)为周期函数,T为它的一个周期.若在所有周期中,有一个最小的正数,贝y这个最小的正数叫做f(x)的最小正周期.2 .正弦函数、余弦函数、正切函数的图象和性质n1、函数 y = cos x + — , x € R( ).3A. 是奇函数B. 是偶函数C. 既不是奇函数也不是偶函数D. 既是奇函数又是偶函数n2.下列函数中,在 2,n 上是增函数的是( ).n3.函数y = cos 2x + 2的图象的一条对称轴方程是(x = —nf ~的值是().A. 0 B . 1 C.— 1 D5.已知函数y = sin x 的定义域为[a,b ],值域为 一1, 2,则b — a 的值不可能是().2n "3C.n 【合作探究】典例精析:一、三角函数的定义域与值域例1、(1)求函数y = lg sin 2 x + ;9 — x 2的定义 域.2n(2)求函数y = cos x + sin x | x | <-4的最大值与最小值.nc. X = 8 Dx =n4.函数 f (x ) = tan3X( 3 > 0)的图象的相邻的两支截直线nny= 7所得线段长为7,则A. y = sin xB. y = cos xC. y = sin 2 xD. y = cos 2 x1 •求三角函数定义域实际上是解简单的三角不等式,常借助三角函数线或三角函数图象来求解.2•求解涉及三角函数的值域(最值)的题目一般常用以下方法:⑴利用sin x, cos x的值域;(2) 化为y= A sin( ®x+ 0 ) + k的形式,逐步分析®x+0的范围,根据正弦函数单调性写出值域;(3) 换元法:把sin x或cos x看作一个整体,可化为求函数在区间上的值域(最值)问题.变式练习1:⑴求函数y= ,sin x- cos x的定义域._ n n n(2)已知函数 f (x) = cos 2x—3 + 2sin x--4 • sin x+ —,求函数f(x)在区间n n—12,~2上的最大值与最小值.二、三角函数的单调性例2、(1 )已知函数f (x) = 2si n( 3x+0 ) ,x€ R,其中0,—nV 0Wn .若f ( x) n的最小正周期为6n,且当x =-时,f(x)取得最大值,则().A. f(x)在区间[—2n, 0]上是增函数B. f (x)在区间[—3n,—n ]上是增函数C. f (x)在区间[3 n, 5 n ]上是减函数D. f (x)在区间[4 n, 6n ]上是减函数2 n n(2)设a€ R, f (x) = cos x(a sin x—cos x) + cos ~2—x 满足f —§ = f (0),求函n 11 n 数f (x)在,上的最大值和最小值.4 241. 熟记y= sin x, y = cos x, y = tan x的单调区间是求复杂的三角函数单调区间的基础.2. 求形如y = A sin( ®x+0 ) + k的单调区间时,只需把®x+0看作一个整体代入y=sin x的相应单调区间即可,注意A的正负以及要先把3化为正数.变式练习2:2 n 一(1)若函数y= 2cos 3x在区间[0 ,百]上递减,且有最小值1,则3的值可以是()1 1A. 2B. -C. 3D.-2 3n(2) __________________________________________________ 函数f(x) = sin —2x +亍的单调减区间为_______________________________________________ .三、三角函数的周期性和奇偶性及对称性例3、设函数f (x) = si n23x + 2 ': 3sin wx • cos wx —cos2®x+ 入(x€ R)的图象关于1直线x=n对称,其中w ,入为常数,且w € 2,1 .(1) 求函数f (x)的最小正周期;n(2) 若y= f (x)的图象经过点4,0,求函数f (x)的值域.规律总结:求三角函数周期的方法:(1) 利用周期函数的定义;2 n(2) 公式法:y=A sin( wx+ 0)和y=A cos( wx+ 0)的最小正周期为,y=tan( wx + 【课堂小结】【当堂达标】1. 若函数f (x) = sin ^^3虫(0 €[0,2 n ])是偶函数,则0 =( ).丨3丨n0 )的最小正周期为;丨3丨变式练习3:已知函数f (x) = (sin x —cos x)sin x, x€ R,则f (x)的最小正周期是_______________ .32. 函数y = In (sin x — cos x )的定义域为n3. 函数y = 2sin x ——的单调递增区间为,, n24. 设函数 f (x ) = cos 2x + — + sin x .3(1)求函数f (x )的最大值和最小正周期.⑵设A, B ,。
山东省平邑县高中数学第一章三角函数1.4三角函数的图象和性质小结导学案(无答案)新人教A版必修4
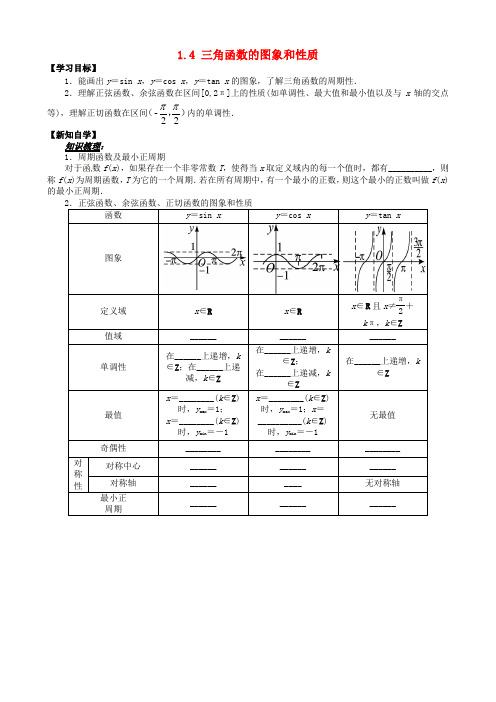
1.4 三角函数的图象和性质【学习目标】1.能画出y =sin x ,y =cos x ,y =tan x 的图象,了解三角函数的周期性.2.理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值以及与x 轴的交点等),理解正切函数在区间),(22-ππ内的单调性. 【新知自学】知识梳理:对于函数f (x ),如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有__________,则称f (x )为周期函数,T 为它的一个周期.若在所有周期中,有一个最小的正数,则这个最小的正数叫做f (x )的最小正周期.x ∈Rx ∈R 且x ≠π2+k π,k ∈Z______对点练习:1、函数y =cos ⎝⎛⎭⎪⎫x +π3,x ∈R ( ).A .是奇函数B .是偶函数C .既不是奇函数也不是偶函数D .既是奇函数又是偶函数2.下列函数中,在⎣⎢⎡⎦⎥⎤π2,π上是增函数的是( ). A .y =sin x B .y =cos x C .y =sin 2x D .y =cos 2x3.函数y =cos ⎝⎛⎭⎪⎫2x +π2的图象的一条对称轴方程是( ). A .x =-π2 B .x =-π4C .x =π8D .x =π4.函数f (x )=tan ωx (ω>0)的图象的相邻的两支截直线y =π4所得线段长为π4,则f ⎝ ⎛⎭⎪⎫π4的值是( ).A .0B .1C .-1D .π45.已知函数y =sin x 的定义域为[a ,b ],值域为⎣⎢⎡⎦⎥⎤-1,12,则b -a 的值不可能是( ). A .π3 B .2π3C .πD .4π3【合作探究】典例精析:例1、(1)求函数y =lg sin 2x +9-x 2的定义域.(2)求函数y =cos 2x +sin x ⎝⎛⎭⎪⎫|x |≤π4的最大值与最小值.规律总结:1.求三角函数定义域实际上是解简单的三角不等式,常借助三角函数线或三角函数图象来求解.2.求解涉及三角函数的值域(最值)的题目一般常用以下方法: (1)利用sin x ,cos x 的值域;(2)化为y =A sin(ωx +φ)+k 的形式,逐步分析ωx +φ的范围,根据正弦函数单调性写出值域;(3)换元法:把sin x 或cos x 看作一个整体,可化为求函数在区间上的值域(最值)问题.变式练习1:(1)求函数y =sin x -cos x 的定义域.(2)已知函数f (x )=cos ⎝ ⎛⎭⎪⎫2x -π3+2sin ⎝ ⎛⎭⎪⎫x -π4·sin ⎝⎛⎭⎪⎫x +π4,求函数f (x )在区间⎣⎢⎡⎦⎥⎤-π12,π2上的最大值与最小值.二、三角函数的单调性 例2、(1)已知函数f (x )=2sin(ωx +φ),x ∈R ,其中ω>0,-π<φ≤π.若f (x )的最小正周期为6π,且当x =π2时,f (x )取得最大值,则( ).A .f (x )在区间 [-2π,0]上是增函数B .f (x )在区间[-3π,-π]上是增函数C .f (x )在区间[3π,5π]上是减函数D .f (x )在区间[4π,6π]上是减函数(2)设a ∈R ,f (x )=cos x (a sin x -cos x )+cos 2⎝ ⎛⎭⎪⎫π2-x 满足f ⎝ ⎛⎭⎪⎫-π3=f (0),求函数f (x )在⎣⎢⎡⎦⎥⎤π4,11π24上的最大值和最小值.规律总结:sin x ,y =cos x ,y =tan x 的单调区间是求复杂的三角函数单调区间的基础.2.求形如y =A sin(ωx +φ)+k 的单调区间时,只需把ωx +φ看作一个整体代入y =sin x 的相应单调区间即可,注意A 的正负以及要先把ω化为正数.变式练习2:(1)若函数y =2cos ωx 在区间[0,2π3]上递减,且有最小值1,则ω的值可以是( )A. 2B. 12C. 3D. 13(2)函数f (x )=sin ⎝⎛⎭⎪⎫-2x +π3的单调减区间为_____________.三、三角函数的周期性和奇偶性及对称性例3、设函数f (x )=sin 2ωx +23sin ωx ·cos ωx -cos 2ωx +λ(x ∈R )的图象关于直线x =π对称,其中ω,λ为常数,且ω∈⎝ ⎛⎭⎪⎫12,1. (1)求函数f (x )的最小正周期;(2)若y =f (x )的图象经过点⎝ ⎛⎭⎪⎫π4,0,求函数f (x )的值域.规律总结:(1)利用周期函数的定义;(2)公式法:y=A sin(ωx +φ)和y=A cos(ωx +φ)的最小正周期为2π|ω|,y=tan(ωx +φ)的最小正周期为π|ω|;变式练习3:已知函数f (x )=(sin x -cos x )sin x ,x ∈R ,则f (x )的最小正周期是________.【课堂小结】【当堂达标】1.若函数f (x )=sinx +φ3(φ∈[0,2π])是偶函数,则φ=( ).A .π2B .2π3C .3π2D .5π32.函数y =ln(sin x -cos x )的定义域为__________.3.函数y =2sin ⎝⎛⎭⎪⎫x -π4的单调递增区间为__________.4.设函数f (x )=cos ⎝⎛⎭⎪⎫2x +π3+sin 2x .(1)求函数f (x )的最大值和最小正周期.(2)设A ,B ,C 为△ABC 的三个内角,若cos B =13,)2C f(=-14,且C 为锐角,求sin A .5.已知函数f (x )=sin x (cos x -3sin x ). (1)求函数f (x )的最小正周期;(2)将函数y =sin 2x 的图象向左平移a ⎝⎛⎭⎪⎫0<a <π2个单位,向下平移b 个单位,得到函数y =f (x )的图象,求a ,b 的值;(3)求函数f (x )的单调增区间.【课时作业】1、已知函数y =sin x 的定义域为[a ,b ],值域为[-1,12],则b -a 的值不可能是( )A. π3B. 2π3C. πD. 4π32、若函数f (x )=sin x +φ3(φ∈[0,2π]) 是偶函数,则φ=( )A. π2B. 2π3C. 3π2D. 5π33、函数y =cos ⎝⎛⎭⎪⎫2x +π3图象的对称轴方程可能是( ). A .x =-π6 B .x =-π12C .x =π6D .x =π124. 如果函数f (x )=sin(ωx +π6)(ω>0)的两个相邻零点之间的距离为π12,则ω的值为( )A. 3B. 6C. 12D. 245.函数f (x )=cos(2x +3π2)(x ∈R ),下面结论不正确的是( )A. 函数f (x )的最小正周期为πB. 函数f (x )的对称中心是(π2,0)C. 函数f (x )的图象关于直线x =π4对称D. 函数f (x )是偶函数6、若0<α<π2,g (x )=sin ⎝ ⎛⎭⎪⎫2x +π4+α是偶函数,则α的值为________.7、函数y =2sin(3x +φ)⎝⎛⎭⎪⎫||φ<π2的一条对称轴为x =π12,则φ=________. 8、函数y =cos(3x +φ)的图象关于原点成中心对称图形.则φ=________.9.若函数f (x )=2tan(kx +π3)的最小正周期T 满足1<T <2,则自然数k 的值为________.10. 设二次函数f (x )=x 2+bx +c (b ,c ∈R ),已知不论α、β为何实数恒有f (sin α)≥0和f (2+cos β)≤0.(1)求证:b +c =-1; (2)求证c ≥3;(3)若函数f (sin α)的最大值为8,求b ,c 的值.11、有一块半径为R ,中心角为45°的扇形铁皮材料,为了获取面积最大的矩形铁皮,工人师傅常让矩形的一边在扇形的半径上,然后作其最大内接矩形,试问:工人师傅是怎样选择矩形的四点的?并求出最大面积值.12、是否存在实数a ,使得函数y =sin 2x +a ·cos x +85a -23在闭区间[0,2π]上的最大值是1?若存在,求出对应的a 值;若不存在,试说明理由.【延伸探究】设f (x )=a sin 2x +b cos 2x ,其中a ,b ∈R ,ab ≠0,若f (x )≤⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π6对一切x ∈R 恒成立,则①f ⎝ ⎛⎭⎪⎫11π12=0 ②⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫7π10<⎪⎪⎪⎪⎪⎪f ⎝ ⎛⎭⎪⎫π5 ③f (x )既不是奇函数也不是偶函数④f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3(k ∈Z ) ⑤存在经过点(a ,b )的直线与函数f (x )的图象不相交. 以上结论正确的是__________(写出正确结论的编号).。
高中数学必修四导学案

高中数学《必修四》导学案班级________ 姓名___________第一章 三角函数 1.1.1 任意角【学习目标】1、 了解任意角的概念;正确理解正角、零角、负角的概念2、 正确理解终边相同的角的概念,并能判断其为第几象限角,熟悉掌握终边相同的角的集合表示【学习重点、难点】 用集合与符号语言正确表示终边相同的角 【自主学习】 一、复习引入问题1:回忆初中我们是如何定义一个角的______________________________________________________ 所学的角的范围是什么______________________________________________________问题2:在体操、跳水中,有“转体0720”这样的动作名词,这里的“0720”,怎么刻画______________________________________________________ 二、建构数学 1.角的概念角可以看成平面内一条______绕着它的_____从一个位置_____到另一个位置所形成的图形。
射线的端点称为角的________,射线旋转的开始位置和终止位置称为角的______和______。
2.角的分类按__________方向旋转形成的角叫做正角, 按顺时针方向旋转形成的角叫做_________。
如果一条射线没有作任何旋转,我们称它形成了一个_________,它的______和_______重合。
这样,我们就把角的概念推广到了_______,包括_______、________和________。
3. 终边相同的角所有与角α终边相同的角,连同角α在内,可构成一个集合_________ ,即任一与角α终边相同的角,都可以表示成。
4.象限角、轴线角的概念我们常在直角坐标系内讨论角。
为了讨论问题的方便,使角的________与__________重合,角的___________与_______________________重合。
高中数学 第一章 三角函数 1.3.2 诱导公式导学案2(无答案)新人教A版必修4(2021年整理)

山东省平邑县高中数学第一章三角函数1.3.2 诱导公式导学案2(无答案)新人教A版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(山东省平邑县高中数学第一章三角函数1.3.2 诱导公式导学案2(无答案)新人教A版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为山东省平邑县高中数学第一章三角函数1.3.2 诱导公式导学案2(无答案)新人教A版必修4的全部内容。
1。
3.2 诱导公式【学习目标】1.借助单位圆,推导出正弦、余弦第五、六组的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题2.通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力。
【新知自学】知识回顾:1、问题1:请同学们回顾一下前一节我们学习的与、、的三角函数关系.2、问题2:如果两个点关于直线y=x对称,它们的坐标之间有什么关系呢?若两个点关于y轴对称呢?新知梳理:1、问题1:如图:设的终边与单位圆相交于点P,则P点坐标为,点P关于直线y=x的轴对称点为M,则M点坐标为 , 点M关于y轴的对称点N,则N的坐标为 ,∠XON的大小与的关系是什么呢?点N的坐标又可以怎么表示呢?学生活动:学生看图口答P(,),M(,),N(-,),∠XON=N(,)(教师在引导学生分析问题过程中,积极观察学生的反映,适时进行激励性评价)2、问题2:观察点N的坐标,你从中发现什么规律了?设置意图:让学生总结出公式=-,=感悟:我们学习了2πα+的诱导公式,还知道2πα-的诱导公式,那么对于32πα+,32πα-又有怎样的诱导公式呢?设置意图:利用已学诱导公式推导新公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2.1任意角的三角函数(第一课时)
【学习目标】1.理解任意角的正弦、余弦、正切的定义,会用定义求任意角的三角函数值;
2. 会用三角函数值的符号解决问题;
3. 掌握并能初步运用定义分析和解决与三角函数值有关的一些问题.
【新知自学】
知识回顾:
1. 弧度制的定义
长度等于__________的圆弧所对的圆心角叫做1弧度角,记作1rad,或1弧度,2.弧度数的求法
一个半径为r的圆的圆心角α所对的弧长是l,那么角α的弧度数的绝对值是:α________.α的正负由__决定.
=
正角的弧度数是一个,负角的弧度数是一个,零角的弧度数是.
3.角度与弧度的换算
(1)3600=________rad;
(2)________=πrad;
新知梳理:
1. 三角函数定义
在直角坐标系中,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
(1)______叫做α的正弦,记作_______,即________;
(2)_______叫做α的余弦,记作_______,即_________;
(3)_______叫做α的正切,记作_______,即_________.
推广:α终边上任意一点P(除了原点)的坐标为(x,y),它与原点的距离为r,那么sinα=____ ;
cosα=___ ____,
tanα=____ _ __.
(三角函数值的大小与P点的位置有关吗?)
2.三角函数的符号
对于第一、二象限为____(y>0,r>0),对于第三、四象限为____(y<0,r>0)
(1)正弦值y
r
(2)余弦值x
对于第一、四象限为_____(x>0,r>0),对于第二、三象限为___ (x<0,r>0)
r
(3)正切值x
y 对于第一、三象限为____(x,y 同号),对于第二、四象限为____(x,y 异号). 记忆口诀:
“第一象限全为正,第二象限正弦正,
第三象限是正切,余弦就在四象正”
对点练习:
1、下列选项中错误的是( )
A .0585sin 0<
B .()0675tan 0>-
C .()0690cos 0<-
D .01010tan 0
<
2、已知角α终边上一点(3,4)P --,求角α的正弦、余弦和正切值。
【合作探究】 典例精析:
例1.求
3
5π的正弦、余弦、正切.
y
函 余 正 切 x o
变式练习(1): 利用三角函数的定义求67π、3
π-的三个三角函数值
例2.已知角α的终边经过点)4,3(0--P ,求角α的正弦、余弦和正切值.
*变式练习(2)已知角α的终边经过点)0)(3,4(≠-a a a P
**变式练习(3)已知角α的终边在直线x y =上,求αααtan ,cos ,sin .
题型二:三角函数的符号规律的应用
例3.求证:当右边不等式组成立时,角θ为第二象限角.反之也对. ⎩⎨⎧<>0
tan 0sin θθ
变式练习:
(1)已知sin 0θ<且tan 0θ<则α是( )
A .第一象限的角
B .第二象限的角
C .第三象限的角
D .第四象限的角
(2)若α为锐角,k ·180°+α)(Z ∈k 所在的象限是____________.
【课堂小结】
【当堂达标】
1.若23
cos -=α,且α的终边经过点)2,(x P ,则点P 的横坐标是(
)
A. 32
B. 32±
C. 22-
D. 32-
2.代数式3cos 53sin ⋅π
的值是( )
A.大于0
B.小于0
C.大于或等于0
D.小于或等于0
3. 若角α的终边过点P (5,-12),则sin α+cos α=________.
4、设点P )4,(n 在角α的终边上,且5
4sin =α,求cos α和tan α的值
【课时作业】
1、角α的终边上有一点P (a ,a ),a ∈R ,a ≠0,则sin α的值是(
) A.22 B.-22
C. 22
或-22
D.1
2、是,则已知ααtan 2=( )
A .正值
B .负值
C .大于等于0
D .不能确定
3、已知角α为第二象限角,则2sin α
为( )
A .正值
B .负值
C .可正可负
D .不能确定
4、已知角α终边上一点
()()值为则且x x P 53sin ,3,=α
A .4
B .-4
C .4±
D .不确定
5.已知点P (tan α,cos α)在第三象限,则角α的终边在第______象限.
6.sin2·cos4·tan6与0的大小关系为_____________.
(填>,<,≥,≤)
7.求下列各式的值:
(1);)647-
(sin π (2)4
17cos π; (3)tan )317(π-.
*8.若角α的终边经过P (-3,b ),且cos α=-35
,判断角α所在的象限,并求sin α、tan α的值.
【延伸探究】
**9. 已知角α的终边经过点P (x ,-2),且cos α=x 3
,求sin α和tan α.。
