统计学回归分析大作业
统计学:相关回归分析习题与答案

一、单选题1、下列哪种关系属于相关关系而非函数关系?()A.销售总额与销售量B.价格与销售量C.工资总额与人均工资D.圆的面积与半径正确答案:B解析: B、函数关系是指现象之间存在的确定性的数量依存关系。
2、若两个变量之间的线性相关系数为0.9,则()。
A.回归系数为0.81B.判定系数为0.81C.回归估计标准误为0.81D.判定系数为0.95正确答案:B3、下列指标一定非负的是()。
A.回归系数bB.相关系数rC.回归估计标准误S yxD.回归常数a正确答案:C4、在回归直线方程中y c=a+bx,b 是直线的斜率,表明()。
A.当x 增加一个单位时,y 增加a的数量B.当y 增加一个单位时,x 的平均增加量C.当y 增加一个单位时,x 增加b的数量D.当x 增加一个单位时,y 的平均增加量正确答案:D5、相关系数r与回归系数b的关系是()。
A. b=r×S x/S yB. b=r×S y/S xC. r=b×S y/S xD. 以上都不对正确答案:B6、当所有的观察值y都落在直线y c=a+bx上时,x与y之间的相关系数是()。
A. r=1B.r=-1C. |r|=1D.r=0正确答案:C解析:当r=1或r=-1时,表示变量之间为完全相关7、相关系数r=0表示()。
A.不存在相关关系B.两变量独立C.不存在线性相关关系D.存在平衡关系正确答案:C8、对相关系数的显著性检验,通常采用的是()。
A.Z检验B.F检验C.χ2检验D.T检验正确答案:D9、线性回归的检验中,检验整个方程显著性的是()。
A.F检验B.DW检验C.t检验D.R检验正确答案:A10、下列现象的相关密切程度高的是A.商品销售额与商业利润率之间的相关系数是0.62B.商品销售额与流通费用率之间的相关系数为-0.76C.某商店职工人数与商品销售额之间的相关系数为0.79D.流通费用率与商业利润率之间的相关系数是-0.89正确答案:D二、多选题1、下列属于负相关的现象是()。
统计学(回归分析)习题

统计学第三次作业(第十章相关与回归分析)计算题1. 为研究年收入水平Y (单位:万元)与受教育程度X (单位:年)之间的关系,现抽取一个包括20个人的随机样本,得到:22239, 72.61, ()422.95()34.83, ()()106.74ttttttX Y X X Y Y X X Y Y ==-=-=--=∑∑∑∑∑试根据以上数据:(1) 计算年收入水平与受教育程度的样本相关系数;(2) 拟合简单线性回归方程,并对回归系数的经济意义作解释; (3) 预测受教育年限为16年时,平均年收入是多少?2. 为研究零食中脂肪含量X (单位:克)与热量Y (单位:卡路里)之间的关系,随机抽查了16种点心食品,得到的数据如下:22189, 3461, 2799907717, 49526, 16tt t tt t X Y X YX Y n ======∑∑∑∑∑试根据以上数据:(1)计算热量与脂肪含量的样本相关系数;(2)拟合热量与脂肪含量的简单线性回归方程,并计算回归方程的决定系数以反映拟合效果;(3)若某糖果条包装上标明含有3克脂肪,预测其含有的热量。
3. 有8个同类企业的生产性固定资产年均价值和工业增加值的资料如下:要求:(计算必须有公式和过程)(1)计算相关系数,说明两变量相关的方向和程度;(2)建立以工业增加值为因变量的直线回归方程,说明方程参数的经济意义;(3)在0.05的显著性水平下,用F检验检验线性回归效果是否显著?(0.05(1,6) 5.987F=)(4)确定生产性固定资产为1100万元时,工业增加值的估计值。
4. 根据甲企业2004年每月的产品销售额Y与广告费支出X数据(单位:元),计算出其估计的回归方程为ŷ=31.98+1.68X,估计结果中R2=0.923,F=230.78,自变量系数的t检验值为3.587;另有一企业乙也进行了同样情况的分析,已知∑X=50, ∑Y=110.8, ∑X2=294, ∑Y2=1465.0, ∑XY=654.9,要求:(1)确定乙企业产品销售额Y与广告费支出X的线性回归方程,并说明βˆ1的含义;(2)若已知乙企业的回归结果中R2=0.847,F=302.5,自变量系数的t检验值为1.7689,试根据所学知识对甲、乙两企业所建立的线性回归方程的优劣进行综合分析。
统计学第七章相关与回归分析试题及答案

统计学第七章相关与回归分析试题及答案第七章相关与回归分析(⼆) 单项选择题1、当⾃变量的数值确定后,因变量的数值也随之完全确定,这种关系属于( B )A 、相关关系B 、函数关系C 、回归关系D 、随机关系2、测定变量之间相关密切程度的代表性指标是(C )A 、估计标准误B 、两个变量的协⽅差C 、相关系数D 、两个变量的标准差3、现象之间的相互关系可以归纳为两种类型,即( A )A 、相关关系和函数关系B 、相关关系和因果关系C 、相关关系和随机关系D 、函数关系和因果关系4、相关系数的取值范围是( C )A 、10≤≤γB 、11<<-γC 、11≤≤-γD 、01≤≤-γ5、变量之间的相关程度越低,则相关系数的数值(B )A 、越⼩B 、越接近于0C 、越接近于-1D 、越接近于16、在价格不变的条件下,商品销售额和销售量之间存在着( D )A 、不完全的依存关系B 、不完全的随机关系C 、完全的随机关系D 、完全的依存关系7、下列哪两个变量之间的相关程度⾼( C )A 、商品销售额和商品销售量的相关系数是0.9;B 、商品销售额与商业利润率的相关系数是0.84;C 、平均流通费⽤率与商业利润率的相关系数是-0.94;D 、商品销售价格与销售量的相关系数是-0.918、回归分析中的两个变量(D )A 、都是随机变量B 、关系是对等的C 、都是给定的量D 、⼀个是⾃变量,⼀个是因变量9、每⼀吨铸铁成本(元)倚铸件废品率(%)变动的回归⽅程为:x y c 856+=,这意味着( C )A 、废品率每增加1%,成本每吨增加64元B 、废品率每增加1%,成本每吨增加8%C 、废品率每增加1%,成本每吨增加8元D 、如果废品率增加1%,则每吨成本为56元。
10、某校对学⽣的考试成绩和学习时间的关系进⾏测定,建⽴了考试成绩倚学习时间的直线回归⽅程为:x y c 5180-=,该⽅程明显有错,错误在于( C )A 、a 值的计算有误,b 值是对的B 、b 值的计算有误,a 值是对的C 、a 值和b 值的计算都有误D 、⾃变量和因变量的关系搞错了11、配合回归⽅程对资料的要求是(B )A 、因变量是给定的数值,⾃变量是随机的B 、⾃变量是给定的数值,因变量是随机的C 、⾃变量和因变量都是随机的D 、⾃变量和因变量都不是随机的。
统计学一元线性回归分析练习题

统计学一元线性回归分析练习题一、内容提要本章介绍了回归分析的基本思想与基本方法。
首先,本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始,建立了回归分析的基本思想。
总体回归函数是对总体变量间关系的定量表述,由总体回归模型在若干基本假设下得到,但它只是建立在理论之上,在现实中只能先从总体中抽取一个样本,获得样本回归函数,并用它对总体回归函数做出统计推断。
本章的一个重点是如何获取线性的样本回归函数,主要涉及到普通最小二乘法的学习与掌握。
同时,也介绍了极大似然估计法以及矩估计法。
本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断,即进行所谓的统计检验。
统计检验包括两个方面,一是先检验样本回归函数与样本点的“拟合优度”,第二是检验样本回归函数与总体回归函数的“接近”程度。
后者又包括两个层次:第一,检验解释变量对被解释变量是否存在着显著的线性影响关系,通过变量的t检验完成;第二,检验回归函数与总体回归函数的“接近”程度,通过参数估计值的“区间检验”完成。
本章还有三方面的内容不容忽视。
其一,若干基本假设。
样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。
其二,参数估计量统计性质的分析,包括小样本性质与大样本性质,尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。
Goss-markov定理表明OLS估计量是最佳线性无偏估计量。
其三,运用样本回归函数进行预测,包括被解释变量条件均值与个值的预测,以及预测置信区间的计算及其变化特征。
二、典型例题分析例1、令kids表示一名妇女生育孩子的数目,educ 表示该妇女接受过教育的年数。
生育率对教育年数的简单回归模型为kids??0??1educ??随机扰动项?包含什么样的因素?它们可能与教育水平相关吗?上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗?请解释。
北师大应用多元统计分析作业——回归分析

应用多元统计分析作业(七)——回归分析4-2:利用回归分析方法分析某种消费品的销售量于相关指标之间的关系。
解:●执行SAS程序代码:data dxiti42;input number x1 x2 x3 x4 Y;cards;1 82.9 92.0 17.1 94.0 8.42 88.0 93.0 21.3 96.0 9.63 99.9 96.0 25.1 97.0 10.44 105.3 94.0 29.0 97.0 11.45 117.7 100.0 34.0 100.0 12.26 131.0 101.0 40.0 101.0 14.27 148.2 105.0 44.0 104.0 15.88 161.8 112.0 49.0 109.0 17.99 174.2 112.0 51.0 111.0 19.610 184.7 112.0 53.0 111.0 20.8;proc reg data=dxiti42;model Y = x1 x2 x3 x4;run;quit;●结果分析:输出结果首先给出了回归模型的方差分析表:Model 4 169.5535 42.38838 1021.41 <.0001Error 5 0.2075 0.0415Corrected Total 9 169.761以及回归模型的一些统计量的值:0.20.9988Dependent Mean14 Adj R‐Sq 0.9978Coeff Var 1.45从以上两表中可以看出,此回归模型的拟合效果较好,R2值达到了0.9978;同时回归模型的F值也很大,为1021.41;并且F的p值很小(<0.0001),小于显著性水平α=0.05。
综上,可以判定此回归模型在α = 0.05 的水平上是显著的。
进一步给出了回归模型参数估计的一些信息:Intercept 1 ‐17.6677 5.9436 ‐2.97 0.0311 x1 1 0.09006 0.02095 4.3 0.0077x2 1 ‐0.23132 0.07132 ‐3.24 0.0229x3 1 0.01806 0.03907 0.46 0.6633x4 1 0.42075 0.11847 3.55 0.0164从上表中的最后一栏可以看出,截距项、x1、x2、x4的回归系数的t统计量的尾概率均小于显著水平α=0.05,而x3的回归系数的t统计量的尾概率大于显著水平α=0.05。
回归分析习题及答案

回归分析习题及答案回归分析习题及答案回归分析是统计学中一种常用的分析方法,用于研究变量之间的关系。
它可以帮助我们了解变量之间的相关性,并预测未来的趋势。
在本文中,我们将提供一些回归分析的习题及其详细解答,帮助读者更好地理解和应用这一方法。
习题一:某公司想要了解其销售额与广告投入之间的关系。
公司收集了过去12个月的数据,包括每个月的广告投入(单位:万元)和当月的销售额(单位:万元)。
请利用这些数据进行回归分析,并给出相关的统计结果。
解答一:首先,我们需要将数据导入统计软件,比如SPSS或Excel。
然后,我们可以使用线性回归模型来分析销售额与广告投入之间的关系。
在SPSS中,可以选择“回归”分析,将销售额作为因变量,广告投入作为自变量,进行线性回归分析。
回归分析的结果包括回归方程、相关系数、显著性检验等。
回归方程可以用来描述销售额与广告投入之间的关系。
相关系数可以告诉我们这两个变量之间的相关程度,取值范围为-1到1,越接近1表示相关性越强。
显著性检验可以告诉我们回归方程是否显著,即广告投入是否对销售额有显著影响。
习题二:某研究人员想要了解学生的考试成绩与他们的学习时间之间的关系。
研究人员随机选择了100名学生,记录了他们的学习时间(单位:小时)和考试成绩(百分制)。
请利用这些数据进行回归分析,并给出相关的统计结果。
解答二:同样地,我们需要将数据导入统计软件,然后进行回归分析。
这次,我们将考试成绩作为因变量,学习时间作为自变量。
除了之前提到的回归方程、相关系数和显著性检验之外,我们还可以通过回归分析的结果来进行预测。
例如,我们可以利用回归方程来预测一个学生在给定学习时间下的考试成绩。
习题三:某研究人员想要了解一个人的身高与体重之间的关系。
研究人员随机选择了200名成年人,记录了他们的身高(单位:厘米)和体重(单位:千克)。
请利用这些数据进行回归分析,并给出相关的统计结果。
解答三:同样地,我们将数据导入统计软件,然后进行回归分析。
统计学实训回归分析报告

一、引言回归分析是统计学中一种重要的分析方法,主要用于研究变量之间的线性关系。
本次实训报告将结合实际数据,运用回归分析方法,探讨变量之间的关系,并分析影响因变量的关键因素。
二、实训目的1. 理解回归分析的基本原理和方法。
2. 掌握使用统计软件进行回归分析的操作步骤。
3. 分析变量之间的关系,并找出影响因变量的关键因素。
三、实训数据本次实训数据来源于某地区2019年居民消费情况调查,包含以下变量:1. 家庭月收入(万元)作为因变量。
2. 家庭人口数、教育程度、住房面积、汽车拥有量、子女数量作为自变量。
四、实训步骤1. 数据整理:将数据录入统计软件,进行数据清洗和整理。
2. 描述性统计:计算各变量的均值、标准差、最大值、最小值等指标。
3. 相关性分析:计算各变量之间的相关系数,分析变量之间的线性关系。
4. 回归分析:建立多元线性回归模型,分析各自变量对因变量的影响程度。
5. 模型检验:进行残差分析、方差分析等,检验模型的可靠性。
五、实训结果与分析1. 描述性统计结果家庭月收入均值为8.5万元,标准差为2.1万元;家庭人口数均值为3.2人,标准差为1.5人;教育程度均值为2.5年,标准差为0.6年;住房面积均值为100平方米,标准差为20平方米;汽车拥有量均值为1.2辆,标准差为0.7辆;子女数量均值为1.5个,标准差为0.8个。
2. 相关性分析结果家庭月收入与家庭人口数、教育程度、住房面积、汽车拥有量、子女数量之间存在显著正相关关系。
3. 回归分析结果建立多元线性回归模型如下:家庭月收入 = 5.6 + 0.3 家庭人口数 + 0.2 教育程度 + 0.1 住房面积 + 0.05 汽车拥有量 + 0.02 子女数量模型检验结果如下:- F统计量:76.23- P值:0.000- R方:0.642模型检验结果表明,该模型具有较好的拟合效果,可以用于分析家庭月收入与其他变量之间的关系。
4. 影响家庭月收入的关键因素分析根据回归分析结果,影响家庭月收入的关键因素包括:(1)家庭人口数:家庭人口数越多,家庭月收入越高。
(完整word版)北航数理统计大作业1-线性回归分析

应用数理统计作业一学号:姓名:电话:二〇一四年十二月国内生产总值的多元线性回归模型摘要:本文首先选取了选取我国自1978至2012年间的国内生产总值为因变量,并选取了7个主要影响因素,进一步利用统计软件SPSS对以上数据进行了多元逐步线性回归。
从而找到了能反映国内生产总值与各因素之间关系的“最优”回归方程.然后利用多重线性的诊断找出存在共线性的自变量,剔除缺失值较多的因子.再次进行主成份线性回归分析,找出最优回归方程。
所得结论与我国当前形势相印证。
关键词:多元线性回归,逐步回归法,多重共线性诊断,主成份分析目录0符号说明 (1)1 介绍 (2)2 统计分析步骤 (3)2。
1 数据的采集和整理 (3)2。
2采用多重逐步回归分析 (7)2.3进行共线性诊断 (17)2。
4进行主成分分析确定所需主成份 (24)2。
5进行主成分逐步回归分析 (27)3 结论 (30)参考文献 (31)致谢 (32)0符号说明1 介绍文中主要应用逐步回归的主成份分析方法,对数据进行分析处理,最终得出能够反映各个因素对国内生产总值影响的最“优”模型及线性回归方程.国内生产总值是指在一定时期内(一个季度或一年),一个国家或地区的经济中所生产出的全部最终产品和劳务的价值,常被公认为衡量国家经济状况的最佳指标.它不但可反映一个国家的经济表现,还可以反映一国的国力与财富。
2012年1月,国家统计局公布2011年重要经济数据,其中GDP增长9.2%,基本符合预期。
2012年10月18日,统计显示,2012年前三季度国内生产总值353480亿元,同比增长7.7%;其中,一季度增长8.1%,二季度增长7。
6%,三季度增长7.4%,三季度增幅创下2009年二季度以来14个季度新低。
中国的GDP核算历史不长,上世纪90年代之前通常用“社会总产值”来衡量经济发展情况。
上世纪80年代初中国开始研究联合国国民经济核算体系的国内生产总值(GDP)指标。
统计学原理-第六章--相关与回归分析习题

A+1 B 0 C 0.5 D [1]5.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( )A线性相关还是非线性相关B正相关还是负相关C完全相关还是不完全相关D单相关还是复相关6.某校经济管理类的学生学习统计学的时间()与考试成绩(y)之x间建立线性回归方程y c=a+b。
经计算,方程为y c=200—0.8x,该方程参数x的计算( )A a值是明显不对的B b值是明显不对的C a值和b值都是不对的 C a值和6值都是正确的7.在线性相关的条件下,自变量的均方差为2,因变量均方差为5,而相关系数为0.8时,则其回归系数为:( )A 8B 0.32C 2D 12.58.进行相关分析,要求相关的两个变量( )A都是随机的B都不是随机的C一个是随机的,一个不是随机的D随机或不随机都可以9.下列关系中,属于正相关关系的有( )A合理限度内,施肥量和平均单产量之间的关系B产品产量与单位产品成本之间的关系C商品的流通费用与销售利润之间的关系D流通费用率与商品销售量之间的关系10.相关分析是研究( )A变量之间的数量关系B变量之间的变动关系C变量之间的相互关系的密切程度D变量之间的因果关系11.在回归直线y c=a+bx,b<0,则x与y之间的相关系数( )A =0B =lC 0<<1D -1<<0r r r r12.在回归直线yc=a+bx中,b表示( )A当x增加一个单位,,y增加a的数量B当y增加一个单位时,x增加b的数量C当x增加一个单位时,y的均增加量D当y增加一个单位时,x的平均增加量13.当相关系数r=0时,表明( )A现象之间完全无关B相关程度较小C现象之间完全相关D无直线相关关系14.下列现象的相关密切程度最高的是( )A某商店的职工人数与商品销售额之间的相关系数0.87B流通费用水平与利润率之间的相关关系为-0.94C商品销售额与利润率之间的相关系数为0.51D商品销售额与流通费用水平的相关系数为-0.8115.估计标准误差是反映( )A平均数代表性的指标B相关关系的指标C回归直线的代表性指标D序时平均数代表性指标三、多项选择题1.下列哪些现象之间的关系为相关关系( )A家庭收入与消费支出关系B圆的面积与它的半径关系C广告支出与商品销售额关系D单位产品成本与利润关系E在价格固定情况下,销售量与商品销售额关系2.相关系数表明两个变量之间的( )A线性关系B因果关系C变异程度D相关方向E相关的密切程度3.对于一元线性回归分析来说( )A两变量之间必须明确哪个是自变量,哪个是因变量B回归方程是据以利用自变量的给定值来估计和预测因变量的平均可能值C可能存在着y依x和x依y的两个回归方程D回归系数只有正号E 确定回归方程时,尽管两个变量也都是随机的,但要求自变量是给定的。
数理统计回归分析大作业

《应用数理统计》第一次大作业回归分析姓名:学号:班级:2014-12-20国家财政收入的多元线性回归模型摘 要:本文以多元线性回归为出发点,选取我国自1990至2009年连续20年的财政收入为因变量,初步选取了7个影响因素,并利用统计软件PASW Statistics 17.0对各影响因素进行了筛选,最终确定了能反映财政收入与各因素之间关系的回归方程:43806.0044.0357.817y x x ++=从而得出了结论,最后我们用2010年的数据进行了验证,得出的结果(86482.00)在误差范围内,表明这个模型可以正确反映影响财政收入的各因素的情况。
关键词:多元线性回归,逐步回归法,财政收入,SPSS0符号说明变 量 符号 财政收入 Y 工 业 X 1 农 业 X 2 进出口总额 X 3 建 筑 业 X 4 人 口 X 5 商品销售额 X 6 国内生产总值X 71 引言定义:所谓回归分析法,是在掌握大量观察数据的基础上,利用数理统计方法建立因变量与自变量之间的回归关系函数表达式(称回归方程式)。
回归分析中,当研究的因果关系只涉及因变量和一个自变量时,叫做一元回归分析;当研究的因果关系涉及因变量和两个或两个以上自变量时,叫做多元回归分析。
此外,回归分析中,又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的,分为线性回归分析和非线性回归分析。
通常线性回归分析法是最基本的分析方法,遇到非线性回归问题可以借助数学手段化为线性回归问题处理。
回归分析法预测是利用回归分析方法,根据一个或一组自变量的变动情况预测与其有相关关系的某随机变量的未来值。
进行回归分析需要建立描述变量间相关关系的回归方程。
根据自变量的个数,可以是一元回归,也可以是多元回归。
根据所研究问题的性质,可以是线性回归,也可以是非线性回归。
本文应用逐步回归的方法进行分析。
中国作为世界第一大发展中国家,要实现中华民族的伟大复兴,必须把发展放在第一位。
回归分析大作业
回归大作业国内旅游消费影响的回归分析一、问题引入我国第三产业发展迅速,在2010年其已占国内生产总值的43.14%,而旅游业在第三产业中占有重要地位,且与餐饮、住宿、休闲、运输等产业联系密切,所以此次分析以探究国内旅游消费的影响为目的,并建立回归模型。
二、模型设计运用多元线性模型拟合,若拟合效果不显著,则进行log或平方根变换或使用多项式拟合等其他模型。
1、相关性分析,首先确定与因变量有相关性的变量。
2、建立全模型多元线性回归,若回归方程F检验未通过,则查找原因、更换模型;若有部分回归系数检验未通过,则进行选元(步骤2),剔除部分变量再继续;若所有检验都良好,则模型初步确立,跳过步骤2。
3、运用逐步回归方法筛选变量,并进行t检验,若效果显著,则可初步确立多元线性回归模型;若仍有部分变量未通过检验,则再单独进行变量筛选,综合运用AIC准则等确定剔除变量,直至所有变量都通过t检验。
4、回归诊断。
进行残差分析,检验残差是否满足正态分布,是否有相关性,也即自变量间是否有自相关性,检验是否存在异常值和强影响值,是否存在异方差性,是否存在多重共线性。
若以上问题存在,则需修改模型,或重新筛选变量,或增减样本。
5、模型最终确立。
数据来源:《中国统计年鉴2011》数据说明:Year:年份。
Income:国民总收入,单位亿元。
Number:旅游人数。
Expense:人均旅游花费,单位元。
Level:居民消费水平指数,以1978年为基年。
Road:公路里程,单位万公里。
Rail:铁路里程,单位万公里。
Air:民航里程,单位万公里。
Roadtran:公路客运量,单位万人。
Railtran:铁路客运量,单位万人。
Shiptran:水路客运量,单位万人。
Airtran:民航客运量,单位万人。
Travel:国内旅游消费总额,单位亿元。
四、回归分析1、相关性首先分析相关性,画出散布阵。
可较为直观地看出,travel与各变量间有较强的相关性,除了road,和shiptran两项,做相关性检验,可见,travel与road是线性相关的,相关系数为0.93,p-value = 4.563e-08,而travel与shiptran不相关,p-value = 0.9983,所以可先排除shiptran,再做回归。
医学统计学考题(按章节)第4题【15分】__回归分析

四、回归分析 15分可能涉及范围:多元线性回归、logistic 回归。
要求: 1、提供某一资料,选择统计分析方法2、偏回归系数、标准偏回归系数、决定系数、校正决定系数、OR 等常用指标的意义与应用3、列回归方程例 27名糖尿病人的血清总胆固醇、甘油三脂、空腹胰岛素、糖化血红蛋白、空腹血糖的测量值如下表:(1)欲分析影响空腹血糖浓度的有关因素,宜采用什么统计分析方法?多元线性回归分析(2)已知甘油三酯(X2)、胰岛素(X3)和糖化血红蛋白(X4)是主要影响因素,现欲比较上述因素对血糖浓度的相对影响强度,应计算何种指标?标准偏回归系数可用来比较各自变量Xj 对Y 的影响强度,有统计意义下,回归系数绝对值越大,对Y 的作用越大。
SPSS 输出的多元回归分析结果中给出的各变量的标准偏回归系数,比较三个标准偏回归系数:甘油三脂0.354: 胰岛素0.360: 糖化血红蛋白0.413≈1:1.02:1.17(倍) 糖化血红蛋白对血糖的影响强度大小依次为:糖化血红蛋白X4、胰岛素X3、甘油三脂X2(3)分析其回归模型的好坏宜选用何种指标?校正决定系数( R 2a )作为评价标准一般说决定系数(R 2)越大越优,但由于R 2是随自变量的增加而增大,因此,不能简单地以R 2作为评价标准,而是用校正决定系数( R 2a )作为评价标准。
R 2a 不会随无意义的自变量增加而增大。
(4)根据给出SPSS 结果,做出正确的结论。
空腹血糖浓度与总胆固醇无关,与甘油三脂、空腹胰岛素、糖化血红蛋白线性相关。
(5)列出回归方程。
最优回归方程为:432663.0287.0402.05.6ˆX X X y+-+= Model Summary(最终模型的拟合优度检验验表)相关分析【完全分析答案】jszb1、此资料包含有四个变量,属于多变量计量资料,为多因素设计。
要分析多因素对空腹血糖浓度的影响,宜采用 多元线性回归分析。
2、根据样本数据求得模型参数β0, β1, β2, β3,β4的估计值b0,b1,b2,b3,b4β0又称为截距,β1, β2, …,βm 称为偏回归系数(partial regressin coefficient )或简称为回归系数。
回归分析练习题及参考答案
求:(1)人均GDP 作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP 为5000元,预测其人均消费水平。
(7)求人均GDP 为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的R 方估计的标准差1 .998(a) 0.996 0.996 247.303a. 预测变量:(常量), 人均GDP(元)。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F 检验:回归系数的检验:t 检验注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型 非标准化系数标准化系数t 显著性B 标准误 Beta1(常量) 734.693 139.540 5.2650.003 人均GDP (元)0.3090.0080.99836.4920.000a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(6)某地区的人均GDP 为5000元,预测其人均消费水平为 734.6930.30950002278.693y =+⨯=(元)。
统计学习题——回归分析

回归分析例1、假定一个4家庭的随机样本的年收入和年节余如下表所示(单位:千元):1) 估计总体回归直线X Y βα+=2) 构造斜率β的95%置信区间;3) 作图画出4个样本点和拟合的直线,然后尽你所能在图中表示由2)的置信区间所给出的可接受的斜率(范围)。
解:(1) 方法1因为X Y βα+=,X =(4.8+7.2+8.5+9.5)/4=7.5 Y =(1.2+3.0+3.5+3.5)/4=2.8 记i x =i X -X ,i y =i Y -Y所以βˆ=∑∑2x iii xy=0.513732(代入数值计算过程略), =αˆY -βˆ*X = -1.052989 即估计总体回归方程为:Y=-1.052989+0.513732X.即估计总体回归方程为:Y=-1.052989+0.513732X. 说明结果一致。
(2)∑2ie =∑2iy-2ˆβ∑2ix=3.58-0.513732*0.513732*12.38=0.312666(与上一致)2Òˆ=2n 2-∑ie =0.156333。
(n =4) Se(βˆ)=∑2Òˆix =0.11237。
所以β的95%置信区间为(βˆ-2/t a * Se(βˆ),βˆ+2/t a * Se(βˆ))=(0.513732-4.3027*0.11237,0.513732+4.3027*0.11237)=(0.0304,1.0027)(自由度为2)(3)在Eviews 中作X-Y 图如下:1.01.52.02.53.03.54.056789XY例2、从某单位随机地抽取了相互独立的两个样本(男、女职工收入),其月收入数据如下:男:2300,2500,3000,2800,2600; 女:2400,2200,2000,2500,2700 用Y 表示收入,用哑变量X 表示性别:其中对于男性X =1,对于女性X =0。
1) 画出Y 对X 的图形;2) 用眼睛拟合一条Y 对X 的回归线;3) 计算Y 对X 的回归线;与2)中用眼睛拟合的相比,后者的精度如何? 4) 构造一个斜率为95%的置信区间,用简单的语言解释一下它的意义; 5) 在 5%的错误水平下,检验收入是否与性别无关; 6) 4)和5)的结果是否度量了该单位对女性的歧视? 解:(1)在Eviews 中作X-Y 图如下:180020002200240026002800300032000.00.20.40.60.81.0XY(2)由上图用眼睛拟合拟合一条Y 对X 的回归线:Y=2390+200X (3) 利用Eviews 进行回归:即回归方程为:Y=2380+280X与(2)中直观看到的:我们发现在斜率差距较大。
统计学 第九章相关与回归分析作业

课外作业:
葡萄酒能降低心脏病死亡率吗
适量饮用葡萄酒可以预防心脏病。
我们来看看一些国家的资料。
表中是10个发达国家一年的葡萄酒消耗量(平均每人喝葡萄酒摄取酒精的升数X)以及一年中因心脏病死亡的人数(每10万人死亡人数Y)。
(1)根据下表中的数据制作一个散点图来说明:一国的葡萄酒消耗量是否有助于解释心脏病的死亡率。
(2)为何在求相关系数和拟合回归方程时经常要做散点图。
(3)计算从葡萄酒得到的酒精和心脏病死亡率两变量间相关系数,并评价两变量的相关关系的程度和方向;以心脏病死亡率为因变量,以从葡萄酒得到的酒精为自变量拟合简单线性回归方程,并解释方程中的两系数的含义。
(4)请简要分析相关系数的意义。
统计学回归分析大作业
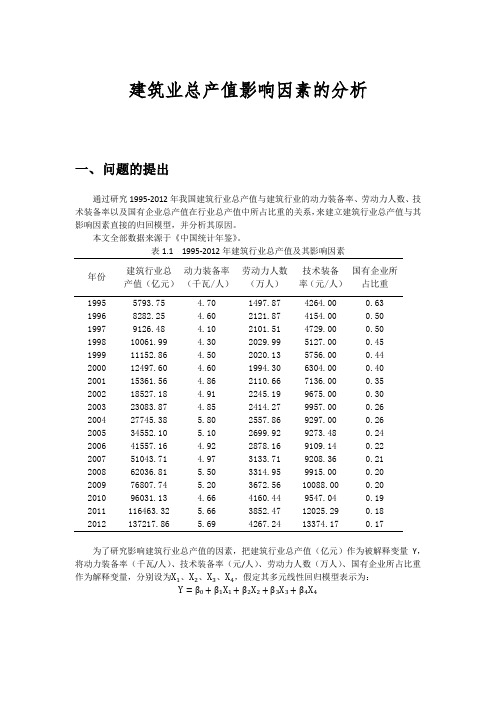
建筑业总产值影响因素的分析一、问题的提出通过研究1995-2012年我国建筑行业总产值与建筑行业的动力装备率、劳动力人数、技术装备率以及国有企业总产值在行业总产值中所占比重的关系,来建立建筑行业总产值与其影响因素直接的归回模型,并分析其原因。
本文全部数据来源于《中国统计年鉴》。
表1.1 1995-2012年建筑行业总产值及其影响因素年份建筑行业总产值(亿元)动力装备率(千瓦/人)劳动力人数(万人)技术装备率(元/人)国有企业所占比重1995 5793.75 4.70 1497.87 4264.00 0.631996 8282.25 4.60 2121.87 4154.00 0.501997 9126.48 4.10 2101.51 4729.00 0.501998 10061.99 4.30 2029.99 5127.00 0.451999 11152.86 4.50 2020.13 5756.00 0.442000 12497.60 4.60 1994.30 6304.00 0.402001 15361.56 4.86 2110.66 7136.00 0.352002 18527.18 4.91 2245.19 9675.00 0.302003 23083.87 4.85 2414.27 9957.00 0.262004 27745.38 5.80 2557.86 9297.00 0.262005 34552.10 5.10 2699.92 9273.48 0.242006 41557.16 4.92 2878.16 9109.14 0.222007 51043.71 4.97 3133.71 9208.36 0.212008 62036.81 5.50 3314.95 9915.00 0.202009 76807.74 5.20 3672.56 10088.00 0.202010 96031.13 4.66 4160.44 9547.04 0.192011 116463.32 5.66 3852.47 12025.29 0.182012 137217.86 5.69 4267.24 13374.17 0.17为了研究影响建筑行业总产值的因素,把建筑行业总产值(亿元)作为被解释变量Y,将动力装备率(千瓦/人)、技术装备率(元/人)、劳动力人数(万人)、国有企业所占比重作为解释变量,分别设为X1、X2、X3、X4,假定其多元线性回归模型表示为:Y=β0+β1X1+β2X2+β3X3+β4X4二、相关性问题图2.1 各变量之间的散点图散点图如图2.1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建筑业总产值影响因素的分析一、问题的提出通过研究1995-2012年我国建筑行业总产值与建筑行业的动力装备率、劳动力人数、技术装备率以及国有企业总产值在行业总产值中所占比重的关系,来建立建筑行业总产值与其影响因素直接的归回模型,并分析其原因。
本文全部数据来源于《中国统计年鉴》。
表1.1 1995-2012年建筑行业总产值及其影响因素年份建筑行业总产值(亿元)动力装备率(千瓦/人)劳动力人数(万人)技术装备率(元/人)国有企业所占比重1995 5793.75 4.70 1497.87 4264.00 0.631996 8282.25 4.60 2121.87 4154.00 0.501997 9126.48 4.10 2101.51 4729.00 0.501998 10061.99 4.30 2029.99 5127.00 0.451999 11152.86 4.50 2020.13 5756.00 0.442000 12497.60 4.60 1994.30 6304.00 0.402001 15361.56 4.86 2110.66 7136.00 0.352002 18527.18 4.91 2245.19 9675.00 0.302003 23083.87 4.85 2414.27 9957.00 0.262004 27745.38 5.80 2557.86 9297.00 0.262005 34552.10 5.10 2699.92 9273.48 0.242006 41557.16 4.92 2878.16 9109.14 0.222007 51043.71 4.97 3133.71 9208.36 0.212008 62036.81 5.50 3314.95 9915.00 0.202009 76807.74 5.20 3672.56 10088.00 0.202010 96031.13 4.66 4160.44 9547.04 0.192011 116463.32 5.66 3852.47 12025.29 0.182012 137217.86 5.69 4267.24 13374.17 0.17为了研究影响建筑行业总产值的因素,把建筑行业总产值(亿元)作为被解释变量Y,将动力装备率(千瓦/人)、技术装备率(元/人)、劳动力人数(万人)、国有企业所占比重作为解释变量,分别设为X1、X2、X3、X4,假定其多元线性回归模型表示为:Y=β0+β1X1+β2X2+β3X3+β4X4二、相关性问题图2.1 各变量之间的散点图散点图如图2.1所示。
简单相关系数如表2.1所示。
表2.1 简单相关系数可以看出,建筑业总产值与劳动力人数相关度很高,与技术装备率和国有企业所占比重相关度也叫较高,而动力装备率相关度一般。
但是由于所有的p值检验都小于0.05,所以变量还是可以用于建模的。
三、建立回归模型利用强行进入发,建立初步模型。
输出结果如下:1.拟合优度检验可以看出,复相关系数R为0.990,样本决定系数为0.981,调整后相关系数为0.975,说明方程拟合良好。
2.回归方程显著性检验由表可知,F为167.393,P值为0,.000,说明回归方程高度显著,各解释变量整体上对被解释变量有高度显著的线形影响。
3.回归系数检验由表可知,动力装备率,即X1P值大于0.05,未通过检验。
其他变量均通过检验。
4.残差分析——正态性检验如图所示,残差与正态分布直接存在较小差距,基本符合正态分布。
5.残差分析——异方差分析有图表可知,被解释变量与残差相关系数为0.055,P 值0.829,可以说没有异方差现象。
6.自相关检验D.W值为1.435.。
查表得,dl=0.574,du=1.631,所以不确定。
有图示可以认为,残差之间不存在自相关性。
7.共线性诊断只有技术装备率的VIF大于10.存在轻微共线性。
所以,需要修改模型。
四、修改模型1.模型存在的问题1.动力装备率X1未经过回归检验;2.有轻微的共线性;2.修改删除X1,再利用强行进入法建立模型。
得到结果如下:Descriptive StatisticsMean Std. Deviation N建筑行业总产值42074.59722 40200.244255 18 劳动力人数(万人)2726.283333 827.8771536 18 技术装备率(元/人)8274.41556 2691.388053 18 国有企业所占比重.3166666667 .137******** 18Correlations国有企业所占比重Pearson Correlation 建筑行业总产值-.747劳动力人数(万人)-.842技术装备率(元/人)-.928国有企业所占比重 1.000 Sig. (1-tailed) 建筑行业总产值.000劳动力人数(万人).000技术装备率(元/人).000国有企业所占比重.N 建筑行业总产值18劳动力人数(万人)18 技术装备率(元/人)18 国有企业所占比重18ANOVA bModel Sum of Squares df Mean Square FSig.1 Regression 2.693E10 3 8.976E9 231.163 .000aResidual 5.436E8 14 38831754.722Total 2.747E10 17a. Predictors: (Constant), 国有企业所占比重, 劳动力人数(万人), 技术装备率(元/人)b. Dependent Variable: 建筑行业总产值1 (Constant) -228727.624 23531.485劳动力人数(万人)50.480 3.486技术装备率(元/人)8.666 1.552国有企业所占比重194120.926 31268.974Coefficients aModel Correlations Collinearity Statistics Part Tolerance VIF1 (Constant)劳动力人数(万人).544 .274 3.647技术装备率(元/人).210 .131 7.635国有企业所占比重.233 .123 8.138 a. Dependent Variable: 建筑行业总产值Coefficient Correlations aModel 国有企业所占比重劳动力人数(万人)技术装备率(元/人)1 Correlations 国有企业所占比重 1.000 .343 .761劳动力人数(万人).343 1.000 -.245技术装备率(元/人).761 -.245 1.000 Covariances 国有企业所占比重9.777E8 37445.783 36909.143 劳动力人数(万人)37445.783 12.156 -1.324技术装备率(元/人)36909.143 -1.324 2.408 a. Dependent Variable: 建筑行业总产值Collinearity Diagnostics aModel Dimension Eigenvalue Condition Index1 1 3.694 1.0002 .289 3.5763 .015 15.9414 .003 36.835Collinearity Diagnostics aModel DimensionVariance Proportions(Constant)劳动力人数(万人)技术装备率(元/人)国有企业所占比重1 1 .00 .00 .00 .002 .00 .01 .01 .043 .01 .88 .32 .004 .99 .11 .67 .96a. Dependent Variable: 建筑行业总产值Residuals Statistics aMinimum Maximum MeanPredicted Value 4224.78906 135586.56250 42074.59722Std. Predicted Value -.951 2.350 .000 Standard Error of PredictedValue2049.747 4660.526 2824.607 Adjusted Predicted Value 3194.88916 133515.82813 42288.54061 Residual -8164.224609 11562.820313 .000000Std. Residual -1.310 1.856 .000Stud. Residual -1.537 2.123 -.016Deleted Residual -11240.480469 15130.299805 -213.943388Stud. Deleted Residual -1.625 2.484 .001Mahal. Distance .895 8.564 2.833Cook's Distance .000 .348 .071 Centered Leverage Value .053 .504 .167Residuals Statistics aStd. Deviation N Predicted Value 39800.509369 18 Std. Predicted Value 1.000 18 Standard Error of Predicted830.159 18 ValueAdjusted Predicted Value 39527.973748 18 Residual 5655.005935 18 Std. Residual .907 18 Stud. Residual 1.022 18 Deleted Residual 7225.228735 18 Stud. Deleted Residual 1.085 18 Mahal. Distance 2.405 18 Cook's Distance .094 18 Centered Leverage Value .141 18a. Dependent Variable: 建筑行业总产值1.拟合优度分析有表可知,调整样本决定系数为0.976,拟合良好。
2.回归方程显著性检测F=231.163。
P=0.000,故明显显著。
3.回归系数显著性检验三个变量t值均大于1.734,P值均为0.000,故通过检验。
4.残差分析——正态性检验有图可以看到,基本符合正态性假设。
5.残差分析——异方差分析由残差图和残差相关系数得知,不存在显著的异方差。
6.自相关性分析。
