水轮机 相似理论
合集下载
水轮机的相似理论
第三章水轮机的相似理论及综合特性曲线§3.1 相似理论概述一、几个基本概念1、水轮机特性水轮机在不同工况下运行时，各运行参数(H，Q，n，N，η，б)及这些参数之间的关系，称水轮机的特性。
水轮机设计、制造、选型、最佳运行方案、限制条件。
由于水轮机水流条件复杂，研究水轮机特性靠理论与实验相结合。
2、模型试验试验研究：原型：尺寸大，试验困难，不经济。
模型：(D: 250～460mm，H：2～6m)快、方便，易测量数据，较准确。
3、相似理论研究相似水轮机之间存在的相似规律，并确立这些参数之间的换算关系的理论。
二、水轮机相似条件保证模型水轮机与原型水轮机相似，只有符合一定的相似条件(水流运动相似)。
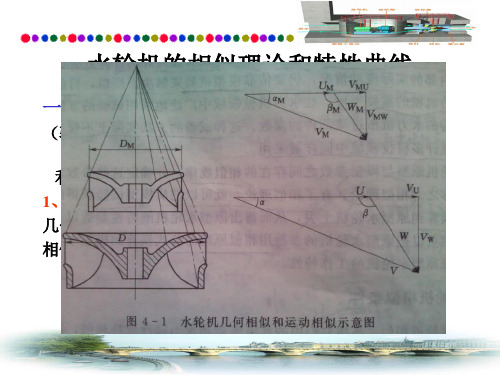
1、几何相似：过流通道几何形状相似(1)、过流通道的对应角相等：βe1＝βe1M ；βe2＝βe2M ；Φ＝ΦM……(2)、对应尺寸成比例：D1/D1M＝b0/b0M＝a0/a0M＝…….(3)、对应部位的相对糙率相等：△/ D1＝△M/D1M几何相似: 大大小小的一套水轮机系列——轮系，同一轮系的水轮机才能建立运动相似和动力相似。
2、运动相似：同一轮系水轮机、工况相似(1)、过流通道的对应点的速度方向相同(2)、过流通道的对应点的速度大小对成比例即速度三角形相似。
3、 动力相似： (压力、惯性力、重力、摩擦力等)同一轮系水轮机，水流对应点所受的作用力是同名力、方向相同、大小成比例。
3.2 水轮机的相似定律、单位参数及比转速一、水轮机的相似定律相似定律：建立模型击原型水轮机各个参数(H 、n 、N 、η)之间的关系。
1． 流量相似律：几何相似、相似工况下流量之间的关系。
(a=a M )=SMM M rMM H DQ ηη21CH DQ Sr =ηη2111,,,D H D H M M 均为固定值，Q M 可以测得，若ηrM 、ηsM 、ηr 、ηs 已知，可求出Q 。
2. 转速相似律：即原型和模型水轮机转速之间的关系。
水轮机的相似理论
第三章水轮机的相似理论及综合特性曲线§3.1 相似理论概述一、几个基本概念1、水轮机特性水轮机在不同工况下运行时，各运行参数(H，Q，n，N，η，б)及这些参数之间的关系，称水轮机的特性。
水轮机设计、制造、选型、最佳运行方案、限制条件。
由于水轮机水流条件复杂，研究水轮机特性靠理论与实验相结合。
2、模型试验试验研究：原型：尺寸大，试验困难，不经济。
模型：(D: 250～460mm，H：2～6m)快、方便，易测量数据，较准确。
3、相似理论研究相似水轮机之间存在的相似规律，并确立这些参数之间的换算关系的理论。
二、水轮机相似条件保证模型水轮机与原型水轮机相似，只有符合一定的相似条件(水流运动相似)。
1、几何相似：过流通道几何形状相似(1)、过流通道的对应角相等：βe1＝βe1M ；βe2＝βe2M ；Φ＝ΦM……(2)、对应尺寸成比例：D1/D1M＝b0/b0M＝a0/a0M＝…….(3)、对应部位的相对糙率相等：△/ D1＝△M/D1M几何相似: 大大小小的一套水轮机系列——轮系，同一轮系的水轮机才能建立运动相似和动力相似。
2、运动相似：同一轮系水轮机、工况相似(1)、过流通道的对应点的速度方向相同(2)、过流通道的对应点的速度大小对成比例即速度三角形相似。
3、 动力相似： (压力、惯性力、重力、摩擦力等)同一轮系水轮机，水流对应点所受的作用力是同名力、方向相同、大小成比例。
3.2 水轮机的相似定律、单位参数及比转速一、水轮机的相似定律相似定律：建立模型击原型水轮机各个参数(H 、n 、N 、η)之间的关系。
1． 流量相似律：几何相似、相似工况下流量之间的关系。
(a=a M )=SMM M rMM H DQ ηη21CH DQ Sr =ηη2111,,,D H D H M M 均为固定值，Q M 可以测得，若ηrM 、ηsM 、ηr 、ηs 已知，可求出Q 。
2. 转速相似律：即原型和模型水轮机转速之间的关系。
第4章 水轮机相似理论与特性曲线
二、单位参数
H=1m的标准水轮机参数 1、定义：指转轮直径D1=1m，水头H=1m的标准水轮机参数。 定义：指转轮直径D =1m，水头H=1m的标准水轮机参数。 称为单位转速，表示转轮直径D =1m，水头H=1m H=1m时水轮机具有的 1）n11—称为单位转速，表示转轮直径D1=1m，水头H=1m时水轮机具有的 7 转速；（ ；（P86 12） 转速；（P86 公式 4-12）
6
第四章 水轮机相似理论与特性曲线 §4.2 相似律与单位参数
水轮机相似律（参数之间关系） 一、 水轮机相似律（参数之间关系）
1、转速相似律：（P85 公式4-8） 转速相似律：（P85 公式4 ：（ 物理含义：表示原型与模型水轮机在相似工况下转速之间的相互关系， 物理含义：表示原型与模型水轮机在相似工况下转速之间的相互关系， 它适用于同一系列的水轮机在相似工况下， 转速与直径成反比 与直径成反比， 它适用于同一系列的水轮机在相似工况下，其转速与直径成反比，与水头平方 根成正比。 根成正比。 流量相似律：（P86公式 10） ：（P86公式4 2、流量相似律：（P86公式4-10） 物理含义：表示原型与模型水轮机在相似工况下流量之间的相互关系， 物理含义：表示原型与模型水轮机在相似工况下流量之间的相互关系， 它适用于同一系列的水轮机在相似工况下， 流量与直径平方成正比 与直径平方成正比， 它适用于同一系列的水轮机在相似工况下，其流量与直径平方成正比，与水头 平方根成正比。 平方根成正比。 出力相似律： P86公式 11） 公式4 3、出力相似律：（P86公式4-11） 物理含义：表示原型与模型水轮机在相似工况下出力之间的相互关系， 物理含义：表示原型与模型水轮机在相似工况下出力之间的相互关系， 它适用于同一系列的水轮机在相似工况下， 出力与直径平方成正比 与直径平方成正比， 它适用于同一系列的水轮机在相似工况下，其出力与直径平方成正比，与水头 平方根的三次方成正比。 平方根的三次方成正比。
第四章水轮机相似理论
见课本P89页（新）或课本P69页（老）
虽然高比转速水轮机存在转轮出口动能损 失大、气蚀不佳等不足之处，但它的能量特性 好是十分明显的，在同样水头下提高比转速是 水轮机的一种发展趋势，它可使水轮机尺寸和 电站开挖量不增加的情况下增加出力。 如：美国大古力三厂第二期工程与第一期一 样，H=86.9米，D1=8.9米，将ns从210提高到 270，出力则由60万kw增大到70万kw。 在世界范围内，从60年代到80年代，HL 式水轮机的ns提高了17%，ZZ式提高了15%， CJ式提高了9%。
二、单位流量
水轮机转轮直径为1m，在有效水头为1m 时，水轮机的实际有效流量，称为单位流量 ，用符号 Q11 表示，单位 m 3 s
QT D
2 1T
H T T
QM D
2 1M
H MM
C Q11
表达式为
Q11
Q D
2 1
H
Q Q11 2 D1 H
上式表明： 在相同转轮直径 D1 和水头
b0 21.47 0.44 D1 ns
轴流式：
②
ns
D1 与转轮进、出口直径比 D2
的关系
依照经验公式
D1 1 D2 0.96 0.00038 n s
可以看出，
D1 ns 在D1相同下D2 D2
③
n s 与转轮叶片数 Z
ns Z
ns
ns
的关系
④
与叶片形状的关系
H
条件下，
单位流量越大，则水轮机的实际过流能力越大 ，因此，在一定出力条件下，选择单位流量大 的机型，可缩小水轮机直经，或在一定直径 D1 下，选择单位流量大的机型，可获得较大的水 轮机出力。
水轮机的相似原理.pptx
e2 e2M
M ，
（2） D1 = b0 = a0 L(常数) D1M b0M a 0M
2、运动相似
前提：几何相似
相似工况 （1） 1 1M 1 1M ，
（2） v1 = u1 = w1 常数 v1M u1M w1M
3、动力相似
p = F = G L(常数) pM FM GM M
二、水轮机的相似定律
相似定律：水轮机在相似工况下运行时，各工 作参数(H、Q、n、N、η)之间的固定关系。 包括转速相似率、流量相似率和出力相似率。
1、 转速相似律：转速 有效水头 直径
Vx kvx 2gHH
转 速 相 似 律
1、 转速相似律：转速 有效水头 直径
Vx kvx 2gHH
n D1M HH C nM D1 H MHM
水轮机的相似原理
知识回顾：
水流在水轮机内运动复杂
H Q n N
试验
原型试验 校核与检测 模型试验 设计与研究 D 1m
问题:
水轮机的相似原理
1 模型如何模拟原相型似水条轮件机？ 相似条件 相似原理
2 模型结果如何应相用似到定原律型中？ 相似定律
一、水轮机相似条件
1、几何相似
轮系
（1） e1 e1M
2、 流量相似律：有效流量 有效水头 直径
流 量 相 似 律
2、 流量相似律：有效流量 有效水头 直径
QV D12 HH C QMVM D1M 2 HMHM
3、出力相似律：出力 有效水头 直径
出 力 相 似 律
3、出力相似律：出力 有效水头 直径
N NM
m D12 mM D12M
(HH )3/2 (H M HM )3/水轮机直径 D1M 0.25m ,模型水头HM 3.5m , 模型效率 M 90% ,相应的模型转速nM 500 r min ， 模型流量 QM 0.15 m3 s
水轮机的相似原理2
∠β 2 ap = ∠β 2 am ∠β 1ap = ∠β 1am D1 p D2 p b0 p = = = 常数） （常数） D1m D2 m b 0m
疆大学电气学 华
轮机
论
水轮机相似： 水轮机相似：两个水流中同名称运动要素特征值 相等或对应特征值比值存在共同的比例。 相等或对应特征值比值存在共同的比例。 一、水轮机相似条件 水轮机相似必须满足水轮机相似条件， 水轮机相似必须满足水轮机相似条件，包括应满 足它们的几何相似 运动相似和动力相似。 几何相似、 足它们的几何相似、运动相似和动力相似。 1. 几何相似 指原型与模型水轮机过流通道的几何形状相似， 指原型与模型水轮机过流通道的几何形状相似， 即所有对应空间角度相等， 即所有对应空间角度相等，并且一切线形尺寸成 一定的比例。 一定的比例。
疆大学电气学 华
节
条件
3. 动力相似 模型和原型流道内各对应点的流体质点所受的同 名称力的方向相同，大小成比例且比值相等。 名称力的方向相同，大小成比例且比值相等。 流体在泵与风机中流动时受到四种力的作用 ①惯性力 ②黏性力 ③重力 ④压力 主导作用 可忽略 表征惯性力和黏性力动力相似的准则数是 雷诺数 若 Rep = Rem 满足动力相似
疆大学电气学 华
节
条件
为了保证流体流动相似，必须具备几何相似、 为了保证流体流动相似，必须具备几何相似、运 几何相似 动相似和动力相似三个条件 三个条件。 动相似和动力相似三个条件。 即必须满足模型和原型中任一对应点上的同一 物理量之间保持比例关系。 物理量之间保持比例关系。 几何尺寸、运动参数和动力参数 几何尺寸、运动参数和 下标“ 表示模型的各参数 下标“ 表示原型 表示模型的各参数， 下标“m”表示模型的各参数，下标“p”表示原型 的各参数。 的各参数。 1. 几何相似 模型和原型各对应点的几何尺寸成比例， 模型和原型各对应点的几何尺寸成比例，且比值 相等，各对应角、叶片数相等。 相等，各对应角、叶片数相等。
疆大学电气学 华
轮机
论
水轮机相似： 水轮机相似：两个水流中同名称运动要素特征值 相等或对应特征值比值存在共同的比例。 相等或对应特征值比值存在共同的比例。 一、水轮机相似条件 水轮机相似必须满足水轮机相似条件， 水轮机相似必须满足水轮机相似条件，包括应满 足它们的几何相似 运动相似和动力相似。 几何相似、 足它们的几何相似、运动相似和动力相似。 1. 几何相似 指原型与模型水轮机过流通道的几何形状相似， 指原型与模型水轮机过流通道的几何形状相似， 即所有对应空间角度相等， 即所有对应空间角度相等，并且一切线形尺寸成 一定的比例。 一定的比例。
疆大学电气学 华
节
条件
3. 动力相似 模型和原型流道内各对应点的流体质点所受的同 名称力的方向相同，大小成比例且比值相等。 名称力的方向相同，大小成比例且比值相等。 流体在泵与风机中流动时受到四种力的作用 ①惯性力 ②黏性力 ③重力 ④压力 主导作用 可忽略 表征惯性力和黏性力动力相似的准则数是 雷诺数 若 Rep = Rem 满足动力相似
疆大学电气学 华
节
条件
为了保证流体流动相似，必须具备几何相似、 为了保证流体流动相似，必须具备几何相似、运 几何相似 动相似和动力相似三个条件 三个条件。 动相似和动力相似三个条件。 即必须满足模型和原型中任一对应点上的同一 物理量之间保持比例关系。 物理量之间保持比例关系。 几何尺寸、运动参数和动力参数 几何尺寸、运动参数和 下标“ 表示模型的各参数 下标“ 表示原型 表示模型的各参数， 下标“m”表示模型的各参数，下标“p”表示原型 的各参数。 的各参数。 1. 几何相似 模型和原型各对应点的几何尺寸成比例， 模型和原型各对应点的几何尺寸成比例，且比值 相等，各对应角、叶片数相等。 相等，各对应角、叶片数相等。
4_水轮机相似理论
vm1 vm1M
2 vm1 Qv D1M 2 vm1M QMvM D1
D13 D1M Q v 3 QmvM D1 M D1
h hM vM v
vm1 u1 D1n v m1M u1M D1M nM nD13 Q v H h QMvM nM D13M H M hM
对于水斗式水轮机，它的单位参数亦可按同样 的方法求得，不过这些参数是用射流直径d0、喷嘴个 数z0和转轮直径D1来表示的。
水斗式水轮机的单位参数分别为：
第三节 原、模型单位参数的换算
一、水轮机的效率换算
模型与原型不可能保持完全的力学相似，雷诺 数并不相等。因此由粘性力引起的水力摩擦相对损 失在原、模型中就不相等。 1.最优工况下的效率修正
单位参数的修正
n11T n11M n11
Q11T Q11M Q11
T 1n11M 3%n11M 在设计中一般规定，若n11 M
单位转速可不予修正，即
n11T n11M
Q11T Q11M
单位流量的修正值一般较小，可不作修正，
★几点说明：
③ 单位参数可由模型试验资料整理得出，这样在 水轮机设计、选型和运行中，可以很方便地应用它们 确定原形水轮机在相应工况下的参数。 ④ 可借助特征工况（如最优工况或限制工况）下 的单位参数，来进行水轮机不同轮系之间的比较。 最优单位参数可表示为：
五、水斗式水轮机的单位参数
以上所得出的相似律公式仅适用于反击式水轮 机。
N D H
2 1 3 2
NM D H M2 M
2 1M 3
1.单位转速： 直径为D1=1m，H1=1m 时，水轮机所具有的转速称为水轮机 的单位转速，单位为r/min.习惯用 n11 表示。 Dn n11 1 H
5水轮机的相似理论和特性曲线解析
水轮机的相似理论和特性曲线
水轮机运转综合特性曲线： • 用水轮机工作参数（P、H、 η）直接表达水轮机运行特性 的曲线。 • 选型设计中方案分析、比较 的依据 • 水电站运行管理、拟定机组 的运行方式及考察机组动力 特性的主要依据 • 机组运行人员检查水轮机运 行情况的依据
水轮机的相似理论和特性曲线
η ——原水轮机的最高效率η max η M——模型最优工况效率η Mmax ②非最优工况下的换算： 采用简化的等差修正法
max M max
M
水轮机的相似理论和特性曲线
2、单位参数的修正 模型与原型水轮机效率不同，单位参数也不完全相同。 单位转速修正（P91修正式） 单位流量修正 3、例析（综合应用） P92 例4-2 思考练习 • P107 2～6题 • 反复看例4-2，理解不同工况参数的分析、计算方法. • 为什么高比转速水轮机只适用于低水头水电站？（P88）
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
混流式水轮机综合特性曲线包含： • 等效率曲线 • 导叶等开度曲线 • 等空化系数曲线 • 5%功率限制线：各单位转速下95%（使水轮机有一定 的功率储备）最大功率工况点的连线。左侧是可运 行区，右侧是不可运行区。 • 不同工况下稳定性的等压力脉动A线 • 飞逸特性曲线 • 模型转轮的流道参数和模型试验条件 水轮机综合特性曲线是正确选择水轮机、分析水轮机性 能的依据。
水轮机的相似理论和特性曲线
④ 提高比转速——设法提高n11、Q11（研究方向） ns 3.13n11 Q11 (m.kw) 提问：为什么高比转速水轮机只适用于低水头水电站？ （P88）
水轮机的相似条件
水轮机的相似条件
1、几何相似：指从蜗壳进口到尾水管出口的过流通道的几何形状相似，尺寸成比例。
过流通道几何形状相似过流通道的对应角相等：βe1=βe1M；βe2=βe2M对应部位的相对糙率相等：/D1=M/D1M几何相似的一套水轮机系列——轮系。
同一轮系的水轮机才能建立运动相似和动力相似。
过流通道的对应点的速度大小对成比例，即速度三角形相似。
2、动力相似：指流道中对应点的流动方向相同，流速大小成比例常称速度三角形相似；压力、惯性力、重力、摩擦力等同一轮系水轮机，水流对应点所受的同名作用力方向相同、大小成比例。
第二节水轮机的相似率、单位参数和比转速一水轮机的相似定律相似定律：水轮机在相似工况下运行时，各工作参数H、n、N、η之间的固定关系。
3、动力相似律：指作用在液体和水轮机部件上的各种力的比率保持相同，即需保持以下准则数相等即参见弗劳德相似准则、雷诺相似准则、韦伯相似准则、斯特劳哈尔相似准则；即原型和模型水轮机出力之间的关系均为固定值QM可以测得若η0M、ηsM、η0、ηj已知，可求出Q。
03 水轮机的相似理论与模型实验
U12
U
2 2
2g
W1
W22 2g
Vx Kvx 2gHs
u1
D1n
60
K u1
2 gH s
nD1 nM D1M 常数
H s
H MsM
Q0 D12 HS
QM0M
D12M H MSM
常数 N
D12 (Hs )3/ 2 j
NM D12M (H M sM )3/ 2 jM
在进行水轮机模型试验时，由于试验装置情况和要求不同， 水轮机的模型直径和试验水头也不相同，因此模型试验得到 的参数也就不可能相同，这样就不便于进行水轮机的性能比 较。为了比较时有一个统一的标准，通常规定把模型试验成 果都统一换算到转轮直径为m,有效水头m时的水轮机参数， 这种参数就称为它为单位参数。
第三章 水轮机的相似理论与模型试验
第1节：水轮机的相似理论与单位参数 第2节：水轮机的效率换算与单位参数修正 第3节：水轮机的比转速
第4节：水轮机的模型试验 第5节：水轮机的飞逸特性
第1节：水轮机的相似理论与单位参数
水轮机系列： 相似理论：研究同系列水轮机的几何尺寸及特性参数间相似规 律、和转换关系的理论。
n11
nD1
H s
Q11
D12
Q
H S
N11
N
D12 (H S )3 / 2
目前在模型中整理试验成果时，或在初步设计时，都采用上述 公式，它应用简便，但比较粗糙，常作近似计算。
因此，单位参数可以表示出相似水轮机的特性，是几何相似水轮机保持 相似工况的一种判别准则。
同时对几何形状不同的各种系列水轮机，利用单位参数可以比较方便地进 行过流能力、转速高低、出力大小的性能比较，选择性能较好的转轮。
水轮机水力设计3-水轮机的相似理论
轴流式水轮机
水流通过转轮叶片的轴向流动 ，适用于中高水头。
冲击式水轮机
水流冲击转轮叶片，适用于高 水头。
比较
比较不同类型水轮机的性能特 点，选择适合特定工程条件的
水轮机类型。
水轮机性能的预测与优化
01
02
03
性能预测
基于相似理论，利用模型 实验数据预测实际水轮机 的性能。
优化设计Байду номын сангаас
根据预测结果，对水轮机 设计进行优化，提高运行 效率、降低能耗。
相似准则的应用
在水轮机设计和优化过程中，利用相似准则对不 同型号、不同工况下的水轮机进行比较和分析。
通过相似准则，可以预测新设计水轮机的性能表 现，为优化设计和改进提供依据。
利用相似准则，可以在实验室内对小型水轮机模 型进行实验，以预测实际大型水轮机的性能。
03
水轮机相似理论的实际应用
模型水轮机与实际水轮机的比较
关注水轮机内部流动的细节，深入研究水轮机的复杂流动结构
03
和机理。
THANKS
感谢观看
实例分析
分析实际工程中水轮机的 运行数据，验证相似理论 的准确性，为后续工程提 供参考。
04
水轮机相似理论的限制与挑战
相似理论的局限性
模型尺寸限制
相似理论要求模型与实际 水轮机在尺寸上保持一致， 但实际中很难实现完全一 致的缩放比例。
流体特性差异
相似理论假设流体是不可 压缩的，忽略了流体压缩 性对水轮机性能的影响。
相似理论在水轮机设计中的重要性
相似理论是水轮机设计的重要理论基 础，通过相似设计，可以在实验室内 对水轮机进行缩尺实验，预测实际运 行中的性能表现。
相似理论有助于实现水轮机设计的标 准化和系列化，提高设计效率，降低 研发成本。
高清图文+水轮机的相似原理、单位参数、比转速及特性曲线
(3) 综合参数：(Q1，n1，N1) ，轴功率N、η、б
(二) 特性曲线：各参数之间的关系曲线 (1) 线性特性曲线：反映2~3个参数之间的关系曲线 (2) 综合特性曲线：表示多个参数之间的关系，能较
完整地描述水轮机各运行工况的特性。
当H和N一定时，ns越高，汽蚀系数越大，增加厂 房开挖。
比转速增加，单位流量增加，b0/D1增大，叶片数 目减少。
水轮机的特性曲线及其绘制
ٛ 一、水轮机参数及特性曲线 (一) 水轮机参数：参数关系反映水轮机特性。 (1) 结构参数：转轮直径D1，导叶高度b0，导叶开度 a0，叶片转角Φ (2) 工作参数：H、Q、n 、Hs
参数n、H、 N之间的关系综合反映出来，代表了水轮机的轮系
特征。
ns随工况变化,一般按H设、N额、n额确定该水轮机轮系的特征参 数。
ns
ne N e
H
5/4 r
讨论：
相似水轮机，工况相似，ns相同，不同的ns ，反 映不同轮系水轮机特征。
当H一定时： ns ↑→N↑→n↑。机组尺寸缩小， 投资减少，因此提高比转速可以降低造价。
3、相似理论 研究相似水轮机之间存在的相似规律，
并确立这些参数之间的换算关系的理论。
二、水轮机相似条件
1、几何相似： 过流通道几何形状相似
(1) 过流通道的对应角相等：βe1＝βe1M ；βe2＝ βe2M ；Φ＝Φ M……
(2) 对应尺寸成比例：D1/D1M＝b0/b0M＝a0/a0M＝…….
(3) 对应部位的相对糙率相等：△/ D1＝△M/D1M 几何相似的大大小小的一套水轮机系列——轮系 同一轮系的水轮机才能建立运动相似和动力相似。
→
M D 1M
(二) 特性曲线：各参数之间的关系曲线 (1) 线性特性曲线：反映2~3个参数之间的关系曲线 (2) 综合特性曲线：表示多个参数之间的关系，能较
完整地描述水轮机各运行工况的特性。
当H和N一定时，ns越高，汽蚀系数越大，增加厂 房开挖。
比转速增加，单位流量增加，b0/D1增大，叶片数 目减少。
水轮机的特性曲线及其绘制
ٛ 一、水轮机参数及特性曲线 (一) 水轮机参数：参数关系反映水轮机特性。 (1) 结构参数：转轮直径D1，导叶高度b0，导叶开度 a0，叶片转角Φ (2) 工作参数：H、Q、n 、Hs
参数n、H、 N之间的关系综合反映出来，代表了水轮机的轮系
特征。
ns随工况变化,一般按H设、N额、n额确定该水轮机轮系的特征参 数。
ns
ne N e
H
5/4 r
讨论：
相似水轮机，工况相似，ns相同，不同的ns ，反 映不同轮系水轮机特征。
当H一定时： ns ↑→N↑→n↑。机组尺寸缩小， 投资减少，因此提高比转速可以降低造价。
3、相似理论 研究相似水轮机之间存在的相似规律，
并确立这些参数之间的换算关系的理论。
二、水轮机相似条件
1、几何相似： 过流通道几何形状相似
(1) 过流通道的对应角相等：βe1＝βe1M ；βe2＝ βe2M ；Φ＝Φ M……
(2) 对应尺寸成比例：D1/D1M＝b0/b0M＝a0/a0M＝…….
(3) 对应部位的相对糙率相等：△/ D1＝△M/D1M 几何相似的大大小小的一套水轮机系列——轮系 同一轮系的水轮机才能建立运动相似和动力相似。
→
M D 1M
水轮机相似原理10
Q11
QV D12 Hh
2021/6/14
2肖1 惠民
三、单位功率
由
P PM P D D11M P2H H 及M P h hM P32、m mM P
D 得1M1m HMhM 1m
P P P P D H P D H M
2 1 P
3 2 PhP
mP
P mP
MmM2
3 2
mM
1 P PhP
2021/6/14
1肖2 惠民
假定 hP ，h可M 得 nP D1M HP nM D1P HM
（4－10）
（4－10）式为转速相似律，即几何相似水轮机在相似工况下，其转速 与直径成反比，与水头的平方根成正比
2021/6/14
1肖3 惠民
二、流量相似律
通过几何相似水轮机的有效流量分别为
Q Q V F
2021/6/14
肖9 惠民
D1 代表 L，1/n 代表 T，V 正比于 H ，考虑 g、 、 是常数，则
欧拉数（压力相似） Eu P V 2 C
→ P idem 压强相似关系（空化试验）
H
斯特洛哈数（惯性力相似）
Sh VT L C
→
nD1 idem 单位转速
H
雷诺数（粘性力相似） Re VLv C → D1 H idem
b1P b1M b2P b2M P M
式中，D1（转轮标称直径）、b0（导叶高度）、a0（导叶开度）为水轮
机的线性尺度，βb1、βb2、 分别为叶片进口、出口安放角、桨叶转角
下标“P”代表原型（ProtoType）水轮机，“M”代表模型（Model
）水轮机
几何相似的水轮机称水轮机系列
2021/6/14
水轮机 相似理论
对直径大于 1 米的水轮机来说，如进行水轮机原
型实验来修正理论计算，既不经济，又非常困难、
不可能实现。
模型试验：在实验室条件下，将水轮机原型按比例 缩小为模型，通过模型试验修正理论计算。
优点：可保证制造速度快，费用低、试验测量方便
且又正确，同时可以进行多个方案的试验，取其最
好的方案。
需解决的关键技术： 1、模型与原型如何保持相似？ 2、模型试验结果如何换算到原型？
M
M
Q11 Q11M
n11 n11 n11M n11M
Q11 Q11 Q11M Q11M
n11M n11M ( 1) M M
Q11M Q11M ( 1) M M
例题一
混 流 式 水 轮 机 模 型 直 径 D1M=0.46m ， 试 验 水 头 HM=4m。最高效率时实测：转速nM=282r/min，流量 QM=0.38m3/s，出力NM=13.1kW。原型水轮机转轮直 径 D1=2m ，工作水头 H=30m ，求最优工况下原型水 轮机的n、P、Q、η。 解：模型水轮机单位参数：
可以不考虑修正，即 n11 n11M Q11 Q11M
n n11 H 30 64.86 178 r min D1 2
Q Q11 D12 H 0.9 2 2 30 19.7m 3 s
P 9.81QH max 9.81 19.7 30 0.911 5281 .7kW
Vx K vx 2 gH s
1.转速相似定律
u1
Vx K vx 2 gH s
D1n
60
21 gH VuK ;V 1 U 1u us2 U 2 ; U1 Vx ; U 2 Vx
第3章 水轮机的相似理论及模型综合特性曲线
2、 运动相似 ★同一轮系水轮机，
过流通道中对应点的速 度成比例、方向相同。
★即对应点的速度 三角形相似，如图3-1， 可表示为：
α1=α1M ；β1=β1M ；α2=α2M ；…… (3-4) V1/V1M＝ U1/U1M ＝ W1/W1M ＝ V2/V2M ……. (3-5)
3、 动力相似 ★同一轮系水轮机，水流在过流部分对应点上
ns 3.13n1 Q1 (m·kW) （3-17）
(ns 30)1.8
200000
（3-18）
② 当H和N一定时，ns↑→σ迅速↑→增加厂房 开挖深度和减小水轮机的使用寿命。
故选择合理的水轮机时，其合理的比转速应 该是经过动能经济比较的。
③ 不同ns反映了不同轮系的能量特征，也就 反映了不同轮系水轮机过流通道的几何形状的特 征，由式3-17可见：
包括几何相似、运动相似和动力相似。 1、 几何相似 模型与原型过流通道的几何形状相似，包括： (1) 过流通道的所有对应角相等： βe1=βe1M ；βe2=βe2M ；Φ=ΦM；…… (3-1)
1、 几何相似 (2) 所有对应尺寸成比例：
D1/D1M＝b0/b0M ＝a0/a0M＝……. (3-2)
N 9.81QH 9.81aKV1
2gHs
sin 1D12
1 r
Hs r j
（1）
(1)式可改写为：
N D12 (Hs )3/ 2 j
9.81aK v1
2g sin 1
（2）
同样，对模型水轮机有：
NM D12M (HMsM )3/ 2 jM
9.81a MK v1M
2g sin 1M
（3）
3、 出力相似律 由前（2）式和（3）式整理有：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数少。 混流式
b0 D1
0.1 0.00065 ns
轴流式
b0 D1
Байду номын сангаас
0.44 21.47
ns
转轮进、出口直径比D1/D2随比转速的增加而减小:
D1
1
D2 0.96 0.00038 ns
ns
nN H54
使用高比转速水轮机能带来经济效益
水轮机：比转速提高，在相同出力与水头条件下，能
解：模型水轮机单位参数：
n11M
nM D1M HM
282 0.46 64.8r
4
min
Q11M
QM D12M H M
0.38 0.9 m3 0.46 2 4
s
模型水轮机最高效率
M max
NM
9.81QM HM
13.1 0.88 9.81 0.38 4
ns 3.13n11 Q11
比转速：同一系列水轮机在相似工况下运行的综合性能。 作为水轮机系列分类的依据。
采用设计工况或最优工况下的比转速作为水轮机分 类的特征参数。
水斗式： 混流式： 斜流式： 轴流式：
ns=10～70 ns=60～350 ns=200～450 ns=400～900
二、比转速与水轮机性能关系
H MsM
84.6Ku1M
nD1 nM D1M 常数
H s
H MsM
2.流量相似定律
Vx Kvx 2gHs
Q0 Vm1F1
Vm1 K vm1 2gH s
F1 D1b0 f fb0 D12 D12
Q 0 D12 H S
K vm1
2g
QM0M D12M H M SM
的原型水轮机。 模型试验优点：
1、模型运转规模比真机运转规模小的多，费用小， 试验方便，可以根据需要随意变动工况。
2、能在较短时间内测出模型水轮机的全面特性。
解决办法：对模型试验所得数据进行修正，从而较准 确地推算出原型效率。
1、最优工况下的效率修正
基本假定 （1）水力损失仅有粘性摩擦损失，比较符合最优工况； （2）粘性摩擦损失类似于圆管中的沿程摩擦损失。
H l V 2
d 2g
（3）水轮机中的流态处于“水力光滑区”，水头损失 系数仅与雷诺数有关，而与管壁粗糙度无关。
单位转速 单位流量
n11
nD1
H s
Q11
D12
Q
H S
单位出力
N11
N
D12 (H S )3/ 2
假定同系列水轮机的效率相同
n11
nD1 H
Q11
Q D12 H
N11
N D12 H 3 / 2
单位转速、单位流量
第一，分别表示惯性力相似和压力相似的准则， 是判别几何相似的两个同型号水轮机运行工况相 似的依据。
N N11 D12 H 3 / 2
n11 N11 n N / H 5 / 4
对于同一系列水轮机，在相似工况下其n11、N11均
为常数，因此 水轮机比转速
ns
nN H54
ns
nN H54
N
9.81HQ,
n n11 H D1
和Q Q11 D12
H
n Q
ns 3.13 3 H4
解：原型最优工况效率
5
10
T 0 1 (1 M 0 ) (0.3 0.7
D1M D1T
φ=+10o时原型最高效率
3.5 ) 0.927 28
5
10
(T 0 ) 1 1 (M 0 ) (0.3 0.7
D1M D1T
3.5 ) 0.916 28
例题二
对直径大于1米的水轮机来说，如进行水轮机原 型实验来修正理论计算，既不经济，又非常困难、 不可能实现。 模型试验：在实验室条件下，将水轮机原型按比例 缩小为模型，通过模型试验修正理论计算。 优点：可保证制造速度快，费用低、试验测量方便 且又正确，同时可以进行多个方案的试验，取其最 好的方案。 需解决的关键技术： 1、模型与原型如何保持相似？ 2、模型试验结果如何换算到原型？
抓住主要矛盾，忽略某些次要条件，待由模型 换算到原型去时，再进行适当的修正。
二、相似定律
相似工况：同一系列水轮机保持运动相似的工况 。
相似数定（律如：水水H头轮、s机流在量g相、V似u转1工r1速况等V下u）2运r之2行间时的，固其定各关工系作。参
Hs
1 g
Vu1U1
Vu2U 2
Q Q11 D12 H
Q110 Q11M0M
s
sM
s 0 0M
Q11 Q11M
M
n11 n11M
M
Q11 Q11M
M
n11 n11M M
Q11 Q11M M
n11 n11 n11M n11M M n11M n11M ( M 1)
2、运动相似 两个水轮机所形成的液流，相应点处的速度
同名者方向相同，大小成比例，相应的夹角相 等。即相应点处的速度三角形相似一般也称其 为等角工况。
V1 u1 W1 V1M u1M W1M
1 1M 1 1M
3、动力相似 两个水轮机所形成的液流中各相应点所受的
力，数量相同、名称相同，且同名力方向一致， 大小成比例。作用在液流上的力主要有压力、 惯性力、粘性力和重力等，同时包括相同的边 界条件。
Vu1 U1; Vu2 U2; U1 Vx ; U2 Vx
Vx Kvx 2gHs
1.转速相似定律
Vx Kvx 2gHs
u1
D1n
60
VuK1 u1 U21g;HVus2
U2;
U1
Vx;
U2
Vx
nD1 60Ku1
H s
2g 84.6Ku1
nM D1M
可以不考虑修正，即 n11 n11M Q11 Q11M
n n11
H D1
64.86
30 178r min
2
Q Q11D12 H 0.9 22 30 19.7 m3 s
P 9.81QHmax 9.8119.730 0.911 5281.7kW
第三章 水轮机的相似理论与模型试验
第一节 水轮机的相似理论与单位参数
对水流在水轮机内的运动规律作了很多研究， 获得了不少成就。实际情况十分复杂，到目前为 止，尚没有完全掌握这种规律。
理论分析不能十分正确地反映水流在水轮机内 的运动规律，原因：引入假设条件。
通过模型试验，对理论计算加以校核。 近年来CFD技术在水轮机中的应用发展迅猛。
够缩减水轮机尺寸，降低水轮机的成本及节约动力厂
房的投资。或者，对既定的水轮机尺寸，在相等水头
条件下，提高比转速能够增加水轮机的出力。
发电机：比转速高则提高了发电机转速，可用较少的
磁极数、缩小发电机尺寸，电机成本降低。
第四节 水轮机的模型试验
一、水轮机模型试验的意义 按相似理论，模型水轮机的工作能反应任何尺寸
混流式
5
T 0 1 (1 M 0 )
D1M D1
5
10
轴流式 T 0 1 (1 M 0 )(0.3 0.7
D1M D1
HM ) H
最优工况下原型、模型效率的差值：
0 T 0 M 0
2、非最优工况下的效率修正
水轮机偏离最优工况时，涡流损失比摩阻损失大 得多，水力效率关系难以确定，效率修正只能采用 简化方法。 简化原则：非最优工况下原模型效率差值与最优工 况时的差值相同。
1、几何相似 两个水轮机过流部分几何形状与表面糙度相同，
并且一切相应的线性尺寸成比例。
几何相似实质：原型与模型水轮机主要过流部件形状 应相同，只是大小不等，其中转轮形状必须相同，叶 片相应的角度相等。
'1 '1M
'2 '2M
D1 b0 a0 D1M b0M a0M
'2 '2M
9.81C
NM
9.81C
D12M (H M sM )3 / 2 jM
N
NM
常数
D12 (H s )3/ 2 j D12M (H M sM )3/ 2 jM
三、单位参数
通常规定把模型试验成果都统一换算到：
转轮直径D1为：1m 有效水头Hηs为：1m
对应有单位转速、单位流量和单位出力。
Q11 Q11 Q11M Q11M M Q11M Q11M ( M 1)
例题一
混 流 式 水 轮 机 模 型 直 径 D1M=0.46m ， 试 验 水 头 HM=4m。最高效率时实测：转速nM=282r/min，流量 QM=0.38m3/s，出力NM=13.1kW。原型水轮机转轮直 径D1=2m，工作水头H=30m，求最优工况下原型水 轮机的n、P、Q、η。
1.比转速与水轮机性能
水轮机性能：水轮机能量、空化等水力性能。
提高比转速，额 σ
定工况、满负荷时 空化系数随之加速 增大。
(ns 30)1.8
20000
n 满负荷时空化系数与比转速的关系
s
二、比转速与水轮机性能关系
2.比转速与水轮机几何参数
比转速越高、单位流量越大。在一定流速下，所需
过流断面面积越大，要求导叶相对高度大、转轮叶片
例题二
轴 流 转 桨 式 水 轮 机 模 型 试 验 数 据 ： D1M=0.46m ， HM=3.5m。在最优工况时(轮叶转角φ=0o)， ηM0=0.89； 当φ=+10o时，最高效率(ηM0)φ=0.872，相应协联工况 时 ηMφ=0.865 。 同 系 列 原 型 水 轮 机 D1T=4.5m ， 求 HT=2.8m时同一最优工况、协联工况运行的效率ηT0 和ηT。