重庆八中2011-2012八年级上期期末模拟考试3(扫描版)
重庆第八中学人教版八年级上册生物期末综合题试卷及答案-百度文库

重庆第八中学人教版八年级上册生物期末综合题试卷及答案-百度文库一、实验探究综合题1.如图A、B、C、D、E是常见的几种动物,据图回答下列问题:(1)D生活在水中,用______呼吸,用______游泳,靠______感知水流和测定方向。
(2)B的身体体表有______,具有保护和支持内部柔软器官、防止水分蒸发等作用。
(3)A的幼体生活在水中用______呼吸;成体水陆两栖生活,用______呼吸。
(4)E的身体呈______型,前肢变成______;它的身体内有发达的______与肺相通,有贮存空气,辅助呼吸的作用。
(5)C是哺乳动物,特有的生殖发育特点是______。
(6)F类动物的主要特征:体表覆盖角质的鳞片或甲:______;在陆地上产卵,卵表面具有______。
(7)上述动物中,体温能保持恒定的是______(填字母)。
2.根据观察蚯蚓实验回答下列问题:(1)蚯蚓身体呈圆筒形,前端和后端可依据[_____] (填序号)的位置来区分。
(2)观察蚯蚓的过程中,应经常用浸湿的棉球轻擦其体表,原因是保持正常_______________。
(3)用放大镜观察蚯蚓的腹面,发现有许多小突起,叫___________,它可以辅助运动。
(4)蚯蚓的身体是由许多环状的体节构成的。
身体分节的意义是_____________________。
(5)蚯蚓能把自然界中一些有机废物分解为无机物,供给绿色植物再利用,因此蚯蚓在生态系统应属于__________者。
3.观察鲫鱼的形态结构,回答问题:(1)鲫鱼的身体可分为__________、_________和尾部三部分。
(2)[①]__________、[③]__________、[⑤]____________。
(3)鲫鱼能够适应水中的生活,从形态结构上来看:大多身体呈流线型;身体表面常常覆盖着____________;表面有滑滑的黏液,它们可以减少游动时水带来的阻力。
重庆第八中学人教版八年级上册生物期末试卷及答案-百度文库

重庆第八中学人教版八年级上册生物期末试卷及答案-百度文库一、选择题1.下列关于水螅的描述,错误的是()A.身体呈辐射对称B.有刺细胞C.有口有肛门D.内胚层细胞具有消化功能2.下雨天,蚯蚓会纷纷从被雨水浸没的土壤中爬出来,这是为了()A.寻找食物B.获得氧气C.繁殖后代D.排出废物3.俗话说“秋风起,蟹脚痒;菊花开,闻蟹来”。
秋天才是吃螃蟹最好的季节,请问螃蟹属于()A.环节动物B.节肢动物C.爬行动物D.哺乳动物4.生物兴趣小组为探究“鲫鱼适应水中生活的外部特征”,进行了一系列的探究实验。
取两条大小相似、同样健壮的鲫鱼,一条不做任何处理,另一条用橡皮筋将图中的①、②、③束起来,再用木板夹住④部位并用绳子捆绑,两条鱼同时放入水中观察。
分析回答,这个实验探究的问题是()A.鱼鳍与运动的关系B.鱼的侧线与运动的关系C.鱼的体型与呼吸的关系D.鱼鳞与呼吸的关系5.图是兔和狼的牙齿示意图,下列说法不正确的是(......).A.兔和狼都有门齿和臼齿B.图甲是兔的牙齿,图乙是狼的牙齿C.图中结构①是犬齿,与肉食性生活相适应D.牙齿的分化提高了哺乳动物摄取食物的能力,又增加了对食物的消化能力6.生物体结构与其生活环境相适应,对此叙述不正确...的是()A.家鸽体表覆羽,前肢变成翼,有气囊辅助肺呼吸,适于空中飞行生活B.蛙幼体生活在水中,用鳃呼吸;成体生活在陆地上,用皮肤呼吸就能满足氧气的需求C.鲫鱼体表覆盖鳞片,用鳃呼吸,通过尾部和躯干部的摆动及鳍的协调游泳,适于水中生活D.龟的卵较大、养料多且含一定的水分,卵外有坚韧的卵壳,能在陆地环境中发育成幼龟7.都属于两栖动物的一组是()A.乌龟、青蛙、鳄鱼B.大鲵、小鲵、乌龟C.蝾螈、大鲵、蟾蜍D.蟾蜍、鳄鱼、水獭8.下列有关“白虎”的描述,你不认同的是()A.白虎体表被毛,体温恒定B.白虎的生殖发育特点为胎生、哺乳C.白虎的盲肠发达D.白虎有门齿、犬齿和臼齿的分化9.下列有关运动的说法中,正确的是()A.哺乳动物的运动系统由骨和肌肉组成B.只要运动系统完好,动物就能正常运动C.每块骨骼肌的两端附着在同一块骨上D.骨骼肌由中间的肌腹和两端的肌腱组成10.小明喜欢用哑铃锻炼上肢。
重庆第八中学人教版八年级上册生物期末综合题试卷及答案-百度文库

重庆第八中学人教版八年级上册生物期末综合题试卷及答案-百度文库一、选择题1.水螅攻击和防御的利器是()A.触手B.刺细胞C.芽体D.口2.下列不属于扁形动物的是()A.涡虫B.华枝睾吸虫C.珊瑚虫D.猪肉绦虫3.下列各项中,依次属于线形动物和环节动物的是()A.蛔虫、涡虫B.蚯蚓、蛔虫C.丝虫、沙蚕D.绦虫、蛲虫4.大雨过后,蚯蚓往往要爬到地面上是因为()A.蚯蚓喜欢干燥的环境B.土中缺氧,无法呼吸C.到地面寻找食物D.穴中浸透雨水太凉5.无脊椎动物中,昆虫分布范围十分广泛,活动范围大,其主要原因是()A.体表有防止体内水分蒸发的外骨骼B.有翅能飞C.具有二对足,尤其是跳跃足D.头部长有多种感觉器官6.下列无脊椎动物与所属类群正确的是A.蚯蚓属于线形动物B.涡虫属于环节动物C.水母属于软体动物D.蝴蝶属于节肢动物7.在水产市场,王强同学发现一种陌生的活体海洋动物(如图),并将其买回家进行研究,若想确定它是否属于鱼类,下列哪项观察无助于...做判断A.是否异养生活B.是否有脊柱C.是否用鳃呼吸D.是否一心房一心室8.下面选项中属于..鱼类的是()A.鲸鱼B.鲨鱼C.娃娃鱼D.河马9.如图是家鸽的呼吸系统示意图,以下说法正确的是()A.①是气管,②是肺,③是气囊B.气囊的存在,有利于提高肺内气体交换的效率C.②和③都能进行气体交换,所以称为“双重呼吸"D.气体进入体内的途径是①→②→③10.如图是比较三种动物特征的示意图,其中金鱼与家鸽交叉部分2表示()A.用鳃呼吸B.卵生C.体温恒定D.体内有脊柱11.恒温动物比变温动物更具有生存优势的原因是A.恒温动物耗氧少B.恒温动物需要的食物少C.恒温动物更适应环境的变化D.恒温动物所需的能量少12.“双飞燕子几时回,夹岸桃花蘸水开”,燕子在飞行中需要消耗大量能量。
下列叙述中,与鸟产生大量能量无关的是()A.心跳频率快,运输能力强B.气囊辅助呼吸,可获得充足氧气C.骨骼轻、薄、坚固,有些骨中空D.食量大,消化能力强13.下列各组动物中,都用鳃呼吸的是()A.河蚌、鲨鱼、鲫鱼B.鲸、蛇、乌龟C.青蛙、青鱼、蝌蚪D.珍珠蚌、鲫鱼、大鲵14.蛙和龟既能在水中游泳,也能在陆地上生活。
重庆八中八年级上学期末数学试卷解析版(1)

重庆八中八年级(上)期末数学试卷、选择题(本大题共 10小题,共40.0 分)3. 函数y 中,自变量x 的取值范围是( )A. B. C.4.下列调查中,适合采用全面调查(普查)方式的是(A. 了解中央电视台“走遍中国栏目的收视率B. 了解某班同学“跳绳”的月考成绩C. 了解全国快递包裹产生包装垃圾的数量D. 了解青海湖斑头雁种群数量5.若a v b ,则下列结论不一定成立的是()A. B. C. - -D.6. 估计— 一的运算结果应在哪两个连续自然数之间()A. 1 和 2B. 2 和 3C. 3 和 4D. 4 和 57.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()8.△' B'C 的位置,再沿 CB 向左平移使点B '落在原三角尺 1.不等式x 》l 的解集在数轴上表示正确的是A. -2 -1 0 12 C.-2-11 2B. D.- ——6 --------- >-2 ^1 0 1 2 2.如图图形中既是中心对称又是轴对称图形的是(------------------ • ----- >-2 -1 0 1 2)D.D.)ABC 的斜边AB 上,则① ② ③如图,斜边长12cm , Z A=30。
的直角三角尺 ABC 绕点C 顺时针方向旋转 90至三角尺向左平移的距离为()(结果保留根号)9. A. B.若点A (a+1, b-2)在第二象限,则点C.B (-a, 1-b )在(A.第一象限B.第二象限C.第三象限D.)D.第四象限10.如图,RtMBC 中,/CAB=90 °A ABD 是等腰三角形, AB=BD=4, CB1BD 交 AD 于 E , BE=1,贝U AC 长为 ( )A.B. C. — D. 614.我校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林活动,为了 了解全校学生的植树情况,学校随机抽查了 100名学生的植树数量情况,将调查数 据整理如表:植树数量(棵) 4 5 6 8 10 人数30222515816. 如图,△ABC ^△X DE ,线段BC 的延长线过点 E ,与线段AD 交于点 F , ZACB= Z AED=105°, /CAD =5° /B=50°则 /DEF 的 度数 . 17. 已知关于x 的不等式2x-m+3 >0的最小整数解为1,则实数m 的取值范围是 _________ . 18. 甲、乙两车同时从 A 地出发,沿同一条笔直的公路匀速前往相距300km 的B 地,半小时后甲发现有东西落在A 地,于是立即以原速返回 A 地取物品,取到物品后立即以原来速度的1.2倍继续前往B 地(所有掉头时间和领取物品的时间忽略不计) , 甲、乙两车之间的距离 y (km )与甲车驶的时间 x (h )之间的部分函数关系如图所 示,当甲车到达 B 地时,乙车离 B 地的距离是 ____________ km .二、填空题(本大题共 11小题,共44.0分) 11. 12. 13. 4是 _____ 的算术平方根. 将直线y=x 沿y 轴正方向平移2个单位后过点(1, a-2) 如图,在矩形ABCD 中,AB=3, AD=2,以点A 为圆心, AD 长为半径画弧, ______ (结果保留 交AB 于点E ,图中阴影部分的面积是 n ) •C71,则a=D15.已知关于x , y 的二元一次方程组,贝H x-y= ___r19. 如图,已知△ABC为等腰直角三角形,AC=BC=4,/BCD=15° AP为CD上的动点,贝U |PA-PB|的最大值为______20. 对于三个数a, b, c,用M{a, b, c}表示这三个数的中位数,用max{a, b, c}表示这三个数中最大的数. 例如:M{-2,-1,0}=-1 ;max{-2,-1,0}=0,max{-2,-1,a}= 根据以上材料,解决下列问题:若max{3,5-3x,2x-6}= M{1,5,3},贝U x 的取值范围为 _______ .21. 如图,点A (2,2)在直线y=x上,过点A j作A1B1/“轴交直线y=-x于点B1,以点A2为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1,再过点C1作A2B2 /y轴,分别交直线y=x和y=-x于A2B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角M2B2C2…,按此规律进行下去,则等腰直角A A4B4C4的面积为_______ .环v=x聲三、计算题(本大题共1小题,共8.0 分)22. (1)解方程组:>(2)解不等式组:四、解答题(本大题共6小题,共58.0分)23. 如图,已知△ABC的三个顶点的坐标分别为A (-2, 3), B (-6, 0), C (-1 , 0).(1)将△ABC向右平移6个单位长度,再向下平移3个单位长度得到A A I B I C I,在图中画出A A I B I C I,平移后点A对应的点A i的坐标是____________ ;D(2) _________ 将A ABC沿y轴翻折得到ZA A2B2C2在图中画出A A2B2C2,翻折后点A对应点A2 的坐标是;(3)求出线段AB在(1)中的平移过程中扫过的面积.24. 学校为奖励在艺术节系列活动中表现优秀的同学,计划购买甲、乙两种奖品•已知购买甲种奖品30件和乙种奖品25件需花费1950元,购买甲种奖品15件和乙种奖品35件需花费1650元.(1)求甲、乙两种奖品的单价;(2)学校计划购买甲、乙两种奖品共1800件,其中购买乙种奖品的件数不超过甲种奖品件数的2倍,学校分别购买甲、乙两种奖品多少件才能使总费用最小?最小费用是多少元?25. 如图,在平面直角坐标系中,直线I仁y=mx+b ( m^0与x轴交于点A (-3, 0),直线I与直线l2:y=nx (m^0交于点B (a, 2),若AB=BO.(1)求直线l i与直线I2的解析式;(2)将直线I2沿x轴水平移动2个单位得到直线13,直线13与x轴交于点C,与l i 直线交于点D,26. 如图,在△ABC中,AC=CB, /ACB=90°在AB上取点F,过A作AB的垂线,使得AD=BF,连接BD、CD、CF, CE是/ACB的角平分线,交BD于点M,交AB 于点E.(1)若AC=6 , AF=2 一,求BD 的长;(2)求证:2CM=AF.27. 如图1,点C把线段AB分成两条线段AC和BC,如果AC=一AB,则称线段AB被点C黄金分割,点C叫做线段AB的黄金“右割“点,根据图形不难发现,线段AB上另有一点D把线段AB分成两条线段AD和BD,若BD=——AB,则称点D是线段AB的黄金“左割”点.请根据以上材科.回答下列问题(1)如图2,若AB=8,点C和点D分别是线段AB的黄金“右割”点、黄金“左害『’点,贝U BC= __ ,DC= ______ .(2)若数轴上有M , P,Q, N四个点,它们分别对应的实数为m, p, q, n,且m v p v q v n, n=3|m|,点Q和点P分别是线段MN的黄金“右割”点、黄金“左割”点,求-的值.* ♦-------- • ---- 1 ------ • --- •---- •DA 5 cB A DC B图1 圉228. 已知直线l i:y=-x+b与x轴交于点A,直线I2:y=-x-—与x轴交于点B,直线l i, I2交与点C,且C点的横坐标为1.图1 图2(1)求直线l i的解析式;(2)如图1,过点A作x轴的垂线,若点P为垂线上的一个动点,点Q (0, 2), 若S/CPQ=4,求此时点P的坐标;(3)如图2,点E的坐标为(-2, 0),将直线l1绕点C逆时针旋转,使旋转后的直线13刚好过点E,过点C作平行于x轴的直线14,点M、N分别为直线13、14上的两个动点,是否存在点M、N,使得MMN是以M点为直角顶点的等腰直角三角形,若存在,直接写出N点的坐标;若不存在,请说明理由.答案和解析1. 【答案】D【解析】解:••x>1•••1处是实心原点,且折线向右.故选:D.根据在数轴上表示不等式解集的方法求解即可.本题考查的是在数轴上表示不等式的解集,熟知“小于向左,大于向右”是解答此题的关键.2. 【答案】D【解析】解:A、••此图形旋转180°后不能与原图形重合,••此图形不是中心对称图形,也不是轴对称图形,故此选项错误;B、••此图形旋转180°后不能与原图形重合,••此图形不是中心对称图形,也不是轴对称图形,故此选项错误;C、此图形旋转180°后不能与原图形重合,此图形不是中心对称图形,也不是轴对称图形,故此选项错误;D、•此图形旋转180°后能与原图形重合,•此图形是中心对称图形,也是轴对称图形,故此选项正确.故选:D.根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.此题主要考查了中心对称图形与轴对称的定义,根据定义得出图形形状是解决问题的关键.3. 【答案】B【解析】解:由题意得,x-2>0解得x>2故选:B.根据被开方数大于等于0列式计算即可得解.本题考查了函数自变量的取值范围,解决本题的关键是二次根式的被开方数是非负数.4. 【答案】B【解析】解:A. 了解中央电视台走遍中国栏目的收视率适合抽样调查;B .了解某班同学跳绳”的月考成绩适合全面调查;C. 了解全国快递包裹产生包装垃圾的数量适合抽样调查;D .了解青海湖斑头雁种群数量适合抽样调查;故选:B.由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普査的意义或价值不大,应选择抽样调查,对于精确度要求高的调查, 事关重大的调查往往选用普查.5. 【答案】D【解析】解:A、由a v b,可得a-2v b-2,成立;B、由a v b,可得-a>-b,成立;C、由a v b,可得-j,成立;D、当a=-5, b=1时,不等式a2v b2不成立,故本选项正确;故选:D.由不等式的性质进行计算并作出正确的判断.考查了不等式的性质.应用不等式的性质应注意的问题:在不等式的两边都乘以(或除以)同一个负数时,一定要改变不等号的方向;当不等式的两边要 乘以(或除以)含有字母的数时,一定要对字母是否大于0进行分类讨论. 6. 【答案】B【解析】解:::* ;-1= --1,••9v 15v 16, ••3v . v 4, ••3-1 v . -1 v 4-1, ••2v . - -1 v 3. 故选:B .先计算出;* ■=】,再估算 】的范围,最后根据不等式的性质即可得 到答案. 本题考查了估算无理数的大小,二次根式的除法运算,不等式的性 质,正确 估算出1技的范围是解题的关键. 7. 【答案】A【解析】解:由于得到的图形的中间是正方形,且顶点在原来的正方形的 对角线上, 故选:A .对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.本题主要考查学生的动手能力及空间想象能力.对于此类问题,学生只要亲 自动手操作,答案就会很直观地呈现. 8.【答案】A【解析】••在 RtMBC 中,AB=12,ZA=30 °I厂••BC= AB=6,AC=6 :, •B C=6••AB ,=ACB ' C=6 -6, •B 他〃 C ;'B ' C=B 〃,C 〃 ••四边形B 〃 C 〃(是矩形, • zAB 〃 B ^z ABC ,皿 TicBri 6v'3 (i即卩,(J解得:B 〃 B' =6…解:如图:连接B' B ;'••B 〃 B 'C,B 〃 B ' =C,〃 BC•C' C=B〃B-2 =6 .故选:A.首先根据题意作图,然后连接B' B;由在RtMBC中,AB=12,/A=30°,即可求得AC与BC的值,则可得AB的值,又由B'C/B〃C; B' C=B C四边形B〃C〃C是矩形,可得MB B^^ABC,然后根据相似三角形的对应边成比例,即可求得答案.此题考查了相似三角形的判定与性质,旋转与平移的性质,以及直角三角形的性质等知识.此题综合性较强,难度适中,解题的关键是数形结合思想的应用.9. 【答案】D【解析】解:••点A a+1,b-2)在第二象限,.'a+1<0, b-2>0,解得:a<-1,b>2,则-a> 1, 1-b< -1,故点B -a,1-b)在第四象限.故选:D.直接利用第二象限横纵坐标的关系得出a,b的符号,进而得出答案.此题主要考查了点的坐标,正确记忆各象限内点的坐标符号是解题关键.10. 【答案】C【解析】解:-.AB=BD=4 ,•••启AE= ZBDE ,•.CBXBD,•••QBE= Z CAB=90° ,•••QEB=90°-ZD, ZCAE=90°-/BAD ,• zCAE= ZDEB,•••ZEA= ZDEB,•••£AE= Z CEA,••AC=EC,•.BE=1,••BC=AC+1 ,2 2 2••AC2+AB2=BC2,••AC2+42= AC+1 )2,• AC=不,故选:C.根据等腰三角形的性质得到ZBAE= ZBDE,根据等式的性质得到ZCAE= ZDEB,求得AC=EC,根据勾股定理列方程即可得至V结论.本题考查了直角三角形的性质,等腰三角形的性质,勾股定理,证得AC=CE 是解题的关键.11. 【答案】16【解析】解:--42=16,••4是16的算术平方根.故答案为:16.如果一个非负数x的平方等于a,那么x是a的算术平方根,由此即可求出结果.此题主要考查了算术平方根的概念,牢记概念是关键.12. 【答案】5【解析】解:将直线y=x沿y轴正方向平移2个单位后得y=x+2,根据题意,将1, a-2)代入,得1 +2=a-2,解得:a=5,故答案为:5.根据平移规律可得,直线y=x沿y轴正方向平移2个单位后得y=x+2,然后把1, a-2)代入即可求出a的值.此题主要考查了坐标与图形变化-平移,直线平移后的解析式有这样的规律左加右减,上加下减”13. 【答案】6-n【解析】解: ••矩形ABCD,••AD=2,•'S 阴影=S 矩形-S 四分之一圆=2X3-冗处26-冗,故答案为:6-n用矩形的面积减去四分之一圆的面积即可求得阴影部分的面 积.本题考查了扇形的面积的计算及矩形的性质,能够了解两个扇形构成半 圆是 解答本题的关键,难度不大.14.【答案】5【解析】解:因为共有100个数,把这组数据从小到大排列,最中间两个数的平均数是 第50个数和第51个数的平均数,所以中位数是(5+5)吃=5.故答案为:.利用中位数的定 义求得中位数即可.本题考查了确定一组数据的中位数的能力.注意找中位数的 时候一定要先排 好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个, 则正 中间的数字即为所求,如果是偶数个则找中间两位数的平均数.15.【答案】一 【解析】解:1 '1 .「‘①>2+②得:5x=k+14,的/曰 *+14解得:x= , 1. I 1 I把X=, 代入①得:5—-—+3y=k+4,in 15 3,,10故答案为: 利用加减消元法解出x 和y 的值,代入x-y 即可得到答案. 本题考查了解二元一次方程 组,正确掌握解二元一次方程 组的方法是解题的 关键.解得:y=k+14 :2- x-y=16. 【答案】30 °【解析】解:•••△CB=105 , ZB=50°,•••£AB=180°-/B-/ACB=180°-50 -105 =25 °.又vzABC望公DE ,•••zEAD= ZCAB=25° .又•/2EAB= ZEAD+ ZCAD+ /CAB , ZCAD=5 ,•••zEAB=25°+5 °25 °55 °•••/EB=180 °-ZEAB- ZB=180 -55 -50 =75 °•••QEF=ZAED- ZAEB=105 °-75 =30 °.故答案为:30°由△ACB的内角和定理求得ZCAB=25 ;然后由全等三角形的对应角相等得到ZEAD= ZCAB=25 •则结合已知条件易求ZEAB的度数;最后利用MEB的内角和是180度和图形来求ZDEF的度数.本题考查全等三角形的性质.全等三角形的性质是证明线段和角相等的理论依据,应用时要会找对应角和对应边.17. 【答案】3舸v 5【解析】解:解不等式2x-m+3>0,得:x>二二’,••不等式有最小整数解1,in-3••0 W V 1,解得:3<mv5,故答案为3<mV 5.先解出不等式,然后根据最小整数解为1得出关于m的不等式组,解之即可求得m的取值范围.本题考查了一元一次不等式的整数解,正确解不等式,求出解集是解答本题的关键.解不等式应根据不等式的基本性质.18. 【答案】20【解析】解:•甲出发到返回用时0.5小时,返回后速度不变,••返回到A地的时刻为x=1,此时y=80••乙的速度为80千米/时设甲重新出发后的速度为v千米/时,列得方程:3-1)v-80)=80解得:v=120设甲在第t分钟到达B地,列得方程:120(-1)=300解得:t=••此时乙行驶的路程为:80 X =280 (千米)离B地距离为:300-280=20 (千米)结合题意分析函数图象:线段OC对应甲乙同时从A地出发到A返回前的过程,此过程为0.5小时;线段CD对应甲返回走到与乙相遇的过程(即甲的速度大于乙的速度);线段DE对应甲与乙相遇后继续返回走至到达A地的过程,因为速度相同,所以甲去和回所用时间相同,即x=1时,甲回到A地,此时甲乙相距80km,即乙1小时行驶80千米;线段EF对应甲从A地重新出发到追上乙的过程,即甲用3-1)小时的时间追上乙,可列方程求出甲此时的速度,进而求出甲到达B地的时刻,再求出此时乙所行驶的路程.本题考查了一次函数与一元一次方程的应用,关键是把条件表述的几个过程对应图象理解清楚,再找出对应x和y表示的数量关系.19. 【答案】4【解析】解:作A关于CD的对称点A ,连接A'B交CD于P,则点P就是使IPA-PB|的值最大的点,|PA-PB|=A' B连接A'C,vzABC为等腰直角三角形,AC=BC=4 ,•••£AB= ZABC=45° , ZACB=90° ,•••启CD=15°, •••△CD=75°, •••£AA' =15,° ••AC=A'C,••A' C=BC/CA' A=CAA' =15,° •••ACA' =150,° •••△CB=90°,•A' CB=60°•ZA' B是等边三角形,/A' B=BC=4故答案为:4.作A关于CD的对称点A',连接A'B交CD于P,则点P就是使|PA-PB|的值最大的点,|PA-PB|=A'B,连接A'C,根据等腰直角三角形的性质得到ZCAB= ZABC=45° , ZACB=90° ,根据三角形的内角和得到ZACD=75°,于是得到/CAA =15°°根据轴对称的性质得到A' C=BC ZCA A=ZCAA =15°°推出Z A BC是腰三角形,根据等边三角形的性质即可得到结论.此题主要考查轴对称--最短路线问题,等腰直角三角形的性质,等边三角形的判定和性质,正确的作出图形是解题的关键.20. 【答案】-$丘【解析】解:'.max{3,5-3x , 2x-6}=M{1 , 5 , 3}=3 ,丨A-lrQ••力一G",第15页,共24页故答案为< x <.由 max{3,5-3x ,2x-6}=M{1 , 5, 3}得 ,解之可得.此题考查了一元一次不等式 组的应用,解题的关键是读懂题意,根据题意得 到不等式去求解,考查综合应用能力.21.【答案】【解析】解:••点A i 2, 2),止1//轴交直线汙「 点B ,••B i 2, 1).•A 1B 1=2-1=1,即△A 1B 1C 1 面积='•A 1C =A 袒1=1,•'A 2 3, 3), 又••A 2B 2//轴,交直线 于点B q ,•B 2 3,),••A 2B 2=, 即^A 2B 2C 2面积= 以此类推,<} r 工站 I 1)H]A sB s =,即△A 3B 3C 3面积=.•., 27 I 27 729A qB q U ,即△A 4B 4C 4 面积=..7J<J 故答案为: 先根据点A 1的坐标以及A 1B 1 /y 轴,求得B 〔的坐标,进而得到A 1B 1的长以及 △A 1B 1C 1面积,再根据A 2的坐标以及A 2B 2/y 轴,求得B 2的坐标,进而得 到A 2B 2的长以及^A 2B 2C 2面积,最后根据根据变换规律,求得A 4B 4的长,进而得出M4B 4C 4的面积即可本题主要考查了一次函数图象上点的坐标特征以及等腰直角三角形的性 质,x < 2 I 2解决问题的关键是通过计算找出变换规律,解题时注意:直线上任意一点的 坐标都满足函数关系式y=kx+b .①疋+②,得:7x=16, 解得:x=—, 将x=一代入①,得: 一-y=3,解得y=—,则方程组的解为(2)解不等式 -x+2>0,得:x >-6,解不等式1 —— 汰+2,得:x <2则不等式组的解集为-6 v X W2.【解析】1) 利用加减消元法求解可得;2) 分别求出每个不等式的解集,再根据 大小小大中间找”可得不等式组的 解集.本题主要考查解二元一次方程 组和一元一次不等式 组,解题的关键是掌握解 二元一次方程 组的两种加减消元法和解一元一次不等式 组的步骤.23.【答案】(4, 0) (2, 3)【解析】 解:10^A 1B 1C 1如图所示.平移后点A 对应的点的坐标是4, 0); 故答案为4,0).22.【答案】解:( 1)① ②,2)^A2B2C2如图所示•翻折后点A对应点A2的坐标是2,3);故答案为2,3)3)求出线段AB在1)中的平移过程中扫过的面积=6X3+3^4=301)分别画出A ,B ,C的对应点A1? B1? C1即可;2)分别画出A ,B ,C的对应点A2,B2,C2即可;3)线段AB在1)中的平移过程中扫过的面积是两个平行四边形的面积之和; 本题考查平移变换、翻折变换、平行四边形的性质等知识,解题的刚开始熟练掌握基本知识,属于中考常考题型.24. 【答案】解:(1)设甲种奖品的单价为x元/件,乙种奖品的单价为y元/件,依题意,得:,解得:答:甲种奖品的单价为40元/件,乙种奖品的单价为30元/件.(2)设购买甲种奖品m件,则购买乙种奖品(1800-m)件,设购买两种奖品的总费用为w, ••购买乙种奖品的件数不超过甲种奖品件数的2倍,.•.1800-m w 2,/m> 600依题意,得:w=40m+30 (1800-m)=10m+54000,••10> 0,•'w随m值的增大而增大,••当学习购买600件甲种奖品、1200件乙种奖品时,总费用最小,最小费用是60000元.【解析】1)设甲种奖品的单价为x元/件,乙种奖品的单价为y元/件,根据购买甲种奖品30件和乙种奖品25件需花费1950元,购买甲种奖品15件和乙种奖品35件需花费1650元”即可得出关于x,y的二元一次方程组,解之即可得出结论;2)设购买甲种奖品m件,则购买乙种奖品1800-m)件,设购买两种奖品的总费用为w,由购买乙种奖品的件数不超过甲种奖品件数的2倍,可得出关于m 的一元一次不等式,解之可得出m的取值范围,再由总价二单价眉数量,可得出w 关于m的函数关系式,利用一次函数的性质即可解决最值问题.本题考查了二元一次方程组的应用、一元一次不等式的应用以及一次函数的性质,解题的关键是:10找准等量关系,正确列出二元一次方程组;2)根据各数量之间的关系,找出w关于m的一次函数关系式.25. 【答案】解:(1)••点A (-3,0),点B (a,2),且AB=BO..•a=-_,.•点 B (--,2),把 A (-3,0),B (--,2)代入y=m x+b 得 _ ,解得 :••直线11:y=-x+4 ;把 B (--,2)代入y=nx 得2=--n,解得n=--,••直线12:y=--x.(2)将直线12沿x轴水平移动2个单位得到直线b为y=-- (x-2)=--x+-,解得,•'D (--,一),由直线13为y=--x+-可知C(2, o), ••AC=5 ,「•ZACD 的面积=-X5 X— =^.【解析】1)由题意得出B (,2),然后根据待定系数法即可求得;2)根据平移的规律求得直线I3为y=p x+冒,结合直线l i :y=吊x+4求得D的11 1 ]■11坐标,由直线l3得到C点的坐标,然后根据三角形面积公式即可求得.本题考查了两条直线相交或平行问题,直线的平移问题,三角形面积以及待定系数法求一次函数的解析式等,求得交点的坐标是解题的关键.26. 【答案】解:(1)-.AC=CB=6,Z ACB=90 °.•AB=6 —••AF=2 —••BF=AB-AF=4 -••AD=BF=4 -在Rt A ADB 中,BD= =2 —(2)-.AC=CB,Z ACB=90°,CE 平分ZACB••AE=BE=CE=-AB,CE 1AB•/zDAB= /MEB=90 ° ZDBA= ZMBE•••ZMBE S QBA••ME=-AD.•ME=-BF••CE=-AB••CM+ME=- (BF+AF)••CM+-BF=-BF+-AF••CM=-AF,即AF=2CM【解析】1)由勾股定理可求AB=6 即可得BF=4二由勾股定理可求BD的长;2)由等腰直角三角形的性质可得AE=BE=CE= . AB , CE 1AB ,由相似三角 形的性质可得ME= AD= BF ,即可得结论.2 7 本题考查了相似三角形的判定和性 质,勾股定理,等腰直角三角形的性质, 熟练运用这些性质进行推理是本题的关键.27. 【答案】12-4 一 8 一-16【解析】解:10 ••点C 和点D 分别是线段AB 的黄金 右割”点、黄金左割”点,••AC=BD= AB= >8=4 -4,•'BC=8- 4 甘、-4) =12-4》:5 ;••DC=BD -BC= 4 ' -4)- 12-4 )=8 1-16;故答案为12-4 ,;8 -16;2)由 1)禾题意可知:门; 一.;:.:; ——••在数轴上,m v p v q v n, n=3|m| .•PN=n -p ; MQ=q-m ; MN=n-m ;_ I /k_ |当 m>0 时,n=3m ;即 3m-p= .. —■:.< : = —•二仙 W 、z••根据被减数-差=减数:p=3m-[/.i-=4m-同理可求q=.当 m v 0 时,n=-3m ; .'3m-p= 八 丨••根据被减数-差=减数:p=3m-;「-心冰= 同理可求q=3m-_.1+2 苗(1+2 祠(3+2诟) 2:4+«^/5;*—2岛—(3-2>/5){3+2\/5)「 111)黄金分割:扌线段AB 分成两条线段AC 和BC AC > BC ),且便C 是AB 和BC 的比例中项(即AB : AC=AC : BC ),叫做扌线段AB 黄金分割,点C 叫做 线段AB 的黄金分割点.其中AC=丄二AB ,并且线段AB 的黄金分割点有两 个.把AB=8代入式子可以AC 和BD ,用减法可以分别求BC 和DC ;2)在数轴上,由于m 的取值不确定,需要分类讨论;同寸根据上述的黄金 右 割”点、黄金左割”点,可以列出:一 ;1 ■ ■; 9 2•的值为•的值为 4m- (」-齿卜\垢_ 5接着求出PN=n-p;MQ=q-m ;MN=n-m ;最后代入求出p和q及;的值;本题考查了黄金分割、分类讨论的思想;把线段AB分成两条线段AC和BCAC >BC),且使\C是AB和BC的比例中项(即AB : AC=AC :BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点•其中AC=「」AB,并2 且线段AB 的黄金分割点有两个•利用分类讨论的思想,全面考虑不同的M值时,的值q28. 【答案】解:(1)直线12:y=- —,令x=1,则y=-4,故点C (1,-4),把点 C (1,-4)代入直线1i:y=-x+b,得:b=-3,则直线h的表达式为:y=-x-3,(2)对于直线y=-x-3,当y=0 时,有-x-3=0,解得x=-3,即 A (-3,0),如图,设直线AC交y轴于点M,设点P坐标为(-3,m),将点P、C的坐标代入一次函数表达式y=sx+t得:,解得,即S A CPQ=-QM X (X C-X P)=- 一,解得:m=12,即点P的坐标为(-3,12);(3)将E、C点坐标代入一次函数表达式,同理可得其表达式为①当点M在直线14上方时,设点N (n,-4),点M (s,--”),点B (4,0),过点N、B分别作y轴的平行线交过点M与x轴的平行线分别交于点R、S,Vz RMN+ /RNM=90 °/RMN + /SMR=90 °•••zSMR= ZRNM ,ZMRN = ZMSB=90 ° MN=MB ,/.Z MSB^ANRM (AAS),••RN=MS, RM=SB,即一- ,解得故点N的坐标为(-16, -4),②当点M在14下方时,如图1,过点M作PQ/X轴,与过点B作y轴的平行线交于Q, 与过点N 作y轴的平行线交于P,即:点N的坐标为(-—,-4)或(-16,-4)【解析】A _1)当x=1时,y=一〒=-4,即点C的坐标为1,-4),将点3的坐标代入直线»:y=-x+b中,即可求解;2)利用S a pQ= . QM K X c-X p)=4,即可求解;3)①当点M在直线l4上方,画出图形,证明△MSB也巫RM AAS ),利用RN=MS ,RM=SB ,即可求解.②当点M在直线14下方时,同①的方法即可得出结论.此题是一次函数图象的综合性问题,考察了直线与坐标轴交点坐标,利用点的坐标求出直线的解析式,在判断是否存在点的时候,借助于全等三角形来转化相等的线段,进而得出数量关系,列方程组求解.。
重庆第八中学人教版八年级上册期末生物期末试卷及答案-百度文库
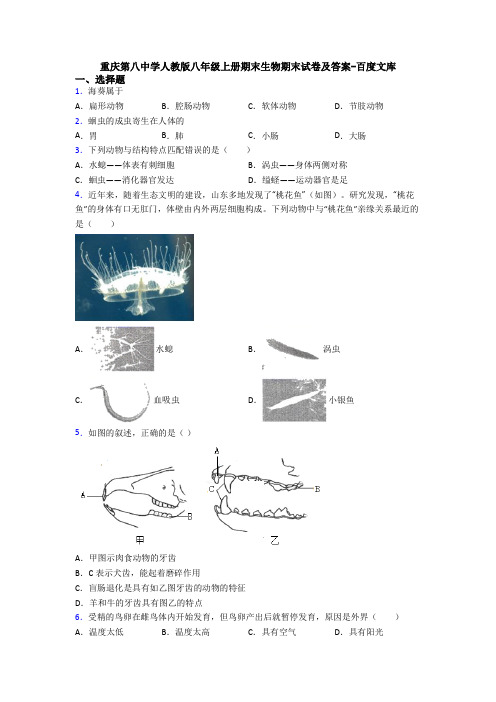
重庆第八中学人教版八年级上册期末生物期末试卷及答案-百度文库一、选择题1.海葵属于A.扁形动物B.腔肠动物C.软体动物D.节肢动物2.蛔虫的成虫寄生在人体的A.胃B.肺C.小肠D.大肠3.下列动物与结构特点匹配错误的是()A.水螅——体表有刺细胞B.涡虫——身体两侧对称C.蛔虫——消化器官发达D.缢蛏——运动器官是足4.近年来,随着生态文明的建设,山东多地发现了“桃花鱼”(如图)。
研究发现,“桃花鱼”的身体有口无肛门,体壁由内外两层细胞构成。
下列动物中与“桃花鱼”亲缘关系最近的是()A.水螅B.涡虫C.血吸虫D.小银鱼5.如图的叙述,正确的是()A.甲图示肉食动物的牙齿B.C表示犬齿,能起着磨碎作用C.盲肠退化是具有如乙图牙齿的动物的特征D.羊和牛的牙齿具有图乙的特点6.受精的鸟卵在雌鸟体内开始发育,但鸟卵产出后就暂停发育,原因是外界()A.温度太低B.温度太高C.具有空气D.具有阳光7.青蛙不能成为真正的陆生脊椎动物的原因是()A.体温不恒定B.用皮肤辅助呼吸C.肺不发达D.生殖和发育离不开水8.以下关于胎生、哺乳的叙述,不正确的是()A.绝大多数哺乳动物以胎生的方式繁殖后代B.哺乳为幼仔成长提供优越的营养条件C.胎生提高了哺乳动物的产仔率D.胎生、哺乳大大降低了幼仔的死亡率9.下列动物中,具有膈这一结构的是()A.大白鲨B.非洲象C.扬子鳄D.丹顶鹤10.观察如图,当你伸肘时,肱二头肌、肱三头肌如何运动()A.肱二头肌收缩,肱三头肌舒张B.肱二头肌收缩,肱三头肌收缩C.肱二头肌舒张,肱三头肌舒张D.肱二头肌舒张,肱三头肌收缩11.如图表示的是人体的屈肘动作。
下列有关叙述,错误的是()A.图中的1、2分别表示肱二头肌和肱三头肌B.前臂骨和上臂骨通过2两端的肌腱连接起来C.完成屈肘动作时,1受神经传来的刺激收缩D.在屈肘动作中1 和2是相互配合活动的12.如图为人体屈肘动作示意图,以下说法错误的是()A.①是肱二头肌,由肌腱和肌腹两部分构成B.屈肘时①处于舒张状态,②处于收缩状态C.完成这个屈肘动作时,③起支点的作用D.屈肘动作的完成需要神经系统的支配13.下图表示关节结构示意图,下列叙述错误的是A.结构③中的滑液能减少骨与骨之间的摩擦B.骨与骨通过关节等方式相连形成骨骼C.结构②是骨骼肌D.肌腱可绕过关节连在不同的骨上14.下列有关动物运动的叙述,错误的是()A.关节腔内有少量滑液,可以减少骨与骨之间的摩擦B.一块骨骼肌的两端肌腱可连接在同一块骨上C.人体任何一个动作的完成,都离不开神经系统的支配D.人在做屈肘动作时,肱二头肌收缩的同时肱三头肌舒张15.下列关于人体运动系统的叙述中,错误的是()A.运动系统由肌肉和骨骼构成B.人体的运动是运动系统在神经系统的支配下完成的C.动物的运动只需运动系统就能够完成D.肌肉收缩所消耗的能量最终来自太阳能16.下列诗词中的动物与其运动方式对应不当的是()A.西塞山前白鹭飞,桃花流水鳜鱼肥——飞行、游泳B.三日雨不止,蚯蚓上我堂——行走C.稻花香里说丰年,听取蛙声片——跳跃D.两个黄鹂鸣翠柳,一行白鹭上青天——飞行17.在一群狒狒组成的“等级社会”中,下列关于首领狒狒的叙述不正确的是()A.优先享有食物和配偶B.优先享有栖息场所C.首领狒狒一般是雌性D.负责指挥整个社群的行动18.动物先天性行为的控制因素是()A.环境因素B.后天“学习”所得C.亲代训练D.遗传物质19.把母鸡正在孵化的鸡蛋换成假鸡蛋,它仍继续孵化,母鸡的这一行为是()①先天性行为②由环境因素决定的③学习行为④由遗传物质决定的.A.①③B.②④C.①④D.②③20.公鸡有好斗的特性,所以人类在家养的鸡群中一般只留一只公鸡,其余公鸡全部阉割。
重庆第八中学人教版八年级上册地理期末试卷及答案-百度文库

重庆第八中学人教版八年级上册地理期末试卷及答案-百度文库一、选择题1.为解决水、土资源配置存在的问题,下列措施正确的是()A.南方地区水资源丰富,应扩大耕地面积B.北方地区相对缺水,应大力缩小耕地面积C.南水北调能从根本上解决我国北方地区缺水问题D.节水与区外引水相结合是北方地区解决缺水问题的长远之策2.有一位外商想在我国投资发展毛纺织工业,仅从接近原料产地方面考虑,下列地点最适宜建厂的是()A.杭州B.郑州C.乌鲁木齐D.沈阳3.上海有一位患者需要移植骨髓,必须在24小时内把骨髓从台北送到上海,需要选择的交通工具是( )A.火车B.轮船C.飞机D.汽车4.我国陆地面积在世界各国中,仅次于()A.俄罗斯、美国B.加拿大、美国C.俄罗斯、加拿大D.美国、巴西5.长江、黄河是中华民族的母亲河,滚滚河水哺育了沿岸亿万儿女,孕育了古老、灿烂的华夏文明。
读图关于两河的叙述正确的是( )A.①是南岭,是长江流域与黄河流域的分水岭B.黄河②处河段形成“地上河”,易引发洪水灾害C.长江中游有众多的支流汇入,其中③是湘江D.长江干流有多座水电站,④是世界上第一大水电站6.据图内容,读图判断①、②、③与乌鲁木齐、拉萨、武汉三地的组合,最有可能的是A.①武汉②乌鲁木齐③拉萨B.①拉萨②乌鲁木齐③武汉C.①武汉②拉萨③乌鲁木齐D.①乌鲁木齐②武汉③拉萨7.一般来说,我国的山区地面崎岖,不利于发展()A.林业B.牧业C.采矿业D.耕作业8.关于南水北调的说法不正确的是()A.为了缓解北方地区严重缺水的问题B.北调的东线主要利用京杭运河北达山东和天津C.中线工程主羹指从丹江口水库引水,北达北京D.西线工程主鬟指把长江中游的水调入黄河,补充西北地区的水资源9.下列省级行政区中有两个简称的是()A.河南省B.湖南省C.甘肃省D.山西省10.某旅游团从辽宁出发,就近进行了“出境游”.他们可能游览了我国下列邻国中的()A.蒙古B.印度C.朝鲜D.越南11.下列重要经线、纬线中,穿过我国的是( )A.赤道B.本初子午线C.北回归线D.北极圈12.对我国影响最大的自然灾害是()A.干旱和泥石流B.台风与干旱C.洪涝与干旱D.台风与寒潮13.读水稻、冬小麦、棉花和油菜分布图,对应正确的是()A.①棉花②油菜③水稻④冬小麦B.①水稻②冬小麦③棉花④油菜C.①油菜②冬小麦③水稻④棉花D.①棉花②冬小麦③水稻④油菜14.下图是中国地形类型构成示意图,该图反映我地形的特点是()A.地形多种多样,平原面积广大B.地形多种多样,高原面积广大C.地形多种多样,山区面积广大D.地形多种多样,盆地面积广大15.我国共设立了5个少数民族自治区,它们名称中所包含的少数民族分别是A.蒙古族回族藏族维吾尔族苗族B.回族藏族布依族满族朝鲜族C.蒙古族回族藏族维吾尔族壮族D.回族白族蒙古族壮族土家族16.我国是一个水资源与人口、耕地匹配欠佳的国家。
重庆第八中学八年级上册期末物理试卷

重庆第八中学八年级上册期末物理试卷一、选择题1.如图所示,用发声音叉触及面颊,发现音叉在振动;一段时间后,音叉停止振动,声音便立即消失。
此现象说明声音()A.是由物体振动产生的B.能够通过空气传播C.不能在真空中传播D.是具有能量的疏密波2.控制噪声是城市环保主要项目之一,下列措施不能减弱噪声的是()A.市区内禁止机动车鸣笛B.规划时,工业区与居住区离得很近C.在汽车的排气管上装消声器D.城市街道两旁和空地多种草、多植树3.今年入夏以来,我市持续严重干旱,气象部门组织实施了多次人工降雨,在空中喷洒干冰是人工降雨的一种方法,干冰使空气中的水蒸气变成小冰粒,小冰粒在下降过程中变成雨滴,其中冰粒变成雨滴的物态变化过程属于()A.熔化B.凝固C.汽化D.升华4.小明同学到南美洲游学,见到一种外表酷似微型西瓜的野生水果,其独特的迷你造型和清爽的口感令人称奇。
图是迷你“西瓜”与一元硬币放在一起的对比照,根据图片信息,估测该迷你“西瓜”的长度约为()A.2mm B.6cm C.6mm D.2cm5.有甲、乙两支温度计,它们下端的玻璃泡的容积相同,内装液体都是煤油,甲玻璃管内径大,乙玻璃管内径小。
用它们同时测量一杯沸水的温度,观察两只温度计的液柱()A.甲上升较快B.乙上升较快C.甲、乙一样快D.无法确定6.如图所示的四种现象中,由光的折射形成的是()A.甲、乙B.丙、丁C.乙、丙D.甲、丁7.关于凸透镜和凹透镜,下列说法中正确的是()A.凸透镜对光有会聚作用,焦距越小,对光的折光本领就越强B.凹透镜对光有发散作用,焦距越小,对光的发散作用就越小C.凸透镜和凹透镜都有两个焦点,且都是实焦点D.经过凸透镜和凹透镜光心的光线,其传播方向会发生改变8.下列关于图中所示光学现象的描述或解释正确的是()A.图甲中,A是水,B是空气B.图乙中,人佩戴凹透镜可以矫正近视眼,是利用了凹透镜的汇聚作用C.图丙中,太阳光通过三棱镜会分解成红橙黄绿蓝靛紫七色光D.图丁中,漫反射的光线杂乱无章不遵循光的反射定律9.如图所示,加油机和战斗机以同样快慢、向同一方向前进。
重庆第八中学物理八年级上册期末试卷

重庆第八中学物理八年级上册期末试卷一、选择题1.中国古诗词文化博大精深,“姑苏城外寒山寺,夜半钟声到客船”,“风声雨声读书声声声入耳,家事国事天下事事事关心”。
下列解释错误的是()A.诗人根据音色判断是钟发出的声音B.钟声可以在空气中传播C.钟声比雨声在空气中传播得快,因为固体传声比液体快D.钟声是由钟体振动产生的2.关于声现象,下列说法正确的是()A.在公路旁植树、安装隔音屏、安装噪声检测仪可以在传播过程中减弱噪声B.大礼堂的四周墙壁都做成凹凸不平像蜂窝状似的,这样做是为了增强声音的反射C.医生用听诊器能听清病人胸腔内的声音是因为听诊器可以减少声音的分散,提高音调D.在教室说话比在操场上说话更响亮,是因为回声可以加强原声3.四季变化,赋予山西的冬天许多特有的景色,如图所示的四个自然现象中,属于凝固的是()A.窗户玻璃“出汗”B.壶口的冰凌C.窗户结冰花D.树枝上雾4.小阳假期和家长一起自驾三厢小轿车到郊外游玩,在路上准备通过一座桥,如图所示,下列对桥的长度估测最接近实际情况的是()A.5m B.10m C.25m D.50m5.如图所示是某种物质熔化时温度随时间变化的图象,根据图象所给的信息,下列叙述中不正确的是()A.该物质是晶体,熔点是48℃B.该物质在第3分钟时是固态C.该物质在熔化过程中不断吸热,温度保持不变D.该物质熔化过程持续了12min6.如图所示的四种现象中,由光的折射形成的是()A.甲、乙B.丙、丁C.乙、丙D.甲、丁7.如图是小涵从生活中收集到的一些光现象实例,以下说法正确的是()A.用放大镜看物体,总是看到放大的虚像B.电视画面的颜色是由红、绿、蓝三种色光组成C.凹透镜能使平行于主光轴的光会聚D.有经验的渔民叉鱼时要对准他看到的鱼8.甲、乙两眼睛的成像示意图如图所示,下列判断正确的是()A.甲是近视眼,应戴凸透镜制成的眼镜矫正B.甲是近视眼,应戴凹透镜制成的眼镜矫正C.乙是近视眼,应戴凸透镜制成的眼镜矫正D.乙是近视眼,应戴凹透镜制成的眼镜矫正9.“朝辞白帝彩云间,千里江陵一日还。
重庆市第八中学初二上学期期末数学试卷(附答案)

5. 如图,△ABC ≌ △DCB,若 AC = 7,BE = 5,则 DE 的长为 ( )
A. 2
B. 3
C. 4
D. 5
6. 如图,已知 △ABC 为等边三角形,BD 为中线,延长 BC 至 E,使 CE = CD,连接 DE, 则 ∠BDE 的度数为 ( )
A. 105◦
B. 120◦
C. 135◦
重庆市第八中学初二上学期期末考试
一选择题 (每小题3 分 1. 下列商标是轴对称图形的是 (
数学
考试时量#!"分钟 满分#!" 分
)
A
B
C
D
2. 下列计算正确的是 ( )
A. a3 + a3 = a6
B. 3a − a = 3
3. 使分式 2 有意义的 x 的取值范围是 ( x−3
A. x ̸= 3
.
15. 如图,在 △ABC 中,∠C = 90◦,∠B = 30◦,DE 垂直平分 AB,分别交 BC,AB 于点 D,
E,若 AD = 2,则 BC =
.
16. 分解因式:a3b − 4ab =
.
17. 如图,在 △ABC 中,∠ABC,∠ACB 的平分线 BE,CD 相交于点 F ,∠ABC = 42◦,∠A = 60◦,
−x ⩽ 1, 2x − 1 <
4
的整数解中选取.
26. 某商家预测一种应季衬衫能畅销市场,就用 13200 元购进了一批这种衬衫,面市后果然供不应求,商家又用 28800 元购进了第二批这种衬衫,所购数量是第一批购进量的 2 倍,但单价贵了 10 元. (1) 该商家购进的第一批衬衫是多少件?
(2) 若两批衬衫按相同的标价销售,最后剩下 50 件按八折优惠卖出,如果两批衬衫全部售完后利润不低于 25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
人教版八年级数学上册重庆三中—期半期试题 .doc

初中数学试卷 马鸣风萧萧重庆三中2011—2012学年上期八年级数学半期试题 题号一、解答题 二、填空题 三、选择题 四、作图题 五、简答题 六、计算题 总分 得分一、解答题1、Rt △ABC 与Rt △FED 是两块全等的含30°、60°角的三角板,按如图①所示拼在一起,CB 与DE 重合.(1)试说明:四边形ABFC 为平行四边形;(2)取BC 中点O ,将△ABC 绕点O 顺时针方向旋转到如图②中△A'B'C'位置,直线B'C'与AB 、CF 分别相交于P 、Q 两点,猜想OQ 、OP 长度的大小关系,并说明你的猜想.(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB 为菱形(不要求说理).2、如图,点O 是等腰直角三角形ABC 内一点,∠ACB =90°,∠AOB =140°,∠AOC =a .将△AOC 绕直角顶点C 按顺时针方向旋转90°得△BDC ,连接OD .(1)说明COD 是等腰直角三角形;评卷人得分(2)当a=95°时,试判断△BOD的形状,并说明理由.二、填空题3、若,则a=______,b=_______.4、比较大小:3______2(填“>”或“<”).5、等边三角形绕着它的中心至少旋转______度后能与自身重合.6、如图,△ABC按顺时针方向转动一个角度后成为△AED,若∠EAB=40°,则∠C=______.7、如图所示,若把△ABC绕点A旋转,能够与△ADE完全重合,其中AB与AD重合,AC与AE重合,若∠EAD=120°,EA⊥AB,则旋转角度为______.8、已知如图所示,梯形ABCD中AB∥CD,AD=BC,AC⊥BD,AB=3,CD=5,则梯形的面积是______.评卷人得分9、在四边形ABCD中,AB=CD,AC交BD于点O.如果想使该四边形成为平行四边形,那么只需添加条件____________________________________:10、已知如图正方形ABCD边长为1 cm,点E在对角线BD上,BE=BC,P是CE上一动点,PF⊥BD,PG⊥BC,PF +PG的值为______.三、选择题评卷人得分11、在天气预报图上,有各种各样表示天气的符号,下列表示天气符号的图形中,既是中心对称图形又是轴对)称图形的是 (12、下列说法:①3是9的平方根;②9的平方根是3;③4是8的平方根;④-8是64的负平方根,其中正确的是 ( )A.1个 B.2个 C.3个 D.4个13、把120.82保留三个有效数字,并用科学记数法表示为 ( )A.1.20×102B.1.2082×102C.12.1×10 D.1.21×10214、已知一个直角三角形的两边长分别为3和4,则第三边长是 ( )A.5 B.25 C . D.5或15、平行四边形不一定具备的性质是 ( )A.对角相等 B.对角线互相平分 C.对边相等 D.对角线相等16、□ABCD的周长为36 cm,AB =BC,则较长边的长为 ( )A.15 cm B.7.5 cm C.10.5 cm D.21 cm17、如图,正方形小方格的面积是1,图中以格点为端点且长度为5的线段有(每个小正方形的顶点都是格点) ( )A.0条 B.2条 C.4条 D.6条18、如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁厚度和小圆孔大小忽略不计)范围是 ( )A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13四、作图题评卷人得分19、图①、图②均为7×6的正方形网格,点A、B、C在格点(小正方形的顶点)上.(1)在图①中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形;(2)在图②中确定格点E,并画出一个以A、B、C、E为顶点的四边形,使其为中心对称图形.五、简答题20、如图,在△ABC 中,∠BAC =45°,AD ⊥BC 于D ,将△ABD 沿AB 所在的直线折叠,使点D 落在点E 处;将△ACD 沿AC 所在的直线折叠,使点D 落在点F 处,分别延长EB 、FC 使其交于点M .(1)判断四边形AEMF 的形状,并说明理由;(2)若BD =2,AD =6,试求DC 的长.六、计算题21、 (2x -3)2=36; 22、参考答案 评卷人得分评卷人得分一、解答题1、(1)略(2)略(3)90°2、(1)略(2)等腰三角形二、填空题3、1 24、>5、1206、70°7、30°8、169、AB//CD10、三、选择题11、A12、B13、D14、D15、D16、C17、B18、A四、作图题19、有以下答案供参考(2) 有以下答案供参考五、简答题20、(1)正方形(2)3六、计算题21、x=或x=-22、-118。
重庆市重庆一中2011-2012学年八年级数学上学期期末考试试题

1、(2014•兰州)给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;(2)如下图(1),请你在图中画出以格点为顶点,OA、OB为勾股边,且对角线相同的所有勾股四边形OAMB.(3)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.①求证:△BCE是等边三角形;②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.思路分析:(1)根据定义和特殊四边形的性质,则有矩形或正方形或直角梯形;(2)①首先证明△ABC≌△BDC,得出AC=DE,BC=BE,连接CE,进一步得出△BCE为等边三角形;②利用等边三角形的性质,进一步得出△DCE是直角三角形,问题得解.例4 解:(1)正方形、矩形、直角梯形均可;(2)画图证明:(3)①∵△ABC≌△DBE,∴BC=BE,∵∠CBE=60°,∴△BCE是等边三角形;②∵△ABC≌△DBE,∴BE=BC,AC=ED;∴△BCE为等边三角形,∴BC=CE,∠BCE=60°,∵∠DCB=30°,∴∠DCE=90°,在Rt△DCE中,DC2+CE2=DE2,∴DC2+BC2=AC2.2、.阅读材料:(1)对于任意两个数的大小比较,有下面的方法:当时,一定有;当时,一定有;当时,一定有.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.(2)对于比较两个正数的大小时,我们还可以用它们的平方进行比较:∵,∴()与()的符号相同当>0时,>0,得当=0时,=0,得当<0时,<0,得解决下列实际问题:(1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2x ,张丽同学的张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且y用纸总面积为W1,李明同学的用纸总面积为W2.回答下列问题:(2)①W1= (用x、y的式子表示)W2= (用x、y的式子表示)(3)②请你分析谁用的纸面积最大.(4)(2)如图1所示,要在燃气管道l上修建一个泵站,分别向A.B两镇供气,已知A.B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=x km,现设计两种方案:方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.方案二:如图3所示,点A'与点A关于l对称,A'B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.①在方案一中,a1= km(用含x的式子表示);②在方案二中,a2= km(用含x的式子表示);③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.(1)解:①W1=3x+7y,W2=2x+8y,故答案为:3x+7y,2x+8y.②解:W1﹣W2=(3x+7y)﹣(2x+8y)=x﹣y,∵x>y,∴x﹣y>0,∴W1﹣W2>0,得W1>W2,所以张丽同学用纸的总面积大.(2)①解:a1=AB+AP=x+3,故答案为:x+3.②解:过B作BM⊥AC于M,则AM=4-3=1,在△ABM中,由勾股定理得:BM2=AB2﹣12=x2﹣1,在△A'MB中,由勾股定理得:AP+BP=A'B==,故答案为:.③解:=(x+3)2﹣()2=x2+6x+9﹣(x2+48)=6x-39,当>0(即a1﹣a2>0,a1>a2)时,6x﹣39>0,解得x>6.5,当=0(即a1﹣a2=0,a1=a2)时,6x﹣39=0,解得x=6.5,当<0(即a1﹣a2<0,a1<a2)时,6x﹣39<0,解得x<6.5,综上所述当x>6.5时,选择方案二,输气管道较短,当x=6.5时,两种方案一样,当0<x<6.5时,选择方案一,输气管道较短3、(2014•苏州模拟)如图①,将一张直角三角形纸片△ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;(3)若一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是什么?. 解:(1)(2)(3)由(2)可得,若一个三角形所折成的“叠加矩形”为正方形,那么三角形的一边长与该边上的高相等的直角三角形或锐角三角形.4、(2013•连云港)小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连接AE并延长交BC的延长线于点F,求证:S四边形ABCD=S△ABF(S表示面积)问题迁移:如图2:在已知锐角∠AOB内有一个定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值,请问当直线MN在什么位置时,△MON的面积最小,并说明理由.5.(2014•珠海)阅读下列材料:解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:解∵x﹣y=2,∴x=y+2又∵x>1,∵y+2>1.∴y>﹣1.又∵y<0,∴﹣1<y<0.…①同理得:1<x<2.…②由①+②得﹣1+1<y+x<0+2∴x+y的取值范围是0<x+y<2请按照上述方法,完成下列问题:(1)已知x﹣y=3,且x>2,y<1,则x+y的取值范围是.(2)已知y>1,x<﹣1,若x﹣y=a成立,求x+y的取值范围(结果用含a的式子表示).4.解:(1)∵x﹣y=3,∴x=y+3,又∵x>2,∴y+3>2,∴y>﹣1.又∵y<1,∴﹣1<y<1,…①同理得:2<x<4,…②由①+②得﹣1+2<y+x<1+4∴x+y的取值范围是1<x+y<5;(2)∵x﹣y=a,∴x=y+a,又∵x<﹣1,∴y+a<﹣1,∴y<﹣a﹣1,又∵y>1,∴1<y<﹣a﹣1,…①同理得:a+1<x<﹣1,…②由①+②得1+a+1<y+x<﹣a﹣1+(﹣1),∴x+y的取值范围是a+2<x+y<﹣a﹣2.6、(2014•自贡)阅读理解:如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.解:(1)∵∠A=∠B=∠DEC=45°,∴∠AED+∠ADE=135°,∠AED+∠CEB=135°∴∠ADE=∠CEB,在△ADE和△BCE中,,∴△ADE∽△BCE,∴点E是否是四边形ABCD的边AB上的相似点.(2)如图所示:点E是四边形ABCD的边AB上的相似点,(3)∵点E是四边形ABCM的边AB上的一个强相似点,∴△AEM∽△BCE∽△ECM,∴∠BCE=∠ECM=∠AEM.由折叠可知:△ECM≌△DCM,∴∠ECM=∠DCM,CE=CD,∴∠BCE=∠BCD=30°,BE=,在Rt△BCE中,tan∠BCE==tan30°=,∴.7.(2014•扬州)对x,y定义一种新运算T,规定:T(x,y)=(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)==B.(1)已知T(1,﹣1)=﹣2,T(4,2)=1.①求a,b的值;②若关于m的不等式组恰好有3个整数解,求实数p的取值范围;(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b 应满足怎样的关系式?6. 解:(1)①根据题意得:T(1,﹣1)==﹣2,即a﹣b=﹣2;T=(4,2)==1,即2a+b=5,解得:a=1,b=3;②根据题意得:,由①得:m≥﹣;由②得:m<,∴不等式组的解集为﹣≤m<,∵不等式组恰好有3个整数解,即m=0,1,2,∴2≤<3,解得:﹣2≤p<﹣;(2)由T(x,y)=T(y,x),得到=,整理得:(x2﹣y2)(2b﹣a)=0,∵T(x,y)=T(y,x)对任意实数x,y都成立,∴2b﹣a=0,即a=2B.逆相似;当点P 在CM 上时,过点P 2只能画出2条截线P 2Q 1、P 2Q 2,分别使∠AP 2Q 1=∠ABC ,∠CP 2Q2=∠ABC ,此时△AP 2Q 1、△Q 2P 2C 都与△ABC 互为逆相似.第三种情况:如图③,点P 在AB (不含点A 、B )上,过点C 作∠BCD=∠A ,∠ACE=∠B ,CD 、CE 分别交AC 于点D 、E .当点P 在AD (不含点D )上时,过点P 只能画出1条截线P 1Q ,使∠AP 1Q=∠ABC ,此时△AQP 1与△ABC 互为逆相似;当点P 在DE 上时,过点P 2只能画出2条截线P 2Q 1、P 2Q 2,分别使∠AP 2Q 1=∠ACB ,∠BP 2Q 2=∠BCA ,此时△AQ 1P 2、△Q 2BP 2都与△ABC 互为逆相似;当点P 在BE (不含点E )上时,过点P 3只能画出1条截线P 3Q′,使∠BP 3Q′=∠BCA ,此时△Q′BP 3与△ABC 互为逆相似.10、阅读:如图1,在ABC ∆和DEF ∆中,90ABC DEF ∠=∠=︒,,AB DE a ==BC EF b ==()b a <,B 、C 、D 、E 四点都在直线m 上,点B 与点D 重合.连接AE 、FC ,我们可以借助于ACE S ∆和FCE S ∆的大小关系证明不等式:222a b ab +>(0b a >>).证明过程如下:∵,,.BC b BE a EC b a ===- ∴11(),22ACE S EC AB b a a ∆=⋅=- 11().22FCES EC FE b a b ∆=⋅=- ∵0b a >>, ∴FCE SACE S ∆∆>. 即a ab b a b )(21)(21->-. ∴22b ab ab a ->-. ∴222a b ab +>. 解决下列问题:(1)现将△DEF 沿直线m 向右平移,设()BD k b a =-,且01k ≤≤.如图2,当BD EC =时, k = .利用此图,仿照上述方法,证明不等式:222a b ab +>(0b a >>).(2)用四个与ABC ∆全等的直角三角形纸板进行拼接,也能够借助图形证明上述不等式.请你画出一个..示意图,并简要说明理由. 答案22.(1)12k =;--------------------------1分 图2证明:连接AD 、BF . 可得1()2BD b a =-. ∴ ()()11112224ABD S BD AB b a a a b a ∆=⋅=⨯⨯-⋅=-,()()11112224FBD S BD FE b a b b b a ∆=⋅=⨯⨯-⋅=-.∵ 0>>a b , ∴ FBD ABD S S ∆∆<, 即 ()14a b a -()14b b a <-.∴ ab b a ab -<-22. ∴ ab b a 222>+.--------------------------2分(2)答案不唯一,图1分,理由1分.举例:如图,理由: 延长BA 、FE 交于点I .∵ 0>>a b , ∴ IBCE ABCD S S >矩形矩形, 即)()(a b a a b b ->-.∴ 22a ab ab b ->-.∴ ab b a 222>+.---------4分 举例:如图,理由: 四个直角三角形的面积和11422S a b ab =⨯⋅=, 大正方形的面积222S a b =+.∵ 0>>a b , ∴ 21S S >. ∴ ab b a 222>+.--------------------------4分11、(2013山西,25,13分)(本题13分)数学活动——求重叠部分的面积。
重庆第八中学人教版八年级上册生物期末试卷及答案-百度文库

重庆第八中学人教版八年级上册生物期末试卷及答案-百度文库一、选择题1.下列不属于扁形动物的是()A.涡虫B.华枝睾吸虫C.珊瑚虫D.猪肉绦虫2.蚯蚓的体壁总是湿润的,这有利于蚯蚓()A.吸收营养B.排出废物C.保持水分D.进行呼吸3.南非周边海域发现一种新甲壳类动物,形似龙虾,体型较小,属于节肢动物。
下列不属于节肢动物的主要特征的是A.身体分节B.体表有外骨骼C.足和触角分节D.有三对足,两对翅4.如图表示鱼和虾生活环境和结构特点的异同,两个圆的重合区域为相同点。
则图中甲区和丙区所示的选项正确的是( )①生活在水中②用鳍游泳③体内有脊柱④用鳃呼吸A.甲区②③ 丙区①④B.甲区①② 丙区③④C.甲区①③ 丙区②④D.甲区①④ 丙区②③5.如图是家鸽的呼吸系统示意图,下列说法正确的是()A.②和③都能进行气体交换B.气体进入体内的途径是①→②→③C.①是气管②是肺③是气囊D.家鸽飞行时,吸气和呼气时都进行了气体交换6.家鸽适应飞翔生活的特点是()①身体分为头、颈、躯干、四肢和尾②身体流线型③前肢变为翼④有坚硬的角质喙⑤长骨中空,充满空气⑥足有四趾⑦胸骨发达,有龙骨突.A.①④⑤⑥B.③⑤⑥⑦C.②③⑤⑦D.②③⑤⑥7.下列与青蛙的发育过程不同的动物是()A.蟾蜍B.大鲵C.蝾螈D.鳄鱼8.下面动物中能在陆地产卵且体温恒定的动物是()A.鳄鱼B.鸽子C.青蛙D.山羊9.当你由伸肘状态变为屈肘状态时(如右图),你的上肢肌肉 X和Y会分别处于什么状态?A.X收缩、Y收缩B.X舒张、Y收缩C.X舒张、Y舒张D.X收缩、Y舒张10.如图表示的是人体的屈肘动作。
下列有关叙述,错误的是()A.图中的1、2分别表示肱二头肌和肱三头肌B.前臂骨和上臂骨通过2两端的肌腱连接起来C.完成屈肘动作时,1受神经传来的刺激收缩D.在屈肘动作中1 和2是相互配合活动的11.地球上动物种类繁多,它们多种多样的运动方式和行为扩大了其活动范围,便于更好的生存和繁術。
重庆第八中学八年级上册压轴题数学模拟试卷含详细答案

重庆第八中学八年级上册压轴题数学模拟试卷含详细答案一、压轴题1.在ABC ∆中,若存在一个内角角度,是另外一个内角角度的n 倍(n 为大于1的正整数),则称ABC ∆为n 倍角三角形.例如,在ABC ∆中,80A ∠=︒,75B ∠=︒,25C ∠=︒,可知3∠=∠B C ,所以ABC ∆为3倍角三角形.(1)在ABC ∆中,55A ∠=︒,25B ∠=︒,则ABC ∆为________倍角三角形;(2)若DEF ∆是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的13,求DEF ∆的最小内角. (3)若MNP ∆是2倍角三角形,且90M N P ∠<∠<∠<︒,请直接写出MNP ∆的最小内角的取值范围.2.直角三角形ABC 中,90ACB ∠=︒,直线l 过点C .(1)当AC BC =时,如图1,分别过点A 和B 作AD ⊥直线l 于点D ,BE ⊥直线l 于点E ,ACD 与CBE △是否全等,并说明理由;(2)当8AC cm =,6BC cm =时,如图2,点B 与点F 关于直线l 对称,连接 BF CF 、,点M 是AC 上一点,点N 是CF 上一点,分别过点M N 、作MD ⊥直线l 于点D ,NE ⊥直线l 于点E ,点M 从A 点出发,以每秒1cm 的速度沿A C →路径运动,终点为C ,点N 从点F 出发,以每秒3cm 的速度沿F C B C F →→→→路径运动,终点为F ,点,M N 同时开始运动,各自达到相应的终点时停止运动,设运动时间为t 秒,当CMN △为等腰直角三角形时,求t 的值.3.如图1,在等边△ABC 中,E 、D 两点分别在边AB 、BC 上,BE =CD ,AD 、CE 相交于点F .(1)求∠AFE 的度数;(2)过点A 作AH ⊥CE 于H ,求证:2FH +FD =CE ;(3)如图2,延长CE 至点P ,连接BP ,∠BPC =30°,且CF =29CP ,求PF AF的值. (提示:可以过点A 作∠KAF =60°,AK 交PC 于点K ,连接KB )4.已知在△ABC 中,AB =AC ,射线BM 、BN 在∠ABC 内部,分别交线段AC 于点G 、H . (1)如图1,若∠ABC =60°,∠MBN =30°,作AE ⊥BN 于点D ,分别交BC 、BM 于点E 、F .①求证:∠1=∠2;②如图2,若BF =2AF ,连接CF ,求证:BF ⊥CF ;(2)如图3,点E 为BC 上一点,AE 交BM 于点F ,连接CF ,若∠BFE =∠BAC =2∠CFE ,求ABFACF S S 的值.5.问题情景:数学课上,老师布置了这样一道题目,如图1,△ABC 是等边三角形,点D 是BC 的中点,且满足∠ADE =60°,DE 交等边三角形外角平分线于点E .试探究AD 与DE 的数量关系.操作发现:(1)小明同学过点D 作DF ∥AC 交AB 于F ,通过构造全等三角形经过推理论证就可以解决问题,请您按照小明同学的方法确定AD 与DE 的数量关系,并进行证明.类比探究:(2)如图2,当点D是线段BC上任意一点(除B、C外),其他条件不变,试猜想AD与DE之间的数量关系,并证明你的结论.拓展应用:(3)当点D在线段BC的延长线上,且满足CD=BC,在图3中补全图形,直接判断△ADE的形状(不要求证明).6.阅读下面材料,完成(1)-(3)题.数学课上,老师出示了这样一道题:如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.同学们经过思考后,交流了自已的想法:小明:“通过观察和度量,发现∠DFC的度数可以求出来.”小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”......老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”(1)求∠DFC 的度数;(2)在图1中探究线段EF 、AF 、DF 之间的数量关系,并证明;(3)在图2中补全图形,探究线段EF 、AF 、DF 之间的数量关系,并证明.7.如图,若要判定纸带两条边线a ,b 是否互相平行,我们可以采用将纸条沿AB 折叠的方式来进行探究.(1)如图1,展开后,测得12∠=∠,则可判定a//b ,请写出判定的依据_________; (2)如图2,若要使a//b ,则1∠与2∠应该满足的关系是_________;(3)如图3,纸带两条边线a ,b 互相平行,折叠后的边线b 与a 交于点C ,若将纸带沿11A B (1A ,1B 分别在边线a ,b 上)再次折叠,折叠后的边线b 与a 交于点1C ,AB//11A B ,137BB AC ==,,求出1AC 的长.8.如图所示,在平面直角坐标系xOy 中,已知点A 的坐标(3,2)-,过A 点作AB x ⊥轴,垂足为点B ,过点(2,0)C 作直线l x ⊥轴,点P 从点B 出发在x 轴上沿着轴的正方向运动.(1)当点P 运动到点O 处,过点P 作AP 的垂线交直线l 于点D ,证明AP DP =,并求此时点D 的坐标;(2)点Q 是直线l 上的动点,问是否存在点P ,使得以P C Q 、、为顶点的三角形和ABP ∆全等,若存在求点P 的坐标以及此时对应的点Q 的坐标,若不存在,请说明理由.9.在△ABC 中,∠BAC =45°,CD ⊥AB ,垂足为点D ,M 为线段DB 上一动点(不包括端点),点N 在直线AC 左上方且∠NCM =135°,CN =CM ,如图①.(1)求证:∠ACN =∠AMC ;(2)记△ANC 得面积为5,记△ABC 得面积为5.求证:12S AC S AB=; (3)延长线段AB 到点P ,使BP =BM ,如图②.探究线段AC 与线段DB 满足什么数量关系时对于满足条件的任意点M ,AN =CP 始终成立?(写出探究过程)10.请按照研究问题的步骤依次完成任务.(问题背景)(1)如图1的图形我们把它称为“8字形”, 请说理证明∠A+∠B=∠C+∠D .(简单应用)(2)如图2,AP 、CP 分别平分∠BAD 、∠BCD ,若∠ABC=20°,∠ADC=26°,求∠P 的度数(可直接使用问题(1)中的结论)(问题探究)(3)如图3,直线AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE , 若∠ABC=36°,∠ADC=16°,猜想∠P 的度数为 ;(拓展延伸)(4)在图4中,若设∠C=x ,∠B=y ,∠CAP=13∠CAB ,∠CDP=13∠CDB ,试问∠P 与∠C 、∠B 之间的数量关系为 (用x 、y 表示∠P ) ;(5)在图5中,AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、D 的关系,直接写出结论 .11.对x y 、定义一种新运算T ,规定:()()(),2T x y mx ny x y =++(其中mn 、均为非零常数).例如:()1,133T m n =+.(1)已知()()1,10,0,28T T -==.①求mn 、的值; ②若关于p 的不等式组()()2,244,32T p p T p p a ⎧->⎪⎨-≤⎪⎩恰好有3个整数解,求a 的取值范围; (2)当22x y ≠时,()(),,T x y T y x =对任意有理数,x y 都成立,请直接写出mn 、满足的关系式.学习参考:①()a b c ab ac +=+,即单项式乘以多项式就是用单项式去乘多项式的每一项,再把所得的结果相加;②()()a b m n am an bm bn ++=+++,即多项式乘以多项式就是用一个多项式的每一项去乘另一个多项式的每一项,再把所得的结果相加.12.如图(1),AB =4cm ,AC ⊥AB ,BD ⊥AB ,AC =BD =3cm .点 P 在线段 AB 上以 1/cm s 的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为 t (s ).(1)若点 Q 的运动速度与点 P 的运动速度相等,当t =1 时,△ACP 与△BPQ 是否全等,请说明理由, 并判断此时线段 PC 和线段 PQ 的位置关系;(2)如图(2),将图(1)中的“AC ⊥AB ,BD ⊥AB”为改“∠CAB =∠DBA =60°”,其他条件不变.设点 Q 的运动速度为x /cm s ,是否存在实数x ,使得△ACP 与△BPQ 全等?若存在,求出相应的x 、t 的值;若不存在,请说明理由.13.如图,△ABC 是等边三角形,△ADC 与△ABC 关于直线AC 对称,AE 与CD 垂直交BC 的延长线于点E ,∠EAF =45°,且AF 与AB 在AE 的两侧,EF ⊥AF .(1)依题意补全图形.(2)①在AE 上找一点P ,使点P 到点B ,点C 的距离和最短;②求证:点D 到AF ,EF 的距离相等.14.数学活动课上,老师出了这样一个题目:“已知:MF NF ⊥于F ,点A 、C 分别在NF 和MF 上,作线段AB 和CD (如图1),使90FAB MCD ∠-∠=︒.求证://AB CD ”.(1)聪聪同学给出一种证明问题的辅助线:如图2,过A 作//AG FM ,交CD 于G .请你根据聪聪同学提供的辅助线(或自己添加其它辅助线),给出问题的证明. (2)若点E 在直线CD 下方,且知30BED ∠=︒,直接写出ABE ∠和CDE ∠之间的数量关系.15.现给出一个结论:直角三角形斜边的中线等于斜边的一半;该结论是正确的,用图形语言可以表示为:如图1在ABC ∆中,90︒∠=C ,若点D 为AB 的中点,则12CD AB =. 请结合上述结论解决如下问题:已知,点P 是射线BA 上一动点(不与A,B 重合)分别过点A,B 向直线CP 作垂线,垂足分别为E,F,其中Q 为AB 的中点(1)如图2,当点P 与点Q 重合时,AE 与BF 的位置关系____________;QE 与QF 的数量关系是__________(2)如图3,当点P 在线段AB 上不与点Q 重合时,试判断QE 与QF 的数量关系,并给予证明.(3)如图4,当点P 在线段BA 的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路.16.小敏与同桌小颖在课下学习中遇到这样一道数学题:“如图(1),在等边三角形ABC 中,点E 在AB 上,点D 在CB 的延长线上,且ED EC =,试确定线段AE 与DB 的大小关系,并说明理由”.小敏与小颖讨论后,进行了如下解答:(1)取特殊情况,探索讨论:当点E 为AB 的中点时,如图(2),确定线段AE 与DB 的大小关系,请你写出结论:AE _____DB (填“>”,“<”或“=”),并说明理由.(2)特例启发,解答题目:解:题目中,AE 与DB 的大小关系是:AE _____DB (填“>”,“<”或“=”).理由如下:如图(3),过点E 作EF ∥BC ,交AC 于点F .(请你将剩余的解答过程完成) (3)拓展结论,设计新题:在等边三角形ABC 中,点E 在直线AB 上,点D 在直线BC 上,且ED EC =,若△ABC 的边长为1,2AE =,求CD 的长(请你画出图形,并直接写出结果).17.(阅读材料):(1)在ABC ∆中,若90C ∠=︒,由“三角形内角和为180°”得1801809090A B C ∠︒+∠=-∠︒︒-=︒=.(2)在ABC ∆中,若90A B ∠+∠=︒,由“三角形内角和为180°”得180()1809090C A B ∠=︒-∠+∠=︒-︒=︒.(解决问题):如图①,在平面直角坐标系中,点C 是x 轴负半轴上的一个动点.已知//AB x 轴,交y 轴于点E ,连接CE ,CF 是∠ECO 的角平分线,交AB 于点F ,交y 轴于点D .过E 点作EM 平分∠CEB ,交CF 于点M .(1)试判断EM 与CF 的位置关系,并说明理由;(2)如图②,过E 点作PE ⊥CE ,交CF 于点P .求证:∠EPC=∠EDP ;(3)在(2)的基础上,作EN 平分∠AEP ,交OC 于点N ,如图③.请问随着C 点的运动,∠NEM 的度数是否发生变化?若不变,求出其值:若变化,请说明理由.18.在△ABC 中,已知∠A =α.(1)如图1,∠ABC 、∠ACB 的平分线相交于点D .求∠BDC 的大小(用含α的代数式表示);(2)如图2,若∠ABC 的平分线与∠ACE 的平分线交于点F ,求∠BFC 的大小(用含α的代数式表示);(3)在(2)的条件下,将△FBC 以直线BC 为对称轴翻折得到△GBC ,∠GBC 的平分线与∠GCB 的平分线交于点M (如图3),求∠BMC 的度数(用含α的代数式表示).19.(1)发现:如图1,ABC ∆的内角ABC ∠的平分线和外角ACD ∠的平分线相交于点O 。
重庆市第八中学2023-2024学年八年级上学期数学期末模拟试题

重庆市第八中学2023-2024学年八年级上学期数学期末模拟试题学校:___________姓名:___________班级:___________考号:___________一、单选题....<,则下列不等式一定成立的是().已知x yA.与小凯相比,小楠5次成绩的方差大B.与小凯相比,小楠C.与小凯相比,小楠的成绩比较稳定D.小凯的极差为6.中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九A.75B10=-和直线8.直线1l:y kx bA.....甲、乙两车从A城出发匀速行驶至城.在整个行驶过程中,甲、乙两车离开y(千米)与甲车行驶的时间(小时)之间的函数关系如图所示,下列结论错误的是()A .A 、B 两城相距300千米B .乙车比甲车晚出发1小时,却早到C .乙车追上甲车时甲车行驶了D .当甲、乙两车相距40千米时,10.如图,直线:2AB y x m =-+与坐标轴交于接AD 且AD y ∥轴,过点()0,6接BD ,BD AB ⊥,将ABD △沿着直线若24ACE S = ,那么BEF S 为(A .3.5B .4二、填空题11.不等式0ax b +>的解集为x <12.已知一组数据12345,,,,a a a a a 的方差是方差是.13.如图,一次函数y kx b =+和y 集是.14.如图,在ABC AB C ''△.若点B '15.若关于x ,y 的二元一次方程组值范围是.16.如图,点D 为等边ABC 外一点,连接120ADC ∠=︒,则BD =.三、解答题17.(1)解方程组:342321x y x y +=⎧⎨-=⎩(2)解不等式组:3(1)521532x x x -≤-⎧⎪-+⎨-⎪⎩18.如图,已知ABC 中,2B ∠=(1)请用基本的尺规作图:作AB AE =,连接DE (不写作法,不下结论,保留作图痕迹)(2)在(1)所作的图形中,探究线段题时,给出了如下的解决思路,请根据小明的思路完成下面的填空.解:AC AB BD =+,理由如下:∵AD 平分BAC ∠,∴BAD ∠=,在ABD △与AED △中,AB AE BAD EAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABD AED ≌,∴B AED DE ∠=∠=,,∵AED EDC C B ∠=∠+∠∠,∴EDC ∠=,(1)b =,m =;(2)根据以上数据分析,你认为该校(八、九年级)年级的学生一分钟跳绳成绩更优秀,请说明理由(写出一条理由即可);(3)若该校八、九年级共有3000名学生参加此次比赛,请你估计这两个年级的学生跳绳个数不少于200个的人数.20.如图,在矩形ABCD 中,2AB =,4=AD ,点E 和F 分别为(1)直接写出y 与x 的函数关系式,并注明自变量x 的取值范围;(2)在直角坐标系中画出y 与x 的函数图象,并写出该函数的一条性质;(3)结合函数图象,当函数y 满足53y ≥,写出x 的取值范围.四、单选题21.已知一次函数(6)1y a x =-+经过第一、二、三象限,且关于1()0232113a x x x ⎧-->⎪⎪⎨+⎪+≥⎪⎩恰有4个整数解,则所有满足条件的整数a 的值的和为(A .9B .11C .15五、填空题23.如图,在ABC 中,E ,交AC 于D ,F 为AC 延长线上,则C D '的长为24.学习完《三角形》章节,某数学小组小花同学给出如下定义:对任意的一个三位数n ,如果n 满足各个数位上的数字均不为零,且该数任意两个数位上的数字之和大于余下数位上的数字,那么我们就把该数称为百位数字作十位得到的两位数,位数字作十位,百位数字作个位得到的两位数,再加上例如:675,是一个“稳定数”,由定义得一个“稳定数”100101s a b =++六、解答题25.爆竹声中一岁除,春风送暖入屠苏.随着春节即将到来,家家户户贴春联,挂灯笼,欢天喜地迎新年.重庆某百货超市计划购进春联和灯笼这两种商品.已知第一次购进5(1)求点D 的坐标;(2)如图2,在直线2l 上存在一点M ,使3ADM AED S S = ,求出点M 的坐标;(3)如图3,将AOB 绕点O 逆时针旋转90︒得到A OB ''△,点P 为直线A B ''上一动点,点Q 为x 轴上一动点,连接PE ,PQ ,EQ ,当PQE V 为以PQ 为腰的等腰直角三角形时,直接写出点P 的坐标.27.如图,等腰三角形ABC 中,AB AC =,D 为AC 边上一点,E 为射线BD 连CE .(1)如图1,点F 在线段BD 上,连AE 、AF .若60BAC ∠=︒,AEF △为等边三角形,AE =2CE =,求BE 的长;(2)如图2,F 为线段CE 的垂直平分线上一点,连接FC 、FE 、AF ,M 为BE 的中点,连接AM 、FM .若90ABC FEC ∠+∠=︒,求证:AM MF ⊥;(3)如图3,60BAC ∠=︒,D 为AC 中点,F 为CE 中点,AF 与BE 交于点G ,将ABG 沿射线BD 方向平移得A B G '''△,连接AB '、A C '.若4AB =,直接写出AB A C ''+的最小值.。
