《图形的位似》图形的相似课件PPT
合集下载
《图形的位似》图形的相似PPT 图文

旧的东西其实极好。学生时代喜欢写信 ,只是 今天书 信似乎 早已被 人遗忘 ,那些 旧的记 忆,被 尘埃轻 轻覆盖 ,曾经 的笔端 洇湿了 笔锋, 告慰着 那时的 心绪。 现在读 来,仿 佛嗅到 时光深 处的香 气,一 朵墨色 小花晕 染了眼 角,眉 梢,是 飞扬的 青春, 无知年 少的轻 狂,这 份带不 走的青 涩,美 丽而忧 伤。
课堂小结
一、定义及性质: 二、位似图形的件确定对应点,并描出对应点 4.顺次连结各对应点,所成的图形就是
所求的图形 三、位似变换与坐标的关系:
在平面直角坐标系中,如果位似变换 是以原点为位似中心,相似比为k, 那么位似图形对应点的坐标的比等于k或-k
-12
-10
B
-8
A
-6
A′
B′ C-4
y
D 6你还有其他办法 4D吗′ ?试试看.
2
-2Co′
C′
2
4B′ 6 8 10 12 x
-2
D′ A′
-4
四边形A′B′C′ D′就是要求的四边 形ABCD的位似图形
-6
1.如图表示△AOB和把它缩小后 得到的△COD,求它们的相似比。
y
6A
4
2C
o -12 -10 -8 -6 -4 -2
小心翼翼珍藏着,和母亲在一起的美好 时光。 母亲身 体一直 不好, 最后的 几年光 景几乎 是在医 院渡过 ,然而 和母亲 在一起 的毎一 刻都是 温暖美 好的。 四年前 ,母亲 还是离 开了这 个世界 ,离开 了我。 生命就 是如此 脆弱, 逝去和 別离, 陈旧的 情绪某 年某月 的那一 刻如水 泻闸。 水在流 ,云在 走,聚 散终有 时,不 贪恋一 生,有 你的这 一程就 是幸运 。那是 地久天 长的在 我的血 液中渗 透,永 远在我 的心中 ,在我 的生命 里。
图形的相似与位似复习课件

3.若△A1B1C1∽△A2B2C2,对应高之比为 n:m,则面积之比为 ; x y z yz 如果 ; 则 4、 4 5 7 x 5若x:4=y:5=z:6,且3x+2y+z=56,则x为( )
A 8 B 10 C 12 D 16
2.下列命题正确的是(
D
)
A.有一角相等且有两边对应成比例的两个三角形相似。 B. △ABC的三边长为3,4,5. △A’B’C’的三边为 a+3,a+4,a+5.则△ABC∽ △A’B’C’。 C.若两个三角形相似,且有一对边相等,则它们的相 似比为1. D.都有一内角为100°的两个等腰三角形相似。
P
.
B
= AP AB
点B把线段AC分成两部分,如果 PB AP 那么称线段AC被点B 黄金分割, 点P为线段AB 的 黄金分割点,
AP与AB的比值约为0.618,这个比值称 为 黄金比.
思考:如何应用二次方程的知识求出黄金比的数值?
1.若 a:3=b:7, 则(a+3b):2b=
;
2.若a=2,b=6,c=4,且a,b,c,d成比 例,则d= ;
∴x=2或x=12
∴x=2或x=12或x=5.6时,以C、D、P为顶点的三 角形与以P、B、A为顶点的三角形相似
巩固提高: 在∆ABC中,AB=8cm,BC=16cm,点P从点A 开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始 沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、 B同时出发,经几秒钟∆BPQ与∆BAC相似?
这个点叫做位似中心.
这时的相似比又称为位似比. 性质:位似图形上任意一对对应点到位似中心的 距离之比等于位似比
1.任取一点O; 2.以点O为端点作射线OA、OB、OC、…; 3.分别在射线OA、OB、OC、 …上取点A’、 B’、C’、 … ,使:
A 8 B 10 C 12 D 16
2.下列命题正确的是(
D
)
A.有一角相等且有两边对应成比例的两个三角形相似。 B. △ABC的三边长为3,4,5. △A’B’C’的三边为 a+3,a+4,a+5.则△ABC∽ △A’B’C’。 C.若两个三角形相似,且有一对边相等,则它们的相 似比为1. D.都有一内角为100°的两个等腰三角形相似。
P
.
B
= AP AB
点B把线段AC分成两部分,如果 PB AP 那么称线段AC被点B 黄金分割, 点P为线段AB 的 黄金分割点,
AP与AB的比值约为0.618,这个比值称 为 黄金比.
思考:如何应用二次方程的知识求出黄金比的数值?
1.若 a:3=b:7, 则(a+3b):2b=
;
2.若a=2,b=6,c=4,且a,b,c,d成比 例,则d= ;
∴x=2或x=12
∴x=2或x=12或x=5.6时,以C、D、P为顶点的三 角形与以P、B、A为顶点的三角形相似
巩固提高: 在∆ABC中,AB=8cm,BC=16cm,点P从点A 开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始 沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、 B同时出发,经几秒钟∆BPQ与∆BAC相似?
这个点叫做位似中心.
这时的相似比又称为位似比. 性质:位似图形上任意一对对应点到位似中心的 距离之比等于位似比
1.任取一点O; 2.以点O为端点作射线OA、OB、OC、…; 3.分别在射线OA、OB、OC、 …上取点A’、 B’、C’、 … ,使:
图形的相似与位似PPT课件 人教版

A(6,2),B(6,0),以原点为位似中心,相似比为1∶3,把线段 AB缩小,则过A点对应点的反比例函数的解析式为( B )
10.(2012中考预测题)如图,△ABC中,CD⊥AB于D,下列 条件一定能确定△ABC为直角三角形的条件的个数是( C )
A.1
B.2
C. 3
D.4
【解析】能确定△ABC为直角三角形的有3个,分 别是①②④.
A A . K 2a B . k 3a
C
5.5
14.(2010中考变式题)如图,△ABC与△A′B′C′是位似图 形,且位似比是1∶2,若AB=2 cm,则A′B′=________cm. 4
15.(2010中考变式题)如图,已知图中的每个小方格都是 边长为1的小正方形,每个小正方形的顶点称为格点,若 △ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中
C)
3.如图,△ABC与△DEF是位似图形,位似比为2
∶3.已知AB=4,则DE的长为
6
.
3
一、选择题(每小题4分,共48分) 1.(2010中考变式题)在中华经典美文阅读中,小明同 学发现自己的一本书的宽与长之比为黄金比.已知这本书 的长为20 cm,则它的宽约为( A )
A.12.36 cm
考点知识精讲
中考典例精析
举一反三
考点训练
考点一
成比例线段与比例的定义及性质
ad=bc
温馨提示: (1)求两条线段的比时,对两条线段要采用同一长度单位.如果单 位不同,那么必须先化成同一单位,然后再比,且两条线段的比是一个实
数、没有单位.
考点二
相似多边形的判断及性质
1.多边形相似的判断:各角对应相等,各边对应成比例. 2.相似多边形的性质
《图形的位似》PPT课件 (共16张PPT)

1对称图形,中心对称与中心对 称图形):对称轴,对称中心. 平移:平移的方向,平移的距离. 旋转:旋转中心,旋转方向,旋转角度. 相似:相似比.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
概念与性质 2. 位似图形的性质
从第 (1),(2)图中,我们可以看到,△OAB∽△O A′B′,
则OOAA′ =OOBB′ =A′ABB′ .从第(3)图中同样可以看到
AF AD
=AAPC
=AABE
=EBPC
=FDPC
性质:位似图形上任意一对对应点到位似中心 的距离之比等于位似比.
• 若△ABC与△A’B’C’的相似比为:1:2, 则OA:OA’=( 1:2 )。
译:同心协力的人,他们的力量足以把坚硬的金属弄断;同心同德的人发表一致的意见,说服力强,人们就像嗅到芬芳的兰花香味,容易接受。
11.君子藏器于身,待时而动。 ——《周易》
译:君子就算有卓越的才能超群的技艺,也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。
12.满招损,谦受益。 ——《尚书》
A’
A
B
B’
O
C
C’
利用位似,可以将一个图形放大或缩小.
例如,要把四边形ABCD缩小到原来的1/2, 1.在四边形外任选一点O(如图),
2.分别在线段OA、OB、OC、OD上取点A'、B'、C'、D', 使得 OA' OB' OC' OD' 1
OA OB OC OD 2 3.顺次连接点A'、B'、C'、D',所得四边形A'B'C'D' 就是所要求的图形.
注:图形这些不同的变换是我们学习几何必不可少的重要 工具,它不但装点了我们的生活,而且是学习后续知识的基础.
概念与性质 2. 位似图形的性质
从第 (1),(2)图中,我们可以看到,△OAB∽△O A′B′,
则OOAA′ =OOBB′ =A′ABB′ .从第(3)图中同样可以看到
AF AD
=AAPC
=AABE
=EBPC
=FDPC
性质:位似图形上任意一对对应点到位似中心 的距离之比等于位似比.
• 若△ABC与△A’B’C’的相似比为:1:2, 则OA:OA’=( 1:2 )。
译:同心协力的人,他们的力量足以把坚硬的金属弄断;同心同德的人发表一致的意见,说服力强,人们就像嗅到芬芳的兰花香味,容易接受。
11.君子藏器于身,待时而动。 ——《周易》
译:君子就算有卓越的才能超群的技艺,也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。
12.满招损,谦受益。 ——《尚书》
A’
A
B
B’
O
C
C’
利用位似,可以将一个图形放大或缩小.
例如,要把四边形ABCD缩小到原来的1/2, 1.在四边形外任选一点O(如图),
2.分别在线段OA、OB、OC、OD上取点A'、B'、C'、D', 使得 OA' OB' OC' OD' 1
OA OB OC OD 2 3.顺次连接点A'、B'、C'、D',所得四边形A'B'C'D' 就是所要求的图形.
25.7 相似多边形和图形的位似 - 第2课时课件(共25张PPT)

知识点2 位似图形的性质
位似图形有哪些性质?
可以发现
对应顶点的直线都相交于位似中心.对应边互相平行或在同一条直线上.
例题示范
例1 如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△ ,以下说法错误的是( )A.△ABC∽△ B.点C,O, 三点在同一直线上C.D.AB∥
创设情境
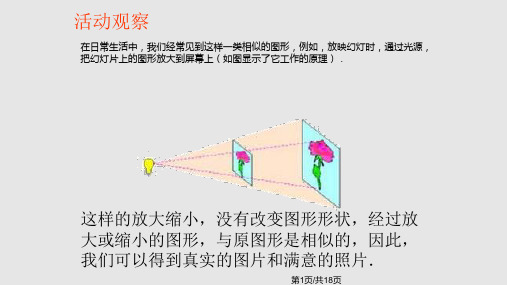
如图是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?连接图片上对应的点,你有什么发现?
探索新知
知识点1 位似图形的概念
一起探究
如图,已知△ABC及△ABC外的一点O.1.请你按如下步骤画出△A'B'C'.(1)画射线OA,OB,OC.(2)分别在OA,OB,OC上截取点A',B',C',使OA'=2OA,OB'=2OB,OC'=2OC.(3)连接A'B',A'C',B'C',得△A'B'C'.2.请你判断AB与A'B'、AC与A'C'、BC与B'C'的位置关系,并说明理由.3.△ABC与△A'B'C'相似吗?为什么?
例3 把四边形ABCD缩小到原来的1/2.
解:(1) 在四边形外任选一点 O (如图);(2) 分别在线段 OA,OB,OC,OD 上取点 A' ,B' , C' ,D' ,使得 ;(3) 顺次连接点 A' ,B' ,C' ,D' ,所得四边形 A' B' C' D' 就是所要求的图形.
C
归纳
位似图形有哪些性质?
可以发现
对应顶点的直线都相交于位似中心.对应边互相平行或在同一条直线上.
例题示范
例1 如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△ ,以下说法错误的是( )A.△ABC∽△ B.点C,O, 三点在同一直线上C.D.AB∥
创设情境
如图是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?连接图片上对应的点,你有什么发现?
探索新知
知识点1 位似图形的概念
一起探究
如图,已知△ABC及△ABC外的一点O.1.请你按如下步骤画出△A'B'C'.(1)画射线OA,OB,OC.(2)分别在OA,OB,OC上截取点A',B',C',使OA'=2OA,OB'=2OB,OC'=2OC.(3)连接A'B',A'C',B'C',得△A'B'C'.2.请你判断AB与A'B'、AC与A'C'、BC与B'C'的位置关系,并说明理由.3.△ABC与△A'B'C'相似吗?为什么?
例3 把四边形ABCD缩小到原来的1/2.
解:(1) 在四边形外任选一点 O (如图);(2) 分别在线段 OA,OB,OC,OD 上取点 A' ,B' , C' ,D' ,使得 ;(3) 顺次连接点 A' ,B' ,C' ,D' ,所得四边形 A' B' C' D' 就是所要求的图形.
C
归纳
位似_相似PPT优秀课件4

A
(2,1)
A'
o
(2,0)
B'
B
x
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为 位似中心,相似比为1:3,把线段AB缩小. y A〞(-2,-1),B〞(-2,0) A′(2,1),B′(2,0)
A
A'
B〞
x o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现? 在平面直角坐标系中,如果位似变换是以原点为位似中心, 相似比为k,那么位似图形对应点的坐标的比等于k或-k.
成比例 3.两个位似图形中的对应角______, 相等 对应线段________, 对应顶点的连线必经过__________ 位似中心 . 4.位似图形上某一对对应点到位似中心的距离分别为5和 10,则它们的位似比为______ 1:2 . 5.四边形ABCD和四边形A′B′C′D′位似,O为位似中
坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它
的一个以原点O为位似中心,相似比为1/2的位似图形.
A
y
D
A′
B
D′ B′
x
C′
C
oABiblioteka ( -3,3 ),B′(-4,1 ), C′( -2,0 ), D′( -1,2 )
你还有其他办法吗?试试看.
如图,表示△AOB和把它缩小后得到的△COD,则它们的相似 比为 5:2 . y
1、你在希望中享受到的乐趣,比将来实际享受的乐趣要大得多。 2、理想不是一只细磁碗,破碎了不有锔补;理想是朵花,谢落了可以重新开放。 3、人类的幸福和欢乐在于奋斗,而最有价值的是为理想而奋斗 4、世界上最快乐的事,莫过于为理想而奋斗 5、理想的实现只靠干,不靠空谈 6、天行健,君子以自强不息 7、心如明镜台,时时勤拂拭 8、理想即寻觅目标的思维。 9、理想是世界的主宰。 10、理想失去了,青春之花也便凋零了。因为理想是青春的光和热。 11、每个人都有一定的理想,这种理想决定着他的努力和判断的方向。 12、理想就在我们自身之中,同时,阴碍我们实现理想的各种障碍,也是在我们自身之中。 13、立志要如山,行道要如水。不如山,不能坚定,不如水,不能曲达。 14、理想是力量的泉源、智慧的摇篮、冲锋的战旗、斩棘的利剑。 15、人生的真正欢乐是致力于一个自己认为是伟大的目标。 16、人的理想志向往往和他的能力成正比。 17、大丈夫行事,论是非,不论利害;论顺逆,不论成败;论万世,不论一生。——(明)黄宗羲 18、生活的理想,就是为了理想的生活。 19、一个人的理想越崇高,生活越纯洁。 20、非淡泊无以明志,非宁静无以致远。 21、理想是反映美的心灵的眼睛。 22、人生最高之理想,在求达于真理。 23、把理想运用到真实的事物上,便有了文明。 24、生当做人杰,死亦为鬼雄。 25、有理想的、充满社会利益的、具有明确目的生活是世界上最美好的和最有意义的生活。 26、人需要理想,但是需要人的符合自然的理想,而不是超自然的理想。 27、生活中没有理想的人,是可怜的。 28、在理想的最美好的世界中,一切都是为美好的目的而设的。 29、理想的人物不仅要在物质需要的满足上,还要在精神旨趣的满足上得到表现。 30、生活不能没有理想。应当有健康的理想,发自内心的理想,来自本国人民的理想。
(2,1)
A'
o
(2,0)
B'
B
x
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为 位似中心,相似比为1:3,把线段AB缩小. y A〞(-2,-1),B〞(-2,0) A′(2,1),B′(2,0)
A
A'
B〞
x o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现? 在平面直角坐标系中,如果位似变换是以原点为位似中心, 相似比为k,那么位似图形对应点的坐标的比等于k或-k.
成比例 3.两个位似图形中的对应角______, 相等 对应线段________, 对应顶点的连线必经过__________ 位似中心 . 4.位似图形上某一对对应点到位似中心的距离分别为5和 10,则它们的位似比为______ 1:2 . 5.四边形ABCD和四边形A′B′C′D′位似,O为位似中
坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它
的一个以原点O为位似中心,相似比为1/2的位似图形.
A
y
D
A′
B
D′ B′
x
C′
C
oABiblioteka ( -3,3 ),B′(-4,1 ), C′( -2,0 ), D′( -1,2 )
你还有其他办法吗?试试看.
如图,表示△AOB和把它缩小后得到的△COD,则它们的相似 比为 5:2 . y
1、你在希望中享受到的乐趣,比将来实际享受的乐趣要大得多。 2、理想不是一只细磁碗,破碎了不有锔补;理想是朵花,谢落了可以重新开放。 3、人类的幸福和欢乐在于奋斗,而最有价值的是为理想而奋斗 4、世界上最快乐的事,莫过于为理想而奋斗 5、理想的实现只靠干,不靠空谈 6、天行健,君子以自强不息 7、心如明镜台,时时勤拂拭 8、理想即寻觅目标的思维。 9、理想是世界的主宰。 10、理想失去了,青春之花也便凋零了。因为理想是青春的光和热。 11、每个人都有一定的理想,这种理想决定着他的努力和判断的方向。 12、理想就在我们自身之中,同时,阴碍我们实现理想的各种障碍,也是在我们自身之中。 13、立志要如山,行道要如水。不如山,不能坚定,不如水,不能曲达。 14、理想是力量的泉源、智慧的摇篮、冲锋的战旗、斩棘的利剑。 15、人生的真正欢乐是致力于一个自己认为是伟大的目标。 16、人的理想志向往往和他的能力成正比。 17、大丈夫行事,论是非,不论利害;论顺逆,不论成败;论万世,不论一生。——(明)黄宗羲 18、生活的理想,就是为了理想的生活。 19、一个人的理想越崇高,生活越纯洁。 20、非淡泊无以明志,非宁静无以致远。 21、理想是反映美的心灵的眼睛。 22、人生最高之理想,在求达于真理。 23、把理想运用到真实的事物上,便有了文明。 24、生当做人杰,死亦为鬼雄。 25、有理想的、充满社会利益的、具有明确目的生活是世界上最美好的和最有意义的生活。 26、人需要理想,但是需要人的符合自然的理想,而不是超自然的理想。 27、生活中没有理想的人,是可怜的。 28、在理想的最美好的世界中,一切都是为美好的目的而设的。 29、理想的人物不仅要在物质需要的满足上,还要在精神旨趣的满足上得到表现。 30、生活不能没有理想。应当有健康的理想,发自内心的理想,来自本国人民的理想。
《图形的位似》图形的相似PPT(第1课时)教学课件

作位似图形:关键是确定位似中心、 相似比和找关键点的对应点.
导入新课
第四章 图形的相似
图形的位似
第2课时
讲授新课
当堂练习
课堂小结
学习目标
1.理解位似图形的坐标变换规律.(难点) 2.能熟练在坐标系中根据坐标的变化规律做出位似图形.(重点)
导入新课
问题:将图(1)图形如何变换得到图(2)?
y
y
O
例1:在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,
0),B(3,6),C(-3,3).以原点O为位似中心,画出四边形OABC的位似图形,使
它与四边形OABC的相似是2:3.
画法一:如右图所示,
解:将四边形OABC各顶点的坐标都
2
乘 ;在平3面直角坐标系中描点
C C'
yB
OA'
连接的直线A相交于点O. OA
, OB' OB
, OC' OC
, OD' OD
,
OE' OE
有什么关系?
A'
B
E
E'
B'
O
D'
D
C'
C
OA' OB' OC' OD' OE' . OA OB OC OD OE
A
A'
B
E
E'
B'
O
如果C两个相似多D边形任意一组对C应' 顶点PD,' P̍ 所在的直线都过同一点O,且
当堂练习
1.选出下面不同于其他三组的图形( B )
A
B
导入新课
第四章 图形的相似
图形的位似
第2课时
讲授新课
当堂练习
课堂小结
学习目标
1.理解位似图形的坐标变换规律.(难点) 2.能熟练在坐标系中根据坐标的变化规律做出位似图形.(重点)
导入新课
问题:将图(1)图形如何变换得到图(2)?
y
y
O
例1:在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,
0),B(3,6),C(-3,3).以原点O为位似中心,画出四边形OABC的位似图形,使
它与四边形OABC的相似是2:3.
画法一:如右图所示,
解:将四边形OABC各顶点的坐标都
2
乘 ;在平3面直角坐标系中描点
C C'
yB
OA'
连接的直线A相交于点O. OA
, OB' OB
, OC' OC
, OD' OD
,
OE' OE
有什么关系?
A'
B
E
E'
B'
O
D'
D
C'
C
OA' OB' OC' OD' OE' . OA OB OC OD OE
A
A'
B
E
E'
B'
O
如果C两个相似多D边形任意一组对C应' 顶点PD,' P̍ 所在的直线都过同一点O,且
当堂练习
1.选出下面不同于其他三组的图形( B )
A
B
图形的位似课件ppt

为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
2、观察下列位似图形 下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似
图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连 线有什么特征?
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
直角坐标系中图形的位似变化与对应点坐标变化的规律
想一想: 1.四边形GCEF与四边形G′C′E′F′具有怎样的对称性? 2.怎样运用像与原像对应点的坐标关系,画出以原点为位
显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
练一练1:判断下列各对图形哪些是位似图形,哪些不是.
(1)五边形ABCDE与五边形A′B′C′D′E′;
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
练一练:判断下列各对图形哪些是位似图形,哪些不是.
(7)扇形ABC与扇形A′B′C′, (B、A 、B′在一条直线上,C、A 、C′在一条直线上)
(8)△ABC与△ADE(①DE∥BC; ②∠AED=∠B)
(1)从上面练习第 1(1)(4)题图中,我们可以看到,△OAB∽△O A′B′ 则OOAA′ =OBO′B =A′ABB′ .从第 2 题的图中同样可以看到AAFD =AACP =AAEB =EBPC =DFCP
《位似》相似PPT课件五

B
x
练一练:
2.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以 原点O为位似中心,将这个三角形放大为原来的2倍.
y
o
x
A
C
B
练一练:
3.如图,写出矩形wxyz各点的坐标,如果矩形STUV相似于wxyz,点S 的坐标为(2,2),按照下列相似比,分别写出T、U、V各点的坐标.
A
C
B
o
x
归纳:
在平面直角坐标系中,如果位似变换是以原点为 位似中心,得到的图形与原图形的相似比为k,那么 与原图形上的点(x,y)对应的位似图形上的点的 坐标为(kx,ky)或(-kx,-ky).
引例.在平面直角坐标系中, 四边形ABCD的四个顶点的坐标
分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个
y A′(2,1),B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原 点O为位似中心,相似比为1:3,把线段AB缩小.
y A′(2,1),B′(2,0)
A〞(-2,-1),B(-2,0)
A
A'
B〞
x
o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现?
探索2:
在平面直角坐标系中, △ABC三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2将 △ABC放大,画它的位似图形.
放大后对应点的坐标分别是多少,你有什么发现?
《位似》相似PPT课件4 (共16张PPT)

①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的 直线都经过同一个点,那么,这两个图形是位似图形; ④位似图形上任意两点与位似中心的距离之比等于位似 比. 【答案】②,③
2.(孝感中考)
( )Biblioteka 【解析】选D.由题意可知∠BOB′=75°,∠BOA=30° ∴∠B′OA=45°∴点B的纵横坐标的绝对值相等,又点B在 第四象限,所以选D.
A
(2,1)
A'
o
(2,0)
B'
B
x
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为 位似中心,相似比为1:3,把线段AB缩小. y A〞(-2,-1),B〞(-2,0) A′(2,1),B′(2,0)
A
A'
B〞
x o
B'
B
A〞
观察对应点之间的坐标的变化,你有什么发现? 在平面直角坐标系中,如果位似变换是以原点为位似中心, 相似比为k,那么位似图形对应点的坐标的比等于k或-k.
成比例 3.两个位似图形中的对应角______, 相等 对应线段________, 对应顶点的连线必经过__________ 位似中心 . 4.位似图形上某一对对应点到位似中心的距离分别为5和 10,则它们的位似比为______ 1:2 . 5.四边形ABCD和四边形A′B′C′D′位似,O为位似中
在平面直角坐标系中, △ABC三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2, 将△ABC放大. 放大后对应点的坐标分别是多少? y A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 ) A
图形的位似变换PPT课件
C' D ' ,使 OA' OB ' OC ' OD' 2;
OA OB OC OD
(4)连接A ' B ',B ' C ',C ' D ',D ' A '.
所得四边形A ' B ' C ' D'即为所求.
第5页/共18页
观察下述图形有什么共同特点?
C
C'
B' A'
O C'
A'
B'
B'
A
BA
第9页/共18页
探索:
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心, 相似比为3:1,把线段AB缩小.
y
A′(2,1),B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现? 第10页/共18页
在平面直角坐标系中,有两点A(6,3),B(6,0),
以原点O为位似中心,相似比为1:3,把线段AB缩小.
y
A C
B
o
x
第14页/共18页
小结:
如果两个图形不仅形状相同,而且每组对应点所在的 直线都经过同一点,那么这样的两个图形叫做位似图 形, 这个点叫做位似中心. 在平面直角坐标系中,如果位似变换是以原点为位 似中心,相似比为k,那么位似图形对应点的坐标的 比等于k或-k.
第15页/共18页
布置作业
课堂作业:P97练习; 家庭作业 : (1)P99习题第2、3题; (2)预习下一节内容.
第16页/共18页
教学反思
第17页/共18页
感谢您的欣赏
第18页/共18页
y
A′(2,1),B′(2,0)
A〞(-2,-1), B〞 (-2,0)
OA OB OC OD
(4)连接A ' B ',B ' C ',C ' D ',D ' A '.
所得四边形A ' B ' C ' D'即为所求.
第5页/共18页
观察下述图形有什么共同特点?
C
C'
B' A'
O C'
A'
B'
B'
A
BA
第9页/共18页
探索:
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心, 相似比为3:1,把线段AB缩小.
y
A′(2,1),B′(2,0)
A
A'
x
o
B'
B
观察对应点之间的坐标的变化,你有什么发现? 第10页/共18页
在平面直角坐标系中,有两点A(6,3),B(6,0),
以原点O为位似中心,相似比为1:3,把线段AB缩小.
y
A C
B
o
x
第14页/共18页
小结:
如果两个图形不仅形状相同,而且每组对应点所在的 直线都经过同一点,那么这样的两个图形叫做位似图 形, 这个点叫做位似中心. 在平面直角坐标系中,如果位似变换是以原点为位 似中心,相似比为k,那么位似图形对应点的坐标的 比等于k或-k.
第15页/共18页
布置作业
课堂作业:P97练习; 家庭作业 : (1)P99习题第2、3题; (2)预习下一节内容.
第16页/共18页
教学反思
第17页/共18页
感谢您的欣赏
第18页/共18页
y
A′(2,1),B′(2,0)
A〞(-2,-1), B〞 (-2,0)
《相似多边形和图形的位似》PPT教学课件(第2课时)

想一想:你还有其他的画法吗?
O
C
F
思考:上面点 O取在两个三角形的同侧,如果点 O在
两个三角形之间呢?能不能画出这时的图形?
解:画射线OA、OB、OC;
沿着射线OA、OB、OE = 2OB,OF = 2OC;
顺次连结D、E、F,使△DEF与△ABC位似,相
解:∵ 四边形ABCD 和四边形A′ B′ C′ D′位似,
∴ 四边形ABCD ∽四边形A′ B′ C′ D′ .
∵ 四边形A′ B′ C′ D′和四边形A″ B″ C″ D″位似,
∴ 四边形A′ B′ C′ D′∽四边形A″ B″ C″ D″ .
∴ 四边形A″ B″ C″ D″∽四边形ABCD.
4. 位似图形上任意一对对应点到位似中心的距离之比等
于相似比.
例2 如图所示,四边形ABCD 和四边形A′ B′ C′ D′位似,相似比1 = 2,四边
形A′ B′ C′D′和四边形A″ B″ C″D″位似,相似比2 = 1. 则四边形A″ B″ C″ D″和
四边形ABCD 是位似图形吗?如果是,请说明理由并求出相似比.
B
似比为2.
O
F
E
D
C
归纳:
画位似图形的一般步骤:
(1)确定位似中心;
(2)分别连接位似中心和能代表原图的关键点并延长;
(3)根据相似比,确定能代表所画的位似图形的关键点;
(4)按照原图的形状,顺次连接上述各点,得到放大或缩
小后的图形.
随堂训练
1.△ABC和△A‘B’C‘是位似图形,且位似之比为1∶3,则△ABC和
E
H
射线OA、OB、OC、OD上分别取
A
点D、E、F,使OE = 2OA , OF =
O
C
F
思考:上面点 O取在两个三角形的同侧,如果点 O在
两个三角形之间呢?能不能画出这时的图形?
解:画射线OA、OB、OC;
沿着射线OA、OB、OE = 2OB,OF = 2OC;
顺次连结D、E、F,使△DEF与△ABC位似,相
解:∵ 四边形ABCD 和四边形A′ B′ C′ D′位似,
∴ 四边形ABCD ∽四边形A′ B′ C′ D′ .
∵ 四边形A′ B′ C′ D′和四边形A″ B″ C″ D″位似,
∴ 四边形A′ B′ C′ D′∽四边形A″ B″ C″ D″ .
∴ 四边形A″ B″ C″ D″∽四边形ABCD.
4. 位似图形上任意一对对应点到位似中心的距离之比等
于相似比.
例2 如图所示,四边形ABCD 和四边形A′ B′ C′ D′位似,相似比1 = 2,四边
形A′ B′ C′D′和四边形A″ B″ C″D″位似,相似比2 = 1. 则四边形A″ B″ C″ D″和
四边形ABCD 是位似图形吗?如果是,请说明理由并求出相似比.
B
似比为2.
O
F
E
D
C
归纳:
画位似图形的一般步骤:
(1)确定位似中心;
(2)分别连接位似中心和能代表原图的关键点并延长;
(3)根据相似比,确定能代表所画的位似图形的关键点;
(4)按照原图的形状,顺次连接上述各点,得到放大或缩
小后的图形.
随堂训练
1.△ABC和△A‘B’C‘是位似图形,且位似之比为1∶3,则△ABC和
E
H
射线OA、OB、OC、OD上分别取
A
点D、E、F,使OE = 2OA , OF =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图,D,E分别AB,AC上的点.
(1)如果DE∥BC,那么∆ADE和 ∆ABC是位似图形吗?为什么? B
A DE
C
(2)如果∆ADE和 ∆ABC是位似图形,那么 DE∥BC吗?为什么?
解:(2) DE∥BC.理由是: ∆ADE和 ∆ABC是位似图形, ∆ADE∽ ∆ABC
∠ADE=∠B
DE∥BC.
A′ C′
B′
下面两副图是相似形吗?认真观察 看它们还有什么特征?
B
A C E O
M
D F
N
探索活动
已知点O和ΔABC
(1)画射线OA、OB、OC,分别在OA、OB、OC
上取点A1、B1 、C1,使
OA 1
OB 1
OC 1
2
OA OB OC
画ΔA1B1C1.
A1
A
C1
.
C
O
B
B1
探索活动
已知点O和ΔABC
A' . A
O.
B
C
B’
C’
将黄色五角星缩 小为原来的一半
。
。
。。
。
。
。
。
。
O
。
。
位似图形特征: 1、位似图形一定是相似形,反之 不一定。 2、判断位似图形时要注意首先它 们必须是相似形,其次每一对对应 点所在直线都经过同一点。
---试一试--- 你发现了什么?
y
3.⑴如图,已知A(2,0),
为了便于学习和使用,本文 档下载后内容可随意修改调 整及打印,欢迎下载。
A1 A
.
C
O
B
B1
C1 B
CO A
A2 C2
B2
1. 在上图中,两个多边形不仅相似,而且 对应顶点的连线交于一点,像这样的两个图形
叫做位似形,这个点叫做位似中 心. (对应边互相平行)
A1
A
.
C
O
B
C1 B
CO A
B1
2.位似形有哪些性质呢?:
A2 C2
B2
(1)两个位似形一定是相似形; (2)对应顶点所在的直线都经过同一点; (3)对应顶点到位似中心的距离之比等于相似比.
---试一试---
请你总结一下:这个问题 有几种解法?
2.如图,已知点O和△ABC
1
以O为位似中心,将△ABC缩小为原来的 2
AADCE NhomakorabeaC
F
O E B
F
O
D
B
将三角形ABC放大一倍。
∆ABC是位似图形吗?为什么? B
C
解:(1) ∆ADE和 ∆ABC是位似图形.理由是:
因为DE∥BC,所以∠ADE和=∠B, ∠AED =∠C.所以∆ADE∽ ∆ABC.
又因为 点A是∆ADE和 ∆ABC的公共点,点D 和点B是对应点,点E和点C是对应点,直线 BD与CE交于点A,所以∆ADE和 ∆ABC是位似 图形.
第五步:过G点作GD⊥BC于点D.四边形 DEFG即为所求作的正方形DEFG.
典例分析
根据以上作图步骤,回答以下问题:
(1)上述所求作的四边形DEFG是正方形吗?为 什么?
(2)在△ABC中,如果BC=10,高AQ=6,求上
述正方形DEFG的边长.
A
G
F
G1 F1
B D1 E1 D
EC
(1)以点P为位似中心,按相似比2:1将图形放大,
DC
A
B
典例分析
5、在给定的锐角△ABC中,求作一个正方 形DEFG,使D、E落在BC上,F、G分别落 在AC、AB边上,作法如下:
第一步:画出一个有3个顶点落在△ABC两边上 的正方形D1E1F1G1; 第二步:连结BF1,并延长交AC于点F; 第三步:过F点作FE⊥BC交AB于点E;
第四步:过F点作FG∥BC交AB于点G;
别观察这五个图,你发现每个图中的两个四边形
各对应点的连线有什么特征?
如果两个相似图形的每组对应点 所在的直线都交于一点,那么这样 的两个图形叫做位似图形, 这个 交点叫做位似中心, 这时两个相 似图形的相似比又叫做它们的位 似比.
观察下图中的五个图,回答下列问题:
(1)在各图中,位似图形的位似中心与这两个图形有
写出B、C的坐标。
CF ′
⑵将A、B、C的横坐标和
纵组成坐△标A都′B乘′C2,′写所出得A′各、点B′、BE′
C′的坐标,画出△A′B′C′
C
B
⑶以O为位似中心,
按比例尺2:1,把
△ABC放大为△DEF O A AD′
x
典例分析
1、下列说法错误的是( )
A、位似图形一定是相似图形 B、相似图形不一定是位似图形 C、位似图形上任意一对对应点到位似中心的距 离之比等于位似比 D、位似图形中每组对应点所在的直线必相互平 行
观察--思考
用点光源将△ABC投影到与其平 行的幕墙上得到△A′B′C′
改变点光源O的位置, 你有什么发现?
O
A C
B
A′ C′
B′
观察--思考
用点光源将△ABC投影到与其平行 的幕墙上 得到△A′B′C′
改变点光源O的位置, 你有什么发现?
A C
O B
① △ABC ∽△A′B′C′ ②对应点的连线相交于一点 ③对应边互相平行
什么位置关系? 位置不一样,位似中心就不一样.
(2)在各图中,任取一对对应点,度量这两个点到位
似中心的距离.它们的比与位似比有什么关系?再换一对
对应点试一试.
相等.
位似图形的对应点和位似中心在 同一条直线上,它们到位似中心的 距离之比等于相似比.
如图,D,E分别AB,AC上的点.
A
(1)如果DE∥BC,那么∆ADE和 D E
典例分析
2、如图,△ABC与 △ABC是位似图形,点O
是位似中心,若 OA 2AA,S△ABC 8 ,则
S△ABC
C1 .
C
A
A1
O B B1
典例分析
3、如图,以O为位似中心,将四边形ABCD 放大为原来的2倍.
C' D'
C D
. O
A
B
A'
B'
典例分析
4、如图在6×6的方格中画出等腰梯形ABCD 的位似图形,位似中心为点A,所画图形与 原等腰梯形ABCD的位似比为2:1.
得图1;
(2)以点Q为位似中心,按相似比1:2将图形缩小,
得图2。
图1与图2的相似比是(
),面积的比是(
)。
P 。Q
小结:
1.以前我们学习了平移、对称、旋转变 换,它们的特点是什么?
2. 位似变换的特点是什么?
观察与思考☞
下列图形中,每个图中的
四边形ABCD和四边形A′B′C′D′都是相似图形.分
分别在OA、OB、OC的反向延长线上取点A2、
B2、C2,使
OA 2
OA
OB 2
OB
OC 2
OC
2 ,画ΔA2B2C2.
A2
B
C2
CO
A B2
合作交流
A1
A2
A
.
C
O
B
B1
C1 B
CO A
C2 B2
(1)ΔABC与ΔA1B1C1及ΔABC与ΔA2B2C2是否 分别相似?为什么?
(2)ΔABC与ΔA1B1C1及ΔABC与ΔA2B2C2在 位置上还有什么特点?
