三次样条插值计算方法上机实验
数值分析实验报告-插值、三次样条

实验报告:牛顿差值多项式&三次样条问题:在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数21()25f x x作多项式插值及三次样条插值,对每个n 值,分别画出插值函数及()f x 的图形。
实验目的:通过编程实现牛顿插值方法和三次样条方法,加深对多项式插值的理解。
应用所编程序解决实际算例。
实验要求:1. 认真分析问题,深刻理解相关理论知识并能熟练应用;2. 编写相关程序并进行实验;3. 调试程序,得到最终结果;4. 分析解释实验结果;5. 按照要求完成实验报告。
实验原理:详见《数值分析 第5版》第二章相关内容。
实验内容:(1)牛顿插值多项式1.1 当n=10时:在Matlab 下编写代码完成计算和画图。
结果如下:代码:clear allclcx1=-1:0.2:1;y1=1./(1+25.*x1.^2);n=length(x1);f=y1(:);for j=2:nfor i=n:-1:jf(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1));endendsyms F x p ;F(1)=1;p(1)=y1(1);for i=2:nF(i)=F(i-1)*(x-x1(i-1));p(i)=f(i)*F(i);endsyms PP=sum(p);P10=vpa(expand(P),5);x0=-1:0.001:1;y0=subs(P,x,x0);y2=subs(1/(1+25*x^2),x,x0);plot(x0,y0,x0,y2)grid onxlabel('x')ylabel('y')P10即我们所求的牛顿插值多项式,其结果为:P10(x)=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36*x^4+2.0202e-1 4*x^3-16.855*x^2-6.6594e-16*x+1.0并且这里也能得到该牛顿插值多项式的在[-1,1]上的图形,并和原函数进行对比(见Fig.1)。
三次样条插值的方法和思路

三次样条插值的方法和思路摘要:1.三次样条插值的基本概念2.三次样条插值的数学原理3.三次样条插值的实现步骤4.三次样条插值的优缺点5.三次样条插值在实际应用中的案例正文:在日常的科学研究和工程应用中,我们经常会遇到需要对一组数据进行插值的问题。
插值方法有很多,其中三次样条插值是一种常见且有效的方法。
本文将从基本概念、数学原理、实现步骤、优缺点以及实际应用案例等方面,全面介绍三次样条插值的方法和思路。
一、三次样条插值的基本概念三次样条插值(Cubic Spline Interpolation)是一种基于分段多项式的插值方法。
它通过在各个节点上构建一条三次多项式曲线,使得这条曲线在节点之间满足插值条件,从而达到拟合数据的目的。
二、三次样条插值的数学原理三次样条插值的数学原理可以分为两个部分:一是分段三次多项式的构建,二是插值条件的满足。
1.分段三次多项式的构建假设有一组数据点序列为(x0,y0),(x1,y1),(x2,y2),(x3,y3),我们可以将这些数据点连接起来,构建一条分段三次多项式曲线。
分段三次多项式在每个子区间上都是一个三次多项式,它们之间通过节点值进行连接。
2.插值条件的满足为了使分段三次多项式在节点之间满足插值条件,我们需要在每个子区间上满足以下四个条件:(1)端点条件:三次多项式在区间的端点上分别等于节点值;(2)二阶导数条件:三次多项式在区间内的二阶导数等于节点间的斜率;(3)三阶导数条件:三次多项式在区间内的三阶导数等于节点间的曲率;(4)内部点条件:三次多项式在区间内部满足插值函数的连续性。
通过求解这四个条件,我们可以得到分段三次多项式的系数,从而实现插值。
三、三次样条插值的实现步骤1.确定插值节点:根据数据点的位置,选取合适的节点;2.构建分段三次多项式:根据节点值和插值条件,求解分段三次多项式的系数;3.计算插值结果:将待插值点的横坐标代入分段三次多项式,得到插值结果。
计算方法大作业1 克服Runge现象

x3
x2
x
1
S1 ( x)
-0.34685
0.2086
0.073964
0.038462
S2 (x)
S (xi 0 ) S x(i 0 )
S
'
(xi
0) S
xi' (
0 )i
S
'
'
x(i
0)S
xi' ' (
0)
1 ,n2, . . . , 1
(1)
这里共有了 3n-3 个条件,再加上条件(2)中的 n+1 个插值条件,共有 4n-2 个条件,
因此还需要 2 个方程才能确定 S (x) .通常可在区间[a, b]的端点 a x0,b xn 上各加一个边
dn1
1
2
Mn
dn
(6)
2 1
2
2
2
1 M1 d1
M2
d2
n 1
2
n
1
M
n
1
dn1
n
n 2 M n dn
由式(1)内点拼接条件,可得
i M i1 2M i i M i1 d j i 1, 2,..., n 1
(3) (4)
其中
i
hi 1 hi1
, hi
i
hi hi 1
三次样条插值方法的应用

CENTRAL SOUTH UNIVERSITY数值分析实验报告三次样条插值方法的应用一、问题背景分段低次插值函数往往具有很好的收敛性,计算过程简单,稳定性好,并且易于在在电子计算机上实现,但其光滑性较差,对于像高速飞机的机翼形线船体放样等型值线往往要求具有二阶光滑度,即有二阶连续导数,早期工程师制图时,把富有弹性的细长木条(即所谓的样条)用压铁固定在样点上,在其他地方让他自由弯曲,然后沿木条画下曲线,称为样条曲线。
样条曲线实际上是由分段三次曲线并接而成,在连接点即样点上要求二阶导数连续,从数学上加以概括就得到数学样条这一概念。
下面我们讨论最常用的三次样条函数及其应用。
二、数学模型样条函数可以给出光滑的插值曲线(面),因此在数值逼近、常微分方程和偏微分方程的数值解及科学和工程的计算中起着重要的作用。
设区间[]b ,a 上给定有关划分b x x n =<<<=Λ10x a ,S 为[]b ,a 上满足下面条件的函数。
● )(b a C S ,2∈;● S 在每个子区间[]1,+i i x x 上是三次多项式。
则称S 为关于划分的三次样条函数。
常用的三次样条函数的边界条件有三种类型:● Ⅰ型 ()()n n n f x S f x S ''0'',==。
● Ⅱ型 ()()n n n f x S f x S ''''0'''',==,其特殊情况为()()0''''==n n x S x S 。
● Ⅲ型 ()()Λ3,2,1,0,0==j x S x S n j j ,此条件称为周期样条函数。
鉴于Ⅱ型三次样条插值函数在实际应用中的重要地位,在此主要对它进行详细介绍。
三、算法及流程按照传统的编程方法,可将公式直接转换为MATLAB可是别的语言即可;另一种是运用矩阵运算,发挥MATLAB在矩阵运算上的优势。
实验四 三次样条插值
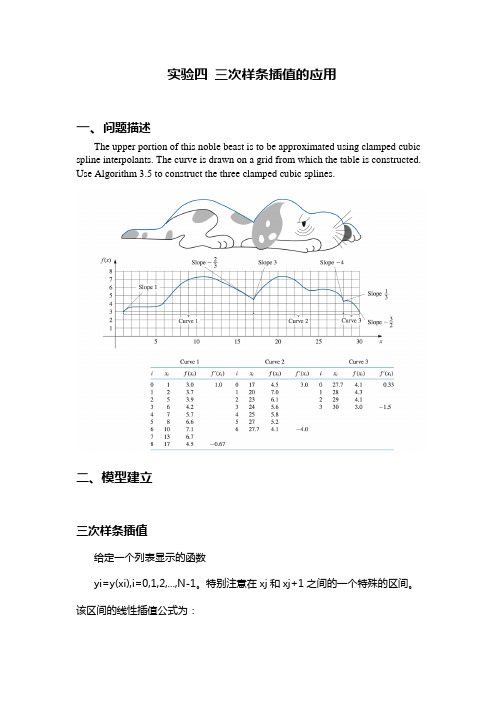
实验四三次样条插值的应用一、问题描述The upper portion of this noble beast is to be approximated using clamped cubic spline interpolants. The curve is drawn on a grid from which the table is constructed. Use Algorithm 3.5 to construct the three clamped cubic splines.二、模型建立三次样条插值给定一个列表显示的函数yi=y(xi),i=0,1,2,...,N-1。
特别注意在xj和xj+1之间的一个特殊的区间。
该区间的线性插值公式为:(3.3.1)式和(3.3.2)式是拉格朗日插值公式(3.1.1)的特殊情况。
因为它是(分段)线性的,(3.3.1)式在每一区间内的二阶导数为零,在横坐标为xj处的二阶导数不定义或无限。
三次样条插值的目的就是要得到一个内插公式,不论在区间内亦或其边界上,其一阶导数平滑,二阶导数连续。
做一个与事实相反的个假设,除yi的列表值之外,我们还有函数二阶导数y"的列表值,即一系列的yi"值,则在每个区间内,可以在(3.3.1)式的右边加上一个三次多项式,其二阶导数从左边的yj"值线性变化到右边的yj+1"值,这么做便得到了所需的连续二阶导数。
如果还将三次多项式构造在xj和xj+1处为零,则不会破坏在终点xj和xj+1处与列表函数值yj和yj+1的一致性。
进行一些辅助计算便可知,仅有一种办法才能进行这种构造,即用注意,(3.3.3)式和(3.3.4)式对自变量x的依赖,是完全通过A和B对x的线性依赖,以及C和D(通过A和B)对x的三次依赖而实现。
可以很容易地验证,y"事实上是该插值多项式的二阶导数。
使用ABCD的定义对x求(3.3.3)式的导数,计算dA/dx dB/dx dC/dx dD/dx,结果为一阶导数因为x=xj是A=1,x=x(i+1)时A=0,而B正相反,则(3.3.6)式表明y"恰为列表函数的二阶导数。
LAB03_三次样条插值实验

Lab03.三次样条插值实验【实验目的和要求】1.使学生深入理解三次样条插值法,深入进行程序设计能力训练;2.对第一与第二种边界条件,按三弯矩法,通过用Matlab 语言设计计算三次样条插值的程序,以提高学生程序设计的能力。
【实验内容】1.根据Matlab 语言特点,描述三次样条插值法。
2.对第一与第二种边界条件,按三弯矩法,用Matlab 语言设计计算三次样条插值的程序。
3对(1) 自然边界条件0)0.1()2.0(=''=''S S ;(2) 第一种边界条件55741.1)0.1( ,20271.0)2.0(='='S S . 输出用追赶法解出的弯矩向量),,(521M M M 和)1.02.0(i S + (i =0,1,…,8)的值,并画出)(x S y =的图形。
4.完成教材P45例8的计算,并将计算结果与Langrage 插值法计算的结果进行比较,由此说明三次样条插值的优越性。
【实验仪器与软件】1.CPU 主频在1GHz 以上,内存在128Mb 以上的PC ;2.Matlab 6.0及以上版本。
实验讲评:实验成绩:评阅教师:2011 年 月 日Lab03.三次样条插值实验一、算法描述1.根据Matlab语言特点,描述三次样条插值法.答:S(x) 在[x j, x j+1](j=1,2,⋯,n-1)上是三次多项式,于是S"(x)在[x j, x j+1] 上是一次多项式,如果S"(x) 在[x j,x j+1](j=1,2,⋯,n-1)两端点上的值已知,设S"(x j)=M j,S"(x j+1)=M j+1,则S"(x) 的表达式为:= ,其中h j =x j+1-x j,对S"(x) 进行两次积分,则得到1 个具有2二、程序设计2.对第一与第二种边界条件,按三弯矩法,用Matlab语言设计计算三次样条插值的程序。
计算方法上机作业——求三次样条插值函数的matlab程序

附录 3 求三次样条插值函数的 matlab 程序 for f = 2:n-1; ly = 0; for g = 1:f-1 ly = ly+l(f,g)*yy(g); end yy(f) = D(f)-ly; end M1(n-1) = yy(n-1)/u(n-1,n-1); for rr=1:n-2 r = n-1-rr; uM1 = 0; for s=r+1:n-1 uM1 = uM1+u(r,s)*M1(s); end M1(r) = (yy(r)-uM1)/u(r,r); end M = [M1(n-1,1);M1]; end ss = 0; for t=1:n-1 S(t,1) = (M(t+1)-M(t))/(6*h(t)); S(t,2) = (M(t)*x(t+1)-M(t+1)*x(t))/(2*h(t)); S(t,3) = (M(t+1)*x(t)^2-M(t)*x(t+1)^2)/(2*h(t))+(y(t+1)-y(t))/h(t)+h(t)*(M(t)-M(t+1))/6; S(t,4) = (M(t)*x(t+1)^3-M(1)*x(t)^3)/(6*h(t))+(y(t)*x(t+1)-y(t+1)*x(t))/h(t)+h(t)*(M(t+1)* x(t)-M(t)*x(t+1))/6; for x1 = x(t):(x(t+1)-x(t))/100:x(t+1) ss = ss+1; xx(ss) = x1; SS(ss) = S(t,1)*x1^3+S(t,2)*x1^2+S(t,3)*x1+S(t,4); end end plot(xx,SS,'-k','linewidth',2); hold on plot(x,y,'*k','markersize',10); hold on xlabel('x'); ylabel('S(x)'); grid; fprintf('\n 所求的三次样条插值函数为:\n'); for uu=1:n-1 fprintf('S(x) = %10.5f*x^3+%10.5f*x^2+%10.5f*x+%10.5f, %8.4f<= x <=%8.4f\n',S(uu,1),S(uu,2),S(uu,3),S(uu,4),x(uu),x(uu+1)); end
三次样条插值算法详解

三次样条插值算法要求数据点数量较多,且在某些情况下可能存在数值不稳定性,如数据 点过多或数据点分布不均等情况。此外,该算法对于离散数据点的拟合效果可能不如其他 插值方法。
对未来研究的展望
01
02
03
改进算法稳定性
针对数值不稳定性问题, 未来研究可以探索改进算 法的数值稳定性,提高算 法的鲁棒性。
3
数据转换
对数据进行必要的转换,如标准化、归一化等, 以适应算法需求。
构建插值函数
确定插值节点
根据数据点确定插值节点,确保插值函数在节点处连续且光滑。
构造插值多项式
根据节点和数据点,构造三次多项式作为插值函数。
确定边界条件
根据实际情况确定插值函数的边界条件,如周期性、对称性等。
求解插值函数
求解线性方程组
06
结论
三次样条插值算法总结
适用性
三次样条插值算法适用于各种连续、光滑、可微的分段函数插值问题,尤其在处理具有复 杂变化趋势的数据时表现出色。
优点
该算法能够保证插值函数在分段连接处连续且具有二阶导数,从而在插值过程中保持数据 的平滑性和连续性。此外,三次样条插值算法具有简单、易实现的特点,且计算效率较高 。
根据数据点的数量和分布,合理分段,确保 拟合的精度和连续性。
求解线性方程组
使用高效的方法求解线性方程组,如高斯消 元法或迭代法。
结果输出
输出拟合得到的插值函数,以及相关的误差 分析和图表。
03
三次样条插值算法步骤
数据准备
1 2
数据收集
收集需要插值的原始数据点,确保数据准确可靠。
数据清洗
对数据进行预处理,如去除异常值、缺失值处理 等。
数值分析实验报告-插值、三次样条

实验报告:牛顿差值多项式&三次样条问题:在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数21()25f x x作多项式插值及三次样条插值,对每个n 值,分别画出插值函数及()f x 的图形。
实验目的:通过编程实现牛顿插值方法和三次样条方法,加深对多项式插值的理解。
应用所编程序解决实际算例。
实验要求:1. 认真分析问题,深刻理解相关理论知识并能熟练应用; 2. 编写相关程序并进行实验; 3. 调试程序,得到最终结果; 4. 分析解释实验结果; 5. 按照要求完成实验报告。
实验原理:详见《数值分析 第5版》第二章相关内容。
实验内容:(1)牛顿插值多项式1.1 当n=10时:在Matlab 下编写代码完成计算和画图。
结果如下:代码:clear allclcx1=-1:0.2:1;y1=1./(1+25.*x1.^2);n=length(x1);f=y1(:);for j=2:nfor i=n:-1:jf(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1));endendsyms F x p;F(1)=1;p(1)=y1(1);for i=2:nF(i)=F(i-1)*(x-x1(i-1));p(i)=f(i)*F(i);endsyms PP=sum(p);P10=vpa(expand(P),5);x0=-1:0.001:1;y0=subs(P,x,x0);y2=subs(1/(1+25*x^2),x,x0);plot(x0,y0,x0,y2)grid onxlabel('x')ylabel('y')P10即我们所求的牛顿插值多项式,其结果为:P10(x)=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36* x^4+2.0202e-14*x^3-16.855*x^2-6.6594e-16*x+1.0并且这里也能得到该牛顿插值多项式的在[-1,1]上的图形,并和原函数进行对比(见Fig.1)。
第二类边界条件三次样条插值实验报告

数值计算实验—实验报告2一、实验项目:第二类边界条件三次样条插值二、实验目的和要求a.通过本实验深入地理解三次样条插值多项式的基本原理b.通过数值算例更好的领会三次样条插值多项式具有较高的准确性三、实验内容1.用调试好的程序解决如下问题:点中点处的函数值,并将计算结果与sinx在相应点的数值相比较。
n=8;p1=0.4794;pn=0.9463;u=[0.6,0.8,1.0,1.2,1.4,1.6,1.8];p=7;x=[0.5,0.7,0.9,1.1,1.3,1.5,1.7,1.9];y=[0.4794,0.6442,0.7833,0.8912,0.9636,0.9975,0.9917,0.9463];for i=1:n-1h(i)=x(i+1)-x(i);enda2(1)=1;g(1)=3*(y(2)-y(1))/h(1)-p1*h(1)/2;for k=2:n-1a1(k-1)=h(k)/(h(k)+h(k-1));a2(k)=h(k-1)/(h(k)+h(k-1));g(k)=3*a2(k)*(y(k+1)-y(k))/h(k)+3*a1(k-1)*(y(k)-y(k-1))/h(k-1); enda1(n-1)=1;g(n)=3*(y(n)-y(n-1))/h(n-1)+pn * h(n-1)/2;%追赶法求三转角方程b1(1)=2;m(1)=g(1)/2;b2(1)=a2(1)/b1(1);for i=2:nb1(i)=2-a1(i-1)*b2(i-1);if(i~=n)b2(i)=a2(i)/b1(i);endm(i)=(g(i)-a1(i-1)*m(i-1))/b1(i);endfor i=n-1:-1:1m(i)=m(i)-b2(i)*m(i+1);endfor j=1:pfor i=1:nif((u(j)>=x(i))&&(u(j)<x(i+1)))k=i;break;endends(j)=0;s(j)=s(j)+(h(k)+2*(u(j)-x(k)))*(u(j)-x(k+1))^2*y(k)/(h(k))^3;s(j)=s(j)+(h(k)-2*(u(j)-x(k+1)))*(u(j)-x(k))^2*y(k+1)/(h(k))^3;s(j)=s(j)+(u(j)-x(k))*(u(j)-x(k+1))^2*m(k)/(h(k))^2;s(j)=s(j)+(u(j)-x(k+1))*(u(j)-x(k))^2*m(k+1)/(h(k))^2;end(2).运行结果3. 根据Lagrange插值多项式基本原理编制程序,并计算下面的数值算例:=-5+kh,其中h=10/n,n=10,20,40.给定函数f(x)=1/(1+x^2)(-5≤x≤5),取等距节点xk边界条件为S''(x0)=f''(x0),S''(x n)=f''(x n).用上述算法计算S10(x),S20(x), S40(x),并与函数f(x)以及10次Lagrange插值多项式L10(x)在给定点处的函数值进行比较。
数值计算方法三次样条插值演示文稿

第14页,共68页。
三次样条插值
对于待定系数a j ,bj , c j .d j j 1,2,...n,即4n个未知系数, 而插值条件为4n 2个,还缺两个,因此须给出两个 条件称为边界条件,有以下三类: 第一类 已知两端点的一阶导数
s( s(
x0 xn
) )
f (x0 ) m0 f (xn ) mn
第12页,共68页。
4.4.2 三次样条插值
定义 设函数f (x)是区间[a,b]上的二次连续可微函数, 在区间[a,b]上给出一个划分
:a x0 x1 ... xn1 xn b 如果函数s( x)满足条件
(1)s(x j ) f (x j ) ( j 0,1,2,...n); (2) 在每个小区间[x j1, x j ]( j 1,2,..., n)上s(x)是不超过
Mi 2!
( xi 1
xi )2
M i1 3!
Mi
( xi 1
xi )2
解得
s(xi )
yi1 yi xi1 xi
(
1 6
M
i 1
2 6
M
i
)( xi 1
xi
)
(1)
第18页,共68页。
三次样条插值
同理在[xi1, xi ]上讨论得
s(xi )
yi xi
yi1 xi1
(
2 6
M
i
1 6 M i1)(xi
第21页,共68页。
三次样条插值
第一类边界条件:s(x0 ) f (x0 ) s(xn ) f (xn )
(1) 式中令i 0得
s(x0 )
y1 x1
y0 x0
(1 6
计算方法大作业——三次样条插值

计算方法上机报告
此完成所有数据的输入。继续按 Enter 键会出现提示“选择封闭方程组的边界条件: 第 一类边界条件输入 1,第二类边界条件输入 2,第三类边界条件输入 3。 ”根据已知情况 选择相应的边界条件,若为自然三次样条插值,则选 1,并将插值区间两端点的二阶导 数值设置为 0。输入完成之后按 Enter 开始求解,程序运行结束后命令窗口会显示要求 的三次样条插值函数,同时会出现该插值函数以及插值节点的图像,便于直接观察。 2.3 算例及计算结果 (1) 《数值分析》课本第 137 页的例题 4.6.1,已知函数 y=f(x)的数值如下表,求它 的自然三次样条插值函数。 xi yi -3 7 -1 11 0 26 3 56 4 29
(2) 给定函数 f ( x)
3 x 1 1 x 0 0 x3 3 x 4
1 (1 x 1) 。取等距节点,构造牛顿插值多项式 N5(x) 1 25x 2 和 N10(x)及三次样条插值函数 S10(x)。分别将三种插值多项式与 f(x)的曲线画在同一个
N10 x
22757 10 5444 8 20216 6 17147 4 3725 2 x x x x x 1 103 11 53 139 221
将牛顿插值多项式 N5(x)和 N10(x)及三次样条插值函数 S10(x)分别与 f(x)的曲线画在 同一个坐标系上进行比较,如图 12。可以看出三次样条函数与原函数符合的非常好, 对于低次的牛顿插值多项式,与原函数的大致趋势相同,而高次的牛顿插值多项式由 于龙格现象的出现,与原函数之间相差比较大。
S ( xi ) S ( xi ), ( xi ) S ( xi ), S S ( x ) S ( x ), i i i 1, 2, , n 1
代数插值实验-三次样条曲线

实验7 代数插值实验-(2)实验类型:●验证性实验 ○综合性实验 ○设计性实验实验目的:进一步熟练掌握spline(样条)插值算法,提高编程能力和解决插值问题的实践技能。
实验内容:编写程序用计算机求解三次压紧样条曲线,经过点(0,0.0),(1,0.5),(2,2.0)和(3,1.5),而且一阶导数边界条件S ’(0)=0.2和S ’(3)=-1实验原理 若已知N+1个点的{}N k k k y x 0),(=及其一阶导数的边界条件S ’(a)=0d 和S ’(b)=N d ,则存在唯一的三次样条曲线。
构造并求解下列线性方程组01112100111122211113(2)3('())22()(2,3,,2)3(2)3('())2k k k k k k k k N N N N N N N N h h m h m u d S x h m h h m h m u k N h m h h m u S x d ---+-------⎧++=--⎪⎪+++==-⎨⎪⎪++=--⎩ 构造分段函数S(x):23,0,1,2,31()()()()()[,]k k k k k k k k k k S x S x s s x x s x x s x x x x x +==+-+-+-∈ k k y s =0, ; 6)2(11,++-=k k k k k m m h d s ; 22,k k m s = ; kk k k h m m s 613,-=+ 实验说明 需要建立两个数组X ,Y 分别存放(1x ,…,)n x ,(1y ,…,)n y ,建立两个变量dxo 、 dxn 分别存放左右端点的一阶导数 dxo = S'(x0) , dxn = S'(xn),上述方程组中10,1,,1k k k h x x k N +=-=- 其中;1()/0,1,,1k k k k d y y h k N +=-=- 16(),1,2,,1k k k u d d k N -=-=- 实验步骤1 要求上机实验前先编写出程序代码2 编辑录入程序3 调试程序并记录调试过程中出现的问题及修改程序的过程4 经反复调试后,运行程序并验证程序运行是否正确。
LAB03_三次样条插值实验

LAB03_三次样条插值实验实验内容1.用三次样条插值的三弯矩法,编制第一与第二种边界条件的程序.已知数据如下:求)(x f 的三次样条插值函数)(x S 满足: (1)自然边界条件''(0.2)''(1.0)0;S S ==(2)第一种边界条件.55741.1)0.1(',20271.0)2.0('==S S 要求输出用追赶法解出的弯矩向量(0M ,1M ,2M ,3M ,4M )及)1.02.0(i S +(i=0,1,2,3,4,5,6,7,8)的值.并画出)(x S y =的图形.实验原理简述我们先利用一阶导数)(x s ''在节点i x (i=1,2,…n-1)上的连 性以及边界条件,列出确定二阶导数)(i i x s M ''=(i=0,1,2,…n-1)的线性方程组(三弯矩方程),并由此解出i M 然后用i M 表达是)`(x s 即可i i i i i i g M M M =+++-112λμ(三弯矩方程) jj j i h h h +=--11μ,jj j i h h h +=-1λ, ,,,1,0n i =[][][]11111,,6,,6+---+=+-=j j j jj jj j j i x x xf h h x x f x x fg .其中有(1+n )个未知数n M M M ,...,10,而方程只有(n-1)个,当满足第一种边界条件时,可的另两个方程[]()010010,62f x x f h M M '-=+, []()n n n n n n x x f f h M M ,62111----'=+如果令[]()[]()n n n n n n x x f f h g f x x f h d ,6,1,,6,111010000---'=='-==μλ,将上述方程综合后的一下矩阵形式:222211110nn n μλμλμλ--nn M M M M 110- =n n g g g g 110-可以证明此方程组满足追赶法的条件,我们用追赶法可得M 的)1(+n 值,将其带入公式即得)(x s对第二种边界条件,直接的端点方程n n f M f M ''=''=,00并且令n n n f d f d ''=''===2,2,0000μλ,则又得三弯矩方程同理即可求得解。
三次样条插值实验报告

x1=0:.01:1;y1=polyval(S1(1,:),x1-X(1)); x2=1:.01:2;y2=polyval(S1(2,:),x2-X(2)); x3=2:.01:3;y3=polyval(S1(3,:),x3-X(3)); x4=3:.01:4;y4=polyval(S1(4,:),x4-X(4)); x5=4:.01:5;y5=polyval(S1(5,:),x5-X(5)); x6=5:.01:6;y6=polyval(S1(6,:),x6-X(6)); >> plot(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x6,y6,X,Y,'.') >> hold on >> x1=0:.01:1;y1=polyval(S2(1,:),x1-X(1)); x2=1:.01:2;y2=polyval(S2(2,:),x2-X(2)); x3=2:.01:3;y3=polyval(S2(3,:),x3-X(3)); x4=3:.01:4;y4=polyval(S2(4,:),x4-X(4)); x5=4:.01:5;y5=polyval(S2(5,:),x5-X(5)); x6=5:.01:6;y6=polyval(S2(6,:),x6-X(6)); >> plot(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x6,y6,X,Y,'.') >> hold on >> x1=0:.01:1;y1=polyval(S3(1,:),x1-X(1)); x2=1:.01:2;y2=polyval(S3(2,:),x2-X(2)); x3=2:.01:3;y3=polyval(S3(3,:),x3-X(3)); x4=3:.01:4;y4=polyval(S3(4,:),x4-X(4)); x5=4:.01:5;y5=polyval(S3(5,:),x5-X(5)); x6=5:.01:6;y6=polyval(S3(6,:),x6-X(6)); >> plot(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x6,y6,X,Y,'.')
三次样条插值法《数值分析》上机实验作业

昆明理工大学研究生《数值分析》上机实验作业姓名:学号:专业:一、 课题名称课题七 三次样条插值法1、问题提出 设已知数据如下:求f(x)的三次样条插值函数S(x)。
2、要求(1)满足自然边界条件0)0.1()2.0(=''=''s s ;(2)满足第一类边界条件20271.0)2.0(='s ,55741.1)0.1(='s 。
(3)打印输出用追赶法解出的弯曲向量(0M ,1M ,2M ,3M ,4M )和)1.02.0(i S + (i=0,1,2,3,4,5,6,7,8)的值。
并画出)(x S y =的图形。
二、 班级、姓名、学号三、目的和意义由于航空、造船等工程设计的需要而发展起来所谓样条插值方法,既保留了分段低次插值多项式的各种优点,又提高了插值函数的光滑性,而且具有较好的稳定性。
今天,样条插值方法已成为数值逼近的一个极其重要的分支,在许多领域里得到越来越广泛地应用。
其中,尤以三次样条插值函数应用最为广泛,如在高速飞机的机翼形体和船体放样等方面的应用,同时在计算机作图方面更是大有作为。
它能够解决一些既有二阶光滑度,又有二阶连续导数的方程,具有良好的收敛性和稳定性。
1. 通过本次实验进一步了解三次样条插值函数,并通过求解三 弯矩方程组得出曲线函数组;2. 通过MATLAB 编程实现求三次样条插值函数的算法,分别考虑 不同的边界条件,同时用追赶法解出弯曲向量和)1.02.0(i S + (i=0,1,2,3,4,5,6,7,8)的值。
四、计算公式首先我们利用)(x S 的二阶导数值),,2,1,0()(j n j M x S j ==''表达)(x S ,因为在区间]x ,[x 1j j +上)()(j x S x S =是不高于三次的多项式,其二阶导数)(x S ''必是线性函数,所以可表示为:]x ,[x x ,h x x M h x x M (x)S 1j j jj1j j1j j+++∈-+-=''对)(x S ''积分两次并利用1j 1j j j y )(x S ,y )(x S ++==,可定出积分 常数,于是得三次样条表达式。
三次样条插值的方法和思路 -回复

三次样条插值的方法和思路-回复三次样条插值是一种常用的插值方法,它可以在已知的离散数据点上构造出一条光滑的曲线。
这种方法被广泛应用在曲线拟合、图像处理、数据分析等领域。
本文将介绍三次样条插值的方法和思路,并详细阐述每个步骤。
第一步是确定插值段数。
在进行三次样条插值时,首先需要将已知数据点划分成若干个插值段。
插值段越多,插值曲线越接近原始数据,但也会使插值算法复杂度增加。
因此,在确定插值段数时需要权衡精度和计算效率。
第二步是计算每个插值段的系数。
对于每个插值段,我们需要计算出一个三次曲线,该曲线会通过该段的两个端点。
具体的计算方法是,假设有n 个插值点,则有n-1个插值段,每个插值段的系数需要通过以下步骤计算:1. 计算边界条件:这是三次样条插值的关键一步。
我们需要根据已知数据点的性质,来确定边界条件是自然边界、固定边界还是其他类型的边界。
自然边界要求二阶导数在两个端点处为0,即S''(x_0) = S''(x_n) = 0。
固定边界要求插值曲线通过端点的给定导数值,即S'(x_0) = d_0、S'(x_n) = d_n。
2. 构建三对角矩阵:三次样条插值的求解过程可以转化为解线性方程组的问题。
为了解这个方程组,我们需要构建一个三对角矩阵。
其中的对角线元素是2,上下对角线元素是1。
3. 计算方程组的右侧:方程组的右侧是一个n-1维的向量,每个元素对应插值段的边界条件。
对于自然边界,右侧元素都是0;对于固定边界,则通过求解给定的导数值得到。
4. 解线性方程组:将三对角矩阵与右侧向量相乘,即可得到每个插值段的系数。
第三步是构造插值曲线。
在前两步中,我们计算得到了每个插值段的系数。
现在,我们需要将这些系数整合起来,构造出整个插值曲线。
具体的构造方法为,对于第i个插值段,其插值函数可表示为:S_i(x) = a_i + b_i(x - x_i) + c_i(x - x_i)^2 + d_i(x - x_i)^3其中x_i和x_{i+1}为插值段的端点,a_i、b_i、c_i、d_i为第i个插值段的系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) di
(4)边界条件选取: M 0 2M i i M i 1 di , i 1, 2,3, , n 1.
(6)解三弯矩方程组得:
S ( x)
( xi x)3 ( x xi 1 )3 h2 x x M i 1 M i ( yi 1 i M i 1 ) i 6hi 6hi 6 hi
4. 算例计算结果 此算例为课本 141 页计算实习求三次样条插值。 运行文件“scyt2.m”, 可得到三次样条插值函数与原函数的曲线, 其中虚线代 表三次样条插值函数曲线, 实线代表原函数曲线。 然后在命令窗口输入“S = scyt(x, y)”,回车后即可得到 S(x)的在各个区间的系数 a, b, c, d 的值。 结果如下: 曲线:
比如当 x 在区间[-1, -0.8]时, S ( x) 0.3417 x3 1.0251x 2 1.1133x 0.4683 , 以此类推可以得到其他区间 S ( x) 的表达式。
hi 2 x xi 1 ( yi Mi ) , 6 hi
2. 程序框图
xi 1 x xi .
开始
输入节 点 x,y
计算 hi
计算μi ,λi
和 di
M0 Mn 0
追赶法解三弯矩方程组 求出 M1—Mn-1
将 M0—Mn 代入三次样 条插值公式
输出对应区 间的三次多 项式 S(X)
结束
3. 程序使用说明 本程序使用 MATLAB 来求解三次样条插值函数 S ( x) . 源程序文件 “scyt.m”为三次样条插值源程序, x,y分别为n+1个插值节点的 横坐标组成的向量和纵坐标组成的向量。 输入节点向量x, y后,在命令窗口输入S = scyt(x, y),回车后即可算出在区间 [ xi 1 , xi ]三次样条插值函数 S ( x) ax3 bx 2 cx d 表达式的系数a, b, c, d的值。 源程序文件 “scyt2.m”是计算实习算例的程序,直接运行即可得到结果。
实验 2 三次样条插值
1. 算法原理 S(x)是分段三次多项式;S(x)的二阶导数在区间[a,b]上连续。 求解步骤如下: (1)计算步长: hi xi xi 1 (2) i
hi hi 1 , i 1 i hi hi 1 hi hi 1
y y y yi 1 6 [ i 1 i i ] 6 f [ xi 1 , xi , xi 1 ], i 1, 2,3, , n 1. hi hi 1 hi 1 hi
系数: S= 0.3417 0.8933 0.8364 13.4083 -54.4694 54.4694 -13.4083 -0.8364 -0.8933 -0.3417 1.0251 2.3488 2.2465 17.3327 -23.3939 -23.3939 17.3327 2.2465 2.3488 1.0251 1.1133 2.1722 2.1108 8.1453 0.0000 0 -8.1453 -2.1108 -2.1722 -1.1133 0.4683 0.7507 0.7384 1.5430 1.0000 1.0000 1.5430 0.7384 0.7507 0.4683
