数学:第四章平面图形及其位置关系复习(北师大版七年级上)PPT课件
合集下载
新北师大版七级数学上册第四章复习PPT课件

A
MN
B
.
17
11.如图,已知BOC=30º,∠AOB=90º,OD 平分∠AOC,求∠BOD的度数。
CB D
A
.
18
12.如图,已知∠AOB=900,BOC=300, OM平分∠AOC,ON平分∠BOC,求 ∠MON的度数。
A
M
O
B
N
.
19
C
13、如图将一张长方形的纸片斜折过去使角的顶点
A落在F处,BC为折痕,然后再把BE折过去使它与 FB重合,折痕为BD,那么两条折痕BC、BD的夹角 是多少度?请说明理由。
D F
C
A
B
E
.
20
14、从九边形的一个顶点出发,能引出________ 条对角线,它们将九边形分成________个三角形,九 边形一共有________条对角线.
15、过多边形的一个顶点的所有对角线把多边形分 成8个三角形,这个多边形是______边形.
.
21
第四章 平面图形及其位置关系
基本概念:
1A.
c
表示为:直线c
2.射线:
O
M
表示为:射线OM,注意端点字母 一定要写在前边.
3.线段:
A
B
表示为:线段AB ,(或)线段BA.
m
表示为: 线段m
4.直线的性质:经过两点有且只有一条直线.
5. 线段的性质: 两点之间,线段最段. 两点之间线段的长度叫两点间的距离.
线段MN 的长.
A
CM N
B
解:∵N 是CB 的中点 ∴CB=2NB=2×5=10
∴AB=AC+CB=6+10=16
又∵M是AB 的中点
北师大版七年级数学上册复习课件 第四章 基本的平面图形 (共39张ppt)

数学·课标版(BS)
第四章复习
方法技巧 通过观察、分析、综合、归纳、概括、推理、判断等一 系列探索活动,解答有关探索规律的问题,探索规律性问题 的特点是问题的结论或条件不直接给出,需要逐步确定所求 的结论和条件.
数学·课标版(BS)
第四章复习
试卷讲练
考
平面图形是七年级数学的重要组成部分,在各类考
(4)分类:小于平角的角可按大小分成三类:当一个角等 于平角的一半时,这个角叫做_直__角__;大于 0°角小于直角的角 叫做_锐__角__;大于直角而小于平角的角叫做__钝__角__.
数学·课标版(BS)__点__引出的一条射线,把这个角分成两 个__相__等___的角,这条射线叫做这个角的平分线.
上 ” , 那 么 小 亮 可 以 对 小 明 说 : “ 你 在 我 的 ________ 方 向
上.”( A )
A.南偏西 30°
B.北偏东 30°
C.北偏东 60°
D.南偏西 60°
2.在一次航海中,在一艘货轮的北偏东 54°的方向上有一 艘渔船,那么货轮在渔船的_南__偏__西__5_4_°_方向上.
[解析] 钟表被分成 12 格,每格的度数是 30°, 30°×2.5=75°.
数学·课标版(BS)
第四章复习
方法技巧 计算钟面上时针与分针的夹角,关键是确定时针
与分针相隔几个格.
数学·课标版(BS)
第四章复习
►考点三 规律探索性问题
如图 4-2,平面内有公共端点 的六条射线 OA,OB,OC,OD,OE, OF,从射线 OA 开始按逆时针方向依 次在射线上写出数字 1,2,3,4,5,6,7,…. 则“17”在射线__O__E__上;“2013”在射 线__O__C__上.
第四章复习
方法技巧 通过观察、分析、综合、归纳、概括、推理、判断等一 系列探索活动,解答有关探索规律的问题,探索规律性问题 的特点是问题的结论或条件不直接给出,需要逐步确定所求 的结论和条件.
数学·课标版(BS)
第四章复习
试卷讲练
考
平面图形是七年级数学的重要组成部分,在各类考
(4)分类:小于平角的角可按大小分成三类:当一个角等 于平角的一半时,这个角叫做_直__角__;大于 0°角小于直角的角 叫做_锐__角__;大于直角而小于平角的角叫做__钝__角__.
数学·课标版(BS)__点__引出的一条射线,把这个角分成两 个__相__等___的角,这条射线叫做这个角的平分线.
上 ” , 那 么 小 亮 可 以 对 小 明 说 : “ 你 在 我 的 ________ 方 向
上.”( A )
A.南偏西 30°
B.北偏东 30°
C.北偏东 60°
D.南偏西 60°
2.在一次航海中,在一艘货轮的北偏东 54°的方向上有一 艘渔船,那么货轮在渔船的_南__偏__西__5_4_°_方向上.
[解析] 钟表被分成 12 格,每格的度数是 30°, 30°×2.5=75°.
数学·课标版(BS)
第四章复习
方法技巧 计算钟面上时针与分针的夹角,关键是确定时针
与分针相隔几个格.
数学·课标版(BS)
第四章复习
►考点三 规律探索性问题
如图 4-2,平面内有公共端点 的六条射线 OA,OB,OC,OD,OE, OF,从射线 OA 开始按逆时针方向依 次在射线上写出数字 1,2,3,4,5,6,7,…. 则“17”在射线__O__E__上;“2013”在射 线__O__C__上.
七年级数学上册课件(北师大版):第四章基本平面图形 (共17张PPT)精品

2020/9/29
最新中小学课件
仅供学习交流!
2020/9/29
最新中小学课件
2020/9/29
◆考点突破 ◆考前过三最关新中小学课(件 ◎第一关 ◎第二关
◎第三关 ) 1
2020/9/29
◆考点突破 ◆考前过三最关新中小学课(件 ◎第一关 ◎第二关
◎第三关 ) 2
2020/9/29
◆考点突破 ◆考前过三最关新中小学课(件 ◎第一关 ◎第二关
◎第三关 ) 3
2020/9/29
◎第三关 ) 7
2020/9/29
◆考点突破 ◆考前过三最关新中小学课(件 ◎第一关 ◎第二关
◎第三关 ) 8
2020/9/29
◆考点突破 ◆考前过三最关新中小学课(件 ◎第一关 ◎第二关
◎第三关 ) 9
2020/9/29
◆考点突破 ◆考前过三最关新中小学课(件 ◎第一关 ◎第二关
◎第三关 ) 10
◆考点突破 ◆考前过三最关新中小学课(件 ◎第一关 ◎第二关
◎第三关 ) 18
谢谢!
墨子,(约前468~前376)名翟,鲁人 ,一说 宋人, 战国初 期思想 家,政 治家, 教育家 ,先秦 堵子散 文代表 作家。 曾为宋 国大夫 。早年 接受儒 家教育 ,后聚 徒讲学 ,创立 与儒家 相对立 的墨家 学派。 主张•兼 爱”“ 非攻“ 尚贤” “节用 ”,反 映了小 生产者 反对兼 并战争 ,要求 改善经 济地位 和社会 地位的 愿望, 他的认 识观点 是唯物 的。但 他一方 面批判 唯心的 宿命论 ,一方 面又提 出同样 是唯心 的“天 志”说 ,认为 天有意 志,并 且相信 鬼神。 墨于的 学说在 当时影 响很大 ,与儒 家并称 为•显 学”。 《墨子》是先秦墨家著作,现存五 十三篇 ,其中 有墨子 自作的 ,有弟 子所记 的墨子 讲学辞 和语录 ,其中 也有后 期墨家 的作品 。《墨 子》是 我国论 辩性散 文的源 头,运 用譬喻 ,类比 、举例 ,推论 的论辩 方法进 行论政 ,逻辑 严密, 说理清 楚。语 言质朴 无华, 多用口 语,在 先秦堵 子散文 中占有 重要的 地位。 公输,名盘,也作•“般”或•“班 ”又称 鲁班, 山东人 ,是我 国古代 传说中 的能工 巧匠。 现在, 鲁班被 人们尊 称为建 筑业的 鼻祖, 其实这 远远不 够.鲁 班不光 在建筑 业,而 且在其 他领域 也颇有 建树。 他发明 了飞鸢 ,是人 类征服 太空的 第一人 ,他发 明了云 梯(重武 器),钩 钜(现 在还用) 以及其 他攻城 武器, 是一位 伟大的 军事科 学家, 在机械 方面, 很早被 人称为 “机械 圣人” ,此外 还有许 多民用 、工艺 等方面 的成就 。鲁班 对人类 的贡献 可以说 是前无 古人, 后无来 者,是 我国当 之无愧 的科技 发明之 父。
北师大版七年级上册数学《第4章 基本平面图形小结与复习》课件

形,这个多边形的边数是___1_0____.
[解析] 设多边形有n条边, 则n-2=8,解得n=10. 所以这个多边形的边数是10.
学生课堂行为规范的内容是: 按时上课,不得无故缺课、迟到、早 退。 遵守课堂礼仪,与老师问候。 上课时衣着要整洁,不得穿无袖背心 、吊带 上衣、 超短裙 、拖鞋 等进入 教室。 尊敬老师,服从任课老师管理。 不做与课堂教学无关的事,保持课堂 良好纪 律秩序 。 听课时有问题,应先举手,经教师同 意后, 起立提 问。 上课期间离开教室须经老师允许后方 可离开 。 上课必须按座位表就坐。 要爱护公共财物,不得在课桌、门窗 、墙壁 上涂写 、刻划 。 要注意保持教室环境卫生。 离开教室要整理好桌椅,并协助老师 关好门 窗、关 闭电源 。
第四章 基本平面图形 小结与复习
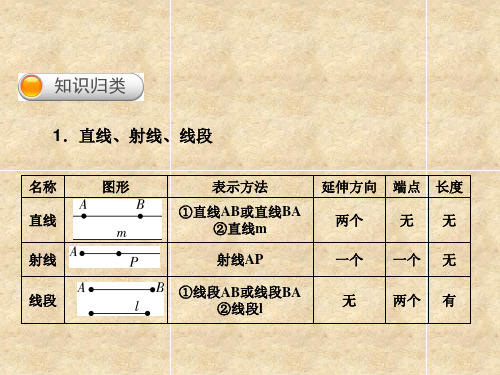
知识回顾 1.直线、射线、线段
名称 直线 射线 线段
图形
表示方法
①直线AB或直线BA
无无
射线AP
一个 一个 无
①线段AB或线段BA ②线段l
无
两个 有
知识回顾 2.直线的基本性质 经过两点有且只有__二__条直线. 3.线段的基本性质 两点之间,__线__段________最短. 4.两点之间的距离 两点之间线段的__长__度____,叫做这两点之间的距离.距离
知识回顾
(3)单位及换算:把周角平均分成360份,每一份就是1°的 角,1°的1/60就是1′,1′的1/60就是1″,即1°= _6_0_′_,1′= __6_0_′____.
(4)分类:小于平角的角可按大小分成三类:当一个角等于 平角的一半时,这个角叫做___直__角___;大于0°角小于直角的角 叫做__锐__角____;大于直角而小于平角的角叫做___钝__角_____.
[解析] 设多边形有n条边, 则n-2=8,解得n=10. 所以这个多边形的边数是10.
学生课堂行为规范的内容是: 按时上课,不得无故缺课、迟到、早 退。 遵守课堂礼仪,与老师问候。 上课时衣着要整洁,不得穿无袖背心 、吊带 上衣、 超短裙 、拖鞋 等进入 教室。 尊敬老师,服从任课老师管理。 不做与课堂教学无关的事,保持课堂 良好纪 律秩序 。 听课时有问题,应先举手,经教师同 意后, 起立提 问。 上课期间离开教室须经老师允许后方 可离开 。 上课必须按座位表就坐。 要爱护公共财物,不得在课桌、门窗 、墙壁 上涂写 、刻划 。 要注意保持教室环境卫生。 离开教室要整理好桌椅,并协助老师 关好门 窗、关 闭电源 。
第四章 基本平面图形 小结与复习
知识回顾 1.直线、射线、线段
名称 直线 射线 线段
图形
表示方法
①直线AB或直线BA
无无
射线AP
一个 一个 无
①线段AB或线段BA ②线段l
无
两个 有
知识回顾 2.直线的基本性质 经过两点有且只有__二__条直线. 3.线段的基本性质 两点之间,__线__段________最短. 4.两点之间的距离 两点之间线段的__长__度____,叫做这两点之间的距离.距离
知识回顾
(3)单位及换算:把周角平均分成360份,每一份就是1°的 角,1°的1/60就是1′,1′的1/60就是1″,即1°= _6_0_′_,1′= __6_0_′____.
(4)分类:小于平角的角可按大小分成三类:当一个角等于 平角的一半时,这个角叫做___直__角___;大于0°角小于直角的角 叫做__锐__角____;大于直角而小于平角的角叫做___钝__角_____.
新北师大版七年级上册第四章基本平面图形复习课件
解:OE与OD是互相垂直的 因为∠AOB +∠BOC=∠AOB =180° 又因为∠AOD =∠BOD ∠BOE=∠COE 所以2∠BOD+2∠BOE=180° 即:∠BOD +∠BOE=90° 所以∠DOE =90° 因此OE与OD互相垂直
1 ∴NB = BC,MB = 2 ∵NB =5,∴BC =10
1 AB 2
1 (AC+BC)=9 ∴MB =9 2 ∴MN=MB-NB=9-5 = 4
D 条. 11.经过E、F、G 三点画直线,可以画____ A. 1 B. 2 C. 3 D. 1或3
分析:三点共线时,可画一条直线,三点 不在同一直线上,根据直线的性质,每过 两点可以画一条直线,共有三条直线. 解:如图.
5.下列说法,正确说法的个数是( C )
①直线AB和直线BA是同一条直线;②射线 AB与射线BA是同一条射线;③线段AB和线 段BA是同一条线段;④图中有两条射线. A.0 B.1 C.2 D.3
6.下列图形中有线段、射线或直线,根据它们 的基本特征可判断出,其中能够相交的有( .C )
A.①② B.①③
知识归类
1.直线、射线、线段
名称 直线 射线 线段 图形 表示方法 ①直线AB或直线BA ②直线m 射线AP ①线段AB或线段BA ②线段l 延伸方向 两个 一个 无 端点 无 一个 两个 长度 无 无 有
2.直线的基本性质
一 条直线. 经过两点有且只有____
3.线段的基本性质
两点之间,____________ 最短. 线段 4.两点之间的距离 两点之间线段的________ 长度 ,叫做这两点之间的距离.距离 是指线段的_______ 长度 ,是一个_______ 数值 ,而不是指线段本身.
1 ∴NB = BC,MB = 2 ∵NB =5,∴BC =10
1 AB 2
1 (AC+BC)=9 ∴MB =9 2 ∴MN=MB-NB=9-5 = 4
D 条. 11.经过E、F、G 三点画直线,可以画____ A. 1 B. 2 C. 3 D. 1或3
分析:三点共线时,可画一条直线,三点 不在同一直线上,根据直线的性质,每过 两点可以画一条直线,共有三条直线. 解:如图.
5.下列说法,正确说法的个数是( C )
①直线AB和直线BA是同一条直线;②射线 AB与射线BA是同一条射线;③线段AB和线 段BA是同一条线段;④图中有两条射线. A.0 B.1 C.2 D.3
6.下列图形中有线段、射线或直线,根据它们 的基本特征可判断出,其中能够相交的有( .C )
A.①② B.①③
知识归类
1.直线、射线、线段
名称 直线 射线 线段 图形 表示方法 ①直线AB或直线BA ②直线m 射线AP ①线段AB或线段BA ②线段l 延伸方向 两个 一个 无 端点 无 一个 两个 长度 无 无 有
2.直线的基本性质
一 条直线. 经过两点有且只有____
3.线段的基本性质
两点之间,____________ 最短. 线段 4.两点之间的距离 两点之间线段的________ 长度 ,叫做这两点之间的距离.距离 是指线段的_______ 长度 ,是一个_______ 数值 ,而不是指线段本身.
北师大版七年级数学上册第四章《基本平面图形》精品复习课件

渝南田家炳中学欢迎您!
课堂练习:
一、图形个数问题
例1 如图,A,B,C,D为平面内每三点都
不在一条直线上的四点,那么过其中任意的两点,
可画出几条直线?若A,B,C,D,E为平面内
每三点都不在一条直线上的五点,则过其中任意 的两点可画几条直线?若是n个点呢?
渝南田家炳中学欢迎您!
解:对于已知四点,A点与其他三点共可确定3条直线,过
渝南田家炳中学欢迎您!
4. 比较线段的长短 线段长度的比较有两种方法: (1)叠合比较法,如比较线段AB,CD的长度,可将线段 AB,CD移到同一条射线上,使它们的端点A,C都与射线的端点重 合,再由点B与点D的位置关系,就可得出线段AB和CD的长度关 系. (2)度量比较法,先用刻度尺度量各线段的长度,再按照度量的 长度比较它们的长短.
渝南田家炳中学欢迎您!
二、线段长度的计算 例2 如图,线段AB=32cm,点C在AB上,
且AC∶CB=5∶3,点D是AC的中点,点O 是AB的中点,求DB与OC的长.
【解析】 从图上可以看出DB=AB-AD,而D是
AC的中点,AD= 1/2 AC,结合AC∶CB=5∶3,AB= 32 cm,故AC和BC可求,OC=OB-BC=1/2AB-BC.
渝南田家炳中学欢迎您!
三、时钟夹角问题
例3 钟表在3点半时,它的时针和分针所 成的锐角是( B )
A.70° B.75° C.85° D.90°
【解析】 可以画出草图,如图所示,要注 意的是3点半时,分针指在正下方6处,而时针 并非指在3处,而是在3与4的正中间,所以分 针和时针的夹角为90°- 1/2×30°=75°.
渝南田家炳中学欢迎您!
四、有关角度的计算
北师大版七年级数学上册第四章:基本平面图形复习课件

30.(1)一个圆和一个扇形的半径相等,已知圆的面积 是30cm2,扇形的圆心角是36°。求扇形的面积。
(2)已知扇形的圆心角为120°,面积为300π.求扇形 的弧长。
由两条直线成的图形
经过两点有且只有一条线段 B.
按下列线段长度,可以确定点A、B、C不在同一条直线上的是( )
两条射线组成的图形叫做角
A.两点之间的连线中,直线最短 平面上有三点A,B,C,如果AB=8,AC=5,BC=3,那么( )
6时30分,时针与分针重合
B.若P是线段AB的中点,则AP=BP A.直线A
B.
如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )
由两条线段组成的图形
两A.条一直条线直C确线.定一若个交AB点P.。一=条射B线P,则P是线段AB的中点
已知点A、B、C在同一条直线上,且AC=5cm,BC=3cm,M、N分别是AC、BC的中点。
A、85° B、75° C、70° D、60°
A.一条直线
B.一条射线
平面上有四点,经过其中的两点画直线最多可画出( )
(提示:未给出图形,注意C点位置有多种可能)
6时30分,时针与分针重合
5 C.
D.两点之间的线段叫作这两点之间的距离 (提示:未给出图形,注意C点位置有多种可能)
下列各直线的表示法中,正确的是( )
直线AB
10.角是指( ) A.由两条线段组成的图形 B.由两条射线组成的图形 C.由两条直线组成的图形 D.有公共端点的两条射线组成的图形
11.下列关于角的说法正确的是( ) A.两条射线组成的图形叫做角 B.延长一个角的两边 C.角的两边是射线,所以角不可以度量 D.角的大小与这个角两边的长短无关
北师大版七年级数学上册第四章 《基本平面图形》课件

11、如图:从一个角的顶点(O)引出的一条射线(OC)
,把这个角分成两个相等的角,这条射线叫做这个角的平
分线。射线OA是 AOB 的平分线,
B
这时, AO C BO C 1 AOB
2
O
或 AOB 2AOC =2 BOC.
C A
12、各边相等,各角也相等的多边形叫做 等边多边形。
基础知识复习
13、平面上,一条线段围绕着它的一个端点旋转一周,另一 个端点形成的图形叫做圆 。固定的端点O称为 圆心 线段OA称为 半径 。圆上任意两点A、B间的部分叫做圆 弧。简称 弧 记作 A B,读作“圆弧AB ”或“弧AB ”。
相等的角,这条射线叫做这个角的平分线。
性质:射线OC是<AOB的平分线。这时,
B
AOC BOC 1A0B 2
O
或 AO 2 A BO 2 B COC
C A
例题:
如下图:OB平分 AOC ,OC平分 BOD ,
且 BOC= 18º,则 AOD是多少度?
D
解:
OB平分 AOC
C
B
OC平分 BOD且 BOC180 A
●
●●
●
A
OB
C
解:因为 AC ABBC437(cm)
o是线段AC的中点
所以AOOC 1 AC 173.5(cm) 22
所以OBOCBC3.53O.5(cm)
考点四:度、分、秒单位换算
【原理】:相邻两个单位之间的进率是60 即:1º=60’ 1’=60”
[例题】1、 1.45º等于多少分?等于多少秒?
A● ●O
B ●
14、由一条弧AB和经扇过形这条弧的端点的两条半径O圆A心、角OB
北师大七年级上册第四章平面图形及其位置关系复习课件

6.想一想
(1)已知:如图,B为线段AC上的一点,点M,N分 别为AB,BC的中点。 填空:MN=( )+( ), MN=( )-( ), MN=( )-( )-( ); (2)已知:如图,B为线段AC上的一点,点M, N分别为AB,BC的中点,AB=m,BC=n,求: MN。
7.做一做
利用方格纸,分别画出MN的平行线段、PQ 的垂线段
七年级数学上册
知识网络
1 选一选
下列说法正确的是( )个。 ①三条直线两两相交有三个交点 ②两条不相交的直线叫平行线 ③经过一点有且只有一条直线与已知直线平行 ④平面内,经过一点有且只有一条直线与已知 直线垂直 ⑤平面内,若线段AB=BC,则B为AC的中点 (A)1 (B)2 (C)3 (D)4
---------------------------------东海路
4.拼一拼
请你用一副三角尺拼出135°,75°,15° 的角
5.算一算
(1)如图:∠AOB=∠COD=90°,那么∠AOC与 ∠BOD相等吗? 若∠BOD=150°,求∠BOC等于多少度? (2)当钟表上的时间是12:30时,时针与分针所 成的角是多少度?
8.辨一辨
如图是一个公园的示意图,下列说法错误的是( )。 (A)海洋世界在大门口的北偏东90° (B)山在大门的正北方向 (C)大象馆在大门的北偏东60° (D)虎豹园在大门的南偏东30°
9.议一议
如图,AOC 为一条直线, OB、OD、OE是三条 射线,且 ∠AOD=∠BOD, ∠COE =∠BOE,请 判断OE与OD是否互相 垂直,为什么?
2.填一填
(1)要把木条水平地钉在墙上至少需要钉钉子,用数学知识 解释为( ) (2)1.6° =( )′=( )″,1800″=( )′=( )° ; (3)两条相交直线所成角相等,那么这两条直线; (4)找找看图中共有( )条线段,( )个小于平角的角。
北师大版七年级上第4章《平面图形及其位置关系》复习课件

D
E
C
1°= 60´=3600"
。
A D
4、角平分线:
B
∵BD是∠ABC的平分线 1 ∴∠ABD=∠CBD= ∠ABC
2
A
C
如图,AE、BD分别是∠BAC、∠ABC的 平分线,∠ABC=60°,∠BAC=72°, 则∠ADB= °,∠CAE= ° B 5、度、分、秒的转化 1800″= ′= ° 2.17°= ° ′ ″ 25°34´+16°40´ = 90°-18°14´= 。 15°25´×3= 。
(1)过一点可作 无数 条直线,过两点可作 1 条直线, 过三个点中的任意两个点最多可作 条直线; 3 (2)三条直线两两相交,有 1或3 个交点。
3、两点之间的所有连线中,线段最短。
4、两点之间的距离:两点之间线段的长度。
将弯曲的河道改直可以缩短航程,用数学知识 可以解释为 。
5、中点:
∵c是AB的中点 1 ∴AC=BC= AB
3、角的分类: 锐角、直角、钝角 特殊角:直角=90°,平角=180°,周角=360°
1 1 1、 平角 直角 4 3
度。
2、指出下列时刻钟表上分针与时针的夹角。 8:00 10:30 6:15
A D
4、角平分线:
B
∵BD是∠ABC的平分线 1 ∴∠ABD=∠CBD= ∠ABC
2
A
C
如图,AE、BD分别是∠BAC、∠ABC的 平分线,∠ABC=60°,∠BAC=72°, 则∠ADB= °,∠CAE= ° B 5、度、分、秒的转化 1800″= ′= ° 2.17°= ° ′ ″ 25°34´+16°40´ = 90°-18°14´= 。 15°25´×3= 。
第四章平面图形及其位置关系复习PPT

• 垂直性质 :平面内,过一点 垂直性质1 平面内, 有且只有一条直线与已知直线 垂直。 垂直。 • 垂直性质 :直线外一点与直线 垂直性质2:直线外一点与 各点连接的所有线段中, 上各点连接的所有线段中,垂 线段最短。 线段最短。 P
A O B C
1、23.2 ° = °= ′ 2、平面上两条直线的位置关系只有 两种, __________和 两种,即__________和_________ 如图,四条表示方向的射线中, 3、如图,四条表示方向的射线中, 表示北偏东60 的是( 60° 表示北偏东60°的是( )
6、如图,已知 、如图, ∶∠3∶∠ ∠1∶∠ ∶∠ ∶∠ ∶∠4=1∶2∶4,∠2= ∶ ∶ ∠ 80°,求∠1、∠3、∠4的度 ° 、 、 的度 数.
7、如图,在三角形 、如图 在三角形 在三角形ABC中,AB=AC, 中 用量角器和三角板按要求画图 到线段BC的距离 (1)画出表示点 到线段 的距离 )画出表示点A到线段 AD; ; A 点作BA的平行线 (2)过D点作 的平行线 交AC ) 点作 的平行线DE交 于点E,并连结BE 于点 ,并连结
3、如图∠ AOB= ∠ COD=900, 、如图∠ 0, ∠ BOC= 340 ; ∠ AOD=146
4、如图:这是A、B两地之间的公 如图:这是A 在公路工程改造计划时, 路,在公路工程改造计划时,为使 A、B两地行程最短,应如何设计 两地行程最短, 线路?在图中画出. 线路?在图中画出.并说明你的理 由. 5、已知线段a、b, 、已知线段 、 , 求作:线段MN,使MN =a + b 求作:线段 , a 不写作法, (不写作法, b 保留作图痕迹) 保留作图痕迹)
A
M
B
角的平分线: 角的平分线:从一个角的顶点引出的 一条射线 射线, 一条射线,把这个角分成两个相 等的角, 等的角,这条射线叫做角的平分 如图, 线。如图, 的角平分线, ∵ OC是∠AOB的角平分线, 是 的角平分线 1 ∴ ∠AOC = ∠BOC = ∠AOB 2
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A.①② B.①③ C.①③ D.③④
8.角就是(D )
A.有公共点的两条直线组成的图形 B.有一个公共点的两条射线组成的图形 C.由一条射线旋转而成的 D.由公共端点的两条射线组成的图形
3.在∠AOB) A
A.∠AOB >∠AOC B.∠AOC >∠BOC C.∠BOC >∠AOC D.∠AOC =∠BOC
1.解:∵M、N 分别是AB、CB 的中点
∴NB = 1BC,MB =
1
AB
2
2
∵NB =5,∴BC =10
12(AC+BC)=9 ∴MB =9
∴MN=MB-NB=9-5 = 4
13.经过E、F、G 三点画直线,可以画__D__条.
A. 1 B. 2 C. 3
D. 1或3
分析:三点共线时,可画一条直线,三点 不在同一直线上,根据直线的性质,每过 两点可以画一条直线,共有三条直线. 解:如图.
11.如图,直线AB、CD相交于点O, OE⊥AB 于O,∠DOE =42°,
则∠BOD 的度数是_4_8_°__.
解:∵OE⊥AB于O ∴∠AOE =∠BOE=90° ∵∠DOE =42° ∴∠BOD =∠BOE- ∠DOE=48° 因此,∠BOD 的度数为48°
12.如图所示,点C是线段AB上一点, AC<CB,M、N分别是AB、CB 的中点, AC=8,NB = 5,求线段MN 的长是__4___.
14. 平行线的表示: A
B
a D
b
直线a∥b或 直线AB∥CD
m C
o
直线m与直线相n交于o.
n
15.平行线的性质:
1.经过直线外一点,有 且只有一条直线与这 条直线平行.
C P· D
A
B
2.如果两条直线都与第
l1
三条直线平行,那么这
两条直线互相平行.
l2
∵ l1 ∥ l2 l3 ∥ l2
l3
∴ l1 ∥ l3
第四章平面图形及其位置关系 复习课件
第四章 平面图形及其位置关系
基本概念:
1.直线:
A
B
表示为:直线AB ,(或)直线BA.
C
表示为:直线C
2.射线:
O
M
表示为:射线OM,注意端点字母 一定要写在前边.
m
表示为: 射线m
3.线段:
A
B
表示为:线段AB ,(或)线段BA.
m
表示为: 线段m
4.直线的性质:经过两点只有一条直线.
16.在线段AB上任取D、C、E 三个点,
那么这个图中共有______1条0线段.
分析:只要有一个端点不相同,就是不同的线段.
解:以A为起点的线段有AC、AD、AE、AB 四条. 以D为起点的线段且与前不重复的有DE、DC、 DB三条. 以E为起点的线段且与前不重复的有EC、EB二条. 以C为起点的线段并且与前不重复的有BC一条.
①直线AB和直线BA是同一条直线;②射线
AB与射线BA是同一条射线;③线段AB和线
段BA是同一条线段;④图中有两条射线.
A.0 B.1 C.2
D.3
6.三条直线AB、CD、EF,若AB∥EF、
CD∥EF,则__A_B__∥__C_D__,理由:
如果两条直线都和第三条直线平行,
那么这两条直线互相平行
7.下列图形中有线段、射线或直线,根据它们 的基本特征可判断出,其中能够相交的有(.C )
5. 线段的性质: 在两点的所有连接的 线中,线段最段. 两点之间线段的长度 叫两点间的距离.
A
B
6. 线段的中点: 把一条线段分成两条 相等的两条线段的点叫作线段的中点.
A
M
B
例如: M是线段AB的中点,
则AM = MB =
1 AB 2
7.角的定义:具有公共端点的两条射
8.角的表示: 线所组成的图形叫做角.
16.垂直的定义:
如果两条直线相交成 直角,那么这两条直 线互相垂直.
17.垂直的表示:
直线AB垂直于直 线CD表示为: AB⊥CD或a⊥b
aC
b
A
B
D
18.垂线的性质:
(1).平面内经过一点有且只有 一条直线和已知直线垂直.
(2).直线外一点与
直线上各点的连线
中,垂线段最短.垂
线段的长度叫做点 到直线的距离.
A
·P CD B
如图:PA>PB>PC>PD, 线段PD的长度 就是P点到直线AB的距离.
1.一条线段有___两__个端点.
2.用度表示:30°45′=__3__0_.7. 5° 3.时钟4点20分,时针和分针所夹的锐角
的度数是_1__0_°_.
4.图中小于平角的角 的个数有__6___个.
5.下列说法,正确说法的个数是( C )
14.如图4,直线AB、CD 相交于O,∠COE是直角,
∠1=57°,则∠2=__3_3_°____.
15.小亮利用星期天搞社会调查活动,早晨 8:00出发,中午12:30到家,问小亮出 发时和到家时时针和分针的夹角各为 ___1_2_0_°__或_1_6_5_°_____度.
答案:出发时的时针和分针的夹角为120°, 回到家时时针与分针的夹角为165°.
A (1). 三个大写字母表示:
∠AOB ∠ABD ∠ABC
O B
A D
∠DBC
B
C
(2). 一个大写字母表示:
C
∠A ∠B ∠C A
B
(3).希腊字母表示:
∠ ∠ ∠
(4). 数字表 示∠:1 ∠2 ∠3
3 2
1
9.角也可以看做是一条射 线绕端点旋转得到的.
10.角的度量: 1°= 60′, 1′= 60″
9.点到直线的距离是指这点到这条直线的(D )
A.垂线段 C.长度
B.垂线的 D.垂线段的长
10.下面说法正确的是( D )
A.在同一平面内,如果两条射线不相交, 那么这两条射线平行
B. 两条直线不平行,必定相交 C. 在同一平面内,两条不相交的线段是平行线 D. 两条射线或线段平行,是指它们所在的直线平行
因此图中共有4+3+2+1=10条线段.
17.如图,用字母A、B、C 表示∠α、∠β. 答案:∠CAB或∠BAC 表示∠α; ∠CBA或∠ABC表示 ∠β.
20.引水渠从M向东流250米到N处, 转向东北方向300米到C 处,再转向 北偏西30°方向,流200米到D处,试
11. 角平分线意义:
从一个角的顶点出发,把这个角 分成相等的两个角的射线叫做 角平分线
∵∠AOC=∠BOC O
1 =2
∠AOB
A C
B
12.点方位:
北
∠1.北偏东60° ∠2.北偏西30° ∠3.西偏南60°
西3 ∠4.南偏东45°
∠5.东偏南45°
21
4 南
5东
13.同一平面内两直线的位置 相交, 平行.
8.角就是(D )
A.有公共点的两条直线组成的图形 B.有一个公共点的两条射线组成的图形 C.由一条射线旋转而成的 D.由公共端点的两条射线组成的图形
3.在∠AOB) A
A.∠AOB >∠AOC B.∠AOC >∠BOC C.∠BOC >∠AOC D.∠AOC =∠BOC
1.解:∵M、N 分别是AB、CB 的中点
∴NB = 1BC,MB =
1
AB
2
2
∵NB =5,∴BC =10
12(AC+BC)=9 ∴MB =9
∴MN=MB-NB=9-5 = 4
13.经过E、F、G 三点画直线,可以画__D__条.
A. 1 B. 2 C. 3
D. 1或3
分析:三点共线时,可画一条直线,三点 不在同一直线上,根据直线的性质,每过 两点可以画一条直线,共有三条直线. 解:如图.
11.如图,直线AB、CD相交于点O, OE⊥AB 于O,∠DOE =42°,
则∠BOD 的度数是_4_8_°__.
解:∵OE⊥AB于O ∴∠AOE =∠BOE=90° ∵∠DOE =42° ∴∠BOD =∠BOE- ∠DOE=48° 因此,∠BOD 的度数为48°
12.如图所示,点C是线段AB上一点, AC<CB,M、N分别是AB、CB 的中点, AC=8,NB = 5,求线段MN 的长是__4___.
14. 平行线的表示: A
B
a D
b
直线a∥b或 直线AB∥CD
m C
o
直线m与直线相n交于o.
n
15.平行线的性质:
1.经过直线外一点,有 且只有一条直线与这 条直线平行.
C P· D
A
B
2.如果两条直线都与第
l1
三条直线平行,那么这
两条直线互相平行.
l2
∵ l1 ∥ l2 l3 ∥ l2
l3
∴ l1 ∥ l3
第四章平面图形及其位置关系 复习课件
第四章 平面图形及其位置关系
基本概念:
1.直线:
A
B
表示为:直线AB ,(或)直线BA.
C
表示为:直线C
2.射线:
O
M
表示为:射线OM,注意端点字母 一定要写在前边.
m
表示为: 射线m
3.线段:
A
B
表示为:线段AB ,(或)线段BA.
m
表示为: 线段m
4.直线的性质:经过两点只有一条直线.
16.在线段AB上任取D、C、E 三个点,
那么这个图中共有______1条0线段.
分析:只要有一个端点不相同,就是不同的线段.
解:以A为起点的线段有AC、AD、AE、AB 四条. 以D为起点的线段且与前不重复的有DE、DC、 DB三条. 以E为起点的线段且与前不重复的有EC、EB二条. 以C为起点的线段并且与前不重复的有BC一条.
①直线AB和直线BA是同一条直线;②射线
AB与射线BA是同一条射线;③线段AB和线
段BA是同一条线段;④图中有两条射线.
A.0 B.1 C.2
D.3
6.三条直线AB、CD、EF,若AB∥EF、
CD∥EF,则__A_B__∥__C_D__,理由:
如果两条直线都和第三条直线平行,
那么这两条直线互相平行
7.下列图形中有线段、射线或直线,根据它们 的基本特征可判断出,其中能够相交的有(.C )
5. 线段的性质: 在两点的所有连接的 线中,线段最段. 两点之间线段的长度 叫两点间的距离.
A
B
6. 线段的中点: 把一条线段分成两条 相等的两条线段的点叫作线段的中点.
A
M
B
例如: M是线段AB的中点,
则AM = MB =
1 AB 2
7.角的定义:具有公共端点的两条射
8.角的表示: 线所组成的图形叫做角.
16.垂直的定义:
如果两条直线相交成 直角,那么这两条直 线互相垂直.
17.垂直的表示:
直线AB垂直于直 线CD表示为: AB⊥CD或a⊥b
aC
b
A
B
D
18.垂线的性质:
(1).平面内经过一点有且只有 一条直线和已知直线垂直.
(2).直线外一点与
直线上各点的连线
中,垂线段最短.垂
线段的长度叫做点 到直线的距离.
A
·P CD B
如图:PA>PB>PC>PD, 线段PD的长度 就是P点到直线AB的距离.
1.一条线段有___两__个端点.
2.用度表示:30°45′=__3__0_.7. 5° 3.时钟4点20分,时针和分针所夹的锐角
的度数是_1__0_°_.
4.图中小于平角的角 的个数有__6___个.
5.下列说法,正确说法的个数是( C )
14.如图4,直线AB、CD 相交于O,∠COE是直角,
∠1=57°,则∠2=__3_3_°____.
15.小亮利用星期天搞社会调查活动,早晨 8:00出发,中午12:30到家,问小亮出 发时和到家时时针和分针的夹角各为 ___1_2_0_°__或_1_6_5_°_____度.
答案:出发时的时针和分针的夹角为120°, 回到家时时针与分针的夹角为165°.
A (1). 三个大写字母表示:
∠AOB ∠ABD ∠ABC
O B
A D
∠DBC
B
C
(2). 一个大写字母表示:
C
∠A ∠B ∠C A
B
(3).希腊字母表示:
∠ ∠ ∠
(4). 数字表 示∠:1 ∠2 ∠3
3 2
1
9.角也可以看做是一条射 线绕端点旋转得到的.
10.角的度量: 1°= 60′, 1′= 60″
9.点到直线的距离是指这点到这条直线的(D )
A.垂线段 C.长度
B.垂线的 D.垂线段的长
10.下面说法正确的是( D )
A.在同一平面内,如果两条射线不相交, 那么这两条射线平行
B. 两条直线不平行,必定相交 C. 在同一平面内,两条不相交的线段是平行线 D. 两条射线或线段平行,是指它们所在的直线平行
因此图中共有4+3+2+1=10条线段.
17.如图,用字母A、B、C 表示∠α、∠β. 答案:∠CAB或∠BAC 表示∠α; ∠CBA或∠ABC表示 ∠β.
20.引水渠从M向东流250米到N处, 转向东北方向300米到C 处,再转向 北偏西30°方向,流200米到D处,试
11. 角平分线意义:
从一个角的顶点出发,把这个角 分成相等的两个角的射线叫做 角平分线
∵∠AOC=∠BOC O
1 =2
∠AOB
A C
B
12.点方位:
北
∠1.北偏东60° ∠2.北偏西30° ∠3.西偏南60°
西3 ∠4.南偏东45°
∠5.东偏南45°
21
4 南
5东
13.同一平面内两直线的位置 相交, 平行.
