2.6.2菱形的判定同步练习含答案

合集下载

菱形的判定同步练习(含答案)

第六章特殊平行四边形1 菱形的性质与判定第2课时菱形的判定基础闯关知识点一：利用定义判定菱形1.如图，四边形ABCD是平行四边形，延长BA到点E,使AE=AB,连接ED,EC,AC.添加一个条件，能使四边形ACDE成为菱形的是( )A.AB=ADB.AB=EDC.CD=AED.EC=AD2.如图,在△ABC中,点D,E,F分别是边BC,CA,AB的中点,要使四边形AFDE为菱形,△ABC应满足的条件是.(添加一个条件即可)知识点二：利用对角线的位置关系判定菱形3.如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，DE=DF.在下列条件中，使四边形BECF是菱形的是( )A.EB⊥ECB.AB⊥ACC.AB=ACD.BF∥CE4.从下图入口处进入，最后到达的是( )A.甲B.乙C.丙D.丁知识点三：利用边的关系判定菱形5.如图,将平行四边形ABCD沿AE翻折,使点B恰好落在AD上的点F处，则下列结论不一定成立的是( )A.AF=EFB.AB=EFC.AE=AFD.AF=BE6.如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件能够判定四边形ABCD为菱形的是( )A.AB=BCB.AC=BCC.∠B=60°D.∠ACB=60°7.如图,在△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.如果AE=4cm,那么四边形AEDF的周长为( )A.12cmB.16cmC.20cmD.22cm8.如图，两条笔直的公路l₁，l₂相交于点O，村庄C的村民在公路的旁边建了三个加工厂A,B,D,已知AB=BC=CD=DA=5千米,村庄C到公路l₁的距离为4千米，则村庄C到公路l₂的距离为.知识点四：菱形判定方法的综合应用9.如图,在▱ABCD中,对角线AC,BD相交于点O，添加下列条件，不能判定▱ABCD是菱形的是( )A.AC⊥BDB.AB=BCC.AC=BDD.∠1=∠210.如图,在▱ABCD中,AE,CF分别是∠BAD和∠BCD的平分线.添加一个条件，仍无法判断四边形AECF为菱形的是( )A.AE=AFB.EF⊥ACC.∠B=60°D.AC是∠EAF的平分线能力提升11.如图，在小正方形组成的网格图中，四边形ABCD的顶点都在格点上，则下列结论错误的是( )A.AD∥BCB.DC=ABC.四边形ABCD是菱形D.将边AD向右平移3格，再向上平移7格就与边BC重合12.如图,▱ABCD中,对角线AC,BD相交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点，下列结论：①BE ⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )A.2B.3C.4D.513.如图，四边形ABCD内有一点E,AE=BE=DE=BC=DC,AB=AD,若∠C=100°,则∠BAD的度数为.14.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D为斜边AB上一点,以CD,CB为边作▱CDEB,当AD=时,▱CDEB为菱形.15.如图,在▱ABCD中,对角线AC与BD相交于点O，过点O的直线EF与BA,DC的延长线分别交于点E,F.(1)求证:AE=CF.(2)请再添加一个条件，使四边形BFDE是菱形，并说明理由.16.如图,▱ABCD中,过点A作AM⊥BC于点M,交BD于点E,过点C作CN⊥AD于点N,交BD于点F,连接AF,CE.(1)求证:△ABE≌△CDF.(2)求证:当AB=AD时,四边形AECF是菱形.17.如图,过▱ABCD对角线AC与BD的交点E作两条互相垂直的直线，分别交边AB,BC,CD,DA 于点P,M,Q,N.(1)求证:△PBE≌△QDE.(2)顺次连接点P,M,Q,N,求证:四边形PMQN是菱形.培优创新【求解中点四边形的关键——中位线】18.如图，在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点，要使四边形EFGH是菱形，则四边形ABCD只需要满足一个条件,是( )A.四边形ABCD是梯形B.四边形ABCD是菱形C.对角线AC=BDD.AD=BC19.如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P,Q,M,N分别为AB,BC,CD,DA的中点，求证：四边形MNPQ是菱形.参考答案1.B2.示例:AB=AC3.C4.D5.C6.A7.B8.4千米9.C 10.C 11.C 12.C 13.50° 14.2.815.(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,BE∥DF,∴∠E=∠F.在△AOE和△COF中,CF.(2)解:示例:当EF⊥BD时,四边形BFDE是菱形.理由:如图,连接BF,DE.∵四边形ABCD是平行四边形,∴OB=OD.∵△AOE≌△COF,∴OE=OF,∴四边形BFDE是平行四边形.∵EF⊥BD,∴四边形BFDE是菱形.16.证明:(1)∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∠ABM=∠CDN,∴∠ABE=∠CDF.∵AM⊥BC,CN⊥AD,∴∠AMB=∠CND=90°,∴∠BAM=∠DCN,在△ABE和△CDF中,∴△ABE≌△CDF(ASA).(2)如图,连接AC.当AB=AD时,四边形ABCD为菱形,则AC⊥BD,AD∥BC.∵△ABE≌△CDF,∴AE=CF.∵AM⊥BC,CN⊥AD,AD∥BC,∴AM∥CN,∴四边形AECF为平行四边形.∵AC⊥EF,∴四边形AECF为菱形.17.证明:(1)∵四边形ABCD是平行四边形,∴EB=ED,AB∥CD,∴∠EBP=∠EDQ.在△PBE和△QDE中,(2)如图所示,∵△PBE≌△QDE,∴EP=EQ.同理,△BME≌△DNE(ASA),∴EM=EN,∴四边形PMQN是平行四边形.∵PQ⊥MN,∴四边形PMQN是菱形.18.D19.证明:如图,连接BD,AC.∵△ADE和△BCE都是等边三角形,∴AE=DE,EC=BE,∠AED=∠BEC=60°,∴∠AEC=∠DEB=120°,∴△AEC≌△DEB(SAS),∴AC=BD.∵M,N是CD,DA的中点,∴MN是△ACD的中位线,即同理可得NP=QM,∴四边形MNPQ是菱形.。

2020年菱形的判定同步练习含试卷及答案解析课后作业

2020年菱形的判定同步练习含试卷及答案解析一．选择题（共3小题）1．已知▭ABCD，添加一个条件能使它成为菱形，下列条件正确的是（）A．AB＝AC B．AB＝CDC．对角线互相垂直D．∠A+∠C＝180°2．下列条件中，能判断四边形是菱形的是（）A．对角线互相垂直且相等的四边形B．对角线互相垂直的四边形C．对角线相等的平行四边形D．对角线互相平分且垂直的四边形3．如图，添加下列条件仍然不能使▱ABCD成为菱形的是（）A．AB＝BC B．AC⊥BD C．∠ABC＝90°D．∠1＝∠2二．填空题（共2小题）4．如图，四边形ABCD是平行四边形，补充一个条件使其成为菱形，你补充条件是（只需填一个即可）．5．如图，剪两张对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是．三．解答题（共6小题）6．如图，在等腰三角形ABC中，AB＝AC，AH⊥BC，点E是AH上一点，延长AH至点F，使FH＝EH．求证：四边形EBFC是菱形．7．如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，AC与BD相交于点O，连接CD．（1）求∠AOD的度数；（2）求证：四边形ABCD是菱形．8．如图，▱ABCD中，AB＝2cm，AC＝5cm，S▱ABCD＝8cm2，E点从B点出发，以1cm每秒的速度，在AB延长线上向右运动，同时，点F从D点出发，以同样的速度在CD延长线上向左运动，运动时间为t秒．（1）在运动过程中，四边形AECF的形状是；（2）t＝时，四边形AECF是矩形；（3）求当t等于多少时，四边形AECF是菱形．9．已知，如图，在▱ABCD中，BF平分∠ABC交AD于点F，AE⊥BF于点O，交BC于点E，连接EF．（1）求证：四边形ABEF是菱形；（2）若AE＝6，BF＝8，CE＝3，求四边形ABCD的面积．10．如图，已知点P为∠ACB平分线上的一点，∠ACB＝60°，PD⊥CA于D，PE⊥CB于E．点M是线段CP上的动点（不与两端点C、P重合），连接DM，EM．（1）求证：DM＝ME；（2）当点M运动到线段CP的什么位置时，四边形PDME为菱形，请说明理由．11．如图，菱形ABCD对角线交于点O，BE∥AC，AE∥BD，EO与AB交于点F．（1）试判断四边形AEBO的形状，并说明你的理由；（2）求证：EO＝DC．2020年菱形的判定同步练习含试卷及答案解析参考答案与试题解析一．选择题（共3小题）1．已知▭ABCD，添加一个条件能使它成为菱形，下列条件正确的是（）A．AB＝AC B．AB＝CDC．对角线互相垂直D．∠A+∠C＝180°【分析】根据菱形的判定方法①一组邻边相等的平行四边形是菱形；②四条边都相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）针对每一个选项进行判断，即可选出正确答案．【解答】解：A、添加AB＝AC，不能证明▱ABCD是菱形，故此选项错误；B、添加AB＝CD，不能证明▱ABCD是菱形，故此选项错误；C、添加对角线互相垂直，可以证明▱ABCD是菱形，故此选项正确；D、添加∠A+∠C＝180°不能证明▱ABCD是菱形，故此选项错误；故选：C．【点评】此题主要考查了菱形的判定，关键是熟练掌握菱形的判定方法．2．下列条件中，能判断四边形是菱形的是（）A．对角线互相垂直且相等的四边形B．对角线互相垂直的四边形C．对角线相等的平行四边形D．对角线互相平分且垂直的四边形【分析】利用菱形的判定方法对各个选项一一进行判断即可．【解答】解：A、对角线互相垂直相等的四边形不一定是菱形，此选项错误；B、对角线互相垂直的四边形不一定是菱形，此选项错误；C、对角线相等的平行四边形也可能是矩形，此选项错误；D、对角线互相平分且垂直的四边形是菱形，此选项正确；故选：D．【点评】本题考查了菱形的判定，平行四边形的性质，熟练运用这些性质是本题的关键．3．如图，添加下列条件仍然不能使▱ABCD成为菱形的是（）A．AB＝BC B．AC⊥BD C．∠ABC＝90°D．∠1＝∠2【分析】根据菱形的性质逐个进行证明，再进行判断即可．【解答】解：A、∵四边形ABCD是平行四边形，AB＝BC，∴平行四边形ABCD是菱形，故本选项错误；B、∵四边形ABCD是平行四边形，AC⊥BD，∴平行四边形ABCD是菱形，故本选项错误；C、∵四边形ABCD是平行四边形和∠ABC＝90°不能推出，平行四边形ABCD是菱形，故本选项正确；D、∵四边形ABCD是平行四边形，∴AB∥CD，∴∠2＝∠ADB，∵∠1＝∠2，∴∠1＝∠ADB，∴AB＝AD，∴平行四边形ABCD是菱形，故本选项错误；故选：C．【点评】本题考查了平行四边形的性质，菱形的判定的应用，注意：菱形的判定定理有：①有一组邻边相等的平行四边形是菱形，②四条边都相等的四边形是菱形，③对角线互相垂直的平行四边形是菱形．二．填空题（共2小题）4．如图，四边形ABCD是平行四边形，补充一个条件使其成为菱形，你补充条件是AB＝BC（答案不唯一）（只需填一个即可）．【分析】根据菱形的判定可得．【解答】解：∵AB＝BC，且四边形ABCD为平行四边形∴四边形ABCD是菱形故答案为：AB＝BC（答案不唯一）【点评】本题考查了菱形的判定，熟练掌握菱形的判定是本题的关键．5．如图，剪两张对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是平行四边形．【分析】由条件可知AB∥CD，AD∥BC，可得四边形ABCD是平行四边形．【解答】解：∵AB∥CD，AD∥BC，∴四边形ABCD是平行四边形．故答案为：平行四边形．【点评】本题考查了平行四边形的判定．关键是掌握平行四边形的判定方法．三．解答题（共6小题）6．如图，在等腰三角形ABC中，AB＝AC，AH⊥BC，点E是AH上一点，延长AH至点F，使FH＝EH．求证：四边形EBFC是菱形．【分析】根据题意可证得△BCE为等腰三角形，由AH⊥CB，则BH＝HC，从而得出四边形EBFC是菱形．【解答】证明：∵AB＝AC，AH⊥CB，∴BH＝HC，∵FH＝EH，∴四边形EBFC是平行四边形，又∵AH⊥CB，∴四边形EBFC是菱形．【点评】本题考查了菱形的判定和性质，以及等腰三角形的性质，是基础知识要熟练掌握．7．如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，AC与BD相交于点O，连接CD．（1）求∠AOD的度数；（2）求证：四边形ABCD是菱形．【分析】（1）首先根据角平分线的性质得到∠DAC＝∠BAC，∠ABD＝∠DBC，然后根据平行线的性质得到∠DAB+∠CBA＝180°，从而得到∠BAC+∠ABD＝（∠DAB+∠ABC）＝×180°＝90°，得到答案∠AOD＝90°；（2）根据平行线的性质得出∠ADB＝∠DBC，∠DAC＝∠BCA，根据角平分线定义得出∠DAC＝∠BAC，∠ABD＝∠DBC，求出∠BAC＝∠ACB，∠ABD＝∠ADB，根据等腰三角形的判定得出AB＝BC＝AD，根据平行四边形的判定得出四边形ABCD是平行四边形，即可得出答案．【解答】解：（1）∵AC、BD分别是∠BAD、∠ABC的平分线，∴∠DAC＝∠BAC，∠ABD＝∠DBC，∵AE∥BF，∴∠DAB+∠CBA，＝180°，∴∠BAC+∠ABD＝（∠DAB+∠ABC）＝×180°＝90°，∴∠AOD＝90°；（2）证明：∵AE∥BF，∴∠ADB＝∠DBC，∠DAC＝∠BCA，∵AC、BD分别是∠BAD、∠ABC的平分线，∴∠DAC＝∠BAC，∠ABD＝∠DBC，∴∠BAC＝∠ACB，∠ABD＝∠ADB，∴AB＝BC，AB＝AD∴AD＝BC，∵AD∥BC，∴四边形ABCD是平行四边形，∵AD＝AB，∴四边形ABCD是菱形．【点评】本题考查了等腰三角形的性质，平行四边形的判定，菱形的判定的应用，能得出四边形ABCD是平行四边形是解此题的关键．8．如图，▱ABCD中，AB＝2cm，AC＝5cm，S▱ABCD＝8cm2，E点从B点出发，以1cm每秒的速度，在AB延长线上向右运动，同时，点F从D点出发，以同样的速度在CD延长线上向左运动，运动时间为t秒．（1）在运动过程中，四边形AECF的形状是平行四边形；（2）t＝1时，四边形AECF是矩形；（3）求当t等于多少时，四边形AECF是菱形．【分析】（1）由平行四边形的性质得出AB＝CD＝2cm，AB∥CD，由已知条件得出CF ＝AE，即可得出四边形AECF是平行四边形；（2）若四边形AECF是矩形，则∠AFC＝90°，得出AF⊥CD，由平行四边形的面积得出AF＝4cm，在Rt△ACF中，由勾股定理得出方程，解方程即可；（3）当AE＝CE时，四边形AECF是菱形．过C作CG⊥BE于G，则CG＝4cm，由勾股定理求出AG，得出GE，由勾股定理得出方程，解方程即可．【解答】解：（1）四边形AECF是平行四边形；理由如下：∵四边形ABCD是平行四边形，∴AB＝CD＝2cm，AB∥CD，∴CF∥AE，∵DF＝BE，∴CF＝AE，∴四边形AECF是平行四边形；故答案为：平行四边形；（2）t＝1时，四边形AECF是矩形；理由如下：若四边形AECF是矩形，∴∠AFC＝90°，∴AF⊥CD，∵S▱ABCD＝CD•AF＝8cm2，∴AF＝4cm，在Rt△ACF中，AF2+CF2＝AC2，即42+（t+2）2＝52，解得：t＝1，或t＝﹣5（舍去），∴t＝1；故答案为：1；（3）依题意得：AE平行且等于CF，∴四边形AECF是平行四边形，故AE＝CE时，四边形AECF是菱形．又∵BE＝tcm，∴AE＝CE＝t+2（cm），过C作CG⊥BE于G，如图所示：则CG＝4cmcm，∵AG＝＝＝3（cm），∴GE＝t+2﹣3＝t﹣1（cm），在△CGE中，由勾股定理得：CG2+GE2＝CE2＝AE2，即42+（t﹣1）2＝（t+2）2，解得：t＝，即t＝s时，四边形AECF是菱形．【点评】本题考查了平行四边形的性质与判定、菱形的判定、矩形的判定、勾股定理等知识；熟练掌握平行四边形的性质，由勾股定理得出方程是解决问题的关键．9．已知，如图，在▱ABCD中，BF平分∠ABC交AD于点F，AE⊥BF于点O，交BC于点E，连接EF．（1）求证：四边形ABEF是菱形；（2）若AE＝6，BF＝8，CE＝3，求四边形ABCD的面积．【分析】（1）先证明四边形ABEF是平行四边形，再证明邻边相等即可证明．（2）作FG⊥BC于G，根据S菱形ABEF＝•AE•BF＝BE•FG，先求出FG即可解决问题．【解答】（1）证明：∵四边形ABCD是平行四边形∴AD∥BC，∴∠EBF＝∠AFB，∵BF平分∠ABC，∴∠ABF＝∠CBF，∴∠ABF＝∠AFB，∴AB＝AF，∵BO⊥AE，∴∠AOB＝∠EOB＝90°，∵BO＝BO，∴△BOA≌△BOE（ASA），∴AB＝BE，∴BE＝AF，BE∥AF，∴四边形ABEF是平行四边形，∵AB＝AF．∴四边形ABEF是菱形．（2）解：作FG⊥BC于G，∵四边形ABEF是菱形，AE＝6，BF＝8，∴AE⊥BF，OE＝AE＝3，OB＝BF＝4，∴BE＝＝5，∵S菱形ABEF＝•AE•BF＝BE•FG，∴GF＝，∴S平行四边形ABCD＝BC•FG＝．【点评】本题考查平行四边形的性质、菱形的判定和性质、勾股定理等知识，解题的关键是利用面积法求出高FG，记住菱形的三种判定方法，属于中考常考题型．10．如图，已知点P为∠ACB平分线上的一点，∠ACB＝60°，PD⊥CA于D，PE⊥CB于E．点M是线段CP上的动点（不与两端点C、P重合），连接DM，EM．（1）求证：DM＝ME；（2）当点M运动到线段CP的什么位置时，四边形PDME为菱形，请说明理由．【分析】（1）先利用角平分线定义得到∠ACP＝∠BCP＝30°，再根据角平分线的性质得PD＝PE，则利用“HL”可证明Rt△DCP≌Rt△ECP得到CD＝CE，然后证明△DCM ≌△ECM得到DM＝ME；（2）利用∠DCP＝30°得到PC＝2PD，∠CPD＝60°，则当DM＝DP时，PD＝PE＝MD＝ME，则四边形DMEP为菱形，由于此时△PDM为等边三角形，所以PD＝PM，从而得到CM＝PM，即当点M运动到线段CP的中点时，四边形PDME为菱形．【解答】（1）证明：∵点P为∠ACB平分线上的一点，∴∠ACP＝∠BCP＝30°，∵PD⊥CA于D，PE⊥CB于E，∴PD＝PE，在Rt△DCP和Rt△ECP中，∴Rt△DCP≌Rt△ECP，∴CD＝CE，在△DCM和△ECM中，∴△DCM≌△ECM，∴DM＝ME；（2）解：当点M运动到线段CP的中点时，四边形PDME为菱形．理由如下：∵∠DCP＝30°，∴PC＝2PD，∠CPD＝60°，∵PD＝PE，MD＝ME，∴当DM＝DP时，PD＝PE＝MD＝ME，则四边形DMEP为菱形，此时△PDM为等边三角形，∴CM＝PM，∴当点M运动到线段CP的中点时，四边形PDME为菱形．【点评】本题考查了菱形的判定：一组邻边相等的平行四边形是菱形（平行四边形+一组邻边相等＝菱形）；四条边都相等的四边形是菱形．也考查了全等三角形的判定与性质和角平分线的性质．11．如图，菱形ABCD对角线交于点O，BE∥AC，AE∥BD，EO与AB交于点F．（1）试判断四边形AEBO的形状，并说明你的理由；（2）求证：EO＝DC．【分析】（1）由菱形的性质可证明∠BOA＝90°，然后再证明四边形AEBO为平行四边形，从而可证明四边形AEBO是矩形；（2）依据矩形的性质可得到EO＝BA，然后依据菱形的性质可得到AB＝CD．【解答】解：（1）四边形AEBO是矩形．证明：∵BE∥AC，AE∥BD∴四边形AEBO是平行四边形．又∵菱形ABCD对角线交于点O∴AC⊥BD，即∠AOB＝90°．∴四边形AEBO是矩形．（2）∵四边形AEBO是矩形∴EO＝AB，在菱形ABCD中，AB＝DC．【点评】本题主要考查的是菱形的性质判定、矩形的性质和判定，熟练掌握相关图形的性质是解题的关键．。

八年级数学下册菱形同步练习、含答案2(含答案)

菱形班级：___________________________姓名：___________________________作业导航理解并掌握菱形的性质及判别方法，会利用菱形的性质和判别方法进行推理说明和有关计算．一、选择题1．菱形具有而一般平行四边形不具有的性质是（）A．对角相等B．对边相等C．对角线互相垂直D．对角线相等2．能够判别一个四边形是菱形的条件是（）A．对角线相等且互相平分B．对角线互相垂直且相等C．对角线互相平分D．一组对角相等且一条对角线平分这组对角3．菱形的周长为100 cm，一条对角线长为14 cm，它的面积是（）A．168 cm2 B．336 cm2 C．672 cm2 D．84 cm24．菱形的周长为16，两邻角度数的比为1：2，此菱形的面积为（）A．43B．83C．103D．1235．下列语句中，错误的是（）A．菱形是轴对称图形，它有两条对称轴B．菱形的两组对边可以通过平移而相互得到C．菱形的两组对边可以通过旋转而相互得到D．菱形的相邻两边可以通过旋转而相互得到二、填空题6．菱形的周长是8 cm，则菱形的一边长是______．7．菱形的一个内角为120°，平分这个内角的对角线长为11厘米，菱形的周长为______．8．菱形的对角线的一半的长分别为8 cm和11 cm，则菱形的面积是_______．9．菱形的面积为24 cm2，一对角线长为6 cm，则另一对角线长为______，边长为______．10．菱形的面积为83平方厘米，两条对角线的比为1：3，那么菱形的边长为_______．三、解答题11．如图，AD是△ABC的角平分线．DE∥AC交AB于E，DF∥AB交AC于F．四边形AEDF是菱形吗？说明你的理由．12．□ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F，四边形AFCE 是否是菱形？为什么？13．菱形ABCD的周长为20 cm，两条对角线的比为3：4，求菱形的面积．14．如图，菱形ABCD的对角线AC、BD交于点O，且AC=16 cm，BD=12 cm，求菱形ABCD的高DH．参考答案一、1．C2．D3．B4．B5．D二、6．2 cm7．44厘米8．176 cm29．8 cm 5 cm10．4 cm三、11．四边形AEDF是菱形，AE=E D．12．□AFCE是菱形，△AOE≌△COF，四边形AFCE是平行四边形，EF⊥AC13．24 cm214．9.6 cm。

湘教版2019年度八年级数学下册第2章2.6菱形2.6.2菱形的判定练习含答案

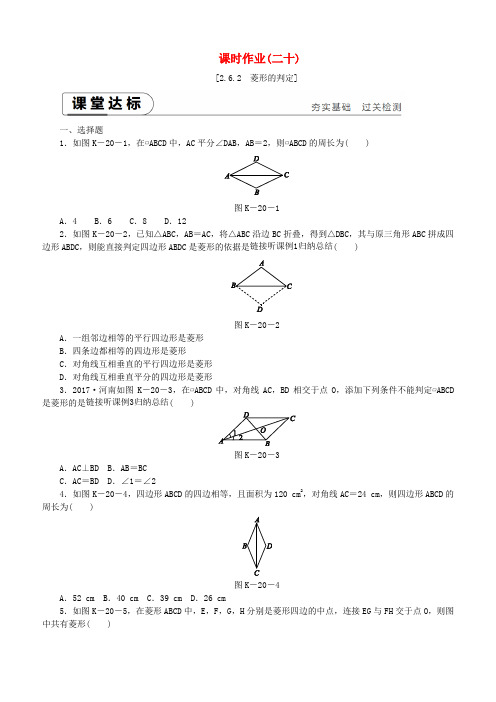
课时作业(二十)[2.6.2 菱形的判定]一、选择题1．如图K－20－1，在▱ABCD中，AC平分∠DAB，AB＝2，则▱ABCD的周长为( )图K－20－1A．4 B．6 C．8 D．122．如图K－20－2，已知△ABC，AB＝AC，将△ABC沿边BC折叠，得到△DBC，其与原三角形ABC拼成四边形ABDC，则能直接判定四边形ABDC是菱形的依据是链接听课例1归纳总结( )图K－20－2A．一组邻边相等的平行四边形是菱形B．四条边都相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．对角线互相垂直平分的四边形是菱形3．2017·河南如图K－20－3，在▱ABCD中，对角线AC，BD相交于点O，添加下列条件不能判定▱ABCD 是菱形的是链接听课例3归纳总结( )图K－20－3A．AC⊥BD B．AB＝BCC．AC＝BD D．∠1＝∠24．如图K－20－4，四边形ABCD的四边相等，且面积为120 cm2，对角线AC＝24 cm，则四边形ABCD的周长为( )图K－20－4A．52 cm B．40 cm C．39 cm D．26 cm5．如图K－20－5，在菱形ABCD中，E，F，G，H分别是菱形四边的中点，连接EG与FH交于点O，则图中共有菱形( )图K－20－5A．4个 B．5个 C．6个 D．7个6．图K－20－6是一张平行四边形纸片ABCD，要求利用所学知识将它变成一个菱形，甲、乙两名同学的作法分别如下，对于甲、乙两人的作法，可判断( )甲：连接AC，作AC的中垂线分别交AD，BC于点E，F，连接AF，CE，则四边形AFCE是菱形．乙：分别作∠BAD与∠ABC的平分线AE，BF，分别交BC，AD于点E，F，则四边形ABEF是菱形．图K－20－6A．甲、乙均正确 B．甲、乙均错误C．甲正确，乙错误 D．甲错误，乙正确二、填空题7．如图K－20－7，在▱ABCD中，AB＝6 cm，AD＝8 cm，点M，N分别在AD，BC上，且DM＝CN＝2 cm，则四边形ABNM是________形，判断的依据是______________________．图K－20－78．如图K－20－8，在△ABC中，D是BC的中点，点E，F分别在线段AD及其延长线上，且DE＝DF，给出下列条件：①BE⊥EC；②BF∥EC；③AB＝AC.从中选择一个条件使四边形BECF是菱形，你认为这个条件是________(只填写序号)．图K－20－8三、解答题9．2018·郴州如图K－20－9，在▱ABCD中，作对角线BD的垂直平分线EF，垂足为O，分别交AD，BC 于点E，F，连接BE，DF.求证：四边形BFDE是菱形．图K－20－910.2018·南京如图K－20－10，在四边形ABCD中，BC＝CD，∠C＝2∠BAD，O是四边形ABCD内的一点，且OA＝OB＝OD.求证：(1)∠BOD＝∠C；(2)四边形OBCD是菱形.链接听课例1归纳总结图K－20－1011．2018·娄底如图K－20－11，在四边形ABCD中，对角线AC，BC相交于点O，且OA＝OC，OB＝OD，过点O作EF⊥BD，分别交AD，BC于点E，F.(1)求证：△AOE≌△COF；(2)判断四边形BEDF的形状，并说明理由．图K－20－1112．如图K－20－12，已知AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F.求证：AD ⊥EF.图K－20－12操作探究小明用两条宽度均为d cm的长方形纸条交错地叠在一起，相交成∠α(如图K－20－13)，设重叠部分是四边形ABCD.(1)他发现：不管∠α是锐角、直角还是钝角，四边形ABCD的形状好像总不变，请你判断它的形状，并说出理由；(2)分别求出当d＝1，∠α＝45°和d＝3，∠α＝60°时重叠部分的面积．图K－20－13详解详析课堂达标 1．C2．[解析] B ∵将△ABC 沿边BC 折叠得到△DBC ，∴AB ＝BD ，AC ＝CD.∵AB ＝AC ，∴AB ＝BD ＝CD ＝AC ，∴四边形ABDC 是菱形．故选B.3．[解析] C A 项，∵四边形ABCD 是平行四边形，AC ⊥BD ，∴▱ABCD 是菱形(对角线互相垂直的平行四边形是菱形)；B 项，∵四边形ABCD 是平行四边形，AB ＝BC ，∴▱ABCD 是菱形(一组邻边相等的平行四边形是菱形)；C 项，∵四边形ABCD 是平行四边形，AC ＝BD ，∴▱ABCD 是矩形(对角线相等的平行四边形是矩形)；D 项，∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠1＝∠ACB.∵∠1＝∠2，∴∠ACB ＝∠2，∴AB ＝BC ，∴▱ABCD 是菱形(一组邻边相等的平行四边形是菱形)．故选C.4．[解析] A 连接BD.∵四边形ABCD 的四边相等，∴四边形ABCD 为菱形．∵它的面积为120 cm 2，对角线AC ＝24 cm ，∴120＝12×24×BD ，∴BD ＝10 cm ，∴AB ＝52＋122＝13(cm)，∴四边形ABCD 的周长为4×13＝52(cm)．故选A.5．[解析] B ∵四边形ABCD 是菱形，E ，F ，G ，H 分别是菱形四边的中点， ∴AE ＝AH ＝HD ＝GD ＝CG ＝CF ＝FB ＝BE ＝OE ＝OG ＝OH ＝OF ，∴四边形AEOH ，HOGD ，EOFB ，OFCG 和ABCD 均为菱形，共5个． 6．[解析] A 甲的作法正确，如图①.∵四边形ABCD 是平行四边形， ∴AD ∥BC ，∴∠EAO ＝∠FCO.∵EF 是AC 的垂直平分线， ∴AO ＝CO.在△AOE 和△COF 中， ⎩⎪⎨⎪⎧∠EAO ＝∠FCO ，AO ＝CO ，∠AOE ＝∠COF ，∴△AOE ≌△COF(ASA)， ∴AE ＝CF. 又∵AE ∥CF ，∴四边形AECF 是平行四边形．又∵EF ⊥AC ，∴四边形AECF 是菱形．乙的作法正确，如图②.∵AD ∥BC ，∴∠1＝∠2，∠5＝∠6. ∵BF 平分∠ABC ，AE 平分∠BAD ， ∴∠2＝∠3，∠4＝∠5， ∴∠1＝∠3，∠4＝∠6，∴AB ＝AF ，AB ＝BE ，∴AF ＝BE. ∵AF ∥BE 且AF ＝BE ，∴四边形ABEF 是平行四边形．又∵AB ＝AF ，∴▱ABEF 是菱形．故选A.7．菱有一组邻边相等的平行四边形是菱形 8．[答案] ③[解析] 需添加条件③.理由：∵D 是BC 的中点，∴BD ＝CD.又∵DE ＝DF ，∴四边形BECF 为平行四边形．∵AB ＝AC ，D 是BC 的中点， ∴AD ⊥BC ，∴▱BECF 为菱形，故答案为③.9．解：如图．∵EF 是BD 的垂直平分线， ∴BE ＝DE ，BF ＝DF ， ∴∠1＝∠2，∠3＝∠4.∵四边形ABCD 是平行四边形， ∴DE ∥BF ，∴∠1＝∠3， ∴∠1＝∠2＝∠3＝∠4，∴BE ∥DF ，∴四边形BFDE 是平行四边形． ∵EF ⊥BD ，∴四边形BFDE 是菱形．10．证明：(1)∵OA ＝OB ＝OD ，∴∠OAB ＝∠OBA ，∠OAD ＝∠ODA ，∠BOD ＝360°－∠AOD －∠AOB ，∠AOB ＝180°－∠OAB －∠OBA ＝180°－2∠OAB ，∠AOD ＝180°－∠OAD －∠ODA ＝180°－3∠OAD ，∴∠BOD ＝360°－(180°－2∠OAD)－(180°－2∠OAB)＝2∠OAD ＋2∠OAB ＝2(∠OAD ＋∠OAB)＝2∠BAD. 又∵∠C ＝2∠BAD ， ∴∠BOD ＝∠C. (2)连接OC.∵OB ＝OD ，CB ＝CD ，OC ＝OC ， ∴△BOC ≌△DOC ，∴∠BOC ＝∠DOC ，∠BCO ＝∠DCO ，∴∠BOC ＝12∠BOD ，∠BCO ＝12∠BCD.由(1)知∠BOD ＝∠C ，∴∠BOC ＝∠BCO ， ∴OB ＝CB.又∵OB ＝OD ，CB ＝CD ， ∴OB ＝BC ＝CD ＝DO ， ∴四边形OBCD 是菱形．11．解：(1)证明：∵OA ＝OC ，OB ＝OD ， ∴四边形ABCD 是平行四边形， ∴AD ∥BC ，∴∠EAO ＝∠FCO.在△AOE 和△COF 中，⎩⎪⎨⎪⎧∠EAO ＝∠FCO ，OA ＝OC ，∠AOE ＝∠COF ，∴△AOE ≌△COF(ASA)．(2)结论：四边形BEDF 是菱形． ∵△AOE ≌△COF ，∴AE ＝CF. ∵四边形ABCD 是平行四边形， ∴AD ＝BC ，AD ∥BC ， ∴DE ＝BF. ∵DE ∥BF ，∴四边形BEDF 是平行四边形． ∵EF ⊥BD ，∴四边形BEDF 是菱形．12．[解析] 要证AD ⊥EF ，可先证明四边形AEDF 为菱形．由题意可得四边形AEDF 为平行四边形，再证一组邻边相等即可．证明：∵DE ∥AC ，DF ∥AB ， ∴四边形AEDF 为平行四边形． ∵AD 是△ABC 的角平分线， ∴∠EAD ＝∠FAD. ∵DE ∥AC ，∴∠FAD ＝∠EDA ， ∴∠EAD ＝∠EDA ， ∴AE ＝DE ，∴四边形AEDF 为菱形， ∴AD ⊥EF. 素养提升解：(1)四边形ABCD 是菱形．理由：∵两长方形纸条对边平行， ∴AB ∥CD ，BC ∥AD ，∴四边形ABCD 是平行四边形．过点A 作AE ⊥BC 于点E ，AF ⊥CD 于点F ，则AE ＝AF ＝d.又∵S ▱ABCD ＝AE·BC＝AF·CD， ∴BC ＝CD ，∴▱ABCD 是菱形．(2)当d ＝1，∠α＝45°时，∠ADF ＝45°， AF ＝1 cm ，而AF ⊥CD ，∴△ADF 是等腰直角三角形且AF ＝DF.又∵AD 2＝AF 2＋DF 2，∴AD ＝ 2 cm ， ∴CD ＝AD ＝ 2 cm ，∴重叠部分的面积＝CD·AF＝2×1＝2(cm 2)．当d ＝3，∠α＝60°时，∠ADF ＝60°，AF ＝ 3 cm ，则DF ＝12AD ，利用勾股定理可得AD ＝2 cm ， ∴CD ＝AD ＝2 cm ，∴重叠部分的面积＝CD·AF＝2×3＝2 3(cm 2)．。

菱形的判定配套练习-含答案

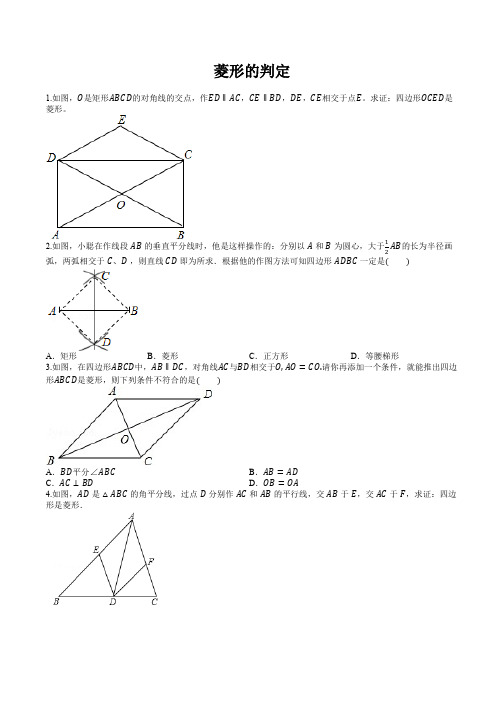
菱形的判定1.如图，O是矩形ABCD的对角线的交点，作ED∥AC，CE∥BD，DE，CE相交于点E。

求证：四边形OCED是菱形。

AB的长为半径画2.如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于12弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是()A．矩形B．菱形C．正方形D．等腰梯形3.如图，在四边形ABCD中，AB∥DC，对角线AC与BD相交于O,AO=CO.请你再添加一个条件，就能推出四边形ABCD是菱形，则下列条件不符合的是()A．BD平分∠ABC B．AB=ADC．AC⊥BD D．OB=OA4.如图，AD是△ABC的角平分线，过点D分别作AC和AB的平行线，交AB于E，交AC于F，求证：四边形是菱形．5.如图，在▱ABCD中，BD是对角线，且DB⊥BC，E,F分别为边AB、CD的中点．求证：四边形DEBF是菱形．6.如图，在△ABC中，AD是∠BAC的平分线，EF垂直平分AD交AB于E，交AC于F．求证：四边形AEDF是菱形．7.如图，在平行四边形ABCD中，E为BC边上的一点，连结AE，BD，且AE=AB.(1) 求证：∠ABE=∠EAD;(2) 若∠AEB=2∠ADB，求证：四边形ABCD是菱形8.如图，在平行四边形ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．(1) 求证：△ABE≅△DFE；(2) 连接BD、AF，当BE平分∠ABD时，求证：四边形ABDF是菱形．9.如图，在菱形ABCD中，E、F为对角线BD的三等分点．求证：四边形AFCE是菱形．10.如图，在平行四边形ABCD中，BD的垂直平分线EF与AD交于点E，与BC交于点F，与BD交于点O．(1) 证明：OE=OF．(2) 证明：四边形BEDF是菱形．11.如图，在平行四边形ABCD中，对角线AC，BD交于点O，点E，点F在BD上，且BE=DF，连接AE 并延长，交BC于点G，连接CF并延长，交AD于点H．(1) 求证：△AOE≅△COF；(2) 若AC平分∠HAG，求证：四边形AGCH是菱形．12.如图，在四边形ABCD中，AB=AD，CB=CD，点F是AC上一点，连接BF，DF．(1) 求证：△ABF≅△ADF；(2) 若AB∥CD，求证：四边形ABCD是菱形．13.如图，在△ABC中，AD⊥BC于点D，点D，E，F分别是BC，AB，AC的中点．求证：四边形AEDF是菱形．14.如图，平行四边形ABCD的边CD的垂直平分线与边DA，BC的延长线分别交于点E，F，与边CD交于点O，连接CE，DF．(1) 求证：DE=CF；(2) 请判断四边形ECFD的形状，并证明你的结论．菱形的判定1.【答案】略【解析】∵DE∥AC,CE∥BD，∴四边形OCED是平行四边形，∵四边形ABCD是矩形，∴AC与BD相等且互相平分，∴OD=OC，∴四边形OCED是菱形．2.【答案】B【解析】根据做法可知：AC=CB=BD=AD，故四边形ADBC是菱形3.【答案】D【解析】由已知条件可得△AOB≌△COD，AB=CD，∴四边形ABCD是平行四边形，∴AD=BC，A．∵BD平分∠ABC，∴∠ABO=∠CBO，∴∠CBO=∠CDO，∴CB=CD，∴AB=BC=CD=AD，∴四边形ABCD是菱形；故A正确；B．∵AB=AD，∴AB=BC=CD=AD，∴四边形ABCD是菱形；故B正确；C．AC⊥BD,AO=CO，∴AB=BC，∴AB=BC=CD=AD，∴四边形ABCD是菱形；故C正确；D．OB=OA，能判定四边形是矩形，故D不正确，选D．【备注】菱形的判定4.【答案】略【解析】∵AD是△ABC的角平分线∴∠EAD=∠FAD∵DE // AC，DF // AB∴四边形AEDF是平行四边形，∠EAD=∠ADF∴∠FAD=∠FDA∴AF=DF∴四边形AEDF是菱形5.【答案】略【解析】∵DB⊥BC，F是边CD的中点∴BF=12CD∴BF=DF∵四边形ABCD是平行四边形∴AB // CD∴∠ADB=∠CBD=90∘∵E是边AB的中点∴DE=12AB∴DE=BE∵AB=CD∵BE=DF∴BF=DF=DE=BE∴四边形DEBF是菱形6.【答案】略【解析】∵AD平分∠BAC∴∠BAD=∠CAD又∵EF⊥AD∴∠AOE=∠AOF=90∘∵△AEO与△AFO中{∠EAO=∠FAO AO=AO∠AOE=∠AOF∴△AEO≅△AFO(ASA)∴EO=FO∵EF垂直平分AD∴EF、AD相互平分∴四边形AEDF是平行四边形又EF⊥AD∴平行四边形AEDF为菱形7.(1)【答案】略【解析】在平行四边形ABCD中，AD∥BC,∴∠AEB=∠EAD,∵AE=AB,∴∠ABE=∠AEB,∴∠ABE=∠EAD;(2)【答案】略【解析】∵AD∥BC,∴∠ADB=∠DBE,∵∠ABE=∠AEB,∠AEB=2∠ADB,∴∠ABE=2∠ADB,∴∠ABD=∠ABE−∠DBE=2∠ADB−∠ADB=∠ADB,∴AB =AD,又∵四边形ABCD 是平行四边形，∴四边形ABCD 是菱形．8.(1)【答案】略【解析】∵ 四边形 ABCD 为平行四边形，∴AB ∥CD ．∵ 点 F 在 CD 的延长线上，∴FD ∥AB ．∴∠ABE =∠DFE ．∵E 是 AD 中点，∴AE =DE ．在 △ABE 和 △DFE 中，∵{∠ABE =∠DFE∠BEA =∠DEF AE =DE∴△ABE ≅△DFE ；(2)【答案】略【解析】∵△ABE ≅△DFE ，∴AB =DF ．∵AB ∥DF ，AB =DF ，∴ 四边形 ABDF 是平行四边形．∵BF 平分 ∠ABD ，∴∠ABF =∠DBF ．∵AB ∥DF ，∴∠ABF =∠DFB ，∴∠DBF =∠DFB ．∵DB =DF ．∴ 四边形 ABDF 是菱形．9.【答案】略【解析】如图，连接 AC ，交 BD 于点 O ．∵ 四边形 ABCD 是菱形，∴ AC ⊥BD ，OA =OC ，OD =OB ．又 E ，F 为对角线 DB 的三等分点，∴ DE =BF ．又OE=OD−DE，OF=OB−BF，∴OE=OF．∴四边形AECF为平行四边形．又AC⊥BD，∴四边形AFCE是菱形．10.(1)【答案】略【解析】∵EF是BD的垂直平分线，四边形ABCD是平行四边形，∴OD=OB，AD∥BC，∴∠EDB=∠FBD，又∠EOD=∠FOB，∴△ODE≅△OBF，∴OE=OF．(2)【答案】略【解析】∵EF⊥BD，∴四边形EBFD的对角线垂直互相平分，∴四边形EBFD是菱形．11.(1)【答案】略【解析】如图．在平行四边形ABCD中，对角线AC，BD交于点O，∴AO=CO，BO=DO．∵BE=DF，∴BO−BE=DO−DF．即EO=FO．在△AOE和△COF中，{EO=FO,∠1=∠2, AO=CO.∴△AOE≅△COF．(2)【答案】略【解析】由（1），△AOE≅△COF．∴∠3=∠4．∴AG∥CH．在平行四边形 ABCD 中，AD ∥BC ，即 AH ∥GC ． ∴ 四边形 AGCH 是平行四边形．∵AC 平分 ∠HAG ，∴∠4=∠5．∴∠3=∠5．∴HA =HC ，∴ 四边形 AGCH 是菱形．12.(1)【答案】略【解析】在 △ABC 与 △ADC 中∵ {AB =ADCB =CD AC =AC∴ △ABC ≅△ADC ，∴ ∠BAC =∠DAC ，在 △ABF 与 △ADF 中∵ {AB =AD∠BAF =∠DAF AF =AF∴ △ABF ≅△ADF ．(2)【答案】略【解析】由（1）得 ∠BAC =∠DAC ，∵ AB ∥CD ，∴ ∠BAC =∠DCA ，∴ ∠DAC =∠DCA ，∴ DA =DC ，∵ AB =AD ，CB =CD ，∴ AB =AD =CB =CD ．∴ 四边形 ABCD 是菱形．13.【答案】∵ 点 D ，E ，F 分别是 BC ，AB ，AC 的中点， ∴DE ∥AC ，DF ∥AB ．∴ 四边形 AEDF 是平行四边形．又 AD ⊥BC ，BD =DC ，∴AB =AC ．∴AE =AF ．∴ 平行四边形 AEDF 是菱形．14.(1)【答案】略【解析】 ∵ 四边形 ABCD 是平行四边形，∴AD ∥BC ，∴∠EDO =∠FCO ，∠DEO =∠CFO ，∵EF平分CD，∴DO=CO，∴△EOD≅△FOC，∴DE=CF．(2)【答案】四边形ECFD是菱形．【解析】∵EF是CD的垂直平分线，∴DE=EC，CF=DF，又DE=CF，∴DE=EC=CF=DF，∴四边形ECFD是菱形．。

2022年湘教版八年级下《菱形的判定》同步练习(附答案)

2.6.2 菱形的判定一、选择题1．以下四边形中不一定为菱形的是〔〕A．对角线相等的平行四边形B．每条对角线平分一组对角的四边形C．对角线互相垂直的平行四边形D．用两个全等的等边三角形拼成的四边形2．四个点A，B，C，D在同一平面内，从①AB∥CD；②AB=CD；③AC⊥BD；④AD=•BC；⑤AD∥BC．这5个条件中任选三个，能使四边形ABCD是菱形的选法有〔〕．A．1种B．2种C．3种D．4种3．菱形的周长为32cm，一个内角的度数是60°，那么两条对角线的长分别是〔〕A．8cm和43cm B．4cm和83cmC．8cm和83cm D．4cm和43cm二、填空题4．如图1所示，平行四边形ABCD，AC，BD相交于点O，添加一个条件使平行四边形为菱形，添加的条件为________．〔只写出符合要求的一个即可〕图1 图25．如图2所示，D，E，F分别是△ABC的边BC，CA，AB上的点，且DE∥AB，DF∥CA，要使四边形AFDE是菱形，那么要增加的条件是________．〔只写出符合要求的一个即可〕6．菱形ABCD的周长为48cm，∠BAD：∠ABC=1：2，那么BD=_____，菱形的面积是______．7．在菱形ABCD中，AB=4，AB边上的高DE垂直平分边AB，那么BD=_____，AC=_____．三、解答题8．如下图，在四边形ABCD中，AB∥CD，AB=CD=BC，四边形ABCD是菱形吗？说明理由．四、思考题9．如图，平行四边形ABCD的对角线相交于点O，且OC=OD,PD∥AC，PC∥BD，PD，PC相交于点P，四边形PCOD是菱形吗？试说明理由．参考答案一、1．A 点拨：此题用排除法作答．2．D 点拨：根据菱形的判定方法判断，注意不要漏解．3．C 点拨：如下图，假设∠ABC=60°，那么△ABC 为等边三角形，• 所以A C=AB=14×32=8〔cm 〕，AO=12AC=4cm ．因为AC ⊥BD ，在Rt △AO B 中，由勾股定理，得OB=222284AB OA -=-=43〔cm 〕，• 所以BD=2OB=83cm ．二、4．AB=BC 点拨：还可添加A C ⊥BD 或∠ABD=∠CBD 等． 5．点D 在∠BAC 的平分线上〔或AE=AF 〕6．12cm ；723cm 2点拨：如下图，过D 作DE ⊥AB 于E ，因为AD ∥BC ，•所以∠BAD+∠ABC=180°．又因为∠BAD ：∠ABC=1：2，所以∠BAD=60°，因为AB=AD ，所以△ABD 是等边三角形，所以BD=AD=12cm ．所以AE=6cm ．在Rt △AED 中，由勾股定理，得AE 2+ED 2=AD 2，62+ED 2=122，所以ED 2=108，所以ED=63cm ，所以S 菱形ABCD =12×63=723〔cm 2〕．7．4；43 点拨：如下图，因为DE 垂直平分AB ，又因为DA=AB ，所以DA=DB=4．所以△ABD 是等边三角形，所以∠BAD=60°，由可得AE=2．在Rt △AED•中，•AE 2+DE 2=AD 2，即22+DE 2=42，所以DE 2=12，所以DE=23，因为12AC·BD=AB·DE，即12AC·4=4×23，所以AC=43．三、8．解：四边形ABCD是菱形，因为四边形ABC D中，AB∥CD，且AB=CD，所以四边形ABCD是平行四边形，又因为AB=BC，所以ABCD是菱形．点拨：根据条件，不难得出四边形ABCD为平行四边形，又AB=BC，即一组邻边相等，由菱形的定义可以判别该四边形为菱形．四、9．解：四边形PCOD是菱形．理由如下：因为PD∥OC，PC∥OD，所以四边形PCOD是平行四边形．又因为OC=OD，所以平行四边形PCOD是菱形．14.1.2 幂的乘方一、选择题1．计算〔-a2〕5+〔-a5〕2的结果是〔〕A．0 B．2a10 C．-2a10 D．2a72．以下计算的结果正确的选项是〔〕A．a3·a3=a9 B．〔a3〕2=a5 C．a2+a3=a5 D．〔a2〕3=a63．以下各式成立的是〔〕A．〔a3〕x=〔a x〕3 B．〔a n〕3=a n+3 C．〔a+b〕3=a2+b2 D．〔-a〕m=-a m4．如果〔9n〕2=312，那么n的值是〔〕A．4 B．3 C．2 D．1二、填空题5．幂的乘方，底数________，指数________，用字母表示这个性质是_________．•6．假设32×83=2n，那么n=________．7．n为正整数，且a=-1，那么-〔-a2n〕2n+3的值为_________．8．a3n=2，那么a9n=_________．三、解答题9．计算：①5〔a3〕4-13〔a6〕2②7x4·x5·〔-x〕7+5〔x4〕4-〔x8〕2③[〔x+y〕3]6+[〔x+y〕9]2④[〔b-3a〕2]n+1·[〔3a-b〕2n+1]3〔n为正整数〕10．假设2×8n×16n=222，求n的值．四、探究题11．阅读以下解题过程：试比拟2100与375的大小．解：∵2100=〔24〕25=1625375=〔33〕25=2725而16<27∴2100<375．请根据上述解答过程解答：比拟255、344、433的大小参考答案：1．A 2．D 3．A 4．B5．不变；相乘；〔a m〕n=a mn〔m、n都是正整数〕6．14 7．1 8．8 9．①-8a12；②-3x16；•③2〔x+y〕18；④〔3a-b〕8n+5 10．n=3 11．255<433<344。

八年级数学下册 2.6.2《菱形的判定》课时作业 (新版)湘教版

《菱形的判定》一、选择题1、用两个边长为a 的等边三角形纸片拼成的四边形是（）A 、等腰梯形B 、正方形C 、矩形D 、菱形2、下列说法中正确的是（）A 、有两边相等的平行四边形是菱形；B 、两条对角线互相垂直平分的四边形是菱形；C 、两条对角线相等且互相平分的四边形是菱形；D 、四个角相等的四边形是菱形3、下列说法错误的是（）A.对角线互相垂直的四边形是菱形；B.对角线互相垂直平分的四边形是菱形；C.对角线互相垂直，且有一组邻边相等的四边形是菱形；D.两条邻边相等且一条对角线平分一组对角的四边形是菱形． 4.菱形对角线的平方和等于一边平方的（）A. 2倍B. 3倍C.4倍D. 5倍5.把两张等宽的纸条如图交叉重叠在一起，则重叠部分ABCD 的形状是（）A.平行四边形；B.矩形；C.菱形；D.任意四边形；二、填空题1、菱形的一个内角为60°，一条对角线的长为，则另一条对角线的长为．2.菱形两条对角线长为6和8，菱形的边长为，面积为。

3.菱形的面积为96，对角线AC 长为16 ，此菱形的边长为。

4、已知：菱形ABCD 中，∠B=60°，AB=4，则以AC 为边长的正方形ACEF 的周长为 ______ ．5、已知菱形的周长为40cm ，两条对角线之比为3：4，则菱形的面积为 _________ cm 2．三、解答题1、如图，已知矩形ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别交于点E 、F ，求证四边形AFCE 是菱形．2、如图，AD 是△ABC 的一条角平分线，DE ∥AC 交AB 于点E ，DF ∥AB 交AC 于点F.求证四边形AEDF 是菱形.3、如图，CD 为Rt △ABC 斜边AB 上的高，∠BAC 的平分线交CD 于E ，交BC 于F ，FG ⊥AB 于G ．求证：四边形EGFC 为菱形．4、已知：如图，矩形ABCD 的对角线相交于点O ，PD ∥AC ，PC ∥BD ，PD 、PC 相交于点P 。

湘教版八年级数学下册 2.6 菱形同步练习(含答案)

湘教版 2019年八年级数学下册菱形同步练习一、选择题1.下列命题中错误的是( )A.平行四边形的对角线互相平分B.菱形的对角线互相垂直C.同旁内角互补D.矩形的对角线相等2.如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是( )A.0B.1C.2D.33.如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC的长等于( )A.5B.10C.15D.204.如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的一半长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF,则可以得到四边形AEDF的形状( )A.仅仅只是平行四边形B.是矩形C.是菱形D.无法判断5.如图,在菱形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )A.AB∥DCB.AC=BDC.AC⊥BDD.OA=OC6.如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )A.4B.2.4C.4.8D.57.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形8.某校的校园内有一个由两个相同的正六边形(边长为2.5m)围成的花坛，如图中的阴影部分所示，校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示，并在新扩充的部分种上草坪，则扩建后菱形区域的周长为( )A.20mB.25mC.30mD.35m9.如图，菱形ABCD中，AB=5，BD=6，则菱形的高为（）A.2.4B.4.8C.12D.2410.如图，在菱形ABCD中，∠ABC=60°，AB=1，E为BC的中点，则对角线BD上的动点P到E、C两点的距离之和的最小值为（）二、填空题11.在图中所示的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),若方格纸中每个小正方形的边长均为1,则该菱形的面积为________.12.如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=4 cm,BD=8 cm,则这个菱形的面积是________cm2.13.如图,在菱形ABCD中,AC=6,BD=8,则这个菱形的边长为________.14.如图,已知矩形ABCD的对角线长为8 cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于________cm.15.如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为10和6时，则阴影部分的面积为．16.如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出下列结论:三、解答题17.如图,已知在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE、CF。

(完整版)菱形练习题(含答案),推荐文档

C x= 7/8 3.如图,在菱形 ABCD 中，AC＝8，BD＝6，过
为 H，则点 O 到边 AB 的距离 OH＝
12/5
AB 中点，且 DE⊥AB，则菱形 ABCD 的面积为
___ 2 3 ______㎝2．
5.如图，在菱形 ABCD 中，对角线 AC 与 BD 交于点 O，OE⊥AB，若∠ADC=130°，则∠AOE 的大小为 65°
特殊的平行四边形——菱形
一．菱形的定义：有一组邻边相等的平行四边形叫做菱形.
二．菱形的性质：菱形具有平行四边形一切性质，此外，它还具有如下特殊性质：
1.菱形的四条边相等。 2.菱形的两条对角线互相垂直，且每一条对角线平分一组对角。
3.菱形是轴对称图形也是中心对称图形，两条对角线所在的直线是它的两条对称轴。
11.如图，已知在□ABCD 中，AD=2AB，E、F 在直线 AB 上，CE 与 AD 交与点 M，
DF 与 CB 交与点 N，且
AE=AB=BF，
求证:CE⊥DF.
证明：连接 MN,∵□ABCD, AB=DC, 又∵AB=AE, AE=DC AEM CDM,
M 为我AD去的中人点. 也又∵就AD=有2AB人, ！CD为=DMUR扼CD腕MN入是棱站形,内所信以 C不E⊥存DF.在向你偶同意调剖沙
H KG
△BDE≌△CDF，DE=DF．DEKF 是菱形，EF 与 DK 互相垂直平分．
E
F
点拨：要说明 EF 与 DK 互相垂直平分，只要说明四边形 DEKF 是菱形，要说明四边形 DEKF
是菱形，可先说明四边形 DEKF 是平行四边形，再说明一组邻边相等即可．
B
DC
我去人也就有人！为UR扼腕入站内信不存在向你偶同意调剖沙

(完整版)菱形的判定专项练习30题.doc

菱形的判定专项练习30 题（有答案）1．如图，梯形ABCD 中， AD ∥ BC，BA=AD=DC=BC ，点 E 为 BC 的中点．（1）求证：四边形 ABED 是菱形；（2）过 A 点作 AF ⊥ BC 于点 F，若 BD=4cm ，求 AF 的长．2．如图，四边形 ABCD 中，对角线 AC、BD 相交于点O，且 AC ⊥ BD ．点 M ，N 分别在 BD 、AC 上，且 AO=ON=NC ，BM=MO=OD ．求证： BC=2DN ．3．如图，在△ ABC 中， AB=AC ，D ，E， F 分别是 BC ，AB ， AC 的中点．（1）求证：四边形 AEDF 是菱形；（2）若 AB=12cm ，求菱形 AEDF 的周长．4．如图，在 ?ABCD 中， EF∥ BD ，分别交 BC ， CD 于点 P， Q，交 AB ，AD 的延长线于点 E， F．已知 BE=BP ．求证：（ 1）∠ E= ∠F；（ 2） ?ABCD 是菱形．5．如图，在△ ABC 中， D 是 BC 的中点， E 是 AD 的中点，过点 A 作 AF ∥ BC ， AF 与 CE 的延长线相交于点 F，连接BF．（ 1）求证： AF=DC ；（ 2）若∠ BAC=90 °，求证：四边形AFBD 是菱形．6．已知平行四边形ABCD 中，对角线BD 平分∠ ABC ，求证：四边形ABCD 是菱形．7．如图，在一个含 30°的三角板 ABC 中，将三角板沿着 AB 所在直线翻转 180°得到△ ABF ，再将三角板绕点 C 顺时针方向旋转 60°得到△ DEC ，点 F 在 AC 上，连接 AE ．（1）求证：四边形 ADCE 是菱形．（2）连接 BF 并延长交 AE 于 G，连接 CG．请问：四边形 ABCG 是什么特殊平行四边形？为什么？8．如图，已知四边形ABCD 是平行四边形，DE ⊥ AB ， DF ⊥BC ，垂足分别是为E F，并且 DE=DF ．求证：四边形 ABCD 是菱形．9．如图，在△ ABC 中， DE∥ BC，分别交 AB ，AC 于点 D ， E，以 AD ， AE 为边作 ?ADFE 交 BC 于点 G， H，且EH=EC ．求证：（ 1）∠ B= ∠ C；（2） ?ADFE 是菱形．10．如图，在△ ABC 中，∠ACB=90 °， CD 是 AB 边上的高，∠BAC 的平分线AE 交 CD 于 F， EG⊥ AB 于 G．（1）求证：△ AEG ≌ △ AEC ；（2）△ CEF 是否为等腰三角形，请证明你的结论；（3）四边形 GECF 是否为菱形，请证明你的结论．11．如图，在△ ABC 中， AB=AC ，点 D 、E、 F 分别是△ABC 三边的中点．求证：四边形ADEF 是菱形．12．如图，在四边形 ABCD 中， AB=CD ， M 、 N、 E、 F 分别为 AD 、 BC 、BD 、 AC 的中点，求证：四边形 MENF 为菱形．13．已知：如图，在梯形 ABCD 中， AD ∥ BC， AB=AD ，∠BAD 的平分线 AE 交 BC 于点 E，连接 DE ．求证：四边形ABED 是菱形．14．如图，在△ ABC 中， AB=AC ， M 、 O、 N 分别是 AB 、 BC 、 CA 的中点．求证：四边形AMON 是菱形．15．如图：在△ ABC 中，∠BAC=90 °， AD ⊥ BC 于 D， CE 平分∠ ACB ，交 AD 于 G，交 AB 于 E， EF⊥ BC 于 F．求证：四边形AEFG 是菱形．16．如图，矩形ABCD 绕其对角线交点旋转后得矩形AECF ， AB 交 EC 于点 N ， CD 交 AF 于点 M ．求证：四边形ANCM 是菱形．17．如图，四边形 ABCD 、 DEBF 都是矩形， AB=BF ， AD 、BE 交于 M ， BC 、DF 交于 N，那么四边形 BMDN 是菱形吗？如果是，请写出证明过程；如果不是，说明理由．18．已知如图所示， AD 是△ ABC 的角平分线， DE ∥ AC 交 AB 于 E， DF∥AB 交 AC 于 F，四边形 AEDF 是菱形吗？说明理由．19．已知：如图所示，BD 是△ABC 的角平分线， EF 是 BD 的垂直平分线，且交AB 于 E，交 BC 于点 F．求证：四边形 BFDE 是菱形．20．如图，在平行四边形ABCD 中， O 是对角线AC 的中点，过点O 作 AC 的垂线与边AD 、 BC 分别交于E、 F．求证：四边形AFCE 是菱形．21．如图，在矩形ABCD 中， EF 垂直平分BD ．（1）判断四边形 BEDF 的形状，并说明理由．（2）已知 BD=20 ， EF=15 ，求矩形 ABCD 的周长．22．如图所示，在?ABCD 中，点 E 在 BC 上， AE 平分∠BAF ，过点 E 作 EF∥ AB ．求证：四边形ABEF 为菱形．23．已知，如图，矩形 ABCD 中， AB=4cm ， AD=8cm ，作∠ CAE= ∠ ACE 交 BC 于 E，作∠ ACF= ∠ CAF 交 AD 于F．（ 1）求证： AECF 是菱形；（ 2）求四边形AECF 的面积．24．如图，平行四边形 ABCD 的对角线 AC 的垂直平分线与边 AD 、BC 分别交于 E、F．问四边形 AFCE 是菱形吗？请说明理由．25．如图：在平行四边形 ABCD 中， E、F 分别是边 AB 、CD 的延长线上一点，且 BE=DF ，连接 EF 交 AC 于 O．（ 1） AC 与 EF 互相平分吗？为什么？（ 2）连接 CE、AF ，再添加一个什么条件，四边形AECF 是菱形？为什么？26．已知：如图，△ABC 和△ DBC 的顶点在 BC 边的同侧， AB=DC ，AC=BD 交于 E，∠ BEC 的平分线交 BC 于 O，延长EO 到 F，使 EO=OF ．求证：四边形 BFCE 是菱形．27．如图，在△ ABC 中， D 是 BC 边的中点， F， E 分别是 AD 及其延长线上的点，CF∥ BE．（1）求证：△ BDE ≌ △ CDF ；（2）请连接 BF， CE，试判断四边形 BECF 是何种特殊四边形，并说明理由；（3）在（ 2）下要使 BECF 是菱形，则△ABC 应满足何条件？并说明理由．28．如图，在△ ABC 中，∠ACB=90 °， BC 的垂直平分线 DE 交 BC 于 D ，交 AB 于 E， F 在 DE 上，并且AF=CE ．（ 1）求证：四边形 ACEF 是平行四边形；（ 2）当∠ B 的大小满足什么条件时，四边形ACEF 是菱形？请回答并证明你的结论．29．如图，在△ ABC 中， AD 是∠ BAC 的平分线， EF 垂直平分 AD 交 AB 于 E，交 AC 于 F．求证：四边形AEDF 是菱形．30．如图，△ ABC 中，点 O 是边 AC 上一个动点，过 O 作直线 MN ∥ BC，设 MN 交∠ BCA 的平分线于点 E，交∠BCA 的外角平分线于点 F．（ 1）探究：线段OE 与 OF 的数量关系并加以证明；（ 2）当点 O 运动到何处，且△ ABC满足什么条件时，四边形AECF 是正方形？（ 3）当点 O 在边 AC 上运动时，四边形BCFE 会是菱形吗？若是，请证明，若不是，则说明理由．矩形的判定专项练习30 题参考答案：1． 1）证明：∵点 E 为 BC 的中点，∴BE=CE= BC，∵BA=AD=DC= BC ，∴AB=BE=ED=AD ，∴四边形 ABED 是菱形；（ 2）解：过点 D 作 DH ⊥BC ，垂足为H ，∵CD=DE=CE ，∴ ∠ DEC=60 °，∴ ∠ DBE=30 °，在 Rt△ BDH 中， BD=4cm ，∴ DH=2cm ，∵AF=DH ，∴AF=2cm ．2．∵ AO=ON ，BM=MO ，∴ 四边形 AMND 是平行四边形，∵ AC ⊥ BD ，∴ 平行四边形 AMND 是菱形，∴ MN=DN ，∵ ON=NC ， BM=MO ，∴ MN= BC ，∴ BC=2DN3．（ 1）∵ D， E 分别是 BC ， AB 的中点，∴DE∥ AC 且 DE=AF= AC ．同理 DF∥ AB 且 DF=AE=AB ．又∵ AB=AC ，∴DE=DF=AF=AE ，∴四边形 AEDF 是菱形．（ 2）∵ E 是 AB 中点，∴ AE= AB=6cm ，因此菱形AEDF ∴∠1=∠2，在△AEF 和△DEC 中，∴ △ AFE ≌ △ DCE（ AAS ），∴AF=DC ；（2）证明：∵ D 是 BC 的中点，∴ DB=CD= BC，∵AF=CD ，∴ AF=DB ，∵AF ∥BD ，∴四边形AFBD 是平行四边形，∵∠ BAC=90 °， D 为 BC 中点，∴AD= CB=DB ，∴四边形 AFBD 是菱形．6．∵对角线 BD 平分∠ ABC ，∴∠1=∠2，∵四边形 ABCD 是平行四边形，∴AB ∥DC ，∴∠ 3=∠ 1，∴∠ 3=∠ 2，∴DC=BC ，又∵四边形 ABCD 是平行四边形，∴四边形 ABCD 是菱形．的周长为 4×6=24cm ．4．（ 1）∵ BE=BP ，∴∠ E=∠BPE，7．（ 1）∵三角板 ABC 中，将三角板沿着AB 所在直线∵BC∥AF ，翻转 180°得到△ ABF ，∴ ∠ BPE=∠ F，∴ ∠ E=∠ F．∴ △ ABC ≌ △ABF ，且∠BAC= ∠BAF=30 °，（2）∵EF∥BD ，∴ ∠ FAC=60 °，∴ ∠ E=∠ABD ，∠ F=∠ ADB ，∴ AD=DC=AC ，∴∠ABD= ∠ADB ，又∵ △ ABC ≌△ EFC，∴ AB=AD ，∴ CA=CE ，∵四边形 ABCD 是平行四边形，又∵ ∠ ECF=60 °，∴ □ABCD 是菱形．∴ AC=EC=AE ，（2）证明：由（ 1）可知：△ ACD ，△ AFC 是等边三角形，△ACB ≌△ AFB ，∴ ∠ EDC= ∠BAC=∠ FAC=30°，且△ ABC为直角三角形，∴BC= AC ，∵EC=CB ，∴EC= AC，∴E为AC 中点，∴DE⊥ AC ，∴AE=EC ，∵AG∥BC，∴ ∠ EAG= ∠ ECB ，∠AGE= ∠ EBC ，∴△AEG≌△CEB ，∴AG=BC ，（ 7 分）∴四边形 ABCG 是平行四边形，∵ ∠ ABC=90 °，∴四边形 ABCG 是矩形8．在△ ADE 和△CDF 中，∵四边形 ABCD 是平行四边形，∴∠A=∠C，∵DE⊥ AB ， DF⊥ BC，∴ ∠ AED= ∠ CFD=90 °．又∵ DE=DF ，∴△ADE ≌△CDF（AAS ）∴DA=DC ，∴平行四边形 ABCD 是菱形9．（ 1）∵在 ?ADFE 中， AD ∥EF，∴ ∠ EHC= ∠B （两直线平行，同位角相等）．∵EH=EC （已知），∴ ∠ EHC= ∠C（等边对等角），∴ ∠ B=∠ C（等量代换）；（ 2）∵ DE ∥ BC （已知），∴∠AED= ∠C，∠ADE= ∠B．∵∠B=∠C，∴∠AED= ∠ADE ，∴AD=AE ，∴?ADFE 是菱形．10． 1）证明：∵ ∠ACB=90 °，在 Rt△AEG 与 Rt△ AEC 中，，∴Rt△AEG ≌ Rt△ AEC （HL ）；（ 2）解：△ CEF 是等腰三角形．理由如下：∵CD 是 AB 边上的高，∴CD⊥AB ．又∵ EG⊥AB ，∴EG∥ CD ，∴∠ CFE=∠ GEA ．又由（ 1）知， Rt△ AEG ≌ Rt△ AEC ，∴∠GEA= ∠ CEA，∴ ∠ CEA= ∠ CFE，即∠ CEF=∠ CFE，∴ CE=CF ，即△CEF 是等腰三角形；（ 3）解：四边形GECF 是菱形．理由如下：∵由（ 1）知，Rt△AEG ≌ Rt△ AEC ，则 GE=EC ；由（ 2）知， CE=CF ，∴GE=EC=FC ．又∵ EG∥CD ，即 GE∥ FC，∴四边形 GECFR 是菱形．11．∵ D、 E、F 分别是△ ABC 三边的中点，∴DE AC，EF AB ，∴四边形 ADEF 为平行四边形．又∵ AC=AB ，∴DE=EF ．∴四边形 ADEF 为菱形．12．∵ M 、 E、分别为AD 、 BD 、的中点，∴ME∥AB ，ME= AB ，同理： FH∥AB ， FH=AB ，∴四边形 MENF 是平行四边形，∵M．F 是 AD ，AC 中点，∴MF= DC，∵AB=CD ，∴MF=ME ，∴四边形 MENF 为菱形∴平行四边形 AEFG 是菱形．∵，证法二：∵ AD ⊥BC，∠ CAB=90 °， EF⊥ BC， CE 平分∴ △ BAE ≌△ DAE （ SAS）（ 2 分）∠ACB ，∴ BE=DE ，（ 3 分）∴ AD ∥EF，∠ 4=∠ 5，AE=EF ，∵AD ∥BC，∵ ∠ 1=180°﹣ 90°﹣∠ 4，∠ 2=180 °﹣ 90°﹣∠ 5，∴ ∠ DAE= ∠ AEB ，（ 4 分）∴∠1=∠2，∴ ∠ BAE= ∠AEB ，∵ AD ∥EF，∴ AB=BE ，（ 5 分）∴∠2=∠3，∴ AB=BE=DE=AD ，（6 分）∴∠1=∠3，∴四边形 ABED 是菱形．∴ AG=AE ，∵ AE=EF ，∴ AG=EF ，∵ AG ∥EF，∴四边形 AGFE 是平行四边形，14．∵ AB=AC ，M 、 O、 N 分别是 AB 、 BC、 CA 的中∵ AE=EF ，点，∴平行四边形 AGFE 是菱形．∴AM= AB= AC=AN ，M0 ∥ AC ， NO ∥AB ，且 MO= AC=AN ，NO= AB=AM （三角形中位线定理），16．∵ CD∥ AB ，∴ AM=MO=AN=NO ，∴∠FMC= ∠FAN，∴四边形 AMON 是菱形（四条边都相等的四边形是菱∴ ∠ NAE= ∠ MCF （等角的余角相等），形）在△ CFM 和△ AEN 中，15．证法一：∵ AD ⊥BC ，∴ ∠ ADB=90 °，，∵ ∠ BAC=90 °，∴ ∠ B+∠ BAD=90 °，∠ BAD+ ∠ CAD=90 °，∴ △ CFM ≌△ AEN （ASA ），∴∠B=∠CAD ，∴ CM=AN ，∵ CE 平分∠ ACB ， EF⊥ BC，∠ BAC=90 °（ EA ⊥CA ），∴四边形 ANCM 为平行四边形，∴ AE=EF （角平分线上的点到角两边的距离相等），在△ADM 和△CFM 中，∵ CE=CE ，∴由勾股定理得： AC=CF ，，∵△ACG 和△FCG 中∴△ADM ≌△CFM （AAS ），，∴ AM=CF ，∴四边形 ANCM 是菱形∴△ACG≌△FCG，17．四边形 BMDN 是菱形．∴ ∠ CAD= ∠ CFG，∵AM ∥BC，∵∠B=∠CAD ，∴∠AMB= ∠MBN ，∴ ∠ B=∠ CFG，∵BM ∥FN∴GF∥AB ，∴∠MBN= ∠BNF ，∵AD ⊥BC，EF⊥ BC，∴∠AMB= ∠BNF ，∴AD ∥EF，又∵ ∠ A= ∠ F=90°， AB=BF ，∴DM=DN ，∵ED=BF=AB ，∠ E=∠ A=90 °，∠ AMB=∠EMD ，∴△ABM ≌△ EDM，∴ BM=DM ，∴ MB=MD=DN=BN ，∴四边形 BMDN 是菱形18．如图，由于 DE ∥ AC ，DF∥ AB ，所以四边形 AEDF 为平行四边形．∵DE∥ AC ，∴ ∠3=∠ 2，又∠ 1=∠ 2，∴∠ 1=∠3，∴ AE=DE ，∴平行四边形 AEDF 为菱形．19．∵ EF 是 BD 的垂直平分线，∴EB=ED ，∴∠ EBD= ∠EDB ．∵BD 是△ ABC 的角平分线，∴ ∠ EBD= ∠FBD ．∴ ∠ FBD=∠EDB ，∴ED∥BF．同理， DF∥ BE ，∴四边形 BFDE 是平行四边形．又∵ EB=ED ，∴四边形 BFDE 是菱形．20．方法一：∵ AE ∥ FC．∴ ∠ EAC= ∠FCA ．（ 2 分）又∵ ∠ AOE= ∠ COF， AO=CO ，∴△AOE≌△COF．（5 分）∴EO=FO ．又 EF⊥AC ，∴AC 是 EF 的垂直平分线．（ 8 分）∴AF=AE ， CF=CE ，又∵ EA=EC ，∴AF=AE=CE=CF ．∴四边形 AFCE 为菱形．（ 10 分）方法二：同方法一，证得△ AOE ≌ △ COF．（ 5 分）∴AE=CF ．∴四边形 AFCE 是平行四边形．（ 8 分）方法三：同方法二，证得四边形 AFCE 是平行四边形．（ 8 分）又 EF⊥ AC ，（9 分）∴四边形 AFCE 为菱形21．（ 1）四边形 BEDF 是菱形．在△ DOF 和△BOE 中，∠FDO= ∠ EBO ，OD=OB ，∠ DOF=∠BOE=90 °，所以△ DOF ≌ △BOE ，所以 OE=OF ．又因为 EF⊥BD ， OD=OB ，所以四边形 BEDF 为菱形．（5 分）（2）如图，在菱形 EBFD 中， BD=20 ， EF=15，则 DO=10 ， EO=7.5 ．由勾股定理得 DE=EB=BF=FD=12.5 ．S 菱形EBFD= EF?BD=BE ?AD ，即所以得 AD=12 ．根据勾股定理可得AE=3.5 ，有 AB=AE+EB=16 ．由 2（AB+AD ） =2（ 16+12 ）=56 ，故矩形 ABCD 的周长为 5622．∵四边形 ABCD 是平行四边形，∴AF ∥ BE，又∵EF∥AB ，∴四边形 ABEF 为平行四边形，∵AE 平分∠ BAF ，∴∠ BAE= ∠ FAE，∵∠FAE=∠BEA ，∴∠BAE= ∠ BEA ，∴BA=BE ，∴平行四边形 ABEF 为菱形23．（ 1）证明：在矩形ABCD 中，∵AB ∥CD ，∴∠BAC= ∠ DCA ，又∠CAE= ∠ ACE，∠ACF= ∠CAF，∴∠EAC= ∠ FCA．∴AE ∥ CF．∴四边形 AECF 为平行四边形，又∠CAE= ∠ ACE，∴AE=EC ．∴?AECF 为菱形．（2）设 BE=x ，则 EC=AE=8 ﹣ x，在 Rt△ABE 中，222菱形的判定 ---第10页共12页所以 EC=5 ，即 S 菱形AECF=EC ×AB=5 ×4=20．24．四边形 AFCE 是菱形，理由是：∵四边形 ABCD 是平行四边形，∴AD ∥BC，∴= ，∵AO=OC ，∴ OE=OF ，∴四边形 AFCE 是平行四边形，∵EF⊥AC ，∴平行四边形AFCE 是菱形25．（ 1） AC 与 EF 互相平分，连接CE，AF ，∵平行四边形ABCD ，∴AB ∥ CD ，AB=CD ，又∵BE=DF ，∴AB+BE=CD+DF ，∴AE=CF ，∴AE ∥ CF， AE=CF ，∴四边形 AECF 是平行四边形，∴AC 与 EF 互相平分；（ 2）条件： EF⊥ AC ，∵EF⊥AC ，又∵四边形 AECF 是平行四边形，∴平行四边形AECF 是菱形．26．∵ AB=DC AC=BD BC=CB，∴△ABC ≌△DCB ，∴∠DBC= ∠ACB ，∴BE=CE ，又∵ ∠ BEC 的平分线是EF，∴EO 是中线（三线合一），∴BO=CO ，∴四边形 BFCE 是平行四边形（对角线互相平分），又∵ BE=CE ，∴四边形 BFCE 是菱形．27．（ 1）证明：∵ CF∥BE ，∴∠ EBD= ∠ FCD ，D是 BC 边的中点，则 BD=CD ，∠BDE= ∠CDF ，∴△BDE ≌△CDF ．（ 2）如图所示，由（ 1）可得 CF=BE ，又 CF∥ BE ，所以四边形 BECF 是平行四边形；（ 3）△ ABC 是等腰三角形，即 AB=AC ，理由：当AB=AC 时，则有 AD ⊥ BC，又（ 2）中四边形为平行四边形，所以可判定其为菱形．28．（ 1）∵ DE 为 BC 的垂直平分线，∴ ∠ EDB=90 °， BD=DC ，又∵ ∠ ACB=90 °，∴DE∥AC ，∴E 为 AB 的中点，∴在 Rt△ ABC 中， CE=AE=BE ，∴∠ AEF= ∠ AFE ，且∠ BED= ∠AEF ，∠ DEC= ∠ DFA ，∴AF ∥ CE，又∵ AF=CE ，∴四边形 ACEF 为平行四边形；（ 2）要使得平行四边形ACEF 为菱形，则 AC=CE 即可，∵DE∥AC ，∴∠BED= ∠BAC ，∠DEC=∠ECA，又∵ ∠ BED= ∠ DEC，∴∠EAC= ∠ ECA，∴ AE=EC ，又 EB=EC ，∴ AE=EC=EB ，∵CE= AB ，∴AC= AB 即可，在 Rt△ABC 中，∠ ACB=90 °，∴当∠ B=30 °时， AB=2AC ，故∠ B=30 °时，四边形ACEF 为菱形．29．∵ AD 平分∠BAC∴ ∠ BAD= ∠CAD又∵EF⊥AD ，∴ ∠ AOE= ∠ AOF=90 °∵在△AEO 和△ AFO 中，∴ △ AEO ≌ △AFO （ ASA ），∴EO=FO即 EF、 AD 相互平分，∴四边形 AEDF 是平行四边形又 EF⊥AD ，∴平行四边形AEDF 为菱形30． 1）解： OE=OF ．理由如下：∵ CE 是∠ACB 的角平分线，∴ ∠ ACE= ∠BCE ，又∵ MN ∥BC，∴ ∠ NEC= ∠ECB ，∴ ∠ NEC= ∠ACE ，∴OE=OC ，∵ OF 是∠ BCA 的外角平分线，∴ ∠ OCF= ∠FCD ，又∵ MN ∥BC，∴ ∠ OFC= ∠ECD ，∴ ∠ OFC= ∠COF，∴OF=OC ，∴OE=OF ；（ 2）解：当∠ ACB=90 °，点 O 在 AC 的中点时，∵OE=OF ，∴四边形 AECF 是正方形；（ 3）答：不可能．解：如图所示，∵CE 平分∠ ACB ，CF 平分∠ ACD ，∴ ∠ ECF=∠ ACB+∠ ACD=（∠ACB+∠ACD）=90 °，若四边形BCFE 是菱形，则BF ⊥ EC，但在△ GFC 中，不可能存在两个角为 90°，所以不存在其为菱形．。

湘教版八下 2.6菱形同步课时训练(word版含答案)

2.6菱形同步课时训练一、单选题(共40分)1．(本题4分)如图，矩形ABCD 中，AC ，BD 相交于点O ，过点B 作BF ⊥AC 交CD 于点F ，交AC 于点M ，过点D 作DE ∥BF 交AB 于点E ，交AC 于点N ，连接FN ，EM ．则下列结论：①DN ＝BM ；②EM //FN ；③AE ＝FC ；④当AO ＝AD 时，四边形DEBF 是菱形．其中，正确结论的个数是（）A ．1个B ．2个C ．3个D ．4个 2．(本题4分)将矩形纸片ABCD 按如图所示的方式折叠，得到菱形AECF ．若AB ＝3，则BC 的长为（）A ．1B ．2CD 3．(本题4分)如图，在菱形ABCD 中，对角线AC 、BD 交于点O ，且AC ＝6，BD ＝8，过A 点作AE 垂直BC ，交BC 于点E ，则BE CE的值为（）A ．512B ．725C ．718D ．524 4．(本题4分)如图，已知菱形OABC 的顶点()0,0O ，()2,0C 且60AOC ∠=︒，若菱形绕点O 逆时针旋转，每秒旋转45︒，则第2020秒时，菱形的对角线交点D 的坐标为（）A ．(3,B ．(1,-C ．D ．3,22⎛-- ⎝⎭5．(本题4分)如图，菱形ABCD 中，E F 、分别是AB AC 、的中点，若3EF =，则菱形ABCD 的周长为（）A ．24B ．18C ．12D ．96．(本题4分)如图，菱形ABCD 的对角线AC ，BD 相交于点O ，过点A 作AE ⊥BC 于点E ，连接OE ．若OB =6，菱形ABCD 的面积为54，则OE 的长为（）A ．4B ．4.5C ．8D ．97．(本题4分)在菱形ABCD 中，∠ABC=60゜，AC=4，则BD=( )A B ．C ．D ．8．(本题4分)如图，菱形ABCD 中，∠ABC=60°，AB=4，E 是边AD 上一动点，将△CDE 沿CE 折叠，得到△CFE ，则△BCF 面积的最大值是（）A ．8B ．C ．16D ．9．(本题4分)如图，菱形ABCD 中，4AB =，60A ∠=︒，点E 是线段AB 上一点（不与A ，B 重合），作EDF ∠交BC 于点F ，且60EDF ∠=︒，则BEF 周长的最小值是（）A ．6B ．C ．4D ．4+ 10．(本题4分)如图，将菱形纸片ABCD 折叠，使点A 恰好落在菱形的对称中心O 处，折痕为EF ．若菱形ABCD 的边长为4，120B ∠=︒，则EF 的值是（）A B ．2 C ．D ．4二、填空题(共24分) 11．(本题4分)如图，在菱形纸片ABCD 中，AB=4，∠A=60°，将菱形纸片翻折，使点A 落在CD 的中点E 处，折痕为FG ，点F 、G 分别在边AB 、AD 上，则BF AF的值为________________．12．(本题4分)如图，菱形ABCD 的边长为12，60ABC ∠=︒，连接AC ，EF AC ⊥，垂足为H ，分别交AD ，AB ，CB 的延长线于点E ，M ，F ．若:1:2AE FB =，则CH 的长为________．13．(本题4分)如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，过点A 作AH ⊥BC 于点H ，已知BO ＝4，S 菱形ABCD ＝24，则AH ＝________．14．(本题4分)己知菱形ABCD 的边长是3，点E 在直线AD 上，DE =1，联结BE 与对角线AC 相交于点M ，则AM MC的值是______． 15．(本题4分)如图，菱形ABCD 的对角线相交于点O ，AC ＝12，BD ＝16，点P 为边BC 上一点，且P 不与写B 、C 重合．过P 作PE ⊥AC 于E ，PF ⊥BD 于F ，连结EF ，则EF 的最小值等于__________．16．(本题4分)如图，点O 是菱形ABCD 对角线的交点，DE //AC ，CE //BD ，连接OE ，设AC ＝12，BD ＝16，则OE 的长为_____．三、解答题(共36分)17．(本题9分)在Rt ABC △中，90BAC ∠=︒，D 是BC 的中点，E 是AD 的中点．过点A 作//BC AF 交BE 的延长线于点F ．（1）求证：AEF≌DEB；（2）证明四边形ADCF是菱形．18．(本题9分)如图，已知菱形ABCD的对角线AC、BD相交于点O，分别过A、D两点作AO、DO的垂线，两垂线交于点E．（1）求证：四边形AODE是矩形；（2）若四边形AODE的面积为12，AD＝5，求四边形AODE的周长．19．(本题9分)如图，在菱形ABCD中，E为对角线BD上一点，且AE＝DE，连接CE．（1）求证：CE＝DE．（2）当BE＝2，CE＝1时，求菱形的边长．20．(本题9分)如图，在直角坐标系中，四边形OABC是矩形，OA＝8，OC＝6，点D 是对角线AC的中点，过点D的直线分别交OA、BC边于点E、F．（1）求证：四边形EAFC是平行四边形；（2）当CE＝CF时，求EF的长；（3）在条件（2）的情况下，P为x轴上一点，当以E，F，P为顶点的三角形为等腰三角形时，请求出点P的坐标．参考答案1．D2．D3．C4．D5．A6．B7．D8．A9．D10．B11．1712．1013．24514．23或43 15．4.816．1017．（1）见解析；（2）见解析．【详解】（1）∵//BC AF ，∴AFE DBE ∠=∠，∵E 是AD 中点，AD 是BC 边上的中线，∴AE DE =，BD CD =，在AFE △和DBE 中，AFE DBE FEA BED AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴AFE △≌DBE （AAS ）．（2）由（1）知AFE △≌DEB ，则AF DB =，∵DB DC =，∴AF CD =，∵//BC AF ，∴四边形ADCF 是平行四边形，∵90BAC ∠=︒，D 是BC 的中点，E 是AD 中点， ∴12AD DC BC ==， ∴四边形ADCF 是菱形．18．（1）见解析（2）14．【详解】解：（1）∵四边形ABCD 是菱形，∴AC ⊥BD ，∴∠AOD=90°，∵EA ⊥AO ，DO ⊥AO ，∴∠EAO=∠DOA=90°，∴四边形AODE 是矩形；(2)由(1)知,四边形AODE 是矩形，∴∠AED=90°，∵AD=5，∵四边形AODE 的面积为12，∴AO×OD=12，在Rt △AOD 中，根据勾股定理得，22OA 25OD +=，∴()2222AO OD AO AO OD OD +=+⨯+=25+24=49．∴AO+OD=7∴四边形AODE 的周长为1419．（1）见解析（2【详解】（1）∵四边形ABCD 是菱形，∴∠ABE ＝∠CBE ，AB ＝CB ，在△ABE 和△CBE 中，AB CB ABE CBE BE BE =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△CBE ，∴AE ＝CE ，∵AE ＝DE ，∴CE ＝DE ；（2）如图，连接AC 交BD 于H ，∵四边形ABCD 是菱形，∴AH ⊥BD ，BH ＝DH ，AH ＝CH ，∵CE ＝DE ＝AE ＝1，∴BD ＝BE+DE ＝2+1＝3，∴BH ＝12BD ＝32，EH ＝BE ﹣BH ＝2﹣32＝12，在Rt △AHE 中，由勾股定理得：AH2，在Rt △AHB 中，由勾股定理得：AB， ∴．20．（1）见解析；（2）152；（3）点P 的坐标为（8，0）或（374，0）或（﹣234，0）或（434，0）【详解】（1）证明：∵四边形OABC 是矩形，∴BC ∥OA ，∴∠FCD ＝∠DAE ，∠CFD ＝∠AED ，∵D 是AC 的中点，∴CD ＝AD ，∴△CDF ≌△ADE （AAS ），∴DF ＝DE ，∴四边形EAFC 是平行四边形；（2）解：∵四边形EAFC 是平行四边形，CE ＝CF ， ∴四边形EAFC 是菱形，∴CE ＝EA ，AC ⊥EF ，设CE ＝AE ＝x ，∵OC 2+OE 2＝CE 2，∴62+（8﹣x ）2＝x 2，∴x ＝254， ∴CE ＝254， ∵OA ＝8，OC ＝6，∴AC 10，∴CD ＝12AC ＝5，∴ED＝154，∴EF＝2ED＝152；（3）由（2）可知，257,44 AE CE OE OA AE===-=，分三种情况：①若PE＝PF，点P与点A重合，∴P（8，0），②若EF＝EP＝152，当点P在x轴的正半轴上，OP＝OE+PE＝71542+＝374，∴P（374，0），当点P在x轴的负半轴上，OP＝PE﹣OE＝15724-＝234，∴P（﹣234，0），③若EF＝FP，过点F作FG⊥AE于点G，则EG＝CF﹣OE＝254﹣74＝92，∴EP＝9，∴OP＝OE+EP＝74+9＝434，∴P（434，0）．综上可得，点P的坐标为（8，0）或（374，0）或（﹣234，0）或（434，0）．答案第5页，总5页。

新人教版八年级下册菱形同步练习、含答案2

2022年湘教版八年级下《菱形的判定2》同步练习(附答案)

2.6.2 菱形的判定1、能够判别一个四边形是菱形的条件是〔〕A. 对角线相等且互相平分B. 对角线互相垂直且相等C. 对角线互相平分D. 一组对角相等且一条对角线平分这组对角2、平行四边形ABCD 的两条对角线AC 、BD 相交于点O, AB=5, AO=2, OB=1. 四边形ABCD 是菱形吗？为什么？3、如图，AD 是△ABC 的角平分线。

DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F.四边形AEDF 是菱形吗？说明你的理由。

4、如图，□ABCD 的对角线AC 的垂直平分线与AD 、BC 分别交于E 、F ，四边形AFCE 是否是菱形？为什么？5、DE ∥AC 、DF ∥AB ，添加以下条件后，不能判断四边形DEAF 为菱形的是〔〕 A. AD 平分∠BACB. AB ＝AC ＝且BD ＝CDC. AD 为中线D. EF ⊥AD6、如右图，四边形ABCD 为菱形，AE＝CF. 求证：四边形BEDF 为F DECBAEO BCF DA 菱形。

7、ABCD 为平行四边形纸片，要想用它剪成一个菱形。

小刚说只要过BD 中点作BD 的垂线交AD 、BC 于E 、F ，沿BE 、DF 剪去两个角，所得的四边形BFDE 为菱形。

你认为小刚的方法对吗？为什么？8、如右上图，两张等宽的纸条交叉重叠在一起，重叠的局部ABCD 是菱形吗？为什么？9、如图，四边形ABCD 中，对角线AC 和BD 相交于点O ，且AC ⊥BD ，点M 、N 分别在BD 、AC 上，且AO ＝ON ＝NC ，BM ＝MO ＝OD. 求证：BC ＝2 DN.F EC DBADACF H E B10、如图，四边形ABCD 为矩形，AD ＝20㎝、AB ＝10㎝。

M 点从D 到A ，P 点从B 到C ，两点的速度都为2㎝/s ；N 点从A 到B ，Q 点从C 到D ，两点的速度都为1㎝/s 。

假设四个点同时出发。

〔1〕判断四边形MNPQ 的形状。

湘教版八年级下册数学第2章 2.6.2 菱形的判定(含答案)

2.6.2 菱形的判定基础题知识点1 四条边都相等的四边形是菱形1．如图，用直尺和圆规作一个菱形，能得到四边形ABCD 是菱形的依据是(B)A ．一组邻边相等的四边形是菱形B ．四边相等的四边形是菱形C ．对角线互相垂直的平行四边形是菱形D ．每条对角线平分一组对角的平行四边形是菱形2．如图，△ABC 为等腰三角形，如果把它沿底边BC 翻折后，得到△DBC ，那么四边形ABDC 为(B)A ．平行四边形B ．菱形C ．矩形D ．以上都不对3．如图，四边形ABCD 内有一点E ，AE ＝BE ＝DE ＝BC ＝DC ，AB ＝AD ，若∠C ＝100°，则∠AED 的大小是(B)A ．120°B ．130°C ．140°D ．150°4．如图，在四边形ABCD 中，E ，F ，G ，H 分别是AB ，BD ，CD ，AC 的中点，AD ＝BC ，求证：四边形EFGH 是菱形．证明：∵E ，F 分别是AB ，BD 的中点， ∴EF ＝12AD.同理可得：GH ＝12AD ，GF ＝12BC ，HE ＝12BC.又∵AD ＝BC ，∴EF ＝GF ＝GH ＝HE. ∴四边形EFGH 是菱形．知识点2 对角线互相垂直的平行四边形是菱形5．如图，四边形ABCD 的对角线AC ，BD 互相垂直，则下列条件能判定四边形ABCD 为菱形的条件是(B)A ．BA ＝BCB ．AC ，BD 互相平分 C ．AC ＝BD D ．AB ∥CD6．(三明中考)如图，在四边形ABCD中，对角线AC，BD交于点O，OA＝OC，OB＝OD，添加一个条件使四边形ABCD 是菱形，那么所添加的条件可以是答案不唯一，如：AB＝AD或AB＝BC或AC⊥BD等(写出一个即可)．7．(镇江中考)如图，在四边形ABCD中，AB＝AD，BC＝DC，AC，BD相交于点O，点E在AO上，且OE＝OC.(1)求证：∠1＝∠2；(2)连接BE，DE，判断四边形BCDE的形状，并说明理由．解：(1)证明：∵在△ADC和△ABC中，AD＝AB，AC＝AC，DC＝BC，∴△ADC≌△ABC(SSS)．∴∠1＝∠2.(2)四边形BCDE是菱形．理由：∵DC＝BC，∠1＝∠2，∴AC垂直平分BD.又∵OE＝OC，∴四边形BCDE是平行四边形．又∵AC⊥BD，∴四边形BCDE是菱形．8．(淮安中考)如图，在△ABC中，AD平分∠BAC，将△ABC折叠，使点A与点D重合，展开后折痕分别交AB，AC 于点E，F，连接DE，DF.求证：四边形AEDF是菱形．证明：连接EF，交AD于点O.∵AD平分∠BAC，∴∠EAO＝∠FAO.∵EF⊥AD，∴∠AOE＝∠AOF＝90°.在△AEO和△AFO中，∠EAO＝∠FAO，AO＝AO，∠AOE＝∠AOF，∴△AEO ≌△AFO(ASA)．∴EO＝FO.∵A点与D点重合，∴AO＝DO.∴EF，AD互相平分．∴四边形AEDF是平行四边形．又∵EF⊥AD，∴四边形AEDF为菱形．中档题9．(海南中考)如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件中能够判定四边形ACED为菱形的条件是(B)A．AB＝BCB．AC＝BCC．∠B＝60°D．∠ACB＝60°10．(防城港中考)如图，在给定的一张平行四边形纸片上作一个菱形，甲、乙两人的作法如下：甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于点M，O，N，连接AN，CM，则四边形ANCM是菱形．乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于点E，F，连接EF，则四边形ABEF是菱形．根据两人的作法可判断(C)A．甲正确，乙错误 B．乙正确，甲错误C．甲、乙均正确 D．甲、乙均错误11．(十堰中考)如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE＝DF，给出下列条件：①BE⊥EC；②BF∥CE；③AB＝AC.从中选择一个条件使四边形BECF是菱形，你认为这个条件是③(填序号)．12．(娄底中考)如图，将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置，AB与A1C1相交于点D，AC与A1C1，BC1分别交于点E，F.(1)求证：△BCF≌△BA1D.(2)当∠C＝α度时，判定四边形A1BCE的形状，并说明理由．解：(1)证明：∵△ABC是等腰三角形，∴AB＝BC，∠A＝∠C.由旋转性质得：A1B＝AB＝BC，∠A＝∠A1＝∠C，∠A1BD＝∠CBF＝α.∴△BCF≌△BA1D(ASA)．(2)四边形A1BCE是菱形．∵∠ADE＝∠A1DB，∠A1＝∠A，∴∠AED＝∠A1BD＝α.∵∠C＝α，∴∠AED＝∠C.∴A1E∥BC.∵∠A＝∠C＝α，∠A1BD＝α，∴∠A＝∠A1BD.∴A1B∥EC.又∵A1E∥BC，∴四边形A1BCE是平行四边形．又∵A1B＝BC，∴四边形A1BCE是菱形．综合题13．(滨州中考)如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG.(1)请判断四边形EBGD的形状，并说明理由；(2)若∠ABC ＝30°，∠C ＝45°，ED ＝210，点H 是BD 上的一个动点，求HG ＋HC 的最小值．解：(1)四边形EBGD 是菱形．理由：∵EG 垂直平分BD ， ∴EB ＝ED ，GB ＝GD ，BF ＝FD. ∴∠EBD ＝∠EDB. ∵∠EBD ＝∠DBC ， ∴∠EDF ＝∠GBF. 又∵∠EFD ＝∠GFB ， ∴△EFD ≌△GFB(ASA)． ∴ED ＝BG.∴BE ＝ED ＝DG ＝GB. ∴四边形EBGD 是菱形． (2)过点E 作EM ⊥BC 于点M ，过点D 作DN ⊥BC 于点N ，连接EC 交BD 于点H ，由轴对称的性质可知此时HG ＋HC 最小．在Rt △EBM 中，∵∠EMB ＝90°，∠EBM ＝30°，EB ＝ED ＝210，∴EM ＝12BE ＝10.∵DE ∥BC ，EM ⊥BC ，DN ⊥BC ， ∴四边形EMND 为矩形，∴EM ＝DN ＝10，MN ＝DE ＝210.在Rt △DNC 中，∵∠DNC ＝90°，∠DCN ＝45°， ∴∠NDC ＝∠DCN ＝45°.∴DN ＝NC ＝10. ∴MC ＝310.∵在Rt △EMC 中，∠EMC ＝90°，EM ＝10，MC ＝310， ∴EC ＝EM 2＋MC 2＝（10）2＋（310）2＝10. ∵HG ＋HC ＝EH ＋HC ＝EC ， ∴HG ＋HC 的最小值为10.。

菱形的判定专项练习30题(有答案)ok

菱形的判定专项练习30题(有答案)ok菱形的判定专项练习30题（有答案）1．如图，梯形ABCD中，AD∥BC，BA=AD=DC=BC，点E为BC的中点．（1）求证：四边形ABED是菱形；（2）过A点作AF⊥BC于点F，若BD=4cm，求AF的长．2．如图，四边形ABCD中，对角线AC、BD相交于点O，且AC⊥BD．点M，N分别在BD、AC上，且AO=ON=NC，BM=MO=OD．求证：BC=2DN．3．如图，在△ABC中，AB=AC，D，E，F分别是BC，AB，AC的中点．（1）求证：四边形AEDF是菱形；（2）若AB=12cm，求菱形AEDF的周长．4．如图，在▱ABCD中，EF∥BD，分别交BC，CD于点P，Q，交AB，AD的延长线于点E，F．已知BE=BP．求证：（1）∠E=∠F；（2）▱ABCD是菱形．5．如图，在△ABC中，D是BC的中点，E是AD的中点，过点A作AF∥BC，AF与CE的延长线相交于点F，连接BF．（1）求证：AF=DC；（2）若∠BAC=90°，求证：四边形AFBD是菱形．6．已知平行四边形ABCD中，对角线BD平分∠ABC，求证：四边形ABCD是菱形．7．如图，在一个含30°的三角板ABC中，将三角板沿着AB所在直线翻转180°得到△ABF，再将三角板绕点C顺时针方向旋转60°得到△DEC，点F在AC上，连接AE．（1）求证：四边形ADCE是菱形．（2）连接BF并延长交AE于G，连接CG．请问：四边形ABCG是什么特殊平行四边形？为什么？8．如图，已知四边形ABCD是平行四边形，DE⊥AB，DF⊥BC，垂足分别是为E F，并且DE=DF．求证：四边形ABCD是菱形．9．如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E，以AD，AE为边作▱ADFE交BC于点G，H，且EH=EC．求证：（1）∠B=∠C；（2）▱ADFE是菱形．10．如图，在△ABC中，∠ACB=90°，CD是AB边上的高，∠BAC的平分线AE交CD于F，EG⊥AB于G．（1）求证：△AEG≌△AEC；（2）△CEF是否为等腰三角形，请证明你的结论；（3）四边形GECF是否为菱形，请证明你的结论．11．如图，在△ABC中，AB=AC，点D、E、F分别是△ABC三边的中点．求证：四边形ADEF是菱形．12．如图，在四边形ABCD中，AB=CD，M、N、E、F分别为AD、BC、BD、AC的中点，求证：四边形MENF 为菱形．13．已知：如图，在梯形ABCD中，AD∥BC，AB=AD，∠BAD的平分线AE交BC于点E，连接DE．求证：四边形ABED是菱形．14．如图，在△ABC中，AB=AC，M、O、N分别是AB、BC、CA的中点．求证：四边形AMON是菱形．15．如图：在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F．求证：四边形AEFG是菱形．16．如图，矩形ABCD绕其对角线交点旋转后得矩形AECF，AB交EC于点N，CD交AF于点M．求证：四边形ANCM是菱形．17．如图，四边形ABCD、DEBF都是矩形，AB=BF，AD、BE交于M，BC、DF交于N，那么四边形BMDN是菱形吗？如果是，请写出证明过程；如果不是，说明理由．18．已知如图所示，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，四边形AEDF是菱形吗？说明理由．19．已知：如图所示，BD是△ABC的角平分线，EF是BD的垂直平分线，且交AB于E，交BC于点F．求证：四边形BFDE是菱形．20．如图，在平行四边形ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AD、BC分别交于E、F．求证：四边形AFCE是菱形．21．如图，在矩形ABCD中，EF垂直平分BD．（1）判断四边形BEDF的形状，并说明理由．（2）已知BD=20，EF=15，求矩形ABCD的周长．22．如图所示，在▱ABCD中，点E在BC上，AE平分∠BAF，过点E作EF∥AB．求证：四边形ABEF为菱形．23．已知，如图，矩形ABCD中，AB=4cm，AD=8cm，作∠CAE=∠ACE交BC于E，作∠ACF=∠CAF交AD于F．（1）求证：AECF是菱形；（2）求四边形AECF的面积．24．如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F．问四边形AFCE是菱形吗？请说明理由．25．如图：在平行四边形ABCD中，E、F分别是边AB、CD的延长线上一点，且BE=DF，连接EF交AC于O．（1）AC与EF互相平分吗？为什么？（2）连接CE、AF，再添加一个什么条件，四边形AECF是菱形？为什么？26．已知：如图，△ABC和△DBC的顶点在BC边的同侧，AB=DC，AC=BD交于E，∠BEC的平分线交BC于O，延长EO到F，使EO=OF．求证：四边形BFCE是菱形．27．如图，在△ABC中，D是BC边的中点，F，E分别是AD及其延长线上的点，CF∥BE．（1）求证：△BDE≌△CDF；（2）请连接BF，CE，试判断四边形BECF是何种特殊四边形，并说明理由；（3）在（2）下要使BECF是菱形，则△ABC应满足何条件？并说明理由．28．如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF=CE．（1）求证：四边形ACEF是平行四边形；（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．29．如图，在△ABC中，AD是∠BAC的平分线，EF垂直平分AD交AB于E，交AC于F．求证：四边形AEDF是菱形．30．如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA 的外角平分线于点F．（1）探究：线段OE与OF的数量关系并加以证明；（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？（3）当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由．参考答案：1．1）证明：∵点E为BC的中点，∴BE=CE=BC，∵BA=AD=DC=BC，∴AB=BE=ED=AD，∴四边形ABED是菱形；（2）解：过点D作DH⊥BC，垂足为H，∵CD=DE=CE，∴∠DEC=60°，∴∠DBE=30°，在Rt△BDH中，BD=4cm，∴DH=2cm，∵AF=DH，∴AF=2cm．2．∵AO=ON，BM=MO，∴四边形AMND是平行四边形，∵AC⊥BD，∴平行四边形AMND是菱形，∴MN=DN，∵ON=NC，BM=MO，∴MN=BC，∴BC=2DN 3．（1）∵D，E分别是BC，AB的中点，∴DE∥AC且DE=AF=AC．同理DF∥AB且DF=AE=AB．又∵AB=AC，∴DE=DF=AF=AE，∴四边形AEDF是菱形．（2）∵E是AB中点，∴AE=AB=6cm，因此菱形AEDF的周长为4×6=24cm．4．（1）∵BE=BP，∴∠E=∠BPE，∵BC∥AF，∴∠BPE=∠F，∴∠E=∠F．（2）∵EF∥BD，∴∠E=∠ABD，∠F=∠ADB，∴∠ABD=∠ADB，∴AB=AD，∵四边形ABCD是平行四边形，∴□ABCD是菱形．5．1）证明：∵E是AD的中点，∴∠1=∠2，在△AEF和△DEC 中，∴△AFE≌△DCE（AAS），∴AF=DC；（2）证明：∵D是BC的中点，∴DB=CD=BC，∵AF=CD，∴AF=DB，∵AF∥BD，∴四边形AFBD是平行四边形，∵∠BAC=90°，D为BC中点，∴AD=CB=DB，∴四边形AFBD是菱形．6．∵对角线BD平分∠ABC，∴∠1=∠2，∵四边形ABCD是平行四边形，∴AB∥DC，∴∠3=∠1，∴∠3=∠2，∴DC=BC，又∵四边形ABCD是平行四边形，∴四边形ABCD是菱形．7．（1）∵三角板ABC中，将三角板沿着AB所在直线翻转180°得到△ABF，∴△ABC≌△ABF，且∠BAC=∠BAF=30°，∴∠FAC=60°，∴AD=DC=AC，又∵△ABC≌△EFC，∴CA=CE，又∵∠ECF=60°，∴AC=EC=AE，∴AD=DC=CE=AE，（2）证明：由（1）可知：△ACD，△AFC是等边三角形，△ACB≌△AFB，∴∠EDC=∠BAC=∠FAC=30°，且△ABC为直角三角形，∴BC=AC，∵EC=CB，∴EC=AC，∴E为AC中点，∴DE⊥AC，∴AE=EC，∵AG∥BC，∴∠EAG=∠ECB，∠AGE=∠EBC，∴△AEG≌△CEB，∴AG=BC，（7分）∴四边形ABCG是平行四边形，∵∠ABC=90°，∴四边形ABCG是矩形8．在△ADE和△CDF中，∵四边形ABCD是平行四边形，∴∠A=∠C，∵DE⊥AB，DF⊥BC，∴∠AED=∠CFD=90°．又∵DE=DF，∴△ADE≌△CDF（AAS）∴DA=DC，∴平行四边形ABCD是菱形9．（1）∵在▱ADFE中，AD∥EF，∴∠EHC=∠B（两直线平行，同位角相等）．∵EH=EC（已知），∴∠EHC=∠C（等边对等角），∴∠B=∠C（等量代换）；（2）∵DE∥BC（已知），∴∠AED=∠C，∠ADE=∠B．∵∠B=∠C，∴∠AED=∠ADE，∴AD=AE，∴▱ADFE是菱形．10．1）证明：∵∠ACB=90°，∴AC⊥EC．在Rt△AEG与Rt△AEC中，，∴Rt△AEG≌Rt△AEC（HL）；（2）解：△CEF是等腰三角形．理由如下：∵CD是AB边上的高，∴CD⊥AB．又∵EG⊥AB，∴EG∥CD，∴∠CFE=∠GEA．又由（1）知，Rt△AEG≌Rt△AEC，∴∠GEA=∠CEA，∴∠CEA=∠CFE，即∠CEF=∠CFE，∴CE=CF，即△CEF是等腰三角形；（3）解：四边形GECF是菱形．理由如下：∵由（1）知，Rt△AEG≌Rt△AEC，则GE=EC；由（2）知，CE=CF，∴GE=EC=FC．又∵EG∥CD，即GE∥FC，∴四边形GECFR是菱形．11．∵D、E、F分别是△ABC三边的中点，∴DE AC，EF AB，∴四边形ADEF为平行四边形．又∵AC=AB，∴DE=EF．∴四边形ADEF为菱形．12．∵M、E、分别为AD、BD、的中点，∴ME∥AB，ME=AB，同理：FH∥AB，FH=AB，∴四边形MENF是平行四边形，∵M．F是AD，AC中点，∴MF=DC，∵AB=CD，∴MF=ME，∴四边形MENF为菱形13．∵AE平分∠BAD，∵，∴△BAE≌△DAE（SAS）…（2分）∴BE=DE，…（3分）∵AD∥BC，∴∠DAE=∠AEB，…（4分）∴∠BAE=∠AEB，∴AB=BE，…（5分）∴AB=BE=DE=AD，…（6分）∴四边形ABED是菱形．14．∵AB=AC，M、O、N分别是AB、BC、CA的中点，∴AM=AB=AC=AN，M0∥AC，NO∥AB，且MO=AC=AN，NO=AB=AM（三角形中位线定理），∴AM=MO=AN=NO，∴四边形AMON是菱形（四条边都相等的四边形是菱形）15．证法一：∵AD⊥BC，∴∠ADB=90°，∵∠BAC=90°，∴∠B+∠BAD=90°，∠BAD+∠CAD=90°，∴∠B=∠CAD，∵CE平分∠ACB，EF⊥BC，∠BAC=90°（EA⊥CA），∴AE=EF（角平分线上的点到角两边的距离相等），∵CE=CE，∴由勾股定理得：AC=CF，∵△ACG和△FCG中，∴△ACG≌△FCG，∴∠CAD=∠CFG，∵∠B=∠CAD，∴∠B=∠CFG，∴GF∥AB，∵AD⊥BC，EF⊥BC，∴AD∥EF，即AG∥EF，AE∥GF，∴平行四边形AEFG是菱形．证法二：∵AD⊥BC，∠CAB=90°，EF⊥BC，CE平分∠ACB，∴AD∥EF，∠4=∠5，AE=EF，∵∠1=180°﹣90°﹣∠4，∠2=180°﹣90°﹣∠5，∴∠1=∠2，∵AD∥EF，∴∠2=∠3，∴∠1=∠3，∴AG=AE，∵AE=EF，∴AG=EF，∵AG∥EF，∴四边形AGFE是平行四边形，∵AE=EF，∴平行四边形AGFE是菱形．16．∵CD∥AB，∴∠FMC=∠FAN，∴∠NAE=∠MCF（等角的余角相等），在△CFM和△AEN中，，∴△CFM≌△AEN（ASA），∴CM=AN，∴四边形ANCM为平行四边形，在△ADM和△CFM中，，∴△ADM≌△CFM（AAS），∴AM=CF，∴四边形ANCM是菱形17．四边形BMDN是菱形．∵AM∥BC，∴∠AMB=∠MBN，∵BM∥FN∴∠MBN=∠BNF，∴∠AMB=∠BNF，又∵∠A=∠F=90°，AB=BF，∴△ABM≌△BFN，∴DM=DN，∵ED=BF=AB，∠E=∠A=90°，∠AMB=∠EMD，∴△ABM≌△EDM，∴BM=DM，∴MB=MD=DN=BN，∴四边形BMDN是菱形18．如图，由于DE∥AC，DF∥AB，所以四边形AEDF 为平行四边形．∵DE∥AC，∴∠3=∠2，又∠1=∠2，∴∠1=∠3，∴AE=DE，∴平行四边形AEDF为菱形．19．∵EF是BD的垂直平分线，∴EB=ED，∴∠EBD=∠EDB．∵BD是△ABC的角平分线，∴∠EBD=∠FBD．∴∠FBD=∠EDB，∴ED∥BF．同理，DF∥BE，∴四边形BFDE是平行四边形．又∵EB=ED，∴四边形BFDE是菱形．20．方法一：∵AE∥FC．∴∠EAC=∠FCA．（2分）又∵∠AOE=∠COF，AO=CO，∴△AOE≌△COF．（5分）∴EO=FO．又EF⊥AC，∴AC是EF的垂直平分线．（8分）∴AF=AE，CF=CE，又∵EA=EC，∴AF=AE=CE=CF．∴四边形AFCE为菱形．（10分）方法二：同方法一，证得△AOE≌△COF．（5分）∴AE=CF．∴四边形AFCE是平行四边形．（8分）又∵EF是AC的垂直平分线，方法三：同方法二，证得四边形AFCE是平行四边形．（8分）又EF⊥AC，（9分）∴四边形AFCE为菱形21．（1）四边形BEDF是菱形．在△DOF和△BOE中，∠FDO=∠EBO，OD=OB，∠DOF=∠BOE=90°，所以△DOF≌△BOE，所以OE=OF．又因为EF⊥BD，OD=OB，所以四边形BEDF为菱形．（5分）（2）如图，在菱形EBFD中，BD=20，EF=15，则DO=10，EO=7.5．由勾股定理得DE=EB=BF=FD=12.5．S菱形EBFD =EF•BD=BE•AD，即所以得AD=12．根据勾股定理可得AE=3.5，有AB=AE+EB=16．由2（AB+AD）=2（16+12）=56，故矩形ABCD的周长为5622．∵四边形ABCD是平行四边形，∴AF∥BE，又∵EF∥AB，∴四边形ABEF为平行四边形，∵AE平分∠BAF，∴∠BAE=∠FAE，∵∠FAE=∠BEA，∴∠BAE=∠BEA，∴BA=BE，∴平行四边形ABEF为菱形23．（1）证明：在矩形ABCD中，∵AB∥CD，∴∠BAC=∠DCA，又∠CAE=∠ACE，∠ACF=∠CAF，∴∠EAC=∠FCA．∴AE∥CF．∴四边形AECF为平行四边形，又∠CAE=∠ACE，∴AE=EC．∴▱AECF为菱形．（2）设BE=x，则EC=AE=8﹣x，在Rt△ABE中，AB2+BE2=AE2，所以EC=5，即S菱形AECF=EC×AB=5×4=20．24．四边形AFCE是菱形，理由是：∵四边形ABCD是平行四边形，∴AD∥BC，∴=，∵AO=OC，∴OE=OF，∴四边形AFCE是平行四边形，∵EF⊥AC，∴平行四边形AFCE是菱形25．（1）AC与EF互相平分，连接CE，AF，∵平行四边形ABCD，∴AB∥CD，AB=CD，又∵BE=DF，∴AB+BE=CD+DF，∴AE=CF，∴AE∥CF，AE=CF，∴四边形AECF是平行四边形，∴AC与EF互相平分；（2）条件：EF⊥AC，∵EF⊥AC，又∵四边形AECF是平行四边形，∴平行四边形AECF是菱形．26．∵AB=DC AC=BD BC=CB，∴△ABC≌△DCB，∴∠DBC=∠ACB，∴BE=CE，又∵∠BEC的平分线是EF，∴EO是中线（三线合一），∴BO=CO，∴四边形BFCE是平行四边形（对角线互相平分），又∵BE=CE，∴四边形BFCE是菱形．27．（1）证明：∵CF∥BE，∴∠EBD=∠FCD，D是BC边的中点，则BD=CD，∠BDE=∠CDF，∴△BDE≌△CDF．（2）如图所示，由（1）可得CF=BE，又CF∥BE，所以四边形BECF是平行四边形；（3）△ABC是等腰三角形，即AB=AC，理由：当AB=AC 时，则有AD⊥BC，又（2）中四边形为平行四边形，所以可判定其为菱形．28．（1）∵DE为BC的垂直平分线，∴∠EDB=90°，BD=DC，又∵∠ACB=90°，∴DE∥AC，∴E为AB的中点，∴在Rt△ABC中，CE=AE=BE，∴∠AEF=∠AFE，且∠BED=∠AEF，∠DEC=∠DFA，∴AF∥CE，又∵AF=CE，∴四边形ACEF为平行四边形；（2）要使得平行四边形ACEF为菱形，则AC=CE即可，∵DE∥AC，∴∠BED=∠BAC，∠DEC=∠ECA，又∵∠BED=∠DEC，∴∠EAC=∠ECA，∴AE=EC，又EB=EC，∴AE=EC=EB，∵CE=AB，∴AC=AB即可，在Rt△ABC中，∠ACB=90°，∴当∠B=30°时，AB=2AC，故∠B=30°时，四边形ACEF为菱形．29．∵AD平分∠BAC∴∠BAD=∠CAD又∵EF⊥AD，∴∠AOE=∠AOF=90°∵在△AEO和△AFO中，∴△AEO≌△AFO（ASA），∴EO=FO即EF、AD相互平分，∴四边形AEDF是平行四边形又EF⊥AD，∴平行四边形AEDF为菱形30．1）解：OE=OF．理由如下：∵CE是∠ACB的角平分线，∴∠ACE=∠BCE，又∵MN∥BC，∴∠NEC=∠ECB，∴∠NEC=∠ACE，∴OE=OC，∵OF是∠BCA的外角平分线，∴∠OCF=∠FCD，又∵MN∥BC，∴∠OFC=∠ECD，∴∠OFC=∠COF，∴OF=OC，∴OE=OF；（2）解：当∠ACB=90°，点O在AC的中点时，∵OE=OF，∴四边形AECF是正方形；（3）答：不可能．解：如图所示，∵CE平分∠ACB，CF平分∠ACD，∴∠ECF=∠ACB+∠ACD=（∠ACB+∠ACD）=90°，若四边形BCFE是菱形，则BF⊥EC，但在△GFC中，不可能存在两个角为90°，所以不存在其为菱形．。