严家騄版工程热力学PPT 第2章 热力学第一定律
合集下载
02工程热力学第二章 热力学第一定律

dU = δQ δW
ห้องสมุดไป่ตู้
δQ = dU + δW
Q1 2 = (U 2 U1 ) + W1 2
δq = du + δw
q1 2 = (u2 u1 ) + w1 2
式中各项的正负号规定为:系统吸热为正,放热为负; 式中各项的正负号规定为:系统吸热为正,放热为负; 系统对外作功为正,外界对系统作功为负. 系统对外作功为正,外界对系统作功为负. 上式既适用于准静态过程,也适用于非准静态过程. 上式既适用于准静态过程,也适用于非准静态过程.
Time τ0 +dτ
引起系统内部能量变化的原因:质量交换和能量交换. 引起系统内部能量变化的原因:质量交换和能量交换.
经历dτ时间后,系统内的质量变化: 经历 时间后,系统内的质量变化: dm = δm1 δm2 时间后 由此可得: 由此可得:
dm δm1 δm2 = dτ dτ dτ dm = qm1 qm2 dτ
第二章 热力学第一定律
5
第二章 热力学第一定律
6
对某同学的"动力机械" 对某同学的"动力机械"的思考
压气机 从大气中取气
压力容器
①按图示系统工作的"动力 按图示系统工作的" 机械"是否有意义? 机械"是否有意义? 输入< 输出, ②设想w输入 w输出,则 设想 输入 输出 该系统是否有可能? 该系统是否有可能?
1
2
δq = du + δw
q1 2 = (u2 u1 ) + w1 2
δq = du + pdv
q1 2 = (u2 u1 ) + ∫ pdv
工程热力学 第2章 热力学第一定律

6
δWtot
δmi ei
δQ
E
δm j e j
E+dE
δQ = dE + ⎡Σ ( ej δmj ) −Σ ( eiδmi ) ⎤ + δWtot ⎣ ⎦
或
τ
τ + dτ
Q = ΔE + ∫ ⎡Σ( ej δmj ) −Σ( eiδmi ) ⎤ +Wtot ⎦ τ1 ⎣
τ2
dE Φ= + ⎡Σ ( ej qmj ) −Σ ( ei qmi ) ⎤ + P ⎣ ⎦ tot dτ
二、总(储存)能(total stored energy of system) 热力学能,内部储存能
E =U+Ek +Ep
宏观动能 宏观位能 总能 外部储存能
e =u+ek +ep
3
外部储存能 宏观动能:质量为m的物体以速度cf运动时,该物 体具有的宏观运动动能为:
1 2 Ek = mc f 2
重力位能:在重力场中质量为m的物体相对于系统 外的参数坐标系的高度为z时,具有的重力位能为:
1 2 q − Δu = Δc f + gΔz + Δ( pv ) + wi 2
维持工质流动所需的流动功
21
稳定能量方程的物理意义:工质在状态变化过程 中,从热能转变而来的机械能总和等于膨胀功。 技术功:技术上可资用的功,其数学表达式为:
由
1 2 wt = wi + Δc f + gΔz 2 q − Δu = w
E p = mgz
4
宏观动能与内动能的区别
三、热力学能是状态参数∂U ⎞ ⎛ ∂U ⎞ dU = ⎜ ⎟ dT + ⎜ ⎟ dV = cV dT + ⎢T ⎜ ⎟ − p ⎥ dV ⎝ ∂T ⎠V ⎝ ∂V ⎠T ⎣ ⎝ ∂T ⎠V ⎦
δWtot
δmi ei
δQ
E
δm j e j
E+dE
δQ = dE + ⎡Σ ( ej δmj ) −Σ ( eiδmi ) ⎤ + δWtot ⎣ ⎦
或
τ
τ + dτ
Q = ΔE + ∫ ⎡Σ( ej δmj ) −Σ( eiδmi ) ⎤ +Wtot ⎦ τ1 ⎣
τ2
dE Φ= + ⎡Σ ( ej qmj ) −Σ ( ei qmi ) ⎤ + P ⎣ ⎦ tot dτ
二、总(储存)能(total stored energy of system) 热力学能,内部储存能
E =U+Ek +Ep
宏观动能 宏观位能 总能 外部储存能
e =u+ek +ep
3
外部储存能 宏观动能:质量为m的物体以速度cf运动时,该物 体具有的宏观运动动能为:
1 2 Ek = mc f 2
重力位能:在重力场中质量为m的物体相对于系统 外的参数坐标系的高度为z时,具有的重力位能为:
1 2 q − Δu = Δc f + gΔz + Δ( pv ) + wi 2
维持工质流动所需的流动功
21
稳定能量方程的物理意义:工质在状态变化过程 中,从热能转变而来的机械能总和等于膨胀功。 技术功:技术上可资用的功,其数学表达式为:
由
1 2 wt = wi + Δc f + gΔz 2 q − Δu = w
E p = mgz
4
宏观动能与内动能的区别
三、热力学能是状态参数∂U ⎞ ⎛ ∂U ⎞ dU = ⎜ ⎟ dT + ⎜ ⎟ dV = cV dT + ⎢T ⎜ ⎟ − p ⎥ dV ⎝ ∂T ⎠V ⎝ ∂V ⎠T ⎣ ⎝ ∂T ⎠V ⎦
工程热力学(第2章--热力学第一定律)

第一篇 工程热力学
第二章 热力学第一定律
本章主要内容
热力学第一定律的实质 系统储存能 闭口系能量方程 状态参数焓 开口系能量方程及其应用
2
2-1 热力学第一定律的实质
➢19世纪30-40年代,迈尔·焦耳(德国医生) 发现并确定了能量转换与守恒定律。恩格斯 将其列为19世纪三大发现之一(细胞学说、 达尔文进化论)。
5
永动机设想?
Q
电
锅 炉
加 热 器
汽轮机 发电机
凝
给水泵
汽
器
Wnet
Qout
6
2-2 系统储存能
➢ 能量是物质运动的度量,运动有各种不同的形 态,相应的就有各种不同的能量。
➢ 系统储存的能量称为储存能,它有内部储存能 与外部储存能之分。
系统储存能
内部储存能 (热力学能)
外部储存能 (宏观机械能)
➢能量转换与守恒定律指出:一切物质都具有 能量。能量既不可能被创造,也不可能被消 灭,它只能在一定的条件下从一种形式转变 为另一种形式。而在转换过程中,能的总量 保持不变。
3
实质:热力学第一定律是能量转换与守恒 定律在热力学中的具体应用。
热功转换可归结为两种运动形式之间的转化:
宏观物体的机械运动 微观分子的热运动
说明:由计算结果可知,将汽轮机的散热量忽略不计时,对汽轮机
功率的影响并不大。所以,将汽轮机内蒸汽的膨胀作功过程看成是绝热 过程来分析是合理的。
30
例2-3 某300MW机组,锅炉的出力为qm=1024×103kg/h,出口蒸
汽锅每焓炉小为的时h效的2=率燃33煤η92量炉.=3B9K?2J%/,kg标,准锅煤炉发进热口量给q水煤=焓29为27h01=K1J1/9k7g.,3K求J/锅kg炉,
第二章 热力学第一定律
本章主要内容
热力学第一定律的实质 系统储存能 闭口系能量方程 状态参数焓 开口系能量方程及其应用
2
2-1 热力学第一定律的实质
➢19世纪30-40年代,迈尔·焦耳(德国医生) 发现并确定了能量转换与守恒定律。恩格斯 将其列为19世纪三大发现之一(细胞学说、 达尔文进化论)。
5
永动机设想?
Q
电
锅 炉
加 热 器
汽轮机 发电机
凝
给水泵
汽
器
Wnet
Qout
6
2-2 系统储存能
➢ 能量是物质运动的度量,运动有各种不同的形 态,相应的就有各种不同的能量。
➢ 系统储存的能量称为储存能,它有内部储存能 与外部储存能之分。
系统储存能
内部储存能 (热力学能)
外部储存能 (宏观机械能)
➢能量转换与守恒定律指出:一切物质都具有 能量。能量既不可能被创造,也不可能被消 灭,它只能在一定的条件下从一种形式转变 为另一种形式。而在转换过程中,能的总量 保持不变。
3
实质:热力学第一定律是能量转换与守恒 定律在热力学中的具体应用。
热功转换可归结为两种运动形式之间的转化:
宏观物体的机械运动 微观分子的热运动
说明:由计算结果可知,将汽轮机的散热量忽略不计时,对汽轮机
功率的影响并不大。所以,将汽轮机内蒸汽的膨胀作功过程看成是绝热 过程来分析是合理的。
30
例2-3 某300MW机组,锅炉的出力为qm=1024×103kg/h,出口蒸
汽锅每焓炉小为的时h效的2=率燃33煤η92量炉.=3B9K?2J%/,kg标,准锅煤炉发进热口量给q水煤=焓29为27h01=K1J1/9k7g.,3K求J/锅kg炉,
02 第二章 热力学第一定律共48页PPT资料

② Q、W不是状态函数,除了与始终态有关外,还 与变化途径有关。
③ W指总功,包括体积功和非体积功。
④ 第一定律只适用于封闭系统。
(五) 功、热、热力学能、焓
(五) 功、热、热力学能、焓 1. 热(heat)系统与环境之间因温差而传递的能量 称为热,用符号Q 表示, δQ = CdT。 Q的取号:
第二章 热力学第一定律及其应用
(二)状态函数(states function) 状态函数是描述系统状态的参数。其数值仅取决于
系统所处的状态,而与系统的历史无关;它的变化值仅 取决于系统的始态和终态,而与变化的途径无关。 1.状态函数的特点: (1)状态一定,状态函数一定。 (2)状态函数改变,状态改变。 (3)状态函数的改变值,只与始终态有关,与变化 的途径无关。 (4)状态函数在数学上具有全微分的性质。
(五) 功、热、热力学能、焓
3. 热力学能:热力学能是系统内部能量的总和,其 中包括平动能(t)、转动能(r)、振动能(υ)、电子能 (e)和核能(n)以及各种粒子之间的相互作用位能等。
热力学能的绝对值不可测,只能测出变化值,这 种能量以热与功的形式表现出来。
ΔU = Q + W
UTT 12CVd
(电功)
δW表面 = -γdA
(表面功)
功的一般表示式 Wp外 dV (Xd YxdZ ydz)
W eW f
从微观角度来说,功是大量质点以有序运动而传递的 能量,而热是大量质点以无序运动方式而传递的能量。
热和功的特点 (1)Q和W都不是状态函数,其数值与变化途径有关。
(2)Q和W的微变都不是全微分,用Q和W表示
2. 可逆过程
系统经过某一过程之后,如果使系统恢复原状的同 时,环境也能恢复到原状而未留下任何永久性的变化, 则该过程称为热力学可逆过程。否则为不可逆过程。
③ W指总功,包括体积功和非体积功。
④ 第一定律只适用于封闭系统。
(五) 功、热、热力学能、焓
(五) 功、热、热力学能、焓 1. 热(heat)系统与环境之间因温差而传递的能量 称为热,用符号Q 表示, δQ = CdT。 Q的取号:
第二章 热力学第一定律及其应用
(二)状态函数(states function) 状态函数是描述系统状态的参数。其数值仅取决于
系统所处的状态,而与系统的历史无关;它的变化值仅 取决于系统的始态和终态,而与变化的途径无关。 1.状态函数的特点: (1)状态一定,状态函数一定。 (2)状态函数改变,状态改变。 (3)状态函数的改变值,只与始终态有关,与变化 的途径无关。 (4)状态函数在数学上具有全微分的性质。
(五) 功、热、热力学能、焓
3. 热力学能:热力学能是系统内部能量的总和,其 中包括平动能(t)、转动能(r)、振动能(υ)、电子能 (e)和核能(n)以及各种粒子之间的相互作用位能等。
热力学能的绝对值不可测,只能测出变化值,这 种能量以热与功的形式表现出来。
ΔU = Q + W
UTT 12CVd
(电功)
δW表面 = -γdA
(表面功)
功的一般表示式 Wp外 dV (Xd YxdZ ydz)
W eW f
从微观角度来说,功是大量质点以有序运动而传递的 能量,而热是大量质点以无序运动方式而传递的能量。
热和功的特点 (1)Q和W都不是状态函数,其数值与变化途径有关。
(2)Q和W的微变都不是全微分,用Q和W表示
2. 可逆过程
系统经过某一过程之后,如果使系统恢复原状的同 时,环境也能恢复到原状而未留下任何永久性的变化, 则该过程称为热力学可逆过程。否则为不可逆过程。
工程热力学 第二章 热力学第一定律

pv p2v2 p1v1
是系统为维持工质流动所需的功
对推动功的说明
1、与宏观流动有关,流动停止,推动功不存在 2、作用过程中,工质仅发生位置变化,无状态变化
3、w推=pv与所处状态有关,是状态量 4、并非工质本身的能量(动能、位能)变化引起, 而由外界做出,流动工质所携带的能量
可理解为:由于工质的进出,外界与系统之间
The work depends on the process path
作功的说明
“作功”是系统与外界间的一种相互作用,是越过系统边
界的能量交换。
功是指作功过程中在传递着的能量的总称,过程一旦结束
就再无所谓功。
机械能与机械功、电能与电功等同吗?
系统可以拥有电能,机械能,但决不会拥有电功、机械功之类的功。 功只不过是特定条件下在过程中传递着的能量。
实质:能量守恒及转换定律在热现象中的应用
• 18世纪初,工业革命,热效率只有1% • 1842年,J.R. Mayer阐述热力学第一定律, 但没有引起重视
• 1840-1849年,Joule用多种实验的一致性 证明热力学第一定律,于1850年发表并得 到公认
热力学第一定律的普遍表达式
第一定律的表述: 热是能的一种,机械能变热能,或热能 变机械能的时候,他们之间的比值是一定的。 或:热可以变为功,功也可以变为热;一定量的热消失时 必定产生相应量的功;消耗一定量的功时,必出现与之相 应量的热。
系统是否作功应以过程在外界所引起的效果来判断,而不
应从系统的内部去寻找依据,对系统的内部来说无所谓 “功”。
功是有序能量传递。
传热
系统与外界之间的另一种相互作 用,是系统与外界之间依靠温差进行 的一种能量传递现象,所传递的能量 称放热为负
是系统为维持工质流动所需的功
对推动功的说明
1、与宏观流动有关,流动停止,推动功不存在 2、作用过程中,工质仅发生位置变化,无状态变化
3、w推=pv与所处状态有关,是状态量 4、并非工质本身的能量(动能、位能)变化引起, 而由外界做出,流动工质所携带的能量
可理解为:由于工质的进出,外界与系统之间
The work depends on the process path
作功的说明
“作功”是系统与外界间的一种相互作用,是越过系统边
界的能量交换。
功是指作功过程中在传递着的能量的总称,过程一旦结束
就再无所谓功。
机械能与机械功、电能与电功等同吗?
系统可以拥有电能,机械能,但决不会拥有电功、机械功之类的功。 功只不过是特定条件下在过程中传递着的能量。
实质:能量守恒及转换定律在热现象中的应用
• 18世纪初,工业革命,热效率只有1% • 1842年,J.R. Mayer阐述热力学第一定律, 但没有引起重视
• 1840-1849年,Joule用多种实验的一致性 证明热力学第一定律,于1850年发表并得 到公认
热力学第一定律的普遍表达式
第一定律的表述: 热是能的一种,机械能变热能,或热能 变机械能的时候,他们之间的比值是一定的。 或:热可以变为功,功也可以变为热;一定量的热消失时 必定产生相应量的功;消耗一定量的功时,必出现与之相 应量的热。
系统是否作功应以过程在外界所引起的效果来判断,而不
应从系统的内部去寻找依据,对系统的内部来说无所谓 “功”。
功是有序能量传递。
传热
系统与外界之间的另一种相互作 用,是系统与外界之间依靠温差进行 的一种能量传递现象,所传递的能量 称放热为负
《工程热力学》第二章 热力学第一定律

热力学第一定律是热力学的基本定律,是热 力过程能量传递与转换分析计算的基本依据。它 普遍适用于任何工质、任何过程。
6
2-2 热力学能和总能
能量是物质运动的度量,运动有各种不同的 形态,相应的就有各种不同的能量。
系统储存的能量称为储存能,它有内部储存 能与外部储存能之分。系统的内部储存能即为热 力学能
Q U W
Q 0 W ? 0 U 0 即U1 U2
强调:功是通过边界传递的能量。
30
h1 a 2
h1 b 2
2
dh
1
h2 h1
dh 0
21
三、焓的意义:
焓是物质进出开口系统时带入或带出的热力学 能与推动功之和,是随物质一起转移的能量。
焓是一种宏观存在的状态参数,不仅在开口系 统中出现,而且在分析闭口系统时,它同样存 在。
焓是随着质量交换而交换的一种“转移能”, 只有在质量跨越边界的前提下,焓的物理意义 及其能量属性才能体现出来。
第二章 热力学第一定律
1
本章基本要求
深刻理解热能、储存能、功的概念,深刻理解内 能、焓的物理意义;
理解膨胀(压缩)功、轴功、技术功、流动功的 联系与区别;
本章重点
熟练应用热力学第一定律解决具体问题
2
2-1 热力学第一定律的实质
19世纪30-40年代,迈耶,焦耳等发现并确 定了能量转换与守恒定律。恩格斯将这列为19世纪 三大发现之一(细胞学说、达尔文进化论)。
在热能与其它形式能的互相转换过程中,能的 总量始终不变。
不花费能量就可以产生功的第一类永动机是不 可能制造成功的。
4
5
进入系统的能量-离开系统的能量 = 系 统储存能量的变化
在工程热力学的范围内,主要考虑热能与机 械能之间的相互转换与守恒,因此热力学第一定 律可表述为:热可以变为功,功也可以变为热, 在相互转变时能的总量是不变的。
6
2-2 热力学能和总能
能量是物质运动的度量,运动有各种不同的 形态,相应的就有各种不同的能量。
系统储存的能量称为储存能,它有内部储存 能与外部储存能之分。系统的内部储存能即为热 力学能
Q U W
Q 0 W ? 0 U 0 即U1 U2
强调:功是通过边界传递的能量。
30
h1 a 2
h1 b 2
2
dh
1
h2 h1
dh 0
21
三、焓的意义:
焓是物质进出开口系统时带入或带出的热力学 能与推动功之和,是随物质一起转移的能量。
焓是一种宏观存在的状态参数,不仅在开口系 统中出现,而且在分析闭口系统时,它同样存 在。
焓是随着质量交换而交换的一种“转移能”, 只有在质量跨越边界的前提下,焓的物理意义 及其能量属性才能体现出来。
第二章 热力学第一定律
1
本章基本要求
深刻理解热能、储存能、功的概念,深刻理解内 能、焓的物理意义;
理解膨胀(压缩)功、轴功、技术功、流动功的 联系与区别;
本章重点
熟练应用热力学第一定律解决具体问题
2
2-1 热力学第一定律的实质
19世纪30-40年代,迈耶,焦耳等发现并确 定了能量转换与守恒定律。恩格斯将这列为19世纪 三大发现之一(细胞学说、达尔文进化论)。
在热能与其它形式能的互相转换过程中,能的 总量始终不变。
不花费能量就可以产生功的第一类永动机是不 可能制造成功的。
4
5
进入系统的能量-离开系统的能量 = 系 统储存能量的变化
在工程热力学的范围内,主要考虑热能与机 械能之间的相互转换与守恒,因此热力学第一定 律可表述为:热可以变为功,功也可以变为热, 在相互转变时能的总量是不变的。
工程热力学第二章热力学第一定律

Macroscopic energy---kinetic energy potential energy
They are related to some outside reference frame。
Kinetic energy is the energy a system possesses as a result of its motion relative to some reference frame. It is denoted as Eke.
移动 translation 分子动能 转动 rotation 振动 vibration 分子位能 binding forces
热力学能
化学能 chemical energy
核能 nuclear energy
(1)Kinetic and potential energies of the molecules
分子的动能和势能
Internal Energy=
internal kinetic energy+internal potential energy
热力学能=内动能+内位能
T
T, v
u is a function of the state of the system. u = u (p, T), or u = u (p, v), or u = u(v,T).
mc E U E ke E p U mgz 2
On a unit mass basis
2
1 2 e u eke e p u c gz 2
§2.2 Energy transfer by Heat, Work and Mass (热量、功量及质量引起的能量传递------传递中的能量)
They are related to some outside reference frame。
Kinetic energy is the energy a system possesses as a result of its motion relative to some reference frame. It is denoted as Eke.
移动 translation 分子动能 转动 rotation 振动 vibration 分子位能 binding forces
热力学能
化学能 chemical energy
核能 nuclear energy
(1)Kinetic and potential energies of the molecules
分子的动能和势能
Internal Energy=
internal kinetic energy+internal potential energy
热力学能=内动能+内位能
T
T, v
u is a function of the state of the system. u = u (p, T), or u = u (p, v), or u = u(v,T).
mc E U E ke E p U mgz 2
On a unit mass basis
2
1 2 e u eke e p u c gz 2
§2.2 Energy transfer by Heat, Work and Mass (热量、功量及质量引起的能量传递------传递中的能量)
工程热力学 第2章 热力学第一定律

6
可逆膨胀过程:
系统内部准静→系统的压力与外界压力相差只是无穷小 →可看作过程中P=Ps→微元过程中系统对外界所作的膨 胀功可完全用系统内部参数表示:
W PdV
对1kg工质的微元过程 对1→2的有限过程
m kg工质:
w Pdv
1 kg工质:
以上公式适用于任何简单可压缩物质可逆过程
2020/1/10
• 系统温度的变化与传热并无必然的联系 • 热能是微观粒子无序紊乱运动的能量;传热是微观粒
子间无序运动能量的传递
2020/1/10
12
⑵ 可逆过程的热量计算
①利用熵参数进行热量计算
热力学状态参数熵的定义
经历可逆的微元过程时,系统的熵变 量dS等于该微元过程中系统所吸入的热 量đQ与吸热当时的热源温度T之比
这时
E=U
2020/1/10
20
§2.5 控制质量(CM)能量分析
⑴热力学第一定律基本表达式
控制质量 热力过程中吸入热量Q, 对外界作功W,热力学能增加∆U 根据热力学第一定律
Q = ∆E + W W——广义功
输入能量 贮能增量 输出能量
若系统固定不动,U=E,则
Q = ∆U + W
对于微元能
⑴状态参数热力学能
物质内部拥有的能量统称为热力学能(内能)
分子平移运动、转动和振动的动能(内动能) 分子间因存在作用力而相应拥有的位能(内位能) 维持一定分子结构的化学能、分子的结合能 U 电偶极子和磁偶极子的偶极矩能 原子核能(原子能) ……(电子的运动能量等)
第2章 热力学第一定律
( The First Law of Thermodynamics )
主要内容
第2章热力学第一定律PPT课件

状态函数:描述体系状态的宏观物理量都叫状态函数 或叫状态性质,例如温度,压力,体积,质量,密度 ,浓度等等都是体系的状态函数。宏观可测性质用来 描述体系的热力学状态,故这些性质又称为热力学变 量。
16
1.2 状态和状态函数 状态
——指静止的,系统内部的状态,是各种宏观 性质的综合体现。也称热力学状态
系统:人们确立的研究对象 环境:系统以外与系统紧密相联的部分
★系统与环境之间可以是有形的物 理界面,也可以是无形的几何界面
★系统与环境之间的联系有物质交 换与能量交换两种形式
敞开系统 封闭系统 隔离系统
物质交换 √ × ×
能量交换 √ √ ×
说明:★热力学中的系统如不特 别注明都是封闭系统
★绝对的隔离系统是不存 在的
三大定律
第一定律 → 化学反应热效应 第二定律 → 化学反应方向和限度、
相平衡、化学平衡 第三定律 → 绝对熵的数值
5
热力学三大特点
1. 热力学研究的对象是由大量质点(原子和分子等)所 构成的集合体,这是热力学的最大特点。这个特点也 就决定了热力学方法的优点和缺点。
2. 对热力学来说,只需知道系统的起始状态和最终状态 以及过程进行的外界条件,就可以进行相应的计算。
1.系统与环境 系统 被划定的研究对象称为系统,亦称 为物系或体系。
环境 与系统密切相关、有相互作用
或影响所能及的部分称为环境。
系统 环境
9
物质交换
能量交换(包括热和功)
系统分类
(1)封闭系统 系统与环境之间无物质交换,但有能量交换。
(2)隔离系统 系统与环境之间既无物质交换,又无能量交换,故 又称为孤立系统。有时把封闭系统和系统影响所及 的环境一起作为孤立系统来考虑。
16
1.2 状态和状态函数 状态
——指静止的,系统内部的状态,是各种宏观 性质的综合体现。也称热力学状态
系统:人们确立的研究对象 环境:系统以外与系统紧密相联的部分
★系统与环境之间可以是有形的物 理界面,也可以是无形的几何界面
★系统与环境之间的联系有物质交 换与能量交换两种形式
敞开系统 封闭系统 隔离系统
物质交换 √ × ×
能量交换 √ √ ×
说明:★热力学中的系统如不特 别注明都是封闭系统
★绝对的隔离系统是不存 在的
三大定律
第一定律 → 化学反应热效应 第二定律 → 化学反应方向和限度、
相平衡、化学平衡 第三定律 → 绝对熵的数值
5
热力学三大特点
1. 热力学研究的对象是由大量质点(原子和分子等)所 构成的集合体,这是热力学的最大特点。这个特点也 就决定了热力学方法的优点和缺点。
2. 对热力学来说,只需知道系统的起始状态和最终状态 以及过程进行的外界条件,就可以进行相应的计算。
1.系统与环境 系统 被划定的研究对象称为系统,亦称 为物系或体系。
环境 与系统密切相关、有相互作用
或影响所能及的部分称为环境。
系统 环境
9
物质交换
能量交换(包括热和功)
系统分类
(1)封闭系统 系统与环境之间无物质交换,但有能量交换。
(2)隔离系统 系统与环境之间既无物质交换,又无能量交换,故 又称为孤立系统。有时把封闭系统和系统影响所及 的环境一起作为孤立系统来考虑。
第二章 热力学第一定律Microsoft PowerPoint 演示文稿
6.热力学第一定律
2-3 恒容热、恒压热、焓
1.恒容热 恒容热是系统在恒容且非体积功为零的过程中 与环境交换的热,其符号为QV
根据热力学第一定律: dU=δQ+δW 恒容,W=0 QV=U 或 δQV=dU (dV=0, W′=0,封闭系统) 表明:在恒容且W′=0的过程中,恒容热等于热力学 能的改变。
Z Z dz dx dy y x y x
以 V = f (p,T ) 为例
V V dV p dp T dT p T
6.热力学平衡态
定义:系统在一定条件下,经足够长的时间,
3.焓的单位:J 或 kJ
4.对于物质量恒定的系统,系统的焓可以表示为温度、压力 的函数 即H=f(T,P) 5.焓的绝对值无法确定
4.盖斯定律:一个化学反应,不管是一步完成还 是几步完成,反应的恒容热与恒压热只取决于
始末状态与途径无关。
例如(1) C(S)+O 2(g)= CO 2 (g) QP,1 (2) C(S) +1/2O 2(g)= CO (g) QP,2 (3) CO (g) +1/2O 2(g)= CO 2 (g) QP,3 QP,1与QP,3能从实验中测得,但QP,2却很难测得 由于QP,1 = △H 1 , QP,2 =△H 2 , QP,3 =△H 3 而状态函数 的改变只与始末状态有关,由反应方程得(2)= (1)- (3) 故△H 2 = △H 1 - △H 3 于是QP,2 = QP,1 - QP,3
第二章 热力学第一定律 2-1 热力学基本概念
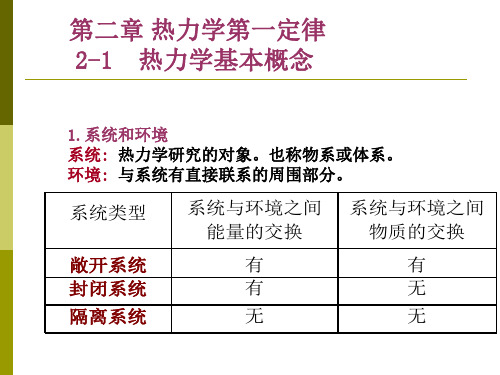
1.系统和环境 系统: 热力学研究的对象。也称物系或体系。 环境: 与系统有直接联系的周围部分。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国民航大学航空工程学院发动机系工程热物理教研室
23
工程热力学——热力学第一定律
推进功的表达式 推进功(流动功、推动功) A
Flow work W推 = p A dl = pV w推= pv
注意:
不是 pdv v 没有变化
2014-12-30
p
p V
dl
中国民航大学航空工程学院发动机系工程热物理教研室
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 25
工程热力学——热力学第一定律
开口系能量方程的推导
uin
pvin gzin Wnet mout uout pvout 1 2 c gzout 2 out
26
min
1 2 cin 2
Q
Q + min(u + c2/2 + gz)in - mout(u + c2/2 + gz)out - Wnet = dEcv
内能总以变化量出现,内能零点人为定
2014-12-30
中国民航大学航空工程学院发动机系工程热物理教研室
13
工程热力学——热力学第一定律
热一律的文字表达式
热一律: 能量守恒与转换定律
进入系统 的能量 Total energy entering the system
2014-12-30
-
离开系统 的能量 Total energy leaving the system
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 6
工程热力学——热力学第一定律
Perpetual –motion machine of the first kind
Q
锅 炉
电 加 热 器
汽轮机
发电机
凝 汽 器
Wnet
给水泵
2014-12-30
Qout
7
中国民航大学航空工程学院发动机系工程热物理教研室
Q dE (e2m2 e1m1 ) Wtot
E U Ek Ep
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 15
工程热力学——热力学第一定律
Energy balance for closed system
一般式 Q = dU + W Q = U + W q = du + w q = u + w
1842年,J.R. Mayer阐述热一律,但没有 引起重视 1840-1849年,Joule用多种实验的一致性 证明热一律,于1850年发表并得到公认
1909年,C. Caratheodory最后完善热一律
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 2
工程热力学——热力学第一定律
w = pdv - dl - dA +…...
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 17
工程热力学——热力学第一定律
闭口系能量方程的通式 q = du + w 若在地球上研究飞行器
q = de + w = du + dek + dep + w
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室
工程热力学——热力学第一定律
开口系能量方程微分式
Q + min(u + pv+c2/2 + gz)in - Wnet - mout(u + pv+c2/2 + gz)out = dEcv
工程上常用流率
Q Q lim 0
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 19
工程热力学——热力学第一定律
门窗紧闭房间用电冰箱降温 以房间为系统 闭口系能量方程 绝热闭口系 Refrigerator Icebox
电 冰 箱
20
Q U W Q0
W 0
U W 0
T
2014-12-30
工质经历循环:
Q W
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 5
工程热力学——热力学第一定律
闭口系循环的热一律表达式
Q W
要想得到功,必须花费热能或其它能量
热一律又可表述为“第一类永动机是
不可能制成的” Perpetual –motion machine of the first kind
系统总能 E = U + Ek + Ep e = u + ek + ep
一般与系统同坐标,常用U, dU, u, du
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 12
工程热力学——热力学第一定律
内能的说明 内能是状态量 state property U : 广延参数 [ kJ ] u : 比参数 [kJ/kg]
状态参数
2014-12-30
( Q W )
1a 2
1b 2
( Q W )
8
中国民航大学航空工程学院发动机系工程热物理教研室
工程热力学——热力学第一定律
内能及闭口系热一律表达式 定义 dU = Q - W 内能U 状态函数
Q = dU + W Q=U+W
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 11
工程热力学——热力学第一定律
系统总能 total energy 外部储存能macroscopic forms of energy
宏观动能 kinetic Ek= mc2/2 宏观位能 potential Ep= mgz 机械能
22
中国民航大学航空工程学院发动机系工程热物理教研室
工程热力学——热力学第一定律
推进功的引入 min 1 2 uin cin 2 gzin
这个结果与实验 不符
Wnet uout mout gzout 1 c 2 out 2
少了推进功
Q
2014-12-30
Q + min(u + c2/2 + gz)in - mout(u + c2/2 + gz)out - Wnet = dEcv
§2-2 闭口系能量方程
Q
W
单位工质
适用条件: 1)任何工质 2) 任何过程
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 16
工程热力学——热力学第一定律
闭口系能量方程中的功 q = du + w 功 ( w) 是广义功 闭口系与外界交换的功量 准静态容积变化功 拉伸功 表面张力功 pdv w拉伸= - dl w表面张力= - dA
工程热力学用此式较少
2014-12-30
中国民航大学航空工程学院发动机系工程热物理教研室
18
工程热力学——热力学第பைடு நூலகம்定律
准静态和可逆闭口系能量方程 简单可压缩系准静态过程 w = p dv q = du + pdv 热一律解析式之一 q = u + pdv 简单可压缩系可逆过程 q = Tds Tds = du + pdv 热力学恒等式 Tds = u + pdv
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 27
工程热力学——热力学第一定律
开口系能量方程微分式 当有多条进出口:
Q dEcv / W net u pv c / 2 gz
2 2 out
m out
u pv c / 2 gz min
u h pv c / 2 gz min
in
开口系能量方程
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 29
工程热力学——热力学第一定律
焓Enthalpy的 说明 定义:h = u + pv H = U + pV
1、焓是状态量 state
[ kJ/kg ] [ kJ ]
24
工程热力学——热力学第一定律
对推进功的说明
1、与宏观流动有关,流动停止,推进功不存在 2、作用过程中,工质仅发生位置变化,无状态变化 3、w推=pv与所处状态有关,是状态量
4、并非工质本身的能量(动能、位能)变化引起,
而由外界做出,流动工质所携带的能量
可理解为:由于工质的进出,外界与系统之
间所传递的一种机械功,表现为流动工质进 出系统时所携带和所传递的一种能量
闭口系热一律表达式
!!!两种特例 绝功系 Q = dU 绝热系 W = - dU
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 9
工程热力学——热力学第一定律
内能U 的物理意义 dU = Q - W
Q
W
dU 代表某微元过程中系统通过边界 交换的微热量与微功量两者之差值,也 即系统内部能量的变化。
U 代表储存于系统内部的能量 内储存能(内能、热力学能)
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 10
工程热力学——热力学第一定律
内能的组成
microscopic forms of energy
移动 translation 分子动能 转动 rotation 振动 vibration 分子位能 binding forces 内能 化学能 chemical energy 核能 nuclear energy
23
工程热力学——热力学第一定律
推进功的表达式 推进功(流动功、推动功) A
Flow work W推 = p A dl = pV w推= pv
注意:
不是 pdv v 没有变化
2014-12-30
p
p V
dl
中国民航大学航空工程学院发动机系工程热物理教研室
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 25
工程热力学——热力学第一定律
开口系能量方程的推导
uin
pvin gzin Wnet mout uout pvout 1 2 c gzout 2 out
26
min
1 2 cin 2
Q
Q + min(u + c2/2 + gz)in - mout(u + c2/2 + gz)out - Wnet = dEcv
内能总以变化量出现,内能零点人为定
2014-12-30
中国民航大学航空工程学院发动机系工程热物理教研室
13
工程热力学——热力学第一定律
热一律的文字表达式
热一律: 能量守恒与转换定律
进入系统 的能量 Total energy entering the system
2014-12-30
-
离开系统 的能量 Total energy leaving the system
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 6
工程热力学——热力学第一定律
Perpetual –motion machine of the first kind
Q
锅 炉
电 加 热 器
汽轮机
发电机
凝 汽 器
Wnet
给水泵
2014-12-30
Qout
7
中国民航大学航空工程学院发动机系工程热物理教研室
Q dE (e2m2 e1m1 ) Wtot
E U Ek Ep
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 15
工程热力学——热力学第一定律
Energy balance for closed system
一般式 Q = dU + W Q = U + W q = du + w q = u + w
1842年,J.R. Mayer阐述热一律,但没有 引起重视 1840-1849年,Joule用多种实验的一致性 证明热一律,于1850年发表并得到公认
1909年,C. Caratheodory最后完善热一律
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 2
工程热力学——热力学第一定律
w = pdv - dl - dA +…...
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 17
工程热力学——热力学第一定律
闭口系能量方程的通式 q = du + w 若在地球上研究飞行器
q = de + w = du + dek + dep + w
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室
工程热力学——热力学第一定律
开口系能量方程微分式
Q + min(u + pv+c2/2 + gz)in - Wnet - mout(u + pv+c2/2 + gz)out = dEcv
工程上常用流率
Q Q lim 0
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 19
工程热力学——热力学第一定律
门窗紧闭房间用电冰箱降温 以房间为系统 闭口系能量方程 绝热闭口系 Refrigerator Icebox
电 冰 箱
20
Q U W Q0
W 0
U W 0
T
2014-12-30
工质经历循环:
Q W
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 5
工程热力学——热力学第一定律
闭口系循环的热一律表达式
Q W
要想得到功,必须花费热能或其它能量
热一律又可表述为“第一类永动机是
不可能制成的” Perpetual –motion machine of the first kind
系统总能 E = U + Ek + Ep e = u + ek + ep
一般与系统同坐标,常用U, dU, u, du
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 12
工程热力学——热力学第一定律
内能的说明 内能是状态量 state property U : 广延参数 [ kJ ] u : 比参数 [kJ/kg]
状态参数
2014-12-30
( Q W )
1a 2
1b 2
( Q W )
8
中国民航大学航空工程学院发动机系工程热物理教研室
工程热力学——热力学第一定律
内能及闭口系热一律表达式 定义 dU = Q - W 内能U 状态函数
Q = dU + W Q=U+W
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 11
工程热力学——热力学第一定律
系统总能 total energy 外部储存能macroscopic forms of energy
宏观动能 kinetic Ek= mc2/2 宏观位能 potential Ep= mgz 机械能
22
中国民航大学航空工程学院发动机系工程热物理教研室
工程热力学——热力学第一定律
推进功的引入 min 1 2 uin cin 2 gzin
这个结果与实验 不符
Wnet uout mout gzout 1 c 2 out 2
少了推进功
Q
2014-12-30
Q + min(u + c2/2 + gz)in - mout(u + c2/2 + gz)out - Wnet = dEcv
§2-2 闭口系能量方程
Q
W
单位工质
适用条件: 1)任何工质 2) 任何过程
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 16
工程热力学——热力学第一定律
闭口系能量方程中的功 q = du + w 功 ( w) 是广义功 闭口系与外界交换的功量 准静态容积变化功 拉伸功 表面张力功 pdv w拉伸= - dl w表面张力= - dA
工程热力学用此式较少
2014-12-30
中国民航大学航空工程学院发动机系工程热物理教研室
18
工程热力学——热力学第பைடு நூலகம்定律
准静态和可逆闭口系能量方程 简单可压缩系准静态过程 w = p dv q = du + pdv 热一律解析式之一 q = u + pdv 简单可压缩系可逆过程 q = Tds Tds = du + pdv 热力学恒等式 Tds = u + pdv
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 27
工程热力学——热力学第一定律
开口系能量方程微分式 当有多条进出口:
Q dEcv / W net u pv c / 2 gz
2 2 out
m out
u pv c / 2 gz min
u h pv c / 2 gz min
in
开口系能量方程
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 29
工程热力学——热力学第一定律
焓Enthalpy的 说明 定义:h = u + pv H = U + pV
1、焓是状态量 state
[ kJ/kg ] [ kJ ]
24
工程热力学——热力学第一定律
对推进功的说明
1、与宏观流动有关,流动停止,推进功不存在 2、作用过程中,工质仅发生位置变化,无状态变化 3、w推=pv与所处状态有关,是状态量
4、并非工质本身的能量(动能、位能)变化引起,
而由外界做出,流动工质所携带的能量
可理解为:由于工质的进出,外界与系统之
间所传递的一种机械功,表现为流动工质进 出系统时所携带和所传递的一种能量
闭口系热一律表达式
!!!两种特例 绝功系 Q = dU 绝热系 W = - dU
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 9
工程热力学——热力学第一定律
内能U 的物理意义 dU = Q - W
Q
W
dU 代表某微元过程中系统通过边界 交换的微热量与微功量两者之差值,也 即系统内部能量的变化。
U 代表储存于系统内部的能量 内储存能(内能、热力学能)
2014-12-30 中国民航大学航空工程学院发动机系工程热物理教研室 10
工程热力学——热力学第一定律
内能的组成
microscopic forms of energy
移动 translation 分子动能 转动 rotation 振动 vibration 分子位能 binding forces 内能 化学能 chemical energy 核能 nuclear energy
