时间延缓长度收缩
相对论、长度收缩、时间延缓讲解

上一章我们讲了狭义相对论中的洛伦兹变换,并且知道了光速是一不同参考系中,长度和时 间的测量都是一样的,比如在S系中有一个一米长的物体,在S'系中测量也是一米, 但是在狭义相对论中结果却有所不同,
图1为S'系相对于S以速度v运动,一观察者在S'系中同时测得木棒两端的坐标为x1' 和x2',于是棒的长度为L' = x2'- x1',通常把木棒相对于观察者静止的长度叫做固 有长度L0,即L0 = L',根据洛伦兹变换式,在同一时刻t1= t2的情况下,木棒两 端的坐标分别为x1'= (x1-vt1)/(1-β^2)^1/2, x2'= (x2-vt1)/(1-β^2)^1/2,则x2'- x1'= (x2- x1)/(1-β^2)^1/2,也就是木棒在 S系中的长度为:
L = x2 - x1 = L0(1-β^2)^1/2,
因为(1-β^2)^1/2是小于1的,因此L的值就要比木棒固有长度L0小,所以当物体 以接近光速的速度运动时,物体将会沿运动方向收缩,这种收缩叫做洛伦兹收缩, 你之所以察觉不到物体的收缩效应,除了眼睛反应不过来以外,还有宏观物体的运 动速度与光速相比太小,长度相对收缩的数量级约为10^-10,完全 可以忽略不计。
现在我们可以得出结论,在狭义相对论中,对空间和时间的测量与惯性系的选择有 关,时间与空间是相互联系的,且与物质有密不可分的关系,不存在孤立的时间, 也不存在孤立的空间,时间、空间、物质三者之间的相互联系反应了时空 的性质。
说完了时间、空间与物质,下一章《从时间延缓效应来看时空穿梭,严格意义上讲 只是在和光速较劲》就说说大家最关心的时空穿越问题,从最理性的角度来看看相 对论中的穿越和影视剧中的穿越到底有什么不同。
第4章 狭义相对论
第4章 狭义相对论一、基本要求1.掌握运动时间延缓和运动长度收缩原理; 2.理解质速关系和质能关系。
二、基本内容(一)本章重点和难点:重点:狭义相对论时空观中运动时间延缓和运动长度收缩。
难点:相对论动力学中质能关系。
(二)知识网络结构图:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧=⎩⎨⎧⎩⎨⎧)(2mc (E )质能关系运动质量变大质速关系相对论动力学运动长度收缩运动时间延缓相对论运动学光速不变原理爱因斯坦相对性原理基本原理(三)容易混淆的概念: 1.静止长度和运动长度静止长度0l ,也称固有长度,即观察者和被测物体在同一参照系所测长度;运动长度l ,即观察者和被测物体不在同一参照系所测长度。
2. 静止时间和运动时间静止时间0τ,也称固有时,即观察者和被测事件在同一参照系所测时间;运动时间τ,即观察者和被测事件不在同一参照系所测时间。
3.总能量、静能量和动能总能量E 由爱因斯坦质能关系式,等于动质量和光速的平方的乘积;静能量0E 等于静质量和光速的平方的乘积;动能k E 即总能量与静能量之差。
(四)主要内容:1.经典力学的相对性原理:一切彼此相对作匀速直线运动的诸惯性系中的力学规律是一样的。
即力学规律的数学形式都是相同的。
2.狭义相对论基本原理:(1)爱因斯坦相对性原理:物理定律在所有惯性参考系内都是等价的。
(2)光速不变原理:在所有惯性系中,光在真空中的速度恒等于c 。
3.洛伦兹变换:若S S 、'分别为两惯性系,S 系相对S '系以v 沿x 轴运动,在0='=t t 时两系重合,则一质点(或一事件)在S 系中的时空坐标(x 、y 、z 、t )与在S '系中的时空坐标(x '、y '、z '、t ')之间的关系为洛伦兹时空变换。
(1)洛伦兹时空变换同一事件在S 系中时空坐标(x 、y 、z 、t )与在S '系中的时空坐标(x '、y '、z '、t ')之间的关系为:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧='='--='--='z z y y c v vt x x c v x c v t t 222)(1)(1逆变换为:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧'='=-+'=-+=z z y y c v vtx x c v x c v t t 222)(1)(1(2)洛伦兹速度变换某质点相对于S 系速度u ,与相对S '系速度u '之间的关系为:PcE 021c vu v u u x x x--=';221)(1c v u c v u u x y y --=';221)(1c v u cvu u x z z --='逆变换为:21c vu v u u x xx '++'=;221)(1c v u c v u u x y y '+-'=;221)(1c v u c v u u x z z '+-'=4.狭义相对论时空观:(为简化公式,可令:22221,11c v cv -=-=βγ) (1)运动时间延缓公式:2201c v -=ττ其中:0τ为静止时间,也称固有时,即观察者和被测事件在同一参照系所测时间;τ为运动时间,即观察者和被测事件不在同一参照系所测时间。
长度收缩时间延缓

12
93 6
d
x2
12 x
93 6
在S′系中观测时间间隔:
Δt 2d c
固有时间: 同一地点发生的 两事件的时间间隔。
在 S 系中观测时间间隔:
Δt 2 d 2 ( v t)2 c 2
t 2d
1v2 c2c Nhomakorabeat
t
1
v2 c2
结论:
(1)固有时间最短
(2)时间延缓是相对的
此棒的长度以及棒与 Ox 轴的夹角是多少?
设 S 系相对 S 系的运动速度 v 3c 2 .
y y' v
l
' y
'
o o'
'
l
' x
'
x'x
解 在 S' 系 ' 45 , l' 1m
l'x' l'y' 2 / 2m
v 3c 2
在 S 系 ly l'y' 2 / 2m
(3)时间延缓不只限于钟变慢,而是指一切发生在 运动物体上的过程相对静止的观测者来说都 变慢了,例如新陈代谢、放射性的衰变、寿命。
例2 设想一光子火箭以 v 0.95c
速率相对地球作直线运动 ,火箭上宇航员 的计时器记录他观测星云用去 10 min , 则 地球上的观察者测此事用去多少时间 ?
vt) (x1
1
v2 c2
vt)
x2 x1
1
v2 c2
l
1
v2 c2
l l0
1
v2 c2
长度收缩时间延缓

例2 设想一光子火箭以 v 0.95c
速率相对地球作直线运动,火箭上宇航员 的计时器记录他观测星云用去 10 min , 则 地球上的观察者测此事用去多少时间?
解 设火箭为 S 系、地球பைடு நூலகம்S 系
Δt' 10min
Δt Δt' 10 min 32.01min
1 2 1 0.952
运动的钟似乎走慢了.
vt)
x2 x1 1 v2
c2
c2
l
1 v2 c2
v2
l l0 1 c2
v
结论:
1 相对于观察者运动的物体长度缩短了 2 长度收缩只发生在运动方向上 3 长度收缩相对的
例1 长为 1 m 的棒静止地放在 O' x' y'
平面内,在 S'系的观察者测得此棒与 O' x' 轴成 45 角,试问从 S 系的观察者来看,
固有时间: 同一地点发生的 两事件的时间间隔。
在 S 系中观测时间间隔:
Δt 2 d 2 ( v t)2 c 2
v2 t 2d 1 c2 c
t
t v2
1 c2
结论:
1 固有时间最短
2 时间延缓是相对的 3 时间延缓不只限于钟变慢,而是指一切发生在
运动物体上的过程相对静止的观测者来说都 变慢了,例如新陈代谢、放射性的衰变、寿命。
此棒的长度以及棒与 Ox 轴的夹角是多少?
设 S 系相对 S 系的运动速度 v 3c 2 .
y y' v
l'
y'
o o'
' lx' 'x'x
解 在 S'系
狭义相对论的时空观

一. 同时性的相对性
1. 地面观测者观测
v
乙
甲
甲接受的信号
乙接受的信号
甲乙接受的信号
地
• 同时接受到前后灯信号,两灯同时亮
面
• 灯同时亮,火车运动使乙首先接受到前灯信号
2. 车上观测者观测
v
乙
甲
甲接受的信号
乙接受的信号
甲乙接受的信号
火
• 先接到前灯信号,所以前灯先亮
车
• 地面的运动抵消了发光的时间差,使甲同时接受到前后灯信号
总结:
先接到前灯信号 前灯先亮
v
同时接受两 灯信号
两灯同时亮
两个异地事件,在一个惯性系中是同时的,在另 一个惯性系中观察,则二者不是同时发生的。
二. 时间延缓
h
u
火车系
车上测者测量
二. 时间延缓
火车系 地面系
甲
地
面 系
车的长度= 车 走过的路程 = 火车速度u 时间0
火
车
系
车的长度= 地面 走过的路程 = 地面速度u 时间
静止长度
(原长)
塔的路程
v
乙
甲
火
车
系
车的长度= 地面 走过的路程 = 地面速度 时间
静止长度
(原长)
三 长度收缩
经开历始了计0时时间
经历了 时间
u
乙
甲
车厢前端和塔相遇——A 事件 后端和塔相遇——B 事件
lh
h
ut
u
在火车上,信号的发出 和接收属同地事件,测
得时间间隔称为原时
• 一对事件,在不同的惯性系中,时间间隔不同;
• 同地事件时间间隔—— 原时t‘ 最短。
钟慢效应和尺缩效应

钟慢效应和尺缩效应
钟慢尺缩:亦称时慢尺缩。
根据爱因斯坦的狭义相对论,特别是其中提出的钟慢尺缩论断。
当一个物体运动速度接近光速时,物体周围的时间会迅速减慢、空间会迅速缩小。
当物体运动速度等于光速时,时间就会停止、空间就会微缩为点,也就是说出现零时空。
只有零静止质量的物体才能达到光速。
没有物体可以超越光速。
狭义相对论认为,时空也具有多普勒效应,钟慢尺缩就是这种效应的一个表现。
当一个物体运动速度接近光速时,物体周围的时间就会迅速变慢,空间会迅速缩小。
当达到光速时,时间就会停止,空间会缩小为零。
这种效应在低速状态下表现得很微小,无法觉察和检测,接近光速时才会明显出现。
因此,在光速飞船上的人,并不会感觉到时间减慢,只不过是没有花时间而已,因为空间已经变成了0,自己没走,怎么会感觉到了时间流逝呢?而在外面观察的人,与飞船里的人不在一个惯性参考系,才能感觉到他们的时间流逝的特别慢。
等这艘飞船到100光年距离的地方转了一圈,地球上已经过了200年,而飞船里的人感觉没花时间。
但这个世界光子能够达到光速,是因为光子不会停止,因此没有静止质量,只有动质量。
光子的动量为p=h/λ=hv/c,其中v为频率,λ为波长,c为光速,h为普朗克常数。
普朗克常数为:h=6.62606896(33)×10^(-34) J·s。
7.5相对论时空观与牛顿力学的局限性高一物理学与练(人教版2019)(原卷版)

7.5 相对论时空观与牛顿力学的局限性(一)课前研读课本,梳理基础知识:一、两个假设 (1)狭义相对性原理:在不同的 参考系中,一切物理规律都是 的。
(2)光速不变原理: 的光速在不同的 参考系中都是相同的,光速和光源、观测者间的 运动没有关系。
二、两个效应(1)时间延缓效应:Δt = (2)长度收缩效应:l =三、质速关系:m =(二)即时练习:【小试牛刀1】如图所示,沿平直铁路线有间距相等的三座铁塔A 、B 和C .假想有一列车沿AC 方向以接近光速的速度行驶,当铁塔B 发出一个闪光,列车上的观测者测得A 、C 两铁塔被照亮的顺序是( )A .同时被照亮B .A 先被照亮C .C 先被照亮D .无法判断【小试牛刀2】(多选)对于公式m =m 01-⎝⎛⎭⎫v c 2,下列说法中正确的是( )A .公式中的m 0是物体以速度v 运动时的质量B .当物体运动速度v >0时,物体的质量m >m 0,即物体的质量改变了,故经典力学不再适用C .当物体以较小的速度运动时,质量变化十分微小,经典力学理论仍然适用,只有当物体以接近光速的速度运动时,质量变化才明显,故经典力学仅适用于低速运动,而不适用于高速运动D.通常由于物体的速度太小,质量的变化不能引起我们的感觉,在分析地球上物体的运动时,不必考虑质量变化【小试牛刀3】π+介子是一不稳定粒子,平均寿命是2.60×10-8s(在它自己参考系中测得).(1)如果此粒子相对于实验室以0.8c的速度运动,那么在实验室坐标系中测量的π+介子寿命多长?(2)π+介子在衰变前运动了多长距离?03【题型一】光速不变原理【典型例题1】如图所示,强强乘坐速度为0.9c(c为光速)的宇宙飞船追赶正前方的壮壮,壮壮的飞行速度为0.5c,强强向壮壮发出一束光进行联络,则壮壮观测到该光束的传播速度为()A.0.4c B.0.5c C.0.9c D.c【典型例题2】关于狭义相对论的说法,不正确的是()A.狭义相对论认为在不同的惯性参考系中,一切物理规律都是相同的B.狭义相对论认为在一切惯性参考系中,光在真空中的速度都等于c,与光源的运动无关C.狭义相对论只涉及无加速运动的惯性系D.狭义相对论任何情况下都适用【对点训练1】如图所示,考虑几个问题:(1)如图所示,参考系O′相对于参考系O静止时,人看到的光速应是多少?(2)参考系O′相对于参考系O以速度v向右运动,人看到的光速应是多少?(3)参考系O相对于参考系O′以速度v向左运动,人看到的光速又是多少?【对点训练2】(多选)设某人在速度为0.5c的飞船上打开一个光源,则下列说法正确的是()A.飞船正前方地面上的观察者看到这一光速为1.5cB.飞船正后方地面上的观察者看到这一光速为0.5cC.在垂直飞船前进方向地面上的观察者看到这一光速是cD.在地面上任何地方的观察者看到的光速都是c【题型二】时间延缓效应【典型例题3】(多选)接近光速飞行的飞船和地球上各有一只相同的铯原子钟,飞船和地球上的人观测这两只钟的快慢,下列说法正确的有()A.飞船上的人观测到飞船上的钟较快B.飞船上的人观测到飞船上的钟较慢C.地球上的人观测到地球上的钟较快D.地球上的人观测到地球上的钟较慢【典型例题4】长度测量与被测物体相对于观察者的运动有关,一艘宇宙飞船的船身长度为l0=90 m,相对地面以v=0.8c的速度在一观测站的上空飞过。
3.3时间延缓和长度收缩_864108022

3.3.2 时间延缓 同时性具有相对性,对不同参考系而言, 同时性具有相对性,对不同参考系而言 ,沿 相对速度方向发生的同样的两个事件之间的时 间间隔是不同的 时间的量度是相对的 时间的量度是相对的 设在S'系中的同一地点x'处 设在 系中的同一地点 处,先、后发生两个 系中的同一地点 ′ ′ ′ ′ 事件 ( x′, t1 ) 和 ( x′, t 2 ) ,时间间隔 ∆t ′ = t 2 − t1 > 0 。 系中这两个事件一定不同地发生, 在S系中这两个事件一定不同地发生,它们的 系中这两个事件一定不同地发生 时间间隔∆ 时间间隔∆t :
−5
因此果律(自学) 】证明狭义相对论符合因果律(自学)
3.3.3 长度收缩 对静止物体长度的测量: 对静止物体长度的测量:测出物体两 端的坐 就是物体的长度( 标,差值 ∆x′ 就是物体的长度(称为物体的原 长),对测量的先后次序没有要求 , 可以不同 对测量的先后次序没有要求, 时测量物体两端的坐标, 时测量物体两端的坐标,t1' 可以不等于 t2'。 。 对运动物体长度的测量: 对运动物体长度的测量:只 有 同 时 测 定 物 体 两端的坐标,t1=t2,差值 ∆x 才是物体的长度。 两端的坐标, 才是物体的长度。 定义两个事件: 定义两个事件:测量物体两端坐标
′ 1 − u2 c 2 ∆l = ∆l
测长最短 对长度收缩效应的更普遍说法
•在涉及某个参考系中两个同时发生的事件的问 在涉及某个参考系中两个同时发生的事件的问 题中,一般应先确定哪个是测长。 题中,一般应先确定哪个是测长。 • 长度收缩与同时性的相对性有关 , 是不同惯 长度收缩与同时性的相对性有关, 性系之间进行时间测量的结果。 性系之间进行时间测量的结果。 • 长度收缩只发生在物体运动的方向上,在垂直 长度收缩只发生在物体运动的方向上, 方向上不收缩 纵向收缩,横向不收缩。 纵向收缩,横向不收缩。 • 长度收缩纯属时空性质,与在热胀冷缩现象中 长度收缩纯属时空性质, 所发生的实际的收缩和膨胀是完全不同的。 所发生的实际的收缩和膨胀是完全不同的。
大学物理:第11章-相对论2-长度收缩和时间延缓
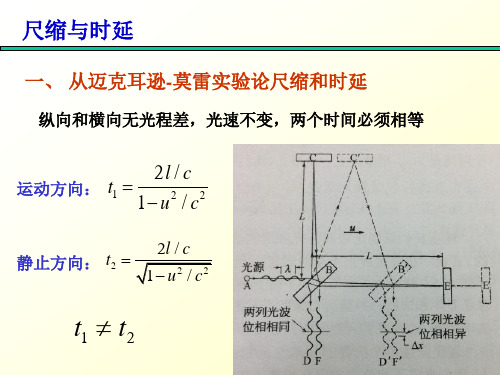
例 一飞船以 u = 9000m/s 的速率相对于地面 ( 假定为
惯性系) 匀速飞行。 飞船上的钟走了 5s 的时间,用地
面上的钟测量经过了多少时间?地面上的钟走了 5s 的
时间,用飞船上的钟测量经过了多少时间?
解:飞船上的钟测量飞船上的时间间隔,首末两个事
件在同一地点发生,所以此时间是固有时, t 5s
解:(1) S’系,非同一地点,不是固有时。
(2) S系,非同一时间,也不能用尺缩的概念, 但是,可以直接用洛仑兹变换
x
x ' ut '
90 0.80c 90
c 270m
1 u2 / c2
1 0.82
例2. 如图所示,一长为1m的棒静止地放在O’x’y’平面内。
在S’系的观察者测得此棒与O’x’轴成450角。试问若S系
的观察者观察,此棒的长度以及棒与Ox轴的夹角是多
S ':自坐标,自己看自己
看静止的对象:地面上看地面上发生的事情 静止地看对象:火车里看火车里发生的事情
是否运动并不能用来区分S和S’ 关键在于区分自和他!
讨论
1.运动的棒长度收缩是空间本身的客观特征。 2.运动的棒长度收缩是一种相对效应。
别人(运动)永远比自己短, 谁都可以是那个“别人”或“自己” 3.纵向效应 运动方向(纵向)
解一:米尺,固有长的角度。
l0 1m 是固有长度 观察者测得的米尺长度,运动长度
l l0 1 u2 / c2 1 1 0.62 0.8m 在观察者参考系中,运动长掠过观察者的时间为
t
l u
0.8 0.6 3 108
4.44 109 s
同一个观察系中 的长度和速度
解二:米尺掠过观察者,固有时角度
5 相对论时空观与牛顿力学的局限性

相对论时空观与牛顿力学的局限性核心素养目标物理观念 知道爱因斯坦的两条假设,了解时间延缓效应、长度收缩效应,认识牛顿力学的成就与局限性。
科学思维 知道牛顿力学的适用范围,认识物理学中理论的相对稳定性,要有质疑精神。
科学探究认识迈克耳孙—莫雷实验对光速不变原理的推动作用,体会实验和理论的相互关系。
知识点一 相对论时空观1.爱因斯坦假设(1)在不同的惯性参考系中,物理规律的形式都是相同的。
(2)真空中的光速在不同的惯性参考系中大小都是相同的。
2.时间延缓效应如果相对于地面以v 运动的惯性参考系上的人观察到与其一起运动的物体完成某个动作的时间间隔为Δτ,地面上的人观察到该物体在同一地点完成这个动作的时间间隔为Δt ,那么两者之间的关系是Δt =Δτ1-⎝ ⎛⎭⎪⎫v c 2 由于1-⎝ ⎛⎭⎪⎫v c 2<1,所以总有Δt >Δτ,此种情况称为时间延缓效应。
3.长度收缩效应如果与杆相对静止的人测得杆长是l 0,沿着杆的方向,以v 相对杆运动的人测得杆长是l ,那么两者之间的关系是l =l 01-⎝ ⎛⎭⎪⎫v c 2 由于1-⎝ ⎛⎭⎪⎫v c 2<1,所以总有l <l 0,此种情况称为长度收缩效应。
惯性参考系凡是牛顿运动定律成立的参考系,称为惯性参考系,简称惯性系。
①所有相对于惯性系做匀速直线运动的参考系都是惯性系。
②所有相对于惯性系做变速运动的参考系都是非惯性系。
运动物体的长度(空间距离)和物理过程的快慢(时间进程)都跟物体的运动状态有关。
知识点二牛顿力学的成就与局限性1.牛顿力学的成就从地面上物体的运动到天体的运动,从拦河筑坝、修建桥梁到设计各种机械,从自行车到汽车、火车、飞机等现代交通工具的运动,从投出篮球到发射导弹、人造地球卫星、宇宙飞船……所有这些都服从牛顿力学的规律。
2.牛顿力学的局限性(1)牛顿力学不适用于高速运动。
(2)物理学研究深入到微观世界,发现了电子、质子、中子等微观粒子,而且发现它们不仅具有粒子性,同时还具有波动性,它们的运动规律在很多情况下不能用牛顿力学来说明。
AE中实现时间延缓效果的技巧

AE中实现时间延缓效果的技巧Adobe After Effects(简称AE)是一款专业的视频合成与特效制作软件,广泛应用于电影制作、广告宣传、动画制作等领域。
在AE中,我们可以通过一些技巧实现时间的延缓效果,使画面变得更加有趣、独特。
本文将介绍一些常用的实现时间延缓效果的技巧。
一、时间伸缩时间伸缩是实现时间延缓效果最常用的方法之一。
在AE中,我们可以通过调整合成层的时间比例来实现。
具体操作如下:1. 选中要进行时间延缓的合成层,在时间轴面板右键点击“时间”选项,选择“时间伸缩”。
2. 在弹出的对话框中,可以设置时间比例。
值为100%表示正常速度播放,小于100%表示减慢速度播放,大于100%表示加快速度播放。
通过时间伸缩技巧,我们可以更改整个合成层的播放速度,从而实现时间延缓的效果。
这种方法在制作慢动作效果时尤为常用。
二、时间倒放时间倒放是另一种常见的实现时间延缓效果的技巧。
通过将合成层的时间反转,可以使画面逆序播放,从而产生时光倒流的效果。
具体操作如下:1. 选中要进行时间延缓的合成层,在时间轴面板右键点击“时间”选项,选择“时间倒放”。
2. 在弹出的对话框中,可以选择倒放范围。
选择“全部倒放”时,整个合成层都将以倒序播放。
时间倒放技巧常用于制作逆向回放、倒影等特效。
通过适当调整倒放范围,可以实现不同的时间延缓效果。
三、帧重复与插入帧帧重复和插入帧是实现时间延缓效果的另外两种常用方法。
通过复制和插入关键帧,我们可以在画面中对某一时间段进行多次重复播放,从而实现时间的延缓效果。
具体操作如下:1. 选中要进行时间延缓的画面或合成层,在时间轴面板中找到关键帧。
2. 通过复制和粘贴关键帧,或者直接插入关键帧的方式,重复播放需要延缓的时间段。
帧重复和插入帧的技巧常用于制作动画中的循环效果、重复运动等。
通过合理调整帧数和关键帧的位置,可以实现不同的时间延缓效果。
四、时间扭曲效果时间扭曲效果是AE中专门用于实现时间延缓效果的一个功能。
广义相对论尺缩钟慢

广义相对论尺缩钟慢
广义相对论是爱因斯坦在20世纪初提出的一种描述引力的理论。
其中,尺缩效应和钟慢效应是广义相对论的两个重要预言。
尺缩效
应指的是物体在引力场中会出现长度缩短的现象,而钟慢效应则是
指在引力场中的时钟会运行得更慢。
在引力场中,物体的长度会发生变化。
这是因为引力场会影响
时空的弯曲,导致物体的长度在引力场中会缩短。
这就是尺缩效应。
例如,如果一个棒子放置在引力场中,它将会变得更短。
这一效应
在实际生活中可能不太容易察觉,但在极端的引力场中,比如黑洞
附近,尺缩效应将会变得非常明显。
另一方面,钟慢效应是指在引力场中的时钟会运行得更慢。
这
是因为引力场同样会影响时空的弯曲,导致时间的流逝变慢。
这一
效应已经在实验中得到了验证,比如在卫星导航系统中,由于卫星
相对地面时钟运行得更慢,需要进行修正。
广义相对论的尺缩效应和钟慢效应不仅仅是理论上的预言,它
们已经在实验中得到了验证。
这些效应的发现不仅深化了我们对引
力的理解,也为我们的科技发展提供了重要的指导。
通过对尺缩效
应和钟慢效应的研究,我们可以更好地理解引力场对时空的影响,为未来的科学研究和技术应用提供更加准确的基础。
时间延缓长度收缩狭义相对论的时空观

时间延缓长度收缩狭义相对论的时空观狭义相对论是爱因斯坦在1905年提出的一种物理学理论,它描述了时空的特殊性质,其中最重要的观点是时间延缓和长度收缩。
然而,需要注意的是,这些观点只适用于特定的条件和参考系。
在其他条件下,我们可能会观察到不同的现象。
首先,让我们来看一下时间延缓的概念。
根据狭义相对论的观点,当一个物体以接近光速的速度运动时,其时间会相对于静止物体来说变得慢。
这意味着,如果一个人在宇宙飞船上以接近光速的速度进行旅行,他将会经历比地面上的观察者更长的时间。
这是因为宇宙飞船上的时钟会比地面上的时钟慢。
这一观点已经在实际的实验中得到了验证,就如同双子佯谬实验中的情况。
然而,需要注意的是,时间延缓目前只适用于速度接近光速的情况。
在低速场景中,时间延缓效应可以忽略不计。
这也意味着,在日常生活中,我们通常无法观察到时间的延缓现象。
因此,时间延缓只在高速运动和强引力场下才会显著发生。
接下来,让我们来讨论长度收缩。
根据狭义相对论的观点,当一个物体以接近光速的速度运动时,其长度会相对于静止物体来说变短。
这意味着,如果我们观察一个接近光速的物体,它看起来比它实际上要短一些。
这种现象在实验中也得到了验证,就像著名的拼轮积木实验一样。
然而,与时间延缓类似,长度收缩效应同样只适用于高速运动的物体,而在低速运动中是无法观察到的。
总的来说,狭义相对论的时空观提出了时间延缓和长度收缩的概念。
这些现象在高速运动和强引力场下才会显著发生。
因此,在我们日常的生活中,我们通常无法观察到这些效应。
然而,通过实验和研究,我们已经证实了这些观点的正确性。
这些理论为我们对时空的理解提供了重要的基础,同时也促进了科学研究的进展。
狭义相对论是爱因斯坦在1905年提出的一种物理学理论,它描述了时空的特殊性质,其中最重要的观点是时间延缓和长度收缩。
这些观点对我们对时空的理解有着重要的影响,但需要注意的是,它们只适用于特定的条件和参考系。
首先,让我们来深入探讨一下时间延缓的概念。
3-3 时间延缓和长度收缩 3-5 相对论动力学基础

速度的定义:
dx dy dz vx , vy , v z dt dt dt dx dy dz vx , vy , vz dt dt dt
vx u vx uv x 1 2 c (课下推导) vy vy 1 u2 c 2 uv x 1 2 c 【例3.6】―追光实验” vz v 1 u2 c 2 z uv x 1 2 c
第3章 狭义相对论
25
m0 c 2 m c 2 Ek m0 0 1 v2 c 2
1 1 v c 2
2 2
3 v c 0.866c 4
第3章 狭义相对论
16
3-5
相对论动力学基础
2 2
E K mc m0c ——高速下(相对论)动能
与经典动能形式完全不同
E K m0 c (
m0v v 1 2 c
2
静质量 m0 :物体相对于惯性系静止时的质量.
第3章 狭义相对论
10
3-5
相对论动力学基础
质速关系式:
m
m0 1 v c
2 2
m0——静止质量 m——相对论质量(动质量)
m v c时 , m0
当 v
c 时, m m0
0
第3章 狭义相对论
11
3-5
第3章 狭义相对论
3
3-3 相对论动力学基础 3-5 时间延缓和长度收缩
三
长度的收缩
标尺相对 s' 系静止 在 s' 系中测量: 固有长度
y
y'
x '1
s s'
u
l0
l0 x'2 x'1 l'
钟慢效应和尺缩效应

钟慢效应和尺缩效应
时钟慢效应指的是一个人在一段时间内,他/她对一件事
情的反应会越来越慢,甚至没有反应。
也就是说,一个人会在一段时间内慢慢地变得无聊或厌恶。
这种现象在实验中表现得最为明显,但也会在工作或研究中发生。
时钟慢效应可以被认为是一种情绪调节和控制机制,它可以帮助人们减少对某事的焦虑和压力,更好地把握现实中的情况。
尺缩效应是指当一个人每次移动到一个新的空间时,他/
她会有一些新的感受和体验。
比如,你可能会有不同的情绪反应,如期待、兴奋或惊讶等。
这种现象可以归结为一个人在新环境中的心理调整过程,也就是说,人们会有新的情绪响应以适应新的环境。
尺缩效应可以帮助人们更好地适应新的环境,并能够从新的环境中获得更多的收获。
从心理学的角度来看,时钟慢效应和尺缩效应是两种具有相似特征的心理现象。
它们都是人们在不同时空背景下的心理调整机制,可以帮助人们更好地适应新的情况并获得更多收获。
尽管它们有着相似的特征,但它们也有不同之处,因此,当讨论心理学时,我们应当正确区分它们,以便更好地了解它们的特征和机理,以便我们能够更好地应用它们。
狭义相对论中的尺缩钟慢效应

狭义相对论中的尺缩钟慢效应【引言】狭义相对论是爱因斯坦提出的一个颠覆性的物理理论,它改变了人类对时间和空间的认识。
其中,尺缩钟慢效应是狭义相对论的核心内容之一。
本文将详细介绍尺缩钟慢效应,并通过实例分析其应用和影响。
【狭义相对论简介】狭义相对论分为两个部分:洛伦兹变换和相对性原理。
洛伦兹变换描述了在不同参考系下物理量的变换规律,如时间、空间和质量等。
相对性原理则表明所有物理定律在所有惯性参考系中都是相同的。
【尺缩效应】尺缩效应是指在高速运动的物体长度会变短。
根据狭义相对论的洛伦兹变换公式,物体在运动方向上的长度会随着速度的增加而减小。
这一现象在微观和宏观世界里都成立,只是影响程度不同。
在极端情况下,如接近光速运动,尺缩效应会更加明显。
【钟慢效应】钟慢效应是指在高速运动的参考系中,钟表走得比在静止参考系中的慢。
这是由于时间的流逝与空间的扩展密切相关,当物体以高速运动时,空间扩展的速度也会增加,从而导致时间流逝的减缓。
【实例分析】假设有一对双胞胎,哥哥在地球静止参考系中,弟弟在高速运动的宇宙飞船上。
当弟弟乘坐飞船回来时,相对于地球,他的年龄会比哥哥小。
这就是因为弟弟在高速运动的飞船上经历了更少的“时间”,而时间延缓效应使得他在地球上的兄弟看来更年轻。
【结论】尺缩钟慢效应是狭义相对论的重要组成部分,它揭示了时间和空间的相互关联,并揭示了高速运动物体的时间延缓和长度收缩现象。
通过深入了解尺缩钟慢效应,我们可以更好地认识和理解相对论的原理,同时也能应用到实际生活中,例如GPS卫星导航系统就需要考虑尺缩钟慢效应来进行精度修正。
洛伦兹变换的详细推导

第三节 洛伦兹变换式教学内容:1. 洛伦兹变换式的推导;2. 狭义相对论的时空观:同时性的相对性、长度的收缩和时间的延缓; 重点难点:狭义相对论时空观的主要结论。
基本要求:1. 了解洛伦兹坐标变换和速度变换的推导;2. 了解狭义相对论中同时性的相对性以及长度收缩和时间延缓概念;3. 理解牛顿力学中的时空观和狭义相对论中的时空观以及两者的差异。
三、洛伦兹坐标变换的推导()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--='='='--='22211c v c vx t t z z y y c v vt x x 或 ()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-'+'='='=-'+'=22211c v c x v t t z z y y c v t v x x据狭义相对论的两个基本假设来推导洛仑兹变换式。
1. 时空坐标间的变换关系作为一条公设,我们认为时间和空间都是均匀的,因此时空坐标间的变换必须是线性的。
对于任意事件P 在S 系和S '系中的时空坐标(x ,y ,z ,t )、(x ',y ',z ',t '),因S ' 相对于S 以平行于 x 轴的速度v 作匀速运动,显然有y '=y , z '=z 。
在S 系中观察S 系的原点,x =0;在S '系中观察该点,x '=-v t ',即x '+v t '=0。
因此x =x '+v t '。
在任意的一个空间点上,可以设:x =k (x '+v t '),k 是—比例常数。
同样地可得到:x '=k '(x -v t )= k '(x +(-v )t )根据相对性原理,惯性系S 系和S '系等价,上面两个等式的形式就应该相同(除正、负号),所以k =k '。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A,B
S'系中是两地时。
B
20
(两地时)
t
t2
t1
x u
t2
x u
A'钟示值
S Su
A,B
B
(原时)
t t
1
u2 c2
t2
t
1
u2 c2
B的示值
21
A'钟示值
t2
x u
3108 5
s
4 3108 4
5
B的示值
t2
t
1
u2 c2
5 1 (4)2 3 s 4 54
22
三、时空不变量
c2 (t)2 [(x)2 (y)2 (z)2 ] c2 (t)2 [(x)2 (y)2 (z)2 ]
2 2
u l0 u
1
u c
2 2
l l0
1
u2 c2
16
5) 当一人高速经过时,你会发现奇怪的 现象:瘦、质量大、反映慢。
6) 长度收缩符合客观事实(火车是否可 避免雷击)(同时的相对性) (1)在地上看 (2)在火车上看
17
注意: (1)原时
一定涉及到一只钟指示的时间间隔;
或说,在使用洛仑兹变换时必须存在的条件:
也称静长 ,只有一个。
棒静止在S'系中 l0 静长
11
S S
u
l0
棒以极高的速度相对S系运动 S系测得棒的长度值是什么呢?
相应的时空坐标
S
S
事件1:测棒的左端 事件2:测棒的右端
x1, t1 x2 , t2
x1, t1 x2 , t2
同时测的条件
t2 t1
x2 x1 ? 12
2.原长最长
S
的立方体u
u2
x
V V0 1 c2
若均匀带电为Q 电量是相对论不变量
Q Q
V
V0
1
u c
2 2
b)运动的棒在与运动方向的夹角变大。
14
3) 在低速下 伽利略变换 4)同时性的相对性的直接结果 l l0
1
u2 c2
一根尺静止在S'系中
静长 与参考
S系中测量这根高速运动的尺 按约定,同时测尺的两端A、B 坐标值差 xB xA 由同时性的相对性, S' 系
两系所测时间间隔的关系? 两只钟 时间间隔由
事件1 ( x1, t1) ( x1, t1)
一只钟测出
事件2 ( x2 , t2 ) (x2 , t2 )
特殊条件
S S u( x1, t1) S( x1, t2 )
x2 x1
( x1, t1)
(x2 , t2 )
2
1. 原时 Proper time 两地时 在某一参考系中,同一地点先后发生的两个
事件之间的时间间隔叫原时,或固有时。
2. 原时最短 时间膨胀 考察S' 中的一只钟
x x2 x1 0 一只钟
t t2 t1 原时
S S ( x1, t1)
S (x1, t1) S( x1, t2 )
t t2 t1 两地时
(x2 , t23 )
由洛仑兹逆变换
t
t
u c2
x
1
u2 c2
t
1
u2 c2
x 0
t
1
1
u2 c2
>< 1
t
原时最短 4
讨论 1) 运动时钟变慢效应是时间本身的客 观特征,适宜一切类型的钟 物理过程 生命过程
化学过程
2) 对同一过程,原时只有一个 固有时 本性时 本征时
例:基本粒子 子的寿命 =?
通过高能物理实验取得的数据是:
运动速度
u 0.9966c
2.2 106 s
基本数据 m 208me e 2.2 106 s
7
3)双生子效应 twin effect 20岁时,哥哥从地球出发乘飞船运行10年后
再回到地球 ,弟兄见面的情景?
飞船速度 u 0.999c
哥哥测的是原时,弟弟测的是两地时
t
1
u2 c2
0.447 y
20.5 岁和 30岁
S
S
u
A l0
系无关 B
认为,测 B 端在先
xA xB xB
xB xA < l0 动长小于静长
15
也可从时间测量的相对性导出长度测量的相对性
S
头过此点 x1 尾过此点 x1
汽车参考系为S系 S系中汽车长度为原长l0 汽车参考系:两地时 地面参考系:原时
地面测的
汽车长度 l ut
uΔ t
1
u c
(2)静长(原长)
x 0 (x 0)
一定涉及到两个同时发生的事件的空间距离 ;
或说,在使用洛仑兹变换时必须存在的条件是:
t 0 (t 0)
18
例** 已知:在 S' 参考系中有两只钟A' B'
与 S 系中的B钟先后相遇。
B'与B相遇时,两钟均指零。
Δx 3108 m u 4c
5 求:A' 与B相遇时,
仙境一天,地面一年
8
20.5 岁和 30岁
若用到一对夫妻身上(丈夫宇航)会怎样呢?
初始 见面时
问题:相对的
加速 -- 非惯性系, 与引力场等价,时 钟变慢。广义相对 论
生命在 于运动
9
利用飞机进行运动时钟变慢效应的实验
10
二、长度收缩
对运动长度的测量问题 怎么测?
S S
u
l0
同时测
1.原长 棒静止时测得的它的长度
从出生到死亡走过的距离 l 8 km
5
解:把 子静止的参考系定为 S' 系 实验室参考系 定为 S 系
S'中是原时 S中是两地时
t
t l u
t
1
u2 c2
S S u S u
l
l u
1
u2 c2
6
t
u2 1 c2
l u
1
u2 c2
8 103
(0.9966c)2
0.9966 3108 1 c2
S Su
A,B
B
B钟指示的时刻, A' 钟指示的时刻
19
解:事件1 B' 与B相遇 ( x1, t1) ( x1, t1) 事件2 A' 与B相遇 (x2 , t2 ) (x2 , t2 )
由已知条件,知 t1 0 t1 0
分析:研究的问题中,S系
S Su
中只涉及一只钟,所以S系 中的两事件时间间隔是原时;
§大学物理课件第6章 时间延缓长度收缩(狭义相对论 一、时间延缓(不同系中描述关系) 运动时钟变慢
考察一只高速运动的时钟
方法:研究一个物理过程的时间间隔, 在两个惯性系中比较:两个事件的时间间隔。 按当地钟测当地时的约定, 研究事件的特点:
1
在某系中(如 S'系),两个事件先后发生在同一地点
在另一系中(如S系),这两个事件发生在两个地点
事件1:测棒的左端 事件2:测棒的右端
x1, t1
x2 , t2
由洛仑兹变换
l x2 x1
t 0
S
x1, t1
x2 , t2
l0 x2 x1
x x ut
1
u c
2 2
l l0
1
u2 c2
13
讨论 1)相对效应
l l01Βιβλιοθήκη u2 c22)纵向效应
高速运动
a a)垂直运动方向长度不变
(火车过隧道)
时空间隔 洛仑兹不变量 四维空间
23
应用
v 1、宇宙飞船相对于地面以速度 做匀速 直线运动。某一时刻飞船头部的宇航员 向船尾发出一光信号,经过 (飞t 船上 钟测量)时间后,被尾部的接收器收到。 由此可知飞船的固有长度为( )
