[泰安一模理数]泰安市2015届高三第一次模拟考数学试题(理)及答案(word版)

合集下载

山东省泰安一模数学试题及答案(理)

山东省泰安一模数学试题及答案(理) 高三第一轮复质量检测数学试题（理科）第I卷一、选择题：本大题共12小题，每小题5分。

共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合A={-10.-9.…。

2}，集合B={y | y=2x-3.x∈A}，则A∩B等于（）。

A。

{-10.-9.…。

-1}B。

{-1}C。

{-1.0 (2)D。

{0 (2)2.若(1-2i)z=5i，则z的值为（）。

A。

3B。

5C。

3+2iD。

5+2i3.在各项均为正数的等比数列{an}中，a6=3，则a4+a8（）。

A。

有最小值6B。

有最大值6C。

有最大值9D。

有最小值34.下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x与相应的生产能耗y的几组对应数据：x | 1 | 2 | 3 | 4 | 5 |y | 18.5 | 28.9 | 38.3 | 47.7 | 57.1 |根据上表可得回归方程y=9.4x+9.1，则表中m的值为（）。

A。

27.9B。

25.5C。

26.9D。

265.阅读右侧程序框图，运行相应程序，则输出i的值为（）。

i = 0while i < 5:if i % 3 == 0:i += 2elif i % 3 == 1:i += 3else:i += 1print(i)A。

3B。

4C。

5D。

66.将函数f(x)=sin(2x+π/3)的图像向右平移π/6个单位，得到函数g(x)的图像，则下列说法不正确的是（）。

A。

g(x)的周期为πB。

g(π/3)=f(0)C。

x=π/6是g(x)的一条对称轴D。

g(x)为奇函数7.以F(0.2√2)为焦点的抛物线C的准线与双曲线x-y=2相交于M、N两点，若△MNF为正三角形，则抛物线C的标准方程为（）。

A。

y2=26xB。

y2=46xC。

x2=46yD。

x2=26y8.a=∫2(-cosx)dx，则ax+2ax2的展开式中项的系数为（）。

[泰安一模理综]泰安市2015届高三第一次模拟考理科综合及答案(word版)

高三第一轮复习质量检测理科综合试题2015.3 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分，共15页，满分300分，考生用时150分钟。

考试结束后，将本试卷和答题卡一并交回。

答卷前，考生务必将自己的姓名、准考证号、考试科目填涂在答题卡规定的地方。

第I卷(必做题，共107分)注意事项：1．每小题选出答案后，用2B铅笔把答题卡上对应的答案标号涂黑，如需改动，用橡皮擦干净以后，再涂写其他答案标号。

不涂答题卡，只答在试卷上不得分。

2．第I卷共20小题，l~13题，每小题5分；14～20题，每小题6分，共107分。

可能用到的相对原子质量：H l C 12 O 16 Si 28 Fe 56一、选择题(本题包括13小题，每小题5分，共65分。

每小题只有一个选项符合题意) 1．下列关于植物生长素(生长素类似物)生理作用的叙述，错误的是A．摘除棉花的顶芽，可降低侧芽处生长素浓度以促进侧芽的生长发育B．扦插月季时，保留芽或者幼叶以产生生长素促进插条生根C．在没有受粉的番茄雌蕊柱头上喷洒一定浓度的2,4-D溶液，可获得无子果实D．不同浓度生长素类似物对玫瑰插条生根的作用效果一定不同2．人工鱼塘里的某淡水鱼，成鱼底栖，捕食贝壳类；幼鱼生活在水体表层，滤食藻类和浮游动物。

下列有关叙述错误的是A．幼鱼与浮游动物可能具有捕食和竞争关系B．幼鱼和成鱼属于该生态系统中的消费者C．该鱼的成鱼和幼鱼在水中的分层分布构成群落的垂直结构D．输入该生态系统的能量大于生产者固定的太阳光能3．右图表示动物细胞分裂各阶段染色体数与核DNA数的比例关系(用实线表示)和细胞质中mRNA含量的变化(用虚线表示)。

下列分析合理的是A．a、c阶段活动旺盛的细胞器有核糖体、内质网、高尔基体、线粒体B．c、d段存在姐妹染色单体，d、e之间的比例关系改变是着丝点分裂引起的C．c阶段细胞两极发出纺锤丝形成纺锤体D．b阶段原癌基因发生突变的频率增加，一旦原癌基因发生突变就会导致细胞癌变4．下列关于生物实验中染色的描述，正确的是A．观察细胞中的脂肪，把苏丹III染液滴到载玻片的花生子叶薄片上染色B．观察植物细胞染色体数目变异，把解离后的洋葱根尖直接放到龙胆紫染液中染色C．观察DNA、RNA在细胞中的分布，取口腔上皮细胞直接放入吡罗红甲基绿染色剂中染色D．观察线粒体．把烘干处理的口腔上皮细胞放在健那绿染液中染色5．埃博拉出血热(EBHF)是由埃博拉病毒(EBV)(一种丝状单链RNA病毒)引起的病毒性出血热，EBV与宿主细胞结合后，将核酸-蛋白复合体释放至细胞质，通过以下途径进行增殖。

山东省泰安市2015届高考模拟高三第一次模拟考试(整理精校版)

山东省泰安市2015届高考模拟高三第一次模拟考试高考模拟试卷0328 21:37：：山东省泰安市2015届高考模拟高三第一次模拟考试语文试题2015高考模拟.03注意事项：1．本试题分为选择题和非选择题两部分，共8页。

满分150分，答题时间150分钟。

2．答题前，考生务必先将密封线内的项目填写清楚。

答第I卷前先将自己的学校、姓名、考号、考试科目用铅笔涂写在答题卡上。

3．选择题的每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，不能答在试题纸或答题纸上。

4．非选择题写在答题纸对应区域内，严禁在试题纸或草稿纸上答题。

5．考试结束后，将试题纸、答题卡和答题纸一并交回。

第I卷(选择题共36分)一、(15分，每小题3分)1．下列词语中加点的字，每对读音都相同的一组是A．慑．服／蹑手蹑．脚陪．绑／烘焙．坊菁．华／泾渭．分明B．裨．益／髀．肉复生道行．／行．道树翁媪．／面有愠．色C．瑰．丽／岿．然不动讥诮．/翘．尾巴炽．热/炙．手可热D．祈祷／歧路亡羊啸傲／肖像画蝉蜕／蟾宫折桂2．下列词语中，没有错别字的一组是A．闲置冷板凳竹暴平安如切如磋，如琢如磨B．盲点印花税功亏一篑盛名之下，其实难符C．陨石西洋景胁肩谄笑将欲取之．必先与之D．休假双规制轻歌曼舞阳春白雪，和者必寡3．依次填入下列句子横线处的词语．最恰当的一组是(1)周立波的“海派清口”与郭德纲的相声，都将自己的艺术视野在原生态的市井小民身上，具有“草根文化”的喜剧属性。

(2)林书豪的成功，为华裔乃至亚洲人，表明除了姚明这样的大个子，普通黄种人也可以在强手如云的篮球世界取得一席之地。

(3)网络拒绝谣言，也拒绝“垄断”，但许多人却这样，以为网络上没有批评，没有质疑，才算工作平妥，才算治理有方。

A．聚集证明误解B．聚焦正名曲解C．聚集正名曲解D．聚焦证明误解4．下列各句中，加点的成语使用恰当的一项是A．早已高调宣布退休的达赖再次向其信徒发出号召，鼓动信徒参与“自焚”等和平运动。

泰安市2015届高三第一次模拟数学试题(理)含答案

高三第一轮复习质量检测数学试题（理科）2015.3一、选择题：本大题共10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}2,,1,2,3,M m N ==则“3m =”是“M N ⊆”的 A.充分而不必条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件2.已知i 是虚数单位，3,,1ia b R a bi i+∈+=-，则a b +等于 A. 1-B.1C.3D.43.设随机变量ξ服从正态分布()()()3,4232N P a P a ξξ<-=>+，若，则实数a 等于 A.73B.53C.5D.34.设等差数列{}n a 的前n 项和为25911,2n S a a a =-+=-，若，则当n S 取最小值时，n 等于 A.9 B.8 C.7D.65.根据如下样本数据得到的回归方程为.7.9y bx a a x =+=若，则$每增加1个单位，y 就 A.增加1.4个单位 B.减少1.4个单位 C.增加1.2个单位D.减少1.2个单位6.已知O 是坐标原点，点()21A -，，若点(),M x y 为平面区域212x y x y +≥⎧⎪≤⎨⎪≤⎩上的一个动点，则OA OM ⋅uu r uuu r的取值范围是A. []0,1B. []0,2C. []1,0-D. []1,2-7.已知,m n 是满足1m n +=，且使19m n+取得最小值的正实数.若曲线y x α=过点2,3P m n ⎛⎫⎪⎝⎭，则α的值为 A. 1-B.12C.2D.38.某校开设A 类课3门，B 类课5门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有 A.15 种 B.30种 C.45种 D.90种 9.如图是函数()2f x x ax b =++的图象，则函数()()ln g x x f x '=+的零点所在的区间是A. 11,42⎛⎫⎪⎝⎭B. ()1,2C. 1,12⎛⎫⎪⎝⎭D. ()2,310.设()f x 是定义在R 上的偶函数，对任意x R ∈，都有()()4f x f x +=，且当[]()12,063xx f x ⎛⎫∈-=- ⎪⎝⎭时，，若在区间(]2,6-内关于x 的()()()log 201a f x x a -+=>恰有3个不同的实数根，则a 的取值范围是A. ()1,2B. ()2,+∞C. (D.)二、填空题：本大题共5个小题，每小题5分，共25分.请把答案填在答题纸的相应位置. 11.已知()sin cos 0,,tan αααπα-=∈=则 ▲ . 12.若关于x 的不等式23mx -<的解集为5166x x ⎧⎫-<<⎨⎬⎩⎭，则m= ▲ . 13.已知双曲线()222210,0x y a b a b-=>>的一条渐近线垂直于直线:250l x y --=，双曲线的一个焦点在l 上，则双曲线的方程为 ▲ .14.执行如图所示的程序框图，若输入n 的值为10，则输出s 的值为 ▲.15.设甲、乙两个圆柱的底面积分别为12S S 、，体积分别为12υυ，，若它们的侧面积相等，且1122169S S υυ=，则的值为 ▲ . 三、解答题：本大题共6个小题，满分75分.解答应写出必要的文字说明、证明过程或演算步骤.请将解答过程写在答题纸的相应位置. 16.（本小题满分12分）已知函数()()21cos cos 0,2f x x x x x R ωωωω=-->∈的图像上相邻两个最高点的距离为π.（I ）求函数()f x 的单调递增区间；（II ）若ABC ∆三个内角A 、B 、C的对边分别为()0,sin a b c c f C B ===、、，且3sin A ，求a ，b 的值.17. （本小题满分12分）已知数列{}n a 前n 项和n S 满足：21n n S a += （I ）求数列{}n a 的通项公式；（II ）设()()11211n n n n a b a a ++=++，数列{}n b 的前n 项和为n T ，求证：14n T <.18. （本小题满分12分）下表为某专业的学生的毕业综合能力测试成绩（百分制）的频率分布表，已知80~90分数段的学生数为21人.（I ）求该专业毕业生综合能力测试成绩在90~95分数段内的人数；（II ）现欲将90~95分数段内的毕业生派往甲、乙、丙三个单位，若向甲单位派往两名毕业生，且其中至少有一名男生的概率分为35.求90~95分数段内男女各几人？（III ）在（II ）的结论下，设随机变量ξ表示派往乙单位的三名学生中男生的人数，求ξ的分布列和数学期望.19. （本小题满分12分）如图正方形ABCD 的边长为BDEF 是平行四边形，BD 与AC 交于点G ，O 为GC 的中点，FO FO =⊥平面ABCD.（I ）求证:AE//平面BCF ；（II ）求证：CF ⊥平面AEF ；（III ）求二面角A CF B --余弦值的大小.20. （本小题满分13分）已知函数()()()ln 0f x x x a a =-+>的最小值为0. （I ）求()f x 的解析式；（II ）若对任意[)0,x ∈+∞不等式()1mxf x x x ≤-+恒成立，求实数m 的取值范围. 21. （本小题满分14分）已知椭圆()2222:10x y C a b a b+=>>的焦距为，点()00,R x y 是椭圆上任意一点，从原点O 引圆()()()222000:22R x x y y x -+-=≠的两条切线分别交椭圆C 于点M 、N.（I ）求椭圆C 的方程；（II ）求四边形OMRN 面积的最大值.。

山东省泰安市高三一模(数学理)(word版)

泰安市高三第一轮复习质量检测数学试题（理科）一、选择题：本大题共12个小题。

每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

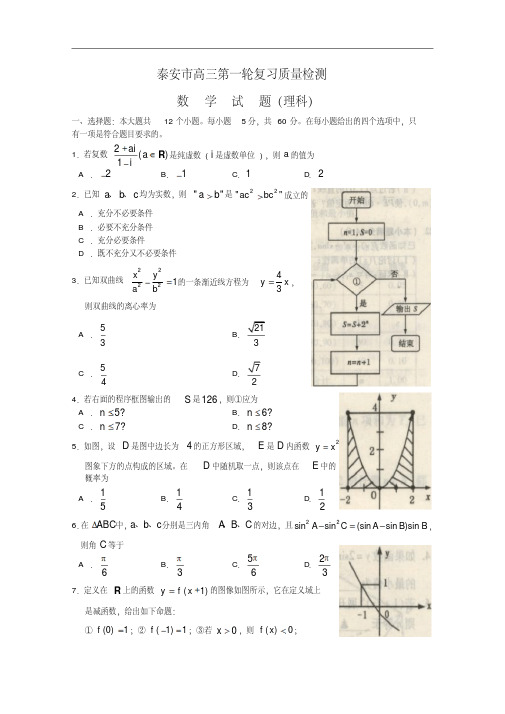
1．若复数2()1aia i+∈-R 是纯虚数(i 是虚数单位)，则a 的值为 A ．2- B ．1- C ．1 D ．22．已知a b c 、、均为实数，则""a b >是22""ac bc >成立的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分又不必要条件3．已知双曲线22221x y a b-=的一条渐近线方程为43y x =，则双曲线的离心率为A ．53 BC ．54D4．若右面的程序框图输出的S 是126，则①应为 A ．5?n ≤ B ．6?n ≤ C ．7?n ≤ D ．8?n ≤5．如图，设D 是图中边长为4的正方形区域，E 是D 内函数2y x = 图象下方的点构成的区域。

在D 中随机取一点，则该点在E 中的概率为 A ．15B ．14C ．13D ．126．在ABC ∆中，a b c 、、分别是三内角A B C 、、的对边，且22sin sin (sin sin )sin A C A B B -=-，则角C 等于A ．6π B ．3π C ．56π D ．23π 7．定义在R 上的函数(1)y f x =+的图像如图所示，它在定义域上是减函数，给出如下命题：①(0)1f =；②(1)1f -=；③若0x >，则()0f x <；④若0x <，则()1f x >。

其中正确的命题是A ．②③B ．①④C ．②④D ．①③8．如图，在棱长均为1的三棱锥S ABC -中，E 为棱SA 的中点，F 为ABC ∆的中心，则直线EF 与平面ABC 所成角的正切值是 A．B ．1CD．29．定义在R 上的函数()f x 满足()()()2(,),(1)2,f x y f x f y xy x y f +=++∈=R 则(2)f -等于 A ．2B ．3C ．6D ．910．已知非零向量,a b 满足：2=||||a b ，若函数3211()32f x x x x =++⋅||a a b 在R 上有极值，设向量,a b 的夹角为θ，则cos θ的取值范围为 A ．[1[,1]2B ．1(,1]2C ．1[1,]2- D ．1[1,)2-11．如果直线1y kx =+与圆2240x y kx my +++-=交于M N 、两点，且M N 、关于直线0x y +=对称，则不等式组 10,0,0,kx y kx my y -+≥-≤≥表示的平面区域的面积是A ．14B ．12C ．1D ．212．某钢厂的年产量由1990年的40万吨增加到2000年的50万吨，如果按照这样的年增长率计算，则该钢厂2010年的年产量约为A ．60万吨B ．61万吨C ．63万吨D ．64万吨二、填空题：本大题共4个小题，每小题4分，共16分。

山东省泰安市2015届高三上学期期末考试数学试题(理科)

山东省泰安市2015届高三上学期期末考试数学试题（理科）【试卷综析】本试卷是高三理科试卷，以基础知识和基本技能为载体，以能力测试为主导，在注重考查学科核心知识的同时，突出考查考纲要求的基本能力，重视学生科学素养的考查.知识考查注重基础、注重常规、注重主干知识，兼顾覆盖面.试题重点考查：集合、不等式、向量、三视图、导数、简单的线性规划、直线与圆、圆锥曲线、数列、函数的性质及图象、三角函数的性质、三角恒等变换与解三角形、充要条件等；考查学生解决实际问题的综合能力，是份较好的试卷.2015.1【题文】一、选择题：本大题共10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.【题文】1.集合{}{}{}3,2,,4a A B a b A B A B ==⋂=⋃，则，则等于A. {}234，， B. {}341，， C. {}0,1,2,3D. {}1,2,3,4【知识点】集合的并集 A1【答案】 A 解析：因为{}4A B ⋂=，所以24a=，解得2a =，由集合B 可得4b =，所以{}{}3,4,2,4A b ==，{}2,3,4A B ⋃=可得故选A .【思路点拨】由{}4A B ⋂=可得2a =进而得到4b =，即可得到集合A,B ，再由并集定义求得. 【题文】2.已知a R ∈，则“2a a <”是“1a <”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【知识点】充分必要条件 A2【答案】 A 解析：因为由2a a <，可得01a <<，所以“2a a <”是“1a <”的充分而不必要条件.故选A. 【思路点拨】找到不等式2a a <的解集为01a <<，然后根据“小范围能推大范围，大范围推不出小范围”进行判断.【题文】3.正项等比数列{}n a 的公比为2，若21016a a =，则9a 的值是 A.8 B.16 C.32 D.64 【知识点】等比数列的性质 D3【答案】 C 解析：因为21016a a =且等比数列各项为正，由等比中项可得64a =，而可得3964832a a q ==⨯=.故选C【思路点拨】由等比中项可得64a =，再由等比数列公式可得3964832a a q ==⨯=.【题文】4.已知命题4:0,4p x x x ∀>+≥：命题001:,22x q x R +∃∈=.则下列判断正确的是 A.p 是假命题B.q 是真命题C.()p q ∧⌝是真命题D.()p q ⌝∧是真命题【知识点】复合命题的真假 A3 【答案】 C 解析：命题4:0,4p x x x ∀>+≥由基本不等式可得为真命题，而命题01:22x q =的解为01x R +=-∉，所以为假命题，由复合命题的真值表可得C 正确.故选C. 【思路点拨】由基本不等式可得命题p 为真命题，解0122x =可得命题q 为假命题，再结合复合命题的真值表可得.【题文】5.已知,m n 为不同的直线，,αβ为不同的平面，则下列说法正确的是 A. ,////m n m n αα⊂⇒B. ,m n m n αα⊂⊥⇒⊥C. ,////m n n m αβαβ⊂⊂⇒D. ,n n βααβ⊂⊥⇒⊥【知识点】空间中的直线与平面的位置关系 G4 G5【答案】 D 解析：A. 因为,////m n m n n ααα⊂⇒⊂或，所以不正确；B. ,m n m α⊂⊥不能确定n α与关系，所以不正确；C. ,//m n n m αβ⊂⊂，若两平面相交且,m n 都平行于交线，也可以满足，所以不正确；D.直线垂直于平面，则过该直线的所有的面都与此面垂直，所以正确.故选D.【思路点拨】A.中直线还可以在平面内；B.中n α与的关系不能确定；C. 若两平面相交且,m n 都平行于交线，也可以满足；D.由线面垂直的性质定理可得正确.【题文】6.若变量,x y 满足条件211y x x y y ≤⎧⎪+≤⎨⎪≥-⎩，则2x y +的取值范围为A. 5,02⎡⎤-⎢⎥⎣⎦B. 50,2⎡⎤⎢⎥⎣⎦C. 55,23⎡⎤-⎢⎥⎣⎦D. 55,22⎡⎤-⎢⎥⎣⎦【知识点】线性规划 E5【答案】 A 解析：根据线性条件画出可行域如图：令2,z x y =+可得22x z y =-+由图像可知当过点1,12B ⎛⎫-- ⎪⎝⎭时，目标函数有最小值为()152122-+⨯-=-.故选A.【思路点拨】由线性条件画出可行域，目标函数为22x zy =-+是一组平行线，可得当过B 点时为最小值. 【题文】7.下列函数中，与函数,0,1,0x x e x y x e ⎧≥⎪=⎨⎛⎫<⎪ ⎪⎝⎭⎩的奇偶性相同，且在(),0-∞上单调性也相同的是A. 1y x =-B. 22y x =+C. 33y x =-D. 1log ey x =【知识点】函数的奇偶性单调性 B3 B4【答案】 B 解析：因为函数,0,1,0x xe x y x e ⎧≥⎪=⎨⎛⎫<⎪ ⎪⎝⎭⎩当0x >时，()()10,x x xf x e f x e -⎛⎫-<-=== ⎪⎝⎭，当0x <时，()()()10,xxx f x e f x e -⎛⎫->-=== ⎪⎝⎭，所以函数为偶函数，排除A,C ，且在(),0-∞上单调减，排除D.故选B. 【思路点拨】由函数的奇偶性可得为偶函数，由函数的性质可得在(),0-∞上单调减，逐一检验即可. 【题文】8.设函数()()sin cos 0f x x x ωωω=+>的最小正周期为π，将()y f x =的图象向左平移8π个单位得函数()y g x =的图象，则 A. ()02g x π⎛⎫⎪⎝⎭在，上单调递减B. ()344g x ππ⎛⎫⎪⎝⎭在，上单调递减 C. ()02g x π⎛⎫⎪⎝⎭在，上单调递增D. ()344g x ππ⎛⎫⎪⎝⎭在，上单调递增【知识点】三角函数的图象与性质 C4【答案】 A 解析：由题意可得：()sin 4f x x πω⎛⎫=+⎪⎝⎭因为最小正周期为π，所以可得2ω=，即()sin 24f x x π⎛⎫=+ ⎪⎝⎭，其图象向左平移8π个单位得函数()sin 2sin 2cos 2842y g x x x x πππ⎛⎫⎛⎫⎛⎫==++=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，由余弦函数图像的性质可得()02g x π⎛⎫⎪⎝⎭在，上单调递减.故选A【思路点拨】由辅助角公式可得()sin 4f x x πω⎛⎫=+⎪⎝⎭，由最小正周期为π，可得()sin 24f x x π⎛⎫=+⎪⎝⎭，由图像的平移变换可得()cos 2g x x =，再由余弦函数图像的性质可得结果.【题文】9.设函数()f x 的零点为()1,422xx g x x =+-的零点为2x ，若()120.25x x f x -≤，则可以是A. ()21f x x =-B. ()24xf x =-C. ()()ln 1f x x =+D. ()82f x x =-【知识点】函数的零点 B9【答案】 D 解析：因为()1310120,0,2120422g g g ⎛⎫⎛⎫=-<=-<=+-> ⎪ ⎪⎝⎭⎝⎭且函数()g x 为增函数，所以零点在区间11,42⎛⎫ ⎪⎝⎭内，又因为120.25x x -≤，所以可得函数()f x 的零点在区间13,24⎛⎫⎪⎝⎭内，只有D 的零点满足.故选D.【思路点拨】根据零点存在性定理可得()g x 零点在区间11,42⎛⎫⎪⎝⎭内，由120.25x x -≤可得函数()f x 的零点在区间13,24⎛⎫⎪⎝⎭内，逐一检验即可. 【题文】10.定义在R 上的函数()f x 满足：()()()()()1,00,f x f x f f x f x ''>-=是的导函数，则不等式()1x x e f x e >-（其中e 为自然对数的底数）的解集为A. ()(),10,-∞-⋃+∞B. ()0,+∞C. ()(),01,-∞⋃+∞D. ()1,-+∞【知识点】导数的应用 B12 【答案】 B 解析：由题意可得：即函数()()()()()()1'10'0x x x f x f x f x f x e f x e f x e '>-⇒+->⇒+->为增函数，而()()0011g f =-=-，所以不等式()1x x e f x e >-的解集，即()1x x e f x e ->-的解集为()0,+∞.故选B.【思路点拨】根据()()1,f x f x '>-构造不等式()()'0x x x e f x e f x e +->，既得函数()()x xg x e f x e =-为增函数，由()()0011g f =-=-，可解得不等式解集.【题文】二、填空题：本大题共5个小题，每小题5分，共25分.请把答案填在答题纸的相应位置. 【题文】11.已知向量()()()3,1,0,1,,3.2m n k t m n k ==-=-若与共线，则t= ▲ .【知识点】向量共线的坐标表示F2 【答案】 1t =解析：由已知可得()23,3m n -=3t =⨯，解得1t =.故答案为1t =【思路点拨】两向量共线的充要条件：1221x y x y =可求得. 【题文】12.设α为锐角，若4cos sin 6512ππαα⎛⎫⎛⎫+=-=⎪ ⎪⎝⎭⎝⎭，则 ▲ . 【知识点】三角变换 C7 【答案】解析：因为α为锐角，所以可得2663πππα<+<，所以有3sin 65πα⎛⎫+= ⎪⎝⎭，而sin sin sin cos cos sin 12646464πππππππαααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=+-=+-+⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭==.故答案为. 【思路点拨】通过凑角由1264πππαα⎛⎫-=+- ⎪⎝⎭，然后利用两角差的正弦展开式求得. 【题文】13.若()()123f x x f x dx =+⎰，则()1f x dx ⎰= ▲ .【知识点】定积分 B13 【答案】 16-解析：因为()()()()()()13111112000000133333x f x dx x f x dx dx f x dx x f x dx =+=+=+⎰⎰⎰⎰⎰，可得()116f x dx =-⎰.故答案为16-.【思路点拨】因为()1f x dx⎰为一个常数，所以对整个函数求定积分可得()()()()()()131111120000133333x f x dxx f x dx dx f x dx x f x dx =+=+=+⎰⎰⎰⎰⎰，整理即可求得.【题文】14.20y -+=100y --=截圆C 所得的弦长均为8，则圆C 的面积是 ▲ . 【知识点】直线与圆的位置关系 H4【答案】 25π解析：因为已知的两条直线平行且截圆C 所得的弦长均为8，所以圆心到直线的距离d 为两直线距离的一半，即3d =，又因为直线截圆C 所得的弦长为8，所以圆的半径5r ==，所以圆C 的面积是25π.故答案为25π【思路点拨】根据题意确定圆心在两平行直线的中间，即圆心到直线的距离d 为两直线距离的一半，由两平行直线的距离求得圆心得到直线的距离，进而由勾股定理可得圆的半径.【题文】15.棱长为4的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是 ▲ .【知识点】三视图正方体的体积 G2【答案】 32解析：如图，红色虚线表示截面，可见这个截面将正方体分为完全相同的两个几何体，则所求几何体的体积即是原正方体的体积的一半，1444322V =⨯⨯⨯=.故答案为32.【思路点拨】由图像的直观图可得，截面将正方体分为完全相同的两个几何体，则所求几何体的体积即是原正方体的体积的一半.【题文】三、解答题：（本大题共6个小题，满分75分，解答应写出必要的文字说明、证明过程或演算步骤.请将解答过程写在答题纸的相应位置.） 16.（本小题满分12分）在ABC ∆中，角A 、B 、C 所对的边分别为,,a b c ，且2cos 2.c A b ⋅= （I ）求角C 的大小；（II ）若b =，ABC ∆2A ，求a 、c 的值.【知识点】解三角形 C8 【答案】（I ）6π；（II ）1.解析：（I ）由2sin 2C A b =可得：2sin cos 2sin C A B A =-即：()2sin cos 2sin C A A C A =+即：2sin cos 2sin cos 2cos sin C A A C A C A =+-整理可得：2sin cos 0C A A =即：(sin 2cos 0A C -=又(),0,,sin 0,cos 6A C A C C ππ∈∴>=∴=；（II ）3,,6b a C π==2111sin ..222ABCSab C a ∴===又2,ABCSA ∴=22sin 4a A ∴=故有：sin 2aA = 即：2sin aA= 由正弦定理可得：,2sin sin sin a c cA C C=∴= 2sin 1c C ∴==，由余弦定理可得：2222cos a b c ab C +-=即：2231 2.a a a +-= 整理可得：222413,1,1a a a a -=∴=∴=【思路点拨】由正弦定理可得2sin cos 2sin C A B A =，再由()sinB sin A c =+化简即可得到cos 6C C π==；由面积公式可得sin 2a A =，有正弦定理可得2sin c C =，由余弦定理可得1a =. 【题文】17.（本小题满分12分）如图所示，在直三棱柱111ABC A B C -中，12,4,3,AA AB AC BC D ====为AB 的中点，且11AB AC ⊥（I ）求证：11AB A D ⊥；（II ）求二面角1A AC D --的平面的正弦值. 【知识点】线线垂直二面角 G5 G11【答案】（I ）略：（II . 解析：如图：三棱柱111ABC A B C -为直三棱柱1AA ABC ∴⊥平面，又CD ⊂平面ABC 1AA CD ∴⊥又,CD CB D =为AB 中点CD AB ∴⊥又1AA AB A ⋂=，CD ∴⊥平面1AB 又1AB ⊂平面1AB1CD AB ∴⊥又111,AB AC CD AC C ⊥⋂= 1AB ∴⊥平面1ACD 又1A D ⊂平面1ACD 11AB A D ∴⊥（II ）由（I ）知，1AB ⊥平面1ACD ，交1A D 于点E ， ∴过A 作1AF AC ⊥与点F,连接EF1AC ∴⊥平面AEF ，1AC EF ∴⊥ 则AEF ∠为所求二面角1A AC D --的平面角在1Rt A AD中，112,2,A A AD A D ===1.AA ADAE AD∴==同理可得：11.AA AC AF A C ==sin AE AFE AF ∴∠==故二面角1A AC D --. 【思路点拨】通过证明1CD AB ⊥， 11AB AC ⊥，1AC CD C ⋂=，证明1AB ⊥平面1A CD ，进而得到11AB A D ⊥；过A 作1AF AC ⊥与点F,连接EF ,则AEF ∠为所求二面角1A AC D --的平面角，在1Rt A AD 中，求得AE =，同理可得：AF =即可求得sin AE AFE AF ∠==. 【题文】18.（本小题满分12分）若数列{}n a 的前n 项和为n S ，且满足：()21262n n n S S S n n N *++++=-∈.（I ）若数列{}n a 是等差数列，求{}n a 的通项公式. （II ）若121a a ==，求50S .【知识点】等差数列的性质数列求和 D2 D4 【答案】（I ）46n a n =-；（II ）4028.解析：（I ）由题意可得：设数列的公差为d ，当n=1时，123624S S S ++=-= 即()()1121231644a a a a a a a d +++++=+= 整理可得：1322a d +=(1)当2n =时，223462222S S S ++=⨯-=即()()()11112334691022a d a d a d a d +++++=+=(2) 由(1)（2）可得：12,4a d =-= 所以46n a n =-所以等差数列的通项公式为46n a n =-；（II ）因为()21262n n n S S S n n N*++++=-∈(1)所以：当2n ≥时，有()211612n n n S S S n -+++=--(2) （1）-（2）可得：()121262n n n a a a n n ++++=-≥，所以()()()50125012345678484950S a a a a a a a a a a a a a a =+++=+++++++++++()()()21236126612486=+⨯-+⨯-++⨯-⎡⎤⎣⎦()2123648616=+⨯++-⨯⎡⎤⎣⎦4028=【思路点拨】分别令1,2n n ==联立解得12,4a d =-=，即可得46n a n =-；由题意当2n ≥时，有()211612n n n S S S n -+++=--与已知式子做差，可得()121262n n n a a a n n ++++=-≥，得到数列的的每三项和的特点，进而求和.【题文】19.（本小题满分12分）某公司研发甲、乙两种新产品，根据市场调查预测，甲产品的利润y （单位：万元）与投资x （单位：万元）满足：()ln 3f x a x bx =-+（,,,a b R a b ∈为常数），且曲线()y f x =与直线y kx =在（1，3）点相切；乙产品的利润与投资的算术平方根成正比，且其图像经过点（4，4）. （I ）分别求甲、乙两种产品的利润与投资资金间的函数关系式；（II ）已知该公司已筹集到40万元资金，并将全部投入甲、乙两种产品的研发，每种产品投资均不少于10万元.问怎样分配这40万元投资，才能使该公司获得最大利润？其最大利润约为多少万元？（参考数据：ln 10 2.303,ln15 2.708,ln 20 2.996,ln 25 3.219,ln 30 3.401======）【知识点】导数的应用 B12【答案】（I ）()()3ln 30f x x x =+>，()g x =；（II ）当甲产品投资15万元，乙产品投资25万元时，公司取得最大利润，最大利润为21.124万元.解析：（I ）函数()f x 的定义域为()0,+∞，且()'af x b x=- 因为点()1,3在直线y kx =上，故有3k = 又曲线()y f x =与直线3y x =在()1,3处相切，故有：()()'133013f a b f =⎧=⎧⎪⇒⎨⎨==⎩⎪⎩ 所以甲产品的利润与投资资金间的函数关系式为：()()3ln 30f x x x =+> 由题意可得乙产品的利润与投资资金间的函数关系式为()g x m =，将点()4,4代入可得2m =，所以乙产品的利润与投资资金间的函数关系式为()g x =；（II ）设甲产品投资x 万元，则乙产品投资（40-x ）万元，且[]10,30x ∈ 则该公司所得利润为：3ln 3y x =++故有'3x y =令'0y >解得1015x ≤< 令'0y <解得1530x ≤<所以15x =为函数的极大值点，也是函数的最大值点，min 3ln15321.124y =++=(万元)所以：当甲产品投资15万元，乙产品投资25万元时，公司取得最大利润，最大利润为21.124万元.【思路点拨】由已知可得()()'1313f f =⎧⎪⎨=⎪⎩解得30a b =⎧⎨=⎩可得()()3ln 30f x x x =+>，将已知点()4,4代入()g x =()g x =；设甲产品投资x 万元，则乙产品投资（40-x ）万元，且[]10,30x ∈则该公司所得利润为：3ln 3y x =++. 【题文】20.（本小题满分13分）已知椭圆()222210x y a b a b +=>>的两个焦点为12F F 、，，直线l 与椭圆相交于A 、B两点，且满足121,2OA OB AF AF K K +=⋅=-O 为坐标原点.（I ）求椭圆的方程; （II ）求OA OB ⋅的最值.【知识点】椭圆方程直线与圆锥曲线 H5 H8【答案】（I ）22184x y +=；（II）. 解析：（I，可得：a =又122a AF AF =+=2,2a c b ∴=∴==所以椭圆方程为：22184x y +=；（II ）设直线AB 的方程为y kx m =+，设()()1122,,,A x y B x y联立22184y kx mx y =+⎧⎪⎨+=⎪⎩ 可得：()222124280kxkmx m +++-=()()()()222224412288840km k m k m =-+-=-+>2121222428,.1212km m x x x x k k --+==++ 21221211.,22OA OBy y b k k a x x =-=-∴=-21212214212m y y x x k-∴=-=-+ 又()()()2222121212122812m k y y kx m kx m k x x km x x m k-=++=+++=+ 2224281212km m k k --∴=++，()2222248,42m m k k m ∴--=-∴+= 2212122222844.2121212m m OA OB x x y y k k k--=+=-=-+++ 所以224.2OAOB -=-≤<当k=0(此时22m =满足上式)，即直线AB 平行于x 轴时，.OAOB 最小值为-2，当斜率不存在时，有2121121221211,,k .k .2OA OB y y y x x y y x x x ====-=- 所以22112x y =将点A 坐标代入椭圆方程，可得：212y = 所以212121.2OAOB x x y y y =+== 所以.OAOB 最大值为2，综上所述：.OAOB 最小值为-2，最大值为2.，可得：a =，由椭圆的定义可得a =可得2121222428,.1212km m x x x x k k --+==++，由221.,2OA OBb k k a =-=-可得121212y y x x =-即21212214212m y y x x k -=-=-+，再由直线可得()()()2222121212122812m k y y kx m kx m k x x km x x m k-=++=+++=+，列的等式解得2242k m +=，因为2212122222844.2121212m m OA OB x x y y k k k--=+=-=-+++，224.2OAOB -=-≤<，当斜率不存在时，.2OAOB =，所以可得其范围.【题文】21.（本小题满分14分）设函数()()11ln .22f x m x x m R x=-+∈. （I ）当54m =时，求()f x 的极值；（II ）设A 、B 是曲线()y f x =上的两个不同点，且曲线在A 、B 两点处的切线均与x 轴平行，直线AB 的斜率为k ，是否存在m ，使得1?m k -=若存在，请求出m 的值，若不存在，请说明理由.【知识点】导数的应用 B12 【答案】（I ）()()()35135=2ln 2,=ln 2.44244f x f f x f ⎛⎫=-+=- ⎪⎝⎭极大值极小值（II ）故不存在这样的m 使得1k m =-.解析：（I ）函数()f x 的定义域为()0,+∞()2221'2x mx f x x-+=- （I ）当54m =时，()()222152122'22x x x x f x x x ⎛⎫---+ ⎪⎝⎭=-=- 令()'0f x =解得：2x =或12x =所以，当x 变化时，()()',f xf x 变化情况如下表：由上表可知：()()()35135=2ln 2,=ln 2.44244f x f f x f ⎛⎫=-+=- ⎪⎝⎭极大值极小值（II ）设()()112212,y ,0A x y B x x x ≤< 令()221g x x mx =-+由题意可得()()12''0f x f x <=，所以()()12''0g x g x == 所以12,x x 为方程2210x mx -+=的两个根故121x x =，且2440m =->即21m >()()121122121111''ln ln 2222f x f x m x x m x x x x -=-+-+- ()()1212ln ln m x x x x =--- 若存在实数m 使得1k m =- 则()()()12121212ln ln 11f x f x m x x k m x x x x --==-=-+--()1212ln ln m x x m x x -=-所以1212n ln 1l x x x x -=-即：1212n ln l x x x x -=-，又1212.1,0,x x x x =<<111112ln 0,01x x x x ∴--=<< 令()12ln ,01h t t t t t=--<<()22121'110h t t t t ⎛⎫=+-=-> ⎪⎝⎭所以()h t 在()0,1上单调递减，所以()()10h t h <= 即：11112ln 0,x x x ∴--<与111112ln 0,01x x x x ∴--=<<矛盾故不存在这样的m 使得1k m =-【思路点拨】对函数求导，令导函数为零，解得零点，由左右单调性判断是否为极值，即可求得极值；令()221g x x mx =-+由题意可得12,x x 为方程2210x mx -+=的两个根，()()12''f x f x -()()1212ln ln m x x x x =---若存在实数m使得1k m =-则()()()12121212ln ln 11f x f x m x x k m x x x x --==-=-+--所以1212n ln 1l x x x x -=-即：1212n ln l x x x x -=-，又1212.1,0,x x x x =<<111112ln 0,01x x x x ∴--=<< 令()12ln ,01h t t t t t=--<<，可证得 ()()10h t h <=，故不存在这样的m 使得1k m =-.。

2015年泰安高三上期期末1月考试

高三年级考试物理试题2015．1 本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分，共6页，满分100分，考试时间90分钟．第I卷(选择题共40分)注意事项：1．答第I卷前，考生务必将自己的姓名、考号、试卷类型、考试科目用铅笔涂写在答题卡上．2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试卷上．3．考试结束后，监考人员将本试卷和答题卡一并收回．一、选择题：(本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，有的只有一个选项正确，有的有多个选项正确。

全部选对的得4分，选对但不全的得2分，有选错的得0分．)1．关于力和运动的关系，下列说法中正确的是A．物体做曲线运动，其速度一定改变B．物体做曲线运动，其加速度可能不变C．物体在恒力作用下运动，其速度方向一定不变D．物体在变力作用下运动，其速度大小一定改变2．利用霍尔效应制作的霍尔元件，广泛应用于测量和自动控制等领域。

如图是霍尔元件的工作原理示意图，磁感应强度B垂直于霍尔元件的工作面向下，通入图示方向的电流I，C、D两侧面会形成电势差U CD，下列说法中正确的是A．电势差U CD仅与材料有关B．仅增大磁感应强度时，C、D两面的电势差变大C．若霍尔元件中定向移动的是自由电子，则电势差U CD>0D．在测定地球赤道上方的地磁场强弱时，元件的工作面应保持水平方向3．如图，用OA、OB两根轻绳将花盆悬于两竖直墙之间，开始时OB绳水平。

现保持O点位置不变，改变OB绳长使绳右端由B点缓慢上移至B’点，此时OB’与OA之间的夹角θ< 90°。

设此过程OA、OB绳的拉力分别为F OA、F OB，则下列说法正确的是A．F OA一直减小B．F OA一直增大C．F OB一直减小D．F OB先减小后增大4．如图两颗卫星1和2的质量相同，都绕地球做匀速圆周运动，卫星2的轨道半径更大些。

2015年山东省高考一模数学试卷(理科)【解析版】

2015年山东省高考数学一模试卷（理科）一、选择题（共10小题，每小题5分，满分50分）1．（5分）复数z＝|（﹣i）i|+i5（i为虚数单位），则复数z的共轭复数为（）A．2﹣i B．2+i C．4﹣i D．4+i2．（5分）若[﹣1，1]⊆{x||x2﹣tx+t|≤1}，则实数t的取值范围是（）A．[﹣1，0]B．[2﹣2，0]C．（﹣∞，﹣2]D．[2﹣2，2+2]3．（5分）已知M（2，m）是抛物线y2＝2px（p＞0）上一点，则“p≥1”是“点M到抛物线焦点的距离不少于3”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条4．（5分）若m是2和8的等比中项，则圆锥曲线x2+的离心率为（）A．B．C．或D．或5．（5分）在△ABC中，若b＝2，A＝120°，三角形的面积S＝，则三角形外接圆的半径为（）A．B．2C．2D．46．（5分）某几何体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此几何体的外接球的表面积为（）A．3πB．4πC．2πD．7．（5分）定义max{a，b}＝，设实数x，y满足约束条件，则z＝max{4x+y，3x﹣y}的取值范围是（）A．[﹣8，10]B．[﹣7，10]C．[﹣6，8]D．[﹣7，8] 8．（5分）函数y＝log3（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A，若点A 在直线mx+ny+1＝0上，其中m，n均大于0，则的最小值为（）A．2B．4C．8D．169．（5分）已知△ABC中，内角A、B、C所对的边分别为a，b，且a cos C+c ＝b，若a＝1，c﹣2b＝1，则角B为（）A．B．C．D．10．（5分）设定义在D上的函数y＝h（x）在点P（x0，h（x0））处的切线方程为l：y＝g（x），当x≠x0时，若＞0在D内恒成立，则称P为函数y＝h（x）的“类对称点”，则f（x）＝x2﹣6x+4lnx的“类对称点”的横坐标是（）A．1B．C．e D．二、填空题：本大题共5小题，每小题5分，共25分．11．（5分）已知函数f（x）＝|2x﹣a|+a，若不等式f（x）≤6的解集为{x|﹣2≤x ≤3}，则实数a的值为．12．（5分）已知点A（2，0）抛物线C：x2＝4y的焦点为F，射线F A与抛物线C相交于点M，与其准线相交于点N，则|FM|：|MN|＝．13．（5分）已知函数则＝．14．（5分）把座位编号为1、2、3、4、5的五张电影票全部分给甲、乙、丙、丁四个人，每人至少一张，至多两张，且分得的两张票必须是连号，那么不同的分法种数为．（用数字作答）15．（5分）已知函数f（x）＝xe x，记f0（x）＝f′（x），f1（x）＝f′（x0），…，f n（x）＝f′n﹣1（x）且x2＞x1，对于下列命题：①函数f（x）存在平行于x轴的切线；②＞0；③f′2012（x）＝xe x+2014e x；④f（x1）+x2＜f（x2）+x1．其中正确的命题序号是（写出所有满足题目条件的序号）．三、解答题：本大题共6小题，共75分，解答时应写出必要的文字说明、证明过程或演算步骤．16．（12分）已知函数f（x）＝2sin x+2sin（x﹣）．（1）求f（x）的单调递增区间；（2）在△ABC中，角A，B，C的对边分别为a，b，c．已知f（A）＝，a＝b，证明：C＝3B．17．（12分）2008年中国北京奥运会吉祥物由5个“中国福娃”组成，分别叫贝贝、晶晶、欢欢、迎迎、妮妮．现有8个相同的盒子，每个盒子中放一只福娃，每种福娃的数量如下表：从中随机地选取5只．（Ⅰ）求选取的5只恰好组成完整“奥运吉祥物”的概率；（Ⅱ）若完整地选取奥运会吉祥物记10分；若选出的5只中仅差一种记8分；差两种记6分；以此类推．设ξ表示所得的分数，求ξ的分布列及数学期望．18．（12分）在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE：EB＝CF：F A＝CP：PB＝1：2（如图1）．将△AEF沿EF折起到△A1EF 的位置，使二面角A1﹣EF﹣B成直二面角，连接A1B、A1P（如图2）（1）求证：A1E⊥平面BEP（2）求直线A1E与平面A1BP所成角的大小；（3）求二面角B﹣A1P﹣F的余弦值．19．（12分）数列{a n}中，a1＝1，当n≥2时，其前n项和为S n，满足S n2＝a n（S n ﹣）．（1）求S n的表达式；（2）设b n＝，数列{b n}的前n项和为T n，不等式T n≥（m2﹣5m）对所有的n∈N*恒成立，求正整数m的最大值．20．（13分）在平面直角坐标系xOy中，椭圆G的中心为坐标原点，左焦点为F1（﹣1，0），P为椭圆G的上顶点，且∠PF1O＝45°．（Ⅰ）求椭圆G的标准方程；（Ⅱ）已知直线l1：y＝kx+m1与椭圆G交于A，B两点，直线l2：y＝kx+m2（m1≠m2）与椭圆G交于C，D两点，且|AB|＝|CD|，如图所示．（ⅰ）证明：m1+m2＝0；（ⅱ）求四边形ABCD的面积S的最大值．21．（14分）已知函数f（x）＝aln（x+1）﹣ax﹣x2．（Ⅰ）若x＝1为函数f（x）的极值点，求a的值；（Ⅱ）讨论f（x）在定义域上的单调性；（Ⅲ）证明：对任意正整数n，ln（n+1）＜2+．2015年山东省高考数学一模试卷（理科）参考答案与试题解析一、选择题（共10小题，每小题5分，满分50分）1．（5分）复数z＝|（﹣i）i|+i5（i为虚数单位），则复数z的共轭复数为（）A．2﹣i B．2+i C．4﹣i D．4+i【解答】解：由z＝|（﹣i）i|+i5＝，得：．故选：A．2．（5分）若[﹣1，1]⊆{x||x2﹣tx+t|≤1}，则实数t的取值范围是（）A．[﹣1，0]B．[2﹣2，0]C．（﹣∞，﹣2]D．[2﹣2，2+2]【解答】解：令y＝x2﹣tx+t，①若t＝0，则{x||x2≤1}＝[﹣1，1]，成立，②若t＞0，则y max＝（﹣1）2﹣t（﹣1）+t＝2t+1≤1，即t≤0，不成立；③若t＜0，则y max＝（1）2﹣t+t＝1≤1，成立，y min＝（）2﹣t•+t≥﹣1，即t2﹣4t﹣4≤0，解得，2﹣2≤t≤2+2，则2﹣2≤t＜0，综上所述，2﹣2≤t≤0．故选：B．3．（5分）已知M（2，m）是抛物线y2＝2px（p＞0）上一点，则“p≥1”是“点M到抛物线焦点的距离不少于3”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条【解答】解：抛物线的交点坐标为F（，0），准线方程为x＝﹣，则点M到抛物线焦点的距离PF＝2﹣（﹣）＝2+，若p≥1，则PF＝2+≥，此时点M到抛物线焦点的距离不少于3不成立，即充分性不成立，若点M到抛物线焦点的距离不少于3，即PF＝2+≥3，即p≥2，则p≥1，成立，即必要性成立，故“p≥1”是“点M到抛物线焦点的距离不少于3”的必要不充分条件，故选：B．4．（5分）若m是2和8的等比中项，则圆锥曲线x2+的离心率为（）A．B．C．或D．或【解答】解：依题意可知m＝±＝±4当m＝4时，曲线为椭圆，a＝2，b＝1，则c＝，e＝＝当m＝﹣4时，曲线为双曲线，a＝1，b＝2，c＝则，e＝故选：D．5．（5分）在△ABC中，若b＝2，A＝120°，三角形的面积S＝，则三角形外接圆的半径为（）A．B．2C．2D．4【解答】解：△ABC中，∵b＝2，A＝120°，三角形的面积S＝＝bc•sin A ＝c•，∴c＝2＝b，故B＝（180°﹣A）＝30°．再由正弦定理可得＝2R＝＝4，∴三角形外接圆的半径R＝2，故选：B．6．（5分）某几何体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此几何体的外接球的表面积为（）A．3πB．4πC．2πD．【解答】解：如图所示，该几何体是正方体的内接正四棱锥．因此此几何体的外接球的直径2R＝正方体的对角线，其表面积S＝4πR2＝3π．故选：A．7．（5分）定义max{a，b}＝，设实数x，y满足约束条件，则z＝max{4x+y，3x﹣y}的取值范围是（）A．[﹣8，10]B．[﹣7，10]C．[﹣6，8]D．[﹣7，8]【解答】解：由约束条件作出可行域如图，由定义max{a，b}＝，得z＝max{4x+y，3x﹣y}＝，当x+2y≥0时，化z＝4x+y为y＝﹣4x+z，当直线y＝﹣4x+z过B（﹣2，1）时z 有最小值为4×（﹣2）+1＝﹣7；当直线y＝﹣4x+z过A（2，2）时z有最大值为4×2+1×2＝10；当x+2y＜0时，化z＝3x﹣y为y＝3x﹣z，当直线y＝3x﹣z过B（﹣2，1）时z 有最小值为3×（﹣2）﹣1＝﹣7；当直线y＝﹣4x+z过C（2，﹣2）时z有最大值为4×2﹣1×（﹣2）＝10．综上，z＝max{4x+y，3x﹣y}的取值范围是[﹣7，10]．故选：B．8．（5分）函数y＝log3（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A，若点A 在直线mx+ny+1＝0上，其中m，n均大于0，则的最小值为（）A．2B．4C．8D．16【解答】解：∵y＝log3（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A，当x+3＝1时，即x＝﹣2时，y＝﹣1，∴A点的坐标为（﹣2，﹣1），∵点A在直线mx+ny+1＝0上，∴﹣2m﹣n+1＝0，即2m+n＝1，∵m，n均大于0，∴＝+＝2+++2≥4+2＝8，当且仅当m＝，n＝时取等号，故的最小值为8，故选：C．9．（5分）已知△ABC中，内角A、B、C所对的边分别为a，b，且a cos C+c ＝b，若a＝1，c﹣2b＝1，则角B为（）A．B．C．D．【解答】解：已知等式利用正弦定理化简得：sin A cos C+sin C＝sin B＝sin（A+C）＝sin A cos C+cos A sin C，由sin C≠0，整理得：cos A＝，即A＝，由余弦定理得：a2＝b2+c2﹣2bc cos A，即1＝b2+c2﹣bc①，与c﹣2b＝1联立，解得：c＝，b＝1，由正弦定理＝，得：sin B＝＝＝，∵b＜c，∴B＜C，则B＝．故选：B．10．（5分）设定义在D上的函数y＝h（x）在点P（x0，h（x0））处的切线方程为l：y＝g（x），当x≠x0时，若＞0在D内恒成立，则称P为函数y＝h（x）的“类对称点”，则f（x）＝x2﹣6x+4lnx的“类对称点”的横坐标是（）A．1B．C．e D．【解答】解：函数y＝f（x）在其图象上一点P（x0，f（x0））处的切线方程为：y＝g（x）＝（2x0+﹣6）（x﹣x0）+x02﹣6x0+4lnx0，设m（x）＝f（x）﹣g（x）＝x2﹣6x+4lnx﹣（2x0+﹣6）（x﹣x0）﹣x02+6x0﹣4lnx0，则m（x0）＝0．m′（x）＝2x+﹣6﹣（2x0+﹣6）＝2（x﹣x0）（1﹣）＝（x﹣x0）（x ﹣）若x0＜，m（x）在（x0，）上单调递减，∴当x∈（x0，）时，m（x）＜m（x0）＝0，此时＜0；若x0，φ（x）在（，x0）上单调递减，∴当x∈（，x0）时，m（x）＞m（x0）＝0，此时＜0；∴y＝f（x）在（0，）∪（，+∞）上不存在“类对称点”．若x0＝，（x﹣）2＞0，∴m（x）在（0，+∞）上是增函数，当x＞x0时，m（x）＞m（x0）＝0，当x＜x0时，m（x）＜m（x0）＝0，故＞0．即此时点P是y＝f（x）的“类对称点”综上，y＝f（x）存在“类对称点”，是一个“类对称点”的横坐标．故选：B．二、填空题：本大题共5小题，每小题5分，共25分．11．（5分）已知函数f（x）＝|2x﹣a|+a，若不等式f（x）≤6的解集为{x|﹣2≤x ≤3}，则实数a的值为a＝1．【解答】解：由题意可得，不等式即|2x﹣a|≤6﹣a，∴a﹣6≤2x﹣a≤6﹣a，解得a﹣3≤x≤3．再由不等式的解集为{x|﹣2≤x≤3}，可得a﹣3＝﹣2，故a＝1，故答案为a＝1．12．（5分）已知点A（2，0）抛物线C：x2＝4y的焦点为F，射线F A与抛物线C相交于点M，与其准线相交于点N，则|FM|：|MN|＝1：．【解答】解：∵抛物线C：x2＝4y的焦点为F（0，1），点A坐标为（2，0），∴抛物线的准线方程为l：y＝﹣1，直线AF的斜率为k＝＝﹣，过M作MP⊥l于P，根据抛物线物定义得|FM|＝|PM|，∵Rt△MPN中，tan∠MNP＝﹣k＝，∴＝，可得|PN|＝2|PM|，得|MN|＝＝|PM|因此可得|FM|：|MN|＝|PM|：|MN|＝1：．故答案为：1：．13．（5分）已知函数则＝．【解答】解：＝，由定积分的几何意义可知：表示上半圆x2+y2＝1（y≥0）的面积，∴＝．又dx＝＝e2﹣e．∴＝＝好．故答案为：．14．（5分）把座位编号为1、2、3、4、5的五张电影票全部分给甲、乙、丙、丁四个人，每人至少一张，至多两张，且分得的两张票必须是连号，那么不同的分法种数为96．（用数字作答）【解答】解：先将票分为符合条件的4份，由题意，4人分5张票，且每人至少一张，至多两张，则三人一张，1人2张，且分得的票必须是连号，相当于将1、2、3、4、5这五个数用3个板子隔开，分为四部分且不存在三连号．在4个空位插3个板子，共有C43＝4种情况，再对应到4个人，有A44＝24种情况，则共有4×24＝96种情况．故答案为96．15．（5分）已知函数f（x）＝xe x，记f0（x）＝f′（x），f1（x）＝f′（x0），…，f n（x）＝f′n﹣1（x）且x2＞x1，对于下列命题：①函数f（x）存在平行于x轴的切线；②＞0；③f′2012（x）＝xe x+2014e x；④f（x1）+x2＜f（x2）+x1．其中正确的命题序号是①③（写出所有满足题目条件的序号）．【解答】解：对于①，因为f′（x）＝（x+1）e x，易知f′（﹣1）＝0，函数f （x）存在平行于x轴的切线，故①正确；对于②，因为f′（x）＝（x+1）e x，所以x∈（﹣∞，﹣1）时，函数f（x）单调递减，x∈（﹣1，+∞）时，函数f（x）单调递增，故＞0不能确定，故②错；对于③，因为f1（x）＝f′（x0）＝xe x+2e x，f2（x）＝f1′（x）＝xe x+3e x，…，f n（x）＝f′n﹣1（x）＝xe x+（n+1）e x，所以f′2012（x）＝f2013（x）＝xe x+2014e x；故③正确；对于④，f（x1）+x2＜f（x2）+x1等价于f（x1）﹣x1＜f（x2）﹣x2，构建函数h（x）＝f（x）﹣x，则h′（x）＝f′（x）﹣1＝（x+1）e x﹣1，易知函数h（x）在R上不单调，故④错；故答案为：①③三、解答题：本大题共6小题，共75分，解答时应写出必要的文字说明、证明过程或演算步骤．16．（12分）已知函数f（x）＝2sin x+2sin（x﹣）．（1）求f（x）的单调递增区间；（2）在△ABC中，角A，B，C的对边分别为a，b，c．已知f（A）＝，a＝b，证明：C＝3B．【解答】（1）解：函数f（x）＝2sin x+2sin（x﹣）＝2（sin x+sin x﹣cos x）＝2（sin x﹣cos x）＝2sin（x﹣），令2kπ﹣≤x﹣≤2k，k∈Z，则2kπ﹣≤x≤2kπ，则f（x）的单调递增区间是[2kπ﹣，2kπ]，k∈Z．（2）证明：由f（A）＝，则sin（A﹣）＝，由0＜A＜π，则﹣＜A﹣＜，则A＝，由＝，a＝b，则sin B＝，由a＞b，A＝，B＝，C＝，故C＝3B．17．（12分）2008年中国北京奥运会吉祥物由5个“中国福娃”组成，分别叫贝贝、晶晶、欢欢、迎迎、妮妮．现有8个相同的盒子，每个盒子中放一只福娃，每种福娃的数量如下表：从中随机地选取5只．（Ⅰ）求选取的5只恰好组成完整“奥运吉祥物”的概率；（Ⅱ）若完整地选取奥运会吉祥物记10分；若选出的5只中仅差一种记8分；差两种记6分；以此类推．设ξ表示所得的分数，求ξ的分布列及数学期望．【解答】解：（Ⅰ）选取的5只恰好组成完整“奥运吉祥物”的概率P＝＝＝，（Ⅱ）ξ的取值为：10，8，6，4．P（ξ＝10）＝＝，P（ξ＝8）＝，P（ξ＝6）＝＝，P（ξ＝4）＝＝ξ的分布列为：﹣Eξ＝＝7.5．18．（12分）在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE：EB＝CF：F A＝CP：PB＝1：2（如图1）．将△AEF沿EF折起到△A1EF 的位置，使二面角A1﹣EF﹣B成直二面角，连接A1B、A1P（如图2）（1）求证：A1E⊥平面BEP（2）求直线A1E与平面A1BP所成角的大小；（3）求二面角B﹣A1P﹣F的余弦值．【解答】（1）证明：不妨设正三角形ABC的边长为3．在图1中，取BE的中点D，连接DF．∵AE：EB＝CF：F A＝1：2，∴AF＝AD＝2，而∠A＝60度，∴△ADF是正三角形，又AE＝DE＝1，∴EF⊥AD．在图2中，A1E⊥EF，BE⊥EF，∴∠A1EB为二面角A1﹣EF﹣B的平面角．由题设条件知此二面角为直二面角，∴A1E⊥BE．又BE∩EF＝E，∴A1E⊥平面BEF，即A1E⊥平面BEP．（2）建立分别以EB、EF、EA为x轴、y轴、z轴的空间直角坐标系，则E（0，0，0），A（0，0，1），B（2，0，0），F（0，，0），P（1，，0），则，．设平面ABP的法向量为，由平面ABP知，，即令，得，．，，∴直线A1E与平面A1BP所成的角为60度．（3），设平面A1FP的法向量为．由平面A1FP知，令y 2＝1，得，．，所以二面角B﹣A1P﹣F的余弦值是．19．（12分）数列{a n}中，a1＝1，当n≥2时，其前n项和为S n，满足S n2＝a n（S n ﹣）．（1）求S n的表达式；（2）设b n＝，数列{b n}的前n项和为T n，不等式T n≥（m2﹣5m）对所有的n∈N*恒成立，求正整数m的最大值．【解答】解：（1）∵S n2＝a n（S n﹣）＝．化为，∴数列是首项为＝＝1，公差为2的等差数列．故＝1+2（n﹣1）＝2n﹣1，∴S n＝．（2）b n＝＝＝，故T n＝+…+＝．又∵不等式T n≥（m2﹣5m）对所有的n∈N*恒成立，∴≥（m2﹣5m），化简得：m2﹣5m﹣6≤0，解得：﹣1≤m≤6．∴正整数m的最大值为6．20．（13分）在平面直角坐标系xOy中，椭圆G的中心为坐标原点，左焦点为F1（﹣1，0），P为椭圆G的上顶点，且∠PF1O＝45°．（Ⅰ）求椭圆G的标准方程；（Ⅱ）已知直线l1：y＝kx+m1与椭圆G交于A，B两点，直线l2：y＝kx+m2（m1≠m2）与椭圆G交于C，D两点，且|AB|＝|CD|，如图所示．（ⅰ）证明：m1+m2＝0；（ⅱ）求四边形ABCD的面积S的最大值．【解答】（Ⅰ）解：设椭圆G的标准方程为．因为F1（﹣1，0），∠PF1O＝45°，所以b＝c＝1．所以，a2＝b2+c2＝2．…（2分）所以，椭圆G的标准方程为．…（3分）（Ⅱ）设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4）．（ⅰ）证明：由消去y得：．则，…（5分）所以＝＝＝．同理．…（7分）因为|AB|＝|CD|，所以．因为m1≠m2，所以m1+m2＝0．…（9分）（ⅱ）解：由题意得四边形ABCD是平行四边形，设两平行线AB，CD间的距离为d，则．因为m1+m2＝0，所以．…（10分）所以＝．（或）所以当时，四边形ABCD的面积S取得最大值为．…（12分）21．（14分）已知函数f（x）＝aln（x+1）﹣ax﹣x2．（Ⅰ）若x＝1为函数f（x）的极值点，求a的值；（Ⅱ）讨论f（x）在定义域上的单调性；（Ⅲ）证明：对任意正整数n，ln（n+1）＜2+．【解答】解：（1）因为，令f'（1）＝0，即，解得a＝﹣4，经检验：此时，x∈（0，1），f'（x）＞0，f（x）递增；x∈（1，+∞），f'（x）＜0，f（x）递减，∴f（x）在x＝1处取极大值．满足题意．（2），令f'（x）＝0，得x＝0，或，又f（x）的定义域为（﹣1，+∞）①当，即a≥0时，若x∈（﹣1，0），则f'（x）＞0，f（x）递增；若x∈（0，+∞），则f'（x）＜0，f（x）递减；②当，即﹣2＜a＜0时，若x∈（﹣1，，则f'（x）＜0，f（x）递减；若，0），则f'（x）＞0，f（x）递增；若x∈（0，+∞），则f'（x）＜0，f（x）递减；③当，即a＝﹣2时，f'（x）≤0，f（x）在（﹣1，+∞）内递减，④当，即a＜﹣2时，若x∈（﹣1，0），则f'（x）＜0，f（x）递减；若x∈（0，，则f'（x）＞0，f（x）递增；若，+∞），则f'（x）＜0，f（x）递减；（3）由（2）知当a＝1时，f（x）在[0，+∞）上递减，∴f（x）≤f（0），即ln （x+1）≤x+x2，∵，∴，i＝1，2，3，…，n，∴，∴．。

山东省泰安一中2015届高三上学期第一次月考数学(理)试题 word版

山东省泰安一中2015届高三上学期第一次月考数学（理）试题注意事项：1. 本试题共分22大题，全卷共150分。

考试时间为120分钟。

2．第I 卷必须使用2B 铅笔填涂答题纸相应题目的答案标号，修改时，要用橡皮擦干净。

3. 第II 卷必须使用0.5毫米的黑色墨水签字笔书写在答题纸的指定位置，在草稿纸和本卷上答题无效。

作图时，可用2B 铅笔，要求字体工整、笔迹清晰。

第I 卷（共60分）一、选择题 (本大题共12个小题；每小题5分，共60分．在每小题给出的4个选项中，只有一项符合题目要求.) 1．已知集合{}{}1,1,124x A B x =-=≤<,则A B ⋂等于（）A ．{}1,0,1-B ．{}1C ．{}1,1-D ．{}0,12．设f (x )＝lg 2＋x 2－x，则f ⎝⎛⎭⎫x 2＋f ⎝⎛⎭⎫2x 的定义域为( ) A ．(－4,0)∪(0,4) B ．(－4，－1)∪(1,4) C ．(－2，－1)∪(1,2) D ．(－4，－2)∪(2,4) 3．命题“所有能被2整除的整数都是偶数”的否定是( )A ．所有不能被2整除的整数都是偶数B ．所有能被2整除的整数都不是偶数C ．存在一个不能被2整除的整数是偶数D ．存在一个能被2整除的整数不是偶数4．设函数⎩⎨⎧>-≤=-1,log 11,2)(21x x x x f x ，则满足2)(≤x f 的x 的取值范围是( )A ．1[-，2]B ．[0，2]C ．[1，+∞)D ．[0，+∞)5．若函数2()()af x x a x=+∈R ，则下列结论正确的是（） A ．a ∀∈R ，()f x 在(0,)+∞上是增函数 B ．a ∀∈R ，()f x 在(0,)+∞上是减函数 C ．a ∃∈R ，()f x 是偶函数 D ．a ∃∈R ，()f x 是奇函数6．一个篮球运动员投篮一次得3分的概率为a ，得2分的概率为b ，不得分的概率为c ，[,,(0,1)]a b c ∈，已知他投篮一次得分的期望是2，则ba 312+的最小值为（） A ．332 B ．328 C ．314 D ．316 7．已知函数()f x 的定义域为(32,1)a a -+,且(1)f x +为偶函数,则实数a 的值可以是（）A ．23B ．2C ．4D ．68．已知函数9()4(1)1f x x x x =-+>-+,当x=a 时,()f x 取得最小值,则在直角坐标系中,函数11()()x g x a+=的大致图象为9．对于集合M 、N ，定义M －N ＝{x |x ∈M 且x ∉N }，M ⊕N ＝(M －N )∪(N －M )，设A ＝{y |y ＝3x ， x ∈R}，B ＝{y |y ＝－(x －1)2＋2，x ∈R}，则A ⊕B 等于( )A ．[0,2)B ．(0,2]C ．(－∞，0]∪(2，＋∞)D ．(－∞，0)∪[2，＋∞)10．已知函数2()23f x x x =-+在区间[0,]t 上有最大值3，最小值2，则t 的取值范围是( ) A ．[1,)+∞B ．[0,2]C ．(,2]-∞D ．[1,2]11．对于任意两个正整数,m n ,定义某种运算“※”如下:当,m n 都为正偶数或正奇数时,m ※n =m n +;当,m n 中一个为正偶数,另一个为正奇数时,m ※n =mn ．则在此定义下,集合{(,)M a b a =※12,,}b a b **=∈∈N N 中的元素个数是( )A ．10个B ．15个C ．16个D ．18个12．已知函数y ＝f (x )的周期为2，当x ∈[－1,1]时f (x )＝x 2，那么函数y ＝f (x )的图象与函数y ＝|lg x |的图象的交点共有( )A ．10个B ．9个C ．8个D ．1个第II 卷（非选择题，共90分）二、填空题(本大题共4小题，每小题4分，共16分,请将答案填在答题纸上)13．已知集合A ＝{(x ，y )|⎩⎪⎨⎪⎧x ≥1，x ≤y ，2x －y ≤1}，集合B ＝{(x ，y )|3x ＋2y －m ＝0}，若A ∩B ≠∅，则实数m 的最小值等于__________．14．若(a ＋1)12-＜(3－2a)12-，则a 的取值范围是__________．15．用二分法求方程x 2＝2的正实根的近似解(精确度0.001)时，如果我们选取初始区间是[1.4,1.5]，则要达到精确度要求至少需要计算的次数是__________次． 16．下列结论中是真命题的是__________(填序号)．①f (x )＝ax 2＋bx ＋c 在[0，＋∞)上是增函数的一个充分条件是－b2a ＜0；②已知甲：x ＋y ≠3，乙：x ≠1或y ≠2，则甲是乙的充分不必要条件； ③数列{a n }(n ∈N *)是等差数列的充要条件是P n ⎝⎛⎭⎫n ，S nn 是共线的．三、解答题:本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤. 17. （本小题满分12分）已知集合A ＝{x ∈R|3x ＋1≥1}，集合B ＝{x ∈R|y ＝－x 2＋x －m ＋m 2}，若A ∪B ＝A ，求实数m的取值范围．18．（本小题满分12分）已知函数f (x )＝x 2＋4ax ＋2a ＋6.(1)若函数f (x )的值域为[0，＋∞)，求a 的值；(2)若函数f (x )的函数值均为非负数，求f (a )＝2－a |a ＋3|的值域． 19．（本小题满分12分）已知函数)()14(log )(4R k kx x f x ∈++=为偶函数. (Ⅰ) 求k 的值;(Ⅱ) 若方程)2(log )(4a a x f x -⋅=有且只有一个根, 求实数a 的取值范围.20．（本小题满分12分）提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度v (单位：千米/小时)是车流密度x (单位：辆/千米)的函数，当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当20≤x ≤200时，车流速度v 是车流密度x 的一次函数．(1)当0≤x ≤200时，求函数v (x )的表达式；(2)当车流密度x 为多大时，车流量(单位时间内通过桥上某观测点的车辆数，单位：辆/小时)f (x )＝x ·v (x )可以达到最大，并求出最大值．(精确到1辆/小时)21．（本小题满分12分）已知p ：∀x ∈R,2x ＞m (x 2＋1)，q ：∃x 0∈R ，x 20＋2x 0－m －1＝0，且p ∧q 为真，求实数m 的取值范围．22．（本小题满分14分）设函数f (θ)＝3sinθ＋cosθ，其中，角θ的顶点与坐标原点重合，始边与x 轴非负半轴重合，终边经过点P(x ，y)，且0≤θ≤π.(1)若点P 的坐标为(12，32)，求f(θ)的值；(2)若点P(x ，y)为平面区域Ω：⎩⎪⎨⎪⎧x ＋y≥1x≤1y≤1，上的一个动点，试确定角θ的取值范围，并求函数f(θ)的最小值和最大值．参考答案一、选择题1. B {}124{02}x B x x x =≤<=≤<,所以{1}A B ⋂=,选B ． 2. B 由202xx+>-，得f(x)的定义域为{x|－2＜x ＜2}. 故－2＜2x ＜2，－2＜2x ＜2.解得x ∈(－4，－1)∪(1, 4)．3 .D 否定原题结论的同时要把量词做相应改变，故选D.4.D5.C 对于0a =时有()2f x x =是一个偶函数.6.D7.B 因为函数(1)f x +为偶函数,所以(1)(1)f x f x -+=+,即函数()f x 关于1x =对称,所以区间(32,1)a a -+关于1x =对称,所以32112a a -++=,即2a =,所以选B ．8 B 9941+511y x x x x =-+=+-++,因为1x >-,所以910,01x x +>>+,所以由均值不等式得91+5511y x x =+-≥=+,当且仅当911x x +=+, 即2(1)9x +=,所以13,2x x +==时取等号,所以2a =,所以1111()()()2x x g x a ++==,又1111(),11()()222,1x x x x g x x +++⎧≥-⎪==⎨⎪<-⎩,所以选B. 9. C 由题可知，集合A ＝{y|y ＞0}，B ＝{y|y≤2}，所以A －B ＝{y|y ＞2}，B －A ＝{y|y≤0}，所以A ⊕B ＝(－∞，0]∪ (2，＋∞)，故选C.10.D 11.B 12 .A 画出两个函数图象可看出交点有10个．二、填空题13. 5 A ∩B≠∅说明直线与平面区域有公共点，因此问题转化为：求当x ，y 满足约束条件x≥1，x≤y ，2x －y≤1时，目标函数m ＝3x ＋2y 的最小值．在平面直角坐标系中画出不等式组表示的可行域．可以求得在点(1,1)处，目标函数m ＝3x ＋2y 取得最小值5.14.23(,)32∵函数12y x -=在定义域(0，＋∞)上递减，∴a ＋1＞0，3－2a ＞0，a ＋1＞3－2a ，即23＜a ＜32. 15. 7 设至少需要计算n 次，则n 满足0.10.0012n <，即2100n >，由于72128=，故要达到精确度要求至少需要计算7次．16. ②③ ①f(x)＝ax 2＋bx ＋c 在[0，＋∞)上是增函数，则必有a ＞0，02ba-≤，故①不正确．②x ＝1且y ＝2，则x ＋y ＝3. 从而逆否命题是充分不必要条件，故②正确． ③若{a n }是等差数列，则S n ＝An 2＋Bn ，即nS n ＝An ＋B ，故③正确．三、解答题17解：由题意得：A ＝{x ∈R|x-20x+1≤}＝(－1,2]， B ＝{x ∈R|x 2－x ＋m －m 2≤0}＝{x ∈R|(x －m)(x －1＋m)≤ 0} 由A ∪B ＝A 知B ⊆A ，得－1＜m≤2，－1＜1－m≤2，解得：－1＜m ＜2. 18解：(1)∵函数的值域为[0，＋∞)，∴Δ＝16a 2－4(2a ＋6)＝0, ∴2a 2－a －3＝0, ∴a ＝－1或a ＝32. (2)∵对一切x ∈R 函数值均为非负，∴Δ＝8 (2a 2－a －3)≤0, ∴－1≤a≤32，∴a ＋3＞0，∴f(a)＝2－a|a ＋3|＝－a 2－3a ＋2＝－23173(a+)(a [-1,])224+∈. ∵二次函数f(a)在3[-1,]2上单调递减，∴3f ()2≤f(a)≤f(－1)，即－194≤f(a)≤4，∴f(a)的值域为[－194，4]. 19解：（1）因为)(x f 为偶函数，所以)()(x f x f =-即=-+-kx x)14(log 44log (41)xkx ++，∴kx xxx 2)14(log 414log 44=+-+ ∴0)12(=+x k ，∴12k =- (2）依题意知： ()f x =x x 21)14(log 4-+1244log (41)log 4x x =+-44log (41)log 2x x =+- ∴由4()log (2)x f x a a =⋅-得4log (41)x +)2(log 4a a x -=4log 2x +∴⎩⎨⎧>-⋅⋅-⋅=+⇒0)2(2)2(14a a a a xx x x ﹡令xt 2= ，则*变为01)1(2=++-at t a 只需其有一正根. (1）1,1-==t a 不合题意(2）*式有一正一负根，⎪⎩⎪⎨⎧<-=>--=∆0110)1(4212a t t a a 经验证满足02>-⋅a a x 1>∴a (3）两相等正根，2220-±=⇒=∆a 经验证02>-⋅a a x 222--=∴a 20解：(1)由题意：当0≤x≤20时，v(x)＝60；当20≤x≤200时，设v(x)＝ax ＋b ，再由已知得200a ＋b ＝0，20a ＋b ＝60，解得a ＝－13，b ＝2003. 故函数v(x)的表达式为60, 0x<20v(x)=1(200x), 20x 2003≤⎧⎪⎨-≤≤⎪⎩(2)依题意并由(1)可得60x, 0x<20f(x)=1x(200x), 20x 2003≤⎧⎪⎨-≤≤⎪⎩. 当0≤x≤20时，f(x)为增函数，故当x ＝20时，其最大值为60×20＝1200；当20≤x≤200时，1f(x)=x(200x)3-≤21x+200x 10000f(x)=()323-=，当且仅当x ＝200－x ，即x ＝100时，等号成立．所以，当x ＝100时，f(x)在区间[20,200]上取得最大值100003. 综上，当x ＝100时，f(x)在区间[0,200]上取得最大值100003≈3333，即当车流密度为100辆/千米时，车流量可以达到最大，最大值约为3333辆/小时． 21解：2x ＞m(x 2＋1) 可化为mx 2－2x ＋m ＜0.若p ：∀x ∈R, 2x ＞m(x 2＋1)为真，则mx 2－2x ＋m ＜0对任意的x ∈R 恒成立．当m ＝0时，不等式可化为－2x ＜0，显然不恒成立；当m≠0时，有m ＜0，Δ= 4－4m 2＜0，∴m ＜－1.若q ：∃x 0∈R ，20x ＋2x 0－m －1＝0为真，则方程x 2＋2x －m －1＝0有实根， ∴Δ=4＋4(m ＋1)≥0，∴m≥－2. 又p ∧q 为真，故p 、q 均为真命题． ∴m ＜－1且m≥－2，∴－2≤m ＜－1.22解：(1)由点P 的坐标和三角函数的定义可得sinθ＝2，cosθ＝12.于是f(θ)＋cos θ12+＝2. (2)作出平面区域Ω(即三角区域ABC)如图所示，其中A(1,0)，B(1,1)，C(0,1)．于是0≤θ≤2π.又f(θ)＋cosθ＝2sin(θ＋6π)，且6π≤θ＋6π≤32π，故当θ＋6π＝2π，即θ＝3π时，f(θ)取得最大值，且最大值等于2 ；当θ＋6π＝6π，即θ＝0时，f(θ)取得最小值，且最小值等于1.。

2015年山东省高考数学一模试卷(理科)含解析答案

2015年山东省高考数学一模试卷（理科）一、选择题（共10小题，每小题5分，满分50分）1．（5分）（2015•山东一模）复数z=|（﹣i）i|+i5（i为虚数单位），则复数z的共轭复数为（）A．2﹣i B．2+i C．4﹣i D．4+i【考点】：复数代数形式的乘除运算．【专题】：数系的扩充和复数．【分析】：直接利用复数模的公式求复数的模，再利用虚数单位i的运算性质化简后得z，则复数z的共轭复数可求．【解析】：解：由z=|（﹣i）i|+i5=，得：．故选：A．【点评】：本题考查复数模的求法，考查了虚数单位i的运算性质，是基础题．2．（5分）（2015•山东一模）若[﹣1，1]⊆{x||x2﹣tx+t|≤1}，则实数t的取值范围是（）A．[﹣1，0] B．[2﹣2，0] C．（﹣∞，﹣2] D．[2﹣2，2+2]【考点】：集合的包含关系判断及应用．【专题】：计算题；函数的性质及应用；集合．【分析】：令y=x2﹣tx+t，由题意，将集合的包含关系可化为求函数的最值的范围．【解析】：解：令y=x2﹣tx+t，①若t=0，则{x||x2≤1}=[﹣1，1]，成立，②若t＞0，则y max=（﹣1）2﹣t（﹣1）+t=2t+1≤1，即t≤0，不成立；③若t＜0，则y max=（1）2﹣t+t=1≤1，成立，y min=（）2﹣t•+t≥﹣1，即t2﹣4t﹣4≤0，解得，2﹣2≤t≤2+2，则2﹣2≤t＜0，综上所述，2﹣2≤t≤0．故选B．【点评】：本题考查了集合的包含关系的应用，属于基础题．3．（5分）（2015•山东一模）已知M（2，m）是抛物线y2=2px（p＞0）上一点，则“p≥1”是“点M到抛物线焦点的距离不少于3”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条【考点】：必要条件、充分条件与充要条件的判断．【专题】：简易逻辑．【分析】：根据抛物线的定义和性质，利用充分条件和必要条件的定义即可得到结论．【解析】：解：抛物线的交点坐标为F（，0），准线方程为x=﹣，则点M到抛物线焦点的距离PF=2﹣（﹣）=2+，若p≥1，则PF=2+≥，此时点M到抛物线焦点的距离不少于3不成立，即充分性不成立，若点M到抛物线焦点的距离不少于3，即PF=2+≥3，即p≥2，则p≥1，成立，即必要性成立，故“p≥1”是“点M到抛物线焦点的距离不少于3”的必要不充分条件，故选：B【点评】：本题主要考查充分条件和必要条件的判断，利用抛物线的定义和性质是解决本题的关键．4．（5分）（2015•山东一模）若m是2和8的等比中项，则圆锥曲线x2+的离心率为（）A．B．C．或D．或【考点】：圆锥曲线的共同特征；等比数列的性质．【专题】：计算题．【分析】：先根据等比中项的性质求得m的值，分别看当m大于0时，曲线为椭圆，进而根据标准方程求得a和b，则c可求得，继而求得离心率．当m＜0，曲线为双曲线，求得a，b和c，则离心率可得．最后综合答案即可．【解析】：解：依题意可知m=±=±4当m=4时，曲线为椭圆，a=2，b=1，则c=，e==当m=﹣4时，曲线为双曲线，a=1，b=2，c=则，e=故选D【点评】：本题主要考查了圆锥曲线的问题，考查了学生对圆锥曲线基础知识的综合运用，对基础的把握程度．5．（5分）（2015•山东一模）在△ABC中，若b=2，A=120°，三角形的面积S=，则三角形外接圆的半径为（）A．B． 2 C．2D． 4【考点】：正弦定理．【专题】：解三角形．【分析】：由条件求得c=2=b，可得B的值，再由正弦定理求得三角形外接圆的半径R的值．【解析】：解：△ABC中，∵b=2，A=120°，三角形的面积S==bc•sinA=c•，∴c=2=b，故B=（180°﹣A）=30°．再由正弦定理可得=2R==4，∴三角形外接圆的半径R=2，故选：B．【点评】：本题主要考查正弦定理的应用，属于基础题．6．（5分）（2015•山东一模）某几何体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此几何体的外接球的表面积为（）A．3π B．4π C．2π D．【考点】：由三视图求面积、体积．【专题】：空间位置关系与距离．【分析】：如图所示，该几何体是正方体的内接正四棱锥．因此此几何体的外接球的直径2R=正方体的对角线，利用球的表面积计算公式即可得出．【解析】：解：如图所示，该几何体是正方体的内接正四棱锥．因此此几何体的外接球的直径2R=正方体的对角线，其表面积S=4πR2=3π．故选：A．【点评】：本题考查了正方体的内接正四棱锥、球的表面积计算公式，考查了推理能力与计算能力，属于基础题．7．（5分）（2015•山东一模）定义max{a，b}=，设实数x，y满足约束条件，则z=max{4x+y，3x﹣y}的取值范围是（）A．[﹣8，10] B．[﹣7，10] C．[﹣6，8] D．[﹣7，8]【考点】：简单线性规划．【专题】：分类讨论；转化思想；不等式的解法及应用．【分析】：由约束条件作出可行域，结合新定义得到目标函数的分段函数，然后化目标函数为直线方程的斜截式，数形结合得到最优解，求出最优解的坐标，代入目标函数得答案．【解析】：解：由约束条件作出可行域如图，由定义max{a，b}=，得z=max{4x+y，3x﹣y}=，当x+2y≥0时，化z=4x+y为y=﹣4x+z，当直线y=﹣4x+z过B（﹣2，1）时z有最小值为4×（﹣2）+1=﹣7；当直线y=﹣4x+z过A（2，2）时z有最大值为4×2+1×2=10；当x+2y＜0时，化z=3x﹣y为y=3x﹣z，当直线y=3x﹣z过B（﹣2，1）时z有最小值为3×（﹣2）﹣1=﹣7；当直线y=﹣4x+z过A（2，﹣2）时z有最大值为4×2﹣1×（﹣2）=10．综上，z=max{4x+y，3x﹣y}的取值范围是[﹣7，10]．故选：B．【点评】：本题是新定义题，考查了简单的线性规划，考查了数形结合及数学转化思想方法，是中档题．8．（5分）（2015•山东一模）函数y=log3（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A，若点A在直线mx+ny+1=0上，其中m，n均大于0，则的最小值为（）A．2 B． 4 C．8 D．16【考点】：基本不等式；对数函数的图像与性质．【专题】：函数的性质及应用；不等式的解法及应用．【分析】：现根据对数函数图象和性质求出点A的坐标，再根据点在直线上，代入化简得到2m+n=1，再根据基本不等式，即可求出结果【解析】：解：∵y=log3（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A，当x+3=1时，即x=﹣2时，y=﹣1，∴A点的坐标为（﹣2，﹣1），∵点A在直线mx+ny+1=0上，∴﹣2m﹣n+1=0，即2m+n=1，∵m，n均大于0，∴=+=2+++2≥4+2=8，当且仅当m=，n=时取等号，故的最小值为8，故选：C【点评】：本题考查了对数函数图象和性质以及基本不等式，属于中档题9．（5分）（2015•山东一模）已知△ABC中，内角A、B、C所对的边分别为a，b，且acosC+c=b，若a=1，c﹣2b=1，则角B为（）A．B．C．D．【考点】：余弦定理；正弦定理．【专题】：解三角形．【分析】：已知等式利用正弦定理化简，整理求出cosA的值，求出A的度数，利用余弦定理列出关系式，把a与sinA的值代入得到关于b与c的方程，与已知等式联立求出b与c 的值，再利用正弦定理求出sinB的值，即可确定出B的度数．【解析】：解：已知等式利用正弦定理化简得：sinAcosC+sinC=sinB=sin（A+C）=sinAcosC+cosAsinC，由sinC≠0，整理得：cosA=，即A=，由余弦定理得：a2=b2+c2﹣2bccosA，即1=b2+c2﹣bc①，与c﹣2b=1联立，解得：c=，b=1，由正弦定理=，得：sinB===，∵b＜c，∴B＜C，则B=．故选：B．【点评】：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．10．（5分）（2015•山东一模）设定义在D上的函数y=h（x）在点P（x0，h（x0））处的切线方程为l：y=g（x），当x≠x0时，若＞0在D内恒成立，则称P为函数y=h（x）的“类对称点”，则f（x）=x2﹣6x+4lnx的“类对称点”的横坐标是（）A．1 B．C．e D．【考点】：利用导数研究曲线上某点切线方程．【专题】：计算题；新定义；导数的概念及应用；导数的综合应用．【分析】：当a=4时，函数y=H（x）在其图象上一点P（x0，f（x0））处的切线方程为y=g （x）=（2x0+﹣6）（x﹣x0）++x02﹣6x0+4lnx0．由此能推导出y=h（x）存在“类对称点”，是一个“类对称点”的横坐标．【解析】：解：当a=4时，函数y=h（x）在其图象上一点P（x0，h（x0））处的切线方程为：y=g（x）=（2x0+﹣6）（x﹣x0）+x02﹣6x0+4lnx0，设m（x）=h（x）﹣g（x）=x2﹣6x+4lnx﹣（2x0+﹣6）（x﹣x0）﹣x02+6x0﹣4lnx0，则m（x0）=0．m′（x）=2x+﹣6﹣（2x0+﹣6）=2（x﹣x0）（1﹣）=（x﹣x0）（x﹣）若x0＜，φ（x）在（x0，）上单调递减，∴当x∈（x0，）时，m（x）＜m（x0）=0，此时＜0；若x0，φ（x）在（，x0）上单调递减，∴当x∈（，x0）时，m（x）＞m（x0）=0，此时＜0；∴y=h（x）在（0，）∪（，+∞）上不存在“类对称点”．若x0=，（x﹣）2＞0，∴m（x）在（0，+∞）上是增函数，当x＞x0时，m（x）＞m（x0）=0，当x＜x0时，m（x）＜m（x0）=0，故＞0．即此时点P是y=f（x）的“类对称点”综上，y=h（x）存在“类对称点”，是一个“类对称点”的横坐标．故选B．【点评】：本题考查函数的单调增区间的求法，探索满足函数在一定零点下的参数的求法，探索函数是否存在“类对称点”．解题时要认真审题，注意分类讨论思想和等价转化思想的合理运用，此题是难题．二、填空题：本大题共5小题，每小题5分，共25分．11．（5分）（2015•山东一模）已知函数f（x）=|2x﹣a|+a，若不等式f（x）≤6的解集为{x|﹣2≤x≤3}，则实数a的值为a=1．【考点】：其他不等式的解法．【专题】：不等式的解法及应用．【分析】：不等式即|2x﹣a|≤6﹣a，解得a﹣3≤x≤3．再由已知不等式的解集为{x|﹣2≤x≤3}，可得a﹣3=﹣2，由此求得实数a的值．【解析】：解：由题意可得，不等式即|2x﹣a|≤6﹣a，∴a﹣6≤2x﹣a≤6﹣a，解得a﹣3≤x≤3．再由不等式的解集为{x|﹣2≤x≤3}，可得a﹣3=﹣2，故a=1，故答案为a=1．【点评】：本题主要考查绝对值不等式的解法，体现了等价转化的数学思想，属于基础题．12．（5分）（2015•山东一模）已知点A（2，0）抛物线C：x2=4y的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，则|FM|：|MN|=1：．【考点】：抛物线的简单性质．【专题】：圆锥曲线的定义、性质与方程．【分析】：求出抛物线C的焦点F的坐标，从而得到AF的斜率k=﹣．过M作MP⊥l于P，根据抛物线物定义得|FM|=|PM|．Rt△MPN中，根据tan∠MNP=，从而得到|PN|=2|PM|，进而算出|MN|=|PM|，由此即可得到|FM|：|MN|的值．【解析】：解：∵抛物线C：x2=4y的焦点为F（0，1），点A坐标为（2，0），∴抛物线的准线方程为l：y=﹣1，直线AF的斜率为k==﹣，过M作MP⊥l于P，根据抛物线物定义得|FM|=|PM|，∵Rt△MPN中，tan∠MNP=﹣k=，∴=，可得|PN|=2|PM|，得|MN|==|PM|因此可得|FM|：|MN|=|PM|：|MN|=1：．故答案为：1：．【点评】：本题给出抛物线方程和射线FA，求线段的比值．着重考查了直线的斜率、抛物线的定义、标准方程和简单几何性质等知识，属于中档题．13．（5分）（2015•山东一模）已知函数则=．【考点】：定积分．【专题】：导数的综合应用．【分析】：=，由定积分的几何意义可知：表示上半圆x2+y2=1（y≥0）的面积，即可得出．利用微积分基本定理即可得出dx=．【解析】：解：=，由定积分的几何意义可知：表示上半圆x2+y2=1（y≥0）的面积，∴=．又dx==e2﹣e．∴==好．故答案为：．【点评】：本题考查了定积分的几何意义、微积分基本定理，属于中档题．14．（5分）（2015•山东一模）把座位编号为1、2、3、4、5的五张电影票全部分给甲、乙、丙、丁四个人，每人至少一张，至多两张，且分得的两张票必须是连号，那么不同的分法种数为96．（用数字作答）【考点】：排列、组合及简单计数问题．【专题】：概率与统计．【分析】：根据题意，先将票分为符合题意要求的4份，可以转化为将1、2、3、4、5这五个数用3个板子隔开，分为四部分且不存在三连号的问题，用插空法易得其情况数目，再将分好的4份对应到4个人，由排列知识可得其情况数目，由分步计数原理，计算可得答案．【解析】：解：先将票分为符合条件的4份，由题意，4人分5张票，且每人至少一张，至多两张，则三人一张，1人2张，且分得的票必须是连号，相当于将1、2、3、4、5这五个数用3个板子隔开，分为四部分且不存在三连号．在4个空位插3个板子，共有C43=4种情况，再对应到4个人，有A44=24种情况，则共有4×24=96种情况．故答案为96．【点评】：本题考查排列、组合的应用，注意将分票的问题转化为将1、2、3、4、5这五个数用3个板子隔开，分为四部分的问题，用插空法进行解决．15．（5分）（2015•山东一模）已知函数f（x）=xe x，记f0（x）=f′（x），f1（x）=f′（x0），…，f n（x）=f′n﹣1（x）且x2＞x1，对于下列命题：①函数f（x）存在平行于x轴的切线；②＞0；③f′2012（x）=xe x+2014e x；④f（x1）+x2＜f（x2）+x1．其中正确的命题序号是①③（写出所有满足题目条件的序号）．【考点】：导数的运算．【专题】：导数的概念及应用．【分析】：根据导数的几何意义判断①正确，根据导数和函数的单调性判断②错；根据导数的运算，得到③正确，根据导数与函数的单调性的关系判断④错【解析】：解：对于①，因为f′（x）=（x+1）e x，易知f′（﹣1）=0，函数f（x）存在平行于x轴的切线，故①正确；对于②，因为f′（x）=（x+1）e x，所以x∈（﹣∞，﹣1）时，函数f（x）单调递减，x∈（﹣1，+∞）时，函数f（x）单调递增，故＞0的正负不能定，故②错；对于③，因为f1（x）=f′（x0）=xe x+2e x，f2（x）=f′（x1）=xe x+3e x，…，f n（x）=f′n﹣1（x）=xe x+（n+1）e x，所以f′2012（x）=f2013（x）=xe x+2014e x；故③正确；对于④，f（x1）+x2＜f（x2）+x1等价于f（x1）﹣x1＜f（x2）﹣x2，构建函数h（x）=f（x）﹣x，则h′（x）=f′（x）﹣1=（x+1）e x﹣1，易知函数h（x）在R上不单调，故④错；故答案为：①③【点评】：本题考查了导数的几何意义以及导数和函数的单调性的关系，以及导数的运算法则，属于中档题三、解答题：本大题共6小题，共75分，解答时应写出必要的文字说明、证明过程或演算步骤．16．（12分）（2015•山东一模）已知函数f（x）=2sinx+2sin（x﹣）．（1）求f（x）的单调递增区间；（2）在△ABC中，角A，B，C的对边分别为a，b，c．已知f（A）=，a=b，证明：C=3B．【考点】：两角和与差的正弦函数；正弦定理．【专题】：计算题；三角函数的图像与性质；解三角形．【分析】：（1）运用两角差的正弦公式，即可化简，再由正弦函数的单调增区间，即可得到；（2）由f（A）=，及0＜A＜π，即可得到A=，再由正弦定理，及边角关系，即可得证．【解析】：（1）解：函数f（x）=2sinx+2sin（x﹣）=2（sinx+sinx﹣cosx）=2（sinx﹣cosx）=2sin（x﹣），令2kπ﹣≤x﹣≤2k，k∈Z，则2kπ﹣≤x≤2kπ，则f（x）的单调递增区间是[2kπ﹣，2kπ]，k∈Z．（2）证明：由f（A）=，则sin（A﹣）=，由0＜A＜π，则﹣＜A﹣＜，则A=，由=，a=b，则sinB=，由a＞b，A=，B=，C=，故C=3B．【点评】：本题考查三角函数的化简，正弦函数的单调区间，考查正弦定理及边角关系，注意角的范围，属于中档题．17．（12分）（2015•山东一模）2008年中国北京奥运会吉祥物由5个“中国福娃”组成，分别叫贝贝、晶晶、欢欢、迎迎、妮妮．现有8个相同的盒子，每个盒子中放一只福娃，每种福娃的数量如下表：福娃名称贝贝晶晶欢欢迎迎妮妮数量1 1 1 2 3从中随机地选取5只．（Ⅰ）求选取的5只恰好组成完整“奥运吉祥物”的概率；（Ⅱ）若完整地选取奥运会吉祥物记10分；若选出的5只中仅差一种记8分；差两种记6分；以此类推．设ξ表示所得的分数，求ξ的分布列及数学期望．【考点】：离散型随机变量及其分布列；离散型随机变量的期望与方差．【专题】：概率与统计．【分析】：（Ⅰ）根据排列组合知识得出P=运算求解即可．（Ⅱ）确定ξ的取值为：10，8，6，4．分别求解P（ξ=10），P（ξ=8），P（ξ=6），P（ξ=4），列出分布列即可．【解析】：解：（Ⅰ）选取的5只恰好组成完整“奥运吉祥物”的概率P===，（Ⅱ）ξ的取值为：10，8，6，4．P（ξ=10）==，P（ξ=8）=，P（ξ=6）==，P（ξ=4）==ξ的分布列为：ξ 10 8 6 4P﹣Eξ==7.5．【点评】：本题综合考查了运用排列组合知识，解决古典概率分布的求解问题，关键是确定随机变量的数值，概率的求解，难度较大，仔细分类确定个数求解概率，属于难题．18．（12分）（2015•山东一模）在正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE：EB=CF：FA=CP：PB=1：2（如图1）．将△AEF沿EF折起到△A1EF的位置，使二面角A1﹣EF﹣B成直二面角，连结A1B、A1P（如图2）（1）求证：A1E⊥平面BEP（2）求直线A1E与平面A1BP所成角的大小；（3）求二面角B﹣A1P﹣F的余弦值．【考点】：与二面角有关的立体几何综合题；直线与平面垂直的判定；直线与平面所成的角．【专题】：空间角．【分析】：（1）设正三角形ABC的边长为3．在图1中，取BE的中点D，连结DF．由已知条件推导出△ADF是正三角形，从而得到EF⊥AD．在图2中，推导出∠A1EB为二面角A1﹣EF﹣B的平面角，且A1E⊥BE．由此能证明A1E⊥平面BEP．（2）建立分别以EB、EF、EA为x轴、y轴、z轴的空间直角坐标系，利用向量法能求出直线A1E与平面A1BP所成的角的大小．（3）分别求出平面A1FP的法向量和平面BA1F的法向量，利用向量法能求出二面角B﹣A1P﹣F的余弦值．【解析】：（1）证明：不妨设正三角形ABC 的边长为3．在图1中，取BE的中点D，连结DF．∵AE：EB=CF：FA=1：2，∴AF=AD=2，而∠A=60度，∴△ADF是正三角形，又AE=DE=1，∴EF⊥AD．在图2中，A1E⊥EF，BE⊥EF，∴∠A1EB为二面角A1﹣EF﹣B的平面角．由题设条件知此二面角为直二面角，∴A1E⊥BE．又BE∩EF=E，∴A1E⊥平面BEF，即A1E⊥平面BEP．（2）建立分别以EB、EF、EA为x轴、y轴、z轴的空间直角坐标系，则E（0，0，0），A（0，0，1），B（2，0，0），F（0，，0），P （1，，0），则，．设平面ABP的法向量为，由平面ABP知，，即令，得，．，，∴直线A1E与平面A1BP所成的角为60度．（3），设平面A1FP的法向量为．由平面A1FP知，令y 2=1，得，．，所以二面角B﹣A1P﹣F的余弦值是．【点评】：本题考查直线与平面垂直的证明，考查直线与平面所成的角的求法，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．19．（12分）（2015•山东一模）数列{a n}中，a1=1，当n≥2时，其前n项和为S n，满足S n2=a n （S n﹣）．（1）求S n的表达式；（2）设b n=，数列{b n}的前n项和为T n，不等式T n≥（m2﹣5m）对所有的n∈N*恒成立，求正整数m的最大值．【考点】：数列的求和；数列递推式．【专题】：等差数列与等比数列．【分析】：（1）当n≥2时，a n=S n﹣S n﹣1，代入利用等差数列的通项公式即可得出；（2）利用“裂项求和”、一元二次不等式的解法即可得出．【解析】：解：（1）∵S n2=a n（S n﹣）=．化为，∴数列是首项为==1，公差为2的等差数列．故=1+2（n﹣1）=2n﹣1，∴S n=．（2）b n===，故T n=+…+=．又∵不等式T n≥（m2﹣5m）对所有的n∈N*恒成立，∴≥（m2﹣5m），化简得：m2﹣5m﹣6≤0，解得：﹣1≤m≤6．∴正整数m的最大值为6．【点评】：本题考查了递推式的应用、“裂项求和”、等差数列的通项公式、一元二次不等式的解法，考查了推理能力与计算能力，属于中档题．20．（13分）（2015•山东一模）在平面直角坐标系xOy中，椭圆G的中心为坐标原点，左焦点为F1（﹣1，0），P为椭圆G的上顶点，且∠PF1O=45°．（Ⅰ）求椭圆G的标准方程；（Ⅱ）已知直线l1：y=kx+m1与椭圆G交于A，B两点，直线l2：y=kx+m2（m1≠m2）与椭圆G交于C，D两点，且|AB|=|CD|，如图所示．（ⅰ）证明：m1+m2=0；（ⅱ）求四边形ABCD的面积S的最大值．【考点】：直线与圆锥曲线的综合问题；椭圆的标准方程．【专题】：综合题．【分析】：（Ⅰ）根据F1（﹣1，0），∠PF1O=45°，可得b=c=1，从而a2=b2+c2=2，故可得椭圆G的标准方程；（Ⅱ）设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4）．（ⅰ）直线l1：y=kx+m1与椭圆G联立，利用韦达定理，可求AB，CD的长，利用|AB|=|CD|，可得结论；（ⅱ）求出两平行线AB，CD间的距离为d，则，表示出四边形ABCD的面积S，利用基本不等式，即可求得四边形ABCD的面积S取得最大值．【解析】：（Ⅰ）解：设椭圆G的标准方程为．因为F1（﹣1，0），∠PF1O=45°，所以b=c=1．所以，a2=b2+c2=2．…（2分）所以，椭圆G的标准方程为．…（3分）（Ⅱ）设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4）．（ⅰ）证明：由消去y得：．则，…（5分）所以===．同理．…（7分）因为|AB|=|CD|，所以．因为m1≠m2，所以m1+m2=0．…（9分）（ⅱ）解：由题意得四边形ABCD是平行四边形，设两平行线AB，CD间的距离为d，则．因为m1+m2=0，所以．…（10分）所以=．（或）所以当时，四边形ABCD的面积S取得最大值为．…（12分）【点评】：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查弦长的计算，考查三角形的面积，同时考查利用基本不等式求最值，正确求弦长，表示出四边形的面积是解题的关键．21．（14分）（2015•山东一模）已知函数f（x）=aln（x+1）﹣ax﹣x2．（Ⅰ）若x=1为函数f（x）的极值点，求a的值；（Ⅱ）讨论f（x）在定义域上的单调性；（Ⅲ）证明：对任意正整数n，ln（n+1）＜2+．【考点】：利用导数求闭区间上函数的最值；利用导数研究函数的单调性；利用导数研究函数的极值．【专题】：导数的综合应用．【分析】：（I）由，f′（1）=0，知，由此能求出a．（Ⅱ）由，令f′（x）=0，得x=0，或，又f（x）的定义域为（﹣1，+∞），讨论两个根及﹣1的大小关系，即可判定函数的单调性；（Ⅲ）当a=1时，f（x）在[0，+∞）上递减，∴f（x）≤f（0），即ln（x+1）≤x+x2，由此能够证明ln（n+1）＜2+．【解析】：解：（1）因为，令f'（1）=0，即，解得a=﹣4，经检验：此时，x∈（0，1），f'（x）＞0，f（x）递增；x∈（1，+∞），f'（x）＜0，f（x）递减，∴f（x）在x=1处取极大值．满足题意．（2），令f'（x）=0，得x=0，或，又f（x）的定义域为（﹣1，+∞）①当，即a≥0时，若x∈（﹣1，0），则f'（x）＞0，f（x）递增；若x∈（0，+∞），则f'（x）＜0，f（x）递减；②当，即﹣2＜a＜0时，若x∈（﹣1，，则f'（x）＜0，f（x）递减；若，0），则f'（x）＞0，f（x）递增；若x∈（0，+∞），则f'（x）＜0，f（x）递减；③当，即a=﹣2时，f'（x）≤0，f（x）在（﹣1，+∞）内递减，④当，即a＜﹣2时，若x∈（﹣1，0），则f'（x）＜0，f（x）递减；若x∈（0，，则f'（x）＞0，f（x）递增；若，+∞），则f'（x）＜0，f（x）递减；（3）由（2）知当a=1时，f（x）在[0，+∞）上递减，∴f（x）≤f（0），即ln（x+1）≤x+x2，∵，∴，i=1，2，3，…，n，∴，∴．【点评】：本题考查函数极值的意义及利用导数研究函数的单调性，证明：对任意的正整数n．解题时要认真审题，注意导数的合理运用，恰当地利用裂项求和法进行解题．。

山东省泰安市高三第一轮复习质量检测(一模)数学(理科)试题

山东省泰安市高三第一轮复习质量检测（一模）数学（理科）试题2013.3一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合{}{}1,1,124x A B x =-=≤<，则A B ⋂等于 A.{}1,0,1- B.{}1C.{}1,1-D.{}0,1【答案】B{}124{02}x B x x x =≤<=≤<，所以{1}A B ⋂=，选B.2.复数311i i-+（i 为虚数单位）的模是B.C.5D.8【答案】A31(31)(1)24121(1)(1)2i i i ii i i i ---+===+++-，所以31121i i i -=+=+ A. 3.如果椭机变量()()21,,310.4N P ζσζ---≤≤-=且，则()1P ζ≥等于 A.0.4B.0.3C.0.2D.0.1【答案】D 因为()()31110.P P ζζ-≤≤-=-≤≤=，所以()()()1311110.40.410.122P P P ζζζ--≤≤---≤≤--≥===，选D.4.下列结论错误．．的是 A.命题“若2340x x --=，则4x =”的逆否命题为“若24,340x x x ≠--≠则”B.“4x =”是“2340x x --=”的充分条件C.命题“若0m >，则方程20x x m +-=有实根”的逆命题为真命题D.命题“若220m n +=，则00m n ==且”的否命题是“若220.00m n m n +≠≠≠则或”【答案】C命题“若0m >，则方程20x x m +-=有实根”的逆命题为“若方程20x x m +-=有实根，则0m >”。

若方程20x x m +-=有实根，则140m ∆=+≥，解得14m ≥-。

所以14m ≥-时，不一定有0m >，所以C 错误。

5.若程序框图如图所示，则该程序运行后输出k 的值是A.4B.5C.6D.7【答案】B第一次35116,1n k =⨯+==；第二次168,22n k ===；第三次84,32n k ===；第四次42,42n k ===；第五次21,52n k ===此时满足条件输出5k =，选B. 6.当4x π=时，函数()()()sin 0f x A x A ϕ=+>取得最小值，则函数34y f x π⎛⎫=-⎪⎝⎭是 A.奇函数且图像关于点,02π⎛⎫⎪⎝⎭对称 B.偶函数且图像关于点(),0π对称C.奇函数且图像关于直线2x π=对称D.偶函数且图像关于点,02π⎛⎫⎪⎝⎭对称【答案】C 当4x π=时，函数()()()sin 0f x A x A ϕ=+>取得最小值，即2,42k k Z ππϕπ+=-+∈，即32,4k k Z πϕπ=-+∈，所以()()3s i n ()04f x A x A π=->，所以333()s i n ()s i n 444y f x A x A x πππ=-=--=-，所以函数为奇函数且图像关于直线2x π=对称，选C.7.在,2ABC AB ∆∠=中,A=60，且ABC ∆BC 的长为B.3D.7【答案】A11sin 6022222S AB AC AC =⨯⋅=⨯⨯=，所以1AC =，所以2222c o s 63BCA BA C AB A C=+-⋅,，所以BC =,选A. 8.已知()1,6,2a b a b a ==⋅-=则向量a b 与的夹角为 A.2π B.3πC.4π D.6π 【答案】B2()2a b a a b a ⋅-=⋅-=，所以3a b ⋅=，所以31cos ,162a b a b a b⋅<>===⨯，所以,3a b π<>=，选B.9.若,,0,a b R ab ∈>且则下列不等式中，恒成立的是A.a b +≥B.11a b +> C.2b a a b +≥ D.222a b ab +> 【答案】C因为0ab >，所以0,0b aa b>>，即2b a a b +≥=，所以选C. 10.设函数()()3402f x x x a a =-+<<有三个零点1x 、x 2、x 3，且123,x x x <<则下列结论正确的是 A.11x >-B.20x <C.32x >D.201x <<【答案】D∵函数()()3402f x x x a a =-+<<，∴f ′（x ）=3x 2﹣4．令f ′（x ）=0，得 x=±．∵当x <'()0f x >；在(上，'()0f x <；在)+∞上，'()0f x >．故函数在(,-∞）上是增函数，在(上是减函数，在)+∞上是增函数．故(3f -是极大值，(3f 是极小值．再由f （x ）的三个零点为x 1，x 2，x 3，且123,x x x <<得 x 1＜﹣，﹣＜x 2，x 3＞．根据f （0）=a ＞0，且f （）=a ﹣＜0，得＞x 2＞0．∴0＜x 2＜1．选D.11.直线()2110x a y +++=的倾斜角的取值范围是 A.0,4π⎡⎤⎢⎥⎣⎦B.3[,)4ππ C.0,,42πππ⎡⎤⎛⎫⋃ ⎪⎢⎥⎣⎦⎝⎭D.3,,424ππππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【答案】B直线的斜截式方程为221111y x a a =--++，所以斜率为211k a =-+，即21tan 1a α=-+，所以1tan 0α-≤<，解得34παπ≤<，即倾斜角的取值范围是3[,)4ππ，选B. 12.设奇函数()[]1,1f x -在上是增函数，且()11f -=-，若函数，()221f x t at ≤-+对所有的[]1,1x ∈-都成立，则当[]1,1a ∈-时t 的取值范围是A.22t -≤≤B.1122t -≤≤ C.202t t t ≤-=≥或或D.11022t t t ≤-=≥或或【答案】C因为奇函数()[]1,1f x -在上是增函数，且()11f -=-，所以最大值为(1)1f =，要使()221f x t at ≤-+对所有的[]1,1x ∈-都成立，则2121t a t ≤-+，即220t at -≥，即(2)0t t a -≥，当0t =时，不等式成立。

山东省泰安市高三数第一次高考模拟考试(理)新人教

已知函数 f (x)
x
a
x ln a ，其中 a
(1,e]
( Ⅰ) 讨论 f (x) 的单调性；
( Ⅱ) 求证：对 x1, x2 [ 1,1] ，都有 | f ( x1 ) f ( x2 ) | e 2 。
泰安市高三第一轮复习质量检测
数学参考答案及评分标准（理科）
一、选择题： ( 每小题 5 分，共 60 分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D B A B C B B C A D A C
b1
椭圆的方程为 x 2 y 2 1 ……………………………………………………
3分
4
( Ⅱ ) 当直线 l 的斜率存在时，设其斜率为 k ，则 l 的方程为： y k( x 1)
x2 y2 1 4 y k( x 1)
(4k 2 1) x2 8k 2 x 4 k 2 4 0
P ( x1, y1), Q (x2 , y2 )
二、填空题： ( 每小题 4 分，共 16 分)
13 ．
14 ．
3
三、解答题：
15 ． 5 16 ． y2
3x’
17．解：（Ⅰ） f ( x) (1 cos2x)2 2cos 2 x 1
cos2 2x
sin( x)sin( x)
4
4
sin( x)cos( x)
4
4
2cos 2 2x
2cos 2 2 x 2cos 2x ………………………………… 4 分
形， AB BC 2CD 。 ( Ⅰ) 在线段 BE 上是否存在一点 F ，使 CF // 平面 ADE ? ( Ⅱ) 求证：平面 ADE 平面 ABE ； ( Ⅲ) 求二面角 A DE B 的正切值。

山东泰安一中2015届高三上学期第一次月考数学(文)试题 word版

山东泰安一中2015届高三上学期第一次月考数学（文）试题注意事项：1. 本试题共分三大题，全卷共150分。

考试时间为120分钟。

2．第I 卷必须使用2B 铅笔填涂答题纸相应题目的答案标号，修改时，要用橡皮擦干净。

3. 第II 卷必须使用0.5毫米的黑色墨水签字笔书写在答题纸的指定位置，在草稿纸和本卷上答题无效。

作图时，可用2B 铅笔，要求字体工整、笔迹清晰。

第I 卷（共60分）一、选择题 (本大题共12个小题；每小题5分，共60分．在每小题给出的4个选项中，只有一项符合题目要求.) 1. 设全集}5,4,3,2,1{=U ，集合}4,3,2{=A ，}5,2{=B ，则=⋃)(A C B U ( ) A.{5} B.{1,2,5} C.}5,4,3,2,1{ D.∅2．定义映射B A f →:，若集合A 中元素在对应法则f 作用下象为3log x ，则A 中元素9的象是( )A ．－3B ．－2C ．3D ． 2 3.已知命题p ：,cos 1,x R x ∀∈≤则（）A ．:,cos 1;p x R x ⌝∃∈≥B ．:,cos 1;p x R x ⌝∀∈≥C ．:,cos 1;p x R x ⌝∃∈>D ．:,cos 1;p x R x ⌝∀∈>4.函数x x f 21)(-=的定义域是（）A ．]0,(-∞B ．),0[+∞C ．)0,(-∞D ．),(+∞-∞ 5.,,A B C 是三个集合，那么“B A =”是“AC B C =”成立的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6．若2313log 3,log 2,2,log 2,,,a b c a b c ===则的大小关系是（）A ．a b c <<B ．b c a <<C ．c b a <<D ．c a b <<7．若)(x f 为奇函数且在+∞,0(）上递增，又0)2(=f ，则0)()(>--xx f x f 的解集是（） A ．)2,0()0,2(⋃- B ．)2,0()2,(⋃-∞C ．),2()0,2(+∞⋃-D ．),2()2,(+∞⋃--∞8.已知命题p ：关于x 的函数234y =x ax -+在[1,)+∞上是增函数，命题q ：函数(21)x y =a -为减函数，若p q ∧为真命题，则实数a 的取值范围是 ( )A ．23a ≤B. 120a << C ．1223a <≤ D. 112a << 9.下列函数中既是奇函数又在区间]1,1[-上单调递减的是（）A ．x y sin =B ．1+-=x yC ．2ln2x y x -=+ D ．)22(21xx y -+= 10．函数2ln 2,(0)()21,(0)x x x x f x x x ⎧-+>=⎨+≤⎩的零点的个数（）A ．4 B. 3C ．2D ．111．已知函数()()()() 0340x a x f x a x a x ⎧<⎪=⎨-+≥⎪⎩，满足对任意12x x ≠，都有()()12120f x f x x x -<-成立，则a 的取值范围是（） A . 1(0,]4 B .(1,2] C. (1，3) D.1(,1)212．若存在负实数使得方程 112-=-x a x成立，则实数a 的取值范围是（）A ．),2(+∞ B. ),0(+∞ C. )2,0( D. )1,0(第II 卷（非选择题，共90分）二、填空题(本大题共4小题，每小题4分，共16分,请将答案填在答题纸上) 13.已知函数()y f x =的图象在(1,(1))M f 处的切线方程是221+=x y ,则(1)(1)f f '+= .14．函数()ln 2f x x x =-的极值点为 .15.已知函数()y =f x 满足(+1)=(-1)f x f x ，且[1,1]x ∈-时，2()=f x x ,则函数()y =f x 与3log y =|x|的图象的交点的个数是 .16.用[]x 表示不超过x 的最大整数，如[][][]00,44.3,31.3=-=-=，设函数[])()(R x x x x f ∈-=，关于函数)(x f 有如下四个命题：①)(x f 的值域为[)1,0； ②)(x f 是偶函数； ③)(x f 是周期函数，最小正周期为1 ； ④)(x f 是增函数.其中正确命题的序号是： .三、解答题:本大题共5小题，共74分，解答应写出文字说明，证明过程或演算步骤.17．（本小题满分12分）已知m R ∈，设命题P ： 353m -≤-≤；命题Q ：函数f （x ）＝3x 2＋2mx ＋m ＋43有两个不同的零点．求使命题“P 或Q ”为真命题的实数m 的取值范围．18.（本小题满分12分）已知函数)(x f 是定义在R 上的偶函数，且0≥x 时，xx f )21()(=,函数)(x f 的值域为集合A .（I ）求)1(-f 的值；（II ）设函数a x a x x g +-+-=)1()(2的定义域为集合B ，若B A ⊆，求实数a 的取值范围.19.（本小题满分12分）已知定义域为R 的函数141)(++=x a x f 是奇函数．（I ）求a 的值；（Ⅱ）判断)(x f 的单调性并证明；（III ）若对任意的R t ∈，不等式0)2()2(22<-+-k t f t t f 恒成立，求k 的取值范围． 20．（本小题满分13分）已知函数32()3.f x x ax x =--（Ⅰ）若()(1,)f x +∞在上是增函数，求实数a 的取值范围。

(整理完)山东省泰安市高三一模考试数学试题(理)

山东省泰安市2009届高三一模考试数学试题数学试题（理科）一、选择题：本大题共12个小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．化简)12(-i i =（）A ．i +-2B ．i +2C ．i +-2D ．i --22．设随机变量ξ服从标准正态分布N （0,1），在某项测量中，已知ξ在(]96.1,-∞-内取值的概率为0.025，则)96.1|(|<ξP = （）A ．0.025B ．0.050C ．0.950D ．0.9753．已知命题p ：“0],2,1[2≥-∈∀a x x ”，命题q ：“022,2=-++∈∃a ax x R x 使”，若命题“p 且q ”是真命题，则实数a 的取值范围是（） A ．}12|{=-≤a a a 或 B ．}11|{≥aC ．}212|{≤≤-≤a a a 或D ．}12|{≤≤-a a4．右面程序运行后，输出的值是（）A ．42B ．43C ．44D ．455．设A 、B 、C 、D 是空间四个不同的点，在下列命题中，不正确的是（） A ．若AC 与BD 共面，则AD 与BC 共面 B ．若AC 与BD 是异面直线，则AD 与BC 是异面直线 C ．若AB=AC ，DB=DC ，则AD ⊥BC D ．若AB=AC ，DB=DC ，则AD=BC 6．若)42sin(),2,4(,310tan 1tan παππααα+∈=+则的值为（）A ．102-B ．102 C ．1025 D ．1027 7．已知实数,x y 满足y x z m y x x y y -=⎪⎩⎪⎨⎧≤+-≤≥如果目标函数,121的最小值为-1，则实数m 等于（） A ．7B ．5C ．4D ．38．按分层抽样的方法，从15个相同的红球和10个相同的黑球中抽出10个球排成一排，则不同的排列方法为（）A ．10101025A CB ．610A C ．410C D ．4466A A9．已知m f m xmx x f m 则实数且,18)1(,27)(,03-≥'+=<等于（）A ．-9B ．-3C ．3D ．910．已知曲线22:x y C =，点A （0，-2）及点B （3，a ），从点A 观察点B ，要使视线不被曲线C 挡住，则实数a 的取值范围是（）A ．),4(+∞B ．)4,(-∞C ．),10(+∞D ．)10,(-∞11．已知数列}{n a 是等差数列，若它的前n 项和S n 有最小值，且0,11011>-<n S a a 则使成立的最小自然数n 的值为（）A ．21B ．20C ．19D ．1112．如图，有一直角墙角，两边的长度足够长，在P 处有一棵树与两墙的距离分别是)120(<<a am 、4m ，不考虑树的粗细。

泰安一模试题理科数学

泰安市高三第一轮复习质量检测数学试题（理科）一、选择题：本大题共 12个小题，每题 5 分，共60 分 .在每题给出的四个选项中，只有一项为哪一项切合题目要求的。

1.已知会合A1,1 ,B x 1 2x4，则 A B 等于A. 1,0,1B. 1C.1,1D.0,12.复数3i 1（i为虚数单位）的模是1 iA.5B.223.假如椭机变量N1, 2, 且P310.4 ，则 P 1 等于4.以下结论错误的是．．A.命题“若x23x40 ，则x 4 ”的逆否命题为“若x 4, 则 x23x 4 0 ”B.“x4” j “x23x40 ”的充足条件C.m0，则方程 x2x m0有实根” 的抗命题命题“若为真命题D.命题“若m2n20 ，则m 0且n0 ”的否命题是“若m2n20.则 m0或 n 0 ”5.若程序框图以下图，则该程序运转后输出k 的值是6.当x4时，函数f x Asin x A 0获得最小值，则函数y f 3x是4A.奇函数且图像对于点, 0对称2B.偶函数且图像对于点,0 对称C.奇函数且图像对于直线x对称2D.偶函数且图像对于点, 0 对称27.在ABC中 , A=60o AB2，且ABC 的面积为32，则 BC 的长为A.3 C.7r r r r8.已知a1, b6, a b a 2 则向量 a与 b 的夹角为A.2B. C. D.6 349.若a,b R,且 ab0, 则以下不等式中，恒建立的是A. a b2abB.112C. ba 2 D. a2b22aba b ab a b10.设函数f x x34x a 0 a 2 有三个零点x1、x2、x3，且x1x2x3 , 则以下结论正确的选项是A. x11B. x20C. x32D. 0 x2111.直线x a2 1 y10 的倾斜角的取值范围是A. 0,4B.3, C. 0,, D.,23, 4424412.设奇函数f x 在1,1上是增函数，且f1 1 ，若函数，f x t 22at 1对所有的 x1,1 都建立，则当 a1,1 时t的取值范围是A.2t2B.11t2 2或或1或t0或 t1t t0t2C.2D.22二、填空题：本大题共 4 个小题，每题 4 分，共 16 分 .请把答案填在答题纸的相应地点 .13.从会合1,2,3,4,5中随机选用3 个不一样的数，这个数能够构成等差数列的概率为▲.1614.二项式3x的睁开式中，常数项等于▲（用数字作答） .x215.已知矩形ABCD 的极点都在半径为 5 的球O 的球面上，且AB 8, BC 2 3 ，则棱锥O ABCD 的体积为▲.16.设双曲线x2y2 1的离心率为2，且一个焦点与抛物线x28 y 的焦点同样，则此双曲m n线的方程为▲.三、解答题：17.（本小题满分12 分）设等比数列a n的前 n 项和为S n,a4a1 9, a5, a3, a4成等差数列.（I）求数列a n的通项公式；（II）证明：对随意R N , S k 2, S k, S k 1成等差数列 .18.（本小题满分12 分）urAsin x, Ar3,cosx, f xur r2.已知 m, n m n,且 f334（ 1）求 A 的值；（ II）设、0,, f 330, f 378, 求 cos的值 .2172519.（本小题满分12 分）如图在多面体 ABCDEF中， ABCD为正方形， ED平面 ABCD，FB//ED，且 AD=DE=2BF=2.（I）求证：AC EF；（II）求二面角 C— EF—D 的大小；（ III）设 G 为 CD 上一动点，试确立G 的地点使得BG// 平面CEF，并证明你的结论.20.（本小题满分12 分）某产品按行业生产标准分红 6 个等级，等级系数挨次为1，2，3，4，5，6，按行业规定产品的等级系数 5 的为一等品，3 5 的为二等品，3的为三等品 .若某工厂生产的产品均切合行业标准，从该厂生产的产品中随机抽取 30 件，相应的等级系数构成一个样本，数据以下；（I）以此 30 件产品的样原来预计该厂产品的整体状况，试分别求出该厂生产原一等品、二等品和三等品的概率；（ II ）已知该厂生产一件产品的收益y（单位：元）与产品的等级系数的关系式为1,3y2,3 5，若从该厂大批产品中任取两件，其收益记为 Z ，求 Z 的散布列和数学希望 .4,521.（本小题满分 13 分）已知椭圆y 2x 2211C 1:1641，椭圆 C 以C 的短轴为长轴，且与C 有同样的离心率 .（ I ）求椭圆 C 2 的方程；（ II ）设直线 l 与椭圆 C 2 订交于不一样的两点A 、B ，已知 A 点的坐标为2,0 ，点 Q 0, y 0 在线段 AB 的垂直均分线上，且 uuur uuur4 ，求直线 l 的方程 .QA QB 22.（本小题满分 13 分）已知函数 f xax 2 bx c e x 且f 01, f 1 0.（ I ）若 fx 在区间 0,1 上单一递减，务实数a 的取值范围；（ II ）当 a=0 时，能否存在实数 m 使不等式2 f x4xe x mx 1x 24x 1 对随意 x R恒建立？若存在，求出 m 的值，若不存在，请说明原因 .。

数学(理)一模备考综合练习(八)2015届泰安

数学（理）一模备考综合练习（八）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设全集{}1,2,3,4,5,6,7,8U =，集合{}1,2,3,5A =，{}2,4,6B =，则右图中的阴影部分表示的集合为A. {}2B. {}4,6C. {}1,3,5D. {}4,6,7,82.设{}n a 是公差为正数的等差数列，若1310a a +=，且1316a a =，则111213a a a ++等于A.75B.90C.105D.1203.已知:04,:p a q <<函数2y x ax a =-+的值恒为正，则p 是q 的 A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件4.下列命题错误．．的是 A.如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β B.如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β C.如果平面α⊥平面γ，平面β⊥平面,l γαβ⋂=，那么l ⊥平面γ D.如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β 5.不等式518x x -++<的解集为 A. (),2-∞B. ()1,5-C. ()6,+∞D. ()2,6-6.已知点12F F 、分别是椭圆22221x y a b+=的左、右焦点，过1F 且垂直于x 轴的直线与椭圆交于M 、N 两点，若2MNF ∆为等腰直角三角形，则该椭圆的离心率e 为A.B.12C. 1-+D.7.设()f x 在定义域内可导，其图象如右图所示，则导函数()f x '的图象可能是8.已知实数,a b 满足23,32a b ==，则()xf x a x b =+-的零点所在的区间是A. ()2,1--B. ()1,0-C. ()0,1D. ()1,29.已知函数()()2sin 10,2f x x πωϕωϕ⎛⎫=++>≤⎪⎝⎭，其图象与直线1y =-相邻两个交点的距离为π.若()1f x >对于任意的,123x ππ⎛⎫∈- ⎪⎝⎭恒成立，则ϕ的取值范围是A. ,63ππ⎡⎤⎢⎥⎣⎦B. ,122ππ⎡⎤⎢⎥⎣⎦C. ,123ππ⎡⎤⎢⎥⎣⎦D. ,62ππ⎛⎤⎥⎝⎦10.已知函数()()()2111x x x f x ex ->-⎧⎪=⎨≤-⎪⎩，若()(),a b f a f b <=，则实数2a b -的取值范围为A. 1,1e⎛⎫-∞- ⎪⎝⎭B. 1,e ⎛⎫-∞- ⎪⎝⎭C. 1,2e⎛⎫-∞-- ⎪⎝⎭D. 1,2e⎛⎤-∞-- ⎥⎝⎦二、填空题：本大题共5个小题，每小题5分，共25分，请把答案填写在答题卡相应位置. 11.若02πα⎛⎫∈ ⎪⎝⎭，，且23cos cos 2,tan 210πααα⎛⎫++==⎪⎝⎭则 ▲ . 12.直线10ax y ++=被圆2220x y ax a +-+=截得弦长为2，则实数a 的值是 ▲ .13.如果实数,x y 满足条件20,220,10,x y x y x -≥⎧⎪+-≥⎨⎪-≤⎩则z x y =+的最小值为 ▲ .14.某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为 ▲ .15.规定记号“*”表示一种运算，a*b=a 2+ab ，设函数()*2f x x =，且关于x 的方程()()ln 11f x x x =+≠-恰有4个互不相等的实数根1234,,,x x x x ，则1234x x x x +++= ▲数学（理）一模备考综合练习（八）答题纸姓名二．填空题11. 12. 13. 14. 15. 三、解答题：本大题共有6小题，满分75分，解答应写出文字说明、证明过程或演算步骤.16.（本小题满分12分）ABC ∆的内角A B C 、、所对的边a b c 、、，且sin cos 0a B A =（I ）求角A （II ）若224AB AC BC BC ++=u u u r u u u r u u u r u u u r g ，求a 的最小值。

山东省泰安市高三数学下学期第一次模拟考试试题理

山东省泰安市2016届高三数学下学期第一次模拟考试试题理一、选择题：本大题共10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集{}1,2,3,4,5U =，集合{}1,2,3A =，集合{}3,4B =，则()U C A B ⋃= A. {}4B. {}2,3,4C. {}3,4,5D. {}2,3,4,52.已知11222,12z z t i z i z =+=-，若为实数，则实数t 的值为 A.1B. 1-C.14D. 14-3.右图是一个程序框图，则输出S 的值是 A.84 B.35 C.26 D.104.下列结论正确的是A.命题“若21x =，则1x =”的否命题为：“若21x =，则1x ≠”B.已知()y f x =是R 上的可导函数，则“()00f x =”是“0x 是函数()y f x =的极值点”的必要不充分条件C.命题“存在x R ∈，使得210x x ++<”的否定是：“对任意x R ∈，均有210x x ++<”D.命题“角α的终边在第一象限角，则α是锐角”的逆否命题为真命题5.高为4的直三棱柱被削去一部分后得到一个几何体，它的直观图和三视图中的侧视图、俯视图如图所示，则该几何体的体积是原直三棱柱的体积的A.34 B. 14C. 12D. 386.已知点()22,0Q -及抛物线24x y =-上一动点(),P x y ，则y PQ +的最小值是A.12B.1C.2D.37.已知()()2,1,0,0A O ，点(),M x y 满足12222x y x y ≤≤⎧⎪≤⎨⎪-≤⎩，则z OA AM =⋅uu r uuu r 的最大值为A. 5-B. 1-C. 0D.18.分别在区间[][]0,01π和，内任取两个实数,x y ，则不等式sin y x ≤恒成立的概率为 A.1πB.2π C.3πD.129.已知函数()()3sin 206f x x πωω⎛⎫=+-> ⎪⎝⎭的图象向右平移23π个单位后与原图象重合，则ω的最小值是 A.3B.32C. 43D.2310.奇函数()f x 的定义域为R ，若()1f x +为偶函数，且()12f =，则()()45f f +的值为A.2B.1C. 1-D. 2-二、填空题：本大题共5个小题，每小题5分，共25分，请把答案填写在答题卡相应位置. 11.若()1cos 753α+=o，则()cos 302α-o 的值为__________. 12.随机抽取100名年龄在[)[)10,20,20,30…，[)50,60年龄段的市民进行问卷调查，由此得到样本的频率分布直方图如图所示，从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人，则在[)50,60年龄段抽取的人数为 ▲ .13.设二项式()60a x a x ⎛⎫-≠ ⎪⎝⎭的展开式中2x 的系数为A ，常数项为B ，若B=44，则a = ▲ .14.已知平面向量,a b r r满足1b =u r ，且a b a -r r r 与的夹角为120°，则a r 的模的取值范围为▲ .15.若函数()32221f x x tx =-++存在唯一的零点，则实数t 的取值范围为 ▲ . 三、解答题：本大题共6个小题，满分75分，解答应写出文字说明、证明过程或演算步骤.16. （本小题满分12分）已知函数()sin cos 16f x x x π⎛⎫=++ ⎪⎝⎭（I ）求函数()f x 的单调递减区间；（II ）在ABC ∆中，,,a b c 分别是角A 、B 、C 的对边，()5,4,124f C b AC BC ==⋅=uuu r uu u r ，求c.17. （本小题满分12分）一个袋中装有7个大小相同的球，其中红球有4个，编号分别为1，2，3，4；蓝球3个，编号为2，4，6，现从袋中任取3个球（假设取到任一球的可能性相同）. （I ）求取出的3个球中，含有编号为2的球的概率；（II ）记ξ为取到的球中红球的个数，求ξ的分布列和数学期望. 18. （本小题满分12分）已知等比数列{}n a 的公比11,1q a >=，且132,,14a a a +成等差数列，数列{}n b 满足：()1122131n n n a b a b a b n ++⋅⋅⋅+=-⋅+ n N ∈.（I ）求数列{}n a 和{}n b 的通项公式；（II ）若8n n ma b ≥-恒成立，求实数m 的最小值. 19. （本小题满分12分）如图，在三棱锥P ABC -中，AB ⊥平面,PAC APC ∠=90°，1,2AB AC ==，E 是AB 的中点，M 是CE 的中点，N 点在PB 上，且4PN PB =. （I ）证明：平面PCE ⊥平面PAB ；（II ）证明：MN//平面PAC ；（III ）若60PAC ∠=o，求二面角P CE A --的大小. 20. （本小题满分13分）如图：A,B,C 是椭圆()222210x y a b a b+=>>的顶点，点(),0F c 为椭圆的右焦点，原点O到直线CF 的距离为12c ，且椭圆过点()23,1. （I ）求椭圆的方程；（II ）若P 是椭圆上除顶点外的任意一点，直线CP 交x 轴于点E ，直线BC 与AP 相交于点D ，连结DE.设直线AP 的斜率为k ，直线DE 的斜率为1k ，问是否存在实数λ，使得112k k λ=+成立，若存在求出λ的值，若不存在，请说明理由.21. （本小题满分14分）已知函数()ln f x x =（I ）若函数()()F x tf x =与函数()21g x x =-在点1x =处有共同的切线l ，求t 的值；（II ）证明：()()12f x f x x x ->+；（III ）若不等式()mf x a x ≥+对所有的230,,1,2m x e ⎡⎤⎡⎤∈∈⎣⎦⎢⎥⎣⎦都成立，求实数a 的取值范围.。

山东省泰安市高三理数第一次统测数学试卷

山东省泰安市高三理数第一次统测数学试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共12分)1. （1分） (2016高二上·衡水期中) 已知集合A={﹣1，0，1}，B={x|x=|a﹣1|，a∈A}，则A∪B中的元素的个数为（）A . 2B . 4C . 6D . 82. （1分）已知是虚数单位，则满足的复数为（）A .B .C .D .3. （1分）已知=（5，-3），C（-1，3），=2，则点D的坐标为（）A . （11，9）B . （4，0）C . （9， 3）D . （9，-3）4. （1分）已知复数，则的最大值为（）A .B .C .D . 35. （1分）具有线性相关关系的变量x、y的一组数据如表所示．若y与x0123y﹣11m6x的回归直线方程为 =3x﹣，则m的值是（）A . 4B .C . 5.5D . 66. （1分） (2019高三上·双流期中) 已知实数，满足不等式组，则的最大值为（）A . 3B . 9C . 22D . 257. （1分） (2018高三上·云南期末) 程序框图如图所示，若输入a的值是虚数单位i ，则输出的结果是（）A .B .C . 0D .8. （1分）设，是两个非零向量，则“•＜0”是“，夹角为钝角”的（）A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件9. （1分）(2016·黄山模拟) 如图为三棱锥S﹣ABC的三视图，其表面积为（）A . 16B . 8 +6C . 16D . 16+610. （1分）(2017·衡阳模拟) 下面是关于公差d＞0的等差数列{an}的四个命题：p1：数列{an}是递增数列；p2：数列{an}的前n项和Sn是递增数列；p3：数列{ }是递增数列；p4：数列{an+nd}是递增数列．其中的真命题为（）A . p1 ， p2B . p3 ， p4C . p2 ， p3D . p1 ， p411. （1分） (2018高二下·龙岩期中) 某天某校的校园卫生清扫轮到高二(5)班，该班劳动委员把班级同学分为5个劳动小组，该校共有A、B、C、D四个区域要清扫，其中A、B、C三个区域各安排一个小组，D区域安排2个小组，则不同的安排方法共有（）A . 240种B . 150种C . 120种D . 60种12. （1分） (2016高三上·怀化期中) 已知一几何体的正视图、俯视图为直角三角形，侧视图为矩形，则该几何体的体积为（）A . 6B . 12C . 18D . 36二、填空题 (共4题；共4分)13. （1分） (2017高二下·临淄期末) 已知随机变量ξ服从正态分布N（2，σ2），且P（ξ＜4）=0.8，则P（0＜ξ＜2）=________．14. （1分）二项式的展开式中，前三项的系数依次成等差数列，则此展开式中有理项有________项．15. （1分）小明通过英语四级测试的概率为，他连续测试3次，那么其中恰有一次获得通过的概率________16. （1分）(2017·南通模拟) 如图，在平面四边形中，为的中点，且OA=3，OC=5．若，则的值是________三、解答题 (共7题；共9分)17. （2分）如图，设长方体ABCD﹣A1B1C1D1中，AB=BC=1，AA1=2，Q是AA1的中点，点P在线段B1D1上；（1）试在线段B1D1上确定点P的位置，使得异面直线QB与DP所成角为60°，并请说明你的理由；（2）在满足（1）的条件下，求四棱锥Q﹣DBB1P的体积．18. （2分）(2017·内江模拟) 某工厂为了解用电量y与气温x℃之间的关系，随机统计了5天的用电量与当天气温，得到如下统计表：8月18日8月25日曰期8月1曰8月7日8月14日平均气温（℃）3330323025用电量（万度）3835413630xiyi=5446， xi2=4538， = ， = ﹣（1）请根据表中的数据，求出y关于x的线性回归方程．据气象預报9月3日的平均气温是23℃，请预测9月3日的用电量；（结果保留整数）（2）请从表中任选两天，记用电量（万度）超过35的天数为ξ，求ξ的概率分布列，并求其数学期望和方差．19. （1分） (2016高一下·新化期中) 如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC= ，O，M分别为AB，VA的中点．（1）求证：VB∥平面MOC；（2）求证：平面MOC⊥平面VAB（3）求三棱锥V﹣ABC的体积．20. （1分）(2017·广西模拟) 某校设计了一个实验学科的实验考查方案：考生从6道备选题中一次性随机抽取3题，按照题目要求独立完成全部实验操作．规定：至少正确完成其中2题获得学分2分，便可通过考察．已知6道备选题中考生甲有4题能正确完成：考生乙每题正确完成的概率都是，且每题正确完成与否互不影响．求：（Ⅰ）分别写出甲、乙两考生正确完成题数的概率分布列，并计算数学期望；（Ⅱ）请你判断两考生的实验操作学科能力，比较他们能通过本次考查的可能性大小．21. （1分） (2019高三上·吉林月考) 如图，三棱柱的侧棱垂直于底面，且，，，，是棱的中点.（1）证明：；（2）求二面角的余弦值.22. （1分）将圆x2+y2=1 每一点的，横坐标保持不变，纵坐标变为原来的2倍，得到曲线C．（1）写出C的参数方程；（2）设直线l:2x+y-2=0 与C的交点为P1,P2 ，以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系，求线段 P1P2 的中点且与 l 垂直的直线的极坐标方程．23. （1分）(2018·南充模拟) 选修4-5：不等式选讲已知函数 .（Ⅰ）解不等式；（Ⅱ）若，且，证明： .参考答案一、单选题 (共12题；共12分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共9分) 17-1、17-2、18-1、18-2、19-1、19-2、19-3、21-1、21-2、22-1、22-2、23-1、。

[泰安一模 理数]泰安市2015届高三第一次模拟考数学试题(理)及答案(word版)

山东省泰安一模数学试题及答案(理)

[泰安一模 理综]泰安市2015届高三第一次模拟考理科综合及答案(word版)

山东省泰安市2015届高考模拟高三第一次模拟考试(整理精校版)

泰安市2015届高三第一次模拟数学试题(理)含答案

山东省泰安市高三一模(数学理)(word版)

山东省泰安市2015届高三上学期期末考试数学试题(理科)

2015年泰安高三上期期末1月考试

2015年山东省高考一模数学试卷(理科)【解析版】

山东省泰安一中2015届高三上学期第一次月考数学(理)试题 word版

2015年山东省高考数学一模试卷(理科)含解析答案

山东省泰安市高三第一轮复习质量检测(一模)数学(理科)试题

山东省泰安市高三数第一次高考模拟考试(理)新人教

山东泰安一中2015届高三上学期第一次月考数学(文)试题 word版

(整理完)山东省泰安市高三一模考试数学试题(理)

泰安一模试题理科数学

数学(理)一模备考综合练习(八)2015届泰安

山东省泰安市高三数学下学期第一次模拟考试试题 理

山东省泰安市高三理数第一次统测数学试卷

[泰安一模理数]泰安市2015届高三第一次模拟考数学试题(理)及答案(word版)

[泰安一模理综]泰安市2015届高三第一次模拟考理科综合及答案(word版)

山东省泰安市高三数学下学期第一次模拟考试试题理