2015年高考数学试题——三角函数
2015年全国各地高考数学试题及解答分类大全(三角函数 三角恒等变换)

4、(2015 全国新课标Ⅰ卷文、理)函数 f (x) cos( x ) 的部分图像如图所示,则 f (x) 的单调
递减区间为( )
(A)(k 1 , k 3), k Z (B)(2k 1 , 2k 3), k Z
4
4
4
4
(C) (k 1 , k 3), k Z 44
(D) (2k 1 , 2k 3), k Z
第 6页 (共 22页)
准确绘制函数图像的能力和灵活运用基础知识解决实际问题的能力. 2.(2015 湖北理)函数 f (x) 4 cos2 x cos( π x) 2sin x | ln(x 1) | 的零点个数为.
22 【答案】2
考点:1.二倍角的正弦、余弦公式,2.诱导公式,3.函数的零点.
.
6
【答案】 .
2
第 9页 (共 22页)
【考点定位】三角恒等变换及特殊角的三角函数值. 【名师点睛】这是一个来自于课本的题,这告诉我们一定要立足于课本.首先将两个角统一为一个
角,然后再化为一个三角函数一般地,有 a sin b cos a2 b2 sin( ) .第二种方法是
直接凑为特殊角,利用特殊角的三角函数值求解.
11 23 1 1 1
1 7
;
23
故选 A.
考点:正切差角公式.
8.(2015
重庆理)若
tan
2 tan
5
,则
cos( 3 ) 10
sin( )
5
A、1
B、2
C、3
D、4
【答案】C
【解析】
()
【考点定位】两角和与差的正弦(余弦)公式,同角间的三角函数关系,三角函数的恒等变换.
2015年全国统一高考数学试卷(理科)(新课标i)附详细解析

2015年全国统一高考数学试卷(理科)(新课标I)一、选择题(共12小题,每小题5分,满分60分)1.(5分)设复数z满足=i,则|z|=()B2n4.(5分)投篮测试中,每人投3次,至少投中2次才能通过测试.己知某同学每次投篮投5.(5分)已知M(x0,y0)是双曲线C:=1上的一点,F1,F2是C的两个焦点,若<0,则y0的取值范围是()....6.(5分)《九章算术》是我国古代内容极为丰富的数学明著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()7.(5分)设D为△ABC所在平面内一点,,则().8.(5分)函数f(x)=cos(ωx+ϕ)的部分图象如图所示,则f(x)的单调递减区间为()﹣,,,)(2k+9.(5分)执行如图的程序框图,如果输入的t=0.01,则输出的n=()255211.(5分)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()12.(5分)设函数f(x)=e x(2x﹣1)﹣ax+a,其中a<l,若存在唯一的整数x0使得f(x0)[[[[二、填空题(本大题共有4小题,每小题5分)13.(5分)若函数f(x)=xln(x+)为偶函数.则a=.14.(5分)一个圆经过椭圆=1的三个顶点.且圆心在x轴的正半轴上.则该圆标准方程为.15.(5分)若x,y满足约束条件.则的最大值为.16.(5分)在平面四边形ABCD中,∠A=∠B=∠C=75°.BC=2,则AB的取值范围是.三、解答题:17.(12分)S n为数列{a n}的前n项和,己知a n>0,a n2+2a n=4S n+3(I)求{a n}的通项公式:(Ⅱ)设b n =,求数列{b n }的前n 项和.18.(12分)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE 丄平面ABCD ,DF 丄平面 ABCD ,BE=2DF ,AE 丄EC . (Ⅰ)证明:平面AEC 丄平面AFC(Ⅱ)求直线AE 与直线CF 所成角的余弦值.19.(12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费x i 和年销售量y i (i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(x i﹣)2(w i ﹣)2(x i ﹣)(y i )(w i ﹣)(y i表中w i =1,=(Ⅰ)根据散点图判断,y=a+bx 与y=c+d 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y 关于x 的回归方程;(Ⅲ)以知这种产品的年利率z与x、y的关系为z=0.2y﹣x.根据(Ⅱ)的结果回答下列问题:(i)年宣传费x=49时,年销售量及年利润的预报值是多少?(ii)年宣传费x为何值时,年利率的预报值最大?附:对于一组数据(u1 v1),(u2 v2)…..(u n v n),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:=,=﹣.20.(12分)在直角坐标系xOy中,曲线C:y=与直线l:y=kx+a(a>0)交于M,N两点.(Ⅰ)当k=0时,分別求C在点M和N处的切线方程.(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?(说明理由)21.(12分)已知函数f(x)=x3+ax+,g(x)=﹣lnx(i)当a为何值时,x轴为曲线y=f(x)的切线;(ii)用min {m,n }表示m,n中的最小值,设函数h(x)=min { f(x),g(x)}(x>0),讨论h(x)零点的个数.选修4一1:几何证明选讲22.(10分)如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.(Ⅰ)若D为AC的中点,证明:DE是⊙O的切线;(Ⅱ)若OA=CE,求∠ACB的大小.选修4一4:坐标系与参数方程23.(10分)(2015春•新乐市校级月考)在直角坐标系xOy中,直线C1:x=﹣2,圆C2:(x﹣1)2+(y﹣2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求C1,C2的极坐标方程;(Ⅱ)若直线C3的极坐标方程为θ=(ρ∈R),设C2与C3的交点为M,N,求△C2MN 的面积.选修4一5:不等式选讲24.(10分)已知函数f(x)=|x+1|﹣2|x﹣a|,a>0.(Ⅰ)当a=1时,求不等式f(x)>1的解集;(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.2015年全国统一高考数学试卷(理科)(新课标I)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)设复数z满足=i,则|z|=()满足=iB.2n4.(5分)投篮测试中,每人投3次,至少投中2次才能通过测试.己知某同学每次投篮投5.(5分)已知M(x0,y0)是双曲线C:=1上的一点,F1,F2是C的两个焦点,若<0,则y0的取值范围是()....=﹣(﹣<<6.(5分)《九章算术》是我国古代内容极为丰富的数学明著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有(),则,××(,÷7.(5分)设D为△ABC所在平面内一点,,则().利用向量的三角形法则首先表示为=本题考查了向量的三角形法则的运用;关键是想法将向量表示为8.(5分)函数f(x)=cos(ωx+ϕ)的部分图象如图所示,则f(x)的单调递减区间为()﹣,,,)(2k+)的部分图象,可得函数的周期为(﹣可得+=,)≤≤2k+)的单调递减区间为()9.(5分)执行如图的程序框图,如果输入的t=0.01,则输出的n=()﹣﹣≤﹣≤﹣=﹣=2552,的通项为=的系数为11.(5分)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()×+22r+12.(5分)设函数f(x)=e x(2x﹣1)﹣ax+a,其中a<l,若存在唯一的整数x0使得f(x0)[[[[<﹣时,,>﹣时,﹣,,解得二、填空题(本大题共有4小题,每小题5分)13.(5分)若函数f(x)=xln(x+)为偶函数.则a=1.x+14.(5分)一个圆经过椭圆=1的三个顶点.且圆心在x轴的正半轴上.则该圆标准方程为(x﹣)2+y2=.解:一个圆经过椭圆,解得,,).)15.(5分)若x,y满足约束条件.则的最大值为3.,则,解得,即=3的最大值为16.(5分)在平面四边形ABCD中,∠A=∠B=∠C=75°.BC=2,则AB的取值范围是(﹣,+).x x xx+m=+AD=x+mx+m=,x+m x=+x的取值范围是(﹣+﹣,)三、解答题:17.(12分)S n为数列{a n}的前n项和,己知a n>0,a n2+2a n=4S n+3(I)求{a n}的通项公式:(Ⅱ)设b n=,求数列{b n}的前n项和.,利用裂项法即可求数列==(﹣(﹣+﹣)(﹣.18.(12分)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,BE=2DF,AE丄EC.(Ⅰ)证明:平面AEC丄平面AFC(Ⅱ)求直线AE与直线CF所成角的余弦值.AG=GC=,且BE=,故,,EF=,),=,)=,﹣,,>=﹣.19.(12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费x i 和年销售量y i (i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(x i ﹣)2(w i ﹣)2(x i ﹣)(y i )(w i ﹣)(y i表中w i=1,=(Ⅰ)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;(Ⅲ)以知这种产品的年利率z与x、y的关系为z=0.2y﹣x.根据(Ⅱ)的结果回答下列问题:(i)年宣传费x=49时,年销售量及年利润的预报值是多少?(ii)年宣传费x为何值时,年利率的预报值最大?附:对于一组数据(u1 v1),(u2 v2)…..(u n v n),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:=,=﹣.w=,建立y=c+dw=的线性回归方程,由于===563的线性回归方程为的回归方程为=100.6+68,的预报值=100.6+68=576.6的预报值的预报值=0.2100.6+68)﹣+20.12=20.(12分)在直角坐标系xOy中,曲线C:y=与直线l:y=kx+a(a>0)交于M,N两点.(Ⅰ)当k=0时,分別求C在点M和N处的切线方程.(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?(说明理由),利用导数的运算法则,利用导数的几何意义、点斜式即可得出切线方程..)联立M Ny=点处的切线斜率为=a=处的切线方程为:,化为==.21.(12分)已知函数f(x)=x3+ax+,g(x)=﹣lnx(i)当a为何值时,x轴为曲线y=f(x)的切线;(ii)用min {m,n }表示m,n中的最小值,设函数h(x)=min { f(x),g(x)}(x>0),讨论h(x)零点的个数.,,即可得出零点的个数;,解得.时,﹣=a+<﹣=a+=,∴当)在内单调递减,在x==,即,则,即,=a+a时,或时,或选修4一1:几何证明选讲22.(10分)如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.(Ⅰ)若D为AC的中点,证明:DE是⊙O的切线;(Ⅱ)若OA=CE,求∠ACB的大小.,BE=选修4一4:坐标系与参数方程23.(10分)(2015春•新乐市校级月考)在直角坐标系xOy中,直线C1:x=﹣2,圆C2:(x﹣1)2+(y﹣2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求C1,C2的极坐标方程;(Ⅱ)若直线C3的极坐标方程为θ=(ρ∈R),设C2与C3的交点为M,N,求△C2MN 的面积.3的面积(3=2=.选修4一5:不等式选讲24.(10分)已知函数f(x)=|x+1|﹣2|x﹣a|,a>0.(Ⅰ)当a=1时,求不等式f(x)>1的解集;(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.,或求得<,a|=,,[2a+1]参与本试卷答题和审题的老师有:刘长柏;qiss;maths;changq;caoqz;cst;lincy;吕静;双曲线;whgcn;孙佑中(排名不分先后)菁优网2015年7月20日。
2015年高考真题解三角形(word精校版)

2015年高考解三角形试题精选(一)1.(广东文科·5)设C ∆AB 的内角A ,B ,C 的对边分别为a ,b ,c .若2a =,23c =,3cos 2A =,且b c <,则b =( )A .3B .2C .22D .32.(安徽文科·12)在ABC ∆中,6=AB , 75=∠A ,45=∠B ,则=AC .3.(北京文科·11)在△ABC 中,a=3,b=,∠A=,∠B=4.(福建理科·12)若锐角ABC △的面积为103 ,且5,8AB AC ==,则BC 等于 . 5.(四川理科·12)=+75sin 15sin . 6.(北京理科·12)在ABC △中,4a =,5b =,6c =,则sin 2sin AC= .7.(重庆文科·13)设ABC ∆的内角A,B,C 的对边分别为a,b,c ,且B A C a sin 2sin 3,41cos ,2=-==,则c=8.(天津理科·13)在ABC ∆ 中,内角,,A B C 所对的边分别为,,a b c ,已知ABC ∆的面积为315 ,12,cos ,4b c A -==- 则a 的值为 .9.(湖北理科·13)如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30的方向上,行驶600m 后到达B 处,测得此山顶在西偏北75的方向上,仰角为30,则此山的高度CD = m .10.(课标Ⅰ理16)在平面四边形ABCD 中,∠A=∠B=∠C=75°,BC=2,则AB 的取值范围是________.11.(课标Ⅰ卷文·17)已知a,b,c 分别为ABC ∆内角A,B,C 的对边,C A B sin sin 2sin 2=. (Ⅰ)若a=b ,求B cos ;(Ⅱ)设2a ,90=︒=且B ,求ABC ∆的面积.ABCD12.(课标Ⅱ卷文·17)△ABC 中D 是BC 上的点,AD 平分∠P AC , BD =2DC . (I )求sin sin BC∠∠ ;(II )若60BAC ∠=,求B ∠.13. (课标Ⅱ卷理·17)∆ABC 中,D 是BC 上的点,AD 平分∠BAC ,∆ABD 是∆ADC 面积的2倍. (Ⅰ)求CB∠∠sin sin ;(Ⅱ)若22,1==DC AD ,求BD 和AC 的长14.(湖南理科·17)设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,tan a b A =,且B 为钝角. (1)证明:2B A π-=(2)求sin sin A C +的取值范围.15.(四川理·19).如图,A,B,C,D 为平面四边形ABCD 的四个内角.(1)证明:1cos tan;2sin A A A-= (2)若180,6,3,4,5,A C AB BC CD AD +=====o求tantan tan tan 2222A B C D+++的值。
2015年三年高考数学(理)真题精编——专题04 三角函数与三角形

一、选择题1. 【2013高考北京理第3题】“φ=π”是“曲线y =sin(2x +φ)过坐标原点”的().A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】A考点:充分必要条件;三角函数值.2.【 2013湖南3】在锐角中ABC ∆,角,A B 所对的边长分别为,a b .若2sin ,a B A =则角等于A .12πB .6πC .4πD .3π【答案】 D【解析】 3=A 223=sinA sinB 3 = sinB 2sinA :得b 3=2asinB 由ππ⇒<⇒⋅⋅A , 选D4. 【 2014湖南9】已知函数()sin(),f x x ϕ=-且230()0,f x dx π=⎰则函数()f x 的图象的一条对称轴是( ) A.56x π=B.712x π=C.3x π=D.6x π= 【答案】A【考点定位】三角函数图像 辅助角公式 定积分5. 【2013山东,理5】将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( ).A .3π4 B .π4 C .0 D .π4- 【答案】:B【解析】:函数y =sin(2x +φ)的图象向左平移π8个单位后变为函数πsin 28y x ϕ⎡⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦=πsin 24x ϕ⎛⎫++ ⎪⎝⎭的图象,又πsin 24y x ϕ⎛⎫++ ⎪⎝⎭=为偶函数,故πππ42k ϕ+=+,k ∈Z ,∴ππ4k ϕ=+,k∈Z .若k =0,则π4ϕ=.故选B. 8. 【2015高考山东,理3】要得到函数sin 43y x π⎛⎫=- ⎪⎝⎭的图象,只需要将函数sin 4y x =的图象( )(A )向左平移12π个单位 (B )向右平移12π个单位(C )向左平移3π个单位 (D )向右平移3π个单位 【答案】B【解析】因为sin 4sin 4312y x x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭ ,所以要得到函数sin 43y x π⎛⎫=- ⎪⎝⎭ 的图象,只需将函数sin 4y x = 的图象向右平移12π个单位.故选B.【考点定位】三角函数的图象变换.9. 【2013山东,理8】函数y =x cos x +sin x 的图象大致为().【答案】:D11. 【2014高考陕西版理第2题】函数()cos(2)6f x x π=-的最小正周期是( ).2A π.B π .2C π .4D π【答案】B 【解析】试题分析:由周期公式2T w π=,又2w =,所以函数()cos(2)6f x x π=-的周期22T ππ==,故选B . 考点:三角函数的最小正周期.12. .【2015高考陕西,理3】如图,某港口一天6时到18时的水深变化曲线近似满足函数3sin()6y x k πϕ=++,据此函数可知,这段时间水深(单位:m )的最大值为( )A .5B .6C .8D .10【答案】C【解析】由图象知:min 2y =,因为min 3y k =-+,所以32k -+=,解得:5k =,所以这段时间水深的最大值是max 3358y k =+=+=,故选C . 【考点定位】三角函数的图象与性质.13. 【2013高考陕西版理第7题】在设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cosB =a sin A ,则△ABC 的形状为( ). A .直角三角形 B .锐角三角形 C .钝角三角形D .不确定 【答案】A考点:正弦定理.14.【2014新课标,理4】钝角三角形ABC 的面积是12,AB=1, ,则AC=( )A. 5B.C. 2D. 1【答案】B【解析】由面积公式得:1122B =,解得sin B =45B =o 或135B =o ,当45B =o 时,由余弦定理得:21245AC =+-o=1,所以1AC =,又因为AB=1,,所以此时ABC ∆为等腰直角三角形,不合题意,舍去;所以135B =o ,由余弦定理得:212AC =+-o=5,所以AC = B.20. 【2013四川,理5】函数()2sin()f x x ωϕ=+(0ω>,22ππϕ-<<)的部分图象如图所示,则ω,ϕ的值分别是( )(A )2,3π- (B )2,6π-(C )4,6π- (D )4,3π【答案】A【考点定位】本题考查正弦型函数()sin()f x A x ωϕ=+的图象与性质,难点是确定初相ϕ的值,关键是理解“五点法”作图.21. .【2014四川,理3】 为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上所有的点( ) A .向左平行移动12个单位长度 B .向右平行移动12个单位长度 C .向左平行移动1个单位长度 D .向右平行移动1个单位长度 【答案】A【考点定位】三角函数图象的变换.22. 【2015高考四川,理4】下列函数中,最小正周期为π且图象关于原点对称的函数是( )()cos(2)2A y x π=+ ()sin(2)2B y x π=+ ()sin 2cos 2C y x x =+ ()sin cos D y x x =+【答案】A【解析】对于选项A ,因为2sin 2,2y x T ππ=-==,且图象关于原点对称,故选A. 【考点定位】三角函数的性质.24. 【2015高考新课标1,理2】o o o o sin 20cos10cos160sin10- =( )(A ) (B (C )12- (D )12【答案】D【解析】原式=o o o o sin 20cos10cos 20sin10+ =o sin 30=12,故选D. 【考点定位】三角函数求值.25. 【2014课标Ⅰ,理6】如图,图O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示成x 的函数)(x f ,则],0[)(π在x f y =的图像大致为( )【答案】CP OAM D POAM D26. 【2014课标Ⅰ,理8】设(0,),(0,),22ππαβ∈∈且1sin tan ,cos βαβ+=则( )(A ) 32παβ-= (B )32παβ+=(C )22παβ-=(D )22παβ+=【答案】C28. 【2015高考新课标1,理8】函数()f x =cos()x ωϕ+的部分图像如图所示,则()f x 的单调递减区间为( )(A)13(,),44k k k Z ππ-+∈ (B)13(2,2),44k k k Z ππ-+∈ (C)13(,),44k k k Z -+∈ (D)13(2,2),44k k k Z -+∈【答案】D【考点定位】三角函数图像与性质31. 【2014年.浙江卷.理4】为了得到函数x x y 3cos 3sin +=的图像,可以将函数x y 3sin 2=的图像( ) A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位答案:D解析:sin 3cos334y x x x π⎛⎫=+=+ ⎪⎝⎭,故只需将3y x =向左平移4π个单位.考点:三角函数化简,图像平移.32. 【2013年.浙江卷.理4】已知函数f (x )=A cos(ωx +φ)(A >0,ω>0,φ∈R ),则“f (x )是奇函数”是“π2ϕ=”的( ). A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】:B 【解析】:若f (x )是奇函数,则φ=k π+π2,k ∈Z ; 若π2ϕ=,则f (x )=A cos(ωx +φ)=-A sin ωx ,显然是奇函数. 所以“f (x )是奇函数”是“π2ϕ=”的必要不充分条件.33. 【2013年.浙江卷.理6】已知α∈R ,sin α+2cos αtan 2α=( ).A .43B .34C .34-D .43-【答案】:C38. 【2013高考重庆理第9题】4cos 50°-tan 40°=().A 2B 23+ C 3 D .221 【答案】C39. 【2014高考重庆理第10题】已知ABC ∆的内角21)sin()sin(2sin ,+--=+-+B A C C B A A C B A 满足,,面积S 满足 C B A c b a S ,,,,21分别为,记≤≤所对的边,则下列不等式一定成立的是( ) A.8)(>+c b bc B.()162ac a b +> C.126≤≤abc D.1224abc ≤≤【答案】A 【解析】试题分析:由题设得:()()1sin 2+sin 2sin 22A B C ππ-=-+1sin 2+sin2B+sin 22A C ⇒= ⇒ ()()1sin 222+sin2B+sin 22BC C π-+=()1sin2B+sin 2sin 222C B C ⇒-+=⇒()()1sin 21cos 2sin 21-cos2B 2B C C -+=()14sin sin sin cos cos sin 2B C B C B C ⇒+=1sin sin sin 8A B C ⇒= (1)由三角形面积公式1sin 2s ab C =及正弦定理得:214sin sin sin 2s R A B C =⨯所以24s R =,又因为12s ≤≤,所以248R ≤≤, 所以()338sin sin sin b c b cbc b c abc R A B C R a a+++=⨯=⨯>恒成立,所以()8bc b c +> 故选A.考点:1、两角和与差的三角函数;2、正弦定理;3、三角形的面积公式.40. 【2015高考重庆,理9】若tan 2tan 5πα=,则3cos()10sin()5παπα-=-( ) A 、1 B 、2 C 、3 D 、4 【答案】C 【解析】由已知,3cos()10sin()5παπα-=-33cos cos sin sin 1010sin cos cos sin 55ππααππαα+-33cos tan sin 1010tan cos sin 55ππαππα+=-33cos 2tan sin 105102tan cos sin555ππππππ+=- 33cos cos2sin sin 510510sin cos 55ππππππ+==155(cos cos )(cos cos )21010101012sin 25πππππ++-3cos 103cos 10ππ==,选C . 【考点定位】两角和与差的正弦(余弦)公式,同角间的三角函数关系,三角函数的恒等变换.42. 【2015高考安徽,理10】已知函数()()sin f x x ωϕ=A +(A ,ω,ϕ均为正的常数)的最小正周期为π,当23x π=时,函数()f x 取得最小值,则下列结论正确的是( ) (A )()()()220f f f <-< (B )()()()022f f f <<- (C )()()()202f f f -<< (D )()()()202f f f <<-【答案】A【考点定位】1.三角函数的图象与应用;2.函数值的大小比较.45.【2013天津,理6】在△ABC 中,∠ABC =π4,AB ,BC =3,则sin ∠BAC =().A BC D 【答案】C48.【2013年普通高等学校招生全国统一考试湖北卷4】将函数()sin y x x x R =+∈的图像向左平移()0m m >个长度单位后,所得到的图像关于y 轴对称,则m 的最小值是( )A.12πB.6π C. 3π D. 56π 【答案】 【解析】试题分析:2cos 6y x π⎛⎫=- ⎪⎝⎭的图像向左平移()0m m >个长度单位后变成2cos 6y x m π⎛⎫=-+ ⎪⎝⎭,所以m 的最小值是6π.故选B. 49. 【2013年普通高等学校招生全国统一考试湖北卷5】已知04πθ<<,则双曲线22122:1cos sin x y C θθ-=与222222:1sin sin tan y x C θθθ-=的( )A.实轴长相等B.虚轴长相等C.焦距相等D. 离心率相等 【答案】D 【解析】试题分析:双曲线1C 的离心率是11cos e θ=,双曲线2C 的离心率是21cos e θ==,故选D.二、填空题3. 【2014高考北京理第14题】设函数()sin()f x A x ωϕ=+(,,A ωϕ是常数,0,0A ω>>).若()f x 在区间[,]62ππ上具有单调性,且2()()()236f f f πππ==-,则()f x 的最小正周期为 . 【答案】π 【解析】试题分析:由)(x f 在区间]2,6[ππ上具有单调性,且)6()2(ππf f -=知,函数)(x f 的对称中心为)0,3(π,由)32()2(ππf f =知函数)(x f 的对称轴为直线127)322(21πππ=+=x ,设函数)(x f 的最小正周期为T , 所以,6221ππ-≥T ,即32π≥T ,所以43127T =-ππ,解得π=T .考点:函数)sin()(ϕω+=x A x f 的对称性、周期性,容易题.4. 【2015高考北京,理12】在ABC △中,4a =,5b =,6c =,则sin 2sin A C=.【答案】1【解析】222sin 22sin cos 2sin sin 2A A A a b c a C C c bc+-==⋅2425361616256⨯+-=⋅=⨯⨯ 考点定位:本题考点为正弦定理、余弦定理的应用及二倍角公式,灵活使用正弦定理、余弦定理进行边化角、角化边.5. 【2014高考广东卷.理.12】在ABC ∆中,角A .B .C 所对应的边分别为a .b .c ,已知b Bc C b 2cos cos =+,则=ba. 【答案】2.【考点定位】本题考查正弦定理中的边角互化思想的应用以及两角和的三角函数,属于中等题.6. 【2015高考广东,理11】设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,若a = 1sin 2B =,6C =π,则b = . 【答案】1. 【解析】因为1sin 2B =且()0,B π∈,所以6B π=或56B π=,又6C π=,所以6B π=, 23A BC ππ=--=,又a =sin sin a b A B =sin 36b π=解得1b =,故应填入1. 【考点定位】三角形的内角和定理,正弦定理应用.10. 【2013江苏,理1】(2013江苏,1)函数π3sin 24y x ⎛⎫=+ ⎪⎝⎭的最小正周期为__________.【答案】π.【解析】函数π3sin 24y x ⎛⎫=+ ⎪⎝⎭的最小正周期2ππ2T ==..11. 【2014江苏,理5】已知函数cos y x =与函数sin(2)(0)y x φφπ=+≤<,它们的图像有一个横坐标为3π的交点,则ϕ的值是 .【答案】6π.12. 【2015江苏高考,8】已知tan 2α=-,()1tan 7αβ+=,则tan β的值为_______.【答案】3【解析】12tan()tan 7tan tan() 3.21tan()tan 17αβαβαβααβα++-=+-===++- 【考点定位】两角差正切公式13. 【2014江苏,理14】若ABC ∆的内角满足sin 2sin A B C +=,则cos C 的最小值是 ..【解析】由已知sin 2sin A B C +=及正弦定理可得2a c +=,222cos 2a b cC ab+-===≥=,当且 仅当2232a b =即a b =时等号成立. 15. 【2014新课标,理14】函数()()()sin 22sin cos f x x x ϕϕϕ=+-+的最大值为_________.【答案】1【解析】由题意知:()()()sin 22sin cos f x x x ϕϕϕ=+-+=()()sin[]2sin cos x x ϕϕϕϕ++-+ =()sin cos x ϕϕ++()cos sin x ϕϕ+-()2sin cos x ϕϕ+=()cos sin x ϕϕ+-()sin cos x ϕϕ+ =()sin[]x ϕϕ+-=sin x ,即()sin f x x =,因为x R ∈,所以()f x 的最大值为1.17. 【2013课标全国Ⅱ,理15】设θ为第二象限角,若π1tan 42θ⎛⎫+= ⎪⎝⎭,则sin θ+cos θ=__________.【答案】:19. 【2013四川,理13】设sin 2sin αα=-,(,)2παπ∈,则tan 2α的值是____________.【考点定位】本题考查同角三角函数间的基本关系,二倍角公式,简单的三角恒等变换,基础题.20. 【2014四川,理13】如图,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为67 ,30 ,此时气球的高是46m ,则河流的宽度BC 约等于 m .(用四舍五入法将结果精确到个位.参考数据:sin 670.92≈ ,cos 670.39≈ ,sin 370.60≈ ,cos370.80≈ 1.73≈)【答案】60 【解析】试题分析:92AC =,46cos 67AB =,sin 37,60sin 30sin 37sin 30AB BC AB BC =∴=≈ . 【考点定位】解三角形.21. 【2015高考四川,理12】=+ 75sin 15sin .【考点定位】三角恒等变换及特殊角的三角函数值.有sin cos )a b αααϕ+=+.第二种方法是直接凑为特殊角,利用特殊角的三角函数值求解.22. 【2014课标Ⅰ,理16】已知c b a ,,分别为ABC ∆三个内角C B A ,,的对边,2=a ,且()C b c B A b sin )()sin (sin 2-=-+,则ABC ∆面积的最大值为____________.【解析】由2=a ,且()C b c B A b sin )()sin (sin 2-=-+,故(a b)(sinA sinB)(c b)sinC +-=-,又根据正弦定理,得(a b)()(c b)a b c +-=-,化简得,222b c a bc +-=,故222b c a 1cosA 2bc 2+-==,所以0A 60=,又22b c 4bc bc +-=≥,故1S bcsinA 2BAC ∆=≤. 24. 【2015高考新课标1,理16】在平面四边形ABCD 中,∠A =∠B =∠C =75°,BC =2,则AB 的取值范围是 .【答案】【考点定位】正余弦定理;数形结合思想25.【2014年.浙江卷.理17】如图,某人在垂直于水平地面的墙面前的点处进行射击训练.已知点到墙面的距离为,某目标点沿墙面的射击线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角的大小.若则的最大值53考点:解三角形,求最值.26.【2013年.浙江卷.理16】在△ABC中,∠C=90°,M是BC的中点.若sin∠BAM=1,则sin∠BAC3=__________.【答案】【解析】:如图以C为原点建立平面直角坐标系,27. 【2015高考浙江,理11】函数2()sin sin cos 1f x x x x =++的最小正周期是 ,单调递减区间是 . 【答案】π,]87,83[ππππk k ++,Z k ∈. 【解析】试题分析:1cos 2sin 23()1)2242x x f x x π-=++=-+,故最小正周期为π,单调递减区间为 ]87,83[ππππk k ++,Z k ∈. 【考点定位】1.三角恒等变形;2.三角函数的性质30.【2015高考重庆,理13】在 ABC 中,B =120o ,AB ,A 的角平分线AD ,则AC =_______.【解析】由正弦定理得sin sin AB ADADB B=∠=,解得sin ADB ∠= 45ADB ∠=︒,从而15BAD DAC ∠=︒=∠,所以1801203030C =︒-︒-︒=︒,2cos30AC AB =︒=【考点定位】解三角形(正弦定理,余弦定理)31. 【2014,安徽理11】若将函数()sin 24f x x π⎛⎫=+ ⎪⎝⎭的图像向右平移ϕ个单位,所得图像关于y 轴对称, 则ϕ的最小正值是________. 【答案】83π.考点:1.三角函数的平移;2.三角函数恒等变换与图象性质.32. 【2013,安徽理12】设ABC ∆的内角,,A B C 所对边的长分别为,,a b c .若2b c a +=,则3sin 5sin ,A B =则角C =_____.【答案】π32. 【解析】由3sin 5sin A B =,得35b a =.又2b c a +=,所以725c a b a =-=.由余弦定理可得 ()2221cos ,0,22a b c C C ab π+-==-∈,所以2.3C π= 【命题立意】考查正弦定理、余弦定理的应用.35. 【2014天津,理12】在ABC D 中,内角,,A B C 所对的边分别是,,a b c .已知14b c a -=,2sin 3sin B C =,则cos A 的值为_______.【答案】14-. 【解析】试题分析:∵32sin 3sin ,23,,2B C b c b c =\=\=代入14b c a -=得2a c =,由余弦定理得2221cos 24b c a A bc +-==-.考点:1.正弦定理;2.余弦定理的推论.36.【2015高考天津,理13】在ABC ∆ 中,内角,,A B C 所对的边分别为,,a b c ,已知ABC ∆的面积为,12,cos ,4b c A -==- 则a 的值为 .【答案】8【解析】因为0A π<<,所以sin A ==又1sin 242ABC S bc A bc ∆===∴=,解方程组224b c bc -=⎧⎨=⎩得6,4b c ==,由余弦定理得 2222212cos 64264644a b c bc A ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭,所以8a =.【考点定位】同角三角函数关系、三角形面积公式、余弦定理.38. 【2015高考湖北,理12】函数2π()4cos cos()2sin |ln(1)|22x f x x x x =---+的零点个数为 .【答案】2【解析】因为2π()4cos cos()2sin |ln(1)|22x f x x x x =---+ |)1ln(|sin 2sin )cos 1(2+--+=x x x x |)1ln(|2sin +-=x x所以函数)(x f 的零点个数为函数x y 2sin =与|)1ln(|+=x y 图象的交点的个数, 函数x y 2sin =与|)1ln(|+=x y 图象如图,由图知,两函数图象有2个交点, 所以函数)(x f 有2个零点.【考点定位】二倍角的正弦、余弦公式,诱导公式,函数的零点.39. 【2015高考湖北,理13】如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30 的方向上,行驶600m 后到达B 处,测得此山顶在西偏北75 的方向上,仰角为30 ,则此山的高度CD = m.【答案】6100【解析】依题意, 30=∠BAC , 105=∠ABC ,在ABC ∆中,由 180=∠+∠+∠ACB BAC ABC ,所以 45=∠ACB ,因为600=AB ,由正弦定理可得30sin 45sin 600BC=,即2300=BC m , 在BCD Rt ∆中,因为 30=∠CBD ,2300=BC ,所以230030tan CD BC CD ==,所以6100=CD m. 【考点定位】三角形三内角和定理,三角函数的定义,有关测量中的的几个术语,正弦定理.40. 【2014 上海,理1】 函数212cos (2)y x =-的最小正周期是.【答案】2π【考点】三角函数的周期.41. 【2013上海,理4】已知△ABC 的内角A 、B 、C 所对的边分别是a 、b 、c .若3a 2+2ab +3b 2-3c 2=0,则角C 的大小是______(结果用反三角函数值表示). 【答案】π-arccos 13【解析】3a 2+2ab +3b 2-3c 2=0⇒c 2=a 2+b 2+23ab ,故cos C =13-,C =1arccos 3π-. 42. 【2013上海,理11】若cos x cos y +sin x sin y =12,sin2x +sin2y =23,则sin(x +y )=______.【答案】23【解析】cos(x -y )=12,sin2x +sin2y =2sin(x +y )cos(x -y )=23,故sin(x +y )=23. 46.【2014福建,理12】在ABC ∆中,60,4,A AC BC =︒==,则ABC ∆的面积等于_________【答案】【解析】试题分析:由正弦定理可得0sin 1,90B B =∴=.所以ABC ∆的面积等于. 考点:1.正弦定理.2.三角形的面积.47.(2013福建,理13)如图,在△ABC 中,已知点D 在BC 边上,AD ⊥AC ,sin ∠BAC ,AB =AD =3,则BD 的长为________.51.【2015高考福建,理12】若锐角ABC ∆的面积为,且5,8AB AC == ,则BC 等于________.【答案】7【解析】由已知得ABC ∆的面积为1sin 20sin 2AB AC A A ⋅==,所以sin A =,(0,)2A π∈,所以3A π=.由余弦定理得2222cos BC AB AC AB AC A =+-⋅=49,7BC =.【考点定位】1、三角形面积公式;2、余弦定理.三、解答题3.【2013高考北京理第15题】(本小题共13分)在△ABC 中,a =3,b =,∠B =2∠A ,(1)求cos A 的值; (2)求c 的值.【答案】解:(1)因为a =3,b =,∠B =2∠A ,所以在△ABC 中,由正弦定理得3sin A =所以2sin cos sin A A A =.故cos A(2)由(1)知,cos A所以sin A =.4. 【2014高考北京理第15题】(本小题满分13分)如图,在ABC ∆中,,83B AB π∠==,点D 在BC 边上,且2CD =,1cos 7ADC ∠=. (1)求sin BAD ∠; (2)求BD ,AC 的长.【答案】(1)1433;(2)7. 【解析】试题分析:(1)由条件,根据1cos sin 22=+αα求ADC ∠sin ,再由两个角的差的正弦公式求BAD ∠sin ; (2)根据正弦定理求出BD ,再由余弦定理求AC . 试题解析:(1)在ADC ∆中,因为71cos =∠ADC ,所以734sin =∠ADC ,所以B ADC B ADC B ADC BAD ∠∠-∠∠=∠-∠=∠sin cos cos sin )sin(sin 1433237121734=⨯-⨯=.考点:同角三角函数的关系,两个角的差的正弦公式,正弦定理与余弦定理.5. 【2015高考北京,理15】已知函数2()cos 222x x xf x =.(Ⅰ) 求()f x 的最小正周期;(Ⅱ) 求()f x 在区间[π0]-,上的最小值. 【答案】(1)2π,(2)1-- 【解析】 (Ⅰ) 211cos ()sincossin sin 22222xxxxf x x -=-=⋅-⋅=sin cos x x =+-sin()4x π=+- (1)()f x 的最小正周期为221T ππ==; (2)30,444x x ππππ-≤≤∴-≤+≤ ,当3,424x x πππ+=-=-时,()f x 取得最小值为:1--考点定位: 本题考点为三角函数式的恒等变形和三角函数图象与性质,要求熟练使用降幂公式与辅助角公式,利用函数解析式研究函数性质,包括周期、最值、单调性等.6. 【2015高考广东,理16】在平面直角坐标系xoy中,已知向量m = ,()sin ,cos n x x =,0,2x π⎛⎫∈ ⎪⎝⎭.(1)若m n ⊥,求tan x 的值;(2)若m 与n 的夹角为3π,求x 的值.【答案】(1)1;(2)512x π=.【考点定位】向量数量积的坐标运算,两角和差公式的逆用,知角求值,知值求角.7. 【2014高考广东卷.理.16】 (本小题满分12分)已知函数()sin 4f x A x π⎛⎫=+ ⎪⎝⎭,x R ∈,且53122f π⎛⎫= ⎪⎝⎭.(1)求A 的值; (2)若()()32f f θθ+-=,0,2πθ⎛⎫∈ ⎪⎝⎭,求34f πθ⎛⎫- ⎪⎝⎭.【答案】(1)A =【解析】(1)5523sin sin sin sin 121243332f A A A A A πππππππ⎛⎫⎛⎫⎛⎫=+==-===⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以A =()4f x x π⎛⎫∴=+ ⎪⎝⎭;【考点定位】本题考查诱导公式.同角三角函数的基本关系以及两角和的三角函数,综合考查三角函数的求值问题,属于中等题.8.【2013高考广东卷.理.16】 (本小题满分12分)已知函数π()12f x x⎛⎫=-⎪⎝⎭,x∈R.(1)求π6f⎛⎫-⎪⎝⎭的值;(2)若cosθ=35,θ∈3π,2π2⎛⎫⎪⎝⎭,求π23fθ⎛⎫+⎪⎝⎭.【答案】(1)1 (2)17 25【解析】(1)πππ6612f⎛⎫⎛⎫-=--⎪ ⎪⎝⎭⎝⎭ππ144⎛⎫-==⎪⎝⎭.(2)πππ223312fθθ⎛⎫⎛⎫+=+-⎪ ⎪⎝⎭⎝⎭π24θ⎛⎫+⎪⎝⎭=cos2θ-sin2θ.因为cosθ=35,θ∈3π,2π2⎛⎫⎪⎝⎭,所以sinθ=45-.所以sin2θ=2sinθcosθ=2425-,cos2θ=cos2θ-sin2θ=725-.所以π23fθ⎛⎫+⎪⎝⎭=cos2θ-sin2θ=72417252525⎛⎫---=⎪⎝⎭.【考点定位】本题考查三角函数中的化简求值,属于能力题12.【 2014湖南18】如图5,在平面四边形ABCD 中,1,2,AD CD AC ===(1)求cos CAD ∠的值;(2)若cos BAD ∠=,sin CBA ∠=,求BC 的长.【答案】(1) cos CAD ∠=(2)3试题解析: (1)由DAC ∆关于CAD ∠的余弦定理可得222cos2AD AC DC CAD AD AC +-∠= ==所以cos CAD ∠=. (2)因为BAD ∠为四边形内角,所以sin 0BAD ∠>且sin 0CAD ∠>,则由正余弦的关系可得sin BAD ∠==且sin CAD ∠==再由正弦的和差角公式可得()sin sin sin cos sin cos BAC BAD CAD BAD CAD CAD BAD ∠=∠-∠=∠∠-∠∠⎛= ⎝==再由ABC ∆的正弦定理可得 sin sin AC BCCBA BAC =∠∠3BC ⇒==. 【考点定位】三角形正余弦定理 正余弦之间的关系与和差角公式13. 【 2013湖南17】已知函数2()sin()cos().()2sin 632x f x x x g x ππ=-+-=。
2015年高考理科数学全国卷1(含答案解析)

绝密★启用前 2015年普通高等学校招生全国统一考试(全国新课标卷1)数学(理科)使用地区:河南、山西、河北、江西本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数z 满足1+z1z-=i ,则|z|=( ) A .1B .2C .3D .2 2.sin20cos10cos160sin10︒︒︒︒-=( )A .32-B .32C .12-D .123.设命题:p n ∃∈Ν,22n n >,则⌝p 为( )A .2n n n ∀∈N 2,>B .2n n n ∃∈N 2,≤C .2n n n ∀∈N 2,≤D .=2n n n ∃∈N 2,4.投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )A .0.648B .0.432C .0.36D .0.3125.已知00()M x y ,是双曲线2212x C y -=:上的一点,F 1,F 2是C 的两个焦点.若120MF MF <,则0y 的取值范围是( )A .33()33-, B .33()66-, C .2222()33-, D .2323()33-, 6. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A .14斛B .22斛C .36斛D .66斛 7.设D 为ABC △所在平面内一点,=3BC CD ,则( )A .1433AD AB AC =-+ B .1433AD AB AC =- C .4133AD AB AC =+ D .4133AD AB AC =-8.函数=cos(+)x f x ωϕ()的部分图象如图所示,则f x ()的单调递减区间为( )A .13π,π+44k k k -∈Z (),B .132π,2π+44k k k -∈Z (),C .13,+44k k k -∈Z (),D .132,2+44k k k -∈Z (),9.执行如图所示的程序框图,如果输入的0.01t =,则输出 的n =( )A .5B .6C .7D .810.25()x x y ++的展开式中,52x y 的系数为( )A .10B .20C .30D .6011.圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r =( )A .1B .2C .4D .812.设函数()()21x f x e x ax a =--+,其中a<1,若存在唯一的整数0x 使得0()0f x <,则a 的取值范围是( )--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________A .3[)21,e-B .43[,)23e -C .3[,)234e D .3[,)21e第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13.若函数2()=()ln f x x a x x ++为偶函数,则a =________. 14.一个圆经过椭圆22=1164x y+的三个顶点,且圆心在x 轴的正半轴上,则该圆的标准方程为________.15.若x ,y 满足约束条件10,0,40,x x y x y -⎧⎪-⎨⎪+-⎩≥≤≤则y x 的最大值为________.16.在平面四边形ABCD 中,==75=A B C ∠∠∠︒,=2BC ,则AB 的取值范围是________. 三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分)n S 为数列{}n a 的前n 项和.已知0n a >,2n n n +2=4+3a a S .(Ⅰ)求{}n a 的通项公式;(Ⅱ)设n n n+11=b a a ,求数列{}n b 的前n 项和.18.(本小题满分12分)如图,四边形ABCD 为菱形,∠ABC =120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC . (Ⅰ)证明:平面AEC ⊥平面AFC ; (Ⅱ)求直线AE 与直线CF 所成角的余弦值.19.(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z(单位:千元)的影响,对近8年的年宣传费i x 和年销售量i y (i =1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.xyω28i=1()ixx -∑28i=1()iωω∑-8i=1()()iiy x x y-∑-8i=1()()ii y y ωω--∑46.65636.8289.8 1.6 1 469108.8表中i ω=i x ,ω=188i i=1ω∑(Ⅰ)根据散点图判断,y a bx =+与y c d x =+哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y 关于x 的回归方程;(Ⅲ)已知这种产品的年利率z 与x ,y 的关系为z=0.2y -x .根据(Ⅱ)的结果回答下列问题:(i )年宣传费x =49时,年销售量及年利润的预报值是多少? (ii )年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据11()u v ,,22(,)u v ,…,(,)n n u v ,其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为121()(),()nii i nii uu v v v u uu βαβ==--==--∑∑.20.(本小题满分12分)在直角坐标系xOy 中,曲线24C y x :=与直线)0(l y kx a a >:=+交于M ,N 两点.(Ⅰ)当k =0时,分别求C 在点M 和N 处的切线方程;(Ⅱ)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM =∠OPN ?说明理由.21.(本小题满分12分)已知函数31()4f x x ax =++,()ln g x x =-. (Ⅰ)当a 为何值时,x 轴为曲线()y f x =的切线;(Ⅱ)用min{,}m n 表示m ,n 中的最小值,设函数()min{(),()}h x f x g x =(0)x >,讨论()h x 零点的个数.请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题记分. 22.(本小题满分10分)选修4—1:几何证明选讲如图,AB 是O 的直径,AC 是O 的切线,BC 交O 于点E . (Ⅰ)若D 为AC 的中点,证明:DE 是O 的切线; (Ⅱ)若OA =3CE ,求∠ACB 的大小.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy 中,直线1C :x =-2,圆2C :(x -1)2+(y -2)2=1,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (Ⅰ)求1C ,2C 的极坐标方程; (Ⅱ)若直线3C 的极坐标方程为()π4θρ=∈R ,设2C 与3C 的交点为M ,N ,求2C MN △的面积.24.(本小题满分10分)选修4—5:不等式选讲已知函数12f x =|||x |x a -+-(),0a >. (Ⅰ)当=1a 时,求不等式1f x >()的解集;(Ⅱ)若f x ()的图象与x 轴围成的三角形面积大于6,求a 的取值范围. 2015年普通高等学校招生全国统一考试(全国新课标卷1)数学(理科)答案解析第Ⅰ卷一、选择题 1.【答案】A 【解析】由1=i 1z z+-,得1i (1i)(1i)=i 1i (1i)(1i)z -+-+-===++-,故1z =,故选C . 【提示】先化简复数,再求模即可. 【考点】复数的运算. 2.【答案】D【解析】原式1sin 20cos10cos20sin10sin302=+==,故选D . 【提示】直接利用诱导公式以及两角和的正弦函数,化简求解即可. 【考点】三角函数的运算. 3.【答案】C【解析】命题的否定是:22n n n ∀∈≤N ,.【提示】根据特称命题的否定是全称命题即可得到结论. 【考点】命题. 4.【答案】A【解析】根据独立重复试验公式可得,该同学通过测试的概率为2233C 0.60.40.6=0.648.⨯+【提示】判断该同学投篮投中是独立重复试验,然后求解概率即可.【考点】概率. 5.【答案】A【解析】由题知12(F F ,,220012x y -=,所以222120000000(3,)(3,)331MF MF x y xy x y y =-----=+-=-<,解得0y <<,故选A . 【提示】利用向量的数量积公式,结合双曲线方程,即可确定0y 的取值范围. 【考点】双曲线. 6.【答案】B【解析】设圆锥底面半径为r ,则116238,43r r ⨯⨯=⇒=所以米堆的体积为 2111632035,4339⎛⎫⨯⨯⨯⨯= ⎪⎝⎭故堆放的米约为320 1.6222,9÷≈故选B . 【考点】圆锥体积.【提示】根据圆锥的体积公式计算出对应的体积即可. 7.【答案】A【解析】由题知1114()3333AD AC CD AC BC AC AC AB AB AC =+=+=+-=-+【提示】将向量AD 利用向量的三角形法则首先表示为AC CD +,然后结合已知表示为AC AC ,的形式.【考点】向量运算. 8.【答案】D【解析】由五点作图知,1π42,53π42ωϕωϕ⎧+=⎪⎪⎨⎪+=⎪⎩解得ππ,4ωϕ==,所以π()cos π,4f x x ⎛⎫=+ ⎪⎝⎭令2ππ2ππ,,4k x k k π<+<+∈Z 解得1322,,44k x k k -<<+∈Z故()f x 的单调递减区间为132,2,44k k k ⎛⎫-+∈ ⎪⎝⎭Z ,故选D .【提示】由周期求出ω,由五点法作图求出ϕ,可得()f x 的解析式,再根据余弦函数的单调性,求得()f x 的减区间. 【考点】三角函数运算. 9.【答案】C【解析】执行第1次,0.01,1,t S ==10,0.5,2n m === 0.5,0.25,2mS S m m =-===1,0.50.01n S t ==>=,是,循环,执行第2次, 0.25,0.125,2mS S m m =-===2,0.250.01n S t ==>=,是,循环,执行第3次,0.125,0.0625,2mS S m m =-===3,0.1250.01n S t ==>=,是,循环,执行第4次,0.0625,0.03125,2mS S m m =-===4,0.06250.01n S t ==>=,是,循环,执行第5次,0.03125,0.015625,2mS S m m =-===5,0.031250.01n S t ==>=,是,循环,执行第6次,0.015625,0.0078125,2mS S m m =-===6,0.0156250.01n S t ==>=,是,循环,执行第7次,0.0078125,S S m =-=2mm =0.00390625=, 7,0.00781250.01n S t ==>=,否,输出7,n =故选C .【提示】由题意依次计算,当7,0.00781250.01,n S t ==>=停止由此可得结论. 【考点】程序框图. 10.【答案】C【解析】在25()x x y ++的五个因式中,2个取因式中2x 剩余的3个因式中1个取x ,其余因式取y ,故52x y 的系数为212532C C C 30,=故选C .【提示】利用展开式的通项进行分析,即可得出结论. 【考点】二项式展开式. 11.【答案】B【解析】由正视图和俯视图知,该几何体是半球和半个圆柱的组合体,圆柱和球的半径都是r ,圆柱的高为2r ,其表面积为222214ππ2π225π41620π2r r r r r r r r ⨯+⨯++⨯=+=+,解得r=2,故选B .【提示】通过三视图可知该几何体是一个半球拼接半个圆柱,计算即可. 【考点】空间几何体的表面积. 12.【答案】D【解析】设()()e 21,,xg x x y ax a =-=-由题知存在唯一的整数0x ,使得0()g x 在直线y ax a =-的下方.因为()e (21)xg'x x =+,所以当12x <-时,'()0g x <,当12x >-,()0,g'x >所以当12x =-时,12min [()]2e g x -=-.当0x =时(0)1g =-,(1)e 0g =>,直线y ax a =-恒过(1,0)且斜率a ,故(0)1a g ->=-,且1(1)3e g a a --=-≥--,解得312ea ≤<,故选D .【提示】设()()e 21,,xg x x y ax a =-=-,问题转化为存在唯一的整数0x 使得0()g x 在直线y ax a =-的下方,由导数可得函数的极值,数形结合可得(0)1a g ->=-且1(1)3e g a a --=-≥--,解关于a 的不等式组可得.【考点】带参函数.第Ⅱ卷二、填空题 13.【答案】1【解析】由题知ln(y x =是奇函数,所以22ln(ln(ln()ln 0x x a x x a +-=+-==,解得 1.a =【提示】由题意可得,()()f x f x -=,代入根据对数的运算性质即可求解 【考点】函数奇偶性.14.【答案】2232524x y ⎛⎫±+= ⎪⎝⎭【解析】设圆心为(,0)a ,则半径为4a -,则222(4)2,a a -=+解得32a =±, 故圆的标准方程为2232524x y ⎛⎫±+= ⎪⎝⎭.【提示】利用椭圆的方程求出顶点坐标,然后求出圆心坐标,求出半径即可得到圆的方程. 【考点】圆的标准方程. 15.【答案】3【解析】做出可行域如图中阴影部分所示,由斜率的意义知,yx是可行域内一点与原点连线的斜率,由图可知,点(1,3)与原点连线的斜率最大,故yx的最大值3.【提示】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定y x的最大值.【考点】线性规划问题.16.【答案】【解析】如下图所示:延长BACD ,交于点E ,则可知在△ADE 中,105DAE ∠=︒,45ADE ∠=︒,30,E ∠=︒∴设12AD x =,2AE x =,4DE x =,CD m =,2BC =,sin151m ⎫∴+︒=⎪⎪⎝⎭⇒m +=∴04x <<,而2AB m x +-,2x∴AB的取值范围是.【提示】如图所示,延长BACD ,交于点,设12AD x =,2AE x =,4DE x =,CD m =m +=AB 的取值范围. 【考点】平面几何问题. 三.解答题17.【答案】(Ⅰ)21n + (Ⅱ)11646n -+ 【解析】(Ⅰ)当1n =时,211112434+3a a S a +=+=,因为0n a >,所以1a =3,当2n ≥时,221122n n n n a a a a --+--=14343n n S S -+--=4n a ,即111()()2()n n n n n n a a a a a a ---+-=+,因为0n a >,所以1n n a a --=2,所以数列{}n a 是首项为3,公差为2的等差数列,所以n a =21n +; (Ⅱ)由(1)知,1111(21)(23)22123n b n n n n ⎛⎫==- ⎪++++⎝⎭,所以数列{}n b 前n 项和为121111111=235572123n b b b n n ⎡⎤⎛⎫⎛⎫⎛⎫+++-+-++- ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎣⎦=11646n -+. 【提示】(Ⅰ)根据数列的递推关系,利用作差法即可求{}n a 的通项公式:(Ⅱ)求出11n n n b a a +=,利用裂项法即可求数列{}n b 的前n 项和.【考点】数列前n 项和与第n 项的关系,等差数列定义与通项公式. 18.【答案】(Ⅰ)答案见解析 【解析】(Ⅰ)连接BD ,设,BDAC G =连接EG FG EF ,,,在菱形ABCD 中,不妨设1GB =,由∠ABC=120°,可得AG GC ==由BE ⊥平面ABCD ,AB BC =,可知AE EC =, 又∵AE EC ⊥,∴EG EG AC =⊥,在Rt EBG △中,可得BE,故DF =在Rt FDG △中,可得FG =在直角梯形BDEF 中,由2BD =,BE,2DF =,可得2EF =, ∴222EG FG EF +=, ∴EG FG ⊥, ∵ACFG G =,∴EG ⊥平面AFC , ∵EG ⊂平面AEC , ∴平面AFC ⊥平面AEC .(Ⅱ)如图,以G 为坐标原点,分别以,GB GC 的方向为x 轴,y 轴正方向,||GB 为单位长度,建立空间直角坐标系G xyz -,由(Ⅰ)可得0,A (,(E,2F ⎛- ⎝⎭,C ,∴AE =,1,CF ⎛=- ⎝⎭.故cos ,3||||AE CFAE CF AE CF <>==-,所以直线AE 与CF .【提示】(Ⅰ)连接BD ,设BD AC G =,连接EG EF FG ,,,运用线面垂直的判定定理得到EG ⊥平面AFC ,再由面面垂直的判定定理,即可得到.(Ⅱ)以G 为坐标原点,分别以GB GC ,为x 轴,y 轴,GB 为单位长度,建立空间直角坐标系G xyz -,求得AE F C ,,,的坐标,运用向量的数量积的定义,计算即可得到所求角的余弦值.【考点】空间垂直判定与性质,异面直线所成角的计算.19.【答案】(Ⅰ)答案见解析 (Ⅱ)答案见解析 (Ⅲ)(i )66.32 (ii )46.24【解析】(Ⅰ)由散点图可以判断,y c =+y 关于年宣传费用x 的回归方程类型.(Ⅱ)令w =先建立y 关于w 的线性回归方程,由于81821()()108.8=68,16()iii ii w w yy d w w ==--==-∑∑ ∴56368 6.8100.6.==c y d w -⨯=-∴y 关于w 的线性回归方程为=100.6+68y w ,y ∴关于x 的回归方程为y (Ⅲ)(i )由(Ⅱ)知,当49x =时,年销量y的预报值576.6y =, 年利润z 的预报值=576.60.249=66.32z ⨯-(ii )根据(Ⅱ)的结果知,年利润z 的预报值20.12z x =x +--,∴13.66.8,2=即46.24x =,z 取得最大值,故宣传费用为46.24千元时,年利润的预保值最大.【提示】(Ⅰ)根据散点图,即可判断出.(Ⅱ)先建立中间量w =y 关于w 的线性回归方程,根据公式求出w ,问题得以解决.(Ⅲ)(Ⅰ)年宣传费49x =时,代入到回归方程,计算即可. (ii )求出预报值得方程,根据函数的性质,即可求出.【考点】线性回归方程求法,利用回归方程进行预报预测. 20.【答案】0y a --=0y a ++=(Ⅱ)答案见解析【解析】(Ⅰ)由题设可得)Ma ,()N a -,或()M a-,)N a .∵12yx '=,故24x y =在x =C在)a 处的切线方程为y a x -=-0y a --=,故24x y =在x =-处的导数值为,C 在()a -处的切线方程为y a x -=+,0y a ++=0y a --=0y a ++=. (Ⅱ)存在符合题意的点,证明如下:设(0,)P b 为符合题意得点,11(,)M x y ,22(,)N x y ,直线PM PN ,的斜率分别为12k k ,.将y kx a =+代入C 得方程整理得2440x kx a --=.∴12124,4x x k x x a +==-.∴1212121212122()()()=y b y b kx x a b x x k a b k k x x x x a--+-+++=+. 当b a =-时,有12k k + =0,则直线PM 的倾斜角与直线PN 的倾斜角互补,故OPM OPN ∠=∠,所以(0,)P a -符合题意.【提示】(Ⅰ)求出C在)a 处的切线方程,故24x y =在x =-即可求出方程.(Ⅱ)存在符合条件的点(0,)P b ,11(,)M x y,22(,)N x y ,直线PM PN ,的斜率分别为12k k ,直线方程与抛物线方程联立化为2440x kx a --=,利用根与系数的关系,斜率计算公式可得12()=k a b k k a++=即可证明. 【考点】抛物线的切线,直线与抛物线位置关系. 21.【答案】(Ⅰ)34a =- (Ⅱ)答案见解析【解析】(Ⅰ)设曲线()y f x =与x 轴相切于点0(,0)x ,则0()0f x =,0()0f x '=,即3002010430x ax x a ⎧++=⎪⎨⎪+=⎩,解得013,24x a ==-,因此,当34a =-时,x 轴是曲线()y f x =的切线. (Ⅱ)当(1,)x ∈+∞时,()ln 0g x x =-<,从而()min{(),()}()0h x f x g x g x =≤<, ∴()h x 在(1,)+∞无零点. 当1x =时,若54a ≥-,则5(1)04f a =+≥,(1)min{(1),(1)}(1)0h f g g ===,故1x =是()h x 的零点;若54a <-,则5(1)04f a =+<,(1)min{(1),(1)}(1)0h f g f ==<,故x =1不是()h x 的零点.当(0,1)x ∈时,()ln 0g x x =->,所以只需考虑()f x 在(0,1)的零点个数.(ⅰ)若3a ≤-或0a ≥,则2()3f x x a '=+在(0,1)无零点,故()f x 在(0,1)单调,而1(0)4f =,5(1)4f a =+,所以当3a ≤-时,()f x 在(0,1)有一个零点;当a ≥0时,()f x 在(0,1)无零点.(ⅱ)若30a -<<,则()f x在⎛ ⎝单调递减,在⎫⎪⎪⎭单调递增,故当x =()f x取的最小值,最小值为14f =.①若0f >,即304x -<<,()f x 在(0,1)无零点.②若0f =,即34a =-,则()f x 在(0,1)有唯一零点;③若0f <,即334a -<<-,由于1(0)4f =,5(1)4f a =+,所以当5344a -<<-时, ()f x 在(0,1)有两个零点;当534a -<≤-时,()f x 在(0,1)有一个零点.综上,当34a >-或54a <-时,()h x 有一个零点;当34a =-或54a =-时,()h x 有两个零点;当5344a -<<-时,()h x 有三个零点.【提示】(Ⅰ)设曲线()y f x =与x 轴相切于点0(,0)x ,则0()0f x =,0()0f x '=解出即可. (Ⅱ)对x 分类讨论:当(1,)x ∈+∞时,()ln 0g x x =-<,可得函数(1)min{(1),(1)}(1)0h f g g ===,即可得出零点的个数.当1x =时,对a 分类讨论利用导数研究其单调性极值即可得出.【考点】利用导数研究曲线的切线,分段函数的零点. 22.【答案】(Ⅰ)答案见解析 (Ⅱ)60ACB ∠=【解析】(Ⅰ)连接AE ,由已知得,AE BC AC AB ⊥⊥,,在Rt AEC △中,由已知得DE DC =,∴DEC DCE ∠=∠,连接OE ,OBE OEB ∠=∠, ∵90ACB ABC ∠+∠=, ∴90DEC OEB ∠+∠=,∴90OED ∠=,∴DE 是圆O 的切线.(Ⅱ)设1CE AE x ==,,由已知得AB =,BE =,由射影定理可得,2AE CE BE =,∴2x =x = ∴60ACB ∠=.【提示】(Ⅰ)连接AE 和OE ,由三角形和圆的知识易得90OED ∠=,可得DE 是O 的切线.(Ⅱ)设1CE AE x ==,,由射影定理可得关于x的方程2x =,解方程可得x 值,可得所求角度.【考点】圆的切线判定与性质,圆周角定理,直角三角形射影定理. 23.【答案】(Ⅰ)22cos 4sin 40ρρθρθ--+= (Ⅱ)12【解析】(Ⅰ)因为cos ,sin x y ρθρθ==, ∴1C 的极坐标方程为cos 2ρθ=-,2C 的极坐标方程为22cos 4sin 40ρρθρθ--+=.(Ⅱ)将=4θπ代入22cos 4sin 40ρρθρθ--+=,得240ρ-+=,解得1ρ=2ρ12=MN ρρ-,因为2C 的半径为1,则2C MN △的面积111sin 45=22⨯.【提示】(Ⅰ)由条件根据cos sin x y ρθρθ==,求得12C C ,的极坐标方程.(Ⅱ)把直线3C 的极坐标方程代入22cos 4sin 40ρρθρθ--+=,求得12ρρ,的值,从而求出2C MN △的面积.【考点】直角坐标方程与极坐标互化,直线与圆的位置关系.24.【答案】(Ⅰ)22.3x x ⎧⎫<<⎨⎬⎩⎭(Ⅱ)(2)+∞,【解析】(Ⅰ)当1a =时,不等式()1f x >化为1211x x +-->,等价于11221x x x ≤⎧⎨--+->⎩或111221x x x -<<⎧⎨++->⎩或11221x x x ≥⎧⎨+-+>⎩,解得223x <<,∴不等式()1f x >的解集为22.3x x ⎧⎫<<⎨⎬⎩⎭(Ⅱ)由题设可得,12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--≤≤⎨⎪-++>⎩,所以函数()f x 的图像与x 轴围成的三角形的三个顶点分别为21,03a A -⎛⎫⎪⎝⎭,(21,0)B a +,(,+1)C a a ,所以ABC △的面积为22(1)3a +, 由题设得22(1)63a +>,解得2a >,所以a 的取值范围为(2)+∞,. 【提示】(Ⅰ)当1a =时,把原不等式去掉绝对值,转化为与之等价的三个不等式组,分别求得每个不等式组的解集,再取并集,即得所求.(Ⅱ)化简函数()f x 的解析式,求得它的图像与x 轴围成的三角形的三个顶点的坐标,从而求得()f x 的图像与x 轴围成的三角形面积;再根据()f x 的图像与x 轴围成的三角形面积大于6,从而求得a 的取值范围.【考点】含绝对值不等式解法,分段函数,一元二次不等式解法.。
2015届高考数学总复习 第三章 第五节三角函数的图象与性质课时精练试题 文(含解析)

1.下列函数中,周期为π2的是()A .y =sin x 2B .y =sin 2xC .y =cos x4D .y =cos 4x解析:利用公式 T =2πω即可得到答案D.答案:D2.(2013·潮州二模)下列函数中,周期为1的奇函数是( )A .y =1-2sin 2πx B .y =sin ⎝⎛⎭⎪⎫2πx +π3C .y =tan π2x D .y =sin πx cos πx解析:因为y =1-2sin 2πx =cos 2πx ,为偶函数,排除A.因为对于函数y =sin ⎝ ⎛⎭⎪⎫2πx +π3,f (-x )=sin ⎝ ⎛⎭⎪⎫-2πx +π3≠-sin ⎝⎛⎭⎪⎫2πx +π3,不是奇函数,排除B.对于y =tan π2x ,T =ππ2=2≠1,排除C.对于y =sin πx cos πx =12sin 2πx ,为奇函数,且T =2π2π=1,满足条件.故选D.答案:D3.(2013·广州一模)函数y =(sin x +cos x )(sin x -cos x )是( )A .奇函数且在⎣⎢⎡⎦⎥⎤0,π2上单调递增B .奇函数且在⎣⎢⎡⎦⎥⎤π2,π上单调递增C .偶函数且在⎣⎢⎡⎦⎥⎤0,π2上单调递增D .偶函数且在⎣⎢⎡⎦⎥⎤π2,π上单调递增解析:y =sin 2x -cos 2x =-cos 2x ,可见它是偶函数,并且在⎣⎢⎡⎦⎥⎤0,π2上是单调递增的.答案:C4.(2013·肇庆二模)已知函数f (x )=A sin ⎝⎛⎭⎪⎫ωx +π6(A >0,ω>0,x ∈R )的最小正周期为2,且f (0)=3,则函数f (3)=( )A .- 3 B. 3 C .-2 D .2解析:由题意可得:函数的最小正周期T =2πω=2,解得ω=π,又f (0)=A sin π6=12A =3,可得A =23,故函数的解析式为:f (x )=23sin ⎝⎛⎭⎪⎫πx +π6.故f (3)=23sin ⎝ ⎛⎭⎪⎫3π+π6=23sin ⎝ ⎛⎭⎪⎫π+π6=-23sin π6=-23×12=- 3.故选A. 答案:A5.(2013·东莞二模)已知函数y =sin x +cos x ,则下列结论正确的是( )A .此函数的图象关于直线x =-π4对称B .此函数的最大值为1C .此函数在区间⎝ ⎛⎭⎪⎫-π4,π4上是增函数 D .此函数的最小正周期为π解析:因为函数y =sin x +cos x =2sin ⎝⎛⎭⎪⎫x +π4,当x =-π4时函数值为0,函数不能取得最值,所以A 不正确;函数y =sin x +cos x =2sin ⎝⎛⎭⎪⎫x +π4,当x =π4时函数取得最大值为2,B 不正确;因为函数x +π4∈⎝ ⎛⎭⎪⎫-π2,π2,即x 在⎝ ⎛⎭⎪⎫-3π4,π4上函数是增函数,所以函数在区间⎝ ⎛⎭⎪⎫-π4,π4上是增函数,C 正确.函数的周期是2π,D 不正确;故选C. 答案:C6.“φ=π”是“函数f (x )=sin(x +φ)是奇函数”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件答案:A7.(2013·惠州模拟)如图,设点A 是单位圆上的一定点,动点P 从A 出发在圆上按逆时针方向转一周,点P 所旋转过的弧AP 的长为l ,弦AP 的长为d ,则函数d =f (l )的图象大致为( )解析:如图,取AP 的中点为D ,设∠DOA =θ,则d =2sin θ,又l =2θR =2θ,所以d =2sin l2,根据正弦函数的图象知,选项C 中的图象符合解析式.故选C.答案:C8.(2013·太原模拟)若函数f (x )=2tan ⎝⎛⎭⎪⎫kx +π3的最小正周期T 满足1<T <2,则自然数k 的值为________.解析:因为T =πk ,所以1<πk <2,即π2<k <π,而k 为自然数,所以k =2或3.答案:2或39.(2013·苏州模拟)函数y =sin x +16-x 2的定义域为________.解析:因为sin x ≥0,所以2k π≤x ≤2k π+π,k ∈Z ,因为16-x 2≥0,所以-4≤x ≤4, 取交集得[-4,-π]∪[0,π]. 答案:[-4,-π]∪[0,π]10. (2012·广东两校联考)设M cos πx 3+cos πx 5,sin πx 3+sin πx5(x ∈R )为坐标平面内一点,O 为坐标原点,记f (x )=|OM |,当x 变化时,函数f (x )的最小正周期是__________.解析:∵f (x )=|OM |= ⎝ ⎛⎭⎪⎫cos πx 3+cos πx 52+⎝ ⎛⎭⎪⎫sin πx 3+sin πx 52=2+2cos ⎝⎛⎭⎪⎫πx 3-πx 5=2⎝ ⎛⎭⎪⎫1+cos 2πx 15=2⎪⎪⎪⎪⎪⎪cos πx 15, 画图易知函数f (x )的最小正周期为15. 答案:1511.函数y =sin 4x +cos 4x 的单调递增区间是____________.答案:⎣⎢⎡⎦⎥⎤k π2-π4,k π2(k ∈Z )(开区间也可)12.(2013·潮州二模)已知函数f (x )=3(sin 2x -cos 2x )-2sin x cos x . (1)求f (x )的最小正周期;(2)设x ∈⎣⎢⎡⎦⎥⎤-π3,π3,求f (x )的值域和单调递增区间.解析:(1)∵f (x )=-3(cos 2x -sin 2x )-2sin x cos x=-3cos 2x -sin 2x =-2sin ⎝⎛⎭⎪⎫2x +π3. ∴f (x )的最小正周期为π.(2)∵x ∈⎣⎢⎡⎦⎥⎤-π3,π3,∴-π3≤2x +π3≤π, ∴-32≤sin ⎝ ⎛⎭⎪⎫2x +π3≤1. ∴f (x )的值域为[-2,3]. ∵当y =sin ⎝⎛⎭⎪⎫2x +π3递减时,f (x )递增. ∴π2≤2x +π3≤π,即π12≤x ≤π3. 故f (x )的递增区间为⎣⎢⎡⎦⎥⎤π12,π3.13.(2013·南通质检)已知a >0,函数f (x )=-2a sin2x +π6+2a +b ,当x ∈⎣⎢⎡⎦⎥⎤0,π2时,-5≤f (x )≤1.(1)求常数a ,b 的值; (2)求f (x )的单调区间.解析:(1)∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴π6≤2x +π6≤76π,∴-12≤sin ⎝⎛⎭⎪⎫2x +π6≤1, 又∵a >0,-5≤f (x )≤1,∴⎩⎪⎨⎪⎧-2a +2a +b =-5,a +2a +b =1,即⎩⎪⎨⎪⎧a =2,b =-5.(2)f (x )=-4sin ⎝⎛⎭⎪⎫2x +π6-1,由-π2+2k π≤2x +π6≤π2+2k π,得-π3+k π≤x ≤π6+k π,k ∈Z ,由π2+2k π≤2x +π6≤32π+2k π,得π6+k π≤x ≤23π+k π,k ∈Z ,∴f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤π6+k π,23π+k π(k ∈Z ), 单调递减区间为⎣⎢⎡⎦⎥⎤-π3+k π,π6+k π(k ∈Z ).14.已知向量a =(sin x ,cos x ), b =(sin x ,sin x ),c =(-1,0).(1)若x =π3,求向量a 与c 的夹角θ;(2)若x ∈⎣⎢⎡⎦⎥⎤-3π8,π4,函数f (x )=λa ·b 的最大值为12,求实数λ的值.解析:(1)当x =π3时,a =⎝ ⎛⎭⎪⎫32,12,所以 cos θ=a ·c |a ||c |=-321×1=-32.因而θ=5π6.(2)f (x )=λ(sin 2x +sin x cos x ) =λ2(1-cos 2x +sin 2x ) =λ2⎣⎢⎡⎦⎥⎤1+2sin ⎝⎛⎭⎪⎫2x -π4, 因为x ∈⎣⎢⎡⎦⎥⎤-3π8,π4,所以2x -π4∈⎣⎢⎡⎦⎥⎤-π,π4.当λ>0时,f (x )max =λ2()1+1=12,即λ=12.当λ<0时,f (x )max =λ2()1-2=12,即λ=-1- 2.所以λ=12或λ=-1- 2.。
2015年高考数学试题分类汇编三角函数

专题三 三角函数1.(15北京理科)已知函数2()cos 222x x xf x .(Ⅰ) 求()f x 的最小正周期;(Ⅱ) 求()f x 在区间[π0]-,上的最小值.【答案】(1)2π,(2)12-- 【解析】试题分析:先用降幂公式和辅助角公式进行三角恒等变形,把函数化为()sin()f x A x m ωϕ=++形式,再利用周期公式2T πω=求出周期,第二步由于0,x π-≤≤则可求出3444x πππ-≤+≤,借助正弦函数图象 找出在这个范围内当42x ππ+=-,即34x π=-时,()f x 取得最小值为:1--.试题解析:(Ⅰ) 211cos ()sincossin sin 22222xxxxf x x -=-=⋅-⋅=sin cos 222x x =+-sin()42x π=+-(1)()f x 的最小正周期为221T ππ==; (2)30,444x x ππππ-≤≤∴-≤+≤ ,当3,424x x πππ+=-=-时,()f x 取得最小值为:1--考点: 1.三角函数式的恒等变形;2.三角函数图像与性质.2.(15北京文科)已知函数()2sin 2x f x x =-. (Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在区间20,3π⎡⎤⎢⎥⎣⎦上的最小值.【答案】(1)2π;(2).考点:倍角公式、两角和的正弦公式、三角函数的周期、三角函数的最值. 3.(15年广东文科)已知tan 2α=.()1求tan 4πα⎛⎫+ ⎪⎝⎭的值;()2求2sin 2sin sin cos cos 21ααααα+--的值.【答案】(1)3-;(2)1.考点:1、两角和的正切公式;2、特殊角的三角函数值;3、二倍角的正、余弦公式;4、同角三角函数的基本关系.4.(15年安徽文科)已知函数2()(sin cos )cos2f x x x x =++ (1)求()f x 最小正周期; (2)求()f x 在区间[0,]2π上的最大值和最小值.【答案】(1)π ;(2)最大值为10考点:1.三角函数的性质;2.三角函数的最值.5.(15年福建理科)已知函数f()x 的图像是由函数()cos g x x =的图像经如下变换得到:先将()g x 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移2p个单位长度. (Ⅰ)求函数f()x 的解析式,并求其图像的对称轴方程;(Ⅱ)已知关于x 的方程f()g()x x m +=在[0,2)p 内有两个不同的解,a b . (1)求实数m 的取值范围;(2)证明:22cos ) 1.5m a b -=-(【答案】(Ⅰ) f()2sin x x =,(k Z).2x k pp =+?;(Ⅱ)(1)(-;(2)详见解析. 【解析】试题分析:(Ⅰ)纵向伸缩或平移: ()()g x kg x →或()()g x g x k →+;横向伸缩或平移:()()g x g x ω→(纵坐标不变,横坐标变为原来的1ω倍),()()g x g x a →+(0a >时,向左平移a 个单位;0a <时,向右平移a个单位);(Ⅱ) (1)由(Ⅰ)得f()2sin x x =,则f()g()2s i n cos x x x x +=+,利用辅助角公式变形为f()g()x x +)x j +(其中sinj j ==),方程f()g()x x m +=在[0,2)p 内有两个不同的解,a b ,等价于直线y m =和函数)y x j +有两个不同交点,数形结合求实数m 的取值范围;(2)结合图像可得+=2()2p a b j -和3+=2()2pa b j -,进而利用诱导公式结合已知条件求解. 试题解析:解法一:(1)将()cos g x x =的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变)得到y 2cos x=的图像,再将y 2cos x =的图像向右平移2p 个单位长度后得到y 2cos()2x p=-的图像,故f()2sin x x =,从而函数f()2sin x x =图像的对称轴方程为(k Z).2x k pp =+?(2)1) f()g()2sin cos )x x x x x x +=+)x j +(其中sinj j =) 依题意,sin(x j +在区间[0,2)p 内有两个不同的解,a b 当且仅当|1<,故m 的取值范围是(-.2)因为,a b )=m x j +在区间[0,2)p 内有两个不同的解, 所以sin(a j +sin(b j +当1£+=2(),2();2pa b j a b p b j --=-+当-时, 3+=2(),32();2pa b j a b p b j --=-+ 所以2222cos )cos 2()2sin ()11 1.5m a b b j b j -=-+=+-=-=-(解法二:(1)同解法一. (2)1) 同解法一.2) 因为,a b )=m x j +在区间[0,2)p 内有两个不同的解,所以sin(a j +sin(b j +当1£+=2(),+();2pa b j a j p b j -=-+即当-时, 3+=2(),+3();2pa b j a j p b j -=-+即 所以cos +)cos()a j b j =-+(于是cos )cos[()()]cos()cos()sin()sin()a b a j b j a j b j a j b j -=+-+=+++++(22222cos ()sin()sin()[1] 1.5m b j a j b j =-++++=--+=-考点:1、三角函数图像变换和性质;2、辅助角公式和诱导公式. 6.(15年福建文科)若5sin 13α=-,且α为第四象限角,则tan α的值等于( ) A .125 B .125- C .512 D .512-【答案】D 【解析】试题分析:由5sin 13α=-,且α为第四象限角,则12cos 13α==,则sin tan cos ααα= 512=-,故选D . 考点:同角三角函数基本关系式.7.(15年福建文科)已知函数()2cos 10cos 222x x x f x =+. (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)将函数()f x 的图象向右平移6π个单位长度,再向下平移a (0a >)个单位长度后得到函数()g x 的图象,且函数()g x 的最大值为2. (ⅰ)求函数()g x 的解析式;(ⅱ)证明:存在无穷多个互不相同的正整数0x ,使得()00g x >. 【答案】(Ⅰ)2π;(Ⅱ)(ⅰ)()10sin 8g x x =-;(ⅱ)详见解析. 【解析】试题分析:(Ⅰ)首先利用证明二倍角公式和余弦降幂公式将()f x 化为()10sin 56f x x π⎛⎫=++ ⎪⎝⎭,然后利用2T πω=求周期;(Ⅱ)由函数()f x 的解析式中给x 减6π,再将所得解析式整体减去a 得()g x 的解析式为()10sin 5g x x a =+-,当sin x 取1的时,()g x 取最大值105a +-,列方程求得13a =,从而()g x 的解析式可求;欲证明存在无穷多个互不相同的正整数0x ,使得()00g x >,可解不等式()00g x >,只需解集的长度大于1,此时解集中一定含有整数,由周期性可得,必存在无穷多个互不相同的正整数0x .试题解析:(I )因为()2cos 10cos 222x x xf x =+5cos 5x x =++10sin 56x π⎛⎫=++ ⎪⎝⎭.所以函数()f x 的最小正周期2πT =. (II )(i )将()f x 的图象向右平移6π个单位长度后得到10sin 5y x =+的图象,再向下平移a (0a >)个单位长度后得到()10sin 5g x x a =+-的图象.又已知函数()g x 的最大值为2,所以1052a +-=,解得13a =. 所以()10sin 8g x x =-.(ii )要证明存在无穷多个互不相同的正整数0x ,使得()00g x >,就是要证明存在无穷多个互不相同的正整数0x ,使得010sin 80x ->,即04sin 5x >.由452<知,存在003πα<<,使得04sin 5α=.由正弦函数的性质可知,当()00,x απα∈-时,均有4sin 5x >. 因为sin y x =的周期为2π,所以当()002,2x k k παππα∈++-(k ∈Z )时,均有4sin 5x >. 因为对任意的整数k ,()()00022213k k πππαπαπα+--+=->>,所以对任意的正整数k ,都存在正整数()002,2k x k k παππα∈++-,使得4sin 5k x >. 亦即存在无穷多个互不相同的正整数0x ,使得()00g x >. 考点:1、三角函数的图像与性质;2、三角不等式.8.(15年新课标1理科)sin20°cos10°-con160°sin10°=(A )2- (B )2(C )12- (D )12【答案】D【解析】原式=sin20°cos10°+cos20°sin10°=sin30°=12,故选D.9.(15年新课标1理科) 函数f(x)=的部分图像如图所示,则f (x )的单调递减区间为(A)(),k (b)(),k(C)(),k (D)(),k【答案】B10.(15年陕西理科)如图,某港口一天6时到18时的水深变化曲线近似满足函数3sin()6y x k πϕ=++,据此函数可知,这段时间水深(单位:m )的最大值为( )A .5B .6C .8D .10【答案】C 【解析】试题分析:由图象知:min 2y =,因为min 3y k =-+,所以32k -+=,解得:5k =,所以这段时间水深的最大值是max 3358y k =+=+=,故选C . 考点:三角函数的图象与性质.11.(15年陕西文科)如图,某港口一天6时到18时的谁深变化曲线近似满足函数y =3sin (6πx +Φ)+k ,据此函数可知,这段时间水深(单位:m )的最大值为____________.【答案】8 【解析】试题分析:由图像得,当sin()16x π+Φ=-时min 2y =,求得5k =,当sin()16x π+Φ=时,max 3158y =⨯+=,故答案为8.考点:三角函数的图像和性质.12.(15年天津理科)已知函数()22sin sin 6f x x x π⎛⎫=--⎪⎝⎭,R x ∈ (I)求()f x 最小正周期; (II)求()f x 在区间[,]34p p-上的最大值和最小值.【答案】(I)π; (II) max ()4f x =,min 1()2f x =-.考点:1.两角和与差的正余弦公式;2.二倍角的正余弦公式;3.三角函数的图象与性质. 13.(15年天津文科)已知函数()()sin cos 0,,f x x x x ωωω=+>∈R 若函数()f x 在区间(),ωω-内单调递增,且函数()f x 的图像关于直线x ω=对称,则ω的值为 .【解析】试题分析:由()f x 在区间(),ωω-内单调递增,且()f x 的图像关于直线x ω=对称,可得π2ωω≤,且()222πsin cos sin 14f ωωωω⎛⎫=+=+= ⎪⎝⎭,所以2ππ42ωω+=⇒= 考点:三角函数的性质.14.(15年湖南理科)A.512πB.3πC.4πD.6π 【答案】D.【解析】试题分析:向右平移ϕ个单位后,得到)22sin()(ϕ-=x x g ,又∵2|)()(|21=-x g x f ,∴不妨 ππk x 2221+=,ππϕm x 22222+-=-,∴πϕπ)(221m k x x -+-=-,又∵12min 3x x π-=, ∴632πϕπϕπ=⇒=-,故选D.考点:三角函数的图象和性质.10.(15年江苏)已知tan 2α=-,()1tan 7αβ+=,则tan β的值为_______. 【答案】3【解析】 试题分析:12tan()tan 7tan tan() 3.21tan()tan 17αβαβαβααβα++-=+-===++- 考点:两角差正切公式11.(15年江苏)在ABC ∆中,已知60,3,2===A AC AB .(1)求BC 的长;(2)求C 2sin 的值.【答案】(12【解析】考点:余弦定理,二倍角公式。
2015年高中数学高考真题分类汇编理科数学C单元 三角函数

数 学C 单元 三角函数C1 角的概念及任意角的三角函数C2 同角三角函数的基本关系式与诱导公式12.B9、C2、C6[2015·湖北卷] 函数f (x )=4cos 2x2·cos ⎝⎛⎭⎫π2-x -2sin x -|ln(x +1)|的零点个数为________.12.2 [解析] f (x )=4cos 2x2sin x -2sin x -|ln(x +1)|=2sin x ⎝⎛⎭⎫2cos 2x 2-1-|ln(x +1)|=sin 2x -|ln(x +1)|.令f (x )=0,得sin 2x =|ln(x +1)|.在同一坐标系中作出函数y =sin 2x 与函数y =|ln(x+1)|的大致图像,如图所示.观察图像可知,两个函数的图像有2个交点,故函数f (x )有2个零点. 19.C2、C5、C8[2015·四川卷] 如图1-4所示,A ,B ,C ,D 为平面四边形ABCD 的四个内角.(1)证明:tan A 2=1-cos Asin A;(2)若A +C =180°,AB =6,BC =3,CD =4,AD =5,求tan A 2+tan B 2+tan C 2+tan D2的值.19.解:(1)证明:tan A2=sinA 2cos A 2=2sin 2A22sin A 2cos A 2=1-cos A sin A.(2)由A +C =180°,得C =180°-A ,D =180°-B .由(1)知, tanA 2+tanB 2+tanC 2+tan D2=1-cos A sin A +1-cos B sin B +1-cos (180°-A )sin (180°-A )+1-cos (180°-B )sin (180°-B )=2sin A +2sin B . 连接BD ,在△ABD 中,有BD 2=AB 2+AD 2-2AB ·AD cos A , 在△BCD 中,有BD 2=BC 2+CD 2-2BC ·CD cos C , 所以AB 2+AD 2-2AB ·AD cos A =BC 2+CD 2+2BC ·CD cos A , 则cos A =AB 2+AD 2-BC 2-CD 22(AB ·AD +BC ·CD )=62+52-32-422×(6×5+3×4)=37.于是sin A =1-cos 2A =1-⎝⎛⎭⎫372=2107.连接AC ,同理可得cos B =AB 2+BC 2-AD 2-CD 22(AB ·BC +AD ·CD )=62+32-52-422×(6×3+5×4)=119,于是sin B =1-cos 2B =1-⎝⎛⎭⎫1192=6 1019.所以tan A 2+tan B 2+tan C 2+tan D2=2sin A +2sin B=2×7210+2×19610=4103.9.C2、C5、C7[2015·重庆卷] 若tan α=2tan π5,则cos α-3π10sin α-π5=( )A .1B .2C .3D .49.C [解析] cos α-3π10sin α-π5=sin α-3π10+π2sin α-π5=sin α+π5sin α-π5=sin αcos π5+cos αsinπ5sin αcos π5-cos αsinπ5=sin αcos αcos π5+sin π5sin αcos αcos π5-sin π5=2·sinπ5cos π5cos π5+sinπ52·sin π5cosπ5cos π5-sinπ5=3sin π5sinπ5=3.18.C2、C3、C5、C6[2015·重庆卷] 已知函数f (x )=sin π2-x sin x -3cos 2x . (1)求f (x )的最小正周期和最大值; (2)讨论f (x )在π6,2π3上的单调性.18.解:(1)f (x )=sin π2-x sin x -3cos 2x =cos x sin x -32(1+cos 2x )=12sin 2x -32cos 2x -32=sin2x -π3-32, 因此f (x )的最小正周期为π,最大值为2-32.(2)当x ∈π6,2π3时,0≤2x -π3≤π,从而当0≤2x -π3≤π2,即π6≤x ≤5π12时,f (x )单调递增;当π2≤2x -π3≤π,即5π12≤x ≤2π3时,f (x )单调递减. 综上可知,f (x )在π6,5π12上单调递增;在5π12,2π3上单调递减.C3 三角函数的图象与性质17.C4、C3[2015·湖北卷] 某同学用“五点法”画函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2在某一个周期内的图像时,列表并填入了部分数据,如下表:(1)请将上表数据补充完整,填写在答题卡上相应位置...........,并直接写出函数f (x )的解析式; (2)将y =f (x )图像上所有点向左平行移动θ(θ>0)个单位长度,得到y =g (x )的图像,若y =g (x )图像的一个对称中心为⎝⎛⎭⎫5π12,0,求θ的最小值. 17.解:(1)根据表中已知数据,解得A =5,ω=2,φ=-π6.数据补全如下表:且函数解析式为f (x )=5sin ⎝⎛⎭⎫2x -π6.(2)由(1)知f (x )=5sin ⎝⎛⎭⎫2x -π6,所以g (x )=5sin ⎝⎛⎭⎫2x +2θ-π6.因为y =sin x 的图像的对称中心为(k π,0),k ∈Z . 所以令2x +2θ-π6=k π,k ∈Z ,解得x =k π2+π12-θ,k ∈Z .由于函数y =g (x )的图像关于点⎝⎛⎭⎫5π12,0成中心对称,所以令k π2+π12-θ=5π12,k ∈Z ,解得θ=k π2-π3,k ∈Z .由θ>0可知,当k =1时,θ取得最小值π6.15.C5,C3[2015·北京卷] 已知函数f (x )=2sin x 2cos x 2-2sin 2x2.(1)求f (x )的最小正周期;(2)求f (x )在区间[-π,0]上的最小值. 15.解:(1)因为f (x )=22sin x -22(1-cos x ) =sin ⎝⎛⎭⎫x +π4-22,所以f (x )的最小正周期为2π.(2)因为-π≤x ≤0,所以-3π4≤x +π4≤π4.当x +π4=-π2,即x =-3π4时,f (x )取得最小值.所以f (x )在区间[-π,0]上的最小值为 f ⎝⎛⎭⎫-3π4=-1-22.12.A3、C3[2015·山东卷] 若“∀x ∈⎣⎡⎦⎤0,π4,tan x ≤m ”是真命题,则实数m 的最小值为________.12.1 [解析] ∵y =tan x 在区间⎣⎡⎦⎤0,π4上单调递增,∴y =tan x ⎝⎛⎭⎫x ∈⎣⎡⎦⎤0,π4的最大值为tan π4=1.又∵“∀x ∈⎣⎡⎦⎤0,π4,tan x ≤m ”是真命题,∴m ≥1.4.C3,C4[2015·四川卷] 下列函数中,最小正周期为π且图像关于原点对称的函数是( )A .y =cos2x +π2B .y =sin2x +π2C .y =sin 2x +cos 2xD .y =sin x +cos x4.A [解析] 选项A 中,y =-sin 2x ,最小正周期为π,且图像关于原点对称;选项B 中,y =cos 2x 是偶函数,图像不关于原点对称;选项C 中,y =2sin ⎝⎛⎭⎫2x +π4,图像不关于原点对称;选项D 中,y =2sin ⎝⎛⎭⎫x +π4,最小正周期为2π.故选A.15.C3、C5、C6[2015·天津卷] 已知函数f (x )=sin 2x -sin 2x -π6,x ∈R .(1)求f (x )的最小正周期;(2)求f (x )在区间-π3,π4上的最大值和最小值.15.解:(1)由已知,有f (x )=1-cos 2x2-1-cos2x -π32=1212cos 2x +32sin 2x -12cos 2x =34sin 2x -14cos 2x =12sin2x -π6. 所以f (x )的最小正周期T =2π2=π.(2)因为f (x )在区间-π3,-π6上是减函数,在区间-π6,π4上是增函数,f -π3=-14,f -π6=-12,f π4=34,所以f (x )在区间-π3,π4上的最大值为34,最小值为-12.18.C2、C3、C5、C6[2015·重庆卷] 已知函数f (x )=sin π2-x sin x -3cos 2x . (1)求f (x )的最小正周期和最大值; (2)讨论f (x )在π6,2π3上的单调性.18.解:(1)f (x )=sin π2-x sin x -3cos 2x =cos x sin x -32(1+cos 2x )=12sin 2x -32cos 2x -32=sin2x -π3-32, 因此f (x )的最小正周期为π,最大值为2-32.(2)当x ∈π6,2π3时,0≤2x -π3≤π,从而当0≤2x -π3≤π2,即π6≤x ≤5π12时,f (x )单调递增;当π2≤2x -π3≤π,即5π12≤x ≤2π3时,f (x )单调递减. 综上可知,f (x )在π6,5π12上单调递增;在5π12,2π3上单调递减.C4 函数sin()y A x ωϕ=+的图象与性质10.C4[2015·安徽卷] 已知函数f (x )=A sin(ωx +φ)(A ,ω,φ均为正的常数)的最小正周期为π,当x =2π3时,函数f (x )取得最小值,则下列结论正确的是( )A .f (2)<f (-2)<f (0)B .f (0)<f (2)<f (-2)C .f (-2)<f (0)<f (2)D .f (2)<f (0)<f (-2)10.A [解析] 依题意得f (x )在⎣⎡⎦⎤π6,2π3上单调递减,且直线x =π6是f (x )的图像的一条对称轴.又f (-2)=f (π-2),f (0)=f ⎝⎛⎭⎫π3,且π6<π3<π-2<2<2π3,所以f (0)=f ⎝⎛⎭⎫π3>f (π-2)=f (-2)>f (2),故选A.17.C4、C3[2015·湖北卷] 某同学用“五点法”画函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2在某一个周期内的图像时,列表并填入了部分数据,如下表:(1)请将上表数据补充完整,填写在答题卡上相应位置...........,并直接写出函数f (x )的解析式; (2)将y =f (x )图像上所有点向左平行移动θ(θ>0)个单位长度,得到y =g (x )的图像,若y =g (x )图像的一个对称中心为⎝⎛⎭⎫5π12,0,求θ的最小值. 17.解:(1)根据表中已知数据,解得A =5,ω=2,φ=-π6.数据补全如下表:且函数解析式为f (x )=5sin ⎝⎛⎭⎫2x -π6.(2)由(1)知f (x )=5sin ⎝⎛⎭⎫2x -π6,所以g (x )=5sin ⎝⎛⎭⎫2x +2θ-π6.因为y =sin x 的图像的对称中心为(k π,0),k ∈Z . 所以令2x +2θ-π6=k π,k ∈Z ,解得x =k π2+π12-θ,k ∈Z .由于函数y =g (x )的图像关于点⎝⎛⎭⎫5π12,0成中心对称,所以令k π2+π12-θ=5π12,k ∈Z ,解得θ=k π2-π3,k ∈Z .由θ>0可知,当k =1时,θ取得最小值π6.8.C4[2015·全国卷Ⅰ] 函数f (x )=cos(ωx +φ)的部分图像如图1-2所示,则f (x )的单调递减区间为( )A.⎝⎛⎭⎫k π-14,k π+34,k ∈Z B.⎝⎛⎭⎫2k π-14,2k π+34,k ∈ZC.⎝⎛⎭⎫k -14,k +34,k ∈Z D.⎝⎛⎭⎫2k -14,2k +34,k ∈Z 8.D [解析] 由图知T 2=54-14=1,所以T =2,即2π||ω=2,所以ω=±π.因为函数f (x )的图像过点⎝⎛⎭⎫14,0,所以当ω=π时,ω4+φ=π2+2k π,k ∈Z ,解得φ=π4+2k π,k ∈Z ;当ω=-π时,ω4+φ=-π2+2k π,k ∈Z ,解得φ=-π4+2k π,k ∈Z .所以f (x )=cos ⎝⎛⎭⎫πx +π4,由2k π<πx +π4<π+2k π解得2k -14<x <2k +34,k ∈Z ,故选D.9.C4、C9[2015·湖南卷] 将函数f (x )=sin 2x 的图像向右平移φ0<φ<π2个单位后得到函数g (x )的图像,若对满足|f (x 1)-g (x 2)|=2的x 1,x 2,有|x 1-x 2|min =π3,则φ=( ) A.5π12 B.π3 C.π4 D.π69.D [解析] 由已知得g (x )=sin(2x -2φ),又|f (x 1)-g (x 2)|=2,0<φ<π2,所以当|x 1-x 2|取最小值时,刚好是取两个函数相邻的最大值与最小值点.令2x 1=π2,2x 2-2φ=-π2,则|x 1-x 2|=⎪⎪⎪⎪π2-φ=π3,得φ=π6.3.C4[2015·山东卷] 要得到函数y =sin ⎝⎛⎭⎫4x -π3的图像,只需将函数y =sin 4x 的图像( )A .向左平移π12个单位B .向右平移π12个单位C .向左平移π3个单位D .向右平移π3个单位3.B [解析] 设将y =sin 4x 的图像向右平移φ个单位,得到y =sin 4(x -φ)=sin(4x -4φ)=sin ⎝⎛⎭⎫4x -π3 ,则φ=π12.3.C4[2015·陕西卷] 如图1-2,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin π6x +φ+k ,据此函数可知,这段时间水深(单位:m)的最大值为( )图1-2A .5B .6C .8D .103.C [解析] 据图可知,-3+k =2,得k =5,所以y max =3+5=8. 4.C3,C4[2015·四川卷] 下列函数中,最小正周期为π且图像关于原点对称的函数是( )A .y =cos2x +π2B .y =sin2x +π2C .y =sin 2x +cos 2xD .y =sin x +cos x4.A [解析] 选项A 中,y =-sin 2x ,最小正周期为π,且图像关于原点对称;选项B 中,y =cos 2x 是偶函数,图像不关于原点对称;选项C 中,y =2sin ⎝⎛⎭⎫2x +π4,图像不关于原点对称;选项D 中,y =2sin ⎝⎛⎭⎫x +π4,最小正周期为2π.故选A.11.C4、C5、C6 [2015·浙江卷] 函数f (x )=sin 2x +sin x cos x +1的最小正周期是____________,单调递减区间是________.11.π ⎣⎡⎦⎤38π+k π,78π+k π(k ∈Z ) [解析] f (x )=1-cos 2x 2+12sin 2x +1=22sin ⎝⎛⎭⎫2x -π4+32,则最小正周期是π.单调递减区间: 2k π+π2≤2x -π4≤2k π+3π2(k ∈Z )⇒k π+3π8≤x ≤k π+7π8(k ∈Z ).C5 两角和与差的正弦、余弦、正切16.F3、C5[2015·广东卷] 在平面直角坐标系xOy 中,已知向量m =⎝⎛⎭⎫22,-22,n =(sin x ,cos x ),x ∈⎝⎛⎭⎫0,π2.(1)若m ⊥n ,求tan x 的值;(2)若m 与n 的夹角为π3,求x 的值.8.C5[2015·江苏卷] 已知tan α=-2,tan(α+β)=17,则tan β的值为________.8.3 [解析] 因为β=(α+β)-α,所以tan β=tan[(α+β)-α]=tan (α+β)-tan α1+tan (α+β)tan α=17+21-27=3.17.C5、C8[2015·全国卷Ⅱ] △ABC 中,D 是BC 上的点,AD 平分∠BAC ,△ABD 面积是△ADC 面积的2倍.(1)求sin ∠Bsin ∠C; (2)若AD =1,DC =22,求BD 和AC 的长. 17.解:(1)S △ABD =12AB ·AD sin ∠BAD ,S △ADC =12AC ·AD sin ∠CAD .因为S △ABD =2S △ADC ,∠BAD =∠CAD , 所以AB =2AC . 由正弦定理可得 sin ∠B sin ∠C =AC AB =12. (2)因为S △ABD ∶S △ADC =BD ∶DC ,所以BD = 2. 在△ABD 和△ADC 中,由余弦定理知 AB 2=AD 2+BD 2-2AD ·BD cos ∠ADB , AC 2=AD 2+DC 2-2AD ·DC cos ∠ADC . 故AB 2+2AC 2=3AD 2+BD 2+2DC 2=6. 由(1)知AB =2AC ,所以AC =1. 2.C5[2015·全国卷Ⅰ] sin 20°cos 10°-cos 160°sin 10°=( )A .-32 B.32C .-12 D.122.D [解析] sin 20°cos 10°-cos 160°sin 10°=sin 20°cos 10°+cos 20°sin 10°=sin 30°=12.15.C5,C3[2015·北京卷] 已知函数f (x )=2sin x 2cos x 2-2sin 2x2.(1)求f (x )的最小正周期;(2)求f (x )在区间[-π,0]上的最小值. 15.解:(1)因为f (x )=22sin x -22(1-cos x ) =sin ⎝⎛⎭⎫x +π4-22,所以f (x )的最小正周期为2π.(2)因为-π≤x ≤0,所以-3π4≤x +π4≤π4.当x +π4=-π2,即x =-3π4时,f (x )取得最小值.所以f (x )在区间[-π,0]上的最小值为 f ⎝⎛⎭⎫-3π4=-1-22.12.C5[2015·四川卷] sin 15°+sin 75°的值是________.12.62[解析] sin 15°+sin 75°=sin 15°+cos 15°=2sin(15°+45°)=2sin 60°=62. 19.C2、C5、C8[2015·四川卷] 如图1-4所示,A ,B ,C ,D 为平面四边形ABCD 的四个内角.(1)证明:tan A 2=1-cos Asin A;(2)若A +C =180°,AB =6,BC =3,CD =4,AD =5,求tan A 2+tan B 2+tan C 2+tan D2的值.19.解:(1)证明:tan A2=sinA 2cos A 2=2sin 2A22sin A 2cos A 2=1-cos A sin A.(2)由A +C =180°,得C =180°-A ,D =180°-B .由(1)知, tanA 2+tanB 2+tanC 2+tan D2=1-cos A sin A +1-cos B sin B +1-cos (180°-A )sin (180°-A )+1-cos (180°-B )sin (180°-B )=2sin A +2sin B . 连接BD ,在△ABD 中,有BD 2=AB 2+AD 2-2AB ·AD cos A , 在△BCD 中,有BD 2=BC 2+CD 2-2BC ·CD cos C , 所以AB 2+AD 2-2AB ·AD cos A =BC 2+CD 2+2BC ·CD cos A , 则cos A =AB 2+AD 2-BC 2-CD 22(AB ·AD +BC ·CD )=62+52-32-422×(6×5+3×4)=37.于是sin A =1-cos 2A =1-⎝⎛⎭⎫372=2107.连接AC ,同理可得cos B =AB 2+BC 2-AD 2-CD 22(AB ·BC +AD ·CD )=62+32-52-422×(6×3+5×4)=119,于是sin B =1-cos 2B =1-⎝⎛⎭⎫1192=6 1019.所以tan A 2+tan B 2+tan C 2+tan D2=2sin A +2sin B=2×7210+2×19610=4103.15.C3、C5、C6[2015·天津卷] 已知函数f (x )=sin 2x -sin 2x -π6,x ∈R .(1)求f (x )的最小正周期;(2)求f (x )在区间-π3,π4上的最大值和最小值.15.解:(1)由已知,有f (x )=1-cos 2x2-1-cos2x -π32=1212cos 2x +32sin 2x -12cos 2x = 34sin 2x -14cos 2x =12sin2x -π6. 所以f (x )的最小正周期T =2π2=π.(2)因为f (x )在区间-π3,-π6上是减函数,在区间-π6,π4上是增函数,f -π3=-14,f -π6=-12,f π4=34,所以f (x )在区间-π3,π4上的最大值为34,最小值为-12.11.C4、C5、C6 [2015·浙江卷] 函数f (x )=sin 2x +sin x cos x +1的最小正周期是____________,单调递减区间是________.11.π ⎣⎡⎦⎤38π+k π,78π+k π(k ∈Z ) [解析] f (x )=1-cos 2x 2+12sin 2x +1=22sin ⎝⎛⎭⎫2x -π4+32,则最小正周期是π.单调递减区间: 2k π+π2≤2x -π4≤2k π+3π2(k ∈Z )⇒k π+3π8≤x ≤k π+7π8(k ∈Z ).9.C2、C5、C7[2015·重庆卷] 若tan α=2tan π5,则cos α-3π10sin α-π5=( )A .1B .2C .3D .49.C [解析] cos α-3π10sin α-π5=sin α-3π10+π2sin α-π5=sin α+π5sin α-π5=sin αcos π5+cos αsinπ5sin αcos π5-cos αsinπ5=sin αcos αcos π5+sin π5sin αcos αcos π5-sin π5=2·sinπ5cos π5cos π5+sinπ52·sin π5cosπ5cos π5-sinπ5=3sin π5sinπ5=3.18.C2、C3、C5、C6[2015·重庆卷] 已知函数f (x )=sin π2-x sin x -3cos 2x . (1)求f (x )的最小正周期和最大值; (2)讨论f (x )在π6,2π3上的单调性.18.解:(1)f (x )=sin π2-x sin x -3cos 2x =cos x sin x -32(1+cos 2x )=12sin 2x -32cos 2x -32=sin2x -π3-32, 因此f (x )的最小正周期为π,最大值为2-32.(2)当x ∈π6,2π3时,0≤2x -π3≤π,从而当0≤2x -π3≤π2,即π6≤x ≤5π12时,f (x )单调递增;当π2≤2x -π3≤π,即5π12≤x ≤2π3时,f (x )单调递减. 综上可知,f (x )在π6,5π12上单调递增;在5π12,2π3上单调递减.C6 二倍角公式12.B9、C2、C6[2015·湖北卷] 函数f (x )=4cos 2x2·cos ⎝⎛⎭⎫π2-x -2sin x -|ln(x +1)|的零点个数为________.12.2 [解析] f (x )=4cos 2x2sin x -2sin x -|ln(x +1)|=2sin x ⎝⎛⎭⎫2cos 2x 2-1-|ln(x +1)|=sin 2x -|ln(x +1)|.令f (x )=0,得sin 2x =|ln(x +1)|.在同一坐标系中作出函数y =sin 2x 与函数y =|ln(x+1)|的大致图像,如图所示.观察图像可知,两个函数的图像有2个交点,故函数f (x )有2个零点.12.C6,C8[2015·北京卷] 在△ABC 中,a =4,b =5,c =6,则sin 2Asin C =________.12.1 [解析] 根据题意,cos A =b 2+c 2-a 22bc =52+62-422×5×6=34.因为0<A <π,所以sin A=1-cos 2A =74.同理可求sin C =3 78,所以sin 2A sin C =2sin A cos Asin C=1. 6.A2、C6[2015·陕西卷] “sin α=cos α”是“cos 2α=0”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件6.A [解析] sin α=cos α时,cos 2α=cos 2α-sin 2α=0,反之cos 2α=0时,sin α=±cos α,故“sin α=cos α”是“cos 2α=0”的充分不必要条件.15.C3、C5、C6[2015·天津卷] 已知函数f (x )=sin 2x -sin 2x -π6,x ∈R .(1)求f (x )的最小正周期;(2)求f (x )在区间-π3,π4上的最大值和最小值.15.解:(1)由已知,有f (x )=1-cos 2x2-1-cos2x -π32=1212cos 2x +32sin 2x -12cos 2x = 34sin 2x -14cos 2x =12sin2x -π6. 所以f (x )的最小正周期T =2π2=π.(2)因为f (x )在区间-π3,-π6上是减函数,在区间-π6,π4上是增函数,f -π3=-14,f -π6=-12,f π4=34,所以f (x )在区间-π3,π4上的最大值为34,最小值为-12.11.C4、C5、C6 [2015·浙江卷] 函数f (x )=sin 2x +sin x cos x +1的最小正周期是____________,单调递减区间是________.11.π ⎣⎡⎦⎤38π+k π,78π+k π(k ∈Z ) [解析] f (x )=1-cos 2x 2+12sin 2x +1=22sin ⎝⎛⎭⎫2x -π4+32,则最小正周期是π.单调递减区间: 2k π+π2≤2x -π4≤2k π+3π2(k ∈Z )⇒k π+3π8≤x ≤k π+7π8(k ∈Z ).18.C2、C3、C5、C6[2015·重庆卷] 已知函数f (x )=sin π2-x sin x -3cos 2x . (1)求f (x )的最小正周期和最大值; (2)讨论f (x )在π6,2π3上的单调性.18.解:(1)f (x )=sin π2-x sin x -3cos 2x =cos x sin x -32(1+cos 2x )=12sin 2x -32cos 2x -32=sin2x -π3-32, 因此f (x )的最小正周期为π,最大值为2-32.(2)当x ∈π6,2π3时,0≤2x -π3≤π,从而当0≤2x -π3≤π2,即π6≤x ≤5π12时,f (x )单调递增;当π2≤2x -π3≤π,即5π12≤x ≤2π3时,f (x )单调递减. 综上可知,f (x )在π6,5π12上单调递增;在5π12,2π3上单调递减.C7 三角函数的求值、化简与证明14.C7、F3[2015·江苏卷] 设向量a k =⎝⎛⎭⎫cos k π6,sin k π6+cos k π6(k =0,1,2,…,12),则k =011(a k ·a k +1)的值为________.14.93 [解析] 因为a k ·a k +1=cosk π6cos (k +1)π6+⎝⎛⎭⎫sin k π6+cos k π6⎣⎡⎦⎤sin (k +1)π6+cos (k +1)π6=2cosk π6cos (k +1)π6+sin k π6sin (k +1)π6+sin k π6cos (k +1)π6+cos k π6sin (k +1)π6=cos k π6cos (k +1)π6+cos π6+sin (2k +1)π6=12cos (2k +1)π6+sin (2k +1)π6+334,所以k =011(a k ·a k +1)=12×334+12k =011c os (2k +1)π6+k =011s in (2k +1)π6=9 3.16.C7、C8[2015·山东卷] 设f (x )=sin x cos x -cos 2⎝⎛⎭⎫x +π4.(1)求f (x )的单调区间;(2)在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若f ⎝⎛⎭⎫A 2=0,a =1,求△ABC 面积的最大值.16.解:(1)由题意知f (x )=sin 2x2-1+cos ⎝⎛⎭⎫2x +π22=sin 2x 2-1-sin 2x 2=sin 2x -12. 由-π2+2k π≤2x ≤π2+2k π,k ∈Z ,可得-π4+k π≤x ≤π4+k π,k ∈Z ;由π2+2k π≤2x ≤3π2+2k π,k ∈Z ,可得π4+k π≤x ≤3π4+k π,k ∈Z . 所以f (x )的单调递增区间是⎣⎡⎦⎤-π4+k π,π4+k π(k ∈Z );单调递减区间是⎣⎡⎦⎤π4+k π,3π4+k π(k ∈Z ).(2)由f ⎝⎛⎭⎫A 2=sin A -12=0,得sin A =12. 由题意知A 为锐角,所以cos A =32. 由余弦定理a 2=b 2+c 2-2bc cos A ,可得1+3bc =b 2+c 2≥2bc ,即bc ≤2+3,当且仅当b =c 时等号成立,因此12bc sin A ≤2+34,所以△ABC 面积的最大值为2+34.图1-29.C2、C5、C7[2015·重庆卷] 若tan α=2tan π5,则cos α-3π10sin α-π5=( )A .1B .2C .3D .49.C [解析] cos α-3π10sin α-π5=sin α-3π10+π2sin α-π5=sin α+π5sin α-π5=sin αcos π5+cos αsinπ5sin αcos π5-cos αsinπ5=sin αcos αcos π5+sin π5sin αcos αcos π5-sin π5=2·sinπ5cos π5cos π5+sinπ52·sin π5cosπ5cos π5-sinπ5=3sin π5sinπ5=3.C8 解三角形16.C8[2015·安徽卷] 在△ABC 中,∠A =3π4,AB =6,AC =32,点D 在BC 边上,AD =BD ,求AD 的长.16.解:设△ABC 的内角A ,B ,C 所对边的长分别是a ,b ,c .由余弦定理得a 2=b 2+c 2-2bc cos ∠BAC =(32)2+62-2×32×6×cos 3π4=18+36-(-36)=90,所以a =310.又由正弦定理得sin B =b sin ∠BAC a =3310=1010,且0<B <π4,所以cos B =1-sin 2B =1-110=31010. 在△ABD 中,由正弦定理得AD =AB ·sin B sin (π-2B )=6sin B 2sin B cos B =3cos B=10.11.C8[2015·广东卷] 设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =3,sin B=12,C =π6,则b =________. 11.1 [解析] ∵sin B =12,∴B =π6或5π6.当B =5π6时,有B +C =π,不符合,∴B =π6=C ,∴b cos π6=a 2=32,∴b =1. 13.C8[2015·湖北卷] 如图1-2,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30°的方向上,行驶600 m 后到达B 处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD =________m.图1-213.1006 [解析] 依题意,在△ABC 中,AB =600,∠BAC =30°,∠ACB =75°-30°=45°.由正弦定理得BC sin ∠BAC =AB sin ∠ACB ,即BC sin 30°=600sin 45°,所以BC =300 2.在△BCD 中,∠CBD =30°,CD =BC tan ∠CBD =3002·tan 30°=100 6.15.C8[2015·江苏卷] 在△ABC 中,已知AB =2,AC =3,A =60°. (1)求BC 的长; (2)求sin 2C 的值.15.解:(1)由余弦定理知,BC 2=AB 2+AC 2-2AB ·AC ·cos A =4+9-2×2×3×12=7,所以BC =7.(2)由正弦定理知,AB sin C =BC sin A ,所以sin C =AB BC ·sin A =2sin 60°7=217. 因为AB <BC ,所以C 为锐角,则cos C =1-sin 2C =1-37=277. 因此sin 2C =2sin C ·cos C =2×217×277=437. 17.C5、C8[2015·全国卷Ⅱ] △ABC 中,D 是BC 上的点,AD 平分∠BAC ,△ABD 面积是△ADC 面积的2倍.(1)求sin ∠Bsin ∠C; (2)若AD =1,DC =22,求BD 和AC 的长. 17.解:(1)S △ABD =12AB ·AD sin ∠BAD ,S △ADC =12AC ·AD sin ∠CAD .因为S △ABD =2S △ADC ,∠BAD =∠CAD ,所以AB =2AC . 由正弦定理可得 sin ∠B sin ∠C =AC AB =12. (2)因为S △ABD ∶S △ADC =BD ∶DC ,所以BD = 2. 在△ABD 和△ADC 中,由余弦定理知 AB 2=AD 2+BD 2-2AD ·BD cos ∠ADB , AC 2=AD 2+DC 2-2AD ·DC cos ∠ADC . 故AB 2+2AC 2=3AD 2+BD 2+2DC 2=6. 由(1)知AB =2AC ,所以AC =1. 16.C8[2015·全国卷Ⅰ] 在平面四边形ABCD 中,∠A =∠B =∠C =75°,BC =2,则AB 的取值范围是________.16.(6-2,6+2) [解析]MB <AB <EB ,在△BMC 中,CB ==30°,由余弦定理知MB 2=22+22-2×2×2cos 30°=8-43=(6-2)2,所以MB =6- 2.在△EBC 中,设EB =x ,由余弦定理知4=x 2+x 2-2×x ×x cos 30°,得x 2=8+43=(6+2)2,所以x =6+2,即EB =6+2,所以6-2<AB <6+ 2.12.C6,C8[2015·北京卷] 在△ABC 中,a =4,b =5,c =6,则sin 2Asin C=________.12.1 [解析] 根据题意,cos A =b 2+c 2-a 22bc =52+62-422×5×6=34.因为0<A <π,所以sin A=1-cos 2A =74.同理可求sin C =3 78,所以sin 2A sin C =2sin A cos Asin C=1. 12.C8[2015·福建卷] 若锐角△ABC 的面积为103,且AB =5,AC =8,则BC 等于________.12.7 [解析] 由S △ABC =12×5×8sin A =103,得sin A =32.又A 为锐角,∴A =π3,∴由余弦定理得BC =25+64-2×5×8cosπ3=49=7. 17.C8[2015·湖南卷] 设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,a =b tan A ,且B 为钝角.(1)证明:B -A =π2;(2)求sin A +sin C 的取值范围.17.解:(1)证明:由a =b tan A 及正弦定理,得sin A cos A =a b =sin Asin B ,所以sin B =cos A ,即sin B =sin π2+A .又B 为钝角,因此π2+A ∈π2,π,故B =π2+A ,即B -A =π2.(2)由(1)知,C =π-(A +B )=π-2A +π2=π2-2A >0,所以A ∈0,π4.于是sin A +sin C =sin A +sinπ2-2A = sin A +cos 2A =-2sin 2A +sin A +1= -2sin A -142+98.因为0<A <π4,所以0<sin A <22,因此22<-2sin A -142+98≤98. 由此可知,sin A +sin C 的取值范围是22,98. 16.C7、C8[2015·山东卷] 设f (x )=sin x cos x -cos 2⎝⎛⎭⎫x +π4.(1)求f (x )的单调区间;(2)在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若f ⎝⎛⎭⎫A 2=0,a =1,求△ABC 面积的最大值.16.解:(1)由题意知f (x )=sin 2x2-1+cos ⎝⎛⎭⎫2x +π22=sin 2x 2-1-sin 2x 2=sin 2x -12. 由-π2+2k π≤2x ≤π2+2k π,k ∈Z ,可得-π4+k π≤x ≤π4+k π,k ∈Z ;由π2+2k π≤2x ≤3π2+2k π,k ∈Z ,可得π4+k π≤x ≤3π4+k π,k ∈Z . 所以f (x )的单调递增区间是⎣⎡⎦⎤-π4+k π,π4+k π(k ∈Z );单调递减区间是⎣⎡⎦⎤π4+k π,3π4+k π(k ∈Z ).(2)由f ⎝⎛⎭⎫A 2=sin A -12=0,得sin A =12. 由题意知A 为锐角,所以cos A =32. 由余弦定理a 2=b 2+c 2-2bc cos A ,可得1+3bc =b 2+c 2≥2bc ,即bc ≤2+3,当且仅当b =c 时等号成立, 因此12bc sin A ≤2+34,所以△ABC 面积的最大值为2+34.17.C8[2015·陕西卷] △ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .向量m =(a ,3b )与n =(cos A ,sin B )平行.(1)求A ;(2)若a =7,b =2,求△ABC 的面积.17.解:(1)因为m ∥n ,所以a sin B -3b cos A =0, 由正弦定理得sin A sin B -3sin B cos A =0, 又sin B ≠0,从而tan A =3, 由于0<A <π,所以A =π3.(2)方法一:由余弦定理得 a 2=b 2+c 2-2bc cos A , 而a =7,b =2,A =π3,得7=4+c 2-2c ,即c 2-2c -3=0, 因为c >0,所以c =3.故△ABC 的面积为12bc sin A =332.方法二:由正弦定理得7sin π3=2sin B ,从而sin B =217, 又由a >b ,知A >B ,所以cos B =277.故sin C =sin(A +B )=sin B +π3= sin B cos π3+cos B sin π3=32114.所以△ABC 的面积为12ab sin C =332.19.C2、C5、C8[2015·四川卷] 如图1-4所示,A ,B ,C ,D 为平面四边形ABCD 的四个内角.(1)证明:tan A 2=1-cos Asin A;(2)若A +C =180°,AB =6,BC =3,CD =4,AD =5,求tan A 2+tan B 2+tan C 2+tan D2的值.19.解:(1)证明:tan A2=sinA 2cos A 2=2sin 2A22sin A 2cos A 2=1-cos A sin A.(2)由A +C =180°,得C =180°-A ,D =180°-B . 由(1)知, tanA 2+tanB 2+tanC 2+tan D2=1-cos A sin A +1-cos B sin B +1-cos (180°-A )sin (180°-A )+1-cos (180°-B )sin (180°-B )=2sin A +2sin B . 连接BD ,在△ABD 中,有BD 2=AB 2+AD 2-2AB ·AD cos A , 在△BCD 中,有BD 2=BC 2+CD 2-2BC ·CD cos C , 所以AB 2+AD 2-2AB ·AD cos A =BC 2+CD 2+2BC ·CD cos A , 则cos A =AB 2+AD 2-BC 2-CD 22(AB ·AD +BC ·CD )=62+52-32-422×(6×5+3×4)=37.于是sin A =1-cos 2A =1-⎝⎛⎭⎫372=2107.连接AC ,同理可得cos B =AB 2+BC 2-AD 2-CD 22(AB ·BC +AD ·CD )=62+32-52-422×(6×3+5×4)=119,于是sin B =1-cos 2B =1-⎝⎛⎭⎫1192=6 1019.所以tan A 2+tan B 2+tan C 2+tan D2=2sin A +2sin B=2×7210+2×19610=4103.13.C8[2015·天津卷] 在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知△ABC的面积为315,b -c =2,cos A =-14,则a 的值为________.13.8 [解析] 在△ABC 中,cos A =-14,则sin A =154,又由△ABC 的面积为315 ,可得12bc sin A =315,求得bc =24,所以a 2=b 2+c 2-2bc cos A =(b -c )2+2bc -2bc -14=64,解得a =8.16.C8[2015·浙江卷] 在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .已知A =π4,b 2-a 2=12c 2.(1)求tan C 的值;(2)若△ABC 的面积为3,求b 的值.16.解:(1)由b 2-a 2=12c 2及正弦定理得sin 2B -12=12sin 2C ,所以-cos 2B =sin 2C .又由A =π4,即B +C =34π,得-cos 2B =sin 2C =2sin C cos C =sin 2C , 解得tan C =2.(2)由tan C =2,C ∈(0,π)得sin C =2 55,cos C =55.又因为sin B =sin(A +C )=sin ⎝⎛⎭⎫π4+C ,所以sin B =31010.由正弦定理得c =2 23b .又因为A =π4,12bc sin A =3,所以bc =6 2,故b =3.13.C8[2015·重庆卷] 在△ABC 中,B =120°,AB =2,A 的角平分线AD =3,则AC =________.13.6 [解析] 在△ABD 中,由正弦定理,得sin ∠ADB =AB ·sin BAD=2×323=22.由题意知0°<∠ADB <60°,所以∠ADB =45°,则∠BAD =15°,所以∠BAC =2∠BAD =30°,所以C =30°,所以BC =AB = 2.由余弦定理,得AC =AB 2+BC 2-2AB ·BC cos B =(2)2+(2)2-22×2cos 120°= 6.C9 单元综合19.C9[2015·福建卷] 已知函数f (x )的图像是由函数g (x )=cos x 的图像经如下变换得到:先将g (x )图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移π2个单位长度. (1)求函数f (x )的解析式,并求其图像的对称轴方程.(2)已知关于x 的方程f (x )+g (x )=m 在[0,2π)内有两个不同的解α,β. (i)求实数m 的取值范围; (ii)证明:cos(α-β)=2m 25-1.19.解:方法一:(1)将g (x )=cos x 的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变)得到y =2cos x 的图像,再将y =2cos x 的图像向右平移π2个单位长度后得到y =2cos ⎝⎛⎭⎫x -π2的图像,故f (x )=2sin x .从而函数f (x )=2sin x 图像的对称轴方程为x =k π+π2(k ∈Z ).(2)(i)f (x )+g (x )=2sin x +cos x=5⎝⎛⎭⎫25sin x +15cos x=5sin(x +φ)⎝⎛⎭⎫其中sin φ=15,cos φ=25.依题意,sin(x +φ)=m5在[0,2π)内有两个不同的解α,β当且仅当⎪⎪⎪⎪m 5<1,故m 的取值范围是(-5,5).(ii)证明:因为α,β是方程5sin(x +φ)=m 在[0,2π)内的两个不同的解,所以sin(α+φ)=m 5,sin(β+φ)=m5.当1≤m <5时,α+β=2⎝⎛⎭⎫π2-φ,即α-β=π-2(β+φ); 当-5<m <1时,α+β=2⎝⎛⎭⎫3π2-φ,即α-β=3π-2(β+φ). 所以cos(α-β)=-cos 2(β+φ)=2sin 2(β+φ)-1=2⎝⎛⎭⎫m 52-1 =2m 25-1.方法二:(1)同方法一. (2)(i)同方法一.(ii)因为α,β是方程5sin(x +φ)=m 在[0,2π)内的两个不同的解,所以sin(α+φ)=m 5,sin(β+φ)=m5.当1≤m <5时,α+β=2⎝⎛⎭⎫π2-φ,即α+φ=π-(β+φ); 当-5<m <1时,α+β=2⎝⎛⎭⎫3π2-φ,即α+φ=3π-(β+φ). 所以cos(α+φ)=-cos(β+φ).于是cos(α-β)=cos[(α+φ)-(β+φ)]=cos(α+φ)cos(β+φ)+sin(α+φ)sin(β+φ) =-cos 2(β+φ)+sin(α+φ)sin(β+φ)=-⎣⎡⎦⎤1-⎝⎛⎭⎫m 52+⎝⎛⎭⎫m 52=2m 25-1.9.C4、C9[2015·湖南卷] 将函数f (x )=sin 2x 的图像向右平移φ0<φ<π2个单位后得到函数g (x )的图像,若对满足|f (x 1)-g (x 2)|=2的x 1,x 2,有|x 1-x 2|min =π3,则φ=( ) A.5π12 B.π3 C.π4 D.π69.D [解析] 由已知得g (x )=sin(2x -2φ),又|f (x 1)-g (x 2)|=2,0<φ<π2,所以当|x 1-x 2|取最小值时,刚好是取两个函数相邻的最大值与最小值点.令2x 1=π2,2x 2-2φ=-π2,则|x 1-x 2|=⎪⎪⎪⎪π2-φ=π3,得φ=π6.7.[2015·杭州质检] 在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知cos 2A +32=2cos A. (1)求角A 的大小;(2)若a =1,求△ABC 的周长l 的取值范围.7.解:(1)根据倍角公式,得2cos 2A +12=2cos A ,即4cos 2A -4cos A +1=0,所以(2cosA -1)2=0,所以cos A =12.因为0<A <π,所以A =π3.(2)由a sin A =b sin B =c sin C ,得b =23sin B ,c =23sin C , 所以l =1+b +c =1+23(sin B +sin C ). 因为A =π3,所以B +C =2π3,所以l =1+23⎣⎡⎦⎤sin B +sin ⎝⎛⎭⎫2π3-B =1+2sin ⎝⎛⎭⎫B +π6.因为0<B <2π3,所以l ∈(2,3].8.[2015·咸阳一模] 已知△ABC 的三个内角A ,B ,C 的对边分别为a ,b ,c ,且△ABC 的面积S =32ac cos B . (1)若c =2a ,求角A ,B ,C 的大小; (2)若a =2,且π4≤A ≤π3,求c 的取值范围.8. 解:由题意可知,12ac sin B =32ac cos B ,化简,得sin B =3cos B ,即tan B =3,又0<B <π,所以B =π3.(1)由余弦定理得,b 2=a 2+c 2-2ac cos B =a 2+4a 2-2a 2=3a 2, ∴b =3a ,∴a ∶b ∶c =1∶3∶2,易求得A =π6,C =π2.(2)由a sin A =c sin C ,得c =a sin C sin A =2sin Csin A .由C =2π3-A ,得c =2sin ⎝⎛⎭⎫2π3-A sin A=2⎝⎛⎭⎫sin 2π3cos A -cos 2π3sin A sin A =3tan A+1.又由π4≤A ≤π3知1≤tan A ≤3,故c ∈[2,3+1].10.[2015·福州期末] 已知函数f (x )=3sin ωx -cos ωx (ω>0)的图像与直线y =2的相邻两个交点之间的距离为π.(1)求函数f (x )的单调递增区间; (2)设△ABC 的内角A ,B ,C 所对的边分别是a ,b ,c ,若f (A )=2,a =3b ,求角B 的大小.10.解:(1)因为f (x )=3sin ωx -cos ωx (ω>0,x ∈R ),所以f (x )=2sin ⎝⎛⎭⎫ωx -π6,所以函数f (x )的最大值为2.因为函数f (x )的图像与直线y =2的相邻两个交点之间的距离为π,所以f (x )的最小正周期T =π,所以2πω=π,解得ω=2,所以f (x )=2sin ⎝⎛⎭⎫2x -π6.令2k π-π2≤2x -π6≤2k π+π2,k ∈Z ,解得k π-π6≤x ≤k π+π3,k ∈Z ,所以函数f (x )的单调递增区间是⎣⎡⎦⎤k π-π6,k π+π3,k ∈Z .(2)由(1)知,f (x )=2sin ⎝⎛⎭⎫2x -π6.在△ABC 中,因为f (A )=2,所以2sin ⎝⎛⎭⎫2A -π6=2,所以sin ⎝⎛⎭⎫2A -π6=1.因为0<A <π,所以A =π3.因为a =3b ,所以sin A =3sin B ,所以sinπ3=3sin B ,所以sin B =12.因为a >b ,所以A >B ,所以0<B <π3,所以B =π6.7.[2015·开封二模] 函数f (x )=sin(ωx + φ)x ∈R ,ω>0, |φ | <π2的部分图像如图K162所示,如果x 1,x 2 ∈⎝⎛⎭⎫-π6,π3,且f (x 1)=f (x 2),则f (x 1+x 2)=( )A.12B.22C.32D .1 7.C [解析] 由图像知,函数的最小正周期T =2⎝⎛⎭⎫π3+π6=π,则ω=2ππ=2.由函数f (x )的图像过点⎝⎛⎭⎫-π6,0,得sin ⎝⎛⎭⎫-π3+φ=0,又|φ|<π2,所以φ=π3,所以f (x )=sin ⎝⎛⎭⎫2x +π3.由x 1,x 2 ∈⎝⎛⎭⎫-π6,π3,且f (x 1)=f (x 2),易得点(x 1,f (x 1))与点(x 2,f (x 2))关于直线x =π12对称,即x 1 + x 2=π6,所以f (x 1+x 2)=sin ⎝⎛⎭⎫π3+π3=32.。
2015年高考数学试卷附详细答案

2015年高考数学试卷一、选择题:本大题共8小题,每小题5分,共40分2015年普通高等学校招生全国统一考试(浙江卷)数学(理科)1.(5分)(2015•原题)已知集合P={x|x2﹣2x≥0},Q={x|1<x≤2},则(∁R P)∩Q=()A .[0,1)B.(0,2] C.(1,2)D.[1,2]2.(5分)(2015•原题)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A .8cm3B.12cm3C.D.3.(5分)(2015•原题)已知{a n}是等差数列,公差d不为零,前n项和是S n,若a3,a4,a8成等比数列,则()A .a1d>0,dS4>0B.a1d<0,dS4<0C.a1d>0,dS4<0D.a1d<0,dS4>04.(5分)(2015•原题)命题“∀n∈N*,f(n)∈N*且f(n)≤n”的否定形式是()A.∀n∈N*,f(n)∉N*且f(n)>n B.∀n∈N*,f(n)∉N*或f(n)>n C.∃n0∈N*,f(n0)∉N*且f(n0)>n0D.∃n0∈N*,f(n0)∉N*或f(n0)>n05.(5分)(2015•原题)如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是()A .B.C.D.6.(5分)(2015•原题)设A,B是有限集,定义:d(A,B)=card(A∪B)﹣card(A∩B),其中card(A)表示有限集A中的元素个数()命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C)A.命题①和命题②都成立B.命题①和命题②都不成立C.命题①成立,命题②不成立D.命题①不成立,命题②成立7.(5分)(2015•原题)存在函数f(x)满足,对任意x∈R都有()A .f(sin2x)=sinxB.f(sin2x)=x2+xC.f(x2+1)=|x+1|D.f(x2+2x)=|x+1|8.(5分)(2015•原题)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′﹣CD﹣B的平面角为α,则()A .∠A′DB≤αB.∠A′DB≥αC.∠A′CB≤αD.∠A′CB≥α二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9.(6分)(2015•原题)双曲线=1的焦距是,渐近线方程是.10.(6分)(2015•原题)已知函数f(x)=,则f(f(﹣3))= ,f(x)的最小值是.11.(6分)(2015•原题)函数f(x)=sin2x+sinxcosx+1的最小正周期是,单调递减区间是.12.(4分)(2015•原题)若a=log43,则2a+2﹣a= .13.(4分)(2015•原题)如图,三棱锥A﹣BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是.14.(4分)(2015•原题)若实数x,y满足x2+y2≤1,则|2x+y﹣2|+|6﹣x﹣3y|的最小值是.15.(6分)(2015•原题)已知是空间单位向量,,若空间向量满足,且对于任意x,y∈R,,则x0= ,y0= ,|= .三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)(2015•原题)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A=,b2﹣a2=c2.(1)求tanC的值;(2)若△ABC的面积为3,求b的值.17.(15分)(2015•原题)如图,在三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.(1)证明:A1D⊥平面A1BC;(2)求二面角A1﹣BD﹣B1的平面角的余弦值.18.(15分)(2015•原题)已知函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在区间[﹣1,1]上的最大值.(1)证明:当|a|≥2时,M(a,b)≥2;(2)当a,b满足M(a,b)≤2时,求|a|+|b|的最大值.19.(15分)(2015•原题)已知椭圆上两个不同的点A,B关于直线y=mx+对称.(1)求实数m的取值范围;(2)求△AOB面积的最大值(O为坐标原点).20.(15分)(2015•原题)已知数列{a n}满足a1=且a n+1=a n﹣a n2(n∈N*)(1)证明:1≤≤2(n∈N*);(2)设数列{a n2}的前n项和为S n,证明(n∈N*).2015年高考数学试卷(理科)答案与试题解析一、选择题:本大题共8小题,每小题5分,共40分2015年普通高等学校招生全国统一考试(原题卷)数学(理科)1.(5分)考点:交、并、补集的混合运算.专题:集合.分析:求出P中不等式的解集确定出P,求出P补集与Q的交集即可.解答:解:由P中不等式变形得:x(x﹣2)≥0,解得:x≤0或x≥2,即P=(﹣∞,0]∪[2,+∞),∴∁R P=(0,2),∵Q=(1,2],∴(∁R P)∩Q=(1,2),故选:C.点评:此题考查了交、并、补集的混合运算,熟练掌握运算法则是解本题的关键.2.(5分)考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:判断几何体的形状,利用三视图的数据,求几何体的体积即可.解答:解:由三视图可知几何体是下部为棱长为2的正方体,上部是底面为边长2的正方形奥为2的正四棱锥,所求几何体的体积为:23+×2×2×2=.故选:C.点评:本题考查三视图与直观图的关系的判断,几何体的体积的求法,考查计算能力.3.(5分)考点:等差数列与等比数列的综合.专题:等差数列与等比数列.分析:由a3,a4,a8成等比数列,得到首项和公差的关系,即可判断a1d和dS4的符号.解答:解:设等差数列{a n}的首项为a1,则a3=a1+2d,a4=a1+3d,a8=a1+7d,由a3,a4,a8成等比数列,得,整理得:.∵d≠0,∴,∴,=<0.故选:B.点评:本题考查了等差数列和等比数列的性质,考查了等差数列的前n项和,是基础题.4.(5分)考点:命题的否定.专题:简易逻辑.分析:根据全称命题的否定是特称命题即可得到结论.解答:解:命题为全称命题,则命题的否定为:∃n0∈N*,f(n0)∉N*或f(n0)>n0,故选:D.点评:本题主要考查含有量词的命题的否定,比较基础.5.(5分)考点:直线与圆锥曲线的关系.专题:圆锥曲线的定义、性质与方程.分析:根据抛物线的定义,将三角形的面积关系转化为的关系进行求解即可.解答:解:如图所示,抛物线的准线DE的方程为x=﹣1,过A,B分别作AE⊥DE于E,交y轴于N,BD⊥DE于E,交y轴于M,由抛物线的定义知BF=BD,AF=AE,则|BM|=|BD|﹣1=|BF|﹣1,|AN|=|AE|﹣1=|AF|﹣1,则===,故选:A点评:本题主要考查三角形的面积关系,利用抛物线的定义进行转化是解决本题的关键.6.(5分)考点:复合命题的真假.专题:集合;简易逻辑.分析:命题①根据充要条件分充分性和必要性判断即可,③借助新定义,根据集合的运算,判断即可.解答:解:命题①:对任意有限集A,B,若“A≠B”,则A∪B≠A∩B,则card(A∪B)>card(A∩B),故“d(A,B)>0”成立,若d(A,B)>0”,则card(A∪B)>card(A∩B),则A∪B≠A∩B,故A≠B成立,故命题①成立,命题②,d(A,B)=card(A∪B)﹣card(A∩B),d(B,C)=card(B∪C)﹣card(B∩C),∴d(A,B)+d(B,C)=card(A∪B)﹣card(A∩B)+card(B∪C)﹣card(B∩C)=[card (A∪B)+card(B∪C)]﹣[card(A∩B)+card(B∩C)]≥card(A∪C)﹣card(A∩C)=d(A,C),故命题②成立,故选:A点评:本题考查了,元素和集合的关系,以及逻辑关系,分清集合之间的关系与各集合元素个数之间的关系,注意本题对充要条件的考查.集合的元素个数,体现两个集合的关系,但仅凭借元素个数不能判断集合间的关系,属于基础题.7.(5分)考点:函数解析式的求解及常用方法.专题:函数的性质及应用.分析:利用x取特殊值,通过函数的定义判断正误即可.解答:解:A.取x=0,则sin2x=0,∴f(0)=0;取x=,则sin2x=0,∴f(0)=1;∴f(0)=0,和1,不符合函数的定义;∴不存在函数f(x),对任意x∈R都有f(sin2x)=sinx;B.取x=0,则f(0)=0;取x=π,则f(0)=π2+π;∴f(0)有两个值,不符合函数的定义;∴该选项错误;C.取x=1,则f(2)=2,取x=﹣1,则f(2)=0;这样f(2)有两个值,不符合函数的定义;∴该选项错误;D.令|x+1|=t,t≥0,则f(t2﹣1)=t;令t2﹣1=x,则t=;∴;即存在函数f(x)=,对任意x∈R,都有f(x2+2x)=|x+1|;∴该选项正确.故选:D.点评:本题考查函数的定义的应用,基本知识的考查,但是思考问题解决问题的方法比较难.8.(5分)考点:二面角的平面角及求法.专题:创新题型;空间角.分析:解:画出图形,分AC=BC,AC≠BC两种情况讨论即可.解答:解:①当AC=BC时,∠A′DB=α;②当AC≠BC时,如图,点A′投影在AE上,α=∠A′OE,连结AA′,易得∠ADA′<∠AOA′,∴∠A′DB>∠A′OE,即∠A′DB>α综上所述,∠A′DB≥α,故选:B.点评:本题考查空间角的大小比较,注意解题方法的积累,属于中档题.二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9.(6分)双曲线的简单性质.考点:计算题;圆锥曲线的定义、性质与方程.专题:确定双曲线中的几何量,即可求出焦距、渐近线方程.分析:解解:双曲线=1中,a=,b=1,c=,答:∴焦距是2c=2,渐近线方程是y=±x.故答案为:2;y=±x.本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.点评:10.(6分)函数的值.考点:计算题;函数的性质及应用.专题:分根据已知函数可先求f(﹣3)=1,然后代入可求f(f(﹣3));由于x≥1时,f(x)=,析:当x<1时,f(x)=lg(x2+1),分别求出每段函数的取值范围,即可求解解答:解:∵f(x)=,∴f(﹣3)=lg10=1,则f(f(﹣3))=f(1)=0,当x≥1时,f(x)=,即最小值,当x<1时,x2+1≥1,(x)=lg(x2+1)≥0最小值0,故f(x)的最小值是.故答案为:0;.本题主要考查了分段函数的函数值的求解,属于基础试题.点评:11.(6分)两角和与差的正弦函数;三角函数的周期性及其求法;正弦函数的单调性.考点:专三角函数的求值.题:分由三角函数公式化简可得f(x)=sin(2x﹣)+,易得最小正周期,解不等析:式2kπ+≤2x﹣≤2kπ+可得函数的单调递减区间.解答:解:化简可得f(x)=sin2x+sinxcosx+1=(1﹣cos2x)+sin2x+1=sin(2x﹣)+,∴原函数的最小正周期为T==π,由2kπ+≤2x﹣≤2kπ+可得kπ+≤x≤kπ+,∴函数的单调递减区间为[kπ+,kπ+](k∈Z)故答案为:π;[kπ+,kπ+](k∈Z)点评:本题考查三角函数的化简,涉及三角函数的周期性和单调性,属基础题.12.(4分)考点:对数的运算性质.专题:函数的性质及应用.分析:直接把a代入2a+2﹣a,然后利用对数的运算性质得答案.解答:解:∵a=log43,可知4a=3,即2a=,所以2a+2﹣a=+=.故答案为:.点评:本题考查对数的运算性质,是基础的计算题.13.(4分)考点:异面直线及其所成的角.专题:空间角.分析:连结ND,取ND 的中点为:E,连结ME说明异面直线AN,CM所成的角就是∠EMC通过解三角形,求解即可.解答:解:连结ND,取ND 的中点为:E,连结ME,则ME∥AN,异面直线AN,CM所成的角就是∠EMC,∵AN=2,∴ME==EN,MC=2,又∵EN⊥NC,∴EC==,∴cos∠EMC===.故答案为:.点评:本题考查异面直线所成角的求法,考查空间想象能力以及计算能力.14.(4分)考点:函数的最值及其几何意义.专题:不等式的解法及应用;直线与圆.分析:根据所给x,y的范围,可得|6﹣x﹣3y|=6﹣x﹣3y,再讨论直线2x+y﹣2=0将圆x2+y2=1分成两部分,分别去绝对值,运用线性规划的知识,平移即可得到最小值.解答:解:由x2+y2≤1,可得6﹣x﹣3y>0,即|6﹣x﹣3y|=6﹣x﹣3y,如图直线2x+y﹣2=0将圆x2+y2=1分成两部分,在直线的上方(含直线),即有2x+y﹣2≥0,即|2+y﹣2|=2x+y﹣2,此时|2x+y﹣2|+|6﹣x﹣3y|=(2x+y﹣2)+(6﹣x﹣3y)=x﹣2y+4,利用线性规划可得在A(,)处取得最小值3;在直线的下方(含直线),即有2x+y﹣2≤0,即|2+y﹣2|=﹣(2x+y﹣2),此时|2x+y﹣2|+|6﹣x﹣3y|=﹣(2x+y﹣2)+(6﹣x﹣3y)=8﹣3x﹣4y,利用线性规划可得在A(,)处取得最小值3.综上可得,当x=,y=时,|2x+y﹣2|+|6﹣x﹣3y|的最小值为3.故答案为:3.点本题考查直线和圆的位置关系,主要考查二元函数在可行域内取得最值的方法,属于中档题.评:15.(6分)空间向量的数量积运算;平面向量数量积的运算.考点:专创新题型;空间向量及应用.题:分由题意和数量积的运算可得<•>=,不妨设=(,,0),=(1,0,0),由析:已知可解=(,,t),可得|﹣(|2=(x+)2+(y﹣2)2+t2,由题意可得当x=x0=1,y=y0=2时,(x+)2+(y﹣2)2+t2取最小值1,由模长公式可得|.解解:∵•=||||cos<•>=cos<•>=,答:∴<•>=,不妨设=(,,0),=(1,0,0),=(m,n,t),则由题意可知=m+n=2,=m=,解得m=,n=,∴=(,,t),∵﹣()=(﹣x﹣y,,t),∴|﹣(|2=(﹣x﹣y)2+()2+t2=x2+xy+y2﹣4x﹣5y+t2+7=(x+)2+(y﹣2)2+t2,由题意当x=x0=1,y=y0=2时,(x+)2+(y﹣2)2+t2取最小值1,此时t2=1,故|==2故答案为:1;2;2点本题考查空间向量的数量积,涉及向量的模长公式,属中档题.评:三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)余弦定理.考点:解三角形.专题:分(1)由余弦定理可得:,已知b2﹣a2=c2.可得,a=.利析:用余弦定理可得cosC.可得sinC=,即可得出tanC=.(2)由=×=3,可得c,即可得出b.解解:(1)∵A=,∴由余弦定理可得:,∴b2﹣a2=bc﹣c2,答:又b2﹣a2=c2.∴bc﹣c2=c2.∴b=c.可得,∴a2=b2﹣=,即a=.∴cosC===.∵C∈(0,π),∴sinC==.∴tanC==2.(2)∵=×=3,解得c=2.∴=3.点评:本题考查了正弦定理余弦定理、同角三角形基本关系式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.17.(15分)考点:二面角的平面角及求法;直线与平面垂直的判定.专题:空间位置关系与距离;空间角.分析:(1)以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系,通过•=•=0及线面垂直的判定定理即得结论;(2)所求值即为平面A1BD的法向量与平面B1BD的法向量的夹角的余弦值的绝对值的相反数,计算即可.解答:(1)证明:如图,以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系.则BC=AC=2,A1O==,易知A1(0,0,),B(,0,0),C(﹣,0,0),A(0,,0),D(0,﹣,),B1(,﹣,),=(0,﹣,0),=(﹣,﹣,),=(﹣,0,0),=(﹣2,0,0),=(0,0,),∵•=0,∴A1D⊥OA1,又∵•=0,∴A1D⊥BC,又∵OA1∩BC=O,∴A1D⊥平面A1BC;(2)解:设平面A1BD的法向量为=(x,y,z),由,得,取z=1,得=(,0,1),设平面B1BD的法向量为=(x,y,z),由,得,取z=1,得=(0,,1),∴cos<,>===,又∵该二面角为钝角,∴二面角A1﹣BD﹣B1的平面角的余弦值为﹣.点评:本题考查空间中线面垂直的判定定理,考查求二面角的三角函数值,注意解题方法的积累,属于中档题.18.(15分)考点:二次函数在闭区间上的最值.专题:函数的性质及应用.分析:(1)明确二次函数的对称轴,区间的端点值,由a的范围明确函数的单调性,结合已知以及三角不等式变形所求得到证明;(2)讨论a=b=0以及分析M(a,b)≤2得到﹣3≤a+b≤1且﹣3≤b﹣a≤1,进一步求出|a|+|b|的求值.解答:解:(1)由已知可得f(1)=1+a+b,f(﹣1)=1﹣a+b,对称轴为x=﹣,因为|a|≥2,所以或≥1,所以函数f(x)在[﹣1,1]上单调,所以M(a,b)=max{|f(1),|f(﹣1)|}=max{|1+a+b|,|1﹣a+b|},所以M(a,b)≥(|1+a+b|+|1﹣a+b|)≥|(1+a+b)﹣(1﹣a+b)|≥|2a|≥2;(2)当a=b=0时,|a|+|b|=0又|a|+|b|≥0,所以0为最小值,符合题意;又对任意x∈[﹣1,1].有﹣2≤x2+ax+b≤2得到﹣3≤a+b≤1且﹣3≤b﹣a≤1,易知|a|+|b|=max{|a﹣b|,|a+b|}=3,在b=﹣1,a=2时符合题意,所以|a|+|b|的最大值为3.点评:本题考查了二次函数闭区间上的最值求法;解答本题的关键是正确理解M(a,b)是|f(x)|在区间[﹣1,1]上的最大值,以及利用三角不等式变形.19.(15分)考点:直线与圆锥曲线的关系.专题:创新题型;圆锥曲线中的最值与范围问题.分析:(1)由题意,可设直线AB的方程为x=﹣my+n,代入椭圆方程可得(m2+2)y2﹣2mny+n2﹣2=0,设A(x1,y1),B(x2,y2).可得△>0,设线段AB的中点P(x0,y0),利用中点坐标公式及其根与系数的可得P,代入直线y=mx+,可得,代入△>0,即可解出.(2)直线AB与x轴交点横坐标为n,可得S△OAB=,再利用均值不等式即可得出.解答:解:(1)由题意,可设直线AB的方程为x=﹣my+n,代入椭圆方程,可得(m2+2)y2﹣2mny+n2﹣2=0,设A(x1,y1),B(x2,y2).由题意,△=4m2n2﹣4(m2+2)(n2﹣2)=8(m2﹣n2+2)>0,设线段AB的中点P(x0,y0),则.x0=﹣m×+n=,由于点P在直线y=mx+上,∴=+,∴,代入△>0,可得3m4+4m2﹣4>0,解得m2,∴或m.(2)直线AB与x轴交点纵坐标为n,∴S△OAB==|n|•=,由均值不等式可得:n2(m2﹣n2+2)=,∴S△AOB=,当且仅当n2=m2﹣n2+2,即2n2=m2+2,又∵,解得m=,当且仅当m=时,S△AOB取得最大值为.点评:本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、线段垂直平分线的性质、三角形面积计算公式、弦长公式、均值不等式的性质,考查了推理能力与计算能力,属于难题.20.(15分)考点:数列的求和;数列与不等式的综合.专题:创新题型;点列、递归数列与数学归纳法.分析:(1)通过题意易得0<a n≤(n∈N*),利用a n﹣a n+1=可得≥1,利用==≤2,即得结论;(2)通过=a n﹣a n+1累加得S n=﹣a n+1,利用数学归纳法可证明≥a n≥(n≥2),从而≥≥,化简即得结论.解答:证明:(1)由题意可知:0<a n≤(n∈N*),又∵a2=a1﹣=,∴==2,又∵a n﹣a n+1=,∴a n>a n+1,∴≥1,∴==≤2,∴1≤≤2(n∈N*);(2)由已知,=a n﹣a n+1,=a n﹣1﹣a n,…,=a1﹣a2,累加,得S n=++…+=a1﹣a n+1=﹣a n+1,易知当n=1时,要证式子显然成立;当n≥2时,=.下面证明:≥a n≥(n≥2).易知当n=2时成立,假设当n=k时也成立,则a k+1=﹣+,由二次函数单调性知:a n+1≥﹣+=≥,a n+1≤﹣+=≤,∴≤≤,即当n=k+1时仍然成立,故对n≥2,均有≥a n≥,∴=≥≥=,即(n∈N*).点评:本题是一道数列与不等式的综合题,考查数学归纳法,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于难题.。
2015年全国高考真题_三角函数(详细答案)

又∵,,∴,故. 23.【2015高考山东,理16】设. (Ⅰ)求的单调区间; (Ⅱ)在锐角中,角的对边分别为,若,求面积的最大值. 【答案】(I)单调递增区间是; 单调递减区间是 (II) 面积的最大值为 【解析】 (I)由题意知 由 可得 由 可得 所以函数 的单调递增区间是 ; 单调递减区间是
(Ⅱ)若,,求和的长. 【答案】(Ⅰ);(Ⅱ). 【解析】(Ⅰ),,因为,,所以.由正弦定理可得. (Ⅱ)因为,所以.在和中,由余弦定理得 ,. .由(Ⅰ)知,所以. 20.【2015江苏高考,15】(本小题满分14分)
在中,已知. (1)求的长;
(2)求的值. 【答案】(1);(2)
21.【2015高考福建,理19】已知函数的图像是由函数的图像经如下变 换得到:先将图像上所有点的纵坐标伸长到原来的2倍(横坐标不 变),再将所得到的图像向右平移个单位长度. (Ⅰ)求函数的解析式,并求其图像的对称轴方程;
∴ ,又, ∴ ,∴ 即,∴ ; (2)由(1)依题知 , ∴ 又, ∴ 即. 32.【2015高考湖南,理17】设的内角,,的对边分别为,,,,且为 钝角. (1)证明:; (2)求的取值范围. 【答案】(1)详见解析;(2).
,∴,于是 ,∵,∴,因此,由此可知的取值范围是.
2015届高考数学一轮总复习 阶段性测试题4(三角函数与三角形)

阶段性测试题四(三角函数与三角形)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分。
考试时间120分钟。
第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(2014·威海期中)角α的终边经过点P (sin10°,-cos10°),则α的可能取值为( ) A .10° B .80° C .-10° D .-80°[答案] D[解析] 由条件知tan α=-cos10°sin10°=-tan80°=tan(-80°),故选D.2.(文)(2014·北京海淀期中)在△ABC 中,若tan A =-2,则cos A =( ) A.55B .-55 C.255 D .-255[答案] B[解析] 在△ABC 中,若tan A =-2,则A ∈(π2,π),cos A =-11+tan 2A=-15=-55,故选B.(理)(2014·三亚市一中月考)若tan α=2,则cos2α+sin2α的值为( ) A .0 B.15 C .1 D.54[答案] B[解析] ∵tan α=2,∴cos2α+sin2α=cos 2α-sin 2α+2sin αcos αsin 2α+cos 2α=1-tan 2α+2tan αtan 2α+1=15.3.(文)(2014·江西临川十中期中)已知sin(θ+π2)=35,则cos2θ等于( )A.1225B .-1225C .-725D.725[答案] C[解析] ∵sin(θ+π2)=cos θ=35,∴cos2θ=2cos 2θ-1=-725.(理)(2014·枣庄市期中)化简cos (π+α)cos (π2+α)cos (11π2-α)cos (π-α)sin (-π-α)sin (9π2+α)的结果是( ) A .-1 B .1 C .tan α D .-tan α[答案] C[解析] 原式=-cos α·(-sin α)·(-sin α)-cos α·sin α·cos α=tan α,故选C.4.(2014·山东省菏泽市期中)要得到y =sin(2x -2π3)的图象,只要将函数y =sin(2x +π3)的图象向右平移( )个单位即可( )A.π3 B .π C.2π3 D.π2 [答案] D[解析] ∵sin[2(x -π2)+π3]=sin(2x -2π3),∴只需将y =sin(2x +π3)的图象向右平移π2个单位可得到y =sin(2x -2π3)的图象.5.(2014·九江市七校联考)在△ABC 中,AC =7,∠B =2π3,△ABC 的面积S =1534,则AB =( )A .5或3B .5C .3D .5或6 [答案] A[解析] 设AB =x ,BC =y ,则x >0,y >0,由条件得,⎩⎨⎧72=x 2+y 2-2xy cos 2π3,12xy sin 2π3=1534,即⎩⎪⎨⎪⎧x 2+y 2+xy =49,xy =15, 则⎩⎪⎨⎪⎧ x =3,y =5,或⎩⎪⎨⎪⎧x =5,y =3,∴AB =3或5. 6.(2014·山东省菏泽市期中)已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是( )A .2B .2sin1C .2sin -11D .sin2[答案] C[解析] 设圆半径为R ,由条件知sin1=1R ,∴R =1sin1,∴l =2R =2sin1,故选C.7.(文)(2014·辽宁师大附中期中)在△ABC 中,角A 、B 均为锐角,且cos A >sin B ,则△ABC 的形状是( )A .直角三角形B .锐角三角形C .钝角三角形D .等腰三角形[答案] C[解析] ∵cos A =sin(π2-A )>sin B,0<π2-A <π2,0<B <π2,∴π2-A >B ,∴A +B <π2,∴C >π2,故选C.(理)(2014·安徽程集中学期中)在△ABC 中,“sin(A -B )cos B +cos(A -B )sin B ≥1”是“△ABC 是直角三角形”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件[答案] A[解析] 由条件式得sin A ≥1,∴sin A =1,∴A 为直角,但△ABC 为直角三角形时,不一定A 为直角,故选A.8.(2014·浙江省五校联考)函数y =2sin(π4-x 2)sin(π4+x2)的图象的一条对称轴为( )A .x =-π2B .x =π2C .x =πD .x =3π2[答案] C[解析] y =2sin(π4-x 2)sin(π4+x 2)=2sin(π4-x 2)cos(π4-x 2)=sin(π2-x )=cos x ,其对称轴方程为x =k π,k ∈Z .9.(文)(2014·江西白鹭洲中学期中)函数y =cos2x 在下列哪个区间上是减函数( ) A .[0,π2]B .[π4,3π4]C .[-π4,π4]D .[π2,π][答案] A[解析] 由2k π≤2x ≤2k π+π得k π≤x ≤k π+π2(k ∈Z ),令k =0知选A.(理)(2014·福州市八县联考)已知ω>0,函数f (x )=sin(ωx +π4)在(π2,π)上单调递减,则ω的取值范围是( )A .[12,54]B .[12,34]C .(0,12]D .(0,2] [答案] A[解析] 由2k π+π2≤ωx +π4≤2k π+3π2及ω>0得,2k πω+π4ω≤x ≤2k πω+5π4ω,k ∈Z . ∵f (x )在(π2,π)上单调递减,∴(π2,π)⊆[2k πω+π4ω,2k πω+5π4ω], ∴k =0,⎩⎨⎧π4ω≤π2,5π4ω≥π.∴12≤ω≤54,故选A. 10.(2014·营口三中期中)函数f (x )=sin(ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,如果x 1,x 2∈(-π6,π3),且f (x 1)=f (x 2),则f (x 1+x 2)=( )A.12B.22C.32D .1[答案] C[解析] ∵x 1,x 2∈(-π6,π3)时,f (x 1)=f (x 2),∴x 1+x 2=-π6+π3=π6,∴f (x 1+x 2)=f (π6),由图象知,T 2=π3-(-π6)=π2,∴T =2πω=π,∴ω=2,∴f (x )=sin(2x +φ),由于f (x )的图象过点(π12,1),∴sin(π6+φ)=1,∴φ=π3,∴f (π6)=sin(2×π6+π3)=sin 2π3=32,故选C.11.(2014·哈六中期中)2sin 225°-1sin20°cos20°的值为( )A .-1B .-2C .1D .2[答案] B[解析] 原式=-cos50°12sin40°=-2.12.(文)(2014·威海期中)函数f (x )=sin x +cos2x 的图象为( )[答案] B[解析] f (0)=sin0+cos0=1,排除A 、D ;f (-π)=sin(-π)+cos(-2π)=1,排除C ,故选B. (理)(2014·山东省菏泽市期中)函数f (x )=2x -tan x 在(-π2,π2)上的图象大致为( )[答案] C[解析] ∵f (-x )=-2x -tan(-x )=-(2x -tan x )=-f (x ), ∴f (x )为奇函数,排除A 、B ; f ′(x )=(2x -sin x cos x )′=2-1cos 2x ,令f ′(x )≥0得,cos 2x ≥12,∴cos x ≥22或cos x ≤-22, ∵x ∈(-π2,π2),∴-π4≤x ≤π4,故选C.第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.) 13.(2014·华安、连城、永安、漳平、泉港一中、龙海二中六校联考)在△ABC 中,三边a 、b 、c 所对的角分别为A 、B 、C ,若a 2+b 2-c 2+2ab =0,则角C 的大小为________.[答案] 135°[解析] ∵a 2+b 2-c 2+2ab =0, ∴cos C =a 2+b 2-c 22ab =-22,∵0°<C <180°,∴C =135°.14.(文)(2014·甘肃临夏中学期中)函数f (x )=3sin(2x -π3)的图象为C ,则如下结论中正确的序号是________.①图象C 关于直线x =1112π对称;②图象C 关于点(2π3,0)对称;③函数f (x )在区间(-π12,5π12)内是增函数;④由y =3sin2x 的图象向右平移π3个单位长度可以得到图象C .[答案] ①②③[解析] ①当x =11π12时,f (11π12)=3sin 3π2=-3,∴正确;②当x =2π3时,f (2π3)=0,∴正确;③由2k π-π2≤2x -π3≤2k π+π2可得k π-π12≤x ≤k π+5π12,k ∈Z ,∴f (x )的单调递增区间为[k π-π12,k π+5π12](k∈Z ),∴正确;④y =3sin2x 的图象向右平移π3个单位长度得到y =3sin2(x -π3),∴④错误.(理)(2014·威海期中)将函数y =sin(x -π3),x ∈[0,2π]的图象上各点的纵坐标不变横坐标伸长到原来的2倍,再向左平移π6个单位,所得函数的单调递增区间为____________.[答案] [-π6,3π2],[7π2,23π6][解析]由2k π-π2≤12x -π4≤2k π+π2得,4k π-π2≤x ≤4k π+3π2,k ∈Z ,由已知函数中x ∈[0,2π]得所求函数的定义域为[-π6,23π6],令k =0得,-π2≤x ≤3π2,令k =1得,7π2≤x ≤11π2,故所求函数的单调增区间为[-π6,3π2]和[7π2,23π6].15.(文)(2014·吉林省实验中学一模)设α为锐角,若cos(α+π6)=45,则sin(2α+π3)=________.[答案]2425[解析] ∵α为锐角,∴0<α+π6<π,∵cos(α+π6)=45,∴sin(α+π6)=35,∴sin(2α+π3)=2sin(α+π6)·cos(α+π6)=2×35×45=2425.(理)(2014·吉林延边州质检)设△ABC 的三个内角A 、B 、C 所对的三边分别为a 、b 、c ,若△ABC 的面积为S =a 2-(b -c )2,则sin A1-cos A=________.[答案] 4[解析] ∵S =12bc sin A ,a 2-(b -c )2=2bc -(b 2+c 2-a 2)=2bc -2bc cos A ,S =a 2-(b -c )2,∴12bc sin A =2bc -2bc cos A ,∴sin A 1-cos A=4. 16.(2014·浙江省五校联考)已知O (0,0),A (cos α,sin α),B (cos β,sin β),C (cos γ,sin γ),若kOA →+(2-k )OB →+OC →=0(0<k <2),则cos(α-β)的最大值是________.[答案] -12[解析] ∵kOA →+(2-k )OB →+OC →=0,OA →=(cos α,sin α),OB →=(cos β,sin β),OC →=(cos γ,sin γ),∴⎩⎪⎨⎪⎧k cos α+(2-k )cos β+cos γ=0,k sin α+(2-k )sin β+sin γ=0, ∵cos 2γ+sin 2γ=1,∴k 2+(2-k )2+2k (2-k )cos αcos β+2k ·(2-k )sin αsin β=1, ∴cos(α-β)=-2k 2+4k -3-2k 2+4k =1+32k 2-4k , ∵0<k <2,∴-2≤2k 2-4k <0,∴cos(α-β)≤-12.三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤.) 17.(本小题满分12分)(文)(2014·甘肃省金昌市二中期中)已知函数f (x )=2sin x (sin x +cos x ). (1)求f (x )的最小正周期;(2)当x ∈[0,π2]时,求f (x )的最大值.[解析] f (x )=2sin x (sin x +cos x )=2sin 2x +2sin x cos x =1-cos2x +sin2x=2(22sin2x -22cos2x )+1 =2sin(2x -π4)+1,(1)f (x )的最小正周期T =2π2=π.(2)∵0≤x ≤π2,∴-π4≤2x -π4≤3π4,∴当2x -π4=π2,即x =3π8时,f (x )取得最大值,且最大值为f (3π8)=2sin π2+1=2+1.(理)(2014·北京东城区联考)已知函数f (x )=3sin x cos x -cos 2x . (1)求f (x )的最小正周期;(2)当x ∈[0,π2]时,求函数f (x )的最大值及相应的x 的值.[解析] (1)因为f (x )=32sin2x -12cos2x -12=sin(2x -π6)-12,所以T =2π2=π,故f (x )的最小正周期为π.(2)因为0≤x ≤π2,所以-π6≤2x -π6≤5π6.所以当2x -π6=π2,即x =π3时,f (x )有最大值12.18.(本小题满分12分)(文)(2014·辽宁师大附中期中)设△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,且cos B =45,b =2.(1)当A =30°时,求a 的值;(2)当△ABC 的面积为3时,求a +c 的值. [解析] (1)∵cos B =45,∴sin B =35.由正弦定理a sin A =b sin B ,可得a sin30°=103.∴a =53.(2)∵△ABC 的面积S =12ac sin B ,sin B =35,S =3,∴ac =10.由余弦定理b 2=a 2+c 2-2ac cos B 得, 4=a 2+c 2-85ac =a 2+c 2-16,即a 2+c 2=20.∴(a +c )2-2ac =20,(a +c )2=40,∴a +c =210.(理)(2014·威海期中)△ABC 的角A ,B ,C 的对边分别为a ,b ,c ,已知a sin A +b sin B -c sin C =a sin B .(1)求角C ;(2)若a +b =5,S △ABC =323,求c 的值.[解析] (1)根据正弦定理a sin A =b sin B =csin C ,原等式可转化为:a 2+b 2-c 2=ab , ∴cos C =a 2+b 2-c 22ab =12,∵0°<C <180°,∴C =60°.(2)S △ABC =12ab sin C =12ab ·32=332,∴ab =6,c 2=a 2+b 2-2ab ·cos C =(a +b )2-3ab =25-18=7, ∴c =7.19.(本小题满分12分)(2014·江西白鹭洲中学期中)在△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边,已知tan A +tan B 1-tan A ·tan B=-3,c =7,三角形面积为332.(1)求∠C 的大小; (2)求a +b 的值.[解析] (1)∵tan(A +B )=tan A +tan B1-tan A tan B =-3,且tan C =tan[π-(A +B )]=-tan(A +B ), ∴tan C =3,又∵0<C <π,∴∠C =π3.(2)由题意可知:S △ABC =12ab sin C =12ab sin π3=34ab =332,∴ab =6.由余弦定理可得:c 2=a 2+b 2-2ab cos C =(a +b )2-3ab , ∴(a +b )2=3ab +c 2=3×6+(7)2=25, 又a >0,b >0,∴a +b =5.20.(本小题满分12分)(文)(2014·马鞍山二中期中)已知A ,B ,C 的坐标分别为A (3,0),B (0,3),C (cos α,sin α),α∈(π2,3π2).(1)若|AC →|=|BC →|,求角α的值;(2)若AC →·BC →=-1,求2sin 2α+sin2α1+tan α的值. [解析] (1)∵AC →=(cos α-3,sin α),BC →=(cos α,sin α-3),∴AC →2=(cos α-3)2+sin 2α=10-6cos α,BC →2=cos 2α+(sin α-3)2=10-6sin α,由|AC →|=|BC →|,可得AC →2=BC →2,即10-6cos α=10-6sin α,得sin α=cos α.又∵α∈(π2,3π2),∴α=5π4. (2)由AC →·BC →=-1,得(cos α-3)cos α+sin α(sin α-3)=-1,∴sin α+cos α=23.① 又2sin 2α+sin2α1+tan α=2sin 2α+2sin αcos α1+sin αcos α=2sin αcos α. 由①式两边分别平方,得1+2sin αcos α=49, ∴2sin αcos α=-59.∴2sin 2α+sin2α1+tan α=-59. (理)(2014·辽宁师大附中期中)已知向量a =(2sin x ,sin x -cos x ),b =(cos x ,3(cos x +sin x )),函数f (x )=a ·b +1.(1)当x ∈[π4,π2]时,求f (x )的最大值和最小值; (2)求f (x )的单调区间.[解析] (1)f (x )=sin2x -3cos2x +1=2sin(2x -π3)+1. ∵π4≤x ≤π2,∴π2≤2x ≤π,∴π6≤2x -π3≤2π3, ∴12≤sin(2x -π3)≤1,∴1≤2sin(2x -π3)≤2, 于是2≤2sin(2x -π3)+1≤3, ∴f (x )的最大值是3,最小值是2.(2)由2k π-π2≤2x -π3≤2k π+π2,k ∈Z 得2k π-π6≤2x ≤2k π+5π6,k ∈Z , ∴k π-π12≤x ≤k π+5π12,k ∈Z , 即f (x )的单调递增区间为[k π-π12,k π+5π12],k ∈Z , 同理由2k π+π2≤2x -π3≤2k π+3π2,k ∈Z 得,f (x )的单调递减区间为[k π+5π12,k π+11π12],k ∈Z . 21.(本小题满分12分)(2014·马鞍山二中期中)如图A 、B 是海面上位于东西方向相距5(3+3)n mile 的两个观测点,现位于A 点北偏东45°,B 点北偏西60°的D 点有一艘轮船发出求救信号,位于B 点南偏西60°且与B 点相距203n mile 的C 点的救援船立即前往营救,其航行速度为30n mile/h ,该救援船到达D 点需要多长时间?[解析] 由题意知AB =5(3+3)n mile ,∠DBA =90°-60°=30°,∠DAB =90°-45°=45°, ∴∠ADB =180°-(45°+30°)=105°,在△DAB 中,由正弦定理得,DB sin ∠DAB =AB sin ∠ADB∴DB =AB ·sin ∠DAB sin ∠ADB=5(3+3)·sin45°sin105°=5(3+3)·sin45°sin45°·cos60°+sin60°·cos45°=53(3+1)3+12=103(n mile). 又∠DBC =∠DBA +∠ABC =30°+(90°-60°)=60°,BC =203(n mile),在△DBC 中,由余弦定理得,CD 2=BD 2+BC 2-2BD ·BC ·cos ∠DBC =300+1200-2×103×203×12=900, ∴CD =30(n mile),则需要的时间t =3030=1(h). 答:救援船到达D 点需要1h.22.(本小题满分14分)(文)(2014·安徽程集中学期中)已知函数f (x )=A cos(ωx +φ)(A >0,ω>0,0<φ<π2)的图象过点(0,12),最小正周期为2π3,且最小值为-1.(1)求函数f (x )的解析式;(2)若x ∈[π6,m ],f (x )的值域是[-1,-32],求m 的取值范围. [解析] (1)由函数的最小值为-1,可得A =1,因为最小正周期为2π3,所以ω=3.可得f (x )=cos(3x +φ),又因为函数的图象过点(0,12),所以cos φ=12,而0<φ<π2,所以φ=π3,故f (x )=cos(3x +π3). (2)由x ∈[π6,m ],可知5π6≤3x +π3≤3m +π3,因为f (π6)=cos 5π6=-32,且cosπ=-1,cos 7π6=-32, 由余弦曲线的性质知,π≤3m +π3≤7π6,得2π9≤m ≤5π18,即m ∈[2π9,5π18]. (理)(2014·浙江省五校联考)已知函数f (x )=(3sin ωx +cos ωx )cos ωx -12,其中ω>0,f (x )的最小正周期为4π.(1)求函数f (x )的单调递增区间;(2)在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且满足(2a -c )cos B =b cos C ,求函数f (A )的取值范围.[解析] f (x )=3sin ωx ·cos ωx +cos 2ωx -12=32sin2ωx +12cos2ωx =sin(2ωx +π6). (1)∵2π2ω=4π,∴ω=14,f (x )=sin(x 2+π6). 由2k π-π2≤x 2+π6≤2k π+π2(k ∈Z )得: 4k π-4π3≤x ≤4k π+2π3. ∴f (x )的单调递增区间是[4k π-4π3,4k π+2π3](k ∈Z ). (2)由正弦定理得,(2sin A -sin C )cos B =sin B ·cos C ,∴2sin A cos B =sin(B +C ),∵sin(B +C )=sin(π-A )=sin A >0,∴cos B =12,∵0<B <π,∴B =π3, ∴0<A <2π3,π6<A 2+π6<π2,∴f (A )∈(12,1).。
2015年全国统一高考真题数学试卷(理科)(新课标ⅰ)(含答案及解析)

2015年全国统一高考数学试卷(理科)(新课标Ⅰ)一、选择题(共12小题,每小题5分,满分60分)1.(5分)设复数z满足=i,则|z|=()A.1B.C.D.22.(5分)sin20°cos10°﹣cos160°sin10°=()A.B.C.D.3.(5分)设命题p:∃n∈N,n2>2n,则¬p为()A.∀n∈N,n2>2n B.∃n∈N,n2≤2nC.∀n∈N,n2≤2n D.∃n∈N,n2=2n4.(5分)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为()A.0.648B.0.432C.0.36D.0.3125.(5分)已知M(x0,y0)是双曲线C:=1上的一点,F1,F2是C的左、右两个焦点,若<0,则y0的取值范围是()A.B.C.D.6.(5分)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛7.(5分)设D为△ABC所在平面内一点,,则()A.B.C.D.8.(5分)函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为()A.(kπ﹣,kπ+),k∈z B.(2kπ﹣,2kπ+),k∈zC.(k﹣,k+),k∈z D.(,2k+),k∈z9.(5分)执行如图所示的程序框图,如果输入的t=0.01,则输出的n=()A.5B.6C.7D.810.(5分)(x2+x+y)5的展开式中,x5y2的系数为()A.10B.20C.30D.6011.(5分)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1B.2C.4D.812.(5分)设函数f(x)=e x(2x﹣1)﹣ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是()A.[)B.[)C.[)D.[)二、填空题(本大题共有4小题,每小题5分)13.(5分)若函数f(x)=xln(x+)为偶函数,则a=.14.(5分)一个圆经过椭圆=1的三个顶点.且圆心在x轴的正半轴上.则该圆标准方程为.15.(5分)若x,y满足约束条件.则的最大值为.16.(5分)在平面四边形ABCD中,∠A=∠B=∠C=75°.BC=2,则AB的取值范围是.三、解答题:17.(12分)S n为数列{a n}的前n项和,已知a n>0,a n2+2a n=4S n+3(I)求{a n}的通项公式:(Ⅱ)设b n=,求数列{b n}的前n项和.18.(12分)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,BE=2DF,AE丄EC.(Ⅰ)证明:平面AEC丄平面AFC(Ⅱ)求直线AE与直线CF所成角的余弦值.19.(12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费x i和年销售量y i(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(x i﹣)2(w i﹣)2(x i﹣)(y i﹣)(w i﹣)(y i﹣)46.6563 6.8289.8 1.61469108.8表中w i=i,=(Ⅰ)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y﹣x.根据(Ⅱ)的结果回答下列问题:(i)年宣传费x=49时,年销售量及年利润的预报值是多少?(ii)年宣传费x为何值时,年利润的预报值最大?附:对于一组数据(u1 v1),(u2 v2)…..(u n v n),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:=,=﹣.20.(12分)在直角坐标系xOy中,曲线C:y=与直线l:y=kx+a(a>0)交于M,N两点.(Ⅰ)当k=0时,分別求C在点M和N处的切线方程.(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?(说明理由)21.(12分)已知函数f(x)=x3+ax+,g(x)=﹣lnx(i)当a为何值时,x轴为曲线y=f(x)的切线;(ii)用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x>0),讨论h(x)零点的个数.选修4一1:几何证明选讲22.(10分)如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.(Ⅰ)若D为AC的中点,证明:DE是⊙O的切线;(Ⅱ)若OA=CE,求∠ACB的大小.选修4一4:坐标系与参数方程23.(10分)在直角坐标系xOy中,直线C1:x=﹣2,圆C2:(x﹣1)2+(y﹣2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求C1,C2的极坐标方程;(Ⅱ)若直线C3的极坐标方程为θ=(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.选修4一5:不等式选讲24.(10分)已知函数f(x)=|x+1|﹣2|x﹣a|,a>0.(Ⅰ)当a=1时,求不等式f(x)>1的解集;(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.2015年全国统一高考数学试卷(理科)(新课标Ⅰ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)设复数z满足=i,则|z|=()A.1B.C.D.2【考点】A8:复数的模.【专题】11:计算题;5N:数系的扩充和复数.【分析】先化简复数,再求模即可.【解答】解:∵复数z满足=i,∴1+z=i﹣zi,∴z(1+i)=i﹣1,∴z==i,∴|z|=1,故选:A.【点评】本题考查复数的运算,考查学生的计算能力,比较基础.2.(5分)sin20°cos10°﹣cos160°sin10°=()A.B.C.D.【考点】GP:两角和与差的三角函数.【专题】56:三角函数的求值.【分析】直接利用诱导公式以及两角和的正弦函数,化简求解即可.【解答】解:sin20°cos10°﹣cos160°sin10°=sin20°cos10°+cos20°sin10°=sin30°=.故选:D.【点评】本题考查诱导公式以及两角和的正弦函数的应用,基本知识的考查.3.(5分)设命题p:∃n∈N,n2>2n,则¬p为()A.∀n∈N,n2>2n B.∃n∈N,n2≤2n C.∀n∈N,n2≤2n D.∃n∈N,n2=2n【考点】2J:命题的否定.【专题】5L:简易逻辑.【分析】根据特称命题的否定是全称命题即可得到结论.【解答】解:命题的否定是:∀n∈N,n2≤2n,故选:C.【点评】本题主要考查含有量词的命题的否定,比较基础.4.(5分)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为()A.0.648B.0.432C.0.36D.0.312【考点】C8:相互独立事件和相互独立事件的概率乘法公式.【专题】5I:概率与统计.【分析】判断该同学投篮投中是独立重复试验,然后求解概率即可.【解答】解:由题意可知:同学3次测试满足X∽B(3,0.6),该同学通过测试的概率为=0.648.故选:A.【点评】本题考查独立重复试验概率的求法,基本知识的考查.5.(5分)已知M(x0,y0)是双曲线C:=1上的一点,F1,F2是C的左、右两个焦点,若<0,则y0的取值范围是()A.B.C.D.【考点】KC:双曲线的性质.【专题】11:计算题;5D:圆锥曲线的定义、性质与方程.【分析】利用向量的数量积公式,结合双曲线方程,即可确定y0的取值范围.【解答】解:由题意,=(﹣﹣x0,﹣y0)•(﹣x0,﹣y0)=x02﹣3+y02=3y02﹣1<0,所以﹣<y0<.故选:A.【点评】本题考查向量的数量积公式,考查双曲线方程,考查学生的计算能力,比较基础.6.(5分)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛【考点】LF:棱柱、棱锥、棱台的体积.【专题】5F:空间位置关系与距离.【分析】根据圆锥的体积公式计算出对应的体积即可.【解答】解:设圆锥的底面半径为r,则r=8,解得r=,故米堆的体积为××π×()2×5≈,∵1斛米的体积约为1.62立方,∴÷1.62≈22,故选:B.【点评】本题主要考查椎体的体积的计算,比较基础.7.(5分)设D为△ABC所在平面内一点,,则()A.B.C.D.【考点】96:平行向量(共线).【专题】5A:平面向量及应用.【分析】将向量利用向量的三角形法则首先表示为,然后结合已知表示为的形式.【解答】解:由已知得到如图由===;故选:A.【点评】本题考查了向量的三角形法则的运用;关键是想法将向量表示为.8.(5分)函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为()A.(kπ﹣,kπ+),k∈z B.(2kπ﹣,2kπ+),k∈zC.(k﹣,k+),k∈z D.(,2k+),k∈z【考点】HA:余弦函数的单调性.【专题】57:三角函数的图像与性质.【分析】由周期求出ω,由五点法作图求出φ,可得f(x)的解析式,再根据余弦函数的单调性,求得f(x)的减区间.【解答】解:由函数f(x)=cos(ωx+ϕ)的部分图象,可得函数的周期为=2(﹣)=2,∴ω=π,f(x)=cos(πx+ϕ).再根据函数的图象以及五点法作图,可得+ϕ=,k∈z,即ϕ=,f(x)=cos (πx+).由2kπ≤πx+≤2kπ+π,求得2k﹣≤x≤2k+,故f(x)的单调递减区间为(,2k+),k∈z,故选:D.【点评】本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值;还考查了余弦函数的单调性,属于基础题.9.(5分)执行如图所示的程序框图,如果输入的t=0.01,则输出的n=()A.5B.6C.7D.8【考点】EF:程序框图.【专题】5K:算法和程序框图.【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量n的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解答】解:第一次执行循环体后,S=,m=,n=1,不满足退出循环的条件;再次执行循环体后,S=,m=,n=2,不满足退出循环的条件;再次执行循环体后,S=,m=,n=3,不满足退出循环的条件;再次执行循环体后,S=,m=,n=4,不满足退出循环的条件;再次执行循环体后,S=,m=,n=5,不满足退出循环的条件;再次执行循环体后,S=,m=,n=6,不满足退出循环的条件;再次执行循环体后,S=,m=,n=7,满足退出循环的条件;故输出的n值为7,故选:C.【点评】本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.10.(5分)(x2+x+y)5的展开式中,x5y2的系数为()A.10B.20C.30D.60【考点】DA:二项式定理.【专题】11:计算题;5P:二项式定理.【分析】利用展开式的通项,即可得出结论.=,【解答】解:(x2+x+y)5的展开式的通项为T r+1令r=2,则(x2+x)3的通项为=,令6﹣k=5,则k=1,∴(x2+x+y)5的展开式中,x5y2的系数为=30.故选:C.【点评】本题考查二项式定理的运用,考查学生的计算能力,确定通项是关键.11.(5分)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1B.2C.4D.8【考点】L!:由三视图求面积、体积.【专题】5Q:立体几何.【分析】通过三视图可知该几何体是一个半球拼接半个圆柱,计算即可.【解答】解:由几何体三视图中的正视图和俯视图可知,截圆柱的平面过圆柱的轴线,该几何体是一个半球拼接半个圆柱,∴其表面积为:×4πr2+×πr22r×2πr+2r×2r+×πr2=5πr2+4r2,又∵该几何体的表面积为16+20π,∴5πr2+4r2=16+20π,解得r=2,故选:B.【点评】本题考查由三视图求表面积问题,考查空间想象能力,注意解题方法的积累,属于中档题.12.(5分)设函数f(x)=e x(2x﹣1)﹣ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是()A.[)B.[)C.[)D.[)【考点】51:函数的零点;6D:利用导数研究函数的极值.【专题】2:创新题型;53:导数的综合应用.【分析】设g(x)=e x(2x﹣1),y=ax﹣a,问题转化为存在唯一的整数x0使得g (x0)在直线y=ax﹣a的下方,求导数可得函数的极值,数形结合可得﹣a>g (0)=﹣1且g(﹣1)=﹣3e﹣1≥﹣a﹣a,解关于a的不等式组可得.【解答】解:设g(x)=e x(2x﹣1),y=ax﹣a,由题意知存在唯一的整数x0使得g(x0)在直线y=ax﹣a的下方,∵g′(x)=e x(2x﹣1)+2e x=e x(2x+1),∴当x<﹣时,g′(x)<0,当x>﹣时,g′(x)>0,∴当x=﹣时,g(x)取最小值﹣2,当x=0时,g(0)=﹣1,当x=1时,g(1)=e>0,直线y=ax﹣a恒过定点(1,0)且斜率为a,故﹣a>g(0)=﹣1且g(﹣1)=﹣3e﹣1≥﹣a﹣a,解得≤a<1故选:D.【点评】本题考查导数和极值,涉及数形结合和转化的思想,属中档题.二、填空题(本大题共有4小题,每小题5分)13.(5分)若函数f(x)=xln(x+)为偶函数,则a=1.【考点】3K:函数奇偶性的性质与判断.【专题】51:函数的性质及应用.【分析】由题意可得,f(﹣x)=f(x),代入根据对数的运算性质即可求解.【解答】解:∵f(x)=xln(x+)为偶函数,∴f(﹣x)=f(x),∴(﹣x)ln(﹣x+)=xln(x+),∴﹣ln(﹣x+)=ln(x+),∴ln(﹣x+)+ln(x+)=0,∴ln(+x)(﹣x)=0,∴lna=0,∴a=1.故答案为:1.【点评】本题主要考查了偶函数的定义及对数的运算性质的简单应用,属于基础试题.14.(5分)一个圆经过椭圆=1的三个顶点.且圆心在x轴的正半轴上.则该圆标准方程为(x﹣)2+y2=.【考点】K3:椭圆的标准方程.【专题】5D:圆锥曲线的定义、性质与方程.【分析】利用椭圆的方程求出顶点坐标,然后求出圆心坐标,求出半径即可得到圆的方程.【解答】解:一个圆经过椭圆=1的三个顶点.且圆心在x轴的正半轴上.可知椭圆的右顶点坐标(4,0),上下顶点坐标(0,±2),设圆的圆心(a,0),则,解得a=,圆的半径为:,所求圆的方程为:(x﹣)2+y2=.故答案为:(x﹣)2+y2=.【点评】本题考查椭圆的简单性质的应用,圆的方程的求法,考查计算能力.15.(5分)若x,y满足约束条件.则的最大值为3.【考点】7C:简单线性规划.【专题】59:不等式的解法及应用.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定的最大值.【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).设k=,则k的几何意义为区域内的点到原点的斜率,由图象知OA的斜率最大,由,解得,即A(1,3),k OA==3,即的最大值为3.故答案为:3.【点评】本题主要考查线性规划的应用,结合目标函数的几何意义以及直线的斜率,利用数形结合的数学思想是解决此类问题的基本方法.16.(5分)在平面四边形ABCD中,∠A=∠B=∠C=75°.BC=2,则AB的取值范围是(﹣,+).【考点】HT:三角形中的几何计算.【专题】15:综合题;2:创新题型;58:解三角形.【分析】如图所示,延长BA,CD交于点E,设AD=x,AE=x,DE=x,CD=m,求出x+m=+,即可求出AB的取值范围.【解答】解:方法一:如图所示,延长BA,CD交于点E,则在△ADE中,∠DAE=105°,∠ADE=45°,∠E=30°,∴设AD=x,AE=x,DE=x,CD=m,∵BC=2,∴(x+m)sin15°=1,∴x+m=+,∴0<x<4,而AB=x+m﹣x=+﹣x,∴AB的取值范围是(﹣,+).故答案为:(﹣,+).方法二:如下图,作出底边BC=2的等腰三角形EBC,B=C=75°,倾斜角为150°的直线在平面内移动,分别交EB、EC于A、D,则四边形ABCD即为满足题意的四边形;当直线移动时,运用极限思想,①直线接近点C时,AB趋近最小,为﹣;②直线接近点E时,AB趋近最大值,为+;故答案为:(﹣,+).【点评】本题考查求AB的取值范围,考查三角形中的几何计算,考查学生的计算能力,属于中档题.三、解答题:17.(12分)S n为数列{a n}的前n项和,已知a n>0,a n2+2a n=4S n+3(I)求{a n}的通项公式:(Ⅱ)设b n=,求数列{b n}的前n项和.【考点】8E:数列的求和;8H:数列递推式.【专题】54:等差数列与等比数列.【分析】(I)根据数列的递推关系,利用作差法即可求{a n}的通项公式:(Ⅱ)求出b n=,利用裂项法即可求数列{b n}的前n项和.【解答】解:(I)由a n2+2a n=4S n+3,可知a n+12+2a n+1=4S n+1+3两式相减得a n+12﹣a n2+2(a n+1﹣a n)=4a n+1,即2(a n+1+a n)=a n+12﹣a n2=(a n+1+a n)(a n+1﹣a n),∵a n>0,∴a n+1﹣a n=2,∵a12+2a1=4a1+3,∴a1=﹣1(舍)或a1=3,则{a n}是首项为3,公差d=2的等差数列,∴{a n}的通项公式a n=3+2(n﹣1)=2n+1:(Ⅱ)∵a n=2n+1,∴b n===(﹣),∴数列{b n}的前n项和T n=(﹣+…+﹣)=(﹣)=.【点评】本题主要考查数列的通项公式以及数列求和的计算,利用裂项法是解决本题的关键.18.(12分)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,BE=2DF,AE丄EC.(Ⅰ)证明:平面AEC丄平面AFC(Ⅱ)求直线AE与直线CF所成角的余弦值.【考点】LM:异面直线及其所成的角;LY:平面与平面垂直.【专题】5F:空间位置关系与距离;5G:空间角;5H:空间向量及应用.【分析】(Ⅰ)连接BD,设BD∩AC=G,连接EG、EF、FG,运用线面垂直的判定定理得到EG⊥平面AFC,再由面面垂直的判定定理,即可得到;(Ⅱ)以G为坐标原点,分别以GB,GC为x轴,y轴,|GB|为单位长度,建立空间直角坐标系G﹣xyz,求得A,E,F,C的坐标,运用向量的数量积的定义,计算即可得到所求角的余弦值.【解答】解:(Ⅰ)连接BD,设BD∩AC=G,连接EG、EF、FG,在菱形ABCD中,不妨设BG=1,由∠ABC=120°,可得AG=GC=,BE⊥平面ABCD,AB=BC=2,可知AE=EC,又AE⊥EC,所以EG=,且EG⊥AC,在直角△EBG中,可得BE=,故DF=,在直角三角形FDG中,可得FG=,在直角梯形BDFE中,由BD=2,BE=,FD=,可得EF==,从而EG2+FG2=EF2,则EG⊥FG,(或由tan∠EGB•tan∠FGD=•=•=1,可得∠EGB+∠FGD=90°,则EG⊥FG)AC∩FG=G,可得EG⊥平面AFC,由EG⊂平面AEC,所以平面AEC⊥平面AFC;(Ⅱ)如图,以G为坐标原点,分别以GB,GC为x轴,y轴,|GB|为单位长度,建立空间直角坐标系G﹣xyz,由(Ⅰ)可得A(0,﹣,0),E(1,0,),F(﹣1,0,),C(0,,0),即有=(1,,),=(﹣1,﹣,),故cos<,>===﹣.则有直线AE与直线CF所成角的余弦值为.【点评】本题考查空间直线和平面的位置关系和空间角的求法,主要考查面面垂直的判定定理和异面直线所成的角的求法:向量法,考查运算能力,属于中档题.19.(12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费x i和年销售量y i(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(x i ﹣)2(w i ﹣)2(x i ﹣)(y i ﹣)(w i ﹣)(y i ﹣)46.6563 6.8289.8 1.61469108.8表中w i =i ,=(Ⅰ)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y﹣x.根据(Ⅱ)的结果回答下列问题:(i)年宣传费x=49时,年销售量及年利润的预报值是多少?(ii)年宣传费x为何值时,年利润的预报值最大?附:对于一组数据(u1 v1),(u2 v2)…..(u n v n),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:=,=﹣.【考点】BK:线性回归方程.【专题】5I:概率与统计.【分析】(Ⅰ)根据散点图,即可判断出,(Ⅱ)先建立中间量w=,建立y关于w的线性回归方程,根据公式求出w,问题得以解决;(Ⅲ)(i)年宣传费x=49时,代入到回归方程,计算即可,(ii)求出预报值得方程,根据函数的性质,即可求出.【解答】解:(Ⅰ)由散点图可以判断,y=c+d适宜作为年销售量y关于年宣传费x的回归方程类型;(Ⅱ)令w=,先建立y关于w的线性回归方程,由于==68,=﹣=563﹣68×6.8=100.6,所以y关于w的线性回归方程为=100.6+68w,因此y关于x的回归方程为=100.6+68,(Ⅲ)(i)由(Ⅱ)知,当x=49时,年销售量y的预报值=100.6+68=576.6,年利润z的预报值=576.6×0.2﹣49=66.32,(ii)根据(Ⅱ)的结果可知,年利润z的预报值=0.2(100.6+68)﹣x=﹣x+13.6+20.12,当==6.8时,即当x=46.24时,年利润的预报值最大.【点评】本题主要考查了线性回归方程和散点图的问题,准确的计算是本题的关键,属于中档题.20.(12分)在直角坐标系xOy中,曲线C:y=与直线l:y=kx+a(a>0)交于M,N两点.(Ⅰ)当k=0时,分別求C在点M和N处的切线方程.(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?(说明理由)【考点】KH:直线与圆锥曲线的综合.【分析】(I)联立,可得交点M,N的坐标,由曲线C:y=,利用导数的运算法则可得:y′=,利用导数的几何意义、点斜式即可得出切线方程.(II)存在符合条件的点(0,﹣a),设P(0,b)满足∠OPM=∠OPN.M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为:k1,k2.直线方程与抛物线方程联立化为x2﹣4kx﹣4a=0,利用根与系数的关系、斜率计算公式可得k1+k2=.k1+k2=0⇔直线PM,PN的倾斜角互补⇔∠OPM=∠OPN.即可证明.【解答】解:(I)联立,不妨取M,N,由曲线C:y=可得:y′=,∴曲线C在M点处的切线斜率为=,其切线方程为:y﹣a=,化为.同理可得曲线C在点N处的切线方程为:.(II)存在符合条件的点(0,﹣a),下面给出证明:设P(0,b)满足∠OPM=∠OPN.M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为:k1,k2.联立,化为x2﹣4kx﹣4a=0,∴x1+x2=4k,x1x2=﹣4a.∴k1+k2=+==.当b=﹣a时,k1+k2=0,直线PM,PN的倾斜角互补,∴∠OPM=∠OPN.∴点P(0,﹣a)符合条件.【点评】本题考查了导数的运算法则、利用导数的几何意义研究切线方程、直线与抛物线相交问题转化为方程联立可得根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于中档题.21.(12分)已知函数f(x)=x3+ax+,g(x)=﹣lnx(i)当a为何值时,x轴为曲线y=f(x)的切线;(ii)用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)}(x>0),讨论h(x)零点的个数.【考点】6E:利用导数研究函数的最值;6H:利用导数研究曲线上某点切线方程.【专题】2:创新题型;53:导数的综合应用.【分析】(i)f′(x)=3x2+a.设曲线y=f(x)与x轴相切于点P(x0,0),则f(x0)=0,f′(x0)=0解出即可.(ii)对x分类讨论:当x∈(1,+∞)时,g(x)=﹣lnx<0,可得函数h(x)=min { f(x),g(x)}≤g(x)<0,即可得出零点的个数.当x=1时,对a分类讨论:a≥﹣,a<﹣,即可得出零点的个数;当x∈(0,1)时,g(x)=﹣lnx>0,因此只考虑f(x)在(0,1)内的零点个数即可.对a分类讨论:①当a≤﹣3或a≥0时,②当﹣3<a<0时,利用导数研究其单调性极值即可得出.【解答】解:(i)f′(x)=3x2+a.设曲线y=f(x)与x轴相切于点P(x0,0),则f(x0)=0,f′(x0)=0,∴,解得,a=.因此当a=﹣时,x轴为曲线y=f(x)的切线;(ii)当x∈(1,+∞)时,g(x)=﹣lnx<0,∴函数h(x)=min { f(x),g(x)}<0,故h(x)在x∈(1,+∞)时无零点.当x=1时,若a≥﹣,则f(1)=a+≥0,∴h(x)=min { f(1),g(1)}=g(1)=0,故x=1是函数h(x)的一个零点;若a<﹣,则f(1)=a+<0,∴h(x)=min { f(1),g(1)}=f(1)<0,故x=1不是函数h(x)的零点;当x∈(0,1)时,g(x)=﹣lnx>0,因此只考虑f(x)在(0,1)内的零点个数即可.①当a≤﹣3或a≥0时,f′(x)=3x2+a在(0,1)内无零点,因此f(x)在区间(0,1)内单调,而f(0)=,f(1)=a+,∴当a≤﹣3时,函数f(x)在区间(0,1)内有一个零点,当a≥0时,函数f(x)在区间(0,1)内没有零点.②当﹣3<a<0时,函数f(x)在内单调递减,在内单调递增,故当x=时,f(x)取得最小值=.若>0,即,则f(x)在(0,1)内无零点.若=0,即a=﹣,则f(x)在(0,1)内有唯一零点.若<0,即,由f(0)=,f(1)=a+,∴当时,f(x)在(0,1)内有两个零点.当﹣3<a时,f(x)在(0,1)内有一个零点.综上可得:a<时,函数h(x)有一个零点.当时,h(x)有一个零点;当a=或时,h(x)有两个零点;当时,函数h(x)有三个零点.【点评】本题考查了导数的运算法则、利用导数的几何意义研究切线方程、利用导数研究函数的单调性极值,考查了分类讨论思想方法、推理能力与计算能力,属于难题.选修4一1:几何证明选讲22.(10分)如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.(Ⅰ)若D为AC的中点,证明:DE是⊙O的切线;(Ⅱ)若OA=CE,求∠ACB的大小.【考点】N9:圆的切线的判定定理的证明.【专题】5B:直线与圆.【分析】(Ⅰ)连接AE和OE,由三角形和圆的知识易得∠OED=90°,可得DE是⊙O的切线;(Ⅱ)设CE=1,AE=x,由射影定理可得关于x的方程x2=,解方程可得x 值,可得所求角度.【解答】解:(Ⅰ)连接AE,由已知得AE⊥BC,AC⊥AB,在RT△ABC中,由已知可得DE=DC,∴∠DEC=∠DCE,连接OE,则∠OBE=∠OEB,又∠ACB+∠ABC=90°,∴∠DEC+∠OEB=90°,∴∠OED=90°,∴DE是⊙O的切线;(Ⅱ)设CE=1,AE=x,由已知得AB=2,BE=,由射影定理可得AE2=CE•BE,∴x2=,即x4+x2﹣12=0,解方程可得x=∴∠ACB=60°【点评】本题考查圆的切线的判定,涉及射影定理和三角形的知识,属基础题.选修4一4:坐标系与参数方程23.(10分)在直角坐标系xOy中,直线C1:x=﹣2,圆C2:(x﹣1)2+(y﹣2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求C1,C2的极坐标方程;(Ⅱ)若直线C3的极坐标方程为θ=(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.【考点】Q4:简单曲线的极坐标方程.【专题】5S:坐标系和参数方程.【分析】(Ⅰ)由条件根据x=ρcosθ,y=ρsinθ求得C1,C2的极坐标方程.(Ⅱ)把直线C3的极坐标方程代入ρ2﹣3ρ+4=0,求得ρ1和ρ2的值,结合圆的半径可得C2M⊥C2N,从而求得△C2MN的面积•C2M•C2N的值.【解答】解:(Ⅰ)由于x=ρcosθ,y=ρsinθ,∴C1:x=﹣2 的极坐标方程为ρcosθ=﹣2,故C2:(x﹣1)2+(y﹣2)2=1的极坐标方程为:(ρcosθ﹣1)2+(ρsinθ﹣2)2=1,化简可得ρ2﹣(2ρcosθ+4ρsinθ)+4=0.(Ⅱ)把直线C3的极坐标方程θ=(ρ∈R)代入圆C2:(x﹣1)2+(y﹣2)2=1,可得ρ2﹣(2ρcosθ+4ρsinθ)+4=0,求得ρ1=2,ρ2=,∴|MN|=|ρ1﹣ρ2|=,由于圆C2的半径为1,∴C2M⊥C2N,△C2MN的面积为•C2M•C2N=•1•1=.【点评】本题主要考查简单曲线的极坐标方程,点的极坐标的定义,属于基础题.选修4一5:不等式选讲24.(10分)已知函数f(x)=|x+1|﹣2|x﹣a|,a>0.(Ⅰ)当a=1时,求不等式f(x)>1的解集;(Ⅱ)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.【考点】R5:绝对值不等式的解法.【专题】59:不等式的解法及应用.【分析】(Ⅰ)当a=1时,把原不等式去掉绝对值,转化为与之等价的三个不等式组,分别求得每个不等式组的解集,再取并集,即得所求.(Ⅱ)化简函数f(x)的解析式,求得它的图象与x轴围成的三角形的三个顶点的坐标,从而求得f(x)的图象与x轴围成的三角形面积;再根据f(x)的图象与x轴围成的三角形面积大于6,从而求得a的取值范围.【解答】解:(Ⅰ)当a=1时,不等式f(x)>1,即|x+1|﹣2|x﹣1|>1,即①,或②,或③.解①求得x∈∅,解②求得<x<1,解③求得1≤x<2.综上可得,原不等式的解集为(,2).(Ⅱ)函数f(x)=|x+1|﹣2|x﹣a|=,由此求得f(x)的图象与x轴的交点A (,0),B(2a+1,0),故f(x)的图象与x轴围成的三角形的第三个顶点C(a,a+1),由△ABC的面积大于6,可得[2a+1﹣]•(a+1)>6,求得a>2.故要求的a的范围为(2,+∞).【点评】本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.。
2015年高考数学三角函数解析-精品PPT

例1.若sin2x>cos2x,则x的取值范围 是 ( D)
(A){x|2kπ-3π/4<x<2kπ+π/4,k∈Z}(B) {x|2kπ+π/4<x<2kπ+5π/4,k∈Z} (C) {x|kπ-π/4<x<kπ+π/4,k∈Z } (D) {x|kπ+π/4<x<kπ+3π/4,k∈Z} 解 : 由 sin2x>cos2x 得 cos2x - sin2x < 0, 即 cos2x <0,所以:π/2+kπ<2x<3π/2+kπ,选D. 另解:数形结合法:由已知得|sinx|>|cosx|, 画出y=|sinx|和y=|cosx|的图象,从图象中可知 选D.
f(-0.5)=-f(0.5)=-0.5,所以选B. 也可由f(x+2)=-f(x),得到周期T=4,所以
f(7.5)=f(-0.5)=-f(0.5)=-0.5.
例3.七人并排站成一行,如果甲、乙两人必需不相
邻,那么不同的排法的种数是(B)
(A)1440 (B)3600 (C)4320 (D)4800
3.已知 sin m 3 ,cos 4 2m ( ),
m5
m5 2
则tan 等于 __D____ .
2
A. m 3 B. | m 3 | C. 1 D.5 9m 9m 3
4.抛物线 y=ax2的准线方程是 y=2,
则a的值为___B___. (2003江苏.2)
A. 1 B. 1 C.8 D. 8
( )B
( A) 4 3 3 10
(B) 4 3 3 10
(C) 4 3 3 10
(D) 4 3 3 10
四、数学选择题的解题思路
要想确保在有限的时间内,对10多条选择 题作出有效的抉择,明晰解题思路是十分 必要的。一般说来, 数学选择题有着特 定的解题思路,具体概括如下:
2015年高考数学二轮微专题4:三角函数的图像与性质(word解析版)

微专题4 三角函数的图象与性质[真题感悟]1.(2013·江苏卷)函数y =3sin ⎝ ⎛⎭⎪⎫2x +π4的最小正周期为 ________. 解析 ω=2,T =2π|ω|=π.答案 π2.(2011·江苏卷)函数f (x )=A sin(ωx +φ),(A ,ω,φ是常数,A >0,ω>0)的部分图象如图所示,则f (0)=________.解析 因为由图象可知振幅A =2,T 4=7π12-π3=π4,所以周期T =π=2πω,解得ω=2,将⎝ ⎛⎭⎪⎫7π12,-2代入,解得一个符合的φ=π3,从而y =2sin ⎝ ⎛⎭⎪⎫2x +π3,∴f (0)=62. 答案 623.(2013·四川卷改编)函数f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)的部分图象如图所示,则ω,φ的值分别是________.解析 34T =5π12-⎝ ⎛⎭⎪⎫-π3,T =π, ∴ω=2,∴2×5π12+φ=2k π+π2,k ∈Z ,∴φ=2k π-π3,k ∈Z ,又φ∈⎝ ⎛⎭⎪⎫-π2,π2, ∴φ=-π3.答案 2,-π34.(2013·新课标全国Ⅰ卷)设当x =θ时,函数f (x )=sin x -2cos x 取得最大值,则cos θ=________.解析 f (x )=sin x -2cos x =5⎝ ⎛⎭⎪⎫55sin x -255cos x =5sin(x -φ),其中sin φ=255,cos φ=55,当x -φ=2k π+π2(k ∈Z )时,函数f (x )取得最大值,即θ=2k π+π2+φ时,函数f (x )取到最大值,所以cos θ=-sin φ=-255.答案 -255[考题分析]三角函数的有关知识大部分是B 级要求,只有函数y =A sin(ωx +φ)的图象与性质是A 级要求;试题类型可能是填空题,同时在解答题中也是必考题,经常与向量综合考查,构成中档题.。
2015年高考真题解答题专项训练:三角函数(理科)

2015年高考真题解答题专项训练:三角函数(理科)1.(1)求()f x 的最小正周期和最大值;(2)讨论()f x 在.2,R x ∈ (Ⅰ)求()f x 最小正周期(Ⅱ)求()f x 在区间上的最大值和最小值.3.(12分)(2015•广东)在平面直角坐标系xOy 中,已知向量=(,﹣),=(sinx ,cosx ),x ∈(0,).(1)若⊥,求tanx 的值;(2)若与的夹角为,求x 的值.4.【2015高考山东,理16 (Ⅰ)求()f x 的单调区间;(Ⅱ)在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,若求ABC ∆面积的最大值.5.(本题满分12分)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,22b a -=(1)求tan C 的值;(2)若ABC ∆的面积为7,求b 的值.6.(本小题13(Ⅰ)求()f x 的最小正周期;7.(本小题满分12分)C ∆AB 的内角A ,B ,C 所对的边分别为a ,b ,c .与()cos ,sin n =A B平行.(Ⅰ)求A ;,2b =求C ∆AB 的面积.8,B ,C 的对边分别为a ,b ,c ,tan a b A =,且B 为钝角. (1(2.9.(本小题满分12分)在ABC ∆点D 在BC 边上,AD BD =,求AD 的长.10.(本题满分12分)ABC ∆中,D 是BC 上的点,AD 平分BAC ∠,ABD ∆面积是ADC ∆面积的2倍.(Ⅰ) (Ⅱ)若1AD =,,求BD 和AC 的长.2015年高考真题解答题专项训练:三角函数参考答案1.(1)最小正周期为p ,最大值为(2)()f x 在上单调递增;()f x 在. 【解析】试题分析:三角函数问题一般方法是把函数转化为一个角,一个函数,一次式,即为sin()A x k εϕ++形式,然后根据正弦函数的性质求得结论,本题利用诱导公式、倍角公式、(1(2上分别是增函数和减函数,因此可得()f x 单调区间.试题解析:(1)因此()f x 的最小正周期为p ,最大值为. 考点:三角函数的恒等变换,周期,最值,单调性,考查运算求解能力.2.(Ⅰ)π; (Ⅱ)【解析】(Ⅰ) 由已知,有所以()f x 的最小正周期 (Ⅱ)因为()f x 在区间上是减函数,在区间上是增函数,,所以()f x 在区间考点:三角恒等变形、三角函数的图象与性质. 3.(1)tanx=1;(2)【解析】试题分析:(1)若⊥,则•=0,结合三角函数的关系式即可求tanx 的值; (2)若与的夹角为,利用向量的数量积的坐标公式进行求解即可求x 的值.解:(1)若⊥, 则•=(,﹣)•(sinx ,cosx )=sinx ﹣cosx=0,即sinx=cosxsinx=cosx ,即tanx=1; (2)∵||=1,||=1,•=(,﹣)•(sinx ,cosx )=sinx ﹣cosx ,∴若与的夹角为, 则•=||•||cos =,即sinx ﹣cosx=, 则sin (x ﹣)=, ∵x ∈(0,).∴x ﹣∈(﹣,).则x ﹣= 即x=+=.点评:本题主要考查向量数量积的定义和坐标公式的应用,考查学生的计算能力,比较基础. 4.(Ⅱ)ABC ∆【解析】试题分析:(Ⅰ)首先利用二倍角公式化简函数()f x 的解析式,再利用正弦函数的单调性求其单调区间;结合(Ⅰ)的结果,确定角A 的值,然后结合余弦定理求出三角形ABC ∆面积的最大值. 试题解析:解:所以函数()f x;由题意知A 为锐角,所以 由余弦定理:2222cos a b c bc A =+-当且仅当b c =时等号成立.所以ABC ∆面积的最大值为考点:1、诱导公式;2、三角函数的二倍角公式;3、余弦定理;4、基本不等式. 5.(1)2;(2)3b =. 【解析】(1)根据正弦定理可将条件中的边之间的关系转化为角之间满足的关系,再将式 子作三角恒等变形即可求解;(2)根据条件首先求得sin B 的值,再结合正弦定理以及三角 形面积的计算公式即可求解.解得tan 2C =;(2)由tan 2C =,(0,)C π∈得,故3b =. 考点:1.三角恒等变形;2.正弦定理.6.(Ⅰ)2π; 【解析】试题解析:先用降幂公式和辅助角公式进行三角恒等变形,把函数化为()sin()f x A x m ωϕ=++0,x π-≤≤时,()f x 取得最小值为: 试题解析:(Ⅰ)()f x 的最小正周期为()f x 取得最小值为:考点:本题考点为三角函数式的恒等变形和三角函数图象与性质,要求熟练使用降幂公式与辅助角公式,利用函数解析式研究函数性质,包括周期、最值、单调性等.7. 【解析】试题分析:(Ⅰ)先利用//m n可得,再利用正弦定理可得tan A 的值,进而可得A 的值;(Ⅱ)由余弦定理可得c 的值,进而利用三角形的面积公式可得C∆AB 的面积.试题解析:(Ⅰ)因为//m n,所以又sin 0B ≠,从而 由于0A π<<,所以(Ⅱ)解法一:由余弦定理,得2222cos a b c bc A =+-得2742c c =+-,即2230c c --=因为0c >,所以3c =.故C ∆AB 的面积为又由a b >,知A B >,所以所以C ∆AB 的面积为考点:1、平行向量的坐标运算;2、正弦定理;3、余弦定理;4、三角形的面积公式.8.(1)详见解析;(2 【解析】试题分析:(1件从而得证;(2)利用(1)中的结论,以及三角恒等变形,转化为只与A 有关的表达式,再利用三角函数的性质即可求解. 试题解析:(1)由tan a b A =,∴sin cos B A =,即(2)由(1)知,()C A B π=-+∴sin sin A C +的取值范围考点:1.正弦定理;2.三角恒等变形;3.三角函数的性质.【名师点睛】本题主要考查了利用正弦定理解三角形以及三角恒等变形等知识点,属于中档题,高考解答题对三角三角函数的考查主要以三角恒等变形,三角函数的图象和性质,利用正余弦定理解三角形为主,难度中等,因此只要掌握基本的解题方法与技巧即可,在三角函数求值问题中,一般运用恒等变换,将未知角变换为已知角求解,在研究三角函数的图象和性质问题时,一般先运用三角恒等变形,将表达式转化为一个角的三角函数的形式求解,对于三角函数与解三角形相结合的题目,要注意通过正余弦定理以及面积公式实现边角互化,求出相关的边和角的大小.9【解析】 试题分析:根据题意,设出ABC ∆的内角,,A B C 所对边的长分别是,,a b c ,由余弦定理求出a 的长度,再由正弦定理求出角B 的大小,在ABD ∆中.利用正弦定理即可求出AD 的长度.试题解析:如图,设ABC ∆的内角,,A B C 所对边的长分别是,,a b c ,由余弦定理得,在ABD ∆中,由正弦定理得 考点:1.正弦定理、余弦定理的应用.10.(Ⅱ)1.【解析】(Ⅰ2ABD ADC S S ∆∆=, (Ⅱ)因为::ABD ADC S S BD DC ∆∆=,所以.在ABD ∆和ADC ∆中,由余弦定理得2222cos AB AD BD AD BD ADB =+-⋅∠,2222cos AC AD DC AD DC ADC =+-⋅∠.222222326AB AC AD BD DC +=++=.由(Ⅰ)知2AB AC =,所以1AC =. 考点:1、三角形面积公式;2、正弦定理和余弦定理.。
2015-三角函数高考真题教师版

2015-2017三角函数高考真题1、(2015全国1卷2题)o o o o sin 20cos10cos160sin10- =( ) (A)(B(C )12- (D )12【答案】D【解析】原式=o o o o sin 20cos10cos 20sin10+ =o sin30=12,故选D. 2、(2015全国1卷8题)函数()f x =cos()x ωϕ+的部分图像如图所示,则()f x 的单调递减区间为( )(A )13(,),44k k k Z ππ-+∈ (B )13(2,2),44k k k Z ππ-+∈ (C )13(,),44k k k Z -+∈ (D )13(2,2),44k k k Z -+∈【答案】D【解析】由五点作图知,1+4253+42πωϕπωϕ⎧=⎪⎪⎨⎪=⎪⎩,解得=ωπ,=4πϕ,所以()cos()4f x x ππ=+,令22,4k x k k Z πππππ<+<+∈,解得124k -<x <324k +,k Z ∈,故单调减区间为(124k -,324k +),k Z ∈,故选D. 考点:三角函数图像与性质3、(2015全国1卷12题)在平面四边形ABCD 中,∠A=∠B=∠C=75°,BC=2,则AB 的取值范围是 .【答案】【解析】如图所示,延长BA ,CD 交于E ,平移AD ,当A 与D 重合与E 点时,AB 最长,在△BCE 中,∠B=∠C=75°,∠E=30°,BC=2,由正弦定理可得sin sin BC BEE C=∠∠,即o o2sin 30sin 75BE=,解得BE,平移AD ,当D 与C 重合时,AB 最短,此时与AB 交于F ,在△BCF 中,∠B=∠BFC =75°,∠FCB=30°,由正弦定理知,sin sin BF BCFCB BFC=∠∠,即o o2sin 30sin 75BF =,解得-AB 的取值范围为).考点:正余弦定理;数形结合思想4、(2015全国2卷10题)如图,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠=.将动P 到A 、B 两点距离之和表示为x 的函数()f x ,则()y f x =的图像大致为( )【解析】由已知得,当点P 在BC 边上运动时,即04x π≤≤时,tan PA PB x +=;当点P 在CD 边上运动时,即3,442x x πππ≤≤≠时,PA PB +=,当2x π=时,PA PB +=当点P 在AD 边上运动时,即34x ππ≤≤时,tan PA PB x +=,从点P 的运动过程可以看出,轨迹关于直线2x π=对称,且()()42f f ππ>,且轨迹非线型,故选B .考点:函数的图象和性质.5、(2015全国2卷17题)ABC ∆中,D 是BC 上的点,AD 平分BAC ∠,ABD ∆面积是ADC ∆面积的2倍.(Ⅰ) 求sin sin BC∠∠; (Ⅱ)若1AD =,2DC =,求BD 和AC 的长.【解析】(Ⅰ)1sin 2ABD S AB AD BAD ∆=⋅∠,1sin 2ADC S AC AD CAD ∆=⋅∠,因为2ABDADC S S ∆∆=,BAD CAD ∠=∠,所以2AB AC =.由正弦定理可得sin 1sin 2B AC C AB ∠==∠.(Ⅱ)因为::ABD ADC S S BD DC ∆∆=,所以BD =ABD ∆和ADC ∆中,由余弦定理得DPCB OAx2222cos AB AD BD AD BD ADB =+-⋅∠,2222cos AC AD DC AD DC ADC =+-⋅∠.222222326AB AC AD BD DC +=++=.由(Ⅰ)知2AB AC =,所以1AC =.考点:1、三角形面积公式;2、正弦定理和余弦定理.6、(2016全国1卷12题)已知函数()sin()(0),24f x x+x ππωϕωϕ=>≤=-, 为()f x 的零点,4x π=为()y f x =图像的对称轴,且()f x 在51836ππ⎛⎫⎪⎝⎭,单调,则ω的最大值为 (A )11 (B )9 (C )7 (D )5 【答案】B考点:三角函数的性质【名师点睛】本题将三角函数单调性与对称性结合在一起进行考查,叙述方式新颖,是一道考查能力的好题.注意本题解法中用到的两个结论:①()()()sin 0,0f x A x A ωϕω=+≠≠的单调区间长度是半个周期;②若()()()sin 0,0f x A x A ωϕω=+≠≠的图像关于直线0x x = 对称,则()0f x A = 或()0f x A =-.7、(2016全国1卷17题)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos (cos cos ).C a B+b A c =(I )求C ; (II )若c ABC =∆求ABC V 的周长. 试题分析:(I )先利用正弦定理进行边角代换化简得得1cos C 2=,故C 3π=;(II )根据1sin C 2ab =.及C 3π=得6ab =.再利用余弦定理得 ()225a b +=.再根据c =可得C ∆AB 的周长为5+.考点:正弦定理、余弦定理及三角形面积公式 【名师点睛】三角形中的三角变换常用到诱导公式,()()sin sin ,cos cos ,A B C A B C +=+=-()tan tan A B C+=-,就是常用的结论,另外利用正弦定理或余弦定理处理条件中含有边或角的等式,常考虑对其实施“边化角”或“角化边.”8、(2016全国2卷7题)若将函数y =2sin 2x 的图像向左平移π12个单位长度,则平移后图象的对称轴为(A )()ππ26k x k =-∈Z (B )()ππ26k x k =+∈Z (C )()ππ212Z k x k =-∈ (D )()ππ212Z k x k =+∈ 解析:平移后图像表达式为,令,得对称轴方程:, 故选B .9、(2016全国2卷9题)若π3cos 45α⎛⎫-= ⎪⎝⎭,则sin2α=(A )725 (B )15(C )15- (D )725-【解析】D ∵,,10、(2016全国2卷13题)ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,若4cos 5A =,5cos 13C =,1a =,则b = .【解析】 ∵,, ,, ,由正弦定理得:解得.11、(2016全国3卷5题)若3tan 4α= ,则2cos 2sin 2αα+=( ) (A)6425 (B) 4825 (C) 1 (D)1625【答案】A【解析】试题分析:由3tan 4α=,得34sin ,cos 55αα==或34sin ,cos 55αα=-=-,所以2161264cos 2sin 24252525αα+=+⨯=,故选A .考点:1、同角三角函数间的基本关系;2、倍角公式.【方法点拨】三角函数求值:①“给角求值”将非特殊角向特殊角转化,通过相消或相约消去非特殊角,进而求出三角函数值;②“给值求值”关键是目标明确,建立已知和所求之间的联系.12、(2016全国3卷8题)在ABC △中,π4B =,BC 边上的高等于13BC ,则cos A =( )(A (B (C )- (D )- 【答案】C 【解析】试题分析:设BC 边上的高线为AD ,则3BC AD =,所以AC ==,AB =.由余弦定理,知222222cos2AB AC BC A AB AC +-===⋅,故选C . 考点:余弦定理.13、(2016全国3卷14题)函数sin y x x =的图像可由函数sin y x x =的图像至少向右平移_____________个单位长度得到. 【答案】32π 考点:1、三角函数图象的平移变换;2、两角和与差的正弦函数.【误区警示】在进行三角函数图象变换时,提倡“先平移,后伸缩”,但“先伸缩,后平移”也经常出现在题目中,所以也必须熟练掌握,无论是哪种变形,切记每一个变换总是对字母x 而言,即图象变换要看“变量”起多大变化,而不是“角”变化多少.14、(2017年全国1卷9题)9、已知曲线1:cos C y x =,22π:sin 23C y x ⎛⎫=+ ⎪⎝⎭,则下面结论正确的是()A .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线2CB .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线2CC .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线2CD .把1C 上各点的横坐标缩短到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线2C 【答案】D【解析】1:cos C y x =,22π:sin 23⎛⎫=+ ⎪⎝⎭C y x首先曲线1C 、2C 统一为一三角函数名,可将1:cos C y x =用诱导公式处理.πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x .横坐标变换需将1=ω变成2=ω,即112πππsin sin 2sin 2224⎛⎫⎛⎫⎛⎫=+−−−−−−−−−→=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C 上各坐短它原y x y x x 点横标缩来 2ππsin 2sin 233⎛⎫⎛⎫−−→=+=+ ⎪ ⎪⎝⎭⎝⎭y x x .注意ω的系数,在右平移需将2=ω提到括号外面,这时π4+x 平移至π3+x , 根据“左加右减”原则,“π4+x ”到“π3+x ”需加上π12,即再向左平移π12. 15、(2017年全国1卷17题)17、ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知ABC △的面积为23sin a A.(1)求sin sin B C ;(2)若6cos cos 1B C =,3a =,求ABC △的周长.【解析】本题主要考查三角函数及其变换,正弦定理,余弦定理等基础知识的综合应用.(1)∵ABC △面积23sin a S A=.且1sin 2S bc A =∴21sin 3sin 2a bc A A = ∴223sin 2a bc A =∵由正弦定理得223sin sin sin sin 2A B C A =,由sin 0A ≠得2sin sin 3B C =. (2)由(1)得2sin sin 3B C =,1cos cos 6B C = ∵πA B C ++=∴()()1cos cos πcos sin sinC cos cos 2A B C B C B B C =--=-+=-=又∵()0πA ∈,∴60A =︒,sin A =1cos 2A =由余弦定理得2229a b c bc =+-= ① 由正弦定理得sin sin a b B A =⋅,sin sin ac C A=⋅ ∴22sin sin 8sin a bc B C A=⋅= ②由①②得b c +=∴3a b c ++=+ABC △周长为316、(2017年全国2卷14题)函数()23sin 4f x x x =-(0,2x π⎡⎤∈⎢⎥⎣⎦)的最大值是 . 【命题意图】本题考查三角函数同角基本关系及函数性质—最值,意在考查考生转化与化归思 想和运算求解能力【解析】∵ ()23sin 0,42f x x x x π⎛⎫⎡⎤=-∈ ⎪⎢⎥⎣⎦⎝⎭,22sin cos 1x x +=∴ ()21cos 4f x x x =-+设cos t x =,[]0,1t ∈,∴ ()214f x t =-+函数对称轴为[]0,1t =,∴ ()max 1f x = 17、(2017年全国2卷17题)ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知2sin()8sin 2BA C +=. (1)求cos B(2)若6a c += , ABC ∆面积为2,求.b 【命题意图】本题考查三角恒等变形,解三角形.【试题分析】在第(Ⅰ)中,利用三角形内角和定理可知A C B π+=-,将2sin 8)sin(2B C A =+转化为角B 的方程,思维方向有两个:①利用降幂公式化简2sin 2B ,结合22sin cos 1B B +=求出cos B ;②利用二倍角公式,化简2sin 8sin 2BB =,两边约去2sin B ,求得2tan B,进而求得B cos .在第(Ⅱ)中,利用(Ⅰ)中结论,利用勾股定理和面积公式求出a c ac +、,从而求出b . (Ⅰ) 【基本解法1】由题设及2sin 8sin ,2BB C B A ==++π,故 sin 4-cosB B =(1)上式两边平方,整理得 217cos B-32cosB+15=0 解得 15cosB=cosB 171(舍去),= 【基本解法2】由题设及2sin 8sin ,2B BC B A ==++π,所以2sin 82cos 2sin 22B B B =,又02sin ≠B,所以412tan =B ,17152tan 12tan 1cos 22=+-=B BB(Ⅱ)由158cosB sin B 1717==得,故14a sin 217ABC S c B ac ∆== 又17=22ABC S ac ∆=,则由余弦定理及a 6c +=得2222b 2cos a 2(1cosB)1715362(1)2174a c ac Bac =+-=-+=-⨯⨯+=(+c )所以b=2【知识拓展】解三角形问题是高考高频考点,命题大多放在解答题的第一题,主要利用三角形的内角和定理,正、余弦定理、三角形面积公式等知识解题,解题时要灵活利用三角形的边角关系进行“边转角”“角转边”,另外要注意22,,a c ac a c ++三者的关系,这样的题目小而活,备受老师和学生的欢迎.18、(2017全国3卷6题)设函数π()cos()3f x x =+,则下列结论错误的是()A .()f x 的一个周期为2π-B .()y f x =的图像关于直线8π3x =对称 C .()f x π+的一个零点为π6x =D .()f x 在π(,π)2单调递减【答案】D【解析】函数()πcos 3f x x ⎛⎫=+ ⎪⎝⎭的图象可由cos y x =向左平移π3个单位得到,如图可知,()f x 在π,π2⎛⎫⎪⎝⎭上先递减后递增,D 选项错误,故选D.19、(2017全国3卷17题)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin 0A A =,a =,2b =.(1)求c ;(2)设D 为BC 边上一点,且AD AC ⊥,求ABD △的面积.【解析】(1)由sin 0A A =得π2sin 03A ⎛⎫+= ⎪⎝⎭,即()ππ3A k k +=∈Z ,又()0,πA ∈, ∴ππ3A +=,得2π3A =.由余弦定理2222cos a b c bc A =+-⋅.又∵12,cos 2a b A ===-代入并整理得()2125c +=,故4c =.(2)∵2,4AC BC AB ===,由余弦定理222cos 2a b c C ab +-==. ∵AC AD ⊥,即ACD △为直角三角形,则cos AC CD C =⋅,得CD =由勾股定理AD =又2π3A =,则2πππ326DAB ∠=-=, 1πsin 26ABD S AD AB =⋅⋅=△。
2015-2019年三角函数高考真题.docx
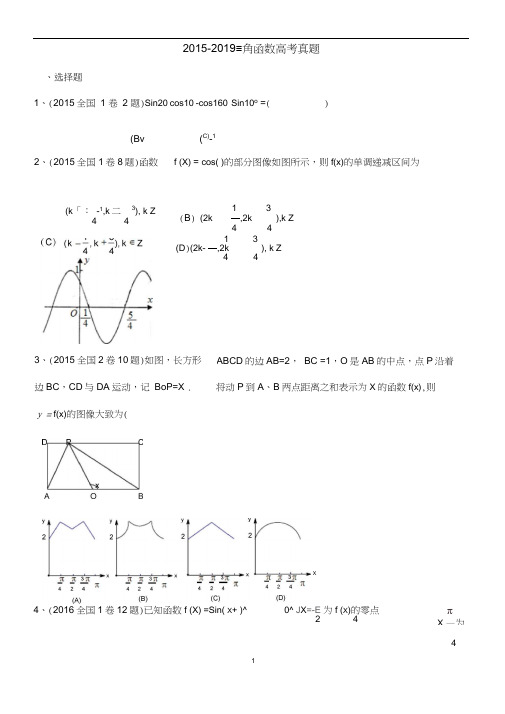
2015-2019≡角函数高考真题、选择题1、(2015全国1 卷2 题)Sin20°cos10°-cos160°Sin10o =( )(Bv (C)-14、(2016全国1卷12题)已知函数f (X) =Sin( X+ )^ 0^ J X=-E 为f (X)的零点2 42、(2015全国1卷8题)函数 f (X) = cos( )的部分图像如图所示,则f(x)的单调递减区间为(k「:-1,k二3), k Z4 41 3(B) (2k —,2k ),k Z4 41 3(D)(2k- —,2k ), k Z4 43、(2015全国2卷10题)如图,长方形ABCD的边AB=2,BC =1,O是AB的中点,点P沿着边BC,CD与DA运动,记BoP=X .将动P到A、B两点距离之和表示为X的函数f(x),则y = f(x)的图像大致为(Xπ,X —为4y=f(x)图像的对称轴且f(x)在任,竺单调,则技的最大值为(18 36 J(A) 11 (B) 9 (C) 7 (D) 55、(2016全国2卷7题)若将函数y=2sin 2x的图像向左平移1∏个单位长度,则平移后图象的对称轴为( )(A) X 斗-∏ k∙ Z (B) x=k∏ 上2 6 2& (2016全国2卷9题)若cos -(A) 25 1(B) 1 (C)5 -k Z(C)J5,15 (D)7、(2016全国3卷5题) ,则X忙訂Z (D) X=Z」k Z2 127252cos ‘:亠2sin2:=64(A)—25 (B)48258、(2016全国3卷8题) 在厶ABC中,(A)迈(B)卫10 109、(2017年全国1卷9题)16(D)—25B= - , BC边上的高等于-BC ,则cosA=( 4 3(D)-辽10(C) 1(C)-卫10、『2 JV已知曲线C i : y =CoSX , O :y =sin 2χ■2-,则下面结论正确的是()A .把G上各点的横坐标伸长到原来的 2 倍, 纵坐标不变,再把得到的曲线向右平移才个单位长度,得到曲线C2B.把G上各点的横坐标伸长到原来的 2 倍, 纵坐标不变,再把得到的曲线向左平移度,得到曲线C2C.把C l上各点的横坐标缩短到原来的纵坐标不变,再把得到的曲线向右平移三个单位长6度,得到曲线C2D .把G上各点的横坐标缩短到原来的 2倍,纵坐标不变,再把得到的曲线向左平移度,得到曲线C2 .10、( 2017全国3卷6题)设函数f(x^cos(x π),则下列结论错误的是()3B. y =f (X)的图像关于直线A. f (x)的一个周期为-2πX哼对称—C. f(χ V)的一个零点为X=- D . f (x)在(∏, ∏单调递减611、(2018年全国1 ∙8)已知函数f X =2cos2χ-sin2x • 2 ,贝U ( )A. f X的最小正周期为π,最大值为3B. f X的最小正周期为π,最大值为4C. f (X )的最小正周期为2π,最大值为3 D . f (X )的最小正周期为2 π,最大值为412. (2018年全国1 • 11)已知角〉的顶点为坐标原点,始边与X轴的非负半轴重合,终边上有两点2A(1, a ), B (2 , b ),且cos2α =—,则a —b =( )3A. -B. -5C. 2-5 D . 15 5 513. (2018 年全国2 • 7).在厶ABC 中,CoSC=逅,BC =1 , AC =5 ,则AB=(2 5A . 4.2 B. .. 30 C. 29 D . 2 514. (2018年全国2 • 10)若f(x) =COSX-sinx在[0, a]是减函数,贝U a的最大值是(A. πB. πC.3πD.π42415. (2018年全国3 • 4) 若Sin「^—,则cos2 :■=()3A 8r 778 A.-B.C. D.999916. (2018年全国3 • 6) 函数f (X)=tan X的最小正周期为 ( )1 tan2XMπ… πA.-B.-C. πD. 24217、(2018年全国3∙ 11) △ ABC的内角A , B , C的对边分别为a , b , C .若△ ABC的面积为2-CJl λJl fAA. -B. -C. —D.-2 3 4 6Sin X + X18、(2019年全国1 • 5)函数f(x)= ------------- 2在[—π,π]的图像大致为cos X 十X19、 (2019年全国1 ∙11)关于函数f(x) =sin∣x∣ |sin x|有下述四个结论:①f(x)是偶函数②f(x)在区间(-√:)单调递增2③f(x)在[-二,二]有4个零点④f(x)的最大值为2其中所有正确结论的编号是A.①②④B.②④C.①④D.①③20、 (2019年全国2 • 9)下列函数中,以二为周期且在区间(二,)单调递增的是2 4 2A. f (X)=∣COS 2x IB. f (X)=∣Sin 2x ∣C. f (X)= COS | X | D . f (X) = Sin | X |___ -JT21、(2019年全国2 • 10)已知α∈0,—」,2sin 2 α= coS∣2 贝α Sin α=()2A. 1B. §C.仝 D .空5 5 3 5二、填空题1、(2015全国1卷12题)在平面四边形ABCD中,∠ A= ∠ B= ∠ C=75 ° , BC=2 ,贝U AB的取值范围是_________ .4 5 2、(2016全国2卷13题)A ABC的内角A, B, C的对边分别为a, b, c,若cosA=-, cosC -,5 13a =1 ,贝Ub =_____ .3、(2016全国3卷14题)函数y =sinx---3cosx的图像可由函数y=sinχ∙ ■■一3cosx的图像至少向右平移______________ 单位长度得到.函数2厂 3 (- 7r ])的最大值是 ____________________.f (x )=sin x +J 3cosx -一 X E :0 二4f 2」5. (2018年全国 1 ∙16) △ ABC 的内角 A , B , C 的对边分别为 a , b , C ,已知 bsinC +csin B =4asin BsinC ,b 2c 2 -a 2 -8 ,则△ ABC 的面积为 _______________ 。
2015年高考数学试卷真题附详细解析

2015年高考数学试卷一、选择题:本大题共8小题,每小题5分,共40分2015年普通高等学校招生全国统一考试(真题卷)数学(理科)1.(5分)(2015•真题)已知集合P={x|x2﹣2x≥0},Q={x|1<x≤2},则(∁R P)∩Q=()A .[0,1)B.(0,2]C.(1,2)D.[1,2]2.(5分)(2015•真题)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A .8cm3B.12cm3C.D.3.(5分)(2015•真题)已知{a n}是等差数列,公差d不为零,前n项和是S n,若a3,a4,a8成等比数列,则()A .a1d>0,dS4>0B.a1d<0,dS4<0C.a1d>0,dS4<0D.a1d<0,dS4>04.(5分)(2015•真题)命题“∀n∈N*,f(n)∈N*且f(n)≤n”的否定形式是()A.∀n∈N*,f(n)∉N*且f(n)>n B.∀n∈N*,f(n)∉N*或f(n)>nC.∂n0∈N*,f(n0)∉N*且f(n0)>n0D.∂n0∈N*,f(n0)∉N*或f(n0)>n05.(5分)(2015•真题)如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是()A .B.C.D.6.(5分)(2015•真题)设A,B是有限集,定义:d(A,B)=card(A∪B)﹣card(A∩B),其中card(A)表示有限集A中的元素个数()命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C)A.命题①和命题②都成立B.命题①和命题②都不成立C.命题①成立,命题②不成立D.命题①不成立,命题②成立7.(5分)(2015•真题)存在函数f(x)满足,对任意x∈R都有()A .f(sin2x)=sinx B.f(sin2x)=x2+xC.f(x2+1)=|x+1| D.f(x2+2x)=|x+1|8.(5分)(2015•真题)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′﹣CD﹣B的平面角为α,则()A .∠A′DB≤αB.∠A′DB≥αC.∠A′CB≤αD.∠A′CB≥α二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9.(6分)(2015•真题)双曲线=1的焦距是,渐近线方程是.10.(6分)(2015•真题)已知函数f(x)=,则f(f(﹣3))=,f(x)的最小值是.11.(6分)(2015•真题)函数f(x)=sin2x+sinxcosx+1的最小正周期是,单调递减区间是.12.(4分)(2015•真题)若a=log43,则2a+2﹣a=.13.(4分)(2015•真题)如图,三棱锥A﹣BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是.14.(4分)(2015•真题)若实数x,y满足x2+y2≤1,则|2x+y﹣2|+|6﹣x﹣3y|的最小值是.15.(6分)(2015•真题)已知是空间单位向量,,若空间向量满足,且对于任意x,y∈R,,则x0=,y0=,|=.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)(2015•真题)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A=,b2﹣a2=c2.(1)求tanC的值;(2)若△ABC的面积为3,求b的值.17.(15分)(2015•真题)如图,在三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.(1)证明:A1D⊥平面A1BC;(2)求二面角A1﹣BD﹣B1的平面角的余弦值.18.(15分)(2015•真题)已知函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在区间[﹣1,1]上的最大值.(1)证明:当|a|≥2时,M(a,b)≥2;(2)当a,b满足M(a,b)≤2时,求|a|+|b|的最大值.19.(15分)(2015•真题)已知椭圆上两个不同的点A,B关于直线y=mx+对称.(1)求实数m的取值范围;(2)求△AOB面积的最大值(O为坐标原点).20.(15分)(2015•真题)已知数列{a n}满足a1=且a n+1=a n﹣a n2(n∈N*)(1)证明:1≤≤2(n∈N*);(2)设数列{a n2}的前n项和为S n,证明(n∈N*).高考数学试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分2015年普通高等学校招生全国统一考试(真题卷)数学(理科)1.(5分)考点:交、并、补集的混合运算.专题:集合.分析:求出P中不等式的解集确定出P,求出P补集与Q的交集即可.解答:解:由P中不等式变形得:x(x﹣2)≥0,解得:x≤0或x≥2,即P=(﹣∞,0]∪[2,+∞),∴∁R P=(0,2),∵Q=(1,2],∴(∁R P)∩Q=(1,2),故选:C.点评:此题考查了交、并、补集的混合运算,熟练掌握运算法则是解本题的关键.2.(5分)考点:由三视图求面积、体积.专题:空间位置关系与距离.分析:判断几何体的形状,利用三视图的数据,求几何体的体积即可.解答:解:由三视图可知几何体是下部为棱长为2的正方体,上部是底面为边长2的正方形奥为2的正四棱锥,所求几何体的体积为:23+×2×2×2=.故选:C.点评:本题考查三视图与直观图的关系的判断,几何体的体积的求法,考查计算能力.3.(5分)考点:等差数列与等比数列的综合.专题:等差数列与等比数列.分析:由a3,a4,a8成等比数列,得到首项和公差的关系,即可判断a1d和dS4的符号.解答:解:设等差数列{a n}的首项为a1,则a3=a1+2d,a4=a1+3d,a8=a1+7d,由a3,a4,a8成等比数列,得,整理得:.∵d≠0,∴,∴,=<0.故选:B.点评:本题考查了等差数列和等比数列的性质,考查了等差数列的前n项和,是基础题.4.(5分)考点:命题的否定.专题:简易逻辑.分析:根据全称命题的否定是特称命题即可得到结论.解答:解:命题为全称命题,则命题的否定为:∂n0∈N*,f(n0)∉N*或f(n0)>n0,故选:D.点评:本题主要考查含有量词的命题的否定,比较基础.5.(5分)考点:直线与圆锥曲线的关系.专题:圆锥曲线的定义、性质与方程.分析:根据抛物线的定义,将三角形的面积关系转化为的关系进行求解即可.解答:解:如图所示,抛物线的准线DE的方程为x=﹣1,过A,B分别作AE⊥DE于E,交y轴于N,BD⊥DE于E,交y轴于M,由抛物线的定义知BF=BD,AF=AE,则|BM|=|BD|﹣1=|BF|﹣1,|AN|=|AE|﹣1=|AF|﹣1,则===,故选:A点评:本题主要考查三角形的面积关系,利用抛物线的定义进行转化是解决本题的关键.6.(5分)考点:复合命题的真假.专题:集合;简易逻辑.分析:命题①根据充要条件分充分性和必要性判断即可,③借助新定义,根据集合的运算,判断即可.解答:解:命题①:对任意有限集A,B,若“A≠B”,则A∪B≠A∩B,则card(A∪B)>card(A∩B),故“d(A,B)>0”成立,若d(A,B)>0”,则card(A∪B)>card(A∩B),则A∪B≠A∩B,故A≠B成立,故命题①成立,命题②,d(A,B)=card(A∪B)﹣card(A∩B),d(B,C)=card(B∪C)﹣card(B∩C),∴d(A,B)+d(B,C)=card(A∪B)﹣card(A∩B)+card(B∪C)﹣card(B∩C)=[card (A∪B)+card(B∪C)]﹣[card(A∩B)+card(B∩C)]≥card(A∪C)﹣card(A∩C)=d(A,C),故命题②成立,故选:A点评:本题考查了,元素和集合的关系,以及逻辑关系,分清集合之间的关系与各集合元素个数之间的关系,注意本题对充要条件的考查.集合的元素个数,体现两个集合的关系,但仅凭借元素个数不能判断集合间的关系,属于基础题.7.(5分)考点:函数解析式的求解及常用方法.专题:函数的性质及应用.分析:利用x取特殊值,通过函数的定义判断正误即可.解答:解:A.取x=0,则sin2x=0,∴f(0)=0;取x=,则sin2x=0,∴f(0)=1;∴f(0)=0,和1,不符合函数的定义;∴不存在函数f(x),对任意x∈R都有f(sin2x)=sinx;B.取x=0,则f(0)=0;取x=π,则f(0)=π2+π;∴f(0)有两个值,不符合函数的定义;∴该选项错误;C.取x=1,则f(2)=2,取x=﹣1,则f(2)=0;这样f(2)有两个值,不符合函数的定义;∴该选项错误;D.令|x+1|=t,t≥0,则f(t2﹣1)=t;令t2﹣1=x,则t=;∴;即存在函数f(x)=,对任意x∈R,都有f(x2+2x)=|x+1|;∴该选项正确.故选:D.点评:本题考查函数的定义的应用,基本知识的考查,但是思考问题解决问题的方法比较难.8.(5分)考点:二面角的平面角及求法.专题:创新题型;空间角.分析:解:画出图形,分AC=BC,AC≠BC两种情况讨论即可.解答:解:①当AC=BC时,∠A′DB=α;②当AC≠BC时,如图,点A′投影在AE上,α=∠A′OE,连结AA′,易得∠ADA′<∠AOA′,∴∠A′DB>∠A′OE,即∠A′DB>α综上所述,∠A′DB≥α,故选:B.点评:本题考查空间角的大小比较,注意解题方法的积累,属于中档题.二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.9.(6分)双曲线的简单性质.考点:计算题;圆锥曲线的定义、性质与方程.专题:确定双曲线中的几何量,即可求出焦距、渐近线方程.分析:解解:双曲线=1中,a=,b=1,c=,答:∴焦距是2c=2,渐近线方程是y=±x.故答案为:2;y=±x.本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.点评:10.(6分)函数的值.考点:计算题;函数的性质及应用.专题:分根据已知函数可先求f(﹣3)=1,然后代入可求f(f(﹣3));由于x≥1时,f(x)=,析:当x<1时,f(x)=lg(x2+1),分别求出每段函数的取值范围,即可求解解答:解:∵f(x)=,∴f(﹣3)=lg10=1,则f(f(﹣3))=f(1)=0,当x≥1时,f(x)=,即最小值,当x<1时,x2+1≥1,(x)=lg(x2+1)≥0最小值0,故f(x)的最小值是.故答案为:0;.本题主要考查了分段函数的函数值的求解,属于基础试题.点评:11.(6分)两角和与差的正弦函数;三角函数的周期性及其求法;正弦函数的单调性.考点:专三角函数的求值.题:分由三角函数公式化简可得f(x)=sin(2x﹣)+,易得最小正周期,解不等析:式2kπ+≤2x﹣≤2kπ+可得函数的单调递减区间.解答:解:化简可得f(x)=sin2x+sinxcosx+1=(1﹣cos2x)+sin2x+1=sin(2x﹣)+,∴原函数的最小正周期为T==π,由2kπ+≤2x﹣≤2kπ+可得kπ+≤x≤kπ+,∴函数的单调递减区间为[kπ+,kπ+](k∈Z)故答案为:π;[kπ+,kπ+](k∈Z)点评:本题考查三角函数的化简,涉及三角函数的周期性和单调性,属基础题.12.(4分)考点:对数的运算性质.专题:函数的性质及应用.分析:直接把a代入2a+2﹣a,然后利用对数的运算性质得答案.解答:解:∵a=log43,可知4a=3,即2a=,所以2a+2﹣a=+=.故答案为:.点评:本题考查对数的运算性质,是基础的计算题.13.(4分)考点:异面直线及其所成的角.专题:空间角.分析:连结ND,取ND 的中点为:E,连结ME说明异面直线AN,CM所成的角就是∠EMC 通过解三角形,求解即可.解答:解:连结ND,取ND 的中点为:E,连结ME,则ME∥AN,异面直线AN,CM所成的角就是∠EMC,∵AN=2,∴ME==EN,MC=2,又∵EN⊥NC,∴EC==,∴cos∠EMC===.故答案为:.点评:本题考查异面直线所成角的求法,考查空间想象能力以及计算能力.14.(4分)考点:函数的最值及其几何意义.专题:不等式的解法及应用;直线与圆.分析:根据所给x,y的范围,可得|6﹣x﹣3y|=6﹣x﹣3y,再讨论直线2x+y﹣2=0将圆x2+y2=1分成两部分,分别去绝对值,运用线性规划的知识,平移即可得到最小值.解答:解:由x2+y2≤1,可得6﹣x﹣3y>0,即|6﹣x﹣3y|=6﹣x﹣3y,如图直线2x+y﹣2=0将圆x2+y2=1分成两部分,在直线的上方(含直线),即有2x+y﹣2≥0,即|2+y﹣2|=2x+y﹣2,此时|2x+y﹣2|+|6﹣x﹣3y|=(2x+y﹣2)+(6﹣x﹣3y)=x﹣2y+4,利用线性规划可得在A(,)处取得最小值3;在直线的下方(含直线),即有2x+y﹣2≤0,即|2+y﹣2|=﹣(2x+y﹣2),此时|2x+y﹣2|+|6﹣x﹣3y|=﹣(2x+y﹣2)+(6﹣x﹣3y)=8﹣3x﹣4y,利用线性规划可得在A(,)处取得最小值3.综上可得,当x=,y=时,|2x+y﹣2|+|6﹣x﹣3y|的最小值为3.故答案为:3.点本题考查直线和圆的位置关系,主要考查二元函数在可行域内取得最值的方法,属于中档题.评:15.(6分)空间向量的数量积运算;平面向量数量积的运算.考点:专创新题型;空间向量及应用.题:分由题意和数量积的运算可得<•>=,不妨设=(,,0),=(1,0,0),析:由已知可解=(,,t),可得|﹣(|2=(x+)2+(y﹣2)2+t2,由题意可得当x=x0=1,y=y0=2时,(x+)2+(y﹣2)2+t2取最小值1,由模长公式可得|.解解:∵•=||||cos<•>=cos<•>=,答:∴<•>=,不妨设=(,,0),=(1,0,0),=(m,n,t),则由题意可知=m+n=2,=m=,解得m=,n=,∴=(,,t),∵﹣()=(﹣x﹣y,,t),∴|﹣(|2=(﹣x﹣y)2+()2+t2=x2+xy+y2﹣4x﹣5y+t2+7=(x+)2+(y﹣2)2+t2,由题意当x=x0=1,y=y0=2时,(x+)2+(y﹣2)2+t2取最小值1,此时t2=1,故|==2故答案为:1;2;2点本题考查空间向量的数量积,涉及向量的模长公式,属中档题.评:三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)余弦定理.考点:解三角形.专题:分(1)由余弦定理可得:,已知b2﹣a2=c2.可得,a=.利析:用余弦定理可得cosC.可得sinC=,即可得出tanC=.(2)由=×=3,可得c,即可得出b.解解:(1)∵A=,∴由余弦定理可得:,∴b2﹣a2=bc﹣c2,答:又b2﹣a2=c2.∴bc﹣c2=c2.∴b=c.可得,∴a2=b2﹣=,即a=.∴cosC===.∵C∈(0,π),∴sinC==.∴tanC==2.(2)∵=×=3,解得c=2.∴=3.点评:本题考查了正弦定理余弦定理、同角三角形基本关系式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.17.(15分)考点:二面角的平面角及求法;直线与平面垂直的判定.专题:空间位置关系与距离;空间角.分析:(1)以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系,通过•=•=0及线面垂直的判定定理即得结论;(2)所求值即为平面A1BD的法向量与平面B1BD的法向量的夹角的余弦值的绝对值的相反数,计算即可.解答:(1)证明:如图,以BC中点O为坐标原点,以OB、OA、OA1所在直线分别为x、y、z轴建系.则BC=AC=2,A1O==,易知A1(0,0,),B(,0,0),C(﹣,0,0),A(0,,0),D(0,﹣,),B1(,﹣,),=(0,﹣,0),=(﹣,﹣,),=(﹣,0,0),=(﹣2,0,0),=(0,0,),∵•=0,∴A1D⊥OA1,又∵•=0,∴A1D⊥BC,又∵OA1∩BC=O,∴A1D⊥平面A1BC;(2)解:设平面A1BD的法向量为=(x,y,z),由,得,取z=1,得=(,0,1),设平面B1BD的法向量为=(x,y,z),由,得,取z=1,得=(0,,1),∴cos<,>===,又∵该二面角为钝角,∴二面角A1﹣BD﹣B1的平面角的余弦值为﹣.点评:本题考查空间中线面垂直的判定定理,考查求二面角的三角函数值,注意解题方法的积累,属于中档题.18.(15分)考点:二次函数在闭区间上的最值.专题:函数的性质及应用.分析:(1)明确二次函数的对称轴,区间的端点值,由a的范围明确函数的单调性,结合已知以及三角不等式变形所求得到证明;(2)讨论a=b=0以及分析M(a,b)≤2得到﹣3≤a+b≤1且﹣3≤b﹣a≤1,进一步求出|a|+|b|的求值.解答:解:(1)由已知可得f(1)=1+a+b,f(﹣1)=1﹣a+b,对称轴为x=﹣,因为|a|≥2,所以或≥1,所以函数f(x)在[﹣1,1]上单调,所以M(a,b)=max{|f(1),|f(﹣1)|}=max{|1+a+b|,|1﹣a+b|},所以M(a,b)≥(|1+a+b|+|1﹣a+b|)≥|(1+a+b)﹣(1﹣a+b)|≥|2a|≥2;(2)当a=b=0时,|a|+|b|=0又|a|+|b|≥0,所以0为最小值,符合题意;又对任意x∈[﹣1,1].有﹣2≤x2+ax+b≤2得到﹣3≤a+b≤1且﹣3≤b﹣a≤1,易知|a|+|b|=max{|a﹣b|,|a+b|}=3,在b=﹣1,a=2时符合题意,所以|a|+|b|的最大值为3.点评:本题考查了二次函数闭区间上的最值求法;解答本题的关键是正确理解M(a,b)是|f(x)|在区间[﹣1,1]上的最大值,以及利用三角不等式变形.19.(15分)考点:直线与圆锥曲线的关系.专题:创新题型;圆锥曲线中的最值与范围问题.分析:(1)由题意,可设直线AB的方程为x=﹣my+n,代入椭圆方程可得(m2+2)y2﹣2mny+n2﹣2=0,设A(x1,y1),B(x2,y2).可得△>0,设线段AB的中点P(x0,y0),利用中点坐标公式及其根与系数的可得P,代入直线y=mx+,可得,代入△>0,即可解出.(2)直线AB与x轴交点横坐标为n,可得S△OAB=,再利用均值不等式即可得出.解答:解:(1)由题意,可设直线AB的方程为x=﹣my+n,代入椭圆方程,可得(m2+2)y2﹣2mny+n2﹣2=0,设A(x1,y1),B(x2,y2).由题意,△=4m2n2﹣4(m2+2)(n2﹣2)=8(m2﹣n2+2)>0,设线段AB的中点P(x0,y0),则.x0=﹣m×+n=,由于点P在直线y=mx+上,∴=+,∴,代入△>0,可得3m4+4m2﹣4>0,解得m2,∴或m.(2)直线AB与x轴交点纵坐标为n,∴S△OAB==|n|•=,由均值不等式可得:n2(m2﹣n2+2)=,∴S△AOB=,当且仅当n2=m2﹣n2+2,即2n2=m2+2,又∵,解得m=,当且仅当m=时,S△AOB取得最大值为.点评:本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、线段垂直平分线的性质、三角形面积计算公式、弦长公式、均值不等式的性质,考查了推理能力与计算能力,属于难题.20.(15分)考点:数列的求和;数列与不等式的综合.专题:创新题型;点列、递归数列与数学归纳法.分析:(1)通过题意易得0<a n≤(n∈N*),利用a n﹣a n+1=可得≥1,利用==≤2,即得结论;(2)通过=a n﹣a n+1累加得S n=﹣a n+1,利用数学归纳法可证明≥a n≥(n≥2),从而≥≥,化简即得结论.解答:证明:(1)由题意可知:0<a n≤(n∈N*),又∵a2=a1﹣=,∴==2,又∵a n﹣a n+1=,∴a n>a n+1,∴≥1,∴==≤2,∴1≤≤2(n∈N*);(2)由已知,=a n﹣a n+1,=a n﹣1﹣a n,…,=a1﹣a2,累加,得S n=++…+=a1﹣a n+1=﹣a n+1,易知当n=1时,要证式子显然成立;当n≥2时,=.下面证明:≥a n≥(n≥2).易知当n=2时成立,假设当n=k时也成立,则a k+1=﹣+,由二次函数单调性知:a n+1≥﹣+=≥,a n+1≤﹣+=≤,∴≤≤,即当n=k+1时仍然成立,故对n≥2,均有≥a n≥,∴=≥≥=,即(n∈N*).点评:本题是一道数列与不等式的综合题,考查数学归纳法,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于难题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年高考数学试题——三角函数1.(15北京理科)已知函数2()cos 222x x xf x .(Ⅰ) 求()f x 的最小正周期;(Ⅱ) 求()f x 在区间[π0]-,上的最小值.【答案】(1)2π,(2)1-- 【解析】试题分析:先用降幂公式和辅助角公式进行三角恒等变形,把函数化为()sin()f x A x mωϕ=++形式,再利用周期公式2T πω=求出周期,第二步由于0,x π-≤≤则可求出3444x πππ-≤+≤,借助正弦函数图象 找出在这个范围内当42x ππ+=-,即34x π=-时,()f x 取得最小值为:12--.试题解析:(Ⅰ) 211cos ()sincossin sin 22222xxxxf x x -=-=⋅-⋅=sin cos x x =+-sin()4x π=+-(1)()f x 的最小正周期为221T ππ==; (2)30,444x x ππππ-≤≤∴-≤+≤,当3,424x x πππ+=-=-时,()f x 取得最小值为:12--考点: 1.三角函数式的恒等变形;2.三角函数图像与性质.2.(15北京文科)已知函数()2sin 2x f x x =-. (Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在区间20,3π⎡⎤⎢⎥⎣⎦上的最小值.【答案】(1)2π;(2)考点:倍角公式、两角和的正弦公式、三角函数的周期、三角函数的最值. 3.(15年广东文科)已知tan 2α=.()1求tan 4πα⎛⎫+ ⎪⎝⎭的值;()2求2sin 2sin sin cos cos 21ααααα+--的值.【答案】(1)3-;(2)1.考点:1、两角和的正切公式;2、特殊角的三角函数值;3、二倍角的正、余弦公式;4、同角三角函数的基本关系.4.(15年安徽文科)已知函数2()(sin cos )cos2f x x x x =++ (1)求()f x 最小正周期; (2)求()f x 在区间[0,]2π上的最大值和最小值.【答案】(1)π ;(2)最大值为10考点:1.三角函数的性质;2.三角函数的最值.5.(15年福建理科)已知函数f()x 的图像是由函数()cos g x x =的图像经如下变换得到:先将()g x 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移2p个单位长度. (Ⅰ)求函数f()x 的解析式,并求其图像的对称轴方程;(Ⅱ)已知关于x 的方程f()g()x x m +=在[0,2)p 内有两个不同的解,a b . (1)求实数m 的取值范围;(2)证明:22cos ) 1.5m a b -=-(【答案】(Ⅰ) f()2sin x x =,(k Z).2x k pp =+ ;(Ⅱ)(1)(;(2)详见解析. 【解析】试题分析:(Ⅰ)纵向伸缩或平移: ()()g x kg x →或()()g x g x k →+;横向伸缩或平移:()()g x g x ω→(纵坐标不变,横坐标变为原来的1ω倍),()()g x g x a →+(0a >时,向左平移a 个单位;0a <时,向右平移a 个单位);(Ⅱ) (1)由(Ⅰ)得f()2sin x x =,则f()g()2sin cos x x x x +=+,利用辅助角公式变形为f()g()x x +)x j +(其中sinj j ),方程f()g()x x m +=在[0,2)p 内有两个不同的解,a b ,等价于直线y m =和函数)y x j +有两个不同交点,数形结合求实数m 的取值范围;(2)结合图像可得+=2()2p a b j -和3+=2()2pa b j -,进而利用诱导公式结合已知条件求解. 试题解析:解法一:(1)将()cos g x x =的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变)得到y 2cos x =的图像,再将y 2cos x =的图像向右平移2p 个单位长度后得到y 2cos()2x p=-的图像,故f()2sin x x =,从而函数f()2sin x x =图像的对称轴方程为(k Z).2x k pp =+(2)1) f()g()2sin cos )x x x x x x +=+)x j +(其中sinj j =) 依题意,sin(x j +在区间[0,2)p 内有两个不同的解,a b 当且仅当|1<,故m 的取值范围是(-.2)因为,a b )=m x j +在区间[0,2)p 内有两个不同的解, 所以sin(a j +,sin()=b j +.当1£+=2(),2();2pa b j a b p b j --=-+当-时, 3+=2(),32();2pa b j a b p b j --=-+ 所以2222cos )cos 2()2sin ()11 1.5m a b b j b j -=-+=+-=-=-(解法二:(1)同解法一. (2)1) 同解法一.2) 因为,a b )=m x j +在区间[0,2)p 内有两个不同的解,所以sin(a j +,sin()=b j +.当1£+=2(),+();2pa b j a j p b j -=-+即当-时, 3+=2(),+3();2pa b j a j p b j -=-+即 所以cos +)cos()a j b j =-+(于是cos )cos[()()]cos()cos()sin()sin()a b a j b j a j b j a j b j -=+-+=+++++(22222cos ()sin()sin()[1] 1.5m b j a j b j =-++++=--+=-考点:1、三角函数图像变换和性质;2、辅助角公式和诱导公式. 6.(15年福建文科)若5sin 13α=-,且α为第四象限角,则tan α的值等于( ) A .125 B .125- C .512 D .512-【答案】D 【解析】试题分析:由5sin 13α=-,且α为第四象限角,则12cos 13α==,则sin tan cos ααα= 512=-,故选D . 考点:同角三角函数基本关系式.7.(15年福建文科)已知函数()2cos 10cos 222x x x f x =+. (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)将函数()f x 的图象向右平移6π个单位长度,再向下平移a (0a >)个单位长度后得到函数()g x 的图象,且函数()g x 的最大值为2. (ⅰ)求函数()g x 的解析式;(ⅱ)证明:存在无穷多个互不相同的正整数0x ,使得()00g x >. 【答案】(Ⅰ)2π;(Ⅱ)(ⅰ)()10sin 8g x x =-;(ⅱ)详见解析. 【解析】试题分析:(Ⅰ)首先利用证明二倍角公式和余弦降幂公式将()f x 化为()10sin 56f x x π⎛⎫=++ ⎪⎝⎭,然后利用2T πω=求周期;(Ⅱ)由函数()f x 的解析式中给x 减6π,再将所得解析式整体减去a 得()g x 的解析式为()10sin 5g x x a =+-,当sin x 取1的时,()g x 取最大值105a +-,列方程求得13a =,从而()g x 的解析式可求;欲证明存在无穷多个互不相同的正整数0x ,使得()00g x >,可解不等式()00g x >,只需解集的长度大于1,此时解集中一定含有整数,由周期性可得,必存在无穷多个互不相同的正整数0x .试题解析:(I )因为()2cos 10cos 222x x xf x =+5cos 5x x =++10sin 56x π⎛⎫=++ ⎪⎝⎭.所以函数()f x 的最小正周期2πT =. (II )(i )将()f x 的图象向右平移6π个单位长度后得到10sin 5y x =+的图象,再向下平移a (0a >)个单位长度后得到()10sin 5g x x a =+-的图象.又已知函数()g x 的最大值为2,所以1052a +-=,解得13a =. 所以()10sin 8g x x =-.(ii )要证明存在无穷多个互不相同的正整数0x ,使得()00g x >,就是要证明存在无穷多个互不相同的正整数0x ,使得010sin 80x ->,即04sin 5x >.由452<知,存在003πα<<,使得04sin 5α=.由正弦函数的性质可知,当()00,x απα∈-时,均有4sin 5x >. 因为sin y x =的周期为2π,所以当()002,2x k k παππα∈++-(k ∈Z )时,均有4sin 5x >. 因为对任意的整数k ,()()00022213k k πππαπαπα+--+=->>,所以对任意的正整数k ,都存在正整数()002,2k x k k παππα∈++-,使得4sin 5k x >. 亦即存在无穷多个互不相同的正整数0x ,使得()00g x >. 考点:1、三角函数的图像与性质;2、三角不等式.8.(15年新课标1理科)sin20°cos10°-con160°sin10°=(A )2- (B )2(C )12- (D )12【答案】D【解析】原式=sin20°cos10°+cos20°sin10°=sin30°=12,故选D.9.(15年新课标1理科) 函数f(x)=的部分图像如图所示,则f (x )的单调递减区间为 (A)(),k(b)(),k(C)(),k (D)(),k【答案】B10.(15年陕西理科)如图,某港口一天6时到18时的水深变化曲线近似满足函数3sin()6y x k πϕ=++,据此函数可知,这段时间水深(单位:m )的最大值为( )A .5B .6C .8D .10【答案】C 【解析】试题分析:由图象知:min 2y =,因为min 3y k =-+,所以32k -+=,解得:5k =,所以这段时间水深的最大值是max 3358y k =+=+=,故选C . 考点:三角函数的图象与性质.11.(15年陕西文科)如图,某港口一天6时到18时的谁深变化曲线近似满足函数y =3sin (6πx +Φ)+k ,据此函数可知,这段时间水深(单位:m )的最大值为____________.【答案】8 【解析】试题分析:由图像得,当sin()16x π+Φ=-时min 2y =,求得5k =,当sin()16x π+Φ=时,max 3158y =⨯+=,故答案为8.考点:三角函数的图像和性质.12.(15年天津理科)已知函数()22sin sin 6f x x x π⎛⎫=--⎪⎝⎭,R x ∈ (I)求()f x 最小正周期; (II)求()f x 在区间[,]34p p-上的最大值和最小值.【答案】(I)π; (II) max ()4f x =,min 1()2f x =-.考点:1.两角和与差的正余弦公式;2.二倍角的正余弦公式;3.三角函数的图象与性质. 13.(15年天津文科)已知函数()()sin cos 0,,f x x x x ωωω=+>∈R 若函数()f x 在区间(),ωω-内单调递增,且函数()f x 的图像关于直线x ω=对称,则ω的值为 .【解析】试题分析:由()f x 在区间(),ωω-内单调递增,且()f x 的图像关于直线x ω=对称,可得π2ωω≤,且()222πsin cos sin 14f ωωωω⎛⎫=+=+= ⎪⎝⎭,所以2ππ42ωω+=⇒= 考点:三角函数的性质.14.(15年湖南理科)A.512πB.3πC.4πD.6π 【答案】D.【解析】试题分析:向右平移ϕ个单位后,得到)22sin()(ϕ-=x x g ,又∵2|)()(|21=-x g x f ,∴不妨 ππk x 2221+=,ππϕm x 22222+-=-,∴πϕπ)(221m k x x -+-=-,又∵12min 3x x π-=, ∴632πϕπϕπ=⇒=-,故选D.考点:三角函数的图象和性质.10.(15年江苏)已知tan 2α=-,()1tan 7αβ+=,则tan β的值为_______. 【答案】3【解析】 试题分析:12tan()tan 7tan tan() 3.21tan()tan 17αβαβαβααβα++-=+-===++- 考点:两角差正切公式11.(15年江苏)在ABC ∆中,已知60,3,2===A AC AB .(1)求BC 的长;(2)求C 2sin 的值.【答案】(12【解析】考点:余弦定理,二倍角公式12.。
