SPSS多重比较方法
平均值的多重比较SPSS操作

平均值的多重比较SPSS操作一、简介多重比较是一个非常重要的统计方法。
在采集大量数据后,通常会对某个变量进行平均值的比较。
但是,如果对数据进行简单的比较可能会存在问题:假设有10个不同的样本,进行10次比较,这将导致多达45个比较(10C2),这个时候难免会出现误差。
多重比较是一种用于调整显著性水平和减少误差的方法,可以在比较中减少错误的拒绝。
二、SPSS操作1、单因素方差分析打开SPSS软件,加载数据并选择“Analyze”菜单,选择“Compare Means”选项,进入子菜单,选择“One-Way ANOVA”,进入单因素方差分析子菜单,如下图所示。
2、设置分析变量在“One-Way ANOVA”对话框中,选择需要分析的变量,并将其添加到右侧区域,如下图所示。
3、添加编辑标签在“Options”标签页中,选择“Descriptive”。
在描述性统计选项卡中,选择“Mean”、“Std. Deviation”和“N”三个选项,并单击“Continue”按钮。
现在我们将为分组变量添加标签。
4、分组变量标签点击“Post Hoc...”按钮进入“Post Hoc Tests”对话框,并选择一个或多个比较类型进行比较,如下图所示。
5、设置显著性水平在“Options”标签页中,将显著性水平设置为0.05,如下图所示。
6、执行分析完成设置后,单击“OK”按钮开始分析过程。
SPSS运行程序并输出结果,如下图所示。
分析结果可以得出:1)整体效应不显著,F(2,54)=2.49,P=0.09。
2)当α = 0.05 时,相应的 Bonferroni 校正后置Hoc比较表明,组1、2和组1、3之间差异不显著,但组2和组3之间差异显著。
3)平均得分方面,在平均得分方面,组1的平均得分小于2和组三的平均得分;组2的平均得分高于组一和组三的平均得分;组三的平均得分最高。
四、总结平均值的多重比较SPSS操作是非常重要的,该方法让我们能够在更复杂的数据集中得出显著的结论。
SPSS如何实现多个样本类型的多重比较

SPSS如何实现多个样本类型的多重比较
SPSS是一种统计分析软件,可以进行多重比较分析。
多重比
较可以在不同样本类型之间进行比较,帮助研究人员发现不同样本
之间的差异。
以下是实现多个样本类型的多重比较的步骤:
1. 在SPSS中加载数据
首先,在SPSS中加载包含所需变量的数据集。
确保数据集包
含多个样本类型的数据,以便进行比较分析。
2. 打开“分析”菜单
在SPSS的菜单栏中,点击“分析”菜单,以打开分析选项。
3. 选择“比较均值”选项
在“分析”菜单中,选择“比较均值”选项,以打开多重比较分析。
4. 选择“GLM方差分析”的子选项
在“比较均值”选项中,选择“GLM方差分析”的子选项。
这将允许您进行多重比较分析。
5. 选择“因子”和“因子水平”
在GLM方差分析窗口中,选择需要进行比较的样本类型的“因子”和“因子水平”。
这些信息将帮助SPSS确定需要进行比较的样本类型。
6. 点击“确定”按钮
完成选择后,点击GLM方差分析窗口中的“确定”按钮。
SPSS 会根据您的选择进行多重比较分析。
7. 查看结果
SPSS将显示多重比较的结果。
您可以查看各个样本类型之间的差异和显著性水平,以了解它们之间的统计差异。
通过按照以上步骤,在SPSS中实现多个样本类型的多重比较分析。
这将帮助您发现不同样本类型之间的差异,并得出有关样本的结论。
用SPSS进行单因素方差分析和多重比较

方差分析方差分析可以用来检验来多个均值之间差异的显著性,可以看成是两样本t检验的扩展。
统计学原理中涉及的方差分析主要包括单因素方差分析、两因素无交互作用的方差分析和两因素有交互作用的方差分析三种情况。
虽然Excel可以进行这三种类型的方差分析,但对数据有一些限制条件,例如不能有缺失值,在两因素方差分析中各个处理要有相等的重复次数等;功能上也有一些不足,例如不能进行多重比较。
而在方差分析方面SPSS的功能特别强大,很多输出结果已经超出了统计学原理的范围。
用SPSS检验数据分布的正态性方差分析需要以下三个假设条件:(1)、在各个总体中因变量都服从正态分布;(2)、在各个总体中因变量的方差都相等;(3)、各个观测值之间是相互独立的。
在SPSS中我们很方便地对前两个条件进行假设检验。
同方差性检验一般与方差分析一起进行,这一小节我们只讨论正态性的检验问题。
[例7.4] 检验生兴趣对考试成绩的影响的例子中各组数据的正态性。
在SPSS中输入数据(或打开数据文件),选择Analyze→Descriptive Statistics→Explore,在Explore对话框中将统计成绩作为因变量,兴趣作为分类变量(Fator),单击Plots按钮,选中“Histogram”复选框和“Normality plots with Test”,单击“Continue”按钮,在单击主对话框中的“OK”,可以得到分类别的描述统计信息。
从数据的茎叶图、直方图和箱线图都可以对数据分布的正态性做出判断,由于这些内容前面已经做过讲解,这里就不再进一步说明了。
图7-2 用Expore过程进行正态性检验top↑输出结果中的Q-Q图是观察数据分布正态性的一种常用图形。
这类图形大致是这样绘制的:计算数据在样本中对应的经验分布函数值(类似于累积分布的函数值,取值在0-1之间);然后计算标准正态分布(或者均值、方差相同的正态分布)对应于经验分布函数值的分位数。
SPSS如何实现多个指标的多重比较

SPSS如何实现多个指标的多重比较在统计学中,多重比较是一种常用的方法,用于比较多个指标之间的差异。
SPSS是一款功能强大的统计分析软件,提供了多种方法来实现多个指标的多重比较。
下面将介绍两种常用的方法:___校正和Tukey HSD法。
___校正Bonferroni校正是一种常见的多重比较校正方法,它的基本原理是将显著性水平除以比较的指标数目。
SPSS提供了简便的方法来进行Bonferroni校正。
1.打开SPSS软件并加载你的数据集。
2.在菜单栏中选择【分析】>【一般线性模型】>【多重比较】。
3.在弹出窗口中,选择你要进行多重比较的自变量和因变量,然后点击【设置】按钮。
4.在设置窗口中,选择Bonferroni校正方法并输入显著性水平。
5.点击【确定】按钮来完成多重比较的分析。
___ HSD法___ HSD法是一种常用的多重比较方法,它基于___'s方法来调整比较的显著性水平。
SPSS也提供了简单的方法来进行TukeyHSD法的分析。
1.打开SPSS软件并加载你的数据集。
2.在菜单栏中选择【分析】>【一般线性模型】>【多重比较】。
3.在弹出窗口中,选择你要进行多重比较的自变量和因变量,然后点击【设置】按钮。
4.在设置窗口中,选择Tukey HSD法,并选择需要比较的指标。
5.点击【确定】按钮来完成多重比较的分析。
结论通过SPSS软件提供的Bonferroni校正和Tukey HSD法,我们可以方便地实现多个指标的多重比较分析。
在进行多重比较时,我们需要选择适当的校正方法,并设定显著性水平,以确保分析结果的可靠性。
用SPSS进行单因素方差分析和多重比较

用SPSS进行单因素方差分析和多重比较在SPSS中进行单因素方差分析和多重比较可以帮助研究人员分析各组之间的差异,并确定是否存在显著性差异。
本文将详细介绍如何使用SPSS进行单因素方差分析和多重比较。
一、单因素方差分析1.数据准备首先,将数据导入SPSS软件。
确保每个观测值都位于独立的行中,并且将每个因素作为一个变量列。
确保每个变量的测量水平正确设置。
对于要进行单因素方差分析的变量,应该是连续型变量。
2.描述性统计在执行方差分析之前,我们需要进行描述性统计,以了解每个组的均值、标准差和样本数量。
在SPSS中,可以通过选择“统计”菜单,然后选择“描述统计”来执行描述性统计。
在弹出的对话框中,选择想要分析的变量,并选择“均值”和“标准差”。
3.单因素方差分析要进行单因素方差分析,在SPSS中选择“分析”菜单,然后选择“一元方差分析”。
在弹出的对话框中,将要分析的变量移入“因素”框中。
然后,点击“选项”按钮,选择想要输出的结果,如方差分析表和均值表。
最后,点击“确定”执行单因素方差分析。
4.结果解读方差分析表提供了重要的统计信息,包括组间和组内的平方和、自由度、均方、F值和p值。
其中,F值表示组间变异性和组内变异性的比值。
p值表示在原假设下观察到的差异是否显著。
如果p值小于设定的显著性水平(通常为0.05),则可以拒绝原假设,即存在显著差异。
二、多重比较当在单因素方差分析中发现存在显著组间差异时,下一步是进行多重比较,以确定哪些组之间存在显著差异。
1.多重比较检验在SPSS中,可以使用多种方法进行多重比较检验,如Tukey HSD、Bonferroni、LSD等。
这些方法可以通过选择“分析”菜单,然后选择“比较手段”来执行。
在弹出的对话框中,选择要进行比较的变量和方法。
点击“确定”执行多重比较检验。
2.结果解读多重比较结果表提供了各组之间的均值差异估计、标准误差、置信区间和p值。
根据p值,可以确定哪些组之间存在显著差异。
用SPSS实现完全随机设计多组比较秩和检验的多重比较

用SPSS实现完全随机设计多组比较秩和检验的多重比较用SPSS实现完全随机设计多组比较秩和检验的多重比较一、引言在实证研究中,为了探讨不同处理或干预对某个变量的影响,常常需要进行多组比较。
多组比较的目的是确定是否存在差异以及差异的大小。
秩和检验是一种用于比较两组或多组样本之间差异的非参数方法,具有一定的优势。
二、方法以SPSS软件为例,我们可以利用其提供的功能实现完全随机设计多组比较秩和检验的多重比较。
以下是具体的步骤:1. 数据准备首先,需要准备好用于分析的数据。
假设有n个处理组,每个处理组有m个观测值。
可以将数据按照处理组进行分类整理,每个处理组的观测值放在一列中。
2. 数据输入打开SPSS软件,创建一个新的数据文件,并将之前准备好的数据输入。
确保每个处理组的观测值对应正确。
3. 非参数检验选择菜单栏中的“分析-非参数检验-维尔科克森-曼-惠特尼U 检验”或“分析-非参数检验-克鲁斯卡尔-华里斯H检验”,根据实验需要选择适当的检验方法。
4. 设置选项在弹出的对话框中,将要比较的变量选择到“因子”框中,将处理组变量选择到“因子标签”框中。
选择需要进行多重比较的处理组,点击“组间对比”按钮。
5. 多重比较在“组间对比”对话框中,选择想要进行多重比较的处理组。
可以点击“加入全部对比”按钮将所有处理组两两比较,也可以手动选择需要比较的处理组。
点击“确定”进行多重比较。
6. 结果输出SPSS将会输出多重比较的结果,包括均值、标准误差、t值、p值等统计指标。
根据p值判断处理组之间是否存在显著差异。
三、示例为了更好地理解上述方法,我们通过一个假想的实验来展示如何使用SPSS进行完全随机设计多组比较秩和检验的多重比较。
假设研究人员想要比较四种不同药物对降压效果的影响。
他们随机地将30名患有高血压的参与者分为四个处理组,分别接受A药物、B药物、C药物和D药物的治疗。
每个处理组的参与者分别测量他们的血压值。
现在,研究人员想要确定这些药物在降压效果上是否有显著差异。
SPSS如何实现多个数据集的多重比较

SPSS如何实现多个数据集的多重比较SPSS(统计分析软件)是一款经常用于数据分析和统计的软件工具。
它拥有强大的功能,可以对多个数据集进行多重比较。
以下是实现多个数据集多重比较的步骤:1. 打开SPSS软件并导入数据集:首先,打开SPSS软件。
然后,选择“文件”菜单并点击“打开”选项。
在弹出的对话框中,选择要进行比较的第一个数据集,并点击“打开”。
2. 创建第一个数据集的副本:在第一个数据集的视图中,选择“数据”菜单并点击“分拆文件”选项。
在弹出的对话框中,选择“分拆文件”选项并点击“添加”按钮。
选择变量或者全部变量,然后点击“OK”。
3. 导入其他数据集:按照第一步的方法将其他需要比较的数据集逐一导入SPSS软件中,并创建副本。
4. 进行多重比较:选择“分析”菜单,并点击“通用线性模型(GLM)”选项。
在弹出的对话框中,将第一个数据集的副本作为因变量,其他数据集的副本作为因子,并点击“添加”按钮。
然后,选择“比较”选项,在弹出的对话框中选择需要进行的多重比较方法,例如Tukey或Bonferroni等。
5. 运行分析:点击“确定”按钮,SPSS将开始进行多重比较分析。
分析完成后,可以查看结果报告和统计输出。
这是一个基本的步骤指南,供您在SPSS中实现多个数据集的多重比较。
然而,具体的步骤可能因SPSS软件版本的不同而略有差异。
因此,在使用SPSS进行多重比较时,建议您参考软件的帮助文档或相关教程,以获得更准确和详细的指导。
请注意,本文档仅提供了一般性的指导,并不涉及具体的数据集或样本。
对于特定的数据分析问题,建议您根据实际情况进行相应的步骤和方法选择。
参考资料:。
SPSS如何实现多个样本率多重比较

SPSS实现多组率的两两比较多组率的比较是在医学研究中常常会遇到的问题,其通常被列为R×2表进行χ2检验,其结果仅能说明多个率间的差别有统计学意义,并不能对两两之间差别做出检验。
而将其分割成2 ×2表虽可行两两比较,但不宜用独立四格表的显著界值。
针对这个问题,本文就如何使用国际通用SPSS软件实现该方法,给出具体解决方案。
如图1一组病例资料。
拟对上述资料进行统计分析。
将上述资料按图2进行SPSS录入。
要求:将各组按观察率从小到大排列,本例有效率恰好已是升序排列,故无需再排序。
经过交叉表对三组资料进行卡方检验后,具有统计学意义。
下一步进行两两比较。
操作步骤①权变量:由于“数据”变量中数据并非真正的每条记录数据,而是频数资料,所以要加权,其步骤如下:Data→Weight Case→选择⊙weight case by单选按钮→将“数据”变量添加到Frequency Variable框内→OK。
②选择记录:根据杜养志法,需分别将G1组与第Gi ( i = 2, 3, ⋯⋯k)组进行非独立2 ×2表,步骤如下:Data→Select Case→选择⊙If condition is satisfied单选按钮→点击其下方的If⋯⋯按钮→在右上方框体内录入引号内的内容:“行变量= 1 or行变量= i”( i根据所比的具体组的序数而定) →continue→OK。
③卡方检验: Analyze →Descrip tive Statisics →Crosstable→将“行变量”放入Row框体中→将“列变量”放入column框体中→Statisics→选择Chi - square→continue→OK。
④重复选择记录步骤,选择新的比较组,再行卡方检验,直到所有组均与G1比较过为止。
经过分析后,得出下图结果。
然后根据下图“杜养志非独立的2 ×2表的χ2 值著界值表”确定界值。
SPSS多重比较方法

SPSS 多重比较方法(信息摘自网络,仅供参考)(一)常用方法总结1. LS D法最小显著差异法,公式为:它其实只是t检验的一个简单变形,并未对检验水准做出任何校正,只是在标准误的计算上充分利用了样本信息, 为所有组的均数统一估计出了一个更为稳健的标准误,其中MS误差是方差分析中计算得来的组内均方,它一般用于计划好的多重比较。
由于单次比较的检验水准仍为α,因此可认为LSD法是最灵敏的。
2. Bonfe rroni法该法又称Bonferro ni t检验,由Bo nferron i提出。
用t检验完成各组间均值的配对比较,但通过设置每个检验的误差率来控制整个误差率。
若每次检验水准为α′,共进行m 次比较,当H0 为真时,犯Ⅰ类错误的累积概率α不超过mα′, 既有B onferro ni不等式α≤mα′成立。
3. Sida k法它实际上就是Sidak校正在LSD法上的应用,即通过Sidak校正降低每两次比较的Ⅰ类错误概率,以达到最终整个比较的Ⅰ类错误概率为α的目的。
即α′=1 - (1 -α) 2 / k ( k- 1),计算t统计量进行多重配对比较。
可以调整显著性水平,比Boff erroni方法的界限要小。
4. Stud ent-Newman-Keuls法(S NK法)它实质上是根据预先制定的准则将各组均数分为多个子集, 利用Studen tiz ed Rang e分布来进行假设检验,并根据所要检验的均数的个数调整总的Ⅰ类错误概率不超过α。
用studentra nge分布进行所有各组均值间的配对比较。
如果各组样本含量相等或者选择了(差异较小的子集)的均值配对比较。
SPSS如何操作方差分析后的多重比较?
SPSS如何操作方差分析后的多重比较?
二组计量数据之间的比较我们采用的是t检验,此时t检验与方差分析是等价的,二组以上的计量数据之间的比较是采用方差分析
此时我们会想到一个问题,比如是三组之间的比较不存在差异,我们可以不再继续研究,但实际上单因素的方差分析并不是这样简单,在研究中我们往往想知道哪些组间存在差异,
很重要的一点,对于不同的需求比较分两种情况
计划好的多重比较在收集数据之前就决定了考察多个组别与特定组别的比较或某几个组织间的彼此差别的分析。
非计划的多重比较是指在单因素方差分析以后,结果有意义才进行的探索性分析
首先,我们来看下如何进行两两比较的操作:
在医学论文写作中很多情况属于非计划的多重比较
首先,我门介绍下如何在SPSS软件中进行操作;
第一步:同上期的【步骤一】,将数据输入并设置变量名后,选择【分析】→【比较均值】→【单因素ANOV A】即可,
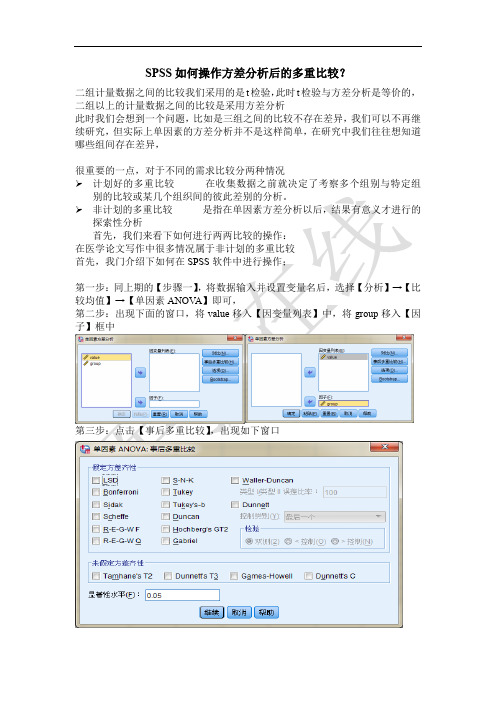
第二步:出现下面的窗口,将value移入【因变量列表】中,将group移入【因子】框中
第三步:点击【事后多重比较】,出现如下窗口
从图中我们可以看到有两种情况下的多重比较方法,即【假定方差齐性】和【未假定方差齐】性,如何选择这两种情况,依据我们之前所做的结果,在整体比较的时候我们已经得到过方差是否齐的检验结果,依次结果选择其中一种情况,但是如果方差不齐,在方法的接受程度和结果的稳健性来讲,结果不是很可靠,仅供参考,建议此时进行变量转换,或者是非参数检验的方法进行代替。
但是我们看到在【假定方差齐】的情况下,也有14种多重比较的方法呈现,那么我们如何选择呢,下期继续介绍几种常用的多重比较的方法。
SPSS如何实现多个变量的多重比较

SPSS如何实现多个变量的多重比较在统计分析中,多重比较是一种常用的方法,用于同时比较多个变量之间的差异。
SPSS是一种功能强大的统计软件,可以实现多个变量的多重比较。
本文将介绍如何使用SPSS进行多重比较的步骤。
1. 准备数据首先,确保你有收集到的相关数据,并将其保存为SPSS能够读取的数据文件格式(如.sav文件)。
2. 打开数据文件在SPSS软件中,找到并打开你准备好的数据文件。
确保数据文件中包含你想要进行多重比较的变量。
3. 执行多重比较分析3.1 选择“分析”菜单在SPSS软件的顶部菜单栏中,选择“分析”菜单。
3.2 选择“比较手段”选项在“分析”菜单中,选择“比较手段”选项。
3.3 选择“多重比较”子选项在“比较手段”选项中,选择“多重比较”子选项。
3.4 选择变量在“多重比较”选项中,将你想要进行多重比较的变量移动到右侧的“变量”框中。
可以使用左侧的箭头按钮实现变量的移动。
3.5 设置参数在“多重比较”选项中,可以设置参数,如显著性水平、调整方法等。
根据你的需求进行设置。
3.6 运行分析完成参数设置后,点击“确定”按钮运行多重比较分析。
SPSS 将会计算并显示多重比较的结果。
4. 解读结果分析完成后,你可以查看SPSS显示的多重比较结果。
通常,多重比较的结果包括各组间的均值差异、显著性水平等。
5. 导出结果如果你希望保存多重比较结果,可以使用SPSS提供的导出功能将结果保存为文件格式,如Excel、Word等。
6. 分享和报告最后,你可以将多重比较结果分享给他人,并在报告或论文中引用这些结果。
确保在引用结果时注明使用的数据分析软件和分析方法。
以上就是使用SPSS进行多个变量的多重比较的简要步骤。
使用SPSS进行多重比较可以帮助你更全面地了解各组间的差异情况,从而得到更准确的分析结果。
希望本文对你有所帮助!。
SPSS如何实现多个条件的多重比较

SPSS如何实现多个条件的多重比较在使用SPSS进行数据分析时,我们常常需要进行多个条件下的多重比较。
SPSS提供了一些简单的策略来实现这一目标。
下面将介绍一些常见的方法。
1. 单因素方差分析(One-way ANOVA)如果我们有一个自变量(组别)和一个因变量(数值型),并且希望比较多个组之间的均值差异,我们可以使用单因素方差分析。
在SPSS中,选择“分析”菜单下的“一元方差分析”选项。
然后将因变量移至“因变量”框中,将自变量移至“因子”框中。
点击“选项”,勾选“描述性统计”和“多重比较”。
2. 重复测量方差分析(Repeated Measures ANOVA)在某些情况下,我们可能有多个因变量,并且希望比较这些因变量在多个时间点或条件下的均值差异。
这时可以使用重复测量方差分析。
在SPSS中,选择“分析”菜单下的“一元方差分析”选项。
在“因变量”框中选择所有的因变量,将自变量(时间点或条件)移至“因子”框中。
点击“选项”,勾选“描述性统计”和“多重比较”。
3. 多元方差分析(Multivariate ANOVA)在某些情况下,我们可能有多个自变量,并且想要比较这些自变量在多个因变量上的均值差异。
这时可以使用多元方差分析。
在SPSS中,选择“分析”菜单下的“一元方差分析”选项。
在“因变量”框中选择所有的因变量,将自变量移至“因子”框中。
点击“选项”,勾选“描述性统计”和“多重比较”。
4. 进一步的多重比较分析除了上述方法,SPSS还提供了更多的多重比较分析方法,如LSD(最小显著差异法)、Bonferroni法、Tukey法等。
这些方法可在上述分析的结果中找到。
需要注意的是,在进行多重比较时,我们应该根据实际情况选择最适合的方法。
在选择方法时,应综合考虑样本大小、数据分布和研究假设等因素。
以上就是在SPSS中实现多个条件的多重比较的一些基本方法。
希望对您有帮助!。
用SPSS进行单因素方差分析和多重比较

SPSS——单因素方差分析单因素方差分析单因素方差分析也称作一维方差分析。
它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。
还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析,即进行均值的多重比较。
One-Way ANOVA过程要求因变量属于正态分布总体。
如果因变量的分布明显的是非正态,不能使用该过程,而应该使用非参数分析过程。
如果几个因变量之间彼此不独立,应该用Repeated Measure 过程。
[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量,数据如表1-1所示。
表1-1 不同水稻品种百丛中稻纵卷叶螟幼虫数图1-2 单因素方差分析窗口3)设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。
本例选择“幼虫”。
因素变量:选择一个因素变量进入“Factor”框中。
本例选择“品种”。
4)设置多项式比较单击“Contrasts”按钮,将打开如图1-3所示的对话框。
该对话框用于设置均值的多项式比较。
图1-3 “Contrasts”对话框定义多项式的步骤为:均值的多项式比较是包括两个或更多个均值的比较。
例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值,检验的假设H0:第一组均值的1. 1倍与第二组的均值相等。
单因素方差分析的“0ne-Way ANOVA”过程允许进行高达5次的均值多项式比较。
多项式的系数需要由读者自己根据研究的需要输入。
具体的操作步骤如下:①选中“Polynomial”复选项,该操作激活其右面的“Degree”参数框。
②单击Degree参数框右面的向下箭头展开阶次菜单,可以选择“Linear”线性、“Quadratic”二次、“Cubic”三次、“4th”四次、“5th”五次多项式。
③为多项式指定各组均值的系数。
方法是在“Coefficients”框中输入一个系数,单击Add按钮,“Coefficients”框中的系数进入下面的方框中。
SPSS如何实现多个因素的多重比较

SPSS如何实现多个因素的多重比较在统计分析中,当我们研究多个因素对结果变量的影响时,常常需要进行多重比较来确定不同因素之间是否存在显著差异。
SPSS 是一种功能强大的统计软件,可以帮助我们实现这种多重比较。
步骤1:创建数据集首先,我们需要在SPSS中创建一个包含所有变量的数据集。
确保变量在SPSS中的类型和测量水平正确,并在数据集中录入相应的数据。
步骤2:进行方差分析(ANOVA)接下来,我们需要进行方差分析来比较不同因素之间的差异是否显著。
在SPSS中,可以通过点击"分析"菜单,然后选择"一元方差分析"来进行方差分析。
在弹出的对话框中,将结果变量放入"因变量"框中,将因素变量放入"因子"框中,并设置其他相关参数。
步骤3:进行多重比较在进行方差分析后,SPSS会生成多个统计指标,包括组间差异的F值和p值。
为了进行多重比较,我们可以采取以下几种方法:LSD法(最小显著差异法)LSD法是最常用的多重比较方法之一。
它通过比较每两个组之间的平均值差异来确定是否存在显著差异。
在SPSS中,可以通过点击"分析"菜单,然后选择"比较手段",再选择"LSD"来进行LSD 法的多重比较。
Bonferroni校正Bonferroni校正也是一种常用的多重比较方法,它通过将显著性水平除以进行比较的组数来校正p值。
在SPSS中,可以通过点击"分析"菜单,然后选择"比较手段",再选择"Bonferroni"来进行Bonferroni校正的多重比较。
Tukey HSD法Tukey HSD法是另一种常用的多重比较方法,它通过比较每两个组之间的平均值差异,并根据样本大小和方差大小来确定是否存在显著差异。
在SPSS中,可以通过点击"分析"菜单,然后选择"比较手段",再选择"Tukey"来进行Tukey HSD法的多重比较。
SPSS如何实现多个样本的多重比较

SPSS如何实现多个样本的多重比较SPSS是一种数据分析软件,可以用于实现多个样本的多重比较。
多重比较是一种统计分析方法,用于比较多个样本之间的差异。
以下是使用SPSS进行多重比较的步骤:步骤一:导入数据首先,您需要在SPSS中导入包含多个样本数据的数据文件。
可以将数据文件保存为CSV或Excel格式,在SPSS中使用导入向导将其导入。
步骤二:选择统计方法在SPSS软件中,您可以使用不同的统计方法来进行多重比较。
以下是一些常用的方法:方差分析(ANOVA):适用于比较多个组的平均值是否有统计学上的显著差异。
___事后检验:适用于在方差分析中发现组间差异的情况下,进行多重比较。
Scheffe事后检验:适用于在方差分析中发现组间差异的情况下,进行多重比较。
LSD事后检验:适用于在方差分析中发现组间差异的情况下,进行多重比较。
Bonferroni校正:适用于在进行多个组间比较时控制整体显著性水平。
根据您的数据和研究设计选择适当的方法进行多重比较。
步骤三:进行多重比较一旦选择了合适的统计方法,您可以按照以下步骤在SPSS中进行多重比较:1.打开数据文件并选择要进行比较的变量。
2.运行相应的统计分析,例如方差分析,以获取组间差异的信息。
3.在得到结果后,选择进行多重比较的方法。
4.根据方法和操作菜单,输入相应的参数和选项。
5.运行多重比较分析,得到相应的结果。
步骤四:解读结果一旦多重比较分析完成,您将得到一些统计指标和结果。
您可以通过分析结果来回答研究问题或验证假设。
这些结果可能包括组间差异的显著性水平、置信区间和效应大小等。
请注意,完成多重比较之前,应该正确地进行数据清洗和预处理。
这将确保分析结果的准确性和可靠性。
以上是使用SPSS实现多个样本的多重比较的基本步骤。
根据您的具体研究问题和数据,可能需要进一步详细了解SPSS的相关功能和操作方法。
SPSS多重比较方式

SPSS 多重比较方法(信息摘自网络,仅供参考)(一)常用方法总结1.LSD法 最小显著差异法,公式为:它其实只是t检验的一个简单变形,并未对检验水准做出任何校正,只是在标准误的计算上充分利用了样本信息, 为所有组的均数统一估计出了一个更为稳健的标准误,其中MS误差是方差分析中计算得来的组内均方,它一般用于计划好的多重比较。
由于单次比较的检验水准仍为α,因此可认为LSD法是最灵敏的。
2.Bonferroni法 该法又称Bonferroni t检验,由Bonferroni提出。
用t检验完成各组间均值的配对比较,但通过设置每个检验的误差率来控制整个误差率。
若每次检验水准为α′,共进行m 次比较,当H0 为真时,犯Ⅰ类错误的累积概率α不超过mα′,既有Bonferroni不等式α≤mα′成立。
3.Sidak法 它实际上就是Sidak校正在LSD法上的应用,即通过Sidak校正降低每两次比较的Ⅰ类错误概率,以达到最终整个比较的Ⅰ类错误概率为α的目的。
即α′= 1 - (1 -α) 2 / k ( k - 1) ,计算t统计量进行多重配对比较。
可以调整显著性水平,比Bofferroni方法的界限要小。
4.Student-Newman-Keuls法( SNK法)它实质上是根据预先制定的准则将各组均数分为多个子集, 利用Studentized Range分布来进行假设检验,并根据所要检验的均数的个数调整总的Ⅰ类错误概率不超过α。
用student range分布进行所有各组均值间的配对比较。
如果各组样本含量相等或者选择了(差异较小的子集)的均值配对比较。
在该比较过程中,各组均值从大到小按顺序排列,最先比较最末端的差异。
5.Dunnett检验常用于多个试验组与一个对照组间的比较,根据算得的t值,误差自由度ν误差、试验组数k - 1以及检验水准α查Dunnett-t界值表,作出推断。
6.Duncan法(新复极差法)(SSR)指定一系列的“range”值,逐步进行计算比较得出结论。
SPSS如何实现多个样本率多重比较

SPSS如何实现多个样本率多重比较SPSS实现多组率的两两比较在医学研究中,多组率的比较是一个常见的问题。
通常,我们会将这些数据列成R×2表进行χ2检验,但是这种方法只能说明多个率之间存在统计学上的差异,而不能对两两之间的差异进行检验。
如果将数据分割成2×2表,虽然可以进行两两比较,但不宜使用独立四格表的显著界值。
因此,本文将介绍如何使用国际通用的SPSS软件实现该方法,并提供具体解决方案。
首先,我们需要有一组病例资料,如图1所示。
接下来,我们需要将这些数据录入SPSS中,按照图2的格式进行录入。
需要注意的是,我们要将各组按观察率从小到大排列,本例中有效率已经是升序排列,因此无需再排序。
经过交叉表对三组资料进行卡方检验后,我们可以得出具有统计学意义的结果。
下一步,我们需要进行两两比较。
具体操作步骤如下:①权变量:由于“数据”变量中的数据并非真正的每条记录的数据,而是频数资料,因此需要加权。
具体步骤为:Data→Weight Case→选择⊙weight case by单选按钮→将“数据”变量添加到Frequency Variable框内→OK。
②选择记录:根据杜养志法,我们需要分别将G1组与第Gi ( i = 2.3,⋯⋯k)组进行非独立2×2表。
具体步骤为:Data→Select Case→选择⊙If n is satisfied单选按钮→点击其下方的If⋯⋯按钮→在右上方框体内录入引号内的内容:“行变量= 1 or行变量= i”( i根据所比的具体组的序数而定)→continue→OK。
③卡方检验:XXX→Descriptive XXX→XXX→将“行变量”放入Row框体中→将“列变量”放入column框体中→Statistics→选择Chi-XXX→continue→OK。
④重复选择记录步骤,选择新的比较组,再行卡方检验,直到所有组均与G1比较过为止。
经过分析后,我们可以得到如下图所示的结果。
SPSS多重比较方法【精品】

SPSS 多重比较方法(信息摘自网络,仅供参考)(一)常用方法总结1. LSD法最小显著差异法,公式为:它其实只是t检验的一个简单变形,并未对检验水准做出任何校正,只是在标准误的计算上充分利用了样本信息, 为所有组的均数统一估计出了一个更为稳健的标准误,其中MS误差是方差分析中计算得来的组内均方,它一般用于计划好的多重比较。
由于单次比较的检验水准仍为α,因此可认为LSD法是最灵敏的。
2. Bonferroni法该法又称Bonferroni t检验,由Bonferroni提出。
用t检验完成各组间均值的配对比较,但通过设置每个检验的误差率来控制整个误差率。
若每次检验水准为α′,共进行m 次比较,当H0 为真时,犯Ⅰ类错误的累积概率α不超过mα′,既有Bonferroni不等式α≤mα′成立。
3. Sidak法它实际上就是Sidak校正在LSD法上的应用,即通过Sidak校正降低每两次比较的Ⅰ类错误概率,以达到最终整个比较的Ⅰ类错误概率为α的目的。
即α′=1 - (1 -α)2 / k ( k - 1) ,计算t统计量进行多重配对比较。
可以调整显著性水平,比Bofferroni方法的界限要小。
4. Student-Newman-Keuls法( SNK法)它实质上是根据预先制定的准则将各组均数分为多个子集, 利用Studentized Range分布来进行假设检验,并根据所要检验的均数的个数调整总的Ⅰ类错误概率不超过α。
用student range分布进行所有各组均值间的配对比较。
如果各组样本含量相等或者选择了(差异较小的子集)的均值配对比较。
在该比较过程中,各组均值从大到小按顺序排列,最先比较最末端的差异。
5. Dunnett检验常用于多个试验组与一个对照组间的比较,根据算得的t值,误差自由度ν误差、试验组数k - 1以及检验水准α查Dunnett-t界值表,作出推断。
6. Duncan法(新复极差法)(SSR)指定一系列的“range”值,逐步进行计算比较得出结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SPSS 多重比较方法(信息摘自网络,仅供参考)(一)常用方法总结1.LSD 法最小显著差异法 ,公式为 :它其实只是 t 检验的一个简单变形 ,并未对检验水准做出任何校正 ,只是在标准误的计算上充分利用了样本信息 , 为所有组的均数统一估计出了一个更为稳健的标准误 ,其中 MS 误差是方差分析中计算得来的组内均方 ,它一般用于计划好的多重比较。
由于单次比较的检验水准仍为α,因此可认为 LSD 法是最灵敏的。
2.Bonferroni 法该法又称 Bonferroni t 检验 ,由 Bonferroni 提出。
用 t 检验完成各组间均值的配对比较,但通过设置每个检验的误差率来控制整个误差率。
若每次检验水准为α′,共进行 m 次比较 ,当 H0为真时 ,犯Ⅰ类错误的累积概率α不超过 mα′,既有 Bonferroni 不等式α≤ mα′成立。
3.Sidak 法它实际上就是 Sidak 校正在 LSD 法上的应用 ,即通过 Sidak 校正降低每两次比较的Ⅰ类错误概率 ,以达到最终整个比较的Ⅰ类错误概率为α的目的。
即α′ =1 - (1 - α )2 / k ( k- 1) ,计算 t 统计量进行多重配对比较。
可以调整显著性水平,比 Bofferroni 方法的界限要小。
4.Student-Newman-Keuls 法 ( SNK 法)它实质上是根据预先制定的准则将各组均数分为多个子集, 利用 StudentizedRange 分布来进行假设检验 ,并根据所要检验的均数的个数调整总的Ⅰ类错误概率不超过α。
用 student range 分布进行所有各组均值间的配对比较。
如果各组样本含量相等或者选择了(差异较小的子集)的均值配对比较。
在该比较过程中,各组均值从大到小按顺序排列,最先比较最末端的差异。
5.Dunnett 检验常用于多个试验组与一个对照组间的比较,根据算得的t 值,误差自由度ν误差、试验组数 k - 1 以及检验水准α查 Dunnett-t 界值表 ,作出推断。
6.Duncan 法 (新复极差法 )( SSR )指定一系列的“range值”,逐步进行计算比较得出结论。
7.Tukey 检验使用学生化的范围统计量进行组间所有成对比较。
将试验误差率设置为所有成对比较的集合的误差率。
Tukey 的应用指征:(1)所有各组的样本数相等;( 2)各组样本均数之间的全面比较;( 3)可能产生较多的假阴性结论。
8.Scheffe 检验为均值的所有可能的成对组合执行并发的联合成对比较。
使用 F 取样分布。
可用来检查组均值的所有可能的线性组合,而非仅限于成对组合。
Scheffe 的应用指征:(1)各组样本数相等或不等均可以,但是以各组样本数不相等使用较多;( 2)如果比较的次数明显地大于均数的个数时, Scheffe 法的检验功效可能优于 Bonferroni 法和 Sidak 法。
如均数的个数等于或小于比较的次数,Bonferroni 方法较 Scheffe 方法佳。
(二)各种方法简介 -11.方差齐时,可选用以下方法:LSD :least significant difference检验法,指用t检验对各组均值间进行配对比较。
对多重比较误差率不进行调整。
Bonferroni :用 t 检验对各组间均值进行配对比较,通过设置每个检验的误差率来控制整个误差率。
Sigdk :为计算 t 统计量进行多重配对比较。
可以调整显著性水平,比 Bonferroni 方法的界限要小。
Scheffe :为对所有可能的配对组合进行同步配对比较。
可以同时检验所有均数的线性组合。
不单纯是配对均值的比较。
R-E-G-W F:为作Ryan-Einot-Gabriel-Welsch F检验法,用 F 检验进行多重比较检验。
R-E-G-W Q:为作Ryan-Einot-Gabriel-Welsch检验法,用t 化极差进行多重配对比较。
S-N-K :为 Student-Newman-Keuls检验法,用t化极差分布进行所有各组均值间的配对比较。
如果各组样本含量相等或者选择了用所有各组样本含量的调和平均数进行样本量估计时,用逐步过程进行齐次子集(差异较小的子集)的均值配对比较。
在该比较过程中,各组均值从大到小的顺序排列。
最先比较极端的差异。
Tukey :为作 Tukey's honestly significant difference检验法,用t化极差统计量进行所有组间均值的配对比较,用所有配对比较误差率作为实验误差率。
Tukey's-b :用 t 化极差分布进行组间均值的配对比较。
其精确值为前两种检验相应值的平均值。
Duncan :为作 Duncan's multiple range检验法指定一系列的t 化极差值,逐步进行计算比较得出结论。
Hochberg's GT2 :用正态最大系数进行多重比较。
Gabriel :用正态标准系数进行配对比较,在单元数较大时,这种方法较自由。
Waller-Duncan :用 t 统计量进行多重比较检验。
使用Bayesian 逼近。
Dunnett :用于多个处理组与一个对照组配对比较。
选定此方法后,激活下面的Control categories 框,选择对照组,有两个选项 Lase(默认选项)和 First 。
Test 框内选择检验的单双侧。
选项 2-side 表示双侧检验(默认选项);选项<control 为单侧检验表示处理组均数小于对照组均数;选项 >control 为单侧检验表示处理组均数大于对照组均数。
2.方差不齐时可以选用以下方法:Tamhane's T2 : t 检验进行配对比较。
Dunnett's T3 :t 化最大值下的配对比较。
Games-Howell :方差不具齐次性时的配对比较,方法较灵活。
Dunnett's C :t 化极差下的配对比较。
注:在 LSD 以及 Duncan 法的计算结果的表示方法为把差异没有显著性意义的比较组列在同一列里。
没有列出的其余各比较组之间差异均有显著性意义。
(三)各种方法简介 -21.假定方差齐性?LSD. 使用 t 检验执行组均值之间的所有成对比较。
对多个比较的误差率不做调整。
LSD 法侧重于减少第二类错误,此法精度较差,易把不该判断为显著的差异错判为显著,敏感度最高。
LSD 法的使用:在进行试验设计时就确定各处理只是固定的两个两个相比,每个处理平均数在比较中只比较一次。
例如,在一个试验中共有 4 个处理,设计时已确定只是处理 1 与处理2、处理 3 与处理 4(或 1 与3、2 与 4;或 1 与4、2 与 3)比较,而其它的处理间不进行比较。
因为这种比较形式实际上不涉及多个均数的极差问题,所以不会增大犯 I 型错误的概率。
?Bonferroni. Bonferroni 提出,设 H0为真,如果进行 m 次显著性水准为α的假设检验时,犯Ⅰ类错误的累积概率α’不超过 mα,即有 Bonferroni 不等式α’≤ mα成立。
所以令各次比较的显著性水准为 a=0.05 /m, 并规定 P≤ 0.05/ m 时拒绝 H0,基于这样的做法,就可以把Ⅰ 类错误的累积概率控制在 0.05 。
这种对检验水准进行修正的方法叫做Bonferroni 调整(Bonferroni adjustment) 法,简称 Bonferroni 法。
使用 t 检验在组均值之间执行成对比较,但通过将每次检验的错误率设置为实验性质的错误率除以检验总数来控制总体误差率。
这样,根据进行多个比较的实情对观察的显著性水平进行调整。
换句话来说, Bonferroni 法由 LSD 修正而来,通过设置每个检验的α水准来控制总的α水准。
但是比较的次数越多,比较的结果越保守。
Bonferroni 法的应用指征:(1)各组的样本数无论相等还是不等;(2)计划好的某两个组间或几个组间作两两比较;(4)当比较次数不多时, Bonferroni 法的效果较好;(5)但当比较次数较多 (例如在 10 次以上 )时,则由于其检验水准选择得过低,结论偏于保守,犯Ⅱ类错误的概率增加,即出现较多的假阴性结果;(6)Bonferroni 法比 LSD 法、 Duncan 法、 SNK 法偏于保守,不过,它比 Tukey 法、 Scheffe 法要敏感。
?Sidak. 基于 t 统计量的成对多重比较检验。
Sidak 调整多重比较的显著性水平,并提供比 Bonferroni 更严密的边界。
?Scheffe. (最常用,不需要样本数目相同)为均值的所有可能的成对组合执行并发的联合成对比较。
使用 F 取样分布。
可用来检查组均值的所有可能的线性组合,而非仅限于成对组合。
Scheffe 的应用指征:(1)各组样本数相等或不等均可以,但是以各组样本数不相等使用较多;(2)如果比较的次数明显地大于均数的个数时, Scheffe 法的检验功效可能优于 Bonferroni 法和 Sidak法。
如均数的个数等于或小于比较的次数,Bonferroni方法较Scheff ’e 方法佳。
? R-E-G-W F.基于 F 检验的Ryan-Einot-Gabriel-Welsch多步进过程。
? R-E-G-W Q. 基于学生化范围的Ryan-Einot-Gabriel-Welsch多步进过程。
?S-N-K. 使用学生化的范围分布在均值之间进行所有成对比较。
它还使用步进式过程比较具有相同样本大小的同类子集内的均值对。
均值按从高到低排序,首先检验极端差分。
?Tukey. (最常用,需要样本数目相同)使用学生化的范围统计量进行组间所有成对比较。
将试验误差率设置为所有成对比较的集合的误差率。
Tukey 的应用指征:( 1)所有各组的样本数相等;(2)各组样本均数之间的全面比较;(3)可能产生较多的假阴性结论。
?Tukey's b. 使用学生化的范围分布在组之间进行成对比较。
临界值是 Tukey's真实显著性差异检验的对应值与Student-Newman-Keuls的平均数。
?Duncan. 使用与 Student-Newman-Keuls 检验所使用的完全一样的逐步顺序成对比较,但要为检验的集合的错误率设置保护水平,而不是为单个检验的错误率设置保护水平。
使用学生化的范围统计量。
? Hochberg's GT2. 使用学生化最大模数的多重比较和范围检验。
与Tukey's 真实显著性差异检验相似。
?Gabriel. 使用学生化最大模数的成对比较检验,并且当单元格大小不相等时,它通常比Hochberg's GT2更为强大。
