大物练习题
大物习题册答案及详解(山东理工大学大二上学期2020版)

4.如图所示,一点电荷q位于正立方体的A角上,则通过侧面abcd的电通量Φe=q/24ε0
考点: 高斯定理公式 (课本118页 6-18) 解法:1.建立一正方体高斯面(补7个如图正方体),使A点位于正中心
考点:电势是一个与引进电荷无关,完全由电场自身的性质和相对位置决定的物理量。电场中某点电势的大小与零 电势点的选取有关。
2.在边长为a的正方体中心处放置一电量为Q的点电荷,设无穷远处为电势零点,则在一个侧面的中心处的电势为
(B)
(A)Q/4πε0a
(B)Q/2πε0a
(C)Q/πε0a
(D)Q/2√2πε0a
q/(1/r-1/r0)/4πε0
考点:电势的计算
解法:U=∫
r0 r
E·dr
=∫
r0 qdr r 4πε0r
2
=q/(1/r-1/r0)/4πε0
(课本122页
6-29b)
பைடு நூலகம்
3.一质量为m、电量为q的小球,在电_场__力__作__用下,从电势为U的a点移动到电势为零的b点,若已知小球在b点的 速率为Vb,则小球在a点的速率Va=√Vb2-2qU/m
②均匀带电球面内的电势UP2=Q/4πε0R(课本123页例6-8结论得), ③UP=UP1+UP2.
6.在带电量为-Q的点电荷A的静电场中,将另一带电量为q的点电荷B从a点移到b点,a、b两点距离点电荷A的距 离分别为r1和r2,如图所示,则移动过程中电场力做的功为(C) (A)-Q(1/r1-1/r2)/4πε0 (B)qQ(1/r1-1/r2)/4πε0 (C)-qQ(1/r1-1/r2)/4πε0 (D)-qQ/4πε0(r2-r1) 考点:电场力的功 解法:Aeab=q(UA-UB)=q(-Q/4πε0r1— -Q/4πε0r2)=-qQ(1/r1-1/r2)/4πε0 (课本123页 6-31)
大物练习题

第十一章真空中的静电场1.如图所示,真空中一长为L的均匀带电细直杆,电荷为q,试求在直杆延长线上距杆的一端距离为d的P点的电场强度.LP2.一个点电荷位于一边长为a的立方体高斯面中心,则通过此高斯面的电通量为ˍˍˍ,通过立方体一面的电场强度通量是ˍˍˍ,如果此电荷移到立方体的一个角上,这时通过(1)包括电荷所在顶角的三个面的每个面电通量是ˍˍˍ,(2)另外三个面每个面的电通量是ˍˍˍ。
3.在场强为E的均匀静电场中,取一半球面,其半径为R,E的方向和半球的轴平行,可求得通过这个半球面的E通量是()A.ER2π B.R22πC. ER22π D. ER221π4.根据高斯定理的数学表达式⎰∑⋅=SqSE/dε可知下述各种说法中,正确的是()(A) 闭合面内的电荷代数和为零时,闭合面上各点场强一定为零.(B) 闭合面内的电荷代数和不为零时,闭合面上各点场强一定处处不为零.(C) 闭合面内的电荷代数和为零时,闭合面上各点场强不一定处处为零.(D) 闭合面上各点场强均为零时,闭合面内一定处处无电荷.5.半径为R的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E与距轴线的距离r的关系曲线为( )图11-2图11-3EOr (A)E ∝1/r6.如图所示, 电荷-Q 均匀分布在半径为R ,长为L 的圆弧上,圆弧的两端有一小空隙,空隙长为)(R L L <<∆∆,则圆弧中心O 点的电场强度和电势分别为( )A.R Q i L R L Q 0204,4πεπε-∆- B.RQ i L R L Q 02024,8πεεπ-∆- C.RQ i L R L Q 0204,4πεπε ∆ D.RL L Qi L R L Q 0204,4πεπε∆-∆-7.如图所示,两同心带电球面,内球面半径为r 1=5 cm ,带电荷q 1=3×10-8 C ;外球面半径为r 2=20 cm , 带电荷q 2=-6×108C ,设无穷远处电势为零,则空间另一电势为零的球面半径r = __________________8. 如图所示,一半径为a 的“无限长”圆柱面上均匀带电,其电荷线密度为λ.在它外面同轴地套一半径为b 的薄金属圆筒,圆筒原先不带电,但与地连接.设地的电势为零,则在内圆柱面里面、距离轴线为r 的P 点的场强大小和电势分别为( )(A) E =0,U =r a ln 20ελπ. (C) E =r 02ελπ,U =rb ln 20ελπ (B) E =0,U =a b ln 20ελπ (D) E =r 02ελπ,U =a b ln 20ελπ.图11-69.如图,在点电荷+Q ,-Q 产生的电场中,abcd 为同一直线上等间距的四个点,若将一点电荷+q 0由b 点移到d 点,则电场力( )A. 作正功;B. 作负功;C.不作功;D.不能确定10.说明下列各式的物理意义(1)l d E ⋅(2)l d E b a ⋅⎰ (3)l d E L ⋅⎰(4)S d E ⋅11.已知某静电场的电势函数)(14121222SI y y x x U --=,由场强和电势梯度的关系式可得点(2,3,0)处的场强E =ˍˍˍi +ˍˍˍj +ˍˍˍk (SI)a c +Q-Q 图11-9答案:1.()d L d q +π04ε 2. 00024,0,6,εεεq q q 3.A4.C5.C ⎪⎪⎩⎪⎪⎨⎧≥=≤=)( 22)( 220020R r R rr R R r r E ρπλπελερερ,或 6. A7. 10cm8.B9.A10. (1)l d E ⋅表示电场力对单位正电荷所做的元功。
大学基础教育《大学物理(上册)》真题练习试题 附解析

大学基础教育《大学物理(上册)》真题练习试题附解析姓名:______ 班级:______ 学号:______考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题(共10小题,每题2分,共20分)1、四根辐条的金属轮子在均匀磁场中转动,转轴与平行,轮子和辐条都是导体,辐条长为R,轮子转速为n,则轮子中心O与轮边缘b之间的感应电动势为______________,电势最高点是在______________处。
2、动量定理的内容是__________,其数学表达式可写__________,动量守恒的条件是__________。
3、图示曲线为处于同一温度T时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中曲线(a)是________气分子的速率分布曲线;曲线(c)是________气分子的速率分布曲线。
4、一条无限长直导线载有10A的电流.在离它 0.5m远的地方它产生的磁感强度B为____________。
一条长直载流导线,在离它1cm处产生的磁感强度是T,它所载的电流为____________。
5、若静电场的某个区域电势等于恒量,则该区域的电场强度为_______________,若电势随空间坐标作线性变化,则该区域的电场强度分布为 _______________。
6、一长为的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动。
抬起另一端使棒向上与水平面呈60°,然后无初转速地将棒释放,已知棒对轴的转动惯量为,则(1) 放手时棒的角加速度为____;(2) 棒转到水平位置时的角加速度为____。
()7、质量为M的物体A静止于水平面上,它与平面之间的滑动摩擦系数为μ,另一质量为的小球B以沿水平方向向右的速度与物体A发生完全非弹性碰撞.则碰后它们在水平方向滑过的距离L=__________。
大一物理习题及答案 (下)
(A) (B) .
(C) (D)
解:
二. 填空题:
1.一段导线被弯成圆心在O点、半径为R的三段圆弧 、 、 ,它们构成了一个闭合回路, 位于XOY平面内, 和 分别位于另两个坐标面中(如图)。均匀磁场 沿X轴正方向穿过圆弧 与坐标轴所围成的平面。设磁感应强度随时间的变化率为K(K>0),则闭合回路a b c a中
5.如图所示的一细螺绕环,它由表面绝缘的导线在铁环上密绕而成,每厘米绕10匝。当导线中的电流I为2.0A时,测得铁环内的磁感应强度的大小B为1.0T,则可求得铁环的相对磁导率 为(真空磁导率 ):[B]
(A) (B)
(C) (D)63.3
解:n=10匝/cm=1000匝/m
二.填空题:
1.铜的相对磁导率 ,其磁化率 ,它是抗磁性磁介质。 ∴
方向:
或:
(2)取顺时针方向为回路L的正方向.
, 的方向与L的正方向一致;
, 的方向与L的正方向相反.
4.如图所示,有一根长直导线,载有直流电流I,近旁有一个两条对边与它平行并与它共面的矩形线圈,以匀速度 沿垂直于导线的方向离开导线.设t=0时,线圈位于图示位置,求:
(1) 在任意时刻t通过矩形线圈的磁通量.
4.关于稳恒磁场的磁场强度 的下列几种说法哪个是正确的?[C]
(A) 仅与传导电流有关。(还与磁化电流有关)
(B)若闭合曲线内没有包围传导电流,则曲线上各点的 必为零。(闭合曲线外有传导电流)
(C)若闭合曲线上各点 均为零,则该曲线所包围传导电流的代数和为零。
高三物理大题练习题

高三物理大题练习题一、选择题1. 下列哪个物理量是标量?A. 力B. 速度C. 加速度D. 位移2. 以下哪个公式描述了牛顿第二定律?A. F = maB. F = mvC. F = msD. F = mp3. 下列哪个描述最准确地解释了动量?A. 物体所具有的质量B. 物体所具有的能量C. 物体改变运动状态的能力D. 物体运动的速度4. 以下哪个现象与牛顿第三定律相对应?A. 月球绕地球运动B. 弹簧的伸缩C. 车辆在路上行驶D. 飞机在空中飞行5. 在光的三原色中,红、绿和蓝分别对应于光的什么特性?A. 频率B. 能量C. 波长D. 速度二、填空题1. 物体自由下落的加速度近似等于 __________。
2. 一个球以10 m/s的初速度向上抛出,最高点的速度是__________。
3. 在抛体运动中,抛出速度的大小等于抛体回到地面时的__________。
4. 音速在哪种介质中传播速度最快? __________。
5. 根据质能方程E = mc^2,其中c代表光速,E代表能量,m代表__________。
三、解答题1. 描述牛顿第一定律。
2. 解释为什么冰上的摩擦力比地面上的小。
3. 列出至少两种能量转换的形式,并给出具体例子。
4. 解释为什么我们可以通过声音来判断物体的位置。
5. 谈谈光的折射现象,并解释为什么折射会发生。
以上为高三物理大题练习题,请您按照题号顺序回答。
祝你好运!。
04《大学物理学》刚体部分练习题(马)

《大学物理学》刚体部分学习材料一、选择题4-1.有两个力作用在有固定转轴的刚体上:(1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零; (2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零; (3)当这两个力的合力为零时,它们对轴的合力矩也一定是零; (4)当这两个力对轴的合力矩为零时,它们的合力也一定是零; 对上述说法,下述判断正确的是:( )(A )只有(1)是正确的; (B )(1)、(2)正确,(3)、(4)错误; (C )(1)、(2)、(3)都正确,(4)错误; (D )(1)、(2)、(3)、(4)都正确。
【提示:(1)如门的重力不能使门转动,平行于轴的力不能提供力矩;(2)垂直于轴的力提供力矩,当两个力提供的力矩大小相等,方向相反时,合力矩就为零】4-2.关于力矩有以下几种说法:(1)对某个定轴转动刚体而言,内力矩不会改变刚体的角加速度; (2)一对作用力和反作用力对同一轴的力矩之和必为零;(3)质量相等,形状和大小不同的两个刚体,在相同力矩的作用下,它们的运动状态一定相同。
对上述说法,下述判断正确的是:( )(A )只有(2)是正确的; (B )(1)、(2)是正确的; (C )(2)、(3)是正确的; (D )(1)、(2)、(3)都是正确的。
【提示:(1)刚体中相邻质元间的一对内力属于作用力和反作用力,作用点相同,则对同一轴的力矩和为零,因而不影响刚体的角加速度和角动量;(2)见上提示;(3)刚体的转动惯量与刚体的质量和大小形状有关,因而在相同力矩的作用下,它们的运动状态可能不同】3.一个力(35)F i j N =+作用于某点上,其作用点的矢径为m j i r )34(-=,则该力对坐标原点的力矩为 ( )(A )3kN m -⋅; (B )29kN m ⋅; (C )29kN m -⋅; (D )3kN m ⋅。
【提示:(43)(35)4302092935i j kM r F i j i j k k k =⨯=-⨯+=-=+=】4-3.均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴 转动,如图所示。
大物电磁学第三章习题静电场中的电介质

第三章 练习题一、选择题1、[ C ]关于D r的高斯定理,下列说法中哪一个是正确的?(A) 高斯面内不包围自由电荷,则面上各点电位移矢量D r为零.(B) 高斯面上D r 处处为零,则面内必不存在自由电荷. (C) 高斯面的D r通量仅与面内自由电荷有关.(D) 以上说法都不正确.2、[ D ]静电场中,关系式 0D E P ε=+r r r(A) 只适用于各向同性线性电介质. (B) 只适用于均匀电介质. (C) 适用于线性电介质. (D) 适用于任何电介质.3、[ B ]一导体球外充满相对介电常量为r ε的均匀电介质,若测得导体表面附近场强为E ,则导体球面上的自由电荷面密度0σ为:(A)0E ε. (B) E ε. (C) r E ε . (D) 0()E εε- .4、[ A ]一平行板电容器中充满相对介电常量为r ε的各向同性的线性电介质.已知介质表面极化电荷面密度为σ'±,则极化电荷在电容器中产生的电场强度的大小为:(A)0σε'. (B) 0r σεε'. (C) 02σε'. (D) rσε'. 5、[ B ]一平行板电容器始终与端电压一定的电源相联.当电容器两极板间为真空时,电场强度为0E r ,电位移为0D r,而当两极板间充满相对介电常量为r ε的各向同性的线性电介质时,电场强度为E r ,电位移为D r,则(A) 00,r E E D D ε==r rr r . (B) 00,r E E D D ε==r r r r.(C) 00,r r E E D D εε==r r r r . (D) 00,E E D D ==r r r r.6、 [ C ]一空气平行板电容器,两极板间距为d ,充电后板间电压为U 。
然后将电源断开,在两板间平行地插入一厚度为d/3的与极板等面积的金属板,则板间电压变为(A )3U . (B)13U . (C) 23U . (D U .7、[ B ]一空气平行板电容器充电后与电源断开,然后在两极板间充满某种各向同性、均匀电介质,则电场强度的大小E 、电容C 、电压U 、电场能量W 四个量各自与充入介质前相比较,增大(↑)或减小(↓)的情形为(A) E ↑,C ↑,U ↑,W ↑. (B) E ↓,C ↑,U ↓,W ↓. (C) E ↓,C ↑,U ↑,W ↓. (D) E ↑,C ↓,U ↓,W ↑.8、[ B ]真空中有“孤立的”均匀带电球体和一“孤立的”的均匀带电球面,如果它们的半径和所带的电荷都相等.则它们的静电能之间的关系是 (A) 球体的静电能等于球面的静电能. (B) 球体的静电能大于球面的静电能. (C) 球体的静电能小于球面的静电能.(D) 球体内的静电能大于球面内的静电能,球体外的静电能小于球面外的静电能. 9、[ B ]如图所示, 一球形导体,带有电荷q ,置于一任意形状的空腔导体中.当用导线将两者连接后,则与未连接前相比系统静电场能量将(A) 增大. (B) 减小. (C) 不变. (D) 如何变化无法确定.10、[ D ]图示为一均匀极化的各向同性电介质圆柱体,已知电极化强度为P ϖ,圆柱体表面上束缚电荷面密度0σ'=的地点是图中的(A) a 点. (B) b 点. (C) c 点. (D) d 点.二、填空题1、分子的正负电荷中心重合的电介质叫做无极分子电介质,在外电场作用下,分子的正负电荷中心发生相对位移,电介质的这种极化形式叫:____ __极化。
大物练习册答案
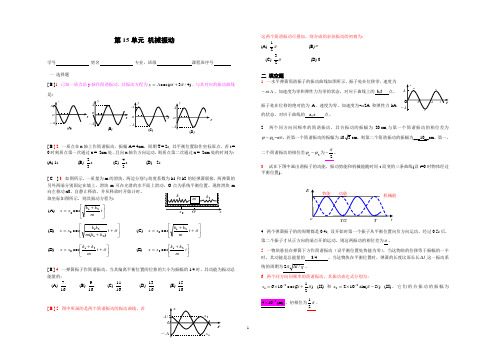
第15单元 机械振动学号 姓名 专业、班级 课程班序号一 选择题[ B ]1. 已知一质点沿y 轴作简谐振动,其振动方程为)4/3cos(πω+=t A y 。
与其对应的振动曲线是:[ B ] 2. 一质点在x 轴上作简谐振动,振幅A = 4cm ,周期T = 2s, 其平衡位置取作坐标原点。
若t = 0时刻质点第一次通过x = -2cm 处,且向x 轴负方向运动,则质点第二次通过x = -2cm 处的时刻为: (A) 1s (B)s 32 (C) s 34(D) 2s[ C ] 3. 如图所示,一质量为m 的滑块,两边分别与劲度系数为k1和k2的轻弹簧联接,两弹簧的另外两端分别固定在墙上。
滑块m 可在光滑的水平面上滑动,O 点为系统平衡位置。
现将滑块m 向左移动x0,自静止释放,并从释放时开始计时。
取坐标如图所示,则其振动方程为: ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210 ⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D)⎥⎦⎤⎢⎣⎡+=t mk k x x 210cos (E)[ E ] 4. 一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的: (A)167 (B) 169 (C) 1611 (D) 1613(E) 1615[ B ] 5. 图中所画的是两个简谐振动的振动曲线,若这两个简谐振动可叠加,则合成的余弦振动的初相为:(A) π21(B)π (C) π23(D) 0二 填空题1. 一水平弹簧简谐振子的振动曲线如图所示,振子处在位移零、速度为A ω-、加速度为零和弹性力为零的状态,对应于曲线上的 b,f 点。
振子处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性力-kA 的状态,对应于曲线的 a, e 点。
大学物理学练习题

第1单元 质点运动学一. 选择题1. 某质点作直线运动的运动学方程为x =3t -5t 3+ 6 (SI),则该质点作[ ]。
(A) 匀加速直线运动,加速度沿x 轴正方向; (B) 匀加速直线运动,加速度沿x 轴负方向; (C) 变加速直线运动,加速度沿x 轴正方向;(D) 变加速直线运动,加速度沿x 轴负方向。
2. 质点作曲线运动,r 表示位置矢量,v 表示速度,a表示加速度,S 表示路程,t a 表示切向加速度,下列表达式中[ ]。
(1) a t d /d v , (2) v t /r d d , (3) v t S d /d , (4) t a t d /d v。
(A) 只有(1)、(4)是对的; (B) 只有(2)、(4)是对的;(C) 只有(2)是对的; (D) 只有(3)是对的。
3. 一质点在平面上运动,已知质点位置矢量的表示式为 j bt i at r 22 (其中a 、b 为常量), 则该质点作[ ]。
(A) 匀速直线运动; (B) 变速直线运动; (C) 抛物线运动; (D)一般曲线运动。
4. 一小球沿斜面向上运动,其运动方程为s=5+4t t 2(SI), 则小球运动到最高点的时刻是[ ]。
(A) t=4s ; (B) t=2s ; (C) t=8s ; (D) t=5s 。
5. 一质点在xy 平面内运动,其位置矢量为j t i t r ˆ)210(ˆ42(SI ),则该质点的位置矢量与速度矢量恰好垂直的时刻为[ ]。
(A) s t 2 ; (B )s t 5; (C )s t 4 ; (D )s t 3 。
6. 某物体的运动规律为t k t 2d /d v v ,式中的k 为大于零的常量。
当0 t 时,初速为v 0,则速度v 与时间t 的函数关系是[ ]。
(A) 0221v vkt ; (B) 0221v v kt ; (C) 02121v v kt ; (D) 02121v vkt 。
大物习题

;。
3.一空气平行板电容器,电容为C,两极板间距离为d。充电后,两极板间相互作用力为F,则两极板间的电势差为______________,极板上的电量为______________。
4.一电容为C的空气平行板电容器,接上电源充电至端电压为V后与电源断开。若把电容器的两个极板的间距增大至原来的3倍,则外力所做的功为。
(3)若外球接地, 和 为多少?(4)若内球接地, 和 为多少?
2.两个同心的薄金属球壳,内、外半径分别为 和 。球壳之间充满两层均匀电介质,其相对电容率分别为 和 ,两层电介质的分界面半径为 。设内球壳带有电荷 ,求电位移、场强分布和两球壳之间的电势差。
3.在极板间距为d的空气平行板电容器中,平行于极板插入一块厚度为 、面积与极板相同的金属板后,其电容为原来电容的多少倍?如果平行插入的是相对电容率为 的与金属板厚度、面积均相同的介质板则又如何?
2.在真空中,电流I由长直导线1沿垂直bc边方向经a点流入一电阻均匀分布的正三角形线框,再由b点沿平行ac边方向流出,经长直导线2返回电源,如图3-4所示。三角形框每边长为l,则在该正三角框中心O点处磁感应强度的大小 。
3.在一根通有电流I的长直导线旁,与之共面地放着一个长、宽各为a和b的矩形线框,线框的长边与载流长直导线平行,且二者相距为b,如图3-5所示。在此情形中,线框内的磁通量 ______________。
2.如图所示,一半径为R的半圆环,右半部均匀带电 ,左半部均匀带电 。问半圆环中心O点的电场强度大小为多少?方向如何?
3.图示为一个均匀带电的球层,其电荷体密度为,球层内表面半径为R1,外表面半径为R2。设无穷远处为电势零点,求该带电系统的场强分布和空腔内任一点的电势。
4.两个带等量异号电荷的均匀带电同心球面,半径分别为 和 。已知两者的电势差为450 V,求内球面上所带的电荷。
《大学物理A1》试练习题及答案

《大学物理A1》试练习题及答案力学部分一、选择题1.某质点作直线运动的运动学方程为x =3t -5t 3 + 6 (SI),则该质点作 DA.匀加速直线运动,加速度沿x 轴正方向.B.匀加速直线运动,加速度沿x 轴负方向.C.变加速直线运动,加速度沿x 轴正方向.D.变加速直线运动,加速度沿x 轴负方向.2.某一滑雪装置,其在水平面上的运动学方程为x =3t 2-5(SI),则该质点作(a=6)AA.匀加速直线运动,加速度沿x 轴正方向.B.匀加速直线运动,加速度沿x 轴负方向.C.匀速直线运动,加速度沿x 轴正方向.D.匀速直线运动,加速度沿x 轴负方向.3.一质点沿x 轴作直线运动,其v -t 曲线如图所示,如t =0时,质点位于坐标原点,则t =4.5 s 时,质点在x 轴上的位置为 B A.5m . B.2m .C.0.D.-2 m . 4.一质点在平面上由静止开始运动,已知质点位置矢量的表示式为 j bt i at r 22+=(其中a 、b 为常量), 则该质点作 BA.匀速直线运动.B. 变速直线运动.C. 抛物线运动.D.一般曲线运动.5.一质点在x 轴上运动,其坐标与时间的变化关系为x =4t-2t 2,式中x 、t 分别以m 、s 为单位,则4秒末质点的速度和加速度为 ( B )A.12m/s 、4m/s 2;B.-12 m/s 、-4 m/s 2 ;C.20 m/s 、4 m/s 2 ;D.-20 m/s 、-4 m/s 2;6.一质点在y 轴上运动,其坐标与时间的变化关系为x =4t 2-2t ,式中x 、t 分别以m 、s 为单位,则2秒末质点的速度和加速度为 ( B )A.14m/s 、-8m/s 2;B.-14 m/s 、-4 m/s 2 ;C.14 m/s 、8m/s 2 ;D.-14 m/s 、-8 m/s 2;7.下列哪一种说法是正确的 C -12A.运动物体加速度越大,速度越快B.作直线运动的物体,加速度越来越小,速度也越来越小C.切向加速度为正值时,质点运动加快D.法向加速度越大,质点运动的法向速度变化越快8.下列哪一个实例中物体和地球构成的系统的机械能不守恒? CA.物体作圆锥摆运动.B.抛出的铁饼作斜抛运动(不计空气阻力).C.物体在拉力作用下沿光滑斜面匀速上升.D.物体在光滑斜面上自由滑下. 9.用水平压力F 把一个物体压着靠在粗糙的竖直墙面上保持静止.当F 逐渐增大时,物体所受的静摩擦力f BA.恒为零.B.不为零,但保持不变.C.随F 成正比地增大.D.开始随F 增大,达到某一最大值后,就保持不变10.谐振动过程中,动能和势能相等的位置的位移等于 A.4A ± B. 2A ± C. 23A ± D. 22A ± 11.质量为20 g 的子弹沿X 轴正向以 500 m/s 的速率射入一木块后,与木块一起仍沿X 轴正向以50 m/s 的速率前进,在此过程中木块所受冲量的大小为 AA.9 N·s . B .-9 N·s .C.10 N·s .D.-10 N·s .12.一质点作匀速率圆周运动时 CA.它的动量不变,对圆心的角动量也不变。
大物习题课练习1

E Ⅱ
EⅢ
I 有 电场的分布为: 由 E 0 Q 在Ⅰ区, EⅠ 方向向左 2 0 S Q 在Ⅱ区, EⅡ 方向向右 2 0 S Q 在Ⅲ区, E Ⅲ 方向向右 2 0 S
Ⅱ
II I
Q Q E1 E2 20 2S 20 2S
1 2 3 4
(2)如果把第二块金属板接地 ,其右表面上的电荷就会分散到 地球表面上,所以
R
4
B
14.一半径为R的无限长半圆柱面导体,其上电流与其轴 线上一无限长直导线的电流等值反向。电流I在半圆柱面 上均匀分布。(1)求轴线上导线单位长度所受的力;(2)若 将另一无限长直导线(通有大小、方向与半圆柱面相同的 电流I)代替圆柱面,产生同样的作用力,该导线应放在 何处? 解:(1)在半圆柱面上沿母线取宽为dl dl 的窄条,其电流 d dI I I R dI dl d x R 它在轴线上一点产生的 I dB I 磁感应强度: y
qH e
qO 2e
1 m H mO 16
1 2 mH vH eU 2 1 1 2 2 m H v H mO v O 2 4
1 2 mO v O 2eU 2
vH mO 2 2 vO 2mH
3. 求无限长均匀带电圆柱面的电场强度(轴对称) 已知:线电荷密度
R + + + + + + + S + + +
对称性分析:E 垂直柱面
选取闭合的柱型高斯面
rR
s ( 柱)
E ds
s ( 上底)
E ds
E ds 0
S
s ( 下底)
大物习题

第一次 质点运动学、牛顿运动定律一、 选择题1.瞬时速度 v 的大小 v可以用下列哪个式子来表示: [ ]A .dt drB .dt r dC . dt r dD . 222⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛dt dz dt dy dt dx2.一质点沿X 轴作直线运动,其v-t 曲线如图所示,t =0时,质点于坐标原点,则t =4.5s 时质点在X 轴上位置为: [ ]A .0mB .5mC .-2mD .2m3. 质点作曲线运动,r (x,y)表示位置矢量,S 表示路程,下列表达式正确是:[ ]A.(1、2、4)B.(3、4、5)C.(1、3、6)D.(2、5、6)1.dv a dt τ=;2.dt dr =υ;3.dt ds =υ;4.dv a dt =;5.22d r a dt =;6.222dv v dt R ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭=a 4.下列说法中正确的是:[ ]A .物体在作曲线运动时,有可能在某时刻的法向加速度为零.B .斜上抛物体,在最高点处的速度最小,加速度最大.C .不管加速度如何,平均速率表达式总可以写成:2/)(21v v v +=.D .物体运动加速度的大小越大,则速率越大.5.某质点作直线运动的运动学方程为3356x t t=-+ (SI),则该质点作 [ ]A .匀加速直线运动,加速度沿x 轴正方向.B .匀加速直线运动,加速度沿x 轴负方向.C .变加速直线运动,加速度沿x 轴正方向.D .变加速直线运动,加速度沿x 轴负方向.6. 一个原来静止的小球受到图示的两个力的作用,设力的作用时间为5秒,问下列哪种情况下小球最终获得的速率最大。
[ ]A .N F 8F ,6N 21==;B .N F 8F 21== ;C .N F 8F ,021==D .0F ,6N 21==F .7.用细绳系一小球使之于竖直平面内做圆周运动。
下面说法正确的是[ ]A .小球在任意位置都有切向加速度;B .小球在任意位置都有法向加速度;C .小球在任意位置绳子拉力和重力合力是惯性离心力的反作用力;D .小球运动到最高点时将受到重力、拉力和离心力的作用.二、填空题1. 质点以速度 )/( 3 2s m t t v +=沿 X 轴做直线运动, 2 s t =时,质点位于 5 m x =处,则该质点的运动学方程为:_____________________-______。
大物习题

选择1、对质点系有下列几种说法:(1)质点系总动量的改变与内力无关;(2)质点系的总动能与内力无关;(3)质点系机械能的改变与保守内力无关。
对于这些说法,下述结论中正确的是(B)B、只有(1)、(3)是正确的2、对质点系的动量和机械能有下述三种说法。
(1)不受外力作用的系统,它的动量和机械能必然同时守恒;(2)内力是保守力的系统,当所受的合外力为零时,其机械能必然守恒;(3)只有保守内力而无外力作用的系统,它的动量和机械能必然守恒。
对于这些说法,下列结论中正确的是(C)C、只有(3)是正确的3、一力学系统由两个质点组成,它们之间只有引力作用。
若两质点所受外力的矢量和为零,则此系统中(C)C、动量守恒,但机械能和对一固定点的角动量是否守恒还不能断定4、关于角动量有以下四种说法,其中正确的是(B)B、一质点做直线运动,相对于直线上的任一点,质点的角动量一定为零5、一个人站在旋转平台的中央,两臂侧平举,整个系统以2πrad/s的角速度旋转,转动惯量为6.0kg·m平方;如果将两臂收回,该系统的转动惯量变为2.0kg·m平方。
此时系统的转动动能与原来的转动动能之比为(C)C、36、对一绕固定水平O轴匀速转动的转盘,沿如图所示的同一水平直线从相反方向射入两粒质量相同、速率相等的子弹,并留在盘中。
则子弹射入后的转盘的角速度应(B)B、减小第9页7、均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动,如图所示。
今使棒从水平位置由静止开始下落。
在棒摆动到竖直位置的过程中,应有(A)A、角速度从小到大,角加速度从大到小8、关于力矩有以下几种说法,其中正确的是(B)B、作用力和反作用力对同一轴的力矩之和必为零9、在相对论的时空观中,以下的判断哪一个是正确的(C)C、在一个惯性系中,两个同时又同地的事件,在另一惯性系中一定同时又同地10、根据狭义相对论观点,下列说法正确的是(C)C、如果光速是无限大,同时的相对性就不会存在了11、根据狭义相对论,有下列几种说法:(1)所有惯性系统对物理基本规律都是等价的;(2)在真空中,光的速度与光的频率、光源的运动状态无关;(3)在任何惯性系中,光在真空中沿任何方向的传播速度都相同。
大物第一章习题及答案

第一章章节测试题一、选择题(每小题3分,共计15分)1.以下四种运动形式中,a保持不变的运动是 ( D ) (A) 单摆的运动 (B) 匀速率圆周运动 (C) 行星的椭圆轨道运动 (D) 抛体运动2.一物体从某一确定高度以0v 的速度水平抛出,已知它落地时的速度为 t v,那么它运动的时间是 ( C ) (A) gt 0v v (B) gt 20v v(C) gt2/1202v v(D) gt22/1202v v3.下列说法中,哪一个是正确的? ( C )(A) 一质点在某时刻的瞬时速度是2 m/s ,说明它在此后1 s 内一定要经过2 m 的路程 (B) 斜向上抛的物体,在最高点处的速度最小,加速度最大 (C) 物体作曲线运动时,有可能在某时刻的法向加速度为零 (D) 物体加速度越大,则速度越大4.一质点沿x 轴运动,其运动方程为2353x t t ,其中t 以s 为单位。
当t=2s 时,该质点正在 ( A ) (A )加速 (B )减速 (C )匀速 (D ) 静止5.下列关于加速度的说法中错误的是 ( C ) (A )质点加速度方向恒定,但其速度的方向仍可能在不断的变化着 (B )质点速度方向恒定,但加速度方向仍可能在不断的变化着(C )某时刻质点加速度的值很大,则该时刻质点速度的值也必定很大(D )质点作曲线运动时,其法向加速度一般不为零,但也有可能在某时刻法向加速度为零 二、填空题(每空2分,共计20分)1.一辆作匀加速直线运动的汽车,在6 s 内通过相隔60 m 远的两点,已知汽车经过第二点时的速率为15 m/s ,则汽车通过第一点时的速率v 1 =__5.00m/s_。
2.质点沿半径为R 的圆周运动,运动学方程为 223t ,则t时刻质点的法向加速度大小为a n = 16Rt 2。
3.一质点沿x 方向运动,其加速度随时间变化关系为:a = 3+2 t ,如果初始时刻质点的速度v 0为5 m/s ,则当t为3s 时,质点的速度 v = 23m/s 。
大物练习题

e2 4pe0r 2
— —
R1 O
r
—
R2
— —
—
两金属圆筒间的电势差为
U Edr ln R2
2 0 R1
—
电子作圆周运动,必有
eE m v 2 eU / ln R2
rr
R1
由上式得
U mv2 ln R2 35.5V e R1
练习14. 如图所示,在静电实验装置中,有一均匀带电圆环,内外半 径分别为R1 0.4m,R2 0.8m,总电量为q -6107 C。现有一电 子沿轴线从无限远处射向带负电的圆环。欲使电子能穿过圆环,它 的初始动能至少多大?
=
me
v2 r
v=
e 4pe0mer
M
=
BIS
=
B
ve 2pr
pr 2
=
Ber 2
v
M = 1 Be2 4
r
pe 0
me
练习2. 1、2是两个完全相同的空气电容器,将其充Байду номын сангаас后与电
源断开,再将一块各向同性均匀电介质插入电容器1的两极板
间,则电容器2的电压U2 将 大、减小或不变)
,电场能量W2 将
。(填增
减少
练习13.如图所示,将半径分别为R1=5cm和R2=10cm的两个很长 的共轴金属圆筒分别连接到直流电源的两极上。今使一电子
大物(2)期末复习

11练习一 静电场中的导体三、计算题1. 已知某静电场在xy 平面内的电势函数为U =Cx/(x 2+y 2)3/2,其中C 为常数.求(1)x 轴上任意一点,(2)y 轴上任意一点电场强度的大小和方向.解:. E x =U/x=C [1/(x 2+y 2)3/2+x (3/2)2x /(x 2+y 2)5/2]= (2x2y 2)C /(x 2+y 2)5/2E y =U/y=Cx (3/2)2y /(x 2+y 2)5/2=3Cxy /(x 2+y 2)5/2x 轴上点(y =0) E x =2Cx 2/x 5=2C /x 3 E y =0E =2C i /x 3y 轴上点(x =0) E x =Cy 2/y 5=C /y 3 E y =0E =C i /y 32.如图,一导体球壳A (内外半径分别为R 2,R 3),同心地罩在一接地导体球B (半径为R 1)上,今给A 球带负电Q , 求B 球所带电荷Q B 及的A 球的电势U A .静电场中的导体答案解: 2. B 球接地,有 U B =U =0, U A =U BAU A =(Q+Q B )/(40R 3)U BA =[Q B /(4)](1/R 21/R 1)得 Q B =QR 1R 2/( R 1R 2+ R 2R 3 R 1R3)U A =[Q/(40R 3)][1+R 1R 2/(R 1R 2+R 2R 3R 1R 3)]图22 =Q (R 2R 1)/[4(R 1R 2+R 2R 3R 1R 3)]练习二 静电场中的电介质三、计算题1. 如图所示,面积均为S =的两金属平板A ,B 平行对称放置,间距为d =1mm,今给A , B 两板分别带电 Q 1=×10-9C, Q 2=×10-9C.忽略边缘效应,求:(1) 两板共四个表面的面电荷密度1,2,3,4;(2) 两板间的电势差V =U A -U B .解:1. 在A 板体内取一点A , B 板体内取一点B ,它们的电场强度是四个表面的电荷产生的,应为零,有E A =1/(2)2/(20)3/(2)4/(2)=0E A =1/(2)+2/(20)+3/(2)4/(2)=0而 S (1+2)=Q 1 S (3+4)=Q 2有 1234=01+2+34=01+2=Q 1/S 3+4=Q 2/S解得1=4=(Q 1+Q 2)/(2S )=108C/m 22=3=(Q 1Q 2)/(2S )=108C/m 2两板间的场强 E=2/=(Q 1Q 2)/(2S )V=U A -U B ⎰⋅=BAl E d=Ed=(Q 1Q 2)d /(2S )=1000V四、证明题导体 图A Q 1图Q 21234331. 如图所示,置于静电场中的一个导体,在静电平衡后,导体表面出现正、负感应电荷.试用静电场的环路定理证明,图中从导体上的正感应电荷出发,终止于同一导体上的负感应电荷的电场线不能存在.解:1. 设在同一导体上有从正感应电荷出发,终止于负感应电荷的电场线.沿电场线ACB 作环路ACBA ,导体内直线BA 的场强为零,ACB 的电场与环路同向于是有=⋅⎰l E d l+⋅⎰ACBl E d ⎰⋅ABl E d 2=⎰⋅ACBlE d 0与静电场的环路定理=⋅⎰l E d l 0相违背,故在同一导体上不存在从正感应电荷出发,终止于负感应电荷的电场线.练习三 电容 静电场的能量三、计算题1. 半径为R 1的导体球带电Q ,球外一层半径为R 2相对电容率为r的同心均匀介质球壳,其余全部空间为空气.如图所示.求:(1)离球心距离为r 1(r 1<R 1), r 2(R 1<r1<R2), r 3(r 1>R 2)处的D 和E ;(2)离球心r 1, r 2, r 3,处的U ;(3)介质球壳内外表面的极化电荷. 解:1. (1)因此电荷与介质均为球对称,电场也球对称,过场点作与金属球同心的球形高斯面,有iSq0d ∑=⋅⎰S D4r 2D=q 0i当r=5cm <R 1, q 0i =0得 D 1=0, E 1=0 当r=15cm(R 1<r <R 1+d ) q 0i =Q=×108C 得D 2=Q /(4r 2)=×108C/m 2E 2=Q /(40rr 2)=×103N/C图R 2BA C当r=25cm(r>R1+d )q 0i=Q=×108C 得D3=Q/(4r2)=×108C/m2E3=Q/(40r2)=×104N/CD和E的方向沿径向.(2) 当r=5cm<R1时U1=⎰∞⋅r lE d⎰=R r r E d1⎰++d RRrE d2⎰∞++dRrE d3=Q/(40r R)Q/[40r(R+d)]+Q/[40(R+d)]=540V当r=15cm<R1时U2=⎰∞⋅r lE d⎰+=d RrrE d2⎰∞++dRrE d3=Q/(40r r)Q/[40r(R+d)]+Q/[40(R+d)]=480V当r=25cm<R1时U3=⎰∞⋅r lE d⎰∞=rrE d3=Q/(40r)=360V(3)在介质的内外表面存在极化电荷,P e=0E=0(r1)E =P e·n r=R处, 介质表面法线指向球心=P e·n =P e cos =0(r 1)Eq =S=0(r1) [Q /(40r R2)]4R2=(r1)Q/r=×108Cr=R+d处, 介质表面法线向外=P e·n =P e cos0=0(r1)Eq=S=0(r1)[Q /(40r(R+d)2]4(R+d)2=(r1)Q/r=×108C44552.两个相距很远可看作孤立的导体球,半径均为10cm ,分别充电至200V 和400V ,然后用一根细导线连接两球,使之达到等电势. 计算变为等势体的过程中,静电力所作的功. 解;2.球形电容器 C =4RQ 1=C 1V 1= 40RV 1 Q 2=C 2V 2= 4RV 2W 0=C 1V 12/2+C 2V 22/2=2R (V 12+V 22)两导体相连后 C =C 1+C 2=8RQ=Q 1+Q 2= C 1V 1+C 2V 2=40R (V 1+V 2)W=Q 2/(2C )= [4R (V 1+V 2)]2/(16R )=R (V 1+V 2)2静电力作功 A=W 0W=2R (V 12+V 22)R (V 1+V 2)2=R (V 1V 2)2=×107J练习六 磁感应强度 毕奥—萨伐尔定律三、计算题1. 如图所示, 一宽为2a 的无限长导体薄片, 沿长度方向的电流I 在导体薄片上均匀分布. 求中心轴线OO上方距导体薄片为a 的磁感强度.解:1.取宽为d x 的无限长电流元d I=I d x/(2a ) d B=0d I/(2r )=I d x/(4ar )d B x =d B cos =[0I d x/(4ar )](a/r )=I dx/(4r 2)= 0I d x/[4(x 2+a2)]xy d Bd IPr OO Ixy zP2a图66 d B y =d B sin =Ix d x/[4a (x 2+a 2)]()⎰⎰-+==aax x a x xI B B 2204d d πμ=[I/(4)](1/a )arctan(x/a )a a-=I/(8a )()⎰⎰-+==aay y ax a xIx B B 2204d d πμ=[I/(8a )]ln(x 2+a 2)a a-=02. 如图所示,半径为R 的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈覆盖住半个球面. 设线圈的总匝数为N ,通过线圈的电流为I . 求球心O 的磁感强度.解:2. 取宽为d L 细圆环电流, d I=I d N=I [N/(R/2)]R d =(2IN/)d d B=d Ir 2/[2(r 2+x 2)3/2]r=R sin x=R cosd B=NI sin 2 d /(R )⎰⎰==πππθθμ220d sin d RNI B B=0NI/(4R )练习七 毕奥—萨伐尔定律(续) 磁场的高斯定理三、计算题1.在无限长直载流导线的右侧有面积为S 1和S 2的两个矩形回路, 回路旋转方向如图所示, 两个回路与长直载流导线在同一平面内, 且矩形回路的一边与长直载流导线平行. 求通过两矩形回路的磁通量及通过S 1回路的磁通量与通过S 2回路的磁通量之比. 解: 1.取窄条面元d S =b d r ,O R 图图2aaaS 2S 1 bx d Bd I77面元上磁场的大小为B =0I /(2r ), 面元法线与磁场方向相反.有1=⎰-=aabIbdr r I 2002ln 2cos 2πμππμ 2=⎰-=aabI bdr r I 42002ln 2cos 2πμππμ 1/2=12. 半径为R 的薄圆盘均匀带电,总电量为Q . 令此盘绕通过盘心且垂直盘面的轴线作匀速转动,角速度为,求轴线上距盘心x 处的磁感强度的大小和旋转圆盘的磁矩. 解;2. 在圆盘上取细圆环电荷元d Q =2r d r , [=Q /(R 2) ],等效电流元为d I =d Q /T =2r d r/(2/)=r d r(1)求磁场, 电流元在中心轴线上激发磁场的方向沿轴线,且与同向,大小为 d B=d Ir 2/[2(x 2+r 2)3/2]=r 3d r /[2(x 2+r 2)3/2]()()()⎰⎰++=+=R Rxrx r r xr rr B 02322222002/32230d 42d σωμσωμ=()()()⎰+++R xrx r x r 0232222220d 4σωμ()()⎰++R xrx r x 023222220d 4σωμ=⎪⎪⎭⎫⎝⎛+++RR x r x xr 022202202σωμ =⎪⎪⎭⎫ ⎝⎛-++x x R x R R Q 222222220πωμ (2)求磁距. 电流元的磁矩 d P m =d IS=r d r r 2=r 2d r ⎰=R m dr r P 03πσω=R 4/4=QR 2/488 练习八 安培环路定律三、计算题1. 如图所示,一根半径为R 的无限长载流直导体,其中电流I 沿轴向流过,并均匀分布在横截面上. 现在导体上有一半径为R 的圆柱形空腔,其轴与直导体的轴平行,两轴相距为 d . 试求空腔中任意一点的磁感强度.解:1. 此电流可认为是由半径为R 的无限长圆柱电流I 1和一个同电流密度的反方向的半径为R 的无限长圆柱电流I 2组成.I 1=J R 2 I 2=J R2J =I/[ (R 2R2)]它们在空腔内产生的磁感强度分别为B 1=0r 1J/2 B 2=0r 2J/2方向如图.有 B x =B 2sin2B 1sin1=(J/2)(r 2sin2r 1sin1)=B y =B 2cos2+B 1cos1=(J/2)(r 2cos 2+r 1cos1)=(J/2)d所以 B = B y = 0dI/[2(R 2-R2)]方向沿y 轴正向2. 设有两无限大平行载流平面,它们的电流密度均为j ,电流流向相反. 求: (1) 载流平面之间的磁感强度; (2) 两面之外空间的磁感强度.解;2. 两无限大平行载流平面的截面如图.平面电流在空间产生的磁场为 B 1=J /2在平面①的上方向右,在平面①的下方向左; 电流②在空间产生的磁场为 B 2=J /2图O 2RdORI 1 I 2① ②OO Irr B B y xRRd在平面②的上方向左,在平面②的下方向右.(1) 两无限大电流流在平面之间产生的磁感强度方向都向左,故有B=B1+B2=0J(2) 两无限大电流流在平面之外产生的磁感强度方向相反,故有B=B1B2=0练习九安培力三、计算题1. 一边长a =10cm的正方形铜导线线圈(铜导线横截面积S=, 铜的密度=cm3), 放在均匀外磁场中. B竖直向上, 且B = 103T, 线圈中电流为I =10A . 线圈在重力场中求:(1) 今使线圈平面保持竖直, 则线圈所受的磁力矩为多少.(2) 假若线圈能以某一条水平边为轴自由摆动,当线圈平衡时,线圈平面与竖直面夹角为多少.解:1. (1) P m=IS=Ia2方向垂直线圈平面.线圈平面保持竖直,即P m与B垂直.有M m=P m×BM m=P m B sin(/2)=Ia2B=×10-4m N(2) 平衡即磁力矩与重力矩等值反向M m=P m B sin(/2-)=Ia 2B cosM G= M G 1 + M G2 + M G 3= mg(a/2)sin+ mga sin+ mg(a/2)sin =2(Sa)ga sin=2Sa2g sinBn/2mgmgmg991010Ia 2B cos =2Sa 2g sintan=IB/(2Sg )==152. 如图所示,半径为R 的半圆线圈ACD 通有电流I 2, 置于电流为I 1的无限长直线电流的磁场中, 直线电流I 1 恰过半圆的直径, 两导线相互绝缘. 求半圆线圈受到长直线电流I 1的磁力.解:2.在圆环上取微元I 2d l = I 2R d该处磁场为B =0I 1/(2R cos )I 2d l 与B 垂直,有d F= I 2d lB sin(/2)d F=0I 1I 2d/(2cos )d F x =d F cos =0I 1I 2d/(2)d F y =d F sin =0I 1I 2sin d/(2cos )⎰-=222102πππθμd I I F x =0I 1I 2/2因对称F y =0.故 F =0I 1I 2/2 方向向右.练习十 洛仑兹力三、计算题1. 如图所示,有一无限大平面导体薄板,自下而上均匀通有电流,已知其面电流密度为i (即单位宽度上通有的电流强度)(1) 试求板外空间任一点磁感强度的大小和方向.(2) 有一质量为m ,带正电量为q 的粒子,以速度v 沿平板法线方向向外运动. 若不计粒子重力.求:(A) 带电粒子最初至少在距板什么位置处才不与大平板碰撞. (B) 需经多长时间,才能回到初始位置.. 解:1. (1)求磁场.用安培环路定律得 B =i/2iv图I 1 I 2图I 1I 2Rx y d F在面电流右边B的方向指向纸面向里,在面电流左边B的方向沿纸面向外.(2) F =q v×B=m a qvB=ma n=mv2/R带电粒子不与平板相撞的条件是粒子运行的圆形轨迹不与平板相交,即带电粒子最初位置与平板的距离应大于轨道半径.R=mv/qB= 2mv/(0iq)(3) 经一个周期时间,粒子回到初始位置.即t=T=2R/v= 4m/(0iq)2. 一带电为Q质量为m的粒子在均匀磁场中由静止开始下落,磁场的方向(z轴方向)与重力方向(y 轴方向)垂直,求粒子下落距离为y 时的速率.并讲清求解方法的理论依据.解:2. 洛伦兹力Q v×B垂直于v,不作功,不改变v的大小;重力作功.依能量守恒有mv2/2=mgy,得v=(2gy)1/2.练习十一磁场中的介质三、计算题1. 一厚度为b的无限大平板中通有一个方向的电流,平板内各点的电导率为,电场强度为E,方向如图所示,平板的相对磁导率为r1,平板两侧充满相对磁导率为r2的各向同性的均匀磁介质,试求板内外任意点的磁感应强度.解:1. 设场点距中心面为x,因磁场面对称以中心面为对称面过场点取矩形安培环路,有⎰⋅l lH d=ΣI0 2LH=ΣI0(1)介质内,0<x<b/2. ΣI0=2x lJ=2x l E,有H=x E B=0r1H=0r1x E(2)介质外,x>b/2. ΣI0=b lJ=b l E,有H=b E/2 B=0r2H=0r2b E/2×EHHl111112122. 一根同轴电缆线由半径为R 1的长导线和套在它外面的半径为R 2的同轴薄导体圆筒组成,中间充满磁化率为m的各向同性均匀非铁磁绝缘介质,如图所示. 传导电流沿导线向上流去, 由圆筒向下流回,电流在截面上均匀分布. 求介质内外表面的磁化电流的大小及方向.解: 2. 因磁场柱对称 取同轴的圆形安培环路,有 ⎰⋅l l H d =ΣI 0在介质中(R 1r R 2),ΣI 0=I ,有2rH = I H = I /(2r )介质内的磁化强度M =mH =mI /(2r )介质内表面的磁化电流J SR 1= M R 1×n R 1= M R 1=mI /(2R 1)I SR 1=J SR 12R 1=mI (与I 同向)介质外表面的磁化电流J SR 2= M R 2×n R 2= M R 2=mI /(2R 2)I SR 2=J SR 22R 2=mI (与I 反向)练习十二 电磁感应定律 动生电动势三、计算题1. 如图所示,长直导线AC 中的电流I 沿导线向上,并以d I /d t = 2 A/s 的变化率均匀增长. 导线附近放一个与之同面的直角三角形线框,其一边与导线平行,位置及线框尺寸如图所示. 求此线框中产生的感应电动势的大小和方向.解: 1. 取顺时针为三角形回路电动势正向,得三角形面法线垂直纸面向里.取窄条面积微元20cm10cm5cm 图bBla图rrrbE图OI图R 1R 21313d S =y d x =[(a+b x )l/b ]d xm=⎰⋅S d S B=()⎰+-+⋅ba abldxx b a x I πμ20 =()⎥⎦⎤⎢⎣⎡-++b a b a b a bIl ln 20πμ εi =dm/d t=()dt dIa b a b a b b l ⎥⎦⎤⎢⎣⎡++-ln 20πμ =×10-8V负号表示逆时针2. 一很长的长方形的U 形导轨,与水平面成 角,裸导线可在导轨上无摩擦地下滑,导轨位于磁感强度B 垂直向上的均匀磁场中,如图所示. 设导线ab 的质量为m ,电阻为R ,长度为l ,导轨的电阻略去不计, abcd 形成电路. t=0时,v=0. 求:(1) 导线ab 下滑的速度v 与时间t 的函数关系; (2) 导线ab 的最大速度v m .解: 2. (1) 导线ab 的动生电动势为εi =lv×B ·d l=vBl sin(/2+)=vBl cos I i =εi /R = vBl cos /R方向由b 到a . 受安培力方向向右,大小为F =l(I i d l×B )= vB 2l 2cos /RF 在导轨上投影沿导轨向上,大小为F = F cos =vB 2l 2cos 2/R重力在导轨上投影沿导轨向下,大小为mg sinmg sin vB 2l 2cos 2/R=ma=m d v /d t dt=d v /[g sin vB 2l 2cos 2/(mR )]1414()[]{}⎰-=vmR l vB g dv t 0222cos sin θθ()()()mR t l B el B mgR v θθθ222cos 2221cos sin --=(2) 导线ab 的最大速度v m =θθ222cos sin l B mgR .练习十三 感生电动势 自感三、计算题1. 在半径为R 的圆柱形空间中存在着均匀磁场B ,B 的方向与柱的轴线平行.有一长为2R 的金属棒MN 放在磁场外且与圆柱形均匀磁场相切,切点为金属棒的中点,金属棒与磁场B 的轴线垂直.如图所示.设B 随时间的变化率d B /d t 为大于零的常量.求:棒上感应电动势的大小,并指出哪一个端点的电势高. (分别用对感生电场的积分εi =l E i·d l 和法拉第电磁感应定律εi =-d /d t 两种方法解)..解:(1) 用对感生电场的积分εi =l E i·d l 解:在棒MN 上取微元d x (R<x<R ),该处感生电场大小为E i =[R 2/(2r )](d B/d t )与棒夹角满足tan =x/Rεi =⎰⋅NMl E i d =⎰NMi x E θcos d=()⎰-⋅RRr R r x t B R 22d d d =⎰-+⋅RR R x xt B R 2232d d d =[R 3(d B/d t )/2](1/R )arctan(x/R )RR-=R 2(d B/d t )/4因εi =>0,故N 点的电势高. (2) 用法拉第电磁感应定律εi =-d /d t 解:图×× × ×OR 2RBa2az图L× ×× ×OBMNd E × ×× ×OB1515沿半径作辅助线OM ,ON 组成三角形回路MONMεi =⎰⋅N Ml E i d =⎰⋅-MNl E i d=⎢⎣⎡⋅⎰M N l E i d +⎰⋅O M l E i d +⎥⎦⎤⋅⎰N O l E i d=-(-dmMONM/d t ) =dmMONM/d t而mMONM=⎰⋅S d S B =R 2B/4故 εi =R 2(d B/d t )/4N 点的电势高.2. 电量Q 均匀分布在半径为a ,长为L (L >>a )的绝缘薄壁长圆筒表面上,圆筒以角速度绕中心轴旋转.一半径为2a ,电阻为R 总匝数为N 的圆线圈套在圆筒上,如图所示.若圆筒转速按=(1t/t 0)的规律(,t 0为已知常数)随时间线性地减小,求圆线圈中感应电流的大小和流向.解:2. .等效于螺线管B 内=nI=[Q /(2)]/L=Q /(2L )B 外=0=SB d S=B a 2=Q a 2 /(2 L )εi =-d /d t=-[Q a 2 /(2 L )]d /d t=Q a 2 /(2 L t 0)I i =εi /R=Q a 2 /(2 LR t 0)方向与旋转方向一致.练习十四 自感(续)互感 磁场的能量三、计算题1. 两半径为a 的长直导线平行放置,相距为d ,组成同一回路,求其单位长度导线的自感系数L 0.1616解:1. 取如图所示的坐标,设回路有电流为I ,则两导线间磁场方向向里,大小为 0≤r ≤a B 1=Ir/(2a 2)+I/[2(d r )]a ≤r ≤d a B 2=0I/(2r )+0I/[2(d r )]d a ≤r ≤d B 3=I/(2r )+I (d r )/(2a 2)取窄条微元d S=l d r ,由m=⎰⋅S S B d 得ml =⎰aa r Irl 0202d πμ+()⎰-a r d rIl 002d πμ +⎰-ad ar r Il πμ2d 0+()⎰--a d ar d r Il πμ2d 0+⎰-ad ar r Il πμ2d 0+()⎰-a d aa rl r -d I 202d πμ =Il/(4)+[0Il/(2)]ln[d/(d a )]+[Il/(2)]ln[(d a )/a ] +[Il/(2)]ln[(d a )/a ]+[Il/(2)]ln[d/(d a )]+Il/(4)=Il/(2)+(Il/)ln(d/a )由L l =l/I ,L 0= L l /l=l/(Il ).得单位长度导线自感 L 0==0l/(2)+(l/)ln(d/a )2 内外半径为R 、r 的环形螺旋管截面为长方形,共有N 匝线圈.另有一矩形导线线圈与其套合,如图(1)所示. 其尺寸标在图(2) 所示的截面图中,求其互感系数.解:2. 设环形螺旋管电流为I , 则管内磁场大小为B =NI/(2) r ≤≤R图(1Rrh a b(21717方向垂直于截面; 管外磁场为零.取窄条微元d S=h d ,由m=⎰⋅S S B d 得m=⎰RrNIh πρρμ2d 0=0NIh ln(R/r )/(2)M =m/I ==Nh ln(R/r )/(2)。
大物质点运动学习题

班级 姓名 学号第一章 质点运动学一 、填空题1.一质点作半径为1.0 m 的圆周运动,它通过的弧长s 按规律 s = t + 2 t 2 变化。
则它在2 s 末的切向加速度为 m/s 2。
法向加速度为 m/s 2。
2.一质点沿x 轴作直线运动,运动方程为324t t x -=,则1 s 末到3 s 末的位移为 m 。
则1 s 末到3 s 末的平均速度为 m/s 。
3.已知质点的运动方程为j t t i t t r)314()2125(32++-+=(SI ),当t = 2 s 时,质点的速度为υ m/s , 质点的加速度=am/s 24.一质点的运动方程为 262t t x +=(SI ),质点在4 s 时的速度大小为 m/s 。
加速度大小为 m/s 25.一质点沿半径R = 1 m 的圆周运动,其路程与时间的关系为 222t s +=(m ),那么,从开始 计时到总加速度a 恰好与半径成45°角时,质点所经过的路程s = m 。
6.一质点在半径为0.20 m 的圆周上运动,其角位置为256t +=θ(SI ),则t = 2.0 s 时质点的速度的大小 v = m/s 。
质点的切向加速度大小为 m /s 2。
质点的法向加速度大小为 m /s 2。
质点的加速度的大小 a = m/s 2。
7.在xoy 平面内有一运动的质点,其运动方程为 j t i t r5sin 105cos 10+=(SI ),则该质点运动的轨迹方程是 。
8.一质点作平面曲线运动,运动方程为 )()(2m j t i t t r+=,在 t = 1s 时质点的切向加速度a t = m/s 2 ; 在 t = 1s 时质点的法向加速度a n = m/s 2。
9.质点沿半径为R 的圆周运动,运动方程223t +=θ(SI ),则t 时刻质点的法向加速度a n = m/s 2; t 时刻质点的角加速度β= rad/s 2。
大物期末温习

练习一 静电场中的导体三、计算题1. 已知某静电场在xy 平面内的电势函数为U =Cx/(x 2+y 2)3/2,其中C 为常数.求(1)x轴上任意一点,(2)y 轴上任意一点电场强度的大小和方向. 解:. E x =U/x=C [1/(x 2+y 2)3/2+x (3/2)2x /(x 2+y 2)5/2]= (2x2y 2)C /(x 2+y 2)5/2E y =U/y=-Cx (-3/2)2y /(x 2+y 2)5/2=3Cxy /(x 2+y 2)5/2x 轴上点(y =0) E x =2Cx 2/x 5=2C /x 3 E y =0 E =2C i /x 3y 轴上点(x =0) E x =-Cy 2/y 5=-C /y 3 E y =0E =-C i /y 32.如图5.6,一导体球壳A (内外半径别离为R 2,R 3),同心地罩在一接地导体球B (半径为R 1)上,今给A 球带负电-Q , 求B 球所带电荷Q B 及的A 球的电势U A .静电场中的导体答案 解: 2. B 球接地,有 U B =U ∞=0, U A =U BAU A =(-Q+Q B )/(4πε0R 3) U BA =[Q B /(4πε0)](1/R 2-1/R 1)得 Q B =QR 1R 2/( R 1R 2+ R 2R 3- R 1R 3)U A =[Q/(4πε0R 3)][-1+R 1R 2/(R 1R 2+R 2R 3-R 1R 3)]=-Q (R 2-R 1)/[4πε0(R 1R 2+R 2R 3-R 1R 3)]练习二 静电场中的电介质三、计算题1. 如图6.6所示,面积均为S =0.1m 2的两金属平板A ,B 平行对称放置,间距为d =1mm,今给A , B 两板别离带电 Q 1=3.54×10-9C, Q 2=1.77×10-9C.忽略边缘效应,求:(1) 两板共四个表面的面电荷密度 σ1, σ2, σ3, σ4;(2) 两板间的电势差V =U A -U B .解:1. 在A 板体内取一点A , B 板体内取一点B ,它们的电场强度是四个表面的电荷产生的,应为零,有E A =σ1/(2ε0)-σ2/(2ε0)-σ3/(2ε0)-σ4/(2ε0)=0E A =σ1/(2ε0)+σ2/(2ε0)+σ3/(2ε0)-σ4/(2ε0)=0而 S (σ1+σ2)=Q 1 S (σ3+σ4)=Q2图5.6A Q 1图6.62σ1 σ2 σ3 4有 σ1-σ2-σ3-σ4=0σ1+σ2+σ3-σ4=0 σ1+σ2=Q 1/S σ3+σ4=Q 2/S解得 σ1=σ4=(Q 1+Q 2)/(2S )=2.66⨯10-8C/m 2σ2=-σ3=(Q 1-Q 2)/(2S )=0.89⨯10-8C/m 2 两板间的场强 E=σ2/ε0=(Q 1-Q 2)/(2ε0S )V=U A -U B ⎰⋅=BAl E d=Ed=(Q 1-Q 2)d /(2ε0S )=1000V四、证明题1. 如图6.7所示,置于静电场中的一个导体,在静电平稳后,导体表面显现正、负感应电荷.试用静电场的环路定理证明,图中从导体上的正感应电荷动身,终止于同一导体上的负感应电荷的电场线不能存在.解:1. 设在同一导体上有从正感应电荷动身,终止于负感应电荷的电场线.沿电场线ACB 作环路ACBA ,导体内直线BA 的场强为零,ACB 的电场与环路同向于是有=⋅⎰l E d l+⋅⎰ACBl E d ⎰⋅ABl E d 2=⎰⋅ACBl E d ≠0与静电场的环路定理=⋅⎰l E d l0相违抗,故在同一导体上不存在从正感应电荷动身,终止于负感应电荷的电场线.练习三 电容 静电场的能量三、计算题1. 半径为R 1的导体球带电Q ,球外一层半径为R 2相对电容率为εr 的同心均匀介质球壳,其余全数空间为空气.如图7.1所示.求:(1)离球心距离为r 1(r 1<R 1), r 2(R 1<r 1<R 2), r 3(r 1>R 2)处的D 和E ;(2)离球心r 1, r 2, r 3,处的U ;(3)介质球壳内外表面的极化电荷. 解:1. (1)因此电荷与介质均为球对称,电场也球对称,过场点作与金属球同心的球形高斯面,有iSq0d ∑=⋅⎰S D4πr 2D=∑q 0i 当r=5cm <R 1, ∑q 0i =0得 D 1=0, E 1=0 当r=15cm(R 1<r <R 1+d ) ∑q 0i =Q=1.0×10-8C 得 D 2=Q /(4πr 2)=3.54×10-8C/m 2 E 2=Q /(4πε0εr r 2)=7.99×103N/C 当r=25cm(r >R 1+d ) ∑q 0i =Q=1.0×10-8C 得 D 3=Q /(4πr 2)=1.27×10-8C/m 2 E 3=Q /(4πε0r 2)=1.44×104N/C D 和E 的方向沿径向. (2) 当r=5cm <R 1时 U 1=⎰∞⋅rlEd图 7.1⎰=R r r E d1⎰++d RRrE d2⎰∞++dRrE d3=Q/(4πε0εr R)-Q/[4πε0εr(R+d)]+Q/[4πε0(R+d)]=540V当r=15cm<R1时U2=⎰∞⋅r lE d⎰+=d RrrE d2⎰∞++dRrE d3=Q/(4πε0εr r)-Q/[4πε0εr(R+d)]+Q/[4πε0(R+d)]=480V当r=25cm<R1时U3=⎰∞⋅r lE d⎰∞=rrE d3=Q/(4πε0r)=360V(3)在介质的内外表面存在极化电荷,P e=ε0χE=ε0(εr-1)E σ'=P e·nr=R处, 介质表面法线指向球心σ'=P e·n =P e cosπ=-ε0(εr-1)Eq'=σ'S=-ε0(εr-1) [Q/(4πε0εr R2)]4πR2=-(εr-1)Q/εr=-0.8×10-8Cr=R+d处, 介质表面法线向外σ'=P e·n =P e cos0=ε0(εr-1)Eq'=σ'S=ε0(εr-1)[Q/(4πε0εr(R+d)2]4π(R+d)2=(εr-1)Q/εr=0.8×10-8C2.两个相距很远可看做孤立的导体球,半径均为10cm,别离充电至200V和400V,然后用一根细导线连接两球,使之达到等电势. 计算变成等势体的进程中,静电力所作的功.解;2.球形电容器C=4πε0RQ1=C1V1=4πε0RV1 Q2=C2V2=4πε0RV2W0=C1V12/2+C2V22/2=2πε0R (V12+V22)两导体相连后C=C1+C2=8πε0RQ=Q1+Q2= C1V1+C2V2=4πε0R(V1+V2)W=Q2/(2C)= [4πε0R(V1+V2)]2/(16πε0R)=πε0R(V1+V2)2静电力作功A=W0-W=2πε0R (V12+V22)-πε0R(V1+V2)2=πε0R(V1-V2)2=1.11×10-7J练习六磁感应强度毕奥—萨伐尔定律三、计算题1. 如图10.7所示, 一宽为2a的无穷长导体薄片, 沿长度方向的电流I在导体薄片上均匀散布. 求中心轴线OO'上方距导体薄片为a 的磁感强度.解:1.取宽为d x的无穷长电流元d I=I d x/(2a)d B=μ0d I/(2πr)=μ0I d x/(4πar)d B x=d B cosα=[μ0I d x/(4πar)](a/r) =μ0I d x/(4πr2)=μ0I d x/[4π(x2+a2)]rd B y =d B sin α= μ0Ix d x/[4πa (x 2+a 2)]()⎰⎰-+==aax x a x xI B B 2204d d πμ=[μ0I/(4π)](1/a )arctan(x/a )a a-=μ0I/(8a )()⎰⎰-+==aay y ax a xIx B B 2204d d πμ=[μ0I/(8πa )]ln(x 2+a 2)a a-=02. 如图10.8所示,半径为R 的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈覆盖住半个球面. 设线圈的总匝数为N ,通过线圈的电流为I . 求球心O 的磁感强度.解:2. 取宽为d L 细圆环电流, d I=I d N=I [N/(πR/2)]R d θ =(2IN/π)d θd B=μ0d Ir 2/[2(r 2+x 2)3/2]r=R sin θ x=R cos θd B=μ0NI sin 2θ d θ /(πR )⎰⎰==πππθθμ20d sin d RNI B B=μ0NI/(4R )练习七 毕奥—萨伐尔定律(续) 磁场的高斯定理三、计算题1.在无穷长直载流导线的右边有面积为S 1和S 2的两个矩形回路, 回路旋转方向如图11.6所示, 两个回路与长直载流导线在同一平面内, 且矩形回路的一边与长直载流导线平行. 求通过两矩形回路的磁通量及通过S 1回路的磁通量与通过S 2回路的磁通量之比.解: 1.取窄条面元d S =b d r , 面元上磁场的大小为B =μ0I /(2πr ), 面元法线与磁场方向相反.有Φ1=⎰-=aabIbdr r I 2002ln 2cos 2πμππμ Φ2=⎰-=aabI bdr r I 42002ln 2cos 2πμππμ Φ1/Φ2=12. 半径为R 的薄圆盘均匀带电,总电量为Q . 令此盘绕通过盘心且垂直盘面的轴线作匀速转动,角速度为ω,求轴线上距盘心x 处的磁感强度的大小和旋转圆盘的磁矩.解;2. 在圆盘上取细圆环电荷元d Q =σ2πr d r , [σ=Q /(πR 2) ],等效电流元为 d I =d Q /T =σ2πr d r/(2π/ω)=σωr d r(1)求磁场, 电流元在中心轴线上激发磁场的方向沿轴线,且与ω同向,大小为图10.8图11.6d B=μ0d Ir2/[2(x2+r2)3/2]=μ0σωr3d r/[2(x2+r2)3/2]()()()⎰⎰++=+=RRx rx r r x r rr B 02322222002/32230d 42d σωμσωμ=()()()⎰+++Rx rx r x r23222222d 4σωμ-()()⎰++Rx rx r x 023222220d 4σωμ=⎪⎪⎭⎫⎝⎛+++RRx r x x r 022202202σωμ =⎪⎪⎭⎫ ⎝⎛-++x x R x R R Q 222222220πωμ (2)求磁距. 电流元的磁矩d P m =d IS=σωr d r πr 2=πσωr 2d r⎰=Rm dr r P 03πσω=πσωR 4/4=ωQR 2/4练习八 安培环路定律三、计算题1. 如图12.5所示,一根半径为R 的无穷长载流直导体,其中电流I 沿轴向流过,并均匀散布在横截面上. 此刻导体上有一半径为R '的圆柱形空腔,其轴与直导体的轴平行,两轴相距为 d . 试求空腔中任意一点的磁感强度.解:1. 此电流能够为是由半径为R 的无穷长圆柱电流I 1和一个同电流密度的反方向的半径为R '的无穷长圆柱电流I 2组成. I 1=J πR 2 I 2=-J πR '2 J =I/[π (R 2-R '2)] 它们在空腔内产生的磁感强度别离为 B 1=μ0r 1J/2 B 2=μ0r 2J/2 方向如图.有B x =B 2sin θ2-B 1sin θ1=(μ0J/2)(r 2sin θ2-r 1sin θ1)=0 B y =B 2cos θ2+B 1cos θ1=(μ0J/2)(r 2cos θ2+r 1cos θ1)=(μ0J/2)d 因此 B = B y = μ0dI/[2π(R 2-R '2)] 方向沿y 轴正向2. 设有两无穷大平行载流平面,它们的电流密度均为j ,电流流向相反. 求: (1) 载流平面之间的磁感强度; (2) 两面之外空间的磁感强度.解;2. 两无穷大平行载流平面的截面如图.平面电流在空间产生的磁场为 B 1=μ0J /2 在平面①的上方向右,在平面①的下方向左;电流②在空间产生的磁场为 B 2=μ0J /2 在平面②的上方向左,在平面②的下方向右.(1) 两无穷大电流流在平面之间产生的磁感强度方向都向左,故有 B=B 1+B 2=μ0J (2) 两无穷大电流流在平面之外产生的磁感强度方向相反,故有 B=B 1-B 2=0图12.5I 1 I 2①②练习九 安培力三、计算题1. 一边长a =10cm 的正方形铜导线线圈(铜导线横截面积S =2.00mm 2, 铜的密度ρ=8.90g/cm 3), 放在均匀外磁场中. B 竖直向上, 且B = 9.40⨯10-3T, 线圈中电流为I =10A . 线圈在重力场中 求:(1) 今使线圈平面维持竖直, 那么线圈所受的磁力矩为多少.(2) 假假设线圈能以某一条水平边为轴自由摆动,当线圈平稳时,线圈平面与竖直面夹角为多少. 解:1. (1) P m =IS=Ia 2 方向垂直线圈平面.线圈平面维持竖直,即P m 与B 垂直.有 M m =P m ×BM m =P m B sin(π/2)=Ia 2B=9.4×10-4m ⋅N(2) 平稳即磁力矩与重力矩等值反向 M m =P m B sin(π/2-θ)=Ia 2B cos θ M G = M G 1 + M G 2 + M G 3= mg (a/2)sin θ+ mga sin θ+ mg (a/2)sin θ =2(ρSa )ga sin θ=2ρSa 2g sin θ Ia 2B cos θ=2ρSa 2g sin θ tan θ=IB/(2ρSg )=0.2694 θ=15︒2. 如图13.5所示,半径为R 的半圆线圈ACD 通有电流I 2, 置于电流为I 1的无穷长直线电流的磁场中, 直线电流I 1 恰过半圆的直径, 两导线彼此绝缘. 求半圆线圈受到长直线电流I 1的磁力.解:2.在圆环上取微元 I 2d l = I 2R d θ 该处磁场为B =μ0I 1/(2πR cos θ)I 2d l 与B 垂直,有d F= I 2d lB sin(π/2) d F=μ0I 1I 2d θ/(2πcos θ) d F x =d F cos θ=μ0I 1I 2d θ /(2π) d F y =d F sin θ=μ0I 1I 2sin θd θ /(2πcos θ)⎰-=222102πππθμd I I F x =μ0I 1I 2/2因对称F y =0.故 F =μ0I 1I 2/2 方向向右.练习十 洛仑兹力I图13.5I三、计算题1. 如图14.6所示,有一无穷大平面导体薄板,自下而上均匀通有电流,已知其面电流密度为i (即单位宽度上通有的电流强度)(1) 试求板外空间任一点磁感强度的大小和方向.(2) 有一质量为m ,带正电量为q 的粒子,以速度v 沿平板法线方向向外运动. 假设不计粒子重力.求:(A) 带电粒子最初至少在距板什么位置处才不与大平板碰撞. (B) 需经多长时刻,才能回到初始位置.. 解:1. (1)求磁场.用安培环路定律得 B =μ0i/2在面电流右边B 的方向指向纸面向里,在面电流左侧B 的方向沿纸面向外.(2) F =q v×B=m a qvB=ma n =mv 2/R带电粒子不与平板相撞的条件是粒子运行的圆形轨迹不与平板相交,即带电粒子最初位置与平板的距离应大于轨道半径.R =mv/qB= 2mv/(μ0iq )(3) 经一个周期时刻,粒子回到初始位置.即 t =T=2πR/v= 4πm/(μ0iq )2. 一带电为Q 质量为m 的粒子在均匀磁场中由静止开始下落,磁场的方向(z 轴方向)与重力方向(y 轴方向)垂直,求粒子下落距离为y 时的速度.并讲清求解方式的理论依据.解:2. 洛伦兹力Q v ×B 垂直于v ,不作功,不改变v 的大小;重力作功.依能量守恒有 mv 2/2=mgy ,得 v =(2gy )1/2.练习十一 磁场中的介质三、计算题1. 一厚度为b 的无穷大平板中通有一个方向的电流,平板内各点的电导率为γ,电场强度为E ,方向如图15.6所示,平板的相对磁导率为μr 1,平板双侧充满相对磁导率为μr 2的各向同性的均匀磁介质,试求板内外任意点的磁感应强度.解:1. 设场点距中心面为x ,因磁场面对称 以中心面为对称面过场点取矩形安培环路,有⎰⋅ll H d =ΣI 0 2∆LH=ΣI 0(1) 介质内,0<x <b/2. ΣI 0=2x ∆lJ =2x ∆l γE ,有 H =x γE B =μ0μr 1H=μ0μr 1x γE(2) 介质外,|x |>b/2. ΣI 0=b ∆lJ =b ∆l γE ,有 H =b γE/2 B =μ0μr 2H=μ0μr 2b γE/22. 一根同轴电缆线由半径为R 1的长导线和套在它外面的半径为R 2的同轴薄导体圆筒组成,中间充满磁化率为χm 的各向同性均匀非铁磁绝缘介质,如图15.7所示. 传导电流沿导线向上流去, 由圆筒向下流回,电流在截面上均匀散布.v•图14.6图15.7求介质内外表面的磁化电流的大小及方向. 解:2. 因磁场柱对称 取同轴的圆形安培环路,有 ⎰⋅ll H d =ΣI 0在介质中(R 1<r <R 2),ΣI 0=I ,有 2πrH = I H = I /(2πr ) 介质内的磁化强度 M =χm H =χm I /(2πr )介质内表面的磁化电流 J SR 1=| M R 1×n R 1|=| M R 1|=χm I /(2πR 1) I SR 1=J SR 1⋅2πR 1=χm I (与I 同向) 介质外表面的磁化电流J SR 2=| M R 2×n R 2|=| M R 2|=χm I /(2πR 2) I SR 2=J SR 2⋅2πR 2=χm I (与I 反向)练习十二 电磁感应定律 动生电动势三、计算题1. 如图17.8所示,长直导线AC 中的电流I 沿导线向上,并以d I /d t = 2 A/s 的转变率均匀增加. 导线周围放一个与之同面的直角三角形线框,其一边与导线平行,位置及线框尺寸如下图. 求此线框中产生的感应电动势的大小和方向.解: 1. 取顺时针为三角形回路电动势正向,得三角形面法线垂直纸面向里.取窄条面积微元 d S =y d x =[(a+b -x )l/b ]d xΦm =⎰⋅S d S B=()⎰+-+⋅ba abldxx b a x I πμ20 =()⎥⎦⎤⎢⎣⎡-++b a b a b a b Il ln 20πμ εi =-d Φm /d t=()dtdIa b a b a b b l ⎥⎦⎤⎢⎣⎡++-ln 20πμ =-5.18×10-8V负号表示逆时针2. 一很长的长方形的U 形导轨,与水平面成θ 角,裸导线可在导轨上无摩擦地下滑,导轨位于磁感强度B 垂直向上的均匀磁场中,如图17.9所示. 设导线ab 的质量为m ,电阻为R ,长度为l ,导轨的电阻略去不计, abcd 形成电路. t=0时,v=0. 求:(1) 导线ab 下滑的速度v 与时刻t 的函数关系; (2) 导线ab 的最大速度v m .解:2. (1) 导线ab 的动生电动势为εi = ⎰l v×B ·d l=vBl sin(π/2+θ)=vBl cos θI i =εi /R = vBl cos θ/R方向由b 到a . 受安培力方向向右,大小为图17.8图17.9F =| ⎰l (I i d l×B )|= vB 2l 2cos θ/RF 在导轨上投影沿导轨向上,大小为F '= F cos θ =vB 2l 2cos 2θ/R重力在导轨上投影沿导轨向下,大小为mg sin θmg sin θ -vB 2l 2cos 2θ/R=ma=m d v /d t dt=d v /[g sin θ -vB 2l 2cos 2θ/(mR )]()[]{}⎰-=vmR l vB g dv t 0222cos sin θθ()()()mR t l B e l B mgR v θθθ222cos 2221cos sin --=(2) 导线ab 的最大速度v m =θθ222cos sin l B mgR .练习十三 感生电动势 自感三、计算题1. 在半径为R 的圆柱形空间中存在着均匀磁场B ,B 的方向与柱的轴线平行.有一长为2R 的金属棒MN 放在磁场外且与圆柱形均匀磁场相切,切点为金属棒的中点,金属棒与磁场B 的轴线垂直.如图18.6所示.设B 随时刻的转变率d B /d t 为大于零的常量.求:棒上感应电动势的大小,并指出哪个端点的电势高.(别离用对感生电场的积分εi =⎰l E i ·d l 和法拉第电磁感应定律εi =-d Φ/d t 两种方式解)..解:(1) 用对感生电场的积分εi =⎰l E i ·d l 解:在棒MN 上取微元d x (-R<x<R ), 该处感生电场大小为E i =[R 2/(2r )](d B/d t )与棒夹角θ知足tan θ=x/Rεi =⎰⋅NMl E i d =⎰NMi x E θcos d=()⎰-⋅RRr R r x t B R 22d d d =⎰-+⋅RR R x xt B R 2232d d d =[R 3(d B/d t )/2](1/R )arctan(x/R )R R-=πR 2(d B/d t )/4因εi =>0,故N 点的电势高. (2) 用法拉第电磁感应定律εi =-d Φ/d t 解: 沿半径作辅助线OM ,ON 组成三角形回路MONM=⎰⋅NMl E i d =⎰⋅-MNlE i d εi图18.6图18.7=-⎢⎣⎡⋅⎰MNl E i d +⎰⋅OM l E i d +⎥⎦⎤⋅⎰N O l E i d =-(-d ΦmMONM /d t ) =d ΦmMONM /d t而 ΦmMONM =⎰⋅Sd S B =πR 2B/4故 εi =πR 2(d B/d t )/4 N 点的电势高.2. 电量Q 均匀散布在半径为a ,长为L (L >>a )的绝缘薄壁长圆筒表面上,圆筒以角速度ω绕中心轴旋转.一半径为2a ,电阻为R 总匝数为N 的圆线骗局在圆筒上,如图18.7所示.假设圆筒转速按ω=ω0(1-t/t 0)的规律(ω0,t 0为已知常数)随时刻线性地减小,求圆线圈中感应电流的大小和流向.解:2. .等效于螺线管B 内=μ0 nI=μ0 [Q ω /(2π)]/L=μ0 Q ω /(2πL )B 外=0Φ=⎰S B ⋅d S=B πa 2=μ0Q ω a 2 /(2 L ) εi =-d Φ/d t=-[μ0Q a 2 /(2 L )]d ω /d t=μ0ω 0Q a 2 /(2 L t 0)I i =εi /R=μ0ω 0Q a 2 /(2 LR t 0)方向与旋转方向一致.练习十四 自感(续)互感 磁场的能量三、计算题1. 两半径为a 的长直导线平行放置,相距为d ,组成同一回路,求其单位长度导线的自感系数L 0. 解:1. 取如下图的坐标,设回路有电流为I ,那么两导线间磁场方向向里,大小为 0≤r ≤a B 1=μ0Ir/(2πa 2)+ μ0I/[2π(d -r )] a ≤r ≤d -a B 2=μ0I/(2πr )+μ0I/[2π(d -r )] d -a ≤r ≤d B 3=μ0I/(2πr )+ μ0I (d -r )/(2πa 2) 取窄条微元d S=l d r ,由Φm =⎰⋅SS B d 得Φml =⎰aa r Irl 0202d πμ+()⎰-a r d r Il 002d πμ +⎰-ad ar r Il πμ2d 0+()⎰--a d ar d rIl πμ2d 0 +⎰-ad ar r Il πμ2d 0+()⎰-a d aa rl r -d I 202d πμ =μ0Il/(4π)+[μ0Il/(2π)]ln[d/(d -a )]+[μ0Il/(2π)]ln[(d -a )/a ] +[μ0Il/(2π)]ln[(d -a )/a ]+[μ0Il/(2π)]ln[d/(d -a )]+μ0Il/(4π)=μ0Il/(2π)+(μ0Il/π)ln(d/a )由L l =Φl /I ,L 0= L l /l=Φl /(Il ).得单位长度导线自感 L 0==μ0l/(2π)+(μ0l/π)ln(d/a )2 内外半径为R 、r 的环形螺旋管截面为长方形,共有N 匝线圈.还有一矩形导线线圈与其套合,如图19.4(1)所示. 其尺寸标在图19.4(2)所示的截面图中,求其互感系数.解:2. 设环形螺旋管电流为I , 那么管内磁场大小为 B =μ0NI/(2πρ) r ≤ρ≤R方向垂直于截面; 管外磁场为零.取窄条微元d S=h d ρ,由Φm =⎰⋅SS B d 得Φm =⎰RrNIh πρρμ2d 0=μ0NIh ln(R/r )/(2π) M =Φm /I ==μ0Nh ln(R/r )/(2π)图19.4(1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如图, 有一半径为 R 质量为 m '的匀质圆盘, 可绕通过盘心 O 垂直盘面的水平轴转动. 转轴与圆盘之间的摩擦略去不计. 圆盘上绕有轻而细的绳索, 绳的一端固定在圆盘上, 另一端系质量为 m 的物体. 试求物体下落时的加速度、绳中的张力和圆盘的角加速度
2、真空中,有一带电为Q ,半径为R 的带电球壳。
试求(1)球壳外两点间的
电势差;(2)球壳内两点间的电势差;(3)球壳外任意点的电势;(4)球壳内任意点的电势。
3、如图所示,长直导线中电流为i ,矩形线框abcd 与长直导线共面,且ad ∥AB ,
dc 边固定,ab 边沿da 及cb 以速度v 无摩擦地匀速平动.t = 0时,ab 边与cd
边重合.设线框自感忽略不计.如i =I 0,求ab 中的感应电动势.ab 两点哪点电势高?
i l 2 b c A B
4、一质量为m 的物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示.轴水平且垂直于轮轴面,其半径为r ,整个装置架在光滑的固定轴承之上.当物体从静止释放后,在时间t 内下降了一段距离S .试求整个轮轴的转动惯量(用m 、r 、t 和S 表示).
5、一长为L 的铜棒在磁感强度为 B 的均匀磁场中, 以角速度 ω 在与磁场方向垂直的平面上绕棒的一端转动,求铜棒两端的感应电动势,并判断哪端的电势高
+ +
+
+
6、如图所示,质量为m1=24kg的匀质圆盘,可绕水平光滑固定轴转动,一轻绳绕于轮上,另一端通过质量为m2=5kg的圆盘形定滑轮悬有m=10kg的物体。
求(1)物体下降过程中的加速度;(2)绳中张力。
(设绳与定滑轮间无相对滑动)。
7、用高斯定理求均匀带正电的无限大平面簿板的场强(设电荷的面密度为 );。
