高考数学(理)一轮复习题库：5.4 平面向量的综合应用

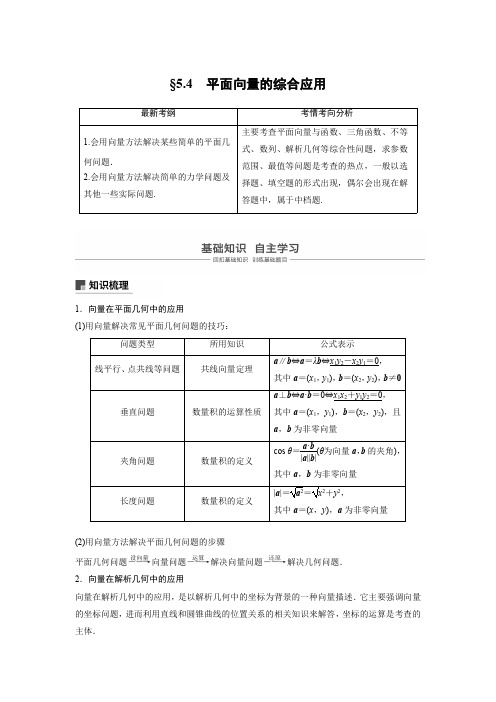
1．向量在平面几何中的应用(1)用向量解决常见平面几何问题的技巧：(2)用向量方法解决平面几何问题的步骤：平面几何问题――→设向量向量问题――→运算解决向量问题――→还原解决几何问题． 2．平面向量在物理中的应用(1)由于物理学中的力、速度、位移都是矢量，它们的分解与合成与向量的加法和减法相似，可以用向量的知识来解决．(2)物理学中的功是一个标量，是力F 与位移s 的数量积，即W ＝F·s ＝|F||s |cos θ(θ为F 与s 的夹角)．3．向量与相关知识的交汇平面向量作为一种工具，常与函数(三角函数)，解析几何结合，常通过向量的线性运算与数量积，向量的共线与垂直求解相关问题． 【知识拓展】1．若G 是△ABC 的重心，则GA →＋GB →＋GC →＝0.2．若直线l 的方程为：Ax ＋By ＋C ＝0，则向量(A ，B )与直线l 垂直，向量(－B ，A )与直线l 平行． 【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”) (1)若AB →∥AC →，则A ，B ，C 三点共线．( √ ) (2)向量b 在向量a 方向上的投影是向量．( × )(3)若a ·b ＞0，则a 和b 的夹角为锐角；若a ·b ＜0，则a 和b 的夹角为钝角．( × ) (4)在△ABC 中，若AB →·BC →<0，则△ABC 为钝角三角形．( × )(5)已知平面直角坐标系内有三个定点A (－2，－1)，B (0，10)，C (8,0)，若动点P 满足：OP →＝OA →＋t (AB →＋AC →)，t ∈R ，则点P 的轨迹方程是x －y ＋1＝0.( √ )1．(教材改编)已知△ABC 的三个顶点的坐标分别为A (3,4)，B (5,2)，C (－1，－4)，则该三角形为( ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．等腰直角三角形答案 B解析 AB →＝(2，－2)，AC →＝(－4，－8)，BC →＝(－6，－6)， ∴|AB →|＝22＋(－2)2＝22，|AC →|＝16＋64＝45， |BC →|＝36＋36＝62， ∴|AB →|2＋|BC →|2＝|AC →|2， ∴△ABC 为直角三角形．2．已知在△ABC 中，|BC →|＝10，AB →·AC →＝－16，D 为边BC 的中点，则|AD →|等于( ) A ．6 B ．5 C ．4 D ．3答案 D解析 在△ABC 中，由余弦定理可得，AB 2＋AC 2－2AB ·AC ·cos A ＝BC 2，又AB →·AC →＝|AB →|·|AC →|·cos A ＝－16，所以AB 2＋AC 2＋32＝100，AB 2＋AC 2＝68.又D 为边BC 的中点，所以AB →＋AC →＝2AD →，两边平方得4|AD →|2＝68－32＝36，解得|AD →|＝3，故选D.3．(2017·武汉质检)平面直角坐标系xOy 中，若定点A (1,2)与动点P (x ，y )满足OP →·OA →＝4，则点P 的轨迹方程是____________． 答案 x ＋2y －4＝0解析 由OP →·OA →＝4，得(x ，y )·(1,2)＝4， 即x ＋2y ＝4.4．(2016·银川模拟)已知向量a ＝(cos θ，sin θ)，b ＝(3，－1)，则|2a －b |的最大值为________． 答案 4解析 设a 与b 夹角为α， ∵|2a －b |2＝4a 2－4a·b ＋b 2 ＝8－4|a||b |cos α＝8－8cos α， ∵α∈[0，π]，∴cos α∈[－1,1]， ∴8－8cos α∈[0,16]，即|2a －b |2∈[0,16]， ∴|2a －b |∈[0,4]． ∴|2a －b |的最大值为4.5．已知一个物体在大小为6 N 的力F 的作用下产生的位移s 的大小为100 m ，且F 与s 的夹角为60°，则力F 所做的功W ＝________ J. 答案 300解析 W ＝F ·s ＝|F ||s |cos 〈F ，s 〉 ＝6×100×cos 60°＝300(J).题型一 向量在平面几何中的应用例1 (1)在平行四边形ABCD 中，AD ＝1，∠BAD ＝60°，E 为CD 的中点．若AC →·BE →＝1，则AB ＝________.(2)已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个动点，若动点P 满足OP →＝OA →＋λ(AB →＋AC →)，λ∈(0，＋∞)，则点P 的轨迹一定通过△ABC 的( ) A ．内心B ．外心 C ．重心D ．垂心 答案 (1)12(2)C解析 (1)在平行四边形ABCD 中，取AB 的中点F ，则BE →＝FD →，∴BE →＝FD →＝AD →－12AB →，又∵AC →＝AD →＋AB →，∴AC →·BE →＝(AD →＋AB →)·(AD →－12AB →)＝AD →2－12AD →·AB →＋AD →·AB →－12AB →2＝|AD →|2＋12|AD →||AB →|cos 60°－12|AB →|2＝1＋12×12|AB →|－12|AB →|2＝1.∴⎝⎛⎭⎫12－|AB →||AB →|＝0，又|AB →|≠0，∴|AB →|＝12. (2)由原等式，得OP →－OA →＝λ(AB →＋AC →)，即AP →＝λ(AB →＋AC →)，根据平行四边形法则，知AB →＋AC →是△ABC 的中线AD (D 为BC 的中点)所对应向量AD →的2倍，所以点P 的轨迹必过△ABC 的重心． 引申探究本例(2)中，若动点P 满足OP →＝OA →＋λ⎝ ⎛⎭⎪⎫AB →|AB →|＋AC →|AC →|，λ∈(0，＋∞)，则点P 的轨迹一定通过△ABC的________． 答案 内心解析 由条件，得OP →－OA →＝λ⎝ ⎛⎭⎪⎫AB →|AB →|＋AC →|AC →|，即AP →＝λ⎝ ⎛⎭⎪⎫AB →|AB →|＋AC →|AC →|，而AB →|AB →|和AC →|AC →|分别表示平行于AB →，AC →的单位向量，故AB →|AB →|＋AC →|AC →|平分∠BAC ，即AP →平分∠BAC ，所以点P 的轨迹必过△ABC 的内心．思维升华 向量与平面几何综合问题的解法 (1)坐标法把几何图形放在适当的坐标系中，则有关点与向量就可以用坐标表示，这样就能进行相应的代数运算和向量运算，从而使问题得到解决． (2)基向量法适当选取一组基底，沟通向量之间的联系，利用向量间的关系构造关于未知量的方程进行求解．(1)在△ABC 中，已知向量AB →与AC →满足(AB →|AB →|＋AC →|AC →|)·BC →＝0，且AB →|AB →|·AC →|AC →|＝12，则△ABC 为( ) A ．等边三角形 B ．直角三角形C ．等腰非等边三角形D ．三边均不相等的三角形(2)已知直角梯形ABCD 中，AD ∥BC ，∠ADC ＝90°，AD ＝2，BC ＝1，P 是腰DC 上的动点，则|P A →＋3PB →|的最小值为________． 答案 (1)A (2)5解析 (1)AB →|AB →|，AC →|AC →|分别为平行于AB →，AC →的单位向量，由平行四边形法则可知AB →|AB →|＋AC →|AC →|为∠BAC 的平分线．因为(AB →|AB →|＋AC →|AC →|)·BC →＝0，所以∠BAC 的平分线垂直于BC ，所以AB ＝AC .又AB →|AB →|·AC →|AC →|＝⎪⎪⎪⎪⎪⎪AB →|AB →|·⎪⎪⎪⎪⎪⎪AC →|AC →|·cos ∠BAC ＝12，所以cos ∠BAC ＝12，又0<∠BAC <π，故∠BAC ＝π3，所以△ABC 为等边三角形． (2)以D 为原点，分别以DA ，DC 所在直线为x 轴、y 轴建立如图所示的平面直角坐标系，设DC ＝a ，DP ＝y .则D (0,0)，A (2,0)，C (0，a )，B (1，a )， P (0，y )，P A →＝(2，－y )，PB →＝(1，a －y )， 则P A →＋3PB →＝(5,3a －4y )， 即|P A →＋3PB →|2＝25＋(3a －4y )2， 由点P 是腰DC 上的动点，知0≤y ≤a . 因此当y ＝34a 时，|P A →＋3PB →|2的最小值为25.故|P A →＋3PB →|的最小值为5. 题型二 向量在解析几何中的应用例2 (1)已知向量OA →＝(k,12)，OB →＝(4,5)，OC →＝(10，k )，且A 、B 、C 三点共线，当k <0时，若k 为直线的斜率，则过点(2，－1)的直线方程为________________．(2)设O 为坐标原点，C 为圆(x －2)2＋y 2＝3的圆心，且圆上有一点M (x ，y )满足OM →·CM →＝0，则yx＝________________________________________________________________________.答案 (1)2x ＋y －3＝0 (2)±3解析 (1)∵AB →＝OB →－OA →＝(4－k ，－7)， BC →＝OC →－OB →＝(6，k －5)，且AB →∥BC →， ∴(4－k )(k －5)＋6×7＝0， 解得k ＝－2或k ＝11.由k <0可知k ＝－2，则过点(2，－1)且斜率为－2的直线方程为y ＋1＝－2(x －2)，即2x ＋y －3＝0.(2)∵OM →·CM →＝0，∴OM ⊥CM ，∴OM 是圆的切线，设OM 的方程为y ＝kx ， 由|2k |1＋k 2＝3，得k ＝±3，即yx ＝±3.思维升华 向量在解析几何中的“两个”作用(1)载体作用：向量在解析几何问题中出现，多用于“包装”，解决此类问题的关键是利用向量的意义、运算脱去“向量外衣”，导出曲线上点的坐标之间的关系，从而解决有关距离、斜率、夹角、轨迹、最值等问题．(2)工具作用：利用a ⊥b ⇔a·b ＝0(a ，b 为非零向量)，a ∥b ⇔a ＝λb (b ≠0)，可解决垂直、平行问题，特别地，向量垂直、平行的坐标表示对于解决解析几何中的垂直、平行问题是一种比较简捷的方法．(2016·合肥模拟)如图所示，半圆的直径AB ＝6，O 为圆心，C 为半圆上不同于A 、B 的任意一点，若P 为半径OC 上的动点，则(P A →＋PB →)·PC →的最小值为________．答案 －92解析 ∵圆心O 是直径AB 的中点，∴P A →＋PB →＝2PO →，∴(P A →＋PB →)·PC →＝2PO →·PC →， ∵PO →与PC →共线且方向相反，∴当大小相等时，乘积最小．由条件知，当PO ＝PC ＝32时，最小值为－2×32×32＝－92.题型三 向量的其他应用 命题点1 向量在不等式中的应用例3 已知x ，y 满足⎩⎪⎨⎪⎧y ≥x ，x ＋y ≤2，x ≥a ，若OA →＝(x,1)，OB →＝(2，y )，且OA →·OB →的最大值是最小值的8倍，则实数a 的值是________． 答案 18解析 因为OA →＝(x,1)，OB →＝(2，y )，所以OA →·OB →＝2x ＋y ，令z ＝2x ＋y ，依题意，不等式组所表示的可行域如图中阴影部分所示(含边界)，观察图象可知，当目标函数z ＝2x ＋y 过点C (1,1)时，z max ＝2×1＋1＝3，目标函数z ＝2x ＋y 过点F (a ，a )时，z min ＝2a ＋a ＝3a ，所以3＝8×3a ，解得a ＝18.命题点2 向量在解三角形中的应用例4 (2016·合肥模拟)在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，若20aBC →＋15bCA →＋12cAB →＝0，则△ABC 最小角的正弦值等于( ) A.45 B.34 C.35 D.74答案 C解析 ∵20aBC →＋15bCA →＋12cAB →＝0， ∴20a (AC →－AB →)＋15bCA →＋12cAB →＝0， ∴(20a －15b )AC →＋(12c －20a )AB →＝0， ∵AC →与AB →不共线，∴⎩⎪⎨⎪⎧20a －15b ＝0，12c －20a ＝0⇒⎩⎨⎧b ＝43a ，c ＝53a ，∴△ABC 最小角为角A ， ∴cos A ＝b 2＋c 2－a 22bc＝169a 2＋259a 2－a 22×43a ×53a ＝45，∴sin A ＝35，故选C.命题点3 向量在物理中的应用例5 如图，一质点受到平面上的三个力F 1，F 2，F 3(单位：牛顿)的作用而处于平衡状态．已知F 1，F 2成60°角，且F 1，F 2的大小分别为2和4，则F 3的大小为()A ．27B ．2 5C ．2D ．6答案 A解析 如题图所示，由已知得F 1＋F 2＋F 3＝0，则F 3＝－(F 1＋F 2)，即F 23＝F 21＋F 22＋2F 1·F 2＝F 21＋F 22＋2|F 1|·|F 2|·cos 60°＝28.故|F 3|＝27. 思维升华 利用向量的载体作用，可以将向量与三角函数、不等式结合起来，解题时通过定义或坐标运算进行转化，使问题的条件结论明晰化．(1)函数y ＝sin(ωx ＋φ)在一个周期内的图象如图所示，M 、N 分别是最高点、最低点，O 为坐标原点，且OM →·ON →＝0，则函数f (x )的最小正周期是______．(2)已知在平面直角坐标系中，O (0,0)，M (1,1)，N (0,1)，Q (2，3)，动点P (x ，y )满足不等式0≤OP →·OM →≤1,0≤OP →·ON →≤1，则z ＝OQ →·OP →的最大值为________． 答案 (1)3 (2)3解析 (1)由图象可知，M ⎝⎛⎭⎫12，1，N ()x N ，－1， 所以OM →·ON →＝⎝⎛⎭⎫12，1·(x N ，－1)＝12x N －1＝0，解得x N ＝2，所以函数f (x )的最小正周期是2×⎝⎛⎭⎫2－12＝3.(2)∵OP →＝(x ，y )，OM →＝(1,1)，ON →＝(0,1)，OQ →＝(2,3)， ∴OP →·OM →＝x ＋y ，OP →·ON →＝y ，OQ →·OP →＝2x ＋3y ，即在⎩⎪⎨⎪⎧0≤x ＋y ≤1，0≤y ≤1条件下，求z ＝2x ＋3y 的最大值，由线性规划知识得，当x ＝0，y ＝1时，z max ＝3.三审图形抓特点典例 (2016·太原一模)已知A ，B ，C ，D 是函数y ＝sin(ωx ＋φ)⎝⎛⎭⎫ω＞0，0＜φ＜π2一个周期内的图象上的四个点，如图所示，A ⎝⎛⎭⎫－π6，0，B 为y 轴上的点，C 为图象上的最低点，E 为该函数图象的一个对称中心，B 与D 关于点E 对称，CD →在x 轴上的投影为π12，则ω，φ的值为( )A ．ω＝2，φ＝π3B ．ω＝2，φ＝π6C ．ω＝12，φ＝π3D ．ω＝12，φ＝π6E 为函数图象的对称中心，C 为图象最低点―――――――――――→作出点C 的对称点MD 、B 两点对称 CD 和MB 对称―――――――――――→CD →在x 轴上的投影是π12BM 在x 轴上的投影OF ＝π12――――――→A (－π6，0)，AF ＝π4―→T ＝π―→ω＝2――――――――→y ＝sin(2x ＋φ)和y ＝sin 2x 图象比较φ2＝π6―→φ＝π3解析 由E 为该函数图象的一个对称中心，作点C 的对称点M ，作MF ⊥x 轴，垂足为F ，如图．B 与D 关于点E 对称，CD →在x 轴上的投影为π12，知OF ＝π12.又A ⎝⎛⎭⎫－π6，0，所以AF ＝T 4＝π2ω＝π4，所以ω＝2.同时函数y ＝sin(ωx ＋φ)图象可以看作是由y ＝sin ωx 的图象向左平移得到，故可知φω＝φ2＝π6，即φ＝π3.答案 A1．在△ABC 中，(BC →＋BA →)·AC →＝|AC →|2，则△ABC 的形状一定是( ) A ．等边三角形 B ．等腰三角形 C ．直角三角形 D ．等腰直角三角形答案 C解析 由(BC →＋BA →)·AC →＝|AC →|2， 得AC →·(BC →＋BA →－AC →)＝0， 即AC →·(BC →＋BA →＋CA →)＝0， 2AC →·BA →＝0， ∴AC →⊥BA →，∴A ＝90°.又根据已知条件不能得到|AB →|＝|AC →|， 故△ABC 一定是直角三角形．2．(2016·山东)已知非零向量m ，n 满足4|m |＝3|n |，cos 〈m ，n 〉＝13.若n ⊥(t m ＋n )，则实数t 的值为( )A ．4B ．－4 C.94 D ．－94答案 B解析 ∵n ⊥(t m ＋n )，∴n ·(t m ＋n )＝0， 即t m ·n ＋n 2＝0，∴t |m ||n |cos 〈m ，n 〉＋|n |2＝0， 由已知得t ×34|n |2×13＋|n |2＝0，解得t ＝－4，故选B.3．(2016·南宁模拟)已知向量a ＝(cos α，－2)，b ＝(sin α，1)且a ∥b ，则sin 2α等于( ) A ．3B ．－3C.45D ．－45答案 D 解析 由a ∥b 得cos α＋2sin α＝0，∴cos α＝－2sin α，又sin 2α＋cos 2α＝1，∴5sin 2α＝1，sin 2α＝15，cos 2α＝45， sin 2α＝2sin αcos α＝－cos 2α＝－45. 4．(2016·武汉模拟)设△ABC 的三个内角为A ，B ，C ，向量m ＝(3sin A ，sin B )，n ＝(cos B ，3cos A )，若m·n ＝1＋cos(A ＋B )，则C 等于( )A.π6B.π3C.2π3D.5π6答案 C解析 依题意得3sin A cos B ＋3cos A sin B ＝1＋cos(A ＋B )，3sin(A ＋B )＝1＋cos(A ＋B )，3sin C ＋cos C ＝1,2sin(C ＋π6)＝1，sin(C ＋π6)＝12. 又π6<C ＋π6<7π6，因此C ＋π6＝5π6，C ＝2π3. 5．已知点A (－2,0)，B (3,0)，动点P (x ，y )满足P A →·PB →＝x 2，则点P 的轨迹是( )A ．圆B ．椭圆C ．双曲线D ．抛物线 答案 D解析 ∵P A →＝(－2－x ，－y )，PB →＝(3－x ，－y )，∴P A →·PB →＝(－2－x )(3－x )＋y 2＝x 2，∴y 2＝x ＋6，即点P 的轨迹是抛物线．*6.若平面向量α，β满足|α|＝1，|β|≤1，且以向量α，β为邻边的平行四边形的面积为12，则α与β的夹角θ的取值范围是________．答案 ⎣⎡⎦⎤π6，5π6解析 如图，向量α与β在单位圆O 内，由于|α|＝1，|β|≤1，且以向量α，β为邻边的平行四边形的面积为12，故以向量α，β为两边的三角形的面积为14，故β的终点在如图所示的线段AB 上(α∥AB →，且圆心O 到AB 的距离为12)，因此夹角θ的取值范围为⎣⎡⎦⎤π6，5π6.7．在菱形ABCD 中，若AC ＝4，则CA →·AB →＝________.答案 －8解析 设∠CAB ＝θ，AB ＝BC ＝a ，由余弦定理得：a 2＝16＋a 2－8a cos θ，∴a cos θ＝2，∴CA →·AB →＝4×a ×cos(π－θ)＝－4a cos θ＝－8.8．已知平面向量a ，b 满足|a |＝1，|b |＝2，a 与b 的夹角为π3.以a ，b 为邻边作平行四边形，则此平行四边形的两条对角线中较短的一条的长度为______．答案 3解析 ∵|a ＋b |2－|a －b |2＝4a·b＝4|a ||b |cos π3＝4>0， ∴|a ＋b |>|a －b |，又|a －b |2＝a 2＋b 2－2a·b ＝3，∴|a －b |＝ 3.9．已知|a |＝2|b |≠0，且关于x 的函数f (x )＝13x 3＋12|a |x 2＋a ·b x 在R 上有极值，则向量a 与b 的夹角的范围是__________．答案 ⎝⎛⎦⎤π3，π解析 设a 与b 的夹角为θ.∵f (x )＝13x 3＋12|a |x 2＋a ·b x ， ∴f ′(x )＝x 2＋|a |x ＋a ·b .∵函数f (x )在R 上有极值，∴方程x 2＋|a |x ＋a ·b ＝0有两个不同的实数根，即Δ＝|a |2－4a ·b ＞0，∴a ·b ＜a 24， 又∵|a |＝2|b |≠0，∴cos θ＝a ·b |a ||b |＜a 24a 22＝12，即cos θ＜12， 又∵θ∈[0，π]，∴θ∈⎝⎛⎦⎤π3，π.*10.已知圆C ：(x －2)2＋y 2＝4，圆M ：(x －2－5cos θ)2＋(y －5sin θ)2＝1(θ∈R )，过圆M 上任意一点P 作圆C 的两条切线PE ，PF ，切点分别为E ，F ，则PE →·PF →的最小值是________．答案 6解析 圆(x －2)2＋y 2＝4的圆心C (2,0)，半径为2，圆M (x －2－5cos θ)2＋(y －5sin θ)2＝1，圆心M (2＋5cos θ，5sin θ)，半径为1，∵CM ＝5＞2＋1，故两圆相离．如图所示，设直线CM 和圆M 交于H ，G 两点，则PE →·PF →最小值是HE →·HF →，HC ＝CM －1＝5－1＝4，HF ＝HE ＝HC 2－CE 2＝16－4＝23，sin ∠CHE ＝CE CH ＝12， ∴cos ∠EHF ＝cos 2∠CHE ＝1－2sin 2∠CHE ＝12， HE →·HF →＝|HE →|·|HF →|·cos ∠EHF ＝23×23×12＝6. 11．已知点P (0，－3)，点A 在x 轴上，点Q 在y 轴的正半轴上，点M 满足P A →·AM →＝0，AM→＝－32MQ →，当点A 在x 轴上移动时，求动点M 的轨迹方程． 解 设M (x ，y )为所求轨迹上任一点，设A (a,0)，Q (0，b )(b ＞0)，则P A →＝(a,3)，AM →＝(x －a ，y )，MQ →＝(－x ，b －y )，由P A →·AM →＝0，得a (x －a )＋3y ＝0.①由AM →＝－32MQ →，得 (x －a ，y )＝－32(－x ，b －y )＝⎝⎛⎭⎫32x ，32(y －b )， ∴⎩⎨⎧ x －a ＝32x ，y ＝32y －32b ，∴⎩⎨⎧ a ＝－x 2，b ＝y 3.∴b ＞0，y ＞0，把a ＝－x 2代入①，得－x 2⎝⎛⎭⎫x ＋x 2＋3y ＝0，整理得y ＝14x 2(x ≠0)． ∴动点M 的轨迹方程为y ＝14x 2(x ≠0)． 12．已知角A ，B ，C 是△ABC 的内角，a ，b ，c 分别是其所对边长，向量m ＝(23sin A 2，cos 2A 2)，n ＝(cos A 2，－2)，m ⊥n . (1)求角A 的大小；(2)若a ＝2，cos B ＝33，求b 的长． 解 (1)已知m ⊥n ，所以m·n ＝(23sin A 2，cos 2A 2)·(cos A 2，－2) ＝3sin A －(cos A ＋1)＝0，即3sin A －cos A ＝1，即sin(A －π6)＝12， 因为0<A <π，所以－π6<A －π6<5π6. 所以A －π6＝π6，所以A ＝π3. (2)在△ABC 中，A ＝π3，a ＝2，cos B ＝33， sin B ＝1－cos 2B ＝1－13＝63. 由正弦定理知a sin A ＝b sin B， 所以b ＝a ·sin B sin A ＝2×6332＝423. *13.已知平面上一定点C (2,0)和直线l ：x ＝8，P 为该平面上一动点，作PQ ⊥l ，垂足为Q ，且(PC →＋12PQ →)·(PC →－12PQ →)＝0. (1)求动点P 的轨迹方程；(2)若EF 为圆N ：x 2＋(y －1)2＝1的任意一条直径，求PE →·PF →的最值．解 (1)设P (x ，y )，则Q (8，y )．由(PC →＋12PQ →)·(PC →－12PQ →)＝0， 得|PC →|2－14|PQ →|2＝0，即(2－x )2＋(－y )2－14(8－x )2＝0， 化简得x 216＋y 212＝1. ∴动点P 在椭圆上，其轨迹方程为x 216＋y 212＝1. (2)∵PE →＝PN →＋NE →，PF →＝PN →＋NF →，且NE →＋NF →＝0.∴PE →·PF →＝PN →2－NE →2＝(－x )2＋(1－y )2－1＝16(1－y 212)＋(y －1)2－1＝－13y 2－2y ＋16 ＝－13(y ＋3)2＋19. ∵－23≤y ≤2 3.∴当y ＝－3时，PE →·PF →的最大值为19，当y ＝23时，PE →·PF →的最小值为12－4 3.综上，PE →·PF →的最大值为19，最小值为12－4 3.。