各种计算公式演示教学
完成率公式演示教学

完成率公式
精品资料
完成率的计算
完成率就是实际完成数值占计划目标完成数值的百分比,是工作中很常用的分析指标,计算公式总结如下:
1、当计划数和实际完成数都为正数时:
完成率公式=(实际/计划)×100%
2、当计划数为负数,实际完成数为正数或者负数时:
完成率公式=(2-实际/计划)×100%
例如:(1)公司计划完成-100,实际完成-50,实际比计划少亏50(可以理解成比计划多赚50),完成率就是〔2-(-50/-100)〕×100%=150%
(2)公司计划完成-100,实际完成50,实际比计划少亏150(可以理解成比计划多赚150),完成率就是〔2-(50/-100)〕×100%=250%
3、当计划数为正数,实际完成数为负数时:
完成率公式=-(计划+实际)/计划×100%
(注:在公式运算中实际完成数取正值计算)
例如:公司计划完成100,实际完成-50,完成率就是-(100+50)/100×100%=-150%
2016年2月
仅供学习与交流,如有侵权请联系网站删除谢谢2。
Excel2016数组公式指南和示例

Excel数组公式指南和示例要成为一名Excel 高级用户,您需要知道如何使用数组公式,它能执行非数组公式所不能执行的计算。
本文内容∙了解数组公式∙了解数组常量∙使用基本数组公式∙使用高级数组公式了解数组公式本节介绍数组公式并解释如何对数组公式进行输入、编辑并解答疑难问题。
为什么要使用数组公式?如果您在Excel 中使用过公式,想必知道利用公式可以执行某些相当复杂的操作。
例如,可以基于给定的年数计算贷款总成本。
但是,如果您确实想精通Excel,还需要掌握如何使用数组公式。
因为使用数组公式可以执行更多复杂的任务,例如:∙计算包含在某个单元格区域中的字符数。
∙仅对满足特定条件的数字求和,例如某一区域中的最小值或介于上限和下限之间的数字。
∙对一系列值中的每第n 个值求和。
数组公式也被称为“CSE 公式”,这是因为可以按Ctrl+Shift+Enter 在工作簿中输入它们。
数组和数组公式简介如果您有过一点编程经验,可能碰到过术语数组。
在本文中,数组是项的集合。
在Excel 中,这些项可以位于一行(称为一维水平数组)中,也可位于一列(称为一维垂直数组)中或多行和多列(二维数组)中。
无法在Excel 中创建三维数组或三维数组公式。
数组公式是指可以在数组的一项或多项上执行多个计算的公式。
数组公式可以返回多个结果,也可返回一个结果。
例如,可以将数组公式放入单元格区域中,并使用数组公式计算列或行的小计。
也可以将数组公式放入单个单元格中,然后计算单个量。
位于多个单元格中的数组公式称为多单元格公式,位于单个单元格中的数组公式称为单个单元格公式。
下节中的示例将演示如何创建多单元格和单个单元格数组公式。
试一试本练习演示如何使用多单元格数组公式和单个单元格数组公式来计算一组销售数据。
第一组操作是使用多单元格公式计算一组小计。
第二组操作是使用单个单元格公式计算总计。
创建多单元格数组公式1.打开一个新的空白工作簿。
2.复制示例工作表数据,并将它粘贴到的新工作簿中(从单元格A1 开始)。
三年级数学下册课件 5.2长方形正方形面积的计算公式 人教版

三年级数学下册课件 5.2长方形正方形面积的计算公式 人教版 (共16张PPT)
三年级数学下册课件 5.2长方形正方形面积的计算公式 人教版 (共16张PPT)
(三)
❖ 提问:长和宽各是多少?
❖
用手中的12个面积单位测量这个长方形的面积,出现了什么问题?
我们手中的面积单位不够了,怎么办?
❖
每排个数、排数与长、宽有什么关系?
❖
5、实验(3)小篇子,第三组长方形:
三年级数学下册课件 5.2长方形正方形面积的计算公式 人教版 (共16张PPT)
米。
❖
4、一个长方形的面积是40平方米,长是8分米,宽是( )分米,这
个长方形的周长是( )。
❖
5、一个正方形的面积是25平方厘米,它的边长是( )厘米,周长是
( )厘米。
❖ 二、判断
❖
1、一个角的面积是10平方分米。( )
❖
2、黑板的长是4平方米。( )
❖
3、把两个长方形拼成一个大长方形,面积不变。( )
❖ 五、板书设计
三年级数学下册课件 5.2长方形正方形面积的计算公式 人教版 (共16张PPT)
典型例题 三年级数学下册课件 5.2长方形正方形面积的计算公式 人教版 (共16张PPT)
(一)
❖
1、一张边长是10厘米的正方形纸板,剪下一个长10厘米,宽6厘米
的长方形。剩下
❖ 的部分是什么形?它的面积是多少平方厘米?
(四) 三年级数学下册课件 5.2长方形正方形面积的计算公式 人教版 (共16张PPT)
❖ 教师提问:这个长方形能不能用我们手中的学具得到这个长方形的面积?
低压出线电缆线路压降计算演示教学

低压出线电缆线路压降计算箱变低压出线电缆线路压降计算贵司G3地块箱变电缆出线电缆至最远点集中电表箱压降计算如下:一、线路压降计算公式:1.R=ρL/S(R电阻、S截面积、L长度、ρ电阻率,铜的电阻率ρ=0.0175)2.I=P/1.732*U*COSØ(I电流、U电压、COSØ功率)根据实测:箱变至G3-1AW6距离为390米,末端用电负荷为240KW,电缆截面为2*(4*120+1*70)I=P/1.732*U*COSØ=240/1.732*0.38*0.8=456.27AR=ρL/S=0.0175*390/(2*120)=0.028欧△U=IR=456.27*0.028=12.77V<26.6V(7%U=0.05*380=26.6)。
箱变至G3-1AW5距离为390米,末端用电负荷为215KW,电缆截面为2*(4* 120+1*70)I=P/1.732*U*COSØ=214/1.732*0.38*0.8=408.75AR=ρL/S=0.0175*390/(2*120)=0.028欧△U=IR=408.75*0.028=11.44V<26.6V(7%U=0.05*380=26.6)。
二、根据《电能质量供电电压允许偏差》(GB12325-90)规定,电力系统在正常运行条件下,用户受电端供电电压的允许偏差为:(1)35kV及以上供电和对电压质量有特殊要求的用户为额定电压的+5%~-5%;(2)10kV及以下高压供电和低压电力用户为额定电压的+7%~-7%;(3)低压照明用户为额定电压的+5%~-10%。
G3地块箱变出线至G3-1AW5、G3-AW6集中电表箱之间的电缆产生的压降,未超出国标(GB12325-90)规定的压降允许值。
综上,贵司G3地块箱变电缆出线电缆至最远点集中电表箱压降符合要求。
海南金盘电气有限公司2015年06月10日。
暴雨产流计算(推理公式-四川省)演示教学
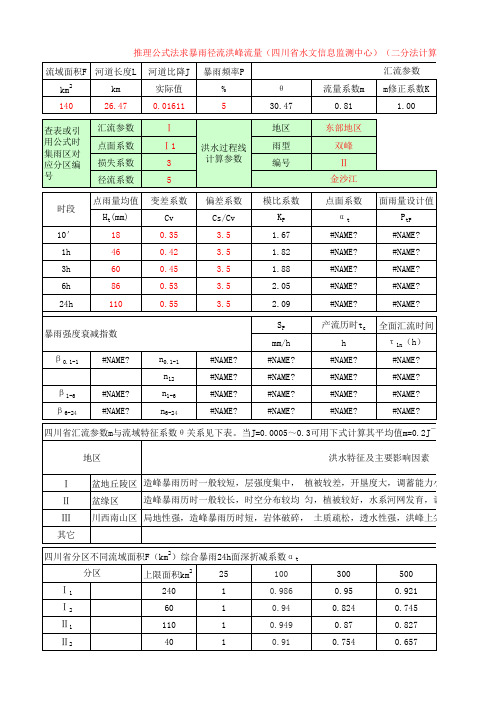
1
0.938
0.835
0.77
1
0.928
0.832
0.771
1
0.972
0.909
0.861
1
0.815
0.539
0.423
1
0.962
0.875
0.81
根据实测资料的对应分析,μ值随集水面积的减小而增大。在四川其平均变化关系为:μ=k·F-0.19,k值变化归
计算编号
地区
流域地形地貌
1
青衣江~鹿头山暴雨区 相对高差在200m以上,地势较陡,切割较深,植被较好,有部分荒山或坡地
9
#NAME?
10
#NAME?
11
#NAME?
12
#NAME?
13
#NAME?
分区名称
分区范围
盆地腹部丘陵区
岷江、沱江中 游及涪江、嘉
岷沱江下游平行岭谷区 岷江、沱江下游及平行岭谷地区
长江南岸区
高县至綦江长江南岸地区
赤水河古蔺区
赤水河古蔺地区
乌江下游及巫山区 乌江下游及巫山地区
沅江区
秀山地区
大巴山暴雨区
1 0.95 0.8 0.6 0.4 0.2 0.1 0.05
0
0.76 0.52
0.79 0.56
单峰
Ⅰ 0 0.2 0.26 0.34 0.4 0.5 0.62 0.75 0.9 0.98 1.09 1.24 1.44 1.79 2.1 2.38 3.1
四川省分区不同流域面积F(km2)综合暴雨24h面深折减系数αt
分区
上限面积km2
25
100
Ⅰ1
240
1
0.986
跨年月数计算公式教学

跨年月数计算公式教学在日常生活中,我们经常需要计算两个日期之间的跨年月数。
这种计算可以用于各种场合,比如计算两个人的年龄差、计算两个事件之间的时间间隔等等。
本文将介绍如何使用公式来计算两个日期之间的跨年月数。
首先,我们需要明确两个日期之间的跨年月数是指从第一个日期到第二个日期之间的完整年份和月份的数量。
例如,从2020年1月1日到2022年3月1日之间的跨年月数是2年2个月。
接下来,我们将介绍两种常用的方法来计算跨年月数的公式。
方法一,利用日期差计算。
首先,我们可以使用日期差的方法来计算跨年月数。
这种方法的基本思路是先计算出两个日期之间的总天数,然后根据这个总天数来计算出跨年月数。
假设我们有两个日期分别为date1和date2,我们可以先计算出两个日期之间的总天数diff_days = date2 date1。
然后,我们可以根据这个总天数来计算出跨年月数。
具体的计算公式如下:跨年月数 = (date2的年份 date1的年份) 12 + (date2的月份 date1的月份)。
需要注意的是,上面的计算公式中,我们需要考虑到跨年的情况。
如果date2的月份小于date1的月份,那么我们需要将(date2的年份 date1的年份)减去1,并且将(date2的月份 date1的月份)加上12。
下面是一个具体的例子,假设我们有两个日期分别为2020年1月1日和2022年3月1日,我们可以先计算出总天数为diff_days = 790天。
然后,根据上面的公式,我们可以计算出跨年月数为2年2个月。
方法二,利用月份差计算。
除了使用日期差的方法来计算跨年月数,我们还可以使用月份差的方法来计算。
这种方法的基本思路是先计算出两个日期之间的总月数,然后根据这个总月数来计算出跨年月数。
假设我们有两个日期分别为date1和date2,我们可以先计算出两个日期之间的总月数diff_months = (date2的年份date1的年份) 12 + (date2的月份date1的月份)。
焊缝受力计算公式教学

焊缝受力计算公式教学在焊接工程中,焊缝受力计算是非常重要的一环。
焊接是将两个或多个材料通过熔化并冷却后形成连接的工艺,焊缝是焊接过程中形成的连接部分。
在实际工程中,焊缝需要承受各种不同方向和大小的受力,因此需要进行受力计算以保证焊缝的安全性和可靠性。
本文将介绍焊缝受力计算的基本公式和教学方法。
焊缝受力计算的基本公式。
在进行焊缝受力计算时,需要考虑到焊缝所承受的拉力、剪力、弯矩等不同受力情况。
以下是焊缝受力计算的基本公式:1. 拉力计算公式。
焊缝在拉力作用下的受力计算公式为:N = F/A。
其中,N为焊缝受力,F为拉力大小,A为焊缝的有效截面积。
2. 剪力计算公式。
焊缝在剪力作用下的受力计算公式为:V = τA。
其中,V为焊缝受力,τ为剪应力大小,A为焊缝的有效截面积。
3. 弯矩计算公式。
焊缝在弯矩作用下的受力计算公式为:M = σS。
其中,M为焊缝受力,σ为弯矩应力大小,S为焊缝的受力臂长。
以上是焊缝受力计算的基本公式,通过这些公式可以计算焊缝在不同受力情况下的受力大小,从而为焊接工程的设计和实施提供参考依据。
焊缝受力计算的教学方法。
在进行焊缝受力计算的教学中,需要从基础知识的讲解开始,逐步引导学生理解和掌握受力计算的方法和技巧。
以下是焊缝受力计算的教学方法:1. 理论知识的讲解。
首先,需要向学生介绍焊缝受力计算的基本理论知识,包括受力的分类、受力计算的基本原理和公式等内容。
通过理论知识的讲解,可以帮助学生建立对焊缝受力计算的基本认识和理解。
2. 实例分析。
其次,可以通过实例分析的方式,向学生展示不同受力情况下焊缝受力计算的具体步骤和方法。
通过实例分析,可以帮助学生将理论知识应用到实际问题中,提高他们的计算能力和实际操作能力。
3. 计算练习。
在教学过程中,可以安排一定数量的焊缝受力计算练习,让学生通过实际操作来巩固和提高他们的受力计算能力。
通过计算练习,可以帮助学生加深对焊缝受力计算方法的理解和掌握。
人教版初中数学八年级上册14.2乘法公式(教案)示例

此外,我发现学生们在解决具体问题时,对于何时使用平方差公式和立方和差公式还不够自信。这可能是因为他们在公式选择和应用上缺乏足够的练习。因此,我计划在下一节课中增加更多针对性的练习,特别是那些涉及公式选择和综合应用的题目。
2.培养学生的数学运算能力,使学生能够熟练运用乘法公式进行简便计算,解决实际问题,增强数学运算的准确性。
3.培养学生的空间想象力和抽象思维能力,通过乘法公式的学习,引导学生从具体实例中提炼出数学规律,提升对数学概念的理解。
4.培养学生的团队协作和交流表达能力,课堂上鼓励学生进行小组讨论,分享乘法公式的发现与应用,提高学生的沟通能力。
-灵活运用乘法公式:学生在解决问题时,可能难以判断何时使用哪个乘法公式,需要通过大量练习和讲解,让学生掌握乘法公式的应用场景。
-识别并分解问题中的乘法结构:学生在面对复杂问题时,可能难以识别其中的乘法结构,需要教师指导如何分解问题,找到适用的乘法公式。
举例:
-难点突破:通过展开(a+b)²和(a-b)²,让学生观察并发现完全平方公式的规律,理解平方差公式的来源。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了乘法公式的基本概念、重要性和应用。通过实践活动和小组讨论,我们加深了对乘法公式的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
在小组讨论环节,我观察到学生们在讨论乘法公式在日常生活中的应用时,能够提出一些很有创意的想法。这表明他们能够将学到的知识应用到实际问题中。然而,我也发现有些小组在讨论时,成员之间的交流并不充分,导致部分学生的参与度不高。在未来的教学中,我需要更加注重引导学生之间的互动,确保每个学生都能积极参与讨论。
完全平方公式与平方差公式-经典教学教辅文档

第8章整式乘法与因式分解8.3 完全平方公式与平方差公式(续表)_________________________________________________________________________________________________________④[习题反思]好题题号_____________________________________________错题题号_____________________________________________第1课时完全平方公式学案1、完全平方公式有两个:(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.即,两数和(或差)的平方,等于这两个数的平方和,加上(或者减去)这两个数的积的2倍.这两个公式叫做完全平方公式.它们可以合写在一同,为(a±b)2=a2±2ab+b2.为便于记忆,可抽象的叙说为:“首平方、尾平方,2倍乘积在中央”.几何背景:如图,大正方形的面积可以表示为(a+b)2,也能够表示为S=SⅠ+ SⅡ+ SⅢ+SⅣ,同时S=a2+ab+ab+b2=a2+2ab+b2.从而验证了完全平方公式(a+b)2=a2+2ab+b2.2、完全平方公式的特点是:左侧是两个相反的二项式相乘,右侧是三项式,是左侧二项式中两项的平方和,加上(这两项相加时)或减去(这两项相减时)这两项乘积的2倍.公式中的字母可以表示具体的数(正数或负数),也能够表示单项式或多项式等代数式.只需符合这一公式的结构特点,就可以运用这一公式.3、在运用完全平方公式时应留意成绩:(1)千万不要发生类似(a±b)2=a 2±b 2的错误;(2)不要与公式(ab )2=a 2b 2混淆;(3)切勿把“乘积项”2ab 中的2漏掉;(4)计算时,应先观察所给标题的特点能否符合公式的条件,如符合,则可以直接套用公式进行计算;如不符合,应先变形为公式的结构特点,再利用公式进行计算,如变形后仍不具备公式的结构特点,则应运用乘法法则进行计算.名师导学互动典例精析:知识点1:改变公式中b a ,的符号:例1、运用完全平方公式计算: ()252y x +-【解题思绪】本例改变了公式中b a ,的符号,处理方法之一:把两式分别变形为()()[]225252y x y x --=+-()252y x -=再用公式计算(反思得:()()()()2222;b a b a a b b a +=---=-);方法二:把两式分别变形为:()()222552x y y x -=+-后直接用公式计算;方法三:把两式分别变形为()()[]225252y x y x +-=+-后直接用公式计算.【解】()252y x +-=()()()22222420252252525x xy y x x y y x y +-=+⨯⨯-=-.【方法归纳】对乘法公式的最初运用是模仿套用,套用的前提是确定能否具备运用公式的条件,关键是正确确定“两数”即“a ”和“b ”.对应练习:()2b a --知识点2:改变公式中的项数 例2、计算:()2c b a ++【解题思绪】完全平方公式的左侧是两个相反的二项式相乘,而本例中出现了三项,故应考虑将其中两项结合运用全体思想看成一项,从而化解矛盾.所以在运用公式时, ()2c b a ++ 可先变形为()[]2c b a ++ 或()[]2c b a ++ 或者()[]2b c a ++ ,再进行计算.【解】()2c b a ++=()[]2c b a ++=()()bc ac ab c b a c c b a b a 222222222+++++=++++.【方法归纳】运用全体思想可以使计算更为简便,快捷. 对应练习:(2a -b +4)2知识点3:改变公式的结构例3、运用公式计算: (1)()()y x y x 22++; (2)()()b a b a --+. 【解题思绪】本例中所给的均是二项式乘以二项式,表面看外观结构不符合公式特点,但仔细观察易发现,只需将其中一个因式作适当变形就可以了.【解】(1)()()y x y x 22++=()2222422y xy x y x ++=+;(2)()()b a b a --+=()2222b ab a b a ---=+-.【方法归纳】观察到两个因式的系数有倍数关系或相反关系是正确变形并利用公式的前提条件. 对应练习:计算:()()a b b a --知识点4:利用公式简便运算 例4:计算:9992【解题思绪】本例中的999接近1000,故可化成两个数的差,从而运用完全平方公式计算.【解】()=+-=+-=-=120001000000120001000110009992222998001. 【方法归纳】有些数学计算可拆成两数(式)平方差、完全平方公式的方式,正用乘法公式可使运算简捷、快速. 对应练习:计算:100.12知识点5:公式的逆用例5、计算: ()()()()2233525++++-+x x x x【解题思绪】本题若直接运用乘法公式和法则较繁琐,仔细分析可发现其结构恰似完全平方公式()2222b ab a b a +-=-的右侧,不妨把公式倒过来用.【解】()()()()2233525++++-+x x x x =()()[]4352=+-+x x .【方法归纳】解题中,•若把留意力和着眼点放在成绩的全体上,多方位考虑、联想、探求,进行全体考虑、全体变形,•从不同的方面确定解题策略,能使成绩迅速获解.对应练习:化简()()()()223372272++++-+a a a a 知识点6:公式的变形例6、已知实数a 、b 满足()1,102==+ab b a .求以下各式的值:(1)22b a +;(2)()2b a -【解题思绪】此例是典型的整式求值成绩,若按常规思想把a 、b 的值分别求出来,非常困难;仔细探求易把这些条件同完全平方公式结合起来,运用完全平方公式的变方式很容易找到解决成绩的途径.【解】(1)22b a +=()822=-+ab b a ; (2)()()ab b a b a 422-+=-=6.【方法归纳】()()ab b a b a 422-+=-()(),422ab b a b a +-=+()()ab b a b a ab b a b a 2,2222222+-=+-+=+熟习完全平方公式的变方式,是相关全体代换求知值的关键. 对应练习:已知:x +y =-1,x 2+y 2=5,求xy 的值. 知识点7:乘法公式的综合运用 例7、计算:()()z y x z y x -+++【解题思绪】此例是三项式乘以三项式,特点是:有些项相反,另外的项互为相反数。
excel表格函数公式教程PPT

用于查找指定单元格范围内的最大值或最小值。
详细描述
MAX函数和MIN函数分别用于查找一系列数字中的最大值和最小值。使用时需要指定起始单元格和结束单元格 的范围,例如MAX(C1:C10)表示查找C1到C10单元格范围内的最大值。
IF函数:条件判断
总结词
根据设定的条件返回不同的结果。
详细描述
IF函数用于在满足特定条件时返回一个值,不满足时返回另一个值。IF函数的语法是IF(condition, value_if_true, value_if_false),其中condition是需要判断的条件,value_if_true是条件为真时返回的值, value_if_false是条件为假时返回的值。
通过使用“名称管理器”或“定义名称”功能,可以为单元格或区域指定一个名称 ,并在公式中直接使用该名称代替单元格地址。
名称定义有助于简化公式,提高可读性和维护性。
自定义函数
Excel允许用户创建自定义函数,以便 扩展Excel内置函数的功能。
自定义函数可以用于实现特定的计算 逻辑或处理复杂的数据关系,以满足 特定需求。
01
02
03
04
随着技术的不断进步,Excel 函数和公式将更加智能化和自
动化。
数据分析和预测功能将更加完 善,为用户提供更准确的决策
支持。
与其他软件的集成将更加紧密 ,实现数据共享和协同工作。
云端存储和在线协作将成为 Excel发展的新趋势。
如何进一步学习和掌握Excel技能
01
02
03
04
参加专业培训课程
函数是Excel内置的公式,用于执行各种计算和分析任务,如 求和、平均、查找等。公式则是由用户自行编写,通过使用 运算符和单元格引用,对数据进行计算、比较和处理。
压电陶瓷频率计算公式教学

压电陶瓷频率计算公式教学压电陶瓷是一种特殊的材料,具有压电效应,即在受到外力作用时会产生电荷。
压电陶瓷广泛应用于传感器、振动器、滤波器等领域。
在实际应用中,我们经常需要计算压电陶瓷的频率,以便设计和调整相应的电路。
本文将介绍压电陶瓷频率计算的基本公式和方法。
压电陶瓷的频率计算涉及到其物理特性和结构参数。
首先,我们需要了解压电陶瓷的压电常数和结构尺寸,这些参数将影响其振动频率。
压电常数是一个描述压电材料电-机械耦合效应的物理量,通常用符号d表示,单位是库仑/牛。
结构尺寸包括压电陶瓷的长度、宽度和厚度等几何参数。
在计算压电陶瓷的频率时,我们可以使用以下的基本公式:\[f = \frac{1}{2L} \sqrt{\frac{Y}{\rho}}\]其中,f是压电陶瓷的频率,L是压电陶瓷的长度,Y是压电陶瓷的杨氏模量,ρ是压电陶瓷的密度。
在这个公式中,频率与压电陶瓷的长度成反比,与杨氏模量和密度的平方根成正比。
这意味着,如果我们想要增加压电陶瓷的频率,可以通过减小长度或增大杨氏模量和密度来实现。
接下来,让我们通过一个具体的例子来演示如何使用上述公式计算压电陶瓷的频率。
假设我们有一块压电陶瓷的尺寸为2cm × 2cm × 0.2cm,杨氏模量为10GPa,密度为7500kg/m³。
我们可以先计算出压电陶瓷的长度L为:\[L = \sqrt[3]{V} = \sqrt[3]{2cm × 2cm × 0.2cm} = 1.26cm\]然后,代入上述公式中,即可计算出压电陶瓷的频率:\[f = \frac{1}{2×1.26cm} \sqrt{\frac{10×10^9Pa}{7500kg/m³}} = 1.58MHz\]通过这个例子,我们可以看到,通过简单的公式计算,我们就可以得到压电陶瓷的频率。
这对于工程师在设计和调整电路时提供了重要的参考。
n个数的平均数和方差的计算公式

(一)n个数的平均数的计算公式平均数(mean)是一组数值的总和除以数值的个数,是描述数据集中心位置的一种统计量。
对于n个数的数据集合,其平均数的计算公式可以表示为:\[\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i\]其中,\(\bar{x}\)表示平均数,\(x_i\)表示数据集中的第i个数值。
(二)n个数的方差的计算公式方差(variance)是一组数据的离散程度的度量,表示数据与其平均数之间的偏离程度。
对于n个数的数据集合,其方差的计算公式可以表示为:\[Var(x) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2\]其中,\(Var(x)\)表示方差,\(x_i\)表示数据集中的第i个数值,\(\bar{x}\)表示数据集的平均数。
(三) n个数的平均数和方差的例子假设有一个数据集合:2, 4, 6, 8, 10。
现在我们来计算其平均数和方差。
1. 平均数的计算数据集合的总和 = 2 + 4 + 6 + 8 + 10 = 30数据集合的个数 = 5平均数 = 30 / 5 = 6数据集合2, 4, 6, 8, 10的平均数为6。
2. 方差的计算将每个数值与平均数的差的平方进行累加,并除以数值的个数:\[\frac{(2-6)^2 + (4-6)^2 + (6-6)^2 + (8-6)^2 + (10-6)^2}{5}\]=\[\frac{16 + 4 + 0 + 4 + 16}{5}\]=\[\frac{40}{5}\]=8数据集合2, 4, 6, 8, 10的方差为8。
通过这个例子可以清楚地看到,平均数和方差是描述一个数据集合的重要统计量,它们可以帮助我们理解数据的中心位置和数据的离散程度。
在实际应用中,我们经常会用到这些统计量来分析和描述数据的特征。
当我们对一组数据进行统计分析时,平均数和方差是最基本的描述统计量之一。
2024年乘法公式2两数和差的平方课件华东师大版

2024年乘法公式 2两数和差的平方课件华东师大版一、教学内容本节课选自华东师大版教材《数学》七年级下册第十章“数的运算”中的“平方差公式”一节。
具体内容包括:理解并掌握平方差公式的含义及其运用,通过实例分析,让学生掌握两数和与两数差的平方关系的转换,并能够运用平方差公式进行相关计算。
二、教学目标1. 让学生理解平方差公式的概念,并能够熟练运用公式进行计算。
2. 培养学生的观察、分析、归纳能力,提高他们解决问题的策略水平。
3. 通过平方差公式的学习,使学生进一步理解乘法分配律的应用,培养他们的逻辑思维能力。
三、教学难点与重点教学难点:平方差公式的推导及其应用。
教学重点:理解并熟练运用平方差公式进行计算。
四、教具与学具准备1. 教具:黑板、粉笔、教学课件。
2. 学具:练习本、铅笔。
五、教学过程1. 实践情景引入:通过生活中的实例,如计算两个数的和与差的平方,引入平方差公式的概念。
2. 探索平方差公式:a. 请学生计算(a+b)^2 和(ab)^2。
b. 引导学生观察两个式子的展开结果,发现它们之间的关系。
c. 归纳平方差公式:(a+b)^2 = a^2 + 2ab + b^2,(ab)^2 = a^2 2ab + b^2。
3. 例题讲解:a. 讲解平方差公式的应用,通过具体例题进行演示。
b. 让学生跟随讲解,进行同步计算,加深理解。
4. 随堂练习:a. 设计一些关于平方差公式的练习题,让学生独立完成。
b. 对学生进行个别辅导,帮助他们解决在练习过程中遇到的问题。
b. 引导学生思考平方差公式与乘法分配律之间的关系。
六、板书设计1. 平方差公式2. 内容:a. 定义:两数和与两数差的平方关系。
b. 公式:(a+b)^2 = a^2 + 2ab + b^2,(ab)^2 = a^2 2ab + b^2。
c. 例题:具体应用平方差公式的例子。
d. 练习题:设计具有代表性的练习题。
七、作业设计1. 作业题目:(1)(3x+4y)^2(2)(5a6b)^2b. 应用题:生活中运用平方差公式的例子。
根号差公式教学设计

根号差公式教学设计引言根号差公式是解二次方程的重要方法之一,通过这个教学设计,旨在帮助学生理解和掌握根号差公式的运用,提高解二次方程的能力。
教学目标- 理解根号差公式的含义和应用场景- 掌握根号差公式的计算步骤和运用方法- 提高解二次方程的能力,解决相关问题教学内容1. 根号差公式的定义和推导过程的讲解2. 根号差公式的计算步骤和运用方法的演示3. 根据实际问题进行练和案例讲解教学步骤步骤一:引入根号差公式- 示例:利用根号差公式求解以下二次方程的解。
- $x^2-5x+6=0$- 引导学生思考如何求解,引出根号差公式。
步骤二:定义和推导根号差公式- 定义根号差公式的含义和作用。
- 推导根号差公式的过程,解释推导的逻辑和思路。
步骤三:介绍根号差公式的计算步骤和运用方法- 示范计算步骤和运用方法,引导学生理解和记忆。
步骤四:练和案例分析- 给学生提供一些练题,巩固根号差公式的运用。
- 分析实际问题,应用根号差公式求解。
教学辅助工具- 讲义:提供定义、推导过程、计算步骤和例题- 教学演示软件:展示根号差公式的计算过程和应用方法- 白板和彩色笔:用于讲解和示范过程- 练题和案例题集:提供给学生练和思考教学评估- 批判性思维问题:提供一些需要综合运用根号差公式解决的问题,考察学生的理解和应用能力。
- 练题考试:通过解题考试,检测学生掌握程度。
教学反思通过这个教学设计,学生可以全面理解根号差公式的应用,掌握解二次方程的方法,提高数学解题的能力。
在教学过程中,要注重引导学生自主思考和合作学习,激发学生兴趣,提高学习效果。
[教学]剪切计算公式
![[教学]剪切计算公式](https://img.taocdn.com/s3/m/8563b0c748649b6648d7c1c708a1284ac85005ac.png)
2.剪切强度计算 (1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sF A ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系:对塑性材料:[]0.60.8[]τσ=对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2s FF =销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4s F A ττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算dmax max2=[]4F F d Aσσπ=≤所以0.034 3.4d m cm≥===(2)钢板的剪切面是直径为d 高为t 的柱表面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算公式1、长方形的周长=(长+宽)×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽 S=ab4、正方形的面积=边长×边长 S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高 S=ah7、梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径 ?=πr11、长方体的表面积=(长×宽+长×高+宽×高)×212、长方体的体积 =长×宽×高 V =abh13、正方体的表面积=棱长×棱长×6 S =6a14、正方体的体积=棱长×棱长×棱长 V=a.a.a= a15、圆柱的侧面积=底面圆的周长×高 S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2)+2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高 V=ShV=πr h=π(d÷2) h=π(C÷2÷π) h18、圆锥的体积=底面积×高÷3V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π) h÷3 19、长方体(正方体、圆柱体)的体1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、 1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数小学数学图形计算公式1 、正方形 C周长 S面积 a边长周长=边长×4C=4a 面积=边长×边长 S=a×a2 、正方体 V:体积 a:棱长表面积=棱长×棱长×6 S表=a ×a×6 体积=棱长×棱长×棱长V=a×a×a3 、长方形C周长 S面积 a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4 、长方体V:体积 s:面积 a:长 b: 宽 h:高(1)表面积(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)(2)体积=长×宽×高V=abh5 三角形s面积 a底 h高面积=底×高÷2s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6 平行四边形s面积 a底 h高面积=底×高s=ah7 梯形s面积 a上底 b下底 h高面积=(上底+下底)×高÷2s=(a+b)×h÷28 圆形S面积 C周长∏ d=直径 r=半径(1)周长=直径×∏=2×∏×半径C=∏d=2∏r(2)面积=半径×半径×∏9 圆柱体v:体积 h:高 s;底面积 r:底面半径 c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10 圆锥体v:体积 h:高s;底面积 r:底面半径体积=底面积×高÷3总数÷总份数=平均数和差问题(和+差)÷2=大数(和-差)÷2=小数和倍问题和÷(倍数-1)=小数小数×倍数=大数(或者和-小数=大数)差倍问题差÷(倍数-1)=小数小数×倍数=大数(或小数+差=大数)植树问题1非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数=段数+1=全长÷株距-1全长=株距×(株数-1)株距=全长÷(株数-1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么:株数=段数=全长÷株距全长=株距×株数株距=全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1全长=株距×(株数+1)株距=全长÷(株数+1)2 封闭线路上的植树问题的数量关系如下株数=段数=全长÷株距全长=株距×株数株距=全长÷株数盈亏问题(盈+亏)÷两次分配量之差=参加分配的份数(大盈-小盈)÷两次分配量之差=参加分配的份数(大亏-小亏)÷两次分配量之差=参加分配的份数相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间流水问题顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷2浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100% 涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1)利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)时间单位换算1世纪=100年 1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时 1时=60分1分=60秒 1时=3600秒积=底面积×高 V=Sh第一部分:概念1、加法交换律:两数相加交换加数的位置,和不变.2、加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变.3、乘法交换律:两数相乘,交换因数的位置,积不变.4、乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变.5、乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变.如:(2+4)×5=2×5+4×56、除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变. O除以任何不是O的数都得O.简便乘法:被乘数、乘数末尾有O的乘法,可以先把O前面的相乘,零不参加运算,有几个零都落下,添在积的末尾.7、什么叫等式?等号左边的数值与等号右边的数值相等的式子叫做等式.等式的基本性质:等式两边同时乘以(或除以)一个相同的数,等式仍然成立.8、什么叫方程式?答:含有未知数的等式叫方程式.9、什么叫一元一次方程式?答:含有一个未知数,并且未知数的次数是一次的等式叫做一元一次方程式.学会一元一次方程式的例法及计算.即例出代有χ的算式并计算.10、分数:把单位“1”平均分成若干份,表示这样的一份或几分的数,叫做分数.11、分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变.异分母的分数相加减,先通分,然后再加减.12、分数大小的比较:同分母的分数相比较,分子大的大,分子小的小.异分母的分数相比较,先通分然后再比较;若分子相同,分母大的反而小.13、分数乘整数,用分数的分子和整数相乘的积作分子,分母不变.14、分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母.15、分数除以整数(0除外),等于分数乘以这个整数的倒数.16、真分数:分子比分母小的分数叫做真分数.17、假分数:分子比分母大或者分子和分母相等的分数叫做假分数.假分数大于或等于1.18、带分数:把假分数写成整数和真分数的形式,叫做带分数.19、分数的基本性质:分数的分子和分母同时乘以或除以同一个数0除外),分数的大小不变.20、一个数除以分数,等于这个数乘以分数的倒数.21、甲数除以乙数(0除外),等于甲数乘以乙数的倒数. 分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变.异分母的分数相加减,先通分,然后再加减.分数的乘法则:用分子的积做分子,用分母的积做分母. 22、什么叫比:两个数相除就叫做两个数的比.如:2÷5或3:6或1/3比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变.23、什么叫比例:表示两个比相等的式子叫做比例.如3:6=9:1824、比例的基本性质:在比例里,两外项之积等于两内项之积.25、解比例:求比例中的未知项,叫做解比例.如3:χ=9:1826、正比例:两种相关联的量,一种量变化,另一种量也随着化,如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系.如:y/x=k(k一定)或kx=y27、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系.如:x×y = k( k一定)或k / x = y28、百分数:表示一个数是另一个数的百分之几的数,叫做百分数.百分数也叫做百分率或百分比.29、把小数化成百分数,只要把小数点向右移动两位,同时在后面添上百分号.其实,把小数化成百分数,只要把这个小数乘以100%就行了.30、把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位.31、把分数化成百分数,通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数.其实,把分数化成百分数,要先把分数化成小数后,再乘以100%就行了. 32、把百分数化成分数,先把百分数改写成分数,能约分的要约成最简分数.33、要学会把小数化成分数和把分数化成小数的化发.34、最大公约数:几个数都能被同一个数一次性整除,这个数就叫做这几个数的最大公约数.(或几个数公有的约数,叫做这几个数的公约数.其中最大的一个,叫做最大公约数.)35、互质数:公约数只有1的两个数,叫做互质数.36、最小公倍数:几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数.37、通分:把异分母分数的分别化成和原来分数相等的同分母的分数,叫做通分.(通分用最小公倍数)38、约分:把一个分数化成同它相等,但分子、分母都比较小的分数,叫做约分.(约分用最大公约数)39、最简分数:分子、分母是互质数的分数,叫做最简分数.40、分数计算到最后,得数必须化成最简分数.41、个位上是0、2、4、6、8的数,都能被2整除,即能用2进行42、约分.个位上是0或者5的数,都能被5整除,即能用5进行约分.在约分时应注意利用.43、偶数和奇数:能被2整除的数叫做偶数.不能被2整除的数叫做奇数.44、质数(素数):一个数,如果只有1和它本身两个约数,这样的数叫做质数(或素数).45、合数:一个数,如果除了1和它本身还有别的约数,这样的数叫做合数.1不是质数,也不是合数.46、利息=本金×利率×时间(时间一般以年或月为单位,应与利率的单位相对应)47、利率:利息与本金的比值叫做利率.一年的利息与本金的比值叫做年利率.一月的利息与本金的比值叫做月利率.48、自然数:用来表示物体个数的整数,叫做自然数.0也是自然数.49、循环小数:一个小数,从小数部分的某一位起,一个数字或几个数字依次不断的重复出现,这样的小数叫做循环小数.如3. 14141450、不循环小数:一个小数,从小数部分起,没有一个数字或几个数字依次不断的重复出现,这样的小数叫做不循环小数.如圆周率:3. 14159265451、无限不循环小数:一个小数,从小数部分起到无限位数,没有一个数字或几个数字依次不断的重复出现,这样的小数叫做无限不循环小数.如3.141592654……52、什么叫代数? 代数就是用字母代替数.53、什么叫代数式?用字母表示的式子叫做代数式.如:3x =ab+c第二部分:定义定理一、算术方面1.加法交换律:两数相加交换加数的位置,和不变.2.加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变.3.乘法交换律:两数相乘,交换因数的位置,积不变.4.乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变.5.乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变.如:(2+4)×5=2×5+4×5.6.除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变.0除以任何不是0的数都得0.7.等式:等号左边的数值与等号右边的数值相等的式子叫做等式.等式的基本性质:等式两边同时乘以(或除以)一个相同的数,等式仍然成立.8.方程式:含有未知数的等式叫方程式.9.一元一次方程式:含有一个未知数,并且未知数的次数是一次的等式叫做一元一次方程式.学会一元一次方程式的例法及计算.即例出代有χ的算式并计算.10.分数:把单位“1”平均分成若干份,表示这样的一份或几分的数,叫做分数.11.分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变.异分母的分数相加减,先通分,然后再加减. 12.分数大小的比较:同分母的分数相比较,分子大的大,分子小的小.异分母的分数相比较,先通分然后再比较;若分子相同,分母大的反而小.13.分数乘整数,用分数的分子和整数相乘的积作分子,分母不变.14.分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母.15.分数除以整数(0除外),等于分数乘以这个整数的倒数.16.真分数:分子比分母小的分数叫做真分数.17.假分数:分子比分母大或者分子和分母相等的分数叫做假分数.假分数大于或等于1.18.带分数:把假分数写成整数和真分数的形式,叫做带分数.19.分数的基本性质:分数的分子和分母同时乘以或除以同一个数(0除外),分数的大小不变.20.一个数除以分数,等于这个数乘以分数的倒数.21.甲数除以乙数(0除外),等于甲数乘以乙数的倒数. 第三部分:几何体1.正方形正方形的周长=边长×4 公式:C=4a正方形的面积=边长×边长公式:S=a×a正方体的体积=边长×边长×边长公式:V=a×a×a2.正方形长方形的周长=(长+宽)×2 公式:C=(a+b)×2长方形的面积=长×宽公式:S=a×b长方体的体积=长×宽×高公式:V=a×b×h3.三角形三角形的面积=底×高÷2. 公式:S= a×h÷24.平行四边形平行四边形的面积=底×高公式:S= a×h5.梯形梯形的面积=(上底+下底)×高÷2 公式:S=(a+b)h÷2 6.圆直径=半径×2公式:d=2r半径=直径÷2 公式:r= d÷2圆的周长=圆周率×直径公式:c=πd =2πr圆的面积=半径×半径×π公式:S=πrr7.圆柱圆柱的侧面积=底面的周长×高. 公式:S=ch=πdh=2πrh圆柱的表面积=底面的周长×高+两头的圆的面积. 公式:S=ch+2s=ch+2πr2圆柱的总体积=底面积×高. 公式:V=Sh8.圆锥圆锥的总体积=底面积×高×1/3 公式:V=1/3Sh三角形内角和=180度.平行线:同一平面内不相交的两条直线叫做平行线垂直:两条直线相交成直角,像这样的两条直线,我们就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足.第四部分:计算公式数量关系式:1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、 1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数时间单位换算:1世纪=100年 1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时 1时=60分1分=60秒1时=3600秒。
