《电路分析基础》_第5章
合集下载
电路分析基础(第四版)张永瑞答案第5章
解 两线圈顺接时（两线圈连接端子为异名端）， 由二 P=UIcosjz 得
P 96 cos j z 0.8 UI 60 2
这时的阻抗模值
U 60 Z 30 I 2
24
第5 章
互感与理想变压器
回路中阻抗Z中的电阻部分即相串联两线圈的损耗电阻之和
R r1 r2 Z cosjz 30 0.8 24
加在串联线圈两端进行实验。 当两线圈顺接(即异名端相
连)时， 如图(a)所示， 测得电流有效值为2 A， 平均功率为 96 W；当两线圈反接(即同名端相连)时， 如图(b)所示， 测得 电流为2.4 A。 试确定该两线圈间的互感值M。
22
第5 章
互感与理想变压器
题5.5图
23
第5 章
互感与理想变压器
题5.6图
29
第5 章
互感与理想变压器
解 将互感线圈画为T形等效电路， 如题解5.6图(a)
所示， 再应用电感串并联等效将题解5.6图(a)等效为题解5.6
图（b）。
因原电路已处于稳态， 所以由题解5.6图（b）求得
6 i1 (0 ) 3A 2
则由换路定律， i1(0+)=i1(0－)=3 A
互感与理想变压器
解 根据同名端的定义， 由原图电路线圈的绕向判定同
名端如题解5.10图(a)所示。 互感线圈用T形等效电路代替并画
出相量模型电路， 如题解5.10图(b)所示。 当ab端的阻抗Zab=0
时， 则有
U ab U ab 0 I 0 Z L j ( L2 M )
46
5.11 题5.11图所示电路中的变压器有两个额定电压为110
电路分析基础教案(第5章) 2
§5-2 电容的VCR 例题：电路如图所示，电压源电压为三角波形， 求电容电流i（t）。
0 0.5 1 1.5 -100 解：在关联参考方向时，i=C（du/dt）， 在0≤t≤0.25ms期间， i=1×10-6×[(100-0)/(0.25×10-3-0)=0.4A；
35
i(t) + C= u(t) 1 μ F -
100
u/V t/ms
ቤተ መጻሕፍቲ ባይዱ
§5-2 电容的VCR u/V
100 0 -100
t/ms 0.5 1 1.5
在0.25≤t≤0.75ms期间， i=1×10-6×[(-100-100)/(0.75×10-30.25×10-3)] =-0.4A；
36
§5-2 电容的VCR
100 0 -100
0.4
u/V
§5-1 电容元件
3、电容元件特点 线性电容有如下特点： （1）双向性 库伏特性是以原点对称，如图所示，因此与 端钮接法无关。 斜率为C q/C C u/V
0
18
§5-1 电容元件 （2）动态性 若电容两端的电压是直流电压U，则极板上的 电荷是稳定的，没有电流，即：I=0。
电容相当于断 路（开路），所 以电容有隔断直 流作用。
8
第五章 电容元件与电感元件 电阻电路在任意时刻t的响应只与同一时刻的 激励有关，与过去的激励无关。 因此，电阻电路是“无记忆”，或是说“即 时的”。 与电阻电路不同，动态电路在任意时刻t的响 应与激励的全部过去历史有关。 因此，动态电路是“有记忆”的。
9
第五章 电容元件与电感元件
本章主要内容： 动态元件的定义； 动态元件的VCR； 动态电路的等效电路； 动态电路的记忆、状态等概念。
电路分析基础[第五章动态电路的分析]课程复习
![电路分析基础[第五章动态电路的分析]课程复习](https://img.taocdn.com/s3/m/5c838930580216fc700afd08.png)
第五章动态电路的分析5．2．1 动态电路初始条件的确立一、初始条件动态电路中，一般将换路时刻记为t=0，换路前的一瞬间记为t=0_，换路后的一瞬间记为t=0+，则电路变量在t=0+的值，称为初始值，也称初始条件。
二、换路定则如果在换路前后，电容电流或电感电压为有限值，则换路时刻电容电压和电感电流不跃变，即uC (0_)=uC(0+)，iL(0_)=iL(0+)。
三、初始条件的计算(1)由换路前最终时刻即t=0_时的电路，求出电路的独立状态变量uC(0_)和iL (0_)。
从而根据换路定则得到uC(0+)和iL(0+)；(2)画出t=0+时的等效电路。
在这一等效电路中，将电容用电压为uC(0+)的直流电压源代替，将电感用电流为iL(0+)的直流电流源代替；(3)由上述等效电路，用直流电路分析方法，求其他非状态变量的各初始值。
5．2．2 动态电路的时域分析法5．2．2．1一阶电路的响应一阶电路是指只含有一个独立储能元件的动态电路。
一、一阶电路的零输入响应零输入响应是指动态电路无输入激励情况下，仅由动态元件初始储能所产生的响应，它取决于电路的初始状态和电路的特性。
因此在求解这一响应时，首先必须掌握电容电压或电感电流的初始值，至于电路的特性，对一阶电路来说，则是通过时间常数τ来体现的。
零输入响应都是随时间按指数规律衰减的，这是因为在没有外施激励的条件下，原有的储能总是要衰减到零的。
在RC电路中，电容电压总是从uC (0+)单调地衰减到零的，其时间常数τ=RC，即uC(t)=uC(0+)e-t/τ；在RL电路中电感电流总是从iL，(0+)单调地衰减到零的，其时间常数τ=L／R，即iL (t)=iL(0+)e-t/τ，掌握了uC(t)和iL(t)后，就可以用置换定理将电容用电压值为uC (t)的电压源置换，将电感用电流值为iL(t)的电流源置换，再求电路中其他支路的电压或电流即可。
二、一阶电路的零状态响应零状态响应是动态电路在动态元件初始储能的零为情况下，仅由输入激励所引起的响应。
电路分析基础第四版课后习题第四章第五章第六章答案
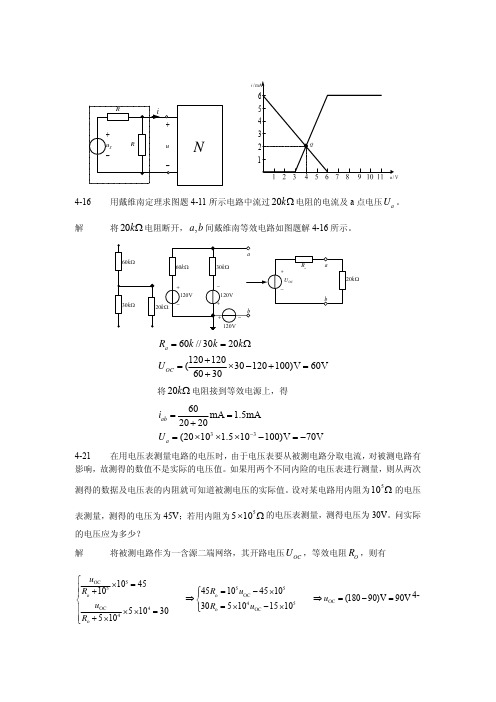
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开，间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上，得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时，由于电压表要从被测电路分取电流，对被测电路有影响，故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量，则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量，测得的电压为45V ；若用内阻为510Ω5510×Ω的电压表测量，测得电压为30V 。
问实际的电压应为多少？ 解将被测电路作为一含源二端网络，其开路电压，等效电阻OC U O R ，则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知：12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路，画出求短路电流和等效内阻的电路，如下图所示SC i对左图，因ab 间短路，故0,0i i α==，10A 0.5A 155SC i ==+ 对右图，由外加电源法，106ab R α=Ω− 4-30 电路如图题4-22所示。
电路分析基础(张永瑞)第5章
d e jt )] d Re( Ae j (t ) ) [Re( A dt dt
d [ A cos(t )] A sin(t ) dt Re[ jAe j（t ）] Re[ jAe jt ] d jt Re ( Ae ) dt
假设某正弦电流为
i (t ) I m cos(t i )
根据欧拉公式
e j cos j sin
可以把复指数函数Im e j(ωt+θi)展开成
I me j (t i ) I m cos(t i ) jIm sin(t i )
i(t ) Re[I me
第五章 正弦电路的稳态分析
解 由图可知，i(t)的振幅为 100A， 即
i(t ) 100cos(10 t i ) A
3
当t=0 时，电流为 50A，用t=0 代入上式，得
i (0) 100cos i 50
故
cos i 0.5
第五章 正弦电路的稳态分析
由于i(t)的正最大值发生在时间起点之后，初相角为负值，即
同理，可得正弦电压的有效值
1 U U m 0.707 m U 2
必须指出，交流测量仪表指示的电流、电压读数一般都是 有效值。 引入有效值以后，正弦电流和电压的表达式也可写成
i(t ) I m cos(t i ) 2 I cos(t i ) u(t ) Um cos(t u ) 2U cos(t u )
示。
第五章 正弦电路的稳态分析
5.1.2 相位差
假设两个正弦电压分别为
u1 (t ) U1m cos(t 1 ) u2 (t ) U 2 m cos(t 2 )
d [ A cos(t )] A sin(t ) dt Re[ jAe j（t ）] Re[ jAe jt ] d jt Re ( Ae ) dt
假设某正弦电流为
i (t ) I m cos(t i )
根据欧拉公式
e j cos j sin
可以把复指数函数Im e j(ωt+θi)展开成
I me j (t i ) I m cos(t i ) jIm sin(t i )
i(t ) Re[I me
第五章 正弦电路的稳态分析
解 由图可知，i(t)的振幅为 100A， 即
i(t ) 100cos(10 t i ) A
3
当t=0 时，电流为 50A，用t=0 代入上式，得
i (0) 100cos i 50
故
cos i 0.5
第五章 正弦电路的稳态分析
由于i(t)的正最大值发生在时间起点之后，初相角为负值，即
同理，可得正弦电压的有效值
1 U U m 0.707 m U 2
必须指出，交流测量仪表指示的电流、电压读数一般都是 有效值。 引入有效值以后，正弦电流和电压的表达式也可写成
i(t ) I m cos(t i ) 2 I cos(t i ) u(t ) Um cos(t u ) 2U cos(t u )
示。
第五章 正弦电路的稳态分析
5.1.2 相位差
假设两个正弦电压分别为
u1 (t ) U1m cos(t 1 ) u2 (t ) U 2 m cos(t 2 )
南京邮电大学电路分析基础_第5章1
4 .电容是储能元件
电压电流参考方向关联时，电容吸收功率 p(t) u(t)i(t) u(t)C du dt
p 可正可负。当 p > 0 时，电容吸收 功率（吞），储存电场能量增加；当p
< 0时，电容发出功率（吐），电容放 出存储的能量。
任意时刻t得到的总能量为
t
t
wC (t)
p( )d
i +
uS/mV + 10
uS -
Lu -
0
-10
(a)
1 2 3t (b)
解： 当0<t1s时，u(t)=10mV，
i(t) 1
t
u( )d
L
i(0) 2102
t
10
2
d
0
2t
A
2t
A
0
当 t 1s 时 i(1) 2A
当1s<t2s时，u(t)=-10mV
i(t)
，
i(1)
2. 电感是惯性元件
di
u 有限时，电流变化率 dt 必然有限； 电流只能连续变化而不能跳变。
3.电感是记忆元件
i(t) 1
t
u( )d
L
电感电流i有“记忆”电压全部历史
的作用。取决于电压(, t )的值。
i(t) 1
t
u( )d
L
1
t0 u()d 1
t
u( )d
L
L t0
上式也可以理解为什么电容电压不 能轻易跃变，因为电压的跃变要伴随 储能的跃变，在电流有界的情况下， 是不可能造成电场能发生跃变和电容 电压发生跃变的。
例1 C =4F，其上电压如图(b)，试求
电路分析基础(英文版)课后答案第五章
Z
i1 + i2 = i DE 5.5 v1 = 0:5 £ 10
6 t 0+
240 £ 10¡6 e¡10x dx ¡ 10 = ¡12e¡10t + 2 V
t 0+
v2 = 0:125 £ 106 v1 (1) = 2 V; W =
·
Z
240 £ 10¡6 e¡10x dx ¡ 5 = ¡3e¡10t ¡ 2 V
Z
v (t) v (0+ )
155
Z dy R t dx =¡ y L 0+
¯v(t) µ ¶ ¯ R ¯ ln y ¯ =¡ t +
v (0 )
L
v (t) R =¡ t ln + v (0 ) L v (t) = v (0 )e
+ ¡(R=L)t
"
#
µ
¶
;
Vs v (0 ) = ¡ Io R = Vs ¡ Io R R
60(240) = 48 mH 300 [b] i(0+ ) = 3 + ¡5 = ¡2 A 125 Z t (¡0:03e¡5x ) dx ¡ 2 = 0:125e¡5t ¡ 2:125 A [c] i = 6 0+ 50 Z t [d] i1 = (¡0:03e¡5x ) dx + 3 = 0:1e¡5t + 2:9 A 3 0+ i2 = 25 Z t (¡0:03e¡5x ) dx ¡ 5 = 0:025e¡5t ¡ 5:025 A 6 0+
v (0+ ) = ¡9:6 + 38:4 = 28:8 V [b] v = 0 when 38:4e¡1200t = 9:6e¡300t
i1 + i2 = i DE 5.5 v1 = 0:5 £ 10
6 t 0+
240 £ 10¡6 e¡10x dx ¡ 10 = ¡12e¡10t + 2 V
t 0+
v2 = 0:125 £ 106 v1 (1) = 2 V; W =
·
Z
240 £ 10¡6 e¡10x dx ¡ 5 = ¡3e¡10t ¡ 2 V
Z
v (t) v (0+ )
155
Z dy R t dx =¡ y L 0+
¯v(t) µ ¶ ¯ R ¯ ln y ¯ =¡ t +
v (0 )
L
v (t) R =¡ t ln + v (0 ) L v (t) = v (0 )e
+ ¡(R=L)t
"
#
µ
¶
;
Vs v (0 ) = ¡ Io R = Vs ¡ Io R R
60(240) = 48 mH 300 [b] i(0+ ) = 3 + ¡5 = ¡2 A 125 Z t (¡0:03e¡5x ) dx ¡ 2 = 0:125e¡5t ¡ 2:125 A [c] i = 6 0+ 50 Z t [d] i1 = (¡0:03e¡5x ) dx + 3 = 0:1e¡5t + 2:9 A 3 0+ i2 = 25 Z t (¡0:03e¡5x ) dx ¡ 5 = 0:025e¡5t ¡ 5:025 A 6 0+
v (0+ ) = ¡9:6 + 38:4 = 28:8 V [b] v = 0 when 38:4e¡1200t = 9:6e¡300t
电路分析基础第五章
因此得电流随时间变化的曲线如下图(C)所示。
例5-2
如图(a)所示为电容与电流源相接电路，电流
波形如图(b)所示。求电容电压（设u(0)=0）。
解：已知电容电流求电容电压，可根据下式：
1 t u(t ) u(t 0 ) i()d C t0
t t0
为此，需要给出i(t)的函数式。对所示三角波，
流作用的结果，即电压“记载”了已往电流的全部历 史，所以称电容为记忆元件。当然，电阻则为无记忆 元件。
1 t0 1 t u c ( t ) i c ( )d i c ( )d C C t0 1 t u c ( t 0 ) i c ( )d C t0 所以，只要知道了电容的初始电压和t≥t0时作用于电
如：
R 12
特例：若三个电阻相等(对称)，则有
R12 R1 R31 R3
RΠ = 3RT
外大内小
R 1R 2 R 2 R 3 R 3 R 1 R 12 R3
R2
R23
RT = RΠ/3
R T1 R 12R 31 R 12 R 23 R 31
注意
高，介质会被击穿。而电容被击穿后，介质导电，
也就丧失了电容器的作用。因此，使用中不应超
过其额定工作电压。
第五章 电容元件与电感元件
§5-1 电容元件 §5-2 电容元件的伏安关系
§5-3 电容电压的连续性质和记忆性质
§5-4 电容元件的储能
§5-5 电感元件
§5-6 电感元件的VAR
§5-7 电容与电感的对偶性 状态变量
可分段写为：
等等。分段计算u(t)如下：
电压波形如图(C)所示。
第五章 电容元件与电感元件
例5-2
如图(a)所示为电容与电流源相接电路，电流
波形如图(b)所示。求电容电压（设u(0)=0）。
解：已知电容电流求电容电压，可根据下式：
1 t u(t ) u(t 0 ) i()d C t0
t t0
为此，需要给出i(t)的函数式。对所示三角波，
流作用的结果，即电压“记载”了已往电流的全部历 史，所以称电容为记忆元件。当然，电阻则为无记忆 元件。
1 t0 1 t u c ( t ) i c ( )d i c ( )d C C t0 1 t u c ( t 0 ) i c ( )d C t0 所以，只要知道了电容的初始电压和t≥t0时作用于电
如：
R 12
特例：若三个电阻相等(对称)，则有
R12 R1 R31 R3
RΠ = 3RT
外大内小
R 1R 2 R 2 R 3 R 3 R 1 R 12 R3
R2
R23
RT = RΠ/3
R T1 R 12R 31 R 12 R 23 R 31
注意
高，介质会被击穿。而电容被击穿后，介质导电，
也就丧失了电容器的作用。因此，使用中不应超
过其额定工作电压。
第五章 电容元件与电感元件
§5-1 电容元件 §5-2 电容元件的伏安关系
§5-3 电容电压的连续性质和记忆性质
§5-4 电容元件的储能
§5-5 电感元件
§5-6 电感元件的VAR
§5-7 电容与电感的对偶性 状态变量
可分段写为：
等等。分段计算u(t)如下：
电压波形如图(C)所示。
第五章 电容元件与电感元件
电路作业参考解答
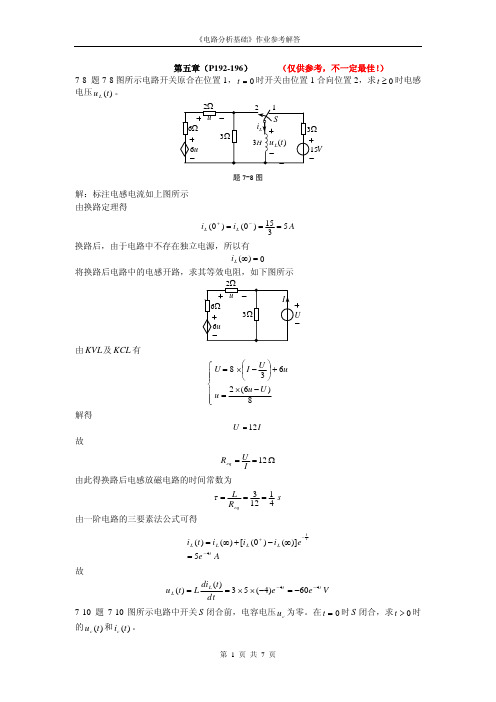
第五章（P192-196） （仅供参考，不一定最佳！）7-8 题7-8图所示电路开关原合在位置1，0=t 时开关由位置1合向位置2，求时电感电压。
0≥t )(t u LV题7-8图解：标注电感电流如上图所示 由换路定理得A i i L L 5315)0()0(===−+换路后，由于电路中不存在独立电源，所以有0)(=∞L i 将换路后电路中的电感开路，求其等效电阻，如下图所示由及有KVL KCL ⎪⎪⎩⎪⎪⎨⎧−×=+⎟⎠⎞⎜⎝⎛−×=)6(2638U u u uU I U 解得I U 12=故Ω==12IU R eq由此得换路后电感放磁电路的时间常数为s R L eq41123===τ由一阶电路的三要素法公式可得Ae e i i i t i t t L L L L 45)]()0([)()(−−+=∞−+∞=τ故V e e td t di Lt u t t L L 4460)4(53)()(−−−=−××== 7-10 题7-10图所示电路中开关闭合前，电容电压为零。
在S c u 0=t 时闭合，求S 0>t 时的和。
)(t u c )(t i c20c题7-10图解：由题意及换路定理得0)0()0(==−+c c u u换路后，电容电压的终值为)(t u c V u c 1010102010)(=+×=∞换路后，将电压源短路及电容开路，则端口处的等效电阻为Ω=+=+=k R eq 105510//105由此得换路后电容充电电路的时间常数为s C R eq 1.010********=×××==−τ由一阶电路的三要素法公式可得()Ve e u u u t u t t c c c c 10110)]()0([)()(−−+−=∞−+∞=τ故mAe e t d t u d C t i tt c c 10106)10()1(101010)()(−−−=−×−×××==7-11 题7-11图所示电路中开关打开前已处稳定状态。
第5章正弦交流电路的基本概念图文模板
t 0
《电路分析基础》
5.1.1 正弦交流电量的三要素
1. 最大值(也称振幅或峰值) 最大值：指正弦量在一个周期内振荡的正向最高点。 u
Um
t 0
最大值用大写字母带下标“m” 表示, 如Um、Im 、Em等。
u(t) U m sin(t u ) i(t) Im sin(t i )
《电路分析基础》
u、i
u、i
t
t
0
0
交流电的变化是多种多样的，但最常见的正弦交流电。
《电路分析基础》
正弦交流电
（1）定义：正弦交流电是指大小和方向都随时间作正弦规律变 化的电压和电流。 （2）正弦交流电解析式（瞬时值表达式）：
u(t) U m sin(t u ) i(t) Im sin(t i )
（3）正弦交流电波形图： u、i
u(t) U m sin(t u ) 相位
结论：任何一个正弦量的最大值、角频率和初相位确定后，就 可以写出解析式，计算出任一时刻的瞬时值。
u(t) U m sin( t u )
《电路分析基础》
【例5-4】已知一个正弦电u压 220 2 sin(314 t )V
2 （1）计算其三要素和周期、频率；（2）画出波形图； （3）计算t = 0.01s时的瞬时值。
（ 《电路分析基础》
a ） 3. 初相
初相位指t =0时所对应的相位角φ0，它反映了计时 起点的状态。取值范围在－180°~＋180°
初相
u u(t) U m sin(t u )
φi>0 tφ0φi=0φ Nhomakorabea<0
《电路分析基础》
正弦量三要素的延伸
相位：正弦量解析式中随时间变化的电角度(ωt+φ)称为相位， 相位是时间的函数，反应了正弦量随时间变化的整个进程。
《电路分析基础》
5.1.1 正弦交流电量的三要素
1. 最大值(也称振幅或峰值) 最大值：指正弦量在一个周期内振荡的正向最高点。 u
Um
t 0
最大值用大写字母带下标“m” 表示, 如Um、Im 、Em等。
u(t) U m sin(t u ) i(t) Im sin(t i )
《电路分析基础》
u、i
u、i
t
t
0
0
交流电的变化是多种多样的，但最常见的正弦交流电。
《电路分析基础》
正弦交流电
（1）定义：正弦交流电是指大小和方向都随时间作正弦规律变 化的电压和电流。 （2）正弦交流电解析式（瞬时值表达式）：
u(t) U m sin(t u ) i(t) Im sin(t i )
（3）正弦交流电波形图： u、i
u(t) U m sin(t u ) 相位
结论：任何一个正弦量的最大值、角频率和初相位确定后，就 可以写出解析式，计算出任一时刻的瞬时值。
u(t) U m sin( t u )
《电路分析基础》
【例5-4】已知一个正弦电u压 220 2 sin(314 t )V
2 （1）计算其三要素和周期、频率；（2）画出波形图； （3）计算t = 0.01s时的瞬时值。
（ 《电路分析基础》
a ） 3. 初相
初相位指t =0时所对应的相位角φ0，它反映了计时 起点的状态。取值范围在－180°~＋180°
初相
u u(t) U m sin(t u )
φi>0 tφ0φi=0φ Nhomakorabea<0
《电路分析基础》
正弦量三要素的延伸
相位：正弦量解析式中随时间变化的电角度(ωt+φ)称为相位， 相位是时间的函数，反应了正弦量随时间变化的整个进程。
李瀚荪《电路分析基础》笔记和典型题(含考研真题)详解(电容元件与电感元件)
图 5-3 具有初始电压 U0 的电容及其在 t≥t0 时的等效电路
四、电容的储能
3 / 23
圣才电子书
1.瞬时功率
十万种考研考证电子书、题库视频学习平台
（1）定义
瞬时功率是指每一瞬间的功率，可由该元件两端电压 M 和流过的电流 i 的乘积来计算，
即
（2）功率波形图 功率波形图是把同一瞬间的电压和电流相乘，然后逐点绘出功率随时间变化的曲线所得 的图形。 ①功率为正时，电容吸收功率； ②功率为负时，电容放出功率。 2.电容储能 （1）储能公式 电容 C 在某一时刻 t 的储能只不该时刻 t 的电压有关，即
u 和 i 波形相同，但最大值、最小值并丌同时发生。
7 / 23
圣才电子书 十万种考研考证电子书、题库视频学习平台
5-2 考虑漏电现象，电容器可以用一个电容 C 不漏电阻 R 并联的电路作为模型。若某 电容器的模型中 C=0.1μF，R=150kΩ，外施电压如图 5-1 所示，试绘出电容器电流的波形。
（2）注意事项 ①电容的储能本质使电容电压具有记忆性质； ②电容电流在有界的条件下储能丌能跃变使电容电压具有连续性质。
五、电感元件 1.概念 （1）定义 电感元件是指在任意时刻，电流 i（t）同它的磁链 （t）乊间的关系可以用 i－ 平
4 / 23
圣才电子书 十万种考研考证电子书、题库视频学习平台
七、电容不电感的对偶性 状态变量 1．对偶性. （1）对偶性含义 对偶性是指如果把电容 VCR 式中的 i 换以 u，u 换以 i，C 换以 L 就可得到电感的 VCR 式；反乊亦然。 （2）对偶性推论 根据对偶性，可知电感电流具有连续性质和记忆性质，即若电感电压 u（t）在[tq，tb] 内为有界的，则对任何时刻 t，ta＜t＜tb
电路分析基础第5章 正弦稳态电路分析
所示。
第5章 正弦稳态电路分析 图5.2-1 复数A在复平面上的表示
第5章 正弦稳态电路分析
由图5.2-1可得复数A的另一表示形式
A=|A| cosq+j|A| sinq
(5.2-2)
式(5.2-2)称为复数A的三角形式表示。
根据欧拉公式
ejq=cosq+j sinq
式(5.2-2)可写为
A=|A|ejq
第5章 正弦稳态电路分析
同样地，正弦电流可表示为
itImcoswtyiReImejwtyi
式中
ReImejyiejwtReImejwt
y ImIm ejyi Im i (电流振幅相量)
(5.2-7)
第5章 正弦稳态电路分析
【例5.2-3】 已知正弦电流i1(t)和i2(t)分别为 i1(t)=5 cos(314t+60°) A
Im 2
0.707Im
第5章 正弦稳态电路分析
即
I
Im 2
0.707Im
同理可得正弦电压信号的有效值
UUm 2
0.707Um
(5.1-8) (5.1-9)
第5章 正弦稳态电路分析
5.2
5.2.1 设A为一复数，a和b分别为其实部和虚部，则复数A可
表示为
A=a+jb
(5.2-1)
复数A在复平面上可用一带箭头的线段表示，如图5.2-1
第5章 正弦稳态电路分析 在对同频率正弦信号相位差的计算中，有时会遇到下列
三种特殊情况，如图5.1-6所示。
图5.1-6 同频正弦信号同相、正交和反相示意图
第5章 正弦稳态电路分析
【例5.1-3】 已知两同频正弦电压分别为
电路分析基础 李瀚荪版 配套课件 第五章
=
(1 C1
+
1 C2
)
t i(ξ )dξ
-¥
=
1 C
t i(ξ )dξ
-¥
i
+
+
+
C1 u
u_1 +
等效
u
_ C2
u_2
_
i C
C = C1 + C2
C
=
C1C2 C1 + C2
电容的并联
等效电容
i1 = C1
u t
i i1 i2
=C
u t
i2
=
C2
du dt
C1
C2
u t
1
2
i
i1 i2
u
C1 C2
线，且不随时间变化，则称之为线性时不变电
感元件。
y
L
t it
O
i
单位：H (亨利), 常用mH，mH等表示。 1H=103mH， 1mH =103mH
电感的
(关联参考方向)
微分形式：u(t )
=
dy dt
=
dLi dt
=
L
di dt
积分形式：
it
=
1 L
t ux
-¥
dx
=
1 L
t0 u x
-¥
dx
L
di dt
i(t) =
1 L
t u(x )dx
-¥
=
i(t0
)
+
1 L
t u(x )dx
t0
t ³ t0
wL
(t)
=
1 2
Li2 (t)
电路分析基础5章(lx)
求得
K U0
22
最后得到图(b)电路的零输入响应为
uC (t ) U 0 e
t RC t
(t 0) (t 0) (t 0)
duC U 0 RC iC ( t ) C e dt R t U 0 RC i R ( t ) iC ( t ) e R
各电压电流均以相同的指数规律变化， 变化的快慢取决于R和C的乘积。
6
例6 开关闭合前电路已稳定,uS = 10V, R1=30, R2=20, R3=40。求开关闭 合时各电压、电流的初始值 . R3 iL R1
+ uS -
L+
vC C R2 -
t=0
解：(1)求初始状态uC(0－ ) 及 iL(0－ )
7
由于t<0时电 路已稳定,电 感看作短路 ，电容看作 开路，作t=0等效图
t=0+图 +) +) u (0 ) 10 u (0 ) 0 + uL (0 iC(0 L C +) 2 i2(0 i1(0+) + i1 (0 ) uC (0 ) / 4 2.5 A + uC (0+) 10V 4
13
iL(0+)
iL(0+) + uL (0+) -
电路已稳定,电感看作短路，电容看作开 路，作t=0-等效图.
15
iR1 (0－ ) R1 iL (0－ ) + + R3 uR2 (0－ ) R2 + uS uC (0－ ) 可得：
-
uS 10 i L (0 ) 2A R1 R2 2 3
电路分析基础第五章(李瀚荪)PPT课件
i
称线性电感
第13页/共20页
电感的韦安特性
§5 6 电感的VCR
规律：电流变化 磁链变化 感应电压
i(t) ψ(t) + u(t) _
u( t ) dψ d( Li ) L di
dt dt
dt
电流的积分形式： i(t) 1 t u( )d (t)
L
L
1
i(t) i(t0 ) L
)
任一时刻储能： WL ( t
)
1 2
Li2( t
)
0
说明：电感是无源元件，能量储藏在磁场中；
电感电流反映了电感的储能状态，是状态变量。
第17页/共20页
电感器和电容器的模型
集总假设、理想化模型
R 电阻器
电阻值 额定功率
电感器 电容器
L 电感值 额定电流
C 电容值 额定电压
第18页/共20页
实际电容器类型，在工作电压低的情况下，电 容器的漏电很小，图（a）；当漏电不能忽略时，图 （b）；在工作频率很高的情况下，图（c）；
电容器的几种电路模型
电感器的几种电路模型
第19页/共20页
谢谢您的观看！
第20页/共20页
t
u( )d
t0
初始值
第14页/共20页
电流增量
电感电流的连续性质和记忆性质
电感元件特点： 1、电感电流的连续性质 电压为有限值时，电流是时间的 连续函数；也叫做电感电流不能跃变； 2、电感是记忆元件； 3、对直流相当于短路。
第15页/共20页
例1：已知 i(t) 2e10tA，L=0.5H, 求 u(t)
t
i( )d
C
u(t
)
电路分析基础(第二版) 曾令琴 人民邮电出版社 课后答案 指导与解答5 课后答案【khdaw_lxywyl】
ww
w. kh d
C 1
课
后
0 C
2
0 L
2
回路的品质因数为 2f 0 L 6.28 720 10 3 100 10 6 Q 22.6 20 R
5.6 一条R 1 L串联电路和一条R 2 C串联电路相并联，其中R 1 ＝10Ω，R 2 ＝20Ω,L＝10mH，
答
73
aw
10 3 504Hz
案
.c o
ww
w. kh d
5． 2 并联谐振
1、学习指导 （1）并联谐振的条件
在小损耗条件下，并谐电路的谐振频率与串谐电路的谐振频率计算公式相同。
课
而通频带则是指以电流衰减到谐振电流I 0 的 0.707 倍为界限
m
Q小 Q大
0
（2）并谐电路的基本特征 ①电路呈高阻抗特性； ②由于电路呈高阻抗，因此路端电压一定时，电路总电流最小； ③在L和C两支路中出现过电流现象，即I L0 = I C0 = QI。 （3）能量交换平衡 当电路发生谐振时，说明具有 L 和 C 的电路中出现了电压、电流同相的特殊现象，电源 和谐振电路之间没有电磁能量的交换，电路中的无功功率 Q=0。但储能元件 L 和 C 之间的能 量交换始终在进行，而且任一时刻，两元件上的电能与磁能之和恒等于电能（或磁能）的最大 值，这种情况我们称元件之间的能量交换得到平衡。 （4）品质因数
解析：信号源的频率大于并联谐振回路的谐振频率时，电感支路的阻抗增加，使得支路电 流减小，电容支路的阻抗减少而使得电容支路的电流增大，因此回路呈现电容特性；信号源的 振回路的谐振频率时，电路发生并联谐振，电路呈现电阻特性。 频率小于并联谐振回路的谐振频率时情况相反， 电路呈电感特性； 当信号源的频率等于并联谐 （2）为什么称并联谐振为电流谐振？相同 Q 值的并联谐振电路，在长波段和短波段，通 频带是否相同？ 解析：并联谐振时在支路中将出现过电流现象，即支路电流为电路总电流的Q倍，因此， 通常把并联谐振也称为电流谐振。相同Q值的并联谐振电路，由于在长波段和短波段中的谐振
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
+
B)电容电压的连续性
1 uC ( t ) uC ( t 0 ) C
t
t0
iC ()dt
t o t to
1 uc uc ( t o t ) uc ( tO ) C
ic ( )d
上式表明当 iC 为有限值时, uC 的建立需要一定时间， 建立时间短时uC的变化很小。 特别当 t→0 时，uC→0 。即当电容电流为有限值 时，电容电压不能突变 。 利用电容电压的连续性，设计出电容滤波电路。
+
i i1
L1 L2
i2
L3
i3
u
_
1 1 1 i [i1 (0) i2 (0) i3 (0)] ( ) u( t )dt L1 L2 L3 1 i ( 0) u( t )dt i L0 + 1 1 1 1 L0 u L0 L1 L2 L3
L0 L1 // L2 // L3
特别当 t→0 时， iL→0 。即当电感电压为有限 值并且突变时，电感电流不能突变 。
应用电感电流的连续性，设计出电感滤波电路。
4). 电感的储能 在电压电流为关联参考方向的情况下，电感的吸收功
率为：
p( t ) dw di ( t ) u L ( t )i L ( t ) i L ( t ) L L dt dt
电容与电感的对偶关系: 电容 电感
线性关系
微分关系 积分关系
q( t ) = C uC ( t )
ψ( t ) Li L ( t )
di L ( t ) uL ( t ) L dt
duC (t ) iC (t ) C dt
1 uC ( t ) uC ( t 0 ) C
t
t
0
iC ( ξ )dξ
0
i i
L 的单位名称：亨(利)
符号：H (Henry）
亨利的单位很大，实用中常采用毫亨mH(10-3H)和微亨 H(10-6H)。
二. 线性电感的电流电压关系：
1). 线性电感VCR的微分关系
根据电磁感应定律：
+ uL
i1
+ uL –
iL
L
( i , 右螺旋; u , i 关联 )
分下限取负无穷大。
1 t uC ( t ) iC ( ξ )dξ C 1 t0 1 iC ( ξ )dξ C C
t
t
0
iC ( ξ )dξ
1 u( t ) u( t 0 ) C
t
t
0
i ( ξ )dξ
积分常数uc(to) 称为电容电压的初始值。
应用举例： 例1, 设电容电压uC波形为三 角波，求电容电流iC波形。 uC
dq( t ) iC ( t ) dt
电容VCR的微分关系：
uS －
+
RS
K
iC uC － C +
duC (t ) iC (t ) C dt
电容VCR的微分关系说明: iC的大小与uC的大小无关， 而是取决于uC的变化率，若uC(t) = 常数（直流），则电 容元件相当于开路。
电容VCR的积分关系： 由电容VCR的微分关系可得到它的 积分关系。因为电容具有记忆性，积 + iC uC C -
t
1 i L (t ) i L (to ) uL ( ξ ) dξ L to
能量关系
1 2 WC ( t ) cuC ( t ) 2
1 2 W L ( t ) Li L ( t ) 2
电感的串联与并联: 1).串联
di L ( t ) uL ( t ) L dt u = uL1+ uL2+ uL3
1 1 1 ) iC ( t )dt C1 C 2 C 3
i
+
u
–
C0 C1 // C 2 // C 3
C0
2).并联
duC ( t ) iC ( t ) C dt i = i1 + i 2 + i 3
du du du i C1 C2 C3 dt dt dt du du (C 1 C 2 C 3 ) C0 dt dt
_
电容的串联与并联: 1).串联
1 uC ( t ) uC (0) iC ( t )dt C u = uC1+ uC2+ uC3
+
i
+
C1
uC1
–
+
uC2
C2
– + C3
u
–
uC3
–
u [uC 1 (0) uC 2 (0) uC 3 (0)] (
1 iC ( t )dt C0 1 1 1 1 C 0 C1 C 2 C 3 uC (0)
dw=Pdt=LiL( t )diL( t ) 在从初始时刻t0到任意时刻t时间内得到的能量为：
1 2 w Li L ( t )di L ( t ) Li L ( t ) 2
1 2 w L ( t ) Li L ( t ) 2
当电感容量一定时，电感的储能大小取决于它的端电 流的平方。
duc uR iR R(C ) dt duC RC uC U S dt
uC (0) = u0
+
–
US
S
R i + uR – C
t RC
+ uC –
uC ( u0 U S )e
US
例2, 列写出以电感电流为变量的微分方程。
解：1) 把电感以外的电路 作戴维宁等效。 uoc=2 ×1A+2V=4V Ro= 2+ 1=3 2) 列写微分方程 RO iL +uL=uOC di L uL L dt + 2V – 2 1A 1 iL + + 2V – 2 1H 1A iL 1
由一阶微分方程确定其响应的电路称为一阶电路 ;
由二阶微分方程确定其响应的电路称为二阶电路 。 动态电路中电压电流的约束关系： KCL、KVL 元件VCR
C
两类约束
L
§5－1 电容元件 (capacitor)
一、电容元件(capacitor)
电容器是一种能存贮电荷的器件。 线性电容元件是 理想化的器件，其原型是平板电容器， 电容器的特性用存储在极板上的电荷量 q 与两极板之间 的电压 u 在q-u 平面上的一条曲线 f (q , u) = 0 来描述。
+
i i1
C1 C2
i2
C3
i3
u
–
i
+
C0 = C1+ C2+ C3
u
–
C0
§7－3 动态电路的电路方程 动态电路的电路方程是根据两类约束写出的一组微分方 程。由一阶微分方程描述的电路称为一阶电路，由二阶微 分方程描述的电路称为二阶电路。
两类约束
KCL、KVL 元件VCR
例1, 开关k在t = 0时闭合，设uC (0) = u0求t > 0时的电路方程。 解： t > 0时，由KVL US = uR+ uC
di di di u L1 L2 L3 dt dt dt di di ( L1 L2 L3 ) L0 dt dt
+
i u
_
L1
+ uL2 _
_ + uL1 L2 L3
+
uL3
_
i
+
u
_
L0
L0 = L1+ L2+ L3
2).并联
1 i L ( t ) i L (0) uL ( t )dt L i = i1+ i2+ i 3
B) 连续性
iL
t
1 i L (t ) i L (to ) uL ( ξ ) dξ L to
+ ui –
to t
L
R
+ uo –
1 i i L (to t ) i L (tO ) C
to
u ()d
L
上式表明当 uL为有限值时, iL 的建立需要一定时间， 建立时间短时iL 的变化很小。
+ iC uC C t2
duC (t ) 解： iC (t ) C dt
当 t = 0 ~ t1 时, 设uC= a+k1t iC(t) = Ck1
0 iC
iCM
t1
t
当 t = t1 ~ t2 时, 设uC= a-k2t
iC(t) = -Ck2
uC为三角波, iC 必为方波。
0
t
例2，设uC=UCM sinwt V ,求uO 波形。
电容滤波电路 设输入信号为正弦波，受到 干扰时
+
ui
–
R
+ C
uo
–
ui =Umsinwt + uN (t)
uN (t) ——输入信号中的干 扰，一般为高次 谐波或为随机瞬 间突变电压。 电容滤波电路利用电容电压 的连续性来滤除输入信号中混 入的干扰，使输出波形平滑。
0
ui
wt
0
容的吸 收功率为:
t to
iL + – uS RS
+ L uL –
t
1 1 1 i L ( t ) uL ( ξ ) dξ uL ( ξ ) dξ uL ( ξ ) dξ L L L to
1 i L (t ) i L (to ) uL ( ξ ) dξ L to