2020届高三数学一轮复习强化训练精品――三角函数及三角恒等变换单元综合测试
2020版高考数学(浙江专用)一轮总复习检测:4.3 三角恒等变换 Word版含解析

( ) ( ) ( ) π
33
π 5π
π
1.(2017 浙江模拟训练冲刺卷五,14)已知 sin ������ + 3 +sin α=
5
,且
α∈
, 3
6
,则 sin ������ +
6
= ,cos α= .
3-4 3 答案 ; 10
25 2.已知 α,β 均为锐角,且 cos α= 5 ,tan β=.
答案 -
( ) ( ) π
π
4.(2017 课标全国Ⅰ文,15,5 分)已知 α∈
0, 2
,tan
α=2,则 cos
������
-
4
= .
3 10 答案 10
考点二 简单的三角恒等变换
1.(2017 课标全国Ⅲ文,4,5 分)已知 sin α-cos α=,则 sin 2α=( )
A.- B.- C. D.
3
3
A.- B. C.-
D.
2
2
答案 D
2.(2018 浙江 9+1 高中联盟期中,12)设 sin 2α=sin α,α∈(0,π),则 cos α= ,tan 2α= . 答案 ;- 3
解析 (1)由(b+c)2-a2=(2+ 2)bc 得 b2+c2-a2= 2bc,
������2 + ������2 - ������2 2
(1)求 a,b,ω 的值;
( ) ( ) 3π
π
������ π
(2)若<x< 4 ,且 f ������ + 6 =,求 f 2 + 6 的值.
解析 (1) f(x)=acos ωx+bsin ωx= ������2 + ������2sin(ωx+θ),
2020年高考数学一轮复习第三章三角函数解三角形质量检测

2020年高考数学一轮复习第三章三角函数解三角形质量检测第三章 三角函数、解三角形(自我评估、考场亮剑,收成成功后进入下一章学习!)(时刻120分钟,总分值150分)一、选择题(本大题共12小题,每题5分,共60分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.)1.cos(-17π4)-sin(-17π4)的值是 ( )A.2 B .- 2 C .0 D.22解析:原式=cos(-4π-π4)-sin(-4π-π4)=cos(-π4)-sin(-π4)=cos π4+sin π4= 2.答案:A2.sin α=2m -5m +1,cos α=-mm +1,且α为第二象限角,那么m 的承诺值为( )A.52<m <6 B .-6<m <52 C .m =4 D .m =4或m =32 解析:由sin 2α+cos 2α=1得,(2m -5m +1)2+(-m m +1)2=1,∴m =4或32,又sin α>0,cos α<0,把m 的值代入检验得,m =4. 答案:C3.sin(x +π4)=-35,那么sin2x 的值等于 ( )A .-725 B.725 C .-1825 D.1825解析:sin(x +π4)=22(sin x +cos x )=-35,因此sin x +cos x =-325,因此(sin x +cos x )2=1+sin2x =1825,故sin2x =-725.答案:A4.设a =sin15°+cos15°,b =sin17°+cos17°,那么以下各式中正确的选项是 ( ) A .a <a 2+b 22<b B .a <b <a 2+b 22C .b <a 2+b 22<aD .b <a <a 2+b 22解析:a =2sin(15°+45°)=2sin60°, b =2sin(17°+45°)=2sin62°,b >a .a 2+b 22=sin 260°+sin 262°>2sin60°sin62°=3sin62°, ∴a 2+b 22>b >a .答案:B5.(2018·惠州模拟)将函数y =sin x 的图象向左平移φ(0≤φ<2π)个单位后,得到函数y =sin(x -π6)的图象,那么φ等于 ( ) A.π6 B.11π6 C.7π6 D.5π6解析:依题意得y =sin(x -π6)=sin(x -π6+2π)=sin(x +11π6),将y =sin x 的图象向左平移11π6个单位后得到y =sin(x +11π6)的图象,即y =sin(x -π6)的图象.答案:B6.在△ABC 中,角A ,B 均为锐角,且cos A >sin B ,那么△ABC 的形状是 ( ) A .直角三角形 B .锐角三角形 C .钝角三角形 D .等腰三角形解析:cos A =sin(π2-A )>sin B ,π2-A ,B 差不多上锐角,那么π2-A >B ,A +B <π2,C >π2.答案:C7.(理)给定性质:①最小正周期为π;②图象关于直线x =π3对称.那么以下四个函数中,同时具有性质①②的是 ( )A .y =sin(x 2+π6)B .y =sin(2x +π6)C .y =sin|x |D .y =sin(2x -π6)解析:∵T =2πω=π,∴ω=2.关于选项D ,又2×π3-π6=π2,因此x =π3为对称轴.答案:D8.(文)假如等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为 ( ) A.518 B.34 C.32 D.78解析:设等腰三角形的底边为a ,顶角为θ,那么腰长为2a . 由余弦定理得cos θ=4a 2+4a 2-a 28a 2=78.答案:D(理)△ABC 的两边长分不为2,3,其夹角的余弦值为13,那么其外接圆的半径为( )A.922B.924C.928 D .9 2解析:由余弦定理得:三角形第三边长为22+32-2×2×3×13=3,且第三边所对角的正弦值为 =223,因此2R =3223⇒R =928.答案:C9.在△ABC 中,角A ,B 所对的边长为a ,b ,那么〝a =b 〞是〝a cos A =b cos B 〞的 ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件解析:a =b ⇒A =B ⇒a cos A =b cos B ,条件是充分的;a cos A =b cos B ⇒sin A cos A =sin B cos B ⇒sin2A =sin2B ⇒2A =2B 或2A +2B =π,即A =B 或A +B =π2,故条件是不必要的.答案:A10.函数f (x )=a sin2x +cos2x (a ∈R)图象的一条对称轴方程为x =π12,那么a 的值为( )A.12B. 3C.33 D .2 解析:函数y =sin x 的对称轴方程为x =kπ+π2,k ∈Z ,f (x )=a 2+1sin(2x +φ),其中tan φ=1a,故函数f (x ) 的对称轴方程为2x +φ=kπ+π2,k ∈Z ,而x =π12是其一条对称轴方程,因此2×π12+φ=kπ+π2,k ∈Z ,解得φ=kπ+π3,k ∈Z ,故tan φ=1a =tan(kπ +π3)=3,因此a =33. 答案:C11.函数f (x )的部分图象如下图,那么f (x )的解析式可能为 ( ) A .f (x )=2cos(x 2-π3)B .f (x )=2cos(4x +π4)C .f (x )=2sin(x 2-π6)D .f (x )=2sin(4x +π4)解析:设函数f (x )=A sin(ωx +φ),由函数的最大值为2知A =2,又由函数图象知该函数的周期T =4×(5π3-2π3)=4π,因此ω=12,将点(0,1)代入得φ=π6,因此f (x )=2sin(12x +π6)=2cos(12x -π3).答案:A12.(2018·抚顺模拟)当0<x <π2时,函数f (x )=1+cos2x +8sin 2x sin2x的最小值为 ( )A .2B .2 3C .4D .4 3 解析:f (x )=1+cos2x +8sin 2x sin2x =2cos 2x +8sin 2x 2sin x cos x =cos x sin x +4sin xcos x≥2cos x sin x ·4sin xcos x=4,当 且仅当cos x sin x =4sin x cos x ,即tan x =12时,取〝=〞,∵0<x <π2,∴存在x 使tan x =12,这时f (x )min =4.答案:C二、填空题(本大题共4小题,每题4分,共16分,将答案填写在题中的横线上)13.在△ABC 中,角A ,B ,C 的对边分不为a ,b ,c ,B =60°,C =75°,a =4,那么b =________.解析:易知A =45°,由正弦定理a sin A =b sin B 得4sin45°=b sin60°,解得b =2 6.答案:2 614.运算:cos10°+3sin10°1-cos80°=________.解析:cos10°+3sin10°1-cos80°=2cos(10°-60°)2sin 240°=2cos50°2sin40°= 2. 答案:215.在△ABC 中,tan A =3tan B ,那么tan(A -B )的最大值为________,现在角A 的大小为________.解析:由于tan(A -B )=tan A -tan B1+tan A tan B =3tan B -tan B1+3tan B ·tan B =2tan B 1+3tan 2B ≤33.当且仅当1=3tan B 时取〝=〞号,那么tan B =33⇒tan A =3⇒A =60°. 答案:3360° 16.如图是函数f (x )=A sin(ωx +φ)(A >0,ω>0,-π<φ<π),x ∈R 的部分图象,那么以下命题中,正确命题的序号为________. ①函数f (x )的最小正周期为π2;②函数f (x )的振幅为23;③函数f (x )的一条对称轴方程为x =7π12;④函数f (x )的单调递增区间为[π12,7π12];⑤函数的解析式为f (x )=3sin(2x -2π3).解析:由图象可知,函数f (x )的最小正周期为(5π6-π3)×2=π,故①不正确;函数f (x )的振幅为3,故②不正确;函数f (x )的一条对称轴方程为x =5π6+π32=7π12,故③正确;④不全面,函数f (x )的单调递增区间应为[π12+2kπ,7π12+2kπ],k ∈Z ;由3sin(2×7π12+φ)=3得2×7π12+φ=π2+2kπ,k ∈Z ,即φ=2kπ-2π3,k ∈Z ,∵-π<φ<π,故k 取0,从而φ=-2π3,故f (x )=3sin(2x -2π3).答案:③⑤三、解答题(本大题共6小题,共74分.解承诺写出文字讲明、证明过程或演算步骤) 17.(本小题总分值12分)tan(α+π4)=-3,α∈(0,π2).(1)求tan α的值;(2)求sin(2α-π3)的值.解:(1)由tan(α+π4)=-3可得tan α+11-tan α=-3.解得tan α=2.(2)由tan α=2,α∈(0,π2),可得sin α=255,cos α=55.因此sin2α=2sin αcos α=45,cos2α=1-2sin 2α=-35,sin(2α-π3)=sin2αcos π3-cos2αsin π3=45×12+35×32=4+3310.18.(文)(本小题总分值12分)sin(π-α)=45,α∈(0,π2).(1)求sin2α-cos 2α2的值;(2)求函数f (x )=56cos αsin2x -12cos2x 的单调递增区间.解:∵sin(π-α)=45,∴sin α=45.又∵α∈(0,π2),∴cos α=35.(1)sin2α-cos 2α2=2sin αcos α-1+cos α2=2×45×35-1+352=425. (2)f (x )=56×35sin2x -12cos2x=22sin(2x -π4). 令2kπ-π2≤2x -π4≤2kπ+π2,k ∈Z ,得kπ-π8≤x ≤kπ+38π,k ∈Z.∴函数f (x )的单调递增区间为[kπ-π8,kπ+38π],k ∈Z.(理)(本小题总分值12分)函数f (x )=2sin x cos x +3(2cos 2x -1).(1)将函数f (x )化为A sin(ωx +φ)(ω>0,|φ|<π2)的形式,填写下表,并画出函数f (x )在区间[-16π,56π]上的图象;x ωx +φ 0 π2 π 32π 2π f (x )(2)求函数f (x )的单调减区间. 解:(1)f (x )=2sin x cos x +3(2cos 2x -1) =sin2x +3cos2x =2sin(2x +π3).x -π6 π12 π3 7π12 5π6 ωx +φ 0 π2 π 32π 2π f (x )2-2图.(2)由2kπ+π2≤2x +π3≤2kπ+3π2(k ∈Z)得kπ+π12≤x ≤kπ+7π12(k ∈Z),故函数f (x )的单调减区间为[kπ+π12,kπ+7π12](k ∈Z).19.(本小题总分值12分)函数f (x )=2sin x cos(π2-x )-3sin(π+x )cos x +sin(π2+x )cos x .(1)求函数y =f (x )的最小正周期和最值;(2)指出y =f (x )图象通过如何样的平移变换后得到的图象关于原点对称. 解:(1)f (x )=2sin 2x +3sin x cos x +cos 2x =1+sin 2x +3sin x cos x =1+1-cos2x 2+32sin2x=sin(2x -π6)+32,y =f (x )最小正周期T =π.y =f (x )的最大值为32+1=52,最小值为32-1=12.(2)∵y =32+sin(2x -π6)的图象1232π−−−−−→左移个单位下移个单位y =sin2x 的图象.20.(本小题总分值12分)在△ABC 中,角A ,B ,C 的对边分不为a ,b ,c ,cosA +C 2=33. (1)求cos B 的值;(2)假设BC BA ·BC =2,b =22,求a 和c 的值. 解:(1)∵cos A +C 2=33,∴sin B 2=sin(π2-A +C 2)=33,∴cos B =1-2sin 2B 2=13.(2)由BA ·BC =2可得a ·c ·cos B =2,又cos B =13,故ac =6,由b 2=a 2+c 2-2ac cos B 可得a 2+c 2=12, ∴(a -c )2=0,故a =c ,∴a =c = 6.21.(本小题总分值12分)如下图,甲船由A 岛动身向北偏东45°的方向做匀速直线航行,速度为152海里/小时,在甲船从A 岛动身的同时,乙船从A 岛正南40海里处的B 岛 动身,朝北偏东θ(tan θ=12)的方向作匀速直线航行,速度为105海里/小时.(1)求动身后3小时两船相距多少海里?(2)求两船动身后多长时刻距离最近?最近距离为多少海里? 解:以A 为原点,BA 所在直线为y 轴建立如下图 的平面直角坐标系.设在t 时刻甲、乙两船分不在P (x 1,y 1),Q (x 2,y 2).那么⎩⎪⎨⎪⎧x 1=152t cos45°=15t y 1=x 1=15t,由tan θ=12可得,cos θ=255,sin θ=55, 故⎩⎪⎨⎪⎧x 2=105t sin θ=10t ,y 2=105t cos θ-40=20t -40.(1)令t =3,P 、Q 两点的坐标分不为(45,45),(30,20), |PQ |=(45-30)2+(45-20)2=850=534.即动身后3小时两船相距534海里. (2)由(1)的解法过程易知: |PQ |=(x 2-x 1)2+(y 2-y 1)2=(10t -15t )2+(20t -40-15t )2 =50t 2-400t +1 600 =50(t -4)2+800≥202,∴当且仅当t =4时,|PQ |取得最小值20 2.即两船动身后4小时时,相距202海里为两船的最近距离.22.(文)(本小题总分值14分)函数f (x )=sin 2x +23sin(x +π4)cos(x -π4)-cos 2x - 3.(1)求函数f (x )的最小正周期和单调递减区间;(2)求函数f (x )在[-π12,2536π]上的最大值和最小值,并指出现在相应的x 的值.(理)(本小题总分值14分)函数f (x )=2cos x sin(x +π3)-32.(1)求函数f (x )的最小正周期T ;(2)假设△ABC 的三边a ,b ,c 满足b 2=ac ,且边b 所对角为B ,试求cos B 的取值范畴,并确定现在f (B )的最大值.解:(1)f (x )=2cos x ·sin(x +π3)-32=2cos x (sin x cos π3+cos x sin π3)-32=2cos x (12sin x +32cos x )-32=sin x cos x +3·cos 2x -32=12sin2x +3· 1+cos2x 2-32 =12sin2x +32cos2x =sin(2x +π3).∴T =2π|ω|=2π2=π.(2)由余弦定理cos B =a 2+c 2-b 22ac 得,cos B =a 2+c 2-ac2ac=a 2+c 22ac -12≥2ac 2ac -12=12,∴12≤cos B <1,而0<B <π,∴0<B ≤π3.函数f (B )=sin(2B +π3),∵π3<2B +π3≤π,当2B +π3=π2, 即B =π12时,f (B )max =1.。
2020年高考数学一轮复习重点突破必刷题——三角函数三角恒等变换【解析版】

2020年高考数学一轮复习重点突破必刷题——三角函数三角恒等变换1.若cos()123απ+=,则sin(2)3απ-= A .79- B .59- C .59D .79【答案】B【解析】由题可得225sin(2)cos(2)2cos ()12()1361239αααπππ-=+=+-=⨯-=-, 故选B .2.已知tan 3α=,则cos(2)2απ+= A .45-B .35- C .35D .45【答案】B【解析】由题可得222π2sin cos 2tan 63cos(2)sin22sin cos 1tan 195αααααααα+=-=-=-=-=-+++. 故选B . 3.若π1cos()42θ-=,则sin2θ=A .12-B .2-C .12D .2【答案】A 【解析】因为π1cos()42θ-=,所以22πππ11sin2cos(2)cos[2()]2cos 12()124422()θθθθ=-=-=--=⨯-=-. 故选A .【名师点睛】本题主要考查了三角函数的化简求值问题,其中解答中利用三角函数的诱导公式和余弦函数的倍角公式,准确化简运算是解答的关键,着重考查了推理与运算能力,属于基础题.由三角函数的诱导公式,化简得2πππsin2cos(2)cos[2()]2cos 124()4θθθθ=-=-=--,即可求解. 4.已知点(3,4)--在角α的终边上,则cos2sin 2αα+=A .3125- B .1725 C .1725-D .3125【答案】B【解析】因为点(3,4)--在角α的终边上,所以4sin 5α=-,3cos 5α=-, 所以cos2sin 2αα+=22343172cos 12sin cos 2()12()()55525ααα-+=⨯--+⨯-⨯-=. 故选B . 5.已知4sin 5α=-,且α是第四象限角,则πsin()4α-的值为A .10B .5C .10D .5【答案】C【解析】由同角三角函数基本关系式可得3cos 5α===,结合两角差的正弦公式可得πππ34sin()sin cos cos sin ()44425510ααα-=-=⨯+=. 故选C .【名师点睛】本题主要考查同角三角函数基本关系,两角差的正弦公式等知识,意在考查学生的转化能力和计算求解能力.首先求得cos α的值,然后结合两角和差正余弦公式求解πsin()4α-的值即可.6.已知cos()48απ+=-,则sin2α= A .58- B .916- C .916D .58【答案】B【解析】因为cos()4απ+=,所以229cos(2)2cos ()12(12416ααππ+=+-=⨯-=,所以9sin 216α=-.故选B . 7.若π1sin()63α-=,则2πcos(2)3α+=A .79B .79-CD .【答案】B【解析】∵ππππ1sin()cos[()]cos()62633ααα-=--=+=, ∴22ππ17cos(2)2cos ()1213399αα+=+-=⨯-=-. 故选B .8.函数2()sin )2f x x x π=-的最小正周期是 A .4πB .2π C .πD .2π【答案】C【解析】易得21cos 2()sin )222x f x x x x π-=-=+112cos 222x x =-+=1sin(2)62x π-+,其最小正周期22T π==π. 故选C .9.若sin 2cos αα=,且(,)2απ∈π,则tan 2α的值是AB .CD .-【答案】B【解析】由sin 2cos αα=可得sin 22sin cos cos αααα==, 因为(,)2απ∈π,所以cos 0α≠,所以1sin 2α=,所以56απ=,所以5tan 2tan tan()tan 333απππ==-=-=. 故选B .10.函数2()sin )([0,])23f x x x x ππ=+-∈的值域是 A .[1,1]- B .1[,1]2-C .3[0,]2D .13[,]22【答案】C【解析】由题可得21cos 21()sin cos(2)sin 2sin 2cos 2222x f x x x x x x π-=-==-+11sin(2)262x π=-+,当[0,]3x π∈时,2[,]662x πππ-∈-,所以1sin(2)[,1]62x π-∈-, 所以13sin(2)[0,]622x π-+∈.故选C . 11.函数2()2coscos()122x f x x π=--+的最小值为A .2B .1C .2D .1+【答案】A【解析】由题可得()cos sin 2)24f x x x x π=-+=++,所以函数()f x 的最小值为2,故选A . 12.若51cos()cos()12124ααππ+-=-,则=+αα2cos 2sin 3 A .3 B .1 C .1-D .3-【答案】C【解析】由题可得5cos()cos()cos()cos()cos()sin()1212121221212ααααααπππππππ+-=++-=++11sin(2)264απ=+=-,即1sin(2)62απ+=-2cos 22sin(2)16αααπ+=+=-, 故选C .13.函数1()2cos()12f x x =π+-的最小正周期为______________.【答案】2【解析】由题可得函数()f x 的最小正周期为22π=π. 14.已知cos(300)2cos αα+︒=,则tan α=______________.【解析】由cos(300)2cos αα+︒=可得cos(60)2cos αα-︒=,15.若4sin()65x π-=,则sin(2)6x π+=______________. 【答案】725-【解析】由题可得2247sin(2)cos(2)cos(2)12sin ()12()6336525x x x x ππππ+=-+=-=--=-⨯=-.16.22tan7.5tan157.5cos 7.5)tan15tan7.5︒⋅︒︒-︒=︒-︒______________.【答案】【解析】原式tan7.5tan15tan15tan7.5︒︒=︒︒-︒sin7.5sin15sin15sin7.5︒︒=︒=︒︒︒2sin(6015)2sin 45=-︒-︒=-︒=【名师点睛】利用弦切互化法和两角差的正弦公式把tan7.5tan15tan15tan7.5︒︒︒-︒化为sin15︒,再利用二倍角公式把22sin 7.5cos 7.5︒-︒化为cos15-︒,最后利用辅助角求值. 利用三角变换公式可以化简一些代数式,常见的方法有:(1)弦切互化法:即把含有正弦和余弦的代数式化成关于正切的代数式,也可以把函数正切的代数式化为关于余弦和正弦的代数式;(2)“1”的代换法:有时可以把1看成22sin cos αα+.(3)升幂降幂法:即利用二倍角公式2222cos2cos sin 2cos 112sin ααααα=-=-=-升幂,利用221cos21cos2cos ,sin 22αααα+-==降幂.(4)辅助角公式:即利用cos sin )a x b x x φ+=+来整合三角函数式. 17.已知πtan()24α+=-,则1sin2cos2αα-=______________. 【答案】12-【解析】因为2221sin2(sin cos )cos sin 1tan cos2cos sin cos sin 1tan αααααααααααα----===-++, 又因为πtan 1tan()241tan ααα++==--,所以1sin21cos22αα-=-. 【名师点睛】三角函数求值的三种类型:(1)给角求值:关键是正确选用公式,以便把非特殊角的三角函数转化为特殊角的三角函数. (2)给值求值:关键是找出已知式与待求式之间的联系及函数的差异. ①一般可以适当变换已知式,求得另外函数式的值,以备应用; ②变换待求式,便于将已知式求得的函数值代入,从而达到解题的目的.(3)给值求角:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,确定角.18.22π(sincos )2sin ()2242ααα++-的值等于 A .2sin α+B .2C .π2)4α+-D .(π2in )4α+【答案】B【解析】2222ππ(sincos )2sin ()sin +2sin cos cos 1cos[2()]2242222242αααααααα++-=⋅++-- π1sin 1cos()1sin 1sin 22αααα=++--=++-=.故选B .【名师点睛】本题考查利用二倍角公式和诱导公式化简计算,属基础题.利用二倍角公式和诱导公式化简计算即可.19.函数()3sin f x x x =+的最大值为A B .2C .D .4【答案】C【解析】由题意可知1π()3sin cos ))26f x x x x x x =+=+=+, π1sin()16x -≤+≤,π)6x ∴-≤+≤故函数()3sin f x x x =的最大值为 故选C .【名师点睛】利用该公式()sin cos )f x a x b x x ωωωϕ=++可以求出: ①函数()f x 的最小正周期2π||ω;②单调区间(利用正弦函数的单调区间可通过解不等式求得);③值域:[; ④对称轴及对称中心(由ππ,2x k k ωϕ+=+∈Z 可得对称轴方程,由π,x k k ωϕ+=∈Z 可得对称中心横坐标).20.已知函数2lg(54)y x x =++的零点为1tan x α=和2tan x β=,则tan()αβ+=A .53B .53-C .52D .52-【答案】C【解析】由2lg(54)0y x x =++=可得2541x x ++=,2530x x ++=, 所以12125,3x x x x +=-=,所以121255tan()1132x x x x αβ+-+===--.故选C .【名师点睛】本题考查两角和正切公式以及根与系数的关系,考查基本求解能力.先求函数零点得零点关系,再根据两角和正切公式求结果.21.已知角α的顶点在坐标原点,始边与x 轴的正半轴重合,角π4α+的终边经过点(-,则sin cos αα+=AB. C.3D.3-【答案】C【解析】因为πsin cos )4ααα+=+,角π4α+的终边经过点(-, 所以πsin()4α+==sin cos αα+== 故选C .22.已知向量(cos ,2)α=-a ,(sin ,1)α=b ,若∥a b ,则πtan()4α-=A .3-B .3C .13D .13-【答案】A【解析】因为向量(cos ,2)α=-a ,(sin ,1)α=b ,∥a b ,所以cos 2sin 0αα+=,所以1tan 2α=-,所以πtan tanπ4tan()3π41tan tan 4ααα--==-+⋅. 故选A .【名师点睛】(1)由∥a b 可得两向量坐标之间的关系cos 2sin 0αα+=,化简可得1tan 2α=-,进而根据两角差的正切公式可求得πtan()4α-的值.(2)平面向量平行应注意两个结论:①数量关系(共线向量定理):若∥a b (≠0b ),则λ=a b ;②若∥a b ,1122(,),(,)x y x y ==a b ,则12210x y x y -=.23.已知角α的顶点在坐标原点,始边与x 轴的正半轴重合,将角α的终边按顺时针方向旋转π6后经过点(4,3)P -,则2πcos(2)3α+= A .725- B .725 C .825D .825-【答案】A【解析】将角α的终边按顺时针方向旋转π6后所得的角为π6α-, 则由三角函数的定义可得π3sin()65α-==,所以22πππcos(2)cos(2)[12sin ()][12336ααα+=--=---=--⨯237()]525-=-. 故选A .24.平面直角坐标系xOy 中,角α的始边在x 轴非负半轴,终边与单位圆交于点34(,)55A ,将其终边绕O 点逆时针旋转3π4后与单位圆交于点B ,则B 的横坐标为A .B .C .D . 【答案】B【解析】设A 点处对应的角度为α,B 点处对应的角度为β, 由题意可得3cos 5α=,4sin 5α=,且3πcos cos()4B x βα==+,由两角和的余弦公式可得3π3π3πcos()cos cos sin sin 444ααα+=-=,即B 的横坐标为10-.故选B . 【名师点睛】本题主要考查三角函数的定义及其应用,两角和差正余弦公式等知识,意在考查学生的转化能力和计算求解能力.由题意结合三角函数的定义和两角和差正余弦公式整理计算即可求得最终结果.25.若,αβ均为锐角,sin 5α=,3sin()5αβ+=,则cos β=ABCD . 【答案】B【解析】∵α为锐角,sin α=α>45°且cos α=,∵3sin()5αβ+=,且13252<,ππ2αβ∴+<<,∴4cos()5αβ+=-,则cos β=cos[(α+β)−α]=cos (α+β)cos α+sin (α+β)sin α43555525=-⨯+⨯= 故选B .【名师点睛】本题考查两角和与差的正弦、余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.利用角的等量代换,β=α+β−α,只要求出α的余弦,α+β的余弦,利用复合角余弦公式展开求之.26.已知324αππ<<,若sin()4απ+=,则sin(2)4απ-=A .10-B .10-C .10D .10【答案】C【解析】因为sin()4απ+=sin cos αα+=, 两边同时平方可得212sin cos 5αα+=,所以3sin 25α=-,因为324αππ<<,所以322αππ<<,所以4cos 25α=-, 所以sin(2)4απ-=(sin 2cos 2)210αα-=, 故选C .27.已知(0,)2απ∈,(0,)2βπ∈,若cos2tan 1sin2βαβ=-,则A .2αβπ+=B .4αβπ+=C .4αβπ-=D .22αβπ+=【答案】C【解析】因为222222cos2cos sin 1tan 1tan tan()1sin2cos sin 2sin cos 1tan 2tan 1tan 4ββββββββββββββ--+π====+-+-+--,所以tan tan()4αβπ=+,又(0,)2απ∈,(0,)2βπ∈,所以4αβπ=+,即4αβπ-=, 故选C .28.若ABC △的内角,A B 满足sin 2cos()sin BA B A=+,则tan B 的最大值为 ABCD【答案】A【解析】在ABC △中,因为sin 0,sin 0A B >>,所以sin 2cos()2cos 0sin BA B C A=+=->,即c o s 0C <, 所以角C 为钝角,且sin 2sin cos B A C =-,又由sin sin()sin cos cos sin B A C A C A C =+=+, 所以sin cos cos sin 2sin cos A C A C A C +=-,即cos sin 3sin cos A C A C =-,所以tan 3tan C A =-,所以2tan tan 2tan tan tan()1tan tan 13tan A C AB AC A C A+=-+=-==-+213tan tan A A+3≤=, 当且仅当13tan tan A A =,即tan 3A =时等号成立,即tan B的最大值为3. 故选A .【名师点睛】本题主要靠考查了同角三角函数的基本关系式,两角和与差的正弦、正切函数的公式,以及基本不等式的运用,其中熟练掌握基本关系式和三角恒等变换的公式,以及合理使用基本不等式是解答的关键,着重考查了推理与运算能力,试题有一定的综合性,属于中档试题.由条件求得cos 0C <,确定C 为钝角,利用诱导公式及三角函数的内角和定理、三角函数恒等变换的公式,化简求得tan 3tan C A =-,代入利用基本不等式即可求解.29.若1sin2,2θ=则2πcos ()4θ+=______________. 【答案】14 【解析】1sin 22θ=,2π1π1sin 21cos ()[1cos(2)]42224θθθ-+=++==. 【名师点睛】本题主要考查了二倍角公式,同角三角函数的基本关系,考查了推理能力和计算能力,属于基础题.根据二倍角公式和诱导公式化简即可. 30.若3sin25α=,(,)42αππ∈,则2sin(2)2cos cos 44ααππ++=______________. 【答案】0【解析】因为(,)42αππ∈,所以2(,)2απ∈π,所以4cos25α==-,所以sin(2)4απ++21cos 22cos cos (sin2cos 2)422ααααπ+=+34sin22()0222552αα=++=-+=. 31.函数2()sin(2)sin 23f x x x π=++,(0,)2x π∈的值域为______________.【答案】(【解析】由题可得函数21()sin(2)sin 2sin 22sin 232f x x x x x x π=++=-++12sin 2sin(2)23x x x π=+=+, 因为(0,)2x π∈,所以42333x πππ<+<,所以sin(2)13x π<+≤,故函数()f x 的值域为(,1]2-. 32.已知228x y +=,则x y +的最大值为______________.【答案】4【解析】因为228x y +=,所以设x =,y αα=,所以x +y =πcos )4sin()4ααα+=+,所以x +y 的最大值为4. 故答案为4.【名师点睛】(1)本题主要考查三角换元和三角恒等变换,考查三角函数的最值,意在考查学生对这些知识的掌握水平和分析推理能力.(2)本题的解题关键是三角换元,设x =,y αα=,即得x +y =cos )αα+,再利用辅助角公式化简即得最大值,大大提高了解题效率.33.当函数cos(10)cos(70),(0,180)y x x x =+︒++︒∈︒︒取得最小值时,x =______________.【答案】140︒【解析】cos(10)cos(70)cos(10)cos(1060)y x x x x =+︒++︒=+︒++︒+︒1cos(10)cos(10)10)2x x x =+︒++︒-+︒3cos(10)10)2x x =+︒-+︒1030)x =+︒+︒40)x =+︒,∴cos(10)cos(70),(0,180)y x x x =+︒++︒∈︒︒取得最小值时,140x =︒.【名师点睛】本题考查了三角函数的化简,观察两角的关系,熟练掌握三角公式是解题关键.将x +70°拆成(x +10°)+60°使用两角和的正弦公式展开合并化简即可.34.【2019年高考全国Ⅰ卷文数】tan255°=A .−2B .−C .2D .【答案】D【解析】tan 255tan(18075)tan 75tan(4530)︒=︒+︒=︒=︒+︒=tan 45tan 301tan 45tan 30︒+︒-︒︒12+==+故选D. 【名师点睛】本题主要考查三角函数的诱导公式、两角和与差的三角函数、特殊角的三角函数值、运算求解能力.首先应用诱导公式,将问题转化成锐角三角函数的计算,进一步应用两角和的正切公式计算求解.题目较易,注重了基础知识、基本计算能力的考查. 35.【2019年高考全国Ⅱ卷文数】已知α∈(0,2π),2sin2α=cos2α+1,则sin α=A .15B5C3D5【答案】B 【解析】2sin 2cos 21αα=+,24sin cos 2cos .(0,),cos 02αααααπ∴⋅=∈∴>,sin 0,α>2sin cos αα∴=,又22sin cos 1αα+=,2215sin 1,sin5αα∴==,又sin 0α>,sin α∴=故选B .【名师点睛】本题是对三角函数中二倍角公式、同角三角函数基本关系式的考查,中等难度,判断正余弦的正负,运算准确性是关键,题目不难,需细心,解决三角函数问题,研究角的范围后得出三角函数值的正负很关键,切记不能凭感觉.解答本题时,先利用二倍角公式得到正余弦关系,再利用角范围及正余弦平方和为1关系得出答案.36.【2019年高考全国Ⅲ卷文数】函数()2sin sin2f x x x =-在[0,2π]的零点个数为A .2B .3C .4D .5【答案】B【解析】由()2sin sin 22sin 2sin cos 2sin (1cos )0f x x x x x x x x =-=-=-=, 得sin 0x =或cos 1x =,[0,2π]x ∈,0πx ∴=、或2π,()f x ∴在[0,2π]的零点个数是3,故选B .【名师点睛】本题考查在一定范围内的函数的零点个数,渗透了直观想象和数学运算素养.令()0f x =,得sin 0x =或cos 1x =,再根据x 的取值范围可求得零点.37.【2018年高考全国Ⅰ卷文数】已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点(1,)A a ,(2,)B b ,且2cos 23α=,则a b -=A .15BCD .1【答案】B【解析】根据条件,可知 三点共线,从而得到 , 因为,解得,即,所以, 故选B.38.【2018年高考全国Ⅲ卷文数】若1sin 3α=,则cos2α=A .89B .79 C .79-D .89-【答案】B【解析】2217cos 212sin 12()39αα=-=-⨯=.故选B . 【名师点睛】本题主要考查三角函数的求值,考查考生的运算求解能力,考查的核心素养是数学运算. 39.【2017年高考全国Ⅲ卷文数】已知4sin cos 3αα-=,则sin 2α=A .79-B .29-C .29D .79【答案】A【解析】由题可得2(sin cos )17sin 22sin cos 19ααααα--===--,故选A.【名师点睛】应用三角公式解决问题的三个变换角度:(1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”.(2)变名:通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”、“升幂与降幂”等. (3)变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有:“常值代换”、“逆用或变用公式”、“通分或约分”、“分解与组合”、“配方与平方”等. 40.【2016年高考全国Ⅲ卷文数】若tan 13θ=,则cos2θ= A .45- B .15- C .15D .45【答案】D【解析】2222222211()cos sin 1tan 43cos 21cos sin 1tan 51()3θθθθθθθ---====+++.故选D. 41.【2019年高考全国Ⅰ卷文数】函数3π()sin(2)3cos 2f x x x =+-的最小值为______________.【答案】4-【解析】23π()sin(2)3cos cos 23cos 2cos 3cos 12f x x x x x x x =+-=--=--+ 23172(cos )48x =-++,1cos 1x -≤≤,∴当cos 1x =时,min ()4f x =-,故函数()f x 的最小值为4-.【名师点睛】本题首先应用诱导公式,转化得到二倍角的余弦,进一步应用二倍角的余弦公式,得到关于cos x 的二次函数,从而得解.注意解答本题的过程中,部分考生易忽视1cos 1x -≤≤的限制,而简单应用二次函数的性质,出现运算错误.42.【2017年高考江苏卷】若π1tan(),46α-=则tan α=______________.【答案】75【解析】由题可得11tan()tan7644tan tan[()]14451tan()tan 1446ααααππ+-+ππ=-+===ππ---. 【名师点睛】三角函数求值的三种类型(1)给角求值:关键是正确选用公式,以便把非特殊角的三角函数转化为特殊角的三角函数. (2)给值求值:关键是找出已知式与待求式之间的联系及函数的差异.一般有如下两种思路: ①适当变换已知式,进而求得待求式的值;②变换待求式,便于将已知式的值代入,从而达到解题的目的.(3)给值求角:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,进而确定角. 43.【2018年高考全国Ⅱ卷文数】已知5π1tan()45α-=,则tan =α______________. 【答案】32【解析】5πtan tan5πtan 114tan()5π41tan 51tan tan 4ααααα---===++⋅,解方程得3tan 2=α. 【名师点睛】本题主要考查三角恒等变换,考查考生的运算求解能力,考查的数学核心素养是数学运算.解答本题时,可直接利用正切函数的差角公式求解;也可灵活利用加减变形技巧加以求解:(1)有意识地考虑“角”与“角”之间的“加减”联系,常见的有2()()=++-ααβαβ,2+=αβ()++αβα,()=--βααβ等;(2)处理有关三角函数问题时,有时需将表示“角”的代数式看作一个整体,然后通过换元,进一步分析、解决问题.44.【2017年高考全国Ⅰ卷文数】已知π(0)2a ∈,,tan α=2,则πcos ()4α-=______________.【解析】由tan 2α=得sin 2cos αα=,又22sin cos 1αα+=,所以21cos 5α=,因为π(0,)2α∈,所以cos ,sin 55αα==,因为πππcos()cos cossin sin 444ααα-=+,所以πcos()4525210α-=+⨯=. 45.【2017年高考全国Ⅱ卷文数】函数()2cos sin f x x x =+的最大值为______________.【解析】()f x ≤=【名师点睛】通过配角公式把三角函数化为sin()y A x B ωϕ=++的形式再借助三角函数图象研究性质,解题时注意观察角、函数名、结构等特征.一般可利用|sin cos |a x b x +≤求最值.46.【2019年高考江苏卷】已知tan 2π3tan()4αα=-+,则πsin(2)4α+的值是______________.【答案】10【解析】由tan tan tan (1tan )2πtan 1tan 13tan()41tan αααααααα-===-+++-,得23tan 5tan 20αα--=,解得tan 2α=或1tan 3α=-.πππsin(2)sin 2cos cos 2sin 444ααα+=+22222sin cos cos sin (sin 2cos 2)()22sin cos αααααααα+-=+=+222tan 1tan ()tan 1ααα+-=+, 当tan 2α=时,上式222212()22110⨯+-==+ 当1tan 3α=-时,上式22112()1()33[]1210()13⨯-+--==-+综上,πsin(2)4α+=.【名师点睛】本题考查三角函数的化简求值,渗透了逻辑推理和数学运算素养.采取转化法,利用分类讨论和转化与化归思想解题.由题意首先求得tan α的值,然后利用两角和的正弦公式和二倍角公式将原问题转化为齐次式求值的问题,最后切化弦求得三角函数式的值即可.。
2020届高三数学一轮复习强化训练精品――三角函数的图象与性质

2020届高三数学一轮复习强化训练精品――三角函数的图象与性质1. ①在(0,2)上递减;②以2为周期;③是奇函数.写出一个同时满足上述条件的函数〔写出一个你认为正确的即可〕. 答案y=-sin x2.〔2018·东海高级中学高三调研〕将函数y=sin 32x 的图象先向左平移3,然后将所得图象上所有的点的横坐标变为原先的2倍〔纵坐标不变〕,那么所得到的图象对应的函数解析式为. 答案y=sin 3x 3.设函数y=acos x+b 〔a 、b 为常数)的最大值是1,最小值是-7,那么acos x+bsin x 的最大值是 . 答案 54.函数y=|sin x|的一个单调增区间是〔写出一个即可〕. 答案23,5.〔2018·全国Ⅱ理〕假设动直线x=a 与函数f (x)=sin x 和g(x)=cos x 的图象分不交于M 、N 两点,那么|MN |的最大值为 . 答案2例1 求以下函数的定义域:〔1〕y=lgsin(cos x);(2)y=x xcos sin . 解〔1〕要使函数有意义,必须使sin(cos x)>0.∵-1≤cos x ≤1,∴0<cos x ≤1.方法一利用余弦函数的简图得知定义域为{x|-2+2k <x <2+2k ,k ∈Z }. 方法二利用单位圆中的余弦线OM ,依题意知0<OM ≤1,∴OM 只能在x 轴的正半轴上,∴其定义域为k k x k x ,2222|.〔2〕要使函数有意义,必须使sin x-cos x ≥0.方法一利用图象.在同一坐标系中画出[0,2]上y=sin x 和y=cosx 的图象,如下图.在[0,2]内,满足sin x=cosx 的x 为4,45,再结合正弦、余弦函数的周期是2, 因此定义域为k k x k x ,24524|.方法二利用三角函数线,如图MN 为正弦线,OM 为余弦线,要使sin x ≥cosx,即MN ≥OM ,那么4≤x ≤45〔在[0,2]内〕.∴定义域为Ζk k x k x ,24524|方法三 sin x-cos x=2sin 4x ≥0,将x-4视为一个整体,由正弦函数y=sin x 的图象和性质可知2k ≤x-4≤+2k ,解得2k +4≤x ≤45+2k ,k ∈Z.因此定义域为Ζk k x kx x ,24542|.例2 求以下函数的值域:〔1〕y=x xx cos 1sin 2sin ;(2)y=sin x+cosx+sin xcos x;(3)y=2cos 3+2cosx.解〔1〕y=x x x x cos 1sin cos sin 2=xx x cos 1)cos 1(cos 22=2cos 2x+2cosx=2221cos -21.因此当且仅当cos x=1时取得y max =4,但cos x ≠1,∴y <4,且y min =-21,当且仅当cos x=-21时取得.故函数值域为4,21.〔2〕令t =sin x+cosx,那么有t 2=1+2sin xcos x,即sin xcosx=212t .有y=f (t )=t +212t =1)1(212t .又t =sin x+cosx=2sin 4x ,∴-2≤t ≤2.故y=f (t )= 1)1(212t (-2≤t ≤2),从而知:f (-1)≤y ≤f (2),即-1≤y ≤2+21.即函数的值域为212,1.〔3〕y=2cos x3+2cos x=2cos 3cos x-2sin 3sin x+2cosx=3cosx-3sin x=23xx sin 21cos 23=23cos 6x .∵6cos x ≤1∴该函数值域为[-23,23].例3 〔14分〕求函数y=2sin x 4的单调区间.解方法一y=2sin x 4化成y=-2sin 4x .1分∵y=sin u(u ∈R )的递增、递减区间分不为22,22k k 〔k ∈Z),232,22k k (k ∈Z),4分∴函数y=-2sin 4x 的递增、递减区间分不由下面的不等式确定2k +2≤x-4≤2k +23〔k ∈Z),即2k +43≤x ≤2k +47〔k ∈Z), 8分2k -2≤x-4≤2k +2〔k ∈Z), 即2k -4≤x ≤2k +43〔k ∈Z). 12分∴函数y=2sinx 4的单调递减区间、单调递增区间分不为432,42k k 〔k ∈Z), 472,432k k 〔k ∈Z). 14分方法二y=2sinx 4可看作是由y=2sin u 与u=x 4复合而成的. 2分又∵u=x 4为减函数,∴由2k -2≤u ≤2k +2〔k ∈Z), -2k -4≤x ≤-2k +43(k ∈Z). 即432,42k k 〔k ∈Z 〕为y=2sin x 4的递减区间. 由2k +2≤u ≤2k +23(k ∈Z),即2k +2≤4-x ≤2k +23(k ∈Z)得-2k -45≤x ≤-2k-4 (k ∈Z), 即42,452k k 〔k ∈Z)为y=2sin x 4的递增区间. 12分综上可知:y=2sinx 4的递增区间为42,452k k 〔k ∈Z 〕;递减区间为432,42k k 〔k ∈Z 〕. 14分1.求f (x)=)2cos(21x 的定义域和值域.解由函数1-2cos x 2≥0,得sin x ≤22,利用单位圆或三角函数的图象,易得所求函数的定义域是k k x k x ,42452|.当sin x=cos x 2=22时,y min =0;当sin x=cos x 2=-1时,y max=21.因此函数的值域为[0,21].2.函数f (x)=xx x 2cos 1cos 3cos 224,求它的定义域和值域,并判定它的奇偶性.解由题意知cos2x ≠0,得2x ≠k +2,解得x ≠42k〔k ∈Z 〕.因此f (x 〕的定义域为k kx x x ,42且,.又f 〔x)= x x x 2cos 1cos 3cos 224=xx x 2cos 1cos )1cos 2(22=cos 2x-1=-sin 2x.又定义域关于原点对称,∴f 〔x 〕是偶函数.明显-sin 2x ∈[-1,0],但∵x ≠42k ,k ∈Z.∴-sin 2x ≠-21.因此原函数的值域为021211|y y y 或.3.〔1〕求函数y=sinx 23的单调递减区间;〔2〕求y=3tan 46x 的周期及单调区间.解〔1〕方法一令u=x 23,y=sin u ,利用复合函数单调性,由2k -2≤-2x+3≤2k +2(k ∈Z),得2k -65≤-2x ≤2k +6〔k ∈Z),-k -12≤x ≤-k +125 (k ∈Z),即k -12≤x ≤k +125〔k ∈Z).∴原函数的单调递减区间为Z Z R125,12k k (k ∈Z).方法二由函数y=-sin 32x ,欲求函数的单调递减区间,只需求y=sin 32x 的单调递增区间. 由2k -2≤2x-3≤2k +2〔k ∈Z), 解得k -12≤x ≤k +125〔k ∈Z).∴原函数的单调递减区间为125,12k k 〔k ∈Z 〕. 〔2〕y=3tan 46x =-3tan64x , ∴T==4,∴y=3tan 46x的周期为4. 由k -2<64x <k +2,得4k -34<x <4k +38(k ∈Z), y=3tan 64x的单调增区间是384,344k k (k ∈Z 〕∴y=3tan46x 的单调递减区间是384,344k k (k ∈Z).一、填空题1.函数y=tanx 在2,2内是减函数,那么的范畴是 . 答案 -1≤<02.〔2018·徐州模拟〕函数f (x)=sin x-3cos x (x ∈[-,0])的单调递增区间是 . 答案0,63.函数f (x)=tanx (>0)的图象的相邻的两支截直线y=4所得线段长为4,那么f 〔4〕的值是 . 答案 04.函数y=2sin 〔6-2x 〕(x ∈[0,])为增函数的区间是 .答案65,35.函数f (x)=lg(sin2x+3cos2x-1)的定义域是 .答案kk x k x ,412|6.给出以下命题:①函数y=cos 232x 是奇函数;②存在实数,使得sin +cos =23;③假设、是第一象限角且<,那么tan <tan ;④x=8是函数y=sin 452x 的一条对称轴方程;⑤函数y=sin 32x 的图象关于点0,12成中心对称图形.其中命题正确的选项是〔填序号〕.答案①④7.〔2018·江苏,1〕f (x)=cos(x-6)最小正周期为5,其中>0,那么= .答案 108.〔2018·东海高级中学高三调研〕定义在R 上的函数f (x):当sin x ≤cos x 时,f (x)=cos x;当sin x >cos x 时,f (x)=sin x.给出以下结论:①f (x)是周期函数②f (x)的最小值为-1③当且仅当x=2k (k ∈Z)时,f (x)取最大值④当且仅当2k -2<x <(2k+1)(k ∈Z)时,f (x)>0⑤f (x)的图象上相邻最低点的距离是2.其中正确命题的序号是 .(把你认为正确命题的序号都填上)答案①④⑤二、解答题9.x ∈3,6,假设方程m cosx-1=cos x+m 有解,试求参数m 的取值范畴.解由m cos x-1=cos x+m 得cosx=11m m ,作出函数y=cosx 的图象〔如下图〕,由图象可得21≤11m m ≤1,解得m ≤-3.10.设a=x x xsin cos ,42sin 2,b=(4sin x,cos x-sin x),f (x)=a ·b.〔1〕求函数f (x)的解析式;〔2〕常数>0,假设y=f (x)在区间32,2上是增函数,求的取值范畴;〔3〕设集合A =326x x ,B ={x||f (x)-m |<2},假设A B ,求实数m 的取值范畴. 解〔1〕f (x)=sin 242x·4sin x+(cos x+sin x)·(cos x-sin x)=4sin x ·22cos1x+cos2x=2sin x(1+sin x)+1-2sin 2x=2sin x+1,∴f (x)=2sin x+1.〔2〕∵f (x)=2sin x+1,>0.由2k -2≤x ≤2k +2,得f (x)的增区间是22,22k k ,k ∈Z.∵f 〔x 〕在32,2上是增函数,∴32,22,2.∴-2≥2且32≤2,∴∈43,0.〔3〕由|f (x)-m |<2,得-2<f (x)-m <2,即f (x)-2<m <f (x)+2.∵A B ,∴当6≤x ≤32时,不等式f (x)-2<m <f (x)+2恒成立.∴f 〔x 〕max -2<m <f (x)min +2,∵f (x)max =f (2)=3,f (x)min =f (6)=2,∴m ∈〔1,4〕.11.定义在R 上的函数f (x)既是偶函数又是周期函数,假设f (x)的最小正周期是,且当x ∈2,0时,f 〔x 〕=sin x. 〔1〕求当x ∈[-,0]时,f (x)的解析式;〔2〕画出函数f (x)在[-,]上的函数简图;〔3〕求当f (x)≥21时,x 的取值范畴.解〔1〕∵f (x)是偶函数,∴f 〔-x 〕=f 〔x 〕. 而当x ∈2,0时,f (x)=sin x.∴当x ∈0,2时,f (x)=f (-x)=sin(-x)=-sin x.又当x ∈2,时,x+∈2,0,∵f 〔x 〕的周期为,∴f 〔x 〕=f (+x)=sin(+x)=-sin x. ∴当x ∈[-,0]时,f (x)=-sin x.〔2〕如图:〔3〕由于f (x 〕的最小正周期为,因此先在[-,0]上来研究f (x)≥21,即-sin x ≥21,∴sin x ≤-21,∴-65≤x ≤-6.由周期性知,当x ∈6,65k k ,k ∈Z 时,f (x)≥21.12.a >0,函数f (x)=-2asin 62x +2a+b,当x ∈2,0时,-5≤f (x)≤1.〔1〕求常数a,b 的值;(2)设g(x)=f 2x 且lg g(x)>0,求g(x)的单调区间. 解〔1〕∵x ∈2,0,∴2x+6∈67,6.∴sin 62x ∈1,21,∴-2asin 62x ∈[-2a,a ].∴f (x)∈[b,3a+b ],又∵-5≤f (x)≤1,因此可得b=-5,3a+b=1, 因此a=2,b=-5.〔2〕由〔1〕知a=2,b=-5,∴f 〔x 〕=-4sin 62x -1,g(x)=f 2x =-4sin 672x -1=4sin 62x -1.又由lg g(x)>0得g(x)>1,∴4sin 62x -1>1,∴sin 62x >21,∴2k +6<2x+6<2k +65,k ∈Z. 由2k +6<2x+6≤2k +2(k ∈Z),得g(x)的单调增区间为:6,k k 〔k ∈Z 〕由2k +2≤2x+6<2k +65,得g(x)的单调减区间为3,6k k 〔k ∈Z 〕.。
2020版高考数学大一轮精准复习精练---三角恒等变换Word版含解析
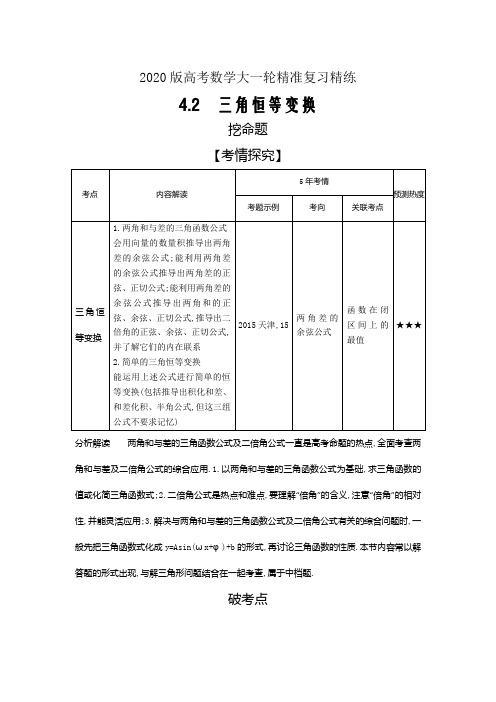
2020版高考数学大一轮精准复习精练4.2 三角恒等变换挖命题【考情探究】分析解读两角和与差的三角函数公式及二倍角公式一直是高考命题的热点,全面考查两角和与差及二倍角公式的综合应用.1.以两角和与差的三角函数公式为基础,求三角函数的值或化简三角函数式;2.二倍角公式是热点和难点,要理解“倍角”的含义,注意“倍角”的相对性,并能灵活应用;3.解决与两角和与差的三角函数公式及二倍角公式有关的综合问题时,一般先把三角函数式化成y=Asin(ωx+φ)+b的形式,再讨论三角函数的性质.本节内容常以解答题的形式出现,与解三角形问题结合在一起考查,属于中档题.破考点【考点集训】考点三角恒等变换1.“sinα+cosα=0”是“cos2α=0”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件答案A2.(2015课标Ⅰ,2,5分)sin20°cos10°-cos160°·sin10°=()A.-B.C.-D.答案D3.若tanα=2tan,则=( )A.1B.2C.3D.4答案C4.(2018课标Ⅱ,15,5分)已知sinα+cosβ=1,cosα+sinβ=0,则sin(α+β)= .答案-炼技法【方法集训】方法1三角函数的化简与求值问题1.(2013课标Ⅱ,6,5分)已知sin2α=,则cos2=( )A. B. C. D.答案A2.已知tanα=2.(1)求tan的值;(2)求的值.解析(1)因为tanα=2,所以tan===-3.(2)因为tanα=2,所以=====1.方法2利用辅助角公式解决问题的方法3.已知2cos2x+sin2x=Asin(ωx+φ)+b(A>0),则A= ,b= .答案;14.已知函数f(x)=(1+tan x)sin2x.(1)求f(x)的定义域;(2)若α∈(0,π),且f(α)=2,求α的值.解析(1)因为函数y=tan x的定义域是x∈R x≠kπ+,k∈Z,所以f(x)的定义域为x∈R x≠kπ+,k∈Z.(2)f(x)=(1+tan x)sin2x=·sin2x=sin2x+2sin2x=sin2x-cos2x+1=sin+1.由f(α)=2,得sin=.因为0<α<π,所以-<2α-<,所以2α-=或2α-=,解得α=或α=(舍去).所以α=.过专题【五年高考】A组自主命题·天津卷题组1.(2015天津,15,13分)已知函数f(x)=sin2x-sin2,x∈R.(1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值.解析(1)由已知,有f(x)=-=-cos2x=sin2x-cos2x=sin.所以,f(x)的最小正周期T==π.(2)因为f(x)在区间上是减函数,在区间上是增函数,f=-,f=-,f=,所以f(x)在区间上的最大值为,最小值为-.2.(2014天津,15,13分)已知函数f(x)=cos x·sin-cos2x+,x∈R.(1)求f(x)的最小正周期;(2)求f(x)在闭区间上的最大值和最小值.解析(1)由已知,有f(x)=cos x·-cos2x+=sin x·cos x-cos2x+=sin2x-(1+cos2x)+=sin2x-cos2x=sin.所以f(x)的最小正周期T==π.(2)因为f(x)在区间上是减函数,在区间上是增函数,f=-,f=-,f=,所以函数f(x)在闭区间上的最大值为,最小值为-.B组统一命题、省(区、市)卷题组1.(2018课标Ⅲ,4,5分)若sinα=,则cos2α=( )A. B. C.- D.-答案B2.(2018课标Ⅱ,15,5分)已知tan=,则tanα= .答案3.(2017江苏,5,5分)若tan=,则tanα= .答案4.(2017课标Ⅰ,15,5分)已知α∈,tanα=2,则cos= .答案5.(2016课标Ⅱ,13,5分)△ABC的内角A,B,C的对边分别为a,b,c,若cos A=,cos C=,a=1,则b= .答案6.(2015四川,12,5分)sin15°+sin75°的值是.答案7.(2018江苏,16,14分)已知α,β为锐角,tanα=,cos(α+β)=-.(1)求cos2α的值;(2)求tan(α-β)的值.解析(1)因为tanα=,tanα=,所以sinα=cosα.因为sin2α+cos2α=1,所以cos2α=,所以cos2α=2cos2α-1=-.(2)因为α,β为锐角,所以α+β∈(0,π).又因为cos(α+β)=-,所以sin(α+β)==,因此tan(α+β)=-2.因为tanα=,所以tan2α==-.因此tan(α-β)=tan[2α-(α+β)]==-.C组教师专用题组1.(2017山东,4,5分)已知cos x=,则cos2x=( )A.-B.C.-D.答案D2.(2016课标Ⅱ,9,5分)若cos=,则sin2α=( )A. B. C.- D.-答案D3.(2014课标Ⅱ,14,5分)函数f(x)=sin(x+2φ)-2sinφcos(x+φ)的最大值为. 答案14.(2014江苏,5,5分)已知函数y=cos x与y=sin(2x+φ)(0≤φ<π),它们的图象有一个横坐标为的交点,则φ的值是.答案5.(2014广东,16,12分)已知函数f(x)=Asin,x∈R,且f=.(1)求A的值;(2)若f(θ)+f(-θ)=,θ∈,求f.解析(1)f=Asin=,∴A·=,解得A=.(2)f(θ)+f(-θ)=sin+sin=,∴=,∴cosθ=,∴cosθ=,又θ∈,∴sinθ==,∴f=sin(π-θ)=sinθ=.【三年模拟】一、选择题(每小题5分,共15分)1.(2018天津河东二模,6)已知函数f(x)=cos2-,在下列区间中f(x)单调递增的为( )A. B. C. D.答案D2.(2019届天津耀华中学第一次月考,6)已知函数f(x)=2sinωxcos2-sinωx(ω>0)的最小值在区间上至少出现两次,则ω的最小值等于( )A.6B.C.D.3答案D3.(2018天津六校联考期中,4)若点P(cosα,sinα)在直线y=-2x上,则sin2α+cos=( )A.0B.C.D.答案D二、填空题(每小题5分,共15分)4.(2019届天津新华中学第一次月考,12)已知α,β∈,sin(α+β)=-,sin=,则cos= .答案-5.(2019届天津武清杨村三中第一次月考,13)函数f(x)=cos x-sin x的单调递增区间为.答案(k∈Z)6.(2018天津南开三模,13)若函数f(x)=sinωx+cosωx(ω≠0)对任意实数x都有f=f,则f的值等于.答案-1三、解答题(共75分)7.(2018天津河西三模,15)已知函数f(x)=2cos2x-cos-1.(1)求函数f(x)的最小正周期和对称轴方程;(2)讨论函数f(x)在上的单调性.解析(1)f(x)=2cos2x-cos-1=cos2x-cos2x+sin2x=sin,∵ω=2,∴函数f(x)的最小正周期T==π.令2x+=kπ+,k∈Z,解得x=+,k∈Z,∴f(x)的对称轴方程为x=+,k∈Z.(2)令2kπ-≤2x+≤2kπ+,k∈Z,解得-+kπ≤x≤+kπ,k∈Z,设A=,B=,可得A∩B=,∴当x∈时,f(x)在区间上单调递增,在区间上单调递减.8.(2017天津红桥二模,15)已知函数f(x)=-sin+6sin xcos x-2cos2x+1,x∈R. (1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值.解析(1)由已知,有f(x)=-sin+6sin xcos x-2cos2x+1=-sin2x-cos2x+3sin2x-(1+cos2x)+1=2sin2x-2cos2x=2sin,∴f(x)的最小正周期T==π.(2)易知f(x)在区间上为增函数,在区间上为减函数,f(0)=-×2=-2, f=×2=2,f=2,∴f(x)在区间上的最大值为2,最小值为-2.9.(2019届天津一中月考,15)设函数f(x)=cos+sin2x.(1)求函数f(x)的最小正周期和最大值;(2)求函数f(x)的单调递减区间;(3)设A,B,C为△ABC的三个内角,若cos B=,f=-,且C为锐角,求sin A.解析(1)由已知,有f(x)=cos2xcos-sin2xsin+=cos2x-sin2x+-cos 2x=-sin2x,所以f(x)的最小正周期T==π.当2x=-+2kπ(k∈Z),即x=-+kπ(k∈Z)时,f(x)取得最大值,最大值为.(2)由-+2kπ≤2x≤+2kπ,k∈Z,得-+kπ≤x≤+kπ,k∈Z,所以f(x)的单调递减区间为(k∈Z).(3)由f=-,即-sin C=-,解得sin C=,又C为锐角,所以C=.由cos B=,得sin B=.因此sin A=sin[π-(B+C)]=sin(B+C)=sin Bcos C+cos Bsin C=×+×=.10.(2018天津部分区县二模,15)已知函数f(x)=cos2ωx+·sin2ωx-(ω>0)的图象上相邻的两最高点间的距离是π.(1)求函数f(x)的解析式;(2)在锐角△ABC中,内角A,B,C满足sin Asin C-sin2C=sin2A-sin2B,求f(A)的取值范围.解析(1)函数f(x)=cos2ωx+sin2ωx-=(1+cos2ωx)+sin2ωx-=sin2ωx+cos2ωx=sin.∵函数f(x)图象上相邻的两最高点间的距离是π,∴T=π,由T==π,且ω>0,解得ω=1,∴f(x)=sin.(2)由sin Asin C-sin2C=sin2A-sin2B得ac-c2=a2-b2,即a2+c2-b2=ac,∴cos B===,又∵B∈,∴B=,在锐角三角形ABC中,A∈,∴<2A+<,∴-<sin<1,∴f(A)∈.11.(2017天津新华中学模拟,15)已知函数f(x)=2sin·sin-2sin xcos(π-x).(1)求f(x)的单调递增区间;(2)将函数y=f(x)的图象向左平移个单位长度,再将所得图象上各点的横坐标变为原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)在上的值域.解析(1)函数f(x)=2sin sin-2sin x·cos(π-x)=cos2x+sin2x=2sin.由2kπ-≤2x+≤2kπ+,k∈Z,得kπ-≤x≤kπ+,k∈Z,所以f(x)的单调递增区间为(k∈Z).(2)由(1)可知f(x)=2sin,将函数y=f(x)的图象向左平移个单位长度,得到y=2sin=2sin的图象,再将所得图象上各点的横坐标变为原来的2倍,纵坐标不变,得到函数y=g(x)=2sin的图象,当x∈时,x+∈,故g(x)∈[-1,2].12.(2017天津和平四模,15)已知函数f(x)=(tan x+1)cos2x.(1)若α∈,且cosα=-,求f(α)的值;(2)讨论函数f(x)在内的单调性.解析(1)∵α∈,且cosα=-,∴sinα==,∴tanα==-2,∴f(α)=(-2+1)×=.(2)易知函数f(x)的定义域为x x∈R,且x≠+kπ,k∈Z.f(x)=(tan x+1)cos2x=sin xcos x+cos2x=sin2x+=sin+,当x∈时,2x+∈,此时函数f(x)单调递减;x∈时,2x+∈,此时函数f(x)在上单调递减,在上单调递增.综上,函数f(x)在区间和区间上单调递减,在区间上单调递增.。
2020届高考数学理一轮考点测试:简单的三角恒等变换

1 cos α = 3,α ∈ ( π , 2π ) ,则
cos
α 2
等于
(
)
6
6
3
3
A. 3 B .- 3 C . 3 D .- 3
答案 B
解析
∵
cosα
=
1 ,α
∈
(
π
,
2π
)
,∴
α
∈
3
2
π 2 ,π
.
∴cos
α 2
=-
1+ cos α 2 =-
1
1+ 3
6
2 =- 3 .故选 B.
π
1
3.若 cos 2 - α =3,则 cos( π - 2α ) =(
)
1
1
1
1
A. 2 B .4 C . 8 D . 16
答案 C
8sin20 °cos20°cos40°cos80° sin160 ° 1
解析 cos20°cos40°cos80°=
8sin20 °
= 8sin20 ° = 8.故选 C.
1 7.已知 cos( x+ 2θ) + 2sin θ sin( x+θ ) = 3,则 cos2 x 的值为 ________.
答案 2 1 解析 ∵ 2cos2x+ sin2 x= 1+ cos2x+ sin2 x
=
2sin
2x+
π 4
+ 1,∴ A=
2, b= 1.
12.(2016 ·全国卷Ⅰ ) 已知 θ 是第四象限角,且
sin
θ
+
π 4
=
3 5,则
tan
θ -π4 = ________.
4 答案 -
【2020】最新高考数学一轮复习第三章三角函数三角恒等变换及解三角形课时训练

(2) 若△AOB为等边三角形,写出与角α终边相同的角β的集合;
(3) 若α∈,请写出弓形AB的面积S与α的函数关系式.
解:(1) 由题意可得B,根据三角函数的定义得tan α==-.
(2) 若△AOB为等边三角形,则∠AOB=.
故与角α终边相同的角β的集合为{β+2kπ,k∈Z}.
10. 已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(4)=3,则f(2 017)的值为________.
答案:-3
解析:∵ f(4)=asin (4π+α)+bcos (4π+β)=asin α+bcos β=3,∴ f(2 017)=asin (2 017π+α)+bcos (2 017π+β)=asin (π+α)+bcos (π+β)=-asin α-bcos β=-(asin α+bcos β)=-3.
答案:
解析:由 sin θ=2cos θ,得 tan θ=2.
sin2θ+sin θ cos θ-2cos2θ====.
9. 设函数f(x)(x∈R)满足f(x+π)=f(x)+sin x,当0≤x<π时,f(x)=0,则f=________.
答案:
解析:由f(x+π)=f(x)+sin x,得f(x+2π)=f(x+π)+sin(x+π)=f(x)+sin x-sin x=f(x),所以f=f=f=f=f+sinπ.因为当0≤x<π时,f(x)=0,所以f=0+=.
二、 解答题
11. 已知=-,求的值.
解:由同角三角函数关系式1-sin2α=cos2α及题意可得cos α≠0,且1-sin α≠0,可得(1+sin α)(1-sin α)=cos αcos α,所以=,所以=-,即=.
高三数学一轮复习强化训练精品――三角函数及三角恒等变换 单元综合测试

高三数学一轮复习强化训练精品――三角函数及三角恒等变换单元综合测试一、填空题(本大题共14小题,每小题5分,共70分)1.定义在R 上的函数f (x )既是偶函数又是周期函数.若f (x )的最小正周期是π,且当x ∈⎥⎦⎤⎢⎣⎡2,0π时,f (x )=sin x ,则f ⎪⎭⎫ ⎝⎛35π的值为 . 答案 23 2.设点P 是函数f (x )=29sin ωx 的图象C 的一个对称中心,若点P 到图象C 的对称轴的距离的最小值是8π,则f (x )的最小正周期是 .答案2π 3.y =sin 2x +2sin x cos x +3cos 2x 的最小正周期和最小值分别为 .答案 π,2-24.(2009·徐州六县一区联考)设sin α=53(2π<α<π),tan(π-β)=21,则tan(α-β)的值等于 . 答案 -112 5.将函数f (x )=3sin2x -cos2x 的图象向右平移θ(θ>0)个单位,所得函数是奇函数,则实数θ的最小值为 . 答案 125π 6.定义运算a *b =⎪⎩⎪⎨⎧>≤+0,0,ab b a ab b a ,则函数f (x )=(sin x )*(cos x )的最小值为 . 答案 -17.cos(α+β)=53,sin ⎪⎭⎫ ⎝⎛-4πβ=135,α,β∈⎪⎭⎫ ⎝⎛2,0π,那么cos ⎪⎭⎫ ⎝⎛+4πα的值为 . 答案 6556 8.已知函数f (x )=a sin x -b cos x (a 、b 为常数,a ≠0,x ∈R )在x =4π处取得最小值,则函数y =f ⎪⎭⎫ ⎝⎛-x 43π是 函数.(用“奇”,“偶”,“非奇非偶”填空)答案 奇9.(2008·重庆理,10)函数f (x )=x x x sin 2cos 231sin ---(0≤x ≤2π)的值域是 .答案 [-1,0] 10.设a =(a 1,a 2),b =(b 1,b 2),定义一种向量积:a ⊗b =(a 1,a 2)⊗(b 1,b 2)=(a 1b 1,a 2b 2).已知m =⎪⎭⎫ ⎝⎛21,2,n =⎪⎭⎫ ⎝⎛0,3π,点P (x ,y )在y =sin x 的图象上运动,点Q 在y =f (x )的图象上运动,且满足OQ =m ⊗OP +n (其中O 为坐标原点),则y =f (x )的最大值A 及最小正周期T 分别为 . 答案 21,4π 11.若cos(α+β)=51,cos(α-β)=53,则tan α·tan β= . 答案 21 12.函数f (x )=sin x +2|sin x |,x ∈[0,2π]的图象与直线y =k 有且仅有两个不同的交点,则k 的取值范围是 . 答案 1<k <313.若f (x )=a sin ⎪⎭⎫ ⎝⎛+4πx +b sin ⎪⎭⎫ ⎝⎛-4πx (ab ≠0)是偶函数,则有序实数对(a ,b )可以是 .(注:只要填满足a +b =0的一组数字即可)答案 (1,-1)14.关于函数f (x )=2sin ⎪⎭⎫ ⎝⎛-π433x ,有下列命题: ①其最小正周期为π32; ②其图象由y =2sin3x 向左平移43个单位而得到; ③在⎥⎦⎤⎢⎣⎡125,12ππ上为单调递增函数,则其中真命题为 (写出你认为正确答案的序号). 答案 ①③二、解答题(本大题共6小题,共90分)15.(14分)已知α∈⎪⎭⎫ ⎝⎛2,0π,β∈⎪⎭⎫ ⎝⎛ππ,2且sin(α+β)=6533,cos β=-135.求sin α. 解 ∵β∈⎪⎭⎫ ⎝⎛ππ,2,cos β=-135,∴sin β=1312. 又∵0<α<2π,2π<β<π,∴2π<α+β<23π, 又sin(α+β)=6533, ∴2π<α+β<π,cos(α+β)=-)(sin 12βα+- =-265331⎪⎭⎫ ⎝⎛-=-6556, ∴sin α=sin [(α+β)-β]=sin(α+β)cos β-cos(α+β)sin β=6533·⎪⎭⎫ ⎝⎛-135-⎪⎭⎫ ⎝⎛-6556·1312=53. 16.(14分)已知函数f (x )=A sin(ωx +ϕ)(A >0, ω>0,|ϕ|<2π) (x ∈R )的部分图象如图所示.(1)求f (x )的表达式;(2)设g (x )=f (x )-3f ⎪⎭⎫ ⎝⎛+4πx ,求函数g (x )的最小值及相应的x 的取值集合. 解 (1)由图象可知:A =1, 函数f (x )的周期T 满足:4T =3π-12π=4π,T =π,∴T =ωπ2=π.∴ω=2.∴f (x )=sin(2x +ϕ).又f (x )图象过点⎪⎭⎫ ⎝⎛1,12π,∴f ⎪⎭⎫⎝⎛12π=sin ⎪⎭⎫ ⎝⎛+ϕπ6=1,ϕπ+6=2k π+2π(k ∈Z ).又|ϕ|<2π,故ϕ=3π.∴f (x )=sin ⎪⎭⎫⎝⎛+32πx .(2)方法一 g (x )=f (x )-3 f ⎪⎭⎫⎝⎛+4πx=sin ⎪⎭⎫ ⎝⎛+32πx -3sin ⎪⎭⎫⎝⎛++322ππx=sin ⎪⎭⎫ ⎝⎛+32πx -3sin ⎪⎭⎫⎝⎛+652πx=21sin2x +23cos2x +23sin2x -23cos2x=2sin2x ,由2x =2k π-2π(k ∈Z ),得x =k π-4π(k ∈Z ),∴g (x )的最小值为-2,相应的x 的取值集合为⎭⎬⎫⎩⎨⎧∈-=k k x x ,4|ππ. 方法二 g (x )=f (x )-3f ⎪⎭⎫⎝⎛+4πx=sin ⎪⎭⎫⎝⎛+32πx -3sin ⎪⎭⎫⎝⎛++322ππx=sin ⎪⎭⎫ ⎝⎛+32πx -3cos ⎪⎭⎫⎝⎛+32πx=2sin ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+332ππx =2sin2x , 由2x =2k π-2π(k ∈Z ),得x =k π-4π(k ∈Z ),∴g (x )的最小值为-2,相应的x 的取值集合为{x |x =k π-4π,k ∈Z }.17.(2008·江苏,15)(14分)如图,在平面直角坐标系xOy 中,以Ox 轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A ,B 两点,已知A ,B 的横坐标分别为102,552.(1)求tan(α+β)的值; Z(2)求α+2β的值.解 由条件得cos α=102,cos β=552. ∵α,β为锐角,∴sin α=α2cos 1-=1027, sin β=β2cos 1-=55. 因此tan α=ααcos sin =7,tan β=ββcos sin =21. (1)tan(α+β)=βαβαtan tan 1tan tan •-+=2171217⨯-+=-3. (2)∵tan2β=ββ2tan 1tan 2-=2)21(1212-⨯=34, ∴tan(α+2β)=βαβα2tan tan 12tan tan •-+=3471347⨯-+=-1.∵α,β为锐角,∴0<α+2β<23π,∴α+2β=43π. 18.(16分)已知tan α、tan β是方程x 2-4x -2=0的两个实根,求:cos 2(α+β)+2sin(α+β)cos(α+β)-3sin 2(α+β)的值.解 由已知有tan α+tan β=4,tan α·tan β=-2,∴tan(α+β)=βαβαtan tan 1tan tan -+=34, cos 2(α+β)+2sin(α+β)cos(α+β)-3sin 2(α+β) =)(sin )(cos )(sin 3)cos()sin(2)(cos 2222βαβαβαβαβαβα++++-++++ =)(tan 1)(tan 3)tan(2122βαβαβα+++-++ =916191633421+⨯-⨯+=-53. 19.(16分)把曲线C :y =sin ⎪⎭⎫ ⎝⎛-x 87π·cos ⎪⎭⎫ ⎝⎛+8πx 向右平移a (a >0)个单位,得到的曲线C ′关于直线x =4π对称. (1)求a 的最小值;(2)就a 的最小值证明:当x ∈⎪⎭⎫ ⎝⎛--89,78ππ时,曲线C ′上的任意两点的直线斜率恒大于零.(1)解 ∵y =sin ⎪⎭⎫ ⎝⎛+•⎪⎭⎫ ⎝⎛-8cos 87ππx x =sin ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+8cos 8ππx x =21sin ⎪⎭⎫ ⎝⎛+42πx , ∴曲线C ′方程为y =21sin ⎥⎦⎤⎢⎣⎡+-4)(2πa x , 它关于直线x =4π对称, ∴21sin ⎥⎦⎤⎢⎣⎡+-4)4(2ππa =±21, 即2⎪⎭⎫ ⎝⎛-a 4π+4π=k π+2π(k ∈Z ), 解得a =8π-2πk (k ∈Z ), ∵a >0,∴a 的最小值是8π. (2)证明 当a =8π时,曲线C ′的方程为y =21sin2x . 由函数y =21sin2x 的图象可知: 当x ∈⎪⎭⎫ ⎝⎛--89,78ππ时,函数y =21sin2x 是增函数, 所以当x 1<x 2时,有y 1<y 2, 所以1212x x y y -->0,即斜率恒大于零. 20.(16分)设函数f (x )=sin (2x +ϕ)(-π<ϕ<0),y =f (x )图象的一条对称轴是直线x =8π. (1)求ϕ;(2)求函数y =f (x )的单调增区间;(3)证明:直线5x -2y +c =0与函数y =f (x )的图象不相切.(1)解 ∵x =8π是函数y =f (x )的图象的对称轴, ∴sin ⎪⎭⎫ ⎝⎛+⨯ϕπ82 =±1, ∴4π+ϕ=k π+2π,k ∈Z . ∵-π<ϕ<0,∴ϕ=-43π. (2)解 由(1)知ϕ=-43π,因此y =sin ⎪⎭⎫ ⎝⎛-432πx . 由题意得2k π-2π≤2x -43π≤2k π+2π,k ∈Z .则k π+8π≤x ≤k π+85π,k ∈Z 所以函数y =sin ⎪⎭⎫ ⎝⎛-432πx 的单调增区间为 ⎥⎦⎤⎢⎣⎡++85,8ππππk k ,k ∈Z . (3)证明 ∵|y ′|=|(sin (432π-x ))′| =|2cos (432π-x )|≤2, ∴曲线y =f (x )的切线斜率的取值范围是[-2,2],而直线5x -2y +c =0的斜率为25>2,所以直线5x -2y +c =0与函数 y =sin (432π-x )的图象不相切.。
2020届高考数学一轮复习单元检测四三角函数解三角形提升卷单元检测理含解析新人教A

A.a>b>c
B.b>c>a
C.c>b>a
D.c>a>b
答案 A
解析 由题可知 b=cos55°=sin35°,因为 sin35°>sin23°,所以 b>c,利用三角函数
线比较 tan35°和 sin35°,易知 tan35°>sin35°,所以 a>b.综上,a>b>c,故选 A.
7.若函数 f(x)= 3sin(2x+θ)+cos(2x+θ)是偶函数,则 θ 的最小正实数值是( )
答案 C
解析 由正弦定理得 2b2=(2a+c)a+(2c+a)c,化简得 a2+c2-b2+ac=0,所以 cosB=
a2+c2-b2 -ac 1
2π
2ac = 2ac =-2,又 B∈(0,π),解得 B= 3 ,故选 C.
1 10.已知函数 f(x)= 3sin2x-2cos2x,将 f(x)的图象上的所有点的横坐标缩短到原来的3,
纵坐标不变,再把所得图象向上平移 1 个单位长度,得到函数 g(x)的图象,若
g(x1)·g(x2)=-4,则|x1-x2|的值可能为( ) πππ
A. 3 B. 4 C. 2 D.π
答案 C
解析 由题意得 f(x)= 3sin2x-cos2x-1
3
( ) ( ) π
π
2π π
2x-
6x-
=2sin 6 -1,则 g(x)=2sin 6 ,故函数 g(x)的最小正周期 T= 6 = 3 .由
若 f(2017)=asin(2 017π+α)+bcos(2 017π+β)=-asinα-bcosβ=-1,则
asinα+bcosβ=1,所以 f(2020)=asin(2020π+α)+bcos(2020π+β)
2020届高三数学一轮复习练习三角恒等变换与解三角形

专题 8三角恒等变换与解三角形一、考点展现1.若 sin1,则 cos 22 =.6332.在 ABC 中,角 A , B , C 所对边的长分别为 a3, b 4,c6 ,则 bc cosAca cosBabcosC 的值为.3.在ABC 中,角 A , B ,C 所对边的长分别为 a, b, c ,若 3b c cos A a cosC ,则 cos A =. 4.在锐角三角形 ABC 中, BC=1,B=2A ,则AC 的值为 , AC 的取值范围为.cos A5.在4,cos B5.ABC 中, cos A,则 cosC =513b a tan C tan C6.在锐角三角形 ABC 中,角 A , B ,C 的对边分别是a,b, c ,若的值a 6 cosC,则tan Bbtan A为.二、例题剖析例 1.已知 0, tan 15 的值 .,求 sin22 tan2 32例 2.如下图:经过乡村 A 有两条夹角为 60 的公路 AB , AC ,依据规划拟在两条公路之间的地区内建一 工厂 P ,分别在两条公路边上建两个库房M , N (异于乡村 A ),要求 PM=PN=MN =2,单位为公义,怎样 设计,使得工厂产生的噪声对居民的影响最小?(即工厂与乡村的距离最远).例 3.已知ABC 的内角 A , B , C 的对边挨次为 a,b, c ,若知足 3 tan A tan B tan A tan B3 .①求角 C 的大小;②若 c 2 ,且ABC 为锐角三角形,求a2b2的取值范围.例 4.等腰三角形ABC 腰上的中线BD 为定长l,当顶角变化时,求三角形ABC 面积的最大值 .三、作业1.若 cos1, cos 3=5 , 则 tan tan.在54, 则边上的高为ABC 中, AB3, BC13, ACAC23. 在 ABC 中,角 A, B, C 所对的边分别是 a,b,c ,假如 a, b, c 成等差数列, B 30 0 , ABC 的面积为 3 ,则 b.24.在 △ABC 中, a4 , b5 , c6 ,则sin 2 A.ABCsin CABCtanC5中,角 A B C的对边分别为 a,b,c,若的面积为 Sa b 2c 2 ,则 .在, ,,且2S的值为.6. 2002 年在北京召开了国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的,弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形,如下图,假如小正方形的面积为1,大正方形的面积为 25,直角三角形中较小的锐角为 ,则 cos2 的值为7.若△ ABC 的内角知足 sin A 2 sin B 2 sin C ,则 cosC 的最小值是.8.已知 cos x2, x 2,3,则 tan x =41049.设 x, y 是锐角,且 tan x 3tan y ,则 xy 的最大值为.10.在 ABC 中 ,内角 A,B,C 所对的边分别为a, b,c , b c 2,cos A1 ABC 的面积为 3 15 ., 已知4①求 a 和 sin C ;②求 cos 2 A6 的值 .11.在ABC 中,内角 A , B , C 所对的边分别为 a, b, c ,已知 a b, c3,cos2 A cos2 B 3 sin A cos A3sin B cos B ;①求角 C 的大小;4②若 sin A,求三角形ABC 的面积5.12.如图 :某农场有一块农田,它的界限由圆O 的一段弧MPN (P 为此圆弧的中点)和线段 MN 组成 ,已知圆 O 的半径为40 米 ,点 P 到 MN 的距离为50 米 ,现规划在此农田上修筑两个温室大棚,大棚 1 内的地块形状为矩形 ABCD ,大棚 2 内的地块形状为三角形 CDP ,要求点 A,B 均在线段 MN 上,点 C,D 均在圆弧上 ,设 OC 与 MN 所成的角为 .⑴用分别表示矩形 ABCD 和三角形CDP 的面积 ,并确立sin 的取值范围 ;4: 3,求⑵若大棚 1 内栽种甲种蔬菜 ,大棚 2 内栽种乙种蔬菜 ,且甲、乙两种蔬菜的单位面历年产值之比为当为什么值时,能使甲、乙两种蔬菜的年总产值最大.。
2020届高三数学一轮复习 第三章三角函数测试题 新人教

第三章 三角函数、解三角形(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.集合M ={x |x =sinnπ3,n ∈Z},N ={x |x =cosnπ2,n ∈N},则M ∩N 等于 ( )A.{-1,0,1}B.{0,1}C.{0}D.∅ 解析:∵M ={x |x =sinnπ3,n ∈Z}={-32,0,32}, N ={-1,0,1},∴M ∩N ={0}. 答案:C2.已知α∈(π2,π),sin α=35,则tan(α+π4)等于 ( )A.17B.7C.-17D.-7 解析:由α∈(π2,π),sin α=35,得tan α=-34,tan(α+π4)=1+tan α1-tan α=17.答案:A3.若函数f (x )=(1+3tan x )cos x,0≤x <π2,则f (x )的最大值为 ( )A.1B.2C.3+1D.3+2 解析:f (x )=(1+3tan x )cos x =cos x +3sin x =2sin(x +π6),∵0≤x <π2,∴f (x )max =2.答案:B4.(2020·温州模拟)函数f (x )=2sin(2x +π6)在[-π2,π2]上对称轴的条数为 ( )A.1B.2C.3 D .0 解析:∵当-π2≤x ≤π2,∵-5π6≤2x +π6≤76π,∴函数的对称轴为:2x +π6=-π2,π2,∴x =-π3,或x =π6.答案:B5.要得到y =sin(2x -π3)的图象,只要将y =sin2x 的图象 ( )A.向左平移π3个单位B.向右平移π3个单位C.向左平移π6个单位 D.向右平移π6个单位 解析:∵y =sin(2x -π3)=sin2(x -π6),∴只要将y =sin2x 的图象向右平移π6个单位便得到y =sin(2x -π3)的图象.答案:D6.使奇函数f (x )=sin(2x +θ)+3cos(2x +θ)在[-π4,0]上为减函数的θ 值为( )A.-π3B.-π6C.5π6D.2π3解析:由已知得:f (x )=2sin(2x +θ+π3),由于函数为奇函数,故有θ+π3=kπ⇒θ=kπ-π3(k ∈Z),可淘汰B 、C 选项,然后分别将A和D 选项代入检验,易知当θ=2π3时,f (x )=-2sin2x 其在区间[-π4,0]上递减,故选D.答案:D7.给定函数①y =x cos(3π2+x ),②y =1+sin 2(π+x ),③y =cos(cos(π2+x ))中,偶函数的个数是 ( )A.3B.2C.1D.0解析:对于①y =x cos(32π+x )=x sin x ,是偶函数,故①正确;对于②y =1+sin 2(π+x )=sin 2x+1,是偶函数,故②正确;对于③y =cos(cos(π2+x ))=cos(-sin x )=cos(sin x ),∵f (-x )=cos(sin(-x ))=cos(-sin x )=cos(sin x )=f (x ), ∴函数是偶函数,故③正确.答案:A8.在△ABC 中,若sin 2A +sin 2B -sin A sin B =sin 2C ,且满足ab =4,则该三角形的面积为( ) A.1 B.2 C. 2 D. 3 解析:∵sin 2A +sin 2B -sin A sin B =sin2C ,∴a 2+b 2-ab =c 2,∴cos C =a 2+b 2-c 22ab =12,∴C =60°,∴S △ABC =12ab sin C =12×4×32= 3.答案:D9.有一种波,其波形为函数y =sin(π2x )的图象,若在区间[0,t ]上至少有2个波峰(图象的最高点),则正整数t 的最小值是 ( ) A.3 B.4 C.5 D.6解析:由T =2πω=2ππ2=4,可知此波形的函数周期为4,显然当0≤x ≤1时函数单调递增,x=0时y =0,x =1时y =1,因此自0开始向右的第一个波峰所对的x 值为1,第二个波峰对应的x 值为5,所以要区间[0,t ]上至少两个波峰,则t 至少为5. 答案:C10.设集合M ={平面内的点(a ,b )},N ={f (x )|f (x )=a cos2x +b sin2x ,x ∈R},给出从M 到N 的映射f :(a ,b )→f (x )=a cos2x +b sin2x ,则点(1,3)的象f (x )的最小正周期为( ) A.π B.π3 C.π2 D.π4解析:f (x )=cos2x +3sin2x =2sin(2x +π6),则最小正周期为π.答案:A11.函数y =sin(2x -π3)在区间[-π2,π]上的简图是 ( )解析:当x =-π2时,y =sin(-π-π3)=sin π3=32>0,排除B 、D ,当x =π6时,y =sin(π3-π3)=sin0=0,排除C. 答案:A12.设函数f (x )=A sin(ωx +φ),(A ≠0,ω>0,-π2<φ<π2)的图象关于直线x =2π3对称,它的周期是π,则 ( ) A.f (x )的图象过点(0,12) B.f (x )的图象在[5π12,2π3]上递减C.f (x )的最大值为AD.f (x )的一个对称中心是点(5π12,0)解析:T =π,∴ω=2.∵图象关于直线x =2π3对称,∴sin(2π3ω+φ)=±1,即2π3×2+φ=π2+kπ,k ∈Z 又∵-π2<φ<π2,∴φ=π6∴f (x )=A sin(2x +π6).再用检验法.答案:D二、填空题(本大题共4小题,每小题4分,共16分.请把正确答案填在题中横线上) 13.已知扇形内切圆半径与扇形半径之比为1∶3,则内切圆面积与扇形面积之比为 . 解析:如图,设内切圆半径为r ,则扇形的半径为3r ,计算可 得扇形中心角为π3,故S 内切圆∶S 扇形=πr 2∶12·3r ·(π3·3r )=2∶3.答案:2∶314.已知函数f (x )=2sin(ωx +φ)的图象如下图所示,则f (7π12)= .解析:由图象知,函数的周期为32×T =π,∴T =2π3.∵f (π4)=0,∴f (7π12)=f (π4+π3)=f (π4+T 2)=-f (π4)=0. 答案:015.设△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c 且a cos B -b cos A =35c .则tan Atan B 的值为 .解析:由a cos B -b cos A =35c 及正弦定理可得sin A cos B -sin B cos A =35sin C ,即sin A cos B -sin B cos A =35sin(A +B ),即5(sin A cos B -sin B cos A )=3(sin A cos B +sin B cos A ),即sin A cos B =4sin B cos A ,因此tan A =4tan B ,所以tan Atan B =4.答案:416.下面有五个命题:①函数y =sin 4x -cos 4x 的最小正周期是π; ②终边在y 轴上的角的集合是{α|α=kπ2,k ∈Z};③在同一坐标系中,函数y =sin x 的图象和函数y =x 的图象有三个公共点; ④把函数y =3sin(2x +π3)的图象向右平移π6个单位得到y =3sin2x 的图象;⑤函数y =sin(x -π2)在[0,π]上是减函数. 其中真命题的序号是 .解析:①y =sin 2x -cos 2x =-cos2x ,故最小正周期为π,①正确; ②k =0时,α=0,则角α终边在x 轴上,故②错;③由y =sin x 在(0,0)处切线为y =x ,所以y =sin x 与y =x 的图象只有一个交点,故③错; ④y =3sin(2x +π3)的图象向右平移π6个单位得到y =3sin[2(x -π6)+π3]=3sin2x ,故④正确;⑤y =sin(x -π2)=-cos x 在[0,π]上为增函数,故⑤错.综上,①④为真命题. 答案:①④三、解答题(本大题共6小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分12分)已知AC u u u r =(cos x 2+sin x 2,-sin x 2),BC u u u r =(cos x 2-sin x 2,2cos x2).(1)设f (x )=AC u u u r ·BC u u u r,求f (x )的最小正周期和单调递减区间;(2)设有不相等的两个实数x 1,x 2∈⎣⎢⎡⎦⎥⎤-2π2,π2,且f (x 1)=f (x 2)=1,求x 1+x 2的值.解:(1)由f (x )=AC u u u r ·BC u u u r得f (x )=(cos x 2+sin x 2)·(cos x 2-sin x 2)+(-sin x 2)·2cos x2=cos 2x2-sin 2x 2-2sin x 2cos x2=cos x -sin x =2cos(x +π4),所以f (x )的最小正周期T =2π. 又由2k π≤x +π4≤π+2k π,k ∈Z ,得-π4+2k π≤x ≤3π4+2k π,k ∈Z.故f (x )的单调递减区间是[-π4+2kπ,3π4+2kπ](k ∈Z).(2)由f (x )=1得2cos(x +π4)=1,故cos(x +π4)=22.又x ∈⎣⎢⎡⎦⎥⎤-π2,π2,于是有x +π4∈⎣⎢⎡⎦⎥⎤-π4,34π,得x 1=0,x 2=-π2, 所以x 1+x 2=-π2.18.(本小题满分12分)在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,tan A =12,cos B =31010.(1)求角C ;(2)若△ABC 的最短边长是5,求最长边的长. 解:(1)∵tan A =12,∴A 为锐角,则cos A =255,sin A =55.又cos B =31010,∴B 为锐角,则sin B =1010,∴cos C =-cos(A +B )=-cos A cos B +sin A sin B =-255×31010+55×1010=-22.又C ∈(0,π),∴C =34π.(2)∵sin A =55>sin B =1010, ∴A >B ,即a >b , ∴b 最小,c 最大, 由正弦定理得b sin B =csin C, 得c =sin C sin B ·b =221010·5=5.19.(本小题满分12分)在△ABC 中,A 、B 为锐角,角A 、B 、C 所对的边分别为a 、b 、c ,且sin A =55,sin B =1010. (1)求A +B 的值;(2)若a -b =2-1,求a 、b 、c 的值. 解:(1)∵A 、B 为锐角,sin A =55,sin B =1010, ∴cos A =1-sin 2A =255, cos B =1-sin 2B =31010,∴cos(A +B )=cos A cos B -sin A sin B =255×31010-55×1010=22.∵0<A +B <π,∴A +B =π4.(2)由(1)知C =3π4,∴sin C =22.由正弦定理αsin A =b sin B =csin C 得5a =10b =2c ,即a =2b ,c =5b , ∵a -b =2-1,∴2b -b =2-1,∴b =1, ∴a =2,c = 5.20.(本小题满分12分)如图,点A ,B 是单位圆上的两点,A ,B 点分别在第一、二象限,点C 是圆与x 轴正半轴的交点,△AOB 是正三角形,若点A 的坐标为(35,45),记∠COA =α.(1)求1+sin2α1+cos2α的值;(2)求|BC |2的值.解:(1)∵A 的坐标为(35,45),根据三角函数的定义可知,sin α=45,cos α=35,∴1+sin2α1+cos2α=1+2sin αcos α2cos 2α=4918. (2)∵△AOB 为正三角形,∴∠AOB =60°.∴cos ∠COB =cos(α+60°)=cos αcos60°-sin αsin60° =35×12-45×32=3-4310, ∴|BC |2=|OC |2+|OB |2-2|OC |·|OB |cos ∠COB =1+1-2×3-4310=7+435.21.(本小题满分12分)已知函数f (x )=A sin(ωx +φ)+B (A >0,ω>0)的一系列对应值如下表:xπ6π35π6 4π3 11π6 7π317π6 y-1131-113(1)根据表格提供的数据求函数f (x )的一个解析式;(2)根据(1)的结果,若函数y =f (kx )(k >0)周期为2π3,当x ∈[0,π3]时,方程f (kx )=m 恰有两个不同的解,求实数m 的取值范围; 解:(1)设f (x )的最小正周期为T ,得T =11π6 -(-π6)=2π,由T =2πω,得ω=1.又32,.11B A A B A B +==⎧⎧⎨⎨-=-=⎩⎩解得令ω·5π6+φ=π2,即5π6+φ=π2,解得φ=-π3,∴f (x )=2sin(x -π3)+1.(2)∵函数y =f (kx )=2sin(kx -π3)+1的周期为2π3,又k >0,∴k =3. 令t =3x -π3,∵x ∈[0,π3],∴t ∈[-π3,2π3]如图sin t =s 在[-π3,2π3]上有两个不同的解的充要条件是s ∈[32,1),∴方程f (kx )=m 在x ∈[0,π3]时恰好有两个不同的解的充要条件是m ∈[3+1,3),即实数m 的取值范围是[3+1,3).22.(本小题满分14分)(2020·长沙模拟)长沙市某棚户区改造 建筑用地平面示意图如图所示.经规划调研确定,棚改规划建 筑用地区域近似地为半径是R 的圆面.该圆面的内接四边形ABCD 是原棚户建筑用地,测量可知边界AB =AD =4万米, BC =6万米,CD =2万米.(1)请计算原棚户区建筑用地ABCD 的面积及圆面的半径R 的值;(2)因地理条件的限制,边界AD 、DC 不能变更,而边界AB 、BC 可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC 上设计一点P ;使得棚户区改造的新建筑用 地APCD 的面积最大,并求最大值.解:(1)因为四边形ABCD 内接于圆,所以∠ABC +∠ADC =180°,连接AC ,由余弦定理:AC 2=42+62-2×4×6×cos∠ABC=42+22-2×2×4cos∠ADC .所以cos∠ABC =12,∵∠ABC ∈(0,π),故∠ABC =60°.S 四边形ABCD =12×4×6×sin60°+12×2×4×sin120°=83(万平方米). 在△ABC 中,由余弦定理:AC 2=AB 2+BC 2-2AB ·BC ·cos∠ABC=16+36-2×4×6×12.AC =27.由正弦定理a sin A =bsin B=2R ,∴2R =AC sin∠ABC =2732=4213,∴R =2213(万米).(2)∵S 四边形APCD =S △ADC +S △APC , 又S △ADC =12AD ·CD ·sin120°=23,设AP =x ,CP =y .则S △APC =12xy ·sin60°=34xy .又由余弦定理AC 2=x 2+y 2-2xy cos60° =x 2+y 2-xy =28.∴x 2+y 2-xy ≥2xy -xy =xy . ∴xy ≤28,当且仅当x =y 时取等号 ∴S 四边形APCD =23+34xy ≤23+34×28=93, ∴最大面积为93万平方米.。
2020高三数学一轮复习三角函数(Ⅴ)单元练习题

高三数学单元练习题:三角函数(V)第I 卷、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代 号填在题后的括号内(本大题共12个小题,每小题5分,共60分)。
C.周期函数, 数小正周期为D.非周期函数1. 使 f(x) sin(2x ),3 cos(2x )为奇函数,且在[0,二]上是减函数的 的一个值A . B. - 6 2 C.3 2. 3. A .A B G 和A 2B 2C 2都是锐角三角形B .A3C 和 A 2B 2C 2都是钝角三角形C. AB 。
!是钝角三角形, A 2 B 2 C 2是锐角三角形D. A BG 疋.锐角三角形,A 2B 2C 2是钝角三角形ABG 的三个内角的余弦值分别等于 A 2B 2C 2的三个内角的正弦值,则 设函数f (x) sin3x | sin3x|,则f(x)为A .周期函数, 最小正周期为 B.周期函数,最小正周期为 一34.ABC 中,若 cosA cosBsinC ,ABC 的形状是5.函数f(x)=sin xcOsx的值域是1sinx cosxA .[-2 --1, 1] U [ — 1, ,2 — 1]B.r <2 1[ ,2 1]22C .[-2-1, 2— 1] D.r <2 1[ ,—1) U (— 1,2226•对任意的锐角a,3,下列不等关系中正确的是A.sin( a + 3 )>sin a +sin 3B. sin( a + 3 )>cos a+cos 3C.cos( a + 3 )< sin a+ sin 3D. cos( a + 3 )< cos a + cos37 .在△ ABC 中,sin A:sinB : sinC = a : (a+1):2a ,则 a 的取值范围是 A.a > 2 D 1 B. a >C. a > 0D. a > 12A .等腰三角形B.等边三角形等腰直角三角形 D •直角三角形C. &已知函数 f(x)=2sin x( >0)在区间[— —]上的最小值是一2,则3 4的最小值等于()9.若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m 则m 的范12.已知 f (x)a cos 2 x bsinxcosx—的最大值是 2—,且 f (_)—,则 f (—)234 3( )1■ 3 1卡 •、3、3A.—B.C.D. 0或242 44第n 卷二、填空题:请把答案填在题中横线上(本大题共 4个小题,每小题4分,共16分)。
2020江苏高考数学一轮配套精练:第25课三角恒等变换

第25课三角恒等变换 一、填空题 A.课时精练 1.已知 a€ 2, n ,sin “=洛则 ta 门“ --------------7t 5.已知 sin a= 2sin 3 tan a= 3tan 3 那么 cos2 a= __________ 6.若 sin(a — 3)cos a- cos(a — 3sin a= m ,且 3为第三象限角,贝U cos 2. (2018珠海一模)已a, B 均为锐角, cos 3= _36? cos( a+ 3 = 2,那么 C0S a= 3. (2018衡水模拟)已i 9nn sin x -14 n, 9 n n 3 cos 7+cosx -石 sin 7 = 5, 7t 8.已知a 是第一象限的角,且 cos a= 存那么 sin a+ 4 cos ( 2 a+ 4 n) 的值为x € 那么tan2x 4.若 a€ 且 sin 2 a+ cos + 2 —cos3的值为_________________________________________________________________________ 7.已知sin x + n = 2,那么sin二、解答题9.已知 a€ 2,兀,且 tan a=— 2.⑴求sin 4+ a 的值;⑵求cos 2^— 2 a 的值.10. (2017 南通调研)已知 tan a= 2, cos 3=—,且 a 氏(0, n ),⑴求COS2 a 的值;⑵求2 a — 3的值.11. (2018 北京卷)已知函数 f(x) = sin 2x + . 3sinxcosx.⑴求f(x)的最小正周期;⑵ 若f(x)在区间一3,m 上的最大值为2,求m 的最小值.B.滚动小练值范围为 _________,匚n … … ..... 一 一. sin B . cos B . tan B2•已知角a= 2k n-尹€ Z ),若角B 与角a 的终边相同,则y =丽广眉+简订 3.已知函数f(x) = e x — ax(e 为自然对数的底数,a 为常数)的图象在点(0, 1)处的切线斜 为—1.(1)求a 的值及函数f(x)的极值;(2)求证:当 x > 0 时,x 2< e x . 1. (2018邯郸一模)若函数f(x)=2x 1,x_1,2 —x ax 1,x : 1在R 上是增函数,则a 的取。
2020年高三文科数学一轮单元卷:第七单元三角恒等变换A卷-(5574)

一轮单元训练金卷?高三?数学卷(A)第七单元三角恒等变换注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.sin75 cos75 的值为()A.14B.12C.18D.12.cos72 cos12 sin72 sin12 ()A.12B.12C.32D.323.sin17 sin223 +cos17 cos 43 等于()A.12B.12C.32D.324.若tan 3,则s in 2cossin cos()A.25B.25C.52D.525.若sin 34,是第二象限角,则sin 2π4()A.2 2 716B.2 2 716C.2 3 1416D.214 1166.已知tan 23,tanπ 16 2,则tanπ6等于()A.14B.78C.18D.797.已知cos cos 12,sin sin13,则cos ()A.5972B.5972C.1336D.13368.1tan151 tan15()A.33B. 3 C.1 D.129.△ABC中A为其内角,设3a,sin A ,21b cos A, ,且a∥b,则sin A cos A()3A.22B. 2 C. 2 D.210.设a sin14 cos14 ,b sin16 cos16 ,6c ,则a ,b ,c 的大小关系是()2A.a b c B.a c bC.b c a D.b a c11.已知 22cos x sin2x Asin ωx φ b A 0,0 φπ,则 A ,φ,b的值分别为()A.A 2 ,πφ,b 1 B.A 2 ,4πφ,b 26C.A 2 ,πφ,b 1 D.A 2 ,6πφ,b 1412.已知ππa sin x ,sin x ,3 6ππb cos x ,cos x ,6 35a b,且13ππx , ,3 6则sin2x 的值为()A.5 3 1226B.5 3 1226C.512 326D.512 326二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上)13.已知sin32,则cos2 __________.14.函数 f x sin x cos x 的最大值为____________.15.若tan12 2,0,π2,则cosα__________.16.已知sin π 36 5,π,π2,则tanπ12________.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10 分)已知cos π 3x ,4 517π7πx .12 4(1)求sin πx 的值;4(2)求sin2 x的值.18.(12 分)已知sin 45,是第四象限角.(1)求tan 和sin2 的值;(2)求tan π4的值.19.(12 分)(1)设为锐角,若cos π 46 5,求sin 2π3的值;(2)已知:π5πcos 3sin2 4,求tantanπ8π8的值.20.(12分)已知:cos π3α,45512sinπβ,413π 3α,π,44πβ0,.4(1)求sin π4α的值;(2)求cosαβ的值.21.(12分)已知函数2f x sin x cosx3sin x.(1)求πf;3(2)设π,π2,13f,求sin的值.24222.(12分)已知:a2cos x,sin x,b3cos x,2cos x.设函数f x a b3,x R,求:(1)f x的最小正周期;(2)f x的对称中心;(3)若ππf f6,且26212π,π2,求.一轮单元训练金卷?高三?数学卷答案(A)第七单元三角恒等变换一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.【答案】A【解析】1 1 1 1 1sin75 cos75 2sin75 cos75 sin1502 2 2 2 4.故选A.2.【答案】B【解析】cos72 cos12 sin72 sin12 cos 72 12 cos60 12,故选B.3.【答案】B【解析】sin17 sin 223 cos17 cos 43 sin17 sin 180 43 cos17 cos43sin17 sin 43 cos17 cos43 cos17 cos43 sin17 sin43 cos60 12,故选B.4.【答案】D【解析】由齐次式可得:sin 2cos tan 2 5 5sin cos tan 1 2 2,故选D.5.【答案】C【解析】由于角为第二象限角,故cos74,所以sin 2 2sin cos3 78,2 1 cos2 1 2sin8 ,故π 2 2 3 14sin 2 sin2 cos24 2 16,故选C.6.【答案】C【解析】π 2 1tan tanππ 6 3 2 1tan tan6 6 2 1 8π1 tan tan 16 3 2,故选C.7.【答案】B【解析】 1c o s c ,o2 sin sin13,分别平方可得2 2 2 1 cos cos cos cos 2cos cos4 , 2 2 21 sin sin sin sin 2sin sin9,两式相加可得 2 2 cos cos sin sin 1336,即cos cos sin sin5972,则cos cos cos sin sin 5972,故选B.8.【答案】A【解析】1tan15 tan45 tan15 3tan301 tan15 1 tan45 tan15 3.故选 A .9.【答案】B【解析】 3a,sin A ,21b cos A, 且a∥b,∴33 1 1sin A cos A ,∴sin2A 1 ,2 3 2∵是锐角,∴2A 90 ,A 45 ,sin A cos A 2 sin A 45 2 sin90 2 ,故选B.10.【答案】 B【解析】 a sin14 cos14 2 sin 14 45 2 sin 59 ,b sin16 cos16 2 sin 16 45 2 sin 61 , 6 3c 2 2sin60 .2 2因为sin59 sin 60 2 sin 61 .所以 a c b.故选B.11.【答案】 D【解析】π2x x x x x .所以 A 2 ,φ,b 1.故选D.2cos sin2 1 cos2 sin2 2 sin 2 14 412.【答案】 B【解析】πππππ 5a b sin x cos x cos x sin x sin 2x ,3 6 3 6 6 13由于ππx , ,所以3 6πππ2x , ,所以6 2 22π 5 12cos 2x 1 ,6 13 13所以ππππππ 5 3 12sin2 x sin 2x sin 2x cos cos 2x sin ,故选B.6 6 6 6 6 6 26二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上)13.【答案】1 2【解析】因为 2 3 1cos2 1 2sin 1 2,故答案为4 2 12 .14.【答案】 2【解析】∵πf x x x x ,故 f x sinx cosx的最大值 2 .sin cos 2sin4 即答案为 2 .15.【答案】3 5【解析】cosαααα1222cos sin1tan132224ααα15222cos sin1tan12224.故答案为35.16.【答案】7【解析】π,π2,π27π,π636,所以πcos06,由sinπ365,可得cos π465,所以tanπsinπ636π4cos6.则ππ3tan tan1πππ644tan tan71264ππ31tan tan1644,故答案为7.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.【答案】(1)45;(2)725.【解析】(1)17π7π5ππ2πsinπ1cos2π 4x x x x.12434445(2)令πt x,则43cost,54sint,5ππ916722sin2x sin2t sin2t cos2t cos t sin t.4225252518.【答案】(1)43,2425;(2)7.【解析】(1)由sin45,是第四象限角,得2243 cos1sin155,则tan s in4cos3,sin22sin cos243245525.(2)π4tan tan1π43tan74π41tan tan143.19.【答案】(1)2425;(2)2.【解析】(1)因为为锐角,∴sinπ365,∴πππ24 sin22sin cos().36625(2)由已知得sin3sin π4,即ππππsin3sin8888,∴ππππ2sin cos4cos sin,故8888tantanπ8π82.20.【答案】(1)35;(2)3365.【解析】(1)∴πππαα,442cosπ3α,45∴ππππ3 sinαsinαcosα.42445(2)∵5ππ12sinπβsinπβsinβ,∴44413sinπ12β,413又∵πβ0,∴4πππβ,∴442cosπ5β,413又∵sin π3α,45π3α,π,∴44ππα,π,∴42cosπ4α,45∴πππcosαβsinαβsinαβ,244ππππ3541233 sinαcosβcosαsinβ.44445135136521.【答案】(1)32;(2)1358.【解析】(1)π3133f3.32222(2)213f x sin x cos x3sin x sin2x1cos2x22133π 3sin2x cos2x sin2x.22232由π313f sin,得23242sinπ134,因为π,π2,所以π5π4π,363,因此cosπ1534,所以ππππππsin sin sin cos cos sin333333 1115313542428.22.【答案】(1)π;(2)kππ,026,k Z;(3)7π或1211π.12【解析】由题意,πf x2sin2x,3(1)函数f x的最小正周期为Tπ;(2)2ππx k,得3kππx,k Z,所以对称中心是26kππ,026,k Z;(3)由题意,sinπ342,得ππ或432π,所以7π或31211π.12。
2020年高考理科数学一轮复习题型归纳与变式演练《三角恒等变换》

2020年高考理科数学一轮复习题型归纳与变式演练《三角恒等变换》【题型一】:正用公式 【题型二】:逆用公式 【题型三】:变用公式【题型四】:三角函数式的化简与求值 【题型一】:正用公式【例1】.若,则( )(A )(B ) (C ) (D )【答案】D【解析】因为3cos()45πα-=,所以2cos 2()2cos ()144ππαα-=--,即237cos(2)sin 22()12525παα-==⨯-=-,即7sin 225α=-.【点评】例1是对公式的正用. 【变式训练】: 【变式1】已知(,0)2x π∈-,4cos 5x =,则tan 2x = . 【答案】247-. 【变式2】已知tan()24x π+=,则tan tan 2xx= . 【答案】19【变式3】已知tan α和tan β是方程2260x x +-=的两个根,求tan()αβ+的值.【答案】18-3cos()45πα-=sin 2α=7251515-725-【解析】由韦达定理,得1tan tan 2αβ+=-, tan tan 3αβ⋅=-,∴ tan tan 1tan()1tan tan 8αβαβαβ++==--⋅.【变式4】某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.(1)22sin 13cos 17sin13cos17︒+︒-︒︒ (2)22sin 15cos 15sin15cos15︒+︒-︒︒ (3)22sin 18cos 12sin18cos12︒+︒-︒︒ (4)22sin (18)cos 48sin(18)cos 48-︒+︒--︒︒ (5)22sin (25)cos 55sin(25)cos55-︒+︒--︒︒ Ⅰ 试从上述五个式子中选择一个,求出这个常数Ⅱ 根据(Ⅰ)的计算结果,将该同学的发现推广三角恒等式,并证明你的结论.【解析】Ⅰ.选择(2)式计算如下2213sin 15cos 15sin15cos151sin 3024︒+︒-︒︒=-︒=Ⅱ.证明:22sin cos (30)sin cos(30)αααα+︒--︒-22sin (cos30cos sin 30sin )sin (cos30cos sin 30sin )αααααα=+︒+︒-︒+︒2222311sin cos cos sin cos sin 442αααααααα=+++-22333sin cos 444αα=+= 【例2】(设1cos 29βα⎛⎫-=- ⎪⎝⎭,2sin 23αβ⎛⎫-= ⎪⎝⎭,且2παπ<<,02πβ<<,则()cos αβ+= .【思路点拨】注意到()()222αββααβ+=---,将()2βα-,()2αβ-看做一个整体运用公式.【答案】239729-【解析】1cos 029βα⎛⎫-=-< ⎪⎝⎭且2παπ<<,02πβ<<22πβαπ∴<-<sin 2βα⎛⎫∴-==⎪⎝⎭ 2sin 23αβ⎛⎫-= ⎪⎝⎭且2παπ<<,02πβ<<422παπβ∴-<-<cos 23αβ⎛⎫-==⎪⎝⎭ sin sin 222sin cos cos sin 22221222939327αββααββαβααβαβ+⎡⎤⎛⎫⎛⎫⎛⎫=--- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫⎛⎫=----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫=--⋅= ⎪⎝⎭()2222239cos 12sin12227729αβαβ+⎛⎫+=-=-⨯=- ⎪⎝⎭【点评】1、给出某些角的三角函数式的值,求另外一些角的三角函数值,解题关键在于“变角”,例2中应用了()()222αββααβ+=---的变换 ,体现了灵活解决问题的能力,应着重体会,常见的变换技巧还有2()()ααβαβ=++-,(),βαβα=+-,1[()()]2ααβαβ=++-,2()()βαβαβ=+--,()424πππαα+=--等. 2、已知某一个(或两个)角的三角函数值,求另一个相关角的三角函数值,基本的解题策略是从“角的关系式”入手切入或突破.角的关系主要有互余(或互补)关系,和差(为特殊角)关系,倍半关系等.对于比较复杂的问题,则需要两种关系的混合运用. 【变式训练】:【变式1】已知3sin 5α=,α是第二象限角,且tan()1αβ+=,求tan 2β的值. 【答案】724-【解析】由3sin 5α=且α是第二象限角,得3tan 4α=-, ∵()αβαβ+-=,∴tan()tan tan tan[()]71tan()tan αβαβαβααβα+-=+-==++.22tan 7tan 21tan 24βββ∴==--【变式2】函数)2cos(10)y x x =+-+的最大值为( )A. B .4 C . 2 D .2+ 【答案】C ;【解析】∵7060(10)x x +=++,60cos(10)cos60sin(10)]2cos(10)cos(10)3sin(10)2sin(40)x x x x x x ∴=+++-+=+++=+原式.所以其最大值为2,故选C.【变式3】若1sin 34πα⎛⎫-= ⎪⎝⎭,则cos 23πα⎛⎫+ ⎪⎝⎭等于( )A. 7-8B. 1-4C. 14D. 78【答案】A 【解析】222cos 2cos 2cos 2cos 233331712sin 213168ππππαπαααπα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=--=-+=-+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤⎛⎫=---=⨯-=-⎪⎢⎥⎝⎭⎣⎦故选A.【变式4】已知παπ434<<,40πβ<<,53)4cos(=-απ,135)43sin(=+βπ,求sin()αβ+的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,k 4
Z
.
方法二 g( x)= f ( x)- 3 f x 4
=sin 2 x
- 3 sin 2x
3
23
=sin 2 x
- 3 cos 2x
3
3
=2sin 2x
=2sin2 x,
33
由 2x=2k - ( k∈Z), 得 x=k - ( k∈Z),
2
4
∴g( x) 的最小值为 -2, 相应的 x 的取值集合为 { x | x =k - , k ∈ Z}. 4
2. 设点 P 是函数 f ( x)=29sin
最小正周期是
.
x 的图象 C 的一个对称中心,假设点 P 到图象 C 的对称轴的距离的最小值是
, 那么 f ( x ) 的 8
答案 2
3. y=sin 2x +2sin xcos x+3cos2x 的最小正周期和最小值分不为
.
答案
,2- 2
4. 〔2018·徐州六县一区联考〕 设 sin = 3 ( < < ),tan(
> 0,| | < ) ( x ∈R) 的部分图象如下图 . 2
〔1〕求 f ( x ) 的表达式;
〔2〕设 g( x )= f ( x)- 3 f x
, 求函数 g( x) 的最小值及相应的 x 的取值集合 .
4
解 〔 1〕由图象可知: A=1,
函数 f ( x) 的周期 T 满足: T = - = ,T= , 4 3 12 4
.
5
5
答案 1 2
12. 函数 f 〔x〕=sin x+2|sin x | ,x ∈[ 0,2 ]的图象与直线 y =k 有且仅有两个不同的交点, 那么 k 的取值范畴是
.
答案 1 <k <3
13. 假设 f 〔x〕=asin x
+bsin x
〔 ab≠ 0〕是偶函数,那么有序实数对〔 a,b〕能够是
- )= 1 , 那么 tan( - ) 的值等于
.
52
2
答案 - 2 11
5. 将函数 f ( x)= 3 sin2 x-cos2 x 的图象向右平移 ( > 0) 个单位,所得函数是奇函数,那么实数
的最小值为
.
答案 5 12
a b, ab 0
6. 定义运算 a* b= a
, 那么函数 f ( x)=(sin x)*(cos x ) 的最小值为
2020 届高三数学一轮复习强化训练精品 ――三角函数及三角恒 等变换单元综合测试
一、填空题 〔本大题共 14 小题,每题 5 分,共 70 分〕
1. 定义在 R 上的函数 f 〔x 〕既是偶函数又是周期函数 . 假设 f 〔 x〕的最小正周期是
那么 f 5 的值为
.
3
答案
3
2
,且当 x∈ 0, 时, f 〔 x 〕=sin x, 2
+ )= 33 , 65
∴ < + < ,cos( + )=- 1 sin 2 (
)
2
〔注:只要
=- 1
2
33 =- 56 ,
65
65
∴ sin =sin(
=sin [( + )cos
+ )-cos(
] + )sin
= 33 · 5 -
65
13
56 · 12 = 3 . 65 13 5
16. 〔14 分〕函数 f ( x )= Asin( x+ )( A> 0 P( x , y) 在 y =sin x
2
3
的图象上运动,点 Q在 y=f ( x) 的图象上运动,且满足 OQ =m OP +n( 其中 O 为坐标原点 ) ,那么 y =f ( x ) 的最大值 A 及最
小正周期 T 分不为 .
答案 1 ,4 2
11. 假设 cos( + )= 1 ,cos( - )= 3 , 那么 tan · tan =
∴T= 2 = . ∴ =2. ∴ f 〔 x 〕=sin(2 x+ ).
又 f 〔x 〕图象过点
,1 ,
12
∴f
=sin
12
6
=1, 6
=2k π+ 〔k ∈Z〕 . 2
又| | < , 故 = . ∴ f 〔x 〕=sin 2x
.
2
3
3
〔2〕 方法一 g( x)= f ( x )- 3 f x 4
〔写出你认为正确答案的序号〕 .
15. 〔14 分〕 ∈ 0, , ∈ , 且 sin(
2
2
+ )= 33 ,cos =- 5 . 求 sin .
65
13
解 ∵ ∈ , ,cos =- 5 , ∴sin = 12 .
2
13
13
又∵ 0< < , < < , ∴ < + < 3 ,
22
2
2
又 sin(
17. (2018 ·江苏, 15) 〔14 分〕如图,在平面直角坐标系 xOy 中,以 Ox 轴为始边作两个锐角 ,
,它们的终边分不与单位圆相交于
〔1〕求 tan( + ) 的值; 〔2〕求 +2 的值 .
A, B 两点, A,B 的横坐标分不为 2 , 2 5 .
.
4
4
填满足 a+b=0 的一组数字即可〕
答案 〔1, -1 〕
14. 关于函数 f ( x)=2sin 3x 3 , 有以下命题: 4
①其最小正周期为 2 ; 3
②其图象由 y=2sin3 x 向左平移 3 个单位而得到; 4
③在 , 5 上为单调递增函数,那么其中真命题为 12 12
答案 ①③ 二、解答题 〔本大题共 6 小题,共 90 分〕
.
, ab 0
b
答案 -1
7.cos( + )= 3 ,sin
= 5 , , ∈ 0, ,那么 cos
的值为
.
5
4 13
2
4
答案 56 65
8. 函数 f ( x)= asin x- bcosx ( a、 b 为常数 , a≠ 0,x∈R) 在 x= 处取得最小值,那么函数 4
〝奇〞,〝偶〞,〝非奇非偶〞填空〕
=sin 2 x
- 3 sin 2x
3
23
=sin 2 x
5 - 3 sin 2x
3
6
= 1 sin2 x + 3 cos2 x + 3 sin2 x - 3 cos2 x
2
2
2
2
=2sin2 x,
由 2x=2k - ( k∈Z), 得 x=k - ( k∈Z),
2
4
∴ g( x) 的最小值为 -2 ,相应的 x 的取值集合为 x | x k
答案 奇
y=f 3 4
x是
函数 . 〔用
9. 〔2018·重庆理, 10〕 函数 f 〔 x〕 =
sin x 1
(0 ≤ x≤ 2 〕的值域是
.
3 2cos x 2 sin x
答案 [-1 ,0]
10. 设 a=( a1, a2), b=〔b1, b2〕,定义一种向量积: a
b=〔a1, a2〕
( b1, b2)=( a1b1, a2b2).
