lomb算法matlab程序

龙格库塔方法及其matlab实现

龙格库塔方法及其m a t l a b实现(总6页)本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March龙格-库塔方法及其matlab实现摘要：本文的目的数值求解微分方程精确解，通过龙格-库塔法，加以利用matlab为工具达到求解目的。

龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法，用于数值求解微分方程。

MatLab软件是由美国Mathworks公司推出的用于数值计算和图形处理的科学计算系统环境。

MatLab是英文MATrix LABoratory（矩阵实验室）的缩写。

在MratLab环境下，用户可以集成地进行程序设计、数值计算、图形绘制、输入输出、文件管理等各项操作。

关键词：龙格-库塔 matlab 微分方程1.前言：知识背景龙格－库塔法（Runge-Kutta）是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。

这些技术由数学家卡尔·龙格和马丁·威尔海姆·库塔于1900年左右发明。

通常所说的龙格库塔方法是相对四阶龙格库塔而言的，成为经典四阶龙格库塔法。

该方法具有精度高，收敛，稳定，计算过程中可以改变步长不需要计算高阶导数等优点，但是仍需计算在一些点上的值，比如四阶龙格-库塔法没计算一步需要计算四步，在实际运用中是有一定复杂性的。

Matlab是在20世纪七十年代后期的事：时任美国新墨西哥大学计算机科学系主任的Cleve Moler教授出于减轻学生编程负担的动机，为学生设计了一组调用LINPACK和EISPACK库程序的“通俗易用”的接口，此即用FORTRAN编写的萌芽状态的MATLAB。

经几年的校际流传，在Little的推动下，由Little、Moler、Steve Bangert合作，于1984年成立了MathWorks公司，并把MATLAB正式推向市场。

matlab算法原理

matlab算法原理MATLAB（Matrix Laboratory）是一种使用矩阵和数组进行数值计算、可视化和编程的高级技术计算语言和环境。

早期发展起来主要用于科学和工程领域的数值计算，现在已经广泛应用于各个领域，如信号处理、图像处理、数据分析等。

MATLAB的主要算法原理包括以下几个方面：1. 数值计算与线性代数：MATLAB基于矩阵运算和线性代数的原理进行数值计算。

其提供了丰富的线性代数函数，如求解线性方程组、矩阵分解、矩阵求逆等。

2. 统计与数据分析：MATLAB提供了统计分析和数据处理的相关函数库，包括数据统计描述、概率分布、假设检验、回归分析等。

这些功能可以用于数据预处理、特征提取和模型建立等应用。

3. 信号处理与滤波技术：MATLAB提供了丰富的信号处理函数，包括傅里叶变换、滤波器设计、频谱分析等。

这些函数可以用于音频信号处理、图像处理和通信系统设计。

4. 图像处理与计算机视觉：MATLAB中集成了图像处理工具箱，提供了各种图像处理函数和算法，如滤波、边缘检测、图像分割等。

计算机视觉方面，可以进行图像特征提取、目标识别和图像重建等操作。

5. 优化与求解器：MATLAB提供了强大的优化工具箱，可以解决各类优化问题，包括线性规划、非线性规划、整数规划等。

这些求解器可以用于设备优化、资源调度和控制系统设计等领域。

6. 微分方程与控制系统：MATLAB支持微分方程求解器和控制系统工具箱，可以对各种模型进行仿真和分析。

这在工程控制领域中非常有用，可以进行系统建模、控制设计和系统响应分析等操作。

综上所述，MATLAB是基于数值计算、线性代数和统计分析原理构建的技术计算环境，具有广泛的应用领域。

通过掌握MATLAB的算法原理，可以进行各种数值计算、数据分析和模拟仿真等工作。

matlab中l-m优化算法

matlab中l-m优化算法
L-M（Levenberg-Marquardt）算法是一种非线性最小二乘优化
算法，用于解决非线性最小化问题。

该算法结合了最速下降法和高
斯-牛顿法的优点，能够在搜索过程中动态调整步长，从而更快地收
敛到最优解。

L-M算法的基本思想是通过不断迭代调整参数，使得目标函数
的值不断减小，直至达到局部最优解。

在每一次迭代中，L-M算法
会根据当前的参数估计值计算出目标函数的梯度和海森矩阵，并结
合这些信息调整参数的取值。

通过这种方式，L-M算法能够有效地
处理非线性最小化问题，并且对初始值的选取不敏感。

在MATLAB中，可以使用内置的lsqnonlin函数来实现L-M算法。

该函数可以通过指定目标函数、初始参数估计值等参数来进行非线
性最小化求解。

此外，MATLAB还提供了许多优化工具箱，其中包括
了更多高级的优化算法和工具，可以帮助用户更方便地进行参数估
计和优化问题的求解。

总的来说，L-M算法是一种非常有效的非线性最小化算法，能
够在MATLAB中得到很好的支持和应用。

通过合理使用MATLAB提供
的工具和函数，可以很方便地对复杂的非线性优化问题进行求解。

希望这个回答能够帮助到你。

MATALB数学建模常用技巧总结

MATALB数学建模常用技巧总结MATLAB数学建模常用技巧总结引言在数学建模领域，MATLAB是一种被广泛应用的工具，其强大的计算能力和丰富的函数库使得它成为许多研究者和工程师的首选。

然而，要充分发挥MATLAB的优势并有效解决问题，我们需要掌握一些常用的技巧。

本文将总结一些MATLAB数学建模中常用的技巧，希望能够对读者有所帮助。

一、数据处理与可视化1. 数据导入与导出在数学建模中，数据处理是一个必不可少的过程。

MATLAB提供了丰富的数据导入与导出函数，可以轻松地从各种文件格式中导入数据，并将结果导出到合适的格式。

2. 数据清洗与处理对于实际问题中复杂的数据，我们常常需要对其进行清洗和处理。

MATLAB 提供了一系列强大的函数，如去除异常值、归一化、滤波等，可以帮助我们对数据进行预处理。

3. 数据可视化数据可视化是理解和传达数据的重要方式。

MATLAB的绘图功能非常强大，可以绘制各种类型的图形，如散点图、曲线图、柱状图等。

此外，还可以通过添加标注、调整颜色和线条等来美化图形。

二、数学建模方法1. 数值求解在实际问题中，我们常常需要求解各种数学方程和微分方程。

MATLAB提供了许多数值求解函数，如fsolve、ode45等，可以帮助我们解决这些问题。

2. 构建模型数学建模的关键在于构建恰当的数学模型。

MATLAB提供了丰富的函数和工具，可以帮助我们构建各种复杂的数学模型，如线性回归、非线性优化等。

3. 参数估计与拟合在实际问题中，我们经常需要根据已有数据来估计模型中的未知参数。

MATLAB提供了多种参数估计和拟合函数，如polyfit、lsqcurvefit等，可以帮助我们进行这些计算。

三、优化与最优化1. 单目标优化在数学建模中，我们常常需要优化某个目标函数。

MATLAB提供了多种优化函数，如fminsearch、fminunc等，可以帮助我们找到目标函数的最小值。

2. 多目标优化在某些情况下，我们可能需要优化多个目标函数。

matlab填充算法

matlab填充算法在MATLAB中，有多种方法可以用来填充数组或矩阵。

这里我将介绍一些常用的方法：1. fill函数：这个函数可以用来填充数组。

```matlabA = fill(array, value);```例如，如果你有一个3x3的零矩阵，并希望将所有元素填充为1，你可以这样做：```matlabA = zeros(3,3);A = fill(A, 1);```2. ones, zeros, ones函数：这些函数可以直接生成填充了特定值的矩阵。

例如，`ones(3,3)`将生成一个3x3的矩阵，所有元素都是1。

3. interp1和interp2函数：这两个函数是用于一维和二维插值的。

你可以创建一个函数，然后使用这些函数来填充矩阵。

4. imfill函数：这个函数用于在二值图像中填充特定的区域。

例如，你可以使用它来填充一个二值图像中的孔洞。

5. imread和imwrite函数：这些函数可以用来读取和写入图像文件。

你可以使用这些函数来填充图像数据。

6. im2bw函数：这个函数可以将彩色图像转换为二值图像。

这对于某些类型的图像处理任务可能很有用。

7. floodfill函数：这个函数类似于在图形编辑器中使用的“填充”工具。

你可以使用它来填充二值图像中的连通区域。

8. str2double函数：这个函数可以将字符串转换为双精度浮点数，这对于处理文本数据并将其转换为数值数据可能很有用。

以上就是在MATLAB中进行数组或矩阵填充的一些常用方法。

具体使用哪种方法取决于你的具体需求和数据类型。

布雷格曼方法matlab

布雷格曼方法matlab
标题：《布雷格曼方法在MATLAB 中的应用指南》
布雷格曼方法（Bregman method）是一种广泛应用于优化问题的迭代算法，尤其在信号处理、机器学习等领域具有重要应用。

MATLAB 作为一种功能强大的数学软件，为布雷格曼方法提供了便捷的实现途径。

本文将详细介绍布雷格曼方法的基本原理及其在MATLAB 中的实现过程。

一、布雷格曼方法简介
1.1 布雷格曼方法的起源
1.2 布雷格曼方法的基本原理
1.3 布雷格曼方法的优势与应用领域
二、MATLAB 实现布雷格曼方法的准备工作
2.1 MATLAB 编程环境配置
2.2 安装相关工具箱
2.3 导入数据与初始化参数
三、布雷格曼方法在MATLAB 中的实现步骤
3.1 目标函数的构建
3.2 梯度计算
3.3 迭代更新公式
3.4 收敛条件设置
3.5 布雷格曼方法MATLAB 代码示例
四、应用案例分析
4.1 图像去噪
4.2 信号重构
4.3 机器学习中的优化问题
五、总结与展望
5.1 布雷格曼方法在MATLAB 中的实现效果
5.2 布雷格曼方法的改进方向
5.3 布雷格曼方法在其他领域的应用潜力
附录：MATLAB 代码详细注释
本文旨在为广大读者提供一个关于布雷格曼方法在MATLAB 中应用的全面指南，帮助读者更好地理解并掌握这一优化方法。

在实际应用中，读者可以根据具体问题调整代码参数，实现问题的有效解决。

爬山算法matlab代码

爬山算法matlab代码爬山算法（Hill Climbing Algorithm）是一种简单而有效的优化算法。

它从一个初始解出发，通过不断地沿着当前最优解方向搜索，来达到局部最优解。

在爬山算法中，我们首先需要定义目标函数。

假设我们的目标是最小化一个函数$f(x)$，其中$x$是一个向量或多个变量的值。

1. 算法过程爬山算法的基本过程如下：（1）初始化当前解$x = x_0$，其中$x_0$可以是随机的。

（2）在初始解$x$的邻域中选择一个新的解$x'$。

（3）如果$f(x')$比$f(x)$更优，则将新解作为当前解$x$，重复步骤2和3，直到找到一个局部最优解或达到指定的停止条件。

注意，在爬山算法中，我们只考虑了当前解的邻域。

这意味着，我们可能会陷入局部最优解，而不是全局最优解。

在实际应用中，我们可以多次运行爬山算法，每次使用不同的初始解。

或者，我们可以使用更加复杂的优化算法，如遗传算法（Genetic Algorithm）或模拟退火算法（Simulated Annealing Algorithm），来找到全局最优解。

2. 算法特点（1）简单易懂，容易实现。

（2）只需要存储当前解和邻域解，不需要存储其他信息，因此占用内存较少。

（3）适用于优化问题较简单、目标函数连续可微的情况。

（4）容易陷入局部最优解，无法保证全局最优解。

3. 算法实现```function [x_opt, f_opt] = hill_climbing(f, x0, step_size, max_iter)% f: 目标函数% x0: 初始解% step_size: 邻域大小% max_iter: 最大迭代次数%% 初始化当前解x_curr = x0;f_curr = f(x_curr);%% 迭代寻找最优解for i = 1:max_iter%% 生成邻域解x_new = x_curr + step_size * randn(size(x0)); f_new = f(x_new);%% 判断邻域解是否更优if f_new < f_currx_curr = x_new;f_curr = f_new;endendend```4. 算法应用举例我们可以使用上述Hill Climbing算法来优化该函数。

MATLAB算法

MATLAB算法以下是一些常见的MATLAB算法：1.插值算法：MATLAB提供了多种插值算法，如线性插值、二次插值和三次样条插值等。

这些算法可以用于填充缺失的数据、重建误差数据和生成平滑曲线等。

2.傅立叶变换：MATLAB提供了一系列用于计算傅立叶变换和逆变换的函数，包括快速傅立叶变换（FFT）算法。

傅立叶变换可以将信号从时域转换到频域，用于频谱分析、滤波和信号压缩等应用。

3.矩阵运算：MATLAB的核心功能是矩阵运算。

它提供了各种矩阵运算函数，如矩阵乘法、矩阵求逆、特征值分解和奇异值分解等。

这些算法可以用于解线性方程组、计算矩阵的特征向量和特征值等。

4.优化算法：MATLAB包含了多种优化算法，如梯度下降、共轭梯度、遗传算法和线性规划等。

这些算法可以用于最小化或最大化目标函数，在工程和经济领域有着广泛的应用。

5.数值积分：MATLAB提供了多种数值积分算法，如梯形法则、辛普森法则和龙贝格积分法。

这些算法可以用于计算函数的定积分，求解微分方程和模拟连续系统等。

6.图像处理：MATLAB拥有丰富的图像处理工具箱，包括图像滤波、边缘检测、图像变换和特征提取等。

这些算法可以用于图像增强、图像恢复和图像分析等应用。

7.机器学习算法：MATLAB提供了多种机器学习算法，如支持向量机、神经网络和决策树等。

这些算法可以用于模式识别、数据挖掘和预测分析等应用。

8.信号处理算法：MATLAB提供了多种信号处理算法，如滤波、谱估计和自适应滤波等。

这些算法可以用于音频处理、语音识别和信号压缩等应用。

9.随机数生成：MATLAB提供了多种随机数生成函数，如均匀分布、正态分布和泊松分布等。

这些算法可以用于模拟随机现象、生成随机样本和进行蒙特卡洛分析等。

10.数值解微分方程：MATLAB提供了多种数值解微分方程的算法，如龙格-库塔法、欧拉法和变步长算法等。

这些算法可以用于求解常微分方程和偏微分方程等。

总之，MATLAB是一个功能强大的数值计算软件和编程语言，拥有丰富的算法库和函数，可以帮助科学和工程领域的研究人员解决各种数学问题。

Matlab实现格子玻尔兹曼方法(Lattice Boltzmann Method,LBM)模拟

Matlab实现格子玻尔兹曼方法(Lattice Boltzmann Method,LBM)模拟%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% cylinder.m: Flow around a cyliner, using LBM %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% This program is free software; you can redistribute it and/or% modify it under the terms of the GNU General Public License% as published by the Free Software Foundation; either version 2% of the License, or (at your option) any later version.% This program is distributed in the hope that it will be useful,% but WITHOUT ANY WARRANTY; without even the implied warranty of % MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the % GNU General Public License for more details.% You should have received a copy of the GNU General Public% License along with this program; if not, write to the Free% Software Foundation, Inc., 51 Franklin Street, Fifth Floor,% Boston, MA 02110-1301, USA. %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%clear% GENERAL FLOW CONSTANTSlx = 250;ly = 51;obst_x = lx/5+1; % position of the cylinder; (exactobst_y = ly/2+1; % y-symmetry is avoided)obst_r = ly/10+1; % radius of the cylinderuMax = 0.02; % maximum velocity of Poiseuille inflowRe = 100; % Reynolds numbernu = uMax * 2.*obst_r / Re; % kinematic viscosityomega = 1. / (3*nu+1./2.); % relaxation parametermaxT = 400000; % total number of iterationstPlot = 5; % cycles% D2Q9 LATTICE CONSTANTSt = [4/9, 1/9,1/9,1/9,1/9, 1/36,1/36,1/36,1/36];cx = [ 0, 1, 0, -1, 0, 1, -1, -1, 1];cy = [ 0, 0, 1, 0, -1, 1, 1, -1, -1];opp = [ 1, 4, 5, 2, 3, 8, 9, 6, 7];col = [2:(ly-1)];[y,x] = meshgrid(1:ly,1:lx);obst = (x-obst_x).^2 + (y-obst_y).^2 <= obst_r.^2;obst(:,[1,ly]) = 1;bbRegion = find(obst);% INITIAL CONDITION: (rho=0, u=0) ==> fIn(i) = t(i)fIn = reshape( t' * ones(1,lx*ly), 9, lx, ly);% MAIN LOOP (TIME CYCLES)for cycle = 1:maxT% MACROSCOPIC VARIABLESrho = sum(fIn);ux = reshape ( ...(cx * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho;uy = reshape ( ...(cy * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho;% MACROSCOPIC (DIRICHLET) BOUNDARY CONDITIONS% Inlet: Poiseuille profileL = ly-2; y = col-1.5;ux(:,1,col) = 4 * uMax / (L*L) * (y.*L-y.*y);uy(:,1,col) = 0;rho(:,1,col) = 1 ./ (1-ux(:,1,col)) .* ( ...sum(fIn([1,3,5],1,col)) + ...2*sum(fIn([4,7,8],1,col)) );% Outlet: Zero gradient on rho/uxrho(:,lx,col) = rho(:,lx-1,col);uy(:,lx,col) = 0;ux(:,lx,col) = ux(:,lx-1,col);% COLLISION STEPfor i=1:9cu = 3*(cx(i)*ux+cy(i)*uy);fEq(i,:,:) = rho .* t(i) .* ...( 1 + cu + 1/2*(cu.*cu) ...- 3/2*(ux.^2+uy.^2) );fOut(i,:,:) = fIn(i,:,:) - ...omega .* (fIn(i,:,:)-fEq(i,:,:));end% MICROSCOPIC BOUNDARY CONDITIONSfor i=1:9% Left boundaryfOut(i,1,col) = fEq(i,1,col) + ...18*t(i)*cx(i)*cy(i)* ( fIn(8,1,col) - ...fIn(7,1,col)-fEq(8,1,col)+fEq(7,1,col) );% Right boundaryfOut(i,lx,col) = fEq(i,lx,col) + ...18*t(i)*cx(i)*cy(i)* ( fIn(6,lx,col) - ...fIn(9,lx,col)-fEq(6,lx,col)+fEq(9,lx,col) );% Bounce back regionfOut(i,bbRegion) = fIn(opp(i),bbRegion);end% STREAMING STEPfor i=1:9fIn(i,:,:) = ...circshift(fOut(i,:,:), [0,cx(i),cy(i)]);end% VISUALIZATIONif (mod(cycle,tPlot)==0)u = reshape(sqrt(ux.^2+uy.^2),lx,ly);u(bbRegion) = nan;imagesc(u');axis equal off; drawnowendend。

如何在MATLAB中使用机器学习算法

如何在MATLAB中使用机器学习算法一、介绍MATLAB与机器学习算法MATLAB是一种专业的科学计算软件，被广泛应用于各个领域中的数据分析、模型建立和算法调试等任务。

机器学习算法是近年来兴起的一类基于数据的算法，可以用于从数据中自动发现模式、进行预测和分类等任务。

在这篇文章中，我们将介绍如何在MATLAB中使用机器学习算法。

二、数据预处理在使用机器学习算法之前，首先需要进行数据预处理。

数据预处理包括数据清洗、特征选择、特征缩放等步骤。

MATLAB提供了丰富的函数和工具箱来实现这些预处理任务。

例如，可以使用`readtable`函数读取数据，并使用`table`数据结构存储数据。

然后，可以使用`fillmissing`函数对数据缺失值进行填充。

此外，MATLAB还提供了`featureSelection`和`featureScaling`等函数来进行特征选择和特征缩放。

三、监督学习算法监督学习算法是一类使用带有标签的训练数据来训练模型的算法。

监督学习算法包括线性回归、逻辑回归、支持向量机等。

在MATLAB中，可以使用`fitlm`函数进行线性回归分析。

该函数可以通过最小二乘法拟合线性模型，并给出相应的系数和拟合优度等信息。

此外，还可以使用`fitcsvm`函数实现支持向量机算法，该函数根据输入数据的标签进行分类训练。

四、无监督学习算法无监督学习算法是一类从无标签数据中发现模式的算法，主要包括聚类算法和降维算法。

在MATLAB中，可以使用`kmeans`函数实现k-means聚类算法。

该函数根据数据点之间的距离进行聚类，并给出每个数据点所属的聚类标签。

此外，还可以使用`pca`函数实现主成分分析算法，该函数将数据投影到新的坐标系中，以降低数据的维度。

五、集成学习算法集成学习算法是一种将多个单一模型组合成一个更强大的模型的算法。

常用的集成学习算法包括随机森林和Adaboost算法。

在MATLAB中，可以使用`TreeBagger`函数实现随机森林算法。

optimproblem在matlab中的用法

optimproblem在matlab中的用法OptimProblem在Matlab中的用法OptimProblem是Matlab中用于定义优化问题的一种数据类型。

它允许用户以数学公式的形式定义目标函数和约束条件，在求解优化问题时提供了很大的便利性。

以下是OptimProblem在Matlab中的一些常见用法的详细讲解。

创建优化问题用户可以通过OptimProblem类创建优化问题对象。

以下是创建优化问题的基本步骤： 1. 导入优化工具箱：首先，在Matlab中导入优化工具箱，以便使用OptimProblem类。

2. 定义目标函数：使用Matlab的符号计算功能，创建一个符号函数，表示优化问题的目标函数。

3. 定义约束条件：使用Matlab的符号计算功能，创建一个符号函数组成的向量，表示优化问题的约束条件。

4. 创建优化问题对象：使用OptimProblem类的构造函数，创建一个优化问题对象，并将目标函数和约束条件作为参数传递给构造函数。

设置优化问题的类型在创建优化问题对象后，用户可以通过设置问题的类型来定义问题的性质。

以下是一些常见的问题类型： - 最小化问题：用户可以设置目标函数的类型为最小化，以使得优化求解器能够找到目标函数的最小值。

- 最大化问题：用户可以设置目标函数的类型为最大化，以使得优化求解器能够找到目标函数的最大值。

- 等式约束问题：用户可以将所有约束条件分组为等式约束，以确定优化问题的可行解集。

- 不等式约束问题：用户可以将所有约束条件分组为不等式约束，以确定优化问题的可行解集。

添加变量优化问题通常涉及到一些变量，用户可以使用OptimProblem对象的addVariable方法来添加变量。

以下是一些添加变量的常用方式：- 添加连续变量：用户可以使用addVariable方法，将连续变量添加到优化问题中。

连续变量没有限制条件，可以取任意实数值。

- 添加离散变量：用户可以使用addVariable方法，并指定变量的取值范围和步长来添加离散变量。

matlab中的一些经典算法

matlab中的一些经典算法在MATLAB中，有许多经典算法可以用于各种数学和工程问题。

以下是一些常见的经典算法：1. 最小二乘法（Least Squares Method），用于拟合数据和解决过定系统的线性方程组。

MATLAB中的`polyfit`和`lsqcurvefit`函数可以实现最小二乘拟合。

2. 快速傅里叶变换（Fast Fourier Transform, FFT），用于信号处理和频域分析。

MATLAB中的`fft`函数可以对信号进行快速傅里叶变换。

3. 线性规划（Linear Programming），用于优化问题的求解，例如最大化/最小化线性目标函数的线性约束问题。

MATLAB中的`linprog`函数可以用于线性规划求解。

4. 非线性最小二乘法（Nonlinear Least Squares），用于拟合非线性模型到数据。

MATLAB中的`lsqnonlin`函数可以用于非线性最小二乘拟合。

5. 最优化算法（Optimization Algorithms），MATLAB提供了许多优化算法，包括梯度下降、共轭梯度、拟牛顿等算法，用于解决无约束和约束优化问题。

6. 插值算法（Interpolation），MATLAB中的`interp1`和`interp2`函数可以用于一维和二维数据的插值。

7. 微分方程求解（Differential Equation Solving），MATLAB中的`ode45`和`ode15s`等函数可以用于求解常微分方程和偏微分方程。

8. 图像处理算法（Image Processing Algorithms），MATLAB提供了丰富的图像处理工具箱，包括滤波、边缘检测、图像分割等经典算法。

以上列举的算法只是 MATLAB 中众多经典算法的一小部分，它们在数学建模、信号处理、优化、图像处理等领域有着广泛的应用。

希望这些信息能够帮助到你。

matlab的哥伦布编码

matlab的哥伦布编码一、简介哥伦布编码（Columbus Coding）是一种用于数据压缩的编码技术，它通过对原始数据进行特殊的编码，使得解码后的数据能够以更少的位数存储或传输。

Matlab是一种广泛应用于工程领域的数学软件，它提供了多种用于数据压缩和编码的算法实现。

二、哥伦布编码算法哥伦布编码算法的基本原理是对原始数据进行分组，并对每个分组进行特定的编码操作。

具体来说，算法会将每个分组的前缀和后缀部分进行编码，并将它们组合在一起形成新的数据序列。

这种编码方式能够有效地减少数据的位数，同时保持原始数据的完整性。

在Matlab中实现哥伦布编码算法需要编写相应的代码，该代码包括对原始数据的分组、前缀和后缀的编码以及组合等操作。

以下是一个简单的哥伦布编码算法实现示例：```matlabfunction encoded_data = columbus_coding(original_data)% 确定分组大小group_size = 5;% 将原始数据按分组大小分割成若干个分组groups = split_data(original_data, group_size);% 对每个分组进行编码for i = 1:length(groups)% 计算前缀和后缀的长度prefix_len = ceil(length(groups(i)) / 2);suffix_len = length(groups(i)) - prefix_len;% 对前缀和后缀进行编码prefix = encode_sequence(groups(i, 1:prefix_len));suffix = encode_sequence(groups(i, prefix_len+1:end));% 将前缀和后缀组合成新的数据序列combined = [prefix, suffix];encoded_data{i} = combined;endend```上述代码中，`split_data`函数用于将原始数据按指定的分组大小分割成若干个分组；`encode_sequence`函数用于对数据进行编码；`encoded_data`是一个结构体数组，用于存储每个分组的编码结果。

itlbo算法matlab代码 -回复

itlbo算法matlab代码-回复\[itlbo算法matlab代码\] 关于ITLBO算法及其在MATLAB中的实现引言：近年来，随着计算机技术的飞速发展，算法在数据处理与分析中起着至关重要的作用。

ITLBO算法（Improved Teaching-Learning-Based Optimization），是一种基于教学学习的优化算法，能够有效地解决复杂的优化问题。

本文将介绍ITLBO算法的原理和在MATLAB中的实现过程，帮助读者深入了解该算法的工作原理和应用方法。

第一部分：ITLBO算法的原理ITLBO算法的核心思想是模拟教学与学习的过程，通过学习个体的经验和教学个体的知识来优化问题的解。

该算法组合了教学过程、学习机制和进化机制，能够在搜索空间中高效地寻找全局最优解。

首先，ITLBO算法将群体分为两个子群体：教师个体群和学生个体群。

教师个体群扮演着教导和引导学生的角色，而学生个体群则通过学习和交流来优化解的质量。

其次，教师个体群的移动由以下三个操作决定：1. 随机移动：教师个体群中的个体根据一定的概率进行随机移动，以提升全局搜索的能力；2. 启发学习：教师个体群中的个体通过其他教师个体的经验进行学习，以增加个体解的质量；3. 突变：教师个体群中的个体根据一定的概率进行突变，以增加搜索空间的多样性。

学生个体群的移动由以下两个操作决定：1. 向教师学习：学生个体群中的个体通过选择教师个体群中最优解进行学习，以获得更优的解；2. 竞争：学生个体群中的个体通过竞争选择来更新自身的位置和解。

以上操作使得教师个体群和学生个体群能够共同进化，通过学习和竞争来不断优化问题的解，从而达到全局最优。

第二部分：ITLBO算法在MATLAB中的实现在MATLAB中实现ITLBO算法，需要对算法的核心操作进行编程。

下面，将详细介绍ITLBO算法在MATLAB中的实现步骤：1. 确定问题的目标函数和约束条件，并将其定义成MATLAB函数。

位置pid算法matlab

位置pid算法matlab位置PID算法是一种广泛应用于工业控制领域的反馈控制算法。

通过比较期望位置与实际位置之间的差异，PID控制器可以调整执行机构的动作，以达到精确控制的目的。

MATLAB作为一种强大的数学工具，为PID控制算法的实现提供了便利。

一、PID控制器设计首先，我们需要设计PID控制器。

在MATLAB中，可以使用`pid`函数来实现。

通过设置比例（P）、积分（I）和微分（D）三个参数，我们可以确定PID控制器的行为。

这三个参数需要根据具体的应用场景进行调整，以达到最佳的控制效果。

二、位置反馈系统设计接下来，我们需要设计位置反馈系统。

该系统通过传感器获取实际位置信息，并将其输入到PID控制器中。

在MATLAB中，可以使用`feedback`函数来实现位置反馈系统。

我们需要将期望位置、实际位置和PID控制器的输出作为系统的输入和输出。

三、MATLAB实现在MATLAB中，我们可以按照以下步骤实现位置PID算法：1.导入必要的库和函数；2.定义期望位置、实际位置和PID控制器的输出；3.使用`feedback`函数创建位置反馈系统；4.将期望位置、实际位置和PID控制器的输出作为系统的输入和输出；5.运行系统并获取控制结果。

下面是一个简单的示例代码：```matlab%导入必要的库和函数globalkP,kI,kD;%设置比例、积分、微分参数k=1;%初始比例系数int=0;%积分项初始值D=zeros(1,1);%微分项初始值为零x=feedback(position_sensor,actual_position,k,int,D);%创建反馈系统%模拟期望位置和实际位置的变化target_position=[0.512];%期望位置向量actual_position=[];%实际位置向量，初始为空position_error=target_position-actual_position;%期望位置与实际位置的误差向量control_signal=k*position_error;%PID控制器的输出信号%控制系统的仿真fort=1:length(target_position)actual_position=actual_position+control_signal(t);%更新实际位置向量fprintf('Time:%d,ActualPosition:%f\n',t,actual_position);%输出当前时间及实际位置end```这段代码中，我们首先定义了比例、积分和微分三个参数，并使用`feedback`函数创建了位置反馈系统。

matlab中模糊规则算法编码

MATLAB中模糊规则算法编码一、概述Matlab作为一种广泛使用的科学计算软件，提供了丰富的工具箱和函数，其中包括模糊逻辑工具箱，可以方便地对模糊逻辑系统进行建模和仿真。

模糊规则算法是模糊逻辑系统中的重要组成部分，本文将介绍在Matlab中如何进行模糊规则算法的编码。

二、模糊逻辑系统概述1. 模糊逻辑系统的基本原理模糊逻辑系统是一种基于模糊集合理论的人工智能技术，它能够处理非精确、模糊性信息，适用于很多实际问题的建模和分析。

模糊逻辑系统由模糊集合、模糊逻辑运算和模糊推理三部分组成，其中模糊规则算法用于描述输入与输出之间的模糊规则。

2. 模糊逻辑系统的应用领域模糊逻辑系统广泛应用于控制系统、模式识别、决策支持系统等领域，例如汽车制动系统、空调控制系统、图像处理等。

三、Matlab中模糊逻辑工具箱MATLAB提供了模糊逻辑工具箱（Fuzzy Logic Toolbox），能够方便地进行模糊系统的建模和仿真。

通过该工具箱，用户可以创建模糊逻辑系统、定义输入输出变量、设计模糊规则等。

四、模糊规则算法编码步骤1. 定义输入输出变量在Matlab中，首先需要定义模糊逻辑系统的输入和输出变量，可以使用fuzzy工具创建模糊逻辑变量，并为其指定隶属函数。

2. 创建模糊逻辑系统通过fuzzy工具创建一个模糊逻辑系统，包括输入、输出变量以及它们之间的模糊规则。

用户可以指定模糊规则的数量和类型，例如模糊if-then规则。

3. 设置模糊规则在创建模糊逻辑系统后，需要为系统定义模糊规则，即输入变量和输出变量之间的映射关系。

用户可以使用fuzzy规则编辑器来编辑和管理模糊规则。

4. 模糊推理一旦模糊规则设置完成，用户可以进行模糊推理，即根据输入变量的模糊值和定义的模糊规则，计算输出变量的模糊值。

5. 非模糊化需要对输出变量的模糊值进行非模糊化处理，得到具体的输出值。

Matlab提供了多种非模糊化方法，如加权平均法、最大值法等。

itlbo算法matlab代码

itlbo算法matlab代码由于您的问题不明确，针对ITLBO（Improved Teaching Learning Based Optimization）算法的Matlab代码，本回答无法提供1200字以上的完整代码，但可以为您提供一个简单的ITLBO算法的伪代码和示例：伪代码：1. 初始化种群数量N、迭代次数MaxIter、学习率alpha等参数2. 根据问题的要求，生成初始种群Pop3.初始化每个个体的学生属性s和教师属性t4. for i = 1 to MaxIter do5. for j = 1 to N do6. for k = 1 to N do7. if k != j then8. if fitness(Pop[k]) > fitness(Pop[j]) then9.更新个体j的学生属性s和教师属性t10. end if11. end for12. 计算每个个体的适应度值fitness13.对适应度值进行排序14.更新个体的位置15. end for16.输出最优解示例代码：function [x_best, f_best] = ITLBO(N, MaxIter, alpha)low_bound = -10; % 问题的解空间下界up_bound = 10; % 问题的解空间上界Pop = low_bound + (up_bound - low_bound) * rand(N, 1); % 初始化种群s = zeros(N, 1); % 初始化每个个体的学生属性st = zeros(N, 1); % 初始化每个个体的教师属性tfitness = zeros(N, 1); % 初始化每个个体的适应度值for i = 1:MaxIterfor j = 1:Nfor k = 1:Nif k ~= jif fitness(k) > fitness(j)s(j) = s(j) + alpha * (Pop(k)-Pop(j)); % 更新学生属性t(j) = t(j) + alpha * (Pop(k)-Pop(j)); % 更新教师属性endendendendfor j = 1:Nfitness(j) = obj_func(Pop(j)); % 计算适应度值end[~, ind] = sort(fitness, 'descend'); % 按降序对适应度值进行排序Pop = Pop(ind); % 根据排序结果更新个体的位置x_best = Pop(1); % 当前迭代最优解f_best = fitness(1); % 当前迭代最优解的适应度值fprintf('Iteration: %d, x_best: %.4f, f_best: %.4f\n', i, x_best, f_best);endendfunction y = obj_func(x)%优化问题的目标函数y=x^2;end在以上示例代码中，ITLBO函数是主函数，它接受三个参数：种群数量N，迭代次数MaxIter，学习率alpha。

itlbo算法matlab代码

itlbo算法matlab代码ITLBO算法（Improved Teaching–Learning-Based Optimization）是一种基于教学学习的优化算法，它模拟了教师和学生之间的互动过程，以解决优化问题。

该算法在matlab中的实现代码如下：% 初始化种群nPop = 50; % 种群大小nVar = 30; % 变量个数VarSize = [1 nVar]; % 变量大小VarMin = -10; % 变量下界VarMax = 10; % 变量上界empty_individual.Position = [];empty_individual.Cost = [];pop = repmat(empty_individual, nPop, 1);for i = 1:nPoppop(i).Position = unifrnd(VarMin, VarMax, VarSize);pop(i).Cost = CostFunction(pop(i).Position);end% 迭代更新for it = 1:nIterations% 排序种群Costs = [pop.Cost];[Costs, SortOrder] = sort(Costs);pop = pop(SortOrder);% 更新教师和学生个体BestSol = pop(1);WorstSol = pop(end);Teacher = BestSol;Student = WorstSol;% 更新学生个体NewSol = empty_individual;NewSol.Position = Student.Position + randn(VarSize) .* abs(Student.Position - 2 * rand(VarSize) .* pop(randi([1 nPop])).Position);NewSol.Position = max(NewSol.Position, VarMin);NewSol.Position = min(NewSol.Position, VarMax);NewSol.Cost = CostFunction(NewSol.Position);% 更新教师个体if NewSol.Cost < Teacher.CostTeacher = NewSol;end% 更新种群for i = 1:nPopif i ~= 1% 选择一个个体作为教师Teacher = pop(randi([1 i]));end% 更新学生个体NewSol = empty_individual;NewSol.Position = pop(i).Position + randn(VarSize) .* abs(Teacher.Position - pop(i).Position);NewSol.Position = max(NewSol.Position, VarMin);NewSol.Position = min(NewSol.Position, VarMax);NewSol.Cost = CostFunction(NewSol.Position);% 更新种群if NewSol.Cost < pop(i).Costpop(i) = NewSol;endendend% 输出结果BestSol = pop(1);以上就是使用matlab实现的ITLBO算法的代码。

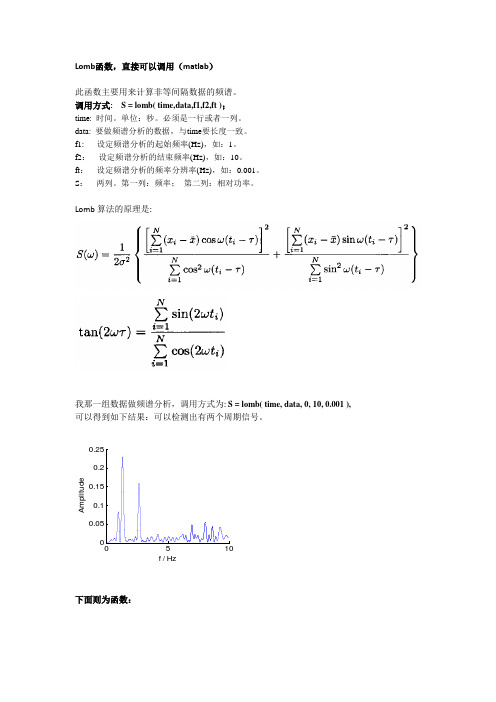
Lomb 函数，直接可以调用（matlab ）此函数主要用来计算非等间隔数据的频谱。

调用方式:S = lomb( time,data,f1,f2,ft )；time: 时间。

单位：秒。

必须是一行或者一列。

data: 要做频谱分析的数据，与time 要长度一致。

f1: 设定频谱分析的起始频率(Hz)，如：1。

f2：设定频谱分析的结束频率(Hz)，如：10。

ft ：设定频谱分析的频率分辨率(Hz)，如：0.001。

S ：两列。

第一列：频率；第二列：相对功率。

Lomb 算法的原理是:我那一组数据做频谱分析，调用方式为: S = lomb( time,data, 0, 10, 0.001 ),可以得到如下结果：可以检测出有两个周期信号。

下面则为函数：05100.050.150.25f / Hz A m p l i t u d efunction S = lomb( time,data,f1,f2,ft )% LOMB Summary% Get frequency spectrum from unequally spaced(in time) data% time: must be in second unit. One row or column.% data: One row or column, must be in the same length of time.% f1: start frequency;% f2: end frequency;% ft: frequency resolution;% S: the first column is frequency; the second column is relative power in frequecy spectrum.time = time - time(1);m = mean(data); % mean valuedata = data -m;j = 1;for f = f1+1e-16:ft:f2 % frequency resolution :ftw = 2*pi*f;% calculate tauk = sum(sin(2*w*time))/sum(cos(2*w*time));tau = atan(k)/(2*w);% get frequency spectrumfen_1 = (sum(data.*cos(w*(time-tau))))^2;mu_1 =sum(cos(w*(time-tau)).^2);fen_2 = (sum(data.*sin(w*(time-tau))))^2;mu_2 =sum(sin(w*(time-tau)).^2);S(j,1) = f;S(j,2) = fen_1/mu_1 + fen_2/mu_2;j = j+1;endend。

蒙特卡洛算法matlab

蒙特卡洛算法matlab蒙特卡洛算法（MonteCarloMethod）是一种随机运行算法，它试图解决复杂问题，通过对有限尝试次数和充分大量的数据随机采样，实现预期的目标。

自上世纪30年代以来，蒙特卡洛方法已经广泛应用在金融、经济学、自然科学和社会科学等领域中。

代表性的应用是软件领域中的机器学习和自动化控制研究；在数据挖掘领域，应用更多的是数据挖掘技术。

蒙特卡洛算法在Matlab中的实现分为两个步骤：第一步是算法的建模，第二步是算法的实施。

在建模过程中，首先需要用户定义解决问题的范围，比如要解决什么类型的问题，背景是什么，以及要使用的算法的参数。

建模完成后，就可以使用MATLAB进行算法的实施，包括数据处理、模型搭建和结果输出等。

Matlab中的蒙特卡洛算法的运用非常广泛，从传统的模拟研究到复杂的机器学习应用，都可以使用它来实现。

其中，传统模拟研究要通过建立蒙特卡洛模型来模拟不同变量对系统状态的影响；而复杂机器学习应用，可以使用蒙特卡洛算法来实现自然语义分析，包括文本分析、图像分析以及视频分析等。

Matlab中的蒙特卡洛方法帮助了许多研究人员和工程师解决了许多复杂的研究问题，它展示了强大的计算机技术，使得研究变得更加高效。

同时，Matlab中的蒙特卡洛方法也能节省研究时间和成本，因此它被广泛应用于金融研究、经济学研究以及工程设计中。

此外，Matlab中蒙特卡洛方法还可以应用于数学建模、深度学习和计算机视觉等领域，帮助企业加快计算机技术的发展，以提高企业的效率和盈利能力。

总的来说，Matlab中的蒙特卡洛方法。

是一种非常强大的算法，它可以有效地解决复杂的计算问题。

它的应用范围广泛，可用于金融学，经济学，自然科学等领域，可以极大地提高企业的效率和盈利能力。

因此，在计算机技术日趋复杂的当今时代，Matlab作为一个强大的工具，可以最大限度的发挥其优势，将蒙特卡洛方法发挥到极致。