第十四章第一节绝对值不等式
第一节 绝对值不等式

文数
课标版
第一节 绝对值不等式
教材研读
栏目索引
1.绝对值不等式的解法 (1)|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法: (i)|ax+b|≤c⇔① -c≤ax+b≤c . (ii)|ax+b|≥c⇔② ax+b≥c或ax+b≤-c . (2)|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法: 解法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想; 解法二:利用“零点分段法”求解,体现了分类讨论的思想; 解法三:通过构造函数,利用函数的图象求解,体现了函数与不等式相结 合的思想.
.
栏目索引
.
考点突破
考点一 绝对值不等式的解法 典例1 已知函数f(x)=|x+a|+|x-2|. (1)当a=-3时,求不等式f(x)≥3的解集; (2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
2x 5, x 2,
解析 (1)当a=-3时, f(x)=1,2 x 3,
栏目索引
2.不等式|2x-a|<b的解集为{x|-1<x<4},则a+b的值为 ( )
A.-2 B.2 C.8 D.-8
答案 C ∵|2x-a|<b的解集为{x|-1<x<4},
∴b>0,
由|2x-a|<b,得
-b<2x-a<b,即 a b <x< a b .
2
2
∴ a b =4,
2
∴a+b=8,故选C.
第一节 绝对值不等式

故原不等式的解集为 {x|x< 1 ∪ } {x| 1 ≤x< 4 ∪ } ∅
={x|x< 4 . }
突 破 点 一 突 破 点 二 课时达标检测
绝对值不等式
结
束
2. 解 不 等 式 x+|2x+3|≥2.
3 3 x<- , x≥- , 2 2 为 解:原 不 等 式 可 化 或 -x-3≥2 3x+3≥2 . 1 解得 x≤-5 或 x≥-3. 所以原不等式的
绝对值不等式
结
束
选修 4-5 不等式选讲
第一节 绝对不等 式
本节主要包2 括 个知识点: 1.绝 对 值 不 等 式 的 解 法 ; 2.绝 对 值 三 角 不 等 . 式
突
破
点
一
突
破
点
二
课时达标检测
绝对值不等式
结
束
突破点(一)
基础联通
绝对值不等式的解法
抓 主 干 知 识“ 的 源” 与“ 流”
突
破
点
一
突
破
点
二
课时达标检测
绝对值不等式
结
束
考点贯通
抓 高 考 命 题“ 的 形” 与“ 神”
绝对值不等式的解法
[典例]
解下列不等式:
( 1 )x |+ 2 1- | 2x | -1 | > 0 . x (2) x+ | 3- | |2 x- 1 | < 2+1 .
[解]
2
( 1 法一: ) 原不等式可化为|2x+1 | > x 2- | 1, | 两边平方
突 破 点 一 突 破 点 二 课时达标检测
绝对值不等式
01绝对值不等式(含经典例题+答案)

绝对值不等式一、绝对值三角不等式1.定理1:如果a,b是实数,则|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.2.定理2:如果a,b,c是实数,则|a-c|≤|a-b|+|b-c|,当且仅当(a-b)(b-c)≥0时,等号成立.二、绝对值不等式的解法(1)|a x+b|≤c⇔-c≤a x+b≤c ;(2)|a x+b|≥c⇔a x+b≥c或a x+b≤-c .3.|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法方法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想.方法二:利用“零点分段法”求解,体现了分类讨论的思想;方法三:通过构造函数,利用函数的图像求解,体现了函数与方程的思想.二、绝对值不等式的解法(1)|a x+b|≤c⇔-c≤ax+b≤c ;(2)|a x+b|≥c⇔ax+b≥c或ax+b≤-c .3.|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法方法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想.方法二:利用“零点分段法”求解,体现了分类讨论的思想;方法三:通过构造函数,利用函数的图像求解,体现了函数与方程的思想.1.不等式|a|-|b|≤|a+b|≤|a|+|b|,右侧“=”成立的条件是ab≥0,左侧“=”成立的条件是ab≤0且|a|≥|b|;不等式|a|-|b|≤|a-b|≤|a|+|b|,右侧“=”成立的条件是ab≤0,左侧“=”成立的条件是ab≥0且|a|≥|b|.2.|x-a|+|x-b|≥c表示到数轴上点A(a),B(b)距离之和大于或等于c的所有点,只要在数轴上确定出具有上述特点的点的位置,就可以得出不等式的解.例4:若不等式|x+1|+|x-2|≥a对任意x∈R恒成立,则a的取值范围是________.解:由于|x+1|+|x-2|≥|(x+1)-(x-2)|=3,所以只需a≤3即可.若本题条件变为“∃x∈R使不等式|x+1|+|x-2|<a成立为假命题”,求a的范围.解:由条件知其等价命题为对∀x∈R,|x+1|+|x-2|≥a恒成立,故a≤(|x+1|+|x-2|)min,又|x+1|+|x-2|≥|(x+1)-(x-2)|=3,∴a≤3.例5:不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是________.解:由绝对值的几何意义知:|x-4|+|x+5|≥9,则log3(|x-4|+|x+5|)≥2所以要使不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则需a<2.例6:某地街道呈现东——西,南——北向的网络状,相邻街距都为1,两街道相交的点称为格点.若以相互垂直的两条街道为轴建立直角坐标系,现有下述格点(-2,2),(3,1),(3,4),(-2,3),(4,5),(6,6)为报刊零售点,请确定一个格点(除零售点外)________为发行站,使6个零售点沿街道到发行站之间的路程的和最短.解:设格点(x,y)(其中x,y∈Z)为发行站,使6个零售点沿街道到发行站之间的路程的和最短,即使(|x+2|+|y-2|+(|x-3|+|y-1|)+(|x-3|+|y-4|)+(|x+2|+|y-3|)+(|x-4|+|y-5|)+(|x-6|+|y-6|)=[(|x+2|+|x-6|)+(|x+2|+|x-4|)+2|x-3|]+[|y-1|+|y-2|+|y-3|+|y-4|+|y-5|+|y-6|]取得最小值的格点(x,y)(其中x,y∈Z).注意到[(|x+2|+|x-6|)+(|x+2|+|x-4|) +2|x-3|]≥|(x+2)-(x-6)|+|(x+2)-(x-4)|+0=14,当且仅当x=3取等号;|y-1|+|y-2|+|y-3|+|y-4|+|y-5|+|y-6|=(|y-1|+|y-6|)+(|y-2|+|y-5|+(|y-3|+|y-4|)≥|(y-1)-(y-6)|+|(y-2)-(y-5)|+|(y-3)-(y-4)|=9,当且仅当y=3或y=4时取等号.因此,应确定格点(3,3)或(3,4)为发行站.又所求格点不能是零售点,所以应确定格点(3,3)为发行站.1.对绝对值三角不等式定理|a|-|b|≤|a±b|≤|a|+|b|中等号成立的条件要深刻理解,特别是用此定理求函数的最值时.2.该定理可以强化为:||a|-|b||≤|a±b|≤|a|+|b|,它经常用于证明含绝对值的不等式.3.对于求y=|x-a|+|x-b|或y=|x+a|-|x-b|型的最值问题利用绝对值三角不等式更简洁、方便.例7:设函数f(x)=|x-a|+3x,其中a>0.(1)当a=1时,求不等式f(x)≥3x+2的解集;(2)若不等式f(x)≤0的例9:已知关于x的不等式|2x+1|+|x-3|>2a-32恒成立,求实数a的取值范围.y =⎩⎪⎨⎪⎧ -3x +2,x <-12,x +4,-12≤x <3,3x -2,x ≥3,∴当x =-12时,y =|2x +1|+|x -3|取最小值72,∴72>2a -32,即得a <52. 例10:已知f (x )=1+x 2,a ≠b ,求证:|f (a )-f (b )|<|a -b |.解:∵|f (a )-f (b )|=|1+a 2-1+b 2|=|a 2-b 2|1+a 2+1+b 2=|a -b ||a +b |1+a 2+1+b 2, 又|a +b |≤|a |+|b |=a 2+b 2<1+a 2+1+b 2,∴|a +b |1+a 2+1+b 2<1.∵a ≠b ,∴|a -b |>0.∴|f (a )-f (b )|<|a -b |.例11:已知a ,b ∈R 且a ≠0,求证:|a |2|a |≥|a |2-|b |2. 证明:①若|a |>|b |,则左边=|a +b |·|a -b |2|a |=|a +b |·|a -b ||a +b +a -b |≥|a +b |·|a -b ||a +b |+|a -b |=11|a +b |+1|a -b |. ∵1|a +b |≤1|a |-|b |,1|a -b |≤1|a |-|b |,∴1|a +b |+1|a -b |≤2|a |-|b |.∴左边≥|a |-|b |2=右边,∴原不等式成立. ②若|a|=|b|,则a 2=b 2,左边=0=右边,∴原不等式成立.③若|a|<|b|,则左边>0,右边<0,原不等式显然成立.综上可知原不等式成立.证明:|f(x)-f(a)|=|x 2-x +43-a 2+a -43|=|(x -a)(x +a -1)|=|x -a|·|x +a -1|.∵|x -a|<1, ∴|x|-|a|≤|x -a|<1.∴|x|<|a|+1.∴|f(x)-f(a)|=|x -a|·|x +a -1|<|x +a -1|≤|x|+|a|+1<2(|a|+1). 例13:已知函数f (x )=log 2(|x -1|+|x -5|-a ).(1)当a =2时,求函数f (x )的最小值;(2)当函数f (x )的定义域为R 时,求实数a 的取值范围.解:函数的定义域满足|x -1|+|x -5|-a >0,即|x -1|+|x -5|>a .(1)当a =2时,f (x )=log 2(|x -1|+|x -5|-2),设g (x )=|x -1|+|x -5|,则g (x )=|x -1|+|x -5|=⎩⎪⎨⎪⎧ 2x -6,x ≥5,4,1<x <5,6-2x ,x ≤1,g (x )min =4,f (x )min =log 2(4-2)=1.(2)由(1)知,g (x )=|x -1|+|x -5|的最小值为4,|x -1|+|x -5|-a >0,∴a <4.∴a 的取值范围是(-∞,4). x -4|-|x -2|>1.解:(1)f (x )=⎩⎪⎨⎪⎧ -2, x >4,-2x +6, 2≤x ≤4,2, x <2.则函数y =f (x )的图像如图所示.(2)由函数y =f (x )的图像容易求得不等式|x -4|-|x -2|>1的解集为5,2⎛⎫-∞ ⎪⎝⎭。
绝对值的不等式

绝对值的不等式绝对值的不等式是数学中的一种重要概念,它在日常生活中也有着广泛的应用。
在不等式中,绝对值表示一个数与0的距离,因此它的结果始终为正数。
绝对值的不等式可以用来描述两个数之间的关系,掌握它的原理和应用对于我们做好数学和生活中的问题都非常有帮助。
首先,我们要了解绝对值的符号,用两条竖线括起来,例如|3|表示3的绝对值,也就是3与0的距离,即3。
如果一个数的绝对值大于另一个数的绝对值,那么这个数的大小也一定更大。
然后,要理解绝对值的不等式。
绝对值不等式的一般形式为|a|<b或|a|>b,其中a和b均为实数。
这意味着,如果|a|<b,那么a必须是一个离0足够近的实数,距离0小于b。
如果|a|>b,那么距离0更远,a的值越大或越小,a绝对值的结果越大。
接着,我们来看绝对值的不等式的应用。
在数学中,绝对值的不等式通常可用于解决不等式问题,如|x+2|<5,就可以用对称的形式把不等式拆分成两个绝对值不等式:-(x+2)<5和x+2<5。
这样,我们就可以得到-x<7和x<3两个解,取它们的交集,就得到了最终的解:-7<x<3。
在生活中,绝对值的不等式也有着广泛的应用。
例如,在购买商品时,我们需要对价格进行比较,绝对值的不等式可以帮助我们快速地比较两个价格的大小。
又如,在交通中,车速的不等式就是一种绝对值不等式,我们需要根据车速限制和实际行驶速度来调整车速,以保证自己和他人的安全。
总之,绝对值的不等式是数学中一个非常重要的概念,它在日常生活中也有着广泛的应用。
通过掌握绝对值的符号、原理和应用,我们可以更好地理解和解决数学问题,也可以更好地应对生活中的各种挑战,成为一个更加全面发展的人。
第一节 绝对值不等式--高考状元之路 (4)-高考状元之路

第二节 证明不等式的基本方法预习设计 基础备考知识梳理1.用比较法证明不等式(1)作差比较法:①理论依据:⇔>b a ⇔<b a ; ,⇔=b a②证明步骤:作差→变形→判断符号→得出结论.(2)作商比较法: ①理论依据:⇒>>1,0b a b ⇒><1,0;ba b ②证明步骤:作商一变形一判断与1的大小关系.2.综合法和分析法 一般地,从 出发,逐步寻求使它成立的充分条件,直至最后,把要证明的不等式归结为判定一个 ,这种证明的方法叫做分析法;而从 出发,利用某些不等式性质或定理,经过一系列的推理论证,最终推导出 成立,这种证明的方法叫做综合法.3.反证法的证明步骤第一步,作出与所证不等式相反的 第二步,从条件和假设出发,应用正确的推理方法,推出 ,否定 ,从而证明原不等式成立.4.放缩法在证明不等式时,有时我们要把所证不等式的一边适当地放大(或缩小)以利化简,并使它与不等式的另一边的不等关系更为明显,从而得到欲证不等式成立,这种方法称为放缩法.典题热身1.已知,0=++c b a 求证:.0≤++ca bc ab2.设a ,b ,c 为正实数,求证:.32111333≥+++abc cb a 课堂设计 方法备考题型一 用比较法证明不等式【例1】证明:(1)当R x ∈时,.221234x x x +≥+(2)当+∈R b a ,时,.2)(b a ab b a b a +≥题型二 用综合法证明不等式【例2】已知),,0(+∞∈b a 、且,1=+b a 求证:;8111)1(≥++abb a;21)2(22≥+b a .811)3(22≥+b a 题型三 用分析法证明不等式【例3】 (2011.江苏模拟)已知,0>a 求证:.212122-+≥-+a a a a 题型四 用放缩法证明不等式【例4】已知*,N n ∈求证:++⨯+⨯<+...32212)1(n n ⋅+<+2)1()1(2n n n 随堂反馈1.已知,0,0>>b a 求证:.22b a ba ab +≥+2.已知),,0(+∞∈b a 、且,1=+b a 求证:;225)1()1)(1(22≥+++b b a a ⋅≥++425)1)(1)(2(b b a a3.若1=+b a 求证:.21212+++b a4.求证:*).(2131211N n n n ∈<++++高效作业 技能备考1.(2011.兰州模拟)已知函数),(log )(2m x x f +=且),0(f )6(),2(f f 成等差数列.(1)求)30(f 的值;(2)若a ,b ,c 是两两不相等的正数,且a ,b ,c 成等比数列,试判断)()(c f a f +与)(2b f 的大小关系,并证明你的结论.2.(2010.江苏高考)设a 、b 是非负实数,求证:).(2233b a ab b a +≥+3.(2010.辽宁高考)已知a ,b ,c 均为正数,证明:+++222c b a ,36)111(2≥++cb a 并确定a ,b ,c 为何值时,等号成立.4.已知a ,b ,c 均为正实数,且,1=++ca bc ab 求证:;)1(k c b a >++).(3)2(c b a abc ac b bc a ++≥++ 5.求证:).,2(121312**********∈≥-<++++<+-N n n n nn 6.已知数列}{n a 中,),2(1>=a a a 对一切=>*∈+1,0,n a a N n π⋅-)1(22n n a a (1)求证:2>n a 且;1n n a a <+(2)求证:).2(221-+<+++a n a a a n。
绝对值不等式的解法

定理2
如果a, b, c是实数,那么
|a-c|≤|a-b|+|b-c|
当且仅当(a-b)(b-c)≥0时,等号成立。 证明:根据绝对值三角不等式有 |a-c|=|(a-b)+(b-c)|≤|a-b|+|b-c| 当且仅当(a-b)(b-c)≥0时,等号成立。
例 : 若 x m , y m , 下列不等式中一定成立 的是( B ) A. x - y C . x y 2 B . x y 2 D. x y
C
)
B.1 a 7 C.a 1 D.a 1 6.设m , 0, x a , y b , a m , y m , 2 2 求证 xy ab m
小结:理解和掌握绝对值不等式的两个定理:
|a+b|≤|a|+|b|(a,b∈R,ab≥0时等号成 立) |a-c|≤|a-b|+|b-c|(a,b,c∈R,
分ab>0和ab<0两种情形讨论:
(1)当ab>0时,如下图可得|a+b|=|a|+|b|
x
O
a
b
a+b
a+b
b
a
O
x
(2)当ab<0时,也分为两种情况:如果a>0,b<0, 如下图可得:|a+b|<|a|+|b|
b
a+b
O
a
x
如果a<0, b>0,如下图可得:|a+b|<|a|+|b|
a
O
a+b
3x 4 1 解 : 原不等式等价于下列不 等式组 3x 4 6 5 x 1或x 3 3 x 4 1或 3 x 4 1 即 6 3 x 4 6 10 x 2 3 3 10 5 2 解得 x 或1 x 3 3 3 2 10 5 故原不等式的解集为 , 1, . 3 3 3
第十四节 第一节 第一节 绝对值不等式

3.设函数f(x)=|2x+1|-|x-4|. .设函数 = + - - (1)解不等式f(x)>2; (1)解不等式f(x)>2; 解不等式 (2)求函数 =f(x)的最小值. 求函数y= 的最小值 的最小值. 求函数
解:(1)令y=|2x+1|-|x-4|,则 令 = + - - ,
y= =
6.含有两个或两个以上绝对值的不等式的解法. .含有两个或两个以上绝对值的不等式的解法. (1)零点分段法,通过讨论去掉绝对值符号. 零点分段法,通过讨论去掉绝对值符号. 零点分段法 (2)利用 -a1|±|x-a2|的几何意义求解 利用|x- ± - 的几何意义求解 的几何意义求解. 利用
解下列不等式; 解下列不等式; (1)1<|x-2|≤3; < - ; (2)|2x+5|>7+x; + > + ; (3)|x2-9|≤x+3; + ; (4)|x-1|+|x+2|<5. - + + <
2. 绝对值不等式的解法 绝对值不等式的解法 (1)|ax+b|≤c、|ax+b|≥c(c>0)型不等式的解法: ) 、 ( > )型不等式的解法:
(2)|x-a|+|x-b|≥c、|x-a|+|x-b|≤c(c>0)型不等式的 ) 、 > 型不等式的 解法: 解法:
1.解不等式2|x|+|x-1|<2. . 不等式 + - < . 解析:如图所示,在直角坐标系 解析:如图所示, 中分别作出函数y= - 和 = 中分别作出函数 =|x-1|和y=2 的图象, -2|x|的图象,由此可得两图象交 的图象 点坐标为(1,0)和(- 和- 点坐标为 ),所以 , ,1). .
2.形如|f(x)|<|g(x)|型不等式. .形如 型不等式. < 型不等式 |f(x)|< |f(x)|<|g(x)|⇔[f(x)]2<[g(x)]2. ⇔ [特别警示 使用平方法去绝对值时要特别小心,非常 特别警示] 使用平方法去绝对值时要特别小心, 特别警示 容易出现增解,必须检查变形的同解性,事实上, 容易出现增解,必须检查变形的同解性,事实上,平 方法去绝对值一般只适用于两边恒正(负)的不等式. 方法去绝对值一般只适用于两边恒正 负 的不等式. 的不等式
绝对值不等式的证明

;
https:/// nba录像集锦
txd38tzu
后生,之前是小青丫头一直拖着不答应人家。现在看来,这门亲事已经是成了。兄弟媳妇很中意这门亲事的,小青丫头也很高 兴。”船老大欲言又止:“哦,这个,她们都高兴就好啊!”耿老爹想一想又说“大哥啊,我们走了以后,兄弟媳妇的生活空 间就大了,你一定要多留意着点儿。她以后的日子还长着呢,需要有一个伴儿啊!”船老大爽快地说:“耿兄弟,这个你只管 放心。我说过的,白兄弟的家眷,我会负责一辈子!如果有合适的好人,我一定会帮忙撮合的。只是,看兄弟媳妇那意思,不 想再考虑这个了呢。没有办法,随缘吧。如果有对了缘分的,也许会成吧。我会记着多操心这事的。还有啊,其他方面,我也 会多多关照的!”耿老爹感激地说:“大哥实在的难得的好人啊!那咱们就此道别吧,我们这就去祭奠白兄弟了。”双方诚恳 地拱手道别。船老大再三嘱咐:“你们返家途径这里时,可一定要来看我啊!”耿老爹连声说:“一定,一定!”在长江边儿 上,耿家父子们把所有的祭品全部放江后,耿老爹含泪向江心拱手说:“白兄弟啊,大哥我明儿个一早就要带着你的这三个侄 儿女离开武昌镇继续南下了,今儿个是特地来向兄弟你辞别的!兄弟一家人对我父子们有大恩啊,但大哥我只能帮你们这些了。 白兄弟你说喜欢耿正,但他在老家已经有心上人了啊,是不可能与小青成婚的。不过你放心,小青和东伢子现在已经好了。东 伢子是个很好的后生!你若在天有灵,一定要保佑她们母女平安幸福啊!”耿正也含泪向江心拱手说:“幺爹啊,我没有答应 做您家的女婿,是我实在不能辜负老家的女娃啊!还请您能够谅解!我今儿个把二胡也带来了。我爹说了,今儿个我们父子四 个每人都要给您拉一段儿曲儿呢!您走得太匆忙了,生前我爹、我妹和我弟都没有来得及为您拉一段儿”耿英朝着江心认真地 施了一个标标准准的万福礼,流着眼泪说:“幺爹啊,我们不想离开娘娘和姐姐,但是,我们必须尽快地离开她们了。希望您 保佑她们,尤其是保佑可怜的娘娘,保佑她的后半生能够幸福安康!”耿直也学着爹爹和哥哥的样子向江心内拱拱手,大声说: “幺爹啊,您可一定要保佑娘娘啊!您知道吗?娘娘说,她要永远住在你们一起住过的那间老房子里呢。幺爹啊,我很想念您, 今儿个也要献丑给您拉一段儿曲儿呢,您可不要笑话我拉得不好啊!”接下来,耿家父子们依次端坐在那块耿正第一次拉二胡 送别白百大时曾经坐过的江边石上,表情肃穆地面向江心各拉了一段儿曲子。耿老爹和耿正拉的是优美动听,但拉奏难度较大 的《江河水》,由耿老爹拉了前半部分,耿正拉了后半部分;耿英和耿直各拉了一小段儿节奏简单明快的地方小曲儿那些在江 面上空展翅飞翔的海鸟们寻声而来,在父子
绝对值不等式公式有哪些该如何解

绝对值不等式公式有哪些该如何解
绝对值不等式是数学中一个重要的知识点,同时也是考试中时常出现的考点。
下面是由编辑为大家整理的“绝对值不等式公式有哪些该如何解”,仅供参考,欢迎大家阅读本文。
绝对值不等式公式
||a|−|b||≤|a±b|≤|a|+|b|;
|ab|=|a||b|,|a/b|=|a|/|b|(b≠0);
|a|<|b| 可推出|b|>|a|;
3、∥a|−Ib∥≤la+b|≤la|+lb|当且仅当ab≤0时左边等号成立,ab≥0时右边等号成立;
4、|a−b|≤|a|+|−b|=|a|+|−1|∗|b|=|a|+|b|
怎样解绝对值不等式
解绝对值不等式的基本方法是去掉绝对值符号
1、平方,比如,|x|=3,可化为x^2=9,绝对值符号没有了;
2、讨论,即x≥0时,|x|=x;x<0时,|x|=-x,绝对值符号也没有了,令绝对值中的式子等于0,分出x的段,然后根据每段讨论得出的x值,取交集,综上所述即可。
14绝对值不等式

2011.10
课前检测
求下列不等式的解集
(1) 2x − 6 ≤ 2
解: 2x≤2+6 : 2x≤8 x≤4 ∴原不等式解集为 {x|x≤4}
(2) 5 − 2x >1
解: -2x>1-5 : 2x>1 5 -2x>-4 x<2 ∴原不等式解集为 {x|x<2}
、绝对值
3
−m
−m
O
m
x
x
O
m
作 业
讨论下列含绝对值不等式的解: (1) |x-1|>0 (2) |2x|<0
− 2 −1 O 1
2
3
x
| 3|= 3
|m|表示对应实数m的点到原点的距离
一、绝对值
?
− 2 −1 O 1
2
3
x
|m|表示对应实数m的点到原点的距离
| 2 |= ?
| −2 |= ?
| 0 |= ?
一、绝对值
?
− 2 −1 O 1
2
3
x
|m|表示对应实数m的点到原点的距离
| 2 |= ?
| −2 |= ?
例2. 解不等式|x-4|<9
−9
练习 (3) |x-2|>2 (4) |x+2|<2 (5) |3x|<12 (6) |4x|>4
O
9
x
解:原不等式等价于 -9 < x-4 < 9 -9+4 < x < 9+4 -5 <x<13 ∴ 原不等式的解集为 {x| -5 <x<13}
例3. 解不等式|2x-3|≤1
含绝对值的不等式及其解法

含绝对值的不等式及其解法一.知识要点:1.绝对值不等式的类型及解法(1)b x f a R b a b x f a <<⇔∈<<+)(,()(或a x f b -<<-)((2))()()()()()(x g x f x g x f x g x f -<>⇔>或 (3))()()()()(x g x f x g x g x f <<-⇔<(4)[][]0)()()()()()()()(22<-⋅+⇔<⇔<x g x f x g x f x g x f x g x f(5)含多个绝对值符号的不等式——采用零点分段法来求解。
2.绝对值的几何意义:(1)x ——表示数轴上的动点x 到原点的距离.(2)b x a x -+-——表示数轴上的动点x 到两定点a 与b 的距离之和,且b x a x -+-b a -≥(3)b x a x ---——表示数轴上的动点x 到两定点a 与b 的距离之差,且≤--b a b x a x ---≤b a -3.绝对值的性质(1)b a ab ⋅=,(2))0(≠=b b a b a ,(3)b a b a b a +≤+≤-当且仅当o ab ≥时右“=”成立,0≤ab 左“=”成立。
(4)b a b a b a +≤-≤-当且仅当0≤ab 时右“=”成立, o ab ≥左“=”成立。
练习题:1. 不等式243<-x 的整数解的个数为( )A . 0B . 1C . 2D .大于22. 若两实数y x ,满足0<xy ,那么总有( ) A y x y x -<+ B y x y x ->+ C y x y x -<-D x y y x -<+3. 已知0,<+>b a b a ,那么( )A . b a >B . b a 11>C . b a <D . ba 11< 4. 不等式13-<-x x 的解是( )A . 52<<xB . 36≥xC . 2>xD . 32≤<x5. 已知,b c a <-且,0≠abc 则( )A . c b a +<B . b c a ->C . c b a +<D . c b a ->6. 不等式652>-x x 的解集为( ). A 1{-<x x 或}6>x B . }32{<<x x C . ∅ D . 1{-<x x 或32<<x 或}6>x7. 若1lg lg ≤-b a ,那么( )A . b a 100≤<B . a b 100≤<C . b a 100≤<或a b 100≤<D .b a b 1010≤≤ 8. 函数22--=x x y 的定义域是( )A . ]2,2[-B . ),2[]2,(+∞--∞C . ),1[]1,(+∞--∞D . ),2[+∞9. 使不等式a x x <-+-34有解的条件是( )A . 1>aB . 1101<<aC . 101<aD . 1010<<a 10. )(13)(R x x x f ∈+=,当b x <-1有),,(4)(+∈<-R b a a x f 则b a ,满足( ) A . 3a b ≤ B . 3b a ≤ C . 3a b > D . 3b a ≥ 11. 不等式b a b a +≤+取等号的条件是 , b a b a +≤-取等号的条件 .12. 不等式x x ->+512的解集是13. 如果不等式21<x 和31>x 同时成立,则x 的取值范围是 14. 不等式xx x x ->-11的解是 13.函数xx x y -+=0)21(的定义域是 14.不等式331≤-<x 的解集是 15.解下列不等式:(1)xx 1<(2)321>++-x x16.解不等式:x x +<-1log 2log 4141。
绝对值不等式(绝对值三角不等式与绝对值不等式的解法)知识讲解

3.若变为|x+1|+|x-2|>k恒成立,则k的取值范围是 4.若变为不等式|x-1|+|x-3|<k的解集为空集,则k的 取值范围是
3、已知 0, x a , y b ,
求证 2x 3y 2a 3b 5
绝对值不等式的解法(一)
2x 4, x 1
例1. 解不等式|x-1|+|x+2|≥5
y
2x 6, x 2 y 2, 2 x 1
2x 4, x 1
如图,作出函数的图象,
函数的零点是-3,2.
-2 1
-3
2x
-2
由图象可知,当x 3或x 2时,y 0,
∴原不等式的解集为{x|x≤-3 或 x≥2}.
取值范围是-(------,--2-]
3.解不等式1<|2x+1|<3. 答案:(-2,-1)∪(0,1)
4.解不等式|x+3|+|x-3|>8. 答案: {x|x<-4或x>4}.
5.解不等式:|x-1|>|x-3|. 答案: {x|x>2}.
6.解不等式|5x- 6|<6-x. 答案:(0,2)
思考四:若变为不等式|x-1|+|x+2|<k的解集 为 ,则k的取值范围是 k 3
练习:解不等式│x+1│–│x–2│≥1
x | x 1
作出f (x) │x +1│–│x – 2│的图像, 并思考f (x)的最大和最小值
│x +1│–│x – 2│ k恒成立,k的取值范围是 │x +1│–│x – 2│ k恒成立,k的取值范围是
绝对值不等式

[证明] ∵|x+5y|=|3(x+y)-2(x-y)|,
∴由绝对值不等式的性质,得
|x+5y|=|3(x+y)-2(x-y)|≤|3(x+y)|+|2(x-y)|
=3|x+y|+2|x-y|≤3×16+2×14=1.
即|x+5y|≤1.
返回
[方法技巧] 绝对值不等式证明的 3 种主要方法
(1)利用绝对值的定义去掉绝对值符号,转化为普通不等 式再证明.
(2018·洛阳第一次统考)已知函数 f(x)=13|x-a|(a∈R ).
返回
(1)当 a=2 时,解不等式x-13+f(x)≥1;
(2)设不等式x-13+f(x)≤x 的解集为 M,若13,12⊆M,求实 数 a 的取值范围.
[ 解] (1)当 a=2 时,原不等式可化为|3x-1|+|x-2|≥3.
全国卷5年考情图解
高考对本章考查主要有以下两个方面: (1)绝对值不等式的求解与函数问题的综合,这是高考命题的热点; (2)绝对值不等式中的恒成立问题与不等式的证明相结合.
返回
突破点一 绝对值不等式的解法
1.绝对值不等式的解法
返回
(1)含绝对值不等式|x|<a 与|x|>a 的解法:
不等式
a>0
2.若对于实数 x,y 有|1-x|≤2,|y+1|≤1, 求|2x+3y+1|的最大值.
解:因为|2x+3y+1|=|2(x-1)+3(y+1)| ≤2|x-1|+3|y+1|≤7, 所以|2x+3y+1|的最大值为 7.
研透高考·深化提能
返回
[全析考法]
考法一 证明绝对值不等式
[例 1] 已知 x,y∈R ,且|x+y|≤16,|x-y|≤14, 求证:|x+5y|≤1.
第1节绝对值不等式

-a<x<a x>a或x<-a
②|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法 |ax+b|≤c⇔ -c≤ax+b≤c (c>0), |ax+b|≥c⇔ ax+b≥c或ax+b≤-c (c>0).
3.|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)不等式的解法 (1)零点分段讨论法:利用绝对值号内式子对应方程的根,将数轴分为(-∞, a],(a,b],(b,+∞)(此处设a<b)三个部分,在每个部分上去掉绝对值号分别列 出对应的不等式求解,然后取各个不等式解集的并集. (2)几何法:利用|x-a|+|x-b|>c(c>0)的几何意义:数轴上到点x1=a和x2=b的 距离之和大于c的点的集合. (3)图像法:作出函数y1=|x-a|+|x-b|和y2=c的图像,结合图像求解.
(3)由绝对值不等式定理还可以推得以下几个不等式
①|a1+a2+…+an|≤|a1|+|a2|+…+|an|. ②||a|-|b||≤|a+b|≤|a|+|b|.
③|a|-|b|≤|a-b|≤|a|+|b|.
2.绝对值不等式的解法 (1)形如|ax+b|≥|cx+d|的不等式,可以利用两边平方的方式转化为二次不等 式求解. (2)①绝对值不等式|x|>a与|x|<a的解集
解:(1)因为|2x-3|≤5, 所以-5≤2x-3≤5, 所以-2≤2x≤8, 所以-1≤x≤4, 所以原不等式的解集为{x|-1≤x≤4}.
绝对值不等式1

O -2
2 x
,3 2, 由 图 象 可 知 原 不 等 式解 的集 为
(2) x a x b c和 x a x b c 型不等式的解法
①利用绝对值不等式的几何意义 ②零点分区间法 ③构造函数法
例 1; 解不等式 1 3x 4 6
(2) x a x b c和 x a x b c 型不等式的解法
例5
解不等式 x 1 x 2 5
A1 -3 A -2 B 1 B1 2 x
2, 那么A, B两点的距离是 3, 因此区间 1上的
数都不是原不等式的解 。 将点A向左移动 1个单位 到点A1, 这时有 A1 A A1 B 5; 同理, 将点B向 右移动一个单位到点 B1, 这时也有 B1 A B1 B 5, 从数轴上可以看到点 A1与B1之间的任何点到点 A, B的距离之和都小于 5; 点A1的左边或点B1的右边 的任何点到点 A,, 的距离之和都大于 。 故原不等 式的解集是 , 3 2,
已知 a , b 是实数,试证明: a b ≤ a b (当且仅当 ab ≥ 0 时,等号成立.)
证明:10 .当ab≥0时,
ab | ab |, | a b | (a b )
2
20. 当ab<0时, ab | ab |,
| a b | (a b )2 a 2 2ab b 2 | a |2 2 | ab | | b |2 | a |2 2 | a || b | | b |2 (| a | | b |)2
证明: |2x+3y-2a-3b|=|(2x-2a)+(3y-3b)| =|2(x-a)+3(y-b)|≤|2(x-a)|+|3(y-b)| =2|x-a|+3|y-b|<2ε +3ε=5ε. 所以 |2x+3y-2a-3b|<5ε .
第十四章 第一节 绝对值不等式

(1)利用公式法转化 利用公式法转化 (2)采用零点分段讨论法,也可用绝对值的几何 采用零点分段讨论法, 采用零点分段讨论法 意义去解. 意义去解.
- + - 解:(1)2|x-3|+|x-4|<2, ,
|x-3|+|x-4|<1,∴x∈. - + - , ∈ (2)|x-3|+|x-4|≥(x-3)-(x-4)=1, - + - - - - = , ∴(|x-3|+|x-4|)min=1, - + - , 又已知不等式的解集不是空集,所以a>1. 又已知不等式的解集不是空集,所以
4.已知a∈R,解关于 的不等式 .已知 ∈ ,解关于x的不等式 的不等式|x|>
解:原不等式等价于x> 原不等式等价于 即 恒成立, ∵x2-ax+6a2>0恒成立, + 恒成立 ∴原不等式等价于x-a>0或 原不等式等价于 - 或 (x-a)(x+2a)(x-3a)<0 - + -
或 x<
当a≥0时,原不等式的解集为:{x|x>a,或x<-2a} 时 原不等式的解集为: , - 当a<0时,原不等式的解集为:{x|x>a,或x<3a}. 时 原不等式的解集为: , .
2.定理 :如果 ,b,c是实数,则 定理2:如果a, , 是实数 是实数, 定理 - + - - - |a-c|≤ |a-b|+|b-c|,当且仅当 (a-b)(b-c)≥0 时, - 等号成立. 等号成立
二、绝对值不等式的解法 1.含绝对值的不等式 含绝对值的不等式|x|<a与|x|>a的解集 含绝对值的不等式 与 的解集 不等式 |x|<a |x|>a a>0 -a<x<a x>a或x<-a 或 - a=0 = x≠0 ≠ a<0 R
第十四章 第一节 绝对值不等式
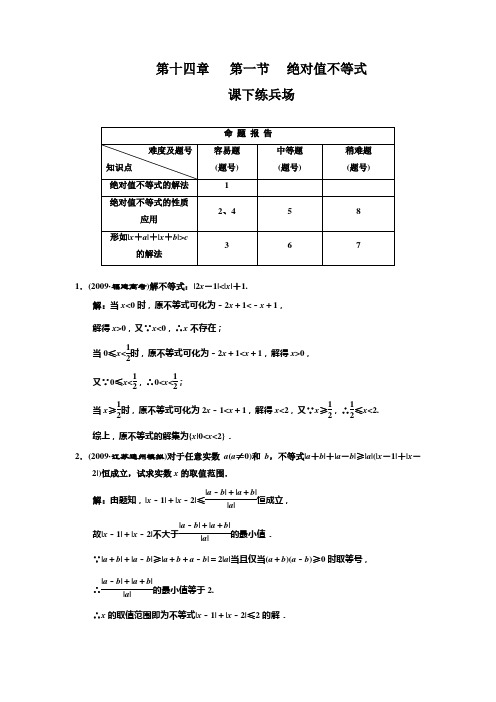
第十四章 第一节 绝对值不等式课下练兵场1.(2009·福建高考)解不等式:|2x -1|<|x |+1.解:当x <0时,原不等式可化为-2x +1<-x +1, 解得x >0,又∵x <0,∴x 不存在;当0≤x <12时,原不等式可化为-2x +1<x +1,解得x >0,又∵0≤x <12,∴0<x <12;当x ≥12时,原不等式可化为2x -1<x +1,解得x <2,又∵x ≥12,∴12≤x <2.综上,原不等式的解集为{x |0<x <2}.2.(2009·江苏通州模拟)对于任意实数a (a ≠0)和b ,不等式|a +b |+|a -b |≥|a |(|x -1|+|x -2|)恒成立,试求实数x 的取值范围. 解:由题知,|x -1|+|x -2|≤|a -b |+|a +b ||a |恒成立,故|x -1|+|x -2|不大于|a -b |+|a +b ||a |的最小值.∵|a +b |+|a -b |≥|a +b +a -b |=2|a |当且仅当(a +b )(a -b )≥0时取等号, ∴|a -b |+|a +b ||a |的最小值等于2.∴x 的取值范围即为不等式|x -1|+|x -2|≤2的解. 解不等式得12≤x ≤52.3.求不等式|x -1|+|2x +1|<2的解集.解:由题意x =1时,|x -1|=0,x =-12时,2x +1=0(以下分类讨论).所以①当x <-12时,原不等式等价于⎩⎪⎨⎪⎧ x <-12,-x +1-2x -1<2,得 -23<x <-12. ②当-12≤x ≤1时,原不等式等价于⎩⎪⎨⎪⎧-12≤x ≤1,-x +1+2x +1<2,得-12≤x <0.③当x >1时,原不等式等价于⎩⎪⎨⎪⎧x >1,x -1+2x +1<2,得x 无解.由①②③得原不等式的解集为{x |-23<x <-12}∪{x |-12≤x <0}∪∅={x |-23<x <0}.4.已知f (x )=1+x 2,a ≠b ,求证:|f (a )-f (b )|<|a -b |.证明:∵|f (a )-f (b )| =|1+a 2-1+b 2| =|a 2-b 2|1+a 2+1+b 2=|a -b ||a +b |1+a 2+1+b 2,又|a +b |≤|a |+|b |=a 2+b 2<1+a 2+1+b 2, ∴|a +b |1+a 2+1+b 2<1.∵a ≠b ,∴|a -b |>0. ∴|f (a )-f (b )|<|a -b |.5.(2009·宁夏、海南高考)如图,O 为数轴的原点,A 、B 、M 为数轴上三点,C 为线段OM 上的动点.设x 表示C 与原点的距离,y 表示C 到A 距离的4倍与C 到B 距离的6倍的和.(1)将y 表示为x 的函数;(2)要使y 的值不超过70,x 应该在什么范围内取值? 解:(1)y =4|x -10|+6|x -20|,0≤x ≤30. (2)依题意,x 满足⎩⎪⎨⎪⎧4|x -10|+6|x -20|≤70, ①0≤x ≤30. 当0≤x <10时,由①得40-4x +120-6x ≤70, 解得x ≥9,即9≤x <10; 当10≤x ≤20时,由①得4x -40+120-6x ≤70, 解得x ≥5, 即10≤x ≤20; 当20<x ≤30时,由①得4x -40+6x -120≤70. 解得x ≤23, 即20<x ≤23. 综上知:x ∈[9,23]. 6.设函数f (x )=|2x +1|-|x -4|.(1)解不等式f (x )>2; (2)求函数y =f (x )的最小值. 解:(1)令y =|2x +1|-|x -4|,则y =⎩⎪⎨⎪⎧-x -5, x ≤-12,3x -3, -12<x <4,x +5, x ≥4.作出函数y =|2x +1|-|x -4|的图象,它与直线y =2的交点为(-7,2)和(53,2).所以|2x +1|-|x -4|>2的解集为 (-∞,-7)∪(53,+∞).(2)由函数y =|2x +1|-|x -4|的图象可知,当x =-12时,y =|2x +1|-|x -4|取得最小值-92. 7.已知函数f (x )=|x -8|-|x -4|.(1)作出函数y =f (x )的图象; (2)解不等式|x -8|-|x -4|>2.解:(1)f (x )=⎩⎪⎨⎪⎧4, x ≤4,-2x +12, 4<x ≤8,-4, x >8.图象如图所示.(2)不等式|x -8|-|x -4|>2,即f (x )>2,由-2x +12=2得x =5.由函数f (x )图象可知,原不等式的解集为(-∞,5). 8.设a ∈R ,函数f (x )=ax 2+x -a (-1≤x ≤1).(1)若|a |≤1,证明|f (x )|≤54;(2)求a 的值,使函数f (x )有最大值178.解:(1)证明:∵|x |≤1,|a |≤1, ∴|f (x )|=|a (x 2-1)+x | ≤|a (x 2-1)|+|x |=|a |·|x 2-1|+|x |≤|x 2-1|+|x | =|1-x 2|+|x |=1-|x |2+|x |=-(|x |-12)2+54≤54.(2)当a =0时,f (x )=x (-1≤x ≤1)的最大值是f (1)=1, 从而a ≠0,故知f (x )是二次函数. ∵f (±1)=±1,∴f (x )=ax 2+x -a (-1≤x ≤1)有最大值178等价于⎩⎪⎨⎪⎧-1<-12a<1,f (-12a )=178,a <0.即⎩⎨⎧a <-12,(a +2)(a +18)=0.∴a =-2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:原不等式等价于x>
或x<
即
∵x2-ax+6a2>0恒成立,
∴原不等式等价于x-a>0或
(x-a)(x+2a)(x-3a)<0
当a≥0时,原不等式的解集为:{x|x>a,或x<-2a}
当a<0时,原不等式的解集为:{x|x>a,或x<3a}.
1.对绝对值三角不等式定理|a|-|b|≤|a±b|≤|a|+|b| 中等号成立的条件要深刻理解,特别是用此定理求函数的 最值时.
当 ab≥0 时,等号成立.
(1)绝对值三角不等式的向量形式及几何意义是什么? (2)不等式|a|-|b|≤|a±b|≤|a|+|b|中“=”成立的条 件分别是什么?
提示:(1)当a,b不共线时,|a+b|<|a|+|b|,它的 几何意义就是三角形的两边之和大于第三边. (2)不等式|a|-|b|≤|a+b|≤|a|+|b|,右侧“=”成立 的条件是ab≥0,左侧“=”成立的条件是ab≤0且 |a|≥|b|;不等式|a|-|b|≤|a-b|≤|a|+|b|,右侧“ =”成立的条件是ab≤0,左侧“=”成立的条件是ab≥0 且|a|≥|b|.
知识点
考纲下载
考情上线
1.理解绝对值的几何意义,并了解下列
不等式成立的几何意义及取等号的 在填空或解答题
条件:
中考查绝对值不
绝对值 (1)|a+b|≤|a|+|b|(a,b∈R).
等式解法与含绝
不等式 (2)|a-b|≤|a-c|+|c-b|(a,b∈R). 对值号的函数的
2.会利用绝对值的几何意义求解以下类 最值,恒成立问
2.该定理可以强化为:||a|-|b||≤|a±b|≤|a|+|b|,它 经常 用于证明含绝对值的不等式.
3.对于y=|x-a|+|x-b|或y=|x+a|-|x-b|型的最值求 法利用该不等式更简洁、方便.
“|x-a|<m,且|y-a|<m”是“|x-y|<2m”(x,y, a,m∈R)的____________________(填充分不必要条件,或 必要不充分条件,或充要条件).
2.解不等式2x+2|x|≥2 解:当x≥0时,有2x+2ห้องสมุดไป่ตู้≥ ∴x≥ 当x<0时,有2x+2-x≥2 , 即(2x)2-2 ·2x+1≥0. 解得2x≤ -1,或2x≥ +1(∵x<0,故舍), ∴x≤log2( -1).∴原不等式解为
3.已知不等式2|x-3|+|x-4|<2a. (1)若a=1,求x的取值范围; (2)若已知不等式解集不是空集,求a的取值范围.
绝对值不等式的常见类型及其解法 1形如|f(x)|<a,|f(x)|>a(a∈R)型不等式
此类不等式的简单解法是等价命题法,即 (1) 当a>0时,|f(x)|<a⇔-a<f(x)<a.
|f(x)|>a⇔f(x)>a或f(x)<-a. (2)当a=0时,|f(x)|<a无解.
|f(x)|>a⇔f(x)≠0. (3)当a<0时,|f(x)|<a无解.
( 2)若已知不等式解集不是空集,求a的取值范围.
解:(1)2|x-3|+|x-4|<2, |x-3|+|x-4|<1,∴x∈∅. (2)|x-3|+|x-4|≥(x-3)-(x-4)=1, ∴(|x-3|+|x-4|)min=1, 又已知不等式的解集不是空集,所以a>1.
4.已知a∈R,解关于x的不等式|x|>
答案:充分不必要条件
1.设f(x)=x2-x+1,实数a满足|x-a|<1,求证: |f(x)-f(a)|<2(|a|+1).
证明:∵f(x)=x2-x+1, ∴|f(x)-f(a)|=|x2-x-a2+a| =|x-a|·|x+a-1|<|x+a-1|, ∵|x+a-1|=|(x-a)+2a-1|≤|x-a|+|2a-1|<1+ |2a|+1=2(|a|+1), ∴|f(x)-f(a)|<2(|a|+1).
型的不等式:|ax+b|≤c,|ax+b|≥c,|x 题.
-c|+|x-b|≥a.
知识点
考纲下载
考情上线
不等式 证明
通过一些简单问题了解 证明不等式的基本方法 :比较法、综合法、分 析法.
考查简单不等式的证 明,多用比较法、综 合法、分析法.
一、绝对值三角不等式 1.定理1:如果a,b是实数,则|a+b|≤ |a|+|b|,当且仅
3.|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式 的解法 方法一:利用绝对值不等式的几何意义求解,体现了数形 结合的思想. 方法二:利用“零点分段法”求解,体现了分类讨论的思想; 方法三:通过构造函数,利用函数的图象求解,体现了函 数与方程的思想.
1.解不等式|x+log2x|<|x|+|log2x|. 解:原不等式成立只需x·log2x<0, 即 ∴解集为{x|0<x<1}.
2.定理2:如果a,b,c是实数,则 |a-c|≤ |a-b|+|b-c|,当且仅当 (a-b)(b-c)≥0 时,
等号成立.
二、绝对值不等式的解法 1.含绝对值的不等式|x|<a与|x|>a的解集
不等式 |x|<a |x|>a
a>0 -a<x<a x>a或x<-a
a=0 a<0
∅
∅
x≠0
R
2.|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法 (1)|ax+b|≤c⇔ -c≤ax+b≤c . (2)|ax+b|≥c⇔ ax+b≥c或ax+b≤-c .
利用绝对值三角不等式,推证 与|x-y|<2m的关系即得答案.
解析:∵|x-y|=|(x-a)-(y-a)|≤|x-a|+|y- a|<m+m=2m, ∴|x-a|<m,且|y-a|<m是|x-y|<2m的充分条件. 取x=3,y=1,a=-2,m=2.5,则有 |x-y|=2<5=2m,但|x-a|=5, 不满足|x-a|<m=2.5, 故|x-a|<m且|y-a|<m不是|x-y|<2m的必要条件.
解:(1)2|x-3|+|x-4|<2, |x-3|+|x-4|<1,∴x∈∅. (2)|x-3|+|x-4|≥(x-3)-(x-4)=1, ∴(|x-3|+|x-4|)min=1, 又已知不等式的解集不是空集,所以a>1.
3.已知不等式2|x-3|+|x-4|<2a.
(1)若a=1,求x的取值范围;
