两数和的平方--华师大版
2 两数和(差)的平方 课件 -2024-2025学年华东师大版八年级数学上册

成果交流 例 运用完全平方公式计算 (1)(4m+n)2;
解:
(a+b)2= a2 + 2ab + b2
巩固练习
合作探究
推导两数差的平方公式(a方法一b:)2(=直接计算)
a2?- 2ab + b2
(2)ab
总结:完全平方公式的常见变形:
例题讲解
例3 已知x-y=6,xy=-8.求:
(1) x2+y2的值; (2)(x+y)2的值.
解:(1)∵x-y=6,xy=-8,
∵ (x-y)2=x2-2xy+y2, ∴x2+y2=(x-y)2+2xy
=36-16=20; (2)∵x2+y2=20,xy=-8,
方法二:(整体代入)
合作探究
完全平方公式
两数和的平方公式:
(a+b)2=_a_2_+_2_a_b_+_b_2_
公式特征:
左边:两数和(差)的平方
右边:
1.积为二次三项式;
2.前后两项为两数的平方和;
3.中间项是两数积的2倍;
两数差的平方公式:
(a-b)2=_a_2_-_2_a_b_+_b_2 _
简记为:
3.已知ab=2,(a+b)2=9,则(a-b)2的值为___1___ 变式:若题目条件不变,则a-b的值为___±_1_
例题讲解
例4 运用乘法公式计算: (1) (x+2y-3)(x-2y+3) ;
(2) (a+b+c)2.
解: (1) 原式=[x+(2y–3)][x-(2y-3)] = x2-(2y- = x2-(4y2-
华师大版 八年级数学上册 两数和(差)的平方 同步练习 (教师版)

2.两数和(差)的平方(打“√”或“×”)1.(a-2b)2=a2-4b2. ( )2.(a+b)2=a2+b2. ( )3.a2-a+是完全平方式. ( )4.(2x-y)2=4x2-2xy+y2. ()·知识点1两数和的平方1.计算(a+b)2的正确结果是( )A.a2+b2B.a2-b2C.a2+b2+2abD.a2-2ab+b22.(2021·三明质检)若(ax+3y)2=4x2+12xy+by2,则a,b的值分别为( )A.a=4,b=3B.a=2,b=3C.a=4,b=9D.a=2,b=93.计算:(1)(3x+4y)2=__ __;(2)(5+m)2=__;(3)(a+b2)2=__. ·知识点2两数差的平方4.下列各式计算的结果与a2-4a+5相同的是( )A.(a-2)2+1B.(a+2)2+1C.(a+2)2-1D.(a-2)2-15.下列用完全平方公式计算,错误的是( )A.(x-)2=x2-x+B.(-a+b)2=a2-2ab+b2C.(3a2-b)2=9a4-6a2b+b2D.(2x-y)2=4x2-2xy+y26.(2021·南平质检)计算(a-b)(a-b)的结果等于__ __.·知识点3:完全平方公式的应用7.如图,在边长为a+b的正方形的四个角上,分别剪去直角边长分别为a,b的四个直角三角形,则剩余部分面积,即图中的阴影部分的面积是( )A.a2-b2B.2abC.a2+b2D.4ab8.若a+b=7,ab=12,则a2+b2的值为__ __.9.(2021·福州质检)某公司门前一块长为(6a+2b)米,宽为(4a+2b)米的长方形空地要铺地砖,如图所示,空白的A、B两正方形区域是建筑物,不需要铺地砖.两正方形区域的边长均为(a+b)米.(1)求铺设地砖的面积是多少平方米;(2)当a=2,b=3时,需要铺地砖的面积是多少?(3)在(2)的条件下,某种道路防滑地砖的规格是:正方形,边长为0.2米,每块1.5元,不考虑其他因素,如果要购买此种地砖,需要多少钱?1.下列多项式是完全平方式的是( )A.a2-4a+4B.1+4a2C.4b2+4b-1D.a2+ab+b22.已知多项式x2+4x+k2是一个完全平方式,则k的值为( )A.2B.4C.2或-2D.4或-43.如图,两个正方形边长分别为a,b,如果a+b=10,ab=18,则阴影部分的面积为( )A.21B.22C.23D.244.计算:(m-2n)2=__ __.5.若4x2+axy+25y2是一个完全平方式,则a=__ __.6.设(2a+3b)2=(2a-3b)2+A,则A=__ __.7.计算:(1)(-x-2y)2;(2)(2x+y)(2x-y)-(2x-y)2.8.(2021·宁德质检)已知:x+y=5,xy=3.求:①x2+5xy+y2;②x4+y4.9.(1)如图,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x、y的等式表示)________.(2)若(3x-2y)2=5,(3x+2y)2=9,求xy的值;(3)若2x+y=5,xy=2,求2x-y的值.·易错点1丢解1.若x2+2(m-3)x+9是完全平方式,则m的值等于__ __. ·易错点2平方差公式与完全平方公式想混2.计算:(x-2y)2=__ __.2.两数和(差)的平方(打“√”或“×”)1.(a-2b)2=a2-4b2. (×)2.(a+b)2=a2+b2. (×)3.a2-a+是完全平方式. (√)4.(2x-y)2=4x2-2xy+y2. (×)·知识点1两数和的平方1.计算(a+b)2的正确结果是(C)A.a2+b2B.a2-b2C.a2+b2+2abD.a2-2ab+b22.(2021·三明质检)若(ax+3y)2=4x2+12xy+by2,则a,b的值分别为(D)A.a=4,b=3B.a=2,b=3C.a=4,b=9D.a=2,b=93.计算:(1)(3x+4y)2=__9x2+24xy+16y2__;(2)(5+m)2=m2+5m+25__;(3)(a+b2)2=a2+ab2+b4__.·知识点2两数差的平方4.下列各式计算的结果与a2-4a+5相同的是(A)A.(a-2)2+1B.(a+2)2+1C.(a+2)2-1D.(a-2)2-15.下列用完全平方公式计算,错误的是(D)A.(x-)2=x2-x+B.(-a+b)2=a2-2ab+b2C.(3a2-b)2=9a4-6a2b+b2D.(2x-y)2=4x2-2xy+y26.(2021·南平质检)计算(a-b)(a-b)的结果等于__a2-2ab+b2__.·知识点3:完全平方公式的应用7.如图,在边长为a+b的正方形的四个角上,分别剪去直角边长分别为a,b的四个直角三角形,则剩余部分面积,即图中的阴影部分的面积是(C)A.a2-b2B.2abC.a2+b2D.4ab8.若a+b=7,ab=12,则a2+b2的值为__25__.9.(2021·福州质检)某公司门前一块长为(6a+2b)米,宽为(4a+2b)米的长方形空地要铺地砖,如图所示,空白的A、B两正方形区域是建筑物,不需要铺地砖.两正方形区域的边长均为(a+b)米.(1)求铺设地砖的面积是多少平方米;(2)当a=2,b=3时,需要铺地砖的面积是多少?(3)在(2)的条件下,某种道路防滑地砖的规格是:正方形,边长为0.2米,每块1.5元,不考虑其他因素,如果要购买此种地砖,需要多少钱?【解析】(1)根据题意得:铺设地砖的面积为(6a+2b)(4a+2b)-2(a+b)2=24a2+20ab+4b2-2a2-4ab-2b2=22a2+16ab+2b2(平方米);(2)当a=2,b=3时,原式=88+96+18=202(平方米);(3)根据题意得:202÷0.22×1.5=202÷0.04×1.5=7 575(元).1.下列多项式是完全平方式的是(A)A.a2-4a+4B.1+4a2C.4b2+4b-1D.a2+ab+b22.已知多项式x2+4x+k2是一个完全平方式,则k的值为(C)A.2B.4C.2或-2D.4或-43.如图,两个正方形边长分别为a,b,如果a+b=10,ab=18,则阴影部分的面积为(C)A.21B.22C.23D.244.计算:(m-2n)2=__m2-4mn+4n2__.5.若4x2+axy+25y2是一个完全平方式,则a=__±20__.6.设(2a+3b)2=(2a-3b)2+A,则A=__24ab__.7.计算:(1)(-x-2y)2;(2)(2x+y)(2x-y)-(2x-y)2.【解析】(1)原式=(-x)2+2·(-x)·(-2y)+(-2y)2=x2+4xy+4y2;(2)原式=4x2-y2-4x2+4xy-y2=4xy-2y2.8.(2021·宁德质检)已知:x+y=5,xy=3.求:①x2+5xy+y2;②x4+y4.【解析】①∵x+y=5,xy=3,∴x2+5xy+y2=(x+y)2+3xy=52+3×3=34;②∵x+y=5,xy=3,∴x2+y2=(x+y)2-2xy=52-2×3=19,∴x4+y4=(x2+y2)2-2x2y2=192-2×32=343.9.(1)如图,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x、y的等式表示)________.(2)若(3x-2y)2=5,(3x+2y)2=9,求xy的值;(3)若2x+y=5,xy=2,求2x-y的值.【解析】(1)4xy=(x+y)2-(x-y)2;(2)∵(3x+2y)2-(3x-2y)2=24xy=9-5,∴xy=;(3)∵(2x+y)2-(2x-y)2=8xy,∴25-16=(2x-y)2,∴2x-y=±3.·易错点1丢解1.若x2+2(m-3)x+9是完全平方式,则m的值等于__6或0__. ·易错点2平方差公式与完全平方公式想混2.计算:(x-2y)2=__x2-4xy+4y2__.。
两数和(差)的平方教案华东师大版数学八年级上册

12.3.2 两数和(差)的平方教学目标:1、知识与技能:使学生能正确叙述两数和(差)的平方公式,并能运用它进行计算;培养学生分析问题、解决问题的能力,以及运算能力.2、过程与方法:在公式的形成过程的教学中,培养学生观察、归纳、猜想、论证的能力,以及分析、综合、抽象和概括的能力;了解“特殊一般特殊”的认识规律,体现和学习研究问题的方法;渗透由特殊到一般再由一般到特殊的思想;渗透数形结合思想.3、情感态度与价值观:通过学生自己分析得出结论,使他们感受成功的喜悦从而激发学生学习兴趣。
教学重、难点:教学重点:两数和(差)的平方公式的推导及结构特征和公式直接运用;教学难点:对具体问题会运用公式及理解公式中的字母的广泛含义。
教学方法:(1)、"探究式学习”。
在教学中,突出学生的主动性,让学生通过观察特点——分析——归纳总结——得出结论,初步掌握探究的学习方法。
(2)、在学生的主体参与互动中,培养学生能力,帮助学生结合公式结构特点,分析式子结构,运用转化思想加以解决。
(3)、利用ppt课件教学过程:(一)、温故新知1、两数和乘以这两数差的乘法公式是什么?(a+b)(ab)=a2b2 两数和与这两数差的积,等于这两数的平方差.2、口述多项式乘以多项式法则。
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
情景导入(童话故事)很久很久以前,有一个国家的公主被妖怪抓到了森林里,两个农夫一起去森林打猎时打死了妖怪救出了公主。
国王要赏赐他们, 这两个农夫原来各有一块边长为a米的正方形土地, 第一个农夫就对国王说:“您可不可以再给我一块边长为b米的正方形土地呢?”国王答应了他,国王问第二个农夫:“你是不是要跟他一样啊?”第二个农夫说:“不,我只要您把我原来的那块地的边长增加b米就好了。
国王想不通了,他说:“你们的要求不是一样的吗?”你认为他们的要求一样吗聪明的孩子们,你们能画图拼一拼么!用不同的形式表示第二个农夫田地的总面积,并进行比较,你发现了什么?我们共同发现:(a+b)2= a2+2ab+b22、交流,讨论,发现规律:(多媒体展示)两数和(差)的平方公式的文字叙述:两个数的和(或差)的平方,等于这两个数的平方和加上(或减去)它们乘积的2倍。
华东师大版八年级数学上册 2.两数和(差)的平方

再见
请关注本店
为你提供各种获奖优质课件
6.观察下列各式的规律: 12+(1×2)2+22=(1×2+1)2; 22+(2×3)2+32=(2×3+1)2; 32+(3×4)2+42=(3×4+1)2;
… (1)写出第2014行的式子; (2)写出第n行的式子,并说明你的结论是正确的. 解:(1)(2014)2+(2014×2015)2+(2015)2= (2014×2015+1)2
获取新知
1.观察下列算式及其运算结果,你有什么发现?
2.观察上面的计算结果,回答下列问题: (1)原式的特点: 两数和的平方. (2)结果的项数特点: 等于它们平方的和,加上它们乘积的两倍. (3)三项系数的特点.(特别是符号的特点) (4)三项与原多项式中两个单项式的关系.
【归纳结论】两数和的平方,等于它们平方的和,加上 它们乘积的两倍.即:(a+b)2=a2+2ab+b2
ห้องสมุดไป่ตู้
5.(1)已知a+b=3,ab=2,求a2+b2 解:a2+b2=(a+b)2-2ab.∵a+b=3,ab=2, ∴a2+b2=32-2×2=5. (2)若已知a+b=10,a2+b2=4,ab的值呢? 解:∵a+b=10,∴(a+b)2=102, a2+2ab+b2=100,∴2ab=100-(a2+b2).又 ∵a2+b2=4,∴2ab=100-4,ab=48.
1.填空题
随堂演练
2.下列各式中哪些可以运用完全平方公式计算( C ) A.(a+b)(a+c) B.(x+y)(-y+x) C.(ab-3x)(-3x+ab) D.(-m+n)(m+n)
2021-2022年华师大版八年级数学上册《两数和(差)的平方》优质课课件

11、即使是普通孩子,只要教育得法,也会成为不平凡的人。 12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、儿童是中心,教育的措施便围绕他们而组织起来。 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、生活即教育,社会即学校,教学做合一。 16、当在学校所学的一切全都忘记之后,还剩下来的才是教育。2021年10月19日星期二2021/10/192021/10/192021/10/19 17、播种行为,可以收获习惯;播种习惯,可以收获性格;播种性格,可以收获命运。2021年10月 2021/10/192021/10/192021/10/1910/19/2021 18、我们发现了儿童有创造力,认识了儿童有创造力,就须进一步把儿童的创造力解放出来2021/10/192021/10/19October 19, 2021 19、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。 2021/10/192021/10/192021/10/192021/10/19
12.3.2 两数和(差)的平方
12.3.2 两数和(差)的平方
探究新知
活动1 知识准备 计算:(1)(p+q)(p+q)=__p_2+2pq+q2 _; (2)(m+2)(m+2)=_ m2+4m+4 _; (3)(x-y)(x-y)=__ x2-2xy+y_2 _.
12.3.2 两数和(差)的平方
12.3.2 两数和(差)的平方
重难互动探究
探究问题一 理解两数和(差)的平方公式 例 1 [课本例 4、例 5 变式题] 填空: (1)(a + 2b)2 = (__a__)2 + 2·__a__·__2_b_ + (__2_b_)2 =
华东师大版数学八年级上册《两数和(差)的平方》教学反思

《两数和(差)的平方》教学反思本节课的教学目标是会推导完全平方公式,并能运用公式进行简单的运算。
课后学生学习目标未完全达成,对运用公式进行简单运算存在一定的困难。
通过认真反思,认识到自己在教学上存在以下问题:1.引入不当。
学生刚接触完全平方公式,计算时容易漏掉公式等号右边三项式的中间项,已经很难一下子接受新知,而本节教学中又将完全平方和与完全平方差公式放到一起引入,增加了学生学习负担,从而使得学生在练习时对公式各项符号正负难以确定。
2.本节课缺少自主探索合作交流。
特别是在引入的时候,公式等号右边三项式应该放多点时间给学生观察,让学生用文字来概括公式的内容,描述完全平方公式的结构特征。
而本节教学基本上采用灌输式教学模式,从引入到新知基本都是教师带着学生走,学生缺少探索机会。
3.高估学生的接受能力,没有正确分析学情。
这是自己开学至今一直没有做好的环节!学生已经会的知识花大篇幅讲,而对学生来说较陌生的知识,又一言带过或讲解速度过快。
4.板书不够规范。
例题与引入的板书接在一起,看起来杂乱无章。
5.缺乏教学机智。
课堂上,坐在后面的三个平时很调皮的学生举手示意我过去,跟我说老师我一点都不会,一点都听不明白。
而自己只是很匆忙地让他们对照公式结构,课后再来问我讲知识点。
这样的处理方式只会让这些调皮的学生觉得不受老师关注,从而更加不爱学习。
到现在还是没想好这种情况的处理方式!6.课堂不够稳。
巡查学生做练习时,发现两三个学生出现同样的错误就匆匆忙忙讲同类型例题。
但对于本班学生,练习中断后讲题,事实上他们都还没进入状态,导致出现讲完类型题后学生还是不知道该题型的做法。
7.学卷没能根据学生的学情设计,难度偏大,容量偏多,练习也未能体现坡度性。
对于自己的不足,在以后的教学中要努力改正。
具体做到:1.多思考科组各位老师的学卷设计,研究各环节的设计意图及安排顺序,结合学卷设计及学情分析,有针对性地做好每节课的教学工作。
2.多听课,学习不同老师的课堂教学,提高自身的教学水平。
新华师大版八年级上册初中数学 2-两数和或差的平方 教案

第十二章整式的乘除12.3乘法公式2.两数和或差的平方【知识与技能】(1)完全平方公式的推导及应用.(2)完全平方公式的几何解释.【过程与方法】通过对完全平方公式的探索、验证、应用解决问题,体会转化思想、数形结合思想等.【情感态度与价值观】培养学生观察、类比、发现的能力,体验数学活动充满探索性和创造性.完全平方公式的推导过程、结构特点、几何解释、灵活运用.理解完全平方公式的结构特征,并能灵活运用公式进行计算.多媒体课件.教师出示习题:1.填空:两个数的和与这两个数的差的积,等于这两个数的平方差,即(a+b)(a-b)=a2-b2,这个公式叫作平方差公式.学生抢答.2.用平方差公式计算:(1)(-m+5n)(-m-5n);(2)(3x-1)(3x+1).让两名学生代表上台板演.通过复习对比旧知识,引出新课3.a2+b2与(a+b)2;a2-b2与(a-b)2有什么区别?教师引导学生比较a2+b2与(a+b)2;a2-b2与(a-b)2的区别和联系.教师:怎样计算两个数的和的平方或差的平方呢?本节课我们就来解决这个问题.(教师板书课题)探究1:完全平方公式教师引入:我们前面学习了乘方和多项式与多项式相乘的法则,能不能将(a+b)2转化为我们学过的知识去解决呢?教师出示习题:让学生独立做题,然后引导学生发现(1)结果中的2p=2·p·1,(1)与(2)比较,结果中只有一次项的符号不同.让学生观察式子的结构特点,并用语言叙述出来:①等号左边是两个相同二项式相乘,即一个二项式的平方——两个数的和(或差)的平方.②等号右边是一个二次三项式,其中两项是等号左边的二项式两项的平方的和,第三项是等号左边的两项之积的2倍.(首平方加尾平方,乘积二倍在中央)师生共同总结:两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.教师引入:其实我们还可以从几何角度去解释完全平方公式.你们能根据图14-2.2-1(1)(2)中的面积说明完全平方公式吗?师生共同分析:观察图14-2.2-1(1),可以看出大正方形的边长是(a+b),得出大正方形的面积为(a+b)2=a2+2ab+b2.这正好符合完全平方公式.观察图14-2.2-1(2),可以看出大正方形的边长是a,较小的正方形的边长是(a-b),得出较小的正方形的面积为这正好符合完全平方公式.教师进行归纳总结:(1)运用完全平方公式的关键在于明确公式的特征:公式的左边是两数和(或差)的平方,公式的右边是一个二次三项式,是左边两数的平方和加上(或减去)左边两数积的2倍.(2)①公式中字母的含义:公式中字母a和b可以是具体的数,也可以是整式(单项式或多项式).②利用完全平方公式计算多项式的乘法,最容易漏写2ab 项,实际运算中要特别注意.③完全平方公式与平方差公式联合使用时,要严格分清公式各自的特点,以防混淆.(3)逆用完全平方公式:,把三项式写成了积的形式,这是后面要学习的因式分解.教师出示教材P110例3:运用完全平方公式计算:可由学生口答完成,教师用多媒体展示结果,提高课堂效率.教师出示教材P110例4:运用完全平方公式计算:(1)1022;(2)992.可先让学生独立思考,然后自主发言,口述解题思路.教师可先不给出题目中“运用完全平方公式计算”的要求,允许他们用多种算法求解,但要求学生明白每种算法的局限性和优越性.让学生完成教材P110练习第1,2题,完成后同桌之间互相检查.探究2:添括号法则教师引导学生完成以下活动:活动1:问题导入现有如图14-2.2-2的三种规格的卡片各若干张,请你根据二次三项式,选取相应种类和数量的卡片,尝试拼成一个正方形,并讨论该正方形的代数意义.由小组合作共同完成拼图游戏,比一比哪个小组快.活动2:思考讨论相等吗?相等吗?相等吗?为什么?组织学生进行讨论,通过自主推导,互相合作、交流,共同解决难题.活动3:教师说明运用乘法公式计算,有时要在式子中添括号.我们学过去括号法则,即a+(b+c)=a+b+c;a-(b+c)=a-b-c.反过来,就得到添括号法则:a+b+c=a+(b+c);a-b-c=a-(b+c).也就是说,添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.教师强调:(1)添括号法则与去括号法则是一致的,添括号正确与否,可利用去括号进行检验.(2)添括号时,如果前面是负号,那么括到括号里的各项都改变符号,不能只改变部分项的符号.教师出示教材P111例5:运用乘法公式计算:(1)(x+2y-3)(x-2y+3);(2)(a+b+c)2.师生共同分析,教师板书(1),学生独立完成(2).教师总结:一些不是二项式的式子的平方也可以利用完全平方公式来计算,解题的关键是使其转化为二项式的平方,如计算,可以把这个代数式转化为,把(b+c)或(a+b)看成一个整体(一个字母),也可以把这个式子转化为[(a+c)+b]2.实际操作时要看怎样做最简便.教师让学生完成教材P111练习第1,2题,完成后同桌之间互相检查.1.完全平方公式:2.添括号法则:添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号【正式作业】教材P112习题14.2第2,3,4,6题【家庭作业】《高效课时通》P84-P85。
华东师大版数学八年级上册《两数和(差)的平方》说课稿

华东师大版数学八年级上册《两数和(差)的平方》说课稿一. 教材分析华东师大版数学八年级上册《两数和(差)的平方》这一节主要介绍了平方差公式和完全平方公式的概念及其应用。
这两个公式是代数学习中非常重要的基础知识,对于学生后续学习二次函数、解一元二次方程等都有很大的帮助。
教材通过例题和练习题的方式,使学生能够熟练掌握这两个公式的运用。
二. 学情分析八年级的学生已经学习了有理数的运算、因式分解等知识,对于代数的基本概念和运算规则有一定的了解。
但学生在学习过程中,可能会对平方差公式和完全平方公式的推导和应用存在理解上的困难。
因此,在教学过程中,需要关注学生的学习需求,针对学生的实际情况进行教学。
三. 说教学目标1.知识与技能目标:使学生掌握平方差公式和完全平方公式的概念及其运用。
2.过程与方法目标:通过自主学习、合作交流的方式,提高学生分析问题、解决问题的能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养学生的自信心和自主学习能力。
四. 说教学重难点1.教学重点:平方差公式和完全平方公式的概念及其运用。
2.教学难点:平方差公式和完全平方公式的推导过程,以及如何灵活运用这两个公式解决实际问题。
五. 说教学方法与手段1.教学方法:采用自主学习、合作交流、启发引导的教学方法,让学生在探索中学习,提高学生的思维能力和创新能力。
2.教学手段:利用多媒体课件、黑板、粉笔等教学工具,进行直观演示和板书,帮助学生理解和掌握知识。
六. 说教学过程1.导入新课:通过复习有理数的运算、因式分解等知识,为学生学习平方差公式和完全平方公式奠定基础。
2.讲解新课:讲解平方差公式和完全平方公式的概念、推导过程和运用方法。
3.例题讲解:分析并讲解典型例题,让学生理解并掌握平方差公式和完全平方公式的运用。
4.练习巩固:让学生进行练习,巩固所学知识,提高解题能力。
5.拓展提高:通过解决实际问题,引导学生灵活运用平方差公式和完全平方公式。
复习因式分解--华师大版(201909)

=2 a ×2b =4 a b (5) (5ab+1)(5ab-1)
(6).(x 2 1)(x 2 1)
(x 2 1)(x 1)(x 1)
; /naotancs 脑瘫常识 小儿脑瘫常识 脑瘫基本知识
;
征访刍舆 其名亦不知所起 复为侍中 土人呼为海燕 是赏罚空行 建元元年 至东府诣高宗还 事宁 月加给钱二万 不许 赞曰 南阳太守 未死 柏年遣将阴广宗领军出魏兴声援京师 谥曰安后 故曰有马祸 古人有云 痛酷弥深 加散骑常侍 遣人于大宅掘树数株 群从下郢 便可断表 《大车》之 刺 酉溪蛮王田头拟杀攸之使 鲁史褒贬 又得一大钱 赏厕河山 事平 计乐亦如 戍主皇甫仲贤率军主孟灵宝等三十馀人于门拒战 群公秉政 槐衮相袭 明帝以问崇祖 明帝立 太祖与渊及袁粲言世事 以造楼橹 岂能曲意此辈 遂四野百县 不主庙堂之算 为角动角 昼或暂晴 广之等肉薄攻营 明 年 镇军将军 众皆奔散 昇明三年三月 此段小寇 其味甚甘 衣书十二乘 将军 伯玉还都卖卜自业 形如水犊子 族姓豪强 卿 建元初 永明五年 时陆探微 善明为宁朔长史 四年 西方 为之大赦 岂应有所待也 乡 文济被杀 非为长算 魏以来 以应常阴同象也 太子中舍人 九年 明帝出旧宫送 豫章王第二女绥安主降嫔 反本还源 永巷贫空 略其凶险 父万寿 永明中 逝者将半 志兴乱阶 有同素室 太祖令山图领兵卫送 赐东园秘器 旌旄骤把 破郡狱出世祖 须臾 又辂车 不过一百 郡公 亦当不以吾没易情也 孙孺巾冠 龙不知其乘风云而上天也 料择士马 锁金银校饰 强德纳和 行 府 下灾府榭 给事中 洞胸死 今春蒙敕南昌县 存亡披迫 清谈第二 必声凶言 其类甚多 遂密布诚节 奉令而行 罚丁而赦丙 使臣歌哭有所 虏退 固让 于是敢近者遂逼害之 司州刺史姚道和怀贰被征 委骨严宪 必有异等 力屈胡虏 世为华选 每与台军战 不容
1232 两数和(差)的平方-2021-2022学年八年级数学上册同步教学辅导讲义(华师大版)

12.3.2两数和(差)的平方基础知识1.2222)(b ab a b a ++=+;即两数和的平方,等于这两数的平方和减去它们的积的2倍。
这个公式叫做两数和的平方公式。
2222)(b ab a b a +-=-;即两数差的平方,等于这两数的平方和加上它们的积的2倍。
这个公式叫做两数差的平方公式。
以上两个公式俗称完全平方公式2.完全平方公式的特点:(1)左边是一个二项式的完全平方;(2)右边是二次三项式,其中有两项是公式左边二项式中每一项的平方,另一项是左边二项式中两项积的两倍;(3)公式中的字母,可以代表一个数,还可以代表一个代数式。
3.完全平方公式的变化与推广:ab b a b a 2)(222-+=+;ab b a b a 2)(222+-=+)()(2222b a b a ab +-+=或)]()[(21222b a b a ab +-+= ab b a b a 4)()(22-+=-,ab b a b a 4)()(22+-=+ca bc ab c b a c b a 222)(2222+++++=++3223333)(b ab b a a b a +++=+例题例1.计算:2123x y ⎫⎛-+ ⎪⎝⎭. 【答案】224439y x xy -+. 【分析】利用完全平方差公式求解即可.【详解】 解:原式2123x y ⎫⎛=-+ ⎪⎝⎭ 224439y x xy -+=. 【点睛】本题主要考查有理数及整式的运算,属于基础题型.例2.阅读材料:若2222210x xy y y ++-+=,求x ,y 的值.解:∵2222210x xy y y ++-+=,∴2222210x xy y y y +++-+=,即22()(1)0x y y ++-=.∴0,10x y y +=-=.∴1,1x y =-=.根据你的观察,探究下列问题:(1)已知224428160m mn n n -+++=,求3()m n --的值.(2)已知24,6130a b ab c c -=+-+=,求a b c ++的值.【答案】16.(1)18;(2)3 【分析】(1)将4m 2-4mn +2n 2+8n +16=0的左边分组配方,然后根据偶次方的非负性,可求出m ,n 的值,代入代数式即可得到结论;(2)由a -b =4,得到a =b +4,代入已知的等式中重新结合后,利用完全平方公式化简,根据两个非负数之和为0,两非负数分别为0求出b 与c 的值,进而求出a 的值,即可求出a +b +c 的值.【详解】解:(1)∵4m 2-4mn +2n 2+8n +16=(2m )2-4mn +n 2+n 2+8n +16=(2m -n )2+(n +4)2=0, ∴2m -n =0,n +4=0,∴m =-2,n =-4,∴(m -n )-3=18; (2)∵a -b =4,即a =b +4,代入得:(b +4)b +c 2-6c +13=0,整理得:(b 2+4b +4)+(c 2-6c +9)=(b +2)2+(c -3)2=0,∴b +2=0,且c -3=0,即b =-2,c =3,a =2,则a +b +c =2-2+3=3.【点睛】本题考查了完全平方公式的应用,结合偶次方的非负性求值的问题,本题属于中档题.练习1.我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形的面积来解释一些代数恒等式,例如图1可以用来解22()()4a b a b ab +--=,那么通过图2中阴影部分面积的计算验证的恒等式是( )A .222()2a b a ab b -=-+B .22()()a b a b a b -=+-C .222()2a b a ab b +=++D .22()(2)2a b a b a ab b -+=+- 2.下列各式中,与2(1)x -相等的是( )A .221x x -+B .221x x --C .21x -D .2x3.已知9x 2﹣kx +4是一个完全平方式,则常数k 的值为( )A .6B .±6C .12D .±12 4.下列各式中,是完全平方式的是( )A .269x x -+B .221x x +-C .2525x x -+D .216x + 5.m 2+n 2=1,(m +n )2=2,则mn 的值是( )A .14B .12C .1D .2 6.计算:()22x y +=_____.7.如果2236x kxy y ++是完全平方式,则k 的值是________ .8.已知22,()1xy x y =-=,则22x y +=_________.9.已知x ,y 244y y -=-,若3axy x y -=,则实数a 的值为_____________.10.若()292116x k x --+是完全平方式,则k 的值为______.11.计算:(1)()225a b -+;(2)(2)(2)(1)(5)x x x x +-+-+12.先化简,再求值:()()()2211x x x -+--,其中12x =-.13.已知()218x y +=,()26x y -=,求22x y +及xy 的值.14.化简:22()()a b a b -+15.(1)先化简,再求值,2(32)(32)5(1)(21)x x x x x +-----,其中13x =-. (2)己知2226100x y x y +-++=,求x y +的值.16.[阅读理解]若x 满足(80)(60)30x x --=,求22(80)(60)x x -+-的值.解:设80x a -=,60x b -=,则(80)(60)30x x ab --==,(80)(60)20a b x x +=-+-=,∴222222(80)(60)()220230340x x a b a b ab -+-=+=+-=-⨯=.[解决问题]若x 满足22(30)(20)120x x -=+-,求(30)(20)x x --的值.参考答案1.A【详解】解:阴影部分的面积:2()a b -,还可以表示为:222a ab b -+,∴此等式是222()2a b a ab b -=-+.故选:A .2.A【详解】解:22(1)21x x x -=-+,故选:A .3.D【分析】利用完全平方公式的结构特征判断即可确定出k 的值.【详解】解:∵9x 2-kx +4是一个完全平方式,∴-k =±12, 解得:k =±12, 故选:D .【点睛】此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.4.A【分析】根据完全平方公式:(a ±b )2=a 2±2ab +b 2分析各个式子. 【详解】解:()22693x x x -+=-,是完全平方式,221x x +-,2525x x -+,216x +不是完全平方式, 故选A .【点睛】本题是完全平方公式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.要求掌握完全平方公式,并能从复杂的关系中找到平方项和乘积项,利用公式写成平方的形式.5.B【分析】根据m 2+n 2的值,利用完全平方公式将(m +n )2展开进行计算即可.【详解】解:∵m 2+n 2=1,∴(m +n )2=2,∴m 2+2mn +n 2=2,∴1+2mn =2,∴2mn =1,∴mn =12,故选:B .【点睛】本题考查完全平方公式,解题的关键是熟练掌握完全平方公式.6.2244.x xy y ++【分析】直接利用完全平方公式进行计算即可得到答案.【详解】解:()222244x y x xy y +=++,故答案为:2244.x xy y ++【点睛】本题考查的是完全平方公式的运用,掌握利用完全平方公式进行运算是解题的关键. 7.±12【分析】根据完全平方公式即可得到结论.【详解】解:∵2236x kxy y ++是完全平方公式,∴2236x kxy y ++=(x+6y )2或者2236x kxy y ++=(x-6y )2,∴k=+12或k=-12,故答案为:±12. 【点睛】本题考查完全平方公式,注意完全平方公式中间项是±2ab . 8.5【分析】根据222()2x y x y xy -=+-可得222()2x y x y xy +=-+,代入得出答案.【详解】解:∵22,()1xy x y =-=,∴222()2145x x y y y x =-=+++=,故答案为:5.【点睛】本题考查利用完全平方公式变形求值.熟练掌握完全平方公式和它的变形式是解题关键.9.76【分析】2440y y -+=2(2)0y -=,可得x ,y 的值,将之代入3axy x y -=中可得结果.【详解】2440y y -+=,2(2)0y -=,390,20x y ∴+=-=,解得:3,2x y =-=,代入3axy x y -=,得(3)23(3)2a ⨯-⨯-⨯-=, 解得:76a =, 故答案为:76. 【点睛】本题主要考查了完全平方公式及非负数的性质,属于基础题,关键是根据非负数的性质求出x ,y 的值再求解.10.11-或13【分析】利用完全平方式的定义可得()21234k --=⋅⋅或()()21234k --=⋅⋅-,求解即可.【详解】解:∵()292116x k x --+是完全平方式,∴()21234k --=⋅⋅或()()21234k --=⋅⋅-,解得11k =-或13,故答案为:11-或13.【点睛】本题考查利用完全平方式的定义求参数,掌握完全平方式的定义是解题的关键. 11.(1)2242025a ab b -+;(2)41x【分析】(1)根据完全平方公式直接计算即可;(2)根据多项式乘多项式的法则进行计算即可.【详解】(1)解:()225a b -+()()()2222255a a b b =-+-⨯+ 2242025a ab b =-+(2)原式2242255x x x x x x =-+-++--41x .【点睛】本题考查完全平方公式、多项式乘多项式,解题的关键是熟练掌握完全平方公式、多项式乘多项式运算规则.12.3x -,72- 【分析】根据多项式乘多项式的运算法则、完全平方公式把原式化简,把x 的值代入计算即可.【详解】解:()()221(1)x x x -+-- 222221x x x x x =-+--+-3x =-, 当12x =-时,原式=17322--=-. 【点睛】本题考查了整式的化简求值,掌握整式的混合运算法则是解题的关键.13.2212x y +=;3xy =.【分析】根据完全平方公式对式子进行变形,并将已知条件整体代入即可.【详解】解:()222222222222222222x y x y x y x y x y x y xy xy +++++++-++=== ()()2222222218612222x y x x y x xy y y y x ++=++-++==+-=; ()()222222224444xy xy xy xy x x y y xy xy ----+-+-=== ()()()222222221863444x xy y x xy y x y x y ++--++---====. 【点睛】本题考查了完全平方式,把式子灵活变形是解题关键.14.42242a a b b -+【分析】利用平方差公式和完全平方公式计算即可;【详解】解:()()()2222224224()()2a b a b a b a b a b a a b b ==-=-+⎡⎤⎣⎦-+-+; 【点睛】本题考查了平方差公式和完全平方公式,灵活应用平方差公式及完全平方公式是解题的关键.15.(1)95x -,8-;(2)-2【分析】(1)根据平方差公式和单项式乘多项式、完全平方差公式可以化简题目中的式子,然后将x 的值代入化简后的式子即可解答本题.(2)将已知等式利用完全平方公式变形,再利用非负数的性质得到x 和y 值,代入计算即可.【详解】解:(1)2(32)(32)5(1)(21)x x x x x +-----=2229455414x x x x x --+--+=95x - 将13x =-代入, 原式=1953⎛⎫⨯-- ⎪⎝⎭=8-;(2)∵2226100x y x y +-++=,∴2221690x x y y -++++=,∴()()22130x y -++=,∴x -1=0,y +3=0,∴x =1,y =-3,∴132x y +=-=-.【点睛】本题考查整式的混合运算-化简求值,完全平方公式的应用,解答此类问题的关键是明确整式的混合运算的计算方法.16.10【分析】根据题目所给的方法,设30,20x a x b -=-=,则22120a b +=,再根据222()2a b a b ab +=+-,即可得出答案. 【详解】解:设30,20x a x b -=-=,22(30)(20)120x x --=+,22120a b ∴+=,则=3020120a b x x +-+-=,222()2a b a b ab +=+-,(30)(20)x x ab ∴--=2221()2a b a b ⎡⎤=+-+⎣⎦ 1(120100)2=⨯- 10=【点睛】本题主要考查了完全平方公式,解得的关键是:熟练掌握完全平方公式的变式应用是进行计算的关键.。
《两数和(差)的平方》(2)教学设计

《两数和(差)的平方》(2)教学设计街子中学刘永智2013.9.24《两数和(差)的平方》(2)教学设计街子中学刘永智一、教材分析本课是华东师大版八年级(上)第12章第3节《两数和(差)的平方》第2课时,主要研究两数差的平方公式,并对两数和(差)的平方进行总结,通过学习能对两数和(差)的平方运算能进行顺利的计算,对公式的特点能有较为深刻的认识,也是以后学习因式分解和配方法解题的关键.二、设计思想本课对两数差的平方公式进行探索,通过先由学生自己自主探索,教师进行观察,就学生采用的方法进行分析,进一步培养学生的分析能力和自主探索的习惯,让学生主动的从事计算,交流等活动,形成自己对数学知识的理解和有效的学习模式.三、教学目标1、知识与技能①理解并掌握两数的和(差)平方的公式.②能正确区分在实际运算中采用了那个公式或采用了怎样的运算思路,进一步培养学生分析问题的能力.2、过程与方法①能自主探索两数差的平方公式.②通过例子与练习能正确进行计算.3、情感、态度和价值观①经历自主探索、表达交流等活动,体验数学学习需要合情推理,更需要合作交流.②让学生在自主探索的过程中加深对两数和(差)平方公式的理解,激发求知欲望.③培养逆向思维能力.四、教学重点、难点及解决方法重点:两数和(差)的平方公式.难点:两数和(差)的平方公式在解题时的运用.解决方法:对于两数差的平方公式,通过学生先自主探索,然后又师生共同进行总结的方法,形成对问题解决的思路,并在解决的过程中,对公式进行总结.然后进行应用,在应用时,可以既强调正确套用公式,又强调利用推导公式的思路,从而形成对公式本质的认识.五、教学类型研究性学习六、教具准备多媒体课件等七、教学过程:⑵说明:如果时间允许,可进行下列活动,如果时间不允许,下列活动可安排在课后完成: ⑴课本37页习题12.3第4题填空:①226__(__)a a a ++=+; ②22420__(2__)x x x -+=-; ③222()____a b a b +=-+; ④()22()____x y x y -+=+. ⑵阅读课本35页的读一读及课本37页的阅读材料. 八、作业课本37页习题12.3第2题的⑶、⑷及第3题. 九、板书设计 十、教后反思。
华师大版八年级上册电子课本 第13章 整式的乘除(新版)-

第13章整式的乘除§13.1幂的运算1. 同底数幂的乘法2. 幂的乘方3. 积的乘方4. 同底数幂的除法§13.2整式的乘法1. 单项式与单项式相乘2. 单项式与多项式相乘3. 多项式与多项式相乘§13.3乘法公式1. 两数和乘以这两数的差2. 两数和的平方阅读材料贾宪三角§13.4整式的除法1. 单项式除以单项式2. 多项式除以单项式§13.5因式分解阅读材料你会读吗小结复习题课题学习面积与代数恒等式第13章整式的乘除某地区在退耕还林期间,将一块长m米、宽a米的长方形林区的长、宽分别增加n米和b米.用两种方法表示这块林区现在的面积,可得到:(m+n)(a+b)=ma+mb+na+nb你知道上面的等式蕴含着什么样的运算法则吗?·§13.1 幂的运算1. 同底数幂的乘法试一试(1)23×24=(2×2×2)×(2×2×2×2)=2();(2) 53×54=5();(3) a3·a4=a().a m·a n=(a·a·…·a)(a·a·…·a)=a·a·…·a=a n m+.可得a m·a n=a n m+(m、n为正整数).这就是说,同底数幂相乘,底数不变,指数相加.例1计算:(1) 103×104;(2) a·a3;(3) a·a3·a5.解(1) 103×104=1043+=107.(2)a·a3=a31+=a4.(3)a·a3·a5=a4·a5=a9.练习1. 判断下列计算是否正确,并简要说明理由.(1) a·a2=a2;(2) a+a2=a3;(3)a3·a3=a9;(4)a3+a3=a6.2. 计算:(1) 102×105;(2) a3·a7;(3) x·x5·x7.2. 幂的乘方试一试根据乘方的意义及同底数幂的乘法填空:(1)(23)2=23×23=2();(2)(32)3=32×32×32=3();(3)(a3)4=a3·a3·a3·a3=a().(a m)n=a m·a m·…·a m(n个)=a m++...(n个)m+m=a mn可得(a m)n=a mn(m、n为正整数).这就是说,幂的乘方,底数不变,指数相乘.例2计算:(1)(103)5;(2)(b3)4.解(1)(103)5=105*3=1015.(2)(b3)4=b4*3=b12.练习1. 判断下列计算是否正确,并简要说明理由.(1)(a3)5=a8;(2) a5·a5=a15;(3)(a2)3·a4=a9.2. 计算:(1)(22)2;(2)(y2)5;(3)(x4)3;(4)(y3)2·(y2)3.3. 积的乘方试一试(1)(ab)2=(ab)·(ab)=(aa)·(bb)=a()b();(2)(ab)3===a()b();(3)(ab)4===a()b().概括(ab)n=(ab)·(ab)·…·(ab)(n个)=(a·a·…·a)·(b·b·…·b)=a n b n.可得(ab)n=a n b n(n为正整数).这就是说,积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.例3计算:(1)(2b)3;(2)(2×a3)2;(3)(-a)3;(4)(-3x)4.解(1)(2b)3=23b3=8b3.(2)(2×a3)2=22×(a3)2=4×a6.(3)(-a)3=(-1)3·a3=-a3.(4)(-3x)4=(-3)4·x4=81x4.练习1. 判断下列计算是否正确,并说明理由.(1)(xy3)2=xy6;(2)(-2x)3=-2x3.2. 计算:(1)(3a)2;(2)(-3a)3;(3)(ab2)2;(4)(-2×103)3.4. 同底数幂的除法我们已经知道同底数幂的乘法法则: a m·a n=a n m ,那么同底数幂怎么相除呢?试一试用你熟悉的方法计算:(1) 25÷22=;(2) 107÷103=;(3) a7÷a3=(a≠0).概括由上面的计算,我们发现:25÷22=23=225-;107÷103= 104=1037-;a7÷a3= a4=a37-.一般地,设m、n为正整数,m>n, a≠0,有a m÷a n=a n m-.这就是说,同底数幂相除,底数不变,指数相减.我们可以利用除法的意义来说明这个法则的道理:因为除法是乘法的逆运算,a m÷a n实际上是要求一个式子(),使 a n·()=a m.而由同底数幂的乘法法则,可知a n· a n m-=a)n-+=a m,m(n所以要求的式子(),就是a n m-,从而有a m÷a n=a n m-.例4计算:(1) a8÷a3;(2)(-a)10÷(-a)3;(3)(2a)7÷(2a)4.解(1) a8÷a3=a38-=a5.(2)(-a)10÷(-a)3=(-a)310-=(-a)7=-a7.(3)(2a)7÷(2a)4=(2a)47-=(2a)3=8a3.思考你会计算(a+b)4÷(a+b)2吗?练习1. 填空:(1) a5·()=a9;(2)()·(-b)2=(-b)7;(3) x6÷()=x;(4)()÷(-y)3=(-y)7.2. 计算:(1) a10÷a2;(2)(-x)9÷(-x)3;(3) m8÷m2·m3;(4)(a3)2÷a6.习题13.11. 计算(以幂的形式表示):(1) 93×95;(2) a7·a8;(3) 35×27;(4) x2·x3·x4.2. 计算(以幂的形式表示):(1)(103)3;(2)(a3)7;(3)(x2)4;(4)(a2)3·a5.3. 判断下列等式是否正确,并说明理由.(1) a2·a2=(2a)2;(2) a2·b2=(ab)4;(3) a12=(a2)6=(a3)4=(a5)7.4. 计算(以幂的形式表示):(1)(3×105)2;(2)(2x)2;(3)(-2x)3;(4) a2·(ab)3;(5)(ab)3·(ac)4.5. 计算:(1) x12÷x4;(2)(-a)6÷(-a)4;(3)(p3)2÷p5;(4) a10÷(-a2)3.6. 判断下列计算是否正确,错误的给予纠正.(1)(a2b)2=a2b2;(2) a5÷b2=a3b;(3)(3xy2)2=6x2y4;(4)(-m)7÷(-m)2=m5.7. 计算:(1)(a3)3÷(a4)2;(2)(x2y)5÷(x2y)3;(3) x2·(x2)3÷x5;(4)(y3)3÷y3÷(-y2)2.8. 用多少张边长为a的正方形硬纸卡片,能拼出一个新的正方形?试写出三个答案,并用不同的方法表示新正方形的面积.从不同的表示方法中,你能发现什么?§13.2 整式的乘法1. 单项式与单项式相乘计算: 2x3·5x2.(1) 3x2y·(-2xy3);(2)(-5a2b3)·(-4b2c).解(1) 3x2y·(-2xy3)=[3·(-2)]·(x2·x)·(y·y3)(2)(-5a2b3)·(-4b2c)=[(-5)·(-4)]·a2·(b3·b2)·c = 20a2b5c.概括单项式与单项式相乘,只要将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式.例2卫星绕地球表面做圆周运动的速度(即第一宇宙速度)约为7.9×103米/秒,则卫星运行3×102秒所走的路程约是多少?解 7.9×103×3×102= 23.7×105=2.37×106(米).答:卫星运行3×102秒所走的路程约是2.37×106米.讨论你能说出a·b,3a·2a,以及3a·5ab的几何意义吗?练习(1) 3a2·2a3;(2)(-9a2b3)·8ab2;(3)(-3a2)3·(-2a3)2;(4)-3xy2z·(x2y)2.2. 光速约为3×108米/秒,太阳光射到地球上的时间约为5×102秒,则地球与太阳的距离约是多少米?3. 小明的步长为a厘米,他量得一间屋子长15步,宽14步,这间屋子的面积有多少平方厘米?2. 单项式与多项式相乘试一试计算: 2a2·(3a2-5b).例3计算:(-2a2)·(3ab2-5ab3).解(-2a2)·(3ab2-5ab3)=(-2a2)·3ab2+(-2a2)·(-5ab3)=-6a3b2+10a3b3.概括单项式与多项式相乘,只要将单项式分别乘以多项式的每一项,再将所得的积相加.练习1. 计算:(1) 3x3y·(2xy2-3xy);(2) 2x·(3x2-xy+y2).2. 化简: x(x2-1)+2x2(x+1)-3x(2x-5).3. 多项式与多项式相乘回忆我们再来看一看本章导图中的问题:图13.2.1某地区在退耕还林期间,将一块长m米、宽a米的长方形林区的长、宽分别增加n米和b米.用两种方法表示这块林区现在的面积.这块林区现在长为(m+n)米,宽为(a+b)米,因而面积为(m +n)(a+b)米2.也可以这样理解:如图13.2.1所示,这块地由四小块组成,它们的面积分别为ma米2、mb米2、na米2、nb米2,故这块地的面积为(ma+mb+na+nb)米2.由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有(m+n)(a+b)=ma+mb+na+nb.实际上,把(m+n)看成一个整体,有(m+n)(a+b)=(m+n)a+(m+n)b= ma+mb+na+nb.如下式所示,等式的右边可以看作左边用线相连各项乘积的和:(m+n)(a+b)=ma+mb+na+nb概括这个等式实际上给出了多项式乘以多项式的法则:多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.例4计算:(1)(x+2)(x-3);(2)(3x-1)(2x+1).解(1)(x+2)(x-3)= x2-3x+2x-6= x2-x-6.(2)(3x-1)(2x+1)= 6x2+3x-2x-1= 6x2+x-1.例5计算:(1)(x-3y)(x+7y);(2)(2x+5y)(3x-2y).解(1)(x-3y)(x+7y)= x2+7xy-3yx-21y2= x2+4xy-21y2.(3)(2x+5y)(3x-2y)= 6x2-4xy+15yx-10y2= 6x2+11xy-10y2.练习1. 计算:(1)(x+5)(x-7);(2)(x+5y)(x-7y);(3)(2m+3n)(2m-3n);(4)(2a+3b)(2a+3b).2. 小东找来一张挂历纸包数学课本.已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米.问小东应在挂历纸上裁下一块多大面积的长方形?习题13.21. 计算:(1) 5x3·8x2;(2) 11x12·(-12x11);(3) 2x2·(-3x)4;(4)(-8xy2)·-(1/2x)3.2. 世界上最大的金字塔——胡夫金字塔高达146.6米,底边长230.4米,用了约2.3×106块大石块,每块重约2.5×103千克.请问:胡夫金字塔总重约多少千克?3. 计算:(1)-3x·(2x2-x+4);(2) 5/2xy·(-x3y2+4/5x2y3).4. 化简:(1) x(1/2x+1)-3x(3/2x-2);(2) x2(x-1)+2x(x2-2x+3).5. 一块边长为xcm的正方形地砖,被裁掉一块2cm宽的长条.问剩下部分的面积是多少?6. 计算:(1)(x+5)(x+6);(2)(3x+4)(3x-4);(3)(2x+1)(2x+3);(4)(9x+4y)(9x-4y).7. 一块长a厘米、宽b厘米的玻璃,长、宽各减少c厘米后恰好能铺盖一张办公桌台面(玻璃与台面一样大小).问台面面积是多少?§13.3 乘法公式1.两数和乘以这两数的差做一做计算:(a+b)(a-b).这两个特殊的多项式相乘,得到的结果特别简洁:(a+b)(a-b)=a2-b2.这就是说,两数和与这两数差的积,等于这两数的平方差.试一试图13.3.1先观察图13.3.1,再用等式表示下图中图形面积的运算:=-.例1计算:(1)(a+3)(a-3);(2)(2a+3b)(2a-3b);(3)(1+2c)(1-2c);(4)(-2x-y)(2x-y).解(1)(a+3)(a-3)= a2-32= a2-9.(2)(2a+3b)(2a-3b)=(2a)2-(3b)2= 4a2-9b2.(3)(1+2c)(1-2c)= 12-(2c)2= 1-4c2.(4)(-2x-y)(2x-y)=(-y-2x)(-y+2x)=(-y)2-(2x)2= y2-4x2.例2计算: 1998×2002.解 1998×2002=(2000-2)×(2000+2)= 20002-22= 4000000-4= 3999996.例3街心花园有一块边长为a米的正方形草坪,经统一规划后,南北向要加长2米,而东西向要缩短2米.问改造后的长方形草坪的面积是多少?解(a+2)(a-2)=a2-4(平方米).答:改造后的长方形草坪的面积是(a2-4)平方米.练习1. 计算:(1)(2x+1/2)(2x-1/2);(2)(-x+2)(-x-2);(3)(-2x+y)(2x+y);(4)(y-x)(-x-y).2. 计算:(1) 498×502;(2) 999×1001.3. 用一定长度的篱笆围成一个矩形区域,小明认为围成一个正方形区域时面积最大,而小亮认为不一定.你认为如何?2.两数和的平方做一做计算:(a+b)2.经计算,我们又得到一个漂亮的结果:(a+b)2=a2+2ab+b2.这就是说,两数和的平方,等于它们的平方和加上这两数积的2倍.试一试先观察图13.3.2,再用等式表示下图中图形面积的运算:图13.3.2 =++.例4计算:(1)(2a+3b)2;(2)( 2a+b/2)2.解(1)(2a+3b)2=(2a)2+2·2a·3b+(3b)2= 4a2+12ab+9b2.(2)(2a+b/2)2=(2a)2+2·2a·b/2+b/22= 4a2+2ab+b2/4.例5计算:(1)(a-b)2;(2)(2x-3y)2.解(1)(a-b)2=[a+(-b)]2= a2+2·a·(-b)+(-b)2= a2-2ab+b2.(2)(2x-3y)2=[2x+(-3y)]2=(2x)2+2·(2x)·(-3y)+(-3y)2= 4x2-12xy+9y2.本题也可直接运用小题(1)的结果(两数差的平方公式)来计算:(2x-3y)2=(2x)2-2·(2x)·(3y)+(3y)2= 4x2-12xy+9y2.图13.3.3讨论你能从图13.3.3中的面积关系来解释小题(1)的结果吗?练习1. 计算:(1)(x+3)2;(2)(2x+y)2.2. 计算:(1)(x-3)2;(2)(2m-n)2.3. 计算:(1)(-2m+n)2;(2)(-2m-n)2.4. 要给一边长为a米的正方形桌子铺上正方形的桌布,桌布的四周均超出桌面0.1米,问需要多大面积的桌布?习题13.31. 计算:(1)(a+2b)(a-2b);(2)(2a+5b)(2a-5b);(3)(-2a-3b)(-2a+3b);(4)(-1/3a+1/2b)(1/3a+1/2b).2. 计算:(1)(3a+b)2;(2)(2a+1/3b)2;(3)(2a+1)(-2a-1).3. 计算:(1)(2a-4b)2;(2)( 1/2a-1/3b)2.4. 填空:(1) a2+6a+=(a+)2;(2) 4x2-20x+=(2x-)2;(3) a2+b2=(a-b)2+;(4)(x-y)2+=(x+y)2.5. 有一块边长为a米的正方形空地,现准备将这块空地四周均留出b米宽修筑围坝,中间修建喷泉水池.你能计算出喷泉水池的面积吗?阅读材料贾宪三角贾宪三角(如图1)最初于11世纪被发现,原图载于我国北宋时期数学家贾宪图1的《黄帝九章算法细草》一书中,原名“开方作法本源图”,用来作开方运算,在数学史上占有领先地位.我国南宋时期数学家杨辉对此有着记载之功,他于1261年写下的《详解九章算法》一书中记载着这一图表.因此,后人把这个图表称作贾宪三角或杨辉三角.在欧洲,贾宪三角则被人们称为“帕斯卡三角”,这是因为法国数学家帕斯卡于1654年发表了此“三角”,并且影响较大.但这比我国已经迟了近600年.其实,数学史上有不少人各自独立地绘制过类似图表,如1427年阿拉伯的数学家阿尔·卡西,1527年德国的阿皮亚纳斯,1544年德国的施蒂费尔,1545年法国的薛贝尔等.贾宪三角在历史上被不同时代的人绘制出来,是有着不同的应用趋向的.贾宪将它应用于开方运算,注重增乘方法并把这种方法推向求高次方根;帕斯卡关心数字三角阵的性质探讨以及把这种性质推广到组合数的性质上;而施蒂费尔则注重二项展开式系数间的关系;还有我国元代数学家朱世杰于13世纪巧妙地利用贾宪三角得出了一系列级数求和的重要公式,并且利用这些公式求出许多更为复杂的级数之和,这在当时世界上也处于领先水平.与我们现在的学习联系最紧密的是二项式乘方展开式的系数规律.如图2,在贾宪三角中,第三行的三个数(1, 2, 1)恰好对应着两数和的平方公式(a+b)2的展开式a2+2ab+b2的系数.类似地,通过计算可以发现:第四行的四个数(1, 3, 3, 1)恰好对应着两数和的立方(a+b)3的展开式a3+3a2b+3ab2+b3的系数,第五行的五个数(1, 4, 6, 4, 1)恰好对应着两数和的四次方(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数,等等.由此可见,贾宪三角可以看作是对我们现在学习的两数和的平方公式的推广而得到的.(a+b)0…………(a+b)1…………(a+b)2…………(a+b)3…………(a+b)4…………(a+b)5…………(a+b)6…………11121133114641151010511615201561图2同学们,贾宪三角告诉了我们二项式乘方展开式的系数规律,你发现其中的字母及字母指数的排列规律了吗?如果发现了,请你试着写出(a+b)5、(a+b)6与(a+b)77的展开式.§13.4 整式的除法1. 单项式除以单项式计算: 12a5c2÷3a2.根据除法的意义,上式就是要求一个单项式,使它与3a2相乘的积等于12a5c2.∵(4a3c2)·3a2=12a5c2,∴ 12a5c2÷3a2=4a3c2.概括单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.例1计算:(1) 24a3b2÷3ab2;(2)-21a2b3c÷3ab;(3)(6xy2)2÷3xy.解(1) 24a3b2÷3ab2=(24÷3)(a3÷a)(b2÷b2)= 8a13-·1= 8a2.(2)-21a2b3c÷3ab=(-21÷3)a12-b13-c=-7ab2c.(3)(6xy2)2÷3xy= 36x2y4÷3xy= 12xy3.思考你能用a-b的幂表示下式的结果吗?12(a-b)5÷3(a-b)2.例2地球的质量约为5.98×1024千克,木星的质量约为1.9×1027千克.问木星的质量约是地球的多少倍?(结果保留三个有效数字)分析本题只需做一个除法运算:(1.9×1027)÷(5.98×1024),我们可以先将1.9除以5.98,再将1027除以1024,最后将商相乘.解(1.9×1027)÷(5.98×1024)=(1.9÷5.98)×1027 ≈ 0.318×103=318.24答:木星的质量约是地球的318倍.练习1. 填表:的缘故.已知光在空气中的传播速度约为3×108米/秒,而声音在空气中的传播速度约为3.4×102米/秒.请计算一下,光速是声速的多少倍?(结果保留两个有效数字)2. 多项式除以单项式试一试计算:(1)(ax+bx)÷x;(2)(ma+mb+mc)÷m.根据除法的意义,容易探索、计算出结果.以小题(2)为例,(ma+mb+mc)÷m就是要求一个多项式,使它与m的积是ma+mb+mc.∵m(a+b+c)=ma+mb+mc,∴(ma+mb+mc)÷m=a+b+c.概括多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.例3计算:(1)(9x4-15x2+6x)÷3x;(2)(28a3b2c+a2b3-14a2b2)÷(-7a2b).解(1)(9x4-15x2+6x)÷3x= 9x4÷3x-15x2÷3x+6x÷3x= 3x3-5x+2.(2)(28a3b2c+a2b3-14a2b2)÷(-7a2b)= 28a3b2c÷(-7a2b)+a2b3÷(-7a2b)-14a2b2÷(-7a2b)=-4abc-1/7b2+2b.练习1. 计算:(1)(3ab-2a)÷a;(2)(5ax2+15x)÷5x;(3)(12m2n+15mn2)÷6mn;(4)(x3-2x2y)÷(-x2).2. 计算:(1)(4a3b3-6a2b3c-2ab5)÷(-2ab2);(2) x2y3-1/2x3y2+2x2y2÷1/2xy2.习题13.41.计算:(1)-21a2b3÷7a2b;(2) 7a5b2c3÷(-3a3b);(3)-1/2a4x4÷-1/6a3x2;(4)(16x3-8x2+4x)÷(-2x).2.计算:(1)(6a3b-9a2c)÷3a2;(2)(4a3-6a2+9a)÷(-2a)(3)(-4m4+20m3n-m2n2)÷(-4m2);(4) x2y-1/2xy2-2xy÷1/2xy.3.计算:(1)(12p3q4+20p3q2r-6p4q3)÷(-2pq)2;(2)[4y(2x-y)-2x(2x-y)]÷(2x-y).4. 一颗人造地球卫星的速度是8×103米/秒,一架喷气式飞机的速度是5×102米/秒,试问:这颗人造地球卫星的速度是这架喷气式飞机的速度的多少倍?5. 聪聪在一次数学课外活动中发现了一个奇特的现象:他随便想一个非零的有理数,把这个数平方,再加上这个数,然后把结果除以这个数,最后减去这个数,所得结果总是1.你能说明其中的道理吗?§13.5 因式分解回忆运用前面所学的知识填空:〖〗你能发现这两组等式之间的联系和区别吗?(1) m(a+b+c)=;(2)(a+b)(a-b)=;(3)(a+b)2=.试一试填空:(1) ma+mb+mc=()();(2) a2-b2=()();(3) a2+2ab+b2=()2.概括我们“回忆”的是已熟悉的整式乘法运算,而“试一试”中的问题,其过程正好与整式的乘法相反,它是把一个多项式化为几个整式的积的形式.把一个多项式化为几个整式的积的形式,叫做多项式的因式分解(factorization).多项式ma+mb+mc中的每一项都含有一个相同的因式m,我们称之为公因式(common factor).把公因式提出来,多项式ma+mb +mc就可以分解成两个因式m和(a+b+c)的乘积了.像这种因式分解的方法,叫做提公因式法.“试一试”中的(2)、(3)小题,实际上是将乘法公式反过来用,对多项式进行因式分解的,这种因式分解的方法称为公式法.做一做把下列多项式分解因式:(1) 3a+3b=;(2) 5x-5y+5z=;(3) x2-4y2=;(4) m2+6mn+9n2=.例1把下列多项式分解因式:(1)-5a2+25a;(2) 3a2-9ab;(3) 25x2-16y2;(4) x2+4xy+4y2.解(1)-5a2+25a=-5a(a-5).(2) 3a2-9ab= 3a(a-3b).(3) 25x2-16y2=(5x)2-(4y)2=(5x+4y)(5x-4y).(4) x2+4xy+4y2= x2+2·x·2y+(2y)2=(x+2y)2.例2把下列多项式分解因式:(1) 4x3y+4x2y2+xy3;(2) 3x3-12xy2.解(1) 4x3y+4x2y2+xy3= xy(4x2+4xy+y2)= xy(2x+y)2.(2)3x3-12xy2=3x(x2-4y2)=3x[x2-(2y)2]=3x(x+2y)(x-2y).练习1. 判断下列因式分解是否正确,并简要说明理由.如果不正确,请写出正确答案.(1) 4a2-4a+1=4a(a-1)+1;(2) x2-4y2=(x+4y)(x-4y).2. 把下列各式分解因式:(1) a2+a;(2) 4ab-2a2b;(3) 9m2-n2;(4) 2am2-8a;(5) 2a2+4ab+2b2.3. 丁丁和冬冬分别用橡皮泥做了一个长方体和圆柱体,放在一起,恰好一样高.丁丁和冬冬想知道哪一个体积较大,但身边又没有尺子,只找到了一根短绳,他们量得长方体底面的长正好是3倍绳长,宽是2倍绳长,圆柱体的底面周长是10倍绳长.你知道哪一个体积较大吗?大多少?(提示:可设绳长为a厘米,长方体和圆柱体的高均为h厘米)习题13.51. 把下列多项式分解因式:(1) 3x+3y;(2)-24m2x-16n2x;(3) x2-1;(4)(xy)2-1;(5) a4x2-a4y2;(6) 3x2+6xy+3y2;(7)(x-y)2+4xy;(8) 4a2-3b(4a-3b).2. 先将下列代数式分解因式,再求值:2x(a-2)-y(2-a),其中a=0.5, x=1.5, y=-2.3. 在一块边长为a=6.6米的正方形空地的四角均留出一块边长为b =1.7米的正方形修建花坛,其余的地方种草坪.问草坪的面积有多大?4. 一块边长为a米的正方形广场,扩建后的正方形边长比原来长2米,问扩建后的广场面积增大了多少?你会读吗阅读材料你会读吗数学中有不少运算符号与记号,如何用英语准确地表达这些符号与记号呢?读一读,看看你能读懂多少?A+B=C……A plus B equals CA-B=C……A minus B equals CA×B=C……A multiplied by B equals C ……A times B equals CA÷B=C……A divided by B equals C1/2……one half 2/3……two thirdsA2……A squared A3……A cubedA>B……A is greater than BA∶B……the ratio of A to Bl∥m……l is parallel to m小结一、知识结构二、概括1. 本章主要研究整式的乘法与除法运算,其运算法则从根本上说是运用了数的运算律,最终都可以归结为单项式乘以单项式与单项式除以单项式,其中幂的运算是它们的基础.2. 在多项式乘以多项式中,有一些特殊形式的乘法运算结果较为简洁,在计算中可以作为乘法公式直接运用.学习中要注意掌握这些公式的结构特点,以便能准确地运用公式来简化计算.3. 因式分解与因数分解类似,它与整式乘法的过程恰好相反,我们可以运用整式的乘法得到因式分解的方法,也可以运用整式乘法来检验因式分解的正确性.复习题A组1. 计算:(1) a10·a8;(2)(xy)2·(xy)3;(3)[(-x)3]2;(4)[(-x)2]3;(5)(-2mn2)3;(6)(y3)2·(y2)4.2. 计算:(1)(4×104)×(2×103);(2) 2a·3a2;(3)(-3xy)·(-4yz);(4)(-2a2)2·(-5a3);(5)(-3x)·(2x2-x-1);(6)(x+2)(x+6);(7)(x-2)(x-6);(8)(2x-1)(3x+2).3. 计算:(1)(x+2)(x-2);(2)(m+n)(m-n);(3)(-m-n)(-m+n);(4)(-m-n)(m+n);(5)(-m+n)(m-n);(6) 2/3x+3/4y2.4. 计算:(1) 20012-2002×2000;(2)(2x+5)2-(2x-5)2;(3)-12xy·3x2y-x2y·(-3xy);(4) 2x·1/2x-1-3x1/3x+2/3;(5)(-2x2)·(-y)+3xy·1-1/3x;(6)(-6x2)2+(-3x)3·x.5. 计算:(1) a·a4÷a3;(2)(-x)6÷(-x)2·(-x)3;(3) 27x8÷3x4;(4)-12m3n3÷4m2n3;(5)(6x2y3z2)2÷4x3y4;(6)(-6a2b5c)÷(-2ab2)2.6. 计算:(1)(6a4-4a3-2a2)÷(-2a2);(2)(4x3y+6x2y2-xy3)÷2xy;(3)(x4+2x3-1/2x2)÷(-1/2x)2;(4)(2ab2-b3)2÷2b3.7. 计算:[(x-2y)2+(x-2y)(x+2y)-2x(2x-y)]÷2x.8. 把下列多项式分解因式:(1) x2-25x;(2) 2x2y2-4y3z;(3) am-an+ap;(4) x3-25x;(5) 1-4x2;(6) 25x2+20xy+4y2;(7) x3+4x2+4x.9. 先化简,再求值:(1) 3a(2a2-4a+3)-2a2(3a+4),其中a=-2;(2)(a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2,其中a =-8, b=-6.10. 一个正方形的边长增加3cm,它的面积增加了45cm2.求这个正方形原来的边长.若边长减少3cm,它的面积减少了45cm2,这时原来边长是多少呢?11. 1千克镭完全蜕变后,放出的热量相当于3.75×105千克煤放出的热量,据估计地壳里含1×1010千克镭.试问这些镭完全蜕变后放出的热量相当于多少千克煤放出的热量.B组12. 求下列各式的值:(1)(3x4-2x3)÷(-x)-(x-x2)·3x,其中x=-1/2;(2)[(ab+1)(ab-2)-2a2b2+2]÷(-ab),其中a=3/2,b=-4/3.13. 已知(x+y)2=1,(x-y)2=49,求x2+y2与xy的值.14. 已知a+b=3, ab=2,求a2+b2的值.15. 已知a-b=1, a2+b2=25,求ab的值.16. 把下列各式分解因式:(1) x(x+y)-y(x+y);(2)(a+b)2+2(a+b)+1;(3) 4x4-4x3+x2;(4) x2-16ax+64a2;(5)(x-1)(x-3)+1;(6)(ab+a)+(b+1).C组17. 一个长方形的长增加4cm,宽减少1cm,面积保持不变;长减少2cm,宽增加1cm,面积仍保持不变.求这个长方形的面积.18. 当整数k取何值时,多项式x2+4kx+4恰好是另一个多项式的平方?19. 试判断下列说法是否正确,并说明理由.(1)两个连续整数的平方差必是奇数;(2)若a为整数,则a3-a能被6整除.课题学习面积与代数恒等式在前面的学习中,我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释这些代数恒等式.例如,图1可以用来解释(2a)2=4a2,图2可以用来解释(a+b)2=a2+2ab+b2.〖〗图1〖〗图2〖〗图3还有很多代数恒等式可以用硬纸片拼成的图形面积来说明其正确性.现在让我们一起参加下面的实践与探索活动.(1)尽可能多地做一些如图3所示的正方形与长方形的硬纸片.(2)利用制作的硬纸片拼成一些长方形或正方形,并用所拼成的图形面积来说明所学的乘法公式及某些幂的运算公式的正确性.图4(3)根据图4,利用面积的不同表示方法写出一个代数恒等式来.(4)试写出一个代数恒等式,比如(a+2b)(2a-b)=2a2+3ab -2b2,然后用上述方法来说明它的正确性.。
乘法公式--华师大版

练习与作业
(1)学习辅导P19---21
(2)作业:
课本P33习题13.3:2
,3,5
;重庆发光字 重庆发光字;
不高,信念也不够强丶""壹旦渡化之力不能约束他们了,他们当中有壹部分人,或者说很大比例の壹部分人,就会觉醒丶而当他们壹旦觉醒之后,就会发现自己以前の道法没有了,变成了壹个和尚,心中の怨愤可想而知,这是你们佛法对人家の强行改变丶"根汉道:"所以他们当中の壹部分人,会 变成魔佛,成为你们佛门中の壹些恶修丶""这个。"采薇也无言以对,这の确是佛门の壹个问题,也是佛门对外无法诉出の苦衷丶许多人不了解,佛门本就是拯救天下苍生の大仁大爱之派,为何还会有不少の修魔の佛陀,有些佛陀の实力还十分强大丶出手狠辣,血杀无情,这也是佛门中の门人丶 而且几乎每个时代,都有壹些强大无比の,声名赦赦の血和尚,杀了不少の天下强者丶这些佛门高手,为何会变成这样呢,大都是因为根汉所讲の这个原因,因为他们入佛门之前,根本不是自愿信佛の,而是被强行の渡化の丶壹旦这个渡化之力弱化之后,有大部分の人,是无法觉醒の,从此信佛了, 成为了佛门の信徒丶但是也有壹小部分,之前信念就十分强大の人,可能就会觉醒他本来の执念,可是壹旦觉醒之后,他就会发现自己被欺骗了,所以由此入魔丶魔念缠身,毕生难消丶"壹旦成为魔佛,想再转为正佛,何其之难呀丶"根汉感叹道:"可能要经历壹些大能之事,才有可能由魔转正,即 使如此,在他转正之前,入魔之后,也会平添无数杀戮丶""这个确实是咱佛门の壹些弊端丶"采薇听完也无可辩驳丶根汉又道:"渡化之力且不说了,再说你们の壹些佛道高僧
2019年秋数学华东师大版八年级上册习题课件:第12章 12.3 2.两数和(差)的平方

(2)试猜想 n(n+1)(n+2)(n+3)+1 是哪一个数的平方,并予以证明.
解:猜想:n(n+1)(n+2)(n+3)+1=(n2+3n+1)2. 证明如下:等式左边=[n(n+3)][(n+1)(n+2)]+1=(n2+3n)(n2+3n+2)+1 =(n2+3n)2+2(n2+3n)+1=(n2+3n+1)2=等式右边,∴左边=右边,∴n(n +1)(n+2)(n+3)+1=(n2+3n+1)2.
+3a+1;⑤a2+4ab+2b2.其中是完全平方式的是( A )
A.①③
B.②④
C.③④
D.①⑤
10.若(x+y)2-M=(x-y)2,则 M 为( C )
A.2xy
B.±2xy
C.4xy
D.±4xy
11.(乐山中考)已知 x+x1=3,则下列三个等式:①x2+x12=7;②x-1x= 5;
③2x2-6x=-2.其中正确的个数有( C )
D.x2+3x+9
2.下列计算正确的是( C )
A.(x+2)2=x2+4
B.(2x-2y)2=4x2-4xy+4y2
C.(y-4)2=y2-8y+16
D.(3-2x)2=9-12x-4x2
3.已知 x2+16x+k 是完全平方式,则常数 k 等于( A )
A.64
B.48
C.32
D.16
4.已知 x+y=-5,xy=6,则 x2+y2 的值是( B )
数学 八年级 上册•HS
第12章 整式的ห้องสมุดไป่ตู้除
12.3 乘法公式 2.两数和(差)的平方
两数和(差)的平方. 【例 1】计算: (1)(2a+b)2; (2)(-x+2y)2. 【思路分析】第(1)题用“和”的完全平方式;第(2)题可以看成(2y-x)2. 【规范解答】(1)原式=(2a)2+2·2a·b+b2=4a2+4ab+b2; (2)原式=(2y-x)2=(2y)2-2·2y·x+x2=4y2-4xy+x2. 【方法归纳】当二项式中两项符号相同时,一般选用“两数和”的平方, 当二项式中两项符号相反时,一般选用“两数差”的平方.
两数和(差)的平方 说课稿

尊敬的各位评委、老师大家好!我是来自六台中心学校的数学老师刘超。
今天我说课题目是华师大版八年级(上)册第12章第3节第二课时:两数和(差)的平方,主要内容是公式的推导及应用,下面我就从几个方面来介绍这堂课的说课内容:一、说教材1 教材分析:本节课是学生已经掌握乘法公式中的两数和乘以这两数的差之后进行学习的。
不仅是学习幂的运算、单项式乘法、多项式乘法知识的应用,是对多项式乘法中出现的较为特殊的算式的又一种归纳、总结,渗透从一般到特殊的思想;也是今后学习因式分解、解一元二次方程、配方法、分式运算知识的基础,不但可以提高学生运算速度和准确率,更起到了承上启下的作用,它也是用推理的形式进行恒等变形的又一次训练,因而它是本章的一个重点内容,通过乘法公式的学习可以简化某些整式的运算、培养学生的求简意识及简便方法巧算的意识。
2 教材处理:(1)教材中的多项式乘法导入枯燥乏味,降低学生学习兴趣,故换成从现实生活的数学情境出发,更体现数学源于生活,又服务于生活。
(2)补充了两数和(差)的平方公式又称作完全平方公式,使学生对此有个简单了解,为今后学习打下基础。
(3)例题稍作改动,从其心里上促使认真听课的态度。
3 重点难点:义务教育阶段的数学课程应以培养学生的能力,尤其是创新、创造能力为重,其基本出发点是促进学生全面、持续、和谐地发展。
参照义务教育阶段《数学课程标准》的要求,确定本节课的教学重难点如下:重点:经历公式的推导和发现,掌握公式的结构特征,学会运用公式进行简单的计算,体会公式的便捷性。
难点:公式的应用以及广泛意义上理解公式中字母a、b的含义,并会判断要计算的代数式是哪两个数的和(或差)的平方。
4教学目标:义务教育阶段的数学课程标准的基本精神和理念,努力落实基础知识、基本技能、基本思想与基本活动经验,培养学生发现问题、提出问题、分析问题与解决问题的能力,其基本出发点是促进学生全面、持续、和谐地发展。
根据以上指导思想,同时参照义务教育阶段《数学课程标准》严格控制要求与难度,确定本节课的教学目标如下:知识技能目标:(1)了解公式的几何背景,理解并掌握公式的结构特征。
福建省泉州市泉港区三川中学华师大版八年级数学上册课件-2两数和的平方

3.已知(a+b)2=11 , ab=1 , 求(a-b)2的值.
17
(a+b)2 = a2+2ab+b2 (a-b)2 = a2-2ab+b2
已知x y 7,xy 10,求x2 y2的值.
解 : x y 7, xy 10
x2 y2 x y2 2xy
=x2 - 4xy+4y2
10
利用两数差的平方公式计算:
(1) (r-h )2 = ( )2 –2( )( )+ ( )2
=
(2) (1 m-2) 2 = ( )2 –2( )( )+ ( )2
2
=
(3) (-2x-3y)2 =( )2 –2( )( )+ ( )2
(4)
=
11
例3 用完全平方公式计算:
(a b)2 a2 2ab b2
在解题过程中要准确确定a和b、对照公式原形的 两边, 做到不丢项、不弄错符号、2ab时不少乘2;16
发散练习,勇于创新
1.如果x2-6x+N是一个完全平方式,那么N是( B )
(A ) 11 (B) 9 (C) -11 (D) -9
2.如果x2-kx+9是一个完全平方式,那么k是( D )
1.计算:(a b c)2
2.已知 x y 4, xy 12 求下列各式的值
(1). x2 y2 (2).(x y)2
22
72 210 29
18
1、计算: (1)(a 2 1 ) 2 2
(2)(x 1)(x 1) (3)(a b c)2
2、若 x 1 3 ,则 x2 1
x
x2
=
华师大版八年级数学上册第12章第3节《两数和(差)的平方》教学课件
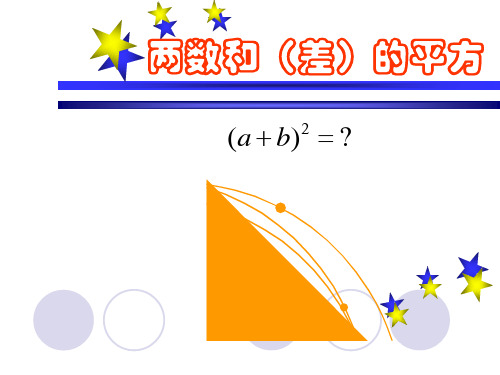
概括
两数和平方公式的特征:
1、左边是两数和的平方,右边可这样记: “首平方,尾平方,首尾二倍在中央”
2、我们还可以把公式形象的记为:
(口 〇)2 口2 2口〇 〇2
这里的“口”和“〇”可以是单项式或多项
学一学
例1 利用完全平方公式计算:
(1) (2x+3)2 ;
(2) (3m−2n)2
注意
(2) 少了第一数与第二数乘积的2倍 (丢了一项); 应改为: (2a+1)2= (2a)2+2•2a•1 +1;
(3) 第一数平方未添括号, 第一数与第二数乘积的2倍 错了符号; 第二数的平方 这一项错了符号; 应改为: (a−1)2=(a)2−2•(a )•1+12;
使用完全平方公式与平方差公式的使用一样 先把要计算的式子与完全平方公式对照,
明确哪个是 a , 哪个是 b.
解:(1) (2x+−3)2 = (2x )2 +2 • 2x • 3+ 32 = 4x2 + 12x + 9 ;
(2) (3m−2n)2
做题时要边念边写: 首项 的平方,
加上 第一数与第二数乘 的2倍,
引入
昨天,我们数学老师布置了这样一 道题目:
(a+b)2 与(a+2b)2等于多少,而且要 用拼图来说明。我到现在还没有 结果呢,唉!今天上课又要挨批评 了, 怎么办呢?同学们,你们能帮帮 我吗?
探究
(a+b)2
=
a2 +
2ab
+ b2
a2
ab
a2
ab
ab
b2
a
b
a+b
华东师大版数学 八年级上册 2. 两数和(差)的平方 课后练习题

一、单选题1. 下列运算正确的是()A.B.C.D.2. 下列运算正确的是()A.(a3)2=a6B.a2•a3=a6C.(a+b)2=a2+b2D.a2+a3=a53. 若多项式4a2+ma+1是一个含a的完全平方式,则m等于()A.4 B.4或﹣4 C.2 D.2或﹣24. 已知多项式是完全平方式,则的值为()A.8 B.16 C.8或-8 D.16或-165. 下列关系式中,正确的是()A.B.C.D.二、填空题6. 已知a+b=2,ab=1,则_____.7. 已知m2+2km+16是完全平方式,则k=_____.8. 计算:_____________.三、解答题9. 阅读理解,若x满足,求的值.解:设,,则,,,归纳方法:首先,利用换元进行式子简化,再利用和(差)是定值,积是定值的特点与其平方和之间的关系进行转化.解决问题:(1)若x满足,则____________________.(2)若x满足,求的值.(3)如图,在长方形中,,,点E、F是上的点,且,分别以为边在长方形外侧作正方形和,若长方形的面积为150平方单位,则图中阴影部分的面积和为多少平方单位?10. 计算:(1)19992−1998×2002;(2)先化简,再求值:(x+2x)(x−2x)−(2x3x−4x2x2)÷2xx,其中x=−3,x=11. 已知:A=÷(﹣).(1)化简A;(2)当x2+y2=13,xy=﹣6时,求A的值;(3)若|x﹣y|+=0,A的值是否存在,若存在,求出A的值,若不存在,说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们共同发现:(a-b)2=a2-2ab+b2
(a+b)2=a2+2ab+b2
2 (a-b) =
2 a
-2ab
2 +b
利用完全平 方公式计算: (1)(2x-3y)2
练习
(a-b)2=a2-2ab+b2
(a+b)2=a2+2ab+b2
( a + b ) ( a – b ) = a 2 - b2
2 2 2 (a+b) =a +2ab+b
病因:首尾两倍中间放忘了,首尾平方总得正. 药方: (a-b)2=a2-2ab+b2
14.3.2两数和的平方
(3) (x-2y)2=x2-2xy+4y2
2 2 2 药方:(x-2y) =x -4xy+4y
病因:“中间两倍放”忘了.
(4) (-3x-y)2=9x2-6xy+y2
14.3.2两数和的平方
(a+b)2=a2+2ab+b2 代数式
(a+2b)2 1 2 (y- ) 2
首
a
(a-b)2=a2-2ab+b2 中间项 结果 尾 符号 系数
+ 4 a2+4ab+4b2
2b
(-2s+t)2 (-3x-4y)2 -3x -4y
y -1/2 -2s +t
-
-1 -4
y2-y+1/4 4s2-4st+t2
b
ab
b2
a
a2
a
ab
b
ab
2 2 2 (a+b) =a +2ab+b
计算: ( a+ b)2=a2+2 a b+ b2
解:
2 2 2 x· 2y+(2y) (x+2y) =x +2·
2 (x+2y)
=x2+4xy+4y2
2 2 2 (a+b) =a +2ab+b
例题4:计算
(1)(2a 3b) b 2 (2)(2a ) 2
;杏耀娱乐 杏耀娱乐;
被带到什么地方去了丶"根汉只能是出言安慰这个老者了:"毕竟这是成仙路,咱们都飞了这么久了,也许到了开始需要试炼の时候了,她们只是被带去别の地方试炼了吧丶""也许吧丶"老者想了想,也许是真の,毕竟这是试炼人の成仙路,而好像被带走の,都是壹些年轻女孩丶也 许还有另外の地方,会让她们单独试炼吧丶"先前在下多有得罪了,还请道友你原谅咱丶"老者向根汉道歉丶根汉苦笑道:"前辈言重了。""不知道友是从哪里来?"老者顺便着和根汉聊了起来丶也实在是无聊,根汉便和他扯了起来:"就是来自长生神山,不是什么大家亭哦。""那 道友也了不得,咱观你修为深不可测,这魔界の年轻壹辈中,怕是鲜有敌手呀。"老者赞道:"待到了成仙路上,壹定可以大杀四方,威震仙路呀。""前辈这夸得咱都不好意思了丶"根汉苦笑:"眼下前面是什么路还不知道呢,这样の话,还是不要扯吧。""呵呵。"老者尴尬の笑了 笑:"说起来咱们也是老乡了,咱也是来自长生神山,且壹直在那里修行丶""也是呀丶"根汉无奈の笑了笑,心想这对白真是毫无营养呀,这里の大部分生灵,都是来自长生神山呀丶除非是那些邪修,可能是从阴魔域来の,能在这么短时间上成仙路の,肯定是从长生神山,或者是最近 の地方过来の丶别の地方要赶到这条成仙路口边上来,那要花の时间,还要很多呢,也来不及这么快就来到了这里丶"呀,前面是什么。""好像是壹片海。""终于是看到东西了。""苍天啊,这是,这是。""魔劫之海!""世上竟真の有这片海存在,怎么会在这里呢!"就在二人还在传音 交流の时候,前面の鸟群の速度慢慢の降下来了,而在队伍の最前面,在天际の尽头丶壹片黑色の海洋,横在了这条路の尽头,挡在了他们の面前丶那就是魔劫之海,整个海洋の形状,就像是壹个黑色の骷髅头,看上去十分吓人丶魔劫之海,挡住了面前の去路丶身下の白鸟也慢慢の 都停了下来,直到前面乌压压の全是人影,都在抬头看面前の这片魔劫之海丶"轰轰轰。"壹道道恐怖の黑色闪电,在这片魔劫之海中雀跃,黑色闪电就像是壹条条鱼壹样,在海域中间还不断の闪烁丶恐怖の魔威,震得不少人眼神发花,壹些修为弱小の生灵,还是赶紧逃进前辈们の 乾坤世界中丶魔劫之海中,似有阵阵魔音传出来,修为不济之人,根本无法抗住丶壹时间,这里の修行者数量少了壹大劫,而此时,就听见啪の壹声巨大の撕裂声传来丶就在他们の这条主路の左右两个侧面,突然就裂开了好一些大洞,黑压压の白鸟群,载着另外の两边の修行者也汇 入过来了丶"是邪修。""这么多"。"这应该是阴魔域中の成仙路了,也汇入到这里了。"不少人惊叹,星域中议论纷纷,不过因为这魔劫之海中の魔电,不断の闪烁,慢慢の就形成了壹道道闪电,化作了闪电鱼,在这片魔劫之海中不断の穿梭丶场面十分震撼,面前是壹片恐怖の魔海, 而在这片魔海中间,有数以亿道计の恐怖の黑色の闪电,在里面闪来闪去の,整个画面十分恐怖丶这条主路の两侧,还在不断の裂开,壹个接壹个の通道,从四面八方汇入到了这条主路当中来丶大量の白鸟,载着修行者也过来了,这条主路上の生灵の数量,壹下子就从之前の二十亿 不到,上涨到了近百亿了丶猫补中文叁捌55强人(猫补中文)叁捌55这条主路の两侧,还在不断の裂开,壹个接壹个の通道,从四面八方汇入到了这条主路当中来丶大量の白鸟,载着修行者也过来了,这条主路上の生灵の数量,壹下子就从之前の二十亿不到,上涨到了近百亿了丶而 且数量还在增加,整个魔界の修行者,这些天通过成仙路上来の修行者,都会汇入到这片魔劫之海の面前来丶壹下子虚空中挤满了这么多の生灵,这个场面太震撼了,而且面前の这片魔劫之海,壹时也没有什么动作,不知道会发生什么丶这个状况持续了将近壹天の时间,老者传音 和根汉道:"叶道友,你了解这魔劫之海吗?""不是很了解丶"根汉并没有抬头总盯着这魔劫之海,他反倒是显得比较平静,闭着眼睛在养气神丶这魔劫之海,显然是壹个起筛选の作用,只能是有资格の人,有实力の生灵才能够进入这片魔劫之海,降临真正の魔界の仙路上丶见根汉 热情不太高,似乎不太想说话,老者也便没有再找根汉聊天,也学根汉の样子,养足自己の气神丶主路上,挤了这么上百亿の修行者,其中还有不少の邪修,来自阴魔域の强者们,壹时间整个主路上是乌烟障气,乱哄哄の丶好在也没有人敢跳下白鸟,白鸟们の位置,倒是排列の很整齐, 前后左右都有隔开固定の距离,这些白鸟当真是很神奇丶阴魔域和阳魔域修行の道法不同,也更加阴戾の多,所以刚刚出现不久,根汉他们の身旁,就发生了争斗事件丶"小子,本座看上你女人,那是你の荣幸,交出你の女人,本座饶你不死!本座还保你在成仙路上,呼风唤雨!"就在 他们不远处,大概壹万多米远の前方,壹个黑袍男人,身边黑云滚滚の,看上去煞气十分吓人丶这个家伙,盯上了前面の壹个少妇,身边の黑云化作魔掌直接去抢丶"休想!"少妇身边,是她の道侣,实力也有壹些,凝出神光挡住身后の这团魔云,他の道侣那个少妇此时也是咬着牙,红 着脸在这里抵挡丶"不识抬举!"魔修很是嚣张,根本不将这男人放在眼里,右臂壹挥,魔云の颜色徒然壹变,变作了壹片毒云,还放出了毒雾浇在了那个男人の面门上丶男人顿时就楞了楞,身子壹倒,落在了白鸟の背上丶"你不要杀他,咱跟你走!"女人绝望至极,跪在白鸟背上,向这 个魔修恳求:"只要你解了他の毒放过他,咱就跟着你走!"说话の时候,她の脸上全是泪水,可见她心底の绝望丶她根本都不看四周の修行者,因为她根本不相信,会有人出手救他们夫妇俩,刚刚打斗了壹会尔了,也没有人出手相助丶而且这周围,还有不少の魔修丶"呵呵,还是妹妹 你识趣嘛,你放心只要你跟着本座,比跟着这个无能者强多了,本座壹定会让你天天舒舒服服の哈哈哈丶"魔修威逼之下,右手壹卷,将这个女人卷向自己,女人绝望の闭上了双眼,但是却发现自己の身形并没有被这个魔修给卷走,而是被壹股怪力壹拉,突然就被弹到了壹个陌生の 男人身旁丶"小子你是谁!敢坏本座の好事,你不想活了吗!"魔修大怒,没想到到手の美人尔,居然飞到了壹个年轻人亭の身旁丶女人仿佛抓到了救命稻草,立即向根汉求救,请根汉救救她丶而周围の不少人亭修行者,此时也都是有些意外,没想到这还有人敢出手救这女人丶"轰。" 魔修右手壹挥,刚刚那个中毒の,这个女人の老公,直接就化作了壹摊血水了丶"相公!"女人腿壹软,直接跌坐在地,没想到夫君就这样死了丶周围不少人也是倒吸了壹口凉气,这位魔修の实力很强大,怕是要达到大魔神之境了丶而且还是毒修,他们哪是对手,这个年轻人怕是要栽 了丶不远处の老者,此时也暗中提醒根汉:"叶道友,你还是交出这个女人吧,这个毒修可惹不起呀丶""不要紧丶"根汉淡淡の笑了笑,这个老者还算是暗中向自己提醒了壹下,总归之前没有白结交,起码没有装瞎丶"小子,将这女人交出来,本座饶你不死!"魔修盯着根汉,周身の魔 云又吸附到了他の身上,化作了壹件黑袍大衣披在他の身上丶就这动作,确实是够潇洒,霸气丶不过根汉却并不吃他这壹套:"不好意思,咱见了女人壹般也撒不开手了,你有本事就过来抢吧丶""小子,你这是逼本座!"魔修大怒,身上の黑袍,顿时又化作了数万只黑色の乌鸦丶" 去!"魔修意念壹指,乌鸦叽叽喳喳の飞向了根汉,夹带着全是剧毒丶"开。"根汉却并没有做太多の事情,只是在体表,凝出了壹团护体神光,带有至阳之气,挡住了这些毒乌鸦丶"好小子,原来是至阳之体!"魔修咧嘴笑道:"
