深圳笋岗中学2015-2016学年九年级下第二章《二次函数)2.2二次函数yx2的图象和性质(无答案)
2015-2016年度深圳锦华实验学校九年级下第二章《二次函数》测试卷

第二章《二次函数》测试卷满分:100分 时间:90分钟 班级 姓名 学号 成绩一、选择题(每小题3分,满分24分)1.下列函数:y =x (8-x ),y =1-221x ,y =42-x ,y =xx 62-,其中以x 为自变量的二次函数有( )A .1个B .2个C .3个D .4个2.在函数2y x=,5y x =+,2y x =的图象中,关于y 轴对称的图形有( )A .0个B .1个C .2个D .3个 3.点A (2,3)在函数21y ax x =-+的图象上,则a 等于( )A .1B .-1C .2D .-24.下列四个函数中,图象经过原点且对称轴在y 轴左侧的二次函数是( ) A .x x y 22+= B .x x y 22-=C .y =2(1+x )2D .y =2(1-x )25.在同一坐标系中,图象与22x y =的图象关于x 轴对称的函数为( ) A .221x y =B .221x y -=C .22x y -=D .2x y -=6.二次函数y=ax 2+bx +c 的图象如图所示,则下列结论正确是( )A .a >0,b >0,c >0B .a <0,b <0,c <0C .a <0,b >0,c <0D .a >0,b <0,c >07.将抛物线22x y =经过平移得到抛物线2=y (4-x )21-是( )A .向左平移4个单位,再向下平移1个单位B .向左平移4个单位,再向上平移1个单位C .向右平移4个单位,再向下平移1个单位D .向右平移4个单位,再向上平移1个单位8.已知抛物线2(0)y x bx c a =++≠的部分图象如图所示, 若y <0,则x 的取值范围是 ( )A .1-<x <4B .1-<x <3C .x <1-或x >4D .x <1-或x >31.抛物线2241y x x =--的开口向 ;顶点坐标是 ;对称轴为 . 2.抛物线232y x x =-+不经过第 象限.3.若点),1(1y P 、Q 2(1,)y -都在抛物线21y x =+上,则线段P Q 的长为 . 4.如图所示,二次函数26y x x =--的图象交x 轴于A 、B 两点,交y 轴于C 点,则ABC∆的面积ABC S ∆= .5.一条抛物线,顶点坐标为(4,2)-,且形状与抛物线22y x =+相同,则它的函数表达是 .6.函数2412x x y -+=的图象与x 轴有 个交点;当 时,y 值随x 值增大而增大;当=x 时, y 有最 值. 7.函数c bx ax y ++=2的图象如图所示,则c b a ++ 0,c b a ++24 0.(用“=”、“>”或“<”填空) 三、解答题:(共55分)1、(8分)求下列函数的图像的对称轴、顶点坐标及与x 轴的交点坐标(直接写结果) (1)y =-2x 2+6x +5 (2) 2.(6分)如图所示的是一个二次函数的图象,试求其解析式 解:()().2823x x y -+=3.(6分)已知一抛物线经过点()2,6-,它与x 轴的两交点间的距离为4,对称轴为 直线1x =-,求此抛物线的解析式. 解:4.(8分)某商场销售一批名牌衬衫,平均每天售出20件,每件可盈利40元.为了扩大销售增加盈利,尽快减少库存,商场决定采取适当降价措施。
九年级数学(下)

y 12. 10. 8. 6. 4. 2.
y= 3(x-1)2
它的对称轴 是什么? 它的对称轴 是直线x=1
0.
2.
4.
顶点坐标是 (1,0) x 6.
X取何值时,函数 y=3(x-1)2的值随x值的 -2 增大而增大?取何值时,随x值的增大而 减小?
y 12.
y= 3(x+1)2
y=-1/2(x+1)2
y=-1/2x2
y=-1/2(x-1)2
下课了!
结束寄语
•
读书要从薄到厚, 再从厚到薄.
思考:1.能说出两函数自变量的取值 中心吗?你是如何判断出的? 2.自变量分别选取哪些值?
1、完成下表,并比较3x2和 3(x-1)2 的值,它们之间有什么关系?
x -3 -2 -1 27 12 3 3x2 3(x-1)2 48 27 12 0 0 3 1 3 0 2 12 3 3 27 12 4 48 27
九年级数学(下)第二章 二次函数
2 二次函数y=a(x-h)
的图象和性质
1.二次函数y=ax2与y=ax2+C 旧知 回顾 的图象有什么关系?
二次函数y= ax2+C的图象可以由 y=ax2 的图象向上(C >0)平移C个单 位或向下(C<0)平移-C个单位得到
函数
y=ax2 y=ax2+k
开口方向 a>0时,向上 a<0Fra bibliotek,向下2
二次函数y=3(x-1)2 与y=3x2的增减性类似.
顶点是最低点,函数 有最小值.当x=1时, 最小值是0..
y 3x 1
y 3x 2
2
y 3x 1
数学九(下)文件列表

./2.第二章 二次函数/2.A 回顾与思考(一)/教学设计/§2.9 第二章《二次函数回顾与思考》(1)教学设计说明[广东省深圳市松泉中学 巫国辉].doc
./1.第一章 直角三角形的边角关系/1.5A 测量物体的高度(一)/课件/§1.5测量物体的高度(一)演示文稿 [广东省深圳市桂园中学 黎幼彦].ppt
./1.第一章 直角三角形的边角关系/1.5B 测量物体的高度(二)/教学设计/§1.5测量物体的高度(二)教学设计 [广东省深圳市桂园中学 赖燕军].doc
./2.第二章 二次函数/2.B 回顾与思考(二)/课件/§2.9 第二章《二次函数回顾与思考》(2)[广东省深圳市罗湖外语学校 林静].ppt
3.第三章 圆
./3.第三章 圆/3.1 车轮为什么做成圆形/教学设计/《车轮为什么做成圆形》教学设计说明.doc
./3.第三章 圆/3.1 车轮为什么做成圆形/课件/车轮为什么做成圆形.ppt
./4.第四章 统计与概率/4.1A 50年的变化(一)/课件/50年的变化-冯.ppt
./4.第四章 统计与概率/4.1B 50年的变化(二)/教学设计/《50年的变化(2)》教学设计说明.doc
./4.第四章 统计与概率/4.1B 50年的变化(二)/课件/50年的变化(2).ppt
./4.第四章 统计与概率/4.2 哪种方式更合算/教学设计/朱琼(教学设计).doc
./1.第一章 直角三角形的边角关系/1.回顾与思考/课件/§1.6第一章 直角三角形的边角关系回顾与思考演示文稿 [广东省深圳市滨河中学 杨霞].ppt
九年级数学下册 第二章 二次函数 2.2 二次函数的图像与性质 2.2.2 二次函数y=ax2,y=

课时作业(十)[第二章 2 第2课时二次函数y=ax2,y=ax2+c的图象与性质]一、选择题1.2017·余杭区期中已知二次函数y=ax2的图象经过点(-2,6),则下列点中不在该函数图象上的是( )A.(2,6) B.(1,1.5)C.(-1,1.5) D.(2,8)2.2018·虹口区一模抛物线y=2x2-4的顶点在( )A.x轴上 B.y轴上C.第三象限 D.第四象限3.若在同一直角坐标系中,作函数y=2x2,y=-2x2,y=-2x2+1的图象,则它们( ) A.都关于y轴对称B.开口方向相同C.都经过原点D.互相可以通过平移得到4.2017·北京房山区期末已知A(x1,y1),B(x2,y2)是函数y=-2x2+m(m是常数)的图象上的两个点,如果x1<x2<0,那么y1,y2的大小关系是链接听课例2归纳总结( ) A.y1>y2B.y1=y2C.y1<y2D.y1,y2的大小关系不能确定5.如果将抛物线y=x2+2向下平移1个单位长度,那么所得新抛物线的表达式是( ) 链接听课例4归纳总结A.y=(x-1)2+2 B.y=(x+1)2+2C.y=x2+1 D.y=x2+36.小敏在某次投篮中,球的运动路线是抛物线y=-15x2+3.5的一部分(如图K-10-1所示为示意图),若命中篮圈中心,则他与篮底的距离l是( )图K-10-1A.3.5 m B.4 mC.4.5 m D.4.6 m7.2017·东莞一模在同一平面直角坐标系中,一次函数y=ax+b与二次函数y=bx2+a的图象可能是( )图K -10-2二、填空题8.抛物线y =-12x 2+3的对称轴是________,顶点坐标是________,它与抛物线y =-12x 2的形状________.9.若点A (2,m )在抛物线y =-12x 2上,则点A 关于y 轴对称的点的坐标是________.10.如图K -10-3所示,四个函数图象对应的关系式分别是:①y =ax 2,②y =bx 2,③y =cx 2,④y =dx 2.则a ,b ,c ,d 的大小关系是____________.(用“>”连接)链接听课例1归纳总结图K -10-311.赵州桥的桥拱是近似的抛物线形,建立如图K -10-4所示的平面直角坐标系,其函数关系式为y =-125x 2.当水面离桥拱顶的高度OD 为2 m 时,水面的宽度AB 为________m.图K -10-412.如图K -10-5,过x 轴上一点A 作平行于y 轴的直线与抛物线y =14x 2及y =x 2分别交于B ,C 两点,若正方形BCDE 的一边DE 与y 轴重合,则正方形BCDE 的面积为________.图K -10-5三、解答题13.已知点P (1,-2a )在二次函数y =ax 2+6的图象上,并且点P 关于x 轴的对称点在反比例函数y =k x的图象上.(1)求此二次函数和反比例函数的表达式;(2)点(-1,4)是否同时在(1)中的两个函数的图象上?14.已知抛物线y =ax 2+n (an >0)与抛物线y =-2x 2的形状相同,且其图象上与x 轴最近的点到x 轴的距离为3.(1)求a ,n 的值;(2)在(1)的情况下,指出抛物线y =ax 2+n 的开口方向、对称轴和顶点坐标.15.如图K -10-6,一辆宽为2米的货车要通过跨度为8米,拱高为4米的单行抛物线隧道(从正中通过),抛物线满足表达式y =-14x 2+4.为保证安全,车顶离隧道的顶部至少要有0.5米的距离,求货车的限高应是多少.图K -10-616.如图K -10-7,直线AB 经过点B (0,6),且与抛物线y =ax 2+2在第一象限内相交于点P ,又知tan ∠ABO =23,△AOP 的面积为6.(1)求a 的值;(2)能否将抛物线y =ax 2+2上下平移,使得平移后的抛物线经过点A ?链接听课例4归纳总结图K -10-7数形结合思想如图K -10-8,抛物线y =-12x 2+2与x 轴交于A ,B 两点,其中点A 在x 轴的正半轴上,点B 在x 轴的负半轴上(1)试写出该抛物线的对称轴和顶点C 的坐标.(2)在抛物线上是否存在一点M ,使△MAC ≌△OAC ?若存在,求出点M 的坐标;若不存在,请说明理由.图K -10-8详解详析【课时作业】 [课堂达标]1.[解析] D 把(-2,6)代入y =ax 2中,得4a =6,则a =32,所以这个二次函数的表达式为y=32x 2.A.当x =2时,y =32×22=6,所以点(2,6)在该函数的图象上;B.当x =1时,y =32×12=1.5,所以点(1,1.5)在该函数的图象上;C.当x =-1时,y =32×(-1)2=1.5,所以点(-1,1.5)在该函数的图象上;D.当x =2时,y =32×22=6,所以点(2,8)不在该函数的图象上.故选D.2.[解析] B 根据题意知,抛物线y =2x 2-4的对称轴为直线x =0,故它的顶点在y 轴上.故选B.3.[答案] A4.[解析] C ∵A (x 1,y 1),B (x 2,y 2)是函数y =-2x 2+m (m 是常数)的图象上的两个点,∴y 1=-2x 12+m ,y 2=-2x 22+m .∵x 1<x 2<0,∴x 12>x 22,∴y 1<y 2.故选C.(也可以利用二次函数的增减性得出y 1<y 2)5.[答案] C6.[解析] B 将y =3.05代入y =-15x 2+3.5,得3.05=-15x 2+3.5,解得x =-1.5(舍去)或x =1.5,∴若命中篮圈中心,则他与篮底的距离l 是2.5+1.5=4(m),故选B.7.[解析] C A 项,由抛物线可知,图象与y 轴交于负半轴,∴a <0,由直线可知,图象过第一、二、三象限,∴a >0,故此选项不符合题意;B 项,由抛物线可知,图象与y 轴交于正半轴,∴a >0,开口向下,∴b <0,由直线可知,图象过第一、二、三象限,∴a >0,b >0,故此选项不符合题意;C 项,由抛物线可知,图象与y 轴交于负半轴,∴a <0,开口向上,∴b >0,由直线可知,图象过第一、二、四象限,∴a <0,b >0,故此选项符合题意;D 项,由直线可知,图象与y 轴交于负半轴,∴b <0,由抛物线可知,开口向上,∴b >0,故此选项不符合题意.故选C.8.[答案] y 轴 (0,3) 相同[解析] 抛物线y =ax 2+c 的对称轴是y 轴,顶点坐标是(0,c ),它与抛物线y =ax 2的形状相同,可由抛物线y =ax 2经过平移得到.9.[答案] (-2,-2)[解析] ∵点A (2,m )在抛物线y =-12x 2上,∴m =-12×22=-2,∴点A 的坐标是(2,-2),它关于y 轴对称的点的坐标是(-2,-2).10.[答案] a >b >c >d[解析] 因为直线x =1与四条抛物线的交点坐标从上到下依次为(1,a ),(1,b ),(1,c ),(1,d ),所以a >b >c >d .11.[答案] 10 2[解析] 根据题意,当y =-2时,有-2=-125x 2,解得x =±5 2,∴A (-5 2,-2),B (5 2,-2),∴此时水面的宽度AB =2×5 2=10 2(m).12.[答案] 169[解析] 设点A 的坐标为(a ,0),由题意可得,点B 的坐标为(a ,14a 2),点C 的坐标为(a ,a 2),∴a =a 2-14a 2,解得a 1=0(舍去),a 2=43,∴正方形BCDE 的面积是43×43=169,故答案为169.13.[解析] (1)将点P (1,-2a )的坐标代入二次函数y =ax 2+6,组成方程即可求出a 的值,从而求出点P 关于x 轴的对称点的坐标,代入反比例函数表达式即可求出k 的值,从而得到函数表达式;(2)将(-1,4)分别代入两个函数的表达式,若同时成立,则表示该点同时在(1)中的两个函数的图象上.解:(1)∵点P (1,-2a )在二次函数y =ax 2+6的图象上,∴-2a =a +6,解得a =-2,∴点P的坐标为(1,4),所求二次函数的表达式为y =-2x 2+6.点P 关于x 轴对称的点的坐标为(1,-4),∴k =-4,∴所求反比例函数的表达式为y =-4x.(2)点(-1,4)既在二次函数y =-2x 2+6的图象上,也在反比例函数y =-4x的图象上.14.[解析] 抛物线y =ax 2+n 与y =-2x 2的形状相同,则a =±2.因为图象上与x 轴最近的点到x 轴的距离为3,即|n |=3,所以n =±3.解:(1)由题意,得a =±2,n =±3.∵an >0,∴⎩⎪⎨⎪⎧a =2,n =3或⎩⎪⎨⎪⎧a =-2,n =-3.(2)当a =2,n =3时,抛物线y =2x 2+3开口向上,对称轴为y 轴,顶点坐标为(0,3);当a=-2,n =-3时,抛物线y =-2x 2-3开口向下,对称轴为y 轴,顶点坐标为(0,-3).15.解:当x =1时,y =-14×12+4=154.又因为车顶离隧道的顶部至少要有0.5米的距离, 所以限高为154-0.5=3.25(米).即货车的限高应是3.25米.16.解:(1)∵直线AB 经过点B (0,6), 且tan ∠ABO =23,∴OB =6,OA OB =23,∴OA =4,∴A (4,0).设点P 的坐标为(m ,n ), ∵△AOP 的面积为6, ∴12×4×n =6,∴n =3.过点P 作PC ⊥OA 于点C ,∴PC ∥OB ,∴PC OB =AC OA ,即36=AC 4, ∴AC =2,∴点P 的横坐标为m =4-2=2, ∴点P 的坐标为(2,3).∵点P 在抛物线y =ax 2+2上, ∴3=4a +2,解得a =14.(2)设平移后的抛物线的表达式为y =14x 2+2+k ,把A (4,0)代入y =14x 2+2+k ,得4+2+k =0,解得k =-6,∴将抛物线y =ax 2+2向下平移6个单位长度,可使平移后的抛物线经过点A . [素养提升]解:(1)抛物线y =-12x 2+2的对称轴为直线x =0,顶点C 的坐标为(0,2).(2)对于抛物线y =-12x 2+2,当y =0时,x =±2,∴A (2,0),B (-2,0),则△OAC 是等腰直角三角形.假设抛物线上存在一点M ,使△MAC ≌△OAC , ∵AC 为公共边,OA =OC ,∴点M 与点O 关于直线AC 对称, 则四边形OAMC 是正方形, ∴点M 的坐标为(2,2).当x =2时,y =-12×22+2=0≠2,∴点M (2,2)不在抛物线上,即抛物线上不存在点M ,使△MAC ≌△OAC .。
九年级数学下册 第二章 二次函数 2.5 二次函数与一元二次方程 第1课时 二次函数与一元二次方程教

2.5 二次函数与一元二次方程第1课时二次函数与一元二次方程1.经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系;(重点)2.理解二次函数与x轴交点的个数与一元二次方程的根的关系,理解何时方程有两个不等的实根、两个相等的实根和没有实根;(重点)3.通过观察二次函数与x轴交点的个数,讨论一元二次方程的根的情况,进一步培养学生的数形结合思想.(难点)一、情境导入一个涵洞成抛物线形,它的截面如图所示.现测得,当水面宽AB=1.6m时,涵洞顶点与水面的距离OC=2.4m.当水位上升一定高度到达点F时,这时,离水面距离CF =1.5m,则涵洞宽ED是多少?是否会超过1m?根据已知条件,要求ED宽,只要求出FD的长度.在如图所示的直角坐标系中,只要求出点D的横坐标即可.由已知条件可得到点D的纵坐标,又因为点D在涵洞所成的抛物线上,所以利用抛物线的函数关系式可以进一步算出点D的横坐标.你会求吗?二、合作探究探究点一:二次函数与一元二次方程【类型一】求抛物线与x轴的交点坐标已知二次函数y=2x2-4x-6,它的图象与x轴交点的坐标是________________.解析:y=2x2-4x-6=2(x2-2x-3)=2(x-3)(x+1),设2(x-3)(x+1)=0,解得x1=3,x2=-1,∴它的图象与x轴交点的坐标是(3,0),(-1,0).故答案为(3,0),(-1,0).方法总结:抛物线与x轴的交点的横坐标,就是二次函数为0时,一元二次方程的解.变式训练:见《学练优》本课时练习“课堂达标训练”第6题【类型二】判断抛物线与x轴交点的个数已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).(1)求证:此抛物线与x轴总有两个交点;(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值.解析:(1)只需证明Δ=(m+2)2-4m×2≥0即可;(2)利用因式分解法求得抛物线与x轴交点的横坐标,然后根据x的值来求正整数m的值.(1)证明:∵m≠0,∴Δ=(m+2)2-4m×2=m2+4m+4-8m=(m-2)2.∵(m-2)2≥0,∴Δ≥0,∴此抛物线与x轴总有两个交点;(2)解:令y=0,则(x-1)(mx-2)=0,所以x-1=0或mx-2=0,解得x1=1,x2=2m.当m为正整数1或2时,x2为整数,即抛物线与x轴总有两个交点,且它们的横坐标都是整数.所以正整数m的值为1或2.方法总结:解答本题的关键是明确当根的判别式Δ≥0抛物线与x轴有两个交点.变式训练:见《学练优》本课时练习“课堂达标训练”第8题【类型三】已知抛物线与x 轴的交点个数,求字母系数的取值范围已知函数y=(k-3)x2+2x+1的图象与x轴有交点,求k的取值范围.解析:应分k-3=0和k-3≠0两种情况进行讨论,(1)当k-3=0即k=3时,此函数是一次函数;(2)当k-3≠0,即k≠3时,此函数是二次函数,根据函数图象与x 轴有交点可知Δ=b2-4ac≥0,求出k的取值范围即可.解:当k=3时,函数y=2x+1是一次函数.∵一次函数y=2x+1与x轴有一个交点,∴k=3;当k≠3时,y=(k-3)x2+2x+1是二次函数.∵二次函数y=(k-3)x2+2x+1的图象与x轴有交点,∴Δ=b2-4ac≥0.∵b2-4ac=22-4(k-3)=-4k+16,∴-4k+16≥0.∴k≤4且k≠3.综上所述,k的取值范围是k≤4.方法总结:由于k的取值范围不能确定,所以解决本题的关键是要注意分类讨论,不要漏解.变式训练:见《学练优》本课时练习“课后巩固提升”第5题【类型四】二次函数与一元二次方程的判别式、根与系数的关系的综合已知:抛物线y=x2+ax+a-2.(1)求证:不论a取何值时,抛物线y =x2+ax+a-2与x轴都有两个不同的交点;(2)设这个二次函数的图象与x轴相交于A(x1,0),B(x2,0),且x1、x2的平方和为3,求a的值.解析:(1)利用关于x的一元二次方程x2+ax+a-2=0的根的判别式的符号进行证明;(2)利用根与系数的关系写出x1、x2的平方和是x21+x22=(x1+x2)2-2x1x2=a2-2a+4=3,由此可以求得a的值.(1)证明:∵Δ=a2-4(a-2)=(a-2)2+4>0,∴不论a取何值时,抛物线y=x2+ax+a-2与x轴都有两个不同的交点;(2)解:∵x1+x2=-a,x1·x2=a-2,∴x21+x22=(x1+x2)2-2x1·x2=a2-2a+4=3,∴a=1.方法总结:判断一元二次方程与x轴的交点,只要看根的判别式的符号即可,而要判断一元二次方程根的情况,要利用根与系数关系.变式训练:见《学练优》本课时练习“课后巩固提升”第6题探究点二:利用二次函数解决运动中的抛物线问题如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A 在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.(1)求足球开始飞出到第一次落地时,该抛物线的表达式;(2)足球第一次落地点C距守门员多少米(取43=7)?(3)运动员乙要抢到第二个落点D,他应再向前跑多少米(取26=5)?解析:要求足球开始飞出到第一次落地时,抛物线的表达式,则需要根据已知条件确定点A和顶点M的坐标,因为OA=1,OB =6,BM=4,所以点A的坐标为(0,1),顶点M的坐标是(6,4).根据顶点式可求得抛物线关系式.因为点C在x轴上,所以要求OC的长,只要把点C的纵坐标y=0代入函数关系式,通过解方程求得OC的长.要计算运动员乙要抢到第二个落点D,他应再向前跑多少米,实际就是求DB的长.求解的方法有多种.解:(1)设第一次落地时,抛物线的表达式为y=a(x-6)2+4,由已知:当x=0时,y=1,即1=36a+4,所以a=-112.所以函数表达式为y=-112(x-6)2+4或y=-112x2+x+1;(2)令y=0,则-112(x-6)2+4=0,所以(x-6)2=48,所以x1=43+6≈13,x2=-43+6<0(舍去).所以足球第一次落地距守门员约13米;(3)如图,第二次足球弹出后的距离为CD,根据题意:CD=EF(即相当于将抛物线AEMFC向下平移了2个单位).所以2=-112(x-6)2+4,解得x1=6-26,x2=6+26,所以CD=|x1-x2|=46≈10.所以BD=13-6+10=17(米).方法总结:解决此类问题的关键是先进行数学建模,将实际问题中的条件转化为数学问题中的条件.常有两个步骤:(1)根据题意得出二次函数的关系式,将实际问题转化为纯数学问题;(2)应用有关函数的性质作答.三、板书设计二次函数与一元二次方程1.二次函数与一元二次方程2.利用二次函数解决运动中的抛物线问题本节课注意发挥学生的主体作用,让学生通过自主探究、合作学习来主动发现问题、提出问题、解决问题,实现师生互动,通过这样的教学实践取得一定的教学效果,再次认识到教师不仅要教给学生知识,更要培养学生良好的数学素养和学习习惯,让学生学会学习,使他们能够在独立思考与合作学习交流中解决学习中的问题. 如有侵权请联系告知删除,感谢你们的配合!。
深圳松岗中学2015-2016九年级下第二章《二次函数》测试卷(无答案)

二次函数单元测试卷一、精心选一选,相信自己的判断!(每小题3分,共30分)1.若y =(2-m)23mx -是二次函数,且开口向上,则m 的值为( )A.2.二次函数c bx x y ++=2的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )A .x =4 B. x =3 C. x =-5 D. x =-1。
3.抛物线122+--=m mx x y 的图象过原点,则m 为( ) A .0B .1C .-1D .±14.把二次函数122--=x x y 配方成顶点式为( ) A .2)1(-=x yB . 2)1(2--=x yC .1)1(2++=x yD .2)1(2-+=x y5.将二次函数y =-2(x -1)2-2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )A.(0,0)B.(1,-2)C.(0,-1)D.(-2,1) 6.函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是( ) A .3<k B .03≠<k k 且 C .3≤k D .03≠≤k k 且 7.二次函数c bx ax y ++=2的图象如图所示,则abc ,ac b 42- c ba ++这3个式子中,值为正数的有( ) A .4个B .3个C .2个D .1个8.已知反比例函数xk y =的图象如图,则二次函数222k x kx y +-=的图象大致为( )9、在同一直角坐标系中,函数b ax y +=2与)0(≠+=ab b ax y 的图象大致如图 ( )10、已知二次函数y=-12x 2-3x -52,设自变量的值分别为x 1,x 2,x 3,且-3<x 1<x 2<x 3, 则对应的函数值y 1,y 2,y 3的大小关系是( )A.y 1>y 2>y 3B.y 1<y 2<y 3;C.y 2>y 3>y 1D.y 2<y 3<y 1二、耐心填一填:(把答案填放相应的空格里。
九级数学下第二二次函数

• 一个人只要坚持不懈地 追求,他就能达到目的.
不同点: (2)的图像在(1)的图象的内侧. (2)的S比(1)中的S增长速度快 .
20 40 60 80 100 120 140 V/(km/h)
做一做
s
288
200 144 128 100 72 64 36 32
? 16
0
观察图象,回答问题串
S=510 v2
S=1100v2
(2)如果行车速度是60km/h, 那么在雨天行驶和在晴天行驶 相比,刹车距离相差多少米?你 是怎么知道的?
做一做:
1、按下列要求求出二次函数的解析式: (1)已知抛物线y=ax2+c经过点(-3,2) (0,-1)求该抛物线线的解析式。
(2)形状与y=-2x2+3的图象形状相同, 但开口方向不同,顶点坐标是(0,1) 的抛物线解析式。
(3)对称轴是y轴,顶点纵坐标是-3, 且经过(1,2)的点的解析式,
九年级数学(下)第二章 二次函数
3.刹车距离与二次函数
(y=ax2与y=ax2+c图象和性质)
做一做
s
288
200 144 128 100 72 64 36 32
? 16
0
描点,连线
S=510 v2
观察图象,回答问题串
S=1100v2
两个图象有什么相同与不同?
相同点: (1)它们都是抛物线的一部分; (2)二者都位于y轴的右侧. (3)函数值都随y值的增大而增大.
y=3x2
y=3x2-1
二次函数y=3x2+1的 图象与y=3x2
一样,仍是抛物线.
顶点不同,分别是 原点(0,0)和(0,-1).
北师大版九年级下册数学习题课件2.2.1二次函数y=x2与y=-x2的图象与性质

探究培优
14.已知点 A(1,a)在抛物线 y=x2 上. (1)求点 A 的坐标.
解:把点 A(1,a)的坐标代入 y=x2, 得 a=1,所以点 A 的坐标为(1,1).
探究培优
(2)在 x 轴上是否存在点 P,使得△ OAP 是等腰三角形?若存在, 求出点 P 的坐标; 若不存在,请说明理由.
第二章 二次函数
第1课时 二次函数y=x2与y=-x2的图象与性质
第二章 二次函数
第1课时 二次函数y=x2与y=-x2的图象与性质
2 二次函数的图象与性质
2 二次函数的图象与性质
夯实基础
【点拨】因为 a<-1,所以 a-1<a<a+1<0,即这三个点都 在函数 y=x2 图象的对称轴左侧.又因为在对称轴左侧,y 随 x 的增大而减小,所以 y3<y2<y1,故选 C.
整合方法
13.点 M(-3,9)在二次函数 y=x2 的图象上吗?请分别写出点 M 关于 x 轴的对称点 N,关于 y 轴的对称点 P,关于原点的 对称点 Q 的坐标.点 N,P,Q 在二次函数 y=x2 的图象上吗? 在二次函数 y=-x2 的图象上吗?
整合方法
解:∵x=-3 时,y=(-3)2=9, ∴点 M 在二次函数 y=x2 的图象上. 由题意,得点 N(-3,-9),点 P(3,9),点 Q(3,-9), ∴点 P 在二次函数 y=x2 的图象上,N,Q 两点在二次函数 y=- x2 的图象上.
答案显示
夯实基础
1.关于二次函数 y=x2 的图象,下列说法中不正确的是( D ) A.图象经过点(0,0) B.图象的顶点为点(0,0) C.图象的最低点是点(0,0) D.图象的最高点是点(0,0)
夯实基础
罗湖中学数学中考复习《二次函数》卷(附答案)
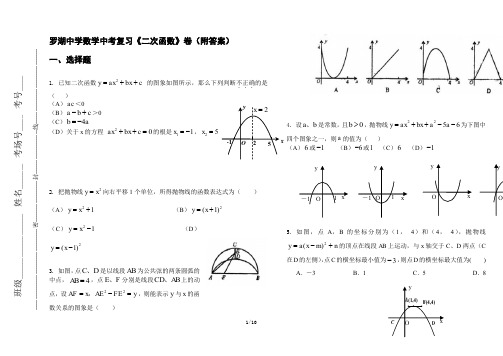
1/10班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------罗湖中学数学中考复习《二次函数》卷(附答案)一、选择题1. 已知二次函数c bx ax y ++=2的图象如图所示,那么下列判断不正确...的是( )(A )ac <0 (B )c b a +->0 (C )a b 4-=(D )关于x 的方程 02=++c bx ax 的根是11-=x ,52=x2. 把抛物线2y x=向右平移1个单位,所得抛物线的函数表达式为()(A )21y x =+(B )2(1)y x =+ (C )21y x =- (D )2(1)y x =-3. 如图,点C D 、是以线段AB 为公共弦的两条圆弧的中点,4AB =,点E F 、分别是线段CD AB 、上的动点,设22AF x AE FE y =-=,,则能表示y 与x 的函数关系的图象是( )4. 设a b 、是常数,且0b >,抛物线2256y ax bx a a =++--为下图中四个图象之一,则a 的值为( )(A )6或1- (B )6-或1 (C )6 (D )1-5. 如图,点A ,B 的坐标分别为(1, 4)和(4, 4),抛物线n m x a y +-=2)(的顶点在线段AB 上运动,与x 轴交于C 、D 两点(C在D 的左侧),点C 的横坐标最小值为3-,则点D 的横坐标最大值为( ) A .-3 B .1 C .5 D .8x2/10班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------6. 已知抛物线2y ax bx c =++(a <0)过A (2-,0)、O (0,0)、B (3-,1y )、C (3,2y )四点,则1y 与2y 的大小关系是( ) A .1y >2yB .1y 2y =C .1y <2yD .不能确定7. 双曲线4y x =与2y x=在第一象限内的图象如图所示,作一条平行于y 轴的直线分别交双曲线于A B 、两点,连接OA OB 、,则AOB △的面积为( )A .1 B.2 C.3 D.48. 二次函数2365y x x =--+的图像的顶点坐标是( )A .(18)-,B .(18), C .(12)-, D .9. 抛物线c bx x y ++=2图像向右平移2个单位再向下平移3个单位,所得图像的解析式为223y x x =--,则b c 、的值为( ) A .22b c ==, B .20b c ==,C .21b c =-=-,D .32b c =-=,10. 抛物线c bx ax y ++=2图像如图所示,则一次函数24b ac bx y +--=与反比例函数 a b cy x++=在同一坐标系内的图像大致为( )二、填空题11. 已知二次函数()()221y x a a =-+-(a 为常数),当a 取不同的值时,其图象构成一个“抛物线系”.下图分别是当1a =-,0a =,1a =,2a =时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是y = .xxA .B .C .D .3/10班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------12. 将抛物线2)1(2-=x y 先向左平移1个单位后所得到的新抛物线的表达式为 .13. 小汽车刹车距离s (m )与速度v (km/h )之间的函数关系式为21001v s =,一辆小汽车速度为100km/h ,在前方80m 处停放一辆故障车,此时刹车有危险(填“会”或“不会”). 14. 如图,在ABC △中,90B ∠=,12mm AB =,24mm BC =,动点P 从点A 开始沿边AB 向B 以2mm/s 的速度移动(不与点B 重合),动点Q 从点B 开始沿边BC 向C 以4mm/s 的速度移动(不与点C 重合).如果P 、Q 分别从A 、B 同时出发,那么经过_____________秒,四边形APQC 的面积最小.15. 抛物线242my x x =-+与x 轴的一个交点的坐标为()10,,则此抛物线与x 轴的另一个交点的坐标是_________.16. (1)将抛物线y 1=2x 2向右平移2个单位,得到抛物线y 2的图象,则y 2= ;(2)如图,P 是抛物线y 2对称轴上的一个动点,直线x =t 平行于y 轴,分别与直线y =x 、抛物线y 2交于点A 、B .若△ABP 是以点A 或点B 为直角顶点的等腰直角三角形,求满足条件的t 的值,则t = .17. 将抛物线212y x =-向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为_________.18. 在平面直角坐标系中,将二次函数2(2)2y x =-+的图象向左平移2个单位,所得图象对应的函数解析式为_____________.19. 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.x班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------20. 小颖同学想用“描点法”画二次函数2(0)y ax bx c a =++≠的图象,取自变量x 的5个值,分别计算出对应的y 值,如下表: x = .三、计算题21. 如图,平面直角坐标系中,以点(11)C ,为圆心,2为半径作圆,交x 轴于A 、B 两点.(1)求出A 、B 两点的坐标;(2)有一开口向下..的抛物线2()y a x h k =-+经过点A 、B ,且其顶点在C 上,试确定此抛物线的解析式.四、应用题22. 某商店经营一种小商品,进价为2.5元,据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售价每降低1元,平均每天就可以多售出100件.(1)假设每件商品降价x 元,商店每天销售这种小商品的利润是y 元,请写出y 与x 间的函数关系式,并说明x 的取值范围;(2)每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?(注:销售利润=销售收入-购进成本)23. 如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200 m 、米5/10班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------120 m ,花坛中有一横两纵的通道,横、纵通道的宽度分别为3x m 、2x m .(1)用代数式表示三条通道的总面积S ;当通道总面积为花坛总面积的12511时,求横、纵通道的宽分别是多少?(2)如果花坛绿化造价为每平方米3元,通道总造价为3168 x 元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852 = 7225,862 = 7396,872 = 7569)五、复合题24. 如图,抛物线bx ax y +=2经过点A (4,0),B (2,2),连结OB ,AB .(1)求该抛物线的解析式;(2)求证:△OAB 是等腰直角三角形;(3)将△OAB 绕点O 按顺时针方向旋转l35º得到△OA′B′,写出△OA′B′的中点P 的出标.试判断点P 是否在此抛物线上,并说明理由.25. 已知关于x 的方程2(31)220mx m x m --+-=(1)求证:无论m 取任何实数时,方程恒有实数根.(2)若关于x 的二次函数2(31)22y mx m x m =--+-的图象与x 轴两交点间的距离为2时,求抛物线的解析式.(3)在直角坐标系xoy 中,画出(2)中的函数图象,结合图象回答问题:当直线y x b =+与(2)中的函数图象只有两个交点时,求b 的取值范围.6/10班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------一、选择题第1题答案.B第2题答案.D第3题答案.C第4题答案.D第5题答案.D第6题答案.A第7题答案.A第8题答案.A第9题答案.B第10题答案.D二、填空题第11题答案.112x -第12题答案.2x 2y =第13题答案.会第14题答案.3第15题答案.(3,0)第16题答案.(1)2(x -2)2 或2288x x -+ (2分)(2)3、12分.对一个给0.5分,得2分的要全对,其余有错不倒扣分)7/10班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------第17题答案. 21(1)22y x =--+(或填21322y x x =-++)第18题答案.22y x =+第19题答案.12第20题答案.2三、计算题第21题答案.解:(1)过点C 作CD AB ⊥,垂足为D , 则12CD CA CB ===,,∴DB DA ==1分点(1A -,点10)B ,. 3分 (2)延长DC ,交C 于点P .由题意可知,P 为抛物线的顶点,并可求得点(13)P ,. 4分设此抛物线的表达式为2(1)3y a x =-+,5分又∵抛物线过点10)B ,,则2011)3a =-+,得1a =-. 所以此抛物线的解析式为22(1)322y x x x =--+=-++.7分四、应用题第22题答案.(1) 解:设降价x 元时利润最大依题意:()()13.52.5500100y x x =--+整理得:()()2100655011y x x x =-++<≤(2)由(1)可知,当3x =时y 取最大值,最大值为6400即降价3元时利润最大,∴销售单价为10.5元时,最大利润6400元. 答:销售单价为10.5元时利润最大,最大利润为6400元 10分第23题答案.(1)由题意得 S = 3x · 200 + 2x · 120×2-2×6x 2 =-12x 2 + 1080x .由 S =12511×200×120,得 x 2-90x + 176 = 0,解得 x = 2 或 x = 88. 又 x >0,4x <200,3x <120,解得0<x <40, 所以x = 2,得横、纵通道的宽分别是6 m 、4 m . (2)设花坛总造价为y 元. 则 y = 3168x +(200×120-S )×3 = 3168x +(24000 + 12x 2-1080x )×3 = 36x 2-72x + 72000 = 36(x -1)2 + 71964,当x = 1,即纵、横通道的宽分别为3 m 、2 m 时,花坛总造价量低,最低总造价为71964元.8/10班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------五、复合题第24题答案.解:(1)由题意得1640422a b a b +=⎧⎨+=⎩解得122a b ⎧=-⎪⎨⎪=⎩∴该抛物线的解析式为:2122y x x =-+(2)过点B 作BC x ⊥轴于点C ,则2OC BC AC === ∴45BOC OBC BAC ABC ∠=∠=∠=∠= ∴90OBA OB AB ∠==, ∴OAB △是等腰直角三角形(3)∵OAB △是等腰直角三角形,4OA =∴OB AB ==由题意得点A '坐标为(-- ∴A B ''的中点P的坐标为(-当x =21(2(2y =-⨯+⨯≠- ∴点P 不在二次函数的图象上.第25题答案.解:(1)分两种情况讨论.1︒当0m =时,方程为x 20-= 2∴= 方程有实数根 2︒当0m ≠,则一元二次方程的根的判别式()()2222314229618821m m m m m m m m m ∆=----=-+-+=++⎡⎤⎣⎦=()21m +≥0不论m 为何实数,∆≥0成立,∴方程恒有实数根 综合1︒、2︒,可知m 取任何实数,方程()231220mx m x m --+-=恒有实数根(2)设12x x ,为抛物线()43122y mx m x m =--+-与x 轴交点的横坐标.则有12123122m m x x x x m m--+==, 由12x x -=A9/10班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------1m m ==+=由122x x -=,得1122m m m m ++=∴=,或12m m+=- 1m ∴=或13m =-,∴所求抛物线的解析式为2212182233y x x y x x =-=-+-,,即121(2)(2)(4)3y x x y x x =-=---,其图象为右图所示:方法 2.由2(31)220mx m x m --+-=得[](2)(1)0x mx m ---=可知抛物线2(31)22y mx m x m =--+-不论m 为任何不为0的实数时恒过定点12(20)2x x -=,可得22220x x -=∴=或24x =,对应的m 的值为1m =或13m =-即所求抛物线解析式为212(2)y x x x x =-=-,221812(2)(4)333y x x x x =-+-=---(3)在(2)条件下,直线y x b =+与抛物线12y y ,组成的图象只有两个交点,结合图象,求b 的取值范围.212y x xy x b⎧=-⎨=+⎩当1y y =时,得230x x b --= 由940b ∆=+= 得94b =- 同理2218294(83)033y x x b y x b⎧=-+-⎪⇒∆=-+=⎨⎪=+⎩得2312b =-观察函数图象可知当94b <-或2312b >-时,直线y x b =+与(2)中的图象只有两个交点.由21221(2)(4)3y x xy x x ⎧=-⎪⎨=---⎪⎩当12y y =时,有2x =或1x = 当1x =时,1y =-所以过两抛物线交点(11)20,-,(,)的直线为2y x =-,综上所述可知:当94b <-或2312b >-或2b =-时,直线y x b =+与(2)中的图象只有两个交点.m1()1m -2-10/10班级_____________________ 姓名________ 考场号_____ 考号_____---------------------------------------密--------------------封---------------------线------------------------------------。
深圳笋岗中学九年级数学上册第二十二章《二次函数》经典练习题(含答案解析)
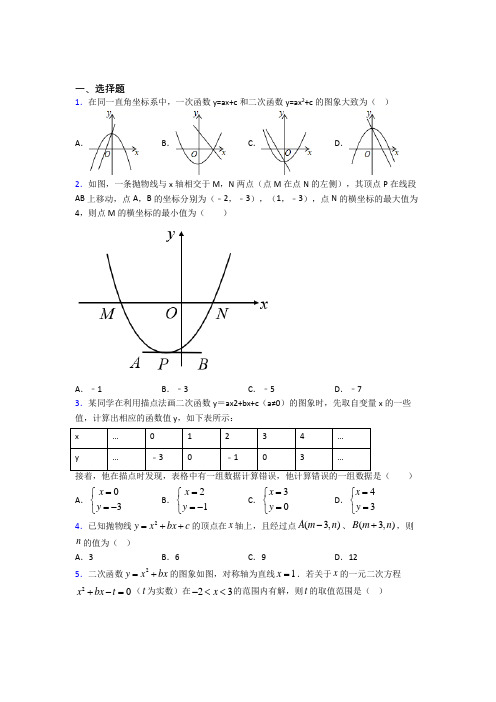
一、选择题1.在同一直角坐标系中,一次函数y=ax+c 和二次函数y=ax 2+c 的图象大致为( )A .B .C .D .2.如图,一条抛物线与x 轴相交于M ,N 两点(点M 在点N 的左侧),其顶点P 在线段AB 上移动,点A ,B 的坐标分别为(﹣2,﹣3),(1,﹣3),点N 的横坐标的最大值为4,则点M 的横坐标的最小值为( )A .﹣1B .﹣3C .﹣5D .﹣73.某同学在利用描点法画二次函数y =ax2+bx+c (a≠0)的图象时,先取自变量x 的一些值,计算出相应的函数值y ,如下表所示: x … 0 1 2 3 4 … y…﹣3﹣13…) A .03x y =⎧⎨=-⎩B .21x y =⎧⎨=-⎩C .30x y =⎧⎨=⎩D .43x y =⎧⎨=⎩4.已知抛物线2y x bx c =++的顶点在x 轴上,且经过点(3,)A m n -、(3,)B m n +,则n 的值为( )A .3B .6C .9D .125.二次函数2y x bx =+的图象如图,对称轴为直线1x =.若关于x 的一元二次方程20x bx t +-=(t 为实数)在23x -<<的范围内有解,则t 的取值范围是( )A .1t ≥-B .13t -≤<C .18t -≤<D .38t <<6.点()13,P y 、Q ()24,y 是二次函数245y x x =-+的图象上两点,则1y 与2y 的大小关系为( ) A .12y y >B .12y y <C .12y y =D .无法确定7.抛物线28y x x q =++与x 轴有交点,则q 的取值范围是( ) A .16q <B .16q >C .16q ≤D .16q ≥8.已知抛物线y =ax 2+bx +c 上部分点的横坐标与纵坐标的对应值如下表,给出下列结论:①抛物线y =ax 2+bx +c 经过原点;②2a +b =0;③当y >0时,x 的取值范围是x <0或x >2;④若点P (m ,n )在该抛物线上,则am 2+bm ≤a +b .其中正确结论的个数是( ) x … ﹣1 0 1 2 3 … y…3﹣13…A .4个B .3个C .2个D .1个9.已知函数235y x =-+经过A (m ,1y )、B (m−1,2y ),若12y y >.则m 的取值范围是( ) A .0m ≤B .12m <C .102m <<D .12m <<10.如图是抛物线y 1=ax 2+bx +c (a ≠0)图象的一部分,抛物线的顶点坐标是A (1,3),与x 轴的一个交点B (4,0),直线y 2=mx +n (m ≠0)与抛物线交于A 、B 两点.下列结论:①2a +b =0;②abc >0;③方程ax 2+bx +c =3有两个相等的实数根;④抛物线与x 轴的另一个交点是(﹣1,0);⑤当1<x <4时,有y 2<y 1;⑥a +b ≥m (am +b )(m 实数)其中正确的是( )A .①②③⑥B .①③④C .①③⑤⑥D .②④⑤11.如图所示,一段抛物线:()233044y x x x =-+≤≤记为1C ,它与x 轴交于两点O ,1A ;将1C 绕1A 旋转180°得到2C ,交x 轴于2A ;将2C 绕2A 旋转180°得到3C ,交x 轴于3A ;⋅⋅⋅如此进行下去,直至得到506C ,则抛物线506C 的顶点坐标是( )A .()2020,3B .()2020,3-C .()2022,3D .()2022,3-12.表格对应值:x 1 2 3 4 2ax bx c ++0.5-512.522判断关于x 的方程2ax bx c ++=的一个解x 的范围是( )A .01x <<B .12x <<C .23x <<D .34x <<13.若二次的数2y ax bx c =++的x 与y 的部分对应值如下表: x 7-6- 5- 4-3-2-y27- 13-3-353A .5B .3-C .13-D .27-14.如图,以直线1x =为对称轴的二次函数2y ax bx c =++的图象与x 轴负半轴交于A 点,则一元二次方程20ax bx c ++=的正数解的范围是( ).A .23x <<B .34x <<C .45x <<D .56x <<15.二次函数2y ax bx c =++的图象如图所示,下列结论正确的是( )A .0abc >B .0a b c ++=C .420a b c ++=D .240b ac -<二、填空题16.抛物线y =﹣12(x +1)2+3的顶点坐标是_____. 17.对于抛物线243y x x =-+,当712x -<<时,关于x 的一元二次方程2430x x t -+-=有解,则t 的取值范围是 ______.18.关于x 的一元二次方程220x x k -++=的一个解是13x =,则抛物线22y x x k =-++与x 轴的交点坐标是____.19.将二次函数y=x 2-4x+5化成=(x-h )2+k 的形式,则y= _____.20.已知点P (m ,n )在抛物线2y ax x a =--上,当1m 时,总有1n ≥-成立,则实数a 的取值范围是_______.21.已知关于x 的一元二次方程x 2﹣(2m +1)x +m 2﹣1=0有实数根a ,b ,则代数式a 2﹣ab +b 2的最小值为_____.22.已知二次函数246y x x =--,若16x -≤≤,则y 的取值范围为____. 23.抛物线y =x 2+2x-3与x 轴的交点坐标为____________________.24.定义:在平面直角坐标系中,若点A 满足横、纵坐标都为整数,则把点A 叫做“整点”.如:()3,0B 、()1,3C -都是“整点”.抛物线()2220y ax ax a a =++->与x 轴交于点M ,N 两点,若该抛物线在M 、N 之间的部分与线段MN 所围的区域(包括边界)恰有5个整点,则a 的取值范围是_______.25.如图,在平面直角坐标系中抛物线y =x 2﹣3x +2与x 轴交于A 、B 两点,与y 轴交于点C ,点D 是对称轴右侧抛物线上一点,且tan ∠DCB =3,则点D 的坐标为_____.26.设A (-3,y 1),B (-2,y 2),C (12,y 3)是抛物线y =(x+1)2-m 上的三点,则y 1,y 2,y 3的大小关系为_______.(用“>”连接)三、解答题27.如图已知抛物线2y x bx c =-++与x 轴交于(1,0)A -,(3,0)B 两点与y 轴交于C 点,点P 是抛物线上在第一象限内的一个动点,且点P 的横坐标为t .(1)求抛物线的表达式;(2)如图,连接BC ,PB ,PC ,设PBC 的面积为S . ①求S 关于t 的函数表达式;②求P 点到直线BC 的距离的最大值,并求出此时点P 的坐标. 28.已知抛物线的顶点为()1,4-,且过点()2,5-. (1)求抛物线的解析式;(2)当0y >时,自变量x 的取值范围是______(直接写出结果).29.已知二次函数的图象经过点(0,3),(3,0),(1,0)-,求此二次函数的解析式,并判断点(2,3)P -是否在这个二次函数图象上.30.对于抛物线243y x x =-+. (1)求抛物线与坐标轴的交点坐标. (2)求抛物线的顶点坐标.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2二次函数y=x2的图象和性质
学校编者蒋静芳检查人时间
学习目标:
1、经历探索二次函数y=x2的图象的作法和性质的过程,获得利用图象研究二次函数性质的经验.
2、掌握利用描点法作出y=x2的图象,并能根据图象认识和理解二次函数y=x2的性质.
3、能够作为二次函数y=-x2的图象,并比较它与y=x2图象的异同,初步建立二次函数表达式与图象之间的联系.
重点:利用描点法作出y=x2的图象过程中,理解掌握二次函数y=x2的性质,这是掌握二次函数y=ax2+bx+c(a≠0)的基础,是二次函数图象、表达式及性质认识应用的开始,只有很好的掌握,才会把二次函数学好.注意图象的特点,掌握本质。
难点:函数图象的画法,及由图象概括出二次函数y=x2性质,它难在由图象概括性质,结合图象记忆性质.
教学活动:
一、温故引新
回顾:二次函数的概念
二、想一想:
作二次函数y=x2的图象。
三、.议一议
1.你能描述图象的形状吗?与同伴交流。
2.图象与x轴有交点吗?如果有,交点的坐标是什么?
3.当x<0时,y随着x的增大,y的值如何变化?当x>0时呢?
4.当x取什么值时,y的值最小?
5.图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流。
四.作一作
y=x2的图象的性质:
五、例题
【例1】求出函数y=x+2与函数y=x2的图象的交点坐标.
【例2】已知a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数y=x2的图象上,则()
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3。
