六年级上册数学第一单元圆的知识结构图
新人教版小学六年级数学上册圆的认识单元知识结构框架

新人教版小学六年级数学上册圆的理解单元知识结构框架在各个学段中,《课程标准》安排了“数与代数”、“空间与图形”、“统计与概率”、“实践与综合应用”四个学习领域。
在空间与图形方面,本册教材安排了《位置》、《圆》两个单元。
在《圆》这个单元中,通过对曲线图形——圆的特征和相关知识的探索与学习,初步理解研究曲线图形的基本方法,促动学生空间观点的进一步发展。
下面,我将从以下几个方面来谈我对这个单元教材的理解和我的主要教学策略:(出示课件)一、课标要求:关于圆,在第一学段(1—3年级)的要求是:1.会辨认长方形、正方形、三角形、平行四边形、圆等简单图形。
2.能用简单的语言描述它的特征。
初步了解它是轴对称图形。
3.能对简单图形实行分类并会用各种平面图形拼图。
在本学段,即第二学段(4—6年级)的要求是:1.通过观察、操作,理解圆,掌握圆的特征,会用圆规画圆;2.知道圆是轴对称图形,进一步理解轴对称图形,能使用平移、轴对称和旋转设计简单的图案。
3.探索并掌握圆的周长和面积公式,能够准确计算圆的周长和面积。
4.经历从实际生活中发现问题、提出问题、解决问题的过程,体会圆的知识在生活中的广泛应用,初步形成综合使用数学知识解决问题的水平。
圆是一种曲线图形,它同直线图形有不同的特点。
在本册之前各册教材出现的平面图形都是直线图形。
所以“圆”的教学是学生系统理解曲线图形特征的开始。
在低年级的教学中虽然也出现过圆,但仅仅直观的理解,比如:人教版一年级上册第四、五单元《理解物体和图形》《分类》,初步理解圆并能够对基本图形实行分类。
一年级下册第三单元《图形的拼组》,尝试用不同的立体图形或平面图形实行设计和拼组。
二年级上册第五单元《观察物体》,初步了解圆是轴对称图形,并知道它有无数条对称轴。
本册的第四单元《圆》,要理解圆的基本特征,会画圆,会计算圆的周长和面积并会灵活应用这些知识解决实际问题。
从学习直线图形到学习曲线图形,不论是内容本身、还是研究问题的方法,都有所变化,教材通过对圆的研究,使学生初步理解研究曲线图形的基本方法,同时,也渗透了曲线图形与直线图形的内在联系。
六年级数学上册 全册知识点 北师大版

北师大版小学数学六年级(上册)知识点第一单元圆1、使学生认识圆的特征:圆的半径、直径、圆心。
认识在同圆内半径和直径的关系。
知道圆是轴对称图形,有无数条对称轴,而这些对称轴都过圆心。
知道生活中有了圆才使我们的生活更美好。
2、认识同心圆、等圆。
知道圆的位置由圆心决定,圆的大小由半径或直径决定。
等圆的半径相等,位置不同;而同心圆的半径不同,位置相同。
3、使学生知道圆的周长和圆周率的含义,掌握圆的周长的计算公式,能够正确地计算圆的周长.介绍祖冲之在圆周率研究上的成就,渗透爱国主义教育。
在运用上,要能根据圆的周长算直径或半径,会算半圆的周长:圆的周长×1/2+直径。
会求组合图形的周长。
4、了解圆的面积的含义,经历圆面积计算公式的推导过程,掌握圆面积计算公式。
5、能正确运用圆的面积公式计算圆的面积,并能运用圆面积知识解决一些简单实际的问题。
会灵活运用圆的面积公式。
已知圆的周长会算圆的面积,会求组合图形的面积。
会算圆环的面积,并且知道在周长相等的情况下,正方形、长方形、圆三种图形中,圆的面积最大。
6、在估一估和探究圆面积公式的活动中,体会“化曲为直”的思想,初步感受极限思想。
第二单元百分数的应用本单元重点讲解百分数在生活中的应用,知识点为:1、知道百分数的意义:表示一个数是另一个数的百分之几的数,叫做百分数。
百分数也叫做百分率或百分比。
百分数通常不写成分数形式,而用百分号“%”表示;百分数有时也定义为分母是100的分数,但百分数与分数是有区别的:分数既可表示具体的量,又可表示两个数量间的倍比关系;然而百分数只能表示两个数量间的倍比关系;所以是不名数,也就是不能带单位的数。
2、在具体情景中理解“增加百分之几”或“减少百分之几”的意义,加深对百分数意义的理解。
3、能解决有关“增加百分之几”或“减少百分之几”的实际问题,提高运用数学解决实际问题的能力,体会百分数与现实生活的密切联系。
4、知道出勤率、出粉率、成活率等百分数的意义及在实际生活中的应用,会计算这种百分数。
北师大版六年级数学上册第一单元《圆》知识点小结

在食指绕拇指旋转一周的过程中,拇指所按的点不变,食指与拇指间的距离不变。
用图钉、线和笔画圆时,图钉要固定好,线要拉直。
用圆规画圆,针尖所在的位置是圆心,两脚间的距离是半径。
1.同一个圆里有无数条半径,长度都相等。
2.直径是圆内最长的线段。
半径一般用字母r表示。
在同一个圆里,所有半径的长度都相等。
(3)直径。
通过圆心并且两端都在圆上的线段叫作直径。
直径一般用字母d表示。
在同一个圆里,所有直径的长度都相等。
4. 圆的各部分之间的关系。
圆有无数条直径,无数条半径;同圆(或等圆)中的直径都相等,半径都相等;直径的长度是半径的2倍,可以表示为d=2r或r=d。
25. 圆心和半径的作用:圆心确定圆的位置,半径决定圆的大小。
6. 圆在生活中的应用。
汽车车轮、自行车的车轮、球、齿轮、方向盘、圆规、井盖、钟表、水杯、环岛……二、圆的认识(二)1. 圆的对称性:圆是轴对称图形,直径所在的直线是圆的对称轴。
圆有无数条对称轴。
2 . 常见的轴对称图形的对称轴的数量。
正方形有4条、长方形有2条、等边三角形有3条、等腰三角形有1条、等腰梯形有1条和圆有无数条。
3. 利用圆的对称性确定圆心的方法。
方法一把圆形纸片按下面的方法对折,两条折痕的交点就是圆心。
方法二把圆形纸片沿不同的方向任意折出两条直径(直径所在的直线即对称轴),两条直径(折痕)的交点就是圆心。
4.圆与内接或外接正多边形组成的组合图形的对称轴是经过圆心的正多边形的对称轴。
三、欣赏与设计综合运用旋转、轴对称和平移的知识设计图案。
四、圆的周长1.圆的周长的意义。
圆的周长就是圆一周的长度,也可以理解为将圆滚动一圈的长度。
直径的长短决定圆周长的大小。
2.圆周长的测量方法。
方法一用滚动法测量圆的周长。
在圆形硬纸板的边缘上点一点A,使点A对准直尺的0刻度,然后使圆形硬纸板在直尺上向右滚动一周,点A所指的新刻度就是这个圆形硬纸板的周长。
方法二用绕线法测量圆的周长。
在圆形硬纸板的边缘上点一点A,使点A对准线的一个点,然后用线从点A开始绕圆形硬纸板一周,做好标记,再拉直并测量绕圆形硬纸板一周的线的长度,该长度就是圆形硬纸板的周长。
北师大六年级上册数学第一单元《圆》重点知识汇总,附习题

北师大六年级上册数学第一单元《圆》重点知识汇总,附习题x一、圆的认识(一)(1).圆的定义:平面上的一种曲线图形。
(2)圆中心的一点叫圆心。
圆心一般用字母O表示。
它到圆上任意一点的距离都相等.(3).半径:连接圆心到圆上任意一点的线段叫做半径。
半径一般用字母r表示。
(4)直径:通过圆心并且两端都在圆上的线段叫做直径。
直径一般用字母d表示。
(5).在同一个圆内,所有的半径都相等,所有的直径都相等。
直径的长度是半径的2倍,半径的长度是直径的一半。
用字母表示为:d=2r用文字表示为:半径=直径÷2 直径=半径×2(6).圆心确定圆的位置,半径确定圆的大小。
在同一个圆内,有无数条半径,有无数条直径。
二.圆的认识(二)(1)将圆沿它的直径对折,我们发现两边完全重合,所以圆是轴对称图形。
(2)圆有无数条直径,所以它也有无数条对称轴。
(3)将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心。
三.欣赏与设计:利用圆可以设计许多美丽的图案。
四.圆的周长及圆周率(1).圆的周长:围成圆的曲线的长度叫做圆的周长。
(2).圆的周长总是直径的3倍多一些,这个比值是一个固定的数。
我们把圆的周长和直径的比值叫做圆周率,用字母π表示。
圆周率是一个无限不循环小数。
在计算时,取π≈3.14。
(3)圆的周长计算:圆的周长:C=πd 或C=2πr(4)我国南北朝时期的数学家祖冲之使用“缀术”计算圆周率。
可惜这种方法早已失传。
据专家推测,“缀术”类似“割圆术”,通过对正24576边形周长的计算来推导。
计算相当繁杂,当时还没有算盘。
最后得出了π的两个分数形式的近似值:,并且精确地算出圆周率在3.1415926和3.1415927之间。
电子计算机的出现带来了计算方面的革命, 的小数点后面的精确数字越来越多。
到2002年,圆周率已经可以计算到小数点后12411亿位。
五.圆的面积(1).圆的面积:圆所占面积的大小叫圆的面积。
北师大版数学六年级上册第一单元圆第4课时圆的周长-课件

cm
cm
第3组
cm
cm
cm
cm
cm
cm
第4组
cm
cm
cm
cm
cm
cm
答:它滚动1圈前进1.884米。
1.884×1000=1884(米)
答:滚动1000圈,前进1884米。
62.8÷3.14=20(米)
5.笑笑绕着花坛边缘走了一周, 走了62.8m,这个花坛的直径 是多少米?
答:这个花坛的直径是20米。
6×3.14÷2=9.42(米)
6.右图是一个一面靠墙,另一 面用篱笆围成的半圆形养鸡 场,这个半圆的直径是6米, 篱笆长是多少米?
组
圆的周长
圆的直径
圆的周长除以直径的商 (结果保留两位小数)
第1组
cm
cm
cm
cm
cm
cm
第2组
cm
cm
cm
cm
圆的周长=直径×圆周率
或
3.14×70=219.8(cm)
答:滚一圈有219.8厘米。
O
3cm
大圆周长的一半:
3×2×3.14÷2=9.42(cm)
小圆周长:
3.14×3=9.42(cm)
9.42+9.42=18.84(cm)
3.14×0.3×2=1.884(米)
4.汽车车轮的半径为0.3m,它滚动1圈前进多少米? 滚动1000圈,前进多少米?
答:篱笆长是9.42米。
7.你能利用圆规把这个圆画完整吗?试一试,并求 出整个圆的周长。
北师大版小学数学六年级上册知识点总结第一单元 圆

北师大版小学数学六年级上册知识点总结第一单元圆1.圆的定义:平面上的一种曲线图形。
2.将一张圆形纸片对折两次,折痕相交于圆中心的一点,这个点叫做圆心。
圆心一般用字母O表示。
它到圆上任意一点的距离都相等.3.半径:连接圆心到圆上任意一点的线段叫做半径。
半径一般用字母r表示。
把圆规两脚分开,两脚之间的距离就是圆的半径。
4.圆心确定圆的位置,半径确定圆的大小。
5.直径:通过圆心并且两端都在圆上的线段叫做直径。
直径一般用字母d表示。
6.在同一个圆内,所有的半径都相等,所有的直径都相等。
7.在同一个圆内,有无数条半径,有无数条直径。
8.在同一个圆内,直径的长度是半径的2倍,半径的长度是直径的一半。
用字母表示为:d=2r r =d用文字表示为:半径=直径÷2直径=半径×29.圆的周长:围成圆的曲线的长度叫做圆的周长。
10.圆的周长总是直径的3倍多一些,这个比值是一个固定的数。
我们把圆的周长和直径的比值叫做圆周率,用字母表示。
圆周率是一个无限不循环小数。
在计算时,取3.14。
世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
11.圆的周长公式:C=d 或C=2r圆周长=×直径圆周长=×半径×212、圆的面积:圆所占面积的大小叫圆的面积。
13.把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,用字母(r)表示,宽相当于圆的半径,用字母(r)表示,因为长方形的面积=长×宽,所以圆的面积= r×r。
圆的面积公式:S=r2。
14.圆的面积公式:S=r2 或者S=(d2)2 或者S=(C 2)215.在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
16.在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。
17.一个环形,外圆的半径是R,内圆的半径是r,它的面积是S=R2-r2 或 S=(R2-r2)。
(其中R=r+环的宽度.)19.半圆的周长等于圆的周长的一半加直径。
六年级上册数学《圆》知识点整理

六年级上册数学《圆》知识点整理1、圆的定义:圆是由曲线围成的一种平面图形。
2、圆心:将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心。
如下图中,中心的一点O 。
一般用字母O 表示。
它到圆上任意一点的距离都相等.(画圆切忌别忘记标圆心0)3、半径:连接圆心到圆上任意一点的线段叫做半径。
一般用字母r 表示。
如下图红色线。
把圆规两脚分开,两脚之间的距离就是圆的半径。
4、直径:通过圆心并且两端都在圆上的线段叫做直径。
一般用字母d 表示。
如下图蓝色线。
直径是一个圆内最长的线段。
85、圆心确定圆的位置,半径确定圆的大小。
如果已知的是直径,我们要把直径除以2换成半径,确定圆心,然后才开始画圆。
(画圆给出半径标半径r=?,给出直径标直径d=?)要比较两圆的大小,就是比较两个圆的直径或半径。
6、在同圆或等圆内,有无数条半径,有无数条直径。
同圆中所有的半径、直径都相等。
7.在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的21。
用字母表示为:d = 2r 或r = 2d 或r=d ÷2 8、轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
折痕所在的这条直线叫做对称轴。
9、长方形、正方形和圆都是对称图形,都有对称轴。
这些图形都是轴对称图形。
10、常见图形的对称轴:只有1一条对称轴的图形有: 角、等腰三角形、等腰梯形、扇形、半圆。
只有2条对称轴的图形是:长方形 只有3条对称轴的图形是:等边三角形只有4条对称轴的图形是:正方形;有无数条对称轴的图形是:圆、圆环。
圆是轴对称图形,有无数条对称轴,对称轴就是直径所在的直线。
11、正方形里最大的圆。
两者联系:边长=直径;圆的面积=78.5%正方形的面积画法:(1)画出正方形的两条对角线;(2)以对角线交点为圆心,以边长为直径画圆。
12、长方形里最大的圆。
两者联系:宽=直径画法:(1)画出长方形的两条对角线;(2)以对角线交点为圆心,以宽为直径画圆。
北师大版六年级上册数学第一单元圆知识点归纳及练习.pptx

A1B2 C无数
4.从圆心到(
)任意一点的线段,叫半径。
A 圆 心 B 圆 外 C 圆 上 5.通过圆心并且两端都
在圆上的( )叫直径。
A直线B线段 C射线
二、 判断题 1、 在同一个圆内,只可以画 100 条直径 ( ) 2、 所 有 的 圆 的 直 径 都 相 等 ( ) 3、 等 圆 的 半 径 都 相 等 ( ) 4、 两 端 都 在 圆 上 的 线 段 叫 做 直 径 ( ) 5、 直径都是半径的 2 倍。 ( ) 6、 同一个圆中,半径都相等。 ( ) 7、 在连接圆上任意两点的线段中,直径最长。 ( ) 8、 水桶是圆形的。( ) 9、 所有的直径都相等。( ) 10、 两个圆的直径相等,它们的半径也一定相等。( )
目标知识点二例题 例 3. 饭店的大厅内挂着一只大钟,它的分针长 48 厘米。这根分针的尖端转动一周所走的路程是多
少厘米?
例 4. 砂子堆在地面上占地正好是圆形,量出它一周的长度是 15.7 米,那么砂子堆的直径是多少 米?
例 5. 一辆自行车轮胎的外直径是 70 厘米,如果每分转 120 周,一小时能行多少千米?(保留整 千米数)
r=4
4
学海无 涯 四、解决问题。
1、一块圆形桌布,半径是 6 分米,给它的周围缝上花边,花边长多少分米?这块桌布用料多少平方 分米?
2、通过一座桥,直径是 1.2 米的车轮需转 500 圈,这座桥长多少米?
3、一根铁丝长 28 厘米,正好在一个圆形线圈上绕了 10 圈,这个圆形线圈的周长是多少厘米?
厘米。( )
A.3.14 B.4.14 C.5.14
()
北师大版六年级数学上册第一单元 圆 1.6 圆的周长(2)

圆的周长(2)
课堂练习
1.一个圆形喷水池的半径是5m,它的周长是多 少米?
2×3.14×5= 31.4(米)
答:它的周长是31.4米。
返回
圆的周长(2)
2.在一个圆形亭子里,小丽沿着直径从一端走12步到达 另一端,每步长大约是55cm。 这个圆的周长大约是多少米?
3.14×(55×12)= 2072.4(cm) 2072.4cm=20.724m
返回
圆的周长(2)
课后作业 1.从教材课后习题中选取; 2.从课时练中选取。
返回
圆的周长(2)
第6课时 圆的周长 圆的周长公式的应用
BS 六年级上册
1圆
返回
圆的周长(2)
提示:点击 进入习题
1
2
3
4
5
6
7
返回
圆的周长(2)
知识点 1 圆的周长公式的应用
1.婷婷家卫生间的墙上有一面圆形镜子,镜子的半径是35cm, 现要给这面镜子围一圈丝带,需要丝带多少米?
返回
圆的周长(2)
7. 文杰和章昊在下图所示的环形跑道上赛跑,文杰 沿外道跑,章昊沿内道跑,这样比赛公平吗?如 果你认为不公平,谁跑得多?多多少米?
不公平。
文杰:3.14×(24+1)×2÷2=78.5(m) 章昊:3.14×24×2÷2=75.36(m) 78.5>75.36 78.5-75.36=3.14(m) 文杰跑得多,多3.14 m。
2×3.14×20×3600= 62.8(cm) 2×3.14×20×4650= 94.2(cm) 答:经过30分钟后分针的尖端所走的路程是62.8cm。 经过45分钟后分针的尖端所走的路程是94.2cm。
返回
六年级数学上册知识点思维导图
求一个数比另一个数
多(或少)百分之几
求常见的百分率
求比一个数多(或少) 百分之几的数是多少
用百分数解决
百分数的意义 和写法
问题
百分数和分数、 小数的互化
第六单元
百分 数
节约用水
扇形统计图
条形统计图
折线统计图
统第
计
七 单
图元
数与形
数 学
第 八
广单
角元
第一单元
位置
与方向
(第二单元)
已知一个数的 几分之几是多 少求这个数的
问题
已知比一个数多 (少)几分之几 是多少求这个数
的问题
分数除法 的意义
解决问题
计算方
法
分数除法
倒数的认识
分
数
混合运算
除
法
第三单元
求一个 数的倒
数
比的基本性质
认识比 比的应用
比
第四单元
圆的周长 圆的面积
认识圆
扇形
第 五 单 元
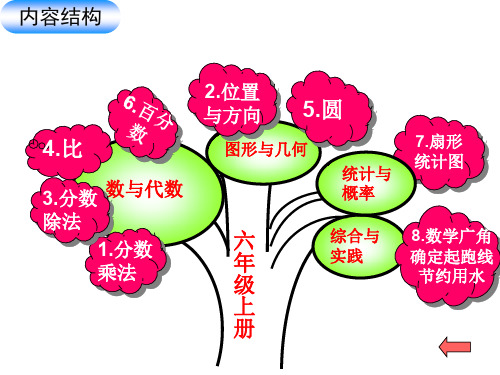
内容结构
4.比
3.分数 数与代数 除法
1.分数 乘法
2.位置 与方向
5.圆
图形与几何
统计与 概率六综合与年实践级
上
册
7.扇形 统计图
8.数学广角 确定起跑线 节约用水
分数乘 整数
分数乘 分数
求一个数的 几分之几是 多少的问题
求比一个数多(少) 几分之几的数是多
少的问题
乘法运算 定律推广
到分数
分 数 乘 法
北师大版小学数学六年级上册第1-7单元思维导图
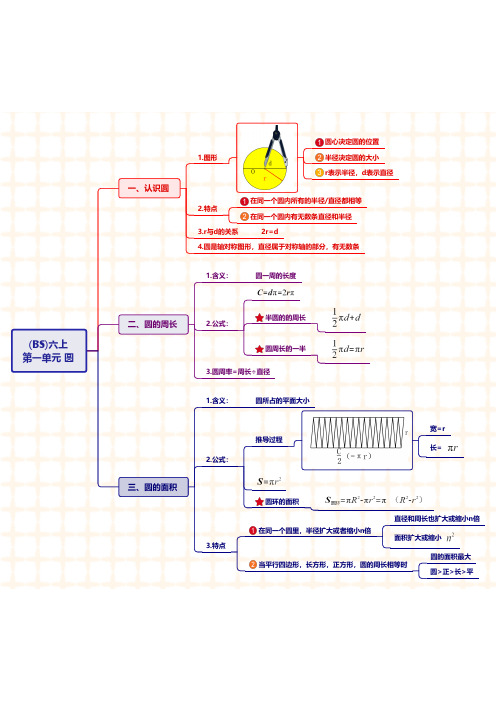
在同一个圆内所有的半径在同一个圆内有无数条直径和半径圆心决定圆的位置半径决定圆的大小2r=dr 圆是轴对称图形,直径属于对称轴的部分,有无数条圆一周的长度周长÷直径半圆的的周长圆周长的一半圆所占的平面大小圆环的面积在同一个圆里,半径扩大或者缩小n 倍当平行四边形,长方形,正方形,圆的周长相等时直径和周长也扩大或缩小面积扩大或缩小圆的面积最大单位单位单位单位量率对应情况不唯一,需要一一列举观察范围随着观察点的变化而变化观察点越高越远,观察范围越大观察点越低越近,观察范围越小(1)拍摄点与照片的位置关系假设自己在拍摄点,联系实际(2)判断连续拍摄一组照片的先后顺序假设自己在拍摄,联系实际2.)读法:百分之八十四)百分数与分数的联系和区别(1)百分率意义(2)常见百分率(3)小数,分数化百分数部分量占总量的百分之几合格率=合格的产品数量÷总数发芽率=发芽种子数量÷总数出勤率=实际出勤人数÷总人数命中率=命中的数量÷总数化成分母为100的分数再写成百分数化成小数x100加上百分号(1)求一个数的百分之几是多少(2)百分数化小数/分数这个数x百分之几去掉百分号,除以100几折注意:八五折(扇形统计图用一个圆作为总体圆内各个扇形大小表示各部分占总体的百分比反映各部分与总体之间的关系条形统计图:清楚表示每个项目的具体数目折线统计图:清楚反映事物变化情况扇形统计图:清楚表示各部分在总体重所占百分比分段整理数据弄清分段标准逐段统计检查,不重复,不遗漏1)分组整理数据比较最大值或最小值比较平均值数据分段比较1)化简比2)比的基本性质求比值按比分配解题方法方法一方法二方法三求总份数--求每份--求各部分量转化成分数乘法解答列方程把一个比化成最简整数比比的前项和后项同时乘或除以一个不为0的数,比值不变计算结果成数列方程算数法利息=本金x利率x时间利率=利息÷本金÷时间。
冀教版六年级上册数学课件-4.1 圆的周长 | (共31张PPT)

学以致用:
一面圆镜的镜面直径是25厘米,在它的边缘镶嵌 着一根金属条,这根金属条的长至少是多少厘米?
3.14×25=78.5(cm)
答:这根金属条的长至少是78.5厘米。
2、在一个圆形亭子里,小丽
走完它的直径需用12步,每 步长大约是55厘米,这个圆 形亭子的周长大约是多少?
3.14×12×55=2072.4(厘米)
方法二:滚动法
0c
10
20
30
m
方法二:滚动法d=10cm0c Nhomakorabea10
20
30
m
方法二:滚动法
0c
10
20
30
m
方法二:滚动法
d=10cm
0c
10
20
30
m
方法二:滚动法
0c
10
20
30
m
圆向右滚动一周,走过的距离 就是圆的周长。
d=10cm
0c
10
20
30
m
转化法:化曲为直
请同学们大胆猜测一下,圆的周长大 约是它直径的几倍?
探究活动要求:
1、小组分工合作,找三个大小不同的圆形物品,分别测量它们 的周长和直径。 2、计算出周长除以直径的结果,填在表中。(可用计算器计算, 除不尽的保留两位小数)
物品
周长 直径 周长÷直径
观察计算的结果,你发现了什么?
————————————————
任何圆的周长总是它直径的3倍多一些。这个倍 数是一个固定不变的数,我们把它叫做圆周率,用字 母“π (读pài)”表示。他是一个无限不循环小数, π= 3.1415926……但在实际应用中一般只取它的近 似值,即π≈3.14。
青岛版六年级上册数学《圆的面积》课件

小力量得一棵树干的周长是 125.6厘米。这棵树干的横 截面积约是多少?
求下图中涂色部分的面积。(单位:米)
80
100
10
10
上图中,O表示( ),OA表示( ), AC表示( )。如果BO=4厘米,那么, 直径AC =( )厘米,圆的周长C=( ) 厘米,圆的面积S=( )平方厘米,半圆 的面积为( )平方厘米。
今天我学习了圆的面积。我知道了 把一个圆平均分成若干等分,然后拼在一 长方形 起,可以拼成一个近似( )。长方形 的宽是圆的( 半径),长是圆的(周长一半 ), 求圆面积用公式表示( S = πr 2 )。
C
2
=πr
r
返回
我的收获
恭喜你! 顺利过关!
圆面积定义
面积公式推导
实践应用
记 忆 宝 库
面积指的是什么?
圆所占平面的大小叫做圆的面积。
返回
记 忆 宝 库
你还记得三角形、梯形 面积的推导过程吗?
记 忆 宝 库
你还记得三角形、梯形 面积的推导过程吗?
猜一猜:圆的面积和什么有关?
将圆分成若干等分
3 4 5 6 7 8 9 10 13 12 11
1
神州五号飞船实际降落范围有 多大?
S = πr2
3.14×52
=3.14×25 =78.5(平方千米) 答:神州五号飞船实际的降落范围 是78.5平方千米。
例3
神州五号飞船实际降落范围比 预定范围小了多少平方千米?
10
圆环面积= 外圆面积-内圆面积 第一步求外圆面积; 第二步求内圆面积; 第三步求环形的面积;
例3
神州五号飞船实际降落范围比预定范围 小了多少平方千米?
圆环面积= 外圆面积-内圆面积 10平方千米
六年级数学上册知识结构网络图

例2
圆的认识和画法
例3
圆的对称特征
2.圆的周长
圆的周长计算公式
练习十五
例1
利用公式计算圆的周长
3.圆的面积
圆的面积计算公式
练习十六
例1
利用圆的面积计算公式求圆的面积
例2
利用圆的面积计算求环形面积
(三)统计与概率
统计(第六单元)
标 题
例 题 安 排
课后练习
统计
引入新知
练习二十五
条形统计图和扇形统计图
练习二十一
例3
求比一个数多(少)百分之几的数是多少
练习二十二
例4
折扣
练习二十三1~3
例5
纳税
练习二十三4、5
例6
利率
练习二十三6~9
(二)空间与图形
1.位置 (第一单元)
标 题
例 题 安 排
课后练习
位置
例1
引入新知
练习一
例2
用数对表示位置
2.圆(第四单元)
标 题
例 题 安 排
课后练习
1.认识圆
例1
想办法画圆,感受圆的曲线特征
练习十二
3.百分数 (第五单元)
标 题
例 题 安 排
课后练习
1.百分数的意义和写法
百分数的意义和写法
练习十八
2.百分数和分数、小数的互化
例1
小数化百分数
练习十九1、2、5、6
例2
百分数化小数
例3
百分数化分数
练习十九3~8
例4
分数化百分数
3.用百分数解决问题
例1
求常见的百分率
练习二十
例2
求一个数比另一个数多(少)百分之几
六年级数学上册圆形知识点

六年级数学上册圆形知识点六年级数学上册圆形知识点一、认识圆形1、圆的定义:圆是由曲线围成的一种平面图形。
2、圆心:将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心。
一般用字母O表示。
它到圆上任意一点的距离都相等.3、半径:连接圆心到圆上任意一点的线段叫做半径。
一般用字母r表示。
把圆规两脚分开,两脚之间的距离就是圆的半径。
4、直径:通过圆心并且两端都在圆上的线段叫做直径。
一般用字母d表示。
直径是一个圆内最长的线段。
5、圆心确定圆的位置,半径确定圆的大小。
6、在同一个圆内或等圆内,有无数条半径,有无数条直径。
所有的半径都相等,所有的直径都相等。
7.在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的1/2。
用字母表示为:d=2r或r=d/28、轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。
折痕所在的这条直线叫做对称轴。
9、长方形、正方形和圆都是对称图形,都有对称轴。
这些图形都是轴对称图形。
10、只有1条对称轴的图形有:角、等腰三角形、等腰梯形、扇形、半圆。
只有2条对称轴的图形是:长方形;只有3条对称轴的图形是:等边三角形;只有4条对称轴的图形是:正方形;有无数条对称轴的图形是:圆、圆环。
11、画对称轴要用铅笔画,同时要用尺子(三角板)画出虚线,这条虚线两端要超出图形一点。
二、圆的周长1、圆的周长:围成圆的曲线的长度叫做圆的周长。
用字母C表示。
2、圆周率实验:(滚动法)在圆形纸片上做个记号,与直尺0刻度对齐,在直尺上滚动一周,得到圆的周长。
或者用线围绕圆形纸片一周量出线的长度就是圆的周长(测绳法)。
发现,圆周长与它直径的比值(圆周长除以直径)是一个固定数即3倍多一点,我们把它叫做圆周率用字母π表示。
3、圆周率:任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率。
用字母π(pai) 表示。
世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
