8位补码表示范围

在计算机科学中，补码是一种用于表示有符号整数的方法。在8位补码表示范围内，可以表示的整数范围是从-128到127。这个范围是由8位二进制数的最高位表示符号位，0表示正数，1表示负数。在8位补码表示范围内，最小的负数是-128，它的二进制表示为10000000。最大的正数是127，它的二进制表示为01111111。这个范围内的所有整数都可以用8位二进制数表示，其中有128个正整数和128个负整数。

补码的表示方法是将一个数的绝对值转换为二进制数，然后将二进制数的每一位取反，最后加1。例如，要表示-5，首先将5转换为二进制数，即101。然后将每一位取反，得到010。最后加1，得到0101，即-5的8位补码表示为11111011。

补码的优点是可以将加法和减法统一为一种操作。在补码中，减法可以转换为加法，即将减数的补码加上被减数的补码，再将结果的补码转换为原码。例如，要计算-5-3，首先将-5和3的补码相加，得到11111011+11111101=11110100。然后将结果的补码转换为原码，得到10001100，即-8。

在8位补码表示范围内，还有一些特殊的数值。其中，0的补码表示为00000000，正数的补码和原码相同，负数的补码是其绝对值的补码。另外，-1的补码表示为11111111，它是唯一一个所有位

都为1的8位补码。

8位补码表示范围内可以表示的整数范围是从-128到127，其中有128个正整数和128个负整数。补码的表示方法可以将加法和减法统一为一种操作，同时还有一些特殊的数值。了解补码的表示方法和范围对于计算机科学的学习和应用都非常重要。

计算机组成原理选择题

A．-127 ～127；B．-128 ～+128；C．-128 ～+127；D．-128 ～+128。

2．设机器数采用补码形式（含1位符号位），若寄存器内容为9BH，则对应的十进制数为______。A．-27；B．-97；C．-101；D．155。答案：

3．设寄存器内容为80H，若它对应的真值是–127，则该机器数是______。

A．原码；B．补码；C．反码；D．移码。答案：

4．若9BH表示移码（含1位符号位）．其对应的十进制数是______。

A．27；B．-27；C．-101；D．101。答案：

5．当定点运算发生溢出时，应______ 。

A．向左规格化；B．向右规格化；C．发出出错信息；D．舍入处理。答案：

6．设寄存器内容为10000000，若它等于-0，则为______。

A．原码；B．补码；C．反码；D．移码。答案：

7．设寄存器内容为11111111，若它等于+127，则为______。

A．原码；B．补码；C．反码；D．移码。答案：

8．在浮点机中，判断原码规格化形式的原则是______。

A．尾数的符号位与第一数位不同；B．尾数的第一数位为1，数符任意；

C．尾数的符号位与第一数位相同；D．阶符与数符不同。答案：

9．浮点数的表示范围和精度取决于______ 。

A．阶码的位数和尾数的机器数形式；B．阶码的机器数形式和尾数的位数；

C．阶码的位数和尾数的位数；D．阶码的机器数形式和尾数的机器数形式。答案：

10. 在定点补码运算器中，若采用双符号位，当______时表示结果溢出。

A．双符号相同B．双符号不同C．两个正数相加D．两个负数相加答案：

二进制原码,反码,补码的基础概念和计算方法

⼆进制原码,反码,补码的基础概念和计算⽅法

⼀. 原码, 反码, 补码的基础概念和计算⽅法.

1. 原码：

原码就是符号位加上真值的绝对值, 即⽤第⼀位表⽰符号, 其余位表⽰值. ⽐如如果是8位⼆进制:

[+1]原 = 0000 0001

[-1]原 = 1000 0001

第⼀位是符号位. 因为第⼀位是符号位, 所以8位⼆进制数的取值范围就是:

[1111 1111 , 0111 1111]

即

[-127 , 127]

2. 反码

反码的表⽰⽅法是:

正数的反码是其本⾝

负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.

[+1] = [00000001]原 = [00000001]反

[-1] = [10000001]原 = [11111110]反

3. 补码

补码的表⽰⽅法是:

正数的补码就是其本⾝

负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1 (即在反码的基础上+1)

[+1] = [00000001]原 = [00000001]反 = [00000001]补

[-1] = [10000001]原 = [11111110]反 = [11111111]补

⼆. 为何要使⽤原码, 反码和补码

计算机可以有三种编码⽅式表⽰⼀个数.

对于正数因为三种编码⽅式的结果都相同:

[+1] = [00000001]原 = [00000001]反 = [00000001]补

但是对于负数:

[-1] = [10000001]原 = [11111110]反 = [11111111]补

机器可以只有加法⽽没有减法

为什么8位二进制的补码取值范围是-128~127

为什么8位有符号数的范围为“-128 —+127”？

（转载加补充）

这是一个困惑了我几年的问题,从我N年前开始摸电脑时,就几乎在每一本C++教科书上都说,8位有符号的取值范围是-128~+127,为什么不是-127~+127呢,后来的java,int的聚值范围,再32位计算,-2^31 ~ +2^31-1。原因没有在工作上或者是什么地方直接遇到它,所以我也一直忽略它,但心里总是有一根刺.直到刚才!!!!

就是刚才,无聊之极,在看汇编的书时,又遇到它了,但一如以往,书上直接地,有心地,明显地绕过了这个问题,真是可恶啊.

几经周折,终于把它搞清楚了:

话说:

用2^8来表示无符号整数的话,全世界的理解都是0 - 255了,那么,有符号呢? 用最高位表示符号,0为+,1为-,那么,正常的理解就是-127 至+127 了.

这就是原码了,值得一提的是,原码的弱点,有2个0,即+0和-0,还有就是,进行异号相加或同号相减时,比较笨蛋,先要判断2个数的绝对值大小,然后进行加减操作,最后运算结果的符号还要与大的符号相同.

于是乎,反码产生了,原因....略,反正,没过多久,反码就成为了过滤产物,也就是,后来补码出现了.

补码的知识不说述,只说有关+127和-128的.

官方的定义[-2^(n-1),2(n-1)-1],补码的0没有正负之分.原因呢?没有一本书上有说,这也是我这么火的原因,但通过思考,google,再思考,很快找到答案:

首先,难不免干点白痴般地事情,穷举一下...

正数,原码跟补码一样

+127, 0111 1111

+1010和-1010对应的8位补码

+1010和-1010对应的8位补码+1010和-1010是两个补码形式的二进制数表示。补码是一种用来表示负数的方法，其基本原理是通过对正数进行逆序取反然后加1的操作来表示对应的负数。

首先来看+1010，它表示的是一个正数。+1010是一个8位的二进制数，可以写成00001010。在补码表示中，正数的补码就是其本身。

接下来看-1010，它表示的是一个负数。如前所述，计算负数的补码的步骤是对正数进行取反然后加1。首先，取反操作是将二进制数的0变成1，1变成0的操作。对于00001010，取反之后得到11110101。然后再对取反后的结果加1，就得到补码。11110101加1等于11110110。所以-1010的8位补码是11110110。

通过这个例子可以看出，+1010和-1010的补码刚好是二进制表示中的翻转，并且负数的补码是正数的补码加1。这种补码表示的方法有几个优点：

1.简化了加减法运算：在补码表示中，负数可以直接通过加减法

运算和正数进行运算，而不需要特殊的处理。这样可以简化计算的步骤，提高计算的效率。

2.没有负零的概念：在补码中，没有负零的概念。也就是说，-00000000和+00000000是一样的。这样可以避免一些运算上的歧义。

3.扩展了二进制表示的范围：在原本的二进制表示中，8位二进制数可以表示的最大正数是11111111，即255。而在补码中，8位二进制数可以表示的最大正数是01111111，即127。这样可以扩展二进制表

示的范围，使得可以表示更大的正数和更小的负数。

8位带符号数表示范围

1. 什么是8位带符号数

8位带符号数是一种数据类型，用8个二进制位来表示一个数值，并且可以表示正

负两种符号。这种数据类型常用于计算机中存储和处理整数。

一位二进制数可以表示0或1，而8位二进制数则可以表示256种不同的数值。当

使用带符号数时，其中一位被用作符号位，用来表示正负。因此，8位带符号数可

以表示的范围是从-128到127。

2. 8位带符号数的表示范围

8位带符号数可以表示的范围可以通过简单的计算得到。其中，最高位表示符号位，剩下的7位用来表示数值。最高位为0表示正数，为1表示负数。

对于正数来说，剩下的7位可以表示的范围是0到127。因此，正数的表示范围为

0到127。

对于负数来说，由于最高位为1，表示的是一个负号。剩下的7位表示了数值。负

数的表示范围可以通过将剩下的7位看作是一个无符号数来计算。对于一个7位的无符号数来说，可以表示的范围是0到127。但是，由于要表示负数，所以负数的

表示范围是从-1到-128。

综上所述，8位带符号数的表示范围是从-128到127。

3. 为什么是-128到127

在计算机内部，数值是以二进制的形式存储的。而对于带符号数来说，最高位被用作符号位，表示正负。由于只有8位，所以最高位只能表示0或1，即表示正数或

负数。

如果希望使用更多位来表示数值范围，可以增加数据类型的位数。例如，使用16

位带符号数可以表示更广范围的整数。

为什么8位带符号数的范围是从-128到127而不是其他范围，是因为在计算机内

部使用补码来表示带符号数。补码是一种表示负数的方法，可以利用正数的表示范围来表示负数。

base8位编码

Base8位编码是指使用8位二进制数来表示数据的方法。它是一种变长编码方式，通常用于表示长度不定的数据。在Base8位编码中，每一位二进制数代表一个八位二进制数，即0到255之间的整数。这种编码方式在计算机科学和电子工程领域中很常见，尤其是在处理图像、音频和视频等多媒体数据时。

Base8位编码的优点在于它可以表示较大的数据范围，同时保持了较好的空间利用率。由于每个八位二进制数都对应一个十进制数，因此可以直接通过索引查找对应的值，提高了数据查找的速度。此外，由于Base8位编码是基于二进制数的变长表示方式，它可以轻松地与其他二进制数据进行合并和比较。

然而，Base8位编码也存在一些缺点。首先，它是一种变长编码方式，因此在处理数据时需要特别注意数据的长度和边界。其次，由于每个八位二进制数的取值范围较小，如果需要表示更大的数据值，就需要使用更多的位数，从而增加了数据的长度和存储空间。最后，由于Base8位编码是基于二进制的，因此对于非技术人员来说可能不太容易理解。

在实际应用中，Base8位编码可以用于各种不同的场景，如图像处理、音频处理、视频处理、网络通信等。在图像处理中，Base8位编码可以用于表示像素的颜色信息；在音频处理中，它可以用于表示音频信号的采样值；在网络通信中，它可以用于表示数据包的长度和内容等信息。

为什么一个字节的补码表示范围是-128~127

为什么⼀个字节的补码表⽰范围是-128~127

我们要先区分⼀下原码、反码和补码的表⽰规则：

0的表⽰：

原码：有正零和负零之分，[+0]补=0000 0000，[-0]补=1000 0000;

反码：同样有两种表⽰⽅法，[+0]反=0000 0000 ，[-0]反=1111 1111；

补码：零只有⼀种表⽰⽅法，不分正负，[0]补=0000 0000；

8为⼆进制表⽰的范围为：

⼀个字节8位，如果采⽤原码表⽰正整数（含0），可以表达0-255，即 2^8=256，⼀共256种状态，从全0到全1的各种排列组合。如果要表⽰负数，则符号位需要占⽤⼀位（最⾼位，1代表负数，0代表正数），因此其绝对值最⼤范围为0-127，即2^7=128，⼀共正负各128种状态，如果不采⽤特殊处理，这时候0占⽤2个编码（10000000和00000000），数据表⽰范围为-127到-0及+0到127，这样总体上⼀个字节只有255种状态，因为其中0具有正0和负0之分，这不符合数学意义也浪费⼀个编码。

除了以上的弊端，还有个原因是，早期硬件很昂贵，⼀位或者⼀个编码的浪费都是不可饶恕的，因此⼈们想到了另⼀种编码把负0利⽤起来，即当遇到负数时，采⽤补码来表⽰就可以解决这个问题，⽽遇到正数或0时还是保留原码表⽰。因此这个负0通过补码算法处理后⾃然⽽然地被利⽤起来，⽤来表⽰-128.

补码的算法为：绝对值的原码各位取反后加1.

例1：负1的补码：绝对值的8位原码为00000001 取反：11111110 加1 ：11111111 此时最⾼位被处理为1，满⾜⾼位为1代表负数的定义。

如果用8位二进制补码表示带符号的定点整数,能表示十进制数的范重点

基础Baidu Nhomakorabea识三
如果用8位二进制补码表示带符号的定点整数，能表示十进制数的范围是。 A、－127~+127 B、-127 ~ +128 C、-128 ~ +127 D、-128 ~ +128 微型计算机中使用的鼠标器是连接在。 A、键盘接口上的 B、显示器接口上的 C、串行接口上的 D、并行接口上的在微型计算机系统中，I/O接口位于之间。 A、主机和总线 B、CPU和内存储器 C、输入/输出设备和总线 D、CPU和输入/输出设备
C
C
C
下面有关计算机毒的说法正确的是。 A、计算机病毒通常不会自己死亡 B、使用防病毒软件后，计算机就不会再感染病毒了 C、使用防病毒卡后，计算机就不会再感染病毒了 D、预种抗病毒疫苗后，计算机就不会再感染病毒了
计算机硬件能直接识别和执行的只有。 A、汇编语言 B、符号语言 C、高级语言
A
D
D、机器语言

-126的8位二进制补码

我们需要了解二进制补码的概念。在计算机中，负数通常使用补码表示。补码的计算方法如下：对于一个给定的负数，首先取其绝对值的二进制表示，然后将其各位取反，最后再加1。以-126为例，首先将126的二进制表示取反，得到反码为01111110，然后将反码加1，得到补码为01111111。

二进制补码的使用主要有以下几个方面的好处：

1. 简化运算：在计算机中，加减乘除等运算可以使用相同的算法来处理正数和负数，不需要额外的逻辑判断。这是因为使用补码表示负数时，负数的加法运算可以转化为正数的加法运算，从而简化了计算过程。

2. 消除溢出：在计算机中，有限的位数限制了数值的表示范围。使用补码表示负数时，可以避免出现溢出的情况。例如，对于8位二进制补码，最大表示范围为-128到127，超出这个范围的计算结果会自动溢出，从而得到正确的结果。

3. 统一处理：在计算机中，所有的数值都以二进制形式存储和处理。使用补码表示负数可以统一处理正数和负数，简化了计算机的硬件设计和编程过程。

除了以上的好处，二进制补码还有一些其他的应用。例如，在数字

信号处理和图像处理中，二进制补码被广泛应用于信号的表示和处理。在嵌入式系统中，二进制补码也被用于控制和通信，实现各种功能和算法。

总结起来，二进制补码是一种计算机中常用的表示负数的方法，具有简化运算、消除溢出和统一处理的优势。在实际应用中，二进制补码被广泛应用于数字信号处理、图像处理和嵌入式系统等领域。通过深入理解二进制补码的原理和应用，可以更好地理解计算机中负数的表示和处理方式，从而提高计算机编程和算法设计的能力。

定点小数的补码表示范围

定点小数的补码表示范围指的是在计算机中用定点数表示小数时，所能表示的最大值和最小值。定点小数表示法是将小数点固定在某个位置上，通常是在数的最高位之后的某个位置，比如在16位的

定点数中，小数点可以固定在第8位，即将16位数分成8位整数部

分和8位小数部分。

定点小数的补码表示法是将小数的补码表示出来，即将小数部分的每一位取反后加1。例如，对于一个8位的定点小数，如果小数部分为0.10100110，那么它的补码为1.01011010。

定点小数的补码表示范围取决于定点数的位数和小数点的位置。对于一个n位的定点小数，如果小数点固定在第m位，则它能表示的最大值和最小值分别为：

最大值：(2^(n-m-1)-1)*(2^(m-1)-2^(-n))

最小值：-2^(n-m-1)*(2^(m-1)-2^(-n))

例如，对于一个16位的定点小数，如果小数点固定在第8位，

那么它能表示的最大值为(2^7-1)*(2^7-2^(-16))=32767.998046875，最小值为-2^7*(2^7-2^(-16))=-32768。

定点小数的补码表示法是一种常见的表示小数的方法，但是它的表示范围相对较小，如果需要表示更大范围的小数，可以考虑使用浮点数表示法。

- 1 -

为什么8位的二进制补码范围是[-128,127]

为什么8位的二进制补码范围是-128-127，而不是-127-127呀？为什么差一个数呀？

数值有正负之分,计算机就用一个数的最高位存放符号(0为正,1为负).这就是机器数的原码了.假设机器能处理的位数为8.即字长为1byte,原码能表示数值的范围为

(-127~-0 +0~127)共256个.

? 有了数值的表示方法就可以对数进行算术运算.但是很快就发现用带符号位的原码进行乘除运算时结果正确,而在加减运算的时候就出现了问题,如下: 假设字长为8bits

( 1 )?10-? ( 1 )10?=? ( 1 )10?+ ( -1 )10?= ?( 0 )10

(00000001)原?+ (10000001)原?= (10000010)原?= ( -2 )?显然不正确.

? 因为在两个整数的加法运算中是没有问题的,于是就发现问题出现在带符号位的负数身上,对除符号位外的其余各位逐位取反就产生了反码.反码的取值空间和原码相同且一一对应. 下面是反码的减法运算:

?( 1 )10?-? ( 1 )?10=? ( 1 )?10+ ( -1 )?10= ?( 0 )10

?(00000001)?反+ (11111110)反?=? (11111111)反?=? ( -0 ) ?有问题.

( 1 )10?-? ( 2)10?=? ( 1 )10?+ ( -2 )10?= ?( -1 )10

(00000001)?反+ (11111101)反?=? (11111110)反?=? ( -1 )?正确

问题出现在(+0)和(-0)上,在人们的计算概念中零是没有正负之分的.(印度人首先将零作为标记并放入运算之中,包含有零号的印度数学和十进制计数对人类文明的贡献极大).

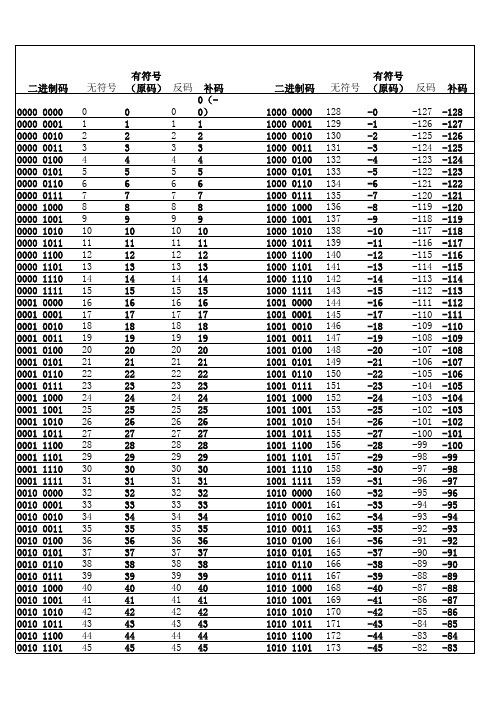
8位补码表

-47 -48 -49 -50 -51 -52 -53 -54 -55 -56 -57 -58 -59 -60 -61 -62 -63 -64 -65 -66 -67 -68 -69 -70 -71 -72 -73 -74 -75 -76 -77 -78 -79 -80 -81 -82 -83 -84 -85 -86 -87 -88 -89 -90 -91 -92 -93 -94 -95 -96 -97
47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97
反码 -127 -126 -125 -124 -123 -122 -121 -120 -119 -118 -117 -116 -115 -114 -113 -112 -111 -110 -109 -108 -107 -106 -105 -104 -103 -102 -101 -100 -99 -98 -97 -96 -95 -94 -93 -92 -91 -90 -89 -88 -87 -86 -85 -84 -83 -82 -81
-80 -79 -78 -77 -76 -75 -74 -73 -72 -71 -70 -69 -68 -67 -66 -65 -64 -63 -62 -61 -60 -59 -58 -57 -56 -55 -54 -53 -52 -51 -50 -49 -48 -47 -46 -45 -44 -43 -42 -41 -40 -39 -38 -37 -36 -35 -34 -33 -32 -31 -30

8种基本数据类型

8种基本数据类型及取值范围:整数类型占位最大值最小值byte 8位补码 0x7f(127) 0x80(-128) short 16位 0x7fff(32767) 0x8000(-32768)int 32位 0x7fffffff(2G-1)2^31-1或21亿 0x80000000(-2G) long 64位 2^63-1 -2^63-1浮点数型：float 占用4字节,范围是-3.403E38~3.403E38,double 占用6字节范围是-1.798E308~1.798E308字符型:charBoolean(布尔)型；booleanint类型的数据能表示的范围比float类型小,int类型数据表示的精度比float大,double精度比int精确,但是不如long;double范围远远大于long引用数据类型:类(class)接口(interface)数组(array)Java标识符命名规则:标识符由字符,下划线"_",美元符"$"或数字组成标识符应以字母,下划线,美元符开头Java标识符大小写敏感,长度无限制约定俗称：Java标识符选取因注意"见名知意"且不能与Java语言的关键字重名Java中一些赋以特定的含义,用做专门用途的字符串称为关键字(keyword)所有Java关键字都是小写英文goto和const虽然从未使用,但也被Java关键字保留Java的常量值用字符串表示,区分为不同的数据类型如整型常量123实型常量3.14字符常量'a'逻辑常量true,false字符串常量"helloworld"Java变量是程序中最基本的存储单元,其要素包括变量名,变量类型和作用域从本质上讲,变量其实是内存中的一小块区域,使用变量名来访问这块区域因此,每一个变量使用前必须要先申请(声明).然后必须进行赋值（填充内容）,才能使用内存分四个区域:code segment 存放代码data segment 静态变量字符串常量stack 局部变量栈heap new出来的东西堆Java变量的分类按被声明的位置划分:局部变量：方法或语句块内部定义的变量成员变量: 方法外部,类的内部定义的变量注意:类外面(与类对应的大括号外面)不能有变量的声明按所属的数据类型划分:逻辑型-boolean类型适于逻辑运算,一般用于程序流程控制boolean类型数据只允许取值true或false,不可以0货非0的整数替代true和false,这点和C语言不同文本型-char整数型-byte,short,int,long浮点数型-float,double字符型charchar型数据用来表示通常意义上"字符"字符常量为用单引号括起来的单个字符,例如:char eChar = 'a';char cChar='中';Java字符采用Unicode编码,每个字符占两个字节,因而可用十六进制编码形式例如:char c1 = '\u0061';注:Unicode是全球语言统一编码Java语言中还允许使用转义字符'\'来将其后的字符转变为其他的含义,例如:char c2='\n';//'\n'代表换行符while &&do while语句while语句为如下形式:while{逻辑表达式,}{语句;...}执行过程先判断逻辑表达式

8位2进制数表示的范围

八位二进制数能表示数的范围以及原码、反码和补码含义

首先八位二进制数0000 0000 ~1111 1111，一共可以表示2^8=256位数，如果表示无符号整数可以表示0~255。计算方法就是二进制与十进制之间的转换。

如果想要表示有符号整数，就要将最前面一个二进制位作为符号位，即0代表正数，1代表负数，后面7位为数值域，这就是原码定义。这样在现实生活中完全没有问题，但在计算机中就出现了问题。

数的表示：

在原码中，0的表示有两种（+0）0000 0000、（-0）1000 0000，这样就产生了编码映射的不唯一性，在计算机上就要区分辨别。然而+0、-0却没有什么现实意义。

数的运算：

为了解决上述数的表示问题，我们可以强制把转换后的10000000强制认定为-128。但这又出现了一个新的问题就是数的运算。数学上，1+(-1)=0，而在二进制中00000001+10000001=10000010，换算成十进制为-2。显然出错了。所以原码的符号位不能直接参与运算，必须和其他位分开，这就增加了硬件的开销和复杂性。

这个时候就要引入补码，补码表示法规定：正数的补码与其原码相同；负数的补码是在其反码的末位加1。反码定义为：正数的反码与其原码相同；负数的反码是对其原码逐位取反，但符号位除外。

1、但为什么要引入补码呢？

2、以及负数补码定义为什么是相对应的正数原码取反加一？

先解决第一个问题，引入补码是为了解决计算机中数的表示和数的运算问题，使用补码，可以将符号位和数值域统一处理，即引用了模运算在数理上对符号位的自动处理，利用模的自动丢弃实现了符号位的自然处理，仅仅通过编码的改变就可以在不更改机器物理架构的基础上完成的预期的要求。

补码的表示范围

补码是计算机中常用的一种表示数字的方式，它是指将原码取反加1的结果。补码的表示范围是由原码的表示范围决定的，其表示范围可以用二进制表示，也可以用十进制表示。

以二进制表示为例，假设原码有n位，那么补码的表示范围就是-2^(n-1)到2^(n-1)-1，其中2^(n-1)表示2的n-1次方，-2^(n-1)表示负2的n-1次方。例如，原码有8位，那么补码的表示范围就是-128到127，即-2^7到2^7-1。

以十进制表示为例，假设原码有m位，那么补码的表示范围就是-2^(m-1)到2^(m-1)-1，其中2^(m-1)表示2的m-1次方，-2^(m-1)表示负2的m-1次方。例如，原码有10位，那么补码的表示范围就是-1024到1023，即-2^9到2^9-1。

补码的表示范围可以用二进制表示，也可以用十进制表示，它们的表示范围都是由原码的表示范围决定的。补码的表示范围可以用来表示计算机中的数字，它可以更有效地表示数字，从而提高计算机的运算效率。