利用导数解决实际问题
应用导数求解实际问题的例子

应用导数求解实际问题的例子篇一:应用导数求解实际问题的例子导数是微积分中的一个重要概念,它可以用来描述函数在某一点的变化率。
应用导数可以帮助我们解决许多实际问题,下面是一个例子:假设我们要设计一个汽车的制动系统,我们希望汽车在制动时可以停下来,并且停下来的时间尽可能短。
为了达到这个目标,我们需要确定合适的制动力大小和时间点。
首先,我们需要建立一个数学模型来描述汽车运动的规律。
假设汽车在t时刻的速度为v(t),我们可以通过导数来描述速度的变化率。
根据牛顿第二定律,汽车的加速度a(t)与施加在汽车上的制动力F(t)之间存在关系:F(t) = m * a(t),其中m是汽车的质量。
我们知道加速度是速度对时间的导数,即a(t) = dv(t)/dt。
将这个等式代入F(t) = m * a(t)中,我们可以得到制动力F(t)与速度v(t)之间的关系。
现在,我们的问题变成了如何确定制动力F(t)使得汽车在尽可能短的时间内停下来。
我们可以通过求解关于时间t的导数来找到答案。
我们需要求解速度v(t)等于0时的时间点t0,即v(t0) = 0。
我们可以通过将v(t)等于0代入导数dv(t)/dt中,得到速度v(t)为0时的时间t0。
通过求解这个方程,我们可以确定汽车停下来的时间点t0。
然后,我们可以根据t0来确定制动力F(t)的大小,使得汽车在这个时间点停下来。
在实际应用中,我们可以通过测量汽车的速度来获取速度随时间的变化情况。
然后,我们可以通过应用导数的方法来确定制动力的大小和时间点,以使得车辆尽快停下来。
这个例子展示了如何应用导数来解决实际问题。
通过建立数学模型,并利用导数的性质,我们可以更好地理解和优化真实世界中的各种现象和过程。
篇二:应用导数是数学中的一个重要概念,它可以帮助我们解决许多实际问题。
下面是一个例子,说明如何使用导数来解决实际问题:假设我们需要确定一个物体在某一时刻的速度。
我们可以通过给定的位置函数来计算。
导数在生活中的应用例子

导数在生活中的应用例子
一、在经济学中
1、供求曲线中的供求应变:当价格发生变化时,需求量会出现波动,
以及需求量对价格的变化也变化,供求曲线受到价格变化的影响。
这
就是导致供求应变的原因,而这个原因可以用微积分的偏导数来证明。
2、市场竞争:随着竞争者数量的增加,市场价格也会发生变化,价格
作为变量,市场最终决定价格时,就会出现供需冲突,从而引起价格
波动,这就用微积分中的导数来分析。
二、在金融学中
1、货币政策传导机制:货币政策的实施使得利率的变化对经济的影响,用微积分的意义来看,利率是一种曲线,当利率变化时,曲线的斜率
也会变化,这就是利率传导机制。
2、投资机会成本:投资机会成本指的是投资者在一定条件下所承担的
投资风险,当利率下降时,投资机会成本也会发生变化,而这一变化
可以用微积分中的导数来进行分析。
三、在制造业中
1、公差计算:在计算机装配工艺中,产品的尺寸关系到了其加工的质量,如果所用的部件的尺寸不符合公差要求,就会出现不良的加工结
果,这时处理的办法就是计算出来最大的容许偏差,而这个最大容许
偏差就是通过微积分的偏微分来计算出来的。
2、工艺优化:为了确保加工出来的产品的质量,就必须对付诸如温度、压力、用料等参数进行优化调整,这可以使用微积分来分析各参数对
最终结果的影响,以达到最优化调整的效果。
导数在实际生活中的运用

导数在实际生活中的运用导数作为微积分中的重要概念,是描述函数变化率的工具之一。
在数学领域中,导数的运用非常广泛,它不仅可以用来解决数学问题,还可以在实际生活中找到许多有趣的应用。
导数在实际生活中的运用,不仅可以帮助我们更好地理解数学知识,还可以为我们的生活带来便利与乐趣。
一、导数在物理学中的应用在物理学中,导数被广泛应用于描述物体运动的规律。
通过对物体位移、速度、加速度等物理量的导数进行分析,可以帮助我们更好地理解物体的运动规律。
以小车匀速运动为例,假设小车在 t 时刻的位置为 s(t),则小车的速度可以表示为 s'(t),而小车的加速度可以表示为 s''(t)。
通过对速度和加速度的分析,可以帮助我们更加深入地理解物体的运动规律,为实际的运动控制提供依据。
在经济学中,导数被广泛应用于描述经济变量的变化规律。
通过对需求函数、供给函数等经济函数的导数进行分析,可以帮助我们更好地理解价格、产量等经济变量的变化规律。
导数还可以用来解决相关的最优化问题,在经济决策中发挥着重要作用。
通过对经济变量的导数进行分析,可以帮助经济学家更好地理解市场运行的规律,为经济政策的制定提供依据。
在工程领域中,导数被广泛应用于描述各种物理现象和工程问题。
在电路设计中,导数可以帮助我们分析电流、电压等电学量的变化规律,为电路的设计提供依据。
在机械设计中,导数可以帮助我们分析力、速度、加速度等物理量的变化规律,为机械系统的设计提供依据。
通过对工程问题中的导数进行分析,可以帮助工程师更好地理解物理现象和工程问题,为工程设计提供科学依据。
除了在物理学、经济学和工程领域中的应用外,导数还可以在生活中的许多其他领域中找到应用。
通过对人口增长率、疾病传播速率等进行导数分析,可以帮助我们更好地理解社会现象和生活问题。
在生产实践中,导数也可以用来描述生产过程中的效率和变化规律。
导数还可以在艺术创作、音乐编排等方面找到应用,帮助我们更好地理解艺术和音乐作品的规律。
求导数的实际应用题

求导数的实际应用题导数作为微积分的重要概念,具有广泛的实际应用价值。
在物理学、经济学、生物学等领域中,求导数可以帮助我们解决一系列实际问题。
本文将以几个实际应用题为例,阐述导数的应用。
1. 速度和加速度假设有一个小车在直线道路上行驶。
我们知道,速度可以看作是位移对时间的导数,即v(t) = ds(t)/dt,其中v(t)表示时刻t的速度,s(t)表示距离。
如果我们已知小车的位移函数s(t),则可以通过求导数的方法得到其速度函数v(t)。
同样地,加速度可以看作速度对时间的导数,即a(t) = dv(t)/dt。
如果我们已知小车的速度函数v(t),可以通过求导数得到其加速度函数a(t)。
这些速度和加速度的函数关系可以帮助我们对行驶中的小车进行分析,如判断是否超速或者行驶过程中是否需要采取制动等措施。
2. 弹簧振动在物理学中,弹簧振动是一个常见的问题。
假设一个弹簧的位置可以用函数x(t)表示,其中x(t)表示时刻t的位置。
根据胡克定律,弹簧受力与其伸长程度成正比。
设弹簧的劲度系数为k,则弹簧的受力可以表示为F = -kx(t)。
根据牛顿第二定律,物体受力与加速度成正比。
设物体的质量为m,则物体的加速度可以表示为a = F/m = -kx(t)/m。
我们可以通过求导数的方法,得到物体的速度v(t) = dx(t)/dt,并进一步求得物体的加速度。
通过对弹簧振动过程的分析,可以了解弹簧在不同时刻的位置、速度以及加速度,从而揭示了弹簧振动的规律。
3. 生物学中的增长问题在生物学中,许多生物群体的增长问题都可以通过求导数来解决。
以细菌繁殖为例,假设初始时刻有N个细菌,细菌的繁殖速率与其当前数量成正比。
设细菌繁殖速率为r,则细菌的繁殖速度可以表示为dN/dt = rN。
将微分方程化简后可得到N(t) = N0 * e^(rt),其中N(t)表示时刻t的细菌数量,N0表示初始时刻的细菌数量。
通过求导数,我们可以得到细菌数量随时间变化的规律,以及在不同时刻细菌数量的增长速度。
导数在实际问题中的应用
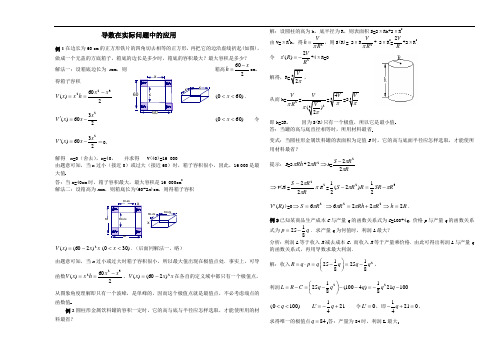
导数在实际问题中的应用例1在边长为60 cm 的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少? 箱高602xh -=cm ,解法一:设箱底边长为x cm ,则得箱子容积260)(322xx h x x V -== )600(<<x .23()602x V x x '=-)600(<<x 令23()602x V x x '=-=0,解得 x=0(舍去),x=40, 并求得 V(40)=16 000由题意可知,当x 过小(接近0)或过大(接近60)时,箱子容积很小,因此,16 000是最大值答:当x=40cm 时,箱子容积最大,最大容积是16 000cm 3解法二:设箱高为x cm ,则箱底长为(60-2x )cm ,则得箱子容积x x x V 2)260()(-=)300(<<x .(后面同解法一,略) 由题意可知,当x 过小或过大时箱子容积很小,所以最大值出现在极值点处.事实上,可导函数260)(322x x h x x V -==、x x x V 2)260()(-=在各自的定义域中都只有一个极值点,从图象角度理解即只有一个波峰,是单峰的,因而这个极值点就是最值点,不必考虑端点的函数值例2圆柱形金属饮料罐的容积一定时,它的高与底与半径应怎样选取,才能使所用的材料最省?解:设圆柱的高为h ,底半径为R ,则表面积S=2πRh+2πR 2由V=πR 2h ,得2V h R π=,则S(R)= 2πR 2V R π+ 2πR 2=2V R+2πR 2令 22()Vs R R'=-+4πR=0 解得,从而h=2VR π即h=2R , 因为S(R)只有一个极值,所以它是最小值 答:当罐的高与底直径相等时,所用材料最省变式:当圆柱形金属饮料罐的表面积为定值S 时,它的高与底面半径应怎样选取,才能使所用材料最省?提示:S =2Rh π+22R π⇒h =RR S ππ222-⇒V (R )=RR S ππ222-πR 2=3221)2(21R SR R R S ππ-=- )('R V )=026R S π=⇒ ⇒R h R Rh R 222622=⇒+=πππ.例3已知某商品生产成本C 与产量q 的函数关系式为C =100+4q ,价格p 与产量q 的函数关系式为q p 8125-=.求产量q 为何值时,利润L 最大? 分析:利润L 等于收入R 减去成本C ,而收入R 等于产量乘价格.由此可得出利润L 与产量q的函数关系式,再用导数求最大利润. 解:收入211252588R q p q q q q ⎛⎫=⋅=-=- ⎪⎝⎭,利润221125(1004)2110088L R C q q q q q ⎛⎫=-=---=-- ⎪⎝⎭(0100)q << 1214L q '=-+ 令0L '=,即12104q -+=,求得唯一的极值点84q =答:产量为84时,利润L 最大。
应用导数解决实际问题

应用导数解决实际问题导数作为微积分的重要概念,广泛应用于解决实际问题中。
它通过研究函数的变化率和极值等特性,为我们提供了解决各种实际问题的有效工具。
本文将通过几个具体问题的探讨,展示导数在实际应用中的重要性。
一、速度、位移和加速度假设我们有一个物体在直线上运动,我们想要计算它在特定时间点的速度。
这时我们可以借助导数的概念来解决这个问题。
设物体在时刻t的位移为s(t),则物体的速度可以通过求解s(t)的导数来得到。
具体地,我们可以使用以下公式来求解速度:v(t) = s'(t)其中v(t)表示物体在时刻t的速度,s'(t)表示s(t)的导数。
通过对位移函数求导,我们可以得到物体在不同时间点的瞬时速度,从而更好地了解其运动情况。
进一步地,我们还可以通过对速度函数求导,得到物体的加速度。
加速度是速度的变化率,通过它我们可以判断物体是在加速还是减速。
设速度函数为v(t),加速度函数为a(t),则加速度可以通过求解v(t)的导数来得到:a(t) = v'(t)通过对速度函数求导,我们可以得到物体在不同时间点的瞬时加速度,进而分析出运动过程中的加速度变化情况。
二、最优问题在实际问题中,我们常常需要寻找优化的解决方案。
这时,我们可以借助导数的概念来找到最优解。
考虑下面一个例子:假设我们要制作一个体积为V的圆形容器,我们想要找到能够最小化表面积的尺寸。
设圆形容器的半径为r,表面积为A,则我们可以通过求解A关于r的导数来得到最优解。
具体地,我们可以使用以下公式来求解表面积的导数:dA/dr = 0通过对表面积函数求导,并令导数等于0,我们可以解得最优解所对应的半径。
这样,我们就能够找到满足实际情况并且表面积最小的容器尺寸。
类似地,我们还可以通过求解函数的导数来解决其他的最优问题。
无论是求职场上的最大收益,还是寻找最短路径,导数都能够帮助我们找到最优解决方案。
三、误差估计在实际测量和计算中,我们难免会遇到误差。
导数与微分实际问题案例

导数与微分实际问题案例导数和微分是微积分中重要的概念,它们在现实世界中有着广泛的应用。
本文将通过一些实际问题案例,详细介绍导数和微分的应用。
案例一:车辆行驶问题假设一辆汽车在一段时间内以匀速行驶。
我们可以通过求解导数来计算汽车的速度。
设汽车的位移函数为s(t),其中t表示时间,s表示位移。
那么汽车的速度可以通过求解导数s'(t)来得到。
例如,假设汽车的位移函数为s(t) = 2t^2 + 3t。
我们可以通过求解导数s'(t)来计算汽车的速度,即s'(t) = 4t + 3。
通过求解导数,我们可以得知汽车的速度在任意时间点上是多少。
这对于研究车辆行驶过程中的加速度、减速度等问题非常有帮助。
案例二:物体移动问题在物理学中,有一类常见的问题是求解物体的运动过程。
通过求解导数,我们可以推导出物体的速度和加速度函数。
设物体的位移函数为s(t),其中t表示时间,s表示位移。
那么物体的速度可以通过求解导数s'(t)来得到,加速度可以通过求解导数s''(t)来得到。
例如,假设物体的位移函数为s(t) = 3t^2 - 4t + 2。
我们可以通过求解导数s'(t)来计算物体的速度,即s'(t) = 6t - 4;通过求解导数s''(t)来计算物体的加速度,即s''(t) = 6。
通过求解导数,我们可以分析物体的运动规律,例如物体的最大速度、加速度的变化情况等。
案例三:利润最大化问题在经济学中,有一个经典的问题是求解利润最大化。
假设某公司生产一种产品,售价为p(单位价格),销量为x(单位数量)。
成本函数可以表示为C(x),那么利润可以表示为P(x) = px - C(x)。
为了求解利润最大化,我们需要计算利润函数P(x)的导数。
通过求解导数P'(x) = p - C'(x),我们可以确定最大利润对应的销量。
重点:利用导数知识解决实际生活中的最优化问题

在确定了所有极值点后,需要比较这些点的函数值,以确定哪个点是最优解。如果目标是最小化函数,则选择函数值最小的极小值点作为最优解;如果目标是最大化函数,则选择函数值最大的极大值点作为最优解。
总结词
导数在最大利润问题中,可以帮助我们找到使利润最大的最优解。
总结词
导数在最大利润问题中,可以帮助我们找到使利润最大的最优解。
详细描述
在商业运营中,最大化利润是一个关键目标。导数的应用可以帮助我们找到使利润最大的最优解。例如,在定价策略中,我们可以通过求导找到最优的定价,以最大化利润。
详细描述
在商业运营中,最大化利润是一个关键目标。导数的应用可以帮助我们找到使利润最大的最优解。例如,在定价策略中,我们可以通过求导找到最优的定价,以最大化利润。
总结词:导数在最优化方案选择问题中,可以帮助我们找到最优的方案。
导数在解决最优化问题中的重要性
CATALOGUE
02
导数大于零的区间内,函数值随自变量增大而增大。
单调递增
导数小于零的区间内,函数值随自变量增大而减小。
单调递减
不等式最值
利用导数研究函数在某区间内的单调性,进而确定不等式成立的条件和最值。
在某些情况下,可能存在多个最优解或没有最优解,这取决于问题的性质和约束条件。
实际案例分析
CATALOGUE
04
总结词
导数在投资回报最大化问题中起到关键作用,通过求导数找到收益函数的最大值点,从而确定最优投资策略。
要点一
要点二
详细描述
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《 走
向
高
告促销和技术改造.经预测,每投入技术改造费
考 》
高
x(百万元),可增加的销售额约为-
1 3
x3+x2+3x(百万
考 总 复 习
·(
元).请设计一个资金分配方案,使该公司由此获得
数 学
配
的收益最大?(注:收益=销售额-投入).
人 教
B
版
)
首页
上页
下页
末页
第三章 导数及其应用
解析:(1)设投入t(百万元)的广告费后增加的收益为
习
·(
数
(2)求函数的导数f ′(x),解方程f ′(x)=0;
学
配
(3)比较函数在区间端点和极值点的函数值大小,最
人 教
B
大(小)者为最大(小)值.
)
版
首页
上页
下页
末页
第三章 导数及其应用
误区警示
《
(1)在求实际问题的最大(小)值时,一定要注意考虑实
走 向
高
际问题的意义,不符合实际意义的值应舍去.
考 》
高
(2)在实际问题中,有时会遇到函数在区间内只有一
考 总
复
个点使f ′(x)=0的情形,如果函数在这点有极大(小)值,那 习
·(
数
么不与端点值比较,也可以知道这就是最大(小)值.
学
配
人
教
B
版
)
首页
上页
下页
末页
第三章 导数及其应用
(3)生活中,经常遇到求利润最大、用料最省、效率
《
最高等问题,这些问题通常称为优化问题.在解决实际优
∴43πr2+2πrh=2rV,S=5π3r2+2rV,-2rV2 =0得,r= 3
3V 5π
·(
习 数 学
配
人
3 代入①中得h=r=
3V 5π
,∴当h=r=
3
3V 5π
时
)
教
B 版
用料最省.
首页
上页
下页
末页
第三章 导数及其应用
《
[例2] 某集团为了获得更大的利益,每年要投入一
《
走
当x∈(80,120]时,f ′(x)>0,f(x)是增函数.
向 高
考
∴当x=80时,f(x)取到极小值f(80)=11.25(升).
》 高
考
总
因为f(x)在(0,120]上只有一个极小值,所以它是
复 习
·(
最小值.
数 学
配
答:当汽车以80千米/小时的速度匀速行驶时,
人 教
B
从甲地到乙地耗油最少,最少为11.25升.
)
版
首页
上页
下页
末页
第三章 导数及其应用
《
走
向
高
某工厂设计一个密闭容器,下部是圆柱体形,上部是
考 》
高
半球形,容积为常数V,当圆柱的底半径r与高h为何值时,
考 总
复
制造这个容器的用料最省?
习
数
学
·(
配 人 教
B 版
)
首页
上页
下页
末页
第三章 导数及其应用
解析:32πr3+πr2h=V①
《 走 向
高
答:当汽车以40千米/小时的速度匀速行驶时,
数 学
配
从甲地到乙地耗油17.5升.
人 教
B
版
)
首页
上页
下页
末页
第三章 导数及其应用
(2)当速度为x千米/小时时,汽车从甲地到乙地行
《
走
驶了10x0小时,设耗油量为f(x)升.
向 高 考 》
高
依题意得f(x)=1281000x3-830x+8·10x 0
第三章 导数及其应用
《 走 向 高 考 》 高 考 总 复 习 数 学 配 人 教 B 版
·(
)
首页
上页
下页
末页
第三章 导数及其应用
《 走 向 高 考 》 高 考 总 复 习 数 学 配 人 教 B 版
·(
)
首页
上页
下页
末页
第三章 导数及其应用
重点难点
《
重点:利用导数解决实际问题中的优化问题
走 向
考 总 复 习
·(
数
=12180x2+80x0-145 (0<x≤120),
学 配 人
教
f ′(x)=64x0-8x020=x63-408x02 3(0<x≤120).
)
B 版
令f ′(x)=0,得x=80.
首页
上页
下页
末页
第三章 导数及其应用
当x∈(0,80)时,f ′(x)<0,f(x)是减函数;
走 向
高
化问题中,不仅要注意将问题中涉及的变量关系用函数关
考 》
高
系式给予表示,还应确定函数关系式中自变量的定义区 考
总
复
间.
习
数 学
·(
配 人 教
B 版
)
首页
上页
下页
末页
第三章 导数及其应用
《 走 向 高 考 》 高 考 总 复 习 数 学 配 人 教 B 版
·(
)
首页
上页
下页
末页
第三章 导数及其应用
[例1] 统计表明,某种型号的汽车在匀速行驶
《 走
向
中每小时耗油量y(升)关于行驶速度x(千米/小时)的
高 考
》
函数解析式可以表示为y=
1 128000
x3-
3 80
x+
高 考 总 复
习
8(0<x≤120).已知甲、乙两地相距100千米.
数
学
·(
(1)当汽车以40千米/小时的速度匀速行驶时,
配
人
从甲地到乙地要耗油多少升?
《
告促销的资金为(3-x)(百万元),又设由此获得的收益
走 向
高
考
是g(x),则有g(x)=(-13x3+x2+3x)+[-(3-x)2+5(3-x)]
》 高 考
总
复
-3=-31x3+4x+3 (0≤x≤3),
习 数 学
·(
∴g′(x)=-x2+4.
配 人
教
高
难点:如何建立数学模型,借助导数求最值
考 》
高
考
总
复
习
·(
数 学
配 人 教
B 版
)
首页
上页
下页
末页
第三章 导数及其应用
知识归纳
《
利用导数解决实际问题中的最值的一般步骤
走 向
高
(1)分析实际问题中各量之间的关系,找出实际问题
考 》
高
的数学模型,写出实际问题中变量之间的函数关系式y=
考 总
复
f(x);
教 B
版
)
(2)当汽车以多大的速度匀速行驶时,从甲地到
乙地耗油最少?最少为多少升?
首页
上页
下页
末页
第三章 导数及其应用
解析:(1)当x=40时,汽车从甲地到乙地行驶了
《 走
向
高
14000=2.5(小时),耗油1281000×403-830×40+8×2.5
考 》 高 考
总
=17.5(升).
复 习
·(
《
f(t)(百万元),则有
走 向
高
f(t)=(-t2+5t)-t=-t2+4t=-(t-2)2+4
(0≤t≤3),
考 》
高
∴当t=2百万元时,f(t)取得最大值4百万元.即投入2
考 总
复
百万元的广告费时,该公司由此获得的收益最大.
习
数 学
·(
配 人 教
B 版
)
首页
上页
下页
末页
第三章 导数及其应用
(2)设用于技术改造的资金为x(百万元),则用于广
走 向 高
定的资金用于广告促销.经调查,每年投入广告费t(百万
考 》
高
元)可增加销售额约为-t2+5t(百万元)(0≤t≤5)
考 总
复
·(
(1)若该公司将当年的广告费控制在三百万元之内,
习 数
学
则应投入多少广告费,才能使该公司由此获得的收益最大? 配
人
教
B
版
)
首页
上页
下页
末页
第三章 导数及其应用
(2)现该公司准备共投入300万元,分别用于广
