测量平差习题
测量平差习题集

第二部分 自测题第一章 自测题一、判断题(每题2分,共20分)1、 通过平差可以消除误差,从而消除观测值之间的矛盾。
( )2、 观测值i L 与其偶然真误差i ∆必定等精度。
( )3、 测量条件相同,观测值的精度相同,它们的中误差、真误差也相同。
( )4、 或然误差为最或然值与观测值之差。
( )5、 若X 、Y 向量的维数相同,则YX XY Q Q =。
( )6、 最小二乘原理要求观测值必须服从正态分布。
( )7、 若真误差向量的数学期望为0,即0=∆)(E ,则表示观测值中仅含偶然误差。
( ) 8、 单位权中误差变化,但权比及中误差均不变。
( ) 9、 权或权倒数可以有单位。
( )10、相关观测值权逆阵Q 的对角线元素ii Q 与权阵P 的对角线元素ii P 之间的关系为1=ii ii P Q 。
( )二、填空题(每空0.5分,共20分)1、测量平差就是在 基础上,依据 原则,对观测值进行合理的调整,即分别给以适当的 ,使矛盾消除,从而得到一组最可靠的结果,并进行 。
2、测量条件包括 、 、 和 ,由于测量条件的不可能绝对理想,使得一切测量结果必然含有 。
3、测量误差定义为 ,按其性质可分为 、 和 。
经典测量平差主要研究的是 误差。
4、偶然误差服从 分布,它的概率特性为 、 和 。
仅含偶然误差的观测值线性函数服从 分布。
5、最优估计量应具有的性质为 、 和 。
若模型为线性模型,则所得最优估计量称为 ,最优估计量主要针对观测值中仅含 误差而言。
要证明某估计量为最优估计量,只需证明其满足 性和 性即可。
6、限差是 的最大误差限,它的概率依据是 ,测量上常用于制定 的误差限。
7、若已知观测值向量L 或其偶然真误差向量∆的协方差阵为∑,则L 或∆的权阵定义为L P =∆P = ,由于验前精度∑难以精确求得,实用中定权公式有 、 、 ,特别是对独立等精度观测向量L 而言,其权阵可简单取为L P = 。
误差理论和测量平差5道经典习题

误差理论和测量平差5道经典习题1、以下对于随机变量的描述,正确的是:A. 其数值的符号和大小均是偶然的B. 其数值的符号和大小均是随机的C. 数值的符号和大小均是无规律的D. 随机变量就其总体来说具有一定的统计规律2、以下关于偶然误差的描述正确的是:A. 在一定的观测条件下,误差的绝对值有一定的限值;B. 绝对值较小的误差比绝对值较大的误差出现的概率大;C. 绝对值相等的正负误差出现概率相同;D. 偶然误差的数学期望为零3、下列关于偶然误差的特性描述正确的是:A 绝对值小的误差比绝对值大的误差出现的概率小B 当偶然误差的个数趋向极大时,偶然误差的代数和趋向零C 误差分布的离散程度是指大部分误差绝对值小于某极限值绝对值的程度D 误差的符号只与观测条件有关4、下列观测中,哪些是具有“多余观测”的观测活动A 对平面三角形的三个内角各观测一测回,以确定三角形形状B 测定直角三角形的两个锐角和一边长,确定该直角三角形的大小及形状C 对两边长各测量一次D 三角高程测量中对水平边和垂直角都进行一次观测第四次作业:1、求随机变量σμ-=x t 的期望和方差2、设随机变量X~N (0,9),求随机变量函数Y=5X 2的均值3、为了鉴定经纬仪的精度,对已知精确测定的水平角α=45°00′00″作12次观测,结果为:45°00′06″ 44°59′55″ 44°59′58″ 45°00′04″ 45°00′03″ 45°00′04″ 45°00′00″ 44°59′58″ 44°59′59″ 44°59′59″ 45°00′06″ 45°00′03″设α没有误差,试求观测值的中误差。
1、对真值为L ~=100.010m 的一段距离以相同的方法进行了10次独立的观测,得到的观测值见下表,试求该组观测值的系统误差、中误差、均方误差。
测量平差所有习题
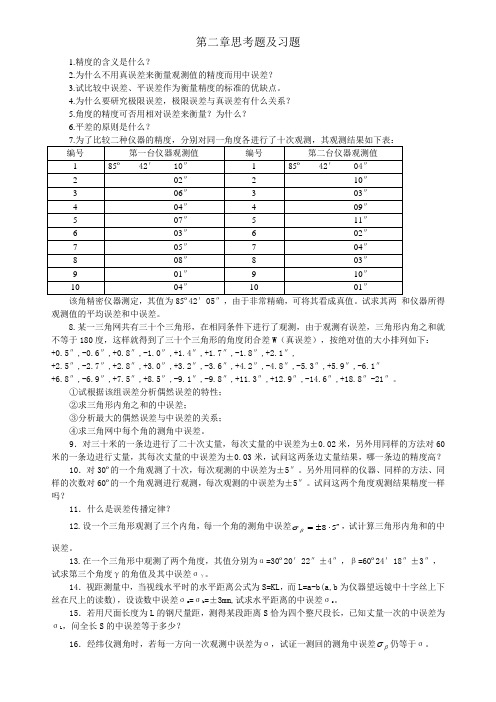
第二章思考题及习题1.精度的含义是什么?2.为什么不用真误差来衡量观测值的精度而用中误差?3.试比较中误差、平误差作为衡量精度的标准的优缺点。
4.为什么要研究极限误差,极限误差与真误差有什么关系?5.角度的精度可否用相对误差来衡量?为什么?6.平差的原则是什么?观测值的平均误差和中误差。
8.某一三角网共有三十个三角形,在相同条件下进行了观测,由于观测有误差,三角形内角之和就不等于180度,这样就得到了三十个三角形的角度闭合差W(真误差),按绝对值的大小排列如下:+0.5″,-0.6″,+0.8″,-1.0″,+1.4″,+1.7″,-1.8″,+2.1″,+2.5″,-2.7″,+2.8″,+3.0″,+3.2″,-3.6″,+4.2″,-4.8″,-5.3″,+5.9″,-6.1″+6.8″,-6.9″,+7.5″,+8.5″,-9.1″,-9.8″,+11.3″,+12.9″,-14.6″,+18.8″-21″。
①试根据该组误差分析偶然误差的特性;②求三角形内角之和的中误差;③分析最大的偶然误差与中误差的关系;④求三角网中每个角的测角中误差。
9.对三十米的一条边进行了二十次丈量,每次丈量的中误差为±0.02米,另外用同样的方法对60米的一条边进行丈量,其每次丈量的中误差为±0.03米,试问这两条边丈量结果,哪一条边的精度高?10.对30º的一个角观测了十次,每次观测的中误差为±5″。
另外用同样的仪器、同样的方法、同样的次数对60º的一个角观测进行观测,每次观测的中误差为±5″。
试问这两个角度观测结果精度一样吗?11.什么是误差传播定律?12.设一个三角形观测了三个内角,每一个角的测角中误差58''⋅±=βσ,试计算三角形内角和的中误差。
13.在一个三角形中观测了两个角度,其值分别为α=30º20′22″±4″,β=60º24′18″±3″,试求第三个角度γ的角值及其中误差σγ。
(完整word版)测量平差经典试卷含答案

一、填空题(每空2分,共20分)1、最优估计量应具有的性质为 、 和 最优估计量主要针对观测值中仅含 误差而言。
2、间接平差中,未知参数的选取要求满足 、 。
3已知条件平差的法方程为024322421=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡k k ,则PV V T = ,μ= , 1k p = ,2k p = 。
4、已知某平差问题,观测值个数为79,必要观测量个数为35,则按间接平差进行求解时,误差方程式个数为 ,法方程式个数为 。
5、已知某平差问题观测值个数为50,必要观测量个数为22,若选6个独立参数按具有参数的条件平差进行求解,则函数模型个数为 ,联系数法方程式的个数为 ;若在22个独立参数的基础上,又选了4个非独立参数按具有条件的参数平差进行求解,则函数模型个数为 ,联系数法方程式的个数为 。
6、条件平差中条件方程的个数等于________________,所选参数的个数等于_______________。
7、已知真误差向量1⨯∆n 及其权阵P ,则单位权中误差公式为 ,当权阵P 为 此公式变为中误差公式。
二、计算题(每题2分,共20分)1、条件平差的法方程等价于:A 、0=+W K Q KB 、0=+W Q K WC 、0=+W P K WD 、0=+W P K K答:______2、水准测量中,10km 观测高差值权为8,则5km 高差之权为:A 、2B 、4C 、8D 、16答:______3、已知⎥⎦⎤⎢⎣⎡=∆3112P ,则2L p 为:A 、2B 、3C 、25D 、35答:______4、间接平差中,L Q ˆ为:A 、TA AN 1- B 、A N A T1-C 、T A AN P11--- D 、A N A P T 11---答:______5、观测条件是指:A)产生观测误差的几个主要因素:仪器,观测者,外界条件等的综合B)测量时的几个基本操作:仪器的对中,整平,照准,度盘配置,读数等要素的综合 C)测量时的外界环境:温度,湿度,气压,大气折光……等因素的综合. D)观测时的天气状况与观测点地理状况诸因素的综合答:______ 6、已知观测向量()L L L T=12的协方差阵为D L =--⎛⎝ ⎫⎭⎪3112,若有观测值函数Y 1=2L 1,Y 2=L 1+L 2,则σy y 12等于?(A)1/4 (B)2 (C)1/2 (D)4 答:_____ 7、已知观测向量()L L L T=12的权阵P L =--⎛⎝ ⎫⎭⎪2113,单位权方差σ025=,则观测值L 1的方差σL 12等于:(A)0.4 (B)2.5 (C)3 (D)253答:____ 8、已知测角网如下图,观测了各三角形的内角,判断下列结果,选出正确答案。
测量平差习题

第一章观测误差与传播率第一节观测误差1、在下列情况下用钢尺丈量距离,使量得的结果产生误差,时判别误差的性质与符号:(1)尺长不准确;(2)尺长检定过程中,尺长与标准尺长比较产生的误差;(3)尺不水平;(4)尺反曲或垂曲;(5)尺端偏离直线方向;(6)估读小数不准确;2、在下列情况下使水准测量中水准尺的读数带有误差,试判别误差的性质与符号:(1)视准轴与水准轴不平行;(2)仪器下沉;(3)读数不准确;(4)水准尺下沉;(5)水准尺竖立不直。
第二节衡量精度的指标3、为检定某经纬仪的测角精度,对已知精确测定的水平角α=58002’00.0”(无误差)进行10次观测,其结果为:58002’03” 58002’01” 58001’58” 58001’57” 58002’04”58001’59” 58001’59” 58002’05” 58002’01” 58001’57”试求测角中误差σ。
4、设有两组观测值X i和Y i,它们的真误差分别为:△x:2,-3,+1,0,+2 △y:0,+3,+1,-2,+3试求观测量X与Y的方差σx2和σy2,哪个测量观测精度高?5、某距离在相同的观测条件下观测20次,得独立观测值(单位:m)为:437.59 437.61 437.60 437.55 437.59 437.62 437.64 437.62437.64 437.61 437.69 437.63 437.61 437.62 437.61 437.60437.56 437.68 437.65 437.58试计算该距离的算术平均值X及其方差与中误差估值。
6、有两段距离S1和S2,经多次观测得观测值及其中误差分别为300.00±2cm和600.00±2cm,试问哪段距离观测精度高?二距离各次观测值的观测真误差是否相同?7、有一段距离,其观测值及其中误差为652.48m±9mm。
(1)试估计该观测值的真误差实际可能出现的范围是多少?(2)试求该观测值的相对中误差。
测量平差试题

B测量平差基础一、 正误判断(正确“T ”,错误“F ”每题1分,共10 分)。
1.已知两段距离的长度及中误差分别为128.286m ±4.5cm 与218.268m ±4.5cm ,则其真误差与精度均相同( )。
2.如果X 与Y 的协方差0xy σ=,则其不相关( )。
3.水准测量中,按公式i icp s =(i s 为水准路线长)来定权,要求每公里高差精度相同( )。
4.可用误差椭圆来确定待定点与待定点之间的某些精度指标( )。
5.在某一平差问题中,观测数为n ,必要观测数为t ,参数个数u <t 且不独立,则该平差问题可采用附有参数的条件平差的函数模型。
( )。
6.由于同一平差问题采用不同的平差方法得到的结果不同,因此为了得到最佳平差结果,必须谨慎选择平差方法( )。
7.根据公式()222220cos sin 0360E F θσθθθ=+≤≤得到的曲线就是误差椭圆( )。
8.对于特定的平面控制网,如果按间接平差法解算,则误差方程的个数是一定的( )。
9.对于同一个观测值来说,若选定一定权常数0σ,则权愈小,其方差愈小,其精度愈高( )。
10.设观测值向量,1n L 彼此不独立,其权为()1,2,,i P i n = ,12(,,,)n Z f L L L = ,则有22211221111Z n nf f f P L P L P L P ⎛⎫⎛⎫⎛⎫∂∂∂=+++ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ ( )。
二、填空题(每空2分,共24分)。
1、设对某三角网进行同精度观测,得三角形角度闭合差分别为:3秒,-3秒,2秒,4秒,-2秒,-1秒,0秒,-4秒,3秒,-2秒,则测角中误差为 秒。
2、某平差问题函数模型)(I Q =为⎪⎪⎩⎪⎪⎨⎧=-=--=+-+=--0ˆ03060515443121x v v v v v v v v ,则该函数模型为平差方法的模型;=n ,=t ,=r ,=c ,=u 。
测量平差试题一

协因数阵为 QXˆXˆ
0.25 0.15
0.15 0.75
,且单位权方差
ˆ
2 0
3.0cm2
,
(1)计算 P1 点纵、横坐标中误差和点位中误差;
(2)计算 P1 点误差椭圆三要素E、E、 F ; (3)计算 P1 点在方位角为 90 方向上的位差。
(17 分)
一、FFFFT 二、相等 三、aabcd
六. (1)ˆx
3 2
cm,,ˆ y
1.5cm
ˆ p
3cm
(2)E =74. 5或254. 5,E, 1.54cm F 0.79cm
(3)
ˆ
90
1.5cm
9.定权时 0 可任意给定,它仅起比例常数的作用( )。
10.设有两个水平角的测角中误差相等,则角度值大的那个水平角相对精度高( )。
二、 用“相等”或“相同”或“不等”填空(8 分)。
已知两段距离的长度及其中误差为 300.158m±3.5cm; 600.686m±3.5cm。则:
1.这两段距离的中误差(
的测回数 N=( )。
a) 25
b) 20
c) 45
QQYXXX
Q XY QYY
=
0.5 0.25
0.25
0.5
单位权方差 0 2 =±2.0。则 P 点误差椭圆的方位角 T=( )。
a) 90
b) 135
c) 120
4.设 L 的权为 1,则乘积 4L 的权 P=( )。
)。
2.这两段距离的误差的最大限差(
)。
3.它们的精度(
)。
4.它们的相对精度(
)。
三、 选择填空。只选择一个正确答案(25 分)。
测量平差复习题答案

测量平差复习题答案一、单项选择题1. 在测量平差中,观测值的改正数与观测值的符号相反,说明该观测值是()。
A. 正误差B. 负误差C. 系统误差D. 偶然误差答案:B2. 测量平差中,观测值的中误差是指()。
A. 观测值的标准差B. 观测值的均值C. 观测值的偏差D. 观测值的最大误差答案:A3. 测量平差中,单位权中误差的计算公式为()。
A. σ0 = √(Σσ²) / nB. σ0 = Σσ² / nC. σ0 = √(Σσ²) / ΣnD. σ0= Σσ² / Σn答案:A二、多项选择题1. 测量平差中,下列哪些因素会影响观测值的精度()。
A. 观测者的技能水平B. 观测仪器的精度C. 观测环境D. 观测时间答案:ABCD2. 在测量平差中,下列哪些方法可以提高观测精度()。
A. 增加观测次数B. 采用高精度仪器C. 改进观测方法D. 延长观测时间答案:ABC三、填空题1. 测量平差中,观测值的中误差是用来衡量观测值的______。
答案:精度2. 测量平差中,单位权中误差是用来衡量观测值的______。
答案:精度3. 在测量平差中,观测值的改正数是用来______观测值的系统误差。
答案:消除四、简答题1. 简述测量平差中,观测值的中误差与观测值的精度之间的关系。
答案:观测值的中误差是观测值精度的一种度量,中误差越小,说明观测值的精度越高。
2. 测量平差中,如何通过观测值的改正数来判断观测值的误差性质?答案:观测值的改正数与观测值的符号相反,说明该观测值是负误差;如果改正数与观测值的符号相同,则说明该观测值是正误差。
五、计算题1. 已知一组观测值的方差分别为2、3、4,计算该组观测值的单位权中误差。
答案:σ0 = √(2+3+4) / 3 = √9 / 3 = √32. 假设在一次测量中,观测者得到了一组观测值,其改正数分别为-0.1、0.2、-0.3,计算该组观测值的平均改正数。
《测量平差习题》word版

第一章观测误差与传播率第一节观测误差1、在下列情况下用钢尺丈量距离,使量得的结果产生误差,时判别误差的性质与符号:(1)尺长不准确;(2)尺长检定过程中,尺长与标准尺长比较产生的误差;(3)尺不水平;(4)尺反曲或垂曲;(5)尺端偏离直线方向;(6)估读小数不准确;2、在下列情况下使水准测量中水准尺的读数带有误差,试判别误差的性质与符号:(1)视准轴与水准轴不平行;(2)仪器下沉;(3)读数不准确;(4)水准尺下沉;(5)水准尺竖立不直。
第二节衡量精度的指标3、为检定某经纬仪的测角精度,对已知精确测定的水平角α=58002’00.0”(无误差)进行10次观测,其结果为:58002’03” 58002’01” 58001’58” 58001’57” 58002’04”58001’59” 58001’59” 58002’05” 58002’01” 58001’57”试求测角中误差σ。
4、设有两组观测值X i和Y i,它们的真误差分别为:△x:2,-3,+1,0,+2 △y:0,+3,+1,-2,+3试求观测量X与Y的方差σx2和σy2,哪个测量观测精度高?5、某距离在相同的观测条件下观测20次,得独立观测值(单位:m)为:437.59 437.61 437.60 437.55 437.59 437.62 437.64 437.62437.64 437.61 437.69 437.63 437.61 437.62 437.61 437.60437.56 437.68 437.65 437.58试计算该距离的算术平均值X及其方差与中误差估值。
6、有两段距离S1和S2,经多次观测得观测值及其中误差分别为300.00±2cm和600.00±2cm,试问哪段距离观测精度高?二距离各次观测值的观测真误差是否相同?7、有一段距离,其观测值及其中误差为652.48m±9mm。
(1)试估计该观测值的真误差实际可能出现的范围是多少?(2)试求该观测值的相对中误差。
(整理)测量平差习题

20、已知观测值向量的权阵为:
(1)试问这三个观测值中有无不相关的观测值,指出哪些是不相关的观测值;
(2)设以L1,L2组成观测向量=,试写出它的权阵PL′及权P3。
21、设已知=,=,Z=,权阵Pz为:
试求权阵Px及Py。
22、设有观测向量Z=,其中,X=,Y=,已知协因数阵Qz为:
38、已知同精度独立观测值的权阵为:
试求算术平均值X=[L]/n的权PX。其中,[L]=L1+L2+…+Ln。
39、已知不等精度独立观测值Li的权为pi(I=1,2,…,n),试求带权平均值Y=[PL]/[P]的权PY。其中,[P]=p1+p2+…+pn。
40、已知随机量X1,X2的函数及其协因数阵为:Y=KX1,Z=FX2,
DL=
试求的方差阵。
30、在高级水准点A,B间(其高程无误差)进行水准测量,如图2-2。路线长为S1=2km,S2=6km,S3=4km,设每里观测高差的中误差为 。试求将闭合差ω=(HB-HA)-(h1+h2+h3),按距离成比例分配后P1至P2点间高差的中误差。
31、已知独立观测值L1,L2的中误差均为σ,试求函数X=2L1+5,Y= L2-2L2,Z=X+Y的中误差σX,σy,σZ。
437.59 437.61 437.60 437.55 437.59 437.62 437.64 437.62
437.64 437.61 437.69 437.63 437.61 437.62 437.61 437.60
437.56 437.68 437.65 437.58
试计算该距离的算术平均值X及其方差与中误差估值。
(整理)测量平差习题集

第二部分 自测题第一章 自测题一、判断题(每题2分,共20分)1、 通过平差可以消除误差,从而消除观测值之间的矛盾。
( )2、 观测值i L 与其偶然真误差i ∆必定等精度。
( )3、 测量条件相同,观测值的精度相同,它们的中误差、真误差也相同。
( )4、 或然误差为最或然值与观测值之差。
( )5、 若X 、Y 向量的维数相同,则YX XY Q Q =。
( )6、 最小二乘原理要求观测值必须服从正态分布。
( )7、 若真误差向量的数学期望为0,即0=∆)(E ,则表示观测值中仅含偶然误差。
( ) 8、 单位权中误差变化,但权比及中误差均不变。
( ) 9、 权或权倒数可以有单位。
( )10、相关观测值权逆阵Q 的对角线元素ii Q 与权阵P 的对角线元素ii P 之间的关系为1=ii ii P Q 。
( )二、填空题(每空0.5分,共20分)1、测量平差就是在 基础上,依据 原则,对观测值进行合理的调整,即分别给以适当的 ,使矛盾消除,从而得到一组最可靠的结果,并进行 。
2、测量条件包括 、 、 和 ,由于测量条件的不可能绝对理想,使得一切测量结果必然含有 。
3、测量误差定义为 ,按其性质可分为 、 和 。
经典测量平差主要研究的是 误差。
4、偶然误差服从 分布,它的概率特性为 、 和 。
仅含偶然误差的观测值线性函数服从 分布。
5、最优估计量应具有的性质为 、 和 。
若模型为线性模型,则所得最优估计量称为 ,最优估计量主要针对观测值中仅含 误差而言。
要证明某估计量为最优估计量,只需证明其满足 性和 性即可。
6、限差是 的最大误差限,它的概率依据是 ,测量上常用于制定 的误差限。
7、若已知观测值向量L 或其偶然真误差向量∆的协方差阵为∑,则L 或∆的权阵定义为L P =∆P = ,由于验前精度∑难以精确求得,实用中定权公式有 、 、,特别是对独立等精度观测向量L 而言,其权阵可简单取为L P = 。
8、已知真误差向量1⨯∆n 及其权阵P ,则单位权中误差公式为 ,当权阵P 为 此公式变为中误差公式。
测量平差习题

第一章观测误差与传播率第一节观测误差1、在下列情况下用钢尺丈量距离,使量得的结果产生误差,时判别误差的性质与符号:(1)尺长不准确;(2)尺长检定过程中,尺长与标准尺长比较产生的误差;(3)尺不水平;(4)尺反曲或垂曲;(5)尺端偏离直线方向;(6)估读小数不准确;2、在下列情况下使水准测量中水准尺的读数带有误差,试判别误差的性质与符号:(1)视准轴与水准轴不平行;(2)仪器下沉;(3)读数不准确;(4)水准尺下沉;(5)水准尺竖立不直。
第二节衡量精度的指标3、为检定某经纬仪的测角精度,对已知精确测定的水平角α=58002’00.0”(无误差)进行10次观测,其结果为:58002’03”58002’01”58001’58”58001’57”58002’04”58001’59”58001’59”58002’05”58002’01”58001’57”试求测角中误差σ。
4、设有两组观测值X i和Y i,它们的真误差分别为:△x:2,-3,+1,0,+2 △y:0,+3,+1,-2,+3试求观测量X与Y的方差σx2和σy2,哪个测量观测精度高?5、某距离在相同的观测条件下观测20次,得独立观测值(单位:m)为:437.59 437.61 437.60 437.55 437.59 437.62 437.64 437.62437.64 437.61 437.69 437.63 437.61 437.62 437.61 437.60437.56 437.68 437.65 437.58试计算该距离的算术平均值X及其方差与中误差估值。
6、有两段距离S1和S2,经多次观测得观测值及其中误差分别为300.00±2cm和600.00±2cm,试问哪段距离观测精度高?二距离各次观测值的观测真误差是否相同?7、有一段距离,其观测值及其中误差为652.48m±9mm。
(1)试估计该观测值的真误差实际可能出现的范围是多少?(2)试求该观测值的相对中误差。
测量平差习题参考答案

第一章 习题参考答案 1题.略2题.解 (1)222194σσ+(2)2221212219)3(σσL L L +-(3) 222212211212212211211")(cos )sin(sin ")(cos )sin(sin )cos(cos σρσρ⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫ ⎝⎛++++L L L L L L L L L L L L L 3题. 解TT TLL XY LL YL LL XL B A AD D BAD D AD D ===,,4题.解 设路线总长S 公里,按照测量学上的附合路线计算步骤,则路线闭合差B A h H h h H f -++=21由于是路线中点,故()B A h H h h H f v v -++-===21212121 则线路中点高程()()B A B A B A A A H H h h H H h h H h h H h H v h H H ++⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=++-=-++-+=-+=2121212121212121ˆ212121111中点设每公里高差观测中误差为0σ,则021)2/(σσσs h h ==按误差传播定律)(16,10425)52/(41)52/(41)2/(41)2/(414141212100212122220202222ˆ21121km S S s s s s h h h h H ≤≤=⋅⨯+⋅⨯=⨯+⨯=+=⎪⎪⎪⎪⎭⎫⎝⎛-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=σσσσσσσ中点5.解 设每个测回的中误差为0σ,需要再增加n 个测回,则)2(2028.0,28.020)1(2042.0,42.0200000+±=±=+±=±=n n σσσσ由上式可解出n.即252023202028.042.020222=-⎪⎭⎫ ⎝⎛⨯=-⨯=n 再增加25个测回6题.解[][][][][][][][][]][][][,100010001...,...)...(2121211212122111⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎣⎡⎥⎦⎤==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎢⎣⎡⎥⎦⎤=+++==p p p p p p p p p P p P p P p Q L L L P p P p P p L p L p L p x n n n p xx n n n n p p pL x][][][][][][p p p p p p p p p p p p p p p nnn⋅⋅++⋅⋅+⋅⋅=1 (1)12221117题。
测量平差习题

第一章 观测误差与传播率第一节 观测误差1、在下列情况下用钢尺丈量距离,使量得的结果产生误差,时判别误差的性质与符号(1)尺长不准确;(2)尺长检定过程中,尺长与标准尺长比较产生的误差;(3)尺不水平; (4)尺反曲或垂曲; ( 5)尺端偏离直线方向; (6)估读小数不准确;2、 在下列情况下使水准测量中水准尺的读数带有误差,试判别误差的性质与符号:1) 视准轴与水准轴不平行; 2) 仪器下沉; 3) 读数不准确; 4) 水准尺下沉; 5) 水准尺竖立不直。
第二节 衡量精度的指标3、为检定某经纬仪的测角精度,对已知精确测定的水平角 a =58°02 00.0”(无误差)进行 10次观测,其结果为:0 ' ” 0 '58002'03”58002'0158002'05” 58002'01” 58001'57试求测角中误差4、设有两组观测值 X i 和Y i ,它们的真误差分别为: △ x:2,-3,+1,0,+2△ y:0,+3,+1,-2,+3试求观测量 X 与Y 的方差d x 2和b y 2,哪个测量观测精度高 ?0 ' ” 0 ' ” 0 ' 58001'58”58001'57”58002'0458001'59” 58001'595、某距离在相同的观测条件下观测 20次,得独立观测值(单位:m )为:437.59 437.6i 437.60 437.55437.59 437.62 437.64 437.62437.64437.6i 437.69 437.63 437.6i 437.62 437.6i 437.60试计算该距离的算术平均值 X 及其方差与中误差估值。
6、有两段距离S i 和S 2,经多次观测得观测值及其中误差分别为 2cm,试问哪段距离观测精度高?二距离各次观测值的观测真误差是否相同7、 有一段距离,其观测值及其中误差为 652.48m ± 9mm 。
测量平差复习题答案

测量平差复习题答案一、选择题1. 平差的目的是什么?A. 确定测量数据的准确度B. 消除测量误差C. 计算未知点的坐标D. 以上都是2. 测量平差中,观测值的权值与什么有关?A. 观测值的精度B. 观测条件C. 测量仪器的精度D. 观测者的经验3. 测量误差的来源主要包括哪些?A. 仪器误差B. 人为误差C. 环境误差D. 所有以上4. 测量平差中,最小二乘法的基本原理是什么?A. 误差平方和最小B. 误差绝对值和最小C. 误差乘积最小D. 误差平均值最小5. 测量平差中,如何确定观测值的权?A. 根据观测者的经验和直觉B. 根据观测值的精度C. 根据测量仪器的精度D. 根据观测条件二、填空题6. 平差过程中,测量误差的改正数通常用________表示。
7. 测量平差中,权的概念是指________。
8. 测量误差的类型包括系统误差和________。
9. 最小二乘法中,观测值的权值通常与________成反比。
10. 测量平差中,常用的权函数有________和________。
三、简答题11. 简述测量平差中,最小二乘法的计算步骤。
12. 说明测量平差中,如何确定观测值的权值。
13. 描述测量平差中,误差传播的概念及其重要性。
四、计算题14. 假设有一组观测数据,其观测值为:x1=100.2mm, x2=100.3mm, x3=100.1mm。
已知观测误差的标准差为σ=0.1mm,试计算这组数据的平均值及其标准误差。
五、论述题15. 论述测量平差在工程测量中的重要性及其应用。
【答案】1. D2. A3. D4. A5. B6. 改正数7. 观测值的相对重要性8. 随机误差9. 观测误差的方差10. 倒数权函数,倒数平方权函数11. 略(根据最小二乘法的基本原理和计算步骤回答)12. 略(根据观测值的精度和误差方差来确定权值)13. 略(描述误差传播的概念,以及在测量平差中的重要性)14. 平均值 = (100.2 + 100.3 + 100.1) / 3 = 100.2mm;标准误差= σ / √3 = 0.1 / √3 mm15. 略(根据测量平差在工程测量中的重要性和应用进行论述)【结束语】测量平差是确保测量结果准确性的重要手段,通过本复习题的练习,希望能够帮助大家更好地理解和掌握测量平差的基本理论、方法和应用。
测量平差复习题及答案

测量平差复习题及答案一、综合题1.已知两段距离(de)长度及中误差分别为cm m 5.4465.300±及cm m 5.4894.660±,试说明这两段距离(de)真误差是否相等他们(de)精度是否相等答:它们(de)真误差不一定相等;相对精度不相等,后者高于前者.2.已知观测值向量⎪⎪⎭⎫ ⎝⎛=2121L L L (de)权阵为⎥⎥⎦⎤⎢⎢⎣⎡=32313132LL P ,现有函数21L L X +=,13L Y =,求观测值(de)权1L P ,2L P ,观测值(de)协因数阵XY Q .答:12/3L P =;22/3L P =;3XY Q =3.在下图所示三角网中,A .B 为已知点,41~P P 为待定点,已知32P P 边(de)边长和方位角分别为0S 和0α,今测得角度1421,,,L L L 和边长21,S S ,若按条件平差法对该网进行平差:(1)共有多少个条件方程各类条件方程各有多少个(2)试列出除图形条件和方位角条件外(de)其它条件方程(非线性条件方程不要求线性化)答:(1)14216,6,10n t r =+=== ,所以图形条件:4个;极条件:2个;边长条件:2个;基线条件:1个;方位角条件:1个 (2)四边形14ABPP (de)极条件(以1P 为极): 34131241314ˆˆˆˆsin()sin sin 1ˆˆˆˆsin sin sin()L L L L L L L L +⋅⋅=+ 四边形1234PP P P (de)极条件(以4P 为极): 10116891167ˆˆˆˆsin()sin sin 1ˆˆˆˆsin sin sin()L L L L L L L L +⋅⋅=+ 边长条件(1ˆAB S S - ):123434ˆˆˆˆˆˆsin()sin()AB S S L L L L L =+++ 边长条件(12ˆˆS S - ):1121314867ˆˆˆsin ˆˆˆˆˆsin()sin sin()S L S L L L L L ⋅=++ 基线条件(0AB S S - ):02101191011ˆˆˆˆˆsin()sin()S S L L L L L =+++4.A .B .C 三点在同一直线上,测出了AB .BC 及AC(de)距离,得到4个独立观测值,m L 010.2001=,m L 050.3002=,m L 070.3003=,m L 090.5004=,若令100米量距(de)权为单位权,试按条件平差法确定A .C 之间各段距离(de)平差值Lˆ.答:ˆ[200.0147,300.0635,300.0635,500.0782]T L=5.在某航测像片上,有一块矩形稻田.为了确定该稻田(de)面积,现用卡规量测了该矩形(de)长为cm L 501=,方差为22136.0cm =σ,宽为cm L 302=,方差为22236.0cm =σ,又用求积仪量测了该矩形(de)面积231535cm L =,方差为42336cm =σ,若设该矩形(de)长为参数1ˆX ,宽为参数2ˆX ,按间接平差法平差:(1)试求出该长方形(de)面积平差值;(2)面积平差值(de)中误差.答:(1)令0111ˆX X x =+,0222ˆX X x =+,011X L =,022X L =,误差方程式为: 1122312ˆˆ305035v xv xv v v ===+-令:10013050B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,0035L ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,单位权方差为2036σ=,则法方程为:T TB PBX B PL=,可得:120.30.5x X x ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,则0111ˆ50.3X X x =+=,0222ˆ30.5X X x =+= 所以面积平差值为2312ˆˆˆ50.3*30.51534L X X cm ===(2)2200.35T V PVcm rσ== ()12112212ˆˆˆˆˆˆˆˆˆdXdS X dX X dX X X dX ⎛⎫=+= ⎪ ⎪⎝⎭,所以ˆˆ98.94SS Q =则2ˆ 3.4814S cm σσ==±6.如图水准网中,A 为已知点,高程为10.000A H m =,观测高差及路线长度为:m h 563.21=,km S 11=;m h 326.12-=,km S 12=;m h 885.33-=,km S 23=;m h 883.34-=,km S 24=;若设参数12334ˆˆˆˆˆˆˆTTBX X X X H h h ⎡⎤⎡⎤==⎣⎦⎣⎦,定权时C= 2 km ,试列出:(1)、误差方程和限制条件; (2)、法方程式.答:(1)误差方程为:112231243ˆˆˆˆ4ˆv xv x v x x v x=⎧⎪=⎪⎨=++⎪⎪=⎩ 限制条件为:13ˆˆ20xx --= (2)法方程为:1234ˆ31004ˆ130140ˆ00110ˆ01102x x xx-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ 7.设对某量进行了两组观测,得到观测值(de)真误差如下: 第一组:3,-3,2,4,-2,-1,0,-4,3,-2 第二组:0,-1,-7,2,1,-1,8,0,-3,1 试回答如下问题:(1)两组值(de)平均误差1ˆθ、2ˆθ和中误差1ˆσ、2ˆσ(2)这两组观测值(de)精度,哪一组精度高,为什么答:(1)1ˆθ=,2ˆθ=;1ˆσ=,2ˆσ=(2)两组观测值(de)平均误差相同,而中误差不同,由于中误差对大(de)误差反应敏感,故通常采用中误差作为衡量精度(de)指标,本题中1ˆσ<2ˆσ,故第一组观测值精度高.8.设对丈量10km(de)距离同精度丈量10次,令其平均值(de)权为5,现以同样等级(de)精度丈量(de)距离.问丈量此距离一次(de)权是多少.(问答题,10分)答:一次观测值(de)权倒数1025N C P === ,所以每次丈量10km 距离(de)权为:100.5P =长度为i S 距离(de)权为:1i i C P S = ,则112.510,2.510C C P P == ,所以15C = 故12.522.5C P == 9.下列各式中(de)()1,2,3i L i =均为等精度独立观测值,其中误差为σ,试求下列函数(de)中误差:(1)()12312X L L L =++;(2)321L L L Y =答:(1)x σ= (2)3x σ=10.在图一所示测角网中,A 、B 、C 为待定点,同精度观测了1L 、2L 、3L 和4L 共四个角度观测值.设平差后BAC ∠为参数Xˆ. (1)试指出采用何种平差模型; (2)写出函数模型和法方程.答:采用附有参数(de)条件平差模型;平差方程为:123ˆˆˆ1800L L L ++-= 34ˆˆ3600L L +-= 1ˆˆ0L X -= 则条件方程为:12313421300ˆ0v v v w v v w v x w +++=⎧⎪++=⎨⎪-+=⎩ ,其中闭合差方程为1123234031w L L L w L L w L X ⎧=++⎪=+⎨⎪=-⎩,建立法方程为: 1122333110120001011ˆ0100k w k w k w x⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎪+= ⎪ ⎪ ⎪- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ 11.有水准网如下图,网中A .B 为已知水准点,高程m H A 013.12+=.m H B 013.10+=可视为无误差,C .D 为待定点,共观测了四个高差,高差观测值及相应水准路线(de)距离为:km S 21=,m h 004.11-=,km S 12=,m h 516.12+=,km S 23=,m h 512.23+=,km S 5.14=,m h 520.14+=.试用条件平差法求C 和D 两点高程(de)平差值.答:4,2n t == ,所以2r = ,条件方程如下:12324ˆˆˆ0ˆˆ0A Bh h h H H h h ⎧+-+-=⎪⎨-=⎪⎩ 以ˆi i ih h v =+ 代入上式,可得上述方程(de)最终形式为: 123411100001014v v v v ⎛⎫⎪-⎛⎫⎛⎫ ⎪-= ⎪ ⎪ ⎪-⎝⎭⎝⎭⎪ ⎪⎝⎭ ,以1km 观测高差为单位权观测,则法方程为: 1212502.540k k k k +=⎧⎨+-=⎩ ,解得120.35, 1.74k k =-= 进而求得()0.74 1.40.7 2.6TV mm =--观测值(de)平差值为:1234ˆˆˆˆ1.0047, 1.5174, 2.5127, 1.5174L m L m L m L m =-=== 则C 、D 两点(de)平差高程为:11.0083,12.5257C D H m H m ==12.设在三角形ABC 中,观测三内角321,,L L L ,将闭合差平均分配后得到(de)各角之值为014489ˆ,025050ˆ,030140ˆ321'''='''='''= L L L ,如下图.它们(de)协方差阵为⎪⎪⎪⎭⎫⎝⎛------=633363336LLD ,已知边长m S 000.15000=(无误差),试求ba S S ,(de)长度和它们(de)协方差SS D .答:013023ˆˆˆˆsin /sin 967.679,sin /sin 1150.573a b S S L L m S S L L m ==== 对函数式取自然对数,并微分得:331213231323ˆˆˆˆcos cos cos cos ˆˆˆˆ,ˆˆˆˆsin sin sin sin a b a b dS L dS L L L dL dL dL dL S S L L L L ====即1132233ˆˆˆ0ˆˆˆ0ˆa a a b b b dLdS S ctgL S ctgL dS dL dS S ctgL S ctgL dL ⎛⎫ ⎪⎛⎫-⎛⎫== ⎪ ⎪ ⎪ ⎪- ⎪⎝⎭⎝⎭ ⎪⎝⎭则23263311460114604 1.860.7713630962096250.77 1.32(20610)33645SS D cm --⎛⎫⎛⎫--⎛⎫⎛⎫ ⎪⎪=--⨯= ⎪ ⎪ ⎪⎪--⨯⎝⎭⎝⎭⎪⎪----⎝⎭⎝⎭。
【精品】测量平差习题

第一章观测误差与传播率第一节观测误差1、在下列情况下用钢尺丈量距离,使量得的结果产生误差,时判别误差的性质与符号:(1)尺长不准确;(2)尺长检定过程中,尺长与标准尺长比较产生的误差;(3)尺不水平;(4)尺反曲或垂曲;(5)尺端偏离直线方向;(6)估读小数不准确;2、在下列情况下使水准测量中水准尺的读数带有误差,试判别误差的性质与符号:(1)视准轴与水准轴不平行;(2)仪器下沉;(3)读数不准确;(4)水准尺下沉;第二节水准尺竖立不直。
第三节衡量精度的指标3、为检定某经纬仪的测角精度,对已知精确测定的水平角α=58002’00。
0”(无误差)进行10次观测,其结果为:58002’03”58002'01”58001’58"58001’57”58002'04”58001’59”58001’59”58002’05"58002’01”58001’57"试求测角中误差σ。
4、设有两组观测值Xi 和Yi,它们的真误差分别为:△x:2,-3,+1,0,+2△y:0,+3,+1,-2,+3试求观测量X与Y的方差σx2和σy2,哪个测量观测精度高?5、某距离在相同的观测条件下观测20次,得独立观测值(单位:m)为:437.59437。
61437。
60437。
55437。
59437.62437.64437。
62 437.64437。
61437.69437.63437。
61437.62437.61437.60437.56437.68437.65437.58试计算该距离的算术平均值X及其方差与中误差估值。
6、有两段距离S1和S2,经多次观测得观测值及其中误差分别为300。
00±2cm和600。
00±2cm,试问哪段距离观测精度高?二距离各次观测值的观测真误差是否相同?7、有一段距离,其观测值及其中误差为652.48m±9mm。
(1)试估计该观测值的真误差实际可能出现的范围是多少?(2)试求该观测值的相对中误差.8、设有观测值L1的权P1=2,其方差为σ12=4,又知观测值L2的方差σ22=1,试求其权P2及协因数Q11和Q22。
测量平差习题

=58002'00.0”(无误差)进行58002'03” 58002'01”58001'5858001'57 58002'04” 58001'5958001'5958002'05”58002'01”58001'575、某距离在相同的观测条件下观测 第一章 观测误差与传播率第一节 观测误差1、在下列情况下用钢尺丈量距离,使量得的结果产生误差,时判别误差的性质与符号(1)尺长不准确;(2)尺长检定过程中,尺长与标准尺长比较产生的误差; (3)尺不水平; (4)尺反曲或垂曲; ( 5)尺端偏离直线方向; (6)估读小数不准确;2、 在下列情况下使水准测量中水准尺的读数带有误差,试判别误差的性质与符号:( 1) 视准轴与水准轴不平行; ( 2) 仪器下沉; ( 3) 读数不准确; ( 4) 水准尺下沉; ( 5) 水准尺竖立不直。
第二节 衡量精度的指标 3、为检定某经纬仪的测角精度,对已知精确测定的水平角a 10 次观测,其结果为:试求测角中误差△x:2,-3,+1,0,+2 △y:0,+3,+1,-2,+3试求观测量X 与Y 的方差b x 2和b y 2,哪个测量观测精度高?4、设有两组观测值 X i 和Y i ,它们的真误差分别为: 437.59 437.61 437.60 437.55 437.59 437.62 437.64 437.62 437.64 437.61 437.69 437.63 437.61 437.62 437.61 437.60 437.56 437.68437.65 437.5820 次,得独立观测值(单位:m )为:试计算该距离的算术平均值X 及其方差与中误差估值。
6、有两段距离S i和S2,经多次观测得观测值及其中误差分别为300.00 ± 2cm和600.00 土2cm,试问哪段距离观测精度高?二距离各次观测值的观测真误差是否相同?7、有一段距离,其观测值及其中误差为652.48m ± 9mm。
测量平差期末考试题及答案

测量平差期末考试题及答案一、选择题(每题2分,共20分)1. 平差的基本目的是()。
A. 确定测量数据的准确度B. 确定测量误差的来源C. 消除测量误差D. 优化测量数据的分布答案:C2. 测量误差的来源主要包括()。
A. 测量仪器的误差B. 测量方法的误差C. 测量环境的误差D. 以上都是答案:D3. 测量平差中,权的概念是指()。
A. 测量数据的可靠性B. 测量数据的准确性C. 测量数据的重要性D. 测量数据的稳定性答案:A4. 测量平差中,最小二乘法的基本原理是()。
A. 使得测量误差的绝对值之和最小B. 使得测量误差的平方和最小C. 使得测量误差的平均值最小D. 使得测量误差的方差最小答案:B5. 在测量平差中,观测值的改正数是指()。
A. 观测值与真值之差B. 观测值与平均值之差C. 观测值与预测值之差D. 观测值与估计值之差答案:A...(此处省略其他选择题)二、填空题(每空2分,共20分)1. 平差的基本任务是_________测量误差,以获得_________的测量结果。
答案:消除或减小;准确可靠2. 测量误差可以分为系统误差和_________误差。
答案:随机3. 权的倒数称为_________。
答案:权的倒数4. 最小二乘法是一种常用的平差方法,其核心思想是使观测值的_________达到最小。
答案:残差平方和5. 测量平差中,观测值的改正数是指观测值与_________之差。
答案:平差值...(此处省略其他填空题)三、简答题(每题10分,共30分)1. 简述最小二乘法在测量平差中的应用。
答案:最小二乘法在测量平差中是一种常用的数据处理方法,它通过最小化观测值的残差平方和来寻找最佳估计值。
在应用时,首先需要建立观测方程,然后通过求解线性方程组来得到未知参数的估计值。
这种方法在处理多个观测数据时,能够合理地分配误差,使得所有观测数据的误差总和最小,从而得到更加准确的测量结果。
2. 解释什么是权,它在测量平差中的作用是什么。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、问答题(每小题4分,共12分)1、对控制网进行间接平差,可否在观测前根据布设的网形的观测方案来估算网中待定点的精度?为什么?2、何所谓控制网的平差基准?根据平差基准数不同,可将控制网的平差分为哪几类?3、经典平差中,精度评定主要包括哪些计算内容? 四、问答题(每小题4分,共12分) 1、(1)可以;(2)对于特定的平面控制网,如果按间接平差法解算,误差方程的个数是一定的,形式也是一定的;误差方程的系数阵B 是控制网网形决定的,观测值的权阵P 是由观测方案决定的,由此可以得到T bb N B PB =,进而可得到1XX bb Q N -=,根据先验方差20σ,便能估算网中待定点的精度。
2、(1)在控制网平差问题中,控制网的起算数据称其平差基准;(2)根据平差基准数不同,可将控制网的平差分为自由网平差与约束网平差两类。
3、测量成果精度包括两个方面:一是观测值实际的精度;二是由观测值经平差得到的观测值函数的精度。
而用来评定精度的方差可用单位权方差和协因数来计算,因而,精度评定主要包括的计算内容有: (1)单位权方差估值计算;(2)平差中基本向量的协因数阵的计算;(3)观测值平差值(参数平差值)函数的协因数计算。
(4)利用单位权方差估值与相应向量的协因数计算其方差(中误差)。
七 检验题(10分)在某地区进行三角观测,共25个三角形,其闭合差(以秒为单位)如下: +0.8 -0.5 +O.5 +0.8 -0.5 -0.8 -1.2 -1.0 -0.6 +0.3 +0.2+1.8 +0.6 -1.1 -1.5 -1.6 +1.2 -1.2 +0.6 +1.3 +0.4 -0.5 -0.6 +0.4 -2.0 现算出08.252w ,正误差平方和为9.07,负误差平方和为16.01,对该闭 合差进行偶然误差特性的检验。
五、综合题(36分) 1(6分)、在间接平差中0T 1T -1TBB ()ˆx (B PB)B Pl=N B Plˆv Bx-l ˆLL V l L f X -=-===+设Q Q LL =,证明ˆV X与统计不相关。
2(10分)、在如图所示的大地四边形中,A 、B 为已知点,C 、D 为未知点,1L ~8L 为角度观测值。
(1)、列出所有的条件方程,非线性的线性化。
(2)、若设未知点的坐标为参数,试写出求CD 边长平差值中误差的权函数式。
共 4 页第3 页3 (10分)、已求得某控制网中P 点误差椭圆参数031570'=E ϕ、dm E 57.1=和dm F 02.1=,已知PA 边坐标方位角032170'=PA α,km S PA 5=,A 为已知点,试求方L 5 L 6L 7 L 8 L 4L 3 L 1L 2B CD A位角中误差PA ασˆ和边长相对中误差PAS S PAσˆ。
4(10分)、如图闭合水准网中,A 为已知点,高程为10.000A H m =, P1,P2为高程未知点,观测高差及路线长度为:h 1=1.352m, S1=2 km ; h 2=-0.531m, S2=2 km ; h 3=-0.826m, S3=1 km ; 试用间接平差求P1,P2点高程的平差值。
五、综合题答案(36分) 1(6分)()()()T 1T -1TBB ll -1T -1T1ˆˆBB BB -1T 1ˆlx BB 11ˆˆˆˆlx ˆx (B PB)B Pl=N B Plˆv Bx-lQ N B P N B P Q N B P Q 0TBBXX BBBB BB VX XX QQ Q N Q BN Q BQ BN BN -----========-=-= 所以,ˆV X与统计不相关共 3页第 1 页2(10分) (1)、n=8,t=4,r=4)sin sin sin sin sin sin sin sin 1(0:1ˆsin ˆsin ˆsin ˆsin ˆsin ˆsin ˆsin ˆsin 0180ˆˆˆˆ0180ˆˆˆˆ0180ˆˆˆˆ86427531887766554433221175318642076540543208321L L L L L L L L W W V ctgL V ctgL V ctgL V ctgL V ctgL V ctgL V ctgL V ctgL L L L L L L L L L L L L L L L L L L L L -''==++-+-+-+-=-=-+++=-+++=-+++ρ线性化Ah3S2h2S1h1P2P1S3(2)()()D CDCD D CD CD C CD CD C CD CD s CDCDCDy S Y x S y S Y x S Y Y X XS CD ˆˆˆˆˆˆˆˆˆˆˆˆ:ˆˆˆˆˆˆ22∆X ∆∆X ∆δ++--=-+-=权函数式为 3(10分)(1),先得求横向中误差μσ,横向中误差μσ的方向μϕ与PA α方向垂直:02222229015000cos sin 2.11()1.45 5.99PA E PAE F dm dm S μμμμμμμμαϕαψϕϕσψψσσσρ=+'=-==+==''''==(2)求纵向误差s σ:022********cos sin 1.397()1.1821:4230PA E s s s PAE F dm dmK S ψαϕσψψσσ'=-==+====边长相对中误差为4 (10分)、n=3,t=2,r=1,选取P1,P2点高程平差值为参数12ˆˆ,X X ,u=2,c=r+u=3。
00112311.352,10.826A b X H h m X H h m =+==-=(1) 列误差方程1121232ˆˆˆˆˆˆˆAAh X H hX X h X H =-=-+=-+1121232ˆˆˆ5ˆv xv xx v x==-++=- 11223100ˆ115ˆ010v x v x v ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=---⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦共 3页第 2 页(2)组成法方程并解算 1231,2,1,1,2,12i iC P C km P P P P S ⎡⎤⎢⎥======⎢⎥⎢⎥⎣⎦则10215,1352ˆ()111.354ˆˆ10.825T TBB BB N B PB W B Pl x N W mm X X x m --⎡⎤⎡⎤====⎢⎥⎢⎥--⎣⎦⎣⎦⎡⎤==⎢⎥-⎣⎦⎡⎤=+=⎢⎥⎣⎦6、如下图所示,为未知P 点误差曲线(图中细线)图和误差椭圆图(图中粗线),A 、B 为已知点。
1)试在误差曲线上作出平差后P A 边的中误差,并说明; 2)试在误差椭圆上作出平差后P A 方位角的中误差,并说明;3)若点P 点位误差的极大值E =5mm ,极小值F =2mm ,且︒=52F ϕ,试计算方位角为102º的PB 边的中误差。
解:1)在误差曲线上作出平差后P A 边的中误差;连接PA 并与误差曲线交点a ,则Pa 长度为平差后P A 边的中误差Pa PA =σˆ 2)在误差椭圆上作出平差后P A 方位角的中误差;作垂直与PA 方向的垂线Pc ,作垂直与Pc 方向的垂线cb ,且与误差椭圆相切,垂足为c 点,则Pc 长度为平差后P A 边的横向误差PA u σˆ 则平差后P A 方位角的中误差:A BPacbρρσσα''=''≈PAPAu S PcS PAPAˆˆ 3)因为︒=52F ϕ 则:︒=142E ϕ则:︒-=︒-︒=-=ψ40142102E ϕα 所以:323.16)40(sin *4)40(cos *25sin cos ˆˆ22222222=︒-+︒-=ψ+ψ==ψF E σσϕ 方位角为102º的PB 边的中误差:mm 04.4ˆˆ±==ψσσϕ证明题如下图所示,A ,B 点为已知高程点,试按条件平差法求证在单一附合水准路线中,平差后高程最弱点在水准路线中央。
h1h2SAB证明:设水准路线全长为S ,h 1水准路线长度为T ,则h 2水准路线长度为S-T ; 设每公里中误差为单位权中误差,则h 1的权为1/T ,h 2的权为1/(S-T);则其权阵为:⎪⎪⎭⎫⎝⎛-=)/(100/1T S T P平差值条件方程式为:HA+0ˆˆ21=-+HB h h 则 A=( 1 1 )S A AP N T ==-1由平差值协因数阵:LL T LL LL L L AQ N A Q Q Q 1ˆˆ--=则高差平差值的协因数阵为:⎪⎪⎭⎫⎝⎛---=-=-1111)(1ˆˆS T S T AQ N A Q Q Q LL T LLLL L L则平差后P 点的高程为:()⎪⎪⎭⎫ ⎝⎛+=+=211ˆˆ01ˆh h H h H H A A P 则平差后P 点的权倒数(协因数)为ST S T f AQ N A fQ f fQ Q T LL T LL T LL P )(1-=-=- 求最弱点位,即为求最大方差,由方差与协因数之间的关系可知,也就是求最大协因数(权倒数),上式对T 求导令其等零,则 02=-STS T=S/2 则在水准路线中央的点位的方差最大,也就是最弱点位,命题得证。
.。
