Transient random walks on graphs and metric spaces with applications to hyperbolic surfaces
Kernels and regularization on graphs

Kernels and Regularization on GraphsAlexander J.Smola1and Risi Kondor21Machine Learning Group,RSISEAustralian National UniversityCanberra,ACT0200,AustraliaAlex.Smola@.au2Department of Computer ScienceColumbia University1214Amsterdam Avenue,M.C.0401New York,NY10027,USArisi@Abstract.We introduce a family of kernels on graphs based on thenotion of regularization operators.This generalizes in a natural way thenotion of regularization and Greens functions,as commonly used forreal valued functions,to graphs.It turns out that diffusion kernels canbe found as a special case of our reasoning.We show that the class ofpositive,monotonically decreasing functions on the unit interval leads tokernels and corresponding regularization operators.1IntroductionThere has recently been a surge of interest in learning algorithms that operate on input spaces X other than R n,specifically,discrete input spaces,such as strings, graphs,trees,automata etc..Since kernel-based algorithms,such as Support Vector Machines,Gaussian Processes,Kernel PCA,etc.capture the structure of X via the kernel K:X×X→R,as long as we can define an appropriate kernel on our discrete input space,these algorithms can be imported wholesale, together with their error analysis,theoretical guarantees and empirical success.One of the most general representations of discrete metric spaces are graphs. Even if all we know about our input space are local pairwise similarities between points x i,x j∈X,distances(e.g shortest path length)on the graph induced by these similarities can give a useful,more global,sense of similarity between objects.In their work on Diffusion Kernels,Kondor and Lafferty[2002]gave a specific construction for a kernel capturing this structure.Belkin and Niyogi [2002]proposed an essentially equivalent construction in the context of approx-imating data lying on surfaces in a high dimensional embedding space,and in the context of leveraging information from unlabeled data.In this paper we put these earlier results into the more principled framework of Regularization Theory.We propose a family of regularization operators(equiv-alently,kernels)on graphs that include Diffusion Kernels as a special case,and show that this family encompasses all possible regularization operators invariant under permutations of the vertices in a particular sense.2Alexander Smola and Risi KondorOutline of the Paper:Section2introduces the concept of the graph Laplacian and relates it to the Laplace operator on real valued functions.Next we define an extended class of regularization operators and show why they have to be es-sentially a function of the Laplacian.An analogy to real valued Greens functions is established in Section3.3,and efficient methods for computing such functions are presented in Section4.We conclude with a discussion.2Laplace OperatorsAn undirected unweighted graph G consists of a set of vertices V numbered1to n,and a set of edges E(i.e.,pairs(i,j)where i,j∈V and(i,j)∈E⇔(j,i)∈E). We will sometimes write i∼j to denote that i and j are neighbors,i.e.(i,j)∈E. The adjacency matrix of G is an n×n real matrix W,with W ij=1if i∼j,and 0otherwise(by construction,W is symmetric and its diagonal entries are zero). These definitions and most of the following theory can trivially be extended toweighted graphs by allowing W ij∈[0,∞).Let D be an n×n diagonal matrix with D ii=jW ij.The Laplacian of Gis defined as L:=D−W and the Normalized Laplacian is˜L:=D−12LD−12= I−D−12W D−12.The following two theorems are well known results from spectral graph theory[Chung-Graham,1997]:Theorem1(Spectrum of˜L).˜L is a symmetric,positive semidefinite matrix, and its eigenvaluesλ1,λ2,...,λn satisfy0≤λi≤2.Furthermore,the number of eigenvalues equal to zero equals to the number of disjoint components in G.The bound on the spectrum follows directly from Gerschgorin’s Theorem.Theorem2(L and˜L for Regular Graphs).Now let G be a regular graph of degree d,that is,a graph in which every vertex has exactly d neighbors.ThenL=d I−W and˜L=I−1d W=1dL.Finally,W,L,˜L share the same eigenvectors{v i},where v i=λ−1iW v i=(d−λi)−1L v i=(1−d−1λi)−1˜L v i for all i.L and˜L can be regarded as linear operators on functions f:V→R,or,equiv-alently,on vectors f=(f1,f2,...,f n) .We could equally well have defined Lbyf,L f =f L f=−12i∼j(f i−f j)2for all f∈R n,(1)which readily generalizes to graphs with a countably infinite number of vertices.The Laplacian derives its name from its analogy with the familiar Laplacianoperator∆=∂2∂x21+∂2∂x22+...+∂2∂x2mon continuous spaces.Regarding(1)asinducing a semi-norm f L= f,L f on R n,the analogous expression for∆defined on a compact spaceΩisf ∆= f,∆f =Ωf(∆f)dω=Ω(∇f)·(∇f)dω.(2)Both(1)and(2)quantify how much f and f vary locally,or how“smooth”they are over their respective domains.Kernels and Regularization on Graphs3 More explicitly,whenΩ=R m,up to a constant,−L is exactly thefinite difference discretization of∆on a regular lattice:∆f(x)=mi=1∂2∂x2if≈mi=1∂∂x if(x+12e i)−∂∂x if(x−12e i)δ≈mi=1f(x+e i)+f(x−e i)−2f(x)δ2=1δ2mi=1(f x1,...,x i+1,...,x m+f x1,...,x i−1,...,x m−2f x1,...,x m)=−1δ2[L f]x1,...,x m,where e1,e2,...,e m is an orthogonal basis for R m normalized to e i =δ, the vertices of the lattice are at x=x1e1+...+x m e m with integer valuedcoordinates x i∈N,and f x1,x2,...,x m=f(x).Moreover,both the continuous and the dis-crete Laplacians are canonical operators on their respective domains,in the sense that they are invariant under certain natural transformations of the underlying space,and in this they are essentially unique.Regular grid in two dimensionsThe Laplace operator∆is the unique self-adjoint linear second order differ-ential operator invariant under transformations of the coordinate system under the action of the special orthogonal group SO m,i.e.invariant under rotations. This well known result can be seen by using Schur’s lemma and the fact that SO m is irreducible on R m.We now show a similar result for L.Here the permutation group plays a similar role to SO m.We need some additional definitions:denote by S n the group of permutations on{1,2,...,n}withπ∈S n being a specific permutation taking i∈{1,2,...n}toπ(i).The so-called defining representation of S n consists of n×n matricesΠπ,such that[Ππ]i,π(i)=1and all other entries ofΠπare zero. Theorem3(Permutation Invariant Linear Functions on Graphs).Let L be an n×n symmetric real matrix,linearly related to the n×n adjacency matrix W,i.e.L=T[W]for some linear operator L in a way invariant to permutations of vertices in the sense thatΠ πT[W]Ππ=TΠ πWΠπ(3)for anyπ∈S n.Then L is related to W by a linear combination of the follow-ing three operations:identity;row/column sums;overall sum;row/column sum restricted to the diagonal of L;overall sum restricted to the diagonal of W. Proof LetL i1i2=T[W]i1i2:=ni3=1ni4=1T i1i2i3i4W i3i4(4)with T∈R n4.Eq.(3)then implies Tπ(i1)π(i2)π(i3)π(i4)=T i1i2i3i4for anyπ∈S n.4Alexander Smola and Risi KondorThe indices of T can be partitioned by the equality relation on their values,e.g.(2,5,2,7)is of the partition type [13|2|4],since i 1=i 3,but i 2=i 1,i 4=i 1and i 2=i 4.The key observation is that under the action of the permutation group,elements of T with a given index partition structure are taken to elements with the same index partition structure,e.g.if i 1=i 3then π(i 1)=π(i 3)and if i 1=i 3,then π(i 1)=π(i 3).Furthermore,an element with a given index index partition structure can be mapped to any other element of T with the same index partition structure by a suitable choice of π.Hence,a necessary and sufficient condition for (4)is that all elements of T of a given index partition structure be equal.Therefore,T must be a linear combination of the following tensors (i.e.multilinear forms):A i 1i 2i 3i 4=1B [1,2]i 1i 2i 3i 4=δi 1i 2B [1,3]i 1i 2i 3i 4=δi 1i 3B [1,4]i 1i 2i 3i 4=δi 1i 4B [2,3]i 1i 2i 3i 4=δi 2i 3B [2,4]i 1i 2i 3i 4=δi 2i 4B [3,4]i 1i 2i 3i 4=δi 3i 4C [1,2,3]i 1i 2i 3i 4=δi 1i 2δi 2i 3C [2,3,4]i 1i 2i 3i 4=δi 2i 3δi 3i 4C [3,4,1]i 1i 2i 3i 4=δi 3i 4δi 4i 1C [4,1,2]i 1i 2i 3i 4=δi 4i 1δi 1i 2D [1,2][3,4]i 1i 2i 3i 4=δi 1i 2δi 3i 4D [1,3][2,4]i 1i 2i 3i 4=δi 1i 3δi 2i 4D [1,4][2,3]i 1i 2i 3i 4=δi 1i 4δi 2i 3E [1,2,3,4]i 1i 2i 3i 4=δi 1i 2δi 1i 3δi 1i 4.The tensor A puts the overall sum in each element of L ,while B [1,2]returns the the same restricted to the diagonal of L .Since W has vanishing diagonal,B [3,4],C [2,3,4],C [3,4,1],D [1,2][3,4]and E [1,2,3,4]produce zero.Without loss of generality we can therefore ignore them.By symmetry of W ,the pairs (B [1,3],B [1,4]),(B [2,3],B [2,4]),(C [1,2,3],C [4,1,2])have the same effect on W ,hence we can set the coefficient of the second member of each to zero.Furthermore,to enforce symmetry on L ,the coefficient of B [1,3]and B [2,3]must be the same (without loss of generality 1)and this will give the row/column sum matrix ( k W ik )+( k W kl ).Similarly,C [1,2,3]and C [4,1,2]must have the same coefficient and this will give the row/column sum restricted to the diagonal:δij [( k W ik )+( k W kl )].Finally,by symmetry of W ,D [1,3][2,4]and D [1,4][2,3]are both equivalent to the identity map.The various row/column sum and overall sum operations are uninteresting from a graph theory point of view,since they do not heed to the topology of the graph.Imposing the conditions that each row and column in L must sum to zero,we recover the graph Laplacian.Hence,up to a constant factor and trivial additive components,the graph Laplacian (or the normalized graph Laplacian if we wish to rescale by the number of edges per vertex)is the only “invariant”differential operator for given W (or its normalized counterpart ˜W ).Unless stated otherwise,all results below hold for both L and ˜L (albeit with a different spectrum)and we will,in the following,focus on ˜Ldue to the fact that its spectrum is contained in [0,2].Kernels and Regularization on Graphs5 3RegularizationThe fact that L induces a semi-norm on f which penalizes the changes between adjacent vertices,as described in(1),indicates that it may serve as a tool to design regularization operators.3.1Regularization via the Laplace OperatorWe begin with a brief overview of translation invariant regularization operators on continuous spaces and show how they can be interpreted as powers of∆.This will allow us to repeat the development almost verbatim with˜L(or L)instead.Some of the most successful regularization functionals on R n,leading to kernels such as the Gaussian RBF,can be written as[Smola et al.,1998]f,P f :=|˜f(ω)|2r( ω 2)dω= f,r(∆)f .(5)Here f∈L2(R n),˜f(ω)denotes the Fourier transform of f,r( ω 2)is a function penalizing frequency components|˜f(ω)|of f,typically increasing in ω 2,and finally,r(∆)is the extension of r to operators simply by applying r to the spectrum of∆[Dunford and Schwartz,1958]f,r(∆)f =if,ψi r(λi) ψi,fwhere{(ψi,λi)}is the eigensystem of∆.The last equality in(5)holds because applications of∆become multiplications by ω 2in Fourier space.Kernels are obtained by solving the self-consistency condition[Smola et al.,1998]k(x,·),P k(x ,·) =k(x,x ).(6) One can show that k(x,x )=κ(x−x ),whereκis equal to the inverse Fourier transform of r−1( ω 2).Several r functions have been known to yield good results.The two most popular are given below:r( ω 2)k(x,x )r(∆)Gaussian RBF expσ22ω 2exp−12σ2x−x 2∞i=0σ2ii!∆iLaplacian RBF1+σ2 ω 2exp−1σx−x1+σ2∆In summary,regularization according to(5)is carried out by penalizing˜f(ω) by a function of the Laplace operator.For many results in regularization theory one requires r( ω 2)→∞for ω 2→∞.3.2Regularization via the Graph LaplacianIn complete analogy to(5),we define a class of regularization functionals on graphs asf,P f := f,r(˜L)f .(7)6Alexander Smola and Risi KondorFig.1.Regularization function r (λ).From left to right:regularized Laplacian (σ2=1),diffusion process (σ2=1),one-step random walk (a =2),4-step random walk (a =2),inverse cosine.Here r (˜L )is understood as applying the scalar valued function r (λ)to the eigen-values of ˜L ,that is,r (˜L ):=m i =1r (λi )v i v i ,(8)where {(λi ,v i )}constitute the eigensystem of ˜L .The normalized graph Lapla-cian ˜Lis preferable to L ,since ˜L ’s spectrum is contained in [0,2].The obvious goal is to gain insight into what functions are appropriate choices for r .–From (1)we infer that v i with large λi correspond to rather uneven functions on the graph G .Consequently,they should be penalized more strongly than v i with small λi .Hence r (λ)should be monotonically increasing in λ.–Requiring that r (˜L) 0imposes the constraint r (λ)≥0for all λ∈[0,2].–Finally,we can limit ourselves to r (λ)expressible as power series,since the latter are dense in the space of C 0functions on bounded domains.In Section 3.5we will present additional motivation for the choice of r (λ)in the context of spectral graph theory and segmentation.As we shall see,the following functions are of particular interest:r (λ)=1+σ2λ(Regularized Laplacian)(9)r (λ)=exp σ2/2λ(Diffusion Process)(10)r (λ)=(aI −λ)−1with a ≥2(One-Step Random Walk)(11)r (λ)=(aI −λ)−p with a ≥2(p -Step Random Walk)(12)r (λ)=(cos λπ/4)−1(Inverse Cosine)(13)Figure 1shows the regularization behavior for the functions (9)-(13).3.3KernelsThe introduction of a regularization matrix P =r (˜L)allows us to define a Hilbert space H on R m via f,f H := f ,P f .We now show that H is a reproducing kernel Hilbert space.Kernels and Regularization on Graphs 7Theorem 4.Denote by P ∈R m ×m a (positive semidefinite)regularization ma-trix and denote by H the image of R m under P .Then H with dot product f,f H := f ,P f is a Reproducing Kernel Hilbert Space and its kernel is k (i,j )= P −1ij ,where P −1denotes the pseudo-inverse if P is not invertible.Proof Since P is a positive semidefinite matrix,we clearly have a Hilbert space on P R m .To show the reproducing property we need to prove thatf (i )= f,k (i,·) H .(14)Note that k (i,j )can take on at most m 2different values (since i,j ∈[1:m ]).In matrix notation (14)means that for all f ∈Hf (i )=f P K i,:for all i ⇐⇒f =f P K.(15)The latter holds if K =P −1and f ∈P R m ,which proves the claim.In other words,K is the Greens function of P ,just as in the continuous case.The notion of Greens functions on graphs was only recently introduced by Chung-Graham and Yau [2000]for L .The above theorem extended this idea to arbitrary regularization operators ˆr (˜L).Corollary 1.Denote by P =r (˜L )a regularization matrix,then the correspond-ing kernel is given by K =r −1(˜L ),where we take the pseudo-inverse wherever necessary.More specifically,if {(v i ,λi )}constitute the eigensystem of ˜L,we have K =mi =1r −1(λi )v i v i where we define 0−1≡0.(16)3.4Examples of KernelsBy virtue of Corollary 1we only need to take (9)-(13)and plug the definition of r (λ)into (16)to obtain formulae for computing K .This yields the following kernel matrices:K =(I +σ2˜L)−1(Regularized Laplacian)(17)K =exp(−σ2/2˜L)(Diffusion Process)(18)K =(aI −˜L)p with a ≥2(p -Step Random Walk)(19)K =cos ˜Lπ/4(Inverse Cosine)(20)Equation (18)corresponds to the diffusion kernel proposed by Kondor and Laf-ferty [2002],for which K (x,x )can be visualized as the quantity of some sub-stance that would accumulate at vertex x after a given amount of time if we injected the substance at vertex x and let it diffuse through the graph along the edges.Note that this involves matrix exponentiation defined via the limit K =exp(B )=lim n →∞(I +B/n )n as opposed to component-wise exponentiation K i,j =exp(B i,j ).8Alexander Smola and Risi KondorFig.2.Thefirst8eigenvectors of the normalized graph Laplacian corresponding to the graph drawn above.Each line attached to a vertex is proportional to the value of the corresponding eigenvector at the vertex.Positive values(red)point up and negative values(blue)point down.Note that the assignment of values becomes less and less uniform with increasing eigenvalue(i.e.from left to right).For(17)it is typically more efficient to deal with the inverse of K,as it avoids the costly inversion of the sparse matrix˜L.Such situations arise,e.g.,in Gaussian Process estimation,where K is the covariance matrix of a stochastic process[Williams,1999].Regarding(19),recall that(aI−˜L)p=((a−1)I+˜W)p is up to scaling terms equiv-alent to a p-step random walk on the graphwith random restarts(see Section A for de-tails).In this sense it is similar to the dif-fusion kernel.However,the fact that K in-volves only afinite number of products ofmatrices makes it much more attractive forpractical purposes.In particular,entries inK ij can be computed cheaply using the factthat˜L is a sparse matrix.A nearest neighbor graph.Finally,the inverse cosine kernel treats lower complexity functions almost equally,with a significant reduction in the upper end of the spectrum.Figure2 shows the leading eigenvectors of the graph drawn above and Figure3provide examples of some of the kernels discussed above.3.5Clustering and Spectral Graph TheoryWe could also have derived r(˜L)directly from spectral graph theory:the eigen-vectors of the graph Laplacian correspond to functions partitioning the graph into clusters,see e.g.,[Chung-Graham,1997,Shi and Malik,1997]and the ref-erences therein.In general,small eigenvalues have associated eigenvectors which vary little between adjacent vertices.Finding the smallest eigenvectors of˜L can be seen as a real-valued relaxation of the min-cut problem.3For instance,the smallest eigenvalue of˜L is0,its corresponding eigenvector is D121n with1n:=(1,...,1)∈R n.The second smallest eigenvalue/eigenvector pair,also often referred to as the Fiedler-vector,can be used to split the graph 3Only recently,algorithms based on the celebrated semidefinite relaxation of the min-cut problem by Goemans and Williamson[1995]have seen wider use[Torr,2003]in segmentation and clustering by use of spectral bundle methods.Kernels and Regularization on Graphs9Fig.3.Top:regularized graph Laplacian;Middle:diffusion kernel with σ=5,Bottom:4-step random walk kernel.Each figure displays K ij for fixed i .The value K ij at vertex i is denoted by a bold line.Note that only adjacent vertices to i bear significant value.into two distinct parts [Weiss,1999,Shi and Malik,1997],and further eigenvec-tors with larger eigenvalues have been used for more finely-grained partitions of the graph.See Figure 2for an example.Such a decomposition into functions of increasing complexity has very de-sirable properties:if we want to perform estimation on the graph,we will wish to bias the estimate towards functions which vary little over large homogeneous portions 4.Consequently,we have the following interpretation of f,f H .As-sume that f = i βi v i ,where {(v i ,λi )}is the eigensystem of ˜L.Then we can rewrite f,f H to yield f ,r (˜L )f = i βi v i , j r (λj )v j v j l βl v l = iβ2i r (λi ).(21)This means that the components of f which vary a lot over coherent clusters in the graph are penalized more strongly,whereas the portions of f ,which are essentially constant over clusters,are preferred.This is exactly what we want.3.6Approximate ComputationOften it is not necessary to know all values of the kernel (e.g.,if we only observe instances from a subset of all positions on the graph).There it would be wasteful to compute the full matrix r (L )−1explicitly,since such operations typically scale with O (n 3).Furthermore,for large n it is not desirable to compute K via (16),that is,by computing the eigensystem of ˜Land assembling K directly.4If we cannot assume a connection between the structure of the graph and the values of the function to be estimated on it,the entire concept of designing kernels on graphs obviously becomes meaningless.10Alexander Smola and Risi KondorInstead,we would like to take advantage of the fact that ˜L is sparse,and con-sequently any operation ˜Lαhas cost at most linear in the number of nonzero ele-ments of ˜L ,hence the cost is bounded by O (|E |+n ).Moreover,if d is the largest degree of the graph,then computing L p e i costs at most |E | p −1i =1(min(d +1,n ))ioperations:at each step the number of non-zeros in the rhs decreases by at most a factor of d +1.This means that as long as we can approximate K =r −1(˜L )by a low order polynomial,say ρ(˜L ):= N i =0βi ˜L i ,significant savings are possible.Note that we need not necessarily require a uniformly good approximation and put the main emphasis on the approximation for small λ.However,we need to ensure that ρ(˜L)is positive semidefinite.Diffusion Kernel:The fact that the series r −1(x )=exp(−βx )= ∞m =0(−β)m x m m !has alternating signs shows that the approximation error at r −1(x )is boundedby (2β)N +1(N +1)!,if we use N terms in the expansion (from Theorem 1we know that ˜L≤2).For instance,for β=1,10terms are sufficient to obtain an error of the order of 10−4.Variational Approximation:In general,if we want to approximate r −1(λ)on[0,2],we need to solve the L ∞([0,2])approximation problemminimize β, subject to N i =0βi λi −r −1(λ) ≤ ∀λ∈[0,2](22)Clearly,(22)is equivalent to minimizing sup ˜L ρ(˜L )−r−1(˜L ) ,since the matrix norm is determined by the largest eigenvalues,and we can find ˜Lsuch that the discrepancy between ρ(λ)and r −1(λ)is attained.Variational problems of this form have been studied in the literature,and their solution may provide much better approximations to r −1(λ)than a truncated power series expansion.4Products of GraphsAs we have already pointed out,it is very expensive to compute K for arbitrary ˆr and ˜L.For special types of graphs and regularization,however,significant computational savings can be made.4.1Factor GraphsThe work of this section is a direct extension of results by Ellis [2002]and Chung-Graham and Yau [2000],who study factor graphs to compute inverses of the graph Laplacian.Definition 1(Factor Graphs).Denote by (V,E )and (V ,E )the vertices V and edges E of two graphs,then the factor graph (V f ,E f ):=(V,E )⊗(V ,E )is defined as the graph where (i,i )∈V f if i ∈V and i ∈V ;and ((i,i ),(j,j ))∈E f if and only if either (i,j )∈E and i =j or (i ,j )∈E and i =j .Kernels and Regularization on Graphs 11For instance,the factor graph of two rings is a torus.The nice property of factor graphs is that we can compute the eigenvalues of the Laplacian on products very easily (see e.g.,Chung-Graham and Yau [2000]):Theorem 5(Eigenvalues of Factor Graphs).The eigenvalues and eigen-vectors of the normalized Laplacian for the factor graph between a regular graph of degree d with eigenvalues {λj }and a regular graph of degree d with eigenvalues {λ l }are of the form:λfact j,l =d d +d λj +d d +d λ l(23)and the eigenvectors satisfy e j,l(i,i )=e j i e l i ,where e j is an eigenvector of ˜L and e l is an eigenvector of ˜L.This allows us to apply Corollary 1to obtain an expansion of K asK =(r (L ))−1=j,l r −1(λjl )e j,l e j,l .(24)While providing an explicit recipe for the computation of K ij without the need to compute the full matrix K ,this still requires O (n 2)operations per entry,which may be more costly than what we want (here n is the number of vertices of the factor graph).Two methods for computing (24)become evident at this point:if r has a special structure,we may exploit this to decompose K into the products and sums of terms depending on one of the two graphs alone and pre-compute these expressions beforehand.Secondly,if one of the two terms in the expansion can be computed for a rather general class of values of r (x ),we can pre-compute this expansion and only carry out the remainder corresponding to (24)explicitly.4.2Product Decomposition of r (x )Central to our reasoning is the observation that for certain r (x ),the term 1r (a +b )can be expressed in terms of a product and sum of terms depending on a and b only.We assume that 1r (a +b )=M m =1ρn (a )˜ρn (b ).(25)In the following we will show that in such situations the kernels on factor graphs can be computed as an analogous combination of products and sums of kernel functions on the terms constituting the ingredients of the factor graph.Before we do so,we briefly check that many r (x )indeed satisfy this property.exp(−β(a +b ))=exp(−βa )exp(−βb )(26)(A −(a +b ))= A 2−a + A 2−b (27)(A −(a +b ))p =p n =0p n A 2−a n A 2−b p −n (28)cos (a +b )π4=cos aπ4cos bπ4−sin aπ4sin bπ4(29)12Alexander Smola and Risi KondorIn a nutshell,we will exploit the fact that for products of graphs the eigenvalues of the joint graph Laplacian can be written as the sum of the eigenvalues of the Laplacians of the constituent graphs.This way we can perform computations on ρn and˜ρn separately without the need to take the other part of the the product of graphs into account.Definek m(i,j):=l ρldλld+de l i e l j and˜k m(i ,j ):=l˜ρldλld+d˜e l i ˜e l j .(30)Then we have the following composition theorem:Theorem6.Denote by(V,E)and(V ,E )connected regular graphs of degrees d with m vertices(and d ,m respectively)and normalized graph Laplacians ˜L,˜L .Furthermore denote by r(x)a rational function with matrix-valued exten-sionˆr(X).In this case the kernel K corresponding to the regularization operator ˆr(L)on the product graph of(V,E)and(V ,E )is given byk((i,i ),(j,j ))=Mm=1k m(i,j)˜k m(i ,j )(31)Proof Plug the expansion of1r(a+b)as given by(25)into(24)and collect terms.From(26)we immediately obtain the corollary(see Kondor and Lafferty[2002]) that for diffusion processes on factor graphs the kernel on the factor graph is given by the product of kernels on the constituents,that is k((i,i ),(j,j ))= k(i,j)k (i ,j ).The kernels k m and˜k m can be computed either by using an analytic solution of the underlying factors of the graph or alternatively they can be computed numerically.If the total number of kernels k n is small in comparison to the number of possible coordinates this is still computationally beneficial.4.3Composition TheoremsIf no expansion as in(31)can be found,we may still be able to compute ker-nels by extending a reasoning from[Ellis,2002].More specifically,the following composition theorem allows us to accelerate the computation in many cases, whenever we can parameterize(ˆr(L+αI))−1in an efficient way.For this pur-pose we introduce two auxiliary functionsKα(i,j):=ˆrdd+dL+αdd+dI−1=lrdλl+αdd+d−1e l(i)e l(j)G α(i,j):=(L +αI)−1=l1λl+αe l(i)e l(j).(32)In some cases Kα(i,j)may be computed in closed form,thus obviating the need to perform expensive matrix inversion,e.g.,in the case where the underlying graph is a chain[Ellis,2002]and Kα=Gα.Kernels and Regularization on Graphs 13Theorem 7.Under the assumptions of Theorem 6we haveK ((j,j ),(l,l ))=12πi C K α(j,l )G −α(j ,l )dα= v K λv (j,l )e v j e v l (33)where C ⊂C is a contour of the C containing the poles of (V ,E )including 0.For practical purposes,the third term of (33)is more amenable to computation.Proof From (24)we haveK ((j,j ),(l,l ))= u,v r dλu +d λv d +d −1e u j e u l e v j e v l (34)=12πi C u r dλu +d αd +d −1e u j e u l v 1λv −αe v j e v l dαHere the second equalityfollows from the fact that the contour integral over a pole p yields C f (α)p −αdα=2πif (p ),and the claim is verified by checking thedefinitions of K αand G α.The last equality can be seen from (34)by splitting up the summation over u and v .5ConclusionsWe have shown that the canonical family of kernels on graphs are of the form of power series in the graph Laplacian.Equivalently,such kernels can be char-acterized by a real valued function of the eigenvalues of the Laplacian.Special cases include diffusion kernels,the regularized Laplacian kernel and p -step ran-dom walk kernels.We have developed the regularization theory of learning on graphs using such kernels and explored methods for efficiently computing and approximating the kernel matrix.Acknowledgments This work was supported by a grant of the ARC.The authors thank Eleazar Eskin,Patrick Haffner,Andrew Ng,Bob Williamson and S.V.N.Vishwanathan for helpful comments and suggestions.A Link AnalysisRather surprisingly,our approach to regularizing functions on graphs bears re-semblance to algorithms for scoring web pages such as PageRank [Page et al.,1998],HITS [Kleinberg,1999],and randomized HITS [Zheng et al.,2001].More specifically,the random walks on graphs used in all three algorithms and the stationary distributions arising from them are closely connected with the eigen-system of L and ˜Lrespectively.We begin with an analysis of PageRank.Given a set of web pages and links between them we construct a directed graph in such a way that pages correspond。
FLUENT中组分输运及化学反应燃烧模拟

混合分数定义
混合分数, f, 写成元素的质量分数形式:
f Zk Zk,O Zk,F Zk,O
其处中的,值。Zk 是元素k的质量分数 ;下标 F 和O 表示燃料和氧化剂进口流
对于简单的 fuel/oxidizer系统, 混合物分数代表计算控制体里的燃料 质量分数.
平衡化学的 PDF模型 层流火焰面模型
进展变量模型
Zimont 模型
有限速率模型
用总包机理反应描述化学反应过程. 求解化学组分输运方程.
求解当地时间平均的各个组分的质量分数, mj.
组分 j的源项 (产生或消耗)是机理中所有k个反应的净反应速率 :
Rj Rjk k
R、jk混(第合k或个涡化旋学破反碎应(生E成BU或)消速耗率的的j 组小分值)。是.根据 Arrhenius速率公式
p(f) can be used to compute time-averaged values of variables that
depend on the mixture fraction, f:
i
1 0
p
(
f
)
i( f )d f
Species mole fractions
Temperature, density
的燃烧过程。.
计算连续相流动场 计算颗粒轨道
更新连续相源项
颗粒弥散: 随机轨道模型
Monte-Carlo方法模拟湍流颗粒弥散 (discrete random walks)
颗粒运动计算中考虑气体的平均速度及随机湍流脉 动速度的影响。
每个轨道包含了一群具有相同特性的颗粒,如相同 的初始直径,密度等.
multisim操作流程步骤

multisim操作流程步骤英文回答:To begin with, the first step in operating Multisim is to open the software on your computer. Once the software is open, you will be presented with a blank canvas where you can start building your circuit. You can choose from a wide range of components such as resistors, capacitors, transistors, and more, to design your circuit.Next, you need to place the components on the canvas and connect them using wires. You can simply drag and drop the components from the component library onto the canvas and use the wire tool to connect them. Multisim provides a variety of wire types such as straight, curved, and orthogonal, which you can choose based on your circuit design.After placing and connecting the components, you can set their values and properties. For example, if you areusing a resistor, you can specify its resistance value. Similarly, for a capacitor, you can set its capacitance value. Multisim allows you to easily modify the properties of the components by double-clicking on them and entering the desired values.Once you have designed your circuit, you can simulate its behavior using Multisim. The software provides various simulation options such as transient analysis, AC analysis, and DC analysis. These simulations allow you to analyze the circuit's response to different inputs and understand its performance.During the simulation, you can observe the voltage and current waveforms, as well as other important parameters of the circuit. Multisim provides a user-friendly interface with customizable plots and graphs to visualize the simulation results. You can also perform interactive measurements and probe the circuit at different points to gather more information.In addition to simulation, Multisim also offersadvanced analysis tools such as Fourier analysis, Monte Carlo analysis, and sensitivity analysis. These tools help you analyze the circuit's behavior in different scenarios and optimize its performance.Once you are satisfied with the circuit design and simulation results, you can proceed to the final step, which is to generate the necessary documentation. Multisim allows you to generate reports, schematics, and bill of materials (BOM) for your circuit design. These documents can be exported in various formats such as PDF, Word, or Excel for further analysis or sharing with others.中文回答:首先,操作Multisim的第一步是在计算机上打开软件。
最最常用JAVA关键字英语大全 带音标
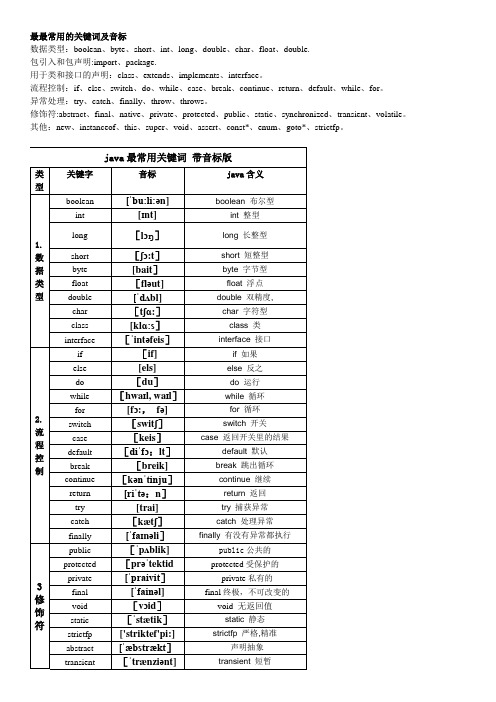
最最常用的关键词及音标数据类型:boolean、byte、short、int、long、double、char、float、double.包引入和包声明:import、package.用于类和接口的声明:class、extends、implements、interface。
流程控制:if、else、switch、do、while、case、break、continue、return、default、while、for。
异常处理:try、catch、finally、throw、throws。
修饰符:abstract、final、native、private、protected、public、static、synchronized、transient、volatile。
其他:new、instanceof、this、super、void、assert、const*、enum、goto*、strictfp。
Java基础常见英语词汇(共70个)['ɔbdʒekt] [’ɔ:rientid]导向的['prəʊɡræmɪŋ]编程OO:object-oriented ,面向对象OOP: object-oriented programming,面向对象编程[dɪ’veləpmənt][kɪt]工具箱['vɜːtjʊəl]虚拟的JDK:Java development kit,java开发工具包JVM:java virtual machine ,java虚拟机['dʒɑːvə] [mə’ʃiːn]机器[kəm’paɪl]Compile:编绎Run:运行[’veərɪəb(ə)l][ɒpə'reɪʃ(ə)n][pə’ræmɪtə]variable:变量operation:操作,运算parameter:参数[’fʌŋ(k)ʃ(ə)n]function:函数member—variable:成员变量member-function:成员函数[dɪ’fɔːlt][’ækses]['pækɪdʒ][ɪm'pɔːt]['stætɪk]default:默认access:访问package:包import:导入static:静态的[vɔid] ['peər(ə)nt][beɪs][’sjuːpə]void:无(返回类型)parent class:父类base class:基类super class:超类[tʃaɪld][di’raivd][əʊvə’raɪd][əʊvə'ləʊd] child class:子类derived class:派生类override:重写,覆盖overload:重载['faɪn(ə)l]['ɪmplɪm(ə)nts]final:最终的,不能改变的implements:实现[rʌn'taim] [æriθ'metik] [ik'sepʃən]Runtime:运行时ArithmeticException:算术异常[ə'rei] ['indeks][baundz][ik’sepʃən][nʌl][’pɔintə]指针ArrayIndexOutOfBoundsException:数组下标越界异常Null Pointer Exception:空引用异常ClassNotFoundException:类没有发现异常[’nʌmbə]['fɔ:mæt]NumberFormatException:数字格式异常(字符串不能转化为数字)[θrəuz]Throws:(投掷)表示强制异常处理Throwable:(可抛出的)表示所有异常类的祖先类[læŋ]['læŋɡwidʒ][ju’til][,dis’plei][ə’rei] [list]Lang:language,语言Util:工具Display:显示ArrayList:(数组列表)表示动态数组[hæʃ][mæp]HashMap: 散列表,哈希表[swiŋ] ['æbstrækt] [’wi ndəu] ['tu:lkit]Swing:轻巧的Awt:abstract window toolkit:抽象窗口工具包[freim] [’pænl][’leiaut][skrəul]['və:tikəl] Frame:窗体Panel:面板Layout:布局Scroll:滚动Vertical:垂直[’hɔri'zɔntəl] ['leibl][tekst][’fi:ld]Horizontal:水平Label:标签TextField:文本框['εəriə] ['bʌtən] [tʃek] [bɔks]TextArea:文本域Button:按钮Checkbox:复选框[’reidiəu] [’kɔmbəu]['lisənə]Radiobutton:单选按钮Combobox:复选框Listener:监听[’bɔ:də] [fləu][ɡrid] [’menju:][bɑ:]Border:边界Flow:流Grid:网格MenuBar:菜单栏[’menju:][’aitəm] [’pɔpʌp]Menu:菜单MenuItem:菜单项PopupMenu:弹出菜单['daiəlɔɡ] [’mesidʒ] ['aikɔn] [nəud]Dialog:对话框Message:消息Icon:图标Node:节点['dʒa:və]['deitəbeis][,kɔnek'tivəti]Jdbc:java database connectivity :java数据库连接[draivə]['mænidʒə] [kə'nekʃən] [’steitmənt]DriverManager:驱动管理器Connection:连接Statement:表示执行对象[pri’peəd] [ri’zʌlt]Preparedstatement:表示预执行对象Resultset:结果集['eksikju:t]['kwiəri]executeQuery:执行查询334157810 这群每日java技术免费分享定期java资料更新Jbuilder中常用英文(共33个)[kləuz] [ik’sept][peinz]Close all except…:除了。
斯普林格数学研究生教材丛书

《斯普林格数学研究生教材丛书》(Graduate Texts in Mathematics)GTM001《Introduction to Axiomatic Set Theory》Gaisi Takeuti, Wilson M.Zaring GTM002《Measure and Category》John C.Oxtoby(测度和范畴)(2ed.)GTM003《Topological Vector Spaces》H.H.Schaefer, M.P.Wolff(2ed.)GTM004《A Course in Homological Algebra》P.J.Hilton, U.Stammbach(2ed.)(同调代数教程)GTM005《Categories for the Working Mathematician》Saunders Mac Lane(2ed.)GTM006《Projective Planes》Daniel R.Hughes, Fred C.Piper(投射平面)GTM007《A Course in Arithmetic》Jean-Pierre Serre(数论教程)GTM008《Axiomatic set theory》Gaisi Takeuti, Wilson M.Zaring(2ed.)GTM009《Introduction to Lie Algebras and Representation Theory》James E.Humphreys(李代数和表示论导论)GTM010《A Course in Simple-Homotopy Theory》M.M CohenGTM011《Functions of One Complex VariableⅠ》John B.ConwayGTM012《Advanced Mathematical Analysis》Richard BealsGTM013《Rings and Categories of Modules》Frank W.Anderson, Kent R.Fuller(环和模的范畴)(2ed.)GTM014《Stable Mappings and Their Singularities》Martin Golubitsky, Victor Guillemin (稳定映射及其奇点)GTM015《Lectures in Functional Analysis and Operator Theory》Sterling K.Berberian GTM016《The Structure of Fields》David J.Winter(域结构)GTM017《Random Processes》Murray RosenblattGTM018《Measure Theory》Paul R.Halmos(测度论)GTM019《A Hilbert Space Problem Book》Paul R.Halmos(希尔伯特问题集)GTM020《Fibre Bundles》Dale Husemoller(纤维丛)GTM021《Linear Algebraic Groups》James E.Humphreys(线性代数群)GTM022《An Algebraic Introduction to Mathematical Logic》Donald W.Barnes, John M.MackGTM023《Linear Algebra》Werner H.Greub(线性代数)GTM024《Geometric Functional Analysis and Its Applications》Paul R.HolmesGTM025《Real and Abstract Analysis》Edwin Hewitt, Karl StrombergGTM026《Algebraic Theories》Ernest G.ManesGTM027《General Topology》John L.Kelley(一般拓扑学)GTM028《Commutative Algebra》VolumeⅠOscar Zariski, Pierre Samuel(交换代数)GTM029《Commutative Algebra》VolumeⅡOscar Zariski, Pierre Samuel(交换代数)GTM030《Lectures in Abstract AlgebraⅠ.Basic Concepts》Nathan Jacobson(抽象代数讲义Ⅰ基本概念分册)GTM031《Lectures in Abstract AlgebraⅡ.Linear Algabra》Nathan.Jacobson(抽象代数讲义Ⅱ线性代数分册)GTM032《Lectures in Abstract AlgebraⅢ.Theory of Fields and Galois Theory》Nathan.Jacobson(抽象代数讲义Ⅲ域和伽罗瓦理论)GTM033《Differential Topology》Morris W.Hirsch(微分拓扑)GTM034《Principles of Random Walk》Frank Spitzer(2ed.)(随机游动原理)GTM035《Several Complex Variables and Banach Algebras》Herbert Alexander, John Wermer(多复变和Banach代数)GTM036《Linear Topological Spaces》John L.Kelley, Isaac Namioka(线性拓扑空间)GTM037《Mathematical Logic》J.Donald Monk(数理逻辑)GTM038《Several Complex Variables》H.Grauert, K.FritzsheGTM039《An Invitation to C*-Algebras》William Arveson(C*-代数引论)GTM040《Denumerable Markov Chains》John G.Kemeny, urie Snell, Anthony W.KnappGTM041《Modular Functions and Dirichlet Series in Number Theory》Tom M.Apostol (数论中的模函数和Dirichlet序列)GTM042《Linear Representations of Finite Groups》Jean-Pierre Serre(有限群的线性表示)GTM043《Rings of Continuous Functions》Leonard Gillman, Meyer JerisonGTM044《Elementary Algebraic Geometry》Keith KendigGTM045《Probability TheoryⅠ》M.Loève(概率论Ⅰ)(4ed.)GTM046《Probability TheoryⅡ》M.Loève(概率论Ⅱ)(4ed.)GTM047《Geometric Topology in Dimensions 2 and 3》Edwin E.MoiseGTM048《General Relativity for Mathematicians》Rainer.K.Sachs, H.Wu伍鸿熙(为数学家写的广义相对论)GTM049《Linear Geometry》K.W.Gruenberg, A.J.Weir(2ed.)GTM050《Fermat's Last Theorem》Harold M.EdwardsGTM051《A Course in Differential Geometry》Wilhelm Klingenberg(微分几何教程)GTM052《Algebraic Geometry》Robin Hartshorne(代数几何)GTM053《A Course in Mathematical Logic for Mathematicians》Yu.I.Manin(2ed.)GTM054《Combinatorics with Emphasis on the Theory of Graphs》Jack E.Graver, Mark E.WatkinsGTM055《Introduction to Operator TheoryⅠ》Arlen Brown, Carl PearcyGTM056《Algebraic Topology:An Introduction》W.S.MasseyGTM057《Introduction to Knot Theory》Richard.H.Crowell, Ralph.H.FoxGTM058《p-adic Numbers, p-adic Analysis, and Zeta-Functions》Neal Koblitz(p-adic 数、p-adic分析和Z函数)GTM059《Cyclotomic Fields》Serge LangGTM060《Mathematical Methods of Classical Mechanics》V.I.Arnold(经典力学的数学方法)(2ed.)GTM061《Elements of Homotopy Theory》George W.Whitehead(同论论基础)GTM062《Fundamentals of the Theory of Groups》M.I.Kargapolov, Ju.I.Merzljakov GTM063《Modern Graph Theory》Béla BollobásGTM064《Fourier Series:A Modern Introduction》VolumeⅠ(2ed.)R.E.Edwards(傅里叶级数)GTM065《Differential Analysis on Complex Manifolds》Raymond O.Wells, Jr.(3ed.)GTM066《Introduction to Affine Group Schemes》William C.Waterhouse(仿射群概型引论)GTM067《Local Fields》Jean-Pierre Serre(局部域)GTM069《Cyclotomic FieldsⅠandⅡ》Serge LangGTM070《Singular Homology Theory》William S.MasseyGTM071《Riemann Surfaces》Herschel M.Farkas, Irwin Kra(黎曼曲面)GTM072《Classical Topology and Combinatorial Group Theory》John Stillwell(经典拓扑和组合群论)GTM073《Algebra》Thomas W.Hungerford(代数)GTM074《Multiplicative Number Theory》Harold Davenport(乘法数论)(3ed.)GTM075《Basic Theory of Algebraic Groups and Lie Algebras》G.P.HochschildGTM076《Algebraic Geometry:An Introduction to Birational Geometry of Algebraic Varieties》Shigeru IitakaGTM077《Lectures on the Theory of Algebraic Numbers》Erich HeckeGTM078《A Course in Universal Algebra》Stanley Burris, H.P.Sankappanavar(泛代数教程)GTM079《An Introduction to Ergodic Theory》Peter Walters(遍历性理论引论)GTM080《A Course in_the Theory of Groups》Derek J.S.RobinsonGTM081《Lectures on Riemann Surfaces》Otto ForsterGTM082《Differential Forms in Algebraic Topology》Raoul Bott, Loring W.Tu(代数拓扑中的微分形式)GTM083《Introduction to Cyclotomic Fields》Lawrence C.Washington(割圆域引论)GTM084《A Classical Introduction to Modern Number Theory》Kenneth Ireland, Michael Rosen(现代数论经典引论)GTM085《Fourier Series A Modern Introduction》Volume 1(2ed.)R.E.Edwards GTM086《Introduction to Coding Theory》J.H.van Lint(3ed .)GTM087《Cohomology of Groups》Kenneth S.Brown(上同调群)GTM088《Associative Algebras》Richard S.PierceGTM089《Introduction to Algebraic and Abelian Functions》Serge Lang(代数和交换函数引论)GTM090《An Introduction to Convex Polytopes》Ame BrondstedGTM091《The Geometry of Discrete Groups》Alan F.BeardonGTM092《Sequences and Series in BanachSpaces》Joseph DiestelGTM093《Modern Geometry-Methods and Applications》(PartⅠ.The of geometry Surfaces Transformation Groups and Fields)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov (现代几何学方法和应用)GTM094《Foundations of Differentiable Manifolds and Lie Groups》Frank W.Warner(可微流形和李群基础)GTM095《Probability》A.N.Shiryaev(2ed.)GTM096《A Course in Functional Analysis》John B.Conway(泛函分析教程)GTM097《Introduction to Elliptic Curves and Modular Forms》Neal Koblitz(椭圆曲线和模形式引论)GTM098《Representations of Compact Lie Groups》Theodor Breöcker, Tammo tom DieckGTM099《Finite Reflection Groups》L.C.Grove, C.T.Benson(2ed.)GTM100《Harmonic Analysis on Semigroups》Christensen Berg, Jens Peter Reus Christensen, Paul ResselGTM101《Galois Theory》Harold M.Edwards(伽罗瓦理论)GTM102《Lie Groups, Lie Algebras, and Their Representation》V.S.Varadarajan(李群、李代数及其表示)GTM103《Complex Analysis》Serge LangGTM104《Modern Geometry-Methods and Applications》(PartⅡ.Geometry and Topology of Manifolds)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov(现代几何学方法和应用)GTM105《SL₂ (R)》Serge Lang(SL₂ (R)群)GTM106《The Arithmetic of Elliptic Curves》Joseph H.Silverman(椭圆曲线的算术理论)GTM107《Applications of Lie Groups to Differential Equations》Peter J.Olver(李群在微分方程中的应用)GTM108《Holomorphic Functions and Integral Representations in Several Complex Variables》R.Michael RangeGTM109《Univalent Functions and Teichmueller Spaces》Lehto OlliGTM110《Algebraic Number Theory》Serge Lang(代数数论)GTM111《Elliptic Curves》Dale Husemoeller(椭圆曲线)GTM112《Elliptic Functions》Serge Lang(椭圆函数)GTM113《Brownian Motion and Stochastic Calculus》Ioannis Karatzas, Steven E.Shreve (布朗运动和随机计算)GTM114《A Course in Number Theory and Cryptography》Neal Koblitz(数论和密码学教程)GTM115《Differential Geometry:Manifolds, Curves, and Surfaces》M.Berger, B.Gostiaux GTM116《Measure and Integral》Volume1 John L.Kelley, T.P.SrinivasanGTM117《Algebraic Groups and Class Fields》Jean-Pierre Serre(代数群和类域)GTM118《Analysis Now》Gert K.Pedersen(现代分析)GTM119《An introduction to Algebraic Topology》Jossph J.Rotman(代数拓扑导论)GTM120《Weakly Differentiable Functions》William P.Ziemer(弱可微函数)GTM121《Cyclotomic Fields》Serge LangGTM122《Theory of Complex Functions》Reinhold RemmertGTM123《Numbers》H.-D.Ebbinghaus, H.Hermes, F.Hirzebruch, M.Koecher, K.Mainzer, J.Neukirch, A.Prestel, R.Remmert(2ed.)GTM124《Modern Geometry-Methods and Applications》(PartⅢ.Introduction to Homology Theory)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov(现代几何学方法和应用)GTM125《Complex Variables:An introduction》Garlos A.Berenstein, Roger Gay GTM126《Linear Algebraic Groups》Armand Borel(线性代数群)GTM127《A Basic Course in Algebraic Topology》William S.Massey(代数拓扑基础教程)GTM128《Partial Differential Equations》Jeffrey RauchGTM129《Representation Theory:A First Course》William Fulton, Joe HarrisGTM130《Tensor Geometry》C.T.J.Dodson, T.Poston(张量几何)GTM131《A First Course in Noncommutative Rings》m(非交换环初级教程)GTM132《Iteration of Rational Functions:Complex Analytic Dynamical Systems》AlanF.Beardon(有理函数的迭代:复解析动力系统)GTM133《Algebraic Geometry:A First Course》Joe Harris(代数几何)GTM134《Coding and Information Theory》Steven RomanGTM135《Advanced Linear Algebra》Steven RomanGTM136《Algebra:An Approach via Module Theory》William A.Adkins, Steven H.WeintraubGTM137《Harmonic Function Theory》Sheldon Axler, Paul Bourdon, Wade Ramey(调和函数理论)GTM138《A Course in Computational Algebraic Number Theory》Henri Cohen(计算代数数论教程)GTM139《Topology and Geometry》Glen E.BredonGTM140《Optima and Equilibria:An Introduction to Nonlinear Analysis》Jean-Pierre AubinGTM141《A Computational Approach to Commutative Algebra》Gröbner Bases, Thomas Becker, Volker Weispfenning, Heinz KredelGTM142《Real and Functional Analysis》Serge Lang(3ed.)GTM143《Measure Theory》J.L.DoobGTM144《Noncommutative Algebra》Benson Farb, R.Keith DennisGTM145《Homology Theory:An Introduction to Algebraic Topology》James W.Vick(同调论:代数拓扑简介)GTM146《Computability:A Mathematical Sketchbook》Douglas S.BridgesGTM147《Algebraic K-Theory and Its Applications》Jonathan Rosenberg(代数K理论及其应用)GTM148《An Introduction to the Theory of Groups》Joseph J.Rotman(群论入门)GTM149《Foundations of Hyperbolic Manifolds》John G.Ratcliffe(双曲流形基础)GTM150《Commutative Algebra with a view toward Algebraic Geometry》David EisenbudGTM151《Advanced Topics in the Arithmetic of Elliptic Curves》Joseph H.Silverman(椭圆曲线的算术高级选题)GTM152《Lectures on Polytopes》Günter M.ZieglerGTM153《Algebraic Topology:A First Course》William Fulton(代数拓扑)GTM154《An introduction to Analysis》Arlen Brown, Carl PearcyGTM155《Quantum Groups》Christian Kassel(量子群)GTM156《Classical Descriptive Set Theory》Alexander S.KechrisGTM157《Integration and Probability》Paul MalliavinGTM158《Field theory》Steven Roman(2ed.)GTM159《Functions of One Complex Variable VolⅡ》John B.ConwayGTM160《Differential and Riemannian Manifolds》Serge Lang(微分流形和黎曼流形)GTM161《Polynomials and Polynomial Inequalities》Peter Borwein, Tamás Erdélyi(多项式和多项式不等式)GTM162《Groups and Representations》J.L.Alperin, Rowen B.Bell(群及其表示)GTM163《Permutation Groups》John D.Dixon, Brian Mortime rGTM164《Additive Number Theory:The Classical Bases》Melvyn B.NathansonGTM165《Additive Number Theory:Inverse Problems and the Geometry of Sumsets》Melvyn B.NathansonGTM166《Differential Geometry:Cartan's Generalization of Klein's Erlangen Program》R.W.SharpeGTM167《Field and Galois Theory》Patrick MorandiGTM168《Combinatorial Convexity and Algebraic Geometry》Günter Ewald(组合凸面体和代数几何)GTM169《Matrix Analysis》Rajendra BhatiaGTM170《Sheaf Theory》Glen E.Bredon(2ed.)GTM171《Riemannian Geometry》Peter Petersen(黎曼几何)GTM172《Classical Topics in Complex Function Theory》Reinhold RemmertGTM173《Graph Theory》Reinhard Diestel(图论)(3ed.)GTM174《Foundations of Real and Abstract Analysis》Douglas S.Bridges(实分析和抽象分析基础)GTM175《An Introduction to Knot Theory》W.B.Raymond LickorishGTM176《Riemannian Manifolds:An Introduction to Curvature》John M.LeeGTM177《Analytic Number Theory》Donald J.Newman(解析数论)GTM178《Nonsmooth Analysis and Control Theory》F.H.clarke, Yu.S.Ledyaev, R.J.Stern, P.R.Wolenski(非光滑分析和控制论)GTM179《Banach Algebra Techniques in Operator Theory》Ronald G.Douglas(2ed.)GTM180《A Course on Borel Sets》S.M.Srivastava(Borel 集教程)GTM181《Numerical Analysis》Rainer KressGTM182《Ordinary Differential Equations》Wolfgang WalterGTM183《An introduction to Banach Spaces》Robert E.MegginsonGTM184《Modern Graph Theory》Béla Bollobás(现代图论)GTM185《Using Algebraic Geomety》David A.Cox, John Little, Donal O’Shea(应用代数几何)GTM186《Fourier Analysis on Number Fields》Dinakar Ramakrishnan, Robert J.Valenza GTM187《Moduli of Curves》Joe Harris, Ian Morrison(曲线模)GTM188《Lectures on the Hyperreals:An Introduction to Nonstandard Analysis》Robert GoldblattGTM189《Lectures on Modules and Rings》m(模和环讲义)GTM190《Problems in Algebraic Number Theory》M.Ram Murty, Jody Esmonde(代数数论中的问题)GTM191《Fundamentals of Differential Geometry》Serge Lang(微分几何基础)GTM192《Elements of Functional Analysis》Francis Hirsch, Gilles LacombeGTM193《Advanced Topics in Computational Number Theory》Henri CohenGTM194《One-Parameter Semigroups for Linear Evolution Equations》Klaus-Jochen Engel, Rainer Nagel(线性发展方程的单参数半群)GTM195《Elementary Methods in Number Theory》Melvyn B.Nathanson(数论中的基本方法)GTM196《Basic Homological Algebra》M.Scott OsborneGTM197《The Geometry of Schemes》David Eisenbud, Joe HarrisGTM198《A Course in p-adic Analysis》Alain M.RobertGTM199《Theory of Bergman Spaces》Hakan Hedenmalm, Boris Korenblum, Kehe Zhu(Bergman空间理论)GTM200《An Introduction to Riemann-Finsler Geometry》D.Bao, S.-S.Chern, Z.Shen GTM201《Diophantine Geometry An Introduction》Marc Hindry, Joseph H.Silverman GTM202《Introduction to Topological Manifolds》John M.LeeGTM203《The Symmetric Group》Bruce E.SaganGTM204《Galois Theory》Jean-Pierre EscofierGTM205《Rational Homotopy Theory》Yves Félix, Stephen Halperin, Jean-Claude Thomas(有理同伦论)GTM206《Problems in Analytic Number Theory》M.Ram MurtyGTM207《Algebraic Graph Theory》Chris Godsil, Gordon Royle(代数图论)GTM208《Analysis for Applied Mathematics》Ward CheneyGTM209《A Short Course on Spectral Theory》William Arveson(谱理论简明教程)GTM210《Number Theory in Function Fields》Michael RosenGTM211《Algebra》Serge Lang(代数)GTM212《Lectures on Discrete Geometry》Jiri Matousek(离散几何讲义)GTM213《From Holomorphic Functions to Complex Manifolds》Klaus Fritzsche, Hans Grauert(从正则函数到复流形)GTM214《Partial Differential Equations》Jüergen Jost(偏微分方程)GTM215《Algebraic Functions and Projective Curves》David M.Goldschmidt(代数函数和投影曲线)GTM216《Matrices:Theory and Applications》Denis Serre(矩阵:理论及应用)GTM217《Model Theory An Introduction》David Marker(模型论引论)GTM218《Introduction to Smooth Manifolds》John M.Lee(光滑流形引论)GTM219《The Arithmetic of Hyperbolic 3-Manifolds》Colin Maclachlan, Alan W.Reid GTM220《Smooth Manifolds and Observables》Jet Nestruev(光滑流形和直观)GTM221《Convex Polytopes》Branko GrüenbaumGTM222《Lie Groups, Lie Algebras, and Representations》Brian C.Hall(李群、李代数和表示)GTM223《Fourier Analysis and its Applications》Anders Vretblad(傅立叶分析及其应用)GTM224《Metric Structures in Differential Geometry》Gerard Walschap(微分几何中的度量结构)GTM225《Lie Groups》Daniel Bump(李群)GTM226《Spaces of Holomorphic Functions in the Unit Ball》Kehe Zhu(单位球内的全纯函数空间)GTM227《Combinatorial Commutative Algebra》Ezra Miller, Bernd Sturmfels(组合交换代数)GTM228《A First Course in Modular Forms》Fred Diamond, Jerry Shurman(模形式初级教程)GTM229《The Geometry of Syzygies》David Eisenbud(合冲几何)GTM230《An Introduction to Markov Processes》Daniel W.Stroock(马尔可夫过程引论)GTM231《Combinatorics of Coxeter Groups》Anders Bjröner, Francesco Brenti(Coxeter 群的组合学)GTM232《An Introduction to Number Theory》Graham Everest, Thomas Ward(数论入门)GTM233《Topics in Banach Space Theory》Fenando Albiac, Nigel J.Kalton(Banach空间理论选题)GTM234《Analysis and Probability:Wavelets, Signals, Fractals》Palle E.T.Jorgensen(分析与概率)GTM235《Compact Lie Groups》Mark R.Sepanski(紧致李群)GTM236《Bounded Analytic Functions》John B.Garnett(有界解析函数)GTM237《An Introduction to Operators on the Hardy-Hilbert Space》Rubén A.Martínez-Avendano, Peter Rosenthal(哈代-希尔伯特空间算子引论)GTM238《A Course in Enumeration》Martin Aigner(枚举教程)GTM239《Number Theory:VolumeⅠTools and Diophantine Equations》Henri Cohen GTM240《Number Theory:VolumeⅡAnalytic and Modern Tools》Henri Cohen GTM241《The Arithmetic of Dynamical Systems》Joseph H.SilvermanGTM242《Abstract Algebra》Pierre Antoine Grillet(抽象代数)GTM243《Topological Methods in Group Theory》Ross GeogheganGTM244《Graph Theory》J.A.Bondy, U.S.R.MurtyGTM245《Complex Analysis:In the Spirit of Lipman Bers》Jane P.Gilman, Irwin Kra, Rubi E.RodriguezGTM246《A Course in Commutative Banach Algebras》Eberhard KaniuthGTM247《Braid Groups》Christian Kassel, Vladimir TuraevGTM248《Buildings Theory and Applications》Peter Abramenko, Kenneth S.Brown GTM249《Classical Fourier Analysis》Loukas Grafakos(经典傅里叶分析)GTM250《Modern Fourier Analysis》Loukas Grafakos(现代傅里叶分析)GTM251《The Finite Simple Groups》Robert A.WilsonGTM252《Distributions and Operators》Gerd GrubbGTM253《Elementary Functional Analysis》Barbara D.MacCluerGTM254《Algebraic Function Fields and Codes》Henning StichtenothGTM255《Symmetry Representations and Invariants》Roe Goodman, Nolan R.Wallach GTM256《A Course in Commutative Algebra》Kemper GregorGTM257《Deformation Theory》Robin HartshorneGTM258《Foundation of Optimization》Osman GülerGTM259《Ergodic Theory:with a view towards Number Theory》Manfred Einsiedler, Thomas WardGTM260《Monomial Ideals》Jurgen Herzog, Takayuki HibiGTM261《Probability and Stochastics》Erhan CinlarGTM262《Essentials of Integration Theory for Analysis》Daniel W.StroockGTM263《Analysis on Fock Spaces》Kehe ZhuGTM264《Functional Analysis, Calculus of Variations and Optimal Control》Francis ClarkeGTM265《Unbounded Self-adjoint Operatorson Hilbert Space》Konrad Schmüdgen GTM266《Calculus Without Derivatives》Jean-Paul PenotGTM267《Quantum Theory for Mathematicians》Brian C.HallGTM268《Geometric Analysis of the Bergman Kernel and Metric》Steven G.Krantz GTM269《Locally Convex Spaces》M.Scott Osborne。
on the evolution of random graphs

by
P. ERD6S and A.
R~NYI
Dedicated to
his 60th birthday.
Profe88m- P. Turdn at
lotroduction
Our aim is to study the probable structure of a ra.ridom gra.ph r,.N which ha.s n given labelled vertices P 1, P2 , ••• , P, and N edges; we suppose that these N edges are chosen a.t random among the (;) possible edges,
' . 1 with Gn.N is - - . If .A is a. property which a. graph may or may not possess,
We denote by p . ...,N (.A) the probability that the A random graph F,.N possesses the property .4, i. e. we put P .. N (A) = 0 n,N where AnN . denotes the
r,.
nected, the pair 0 1 (n) =_!_n log n, 0 11(n) = n is a. pair of strong threshold functions for the property and the corresponding sharp-threshold distribution function is e-r-2ll'; thus we have proved1 that putting 1 N(n) = - n log n + y n+ o(n) we have
Finding community structure in networks using the eigenvectors of matrices

M. E. J. Newman
Department of Physics and Center for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109–1040
We consider the problem of detecting communities or modules in networks, groups of vertices with a higher-than-average density of edges connecting them. Previous work indicates that a robust approach to this problem is the maximization of the benefit function known as “modularity” over possible divisions of a network. Here we show that this maximization process can be written in terms of the eigenspectrum of a matrix we call the modularity matrix, which plays a role in community detection similar to that played by the graph Laplacian in graph partitioning calculations. This result leads us to a number of possible algorithms for detecting community structure, as well as several other results, including a spectral measure of bipartite structure in neteasure that identifies those vertices that occupy central positions within the communities to which they belong. The algorithms and measures proposed are illustrated with applications to a variety of real-world complex networks.
西门子PLM软件NX数字模拟产品功能说明书
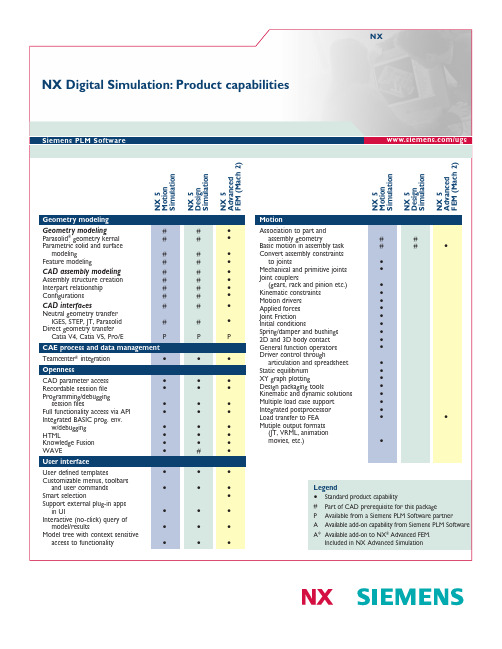
Legend•Standard product capability#Part of CAD prerequisite for this packageP Available from a Siemens PLM Software partnerA Available add-on capability from Siemens PLM Software A*Available add-on to NX ®Advanced FEM.Included in NX Advanced SimulationNX Digital Simulation:Product capabilitiesNX/ugsSiemens PLM Software MotionAssociation to part and assembly geometry##Basic motion in assembly task ##•Convert assembly constraints to joints•Mechanical and primitive joints •Joint couplers(gears,rack and pinion etc.)•Kinematic constraints •Motion drivers •Applied forces •Joint Friction •Initial conditions•Spring/damper and bushings •2D and 3D body contact •General function operators •Driver control througharticulation and spreadsheet •Static equilibrium •XY graph plotting •Design packaging tools•Kinematic and dynamic solutions •Multiple load case support •Integrated postprocessor •Load transfer to FEA ••Mutiple output formats (JT,VRML,animation movies,etc.)•N X 5D e s i g n S i m u l a t i o nN X 5A d v a n c e d F E M (M a c h 2)N X 5M o t i o n S i m u l a t i o nN X 5M o t i o n S i m u l a t i o nN X 5D e s i g n S i m u l a t i o nN X 5A d v a n c e d F E M (M a c h 2)Geometry modelingGeometry modeling##•Parasolid ®geometry kernal ##•Parametric solid and surface modeling##•Feature modeling##•CAD assembly modeling##•Assembly structure creation ##•Interpart relationship ##•Configurations##•CAD interfaces##•Neutral geometry transfer IGES,STEP,JT,Parasolid ##•Direct geometry transfer Catia V4,Catia V5,Pro/EPPPCAE process and data management Teamcenter ®integration •••OpennessCAD parameter access •••Recordable session file •••Programming/debugging session files•••Full functionality access via API •••Integrated BASIC prog.env.w/debugging •••HTML•••Knowledge Fusion •••WAVE •#•User interfaceUser defined templates•••Customizable menus,toolbars and user commands •••Smart selection•Support external plug-in apps in UI•••Interactive (no-click)query of model/results•••Model tree with context sensitive access to functionality•••N X 5D e s i g n S i m u l a t i o nN X 5A d v a n c e d F E M (M a c h 2)N X 5D e s i g n S i m u l a t i o nN X 5A d v a n c e d F E M (M a c h 2)FE model building Geometry defeature tools –topologydiagnosis,geometry repair,CAD featuresuppression,stitch surface,remove hole/fillet,partition••Non-manifold topology generation for volumes•CAE topology•CAE geometry –creation and deletion,mid-surfacing (constant and variable thicknesses)•Automatic topology abstraction –abstraction control,auto stitch geometry,auto merge small regions,auto pinch••Manual topology modification tools•Meshing••0D,1D,and 2D elements •2D mapped meshing •3D elements••Automatic meshing asst.–geometric abstraction and mesh generation in one tool/step ••Batch meshing •Transition meshing•Manual meshing tools –sweeping,revolve,surface coating,interactive controls,etc.•Automatic meshing controls –local element sizing,curvature control•General modeling tools••Axi-symmetric meshing•Mesh display and control –display filters••Material property creation and management –isotropic,anisotropic,orthotropic,linear,nonlinear,thermal,etc.••Mass property calculations •Load summation•Physical property creation and management ••Mesh quality checks –coincident nodes,free edge checks,element shape checks,etc.••FE grouping –by association to geometry,bc’s,material,etc.)•FE collectors and sets •FE append•FEM on assembly••FE model on CAD assembly••Beam modeling•Model update from CAD••FEM model update based on geometry change ••FEM model update based on assembly change••FE model buildingBoundary conditions••Application methods ••On geometry••Local coordinate system ••On FE entities •Friction definition •Time variation•Constraints –statics,dynamics,thermal,symmetric,contact,etc.••Structural loads••Structural thermal –flux,radiation,generation••Advanced thermal –convection,temperature –linear and nonlinear,simple radiation,thermal coupling,adv.radiation•Flow –bc’s,flow surface/blockage/screen definition,fluid domain definition •Axi-symmetric boundary conditions •Automatic contact detection and setup ••Automated load transfer •Laminate composites ASolution setupStructural linearStatic and buckling analysis••Structural linear dynamicsNormal modes••Direct frequency response •Direct transient response •Modal frequency response •Modal transient response•Structural nonlinearStatic,transient,geometric,elastic/plastic material ••Implicit solver •Explicit solver•Structural contact and connection modelingSurface-to-surface contact ••Node-to-node contact •Rigid elements•Constraint elements •Glue connection••ThermalSteady-state•Diurnal solar heatingA Rigid-body transient motion A Transient A Conduction A Convection A RadiationAN X 5D e s i g n S i m u l a t i o nN X 5A d v a n c e d F E M (M a c h 2)N X 5D e s i g n S i m u l a t i o nN X 5A d v a n c e d F E M (M a c h 2)Solution setup Fluid dynamicsSteady-state/transient flow A Incompressible flow A Compressible flow A Laminar/turbulent flow A Internal/external flow A Motion-induced flowA Multiple rotational frames of reference A Forced and natural convectionA Conjugate and radiation heat transferACoupled physicsThermal-structural •A Fluid-thermalA FE data export••Abaqus (inp)A Ansys A Nastran•A*FE data import••Abaqus (fil,inp)A Ansys (rst)A Nastran (op2,dat)•A*NX I-deas ®(unv,afu,bun)•FE results visualizationContour displays (continuous or iso-lines)••Vector displays ••Isosurface displays ••Cutting planes••Advanced lighting control ••Animations••Complex dynamic response results •Multiple viewports••Probing of results on nodes••Postprocessing data table w/sort/criteria ••Results listings••Transparency display ••Local coordinate system ••XY graphing•Synchronized contour and XY plotting displays •Annotated graphs•Output (JT,VMRL,postscript,tif,etc.)••Meta solutionDurability••FE parameter optimization••Dynamic forced response simulation A Laminate composites analysisAN X N a s t r a nN X M u l t i -p h y s i c sN X N a s t r a nN X M u l t i -p h y s i c sSolutions Structural linearStatic •Modal •Buckling•Structural nonlinearStatic •Transient •Geometric•Elastic/plastic material •Hyperelastic material •Gasket material •Nonlinear buckling •Implicit solver •Explicit solver•Structural contact and connection modelingSurface-to-surface contact •Node-to-node contact •Spot welds •Rigid elements•Constraint elements •Glue connection•Structural linear dynamicsModal transient •Modal frequency •Direct transient •Direct frequency •Shock spectrum •Random vibration •Rotor dynamics•ThermalSteady-state,transient••Temperature-dependent properties ••Nonlinear thermal contact•Thermal couplings (welded,bolted,bonded)•Disjoint meshes support in assembly modeling•Surface-to-surface radiative heat transfer ••Hemicube-based view factor calculation •Radiation in participating media •Radiation enclosures•Environmental radiative heating •Orbital modeling and analysis •Specular,transmissive surfaces ••Convection••Forced and natural convection correlations •Hydraulic fluid networks •Joule heating •Phase change•Heater and thermostat modeling ••Material charring and ablation •Transient rigid body motion •Peltier cooler modeling•Heat sink models and modeler•PCB modeler/xchange (ECAD/MCAD)ASolutionsFluid dynamicsSteady-state/transient flow •Incompressible flow •Compressible flow •Laminar/turbulent flow•Forced and natural convection•Conjugate and radiation heat transfer •Porous media modeling •Nonlinear fluid properties •Humidity and condensation•Automatic fluid domain and boundary layer meshing•Flow induced by rigid body motion •Automated connection of disjoint fluid meshes •Fan models•Embedded 2D/3D flow blockages •General scalars and particle tracking •Non-Newtonian fluids•Multiple rotating frames-of-reference•Coupled physicsAcoustics•Acoustics-structural •Subsonic aeroelastic •Supersonic aeroelastic •Fluid-thermal•Thermal-structural ••Fluid-structural•Interface to multi-body dynamics (ADAMS and RecurDyn)•SolversIterative ••Sparse direct•Shared memory processing •Distributed memory processing •(1)•Optimization ••Cyclic symmetry ••Axi-symmetric••FE-based finite volume solver•Advanced capabilitySuperelement/substructuring ••Solution customization (DMAP)•Solution customization (user subroutine)•(1)Available in Enterprise versions only.Note:The NX Nastran and NX Multi-Physics solver suites are comprised of multiple products.Please check the individual product fact sheets to determine the simulation capabilities contained in each core bundle or add-on module.ContactSiemens PLM SoftwareAmericas8004985351Europe+44(0)1276702000Asia-Pacific852********/plm©2007.Siemens Product Lifecycle Management Software Inc.All rights reserved.Siemens and the Siemens logo are registered trademarks of Siemens AG. Teamcenter,NX,Solid Edge,Tecnomatix,Parasolid,Femap,I-deas,JT,UGS Velocity Series,Geolus and the Signs of Innovation trade dress are trademarks or registered trademarks of Siemens Product Lifecycle Management Software Inc.or its subsidiaries in the United States and in other countries.All other logos,trademarks,registered trademarks or service marks used herein are the property of their respective holders.9/07。
随机游走演示课件

问题直观:
•有个醉汉走在回家路上,由于酒醉未醒,分不清家往哪边走。假如家 在东面n的位置,醉汉处在m(m<n)位置。醉汉每一个时间单位走一 步,向东(家的方向)或者向西(酒吧的方向)的概率皆为1/2。 这 个醉汉的行为就可用random walk 来模拟。
这是一个简单的一维随机游走问题模型,从这个模型中我们可以对随机游走 有一个直观上的感受:每一步都是随机的。
1
什么是随机游走
随机游走是由一系列随机步伐(steps)所形成的活动模型。 比如: 液体或空气中分子的运动; 动物的觅食; 股票的价格波动; 一个赌徒的财产状况…
这些都可以模型为random walks(尽管现实中他们可能不是真 正的随机) •Karl Pearson在1905年第一次提出了random walk,如今已被应 用在诸多领域:生态学、经济学、心理学、计算机科学、物理 学、化学、生物学等。
2
随机游走概述 •
3
一维随机游走 •
4
一维随机游走
上述问题可以用杨辉三角来看:
当n趋于无穷的时候,就可以与中心极限定理相联系
一维随机游走模拟结果图:
5
高维随机游走模拟
二维模拟:
一个25000步伐的二维随机游走
三维模拟:
6
高斯随机游走 •
7
带重启的随机游走(RWR)
•Random walk with restart :从一个节点开始,在每一步游走 时面临两个选择:或者移动到一个随机选择的邻点;或者跳 回起点。 •RWR最初是为图像分割而提出的一个算法,它反复的探究一 个网络的总体结构去估计两个节点之间的亲和力程度(亲和 力分数),这个算法只考虑一个参数 r :“重启概率”(1-r的 概率移动到某个邻点) 这个过程反复迭代进行下去直到走遍所有节点,此时得到的 概率向量包含所有节点与起点的亲和力分数。 另外,RWR的起点也可以选择一个起点集合(多个起点组成 的集合)。
Nelson-Aalen估计器的多状态模型累积危险估计说明书

Package‘mvna’October13,2022Title Nelson-Aalen Estimator of the Cumulative Hazard in MultistateModelsVersion2.0.1Author Arthur AllignolDescription Computes the Nelson-Aalen estimator of the cumulative transition hazard for arbi-trary Markov multistate models<ISBN:978-0-387-68560-1>.Maintainer Arthur Allignol<*************************>License MIT+file LICENSEImports latticeNeedsCompilation yesRepository CRANDate/Publication2017-09-1123:21:40UTCR topics documented:abortion (2)lines.mvna (2)mvna (4)plot.mvna (6)predict.mvna (8)print.mvna (10)sir.adm (11)sir.cont (12)summary.mvna (14)xyplot.mvna (15)Index171abortion Pregnancies exposed to coumarin derivativesDescriptionOutcomes of pregnancies exposed to coumarin derivatives.The aim is to investigate whether ex-position to coumarin derivatives increases the probability of spontaneous abortions.Apart from spontaneous abortion,pregnancy may end in induced abortion or live birth.Moreover,data are left-truncated as women usually enter the study several weeks after conception.Usagedata(abortion)FormatA data frame with1186observations on the following5variables.id Identification numberentry Entry times into the cohortexit Event timesgroup Group.0:control,1:exposed to coumarin derivativescause Cause of failure.1:induced abortion,2:life birth,3:spontaneous abortionSourceMeiester,R.and Schaefer,C(2008).Statistical methods for estimating the probability of sponta-neous abortion in observational studies–Analyzing pregnancies exposed to coumarin derivatives.Reproductive Toxicology,26,31–35Examplesdata(abortion)lines.mvna Lines method for’mvna’objectsDescriptionLines method for mvna objects.Usage##S3method for class mvnalines(x,tr.choice,col=1,lty,conf.int=FALSE,level=0.95,var.type=c("aalen","greenwood"),ci.fun=c("log","linear","arcsin"),ci.col=col,ci.lty=3,...)Argumentsx An object of class mvna.tr.choice A character vector of the form c("from to","from to")specifying which tran-sitions should be displayed.By default,all the transition hazards are plotted.col A vector of colours.Default is black.lty A vector of line types.Default is1:number of transitions.conf.int Logical.Indicates whether to display pointwise confidence interval.Default is FALSE.level Level of the confidence interval.Default is0.95.var.type Specifies the variance estimator that should be used to compute the confidence interval.One of"aalen"or"greenwood".Default is"aalen".ci.fun Specifies the transformation applied to the confidence interval.Choices are"lin-ear","log","arcsin".Default is"log".ci.col Colours of the confidence interval lines.By default,ci.col equals col.ci.lty Line types for the confidence intervals.Default is3....Further arguments for lines.ValueNo value returned.Author(s)Arthur Allignol,<*************************>See Alsomvna,plot.mvnaExamplesdata(sir.adm)##data set transformationdata(sir.adm)id<-sir.adm$idfrom<-sir.adm$pneuto<-ifelse(sir.adm$status==0,"cens",sir.adm$status+1)times<-sir.adm$time4mvnadat.sir<-data.frame(id,from,to,time=times)##Possible transitionstra<-matrix(ncol=4,nrow=4,FALSE)tra[1:2,3:4]<-TRUEna.pneu<-mvna(dat.sir,c("0","1","2","3"),tra,"cens")plot(na.pneu,tr.choice=c("02"),conf.int=TRUE,col=1,lty=1,legend=FALSE)lines(na.pneu,tr.choice=c("12"),conf.int=TRUE,col=2,lty=1)mvna Nelson-Aalen estimator in multistate modelsDescriptionThis function computes the multivariate Nelson-Aalen estimator of the cumulative transition haz-ards in multistate models,that is,for each possible transition,it computes an estimate of the cumu-lative hazard.Usagemvna(data,s,tra,)Argumentsdata A data.frame of the form data.frame(id,from,to,time)or(id,from,to,entry,exit) id:patient idfrom:the state from where the transition occursto:the state to which a transition occurstime:time when a transition occursentry:entry time in a stateexit:exit time from a stateThis data.frame is transition-oriented,i.e.it contains one row per transition,andpossibly several rows per patient.Specifying an entry and exit time permits totake into account left-truncation.s A vector of character giving the states names.tra A quadratic matrix of logical values describing the possible transitions within the multistate model. A character giving the code for censored observations in the column to of data.If there is no censored observations in your data,put NULL.mvna5DetailsThis functions computes the Nelson-Aalen estimator as described in Anderson et al.(1993),along with the two variance estimators described in eq.(4.1.6)and(4.1.7)of Andersen et al.(1993)at each transition time.ValueReturns a list named after the possible transitions,e.g.if we define a multistate model with two possible transitions:from state0to state1,and from state0to state2,the returned list will have two parts named"01"and"02".Each part contains a data.frame with columns:na Nelson-Aalen estimates at each transition times.var.aalen Variance estimator given in eq.(4.1.6)of Andersen et al.(1993).var.greenwood Variance estimator given in eq.(4.1.7)of Andersen et al.(1993).time The transition times.The list also contains:time All the event times.n.risk A matrix giving the number at individual at risk in the transient states just before an event.n.event An array which gives the number of transitions at each event times.n.cens A matrix giving the number a censored observations at each event times.s The same as in the function call. The same as in the function call.trans A data frame,with columns from and to,that gives the possible transitions. NoteThe variance estimator(4.1.6)may overestimate the true variance,and the one defined eq.(4.1.7) may underestimate the true variance(see Klein(1991)and Andersen et al.(example IV.1.1,1993)), especially with small sample set.Klein(1991)recommends the use of the variance estimator of eq.(4.1.6,"aalen")because he found it to be less biased.Author(s)Arthur Allignol,<*************************>ReferencesAndersen,P.K.,Borgan,O.,Gill,R.D.and Keiding,N.(1993).Statistical models based on counting processes.Springer Series in Statistics.New York,NY:Springer.Beyersmann J,Allignol A,Schumacher M:Competing Risks and Multistate Models with R(Use R!),Springer Verlag,2012(Use R!)Klein,J.P.Small sample moments of some estimators of the variance of the Kaplan-Meier and Nelson-Aalen estimators.Scandinavian Journal of Statistics,18:333–340,1991.See Alsosir.adm,sir.contExamplesdata(sir.cont)#Modification for patients entering and leaving a state#at the same datesir.cont<-sir.cont[order(sir.cont$id,sir.cont$time),]for(i in2:nrow(sir.cont)){if(sir.cont$id[i]==sir.cont$id[i-1]){if(sir.cont$time[i]==sir.cont$time[i-1]){sir.cont$time[i-1]<-sir.cont$time[i-1]-0.5}}}#Matrix of logical giving the possible transitionstra<-matrix(ncol=3,nrow=3,FALSE)tra[1,2:3]<-TRUEtra[2,c(1,3)]<-TRUE#Computation of the Nelson-Aalen estimatesna<-mvna(sir.cont,c("0","1","2"),tra,"cens")#plotif(require(lattice))xyplot(na)###example with left-truncationdata(abortion)#Data set modification in order to be used by mvnanames(abortion)<-c("id","entry","exit","from","to")abortion$to<-abortion$to+1##computation of the matrix giving the possible transitions tra<-matrix(FALSE,nrow=5,ncol=5)tra[1:2,3:5]<-TRUEna.abortion<-mvna(abortion,as.character(0:4),tra,NULL) plot(na.abortion,tr.choice=c("04","14"),curvlab=c("Control","Exposed"),bty="n",legend.pos="topleft")plot.mvna Plot method for a mvna objectDescriptionPlot method for an object of class mvna.This function plots estimates of the cumulative transition hazards in one panel.Usage##S3method for class mvnaplot(x,tr.choice,xlab="Time",ylab="Cumulative Hazard",col=1,lty,xlim,ylim,conf.int=FALSE,level=0.95,var.type=c("aalen","greenwood"),ci.fun=c("log","linear","arcsin"),ci.col=col,ci.lty=3,legend=TRUE,legend.pos,curvlab,legend.bty="n",...)Argumentsx An object of class mvna.tr.choice A character vector of the form c("from to","from to")specifying which tran-sitions should be plotted.Default,all the cumulative transition hazards are plot-ted.xlab x-axis label.Default is"Time".ylab y-axis label.Default is"Cumulative Hazard".col Vector of colour.Default is black.lty Vector of line type.Default is1:number of transitionsxlim Limits of x-axis for the plotylim Limits of y-axis for the plotconf.int Logical.Whether to display pointwise confidence intervals.Default is FALSE.level Level of the pointwise confidence intervals.Default is0.95.var.type A character vector specifying the variance that should be used to compute the pointwise confidence intervals.Choices are"aalen"or"greenwood".Default is"aalen".ci.fun One of"log","linear"or"arcsin".Indicates which transformation to apply to the confidence intervals.ci.col Colour for the confidence intervals.By default,the colour specified by col is used.ci.lty Line type for the confidence intervals.Default is3.legend A logical specifying if a legend should be addedlegend.pos A vector giving the legend’s position.See legend for further details.curvlab A character or expression vector to appear in the legend.Default is the name of the transitions.legend.bty Box type for the legend....Further arguments for plot method.DetailsThis plot method permits to draw several cumulative transition hazards on the same panel.ValueNo value returnedAuthor(s)Arthur Allignol<*************************>See AlsomvnaExamplesdata(sir.cont)#Modification for patients entering and leaving a state#at the same datesir.cont<-sir.cont[order(sir.cont$id,sir.cont$time),]for(i in2:nrow(sir.cont)){if(sir.cont$id[i]==sir.cont$id[i-1]){if(sir.cont$time[i]==sir.cont$time[i-1]){sir.cont$time[i-1]<-sir.cont$time[i-1]-0.5}}}tra<-matrix(ncol=3,nrow=3,FALSE)tra[1,2:3]<-TRUEtra[2,c(1,3)]<-TRUEna.cont<-mvna(sir.cont,c("0","1","2"),tra,"cens")plot(na.cont,tr.choice=c("02","12"))predict.mvna Calculates Nelson-Aalen estimates at specified time-pointsDescriptionThis function gives the Nelson-Aalen estimates at time-points specified by the user.Usage##S3method for class mvnapredict(object,times,tr.choice,level=0.95,var.type=c("aalen","greenwood"),ci.fun=c("log","linear","arcsin"),...)Argumentsobject An object of class mvnatimes Time-points at which one wants the estimatestr.choice A vector of character giving for which transitions one wants estimates.By de-fault,the function will give the Nelson-Aalen estimates for all transitions.level Level of the pointwise confidence intervals.Default is0.95.var.type Variance estimator displayed and used to compute the pointwise confidence in-tervals.One of"aalen"or"greenwood".Default is"aalen".ci.fun Which transformation to apply for the confidence intervals.Choices are"linear", "log"or"arcsin".Default is"log"....Other arguments to predictValueReturns a list named after the possible transitions,e.g.if we define a multistate model with two possible transitions:from state0to state1,and from state0to state2,the returned list will have two parts named"01"and"02".Each part contains a data.frame with columns:times Time points specified by the user.na Nelson-Aalen estimates at the specified times.var.aalen or var.greenwoodDepending on what was specified in var.type.lower Lower bound of the pointwise confidence intervals.upper Upper bound.Author(s)Arthur Allignol,<*************************>ReferencesAndersen,P.K.,Borgan,O.,Gill,R.D.and Keiding,N.(1993).Statistical models based on counting processes.Springer Series in Statistics.New York,NY:Springer.See Alsomvna,summary.mvna10print.mvnaExamplesdata(sir.cont)#Modification for patients entering and leaving a state#at the same datesir.cont<-sir.cont[order(sir.cont$id,sir.cont$time),]for(i in2:nrow(sir.cont)){if(sir.cont$id[i]==sir.cont$id[i-1]){if(sir.cont$time[i]==sir.cont$time[i-1]){sir.cont$time[i-1]<-sir.cont$time[i-1]-0.5}}}#Matrix of logical giving the possible transitionstra<-matrix(ncol=3,nrow=3,FALSE)tra[1,2:3]<-TRUEtra[2,c(1,3)]<-TRUE#Computation of the Nelson-Aalen estimatesna<-mvna(sir.cont,c("0","1","2"),tra,"cens")#Using predictpredict(na,times=c(1,5,10,15))print.mvna Print method for’mvna’objectDescriptionPrint method for an object of class mvna.It prints estimates of the cumulative hazard along with estimates of the variance described in eq.(4.1.6)and(4.1.7)of Andersen et al.(1993)at several time points obtained with the quantile function.Usage##S3method for class mvnaprint(x,...)Argumentsx An object of class mvna...Other arguments for print methodValueNo value returned.sir.adm11Author(s)Arthur Allignol,<*******************************>See Alsomvnasir.adm Pneumonia on admission in intenive care unit patientsDescriptionPneumonia status on admission for intensive care unit(ICU)patients,a random sample from the SIR-3study.Usagedata(sir.adm)FormatThe data contains747rows and4variables:id:Randomly generated patient idpneu:Pneumonia indicator.0:No pneumonia,1:Pneumoniastatus Status indicator.0:censored observation,1:discharged,2:deadtime:Follow-up time in dayage:Age at inclusionsex:Sex.F for female and M for maleSourceBeyersmann,J.,Gastmeier,P.,Grundmann,H.,Baerwolff,S.,Geffers,C.,Behnke,M.,Rueden,H., and Schumacher,e of multistate models to assess prolongation of intensive care unit stay due to nosocomial infection.Infection Control and Hospital Epidemiology,27:493-499,2006. Examples#data set transformationdata(sir.adm)id<-sir.adm$idfrom<-sir.adm$pneuto<-ifelse(sir.adm$status==0,"cens",sir.adm$status+1)times<-sir.adm$timedat.sir<-data.frame(id,from,to,time=times)#Possible transitionstra<-matrix(ncol=4,nrow=4,FALSE)tra[1:2,3:4]<-TRUEna.pneu<-mvna(dat.sir,c("0","1","2","3"),tra,"cens")if(require("lattice")){xyplot(na.pneu,tr.choice=c("02","12","03","13"),aspect=1,strip=strip.custom(bg="white",factor.levels=c("No pneumonia on admission--Discharge","Pneumonia on admission--Discharge","No pneumonia on admission--Death","Pneumonia on admission--Death"),par.strip.text=list(cex=0.9)),scales=list(alternating=1),xlab="Days",ylab="Nelson-Aalen esimates")}sir.cont Ventilation status in intensive care unit patientsDescriptionTime-dependent ventilation status for intensive care unit(ICU)patients,a random sample from the SIR-3study.Usagedata(sir.cont)FormatA data frame with1141rows and6columns:id:Randomly generated patient idfrom:State from which a transition occursto:State to which a transition occurstime:Time when a transition occursage:Age at inclusionsex:Sex.F for female and M for maleThe possible states are:0:No ventilation1:Ventilation2:End of stay.And cens stands for censored observations.DetailsThis data frame consists in a random sample of the SIR-3cohort data.It focuses on the effect of ven-tilation on the length of stay(combined endpoint discharge/death).Ventilation status is considered as a transcient state in an illness-death model.The data frame is directly formated to be used with the mvna function,i.e.,it is transition-oriented with one row per transition.SourceBeyersmann,J.,Gastmeier,P.,Grundmann,H.,Baerwolff,S.,Geffers,C.,Behnke,M.,Rueden,H., and Schumacher,e of multistate models to assess prolongation of intensive care unit stay due to nosocomial infection.Infection Control and Hospital Epidemiology,27:493-499,2006. Examplesdata(sir.cont)#Matrix of possible transitionstra<-matrix(ncol=3,nrow=3,FALSE)tra[1,2:3]<-TRUEtra[2,c(1,3)]<-TRUE#Modification for patients entering and leaving a state#at the same datesir.cont<-sir.cont[order(sir.cont$id,sir.cont$time),]for(i in2:nrow(sir.cont)){if(sir.cont$id[i]==sir.cont$id[i-1]){if(sir.cont$time[i]==sir.cont$time[i-1]){sir.cont$time[i-1]<-sir.cont$time[i-1]-0.5}}}#Computation of the Nelson-Aalen estimatesna.cont<-mvna(sir.cont,c("0","1","2"),tra,"cens")if(require("lattice")){xyplot(na.cont,tr.choice=c("02","12"),aspect=1,strip=strip.custom(bg="white",factor.levels=c("No ventilation--Discharge/Death","Ventilation--Discharge/Death"),par.strip.text=list(cex=0.9)),scales=list(alternating=1),xlab="Days",ylab="Nelson-Aalen estimates")}14summary.mvna summary.mvna Summary method for objects of class’mvna’DescriptionSummary method for mvna objects.The function returns a list containing the cumulative transition hazards,variance and other informations.Usage##S3method for class mvnasummary(object,level=0.95,var.type=c("aalen","greenwood"),ci.fun=c("log","linear","arcsin"),...)##S3method for class mvnaprint.summary(x,...)Argumentsobject An object of class mvna.level Level of the pointwise confidence interval.Default is0.95.var.type Which of the"aalen"or"greenwood"variance estimator should be displayed and used to compute the pointwise confidence intervals.Default is"aalen".ci.fun Which transformation to apply to the confidence intervals.One of"linear", "log","arcsin".Default is"log"....Further arguments.x An object of class summary.mvna.ValueReturns an object of class mvna which is a list of data frames named after the possible transitions.Each data frame contains the following columns:time Event times at which the cumulative hazards are estimated.na Estimated cumulative transition hazards.var.aalen or var.greenwoodVariance estimates.The name depends on the var.type argument.Default willbe var.aalen.lower Lower bound of the pointwise confidence interval.upper Upper bound.n.risk Number of individuals at risk of experiencing an event just before t.n.event Number of transitions at time t.Author(s)Arthur Allignol,<*************************>See AlsomvnaExamplesdata(sir.adm)##data set transformationdata(sir.adm)id<-sir.adm$idfrom<-sir.adm$pneuto<-ifelse(sir.adm$status==0,"cens",sir.adm$status+1)times<-sir.adm$timedat.sir<-data.frame(id,from,to,time=times)##Possible transitionstra<-matrix(ncol=4,nrow=4,FALSE)tra[1:2,3:4]<-TRUEna.pneu<-mvna(dat.sir,c("0","1","2","3"),tra,"cens")summ.na.pneu<-summary(na.pneu)##cumulative hazard for0->2transition:summ.na.pneu$"02"$naxyplot.mvna Panel plots for object of class’mvna’Descriptionxyplot function for objects of class mvna.Estimates of the cumulative hazards are plotted as a function of time for all the transitions specified by the user.The function can also plot several types of pointwise confidence interval(see Andersen et al.(1993)p.208).Usage##S3method for class mvnaxyplot(x,data=NULL,xlab="Time",ylab="Cumulative Hazard",tr.choice="all",conf.int=TRUE,var.type=c("aalen","greenwood"),ci.fun=c("log","linear","arcsin"),level=0.95,col=c(1,1,1),lty=c(1,3,3),ci.type=c(1,2),...)Argumentsx An object of class mvna.data Useless.xlab x-axis label.Default is"Time".ylab y-axis label.Default is"Cumulative Hazard"tr.choice A character vector of the form c("from to","from to")specifying which tran-sitions should be plotted.Default is"all".conf.int A logical whether plot pointwise confidence interval.Default is TRUEvar.type One of"aalen"or"greenwood".Specifies which variance estimator is used to compute the confidence intervals.ci.fun One of"log","linear"or"arcsin".Indicates the transformation applied to the pointwise confidence intervals.Default is"log".level Level of the confidence interval.Default is0.95.col Vector of colour for the plot.Default is black.lty Vector of line type.Default is c(1,3,3).ci.type DEPRECATED...Other arguments for xyplot.ValueAn object of class trellis.NoteThese plots are highly customizable,see Lattice and xyplot.For example,if one want to change strip background color and the title of each strip,it can be added’strip=strip.custom(bg="a color",factor.levels="a title","another title")’.One can use’aspect="1"’to get the size of the panels isometric.Author(s)Arthur Allignol,<*******************************>ReferencesAndersen,P.K.,Borgan,O.,Gill,R.D.and Keiding,N.(1993).Statistical models based on counting processes.Springer Series in Statistics.New York,NY:Springer.Deepayan Sarkar(2006).lattice:Lattice Graphics.R package version0.13-8.See Alsoxyplot,mvna,sir.adm,sir.contIndex∗aplotlines.mvna,2∗datasetsabortion,2sir.adm,11sir.cont,12∗hplotplot.mvna,6xyplot.mvna,15∗printprint.mvna,10∗survivalabortion,2lines.mvna,2mvna,4plot.mvna,6predict.mvna,8print.mvna,10sir.adm,11sir.cont,12summary.mvna,14xyplot.mvna,15abortion,2Lattice,16legend,7lines.mvna,2mvna,3,4,8,9,11,15,16plot.mvna,3,6predict.mvna,8print.mvna,10print.summary.mvna(summary.mvna),14sir.adm,6,11,16sir.cont,6,12,16summary.mvna,9,14xyplot,16xyplot.mvna,1517。
同学捡到尺子英语作文

同学捡到尺子英语作文Title: The Found Ruler。
One ordinary day, while walking through the bustling school corridor, something caught my eye—a gleam of metal on the ground. Upon closer inspection, I discovered it was a ruler, seemingly abandoned and forgotten. Holding it in my hand, I couldn't help but wonder about its story. How did it end up here? Whose was it? Questions swirled in my mind as I embarked on a journey of imagination.The ruler, an instrument of measurement, symbolizes precision and accuracy. As I pondered its significance, I couldn't help but draw parallels between the ruler and life itself. Just as we strive for precision and accuracy in our actions, the ruler serves as a reminder of the importance of exactness in our endeavors.With each passing day, the ruler became more than just a piece of stationery—it became a source of inspiration.Its sleek lines and markings whispered tales of diligence and meticulousness. I found myself drawn to its simplicity yet profound utility.In the classroom, the ruler became a tool for learning. Its straight edge guided my hand as I drew graphs and diagrams, ensuring accuracy in my work. With each measurement, I embraced the discipline it represented, striving for excellence in my studies.Beyond academics, the ruler took on a deeper significance in my life. It became a metaphor for personal growth, reminding me to measure my progress with precision and honesty. Just as each inch on the ruler represents a unit of length, each step I take symbolizes progress on my journey of self-improvement.Yet, amidst the lessons learned and the inspiration gained, a nagging question lingered—who did the ruler belong to? Was it lost or discarded intentionally? The mystery added an intriguing layer to my fascination with the seemingly mundane object.As days turned into weeks and weeks into months, the ruler remained a constant companion, a silent witness to my experiences. Its presence served as a reminder of the transient nature of life and the importance of seizing every moment.In the end, the story of the found ruler is not just about a chance discovery in a school corridor. It is a reflection of the serendipitous moments that shape our lives—the unexpected encounters, the lessons learned, and the connections made along the way.As I reflect on my journey with the ruler, I realize that its true value lies not in its material form but in the meaning I've attributed to it. It is a symbol of resilience, adaptability, and the beauty of the unexpected. And though its origins may remain a mystery, its impact on my life is undeniable.So, to whoever lost or abandoned the ruler, I offer my gratitude. Thank you for inadvertently enriching my lifewith your absence. And to the ruler itself, I say this—though you may be just a simple piece of stationery, your significance transcends the physical realm. You are a testament to the power of chance and the beauty of the unknown.。
Random Walk Definition - Boston University随机游走的定义-波士顿大学

1i n, i 0
– for 1i n, fii1anhd ii1/i
– Given N(i,t) number of time chain visits state i in t steps
V2 (1/2, 0, 1/4, 3/8, ...)
• Consider probabilities of being at a particular vertex at each step in walk.
• Each of these can be consider a vector,
V (1 ,o 0 ,0 )V , (1 1 /2 ,1 /4 ,1 /4 ),...
Almost there
• A strong component of a directed graph G is a subgraph C of G where for each edge eij there is a directed path from i to j and from j to i.
• Notice that we can then calculate everything given q0 and P.
More Definitions
• Consider question where am I after t steps, define t-step probability P i(tj)PX rt[j|X oi]
• We can express hitting time in terms of
commute time as
[4] H. B. Bakoglu, Circuits, Interconnections and Packaging for VLSI, Addison-Wesley, 1990,
![[4] H. B. Bakoglu, Circuits, Interconnections and Packaging for VLSI, Addison-Wesley, 1990,](https://img.taocdn.com/s3/m/d2ff5605e87101f69e3195b8.png)
NX 8.0 模拟产品功能概述说明书

•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
•
•
#
#
#
#
#
#
#
#
#
#
#
数据科学基础-随机游走

23
Rejection Sampling
设定一个方便采样的常用概率分布函数 q(x),以及 一个常量 k,使得 p(x) 总在 kq(x) 的下方 中采采样样得得到到q(一x)的个一值个u。样如本果z0。u落从在均了匀上分图布中(的0,灰kq色(z0区)) 域,则拒绝这次抽样,否则接受这个样本z0 重复以上过程得到n个接受的样本z0,z1,...zn−1
9
转移概率与顶点概率质量
马尔可夫链中两个状态间的转移概率( transition probability)与转 移概率矩阵
◦ 对于一组状态x和y,从x到y的转移概率记为pxy,并且 ◦ 由pxy 组成的矩阵P称为转移概率矩阵
图G顶点概率质量向量
◦ p(t) 是一个向量, 其维度pi(t)表示 顶点i(状态i)在t时刻的概率质量
,则π 是马尔可夫链的平稳分
14
主要内容
Introduction Stationary Distribution The Web as a Markov Chain Markov Chain Monte Carlo Applications - Areas and Volumes Convergence of Random Walks on Undirected Graphs Random Walks on Undirected Graphs with Unit Edge Weights Hidden Markov Model
◦ 设顶点i只有一条从j进入的边,以及一条出边,π为平稳概率,
则
,
。若i增加1个自循环,则有
,
即
;若增加k个自循环,则
,即
Social games in a social network

a r X i v :n l i n /0010015v 1 [n l i n .A O ] 5 O c t 2000Social games in a social networkGuillermo Abramson 1,2∗and Marcelo Kuperman 1†1Centro At´o mico Bariloche and Instituto Balseiro,8400S.C.de Bariloche,Argentina2Consejo Nacional de Investigaciones Cient´ıficas y T´e cnicas,ArgentinaWe study an evolutionary version of the Prisoner’sDilemma game,played by agents placed in a small-world net-work.Agents are able to change their strategy,imitating that of the most successful neighbor.We observe that different topologies,ranging from regular lattices to random graphs,produce a variety of emergent behaviors.This is a contribu-tion towards the study of social phenomena and transitions governed by the topology of the community.PACS numbers:87.23.Ge,02.50.Le,87.23.KgThe search for models that account for the complex behavior of biological,social and economic systems has been the motivation of much interdisciplinary work in the last decade [1].In particular,the emergence of altruis-tic or cooperative behavior is a favorite problem of game theoretical approaches [2].In this context,the Prisoner’s Dilemma game [3]has been widely studied in different versions,as a standard model for the confrontation be-tween cooperative and selfish behaviors,the later man-ifested by a defecting attitude,aspiring to obtain the greatest benefit from the interaction with another indi-vidual.It is usually implemented in zero dimensional systems,where every player can interact with any other.It has also been studied on a regular lattice,where a player can interact with its nearest neighbors in an array [4].In a regular lattice the concept of a k -neighborhood is straightforward.It is composed of the k nearest individ-uals to a given one.However,social situations are rarely well described by such extreme networks.The topology of social communities is much better described by what has been called small-world networks [5,6].In the version of small worlds that we use in this work,the “regular”k -neighborhood of an individual is modified by breaking a fraction of its k original links.An equal amount of new links are created,adding to the neighborhood a set of individuals randomly selected from the whole system.We have studied a simple model of an evolutionary version of the Prisoner’s Dilemma game played in small-world networks.The Prisoner’s Dilemma was chosen as a paradigm of a system capable to display both cooperative and competitive behaviors [7].The evolutionary dynam-ics is implemented by an imitation behavior.It is im-C Cstwhere Ωi is the set of neighbors of element i .P i is the profit earned by a player in a time step,and it is not accumulated from round to round.After this,the players are allowed to inspect the profit collected by its neighbors in that round,adopting the strategy of the wealthiest among them for the next round of play.If there is a draw between more than one neigh-bor,one of them is chosen at random to be imitated.If the element under consideration is itself one of the win-ners of the round,it keeps its own strategy.That is,explicitly writing the time dependence of the strategies:x i (τ+1)=x i (τ)if P i (τ)≥max(P ∈Ωi )x j (τ)if j ∈Ωi and P j (τ)=max(P ∈Ωi ).We have found that a small amount of noise is essen-tial to prevent the system from falling in a frozen state.After a round of play,we chose one element at random and flip its strategy.This is enough to keep the system out of equilibrium and allow transitions between different states.As a playground for our system,we have used a familyof small-world networks that depend on a parameter ǫ[6].We start from a regular,one-dimensional,periodic lattice of coordination number 2K .We then run sequen-tially through each of the sites,rewiring K of its links with probability ǫ.Running from 0to 1,this parame-ter changes the wiring properties of the network,ranging from a completely ordered lattice at ǫ=0,to a ran-dom network at ǫ=1.Intermediate values of ǫproduce a continuous spectrum of small-world networks.Double connections between sites,as well as the connection of a site with itself,are avoided in the construction of the network.Since we neither destroy nor create links,the resulting network has an average coordination number 2K ,equal to the initial one.This method,however,can produce disconnected graphs,that we have avoided in our analysis.Note that ǫis related to the fraction of modified regular links.Two magnitudes characterize the topological proper-ties of the small-world networks generated by the indi-cated procedure.One of them,L (ǫ),measures the typical separation between any pair of elements in the network.The other,C (ǫ),measures the clustering of an element’s neighborhood [6].Ordered lattices are highly clustered,and have large L .Random graphs have short character-istic length and small clusterization.In between,small worlds can be characterized by a high clusterization (like lattices)and short path lengths (like random networks).The opposing tendencies of cooperation and defection perform differently for different payofftables and differ-ent topologies,through the values of t and ǫ.Disregard-ing ǫ,one may qualitatively expect that,for sufficiently high values of t it would pay to defect while,for low val-ues of t ,it would be worth to cooperate.In either of these two extremes,the system would collapse to a stateformed only by defectors (in the first case)or only by co-operators (in the second case).For intermediate values of t the system would settle into a mixed state consisting in cooperators and defectors.Cooperators would thrive through the formation of clusters,that can resist the in-vasion by defectors.The dependency on the topology of the network appears on top of these three regimes.From the structure of the payoffmatrix one may conjecture that the high values of t referred to above will be around t =2(where a defector earns twice as much as a pair of cooperators).Correspondingly,the low values of t will be around t =1(where a single cooperator earns more than a defector).In the following we show the results of simulations per-formed in systems with 1000elements.The initial strate-gies are assigned at random with equal probability.Then several hundred rounds are played to allow for an asymp-totic regime to be achieved.All the results shown are averages over realizations where both the networks and the initial conditions are randomly chosen,excluding all disconnected graphs from our analysis.d e f e c t o r sthe tempta-probability to 10in-500rounds of t ex-a proper The number of cooperators and defectors are fluctu-ating variables,with bell shaped distributions.In figure 1we show the average fraction of defectors in systems with K =2,that is,systems with an average coordina-tion number of four.Four curves are shown as a function of the parameter t .Each curve corresponds to a network characterized by the parameter ǫshown in the legend.All the curves show a growth in the fraction of defectors for growing values of t ,as expected.We can see however,that the small world corresponding to ǫ=0.1displays an enhanced number of defectors at values of t around 1.2.For systems with a fixed K and a fixed t ,this meansthat the existence of a small world topology with ǫ∼0.1represents that nearly 40%of the population adopts the defecting strategy,against the 20%ofmoreregular or more random networks.(Note that,in fig.1,we have included values of t lower than 1,where the game is not a proper Prisoner’s Dilemma,since the reward for coop-eration is greater that the temptation to defect.We have done so because the state of the system at t =1,for all values of ǫ,still contains a small fraction of defectors.We wanted to stress that for low enough values of t the state is complete cooperation.)1the rewiring in the leg-realizations of 1000but with emphasize the changes in behavior as the structure of the network varies.The four curves correspond to different coordina-tion numbers.The game corresponds to the value t =1.2in the payoffmatrix,so that the curve with K =2is a slice of figure 1cut at t =1.2.Note that only this curve has a clear high peak of defectors centered near ǫ=0.1.Systems with K =3have a downward peak instead,in the region of small worlds,indicating a slight enhance-ment of the cooperative strategy.For K =4we can see again a small peak of defectors.Systems with K =5and greater (not shown)display a monotonous behavior in ǫ.Some conjecture on the origin of these features may be appropriate here.We think that the competition between the stability of clusters of cooperators and their exploita-tion by neighbor defectors at the borders contributes to the features observed here.When K =2,the coopera-tors survive in small compact groups.As ǫgrows,these groups can be formed by elements widely dispersed in the system,where they will have more defector neighbors to compete with.In this way,there will be less configura-tions to support them and,consequently,more defectorsin the system.For ǫeven greater,and more long range links,cooperators may start to reconnect and survive the competition with the defectors.When K >2,the coop-erators can only survive in larger groups,because de-fecting neighbors at the border of a group can penetrate deeper.When ǫgrows,cooperators belonging to faraway groups may become connected to form large clusters able to survive.The fact that K =3,at t =1.2shows a slight decrease in the fraction of defectors at intermediate val-ues of ǫremains,however,unexplained in this picture.At other values of t ,we observed that the system with K =3performs like that with K =2,namely with an enhancement of defector at intermediate values of ǫ.ac-in-that change their strategy.There is a Gaussian distribution of these unsatisfied elements,whose mean increases with ǫ,as shown in figure 3.This behavior is observed for all values of K and of t ,namely that regular lattices contain a smaller number of unsatisfied elements than random networks,with small worlds in between.Most of what is analytically known about small worlds refers to the distribution of shortest paths between pairs of elements (see for example [8–10]).It is known that reg-ular lattices stand apart from even infinitesimally rewired small worlds,that behave like random networks.The ex-istence of a phenomenon like the enhancement of defec-tors density at a finite value of ǫ,as shown in this work,points to the existence of an interesting phenomenology in small worlds.The broad spectrum of behaviors of a given system as a function of the topological features of the network is the main aspect that we want to empha-size.This suggests the possibility of modelling a certain system featuring well known interactions and analyzing the influence of the particular organization the commu-nity.Moreover,the possibility of a self organizing net-work with changing links opens the possibility of mod-elling more realistically social and economical situations [11].At this point we can state that the self organization of the network can lead to a nontrivial behavior of the whole system.Another interesting example of this state-ment would be a simple SIR model for the propagation of an epidemic.This is the subject of work under way [12].The authors thank Dami´a n H.Zanette for interesting discussions.。
基于随机游走和混合高斯模型的运动目标检测

基于随机游走和混合高斯模型的运动目标检测李强;陈光化;余渊【摘要】Since the conventional Gaussian mixture background modeling algorithm does not consider the correlation between adjacent pixels in the same frame,which cannot accurately capture the contour of moving objects,a foreground target detection method combined with random walk and Gaussian mixture model has been proposed.The background of the video source image has been modeled with the mixed Gauss model firstly,and the initial moving object has been obtained.Then,the number of seed points is determined by analyzing the segmentation result and the processing time of the random walk algorithm.The seed points have been labeled with the initial moving object,and the video source image is segmented by random walk algorithm.The obtained segmentation target and the initial moving object have been computed with logic AND operation.The morphological processing has been carried out to get the final moving target.In order to verify the effectiveness of the proposed algorithm, the four selected sequences of videos have been tested by Matlab.The test results show that the proposed method has solved the edge blurring problem of Gaussian mixture algorithm,and reduced the foreground noise.%针对传统的混合高斯背景建模算法未考虑同一帧内相邻像素之间的联系而导致无法准确地捕捉到运动物体轮廓的问题,提出了一种将随机游走和混合高斯模型相结合的前景目标检测算法.该算法利用混合高斯模型对视频源图像进行背景建模,从而获得初始运动目标,应用随机游走算法的分割效果及处理时间来确定种子点数量,结合初始运动目标对种子点进行标记,采用随机游走算法对视频源图像进行分割,将所得到的分割目标再与初始运动目标进行"与"运算,通过形态学处理得到作为结果的运动目标.为验证所提出算法的有效性,基于Matlab对所选取的4段视频进行了仿真检测.验证实验结果表明,所提出的前景目标检测算法较好地解决了混合高斯算法所产生的边缘模糊问题,同时也明显降低了前景噪声.【期刊名称】《计算机技术与发展》【年(卷),期】2017(027)006【总页数】6页(P11-16)【关键词】混合高斯模型;随机游走;运动目标检测;种子点【作者】李强;陈光化;余渊【作者单位】上海大学机电工程与自动化学院,上海200070;上海大学机电工程与自动化学院,上海200070;上海电器科学研究所(集团)有限公司,上海 200333【正文语种】中文【中图分类】TP301.6运动目标检测是分析视频过程中一个基础而又关键的任务[1]。
Bourns TBU-KE系列高速过电压保护器产品说明文档说明书

TBU-KE Series - TBU *RoHS Directive 2002/95/EC Jan. 27, 2003 including annex and RoHS Recast 2011/65/EU June 8, 2011. Specifi cations are subject to change without notice.The device characteristics and parameters in this data sheet can and do vary in different applications and actual device performance may vary over ers should verify actual device performance in their specifi c applications.The TBU-KE Series of Bourns ® TBU ®(Transient Blocking Unit) products are verylow capacitance unidirectional high-speedsurge protection components designed to protect against faults caused by short circuits, AC power cross, induction and lightning surges.The TBU-KE is a unidirectional TBU ® device: the TBU ® protector will trip in less than 1 μs when the current reaches the maximum value in one direction only, that is when Pin 1 is positive in voltage with respect to Pin 2. No current limiting exists in the oppo-site polarity, and the TBU ® protector appears as resistive in nature. The reverse current should not exceed the maximum trigger current level of the TBU ® device. An external diode may be used to prevent reverse current in DC biased applications.The TBU ® protector blocks surges and provides an effective barrier behind which sensi-tive electronics will not be exposed to large voltages or currents during surge events. After the surge, the TBU ® device resets when the voltage across the TBU ® device falls to the V reset level. The TBU ® device will automatically reset on lines which have no DC bias or have DC bias below V reset (such as unpowered signal lines).The TBU ® device is provided in a surface mount DFN package and meets industry standard requirements such as RoHS and Pb Free solder refl ow profi les.DescriptionULFile Number: E315805Absolute Maximum Ratings (@ T A = 25 °C Unless Otherwise Noted)Symbol ParameterPart NumberValue Unit V impPeak impulse voltage withstand with duration less than 10 msTBU-KE025-xxx-WH TBU-KE040-xxx-WH TBU-KE050-xxx-WH 250400500VV rms Continuous A.C. RMS voltage TBU-KE025-xxx-WH TBU-KE040-xxx-WH TBU-KE050-xxx-WH100200250V T op Operating temperature range -40 to +125°C T stgStorage temperature range-65 to +150°C*R o H S CO MP L I A NTE 25500072TBU ®DeviceLine Side 12Load SideAsia-Pacifi c: Tel: +886-2 2562-4117 • Fax: +886-2 2562-4116EMEA: Tel: +36 88 520 390 • Fax: +36 88 520 211The Americas: Tel: +1-951 781-5500 • Fax: +1-951 OB S O L E T ESpecifi cations are subject to change without notice.The device characteristics and parameters in this data sheet can and do vary in different applications and actual device performance may vary over time.Users should verify actual device performance in their specifi c applications.Electrical Characteristics (@ T A = 25 °C Unless Otherwise Noted)Symbol ParameterPart Number Min. T yp. Max. Unit I triggerCurrent required for the device to go from operating state to protected stateTBU-KExxx-050-WHTBU-KExxx-100-WH TBU-KExxx-200-WH TBU-KExxx-300-WH TBU-KExxx-500-WH 50100200300500751503004507501002004006001000mAR deviceSeries resistance of the TBU ® deviceV imp = 250 V I trigger (min.) = 50 mA V imp = 250 V I trigger (min.) = 100 mA V imp = 250 V I trigger (min.) = 200 mA V imp = 250 V I trigger (min.) = 300 mA V imp = 250 V I trigger (min.) = 500 mAV imp = 400 V I trigger (min.) = 50 mAV imp = 400 V I trigger (min.) = 100 mA V imp = 400 V I trigger (min.) = 200 mA V imp = 400 V I trigger (min.) = 300 mA V imp = 400 V I trigger (min.) = 500 mA V imp = 500 V I trigger (min.) = 50 mA V imp = 500 V I trigger (min.) = 100 mA V imp = 500 V I trigger (min.) = 200 mA V imp = 500 V I trigger (min.) = 300 mA V imp = 500 V I trigger (min.) = 500 mATBU-KE025-050-WH TBU-KE025-100-WH TBU-KE025-200-WH TBU-KE025-300-WH TBU-KE025-500-WH TBU-KE040-050-WH TBU-KE040-100-WH TBU-KE040-200-WH TBU-KE040-300-WH TBU-KE040-500-WH TBU-KE050-050-WH TBU-KE050-100-WH TBU-KE050-200-WH TBU-KE050-300-WH TBU-KE050-500-WH12.56.33.42.41.813.06.83.93.02.313.77.54.63.63.014.67.54.13.12.315.28.14.73.72.916.08.95.54.53.6Ωt block Time for the device to go from normal operating state to protected state 1µs I Q Current through the triggered TBU ® device with 50 Vdc circuit voltage 0.250.50 1.00mA V reset Voltage below which the triggered TBU ® device will transition to normal operating state 101418V R th(j-l)Junction to package pads - FR4 using recommended pad layout116°C/W R th(j-l)Junction to package pads - FR4 using heat sink on board (6 cm 2)96°C/WApplications■ Set top box LNB ports ■ Protection modules and dongles ■ Process control equipment ■ Test and measurement equipment ■ General electronicsOB S O L E T ESpecifi cations are subject to change without notice.The device characteristics and parameters in this data sheet can and do vary in different applications and actual device performance may vary over ers should verify actual device performance in their specifi c applications.Reference ApplicationThe TBU ® device can be used to protect against excessive voltage surges in DC biased equipment, as shown in the fi gure below. Diode D1 prevents reverse voltage surges from damaging the equipment, and the TBU ® protector prevents any positive surges from causing damage. An overvoltage protection device, such as an MOV, may be used to provide additional overvoltage protection if the surge voltage is likely to be above the maximum rating of the TBU ® device. D1 reverse voltage rating should be greater than that of the OVP device at the maximum surge cur-rent level. Typically, a 1N4007 is a suitable choice. D2 should be chosen to be above the normal working voltage of the protected device, but below its absolute maximum rating.The TBU ® device is a silicon-based, solid-state, resettable device which is placed in series with a signal path. The TBU ® device operates in approximately 1 µs - once line current exceeds the TBU ® device’s trigger current I trigger . When oper-ated, the TBU ® device restricts line current to less than 1 mA typically. When operated, the TBU ® device will block all system voltages and any other voltages including the surge up to rated limits.After the surge, the TBU ® device resets when the voltage across the TBU ® device falls to the V reset level. The TBU ®device will automatically reset on lines which have no DC bias or have DC bias below V reset (such as unpowered signal lines). If the line has a normal DC bias above V reset , the voltage across the TBU ® device may not fall below V reset after thesurge. In such cases, special care needs to be taken to ensure that the TBU ® device will reset, otherwise an automatic or manual power down will be required. Bourns application engineers can provide further assistance.Basic TBU OperationPerformance GraphsV-I Characteristic - TBU-KE050-300-WH (Pin 2-1)Typical Trigger Current vs. Temperature1.81.61.41.21.00.80.60.40.20.0-75-50-250255075100125150Junction Temperature (°C)N o r m a l i z e d T r i p C u r r e n t (A )Line SideOB S O L E T ERefl ow Profi leProfi le FeaturePb-Free Assembly Average Ramp-Up Rate (Tsmax to Tp) 3 °C/sec. max. Preheat- Temperature Min. (Tsmin) - Temperature Max. (Tsmax) - Time (tsmin to tsmax)150 °C 200 °C60-180 sec.Time maintained above: - Temperature (TL) - Time (tL)217 °C60-150 sec.Peak/Classifi cation Temperature (Tp)260 °C Time within 5 °C of Actual Peak Temp. (tp) 20-40 sec. Ramp-Down Rate6 °C/sec. max. Time 25 °C to Peak Temperature8 min. max.Performance Graphs (Continued)Power Derating CurveTypical Resistance vs. TemperatureJunction Temperature (°C)203.02.52.01.51.00.50.0406080100120140T o t a l M a x . P o w e r (W )2.21.61.82.01.41.21.00.80.60.40.20.0-75-50-250255075100125150Junction Temperature (°C)N o r m a l i z e d R e s i s t a n c e (Ω)Specifi cations are subject to change without notice.The device characteristics and parameters in this data sheet can and do vary in different applications and actual device performance may vary over time.Users should verify actual device performance in their specifi c applications.OB S O L E T E2.50 ± 0.10(.098 ± .004)PIN 10.25(.010)Product DimensionsPad #Pin Out 1Line Side 2Load SidePad Designation DIMENSIONS:MM(INCHES)Recommended Pad LayoutDark grey areas show added PCB copper area for better thermal resistance.Thermal Resistance vs. Additional PCB Cu AreaAdded Cu Area (Sq. In.)0.20.40.60.81.01.21.41.61.82.010090806040200T h e r m a l R e s i s ta n c e t o A mb i e n t (°C /W )10305070TBU ® High-Speed Protectors have a 100 % matte-tin termination fi nish. For improved thermal dissipation, the recommended layout uses PCB copper areas which extend beyond the exposed solder pad. The exposed solder pads should be defi ned by a solder mask which matches the pad layout of the TBU ® device in size and spac-ing. It is recommended that they should be the same dimension as the TBU ® pads but if smaller solder pads are used, they should be centered on the TBU ® package terminal pads and not more than 0.10-0.12 mm (0.004-0.005 in.) smaller in overall width or length. Solder pad areas should not be larger than the TBU ® pad sizes to ensure adequate clearance is maintained. The recommendedstencil thickness is 0.10-0.12 mm (0.004-0.005 in.) with a stencil opening size 0.025 mm (0.0010 in.) less than the solder pad size. Extended copper areas beyond the solder pad signifi cantly improve the junction to ambient thermal resistance, resulting in operation at lower junction temperatures with a corresponding benefi t of reliability. All pads should soldered to the PCB, includ-ing pads marked as NC or NU but no electrical connection should be made to these pads. For minimum parasitic capacitance, it is recommended that signal, ground or power signals are not routed beneath any pad.Specifi cations are subject to change without notice.The device characteristics and parameters in this data sheet can and do vary in different applications and actual device performance may vary over ers should verify actual device performance in their specifi c applications.OB S O L E T EHow to OrderTBU - KE 025 - 500 - WHTBU® ProductSeriesKE = Uni-SeriesImpulse Voltage Rating025 = 250 V040 = 400 V050 = 500 VTrigger Current050 = 50 mA100 = 100 mA200 = 200 mA300 = 300 mA500 = 500 mAHold to Trip Ratio Suffi xW = Hold to Trip RatioPackage Suffi xH = DFN PackageTypical Part Marking“TBU” is a registered trademark of Bourns, Inc. in the United States and other countries.REV. 04/15Packaging Specifi cationsDIMENSIONS:MM(INCHES)A B C DGN Min.Max.Min.Max.Min.Max.Min.Max.Ref.Ref.176(6.929)178(7.008)1.5(.059)2.5(.098)12.8(.504)13.5(.531)20.2(.795)-16.5(.650)102(4.016)A0B0 D D1 E F Min.Max.Min.Max.Min.Max.Min.Max.Min.Max.Min.max.2.8(.110)3.0(.118)5.4(.212)5.6(.220)1.5(.059)1.6(.063)1.5(.059)-1.65(.065)1.85(.073)5.45(.214)5.55(.218) K0P P0P2 t W Min.Max.Min.Max.Min.Max.Min.Max.Min.Max.Min.Max.1.1(.043)1.3(.051)3.8(.150)4.2(.165)3.8(.150)4.2(.165)1.95(.077)2.05(.081)0.25(.010)0.35(.014)11.7(.461)12.3(.484)QUANTITY: 3000 PIECES PER REEL- 1ST DIGIT INDICATES THE YEAR’S 6-MONTH PERIOD.- 2ND DIGIT INDICATES THE WEEK NUMBER IN THE 6-MONTH PERIOD.- 3RD & 4TH DIGITS INDICATE SPECIFIC LOT FOR THE WEEK.6-MONTH PERIOD CODES:A = JAN-JUN 2009 C = JAN-JUN 2010 E = JAN-JUN 2011B = JUL-DEC 2009D = JUL-DEC 2010 F = JUL-DEC 2011- 2ND & 3RD DIGITS INDICATE IMPULSE VOLTAGE:Specifi cations are subject to change without notice.The device characteristics and parameters in this data sheet can and do vary in different applications and actual device performance may vary over time.Users should verify actual device performance in their specifi c applications.O LE TE。
EMH和行为金融(1)

➢ 价格变动的随机性≠价格水平的无理性
➢ 1959年,罗伯茨和奥斯本将“随机游走”和“布朗运 动”概念正式应用于股市,他们在论文中再次肯定了 股价的对数序列是随机游走,或者股价遵循几何布朗 运动。
投资收益(%)
11.5 5.5 0.2 -1.7 0.1 -1.9 1.3 0.8 1.7 1.9 3.0 5.3 3.9 4.2 3.6 4.3
买入并持有 投资收益(%)
10.4 10.3 10.3 10.1 10.1 10.0 9.7 9.6 9.6 9.6 9.6 9.4 10.3 10.3 10.0 9.8
小公司一月份
公司规模或小公司效应最早由Banz(1981)提 出,NYSE按公司规模划分为10组,小公司 的平均年收益持续处于较高水平。第10组 (最大规模)与第1组(最小规模)的平均 年收益之差为8.59%。经过风险调整后,最 小规模组与最大规模组平均收益高4.3%。
原因年底为减少纳税而结清亏损密切相关。
交易次数
12514 8660 4764 2994 2013 1484 1071 828 653 539 435 289 224 172 139 110
考虑交易成本的 的收益 -103.6 -74.9 -45.2 -30.5 -19.5 -16.6 -9.4 -7.4 -5.0 -3.6 -1.4 2.3 1.4 2.3 2.0 3.0
四、EMH的理论基础
EMH理论基于三个逐渐放松的假设之上:
(1)投资者理性; (2)即使某种程度上某些投资者非理性,非理性
部分相互抵消;
(3)市场力量会自动消除同方向的非理性。(套 利力量)。
920i

®800-472-6703PROGRAMMABLEINDICATOR/CONTROLLER®PROGRAMMABLE INDICATOR/CONTROLLERBar graphs and visualcues inform userswhen a batch or fill isin process and whenit’s approachingtarget weights.Customizeddatabase programsallow you to store,access and analyzecritical productioninformation.A 32-channel displaycapability allowsviewing of weight onan individual scaleand a combinationof totalized scales. Flexibility. Intelligence. Programmability.It’s all in the box.The 920i® weight indicator and process controller blends revolutionary user interfaces, totalflexibility and processing performance with the simplicity of a basic weight indicator. A crisp,highly customizable LCD graphical display, programmable softkeys and industry-recognizedelectronics are surrounded by a virtually indestructible enclosure to create one of the indus-try’s most trusted weight indicators and process controllers.Adding an entirely new dimension in flexibility for solution providers and users alike,the 920i indicator/controller brings simplified customization at a fraction of the cost oftraditional process instrumentation. From tailored basic weighing to complex processautomation, the 920i gives you features, programmability and power for your process.Typical LoopProcessingEvent BasedProcessingUncompleted TasksCompleted TasksThe 920i utilizesevent based processing,which identifies, prioritizesand executes events ratherthan processing a whole sequenceof events. This results in increasedefficiency and multi-tasking.Loop Processingfollows a specificsequence of instructionswhich can cause programdelays or systems tobecome unresponsive.• 100 configurable setpoints and six onboard digital I/O • T wo onboard option card slots (expandable to 14) for increased functionality, including communication protocols such as DeviceNet™, Allen-Bradley® Remote I/O, Ethernet/IP™, ControlNet™, Profibus®, Ethernet TCP/IP and Wi-FiCustomization puts increased productivity at your fingertips. The 920i features versatile programming options for increased process efficiency in virtually any application.• Up to 10 different screens can change with any given process • Real-time bar graphs show progress of filling or batching systems • Graphic icons and messages show user alerts and function status • Customizable softkeys give instant access to frequently used functions• Use Rice Lake’s iRite® software to bring a new level of sophistication to your operation with custom applicationsThe 920i delivers the speed, responsiveness and accuracy you need to stay ahead of the competition.• Simultaneously view up to 32 scale/sensor inputs, or up to four Legal for Trade scales • Single or multiple A/Ds feature selectable rates from 7.5 to 960 updates per second• E vent Sequential Protocol (ESP) technology identifies, prioritizes and executes events for increased efficiency and multi-tasking• Power for (16) 350Ω load cells per A/D board • Digital filtering and a selectable display update rate ensure accurate, stable weighments • S afe shutdown, increased input and transient voltage protection assure data is safeguardedin unreliable power environments.The 920i combines recognized performance, simplified architecture and intuitive features to provide a powerful instrument that is remarkably easy to use.• Large 4.6" W x 3.4" H, 320 x 240 pixel backlit LCD graphical display • I ntegrated PS/2 or USB port allows for quick data entry from a keyboard and seamless communication with a PC or other peripheral device • NEMA Type 4X, IP66 stainless steel enclosureLeading DesignThe Power of ProgrammabilityProven PerformanceSOFTKEYSHeavy-duty, stainless steelenclosure for enhanced protectionin harsh environments.CUSTOMIZED SCREENS Customize up to 10 screens with scales, bitmaps, bar graphs,text boxes and symbols.NAV-PAD®HEADQUARTERS230 West Coleman StreetRice Lake, Wisconsin 54868 - USA Tel: (715) 234 9171 | Fax: (715) 234 6967STANDARD FEATURES• Large 4.6" W x 3.4" H, 320 x 240 pixel back-lit LCD graphical display• Selectable character sizes from .25" to 1.2"• Display up to four scale channels with required Legal for Trade information per screen• Five displayed softkeys with 10 user-defined and 14 preset functions per screen• Selectable A/D measurement rate up to 960/second • Power for (16) 350 Ω load cells per A/D board • Peak hold, rate of change• Audit trail tracking and alibi storage • Multiple range/interval weighing • Four bidirectional communication ports • Local/remote keypress operation • Operator prompts/256 widgets• Multiple screens (program control)• Eight onboard databases • Six onboard digital I/O• 100 configurable setpoints, 30 types • Two onboard option card slots• 1,000-ID truck registers for in/out weighing • Programmable ticket formats 20 auxiliary print formats• ESP event-driven processing• User programmable 128 K flash memory • iQUBE2® connectivity• 32 individual scale accumulators• NEMA Type 4X/IP66 stainless steel enclosure •PS/2 or USB keyboard port for data entryOPTIONS/ACCESSORIES•Digital I/O, 24 channel • A/D dual or single channel • 0-4 kHz pulse input• Analog output selectable (0-10 V, 0-20 mA), single or dual • Analog input (-/+ 10V DC, 0-20 mA)• Thermocouple (E, J, K, N, T)• Memory, 1 MB (14 MB optional)• Two channel serial (RS-232, RS-485)• Two-card expansion board for deep, wall and panel mount • Six-card expansion boards, wall mount only • DC-DC 9-36 converter • PS/2 or USB keyboard • Fiber optic interface• Trans-flective display for sunlight applications Communication protocol cards• DeviceNet™• Allen-Bradley® Remote I/O • EtherNet/IP™• ControlNet™• Profibus® DP • PROFINET®• Ethernet TCP/IP 10/100 Base-T •Wireless LAN (Wi-Fi)SPECIFICATIONSPOWER:AC voltages: 100-240 VAC Frequency: 50-60 Hz DC voltages: 12-24 VDCConsumption: A C: 25W (universal) or 65W (others)DC: 25W for all modelsCOMMUNICATION PORTS: F our ports on CPU board support up to 115,200bpsPort 1: Full duplex RS-232Port 2: RS-232 with CTS/RTS; PS/2 keyboard interface or USB type A and B connectors Port 3: Full duplex RS-232, 20mAPort 4: Full duplex RS-232, 2-wire RS-485, 20mA Optional dual-channel serial expansion boards Channel A: RS-232, RS-485, 20 mA Channel B: RS-232, 20 mAKEYS/BUTTONS: 27-key membrane panel, tactile feel, PS/2 or USB port for externalkeyboard connectionTEMPERATURE RANGE: C ertified: 14°F to 104°F (-10°C to +40˚C)Operating: 14°F to 122°F (-10°C to +50˚C)WEIGHT: U niversal enclosure: 9.5 lb (4.3 kg)Wall mount enclosure: 23.0 lb (10.4 kg) Panel mount enclosure: 8.5 lb (3.9 kg) Deep universal: 11 lb (5.0 kg)EMC IMMUNITY: EN 50082 Part 2 IEC EN 61000-4-2, 3, 4, 5, 6, 8, 11 and 10 V/mAPPROVALSCC #01-088Accuracy Class III/IIIL n10,000Wall Mount UL/cUL Listed Custom Wall Mount UL/cUL Listed 508APanel Mount UL/cUL RecognizedMeasurement Canada ApprovedAM-5426Accuracy Class III/IIIHD nmax: 10,000UK 2658Accuracy Class III nmax: 6000/10,000PROGRAMMABLE INDICATOR/CONTROLLERAn ISO 9001 registered company Specifications subject to change without notice. © 2020 Rice Lake Weighing Systems PN 69119 en-US 1/20 REV-BUniversal Mount Deep Universal MountPanel MountWall MountSALES AND TECHNICAL ASSISTANCE。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
STEEN MARKVORSEN, SEAN McGUINNESS,andΒιβλιοθήκη CARSTEN THOMASSEN
[Received 1 October 1990]
ABSTRACT
We introduce an (r, /?)-net (0 < 2r < R) of a metric space M as a maximal graph whose vertices are elements in M of pairwise distance at least r such that any two vertices of distance at most R are adjacent. We show that, for a large class of metric spaces, including many Riemannian manifolds, the property of transience of a net and the property of the net carrying a non-constant harmonic function of bounded energy is independent of the choice of the net. We give a new necessary and sufficient condition for a graph with bounded degrees and satisfying an isoperimetric inequality to have no non-constant harmonic functions. For this purpose we develop equivalent analytic conditions for graphs satisfying an isoperimetric inequality. Some of these results have been discovered recently by others in more general settings, but our treatment here is specific and self-contained. We use graph transience to prove that Scherk's surface is hyperbolic, a problem posed by Osserman in 1965.
The second author is a postdoctoral fellow from Canada. 1991 Mathematics Subject Classification: 05C75, 60J15, 51K10.
Proc. London Math. Soc. (3) 64 (1992) 1-20.
2
S. MARKVORSEN, S. McGUINNESS AND C. THOMASSEN
is transient if and only if some net is transient. We prove that the nets of Scherk's surface are transient. Combined with Kanai's results, this shows that Scherk's surface is hyperbolic. This settles a problem of Osserman [17]. A harmonic function on a graph G is a real function <j) defined on the vertex set such that, for each vertex v, <p(v) equals the average of <f>(u), taken on all neighbours of v; that is, < is harmonic at v for all v. The energy of <f> is the sum / > E (0(w) - 0(^)) 2 taken over all edges uv of G. A harmonic function on a graph is a discrete version of a harmonic function on a manifold. We prove that if G and G' are nets on a slim and well-behaved metric space, then G satisfies an £-isoperimetric inequality (e>0) if and only if G' does. If, in addition, G has a non-constant harmonic function of finite energy, then also G' has such a function. This is in contrast to a result of Lyons [14] which shows that such a result does not hold for 'bounded harmonic functions' instead of 'harmonic functions of finite energy'. 2. Definitions and terminology A graph G is a pair V(G), E(G) where V(G) is a set of elements called vertices and E(G) is a set of unordered pairs uv of vertices called edges. If the edge uv is present, we say that it joins u and v and that u and v are neighbours. The number degc(w) (or just deg(w)) of neighbours of u is called the degree of u in G. The set of neighbours is denoted N(u, G) or just N(u). We shall assume that G is locally finite; that is, all degrees are finite. A finite path (from u, to vk+l) consists of vertices v1)v2,...,vk+1 and edges i>,u/+1 (1 *£/«=/:). The number k is called the length of the path. A one-way infinite or two-way infinite path is defined analogously. A graph is connected if any two vertices are connected by a path. A (connected) component of a disconnected graph is a maximal connected subgraph. The distance dist(w, v, G) (or just dist(u, v)) is the length of a shortest path from u to v. Clearly, distance defines a metric on V(G). Let v be a vertex in G. A flow from v is an assignment of a direction and a non-negative real number to every edge such that, at each vertex distinct from v, the incoming flow equals the outgoing flow. The value of / i s the net flow leaving v. The square sum
1. Introduction Consider a random walk defined on a connected, infinite graph such that, at each vertex v, the walk proceeds to a neighbour chosen with probability l/deg(u) where deg(t>) is the number of neighbours of v. The graph is transient if there is a positive probability that the walk never returns to the origin. There are several equivalent versions of this definition. In this paper we focus on the network flow definition (described in the next section). We say that a graph G satisfies an e-isoperimetric inequality (where £ is a non-negative real number) if there exists a positive real constant c such that, for each finite vertex set V, there are at least c |V| 5+e vertices of V which have neighbours outside V. The 2-dimensional grid Z2 satisfies an e-isoperimetric inequality for e = 0 and it is recurrent (i.e. non-transient). Varopoulos [22] proved by analytic methods (and a more general result by network flow methods is presented in [20] and a related result in the continuous case is proved in [7]) that every graph with bounded degrees satisfying an e-isoperimetric inequality, for some e > 0 , is transient. For e = \ this was proved by Dodziuk [3], and recently Kaimanovich [8] has also observed this relation in general for Markov operators on measure spaces. In this paper, we present an analytic result on lp spaces defined on graphs satisfying an e-isoperimetric inequality. We derive from this the transience result of Varopoulos and apply the results in two directions. Kanai [10] and others (Lyons and Sullivan [13], and Varopoulos [21,22]) showed that there is a close relation between hyperbolicity of certain Riemannian manifolds and transience of their associated nets (defined in the abstract). We extend the concept of a net to metric spaces in general and show that for certain metric spaces which we call slim and well-behaved (see the next section), each net
