电力拖动自动控制系统论文
电力拖动自动控制系统实验报告
电⼒拖动⾃动控制系统实验报告电⼒拖动⾃动控制系统实验实验⼀转速反馈控制直流调速系统的仿真⼀、实验⽬的1、了解MATLAB下SIMULINK软件的操作环境和使⽤⽅法。
2、对转速反馈控制直流调速系统进⾏仿真和参数的调整。
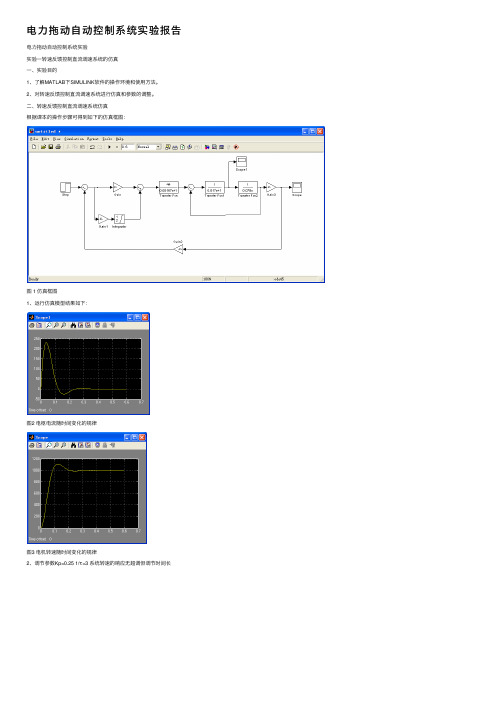
⼆、转速反馈控制直流调速系统仿真根据课本的操作步骤可得到如下的仿真框图:图 1 仿真框图1、运⾏仿真模型结果如下:图2 电枢电流随时间变化的规律图3 电机转速随时间变化的规律2、调节参数Kp=0.25 1/τ=3 系统转速的响应⽆超调但调节时间长3、调节参数Kp=0.8 1/τ=15 系统转速的响应的超调较⼤,但快速性较好实验⼩结通过本次实验初步了解了MATLAB下SIMULINK的基本功能,对仿真图的建⽴了解了相关模块的作⽤和参数设置。
并可将其⽅法推⼴到其他类型控制系统的仿真中。
实验⼆转速、电流反馈控制直流调速系统仿真⼀、实验⽬的及内容了解使⽤调节器的⼯程设计⽅法,是设计⽅法规范化,⼤⼤减少⼯作计算量,但⼯程设计是在⼀定近似条件下得到的,⽤MATLAB仿真可根据仿真结果对设计参数进⾏必要的修正和调整。
转速、电流反馈控制的直流调速系统是静、动态性能优良、应⽤最⼴泛的直流调速系统,对于需要快速正、反转运⾏的调速系统,缩短起动、制动过程的时间成为提⾼⽣产效率的关键。
为了使转速和电流两种负反馈分别起作⽤,可在系统⾥设置两个调节器,组成串级控制。
⼀、双闭环直流调速系统两个调节器的作⽤1)转速调节器的作⽤(1)使转速n跟随给定电压*mU变化,当偏差电压为零时,实现稳态⽆静差。
(2)对负载变化起抗扰作⽤。
(3)其输出限幅值决定允许的最⼤电流。
2)电流调节器的作⽤(1)在转速调节过程中,使电流跟随其给定电压*iU变化。
(2)对电⽹电压波动起及时抗扰作⽤。
(3)起动时保证获得允许的最⼤电流,使系统获得最⼤加速度起动。
(4)当电机过载甚⾄于堵转时,限制电枢电流的最⼤值,从⽽起⼤快速的安全保护作⽤。
当故障消失时,系统能够⾃动恢复正常。
电力系统自动化新技术论文

电力系统自动化新技术论文电力系统实现全面的自动化、一体化的管理是适应市场经济建设需求、促进社会可持续发展的重要保证。
店铺为大家整理的电力系统自动化新技术论文,希望你们喜欢。
电力系统自动化新技术论文篇一浅谈电力系统自动化技术[摘要]电力系统实现全面的自动化、一体化的管理是适应市场经济建设需求、促进社会可持续发展的重要保证。
在电力系统的广泛运营中,自动化控制体系的建立是管理水平、制度水平、科技水平、智能化水平、人性化水平的最真实、有效的反应,也是电力系统生产效能、服务效率提升的重要影响因素。
[关键词]电力;系统;自动化;技术控制中图分类号:F407.67 文献标识码:A 文章编号:1009-914X(2014)44-0098-01电力系统自动化是对电能生产、传输和管理实现自动控制、自动调度和自动化管理。
电力系统是一个地域分布辽阔,由发电厂、变电站、输配电网络和用户组成的统一调度和运行的复杂大系统。
电力系统自动化建设的主要目标是要实现电力在生产环节、供应环节的及时、稳定、安全、迅速、可持续,同时也是实现提高生产效率、降低运营成本,实现自动化、一体化、节约化、安全化管理的重要核心。
自动化系统的建立包含着现代化生产技术、计算机科学技术、网络共享技术的综合应用,对于电力系统而言,自动化的生产包含着发电厂、变电站、送电分配系统、计算机监控系统、网络覆盖系统等众多环节的综合摔制与协调,从而形成实时监控、指令及时传输、信息实时反馈的高实效性综合管理。
一、电力系统自动化控制的特点(1)电力系统的可靠性、安全性运行是建立系统全面自动化的重要保证。
因此我们首先应在电力系统送电服务的初期,经过系统的调研,努力的收集、严密的检测对电力系统的各个单元、部件、安全运行参数进行科学的处理。
(2)接着我们应参照电力自动化系统建立的相关技术要求,根据可行性分析及电力系统实时运行状态的考察进行合理的调控及提供有利的决策支持,对各个部件、整个系统进行微观及宏观的综合调控。
电力电气论文

电力电气论文篇一:电气工程及其自动化专业论文选题电气工程及其自动化专业毕业(论文)选题资料电气工程及其自动化专业研究方向主要包括电力拖动与控制方向和电力系统及其自动化方向。
本专业本科学生选题可以参考所列研究方向结合自己工作实际合理选题,开展论文写作。
方向一、电力拖动与控制电力拖动与控制方向论文可以写成文献综述型、理论研究型、实验研究型、工程设计型论文,主要围绕电力电子技术应用、电力拖动自动控制系统、交流调速系统、交直流电机拖动控制、微机数字控制系统、数字变频电源设计、电气接触控制、PLC控制系统设计、电气测量技术等。
写作过程中注意选题的可行性,选择自己熟悉领域,考虑选题大小难易程度,合理选择切入点。
方向二、电力系统及其自动化电力系统及其自动化方向论文可以写成文献综述型、理论研究型、实验研究型、工程设计型论文,主要围绕电力系统稳定分析与控制、电力系统潮流优化、电力系统过电压及其防护、电力系统无功优化与补偿技术、电力系统继电保护、电力系统安全自动装置、电力系统故障自愈技术、供配电系统工程设计等。
写作过程中注意选题的可行性,选择自己熟悉领域,考虑选题大小难易程度,合理选择切入点。
注:以上题目作为学生选题的参考,可选择作为论文题目,也可就自己感兴趣或平时关注的其他问题与指导教师交流另行选题,但选题应在专业范围之内。
另外需要注意部分选题并不是一个完整题目,需补充完整。
篇二:电气论文参考文献参考文献[1]王仁祥. 电力新技术概论[M]. 北京:中国电力出版社,2009.[2]戈东方. 电力工程电气设计手册.第1册,电气一次部分[M]. 北京:中国电力出版社,1989.[3]丁毓山、雷振山. 中小型变电所使用设计手册[M]. 北京:中国水利水电出版社,2000.[4]姚志松、姚磊. 中小型变压器实用手册[M]. 机械工业出版社,2008.[5]祝淑萍. 工业企业电力网际变电设备[M]. 北京:冶金工业出版社,2003 43-54.[6]刘百昆. 实用电工技术问卷[J]. 内蒙古:内蒙古人民出版社,1992. [7]傅知兰主编. 电力系统电气设备选择与实用计算[M]. 北京:中国电力出版社,2004.[8]李金伴、陆一心. 电气材料手册[M]. 化学工业出版社,2005.[9]清华大学高压教研组. 高压断路器[M]. 北京:水利电力出版社,1978. [10]华东电气. SF6金属封闭组合电器[M]. 北京:华东电气股份有限公,1997. [11]熊信银. 发电厂电气部分[M]. 北京:中国电力出版社,2009. [12]刘学军. 继电保护原理[M]. 北京:中国电力出版社,2007.[13]谷水清主编. 电力系统继电保护[M]. 北京:中国电力出版社,2005. [14]马福. 雷击变电所地电位干扰及防护措施研究[M]. 长沙:长沙理工大学, 2009.[15]李骏年. 电力系统继电保护[M]. 北京:中国电力出版社,1992 26-35. [16]吴华. 浅谈总降压变电所的防雷[J]. 科技风,2009年,第15期. [17]解广润. 电力系统过电压[M]. 北京:水利电力出版社,1991.[18]韩笑. 电气工程专业毕业设计指南-继电保护分册[M]. 北京:中国水利水电出版社,2003.[19]刘介才. 工厂供电设计指导[M]. 北京:机械工业出版社,2003 32-36. [20]刘天琪、邱晓燕. 电力系统分析理论[M]. 北京:科学出版社,2005. [21]中国机械工业协会. 工厂供电[M]. 北京:机械工业出版社,2002. [22]刘介才. 工厂供电[M]. 北京:机械工业出版社,1983.[23]李宗纲. 工厂供电设计[M]. 吉林:吉林科学技术出版社,1985. [24]GB 50059-1992.35~110KV变电所设计规范[S][25]卓乐友. 电力工程电气设计手册.第2册,电气二次部分[M]. 北京:水利电力出版社,1991.[26]陈跃. 电气工程专业毕业设计指南·电力系统分册[M]. 北京:中国水利水电出版社,2003.[27]王士政. 电力工程类专题课程设计与毕业设计指导教程[M]. 中国水利水电出版社,2007.[28]王超、严敏、王凡、唐培康、胡月丹、徐桥安. 降压变电所电气设计[J]. 上海船舶运输科学研究所学报[J],2021年,第1期.[29]范锡普. 发电厂电气部分[M]. 北京:水利电力出版社,1987.[30]Marvin Gerth. Transformers for the Electrician[M]. Cengage Learning,2021.[31]Stanley H.Horowitz、Arun G.Phadke. Power System Relaying[M]. WileyBlackwell,2008.[32]Robert L Smith 、Stephen L.Herman Electrical WiringIndustrial[M].Delmar Cengage Learning,2021.篇三:电气专业技师职业技能鉴定技师论文变压器的运行及维护姓名:周凌云身份证号:653202************职业工种:发电机运行工所在单位:新疆昌源水务准东供水有限公司二零一三年三月五日变压器的运行及维护周凌云摘要:由于每台变压器负荷大小、冷却条件及季节不同,运行中不仅要以上层油温允许值为依据,还应根据以往运行经验及在上述情况下与上次的油温比较。
基于Simulink的直流调速系统的设计与仿真毕业论文

基于Simulink的直流调速系统的设计与仿真摘要调速系统做为当今电力拖动自动控制系统中应用最广泛的一种系统,随着生产工艺、产品质量要求不断提高和产量的增长,使得越来越多的生产机械要求能实现自动调速。
当前控制系统已进入了计算机时代,在许多领域已实现了智能化控制。
直流调速系统凭借优良的调速特性,调速平滑、围宽、精度高、过载能力大、动态性能好、易于控制以及良好的起、制动性能等优点,能满足生产过程自动化系统中各种不同的特殊运行要求,所以研究直流调速系统有着十分必要和重要的意义。
本文以直流调速系统为主要研究对象,首先阐明了该课题研究的目的与意义,具体介绍了开环,单闭环和双闭环直流调速系统的设计和建立Matlab/Simulink 仿真模型的过程,得出转速及电流的仿真波形并与理想启动的转速及电流波形做对比。
分析并比较开环,单闭环和双闭环的优缺点。
关键词:直流调速系统;Simulink;开环;单闭环;双闭环DC SPEED CONTROL SYSTEM BASED ON SIMULINK DESIGN AND SIMULINKAbstractAs today's electric drive speed control system automatic control system of the most widely used system, with the production process, and continuously improve product quality requirements and production growth, making more and more production machinery required to achieve automatic speed . Current control system has entered the computer age, has been achieved in many areas of intelligent control. DC drive system with excellent speed characteristics, smooth speed, wide range, high precision, large overload capacity, good dynamic performance, easy to control and good starting and braking performance, etc., can meet the production process automation system each different kinds of specific operational requirements, the study DC speed control system has a very necessary and important. In this paper, DC speed control system as the main research object, first to clarify the purpose and significance of the research, specifically describes the open-loop, single-loop and double-loop DC speed control system design and build Matlab / Simulink simulation model of the process, too the speed and current simulation waveform and the ideal starting speed and current waveforms do comparison. Analyze and compare the open-loop, single loop and double loop advantages and disadvantages. Experimental results show that the simulation speedperformance with consistent theoretical derivation.Keywords: DC speed control system;Open-loop system;Single-loop system;Double-loop system目录摘要 (I)Abstract (II)1绪论 (1)1.1 课题背景 (1)1.2概述 (1)1.3论文容 (2)1.4本章小结 (2)2直流调速系统的理论基础 (3)2.1 Matlab/Simulink仿真软件 (3)2.2 直流调速的理论基础 (3)2.3 开环系统的电气原理 (6)2.4 单闭环系统的电气原理 (7)2.5 双闭环系统的电气原理 (8)2.6 本章小结 (8)3 调速系统的建模与仿真 (8)3.1 开环调速系统的建模与仿真 (9)3.1.1 开环建模过程 (9)3.1.2 开环系统的仿真 (12)3.2 单闭环调速系统的建模与仿真 (14)3.2.1 单闭环系统的建模 (14)3.2.2 单闭环系统的仿真 (16)3.3 双闭环调速系统的建模与仿真 (18)3.3.1 双闭环系统的建模 (18)3.3.2 双闭环系统的仿真 (20)3.4 本章小结 (22)4 结论与展望 (23)致 (24)参考文献 (25)1绪论1.1 课题背景现代化的工业过程中,几乎无处不使用电力传动装置,尤其是在石油,化工,冶金,轻工,机械等工业生产中对电动机的控制更是起着举足轻重的作用[1]。
电力拖动自动控制系统陈伯时

第一章习题1-1为什么PWM-电动机系统比晶闸管-电动机系统能够获得更好的动态特性?解:省掉了平波电抗器,电磁时间常数小;开关频率高,时间响应滞后时间短,动态响应加快,抗干扰能力增强,提高了系统动态性能。
1-2试分析有制动通路的不可逆PWM 变换器进行制动时,两个VT 是如何工作的。
解:制动时:当Ug1为正时,由于VD1的续流作用,VT1不能导通,Ug2为负,VT2截止;当Ug1为负时,VT1截止,此时Ug2为正,VT2导通。
1-3调速范围和静差率的定义是什么?调速范围、静态速降和最小静差率之间有什么关系?为什么说“脱离了调速范围,要满足给定的静差率也就容易得多了?”解:调速范围:生产机械对电动机所提出的最高转速nmax 与最低转速nmin 之比叫做调速范围,用字母D 来表示。
nmax 与nmin 通常指额定负载下的转速。
静差率:负载由理想空载增加到额定负载所产生的转速降落ΔnN ,与理想空载转速n0的比值,称作静差率,用字母s 表示,一般用百分数表示。
调速范围、静态速降和最小静差率之间的关系如下式:最低转速越高,对应s 值越小,当要求的s 值一定时,如果没有调速范围限制,可以容易的通过提高最低转速来满足对s 的要求。
1-4某一调速系统,测得的最高转速特性为n0max=1500r/min, 最低转速特性为n0min=150r/min ,带额定负载时的转速降落ΔnN=15r/min ,且在不同转速下ΔnN 不变,试问系统能够达到的调速范围有多大?系统允许的静差率是多少? 解:1-5 某闭环调速系统的调速范围是1500~150r/min ,要求系统的静差率s ≤2%,那么系统容许的静态速降是多少?如果开环系统的静态速降是100r/min,则闭环系统的开环放大倍数应有多大?解:1-6某闭环调速系统的开环放大倍数为15时,额定负载下电动机的速降为8r/min ,如果将开环放大倍数提高到30,它的速降为多少?在同样静差率要求下,调速范围可以扩大多少倍? 解:扩大的倍数为:1-7某调速系统的调速范围D=20,额定转速nN=1500r/min ,开环转速降落ΔnNop=240r/min ,若要求系统的静差率由10%降到5%,则系统的开环增益将如何变化? 解: ()s n sn D N N -∆=1=∆-∆-==N N n n n n n n D min 0max 0min max NN Nn D n n D s ∆+∆=()()min /06.38.9301150150015001r s s s D s n n Nb ==-=-⨯=∆1-∆∆=b k n n K ()128111=+∆=∆K n n b k ()13.4122=+∆=∆K n n kb 937.121=∆∆b b n n()8.2711.01.01n D Nop 1=-⨯-∆=N n K ()8.59105.005.012=-⨯-∆=N Nop n n D K1-8转速单闭环调速系统有哪些特点?改变给定电压能否改变电动机的转速?为什么?如果给定电压不变,调节测速反馈电位器的分压比是否能够改变转速?为什么?如果测速发电机的励磁发生了变化,系统有无克服这种干扰的能力?解:闭环调速系统可以得到比开环调速系统硬的多的稳态特性,从而在保证一定静差率要求的情况下,能够提高调速范围,代价是增设放大器以及检测和反馈装置。
电流环的设计

中国农业大学 课程设计(2010-2011学年春季学期)论文题目:基于双闭环的直流脉宽调速系统计算书课程名称: 电力拖动自动控制系统 任课教师: *** 班 级: 自动化081 学 号: 0808140823 姓 名: 李璐基于双闭环的直流脉宽调速系统建模及调节器设计一、设计总体要求:要求设计双闭环直流脉宽调速系统,可完成以下任务:(1) 该调速系统能进行平滑的速度调节,负载电机可逆运行,具有较宽的调速范围(D≥10),系统在工作范围内能稳定工作;(2) 系统静特性良好,无静差(静差率s≤2);(3) 动态性能指标:转速超调量δn <8%,电流超调量δi<5%,动态速降Δn≤10%,调速系统的过渡过程时间(调节时间)ts≤1s ;(4) 系统在5%负载以上变化的运行范围内电流连续;(5) 调速系统中设置有过电压、过电流等保护,并且有制动措施。
电路设计及分析根据设计任务可知,要求系统在稳定的前提下实现无静差调速,并要求较好的动态性能,可选择PI控制的转速、电流双闭环直流调速系统,以完全达到系统需要。
转速、电流双闭环直流调速系统框图如图1-1所示。
图1-1 转速、电流双闭环调速系统系统框图两个调节器的输出均带限幅作用的,转速调节器ASR的输出限幅电压决定了电流给定电压的最大值,电流调节器ACR的输出限幅电压限制了电力电子电换器的最大输出电压。
双闭环直流调速系统原理框图如下图1-2所示:图1-2 双闭环直流调速系统原理框图由此得到系统电气原理图见附图1。
二、电流调节器设计电流调节器使电流紧紧跟随其给定电压(即外环调节器的输出量)变化。
对电网电压的波动起及时抗扰的作用。
在转速动态过程中,保证获得电机允许的最大电流,从而加快动态过程。
由于电流检测中常常含有交流分量,为使其不影响调节器的输入,需加低通滤波。
转速调节器是调速系统的主导调节器,它使转速n很快地跟随给定电压变化,稳态时可减小转速误差,如果采用PI调节器,则可实现无静差。
电力拖动自动控制系统陈伯时一

电力电拖力动传动自动控控制制系统系统
▲第二代电力电子器件构成的VVVF装置主要的控制模 式是模拟和数字电路实现的矢量控制。
▲第三代电力电子器件构成的VVVF 装置主要的控制 模式是数字电路及软件实现的矢量控制、解耦控制、 模糊控制等。
电力电拖力动传动自动控控制制系统系统
17
6. 课程的性质、任务和内容
◆本课程性质及其特点:
▲本课程属于专业必修课
▲硬件设备标准化、模块化。采用微处理
机扩大存储器容量的基础上,将硬件设备(
包括微处理器、存储器、I/O、各种接口、
电源等)标准化、模块化,以增强通用性和
提高柔性。
▲软件标准化、模块化,并采用可编程方
式大力开发软件
▲现代控制理论及新型控制技术的开发应
用。现代控制理论与微处理机技术相结合,
实现了自适应调节、观测器等。
电力电拖力动传动自动控控制制系统系统
3
2.构成
♦ 电力拖动控制技术是以电动机为对象,以 电力电子技术功率变换器为弱电控制强电的 媒质,以自动控制理论为分析和设计基础, 以电子线路或计算机为控制手段,掌握运动 控制系统的控制规律及设计方法。
以控制规律为主线,根据实际学时,按照 循序渐进的原则组织教学内容。
8
♦ 位置控制系统:即位置随动(伺服)系统。例如:液面位置
的控制,雷达方位角的控制,火炮角位置的控制,机械加 工小的轨迹控制等等。
《电力拖动自动控制系统》学习心得

《电力拖动自动控制系统》学习心得电力拖动自动控制系统是现代工业生产中广泛应用的一种自动控制方式。
我在学习这门学科期间,深入了解了电力拖动自动控制系统的原理、组成及其在实际工程中的应用。
通过理论学习和实际操作实践,我对这门学科有了更加深入的理解,并且掌握了一定的应用技巧。
在学习的初期,我系统地学习了电力拖动自动控制系统的基本原理。
了解到电力拖动是通过电动机作为执行机构,实现对机械设备的控制和传动的过程。
而自动控制则是通过传感器、控制器和执行机构相互配合,实现对工艺过程的自动调节。
这让我对电力拖动自动控制系统有了一个整体的认识。
在理论学习的过程中,我主要学习了电力拖动系统的组成部分。
包括电源、电动机、控制器、传感器和负载等。
其中,电源为电动机提供所需的动力,电动机将电能转化为机械能;控制器根据传感器反馈的信号实现对电动机的控制;传感器用于监测工艺过程的参数,并将信号送回控制器;负载则是电动机动力转化的目标对象。
通过学习这些组成部分,我能够知道各个部分的功能和作用,从而更好地理解电力拖动自动控制系统的工作原理。
在学习的过程中,我还深入了解了电力拖动自动控制系统在实际工程中的应用。
其中,我主要了解了电力拖动在机械、冶金、石化和电力等行业的应用。
如在机械行业中,电力拖动可以应用于起重机械、工程机械和数控机床等设备;在冶金行业中,电力拖动可以应用于转炉和连铸设备等;在石化行业中,电力拖动可以应用于石油和化工设备等;在电力行业中,电力拖动可以应用于发电机组和变电站等。
通过了解这些应用案例,我更加深入地认识到电力拖动自动控制系统在实际工程中的重要性和广泛应用性。
除了理论学习,我还进行了一些实际操作的实践。
在实验室中,我学习了电力拖动自动控制系统的搭建和调试。
通过实际操作,我对电力拖动自动控制系统的不同部分有了更加直观的认识,并且学会了一些实际应用技巧。
在实验过程中,我还发现了一些问题,如电源电压不稳定、控制器参数设置不准确等,这让我更加深刻地认识到了实践中的一些难点和挑战。
《电力拖动自动控制系统》学习心得标准(四篇)

《电力拖动自动控制系统》学习心得标准学习心得:《电力拖动自动控制系统》在学习《电力拖动自动控制系统》这门课程期间,我深刻领会到了电力拖动自动控制系统在现代工业中的重要性,以及它的基本原理、组成结构和应用技术。
通过学习这门课程,我对电力拖动自动控制系统有了更深的了解,并且在实践中提高了自己的技能和能力。
以下是我在学习过程中的一些心得和体会。
首先,我学到了电力拖动自动控制系统的基本原理和基本组成。
电力拖动自动控制系统是由电力拖动装置、控制装置和保护装置组成的。
电力拖动装置是通过电动机驱动机械负载运动的组件,控制装置则根据系统要求对电力拖动装置进行控制,而保护装置则是为了确保电力拖动自动控制系统的安全可靠运行。
同时,通过学习还了解到了电力拖动自动控制系统的工作原理和调试方法,以及电力拖动装置的常用控制方式和控制技术,进一步提高了自己的专业知识。
其次,我了解了电力拖动自动控制系统在实际应用中的重要性。
电力拖动自动控制系统广泛应用于工业生产中的各种设备和机械,如机床、起重机械、输送机械等。
它可以实现对设备和机械的精确控制,提高生产效率和产品质量,降低人工成本,减少生产事故的发生。
特别是在自动化生产的背景下,电力拖动自动控制系统具备了更大的优势。
通过学习这门课程,我对电力拖动自动控制系统的应用前景有了更清晰的认识,也对自动化控制技术有了更深的理解。
然后,我通过实践项目更加深入地了解了电力拖动自动控制系统的实际运行。
在实践项目中,我通过搭建简单的电力拖动自动控制系统,对其进行调试和运行,理解了控制系统的输入输出关系和运行过程。
通过实践,我熟悉了电力拖动自动控制系统的调试方法和技巧,掌握了如何判断系统运转是否正常,并且了解了系统故障的排查和处理方法。
实践项目的开展使我对电力拖动自动控制系统的运行机理和实际操作有了更深入的了解,也锻炼了我的实践能力和创新思维。
最后,我对自己在学习《电力拖动自动控制系统》这门课程中取得的成绩感到非常满意。
《电力拖动自动控制系统》课程思政探索与实践

主题一:物理化学的研究对象、 研究方法与基本原理
物理化学是以物理学的基本理论为基础,研究化学现象和化学反应的内在规律 和机制的科学。它从微观到宏观的角度,帮助学生理解化学反应的本质和化学 现象的原理。在课程思政中,物理化学的研究对象、研究方法和基本原理可以 作为引导学生树立正确世界观、价值观和人生观的载体。例如,通过讲解物理 化学中的对立统一规律,可以培养学生的辩证思维;通过探讨化学反应的方向 和限度,可以引导学生树立科学的发展观。
五、结论与建议
通过本次演示的探讨,我们可以得出以下结论:《自动控制原理》课程的思政 建设是必要的,可以提高学生的综合素质和创新能力;增加思政教育内容、强 化教师育人职责和创新教学方法是实现课程思政建设的重要途径;实践验证表 明这些措施是有效的。因此,建议在《自动控制原理》课程中实施思政教育内 容,以培养更多的高素质人才。
谢谢观看
3、增强安全意识:通过分析电力拖动系统的安全操作规程和事故案例,让学 生认识到安全意识的重要性,提高他们的安全防范意识和自我保护能力。
4、传承文化自信:结合我国在电力拖动领域的发展成就,让学生了解我国在 科技创新方面的强大实力和文化自信,激发他们的爱国热情和民族自豪感。
5、培养团队协作精神:在课程实践环节中,通过分组合作、团队讨论等方式, 培养学生的团队协作意识和沟通能力,提高他们的综合素质。
结论
课程思政是一项系统性和长期性的工作,需要教师在教学过程中不断探索和实 践。《物理化学》作为一门基础学科课程,具有其独特的研究对象、研究方法 和基本原理,为思政教育提供了丰富的素材和载体。在实践中,教师应深入挖 掘思政元素,将其有机融入课程中,发挥物理化学课程思政的重要作用。教师 还应注重思政教育的系统性和连贯性,确保学生在学习专业知识的能够树立正 确的世界观、价值观和人生观。
电力拖动自动控制系统介绍

电力拖动自动控制系统介绍电力拖动自动控制系统是一种基于电力传动原理的自动控制系统,广泛应用于机械设备的驱动和控制中。
该系统通过电动机将电能转化为机械能来驱动机械设备,利用传感器感知环境信号并通过自动控制器对电机进行控制,实现对机械设备的自动化控制。
电力拖动自动控制系统主要由电动机、传感器、自动控制器和驱动装置组成。
电动机是系统的动力源,通过电能转换为机械能来驱动机械设备。
传感器用于感知机械设备的状态和环境参数,如位置、速度、力等。
自动控制器负责接收传感器的信号并根据预设的控制策略对电动机进行控制,实现对机械设备的自动化控制。
驱动装置用于将控制信号转化为电机驱动信号,控制电机的启停、转速和转向。
首先,系统的控制精度高。
由于电力传动具有快速响应、高精度和可调性的特点,可以实现对机械设备的精确控制。
其次,系统的抗干扰能力强。
电力传动系统能够通过电机的转矩调节来适应外部负载的变化,从而保持机械设备的稳定运行。
再次,系统的可靠性高。
电力拖动系统中的关键部件如电动机和传感器都经过严格的测试和筛选,能够在长时间运行过程中保持稳定和可靠的性能。
此外,电力拖动自动控制系统还具有节能和环保的优势。
通过合理的控制策略和调节机制,可以减少系统的能耗,并减少对环境的影响。
电力拖动自动控制系统广泛应用于各个领域,如工业制造、交通运输、石油化工等。
以工业制造为例,电力拖动系统可以用于汽车生产线、机械加工设备、输送线等机械设备的驱动和控制。
通过自动控制,可以提高生产效率和产品质量,减少人力投入和人为错误,实现机械设备的自动化生产。
总之,电力拖动自动控制系统是一种利用电力传动原理实现对机械设备自动化控制的系统。
它具有控制精度高、抗干扰能力强、可靠性高、节能环保等优势。
在工业制造、交通运输、石油化工等领域得到广泛应用,为提高生产效率和产品质量发挥了重要作用。
电力拖动制动控制系统

电气工程及其自动化专业实验实验名称:不可逆单闭环直流调速系统静特性的研究实验报告书科目:电力拖动自动控制系统专业:电气工程及其自动化班级:05111001学号:***********名:***重庆邮电大学移通学院2013年6月实验一不可逆单闭环直流调速系统静特性的研究一.实验目的1.研究晶闸管直流电动机调速系统在反馈控制下的工作。
2.研究直流调速系统中速度调节器ASR的工作及其对系统静特性的影响。
3.学习反馈控制系统的调试技术。
二.预习要求1.了解速度调节器在比例工作与比例—积分工作时的输入—输出特性。
2.弄清不可逆单闭环直流调速系统的工作原理。
三.实验线路及原理四.实验设备及仪表1.MCL系列教学实验台主控制屏。
2.MCL—31A组件(适合MCL—Ⅲ)。
3.MCL—33(A)组件4.MEL-11挂箱5.MEL—03三相可调电阻(或自配滑线变阻器)。
6.电机导轨及测速发电机、直流发电机M01(或电机导轨及测功机、MEL—13组件)。
7.直流电动机M03。
8.双踪示波器。
五.注意事项1.直流电动机工作前,必须先加上直流励磁。
2.接入ASR构成转速负反馈时,为了防止振荡,可预先把ASR的RP3电位器逆时针旋到底,使调节器放大倍数最小,同时,ASR的“5”、“6”端接入可调电容(预置7μF)。
3.测取静特性时,须注意主电路电流不许超过电机的额定值(1A)。
4.三相主电源连线时需注意,不可换错相序。
5.电源开关闭合时,过流保护发光二极管可能会亮,只需按下对应的复位开关SB1即可正常工作。
6.系统开环连接时,不允许突加给定信号Ug起动电机。
7.起动电机时,需把MEL-13的测功机加载旋钮逆时针旋到底,以免带负载起动。
8.改变接线时,必须先按下主控制屏总电源开关的“断开”红色按钮,同时使系统的给定为零。
9.双踪示波器的两个探头地线通过示波器外壳短接,故在使用时,必须使两探头的地线同电位(只用一根地线即可),以免造成短路事故。
电力拖动技术的应用与发展趋势

电力拖动技术的应用与发展趋势近年来,随着科技的快速发展和工业化进程的加快,电力拖动技术在工业领域得到了广泛的应用。
电力拖动技术是指利用电动机作为动力源,通过电力传动系统实现机械运动的一种技术。
本文将探讨电力拖动技术的应用和发展趋势,以及其对工业生产的影响。
一、电力拖动技术的应用领域电力拖动技术在各个工业领域都具有广泛的应用。
首先,在制造业中,电力拖动技术广泛用于机床、输送设备、自动化生产线等。
比如,电力拖动技术能够实现机床刀具的高精度运动,提升加工精度和生产效率。
其次,在交通运输领域,电力拖动技术被广泛应用于电动车辆、电动轨道交通等。
电动车辆具有低噪音、零排放等优点,电力拖动技术的应用能够有效降低汽车尾气排放,改善环境。
此外,电力拖动技术还被应用于航空航天、电力系统、矿山等领域。
二、电力拖动技术的发展趋势1. 高效节能:随着能源短缺和环境保护意识的增强,电力拖动技术将越来越注重高效节能。
未来,电力拖动技术将致力于提高系统的能量转换效率,减少能源的消耗。
2. 智能化:随着物联网和人工智能的发展,电力拖动技术将更加智能化。
通过传感器、数据采集和分析等技术,实现对电力拖动系统的智能监测和控制,提高系统的自动化程度和工作效率。
3. 高可靠性:电力拖动技术在工业生产中的可靠性和稳定性要求极高。
未来,电力拖动技术将朝着高可靠性方向发展,提高系统的抗干扰能力和故障诊断能力。
4. 多功能化:电力拖动技术将趋向于多功能化。
未来的拖动系统将不仅仅实现简单的运动控制,还将集成其他功能,如智能监测、故障预警、安全保护等。
5. 绿色环保:电力拖动技术将进一步提升对环境的友好性。
采用低噪音、零排放的电动机和电力传动装置,减少对环境的污染,实现绿色生产。
三、电力拖动技术对工业生产的影响电力拖动技术的应用对工业生产具有显著的影响。
首先,电力拖动技术能够提高工业生产的自动化水平,减少人工操作,提高生产效率和质量。
其次,电力拖动技术能够实现精确的运动控制,可在机械加工过程中实现高精度加工和复杂轮廓的制造。
电力拖动自动控制系统

电力拖动自动控制系统1. 系统简介电力拖动自动控制系统是一种基于电力传动和自动控制的系统,用于驱动和控制各种机械设备的运动。
该系统通过电动机将电能转化为机械能,实现对设备的拖动和控制。
电力拖动自动控制系统广泛应用于工业生产、交通运输、能源领域等各个行业。
2. 系统架构电力拖动自动控制系统主要由以下几个部分组成:2.1 电动机电力拖动自动控制系统的核心部件是电动机。
电动机负责将电能转化为机械能,驱动机械设备的运动。
根据实际需求,电动机可以采用不同的类型,如直流电动机、交流电动机等。
2.2 控制器控制器是电力拖动自动控制系统的核心部分,用于监测和控制电动机的运行。
控制器接收来自传感器的反馈信号,根据预设的控制算法和逻辑,控制电动机的启动、停止、速度调节等操作。
2.3 传感器传感器用于获取与机械设备运动相关的物理量信息,如速度、位置、温度等。
传感器通过将物理量转化为电信号,传递给控制器进行处理和决策。
2.4 电源系统电源系统为电力拖动自动控制系统提供稳定可靠的电能供应。
电源系统可以采用市电供电、蓄电池供电或者发电机供电等多种方式,以满足不同场景的需求。
2.5 人机界面人机界面是用户与电力拖动自动控制系统进行交互的窗口。
通过人机界面,用户可以设置运行参数、监测系统状态、获取报警信息等。
人机界面通常采用触摸屏、按钮、指示灯等形式,具备直观、便捷的操作方式。
3. 工作原理电力拖动自动控制系统的工作原理如下:1.用户通过人机界面设置运行参数,如设备运行速度、运行时间等。
2.人机界面将参数传递给控制器。
3.控制器根据参数和实时反馈信号来控制电动机的启动、停止和调速。
4.传感器将机械设备运动相关的物理量信息转换为电信号,传递给控制器。
5.控制器根据传感器的反馈信号进行实时监测和控制,调整电动机的运行状态。
6.电动机将电能转化为机械能,驱动机械设备的运动。
7.控制器不断与人机界面进行信息交互,向用户显示设备状态、报警信息等。
基于单片机的PWM直流电机调速系统设计论文(附电路图、程序清单)

图 2.2 直流电机原理图
2.2 直流电机的调速方法
根据直流电机的基本原理,由感应电势、电磁转矩以及机械特性方程式可知,直 流电动机的调速方法有三种: (1)调节电枢供电电压 U。改变电枢电压主要是从额定电压往下降低电枢电压, 从电动机额定转速向下变速,属恒转矩调速方法。对于要求在一定范围内无级平滑调 速的系统来说,这种方法最好。 大容量可调直流电源。 (2)改变电动机主磁通 。改变磁通可以实现无级平滑调速,但只能减弱磁通进 变化时间 变化遇到的时间常数较小,能快速响应,但是需要
第1章 引 1.1 概况
言
现代工业的电力拖动一般都要求局部或全部的自动化,因此必然要与各种控制元 件组成的自动控制系统联系起来,而电力拖动则可视为自动化电力拖动系统的简称。 在这一系统中可对生产机械进行自动控制。 随着近代电力电子技术和计算机技术的发展以及现代控制理论的应用,自动化电 力拖动正朝着计算机控制的生产过程自动化的方向迈进。以达到高速、优质、高效率 地生产。在大多数综合自动化系统中,自动化的电力拖动系统仍然是不可缺少的组成 部分。另外,低成本自动化技术与设备的开发,越来越引起国内外的注意。特别对于 小型企业,应用适用技术的设备,不仅有益于获得经济效益,而且能提高生产率、可 靠性与柔性,还有易于应用的优点。自动化的电力拖动系统更是低成本自动化系统的 重要组成部分。 在如今的现实生活中,自动化控制系统已在各行各业得到广泛的应用和发展,其 中自动调速系统的应用则起着尤为重要的作用。虽然直流电机不如交流电机那样结构 简单、价格便宜、制造方便、容易维护,但是它具有良好的起、制动性能,宜于在广 泛的范围内平滑调速,所以直流调速系统至今仍是自动调速系统中的主要形式。现在 电动机的控制从简单走向复杂,并逐渐成熟成为主流。其应用领域极为广泛,例如: 军事和宇航方面的雷达天线、火炮瞄准、惯性导航等的控制;工业方面的数控机床、 工业机器人、印刷机械等设备的控制;计算机外围设备和办公设备中的打印机、传真 机、复印机、扫描仪等的控制;音像设备和家用电器中的录音机、数码相机、洗衣机、 空调等的控制。 随着电力电子技术的发展, 开关速度更快、 控制更容易的全控型功率器件MOSFET 和IGBT成为主流,脉宽调制技术表现出较大的优越性:主电路线路简单,需要用的功 率元件少;开关频率高,电流容易连续,谐波少,电机损耗和发热都较小;低速性能 好,稳速精度高,因而调速范围宽;系统快速响应性能好,动态抗扰能力强;主电路 元件工作在开关状态,导通损耗小,装置效率较高;近年来,微型计算机技术发展速
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AC1 异步电机的矢量控制理论本章首先阐述异步电动机的三相坐标系下的数学模型,然后根据坐标变换理论,得到了它在两相静止坐标系下和两相同步坐标系下的数学方程,在此基础之上介绍了异步电机的矢量控制原理【14】。
1.1 异步电机的数学模型由于异步电机矢量控制调速系统的控制方式比较复杂,要确定最佳的方式,必须对系统动静态特性进行充分的研究。
异步电机本质上是一个高阶、非线性、强耦合的多变量系统,为了便于研究,一般进行如下假设:(1)三相定子绕组和转子绕组在空间均分布,即在空间互差所产生的磁动势沿气隙圆周按正弦分布,并忽略空间谐波;(2)各相绕组的自感和互感都是线性的,即忽略磁路饱和的影响; (3)不考虑频率和温度变化对电阻的影响; (4)忽略铁耗的影响。
无论三相异步电动机转子绕组为绕线型还是笼型,均将它等效为绕线转子,并将转子参数换算到定子侧,换算后的每相绕组匝数都相等。
这样异步电机数模型等效电路如图1.1所示。
120oAA A sA s AB B B s B s BC C C s C s C d u i R i R p dtd u i R i R p dt d u i R i R p dt ψψψψψψ⎧=+=+⎪⎪⎪=+=+⎨⎪⎪=+=+⎪⎩图1.1 异步电机的物理模型图1.1中,定子三相对称绕组轴线A 、B, C 在空间上固定并且互差 ,转子对称绕组的轴线a 、b 、 c 随转子一起旋转。
我们把定子A 相绕组的轴线作为空间参考坐标轴,转子a 轴和定子A 轴间的角度作为空间角位移变量。
规定各绕组相电压、电流及磁链的正方向符合电动机惯例和右手螺旋定则。
这样,我们可以得到异步电机在三相静止坐标系下的电压方程、磁链方程、转矩方程和运动方程。
1.1.1 异步电机在三相静止坐标系下的数学模型 1、三相定子绕组的电压平衡方程为120oθa a a ra r ab b b r b r bc c c r c r cd u i R i R p dtd u i R i R p dt d u i R i R p dt ψψψψψψ⎧=+=+⎪⎪⎪=+=+⎨⎪⎪=+=+⎪⎩/du dt(1-1)式中以微分算子P 代替微分符号相应地,三相转子绕组折算到定子侧的电压方程(1-2)式中:为定子和转子相电压的瞬时值;为定子和转子相电流的瞬时值;为定子和转子相磁链的瞬时值;为定子和转子电阻。
将定子和转子电压方程写成矩阵形式:,,,,,A B C a b cu u u u u u ,,,,,A B C a b ci i i i i i ,,,,,A B C a b cψψψψψψ,s rR R000000000000000000000000000000u i R A A A s u i R B B B su i R C C C s p u i R a a a r R u i r b b b R u i r c c c ψψψψψψ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦A A AAABAC Aa Ab Ac B B BA BB BC Aa Ab Ac C C CA CB CC Ca Cb Cc aA aB aC aa ab ac a a bA bB cC ba bb bc b b cA cB cC ca cbcc c c i L L L L L L i L L L L L L i L L L L L L L L L L L L i L L L L L L i L L L L L L i ψψψψψψ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(1-3)2、磁链方程由于绕组的磁链是它本身的自感磁链和其它绕组对它的互感磁链之和,因此,根据图1-1可列出三相异步电机的磁链方程(1-4)Liψ=()sin ()sin(120)()sin(120)e n m A a B b C c A b B c C a A c B a C b T p L i i i i i i i i i i i i i i i i i i οοθθθ⎡=++++++⎣⎤+++-⎦或者写成: (1-5) 式中L 是6x6电感矩阵,其中对角线上元素是各绕组的自感,其余元素是各烧组间的互感。
与电机绕组交链的磁通主要有两类:一类是只与一相绕组交链而不穿过气隙的漏磁通;另一类是穿过气隙的互感磁通,称为主磁通。
对于各相绕组,它所交链的磁通是主磁通与漏磁通之和,因此 定子各相自感为(1-6)转子各相自感为:aa bb cc m sr L L L L L ===+(1-7)在假设气息磁通为正线分布的条件下,两相绕组间的互感为:(1-8)(1-9)(1-10)(1-11)(1-12)从以上方程可知,定子绕组和转子绕组之间的互感与转子位置角 有关,它们是变参量,这是系统非线性的一个根源。
将方程(1-8)--(1-12)带入式(1-4),即可得到磁链方程。
3、电磁转矩方程由机电能量转换原理,可得到电磁转矩方程 (1-13)AA BB CC m ssL L L L L ===+/2AB AC BC BA CA CB m L L L L L L L ======-/2ab ac bc ba ca cb m L L L L L L L ======-cos Aa Bb Cc aA bB cC m L L L L L L L θ======-cos(120)Ab Ba Bc cB Ca aC m L L L L L L L οθ======-+(240)Ac cA Ba aB Cb bC m L L L L L L L οθ======-+θre l n d J T T P dtω=+11122022A B C ii i i i αβ⎡⎤⎡⎤--⎢⎥⎡⎤⎢⎥⎢=⎢⎥⎢⎥⎢⎣⎦⎢⎥-⎣⎦⎢⎣⎦从上式可以看出,电磁转矩是定子电流、转子电流及角的函数,是一个多变量,非线性且强耦合的函数。
4、运动方程电机的运动方程为(1-14)式中为负载转矩; 为转动惯量。
对于恒转矩负载,阻尼系数D=0,则有(1-15)1.1.2 坐标变换及变换矩阵如果将交流电机的物理模型等效地变换成类似直流电机的模式,分析和控制问题就可以大为简化。
上节中得到的异步电机动态数学模型非常复杂,要分析和求解这些非线性方程显然是非常困难的,即便是做了一些假设,要画出清晰的结构图也并不容易。
采用坐标变换的方法可以使变换后的数学模型容易处理一些,有利于异步电机的分析和控制。
因此,坐标变换是实现矢量控制的关键。
由异步电动机坐标系可以看到,它涉及到了两种坐标变换式:3s/2s 变换和2s/2r 旋转变换,又称克拉克(Clark)变换和2s/2r 变换即派克(Park)变换。
通过坐标变换的方法,使得变化后的数学模型得到简化。
1. 3/2变换(Clark 变换)由电机学原理可知,交流电机三相对称的静止绕组A 、B 、C ,通以三相平衡的正弦电流 、 、 时,产生的合成磁动势是旋转磁动势F ,且以同步转速旋转。
两相绕组的轴线分别为、 ,空间位置相差,构成、 两相静止坐标系(坐标轴逆时针超前坐标轴)。
在该两相固定绕组 、中,加时间上相差的两相平衡交流电流 、时,同样也可以产生与三相定子合成磁动势相同的空间矢量F ,且同步角频率为 。
三相异步电动机的定子三相绕组和与之等效的两相异步电动机定子绕组、 ,各相磁势矢量的空间位置如图1.2所示。
根据变换前后总磁动势不变和变换前后总功率相等的原则,3s/2s 变换用矩阵可表示为θ(/)(/)(/)e l N r n rT T J P d dt D p ωω=++lT J A i B i C i1ωαβ90οαββα90οαβ90οi αi β1ωαβ10122122A B C i i i i i αβ⎡⎤⎢⎥⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎣⎦⎢--⎢⎣⎦(1-16)α图1.2 三相静止到两相静止变换其反变换式如下:(2-17)因此,经过3s/2s 变换,可以将三相异步电机模型变换为两相正交的异步电机模型。
2、旋转变换(Park 变换)从图1.3中的两相静止坐标系到两相旋转坐标系M, T 的变换称作Park 变换,简称2s/2r 变换,其中s 表示静止,r 表示旋转。
如图1-3所示,其中,静止坐标系的两相交流分量和旋转坐标系的两个直流分量产生同样大小的同步旋转磁动势。
cos sin sin cos M T i i i i αβθθθθ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦cos sin sin cos M T i i i i αβθθθθ⎡⎤-⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦0000s s s s m s s s s m m r m r r r r r r r m m r r r r r r u i R L p L p u i R L p L p L p L R L p L u i L L p L R L p u i ααββααββωωωω⎡⎤⎡⎤+⎡⎤⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥--+⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦图1.3 两相静止到两相旋转变换根据图1.3的几何关系写成矩阵形式如下(1-18)旋转反变换如下:(1-19)其中为M-T 坐标和静止的夹角 1.1.3 异步电机在两相坐标系下的数学模型上面分析得到了异步电机的动态数学模型,为了矢量控制分析,必须把它转换为M-T 旋转坐标系下的数学模型,因此,必须先将三相静止坐标系下的模型转换为两相静止坐标系下的模型。
然后,通过旋转变换将异步电机模型转换到M-T 坐标系中,其结果如下所示。
1、异步电机在两相静止坐标系的数学模型经过3s/2s 变换,就得到了三相异步电机在两相静止坐标系下的数学模型。
(1) 电压方程θαβ-αβ-s s s m r s s s m r r s s m r r s s m r L i L i L i L i L i L i L i L i αααβββαααβββψψψψ=+⎧⎪=+⎪⎨=+⎪⎪=+⎩re l n d J T T p dtω=+(1-20(2)磁链方程(1-21)(3)电磁转矩方程(1-22)(4)运动方程(1-23)在 坐标系中绕组都落在两根相互垂直的轴上,两组绕组间没有耦合,矩阵中所有元素均为常系数,消除了异步电动机在三相静止坐标系上的数学模型()e n m s r s r T p L i i i i βααβ=-αβ-11sm sm s s sm m st st e s s s e m m m s m r r r r rm rm s mm s r r r rt rt u i R L p L L p L u i L R L p L L p L p L R L p L u i L L p L R L p u i ωωωωωωωω+--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-+-⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦⎣⎦sm s sm m rmst s st m rtrm r rm m sm rt r rt m stL i L i L i L iL i L i L i L i ψψψψ=+⎧⎪=+⎪⎨=+⎪⎪=+⎩r e l n d J T T p dtω=+中的一个非线性的根源。
