北师大版2014中考数学二次函数压轴题18道精选复习用

合集下载

2014年中考二次函数压轴题

2014年中考数学总复习《二次函数》一．解答题（共30小题）1．（2013•自贡）如图，已知抛物线y=ax2+bx﹣2（a≠0）与x轴交于A、B两点，与y轴交于C点，直线BD 交抛物线于点D，并且D（2，3），tan∠DBA=．（1）求抛物线的解析式；（2）已知点M为抛物线上一动点，且在第三象限，顺次连接点B、M、C、A，求四边形BMCA面积的最大值；（3）在（2）中四边形BMCA面积最大的条件下，过点M作直线平行于y轴，在这条直线上是否存在一个以Q 点为圆心，OQ为半径且与直线AC相切的圆？若存在，求出圆心Q的坐标；若不存在，请说明理由．2．（2013•株洲）已知抛物线C1的顶点为P（1，0），且过点（0，）．将抛物线C1向下平移h个单位（h＞0）得到抛物线C2．一条平行于x轴的直线与两条抛物线交于A、B、C、D四点（如图），且点A、C关于y轴对称，直线AB与x轴的距离是m2（m＞0）．（1）求抛物线C1的解析式的一般形式；（2）当m=2时，求h的值；（3）若抛物线C1的对称轴与直线AB交于点E，与抛物线C2交于点F．求证：tan∠EDF﹣tan∠ECP=．3．（2013•舟山）如图，在平面直角坐标系xOy中，抛物线y=（x﹣m）2﹣m2+m的顶点为A，与y轴的交点为B，连结AB，AC⊥AB，交y轴于点C，延长CA到点D，使AD=AC，连结BD．作AE∥x轴，DE∥y轴．（1）当m=2时，求点B的坐标；（2）求DE的长？（3）①设点D的坐标为（x，y），求y关于x的函数关系式？②过点D作AB的平行线，与第（3）①题确定的函数图象的另一个交点为P，当m为何值时，以，A，B，D，P为顶点的四边形是平行四边形？4．（2013•重庆）如图，对称轴为直线x=﹣1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A、B两点，其中点A 的坐标为（﹣3，0）．（1）求点B的坐标；（2）已知a=1，C为抛物线与y轴的交点．①若点P在抛物线上，且S△POC=4S△BOC．求点P的坐标；②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．5．（2013•张家界）如图，抛物线y=ax2+bx+c（a≠0）的图象过点C（0，1），顶点为Q（2，3），点D在x轴正半轴上，且OD=OC．（1）求直线CD的解析式；（2）求抛物线的解析式；（3）将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E，求证：△CEQ∽△CDO；（4）在（3）的条件下，若点P是线段QE上的动点，点F是线段OD上的动点，问：在P点和F点移动过程中，△PCF的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．6．（2013•湛江）如图，在平面直角坐标系中，顶点为（3，4）的抛物线交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，﹣5）．（1）求此抛物线的解析式；（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有什么位置关系，并给出证明；（3）在抛物线上是否存在一点P，使△ACP是以AC为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．7．（2013•枣庄）如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．（1）求这个二次函数的表达式．（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．8．（2013•岳阳）如图，已知以E（3，0）为圆心，以5为半径的⊙E与x轴交于A，B两点，与y轴交于C 点，抛物线y=ax2+bx+c经过A，B，C三点，顶点为F．（1）求A，B，C三点的坐标；（2）求抛物线的解析式及顶点F的坐标；（3）已知M为抛物线上一动点（不与C点重合），试探究：①使得以A，B，M为顶点的三角形面积与△ABC的面积相等，求所有符合条件的点M的坐标；②若探究①中的M点位于第四象限，连接M点与抛物线顶点F，试判断直线MF与⊙E的位置关系，并说明理由．9．（2013•玉林）如图，抛物线y=﹣（x﹣1）2+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．（1）求点B，C的坐标；（2）判断△CDB的形状并说明理由；（3）将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．10．（2013•营口）如图，抛物线与x轴交于A（1，0）、B（﹣3，0）两点，与y轴交于点C（0，3），设抛物线的顶点为D．（1）求该抛物线的解析式与顶点D的坐标．（2）试判断△BCD的形状，并说明理由．（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCD相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．11．（2013•益阳）阅读材料：如图1，在平面直角坐标系中，A、B两点的坐标分别为A（x1，y1），B（x2，y2），AB中点P的坐标为（x p，y p）．由x p﹣x1=x2﹣x p，得x p=，同理，所以AB的中点坐标为．由勾股定理得AB2=，所以A、B两点间的距离公式为．注：上述公式对A、B在平面直角坐标系中其它位置也成立．解答下列问题：如图2，直线l：y=2x+2与抛物线y=2x2交于A、B两点，P为AB的中点，过P作x轴的垂线交抛物线于点C．（1）求A、B两点的坐标及C点的坐标；（2）连结AB、AC，求证△ABC为直角三角形；（3）将直线l平移到C点时得到直线l′，求两直线l与l′的距离．12．（2013•烟台）如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，二次函数y=ax2+bx+c的图象经过点A，B，与x轴分别交于点E，F，且点E的坐标为（﹣，0），以0C为直径作半圆，圆心为D．（1）求二次函数的解析式；（2）求证：直线BE是⊙D的切线；（3）若直线BE与抛物线的对称轴交点为P，M是线段CB上的一个动点（点M与点B，C不重合），过点M作MN∥BE交x轴与点N，连结PM，PN，设CM的长为t，△PMN的面积为S，求S与t的函数关系式，并写出自变量t的取值范围．S是否存在着最大值？若存在，求出最大值；若不存在，请说明理由．13．（2013•孝感）如图1，已知正方形ABCD的边长为1，点E在边BC上，若∠AEF=90°，且EF交正方形外角的平分线CF于点F．（1）图1中若点E是边BC的中点，我们可以构造两个三角形全等来证明AE=EF，请叙述你的一个构造方案，并指出是哪两个三角形全等（不要求证明）；（2）如图2，若点E在线段BC上滑动（不与点B，C重合）．①AE=EF是否总成立？请给出证明；②在如图2的直角坐标系中，当点E滑动到某处时，点F恰好落在抛物线y=﹣x2+x+1上，求此时点F的坐标．14．（2013•湘西州）如图，已知抛物线y=﹣x2+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．（1）求抛物线的解析式及它的对称轴方程；（2）求点C的坐标，连接AC、BC并求线段BC所在直线的解析式；（3）试判断△AOC与△COB是否相似？并说明理由；（4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．15．（2013•湘潭）如图，在坐标系xOy中，△ABC是等腰直角三角形，∠BAC=90°，A（1，0），B（0，2），抛物线y=x2+bx﹣2的图象过C点．（1）求抛物线的解析式；（2）平移该抛物线的对称轴所在直线l．当l移动到何处时，恰好将△ABC的面积分为相等的两部分？（3）点P是抛物线上一动点，是否存在点P，使四边形PACB为平行四边形？若存在，求出P点坐标；若不存在，说明理由．16．（2013•咸宁）为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：y=﹣10x+500．（1）李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元？（2）设李明获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？（3）物价部门规定，这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元？17．（2013•梧州）如图，抛物线y=a（x﹣h）2+k经过点A（0，1），且顶点坐标为B（1，2），它的对称轴与x 轴交于点C．（1）求此抛物线的解析式．（2）在第一象限内的抛物线上求点P，使得△ACP是以AC为底的等腰三角形，请求出此时点P的坐标．（3）上述点是否是第一象限内此抛物线上与AC距离最远的点？若是，请说明理由；若不是，请求出第一象限内此抛物线上与AC距离最远的点的坐标．18．（2013•无锡）如图，直线x=﹣4与x轴交于点E，一开口向上的抛物线过原点交线段OE于点A，交直线x=﹣4于点B，过B且平行于x轴的直线与抛物线交于点C，直线OC交直线AB于D，且AD：BD=1：3．（1）求点A的坐标；（2）若△OBC是等腰三角形，求此抛物线的函数关系式．19．（2013•乌鲁木齐）如图．在平面直角坐标系中，边长为的正方形ABCD的顶点A、B在x轴上，连接OD、BD、△BOD的外心I在中线BF上，BF与AD交于点E．（1）求证：△OAD≌△EAB；（2）求过点O、E、B的抛物线所表示的二次函数解析式；（3）在（2）中的抛物线上是否存在点P，其关于直线BF的对称点在x轴上？若有，求出点P的坐标；（4）连接OE，若点M是直线BF上的一动点，且△BMD与△OED相似，求点M的坐标．20．（2013•潍坊）如图，抛物线y=ax2+bx+c关于直线x=1对称，与坐标轴交与A，B，C三点，且AB=4，点D（2，）在抛物线上，直线l是一次函数y=kx﹣2（k≠0）的图象，点O是坐标原点．（1）求抛物线的解析式；（2）若直线l平分四边形OBDC的面积，求k的值；（3）把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线与直线l交于M，N两点，问在y轴正半轴上是否存在一定点P，使得不论k取何值，直线PM与PN总是关于y轴对称？若存在，求出P点坐标；若不存在，请说明理由．21．（2013•铜仁地区）如图，已知直线y=3x﹣3分别交x轴、y轴于A、B两点，抛物线y=x2+bx+c经过A、B两点，点C是抛物线与x轴的另一个交点（与A点不重合）．（1）求抛物线的解析式；（2）求△ABC的面积；（3）在抛物线的对称轴上，是否存在点M，使△ABM为等腰三角形？若不存在，请说明理由；若存在，求出点M的坐标．22．（2013•铁岭）某商家独家销售具有地方特色的某种商品，每件进价为40元．经过市场调查，一周的销售量y（1的函数关系式：_________（2）设一周的销售利润为S元，请求出S与x的函数关系式，并确定当销售单价在什么范围内变化时，一周的销售利润随着销售单价的增大而增大？（3）雅安地震牵动亿万人民的心，商家决定将商品一周的销售利润全部寄往灾区，在商家购进该商品的贷款不超过10000元情况下，请你求出该商家最大捐款数额是多少元？23．（2013•天津）已知抛物线y1=ax2+bx+c（a≠0）的对称轴是直线l，顶点为点M．若自变量x和函数值y1的部分对应值如下表所示：（Ⅰ）求y1与x之间的函数关系式；（Ⅱ）若经过点T（0，t）作垂直于y轴的直线l′，A为直线l′上的动点，线段AM的垂直平分线交直线l于点B，点B关于直线AM的对称点为P，记P（x，y2）．（1）求y2与x之间的函数关系式；（2）当x24．（2013•泰安）如图，抛物线y=x2+bx+c与y轴交于点C（0，﹣4），与x轴交于点A，B，且B点的坐标为（2，0）.（1）求该抛物线的解析式．（2）若点P是AB上的一动点，过点P作PE∥AC，交BC于E，连接CP，求△PCE面积的最大值．（3）若点D为OA的中点，点M是线段AC上一点，且△OMD为等腰三角形，求M点的坐标．25．（2013•太原）综合与探究：如图，抛物线y=x2﹣x﹣4与x轴交与A，B两点（点B在点A的右侧），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．（1）求点A，B，C的坐标．（2）当点P在线段OB上运动时，直线l分别交BD，BC于点M，N．试探究m为何值时，四边形CQMD是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．（3）当点P在线段EB上运动时，是否存在点Q，使△BDQ为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．26．（2013•台州）如图1，已知直线l：y=﹣x+2与y轴交于点A，抛物线y=（x﹣1）2+k经过点A，其顶点为B，另一抛物线y=（x﹣h）2+2﹣h（h＞1）的顶点为D，两抛物线相交于点C．（1）求点B的坐标，并说明点D在直线l上的理由；（2）设交点C的横坐标为m．①交点C的纵坐标可以表示为：_________或_________，由此进一步探究m关于h的函数关系式；②如图2，若∠ACD=90°，求m的值．27．（2013•遂宁）如图，抛物线y=x2+bx+c与x轴交于点A（2，0），交y轴于点B（0，）．直线y=kx过点A与y轴交于点C，与抛物线的另一个交点是D．（1）求抛物线y=x2+bx+c与直线y=kx的解析式；（2）设点P是直线AD上方的抛物线上一动点（不与点A、D重合），过点P作y轴的平行线，交直线AD于点M，作DE⊥y轴于点E．探究：是否存在这样的点P，使四边形PMEC是平行四边形？若存在请求出点P的坐标；若不存在，请说明理由；（3）在（2）的条件下，作PN⊥AD于点N，设△PMN的周长为l，点P的横坐标为x，求l与x的函数关系式，并求出l的最大值．28．（2013•绥化）如图，已知抛物线y=（x﹣2）（x+a）（a＞0）与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．（1）若抛物线过点M（﹣2，﹣2），求实数a的值；（2）在（1）的条件下，解答下列问题；①求出△BCE的面积；②在抛物线的对称轴上找一点H，使CH+EH的值最小，直接写出点H的坐标．29．（2013•宿迁）如图，在平面直角坐标系xOy中，二次函数y=ax2+bx﹣3（a，b是常数）的图象与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点C．动直线y=t（t为常数）与抛物线交于不同的两点P、Q．（1）求a和b的值；（2）求t的取值范围；（3）若∠PCQ=90°，求t的值．30．（2013•深圳）如图1，过点A（0，4）的圆的圆心坐标为C（2，0），B是第一象限圆弧上的一点，且BC⊥AC，抛物线y=x2+bx+c经过C、B两点，与x轴的另一交点为D．（1）点B的坐标为（_________，_________），抛物线的表达式为_________；（2）如图2，求证：BD∥AC；（3）如图3，点Q为线段BC上一点，且AQ=5，直线AQ交⊙C于点P，求AP的长．。

中考数学二次函数压轴题集锦(50道含解析)

中考数学二次函数压轴题集锦1．如图1，已知二次函数y=ax2+x+c（a≠0）的图象与y轴交于点A（0，4），与x轴交于点B、C，点C坐标为（8，0），连接AB、AC．（1）请直接写出二次函数y=ax2+x+c的表达式；（2）判断△ABC的形状，并说明理由；（3）若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，请写出此时点N的坐标；（4）如图2，若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标．2．对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“闭距离“，记作d（M，N）．已知点A（﹣2，6），B（﹣2，﹣2），C（6，﹣2）．（1）求d（点O，△ABC）；（2）记函数y=kx（﹣1≤x≤1，k≠0）的图象为图形G．若d（G，△ABC）=1，直接写出k的取值范围；（3）⊙T的圆心为T（t，0），半径为1．若d（⊙T，△ABC）=1，直接写出t 的取值范围．3．如图，在平面直角坐标系中，点A在抛物线y=﹣x2+4x上，且横坐标为1，点B与点A关于抛物线的对称轴对称，直线AB与y轴交于点C，点D为抛物线的顶点，点E的坐标为（1，1）．（1）求线段AB的长；（2）点P为线段AB上方抛物线上的任意一点，过点P作AB的垂线交AB于点H，点F为y轴上一点，当△PBE的面积最大时，求PH+HF+FO的最小值；（3）在（2）中，PH+HF+FO取得最小值时，将△CFH绕点C顺时针旋转60°后得到△CF′H′，过点F'作CF′的垂线与直线AB交于点Q，点R为抛物线对称轴上的一点，在平面直角坐标系中是否存在点S，使以点D，Q，R，S为顶点的四边形为菱形，若存在，请直接写出点S的坐标，若不存在，请说明理由．4．如图，抛物线y=ax2+6x+c交x轴于A，B两点，交y轴于点C．直线y=x﹣5经过点B，C．（1）求抛物线的解析式；（2）过点A的直线交直线BC于点M．①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M 的坐标．5．如图，在平面直角坐标系xOy中，以直线x=对称轴的抛物线y=ax2+bx+c与直线l：y=kx+m（k＞0）交于A（1，1），B两点，与y轴交于C（0，5），直线l 与y轴交于点D．（1）求抛物线的函数表达式；（2）设直线l与抛物线的对称轴的交点为F，G是抛物线上位于对称轴右侧的一点，若=，且△BCG与△BCD面积相等，求点G的坐标；（3）若在x轴上有且仅有一点P，使∠APB=90°，求k的值．6．如图，抛物线y=ax2+bx（a＜0）过点E（10，0），矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A（t，0），当t=2时，AD=4．（1）求抛物线的函数表达式．（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．7．抛物线L：y=﹣x2+bx+c经过点A（0，1），与它的对称轴直线x=1交于点B．（1）直接写出抛物线L的解析式；（2）如图1，过定点的直线y=kx﹣k+4（k＜0）与抛物线L交于点M、N．若△BMN的面积等于1，求k的值；（3）如图2，将抛物线L向上平移m（m＞0）个单位长度得到抛物线L1，抛物线L 1与y轴交于点C，过点C作y轴的垂线交抛物线L1于另一点D．F为抛物线L1的对称轴与x轴的交点，P为线段OC上一点．若△PCD与△POF相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标．8．在平面直角坐标系中，点O（0，0），点A（1，0）．已知抛物线y=x2+mx﹣2m （m是常数），顶点为P．（Ⅰ）当抛物线经过点A时，求顶点P的坐标；（Ⅱ）若点P在x轴下方，当∠AOP=45°时，求抛物线的解析式；（Ⅲ）无论m取何值，该抛物线都经过定点H．当∠AHP=45°时，求抛物线的解析式．9．如图1，四边形OABC是矩形，点A的坐标为（3，0），点C的坐标为（0，6），点P从点O出发，沿OA以每秒1个单位长度的速度向点A出发，同时点Q从点A出发，沿AB以每秒2个单位长度的速度向点B运动，当点P与点A重合时运动停止．设运动时间为t秒．（1）当t=2时，线段PQ的中点坐标为；（2）当△CBQ与△PAQ相似时，求t的值；（3）当t=1时，抛物线y=x2+bx+c经过P，Q两点，与y轴交于点M，抛物线的顶点为K，如图2所示，问该抛物线上是否存在点D，使∠MQD=∠MKQ？若存在，求出所有满足条件的D的坐标；若不存在，说明理由．10．如图①，在平面直角坐标系中，圆心为P（x，y）的动圆经过点A（1，2）且与x轴相切于点B．（1）当x=2时，求⊙P的半径；（2）求y关于x的函数解析式，请判断此函数图象的形状，并在图②中画出此函数的图象；（3）请类比圆的定义（圆可以看成是到定点的距离等于定长的所有点的集合），给（2）中所得函数图象进行定义：此函数图象可以看成是到的距离等于到的距离的所有点的集合．（4）当⊙P的半径为1时，若⊙P与以上（2）中所得函数图象相交于点C、D，其中交点D（m，n）在点C的右侧，请利用图②，求cos∠APD的大小．11．已知顶点为A抛物线经过点，点．（1）求抛物线的解析式；（2）如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠OPM=∠MAF，求△POE的面积；（3）如图2，点Q是折线A﹣B﹣C上一点，过点Q作QN∥y轴，过点E作EN∥x 轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN1，若点N1落在x轴上，请直接写出Q点的坐标．12．在平面直角坐标系xOy中（如图）．已知抛物线y=﹣x2+bx+c经过点A（﹣1，0）和点B（0，），顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．（1）求这条抛物线的表达式；（2）求线段CD的长；（3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．13．如图1，图形ABCD是由两个二次函数y1=kx2+m（k＜0）与y2=ax2+b（a＞0）的部分图象围成的封闭图形．已知A（1，0）、B（0，1）、D（0，﹣3）．（1）直接写出这两个二次函数的表达式；（2）判断图形ABCD是否存在内接正方形（正方形的四个顶点在图形ABCD上），并说明理由；（3）如图2，连接BC，CD，AD，在坐标平面内，求使得△BDC与△ADE相似（其中点C与点E是对应顶点）的点E的坐标14．小贤与小杰在探究某类二次函数问题时，经历了如下过程：求解体验：（1）已知抛物线y=﹣x2+bx﹣3经过点（﹣1，0），则b= ，顶点坐标为，该抛物线关于点（0，1）成中心对称的抛物线表达式是．抽象感悟：我们定义：对于抛物线y=ax2+bx+c（a≠0），以y轴上的点M（0，m）为中心，作该抛物线关于点M对称的抛物线y′，则我们又称抛物线y′为抛物线y的“衍生抛物线”，点M为“衍生中心”．（2）已知抛物线y=﹣x2﹣2x+5关于点（0，m）的衍生抛物线为y′，若这两条抛物线有交点，求m的取值范围．问题解决：（3）已知抛物线y=ax2+2ax﹣b（a≠0）①若抛物线y的衍生抛物线为y′=bx2﹣2bx+a2（b≠0），两抛物线有两个交点，且恰好是它们的顶点，求a、b的值及衍生中心的坐标；②若抛物线y关于点（0，k+12）的衍生抛物线为y1，其顶点为A1；关于点（0，k+22）的衍生抛物线为y2，其顶点为A2；…；关于点（0，k+n2）的衍生抛物线为y n ，其顶点为An…（n为正整数）．求AnAn+1的长（用含n的式子表示）．15．如图，已知抛物线y=ax2+bx（a≠0）过点A（，﹣3）和点B（3，0）．过点A作直线AC∥x轴，交y轴于点C．（1）求抛物线的解析式；（2）在抛物线上取一点P，过点P作直线AC的垂线，垂足为D．连接OA，使得以A，D，P为顶点的三角形与△AOC相似，求出对应点P的坐标；（3）抛物线上是否存在点Q，使得S△AOC =S△AOQ？若存在，求出点Q的坐标；若不存在，请说明理由．16．如图，已知抛物线y=x2﹣4与x轴交于点A，B（点A位于点B的左侧），C 为顶点，直线y=x+m经过点A，与y轴交于点D．（1）求线段AD的长；（2）平移该抛物线得到一条新拋物线，设新抛物线的顶点为C′．若新抛物线经过点D，并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD，求新抛物线对应的函数表达式．17．如图①，在平面直角坐标系xOy中，抛物线y=ax2+bx+3经过点A（﹣1，0）、B（3，0）两点，且与y轴交于点C．（1）求抛物线的表达式；（2）如图②，用宽为4个单位长度的直尺垂直于x轴，并沿x轴左右平移，直尺的左右两边所在的直线与抛物线相交于P、Q两点（点P在点Q的左侧），连接PQ，在线段PQ上方抛物线上有一动点D，连接DP、DQ．（1）若点P的横坐标为﹣，求△DPQ面积的最大值，并求此时点D的坐标；（Ⅱ）直尺在平移过程中，△DPQ面积是否有最大值？若有，求出面积的最大值；若没有，请说明理由．18．已知抛物线y=ax2+bx+c过点A（0，2）．（1）若点（﹣，0）也在该抛物线上，求a，b满足的关系式；（2）若该抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为心，OA为半径的圆与拋物线的另两个交点为B，C，且△ABC有一个内角为60°．①求抛物线的解析式；②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．19．如图，在平面直角坐标系中，∠ACB=90°，OC=2OB，tan∠ABC=2，点B的坐标为（1，0）．抛物线y=﹣x2+bx+c经过A、B两点．（1）求抛物线的解析式；（2）点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使PE=DE．①求点P的坐标；②在直线PD上是否存在点M，使△ABM为直角三角形？若存在，求出符合条件的所有点M的坐标；若不存在，请说明理由．20．我们不妨约定：对角线互相垂直的凸四边形叫做“十字形”．（1）①在“平行四边形，矩形，菱形，正方形”中，一定是“十字形”的有；②在凸四边形ABCD中，AB=AD且CB≠CD，则该四边形“十字形”．（填“是”或“不是”）（2）如图1，A，B，C，D是半径为1的⊙O上按逆时针方向排列的四个动点，AC与BD交于点E，∠ADB﹣∠CDB=∠ABD﹣∠CBD，当6≤AC2+BD2≤7时，求OE 的取值范围；（3）如图2，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a，b，c为常数，a＞0，c＜0）与x轴交于A，C两点（点A在点C的左侧），B是抛物线与y轴的交点，点D的坐标为（0，﹣ac），记“十字形”ABCD的面积为S，记△AOB，△COD，△AOD，△BOC的面积分别为S1，S2，S3，S4．求同时满足下列三个条件的抛物线的解析式；①=；②=；③“十字形”ABCD的周长为12．21．如图1，抛物线y1=ax2﹣x+c与x轴交于点A和点B（1，0），与y轴交于点C（0，），抛物线y1的顶点为G，GM⊥x轴于点M．将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2．（1）求抛物线y2的解析式；（2）如图2，在直线l上是否存在点T，使△TAC是等腰三角形？若存在，请求出所有点T的坐标；若不存在，请说明理由；（3）点P为抛物线y1上一动点，过点P作y轴的平行线交抛物线y2于点Q，点Q关于直线l的对称点为R，若以P，Q，R为顶点的三角形与△AMG全等，求直线PR的解析式．22．如图，已知直线y=﹣2x+4分别交x轴、y轴于点A、B，抛物线过A，B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．（1）若抛物线的解析式为y=﹣2x2+2x+4，设其顶点为M，其对称轴交AB于点N．①求点M、N的坐标；②是否存在点P，使四边形MNPD为菱形？并说明理由；（2）当点P的横坐标为1时，是否存在这样的抛物线，使得以B、P、D为顶点的三角形与△AOB相似？若存在，求出满足条件的抛物线的解析式；若不存在，请说明理由．23．如图，抛物线y=ax2+bx经过△OAB的三个顶点，其中点A（1，），点B（3，﹣），O为坐标原点．（1）求这条抛物线所对应的函数表达式；（2）若P（4，m），Q（t，n）为该抛物线上的两点，且n＜m，求t的取值范围；（3）若C为线段AB上的一个动点，当点A，点B到直线OC的距离之和最大时，求∠BOC的大小及点C的坐标．24．如图，在平面直角坐标系中，抛物线C1：y=ax2+bx﹣1经过点A（﹣2，1）和点B（﹣1，﹣1），抛物线C2：y=2x2+x+1，动直线x=t与抛物线C1交于点N，与抛物线C2交于点M．（1）求抛物线C1的表达式；（2）直接用含t的代数式表示线段MN的长；（3）当△AMN是以MN为直角边的等腰直角三角形时，求t的值；（4）在（3）的条件下，设抛物线C1与y轴交于点P，点M在y轴右侧的抛物线C2上，连接AM交y轴于点K，连接KN，在平面内有一点Q，连接KQ和QN，当KQ=1且∠KNQ=∠BNP时，请直接写出点Q的坐标．25．在平面直角坐标系xOy中，已知抛物线的顶点坐标为（2，0），且经过点（4，1），如图，直线y=x与抛物线交于A、B两点，直线l为y=﹣1．（1）求抛物线的解析式；（2）在l上是否存在一点P，使PA+PB取得最小值？若存在，求出点P的坐标；若不存在，请说明理由．（3）知F（x0，y）为平面内一定点，M（m，n）为抛物线上一动点，且点M到直线l的距离与点M到点F的距离总是相等，求定点F的坐标．26．如图，在平面直角坐标系中，二次函数y=ax2+bx+c交x轴于点A（﹣4，0）、B（2，0），交y轴于点C（0，6），在y轴上有一点E（0，﹣2），连接AE．（1）求二次函数的表达式；（2）若点D为抛物线在x轴负半轴上方的一个动点，求△ADE面积的最大值；（3）抛物线对称轴上是否存在点P，使△AEP为等腰三角形？若存在，请直接写出所有P点的坐标，若不存在请说明理由．27．如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣4，0），B（2，0），与y轴交于点C（0，4），线段BC的中垂线与对称轴l交于点D，与x轴交于点F，与BC交于点E，对称轴l与x轴交于点H．（1）求抛物线的函数表达式；（2）求点D的坐标；（3）点P为x轴上一点，⊙P与直线BC相切于点Q，与直线DE相切于点R．求点P的坐标；（4）点M为x轴上方抛物线上的点，在对称轴l上是否存在一点N，使得以点D，P，M，N为顶点的四边形是平行四边形？若存在，则直接写出N点坐标；若不存在，请说明理由．28．如图，抛物线y=ax2+bx（a≠0）交x轴正半轴于点A，直线y=2x经过抛物线的顶点M．已知该抛物线的对称轴为直线x=2，交x轴于点B．（1）求a，b的值．（2）P是第一象限内抛物线上的一点，且在对称轴的右侧，连接OP，BP．设点P的横坐标为m，△OBP的面积为S，记K=．求K关于m的函数表达式及K的范围．29．抛物线y=﹣x2﹣x+与x轴交于点A，B（点A在点B的左边），与y轴交于点C，点D是该抛物线的顶点．（1）如图1，连接CD，求线段CD的长；（2）如图2，点P是直线AC上方抛物线上一点，PF⊥x轴于点F，PF与线段AC交于点E；将线段OB沿x轴左右平移，线段OB的对应线段是O1B1，当PE+EC的值最大时，求四边形PO1B1C周长的最小值，并求出对应的点O1的坐标；（3）如图3，点H是线段AB的中点，连接CH，将△OBC沿直线CH翻折至△O2B 2 C的位置，再将△O2B2C绕点B2旋转一周，在旋转过程中，点O2，C的对应点分别是点O3，C1，直线O3C1分别与直线AC，x轴交于点M，N．那么，在△O2B2C的整个旋转过程中，是否存在恰当的位置，使△AMN是以MN为腰的等腰三角形？若存在，请直接写出所有符合条件的线段O2M的长；若不存在，请说明理由．30．综合与探究如图，抛物线y=x﹣4与x轴交于A，B两点（点A在点B的左侧），与y 轴交于点C，连接AC，BC．点P是第四象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q，过点P作PE∥AC交x轴于点E，交BC于点F．（1）求A，B，C三点的坐标；（2）试探究在点P运动的过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请直接写出此时点Q的坐标；若不存在，请说明理由；（3）请用含m的代数式表示线段QF的长，并求出m为何值时QF有最大值．31．如图，二次函数y=﹣+bx+2的图象与x轴交于点A、B，与y轴交于点C，点A的坐标为（﹣4，0），P是抛物线上一点（点P与点A、B、C不重合）．（1）b= ，点B的坐标是；（2）设直线PB与直线AC相交于点M，是否存在这样的点P，使得PM：MB=1：2？若存在，求出点P的横坐标；若不存在，请说明理由；（3）连接AC、BC，判断∠CAB和∠CBA的数量关系，并说明理由．32．如图，在平面直角坐标系中，二次函数y=（x﹣a）（x﹣3）（0＜a＜3）的图象与x轴交于点A、B（点A在点B的左侧），与y轴交于点D，过其顶点C作直线CP⊥x轴，垂足为点P，连接AD、BC．（1）求点A、B、D的坐标；（2）若△AOD与△BPC相似，求a的值；（3）点D、O、C、B能否在同一个圆上？若能，求出a的值；若不能，请说明理由．33．如图，已知二次函数y=ax2﹣（2a﹣）x+3的图象经过点A（4，0），与y 轴交于点B．在x轴上有一动点C（m，0）（0＜m＜4），过点C作x轴的垂线交直线AB于点E，交该二次函数图象于点D．（1）求a的值和直线AB的解析式；（2）过点D作DF⊥AB于点F，设△ACE，△DEF的面积分别为S1，S2，若S1=4S2，求m的值；（3）点H是该二次函数图象上位于第一象限的动点，点G是线段AB上的动点，当四边形DEGH是平行四边形，且▱DEGH周长取最大值时，求点G的坐标．34．已知，点M为二次函数y=﹣（x﹣b）2+4b+1图象的顶点，直线y=mx+5分别交x轴正半轴，y轴于点A，B．（1）判断顶点M是否在直线y=4x+1上，并说明理由．（2）如图1，若二次函数图象也经过点A，B，且mx+5＞﹣（x﹣b）2+4b+1，根据图象，写出x的取值范围．（3）如图2，点A坐标为（5，0），点M在△AOB内，若点C（，y1），D（，y 2）都在二次函数图象上，试比较y1与y2的大小．35．如图，在平面直角坐标系中，抛物线y=ax2+bx﹣5交y轴于点A，交x轴于点B（﹣5，0）和点C（1，0），过点A作AD∥x轴交抛物线于点D．（1）求此抛物线的表达式；（2）点E是抛物线上一点，且点E关于x轴的对称点在直线AD上，求△EAD的面积；（3）若点P是直线AB下方的抛物线上一动点，当点P运动到某一位置时，△ABP 的面积最大，求出此时点P的坐标和△ABP的最大面积．36．已知抛物线F：y=x2+bx+c的图象经过坐标原点O，且与x轴另一交点为（﹣，0）．（1）求抛物线F的解析式；（2）如图1，直线l：y=x+m（m＞0）与抛物线F相交于点A（x1，y1）和点B（x2，y2）（点A在第二象限），求y2﹣y1的值（用含m的式子表示）；（3）在（2）中，若m=，设点A′是点A关于原点O的对称点，如图2．①判断△AA′B的形状，并说明理由；②平面内是否存在点P，使得以点A、B、A′、P为顶点的四边形是菱形？若存在，求出点P的坐标；若不存在，请说明理由．37．直线y=﹣x+3交x轴于点A，交y轴于点B，顶点为D的抛物线y=﹣x2+2mx ﹣3m经过点A，交x轴于另一点C，连接BD，AD，CD，如图所示．（1）直接写出抛物线的解析式和点A，C，D的坐标；（2）动点P在BD上以每秒2个单位长的速度由点B向点D运动，同时动点Q 在CA上以每秒3个单位长的速度由点C向点A运动，当其中一个点到达终点停止运动时，另一个点也随之停止运动，设运动时间为t秒．PQ交线段AD于点E．①当∠DPE=∠CAD时，求t的值；②过点E作EM⊥BD，垂足为点M，过点P作PN⊥BD交线段AB或AD于点N，当PN=EM时，求t的值．38．如图1，在平面直角坐标系中，直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点，其中A（m，0）、B（4，n），该抛物线与y轴交于点C，与x轴交于另一点D．（1）求m、n的值及该抛物线的解析式；（2）如图2，若点P为线段AD上的一动点（不与A、D重合），分别以AP、DP 为斜边，在直线AD的同侧作等腰直角△APM和等腰直角△DPN，连接MN，试确定△MPN面积最大时P点的坐标；（3）如图3，连接BD、CD，在线段CD上是否存在点Q，使得以A、D、Q为顶点的三角形与△ABD相似，若存在，请直接写出点Q的坐标；若不存在，请说明理由．39．如图，点A，B，C都在抛物线y=ax2﹣2amx+am2+2m﹣5（其中﹣＜a＜0）上，AB∥x轴，∠ABC=135°，且AB=4．（1）填空：抛物线的顶点坐标为（用含m的代数式表示）；（2）求△ABC的面积（用含a的代数式表示）；（3）若△ABC的面积为2，当2m﹣5≤x≤2m﹣2时，y的最大值为2，求m的值．40．如图1，在平面直角坐标系xOy中，已知点A和点B的坐标分别为A（﹣2，0），B（0，﹣6），将Rt△AOB绕点O按顺时针方向分别旋转90°，180°得到Rt△A1OC，Rt△EOF．抛物线C1经过点C，A，B；抛物线C2经过点C，E，F．（1）点C的坐标为，点E的坐标为；抛物线C的解析式1的解析式为；为．抛物线C2上的一个动点．（2）如果点P（x，y）是直线BC上方抛物线C1①若∠PCA=∠ABO时，求P点的坐标；②如图2，过点P作x轴的垂线交直线BC于点M，交抛物线C于点N，记2h=PM+NM+BM，求h与x的函数关系式，当﹣5≤x≤﹣2时，求h的取值范围．41．如图，抛物线y=ax2+bx+c与两坐标轴相交于点A（﹣1，0）、B（3，0）、C （0，3），D是抛物线的顶点，E是线段AB的中点．（1）求抛物线的解析式，并写出D点的坐标；（2）F（x，y）是抛物线上的动点：①当x＞1，y＞0时，求△BDF的面积的最大值；②当∠AEF=∠DBE时，求点F的坐标．42．如图，在平面直角坐标系中，矩形ABCD的对称中心为坐标原点O，AD⊥y 轴于点E（点A在点D的左侧），经过E、D两点的函数y=﹣x2+mx+1（x≥0）的图象记为G1，函数y=﹣x2﹣mx﹣1（x＜0）的图象记为G2，其中m是常数，图象G1、G2合起来得到的图象记为G．设矩形ABCD的周长为L．（1）当点A的横坐标为﹣1时，求m的值；（2）求L与m之间的函数关系式；（3）当G2与矩形ABCD恰好有两个公共点时，求L的值；（4）设G在﹣4≤x≤2上最高点的纵坐标为y0，当≤y≤9时，直接写出L的取值范围．43．已知抛物线y=ax2+bx+c过点A（0，2），且抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且B在C的左侧，△ABC有一个内角为60°．（1）求抛物线的解析式；（2）若MN与直线y=﹣2x平行，且M，N位于直线BC的两侧，y1＞y2，解决以下问题：①求证：BC平分∠MBN；②求△MBC外心的纵坐标的取值范围．44．如图，抛物线y=x2+bx+c与x轴交于A、B两点，B点坐标为（4，0），与y 轴交于点C（0，4）．（1）求抛物线的解析式；（2）点P在x轴下方的抛物线上，过点P的直线y=x+m与直线BC交于点E，与y轴交于点F，求PE+EF的最大值；（3）点D为抛物线对称轴上一点．①当△BCD是以BC为直角边的直角三角形时，直接写出点D的坐标；②若△BCD是锐角三角形，直接写出点D的纵坐标n的取值范围．45．如图1，抛物线y=ax2+2x+c与x轴交于A（﹣4，0），B（1，0）两点，过点B的直线y=kx+分别与y轴及抛物线交于点C，D．（1）求直线和抛物线的表达式；（2）动点P从点O出发，在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动，设运动时间为t秒，当t为何值时，△PDC为直角三角形？请直接写出所有满足条件的t的值；（3）如图2，将直线BD沿y轴向下平移4个单位后，与x轴，y轴分别交于E，F两点，在抛物线的对称轴上是否存在点M，在直线EF上是否存在点N，使DM+MN 的值最小？若存在，求出其最小值及点M，N的坐标；若不存在，请说明理由．46．如图，已知抛物线y=ax2+bx﹣3与x轴交于点A（﹣3，0）和点B（1，0），交y轴于点C，过点C作CD∥x轴，交抛物线于点D．（1）求抛物线的解析式；（2）若直线y=m（﹣3＜m＜0）与线段AD、BD分别交于G、H两点，过G点作EG⊥x轴于点E，过点H作HF⊥x轴于点F，求矩形GEFH的最大面积；（3）若直线y=kx+1将四边形ABCD分成左、右两个部分，面积分别为S1，S2，且S1：S2=4：5，求k的值．47．如图，抛物线顶点P（1，4），与y轴交于点C（0，3），与x轴交于点A，B．（1）求抛物线的解析式．（2）Q是抛物线上除点P外一点，△BCQ与△BCP的面积相等，求点Q的坐标．（3）若M，N为抛物线上两个动点，分别过点M，N作直线BC的垂线段，垂足分别为D，E．是否存在点M，N使四边形MNED为正方形？如果存在，求正方形MNED 的边长；如果不存在，请说明理由．48．如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线与x轴交于A、B两点，与y轴交于C点，其中A（1，0），C（0，3）．（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；（2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；（3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．49．在平面直角坐标系中，二次函数y=ax2+x+c的图象经过点C（0，2）和点D （4，﹣2）．点E是直线y=﹣x+2与二次函数图象在第一象限内的交点．（1）求二次函数的解析式及点E的坐标．（2）如图①，若点M是二次函数图象上的点，且在直线CE的上方，连接MC，OE，ME．求四边形COEM面积的最大值及此时点M的坐标．（3）如图②，经过A、B、C三点的圆交y轴于点F，求点F的坐标．50．如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．（1）求线段OC的长度；（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；（3）在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC 面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．一．解答题（共50小题）1．如图1，已知二次函数y=ax2+x+c（a≠0）的图象与y轴交于点A（0，4），与x轴交于点B、C，点C坐标为（8，0），连接AB、AC．（1）请直接写出二次函数y=ax2+x+c的表达式；（2）判断△ABC的形状，并说明理由；（3）若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，请写出此时点N的坐标；（4）如图2，若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标．【分析】（1）根据待定系数法即可求得；（2）根据抛物线的解析式求得B的坐标，然后根据勾股定理分别求得AB2=20，AC2=80，BC10，然后根据勾股定理的逆定理即可证得△ABC是直角三角形．（3）分别以A、C两点为圆心，AC长为半径画弧，与x轴交于三个点，由AC的垂直平分线与x轴交于一个点，即可求得点N的坐标；（4）设点N的坐标为（n，0），则BN=n+2，过M点作MD⊥x轴于点D，根据三角形相似对应边成比例求得MD=（n+2），然后根据S△AMN =S△ABN﹣S△BMN得出关于n的二次函数，根据函数解析式求得即可．【解答】解：（1）∵二次函数y=ax2+x+c的图象与y轴交于点A（0，4），与x 轴交于点B、C，点C坐标为（8，0），∴，解得．∴抛物线表达式：y=﹣x2+x+4；（2）△ABC是直角三角形．令y=0，则﹣x2+x+4=0，解得x1=8，x2=﹣2，∴点B的坐标为（﹣2，0），由已知可得，在Rt△ABO中AB2=BO2+AO2=22+42=20，在Rt△AOC中AC2=AO2+CO2=42+82=80，又∵BC=OB+OC=2+8=10，∴在△ABC中AB2+AC2=20+80=102=BC2∴△ABC是直角三角形．（3）∵A（0，4），C（8，0），∴AC==4，①以A为圆心，以AC长为半径作圆，交x轴于N，此时N的坐标为（﹣8，0），②以C为圆心，以AC长为半径作圆，交x轴于N，此时N的坐标为（8﹣4，0）或（8+4，0）③作AC的垂直平分线，交x轴于N，此时N的坐标为（3，0），综上，若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，点N的坐标分别为（﹣8，0）、（8﹣4，0）、（3，0）、（8+4，0）．（4）如图，AB==2，BC=8﹣（﹣2）=10，AC==4，∴AB2+AC2=BC2，∴∠BAC=90°．∴AC⊥AB．∵AC∥MN，∴MN⊥AB．设点N的坐标为（n，0），则BN=n+2，∵MN∥AC，△BMN∽△BAC∴=，∴=，BM==，MN==，AM=AB﹣BM=2﹣==AM•MN∵S△AMN=××=﹣（n﹣3）2+5，当n=3时，△AMN面积最大是5，∴N点坐标为（3，0）．∴当△AMN面积最大时，N点坐标为（3，0）．【点评】本题是二次函数的综合题，解（1）的关键是待定系数法求解析式，解（2）的关键是勾股定理和逆定理，解（3）的关键是等腰三角形的性质，解（4）的关键是三角形相似的判定和性质以及函数的最值等．2．对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“闭距离“，记作d（M，N）．已知点A（﹣2，6），B（﹣2，﹣2），C（6，﹣2）．（1）求d（点O，△ABC）；（2）记函数y=kx（﹣1≤x≤1，k≠0）的图象为图形G．若d（G，△ABC）=1，直接写出k的取值范围；（3）⊙T的圆心为T（t，0），半径为1．若d（⊙T，△ABC）=1，直接写出t 的取值范围．【分析】（1）根据点A、B、C三点的坐标作出△ABC，利用“闭距离”的定义即可得；（2）由题意知y=kx在﹣1≤x≤1范围内函数图象为过原点的线段，再分别求得经过（1，﹣1）和（﹣1，﹣1）时k的值即可得；（3）分⊙T在△ABC的左侧、内部和右侧三种情况，利用“闭距离”的定义逐一判断即可得．【解答】解：（1）如图所示，点O到△ABC的距离的最小值为2，∴d（点O，△ABC）=2；（2）y=kx（k≠0）经过原点，在﹣1≤x≤1范围内，函数图象为线段，当y=kx（﹣1≤x≤1，k≠0）经过（1，﹣1）时，k=﹣1，此时d（G，△ABC）=1；当y=kx（﹣1≤x≤1，k≠0）经过（﹣1，﹣1）时，k=1，此时d（G，△ABC）=1；∴﹣1≤k≤1，∵k≠0，∴﹣1≤k≤1且k≠0；。

北师大版九年级数学下册第二章二次函数压轴题综合复习练习题

16．如图1，直线L：y＝﹣x+1与x轴，y轴分别交于点B，点E，抛物线L1：y＝ax2+bx+c经过点B，点A（﹣3，0）和点C（0，﹣3），并与直线L交于另一点D．
（1）求抛物线L1的解析式；
（2）如图2，点P为x轴上一动点，连接AD，AC，CP，当∠PCA＝∠ADB时，求点P的坐标；
（3）如图3，将抛物线L1平移，使其顶点是坐标原点O，得到抛物线L2，将直线DB向下平移经过坐标原点O，交抛物线L2于另一点F，点M（，0），点N是L2上且位于第一象限内一动点，MN交L2于Q点，QR∥x轴分别交OF，ON于S，R，试说明：QS与SR存在一个确定的数量关系．
5．已知抛物线L：y＝x2+bx+c经过点A（﹣1，0）和（1，﹣2）两点，抛物线L关于原点O的对称的为抛物线L′，点A的对应点为点A′．
（1）求抛物线L和L′的表达式；
（2）是否在抛物线L上存在一点P，抛物线L′上存在一点Q，使得以AA′为边，且以A、A′、P、Q为顶点的四边形是平行四边形？若存在，求出P点坐标；若不存在，请说明理由．
∵∠ABQ＝2∠ABC，则BC是∠ABH的角平分线，则△RQB为等腰三角形，
则点C是RQ的中点，
在△BOC中，tan∠OBC＝＝＝tan∠ROC＝，
则设RC＝x＝QB，则BC＝2x，则RB＝＝ x＝BQ，
在△QRB中，S△RQB＝ ×QR•BC＝ BR•QK，即 2x•2x＝ KQ• x，解得：KQ＝，
11．如图，抛物线与x轴相交于点A（﹣3，0）、点B（1，0），与y轴交于点C（0，3），点D是第二象限内抛物线上一动点．F点坐标为（﹣4，0）．
（1）求这条抛物线的解析式；并写出顶点坐标；
（2）当D为抛物线的顶点时，求△ACD的面积；

2014年中考数学压轴题精选(二次函数)(16题)-附详细解答和评分标准.doc

1、（08广东茂名25题）（本题满分10分）如图，在平面直角坐标系中，抛物线y =－32x 2+b x +c 经过A （0，－4）、B （x 1，0）、 C （x 2，0）三点，且x 2-x 1=5．（1）求b 、c 的值；（4分）（2）在抛物线上求一点D ，使得四边形BDCE 是以BC 为对角线的菱形；（3分）（3）在抛物线上是否存在一点P ，使得四边形B P O H 是以OB 为对角线的菱形？若存在，求出点P 的坐标，并判断这个菱形是否为正方形？若不存在，请说明理由．（3分）解：（08广东茂名25题解析）解：（1）解法一： ∵抛物线y =－32x 2+b x +c 经过点A （0，－4）， ∴c =－4 ……1分又由题意可知，x 1、x 2是方程－32x 2+b x +c =0的两个根， ∴x 1+x 2=23b ， x 1x 2=－23c =6 ·························································· 2分由已知得（x 2-x 1）2=25 又（x 2-x 1）2=（x 2+x 1）2－4x1x 2=49b 2－24 ∴49b 2－24=25 解得b =±314···························································································· 3分当b =314时，抛物线与x 轴的交点在x 轴的正半轴上，不合题意，舍去．∴b =－314． ··························································································· 4分解法二：∵x 1、x 2是方程－32x 2+b x +c=0的两个根，即方程2x 2－3b x +12=0的两个根．∴x =4969b 32-±b ， ································································· 2分（第25题图）x∴x 2－x 1=2969b 2-=5，解得 b =±314 ·················································································· 3分（以下与解法一相同．）（2）∵四边形BDCE 是以BC 为对角线的菱形，根据菱形的性质，点D 必在抛物线的对称轴上， ···················································································· 5分又∵y =－32x 2－314x －4=－32（x +27）2+625····························· 6分 ∴抛物线的顶点（－27，625）即为所求的点D ． ································· 7分（3）∵四边形BPOH 是以OB 为对角线的菱形，点B 的坐标为（－6，0），根据菱形的性质，点P 必是直线x =-3与抛物线y =－32x 2-314x -4的交点， ···················································· 8分∴当x =－3时，y =－32×（－3）2－314×（－3）－4=4，∴在抛物线上存在一点P （－3，4），使得四边形BPOH 为菱形． ··············· 9分四边形BPOH 不能成为正方形，因为如果四边形BPOH 为正方形，点P 的坐标只能是（－3，3），但这一点不在抛物线上． ············································· 10分 2、（08广东肇庆25题）（本小题满分10分）已知点A （a ，1y ）、B （2a ，y 2）、C （3a ，y 3）都在抛物线x x y 1252+=上. （1）求抛物线与x 轴的交点坐标；（2）当a =1时，求△ABC 的面积；（3）是否存在含有1y 、y 2、y 3，且与a 无关的等式？如果存在，试给出一个，并加以证明；如果不存在，说明理由.（08广东肇庆25题解析）（本小题满分10分）解：（1）由5x x 122+=0， ··································································· （1分）得01=x ，5122-=x ． ······································································· （2分） ∴抛物线与x 轴的交点坐标为（0，0）、（512-，0）． ································· （3分）（2）当a =1时，得A （1，17）、B （2，44）、C （3，81）， ·························· （4分）分别过点A 、B 、C 作x 轴的垂线，垂足分别为D 、E 、F ，则有ABC S ∆=S ADFC 梯形 -ADEB S 梯形 -BEFC S 梯形 ············································· （5分）=22)8117(⨯+-21)4417(⨯+-21)8144(⨯+ ······························· （6分）=5（个单位面积） ······························································ （7分）（3）如：)(3123y y y -=． ······························································· （8分）事实上，)3(12)3(523a a y ⨯+⨯= =45a 2+36a ．3（12y y -）=3[5×（2a ）2+12×2a -（5a 2+12a ）] =45a 2+36a ． ··········· （9分） ∴)(3123y y y -=． ········································································ （10分） 3、（08辽宁沈阳26题）（本题14分）26．如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，OB =，矩形ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B的对应点为点F ，点C 的对应点为点D ，抛物线2y ax bx c =++过点A E D ，，．（1）判断点E 是否在y 轴上，并说明理由；（2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．（08辽宁沈阳26题解析）解：（1）点E 在y 轴上 ············································ 1分理由如下：连接AO ，如图所示，在Rt ABO △中，1AB =，BO =，2AO ∴=1sin 2AOB ∴∠=，30AOB ∴∠= 由题意可知：60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上，∴点E 在y 轴上． ······························································· 3分（2）过点D 作DM x ⊥轴于点M1OD =，30DOM ∠=x第26题图∴在Rt DOM △中，12DM =，2OM =点D 在第一象限，∴点D 的坐标为12⎫⎪⎪⎝⎭， ············································································· 5分由（1）知2EO AO ==，点E 在y 轴的正半轴上∴点E 的坐标为(02)，∴点A的坐标为( ··············································································· 6分抛物线2y ax bx c =++经过点E ，2c ∴=由题意，将(A ，12D ⎫⎪⎪⎝⎭，代入22y ax bx =++中得321312422a a ⎧-+=⎪⎨++=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为：2829y x x =-+ ················································ 9分（3）存在符合条件的点P ，点Q ． ······························································ 10分理由如下：矩形ABOC 的面积3AB BO ==∴以O B P Q ，，，为顶点的平行四边形面积为由题意可知OB 为此平行四边形一边，又3OB =OB ∴边上的高为2 ···················································································· 11分依题意设点P 的坐标为(2)m ，点P在抛物线2829y x x =-+上28229m ∴--+=解得，10m =，28m =-1(02)P ∴，，228P ⎛⎫- ⎪ ⎪⎝⎭以O B P Q ，，，为顶点的四边形是平行四边形，PQ OB ∴∥，PQ OB == ∴当点1P 的坐标为(02)，时，点Q的坐标分别为1(2)Q，2Q ；当点2P的坐标为2⎛⎫⎪ ⎪⎝⎭时，点Q的坐标分别为32Q ⎛⎫ ⎪ ⎪⎝⎭，42Q ⎫⎪⎪⎝⎭． ········································ 14分4、（08辽宁12市26题）（本题14分）26．如图16，在平面直角坐标系中，直线y =与x 轴交于点A ，与y 轴交于点C ，抛物线2(0)3y ax x c a =-+≠经过A B C ，，三点．（1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．（08辽宁12市26题解析）解：（1）直线y =与x 轴交于点A ，与y 轴交于点C ．(10)A ∴-，，(0C ， ············································································· 1分点A C ，都在抛物线上，03a c c⎧=++⎪∴⎨⎪=⎩3a c ⎧=⎪∴⎨⎪=⎩ ∴抛物线的解析式为2y x x =-················································· 3分x∴顶点13F ⎛- ⎝⎭， ·················································································· 4分（2）存在 ································································································ 5分1(0P ······························································································ 7分2(2P ····························································································· 9分（3）存在 ······························································································ 10分理由：解法一：延长BC 到点B '，使B C BC '=，连接B F '交直线AC 于点M ，则点M 就是所求的点． ········································································· 11分过点B '作B H AB '⊥于点H ．B点在抛物线2y x x =(30)B ∴，在Rt BOC △中，tan OBC ∠=，30OBC ∴∠=，BC =在Rt BB H '△中，12B H BB ''==6BH H '==，3OH ∴=，(3B '∴--， ········································ 12分设直线B F '的解析式为y kx b =+3k b k b ⎧-=-+⎪∴⎨=+⎪⎩解得2k b ⎧=⎪⎪⎨⎪=-⎪⎩62y x ∴=- ·················································································· 13分62y y x ⎧=⎪∴⎨=-⎪⎩解得377x y ⎧=⎪⎪⎨⎪=-⎪⎩37M ⎛∴ ⎝⎭ ∴在直线AC 上存在点M ，使得MBF △的周长最小，此时37M ⎛- ⎝⎭，． ·· 14分x5、（08青海西宁28题）如图14，已知半径为1的1O 与x 轴交于A B ，两点，OM 为1O 的切线，切点为M ，圆心1O 的坐标为(20)，，二次函数2y x bx c =-++的图象经过A B ，两点．（1）求二次函数的解析式；（2）求切线OM 的函数解析式；（3）线段OM 上是否存在一点P ，使得以P O A ，，为顶点的三角形与1OO M △相似．若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．（08青海西宁28题解析）解：（1）圆心1O 的坐标为(20)，，1O 半径为1，(10)A ∴，，(30)B ，……1分二次函数2y x bx c =-++的图象经过点A B ，，∴可得方程组10930b c b c -++=⎧⎨-++=⎩····································································· 2分解得：43b c =⎧⎨=-⎩∴二次函数解析式为243y x x =-+- ······································· 3分（2）过点M 作MF x ⊥轴，垂足为F ． ······················································ 4分OM 是1O 的切线，M 为切点，1O M OM ∴⊥（圆的切线垂直于经过切点的半径）．在1Rt OO M △中，1111sin 2O M O OM OO ∠== 1O OM ∠为锐角，130O OM ∴∠= ························ 5分1cos3022OM OO ∴==⨯=，在Rt MOF △中，3cos3032OF OM ===．1sin 3032MF OM ===． ∴点M 坐标为322⎛ ⎝⎭， ············································································· 6分图14设切线OM 的函数解析式为(0)y kx k =≠，由题意可知3322k =，33k ∴= ····· 7分 ∴切线OM 的函数解析式为33y x =··························································· 8分（3）存在． ····························································································· 9分 ①过点A 作1AP x ⊥轴，与OM 交于点1P ．可得11Rt Rt APO MO O △∽△（两角对应相等两三角形相似）113tan tan 30P A OA AOP =∠==，1313P ⎛⎫∴ ⎪ ⎪⎝⎭， ····································· 10分 ②过点A 作2AP OM ⊥，垂足为2P ，过2P 点作2P H OA ⊥，垂足为H ．可得21Rt Rt AP O O MO △∽△（两角对应相等两三角开相似）在2Rt OP A △中，1OA =，23cos30OP OA ∴==，在2Rt OP H △中，22333cos 224OH OP AOP =∠=⨯=， 222313sin 224P H OP AOP =∠=⨯=，23344P ⎛⎫∴ ⎪ ⎪⎝⎭， ································· 11分∴符合条件的P 点坐标有31⎛⎫ ⎪ ⎪⎝⎭，，334⎛⎫⎪ ⎪⎝⎭， ·············································· 12分6、（08山东济宁26题）（12分）ABC △中，90C ∠=，60A ∠=，2AC =cm ．长为1cm 的线段MN 在ABC △的边AB 上沿AB 方向以1cm/s 的速度向点B 运动（运动前点M 与点A 重合）．过M N ，分别作AB 的垂线交直角边于P Q ，两点，线段MN 运动的时间为t s ．（1）若AMP △的面积为y ，写出y 与t 的函数关系式（写出自变量t 的取值范围）；（2）线段MN 运动过程中，四边形MNQP 有可能成为矩形吗？若有可能，求出此时t 的值；若不可能，说明理由；（3）t 为何值时，以C P Q ，，为顶点的三角形与ABC △相似？（08山东济宁26题解析）解：（1）当点P 在AC 上时，AM t =，tg 603PM AM t ∴==．2133(01)22y tt t t ∴==≤≤． ······························································ 2分当点P 在BC 上时，3tan 30(4)3PM BM t ==-．213(4)(13)2y t t t =-=+≤≤． ··········································· 4分（2）2AC =，4AB ∴=．413BN AB AM MN t t ∴=--=--=-．3tan 30(3)3QN BN t ∴==-． ······························································ 6分由条件知，若四边形MNQP 为矩形，需PM QN =)3t =-， 34t ∴=． ∴当34t =s 时，四边形MNQP 为矩形．························································ 8分（3）由（2）知，当34t =s 时，四边形MNQP 为矩形，此时PQ AB ∥，PQC ABC ∴△∽△．··············································································· 9分除此之外，当30CPQ B ∠=∠=时，QPC ABC △∽△，此时3tan 30CQ CP ==． 1cos602AM AP ==，22AP AM t ∴==．22CP t ∴=-． ························ 10分3cos302BN BQ ==，)3BQt ∴==-．又2BC =)33CQ t ∴=-=． ·································· 11分 322t ∴=-，12t =．∴当12t =s 或34s 时，以C P Q ，，为顶点的三角形与ABC △相似． ··············· 12分7、（08四川巴中30题）（12分）30．已知：如图14，抛物线2334y x =-+与x 轴交于点A ，点B ，与直线34y x b =-+相交于点B ，点C ，直线34y x b =-+与y 轴交于点E ．（1）写出直线BC 的解析式．（2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB △的面积最大，最大面积是多少？（08四川巴中30题解析）解：（1）在2334y x =-+中，令0y = 23304x ∴-+=12x ∴=，22x =-(20)A ∴-，，(20)B ， ········································· 1分又点B 在34y x b =-+上 302b ∴=-+32b =BC ∴的解析式为3342y x =-+ ··································································· 2分（2）由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩，得11194x y =-⎧⎪⎨=⎪⎩2220x y =⎧⎨=⎩ ············································· 4分 914C ⎛⎫∴- ⎪⎝⎭，，(20)B ，xyAB CEM D P NO。

中考数学二次函数压轴题16道

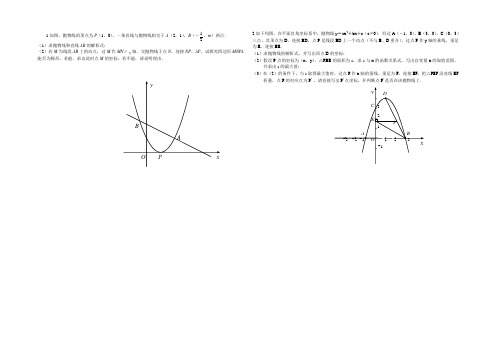
1.如图，抛物线的顶点为P （1，0），一条直线与抛物线相交于A （2，1），B （－21，m ）两点．（1）求抛物线和直线AB 的解析式；（2）若M 为线段AB 上的动点，过M 作MN ∥y 轴，交抛物线于点N ，连接NP 、AP ，试探究四边形MNP A 能否为梯形，若能，求出此时点M 的坐标；若不能，请说明理由．2.如下列图，在平面直角坐标系中，抛物线y ＝ax2＋bx ＋c （a ≠0）．经过A （－1，0）、B （3，0）、C （0，3）三点，其顶点为D ，连接BD ，点P 是线段BD 上一个动点（不与B 、D 重合），过点P 作y 轴的垂线，垂足为E ，连接BE ．（1）求抛物线的解析式，并写出顶点D 的坐标；（2）假设P 点的坐标为（x ，y ），△PBE 的面积为s ，求s 与x 的函数关系式，写出自变量x 的取值范围，并求出s 的最大值；（3）在（2）的条件下，当s 取得最大值时，过点P 作x 轴的垂线，垂足为F ，连接EF ，把△PEF 沿直线EF折叠，点P 的对应点为P ′ ，请直接写出P ′点坐标，并判断点P ′是否在该抛物线上．3．如图，抛物线与x轴交于A（x1，0），B（x2，0）两点，且x1＞x2，与y轴交于点C（0，4），其中x1，x2是方程x2－2x－8＝0的两个根．（1）求这条抛物线的解析式；（2）点P是线段AB上的动点，过点P作PE∥AC，交BC于点E，连接CP，当△CPE的面积最大时，求点P的坐标；（3）探究：若点Q是抛物线对称轴上的点，是否存有这样的点Q，使△QBC成为等腰三角形，若存有，请直接写出所有符合条件的点Q的坐标；若不存有，请说明理由．4．已知：如下列图，关于x的抛物线y＝ax2＋x＋c（a≠0）与x轴交于点A（－2，0），点B（6，0），与y 轴交于点C．（1）求出此抛物线的解析式，并写出顶点坐标；（2）在抛物线上有一点D，使四边形ABDC为等腰梯形，写出点D的坐标，并求出直线AD的解析式；（3）在（2）中的直线AD交抛物线的对称轴于点M，抛物线上有一动点P，x轴上有一动点Q．是否存有以A、M、P、Q为顶点的平行四边形？假设存有，请直接写出点Q的坐标；假设不存有，请说明理由．5．如图，矩形OABC 的两边OA 、OC 分别在x 轴和y 轴上，A （－3，0），过点C 的直线y ＝－2x ＋4与x 轴交于点D ，二次函数y ＝－21x2＋bx ＋c 的图象经过B 、C 两点．（1）求B 、C 两点的坐标；（2）求二次函数的解析式；（3）若点P 是CD 的中点，求证：AP ⊥CD ；（4）在二次函数的图象上是否存有这样的点M ，使以A 、P 、C 、M 为顶点的四边形为矩形？若存有，求出点M 的坐标；若不存有，请说明理由．6．已知：抛物线y ＝ax2＋bx ＋c （a ≠0）的对称轴为x ＝－1，与x 轴交于A 、B 两点，与y 轴交于点C ，其中A （－3，0）、C （0，－2）．（1）求这条抛物线的函数表达式．（2）已知在对称轴上存有一点P ，使得△PBC 的周长最小．请求出点P 的坐标．（3）若点D 是线段OC 上的一个动点（不与点O 、点C 重合）．过点D 作DE ∥PC 交x 轴于点E ，连接PD 、PE ．设CD 的长为m ，△PDE 的面积为S ．求S 与m 之间的函数关系式．试说明S 是否存有最大值，若存有，请求出最大值；若不存有，请说明理由．7.如图，已知抛物线y＝x2－1与x轴交于A、B两点，与y轴交于点C．（1）求A、B、C三点的坐标．（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．（3）在x轴上方的抛物线上是否存有一点M，过M作MG⊥x轴于点G，使以A、M、G三点为顶点的三角形与△PCA相似？若存有，请求出M点的坐标；否则，请说明理由．8．如图，抛物线y＝ax2＋bx－3与x轴交于A，B两点，与y轴交于C点，且经过点（2，－3a），对称轴是直线x＝1，顶点是M．（1）求抛物线对应的函数表达式；（2）经过C，M两点作直线与x轴交于点N，在抛物线上是否存有这样的点P，使以点P，A，C，N为顶点的四边形为平行四边形？若存有，请求出点P的坐标；若不存有，请说明理由；（3）设直线y＝－x＋3与y轴的交点是D，在线段BD上任取一点E（不与B，D重合），经过A，B，E 三点的圆交直线BC于点F，试判断△AEF的形状，并说明理由；（4）当E是直线y＝－x＋3上任意一点时，（3）中的结论是否成立？（请直接写出结论）9．如图，已知抛物线y＝ax2＋bx＋c与y轴交于点A(0，3)，与x轴分别交于B(1，0)、C(5，0)两点．（1）求此抛物线的解析式；（2）若点D为线段OA的一个三等分点，求直线DC的解析式；（3）若一个动点P自OA的中点M出发，先到达x轴上的某点（设为点E），再到达抛物线的对称轴上某点（设为点F），最后运动到点A．求使点P运动的总路径最短的点E、点F的坐标，并求出这个最短总路径的长．10．如图，在平面直角坐标系中，以点A(－3，0)为圆心、5为半径的圆与x轴相交于点B、C两点（点B在点C的左边），与y轴相交于D、M两点（点D在点M的下方）．（1）求以直线x＝－3为对称轴、且经过D、C两点的抛物线的解析式；（2）若点P是这条抛物线对称轴上的一个动点，求PC＋PD的取值范围；（3）若点E为这条抛物线对称轴上的点，则在抛物线上是否存有这样的点F，使得以点B、C、E、F 为顶点的四边形是平行四边形？若存有，求出点F的坐标；若不存有，说明理由．11．如图，已知抛物线y＝ax2＋bx－4与直线y＝x交于点A、B两点，A、B的横坐标分别为－1和4．（1）求此抛物线的解析式．（2）若平行于y轴的直线x＝m（0＜m＜5＋1）与抛物线交于点M，与直线y＝x交于点N，交x轴于点P，求线段MN的长（用含m的代数式表示）．（3）在（2）的条件下，连接OM、BM，是否存有m的值，使得△BOM的面积S最大？若存有，请求出m 的值，若不存有，请说明理由．12．如图，抛物线经过A（4，0），B（1，0），C（0，－2）三点．（1）求此抛物线的解析式；（2）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存有P点，使得以A、P、M为顶点的三角形与△OAC相似？若存有，请求出符合条件的点P的坐标；若不存有，请说明理由；（3）在直线AC上方的抛物线上有一点D，使得△DCA的面积最大，求出点D的坐标．13. 如图（1），抛物线42y x x =+-与y 轴交于点A ，E （0，b ）为y 轴上一动点，过点E 的直线y x b =+与抛物线交于点B 、C .b ；若不存有，说明理由.14.如图，已知抛物线212y x bx c x =++与轴交于点A （-4，0）和B （1，0）两点，与y 轴交于C 点. (1)求此抛物线的解析式；(2)设E 是线段AB 上的动点，作EF ∥AC 交BC 于F ，连接CE ，当△CEF 的面积是△BEF 面积的2倍时，求E 点的坐标；(3)若P 为抛物线上A 、C 两点间的一个动点，过P 作y 轴的平行线，交AC 于Q ，当P 点运动到什么位置时，线段PQ 的值最大，并求此时P 点的坐标.x15.如图，在平面直角坐标系中，二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），与y 轴交于C （0，-3）点，点P 是直线BC 下方的抛物线上一动点. （1）求这个二次函数的表达式．（2）连结PO 、PC ，并把△POC 沿CO 翻折，得到四边形POP /C ，那么是否存有点P ，使四边形POP /C 为菱形？若存有，请求出此时点P 的坐标；若不存有，请说明理由．（3）当点P 运动到什么位置时，四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.16.在平面直角坐标系xOy 中，抛物线2y ax bx c =++与x 轴交于A B 、两点（点A 在点B 的左侧），与y 轴交于点C ，点A 的坐标为(30)-，，若将经过A C 、两点的直线1y kx b =+沿y 轴向下平移3个单位后恰好经过原点，且抛物线的对称轴是直线2x =-．（1）求直线AC 及抛物线的函数表达式；（2）假如P 是线段AC 上一点，设ABP ∆、BPC ∆的面积分别为ABP S ∆、BPC S ∆，且:2:3ABP BPC S S ∆∆=，求点P 的坐标；（3）设Q 的半径为l ，圆心Q 在抛物线上运动，则在运动过程中是否存有Q 与坐标轴相切的情况？若存有，求出圆心Q 的坐标；若不存有，请说明理由．并探究：若设⊙Q 的半径为r ，圆心Q 在抛物线上运动，则当r 取何值时，⊙Q 与两坐轴同时相切？。

中考数学总复习《二次函数与三角函数综合压轴题》专项训练题(附有答案)

中考数学总复习《二次函数与三角函数综合压轴题》专项训练题(附有答案)学校:___________班级：___________姓名：___________考号：___________1．如图1，抛物线y＝ax2+bx+c的顶点坐标为A（1，2），与x轴交于点B（﹣1，0），C两点，点P是抛物线上的动点．（1）求这条抛物线的函数表达式；（2）如图2，连接CD，点E在CD上，且∠PEC＝90°，求线段PE长度的最大值；（3）如图3，连接AB、AC，已知∠ACB+∠PCB＝α，使得tanα＝2？若存在，求出点P 的横坐标，请说明理由．2．抛物线y＝ax2+bx+c（a＞0）的对称轴是y轴，与x轴交于A、B两点且A点坐标是（﹣2，0），且OB＝2OC．（1）如图1，求抛物线的解析式；（2）如图2，若M（﹣4，m），N是抛物线上的两点．求N点坐标；（3）如图3，D是B点右侧抛物线上的一动点，D、E两点关于y轴对称．直线DB、EB 分别交直线x＝﹣1于G、Q两点，请问PG﹣PQ是定值吗？若是请直接写出此定值．3．如图，在平面直角坐标系中，点O为坐标原点2+x+8交x轴于点A（﹣4，0）、B，交y 轴于点C．（1）求点B的坐标；（2）点D是第一象限抛物线上的一点，连接AD交y轴于点E，设点D的横坐标为t，求d与t之间的函数解析式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，当4＜t＜8时，且横坐标为﹣t，连接BF交y轴于点G，点H 为线段BG的中点，连接AG，若AG＝EH，求tan∠CMD的值．4．二次函数y＝ax2+bx﹣3的图象交x轴于点A（﹣1，0），点B（3，0），交y轴于点C （1）求二次函数的解析式；（2）如图1，点P是抛物线上的一点，设点P的横坐标为m（m＞3），且AQ⊥PQ，若AQ＝2PQ；（3）如图2，将抛物线绕x轴正半轴上一点R旋转180°得到新抛物线C1交x轴于D、E两点，点A的对应点为点E，点B的对应点为点D．若sin∠BME＝5．如图，已知抛物线过平面直角坐标系中A（1，0）、B（3，0）（0，3）三个点．（1）求抛物线的表达式及顶点D的坐标．（2）如图②连接BC、BD、CD，求△BCD的面积．（3）点P是抛物线上的一点，已知，求满足条件的P点的坐标．6．在平面直角坐标系中，将二次函数y＝ax2（a＞0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线（点A在点B的左侧），OA＝1，经过点A的一次函数y＝kx+b（k≠0），且与抛物线的另一个交点为D，△ABD的面积为5．（1）求抛物线和一次函数的解析式；（2）抛物线上的动点E在一次函数的图象下方，当△ACE面积的最大值时，求出此时点E的坐标；（3）点Q是直线上的一动点，连接OQ，设△OQF外接圆的圆心为M，当sin∠OQF 最大时（直接写答案）．7．在平面直角坐标系中，已知抛物线与x轴交于点A（1，0），与y轴交于点C（0，﹣4）．（1）求这条抛物线的函数解析式；（2）P是抛物线上一动点（不与点A，B，C重合），作PD⊥x轴，垂足为D①如图，若点P在第三象限，且tan∠CPD＝2；②直线PD交直线BC于点E，当点E关于直线PC的对称点E′落在y轴上时，请直接写出四边形PECE'的周长．8．如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+1交y轴于点A，直线y＝﹣x+2交抛物线于B（点B在点C的左侧），交y轴于点D，交x轴于点E．（1）求点D，E，C的坐标；（2）F是线段OE上一点（OF＜EF），连接AF，DF，且AF2+EF2＝21．①求证：△DFC是直角三角形；②∠DFC的平分线FK交线段DC于点K，P是直线BC上方抛物线上一动点，当3tan∠PFK＝1时9．已知抛物线y＝ax2+bx+4与x轴相交于点A（1，0），B（4，0），与y轴相交于点C．（1）求抛物线的表达式；（2）如图1，点P是抛物线的对称轴l上的一个动点，当△P AC的周长最小时，求；（3）如图2，取线段OC的中点D，在抛物线上是否存在点Q？若存在，求出点Q的坐标，请说明理由．10．在平面直角坐标系xOy中，抛物线y＝ax2+x+c与y轴交于点C，与x轴交于A、B两点（点A在点B的左侧）（﹣，0），tan∠ACO＝．（1）求抛物线的解析式；（2）线段OB上有一动点P，连接CP，当CP+，请直接写出此时点P的坐标和CP+ PB的最小值．（3）如图2，点D为直线BC上方抛物线上一点，连接AD、BC交于点E，记△BDE的面积为S1，△ABE的面积为S2，求的最大值．11．如图，已知一次函数y1＝kx+m的图象经过A（﹣1，﹣5），B（0，﹣4）两点，且与x 轴交于点C2＝ax2+bx+4的图象经过点A，C，连接OA．（1）求一次函数和二次函数的解析式．（2）求∠OAB的正弦值．（3）在点C右侧的x轴上是否存在一点D，使得△BCD与△OAB相似？若存在，求出点D的坐标，请说明理由．12．如图，边长为4的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，过点P作PE⊥OA于点E，点Q的坐标为（0，3）（1）求抛物线的解析式；（2）①当PQ∥EQ时，PQ+PE＝；②某班数学科代表经过一番探究后发现：对于A、C间的任意一点P，PQ与PE之和为定值，你是否同意他的观点？请说明理由；（3）延长EP交BC于点F，当∠FPQ为锐角，且时，求点P的坐标．13．如图，已知二次函数y＝﹣x2+2x+3的图象交x轴分别于A，D两点，交y轴于B点（1）求抛物线的对称轴；（2）求tan∠BAC；（3）在y轴上是否存在一点P，使得以P，B，D三点为顶点的三角形与△ABC相似？如果存在；如果不存在，请说明理由．14．抛物线y＝﹣x2+bx+c与x轴交于点A（3，0）、B（﹣1，0），与y轴交于点C．（1）求抛物线解析式；（2）如图，连接AC，点P在线段AC上，与抛物线交于点Q．以线段PQ为边构造矩形PQMN，边MN在y轴上．①当矩形PQMN周长最大时，求点P坐标．②在①的条件下，点T在第四象限内，作射线AT，求tan∠TAO的值．15．如图，在平面直角坐标系中，O为原点，OQ＝18，点P是x轴正半轴上一点，连接PQ，⊙A经过点O且与QP相切于点P（1）若圆心A在x轴上，求⊙A的半径；（2）若圆心A在x轴的上方，且圆心A到x轴的距离为2，求⊙A的半径；（3）在（2）的条件下，若OP＜10，D，P的抛物线上的一个动点，点F为x轴上的一个动点的点M共有4个，求点F的横坐标的取值范围．参考答案1．解：（1）由题可设抛物线解析式为y＝a（x﹣1）2+6代入点B，得4a+2＝2∴a＝∴抛物线解析式为：；（2）如图1，过P作PF⊥x轴于F∵PE⊥CD∴∠PEH＝∠PFC＝90°∴∠PHE+∠EPH＝∠CHF+DCB＝90°∵∠PHE＝∠CHF∴∠EPH＝∠DCB令x＝6，则y＝＝∴D（0，）令y＝0，则解得x＝﹣2或3∴C（3，5）∴DO＝，CO＝7∴∴cos∠EPH＝cos∠DCB＝设直线CD为y＝kx+代入点C，得k＝∴直线CD为设P（），则H（）∴∵cos∠EPH＝∴PE＝＝∵P在第一象限∴0＜m＜6∴时，PE最大值为；（3）①如图2，当P在x轴下方时延长AB交CP延长线于K，过A作x轴平行线，两线交于点Q 过C作CR⊥AQ于R∵A（7，2），0），5）∴AB＝同理，AC＝∴AB2+AC2＝BC6，AB＝AC∴∠BAC＝90°∵∠AKQ+∠QAK＝∠QAK+∠RAC＝90°∴∠AKQ＝∠RAC又∠AQK＝∠CRA＝90°∴△AQK∽△CRA∴又tan∠ACK＝∴又AR＝CR＝8∴QK＝AQ＝4∴K（﹣3，﹣2）设直线CK为y＝k1（x﹣3），代入点K解得∴直线CK为联立∴3x3﹣4x﹣15＝0解得x＝或3∴P的横坐标为②如图3，当P在x轴上方时，则K′（﹣2，2）连接CK′交抛物线于点P可设直线CK′为y＝k2（x﹣5），代入点K′解得∴直线CK′为y＝联立∴6x2+4x﹣6＝0∴x＝或3∴P的横坐标为综上，P的横坐标为或．2．解：（1）∵抛物线y＝ax2+bx+c（a＞0）的对称轴是y轴∴b＝3∵A点坐标是（﹣2，0）∴B点坐标是（2，0）∴OB＝2∵OB＝5OC∴OC＝1∴C（0，﹣4）∴c＝﹣1把A（﹣2，5）代入y＝ax2﹣1，得5a﹣1＝0解得：a＝∴该抛物线的解析式为y＝x2﹣1；（2）当x＝﹣5时，y＝4﹣1＝3∴M（﹣8，3）过点M作MG⊥x轴于点G则MG＝3，OG＝5在Rt△OMG中，OM＝＝过点O作FK⊥OM，使OF＝OK＝，如图，过点K作KL⊥x轴于点L连接MF交抛物线于点N，连接MK交抛物线于点N′则∠MGO＝∠FHO＝∠KLO＝∠MOF＝∠MOK＝90°，tan∠OMN＝＝＝∵∠MOG+∠FOH＝90°，∠OFH+∠FOH＝90°∴∠OFH＝∠MOG∴△FOH∽△OMG∴＝＝，即＝＝∴OH＝1，FH＝∴F（1，）设直线MF的解析式为y＝kx+n，则解得：∴直线MF的解析式为y＝﹣x+与抛物线y＝x2﹣1联立，得：x2﹣6＝﹣x+解得：x1＝﹣8（舍去），x2＝当x＝时，y＝﹣×+＝∴N（，）；同理可得K（﹣2，﹣），直线MK的解析式为y＝﹣与抛物线y＝x2﹣1联立，得：x2﹣8＝﹣x﹣解得：x6＝﹣4（舍去），x2＝﹣当x＝﹣时，y＝﹣）﹣∴N′（﹣，﹣）；综上所述，N点坐标为（，，﹣）；（3）由（1）知：A（﹣2，7），0）∵D、E两点关于y轴对称设D（m，m2﹣1），则E（﹣m，m2﹣6）设直线BD的解析式为y＝k1x+b1则解得：∴直线BD的解析式为y＝x﹣当x＝﹣1时，y＝﹣﹣∴G（﹣1，﹣）同理可得：直线BE的解析式为y＝x+当x＝﹣8时，y＝∴Q（﹣1，）∵P（﹣1，4）∴PG＝0﹣（﹣）＝∴PG﹣PQ＝﹣＝3故PG﹣PQ的值为5．3．解：（1）∵抛物线y＝ax2+x+8交x轴于点A（﹣5，0）∴0＝（﹣4）2+（﹣4）+8解得a＝﹣∴y＝﹣x2+x+2当y＝0时，0＝﹣x2+x+4解得x1＝﹣4，x6＝8∴B（8，5）；（2）如图1，过D作DP⊥x轴于P∵点D的横坐标为t，点D是第一象限抛物线上的一点∴D（t，﹣x2+x+8）∴PD＝﹣x2+x+7，AP＝t+4在Rt△P AD中，tan∠P AD＝＝（t﹣8）在Rt△AOE中，tan∠OAE＝∴OE＝8﹣t在y＝﹣x2+x+8中，令x＝2∴C（0，8）∴OC＝3∴d＝CE＝OC﹣OE＝8﹣（8﹣t）＝t；（3）如图7，连接BC，FT⊥y轴于T在Rt△ABC中，∵OB＝OC＝8∴∠OBC＝∠OCB，BC＝∵∠OBC+∠OCB＝90°∴∠OBC＝∠OCB＝45°∵点F的横坐标为﹣t，点F在抛物线上∴F（﹣t，﹣t2﹣t+4）∴t6+t﹣8，BR﹣8+t在Rt△BFR中，tan∠FBR＝＝在Rt△BOG中，tan∠OBG＝∴OG＝2t﹣8∴EG＝OE+OG＝6﹣t+2t﹣8＝t＝CE．∵点H为线段BG的中点∴EH∥BC，EH＝∴AG＝EH＝6在Rt△OAG中，OG＝∴∠OAG＝∠OGA∵∠OAG+∠OGA＝90°∴∠OAG＝∠OGA＝45°＝∠OBC∴AE∥GH∴∠CMD＝∠CFB∵OG＝7t﹣8＝4∴t＝4∴﹣t5﹣t+8＝﹣7，CE＝3t＝12∴F（﹣6，﹣7）∴FT＝7，GT＝OT﹣OG＝7﹣4＝6在Rt△FGT中，FG＝＝在Rt△BOG中，BG＝在Rt△CGN中，sin∠CGN＝∴CN＝∴GN＝∴FN＝FG+GN＝3+在Rt△CFN中，tan∠CFN＝＝∴tan∠CMD＝tan∠CFN＝．4．解：（1）将A（﹣1，0），7）解得：∴这个二次函数的表达式是y＝x6﹣2x﹣3；（2）过点Q作x轴的平行线交过点P与y轴的平行线与点N，交过点A与y轴的平行线于点M∵∠NQP+∠MQA＝90°，∠MQA+∠QAM＝90°∴∠NQP＝∠QAM∵∠AMQ＝∠QNP＝90°∴△AMQ∽△QNP∴设点Q的坐标为（1，t），m2﹣6m﹣3）则AM＝t，QN＝m﹣1，NP＝t﹣m8+2m+3即解得m＝6（舍去）或4故m＝4；（3）过点E作EH⊥MB交MB的延长线于点H由抛物线的表达式知，点M（4，BM＝2则tan∠OBM＝＝3＝tan∠HBE∵sin∠BME＝，故tan∠BME＝故设BH＝x，则HE＝2x在Rt△HEM中，tan∠BME＝则tan∠BME＝＝＝，解得x＝在Rt△BHE中，BE＝＝故点E的坐标为（9，0）由旋转的定义知，点R是点A则x R＝（9﹣3）＝4故点R的坐标为（4，8）．5．解：（1）设抛物线的表达式为y＝ax2+bx+c 把A（1，2），0），3）代入得解方程组得：∴y＝x2﹣6x+3配方得：y＝（x﹣2）2﹣1顶点D的坐标为（2，﹣2）；（2）设直线CD的表达式为y＝kx+m把C（0，3），﹣6）代入得解方程组得：∴y＝﹣7x+3如图（2），设直线y＝﹣2x+8交x轴于点E当y＝0时，﹣2x+7＝0∴点E坐标为：（，2）∴BE＝3﹣过D作DF⊥x轴于点F∴；（3）∵BC5＝32+62＝18，BD2＝72+18＝2，CD2＝72+42＝20∴BC2+BD2＝CD7∴△BCD为直角三角形，∠CBD＝90°又∵tan∠BCP＝，即点D为满足条件的点P7（2，﹣1）如图（3），延长DB至点H，得H（2连接CH交抛物线于点P，所得的∠PCB＝∠BCD设直线CH的表达式为y＝k1x+n把C（0，7），1）代入得解得则直线CH的表达式为：由题意得：解得x＝0或当时，∴点满足条件的P点的坐标有P1（2，﹣3），．6．解：（1）将二次函数y＝ax2（a＞0）的图象向右平移4个单位，再向下平移2个单位2﹣2∵OA＝1∴点A的坐标为（﹣1，3），4a﹣2＝2∴∴抛物线的解析式为，即．令y＝0，则解得：x1＝﹣5，x2＝3∴B（5，0）；∴AB＝OA+OB＝4∵△ABD的面积为4∴∴∴解得：x1＝﹣2，x8＝4∴．设直线AD的解析式为y＝kx+b，则有解得：∴直线AD的解析式为．（2）如图，过点E作EM∥y轴交AD于M设，则∴∴S△ACE＝S△AME﹣S△CME＝＝＝＝．∴当此时E点坐标为．（3）如图，H是OF的中点上运动∴∠OQF＝∠OMH∴∴当OM取得最小值时，sin∠OQF的值最大∵MO＝MQ∴当MQ取得最小值时，sin∠OQF的值最大∵当MQ垂直直线时，MQ取得最小值∴此时M、Q在二次函数的对称轴直线x＝7上∴根据对称性，存在故：或．7．解：（1）∵抛物线与x轴交于点A（1，与y轴交于点C（4∴解得∴抛物线的解析式为．答：抛物线的解析式为．（2）①设P（x，），如图∴∠PEC＝∠CED＝90°∵C（0，﹣2）∴OC＝4∵PD⊥x轴∴∠PDO＝90°∵∠DOC＝90°∴四边形DOCE是矩形∴DE＝OC＝4，OD＝CE＝﹣x∴＝∵∴∴（舍去）∴＝∴P（﹣．②设P（m，）对于，当y＝4时，解得x1＝7，x2＝﹣3∴B（﹣5，0）∵OC＝4∴当点P在第三象限时，如图则四边形DEFO是矩形∴EF＝OD＝﹣m∵点E与点E′关于PC对称∴∠ECP＝∠E′CP，CE＝CE′∵PE∥y轴∴∠EPC＝∠PCE′∴PE＝CE∴PE＝CE′∴四边形PECE′是菱形∵EF∥OA∴△CEF∽△CBO∴∴∴设直线BC的解析式为y＝kx+b∴解得∴直线BC的解析式为y＝﹣x﹣2∴∴＝∵，PE＝CE∴解得（舍去）∴∴四边形PECE′的周长C＝4CE＝4×＝当点P在第二象限时，如图同理可得解得（舍去）∴∴四边形PECE′的周长C＝4CE＝3×＝综上，四边形PECE′的周长为或．8．（1）解：∵直线y＝﹣x+8交y轴于点D 当x＝0时，y＝2∴D（4，2）当y＝0时，x＝5∴E（6，0）∵直线y＝﹣x+2交抛物线于B∴﹣x7+3x+1＝﹣x+2∴7x2﹣10x+3＝8解得∵点B在点C的左侧∴点C的横坐标为6，当x＝3时∴C（3，3）答：C（3，1），8），0）．（2）如图①证明：∵抛物线y＝﹣x2+5x+1交y轴于点A 当x＝0时，y＝4∴A（0，1）∴OA＝6在Rt△AOF中，∠AOF＝90°∴AF2＝OA2+OF3设F（m，0）∴OF＝m∴AF2＝5+m2∵E（6，2）∴OE＝6∴EF＝OE﹣OF＝6﹣m∵AF5+EF2＝21∴1+m8+（6﹣m）2＝21∴m2＝2，m2＝7∵OF＜EF∴m＝2∴OF＝2∴F（4，0）∵D（0，4）∴OD＝2∴OD＝OF∴△DOF是等腰直角三角形∴∠OFD＝45°过点C作CG⊥x轴于G∵C（3，6）∴CG＝1，OG＝3∵GF＝OG﹣OF＝3∴CG＝GF∴△CGF是等腰直角三角形∴∠GFC＝45°∴∠DFC＝90°∴△DFC是直角三角形．②解：∵FK平分∠DFC，∠DFC＝90°∴∠DEK＝∠CFK＝45°∴∠OFK＝∠OFD+∠DFK＝90°∴FK∥y轴∵3tan∠PFK＝1∴设点P的坐标为（t，﹣t2+5t+1），根据题意得．（i）当点P在直线KF的左侧抛物线上时，．过点P1作P6H⊥x轴于H∴P1H∥KF∴∠HP1F＝∠P8FK∴∵HF＝OF﹣OH∴HF＝2﹣t在Rt△P1HF中，∵∴P1H＝3HF∵∴﹣t2+3t+6＝3（2﹣t）∴t3﹣6t+5＝3∴t1＝1，t5＝5（舍去）当t＝1时，﹣t7+3t+1＝2∴P1（1，7）．（ii）当点P在直线KF的右侧抛物线上时，过点P7作P2M⊥x轴于M∴P2M∥KF∴∠MP8F＝∠P2FK∴∴P3M＝3MF∵∴﹣t7+3t+1＝6（t﹣2）∴（舍去）当t＝时，∴．∴点P的坐标为（3，3）或（）．9．解：（1）∵抛物线y＝ax2+bx+4与x轴相交于点A（7，0），0）解得：∴抛物线的表达式为y＝x2﹣5x+2；（2）由（1）知y＝x2﹣5x+2，当x＝0时∴C（0，3）∵△P AC的周长等于P A+PC+AC，AC为定长∴当P A+PC的值最小时，△P AC的周长最小∵A，B关于抛物线的对称轴对称∴P A+PC＝PB+PC≥BC，当P，B，P A+PC的值最小，此时点P为直线BC与对称轴的交点设直线BC的解析式为：y＝mx+n则：解得：∴直线BC的解析式为y＝﹣x+4当时，∴∵A（1，8），4）∴P A＝＝，PC＝＝∴；（3）存在∵D为OC的中点∴D（5，2）∴OD＝2∵B（3，0）∴OB＝4在Rt△BOD中，∴∠QDB＝∠OBD；①当Q点在D点上方时：过点D作DQ∥OB，交抛物线于点Q，此时Q点纵坐标为2设Q点横坐标为t，则：t2﹣5t+4＝2，解得：∴Q（，2）或（；②当点Q在D点下方时：设DQ与x轴交于点E则：DE＝BE设E（p，0）2＝OE4+OD2＝p2+7，BE2＝（4﹣p）6∴p2+4＝（6﹣p）2解得：∴设DE的解析式为：y＝kx+q则：解得：∴联立解得：或∴Q（3，﹣2）或；综上所述，或（，﹣2）或．10．解：（1）∵A（﹣，0）∴OA＝∵tan∠ACO＝∴OC＝4∴C（0，3）将A，C的坐标代入y＝ax3+x+c得，∴∴抛物线的解析式为：y＝﹣x2+x+3；（2）令y＝4，则y＝﹣x3+x+3＝0解得x＝﹣或x＝3∴B（8，0）∴OC＝6，OB＝3∴tan∠OBC＝＝∴∠OBC＝30°，∠OCB＝60°；如图1，作点C关于x轴的对称点C′，C′H与x轴的交点即为所求点P∴PH＝PB∴CP+PB＝CP+PH＝C′P+PH＝C′H∵OC＝OC′＝3∴CC′＝6∴C′H＝6；连接CP∴C′P＝CP，∠PCC′＝∠PC′C＝30°∴OP＝综上，当P（，CP+；（3）如图2，过点D作DG⊥x轴于点G，过点A作AK⊥x轴交BC的延长线于点K ∴△DEF∽△AEK∴＝∵C（0，3），0）∴直线BC的解析式为：y＝﹣x+3；设点D的横坐标为t∴D（t，﹣t2+t+3）∴F（t，﹣t+3），4）∴AF＝4，DF＝﹣t2+t+4﹣（﹣t2+t；∴＝＝﹣t2+t＝﹣）2+∴当t＝时，的最大值为．11．解：（1）将A（﹣1，﹣5），﹣3）代入y1＝kx+m ∴解得∴y＝x﹣5令y＝0，则x＝4∴C（6，0）将A（﹣1，﹣2），0）代入y2＝ax2+bx+4∴解得∴y＝﹣2x2+7x+7；（2）过点O作OH⊥AC交于H∵B（0，﹣4），2）∴∠OCB＝45°∵OC＝4∴OH＝CH＝2∵AC＝5∴AH＝8∴AO＝∴sin∠AOB＝＝；（3）存在点D，使得△BCD与△OAB相似∵D点在C点右侧∴∠BCD＝135°∵∠ABO＝135°∴∠CBD＝∠OAB或∠CDB＝∠OAB当∠OAB＝∠CBD时，△OAB∽△DBC∴＝∵OB＝4，BC＝2∴CD＝16∴D（20，6）；当∠OAB＝∠BCD时，△OAB∽△BDC∴＝∴CD＝2∴D（6，6）；综上所述：D点坐标为（20，0）或（6．12．解：（1）∵边长为4的正方形OABC的两边在坐标轴上∴点C坐标为（0，8），0）根据抛物线的点C为顶点，设该抛物线的解析式为：y＝ax2+6将点A（﹣4，0）代入可得16a+3＝0解得a＝﹣∴此抛物线关系式为：y＝﹣x3+4；（2）①当点P与点A重合时，PQ+PE＝AQ＝当点P与点C重合时，PQ+PE＝CQ+CO＝2+4＝5故答案为：2；②对于A，C间的任意一点P理由如下：过点P作PD⊥y轴于点D设点P的坐标为（m，﹣m7+4）∵点P是抛物线上点A，C间的一个动点∴PD＝﹣m，QD＝|﹣m2+4﹣4|∴PQ＝＝m2+1∴PQ+PE＝m2+6+（﹣m3+4）＝5；（3）由（2）得PQ+PE＝6设点P的坐标为（x，y）∴PE＝y，PQ＝5﹣y∵∠FPQ为锐角，则y＜3∴QD＝8﹣y∵cos∠FPQ＝而∠FPQ＝∠DQP∴＝解得：y＝1把y＝1代入抛物线解析式得y＝﹣x2+5＝1解得x＝±2∵点P在AC段上∴x＝﹣2∴点P坐标为（﹣6，1）．13．解（1）∵二次函数y＝﹣x2+2x+3∴抛物线的对称轴x＝﹣＝﹣∴抛物线的对称轴为直线x＝1；（2）∵二次函数y＝﹣x3+2x+3＝﹣（x﹣6）2+4∴C（7，4），3）把y＝3代入y＝﹣x2+2x+8解得：x1＝﹣1，x7＝3∴D（﹣1，5），0）过点C作CE⊥y轴，垂足为点E则BE＝4﹣3＝1，CE＝1∴BC＝，∠EBC＝∠ECB＝45°又∵OB＝OA＝3∴AB＝3，∠OBA＝∠OAB＝45°∴∠CBA＝180°﹣45°﹣45°＝90°又∵BC＝，AB＝3∴tan∠BAC＝＝；（3）存在，P（6，（0，﹣）当点P在原点时，∠BPD＝90°，∴，∠BPD＝∠ABC则△BPD∽△ABC；在Rt△ABC中，BC＝∴AC＝2在Rt△BOD中，OD＝1∴BD＝当PD⊥BD时，设点P的坐标为（0若△BDP∽△ABC，则，即＝解得y＝﹣∴点P的坐标为（0，﹣）∴当P的坐标为（0，0）或（3，﹣，以P、B．14．解：（1）由题意得，抛物线的表达式为：y＝﹣（x﹣3）（x+1）＝﹣（x6﹣2x﹣3）＝﹣x2+2x+3；（2）①由点A、C的坐标得设点P（x，﹣x+3），﹣x2+2x+6）则PQ＝（﹣x2+2x+5）﹣（﹣x+3）＝﹣x2+3x则矩形PQMN的周长＝2（PQ+PN）＝2（﹣x6+3x+x）＝﹣2（x8﹣4x）∵﹣2＜7，故矩形PQMN的周长有最大值即点P（2，1）；②由①知，点P的坐标为（7，则NP＝2当x＝2时，PQ＝﹣x2+3x＝2故PQ＝PQ＝5＝PN故矩形PQMN为正方形，如图连接AQ、AN，设CP交AQ于点M由正方形轴对称性知，AQ＝AN∵∠TAQ＝3∠P AN∴∠TAN＝∠P AN设AT交y轴于点H，即∠HAN＝∠P AN在等腰Rt△MNP中，PN＝2由点P、A的坐标得则tan∠P AN＝＝＝＝tan∠NAH过点H作HK⊥AN于点K在Rt△ONA中，tan∠ONA＝设HK＝3t，则NK＝t在Rt△AHK中，tan∠NAH＝则AK＝6t则AN＝NK+AK＝t+6t＝＝则t＝则HN＝t＝则OH＝HN﹣ON＝﹣1＝则tan∠TAO＝＝＝．15．解：（1）∵圆心A在x轴上，⊙A经过点O且与QP相切于点P ∴PQ⊥x轴，OP为直径∵tan∠POC＝1，∴PQ＝OP∵在Rt△OPQ中，．∴OP＝18．∴⊙A的半径为9；（2）如图所示，过点A作AM⊥x轴于点M，连接AP∵PQ是⊙A的切线∴AP⊥PQ，则∠APQ＝90°∵AM⊥x轴，QB⊥x轴∴∠AMP＝∠PBC＝90°∴∠P AM＝90°﹣∠APM＝∠QPB∴△APM∽△PBQ∴∵tan∠POC＝1，QB＝18∴OB＝QB＝18∵AM＝2，设MP＝MO＝x∴PB＝18﹣2x∴解得x＝3或x＝6∴MO＝3或MO＝x∴A（3，3）或A（6∴AP＝＝或AP＝．∴半径为或2．（3）∵OP＜10∴BO＝3，P（8∴A（3，2）∵tan∠POC＝6，设D（a∵∴（3﹣a）2+（7﹣a）2＝13解得：a＝0或a＝5∴D（5，5）设抛物线解析式为y＝ax7+bx将点P（6，0），2）代入得，解得：∴y＝﹣x2+6x∵点F可能在点O的左边或点P的右边，则|K FM|＝设直线MF：或联立，得或当或解得：或∴直线MF：或令y＝0，解得：或∴或．。

中考数学二次函数-经典压轴题附详细答案

中考数学二次函数-经典压轴题附详细答案一、二次函数1．如图，已知抛物线2(0)y ax bx c a =++≠的对称轴为直线1x =-，且抛物线与x 轴交于A 、B 两点，与y 轴交于C 点，其中(1,0)A ，(0,3)C .（1）若直线y mx n =+经过B 、C 两点，求直线BC 和抛物线的解析式；（2）在抛物线的对称轴1x =-上找一点M ，使点M 到点A 的距离与到点C 的距离之和最小，求出点M 的坐标；（3）设点P 为抛物线的对称轴1x =-上的一个动点，求使BPC ∆为直角三角形的点P 的坐标.【答案】（1）抛物线的解析式为223y x x =--+，直线的解析式为3y x =+.（2）(1,2)M -；（3）P 的坐标为(1,2)--或(1,4)-或317(+-或317()--. 【解析】分析：（1）先把点A ，C 的坐标分别代入抛物线解析式得到a 和b ，c 的关系式，再根据抛物线的对称轴方程可得a 和b 的关系，再联立得到方程组，解方程组，求出a ，b ，c 的值即可得到抛物线解析式；把B 、C 两点的坐标代入直线y=mx+n ，解方程组求出m 和n 的值即可得到直线解析式；（2）设直线BC 与对称轴x=-1的交点为M ，此时MA+MC 的值最小．把x=-1代入直线y=x+3得y 的值，即可求出点M 坐标；（3）设P （-1，t ），又因为B （-3，0），C （0，3），所以可得BC 2=18，PB 2=（-1+3）2+t 2=4+t 2，PC 2=（-1）2+（t-3）2=t 2-6t+10，再分三种情况分别讨论求出符合题意t 值即可求出点P 的坐标．详解：（1）依题意得：1203b a a b c c ⎧-=-⎪⎪++=⎨⎪=⎪⎩，解得：123a b c =-⎧⎪=-⎨⎪=⎩，∴抛物线的解析式为223y x x =--+.∵对称轴为1x =-，且抛物线经过()1,0A ，∴把()3,0B -、()0,3C 分别代入直线y mx n =+，得303m n n -+=⎧⎨=⎩，解之得：13m n =⎧⎨=⎩， ∴直线y mx n =+的解析式为3y x =+.（2）直线BC 与对称轴1x =-的交点为M ，则此时MA MC +的值最小，把1x =-代入直线3y x =+得2y =，∴()1,2M -.即当点M 到点A 的距离与到点C 的距离之和最小时M 的坐标为()1,2-. （注：本题只求M 坐标没说要求证明为何此时MA MC +的值最小，所以答案未证明MA MC +的值最小的原因）.（3）设()1,P t -，又()3,0B -，()0,3C ，∴218BC =，()2222134PB t t =-++=+，()()222213610PC t t t =-+-=-+， ①若点B 为直角顶点，则222BC PB PC +=，即：22184610t t t ++=-+解得：2t =-，②若点C 为直角顶点，则222BC PC PB +=，即：22186104t t t +-+=+解得：4t =，③若点P 为直角顶点，则222PB PC BC +=，即：22461018t t t ++-+=解得： 1317t +=2317t -=. 综上所述P 的坐标为()1,2--或()1,4-或3171,2⎛+- ⎝⎭或3171,2⎛- ⎝⎭. 点睛：本题综合考查了二次函数的图象与性质、待定系数法求函数（二次函数和一次函数）的解析式、利用轴对称性质确定线段的最小长度、难度不是很大，是一道不错的中考压轴题．2．已知如图，抛物线y =x 2+bx +c 过点A （3，0），B （1，0），交y 轴于点C ，点P 是该抛物线上一动点，点P 从C 点沿抛物线向A 点运动（点P 不与点A 重合），过点P 作PD ∥y 轴交直线AC 于点D ．（1）求抛物线的解析式；（2）求点P 在运动的过程中线段PD 长度的最大值；（3）△APD 能否构成直角三角形？若能请直接写出点P 坐标，若不能请说明理由；（4）在抛物线对称轴上是否存在点M使|MA﹣MC|最大？若存在请求出点M的坐标，若不存在请说明理由．【答案】（1）y=x2﹣4x+3；（2）94；（3）点P（1，0）或（2，﹣1）；（4）M（2，﹣3）．【解析】试题分析：（1）把点A、B的坐标代入抛物线解析式，解方程组得到b、c的值，即可得解；（2）求出点C的坐标，再利用待定系数法求出直线AC的解析式，再根据抛物线解析式设出点P的坐标，然后表示出PD的长度，再根据二次函数的最值问题解答；（3）①∠APD是直角时，点P与点B重合，②求出抛物线顶点坐标，然后判断出点P为在抛物线顶点时，∠PAD是直角，分别写出点P的坐标即可；（4）根据抛物线的对称性可知MA=MB，再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时，|MA﹣MC|最大，然后利用待定系数法求出直线BC的解析式，再求解即可．试题解析：解：（1）∵抛物线y=x2+bx+c过点A（3，0），B（1，0），∴93010b cb c++=⎧⎨++=⎩，解得43bc=-⎧⎨=⎩，∴抛物线解析式为y=x2﹣4x+3；（2）令x=0，则y=3，∴点C（0，3），则直线AC的解析式为y=﹣x+3，设点P（x，x2﹣4x+3）．∵PD∥y轴，∴点D（x，﹣x+3），∴PD=（﹣x+3）﹣（x2﹣4x+3）=﹣x2+3x=﹣（x﹣32）2+94．∵a=﹣1＜0，∴当x=32时，线段PD的长度有最大值94；（3）①∠APD是直角时，点P与点B重合，此时，点P（1，0），②∵y=x2﹣4x+3=（x ﹣2）2﹣1，∴抛物线的顶点坐标为（2，﹣1）．∵A（3，0），∴点P为在抛物线顶点时，∠PAD=45°+45°=90°，此时，点P（2，﹣1）．综上所述：点P（1，0）或（2，﹣1）时，△APD能构成直角三角形；（4）由抛物线的对称性，对称轴垂直平分AB，∴MA=MB，由三角形的三边关系，|MA﹣MC|＜BC，∴当M、B、C三点共线时，|MA﹣MC|最大，为BC的长度，设直线BC的解析式为y=kx+b（k≠0），则3k bb+=⎧⎨=⎩，解得：33kb=-⎧⎨=⎩，∴直线BC的解析式为y=﹣3x+3．∵抛物线y=x2﹣4x+3的对称轴为直线x=2，∴当x=2时，y=﹣3×2+3=﹣3，∴点M （2，﹣3），即，抛物线对称轴上存在点M（2，﹣3），使|MA﹣MC|最大．点睛：本题是二次函数综合题，主要利用了待定系数法求二次函数解析式，二次函数的最值问题，二次函数的对称性以及顶点坐标的求解，（2）整理出PD的表达式是解题的关键，（3）关键在于利用点的坐标特征作出判断，（4）根据抛物线的对称性和三角形的三边关系判断出点M的位置是解题的关键．3．在平面直角坐标系xOy中，已知抛物线的顶点坐标为（2，0），且经过点（4，1），如图，直线y=14x与抛物线交于A、B两点，直线l为y=﹣1．（1）求抛物线的解析式；（2）在l上是否存在一点P，使PA+PB取得最小值？若存在，求出点P的坐标；若不存在，请说明理由．（3）知F（x0，y0）为平面内一定点，M（m，n）为抛物线上一动点，且点M到直线l的距离与点M到点F的距离总是相等，求定点F的坐标．【答案】（1）抛物线的解析式为y=14x2﹣x+1．（2）点P的坐标为（2813，﹣1）．（3）定点F的坐标为（2，1）．【解析】分析：（1）由抛物线的顶点坐标为（2，0），可设抛物线的解析式为y=a（x-2）2，由抛物线过点（4，1），利用待定系数法即可求出抛物线的解析式；（2）联立直线AB与抛物线解析式成方程组，通过解方程组可求出点A、B的坐标，作点B关于直线l的对称点B′，连接AB′交直线l于点P，此时PA+PB取得最小值，根据点B的坐标可得出点B′的坐标，根据点A、B′的坐标利用待定系数法可求出直线AB′的解析式，再利用一次函数图象上点的坐标特征即可求出点P的坐标；（3）由点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征，即可得出（1-12-12y0）m2+（2-2x0+2y0）m+x02+y02-2y0-3=0，由m的任意性可得出关于x0、y0的方程组，解之即可求出顶点F的坐标．详解：（1）∵抛物线的顶点坐标为（2，0），设抛物线的解析式为y=a（x-2）2．∵该抛物线经过点（4，1），∴1=4a，解得：a=14，∴抛物线的解析式为y=14（x-2）2=14x2-x+1．（2）联立直线AB与抛物线解析式成方程组，得：214114y xy x x⎧⎪⎪⎨⎪-+⎪⎩＝＝，解得：11114xy⎧⎪⎨⎪⎩＝＝，2241xy⎧⎨⎩＝＝，∴点A的坐标为（1，14），点B的坐标为（4，1）．作点B关于直线l的对称点B′，连接AB′交直线l于点P，此时PA+PB取得最小值（如图1所示）．∵点B（4，1），直线l为y=-1，∴点B′的坐标为（4，-3）．设直线AB′的解析式为y=kx+b（k≠0），将A（1，14）、B′（4，-3）代入y=kx+b，得：1443k bk b⎧+⎪⎨⎪+-⎩＝＝，解得：131243kb⎧-⎪⎪⎨⎪⎪⎩＝＝，∴直线AB′的解析式为y=-1312x+43，当y=-1时，有-1312x+43=-1，解得：x=2813， ∴点P 的坐标为（2813，-1）．（3）∵点M 到直线l 的距离与点M 到点F 的距离总是相等，∴（m-x 0）2+（n-y 0）2=（n+1）2，∴m 2-2x 0m+x 02-2y 0n+y 02=2n+1．∵M （m ，n ）为抛物线上一动点，∴n=14m 2-m+1， ∴m 2-2x 0m+x 02-2y 0（14m 2-m+1）+y 02=2（14m 2-m+1）+1，整理得：（1-12-12y 0）m 2+（2-2x 0+2y 0）m+x 02+y 02-2y 0-3=0． ∵m 为任意值， ∴000220001110222220230y x y x y y ⎧--⎪⎪-+⎨⎪+--⎪⎩＝＝＝，∴0021x y ⎧⎨⎩＝＝， ∴定点F 的坐标为（2，1）．点睛：本题考查了待定系数法求二次（一次）函数解析式、二次（一次）函数图象上点的坐标特征、轴对称中的最短路径问题以及解方程组，解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数解析式；（2）利用两点之间线段最短找出点P 的位置；（3）根据点M 到直线l 的距离与点M 到点F 的距离总是相等结合二次函数图象上点的坐标特征，找出关于x 0、y 0的方程组．4．如图，在平面直角坐标系中，∠ACB=90°，OC=2OB ，tan ∠ABC=2，点B 的坐标为（1，0）．抛物线y=﹣x 2+bx+c 经过A 、B 两点．（1）求抛物线的解析式；（2）点P 是直线AB 上方抛物线上的一点，过点P 作PD 垂直x 轴于点D ，交线段AB 于点E ，使PE=12DE ．①求点P 的坐标；②在直线PD 上是否存在点M ，使△ABM 为直角三角形？若存在，求出符合条件的所有点M 的坐标；若不存在，请说明理由．【答案】（1）y=﹣x 2﹣3x+4；（2）①P （﹣1，6），②存在，M （﹣1，11）或（﹣1，311）或（﹣1，﹣1）或（﹣1，132）．【解析】【分析】（1）先根据已知求点A 的坐标，利用待定系数法求二次函数的解析式；（2）①先得AB 的解析式为：y=-2x+2，根据PD ⊥x 轴，设P （x ，-x 2-3x+4），则E （x ，-2x+2），根据PE=12DE ，列方程可得P 的坐标； ②先设点M 的坐标，根据两点距离公式可得AB ，AM ，BM 的长，分三种情况：△ABM 为直角三角形时，分别以A 、B 、M 为直角顶点时，利用勾股定理列方程可得点M 的坐标．【详解】解：（1）∵B （1，0），∴OB=1，∵OC=2OB=2，∴C （﹣2，0），Rt △ABC 中，tan ∠ABC=2， ∴AC 2BC =， ∴AC 23=， ∴AC=6， ∴A （﹣2，6），把A （﹣2，6）和B （1，0）代入y=﹣x 2+bx+c 得：42610b c b c --+=⎧⎨-++=⎩，解得：34b c =-⎧⎨=⎩， ∴抛物线的解析式为：y=﹣x 2﹣3x+4；（2）①∵A （﹣2，6），B （1，0），∴AB 的解析式为：y=﹣2x+2，设P（x，﹣x2﹣3x+4），则E（x，﹣2x+2），∵PE=12DE，∴﹣x2﹣3x+4﹣（﹣2x+2）=12（﹣2x+2），∴x=-1或1（舍），∴P（﹣1，6）；②∵M在直线PD上，且P（﹣1，6），设M（﹣1，y），∵B（1，0），A（﹣2，6）∴AM2=（﹣1+2）2+（y﹣6）2=1+（y﹣6）2，BM2=（1+1）2+y2=4+y2，AB2=（1+2）2+62=45，分三种情况：i）当∠AMB=90°时，有AM2+BM2=AB2，∴1+（y﹣6）2+4+y2=45，解得：y=311，∴M（﹣1，11）或（﹣1，311ii）当∠ABM=90°时，有AB2+BM2=AM2，∴45+4+y2=1+（y﹣6）2，∴y=﹣1，∴M（﹣1，﹣1），iii）当∠BAM=90°时，有AM2+AB2=BM2，∴1+（y﹣6）2+45=4+y2，∴y=132，∴M（﹣1，132）；综上所述，点M的坐标为：∴M（﹣1，11）或（﹣1，311）或（﹣1，﹣1）或（﹣1，132）．【点睛】此题是二次函数的综合题，考查了待定系数法求二次函数的解析式，铅直高度和勾股定理的运用，直角三角形的判定等知识．此题难度适中，解题的关键是注意方程思想与分类讨论思想的应用．5．如图，已知A （﹣2，0），B （4，0），抛物线y=ax 2+bx ﹣1过A 、B 两点，并与过A 点的直线y=﹣12x ﹣1交于点C ．（1）求抛物线解析式及对称轴；（2）在抛物线的对称轴上是否存在一点P ，使四边形ACPO 的周长最小？若存在，求出点P 的坐标，若不存在，请说明理由；（3）点M 为y 轴右侧抛物线上一点，过点M 作直线AC 的垂线，垂足为N ．问：是否存在这样的点N ，使以点M 、N 、C 为顶点的三角形与△AOC 相似，若存在，求出点N 的坐标，若不存在，请说明理由．【答案】（1）抛物线解析式为：y=211184x x --，抛物线对称轴为直线x=1；（2）存在P 点坐标为（1，﹣12）；（3）N 点坐标为（4，﹣3）或（2，﹣1）【解析】分析：（1）由待定系数法求解即可；（2）将四边形周长最小转化为PC+PO 最小即可；（3）利用相似三角形对应点进行分类讨论，构造图形．设出点N 坐标，表示点M 坐标代入抛物线解析式即可．详解：（1）把A （-2，0），B （4，0）代入抛物线y=ax 2+bx-1，得 042101641a b a b --⎧⎨+-⎩＝＝解得1814a b ⎧⎪⎪⎨⎪-⎪⎩＝＝ ∴抛物线解析式为：y=18x 2−14x−1∴抛物线对称轴为直线x=-141 228ba-=-⨯＝1（2）存在使四边形ACPO的周长最小，只需PC+PO最小∴取点C（0，-1）关于直线x=1的对称点C′（2，-1），连C′O与直线x=1的交点即为P 点．设过点C′、O直线解析式为：y=kx∴k=-12∴y=-12x则P点坐标为（1，-12）（3）当△AOC∽△MNC时，如图，延长MN交y轴于点D，过点N作NE⊥y轴于点E∵∠ACO=∠NCD，∠AOC=∠CND=90°∴∠CDN=∠CAO由相似，∠CAO=∠CMN∴∠CDN=∠CMN∵MN⊥AC∴M、D关于AN对称，则N为DM中点设点N坐标为（a，-12a-1）由△EDN∽△OAC∴ED=2a∴点D坐标为（0，-52a−1）∵N为DM中点∴点M坐标为（2a，32a−1）把M代入y=18x2−14x−1，解得a=4则N点坐标为（4，-3）当△AOC∽△CNM时，∠CAO=∠NCM∴CM∥AB则点C关于直线x=1的对称点C′即为点N由（2）N（2，-1）∴N点坐标为（4，-3）或（2，-1）点睛：本题为代数几何综合题，考查了待定系数、两点之间线段最短的数学模型构造、三角形相似．解答时，应用了数形结合和分类讨论的数学思想．6．（12分）如图所示是隧道的截面由抛物线和长方形构成，长方形的长是12 m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y=16-x2+bx+c表示，且抛物线上的点C到OB的水平距离为3 m，到地面OA的距离为172m.（1）求抛物线的函数关系式，并计算出拱顶D到地面OA的距离；（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向车道，那么这辆货车能否安全通过？（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？【答案】（1）抛物线的函数关系式为y=16-x2+2x+4，拱顶D到地面OA的距离为10 m；(2)两排灯的水平距离最小是3．【解析】【详解】试题分析：根据点B和点C在函数图象上，利用待定系数法求出b和c的值，从而得出函数解析式，根据解析式求出顶点坐标，得出最大值；根据题意得出车最外侧与地面OA的交点为（2,0）（或（10,0）），然后求出当x=2或x=10时y的值，与6进行比较大小，比6大就可以通过，比6小就不能通过；将y=8代入函数，得出x的值，然后进行做差得出最小值．试题解析：（1）由题知点17(0,4),3,2B C⎛⎫⎪⎝⎭在抛物线上所以41719326cb c=⎧⎪⎨=-⨯++⎪⎩，解得24bc=⎧⎨=⎩，所以21246y x x=-++所以，当62bxa=-=时，10ty=≦答：21246y x x=-++，拱顶D到地面OA的距离为10米（2）由题知车最外侧与地面OA的交点为（2,0）（或（10,0））当x=2或x=10时，2263y=>，所以可以通过（3）令8y=，即212486x x-++=，可得212240x x-+=，解得12623,623x x=+=-1243x x-=答：两排灯的水平距离最小是43考点：二次函数的实际应用．7．如图，抛物线212222y x x=-++与x轴相交于A B，两点，（点A在B点左侧）与y轴交于点C.（Ⅰ）求A B，两点坐标.（Ⅱ）连结AC，若点P在第一象限的抛物线上，P的横坐标为t，四边形ABPC的面积为S.试用含t的式子表示S，并求t为何值时，S最大.（Ⅲ）在（Ⅱ）的基础上，若点,G H分别为抛物线及其对称轴上的点，点G的横坐标为m，点H的纵坐标为n，且使得以,,,A G H P四点构成的四边形为平行四边形，求满足条件的,m n的值.【答案】（Ⅰ）(A B ；（Ⅱ）2(2S t t =--+<<,当t =时，S =最大；（Ⅲ）满足条件的点m n 、的值为：34m n ==，或1524m n ==-，或124m n =-= 【解析】【分析】（Ⅰ）令y=0，建立方程求解即可得出结论；（Ⅱ）设出点P 的坐标，利用S=S △AOC +S 梯形OCPQ +S △PQB ，即可得出结论；（Ⅲ）分三种情况，利用平行四边形的性质对角线互相平分和中点坐标公式建立方程组即可得出结论．【详解】解：（Ⅰ）抛物线21222y x x =-++，令0y =，则212022x x -++=，解得：x =x =∴((,A B（Ⅱ）由抛物线21222y x x =-++，令0x =，∴2y =，∴()0,2C ，如图1，点P 作PQ x ⊥轴于Q ， ∵P 的横坐标为t ，∴设(),P t p ，∴212,,22p t PQ p BQ t OQ t =-++===，∴()()11122222AOC PQB OCPQ S S S S p t t p =++=++⨯+⨯⨯V V 梯形 1122t pt pt t =++-=++21222t t ⎫=-+++⎪⎪⎭2t t =+<<，∴当t =时，S =最大（Ⅲ）由（Ⅱ）知，2t =，∴)2,2P，∵抛物线212222y x x =-++的对称轴为22x =， ∴设2122,2,2G m m H n ⎛⎫⎫-++ ⎪⎪ ⎪⎪⎝⎭⎝⎭以,,,A G H P 四点构成的四边形为平行四边形，()2,0A ， ①当AP 和HG 为对角线时，∴()2112111222,2022222222m m m n ⎛⎫⎛⎫=++=-+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， ∴2324m n =-=， ②当AG 和PH 是对角线时，∴(()2112112122,2022222222m m m n ⎫⎛⎫=-+++=+⎪ ⎪⎪ ⎪⎭⎝⎭， ∴215,24m n ==-， ③AH 和PG 为对角线时，∴(()2121112122,2202222222m m m n ⎛⎫⎛⎫-=+-+++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， ∴32124m n =-=，即：满足条件的点m n 、的值为：234m n ==，或52154m n ==-，或3214m n == 【点睛】此题是二次函数综合题，主要考查了坐标轴上点的特点，三角形的面积公式，梯形的面积公式，平行四边形的性质，中点坐标公式，用方程的思想解决问题是解本题的关键．8．如图，抛物线y＝ax2＋bx（a≠0）过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．（1）求抛物线的表达式；（2）直接写出点C的坐标，并求出△ABC的面积；（3）点P是抛物线上一动点，且位于第四象限，是否存在这样的点P，使得△ABP的面积为△ABC面积的2倍？若存在，求出点P的坐标，若不存在，请说明理由；（4）若点M在直线BH上运动，点N在x轴正半轴上运动，当以点C，M，N为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN的面积．【答案】（1）y＝－x2＋4x；（2）C（3，3），面积为3；（3）P的坐标为（5，－5）；（4）52或5．【解析】试题分析：（1）利用待定系数法进行求解即可；（2）先求出抛物线的对称轴，利用对称性即可写出点C的坐标，利用三角形面积公式即可求面积；（3）利用三角形的面积以及点P所处象限的特点即可求；（4）分情况进行讨论，确定点M、N，然后三角形的面积公式即可求.试题解析：（1）将A（4，0），B（1，3）代入到y＝ax2＋bx中，得16403a ba b+=⎧⎨+=⎩，解得14ab=-⎧⎨=⎩，∴抛物线的表达式为y＝－x2＋4x．（2）∵抛物线的表达式为y＝－x2＋4x，∴抛物线的对称轴为直线x＝2．又C，B关于对称轴对称，∴C（3，3）．∴BC＝2，∴S△ABC＝12×2×3＝3．（3）存在点P．作PQ⊥BH于点Q，设P（m，－m2＋4m）．∵S△ABP＝2S△ABC，S△ABC＝3，∴S△ABP＝6．∵S△ABP＋S△BPQ＝S△ABH＋S梯形AHQP∴6＋12×（m－1）×（3＋m2－4m）＝12×3×3＋12×（3＋m－1）（m2－4m）整理得m2－5m＝0，解得m1＝0（舍），m2＝5，∴点P的坐标为（5，－5）．（4）52或5．提示：①当以M为直角顶点，则S△CMN＝52；②当以N为直角顶点，S△CMN＝5；③当以C为直角顶点时，此种情况不存在．【点睛】本题是二次函数的综合题，主要考查待定系数法求解析式，三角形面积、直角三角形的判定等，能正确地根据题意确定图形，分情况进行讨论是解题的关键.9．对于某一函数给出如下定义：若存在实数m，当其自变量的值为m时，其函数值等于﹣m，则称﹣m为这个函数的反向值．在函数存在反向值时，该函数的最大反向值与最小反向值之差n称为这个函数的反向距离．特别地，当函数只有一个反向值时，其反向距离n为零．例如，图中的函数有4，﹣1两个反向值，其反向距离n等于5．（1）分别判断函数y＝﹣x+1，y＝1x-，y＝x2有没有反向值？如果有，直接写出其反向距离；（2）对于函数y＝x2﹣b2x，①若其反向距离为零，求b的值；②若﹣1≤b≤3，求其反向距离n的取值范围；（3）若函数y＝223()3()x x x mx x x m⎧-≥⎨--<⎩请直接写出这个函数的反向距离的所有可能值，并写出相应m的取值范围．【答案】（1）y＝−1x有反向值，反向距离为2；y＝x2有反向值，反向距离是1；（2）①b＝±1；②0≤n≤8；（3）当m＞2或m≤﹣2时，n＝2，当﹣2＜m≤2时，n＝4．【解析】【分析】(1)根据题目中的新定义可以分别计算出各个函数是否有方向值，有反向值的可以求出相应的反向距离；(2)①根据题意可以求得相应的b的值；②根据题意和b的取值范围可以求得相应的n的取值范围；(3)根据题目中的函数解析式和题意可以解答本题．【详解】(1)由题意可得，当﹣m＝﹣m+1时，该方程无解，故函数y＝﹣x+1没有反向值，当﹣m＝1m-时，m＝±1，∴n＝1﹣(﹣1)＝2，故y＝1x-有反向值，反向距离为2，当﹣m＝m2，得m＝0或m＝﹣1，∴n＝0﹣(﹣1)＝1，故y＝x2有反向值，反向距离是1；(2)①令﹣m＝m2﹣b2m，解得，m＝0或m＝b2﹣1，∵反向距离为零，∴|b2﹣1﹣0|＝0，解得，b＝±1；②令﹣m＝m2﹣b2m，解得，m＝0或m＝b2﹣1，∴n＝|b2﹣1﹣0|＝|b2﹣1|，∵﹣1≤b≤3，∴0≤n≤8；(3)∵y＝223()3() x x x mx x x m⎧-≥⎨--<⎩，∴当x≥m时，﹣m＝m2﹣3m，得m＝0或m＝2，∴n＝2﹣0＝2，∴m＞2或m≤﹣2；当x＜m时，﹣m ＝﹣m 2﹣3m ，解得，m ＝0或m ＝﹣4， ∴n ＝0﹣(﹣4)＝4， ∴﹣2＜m ≤2，由上可得，当m ＞2或m ≤﹣2时，n ＝2，当﹣2＜m ≤2时，n ＝4．【点睛】本题是一道二次函数综合题，解答本题的关键是明确题目中的新定义，找出所求问题需要的条件，利用新定义解答相关问题．10．已知关于x 的一元二次方程x 2﹣（2k +1）x +k 2＝0有两个实数根．（1）求k 的取值范围；（2）设x 1，x 2是方程两根，且121111x x k +=-，求k 的值．【答案】（1）k ≥﹣14；（2）k【解析】【分析】（1）根据方程有两个实数根可以得到△≥0，从而求得k 的取值范围；（2）利用根与系数的关系将两根之和和两根之积代入代数式求k 的值即可. 【详解】解：（1）△＝（2k +1）2﹣4k 2＝4k 2+4k +1﹣4k 2＝4k +1 ∵△≥0 ∴4k +1≥0 ∴k ≥﹣14；（2）∵x 1，x 2是方程两根， ∴x 1+x 2＝2k +1 x 1x 2＝k 2，又∵121111x x k +=-， ∴121211x x x x k +=⋅-，即22111k k k +=+ ，解得：12k k ==又∵k ≥﹣14，即：k＝152-．【点睛】本题考查了根与系数的关系以及一元二次方程的解，根的判别式等知识，牢记“两根之和等于ba-，两根之积等于ca”是解题的关键.11．已知点A（﹣1，2）、B（3，6）在抛物线y=ax2+bx上(1)求抛物线的解析式；(2)如图1，点F的坐标为（0，m）（m＞2），直线AF交抛物线于另一点G，过点G作x 轴的垂线，垂足为H．设抛物线与x轴的正半轴交于点E，连接FH、AE，求证：FH∥AE；(3)如图2，直线AB分别交x轴、y轴于C、D两点．点P从点C出发，沿射线CD方向匀速运动，速度为每秒个单位长度；同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM=2PM，直接写出t的值．【答案】(1)抛物线的解析式为y=x2﹣x；(2)证明见解析；(3)当运动时间为或秒时，QM=2PM．【解析】【分析】（1）（1）A，B的坐标代入抛物线y=ax2+bx中确定解析式；（2）把A点坐标代入所设的AF的解析式，与抛物线的解析式构成方程组，解得G点坐标，再通过证明三角形相似，得到同位角相等，两直线平行；（3）具体见详解.【详解】．解：（1）将点A（﹣1，2）、B（3，6）代入中，，解得：，∴抛物线的解析式为y=x2﹣x．（2）证明：设直线AF的解析式为y=kx+m，将点A（﹣1，2）代入y=kx+m中，即﹣k+m=2，∴k=m﹣2，∴直线AF的解析式为y=（m﹣2）x+m．联立直线AF和抛物线解析式成方程组，，解得：或，∴点G的坐标为（m，m2﹣m）．∵GH⊥x轴，∴点H的坐标为（m，0）．∵抛物线的解析式为y=x2﹣x=x（x﹣1），∴点E的坐标为（1，0）．过点A作AA′⊥x轴，垂足为点A′，如图1所示．∵点A（﹣1，2），∴A′（﹣1，0），∴AE=2，AA′=2．∴ =1， = =1，∴= ，∵∠AA′E=∠FOH，∴△AA′E∽△FOH，∴∠AEA′=∠FHO，∴FH∥AE．（3）设直线AB的解析式为y=k0x+b0，将A（﹣1，2）、B（3，6）代入y=k0x+b0中，得，解得：，∴直线AB的解析式为y=x+3，当运动时间为t秒时，点P的坐标为（t﹣3，t），点Q的坐标为（t，0）．当点M在线段PQ上时，过点P作PP′⊥x轴于点P′，过点M作MM′⊥x轴于点M′，则△PQP′∽△MQM′，如图2所示，∵QM=2PM，∴ =，∴QM′=QP'=2，MM′=PP'=t，∴点M的坐标为（t﹣2， t）．又∵点M在抛物线y=x2﹣x上，∴ t=（t﹣2）2﹣（t﹣2），解得：t=；当点M在线段QP的延长线上时，同理可得出点M的坐标为（t﹣6，2t），∵点M在抛物线y=x2﹣x上，∴2t=（t﹣6）2﹣（t﹣6），解得：t=．综上所述：当运动时间秒或时，QM=2PM．【点睛】本题考查二次函数综合运用，综合能力是解题关键.12．如图，已知抛物线经过原点O，顶点A（1，﹣1），且与直线y＝kx+2相交于B（2，0）和C两点（1）求抛物线和直线BC的解析式；（2）求证：△ABC是直角三角形；（3）抛物线上存在点E（点E不与点A重合），使∠BCE＝∠ACB，求出点E的坐标；（4）在抛物线的对称轴上是否存在点F，使△BDF是等腰三角形？若存在，请直接写出点F的坐标．【答案】（1）y ＝x 2﹣2x ，y ＝﹣x +2；（2）详见解析；（3）E （5524,）；（4）符合条件的点F 的坐标（17171，71，27【解析】【分析】（1）将B （2，0）代入设抛物线解析式y ＝a （x ﹣1）2﹣1，求得a ，将B （2，0）代入y ＝kx +2，求得k ；（2）分别求出AB 2、BC 2、AC 2，根据勾股定理逆定理即可证明；（3）作∠BCE ＝∠ACB ，与抛物线交于点E ，延长AB ，与CE 的延长线交于点A '，过A '作A 'H 垂直x 轴于点H ，设二次函数对称轴于x 轴交于点G ．根据对称与三角形全等，求得A '（3，1），然后求出A 'C 解析式，与抛物线解析式联立，求得点E 坐标；（4）设F （1，m ），分三种情况讨论：①当BF ＝BD 2122m +=②当DF ＝BD 24522m m -+=，③当BF ＝DF 22145m m m +-+m ＝1，然后代入即可．【详解】（1）设抛物线解析式y ＝a （x ﹣1）2﹣1，将B （2，0）代入，0＝a （2﹣1）2﹣1，∴a ＝1，抛物线解析式：y ＝（x ﹣1）2﹣1＝x 2﹣2x ，将B （2，0）代入y ＝kx +2，0＝2k +2，k ＝﹣1，∴直线BC 的解析式：y ＝﹣x +2；（2）联立222y x y x x =-+⎧⎨=-⎩，解得1113x y =-⎧⎨=⎩，2220x y =⎧⎨=⎩， ∴C （﹣1，3），∵A （1，﹣1），B （2，0），∴AB 2＝（1﹣2）2+（﹣1﹣0）2＝2，AC 2＝[1﹣（﹣1）]2+（﹣1﹣3）2＝20，BC 2＝[2﹣（﹣1）]2+（0﹣3）2＝18，∴AB 2+BC 2＝AC 2，∴△ABC 是直角三角形；（3）如图，作∠BCE ＝∠ACB ，与抛物线交于点E ，延长AB ，与CE 的延长线交于点A '，过A '作A 'H 垂直x 轴于点H ，设二次函数对称轴于x 轴交于点G ．∵∠BCE ＝∠ACB ，∠ABC ＝90°，∴点A 与A '关于直线BC 对称，AB ＝A 'B ，可知△AFB ≌△A 'HB （AAS ），∵A （1，﹣1），B （2，0）∴AG ＝1，BG ＝OG ＝1，∴BH ＝1，A 'H ＝1，OH ＝3，∴A '（3，1），∵C （﹣1，3），∴直线A 'C ：1522y x =-+，联立：215222y x y x x⎧=-+⎪⎨⎪=-⎩，解得13x y =-⎧⎨=⎩或5254x y ⎧=⎪⎪⎨⎪=⎪⎩， ∴E （52，54）；（4）∵抛物线的对称轴：直线x ＝1，∴设F （1，m ），直线BC 的解析式：y ＝﹣x +2；∴D （0，2）∵B （2，0），∴BD ＝12x x 222(21)(0)1BF m m =-+-=+，222(10)(2)45DF m m m =-+-=-+，①当BF ＝BD 时，2122m +=，m ＝±7，∴F 坐标（1，7）或（1，﹣7）②当DF ＝BD 时，24522m m -+=，m ＝2±7，∴F 坐标（1，2+7）或（1，2﹣7）③当BF ＝DF 时，22145m m m +=-+，m ＝1，F （1，1），此时B 、D 、F 在同一直线上，不符合题意．综上，符合条件的点F 的坐标（1，7）或（1，﹣7）或（1，2+7）或（1，2﹣7）．【点睛】考查了二次函数，熟练掌握二次函数的性质是解题的关键．13．如图，抛物线y ＝﹣x 2+bx +c 经过A （﹣1，0），B （3，0）两点，且与y 轴交于点C ，点D 是抛物线的顶点，抛物线对称轴DE 交x 轴于点E ，连接BD ．（1）求经过A ，B ，C 三点的抛物线的函数表达式；（2）点P 是线段BD 上一点，当PE ＝PC 时，求点P 的坐标．【答案】（1）y ＝﹣x 2+2x +3；（2）点P 的坐标为（2，2）．【解析】【分析】（1）利用待定系数法求出过A ，B ，C 三点的抛物线的函数表达式；（2）连接PC 、PE ，利用公式求出顶点D 的坐标，利用待定系数法求出直线BD 的解析式，设出点P 的坐标为（x ，﹣2x +6），利用勾股定理表示出PC 2和PE 2，根据题意列出方程，解方程求出x的值，计算求出点P的坐标．【详解】解：（1）∵抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，∴10930b cb c--+=⎧⎨-++=⎩，解得23bc=⎧⎨=⎩，∴所求的抛物线的函数表达式为y＝﹣x2+2x+3；（2）如图，连接PC，PE．抛物线的对称轴为x＝222(1)ba-=-⨯-＝1．当x＝1时，y＝4，∴点D的坐标为（1，4）．设直线BD的解析式为y＝kx+b，则430 k bk b+=⎧⎨+=⎩，解得26kb=-⎧⎨=⎩．∴直线BD的解析式为：y＝2x+6，设点P的坐标为（x，﹣2x+6），又C（0，3），E（1，0），则PC2＝x2+（3+2x﹣6）2，PE2＝（x﹣1）2+（﹣2x+6）2，∵PC＝PE，∴x2+（3+2x﹣6）2＝（x﹣1）2+（﹣2x+6）2，解得，x＝2，则y＝﹣2×2+6＝2，∴点P的坐标为（2，2）．【点睛】本题考查的是二次函数的图象和性质、待定系数法求函数解析式，掌握二次函数的图象和性质、灵活运用待定系数法是解题的关键．14．如图，若b是正数，直线l：y=b与y轴交于点A；直线a：y=x﹣b与y轴交于点B；抛物线L ：y =﹣x 2+bx 的顶点为C ，且L 与x 轴右交点为D ．（1）若AB =8，求b 的值，并求此时L 的对称轴与a 的交点坐标；（2）当点C 在l 下方时，求点C 与l 距离的最大值；（3）设x 0≠0，点（x 0，y 1），（x 0，y 2），（x 0，y 3）分别在l ，a 和L 上，且y 3是y 1，y 2的平均数，求点（x 0，0）与点D 间的距离；（4）在L 和a 所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出b =2019和b =2019.5时“美点”的个数．【答案】（1）b =4，（2，﹣2 ）；（2）1；（3）12；（4）当b =2019时“美点”的个数为4040个，b =2019.5时“美点”的个数为1010个．【解析】【分析】（1）求出A 、B 的坐标，由AB =8，可求出b 的值．从而得到L 的解析式，找出L 的对称轴与a 的交点即可；（2）通过配方，求出L 的顶点坐标，由于点C 在l 下方，则C 与l 的距离24b b -，配方即可得出结论；（3）由題意得y 1+y 2=2y 3，进而有b +x 0﹣b =2（﹣x 02+bx 0）解得x 0的值，求出L 与x 轴右交点为D 的坐标，即可得出结论；（4）①当b =2019时，抛物线解析式L ：y =﹣x 2+2019x 直线解析式a ：y =x ﹣2019，美点”总计4040个点，②当b =2019.5时，抛物线解析式L ：y =﹣x 2+2019.5x ，直线解析式a ：y =x ﹣2019.5，“美点”共有1010个．【详解】（1）当x =0吋，y =x ﹣b =﹣b ，∴B （0，﹣b ）．∵AB =8，而A （0，b ），∴b ﹣（﹣b ）=8，∴b =4，∴L ：y =﹣x 2+4x ，∴L 的对称轴x =2，当x =2时，y =x ﹣4=﹣2，∴L 的对称轴与a 的交点为（2，﹣2 ）；（2）y =﹣（x 2b -）224b +，∴L 的顶点C （2b ，24b ）． ∵点C 在l 下方，∴C 与l 的距离b 2144b -=-（b ﹣2）2+1≤1，∴点C 与l 距离的最大值为1；（3）∵y 3是y 1，y 2的平均数，∴y 1+y 2=2y 3，∴b +x 0﹣b =2（﹣x 02+bx 0），解得：x 0=0或x 0=b 12-． ∵x 0≠0，∴x 0=b 12-，对于L ，当y =0吋，0=﹣x 2+bx ，即0=﹣x （x ﹣b ），解得：x 1=0，x 2=b ． ∵b ＞0，∴右交点D （b ，0），∴点（x 0，0）与点D 间的距离b ﹣（b 12-）12=．（4）①当b =2019时，抛物线解析式L ：y =﹣x 2+2019x ，直线解析式a ：y =x ﹣2019．联立上述两个解析式可得：x 1=﹣1，x 2=2019，∴可知每一个整数x 的值都对应的一个整数y 值，且﹣1和2019之间（包括﹣1和﹣2019）共有2021个整数；∵另外要知道所围成的封闭图形边界分两部分：线段和抛物线，∴线段和抛物线上各有2021个整数点，∴总计4042个点．∵这两段图象交点有2个点重复，∴美点”的个数：4042﹣2=4040（个）；②当b =2019.5时，抛物线解析式L ：y =﹣x 2+2019.5x ，直线解析式a ：y =x ﹣2019.5，联立上述两个解析式可得：x 1=﹣1，x 2=2019.5，∴当x 取整数时，在一次函数y =x ﹣2019.5上，y 取不到整数值，因此在该图象上“美点”为0，在二次函数y =x 2+2019.5x 图象上，当x 为偶数时，函数值y 可取整数，可知﹣1到2019.5之间有1010个偶数，因此“美点”共有1010个．故b =2019时“美点”的个数为4040个，b =2019.5时“美点”的个数为1010个．【点睛】本题考查了二次函数，熟练运用二次函数的性质以及待定系数法求函数解析式是解题的关键．15．如图，已知直线AB 与抛物线C ：2y ax 2x c =++ 相交于()1,0A -和点()B 2,3两点.⑴求抛物线C 的函数表达式；⑵若点M 是位于直线AB 上方抛物线上的一动点，以MA MB 、为相邻两边作平行四边形MANB ,当平行四边形MANB 的面积最大时，求此时四边形MANB 的面积S 及点M 的坐标；⑶在抛物线C 的对称轴上是否存在定点F ,使抛物线C 上任意一点P 到点F 的距离等于到直线17y 4=的距离，若存在，求出定点F 的坐标；若不存在，请说明理由. 【答案】⑴2y x 2x 3=-++；⑵当12a =，S □MANB =2S △ABM =274 ，此时115M ,24⎛⎫ ⎪⎝⎭；⑶存在. 当15F 1,4⎛⎫ ⎪⎝⎭时，无论x 取任何实数，均有PG PF =. 理由见解析. 【解析】【分析】（1）利用待定系数法，将A ，B 的坐标代入y=ax 2+2x+c 即可求得二次函数的解析式；（2）过点M 作MH ⊥x 轴于H ，交直线AB 于K ，求出直线AB 的解析式，设点M （a ，-a 2+2a+3），则K （a ，a+1），利用函数思想求出MK 的最大值，再求出△AMB 面积的最大值，可推出此时平行四边形MANB 的面积S 及点M 的坐标；（3）如图2，分别过点B ，C 作直线y=174的垂线，垂足为N ，H ，设抛物线对称轴上存在点F ，使抛物线C 上任意一点P 到点F 的距离等于到直线y=174的距离，其中F （1，a ），连接BF ，CF ，则可根据BF=BN ，CF=CN 两组等量关系列出关于a 的方程组，解方程组即可．【详解】（1）由题意把点（-1，0）、（2，3）代入y=ax 2+2x+c ，得，20443a c a c -+=⎧⎨++=⎩，解得a=-1，c=3，∴此抛物线C 函数表达式为：y=-x 2+2x+3；（2）如图1，过点M 作MH ⊥x 轴于H ，交直线AB 于K ，将点（-1，0）、（2，3）代入y=kx+b 中，得，0 23k bk b-+⎧⎨+⎩＝＝，解得，k=1，b=1，∴y AB=x+1，设点M（a，-a2+2a+3），则K（a，a+1），则MK=-a2+2a+3-（a+1）=-（a-12）2+94，根据二次函数的性质可知，当a=12时，MK有最大长度94，∴S△AMB最大=S△AMK+S△BMK=12MK•AH+12MK•（x B-x H）=12MK•（x B-x A）=12×94×3=278，∴以MA、MB为相邻的两边作平行四边形MANB，当平行四边形MANB的面积最大时，S最大=2S△AMB最大=2×278=274，M（12，154）；（3）存在点F，∵y=-x2+2x+3=-（x-1）2+4，∴对称轴为直线x=1，当y=0时，x1=-1，x2=3，∴抛物线与点x轴正半轴交于点C（3，0），如图2，分别过点B，C作直线y=174的垂线，垂足为N，H，。

中考数学压轴题专题二次函数的经典综合题含详细答案

一、二次函数真题与模拟题分类汇编（难题易错题）1．已知，抛物线y=x 2+2mx(m 为常数且m≠0）．（1）判断该抛物线与x 轴的交点个数，并说明理由．（2）若点A （-n+5，0），B(n-1，0)在该抛物线上，点M 为抛物线的顶点，求△ABM 的面积．（3）若点（2，p)，（3，g ），（4，r)均在该抛物线上，且p<g<r ，求m 的取值范围．【答案】（1）抛物线与x 轴有2个交点，理由见解析；（2）△ABM 的面积为8；（3）m 的取值范围m>-2.5【解析】【分析】（1）首先算出根的判别式b 2-4ac 的值，根据偶数次幂的非负性，判断该值一定大于0，从而根据抛物线与x 轴交点个数与根的判别式的关系即可得出结论；（2）根据抛物线的对称性及A,B 两点的坐标特点求出抛物线的对称轴直线为x=2.从而再根据抛物线对称轴直线公式建立方程，求解算出m 的值，进而求出抛物线的解析式，得出A,B,M 三点的坐标，根据三角形的面积计算方法，即可算出答案；（3）方法一（图象法）：根据抛物线的对称轴直线及开口方向判断出当对称轴在直线x=3的右边时，显然不符合题目条件；当对称轴在直线x=2的左边时，显然符合题目条件（如图2），从而列出不等式得出m 的取值范围；当对称轴在直线x=2和x=3之间时，满足3-（-m)>-m-2即可（如图3），再列出不等式得出m 的取值范围，综上所述，求出m 的取值范围；方法二（代数法）：将三点的横坐标分贝代入抛物线的解析式，用含m 的式子表示出p,g,r ，再代入 p<g<r 即可列出关于m 的不等式组，求解即可。

【详解】（1）解：抛物线与x 轴有2个交点。

理由如下：∵m≠0，∴b 2-4ac =（2m ）2-4×1×0=4m 2>0．∴抛物线与x 轴有2个交点（2）解：∵点A （-n+5，0），B(n-1，0)在抛物线上∴抛物线的对称轴x=5122n n -++-= ∴ 221m ⨯=2,即m=-2． ∴抛物线的表达式为y=x 2-4x ．∴点A （0，0），点B （4，0）或点A （4，0），点B （0，0），点M （2，-4） ∴△ABM 的面积为12×4×4=8 （3）解：方法一（图象法）：∵抛物线y=x 2+2mx 的对称轴为x=-m ，开口向上。

2014年北师大九年级数学上下册精选题练习(圆除外,主要二次函数)(含答案)

2014年北师大九年级数学上下册精选题练习一．选择题（共20小题）22．（2014•广东）二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（），3．（2014•兰州）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，则下列四个结论错误的是（）4．（2014•达州）如图是二次函数y=ax2+bx+c的图象的一部分，对称轴是直线x=1．①b2＞4ac；②4a﹣2b+c＜0；③不等式ax2+bx+c＞0的解集是x≥3.5；④若（﹣2，y1），（5，y2）是抛物线上的两点，则y1＜y2．上述4个判断中，正确的是（）5．（2014•黔东南州）如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列4个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0其中正确结论的有（）6．（2014•资阳）二次函数y=ax 2+bx+c （a ≠0）的图象如图，给出下列四个结论：①4ac ﹣b 2＜0；②4a+c ＜2b ；③3b+2c ＜0；④m （am+b ）+b ＜a （m ≠﹣1），其中正确结论的个数是（）7．（2014•北海）函数y=ax 2+1与y=（a ≠0）在同一平面直角坐标系中的图象可能是（）．CD ．8．（2014•威海）如图，在下列网格中，小正方形的边长均为1，点A 、B 、O 都在格点上，则∠AOB 的正弦值是（）．CD ．2D ．10．（2014•凉山州）拦水坝横断面如图所示，迎水坡AB 的坡比是1：，坝高BC=10m ，则坡面AB 的长度是（）m m．C D．13．（2014•牡丹江）若x：y=1：3，2y=3z，则的值是（）D22216．（2014•玉林）x1，x2是关于x的一元二次方程x2﹣mx+m﹣2=0的两个实数根，是否存在实数m使+=022218．（2014•杭州）让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则两个数的和是2的倍数或是3的倍数的概率等于（）．C D．20．（2014•上海）如图，已知AC、BD是菱形ABCD的对角线，那么下列结论一定正确的是（）二．解答题（共5小题）21．（2014•南京）已知二次函数y=x2﹣2mx+m2+3（m是常数）．（1）求证：不论m为何值，该函数的图象与x轴没有公共点；（2）把该函数的图象沿y轴向下平移多少个单位长度后，得到的函数的图象与x轴只有一个公共点？22．（2014•广东）如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0.1m）．（参考数据：≈1.414，≈1.732）23．如图，Rt△ABC中，∠ACB=90°，AC=8，BC=6，矩形PQMN的顶点P、N分别在AC、BC上，Q、M在边AB 上．（1）求△ABC中AB边上的高h；（2）设PQ=x，用x的代数式表示矩形PQMN的面积．24．（2015•本溪模拟）某机械公司经销一种零件，已知这种零件的成本为每件20元，调查发现当销售价为24元时，平均每天能售出32件，而当销售价每上涨2元，平均每天就少售出4件．（1）若公司每天的现售价为x元时则每天销售量为多少？（2）如果物价部门规定这种零件的销售价不得高于每件28元，该公司想要每天获得150元的销售利润，销售价应当为多少元？25．（2014•宁波）如图，已知二次函数y=ax2+bx+c的图象过A（2，0），B（0，﹣1）和C（4，5）三点．（1）求二次函数的解析式；（2）设二次函数的图象与x轴的另一个交点为D，求点D的坐标；（3）在同一坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值．2014年北师大九年级数学上下册精选题练习参考答案与试题解析一．选择题（共20小题）2）+坐标是（﹣，2．（2014•广东）二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（），，正确，故3．（2014•兰州）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，则下列四个结论错误的是（）﹣4．（2014•达州）如图是二次函数y=ax2+bx+c的图象的一部分，对称轴是直线x=1．①b2＞4ac；②4a﹣2b+c＜0；③不等式ax2+bx+c＞0的解集是x≥3.5；④若（﹣2，y1），（5，y2）是抛物线上的两点，则y1＜y2．上述4个判断中，正确的是（）5．（2014•黔东南州）如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列4个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0其中正确结论的有（）6．（2014•资阳）二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac﹣b2＜0；②4a+c＜2b；③3b+2c＜0；④m（am+b）+b＜a（m≠﹣1），其中正确结论的个数是（）7．（2014•北海）函数y=ax 2+1与y=（a ≠0）在同一平面直角坐标系中的图象可能是（）．CD ．8．（2014•威海）如图，在下列网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠AOB的正弦值是（）．C D．，==2AOB==．2D．×10．（2014•凉山州）拦水坝横断面如图所示，迎水坡AB的坡比是1：，坝高BC=10m，则坡面AB的长度是（）m m：tanA=10AB=．C D．∴周长之比为13．（2014•牡丹江）若x：y=1：3，2y=3z，则的值是（）D∴=22216．（2014•玉林）x1，x2是关于x的一元二次方程x2﹣mx+m﹣2=0的两个实数根，是否存在实数m使+=0使++成立，则∴222，=18．（2014•杭州）让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则两个数的和是2的倍数或是3的倍数的概率等于（）．C D．=．20．（2014•上海）如图，已知AC、BD是菱形ABCD的对角线，那么下列结论一定正确的是（）S=、菱形的面积等于两条对角线之积的，故此选项错误；二．解答题（共5小题）21．（2014•南京）已知二次函数y=x2﹣2mx+m2+3（m是常数）．（1）求证：不论m为何值，该函数的图象与x轴没有公共点；（2）把该函数的图象沿y轴向下平移多少个单位长度后，得到的函数的图象与x轴只有一个公共点？22．（2014•广东）如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0.1m）．（参考数据：≈1.414，≈1.732）×≈23．如图，Rt△ABC中，∠ACB=90°，AC=8，BC=6，矩形PQMN的顶点P、N分别在AC、BC上，Q、M在边AB 上．（1）求△ABC中AB边上的高h；（2）设PQ=x，用x的代数式表示矩形PQMN的面积．CH=h==∴，PN==10﹣x24．（2015•本溪模拟）某机械公司经销一种零件，已知这种零件的成本为每件20元，调查发现当销售价为24元时，平均每天能售出32件，而当销售价每上涨2元，平均每天就少售出4件．（1）若公司每天的现售价为x元时则每天销售量为多少？（2）如果物价部门规定这种零件的销售价不得高于每件28元，该公司想要每天获得150元的销售利润，销售价应当为多少元？×25．（2014•宁波）如图，已知二次函数y=ax2+bx+c的图象过A（2，0），B（0，﹣1）和C（4，5）三点．（1）求二次函数的解析式；（2）设二次函数的图象与x轴的另一个交点为D，求点D的坐标；（3）在同一坐标系中画出直线y=x+1，并写出当x在什么范围内时，一次函数的值大于二次函数的值．∴a=，x x时，得﹣。

中考数学—二次函数的综合压轴题专题复习及详细答案

中考数学—二次函数的综合压轴题专题复习及详细答案一、二次函数1．如图1，抛物线y=ax 2+bx+c （a≠0）与x 轴交于点A （﹣1，0）、B （4，0）两点，与y 轴交于点C ，且OC=3OA ．点P 是抛物线上的一个动点，过点P 作PE ⊥x 轴于点E ，交直线BC 于点D ，连接PC ．（1）求抛物线的解析式；（2）如图2，当动点P 只在第一象限的抛物线上运动时，求过点P 作PF ⊥BC 于点F ，试问△PDF 的周长是否有最大值？如果有，请求出其最大值，如果没有，请说明理由．（3）当点P 在抛物线上运动时，将△CPD 沿直线CP 翻折，点D 的对应点为点Q ，试问，四边形CDPQ 是否成为菱形？如果能，请求出此时点P 的坐标，如果不能，请说明理由．【答案】(1) y=﹣234x +94x+3；(2) 有最大值,365;(3) 存在这样的Q 点，使得四边形CDPQ 是菱形，此时点P 的坐标为（73，256）或（173，﹣253）．【解析】试题分析: （1）利用待定系数法求二次函数的解析式；（2）设P （m ，﹣34m 2+94m+3），△PFD 的周长为L ，再利用待定系数法求直线BC 的解析式为：y=﹣34x+3，表示PD=﹣2334m m ，证明△PFD ∽△BOC ，根据周长比等于对应边的比得：=PED PD BOC BC V V 的周长的周长，代入得：L=﹣95（m ﹣2）2+365，求L 的最大值即可；（3）如图3，当点Q 落在y 轴上时，四边形CDPQ 是菱形，根据翻折的性质知：CD=CQ ，PQ=PD ，∠PCQ=∠PCD ，又知Q 落在y 轴上时，则CQ ∥PD ，由四边相等：CD=DP=PQ=QC ，得四边形CDPQ 是菱形，表示P （n ，﹣23n 4 +94n+3），则D （n ，﹣34n+3），G （0，﹣34n+3），利用勾股定理表示PD 和CD 的长并列式可得结论．试题解析:（1）由OC=3OA ，有C （0，3），将A （﹣1，0），B （4，0），C （0，3）代入y=ax 2+bx+c 中，得：016403a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得：34943a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩，故抛物线的解析式为：y=﹣234x +94x+3；（2）如图2，设P （m ，﹣34m 2+94m+3），△PFD 的周长为L ，∵直线BC 经过B （4，0），C （0，3），设直线BC 的解析式为：y=kx+b ，则403k b b +=⎧⎨=⎩解得：343k b ⎧=-⎪⎨⎪=⎩∴直线BC 的解析式为：y=﹣34x+3，则D （m ，﹣334m +），PD=﹣2334m m +，∵PE ⊥x 轴，PE ∥OC ， ∴∠BDE=∠BCO ， ∵∠BDE=∠PDF ， ∴∠PDF=∠BCO ， ∵∠PFD=∠BOC=90°， ∴△PFD ∽△BOC ，∴=PED PDBOC BCV V 的周长的周长，由（1）得：OC=3，OB=4，BC=5，故△BOC 的周长=12，∴2334125m mL -+=，即L=﹣95（m ﹣2）2+365，∴当m=2时，L 最大=365；（3）存在这样的Q 点，使得四边形CDPQ 是菱形，如图3，当点Q 落在y 轴上时，四边形CDPQ 是菱形，理由是：由轴对称的性质知：CD=CQ ，PQ=PD ，∠PCQ=∠PCD ，当点Q 落在y 轴上时，CQ ∥PD ， ∴∠PCQ=∠CPD ， ∴∠PCD=∠CPD ， ∴CD=PD ， ∴CD=DP=PQ=QC ， ∴四边形CDPQ 是菱形，过D 作DG ⊥y 轴于点G ，设P （n ，﹣234n +94n+3），则D （n ，﹣34n+3），G （0，﹣334n +），在Rt △CGD 中，CD 2=CG 2+GD 2=[（﹣34n+3）﹣3]2+n 2=22516n ，而|PD|=|（﹣239344n n ++ 3n ++）﹣（﹣34n+3）|=|﹣234n +3n|，∵PD=CD ， ∴﹣235344n n n +=①， ﹣235344n n n +=-②，解方程①得：n=73或0（不符合条件，舍去），解方程②得：n=173或0（不符合条件，舍去），当n=73时，P （73，256），如图3，当n=173时，P （173，﹣253），如图4，综上所述，存在这样的Q 点，使得四边形CDPQ 是菱形，此时点P 的坐标为（73，256）或（173，﹣253）．点睛: 本题是二次函数的综合题，考查了利用待定系数法求函数的解析式、菱形的性质和判定、三角形相似的性质和判定，将周长的最值问题转化为二次函数的最值问题，此类问题要熟练掌握利用解析式表示线段的长，并利用相似比或勾股定理列方程解决问题．2．某厂家生产一种新型电子产品，制造时每件的成本为40元，通过试销发现，销售量(y 万件)与销售单价(x 元)之间符合一次函数关系，其图象如图所示．()1求y 与x 的函数关系式；()2物价部门规定：这种电子产品销售单价不得超过每件80元，那么，当销售单价x 定为每件多少元时，厂家每月获得的利润()w 最大？最大利润是多少？【答案】（1）2280y x =-+；（2）当销售单价x 定为每件80元时，厂家每月获得的利润()w 最大，最大利润是4800元．【解析】【分析】()1根据函数图象经过点()40,200和点()60,160，利用待定系数法即可求出y 与x 的函数关系式；()2先根据利润=销售数量(⨯销售单价-成本)，由试销期间销售单价不低于成本单价，也不高于每千克80元，结合电子产品的成本价即可得出x 的取值范围，根据二次函数的增减性可得最值．【详解】解：()1设y 与x 的函数关系式为()0y kx b k =+≠，Q 函数图象经过点()40,200和点()60,160，{4020060160k b k b +=∴+=，解得：{2280k b =-=，y ∴与x 的函数关系式为2280y x =-+．()2由题意得：()()224022802360112002(90)5000w x x x x x =--+=-+-=--+．Q 试销期间销售单价不低于成本单价，也不高于每千克80元，且电子产品的成本为每千克40元，∴自变量x 的取值范围是4080x ≤≤．20-<Q ，∴当90x <时，w 随x 的增大而增大， 80x ∴=时，w 有最大值，当80x =时，4800w =，答：当销售单价x 定为每件80元时，厂家每月获得的利润()w 最大，最大利润是4800元．【点睛】本题考查了一次函数和二次函数的应用，根据点的坐标利用待定系数法求出函数关系式是解题的关键，并注意最值的求法．3．如图，某足球运动员站在点O 处练习射门，将足球从离地面0.5m 的A 处正对球门踢出(点A 在y 轴上)，足球的飞行高度y(单位：m )与飞行时间t(单位：s )之间满足函数关系y ＝at 2＋5t ＋c ，已知足球飞行0.8s 时，离地面的高度为3.5m . (1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？(2)若足球飞行的水平距离x(单位：m )与飞行时间t(单位：s )之间具有函数关系x ＝10t ，已知球门的高度为2.44m ，如果该运动员正对球门射门时，离球门的水平距离为28m ，他能否将球直接射入球门？【答案】（1）足球飞行的时间是85s 时，足球离地面最高，最大高度是4.5m ；（2）能. 【解析】试题分析：（1）由题意得：函数y=at 2+5t+c 的图象经过（0，0.5）（0.8，3.5），于是得到，求得抛物线的解析式为：y=﹣t2+5t+，当t=时，y最大=4.5；（2）把x=28代入x=10t得t=2.8，当t=2.8时，y=﹣×2.82+5×2.8+=2.25＜2.44，于是得到他能将球直接射入球门．解：（1）由题意得：函数y=at2+5t+c的图象经过（0，0.5）（0.8，3.5），∴，解得：，∴抛物线的解析式为：y=﹣t2+5t+，∴当t=时，y最大=4.5；（2）把x=28代入x=10t得t=2.8，∴当t=2.8时，y=﹣×2.82+5×2.8+=2.25＜2.44，∴他能将球直接射入球门．考点：二次函数的应用．4．（12分）如图所示是隧道的截面由抛物线和长方形构成，长方形的长是12 m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y=16x2+bx+c表示，且抛物线上的点C到OB的水平距离为3 m，到地面OA的距离为172m.（1）求抛物线的函数关系式，并计算出拱顶D到地面OA的距离；（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向车道，那么这辆货车能否安全通过？（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？【答案】（1）抛物线的函数关系式为y=16-x 2+2x+4，拱顶D 到地面OA 的距离为10 m ；(2)两排灯的水平距离最小是．【解析】【详解】试题分析：根据点B 和点C 在函数图象上，利用待定系数法求出b 和c 的值，从而得出函数解析式，根据解析式求出顶点坐标，得出最大值；根据题意得出车最外侧与地面OA 的交点为（2,0）（或（10,0）），然后求出当x=2或x=10时y 的值，与6进行比较大小，比6大就可以通过，比6小就不能通过；将y=8代入函数，得出x 的值，然后进行做差得出最小值．试题解析：（1）由题知点17(0,4),3,2B C ⎛⎫⎪⎝⎭在抛物线上所以41719326c b c =⎧⎪⎨=-⨯++⎪⎩，解得24b c =⎧⎨=⎩，所以21246y x x =-++ 所以，当62bx a=-=时，10t y =≦ 答：21246y x x =-++，拱顶D 到地面OA 的距离为10米（2）由题知车最外侧与地面OA 的交点为（2,0）（或（10,0））当x=2或x=10时，2263y =>，所以可以通过（3）令8y =，即212486x x -++=，可得212240x x -+=，解得1266x x =+=-12x x -=答：两排灯的水平距离最小是考点：二次函数的实际应用．5．在平面直角坐标系中，有两点(),A a b 、(),B c d ，若满足：当a b ≥时，c a =，2d b =-；当a b <时，c a <-，d b <，则称点为点的“友好点”.（1）点()4,1的“友好点”的坐标是_______.（2）点(),A a b 是直线2y x =-上的一点，点B 是点A 的“友好点”. ①当B 点与A 点重合时，求点A 的坐标.②当A 点与A 点不重合时，求线段AB 的长度随着a 的增大而减小时，a 的取值范围.【答案】（1）()41-,；（2）①点A 的坐标是()2,0或()1,1-；②当1a <或322a ≤<时，AB 的长度随着a 的增大而减小；【解析】【分析】（1）直接利用“友好点”定义进行解题即可；（2）先利用 “友好点”定义求出B 点坐标，A 点又在直线2y x =-上，得到2b a =-；①当点A 和点B 重合，得2b b =-．解出即可，②当点A 和点B 不重合， 1a ≠且2a ≠．所以对a 分情况讨论，1°、当1a <或2a >时，()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭，所以当a ≤32时，AB 的长度随着a 的增大而减小，即取1a <．2°当12a <<时，()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭，当32a ≥时，AB 的长度随着a 的增大而减小，即取322a ≤<．综上，当1a <或322a ≤<时，AB 的长度随着a 的增大而减小．【详解】（1）点()4,1，4＞1，根据“友好点”定义，得到点()4,1的“友好点”的坐标是()41-, （2）Q 点(),A a b 是直线2y x =-上的一点，∴2b a =-．Q 2a a >-，根据友好点的定义，点B 的坐标为()2,B a b -，①当点A 和点B 重合，∴2b b =-．解得0b =或1b =-．当0b =时，2a =；当1b =-时，1a =，∴点A 的坐标是()2,0或()1,1-．②当点A 和点B 不重合，1a ≠且2a ≠．当1a <或2a >时，()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭． ∴当a ≤32时，AB 的长度随着a 的增大而减小， ∴取1a <．当12a <<时， ()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭ ．∴当32a ≥时，AB 的长度随着a 的增大而减小， ∴取322a ≤<．综上，当1a <或322a ≤<时，AB 的长度随着a 的增大而减小．【点睛】本题属于阅读理解题型，结合二次函数的基本性质进行解题，第二问的第二小问的关键是求出AB 的长用a 进行表示，然后利用二次函数基本性质进行分类讨论6．已知关于x 的一元二次方程x 2﹣（2k +1）x +k 2＝0有两个实数根．（1）求k 的取值范围；（2）设x 1，x 2是方程两根，且121111x x k +=-，求k 的值．【答案】（1）k ≥﹣14；（2）k【解析】【分析】（1）根据方程有两个实数根可以得到△≥0，从而求得k 的取值范围；（2）利用根与系数的关系将两根之和和两根之积代入代数式求k 的值即可. 【详解】解：（1）△＝（2k +1）2﹣4k 2＝4k 2+4k +1﹣4k 2＝4k +1 ∵△≥0 ∴4k +1≥0 ∴k ≥﹣14；（2）∵x 1，x 2是方程两根， ∴x 1+x 2＝2k +1 x 1x 2＝k 2，又∵121111x x k +=-， ∴121211x x x x k +=⋅-，即22111k k k +=+ ，解得：12k k ==又∵k ≥﹣14，即：k【点睛】本题考查了根与系数的关系以及一元二次方程的解，根的判别式等知识，牢记“两根之和等于b a -，两根之积等于ca”是解题的关键.7．已知抛物线2(5)6y x m x m =-+-+-. （1）求证：该抛物线与x 轴总有交点；（2）若该抛物线与x 轴有一个交点的横坐标大于3且小于5，求m 的取值范围；（3）设抛物线2(5)6y x m x m =-+-+-与y 轴交于点M ，若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ，求m 的值.【答案】（1）证明见解析；（2）1?<?m?3<；（3）56m m ==或【解析】【分析】（1）本题需先根据判别式解出无论m 为任何实数都不小于零，再判断出物线与x 轴总有交点．（2）根据公式法解方程，利用已有的条件，就能确定出m 的取值范围，即可得到结果．（3）根据抛物线y=-x 2+（5-m ）x+6-m ，求出与y 轴的交点M 的坐标，再确定抛物线与x 轴的两个交点关于直线y=-x 的对称点的坐标，列方程可得结论．【详解】（1）证明：∵()()()222454670b ac m m m ∆=-=-+-=-≥ ∴抛物线与x 轴总有交点.（2）解：由（1）()27m ∆=-，根据求根公式可知，方程的两根为：x =即1216x x m =-=-+，由题意，有 3<-m 6<5+1<?m 3∴<(3)解：令 x = 0， y =6m -+ ∴ M （0，6m -+）由（2）可知抛物线与x 轴的交点为（-1，0）和（6m -+，0），它们关于直线y x =-的对称点分别为（0 ， 1）和（0， 6m -），由题意，可得：6166m m m 或-+=-+=- 56m m ∴==或【点睛】本题考查对抛物线与x 轴的交点，解一元一次方程，解一元一次不等式，根的判别式，对称等，解题关键是熟练理解和掌握以上性质，并能综合运用这些性质进行计算．8．如图，已知直线y＝﹣2x+4分别交x轴、y轴于点A、B．抛物线过A、B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．（1）如图1，设抛物线顶点为M，且M的坐标是（12，92），对称轴交AB于点N．①求抛物线的解析式；②是否存在点P，使四边形MNPD为菱形？并说明理由；（2）是否存在这样的点D，使得四边形BOAD的面积最大？若存在，求出此时点D的坐标；若不存在，请说明理由．【答案】（1）①y＝﹣2x2+2x+4；；②不存在点P，使四边形MNPD为菱形；；（2）存在，点D的坐标是（1，4）．【解析】【分析】（1）①由一次函数图象上点的坐标特征求得点B的坐标，设抛物线解析式为y＝a21922x⎛⎫-+⎪⎝⎭，把点B的坐标代入求得a的值即可；②不存在点P，使四边形MNPD为菱形．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），根据题意知PD∥MN，所以当PD＝MN时，四边形MNPD为平行四边形，根据该等量关系列出方程﹣2m2+4m＝32，通过解方程求得m的值，易得点N、P的坐标，然后推知PN＝MN是否成立即可；（2）设点D的坐标是（n，﹣2n2+2n+4），P（n，﹣2n+4）．根据S四边形BOAD＝S△BOA+S△ABD ＝4+S△ABD，则当S△ABD取最大值时，S四边形BOAD最大．根据三角形的面积公式得到函数S△ABD＝﹣2（n﹣1）2+2．由二次函数的性质求得最值．【详解】解：①如图1，∵顶点M的坐标是19,22⎛⎫ ⎪⎝⎭，∴设抛物线解析式为y＝21922a x⎛⎫-+⎪⎝⎭（a≠0）．∵直线y＝﹣2x+4交y轴于点B，∴点B的坐标是（0，4）．又∵点B在该抛物线上，∴21922a⎛⎫-+⎪⎝⎭＝4，解得a＝﹣2．故该抛物线的解析式为：y＝219222x⎛⎫--+⎪⎝⎭＝﹣2x2+2x+4；②不存在．理由如下：∵抛物线y＝219222x⎛⎫--+⎪⎝⎭的对称轴是直线x＝12，且该直线与直线AB交于点N，∴点N的坐标是1,32⎛⎫ ⎪⎝⎭．∴93322MN=-=．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），∴PD＝（﹣2m2+2m+4）﹣（﹣2m+4）＝﹣2m2+4m．∵PD∥MN．当PD＝MN时，四边形MNPD是平行四边形，即﹣2m2+4m＝32．解得 m1＝12（舍去），m2＝32．此时P（32，1）．∵PN∴PN≠MN，∴平行四边形MNPD不是菱形．∴不存在点P，使四边形MNPD为菱形；（2）存在，理由如下：设点D的坐标是（n，﹣2n2+2n+4），∵点P在线段AB上且直线PD⊥x轴，∴P（n，﹣2n+4）．由图可知S四边形BOAD＝S△BOA+S△ABD．其中S△BOA＝12OB•OA＝12×4×2＝4．则当S△ABD取最大值时，S四边形BOAD最大．S△ABD＝12（y D﹣y P）（x A﹣x B）＝y D﹣y P＝﹣2n2+2n+4﹣（﹣2n+4）＝﹣2n2+4n＝﹣2（n﹣1）2+2．当n＝1时，S△ABD取得最大值2，S四边形BOAD有最大值．此时点D的坐标是（1，4）．【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．9．如图，在直角坐标系xOy中，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．（1）求这个二次函数的解析式；（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标；（3）对于（2）中的点B，在此抛物线上是否存在点P，使∠POB=90°？若存在，求出点P 的坐标，并求出△POB的面积；若不存在，请说明理由．【答案】（1）y=x2﹣3x。

北师大版九下数学二次函数压轴题分类训练

二次函数压轴题分类训练类型1二次函数与相似三角形的存在性问题1．如图，已知抛物线y＝ax2＋bx＋c(a≠0)经过A(－1，0)，B(4，0)，C(0，2)三点．(1)求这条抛物线的解析式；(2)P为线段BC上的一个动点，过P作PE垂直于x轴与抛物线交于点E，设P点横坐标为m，PE长度为y，请写出y与m的函数关系式，并求出PE的最大值；(3)D为抛物线上一动点，是否存在点D使以A、B、D为顶点的三角形与△COB相似？若存在，试求出点D的坐标；若不存在，请说明理由．2．如图，在平面直角坐标系xOy中，直线y＝x＋4与坐标轴分别交于A，B两点，过A，B两点的抛物线为y＝－x2＋bx＋c.点D为线段AB上一动点，过点D作CD⊥x轴于点C，交抛物线于点E.(1)求抛物线的解析式；(2)当DE＝4时，求四边形CAEB的面积；(3)连接BE，是否存在点D，使得△DBE和△DAC相似？若存在，求出D点坐标；若不存在，说明理由．3．边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E在第一象限，且DE⊥DC，DE＝DC.以直线AB为对称轴的抛物线过C，E两点．(1)求抛物线的解析式；(2)点P从点C出发，沿射线CB以每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD 于点F.当t为何值时，以点P，F，D为顶点的三角形与△COD相似？(3)点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E 为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．类型2 二次函数与平行四边形的存在性问题1．如图，抛物线y ＝ax 2＋bx ＋c 与坐标轴分别交于A (－3，0)，B (1，0)，C (0，3)三点，D 是抛物线顶点，E 是对称轴与x 轴的交点．(1)求抛物线的解析式；(2)F 是抛物线对称轴上一点，且tan ∠AFE ＝12，求点O 到直线AF 的距离； (3)点P 是x 轴上的一个动点，过P 作PQ ∥OF 交抛物线于点Q ，是否存在以点O ，F ，P ，Q 为顶点的平行四边形？若存在，求出P 点坐标；若不存在，请说明理由．2.如图，矩形OABC在平面直角坐标系xOy中，点A在x轴的正半轴上，点C在y轴的正半轴上，OA ＝4，OC＝3，若抛物线的顶点在BC边上，且抛物线经过O，A两点，直线AC交抛物线于点D.(1)求抛物线的解析式；(2)求点D的坐标；(3)若点M在抛物线上，点N在x轴上，是否存在以点A，D，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．3．如图，抛物线y＝x2－2x－3与x轴交于A、B两点(A点在B点左侧)，直线l与抛物线交于A、C 两点，其中C点的横坐标为2.(1)求A、B、C三点的坐标；(2)在抛物线的对称轴上找到点P，使得△PBC的周长最小，并求出点P的坐标；(3)点G是抛物线上的动点，在x轴上是否存在点F，使A、C、F、G为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F点坐标；如果不存在，请说明理由．类型3二次函数与直角三角形的存在性问题1．如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c(a≠0)与x轴相交于A、B两点，与y轴相交于点C，直线y＝kx＋n(k≠0)经过B、C两点，已知A(1，0)，C(0，3)，且BC＝5.(1)分别求直线BC和抛物线的解析式(关系式)；(2)在抛物线的对称轴上是否存在点P，使得以B、C、P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．2．如图，已知抛物线y＝ax2＋bx＋c(a≠0) 的对称轴为x＝－1，且抛物线经过A(1，0)，C(0，3)两点，与x轴交于点B.(1)若直线y＝mx＋n经过B、C两点，求线段BC所在直线的解析式；(2)在抛物线的对称轴x＝－1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出此点M的坐标；(3)设点P为抛物线的对称轴x＝－1上的一个动点，求使△BPC为直角三角形的点P的坐标．3．已知抛物线E1：y＝x2经过点A(1，m)，以原点为顶点的抛物线E2经过点B(2，2)，点A、B关于y 轴的对称点分别为点A′，B′.(1)求m的值及抛物线E2所表示的二次函数的表达式；(2)如图，在第一象限内，抛物线E1上是否存在点Q，使得以点Q、B、B′为顶点的三角形为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由；(3)如图，P为第一象限内的抛物线E1上与点A不重合的一点，连接OP并延长与抛物线E2相交于点P′，求△P AA′与△P′BB′的面积之比．类型4 二次函数与等腰三角形的存在性问题1．如图，已知二次函数y 1＝－x 2＋134x ＋c 的图象与x 轴的一个交点为A (4，0)，与y 轴的交点为B ，过A 、B 的直线为y 2＝kx ＋b .(1)求二次函数y 1的解析式及点B 的坐标；(2)由图象写出满足y 1<y 2的自变量x 的取值范围；(3)在两坐标轴上是否存在点P ，使得△ABP 是以AB 为底边的等腰三角形？若存在，求出点P 的坐标；若不存在，说明理由．2．如图，抛物线与x轴交于A，B两点，直线y＝kx－1与抛物线交于A，C两点，其中A(－1，0)，B(3，0)，点C的纵坐标为－3.(1)求k值；(2)求抛物线的解析式；(3)抛物线上是否存在点P，使得△ACP是以AC为底边的等腰三角形？如果存在，写出所有满足条件的点P的坐标；如果不存在，请说明理由．3．如图，已知抛物线y＝ax2＋bx＋c(a≠0)交于x轴于A(－1，0)，B(5，0)两点，与y轴交于点C(0，2)．(1)求抛物线的解析式；(2)若点M为抛物线的顶点，连接BC、CM、BM，求△BCM的面积；(3)连接AC，在x轴上是否存在点P，使△ACP为等腰三角形；若存在，请求出点P的坐标；若不存在，请说明理由．类型5二次函数与图形面积问题1．如图，在平面直角坐标系中，抛物线y＝ax2＋bx－3(a≠0)与x轴交于点A(－2，0)，B(4，0)两点，与y轴交于点C.(1)求抛物线的解析式；(2)点P从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动．其中一个点到达终点时，另一个点也停止运动．当△PBQ存在时，求运动多少秒使△PBQ的面积最大，最大面积是多少？(3)当△PBQ的面积最大时，在BC下方的抛物线上存在点K，使S△CBK∶S△PBQ＝5∶2，求K点坐标．2．如图所示，抛物线y ＝ax 2＋bx (a ＜0)与双曲线y ＝k x相交于点A 、B ，点A 的坐标为(－2，2)，点B 在第四象限内，过点B 作直线BC ∥x 轴，直线BC 与抛物线的另一交点为点C ，已知直线BC 与x 轴之间的距离是点B 到y 轴的距离的4倍，记抛物线的顶点为E .(1)求双曲线和抛物线的解析式；(2)计算△ABC 与△ABE 的面积；(3)在抛物线上是否存在点D ，使△ABD 的面积等于△ABE 的面积的8倍？若存在，请求出点D 的坐标；若不存在，请说明理由．类型6二次函数与最值问题1．如图，对称轴为直线x＝2的抛物线经过A(－1，0)，C(0，5)两点，与x轴另一交点为B，已知M(0，1)，E(a，0)，F(a＋1，0)，点P是第一象限内的抛物线上的动点．(1)求抛物线的解析式；(2)当a＝1时，求四边形MEFP的面积最大值，并求此时点P的坐标；(3)若△PCM是以点P为顶点的等腰三角形，求a为何值时，四边形PMEF周长最小？请说明理由．2．如图，顶点为A的抛物线y＝a(x＋2)2－4交x轴于点B(1，0)，连接AB，过原点O作射线OM∥AB，过点A作AD∥x轴交OM于点D，点C为抛物线与x轴的另一个交点，连接CD.(1)求抛物线的解析式(关系式)；(2)求点A，B所在的直线的解析式(关系式)；(3)若动点P从点O出发，以每秒1个单位长度的速度沿着射线OM运动，设点P运动的时间为t秒，问：当t为何值时，四边形ABOP分别为平行四边形？(4)若动点P从点O出发，以每秒1个单位长度的速度沿线段OD向点D运动，同时动点Q从点C出发，以每秒2个单位长度的速度沿线段CO向点O运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动时间为t秒，连接PQ.问：当t为何值时，四边形CDPQ的面积最小？并求此时PQ的长．类型7二次函数与根的判别式问题1．如图，顶点M在y轴上的抛物线与直线y＝x＋1相交于A、B两点，且点A在x轴上，点B的横坐标为2，连接AM、BM.(1)求抛物线的函数关系式；(2)判断△ABM的形状，并说明理由；(3)把抛物线与直线y＝x的交点称为抛物线的不动点．若将(1)中抛物线平移，使其顶点为(m，2m)，当m满足什么条件时，平移后的抛物线总有不动点？类型8二次函数与圆1．如图，已知以E(3，0)为圆心，以5为半径的⊙E与x轴交于点A，B两点，与y轴交于C点，抛物线y＝ax2＋bx＋c经过A，B，C三点，顶点为F.(1)求A，B，C三点的坐标；(2)求抛物线的解析式及顶点F的坐标；(3)已知M为抛物线上一动点(不与C点重合)．试探究：①使得以A，B，M为顶点的三角形面积与△ABC的面积相等，求所有符合条件的点M的坐标；②若探究①中的M点位于第四象限，连接M点与抛物线顶点F，试判断直线MF与⊙E的位置关系，并说明理由．2．如图，在平面直角坐标系xOy中，直线l⊥y轴于点B(0，－2)，A为OB的中点，以A为顶点的抛物线y＝ax2＋c(a≠0)与x轴分别交于C、D两点，且CD＝4.点P为抛物线上的一个动点，以P为圆心，PO 为半径画圆．(1)求抛物线的解析式；(2)若⊙P与y轴的另一交点为E，且OE＝2，求点P的坐标；(3)判断直线l与⊙P的位置关系，并说明理由．。

北师大版初中中考数学压轴题及答案学习资料

(注：抛物线y=a/+bx+c(aM0)的顶点坐标为
2.如图，在Rt△ABC中,
A 90o，AB 6，AC
8，D，E分别是边AB，AC的中点，点P从点D出发沿Dຫໍສະໝຸດ 方向运动，过点P作PQBC于
Q，过点Q作QR//BA交AC于
R，当点Q与点C重合时，点P停止运动•设BQ x，QR y.
(1)求点D到BC的距离DH的长;
按逆时针方向旋转•使边AO与AB重合.得到△ABD.(1)求直线AB的解析式；(2)当点P运动到点(.3，0)时，求此时DP的长及点
存在点卩，使厶OPD勺面积等于3，若存在，请求出符合条件的点P的坐标；若不存在，请说明理由
4
北师大版初中中考数
学压轴题及答案
中考数学专题复习
1•已知:如图，抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点，其顶点为D.
(1)求该抛物线的解析式；
(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积；
(3) △AOB与厶BDE是否相似？如果相似，请予以证明；如果不相似，请说明理由
O0内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示AMNP的面积S;
(2)当x为何值时，O0与直线BC相切？
(3) 在动点M的运动过程中，记AMNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式，并求x为何值时,
多少?
图1
4.如图1，在平面直角坐标系中，己知△AOB是等边三角形，点A的坐标是(0,4)，点B在第一象限，点P是x轴上的一个动点，连结
(2)求y关于x的函数关系式(不要求写出自变量的取值范围)；
(3)是否存在点P，使△PQR为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由.