2019国家公务员考试行测数量关系中的三者容斥

合集下载

公务员考试行测技巧：容斥原理公式及运用

如果被计数的事物有A、B两类，那么，先把A、B两个集合的元素个数相加，发现既是A类又是B类的部分重复计算了一次，所以要减去。如下图所示。
【示例1】一次期末考试，某班有15人数学得满分，有12人语文得满分，并且有4人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？
数学得满分人数→A，语文得满分人数→B，数学、语文都是满分人数→A∩B，至少有一门得满分人数→A∪B。A∪B=15+12-4=23，共有23人至少有一门得满分。
【示例2】某班有学生45人，每人都参加体育训练队，其中参加足球队的有25人，游泳都参加的有9人，排球、游泳都参加的有8人，问：三项都参加的有多少人？
参加足球队→A，参加排球队→B，参加游泳队→C，足球、排球都参加的→A∩B，足球、游泳都参加的→C∩A，排球、游泳都参加的→B∩C，三项都参加的→A∩B∩C。三项都参加的有A∩B∩C=A∪B∪C-A-B-C+A∩B+B∩C+C∩A=45-25-22-24+12+9+8=3人。
在计数时，必须注意无一重复，无一遗漏。为了使重叠部分不被重复计算，中公教育专家研究出一种新的计数方法。这种方法的基本思路是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。
一、容斥原理1：两个集合的容斥原理
二、容斥原理2：三个集合的容斥原理
如果被计数的事物有A、B、C三类，那么，将A、B、C三个集合的元素个数相加后发现两两重叠的部分重复计算了1次，三个集合公共部分被重复计算了2次。
如下图所示，灰色部分A∩B-A∩B∩C、B∩C-A∩B∩C、C∩A-A∩B∩C都被重复计算了1次，黑色部分A∩B∩C被重复计算了2次，因此总数A∪B∪C=A+B+C-（A∩B-A∩B∩C）-（B∩C-A∩B∩C）-（C∩A-A∩B∩C）-2A∩B∩C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C。即得到：

公务员考试数量关系之三集合容斥问题

公务员考试数量关系之三集合容斥问题在最近几年的公务员考试中，考察了相关的三集合容斥问题，对于这样的一个问题，华图教研中心提醒你，在复习三集合容斥问题时一定不能停留在表面，一定要从实质上理解它，因为现在在考察容斥问题时，考的比较细致。

但是题目难度并不是很大，只要能够掌握它的实质，熟练运用我们的解题方法，那么这种问题肯定能够轻松应对。

一浅识三集合容斥问题对于三集合容斥问题，一定要弄清楚它题目的关键词语及问法。

A+B+C-AB-AC-BC-ABC=总数-三个条件都不满足的情形A+B+C-满足两个条件-2满足三个条件=总数-三个条件都不满足的情形二真题回放1.某公司招聘员工，按规定每人至多可投考两个职位，结果共42人报名，甲、乙、丙三个职位报名人数分别是22人、16人、25人，其中同时报甲、乙职位的人数为8人，同时报甲、丙职位的人数为6人，那么同时报乙、丙职位的人数为：A. 7人B. 8人C. 5人D. 6人【华图解析】根据题意，“按规定每人至多可投考两个职位”则表明这次招聘中不存在有人报考三个职位的情形，共有42人报名，也表明不存在一个人是三个职位都不报考的情形。

故可以直接代入三集合的标准形公式即可。

22+16+25-8-6-x=42 x=7，故选择A选项。

2.某通讯公司对3542个上网客户的上网方式进行调查，其中1258个客户使用手机上网，1852个客户使用有线网络上网，932个客户使用无线网络上网。

如果使用不只一种上网方式的有352个客户，那么三种上网方式都使用的客户有多少个?（）A. 148B. 248C. 350D. 500【华图解析】设三种上网方式都使用的客户有x个，则使用两种上网方式的就有352-x,根据三集合容斥问题的公式，可以得到 1258+1852+932-（352-x）—2x=3542 解得x=148 故答案选择A3. 某市对52种建筑防水卷材产品进行质量抽检，其中有8种产品的低温柔度不合格，10种产品的可溶物含量不达标，9种产品的接缝剪切性能不合格，同时两项不合格的有7种，有1种产品这三项都不合格。

行测答题技巧：容斥原理之三者容斥问题

中公教育考试研究院宋丽娜：容斥原理是行测数学运算中常考知识点。

容斥原理是指在计数时，必须注意无一重复，且无遗漏。

这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

例1：一个班级的学生数学和语文每人至少喜欢其中一种，其中喜欢数学课的有49人，喜欢语文课的有52人，二者都喜欢的有21人，则这个班级有多少人?中公点拨：本题就是一个容斥问题，解决此问题的方法就是先算：49+52=101(把含于某内容中的所有对象的数目先计算出来)，然后再把计数时重复计算的数目排斥出去即：101-21=80人，则整个班级的人数就有80人。

三者容斥问题是行测数学运算中常考也相对较复杂的容斥问题。

所谓三者容斥是指在题干中有三种集合(集合就是具有共同属性所以元素的的整体，例如上题中喜欢数学的人构成一个集合)。

三者容斥问题有一个基本公式：A，B，C代表三个集合，则有A∪BUC=A+B+C-A∩B-A∩C-B∩C+ A∩B∩C这个公式表达的含义是，A+B+C再减去两两相交之后，中间E(即A∩B∩C)这部分被减没了。

而容斥原理的基本思想是计数时不重复不漏掉，故要再加回来，所以又加了一个A∩B∩C。

例2. 实验小学的小记者对本校100名同学进行调查，调查他们对三种大球(篮球、足球、排球)的与否。

结果显示：他们都至少喜欢三种大球中的一种，其中有58人喜欢篮球，有68人喜欢足球，有62人喜欢排球，而且，篮球和足球都喜欢的有45人，足球和排球都喜欢的有33人，三种球都喜欢的有12人。

篮球和排球都喜欢的多少人?中公教育解析：由题意可画图如下：则有上述公式可知：58+68+62-45-33-篮球和排球都喜欢+12=100人故喜欢篮球和排球的人有22人。

例3. 实验小学的小记者对本校100名同学进行调查，调查他们对三种大球(篮球、足球、排球)的与否。

行测数量关系技巧：容斥问题求极值

行测数量关系技巧：容斥问题求极值在考场上人与人拉开差距的除了平常的知识点的积累，还有面对考试题型能够有一个更好的解答思路，下面为你精心准备了“行测数量关系技巧：容斥问题求极值”，持续关注本站将可以持续获取的考试资讯！行测数量关系技巧：容斥问题求极值对于绝大部分考生而言，行测数量关系一直是比较难的专项，但是要想真正在笔试中遥遥领先数量部分还是要去攻破的。

因此，针对数量所考察的所有题型我们也要由易到难的逐步攻破，在考场考试时学会挑出自己平时擅长的题型先入手。

所以，今天就给大家分享下容斥这一考点。

容斥问题常规的考点有二者容斥和三者容斥问题，利用一些公式以及文氏图能够轻松地解决。

今天我们就把这个题型深入挖掘探讨。

容斥问题也会涉及到求极值的问题，接下来我们就以题目为例讲解下容斥中求极值问题怎么处理。

例题1、某一学校有500人，其中选修数学的有359人，选修文学的有408人，那么两种课程都选的学生至少有多少人?A.165B.203C.267D.199【答案】C。

读完题目我们就能判断出考察容斥问题中的二者容斥问题，但是有涉及到求极值问题。

解极值问题我们可以通过逆向思维来求解，题目要求两种课程都选的至少，即求没选课程的人数最多。

通过这个表格我们可以得出要想不选课程的人数最多，即未选数学的141人和未选文学的92人不重复，因此不选课程的人数最多为141+92，因此题目所求的两种都选的最少=500-(141+92)=267人，故选C。

例题2、阅览室有100本杂志。

小赵借阅过其中75本，小王借阅过70本，小刘借阅过60本，则三人共同借阅过的杂志最少有()本。

A.5B.10C.15D.30【答案】A。

读完题目我们也可以判断出事考察三者容斥中的极值问题，那么我们也可以利用逆向思维来求解，所以我们也能知道未借阅的杂志最多=25+30+40，那么题目所求=100-(25+30+40)=5，因此选A。

通过这2道例题的讲解我们了解到容斥问题的极值问题其实也可以很简单，求N部分都包含的至少=(A+B+C+D+...+N)-(N-1)×I，后期我们碰到这样的问题直接带入公式求解就可以啦。

三者容斥问题3个公式

容斥问题其实是一种在考试中比较常见且简单的题型，它考察的是集合之间彼此的交集问题，一般来说解决容斥问题最常用的两种方法就是文氏图法和公式法。

下面国家公务员考试网为大家讲解。

让我们先从一个生活上的小例子来理解什么是容斥：AB是两个同居室友，有一天A下班回家时在路上买了香蕉、苹果、菠萝三种水果，B回家路上买了菠萝、葡萄、西瓜三种水果，那么家里现在一共有多少种水果?答案很简单，因为尽管两个人各买了三种水果，但其中菠萝是重复的，所以我们在3+3之后还需要把多算了一遍的菠萝减下去，而这就是容斥问题的本质：减去多算的，补上空白的。

在行测的容斥问题里，较常考的是三者容斥，也就是三个集合之间的关系，我们把三个集合分别称作A、B、C，三个集合的总集称作U，就可以得到三者容斥的公式：U=A+B+C-A∩B-B∩C-A∩C+A∩B∩C+三者都没有的在做题的时候只需要找到题干中给定的各个条件，选择直接套用，然后就可以求出公式中缺少的项，从而快速得到答案。

以一道题目为例：18名游泳运动员中，有8名参加仰泳，有10名参加蛙泳，有12名参加自由泳，有4名既参加仰泳又参加蛙泳，有6名既参加蛙泳又参加自由泳，有5名既参加仰泳又参加自由泳，有两名这三个项目都参加。

三个项目都没有参加的有多少名?在题目中，ABC即对应仰泳、蛙泳、自由泳，那么A、B、C、A∩B，B∩C，A∩B∩C都是已知的，求都没有参加，即求剩下的项，首先，我们先把题目中已经给的数据填入公式：18=8+10+12-4-6-2+2+x在这个方程中，我们解得x=1，也就是三个项目都没有参加的有一个人。

而公式法虽然简单，但有的时候可能会觉得有些眼花缭乱，这种时候文氏图法就显得更为直观，我们一起来感受一下文氏图法在题目中的应用：按照从内向外依次填充的方式，在文氏图中填写不同区域对应的数据，这样题目无论是求哪个部分，又或是其中一些部分的和、差关系(比如只会游一种泳的、只会游两种泳的、只会自由泳的人比只会蛙泳的多多少)，我们就都不怕了。

行测数量关系备考：容斥问题

行测数量关系备考：容斥问题行测数量关系备考：容斥问题容斥问题一直是行测数量关系考试当中的“常客”，而如此“文艺”的名字之下，本质研究的其实就只是集合间关系的一类问题。

那么集合间的关系都有哪些呢?一般来说，我们把容斥问题分成三大类研究，分别是二者容斥、三者容斥和容斥极值，其中以三者容斥问题最为常考，也是相对来说最难理解的一类问题。

今天就为大家解释什么是三者容斥?它又难在哪里?【例2】某研究中心就消费者对红、黄、蓝三种颜色的偏好情况进展市场调查，共抽取了40名消费者，发现其中有20人喜欢红色、20人喜欢黄色、15人喜欢蓝色，至少喜欢两种颜色的有19人，喜欢三种颜色的有3人，问三种颜色都不喜欢的有几人?A.1B.3C.5D.7通过以上两道题目，我们不难发现，容斥问题本身难度并不是很大，只要找到题目中数据描绘的特点，对应正确的公式，还是很容易解决的。

比例统一的方法如下：1.找不同比例当中都出现的不变量(某个量、总量、差量等)2.将不变量的份数统一为最小公倍数3.其他量保持比例不变同倍数变化理解完以上相关的方法，我们就详细来看题目感受一下。

【例1】A：B=2：3，B：C=2：3，C比A多10，那么A+B+C=?A.35B.36C.37D.38【解析】答案：D。

根据题干信息可知，给出了一个实际量C比A多10，那么我们就需要找到实际量10所对应的比例份数进展相关的解题，同时我们可以发现题干给出了两个比例，两个比例都出现了B这个不变量，在和A做比的时候是3份，在和C做比的时候是2份，但是B所代表的实际量是一样的，所以把B分成不同的份数每一份所代表的实际量就不一样。

那么我们将B的份数变成一样即可，所以将B统一为最小公倍数6，那么其他量保持比例不变同倍数变化。

得到A:B:C=4:6:9，可以发现C比A多了5份，这5份正是对应的10，题目求A+B+C，通过比例可以知道共有19份，所以答案为38，选D。

【例2】林先生的水果摊销售苹果、芒果、香蕉三种水果，第一天苹果、芒果、香蕉三种水果的收入之比为8:7:5，第二天的收入之比7:9:14.假设第二天苹果的销售收入减少了100元，但这三种水果的总收入不变，问第二天香蕉的收入为多少元?A.180B.200C.280D.360【解析】答案：C。

三者容斥问题3个公式

公务员行测容斥原理容斥原理公式为：三个集合的容斥关系公式：A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C某校六（1）班有学生45人，每人在暑假里都参加体育训练队，其中参加足球队的有25人，参加排球队的有22人，参加游泳队的有24人，足球、排球都参加的有12人，足球、游泳都参加的有9人，排球、游泳都参加的有8人，问：三项都参加的有多少人？答案：25+22+24-12-9-8+X=45 解得X=3问题：某调查公司对甲乙丙三部电影的收看情况向125人进行调查，有89人看过甲电影，47人看过乙电影，63人看过丙电影，其中有24人三部电影全看过，20人一部也没看过，求只看过两部电影的人数？为什么这道题我用容斥原理去解答得到的答案是错误的，而且和上面的例题相比较，两道题几乎一样，谁能告诉我原因？就是用容斥原理去解答错误出现在什么地方公式一：若条件给出A∩B，A∩C，B∩C，A∩B∩C的值对于图中的全集I来说相当于整个图中所有部分之和，即I=A∪B∪C+D（D为非A非B非C的区域），那么这里面我们算得A∪B ∪C需要把其A、B、C中重复的区域扣除，如果我们把A,B,C加在一起，其中对于A∩B（①+②）的区域是在A,B中各参与计算一次，需要减一个A∩B，同样的道理对于A∩C（①+③），B∩C（①+④）均需要减去一个，对于重复的A∩B∩C（①）在我们把A、B、C加和时计算了三次，在减去A∩B，A∩C，B∩C均包含①区域则又减去三次，要保证没有遗漏需要在加回一次A∩B∩C，则A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C。

公式总结：A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩CI=A∪B∪C+D=A+B+C-A∩B-A∩C-B∩C+A∩B∩C+D公式二：若条件给出包含两种元素（②+③+④）和包含三种元素（①）的值同样的I=A∪B∪C+D，那么这里面我们算得A∪B∪C依旧需要把其A、B、C中重复的区域扣除，那么对于包含两种元素（②+③+④）的区域，②在A、B中各加一次，重复一次；③在A、C中各加一次，重复一次；④在B,C中各加一次，重复一次,均重复一次，则需整体减去一倍的包含两种元素（②+③+④），对于重复的包含三种元素（①）在我们把A.B.C加和时计算了三次，则需要减去2倍的包含三种元素（①），即A∪B∪C=A+B+C-含有两种元素-2*含有三种元素公式总结：A∪B∪C=A+B+C-含有两种元素-2*含有三种元素I=A∪B∪C+D=A+B+C-含有两种元素-2*含有三种元素+D【例1】：某调查公司对甲、乙、丙三部电影的收看情况向135人进行调查，有89人看过甲片，有47人看过乙片，有63人看过丙片，既看过甲、乙片为30人，既看过乙、丙片为31人，既看过甲、丙片为32人，其中有24人三部电影都看过，问多少人一部也没有看过呢?【解析】：既看过甲、乙片为30人是包含只看过甲乙还有甲乙丙三人两个部分，以M、N、W为既看过甲、乙片的人，N既看过乙、丙片的人，既看过甲、丙片的人，X为三部都看过的人数，这里面W、N、X都是有包含三者这个区域，根据把重复数的次数变为1次，或者说把重叠的面积变为一层，做到不重不漏的原则，则公式转化为I=A+B+C-(M+N+W)+X+Y，135=89+47+63-(30+31+32)+ 24+Y，Y=5人。

2019公考行测备考：三者容斥问题解题技巧

2019公考行测备考：三者容斥问题解题技巧公务员考试的过程中，容斥问题是行测中比较常考的一道题。

这类题型总是令很多考生头疼不已，因为容斥问题看起来复杂多变，让考生一时找不到头绪。

中公教育专家提醒考生，这类题有非常明显的内在规律，只要够掌握内在规律，看似复杂的问题就能迎刃而解。

对于二者容斥问题一般可以用文氏图或者直接用公式来解决，下面我们总结一下二者容斥的公式。

容斥问题是一种计数类问题，在计数的过程中重点是每个部分只能计一次，不能重复，如下图I表示全集也就是总数，A、B表示两个集合，A、B重叠的部分我们叫做集合的交集，用A∩B表示，Y表示在整体中但不在A、B里面的部分，那么全集I 就可以表示成A+B-A∩B+Y，这就是二者容斥的简单公式。

【例1】公司某个部门有80%的员工有硕士以上学历，有50%的员工有销售经验，该部门既有硕士以上学历，又有销售经验的员工至少占员工的( )?A 20%B 30%C 40%D 50%【答案】选B【中公解析】此题考查的是二者容斥极值问题，求两个集合交集的最小值，用两个集合相加减去全集，所求=80%+50%-100%=30%。

【例2】现有50名学生都做物力、化学实验，如果物理实验做正确的有40人，化学实验做正确的有31人，两种实验都错的有4人，则两种实验都做对的有( )A 27人B 25人C 19人D 10人【答案】选B【中公解析】根据二者容斥的公式直接带入数值，两种实验都做对的=(40+31+4)-50=25。

【例3】体育课上老师要求全班50名同学按顺序报数，报4的倍数的同学向后转，报6的倍数的同学再向后转，那么现在面向老师的有几人( )A 26人B 30人C 34人D 38人【答案】选D【中公解析】在报数之后面向老师的学生分为两类，一类是报的数字既不是4也不是6的倍数，一类是报的数字既是4也是6的倍数的同学。

设A=“报数是4的倍数的人”=12，B=“报数是6的倍数的人”=8，两者交集=“报数既是4也是6倍数的人”=4，第一类人=50-(12+8-4)=34，所以面向老师的同学有34+4=38人。

国考行测三集合容斥原理

国考行测三集合容斥原理
集合容斥原理是组合数学中的一种常用原理，常用于解决集合问题。

在国家公务员考试中，行测部分经常涉及与集合相关的题目，而集合容斥原理则是解决这类问题的一种有效方法。

集合容斥原理描述了多个集合之间的差集和交集的关系。

具体来说，对于给定的n个集合A1、A2、...、An，集合容斥原理
可以帮助我们计算出这些集合的并集的元素个数。

集合容斥原理的公式为：
|A1 ∪ A2 ∪ ... ∪ An| = |A1| + |A2| + ... + |An| - |A1 ∩ A2| - |A1
∩ A3| - ... + (-1)^n-1 |A1 ∩ A2 ∩ ... ∩ An|
其中，|A|表示集合A的元素个数。

在国考行测中，集合容斥原理常常可以用于解决关于人员分组、选修课程、考试通过等问题。

通过运用集合容斥原理，我们可以得到相应的计算式，从而求得准确的答案。

需要注意的是，在实际运用中，对于给定的具体问题，我们需要根据情况决定要包含哪些集合以及如何计算交集和差集。

并且，根据具体情况，可能需要结合其他的解题方法进行综合运用。

总的来说，集合容斥原理在国考行测中是一种非常有用的解题方法，能够帮助我们清晰地分析问题，准确地求解答案。

因此，对集合容斥原理的理解和掌握对于国考行测的备考非常重要。

三者容斥问题3个公式

三者容斥问题3个公式容斥问题一直是公务员考试备考中不可缺少的一部分。

很多同学在做容斥问题，尤其是三者容斥问题的时候常常会考虑不周，缺了一个部分又多了一个部分。

所以接下来要给大家提供一个万能型的容斥公式，所有的三者容斥问题就迎刃而解了。

如图所示，我们用同一字母表示同一属性的区域。

斜线部分：表示只喜欢一者，用“a”来表示;打点部分：表示只喜欢两者，用“b”来表示;空白部分：表示三者都喜欢，用“c”来表示;而集合外的部分表示三者都不喜欢，用“d”来表示。

因此，根据图形，就有了以下几个公式：1.a+b+c+d=I(只喜欢1者+只喜欢2者+3者都喜欢+3者都不喜欢=总集)2.a+2b+3c=A+B+C(三个集合相加时，喜欢1者的部分加了1次，2者的部分加了2次，喜欢3者的部分加了3次)3.b+3c=X+Y+Z(题目中的固定表达方式为喜欢A和B的有X人、喜欢A和C 的有Y人，喜欢B和C的有Z人)那么我们接下来就利用这个公式来练习几道题目：例1某专业有若干学生，现开设有甲、乙、丙三门选修课。

有40人选修甲课程、36人选修乙课程、30人选修丙课程，兼选甲、乙课程的有28人、兼选甲、丙两门课程的有26人、兼选乙、丙两门课程的有24人、甲乙丙三门课程均选的有20人，三门课程均未选的有2人。

该专业共有学生多少人?A .48 B. 50 C. 52 D.54解析：直接套用公式:(1)根据题中“有40人选修甲课程、36人选修乙课程、30人选修丙课程”得：a+2b+3c=40+36+30=106(2)根据题中“兼选甲、乙课程的有28人、兼选甲、丙两门课程的有26人、兼选乙、丙两门课程的有24人”得：b+3c=28+26+24=78(3) 根据题中“甲乙丙三门课程均选的有20人”得：c=20(4)根据题中“三门课程均未选的有2人”得：d=2.最终求出总集I=a+b+c+d=10+18+20+2=50人，所以答案为B例2 某服装公司就消费者对红、黄、蓝三种颜色的偏好情况进行市场调查、共抽取了40名消费者、发现其中有20人喜欢红色、20人喜欢黄色、15人喜欢蓝色，至少喜欢两种颜色的有19人，喜欢三种颜色的有3人，问三种颜色都不喜欢的几个人?A. 1B.3C.5D.7解析：套用公式:(1)根据题中“共抽取了40名消费者”a+b+c+d=40(2)根据题中“发现其中有20人喜欢红色、20人喜欢黄色、15人喜欢蓝色”a+2b+3c=20+20+15=55(3)根据题中“至少喜欢两种颜色的有19人”b+c=19(4)根据题中“喜欢三种颜色的有3人”c=3.求d=?根据列出的四个式子，可求得d=40-14-16-3=7人答案选B通过这两道题目，同学们可以发现，掌握好这个公式，题目中的每句话就可以列出一个式子，就可以达到机械化解题的效果，减少思考时间。

国考笔试资料数量关系之容斥问题

行测高频考点技巧荟萃第6期：数量关系之容斥问题在公务员、政法干警、选调生等行测考试中会经常考察到容斥问题，所以考生一定要给予重视。

难度也逐渐增大，不再拘泥于最常规的两个集合和三个集合的考查方式。

在各省市的公务员考试中，容斥问题仍然出现活跃。

因此，这一题型还是需要重点关注。

二、基本概念涉及多个相互关联的集合，要求根据集合间的相互关系计算集合中元素个数的问题称为“容斥原理”问题。

难度也逐渐增大，不再拘泥于最常规的两个集合和三个集合的考查方式。

在各省市的公务员考试中，容斥问题仍然出现活跃。

因此，这一题型还是需要重点关注。

二、基本概念涉及多个相互关联的集合，要求根据集合间的相互关系计算集合中元素个数的问题称为“容斥原理”问题。

2019国家公务员考试行测答题技巧：容斥问题求交集、补集和全集

2019国家公务员考试行测答题技巧：容斥问题求交
集、补集和全集
容斥问题是指集合与集合元素之间的相容与相斥问题，在国家公务员考试中容斥问题是一类重要的题型，其中又以求集合之间交集、补集和全集为重点和难点，想要突破这一难点，就必须要掌握这类题型的解题方法与技巧。

中公教育专家为大家总结了求集合交集、补集和全集的方法。

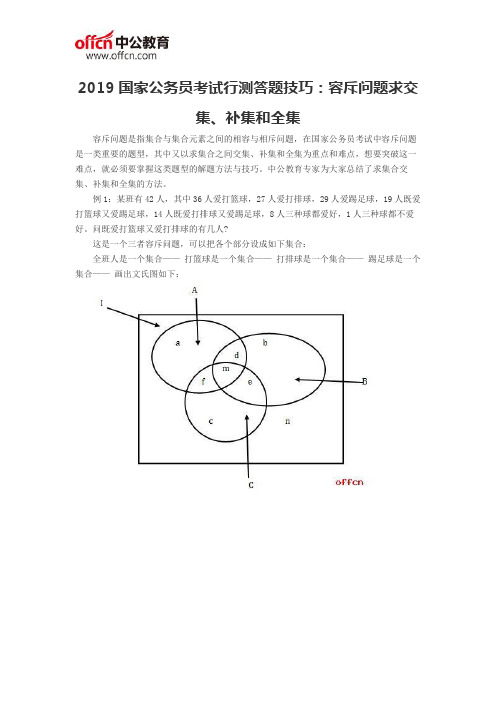
例1：某班有42人，其中36人爱打篮球，27人爱打排球，29人爱踢足球，19人既爱打篮球又爱踢足球，14人既爱打排球又爱踢足球，8人三种球都爱好，1人三种球都不爱好。

问既爱打篮球又爱打排球的有几人?
这是一个三者容斥问题，可以把各个部分设成如下集合：
全班人是一个集合——打篮球是一个集合——打排球是一个集合——踢足球是一个集合——画出文氏图如下：
容斥问题中求交集、补集和全集的题目只要按照本文所给的方法去多加练习，做到熟练运用，就不再困难!。

国家公务员考试行测容斥问题详解

国家公务员考试行测容斥问题详解国家公务员考试行测容斥问题详解：容斥问题容斥问题即包含与排斥问题，它是一种计数问题。

在计数时，几个计数部分有重复包含时，为了不重复计数，应从他们的和中排除重复部分，采用这种计数方法的题型称为容斥问题。

国家公务员考试行测容斥问题详解：题目特点题目中给出多个概念，概念之间存在交叉关系。

国家公务员考试行测容斥问题详解：常考题型1、二者容斥问题公式：覆盖面积=A+B-A与B的交集例1:大学四年级某班有50名同学，其中奥运会志愿者10人，全运会志愿者17人，30人两种志愿者都不是，则班内是全运会志愿者且奥运会志愿者的同学是多少?A.6B.7C.8D.9解析：两个概念分别的奥运会志愿者和全运会志愿者，设班内是全运会志愿者且奥运会志愿者的同学有X人，则有10+17-X+30= 50,所以X=7,即班内是全运会志愿者且奥运会志愿者的同学有7人。

2.三者容斥问题公式：覆盖面积=A+B+C-两者交-2三者交例2:某调查公司对甲、乙、丙三部电影的收看情况向125人进行调查，有89人看过甲片，有47人看过乙片，有63人看过丙片，其中有24人三部电影都看过，20人一部也没有看过，则只看过其中两部电影的人数是多少人?A、69B、65C、57D、46解析：三个概念分别是甲片、乙片、丙片，假设只看过其中两部电影的人数有X人，则89+47+63-X-224+20=125.所以X=46.即只看过其中两部电影的人数有46人。

3.容斥极值问题容斥极值最常考的就是容斥交集的最小值，我们可以套用公式解决。

①(AB)=A+B-I (I表示全集)②(ABC)=A+B+C-2I③(ABCD)=A+B+C+D-3I例3:小明、小刚、小红、小英四人一起参加一次英语考试，已知考试共有100道题，且小明做对了79题，小刚做对了88题，小红做对了91题，小英作对了89.问题：①小明和小刚都最对的题目至少有几题?②小明、小刚、小红都最对的题目至少有几题?③小明、小刚、小红、小英四人最对的题目至少有几题?解析：①小明和小刚都最对的题目至少有79+88-100=67人②小明、小刚、小红都最对的题目至少有79+88+91-2100=58人③小明、小刚、小红、小英四人最对的题目至少有79+88+91+89-3100=47人。

国考行测数学运算中的集合容斥问题

国考行测数学运算中的集合容斥问题三集合容斥问题主要有以下三种题型：1、三集合标准型核心公式2、三集合图示标数型(文氏图或者叫做韦恩图法)a.特别注意“满足某条件”和“只满足某条件”的区别;b.特别注意有没有“三个条件都不满足的情形”;3、三集合整体重复型核心公式三集合容斥问题中，有些条件未知时，就不能直接使用标准型公式，而是运用整体重复型公式同样可以解答。

特别当题目中说明分别满足一种、两种、三种条件的个数时，使用整体重复型公式。

并且，三集合整体重复型公式是现在国家公务员考试考查三集合容斥问题的重点。

另外，可利用尾数法进行快速求解。

原理：在三集合题型中，假设满足三个条件的元素数量分别时A、B和C，而至少满足三个条件之一的元素的总量为W。

其中，满足一个条件的元素数量为x，满足两个条件的元素数量为y，满足三个条件的元素数量为z，根据右图可以得到下满两个等式：W=x+y+zA+B+C=x×1+y×2+z×3通过几个例题阐述三集合容斥的相关内容：由题意我们有 27=8+3+6+2+2+1+X, 解得X=5。

【例3】某高校对一些学生进行问卷调查。

在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备选择两种考试都参加的有46人，不参加其中任何一种考试的都15人。

问接受调查的学生共有多少人?( ) A.120 B.144 C.177 D.192 【解析】根据题意，分别已知两种条件、三种条件都满足的个数，设所有准备参加考试的学生人数为W，只准备参加一门考试的学生人数为X。

使用三集合整体重复型公式：W=X+46+24 63+89+47=X+2×46+3×24根据尾数法，解得x尾数是5，W尾数是5。

因此，学生总数=W+15，尾数为0，选A。

【例4】某市对52种建筑防水卷材产品进行质量抽检，其中有8种产品的低温柔度不合格，10种产品的可溶物含量不达标，9种产品的接缝剪切性能不合格，同时两项不合格的有7种，有1种产品这三项都不合格。

2019漳州事业单位数量关系：三者容斥那些事儿

2019漳州事业单位数量关系：三者容斥那些事儿【导读】中公事业单位为帮助各位考生顺利通过事业单位招聘考试！今天为大家带来数量关系解题技巧：三者容斥那些事儿。

事业单位考试中，容斥问题是一类常考的题型，尤其是三者容斥问题。

此类题目，看起来很复杂，很难解，但实际上是有章可循的，尤其在事业单位考试中，考查的题目一般多数都是利用基本公式就能快速解题的。

因此，只要把基础公式熟烂于心，内化为自己的知识，一定能取得质的突破。

一、基本公式：1.I=A∪B∪C+x=A+B+C-A∩B-A∩C-B∩C+A∩B∩C+x2.I=A+B+C-只包含于两个集合的元素-2×包含于3个集合的元素+x注：x为A、B、C集合之外的部分。

二、例题展示：例题1.对39种食物中是否含有甲、乙、丙三种维生素进行调查，结果如下：含甲的有17种，含乙的有18种，含丙的有15种，含甲、乙的有7种，含甲、丙的有6种，含乙、丙的有9种，三种维生素都不含的有7种，则三种维生素都含的有多少种?A.4B.6C.7D.9中公解析：【答案】A。

解析：首先判断出是容斥问题中的三者容斥问题，设三种维生素都含的食物有m种，根据公式，15+18+17-7-6-9+m+7=39，解得m=4。

所以答案为A。

例题2.某乡镇对集贸市场36种食品进行检查，发现超过保质期的7种，防腐添加剂不合格的9种，产品外包装标识不规范的6种。

其中，两项同时不合格的5种，三项同时不合格的2种。

问三项全部合格的食品有多少种?A.14B.21C.23D.32中公解析：【答案】C。

解析：首先判断出是容斥问题中的三者容斥问题，则根据公式不合格的食品共有7+9+6-5-2×2=13种，则三项全部合格的食品有36-13=23种。

所以答案为C。

例题3.如图所示，X、Y、Z分别是面积为64、180、160的三张不同形状的纸片。

它们部分重叠放在一起盖在桌面上，总共盖住的面积为290。

且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36。

2019国考行测辅导：容斥问题解题技巧

2019国考行测辅导：容斥问题解题技巧容斥问题是国考的必考点，这样的题型如何解答呢？本网为大家整理了2019国考行测辅导：容斥问题解题技巧，供考生们参考，资讯请关注更新。

2019国考行测辅导：容斥问题解题技巧一、概念容斥问题即包含与排斥问题，它是一种计数问题。

在计数时，几个计数部分有重复包含时，为了不重复计数，应从他们的和中排除重复部分，采用这种计数方法的题型称为容斥问题。

简单来说就是要做到不重不漏。

此类题目的题目特点为：题中给出多个概念，各个概念之间有集合关联。

二、解题原则将重复计数的次数变为一次，或者说是把重叠的面积变为一层，做到不重不漏。

即先不考虑重叠的情况，把包含于某内容中的所有对象的数量先计算出来，然后再把计数时重复计算的数量剔除掉，把遗漏的数量补上，使得计算结果既无遗漏又无重复。

三、解题方法——公式法1.两者容斥：2.三者容斥：3.容斥极值：四、经典例题【例1】某科研单位共有68名科研人员，其中45人具有硕士以上学历，30人具有高级职称，12人兼而有之。

既没有高级职称也没有硕士以上学历的科研人员有多少人？A.13B.10C.5D.8【解析】C。

根据题目可知题中涉及的项目共有两个，属于二者容斥的问题。

直接利用两者容斥的公式将相关数据带入可得：，求得。

选择C选项。

【例2】学校开设三门选修课，某年级有240人，其中有120人选择英语写作，有95人选择书法，有78人选择精算学，其中有105人选择三种学科中的至少两种，30人三中学科都选择了，问该年级三种都没选的有多少人？A.122B.82C.112D.216【解析】B。

认真分析题目不难发现题中共出现了三个项目，因此该题为三者容斥问题。

在该题中要注意的是题中说有105人选择三种学科中的至少两种，至少两种包含了两种及三种两种情况。

因此根据公式结合不重不漏的原则可得：，将相关数据带入可以求得：。

故选择B。

【例3】一次考试共有200人参加，试卷共5道题，凡答对3题或3题以上就为合格。

2019国家公务员考试行测数量关系中的三者容斥

公务员考试行测技巧：容斥原理公式及运用

公务员考试数量关系之三集合容斥问题

行测答题技巧：容斥原理之三者容斥问题

行测数量关系技巧：容斥问题求极值

三者容斥问题3个公式

行测数量关系备考：容斥问题

三者容斥问题3个公式

最新完美版国考笔试资料数量关系之容斥问题

2019公考行测备考：三者容斥问题解题技巧

国考行测三集合容斥原理

三者容斥问题3个公式

国考笔试资料数量关系之容斥问题

2019国家公务员考试行测答题技巧：容斥问题求交集、补集和全集

国家公务员考试行测容斥问题详解

国考行测数学运算中的集合容斥问题

2019漳州事业单位数量关系：三者容斥那些事儿

2019国考行测辅导：容斥问题解题技巧