工程光学习题参考答案第四章 光学系统中的光束限制(借鉴分享)
工程光学基础第4章光学系统的光束限制.pptx

光学系统中的渐晕
一、轴外物点的渐晕 二、消除渐晕的条件 三、渐晕系数
想一想:为什么看许多照片时感觉远近都清楚?
理论上,只有共轭的物平面才能在像平面上成 清晰像,其他物点所成的像均为弥散斑。但当此斑 对眼睛的张角小于眼睛的最小分辨角1’时,人眼看 起来仍为一点。此时,该弥散斑可认为是空间点在 平面上的像。
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other fam ous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
10、人的志向通常和他们的能力成正比例。14:13:1114:13:1114:1311/25/2020 2:13:11 PM 11、夫学须志也,才须学也,非学无以广才,非志无以成学。20.11.2514:13:1114:13Nov-2025-Nov-20 12、越是无能的人,越喜欢挑剔别人的错儿。14:13:1114:13:1114:13Wednesday, November 25, 2020 13、志不立,天下无可成之事。20.11.2520.11.2514:13:1114:13:11November 25, 2020
(一)长景深的照片
要拍摄大景深的照片,如远景镜头,应选择短焦距、 小的相对孔径即大的光圈数,对准距离远。
工程光学习题答案(附试题样本)

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学 第4章 光学系统中的光束限制
2,物镜上 hz物=0mm hz分=8mm hz目=9.35mm
lz'=21mm
3,物镜右侧10mm hz物=0.82mm hz分=8mm hz目=9.51mm
lz'=21.3mm
三、阑位对轴外光束位置的选择
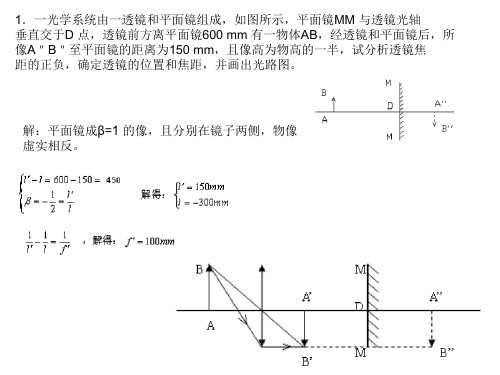
2. 用焦距=450mm 的翻拍物镜拍摄文件,文件上压一块折射率n=1.5,厚度
d=15mm 的玻璃平板,若拍摄倍率
,试求物镜后主面到平板玻璃第一面的距
离。
解:
此为平板平移后的像。
3. 画出经图中棱镜后的输出坐标系
第四章 光学系统中的光束限制
➢光阑 ➢照相系统中的光阑 ➢望远镜系统成像光束的选择 ➢显微系统中的光束限制与分析 ➢光学系统的景深
下,我们都用半视场ω来表示。
2、入射窗、出射窗 1)入射窗:视场光阑经前面的光组在物空间所 成的像; 2)出射窗:视场光阑经后面的光组在像空间所 成的像;
3)判断入射窗的方法: 将光学系统中所有的光学元件的通光口径分别 对其前(后)面的光学系统成像到系统的物 (像)空间去,并根据各像的位置及大小求出 它们对入(出)瞳中心的张角,其中张角最小 者为入射窗(出射窗)。
为圆形或矩形。
孔径光阑位置
第三节 望远系统中成像光束的选择
一、望远系统的基本结构和光学数据:
1、光学结构 2、光学数据:视角放大率Γ、视场角2W、出瞳
直径D’、出瞳距离lZ’ 、物镜焦距f物’、目镜 焦距f目’
双目望远镜系统
望远镜系统简化图
分划板(视场光阑)
孔径光阑
出瞳
二、望远系统中的光束限制:
第一节 光阑
一、概念: 光阑、孔径光阑、视场光阑
1、定义:光学系统中设置的带有内孔的金属薄 片
工程光学习题参考答案第四章-光学系统中的光束限制

第四章 光学系统中的光束限制1.设照相物镜的焦距等于75mm ,底片尺寸为55×55㎜2,求该照相物镜的最大视场角等于多少?解:3.假定显微镜目镜的视角放大率Γ目=15⨯,物镜的倍率β=2.5⨯,求物镜的焦距和要求的通光口径。
如该显微镜用于测量,问物镜的通光口径需要多大(u =-︒3.42y =8mm 显微镜物镜的物平面到像平面的距离为180mm )? 解: (1)5.2'-==ll β mm l 428.51-=180'=-l l mm l 57.128'=‘物f l l 111'=- mm f 73.36=‘物 在此情况下,物镜即为显微镜的孔径光阑︒-=3.4u mm tg ltgu D 734.73.4428.5122=⨯⨯==︒物(2)用于测量时,系统中加入了孔径光阑,目镜是视场光阑 由于u 已知,根据u 可确定孔径光阑的大小 mm tg tgu L OM A 8668.33.4428.51=︒⨯=⋅=OA PA OM D A ’‘孔=2L 目-目fL ‘Zmm OM L f L D A 52.58668.357.12873.3657.12822'=⨯-⨯=⨯-⨯=∴’‘物孔在中M M B B '∆ OA P AB A O M B A D B ‘‘’‘’‘孔=++21 mm y 1045.2'=⨯= mm O M B 863.7=∴ mm D 726.15=物答:物镜的焦距为36.73mm ,物镜的孔径为7.734mm ,用于测量时物镜孔径为15.726mm 。
4. 在本章第二节中的双目望远镜系统中,假定物镜的口径为30mm ,目镜的通光口径为20mm ,如果系统中没有视场光阑,问该望远镜最大的极限视场角等于多少?渐晕系数k =0.5的视场角等于多少? 解:(1)151018108=++x xmm x 252=1081825218252108181815+++=+++=x x y714286.10=y︒=33.112目ω (2)0793651.0181081021=+=+=’目‘物目f f D tg ω ︒︒==∴08.932492‘’‘ω答:极限视场角等于11.33︒渐晕系数为0.5的视场角为9.08︒。
工程光学习题答案

工程光学习题答案第一章习题及答案1、已知真空中的光速c=3*108m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中, n=1.333 时,v=2.25*108m/s,当光在冕牌玻璃中,n=1.51 时,v=1.99*108m/s,当光在火石玻璃中,n=1.65 时,v=1.82*108m/s,当光在加拿大树胶中,n=1.526 时,v=1.97*108m/s,当光在金刚石中,n=2.417 时,v=1.24*108m/s。
2、一物体经针孔相机在屏上成一60mm 大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm 即屏到针孔的初始距离为300mm。
3、一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
工程光学习题解答__第四章_光学系统中的光束限制-推荐下载

解:(1)
ω目
x
108 18 x 15
x 252mm
10
f‘物
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力通根保1据护过生高管产中线工资0不艺料仅高试可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时各卷,类调需管控要路试在习验最题;大到对限位设度。备内在进来管行确路调保敷整机设使组过其高程在中1正资中常料,工试要况卷加下安强与全看过,25度并52工且22作尽护下可1关都能于可地管以缩路正小高常故中工障资作高料;中试对资卷于料连继试接电卷管保破口护坏处进范理行围高整,中核或资对者料定对试值某卷,些弯审异扁核常度与高固校中定对资盒图料位纸试置,卷.编工保写况护复进层杂行防设自腐备动跨与处接装理地置,线高尤弯中其曲资要半料避径试免标卷错高调误等试高,方中要案资求,料技编试术5写、卷交重电保底要气护。设设装管备备置线4高调、动敷中试电作设资高气,技料中课并术3试资件且、中卷料中拒管包试试调绝路含验卷试动敷线方技作设槽案术,技、以来术管及避架系免等统不多启必项动要方方高式案中,;资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资,中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置,作调合并试理且技利进术用行,管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵:导活在。。分对对线于于盒调差处试动,过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调,问试应题技采,术用作是金为指属调发隔试电板人机进员一行,变隔需压开要器处在组理事在;前发同掌生一握内线图部槽纸故内资障,料时强、,电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料,试试线卷卷缆试切敷验除设报从完告而毕与采,相用要关高进技中行术资检资料查料试和,卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
工程光学基础教程 习题参考答案

第一章 几何光学基本定律1. 已知真空中的光速c =3810⨯m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s ,当光在金刚石中,n=2.417时,v=1.24 m/s 。
2. 一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. 一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学习题答案

,斜入射照明,问:
5. 有一生物显微镜,物镜数值孔径 NA=0.5,物体大小 2y=0.4mm,照明灯丝面积 距离 100mm,采用临界照明,求聚光镜焦距和通光孔径。
解:
,灯丝到物面的
视场光阑决定了物面大小,而物面又决定了照明 的大小
第 19 页 共 21 页
工程光学答案
6.为看清 4km 处相隔 150mm 的两个点(设
解:
8、一球面镜半径 r=-100mm,求 =0 ,-0.1 ,-0.2 ,-1 ,1 ,5,10,∝时的物距像距。 解:(1)
第 4 页 共 21 页
(2) 同理,
工程光学答案
(3)同理,
(4)同理,
(5)同理,
(6)同理,
(7)同理,
(8)同理, 9、一物体位于半径为 r 的凹面镜前什么位置时,可分别得到:放大 4 倍的实像,当大 4 倍的虚像、缩小 4 倍的实像和 缩小 4 倍的虚像?
可以根据三角形相似得出: 所以 x=300mm 即屏到针孔的初始距离为 300mm。
3、一厚度为 200mm 的平行平板玻璃(设 n=1.5),下面放一直径为 1mm 的金属片。若在玻璃板上盖一圆形纸片, 要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?
解:令纸片最小半径为 x, 则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正 是由于这个原因导致在玻璃板上方看不到金属片。而全反射临界角求取方法为:
2.设平行光管物镜 L 的焦距 =1000mm,顶杆与光轴的距离 a=10 mm,如果推动顶杆使平面镜倾斜,物镜焦点 F 的自 准直像相对于 F 产生了 y=2 mm 的位移,问平面镜的倾角为多少?顶杆的移动量为多少?
工程光学习题答案(附试题样本)

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
光学系统的光阑与光束限制(第四章)

光学系统的光阑与光束限制(第四章)第四章光学系统的光阑与光束限制一、填空题I级I级1空1、在光学系统中,对光束起限制作用的光学元件通称为[1]。
光阑2、限制轴上物点成像光束大小的光阑称为[1]。
孔径光阑3、孔径光阑经过前面的光学系统在物空间所成的像称为[1]。
入射光瞳4、孔径光阑经过后面的光学系统在像空间所成的像称为[1]。
出射光瞳5、一般安置在物平面或像平面上,以限制成像范围的光阑称为[1]。
视场光阑6、视场光阑经其前面的光学系统所成的像称为[1]。
入射窗7、视场光阑经过后面的光学系统所成的像称为[1]。
出射窗8、轴外点发出的充满入瞳的光束受到透镜通光口径的限制,而部分被遮拦的现象称为[1]。
渐晕9、孔径光阑位于光学系统像方焦面处,光学系统的物方主光线平行于光轴,主光线汇聚中心位于物方无限远处,这样的光路称为[1]。
物方远心光路10、孔径光阑位于光学系统物方焦面处,光学系统的像方主光线平行于光轴,主光线汇聚中心位于像方无限远处,这样的光路称为[1]。
像方远心光路11、在长光路系统中,往往利用[1]达到前后系统的光瞳衔接,以减小光学零件的口径。
场镜12、在像平面上所获得的成清晰像的物空间深度称为成像空间的[1]。
景深13、像面边缘比中心暗的现象称为[1]。
渐晕14、为了减少测量误差,测量仪器一般采用[1]光路。
远心15、渐晕大小用渐晕系数衡量,线渐晕系数定义为轴外点成像光束与轴上点成像光束在[1]上线度之比。
入瞳16、与入射窗共轭的物是[1]。
视场光阑17、与入瞳共轭的物是[1]。
孔径光阑I 级2空1、在放大镜和人眼组成的光学系统中,放大镜的镜框是(),人眼是()。
视场光阑,孔径光阑2、一个10倍的放大镜,通光直径为20mm ,人眼离透镜15mm ,眼瞳直径为3mm ,当渐晕系数为0.5时,人眼观察到的线视场为()mm ;无渐晕时,线视场为()mm 。
33.33,28.333、开普勒望远系统加场镜后,视放大率不变,目镜通光口径(),出瞳离目镜距离()。
工程光学习题解答

6.希望得到一个对无限远成像的长焦距物镜,焦距 =1200mm,由物镜顶点到像面的距离L=700 mm,由系统最后一面到像平面的距离(工作距)为 ,按最简单结构的薄透镜系统考虑,求系统结构,并画出光路图。
解:
7.一短焦距物镜,已知其焦距为35 mm,筒长L=65 mm,工作距 ,按最简单结构的薄透镜系统考虑,求系统结构。
(1) 其远点距离;
(2) 其近点距离;
(3) 配带100度的近视镜,求该镜的焦距;
(4) 戴上该近视镜后,求看清的远点距离;
(5) 戴上该近视镜后,求看清的近点距离。
解:远点距离的倒数表示近视程度
2.一放大镜焦距 ,通光孔径 ,眼睛距放大镜为50mm,像距离眼睛在明视距离250mm,渐晕系数K=50%,试求:(1)视觉放大率;(2)线视场;(3)物体的位置。
4.用焦距=450mm的翻拍物镜拍摄文件,文件上压一块折射率n=1.5,厚度d=15mm的玻璃平板,若拍摄倍率 ,试求物镜后主面到平板玻璃第一面的距离。
解:
此为平板平移后的像。
5.棱镜折射角 ,C光的最小偏向角 ,试求棱镜光学材料的折射率。
解:
6.白光经过顶角 的色散棱镜,n=1.51的色光处于最小偏向角,试求其最小偏向角值及n=1.52的色光相对于n=1.51的色光间的交角。
解:该题可以应用单个折射面的高斯公式来解决,
设凸面为第一面,凹面为第二面。
(1)首先考虑光束射入玻璃球第一面时的状态,使用高斯公式:
会聚点位于第二面后15mm处。
(2) 将第一面镀膜,就相当于凸面镜
像位于第一面的右侧,只是延长线的交点,因此是虚像。
还可以用β正负判断:
(3)光线经过第一面折射: , 虚像
工程光学基础教程 习题答案(完整)

第一章 几何光学基本定律1. 已知真空中的光速c =3810⨯m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s ,当光在金刚石中,n=2.417时,v=1.24 m/s 。
2. 一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. 一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。
(工程光学教学课件)第4章 光学系统中的光束限制

★入射光瞳:孔径光阑经其前面光学系统所成的像(物空间)
决定光学系统的入射光束的孔径角。
★出射光瞳:孔径光阑经其后面光学系统所成的像(像空间)
决定光学系统的出射光束的孔径角。
【例1】单个薄透镜系统
孔径光阑 (入瞳)
出瞳
入瞳
孔径光阑 (出瞳)
★ 如果孔径光阑就安放在透镜上,则孔径光阑本身既是系统 的入瞳,也是系统的出瞳。
例:有一个由三个光学零件组成的光组,透镜O1, 其口径D1=4mm.f’1=36mm,透镜O2,其口径 D2=12mm,f’2=15mm,二透镜间隔195mm,在 离透镜O1右180mm处设有一光孔D3=10mm,物 点离透镜Ol为-45mm.1)求孔径光阑和入瞳出 瞳的大小和位置?2)求视场光阑和入窗出窗的大 小和位置?
第一节 光阑(Stops)
光阑——光学系统中用一些中心开孔的薄金属片来合 理地限制成像光束的宽度、位置和成像范围,此薄金属 片称为光阑。
★含义3:孔径光阑的位置不同,则对应于选择轴外物点 发出光束的不同部分参与成像。
★ 孔径光阑的定义: 1)限制轴上物点成像光束孔径角的大小(宽度); 2)选择轴外物点成像光束的位置。
180
195
D2=12mm
O2
பைடு நூலகம்
(1)求孔径光阑、入瞳、出瞳
2 tgU1 450.044
tg2U425.742/4 .2151.6
tgU3 2.50/2
U1最小,故物镜框O1是入瞳,也是孔径光阑。它经 O2的像为出瞳。
l'1l1l1 f'f2'2
19155 1.2 6m 5 191 55
m D'1ll'11•D111.6295 540.3m 3 m
工程光学基础教程_习题参考答案

工程光学基础教程_习题参考答案工程光学基础教程_习题参考答案第一章光学基本知识与技术1.1 什么是光学?光学在人类生活中有哪些应用?答:光学是研究光的行为和性质的物理学科。
它涉及到光的产生、传播、变换、干涉、衍射、偏振以及光在介质中的行为等问题。
光学在人类生活中有着广泛的应用,如眼镜、镜头、显示器、照明、医疗器械、天文望远镜等。
1.2 光的波动性是如何描述的?答:光的波动性是指光是一种电磁波,具有振幅、频率、波长等特征。
它可以在空间中传播,并且可以表现出干涉、衍射等波动性质。
光的波动性可以通过波长、频率、振幅等参数进行描述。
1.3 什么是光的干涉?举例说明其应用。
答:光的干涉是指两列或两列以上的光波在空间中叠加时,由于光波的叠加产生明暗相间的干涉条纹的现象。
光的干涉在很多领域都有应用,例如光学干涉仪、双缝干涉实验、全息照相、光学通信等。
1.4 什么是光的衍射?举例说明其应用。
答:光的衍射是指光在遇到障碍物或孔径时,会绕过障碍物或孔径边缘,产生明暗相间的衍射图案的现象。
光的衍射在很多领域也有应用,例如光学透镜、衍射光学器件、全息照相、光学存储等。
1.5 什么是光的偏振?举例说明其应用。
答:光的偏振是指光波的电矢量在振动时,只在某个方向上振动,而在其他方向上振动为零的现象。
光的偏振在很多领域也有应用,例如偏振眼镜、偏振片、偏振光学器件等。
第二章光学透镜与成像2.1 什么是透镜?列举几种常见的透镜及其特点。
答:透镜是一种光学器件,它由一块透明材料制成,可以聚焦或发散光线。
常见的透镜包括凸透镜、凹透镜、平凸透镜、平凹透镜等。
2.2 凸透镜的成像原理是什么?如何计算凸透镜的焦距?答:凸透镜的成像原理是光线经过凸透镜后,平行于主轴的光线会聚于一点,这个点称为焦点。
焦距是指从透镜中心到焦点的距离。
凸透镜的焦距可以通过公式 f=1/v+1/u 进行计算,其中f为焦距,u为物距,v为像距。
2.3 凹透镜的成像原理是什么?如何计算凹透镜的焦距?答:凹透镜的成像原理是光线经过凹透镜后,平行于主轴的光线会朝透镜中心方向会聚于一点,这个点称为虚焦点。
工程光学第四章光学系统中的光阑和光束限制

设置方法:
光圈优先:指由机器自动测光系统计算出曝光量的值,然后根据你选定的光圈大小自动决定用多少的快门。手动设置光圈值,由测光结果自动调整快门速度。
★入射光瞳:孔径光阑经其前面光学系统所成的像(物空间) ★出射光瞳:孔径光阑经其后面光学系统所成的像(像空间)
照相机镜头中的孔径光阑
孔径光阑
孔径光阑
物像关系
后面 光学 系统
入瞳
出瞳
孔径光阑
前面 光学 系统
整 个 光 学 系 统
出瞳
孔径 光阑
入瞳
出瞳:决定光学系统的像方光束的孔径角。
入瞳:决定光学系统的物方光束的孔径角。
2
没有对光学零件的大小加以限制
3
01
通常光学系统中用一些中心开孔的薄金属片来合理地限制成像光束的宽度、位置和成像范围。这些限制成像光束和成像范围的薄金属片称为光阑。
02
如果光学系统中安放光阑的位置与光学元件的某一面重合,则光学系统的边框就是光阑
4-1 光阑
使用光圈优先模式的目的是,使用者可以自己控制景深。在风景摄影中,当使用者希望近处和远处的画质都要清晰,而快门速度并不重要的时候,需要设定一个较小的光圈值。在人物摄影中,相机使用者更希望一个较大的光圈值,使得人物的背景失焦,用以强调人物主题而淡化背景。
02
使用光圈优先的另一个目的是让相机选择快门速度,以防止不恰当的曝光时间。在风景摄影中,使用者当为瀑布拍照时,会选用较大的光圈值,也就是较小的光圈配合较长快门时间,使得瀑布的水滴变得模糊。但当在较暗的灯光下摄影时,一个较小的光圈值,也就是获得更大的光圈,使更多的光线进入镜头。
工程光学习题答案

第一章习题及答案1、已知真空中的光速c=3*108m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中, n=1.333 时,v=2.25*108m/s,当光在冕牌玻璃中,n=1.51 时,v=1.99*108m/s,当光在火石玻璃中,n=1.65 时,v=1.82*108m/s,当光在加拿大树胶中,n=1.526 时,v=1.97*108m/s,当光在金刚石中,n=2.417 时,v=1.24*108m/s。
2、一物体经针孔相机在屏上成一60mm 大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2 sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5 的玻璃球上,求其会聚点的位置。
工程光学习题答案

第一章习题及答案1、已知真空中的光速c=3*108m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中, n=1.333 时,v=2.25*108m/s,当光在冕牌玻璃中,n=1.51 时,v=1.99*108m/s,当光在火石玻璃中,n=1.65 时,v=1.82*108m/s,当光在加拿大树胶中,n=1.526 时,v=1.97*108m/s,当光在金刚石中,n=2.417 时,v=1.24*108m/s。
2、一物体经针孔相机在屏上成一60mm 大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2 sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5 的玻璃球上,求其会聚点的位置。
工程光学基础教程课后重点习题答案

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学习题解答

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学习题解答

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 光学系统中的光束限制
1.设照相物镜的焦距等于75mm ,底片尺寸为55×55㎜2,求该照相物镜的最大视场角等于多少?
解:
3.假定显微镜目镜的视角放大率Γ目=15⨯
,物镜的倍率β=2.5⨯
,求物镜的焦距和要求的通光口径。
如该显微镜用于测量,问物镜的通光口径需要多大(u =-︒3.42y =8mm 显微镜物镜的物平面到像平面的距离为180mm )? 解: (1)
5.2'
-==l
l β mm l 428.51-=
180'
=-l l mm l 57.128'
=
‘物
f l l 111'=- mm f 73.36=‘物 在此情况下,物镜即为显微镜的孔径光阑
-ω
f '
︒-=3.4u mm tg ltgu D 734.73.4428.5122=⨯⨯==︒物
(2)
用于测量时,系统中加入了孔径光阑,目镜是视场光阑 由于u 已知,根据u 可确定孔径光阑的大小 mm tg tgu L OM A 8668.33.4428.51=︒⨯=⋅=
A ’
F 2
出瞳
L 目
α
ω'
F '1
f ‘
物
L 目
L 物
A
B
A '
B '
-u
O
A B
M A
M B
M
'
-目f
L ‘
Z
-u
O
B
‘
L 物
O
A P
A OM D A ’‘孔
=2
mm OM L f L D A 52.58668.357
.12873
.3657.12822'=⨯-⨯
=⨯-⨯
=∴’
‘物
孔
在中M M B B '∆ O
A P A
B A O M B A D B ‘
‘
’‘’‘孔=++21 mm y 1045.2'
=⨯= mm O M B 863.7=∴ mm D 726.15=物
答:物镜的焦距为36.73mm ,物镜的孔径为7.734mm ,用于测量时物镜孔径为
15.726mm 。
4. 在本章第二节中的双目望远镜系统中,假定物镜的口径为30mm ,目镜的通光口径为20mm ,
如果系统中没有视场光阑,问该望远镜最大的极限视场角等于多少?渐晕系数k =0.5的视场角等于多少? 解:(1)
y
-f 目
ω目
x
f ‘
物
15
10
18108=++x x
mm x 252=
108
1825218
252108181815+++=
+++=x x y
714286.10=y
︒=33.112目ω (2)
0793651.018
1081021=+=+=’
目‘
物目
f f D t
g ω ︒
︒==∴08.932492‘’
‘
ω
答:极限视场角等于11.33︒
渐晕系数为0.5的视场角为9.08︒。
5. 如果要求上述系统的出射瞳孔离开目镜像方主面的距离为15mm ,求在物镜焦面上加入的
场镜焦距。
ω
f ‘
物
-f 目
解:
D 物对场镜成像,位置为mm f l 1081-=-=’
物
对目镜有
’目
f l l 1112'2=- l mm l Z 15'
'2== mm f 18=‘
目 可得 mm l 902=
21l l d -=’
mm l d l 108901821=+=+‘
对场镜
‘场
f l l 1111'1=- mm l 108'1= mm l 1081-= mm f 54=∴‘场
答:场镜焦距为54mm 。
6.思考题:当物点在垂直光轴方向上下移动时,系统的孔径光阑是否改变?
答:当物点在垂直光轴方向上下移动时,孔径光阑对来自不同点的成像光束 口径限制最大,所以系统的孔径光阑不变。
D 场
D 目
D 目
f ‘
物
-f 目
L ’
Z。
