北京海淀区第一零一中学2010-2011学年初二第二学期数学期中试卷
北京一零一中2010-2011学年度第二学期期末考试初二数学(精)

北京一零一中2010-2011学年度第二学期期末考试初二数学试题及答案考试时间:120分钟满分:140分一、选择题:在每小题给出的四个选项中,只有一项符合题意,请把你认为正确的选项填入表格内。
本大题共10小题,共40分。
1. 下列根式中,是最简二次根式的是(A.8B.12C. 6D. 272. 在平面直角坐标系中,点P (2,-3关于原点对称的点'P 的坐标是( A. (-2,3 B. (3,-2 C. (-2,-3 D. (2,3 3. 关于x 的一元二次方程22(110a x x a -++-=的一个根是0,则a 的值为(A. 1B. -1C. 1或-1D. 04. 在下列图形中,既是轴对称图形,又是中心对称图形的是( A. 等腰梯形 B. 正三角形 C. 平行四边形 D. 菱形5. 下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( A. 3,4,5 B. 6,8,10 C. 325 D. 1,126. 如图1所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B 恰好碰到地面,经测量AB =2米,则树高为(A.5米 B.3米 C. (5+1米 D. 3 米7. 如图2,在正方形A B C D 的外侧作等边A D E △,则A E B ∠的度数为( A. 10° B. 12.5° C. 15° D. 20°8. 如图3,△ABC 中,ABDE //交AC 于D ,交BC 于E ,若AD =2,CD =3,DE =4,则A B =(A.83B.203C.125D. 69. 如图4,等边三角形A B C 的边长为3,D 、E 分别是A B 、A C 上的点,且2AD AE ==,将A D E △沿直线D E 折叠,点A 的落点记为A ',则四边形A D A E '的面积1S 与A B C △的面积2S 之间的关系是(A.1212S S =B.1278S S =C.1234S S =D.1289S S =A E D BCA '图410. 如图5,矩形ABCD 中,AB >AD ,AB =a ,AN 平分∠DAB ,DM ⊥AN 于点M ,CN ⊥AN 于点N 。
海淀区2010-2011学年第二学期初三期中数学试题及参考答案

海淀区九年级第二学期期中练习数 学 2011.5一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.-2的相反数是A .12-B . 12C. -2D. 22.据报道,北京市今年开工及建设启动的8条轨道交通线路,总投资约82 000 000 000元. 将82 000 000 000 用科学计数法表示为A .110.8210⨯B .108.210⨯C .98.210⨯D .98210⨯ 3.在下列几何体中,主视图、左视图和俯视图形状都相同的可能是4. 一个布袋中有1个红球,3个黄球,4个蓝球,它们除颜色外完全相同. 从袋中随机取出一个球,取到黄球的概率是 A.18 B. 38 C. 13D. 125. 用配方法把代数式245x x -+变形,所得结果是A .2(2)1x -+B .2(2)9x --C .2(2)1x +-D .2(2)5x +-6. 如图,ABCD 中,AB =10,BC =6,E 、F 分别是AD 、DC的中点,若EF =7,则四边形EACF 的周长是A .20B .22C .29D .317.有20名同学参加“英语拼词”比赛,他们的成绩各不相同,按成绩取前10名参加复赛. 若小新知道了自己的成绩,则由其他19名同学的成绩得到的下列统计量中,可判断小新能否进入复赛的是 A .平均数 B .极差 C .中位数 D .方差ABD CE F B CDA8.如图,在Rt ABC △中,∠C =90°,AB =5cm ,BC =3cm ,动点P 从点A 出发, 以每秒1cm 的速度,沿A →B →C 的方向运动,到达点C 时停止.设2y PC =, 运动时间为t 秒,则能反映y 与t 之间函数关系的大致图象是二、填空题(本题共16分,每小题4分) 9.若分式14x -有意义,则x 的取值范围是 . 10. 分解因式: 269mx mx m -+= .11. 如图,CD 是⊙O 的直径,弦AB ⊥CD 于点H ,若∠D =30°, CH =1cm ,则AB = cm .12.如图,矩形纸片ABCD中,AB BC =第一次将纸片折叠,使点B 与点D 重合,折痕与BD 交于点1O ;设1O D 的中点为1D ,第二次将纸片折叠使点B 与点1D 重合,折痕与BD 交于点2O ;设21O D 的中点 为2D ,第三次将纸片折叠使点B 与点2D 重合,折痕与BD 交于点3O ,… .按上述方法折叠,第n 次折叠后的折痕与BD 交于点n O ,则1BO = ,n BO = .…第一次折叠 第二次折叠 第三次折叠 …CDC A B DBADCBBAD BAD三、解答题(本题共30分,每小题5分)130211)()4sin 452-+-︒.14.解不等式组:48011.32x x x -<⎧⎪+⎨-<⎪⎩,15.如图,点C 、D 在线段AB 上,E 、F 在AB 同侧,DE 与CF 相交于点O ,且AC =BD , CO =DO ,A B ∠=∠. 求证:AE =BF .16.已知m 是方程220x x --=的一个实数根,求代数式22()(1)m m m m--+的值.17.如图,一次函数y kx b =+与反比例函数my x=的图象交于A (2,1),B (-1,n )两点. (1)求k 和b 的值; (2)结合图象直接写出不等式0mkx b x+->的解集.18.列方程或方程组解应用题:“五一”节日期间,某超市进行积分兑换活动,具体兑换方法见右表. 爸爸拿出自己的积分卡,对小华说:“这里积有8200 分,你去给咱家兑换礼品吧”.小华兑换了两种礼品,共10件,还剩下了200分,请问她兑换了哪两种礼品,各多少件?A C D BEFO四、解答题(本题共20分,每小题5分)19.如图,在梯形ABCD 中,AD ∥BC ,∠B=60°,∠ADC=105°,AD =6,且AC ⊥AB ,求AB 的长.20. 如图,AB 为⊙O 的直径,AB =4,点C 在⊙O 上, CF ⊥OC ,且CF =BF . (1)证明BF 是⊙O 的切线;(2)设AC 与BF 的延长线交于点M ,若MC =6,求∠MCF 的大小.21.为了解学生的课余生活情况,某中学在全校范围内随机抽取部分学生进行问卷调查. 问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类,调查后将数据绘制成扇形统计图和条形统计图(如图所示).(1)请根据所给的扇形图和条形图,填写出扇形图中缺失的数据,并把条形图补充完整; (2)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率; (3)如果该学校有500名学生,请你估计该学校中最喜欢体育运动的学生约有多少名?A D CB A FC OBM 32%其他16%音乐12%美术%体育音乐美术体育其他类别扇形统计图条形统计图合),记△DEF 的周长为p .(1)若D 、E 、F 分别是AB 、BC 、AC 边上的中点,则p =_______;(2)若D 、E 、F 分别是AB 、BC 、AC 边上任意点,则p 的取值范围是 .小亮和小明对第(2)问中的最小值进行了讨论,小亮先提出了自己的想法:将ABC △以AC 边为轴翻折一次得1AB C △,再将1AB C △以1B C 为轴翻折一次得11A B C △,如图2所示. 则由轴对称的性质可知,112DF FE E D p ++=,根据两点之间线段最短,可得2p DD ≥. 老师听了后说:“你的想法很好,但2DD 的长度会因点D 的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的方程2(3)40x m x m --+-=.(1)求证:方程总有两个实数根;(2)若方程有一个根大于4且小于8,求m 的取值范围;(3)设抛物线2(3)4y x m x m =--+-与y 轴交于点M ,若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ,求m 的值.A BD FC E 1图AB D FC E 1F 1A 1B 2D 1D 1E 2图24.已知平面直角坐标系xOy 中, 抛物线2(1)y ax a x =-+与直线y kx =的一个公共点为(4,8)A . (1)求此抛物线和直线的解析式;(2)若点P 在线段OA 上,过点P 作y 轴的平行线交(1)中抛物线于点Q ,求线段PQ 长度的最大值; (3)记(1)中抛物线的顶点为M ,点N 在此抛物线上,若四边形AOMN 恰好是梯形,求点N 的坐标及梯形AOMN 的面积.25.在Rt △ABC 中,∠ACB =90°,tan ∠BAC =12. 点D 在边AC 上(不与A ,C 重合),连结BD ,F 为BD 中点.(1)若过点D 作DE ⊥AB 于E ,连结CF 、EF 、CE ,如图1. 设CF kEF =,则k = ;(2)若将图1中的△ADE 绕点A 旋转,使得D 、E 、B 三点共线,点F 仍为BD 中点,如图2所示.求证:BE -DE =2CF ;(3)若BC =6,点D 在边AC 的三等分点处,将线段AD 绕点A 旋转,点F 始终为BD 中点,求线段CF长度的最大值.(备图1)(备图2)BCA DEFBDEA FC BAC1图2图备图海淀区九年级第二学期期中练习数 学参考答案及评分标准 2011.5说明: 合理答案均可酌情给分,但不得超过原题分数 一、选择题(本题共32分,每小题4分)二、填空题(本题共16分,每小题4分)注:第12题答对一个给2分,答对两个给4分 三、解答题(本题共30分,每小题5分) 13.解:原式=14+-…………………………….……………………………4分 = 3.…………………………….……………………………5分 14.解:解不等式480x -<,得 2x <,…………………………….……………………………2分解不等式1132x x+-<,得 2263x x +-<, 即 4x >-, …………………………….……………………………4分 所以,这个不等式组的解集是42x -<<. …………………………….……………………………5分15.证明:在△COD 中,∵ CO =DO ,∴ ∠ODC =∠OCD . …………………………….……………………………1分 ∵ AC =BD ,∴ AD =BC . …………………………….……………………………2分 在△ADE 和△BCF 中,∵,,,A B AD BC EDA FCB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ △ADE ≌△BCF . …………………………….……………………………4分 ∴ AE =BF .…………………………….……………………………5分16.解:∵ m 是方程220x x --=的一个根,∴ 220m m --=.∴ 22m m -=,22m m -=. …………………………….……………………………2分 ∴ 原式=222()(1)m m m m--+…………………………….……………………………3分 =2(1)mm⨯+ …………………………….……………………………4分 =22⨯=4.…………………………….……………………………5分17.解:(1)∵ 反比例函数my x =的图象过点A (2,1), ∴ m =2.…………………………….……………………………1分∵ 点B (-1,n )在反比例函数2y x=的图象上, ∴ n = -2 .∴ 点B 的坐标为(-1,-2).…………………………….……………………………2分∵ 直线y kx b =+过点A (2,1),B (-1,-2), ∴ 21,2.k b k b +=⎧⎨-+=-⎩解得1,1.k b =⎧⎨=-⎩…………………………….……………………………3分(2)10x -<<或2x >. (写对1个给1分) …………….……………………………5分18.解:因为积分卡中只有8200分,要兑换10件礼品,所以不能选择兑换电茶壶.设小华兑换了x 个保温杯和y 支牙膏, …………….……………………………1分 依题意,得10,20005008200200.x y x y +=⎧⎨+=-⎩…………….……………………………3分解得2,8.x y =⎧⎨=⎩…………….……………………………4分答:小华兑换了2个保温杯和8支牙膏.…………….……………………………5分四、解答题(本题共20分,每小题5分)19.解:过点D 作DE ⊥AC 于点E ,则∠AED =∠DEC =90°.………….……………………1分∵ AC ⊥AB ,∴ ∠BAC =90°. ∵ ∠B =60°,∴ ∠ACB =30°.ADE∴ ∠DAC =∠ACB =30°.………….……………………2分∴ 在Rt △ADE 中,DE =12AD =3,AE=,∠ADE =60°.….………3分∵ ∠ADC=105°, ∴ ∠EDC =45°.∴ 在Rt △CDE 中, CE =DE =3.…………….……………………………4分∴ AC =AE +CE=3.∴ 在Rt △ABC 中,AB =AC ⋅tan ∠ACB=3)3=+ …….……………………5分20.证明:连接OF . (1) ∵ CF ⊥OC,∴ ∠FCO =90°. ∵ OC =OB , ∴ ∠BCO =∠CBO . ∵ FC =FB , ∴ ∠FCB =∠FBC .…………………………..1分∴ ∠BCO +∠FCB =∠CBO +∠FBC . 即 ∠FBO =∠FCO =90°. ∴ OB ⊥BF . ∵ OB 是⊙O 的半径, ∴ BF 是⊙O 的切线.…………………………..2分(2) ∵ ∠FBO =∠FCO =90°,∴ ∠MCF +∠ACO =90°,∠M +∠A =90°. ∵ OA =OC , ∴ ∠ACO =∠A. ∴ ∠FCM =∠M.……………………………………3分易证△ACB ∽△ABM, ∴AC ABAB AM=. ∵ AB =4,MC =6, ∴ AC =2.………………………………………………..4分∴ AM =8,BM . ∴cos ∠MC F = cos M =BM AM. ∴ ∠MCF =30°.………………………………………………..5分AFCOBM21.(1)…………………………….……………………………2分(2)易知选择音乐类的有4人,选择美术类的有3人.记选择音乐类的4人分别是12,,,A A A 小丁;选择美术类的3人分别是12,,B B 小李.可画出树状图如下:由树状图可知共有12中选取方法,小丁和小李都被选中的情况仅有1种,所以小丁和小李恰好都被选中的概率是112. .…………………………….……………………………4分由表可知共有12中选取方法,小丁和小李都被选中的情况仅有1种,所以小丁和小李恰好都被选中的概率是112..…………………………….……………………………4分 (3)由(1)可知问卷中最喜欢体育运动的的学生占40%,得 50040%200⨯=所以该年级中最喜欢体育运动的学生约有200名.…………….……………………………5分22. 解:(1)32p =; .…………………………….……………………………2分 (2)332p <≤..…………………………….……………………………5分音乐美术体育其他类别扇形统计图条形统计图32%其他16%音乐12%美术40%体育1A 1B 2B 小李2A 1B 2B 小李3A 1B 2B 小李1B 2B 小李小丁五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.证明:(1)22224(3)4(4)1025(5)b ac m m m m m ∆=-=---=-+=-≥0,所以方程总有两个实数根..…………………………….……………………………2分解:(2)由(1)2(5)m ∆=-,根据求根公式可知,方程的两根为:x =即:11x =,24x m =-,由题意,有448m <-<,即812m <<.……………………….……………………………5分(3)易知,抛物线2(3)4y x m x m =--+-与y 轴交点为M (0,4m -),由(2)可知抛物线与x 轴的交点为(1,0)和(4m -,0),它们关于直线y x =-的对称点分别为(0,1-)和(0, 4m -), 由题意,可得:14m -=-或44m m -=-,即3m =或4m =.……….……………………………7分24.解:(1)由题意,可得8164(1)a a =-+及84k =,解得1,2a k ==,所以,抛物线的解析式为22y x x =-,直线的解析式为2y x =.…………………………2分(2)设点P 的坐标为4(,2)(0)t t t ≤≤,可得点Q 的坐标为2(,2)t t t -,则 2222(2)4(2)4PQ t t t t t t =--=-=--+ 所以,当2t =时,PQ 的长度取得最大值为4.………………………………4分(3)易知点M 的坐标为(1,-1).过点M 作直线OA 的平行线交抛物线于点N ,如图所示,四边形AOMN为梯形.直线MN 可看成是由直线OA 向下平移b 个单位得到,所以直线MN 的方程为2y x b =-.因为点M 在直线2y x b =-上,解得b =3,即直线MN 的方程为23y x =-,将其代入22y x x =-,可得 2232x x x -=-即 2430x x -+= 解得 11x =,23x = 易得 11y =-,23y =所以,直线MN 与抛物线的交点N 的坐标为(3,3).…………5分如图,分别过点M 、N 作y 轴的平行线交直线OA 于点显然四边形MNHG 是平行四边形.可得点G (1,2),H (113(10)[2(1)]222OMG S MG =⨯-⨯=⨯--=△113(43)(63)222ANH S NH =⨯-⨯=⨯-=△(31)236MNHG S NH =-⨯=⨯=△所以,梯形AOMN 的面积9OMG MNHG ANH AOMN S S S S =++=△△△梯形. ……………………7分25. 解:(1)k =1;……………………….……………………………2分(2)如图2,过点C 作CE 的垂线交BD 于点G ,设BD 与AC 的交点为Q .由题意,tan ∠BAC =12, ∴12BC DE AC AE ==. ∵ D 、E 、B 三点共线, ∴ AE ⊥DB .∵ ∠BQC =∠AQD ,∠ACB =90°,∴ ∠QBC =∠EAQ.∵ ∠ECA+∠ACG =90°,∠BCG+∠ACG =90°, ∴ ∠ECA =∠BCG . ∴ BCG ACE △∽△. ∴12BC GB AC AE ==. ∴ GB =DE. ∵ F 是BD 中点, ∴ F 是EG 中点. 在Rt ECG △中,12CF EG =, ∴ 2BE DE EG CF -==..…………………………….……………………………5分(3)情况1:如图,当AD =13AC 时,取AB 的中点M ,连结MF 和CM ,∵∠ACB =90°, tan ∠BAC =12,且BC = 6, ∴AC =12,AB=.∵M 为AB 中点,∴CM=∵AD =13AC ,∴AD =4.∵M 为AB 中点,F 为BD 中点,∴FM =12AD = 2.B2图BD EAFC GQ∴当且仅当M、F、C三点共线且M在线段CF上时CF最大,此时CF=CM+FM=2+. .…………………………….……………………………6分情况2:如图,当AD=23AC时,取AB的中点M,连结MF和CM,类似于情况1,可知CF的最大值为4+………….……………………………7分综合情况1与情况2,可知当点D在靠近点C的三等分点时,线段CF的长度取得最大值为4+.…………………………….……………………………8分。
北京市101中学20092010学年下学期初二年级

北京市101中学2009-2010学年下学期初二年级期末考试数学试卷(考试时间:100分钟 满分:120分)一、选择题:本大题共8小题,共32分。
(下列每小题中有四个备选答案,其中只有一个是符合题意的,请将正确选项前的字母填在相应的位置上)。
1. 下列各式中正确的是( ) A. 532=+ B. 3232=+ C.169169⨯=⨯D.236=÷2. 把18化成最简二次根式,结果为( ) A. 32B. 36C. 23D. 293. 一元二次方程04x 3x 2=+-的根的情况是( ) A. 无实数根B. 有两个相等的实数根C. 有两个不相等的实数根D. 有一个实数根4. 某中学人数相等的甲、乙两班学生参加了同一次数学测验,各班平均分和方差分别为190S ,245S ,82x ,82x 22====乙甲乙甲,那么成绩比较整齐的班级是( ) A. 甲班 B. 乙班C. 两班成绩一样整齐D. 无法确定5. 在某次数学测验中,随机抽取了10份试卷,其成绩如下:85,81,89,82,72,82,81,81,79,83,则这组数据的众数、中位数分别为( )A. 81,81.5B. 81,81C. 82,82D. 82,776. 下列说法中,错误的是( ) A. 四个角都相等的四边形是矩形B. 一组对边平行且相等的四边形是平行四边形C. 四条边相等的四边形是正方形D. 两条对角线互相垂直且平分的四边形是菱形7. 如图,菱形ABCD 中,∠A =30°,AD=2,若菱形FBCE 与菱形ABCD 关于BC 所在直线对称,连接AF ,则线段AF 的长等于( )A.2 B.3 C. 2 D. 48. 小明将一张正方形包装纸剪成图1所示形状,用它包在一个棱长为10的正方体的表面(不考虑接缝),如图2所示,小明所用正方形包装纸的边长至少..为( ) A. 40B. 220C. 2230+D. 21010+二、填空题:本大题共8小题,共24分。
北京101中学2011-2012学年度第二学期期末考试 初二年级数学

北京101中学2011-2012学年度第二学期期末考试初二年级数学一、选择题:本大题共10小题,共40分.1. 下列二次根式中,属于最简二次根式的是( ). A.x2B.8 C. x 2D.x 21+2. 函数y =x 的取值范围为( ). A. x ≥2 B. x ≤2 C. x >2 D. x <23. 下列图形中,既是中心对称图形又是轴对称图形的是( ).A. 梯形B. 等腰三角形C. 平行四边形D. 圆4. 关于x 的方程0162=-+-m x x 有两个不相等的实数根,则m 的取值范围是( ).A. 10<mB. 10=mC. 10>mD. 10≥m 5. 如图,AB 是⊙O 的弦,OD ⊥AB 于D ,交⊙O 于E ,则下列说法错误..的是( ).A. AD =BDB.C. OD =DED. ∠ACB =∠AOE6. 用配方法解方程2620x x -+=时,下列配方正确的是( ).A. 2(3)9x -= B. 2(3)7x -= C. 2(9)9x -= D. 2(9)7x -=7. 如果两圆的半径分别为3cm 和5cm ,圆心距为5cm ,那么这两个圆的位置关系是( ). A. 内切 B. 相交 C. 外切 D. 外离8. 如图,P A 、PB 分别切⊙O 于点A 、B ,若∠APB =60°,半径是3,则劣弧AB 的长为( ).A.2πB. πC. 2πD. 4π 9. 如图,直角三角形纸片ABC 中,∠C =90°,将三角形纸片沿着图示的中位线DE 剪开,然后把剪开的两部分重新拼接成不重叠的图形,下列选项中不能..拼出的图形是( ).A. 平行四边形B. 矩形C. 等腰梯形D. 直角梯形10. 已知:如图,在正方形ABCD 外取一点E ,连接,,AE BE DE .过点A 作AE 的垂线交DE 于点P .若1,AE AP PB ===.下列结论:①△APD ≌△AEB ;②点B 到直线AE 的距离为;③EB ⊥ED ;④61+=+∆∆APD APB S S ;⑤ABCD S 正方形 ).A. ①③④B. ①②⑤C. ③④⑤D. ①③⑤二、填空题:本大题共6小题,共24分.11. 2(1)0n -=,则3m n +的值为 .12. 如图,△ABC 是等腰直角三角形,BC 是斜边,将△ABP 绕点A 逆时针旋转后,能与△ACD 重合,如果APPD 的长等于 .13. 关于x 的一元二次方程022=+-m mx x 的一个根为1,则m 的值为 .14. 菱形的面积是12,一条对角线的长为4,则另一条对角线长为 . 15. 圆锥的高为12,母线长为13,则该圆锥的侧面积等于 .16. 在平面直角坐标系xOy 中, 正方形A 1B 1C 1D 1,A 2B 2C 2D 2,A 3B 3C 3D 3,…,按下图所示的方式放置. 点A 1,A 2,A 3, …和 O 1,O 2,O 3,…分别在直线y =kx +b 和x 轴上.已知11(,0)2O ,2(2,0)O ,则点A 3的坐标是 ;点A n 的坐标是 .三、解答题:本大题共8小题,共56分.17. 计算: 101()2|2)2-- 18. 解方程:24120x x --=19. 先化简,再求值:2221412211a a a a a a --⋅÷+-+-,其中a 是方程250x x --=的根. 20. 某楼盘准备以6000元/米2的均价对外销售,但为了加快资金周转,开发商两次下调价格后,决定以4860元/米2的均价开盘销售,求平均每次下调的百分率.21. 已知:如图,在梯形ABCD 中,AD ∥BC ,∠B =45°,∠BAC =105°,AD =CD =4. 求BC 的长.22. 如图,四边形ABCD 内接于⊙O ,BD 是⊙O 的直径,AE CD ⊥,垂足为E ,DA 平分BDE ∠.(1)判断直线AE 与⊙O 的位置关系,并证明; (2)若30,1DBC DE ∠=︒=,求AB 的长.23. 阅读下列材料:若关于x 的一元二次方程20ax bx c ++=(0a ≠)的两个实数根分别为12,x x ,则12b x x a +=-,12cx x a=,此结论称为韦达定理.利用此结论解决以下问题:(1)关于x 的一元二次方程222(1)20x k x k -+++=的两根为123,9x x ==,则k = ;(2)关于x 的方程2(1)(1)0kx k x k +++-=的根是整数,求整数k 的值; (3)已知,x y 是正整数,并且2223,120xy x y x y xy ++=+=,求22x y +的值.24. 已知:△ABC 中,AC =BC ,∠ACB =90°,在直角边AC 上任取一点E (E 不与点A ,B 重合),以线段AE 为对角线作正方形ADEF ,连结BE ,取BE 的中点G ,连结FG ,CG .(1)如图①所示,判断FG 与CG 的位置关系与数量关系(直接作答....,不必证明....); (2)将图①中的正方形ADEF 绕点A 逆时针旋转45°,如图②所示,取BE 中点G ,连接FG ,CG .问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3)将图①中正方形ADEF 绕点A 逆时针旋转角α(0°<α<180°),如图③所示,再连结BE ,取BE 的中点G ,连结FG ,CG .问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.25. 如图,将OA = 6,AB = 4的矩形OABC 放在直角坐标系中,动点M ,N 以每秒1个单位的速度分别从点A ,C 同时出发,其中,点M 沿AO 向终点O 运动,点N 沿CB 向终点B 运动,当两个动点运动了t 秒时,过点N 作NP ⊥BC ,交OB 于点P ,连接MP .(1)直线OB 的解析式为 ;用含t 的代数式表示点P 的坐标为 ;(2)在M ,N 的运动过程中,以O ,M ,N 三点为顶点的三角形能否构成等腰三角形,若可以,请求出t 的值;若不能,请说明理由;(3)试探究:在上述运动过程中,过M 点作MQ ⊥OA ,交OB 于点Q ,连接NQ .设以P ,Q ,M ,N 四点为顶点的四边形面积为y ,求y 与t 的函数关系式,并分析此函数与一次函数4y t b =-+的图像的交点个数.【试题答案】一、选择题:本大题共10小题,每小题4分,共40分.二、填空题:本大题共6小题,每小题4分,共24分. 11. 1 12. 2 13. -114. 6 15. 65π 16. 12(3,2),(21,2)n n ---三、解答题:本大题共8小题,共56分.17. (5分)计算:101()|2|2)2--2213=-=-18. (5分)解:126,2x x ==-(5分)19. (5分)解:原式22a a =--(3分),∵2250,5a a a a --=∴-=(4分), ∴原式=3(5分)20. (5分)解:设平均每次下调的百分率为x ,∴26000(1)4860x -=(2分),解得: 120.1, 1.9x x ==(舍)(4分),答:平均每次下调的百分率为10%(5分). 21. (6分)解:分别过A ,D 作BC 的垂线段AE ,DF , ∵∠B =45°,∠BAC =105°,∴∠ACB =30°,∵AD ∥BC ,∴∠CAD =30°,∵AD =CD =4,∴∠ACD =30°,∴∠DCB =60°(2分),∴CF =2,DF=3分),∵∠AEF =∠DFE =∠ADF =90°,∴四边形AEFD 为矩形,∴EF =AD =4,AE =DF=4分),在直角△ABE 中,BE =AE=5分),∴BC =6+6分). 22. (6分)解:(1)直线AE 与⊙O 相切.证明:连结AO ,∵DA 平分BDE ∠,∴∠1=∠2,∵OA =OD ,∴∠1=∠3,∴∠2=∠3,∴AO ∥DE ,∵AE ⊥DE ,∴∠AED =90°,∴∠OAE =180°-90°=90°,∴AE ⊥OA ,∴直线AE 与⊙O 相切(3分); (2)∵BD 是直径,∴∠C =∠BAD =90°,∵∠4=30°,∴∠5=60°,∴∠1=∠2=60°(4分),∵DE =1,∴AD =2(5分),∴AB=6分).23. (8分)解:(1) 122(1)3912x x k +=+=+=, 解得5k =,22[2(1)]4(2)k k ∆=-+-+84360k =-=>,所以5k =(2分).(2)情况一:当0k =时,方程是一元一次方程,此时的解为1x =,成立(3分); 情况二:当0k ≠时,方程是一元二次方程,【方法一】由韦达定理得:12111k x x k k ++=-=--,12111k x x k k-==-,∵12,x x 都是整数,∴1212,x x x x +都是整数,∴1k =±(3分),当1k =时,方程为220x x +=,两根分别为0,-2,成立(4分);当1k =-时,方程为220x --=,即220x +=,无解;综上所述:0,1k k ==(5分).【方法二】设方程的两根为,方程①-方程②得:12122x x x x +-=-(3分),可变形为 12(1)(1)3x x --=, ∴ 111122221113111313111311x x x x x x x x -=-=-=--=-⎧⎧⎧⎧⎨⎨⎨⎨-=-=-=--=-⎩⎩⎩⎩(4分),解得: 122417x x k ⎧⎪=⎪=⎨⎪⎪=-⎩,124217x x k ⎧⎪=⎪=⎨⎪⎪=-⎩,12021x x k =⎧⎪=-⎨⎪=⎩,12201x x k =-⎧⎪=⎨⎪=⎩,综上所述:0,1k k ==(5分);(3)【方法一】原等式可变形为()12023xy x y xy x y +=⎧⎨++=⎩(6分),令12,xy t x y t =+=,∴121212023t t t t =⎧⎨+=⎩,构造方程2231200t t -+=(7分),解得12815t t ⎧=⎨=⎩(舍),或者12158t t =⎧⎨=⎩,即158xy x y =⎧⎨+=⎩,∴222()234x y x y xy +=+-=(8分);【方法二】将23x y xy +=-代入()120xy x y +=得:(23)120xy xy -=,整理得:2()231200xy xy -+=,解得15,8xy xy ==(6分),∴158xy x y =⎧⎨+=⎩或者815xy x y =⎧⎨+=⎩,同理得到(8)15x x -=或者(15)8x x -=(7分),∵,x y 都是正整数,∴得到的无理根或负根舍去,∴53x y =⎧⎨=⎩,或者35x y =⎧⎨=⎩,∴2234x y +=(8分).24. (8分)解:(1)FG ⊥CG ,FG =CG (1分); (2)成立(2分)【方法一】如图①,延长FG 交过B 所作的EF 的平行线于点H ,连结CF ,CH ,第一步:证明△GEF ≌△GBH ,∴HG =FG ,BH =EF (3分),第二步:证明△ACF ≌△BCH ,∴CF =CH ,∴∠1=∠2(4分),∴∠FCH =∠2+∠FCB =∠1+∠FCB =∠ACB =90°,∴FG ⊥CG ,FG =CG (5分);【方法二】如图②,延长FE 交CB 于点H ,连结GH ,第一步:证明△EHB 是等腰直角三角形,∵G 是BE 的中点,∴BG =GH ,∠B =∠3,FH =BC (3分),第二步:证明△FGH ≌△BGC ,∴FG =CG ,∠BGC =∠FGH (4分),∴∠FGC =∠FGH -∠CGH =∠BGC -∠CGH=∠BGH =90°,∴FG ⊥CG (5分);【方法三】如图③,过点B 作AC 的平行线,交AF 的延长线于点H ,取FH 的中点K ,连结GH ,GK ,第一步:证明四边形是正方形,∴BH =BC ,∠4=∠5(3分),第二步:证明△BHG ≌△BGC ,∴GC =GH ,∠6=∠7(4分),第三步:梯形中位线KG ∥BH , ∴∠GKA =∠BHA =90°,∴GK ⊥HF ,∴GF =GH ,∴FG =HG =CG ,∴∠8=∠9,∴∠6=∠10,∴∠FGC =360°-∠10-∠11-90°×2=360°-∠10-(90°-∠7)-90°×2=90°,∴FG ⊥CG (5分).(3)成立.如图④,延长FG 交过B 所作的EF 的平行线于点H ,连结CH ,CF ,BH , 第一步:证明△GEF ≌△GBH ,∴HG =FG ,∠FEB =∠GBH (6分), 第二步:∠HBC =360°-∠GBH -∠1-∠2,∠F AC =∠4+∠5+∠DAB ,可证明: ∠D =∠1+∠3+∠DAB ,∠2=∠4=45°,∠5=90°,在四边形BEF A 中,∠1+∠3+3×90°+∠DAB =360°,∴∠HBC =∠F AC (7分),第三步:证明△F AC ≌△HBC ,∴FC =HC ,∠6=∠7,∴∠FCH =90°,∴在等腰Rt △FCH 中,FG ⊥CG ,FG =CG (8分).25. (8分)(1)直线OB 的解析式:23y x =,点)32,(t t P (2分);(2) 由题可得:(6,0)M t -,(,4)N t ,(0,0)O ;当NO NM =时,62t t -=,解得2t =(3分);当OM ON =时,6t -= 53t =;当MO MN =时(4分),6t -=,无实数解;综上所述,t 的取值是2或53(5分);(3)当3,6t t ==时构不成四边形;当03t <<时,四边形MQNP 是平行四边形,面积为:2412243y t t =-+; 当36t <<时,四边形MQNP 是平行四边形,面积为:2412243y t t =-+-;所以函数解析式是2241224 (03)341224 (36)3t t t y t t t ⎧-+<<⎪⎪=⎨⎪-+-<<⎪⎩(6分)以下考虑其与直线的位置关系: (Ⅰ)03t <<时,联立方程得24122443t t t b -+=-+,整理得: 24247230t t b -+-=①,∴212416(723)48(12)b b ∆=-⨯-=-,(ⅰ)当10∆=时,12b =,此时方程①有两个相同的解123t t ==,但03t <<,∴12b ≠;(ⅱ)当10∆>时,12b >,此时方程①有两个不同的解,∴两函数图像有两个交点,(此时两交点的横坐标的和等于6,其积等于7234b-且必须大于零,否则不成立); (ⅲ)当10∆<时,12b <,此时方程①无解,∴两函数图像无交点,∴舍去; ∴12b >(7分);(Ⅱ)36t <<时,联立方程:24122443t t t b -+-=-+,整理得03724842=++-b t t ②∴224816(723)48(24)b b ∆=-⨯+=⨯-,(ⅰ)当20∆=时,24b =,此时方程②有两个相同的解126t t ==,但36t <<,∴24b ≠;(ⅱ)当20∆>时,24b <,此时方程②有两个不同的解,∴两函数图像有两个交点,(此时,两交点的横坐标的和等于12,其积等于7234b+且必须大于零,否则不成立); (ⅲ)当20∆<时,24b >,此时方程②无解,∴两函数图像无交点,∴舍去;∴24b <;综上所述,当1224b <<时,两函数图像的交点个数为2个;当不在上述范围时,两函数图像的交点个数为0个(8分).。
2013年北京市101中学八年级下数学期中考试模拟试题
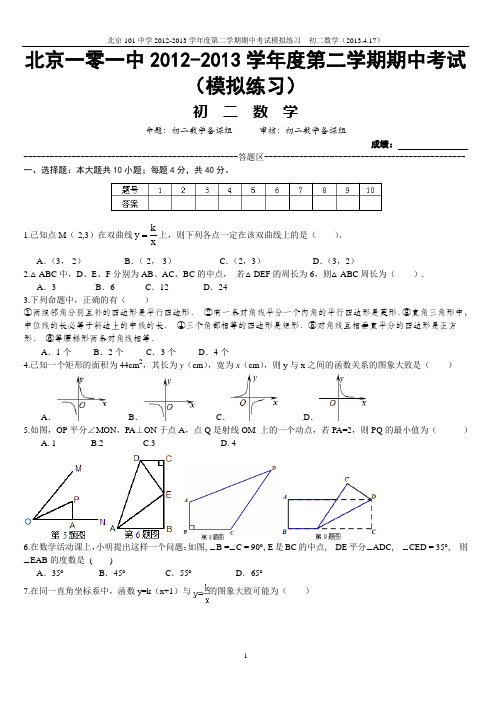
北京一零一中2012-2013学年度第二学期期中考试(模拟练习)初 二 数 学命题:初二数学备课组 审核:初二数学备课组成绩:-------------------------------------------------答题区---------------------------------------------- 一、选择题:本大题共10小题;每题4分,共40分。
1.已知点M (-2,3)在双曲线xky =上,则下列各点一定在该双曲线上的是( )。
A .(3,-2) B .(-2,-3) C .(2,3) D .(3,2)2.△ABC 中,D 、E 、F 分别为AB 、AC 、BC 的中点, 若△DEF 的周长为6,则△ABC 周长为( ). A .3 B .6 C .12 D .243.下列命题中,正确的有( )①两组邻角分别互补的四边形是平行四边形. ②有一条对角线平分一个内角的平行四边形是菱形.③直角三角形中,中位线的长必等于斜边上的中线的长. ④三个角都相等的四边形是矩形.⑤对角线互相垂直平分的四边形是正方形. ⑥等腰梯形两条对角线相等.A .1个B .2个C .3个D .4个4.已知一个矩形的面积为44cm 2,其长为y (cm ),宽为x (cm ),则y 与x 之间的函数关系的图象大致是( )A .B .C .D .5.如图,OP 平分∠MON ,PA ⊥ON 于点A ,点Q 是射线OM 上的一个动点,若PA=2,则PQ 的最小值为( ) A. 1 B.2 C.3 D. 46.在数学活动课上,小明提出这样一个问题:如图, ∠B =∠C = 90︒, E 是BC 的中点, DE 平分∠ADC, ∠CED = 35︒, 则∠EAB 的度数是 ( )A .35︒B .45︒C .55︒D .65︒ 7.在同一直角坐标系中,函数y=k (x+1)与的图象大致可能为( )8.园丁住宅小区有一块草坪如图所示,已知AB=3米,BC=4米,CD=12米,DA=13米,且AB ⊥BC ,这块草坪的面积是( )A .24平方米B .36平方米C .48平方米D .72平方米9.将一张矩形纸片ABCD 如图那样折起,使顶点C 落在C’处,其中AB=4,若∠C’ED=30°,则折痕ED 的长为( ) A .4 B .34 C .8 D .3510.如图,矩形ABCD 的面积为5,它的两条对角线交于点O 1,以AB 、AO 1为两邻边作平行四边形ABC 1O 1,平行四边形ABC 1O 1的对角线交于点O 2,同样以AB 、AO 2为两邻边作平行四边形ABC 2O 2,…,依次类推,则平行四边形ABC a O a 的面积为( )A .B .C .D .二、填空题:本大题共8小题;每题4分,共32分。
2022北京海淀一零一初二(下)期中数学试题及答案

数学
(本卷满分 100 分,考试时间 90 分钟)
命题:初二备课组
审核:初中数学组
一、选择题:(本大题共 8 小题,每小题 3 分,共 24 分)
.1. 下列二次根式中,最简二次根式是( )
A. − 2
B. 1 3
C. 18
2. 在□ABCD 中,∠A∶∠B∶∠C∶∠D 的值可以是( )
5. 下列条件中,不能判断四边形 ABCD 是平行四边形的是( )
A. A = C, B = D
B. AB / /CD, AB = CD
C. AB = CD, AD / /BC
D. AB / /CD, AD / /BC
【答案】C
【解析】
【分析】根据平行四边形的判断方法一一判断即可解决问题.
【详解】解:A、∵∠A=∠C,∠B=∠D,
25. 小明在解方程 24 − x − 8 − x=2 时采用了下面 方法:
24 − x − 8 − x
24 − x+ 8 − x = (24 − x)2 −
2
8− x
=(24 − x) − (8 − x)=16
24 − x − 8 − x = 2 , 24 − x + 8 − x = 8 .
将这两式相加可得
2
(1)求证:四边形 BECF 平行四边形;
( )( 是) ( 的) (2)若 AB=6,AD=4,∠A=60°,求 CE的长.
23. 已知 x = 2 2 + 7 , y = 2 2 − 7 ,试求代数式 x2 − 5xy + y2 的值.
24. 已知 y = x2 −10x + 25 − x + 6 ,当 x 分别取1, 2 , 3 ,…, 2022 时,求所对应 y 值的总和.
北京市海淀区一零一中学2024届数学八年级第二学期期末监测试题含解析

北京市海淀区一零一中学2024届数学八年级第二学期期末监测试题请考生注意:1.请用2B 铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每题4分,共48分)1.数据1,3,5,7,9的方差是( ).A .2B .4C .8D .162.下面调查中,适合采用普查的是( )A .调查全国中学生心理健康现状B .调查你所在的班级同学的身高情况C .调查我市食品合格情况D .调查九江市电视台《九江新闻》收视率 3.下列函数中,一次函数是( ).A .y x =B .y kx b =+C .11y x =+D .22y x x =-4.已知一元二次方程2x 2﹣5x +1=0的两根为x 1,x 2,下列结论正确的是( )A .两根之和等于﹣52,两根之积等于1 B .x 1,x 2都是有理数C .x 1,x 2为一正一负根D .x 1,x 2都是正数5.若分式-22x x +的值为0,则x 的值是( ) A .2 B .0 C .﹣2 D .任意实数6.在同一条道路上,甲车从A 地到B 地,乙车从B 地到A 地,乙先出发,图中的折线段表示甲、乙两车之间的距离y (千米)与行驶时间x (小时)的函数关系的图象,下列说法错误的是( )A .乙先出发的时间为0.5小时B .甲的速度是80千米/小时C .甲出发0.5小时后两车相遇D .甲到B 地比乙到A 地早112小时 7.矩形ABCD 中AB=10,BC=8,E 为AD 边上一点,沿CE 将△CDE 对折,点D 正好落在AB 边上的F 点.则AE的长是( )A .3B .4C .5D .68.如图,以正方形ABCD 的顶点B 为直角顶点,作等腰直角三角形BEF ,连接AF 、FC ,当E 、F 、C 三点在--条直线上时,若2BE =,3AF =,则正方形ABCD 的面积是( )A .10B .14C .5D .79.下列多项式中,不能运用公式法进行因式分解的是( )A .x 2+2xy +y 2B .x 2﹣9C .m 2﹣n 2D .a 2+b 210.已知一次函数y =kx +b (k ≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为 ( ) A .y = x +2 B .y = ﹣x +2 C .y = x +2或y =﹣x +2 D .y = - x +2或y = x -211.某鞋厂调查了商场一个月内不同尺码男鞋的销量,在以下统计量中,该鞋厂最关注的是( ) A .平均数 B .中位数 C .众数 D .方差 12.计算()21412π-⎛⎫-++-- ⎪⎝⎭的值为( ) A .9 B .1 C .4 D .0二、填空题(每题4分,共24分)13.现有四根长30cm ,40cm ,70cm ,90cm 的木棒,任取其中的三根,首尾顺次相连后,能组成三角形的概率为______.14.在平行四边形ABCD 中,AD=13,∠BAD 和∠ADC 的角平分线分别交BC 于E ,F ,且EF=6,则平行四边形的周长是____________________154x -x 的取值范围是__________.16.如图,三个正比例函数的图象分别对应表达式:①y=ax ,②y=bx ,③y=cx ,将a ,b ,c 从小到大排列并用“<”连接为_____.17.如图1,是一个三节段式伸缩晾衣架,如图2,是其衣架侧面示意图,MN 为衣架的墙角固定端,A 为固定支点,B 为滑动支点,四边形DFGI 和四边形EIJH 是菱形,且AF BF CH DF EH ====,点B 在AN 上滑动时,衣架外延钢体发生角度形变,其外延长度(点A 和点C 间的距离)也随之变化,形成衣架伸缩效果,伸缩衣架为初始状态时,衣架外延长度为42cm ,当点B 向点A 移动8cm 时,外延长度为90cm .(1)则菱形DFGI 的边长为______cm .(2)如图3,当60ABF ∠=︒时,M 为对角线(不含H 点)上任意一点,则EM HM JM ++的最小值为______.18. 已知平行四边形ABCD 中,AB =5,AE 平分∠DAB 交BC 所在直线于点E ,CE =2,则AD =_____.三、解答题(共78分)19.(8分)如图,将一张矩形纸片ABCD 沿直线MN 折叠,使点C 落在点A 处,点D 落在点E 处,直线MN 交BC 于点M ,交AD 于点N .(1)求证:CM CN =;(2)若CMN ∆的面积与CDN ∆的面积比为3:1,1ND =.①求MC 的长.②求MN 的长.20.(8分)我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.21.(8分)小丽学完统计知识后,随机调查了她所在辖区若干名居民的年龄,并绘制成如下统计图.请根据统计图提供的信息,解答下列问题(1)小丽共调查了 名居民的年龄,扇形统计图中a = %,b = %;(2)补全条形统计图;(3)若该辖区0~14岁的居民约有3500人,请估计年龄在60岁以上的居民人数.22.(10分)已知:如图,在Rt △ABC 中,∠C=90°,AB=5cm ,AC=3cm ,动点P 从点B 出发沿射线BC 以1cm/s 的速度移动,设运动的时间为t 秒.(1)求BC 边的长;(2)当△ABP 为直角三角形时,求t 的值;(3)当△ABP 为等腰三角形时,求t 的值23.(10分) (1)1483243(2)已知23x =+2(23)1x x --+的值。
2010年北京一零一中第二学期期中考试初一数学及答案

北京-冬•屮2010 -2011学年度第一孑期期屮占试初一数学命邂:杨辉审核:初一铁学备课组友牯提示:下面的銭学问題是为了展示同学们的学习成果,请放松心态,仔细审題,认典作题号12345678910签案4401.卜•列&度的三条线段能组成二角形的足()A 3,4.8 B.5,6, 11 C.1,2.3 D.5,6, 102•已知次于x的不等式2*-加》-3的解集如图2所示•则加的值为()4・•个三和形三个内角的浚数是三个连续的格数.则这个三角形二个内和的度数是()A.2B. IC.0 1).-13.卜列图中能说明Z1>Z2的是()A. 44\45\9fB. 49\59\69eC. 59)60*6°D. 57V59,d的解是(2x + y = 52-1[x = 2X = 12 B.< C.DJ卜=2y = ■],26.已知兰=2 3A 3X - 12丁3 3B. y = —x-3C. y =——x +1D. v = 一一x+ 3 Z 27•“数4“异号. 且其中正数绝对值较夫”•可川不笛式农小为()A. «/> < 0 H I 67 I > I IC. < 0 lLw 4 A < 0B. ah <011a b > 0D. ab <0 11«2+/「工00 3 4 55•方程组用含x的代数式表示y得x = 2&川种工2辺形仙滿血血.不年询满笛恣(B. “…:"I旳C. ||•方形D. il:六边形9 •芳 |* v6| + ix-F + 3 片()•则x 的值为( )9 3A•— B.6 C•— D - 62 210. MBC + . Z^ = ZGDs E分别AH. AC上的点.右AADE "AED • Z.BAD = 20°. Z£DC = 10v.则ZDAE度数•宦足( )A.20"B.40°C.60°D•不能啡••确定一、填空範(Wtt4分,共28分〉11.若x<l .则一2x + 2 0 (用或号城空)・12•—个£也形的何…个外角都绘30。
北京101中学初二期中考试试卷

北京市101中学=上学期初中八年级期中考试数学试卷一、选择题:(本大题共10小题,每小题4分,共40分)(下列每小题中有四个备选答案,其中只有一个....是符合题意的,请将正确选项前的字母填在第三页表格中相应的位置上) 1. 下列图案是轴对称图形的有( )A. 1个B. 2个C. 3个D. 4个 2. 在实数:..12.4,π,-2,722,0.6732323232……,37-中,无理数的个数有( ) A. 1个 B. 2个 C. 3个 D. 4个3. 下列图形不能体现y 是x 的函数的是( )4. 将点A (-2,3)向右平移3个单位得到点B ,则点B 的坐标是( ) A. (1,3) B. (-2,6) C. (-5,3) D. (-2,0)5. 如图,已知A D ∠=∠,要使⊿ABC ≌⊿DCB ,可以增加的一个条件是( )A. AC=BDB. AB=DCC. ACB DBC ∠=∠D. ABE DCE ∠=∠6. 若一次函数y kx b =+中,0,0,k b <<则它的图像大致为( )A B C D7. 下图是象棋盘的一部分,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点( )上。
A. (-1,1)B. (-1,2)C. (-2,1)D. (-2,2)8. 有个数值转换器,原理如下:当输入x 为64时,输出y 的值是( )A. 4B.C.3D.329. 如图,D E ,分别为ABC △的AC ,BC 边的中点,将此三角形沿DE 折叠,使点C 落在AB 边上的点P 处。
若48CDE ∠=°,则APD ∠等于( )A. 42°B. 48°C. 52°D. 58°10. 如图,在平行四边形ABCD 中,∠DAB =30°,AB =6,BC =4,点P 从点D 出发,沿DC 、CB 向终点B 匀速运动。
北京市第一零一中学2023-2024学年八年级下学期期中数学试题(解析版)

北京一零一中2023-2024学年度第二学期期中练习初二数学一、选择题(本大题共8小题,共24分)在下列各题的四个选项中,只有一个是符合题意的.1. 函数中,自变量x 的取值范围是( )A. x >5B. x <5C. x≥5D. x≤5【答案】C【解析】【详解】根据题意得x-5≥0,所以x≥5,故选C.2. 在中,,,的对边分别是a ,b ,c ,下列条件中,不能判定是直角三角形的是( )A. B. C. ,, D. ,,【答案】C【解析】【分析】本题主要考查了直角三角形的判断,分别根据有一个角是直角的三角形是直角三角形,勾股定理的逆定理判断即可.【详解】∵,∴,∴是直角三角形.则A 不符合题意;设,,,根据题意,得,解得,,即,所以是直角三角形.ABC A ∠B ∠C ∠ABC A B ∠∠=︒+90::3:2:1A B C ∠∠∠=1a =1b =1c =1a =b =2c =A B ∠∠=︒+90=90C ∠︒ABC 3A x ∠=2B x ∠=C x ∠=23180x x x ++=︒30x =︒390x =︒=90A ∠︒ABC则B 不符合题意;∵,∴是等边三角形.则C 符合题意;∵,∴是直角三角形;则D 不符合题意.故选:C .3. 将一次函数的图象沿y 轴向上平移4个单位长度,所得直线的解析式为( )A. B. C. D. 【答案】A【解析】【分析】本题考查的是一次函数图象的平移,熟练掌握“左加右减,上加下减”是解答本题的关键.根据平移的性质“左加右减,上加下减”,即可找出平移后的直线解析式.【详解】解: 一次函数的图象沿y 轴向上平移4个单位长度, 所得直线的解析式为.故选A .4. 在平行四边形中,,则的度数为( )A. B. C. D. 【答案】D【解析】【分析】本题主要考查了平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.根据平行四边形的对角相等、邻角互补以及图形可知与是对角,即可求出和的度数;再根据与是邻角,即可求得.【详解】解:如图:∵四边形为平行四边形,a b c ==ABC 2224a b c +==ABC 21y x =-23y x =+25y x =-24y x =-24y x =+ 21y x =-∴21423y x x =-+=+ABCD 100A C ∠+∠=︒B ∠50︒80︒100︒130︒A ∠C ∠A ∠C ∠B ∠A ∠B ∠ABCD∴.∵,∴,∴.故选D .5. 下列各曲线中,不能表示y 是x 的函数的是( )A. B. C. D.【答案】B【解析】【分析】本题考查了函数的概念,“一般地,在一个变化过程中,如果有两个变量与,并且对于的每一个确定的值,都有唯一确定的值与其对应,那么我们就说是自变量,是的函数”,熟悉函数的定义是解决问题的关键.根据定义,逐一判定是否对于的每一个确定的值,都有唯一确定的值与其对应,即可解决问题.【详解】解:A :对于x 的每一个取值,y 都有唯一确定的值与之对应,是的函数,该选项不符合题意;B :在x 正半轴一段范围,对于x 的每一个取值,y 有两个值与之对应,不是的函数,该选项符合题意;C :对于x 的每一个取值,y 都有唯一确定的值与之对应,是的函数,该选项不符合题意;D :对于x 的每一个取值,y 都有唯一确定的值与之对应,是的函数,该选项不符合题意;故选:B .6. 如图,在菱形中,对角线,相交于点O ,E 是的中点,连接,若,.则四边形的周长为( )A. 8B. C. D. 【答案】C 180A B A C ∠+∠=︒∠=∠,100A C ∠+∠=︒50A ∠=︒130B ∠=︒x y x y x y x x y y x y x y x y x ABCD AC BD ABEO OB =120BAD ∠=︒AEOD 6+8+【分析】本题考查了菱形的性质,直角三角形斜边中线等于斜边一半的性质以及勾股定理的应用,熟练掌握相关知识点是解题的关键.利用菱形的性质和勾股定理求出菱形的边长,利用直角三角形的中位线定理得出的长,即可计算出菱形的周长.【详解】解: 为菱形,,对角线,相交于点O ,,,,在中,,,,设,则,利用勾股定理得,,即,解得,(舍去), ,E 是的中点,, 四边形的周长为:.故选:C .7. 能说明命题“若x 为无理数,则也是无理数”是假命题的反例是( )A. B. C. D. 【答案】B【解析】【分析】本题考查了无理数的概念以及二次根式的运算,熟练掌握运算法则和定义是解题的关键.逐一计算每个选项的平方数,按照无理数定义验证即可解决问题.【详解】解:A :,是无理数,不符合题意;B :,不是无理数,符合题意;C :,是无理数,不符合题意;D :EO ABCD ABCD 120BAD ∠=︒AC BD ∴AC BD ⊥60BAO DAO ∠=∠= AB AD BC CD ===OB OD ==Rt AOB △ 60BAO ∠= ∴30ABO = ∠∴12AO AB =AO x =2AB x =222OB AO AB +=222((2)x x +=12x =22x =-∴4AB AD == AB ∴122AE EO AB ===∴AEOD 2248AE EO AD OD +++=+++=+2x π122πx =2212x ==221)6x =-=-225x =+=+8. 如图,某自动感应门的正上方A 处装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高米的学生正对门,缓慢走到离门米的地方时(米),感应门自动打开,则人头顶离感应器的距离等于( )A. 米B. 米C. 2米D. 米【答案】A【解析】【分析】本题考查了矩形的判定与性质,勾股定理.熟练掌握矩形的判定与性质,勾股定理是解题的关键.如图,作于,则四边形是矩形,,,,由勾股定理得,【详解】解:如图,作于,则四边形是矩形,∴,,∴,由勾股定理得,,故选:A .二、填空题(本大题共8小题,共24分)9. 已知点,,在一次函数的图象上,则,的大小关系是______.【答案】【解析】2.5AB =1.6CD 1.21.2BC =AD 1.5 1.8 2.4DE AB ⊥E BCDE 1.2DE BC == 1.6BE CD ==0.9AE =AD =DE AB ⊥E BCDE 1.2DE BC == 1.6BE CD ==0.9AE = 1.5AD ==()11,A y -()23,B y 2y x =-+1y 2y 12y y >【分析】本题主要考查了比较一次函数值的大小,根据解析式得到y 随x 增大而减小,再由即可得到答案.【详解】解:∵一次函数解析式为,,∴y 随x 增大而减小,∵知点,,在一次函数的图象上,且,∴,故答案为:.10. 已知x+1,则代数式x 2﹣2x +1的值为____.【答案】2【解析】【分析】利用完全平方公式将所求的代数式进行变形,然后代入求值即可.【详解】解:原式为:,将代入上式,原式故答案为:2.【点睛】此题考查了完全平方公式的计算,二次根式的性质.利用完全平方公式将所求代数式进行变形是解答此题的关键.11. 如图,在平面直角坐标系中,函数与的图象相交于点,则关于x 的不等式的解集是______.【答案】13-<2y x =-+10k =-<()11,A y -()23,B y 2y x =-+13-<12y y >12y y >221x x -+()2=1x -1x =+)22=(1)=11=2x -+-xOy 1y kx =23y ax =+()1,2A -3kx ax <+1x >-【解析】【分析】本题考查了一次函数与一元一次不等式的关系,观察图象写出直线在直线下方所对应的自变量的范围即可.【详解】解:观察图象可知,当时,直线在直线下方,故关于x 的不等式的解集是,故答案为:.12. 如图1,将长为,宽为的矩形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图2),得到大小两个正方形.若图2中阴影小正方形的面积为49.则a 的值为______.【答案】4【解析】【分析】本题主要考查了正方形的性质,全等三角形的性质,根据题意可得图2中阴影小正方形的边长为,再由图2中阴影小正方形的面积为49即可求出答案.【详解】解:由题意得,图2中阴影小正方形的边长为,∵图2中阴影小正方形的面积为49,∴图2中阴影小正方形的边长为7,∴,∴,故答案为:4.13. 如图,将有一边重合两张直角三角形纸片放在数轴上,纸片上的点A 表示的数是,若以点为圆心,的长为半径画弧,与数轴交于点(点位于点右侧),则点表示的数为________.1y kx =23y ax =+1x >-1y kx =23y ax =+3kx ax <+1x >-1x >-23a +2a 233a a a +-=+233a a a +-=+37a +=4a =1AC BC BD ===2-A AD E E A E【答案】【解析】【分析】根据勾股定理可以求得和的长,再根据和,点表示的数为,即可写出点表示的数.【详解】解:,,,,,点表示的数是,点表示的数为故答案为:【点睛】本题考查勾股定理、实数与数轴,解答本题的关键是明确题意,利用数形结合的思想解答.14. 已知平面直角坐标系下,点A 、C 的坐标为,,点B 的坐标为.若的面积为5,则b 的值为______.【答案】8或【解析】【分析】本题考查了平面直角坐标系中的坐标与图形,利用横、纵坐标得到线段的长度解题的关键.根据点B 、C 的坐标三角形的底,根据点A 的坐标可知边上的高,利用三角形面积计算公式求解即可.【详解】点A 、C 的坐标为,,点B 的坐标为,的底为,高为2,的面积为5,2-+AB AD AD AE A 2-E 1AC BC BD === 90ACB ABD ∠=∠=︒AB ∴===AD ∴===AD AE = AE ∴= A 2-∴E 2-+2-()1,2A ()3,0C (),0Bb ABC 2-BC ()1,2A ()3,0C (),0B b ∴ABC 3BA b =- ABC,,或,故答案为:8或.15. 漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位是时间的一次函数,如表是小明记录的部分数据,则时.h 的值为______.…1235…… 2.4 2.8 3.24…【答案】3.6【解析】【分析】本题考查了待定系数法求一次函数解析式,解二元一次方程组,掌握待定系数法求一次函数解析式是解题的关键.设水位h (cm )是时间t (min )的一次函数解析式为,根据表格代入数据解方程组即可求出解析式,将代入即可求解.【详解】解:设水位h (cm )是时间t (min )的一次函数解析式为,根据表格得,解得,一次函数解析式为,当,.故答案为:3.6.16. 如图,在中,,于点E ,于点F ,、交于点H ,、的延长线交于G ,给出下列结论:①;②点D 是中点:③;④若平分,则;其中一定正确的结论有______.(填序号)1|3|252ABC S b =⨯-⨯=△∴|3|5b -=8b ∴=2b =-2-()cm h ()min t 4t =cm ()min t ()cm h h kt b =+4t =h kt b =+2.42 2.8k b k b +=⎧⎨+=⎩0.42k b =⎧⎨=⎩∴0.42h t =+4t =0.442 3.6h =⨯+=ABCD Y 45DBC∠=︒DE BC ⊥BF CD ⊥DE BF AD BF A BHE ∠=∠AG AB BH =BG DBC ∠)1BE CE =【答案】①③④【解析】【分析】本题考查了平行四边形的性质、等腰三角形的性质,全等三角形的性质和判定,①由证明即可;③先证明,从而得到,然后由平行四边形的性质可知;④连接,证是等腰直角三角形,,设,得出,进而得出.②无法证明点D 是中点.【详解】解:,,,,四边形是平行四边形,,,故①正确;和中,,,,,正确;连接,如图:平分,,在HBE CBF HEB CFB ∠=∠∠=∠,BHE DEC △≌△BH DC =AB BH =CH CEH △DH CH =EH EC a ==DH CH ===)1BE DE EC ==+AG DE BC BF CD ⊥⊥ ,90DEC HFD ∴∠=∠=︒9090DHF EDC EDC C ∴∠+∠=︒∠+∠=︒,DHF C ∴∠=∠ ABCD AB CD A C ∴=∠=∠,DHF BHE ∠=∠ A BHE∴∠=∠BHE DCE △HBE CDE BE DEBEH DEC ∠=∠⎧⎪=⎨⎪∠=∠⎩()ASA BHE DCE ∴ ≌BH DC EH EC ∴==,AB CD = AB BH ∴=,③CH BG 45DBC DBC ∠∠=︒,22.5HBE ∴∠=︒,,是等腰直角三角形,,,,设,,,,④正确∵是平行四边形,∴,∴,,又,∴三个角对应相等无法证明全等,∴无法证明,即无法证明点D 是中点,故②错误,综上①③④正确,故答案为:①③④.三、解答题:(本大题共10小题,共52分)解答应写出文字说明、演算步骤或证明过程.17. 计算:(1(2)【答案】(1)(222.5CDE ∴∠=︒90EH EC DEC =∠=︒ ,CEH ∴ 45EHC CDE HCD ∴∠=︒=∠+∠22.5HCD CDE ∴∠=︒=∠DH CH ∴=EH EC a ==DH CH ∴===)1DE DH HE a a ∴=+=+=+))11BE DE a EC ∴===ABCD AG BC DGF CBF ∠=∠GDF BCF ∠=∠90DFG CFB ∠=∠=︒DFG CFB DG CB =AG +2+4【解析】【分析】本题主要考查二次根式的混合运算,解题的关键是熟练掌握二次根式的性质和运算法则.(1)先根据二次根式的乘除法逐项化简,再合并同类二次根式即可.(2)先将转化为再利用平方差公式,即可求解.【小问1详解】;【小问2详解】18. 如图,在平行四边形中,点E ,F 对角线上,且,连接、、、、求证:四边形是平行四边形.【答案】证明见解析【解析】【分析】根据平行四边形的性质,得到,,进而得到,即可证明四边形是平行四边形.【详解】证明:连接交于点O,2+=+4=+2=+22⎡⎤=-⎢⎥⎣⎦()32=-=ABCD AC AE CF =DE EB BF FD DEBF OA OC =OB OD =OE OF =DEBF BD AC四边形为平行四边形,,,,,四边形为平行四边形.【点睛】本题考查了平行四边形的性质与判定,熟练掌握相关性质与判定定理是解题关键.19.(1)直接写出和的值:______,______;(2)求的值.【答案】(11.(2)1.【解析】【分析】本题考查二次根式的混合运算和异分母分式的加法运算.(1)分别把,和进行计算即可;(2)先进行异分母分式的加法运算,再将和的值代入即可.【小问1详解】解:由已知,,1. ABCD OA OC ∴=OB OD =AE CF = OE OF ∴=∴DEBF a =b =a b +ab a b +=ab =1111s a b=+++a =b =a b +ab a b +ab a b +==1ab ===【小问2详解】解:.20. 如图,已知网格中有一个,顶点A 、B 、C 、D 都在格点上,要求仅利用已有的格点和无刻度直尺作图(注意:不能用圆规),找出格点P (一个即可),使平分.小明和小天分别采用了不同的方法:小明:在边上找到格点P ,连接,可知平分.小天:在边上找到某个格点E ,连接,发现线段上存在格点P ,使平分.请根据两人的思路,分别在图1和图2中完成小明和小天的图形(标出两人所说的点,画出相应的图形)【答案】见解析【解析】【分析】本题主要考查了等腰三角形的性质与判定,平行四边形的性质,根据两人的思路进行作图求解即可.【详解】解:如图1和图2所示,即为所求;图1中易证明,则,再由平行四边形的性质结合平行线的性质可得,则,则点P 即为所求;图2中,易证明,点P 为的中点,则由三线合一定理可得平分.21. 如图.在中,点D 、E 、F 分别是边、、的中点,且.求证:四边形为矩形.()()11112111111b a a b s a b a b a b ab +++++=+====+++++++ABCD Y BP ABC ∠AD BP BP ABC ∠BC AE AE BP ABC ∠AB AP =ABP APB ∠=∠APB CBP ∠=∠ABP CBP ∠=∠AB BE =AE BP ABC ∠ABC AB AC BC 2BC AF =ADFE【答案】见解析【解析】【分析】本题考查了三角形中位线的性质、矩形的判定、等腰三角形的性质以及三角形的内角和.先根据中位线的性质得到,得到四边形为平行四边形,再利用等腰三角形的性质和三角形内角和证明,则求证可证.【详解】证明:∵点D 、E 、F 分别是边、、的中点,∴,,∴四边形为平行四边形,∵F 为中点,,∴,∴,∵,∴,则,即,∴四边形为矩形.22. 探究函数性质时,我们经历了列表、描点、连线画出函数的图象,观察分析图象特征,概括函数性质的过程.小玉同学根据学习函数的经验,对函数进行了探究.下面是小玉的探究过程,请补充完整:(1)函数的自变量取值范围是全体实数;(2)绘制函数图象①列表:下表是x 与的几组对应值:x…01234…EF AB ∥DF AC ∥ADFE 90BAC ∠=︒AB AC BC EF AB ∥DF AC ∥ADFE BC 2BC AF =BF AF CF ==,B BAF FAC C ∠=∠∠=∠180B BAF FAC C ∠+∠+∠+∠=︒()2180BAF FAC ∠+∠=︒90BAF FAC ∠+∠=︒90BAC ∠=︒ADFE 112y x =-+112y x =-+1y 2-1-…543b 345…其中,______;②描点、连线:在同一平面直角坐标系中,描出上表中各组数值所对应的点,并画出函数的图象;(3)结合函数图象,探究函数性质①函数图象上的最低点坐标是______;②的数图象关于直线______对称;(4)已知函数图象和函数的图象无交点,直接写出m 的取值范围是______.【答案】(1)原说法正确,理由见详解 (2)①2,②见详解(3)①,②1. (4)【解析】【分析】本题主要考查了函数的图像和性质.(1)根据对于任意x ,是否有意义回答即可.(2)①把代入函数即可求出b的值. ②描点画出函数图像即可.(3)①根据函数图像即可得出答案,②根据函数图像即可得出答案,(4)根据可得出当时,即可求出m 取值范围.【小问1详解】解:对于任意x ,均有意义上.的1y b =xOy ()1,x y 1y 1y 1y x =22x y m =+112y x =-+()1,232m <1y 1x =1122y x =-+≥1x =122m +<1y∴函数的自变量取值范围是全体实数【小问2详解】①当时,,∴,故答案为:2.②的图象如下:【小问3详解】①函数图象上的最低点坐标是,故答案为:②函数图象关于直线对称,故答案为:1.【小问4详解】∵,且当时,,∴当时,,即,解得:,故答案为:.23. 一次函数的图像与轴交于点,且经过点.(1)当时,求一次函数的解析式及点的坐标;112y x =-+1x =1121122y x =-+=-+=2b =1y 1y ()1,2()1,21y 1x =1122y x =-+≥1x =12y =1x =22y <122m +<32m <32m <()40y kx k k =+≠x A ()2,B m =2m A(2)当时,对于的每一个值,函数的值大于一次函数的值,直接写出的取值范围.【答案】(1)y=x +,点A 的坐标为(-4,0) (2)【解析】【分析】(1)当m =2时,把点C 的坐标代入y =kx +4k (k ≠0),即可求得k 的值,得到一次函数表达式,再求出点A 的坐标即可;(2)根据图像得到不等式,解不等式即可.【小问1详解】解:∵m =2,∴将点C (2,2)代入y =kx +4k ,解得k =;∴一次函数表达式y =x +,当y =0时,x +=0,解得x =-4∵一次函数y =x +的图像与x 轴交于点A ,∴点A 的坐标为(-4,0).【小问2详解】解:如图,y =kx +4k (k ≠0)过定点,∵当时,,对于x 的每一个值,函数的值大于一次函数y =kx +4k (k ≠0)的为1x >-x =y x ()40y kx k k =+≠k 134313k ≤-13134313431343()=+4k x ()4,0-1x =-1y x ==-=y x ()=+4k x值,∴,,解得k ≤−.∴k≤−.【点睛】本题考查了待定系数法求一次函数解析式,利用函数图像解不等式,数形结合是解答本题的关键.24. 如图,一次函数的图象与x 轴交于点A ,与y 轴交于点B ,点D 为x 轴上的点(在点A 右侧),为的垂直平分线,垂足为点E,且,连接.(1)求证:四边形是菱形;(2)连接,求的长.【答案】(1)证明见解析(2)【解析】【分析】本题考查了菱形的判定和性质,勾股定理,平行四边形的判定和性质,直角三角形的性质,熟练掌握菱形的判定与性质是解题的关键;(1)根据为的垂直平分线,得E 为中点,,根据,再证,得,判定四边形是平行四边形,根据对角线互相垂直的平行四边形是菱形,即可得出结论;(2)根据一次函数与x 、y 轴交点得出,,再根据勾股定理求出,根据菱形的性质求出,再次利用勾股定理求出,依据直角三角形的性质定理即可得出.【小问1详解】为的垂直平分线,,,,,1x =-41k k -+≤-1313443y x =-+AC BD BC OD ∥CD ABCD OE OE AC BD BD 90BEC DEC DEA ∠=∠==︒BC OD ∥BEC DEA △≌△BC DA =ABCD OA OB AB AD BD OE AC BD BE DE ∴=90BEC DEC DEA ∠=∠==︒ BC OD ∥BCE DAE ∴∠=∠在和中,,,四边形是平行四边形,为的垂直平分线,四边形是菱形;【小问2详解】一次函数的图象与x 轴交于点A ,与y 轴交于点B ,点A 坐标为,点B 坐标为,,,在中,由(1)得:四边形是菱形,,E 为中点,,在中,E 为中点,连接,.25. 已知,矩形,,对角线、交于点O ,,点M 在射线上,满足,作于E ,的延长线交于F BEC DEA △BEC DEA BE DEBCE DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BEC DEA △≌△BC DA ∴=∴ABCD AC BD ∴ABCD 443y x =-+∴()3,0()0,4∴3OA =4OB =Rt AOB△5AB ===ABCD 5AD AB ∴==BD 8OD OA AD ∴=+=Rt AOB△AB === BDOE 12OE AB ∴===ABCD AD AB >AC BD DAC α∠=BC 2DMC α∠=DE AC ⊥DE BC(1)如图1,点M 在线段上①依题意补全图形,并直接写出______(用含的式子表示)②连接,请用等式表示线段与的数量关系,并证明.(2)当时,设,,请直接写出线段的长(用含m 、n 的式子表示)【答案】(1)①画图见解析,;②,证明见解析 (2)或或【解析】【分析】(1)①根据题意先补全图形,由矩形的性质得到,再根据同角的余角相等得到;②如图所示,延长交于N ,设交于G ,由矩形的性质可得,,先证明,再证明,得到,则;再证明,得到,可得;证明,得到,即可推出;(2)分当点M 在上,且时,当点M 在上,且时,当点M 在线段延长线上时,三种情况画出对应的图形讨论求解即可.【小问1详解】解:①补全图形如下:∵四边形是矩形,∴,∴,∵,∴,∴;BC CDF ∠=αOM OM DF 30α≠︒AD m =CF n =FM α12OM DF =32n m -32m n -2m n +90ADC ∠=︒CDF DAC α==∠∠MO AD MO DF AC BD OA OB OC OD ====,90BAD ∠=︒DBC α∠=BDM DBM α∠==∠BM DM =MO BD ⊥GFM GMF GND GDN ==∠∠,∠∠GF GM GN GD ==,DF MN =()AAS AON COM ≌ON OM =12OM DF =BC FC MC >BC FC MC <BC ABCD 90ADC ∠=︒90DAC DCA ∠+∠=︒DE AC ⊥90CDF DCE ∠+∠=︒CDF DAC α==∠∠故答案为:;②,证明如下:如图所示,延长交于N ,设交于G ,∵四边形是矩形,∴,,∵,∴,∵,∴,∴,∵,∴,∴,∴,∵,∴,,∴,∴,∴,即;∵,∴,又∵,∴,∴,α12OM DF =MO AD MO DF ABCD AC BD OA OB OC OD ====,90BAD ∠=︒DAC α∠=90OAB OBA α==︒-∠∠AB CD 90OAB OBA ODC OCD α====︒-∠∠∠∠DBC α∠=2DMC DBM BDM α=+=∠∠∠BDM DBM α∠==∠BM DM =MO BD ⊥DF AC AD BC ⊥,∥90DFC ADE α==︒-∠∠90DNM NMB α==︒-∠∠GFM GMF GND GDN ==∠∠,∠∠GF GM GN GD ==,GF GD GM GN +=+DF MN =AD BC ∥OAN OCM ONA OMC ==∠∠,∠∠OA OC =()AAS AON COM ≌ON OM =∴,即;【小问2详解】解:如图所示,当点M 在上,且时,取线段的中点N ,连接,则是的中位线,∴,;由矩形的性质可得,∴,∴,由(1)得,∴,∴,∴四边形是平行四边形,∴,∴;如图所示,当点M 在上,且时,取线段的中点N ,连接,则是的中位线,∴,;由矩形的性质可得,2DF MN OM ==12OM DF =BC FC MC >DF ON CN ,ON DBF 12ON BF =ON BF ∥90BC AD m DCF ===︒,∠12CN FN DF ==90CN OM NCF NFC α===︒-,∠∠90EMF α=︒-∠EMF NCF =∠∠CN OM ∥ONCM 12CM ON BF ==()333222n m FM BC BF CM BC BF m m n -=--=-=--=BC FC MC <DF ON CN ,ON DBF 12ON BF =ON BF ∥90BC AD m DCF ===︒,∠∴,∴,由(1)得,∴,∴,∴,∴四边形是平行四边形,∴,∴;如图所示,当点M 线段延长线上时,延长交于N ,∵,∴,∴,∵,∴,∴,∵,∴,∴,∴,∴,∴,在12CN FN DF ==90CN OM NCF NFC α===︒-,∠∠OBM OM BD α=∠,⊥90OMB α=︒-∠EMF NCF =∠∠CN OM ∥ONCM 12CM ON BF ==()333222m n FM BF CM BC BF BC m n m -=+-=-=--=BC AC DM ,AD BC ∥ACB DAC α∠=∠=MCN ACB α==∠∠2DMC N MCN α=+=∠∠∠N MCN DAC α===∠∠∠CM MN DA DN m ===,90DFM α=︒-∠18090290FDM ααα=︒-︒+-=︒-∠FDM DFM ∠=∠MF DM =n CM m CM +=-2m n CM -=∴;综上所述,的长为或或.【点睛】本题主要考查了全等三角形的性质与判定,等腰三角形的性质与判定,矩形的性质,三角形中位线定理,平行四边形的性质与判定等等,利用分类讨论的思想求解是解题的关键.26. 在平面直角坐标系中,对于点和直线.作点关于的对称点,点是直线上一点,作线段满足且,如果线段与直线有交点,则称点是点关于直线和点的“垂对点”.如下图所示,点是点关于直线和点的“垂对点”.2m n MF CF CM +=+=FM 32n m -32m n -2m n +xOy M l M l M 'N l M P 'M P M N ''=90PM N '∠=︒M P 'l P M l N P M l N(1)如图1,已知点,若点,则点关于轴和点的“垂对点”的坐标为______;若点,求点关于轴和点的“垂对点”的坐标;(2)若点、点是直线上的点,点,且满足点是点关于轴和点的“垂对点”,直接写出点的坐标______;(3)已知点,,,,其中.点在四边形的边上,直线,若四边形的边上存在点是点关于直线和点的“垂对点”,请直接写出的取值范围(用含的式子表示)______.【答案】(1)①;②(2)点的坐标为:或 (3)【解析】分析】(1)①根据“垂对点”定义,结合坐标系,即可求解;②点,作关于轴的对称点,过点作轴,过点作的垂【()2,0M -①()10,2N -M y 1N ②()20,4N M y 2N P M P 2y x =--()5,0N -P M x N M (),0A a -(),0B a (),2C a a (),2D a a -0a >M ABCD :l y x t =+ABCD P M l N t a ()0,2()2,2-P ()20-,()1,3-55a t a-≤≤()20,4N ()2,0M -y ()2,0M 'M 'AB y ∥2,P N AB线段,垂足分别为,进而根据“垂对点”定义,结合坐标系,证明,得出的坐标为,即可求解;(2)当在轴上方时,过点作轴,过点作的垂线段,垂足分别为,同(1)可得,得出,根据在上,代入即可求解,当在轴下方时,同法可求;(3)当时,设正方形的中心为,得出,,将绕点逆时针旋转得到,与交于点,证明四边形是正方形,得出是等腰直角三角形,确定点的轨迹,进而根据点与点重合时为临界点,连接,进而得出,结合图形可得当时,存在点是点关于直线和点的“垂对点”,根据对称性即可得出.【小问1详解】解:①如图所示,点,则点关于轴和点的“垂对点”的坐标为如图所示,点,作关于轴的对称点,过点作轴,过点作的垂线段,垂足分别为,,B A ()2AAS AN M BM P ''≌P ()2,2-M x M 'AB x ∥,P N AB ,B A ()AAS ANM BMP ' ≌()2,27P m -+P 2y x =--M x 0t >ABCD Q ()0,Q a (),Q a t t '-M SN ' M '90︒M TP ' EN TP E M SET 'EHK P P C D E '5t a =5t a ≤P M l N 55a t a -≤≤()10,2N -M y 1N ()0,2()20,4N ()2,0M -y ()2,0M 'M 'AB y ∥2,P N AB ,B A根据新定义可得:,∴,∴,∴,∴的坐标为,∴点关于轴和点的“垂对点”的坐标为【小问2详解】解:如图所示,当在轴上方时,过点作轴,过点作的垂线段,垂足分别为,2290,N M P N M PM '''∠=︒=290AM N PM B M PB '''∠=︒-∠=∠()2AAS AN M BM P ''≌24,2AM PB AN BM ''====P ()2,2-M y 2N P ()2,2-M x M 'AB x ∥,P N AB ,B A同(1)可得,∴∵点、点是直线上的点,设,则,∵点,∴∴,即又∵在上,∴,解得:∴;当在轴下方时,如图所示,()AAS ANM BMP ' ≌,AN M B AM PB ''==M P 2y x =--(),2M m m --(),2M m m '+()5,0N -5,2AM m AN m '=+=--()()()225P m n m m +--+++,()2,27P m -+P 2y x =--2722m +=-72m =-()2,0P -M x∵点、点是直线上的点,设,则,∵点,∴∴,,∴,即又∵在上,∴,解得:∴综上所述,点的坐标为:或【小问3详解】解:如图所示,当时,M P 2y x =--(),2M m m --(),2M m m '+()5,0N -5,2AM m AN m '=+=+52AB m m =+--5BP AM m ==+()()225P m m m m +++-+,()22,3P m +-P 2y x =--()3222m -=-+-12m =-()1,3P -P ()20-,()1,3-0t >设正方形的中心为,∵点,,,,其中.∴即,∵关于直线直线的对称点为,则∴,∴,设直线与坐标轴的交点分别为则,∴,则是等腰直角三角形,则∵在直线上,设绕点逆时针旋转(根据新定义,与直线有交点)得到,∴是等腰直角三角形,∵点是点关于直线和点的“垂对点”,∴是等腰直角三角形,设与的交点为,将绕点逆时针旋转得到,与交于点,如图所示,ABCD Q (),0A a -(),0B a (),2C a a (),2D a a -0a >02,20a a a Q -++⎛⎫ ⎪⎝⎭()0,Q a Q :l y x t =+Q '90Q FQ '∠=︒FQ FQ t a '==-(),Q a t t '-:l y x t =+,F H()()0,,,0F t H t -OF OH =OFH 45HFQ ∠=︒N :l y x t =+N Q '90︒Q N ''l N 'NQN ' P M l N M NP ' MM 'FN S M SN ' M '90︒M TP ' EN TP E∴∵∴,∴四边形是矩形又∵∴四边形是正方形,∴∵设与轴的交点为,与轴的交点为点,则,,是等腰直角三角形,当在正方形的边上运动时,在正方形上运动,当点在上运动时,在直线上运动,∴当点与正方形有交点时,存在点是点关于直线和点的“垂对点”,即点与点重合时为临界点,连接,如图所示,90M SN M TP ''∠=∠=︒M S ST'⊥90M SN M SE ''∠=∠=︒M SET 'M S M T''=M SET 'TP NE⊥45FHO ∠=°TP x K y G EHK OKG EFG M ABCD M 'A B C D ''''N y x t =+P TE P ABCD P M l N P C D E '∵四边形是正方形,又∴轴,∵是等腰直角三角形,又,,则的纵坐标之差为,∴,,∵是等腰直角三角形,∴,∴∴当时,存在点是点关于直线和点的“垂对点”,根据对称性可得,故答案为:.【点睛】本题考查了坐标与图形,一次函数与坐标轴交点问题,等腰直角三角形的性质与判定,正方形的性质,全等三角形的性质与判定,轴对称的性质,熟练掌握一线三等角证明全等三角三角形确定点的坐标是解题的关键.M TES '45M ES EHK'∠=︒=∠D E x '∥EFG (),Q a t t '-Q F D E ''∥,F E a (),E a t a --2FG a =GKO 3OG OK OB BK OB BC a ==+=+=5t a=5t a ≤P M l N 55a t a -≤≤55a t a -≤≤。
北京市海淀区中学2010-2011学年下学期初中八年级期中抽测数学试卷

长江中学八年级数学组长江中学八年级数学第二学期期末复习试卷7一、选择题(每题3 分,共 30 分)1. 函数 yx 2 的自变量的取值范围是() A.x 2B. x 2C. x 0D. x 02. 在平面直角坐标系中,将点 P ( -2, 3)沿 x 轴正方向向右平移3 个单位获得点 Q ,则点 Q 对于 x 轴的对称点的坐标是() A. (-1,3)B. ( 5,3)C. ( -5, -3)D. (1, -3)3. 已知点 A (-1, y 1 ), B ( 1, y 2 ), C ( 2, y 3 )在反比率函数 y k(k 0) 的图象上,则 y 1 、 y 2 、 y 3 的x大小关系为() A. y 2 y 3 y 1 B. y 1 y 3 y 2 C. y 1 y 2 y 3 D. y 2 y 1 y 34. 函数 y 6 x 与函数 y 40) 的图象交于 A 、B 两点,设点 A 的坐标为( x 1 , y 1 ),则边长分别为x 1 , y 1(x x 的矩形面积和周长分别为( )A. 4 ,12 B. 4,6 C. 8, 12 D. 8,6 5. 化简a 3 等于( ) A.aB.a C.aD.a aa6. 在平行四边形ABCD 中,已知 BC=12cm ,CD=8cm ,BE 均分∠ ABC 交 AD 于 E ,那么 ED 的长为( )A. 2cmB. 3cmC. 4cmD. 5cm7. 在菱形 ABCD 中, E 、 F 分别是 BC 和 CD 的中点,且 AE ⊥BC , AF ⊥CD ,那么∠ EAF 等于()A. 45°B. 55°C. 60°D. 75°8. 若正方形 ABCD 的边长为6, E 为 BC 边上一点, BE=4 ,M 为线段 AE 上一点,射线 BM 交正方形的 AD 边于点 F ,且 BF=AE ,则 BM 的长为()A.213B.13C.12 13 12 13D. 13或13 13 9. 如图,矩形 ABCD 中, AB AD , AB a , AN 均分∠ DAB ,则 C 、 D 两点到直线 AN 的距离之和是()A. aB.4a C.2a D. 3 a5 2210. 如图,在平行四边形 ABCD 中,∠ DAB=60 °, AB=5 , BC=3 ,点 P 从起点 D 出发,沿 DC 、CB 向终点B 匀速运动,设点 P 所走过的行程为 x ,点 P 所经过的线段与线段 AD 、 AP 所围成图形的面积为 y ,y 随 x 的变化而变化。
北京市一零一中八年级数学下学期期中试卷(含解析)

北京市一零一中八年级数学下学期期中试卷一、选择题:共10小题.1.下列各曲线中表示y是x的函数的是()A. B. C. D.【答案】D【解析】根据函数的意义可知:对于自变量x的任何值,y都有唯一的值与之相对应,故D正确.故选D.2.若点P(﹣1,3)在函数y=kx的图象上,则k的值为()A. ﹣3B. 3C.D. -【答案】A【解析】【分析】利用待定系数法即可解决问题.【详解】解:∵点P(﹣1,3)在函数y=kx的图象上,∴3=﹣k,∴k=﹣3,故选:A.【点睛】本题考查了一次函数图象上的点的坐标特征,待定系数法等知识,解题的关键是熟练掌握基本知识.3.已知,一次函数y=kx+b图象如图所示,则不等式kx+b>0的解集为()A. x>﹣1B. x<﹣1C. x>2D. x<2【答案】A【分析】不等式kx+b>0的解集为直线y=kx+b落在x轴上方的部分对应的x的取值范围.【详解】解:从图象得知一次函数y=kx+b(k,b是常数,k≠0)的图象经过点(﹣1,0),并且函数值y 随x的增大而增大,因而则不等式kx+b>0的解集是x>﹣1.故选:A.【点睛】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b 的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.4.已知P1(-3,y1),P2(2,y2)是一次函数y=2x+1的图象上的两个点,则y1, y2的大小关系是( )A. y1>y2B. y1<y2C. y1= y2D. 不能确定【答案】B【解析】【分析】先根据一次函数y=2x+1中k=2判断出函数的增减性,再根据-3<2进行解答即可.【详解】∵一次函数y=2x+1中k=2>0,∴此函数是增函数,∵−3<2,∴y1<y2.故选B.【点睛】本题考查了一次函数的知识点,解题的关键是熟练的掌握一次函数的性质与其图象上点的坐标特征.5.已知2是关于x的方程3x2﹣2a=0的一个解,则a的值是()A. 3B. 4C. 5D. 6【答案】D【解析】【分析】利用一元二次方程解的定义,把x=2代入方程3x2﹣2a=0得12﹣2a=0,然后解关于a的方程即可.【详解】解:把x=2代入方程3x2﹣2a=0得3×4﹣2a=0,解得a=6.【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.6.如图,若DE是△ABC的中位线,△ABC的周长为1,则△ADE的周长为()A. 1B. 2C.D.【答案】C【解析】【分析】根据三角形的中位线定理,DE是△ABC的中位线,△ABC的周长为1,得DE=,AD=,AE=而解得.【详解】解:∵DE是△ABC的中位线,△ABC的周长为1,∴DE=,AD=,AE=∴△ADE的周长为.故选:C.【点睛】根据三角形的中位线定理,得三角形ADE的边长是三角形ABC边长的.本题主要是根据三角形的中位线定理进行分析计算.7.若m<﹣1,则一次函数y=(m+1)x+m﹣1的图象不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】A【解析】【分析】根据一次函数的性质,可得答案.【详解】解:当m<﹣1时,m+1<0,m﹣1<2,一次函数y=(m+1)x+m﹣1的图象不经过第一象限,故选:A.【点睛】本题考查了一次函数的性质,利用一次函数的性质:y=kx+b,k<0,b<0时,图象经过二三四象限是解题关键.8.将矩形纸片ABCD按如图所示的方式折叠,AE.EF为折痕,∠BAE=30°,BE=1,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则EC的长为()A. B. 2 C. 3 D. 2【答案】B【解析】【分析】根据直角三角形30°角所对的直角边等于斜边的一半求出AE=2,再根据直角三角形两锐角互余求出∠AEB =60°,根据翻折变换的性质可得∠AEB1=∠AEB,根据两直线平行,内错角相等可得∠EAC1=∠AEB1=60°,然后判断出△AEC1是等边三角形,根据等边三角形的性质可得BC1=AE,再根据翻折变换的性质可得EC=BC1.【详解】解:∵矩形纸片ABCD,∠BAE=30°,∴AE=2BE=2×1=2,∠AEB=90°﹣∠BAE=90°﹣30°=60°,∵AB沿AE翻折点B落在EC1边上的B1处,∴∠AEB1=∠AEB=60°,∵矩形对边AD∥BC,∴∠EAC1=∠AEB1=60°,∴△AEC1是等边三角形,∴BC1=AE=2,∵EC沿BF翻折点C落在AD边上的C1处,∴EC=BC1=2.故选:B.【点睛】本题考查了翻折变换,直角三角形30°角所对的直角边等于斜边的一半,等边三角形的判定与性质,熟记翻折前后对应边相等,对应角相等是解题的关键.9.如图,▱ABCD的对角线AC.BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=BC,成立的个数有()A. 1个B. 2个C. 3个D. 4个【答案】C【解析】试题分析:由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=BC,得到AE=BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到S▱ABCD=AB•AC,故②正确,根据AB=BC,OB=BD,且BD>BC,得到AB<OB,故③错误;根据三角形的中位线定理得到OE=AB,于是得到OE=BC,故④正确.解:∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,∴AE=AB=BE,∵AB=BC,∴AE=BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;∵AC⊥AB,∴S▱ABCD=AB•AC,故②正确,∵AB=BC,OB=BD,且BD>BC,∴AB<OB,故③错误;∵CE=BE,CO=OA,∴OE=AB,∴OE=BC,故④正确.故选:C.【此处有视频,请去附件查看】10.如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是()A. 当x=2时,y=5B. 矩形MNPQ的面积是20C. 当x=6时,y=10D. 当y=时,x=10【答案】D【解析】试题分析:由图2可知:PN=4,PQ=5.A.当x=2时,y=×MN×RN=×5×2=5,故A正确,与要求不符;B.矩形的面积=MN•PN=4×5=20,故B正确,与要求不符;C.当x=6时,点R在QP上,y=×MN×RN=10,故C正确,与要求不符;D.当y=时,x=3或x=10,故错误,与要求相符.故选:D.考点:动点问题的函数图象.二、填空题:共8小题.11.函数中自变量x的取值范围是_____.【答案】x≥﹣5【解析】【分析】根据二次根式的性质,被开方数大于等于0可知:x+5≥0,解不等式求x的范围.【详解】解:根据题意得:x+5≥0,解得x≥﹣5.【点睛】本题考查了函数自变量取值范围的求法.函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.12.若一元二次方程 x2﹣2x﹣m=0 无实根,则 m 的取值范围是________.【答案】m<﹣1【解析】【分析】根据根的判别式,得到△0,代入求解即可解题.【详解】解:∵一元二次方程 x2﹣2x﹣m=0 无实根,∴△=4+4m0,解得:m<﹣1.【点睛】本题考查了根的判别式,属于简单题,熟悉根的判别式的概念是解题关键.13.将函数y=2x+1的图象向上平移2个单位,所得的函数图象的解析式为_____.【答案】y=2x+3【解析】【分析】根据一次函数图象平移时“上加、下减”的原则进行解答即可.【详解】解:由“上加下减”的原则可知,将函数y=2x+1的图象向上平移2个单位所得函数的解析式为y=2x+3.故答案为:y=2x+3.【点睛】本题考查了一次函数的图象与几何变换,掌握“上加下减”的原则是解题的关键.14.如图,等边三角形在正方形内,连接,则__________.【答案】15°【解析】∵∵△是正三角形,∴,.又∵正方形,∴,,∴,,∴,∴15.如图,在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3.若平行四边形ABCD的周长是16,则EC的长为________.【答案】2【解析】试题分析:由平行四边形的性质和已知条件证出∠BAE=∠BEA,证出AB=BE=3;求出AB+BC=8,得出BC=5,即可得出EC的长.∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD,AD=BC,∴∠AEB=∠DAE,∵平行四边形ABCD的周长是16,∴AB+BC=8,∵AE是∠BAD的平分线,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=BE=3,∴BC=5,∴EC=BC﹣BE=5﹣3=2;考点:平行四边形的性质16.根据如图所示的程序计算函数值,若输入x的值为,则输出的y值为_____.【答案】【解析】【分析】根据x的值选择相应的函数关系式,计算即可得解.【详解】解:x=时,y=﹣x+2=﹣+2=.故答案为:.【点睛】本题考查了函数值,理解图表信息准确选择相应的函数关系式是解题的关键.17.已知点A(2,﹣4),直线y=﹣x﹣2与y轴交于点B,在x轴上存在一点P,使得PA+PB的值最小,则点P的坐标为_____.【答案】(,0)【解析】【分析】作点B关于x轴的对称点B′,连接AB′,交x轴于P,连接PB,此时PA+PB的值最小.求出直线AB′的解析式即可解决问题.【详解】作点B关于x轴的对称点B′,连接AB′,交x轴于P,连接PB,此时PA+PB的值最小.设直线AB′的解析式为y=kx+b,把A(2,﹣4),B′(0,2)代入得:,解得:,∴直线AB′的解析式为y=﹣3x+2,令y=0,得:x,∴P(,0).故答案为:(,0).【点睛】本题考查了一次函数图象上的点的特征,轴对称最短问题等知识,解题的关键是学会利用轴对称解决最短问题,属于中考常考题型.18.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B3的坐标是_____;点B2018的坐标是_____.【答案】 (1). (7,4) (2). (22018﹣1,22017)【解析】【分析】首先求得直线的解析式,分别求得B1,B2,B3…的坐标,可以得到一定的规律,据此即可求解.【详解】解:∵B1的坐标为(1,1),点B2的坐标为(3,2),∴正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2,∴A1的坐标是(0,1),A2的坐标是:(1,2),代入y=kx+b得,解得:.则直线的解析式是:y=x+1.∵点B1的坐标为(1,1),点B2的坐标为(3,2),∴点B3的坐标为(7,4),…,∴Bn的横坐标是:2n-1,纵坐标是:2n-1.Bn的坐标是(2n-1,2n-1)∴B2018的坐标是(22018-1,22017).故答案为:(7,4),(22018-1,22017).【点睛】此题考查的是一次函数图象上点的坐标特点及用待定系数法求函数解析式和坐标的变化规律,正确得到点的坐标的规律是解题的关键.三、解答题共8小题.19.解一元二次方程:(1)(2x+1)2=9;(2)x2+4x﹣2=0;(3)x2﹣6x+12=0;(4)3x(2x+1)=4x+2.【答案】(1)x1=1,x2=﹣2;(2)x1=﹣2+,x2=﹣2﹣;(3)方程没有实数解;(4)x1=﹣,x2=.【解析】【分析】(1)利用直接开平方法解方程;(2)利用配方法解方程;(3)根据判别式的意义判断方程没有实数解;(4)先移项得到3x(2x+1)﹣2(2x+1)=0,然后利用因式分解法解方程.【详解】解:(1)2x+1=±3,所以x1=1,x2=﹣2;(2)x2+4x=2,x2+4x+4=6,(x+2)2=6,x+2=±,所以x1=﹣2+,x2=﹣2﹣;(3)△=(﹣6)2﹣4×1×12<0,所以方程没有实数解;(4)3x(2x+1)﹣2(2x+1)=0,(2x+1)(3x﹣2)=0,2x+1=0或3x﹣2=0,所以x1=﹣,x2=.【点睛】本题考查了解一元二次方程﹣因式分解法:因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解方程.20.已知,m是方程x2﹣x﹣3=0的一个实数根,求代数式(m2﹣m)(m﹣ +1)的值.【答案】6【解析】【分析】根据一元二次方程解的定义得到m²﹣m﹣3=0,则m²﹣2m=3,把m²﹣m﹣3=0两边都除以m得m﹣1﹣=0,则m﹣=1,然后利用整体代入的方法计算代数式的值.【详解】解:∵m是方程x2﹣x﹣3=0的一个实数根,∴m2﹣m﹣3=0,∴m2﹣m=3,m﹣1﹣=0,即m﹣=1,∴(m2﹣m)(m﹣+1)=3×(1+1)=6.【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.21.已知直线l1的函数解析式为y=x+1,且l1与x轴交于点A,直线l2经过点B,D,直线l1,l2交于点C.(1)求点A的坐标;(2)求直线l2的解析式;(3)求S△ABC的面积.【答案】(1)A(﹣1,0);(2)y=﹣2x+6;(3).【解析】【分析】(1)在y=x+1中,令y=0,则x=﹣1,即可得到点A的坐标;(2)利用待定系数法,即可得到直线l2的解析式;(3)解方程组求得C(,),即可得到S△ABC的面积.【详解】解:(1)在y=x+1中,令y=0,则x=﹣1,∴A(﹣1,0);(2)设直线l2的解析式为y=kx+b,则,解得,∴y=﹣2x+6;(3)解方程组,可得,∴C(,),∴S△ABC=×(3+1)×=.【点睛】本题考查了两直线相交的问题,直线与坐标轴的交点的求解,待定系数法求一次函数解析式,要注意两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.22.如图,在△ABC中,AB=AC,D是BC边的中点,点E,F分别在AD及其延长线上,且CE∥BF,连接BE,CF.(1)求证:四边形EBFC是菱形;(2)若BD=4,BE=5,求四边形EBFC的面积.【答案】(1)见解析;(2)24.【解析】【分析】(1)由D是BC边的中点,CE∥BF,利用ASA易证得△BDF≌△CDE,即可得CE=BF,然后由一组对边平行且相等的四边形是平行四边形,证得四边形BFCE是平行四边形;由AB=AC,D是BC边的中点,即可得AD⊥BC,又由四边形BFCE是平行四边形,根据对角线互相垂直的平行四边形是菱形,即可证得四边形BFCE是菱形.(2)求出BC.EF即可解决问题;【详解】(1)证明:∵D是BC边的中点,∴BD=CD,∵CE∥BF,∴∠DBF=∠ECD,在△BDF和△CDE中,,∴△BDF≌△CDE(ASA),∴CE=BF,又∵CE∥BF,∴四边形BFCE是平行四边形;∵AB=AC,D是BC的中点,∴AD⊥BC,又∵四边形BFCE是平行四边形,∴四边形BFCE是菱形.(2)解:在Rt△BDE中,BE=5,BD=4,∴DE==3,∵四边形BECF是菱形,∴EF=2DE=6,BC=2BD=8,∴菱形BECF的面积=×6×8=24.【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、等腰三角形的性质以及菱形的判定.此题难度适中,注意掌握数形结合思想的应用.23.已知:关于x的一元二次方程x2+(m+1)x+m=0(1)求证:无论m为何值,方程总有两个实数根;(2)若x为方程的一个根,且满足0<x<3,求整数m的值.【答案】(1)见解析;(2)整数m的值为﹣2.﹣1.【解析】【分析】(1)根据根的判别式求出△的值,再进行判断即可;(2)利用因式分解法求得x1=﹣1.x2=﹣m,利用0<x<3得出0<﹣m<3,据此求得m的取值范围,从而得出答案.【详解】解:(1)∵△=(m+1)2﹣4×1×m=m2+2m+1﹣4m=m2﹣2m+1=(m﹣1)2≥0,∴无论m为何值,方程总有两个实数根;(2)∵(x+1)(x+m)=0,∴x+1=0或x+m=0,即x1=﹣1.x2=﹣m,∵0<x<3,∴0<﹣m<3,解得:﹣3<m<0,则整数m的值为﹣2.﹣1.【点睛】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.24.某游乐场普通门票价格40元/张,为了促销,新推出两种办卡方式:①白金卡售价200元/张,每次凭卡另收取20元;②钻石卡售价1000元/张,每次凭卡不再收费.促销期间普通门票正常出售,两种优惠卡不限次数,设去游乐场玩x次时,所需总费用为y元.(1)分别写出选择白金卡、普通门票消费时,y与x之间的函数关系式.(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点B,C的坐标.(3)请根据图象,直接写出选择哪种消费方式更合算.【答案】(1)白金卡:y=20x+200.门票:y=40x;(2)B(10,400),C(40,1000);(3)见解析. 【解析】【分析】(1)根据白金卡售价200元/张,每次凭卡另收取20元,普通门票正常出售,设消费x次时,分别得出所需总费用为y与x之间的关系式即可;(2)利用函数交点坐标求法分别得出即可;(3)根据图象解答即可.【详解】解:(1)根据题意可得:白金卡:y=20x+200.门票:y=40x(2)将y=40x代入y=200+20x,得40x=200+20x,解得x=10,把x=10代入y=40x,得y=400,所以B(10,400),把y=1000代入y=200+20x,得1000=200+20x,解得x=40,所以C(40,1000);(3)当0<x<10时,选普通门票;当x=10时,选普通门票和白金卡;当10<x<40时,选白金卡;当x=40时,选白金卡和钻石卡;当x>40时,选钻石卡【点睛】本题考查了一次函数的应用,两函数交点坐标的求法.进行分类讨论是解题的关键.25.在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.已知点A的坐标为(1,0),(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.【答案】(1)2;(2)直线AC的表达式为y=x﹣1或y=﹣x+1;(3)b>0或b<﹣8.【解析】【分析】(1)由相关矩形的定义可知:要求A与B的相关矩形面积,则AB必为对角线,利用A.B两点的坐标即可求出该矩形的底与高的长度,进而可求出该矩形的面积;(2)由定义可知,AC必为正方形的对角线,所以AC与x轴的夹角必为45,设直线AC的解析式为;y=kx+b,由此可知k=±1,再(1,0)代入y=kx+b,即可求出b的值;(3)分别把点A.D点的坐标代入y=2x+b±2,求得b的数值即可.【详解】解:(1)∵A(1,0),B(3,1)由定义可知:点A,B的“相关矩形”的底与高分别为2和1,∴点A,B的“相关矩形”的面积为2×1=2;(2)由定义可知:AC是点A,C的“相关矩形”的对角线,又∵点A,C的“相关矩形”为正方形∴直线AC与x轴的夹角为45°,设直线AC的解析为:y=x+m或y=﹣x+n把(1,0)分别y=x+m,∴m=﹣1,∴直线AC的解析为:y=x﹣1,把(1,0)代入y=﹣x+n,∴n=1,∴y=﹣x+1,综上所述,若点A,C的“相关矩形”为正方形,直线AC的表达式为y=x﹣1或y=﹣x+1;(3)把A(1,0),D(4,2)分别代入y=2x+b±2,得出b=0,或b=﹣8,∴b>0或b<﹣8【点睛】本题是一次函数综合题,考查了待定系数法,新定义的理解和应用,矩形的面积公式,找出分界点是解题的关键.26.在矩形ABCD中,AB=1,BC=2,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C'.(1)如果C'落在线段AB的延长线上.①在图①中补全图形;②求线段BP的长度;(2)如图②,设直线AP与CC'的交点为M,求证:BM⊥DM.【答案】(1)①见解析;②PB=;(2)见解析.【解析】【分析】(1)①根据要求画出图形即可;②连接AC,作PH⊥AC于H.则△APB≌△APH,同侧AB=AH=1,PB=PH,设PB=PH=x,利用勾股定理构建方程即可;(2)如图②中,连接AC.BD交于点O.连接OM.只要证明A.B.M、C.D五点共圆,即可解决问题;【详解】解:(1)①如图①所示:②连接AC,作PH⊥AC于H.则△APB≌△APH,∴AB=AH=1,PB=PH,设PB=PH=x,∵AC==,∴CH=﹣1,在Rt△PCH中,x2+(﹣1)2=(2﹣x)2,解得x=,∴PB=.(2)如图②中,连接AC.BD交于点O.连接OM.∵四边形ABCD是矩形,∴OA=OB=OC=OD,∵∠AMC=90°,∴OM=OA=OB=OC=OD,∴A.B.M、C.D五点共圆,∵BD是直径,∴∠BMD=90°,∴BM⊥DM.【点睛】本题考查作图﹣轴对称变换,矩形的性质,五点共圆等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用辅助圆解决问题.。
北京101初二上册期中考试数学(含解析).docx

北京101初二(上)期中数学试卷一、选择题(本题共30分,每小题3分)1.下列有4个汽车标志图案,其中不是轴对称图形的是( ).A .B .C .D .2.下列计算中正确的是( ). A .235x y xy += B .44x x x ⋅= C .824x x x ÷=D .2363()x y x y =3.一种细菌的半径是0.00004mm ,用科学记数法把它表示为( ). A .40.410mm -⨯ B .40.410mm --⨯ C .5410mm -⨯ D .5410mm --⨯4.如果把分式3xx y+中的x ,y 都扩大10倍,则分式的值( ). A .扩大100倍B .扩大10倍C .不变D .扩大20倍5.一个等腰三角形的两边长分别是3和7,则它的周长为( ). A .17 B .15 C .13 D .13或176.若9393m ⨯=,则m 的值是( ). A .3 B .4 C .5 D .67.若分式241x x -+的值为0,则x 的值为( ). A .2B .1-C .1D .2或1-8.下列各式从左到右的变形,属于因式分解的是( ). A .2(1)(1)1x x x +-=- B .221(2)1x x x x -+=-+C .22()()a b a b a b -=+-D .()()mx my nx ny m x y n x y +++=+++9.如图,在ABC △中,AB AC =,36BAC ∠=︒,作出AB 边的垂直平分线DE ,交AC 于点D ,交AB 于点E ,连接BD ,下列结论正确的是( ). ①BD 平分ABC ∠;②AD BD BC ==;③BDC △的周长等于AB BC +;④点D 是AC 中点 A .②③ B .①②④ C .①②③D .①②③④10.方程2270xy x y --+=的整数解有( ). A .1组 B .2组C .3组D .4组CBA二、填空题(本题共24分,每小题4分)11.若分式11x -有意义,则x 的取值范围是__________.12.因式分解:3269x x x -+=____________________.13.已知222450a b a b ++-+=,则a =__________,b =__________.14.在ABC △中,AB AC =,AB 的中垂线与AC 所在的直线相交所得的锐角为50︒,则底角B 的大小为__________.15.已知:如图,点P 为AOB ∠内一点,分别作出P 点关于OA ,OB 的对称点1P ,2P ,连接12P P ,交OA于点M ,交OB 于点N ,1215PP =,则PMN △的周长为__________;若40O ∠=︒,则MPN ∠=__________.16.跟我学剪五角星:如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC 剪下ABC △,展开即可得到一个五角星.若想得到一个正五角星(如图④,正五角星的5个角都是36︒),则在图③中BAC ∠的度数为__________,应沿什么角度剪,即ABC ∠的度数为__________.三、解答题(共9小题)17.计算:(1)0131(71)()25(2)3--++-+-;(2)()()(2)()x y x y x y x y +-+++;(3)221a ab a b--+;(4)解分式方程:22142xx x +=--.B④③②①AC POP 2P1NM AB18.如图,ABC △中,AB AC =,D ,E 两点在BC 边上,且AD AE =.求证:BD CE =.19.已知50x y -=,求222232x y x yx xy y x y-+⋅-++得值.20.列方程(组)解应用题:某建筑集团完成一路段的高架桥铺设任务,在合同期内高效完成了任务,这是记者与该集团工程师的一段对话:记者:你们是用9天完成4800米长的高架桥铺设任务的?工程师:我们铺设600米后,采用新的铺设技术,这样每天铺设长度是原来的2倍. 通过这段对话,请你求出该建筑集团原来每天铺设的米数.21.已知210x x +-=,求3223x x ++的值.台球桌的形状是一个长方形,当母球被击打后可能在不同的边上反弹,为了使母球最终击中目标球,击球者需作出不同的设计,确定击球方向,如图,目标球从A 点出发经B 点到C 点,相当于从A 点出发直接击打目标球C ,其实质上是图形的轴对称变换,关键是找母球关于桌边的对称点的位置.(1)如下图,小球起始点位于点(3,0),沿所示的方向击球,小球运动的轨迹如图所示,如果小球起始时位于点(2,0)处,仍按原来的方向击球,那么在点A ,B ,C ,D ,E ,F ,G ,H 中,小球会击中的点是__________.(2)在下图中,请你设计一条路径,使得球P 依次撞击台球桌边AB ,BC 反射后,撞到求Q .(不写作法,保留作图痕迹)EF HDA'ABC把多项式2310x x --分解因式得(5)(2)x x -+,由此方程23100x x --=可以变形为(5)(2)0x x -+=,解得5x =或2x =-.观察多项式2310x x --的因式(5)x -,(2)x +与方程23100x x --=的解5x =或2x =-之间的关系,可以发现,如果5x =,2x =-是方程23100x x --=的解,那么(5)x -,(2)x +是多项式2310x x --的因式.这样,若要把一个多项式分解因式,可以通过其对应方程的解来确定其中的因式.例如:对于多项式332x x -+,观察可知,当1x =时,3320x x -+=,则332(1)x x x A -+=-,其中A 为整式,即(1)x -是多项式332x x -+的一个因式.若要确定整式A ,则可用竖式除法:23232222103232222x x x x x x x x x x x x x x +--+⋅-+----+-+所以32232(1)(2)(1)(1)(2)(1)(2)x x x x x x x x x x -+=-+-=--+=-+ 根据阅读材料,请回答下列问题(直接填空): (1)因式分解:22x x --=_______________;(2)观察可知,当x =__________时,32530x x x +-+=,可得__________是多项式3253x x x +-+的一个因式,分解因式:3253x x x +-+=____________________.(3)已知:32(1)x mx x B +-=+,其中B 为整式,则分解因式:32x mx +-=____________________. 24.如图:在ABC △中,AC BC =,90ACB ∠=︒,D 为ABC △内一点,15BAD ∠=︒,AD AC =,CE AD⊥于点E ,且5CE =. (1)求BC 的长;(2)求证:DCE DCB ∠=∠; (3)求证:BD CD =.25.已知:如图1,在直角坐标系中,点(1,3)A ,点B 与A 关于y 轴对称,将B 沿y 轴正方向平移一个单位得到点C ,点D 与O 关于直线AB 对称,P 是直线AB 上的动点. (1)点B 的坐标为__________,点C 的坐标为__________;(2)点(5,0)E ,当POE △时等腰三角形,符合条件的P 的个数为__________; (3)点Q 是y 轴上的动点,当25BQC ∠=︒时,求OBQ QCD ∠+∠的度数.北京101初二(上)期中数学试卷答案一、选择题(本题共30分,每小题3分)题号 1 2 3 4 5 6 7 8 9 10 答案 DDCCABACCD二、填空题(本题共24分,每小题4分)11.1x ≠ 12.2(3)x x - 13.1-,2 14.20︒或70︒ 15.15,100︒ 16.36︒,126︒三、解答题(共9小题)17.解:(1)原式13528=++-- 56=-;(2)原式222222x y x xy xy y =-++++233x xy =+;(3)原式()()()()a a ba b a b a b a b -=-+-+-()()a a ba b a b -+=+-22ba b =-;(4)去分母,得22(2)4x x x ++=-, 去括号,得22224x x x ++=-, 整理,得26x =-, 解得3x =-.经检验3x =-为原方程的解.18.证明:∵AB AC =,∴B C ∠=∠. ∵AD AE =, ∴ADE AED ∠=∠, ∴ADB AEC ∠=∠. 在ABD △和ACE △中, B C ADB AEC AD AE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴ABD △≌ACE △(AAS ). ∴BD CE =.19.解:222232x y x yx xy y x y-+⋅-++ 2()()3()x y x y x yx y x y +-+=⋅-+ 3x yx y+=-. ∵50x y -=, ∴5x y =. ∴原式538254y y yy y y+===-.20.解:设原来每天铺设x 米, 根据题意,得600480060092x x-+=. 解得:300x =.经检验:300x =是分式方程的解,并且符合实际意义. 答:该建筑集团原来每天铺设300米.21.解:∵210x x +-=, ∴21x x +=. 3223x x ++22()3x x x x =+++ 23x x =++ 13=+ 4=.22.解:(1)B 和F ; (2)如图所示:23.解:(1)(1)(2)x x +-; (2)1,1x -,2(1)(3)x x -+; (3)2(1)(2)x x +-.QPADBC24.解:(1)∵AC BC =,90ACB ∠=︒, ∴45BAC CBA ∠=∠=︒, ∵15BAD ∠=︒, ∴30DAC ∠=︒. ∵CE AD ⊥, ∴90CEA ∠=︒, ∴210AC CE ==. ∴10BC AC ==.(2)∵AD AC =,30DAC ∠=︒, ∴75DCA CDA ∠=∠=︒, ∵9060ECA EAC ∠=︒-∠=︒, ∴15DCE DCA ECA ∠=∠-∠=︒, 又∵9015DCB DCA ∠=︒-∠=︒, ∴DCE DCB ∠=∠.(3)过点D 作DH BC ⊥于点H . 在CDE △和CDH △中, 90DCE DCBCED CHD CD CD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, ∴CDE △≌CDH △(AAS ). ∴HC CE =, ∵12CE AC =, ∴1122HC AC AB ==,∴HB HC =,∴BD CD =.下面提供其余几种证明方法,仅供参考: ①如图1,构造AGD △≌CDB △. ②如图2,构造正方形.③如图3,构造CMD △≌CDB △.④如图4,构造AEC △关于AD 的对称图形. ⑤如图5,作ABD △的对称图形APC △.G图1ABCDE N图2ABCDEM图3ABCDE HABCDE25.解:(1)如图1所示,点B 的坐标为(1,3)-,点C 的坐标为(1,4)-;(2)如图2所示,符合条件的P 的个数为5.(3)如图3所示,连接AB ,BC ,AD ,AC ,过点C 作CH y ⊥轴于点H . 易证明ABC △≌DHC △,OBF △≌DAF △. ∴CD CA =,DCH ACB ∠=∠,ADF BOF ∠=∠. ∵CH AB ∥, ∴HCA CAB ∠=∠,∴90DCA DCH HCA BCA BAC ∠=∠+∠=∠+∠=︒, ∴45CDA ∠=︒,∴45CDH BOQ ∠+∠=︒. 又∵CH AB ∥,易得25QCH QBF BQC ∠-∠=∠=︒.∴OBQ QCD HCD FBO QCH QBF ∠+∠=∠+∠+∠-∠ 909025BOQ CDH =︒-∠+︒-∠+︒ 1804525=︒-︒+︒ 160=︒.M图4ABCDE P图5ABCDEC BA图1Oyx1P 5P 4P 3P 2P 1EBA图2Oyx1G FH AQ BC D 图3Oyx1北京101初二(上)期中数学试卷部分答案解析一、选择题1.【答案】D【解析】观察图形可知,只有D 中的图案不是轴对称图形.2.【答案】D【解析】2x 与3y 不是同类项,不能合并;45x x x ⋅=;826x x x ÷=.3.【答案】C【解析】0.00004mm 用科学记数法表示为5410mm -⨯4.【答案】C 【解析】把分式3x x y+中的x ,y 都扩大10倍,得3031010x x x y x y =++,分式的值不变.5.【答案】A【解析】一个等腰三角形的两边长分别是3和7,则腰长为7,底边长为3,故周长为17.6.【答案】B【解析】∵2193933m m +⨯==,∴219m +=,∴4m =.7.【答案】A【解析】由题意得240x -=,10x +≠,解得2x =.8.【答案】C【解析】观察可知,只有C 选项的结果为整式的乘积,故只有C 选项的变形属于因式分解.9.【答案】C【解析】如图所示,∵AB AC =,36BAC ∠=︒,∴72ABC C ∠=∠=︒.∵DE 为AB 的垂直平分线,∴BD AD =,∴36ABD A ∠=∠=︒,∴36CBD ∠=︒,∴BD 平分ABC ∠.∴72BDC ∠=︒,∴BDC C ∠=∠,∴BC BD =,∴AD BD BC ==.BDC △的周长等于BD BC DC AD DC BC AC BC AB BC ++=++=+=+. 故①②③均正确.10.【答案】D【解析】∵2270xy x y --+=,∴(2)27x y x -=-,∴273222x y x x -==---. ∵x ,y 均为整数,∴32x -为整数,∴2x -能被3整除,∴21x -=±或23x -=±. ∴31x y =⎧⎨=⎩或13x y =⎧⎨=⎩或51x y =⎧⎨=-⎩或15x y =-⎧⎨=⎩.共有4组整数解.二、填空题(本题共24分,每小题4分)11.【答案】1x ≠【解析】由题意得10x -≠,解得1x ≠.12.【答案】2(3)x x -【解析】因式分解:322269(69)(3)x x x x x x x x -+=-+=-.13.【答案】1-,2【解析】2222245(1)(2)0a b a b a b ++-+=++-=,∴1a =-,2b =.14.【答案】20︒或70︒【解析】如图1,易得此时140BAC ∠=︒,∴20B ∠=︒.如图2,易得此时40BAC ∠=︒,∴70B ∠=︒.15.【答案】15,100︒【解析】连接OP ,1OP ,2OP ,1PP ,2PP .由对称可知,1MP MP =,2NP NP =,∴PMN △的周长为121215MN MP NP MN MP NP PP ++=++==. 由对称可知,1OPM OPM ∠=∠,2OPN OP N ∠=∠,∴121802100MPN OPM OPN OPM OP N O ∠=∠+∠=∠+∠=︒-∠=︒.16.【答案】36︒,108︒ 【解析】180365BAC ︒∠==︒;由于五角星的角为36︒,∴图③中,18ACB ∠=︒,∴126ABC ∠=︒.图150°CB A图250°CBA。
北京一零一中20082009学年度第二学期期中考

N x D N O x
图 2
图 3
答案: (1)证明: 分别过点 C,D, 作 CG⊥AB , DH⊥AB, 垂足为 G,H,则 ∠CGA=∠DHB= 90° .……1 分
∴ CG∥DH. ∵ △ABC 与△ABD 的面积相等, ∴ CG=DH. …………………………2 分 ∴ 四边形 CGHD 为平行四边形. ∴ AB∥CD. ……………………………3 分 (2)①证明:连结 MF,NE. …………………4 分 设点 M 的坐标为(x1,y1) ,点 N 的坐标为(x2,y2) . ∵ 点 M,N 在反比例函数 y ∴ x1 y1 k , x2 y2 k . ∵ ME⊥y 轴,NF⊥x 轴, ∴ OE=y1,OF=x2. ∴ S△EFM= S△EFN=
=
m 1 (m 2)(m 2) (m 1)(m 1) -------------------------3 分 m2 (m 1)2
= (m 2)(m 1) = m m 2 .--------------------------------------------------------------5 分
1 ( ) 2 27 ( 3
.
解:
m 1 m2 4 1 2 2 20. 先化简再求值: ,其中 m 3 . m 2 m 2m 1 m 1
解:
21.如图,已知四边形 ABCD 中,AB=CD,连结对角线 AC、BD,E、F、G、H 分别是 AD、BD、BC、AC 的中 点.求证:四边形 EFGH 是菱形. 证明:
N 图 3
25. 如图,在平面直角坐标系 xOy 中,直线 y
北京市海淀区八年级数学下册期中综合试卷(含答案解析)

北京市海淀区20**八年级数学下册期中综合试卷(含答案解析) 北京市海淀区20**八年级数学下册期中综合试卷(含答案解析)一、选择题1.下列方程,是一元二次方程的是()①3x2+x=20,②2x2-3xy+4=0,③x2-=4,④x2=0,⑤x2-+3=0A.①② B.①②④⑤ C.①③④ D.①④⑤2.若,则x的取值范围是()A.x B.x≤3 C.0≤x D.x≥03.若=7-x,则x的取值范围是()A.x≥7 B.x≤7 C.x D.x74.当x取某一范围的实数时,代数式+的值是一个常数,该常数是()A.29 B.16 C.13 D.35.方程(x-3)2=(x-3)的根为()A.3 B.4 C.4或3 D.-4或36.如果代数式x2+4x+4的值是16,则x的值一定是()A.-2 B.2,-2 C.2,-6 D.30,-347.若c(c≠0)为关于x的一元二次方程x2+bx+c=0的根,则c+b的值为()A.1 B.-1 C.2 D.-28.从正方形铁片上截去2cm宽的一个长方形,剩余矩形的面积为80cm2,•则原来正方形的面积为()A.100cm2 B.121cm2 C.144cm2 D.169cm29.方程x2+3x-6=0与x2-6x+3=0所有根的乘积等于()A.-18 B.18 C.-3 D.310.三角形两边长分别是8和6,第三边长是一元二次方程x2-16x+60=0一个实数根,则该三角形的面积是()A.24 B.48 C.24或8 D.8二、填空题11.若=3,=2,且ab0,则a-b=_______.12.化简=________.13.的整数部分为________.14.在两个持续整数a和b之间,且ab,那么a、b的值分别是______.15.x2-10x+________=(x-________)2.16.若关于x的一元二次方程(m+3)x2+5x+m2+2m-3=0有一个根为0,则m=______,•另一根为________.17.方程x2-3x-10=0的两根之比为_______.18.已知方程x2-7x+12=0的两根恰好是Rt△ABC的两条边的长,则Rt△ABC•的第三边长为________.19.一个两位数,个位数字比十位数字大3,个位数字的平方刚好等于这个两位数,则这个两位数是________.20.某超市从我国西部某城市运进两种糖果,甲种a千克,每千克x元,乙种b千克,每千克y元,如果把这两种糖果混合后销售,保本价是_________元/千克.三、解答题21.计算(每小题3分,共6分)(1)(+)-(-)(2)(+)÷22.用合适的方法解下列方程(每小题3分,共12分)(1)(3x-1)2=(x+1)2(2)2x2+x- =0(3)用配方法解方程:x2-4x+1=0;p(4)用换元法解方程:(x2+x)2+(x2+x)=623.(6分)已知方程2(m+1)x2+4mx+3m=2,根据下列条件之一求m的值.(1)方程有两个相等的实数根;(2)方程有两个相反的实数根;(3)方程的一个根为0.24.(5分)已知x1,x2是一元二次方程2x2-2x+m+1=0的两个实数根.(1)求实数m的取值范围;(2)如果x1,x2满足不等式7+4x1x2x12+x22,且m为整数,求m的值.25.(5分)已知x=,求代数式x3+2x2-1的值.26.(6分)半径为R的圆的面积恰好是半径为5与半径为2的两个圆的面积之差,求R的值.27.(6分)某次商品交易会上,所有参加会议的商家之间都签订了一份合同,共签订合同36份,求共有多少商家参加了交易会?28.(7分)有100•米长的篱笆材料,•想围成一个矩形露天仓库,•要求面积不小于600平方米,在场地的北面有一堵长为50米的旧墙,有人用这个篱笆围成一个长40米,宽10米的矩形仓库,但面积只有400平方米,不合要求,•现请你设计矩形仓库的长和宽,使它符合要求.29.(7分)“国运兴衰,系于教育”图中给出了我国从20**─20**年每年教育经费投入的情况.(1)由图可见,20**─20**年的五年内,我国教育经费投入呈现出_______趋势;(2)根据图中所给数据,求我国从20**年到20**年教育经费的年平衡数;(3)如果我国的教育经费从20**年的5480亿元,增加到20**年7891亿元,那么这两年的教育经费平衡年增长率为多少?(结果精准到0.01,=1.200)北京市海淀区20**八年级数学下册期中综合试卷(含答案解析)参考答案:1.D 2.C 3.B 4.D 5.C 6.C 7.B 8.A 9.A 10.C11.-7 12.2- 13.4 14.a=3,b=4 15.25,5 16.1,-17.-或- 18.5或19.25或36 20.21.(1)-;(2)+22.(1)x1=0,x2=1;(2)x=-± ;(3)(x-2)2=3,x1=2+,x2=2-;(4)设x2+x=y,则y2+y=6,y1=-•3,y2=2,则x2+x=-3无解,x2+x=2,x1=-2,x2=1.23.△=16m2-8(m+1)(3m-2)=-8m2-8m+16,(1)方程有两个相等的实数根,∴△=0,即-8m2-8m+16=0,求得m1=-2,m2=1;(2)因为方程有两个相等的实数根,所以两根之和为0且△≥0,则- =0,求得m=0;(3)∵方程有一根为0,∴3m-2=0得m=.24.(1)△=-8m-4≥0,∴m≤-;(2)m=-2,-125.0 26.27.9个28.方案一:设计为矩形(长和宽均用材料:列方程可求长为30米,宽为20米);•方案二:设计为正方形.在周长相等的条件下,正方形的面积大于长方形的面积,它的边长为25米;方案三:利用旧墙的一部分:如果利用场地北面的那堵旧墙,取矩形的长与旧墙平行,设与墙垂直的矩形一边长为x米,则另一边为(100-2x)米,•可求一边长为(25+5)米(约43米),另一边长为14•米;•方案四:•充分利用北面旧墙,•这时面积可达1250平方米.29.(1)由图可见,20**~20**年的五年内,我国教育经费投入呈现出逐年增加的趋势;(2)我国从20**年到20**年教育经费的平衡数为:=4053(亿元);(3)设从20**年到20**年这两年的教育经费平衡年增长率为x,则由题意,得5480(1+x2)=7891,解之得x≈20%.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京海淀区海淀外国语初二第二学期数学试卷一、选择题:在每小题给出的四个选项中,只有一项符合题意,请把你认为正确的选项填入括号中。
本大题共10小 题,共40分. 1.化简二次根式2)3(-等于A .3B .-3C .±3D .9 2.若实数x 、y 满足2(2)30x y -++=,则xy 的值为A .-5B .5C .-6D .6 3.在下列图形中,既是中心对称图形又是轴对称图形的是A .等腰三角形B .正方形C .平行四边形D .等腰梯形 4.函数11-+=x x y 的自变量x 的取值范围为 A .x ≠1 B .x ≥-1 C .x >-1且x ≠1 D .x ≥-1且x ≠1 5.下列二次根式中,与3是同类二次根式的是 A .13B .9C .18D .24 6.如图是一个中心对称图形,点A 为对称中心,若∠C =90°,∠B =30°,BC =1,则BB ′的长为 A .4 B .33 C .332 D .334 7.菱形的两条对角线的长分别是6和8,则这个菱形的周长是A .5B .20C .24D .40 8.下列命题正确的是A .平行四边形的对角线相等B .矩形的对角线互相平分C .菱形的对角线相等且互相平分D .等腰梯形的一组对边相等且平行9.已知点A 的坐标为()a b ,,O 为坐标原点,连结OA ,将线段OA 绕点O 按逆时针方向旋转90得1OA ,则点1A 的坐标为A .()a b -,B .()a b -,C .()b a -,D .()b a -,10.图1中的“箭头”是以AC 所在直线为对称轴的轴对称图形,90BAD ∠=︒,2AB =.图2到图4是将“箭头”沿虚线剪拼成正方形的过程,则图1中BC 的长为A .1B .5C .2D .25二、填空题:请把你认为正确的选项填入表格内.本大题共6小题,每空4分,共36分. 11. 计算:b a 527=____________,714=___________,65⨯=____________.12. 在梯形ABCD 中,AD ∥BC ,点E 、F 分别是AB 、CD 的中点,若AD =5,BC =7,则EF = . 13. 一块木板如图所示,已知AB =4,BC =3,DC =12,AD =13,∠B =90°,木板的面积为 .14. 在平行四边形ABCD 中,AB =5,BC =7,∠B 、∠C 的平分线分别交AD 于E 、F ,则EF = . 15. 如图,Rt △ABC 中,∠C =90°,AC =3,BC =4,点P 为AB 边上任一点,过P 分别作PE ⊥AC 于E ,PF ⊥BC 于F , 则线段EF 的最小值是 . 16. 如图,在平面直角坐标系xOy 中,1B (0,1),2B (0,3),3B (0,6),4B (0,10),…,以12B B 为对角线作第一个正方形1112A B C B ,以23B B 为对角线作第二个正方形2223A B C B ,以34B B 为对角线作第三个正方形3334A B C B ,…, 如果所作正方形的对角线1n n B B +都在y 轴上,且1n n B B +的长度依次增加1个单位,顶点n A 都在第一象限内 (n ≥1,且n 为整数).那么1A 的纵坐标...为 ;用n 的代数式表示n A 的纵坐标...为 .三、解答题:本大题共7小题,共44分. 17.(5分)计算:10112()31(2)3π-+-----.18.(5分)计算:(235)(31)--.19.(6分)已知:如图,梯形ABCD 中,AD ∥BC ,30B ∠=︒,60C ∠=︒,2AD =,6BC =,点E 为AB 中点,BC EF ⊥于点F ,求EF 的长. 20.(6分)列分式方程解应用题:小明乘坐火车从某地到上海去参观世博园,已知此次行程为2160千米,城际直达动车组的平均时速是特快列车的1.6倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时.求小明乘坐动车组到上海需要的时间. 21.(7分) 阅读理解:对于任意正实数a b 、,2()0a b -≥,20a ab b ∴-+≥.2a b ab ∴+≥,只有当a b =时,等号成立.结论:在2a b ab +≥(a b 、均为正实数)中,若ab 为定值p ,则2a b p +≥, 只有当a b =时,a b +有最小值2p . 根据上述内容,回答下列问题:(1)若0m >,只有当m = 时,1m m+有最小值 . (2)探索应用:已知(30)A -,,(04)B -,,点P 为双曲线12(0)y x x=>上的任意一点,过点P 作PC x ⊥轴 于点C ,PD y ⊥轴于点D .求四边形ABCD 面积的最小值,并说明此时四边形ABCD 的形状.22.(8分)如图,在平面直角坐标系中,O为坐标原点,△AOB 为等边三角形,点A的坐标是(34,0),点B在第一象限,AC是∠OAB的平分线,并且与y轴交于点E,点M为直线AC上一个动点,把△AOM绕点A顺时针旋转,使边AO与边AB重合,得到△ABD.(1)求直线OB的解析式;(2)当点M与点E重合时,求此时点D的坐标;(3)设点M的纵坐标为m,求△OMD的面积S关于m的函数解析式.23.(7分)已知,正方形ABCD中,△BEF为等腰直角三角形,且BF为底,取DF的中点G,连接EG、CG.(1)如图1,若△BEF的底边BF在BC上,猜想EG和CG的数量关系为;(2)如图2,若△BEF的直角边BE在BC上,则(1)中的结论是否还成立?请说明理由;(3)如图3,若△BEF的直角边BE在∠DBC内,则(1)中的结论是否还成立?说明理由.GEB DAC FGEBDACFGFBDACEGFBAEGFBDACE图1 图2 图3北京海淀区第一零一中学2010-2011学年初二第二学期数学期中试卷参考答案一、选择题:在每小题给出的四个选项中,只有一项符合题意.本大题共10小题,共40分.题号 1 2 3 4 5 6 7 8 9 10 答案ACBDADBBCD二、填空题:本大题共6小题,共36分.题号111213141516答案 233aab 27 30 6 24 3 12522(1)2n +三、解答题:本大题共7小题,共44分.17.解: 原式=233311--+-…………………………………………4分 =33-.…………………………………………5分18.解:原式=623535--+…………………………………………4分 =1173-.…………………………………………5分19.解:过点A 作AG ∥DC ,交BC 于点G .……………………………1分 ∴ ︒=∠=∠601C . ∵ AD ∥BC ,∴ 四边形AGCD 为平行四边形.……………………………………2分 ∴ 2CG AD ==. ∵ 6=BC ,∴ 4=BG .……………………………………3分 ∵ 12180B ∠+∠+∠=︒,30B ∠=︒, ∴ ︒=∠902.∴ 在△BAG 中,34232AB =⨯=.……………………………………4分 又∵ E 为AB 中点,∴ 321==AB BE .……………………………………5分 ∵ BC EF ⊥于F ,∴ 2321==BE EF .……………………………………6分(若学生使用其他方法,只要解法正确,皆给分.) 20.解:设小明乘坐动车组到上海需要x 小时.……………1分 依题意,得6.1621602160⨯+=x x .…………………………3分 解得 10=x .……………………………………4分 经检验:10x =是方程的解,且满足实际意义.………5分 答:小明乘坐动车组到上海需要10小时.………6分 21.解:(1) m = 1 (填1m不扣分),最小值为 2 ; ……………………2分 (2)设12(,)P x x ,则12(,0),(0,)C x D x, 123,4CA x DB x∴=+=+, ………………………………………………………3分 1112(3)(4)22ABCD S CA DB x x∴=⨯=+⨯+四边形,化简得:92()12S x x=++, ………………………………………………4分990,06x x x x >>∴+≥=, 只有当9,3x x x==即时,等号成立.…………………………………………………5分 ∴S ≥2×6+12=24.∴S 四边形ABCD 有最小值24.……………………………………………………6分 此时,P (3,4),C (3,0),D (0,4), ∴ AB =BC =CD =DA =5,∴ 四边形ABCD 是菱形.……………………………………………………7分 22.解:(1)B (32,6); …………………………………………………1分OB l :x y 3=.……………………………………………………2分(2)如图1,由题意x DA ⊥轴,︒=∠=∠30BAD EAO .则点D 的横坐标为34; ……………………………………3分 此时 823===OA AE DA ,即点D (34,8).……………………………4分(3)过M 作x MN ⊥轴,设a MN =, 如图2,当4m >时,S =111(2)3(343)432222m m m m m m +⋅--⋅-⋅⋅ 2323m m =-.………………………………………5分 如图3,当24m <≤时,由︒=∠30OAM ,∴ a MA 2=,a NA 3=.S =111(433)(2)3432222m m m m m m -⋅++⋅-⋅⋅ 2323m m =-.……………………………………………6分 如图4,当02m ≤≤时, S =111(433)(2)3432222m m m m m m -⋅++⋅-⋅⋅ 2323m m =-+.……………………………………………7分 如图5,当0m <时,由︒=∠30NAM ,∴ a MA 2=,a NA 3=.S =111432(2)3(433)222m m m m m m ⋅⋅++⋅-+⋅. 2323m m =+.……………………………………………8分∴ ()2223232,323(02),323(0).m m m S m mm m m m ⎧->⎪⎪=-+≤≤⎨⎪+<⎪⎩(四种情况讨论正确一种给1分) 23.(1)GC =EG .……………………………………………………………1分 (2)如图,延长EG 交CD 于M , 易证△GEF ≌△GMD ,得G 为EM 的中点. 易得CG 为直角△ECM 的斜边上的中线.于是有GC =GE .……………………………………………3分 (3)如图,延长EG 到M ,使EG =GM ,连接CM 、CE .易证△EFG ≌△MDG ,则EF =DM 、∠EFG =∠MDG . ∵∠DBE +∠DFE +∠BDF =90°,∴∠DBE +∠GDM +∠BDF =90°.∴∠MDC +∠DBE =45°.∵∠EBC +∠DBE =45°, ∴∠EBC =∠MDC . 进而易证△CBE ≌△CDM , ∴EC =CM 、∠ECB =∠MCD . 易得∠ECM =90°, ∴CG 为直角△ECM 斜边EM 的中线. ∴EG =GC .………………………………………………………3分其他证法:(1)EG =CG .………………………………………………………1分 (2)成立.……………………………………………………………2分 证明:过点F 作BC 的平行线交DC 的延长线于点M ,连结MG . ∴EF =CM ,易证EFMC 为矩形 ∴∠EFG =∠GDM . 在直角三角形FMD 中, ∴DG =GF , ∴FG =GM =GD . ∴∠GMD =∠GDM .∴∠EFG =∠GMD . ∴△EFG ≌△GCM .∴EG =CG .……………………………………………………………4分 (3)成立.取BF 的中点H ,连结EH ,GH ,取BD 的中点O ,连结OG ,OC . ∵CB =CD ,∠DCB =90°,∴12CO BD =. ∵DG =GF ,1//,.21//,.2GH BD GH BD OG BF OG BF ∴=∴=且且 ∴CO =GH .∵△BEF 为等腰直角三角形. ∴12EH BF =.∴EH =OG . ∵四边形OBHG 为平行四边形, ∴∠BOG =∠BHG .∵∠BOC =∠BHE =90°. ∴∠GOC =∠EHG .∴△GOC ≌△EHG .∴EG =GC .……………………………………………………………7分 (若学生使用其他方法,只要解法正确,皆给分.)。
