求解矩阵特征值的混合人工鱼群算法
人工鱼群算法ppt

行业PPT模板:/hangye/ PPT素材下载:/sucai/ PPT图表下载:/tubiao/ PPT教程: /powerpoint/ Excel教程:/excel/ PPT课件下载:/kejian/ 试卷下载:/shiti/ PPT论坛:
Y=f(X),其中Y 。
Xnext X
XV X XV X
Step Rand
定义相关参数: (1)N:人工鱼群的规模,作为一种多智能体算法,群体的 概念是最基本的特性;
(2)visual:人工鱼的感知距离,也就是在寻优过程中,人工 鱼的视野范围;
(3)Step:人工鱼的移动步长,人工鱼在移动过程中,向下 一个状态前进的步长的最大值;
拥挤度因子(δ):
拥挤度因子的引入是为了 避免过度拥挤而陷入局部 极值。
拥挤度因子的定义:
对于极大值问题: 1/ nmax, 0,1
对于极小值问题: nmax, 0,1
式中,、nmax 分别为极值接近水平和期望在该邻域内聚集的最大人工鱼数 目。
拥挤度因子对算法的影响(以极大值为例):
① 拥挤度因子越大,表明允许拥挤的程度越小,摆脱局部极值的能 力越强,但收敛速度减缓。
若 Yj f X j Yi f Xi ,则
Xt1 i
Xti
X j Xit X j Xit
Step Rand
否则,重新随机选择Xj,判断是否满足前进条件,尝试Try-number次后,若还不满足 ,则随机前进一步
Xt 1 i
Xti
Visual
Rand
聚集行为
这是鱼群生存和躲避危害的一种生活习性。在鱼群算法中,一般规定两条,一是尽量 向邻近伙伴的中心移动,二是避免过分拥挤。
人工鱼群算法基本原理讲解
人工鱼群算法1

人工鱼群算法实例
• 然后先进行追尾活动,每条鱼Xi都查看在自己可视域范围内 (即距离小于visual,visual根据搜索空间的大小而定)的 其它鱼,从中找到适应函数值最小的一个Xj ,其适应度函 数值记为Yj,Xj周围可视域内的其它个体数量记为nf,若 Yj*nf<δ*Yi (δ为拥挤度因子,此处取1),则表明Xj周围 “食物”较多且不太拥挤,这时Xi对每一个自己和Xj的不同 的位重新随机取值(例如Xi为1001,而Xj为1100,那么就 对Xi的第2,4位重新随机取值),从而向Xj靠近。追尾活动 若不成功,则进行聚群行为,每条鱼都先找出自己周围可 视域内的其它鱼,形成一个小鱼群,然后找出这群鱼的中 心点,这里中心点的确定方法是,若鱼群中半数以上的鱼 在第i位上取1,则中心点的第i位也为1,否则为0,接 着采用和前面相同方法查看中心点的“食物”是否较多, 是否拥挤,据此决定是行为(AF-follow)指鱼向其可视区域 内的最优方向移动的一种行为。人工鱼Xi搜 索其视野内所有伙伴中的函数最优伙伴Xj, 如果 Yj/ nf > δYi,表明最优伙伴的周围不太 拥挤,则Xi朝此伙伴移动一步,否则执行觅 食行为。
算法介绍 伪代码
• • • • • • • • •
算法介绍 代码
function [XXnext] = gmjprey(XX,Try_number,Visual,Step) pp=0; for j=1:Try_number XXj=XX+rand*Step*Visual; if(maxf(XX)<maxf(XXj)) XXnext=XX+rand*Step*(XXj-XX)/norm(XXj-XX); pp=1; break end end if(~pp) XXnext=XX+rand*Step; end
鱼群算法的介绍
无审视环节的实验效果图:公告板得 到的结果是(0.046247,0.005745) , f(x,y)max=0.9996。
有审视环节的实验效果图:公告板显 示的结果:(-0.023021,0.007922), f(x,y)max=0.9999。
2、聚群行为:搜寻视野范内的同伴,判断视野范围内的鱼群 中心的食物量是否比当前自己拥有的食物量多。如果多则往鱼群中心方 向移动,少则执行觅食行为。
3、追尾行为:搜寻视野范围内的同伴,找出拥有食物量最多 的个体。并判断拥有食物量最多的个体的周围是否有太多的鱼。如果少 则说明值得往食物量最多的鱼方向移动,如果太多则说明不值得向食物 量最多的鱼方向移动,还是自己找食物好(即执行觅食行为。)。(这 里的多和少是有拥挤因子决定的。)
如果 且Yv1<Yv2,表明伙伴Xv2的状态具有较高的食物浓度并且其周围不太拥挤,朝伙伴Xv2的方 向前进一步;否则执行觅食行为。如果 也执行觅食行为。
2.4 随机行为
随机行为:随机行为的实现比较简单,就是在视野中随机选择一个状态,然后向该方向移动,其实 它是觅食行为的一个缺省行为。根据所要解决的问题性质, 对人工鱼当前所处的环境进行评价,从 而选一种行为。较常用的评估方法是:选择各行为中使得向最优方向前进最大的方向,也就是各行 为中使得人工鱼的下一个状态最优的行为,如果没有能使下一个状态优于当前状态的行为,则采用 随机行为。
先提一下鱼群算法里面的各种参数: 1、visual 表示人工鱼的感知距离(即视野范围)。 2、step 表示人工鱼移动的最大步长。 3、 δ 表示拥挤因子 4、try—number是人工鱼在觅食行为中的移动次数。 5、friend—number表示人工鱼数量。
基本人工鱼群算法

基本人工鱼群算法摘要人工鱼群算法(Artificial Fish-Swarm Algorithm,AFSA)是由李晓磊等在2002年提出的,源于对鱼群运动行为的研究,是一种新型的智能仿生优化算法。
它具有较强的鲁棒性、优良的分布式计算机制易于和其他方法结合等优点。
目前对该算法的研究、应用已经渗透到多个应用领域,并由解决一维静态优化问题发展到解决多维动态组合优化问题。
人工鱼群算法已经成为交叉学科中一个非常活跃的前沿性学科。
本文主要对鱼群算法进行了概述,引入鱼群模式的概念,然后给出了人工鱼的结构,接下来总结出了人工鱼的寻优原理,并对人工鱼群算法的寻优过程进行仿真,通过四个标准函数选取不同的拥挤度因子进行仿真实验,证实了利用人工鱼群算法进行全局寻优确实是有效的。
关键词:人工鱼群算法;拥挤度因子;寻优0 引言动物在进化过程中,经过漫长的优胜劣汰,形成了形形色色的觅食和生存方式,这些方式为人类解决生产生活中的问题带来了不少启发和灵感。
动物不具备复杂逻辑推理能力和综合判断等高级智能,但他们通过个体的简单行为和相互影响,实现了群体的生存和进化。
动物行为具有以下几个特点。
(1)适应性:动物通过感觉器官来感知外界环境,并应激性的做出各种反应,从而影响环境,表现出与环境交互的能力。
(2)自治性:在不同的时刻和不同的环境中能够自主的选取某种行为,而无需外界的控制或指导。
(3)盲目性:单个个体的行为是独立的,与总目标之间没有直接的关系。
(4)突现性:总目标的完成是在个体行为的运动过程中突现出来的。
(5)并行性:各个个体的行为是并行进行的。
人工鱼群算法是根据鱼类的活动特点提出的一种基于动物行为的自治体寻优模式。
1 鱼群模式描述1.1 鱼群模式的提出20世纪90年代以来,群智能(swarm intelligence,SI)的研究引起了众多学者的极大关注,并出现了蚁群优化、粒子群优化等一些著名的群智能方法。
集群是生物界中常见的一种现象,如昆虫、鸟类、鱼类、微生物乃至人类等等。
人工鱼群算法的分析及改进

1、引入动态调整策略
在AFSO算法中,随着迭代次数的增加,鱼群的全局最优解可能逐渐偏离真正 的最优解。这是由于在寻优过程中,鱼群可能会陷入局部最优陷阱。为了解决这 个问题,我们引入了动态调整策略,即根据算法的迭代次数和当前的最优解,动 态地调整鱼群的搜索范围和搜索速度。
2、增加随机扰动
在AFSO算法中,鱼群通常会向当前的全局最优解集中。这可能会导致算法过 早地陷入局部最优陷阱。为了解决这个问题,我们引入了随机扰动。即在每次迭 代时,随机选择一部分鱼,将其位置和速度进行随机扰动,以增加算法的探索能 力。
2、计算适应度:对于每一条鱼,计算其适应度函数值(通常是目标函数 值),这个值代表了这条鱼的“健康”状况。
3、比较适应度:将每条鱼的适应度与全局最优解进行比较,更新全局最优 解。
4、更新领头鱼:随机选择一条鱼作为领头鱼,然后根据一定的规则,如最 小距离规则,选择其他鱼跟随领头鱼。
5、更新鱼群:根据领头鱼的位置和行为,更新其他鱼的位置和行为。
4、多种群并行搜索:通过将搜索空间划分为多个子空间,并在每个子空间 中独立运行AFSA,我们可以实现多种群的并行搜索。这种并行搜索方法可以显著 提高算法的搜索速度和效率。
四、结论
本次演示对人工鱼群算法进行了详细的分析和改进。通过引入混沌理论、变 异机制和自适应调整参数等方法,我们可以有效地提高AFSA的全局搜索能力和效 率,避免算法过早地陷入局部最优解。多种群并行搜索方法也可以显著提高算法 的搜索速度和效率。这些改进方案为AFSA在实际应用中的广泛应用提供了有力的 支持。
感谢观看
3、引入学习因子
在AFSO算法中,每个鱼会根据自身经验和群体行为来调整自己的方向和位置。 然而,这个学习因子通常是固定的。为了提高算法的收敛速度和精度,我们引入 了可变的学习因子。即根据算法的迭代次数和当前的最优解,动态地调整学习因 子的大小。
基于MATLAB的人工鱼群混合改进算法

I
r a n d o m ( X)
e l s e
1基 本人 工鱼 群算 法
人 工鱼 群 算法 [ m ]( A r t i i f c i a l F i s h S wa r m Al g o r i t h m, A F S A) 是根 据 鱼 类 活 动 特 点 提 出 的一 种 基 于 动 物 行 为 的 自 治 体 寻 优 方 法 ,具 有 良好 的求 取 全 局 极 值 的 能 力 ,且对 初值 和参数选择不敏感 , 简 单、 易 实现 、 鲁棒性 强、 可并 行 处 理 。 1 . 1算 法 描 述 假 设在一个n 维 目标 搜 索 空 间 中 , 有Ⅳ条 人 工 鱼 组 成 一 个 群 体 ,人 工 鱼 个 体 状 态 可表 示 为 向 量 : , x 9 , . . o 9 ) , 其 中x l ( i : 1 , 2 , …. , z 1 为优 化 变 量 ; 人 工鱼 当 前 所 在 位 置 的食 物浓度表示为 Y:f ( X、 ,其 中y 为 目标 函 数 ;人 工 鱼 个 体 之
Mi c r o c o mp u t e r Ap p l i c a t i o n s V o 1 . 3 1 , N o . 8 , 2 0 1 5
文章编号: 1 0 0 7 — 7 5 7 X( 2 0 1 5 ) 0 8 — 0 0 2 8 — 0 3
研 究与 设计
微 型 电脑 应 用 2 0 1 5 年第 3 1 卷第 8 期
象 ,综 合 应 用 上 述 两 种 思 路 对 其 进 行 改 进 , 得 到 一 种 融 入
则执行 随机 行为,可用函数表 示如公式 ( 2 ) :
p . +r a n d 0* s t e p* , Xj - X  ̄
人工鱼群算法ppt全

XX大学
汇报人:XX
目录
Here is your Content
>
1 引言
2 鱼群模式概论
3 鱼群算法的寻优原理
4 鱼群算法的实现
5 算法的收敛性分析
6 总结
>
LOGO
1
引言
在自然界中,多样的物种共同生活在一起,通过漫长的自然界的优胜劣汰,形成 了各自的觅食和生存方式。但是动物一般不具有人类复杂的逻辑思维和判断能力 的高级智能,它们只具有简单的行为能力,这些为人类解决问题的思路带来了不 少启发和鼓舞。动物行为具有以下的特点:
设人工鱼当前状态为Xi,探索当前邻域内的伙伴数目nf及中心位置Xc。
若 Yc / n f Y,i 表明伙伴中心有较多食物且不太拥挤,则朝伙伴的中心位置方向前进
一步,即
X t 1 i
Xti
Xc
X
t i
Xc Xti
Step Rand
否则,执行觅食行为。
追尾行为
• 追尾行为
鱼群在游动过程中,当其中一条鱼或几条鱼发现食物时,其邻近的伙伴会尾随
XV X XV X
Step Rand
其中Rand()函数为产生0到1之间的随机数;Step为步长
参数系统
人工鱼个体的状态可表示为向量
,其中
为欲
X寻 为V 优 目 X的 标变 函Vis量 数ua; 值l 人 ;Ra工 人nd鱼 工 当 鱼前 个所 体在 之位间置的的距食离物表浓示度为表示为
觅食行为
聚群行为
追尾行为
随机行为
鱼群算法在对以上四种行为进行评价后,自动选择合适的行为,从而形成了一种高 效快速的寻优策略。
求解矩阵特征值的混合人工鱼群算法

就是相对于 A S F A的全局搜索能力 ,它的局部搜索能 力较差 ,
收敛 速度较 慢 。针对 这一 不足 ,该 文把 具有 强局部 搜索 的
H o eJee 模式搜索方法 『 作为 A S ok —evs I F A的一个局部搜 索算
子 , 出一种 混合 人工 鱼群算法 , 提 并用此混合算法来求解矩阵 特 征值 。 实验表明 , A S 与 F A相 比, 该混合算法能在更短的时问
广西 民族大学 数学与计算机科学学院 , 南宁 5 00 306
C l g f Ma h mai s a d C mp tr S in e, a g i Unv r i o t n l i s N n i g 5 0 0 C i a ol e o t e t n o ue ce c Gu n x ie st f r Na i ai e , a nn 3 0 6, h n e c y o t
5 6
2 1 ,6 6 00 4 ( )
C m u rE gnei n p l ai s o p t nier g adA pi t n 计算机工程与应用 e n c o
求解矩阵特征值 的混合人工鱼群算法
黄 华娟 , 周永权 , 韦杏琼 , 罗德相
H A G H a ja ,HO 0 g q a , IX n - i g L O D — i g U N u -u n Z U Y n - u n WE ig qo , U e x n n a
G r hoi es gr c n圆盘定理 、 yF n定理 、 so si K a O t w k 定理等都可 以从 r
有 良好的全局搜索能力 , 并具有对初值 、 参数选择不敏感 、 鲁棒 性强 、 简单 、 易实现等优点 。与遗传算法 , 粒子群算法等其他单
人工鱼群算法

人工鱼群算法基本思想
首先放置36条鱼,每一条鱼分别位于每个格子的中心;依次对鱼执行觅食行为,确定鱼的下—步位置,36条鱼的下一步位置计算完以后,这个过程称为一轮;再执行下一轮的计算,直到鱼群的位置不再改变,算法结束。
算法的细节说明如下:
(1)格子的中心点有鱼表示当前格子内有一个以格子中心点为圆心半径为20 m的空洞。
(2)鱼的位置只能位于格子的中心点,鱼可以从当前格子走到其他任何—个格子的中心点上。
(3) 36条鱼的位置对应空洞的分布情况,空洞的分布确定后可以计算出波在98条线段上的传播时间(理论时间),进而得到理论时问与观测时间的误差,所以36条鱼的位置对应于—个误差。
当36条鱼的位置对应的空洞分布最逼近于空洞分布的真实情况时,得到的误差应是最小的;当误差最小时,此时鱼群位置被认为是真实的空洞位置。
(4)针对一条鱼而言,若它游到下—步后鱼群位置所对应的误差小于当前鱼群位置所对应误差,那么这条鱼就允许移到下一步。
(5)第i条鱼下一步的位置确定以后,第f+1条鱼的位置在第i条鱼下—步位置的基础上计算出来的,即第f+l条鱼的下一步位置依赖于第f条鱼的下一步位置。
本算法中鱼的行动不是同时进行的,而是依次序进行。
群体智能优化算法-鱼群优化算法

AF_Follow的伪代码如下:
functionAF_Follow()
{
fmax=-∞;
for (j=0;j<friend_num;j++)
{
if (di,j<Visual andf(Xj)>fmax)
{
fmax=f(Xj);Xmax=Xj;
}
}
nf=0;
for (j=0;j<friend_num;j++)
对Xi(t)执行觅食行为,计算Xi,prey。
ifmin(f(Xi,swarm),f(Xi,follow),f(Xi,prey))<f(Xi)then
Xi(t+1)=argmin(f(Xi,swarm),f(Xi,follow),f(Xi,prey));
end if
endfor
End
参考文献
1.Yazdani, D., A. Nadjaran Toosi, and M.R. Meybodi.Fuzzy Adaptive Artificial Fish Swarm Algorithm. inAI 2010: Advances in Artificial Intelligence. 2011. Berlin, Heidelberg: Springer Berlin Heidelberg.
(4)
AF_Swarm的伪代码如下:
function AF_Swarm()
{
nf=0;Xc=0;
for (j=0;j<fried_num;j++)
{
if (di,j<Visual)
{
nf++;Xc+=Xj;
人工鱼群算法课件

面临的挑战与问题
局部最优解
人工鱼群算法容易陷入局部最优解,导致搜索过程停滞不前。
参数设置
人工鱼群算法的参数设置对搜索结果影响较大,如何合理设置参数 是关键问题。
适用性问题
人工鱼群算法在处理大规模、高维度问题时性能下降,需要改进算 法以适应更复杂的问题。
解决方案与建议
混合优化算法
将人工鱼群算法与其他 优化算法结合,如遗传 算法、粒子群算法等, 以提高搜索性能。
03
人工鱼群算法的实现过程
初始化
随机初始化鱼群
在解空间中随机生成一定数量的鱼, 每条鱼代表一个潜在的解。
设置初始参数
包括最大迭代次数、视野范围、步长 等,这些参数对算法的性能和收敛速 度有重要影响。
行为模拟
觅食行为
01
每条鱼根据自身的感知能力在解空间中随机游动,寻找更优的
解。
聚群行为
02
根据鱼群中其他鱼的分布情况,判断是否聚集到中心区域,以
自适应参数调整
根据搜索过程动态调整 人工鱼群算法的参数, 以避免陷入局部最优解 。
强化学习
借鉴强化学习的思想, 通过与环境的交互不断 调整策略,提高搜索性 能。
THANK YOU
详细描述
多群体协同进化策略将问题划分为多个子问题,并为每个子问题分配一个独立的鱼群进行优化。每个鱼群采用不 同的优化策略和参数,以适应其对应的子问题的特性。通过多群体协同进化,算法能够同时从多个角度探索解空 间,提高全局搜索能力和收敛速度。
混合优化策略
总结词
混合优化策略结合了多种优化算法的优点, 以提高人工鱼群算法的性能。通过将不同的 优化算法与人工鱼群算法相结合,可以弥补 人工鱼群算法的不足,提高其求解复杂问题 的能力。
《基于多算法融合的改进人工鱼群算法及其应用》

《基于多算法融合的改进人工鱼群算法及其应用》一、引言在现实世界的优化问题中,人工智能算法因其出色的寻优能力得到了广泛应用。
人工鱼群算法作为其中一种仿生优化算法,已在许多领域取得显著成果。
然而,单一算法的应用在处理复杂问题时可能存在局限性。
本文旨在探讨基于多算法融合的改进人工鱼群算法,并探讨其在实际应用中的效果。
二、人工鱼群算法概述人工鱼群算法是一种模拟鱼群行为、进行全局寻优的智能算法。
该算法以人工鱼作为基本单位,通过模拟鱼群的觅食、聚群、追尾等行为,在解空间中搜索最优解。
人工鱼群算法具有并行性、鲁棒性等优点,在函数优化、路径规划等领域得到广泛应用。
三、多算法融合的改进人工鱼群算法为了进一步提高人工鱼群算法的寻优能力和适应性,本文提出了一种基于多算法融合的改进人工鱼群算法。
该算法将多种优化算法与人工鱼群算法相结合,通过相互补充和协同作用,提高算法的全局寻优能力和局部搜索能力。
1. 融合差分进化算法差分进化算法是一种基于差分向量的优化算法,具有较强的全局寻优能力。
将差分进化算法与人工鱼群算法相结合,可以扩大搜索范围,提高全局寻优能力。
在改进的人工鱼群算法中,引入差分进化算法的变异操作,对人工鱼的位置进行随机扰动,以增强全局搜索能力。
2. 融合粒子群优化算法粒子群优化算法是一种基于群体行为的优化算法,通过粒子间的协作与竞争实现寻优。
将粒子群优化算法与人工鱼群算法相结合,可以增强局部搜索能力和收敛速度。
在改进的人工鱼群算法中,引入粒子群优化算法的粒子更新机制,对人工鱼的状态进行更新,以加快收敛速度。
四、应用分析本文将改进的人工鱼群算法应用于两个典型领域:函数优化和路径规划。
通过与经典算法进行比较,验证了改进人工鱼群算法的有效性和优越性。
1. 函数优化应用在函数优化问题中,改进的人工鱼群算法能够快速找到全局最优解,且具有较好的鲁棒性。
与经典的人工鱼群算法相比,改进算法在寻优速度和精度方面均有明显提升。
2. 路径规划应用在路径规划问题中,改进的人工鱼群算法能够根据环境信息自主规划出最优路径。
人工鱼群算法综述

人工鱼群算法综述人工鱼群改进算法研究综述摘要:人工鱼群算法源于对鱼群运动行为的研究,是一种新型的群体智能随机全局优化算法,人工鱼群算法(AFSA)起步较晚,还存在着许多不足之处。
因此本文主要通过阐述鱼群算法的基本理论的同时,对人工鱼群算法的改进方法进行文献综述,并根据这些改进方法指出了人工鱼群算法未来的改进与研究方向。
关键词:人工鱼群算法算法改进综述1.引言1.1 人工鱼群算法的基本概念人工鱼群算法是李晓磊等[1]人于2002年提出的一种基于动物自治体[2-3]的优化方法,是集群智能思想[4]的一个具体应用,该算法根据水域中鱼生存数目最多的地方就是本水域中富含营养物质最多的地方这一特点来模拟鱼群的觅食行为而实现寻优。
它的主要特点是不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工鱼个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度[5]。
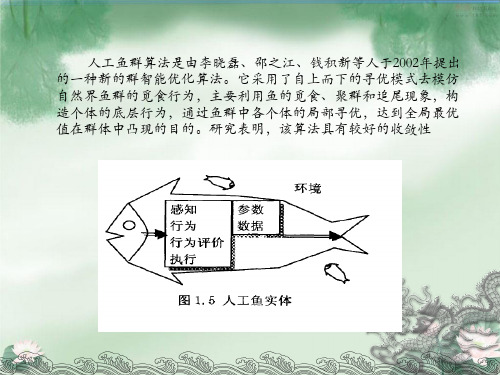
人工鱼群算法主要利用鱼的三大基本行为:觅食、聚群和追尾行为,采用自上而下的寻优模式从构造个体的底层行为开始,通过鱼群中各个体的局部寻优,达到全局最优值在群体中凸显出来的目的[6]。
(1)觅食行为:这是鱼趋向食物的一种活动,一般认为它是通过视觉或味觉来感知水中的食物两或食物浓度来选择行动的方向[6]。
(2)聚群行为:大量或少量的鱼聚集成群,进行集体觅食和躲避敌害,这是它们在进化过程中形成的一种生存方式[6]。
(3)追尾行为:当某一条鱼或几条鱼发现食物时,它们附近的鱼会尾随而来,导致更远处的鱼也会尾随过来[6]。
人工鱼群算法就是通过模拟鱼类的觅食、聚群、追尾等行为在搜索域中进行寻优的。
1.2 人工鱼群算法的行为描述觅食行为:设置人工鱼当前状态,并在其感知范围内随机选择另一个状态,如果得到的状态的目标函数大于当前的状态,则向新选择得到的状态靠近一步,反之,重新选取新状态,判断是否满足条件,选择次数达到一定数量后,如果仍然不满足条件,则随机移动一步[6]。
人工鱼群算法的简介及应用

德州律师人工鱼群算法是根据鱼在水中寻找食物的行为演化而来。
我们知道,在鱼塘里对着某一区域撒下食物,不一会儿就会有大量的鱼儿集中过来,鱼儿在水中一般有觅食,聚群,追尾三种行为,以下是这些行为的描述:(1)觅食行为:鱼一般会呆在食物较多的地方。
一般在水里游的鱼,当它发现食物时,会向其游去。
(2)聚群行为:鱼在水中大多是群聚在一起,这样是为了能够更好的在水中生存,观察鱼群不难发现,鱼群中每条鱼之间都保持有一定的距离,而且它们会尽量保持方向一致,而外围的鱼也都是不断像中心的位置靠近。
(3) 追尾行为:在鱼群中,当一条鱼或者几条鱼发现食物时,其它的鱼也会尾随其快速的游到食物分布较多的地方。
1.人工鱼群算法原理1.1人工鱼群算法具的特点(1)收敛速度较快,可以用来解决有实时性要求的问题;(2)针对一些精度要求不高的情况,可以用来快速的得到一个可行解;(3)不需要问题的严格机理模型,甚至不需要问题的精确描述,这使得它的应用范围得以扩展。
1.2人工鱼群算法常用终止条件(1) 判断连续多次所得的均方差小于允许的误差。
(2)判断一些区域的人工鱼群的数量达到某个比率。
(3)连续多次所获取的值均不得超过已寻找的极值。
(4)迭代次数到达设定的最大次数1.3人工鱼群算法的基本流程人工鱼群算法演化到具体计算技术,具体流程如下:为两个体之间的距离,xp(v1,v2……vn)个体的当前位置,visual一只鱼的感知距离。
@拥挤度因子。
(1)觅食人工鱼当前位置为Xi,在可见域内随机选择一个位置Xj(d(ij) <=visual),如xj优于xi向xj前进一步,否则随机移动一步。
如出现不满足约束则剪去。
不变,else =随机(0,1)}。
(2)聚群:xi可见域内共有nf1条鱼。
形成集和KJi,,if KJi不为空,then(xjk属于kji),若:(FCc为中心食物浓度,FCi为Xi点食物浓度)则:向中心移动:X(i+1,k)=不变,当Xik=X(center,k)时,Xik=随机(0,1),当Xik!=X(center,k)时,若:FCc/n-[论文网]f1<@FCi则:进行觅食。
求解矩阵特征值的捕鱼算法

求解 矩阵特征值 的捕鱼算法
陈建荣 陈建华 王 勇 文志娟 , , , C N J no g, H N ah a WANGY n WE Z i a HE arn C E J n u 2 i i , og, N h u n j
2. w a Ne Rur lCoo e a i eM e i a a a e n n e , ie Gu n xi 3 00 Ch n p r tv d c l M n g me tCe t r Ba s , a g 53 0 , i a
3Co lg f t e t s n mp trS in e Gu n x iest r t n l is Na n n 3 0 6 C ia . l eo Mah mai dCo u e ce c , a g i v ri f i aie , n ig5 0 0 , hn e ca Un y o Na o t
寻优 区域 , 用捕鱼算法在 复数域 内求解任意数值矩阵特征值 的近似值 。数值 实验表 明, 该算法具有收敛速度 快, 计算精度 高的优点。因此 , 该算法是有效和可行 的。
关键词 : 圆盘定理; 矩阵; 特征值 ; 捕鱼算法 文 章编 号 :0283 (022 050 文 献标 识码 : 10 —3 12 1)005.4 A 中图分 类 号 :P 1 T 31
Ke r s c r u a ik t e r m ; ti ; i e v l e ; s i g a g rt m y wo d : ic l r s o e marx eg n au s f h n l o h d h i i
摘
要 : 据 圆盘 定 理 以及 矩 阵特征 值 的性质 , 求 解 特征 值 的 问题 转化 为 最 小化 问题 。通 过 圆盘 定理 确 定 根 将
人工鱼群算法与遗传算法融合求解聚类问题研究

本集有 k个模式分 类。聚 类问题就是要找一个划分 C =
k
{ C1 , C2 , …, Ck }, 满足 : x = ∪Ci, Ci ≠Φ, i = 1, 2, …, k, Ci ICj = i =1
聚类分析是数据挖掘中一个非常重要的内容 ,是一种重 要的人类行为 。简单地讲 ,聚类分析就是将数据对象分组成 为多个类或簇 ,在同一个簇中的对象之间具有较高的相似度 而不同簇中的对象具有较大的差别 [ 6] 。从机器学习观点来
基金项目 安徽省教育厅自然科学基金项目 ( KJ2008B021) 。 作者简介 陈祥 生 (1978 - ) , 男 , 安 徽 安 庆 人 , 讲 师 , 从 事 智 能 计算
责任编辑 姜丽 责任校对 李岩
人工鱼群算法与遗传算法融合求解聚类问题研究
陈祥生 1, 2 ,梁 栋 2 ,王会颖 1
(1. 安徽财贸职业学院电子信息系 ,安徽合肥 230061; 2. 安徽大学电子科学与技术学院 ,安徽合肥 230039)
摘要 人工鱼群算法 (AFSA )是一种新提出的新型仿生优化算法。遗传算法是一种基于生物自然选择与遗传机理的随机搜索与优化方 法。聚类在数据挖掘、统计学和机器学习等很多领域都有广泛应用。聚类问题实质是一个全局优化问题。将遗传算法中的选择和变异 融合到人工鱼群算法 ,提出一种人工鱼群算法与遗传算法的融合算法 , 并应用于求解聚类问题 ,结果该算法保持了 A FSA 算法简单、易 实现的特点 ,仿真试验取得了较好的效果。 关键词 人工鱼群算法 ;遗传算法 ;聚类 ;优化 中图分类号 TP 301 文献标识码 A 文章编号 0517 - 6611 (2010 ) 36 - 21068 - 04
一种融合K-means算法和人工鱼群算法的聚类方法

一种融合K-means算法和人工鱼群算法的聚类方法吕少娟;张桂珠【摘要】Aiming at the problems of K-means clustering being subject to local optimum and sensitive to initial value,and the problems of artificial fish swarm algorithm having high convergence rate,being insensitive to initial values and self-organising behaviour,we propose a clustering method which combines K-means and artificial fish swarm algorithm.The algorithm first slightly improves the standard artificial fish swarm algorithm with self-adaptive strategy:i.e.in early iteration of artificial fish swarm algorithm it uses the fixed visual perspective,with the increase of iteration times,is adopts the self-adaptive decreasing visual perspective value.Based on this,it integrates K-means algorithm to artificial fishes ofthe improved artificial fish swarm algorithm,part of the artificial fishes randomly generated will go through the iteration of K-means once after finishing each iteration in artificial fish algorithm.Experimental results prove that the new algorithm is obviously superior to the particle swarm optimisation,K-means and the improved AFSA,and it will be effectively applied in data clustering.%针对K-means易收敛于局部最优以及对初始值敏感和人工鱼群算法收敛速度快,对初始值不敏感及自组织行为的问题,提出一种K-means和人工鱼群算法融合的聚类方法。
混合变异算子的人工鱼群算法

混合变异算子的人工鱼群算法502008,44(35)ComputerEngineeringandApplications计算机工程与应用混合变异算子的人工鱼群算法曲良东,何登旭QULiang-dong,HEDeng-xu广西民族大学数学与计算机科学学院,南宁530006CollegeofMathematicsandComputerScience,Guan野iUniversityforNationlities,Nanning530006,ChinaQuLiang-dong.HEDeng—xu.Artificialfish-schoolalgorithmbasedonhybridmutationoperators.ComputerEngineeringandApplications。
2008.44(35):50—52.Abstract:AfteranalyzingthedisadvantagesofArtificialFish-SchoolAlgorithm(AFSA),thispaperpresentsahybridartificialfish-schoolalgorithmbasedONGaussmutationanddifferentialevolutionmutation.ByaddingmutationoperatorstoAFSAinevo-lutionprocess,theabilityofAFSAtobreakawayfromartificialfishstochasticmovingwithoutadefinitepurposeorheavygettingtogetherroundthelocaloptimumsolutionisgreatlyimprove.TheproposedalgorithmCallgreatlyimprovetheabilityofseekingtheglobalexeeUentresultandconvergencepropertyandaccuracy.Severalcomputersimulationresult8showthattheproposedal-gorithmissignificantlysuperiortooriginalAFSA.Keywords:ArtificialFish—SchoolAlgorithm(AFSA);Gaussmutationoperator;differentialevolutionmutationoperator摘要:在分析基本人工鱼群算法存在不足的基础上,提出了基于高斯变异算子与差分进化变异算子相结合的人工鱼群算法,该算法克服了人工鱼漫无目的随机游动或在非全局极值点的大量聚集,显著提高了求解质量和运行效率.通过仿真实验测试验证。
人工鱼群算法全解

人工鱼群算法概述
• 2003年李晓磊、邵之江等提出的人工鱼群 算法(Atificial Fish-Swarm Algorithm, AFSA),它利用自上而下的寻优模式模仿自 然界鱼群觅食行为,主要利用鱼的觅食、 聚群和追尾行为,构造个体底层行为;通 过鱼群中各个体的局部寻优,达到全局最 优值在群体中凸现出来的目的。在基本运 算中引入鱼群的生存机制、竞争机制以及 鱼群的协调机制,提高算法的有效效率。
人工鱼群算法实例
• 聚群行为:每条鱼都先找出自己周围可视域内的 其它鱼,形成一个小鱼群,然后找出这群鱼的中 心点,这里中心点的确定方法是,若鱼群中半数 以上的鱼在第i位上取1,则中心点的第i位也 为1,否则为0,接着采用和前面相同方法查看中 心点的“食物”是否较多,是否拥挤,据此决定 是否向中心点靠近。如果聚群行为不成功,则进 行觅食活动。
;
else } retum AF_foodeonsistenee(Xinext ); } Random(N(Xi,Visual))表示在Xi 的Visual一距 离的邻域内随机取一个邻居.
Xinext Xi Random ( step)
;
人工鱼群算法概述
• (3)聚群行为(AF-swarm):鱼在游动 过程中为了保证自身的生存和躲避危害会 自然地聚集成群 。鱼聚群时所遵守的规则 有三条:分隔规则:尽量避免与临近伙伴过于 拥挤;对准规则:尽量与临近伙伴的平均方向 一致;内聚规则:尽量朝临近伙伴的中心移动。 人工鱼Xi搜索其视野内的伙伴数目nf及中心 位置Xc,若Yc/ nf > δYi,表明伙伴中心位置 状态较优且不太拥挤,则Xi朝伙伴的中心位 置移动一步,否则执行觅食行为:
工鱼群算法概述
• (5)公告板:是记录最优人工鱼个体状态 的地方。每条人工鱼在执行完一次迭代后 将自身当前状态与公告板中记录的状态进 行比较,如果优于公告板中的状态则用自 身状态更新公告板中的状态,否则公告板 的状态不变。当整个算法的迭代结束后, 输出公告板的值,就是我们所求的最优值。
人工鱼群算法共26页

鱼群特点: 在一片水域中,鱼存在的数目最多的地方就是本水域中富 含营养物质最多的地方。
算法作用:全局择优 鱼群行为:觅食,聚群,追尾。
1
算法描述
2
人工鱼的视觉描述
其中Rand()函数为产生0到1之间 的随机数;Step为步长
3
序号 变量名
变量含义
1
N
人工鱼群个体大小
2
{Xi}
人工鱼个体的状态位置、Xi=(x1,x1,···,xn),其中xi=(1,2,···,n)为待 优化变量
23
▪ ⑴视野的改进 ▪ ⑵分段优化方法 ▪ ⑶混合优化方法
24
Thank you!
25
NO
Yi<Yj
NO
YES
Xi|next =Xi + rand * Step * X j X i
|| X
j X
||
i
n>=try_number YES
Xi|next =Xi + rand * Step
人工鱼Xi在其视野内随机 选择一个状态Xj,分别计算它 们的目标函数值进行比较,如 果发现Yj比Yi优,则Xi向Xj的 方向移动一步
否则,执行觅食行为
11
▪
12
▪
参数
人工鱼数 最大迭代次数 觅食最大试探次数
取值
50 50 100
参数
感知距离 拥挤度因子 移动步长
取值
1 0.618 0.1
13
14
▪
参数
人工鱼数 最大迭代次数 觅食最大试探次数
取值
100 50 100
参数
感知距离 拥挤度因子 移动步长
取值
2.5 0.618 0.3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1引言在自然科学的研究中,特征值理论及其应用已经渗透到许多学科领域内,如解决数学物理方程、差分方程、Markov过程等问题[1-2]都涉及到矩阵特征值的求解问题。
目前,关于矩阵特征值的研究主要有两方面:(1)特征值分布理论的研究;(2)特征值近似值求解问题的研究。
为了解决第一个问题,数值代数给出了一系列估计特征值分布区域的定理。
对于一般复矩阵,Gerschgorin圆盘定理、Ky Fan定理、Ostrowski定理等都可以从矩阵本身的数据出发,给出一些几何图形去覆盖特征值的分布区域,从而得到了特征值所在的区域范围[3]。
对于矩阵特征值近似值的求解问题,许多学者已经做了大量的研究工作,常用的方法有变换法和幂法等。
变换法可以直接对矩阵进行处理,但计算速度慢;幂法只能求极端特征值,且算法的稳定性依赖于特征值的分布情况[4]。
1999年华人女学者涂晓媛博士将该方法引入到计算机动画的创作中,利用动物形态、习性和行为模型成功地制作了“人工鱼”,用计算机动画实现了“人工动物”共有的基本特征—生物力学、运动、感知和行为,被学术界称为“Xiaoyuan’Fish”[5]。
在2002年李晓磊[6]等人提出了一类群智能优化算法,即人工鱼群算法(Artificial Fish School Algorithm,AFSA)。
该算法具有良好的全局搜索能力,并具有对初值、参数选择不敏感、鲁棒性强、简单、易实现等优点。
与遗传算法,粒子群算法等其他单一群智能算法一样,AFSA也具有自己的不足。
其中一个不足就是相对于AFSA的全局搜索能力,它的局部搜索能力较差,收敛速度较慢。
针对这一不足,该文把具有强局部搜索的Hooke-Jeeves模式搜索方法[7]作为AFSA的一个局部搜索算子,提出一种混合人工鱼群算法,并用此混合算法来求解矩阵特征值。
实验表明,与AFSA相比,该混合算法能在更短的时间内求出更精确的解。
2矩阵特征值的分布理论2.1关于矩阵特征值的定义设矩阵A=(aij)∈C n×n,如果存在λ∈C,且X≠0满足AX=λX,则λ称为方阵A的特征值,X为对应λ的特征向量。
定义1设矩阵A=(aij)∈C n×n,称Ri=nj=1Σj≠i|aij|为矩阵A的第i行半径,以aii为圆心,Ri为半径的圆称为矩阵的第i行圆盘si,即si={λ∈C|λ-a ii≤Ri}。
求解矩阵特征值的混合人工鱼群算法黄华娟,周永权,韦杏琼,罗德相HUANG Hua-juan,ZHOU Yong-quan,WEI Xing-qiong,LUO De-xiang广西民族大学数学与计算机科学学院,南宁530006College of Mathematics and Computer Science,Guangxi University for Nationalities,Nanning530006,ChinaE-mail:hhj-025@HUANG Hua-juan,ZHOU Yong-quan,WEI Xing-qiong,et al.Hybrid artificial fish school algorithm for solving matrix puter Engineering and Applications,2010,46(6):56-59.Abstract:Based on the distribution about eigenvalues of matrix,the approximately distributed region of matrix eigenvalues is de-terminated,using hybrid artificial fish school algorithm to solve approximate eigenvalues of matrix.Several experimental results show that the proposed hybrid artificial fish school algorithm is efficient in solving the matrix’s eigenvalues and can reach a certain precision.Key words:matrix;eigenvalues;circular disc theorem;hybrid artificial fish school algorithm摘要:根据矩阵特征值的分布理论,通过确定矩阵特征值的分布区域,用混合人工鱼群算法来求解任意数值矩阵特征值的近似值。
实验结果表明,这种基于混合人工鱼群求解矩阵特征值的算法,可达到一定的精度,能够有效地获得任意矩阵的特征值。
关键词:矩阵;特征值;圆盘定理;混合人工鱼群算法DOI:10.3778/j.issn.1002-8331.2010.06.016文章编号:1002-8331(2010)06-0056-04文献标识码:A中图分类号:TP18基金项目:国家自然科学基金(the National Natural Science Foundation of China under Grant No.60461001);广西自然科学基金(the Natural Sci-ence Foundation of Guangxi of China under Grant No.0832082);国家民委科研基金(No.08GX01);广西民族大学科研项目启动基金资助项目。
作者简介:黄华娟(1984-),女,硕士,主要研究方向:计算智能及其应用;周永权(1962-),男,博士,教授,主要研究方向:计算智能、神经网络及应用;韦杏琼(1983-),女,硕士,主要研究方向:计算智能及其应用;罗德相(1980-),男,硕士,主要研究方向:计算智能及其应用。
收稿日期:2008-09-23修回日期:2008-12-22定义2设矩阵A =(a ij )∈Cn ×n,称R i ′=nj =1Σj ≠i|a ij |为矩阵A 的第j 列半径,以a ii 为圆心,R i ′为半径的圆称为矩阵的第j 列圆盘s i ′,s i ′={λ∈C |λ-a ii ≤R i ′}。
2.2Gerschgorin 圆盘定理设矩阵A =(a ij )∈Cn ×n,则A 的所有特征值λ1,λ2,…,λn(可相重)都落在复平面上的n 个圆盘s i (A )={λ∈C |λ-a ii ≤R i },i =1,2,…,n 的并集中,并且若A 的n 个圆盘中有k 个圆盘构成一个连通域G ,与其余n-k 个圆盘互不相交,则A 中有且仅有k 个特征值落在G 内。
从Gerschgorin 圆盘定理[8]可以得出以下两个推论[3]:推论1孤立的G 氏圆盘中含有且仅含有一个特征值,而k 个连通的G 氏圆盘中恰含有k 个特征值,而不保证每个圆盘都一定会含有A 的特征值;推论2如果A 的n 个圆盘两两互不相交,则A 有n 个互异的特征值,且每一特征值恰好在孤立的圆盘内。
3求解矩阵特征值的混合人工鱼群算法3.1基本人工鱼群算法人工鱼群算法其主要原理是模拟自然界中鱼的觅食、聚群和追尾行为以及鱼群之间的相互协助从而达到全局寻优的目的,其数学模型描述如下:假设在一个n 维的目标搜索空间中,有N 条组成一个群体的人工鱼,每条人工鱼个体的状态可表示为向量X =(x 1,x 2,…,x n ),其中x i (i =1,2,…,n )为欲寻优的变量;人工鱼当前所在位置的食物浓度表示为Y =f (X ),其中Y 为目标函数;人工鱼个体之间的距离表示为d i ,j =‖X i -X j ‖;visual 表示人工鱼的感知范围,step 为人工鱼移动的步长,δ为拥挤度因子;try-number 表示人工鱼每次觅食最大的试探次数。
3.1.1行为描述在每次迭代过程中,人工鱼主要是通过觅食、聚群和追尾等行为来更新自己,从而实现寻优,具体的行为描述如下:(1)随机行为(AF-Random ):指人工鱼会在其视野visual 内随机的移动,当发现食物时,会向食物逐渐增多的方向快速的移去。
(2)觅食行为(AF-prey ):指鱼循着食物多的方向游动的一种行为,人工鱼X i 在其视野内随机选择一个状态X j ,分别计算它们的目标函数值进行比较,如果发现Y j 比Y i 优,则X i 向X j 的方向移动一步;否则,X i 继续在其视野范围内随机移动选择状态X j ,判断是否满足前进条件,反复尝试try-number 次之后,仍没有满足前进条件,则随机移动一步使得X i 到达一个新的状态。
(3)聚群行为(AF-swarm ):指每条鱼在游动过程中尽量向临近伙伴的中心移动并避免过分拥挤的一种寻优行为。
人工鱼X i 搜索其视野内的伙伴数目nf 及中心位置X c ,若Y c /nf >δY i ,表明伙伴中心位置状态较优且不太拥挤,则X i 朝伙伴的中心位置移动一步,否则执行觅食行为。
(4)追尾行为(AF-follow ):指鱼向其可视域范围内的最优方向移动的一种行为。
人工鱼X i 搜索其视野内的所有伙伴中函数值最优的伙伴X j ,如果Y j /nf >δY i ,表明最优伙伴的周围不太拥挤,则X i 朝此伙伴移动一步,否则执行觅食行为。
3.1.2行为选择根据所要解决的问题性质,每条人工鱼对当前所处的环境进行评价,从而选择一种合适的行为来执行。
如对于求最大值问题,最简单的就是先模拟执行聚群、追尾等行为,然后评价行动后的值,选择其中的最大者来实际执行,缺省的行为方式为觅食行为。
最终,大量人工鱼会聚集在几个局部极值的周围,这有助于获取全局极值域,而值较优的极值区域周围一般会聚集大量的人工鱼,这有助于获取全局极值,从而达到了寻优的目的。
3.2Hooke-Jeeves 方法Hooke-Jeeves(HJ )方法[7]是Hooke 和Jeeves 在1961年提出的一种直接搜索方法。
该方法收敛速度快,具有很强的局部收敛性,但收敛结果的优劣依赖于初值的选取。
HJ 直接搜索法的具体步骤如下:(1)设初始点和初始步长分别为x (1)和d ,e 1,e 2,…,e n 为坐标向量,加速因子和计算精度分别为α>0和ε>0。
令y (1)=x (1),k =j =1;(2)若f (y (j )+de j )<f (y (j )),则称为实验成功,令y (j +1)=y (j )+de j ,转(3);否则,若f (y (j )+de j )≥f (y (j )),成为实验失败,此时,若f (y (j )-de j )<f (y (j )),令y (j +1)=y (j )-de j ,转(3);若f (y (j )-de j )≥f (y (j )),y(j +1)=y (j ),转(3);(3)若j<n ,令j =j +1,返回(2);否则j=n ,若f (y (n +1))≥f (x (k )),转(5);若f (y(n +1))<f (x (k )),则转(4);(4)令x (k +1)=y(n +1),y (1)=x (k +1)+α(x (k +1)-x (k )),k =k +1,再令j =1,返回(2);(5)若d ≤ε,则计算结束,取x *≈x (k );否则,令d=d /2,y (1)=x (k ),x(k +1)=x (k ),k =k +1,再令j =1,返回(2)。
