初二数学科尖子生辅导训练题
整式的除法(限时满分培优训练)-八年级数学上册尖子生培优必刷题【人教版】(原卷版)

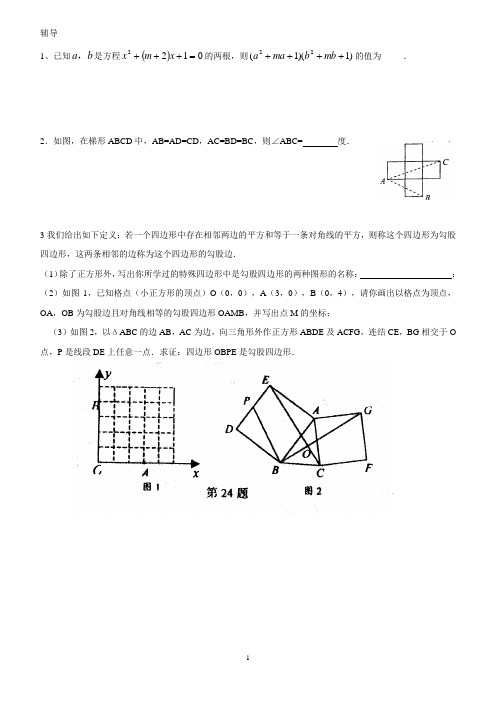
【拔尖特训】2023-2024学年八年级数学上册尖子生培优必刷题【人教版】专题14.8整式的除法班级:_____________ 姓名:_____________ 得分:_____________本试卷满分100分,建议时间:30分钟.试题共23题,其中选择10道、填空6道、解答7道.试题包含基础题、易错题、培优题、压轴题、创新题等类型,没有标记的为基础过关性题目.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022秋•双阳区期末)计算(﹣4a 2+12a 3b )÷(﹣4a 2)的结果是( )A .1﹣3abB .﹣3abC .1+3abD .﹣1﹣3ab 2.(2023春•雅安期末)计算:−13a 2b 2÷(ab)=( )A .13abB .13a 2b 2C .−13abD .−13a 2b 2 3.(2022秋•清河区校级期末)面积为9a 2﹣6ab +3a 的长方形一边长为3a ,另一边长为( )A .3a ﹣2b +1B .2a ﹣3bC .2a ﹣3b +1D .3a ﹣2b4.(易错题)(2023春•遵化市期中)若×4ab 2=﹣12ab 3c ,那么代表的整式是( ) A .﹣3abc B .﹣3ab 2c C .﹣3bcD .bc 5.(易错题)(2023•桃城区校级二模)已知( )÷12ab 2=8a ,则括号内应填( )A .16ab 2B .4ab 2C .16a 2b 2D .4a 2b 26.(2022秋•西丰县期末)长方形的面积是12a 2﹣6ab +3a 3,一边长是3a ,则它的另一边长是( )A .4a 2﹣2b +a 3B .2b ﹣4a +a 2C .a 2+4a ﹣2bD .4a 2﹣2b +a 7.(易错题)(2019春•招远市期末)若x m y n ÷14x 3y =4x 3y ,则m ,n 满足( )A .m =6,n =1B .m =6,n =2C .m =5,n =0D .m =5,n =28.(易错题)(2022春•宁远县期中)墨迹污染了等式12x 3★3x =4x 2(x ≠0)中的运算符号,则污染的运算符号是( )A .+B .﹣C .×D .÷9.(培优题)(2022春•碑林区校级月考)小明在做作业的时候,不小心把墨水滴到了作业本上,■×2ab =4ab +2ab 3,阴影部分即为被墨汁弄污的部分,那么被墨汁遮住的一项是( )A .(2+b 2)B .(a +2b )C .(3ab +2b 2)D .(2ab +b 2)10.(培优题)(2022春•诸暨市期末)若A 、B 、C 均为整式,如果A •B =C ,则称A 能整除C ,例如由(x +3)(x ﹣2)=x 2+x ﹣6,可知x ﹣2能整除x 2+x ﹣6.若已知x ﹣3能整除x 2+kx ﹣7,则k 的值为( )A .−73B .−23C .43D .23 二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上11.(易错题)(2022秋•上海期末)计算(9x 3﹣3x 2)÷(﹣3x 2)= .12.(易错题)(2023春•达州期中)已知A =2x ,B 是多项式,在计算B +A 时,小马虎同学把B +A 看成了B ÷A ;结果得x 2+x ,则B +A = .13.(易错题)(2022秋•兴城市期末)若(﹣25y 3+15y 2﹣5y )÷M =﹣5y ,则M = .14.(培优题)(2023春•福山区期中)如图1.将一张长方形纸板四角各切去一个同样的正方形,制成如图2的无盖纸盒,若纸盒的容积为4a 2b ,则图2中纸盒底部长方形的周长为 .15.(培优题)(2023春•龙口市期末)若n 是正整数,且x 2n =5,则(2x 3n )2÷(4x 2n )= .16.(培优题)(2023春•威海期末)已知9m ÷32m+2=(13)n ,n 的值是 .三、解答题(本大题共7小题,共52分.解答时应写出文字说明、证明过程或演算步骤)17.计算:(1)(7+x )8÷(7+x )7.(2)(abc )5÷(abc )3.(3)(12)7÷(−12)3. (4)(y 10)÷(y 4÷y 2).18.计算:(1)(6a 2b +3a )÷a ;(2)(4x 3y 2﹣x 2y 2)÷(﹣2x 2y );(3)(20m 4n 3﹣12m 3n 2+3m 2n )÷(﹣4m 2n ):(4)[15(a+b)3﹣9(a+b)2]÷3(a+b)2.19.(易错题)(2023春•兴平市期末)已知4m2﹣7m+6=0,求代数式(3m2﹣2m)÷m﹣(2m﹣1)2的值.20.(易错题)(2023春•武功县期中)学习了《整式的乘除》这一章之后,小明联想到小学除法运算时,会碰到余数的问题,那么类比多项式除法也会出现余式的问题.例如,如果一个多项式(设该多项式为A)除以2x2的商为3x+4,余式为x﹣1,那么这个多项式是多少?他通过类比小学除法的运算法则:被除数=除数×商+余数,推理出多项式除法法则:被除式=除式×商+余式.请根据以上材料,解决下列问题:(1)请你帮小明求出多项式A;(2)小明继续探索,如果一个多项式除以3x的商为2x2+x﹣1,余式为x+3,请你根据以上法则求出该多项式.21.(培优题)(2023春•和平区校级月考)(1)若(x2+nx+3)(x2﹣3x+m)的结果中不含x2和x3项,求2m+n ﹣1的值;(2)已知单项式A=4x,B是多项式,小虎计算B+A时,看成了B÷A,结果得x2+12x,求正确的结果.22.(培优题)(2021春•盐湖区校级期末)观察下列各式:(x﹣1)÷(x﹣1)=1;(x2﹣1)÷(x﹣1)=x+1;(x3﹣1)÷(x﹣1)=x2+x+1;(x4﹣1)÷(x﹣1)=x3+x2+x+1;…(x8﹣1)÷(x﹣1)=x7+x6+x5+…+x+1.(1)根据以上各式的规律填空:①(x2018﹣1)÷(x﹣1)=;②(x n﹣1)÷(x﹣1)=.(2)利用②中的结论求22018+22017+22016+…+2+1的值;(3)若1+x+x2+…+x2016+x2017=0,求x2018的值.23.(创新题)(2023春•姜堰区期中)阅读理解:由两个或两类对象在某些方面的相同或相似,得出它们在其他方面也可能相同或相似的推理方法叫类比法.多项式除以多项式可以类比于多位数的除法进行计算.如图1:∴278÷12=23…2,∴(x3+2x2﹣3)÷(x﹣1)=x2+3x+3即多项式除以多项式用竖式计算,步骤如下:①把被除式和除式按同一字母的指数从大到小依次排列(若有缺项用零补齐).②用竖式进行运算.③当余式的次数低于除式的次数时,运算终止,得到商式和余式.若余式为零,说明被除式能被除式整除.例如:(x3+2x2﹣3)÷(x﹣1)=x2+3x+3∵余式为0∴x3+2x﹣3能被x﹣1整除.根据阅读材料,请回答下列问题:(1)多项式x2+5x+6除以多项式x+2,所得的商式为;(2)已知关于x的二次多项式除以x+1,商式是2x﹣2,余式是﹣1,求这个多项式;(3)已知x3+2x2﹣ax﹣10能被x﹣2整除,则a=;(4)如图2,有2张A卡片,3张B卡片,1张C卡片,能否将这6张卡片拼成一个与原来总面积相等且一边长为(a+b)的长方形?若能,求出另一边长;若不能,请说明理由.。
苏科版 八年级数学下册尖子生培优必刷题 专题10.6分式的混合运算大题专练(重难点培优30题)(原卷

【拔尖特训】2023-2024学年八年级数学下册尖子生培优必刷题【苏科版】专题10.6分式的混合运算大题专练(重难点培优30题)班级:___________________ 姓名:_________________ 得分:_______________ 注意事项:本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一.解答题(共30小题)1.(2023秋•苏州期末)化简:(1)a 2a−1−1a−1;(2)(m −3−7m+3)÷m 2−4m 2m+6.2.(2023•泉山区校级三模)(1)计算(π−3.14)0+(13)−2−(−2)3;(2)化简:(1a+1−1a 2−1)÷a−3a+1. 3.(2023春•六合区校级月考)计算.(1)4a 3b ⋅b 2a 3;(2)1−a−2a ÷a 2−4a 2+a. 4.(2023秋•崇川区校级月考)计算:(1)(π−3)0+(−13)−1−√(−2)2;(2)6a 6b 4÷3a 3b 4+a 2⋅(﹣5a );(3)(2y x )−2⋅xy x 2−xy 2xy 2÷2x ; (4)(a −1−2a−1a+1)÷a 2−4a+42+2a5.(2023春•宜兴市校级期中)计算(1)x 2x+2−x +2; (2)x 2−16x+4÷2x−84x .6.(2023春•梁溪区校级期中)计算:(1)6xy 2÷2y 2x ;(2)2x−1x−1−1x−1; (3)x x 2−4−12x−4; (4)x−y x ÷(x −2xy−y 2x) 7.(2023•徐州)计算:(1)(﹣1)2022+|√3−3|﹣(13)﹣1+√9; (2)(1+2x )÷x 2+4x+4x 2. 8.(2023春•溧阳市期中)计算:(1)a 2bc ⋅(−bc 2a ); (2)a−2a+3×2a+6a 2−4; (3)a 22a−4−2a−2; (4)(4x−2−x +2)÷(x−4x−2). 9.(2023•兴化市开学)(1)计算:(√3)2﹣(π−√5)0−√27−|√3−2|;(2)化简:ba 2−b 2÷(1−a a+b ). 10.(2023春•滨湖区校级期中)化简:(1)b 2−27a 3÷2b 9a ⋅3ab b 4; (2)4x 22x−3+93−2x ; (3)m 2m+2−m +2.11.(2023春•东海县期末)计算:(1)a 2bc ⋅(−bc 2a ); (2)a 22a−4−2a−2. 12.(2023春•丹阳市期末)化简:(1)2xx 2−4−1x−2;(2)(1−1a )÷a 2−2a+1a 2−1.13.(2023春•常州期末)计算:(1)8x 3÷32x 2; (2)a−c a−b −c−b b−a. 14.(2023春•溧阳市期末)化简:(1)(−m n 2)•n m; (2)a a−1÷(a 2a 2−1−a a+1).15.(2023秋•环翠区校级月考)分式计算:(1)3x 2y ⋅512ab 2÷(−5a 4b ); (2)(−a 2bc )3⋅(−c 2a 2)2÷(−bc a )4; (3)a+31−a ÷a 2+3aa 2−2a+1; (4)(ab −b 2)÷a 2−b 2a+b. 16.(2023秋•张店区校级月考)分式的计算:(1)(1x−1−1x 2−1)÷x 2−x x 2−2x+1; (2)2x−6x−2÷(5x−2−x −2).17.(2023春•南关区校级月考)计算:(1)x x 2−1⋅x+1x 2; (2)(a+b)2ab −a 2+b 2ab. 18.(2023秋•和平区校级期末)计算:(1)(−4m 3n 3t )2÷n mt(2)x 2−4x 2−4x+4÷x+2x+1−x x−219.(2023春•罗湖区校级期末)计算(1)3x (x−3)2−x 3−x (2)1x+1+1x−1−x 2+1x 2−1x −1x−120.(2023春•南阳月考)化简:(1)(a ﹣1−4a−1a+1)÷a 2−8a+16a+1; (2)(x+2x 2−2x −x−1x 2−4x+4)÷x−4x . 21.(2023秋•青龙县期中)计算:(1)a 2a−b +b 2a−b −2ab a−b ;(2)(1−1a+1)÷a a 2+2a+1. 22.(2023春•沈北新区期末)化简:(1)(x 2﹣4y 2)÷2y+x xy •1x(2y−x); (2)2x x 2−4−1x−2.23.(2023•九龙坡区校级开学)分式化简:(1)16−x 2x 2+4x+4÷x 2x+4⋅x+2x+4; (2)1a+1−3−aa 2−6a+9÷a 2+a a−3. 24.(2023秋•寻甸县期末)计算与化简(1)32m−n −2m−n(2m−n)2;(2)(a +2−5a−2)÷3−a 2a−4. 25.(2023秋•沂水县期末)化简:(1)x x−1+3x−11−x 2; (2)(2m m−1−m m+1)÷m m 2−1. 26.(2023秋•天津期末)计算:(1)(﹣3xy )÷2y 23x •(y x)2; (2)(x x+y −2y x+y )÷x−2y xy •(1x +1y ). 27.(2023春•沙坪坝区校级月考)计算:(1)2y−x x−y +y y−x +x x−y ;28.(2023秋•沙坪坝区校级期末)计算:(1)(a +b )2+a (a ﹣2b );(2)(1−x x+2)÷x 2−4x+4x 2−4. 29.(2023秋•荔湾区期末)计算:(1)a−1a−b −1+b b−a ;(2)(4−a 2a−1+a )÷a 2−16a−1. 30.(2023秋•永年区期末)上课时老师在黑板上书写了一个分式的正确化简结果,随后用手掌盖住了一部分,形式如下: •y 2x 2−xy −y 2−x 2x 2−2xy+y 2=x x−y(1)聪明的你请求出盖住部分化简后的结果;(2)当x =2时,y 等于何值时,原分式的值为5.【拔尖特训】2023-2024学年八年级数学下册尖子生培优必刷题【苏科版】专题10.6分式的混合运算大题专练(重难点培优30题) 班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一.解答题(共30小题)1.(2023秋•苏州期末)化简:(1)a 2a−1−1a−1;(2)(m −3−7m+3)÷m 2−4m 2m+6.【分析】(1)根据分式的减法法则进行计算,再化成最简分式即可;(2)先根据分式的减法法则进行计算,再根据分式的除法法则把除法变成乘法,最后根据分式的乘法法则进行计算即可.【解答】解:(1)原式=a 2−1a−1=(a+1)(a−1)a−1 =a +1;(2)原式=[(m−3)(m+3)m+3−7m+3]•2(m+3)m(m−4) =m 2−9−7m+3•2(m+3)m(m−4)=(m+4)(m−4)m+3•2(m+3)m(m−4)=2(m+4)m=2m+8m . 2.(2023•泉山区校级三模)(1)计算(π−3.14)0+(13)−2−(−2)3;(2)化简:(1a+1−1a 2−1)÷a−3a+1. 【分析】(1)根据零指数幂、负整数指数幂和有理数的乘方计算即可;(2)先算括号内的式子,再计算括号外的除法即可.【解答】解:(1)(π−3.14)0+(13)−2−(−2)3=1+9﹣(﹣8)=1+9+8=18;(2)(1a+1−1a 2−1)÷a−3a+1 =a−1−1(a+1)(a−1)•a+1a−3=a−2(a−1)(a−3)=a−2a 2−4a+3. 3.(2023春•六合区校级月考)计算. (1)4a 3b ⋅b 2a 3;(2)1−a−2a ÷a 2−4a 2+a. 【分析】(1)根据分式的乘法运算即可求出答案.(2)根据分式的乘除运算以及加减运算法则即可求出答案.【解答】解:(1)原式=4ab 6a 3b =23a 2. (2)原式=1−a−2a ×a 2+a a 2−4 =1−a−2a ×a(a+1)(a+2)(a−2)=1−a+1a+2=a+2a+2−a+1a+2=1a+2. 4.(2023秋•崇川区校级月考)计算:(1)(π−3)0+(−13)−1−√(−2)2;(2)6a 6b 4÷3a 3b 4+a 2⋅(﹣5a );(3)(2y x )−2⋅xy x 2−xy 2xy 2÷2x; (4)(a −1−2a−1a+1)÷a 2−4a+42+2a 【分析】(1)利用零指数幂,负指数幂和算术平方根的性质进行计算即可;(2)先利用整式的除法法则,乘法法则进行计算,然后再进行合并即可;(3)先分别利用负指数幂,分式的乘方,分式的乘法法则,除法法则进行计算,然后再进行减法运算;(4)先算括号内的减法,然后再将括号外分式的分子分母进行因式分解,将除法化为乘法再进行约分,最后化为最简分式即可.【解答】解:(1)(π−3)0+(−13)−1−√(−2)2=1+(﹣3)﹣2=﹣4;(2)6a 6b 4÷3a 3b 4+a 2⋅(﹣5a )=2a 3﹣5a 3=﹣3a 3;(3)(2y x )−2⋅xy x 2−xy 2xy 2÷2x =x 24y 2⋅xy x 2−xy 2xy 2⋅x 2=x 4y −x 4y=0;(4)(a −1−2a−1a+1)÷a 2−4a+42+2a=(a+1)(a−1)−(2a−1)a+1÷(a−2)22(a+1) =a(a−2)a+1⋅2(a+1)(a−2)2 =2a a−2. 5.(2023春•宜兴市校级期中)计算(1)x 2x+2−x +2; (2)x 2−16x+4÷2x−84x .【分析】(1)先通分再加减即可;(2)先因式分解,再根据除法法则计算即可.【解答】解:(1)x 2x+2−x +2 =x 2x+2−x 2+2x x+2+2x+4x+2 =4x+2;(2)x 2−16x+4÷2x−84x =(x+4)(x−4)x+4•4x 2(x−4)=2x .6.(2023春•梁溪区校级期中)计算:(1)6xy 2÷2y 2x ; (2)2x−1x−1−1x−1; (3)x x 2−4−12x−4; (4)x−y x ÷(x −2xy−y 2x) 【分析】(1)把除法转为乘法,再约分即可;(2)利用分式的减法法则进行运算即可;(3)先通分,再进行运算即可;(4)先通分,把能分解的进行分解,除法转为乘法,再约分即可.【解答】解:(1)6xy 2÷2y 2x=6xy 2⋅x 2y 2 =3x 2;(2)2x−1x−1−1x−1 =2x−1−1x−1=2(x−1)x−1=2;(3)x x 2−4−12x−4 =2x 2(x−2)(x+2)−x+22(x−2)(x+2) =x−22(x−2)(x+2)=12(x+2)=12x+4;(4)x−y x ÷(x −2xy−y 2x ) =x−y x ÷x 2−2xy+y 2x =x−y x ⋅x(x−y)2 =1x−y .7.(2023•徐州)计算:(1)(﹣1)2022+|√3−3|﹣(13)﹣1+√9; (2)(1+2x )÷x 2+4x+4x 2. 【分析】(1)根据有理数的乘方、绝对值和负整数指数幂可以解答本题;(2)先算括号内的式子,然后计算括号外的除法即可.【解答】解:(1)(﹣1)2022+|√3−3|﹣(13)﹣1+√9 =1+3−√3−3+3=4−√3;(2)(1+2x )÷x 2+4x+4x 2=x+2x •x 2(x+2)2=x x+2.8.(2023春•溧阳市期中)计算:(1)a 2bc ⋅(−bc 2a ); (2)a−2a+3×2a+6a 2−4; (3)a 22a−4−2a−2;(4)(4x−2−x +2)÷(x−4x−2).【分析】(1)根据分式的约分可以解答本题;(2)先对分式的分子分母分解因式,再约分即可;(3)先通分,然后再分解因式,最后约分即可;(4)先对括号内的式子通分,然后计算括号外的除法即可.【解答】解:(1)a 2bc ⋅(−bc 2a )=−a 2; (2)a−2a+3×2a+6a 2−4=a−2a+3•2(a+3)(a+2)(a−2) =2a+2;(3)a 22a−4−2a−2=a 2−42(a−2)=(a+2)(a−2)2(a−2)=a+22;(4)(4x−2−x +2)÷(x−4x−2) =4−(x−2)(x−2)x−2•x−2x−4=4−x 2+4x−4x−4=−x(x−4)x−4 =﹣x .9.(2023•兴化市开学)(1)计算:(√3)2﹣(π−√5)0−√27−|√3−2|;(2)化简:ba 2−b 2÷(1−a a+b). 【分析】(1)先化简各式,然后再进行计算即可解答;(2)先利用异分母分式加减法计算括号里,再算括号外,即可解答.【解答】解:(1)原式=3﹣1﹣3√3−2+√3=﹣2√3;(2)原式=b (a+b)(a−b)÷(a+b−a a+b ) =b (a+b)(a−b)⋅a+b b=1a−b. 10.(2023春•滨湖区校级期中)化简: (1)b 2−27a 3÷2b 9a ⋅3ab b 4; (2)4x 22x−3+93−2x ; (3)m 2m+2−m +2.【分析】(1)先把除法转化为乘法,然后约分化简即可;(2)把第二个分母变形后根据同分母分式的加减法法则计算;(3)先通分,然后根据同分母分式的加减法法则计算.【解答】解:(1)原式=b 2−27a 3⋅9a 2b ⋅3ab b 4 =−12ab 2;(2)原式=4x 22x−3−92x−3=4x 2−92x−3=(2x−3)(2x+3)2x−3=2x +3; (3)原式=m 2m+2−(m −2)=m 2m+2−m 2−4m+2=m 2−m 2+4m+2=4m+2. 11.(2023春•东海县期末)计算:(1)a 2bc ⋅(−bc 2a ); (2)a 22a−4−2a−2. 【分析】(1)根据分式的乘法运算即可求出答案.(2)根据分式的加减运算即可求出答案.【解答】解:(1)原式=−a 2.(2)原式=a 22(a−2)−42(a−2)=a 2−42(a−2) =(a−2)(a+2)2(a−2)=a+22.12.(2023春•丹阳市期末)化简:(1)2xx 2−4−1x−2;(2)(1−1a )÷a 2−2a+1a 2−1. 【分析】(1)原式通分并利用同分母分式的减法法则计算,约分即可得到结果;(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.【解答】解:(1)原式=2x (x+2)(x−2)−x+2(x+2)(x−2)=2x−(x+2)(x+2)(x−2)=2x−x−2(x+2)(x−2)=x−2(x+2)(x−2)=1x+2;(2)原式=a−1a ÷(a−1)2(a+1)(a−1) =a−1a •(a+1)(a−1)(a−1)2=a+1a .13.(2023春•常州期末)计算:(1)8x 3÷32x 2; (2)a−c a−b −c−b b−a. 【分析】(1)根据分式的除法运算进行化简即可求出答案.(2)根据分式的加减运算进行化简即可求出答案.【解答】解:(1)原式=8x 3⋅x 232 =14x. (2)原式=a−c+b−c a−b =a+b a−b . 14.(2023春•溧阳市期末)化简:(1)(−m n 2)•n m; (2)a a−1÷(a 2a 2−1−a a+1).【分析】(1)根据分式的乘法计算即可;(2)先算括号内的式子,然后计算括号外的除法即可.【解答】解:(1)(−m n 2)•n m =﹣(m n 2•n m ) =−1n ;(2)a a−1÷(a 2a 2−1−a a+1) =a a−1÷a 2−a(a−1)(a+1)(a−1)=a a−1⋅(a+1)(a−1)a 2−a 2+a=a a−1⋅(a+1)(a−1)a =a +1.15.(2023秋•环翠区校级月考)分式计算:(1)3x 2y ⋅512ab 2÷(−5a 4b ); (2)(−a 2b c )3⋅(−c 2a 2)2÷(−bc a )4; (3)a+31−a ÷a 2+3aa 2−2a+1; (4)(ab −b 2)÷a 2−b 2a+b .【分析】(1)按照从左到右的顺序,进行计算即可解答;(2)先算乘方,再算乘除,即可解答;(3)先把除法转化为乘法,进行计算即可解答;(4)先把除法转化为乘法,进行计算即可解答.【解答】解:(1)3x 2y ⋅512ab 2÷(−5a 4b ) =15x 2y12ab 2•(−4b 5a ) =−x 2y a 2b; (2)(−a 2b c )3⋅(−c 2a 2)2÷(−bc a )4; =−a 6b 3c 3•c 4a 4÷b 4c 4a 4 =−a 6b 3c 3•c 4a 4•a 4b 4c 4 =−a 6c 3b; (3)a+31−a ÷a 2+3aa 2−2a+1=a+31−a •(a−1)2a(a+3)=1−a a ;(4)(ab −b 2)÷a 2−b 2a+b =b (a ﹣b )•a+b (a+b)(a−b)=b .16.(2023秋•张店区校级月考)分式的计算:(1)(1x−1−1x 2−1)÷x 2−x x 2−2x+1; (2)2x−6x−2÷(5x−2−x −2).【分析】(1)分式的加减运算以及乘除运算法则即可求出答案.(2)分式的加减运算以及乘除运算法则即可求出答案.【解答】解:(1)原式=x+1−1(x−1)(x+1)•(x−1)2x(x−1)=x (x−1)(x+1)•x−1x=1x+1.(2)原式=2(x−3)x−2÷5−(x+2)(x−2)(x−2) =2(x−3)x−2•x−29−x 2=−2(x−3)(x+3)(x−3) =−2x+3. 17.(2023春•南关区校级月考)计算: (1)x x 2−1⋅x+1x 2; (2)(a+b)2ab −a 2+b 2ab. 【分析】(1)先分解因式,然后再约分.(2)同分母相减,分母不变,分子相减即可求出答案.【解答】解:(1)原式=x (x+1)(x−1)•x+1x 2=1x(x−1). (2)原式=a 2+2ab+b 2−a 2−b 2ab =2ab ab=2. 18.(2023秋•和平区校级期末)计算:(1)(−4m 3n 3t )2÷n mt(2)x 2−4x 2−4x+4÷x+2x+1−x x−2【分析】(1)先计算乘方,再计算除法即可;(2)先按分式除法法则计算,再按分式减法法则计算即可.【解答】解:(1)原式=16m 6n 29t 2÷n mt=16m 6n 29t 2×mt n =16m 7n 9t; (2)原式=(x+2)(x−2)(x−2)2−x+1x+2−x x−2 =x+1x−2−x x−2=1x−2. 19.(2023春•罗湖区校级期末)计算(1)3x (x−3)2−x 3−x (2)1x+1+1x−1−x 2+1x 2−1(3)(x+1x 2−1+x x−1)÷x+1x 2−2x+1【分析】(1)直接进行通分运算进而得出答案;(2)直接进行通分运算进而得出答案;(3)直接利用分式的性质化简,再利用分式的混合运算法则计算得出答案.【解答】解:(1)3x (x−3)2−x 3−x =3x (x−3)2+x(x−3)(x−3)2 =x 2(x−3)2;(2)1x+1+1x−1−x 2+1x 2−1=x−1x 2−1+x+1x 2−1−x 2+1x 2−1=−x 2+2x−1(x+1)(x−1)=−(x−1)2(x+1)(x−1)=−x−1x+1;(3)(x+1x 2−1+x x−1)÷x+1x 2−2x+1 =1+x x−1•(x−1)2x+1=x ﹣1.20.(2023春•南阳月考)化简:(1)(a ﹣1−4a−1a+1)÷a 2−8a+16a+1; (2)(x+2x 2−2x −x−1x 2−4x+4)÷x−4x . 【分析】(1)先算括号内的减法,把除法变成乘法,再算乘法即可;(2)先算括号内的减法,把除法变成乘法,再算乘法即可.【解答】解:(1)原式=(a−1)(a+1)−(4a−1)a+1•a+1(a−4)2=a 2−1−4a+1a+1=a 2−4a a+1•a+1(a−4)2 =a(a−4)a+1•a+1(a−4)2=a a−4;(2)原式=[x+2x(x−2)−x−1(x−2)2]•x x−4 =(x+2)(x−2)−x(x−1)x(x−2)2•x x−4 =x 2−4−x 2+x x(x−2)2 =x−4x(x−2)2⋅x x−4 =1(x−2)2 =1x 2−4x+4. 21.(2023秋•青龙县期中)计算: (1)a 2a−b +b 2a−b −2ab a−b; (2)(1−1a+1)÷a a 2+2a+1. 【分析】(1)根据同分母分式加减法则进行计算;(2)先通分计算括号内的减法,再把除法转化为乘法,约分计算便可.【解答】解:(1)a 2a−b +b 2a−b −2ab a−b=a 2+b 2−2ab a−b=(a−b)2a−b =a ﹣b ;(2)(1−1a+1)÷aa 2+2a+1 =a a+1×(a+1)2a =a +1.22.(2023春•沈北新区期末)化简:(1)(x 2﹣4y 2)÷2y+x xy •1x(2y−x); (2)2xx 2−4−1x−2.【分析】(1)先算小括号里面的,然后再算括号外面的;(2)先通分,然后按同分母分式加减法法则进行计算求解.【解答】解:(1)原式=(x +2y )(x ﹣2y )•xy 2y+x ⋅1x(2y−x) =﹣y ;(2)原式=2x (x+2)(x−2)−x+2(x+2)(x−2)=2x−x−2(x+2)(x−2) =1x+2. 23.(2023•九龙坡区校级开学)分式化简: (1)16−x 2x 2+4x+4÷x 2x+4⋅x+2x+4; (2)1a+1−3−aa 2−6a+9÷a 2+a a−3. 【分析】(1)根据分式的乘除法可以解答本题;(2)根据分式的除法和减法可以解答本题.【解答】解:(1)16−x 2x 2+4x+4÷x 2x+4⋅x+2x+4 =(4+x)(4−x)(x+2)2⋅2(x+2)x ⋅x+2x+4 =2(4−x)x=8−2x x ;(2)1a+1−3−aa 2−6a+9÷a 2+a a−3=1a+1−3−a (a−3)2⋅a−3a(a+1) =1a+1+1a(a+1) =a+1a(a+1)=1a .24.(2023秋•寻甸县期末)计算与化简(1)32m−n −2m−n (2m−n)2; (2)(a +2−5a−2)÷3−a 2a−4.【分析】(1)先约分,再根据分式的减法法则进行计算即可;(2)先算括号内的加减,把除法变成乘法,再根据分式的乘法法则求出答案即可.【解答】解:(1)原式=32m−n −12m−n=3−12m−n=22m−n ;(2)原式=(a+2)(a−2)−5a−2÷−(a−3)2(a−2) =a 2−9a−2•2(a−2)−(a−3) =(a+3)(a−3)a−2•2(a−2)−(a−3)=﹣2(a +3)=﹣2a ﹣6.25.(2023秋•沂水县期末)化简:(1)x x−1+3x−11−x 2; (2)(2m m−1−m m+1)÷m m 2−1. 【分析】(1)先通分,再根据同分母分式相加法则求出答案即可;(2)先算括号内的减法,把除法变成乘法,再算乘法即可.【解答】解:(1)x x−1+3x−11−x 2 =x(x+1)(x+1)(x−1)−3x−1(x+1)(x−1)=x 2+x−3x+1(x+1)(x−1)=x 2−2x+1(x+1)(x−1)=(x−1)2(x+1)(x−1) =x−1x+1; (2)(2m m−1−m m+1)÷m m 2−1 =2m(m+1)−m(m−1)(m+1)(m−1)•(m+1)(m−1)m =m 2+3m (m+1)(m−1)•(m+1)(m−1)m =m(m+3)(m+1)(m−1)•(m+1)(m−1)m=m +3.26.(2023秋•天津期末)计算:(1)(﹣3xy )÷2y 23x •(y x)2; (2)(x x+y −2y x+y )÷x−2y xy •(1x +1y ). 【分析】(1)先算乘方,把除法变成乘法,最后根据分式的乘法法则求出答案即可;(2)先算括号内的加减,再把除法变成乘法,最后根据分式的乘法法则求出答案即可.【解答】解:(1)原式=(﹣3xy )÷2y 23x •y 2x 2 =(﹣3xy )•3x 2y 2•y 2x 2=−9y 2;(2)原式=x−2y x+y ÷x−2y xy •x+y xy=x−2y x+y •xy x−2y •x+y xy =1.27.(2023春•沙坪坝区校级月考)计算:(1)2y−x x−y +y y−x +x x−y ;(2)(x +1−8x−1)÷x 3−9x x 2−2x+1. 【分析】(1)先变形为同分母分式的加减运算,再根据法则计算即可;(2)先计算括号内分式的减法、将除式的分子、分母因式分解,继而将除法转化为乘法,然后约分即可.【解答】解:(1)原式=2y−x x−y −y x−y +x x−y =2y−x−y+x x−y=y x−y ;(2)原式=(x 2−1x−1−8x−1)÷x(x+3)(x−3)(x−1)2=(x+3)(x−3)x−1•(x−1)2x(x+3)(x−3)=x−1x .28.(2023秋•沙坪坝区校级期末)计算:(1)(a +b )2+a (a ﹣2b );(2)(1−x x+2)÷x 2−4x+4x 2−4. 【分析】(1)根据完全平方公式.单项式乘多项式可以解答本题;(2)先算括号内的减法,然后计算括号外的除法即可.【解答】解:(1)(a +b )2+a (a ﹣2b );=a 2+2ab +b 2+a 2﹣2ab=2a 2+b 2;(2)(1−x x+2)÷x 2−4x+4x 2−4=x+2−x x+2×(x+2)(x−2)(x−2)2 =2x−2. 29.(2023秋•荔湾区期末)计算: (1)a−1a−b −1+b b−a ;(2)(4−a 2a−1+a )÷a 2−16a−1. 【分析】(1)原式变形后,利用同分母分式的加法法则计算即可求出值;(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果.【解答】解:(1)原式=a−1a−b +1+b a−b=a+b a−b;(2)原式=4−a2+a2−aa−1•a−1(a+4)(a−4)=−a−4a−1•a−1 (a+4)(a−4)=−1a+4.30.(2023秋•永年区期末)上课时老师在黑板上书写了一个分式的正确化简结果,随后用手掌盖住了一部分,形式如下:•y2x2−xy−y2−x2x2−2xy+y2=xx−y(1)聪明的你请求出盖住部分化简后的结果;(2)当x=2时,y等于何值时,原分式的值为5.【分析】(1)根据被减数、减数、差及因数与积的关系,化简分式求出盖住的部分即可;(2)根据x=2时分式的值是5,得关于y的方程,求解即可.【解答】解:(1)∵(xx−y +y2−x2x2−2xy+y2)÷y2x2−xy=[xx−y +(y+x)(y−x)(x−y)2]×x(x−y)y2=−y x−y ×x(x−y)y2=−x y∴盖住部分化简后的结果为−x y;(2)∵x=2时,原分式的值为5,即22−y=5,∴10﹣5y=2解得y=8 5经检验,y=85是原方程的解.所以当x=2,y=85时,原分式的值为5.。
八年级尖子生数学辅导必备
(3)如图2,以ΔABC的边AB,AC为边,向三角形外作正方形ABDE及ACFG,连结CE,BG相交于O点,P是线段DE上任意一点.求证:四边形OBPE是勾股四边形.
综合以上∵0<15<16,0<9<16
∴当t=9(s)或t=15(s)时,以C,D,Q,P为顶点的梯形面积等于60cm2
(3)是否存在点P,使△PQD是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
解:由题可得0<t<16
做QM⊥BC,DN⊥BC
可得矩形ABMQ,ABND
∴BM=AQ=t;BN=AD=16;
x2=;
∴当x=时,△PQD是等腰三角形;
状态2:QD=PD
当QD=PD
C
QD²=PD²;
即(16-t)²=(16-2t)²+12²
该方程无解;
状态3:QP=QD
当QP=QD时
C
QP²=QD²;
即t²+12²=(16-t)²
256-32t-144=0
x=3.5;
∴当x=3.5时,△PQD是等腰三角形;
综合以上,当x=3.5或xC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=300,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是。
(1)当t=2时,求△APQ的面积;
(2)若四边形ABQP为平行四边形,求运动时间t;
八年级《数学》下册尖子生强化训练题及解析答案:二次根式(3套).docx

tj|r>全国重点高中提前招生考试八年级下学期同步强化训练卷(一)(二次根式的性质和化简专题测试)总分:120分时间:120分钟—、选择题(每小题5分,共30分)1.若代数式謬矗有意义,则a■的取值范围是()A. x<2020B. x<2020 且± 2019C. x<2020 且乂工2019D. x<2020 且乂工一2019(“希望杯”竞赛试题改编)2.若化简11 —X I —A/JC2-8x+16的结果为2乂一5,则x的取值范围是()A.才为任意实数B. l<x<4 D.3.把(a-b'Jb'a根号外的因式移到根号内的结果为()D. —V a—b(华中师大一附中招生试题)4.已知实数a、b满足A/(a— I)2 + V(a—6)2 = 10 — | b + 3 | — I b— 2 | ,则a2 ~\~lr的最大值为()A. 50B. 45C. 40D. 0(芜湖一中理科实验班自主招生试题)5.已知y = +』5 —2丁一3,则2.z-y 的值为()15A. —15B. 15C. —6.计算4 丿3+2 血一丿41+24© =()A. 72-1B. 1C.V2二、填空题(5分X6 = 30分)D. 2(全国初中联赛试题)7.如果实数u、b、c在数轴上的位置如图1-1所示.那么代数式-/^-\a+h\ + /G—万尹+“+c何化简为—b " 0 c图1-1(全国初中竞赛题)&若实数.r、y满足|j—4| + ^7=8=0,则以y的值为边长的等腰三角形的周长为_9. __________________________________________________________ 已知实数m满足丨2019—rn \ + Jm—2020=加,那么m— 2019?= __________________________ .(重庆市竞赛试题)11. _______________________________________________ 若工+y= J3 V5—JC—y= V3 42—75 •则xy= ____________________________________________________ ・(天津市竞赛试题)12.若77— = —2,则F的值为.77 十 --------(天津市竞赛试题)三、解答题13.(12分)若」^的整数部分是a.小数部分是儿求a2 + (l+V7)a6的值.3—7711.( 13分)(1)先化简再求值:才存缶一(1一与护),其中a = 2+尽b=2—胚(2)已知a、b、c为ZSABC 的三边,化简:丿(a+6+c)2 + 丿―严 + jQ>_a—cV15.(11分)已知正实数a』满足:a+O=l,1—专+茫+】_茫—茫=_4,求:华的值.1—Jb—Jci 1—76+Va Jb16.(12分)已知7^=石+*(0<0<1),求代数式F+JT—6 . JT+317.(12分)先阅读再化简求值.(1)在化简丿匸刀而的过程中,小王和小李的化简结果不一样:小王的化简过程如下:原式=A/2-2 /2X^+5 = 7(T2)2-2V2 - 75 + (75)2 =丿近二丽=施一岳.小李的化简过程如下:原式=V(-/2)2-2V2 • V5 + (V5)2 = 7(72-75)2 =^-V2.请判断谁的化简结果正确,并说明理由.⑵化简求值:已知乂=“6 —2腐,求(上+*) • 2乙二;)的值(结果保留根号).全国重点高中提前招生考试 八年级下学期同步强化训练卷(二)(二次根式的化简求值专题测试) 总分:120分时间:120分钟一、选择题(5分X6 = 30分)1 •计算 14 + 6 75 — 14 6 75 的值是() A. 1 B.75C. 2 75D. 5(全国初中竞赛试题)2.已知非零实数 a 、b 满足 I 2a —4 | + | b+2 I + J (a — 3)624- 4 = 2a ,则 a~\~h 等于()3.化简J1+古+(”,1)2("〉0或1)所得的结果为()tj|r>A. -1B.0C. 1D. 2A.H 1'1w+1C. 141 1n+1D. 1—丄—一*(武汉市选拔赛试题)4.已知 2x-3 /亦一2y=0(z>0),则;;二器2的值是(16 -25A-fD-27(太原市竞赛题)5•设Dr]表示最接近的整数QHx+0・ 5,77为整数),则[/TX2] + Ly2X3] + L 5/3X4] + - +E7iooxioi]的值为( )C.5150D.5151(“五羊杯”竞赛题)6. 已知,=好兀+ 石弓均为实数).则y 的最大值与最小值的差为( )A. 2^2-2B. 4-2 72C. 3—2©D. 2 V2-1二、填空题(5分X6 = 30分)7. 计算 72017X2018X2019X2020+1-20182 的结果是 ________________ .&已知 a= 72018- v /2017.Z>= 72019- 72018.c= 72020-^/硕©,则 a 、b 、c 三者的大小关 系为.(武汉市竞赛试题改编)9.若实数"』满足乂2+$2_滋_2》+5=0.则石+$ 的值是 ____________________ .V3^—2 77(“希望杯”竞赛试题)华土华】=华二理.则兰+上=V3-V2 V3+V2 y &(“希望杯”竞赛试题)A /5+2 A /6 V 7+4 V3(湖北省黄冈中学理科实验班预录试题)12. [a]表示不大于a 的最大整数,{a}=a —[a].设a =[帚+斤],6=•则^ + (1+77)ab= _________・(鄂州高中自主招生考试数学试题)三、解答题13. (12分)计算与求值.(1)已知°=宀,求护_20 + 1_绍渔土1的值.2+V3 aTa L~a(244-4)<44+4)<64+4)<8<+4-)(104+-7-)4 4 4 4 4(r+4)<34+4-)<54+4-X74+-r )(94+-r )4 4 4 44(湖北黄冈中学理科实验班预录试题)10.已知x= (2)计算:14. (12分)正数心满足,”+4厉-2扁-皿+4,尸3.求倉豐爲的值.(北京市竞赛题)⑵设⑴册'求"2"曲7 + 18「17的值.16. (12 分)设 x= — . y = jZEEElzb/E, 为何值吋.代数式 20才 + 41>ry + 20b 的值 Vi+ 1+7? Jt +l —Jt为 2001.(全国初中数学联赛试题)15. (12 分)(1)化简:用十4血+3匹松)(腐_______________ 117. (12 分)定义/(JC)=求/(l)+/(3)+/(5)H ----------------- 1-■Z?-FZr+T+ \/ x2— 1+ 步卡一2JC+1/(2怡一1)+/(999)的值.(上海市竞赛试题)5. 已知 J25—yi5-x 2=2,则丿25—F + J15—F 的值为(A. 3B. 4C. 5(山东省竞赛题)6-设$=/+*+寺+/+*+* + J1++++ +…+/+壽 +誌?,则与5最接近 的数是( )A.2017B. 2018C. 2019D. 2020二、填空题(5分X6=30分)7.若 u+b —2 Va —1~4 "―2 = 3 J c —3— c ——5,贝9 a+〃+e= _______________ .(武汉市竞赛题)9. _____________________________________________________________ 若的最大值是a,最小值是几则a 2+62的值为 _______________________________________________________ .(全国初中数学竞赛试题)10. 已知a= V7-1.则代数式3a 3 + 12a 2-6a-12的值为 ________________ .(全国初中数学联赛试题)全国重点高中提前招生考试 八年级下学期同步强化训练卷(三)(二次根式综合测试) 总分:120分时间:120分钟―、选择题(5分X6 = 30分)1.已知 7x 2-4 + 727+3^=0.则 乂一y 的值为( ) A. 2B. 6C. 2 或一22.计算(721-3)(73+ 710-77)的值等于( )A. 6^7B. -6V7C. 20 73 + 6^73. 已知/+丄=7(0VzVl ),则石一-的值为()D. 6 或一6D. 20 73-6/7B. —-75D.V5(天津市竞赛试题)4. 已知整数.r 、y 满足点+2心=丿丽,那么整数对(_r,y )的个数是(A. 0B. 1C. 2D. 3(江苏省竞赛题)D. 68-当―点时•化简牛严+今芋1的结果是11.非零实数满足(Z?+2019-J-)(+2019—y) =2019,则孟洛¥;=_(湖北省鄂州市自主招生试题改编)12.已知a、Z>为有理数分别表示5-V7的整数部分和小数部分,且a>nn+bn2 = l.则2a+b三、解答题13.(12分)化简:丿37+20站+丿37-20箱.14. (12分)先化简.再求值:(弄务 a — 1-宦,其中"=血一1・«2+4a+415.(12 分)若〃201172012-1,求m 5— 2m 4—201 lzn 3 的值. 求n 的值.16. (12 分)乂=为自然数,如果2乂2 + 197刊+2)2 = 1993成立,17. ( 12分)求和:S = J1+令+壬 + J1+贪+令 + J1+寺+壬 + J1+令+右 + …4 1224 102参考答案全国重点高中提前招生考试八年级下学期同步强化训练卷(一)(二次根式的性质和化简专题测试)(2020-Q0 (J <20201. B 提示:由条件可知:「 则:,, 故工£2020且;rH±2019.I 1^-1-2019^0, I |却工2019.2. B 提示:•・•丨 1—工| 一 J£ -8工+16= 11—工| 一 丿(乂一4严=11一工| 一 |工一41 •则丨1一却一"一4|=2工一5,I x —1^011—^| =乂一 1, — b —41 =x —4.因此即 1 £乂=4・4—4W0.3. C 提示:由条件可甸:乙」石>0,・°・b —a>0, ・°・a — b<0.故原式=—(5_0)丿方二 =_『(/>_* • =—Jb —a.故选 C.4. B 提示:化简得:\a — l| + |a — 6 | + 16+3 | + “一2 | =10,由绝对值的意义可知・lWa£6・一3Wb 《2,所以 a=6“= —3时.a 2+62有最大值且为45.(2x —5^0cc5. A 提示:由二次根式的非负性得: ・・・工=可,,=一3.故2Q=2X_yX(—3) = —15.【5—2心0, 2 26. B 提示:原式=4 7( 7FFT)2- 7(4 72+3)2 =4(72 + 1)-(4 72+3) = 1.7. —a 提示:由实数aJ )-c 在数轴上的位置口]知:XCaVOVc.且“|>c,所以/—la+引+ J (c —a)? + |b+c| =—(a+6)+ (c —a) —(6-Fc) = —a.I x —4=0.(jr=4 8. 20提示:由题意得:解得:(1)若4是腰长,则三角形三边长分别为4,4,8不能组成三角丨夕一8=0,b=&形.(2)若4是底边长,则腰长为8•能组成三角形,周长为4+8+8=20.9. 2020 提示:由条件可知加$2020,・・・2019—加V0,・•・原等式可化为加一2019+丿加—2020=加,/.丿加一2020 =2019. .\T ?7-2020=20192.故 w-20192 =2020.卡_2>05«r —4"…2_a5 z _ 1则有•r2=2*3,= 2.j?2+y = 2+22 =6.fMwo 5^—411. 用—血 提示:由Q+_y)2 —(彳―$)2=4才〃得:4才3;=(虫岛一血)_(丿17兀騎)'=3站—血一(3血—75)=4頁—4 42.故 _J2.12. —2472 提示:(石'— )2 = ( —2尸=4,即 x ---—2 = 4,乂 -- =6.・°・.才--+2 = 8,即-- )2 =&77 乂 •!•工 77J~r~\-- =2 5/2» /. J ~2— =(无+丄)■(右 -- )•(岛— )=—24 J2.77 工 工 丘 丘 呼.又 2<疗<3..・.5<3+疗<6....2<呼<3..“2.=呼-13. 解:•••占=?3=^7)=10. 6提示:因为y3+疗14.解:(1)原式=(g—b)ab(a~\~b—2ab = 2(cz—6)2a~b'2=^=^ ・・・・/ + (1+疗)肪=2'+(1+疗)><2><^^=4+(7一1) = 10.______ 2 _______ = _ _ =_V3 (2+ 站)一(2—站)_ 2侑_3'(2)由三角形三边关系可知:a-b-cV0,b —a — cV0,c —a —b<0,.・・ V(a-b~c)2 =b-\~c~a, VCb-a-c)2 =a+c~b. V(c-b~a)2=a-^b-c.:.原式= (a+b+c) + (b+c —a) + (a+(—") —(“+"—小=心・ 15.解:原式=(1—心+俾 +(1 一片皿 =_4.即2[(1—心严+(石)右=—4[(]—乔严_(岛旧,整理得: (1—V6)z —(Va)z6(1—0)2=2°,即 3(1—石)2=a ・由于 4+〃=1,・・・3(1—心)2 = 1—〃=(1一心)(1+心),整理得:(1一亦)(3— 376 — 1—76)=0,1—7^=0 或 2—476=0.当 1—心=0,即 6=1 时,a=0,不合题意.当 2 — 476 = 0,即 b=.1 丄11 a 十十〒 1 1a 2 H — +2 * =a 2 H — +2 =a 2 +2.a 2 丄1丄 1 a aa ~\ aa a17.解:(1)小李的化简正确.(2) g = V (>/5 — I )2 =4^— 1,原式=-7 = [—-- = 3 +岳 无—1 V5-1-1全国重点高中提前招生考试八年级下学期同步强化训练卷(二)(二次根式的化简求值专题测试)1. C 提示:原式=V(3+V5)2 — V (3—V5)2 = 3 +站一3 +站=275.2. C 提示:由题设可知"$3,所以题设等式可化为:2a — 4+|b + 2| + J (a —3)圧+4 = 2°,即|方十2| + J (a —3)// =0,・°・b+2 = 0 且(a —3)Z>2 =0,・°・a = 3,b= —2,・°・a+〃=l,故选 C.4. D 提示:由 2JT —3 V xy —2)=0(工〉0)得:2(V^)2 — 3 V xy —2(Vj^)2 =0, /. (2 (-Zr —2 ^/y) =0.*•*2 V7 IVy>0・・2/y = 0. /.V7=2/y. A.r=4^.故原式=(塔=普・ 5. B 提示:设 x 为正整数,考察积.r(j —Fl).Vj*2<Cx(jr +l) = (jr+0. 5)2—0. 25V(«r+0. 5)2».\x<Z A /JT (才+1) VLr+O. 5,・°・[5/工(无+1)]=不,故原式=1+2+3 +…+ 100=5050.故选 B.6. A 提7B :J /=4 + 2 J —(立一6;r+5) =4 + 2 -J —(工一3严+ 4,当工=3时,西大值=2返,当工=1或5时, »最小值=2 •所求值为2 42 — 2 ♦选A.7. 2017 提示:设工=2018,则原式=J (&—1).疋(工+1)(工+2) + 1_.z 2 = A /[(G •—1)(/+2)][工(工+1)] + 1—JT 2rs-4-丄I a+丄 +1 1 1 ca 1 a —— 1 2 1 Z 1 a 丄] a n ------ 1 a ----- a 3. C 提示:原式(1+T )2_f +(^+T7 (1+X )2_2X n±l._X_+ 册"l+十—治S>0或D •故选C.・°・原式=広=壬2+乂一 1 —工2 =乂—i=2oi8—1 = 2017,9. 3 + 2 V2 提示:由已知条件可知:(債•一2)' + (»—I 2) =0・•°・」=2・』=1.故原式=~ =—=V 3-2 72 V(72-l)2^^1 = 3+2 血.V2-110. 98 提示:乂 =冬土纟= 5 + 2 76» y =冬一李=5 — 2 用,.I 工 + y = 10,刊=1, /. — + ^-= 十必=V3-V2V3+V2,龙 对(工+孙―2 可=1O2 = 2X1 = ]OO _2=9&11.2—72*提7F: *.* J 5+2 庇=J («/^+返')?=胚~\~匝、A /7 + 4 胚=J (2+>/^)? =2+>/§".故原式= ~~ +V3+V2—=庇—41 + 2 —厄=2 —42,2+7312. 10 提示:a=2、b= 7?13. 解:(1)原式=° — 1 賈一 =a — l --.当 a = 2~4^时,代入得:a —1 — =2—后一1+2+府=3.a(a —1) a a(1X2+*)(2X3+4_)(3X4+¥)(4X5+-|-)・・・(9X1O+4~)(1OX11+-|') lOXll+与(2)原式= ---------- 台 ------- 台 -------- 台 -------- 台 ----------- f ----------------- 严一= ------ =(0XH-y)(lX2+y)(2X3+y)(3X4+y )M.(8X9+y)(9X10+y) OXl+y 221.此题用到公式”++ =(点+卡)2—沪=(〃2+卄*)(”2—卄今)=[心一i )+g_][讥卄])+*]. 14.解:原式变形为:(^frn + 2 Vn — 3)( Vm + 2石+ 1) = 0.・°・+ 2 石=3,・°・ _8_ = _A —§_斥+2 石+2002 3+20021_401-15-S?:<1'用+翁)爲+②+(用;為游:血厂用—反(2) *• a =~_-— = V 17 — 1,「•a +1 = -/17,•:/ +2a +1 = 17,故 a 2 -\~2a —16 = 0,・:原式=(a' 2d' — /I7 + 116a 3) — («3 -\~2a 2 — 16a) + (a 2 +2a —16) — l=a 3 (a? +2Q —16)—a(.a 2 +2a —16) + (/ +2a —16) — 1 = — 1.16. 解:巧/=1口+,=虹+2,于是 20K2+4Lry+20b=20Gr+y)2+Hy=20(4r+2)2+l = 2001,・・・4r+2=±10, t = 2或z =—3(舍去)・・°・£=2.17. 解:./ (.r) -^====q-^=r===^y===-____________________ ^TT — __________________________ C 敦卄1严 + »Cr+l)Cr —1)+ »Cr —1严](vCTl-8. a>b>c提不:*•* a =]72018+72017 ] .72019+72018^ 13(兀+亦扬;血 J(5)=兀;弭,…,/(999) = J •'/W. .・./(i)+f(3)-------------- ---------------------- /(999) = 全国重点高中提前招生考试八年级下学期同步强化训练卷(三)(二次根式综合测试)(无2—4:=0 (工^2 (—21.D提示:由条件可知:或故x~y=6或一6.(2工+夕=0, »=—4, »=4,2. A 提示:原式=箱(质+疗一箱)(站+ /10-V7)7T0 + (V7-V3)]E 710-(V7~V3)]=A/3[( 7T0)2-(V7-V3)2]=V3(10-10+2 721)=73X2 721 = 677,故选A.3. B 提示:(7^ )2 =工+ 2 = 5(0<«rVl),故=—A/5*.77 & 77严+4 屈=5 屈,(a,y) = (2・8)4. D 提示:质=5施・•・•- 3血+2屈=5血,・・・(工,歹)=(18・2)故(工*)的个数是3•故选D.V572+0=55/2 Cr,y)=(50・0),近寺丸^=2.故血乞+砖7=5.6.B 提示:•••V1+J+(5TP=1+V_^+i'AS=1+l_T+1+T_l+1+l_l+'"+1+2M7—金=2018—佥.故选B.提示:(Va— 1 — I)2 + ( Jb一2 — 2严+*( \/c—3—3)'=0.・°・a = 2・b=6,c=12. .•・a+Z>+c=20.提示:a = 2-A<0.原式=年书=仏二3—丄=1a—3 aka—1) a—3 a(a—1) a5.C 提示:••• E- (冒9-1 提示:由1 — Jr 0.且工0«x1,则"=*十2 一#+歩-卡=* + 27. 20a—3v 25—jc l + v 15—J?214.解:原式=[a —2a(a+2)1 . a — 4_a?—4—a?+aa+2 a (a+2)''.a+2_ ]a—4 a(.a—2) (72-1)(72-1+2)、/_Q严+寻・丁*<■!■< 1,・°・当尤=号时取最大值1 •故a = l;当/=*或取最小值g■,故b 42・2..23 =1■…E =百10.24 提示:原式=3Q(Q2+2a)+6疋一6a —12=Qa2 ~\~\2a—12 = 6X6—12 = 24.11.—1提示:由题意可知%=—』.12.y 提示:•••2</7V3・・・・一3V-V7V—2,・・・2V5—V7V3,S = 2" = 5—V7—2 = 3—V7,・・・aX2X(3—疗)+风3—疗)2 = 1,.・・4(6—2存)+久16 — 6疗)=1,・・・ 6«-2 V7a +166-6 41b= 1, A (6a+ 16Z>) - (2tz += _3_l (6a+16b=l a~~2o 166)77 = 1.根据等式两边对应系数相等,得:解得:2 ・・・2a+b=2X号一£ = 3 —l-(2a+6b)=0. . 1 2 21 _ 5~2~~2'13 .解:原式=725+20 V3 + 12 + 725-20 73 + 12 = 7(5+2 V3)2 + 丿(5—2 府严=5+2 膚+5—2 用=10.1L 5 ••20ll 2011 X ( •/20l2~\~ l) /ccr c I i •1/eel c • 2 c I i ccic15.M: . m= — = ----------- /,---- =』2012 + ]…加一1= J2012…亦一2加+] = 20]2,V2012 — 1( 72012)2-1m2—2m—2011=0. 原式=加3 (?w2—2m—2011) =0.16.解:x=(2n+l)-2 %AiG+l),_y=(2 卄1)+2 /?G+1),工+ y = 4n + 2,£y= 1,又2(工+ 3^ + 193工夕= 1993,得2(4w+2)24-193=1993,(4n+2)z=900,n>0,得宛=7.17.解:A“=Jl+* + d)2 = 1 + —^^2s=Ai +A2 +A3 H ------------------------- An, = (1+ ) + (1+ ) +9 9 9 9 9 9 9 9n-\~—----- )-1-…+O+ ---------- )= io+二 + --------- -- =1?—3 5 10 12 1 2 11 12 66°。
初二数学科尖子生辅导训练题

x《一次函数》测试题一、精心选一选1.下列各点中在函数y=x 21+3的图象上的是( ) (A)(3,-2) (B)(32,3) (C)(-4,1) (D)(5, 25)2.正比例函数y=kx ,当时k >0,下面结论正确的是( )A 、永远是正值B 、永远是负值C 、随着k 的增大而减小D 、随着k 的增大而增大 3.函数y=-11 x 中自变量的取值范围是( )A 、x ≠0B 、x <-1C 、x ≠-1D 、x >-14. 已知点(-4,y 1),(2,y 2)都在直线y=- 12 x+2上,则y 1 y 2大小关系是( )(A )y 1 > y 2 (B )y 1 = y 2 (C )y 1 < y 2 (D )不能比较 5.若一次函数y=(3+k)x+18-2k 2图象经过原点,则k 为( ) A 、3 B 、-2 C 、±3 D 、任何实数6.一根蜡烛长20cm ,点燃后每小时燃烧5cm ,燃烧时剩下的高度(cm)与燃烧时间(小时)的函数关系用图象表示为( )7.已知正比例函数y=kx(k ≠0)的函数值随x的增大而增大,则一次函数y=x+k 的图象大致是( )8.如图是一次函数y=kx+b 的图象,当x <1时,y 的取值范围是( )xAxBxCxDABxCxDxA 、y >0B 、y <0C 、-2 <y <0D 、-2 <y <2二、细心填一填9.若函数y= -2x m+2是正比例函数,则m 的值是 。
10.已知一次函数y=kx+5的图象经过点(-1,2),则k= 。
11.点P (a ,b )在第二象限,则直线y=ax+b 不经过第 象限。
12.已知一次函数y=kx-k+4的图象与y 轴的交点坐标是(0,-2),那么这个一次函数的表达式是______________。
13.一次函数y=kx+b 与y=2x+1平行,且经过点(-3,4),则表达式为: 。
全等三角形的判定(限时满分培优训练)-八年级数学上册尖子生培优必刷题(原卷版)【人教版】

【拔尖特训】2023-2024学年八年级数学上册尖子生培优必刷题(人教版)专题12.6全等三角形的判定(限时满分培优训练)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷满分100分,试题共23题,其中选择10道、填空6道、解答7道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2023春•洋县期末)如图,点B,F,C,E在一条直线上,∠B=∠E,BF=EC,添加下列一个条件,仍不能判断△ABC≌△DEF的是()A.AB=DE B.∠A=∠D C.AC=DF D.AC∥DF2.(2023春•新晃县期末)如图,PD⊥AB,PE⊥AC,垂足分别为D、E,且PD=PE,则△APD与△APE 全等的直接理由是()A.SSS B.AAS C.HL D.ASA3.(2023•凉山州)如图,点E、点F在BC上,BE=CF,∠B=∠C,添加一个条件,不能证明△ABF≌△DCE的是()A.∠A=∠D B.∠AFB=∠DEC C.AB=DC D.AF=DE4.(2023春•天桥区期末)如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是()A.SSS B.SAS C.AAS D.ASA5.(2023春•高碑店市校级月考)如图是嘉淇测量水池AB宽度的方案,下列说法不正确的是()A.△代表BC=CD B.□代表ACC.☆代表DM D.该方案的依据是SAS6.(2023春•兴宁市校级期末)小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是()A.1m B.1.6m C.1.8m D.1.4m7.(2023春•高碑店市校级月考)如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD,AC,BD交于点M,关于结论Ⅰ,Ⅱ,下列判断正确的是()结论Ⅰ:AC=BD;结论Ⅱ:∠CMD>∠CODA.Ⅰ对,Ⅱ错B.Ⅰ错,Ⅱ对C.1,Ⅱ都对D.Ⅰ,Ⅱ都错8.(2023春•达川区校级期末)如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是()A.DE=DF B.BD=FD C.∠1=∠2D.AB=AC9.(2023春•雅安期末)如图,EF=CF,BF=DF,则下列结论错误的是()A.△BEF≌△DCF B.△ABC≌△ADE C.AB=AD D.DC=AC10.(2023春•盐湖区期末)如图,在△ABC中,AD为中线,过点B作BE⊥AD于点E,过点C作CF⊥AD 于点F.在DA延长线上取一点G,连接GC,使∠G=∠BAD.下列结论中正确的个数为()①BE=CF;②AG=2DE;③S△ABD+S△CDF=S△GCF;④S△AGC=2S△BDE.A.1个B.2个C.3个D.4个二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上11.(2023•鹿城区校级开学)如图,AD∥BC,AD=BC,请你添加一个条件:,使△ADE≌△CBF.(写出一个条件即可)12.(2023•海淀区开学)如图,已知OB=OC,若以“SAS”为依据证明△AOB≌△DOC,还需要添加的条件是.13.(2022秋•启东市期末)如图,已知线段AB=20m,MA⊥AB于点A,MA=6m,射线BD⊥AB于B,P 点从B点向A运动,每秒走1m,Q点从B点向D运动,每秒走3m,P,Q同时从B出发,则出发秒后,在线段MA上有一点C,使△CAP与△PBQ全等.14.(2023春•渠县校级期末)如图,在△ABC中,∠C=90°,DE⊥AB于D,交AC于点E,若BC=BD,AC=6cm,BC=8cm,AB=10cm,则△ADE的周长是.15.(2023春•茂名期末)如图,在△ABC中,AD为BC边的中线,E为AD上一点,连接BE并延长交AC 于点F,若∠AEF=∠F AE,BE=4,EF=1.6,则CF的长为.16.(2022秋•柳州期末)如图,点A坐标为(﹣1,0),点B坐标为(0,2),若在y轴右侧有一点C使得△BOC与△BOA全等,则点C的坐标为.三、解答题(本大题共7小题,共52分.解答时应写出文字说明、证明过程或演算步骤)17.(2023•贵州模拟)如图,点D在BC上,∠ADB=∠B,∠BAD=∠CAE.(1)添加条件:(只需写出一个),使△ABC≌△ADE;(2)根据你添加的条件,写出证明过程.18.(2023•荔湾区一模)如图,在四边形ABCD中,AD∥BC,∠B=∠D,连接AC.求证:△ABC≌△CDA.19.(2023•工业园区校级模拟)如图,点C、D在线段AB上,且AC=BD,AE=BF,AE∥BF,连接CE、DE、CF、DF,求证CF=DE.20.(2023•衢江区三模)已知:如图,△ABC与△ADE的顶点A重合,BC=DE,∠C=∠E,∠B=∠D.求证:∠1=∠2.21.(2022秋•内乡县期末)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC 上,且AE=CF.(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30°,求∠ACF的度数.22.(2022秋•东营区校级期末)如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.(1)求证:△ABD≌△EDC;(2)若AB=2,BE=3,求CD的长.23.(2023春•丰城市期末)如图,做一个“U”字形框架P ABQ,其中AB=42cm,AP、BQ足够长,P A⊥AB,QB⊥AB,点M从点B出发,向点A运动,同时点N从点B出发,向点Q运动,点M、N运动的速度之比为3:4,当M、N两点运动到某一瞬间同时停止,此时在射线AP上取点C,使△ACM与△BMN 全等,求此时线段AC的长是多少?。
专题1.1全等图形-2022-2023学年八年级数学上册尖子生同步培优题典(原卷版)【苏科版】

2022-2023学年八年级数学上册尖子生同步培优题典【苏科版】专题1.1全等图形【名师点睛】(1)全等形的概念能够完全重合的两个图形叫做全等形.(2)全等三角形能够完全重合的两个三角形叫做全等三角形.(3)三角形全等的符号“全等”用符号“≌”表示.注意:在记两个三角形全等时,通常把对应顶点写在对应位置上.(4)对应顶点、对应边、对应角把两个全等三角形重合到一起,重合的顶点叫做对应顶点;重合的边叫做对应边;重合的角叫做对应角.【典例剖析】【知识点1】全等图形的识别【例1】(2021·江苏·淮安市洪泽实验中学八年级期中)下列各组的两个图形属于全等图形的是()A.B.C.D.【变式1.1】(2021·江苏连云港·八年级阶段练习)下列各组两个图形属于全等图形的是()A.B.C.D.【变式1.2】(2021·江苏盐城·八年级期中)下列说法正确的是()A.两个等边三角形一定是全等图形B.两个全等图形面积一定相等C.形状相同的两个图形一定全等D.两个正方形一定是全等图形【知识点2】利用全等图形求角度【例2】(2021·江苏·南京市第十二初级中学八年级期中)如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是______.【变式2.1】(2020·江苏省灌云高级中学城西分校八年级阶段练习)如图,由4个相同的小正方形组成的格点图中,∠1+∠2+∠3=________度.【变式2.2】(2021·江苏·沭阳县怀文中学八年级阶段练习)如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4=________.【知识点3】分割成几个全等图形【例3】(2020·江苏苏州·七年级期末)如图,用三种不同的方法沿网格线把正方形分割成4个全等的图形(三种方法得到的图形相互间不全等).【变式3.1】(2018·江苏·洪泽新区中学八年级阶段练习)如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.【满分训练】一.选择题(共10小题)1.(2021秋•靖西市期末)下列各组图形中,属于全等图形的是( )A.B.C.D.2.(2021秋•宿豫区期中)下列两个图形是全等图形的是( )A.两张同底版的照片B.周长相等的两个长方形C.面积相等的两个正方形D.面积相等的两个三角形3.(2021春•淮阳区期末)全等形是指两个图形( )A.大小相等B.可以完全重合C.形状相同D.以上都不对4.(2021春•姑苏区期末)下列说法正确的是( )A.两个等边三角形一定是全等图形B.两个全等图形面积一定相等C.形状相同的两个图形一定全等D.两个正方形一定是全等图形5.(2021春•商水县期末)下列说法不正确的是( )A.如果两个图形全等,那么它们的形状和大小一定相同B.面积相等的两个图形是全等图形C.图形全等,只与形状、大小有关,而与它们的位置无关D.全等三角形的对应边相等,对应角相等6.(2020春•天桥区期末)如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为( )A .45°B .60°C .90°D .100°7.(2019秋•临西县期末)下列图形中,和所给图全等的图形是( )A .B .C .D .8.(2020秋•涿鹿县期中)下列图形中与如图图形全等的是( )A .B .C .D .9.(2019秋•迁安市期末)小明学习了全等三角形后总结了以下结论:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等、对应角相等;③面积相等的两个三角形是全等图形;④全等三角形的周长相等.其中正确的结论个数是( )A .1B .2C .3D .410.(2018春•太原期末)下列说法:(1)全等图形的形状相同,大小相等;(2)全等三角形的对应边相等;(3)全等图形的周长相等,面积相等;(4)面积相等的两个三角形全等.其中正确的是( )A .( 1 )( 3)( 4 )B .( 2)( 3 )( 4 )C .( 1 )( 2 )( 3 )D .( 1 )( 2)( 3 )( 4 )11.(2021秋•雨花区期末)如图,四边形ABCD≌四边形A′B′C′D′,则∠A的大小是 .12.(2020春•石狮市期末)如图,四边形ABCD≌四边形A'B'C'D',则∠A的大小是 .13.(2021秋•常州期中)如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= .14.(2019秋•越城区期末)下列图形中全等图形是 (填标号).15.(2019秋•东台市月考)如图①,已知△ABC的六个元素,则图②中甲、乙、丙三个三角形中与图①中△ABC全等的图形是 .16.(2019秋•常州期中)下列4个图形中,属于全等的2个图形是 .(填序号)17.观察图中图形,它们是不是全等形?为什么?18.找出图中的全等图形.19.(2019秋•孝义市校级月考)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).20.沿着图中的虚线,请把如图的图形划分为4个全等图形,把你的方案画在图中.21.图中所示的是两个全等的五边形,AB=8,AE=5,DE=11,HI=12,IJ=10,∠C=90°,∠G=115°,点B与点H、点D与点J分别是对应顶点,指出它们之间其他的对应顶点、对应边与对应角,并说出图中标的a、b、c、d、e、α、β各字母所表示的值.22.(2018秋•洪泽区校级月考)如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.。
第12章 全等三角形 人教版八年级上册数学尖子生训练题(含答案)

第十二章《全等三角形》尖子生训练题满分:100分时间:90分钟一.选择题(每题3分,共30分)1.△ABC的三边AB,BC,CA的长分别为6cm,4cm,4cm,P为三条角平分线的交点,则△ABP,△BCP,△ACP的面积比等于()A.1:1:1 B.2:2:3 C.2:3:2 D.3:2:22.如图,DE⊥AC,BF⊥AC,垂足分别是E,F,且DE=BF,若利用“HL”证明△DEC≌△BFA,则需添加的条件是()A.EC=FA B.DC=BA C.∠D=∠B D.∠DCE=∠BAF 3.下列数据能唯一确定三角形的形状和大小的是()A.AB=4,BC=5,∠C=60°B.AB=6,∠C=60°,∠B=70°C.AB=4,BC=5,CA=10 D.∠C=60°,∠B=70°,∠A=50°4.如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是()A.SSS B.SAS C.ASA D.AAS5.如图所示,在下列条件中,不能判断△ABD≌△BAC的条件是()A.∠D=∠C,∠BAD=∠ABC B.∠BAD=∠ABC,∠ABD=∠BACC.BD=AC,∠BAD=∠ABC D.AD=BC,BD=AC6.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是()A.角的内部到角的两边的距离相等的点在角的平分线上B.角平分线上的点到这个角两边的距离相等C.三角形三条角平分线的交点到三条边的距离相等D.以上均不正确7.如图,已知:在△AFD和△CEB,点A、E、F、C在同一直线上,在给出的下列条件中,①AE=CF,②∠D=∠B,③AD=CB,④DF∥BE,选出三个条件可以证明△AFD≌△CEB的有()组.A.4 B.3 C.2 D.18.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤S△BDE :S△ACD=BD:AC,其中正确的个数为()A.5个B.4个C.3个D.2个9.如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有()A.一处B.两处C.三处D.四处10.如图,已知∠1=∠2,AC=AD,增加下列条件之一:①AB=AE;②BC=ED;③∠C =∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()A.1个B.2个C.3个D.4个二.填空题(每题4分,共20分)11.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,需添加一个条件是.(只需添加一个条件即可)12.在△ABC中,已知∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O,∠BOC的平分线交BC于F,则下列说法中正确的是.①∠BOE=60°,②∠ABD=∠ACE,③OE=OD④BC=BE+CD13.如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,若BD=5,BD:CD=5:3,AB=10,则△ABD的面积是.14.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.这种做法是利用了全等三角形对应角相等,图中判断三角形全等的依据是.15.如图,在△ABC中,AB=10,AC=5,AD是角平分线,CE是高,过点D作DF⊥AB,垂足为F,若DF=,则线段CE的长是.三.解答题(每题10分,共50分)16.如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.(1)求证:AE=CD;(2)求证:AE⊥CD;(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有(请写序号,少选、错选均不得分).17.如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.18.如图所示,在△ABE和△ACD中,给出以下4个论断:(1)AB=AC;(2)AD=AE;(3)BE=CD;(4)∠DAM=∠EAN.以其中3个论断为题设,填入下面的“已知”栏中,1个论断为结论,填入下面的“求证”栏中,使之组成一个正确的命题,并写出证明过程.已知:;求证:.19.如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)(1)运动秒时,AE=DC;(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;(3)若△ABD≌△DCE,∠BAC=α,则∠ADE=(用含α的式子表示).20.如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B (n,0),且|m﹣n﹣3|+=0,点P从A出发,以每秒1个单位的速度沿射线AO 匀速运动,设点P的运动时间为t秒.(1)求OA、OB的长;(2)连接PB,设△POB的面积为S,用t的式子表示S;(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.参考答案一.选择题1.解:∵P为三条角平分线的交点,∴点P到△ABC三边的距离相等,∵AB,BC,CA的长分别为6cm,4cm,4cm,∴△ABP,△BCP,△ACP的面积比=6:4:4=3:2:2.故选:D.2.解:∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°,∵DE=BF,∴当添加条件DC=BA时,可利用“HL”证明△DEC≌△BFA.故选:B.3.解:A、若已知AB、BC与∠B的大小,则根据SAS可判定其形状和大小,故本选项错误;B、有两个角的大小,也就相当于有了三角形的三个角,又有一边的长,所以根据AAS或ASA可确定三角形的大小和形状,故本选项正确.C、由于AB=4,BC=5,CA=10,所以AB+BC<10,三角形不存在,故本选项错误;D、有三个角的大小,但又没有边长,故其形状也不确定,故本选项错误.故选:B.4.解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.故选:C.5.解:A、符合AAS,能判断△ABD≌△BAC;B、符合ASA,能判断△ABD≌△BAC;C、不能判断△ABD≌△BAC;D、符合SSS,能判断△ABD≌△BAC.故选:C.6.解:(1)如图所示:过两把直尺的交点P作PE⊥AO,PF⊥BO,∵两把完全相同的长方形直尺,∴PE =PF ,∴OP 平分∠AOB (角的内部到角的两边的距离相等的点在这个角的平分线上), 故选:A .7.解:∵AE =CF ,∴AE +EF =CF +EF ,∴AF =CE ,∵DF ∥BE ,∴∠DFA =∠BEC ,∴若①②③为条件,不能证明△AFD ≌△CEB ,若①②④为条件,能证明△AFD ≌△CEB (AAS ),若①③④为条件,不能证明△AFD ≌△CEB ,若②③④为条件,能证明△AFD ≌△CEB (AAS ),故选:C .8.解:①正确,∵在△ABC 中,∠C =90°,AD 平分∠BAC ,DE ⊥AB 于E ,∴CD =ED ;②正确,因为由HL 可知△ADC ≌△ADE ,所以AC =AE ,即AC +BE =AB ;③正确,因为∠BDE 和∠BAC 都与∠B 互余,根据同角的补角相等,所以∠BDE =∠BAC ;④错误,因为∠B 的度数不确定,故BE 不一定等于DE ;⑤错误,因为CD =ED ,△ABD 和△ACD 的高相等,所以S △BDE :S △ACD =BE :AC . 故选:C .9.解:∵△ABC 内角平分线的交点到三角形三边的距离相等,∴△ABC 内角平分线的交点满足条件;如图:点P是△ABC两条外角平分线的交点,过点P作PE⊥AB,PD⊥BC,PF⊥AC,∴PE=PF,PF=PD,∴PE=PF=PD,∴点P到△ABC的三边的距离相等,∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;综上,到三条公路的距离相等的点有4个,∴可供选择的地址有4个.故选:D.10.解:∵∠1=∠2,∴∠CAB=∠DAE,∵AC=AD,∴当AB=AE时,可根据“SAS”判断△ABC≌△AED;当BC=ED时,不能判断△ABC≌△AED;当∠C=∠D时,可根据“ASA”判断△ABC≌△AED;当∠B=∠E时,可根据“AAS”判断△ABC≌△AED.故选:C.二.填空题(共5小题)11.解:当∠D=∠B时,在△ADF和△CBE中∵,∴△ADF≌△CBE(SAS),故答案为:∠D=∠B.(答案不唯一)12.解:①如图,∵∠A=60°,∴∠ABC+∠ACB=180°﹣60°=120°,∵BD、CE分别是∠ABC和∠BCA的平分线,∴∠OBC+∠OCB=×120°=60°,∴∠BOE=∠OBC+∠OCB=60°故①正确;②∵BD、CE分别是∠ABC和∠BCA的平分线,∴∠ABD=∠ABC,∠ACE=∠ACB,当AB=AC时,∠ABC=∠ACB,而已知AB和AC没有相等关系,故②不正确;③∵∠OBC+∠OCB=60°,∴∠BOC=120°,∵OF平分∠BOC,∴∠BOF=∠COF=60°,∴∠BOE=60°,∴∠BOE=∠BOF,在△BOE和△BOF中,∵,∴△BOE≌△BOF(ASA),∴OE=OF,同理得:△CDO≌△CFO,∴OD=OF,∴OD=OE,故③正确;④∵△BOE≌△BOF,△CDO≌△CFO,∴BF=BE,CF=CD,∴BC=CF+BF=BE+CD,故④正确;则下列说法中正确的是:①③④故答案为①③④.13.解:过D作DE⊥AB于E,∵AD平分∠BAC,∠C=90°,∴DE=DC,∵BD=5,BD:CD=5:3,∴CD=3,∵在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,∴DE=CD=3,∵AB=10,∴△ABD的面积是:AB•DE=×10×3=15.故答案为:15.14.解:由图可知,CM=CN,又OM=ON,∵在△MCO和△NCO中,∴△COM≌△CON(SSS),∴∠AOC=∠BOC,即OC是∠AOB的平分线.故答案为:SSS.15.解:∵AD是角平分线,∴===2,∵CE是高,DF⊥AB,∴DF⊥CE,∴==,∴CE=DF=×=4.故答案为4.三.解答题(共5小题)16.(1)证明:∵∠ABC =∠DBE ,∴∠ABC +∠CBE =∠DBE +∠CBE ,即∠ABE =∠CBD ,在△ABE 和△CBD 中,,∴△ABE ≌△CBD ,∴AE =CD .(2)∵△ABE ≌△CBD ,∴∠BAE =∠BCD ,∵∠NMC =180°﹣∠BCD ﹣∠CNM ,∠ABC =180°﹣∠BAE ﹣∠ANB , 又∠CNM =∠ANB ,∵∠ABC =90°,∴∠NMC =90°,∴AE ⊥CD .(3)结论:②理由:作BK ⊥AE 于K ,BJ ⊥CD 于J .∵△ABE ≌△CBD ,∴AE =CD ,S △ABE =S △CDB ,∴•AE •BK =•CD •BJ ,∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,∴BM平分∠AMD.不妨设①成立,则△CBM≌△EBM,则AB=BD,显然不可能,故①错误.故答案为②.17.证明:∵AB⊥BD,ED⊥BD,AC⊥CE,∴∠ACE=∠ABC=∠CDE=90°,∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,∴∠ACB=∠CED.在△ABC和△CDE中,,∴△ABC≌△CDE(ASA),∴AB=CD.18.解:已知:AB=AC,AD=AE,BE=CD.求证:∠DAM=∠EAN.证明:在△ADC和△AEB中,,∴△ADC≌△AEB(SSS),∴∠DAC=∠EAB,即∠DAM+∠BAC=∠EAN+∠BAC,则∠DAM=∠EAN.故答案为:AB=AC,AD=AE,BE=CD;∠DAM=∠EAN.19.解:(1)由题可得,BD=CE=2t,∴CD=12﹣2t,AE=8﹣2t,∴当AE=DC,时,8﹣2t=(12﹣2t),解得t=3,故答案为:3;(2)当△ABD≌△DCE成立时,AB=CD=8,∴12﹣2t=8,解得t=2,∴运动2秒时,△ABD≌△DCE能成立;(3)当△ABD≌△DCE时,∠CDE=∠BAD,又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,∴∠ADE=∠B,又∵∠BAC=α,AB=AC,∴∠ADE=∠B=(180°﹣α)=90°﹣α.故答案为:90°﹣α.20.解:(1)∵|m﹣n﹣3|+=0,且|m﹣n﹣3|≥0,≥0∴|m﹣n﹣3|==0,∴n=3,m=6,∴点A(0,6),点B(3,0).∴OA=6,OB=3;(2)连接PB,t秒后,AP=t,OP=|6﹣t|,∴S=OP•OB=|6﹣t|;(t≥0)(3)作出图形,∵∠OAB+∠OBA=90°,∠OAB+∠APD=90°,∠OPE=∠APD,∴∠OBA=∠OPE,∴只要OP=OB,即可求证△EOP≌△AOB,∴AP=AO﹣OP=3,或AP′=OA+OP′=9∴t=3或9.。
八年级《数学》下册尖子生强化训练题及解析答案:勾股定理及逆定理(2套).docx

全国重点高中提前招生考试八年级下学期同步强化训练卷(四)(勾股定理专题测试)总分:120分时间:120分钟―、选择题(5分X6 = 30分)1.设“、心是直角三角形的两直角边,若该三角形周长为6,斜边为2. 5,则ab的值为()A. 1. 5B. 2C. 2. 5D. 3 2.如图4-1,在四边形ABCD 中,ZB=135O,ZC=120°,AB=V6,BC=3-V3,CD=6,则AD边的长为()A. 6 V33.如图4-2,在直线/上依次摆放七个正方形.已知斜放置的三个正方形的面积分别为1,2,3.正放置的四个正方形的面积依次是S、S?、S3 S ,则S +2Sz + 2S:,+Si=()A. 5B. 4C. 6D. 164.如图4-3,在等腰RtAABC中,AC=BC.以斜边AB为一边作等边△ABD,使点C、D在AB 的同侧;再以CD为一边作等边使点C、E在AD的异侧.若AE=1,则CD的长为A. V3一15.如图4-4,在ZWBC中,AB=AC=4,P是BC上异于B、C的一点,则AP2+BP • PC的值是A. 16B. 20C. 25D. 306,如图4-5所示,长方体的长为15,宽为10.高为20,点B离点C的距离为5, 一只蚂蚁如果要沿着长方体的表面从点B爬到点A ,需要爬行的最短的距离是()A. 5 72TB. 25C. 10 75+5D. 35二、填空题7.如图4-6 .将长方形纸片ABCD折叠.使边DC落在对角线AC上,折痕为CE.且D点落在对角线D'处.若AB=3,AD=4.则ED的长为.8.如图4-7是一种“羊头”形图案。
其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②',…,依此类推.若正方形① 的边长为64 cm.则正方形⑦的边长为E DD'U图4-69.如图4-8, 一只小猫沿着斜立在墙角的木板往上爬,木板底端距离墙角0. 7 m,当小猫从木板底端爬到顶端时.木板底端向左滑动了 1. 3 m,木板顶端向下滑了0. 9 m,则小猫在木板上爬动了m.10.已知二角形相邻两边长分别为20 cm和30 cm,第三边上的高为10 cm,则此三角形的面积为cm2.11.勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了一枚以勾股图为背景的邮票(如图4-9(1)).所谓勾股图是指以直角三角形的三边为边向外作正方形构成的图形。
人教版八年级数学下册尖子生培优必刷题 专题16.4二次根式的计算大题提升训练(重难点培优30题)(

专题16.4二次根式的计算大题提升训练(重难点培优30题)班级:___________________ 姓名:_________________ 得分:_______________ 注意事项:本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一.解答题(共30小题)1.(2023秋•武侯区校级月考)计算:(1)√18÷√23×√43.(2)√48÷√3−√12×√12+√24.(3)(1+√5)(1−√5)+(1+√5)2.(4)√12+|√3−2|+(π﹣3.14)02√3−1. 2.(2023秋•黑山县期中)计算:(1)2√8+13√18−34√32; (2)(√48−4√18)﹣(3√13−2√0.5); (3)√50×√8√6×√3√2; (4)(√3+√2)(√3−√2)﹣(√5−1)2. 3.(2023春•藁城区校级月考)计算:(1)√54−(√23+2√12−√32);(2)−3√827÷√34×√27; (3)(3√2−2√6)×(−3√2−2√6);(4)(2√7+5√2)2−(2√7−5√2)2. 4.(2023秋•成华区校级月考)(1)(√5)2﹣|﹣2|−√273; (2)(√6−√3)×√12;(3)√48÷√3−√12×√12−√24;(4)(3+√5)(3−√5)﹣(√2−1)0+(−13)﹣2. 5.(2023秋•金水区校级月考)(1)√15+√60√3−3√5;(2)(√7−1)2−(√14−√2)(√14+√2);(3)(2√2+3)2011(2√2−3)2012−4√18−√(1−√2)2;(4)(2√5−√2)0+|2−√5|+(−1)2019−13×√45.6.(2023秋•北碚区校级月考)计算:(1)(√48+√20)−(√12−√5);(2)√20+√5(2+√5);(3)√48÷√3−2√15×√30+(2√2+√3)2;(4)(2−√3)2017(2+√3)2018−|−√3|−(−√2)0.7.(2023春•新宾县期中)计算:(1)√27−3√12+√48;(2)√75÷√15×√135;(3)(3√20−2√15)×√5; (4)(√6+√2)(√6−√2)+(√2−√3)2.8.(2023秋•驻马店期中)计算(1)(√6−√2)÷√2;(2)(√6−2√15)×√3−6√12;(3)√24+√216√6+5; (4)(√2−√3)2+(√3+2)×(√3−2). 9.计算:(1)(2√12−3√13)×√6(2)(√82−√25)(5√12−√5) (3)(2√5+3√2)(2√5−3√2) (4)(√3+√2+√5)(√3−√2−√5) 10.(2023秋•雁塔区校级期中)计算:(1)√8−3√12+|1−√2|;(2)(√6+2√27)×√3−√83;(3)√12×2√3√3−√488+(π﹣3.14)0; (4)(√5+2)2022(√5−2)2023.11.(2023秋•平南县期末)计算:(13)﹣2+(π﹣2022)0−√9+|2−√5|. (2)√24÷√112−√13×√12+√48. 12.(2023秋•福田区期末)计算:(1)√12−√27√3−(π﹣3)0; (2)√2×√3+3√23−√54.13.计算. (1)2√18−√50+12√32; (2)(√12+√3)×√6−2√12. 14.(2023秋•海淀区校级期末)计算:(1)√18−√32+√12×√6;(2)|√3−4|+2﹣1+(2023﹣π)0. 15.(2023秋•绥化期末)计算: (1)(√3+√2)(√3−√2);(2)2√12−2√3+12√3.16.(2023秋•淮阴区期末)化简:(1)√6×12×18;(2)(2√3−5√2)(2√3+5√2); (3)√27−2√3+√45;(4)(2√12−3√13)×√6. 17.(2023秋•中山区期末)计算:(1)2√12−6√13+3√48;(2)(√3+3)(√3−2). 18.(2023秋•万源市校级月考)(1)(12)−2+√8−√12;(2)(√3−√2)2−(√3+√2)(√3−√2). 19.(2023秋•龙岗区校级期末)计算 (1)√18−√72+√50;(2)(2√3−1)2+(√3+2)(√3−2).20.(2023秋•铁岭期中)计算.(1)√8+3√2−√18(2)(√10+3)(√10−3)﹣221.(2023秋•芦溪县期中)计算:(1)(2−√3)(√3+2).(2)(√5)2+√(−3)2−(﹣2022)0+(13)﹣1. 22.(2023秋•方城县月考)计算:(1)√(−3)2×(﹣1)2018+√8×√12−|2−√6|;(2)4√2(√18−√6)−√48÷√3+(√3+1)2.23.(2023秋•城阳区期末)计算 (1)2√2×√6√3−√12×√3;(2)√40−5√110+√10.24.(2023秋•青岛期末)(1)计算:√20−√15;(2)计算:(2√3+√2)(2√3−√2)﹣10.25.(2023秋•即墨区期末)计算(1)√27+√12√3−√6×√3√2; (2)(√3−2)2﹣(√2+1)(√2−1).26.(2023秋•高新区校级月考)计算:(1)√16÷√2−√13×√6;(2)32√4x +2√x 9−x √1x +4√x 4. 27.(2023秋•成县期中)(1)√48−6√13+(√3+2)(√3−2);(2)(6√2−4√6)÷2√6+(√6−2)0.28.(2023秋•碑林区校级月考)计算:(1)√8+√18√2; (2)√3−(2−√3)(√3+2).29.(2023秋•沙坪坝区校级月考)计算: (1)3√3+√8−√2−√27;(2)√48÷√3−√12×√12+√24. 30.(2023春•靖江市月考)计算:(1)√27−√12+√32; (2)(√48−√75)×√113; (3)√18−√92−√3+√6√3+(√3−2)0+√(1−√2)2.专题16.4二次根式的计算大题提升训练(重难点培优30题)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一.解答题(共30小题)1.(2023秋•武侯区校级月考)计算:(1)√18÷√23×√43.(2)√48÷√3−√12×√12+√24.(3)(1+√5)(1−√5)+(1+√5)2.(4)√12+|√3−2|+(π﹣3.14)0√3−1.【分析】(1)利用二次根式的乘除法则运算;(2)利用二次根式的乘除法则运算,然后化简后合并即可;(3)利用平方差公式和完全平方公式计算;(4)先根据绝对值、零指数幂的意义进行计算,然后分母有理化后合并即可.【解答】解:(1)原式=√18×32×43=6;(2)原式=√48÷3−√12×12+2√6=4−√6+2√6=4+√6;(3)原式=1﹣5+1+2√5+5=2+2√5;(4)原式=2√3+2−√3+1﹣(√3+1)=2√3+2−√3+1−√3−1=2.2.(2023秋•黑山县期中)计算:(1)2√8+13√18−34√32;(2)(√48−4√18)﹣(3√13−2√0.5);(3)√50×√8√6×√3√2;(4)(√3+√2)(√3−√2)﹣(√5−1)2.【分析】(1)直接化简二次根式,再利用二次根式的混合运算法则计算得出答案;(2)直接化简二次根式,再利用二次根式的加减运算法则计算得出答案;(3)直接化简二次根式,再利用二次根式的混合运算法则计算得出答案;(4)直接利用乘法公式化简,再计算得出答案.【解答】解:(1)原式=2×2√2+13×3√2−34×4√2=4√2+√2−3√2=2√2;(2)原式=(4√3−4×√24)﹣(3×√33−2×√22)=4√3−√2−√3+√2=3√3;(3)原式=5√2×2√2√2√2=10×2﹣3=17;(4)原式=3﹣2﹣(5+1﹣2√5)=3﹣2﹣6+2√5=﹣5+2√5.3.(2023春•藁城区校级月考)计算:(1)√54−(√23+2√12−√32);(2)−3√827÷√34×√27;(3)(3√2−2√6)×(−3√2−2√6);(4)(2√7+5√2)2−(2√7−5√2)2.【分析】(1)先将原式中的二次根式化为最简二次根式,再去括号合并即可得到结果;(2)原式根据二次根式的乘除运算法则即可得到结果;(3)原式根据平方差公式计算即可得到结果;(4)原式先根据完全平方公式计算,再去括号、合并即可得到结果.【解答】解:(1)原式=3√6−(√63+2×√22−4√2)=3√6−√63−√2+4√2 =8√63+3√2;(2)原式=−3×√827×43×27 =−3×4√63=−4√6;(3)原式=(−2√6)2−(3√2)2=24﹣18=6;(4)原式=28+20√14+50−(28−20√14+50)=28+20√14+50﹣28+20√14−50=40√14.4.(2023秋•成华区校级月考)(1)(√5)2﹣|﹣2|−√273; (2)(√6−√3)×√12;(3)√48÷√3−√12×√12−√24;(4)(3+√5)(3−√5)﹣(√2−1)0+(−13)﹣2. 【分析】(1)利用二次根式的性质、绝对值的意义和立方根的定义计算;(2)先把√12化简,然后根据二次根式的乘法法则运算;(3)根据二次根式的乘除法则运算;(4)利用平方差公式、零指数幂和负整数指数幂的意义计算.【解答】解:(1)原式=5﹣2﹣3=0;(2)原式=(√6−√3)×2√3=6√2−6;(3)原式=√48÷3−√12×12−2√6=4−√6−2√6=4﹣3√6;(4)原式=9﹣5﹣1+9=12.5.(2023秋•金水区校级月考)(1)√15+√60√3−3√5;(3)(2√2+3)2011(2√2−3)2012−4√18−√(1−√2)2;(4)(2√5−√2)0+|2−√5|+(−1)2019−13×√45.【分析】(1)先进行二次根式的除法运算.然后把二次根式化为最简二次根式后合并即可;(2)利用平方差公式和完全平方公式计算;(3)先利用积的乘方和二次根式的性质得到原式=[(2√2−3)(2√2+3)]2011•(2√2−3)−√2+1−√2,然后利用平方差公式计算;(4)利用零指数幂的意义、绝对值的意义和乘方的意义计算.【解答】解:(1)原式=√153+√603−3√5=√5+2√5−3√5=0;(2)原式=7﹣2√7+1﹣(14﹣2)=8﹣2√7−12=﹣4﹣2√7;(3)原式=[(2√2+3)(2√2−3)]2011•(2√2−3)−√2+1−√2=(8﹣9)]2011•(2√2−3)−√2+1−√2=﹣2√2+3−√2+1−√2=﹣4√2+4;(4)原式=1+√5−2﹣1−√5=﹣2.6.(2023秋•北碚区校级月考)计算:(1)(√48+√20)−(√12−√5);(2)√20+√5(2+√5);(3)√48÷√3−2√15×√30+(2√2+√3)2;(4)(2−√3)2017(2+√3)2018−|−√3|−(−√2)0.【分析】(1)先化简各个根式,再进行二次根式的加减运算即可;(2)利用二次根式的性质以及二次根式的乘法和加法运算法则求解即可;(3)利用二次根式的性质和二次根式的混合运算法则求解即可;(4)利用积的乘方的逆运算、平方差公式、绝对值、零指数幂、有理数的乘方的运算法则计算即可.=4√3+2√5−2√3+√5 =2√3+3√5;(2)√20+√5(2+√5) =2√5+2√5+√5×√5 =4√5+5;(3)√48÷√3−2√15×√30+(2√2+√3)2=√48÷3−2√15×30+(2√2)2+2×2√2×√3+(√3)2 =√16−2√6+8+4√6+3=15+2√6;(4)(2−√3)2017(2+√3)2018−|−√3|−(−√2)0=[(2−√3)(2+√3)]2017(2+√3)−√3−1=(4−3)2017(2+√3)−√3−1=1.7.(2023春•新宾县期中)计算:(1)√27−3√12+√48;(2)√75÷√15×√13 5;(3)(3√20−2√15)×√5;(4)(√6+√2)(√6−√2)+(√2−√3)2.【分析】(1)根据二次根式的加减运算法则即可求出答案.(2)根据二次根式的乘除运算法则即可求出答案.(3)根据乘法分配律即可取出答案.(4)根据平方差公式以及完全平方公式即可求出答案.【解答】解:(1)原式=3√3−6√3+4√3=√3.(2)原式=√5×√8 5=√8=2√2.(3)原式=3×√20×√5−2×√15×√5=3×10﹣2=30﹣2=28.(4)原式=6﹣2+(2﹣2√6+3)=4+5﹣2√6=9﹣2√6.8.(2023秋•驻马店期中)计算(1)(√6−√2)÷√2;(2)(√6−2√15)×√3−6√12;(3)√24+√216√6+5; (4)(√2−√3)2+(√3+2)×(√3−2).【分析】(1)可利用多项式除以单项式法则计算,亦可通过分母有理化求解;(2)利用乘法的分配律计算(√6−2√15)×√3,利用分数的性质和二次根式的性质化简6√12;(3)可利用多项式除以单项式法则计算,亦可通过分母有理化求解;(4)先利用完全平方公式、平方差公式,再求和.【解答】解:(1)(√6−√2)÷√2=√6÷√2−√2÷√2=√3−1;(2)(√6−2√15)×√3−6√12=√6×√3−2√15×√3−6√1×22×2=√18−2√45−6√24=3√2−6√5−3√2=6√5;(3)√24+√216√6+5 =(√24÷√6+√216÷√6)+5=(√4+√36)+5=2+6+5 =13; (4)(√2−√3)2+(√3+2)×(√3−2)=(√2)2﹣2×√2×√3+(√3)2+(√3)2﹣22=2﹣2√6+3+3﹣4=4﹣2√6.9.计算:(1)(2√12−3√13)×√6(2)(√82−√25)(5√12−√5) (3)(2√5+3√2)(2√5−3√2)(4)(√3+√2+√5)(√3−√2−√5)【分析】(1)先用乘法的分配律进行计算,再合并同类二次根式;(2)先化简括号内各个根式,再进行二次根式乘法运算去括号计算便可;(3)运用平方差公式进行简便运算;(4)运用平方差和完全平方公式进行计算.【解答】解:(1)原式=4√3×√6−√3×√6 =12√2−3√2=−√2;(2)原式=(√2−15√10)(52√2−15√5)=5−15√10−√5+15√2;(3)原式=(2√5)2−(3√2)2=20−18=2;(4)原式=[√3+(√2+√5)][√3−(√2+√5)]=3−(√2+√5)2=3−(2+2√10+5)=−4−2√10.10.(2023秋•雁塔区校级期中)计算:(1)√8−3√12+|1−√2|;(2)(√6+2√27)×√3−√83;(3)√12×2√3√3−√488+(π﹣3.14)0; (4)(√5+2)2022(√5−2)2023.【分析】(1)先化简各式,然后再进行计算即可解答;(2)先计算二次根式的乘法,再算加减,即可解答;(3)先计算二次根式的乘除法,再算加减,即可解答;(4)利用幂的乘方与积的乘方的运算法则,进行计算即可解答.【解答】解:(1)√8−3√12+|1−√2|=2√2−32√2+√2−1 =32√2−1;(2)(√6+2√27)×√3−√83=√18+2√81−2=3√2+18﹣2=3√2+16;(3)√12×2√3√3−√488+(π﹣3.14)0 =2√12−4√38+1=4√3−12√3+1=72√3+1;(4)(√5+2)2022(√5−2)2023=(√5+2)2022(√5−2)2022×(√5−2)=[(√5+2)(√5−2)]2022×(√5−2)=(5﹣4)2022×(√5−2)=12022×(√5−2)=1×(√5−2)=√5−2.11.(2023秋•平南县期末)计算:(13)﹣2+(π﹣2022)0−√9+|2−√5|. (2)√24÷√112−√13×√12+√48.【分析】(1)先计算负整数指数幂、零指数幂、算术平方根和绝对值,再计算加减法即可得到结果.(2)先算乘除法,再将二次根式化为最简二次根式,最后算加减法即可得到结果.【解答】(1)解:原式=9+1−3+(√5−2)=5+√5. (2)解:原式=√24×23−√13×12+4√3=4−2+4√3=2+4√3.12.(2023秋•福田区期末)计算:(1)√12−√27√3−(π﹣3)0; (2)√2×√3+3√23−√54.【分析】(1)直接利用二次根式的性质化简、零指数幂的性质化简,进而计算得出答案;(2)直接利用二次根式的性质、二次根式的乘法运算法则化简,进而得出答案.【解答】解:(1)原式=√3−3√3√31 =√3√3−1 =﹣1﹣1=﹣2;(2)原式=√6+3×√63−3√6 =√6+√6−3√6=−√6.13.计算. (1)2√18−√50+12√32; (2)(√12+√3)×√6−2√12.【分析】(1)先化简,然后合并同类二次根式即可;(2)根据乘法分配律先去掉括号,然后化简,再合并同类二次根式即可.【解答】解:(1)2√18−√50+12√32=6√2−5√2+2√2=3√2; (2)(√12+√3)×√6−2√12=√72+√18−√2=6√2+3√2−√2=8√2. 14.(2023秋•海淀区校级期末)计算:(1)√18−√32+√12×√6;(2)|√3−4|+2﹣1+(2023﹣π)0. 【分析】(1)先算乘法,再合并同类二次根式即可;(2)先根据绝对值、负整数指数幂、零指数幂的意义化简,再进行加减运算即可.【解答】解:(1)√18−√32+√12×√6=3√2−4√2+6√2=5√2;(2)|√3−4|+2﹣1+(2023﹣π)0=4−√3+12+1=112−√3.15.(2023秋•绥化期末)计算:(1)(√3+√2)(√3−√2);(2)2√12−2√3+12√3.【分析】(1)利用平方差公式进行运算较简便;(2)先化简,再进行加减运算即可.【解答】解:(1)(√3+√2)(√3−√2)=(√3)2−(√2)2=3﹣2=1;(2)2√12−2√3+12√3=2×2√3−2√3+12√3=4√3−2√3+12√3=14√3.16.(2023秋•淮阴区期末)化简:(1)√6×12×18;(2)(2√3−5√2)(2√3+5√2);(3)√27−2√3+√45;(4)(2√12−3√13)×√6.【分析】(1)利用二次根式的乘法法则和二次根式的性质进行;(2)利用平方差公式计算;(3)先把各二次根式化为最简二次根式,然后合并即可;(4)先把各二次根式化为最简二次根式,再把括号内合并,然后进行二次根式的乘法运算.【解答】解:(1)原式=√6×6×2×18=√36×36=36;(2)原式=(2√3)2﹣(5√2)2=12﹣50=﹣38;(3)原式=3√3−2√3+3√5=√3+3√5;(4)原式=(4√3−√3)×√6=3√3×√6=3×3√2=9√2.17.(2023秋•中山区期末)计算:(1)2√12−6√13+3√48;(2)(√3+3)(√3−2).【分析】(1)直接利用二次根式的性质化简,进而计算得出答案;(2)直接利用二次根式的乘法运算法则计算得出答案.【解答】解:(1)原式=2×2√3−6×√33+3×4√3=4√3−2√3+12√3=14√3;(2)原式=3﹣2√3+3√3−6 =√3−3.18.(2023秋•万源市校级月考)(1)(12)−2+√8−√12;(2)(√3−√2)2−(√3+√2)(√3−√2).【分析】(1)先算负整数指数幂,二次根式的化简,再算加减即可;(2)利用完全平方公式及平方差公式进行运算,再进行二次根式的加减运算即可.【解答】解:(1)(12)−2+√8−√12=4+2√2−√2 2=4+3√2 2;(2)(√3−√2)2−(√3+√2)(√3−√2)=3﹣2√6+2﹣(3﹣2)=3﹣2√6+2﹣1=4﹣2√6.19.(2023秋•龙岗区校级期末)计算(1)√18−√72+√50;(2)(2√3−1)2+(√3+2)(√3−2).【分析】(1)先化简,然后合并同类二次根式即可;(2)根据完全平方公式和平方差公式将题目中的式子展开,然后合并同类项和同类二次根式即可.【解答】解:(1)√18−√72+√50=3√2−6√2+5√2=2√2;(2)(2√3−1)2+(√3+2)(√3−2)=12﹣4√3+1+3﹣4=12﹣4√3.20.(2023秋•铁岭期中)计算.(1)√8+3√2−√18(2)(√10+3)(√10−3)﹣2【分析】(1)先将原式中的二次根式化为最简二次根式,再根据二次根式的加减运算法则计算即可得到结果;(2)原式先利用平方差公式计算,再根据有理数的加减运算法则计算即可得到结果.【解答】解:(1)原式=2√2+3√2−3√2=2√2;(2)原式=(√10)2−32−2=10﹣9﹣2=﹣1.21.(2023秋•芦溪县期中)计算:(1)(2−√3)(√3+2).(2)(√5)2+√(−3)2−(﹣2022)0+(13)﹣1. 【分析】(1)利用平方差公式计算;(2)先根据二次根式的性质、零指数幂和负整数指数幂的意义计算,然后计算有理数的加减运算.【解答】解:(1)原式=22﹣(√3)2=4﹣3=1;(2)原式=5+3﹣1+3=10.22.(2023秋•方城县月考)计算:(1)√(−3)2×(﹣1)2018+√8×√12−|2−√6|; (2)4√2(√18−√6)−√48÷√3+(√3+1)2.【分析】(1)先利用二次根式的性质和二次根式的乘法法则运算,然后去绝对值后合并即可;(2)先根据二次根式的乘法法则和完全平方公式计算,然后合并即可.【解答】解:(1)√(−3)2×(﹣1)2018+√8×√12−|2−√6|=3×1+2√2×2√3−(√6−2)=3+4√6−√6+2=5+3√6; (2)4√2(√18−√6)−√48÷√3+(√3+1)2=4√2×18−4√2×√6−4√3÷√3+3+1+2√3=2﹣8√3−4+4+2√3=2﹣6√3.23.(2023秋•城阳区期末)计算(1)2√2×√6√3−√12×√3;(2)√40−5√110+√10.【分析】(1)直接利用二次根式的乘除运算法则化简,进而得出答案;(2)直接利用二次根式的性质化简,进而得出答案.【解答】解:(1)原式=2√2×√2−2√3×√3=2×2﹣2×3=4﹣6=﹣2;(2)原式=2√10−5×√1010+√10=52√10.24.(2023秋•青岛期末)(1)计算:√20−√15;(2)计算:(2√3+√2)(2√3−√2)﹣10.【分析】(1)直接化简二次根式,进而计算得出答案;(2)直接利用平方差公式化简,进而得出答案.【解答】解:(1)原式=2√5−√55=9√55;(2)原式=(2√3)2﹣(√2)2﹣10=12﹣2﹣10=0.25.(2023秋•即墨区期末)计算(1)√27+√12√3−√6×√3√2; (2)(√3−2)2﹣(√2+1)(√2−1).【分析】(1)先化简,然后合并同类二次根式即可; (2)先根据完全平方公式和平方差公式将题目中的式子展开,然后合并同类项即可.【解答】解:(1)√27+√12√3−√6×√3√2 =√3+2√3√3√18√2 =√3√3−√9 =5﹣3 =2;(2)(√3−2)2﹣(√2+1)(√2−1)=3﹣4√3+4﹣(2﹣1)=3﹣4√3+4﹣1=6﹣4√3. 26.(2023秋•高新区校级月考)计算:(1)√16÷√2−√13×√6; (2)32√4x +2√x 9−x √1x +4√x4. 【分析】(1)先算乘除,再合并同类二次根式;(2)先化简,再合并同类二次根式.【解答】解:(1)原式=√16÷2−√13×6=2√2−√2=√2;(2)原式=3√x +23√x −√x +2√x =143√x .27.(2023秋•成县期中)(1)√48−6√13+(√3+2)(√3−2);(2)(6√2−4√6)÷2√6+(√6−2)0.【分析】(1)直接化简二次根式,再利用平方差公式计算,进而得出答案;(2)直接利用二次根式的除法运算法则以及零指数幂的性质分别化简,进而得出答案.【解答】解:(1)原式=4√3−6×√33+3﹣4 =4√3−2√3+3﹣4=2√3−1;(2)原式=6√2÷2√6−4√6÷2√6+1=√3−2+1=√3−1.28.(2023秋•碑林区校级月考)计算:(1)√8+√18√2; (2)√3−(2−√3)(√3+2).【分析】(1)先根据二次根式性质进行化简,然后根据二次根式除法运算法则进行计算即可; (2)根据二次根式混合运算法则进行计算即可.【解答】解:(1)√8+√18√2 =√2+3√2√2 =√2√2=5; (2)√3−(2−√3)(√3+2)=√3−[22−(√3)2]=√3−(4−3)=√3−1.29.(2023秋•沙坪坝区校级月考)计算:(1)3√3+√8−√2−√27;(2)√48÷√3−√12×√12+√24.【分析】(1)根据二次根式的化简,加减法即可求解;(2)化简二次根式,根据二次根式的乘除法,加减法即可求解.【解答】解:(1)3√3+√8−√2−√27=3√3+2√2−√2−3√3=3√3−3√3+(2√2−√2)=√2.(2)√48÷√3−√12×√12+√24=√48÷3−√12×12+2√6=√16−√6+2√6==4+√6.30.(2023春•靖江市月考)计算:(1)√27−√12+√32;(2)(√48−√75)×√11 3;(3)√18−√92√3+√6√3+(√3−2)0+√(1−√2)2.【分析】(1)直接化简二次根式,进而合并得出答案;(2)直接化简二次根式,再合并,利用二次根式的乘法运算法则计算得出答案;(3)直接化简二次根式,结合零指数幂的性质以及二次根式的除法运算法则化简,进而合并得出答案.【解答】解:(1)原式=3√3−2√3+4√2=√3+4√2;(2)原式=(4√3−5√3)×√4 3=−√3×√43 =−√3×43=−√4=﹣2;(3)原式=3√2−3√22−(1+√2)+1+√2−1=3√2−3√22−1−√2+1+√2−1=3√22−1.。
八年级上册数学试卷尖子生

一、选择题(每题5分,共25分)1. 下列各数中,不是有理数的是()A. 2.5B. -3C. √9D. π2. 若a、b是方程x^2 - 4x + 3 = 0的两个根,则a + b的值是()A. 1B. 2C. 3D. 43. 下列函数中,自变量x的取值范围正确的是()A. y = √(x - 1)B. y = √(x^2 - 1)C. y = √(1 - x^2)D. y = √(x + 1)4. 在直角坐标系中,点P(2, -3)关于y轴的对称点坐标是()A. (2, 3)B. (-2, 3)C. (-2, -3)D. (2, -3)5. 若a、b是方程2x^2 - 5x + 2 = 0的两个根,则a^2 + b^2的值是()A. 5B. 10C. 15D. 20二、填空题(每题5分,共25分)6. 已知x^2 - 3x + 2 = 0,则x的值为______。
7. 若a、b是方程ax^2 + bx + c = 0的两个根,且a + b = 0,则方程的解为______。
8. 函数y = 2x - 1的图像是______。
9. 在直角坐标系中,点A(1, 2)关于原点的对称点坐标是______。
10. 若m、n是方程m^2 - 2m - 3 = 0的两个根,则m^2 + n^2的值是______。
三、解答题(每题15分,共45分)11. (15分)解下列方程:(1)2x^2 - 5x + 2 = 0;(2)√(x + 1) - √(x - 1) = 2。
12. (15分)已知函数y = kx + b的图像经过点A(2, 3)和点B(-1, 0),求函数的表达式。
13. (15分)在直角坐标系中,点P(a, b)在直线y = x上,且a + b = 3,求点P的坐标。
四、附加题(共10分)14. (5分)已知函数y = -2x + 1的图像与x轴、y轴分别交于点A、B,求三角形AOB的面积。
初二数学尖子班练习题

初二数学尖子班练习题第一节:代数与函数1. 解方程:已知方程 3x + 5 = 20,求解 x 的值。
解:由题意可列方程:3x + 5 = 20移项得:3x = 20 - 53x = 15化简得:x = 15 ÷ 3x = 5所以,方程的解为 x = 5。
2. 计算函数值:已知函数 f(x) = 2x² + 5x - 3,求当 x = 2 时 f(x) 的值。
解:将 x = 2 代入函数 f(x),得:f(2) = 2(2)² + 5(2) - 3= 2(4) + 10 - 3= 8 + 10 - 3= 18所以,当 x = 2 时,f(x) 的值为 18。
第二节:几何与图形1. 求三角形面积:已知三角形 ABC,其中 AB = 4cm,AC = 6cm,且∠BAC = 60°,求三角形 ABC 的面积。
解:首先,根据正弦定理可以求得∠ABC 和∠ACB 的值:∠ABC = arcsin(AB × sin(∠BAC) ÷ AC)= arcsin(4 × sin(60°) ÷ 6)≈ arcsin(0.866)≈ 60°∠ACB = 180° - ∠BAC - ∠ABC= 180° - 60° - 60°= 60°由此可知,三角形 ABC 是等边三角形。
故三角形 ABC 的高为√3/2 × AB = √3/2 × 4 = 2√3 cm。
因此,三角形 ABC 的面积为:S = 1/2 × AB × AC × sin(∠BAC)= 1/2 × 4 × 6 × sin(60°)= 1/2 × 4 × 6 × (√3/2)= 6√3 cm²所以,三角形 ABC 的面积为6√3 平方厘米。
数学尖子生初二练习题

数学尖子生初二练习题数学是一门需要不断练习和巩固的学科,尤其对于数学尖子生来说,初二阶段的练习就显得尤为关键。
本文将为数学尖子生提供一些初二阶段的练习题,旨在帮助他们进一步巩固数学知识并提高解题能力。
1. 简单方程求解(1)解方程:3(x + 2) = 2(x - 3) + 9(2)解方程:4(x - 5) = 2(x + 3) - 52. 分式运算(1)计算:(2/3) ÷ (4/5)(2)计算:(5/6) + (2/9) - (1/3)3. 数列问题(1)求等差数列的通项公式,已知首项 a1 = 3,公差 d = 2,求第 n 项 an(2)求等比数列的通项公式,已知首项 a1 = 2,公比 q = 3,求第 n 项 an4. 几何图形(1)已知正方形 ABCD,边长为 6cm,E、F、G、H 分别为 AB、BC、CD、DA 上的点,连接 EF、FG、GH、HE,求四边形 EFGH 的周长。
(2)已知直角三角形 ABC,∠C = 90°,AC = 3cm,BC = 4cm,求AB 的长。
5. 概率问题(1)一枚正六面体骰子,点数均匀分布,掷一次,求出现奇数点数的概率。
(2)从有 5 个红球和 3 个蓝球的袋子中,随机抽取 2 个球,求两个球颜色相同的概率。
6. 坐标系中的问题(1)在平面直角坐标系中,A(1, 2)、B(4, 3)、C(3, 6) 为三角形ABC 的顶点,求三角形 ABC 的周长。
(2)已知平面直角坐标系中一动点 P 的坐标为 (2t, 3t),t 为实数,当 t 取何值时,点 P 在直线 y = 2x + 1 上。
以上是一些数学尖子生初二阶段的练习题,希望能够对数学尖子生的学习有所帮助。
通过不断练习和思考,相信数学尖子生们能够不断提高数学水平,取得优异的成绩。
加油!。
数学尖子生初二练习题

数学尖子生初二练习题1. 有如下算术题,请计算并写出结果:a) 35 + 47b) 63 - 28c) 14 × 5d) 60 ÷ 42. 简化下列分式,并写出结果:a) $\frac{14}{28}$b) $\frac{36}{48}$c) $\frac{50}{75}$d) $\frac{24}{36}$3. 求下列等式的解:a) $2x + 5 = 15$b) $3y - 7 = 10$c) $4z + 6 = 22$d) $5w - 9 = 26$4. 将下列百分数改写为分数,并写出结果:a) 25%b) 50%c) 75%d) 80%5. 求下列数字的平方根,并写出结果:a) 9b) 16c) 25d) 366. 画出下列几何图形,并标明图中所给的线段或角度:a) 直角三角形b) 等边三角形c) 钝角d) 平行四边形7. 解下列不等式,并写出结果的数轴表示:a) $2x + 5 > 10$b) $3y - 7 < 20$c) $4z + 6 ≥ 18$d) $5w - 9 ≤ 15$8. 按照给出的图形信息,求解图中角度的度数:a) 直角b) 钝角c) 锐角d) 平角9. 计算下列立体图形的体积,并写出结果:a) 边长为6cm的正方体b) 半径为5cm的球体c) 半径为4cm,高度为10cm的圆柱体d) 边长为3cm的正立方体10. 求下列线段的长度,并写出结果:a) 端点坐标分别为A(3,4)和B(7,9)的线段ABb) 端点坐标分别为C(-2,1)和D(4,-2)的线段CDc) 端点坐标分别为E(0,0)和F(3,3)的线段EFd) 端点坐标分别为G(-5,3)和H(1,-4)的线段GH以上为数学尖子生初二练习题,希望能对你的学习有所帮助。
2023-2024学年苏科版八年级数学下册期末备考尖子生集训试题

2023-2024学年苏科版八年级数学下册期末备考尖子生集训试题一、单选题1.某学校准备为七年级学生开设,,,,,A B C D E F 共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).下列说法不正确的是( )A .这次被调查的学生人数为400人B .E 对应扇形的圆心角为80︒C .喜欢选修课F 的人数为72人D .喜欢选修课A 的人数最少2.如图,点P 是正方形ABCD 的对角线BD 上一点,PE BC ⊥于点E ,PF DC ⊥于点F ,连接EF ,给出下列四个结论:①AP EF =;②AP EF ⊥;③PFE BAP ∠=∠;④PD ,其中正确的是( )A .1个B .2个C .3个D .4个3.如图,在平面直角坐标系中,点()0,2A 点B 在x 轴的正半轴上,30ABO ∠=︒,现把AOB V绕点O 顺时针旋转30°得到A OB ''△,点B '恰好落在一次函数y b +的图象上,则b 的值为( )A .1B .C .2D .-4.如图,在▱ABCD 中,BE 垂直平分CD 于点E ,且∠BAD =45°,AD =3,则▱ABCD 的对角线AC 的长为( )A .B .C .D .5.在数学拓展课《折叠矩形纸片》上,小林发现折叠矩形纸片ABCD 可以进行如下操作:①把ABF △翻折,点B 落在C 边上的点E 处,折痕为AF ,点F 在BC 边上;②把ADH V 翻折,点D 落在AE 边上的点G 处,折痕为AH ,点H 在CD 边上,若610AD CD ==,,则EHEF=( )A .32B .53C .43D .546.如图,ABCD Y 的对角线AC 、BD 交于点O ,AE 平分BAD 交BC 于点E ,且A D C 60∠=o,12AB BC =,连接OE .下列结论:①AE CE >;②ABC S AB AC =⋅V ;③ABE AOE S S =V V ;④14OE BC =;成立的个数有( )A .1个B .2个C .3个D .4个7.如图,点B 为x 轴上一点,以OB 为边作等腰三角形OBA ,且2AB O B ==,150ABO ∠=o .现将OBA △绕点O 逆时针旋转,第1次旋转30°,第2次旋转60°,第3次旋转30°,第4次旋转60°……依此进行下去,则第60次旋转结束后点A 的坐标为( )A.()21-B.()21--C.(0,D.)8.如图,ABCD Y 的对角线AC ,BD 交于点O ,AE 平分BAD ∠,交BC 于点E ,且160,2ADC AB BC ︒∠==,连接OE ,下列结论①30︒∠=CAD ;②OD=AB ;③ABCD S AC CD =⋅Y ;④32OECD AOD S S ∆=;其中成立的个数是( )A .1个B .2个C .3个D .4个9.若整数a 使得关于x 的不等式组341242()x x x a x +⎧+>⎪⎨⎪-≤-⎩的解集为2x <-,且关于y 的分式方程2311a yy y -=+++的解为负数,则所有符合条件的整数a 的和为( ) A .0 B .-3 C .-5 D .-810.若关于x 的分式方程61x x -=3+1axx -的解为整数,且一次函数y =(10﹣a )x +a 的图象不经过第四象限,则符合题意的整数a 的个数为( )A .1B .2C .3D .411.如图,在平面直角坐标系中,矩形ABCD 的对角线AC 的中点与坐标原点重合,点E 是x 轴上一点,连接AD ,若AD 平分OAE ∠,反比例函数(0,0)k y k x x=>>的图象经过AE 上的两点,A F ,且AF EF =,若ABE V 的面积为24,则k 的值为( )A .8B .16C .18D .2412.如图,在平面直角坐标系中,菱形OABC 的边OC 在x 轴上,点()4B a ,,点()50.C ,若反比例函数(0,0)ky k x x=>>经过点A ,则k 的值等于( )A .25B .24C .12D .513.如图,在平面直角坐标系中,正方形OBCD 的顶点O 在坐标原点,点B 的坐标为(2,5),点A 在第二象限,反比例函数 的图象经过点A ,则k 的值是( )A .421B .421-C .214D .214-14.如图,点A ,B ,C 三点在x 轴的正半轴上,且OA AB BC ==,过点A ,B ,C 分别作x 轴的垂线交反比例函数(0)ky k x=>的图象于点D ,E ,F ,连结OD ,AE ,BF ,则::OAD ABE BCF S S S △△△为( )A .12∶7∶4B .3∶2∶1C .6∶3∶2D .12∶5∶415.如图,正方形ABCO 和正方形DEFO 的顶点,,A E О在同一直线l 上,且3EF AB ==,给出下列结论:①45COD ∠=︒,②5AE =,③CF BD =④3COF S =△,其中正确的个数为( )A .1个B .2个C .3个D .4个二、填空题16.某中学有270名学生,为了了解学生们的上学方式,抽取部分学生做调查后绘制了如图所示的条形图,那么此次调查的样本容量为.17.在矩形ABCD 中,1AB =, BC =P 是对角线AC 上一点,若以P ,A ,B 三点为顶点的三角形是等腰三角形,则PAB V 的面积是.18.如图,在ABCD Y 中,602B BC AB ∠=︒=,,将AB 绕点A 逆时针旋转角α(0360α︒<<︒)得到AP ,连接PC ,PD .当PCD △为直角三角形时,旋转角α的度数为.19.如图,在矩形纸片ABCD 中,3AD =,9CD =,折叠纸片,使点D 刚好落在线段AB 上,且折痕分别与AB ,CD 相交,设折叠后点A ,D 的对应点分别为点G ,H ,折痕分别与AB ,CD 相交于点E ,F ,则线段CF 的整数值.20.如图,在正方形ABCB 1中,AB =1,AB 与直线l 的夹角为30°,延长CB 1交直线l 于点A 1,作正方形A 1B 1C 1B 2,延长C 1B 2交直线l 于点A 2,作正方形A 2B 2C 2B 3;延长C 2B 3交直线l 于点A 3,…,依次规律,则A 2021B 2021=.21.如图,正方形ABCD 中,点E 在边AD 上,点F 在边CD 上,若BEF EBC ∠=∠,3AB AE =,则下列结论:①DF FC =;②AE DF EF +=;③45ABE CBF ∠+∠=︒;④::3:4:5DF DE EF =;其中结论正确的序号有.22.如图,菱形ABCD 的边长为1, 60ABC ∠=︒.,E F 分别是,BC BD 上的动点,且CE DF =,则AE AF +的最小值为.23.如图,在平行四边形ABCD 中,点F 在AD 上,5,11,AF cm BF cm FBD CBD ==∠=∠,点E 是BC 的中点,若点P 以1厘米/秒的速度从A 点出发,沿AD 向点F 运动;点Q 同时以2厘米/秒的速度从C 点出发,沿CB 向点B 运动,点P 运动到F 停止运动,点Q 也同时停止运动,当点P 运动时间是秒时,以点P Q E F 、、、为顶点的四边形是平行四边形.24.如图,矩形ABCD 中,6AB =,8BC =,E 是AD 边上一点,连接CE ,将CDE ∆沿CE 翻折,点D 的对应点是F ,连接AF ,当AEF ∆是直角三角形时,则DE 的值是25.如图所示,一个长方形窗框ABCD 被EF 分成上下两个长方形,上部分长方形又被分成三个小长方形,其中G ,H 为AD 的四等分点(G 在H 左侧)且AG HD =.一根晾衣杆斜靠在窗框上的PG 位置,P 为BC 中点,若4BC =,PG 分长方形BEFC 的左右面积之比为:a b ,则PG 分长方形AEFD 的左右面积之比为(用含a ,b 的代数式表示).26.已知:如图,点B 、点C 是反比例函数)0y x =>图象上的两点,过点C 作CD x ⊥轴于点D .过点B 作BA x ⊥轴于点A ,连接OC ,交AB 于点E ,连接.OB BC 、当A 为OD 中点且90OBC ︒∠=时,点C 的坐标为.27.如图,在平面直角坐标系中,正方形OABC 的顶点O 与坐标原点重合,点C 的坐标为(0,3),点A 在x 轴的正半轴上.直线1y x =-分别与边,AB OA 相交于,D M 两点,反比例函数(0)ky x x=>的图象经过点D 并与边BC 相交于点N ,连接MN .点P 是直线DM 上的动点,当CP MN =时,点P 的坐标是.28.双曲线k y x =和1y x =在第一象限内的图象如图所示,P 在k y x=的图象上,PC x ⊥轴于C ,交1y x=的图象于A ,PD y ⊥轴于D ,交1y x=的图象于B ,当P 点在ky x=的图象上运动时,下列结论:①OBD V 与OAC V 的面积相等;②四边形PAOB 的面积保持不变;③PA PB =;④若A 是PC 的中点,则B 是DP 的中点.其中一定正确的的序号是.29.阅读下列解题过程:===+L .三、解答题30.如图,点E 为正方形ABCD 边BC 上的一点,CG 平分正方形的外角DCF ∠,将线段AE 绕点E 顺时针旋,点A 的对应点为点H .(1)当点H 落在边CD 上且CE CH =时,求AEH ∠的度数; (2)当点H 落在射线CG 上时,求证:AE EH ⊥;(3)在(2)的条件下,连接AH 并与CD 交于点P ,连接EP ,探究2AP ,2EP 与2HP 之间的数量关系,并说明理由.31.一副三角板如图1摆放,90C DFE ∠=∠=︒,30B ∠=︒,45E ∠=︒,点F 在BC 上,点A 在DF 上,且AF 平分CAB ∠,现将三角板DFE 绕点F 以每秒5︒的速度顺时针旋转(当点D 落在射线FB 上时停止旋转),设旋转时间为t 秒.(1)当t = 秒时,DE AB ∥;当t = 秒时,DE AB ⊥;(2)在旋转过程中,DF 与AB 的交点记为P ,如图2,若AFP V 有两个内角相等,求t 的值;(3)当边DE 与边AB 、BC 分别交于点M 、N 时,如图3,连接AE ,设B A E x ∠=︒,AED y ∠=︒,DFB z ∠=︒,试问x y z ++是否为定值?若是,请求出定值;若不是,请说明理由.32.在数学活动课上,老师出示了以下两个问题,请你解答老师提出的问题:(1)如图①,在A B C D Y 中,BE AD ⊥,垂足为E ,F 是CD 边上一点,连接EF ,BF ,若E F B F =,试判断DF 与CF 的数量关系,并加以证明.(2)如图②,若F 是ABCD Y 边CD 上一点,连接BF ,将CBF V 沿着边BF 所在的直线折叠,点C 的对应点为C ',连接DC '并延长交AB 于点G ,若AG BG =,试判断DF 与CF 的数量关系,并加以证明.33.如图1,四边形ABCD 为正方形,△AEF 为等腰直角三角形,∠EAF =90°,连接BE 、DF .(1)求证:△ABE ≌△ADF ;(2)如图2,延长DF 交AB 于点G ,交BE 于点H ,连结AH . ①求∠EHA 的度数;②过点D 作DM ⊥HA 交HA 的延长线于点M ,请你写出线段AM 与BH 之间的数量关系,并证明你的结论.34.如图,在平面直角坐标系中,四边形ABCO是矩形,已知点B坐标为(10,8),M,N 分别是OC,AB的中点.(1)求证:四边形BCMN是矩形;(2)点F是直线BC上一点,连接OF交直线MN于点E,当OF=OA时,求直线AF的解析式;(3)在(2)的条件下,直线l经过点A,且解析式为y=kx+b(k≠0),若直线l与线段EM 相交,求k的取值范围.35.某果园实验基地推广甲、乙两种芒果苗,已知乙种芒果苗比甲种芒果苗每株贵2元,且用240元钱购买甲种芒果苗的株数与用360元钱购买乙种芒果苗的株数刚好相同.(1)求甲、乙两种芒果苗每株的价格;(2)果农A准备从甲、乙两种芒果苗中选购一种,已知购买数量相同且数量不少于500株,该果园实验基地负责人可给予以下优惠:购买甲种芒果苗每株按原售价九折优惠;购买乙种芒果苗,不多于500株按原售价付款不优惠,超过500株每株按原售价五折优惠.请帮助果农A 判断购买哪种芒果苗更省钱.(3)果农B 计划购买甲、乙两种芒果苗共300株.调查统计发现,甲、乙两种芒果苗的成活率分别为90%、95%,要使这批芒果苗的成活率不低于93%,且使购买芒果苗的费用最低,应如何选购芒果苗?最低费用是多少?36.如图,直线y =﹣23x +4与x 轴交于点A ,与y 轴交于点B ,反比例函数y 1=k x(x >0)的图象经过线段AB 的中点C .(1)求反比例函数的表达式;(2)将直线y =﹣23x +4向右平移4个单位长度后得到直线y 2=ax +b ,直线y 2交x 轴于点D ,交反比例函数y 1=k x(x >0)的图象于点E ,F ,连接CE ,CF ,求△CEF 的面积; (3)请结合图象,直接写出不等式y 1<y 2的解集.37.如图,在平面直角坐标系中,点()()3,0,0,4A B -- ,把线段AB 绕点A 逆时针旋转90︒到AC ,AC 交y 轴于点D ,反比例函数()0ky x x=>的图象经过点C .(1)求k 的值;(2)连接BC ,若点P 在反比例函数k y x=(0)x >的图象上BDP ABC S S =V V ,求点P 的坐标. 38.如图,一次函数y =12x +b 与反比例函数y =k x 的图象交于点A (4,a )、B (﹣8,﹣2).(1)求k、a、b的值;(2)求关于x的不等式12x+b>kx的解集;(3)若点P在y轴上,点Q在反比例函数y=kx的图象上,且A、B、P、Q恰好是一个平行四边形的四个顶点,试求点P的坐标.39.如图,已知直线y x=与双曲线kyx=交于A、B 两点,且点A的横坐标3.(1)求k 的值;(2)若双曲线kyx=上点C的纵坐标为3,求△AOC的面积;(3)在y轴上有一点M,在直线AB上有一点P,在双曲线kyx=上有一点N,若四边形OPNM 是有一组对角为60°的菱形,请写出所有满足条件的点P 的坐标.40.如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数kyx=的图象上.(1)求m ,k 的值;(2)如果M 为x 轴上一点,N 为y 轴上一点, 以点A ,B ,M ,N 为顶点的四边形是平行四边形,试求直线MN 的函数表达式.41.【阅读材料】像3=()0a a =≥,)()1110b b =-≥,…, 两个含有二次模式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.11,…,等都是互为有理化因式,进行二次根式计算时,利用有理化因式,可以化去分母中的根号.【解决问题】 (1)2______;(2)(3)①如图1是44⨯的正方形网格,每个小正方形边长都为1,ABC V 三个顶点都在格点上,则点A 到BC 边的距离为______;②如图2,ABC V 中,ABC ∠与ACB ∠的角平分线相交于点P ,若ABC V 的周长为4,面积为3,求点P 到BC 边的距离.。
2022-2023 学年北师大版八年级数学上册尖子生同步培优试题:专题1

2022-2023 学年八年级数学上册尖子生同步培优题典【北师大版】专题 1.4勾股定理与最短路径问题(重难点培优)姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共 10小题,每小题 3分,共 30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2020秋•禅城区期末)如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁沿侧面爬行,想吃到 B 点的食物,需要爬行的最短路径是()A.9 B.13 C.14 D.25【分析】要想求得最短路程,首先要把A和B展开到一个平面内.根据两点之间,线段最短求出蚂蚁爬行的最短路程.【解析】展开圆柱的半个侧面是矩形,矩形的长是圆柱的底面周长的一半,即为12,矩形的宽是圆柱的高5.根据两点之间线段最短,知最短路程是矩形的对角线的长,即13,故选:B.2.(2020秋•太原期末)如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为()A.12cm B.14cm C.20cm D.24cm【分析】将容器侧面展开,建立A关于EG的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【解析】如图:将圆柱展开,EG为上底面圆周长的一半,作A关于E的对称点A',连接A'B交EG于F,则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF的长,即AF+BF=A'B=20cm,延长BG,过A'作A'D⊥BG于D,∵AE=A'E=DG=4cm,∴BD=16cm,Rt△A'DB中,由勾股定理得:A'D 12cm,∴则该圆柱底面周长为24cm.故选:D.3.(2020秋•金牛区校级月考)如图所示的圆柱体中底面圆的半径是,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是()A.5 B.C.D.4【分析】先将圆柱体展开,再根据两点之间线段最短,由勾股定理即可求出结果.【解析】圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高等于圆柱的母线长.∵AB=π∴AC 4,CB=3,5,故选:A.4.(2020秋•太原期中)今年9月22日是第三个中国农民丰收节,小彬用3D打印机制作了一个底面周长为20cm,高为10cm的圆柱粮仓模型,如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为()A.20πcm B.40πcm C.10 cm D.20 cm【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.【解析】如图,圆柱的侧面展开图为长方形,AC=A'C,且点C为BB'的中点,∵AB=10,BC 20=10,∴装饰带的长度=2AC=2故选:D.20 (cm),5.(2020秋•峄城区期中)已知长方体的长2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从 A 点爬到B′点,那么沿哪条路最近,最短的路程是()A.cm B.5cm C.cm D.4.5cm【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.【解析】根据题意,如图所示,最短路径有以下三种情况:(1)沿AA′,A′C′,C′B′,B′B剪开,得图1:AB′2=AB2+BB′2=(2+1)2+42=25;(2)沿AC,CC′,C′B′,B′D′,D′A′,A′A剪开,得图2:AB′2=AC2+B′C2=22+(4+1)2=4+25=29;(3)沿AD,DD′,B′D′,C′B′,C′A′,AA′剪开,得图3:AB′2=AD2+B′D2=12+(4+2)2=1+36=37;综上所述,最短路径应为(1)所示,所以AB′2=25,即AB′=5cm,故选:B.6.(2020秋•市南区校级期中)某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为()A.8cm B.10cm C.12cm D.15cm【分析】画出三棱柱的侧面展开图,利用勾股定理求解即可.【解析】将三棱柱沿AA′展开,其展开图如图,则AA′15(cm).故选:D.7.(2020秋•沙坪坝区校级期中)小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为()米.A.16 B.8 C.D.【分析】将长方体展开,根据两点之间线段最短,构造出直角三角形,进而根据勾股定理求出AB的长.【解析】如图:AC=5+3=8,BC=8,在Rt△ABC中,AB 8 .米.即从点A攀爬到点B的最短路径为 8故选:B.8.(2021春•江岸区校级月考)如图,桌面上的长方体长为8,宽为6,高为4,B为CD的中点.一只蚂蚁从A点出发沿长方体的表面到达B点,则它运动的最短路程为()A.B.C.10 D.【分析】根据题意画出长方体的侧面展开图,连接AB,根据勾股定理求出AB的长即可.【解析】如图1所示,则 AB 2 ;如图2所示,AB 10,故它运动的最短路程为10,故选:C.9.(2021春•下城区校级期中)如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到 B 点,最短路程是()A.10 B.50 C.120 D.130【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【解析】如图所示,∵它的每一级的长宽高为20cm,宽30cm,长50cm,∴AB 50 (cm).答:蚂蚁沿着台阶面爬行到点B的最短路程是50 cm,故选:B.10.(2021春•天河区校级期中)如图,圆柱的高为4cm,底面半径为cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径、问:蚂蚁食到食物爬行的最短距离是()cm.A.5 B.5πC.3 D.3【分析】求至少要爬多少路程,根据两点之间直线最短,把圆柱体展开,在得到的矩形上连接两点,求出距离即可.【解析】把圆柱体沿着AC直线剪开,得到矩形如下:则AB的长度为所求的最短距离,根据题意圆柱的高为4cm,底面半径为cm,则可以知道AC=4cm,BC ∵底面周长为2πr=2×π∴BC=3cm,底面周长,6(cm),∴根据勾股定理得出AB2=AC2+BC2,即AB2=42+32,∴AB=5(cm).答:蚂蚁至少要爬行5cm路程才能食到食物,故选:A.二、填空题(本大题共 8小题,每小题 3分,共 24分)请把答案直接填写在横线上11.(2020秋•武侯区校级月考)如图,一个长方体盒子的长、宽、高分别为5cm、4cm、3cm,有一只甲虫从顶点A沿盒的表面爬到顶点B处,那么它所爬行的最短路线的长是cm.【分析】把此长方体的一面展开,在平面内,两点之间线段最短.利用勾股定理求点A和B点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形中,一条直角边长等于长方体的高,另一条直角边长等于长方体的长宽之和,利用勾股定理可求得.【解析】因为平面展开图不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面、右面,由勾股定理得AB2=(5+4)2+32=90;(2)展开前面、上面,由勾股定理得AB2=(3+4)2+52=74;(3)展开左面、上面,由勾股定理得AB2=(3+5)2+42=80;∵74<80<90,所以最短路径长为cm.故答案为:.12.(2020秋•南海区期中)如图所示,一圆柱高AB为2cm,底面直径BC为4cm,一只蚂蚁从点A出发沿圆柱表面爬行到点C,则蚂蚁爬行的最短路程是cm(π取3).6【分析】首先画出示意图,连接AC,根据圆的周长公式算出底面圆的周长,BC 底面圆的周长,再在Rt△ACB中利用勾股定理算出AC的长即可,再计算AB+BC=8,比较两种情形的数值的大小即可判断;【解析】将圆柱体的侧面展开并连接AC.∵圆柱的直径为4cm,∴BC4•π≈6(cm),在 Rt△ACB中,AC2=AB2+CB2=22+62=40,∴AC=2 (cm).∵高 AB为 2cm,底面直径 BC为 4cm,∴走高 AB再走直径 BC,其距离为 6cm,∵6<2 ,∴蚂蚁爬行的最短的路线长是 6cm.故答案为:6.13.(2020秋•中牟县期中)如图所示是一个长方体纸盒,纸盒的长为 12cm,宽为 9cm,高为 5cm,一只蚂蚁想从盒底的点 A沿盒的表面爬到盒顶的点 G,蚂蚁爬行的最短路程是 2 cm.【分析】分为三种情况展开,根据勾股定理求出线段 AB的长度,再进行比较即可.【解析】①如图 1,展开后连接 AG,则 AG就是在表面上 A到 G的最短距离,∵∠ACG=90°,AC=12+9=21,CG=5,在 Rt△ACG中,由勾股定理得:AG (cm);②如图 2,展开后连接 AG,则 AG就是在表面上 A到 G的最短距离,∵∠ABG=90°,AB=12,BG=9+5=14,在 Rt△ACBG中,由勾股定理得:AG 2 (cm);③如图 3,展开后连接 AG,则 AG就是在表面上 A到 G的最短距离,∵∠AFG=90°,AF=5+12=17,FG=9,在 Rt△AFG中,由勾股定理得:AG ∴蚂蚁爬行的最短路程是 2 cm,故答案为:2 (cm)..14.(2020秋•青羊区校级期中)如图,圆柱形容器高为 16cm,底面周长为 24cm,在杯内壁离杯底的点 B 处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点 A处,则蚂蚁 A处到达 B处的最短距离为20cm.【分析】先将圆柱的侧面展开,再根据勾股定理求解即可.【解析】如图所示,∵圆柱形玻容器,高 16cm,底面周长为 24cm,∴BD=12cm,∴AB 20(cm).∴蚂蚁 A处到达 B处的最短距离为 20cm,故答案为:20cm.15.(2020秋•莱州市期中)如图,长方体盒子的长、宽、高分别是 9cm,9cm,24cm,一只蚂蚁想从盒底的 A点爬到盒顶的 B点,它至少要爬行30 cm.【分析】将长方形的盒子按不同方式展开,得到不同的矩形,求出不同矩形的对角线,最短者即为正确答案.【解析】如图 1所示,AB 30(cm),如图 2所示:AB (cm).∵30 ,∴蚂蚁爬行的最短路程是 30cm.故答案为:30.16.(2021春•孝南区月考)如图所示,有一个正方体盒子,其棱长为 2dm,一只虫子在顶点 A处,一只蜘蛛在顶点B处,蜘蛛沿着盒子表面准备偷袭虫子,那么蜘蛛要想最快地捉住虫子,它所走的最短路程是2 dm.(结果保留根号)【分析】由于纸箱为正方体,且 A、B两点对称,故将其按任意方式展开,连接 A、B即可求得蚂蚁爬行的最短路程.【解析】如图:因为 BC=2dm,AC=2×2=4(dm),所以 AB 2 (dm).故答案为:2 .17.(2021春•合川区校级月考)如图,圆柱形容器外壁距离下底面 3cm的 A处有一只蚂蚁,它想吃到正对面外壁距离上底面 3cm的 B处的米粒,若圆柱的高为 12cm,底面周长为 24cm.则蚂蚁爬行的最短距离为 6 cm.【分析】先把圆柱的侧面展开得其侧面展开图,由勾股定理求得 AB的长.【解析】如图,将圆柱的侧面沿过 A点的一条母线剪开,得到长方形,连接 AB,则线段 AB的长就是蚂蚁爬行的最短距离,故 AB 6 (cm).故答案为:6 .18.(2021春•江汉区月考)如图,现有一长方体的实心木块,有一蚂蚁从 A处出发沿长方体表面爬行到 C '处,若长方体的长 AB=4cm,宽 BC=2cm,高 BB'=1cm,则蚂蚁爬行的最短路径长是 5cm.【分析】连接 AC′,求出 AC′的长即可,分为三种情况:画出图形,根据勾股定理求出每种情况时 AC ′的长,再找出最短的即可.【解析】展开成平面后,连接 AC′,则 AC′的长就是绳子最短时的长度,分为三种情况:如图 1,AB=4,BC′=2+1=3,在 Rt△ABC′中,由勾股定理得:AC′(cm);如图 2,AC=4+2=6,CC′=1,在 Rt△ACC′中,由勾股定理得:AC′,如图 3,同法可求 AC′,即绳子最短时的长度是 5cm,故答案为:5cm.三、解答题(本大题共 6小题,共 46分.解答时应写出文字说明、证明过程或演算步骤)19.(2020秋•高州市期中)如图,一个圆柱体高 20cm,底面半径为 5cm,在圆柱体下底面的 A点处有一只蜘蛛,它想吃到上底面与 A点相对的 B点处的一只已被粘住的苍蝇,这只蜘蛛从 A点出发,沿着圆柱体的侧面爬到 B点,最短路程是多少?(π取 3)【分析】要求需要爬行的最短路程首先要把圆柱的侧面展开,得到一个矩形,然后利用勾股定理求两点间的距离即可.【解析】如图所示,将圆柱体侧面展开,连接 AB,则 AB的长即为蜘蛛爬行的最短路程.根据题意得 AC=20cm,BC=πR=5π=5×3=15cm,在 Rt△ABC中,由勾股定理得 AB2=BC2+AC2=152+202=625,所以 AB=25cm,即最短路程是 25cm.20.(2020秋•淅川县期末)如图是放在地面上的一个长方体盒子,其中 AB=18cm,BC=12cm,BF=10cm,点 M在棱 AB上,且 AM=6cm,点 N是 FG的中点,一只蚂蚁要沿着长方体盒子的表面从点 M爬行到点 N,它需要爬行的最短路程是多少?【分析】利用平面展开图有三种情况,画出图形利用勾股定理求出 MN的长即可.【解析】如图 1,∵AB=18cm,BC=GF=12cm,BF=10cm,∴BM=18﹣6=12,BN=10+6=16,∴MN 20(cm);如图 2,∵AB=18cm,BC=GF=12cm,BF=10cm,∴PM=18﹣6+6=18,NP=10,∴MN 2 (cm).如图 3中,MN 2 (cm),∵20<2 2 ,∴蚂蚁沿长方体表面爬到米粒处的最短距离为 20cm.21.(2020秋•长春期末)如图所示,有一个圆柱,底面圆的直径 AB ,高 BC=12cm,在 BC的中点 P 处有一块蜂蜜,聪明的蚂蚁总能找到距离食物的最短路径,求蚂蚁从 A点爬到 P点的最短距离.【分析】化“曲”为“平”,在平面内,得到两点的位置,再根据两点之间线段最短和勾股定理求解即可.【解析】将圆柱体的侧面展开,如图所示:AB 底面周长π8(cm),AP BC=6(cm),所以 AP 10(cm),故蚂蚁从 A点爬到 P点的最短距离为 10cm.22.(2020秋•郫都区期中)如图,长方体的长为 20cm,宽为 10cm,高为 15cm,点 B与点 C之间的距离为5cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点 B去吃一滴蜜糖.(1)求出点 A到点 B的距离;(2)求蚂蚁从点 A爬到点 B的最短路程是多少?【分析】(1)分三种情况讨论:把左侧面展开到水平面上,连接 AB ,如图 1;把右侧面展开到正面上, 连接 AB ,如图 2;把向上的面展开到正面上,连接 AB ,如图 3,然后利用勾股定理分别计算各情况下的 AB 即可;(2)根据(1)的结果进行大小比较即可得到结论.【解析】(1)将长方体沿 CF 、FG 、GH 剪开,向右翻折,使面 FCHG 和面 ADCH 在同一个平面内, 连接 AB ,如图 1,由题意可得:BD =BC+CD =5+10=15cm ,AD =CH =15cm ,在 Rt △ABD 中,根据勾股定理得:AB 15 cm ;将长方体沿 DE 、EF 、FC 剪开,向上翻折,使面 DEFC 和面 ADCH 在同一个平面内,连接 AB ,如图 2,由题意得:BH =BC+CH =5+15=20cm ,AH =10cm ,在 Rt △ABH 中,根据勾股定理得:AB则需要爬行的最短距离是 15 cm .10 cm , 连接 AB ,如图 3,由题意可得:BB ′=B ′E+BE =15+10=25cm ,AB ′=BC =5cm ,在 Rt △AB ′B 中,根据勾股定理得:AB5 cm , 综上所述,点 A 到点 B 的距离为:15 cm ,10 cm ,5 (2)由(1)知,∵点 A 到点 B 的距离为:15 cm ,10 cm ,5∴15 ∴则需要爬行的最短距离是 15 cm .cm ;cm ; 10 5 ,23.(2020秋•碑林区校级月考)如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为 16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上底面距离为4cm 的点 A处,若蚂蚁吃到蜂蜜需爬行的最短路径为 20cm,则该圆柱底面周长为多少?【分析】将容器侧面展开,建立 A关于 EG的对称点 A′,根据两点之间线段最短可知 A′B的长度即为所求.【解析】如图:将圆柱展开,EG为上底面圆周长的一半,作 A关于 E的对称点 A',连接 A'B交 EG于 F,则蚂蚁吃到蜂蜜需爬行的最短路径为 AF+BF的长,即AF+BF=A'B=20cm,延长 BG,过 A'作 A'D⊥BG于 D,∵AE=A'E=DG=4cm,∴BD=16cm,12(cm),Rt△A'DB中,由勾股定理得:A'D则该圆柱底面周长为 24cm.24.(2020秋•龙泉驿区期中)如图所示,一个无盖四棱柱容器,其底面是一个边长为 3cm的正方形,高为20cm.现有一根彩带,从底面 A点开始缠绕四棱柱,刚好缠绕 4周到达 B点(假设彩带完美贴合四棱柱).(1)请问彩带的长度是多少?(2)如图所示,一只蚂蚁在容器外 A点发现容器的内部距离顶部 2cm处有一滴蜂蜜,它想以最短的路程到达 C处.请问蚂蚁走的最短路程是多少呢?(注:以上两问均要画出平面展开示意图,再解答)【分析】(1)如果从点 A开始缠绕四棱柱,刚好缠绕 4周到达点 B,相当于直角三角形的两条直角边分别是 12和 5,再根据勾股定理求出斜边长即可;(2)求四棱柱中两点之间的最短路径,最直接的作法,就是将四棱柱展开,然后利用两点之间线段最短解答.【解析】(1)如图,将长方体的侧面沿 AB展开,取 A′B′的四等分点 C、D、E,取 AB的四等分点 C′、D′、E′,连接B′E′,D′E,C′D,AC,则 AC+C′D+D′E+E′B′=4AC为所求的最短细线长,∵AC2=AA′2+A′C2,AC 13,∴AC+C′D+D′E+E′B′=4AC=52,答:彩带的长度是 52cm;(2)如图,将四棱柱展开,找到 C的对称点 C′,连接 AC′,则 AC′即为蚂蚁走的最段路程,在直角△AMC中,AM=6cm,MC′=20+(20﹣18)=22cm,由勾股定理得:AC′2=AM2+MC′2=62+222=520,则 AC′=2 cm,答:蚂蚁走的最短路程是 2cm.专题 1.4勾股定理与最短路径问题(重难点培优)姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共 10小题,每小题 3分,共 30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2020秋•禅城区期末)如图,圆柱的底面周长是 24,高是 5,一只在 A点的蚂蚁沿侧面爬行,想吃到 B 点的食物,需要爬行的最短路径是()A.9 B.13 C.14 D.252.(2020秋•太原期末)如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为 16cm,在容器内壁离容器底部 4cm的点 B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿 4cm的点 A处,若蚂蚁吃到蜂蜜需爬行的最短路径为 20cm,则该圆柱底面周长为()A.12cm B.14cm C.20cm D.24cm3.(2020秋•金牛区校级月考)如图所示的圆柱体中底面圆的半径是,高为 3,若一只小虫从 A点出发沿着圆柱体的侧面爬行到 C点,则小虫爬行的最短路程是()A.5 B.C.D.44.(2020秋•太原期中)今年 9月 22日是第三个中国农民丰收节,小彬用 3D打印机制作了一个底面周长为 20cm ,高为 10cm 的圆柱粮仓模型,如图 BC 是底面直径,AB 是高.现要在此模型的侧面贴一圈彩色 装饰带,使装饰带经过 A ,C 两点(接头不计),则装饰带的长度最短为( )A .20πcm 5.(2020秋•峄城区期中)已知长方体的长 2cm 、宽为 1cm 、高为 4cm ,一只蚂蚁如果沿长方体的表面从 A 点爬到B ′点,那么沿哪条路最近,最短的路程是( B .40πcmC .10 cmD .20 cm)A . cmB .5cmC . cmD .4.5cm6.(2020秋•市南区校级期中)某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三 棱镜的侧面上,从顶点 A 到顶点 A ′镶有一圈金属丝,已知此三棱镜的高为 9cm ,底面边长为 4cm ,则 这圈金属丝的长度至少为( )A .8cmB .10cmC .12cmD .15cm7.(2020秋•沙坪坝区校级期中)小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两 个侧面,如图所示,他根据学过的数学知识准确地判断出:从点 A 攀爬到点 B 的最短路径为( )米.A .16 8.(2021春•江岸区校级月考)如图,桌面上的长方体长为 8,宽为 6,高为 4,B 为 CD 的中点.一只蚂蚁 从 A 点出发沿长方体的表面到达 B 点,则它运动的最短路程为( B .8C .D .)A .B .C .10D .9.(2021春•下城区校级期中)如图,台阶阶梯每一层高 20cm ,宽 30cm ,长 50cm ,一只蚂蚁从 A 点爬到 B 点,最短路程是( )A .10B .50C .120D .13010.(2021春•天河区校级期中)如图,圆柱的高为 4cm ,底面半径为 cm ,在圆柱下底面的 A 点处有一只 蚂蚁,它想吃到上底面 B 处的食物,已知四边形 ADBC 的边 AD 、BC 恰好是上、下底面的直径、问:蚂 蚁食到食物爬行的最短距离是( )cm .A .5B .5πC .3D .3二、填空题(本大题共 8小题,每小题 3分,共 24分)请把答案直接填写在横线上11.(2020秋•武侯区校级月考)如图,一个长方体盒子的长、宽、高分别为 5cm、4cm、3cm,有一只甲虫从顶点 A沿盒的表面爬到顶点 B处,那么它所爬行的最短路线的长是 cm.12.(2020秋•南海区期中)如图所示,一圆柱高 AB为 2cm,底面直径 BC为 4cm,一只蚂蚁从点 A出发沿圆柱表面爬行到点 C,则蚂蚁爬行的最短路程是 cm(π取 3).13.(2020秋•中牟县期中)如图所示是一个长方体纸盒,纸盒的长为 12cm,宽为 9cm,高为 5cm,一只蚂蚁想从盒底的点 A沿盒的表面爬到盒顶的点 G,蚂蚁爬行的最短路程是 cm.14.(2020秋•青羊区校级期中)如图,圆柱形容器高为 16cm,底面周长为 24cm,在杯内壁离杯底的点 B 处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点 A处,则蚂蚁 A处到达 B处的最短距离为.15.(2020秋•莱州市期中)如图,长方体盒子的长、宽、高分别是 9cm,9cm,24cm,一只蚂蚁想从盒底的 A点爬到盒顶的 B点,它至少要爬行 cm.16.(2021春•孝南区月考)如图所示,有一个正方体盒子,其棱长为 2dm,一只虫子在顶点 A处,一只蜘蛛在顶点 B处,蜘蛛沿着盒子表面准备偷袭虫子,那么蜘蛛要想最快地捉住虫子,它所走的最短路程是dm.(结果保留根号)17.(2021春•合川区校级月考)如图,圆柱形容器外壁距离下底面 3cm的 A处有一只蚂蚁,它想吃到正对面外壁距离上底面 3cm的 B处的米粒,若圆柱的高为 12cm,底面周长为 24cm.则蚂蚁爬行的最短距离为cm.18.(2021春•江汉区月考)如图,现有一长方体的实心木块,有一蚂蚁从 A处出发沿长方体表面爬行到 C '处,若长方体的长 AB=4cm,宽 BC=2cm,高 BB'=1cm,则蚂蚁爬行的最短路径长是.三、解答题(本大题共 6小题,共 46分.解答时应写出文字说明、证明过程或演算步骤)19.(2020秋•高州市期中)如图,一个圆柱体高 20cm,底面半径为 5cm,在圆柱体下底面的 A点处有一只蜘蛛,它想吃到上底面与 A点相对的 B点处的一只已被粘住的苍蝇,这只蜘蛛从 A点出发,沿着圆柱体的侧面爬到 B点,最短路程是多少?(π取 3)20.(2020秋•淅川县期末)如图是放在地面上的一个长方体盒子,其中 AB=18cm,BC=12cm,BF=10cm ,点 M在棱 AB上,且 AM=6cm,点 N是 FG的中点,一只蚂蚁要沿着长方体盒子的表面从点 M爬行到点 N,它需要爬行的最短路程是多少?21.(2020秋•长春期末)如图所示,有一个圆柱,底面圆的直径 AB ,高 BC=12cm,在 BC的中点 P 处有一块蜂蜜,聪明的蚂蚁总能找到距离食物的最短路径,求蚂蚁从 A点爬到 P点的最短距离.22.(2020秋•郫都区期中)如图,长方体的长为 20cm,宽为 10cm,高为 15cm,点 B与点 C之间的距离为5cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点 B去吃一滴蜜糖.(1)求出点 A到点 B的距离;(2)求蚂蚁从点 A爬到点 B的最短路程是多少?23.(2020秋•碑林区校级月考)如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为 16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上底面距离为4cm 的点 A处,若蚂蚁吃到蜂蜜需爬行的最短路径为 20cm,则该圆柱底面周长为多少?24.(2020秋•龙泉驿区期中)如图所示,一个无盖四棱柱容器,其底面是一个边长为 3cm的正方形,高为20cm.现有一根彩带,从底面 A点开始缠绕四棱柱,刚好缠绕 4周到达 B点(假设彩带完美贴合四棱柱).(1)请问彩带的长度是多少?(2)如图所示,一只蚂蚁在容器外 A点发现容器的内部距离顶部 2cm处有一滴蜂蜜,它想以最短的路程到达 C处.请问蚂蚁走的最短路程是多少呢?(注:以上两问均要画出平面展开示意图,再解答)。
专题13.6等边三角形的判定(限时满分培优训练)-八年级数学上册尖子生培优必刷题【人教版】

【拔尖特训】2023-2024学年八年级数学上册尖子生培优必刷题(人教版)专题13.6等边三角形的判定(限时满分培优训练)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷满分100分,试题共23题,其中选择10道、填空6道、解答7道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2023春•扶风县期中)在△ABC中,若AB=AC=5,∠B=60°,则BC的值为()A.3B.4C.5D.62.(2023春•碑林区校级期末)下列推理中,不能判断△ABC是等边三角形的是()A.∠A=∠B=∠C B.AB=AC,∠B=60°C.∠A=60°,∠B=60°D.AB=AC,且∠B=∠C3.(2023春•漳州期中)若一个三角形有两条边相等,且有一内角为60°,那么这个三角形一定为()A.钝角三角形B.等腰三角形C.直角三角形D.正三角形4.(2022秋•邹城市校级期末)已知:在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:①如果添加条件“AB=AC”,那么△ABC是等边三角形;②如果添加条件“∠B=∠C”,那么△ABC是等边三角形;③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形.上述说法中,正确的有()A.3个B.2个C.1个D.0个5.(2022春•海州区校级期中)下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中是等边三角形的有()A.①②③B.①②④C.①③D.①②③④6.(2022秋•鄱阳县月考)下列对△ABC的判断,错误的是()A.若AB=AC,∠B=60°,则△ABC是等边三角形B.若∠A:∠B:∠C=3:4:7,则△ABC是直角三角形C.若∠A=20°,∠B=80°,则△ABC是等腰三角形D.若AB=BC,∠C=40°,则∠B=40°7.(易错题)(2023春•淄博期末)如图,D是等边△ABC的边AC上的一点,E是等边△ABC外一点,若BD=CE,∠1=∠2,则对△ADE的形状最准确的是()A.等腰三角形B.直角三角形C.等边三角形D.不等边三角形8.(易错题)(2023春•高州市期末)如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一条直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,连接FH.给出下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形.其中正确结论的个数是()A.1B.2C.3D.49.(培优题)(2021•西陵区二模)如图,在△ABC中,AB=AC,尺规作图:(1)分别以B,C为圆心,BC 长为半径作弧,两弧交于点D;(2)作射线AD,连接BD,CD.则下列结论中错误的是()A.∠BAD=∠CAD B.△BCD是等边三角形C.AD垂直平分BC D.S四边形ABDC=AD⋅BC10.(压轴题)(2021秋•霍林郭勒市期末)如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP ≌△QSP.正确的有()A.1个B.2个C.3个D.4个二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上11.(2023春•尤溪县期中)若△ABC,∠B=∠C,请添加一个条件使△ABC是等边三角形,则添加的条件可以是.(写出一个即可)12.(2021秋•绥滨县期末)如图,用圆规以直角顶点O为圆心,以适当半径画一条弧交直角两边于A,B 两点,若再以A为圆心,以OA为半径画弧,与弧AB交于点C,则△AOC的形状为.13.(培优题)(2022秋•灌阳县期中)如图,∠AOB=60°,点C是BO延长线上的一点,OC=6cm,动点P从点C出发沿射线CB以2cm/s的速度移动,动点Q从点O出发沿射线OA以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=s时,△POQ是等边三角形.14.(易错题)(2020秋•遂宁期末)如图,将含有30°角的直角三角尺ABC绕直角顶点A逆时针旋转到ADE 的位置,使B点的对应点D落在BC边上,连接EB,EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③EB平分∠AED;④△ABD为等边三角形.其中正确的是.(填序号)15.(易错题)(2008秋•江岸区期中)如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE 交∠C的外角平分线于E,则△ADE是三角形.16.(培优题)(2021秋•新吴区期中)如图,过边长为4的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当P A=CQ时,连PQ交AC边于D,则DE的长为.三、解答题(本大题共7小题,共52分.解答时应写出文字说明、证明过程或演算步骤)17.(2023春•渠县校级期末)如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC 于点F,DE=DF.求证:△ABC是等边三角形.18.(易错题)(2022秋•丛台区校级期末)如图,△ABC中,AB=AC,∠BAC=120°.点D,E在BC边上,且AD⊥AC,AE⊥AB.(1)求∠C的度数;(2)求证:△ADE是等边三角形.19.(易错题)(2023春•宽甸县期末)如图所示,在等腰△ABC中,AB=AC,AF为BC的中线,D为AF 上的一点,且BD的垂直平分线过点C并交BD于E.求证:△BCD是等边三角形.20.(易错题)(2023春•市北区期中)如图,△ABC中,D为AC边上一点,DE⊥AB于E,ED的延长线交BC的延长线于F,且CD=CF.(1)求证:△ABC是等腰三角形;(2)当∠F=度时,△ABC是等边三角形?请证明你的结论.21.(易错题)(2020秋•惠州期中)已知:如图,在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF ⊥BC,垂足分别为E,F,且DE=DF.求证:(1)∠B=∠C;(2)△ABC是等边三角形.22.(培优题)(2020秋•赣榆区期中)如图,在△ABC中,AB=AC,∠BAC=120°,点D、E在BC上,且AE=BE.(1)求∠CAE的度数;(2)若点D为线段EC的中点,求证:△ADE是等边三角形.23.(压轴题)(2023春•宣汉县校级期末)在边长为9的等边三角形ABC中,点P是AB上一动点,以每秒1个单位长度的速度从点A向点B运动,设运动时间为t秒.(1)如图1,若点Q是BC上一定点,BQ=6,PQ∥AC,求t的值;(2)如图2,若点P从点A向点B运动,同时点Q以每秒2个单位长度的速度从点B经点C向点A运动,当t为何值时,△APQ为等边三角形?。
“A字”模型经典问题特殊训练(重难点培优)-八年级数学上册尖子生培优必刷题(原卷版)【人教版】

【拔尖特训】2023-2024学年八年级数学上册尖子生培优必刷题(人教版)专题11.9“A字”模型经典问题特殊训练(重难点培优)班级:___________________ 姓名:_________________ 得分:_______________注意事项:一.选择题(共6小题)1.如图,在△ABC中,∠B=90°,若按图中虚线剪去∠B,则∠1+∠2等于()A.90°B.135°C.270°D.315°2.如图所示,在△ABC中,CD、BE分别是AB、AC边上的高,并且CD、BE交于点P,若∠A=60°,则∠BPC等于()A.90°B.120°C.150°D.160°3.在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是()A.B.C.D.4.一天,爸爸带小明到建筑工地玩,看见一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于130°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是()A.50°B.65°C.90°D.130°5.如图,已知四边形ABCD中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.90°B.135°C.270°D.315°6.如图,已知△ABC为等边三角形,若沿图中虚线剪去∠B,则∠1+∠2等于()A.120°B.135°C.240°D.315°二.填空题(共10小题)7.如图,四边形ABOC中,∠BAC与∠BOC的角平分线相交于点P,若∠B=16°,∠C=42°,则∠P =°.8.如图,△ABC中,∠B=80°,∠C=70°,将△ABC沿EF折叠,A点落在形内的A′,则∠1+∠2的度数为.9.如图,在三角形纸片ABC中∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=50°,则∠2的度数为.10.如图,∠1+∠2+∠3+∠4=°.11.如图,在△ABC中,E、F分别是AB、AC上的两点,∠1+∠2=235°,则∠A=度.12.如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,S△BCF=2cm2,则S△ABC=cm2.13.如图,在△ABC中,E,F分别是AB,AC上的两点,∠1+∠2=214°,则∠A=度.14.如图是某建筑工地上的人字架.这个人字架夹角∠1=120°,那么∠3﹣∠2的度数为.15.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2,…,∠A2020BC和∠A2020CD的平分线交于点A2021,得∠A2021,∠A2021BC 和∠A2021CD的平分线交于点A2022,得∠A2022,则∠A2022=度.16.已知△ABC中,∠A=α.在图(1)中∠B、∠C的角平分线交于点O1,则可计算得∠BO1C=90°+12α;在图(2)中,设∠B、∠C的两条三等分角线分别对应交于O1、O2,则∠BO2C=60°+23α;请你猜想,当∠B、∠C同时n等分时,(n﹣1)条等分角线分别对应交于O1,O2,…,O n﹣1,如图(3),则∠BO n ﹣1C=(用含n和α的代数式表示)三.解答题(共8小题)17.如图,D、E、F、G是△ABC边上的点,DE∥BC,∠1=∠2.求证:DG∥FC.18.如图,在△ABC中,AD是∠BAC的平分线,∠2=35°,∠4=65°,求∠ADB的度数.19.如图,点A、B、C、D是平面内四个点.连接AB、AC、BD、CD.(1)如图1,求证:∠BDC=∠A+∠B+∠C;(2)如图2,若BF平分∠ABD,CE平分∠ACD,BF与CE交于G,∠BDC=m°,∠BGC=n°,求∠A的度数.(用m,n表示)20.探究题(1)如图1,∠1+∠2与∠B+∠C有什么关系?为什么?(2)把图1中△ABC沿DE折叠,得到图2,填空:∠1+∠2 ∠B+∠C(填“>”“<”“=”),当∠A=30°时,∠B+∠C+∠1+∠2=.(3)如图2,是由图1的△ABC沿DB折叠得到的,如果∠A=40°,则∠BDA+∠CEA=360°﹣(∠B+∠C+∠1+∠2)=,猜想:∠BDA+∠CEA与∠A有什么关系?为什么?21.探索归纳:(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于A.90°B.135℃.270°D.315°(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.22.如图1,AD平分∠BAC,AE⊥BC,∠B=38°,∠C=64°.(1)求∠DAE的度数;(2)如图2,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”∠B=α,∠C=β(α>β),请用α、β的代数式表示∠DFE.23.旧知新意:我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?初步应用:(2)如图2,在△ABC纸片中剪去△CDE,得到四边形ABDE,∠1=130°,则∠2﹣∠C=;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案.拓展提升:(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由.)24.[尝试探究]如图1,在一张三角形纸片上,剪去△ABC,得到四边形BCHG,∠1与∠2分别为△ABC的两个外角(1)请你试着说明:∠1+∠2=180°+∠A(2)如图2,如果沿着EF再剪一刀,∠3与∠4分别为△AEF的两个外角,那么∠1+∠2和∠3+∠4的数量关系为(3)如图3,EP,FP分别平分外角∠FEG、∠EFH,求∠EPF与∠A的数量关系:[拓展提升]如图4,在四边形BCFE中,EP、FP分别平分外分∠FEG、∠EFH,请写出∠EPF,∠1、∠2这三个角的数量关系,并说明理由.。
专题3.3方差和标准差专项提升训练(重难点培优)-八年级数学下册尖子生培优必刷题(原卷版)【浙教版】

【拔尖特训】2022-2023学年八年级数学下册尖子生培优必刷题【浙教版】专题3.3方差和标准差专项提升训练(重难点培优)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷满分120分,试题共23题,其中选择10道、填空6道、解答7道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2021秋•雅安期末)人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:x甲=x乙=83,s甲2=200,s乙2=180,则成绩较为稳定的班级是()A.甲班B.乙班C.两班成绩一样稳定D.无法确定2.(2022春•温州校级期中)下表记录了甲、乙、丙、丁四位选手各10次射击成绩的数据信息,请你根据表中数据选一人参加比赛,最合适的人选是()选手甲乙丙丁平均数(环)9.29.39.39.2方差(环2)0.0350.0150.0350.015 A.甲B.乙C.丙D.丁3.(2022春•鼓楼区校级期中)若样本x1,x2,x3,…,x n的平均数为8,方差为4,则对于样本x1﹣3,x2﹣3,x3﹣3,…x n﹣3,下列结论正确的是()A.平均数为8,方差为1B.平均数为5,方差为1C.中位数变小,方差不变D.众数不变,方差为44.(2022•拱墅区校级开学)某校六一活动中,10位评委给某个节目的评分各不相同,去掉1个最高分和1个最低分,剩下的8个评分与原始的10个评分相比一定不发生变化的是()A.平均数B.中位数C.方差D.众数5.(2022•靖江市校级模拟)在2,3,4,4,7这组数据中,去掉一个数后,余下的数据的中位数不变,且方差变小,则去掉的数是()A.2B.3C.4D.76.(2021秋•萍乡期末)若一组数据x1+1,x2+1,⋯,x n+1的平均数为17,方差为2,则另一组数据x1+2,x2+2,⋯,x n+2的平均数和方差分别为()A .17,2B .17,3C .18,1D .18,27.(2022•镇江)第1组数据为:0、0、0、1、1、1,第2组数据为:0、0、⋯、0︷m 个0、1、1、⋯、1︷n 个1,其中m 、n 是正整数下列结论:①当m =n 时,两组数据的平均数相等;②当m >n 时,第1组数据的平均数小于第2组数据的平均数;③当m <n 时,第1组数据的中位数小于第2组数据的中位数;④当m =n 时,第2组数据的方差小于第1组数据的方差.其中正确的是( ) A .①②B .①③C .①④D .③④8.(2021秋•烟台期末)已知一组数据x 1,x 2,x 3,……,x n 的平均数是50、方差是1,则另一组数据2x 1+3,2x 2+3,2x 3+3,……,2x n +3的平均数和标准差分别是( ) A .53,2B .103,2C .100,4D .103,49.(2022•泰安二模)泰安市某学校学生会为了贯彻“减负增效”精神,了解九年级学生每天的自主学习情况,随机抽查了九年级一班10名学生每天自主学习的时间情况,得到的数据如表所示,下列说法正确的是( ) 自主学习时间/h0.5 1 1.5 2 2.5 人数/人12421A .本次调查学生自主学习时间的中位数是4B .本次调查学生自主学习时间的平均数是1C .本次调查学生自主学习时间的方差是0.3D .本次调查学生自主学习时间的标准差是3√5510.(2021秋•汝州市期末)描述一组数据的离散程度,我们还可以用“平均差”.在一组数x 1、x 2、x 3、…、x n 中,各数据与它们的平均数x 的差的绝对值的平均数,即T =1n (|x 1﹣x |+|x 2﹣x |+…+|x n ﹣x |)叫做这组数据的“平均差”.“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大,稳定性越小.现有甲、乙两组数据,如表所示,则下列说法错误的是( )甲 12 13 11 15 13 14 乙10161018177A .甲、乙两组数据的平均数相同B .乙组数据的平均差为4C .甲组数据的平均差是2D.甲组数据更加稳定二、填空题(本大题共6小题,每小题4分,共24分)请把答案直接填写在横线上11.(2022春•长兴县期中)下列五个数:11,12,13,14,15的标准差为.12.(2022秋•中牟县校级月考)如果一组数据3,5,x,6,8的众数为3,那么这组数据的方差为.13.(2022•扬州)某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两选手成绩的方差分别记为S甲2、S乙2,则S甲2S乙2.(填“>”“<”或“=”)14.(2021秋•福田区期末)新兴农场果农随机从甲、乙、丙三个品种的枇杷树中各选10棵,每棵产量的平均数x(单位:千克)及方差(单位:千克2)如下表所示,他准备从这三个品种中选出一种产量既高又稳定的枇杷树进行种植,则应选的品种是.甲乙丙x444442S2 1.7 1.5 1.7 15.(2022春•沂南县期末)数据x1,x2,x3,x4的平均数是4,方差是3,则数据x1+1,x2+1,x3+1,x4+1的平均数和方差分别是.16.(2022秋•文登区期中)已知数据x1,x2,…x n的方差是4,则3x1﹣2,3x2﹣2,…,3x n﹣2的标准差为.三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)17.(2022秋•青岛期末)为提高学生对计算机的兴趣,某校举办计算机汉字输入比赛.甲、乙两组各有10名学生参赛,两组学生每分钟输入汉字的个数如表:输入汉字(个)132133134135136137甲组人数(人)101521乙组人数(人)014122(1)请将表中的相关数据补充完整:组别众数(个)中位数(个)平均数(个)方差甲组135135乙组134.5 1.8(2)请根据所学的统计知识,从两个不同角度对甲、乙两组学生的比赛成绩进行分析.18.(2022秋•城阳区期末)某校计划选一名跳高运动员参加区级比赛,对甲、乙两名跳高运动员进行了8次选拔比赛,他们的成绩(单位:cm)如表:甲169164167168171172167166乙160173172161161171171175体育老师对这些数据进行了分析处理,求得:乙运动员的平均成绩为168cm,方差为33.75;甲运动员的平均成绩为168cm.(1)求甲运动员这8次比赛成绩的方差;(2)这两人中谁的成绩更稳定?说明理由;(3)据预测,在区级比赛中需跳过165cm就可能获得冠军,该校为了获得跳高比赛冠军,你认为可能选择哪位运动员参赛?说明理由.19.(2021秋•马关县期末)下表是小明这一学期数学成绩测试记录,根据表格提供的信息,回答下列问题:测试平时成绩期中测试期末测试练习一练习二练习三练习四成绩889290869096(1)求小明6次成绩的众数与中位数;(2)若把四次练习成绩的平均分作为平时成绩,求小明的平时成绩;(3)按照学校规定,本学期的综合成绩的权重如图所示,请求出小明本学期的综合成绩;(注意:把四次练习成绩的平均分作为平时成绩)(4)若全班共有45名同学,综合成绩排名前23的同学可以获得奖励,小明知道了自己的分数后,想知道自己能不能获奖,还需知道全班同学综合成绩的.(填“平均数、中位数、众数、方差”)20.(2022秋•淄川区期中)八(1)班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛,在相同的条件下,分别对两名男生进行了八分钟一次的跳绳比赛,现将测试结果绘制成如下不完整的统计图表:平均数中位数众数方差甲175a b93.75乙175175180,175,170c请根据统计图表中的信息解答下列问题:(1)a=,b=,c=;(2)根据以上的数据分析,请你运用所学的统计知识,任选两个角度评价甲、乙两名男生一分钟跳绳成绩谁优.21.(2021秋•东平县期末)为弘扬泰山文化,我市某校举办了“泰山诗文大赛”活动,小学、初中部根据初赛成绩,各选出5名选手组成小学代表队和初中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.(1)根据图示填写图表;平均数(分)中位数(分)众数(分)小学部85初中部85100(2)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.22.(2021秋•王益区期末)某校组织八年级学生电脑技能竞赛,每班选派相同人数去参加竞赛,竞赛成绩分A、B、C、D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.将八年级(1)班和(2)班的成绩整理并绘制成统计图表如下:竞赛成绩分析表平均数(分)中位数(分)众数(分)方差(1)班a90b26.25(2)班c d100136根据以上信息,解答下列问题:(1)b=分.d=分;(2)分别求两班此次竞赛成绩的平均分;(3)分析上述数据,请问八年级(1)班和八年级(2)班哪个表现更稳定一些?并说明理由.23.(2022秋•晋州市期中)甲、乙两名队员参加射击选拔赛,射击成绩见统计图:根据以上信息,整理分析数据如下:队员平均数(环)中位数(环)众数(环)方差(环2)甲7.9b c 4.09乙a77d(1)直接写出表格中a、b,c的值;(2)求出d的值;(3)若从甲、乙两名队员中选派其中一名队员参赛,你认为应选哪名队员?请结合表中的四个统计量,作出简要分析.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
《一次函数》测试题
一、精心选一选
1.下列各点中在函数y=
x 21
+3的图象上的是( ) (A)(3,-2) (B)(32,3) (C)(-4,1) (D)(5, 2
5
)
2.正比例函数y=kx ,当时k >0,下面结论正确的是( )
A 、永远是正值
B 、永远是负值
C 、随着k 的增大而减小
D 、随着k 的增大而增大 3.函数y=-
1
1 x 中自变量的取值范围是( )
A 、x ≠0
B 、x <-1
C 、x ≠-1
D 、x >-1
4. 已知点(-4,y 1),(2,y 2)都在直线y=- 1
2 x+2上,则y 1 y 2大小关系是( )
(A )y 1 > y 2 (B )y 1 = y 2 (C )y 1 < y 2 (D )不能比较 5.若一次函数y=(3+k)x+18-2k 2图象经过原点,则k 为( ) A 、3 B 、-2 C 、±3 D 、任何实数
6.一根蜡烛长20cm ,点燃后每小时燃烧5cm ,燃烧时剩下的高度(cm)与燃烧时间(小时)的函数关系用图象表示为( )
7.已知正比例函数y=kx(k ≠
0)
的函数值随x
的增大而增大,则一次函数y=x+k 的图象大致是( )
8.如图是一次函数y=kx+b 的图象,
当x <1时,y 的取值范围是( )
x
A
x
B
x
C
x
D
A
B
x
C
x
D
x
A 、y >0
B 、y <0
C 、-2 <y <0
D 、-2 <y <2
二、细心填一填
9.若函数y= -2x m+2是正比例函数,则m 的值是 。
10.已知一次函数y=kx+5的图象经过点(-1,2),则k= 。
11.点P (a ,b )在第二象限,则直线y=ax+b 不经过第 象限。
12.已知一次函数y=kx-k+4的图象与y 轴的交点坐标是(0,-2),那么这个一次函数的表达式是______________。
13.一次函数y=kx+b 与y=2x+1平行,且经过点(-3,4),则表达式为: 。
三、耐心做一做
14. 已知一个一次函数,当3x =时,2y =-;当2x =时,3y =-,求这个一次函数的解析式。
15. 已知一次函数的图象经过(3,5)和(-4,-9)两点。
(1)求此一次函数的解析式. (2)若点(a ,2)在函数图象上,求a 的值
16. 直线y=2x+m 和直线y=3x+3的交点在第二象限,求m 的取值范围.
17.已知一次函数y=kx+b 的图象经过点(-1, -5),且与正比例函数y= 1
2 x 的图象相交
于点(2,a),求 (1)a 的值 (2)k ,b 的值
(3)这两个函数图象与x 轴所围成的三角形的面积。
18.(12分)一次函数y=kx+b 的图象如图所示:(1)求出该一次函数的表达式; (2)当x=10时,y 的值是多少? (3)当y=12时,•x 的值是多少?
19、某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用
水每吨收费1.8元,超计划部分每吨按2.0元收费。
(1)写出该单位水费y (元)与每月用水量x (吨)之间的函数关系式:
①当用水量小于等于3000吨 ;②当用水量大于3000吨 。
(2)某月该单位用水3200吨,水费是 元;若用水2800吨,水费 元。
(3)若某月该单位缴纳水费9400元,则该单位用水多少吨?
20、如图是某市出租车单程收费y (元)与行驶路程x (千米)之间的函数关系图象,根据图象回答下列问题: (1)当行使路程为8千米时,收费应为 元; (2)从图象上你能获得哪些信息?(请写出2条)
①
② (3)求出收费y (元)与行使路程x (千米) (x ≥3)之间的函数关系式。
21.甲、乙两人分别骑自行车和摩托车从甲地到乙地
(1)谁出发较早,早多长时间?谁到达乙地早?早多长时间?
(2)两人行驶速度分别是多少?
(3)分别求出自行车和摩托车行驶过程的函数解析式?
22. 某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
注:利润=售价-成本
(1)该公司对这两种户型住房有哪几种建房方案?
(2)该公司如何建房获得利润最大?
(3)根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a 万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?。
