改进分析过程的模态pushover分析
midas关于Pushover分析总结
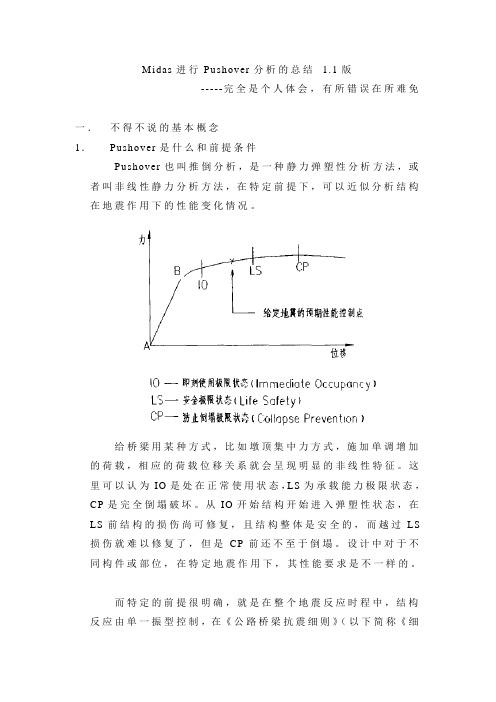
M i das进行P ushover分析的总结 1.1版-----完全是个人体会,有所错误在所难免一.不得不说的基本概念1.P ushover是什么和前提条件P ushover也叫推倒分析,是一种静力弹塑性分析方法,或者叫非线性静力分析方法,在特定前提下,可以近似分析结构在地震作用下的性能变化情况。
给桥梁用某种方式,比如墩顶集中力方式,施加单调增加的荷载,相应的荷载位移关系就会呈现明显的非线性特征。
这里可以认为IO是处在正常使用状态,LS为承载能力极限状态,CP是完全倒塌破坏。
从IO开始结构开始进入弹塑性状态,在LS前结构的损伤尚可修复,且结构整体是安全的,而越过LS 损伤就难以修复了,但是CP前还不至于倒塌。
设计中对于不同构件或部位,在特定地震作用下,其性能要求是不一样的。
而特定的前提很明确,就是在整个地震反应时程中,结构反应由单一振型控制,在《公路桥梁抗震细则》(以下简称《细则》)中,认为常规桥梁中的规则桥梁都满足这一条件(条文说明 6.3.4),因此E1地震可以采用简化反应谱方法,也可用一般的多振型反应谱方法,E2则用Pus hover。
2.P ushover的分析目的在E2地震作用下,《细则》要求:可见,对于规则桥梁,只需要检算墩顶位移就可以了。
对于单柱墩,容许位移可按7.4.7条推荐的公式进行计算,而双柱墩按7.4.8条要求进行Pus hover分析根据塑性铰的最大容许转角(7.4.3)得到。
而无论是7.4.3还是7.4.7都要用到Φy和Φu,对于圆形或者矩形截面可按附录B计算,而特殊的截面,可按7.4.4和7.4.5的要求计算。
计算方法可以自己编程实现,也可用现成的软件如R es ponse2000等来作为工具。
而对于在特定的E2地震作用下,墩顶的位移,都需要用P ushover的能力谱法得到。
所以Pus hover的目的一个是画出荷载位移曲线后,找到塑性铰达到最大容许转角时的曲线点,计算出墩顶容许位移,第2个目的是应用能力谱法,找到性能点,得到E2地震作用下,墩顶的位移。
Pushover分析方法一般过程

Pushover分析是基于性能设计的有力工具。
基于性能的设计可以使工程师更深入的理解和控制不同荷载水平下的结构行为。
SAP2000的非线性版本提供了Pushover分析功能。
进行Pushover分析的一般过程如下。
下面列出了Pushover分析的一般步骤,注意,其中某些步骤是由SAP2000自动完成的。
1)建立结构和构件的计算模型。
2)定义框架铰属性并指定其给框架/索单元。
3)定义钢或混凝土设计可能需要的任意荷载工况和静力与动力分析工况,特别是使用默认铰时。
4)运行设计需要的分析。
5)若任何混凝土铰属性是基于程序计算的默认值时,必须进行混凝土设计,这样确定配筋。
6)若任何钢铰基于程序对于自动选择框架界面计算的默认值,必须进行钢设计且接受程序选择的截面。
7)定义Pushover分析所需的荷载工况,包括:ν重力荷载和其他可能在施加横向地震荷载前作用在结构的荷载。
可能在前面对于设计已经定义了这些荷载工况。
ν用来推结构的横向荷载。
若准备使用加速度荷载或模态荷载,不需要任何新的荷载工况,虽然模态荷载需要定义一个模态分析工况。
8)定义Pushover分析使用的非线性静力分析工况,包括:ν一系列的一个或多个使用荷载控制的从零开始施加重力和其他固定荷载的工况。
这些工况包括阶段施工和几何非线性。
ν从此系列开始并施加横向Pushover荷载的一个或多个Pushover工况。
这些荷载应使用位移控制。
被监测的位移通常位于结构的顶部,将用来绘制Pushover曲线。
9)运行Pushover分析工况。
10)审阅Pushover结果:绘制Pushover曲线、显示铰状态的变形形状、力和弯矩图形,且打印或显示需要的结果。
11)按需要修改模型并重复。
应考虑几种不同的横向Pushover工况来代表可能在动力加载时发生的不同顺序的响应,这是很重要的。
特别地,应在X和Y两个方向推结构,且可能在两者间有角度。
对于非对称结构,在正和负方向推结构可能产生不同的结果。
[精品文档]静力弹塑性分析方法(Pushover方法)与动力弹塑性分析方..
![[精品文档]静力弹塑性分析方法(Pushover方法)与动力弹塑性分析方..](https://img.taocdn.com/s3/m/91f1bffa0875f46527d3240c844769eae009a32a.png)
静力弹塑性分析方法(Pushover方法)与动力弹塑性分析方法的优缺点比较一、Pushover分析法1、Pushover分析法优点:(1)作为一种简化的非线性分析方法,Pushover方法能够从整体上把握结构的抗侧力性能,可以对结构关键机构及单元进行评估,找到结构的薄弱环节,从而为设计改进提供参考。
(2)非线性静力分析可以获得较为稳定的分析结果,减小分析结果的偶然性,同时花费较少的时间和劳力,较之时程分析方法有较强的实际应用价值。
2、Pushover分析法缺点:(1)它假定所有的多自由度体系均可简化为等效单自由度体系,这一理论假定没有十分严密的理论基础。
(2)对建筑物进行Pushover分析时首先要确定一个合理的目标位移和水平加载方式,其分析结果的精确度很大程度上依赖于这两者的选择。
(3)只能从整体上考察结构的性能,得到的结果较为粗糙。
且在过程中未考虑结构在反复加载过程中损伤的累积及刚度的变化。
不能完全真实反应结构在地震作用下性状。
二、弹塑性时程分析法1、时程分析法优点:(1)采用地震动加速度时程曲线作为输入,进行结构地震反应分析,从而全面考虑了强震三要素,也自然地考虑了地震动丰富的长周期分量对高层建筑的不利影响。
(2)采用结构弹塑性全过程恢复力特性曲线来表征结构的力学性质,从而比较确切地、具体地和细致地给出结构的弹塑性地震反应。
(3)能给出结构中各构件和杆件出现塑性铰的时刻和顺序,从而可以判明结构的屈服机制。
(4)对于非等强结构,能找出结构的薄弱环节,并能计算出柔弱楼层的塑性变形集中效应。
2、时程分析法缺点:(1)时程分析的最大缺点在于时程分析的结果与所选取的地震动输入有关,地震动时称所含频频成分对结构的模态n向应有选择放大作用,所以不同时称输入结果差异很大。
(2)时程分析法采用逐步积分的方法对动力方程进行直接积分,从而求得结构在地震过程中每一瞬时的位移、速度和加速度反应。
所以此法的计算工作十分繁重,必须借助于计算机才能完成。
静力弹塑性分析(Pushover分析)两种方法剖析
静力弹塑性分析(Pushover分析)■简介Pushover分析是考虑构件的材料非线性特点,分析构件进入弹塑性状态直至到达极限状态时结构响应的方法。
Pushover分析是最近在地震研究及耐震设计中经常采用的基于性能的耐震设计(Performance-BasedSeismicDesign,PBSD)方法中最具代表性的分析方法。
所谓基于性能的耐震设计就是由用户及设计人员设定结构的目标性能(targetperformance),并使结构设计能满足该目标性能的方法。
Pushover分析前要经过一般设计方法先进行耐震设计使结构满足小震不坏、中震可修的规范要求,然后再通过pushover分析评价结构在大震作用下是否能满足预先设定的目标性能。
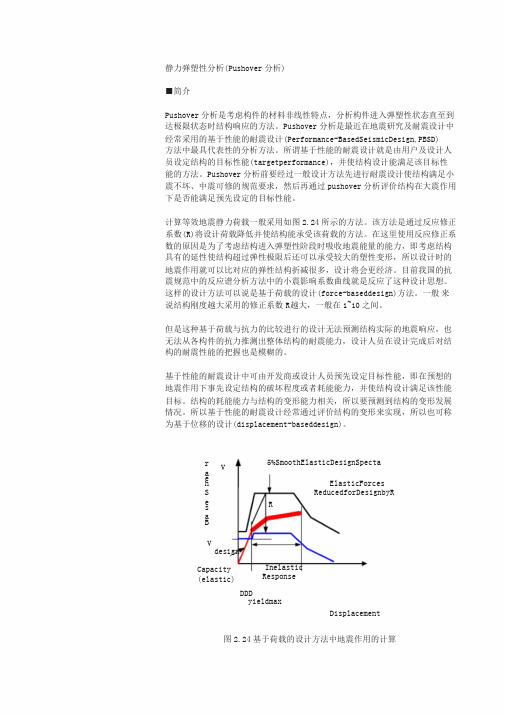
计算等效地震静力荷载一般采用如图2.24所示的方法。
该方法是通过反应修正系数(R)将设计荷载降低并使结构能承受该荷载的方法。
在这里使用反应修正系数的原因是为了考虑结构进入弹塑性阶段时吸收地震能量的能力,即考虑结构具有的延性使结构超过弹性极限后还可以承受较大的塑性变形,所以设计时的地震作用就可以比对应的弹性结构折减很多,设计将会更经济。
目前我国的抗震规范中的反应谱分析方法中的小震影响系数曲线就是反应了这种设计思想。
这样的设计方法可以说是基于荷载的设计(force-baseddesign)方法。
一般来说结构刚度越大采用的修正系数R越大,一般在1~10之间。
但是这种基于荷载与抗力的比较进行的设计无法预测结构实际的地震响应,也无法从各构件的抗力推测出整体结构的耐震能力,设计人员在设计完成后对结构的耐震性能的把握也是模糊的。
基于性能的耐震设计中可由开发商或设计人员预先设定目标性能,即在预想的地震作用下事先设定结构的破坏程度或者耗能能力,并使结构设计满足该性能目标。
结构的耗能能力与结构的变形能力相关,所以要预测到结构的变形发展情况。
所以基于性能的耐震设计经常通过评价结构的变形来实现,所以也可称为基于位移的设计(displacement-baseddesign)。
关于改进模态Pushover方法的探讨

fr n eg t r n lz d u igb t n -tg n wo sa eM PA r cd r .Th e ut h w h t e e th ih saea ay e sn o ho esa ea d t ~t g poeue er s lss o t a t - tg P p o e u eh sb te c u a yi h n lsso al ul ig,a di c nas eu e wosa eM A r c d r a e tra c r c t ea ay i ftl b i n n d n a lob s di t n
第1 8卷 第 6期
21 0 0年 1 2月
安 徽 建 筑 工业 学 学 报 ( 院 自然科学版)
n u ty J u n l fAn u n ttt fArhtcu e& Id sr o r a h iIsiueo c iet r o
Vo. 8 No 6 11 .
De. 2 0 c 01
t r s n t i p p r h a ea o d n d AS u e .I h s a e ,t eltr lla ig mo ei I PA t o e lc d b h n P p o e n me h di r pa e y t eo ei M A r c 一 s n 一
关 于 改 进 模 态 P s o e 方 法 的探 讨 u h vr
孙 场 , 冯仲 齐
705) 10 5 ( 安 建 筑科 技 大 学 理 学 院 , 西 西安
摘
要: 近年来 , 静力弹塑性分析方 法得 到了深入 的研究和广泛 的应用 。为了使静力弹塑性分 析 P so e 方 u e d n c e itc fe il i g,t eM P l a i g mo e i d v d d i t wo s a e . An wo f a swih d f h A d n d i i e o t t g s o s n d t r me t i —
PUSHOVER分析方法全攻略

PUSHOVER分析方法全攻略作为一种常用的风险评估方法,PUSHOVER分析(Pushover Analysis)是一种基于位移的结构性能评估方法,可用于评估结构在地震等外部力作用下的破坏性能。
PUSHOVER分析的基本原理是通过对结构进行逐步加载,计算结构的位移响应,并在每个加载级别上评估结构的非弹性变形。
其中,位移响应与荷载之间的关系被表示为荷载位移曲线(Load-displacement Curve),曲线上的各点对应于结构在不同荷载水平上的位移响应。
为了进行PUSHOVER分析,以下是一些主要步骤和技术,供参考:1.结构模型准备首先,需要准备一个精确的结构模型,包括准确的几何形状、结构材料性质以及荷载。
模型可以通过各种建模软件进行创建,如ETABS、SAP2000等。
2.定义截面性能曲线对于每个结构构件,需要定义其截面的性能曲线。
这些曲线一般采用双切模型(Bi-linear Model)或多切模型(Multi-linear Model)来表示构件的力-位移响应。
3.建立非线性弹簧模型根据结构的截面性能曲线,需要建立每个构件的非线性弹簧模型。
这些弹簧模型可以通过弹簧刚度系数和屈服强度等参数来表示。
4.定义加载方式定义结构的加载方式,包括单项或多项加载。
在推进分析中,通常采用单项加载,即逐步增加水平荷载。
5.设定分析参数根据需要,设定分析的参数,包括推进步长、最大推进步数以及各构件的水平刚度。
6.进行PUSHOVER分析根据设定的加载方式和分析参数,进行PUSHOVER分析。
在每个加载步骤中,计算结构的位移响应,并绘制荷载位移曲线。
7.评估结构性能根据荷载位移曲线,评估结构的性能,包括塑性铰的形成、破坏模式以及结构的侧向刚度退化等。
8.修正分析结果在分析过程中,根据实际情况对模型进行修正。
例如,在形成塑性铰后,可以调整结构的刚度或强度参数。
9.分析结果报告最后,将分析结果整理成报告,包括结构的性能评估、塑性铰的位置和破坏模式等信息。
Pushover分析(弹塑性分析)

Pushover曲线 能力谱加速度Sa 基底剪力Vb
能力谱曲线
V Sa G1
(Sdt,sat)
Sd
top
1 X top ,1
顶点位移Dt
能力谱位移Sd
有效质量比
1
[ (Gi X i1 ) / g ]2
i 1
n
Sd T 2 Sa G
Gi 为结构第i楼层重量
[ Gi / g ][ (Gi X i2 1) / g]
Push-over的基本问题可以概括为三个方面:
如何求得结构的能力曲线? 如何确定结构的目标位移? 如何对计算结果进行评价?
结构能力曲线的计算包括两个方面的主要内容 一 计算模型的建立 二 侧向力的分布形式
结构计算模型—纤维模型
基于平截面假定,将梁柱的内力-变形关系转化成混凝土与钢 筋的单轴应力-应变关系。
为阻尼修正系数,取0.3~1.0
ED为阻尼所消耗的能量(图中虚线部分平行四边形的面积) EE为最大应变能(图中斜线阴影部分的三角形的面积)
Sa A1 A2 T 能力谱曲线 Sa api ay T 能力谱曲线 P EE
P
dy Sd ED
dpi
Sd
用双线型代替能力谱曲线的条件:A1=A2
Teq
T 1
T 2 Sdp Sd ( ) Sa R R 2
R表示由于结构的非弹性变 形对弹性地震力的折减系数
R ( 1) T 1 T T0 T0
R T T0
T0 0.65 0.3Tg Tg
采用Push-over方法对 抗震性能进行评估
最简单的方法是直接得到目标位移点(性能点)与结构的能力曲线。 得到性能点后,经过转化可以得到能力曲线上相应的点,能力曲线上的每 一个点都对应着结构的一个变形状态。根据性能点对应的变形,可以对结 构进行以下方面的评价:顶点侧移和层间位移角是否满足抗震规范规定的 位移限值;构件的局部变形(指梁、柱等构件的塑性铰变形),检验他是 否超过建筑某一性能水平下的允许变形;结构构件的塑性铰分布是否构成 倒塌机构。
Push-over方法的理论与应用

Push-over方法的理论与应用专业品质权威编制人:______________审核人:______________审批人:______________编制单位:____________编制时间:____________序言下载提示:该文档是本团队精心编制而成,期望大家下载或复制使用后,能够解决实际问题。
文档全文可编辑,以便您下载后可定制修改,请依据实际需要进行调整和使用,感谢!同时,本团队为大家提供各种类型的经典资料,如办公资料、职场资料、生活资料、进修资料、教室资料、阅读资料、知识资料、党建资料、教育资料、其他资料等等,想进修、参考、使用不同格式和写法的资料,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of classic materials for everyone, such as office materials, workplace materials, lifestyle materials, learning materials, classroom materials, reading materials, knowledge materials, party building materials, educational materials, other materials, etc. If you want to learn about different data formats and writing methods, please pay attention!Push-over方法的理论与应用Push-over方法是一种常用于结构抗震性能评估和设计的分析方法,它通过模拟结构在地震作用下的非线性行为,为工程师提供了便捷且较准确的结构性能分析工具。
建筑结构的Pushover方法分析研究的开题报告

建筑结构的Pushover方法分析研究的开题报告一、选题背景随着建筑结构设计、施工技术和建筑材料的飞速发展,大型建筑结构的复杂性不断增加,需要更加精细和严谨的分析和设计手段。
建筑结构的可靠性、安全性是极其重要的关键问题,需要进行定量分析和评估。
而Pushover方法作为一种比传统地震响应谱分析更加有效且易于有效实施的非线性静力分析方法,近年来在建筑结构领域越来越受到重视。
本文旨在探讨Pushover方法在建筑结构分析中的应用,为建筑结构可靠性与安全性的提高提供指导。
二、研究目的1. 推广Pushover方法的优势,掌握该方法的基本理论和实现方法。
2. 分析Pushover方法的可靠性和实用性,探究其在建筑结构分析中的应用前景。
3. 通过实例给出Pushover方法在建筑结构分析中的计算过程和结果分析,验证其实际应用价值。
三、研究内容1. Pushover方法的基本原理和理论。
2. Pushover方法在建筑结构典型结构中的应用研究。
3. 基于Pushover方法的建筑结构抗震性能评估。
4. 如何选择适合的Pushover软件进行模拟分析。
5. 实例分析,选择典型建筑进行计算分析,得出具体的结果,并进行实验验证。
四、期望研究结果1. 对Pushover方法基本原理、模拟分析方法和实现过程有深刻理解。
2. 掌握Pushover方法对于建筑结构有非常大的应用前景,提高该方法在建筑结构领域的推广和应用。
3. 进行实例分析,得出实际结果并进行验证。
4. 为建筑结构优化设计和工程实践提供有效方法和方向。
五、研究方法1. 文献综述:系统地查阅学术文献,了解国内外学界对于Pushover方法在建筑结构领域的研究现状,确定研究问题的具体方向。
2. 数值分析:选择适合的Pushover软件,对建筑结构进行模拟分析,得出具体的数据与结果。
3. 实践验证:选取典型建筑进行实验验证,对比分析实验真实结果和模拟计算结果,验证分析模型的准确性和实用性。
改进模态pushover法应用于高墩桥梁抗震分析

得 到 整个结 构 的反应
在 结构 静力 弹塑性 地震 反应 分 析 中 .高 阶振 型对 高墩抗 震能 力 的影响体 现 在高 阶振 型对 高墩 位移延 性 能力 的影 响 国内外一 些研 究者 提 出 的一 些 可 以考 虑
方 法进行 改进 .研 究在 桥梁 领域 内高阶振 型对 高墩 位 移延 性 能力 的影 响 。p s0 e 分 析方 法从 本 质上 说 是 uh vr
一
式 中 : 为 体系 质量 :C为 体 系特 征 阻尼 ; 为 单位 为与 结构 位移 时程 有关 的恢 复 力模 型 , = s f
多 自由度 弹塑 性结 构在 地震 地面 运动 下 的动力方 程 为[: 2 1
“ &+ u & C& 向量 ;
.
( U,s n &)= ML && i U g - u g
() 1
高 阶振 型 作用 的位移 延 性 能力 分 析 方法 [ 1 ] .主要 被 用 于对 高 层建 筑 的抗震 研究 本文 将其 中模 态 p so e uh vr
1 常规 加载 p s o e 分 析方 法 uhvr
过程 和计 算成果 常 规 加 载 D soe 分 析 方 法 是 选 择 适 当 的侧 向 uh v r 荷载分 布模 式 .结构 在这 些侧 向荷 载 的作用 下逐 步达
同 自振 周期 和振 型 的线 弹性体 系等 价 ,即线 弹性 的假
( U,s n &) & i U ;M ()为地 面地 震动 输入 。 g t
我 们认 为在 振 幅较小 的 时候 .弹性 体 系的 刚度 和
弹塑 性体 系 的初始 刚度 相 同 .且 两 种体 系有 相 同的质 量 和 阻尼 比时 .弹塑性 结 构体 系 的振动 特性 和具有 相
静力弹塑性分析方法(Pushover方法)与动力弹塑性分析方法的优缺点比较

静力弹塑性分析方法(Pushover方法)与动力弹塑性分析方法的优缺点比较一、Pushover分析法1、Pushover分析法优点:(1)作为一种简化的非线性分析方法,Pushover方法能够从整体上把握结构的抗侧力性能,可以对结构关键机构及单元进行评估,找到结构的薄弱环节,从而为设计改进提供参考。
(2)非线性静力分析可以获得较为稳定的分析结果,减小分析结果的偶然性,同时花费较少的时间和劳力,较之时程分析方法有较强的实际应用价值。
2、Pushover分析法缺点:(1)它假定所有的多自由度体系均可简化为等效单自由度体系,这一理论假定没有十分严密的理论基础。
(2)对建筑物进行Pushover分析时首先要确定一个合理的目标位移和水平加载方式,其分析结果的精确度很大程度上依赖于这两者的选择。
(3)只能从整体上考察结构的性能,得到的结果较为粗糙。
且在过程中未考虑结构在反复加载过程中损伤的累积及刚度的变化。
不能完全真实反应结构在地震作用下性状。
二、弹塑性时程分析法1、时程分析法优点:(1)采用地震动加速度时程曲线作为输入,进行结构地震反应分析,从而全面考虑了强震三要素,也自然地考虑了地震动丰富的长周期分量对高层建筑的不利影响。
(2)采用结构弹塑性全过程恢复力特性曲线来表征结构的力学性质,从而比较确切地、具体地和细致地给出结构的弹塑性地震反应。
(3)能给出结构中各构件和杆件出现塑性铰的时刻和顺序,从而可以判明结构的屈服机制。
(4)对于非等强结构,能找出结构的薄弱环节,并能计算出柔弱楼层的塑性变形集中效应。
2、时程分析法缺点:(1)时程分析的最大缺点在于时程分析的结果与所选取的地震动输入有关,地震动时称所含频频成分对结构的模态n向应有选择放大作用,所以不同时称输入结果差异很大。
(2)时程分析法采用逐步积分的方法对动力方程进行直接积分,从而求得结构在地震过程中每一瞬时的位移、速度和加速度反应。
所以此法的计算工作十分繁重,必须借助于计算机才能完成。
pushover分析

目标位移反映了结构在特定地震作用水平下可能达到的最大位 移,问题的核心实际上是反应谱(需求谱)的确定。
能力谱法
2021/10/10
26
结构能力曲线的分析步骤
(1)建立结构的计算模型,模型中应考虑所有对结构刚度、质量、强度 以及抗震性能有重要作用的构件。然后给结构加上重力荷载,重力荷载 包括全部恒载和部分静载。
(2)施加沿高度分布的某种水平荷载 静力弹塑性分析时所采用的水平侧力加载模式代表结构上地震惯
性力的分布,水平侧力加载模式直接影响分析结果。 水平侧力加载模式主要有均匀加载、倒三角形加载、基本振型加
xyrMr Qyr
将多自由度体系等效为单自由度体系的目的: 以单自由度体系的弹性、弹塑性反应反推多自由度体系的弹性、 弹塑性反应。 优点: 利用反应谱进行弹性范围内的计算,单自由度体系在理论上是 严密的;可以将反应谱的概念推广到弹塑性阶段,亦即所谓的 “弹塑性反应谱”; 针对单自由度体系的工作量大大少于针对多自由度体系的工作 量。上述这种基于振型向量与结构反应水平无关的等效方法最 为常见。
Chopra提出的弹塑性反应谱曲线 (不需要迭代求解)
Sdp
RSd
R(2T)2Sa
R表示由于结构的非弹性变 形对弹性地震力的折减系数
R(1)T 1
T0
TT0
R TT0
T00.650.3Tg Tg
采用Push-over方法对 抗震性能进行评估
最简单的方法是直接得到目标位移点(性能点)与结构的能力曲线。 得到性能点后,经过转化可以得到能力曲线上相应的点,能力曲线上的每 一个点都对应着结构的一个变形状态。根据性能点对应的变形,可以对结 构进行以下方面的评价:顶点侧移和层间位移角是否满足抗震规范规定的 位移限值;构件的局部变形(指梁、柱等构件的塑性铰变形),检验他是 否超过建筑某一性能水平下的允许变形;结构构件的塑性铰分布是否构成 倒塌机构。
采用MidasGen进行结构Pushover科学分析的方法

Tn2 42
Sa
transform
Tn,2
Tn
Response Spectrum
Demand Spectrum Sd
5% Elastic
Sa Spectrum
Performance Point Demand Spectrum
Amax
Capacity Spectrum
Dmax
Sd
具体地说,就是在结构计算模型 上施加按某种规则分布的水平侧向力, 单调加载并逐级加大;一旦有构件开 裂(或屈服)即修改其刚度(或使其 退出工作),进而修改结构总刚度矩 阵,进行下一步计算,依次循环直到 结构达到预定的状态(成为机构、位 移超限或达到目标位移),得到荷载 -位移曲线。
重新定义; • 需要定义自重、质量; • 需要定义层信息,以及墙编号;
此外,应注意比较SATWE的质量与Midas/Gen的质量, 并比较两者计算的周期结果是否一致。
2、输入Pushover分析控制用数据
荷载最大增幅次数用于定义达到设定的目标位移 (或荷载)的分步数,一般来说,分步越多,每次的增 幅越小,最终得到的能力谱曲线越平滑。但是分步过多 带来计算时间上的大大增加,所以取值应该由少至多进 行试算,直到取得满意的曲线结果为止。
可显示不同颜色区分铰的各个阶段,并可在图例中看到各阶 段的铰所占比例。
对梁分配弯矩铰,对柱和剪力墙分配轴力-弯矩铰。剪 力墙除分配轴力-弯矩铰之外,还须指定剪切铰。
5、分析结果
Pushover曲线输出结果如下图所示
可以在 变形形状 菜单中查看结构在整个 Pushover过程中的变形以及铰生成情况:
图1 10分步,每步最大10次迭代结果 图2 20分步,每步最大10次迭代结果
pushover分析

(a)倒三角形加载
(b)抛物线加载
均匀加载
Pj
V n
(c)均匀加载
此模式适宜于刚度与质量沿高度分布较均匀,且薄弱层为底层的结构。
(d)变振形加载
(a)倒三角形加载
(b)抛物线加载
(c)均匀加载
(d)变振形加载
倒三角加载(底部剪力法模式)
Pj
Wjhj
n
V
Wi hi
i 1
此模式适宜于高度不大于40米,以剪切变形为主且刚度与质量沿高度分布较均匀的结构。
由Pushover方法基本假定(2)可知,结构的高度变形由结
构的形状向量{Φ}表示,并且在整个加载过程中,结构的形
状向量是固定不变的。
假定结构的相对位移向量可由结构顶点位移xtop 和形状向量
{Φ}表示:
x xtop
[M ] xtop [C] xtop R [M ]I xg (t)
Push-over的基本问题可以概括为三个方面:
如何求得结构的能力曲线? 如何确定结构的目标位移? 如何对计算结果进行评价?
结构能力曲线的计算包括两个方面的主要内容 一 计算模型的建立 二 侧向力的分布形式
结构计算模型—纤维模型
基于平截面假定,将梁柱的内力-变形关系转化成混凝土与钢筋的单轴应力-应变关系。
静力弹塑性(Pushover)分析方法
静力推覆分析是结构分析模型在一个沿结构高度为某种 规定分布形式且逐渐增加的侧向力或侧向位移作用下,采用 荷载控制或位移控制的方式,在加载过程中根据构件屈服程 度不断调整结构刚度矩阵,直至结构模型控制点达到目标位 移或结构倾覆为止,得到结构的基底剪力—顶点位移能力谱 曲线。
浅谈静力弹塑性分析(Pushover)及理解与应用

浅谈静力弹塑性分析(Pushover )的理解与应用摘要:本文首先介绍采用静力弹塑性分析(Pushover )的主要理论基础和分析方法,以Midas/Gen 程序为例,采用计算实例进行具体说明弹塑性分析的步骤和过程,表明Pushover 是罕遇地震作用下结构分析的有效方法。
关键词:静力弹塑性 Pushover Midas/Gen 能力谱 需求谱 性能点一、基本理论静力弹塑性分析方法,也称Pushover 分析法,是基于性能评估现有结构和设计新结构的一种静力分析方法,在一定精度范围内对结构在罕遇地震作用下进行弹塑性变形分析。
简要地说,在结构计算模型上施加按某种规则分布的水平侧向力或侧向位移,单调加荷载(或位移)并逐级加大;一旦有构件开裂(或屈服)即修改其刚度(或使其退出工作),进而修改结构总刚度矩阵,进行下一步计算,依次循环直到控制点达到目标位移或建筑物倾覆为止,得到结构能力曲线,之后对照确定条件下的需求谱,并判断是否出现性能点,从而评价结构是否能满足目标性能要求。
Pushover 分析的基本要素是能力谱曲线和需求谱曲线,将两条曲线放在同一张图上,得出交会点的位移值,同位移容许值比较,检验是否满足特定地震作用下的弹塑性变形要求。
能力谱曲线由能力曲线(基底剪力-顶点位移曲线)转化而来(图1)。
与地震作用相应的结构基底剪力与结构加速度为正相关关系,顶点位移与谱位移为正相关关系,两种曲线形状一致。
其对应关系为:1/αG V S a =roofroof d X S ,11γ∆=,图1 基底剪力-顶点位移曲线转换为能力谱曲线其中1α、1γ、roof X ,1分别为第一阵型的质量系数,参与系数、顶点位移。
该曲线与主要建筑材料的本构关系曲线具有相似性,其实其物理意义亦有对应,在初始阶段作用力与变形为线性关系,随着作用力的增大,逐渐进入弹塑性阶段,变形显著增长,不论对于构件,还是结构整体,都是这个规律。
需求谱曲线由标准的加速度响应谱曲线转化而来。
PUSHOVER方法

PUSHOVER方法PUSHOVER方法(PUSHOVER method)是一种简单、经济、直观且有效的方法,用于对结构的强度和刚度进行初步评估。
它是结构工程师在设计过程中常用的一种方法,特别适用于预制结构、短周期结构和轻型结构等。
PUSHOVER方法基于弹塑性分析原理,通过分析结构在地震荷载下的非线性行为,直观地展示结构在不同荷载水平下的变形和受力情况。
在PUSHOVER方法中,结构被简化为一维弹塑性模型,并进行单方向的静力分析。
结构的非线性行为通过增量形式的弹塑性模型来表示,荷载由小到大逐步增加,直至结构达到破坏。
1.确定结构模型:首先,需要将结构转化为一维、双向的框架模型,包括主要的水平和垂直支撑、梁和柱等。
通常,无溶接链接使用简化的接头,而有溶接链接使用精确的模型。
2.选择地震荷载曲线:根据结构所在地区的地震参数和设计要求,选择适当的地震荷载曲线。
常用的荷载曲线包括线性弹性荷载、等效静力荷载和增量动力荷载等。
3.设定分析参数:确定分析所需的参数,如荷载递增步长、分析区间和结构材料的损伤模型等。
4.进行弹塑性分析:根据设定的荷载递增步长,以及结构的初始状态,进行弹塑性分析。
在每个荷载步骤中,根据结构的初始刚度和荷载作用,计算结构的变形、内力和屈服状态。
5.绘制PUSHOVER曲线:根据分析结果,绘制PUSHOVER曲线。
PUSHOVER曲线是结构侧向位移与结构侧向剪力的函数关系图。
它直观地展示了结构在不同荷载水平下的响应。
通过PUSHOVER曲线,结构工程师可以评估结构的强度储备和抗震性能,并确定结构在不同限额位移水平下的塌陷载荷。
这对于设计抗震设防和结构强度调整具有重要意义。
PUSHOVER方法的优点在于其简单性、经济性和直观性。
相对于复杂的动力分析方法,PUSHOVER方法可以在较短的时间内得到合理的结果。
另外,PUSHOVER方法还可以用于实际结构的性能评估和性能矫正,使结构工程师可以方便地进行结构设计和优化。
基于改进的模态往复 pushover 法的拱桥抗震性能评估

基于改进的模态往复 pushover 法的拱桥抗震性能评估禹奇才;林加爵;刘爱荣;邓江东【摘要】针对目前拱桥抗震性能评估方法的不足以及抗震设计规范的局限性,引入改进的模态往复pushover分析,利用Ghobarah隐式双参数指标进行拱桥结构损伤评估.建立了3组刚架拱结构的有限元模型,拱肋均采用跨度为5.4m的钢管拱肋,桥墩分别为钢筋、钢骨以及钢管混凝土桥墩.对3组刚架拱结构采用倒三角荷载分布形式的侧向力,进行了OBG、SFS、TAR等3条地震波的MMCP法分析和动力时程分析,得到墩顶位移、滞回耗能和损伤指标曲线.研究结果表明:①MMCP法可用于拱结构的抗震性能评估;②MMCP法能够准确地预测拱结构整体的损伤情况;③MMCP法可与桥梁规范的设计反应谱相联系,使评估结果具有一定的普适性、安全度.%In view of the limitations of current seismic performance assessment methods and the seismic design specifications , a modified modal cyclic pushover ( MMCP ) analysis is introduced in this paper for damage as-sessment in the arch bridge structure by using Ghobarah implicit two-parameter indicator .The finite element (FE) models of three different rigid frame arch structures ( span of arch ribs is 5.4 m)are established, in which the piers are reinforced , steel and concrete , respectively .The lateral force which is distributed as invert-ed triangle is added on the three arc structure FE models and MMCP analysis as well as the dynamic analysis process are performed to analyze three earthquake waves including OBG , SFS, TAR, to obtain the vertex dis-placement , hysteretic energy , and damage indicators curves .The results showthat:①MMCP can be applied in seismic performance evaluation of archstructures; ②MMCP can predict the overall damage situation of arcstr uctures accurately;③MMCP can be related to the design response spectrum of bridge specifications , indica-ting that to a certain extent , the assessment results own universality and safety .【期刊名称】《广州大学学报(自然科学版)》【年(卷),期】2014(000)004【总页数】6页(P53-58)【关键词】刚架拱;抗震性能;损伤评估;多模态;往复pushover法【作者】禹奇才;林加爵;刘爱荣;邓江东【作者单位】广州大学-淡江大学工程结构灾害与控制联合研究中心,广东广州510006; 广东省高校结构安全与健康监测工程技术研究中心,广东广州 510006; 广州市结构安全与健康监测重点实验室,广东广州 510006;广州大学-淡江大学工程结构灾害与控制联合研究中心,广东广州 510006; 广东省高校结构安全与健康监测工程技术研究中心,广东广州 510006; 广州市结构安全与健康监测重点实验室,广东广州 510006;广州大学-淡江大学工程结构灾害与控制联合研究中心,广东广州 510006; 广东省高校结构安全与健康监测工程技术研究中心,广东广州510006; 广州市结构安全与健康监测重点实验室,广东广州 510006;广东省高校结构安全与健康监测工程技术研究中心,广东广州 510006; 广州市结构安全与健康监测重点实验室,广东广州 510006【正文语种】中文【中图分类】U443.22;TU375.3拱桥以其跨越能力强、承载能力高、造价低、外观优美等优势成为目前最具竞争力的桥型.大跨度拱桥由于其建设时间短,其地震破坏隐患尚未彰显,相关研究也较少.然而拱桥一旦在地震作用下发生破坏,将产生不可弥补的经济损失,甚至人员伤亡.目前我国的抗震规范《公路工程抗震设计规范》和《公路桥梁抗震设计细则》还远远无法满足实际工程的需求,因此其抗震性能评估的研究具有必要性和迫切性[1-2].本文针对目前拱桥抗震性能评估方法的不足以及抗震设计规范的局限性,引入基于能量与位移双重准则的改进的模态往复pushoveR分析[3-5],利用GhobaRah隐式双参数指标进行刚架拱结构的地震损伤评估.传统的pushoveR 分析是对结构进行单向加载,依据结构在不同塑性阶段的反应对其抗震性能进行评估.然而真实的地震反应是一种往复运动过程,单向pushoveR 方法存在一个本质缺陷:无法考虑结构在往复地震作用下的滞回耗能以及由此引起的刚度与强度退化特性,使得评估结果产生较大的误差.文献[6-7]考虑高阶模态及动力特性改变对结构地震反应的影响,采用基于能量准则的能力谱和弹塑性需求谱计算结构最大顶点位移,利用多模态ESDOF体系的概念评估结构滞回耗能需求.在此基础上,提出了改进模态往复pushoveR分析方法(MMCP),采用隐式双参数模型评估结构地震损伤.MMCP分析在一定程度上模拟了地震作用,能够准确地预测结构整体损伤.MMCP法还可以与设计反应谱相联系,使评估结果具有一定的普遍性和安全度.基于以上原因,将MMCP法引入拱桥的抗震性能评估. 1.1 多自由度(MDOF)体系地震最大位移评估式中,FI,n、ΔuI,n分别为第I层结构的第n 阶模态水平推力和位移增量; m 为结构层数.根据能量原理可以得到ESDOF谱位移:基于能量准则的转化更加稳定,而且能够消除高阶模态下可能出现的能力曲线反向问题[8-10];采用弹塑性反应谱取代等效高阻尼弹性反应谱计算,避免高阻尼弹性谱带来的问题.1.2 多自由度(MDOF)体系滞回耗能评估KHASHAEE[6]在对大量地震波的统计分析基础上,建立了单自由度体系滞回耗能的计算方法:由原MDOF体系能量方程可知,MDOF体系第n阶模态条件下滞回耗能为因此Γn为第n阶振型参与系数.借鉴多模态ESDOF的思想,利用式(6)、(7)便可计算MDOF体系各阶模态对应的滞回耗能需求Eh,1,Eh,2,Eh,3…,由于结构滞回耗能总是在最后时刻达到最大,因此将上述各模态能量相加即得到原结构滞回耗能需求Eh.通过MMCP法分析与动力时程分析结果进行对比,得出MMCP法在拱桥结构的适应性,算例模型采用文献[7]拟静力试验分析的试件进行建模计算.构件尺寸是通过现实中的大跨度拱桥结构按一定比例进行模拟,分别采用钢筋混凝土桥墩、钢骨混凝土桥墩和钢管混凝土桥墩,拱肋均采用截面直径为165 mm、跨度为5.4 m 的钢管拱肋,桥墩高度均为1.9 m,配筋率均为2.7%,钢骨混凝土桥墩和普通钢筋混凝土桥墩截面尺寸为300 mm×300 mm,钢管混凝土桥墩直径D为300 mm,计算模型见图1,桥墩截面纤维单元模型见图2.采用非线性分析程序MIDas gen 8.0和数学分析软件oRIgInpRo进行计算和分析.3组拱桥均采用非线性纤维单元模拟(图2),混凝土纤维使用KENT和PARK提出的受压混凝土的包络曲线(enveLope cuRve)的本构模型;钢纤维的本构模型为双折线型的随动硬化(KInematIc haRDenIng)曲线,钢筋强化系数取0.01.结构阻尼比ζ取为0.05.2.1 采用不同地震波的动力时程分析与MMCP法分析结果对比由于下文将会对利用设计反应谱的MMCP法与本节所计算的MMCP法做比较,因此,先假设一个场地类型和区域划分,以与该场地的设计反应谱作比较.此处选取了3条特征周期为一区的Ⅱ类场地的地震波记录(表1),数据由太平洋地震工程中心地震记录库中提供.表2~4为3组拱桥结构在地震作用下,按动力时程方法和MMCP法得到的结构最大顶点位移与滞回耗能需求,其中,MMCP法采用3条地震波所对应的反应谱.经过分析,利用倒三角侧向荷载分布的MMCP法在拱桥结构分析中同样存在适用性.由图3可见,由于MMCP分析中的顶点位移大于动力时程结果,所以得到的损伤值也偏大,但总体看来两者吻合较好,MMCP法能够准确地评估拱桥结构整体损伤.综合3条地震波的分析,可以得到如下结论:利用MMCP 法得到的结构损伤误差主要取决于最大变形评估精度,拱桥结构损伤对于变形的灵敏度要大于滞回耗能.从图4可见,在3条地震波的作用下,整体损伤达到0.15时(轻微损伤),钢筋拱桥能承受0.10~0.15 g,钢骨拱桥能承受0.13~0.21 g,钢管拱桥能承受0.17~0.23 g;当整体损伤达到0.3时(可修复中等损伤)钢筋拱桥能承受0.2~0.32 g,钢骨拱桥能承受0.23~0.35 g,钢管拱桥能承受0.29~0.44 g. 当地震强度(EPA)相同时,钢管拱桥结构抗震性能最好,钢骨拱桥结构次之,钢筋拱桥结构较差.2.2 采用设计反应谱的MMCP法与动力时程分析结果对比采用设计反应谱的MMCP法的钢筋拱桥结构与钢骨拱桥结构在小震EPA=0.3时,结构损伤均接近损伤下限,随着EPA增大,损伤值都逐渐与动力时程分析的上限贴近;而钢管拱桥结构虽然大部分范围都大于损伤上限,但是相差不到10%,当整体损伤达到0.3(可修复中等损伤)钢筋拱桥能承受0.33 g,钢骨拱桥能承受0.34 g,钢管拱桥能承受0.35 g;当整体损伤达到0.6 g(接近倒塌)钢筋拱桥能承受0.49 g,钢骨拱桥能承受0.62 g,钢管拱桥能承受0.65 g.总的来说,采用设计反应谱具有一定的安全度和经济性.本文利用模态pushoveR分析考虑高阶振型的影响,对3个多自由度的拱结构分别进行改进的模态往复pushoveR方法和动力时程分析,通过计算分析,得出以下结论:(1)采用OBG、SFS和TAR 3条地震波加速度反应谱的MMCP法与动力时程反应结果比较二者较为吻合,误差均小于10%,表明MMCP法能够准确地评估拱桥结构整体损伤.(2)采用桥梁抗震规范的设计反应谱评估拱桥的抗震性能具有一定的安全度和经济性.【相关文献】[1] 禹奇才,刘爱荣,唐潘,等.大跨度拱桥随机地震响应分析[J].中山大学学报,2011,50(4):32-36. YU Q C, LIU A R, TANG P, et aL. Long-span aRch bRIDge RanDom seIsmIc Response anaLysIs[J]. J Sun Yat-sen UnIv, 2011,50(4):32-36.[2] 禹奇才, 禹辉君, 刘爱荣.地震三要素对拱桥能量响应的影响[J].广州大学学报:自然科学版, 2012,11(4):37- 43.YU Q C, YU H J, LIU A R. EneRgy Response FoR aRch-bRIDge InFLuenceD by thRee eLements oF eaRthquaKe[J].J Guangzhou UnIv: Nat ScI EDI,2012,11(4):37- 43.[3] 赵静, 李睿. PushoveR法的独柱墩桥梁抗震性能研究[J].科学技术与工程学报,2011,11(2):415- 418.ZHAO J, LI R. ReseaRch on eaRthquaKe-ResIstant oF sIngLe coLumn pIeR baseD on pushoveR[J]. ScI Tech EngIn, 2011,11(2):415- 418.[4] 王占飞, 庞辉, 李帼昌, 等.基于pushoveR分析的刚构桥抗震设计方法研究[J].工程力学, 2012,29:128-132.WANG Z F, PANG H, LI G C, et aL. SeIsmIc DesIgn oF RIgID FRame bRIDge baseD on pushoveR anaLysIs appRoach[J]. EngIn Mech, 2012,29:128-132.[5] 于琦, 孟少平,吴京. 基于变形与能量双重准则的钢筋混凝土结构地震损伤评估[J].土木工程学报,2011,44(5):16-23.YU Q, MENG S P, WU J. EaRthquaKe Damage assessment oF ReInFoRceD concRete stRuctuRes baseD on DeFoRmatIon anD eneRgy DuaL cRIteRIon[J]. ChIna CIvIL EngIn J, 2011,44(5):16-23.[6] KHASHAEE P. EneRgy-baseD seIsmIc DesIgn anD Damage assessment FoR stRuctuRes[D]. DaLLas,Texas: SoutheRn MethoDIst UnIveRsIty, 2004.[7] 龚泳联. 考虑强余震影响的大跨度拱桥抗震性能的评估方法[D]. 广州:广州大学,2012. GONG Y L. A Long-span aRch bRIDge seIsmIc peRFoRmance evaLuatIon methoDconsIDeRIng the eFFects oF stRong aFteRshocK[D]. Guangzhou: Guangzhou UnIveRsIty, 2012.[8] FAJFAR P. EquIvaLent DuctILIty FactoRs, taKIng Into account Low-cycLe FatIgue[J]. EaRthq EngIn StRuct Dyn,1992,21(10): 837-848.[9] FAJFAR P. CapacIty spectRum methoD baseD on IneLastIc DemanD spectRum[J]. EaRthq EngIn StRuct Dyn,1999,28(9): 979-993.[10]牛荻涛, 任利杰. 改进的钢筋混凝土结构双参数地震破坏模型[J]. 地震工程与工程振动, 1996, 16(4): 44-54.NIU D T, REN L J. ImpRoveD two-paRameteR eaRthquaKe Damage moDeL oF ReInFoRceD concRete stRuctuRes[J]. EaRthq EngIn EngIn VIbRat, 1996,16(4):44-54.[11]NAKASHIMA M, SABURI K, TSUJI B. EneRgy Input anD DIssIpatIon behavIoR oF stRuctuRes wIth hysteRetIc DampeRs[J]. EaRthq EngIn StRuct Dyn, 1996, 25(5): 483- 496.。
模态pushover分析方法的研究和改进_毛建猛

顶端位移关系曲
线 ) 。M 表示结构质量矩阵。 ( 3) 将 pushover曲线简化为双折线曲线 ( 如图 1 ( a ) 所示 ) 。一种简化方法是首先估 计基底屈服剪力 Vbny , 取 60 % Vbny 处的割线刚度作为有效初始刚度, 然后逐步迭代, 直到误差小于预定范围。 ( 4) 利用公式 ( 1), 将简化的 pushover曲线转化为 n 阶振型弹塑性单自由度体系力 - 位移曲线 ( 如图 1b 所示 )。 F sn = 显然, F sn /L sn与 D n 的屈服值表达式如下: F sny Vbny u rny = * , D ny = Ln Mn n rn ( 2) Vbn
51
向量 表示 , 且在整个地震反应过程中 , 不管结构的变形大小 , 形状向量 over方法不能考虑高阶振型的贡献, 难以应用到高层结构中。 方法 模态 pushover方法 (M PA)
[ 1]
保持不变。显然, 传统的 push -
Chopra( 2001) 及其合作者基于结构动力学理论, 考虑高阶振型对结构的影响 , 提出的一种新的 pushover 。该方法采用各阶振型的固定水平荷载模式对结构进行推覆分析, 最 后采用一定法则 ( 如 SRSS) , 确定多阶振型影响的结构目标位移。由于该方法考虑了结构的高阶振型影响, 与实际情况更为符合 , 能使计算精度相对提高 , 但是该方法在计算各阶振型等效单自由度体系的弹塑性静力 反应时 , 水平荷载仍取固定不变模式 , 还是难以解决传统 pushover 方法中假定二所带来的问题。为此 , 本文 通过考虑结构屈服后地震作用发生变化这一特性, 对该方法进行了改进。
引言
上个世纪 90 年代 , 美国科学家和工程师提出了基于性态及基于位移的设计方法。该方法一经提出, 立 即引起全世界各国科学家的关注, 有望代替规范中传统的基于承载力的抗震设计方法。作为结构非线性反 应的简化计算方法, Pushover Analysis( POA ) 由于其相对较高的精度及简单的工作量引起了广大学者和设计 人员的兴趣 , 该方法得到了深入的研究和广泛的应用。简单地说 , POA 方法的优点集中体现在两个方面: 1 . 它较底部剪力法和振型分解反应谱法考虑了结构的弹塑性特征 ( 材料非线性 ) , 精度较高; 2 . 它较非线性 时程分析法计算简单 , 工作量较小。总之 , 在实际的工程设计中, 往往要求计算方法具有一定的精度 , 同时应 力求简单和规范。 Pushover方法正具备这个条件, 因而才在全世界范围内得到了蓬勃发展和广泛应用 , 甚至 在有些国家已经被抗震实际规范所采用。 然而, 传统 pushover方法的理论基础是建立在两个基本假定上的: 1 . 结构的响应与一等效单自由度体系 ( SDOF )相关。在实际计算中 , 通常假定结构的反应仅由结构的第 1 振型控制。 2 . 结构沿高度的变形由形状
基于能量平衡的多模态Pushover分析方法的改进的开题报告

基于能量平衡的多模态Pushover分析方法的改进的开题报告一、研究背景随着建筑物的不断发展,其抗震性能的要求也越来越高。
通过分析建筑的震动反应,可以预测其在地震中的性能。
Pushover分析方法是一种简单有效的抗震分析方法,在工程实践中广泛应用。
然而,在Pushover分析中存在一定的缺陷,例如不能考虑结构的瞬时非线性性、能量耗散机制等。
因此,需要对Pushover分析方法进行改进,提高其分析精度和适用范围。
二、研究意义本研究旨在改进基于能量平衡的多模态Pushover分析方法,提高其准确性和实用性。
研究结果将有助于优化建筑的抗震设计,减少地震对建筑物的危害,保护人民的生命财产安全。
三、研究内容本研究拟从以下几个方面展开:1. 分析当前Pushover分析方法的不足之处,明确改进的方向和目标;2. 探究能量平衡法在Pushover分析中的应用,并对其进行详细分析和优化;3. 基于多模态的Pushover分析方法进行改进,采用合适的模态展开形式和参数设置方法,提高其分析效率和准确性;4. 进行算例分析和验证,评估改进后的多模态Pushover分析方法的可靠性和适用性;5. 利用改进后的方法分析实际工程案例,并比较其与传统Pushover 分析结果的差异和优劣。
四、研究方法本研究将采用文献研究、理论分析和数值模拟相结合的方法,详细分析和探究基于能量平衡的多模态Pushover分析方法的改进。
在此基础上,进行算例分析和验证,并对实际工程案例进行分析和比较,验证改进后方法的可靠性和实用性。
五、预期结果预计本研究的主要结果如下:1. 分析当前Pushover分析方法的不足之处,明确改进的方向和目标;2. 探究能量平衡法在Pushover分析中的应用,并对其进行详细分析和优化;3. 基于多模态的Pushover分析方法进行改进,提高其分析效率和准确性;4. 通过算例分析和验证,评估改进后的Pushover分析方法的可靠性和适用性;5. 利用改进后的方法分析实际工程案例,并比较其与传统Pushover 分析结果的差异和优劣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K e wo d : eea t - pa tca ay i Th d l u h v ra ay i H ih mo a y r s Th lsi c lsi n lss emo a s o e n lss p g- dl
一
、
前 言
都是近似成立的 , 但是这种方法对低层 和中等高度结构 弹塑性 行 为的评估 结果却使人 比较满意 。对高层结构 弹塑性行为 的 评估 结果 却不 能令人信 服 , 主要是 因为 高阶振型对高层结构 的
( h a Xi a w y I si t 7 4 0 ) S a n i a t u e 1 0 0 R l n t
Ab ta tT emo a p s oe n ls A )sg etdb h pag t tero i lcmetad tevleo h te e sr c : h d l uh vra a i f y s MP ug se yC o r es h o fds ae n n h au fteoh rr p
进 行修 复 和加 强 , 不 需 要 改 变 整 体 结 构 的性 能 , 能 使 整 体 而 就
结构达到预定的使用功能 ; 而利用 传统 的弹性分 析 , 对不能满
适应分 布可能得 到较好 的抗震性 能评估 , 但是他们对实际工程 人员来说概念 复杂 , 计算量大 , 利于实际应用 [l 。 不 5 】 C o r 模态 p so e 分析l 把结构离散成多质点的多 自 h pa uh vr 7 由度体 系后 , 用振型分解反应 谱理论 把结构 的振型进 行分解 ,
反应 贡献 比 较 大 , 能 被 忽 略 _ 。 在 解 决 高 阶 振 型 影 响 方 不 3 n 面 , 很 多 人 进 行 了深 入 研 究 。其 中有 人 提 出 了横 向力 的 自适 有 应分 布模 式 , 图尽 量 接 近惯 性 力 分 布 的 时 变 性 , 然 这 种 自 试 虽
吕秋 鸿
( 西铁路工程职业技术学院 陕 摘
740) 10 0
Hale Waihona Puke 要 : h pa的模 态 p so e 分 析 需 要 求 解各 振 型 等效 单 自由度 体 系 动 力 方程 , Cor uh v r 以得 到 结 构 对 应振 型 p s oe 分 析 的终 止 目 uh v r
标位移 , 而求解对应 多 自由度体系 的各 阶振型下楼层 的位移。本文对 C o r 进 h pa的模 态 p so e 分析过程进 行 了改进 , uh vr 通过振 型
wa e S P2 0 a e l e t e mo a o d n . o t i p p ra t mp O r a i h mp o e d l u h v r b AP2 0 . r A 0 0 c n r a i h d l a ig S h s a e te tt e l e t e i r v d mo a s o e y S z l z p 0 0
阶振 型 影 响 。
关键词 :静力弹塑性分析 模 态 p so e 高 阶振型 u h vr
中 图分 类号 : TU3 2 1 5. I 文献标识码 : A 文 章 编 号 :0 4 63 (0 0 0 —0 5 - 0 1 0 — 1 5 2 1 )5 0 1 3
A n l ssOfTh o e sO fI pr v n e M o lPu ho e n l ss a y i e Pr c s m o i g Th da s v rA a y i L uog v Qih n
利 用 静 力 弹 塑 性 分 析 ( uh v r a s )1进 行 结 构 抗 P so e l i [ An y s 能 性 能评 估 的优 点 在 于 : 能 对 结 构 在 多 遇 地震 下 的 弹性 设 计 既
进行校 核 , 也能够确定结构在 罕遇地震 下潜在 的破坏机 制 , 找 到最先破坏 的薄弱环节 , 从而使设 计者可以仅对局部薄弱环节
s o s y s l ig t e e u t n o h t 一 ” d l e u v ln DF s s e p n e b o v n h q a i ft e n h o mo a ” q ia e tS y t m. Th m p o e d lp s o e n l s s s g e t d b e i r v d mo a u h v r a a y i u g s e y t i a e e s t ep ro ma c o n sb h u h v r c r e a d t e ea t - p a t p c r lc r e At t e s me t h s p p rg t h e f r n ep i t y t e p s o e u v n h ls i c ls i s e ta u v . c h a i ,t e s f— me h o t
p so e uh vr曲线 与弹 塑 性 反 应 谱 相 交 的 性 能 点 来 求 解 对 应 多 自由度 体 系 各 阶 振 型 下 的 楼 层 位 移 , 以考 虑 高 阶振 型对 静 力 弹 塑 性分
析方法 的影响。并通过 S 20 AP 0 0实现改进模态 p so e 分析过程 , uh vr 计算结果表 明改进 的模态 p so e 分析 可 以有 效的考虑 高 uh v r
21 年第 5 00 期 总第 1 3 4 期
福
建
建
筑
N o ・2 O 5 O1
F j nAr htcu e& C n t ci ui c i tr a e o sr t n u o
Vo .1 3 1 4
改 进 分 析 过 程 的 模 态 p s o e 分 析 uh vr
