第九章二重抽样
其他抽样方法

其他抽样方法一、二重抽样二重抽样是指在抽样时分两步抽取样本,每一步抽取一个样本。
一般情况下,先从总体N 中抽取一个较大的样本n ',称为第一重样本,对之进行调查以获得总体的某些辅助信息,为下一步的抽样估计提供条件。
然后进行第二重抽样,第二重抽样所抽的样本n 相对较小,但是第二重抽样调查才是主调查。
一般地,第二重样本是从第一重样本中抽取的,即第一重样本的子样本,但是有时也可以从总体中独立抽取。
二重抽样与两阶段抽样在概念上很容易引起混淆。
虽然二者都可以被视为分阶段抽样方法,但是二重抽样与两阶段抽样的差异还是很显著的。
首先,两阶段抽样是先从总体N 个单元(初级单元)中抽出n 个样本单元,却并不对这n 个样本单元中的所有小单元(二级单元)都进行调查,而是在其中再抽出若干个二级单元进行调查;二重抽样则不同,要对第一重样本进行调查以获取总体的某些辅助信息,并且要利用这些辅助信息进行排序、分层、抽样或估计。
其次,两阶段抽样的第一阶段抽样单位和第二阶段抽样单位往往是不同的,比如第一阶段抽样单位是居委会,第二阶段抽样单位是住户;而二重抽样的第二重样本则往往是第一重样本的子样本,两次抽样的单位是相同的。
二、分层的二重抽样进行分层抽样有一个前提,即需要将总体N 个单元划分为L 个互不重叠的层,而且需要知道各层的权重NN W hh =。
如果事先无法知道总体的权层,则可采用二重分层抽样方法。
1、符号说明用下标h 表示层数,L h ,,2,1 =h N :总体第h 层的单元数;总体单元数∑==Lh h N N 1hn ':第一重样本第h 层的单元数;第一重样本单元数∑='='Lh h n n 1 h n :第二重样本第h 层的单元数;第二重样本单元数∑==Lh h n n 1N N W h h =:总体单元第h 层的权重;n n w h h''=':第一重样本第h 层的权重 hhhD n n f '=:第二重样本第h 层的抽样比,10≤<hD f hj y :第二重样本第h 层j 单元的观测值,L h n j h ,,2,1;,,2,1 ==∑==hn j hjhh yn y 11:第二重样本第h 层样本单元的平均数2S :总体方差;2h S :第h 层的总方差;2hs ':第一重样本第h 层方差 ∑=--=hn j h hj h hy y n s 122)(11:第二重样本第h 层方差 2、抽样方法第一步:利用简单随机抽样,从总体的N 个单位中随机抽取第一重样本,样本单位数为n ';根据已知的分层标志将第一重样本分层,令nn w hh''='L h ,,2,1 =,则hw '是总体权层h W 的无偏估计。
高中数学必修二 9 1 2 分层随机抽样 教学设计

9.1.2 分层随机抽样本节《普通高中课程标准数学教科书-必修二(人教A版)第九章《9.1.2 分层抽样》,本节的主要内容在本章的结构上,通过大背景的“串联”,从大背景中不断提出新问题,从而通过问题链进行探究学习,合理选择抽样方法的必要性并掌握分层抽样方法。
从而发展学生的直观想象、逻辑推理、数学建模的核心素养。
1.数学建模:结合实际问题情景,理解分层抽样的必要性和重要性;2.逻辑推理:学会用分层抽样的方法从总体中抽取样本;3.直观想象:对简单随机抽样、分层抽样方法进行比较,揭示其相互关系.4.数学运算:总体平均数的估计方法1.教学重点:理解分层抽样的基本思想和适用情形..2.教学难点:掌握分层抽样的实施步骤,会计算总体平均数.多媒体形?3.为什么会出现这种“极端样本”?4.如何避免这种“极端样本”?样本代表性;会;抽样结果的随机性个体差异较大;分组抽样,减少组内差距在树人中学高一年级的712 名学生中,男生有326 名、女生有386 名。
样本量在男生、女生中应如何分配?假设某地区有高中生2400人,初中生10900人,小学生11000人,此地教育部门为了了解本地区中小学的近视情况及其形成原因,要从本地区的小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本?你认为哪些因素影响学生视力?抽样要考虑哪些因素?分层抽样每一层抽取的样本数=一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样(stratified random sampling),每一个子总体称为层.在分层随机抽样中,如果每层样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配.×总样本量做一做1.下列问题中,最适合用分层抽样抽取样本的是()A.从10名同学中抽取3人参加座谈会B.某社区有500个家庭,其中高收入的家庭125个,中等收入的家让学生感受分层抽样的概念及方法,发展学生数学抽象、逻辑推理的核心素养。
第8-9章-多阶段抽样和二重抽样

ˆ ˆ E E E E
2
2
1
2
E 2 E E 2 V E ˆ ˆ E1 2 ˆ 1 2 1 2
E 2 E E 2 ˆ ˆ V1 E2 E1 2 ˆ 1 2 ˆ ˆ V1 E2 E1 V2
2 S2 V ( y ) S12 m
2 当n=1时, V1 (Yi ) S1
这时, 若以n个
yi 的均值 y 推断 Y
,其方差为
2 2 S1 S2 V ( y) n nm
再考虑fpc,则(1)式成立。
V y 的无偏估计为:
证明:
2 1
E (s ) S
2 2
1 f1 2 f1 1 f 2 2 v y s1 s2 n nm
1 1 n 1 1 E1 M iYi M n i 1 MN
M iYi Y i 1
N
估计量的方差为:
1 f1 M i 1 V y M Yi Y nNM 2 nN i 1 i 1
N N
二.按不等概抽初级单元
1.按PPS抽取初级单元 N 第i个单元被选中概率 Z i ,( Z i 1 ) i 1 以总量估计为例,利用Hansen-Hurwitz估计量 ˆ Y的估计: 1 n Y 1 n M y
ˆ YHH
z n
i 1
i
i
n
i 1
i
i
zi
ˆ 可以证明 YHH是Y的无偏估计
抽样调查-第9章 二重抽样

二、二重抽样与两阶段抽样的区别
1.两阶段抽样是先从总体N个单元中抽出n个样本 单元,却并不对n个样本都进行调查,而是从中再抽出 若干个二级单元进行调查。
返回
2。两阶段抽样的第二阶段抽样单元与第一阶段抽样 单元往往是不同的。而二重抽样的第二重样本往往是 第一重样本的子样本。
三、二重抽样的作用
(一)有利于筛选主调查对象 (二)节约调查费用 (三)提高抽样效率
80 60 40 20 200 2 7 15 40
2 yij j
2 j
s
400 3100 9600 45120
1.01 2.71 15.38 690.53
解
w1
根据上表可计算各层的权重:
540 0.32, w3 0.10, w4 0.04 0.54, w2 1000
第一重样本第h层方差:sh
2
nh 1 2 2 第二重样本第h层方差:sh ( y y ) hj h nh 1 j 1
二、抽样方法
第一步: 利用简单随机抽样,从总体的N个单元中随机 抽取第一重样本,样本单元数为 n ;根据已知的分层标 n 志将第一重样本分层,令 wh h , (h 1,2,, L) ,则 n 是总体层权 W 的无偏估计。 wh
L
而总体均值估计量的方差为:
1 1 2 L Wh S h2 1 V ( y stD ) ( ) S ( 1) n N n f hD h 1
返回
要在一定的费用约束下使估计方差最小化,则有
L V ( y stD ) (C c1n n c2 h f hDWh )
§9.1 引言
一、二重抽样的定义
二重抽样(double sampling),也称二相抽样,是指分 两步抽取样本。先从总体N中抽样一个较大的 样本 n ,称为第一重样本,对其进行调查以获 取总体的某些信息,为下一步的抽样估计提供 条件;然后在第一重样本中再进行第二次抽样。 这种抽样方法称为二重抽样。
二重抽样

6.1概述 概述
6.1.1二重抽样的定义 二重抽样的定义 二重抽样(也叫二相抽样),抽样过程分两 二重抽样(也叫二相抽样),抽样过程分两 ),抽样过程分 进行: 步进行:
第一步称为第一 第一步称为第一重(相)抽样,是从总体中抽取 抽样, 一个比较大的样本,称为第一重( 比较大的样本 样本。 一个比较大的样本,称为第一重(相)样本。目 的是获取有关总体的某些辅助信息 辅助信息, 的是获取有关总体的某些辅助信息,为下一步的 第二重抽样估计提供条件。 第二重抽样估计提供条件。 第二步称为第二 抽样, 第二步称为第二重(相)抽样,是从第一重样本 中抽取的相对较小的样本,称为第二重( 较小的样本 中抽取的相对较小的样本,称为第二重(相)样 它是第一重样本的一个子样本, 本。它是第一重样本的一个子样本,对它进行的 调查是主调查。 调查是主调查。
Y
′ ystD = ∑ wh yh
h =1
L
性质: 性质:
(1)
E ( ystD ) = Y
1 1 1 2 2 1 (2)V ( ystD ) = − S + ∑ Wh S h − 1 n′ N h n′ γh
V 的一个近似无偏估计: (3) ( ystD ) 的一个近似无偏估计:
1 1 22 1 1 2 ′ v ( ystD ) = ∑ − w′h sh + − ∑ wh ( yh − ystD ) ′ nh n′ N h h nh
证明: 证明:
K (1)E( y ) = E E ( y ) = E E ′ 1 2 ∑ wh yh stD 1 2 stD h=1
二重抽样

表7-1
某银行客户的样本数据
2 2 2 (2 6.42) 0.32 (7 6.42) 0.1 ( 15 6.42) 1 1 L ' 1 1 0.54 2 ( ' ) h ( y h y stD ) ( ) 2 n N h 1 1000 800 0 . 04 ( 40 6 . 42 )
h
y h )] E ( y stD ) E1 [ E 2 ( y stD )] E1 [ E 2 ( wh
h 1
L
y h ) E1 ( y ) Y E1 ( wh
h 1
L
定理7.2
y stD 的方差为:
2 1 1 2 L Wh S h 1 V ( y stD ) ( )S ( 1) n N n f hD h 1 2 f hD 是第二重样本第h 式中,S2是总体方差;S h 是第h层的总体方差;
6.3 不等概率系统抽样
行政村编号 1
人数 134
累计人数 134
抽中代码 100
2 3
4
376 202
106
510 712
818
5
6 7 8 9 10
634
397 306 247 95 588
1452
1849 2155 2402 2497 3085
1128
2156
7.1 二重抽样
前面介绍的抽样技术中,大多需要事先了解关于总体的 信息,例如分层抽样需要事先知道各层权重,比率估计 和回归估计需要知道总体的某些辅助信息,但在有些情 况下,这些信息在调查前无法预知。这时,可以先从总 体中抽取一个大的初始样本,获得总体的辅助信息,然 后再从初始样本或总体中抽取一个子样本,这种方法就 是二重抽样。
第九章 二重抽样

第十章 二重抽样第一节 二重抽样综述一、二重抽样的概念二重抽样也称二相抽样。
其基本做法是:对于一个大总体,先从总体中随机抽取一个较大的样本(第一重样本),由此估计有关总体的结构或辅助指标以及其他有关信息,为第二重抽样估计提供条件;然后再从第一重样本中随机抽取一个较小的样本(第二重样本),利用这第二重样本,对总体所研究变量进行抽样推断。
在某些情况下,也可在第二重样本中再抽第三重、第四重样本,由此形成多重抽样。
其中二重抽样是最为常用的。
二、二重抽样的作用在社会经济抽样调查中,二重抽样的主要作用有下列几方面:第一,用于从总体所有基本单元中筛选确定出主调查对象。
第二,用于经常性调查。
第三,用于了解陌生总体内在结构或分布的大致情况,为抽样方法和抽样组织形式的选择提供依据。
第四,为分层抽样推断提供层权资料。
第五,为比率估计和回归估计提供辅助资料。
第六,在经常性的多项目抽样调查中,用于解决不同调查项目需要不同样本容量的问题。
第七,用于研究样本轮换中的某些问题。
第二节 二重分层抽样一、二重分层抽样概述在分层抽样中,我们要求总体各层的层权应事先已知,如果层权未知或不能事先确定,则分层抽样在精度上的得益可能会在很大程度上被抵消掉,此时,选择二重分层抽样可以较好地解决层权问题。
二重分层抽样是先在总体中随机抽取第一重样本n ′,对这个样本各单元进行分层后求各层的层权,然后从第一重样本中用分层随机抽样法抽取第二重样本n ,用于估计总体指标。
由于第一重简单随机抽样,第二重分层抽样,故其误差同二重的抽样都有关。
二、估计量及其方差总体均值估计量为∑===Lh h h stD stD y w y Y 1ˆ其中∑==hn j hjhh yn y 11为第一重样本第h 层均值的无偏估计。
可以证明stD y 是总体均值stD Y 的无偏估计量。
如果第一重样本是随机样本,第二重样本为第一重样本的随机子样本,则估计量的方差为∑∑==-+-=-+-=+=Lh h h h Lh h h h h stD v n S W N n S n n n S W N n n S y V E y V Y V 1221222211)11(')1'1()1'(')'1(')]([)'()ˆ( 其中)'(1y V 为第一重抽样之方差,)(2y V 为第二重抽样之方差。
抽样调查-第9节二重抽样

s(Y ) Ns( ystD ) N v( ystD ) 2427.32 (百万元)
四、二重分层抽样样本量的最优分配
二重分层抽样中有两次抽样,这两次抽样的样本量
即n和n ,直接影响估计的精度。第一重抽样n越大,
对分层信息的了解和估计就越精确,从而可以减少估计
量的误差;同样,第二重抽样 n 越大,估计量的方差越
采用二重分层抽样,对总体均值Y 的估计量为:
Байду номын сангаас
L
ystD wh yh
h1
(二)均值估计量 ystD 的性质
性质1 估计量 y stD是 Y的无偏估计。即 E( ystD ) Y
因为
E(yh)
y
h
L
所以有 E( ystD ) E1[E2 ( ystD )] E1[E2 ( wh yh )]
h1
j 1,2, , nh;h 1,2, , L
第二重样本第h层样本单元的平均数: yh
总体方差:S 2
,第h层的总体方差:
S
2 h
1 nh
nh
yhj
j 1
返回
第一重样本第h层方差:sh 2
第二重样本第h层方差:sh2
1 nh 1
nh
( yhj
j 1
yh )2
二、抽样方法
第一步: 利用简单随机抽样,从总体的N个单元中随机
h1
(1 nh
1 nh
)wh 2sh2
(1 n
1 N
L
)
h1
wh
(
yh
y stD
)2
式中,v( ystD )为V ( ystD ) 的近似无偏估计;sh2为第二重样
抽样检验中的双重抽样方法与效果评估

抽样检验中的双重抽样方法与效果评估抽样检验是统计学中一种重要的数据分析方法,用于判断样本数据是否代表总体,并进行统计推断。
抽样检验的精确性和准确性对研究结果的可靠性起着至关重要的作用。
为了增加抽样检验的效果评估,双重抽样方法被广泛采用。
本文将探讨双重抽样方法及其在抽样检验中的效果评估。
一、双重抽样方法的概念和原理双重抽样方法指的是采用两次独立的抽样过程,通过分别对两个抽样集合进行统计分析,来对总体进行推断。
这样的双重抽样方法能够在保证数据的可靠性的同时提高推断的准确性。
在使用双重抽样方法时,第一次抽样通常是从总体中随机选择样本,这个样本称为一级样本。
然后,从一级样本中再次随机选择一部分样本,形成二级样本。
通过对一级样本和二级样本的统计分析,可以得到更加精确的估计结果。
双重抽样方法的基本原理就是通过两次独立的抽样,减小抽样误差,提高估计的准确性。
二、双重抽样方法的应用双重抽样方法被广泛应用于各个领域的统计研究中。
下面将介绍其中两个常见的应用案例。
1.医学研究中的双重抽样方法在医学研究中,为了对新药的疗效进行评估,常常采用对患者进行双重随机抽样的方法。
首先,在一级样本中随机选择一部分患者,将其分为实验组和对照组。
然后,在实验组和对照组中再次随机选择一部分患者进行观察和数据采集。
通过对数据的统计分析,可以判断新药的疗效和安全性。
2.社会调查中的双重抽样方法在社会调查中,为了保证样本的多样性和代表性,常常采用双重抽样方法。
首先,在一级样本中随机选择一部分个体,然后在这些个体中进行二级随机抽样,得到用于调查的最终样本。
通过对最终样本的数据分析,可以对总体进行推断,得出调查结果。
三、双重抽样方法的效果评估为了评估双重抽样方法的效果,需要进行有效的效果评估。
下面将介绍两种常见的双重抽样方法的效果评估方式。
1.重抽样法重抽样法是一种用于评估双重抽样效果的常用方法。
在重抽样法中,通过对已有数据进行重复随机抽样,得到同等大小的样本,然后利用这些样本进行统计分析。
第九章二阶与多阶抽样抽样调查理论与方法北京商学院
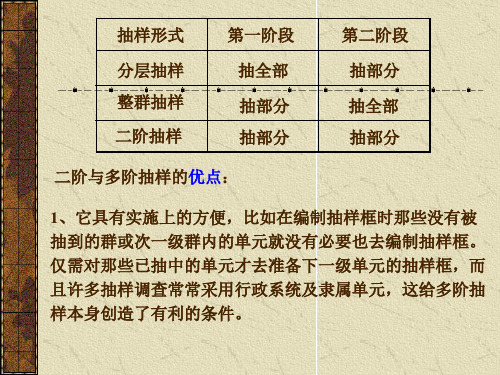
2、能够满足各级政府部门对抽样调查资料的需求。因为各 级政府领导都关心全国和本地区、本部门的社会经济发展状
况,希望抽样调查能同时满足全国性和地方性的需要。因而
采用二阶或多阶抽样,在一定程度上能够满足各级政府、部
门对调查资料的需求。
3、有利于减少抽样误差、提高抽样估计精度。这种抽样调查 方法,可以使每个一阶样本单位分布比较均匀,具有很好的
方差及其方差估计是已知的,因此:
Var( yst )
k h1
Wh2
(
1
f1h nh
S12h
1 f2h nhmh
S22h )
(9.11)
v(
yst
)
k h1
Wh2
(
1
f1h nh
s12h
f1h (1 f2h nhmh
)
s22h
)
(9.12)
其中
f1h
nh Nh
、f2h
mh Mh
分别为第 h 层中的两个抽样比。
S0
S2 c1
m
c2m
或者m的最优取值为:
mopt
S2 S0
c1 c2
(9.7)
一般地, mopt不是整数,记 [mopt ]为 mopt的最小整数部分,那 么 mopt [mopt ] a ( a 为 mopt的小数部分,且 a 0 )。
如果a2 (1 2a)[mopt ] ,则取 m [mopt ] 1
S22i
1 Mi 1
Mi
(Yij
j 1
Yi )2
—第
i 初级单元内方差
Байду номын сангаас
1、只抽取一个初级单元情形(n=1)
先考虑从 N 个初级单元中随机选取 1 个以推断总体. 这种情形看起来似乎很特殊,但在生活中也不少见,例如在 随机地选的一个班级中抽取几个人进行考试以测试全年级的 教育质量。只选取 1 个单元,仍有等概率与不等概率之分.
第九章抽样与抽样估计ppt文档

2、特点 (1) 抽样调查建立在随机取样的基础上。
(2)它是由部分推断整体的一种认识方 法。
(3)抽样调查的误差可以事先计算并加以 控制。
3、抽样调查的适用范围
抽样调查方法是市场经济国家在 调查方法上的必然选择,和普查相比, 它具有准确度高、成本低、速度快、 应用面广等优点。
参数估计 二、抽样推断的内容
假设检验 三、有关抽样的基本概念
(一)总体和样本
总体:也称全及总体。指所要认识的研究对 象全体。总体单位总数用“N”表示。
样本: 也称抽样总体,是抽出的单位组成 的整体。样本单位总数用“n”表示。
(二)参数和统计量 1、针对总体计算的指标叫总体参数,也叫全及 指标。参数的值是定值
2、非概率抽样:也叫非随机抽样,是指从 研究目的出发,根据调查者的经验或判 断,从总体中有意识地抽取若干单位构 成样本。重点调查、典型调查、配额调 查等属于非随机抽样。
(六)、抽样框
1、抽样框是包括全部抽样单位的名单框架。编 制抽样框是实施抽样的基础。抽样框的好坏通常 会直接影响到抽样调查的随机性和调查的效果。 2、抽样框主要有三种形式:
以 N 1 代表N个总体单位中具 有某种特征的单位数,N 0 代表N 个
总体单位中不具有某种特征的单位
数,N=N1+N0。有 P N 1 N
从总体中随机抽出容量为n的样本,
n 具有某种特征的单位数为 ,则样本的成
数为 p n1 。
1
例如,n 某工厂生产某种电子元件,某
批产品共10000件,其中不合格品100件,
①系统误差是非随机因素引起的误差, 它系统性偏高或偏低,也称偏差。
② 随机误差也叫偶然误差。它是由偶 然性因素引起的代表性误差。它不可 避免,但可计算与控制。抽样估计中 的抽样误差,就是指这种随机误差。
抽样调查-第9章 二重抽样

s(Y ) Ns( ystD ) N v( ystD ) 2427.32 (百万元)
四、二重分层抽样样本量的最优分配
二重分层抽样中有两次抽样,这两次抽样的样本量
即n和n ,直接影响估计的精度。第一重抽样n越大,
对分层信息的了解和估计就越精确,从而可以减少估计
量的误差;同样,第二重抽样 n 越大,估计量的方差越
h1
得有关数据如下表,试估计该银行所有客户的资产总额 及其抽样标准误差。
返回
分层
300万元以下 300~1000 1000~2000 2000万元以上 合计
第一重 样本
540 320 100 40 1000
第二重 样本均值
样本
yh
80
2
60
7
40
15
20
40
200
y2 ij j
400 3100 9600 45120
j 1,2, , nh;h 1,2, , L
第二重样本第h层样本单元的平均数: yh
总体方差:S 2
,第h层的总体方差:
S
2 h
1 nh
nh
yhj
j 1
返回
第一重样本第h层方差:sh 2
第二重样本第h层方差:sh2
1 nh 1
nh
( yhj
j 1
yh )2
二、抽样方法
第一步: 利用简单随机抽样,从总体的N个单元中随机
L
CT E(CT ) c1n n c2h f W hD h
h1
而总体均值估计量的方差为:
V
( y stD
)
(1 n
1 N
)S
2
L
Wh
S
计量经济学第九章二重抽样

第九章二重抽样前面各章介绍的几种抽样技术中,大都需要事先了解一些关于总体的信息,例如分层抽样需要事先知道各层权重,比率估计和回归估计中需要知道总体的某些辅助信息但在一些情况下,这些资料在调查前无法预知。
这时,我们可以先从总体中抽取一个大的初始样本,从而获得总体的辅助信息,然后再从初始样本或从总体中再抽一个子样本,这种方法就是二重抽样。
本章第一节介绍二重抽样的定义、作用及其与两阶段抽样的区别,第二节介绍为分层抽样进行的二重抽样,第三节介绍为比率估计进行的二重抽样,第四节介绍为回归估计进行的二重抽样。
§9.1 引言一、定义二重抽样(double sampling),也称二相抽样或两相抽样(two-phase sampling),是指在抽样时分两步抽取样本。
一般情况下,先从总体N中抽取一个较大的样本'n,称为第一重(相)样本(the first phase sample),对之进行调查以获取总体的某些辅助信息,为下一步的抽样估计提供条件;然后进行第二重(相)抽样(the second phase sample)。
第二重抽样所抽的样本n相对较小,但是第二重抽样调查才是主调查。
一般地,第二重样本(the second phase sample)是从第一重样本中抽取的,也即第一重样本的子样本,但有时也可以从总体中独立地抽取。
由于样本是分两次抽取的,因此称做二重抽样。
例如,欲对某城市体育场馆的营业状况进行抽样调查,鉴于不同场馆功能和面积差异较大,拟采用分层抽样,但由于缺乏分层资料,故先随机抽选一个较大的样本,对该样本仅进行分层及进行层权估计,费用相对较低;然后利用第一次调查获得的分层资料,进行一次较小样本的分层抽样,对该样本进行一次正式调查。
这就是二重抽样。
显然,二重抽样方法也可以推广到多次抽取样本,然后结合起来对总体的有关标志值进行估计,这就是多重抽样或多相抽样。
本章主要讨论二重抽样。
二、二重抽样与两阶段抽样二重抽样和两阶段抽样,在名称上很容易引起混淆。
09-第九章 二阶及多阶抽样

1 M å (Yij - Y i ) 2 M - 1 j =1
则
2 S2 =
1 N
åS
i =1
N
2 2i
9.2.2 总体均值 Y 的估计量及其性质 如果二阶抽样中的每一阶抽样都是简单随机的, 且对每个初级单元, 第 二阶抽样是相互独立的,则样本按次级单元的均值
y=
1 n m 1 n yij = å y i åå nm i =1 j =1 n i =1
=W 2å =W 2å
N
1- f 2 Si m i =1 1- f m i =1
é 1 M ù (Yij - Y i )2 ú å ê ë M - 1 j =1 û N M 1- f 1 (Yij - Y i ) 2 =W 2 åå m M - 1 i =1 j =1 = 1 N2 1m N M M 1 (Yij - Y i ) 2 åå m M - 1 i =1 j =1
(9.1)
作为总体均值
Y=
1 NM
åå Yij =
i =1 j =1
N
N
1 N
åY
i =1
N
i
(9.2)
3
的估计,有如下性质:
E( y) = Y V ( y) = 1 - f1 2 1 - f 2 2 S1 + S2 n mn
(9.3) (9.4)
为证明上述性质, 注意到二阶抽样是分两步进行的, 因此对估计量求均 值与方差需按第六章给出的下述一般公式进行,即:
V ( y) =
将 n = N 代入,有
1 - f2 2 S2 mn 1 - f2 2 S2 mN
V ( y) =
其中 f 2 =
m ,则 M
抽样调查09

9.3初级单元大小不等时的二阶抽样(I)
• 9.3.1记号
N
记:Yiji=1,K , N,j=1,K , Mi, M0 Mi
i 1
为总体中第i个初级单元中第j个次级单元的指标值,
记:yiji=1,K , n,j=1,K , mi 为样本中第i个初级单元中第j个次级单元的指标值
f1
n N
,f2i
Yˆ HH =
1 n
n i=1
Miyi zi
Var(Yˆ HH )=
1 n
N i=1
Zi
Yi Zi
2
Y
1 n
N
M
2 i
i=1
1 f2i Zi
S22i
v(Yˆ HH )=
1
n n-1
n i=1
Miyi zi
Yˆ HH
2
(9.22) (9.23) (9.24)
9.3初级单元大小不等时的二阶抽样(I)
nm
n i=1
m
yij
j=1
1 n
n
yi
i=1
作为总体均值的估计
Y= 1
NM
N i=1
M
Yij
j=1
1 N
N
Yi
i=1
的估计,有如下性质:
1. Ey Y
2.
Var(y)= 1-f1 n
S12
1-f2 mn
S22
(9.3) (9.4)
9.2初级单元大小相等时的二阶抽样
• 9.2.2总体均值的估计及其性质
一般意义而言,两次抽样的期望和方差公式为:
1. 期望: Eˆ=E1E2ˆ
(9.5)
2.方差:
Var(ˆ)=V1 E2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章 二重抽样
第一节 二重抽样综述
一、二重抽样的概念
二重抽样也称二相抽样。
其基本做法是:对于一个大总体,先从总体中随机抽取一个较大的样本(第一重样本),由此估计有关总体的结构或辅助指标以及其他有关信息,为第二重抽样估计提供条件;然后再从第一重样本中随机抽取一个较小的样本(第二重样本),利用这第二重样本,对总体所研究变量进行抽样推断。
在某些情况下,也可在第二重样本中再抽第三重、第四重样本,由此形成多重抽样。
其中二重抽样是最为常用的。
二、二重抽样的作用
在社会经济抽样调查中,二重抽样的主要作用有下列几方面:
第一,用于从总体所有基本单元中筛选确定出主调查对象。
第二,用于经常性调查。
第三,用于了解陌生总体内在结构或分布的大致情况,为抽样方法和抽样组织形式的选择提供依据。
第四,为分层抽样推断提供层权资料。
第五,为比率估计和回归估计提供辅助资料。
第六,在经常性的多项目抽样调查中,用于解决不同调查项目需要不同样本容量的问题。
第七,用于研究样本轮换中的某些问题。
第二节 二重分层抽样
一、二重分层抽样概述
在分层抽样中,我们要求总体各层的层权应事先已知,如果层权未知或不能事先确定,则分层抽样在精度上的得益可能会在很大程度上被抵消掉,此时,选择二重分层抽样可以较好地解决层权问题。
二重分层抽样是先在总体中随机抽取第一重样本n ′,对这个样本各单元进行分层后求各层的层权,然后从第一重样本中用分层随机抽样法抽取第二重样本n ,用于估计总体指标。
由于第一重简单随机抽样,第二重分层抽样,故其误差同二重的抽样都有关。
二、估计量及其方差
总体均值估计量为
∑===L h h h stD stD y w y Y 1
ˆ
其中
∑==h n j hj h
h y n y 11
为第一重样本第h 层均值的无偏估计。
可以证明stD y 是总体均值stD Y 的无偏估计量。
如果第一重样本是随机样本,第二重样本为第一重样本的随机子样本,则估计量的方差为
∑∑==-+-=-+-=+=L h h h h L h h h h h stD v n S W N n S n n n S W N n n S y V E y V Y V 122
1
222211)11(')1'1()1'(')'1(')]
([)'()ˆ( 其中)'(1y V 为第一重抽样之方差,)(2y V 为第二重抽样之方差。
以各层的样本方差代替各层的总体方差,以样本各层间方差代替总体方差,则可得方差的近似无偏估计量为
)'11()()1'1()ˆ(ˆ1
2212h L h h h h L h stD h h stD n n s w y y w N n Y V ∑∑==-+--= 第三节 二重比估计与回归估计
一、二重比估计
在使用比估计量时,要求作为辅助变量的总体均值或总和应事先已知,但在实际中可能并不掌握关于辅助变量的资料,此时,就要考虑采用二重比估计的方法。
二重比估计的基本思路是先在总体中抽第一重样本用以估计总体辅助变量指标,再在一重样本中抽第二重样本按比估计法推断总体调查变量的数值。
用二重比估计法估计Y 的一般形式为
'ˆ'ˆX R X y
x Y RD == 其中y x R =ˆ,是总体比率R 的有偏估计量,∑=='1
'1'n i i x n X ,因为R ˆ是有偏的,故RD Y ˆ也为有偏的,但当n 充分大时,RD
Y ˆ为近似无偏的。
当n ′和n 均为简单随机样本时,其方差为 222222222221211)2('1)2(1)2('
11)1'1(
)]ˆ([)]ˆ([)ˆ(y x xy x xy y x xy y y RD
RD RD S N
S R RS n S R RS S n S R RS S n n S N n Y V E Y E V Y V --++-=+--+-≈+= 当n 为n ′的子样本时,方差估计量为
)ˆˆ2('
1)ˆˆ2(1)ˆ(ˆ22222x xy x xy y RD s R s R n s R s R s n Y V -++-= 科克伦曾经证明,在n ′与n 相互独立,且均为简单随机样本时,方差估计量为
22222ˆ'
1)ˆˆ2(1)ˆ(ˆx x xy y RD s R n s R s R s n Y V ++-= 显然:
①当n ′远大于n 时,两种估计之间的差异很小,并且当n 是n ′的子样本时的方差比n 与n ′相互独立时的方差要小。
②二重比估计的结果R
Y ˆ和)ˆ(ˆR Y V 都是有偏估计量,但随样本量的增大,这些偏差会减小,故它们是近似无偏的,且当n ′较大时,二重比估计的精度比较高。
③当n ′=N 时,二重比估计的估计精度与一般的估计相同。
但由于n ′<N ,故二重比估计的精度会低于一般比估计。
当n=n ′时,二重比估计的估计精度会低于简单随机抽样。
原因是二重比估计增加了第一重样本关于辅助变量的误差。
一般情况下,二重抽样中,n<n ′。
④若第一重和第二重样本是各自独立抽取的,也即先从总体中抽取第一重样本n ′,用以估计辅助信息,然后再从总体中,而不是从一重样本中,抽取第二重样本n ,用以调查和推断总体研究变量,则其精度会更高,但抽样工作量却会大大增加。
二、二重回归估计
在使用回归估计量时,需要掌握有关辅助变量的资料,当其未知时,一个可行的办法是采用二重抽样加以估计。
二重回归估计的基本思路是先在总体中抽第一重样本作简单测试以估计辅助变量的总体资;再在第一重样本中抽取第二重样本用以对调查变量的总体指标进行估计。
二重回归估计可以采用多种形式,这里只涉及一元线性回归估计,此时,对总体均值的二重回归估计可采用以下形式
)'(ˆx X b y Y lrD
-+= 当n 充分大时
Y Y E lrD
=)ˆ( 其中
∑∑==---=n i i n i i i x x
y y x x b 121
)()
)((
若n ′和n 均为简单随机样本,则估计量的方差为
N S n S n S Y V y
y
y lrD 22222')1()ˆ(-+-≈ρρ
当∞→N 时,估计量的方差可按以下形式进行估计
'
)1()ˆ(ˆ2222n s r n r s Y V y y lrD +-≈ 其中
∑∑∑==----=n i i n
i i n i i i y y x x y y x x r 12
21)()()
)(( 由此可见:
①若n ′=N ,则二重回归估计与一般回归估计的效果相同。
若n ′=n ,则二重回归估计的估计效果同简单随机抽样的相同。
因为,在一般情况下,回归估计优于简单随机抽样,所以,n ′越大,则估计效果越好。
②相关系数ρ对抽样方差影响较大,ρ越大,抽样方差越小,所以有效地利用辅助变量,对提高抽样估计效果是很有帮助的。
③通常二重回归估计的估计精度是低于一般回归估计,原因是二重抽样中,以第一重抽样所估计的'X 代替了总体X ,因而使抽样方差增加,故二重回归估计精度总比一般回归估计差。
但当n ′增大时,特别当N n →',或者当'X =X 时,二重回归估计与一般回归估计精度一致。
三、二重分层估计、比估计和回归估计的比较
1、在回归估计中,一般要求调查变量与辅助变量之间要有很高的相关关系,并且用于辅助资料的费用很低,实际中,这些条件常常难以满足。
另外,回归估计的计算过程远比比估计和分层估计要复杂。
2、比估计不是无偏的,一般比回归估计有较大的方差。
3、如果调查变量与分层变量是线性相关的,则按比例分层的得益与回归估计基本一致。
此时,使用分层方法还是回归估计法取决于回归方法的计算量带来的费用和分层方法的分层费用的多少。
4、分层抽样常比回归和比率均值有特殊的优越性,特别是在调查变量与辅助变量为非线性关系时,按比例分层能得到更大的得益;若分层变量不是数值型时,分层方法仍然可以使用,而回归和比估计方法则不能用。
5、如果辅助变量的总体均值是已知的,则回归和比估计可以在独立于辅助变量的n次抽选的样本上进行,而在分层抽样中,样本n必须是第一重样本n′的子样本。
