20第五章 PID调节器的数字化实现
2023年大学_计算机控制技术第二版(温希东著)课后答案下载

2023年计算机控制技术第二版(温希东著)课后答案下载2023年计算机控制技术第二版(温希东著)课后答案下载本书全面系统地介绍了计算机控制系统的基本组成和在工业控制中的应用技术,并结合实际深入浅出地介绍了几种典型的控制系统和控制技术。
主要内容包括:计算机控制系统概述、开关量输入/输出通道与人机接口、顺序控制与数字控制、模拟量输入/输出通道、PID调节器的数字化实现、计算机控制系统的抗干扰技术及工业控制微型计算机。
为了帮助读者掌握各部分内容,书中每章后面都附有习题。
本书可作为高职高专院校应用电子技术、自动化、机电一体化、电气工程等专业的计算机控制技术课程的教材,也可作为从事计算机控制工作的工程技术人员的参考书。
计算机控制技术第二版(温希东著):内容简介点击此处下载计算机控制技术第二版(温希东著)课后答案计算机控制技术第二版(温希东著):目录第1章计算机控制系统概述 11.1 计算机控制系统的组成 11.1.1 计算机控制系统的硬件组成 31.1.2 计算机控制系统的软件 41.2 工业控制计算机的特点 41.3 微型计算机控制系统的主要结构类型 51.3.1 计算机操作指导控制系统 51.3.2 直接数字控制系统 51.3.3 监督计算机控制系统 61.3.4 集散型控制系统 61.3.5 现场总线控制系统 71.3.6 工业过程计算机集成制造系统 81.4 微型计算机控制系统的发展 91.4.1 计算机控制系统的发展过程 91.4.2 近年来计算机控制系统在我国的发展趋势 9 习题 13第2章开关量输入/输出通道与人机接口 142.1 过程通道的分类 142.2 开关量输入/输出通道 152.2.1 开关量输入/输出通道的一般结构形式 15 2.2.2 开关量输入信号的调理 162.2.3 开关量输出驱动电路 192.2.4 开关量输入/输出通道的设计 21 2.3 人机接口——键盘 222.3.1 非编码键盘 232.3.2 编码键盘 282.4 人机接口——数字显示方法 312.4.1 发光二极管LED显示 312.4.2 LCD显示接口技术 38习题 81第3章顺序控制与数字控制 833.1 顺序控制 833.1.1 顺序控制系统的类型 833.1.2 顺序控制系统的组成 853.1.3 顺序控制系统的应用领域 853.1.4 顺序控制的应用实例 863.2 数字程序控制 883.2.1 数值插补计算方法 883.2.2 逐点比较法直线插补 893.2.3 逐点比较法圆弧插补 943.2.4 步进电机工作原理 993.2.5 步进电机控制系统原理 1013.2.6 步进电机与微型机的接口及程序设计 103 3.2.7 步进电机步数及速度的计算方法 1083.2.8 步进电机的变速控制 109习题 110[1]第4章模拟量输入/输出通道 1124.1 模拟量输入通道 1124.1.1 输入信号的处理 1124.1.2 多路开关 1134.1.3 放大器 1174.1.4 采样保持器(S/H) 1194.1.5 模/数(A/D)转换器及其应用 1204.2 模拟量输出通道 1284.2.1 DAC的工作原理 1284.2.2 多路模拟量输出通道的结构形式 1304.2.3 D/A输出方式 1314.2.4 失电保护和手动/自动无扰动切换 1324.2.5 DAC的主要技术指标 1324.2.6 典型应用例子 133习题 135第5章 PID调节器的数字化实现 1375.1 PID调节器 1385.1.1 PID调节器的优点 1385.1.2 PID调节器的作用 1385.2 数字PID控制器的设计 1415.2.1 PID控制规律的离散化 1425.2.2 PID数字控制器的实现 1435.3 数字PID控制器参数的整定 1455.3.1 采样周期的选择 1455.3.2 PID控制器参数的整定 146习题 150第6章计算机控制系统的抗干扰技术 152 6.1 干扰信号的类型及其传输形式 1526.2 抗干扰技术 1536.2.1 接地技术 1546.2.2 屏蔽技术 1556.2.3 隔离技术 1566.2.4 串模干扰的'抑制 1566.2.5 共模干扰的抑制 1576.2.6 长线传输中的抗干扰问题 157[1] 6.3 电源干扰的抑制 1586.3.1 电源干扰的基本类型 1586.3.2 电源抗干扰的基本方法 1596.4 CPU软件抗干扰技术 1616.4.1 人工复位 1626.4.2 掉电保护 1626.4.3 睡眠抗干扰 1636.4.4 指令冗余 1646.4.5 软件陷阱 1646.4.6 程序运行监视系统(WATCHDOG) 167 6.5 数字信号的软件抗干扰措施 1706.5.1 数字信号的输入方法 1706.5.2 数字信号的输出方法 1716.5.3 数字滤波 172习题 176第7章工业控制微型计算机 1777.1 工业控制计算机的特点 1777.2 总线式工控机的组成结构 1787.3 常用工控总线(STD/VME/IPC工控机) 179 7.3.1 STD总线工控机 1797.3.2 MC6800/MC68000工控机 1797.3.3 IPC总线工控机 1797.4 IPC的主要外部结构形式 1807.4.1 台式IPC 1807.4.2 盘装式IPC 1817.4.3 IPC工作站 1817.4.4 插箱式IPC 1827.4.5 嵌入式IPC 1837.5 IPC总线工控机内部典型构成形式 1847.5.1 工业控制计算机的组成 1847.5.2 工业控制计算机系统的组成 1857.6 IPC总线工业控制计算机常用板卡介绍 186 7.6.1 IPC总线工业控制计算机的概念 1867.6.2 工业控制计算机I/O接口信号板卡 187 习题 192附录 ST7920GB中文字型码表 193参考文献 198。
电机控制系统PID调节器设计与实现

电机控制系统PID调节器设计与实现一、引言随着电机在工业、农业、交通等领域的广泛应用,如何实现电机的精确控制成为了一项重要挑战。
PID调节器作为一种常用的控制算法,被广泛应用于电机控制系统中。
本文将介绍电机控制系统中PID调节器的设计与实现。
二、PID调节器原理及控制策略PID调节器是一种常用的闭环控制算法,它包含比例控制、积分控制和微分控制三个部分。
比例控制是根据误差信号的大小进行控制,积分控制是处理误差信号的累计值,微分控制是根据误差信号的变化率进行控制。
PID调节器结合了三个控制策略,可以实现对系统的快速响应、精确控制等优秀特性。
三、PID调节器的实现方法PID调节器的实现方法取决于电机控制系统的具体应用场景与控制需求。
一般来说,PID调节器可以分为模拟PID和数字PID 两种实现方法。
1、模拟PID调节器模拟PID调节器是基于传统的模拟电路进行实现的,它需要使用模拟运算放大器等元器件实现PID调节器的比例、积分和微分计算。
模拟PID调节器的优点是响应速度快、控制精度高,但缺点是难以实现复杂的控制算法。
因此,模拟PID调节器通常仅适用于简单的电机控制系统。
2、数字PID调节器数字PID调节器是基于数字信号处理器(DSP)等器件进行实现的,它可以通过编程实现PID调节器的比例、积分和微分运算。
数字PID调节器的优点是可以实现复杂的控制算法、易于开发和调试。
数字PID调节器通常适用于电机控制系统的高级控制或者涉及多轴控制的应用场景。
四、电机控制系统PID调节器设计实例本文以直流电机控制系统为例,介绍PID调节器的设计方法。
1、控制系统模型建立假设直流电机的控制系统如图1所示,它由电气子系统和机械子系统组成。
电气子系统包含直流电机、电源、电阻和感性电路。
机械子系统包含电机机械负载、转动惯量和摩擦阻力等。
图1 直流电机控制系统示意图则直流电机控制系统的传递函数为:G(s) = K / (Ls + R) * 1 / (Js2 + bs)其中,K是电机的电磁功率常数,L是电机的电感,R是电机的电阻,J是电机的转动惯量,b是电机的摩擦系数。
(完整版)数字PID及其算法
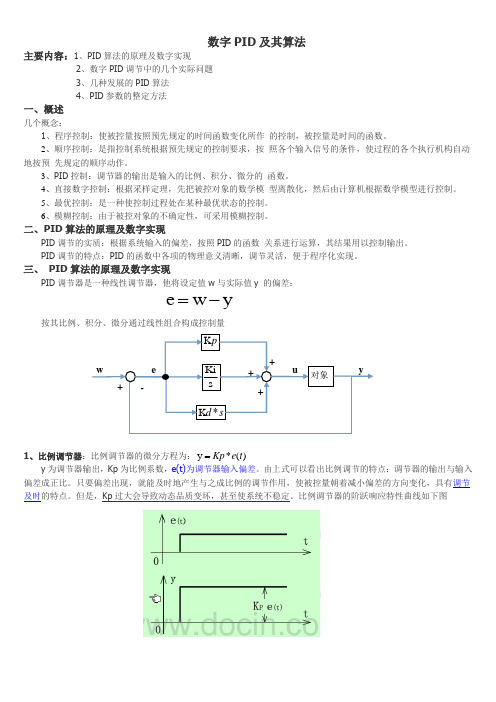
数字PID 及其算法主要内容:1、PID 算法的原理及数字实现2、数字PID 调节中的几个实际问题3、几种发展的PID 算法4、PID 参数的整定方法一、概述几个概念:1、程序控制:使被控量按照预先规定的时间函数变化所作 的控制,被控量是时间的函数。
2、顺序控制:是指控制系统根据预先规定的控制要求,按 照各个输入信号的条件,使过程的各个执行机构自动地按预 先规定的顺序动作。
3、PID 控制:调节器的输出是输入的比例、积分、微分的 函数。
4、直接数字控制:根据采样定理,先把被控对象的数学模 型离散化,然后由计算机根据数学模型进行控制。
5、最优控制:是一种使控制过程处在某种最优状态的控制。
6、模糊控制:由于被控对象的不确定性,可采用模糊控制。
二、PID 算法的原理及数字实现PID 调节的实质:根据系统输入的偏差,按照PID 的函数 关系进行运算,其结果用以控制输出。
PID 调节的特点:PID 的函数中各项的物理意义清晰,调节灵活,便于程序化实现。
三、 PID 算法的原理及数字实现PID 调节器是一种线性调节器,他将设定值w 与实际值y 的偏差:按其比例、积分、微分通过线性组合构成控制量1、比例调节器:比例调节器的微分方程为:)(*y t e Kp =y 为调节器输出,Kp 为比例系数,e(t)为调节器输入偏差。
由上式可以看出比例调节的特点:调节器的输出与输入偏差成正比。
只要偏差出现,就能及时地产生与之成比例的调节作用,使被控量朝着减小偏差的方向变化,具有调节及时的特点。
但是,Kp 过大会导致动态品质变坏,甚至使系统不稳定。
比例调节器的阶跃响应特性曲线如下图yw e -=sd *K s Ki pK 对象 we + - + + + u y2、积分调节器:积分作用是指调节器的输出与输入偏差的积分成比例的作用,其作用是消除静差。
积分方程为:TI 是积分时间常数,它表示积分速度的大小,TI 越大,积分速度越慢,积分作用越弱。
pid调节器工作原理

pid调节器工作原理
PID调节器是一种常用的控制器,用于自动调节系统的输出以
使其接近设定值。
它的工作原理主要包括三个部分:比例、积分和微分。
首先,比例部分根据当前的测量值与设定值之间的差距,计算出一个比例调节量。
比例调节量与差距成正比,即差距越大,比例调节量越大。
这样可以快速地减小差距,但由于比例关系较简单,会使得系统出现超调现象。
接着,积分部分根据过去一段时间内的差距积累计算出一个积分调节量。
积分调节量与差距的积分成正比,即差距积分越大,积分调节量越大。
通过积分部分的作用,可以消除系统的稳态误差,但积分时间过长会导致系统响应速度变慢。
最后,微分部分根据当前的差距变化率计算出一个微分调节量。
微分调节量与差距的微分成正比,即差距变化越快,微分调节量越大。
微分部分可以提高系统的稳定性和响应速度,但过大的微分调节量会引入噪声和振荡。
将比例、积分和微分的调节量相加,即可得到最终的输出信号,用于控制系统的执行器,使系统的输出接近设定值。
PID调节
器根据实际需要,通过调整三个调节参数的数值大小,可以实现不同的控制效果。
总之,PID调节器通过比例、积分和微分三个部分的配合作用,
根据系统的实际情况动态调整输出信号,以实现系统的自动调节和控制。
PID控制算法介绍与实现

PID控制算法介绍与实现一、PID的数学模型在工业应用中PID及其衍生算法是应用最广泛的算法之一,是当之无愧的万能算法,如果能够熟练掌握PID算法的设计与实现过程,对于一般的研发人员来讲,应该是足够应对一般研发问题了,而难能可贵的是,在很多控制算法当中,PID控制算法又是最简单,最能体现反馈思想的控制算法,可谓经典中的经典。
经典的未必是复杂的,经典的东西常常是简单的,而且是最简单的。
PID算法的一般形式:PID算法通过误差信号控制被控量,而控制器本身就是比例、积分、微分三个环节的加和。
这里我们规定(在t时刻):1.输入量为2.输出量为3.偏差量为二、PID算法的数字离散化假设采样间隔为T,则在第K个T时刻:偏差= -积分环节用加和的形式表示,即 + + …微分环节用斜率的形式表示,即[- ]/T;PID算法离散化后的式子:则可表示成为:其中式中:比例参数:控制器的输出与输入偏差值成比例关系。
系统一旦出现偏差,比例调节立即产生调节作用以减少偏差。
特点:过程简单快速、比例作用大,可以加快调节,减小误差;但是使系统稳定性下降,造成不稳定,有余差。
积分参数:积分环节主要是用来消除静差,所谓静差,就是系统稳定后输出值和设定值之间的差值,积分环节实际上就是偏差累计的过程,把累计的误差加到原有系统上以抵消系统造成的静差。
微分参数:微分信号则反应了偏差信号的变化规律,或者说是变化趋势,根据偏差信号的变化趋势来进行超前调节,从而增加了系统的快速性。
PID的基本离散表示形式如上。
目前的这种表述形式属于位置型PID,另外一种表述方式为增量式PID,由上述表达式可以轻易得到:那么:上式就是离散化PID的增量式表示方式,由公式可以看出,增量式的表达结果和最近三次的偏差有关,这样就大大提高了系统的稳定性。
需要注意的是最终的输出结果应该为:输出量 = + 增量调节值三、PID的C语言实现1.位置式PID的C语言实现上边已经抽象出了位置性PID和增量型PID的数学表达式,这里重点讲解C语言代码的实现过程。
PID调节器的电路

采用可编程逻辑控制器(PLC)或微控制器(MCU),可以实现PID调节器电路的远程控制和编程控制, 方便系统的集成和扩展。
THANKS FOR WATCHING
感谢您的观看
比例调节器
根据输入信号与设定值的偏差,按比例输出控制 信号。
积分调节器
对输入信号与设定值之间的偏差进行积分运算, 以消除稳态误差。
微分调节器
对输入信号的变化率进行运算,以减小系统的动 态误差。
03
PID调节器电路的实现
硬件实现
模拟电路实现
通过使用电阻、电容和运算放大器等模拟元件,搭建PID调节器的硬件电路。 这种实现方式具有实时性好、稳定性高的优点,但调试复杂且容易受到环境温 度和元件老化等因素的影响。
电机控制系统
PID调节器电路用于控制电机的速度、 位置和转矩,广泛应用于数控机床、 机器人等领域。
家电领域
空调系统
PID调节器电路用于控制空调系统的温度和湿度,提供舒适的生活环境。
热水器
PID调节器电路用于控制热水器的加热温度,实现快速加热和节能的效果。
汽车领域
燃油喷射系统
PID调节器电路用于控制燃油喷射系统的喷 油量,提高燃油经济性和排放性能。
VS
详细描述
PID调节器由比例、积分和微分三个环节 组成。比例环节根据误差信号调整输出值 ,以减小误差;积分环节根据误差信号的 积分调整输出值,以消除长期误差;微分 环节根据误差信号的变化率调整输出值, 以提前预测并减小误差。三个环节协同作 用,实现PID调节器的控制效果。
PID调节器的特点
总结词
02
PID调节器电路的组成
输入部分
信号采集
负责采集系统或设备的状态信息 ,并将其转换为电信号。
第5章数字PID及其算法

第5章数字PID及其算法数字PID是指使用数字信号处理器(DSP)或微处理器实现的PID控制算法。
它将传统的模拟PID控制器转换为数字信号,通过数值计算和运算来实现对控制系统的稳定和优化。
本章将介绍数字PID的基本原理和常用的数字PID算法。
一、数字PID的基本原理数字PID与传统的模拟PID控制器在基本原理上是一致的,都是通过调整控制器的输出来实现对系统的控制。
数字PID的基本原理包括三个部分:1. 比例(Proportional)部分:根据系统的偏差(即期望值与实际值之差)与设定的比例增益,计算出控制器的比例调节量。
比例调节量通过放大或缩小偏差,反映了控制器对于系统偏差的敏感程度。
2. 积分(Integral)部分:通过对偏差的积分,将系统之前的误差累积起来。
积分调节量考虑了系统在一段时间内的偏差总和,用于消除系统的稳态误差。
3. 微分(Derivative)部分:通过对偏差的微分,计算出系统的变化速率。
微分调节量根据偏差的变化率来预测系统的未来变化趋势,并对控制器的输出进行调整,以减少系统的震荡和振荡。
通过比例、积分和微分三个部分的调节,数字PID可以实现对系统的稳定和响应速度的平衡。
二、常用的数字PID算法1. Ziegler-Nichols算法:Ziegler-Nichols算法是最为常用的数字PID调参方法之一、该算法通过开环试验,观察系统的响应曲线,从而确定合适的比例增益和积分时间。
2. Pole-Zero Canceling算法:Pole-Zero Canceling算法是一种基于系统分析的数字PID调参方法。
它通过分析系统的传递函数,在前向通路中取消极点和零点,从而得到更稳定的闭环系统。
3. Smith Predictor算法:Smith Predictor算法是一种针对具有时延的系统的数字PID调参方法。
它通过引入状态估计器,对系统的时延进行补偿,从而提高系统的响应速度和稳定性。
自动化控制系统中的PID调节器原理与应用

自动化控制系统中的PID调节器原理与应用在自动化控制系统中,PID(比例积分微分)调节器是一种常用的控制器,广泛应用于各行各业的控制系统中。
本文将详细介绍PID调节器的原理与应用。
一、PID调节器的原理PID调节器是通过测量系统输出的反馈信号(通常是被控变量)与设定值之间的误差,来生成控制输出信号,从而实现控制系统的稳定。
PID调节器基于比例、积分和微分三个部分组成,具体如下:1. 比例部分(P部分):根据误差的大小,产生一个与误差成正比的输出信号。
比例控制的作用是使系统能够快速地响应误差的变化,但是它无法完全消除误差。
2. 积分部分(I部分):将误差的累积值相乘以一个比例系数,产生一个输出信号。
积分控制的作用是弥补比例控制无法完全消除的误差,保证系统的稳定性。
3. 微分部分(D部分):根据误差变化的速度,产生一个与误差变化率成正比的输出信号。
微分控制的作用是预测误差的变化趋势,使系统能够更快地收敛到设定值。
PID调节器的输出信号是这三个部分的加权和,称为控制输出。
通过调节这三个部分的权重系数,可以实现对系统的不同要求,例如响应速度、稳定性和抗干扰能力等。
二、PID调节器的应用PID调节器有广泛的应用领域,以下是几个常见的应用示例:1. 温度控制:在工业生产中,往往需要对温度进行精确控制。
PID调节器可以通过测量温度变化与设定值之间的误差来控制加热或冷却系统,使温度稳定在设定值附近。
2. 速度控制:在机械系统中,需要对电机的转速进行控制。
PID调节器可以根据实际转速与目标转速之间的误差来调节电机的控制信号,实现精确控制。
3. 液位控制:在油田开采、化工等领域,需要对液体的液位进行控制。
PID调节器可以测量液位与设定值之间的误差,并通过控制阀门的开度来调节流量,实现液位的稳定控制。
4. 压力控制:在工业生产中,需要对气体或液体的压力进行控制。
PID调节器可以根据实际压力与目标压力之间的误差来调节控制阀门或泵的操作,保持压力稳定。
pid调节原理

pid调节原理
PID调节原理是一种常用的控制策略,它以反馈控制为基础,
通过调整系统的输出来使得系统的反馈信号与设定值之间的差异最小化。
PID调节器根据系统当前的误差(偏差)信号分别
计算出比例、积分和微分的作用量,并把它们加权叠加起来得到最后的控制量。
比例(P)作用是根据误差信号的大小来进行比例放大,将误
差乘以一个比例增益系数Kp得到一个与误差成正比的控制量,该控制量越大,系统的响应越快。
但是纯比例控制对于补偿系统的稳定性和静态误差校正有一定的限制。
积分(I)作用是对误差信号的积分进行放大,该作用量可以
消除系统的静态误差。
积分控制器通过累加误差信号的面积得到一个与误差信号积分值成正比的控制量,该控制量改变系统的偏差,使得系统最终趋于稳定。
微分(D)作用是对误差信号的变化率进行放大,该作用量可
以改善系统的动态响应特性。
微分控制器通过对误差信号的微分值进行放大,得到一个与误差变化率成正比的控制量,该控制量与系统的响应速度成反比。
对于PID控制器来说,比例、积分和微分三个作用量的选择
及其权重的确定是一个重要的问题。
一般来说,比例作用对于系统的响应速度和稳定性有较大的影响;积分作用可以消除系统的稳态误差,但是也容易引起系统的超调和震荡;微分作用可以提高系统的响应速度和稳定性,但是对于噪声和干扰信号
较为敏感。
PID调节器通过权衡比例、积分和微分三个作用量的作用,可
以实现系统的快速响应、准确控制和良好的稳定性。
在现代工业自动化控制系统中,PID调节器被广泛应用于各种控制环节,提高了系统的控制精度和稳定性。
模拟-数字PID调节器

积分作用
积分调节器的作用是把偏差积累的结果, 作为它的输出。在调节过程中,只要偏 差存在,积分器的输出就会不断增大, 直到偏差e等于0,输出u才能维持某一常 量,使系统趋于稳态。积分调节虽然可 以消除静差,但会降低系统的响应速度, 增加系统输出的超调。
微分作用
微分控制器的作用是阻止偏差的变化, 偏差变化越快,微分调节器的输出也越 大。因此微分作用的加入有助于减小超 调,克服振荡,使系统趋于稳定。但微 分环节对噪声有敏感的反应,所以在电 机控制中,一般不加入微分环节,只采 用PI调节器 。
比例作用
PID控制器中比例调节器的作用是对于偏 差做出瞬间快速反应。偏差一旦产生, 调节器立即产生控制作用使控制量向着 减小偏差的方向变化,控制作用的强、 弱取决于比例系数Kp。增大Kp,将加快 系统的响应速度,有利于减少静差。但 过大的比例系数会使系统有较大的超调, 并可能产生振荡,使稳定性变坏。
入口 计算偏差ei
计算比例项
加上前面累 积的积分项
ui 1 umax ? N Y ui 1 umin ? N N
Y
ei 0?NBiblioteka ei 0?计算积分项
比例、积分项相加,得到控制量 出口
PI调节器改进
(2) 积分分离法 积分分离法的基本思想是当输入误差的 绝对值大于某个门限值ε时,不做积分调 节,只做比例调节,避免PI调节器深度 饱和,同时有利于PI退饱和。当输入误 差较小时,才引入积分作用,以消除静 差。
数字PID调节器
积分:
e(t )dt Te(k )
t 0 i 0
k
微分:
de (t ) e(k ) e(k 1) dt T
数字PID控制器ppt课件

R2
R1 -
ui(t)
+
uo(t)
Gc(s)U Uoi((ss))R R12 KP
精选ppt
23
控制器的输出信号u与输入偏差信号e成比例关系
u(t)Kce(t)u0
比例增益
控制器输出信号 的起始值
增量形式 u(t)Kce(t)
精选ppt
24
比例调节器
e
控制规律:
u(t)KPe(t)u0 其中K:P 为比例系数;
香农采样定理给出了从采样信号恢复连续信号的最低采样频率。在计算
机控制系统中,完成信号恢复功能一般由零阶保持器H(s)来实现。零阶保
持器的传递函数为:
其频率特性为
H (s) 1 esT
s
H ( j ) 1 e jT 2e jT 2 (e jT 2 e jT 2 )
j
2 j
T
sin T
2
T
e jT 2
精选ppt
13
(3)后向差分法
利用级数展开还可将Z=esT
z esT
1 e sT
1 1 sT
s z 1
Tz
D(z) D(s) s z1 Tz
精选ppt
14
4.设计由计算机实现的控制算法
数字控制器D(Z)的一般形式为下式,其中n≥m,各 系数ai,bi为实数,且有n个极点和m
D(z)
U (z) E(z)
精选ppt
33
1. PID控制原理---比例控制
特点
(2)比例控制的稳 态误差随比例带的增 大而增大
增大比例增益Kc,会使系统振荡加剧,稳定性变差,但是可以减小 系统的稳态误差,加快系统的响应速度。
精选ppt
模拟PID-调节器设计及数字化实现

模拟PID 调节器设计及数字化实现摘要:本文首先对现代工控系统中比较常用的PID 调节器原理作了详细的阐述,然后对各个环节进行了硬件电路的设计,并通过MATLAB、EWB 等EDA 软件对各个环节及整个调节电路进行了验证摘要:本文首先对现代工控系统中比较常用的PID 调节器原理作了详细的阐述,然后对各个环节进行了硬件电路的设计,并通过MATLAB、EWB 等EDA 软件对各个环节及整个调节电路进行了验证仿真。
通过分析,得出了PID 调节器的优点及缺陷。
最后,对数字化实现PID 调节器的工作过程进行了概述。
关键词: PID;硬件设计;数字实现;EDA 仿真引言随着工业自动化的不断发展,人们对于生产过程的要求越来越高,这就促使人们在生产实践中不断探求新的控制方案。
而在控制方案的选择中,控制规律的选择尤为重要。
控制规律的恰当与否将直接决定生产线的安全、产品的质量以及生产的效率等。
据不完全统计,目前在各种工业控制中,PID 调节或基于PID 调节的控制方式占90%。
调节规律作为应用时间最长、生命力最强的控制方式,主要有以下优点:(1)原理简单,使用方便(2)适应性强(3)鲁棒性强。
既然PID 调节在工业控制中的地位如此重要,那么,PID 的设计问题就显得颇为重要了。
硬件电路设计方案控制器是一种线性控制器。
它根据给定值x (t )与实际输出值y (t )构成控制偏差e(t),即表示e(t) = x (t) ? y (t)。
将偏差的比例、积分和微分通过线性组合构成控制量,对被控对象进行控制,故称PID 控制器。
其控制规律为模拟PID 调节器主要由三个部分组成,即P 调节、I 调节、D 调节,当然,作为工业应用,还必须有输入、输出电路,手动调节电路,下面给出各部分电路的硬件设计方案。
输入电路主要作用:获得偏差信号,并以VB=10V 为参考点进行电平迁移。
分析:如图2 所示,设A1 为理想放大器,即输入阻抗无穷大,输出阻抗为零。
pid控制原理及编程方法

pid控制原理及编程方法PID控制是一种常用的控制算法,可以根据给定的目标值和实际值,通过不断调整输出值,使得实际值尽可能接近目标值。
PID控制的原理可以通过以下几个步骤来理解和实现。
1. 比例控制(P控制):根据目标值和实际值的偏差,乘以一个比例增益系数Kp得到控制量的变化量,作为输出。
控制量的变化量 = Kp * (目标值 - 实际值)2. 积分控制(I控制):将偏差的累积值乘以一个积分增益系数Ki得到控制量的变化量,作为输出。
这个步骤主要是为了解决系统存在的偏差问题。
控制量的变化量 += Ki * (目标值 - 实际值)* Δt3. 微分控制(D控制):根据偏差的变化率乘以一个微分增益系数Kd得到控制量的变化量,作为输出。
这个步骤主要是为了解决系统存在的过渡问题。
控制量的变化量 += Kd * (目标值变化率 - 实际值变化率) / Δt以上三个步骤得到的控制量的变化量之和即为最终的输出。
在编程实现PID控制时,可以按照以下步骤进行:1. 定义并初始化相关变量,包括比例增益系数Kp、积分增益系数Ki、微分增益系数Kd、目标值、实际值、偏差、偏差的累积值、上次偏差等。
2. 循环执行以下操作:a. 更新实际值。
b. 计算偏差(目标值 - 实际值)。
c. 计算控制量的变化量,包括比例控制量、积分控制量和微分控制量。
d. 更新偏差的累积值。
e. 计算最终输出值。
f. 控制执行相应操作(根据最终输出值控制系统)。
g. 等待一定时间间隔。
3. 重复步骤2直至达到控制目标。
需要注意的是,PID控制算法需要根据具体的应用场景,仔细选择合适的增益系数,以达到良好的控制效果。
自动化控制系统中的PID调节器设计与参数配置

自动化控制系统中的PID调节器设计与参数配置在自动化控制系统中,PID(比例-积分-微分)调节器是一种常见且重要的控制机制。
它通过对系统输出与预期设定值之间的差异进行计算,使得系统能够实时调整输入信号以使输出更加稳定。
本文将详细介绍PID调节器的设计原理和参数配置方法。
一、PID调节器的设计原理PID调节器是基于反馈原理的控制器,通过不断对比被控对象的实际输出与期望输出之间的偏差,即误差,来调整输出信号,使误差趋向于零。
具体而言,PID调节器由比例控制、积分控制和微分控制三个部分组成。
1.比例控制(P)比例控制器根据误差的大小,按比例调整输出信号,即输出与误差成正比。
它能够快速响应系统的变化,但对于变异性较大的被控对象,单独使用比例控制往往无法将输出稳定在期望值附近。
2.积分控制(I)积分控制器根据误差的积分值,按一定比例调整输出信号,以消除偏差的累积效应。
积分控制能够消除稳态误差,但会导致系统的过冲和超调。
3.微分控制(D)微分控制器根据误差的变化率,按一定比例调整输出信号。
微分控制器可以预测系统的变化趋势,对快速变化的被控对象能够提供稳定的输出,但过度依赖微分控制可能导致噪声信号的放大。
二、参数配置方法PID调节器的性能取决于三个参数:比例增益(Kp)、积分时间(Ti)和微分时间(Td)。
为了提高系统的响应速度和稳定性,需要对这些参数进行适当的配置。
1.比例增益(Kp)比例增益决定了输出与误差之间的关系,过大或过小的Kp值都会导致系统的不稳定。
一般情况下,可以通过试探法逐渐增加Kp值,观察输出的响应速度和稳定性,找到合适的值。
此外,比例增益也可以根据被控对象的特性进行计算,如增益裕度法等。
2.积分时间(Ti)积分时间决定了积分控制的灵敏度,过大的Ti值会导致系统的超调和震荡,过小的Ti值则会导致系统的稳态误差。
一般而言,可以通过调整Ti值来平衡系统的响应速度和稳态误差。
较小的Ti值适合要求较高的响应速度,而较大的Ti值适合要求较低的稳态误差。
PID调节原理与PID参数整定方法

PID调节原理与PID参数整定方法PID调节原理与参数整定方法是自动控制系统中常用的调节算法和方法之一、PID调节器是一种反馈调节控制器,利用当前的偏差值、偏差累积值和偏差变化率来产生控制输出,进而改变被控对象的状态,使其尽可能地满足设定值。
PID调节器由三个部分组成:比例(P)调节器、积分(I)调节器和微分(D)调节器。
P调节器根据偏差值来产生控制信号;I调节器根据偏差累积值来产生控制信号;D调节器根据偏差变化率来产生控制信号。
这三个调节器的输出都与偏差成比例,然后将它们相加得到最终的控制输出。
PID控制器的数学表达式为:u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt其中,u(t)是控制输出,Kp、Ki和Kd是调节器的增益参数,e(t)是偏差,t是时间。
参数整定是指选择合适的PID控制参数以实现系统良好性能。
对于PID参数整定,常用的方法有以下几种:1.经验法:根据经验和实际应用中相似系统的参数进行估计和调整。
这种方法简单易行,但对于不同系统的参数整定效果不一致。
2. Ziegler-Nichols方法:此方法通过实验获取系统的临界增益(Kcr)和临界周期(Pcr),然后根据不同的整定规则选择PID参数。
常用的整定规则有:P控制器(Kp = 0.5 * Kcr)、PI控制器(Kp = 0.45* Kcr,Ki = 1.2 / Pcr)和PID控制器(Kp = 0.6 * Kcr,Ki = 2 / Pcr,Kd = 8 / Pcr)。
3.最小二乘法:通过最小化系统的输出与设定值之间的误差,来确定合适的PID参数。
这种方法需要进行大量的计算,适用于精确调节和要求高性能的系统。
4.频响法:通过系统的频率响应曲线来进行参数整定。
此方法需要对系统进行频率扫描,可以获得系统的幅频特性和相频特性,然后根据相应的调节规则选择PID参数。
总结来说,PID调节原理是利用当前的偏差值、偏差累积值和偏差变化率来产生控制输出;而PID参数整定方法可以通过经验法、Ziegler-Nichols方法、最小二乘法和频响法等多种方法来选择合适的参数,以实现系统的稳定性和性能要求。
20第五章 PID调节器的数字化实现

第五章PID调节器的数字化实现一、授课时间:年月日第20 次二、教学目的:1、掌握PID调节器的优点2、掌握PID调节器的作用For personal use only in study and research; not for commercial use三、教学的重点及难点:重点:PID调节器的作用。
难点:PID调节器的作用。
四、教学内容及过程:5.1 PID调节器5.1.1 PID调节器的优点1.技术成熟PID调节是连续系统理论中技术最成熟,应用最广泛的一种控制方法。
2.易被人们熟悉和掌握生产技术人员及操作人员都比较熟悉它,并在实践中积累了丰富的经验,特别是一些工作时间较长的工程技术人员。
3.不需要建立数学模型目前,有许多工业对象得不到或很难得到精确的数学模型,因此,应用直接数字控制方法比较困难或根本不可能,所以,必须用PID算法。
4.控制效果好虽然计算机控制是断续的,但对于时间常数比较大的系统来说,其近似于是连续变化的。
因此,用数字PID完全可以代替模拟调节器,并得到比较满意的效果。
5.1.2 PID调节器的作用1.比例调节器比例调节器的微分方程为Y=Kpe(t) (5-1)式中:Y为调节器输出;Kp为比例系数;e(t)为调节器输入偏差。
由上式可以看出,调节器的输出与输入偏差成正比。
因此,只要偏差出现,就能及时地产生与之成比例的调节作用,具有调节及时的特点。
比例调节器的特性曲线如图5-1所示。
图5-1 阶跃响应特性曲线比例调节作用的大小,除了与偏差有关,主要取决于比例系数。
比例系数越大,调节作用越强,动态特性也越好。
反之,比例系数越小,调节作用越弱。
但对于多数惯性环节,Kp太大时,会引起自激振荡。
比例调节器的主要缺点是存在静差,因此,对于扰动较大, 惯性较大的系统,若采用单纯的比例调节器,就难于兼顾动态和静态特性,因此,需要用调节规律比较复杂的调节器。
2. 比例积分调节器所谓积分作用是指调节器的输出与输入偏差的积分成比例的作用。
ID调节器的数字化实现

微分作用的特点是:输 出只能反映偏差输入变 化的速度,而对于一个 固定不变的偏差,不管 其值多大,根本不会有 微分作用输出。
• 4.比例积分微分调节器
1t
de(t)
y
K
p
e(t )
Ti
e(t)dt TD
0
dt
在阶跃信号作用下,首先是比例和微分作用,使其 调节作用加强,然后再进行积分,直到最后消除静 差为止。
感谢下 载
感谢下 载
e(k
1)
T Ti
e(k )
TD T
[e(k )
2e(k
1)
e(k
2)]
5.2.2 PID数字控制器的实 现
• 公式简化得:
u
(k )
u
(k
1)
K
p
1
T Ti
TD T
e(k
)
K
p
1
2TD T
e(k
1)
Kp
TD T
e(k
2)
u (k 1) a0e(k ) a1e(k 1) a2e(k 2)
5.2 数字PID控制器的设计
5.2.1 PID控制规律的离散化
• 在连续控制系统中,模拟调节器最常用的控制规律 是PID控制,其控制规律如下:
式中: u
(te)(t)K:调p 节e(器t) 输 T入1i 函0t e数(t)dt
TD
de(t)
dt
•
u(t):调节器输出函数
•
Kp :比例系数
u•( k整理1后):
K
p
e(k
1)
1 Ti
k 1
e(i)T
PID控制器的数字化

模拟量PID 控制器的输出表达式:
M dt t dev T dt t ev T t ev K t mv d P +⨯+⨯+=⎰])()(1)([)(1 (8-1)
式中,误差信号)()()(t pv t sv t ev -=;)(t mv 是控制器的输出信号;P K 是调节器的比例系数;I T 和D T 分别是积分时间常数和微分时间常数;M 是积分部分的初始值;等号右边的前三项分别是比例、积分、微分部分,它们分别与误差、误差的积分、误差的微分成正比。
直接采用式(8-1)计算,计算量将会很大 ,所以我们采用近似的方法来求得积分和微分部分。
积分部分曲线)(t ev 与坐标轴包围的面积,一般用矩形积分来近似精确积分,每块矩形的面积为s s T jT e ⨯)(,s T 是采样周期,即执行PID 的控制循序的时间间隔;微分部分则可近似用差分来近似:s T n ev n ev t t ev dt t dev )1()()()(--=∆∆≈
将积分,微分的近似式代入(8-1),那么第n 次采样时控制器的输出
为 M n ev n ev T T j ev T T n ev K t mv n j S D I S P +--+⨯+=∑=)]}1()([)()({)(1 (8-2)
式中,)1(-n ev 是第n-1次采样时的误差值,上式可改写为 M
n ev n ev K j ev K n ev K n mv d n j I P +--+⨯+⨯=∑=)]1()([)()()(1 (8-3) 式中I S P I T T K K =、S D P d T T K K =分别是积分系数和微分系数。
数字PID控制算法

INC
MOV CPL
R0
A,@R0 A
ADDC A,#00H
返回本节
4.3 PID算法的几种发展
4.3.1 积分分离的PID控制 4.3.2 变速积分的PID控制
返回本章首页
4.3.1 积分分离的PID控制
Y(t)
1 P
2 一般PID
开始引入积分作用
积分分离PID
t
0
图4-10 具有积分分离作用的控制过程曲线
;取e(n) ;取e(n-1)
ACALL CPL1 ACALL DSUM MOV MOV MOV MOV MOV A,R7
;求e(n-1)的补码 ;求PP=Δe(n)=e(n)-e(n-1)
R5,A ;存Δe(n) A,R6 R4,A R3,4BH ;取PI
MOV
R2,4AH
;求PI+ PP
ACALL DSUM
ACALL DSUM
MOV
MOV MOV MOV RET
3DH,3BH
3EH,3CH 3BH,39H 3CH,3AH
;e(n-1)送入e(n-2)单元
;e(n)送入e(n-1)单元
MOV MOV MOV MOV MOV MOV
R5,37H R4,38H R0,#46H R5,47H R6,46H R3,4BH
入口
计算误差
e
i
根据增量式PID算式计算比例及微分项
y
( n )> 否
y
max
否 ?
是
是
图 4 11
PID
y
否
( n )< 否
y
min
ቤተ መጻሕፍቲ ባይዱ
否 ?
PID调节器的选型与参数调优实现最佳控制性能

PID调节器的选型与参数调优实现最佳控制性能PID(Proportional-Integral-Derivative)调节器是一种经典且广泛应用的控制算法,被广泛用于工业过程控制、机器人控制、自动驾驶等领域。
本文将探讨PID调节器的选型方法以及参数调优策略,以实现最佳的控制性能。
一、PID调节器的选型方法PID调节器的选型需要考虑多个因素,包括系统的物理特性、控制需求以及实际应用环境等。
下面将介绍几种常用的PID调节器选型方法。
1. 手动调节法手动调节法是最常见的PID调节器选型方法,它要求用户通过实际观察系统的响应曲线,逐步调整PID参数以达到期望的控制效果。
手动调节法的优点是简单易行,无需过多的理论知识。
然而,缺点是需要耗费较长的时间,并且对操作者的经验要求较高。
2. Ziegler-Nichols 方法Ziegler-Nichols方法是一种经验参数整定法,它通过系统单位阶跃响应曲线的特性,确定PID参数。
具体而言,Ziegler-Nichols方法包括了三种参数整定方式,分别是P(Proportional)整定、PI (Proportional-Integral)整定以及PID整定。
选择哪种参数整定方式,取决于系统的响应特性和控制需求。
3. 理论模型法理论模型法是一种根据系统的数学模型,通过计算或仿真得到合适的PID参数。
这种方法需要系统的数学模型,通常用传递函数或状态空间模型表示。
将模型参数代入PID调节器的传递函数中,进行数字仿真或者计算,以得到最佳的PID参数。
理论模型法适用于对系统有较深入了解并且有相应模型的情况。
二、PID参数调优策略PID参数的调优是为了使得控制系统具有更好的稳定性、快速响应以及抗干扰能力。
下面将介绍几种常用的PID参数调优策略。
1. 经验法调优经验法是一种基于操作经验的PID参数调优方法,通过人为调整PID参数,以观察系统响应曲线的变化,并不断优化参数。
其中,最常用的经验法是逐步逼近法,即先通过P参数进行调整,再逐渐增加I和D参数,直到达到最佳控制性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章PID调节器的数字化实现一、授课时间:年月日第20 次二、教学目的:1、掌握PID调节器的优点2、掌握PID调节器的作用三、教学的重点及难点:重点:PID调节器的作用。
难点:PID调节器的作用。
四、教学内容及过程:5.1 PID调节器5.1.1 PID调节器的优点1.技术成熟PID调节是连续系统理论中技术最成熟,应用最广泛的一种控制方法。
2.易被人们熟悉和掌握生产技术人员及操作人员都比较熟悉它,并在实践中积累了丰富的经验,特别是一些工作时间较长的工程技术人员。
3.不需要建立数学模型目前,有许多工业对象得不到或很难得到精确的数学模型,因此,应用直接数字控制方法比较困难或根本不可能,所以,必须用PID算法。
4.控制效果好虽然计算机控制是断续的,但对于时间常数比较大的系统来说,其近似于是连续变化的。
因此,用数字PID完全可以代替模拟调节器,并得到比较满意的效果。
5.1.2 PID调节器的作用1.比例调节器比例调节器的微分方程为Y=Kpe(t) (5-1)式中:Y为调节器输出;Kp为比例系数;e(t)为调节器输入偏差。
由上式可以看出,调节器的输出与输入偏差成正比。
因此,只要偏差出现,就能及时地产生与之成比例的调节作用,具有调节及时的特点。
比例调节器的特性曲线如图5-1所示。
图5-1 阶跃响应特性曲线比例调节作用的大小,除了与偏差有关,主要取决于比例系数。
比例系数越大,调节作用越强,动态特性也越好。
反之,比例系数越小,调节作用越弱。
但对于多数惯性环节,Kp太大时,会引起自激振荡。
比例调节器的主要缺点是存在静差,因此,对于扰动较大,惯性较大的系统,若采用单纯的比例调节器,就难于兼顾动态和静态特性,因此,需要用调节规律比较复杂的调节器。
2.比例积分调节器所谓积分作用是指调节器的输出与输入偏差的积分成比例的作用。
积分方程为(5-2)式中:Ti 是积分时间常数,它表示积分速度的大小, Ti 越大, 积分速度越慢,积分作用越弱。
若将比例和积分两种作用结合起来,就构成PI 调节器,调节规律为(5-3)图5-3 调节器的输出特性曲线由图5-3可以看出,对于PI 调节器,当有一阶跃作用时, 开始瞬时有一比例输出y1,随后在同一方向,在y1的基础上输出值不断增大,这就是积分作用y2。
由于积分作用不是无穷大, 而是具有饱和作用,因此经过一段时间后,PI 调节器的输出趋于稳定值KiKpe(t),其中,系数KiKp 是时间t 趋于无穷时的增益, 称之为静态增益。
由此可见,这样的调节器,既克服了单纯比例调节有静差存在的缺点,又避免了积分调节器响应慢的缺点, 静态和动态特性均得到了改善。
3. 比例微分调节器 ⎰=t t e T y d )(1iPI调节器虽然动作快,可以消除静态误差,但当控制对象具有较大的惯性时,用PI调节器就无法得到很好的调节品质。
这时,若在调节器中加入微分作用,即在偏差刚刚出现,偏差值尚不大时,根据偏差变化的趋势(速度),提前给出较大的调节作用,这样可使偏差尽快消除。
微分调节器的微分方程为(5-4)式中TD为微分时间常数。
微分作用响应曲线如图5-4所示。
从图中可以看出,在t=t0时加入阶跃信号,此时输出值y变化的速度很大:当t>t0时,其输出值y迅速变为0。
微分作用的特点是,输出只能反应偏差输入变化的速度,而对于一个固定不变的偏差,不管其数值多大,根本不会有微分作用输出。
因此,微分作用不能消除静差,而只能在偏差刚刚出现时产生一个很大的调节作用。
它一般不单独使用,需要与比例调节器配合使用,构成PD调节器。
PD 调节器的阶跃响应曲线如图5-5所示。
图5-4 微分作用响应特性曲线图5-5 PD调节器的阶跃响应曲线从图中可以看出,当偏差刚一出现的瞬间,PD调节器输出一个很大的阶跃信号,然后,按指数下降,以致最后微分作用完全消失,变成一个纯比例环节。
通过改变微分时间常数TD,可以调节微分作用的强弱。
4.比例积分微分调节器为了进一步改善调节品质,往往把比例、积分、微分三种作用组合起来,形成PID调节器。
理想的PID微分方程为(5-5)PID调节器对阶跃信号的响应曲线如图5-6所示。
由图可以看出,对于PID调节器,在阶跃信号作用下,首先是比例和微分作用,使其调节作用加强,然后再进行积分,直到最后消除静差为止。
因此,采用PID调节器,无论从静态还是从动态的角度来说,调节品质均得到了改善,从而使得PID调节器成为一种应用最为广泛的调节器。
图5-6 PID调节器对阶跃信号的响应特性曲线直接数字控制系统即DDC系统,是目前广为应用的一种微型计算机控制系统,DDC系统是通过用数字控制器取代模拟调节器,并配以适当的装置(如A/D、D/A转换器等)实现对工业生产过程进行控制。
因此,数字控制器是DDC系统的核心。
五、课堂小结:1、PID调节器的优点2、PID调节器的作用六、布置作业:P120 第2题,第4题一、授课时间:年月日第21 次二、教学目的:1、掌握数字PID控制器的设计2、掌握PID数字控制器的实现三、教学的重点及难点:重点:PID控制规律的离散化。
难点:PID数字控制器的实现。
四、教学内容及过程:复习上节课内容1、PID调节器的优点2、PID调节器的作用导入新课5.2数字PID控制器的设计图5-7示出了用计算机实现数字控制器的框图。
图中,W(s)为反映控制规律的调节器的传递函数。
输入函数x(t)为连续信号,由于计算机只能对数字量进行控制,因此连续信号x(t) 需经采样器进行采样,采样后的x(t)变成脉冲信号序列x*(t)。
设置的保持器h(t) 使x*(t)变成近似于x(t)的信号xh(t), xh(t)就是计算机控制器的输出信号,输出信号通过调节器进行控制。
图5-7 用计算机实现数字控制器的框图图中D(z)表示数字控制器的脉冲传递函数,可以用计算机来实现。
按图5-7所示的原理,得到数字控制器的实现方法,该方法称为模拟控制规律的离散化设计法。
该方法的实现步骤是:先根据连续系统控制理论得出的控制规律,再进行离散化得到计算机能实现的控制算式,然后编成程序在计算机上实现。
本章通过对连续系统中技术成熟、应用广泛的比例、积分、微分控制即PID控制规律的离散化,PID算式的程序实现来介绍这种设计方法。
进行数字控制器设计,还有另一种方法,称为直接设计法,该方法是,根据系统的性能要求,运用离散系统控制理论,直接进行数字控制器的设计。
5.2.1 PID控制规律的离散化在连续控制系统中,模拟调节器最常用的控制规律是PID控制,其控制规律形式如下:(5-6)式中: e(t)是调节器输入函数,即给定量与输出量的偏差;u(t)是调节器输出函数;Kp是比例系数;Ti是积分时间常数;TD是微分时间常数。
因为式(5-6)表示的调节器的输入函数及输出函数均为模拟量,所以计算机是无法对其进行直接运算的。
为此,必须将连续形式的微分方程化成离散形式的差分方程。
取T为采样周期,k为采样序号,k=0,1,2,…,i,…,k,因采样周期T相对于信号变化周期是很小的,这样可以用矩形法算面积,用向后差分代替微分,即(5-7)(5-8)于是式(5-6)可写成(5-9)式中: u(k)是采样时刻k时的输出值;e(k)是采样时刻k时的偏差值;e(k-1)是采样时刻k-1时的偏差值。
式(5-9)中的输出量u(k)为全量输出。
它对应于被控对象的执行机构(如调节阀)每次采样时刻应达到的位置,因此,式(5-9)称为PID位置控制算式。
这即是PID控制规律的离散化形式。
应指出的是,按式(5-9)计算u(k)时,输出值与过去所有状态有关,计算时要占用大量的内存和花费大量的时间,为此,将式(5-9)化成递推形式:(5-10)用式(5-9)减去式(5-10),经整理后可得(5-11)按式(5-11)计算在时刻k时的输出量u(k),只需用到采样时刻k的偏差值e(k),以及向前递推一次及两次的偏差值e(k-1)、e(k-2)和向前递推一次的输出值u(k-1),这大大节约了内存和计算时间。
应该注意的是,按PID的位置控制算式计算输出量u(k)时,若计算机出现故障,输出量的大幅度变化,将显著改变被控对象的位置(如调节阀门突然加大或减小),可能会给生产造成损失。
为此,常采用增量型控制,即输出量是两个采样周期之间,控制器的输出增量Δu(k)。
由式(5-11),可得:(5-12)式(5-12)称为PID增量式控制算式。
式(5-11)和式(5-12)在本质上是一样的,但增量式算式具有下述优点:(1) 计算机只输出控制增量,即执行机构位置的变化部分,误动作影响小。
(2) 在进行手动/自动切换时,控制量冲击小,能够较平滑地过渡。
5.2.2 PID数字控制器的实现控制生产过程的计算机要求有很强的实时性,用微型计算机作为数字控制器时,由于其字长和运算速度的限制,必须采用一些方法来加快计算速度。
常用的方法有:简化算式法、查表法、硬件乘法器法。
现仅进行算式简化。
式(5-11)是PID位置控制算式。
按照这个算式,微型计算机每输出u(k)一次,要作四次加法、两次减法、四次乘法和两次除法。
若将该式稍加合并整理可写成如下形式:(5-13)式中, 系数a0、a1、a2可先进行计算,然后代入式(5-13)再进行计算机程序运算,微型计算机每输出u(k)一次,只需作三次乘法、两次加法、一次减法。
按式(5-13)编制位置式数字控制器的程序框图如图5-8所示。
图5-8 位置式数字控制器程序框图五、课堂小结:1、数字PID控制器的设计2、PID数字控制器的实现六、布置作业:P105 第一题,第三题一、授课时间:年月日第22 次二、教学目的:1、掌握数字PID控制器参数的整定2、掌握采样周期的选择三、教学的重点及难点:重点:数字PID控制器参数的整定。
难点:数字PID控制器参数的整定。
四、教学内容及过程:复习上节课内容1、数字PID控制器的设计2、PID数字控制器的实现5.3 数字PID控制器参数的整定5.3.1 采样周期的选择从Shannon采样定理可知,只有当采样频率达到系统信号最高频率的两倍或两倍以上时,才能使采样信号不失真地复现原来的信号。
由于被控对象的物理过程及参数变化比较复杂,因此系统有用信号的最高频率是很难确定的。
采样定理仅从理论上给出了采样周期的上限,实际采样周期要受到多方面因素的制约。
从系统控制质量的要求来看,希望采样周期取得小些,这样更接近于连续控制,使控制效果好些。
从执行机构的特性要求来看,由于过程控制中通常采用电动调节阀或气动调节阀,因此它们的响应速度较低。
如果采样周期过短,执行机构来不及响应,仍然达不到控制的目的。
所以,采样周期不能过短。
从系统的快速性和抗干扰的要求出发,要求采样周期短些;从计算工作量来看,则又希望采样周期长些,这样可以控制更多的回路,保证每个回路有足够的时间来完成必要的运算。
